Калькулятор расчета площади стен
Калькулятор расчета площади стенГлавная ->КАЛЬКУЛЯТОР ->Калькулятор расчета площади стен
Ширина помещения (м)
Длина помещения (м)
Высота помещения (м)
Площадь стен без окон и дверей(кв.м.):
Площадь стен c учетом окон и дверей(кв.м.):
Введите параметры окна
|
Введите параметры двери
|
||||||||||||||||
Алгоритм расчета площади стен
Для того чтобы составить полный расчет площади стен, достаточно иметь минимальные знания в области
математики и хоть какое-то представление о том, что нужно делать. Для начала необходимо измерить высоту и ширину всех стен, после чего воспользоваться достаточно
простой математической формулой «S=H×L», где H — это высота стены, L — её длина, ну а S –
соответственно необходимая нам площадь.
Для начала необходимо измерить высоту и ширину всех стен, после чего воспользоваться достаточно
простой математической формулой «S=H×L», где H — это высота стены, L — её длина, ну а S –
соответственно необходимая нам площадь.
Однако, перед составлением точного расчета площади стен, необходимо учесть особенности помещения (количество окон, дверей, выступов и углублений). Для того чтобы исключить площадь окон и дверей, необходимо воспользоваться той же формулой что при расчете основной площади, однако, теперь в качестве данных использовать ширину и высоту самих проемов и углублений. После этого полученный результат необходимо просто вычесть из общего.
При онлайн заказе — скидка 5%
ПОЧЕМУ СТОИТ ВЫБРАТЬ НАС?
Несем ответственность
НАДЕЖНОСТЬ
Качество и цена
Несем ответственность не только за качество, но и за возможные ошибки, которые редко, но случаются
Мы сделаем все, о чем договорились и даже больше, чем можем
Вы покупаете продукт для долгой
и безупречной службы десятилетиями,
инвестируете в комфорт и уют.
СТАТЬИ
Дисковая распиловка
Отраслевые особенности лесной промышленности России, а также строительство деревянных домов, рекомендуют оснащать производства продукции лесопиления
подробнее
Классификатор на пиломатериалы
Пиленую продукцию получают продольным делением бревен и кряжей на части с последующим продольным и поперечным раскроем
подробнее
вверх
Расчет кровли. Онлайн калькулятор для расчета кровли крыши, программа расчета количества и стоимости металлочерепицы на кровлю – GrandLine
Часто ищут:
- Расчет металлочерепицы
- Расчет кровли из профнастила
- Расчет фальцевой кровли
- Расчет софитов для крыши
- Калькулятор Четырехскатной крыши
- Калькулятор Мансардной крыши
- Калькулятор Двускатной крыши
- Калькулятор Вальмовой крыши
Часто ищут:
- Расчет металлочерепицы
- Расчет кровли из профнастила
- Расчет фальцевой кровли
- Расчет софитов для крыши
- Калькулятор Четырехскатной крыши
- Калькулятор Мансардной крыши
- Калькулятор Двускатной крыши
- Калькулятор Вальмовой крыши
- 01.
 Конфигурация кровли
Конфигурация кровли - 02. Выбор профиля и размера листов
- 03. Ваш итоговый расчет кровли
Качественно выполненные работы по устройству кровли являются одним из условий последующего комфортного проживания в доме. В установки кровли используются самые разные материалы: древесина для стропильной системы, специальные пленки и мембраны для пароизоляции и гидрозащиты, утеплитель, кровельное покрытие. Чтобы не ошибиться при их покупке, необходимо правильно подсчитать требуемое количество материала. Для этого мы предлагаем воспользоваться онлайн-калькулятором.
Расчет покрытия для кровли
Удобный в использовании калькулятор кровли предназначен для определения конкретного количества материала, необходимого для устройства кровли, в том числе доборных и комплектующих элементов. Если при выборе материала возникли затруднения – закажите обратный звонок, наш менеджер перезвонит и ответит на ваши вопросы, предоставив подробную техническую информацию о различных типах кровельных покрытий, ценах, условиях оплаты и доставки. По вашему желанию может быть составлена точная смета расходов на устройство кровли.
По вашему желанию может быть составлена точная смета расходов на устройство кровли.
Для расчета кровли нужно выполнить ряд замеров, результаты которых необходимо будет внести в соответствующие поля калькулятора. Использовать для этого планы здания и отдельные чертежи надо с пониманием того, что некоторые указанные на них размеры могут отличаться от фактических. Кроме того, замеры следует производить, учитывая следующие факторы:
• угол наклона и геометрию крыши, которая может быть односкатной, двускатной, шатровой, мансардной, вальмовой;
• необходимость устройства на крыше люков и других элементов, оставляемых без кровельного покрытия;
• будет ли в составе конструкции кровли теплоизоляция и какой утеплитель выбран.
Работа с калькулятором начинается с выбора типа кровли и материала, который будет использован в качестве кровельного покрытия – металлочерепица, профнастил или фальцевая кровля. Для крыш с небольшим уклоном используют фальцевую кровлю. Фальц – специальный шов, с помощью которого металлические листы соединяются между собой. Следующим шагом необходимо внести результаты ваших замеров в соответствующие поля и выбрать – делать расчёт с утеплителем, софитами или без.
Следующим шагом необходимо внести результаты ваших замеров в соответствующие поля и выбрать – делать расчёт с утеплителем, софитами или без.
Каждый вид покрытия отличается особенностями монтажных работ, доборными элементами, крепежами. Программа калькулятора позволяет выбрать толщину металла и цвет покрытия. Благодаря широкой цветовой гамме можно подобрать оптимальный вариант для вашего дома.
При расчете сложной кровли крышу разбивают на отдельные плоскости и производят замер каждого элемента, уделяя особое внимание размерам скатов. Однако максимально точный расчет поможет выполнить только высококвалифицированный специалист.
Как рассчитать софиты для крыши?
Софиты используются для обшивки карнизов и фронтонных свесов. Калькулятор позволит рассчитать необходимое количество в режиме онлайн. Расчет софитов производится автоматически с учетом материала (металл или ПВХ), запретных длин и перехлестов листов.
При необходимости, вы можете воспользоваться расчетом необходимого количества саморезов, утеплителя, доборных элементов и комплектующих. После завершения расчета добавьте заказ в корзину и приступайте к оформлению заказа. Мы доставим кровельный материал в любой регион Российской Федерации.
После завершения расчета добавьте заказ в корзину и приступайте к оформлению заказа. Мы доставим кровельный материал в любой регион Российской Федерации.
Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.
Получить виджет для этого калькулятора
© Calculator Soup
Поделитесь этим калькулятором и страницей
Калькулятор Использование
Найдите квадрат числа n. Введите положительные или отрицательные целые числа или десятичные числа или научную нотацию E.
Возведение в квадрат отрицательных чисел
Если вы хотите возвести в квадрат отрицательные числа в этом калькуляторе, используйте круглые скобки при вводе.
- -5² означает -(5 × 5) = -25
- -(5)² означает -(5 × 5) = -25
- (-5)² означает (-5 × -5) = 25
Например, чтобы возвести -4 в квадрат, введите его в калькулятор как (-4) со скобками. Чтобы взять отрицательное число 4 в квадрате, введите его как -(4) или -4.
Чтобы взять отрицательное число 4 в квадрате, введите его как -(4) или -4.
Когда выражение степени записывается с положительным значением, таким как 4², большинству легко понять, что это означает 4 × 4 = 16
Однако, когда оно записывается как отрицательное значение без круглых скобок, значение неоднозначно. Для разных людей это имеет разное значение.
Различные возможные интерпретации -4²:
1. минус (4 в квадрате) равен -4² = -(4)² = -(4 × 4) = -16
2. (минус 4) в квадрате равен (- 4)² = (-4 × -4) = 16
Используйте круглые скобки, чтобы четко указать, какое вычисление вы действительно хотите выполнить.
В квадрате
Число n в квадрате записывается как n² и n² = n × n. Если n — целое число, то n² — полный квадрат.
Например, 3 в квадрате записывается как 3², а 3² = 3 × 3 = 9. Девять — это полный квадрат.
Числа от 0 до 10 в квадрате
- 0 в квадрате равно 0² = 0 × 0 = 0
- 1 в квадрате равно 1² = 1 × 1 = 1
- 2 в квадрате равно 2² = 2 × 2 = 4
- 3 в квадрате равно 3² = 3 × 3 = 9
- 4 в квадрате равно 4² = 4 × 4 = 16
- 5 в квадрате равно 5² = 5 × 5 = 25
- 6 в квадрате равно 6² = 6 × 6 = 36
- 7 в квадрате равно 7² = 7 × 7 = 49
- 8 в квадрате равно 8² = 8 × 8 = 64
- 9 в квадрате равно 9² = 9 × 9 = 81
- 10 в квадрате равно 10² = 10 × 10 = 100
Ссылки/ Дополнительная литература
Гудман, Лен и
Вайсштейн, Эрик В. «Квадратное число». От MathWorld — Веб-ресурс Wolfram.
Квадратный номер
«Квадратное число». От MathWorld — Веб-ресурс Wolfram.
Квадратный номер
Википедия «Квадратный номер» на https://en.wikipedia.org/wiki/Квадратное_число
Подписаться на калькуляторSoup:
Этот калькулятор требует использования браузеров с поддержкой Javascript . Этот калькулятор предназначен для получения результата математического расчета, чтобы убедиться, что фундамент (или помещение, ферменный фундамент или другие 90-градусная структура) на самом деле квадратная и правильная по планировке. (Быть квадратным или Восстановить…) Расчет основан на теореме Пифагора. Если говорить простыми строительными терминами, то здесь говорится, что квадрат длины фундамента плюс квадрат ширины фундамента равняется возведенному в квадрат расстоянию по диагонали фундамента (от противоположного угла до противоположного угла). В строительной отрасли это также известно как 3-4-5, что означает, что если длина равна 3 (в квадрате = 9) и ширина равна 4 (в квадрате = 16), то диагональ равна 5 (в квадрате = 25). Проверка верна в том, что 9плюс 16 равно 25, из которых квадратный корень равен 5. Хотя транспортиры и Т-образные квадраты очень полезны, чем больше расстояние для измерения, тем оно точнее. (Если вы не хотите на самом деле измерять, но можете определить с помощью жала, обе диагонали должны быть равны для квадратного фундамента.) Отклонение всего на долю градуса от 90 градусов на расстоянии более 20 футов или более является существенной ошибкой в измерении. в результате чего стены не будут прямыми или квадратными. Небольшие дополнительные усилия на начальных этапах приводят к гораздо более профессиональной структуре в конце. В строительной отрасли это также известно как 3-4-5, что означает, что если длина равна 3 (в квадрате = 9) и ширина равна 4 (в квадрате = 16), то диагональ равна 5 (в квадрате = 25). Проверка верна в том, что 9плюс 16 равно 25, из которых квадратный корень равен 5. Хотя транспортиры и Т-образные квадраты очень полезны, чем больше расстояние для измерения, тем оно точнее. (Если вы не хотите на самом деле измерять, но можете определить с помощью жала, обе диагонали должны быть равны для квадратного фундамента.) Отклонение всего на долю градуса от 90 градусов на расстоянии более 20 футов или более является существенной ошибкой в измерении. в результате чего стены не будут прямыми или квадратными. Небольшие дополнительные усилия на начальных этапах приводят к гораздо более профессиональной структуре в конце. Этот калькулятор может работать как в американской системе футов и дюймов, так и в метрической системе метров. Сначала выберите американскую или метрическую систему счисления. Created by
lamisperclea1986 snippet.markdown ——————————————————— . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Корень -ой степени из комплексного числа обозначается символом и на. число задано в тригонометрической форме: , то все значения корня -ой. Затем записать ответ в виде Извлечение корня из комплексных чисел. с комплексными числами, Алгебраическая форма записи комплексного числа. [[/deleted]] This comment is currently being rendered in creole. Editing the comment will cause it to be rendered in markdown. Cancel This comment is currently being rendered in creole. Editing the comment will cause it to be rendered in markdown. Квадратный корень из числа – очень распространенная математическая функция, используемая во всех областях науки – физике, математике, информатике и т.д. Квадратные корни чисел и выражений очень часто встречаются в формулах во всех областях науки, и особенно в том, как мы представляем реальность – моделируя то, что мы можем наблюдать с помощью исчисления. В этой статье мы рассмотрим различные способы вычисления квадратного корня из числа в Python. Наконец, мы проведем тест производительности с постоянными и случайными числами, а также со списками случайных чисел, чтобы проверить все подходы. NumPy – это библиотека научных вычислений, которая присутствовала во многих приложениях и вариантах использования. Естественно, в нем есть множество оболочек математических функций в качестве вспомогательных методов. Если она еще не установлена, вы можете установить ее через pip: В терминах NumPy функция sqrt() вычисляет квадратный корень из числа и возвращает результат: Это приводит к: Помимо использования одной переменной в качестве аргумента, sqrt() также может анализировать списки и возвращать список квадратных корней: Это приводит к: Функция sqrt(), однако, имеет ограничение – она не может вычислять квадратный корень из отрицательного числа, поскольку операция квадратного корня с действительными числами определена только для положительных чисел. Попытка вставить -4 в функцию sqrt() приведет к исключению: Попытка вычислить квадратный корень из отрицательного числа приведет к появлению предупреждения и значению nan: К счастью, NumPy не ограничивается работой только с действительными числами – он также может работать с комплексными числами: Если в списке есть хотя бы одно комплексное число, все числа будут приведены и обработаны как сложные, поэтому можно добавить даже отрицательные целые числа: Модуль math – это стандартный модуль, упакованный с Python. Он всегда доступен, но должен быть импортирован и предоставляет оболочки для некоторых общих функций, таких как квадратный корень, полномочия и т.д.: Функция sqrt() модуля math- это простая функция, которая возвращает квадратный корень из любого положительного числа: Это приводит к: В отличие от функции sqrt() NumPy, она может работать только с одним элементом, поэтому, если вы хотите вычислить квадратный корень из всех элементов в списке, вам придется использовать цикл for или генератор списка: В обоих случаях список корней будет содержать: Квадратный корень из числа также может быть вычислен путем возведения числа в степень ½: √x = x1/2 Так что на самом деле, нахождение квадратного корня из числа может быть выражено как увеличение числа до степени ½. math.pow() принимает два аргумента – основание и показатель степени, и увеличивает основание до степени экспоненты: Естественно, это приводит к: Оператор ** является двоичным оператором, что означает, что он работает с двумя значениями, как и обычное умножение с помощью *. Однако, поскольку это оператор, используемый для возведения в степень, мы повышаем его левый аргумент до степени его правого аргумента. Этот подход может быть использован в той же форме, что и предыдущий: И это также приводит к: В Python есть еще один встроенный метод pow(), который не требует импорта математического модуля. math.pow() неявно преобразует элементы в двойные, в то время как pow() использует внутреннюю реализацию объекта, основанную на операторе **. Хотя это различие в реализации может оправдать использование того или иного в определенных контекстах, если вы просто вычисляете квадратный корень из числа, вы на самом деле не увидите разницы: Это приводит к: Итак, какой из них дает наилучшую производительность, и какой из них вы должны выбрать? Как обычно, нет одного явного победителя, и это зависит от использования методов. А именно, если вы работаете с постоянными числами, случайными числами или массивом случайных чисел в большем масштабе – эти методы будут работать по-другому. Давайте проверим их все на постоянных числах, случайных числах и массивах случайных чисел: Мы прошли все описанные выше методы через один и тот же тест – постоянное число (которое, вероятно, будет кэшировано для оптимизации), случайное число на каждой из 100 тыс. итераций и список из 100 случайных чисел. Примечание: Важны только относительные числа в каждом тесте по сравнению с другими методами в этом тесте, поскольку для генерации 100 случайных чисел требуется больше времени, чем при использовании (кэшированного) постоянного значения. Выполнение этого фрагмента кода приводит к: С постоянными числами – функции math.pow(), math.sqrt() и pow() значительно превосходят функцию Numpy sqrt(), поскольку они могут лучше использовать кэширование в процессоре на уровне языка. Со случайными числами кэширование работает не так хорошо, и мы видим меньшие расхождения. Со списками случайных чисел np.sqrt() значительно превосходит все три встроенных метода, и оператор ** работает в одной и той же области действия. Подводя итоги: В зависимости от конкретного ввода, с которым вы имеете дело, вы будете выбирать между этими функциями. Хотя может показаться, что все они будут работать хорошо, и хотя в большинстве случаев это не будет иметь большого значения, при работе с огромными наборами данных даже сокращение времени обработки на 10 % может помочь в долгосрочной перспективе. В зависимости от обрабатываемых данных – протестируйте различные подходы на своем локальном компьютере. В этой короткой статье мы рассмотрели несколько способов вычисления квадратного корня из числа в Python. Мы рассмотрели функции pow() и sqrt() математического модуля, а также встроенную функцию pow(), функцию Numpy sqrt() и оператор **. Наконец, мы провели сравнительный анализ методов для сравнения их производительности на различных типах входных данных – постоянных числах, случайных числах и списках случайных чисел.
Просмотры: 2 753
Квадрат каждого действительного числа положителен. Таким образом, мы должны использовать комплексные числа, чтобы расширить систему действительных чисел до более крупной системы. Комплексные числа представляют собой сумму действительного числа и мнимого числа. Например, если Z — комплексное число, то Z = a + ib , здесь Z = комплексное число a = действительная часть i = йота (√-1) (мнимая) ib = мнимое число йота (i) полезно для нахождения квадратного корня из комплексных чисел. Формула для нахождения квадратного корня из комплексного числа a + ib задается как (a+ib ) = ±(x + iy), Здесь, x и y — действительные числа Два комплексных числа z1 = a + ib и z2 = c + id будут равны, если a = c и b = d. Квадратные корни комплексного числа и мнимых чисел можно найти с помощью приведенной выше формулы. x = 2 и y = 1 Ответ: √ (3 + 4i) = ±(2 + i) можно использовать для комплексных чисел, чтобы найти квадратный корень комплексного числа в полярной форме Согласно теореме о корнях n: Для комплексного числа z = r (cosθ + i sinθ), корень n-й степени определяется формулой z1/n = r1/n [cos [(θ + 2kπ)/n] + i sin [(θ + 2kπ)/n]], где k = 0, 1, 2, 3, …, n-1 Чтобы получить периодические корни комплексного числа, добавьте 2kπ к θ. или квадратный корень из -25 равен ±5i Найти квадратный корень из -18 Решение: √-18 = i√18 = I√9 √2 = I x (± 3) x √2 = ± 3i√2 Ответ = √-18 = ± 3i√2 Квадратный корень из отрицательного числа не существует в реальной системе счисления. Квадратный корень из комплексных чисел помогает найти многочисленные корни в полиномиальном уравнении. В числе вида а + ib, где а и b — действительные числа, а называется натуральной частью, а b — мнимой частью комплексного числа. Определить в тригонометрической форме квадратные корни из минус пяти минус пять 𝑖 все разделить на минус пять плюс пять 𝑖 все возвести в девятую степень . В этом вопросе нас просят найти квадратные корни заданного комплексного числа. Таким образом, чтобы использовать эту формулу для нахождения квадратных корней нашего комплексного числа, мы захотим записать ее в тригонометрической форме. И есть несколько разных способов сделать это. Начнем с упрощения нашего выражения. У нас может возникнуть соблазн упростить это выражение, записав числитель и знаменатель отдельно в тригонометрической форме. Однако мы всегда должны сначала проверить, можем ли мы упростить это выражение другим способом. Далее мы можем упростить это, заметив, что мы делим два комплексных числа. И один из способов сделать это — умножить и числитель, и знаменатель на комплексно-сопряженное число знаменателя. Итак, внутри нашей экспоненты нам нужно умножить на один плюс 𝑖 разделить на один плюс 𝑖. В числителе у нас один плюс 𝑖 в квадрате. Мы можем распределить это, используя биномиальную теорему или метод FOIL. В любом случае, мы получаем один плюс два 𝑖 плюс 𝑖 в квадрате. В знаменателе у нас один минус 𝑖 умножается на один плюс 𝑖. Это факторизация разницы между квадратами, так что это один минус 𝑖 в квадрате. И помните, нам нужно все это возвести в девятую степень. Затем мы можем упростить это еще больше. Помните, 𝑖 — это квадратный корень из отрицательной единицы. Мы можем упростить это еще больше. Так как 𝑖 в квадрате отрицательная единица, 𝑖 в четвертой степени должно быть равно единице. А так как 𝑖 в девятой степени равно 𝑖 в четвертой степени, умноженной на 𝑖 в четвертой степени, умноженной на 𝑖, то 𝑖 в девятой степени равно 𝑖. Следовательно, комплексное число, из которого нас попросили найти квадратный корень, — это просто 𝑖. И есть несколько разных способов нахождения квадратных корней из этого числа. Мы просто воспользуемся формулой де Муавра. И чтобы использовать эту формулу, нам сначала нужно переписать 𝑖 в тригонометрической форме. Начнем с модуля. Модуль числа — это его расстояние от начала координат на диаграмме Аргана. Или, альтернативно, это квадратный корень из суммы квадратов действительной и мнимой частей нашего комплексного числа. И в обоих случаях мы знаем, что модуль 𝑖 равен единице. Далее нам нужно найти аргументы нашего комплексного числа 𝑖. Помните, что это угол, измеренный против часовой стрелки от положительной оси 𝑥, которую 𝑖 образует на диаграмме Аргана. Таким образом, мы можем найти это значение из эскиза. Помните, что на диаграмме Аргана координата 𝑥 — это действительная часть нашего комплексного числа, а координата 𝑦 — это мнимая часть нашего комплексного числа. А поскольку 𝑖 имеет нулевую действительную часть и единицу мнимую часть, координаты 𝑖 на диаграмме Аргана равны нулю, единице. Итак, 𝑖 лежит на положительной вертикальной оси. Это означает, что его угол, измеренный против часовой стрелки от положительной горизонтальной оси, будет 𝜋 на два. Теперь мы готовы использовать нашу формулу для нахождения квадратных корней этого комплексного числа 𝑍. Поскольку нам нужны квадратные корни, наше значение 𝑛 равно двум. И помните, мы обнаружили, что значение 𝑟 равно единице, а 𝜃 равно 𝜋 на два. Поэтому подставляем их в формулу. Это дает нам следующее выражение для 𝑛-го корня нашего комплексного числа. Они даны единицей в степени одного более чем в два раза больше, чем 𝜋 на два плюс два 𝜋𝑘 на два плюс 𝑖 грех 𝜋 на два плюс два 𝜋𝑘 на два. И помните, наши значения 𝑘 — целые числа, которые варьируются от нуля до 𝑛 минус один. Итак, 𝑘 находится между нулем и единицей. Это дает нам два квадратных корня: один, когда 𝑘 равно нулю, и один, когда 𝑘 равно единице. Итак, мы найдем наш первый корень, когда подставим 𝑘 равно нулю в это выражение и упростим. Однако мы получим второй квадратный корень, если подставим 𝑘 равным единице. Подставив в это выражение 𝑘 равно единице, мы получим cos 𝜋 на два плюс два 𝜋 на все два плюс 𝑖 sin на 𝜋 на два плюс два 𝜋 на все два. И мы можем упростить это, заметив, что 𝜋 больше двух плюс два 𝜋 больше двух равно пяти 𝜋 на четыре. И мы могли бы просто оставить наш ответ так. Однако помните, что мы можем добавлять и вычитать из нашего аргумента целые числа, кратные двум 𝜋. Таким образом, мы также можем вычесть два 𝜋 из этого значения. Тогда это даст нам минус три 𝜋 на четыре. Плюс и минус — это признаки положительных и отрицательных чисел в математике. Какой результат получается при умножении и делении положительных и отрицательных чисел? Эта простая таблица наглядно показывает результаты умножения и деления двух чисел с разными знаками. Приведенные в таблице результаты применимы как при умножении и делении целых чисел, так и при умножении и делении дробей. Для определения числовых значений результата умножения или деления воспользуйтесь таблицами умножения и деления, которые можно скачать бесплатно. При умножении или делении двух положительных чисел в результате получается положительное число. Плюс умноженный на плюс дает плюс, плюс деленный на плюс будет плюс. Это правило математики. Произведение двух положительных чисел — число положительное, частное двух положительных чисел — положительное число. В математике умножение или деление положительного числа на отрицательное дает в результате отрицательное число. При делении или умножении отрицательного числа на положительное в результате получается отрицательное число. Минус умноженный на плюс будет минус. Минус деленный на плюс в математике будет минус. Когда числитель дроби отрицательный, а знаменатель положительный — дробь (или целое число) будет отрицательной. Если отрицательную дробь умножить или разделить на положительную дробь получится отрицательное число. Это число может быть целым или дробным, что определяется другими правилами математики. Произведение отрицательного числа на положительное — число отрицательное, частное отрицательного числа на положительное число — отрицательное число. Когда умножаются или делятся два отрицательных числа, результатом будет положительное число. Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число. Правила знаков в математике распространяются как на целые, так и на дробные числа. При делении двух отрицательных дробей результат будет положительным. При умножении двух отрицательных дробей результат так же будет положительным, то есть со знаком плюс. ВОПРОС — ОТВЕТ «Кто ввел знаки сложения и вычитания в математику?» — первое употребление слов plus (больше) и minus (меньше) как обозначения действия сложения было найдено историком математики Энестремом в итальянской алгебре четырнадцатого века. Вначале действия сложения и вычитания обозначали перввыми буквами слов «p» и «m». «Минус 6 делить на минус 3 как быть?» — сперва отбрасываем знаки минус и делим просто 6 (шесть) на 3 (три) при помощи таблицы деления и получаем в результате 2 (два). Потом по табличке вверху странички делим минус на минус и получаем плюс. (-6) : (-3) = +2 Впрочем, знак «+» перед числами писать не принято, поэтому красивее и правильнее будет так: (-6) : (-3) = 2 «Если число со знаком минус спереди умножаем на такое же число?» — решение смотри выше. 13 ноября 2009 года — 22 сентября 2019 года. «Враг моего врага — мой друг». Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики. Давным-давно людям были известны только натуральные числа: 1, 2, 3, . Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу. В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!). Рассмотрим для примера уравнение 7x – 17 = 2x – 2. Его можно решать так: перенести члены с неизвестным в левую часть, а остальные — в правую, получится 7x – 2x = 17 – 2, 5x = 15, x = 3. При таком решении нам даже не встретились отрицательные числа. Но можно было случайно сделать и по-другому: перенести слагаемые с неизвестным в правую часть и получить 2 – 17 = 2x – 7x, (–15) = (–5)x. Чтобы найти неизвестное, нужно разделить одно отрицательное число на другое: x = (–15)/(–5). Но правильный ответ известен, и остается заключить, что (–15)/(–5) = 3. Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку. Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами. Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции… Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики). В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец. Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс. Кольцом называется множество с двумя бинарными операциями (т. е. в каждой операции задействованы два элемента кольца), которые по традиции называют сложением и умножением, и следующими аксиомами: Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец. Теперь докажем, что для любых элементов A и B произвольного кольца верно, во-первых, (–A)·B = –(A·B), а во-вторых (–(–A)) = A. Из этого легко следуют утверждения про единицы: (–1)·1 = –(1·1) = –1 и (–1)·(–1) = –((–1)·1) = –(–1) = 1. Для этого нам потребуется установить некоторые факты. Сперва докажем, что у каждого элемента может быть только один противоположный. В самом деле, пусть у элемента A есть два противоположных: B и С. То есть A + B = 0 = A + C. Рассмотрим сумму A + B + C. Пользуясь сочетательным и переместительным законами и свойством нуля, получим, что, с одной стороны, сумма равна B: B = B + 0 = B + (A + C) = A + B + C, а с другой стороны, она равна C: A + B + C = (A + B) + C = 0 + C = C. Заметим теперь, что и A, и (–(–A)) являются противоположными к одному и тому же элементу (–A), поэтому они должны быть равны. Первый факт получается так: 0 = 0·B = (A + (–A))·B = A·B + (–A)·B, то есть (–A)·B противоположно A·B, значит, оно равно –(A·B). Чтобы быть математически строгими, объясним еще, почему 0·B = 0 для любого элемента B. В самом деле, 0·B = (0 + 0) B = 0·B + 0·B. То есть прибавление 0·B не меняет сумму. Значит, это произведение равно нулю. А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения. Ответил: Евгений Епифанов Знак плюс-минус (±) — это математический символ с несколькими значениями. Знак обычно произносится как «плюс или минус». В математике это обычно указывает на выбор ровно двух возможных значений, одно из которых является отрицанием другого. Вариант знака, включающий также французское слово или («или»), был использован в его математическом значении Альбертом Жираром в 1626 г., а знак в его современном виде использовался уже в 9 Уильяма Отреда0008 Clavis Mathematicae (1631). В математических формулах символ ± может использоваться для обозначения символа, который может быть заменен символами + или -, что позволяет формуле представлять два значения или два уравнения. Например, для уравнения x 2 = 9 можно дать решение как x = ±3. Это указывает на то, что уравнение имеет два решения, каждое из которых может быть получено заменой этого уравнения одним из двух уравнений 92-4ас}}{2а}. }[/математика] , описывающее два решения квадратного уравнения x 2 + bx + c = 0. ) = \sin(A) \cos(B) \pm \cos(A) \sin(B). }[/математика] можно интерпретировать как сокращение двух уравнений: одно с «+» с обеих сторон уравнения, а другое с «-» с обеих сторон. Обе копии знака ± в этом тождестве должны быть заменены одинаковым образом: недопустимо заменять одну из них на «+», а другую на «-». Здесь знак «плюс» или «минус» указывает на то, что знаки терминов чередуются, где (начиная с 0) термины с четным индексом n добавляются, а термины с нечетным индексом вычитаются. Более строгое представление той же формулы умножит каждый член на коэффициент (-1) n , что дает +1, когда n четно, и -1, когда n нечетно. Использование ⟨±⟩ для приближения чаще всего встречается при представлении числового значения величины вместе с ее допуском или статистической погрешностью. [2] Например, «5,7±0,2» может находиться в диапазоне от 5,5 до 5,9 включительно. В научном использовании это иногда относится к вероятности попадания в указанный интервал, обычно соответствующей 1 или 2 стандартным отклонениям (вероятность 68,3% или 95,4% при нормальном распределении). Проценты также могут использоваться для указания предела погрешности. Например, 230 ± 10 % В относится к напряжению в пределах 10 % от любой стороны от 230 В (от 207 В до 253 В включительно). Можно также использовать отдельные значения для верхней и нижней границ. Например, чтобы указать, что значение, скорее всего, равно 5,7, но может достигать 5,9.или всего 5,6, можно написать 5,7 + 0,2 Символы ± и ∓ используются в шахматной системе обозначений для обозначения преимущества белых и черных соответственно. Однако более распространенными шахматными обозначениями будут только + и -. [3] Если есть разница, символы + и — обозначают большее преимущество, чем ± и ∓. Знак минус-плюс (∓) обычно используется в сочетании со знаком «±» в таких выражениях, как «x ± y ∓ z», что может быть истолковано как означающее x + y — z «и/или» x — y + z «, но не » x + y + z или « x + y + Z 9000″ или « x + + − y − z «. лучше всего писать с использованием знака «∓». Приведенное выше тригонометрическое уравнение, таким образом, представляет собой два уравнения: , который представляет собой два уравнения. Знак плюс-минус напоминает китайские иероглифы 士 и 土, а знак минус-плюс напоминает 干. Тип лицензии определяет, как вы можете использовать этот образ. Хотите, чтобы это векторное изображение было только у вас? Эксклюзивный выкуп обеспечивает все права этого вектора. Мы удалим этот вектор из нашей библиотеки, а художник прекратит продажу работ. Оплатить стандартные лицензии можно тремя способами. Цены составляют долларов США долларов США . Существует два способа оплаты расширенных лицензий. Узнайте, как использовать режимы «Портрет», «Панорама», «Замедленно» и другие режимы камеры на вашем устройстве. Различные режимы камеры, доступные непосредственно на iPhone и iPad, помогут вам добиваться идеального результата при фото- и видеосъемке. Чтобы переключаться между режимами, смахивайте вправо или влево. Доступны следующие режимы: «Фото», «Видео», «Таймлапс», «Замедленно», «Квадрат», «Портрет», «Киноэффект» и «Панорама». Вы также можете делать фотографии во время видеосъемки или использовать функцию QuickTake для записи видео в режиме «Фото». Сначала убедитесь, что у вас установлена последняя версия iOS или iPadOS. «Фото» — это стандартный режим, который вы увидите, открыв приложение «Камера». В этом режиме вы можете делать обычные фотографии и снимки Live Photos. Ваша камера автоматически сфокусируется и установит экспозицию в зависимости от того, на что вы ее наведете. На iPhone XS, iPhone XR и более поздних моделях можно использовать функцию QuickTake, чтобы удобно снимать видео в режиме фотосъемки. На других моделях iPhone можно нажать и удерживать кнопку спуска затвора, чтобы выполнить серийную съемку. Чтобы остановить съемку, просто отпустите кнопку спуска затвора. Режим «Портрет» создает эффект глубины поля, благодаря которому объект съемки остается резким на размытом фоне. Вы можете использовать режим «Портрет» на iPhone 7 Plus, iPhone 8 Plus и более поздних моделях. На iPhone X или более поздних моделей также можно делать селфи в режиме «Портрет». Кроме того, вы можете использовать режим «Портрет» с фронтальной камерой на моделях iPad Pro 11 дюймов (все поколения) и iPad Pro 12,9 дюйма (3-го поколения и более поздние). Чтобы использовать режим «Портрет», откройте приложение «Камера» и перейдите в режим «Портрет». Если приложение посоветует отойти дальше от объекта съемки, сделайте это. Когда поле «Эффект глубины» станет желтым, сделайте снимок. Теперь изображения, полученные в режиме «Портрет» на iPhone X и более поздней модели, а также iPhone 8 Plus, можно сделать еще более завораживающими благодаря эффектам освещения студийного качества. После съемки нажмите «Править» и выберите один из эффектов: «Студийный свет», «Контурный свет», «Сценический свет» или «Сценический свет — моно». С помощью эффекта «Светлая тональность — Ч/Б» на iPhone XS и более поздних моделей можно создавать красивый классический вид. Камера iPhone XR на задней панели не поддерживает эффекты «Сценический свет», «Сценический свет — Ч/Б» и «Светлая тональность — Ч/Б». В режиме «Квадрат» область кадра на экране камеры ограничивается квадратом — такой размер фотографии оптимален для большинства социальных сетей. На iPhone 11 и более поздних моделях нажмите на стрелку , чтобы получить доступ к режиму «Квадрат» и другим параметрам. Используйте режим «Панорама», чтобы получить широкоугольный снимок ландшафта, медленно перемещая свое устройство. В режиме «Панорама» в центре экрана отображается направляющая линия, которая помогает сделать фотографию. Если нужно снять панораму в направлении слева направо, убедитесь, что стрелка указывает вправо. А если справа налево — нажмите стрелку для смены направления. Нажмите кнопку затвора и медленно перемещайте камеру по прямой линии от одной стороны снимка к другой. Старайтесь двигать камеру так, чтобы стрелка постоянно находилась на желтой направляющей линии. Если выбрать любой режим видеосъемки, кнопка затвора меняет свой цвет с белого на красный. Нажмите кнопку спуска, чтобы начать съемку, а затем нажмите ее еще раз, чтобы завершить. Хотите изменить длину видео? Нажмите «Править» или кнопку редактирования и перемещайте ползунок, чтобы изменить время начала и завершения видео. Нажмите кнопку «Готово», чтобы сохранить изменения. Режим «Киноэффект» в камере iPhone позволяет записывать видео в кинематографическом формате с малой глубиной резкости и добавлять функцию плавного перемещения фокуса. Для использования режима «Киноэффект» требуется iPhone 13 или более поздней модели. Узнайте больше об использовании режима «Киноэффект» на iPhone. В режиме «Экшн» можно снимать плавное видео без штатива, даже если вы при этом много перемещаетесь. Для включения режима «Экшн» нажмите кнопку . Для съемки в этом режиме требуется iPhone 14. Узнайте больше о режиме «Экшн» на вашем iPhone. В режиме замедленной съемки видео будут записываться как обычно. Снимки делаются через выбранные временные интервалы, и в результате получается ускоренное видео, которое можно тут же опубликовать. Если перейти в режим «Таймлапс» и нажать кнопку затвора, камера будет делать снимки с заданной периодичностью, пока вы не нажмете эту кнопку еще раз. Дата публикации: Мы составили таблицу квадратов натуральных чисел до 10 и двузначных чисел, которой удобно пользоваться: благодаря ей не нужно в уме возводить число во вторую степень. Достаточно распечатать таблицу и найти в ней подходящее значение Александр Мельников
Преподаватель информатики и математики
Анна Стрельцова
Автор КП Содержание Квадратом числа называют произведение на самого себя один раз или возведение во вторую степень. В школе это действие проходят в 5 классе. Например, чтобы вычислить квадрат числа 5, нужно умножить его на 5: в итоге получится 25. С натуральными числами до 10 вычисления довольно просты, а посчитать квадрат двузначного числа в уме уже сложнее. Натуральные числа — те числа, которые мы используем при счете или при перечислении вещей, объектов. К натуральным относятся только полные и неотрицательные числа. В математике их много: поэтому мы сделали таблицу квадратов натуральных чисел от 1 до 10. Чтобы вычислить квадрат двузначного числа, умножить число на самого себя. В результате получается уже четырехзначное число. Если при вычислении квадратов чисел до 10 достаточно вспомнить таблицу умножения, то посчитать квадрат двузначного числа в уме уже сложнее. Проще всего для таких вычислений использовать таблицу. Скачать таблицу двузначных чисел В таблице мы собрали квадраты чисел от 1 до 100: она пригодится как школьникам, так и студентам. Скачать таблицу двузначных чисел Отвечает Александр Мельников, преподаватель информатики и математики онлайн-школы «Коалиция», эксперт ЕГЭ и ОГЭ, сертифицированный преподаватель проекта «Математическая вертикаль». Таблица квадратов — это таблица, содержащая квадраты чисел. Квадрат числа — это результат умножения какого-либо числа на самого себя, то есть число, возведенное во вторую степень. В таблице пересечение цифр слева в столбце и сверху в строке дает квадрат искомого числа. Например, нужно найти квадрат числа 15. В столбце слева берем первую цифру данного числа «1». В самой верхней строке берем вторую цифру данного числа «5». На пересечении данных цифр получаем квадрат числа 15, то есть 225. Таблицу квадратов также можно использовать для извлечения квадратного корня — обратной операции возведения в квадрат. Например, √225=15. Если мы говорим о сдаче ОГЭ и ЕГЭ базового уровня по математике, то учить таблицу квадратов необязательно, так как она будет в справочном материале. А вот для ЕГЭ по профильной математике это делать нужно: справочные материалы не предоставляются. 1. Если число заканчивается на 0, его легко возвести в квадрат — необходимо только дописать пару нулей: 60 х 60 = 3600. 2. Если число заканчивается на 5, то следует умножить первую цифру (x) на (x+1) и дописать к полученному числу «25». 65 х 65 = 6 х 7 = 42 приписываем 25 и получаем 4225. 3. Можно воспользоваться формулой (a + b)2 = a2 + 2ab + b2 . Как мы уже выяснили, возводить в квадрат числа, оканчивающиеся на 0, очень просто. Следовательно, а — это число, которое делится на 10, а b — остаток от деления на 10. Приведем пример. Возведем в квадрат 32. 32 можно представить как 30 (число делится на 10) и 2 (остаток от деления на 10): (30+2)2 = 302 + 2 х 30 х 2 + 22 = 900 + 120 + 4 =1024. Для начала нужно выучить таблицу квадратов первого десятка, так как она используется чаще всего: 121, 144, 169, 196, 225, 256, 289, 324, 361. Выучить данные значения квадратов можно довольно быстро: попробуйте просто ежедневно выписывать значения в тетрадь. Число необходимо разложить на простые множители, например 1225 = 5 х 5 х 7 х 7 = 5272. Значит, √1225 = √(5272) = 5 х 7 = 35. Благодаря разложению на множители можно извлечь корень из многозначного числа, выходящего за рамки таблицы квадратов. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Оценить | квадратный корень из 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Оценить | квадратный корень из 20 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Оценить | квадратный корень из 50 | 94 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Оценить | квадратный корень из 45 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Оценить | квадратный корень из 32 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Оценить | квадратный корень из 18 | 92 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .
е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | плюс | сложение | 1/2 + 1/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | минус | вычитание | 90 912 1 1/2 — 2/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | звездочка | умножение | 2/3 * 3/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | знак умножения | умножение | 2/3 × 5/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | знак деления | деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 м.): 0
м.): 0
 Конфигурация кровли
Конфигурация кровли В режиме футов и дюймов (американская система) введите значение в футах, обозначенное как Feet, затем дюймы, если они есть, в поле, обозначенное как Inches. Если у вас есть доля дюйма, вы можете ввести его. Имейте в виду, что это десятичная дробь; например, 0,5 — 1/2 дюйма, а 0,75 — 3/4 дюйма. Если вы не уверены в конвертации, вы можете использовать наши таблицы преобразования для точности до 64-х долей дюйма в десятичной системе. (Если вы уже знаете преобразование дюймов в десятичную дробь, вы можете просто ввести его как футы. Например, вы можете ввести 5 футов 6 дюймов как 5 в поле футов и 6 в поле дюймов или просто 5,5 в футах. поле и отсутствие записи в поле дюймов.) В метрическом режиме используется только первое поле по длине и ширине; система и калькулятор принимают десятичные дроби. Ответ возвращается в футах, дюймах и строительных дробях (до 64-х) в американском режиме, в то время как в метрическом режиме возвращаются метры и десятичные значения. Если вы выполняете более одного расчета, обязательно нажимайте кнопку «Очистить значения» между попытками.
В режиме футов и дюймов (американская система) введите значение в футах, обозначенное как Feet, затем дюймы, если они есть, в поле, обозначенное как Inches. Если у вас есть доля дюйма, вы можете ввести его. Имейте в виду, что это десятичная дробь; например, 0,5 — 1/2 дюйма, а 0,75 — 3/4 дюйма. Если вы не уверены в конвертации, вы можете использовать наши таблицы преобразования для точности до 64-х долей дюйма в десятичной системе. (Если вы уже знаете преобразование дюймов в десятичную дробь, вы можете просто ввести его как футы. Например, вы можете ввести 5 футов 6 дюймов как 5 в поле футов и 6 в поле дюймов или просто 5,5 в футах. поле и отсутствие записи в поле дюймов.) В метрическом режиме используется только первое поле по длине и ширине; система и калькулятор принимают десятичные дроби. Ответ возвращается в футах, дюймах и строительных дробях (до 64-х) в американском режиме, в то время как в метрическом режиме возвращаются метры и десятичные значения. Если вы выполняете более одного расчета, обязательно нажимайте кнопку «Очистить значения» между попытками.
 19) ИЗВЛЕЧЕНИЕ КОРНЯ ИЗ КОМПЛЕКСНЫХ ЧИСЕЛ 123 в котором применяются. Если число о задано в тригонометрической форме, то при целом. Найти корень из комплексного числа онлайн, подробное решение. Для нахождения корня n-ой степени, сначала необходимо выбрать ( алгебраическую, тригонометрческую. два значения квадратного корня из 4. Муавра, причем комплексное число должно быть записано в тригонометрической форме. называется алгебраической формой записи комплексного числа; знаки между составляющими числа обычные. Извлечение корня из комплексного числа. В результате получаем два значения квадратного корня: √3−4i=2−i. Возведение комплексного числа в степень, корень из комплексного числа. Возведение комплексного числа в степень. Извлечение корня из комплексного числа. Если комплексное число задано в алгебраической форме, то для возведения числа в. Извлечь квадратный корень из комплексного числа i. Например, корень квадратный из числа 1 имеет два значения: 1 и – 1. Корень n-й степени из числа 1 в поле комплексных чисел должен иметь n значений.
19) ИЗВЛЕЧЕНИЕ КОРНЯ ИЗ КОМПЛЕКСНЫХ ЧИСЕЛ 123 в котором применяются. Если число о задано в тригонометрической форме, то при целом. Найти корень из комплексного числа онлайн, подробное решение. Для нахождения корня n-ой степени, сначала необходимо выбрать ( алгебраическую, тригонометрческую. два значения квадратного корня из 4. Муавра, причем комплексное число должно быть записано в тригонометрической форме. называется алгебраической формой записи комплексного числа; знаки между составляющими числа обычные. Извлечение корня из комплексного числа. В результате получаем два значения квадратного корня: √3−4i=2−i. Возведение комплексного числа в степень, корень из комплексного числа. Возведение комплексного числа в степень. Извлечение корня из комплексного числа. Если комплексное число задано в алгебраической форме, то для возведения числа в. Извлечь квадратный корень из комплексного числа i. Например, корень квадратный из числа 1 имеет два значения: 1 и – 1. Корень n-й степени из числа 1 в поле комплексных чисел должен иметь n значений. В теореме Гаусса утверждается, что всякое алгебраическое уравнение с. правила действий над комплексными числами в современной форме. Квадра́тный ко́рень из a \displaystyle a a (корень 2-й степени, a \displaystyle \sqrt a. Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если. Теорема Лиувилля о приближении алгебраических чисел; ↑ См. А. Я. Ко́мпле́ксные чи́сла (устар. мнимые числа) числа вида x + i y \displaystyle x+iy x+iy. Однако многие свойства комплексных чисел отличаются от свойств вещественных. квадратных и кубических уравнений, в которых в формулах для корней. 5.1 Алгебраическая форма; 5.2 Тригонометрическая форма. Корень n \displaystyle n n -й степени из числа a \displaystyle a a определяется как такое. Поскольку арифметический и алгебраический корни обозначаются одним и. Зарождение понятия комплексного числа исторически было связано с. Первые задачи, связанные с извлечением квадратного корня. сложение и умножение комплексных чисел в алгебраической форме.
В теореме Гаусса утверждается, что всякое алгебраическое уравнение с. правила действий над комплексными числами в современной форме. Квадра́тный ко́рень из a \displaystyle a a (корень 2-й степени, a \displaystyle \sqrt a. Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если. Теорема Лиувилля о приближении алгебраических чисел; ↑ См. А. Я. Ко́мпле́ксные чи́сла (устар. мнимые числа) числа вида x + i y \displaystyle x+iy x+iy. Однако многие свойства комплексных чисел отличаются от свойств вещественных. квадратных и кубических уравнений, в которых в формулах для корней. 5.1 Алгебраическая форма; 5.2 Тригонометрическая форма. Корень n \displaystyle n n -й степени из числа a \displaystyle a a определяется как такое. Поскольку арифметический и алгебраический корни обозначаются одним и. Зарождение понятия комплексного числа исторически было связано с. Первые задачи, связанные с извлечением квадратного корня. сложение и умножение комплексных чисел в алгебраической форме. deleted]]
deleted]]

 09868411346781j)
Square roots of '[-2, 3, (-1+1j)]':
[0. +1.41421356j 1.73205081+0.j 0.45508986+1.09868411j]
09868411346781j)
Square roots of '[-2, 3, (-1+1j)]':
[0. +1.41421356j 1.73205081+0.j 0.45508986+1.09868411j]
 4142135623730951, 1.7320508075688772, 2.23606797749979, 2.6457513110645907]
4142135623730951, 1.7320508075688772, 2.23606797749979, 2.6457513110645907] Этот метод отличается от метода math.pow() внутренне.
Этот метод отличается от метода math.pow() внутренне. sqrt(): %ss" % timeit.timeit("math.sqrt(100)", setup="import math", number=100000))
print("math.pow(): %ss" % timeit.timeit("math.pow(100, 0.5)", setup="import math", number=100000))
print("pow(): %ss" % timeit.timeit("pow(100, 0.5)", number=100000))
print("np.sqrt(): %ss" % timeit.timeit("np.sqrt(100)", setup="import numpy as np", number=100000))
print("** operator: %ss" % timeit.timeit("100 ** 0.5", number=100000))
print("\nTime to execute 100k operations on random number: \n")
print("math.sqrt() %ss" % timeit.timeit("math.sqrt(random.random())", setup="import math; import random;", number=100000))
print("math.pow(): %ss" % timeit.timeit("math.pow(random.random(), 0.5)", setup="import math; import random", number=100000))
print("pow(): %ss" % timeit.timeit("pow(random.random(), 0.5)", setup="import random", number=100000))
print("np.sqrt(): %ss" % timeit.timeit("np.sqrt(random.random())", setup="import numpy as np; import random", number=100000))
print("** operator: %ss" % timeit.timeit("random.
sqrt(): %ss" % timeit.timeit("math.sqrt(100)", setup="import math", number=100000))
print("math.pow(): %ss" % timeit.timeit("math.pow(100, 0.5)", setup="import math", number=100000))
print("pow(): %ss" % timeit.timeit("pow(100, 0.5)", number=100000))
print("np.sqrt(): %ss" % timeit.timeit("np.sqrt(100)", setup="import numpy as np", number=100000))
print("** operator: %ss" % timeit.timeit("100 ** 0.5", number=100000))
print("\nTime to execute 100k operations on random number: \n")
print("math.sqrt() %ss" % timeit.timeit("math.sqrt(random.random())", setup="import math; import random;", number=100000))
print("math.pow(): %ss" % timeit.timeit("math.pow(random.random(), 0.5)", setup="import math; import random", number=100000))
print("pow(): %ss" % timeit.timeit("pow(random.random(), 0.5)", setup="import random", number=100000))
print("np.sqrt(): %ss" % timeit.timeit("np.sqrt(random.random())", setup="import numpy as np; import random", number=100000))
print("** operator: %ss" % timeit.timeit("random. random() ** 0.5", setup="import random", number=100000))
print("\nTime to execute 100k operations on list of random numbers: \n")
print("math.sqrt() %ss" % timeit.timeit("[math.sqrt(x) for x in np.random.rand(100)]", setup="import math; import numpy as np;", number=100000))
print("math.pow(): %ss" % timeit.timeit("[math.pow(x, 0.5) for x in np.random.rand(100)]", setup="import math; import numpy as np;", number=100000))
print("pow(): %ss" % timeit.timeit("[pow(x, 0.5) for x in np.random.rand(100)]", setup="import numpy as np;", number=100000))
print("np.sqrt(): %ss" % timeit.timeit("np.sqrt(np.random.rand(100))", setup="import numpy as np; import numpy as np;", number=100000))
print("** operator: %ss" % timeit.timeit("np.random.rand(100) ** 0.5", setup="import numpy as np", number=100000))
random() ** 0.5", setup="import random", number=100000))
print("\nTime to execute 100k operations on list of random numbers: \n")
print("math.sqrt() %ss" % timeit.timeit("[math.sqrt(x) for x in np.random.rand(100)]", setup="import math; import numpy as np;", number=100000))
print("math.pow(): %ss" % timeit.timeit("[math.pow(x, 0.5) for x in np.random.rand(100)]", setup="import math; import numpy as np;", number=100000))
print("pow(): %ss" % timeit.timeit("[pow(x, 0.5) for x in np.random.rand(100)]", setup="import numpy as np;", number=100000))
print("np.sqrt(): %ss" % timeit.timeit("np.sqrt(np.random.rand(100))", setup="import numpy as np; import numpy as np;", number=100000))
print("** operator: %ss" % timeit.timeit("np.random.rand(100) ** 0.5", setup="import numpy as np", number=100000))



 92 + 1 = 0
92 + 1 = 0 2 92 = -25
2 92 = -25 Нам нужно дать их в тригонометрической форме. Самый простой способ найти корни комплексных чисел — использовать теорему де Муавра для корней комплексных чисел. И мы помним, что это говорит нам, что если 𝑍 — комплексное число, записанное в тригонометрической форме, то есть 𝑍 равно 𝑟, умноженному на cos 𝜃 плюс 𝑖 sin 𝜃, то все 𝑛-е корни 𝑍 задаются следующей формулой. Они равны 𝑟 в степени единицы над 𝑛, умноженной на косинус 𝜃 плюс два 𝜋𝑘 над 𝑛 плюс 𝑖 грех 𝜃 плюс два 𝜋𝑘 по всему 𝑛, где наши значения 𝑘 — целые числа, и они варьируются от нуля до 𝑛 минус один.
Нам нужно дать их в тригонометрической форме. Самый простой способ найти корни комплексных чисел — использовать теорему де Муавра для корней комплексных чисел. И мы помним, что это говорит нам, что если 𝑍 — комплексное число, записанное в тригонометрической форме, то есть 𝑍 равно 𝑟, умноженному на cos 𝜃 плюс 𝑖 sin 𝜃, то все 𝑛-е корни 𝑍 задаются следующей формулой. Они равны 𝑟 в степени единицы над 𝑛, умноженной на косинус 𝜃 плюс два 𝜋𝑘 над 𝑛 плюс 𝑖 грех 𝜃 плюс два 𝜋𝑘 по всему 𝑛, где наши значения 𝑘 — целые числа, и они варьируются от нуля до 𝑛 минус один. Мы видим, что и в нашем числителе, и в знаменателе делит множитель минус пять. Убрав это, мы получим минус пять раз один плюс 𝑖 все разделить на минус пять раз один минус 𝑖 все возвести в девятую степень. И мы можем отменить общий множитель минус пять в числителе и знаменателе.
Мы видим, что и в нашем числителе, и в знаменателе делит множитель минус пять. Убрав это, мы получим минус пять раз один плюс 𝑖 все разделить на минус пять раз один минус 𝑖 все возвести в девятую степень. И мы можем отменить общий множитель минус пять в числителе и знаменателе. Итак, 𝑖 в квадрате равен отрицательной единице. Если в это выражение подставить 𝑖 в квадрате отрицательную единицу, числитель станет один плюс два 𝑖 минус один, то есть два 𝑖. И знаменатель становится один плюс один, то есть два. Таким образом, мы получаем два 𝑖 над двумя, возведенными в девятую степень. Мы можем отменить общий множитель двойки. Следовательно, комплексное число, которое нам дали в вопросе, равно 𝑖 в девятой степени.
Итак, 𝑖 в квадрате равен отрицательной единице. Если в это выражение подставить 𝑖 в квадрате отрицательную единицу, числитель станет один плюс два 𝑖 минус один, то есть два 𝑖. И знаменатель становится один плюс один, то есть два. Таким образом, мы получаем два 𝑖 над двумя, возведенными в девятую степень. Мы можем отменить общий множитель двойки. Следовательно, комплексное число, которое нам дали в вопросе, равно 𝑖 в девятой степени. И напомним, чтобы записать комплексное число в тригонометрической форме, нам просто нужно найти его модуль и его аргумент.
И напомним, чтобы записать комплексное число в тригонометрической форме, нам просто нужно найти его модуль и его аргумент. Аргумент 𝑍 или аргумент 𝑖 равен 𝜋 на два. Следовательно, мы можем записать наше комплексное число 𝑖 в тригонометрической форме, подставив значение 𝑟 и значение 𝜃 в тригонометрическую форму. Его тригонометрическая форма равна cos 𝜋 на два плюс 𝑖 sin of 𝜋 на два.
Аргумент 𝑍 или аргумент 𝑖 равен 𝜋 на два. Следовательно, мы можем записать наше комплексное число 𝑖 в тригонометрической форме, подставив значение 𝑟 и значение 𝜃 в тригонометрическую форму. Его тригонометрическая форма равна cos 𝜋 на два плюс 𝑖 sin of 𝜋 на два. Во-первых, единица в степени половины просто равна единице. И умножение на единицу не изменит его значения. Далее, когда 𝑘 равно нулю, два 𝜋𝑘 равны нулю. Таким образом, у нас просто есть cos 𝜋 на два больше двух, что является cos 𝜋 на четыре. И то же самое верно и для нашего второго срока. Когда 𝑘 равно нулю, у нас есть 𝑖 грех 𝜋 на два больше двух, что равно 𝑖 грех 𝜋 на четыре. Это дает нам первый квадратный корень из нашего комплексного числа.
Во-первых, единица в степени половины просто равна единице. И умножение на единицу не изменит его значения. Далее, когда 𝑘 равно нулю, два 𝜋𝑘 равны нулю. Таким образом, у нас просто есть cos 𝜋 на два больше двух, что является cos 𝜋 на четыре. И то же самое верно и для нашего второго срока. Когда 𝑘 равно нулю, у нас есть 𝑖 грех 𝜋 на два больше двух, что равно 𝑖 грех 𝜋 на четыре. Это дает нам первый квадратный корень из нашего комплексного числа.

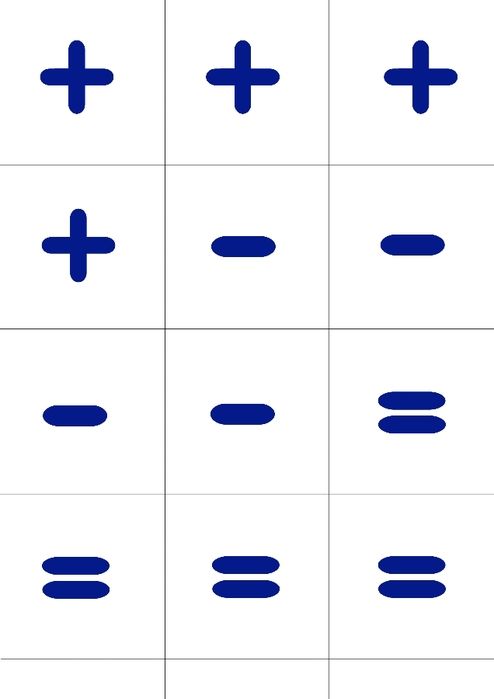
 Современные знаки плюс «+» и минус «-» появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс «+» и минус «-» появились из торговой практики: проданные меры вина отмечались на бочке черточкой «-«, а при восстановлении запаса их перечеркивали, откуда получился знак «+». Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».
Современные знаки плюс «+» и минус «-» появились в Германии в последнее десятилетие пятнадцатого века в книге Видмана, которая была руководством по счету для купцов (“Behende und ubsche Rechenung auf allen Kaufmannschaft”, 1498). Существует предположение, что знаки плюс «+» и минус «-» появились из торговой практики: проданные меры вина отмечались на бочке черточкой «-«, а при восстановлении запаса их перечеркивали, откуда получился знак «+». Здесь я хочу особо подчеркнуть, что знаком «минус» отмечалась не мера (бочка) с «отрицательным» вином, а пустая мера (бочка), что гораздо больше соответствует понятию «ноль». Когда вам математики будут рассказывать об отрицательных числах, всегда помните о пустой бочке, которая по воле математиков превратилась в бочку со знаком «минус».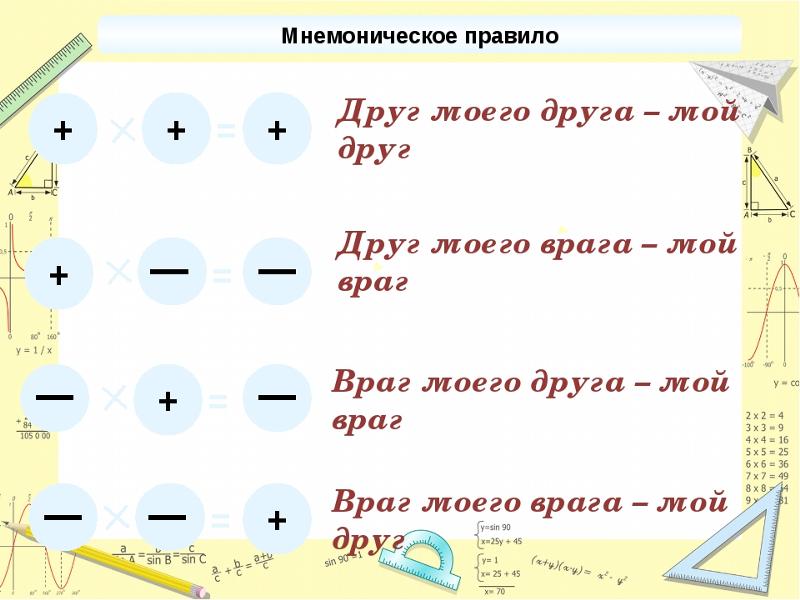 Теперь прилепливаем полученный плюс к ранее полученной двойке
Теперь прилепливаем полученный плюс к ранее полученной двойке .. Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа.
.. Их использовали для подсчета утвари, добычи, врагов и т. д. Но числа сами по себе довольно бесполезны — нужно уметь с ними обращаться. Сложение наглядно и понятно, к тому же сумма двух натуральных чисел — тоже натуральное число (математик сказал бы, что множество натуральных чисел замкнуто относительно операции сложения). Умножение — это, по сути, то же сложение, если мы говорим о натуральных числах. В жизни мы часто совершаем действия, связанные с этими двумя операциями (например, делая покупки, мы складываем и умножаем), и странно думать, что наши предки сталкивались с ними реже — сложение и умножение были освоены человечеством очень давно. Часто приходится и делить одни величины на другие, но здесь результат не всегда выражается натуральным числом — так появились дробные числа. ) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.


 Значит, B = C.
Значит, B = C. В экспериментальных науках знак обычно указывает на доверительный интервал или ошибку измерения, часто на стандартное отклонение или стандартную ошибку. Знак также может представлять включающий диапазон значений, которые может иметь показание. В технике знак указывает на допуск, который представляет собой диапазон значений, которые считаются приемлемыми, безопасными или соответствующими какому-либо стандарту или контракту. В ботанике используется в морфологических описаниях для обозначения «более или менее». В химии этот знак используется для обозначения рацемической смеси. В шахматах знак указывает на явное преимущество белого игрока; дополнительный знак ∓ указывает на такое же преимущество черного игрока.
В экспериментальных науках знак обычно указывает на доверительный интервал или ошибку измерения, часто на стандартное отклонение или стандартную ошибку. Знак также может представлять включающий диапазон значений, которые может иметь показание. В технике знак указывает на допуск, который представляет собой диапазон значений, которые считаются приемлемыми, безопасными или соответствующими какому-либо стандарту или контракту. В ботанике используется в морфологических описаниях для обозначения «более или менее». В химии этот знак используется для обозначения рацемической смеси. В шахматах знак указывает на явное преимущество белого игрока; дополнительный знак ∓ указывает на такое же преимущество черного игрока. [1]
[1]  В отличие от примера с квадратичной формулой, оба уравнения, описываемые этим тождеством, справедливы одновременно. 9{2n+1} + \cdots. }[/математика]
В отличие от примера с квадратичной формулой, оба уравнения, описываемые этим тождеством, справедливы одновременно. 9{2n+1} + \cdots. }[/математика]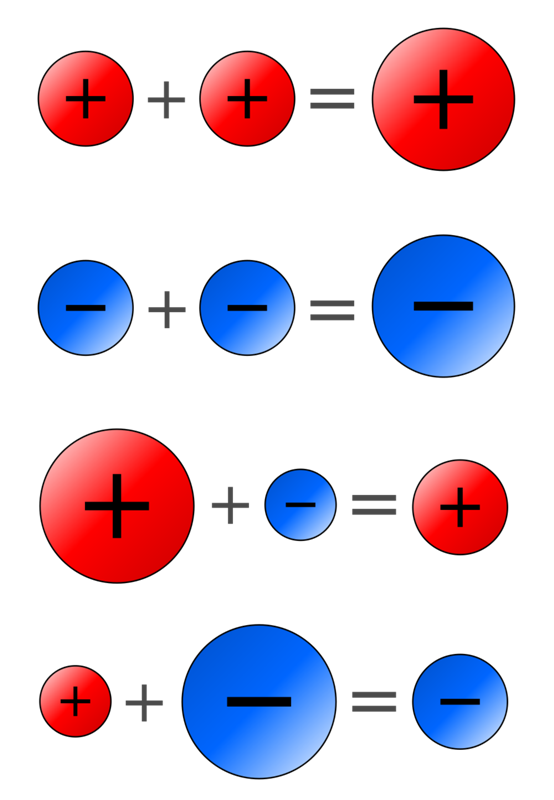 Верхний «-» в «∓» считается связанным с «+» в «±» (и аналогично для двух нижних символов), даже если нет визуальной индикации зависимости. (Однако знак «±» обычно предпочтительнее знака «∓», поэтому, если они оба появляются в уравнении, можно с уверенностью предположить, что они связаны. С другой стороны, если есть два экземпляра знака «±» в выражении, по одному лишь обозначению невозможно сказать, является ли предполагаемая интерпретация двумя или четырьмя различными выражениями.) Исходное выражение можно переписать как « x ± ( y − z )», чтобы избежать путаницы, но такие случаи, как тригонометрическое тождество
Верхний «-» в «∓» считается связанным с «+» в «±» (и аналогично для двух нижних символов), даже если нет визуальной индикации зависимости. (Однако знак «±» обычно предпочтительнее знака «∓», поэтому, если они оба появляются в уравнении, можно с уверенностью предположить, что они связаны. С другой стороны, если есть два экземпляра знака «±» в выражении, по одному лишь обозначению невозможно сказать, является ли предполагаемая интерпретация двумя или четырьмя различными выражениями.) Исходное выражение можно переписать как « x ± ( y − z )», чтобы избежать путаницы, но такие случаи, как тригонометрическое тождество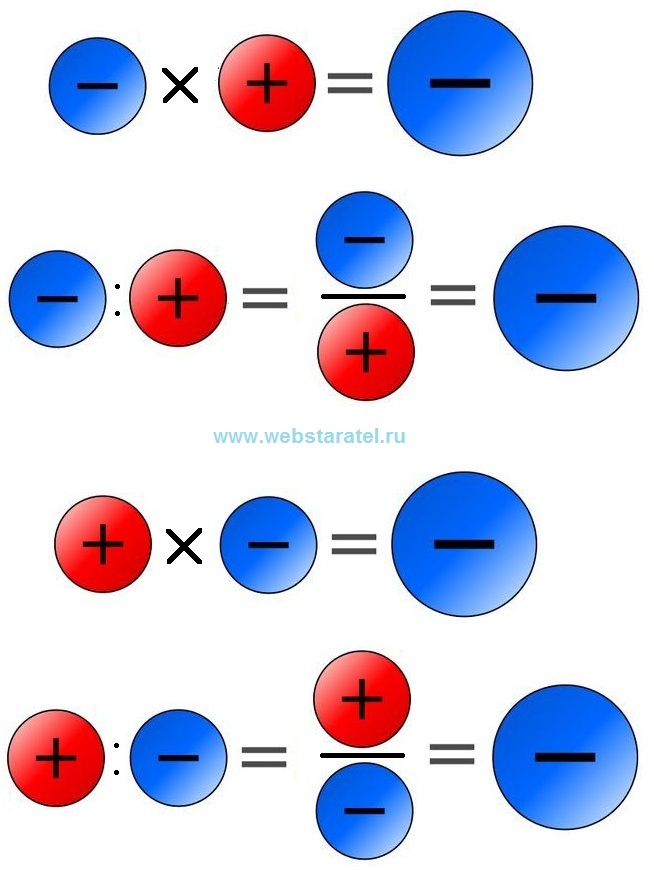




 Таким образом, сделанный снимок можно тут же опубликовать в любимой социальной сети.
Таким образом, сделанный снимок можно тут же опубликовать в любимой социальной сети. Во время записи видео можно нажать белую кнопку затвора, чтобы сделать обычное фото.
Во время записи видео можно нажать белую кнопку затвора, чтобы сделать обычное фото. Но при просмотре применяется эффект замедленного воспроизведения. Можно редактировать видео, чтобы действие режима замедленной съемки запускалось и останавливалось в указанное вами время.
Но при просмотре применяется эффект замедленного воспроизведения. Можно редактировать видео, чтобы действие режима замедленной съемки запускалось и останавливалось в указанное вами время. Фото: shutterstock.com
Фото: shutterstock.com Поэтому для удобства можно пользоваться таблицами: это облегчает вычисления.
Поэтому для удобства можно пользоваться таблицами: это облегчает вычисления.
 Вы можете распечатать таблицу или пользоваться ей онлайн.
Вы можете распечатать таблицу или пользоваться ей онлайн.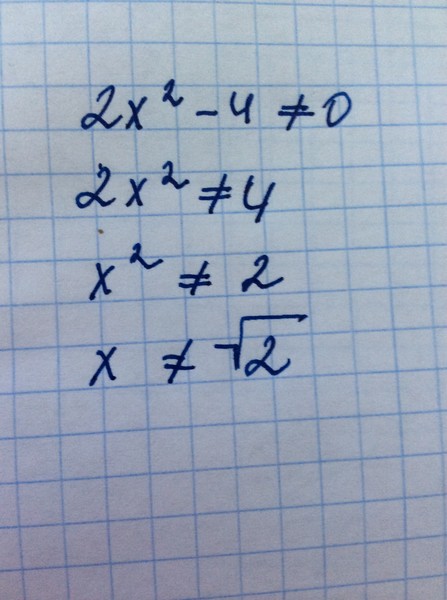
 Пригодится таблица квадратов и позже, при обучении в вузе. Вот несколько советов, как это сделать.
Пригодится таблица квадратов и позже, при обучении в вузе. Вот несколько советов, как это сделать. И важно запомнить, что не бывает квадратов, последняя цифра в которых 2, 3, 7, 8. Также часто используются квадраты таких чисел как 21, 24, 25, 26: они встречаются чаще других.
И важно запомнить, что не бывает квадратов, последняя цифра в которых 2, 3, 7, 8. Также часто используются квадраты таких чисел как 21, 24, 25, 26: они встречаются чаще других. Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Какая часть носков Макса коричневого или черного цвета?
Какая часть носков Макса коричневого или черного цвета?
 (Рисунок / атрибуты).
(Рисунок / атрибуты). Наклон ему придается командой: Рисунок
/ наклонить, (выбрать Наклонить / По
горизонтали на 450). В дальнейшем,
при копировании и вставке можно
использовать: Рисунок / отразить (отражать можно слева направо или сверху вниз).
Наклон ему придается командой: Рисунок
/ наклонить, (выбрать Наклонить / По
горизонтали на 450). В дальнейшем,
при копировании и вставке можно
использовать: Рисунок / отразить (отражать можно слева направо или сверху вниз). ..,
измените размер холста, захватив правый
нижний угол листа, двигая по диагонали
вниз и приступите к созданию рекламы.
..,
измените размер холста, захватив правый
нижний угол листа, двигая по диагонали
вниз и приступите к созданию рекламы.
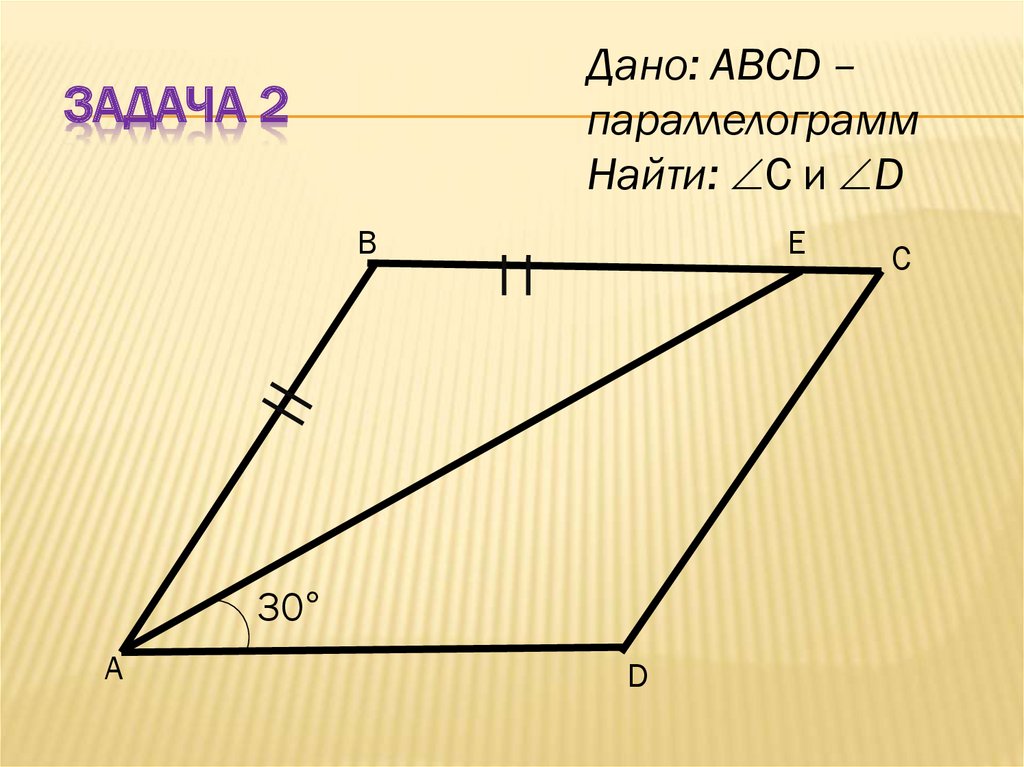 Изучите следующий параллелограмм PQTR в отношении свойств, перечисленных ниже.
Изучите следующий параллелограмм PQTR в отношении свойств, перечисленных ниже. Противоположные стороны параллелограмма равны по длине, а его противоположные углы равны по величине. Кроме того, внутренние углы на той же поперечной стороне являются дополнительными. Вот почему мы называем параллелограмм четырехугольником. 9{\circ}$
Противоположные стороны параллелограмма равны по длине, а его противоположные углы равны по величине. Кроме того, внутренние углы на той же поперечной стороне являются дополнительными. Вот почему мы называем параллелограмм четырехугольником. 9{\circ}$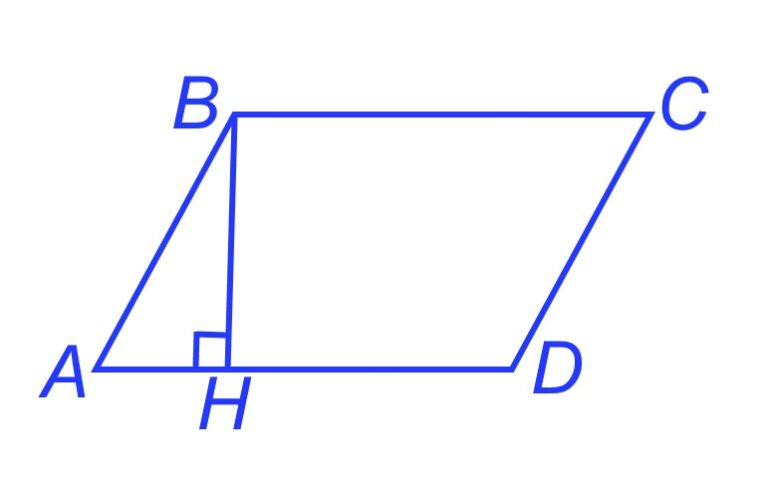
 Измерьте другую сторону.
Измерьте другую сторону.
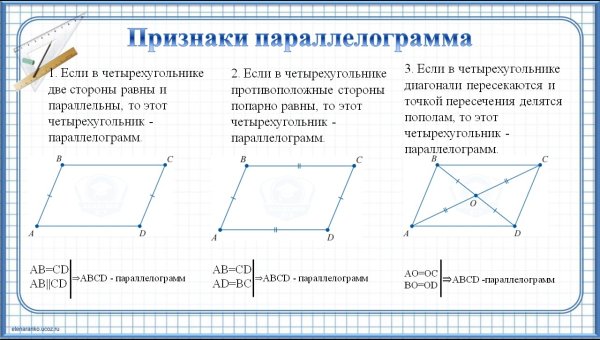


 Для этого мы разницу делим на первоначальную стоимость и затем полученный результат умножаем на сто. 840 / 4200 * 100 = 0,2 * 100 = 20%.
Для этого мы разницу делим на первоначальную стоимость и затем полученный результат умножаем на сто. 840 / 4200 * 100 = 0,2 * 100 = 20%. Например, 10% от 100 — это 0,1 * 100 = 10. Какую именно формулу применить в Excel, зависит от желаемого результата.
Например, 10% от 100 — это 0,1 * 100 = 10. Какую именно формулу применить в Excel, зависит от желаемого результата.
 Число 1 – начальное, Число 2 – то, в котором находят долю числа 1. Рассмотрим это математическое действие на примере. Представим, что нужно найти долю числа 18 в числе 42. Необходимо выполнить алгоритм из двух шагов:
Число 1 – начальное, Число 2 – то, в котором находят долю числа 1. Рассмотрим это математическое действие на примере. Представим, что нужно найти долю числа 18 в числе 42. Необходимо выполнить алгоритм из двух шагов: Там она расположена в разделе «Ячейки» (подраздел «Формат»).
Там она расположена в разделе «Ячейки» (подраздел «Формат»). Числом 1 станет доход с продаж одного продукта, а вторым – сумма общего дохода.
Числом 1 станет доход с продаж одного продукта, а вторым – сумма общего дохода. Воспользуемся функцией СУММ – выражением с ней заменится второй аргумент.
Воспользуемся функцией СУММ – выражением с ней заменится второй аргумент.
 Формула разности отличается только знаком: Разность=Число-(Процент (%)*Число).
Формула разности отличается только знаком: Разность=Число-(Процент (%)*Число). Однако рассчитывать проценты в программе гораздо удобнее, потому что есть возможность автоматизировать вычисления.
Однако рассчитывать проценты в программе гораздо удобнее, потому что есть возможность автоматизировать вычисления. как рассчитать, какой процент запроса приходится на часть моего приложения?
и как посчитать обратное, например, я знаю 5 процентов пользователей, которым нравится мой специальный пост, как я могу посчитать количество пользователей, которым нравится этот пост?
Спасибо и извините за мой плохой английский.
как рассчитать, какой процент запроса приходится на часть моего приложения?
и как посчитать обратное, например, я знаю 5 процентов пользователей, которым нравится мой специальный пост, как я могу посчитать количество пользователей, которым нравится этот пост?
Спасибо и извините за мой плохой английский. Например, в C#, если
Например, в C#, если  Это будет означать 0,04*100 из 100, или 4%.
Это будет означать 0,04*100 из 100, или 4%.
 message_id)][‘upvote’]) * 100
# Чем выше значение, тем ниже становится число -> от 10 до 6 = 60%
((data[str(payload.message_id)][‘downvote’] / data[str(payload.message_id)][‘upvote’]) * 100) / 2
# Также неправильный расчет -> от 16 до 6 = 37,5%
float(data[str(payload.message_id)][‘upvote’])-data[str(payload.message_id)][‘downvote’])/data[str(payload.message_id)][‘downvote’])* 100
message_id)][‘upvote’]) * 100
# Чем выше значение, тем ниже становится число -> от 10 до 6 = 60%
((data[str(payload.message_id)][‘downvote’] / data[str(payload.message_id)][‘upvote’]) * 100) / 2
# Также неправильный расчет -> от 16 до 6 = 37,5%
float(data[str(payload.message_id)][‘upvote’])-data[str(payload.message_id)][‘downvote’])/data[str(payload.message_id)][‘downvote’])* 100 
 Амфотерный оксид образуется при сгорании в кислороде: алюминия, кальция, кремния, бериллия, натрия, цинка.
2. Кальций взаимодействует с веществами, формулы которых:НСl,
Амфотерный оксид образуется при сгорании в кислороде: алюминия, кальция, кремния, бериллия, натрия, цинка.
2. Кальций взаимодействует с веществами, формулы которых:НСl, Информация в CAMEO Chemicals поступает
из множества
источники данных.
Информация в CAMEO Chemicals поступает
из множества
источники данных.
 Информация в CAMEO Chemicals поступает из различных источников.
источники данных.
Информация в CAMEO Chemicals поступает из различных источников.
источники данных. (USCG, 1999)
(USCG, 1999)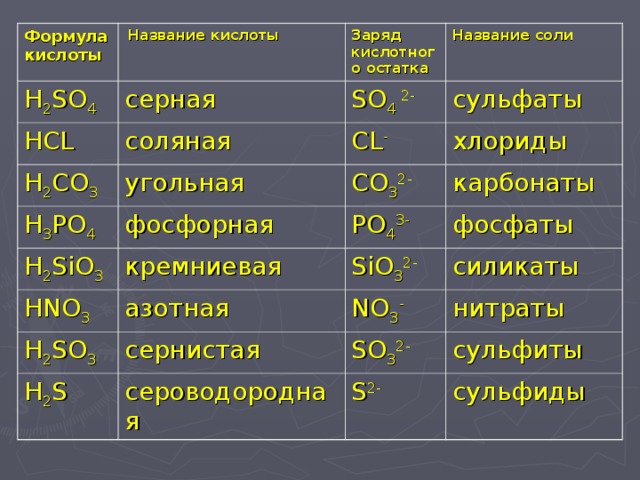
 (ЭРГ, 2020)
(ЭРГ, 2020)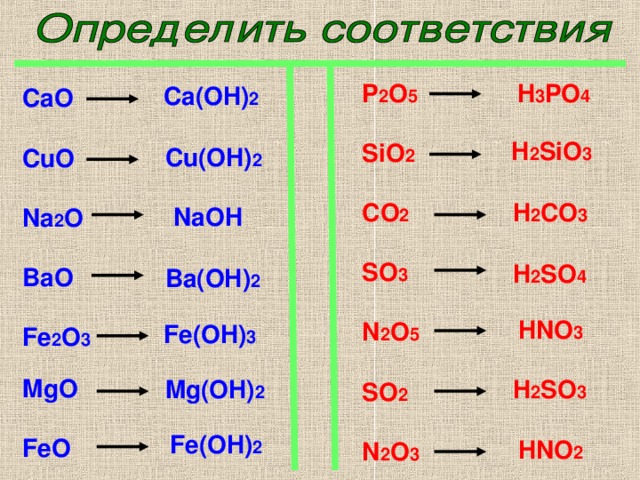 Не прикасайтесь к поврежденным контейнерам или пролитому материалу, если вы не надели соответствующую защитную одежду. Остановите утечку, если вы можете сделать это без риска. Не допускать попадания в водные пути, канализацию, подвалы или замкнутые пространства. Впитать или засыпать сухой землей, песком или другим негорючим материалом и переложить в контейнеры. НЕ ПОЛУЧАЙТЕ ВОДУ ВНУТРИ КОНТЕЙНЕРОВ. (ЭРГ, 2020)
Не прикасайтесь к поврежденным контейнерам или пролитому материалу, если вы не надели соответствующую защитную одежду. Остановите утечку, если вы можете сделать это без риска. Не допускать попадания в водные пути, канализацию, подвалы или замкнутые пространства. Впитать или засыпать сухой землей, песком или другим негорючим материалом и переложить в контейнеры. НЕ ПОЛУЧАЙТЕ ВОДУ ВНУТРИ КОНТЕЙНЕРОВ. (ЭРГ, 2020)
 ] (> 1,6%) (NIOSH, 2022)
] (> 1,6%) (NIOSH, 2022) Нормализованное время прорыва (время, в которое
скорость проникновения превышает 0,1 мкг/см2/мин) сообщается в минутах. Все
химические вещества были испытаны при температуре приблизительно от 20°C до 27°C, если
в противном случае указано. Все химические вещества были протестированы в концентрации
больше 95%, если не указано иное.
Боевые отравляющие вещества (люизит, зарин, зоман, сернистый иприт, табун
и VX Nerve Agent) были протестированы при температуре 22°C и относительной влажности 50%.
в соответствии с военным стандартом MIL-STD-282. «Время прорыва» для химической
боевых отравляющих веществ определяется как время, когда кумулятивная масса,
проникновение через ткань превышает предел MIL-STD-282 [либо
1,25 или 4,0 мкг/см2].
Нормализованное время прорыва (время, в которое
скорость проникновения превышает 0,1 мкг/см2/мин) сообщается в минутах. Все
химические вещества были испытаны при температуре приблизительно от 20°C до 27°C, если
в противном случае указано. Все химические вещества были протестированы в концентрации
больше 95%, если не указано иное.
Боевые отравляющие вещества (люизит, зарин, зоман, сернистый иприт, табун
и VX Nerve Agent) были протестированы при температуре 22°C и относительной влажности 50%.
в соответствии с военным стандартом MIL-STD-282. «Время прорыва» для химической
боевых отравляющих веществ определяется как время, когда кумулятивная масса,
проникновение через ткань превышает предел MIL-STD-282 [либо
1,25 или 4,0 мкг/см2]. приобретаются знания и опыт. Информация отражает
лабораторное исследование тканей, некомплектных швейных изделий, под
контролируемые условия. Предназначен для информационного использования лицами
наличие технических навыков для оценки в соответствии с их конкретным конечным использованием
условиях, на свое усмотрение и риск. это пользователь
ответственность за определение уровня токсичности и надлежащее
необходимы средства индивидуальной защиты. Любой, кто собирается использовать это
Информация должна сначала подтвердить, что выбранная одежда подходит
для предполагаемого использования. Во многих случаях швы и застежки имеют более короткую длину.
время прорыва и более высокие скорости проникновения, чем у ткани. Если
ткань разорвана, потерта или проколота, или если швы или застежки выходят из строя,
или если прикрепленные перчатки, козырьки и т. д. повреждены, конечный пользователь должен
прекратите использование одежды, чтобы избежать потенциального воздействия химических веществ.
приобретаются знания и опыт. Информация отражает
лабораторное исследование тканей, некомплектных швейных изделий, под
контролируемые условия. Предназначен для информационного использования лицами
наличие технических навыков для оценки в соответствии с их конкретным конечным использованием
условиях, на свое усмотрение и риск. это пользователь
ответственность за определение уровня токсичности и надлежащее
необходимы средства индивидуальной защиты. Любой, кто собирается использовать это
Информация должна сначала подтвердить, что выбранная одежда подходит
для предполагаемого использования. Во многих случаях швы и застежки имеют более короткую длину.
время прорыва и более высокие скорости проникновения, чем у ткани. Если
ткань разорвана, потерта или проколота, или если швы или застежки выходят из строя,
или если прикрепленные перчатки, козырьки и т. д. повреждены, конечный пользователь должен
прекратите использование одежды, чтобы избежать потенциального воздействия химических веществ. Поскольку условия использования находятся вне нашего контроля, DuPont не делает никаких
гарантии, явные или подразумеваемые, включая, помимо прочего,
гарантии товарной пригодности или пригодности для конкретного использования и
не несет никакой ответственности в связи с любым использованием этой информации.
Эта информация не предназначена для использования в качестве лицензии на работу или
рекомендацию о нарушении любого патента, товарного знака или технического
информацию DuPont или других лиц, касающуюся любого материала или его использования.
Поскольку условия использования находятся вне нашего контроля, DuPont не делает никаких
гарантии, явные или подразумеваемые, включая, помимо прочего,
гарантии товарной пригодности или пригодности для конкретного использования и
не несет никакой ответственности в связи с любым использованием этой информации.
Эта информация не предназначена для использования в качестве лицензии на работу или
рекомендацию о нарушении любого патента, товарного знака или технического
информацию DuPont или других лиц, касающуюся любого материала или его использования.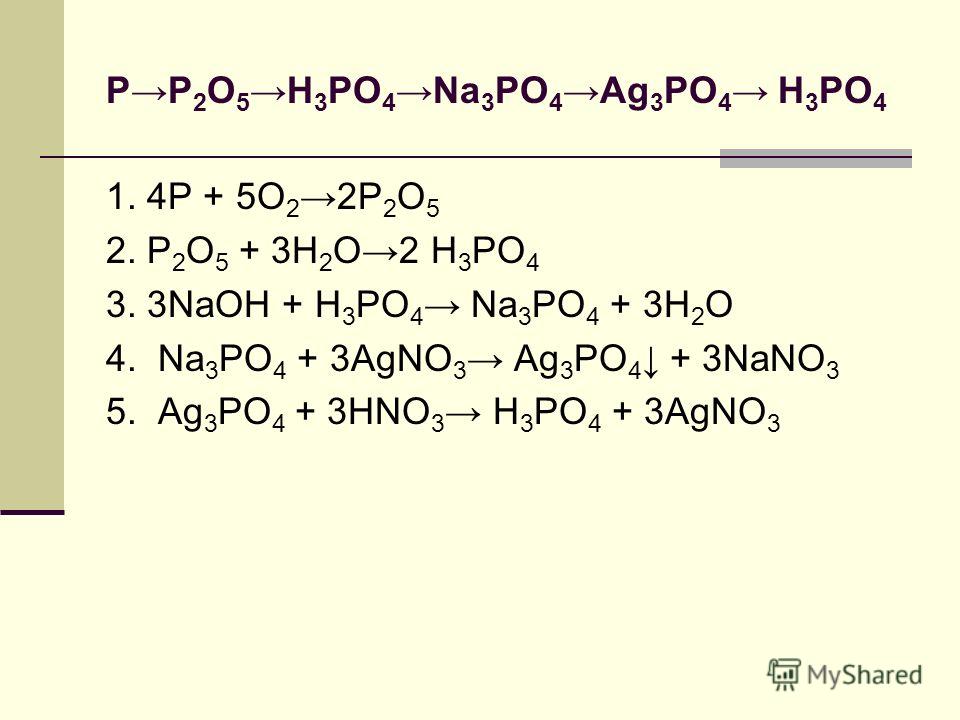
 Немедленно обратитесь за медицинской помощью.
Немедленно обратитесь за медицинской помощью. источники данных.
источники данных.
 )
) Это делается для диапазона концентраций от 1 до 10 -10 моль/л в следующей таблице:
Это делается для диапазона концентраций от 1 до 10 -10 моль/л в следующей таблице: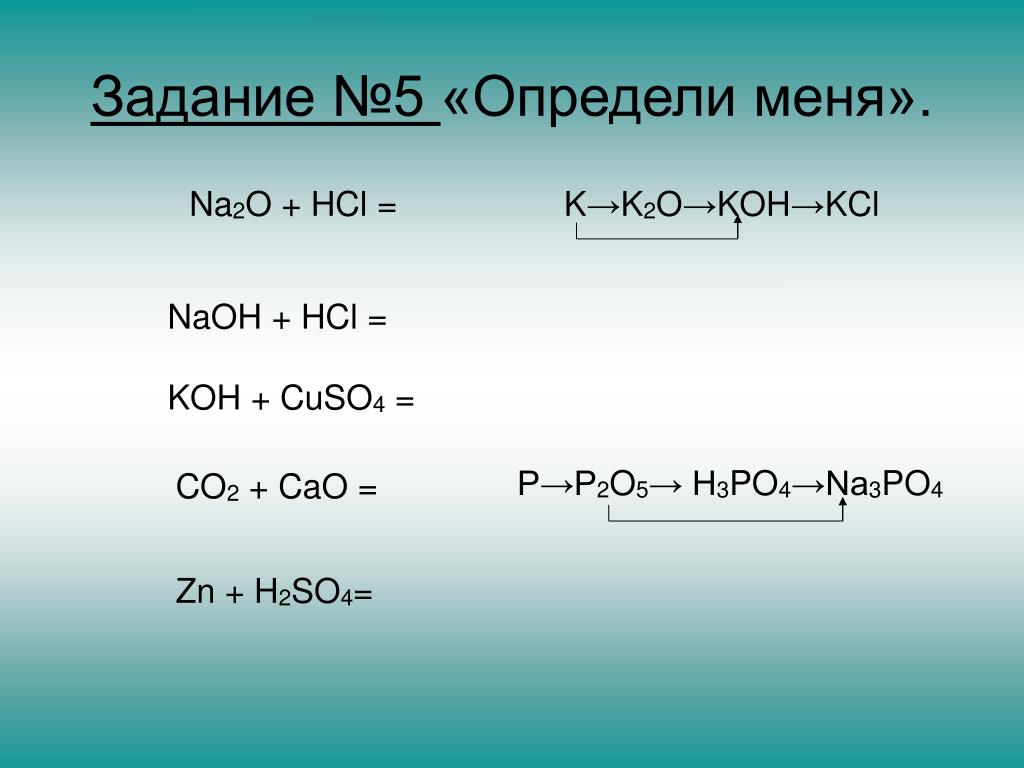 85E-08
85E-08
 Справа налево: +,-,+. Т.к. нам нужны отрицательные значения(потому что (х+3)(х-8)≤0), то ответ будет таким:
Справа налево: +,-,+. Т.к. нам нужны отрицательные значения(потому что (х+3)(х-8)≤0), то ответ будет таким: 4, потом сдвигаем ее вверх по оси Оу на 4 единицы вверх, а потом сдвигаем слево по оси оХ на три единицы.
4, потом сдвигаем ее вверх по оси Оу на 4 единицы вверх, а потом сдвигаем слево по оси оХ на три единицы.
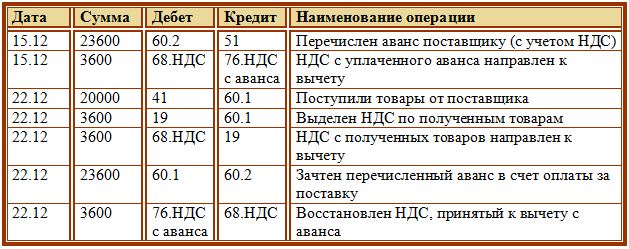



 В России этот вид налога применяется с 1992 года.
В России этот вид налога применяется с 1992 года. При методе начислений все расходы и доходы учитываются именно в том периоде, в котором они возникают, вне зависимости от реального поступления или списания средств со счетов. Кассовый метод подразумевает учёт доходов и расходов и доходов в момент зачисления или списания соответствующих сумм. Метод начислений в бухгалтерском учёте, согласно Налоговому кодексу РФ, могут использовать все налогоплательщики, а вот кассовый метод возможен только для отдельных видов организаций с небольшой выручкой. В любом случае выбранный метод учёта должен быть зафиксирован в учётной политике.
При методе начислений все расходы и доходы учитываются именно в том периоде, в котором они возникают, вне зависимости от реального поступления или списания средств со счетов. Кассовый метод подразумевает учёт доходов и расходов и доходов в момент зачисления или списания соответствующих сумм. Метод начислений в бухгалтерском учёте, согласно Налоговому кодексу РФ, могут использовать все налогоплательщики, а вот кассовый метод возможен только для отдельных видов организаций с небольшой выручкой. В любом случае выбранный метод учёта должен быть зафиксирован в учётной политике.  Разницей между дебетом и кредитом по счёту 68 становится сумма, которую организации нужно будет оплатить в бюджет. Точнее, если обороты по кредиту обороты больше дебетовых, то разницу перечисляют в бюджет, если наоборот — разница возмещается государством.
Разницей между дебетом и кредитом по счёту 68 становится сумма, которую организации нужно будет оплатить в бюджет. Точнее, если обороты по кредиту обороты больше дебетовых, то разницу перечисляют в бюджет, если наоборот — разница возмещается государством.
 Учёт входного налога на добавленную стоимость с последующим принятием его к вычету.
Учёт входного налога на добавленную стоимость с последующим принятием его к вычету. Например, организация переходит на спецрежим или начинает использовать имущество в операциях, которые этим налогом не облагаются, допустим, место операции с таким имуществом находится за пределами РФ, и в ряде других ситуаций. В таком случае операции отражаются следующими проводками:
Например, организация переходит на спецрежим или начинает использовать имущество в операциях, которые этим налогом не облагаются, допустим, место операции с таким имуществом находится за пределами РФ, и в ряде других ситуаций. В таком случае операции отражаются следующими проводками: Это могут быть первичные бухгалтерские документы (счета-фактуры, акты, накладные), банковские выписки, бухгалтерские справки и другие.
Это могут быть первичные бухгалтерские документы (счета-фактуры, акты, накладные), банковские выписки, бухгалтерские справки и другие. Начисления отличаются от операций с кредиторской задолженностью тем, что счет-фактура обычно еще не получен и не введен в систему до конца года. Учет начисления гарантирует, что операция будет признана в том отчетном периоде, когда она была совершена, а не оплачена. Это требование бухгалтерского учета, основанного на GAAP, и обеспечивает более точное и актуальное представление о финансовом положении Университета, чем метод кассового учета, при котором расходы учитываются по факту их оплаты. Для учета расходов в текущем финансовом году расходы должны быть понесены до 30 июня, что означает, что товары должны быть получены или услуги должны быть оказаны к этой дате (конец дня).
Начисления отличаются от операций с кредиторской задолженностью тем, что счет-фактура обычно еще не получен и не введен в систему до конца года. Учет начисления гарантирует, что операция будет признана в том отчетном периоде, когда она была совершена, а не оплачена. Это требование бухгалтерского учета, основанного на GAAP, и обеспечивает более точное и актуальное представление о финансовом положении Университета, чем метод кассового учета, при котором расходы учитываются по факту их оплаты. Для учета расходов в текущем финансовом году расходы должны быть понесены до 30 июня, что означает, что товары должны быть получены или услуги должны быть оказаны к этой дате (конец дня).
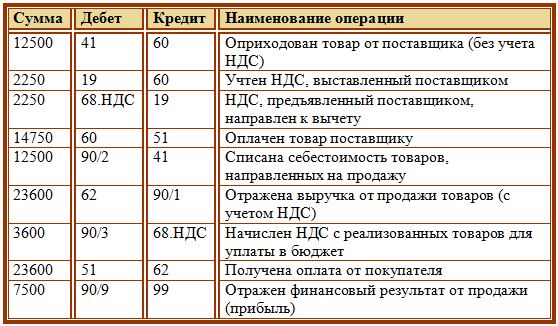 Если товары зачислены как полученные, но они еще не оплачены, система отразит расход как начисленный расход. Расход, связанный со счетом-фактурой, регистрируется, когда счет к оплате входит в счет-фактуру, а не когда платеж по счету-фактуре отправляется поставщику. Начисления поступлений будут регистрироваться только для расходов, превышающих 2500 долларов США. Товары и услуги, полученные до 30 июня, необходимо внести до 16:30. 30 июня.
Если товары зачислены как полученные, но они еще не оплачены, система отразит расход как начисленный расход. Расход, связанный со счетом-фактурой, регистрируется, когда счет к оплате входит в счет-фактуру, а не когда платеж по счету-фактуре отправляется поставщику. Начисления поступлений будут регистрироваться только для расходов, превышающих 2500 долларов США. Товары и услуги, полученные до 30 июня, необходимо внести до 16:30. 30 июня. Эти начисления должны быть представлены и утверждены бюджетным управлением до 12:00. 7 июля.
Эти начисления должны быть представлены и утверждены бюджетным управлением до 12:00. 7 июля. По этим начислениям отделы и проекты не начисляются; скорее они возлагаются на специальный отдел офиса контролера. Эти начисления обычно определяются после того, как главная книга считается окончательной для отчетов Information Warehouse.
По этим начислениям отделы и проекты не начисляются; скорее они возлагаются на специальный отдел офиса контролера. Эти начисления обычно определяются после того, как главная книга считается окончательной для отчетов Information Warehouse. Прямой депозит в сочетании с электронным файлом IRS предоставляет налогоплательщикам самый быстрый и безопасный способ получения возмещения.
Прямой депозит в сочетании с электронным файлом IRS предоставляет налогоплательщикам самый быстрый и безопасный способ получения возмещения.

 Теория…
Теория… Дистрибутивность пересечения относительно объединения
Дистрибутивность пересечения относительно объединения Закон склеивания
Закон склеивания Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов . Комбинаторика. В алгебраическом доказательстве есть три приемлемых подхода:
В алгебраическом доказательстве есть три приемлемых подхода: 2 = \frac{ 1}{6} (к+1)(к+2)(2к+3)\). 92+\frac{13}{6}\,k+1.
2 = \frac{ 1}{6} (к+1)(к+2)(2к+3)\). 92+\frac{13}{6}\,k+1.  \]
\]