Сумма и произведение цифр числа. Решение задачи на Python
Одной из часто используемых задач для начинающих изучать программирование является нахождение суммы и произведения цифр числа. Число может вводиться с клавиатуры или генерироваться случайно. Задача формулируется так:
Дано число. Найти сумму и произведение его цифр.
Например, сумма цифр числа 253 равна 10-ти, так как 2 + 5 + 3 = 10. Произведение цифр числа 253 равно 30-ти, так как 2 * 5 * 3 = 30.
В данном случае задача осложняется тем, что количество разрядов числа заранее (на момент написания программы) не известно. Это может быть и трехзначное число, как в примере выше, и восьмизначное, и однозначное.
Обычно предполагается, что данная задача должна быть решена арифметическим способом и с использованием цикла. То есть с заданным число должны последовательно выполняться определенные арифметические действия, позволяющие извлечь из него все цифры, затем сложить их и перемножить.
При этом используются операции деления нацело и нахождения остатка. Если число разделить нацело на 10, произойдет «потеря» последней цифры числа. Например, 253 ÷ 10 = 25 (остаток 3). С другой стороны, эта потерянная цифра есть остаток от деления. Получив эту цифру, мы можем добавить ее к сумме цифр и умножить на нее произведение цифр числа.
Пусть n – само число, suma – сумма его цифр, а mult – произведение. Тогда алгоритм нахождения суммы и произведения цифр можно словесно описать так:
- Переменной suma присвоить ноль.
- Переменной mult присвоить единицу. Присваивать 0 нельзя, так как при умножении на ноль результат будет нулевым.
- Пока значение переменной n больше нуля повторять следующие действия:
- Найти остаток от деления значения n на 10, то есть извлечь последнюю цифру числа.
- Добавить извлеченную цифру к сумме и увеличить на эту цифру произведение.

- Избавиться от последнего разряда числа n путем деления нацело на 10.
В языке Python операция нахождения остатка от деления обозначается знаком процента — %. Деление нацело — двумя слэшами — //.
Код программы на языке Python
n = int(input())
suma = 0
mult = 1
while n > 0:
digit = n % 10
suma = suma + digit
mult = mult * digit
n = n // 10
print("Сумма:", suma)
print("Произведение:", mult)Пример выполнения:
253 Сумма: 10 Произведение: 30
Изменение значений переменных можно записать в сокращенном виде:
...
while n > 0:
digit = n % 10
suma += digit
mult *= digit
n //= 10
...Приведенная выше программа подходит только для нахождения суммы и произведения цифр натуральных чисел, то есть целых чисел больше нуля. Если исходное число может быть любым целым, следует учесть обработку отрицательных чисел и нуля.
Если число отрицательное, это не влияет на сумму его цифр. В таком случае достаточно будет использовать встроенную в Python функции abc, которая возвращает абсолютное значение переданного ей аргумента. Она превратит отрицательное число в положительное, и цикл while с его условием n > 0 будет работать как и прежде.
Если число равно нулю, то по логике вещей сумма его цифр и их произведение должны иметь нулевые значения. Цикл срабатывать не будет. Поскольку исходное значение mult — это 1, следует добавить проверку на случай, если заданное число — это ноль.
Программа, обрабатывающая все целые числа, может начинаться так:
n = abs(int(input()))
suma = 0
mult = 1
if n == 0:
mult = 0
...Заметим, если в самом числе встречается цифра 0 (например, 503), то произведение всех цифр будет равно нулю. Усложним задачу:
Вводится натуральное число. Найти сумму и произведение цифр, из которых состоит это число.
При этом если в числе встречается цифра 0, то ее не надо учитывать при нахождении произведения.
Для решения такой задачи в цикл добавляется проверка извлеченной цифры на ее неравенство нулю. Делать это надо до умножения на нее значения переменной-произведения.
n = int(input())
suma = 0
mult = 1
while n > 0:
digit = n % 10
if digit != 0:
suma += digit
mult *= digit
n = n // 10
print("Сумма:", suma)
print("Произведение:", mult)Обратим внимание, что заголовок условного оператора if digit != 0: в Python можно сократить до просто if digit:. Потому что 0 — это False. Все остальные числа считаются истиной.
Приведенный выше математический алгоритм нахождения суммы и произведения цифр числа можно назвать классическим, или универсальным. Подобным способом задачу можно решить на всех императивных языках, независимо от богатства их инструментария. Однако средства языка программирования могут позволить решить задачу другим, зачастую более простым, путем. Например, в Python можно не преобразовывать введенную строку к числу, а извлекать из нее отдельные символы, которые преобразовывать к целочисленному типу
Например, в Python можно не преобразовывать введенную строку к числу, а извлекать из нее отдельные символы, которые преобразовывать к целочисленному типу int:
a = input()
suma = 0
mult = 1
for digit in a:
suma += int(digit)
mult *= int(digit)
print("Сумма:", suma)
print("Произведение:", mult)Если добавить в код проверку, что извлеченный символ строки действительно является цифрой, то программа станет более универсальной. С ее помощью можно будет считать не только сумму и произведение цифр целых чисел, но и вещественных, а также цифр, извлекаемых из произвольной строки.
n = input()
suma = 0
mult = 1
for digit in n:
if digit.isdigit():
suma += int(digit)
mult *= int(digit)
print("Сумма:", suma)
print("Произведение:", mult)Пример выполнения:
это3 чи3с9ло! Сумма: 15 Произведение: 81
Строковый метод isdigit проверяет, состоит ли строка только из цифр. В нашем случае роль строки играет одиночный, извлеченный на текущей итерации цикла, символ.
Глубокое знание языка Python позволяет решить задачу более экзотическими способами:
import functools
n = input()
n = [int(digit) for digit in n]
suma = sum(n)
mult = functools.reduce(lambda x, y: x*y, n)
print("Сумма:", suma)
print("Произведение:", mult)Выражение [int(digit) for digit in n] представляет собой генератор списка. Если была введена строка "234", будет получен список чисел: [2, 3, 4].
Встроенная функция sum считает сумму элементов переданного ей аргумента.
Функция reduce модуля functools принимает два аргумента — лямбда-выражение и в данном случае список. Здесь в переменной x происходит накопление произведения, а y принимает каждое следующее значение списка.
Больше задач в PDF
Открытая Математика. Алгебра. Обыкновенные дроби
Обыкновенные дроби
Можно еще больше расширить числовое множество – так, чтобы операция деления над натуральными числами была выполнима всегда. Для этого введем понятие дроби.
Для этого введем понятие дроби.
Обыкновенной дробью называется число вида mn, где m и n – натуральные числа. Число m называется числителем этой дроби, а число n – её знаменателем.
Если n = 1, то дробь имеет вид m1, и её часто записывают просто m. Отсюда, в частности, следует, что любое натуральное число представимо в виде обыкновенной дроби со знаменателем 1.
Две дроби ab и cd называются равными, если ad=bc.
Например, 23=812, так как 2ċ12=3ċ8. Из этого определения следует, что дробь ab равна любой дроби вида ambm, где m – натуральное число. В самом деле, так как aċbm=bċam, то ab=ambm. Итак, мы готовы сформулировать следующее правило.
Если числитель и знаменатель данной дроби умножить или разделить на одно и то же число, неравное нулю, то получится дробь, равная данной.
С помощью основного свойства дроби можно заменить данную дробь другой дробью, равной данной, но с меньшими числителем и знаменателем. Такая замена называется сокращением дроби. Например, 812=46=23
(здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например, 45
– несократимая дробь.
Такая замена называется сокращением дроби. Например, 812=46=23
(здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например, 45
– несократимая дробь.
Обыкновенная дробь mn называется правильной, если её числитель меньше её знаменателя, то есть m < n. Обыкновенная дробь называется неправильной, если её числитель больше её знаменателя, то есть m > n.
Справедливо следующее утверждение (его мы докажем ниже):
Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби.
Из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше. Например, 37<57, 58<68. Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например, 12>15, 38<34.
Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.
Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например, 12>15, 38<34.
Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.
Теперь знаменатели этих дробей одинаковы, значит, 2128>2028.
Следовательно, 34>57.
Ясно, что две дроби можно привести не к единственному общему знаменателю. Так, в нашем примере дроби 34
и 57
можно привести к знаменателю 56. В самом деле:
34=3ċ144ċ14=4256, 57=5ċ87ċ8=4056. Понятно, что эти две дроби можно привести к любому знаменателю, делящемуся одновременно на 4 и 7. Однако обычно стараются привести дроби к наименьшему общему знаменателю, который равен наименьшему общему кратному знаменателей двух данных дробей.
Понятно, что эти две дроби можно привести к любому знаменателю, делящемуся одновременно на 4 и 7. Однако обычно стараются привести дроби к наименьшему общему знаменателю, который равен наименьшему общему кратному знаменателей двух данных дробей.
Привести дроби к наименьшему общему знаменателю: 1215 и 720.
Найдём сперва наименьшее общее кратное чисел 15 и 20. НОК (15, 20) = 60.
Так как 60 : 15 = 4, то числитель и знаменатель дроби 1215 нужно умножить на 4: 1215=12ċ415ċ4=4860. Поскольку 60 : 20 = 3, то числитель и знаменатель второй дроби нужно умножить на 3: 720=7ċ320ċ3=2160. Итак, дроби приведены к общему знаменателю: 1215=4860 и 720=2160.Ответ. 1215=4860, 720=2160.
В рассмотренном примере числа 4 и 3 называют дополнительными множителями для первой и второй дроби соответственно.
Теперь мы можем определить арифметические действия с дробями.
Сложение. Если знаменатели дробей одинаковы, то чтобы сложить эти дроби, нужно сложить их числители; знаменатель остаётся прежним, то есть
ab+cb=a+cb.
Если знаменатели данных дробей разные, то дроби нужно сначала привести к общему знаменателю, а потом поступить, как описано выше.
Если знаменатели дробей одинаковы, то чтобы сложить эти дроби, нужно сложить их числители; знаменатель остаётся прежним, то есть
ab+cb=a+cb.
Если знаменатели данных дробей разные, то дроби нужно сначала привести к общему знаменателю, а потом поступить, как описано выше.
Вычитание. Если две дроби имеют одинаковые знаменатели, то ab-cb=a-cb. Если знаменатели данных дробей различны, то сперва приводят дроби к общему знаменателю, а потом вычитают их по вышеприведённой формуле.
Умножение. Произведение двух дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению их знаменателей, то есть abċcd=acbd. Например, 23ċ47=2ċ43ċ7=821.
Деление. Деление дробей осуществляют следующим образом: ab:cd=adbc. Например, 35:27=3ċ75ċ2=2110.
В случае умножения и деления смешанных чисел всегда удобно переходить к неправильным дробям.
Сложить две дроби 37 и 57. Ответ представить в виде неправильной дроби.
Имеем:
37+57=3+57=87.
Ответ. 87.
Сложить две дроби 1215 и 720. Ответ представить в виде неправильной дроби.
Имеем:
1215+720=4860+2160=48+2160=6960.
Ответ. 6960.
Теперь можно показать, что любую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби (или в виде натурального числа, если дробь mn такова, что число m кратно n, например, 123=4).
Представить неправильную дробь в виде суммы натурального числа и правильной дроби: 1) 257; 2) 3712.
Имеем:
1) 257=21+47=217+47=3+47.
2) 3712=36+112=3612+112=3+112.
Обычно сумму натурального числа и правильной дроби пишут без знака сложения, то есть вместо 3+47
пишут просто 347. Неправильная дробь, записанная в такой форме, называется смешанным числом. Говорят, что целая часть этого числа равна 3, а дробная – 47.
Неправильная дробь, записанная в такой форме, называется смешанным числом. Говорят, что целая часть этого числа равна 3, а дробная – 47.
Ответ. 347, 3112.
Всякую неправильную дробь можно представить в виде смешанного числа (или в виде натурального числа). Понятно также, что верно и обратное: всякое смешанное число может быть представлено в виде неправильной дроби. Например, 435=4+35=205+35=20+35=235.
Выполнить действия. 1) 413-234; 2) 323ċ415; 3) 323:415.
Имеем:
- 413-234=4+13-(2+34)=4+13-2-34=(4-2)+13-34=2+4-912==2-512=1+1212-512=1+12-512=1+712=1712.
- 323ċ415=(3+23)ċ(4+15)=113ċ215=23115=225+615=15615.
- 323:415=113:215=113ċ521=5563.
Ответ. 1) 1712; 2) 15615; 3) 5563.
| Купить входную дверь |
| masterdveri74.ru |
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия. {30}$, чтобы увидеть, насколько они велики на самом деле. 9м$$
{30}$, чтобы увидеть, насколько они велики на самом деле. 9м$$
Это не ответ, мне просто нужно показать график. Я забыл пометить ось. Горизонтальный — $n$, а второй — $m$
Надеюсь, вам понравится
$\endgroup$ 4 $\begingroup$Еще одна попытка: 9н$.
$\endgroup$ 3Алгебраические выражения | ChiliMath
Математика, как и любой другой язык, имеет способ передачи идей. Алгебраическое выражение — это краткий способ описания математических объектов с помощью чисел, переменных (букв) и арифметических операций, таких как сложение, вычитание, умножение и деление.
Тремя основными компонентами алгебраических выражений являются числа , переменные и арифметические операции .
- Числа или константы
Примеры: [латекс]1[/латекс], [латекс]6[/латекс], [латекс]8[/латекс], [латекс]27[/латекс], [латекс] 32[/latex] и т. д.
- Переменные или буквы
Примеры: [latex]x[/latex], [latex]y[/latex], [latex]a[/latex], [latex]h [/latex], [latex]p[/latex] и т. д.
- Арифметические операции
Примеры: [latex]+[/latex] (сложение), [latex] – [/latex] (вычитание) , [латекс] \times[/латекс] (умножение) , [латекс]÷[/латекс] (деление)
Ниже приведены простые примеры, которые помогут вам ознакомиться с операциями сложения, вычитания, умножения и деления.
- Сложение
сумма [латекс]х[/латекс] и [латекс]5[/латекс] → [латекс]х+5[/латекс]
- Вычитание 90 020
разность [латекс]у[/латекс] и [латекс]3[/латекс] → [латекс]у-3[/латекс]
- Умножение
произведение [латекс]n[/латекс] и [латекс]2[/латекс] → [латекс]2n[/латекс]
- Деление
частное [латекс]k[/латекс] и [латекс]7[/латекс] → [латекс]\большой{{к \более 7}}[/латекс]
Пошаговые примеры написания алгебраических выражений
Давайте рассмотрим больше примеров.
Пример 1: Сумма удвоенного числа и [латекс]3[/латекс]
Ответ: Пусть переменная [латекс]х[/латекс] будет неизвестным числом. Таким образом, удвоение числа означает [латекс]2x[/латекс]. Сумма (используйте символ плюс) удвоенного числа и [латекс]3[/латекс] может быть записана как [латекс]2x+3[/латекс].
Пример 2: Разница тройного числа a и [latex]5[/latex]
Ответ: Пусть переменная [latex]y[/latex] будет неизвестным числом. Таким образом, тройное число означает [латекс]3г[/латекс]. Разность (используйте символ минус) тройного числа и [латекс]5[/латекс] должна быть записана как [латекс]3у – 5[/латекс].
Пример 3: Сумма частного [латекс]m[/латекс] и [латекс]2[/латекс] и произведение [латекс]4[/латекс] и [латекс]n[ /латекс].
Ответ: В этом случае неизвестные номера уже указаны как [latex]m[/latex] и [latex]n[/latex]. Это одним поводом для беспокойства меньше.
Это одним поводом для беспокойства меньше.
Ключ в том, чтобы признать, что мы собираемся добавить частное и произведение.
- частное [латекс]m[/латекс] и [латекс]2[/латекс] выражается как [латекс]\большой{{м \более 2}}[/латекс]
- [латекс]4[/латекс] и [латекс]n[/латекс] выражается как [латекс]4n[/латекс]
Таким образом, сумма частного и произведения равна [латекс] {\ большой {{м \ более 2}}} + 4n[/латекс].
Пример 4: Разность произведения [латекс]7[/латекс] и [латекс]w[/латекс] и частного [латекс]2[/латекс] и [латекс]v[ /латекс].
Ответ: В этом случае неизвестным номерам были присвоены соответствующие переменные: [latex]w[/latex] и [latex]v[/latex].
Ключ в том, чтобы признать, что мы собираемся вычесть произведение на частное некоторых выражений.
- произведение [латекс]7[/латекс] и [латекс]в[/латекс] выражается как [латекс]7в[/латекс]
- частное [латекс]2[/латекс] и [latex]v[/latex] выражается как [latex]\Large{{2 \over v}}[/latex]
Следовательно, разница между произведением и частным равна [latex]7w – {\Large{ {2 \over v}}}[/latex].
Общие слова или термины для обозначения сложения, вычитания, умножения и деления
Давайте рассмотрим некоторые распространенные слова или фразы, описывающие четыре арифметических операции. Очень важно, чтобы вы понимали эти слова или фразы, чтобы успешно написать или интерпретировать любое заданное алгебраическое выражение.
Преобразование математических фраз в алгебраические выражения
Ключом к обучению является изучение МНОГО примеров!
| МАТЕМАТИЧЕСКИЕ ФРАЗЫ | АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ | |
|---|---|---|
| число плюс 9 | у + 9 | |
| сумма числа и 10 | м + 10 | |
| б + 5 | ||
| число увеличить на 4 | х + 4 | |
| ч отнять 2 | ч − 2 | |
| 2 убери по номеру | 2 − ч | |
| а число минус 11 | k − 11 | |
| 11 минус число | 11 − k | |
| число уменьшилось на 7 903 15 | y − 7 | |
| разница n и 25 | n − 25 | |
| разница 25 и n | 25 − n | |
| 5 меньше числа | 9031 4 x − 5||
| x меньше числа 5 | 5 − x | |
| произведение r и 4 | 4r | |
| 7 раз число | 7 шт. 2 корень квадратный из 3: Mathway | Популярные задачи 2 |
Три простых правила относительно квадратного корня. Часть 3
GRE Mathematics
уделяет особое внимание заданиям на квадратный корень. В двух предыдущих частях статьи, мы рассматривали, что делать, если все числа в задании положительные. Если же это не так, то следует применять ещё 2 правила GRE Maths.
Правило №2: если x2 = 9, то x = 3, x = -3
Эта ситуация отлична от описанных ранее . Мы больше не имеем знака квадратного корня, зато здесь есть показатель степени. Если 3 возвести в квадрат, то мы получим 9. Если мы возведем -3 в квадрат – мы также получим 9. Следовательно, оба числа являются возможным значением x, потому что оба делают равенство верным.
С математической точки зрения, мы бы сказали, что x = 3 или x = -3. Если вы выполняете задание в разделе Quantitative Comparison, подумайте об этом следующим образом: если одно из них является возможным значением x, то оба варианта должны быть рассмотрены возможными значениями при сравнении Величины А и Величины В.
Правило №3: √(x)2 = 3, если x = 3, x = -3
Итак, вернемся к знаку квадратного корня, но теперь у нас есть и показатель степени! Что дальше? Указывать только положительное число, потому что мы имеем знак корня? Или указывать оба значения, потому что есть показатель степени?
Сначала вычислите значение x: возведите в степень оба значения √(x)2 = 3, чтобы получить x2 = 9. Вычислите квадратный корень, чтобы получить x = 3, x = -3 (как в правиле №2).
Подставьте оба числа в данное равенство, √x2 = 3, и посмотрите, делают ли они равенство верным. Если мы подставим 3 в равенство √x2 = 3, мы получим: √(3)2 = 3. Верно ли это? Да: √(3)2 = √9 и это действительно равняется 3.
Теперь подставьте в равенство -3: √(-3)2= 3. Под корнем у нас стоит отрицательное число, но также в скобках у нас есть квадратная степень. Следуйте установленному порядку действий: возведите число в квадрат, чтобы получить √9. Больше нет никаких отрицательных чисел под знаком корня! Заканчивая решение задачи, мы получаем √9, и снова это должно равняться 3, поэтому -3 тоже является возможным значением x. X может быть равен как 3, так и -3.
Больше нет никаких отрицательных чисел под знаком корня! Заканчивая решение задачи, мы получаем √9, и снова это должно равняться 3, поэтому -3 тоже является возможным значением x. X может быть равен как 3, так и -3.
Запомните: в первом примере представлено либо действительное число, либо очевидная переменная (не возведение в степень!) под знаком квадратного корня. В обоих случаях мы должны получить решение с положительными значениями корня, но не отрицательными.
Второй и третий примеры имеют квадратную степень. Во втором правиле нет знака квадратного корня – в этом случае мы можем получить и положительный, и отрицательный ответ. В нашем третьем правиле есть и знак квадратного корня, и степень в квадрате. В этой ситуации мы должны произвести расчеты, как показано в примере. Сначала мы решаем оба варианта, а затем подставляем их в исходное равенство. Если эти варианты делают равенство верным, то это и есть правильный ответ.
Подготовка к GRE Test включает в себя штудирование не только официальных учебников, но также изучение советов и подсказок, которые представлены здесь. Возможно, на самом тесте вам пригодятся именно они! Успехов!
Возможно, на самом тесте вам пригодятся именно они! Успехов!
Пример несложного задания на квадратные корни в тесте GRE:
По материалам сайта: www.manhattanprep.com
3-8Квадратный корень из 3 — Как найти квадратный корень из 3?
LearnPracticeDownload
Квадратный корень из 3 выражается как √3 в радикальной форме и как (3) ½ или (3) 0,5 в экспоненциальной форме. Квадратный корень из 3, округленный до 7 знаков после запятой, равен 1,7320508. Это положительное решение уравнения x 2 = 3.
Квадратный корень из 3, округленный до 7 знаков после запятой, равен 1,7320508. Это положительное решение уравнения x 2 = 3.
- Корень квадратный из 3: 1,7320508075688772 909:20
- Квадратный корень из 3 в экспоненциальной форме: (3) ½ или (3) 0,5
- Квадратный корень из 3 в подкоренной форме: √3
| 1. | Что такое квадратный корень из 3? |
| 2. | Является ли квадратный корень из 3 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 3? |
| 4. | Важные примечания |
| 5. | Часто задаваемые вопросы о квадратном корне из 3 |
| 6. | Сложные вопросы |
Что такое квадратный корень из 3?
Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число. Например, квадратный корень из 25 равен 5, так как 5 умножить на 5 дает 25. Однако у вас также могут быть квадратные корни некоторых чисел, которые не дают целых чисел, например 3. Мы можем выразить квадратный корень из 3 по-разному
Например, квадратный корень из 25 равен 5, так как 5 умножить на 5 дает 25. Однако у вас также могут быть квадратные корни некоторых чисел, которые не дают целых чисел, например 3. Мы можем выразить квадратный корень из 3 по-разному
- Десятичная форма: 1,732.
- Радикальная форма: √3
- Форма экспонента: 3 1/2
Является ли квадратный корень из 3 рациональным или иррациональным?
- Десятичная часть квадратного корня из 3 не является конечной. Это определение иррационального числа.
- Глядя на десятичную форму корня 3, мы видим, что она бесконечна —
√3 = 1,732050807……. - Следовательно, мы можем заключить, что Квадратный корень из 3 иррационален
Как найти квадратный корень из 3?
Поскольку мы пришли к выводу, что квадратный корень из 3 не является конечным, мы можем использовать только метод длинного деления для вычисления его значения.
- Шаг 1: Для начала запишем 3 как 3.000000 и сгруппируем 0 после запятой в пары по 2 слева направо, как показано ниже. (для цифр слева от запятой соединяйте их справа налево) 909:20
- Шаг 2: Задумайте число, которое при умножении само на себя меньше или равно 3. В этом случае это число будет 1.
- Шаг 3: Разделив 3 на 1 с частным, равным 1, мы получим остаток 2.
- Шаг 4: Перетащите пару нулей вниз и закрасьте ее рядом с 2 , чтобы получить делимое 200.
- Шаг 5: Делитель, который здесь равен 1, добавляется к самому себе и записывается ниже. Теперь у нас есть 2X в качестве нового делителя, и нам нужно найти значение X, которое делает произведение 2X × X меньше или равным 200. В этом случае 27 — это искомое значение 9.09:20
- Шаг 6: Число 7 ставится в частном после запятой. Новый делитель для следующего деления будет 2X + X, что в данном случае равно 34.

Действуя таким же образом и повторяя с шага 4, мы можем вычислить остальные десятичные дроби.
Изучение квадратных корней с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 4
- Квадратный корень из 2
- Квадратный корень из 5
- Квадратный корень из 9
- Квадратный корень из 15
Важные примечания
- Действительные корни √3 равны ± 1,732.
- Квадратный корень из полного квадрата — это всегда рациональное целое число, а корень других чисел всегда иррационален. Например, √16 = 4, а √17 = 4,1231… .
Загадочные вопросы
- Найдите значение √√3.
- Какова длина стороны квадрата площадью 10? (Подсказка: используйте метод длинного деления)
- Найдите квадратный корень из 33.
Пример 1
Джон интересовался, совпадает ли значение -√3 с √-3.
 Что вы думаете?
Что вы думаете?Решение
Отрицательные квадратные корни не могут быть действительными числами.
-√3 — действительное число.
Но √-3 — мнимое число.
Следовательно, они не совпадают, а -√3 не совпадает с √-3.Пример 2
Майкл едет по шоссе со средней скоростью 50√3 км/ч ровно 1 час. Какое расстояние он преодолевает?
Решение
Нам нужно использовать формулу Расстояние = Скорость * Время
Скорость = 50√3 = 86,603 км/ч
Время = 1 час
Используя формулу, Расстояние = 86,603 * 1 = 86,603Следовательно, Майкл преодолевает расстояние 86,603 км
Пример: Если площадь круга равна 3π в 2 . Найдите радиус окружности.
Решение:
Пусть ‘r’ будет радиусом окружности.
⇒ Площадь круга = πr 2 = 3π в 2
⇒ г = ±√3 в
Так как радиус не может быть отрицательным,
⇒ г = √3
Квадратный корень из 3 равен 1,732.
⇒ г = 1,732 в
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу для изучения математики?
Выйдите за рамки заучивания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о квадратном корне из 3
Каково значение квадратного корня из 3?
Квадратный корень из 3 равен 1,73205.
Почему квадратный корень из 3 является иррациональным числом?
Число 3 простое. Отсюда следует, что число 3 беспарное и не находится в степени двойки. Следовательно, квадратный корень из 3 иррационален.
Если квадратный корень из 3 равен 1,732. Найдите значение квадратного корня из 0,03.
Представим √0,03 в форме p/q, т.е. √(3/100) = 0,03/10 = 0,173. Следовательно, значение √0,03 = 0,173
Вычислить 14 плюс 16 квадратный корень 3
Данное выражение равно 14 + 16 √3.


 При этом если в числе встречается цифра 0, то ее не надо учитывать при нахождении произведения.
При этом если в числе встречается цифра 0, то ее не надо учитывать при нахождении произведения.
 Что вы думаете?
Что вы думаете?
 ..ЧастотаЭквивалентная дозаЭкспозиционная дозаЭлектрическая эластичностьЭлектрический дипольный моментЭлектрический зарядЭлектрический токЭлектрическое напряжениеЭлектрическое сопротивлениеЭлектрической проводимостиЭнергияЯркостьFuel consumption
..ЧастотаЭквивалентная дозаЭкспозиционная дозаЭлектрическая эластичностьЭлектрический дипольный моментЭлектрический зарядЭлектрический токЭлектрическое напряжениеЭлектрическое сопротивлениеЭлектрической проводимостиЭнергияЯркостьFuel consumption 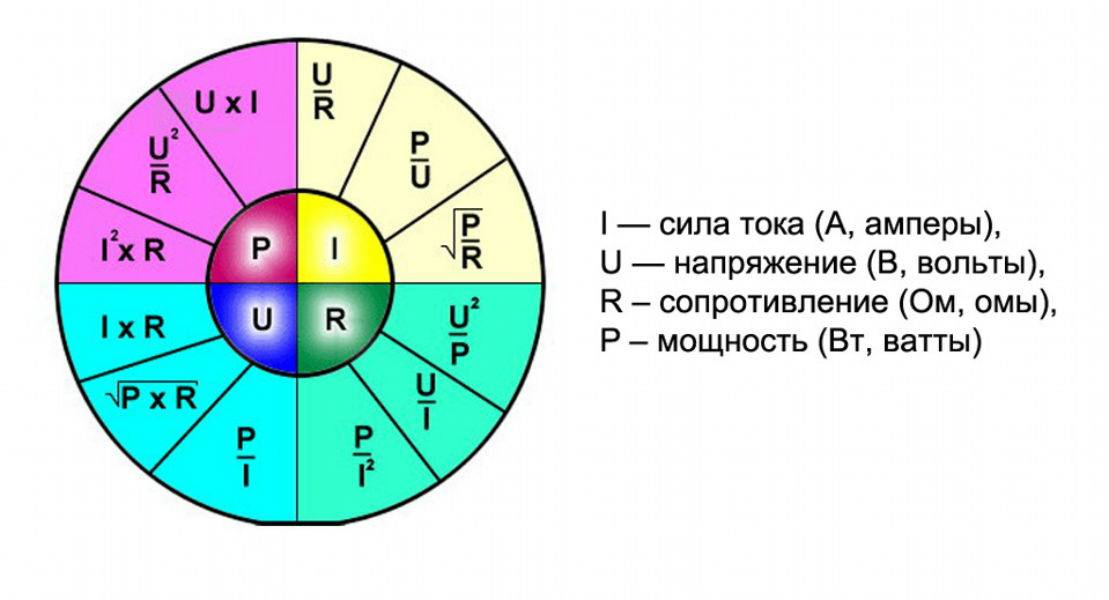 С помощью этих измерений могут быть рассчитаны расстояния. И это далеко не все возможные измерения, а лишь наиболее распространенные из них.
В случаях измерений площади (квадратный метр, квадратный километр, ар, гектар, морган, акр и другие), температуры
(в градусах по Цельсию, по Кельвину, по Фаренгейту), скорости (м/с, км/час, миль/ч, узлы, мах), веса
(центнер, килограмм, метрическая тонна, американская тонна, стандартная тонна, фунт и другие) и объема
(кубический метр, гектолитр, английский галлон жидкости, американский жидкий галлон, американский сухой галлон, баррель и другие)
ситуация не намного лучше. А если всего этого вам показалось мало — большинство из этих единиц также имеют подразделения и высшие единицы
(например, милли-, санти-, деци-). Короче говоря, хаос, в котором так трудно разобраться без помощи справочника или других средств.
Данный калькулятор единиц измерения идеально подходит для перевода данных единиц.
С помощью этих измерений могут быть рассчитаны расстояния. И это далеко не все возможные измерения, а лишь наиболее распространенные из них.
В случаях измерений площади (квадратный метр, квадратный километр, ар, гектар, морган, акр и другие), температуры
(в градусах по Цельсию, по Кельвину, по Фаренгейту), скорости (м/с, км/час, миль/ч, узлы, мах), веса
(центнер, килограмм, метрическая тонна, американская тонна, стандартная тонна, фунт и другие) и объема
(кубический метр, гектолитр, английский галлон жидкости, американский жидкий галлон, американский сухой галлон, баррель и другие)
ситуация не намного лучше. А если всего этого вам показалось мало — большинство из этих единиц также имеют подразделения и высшие единицы
(например, милли-, санти-, деци-). Короче говоря, хаос, в котором так трудно разобраться без помощи справочника или других средств.
Данный калькулятор единиц измерения идеально подходит для перевода данных единиц.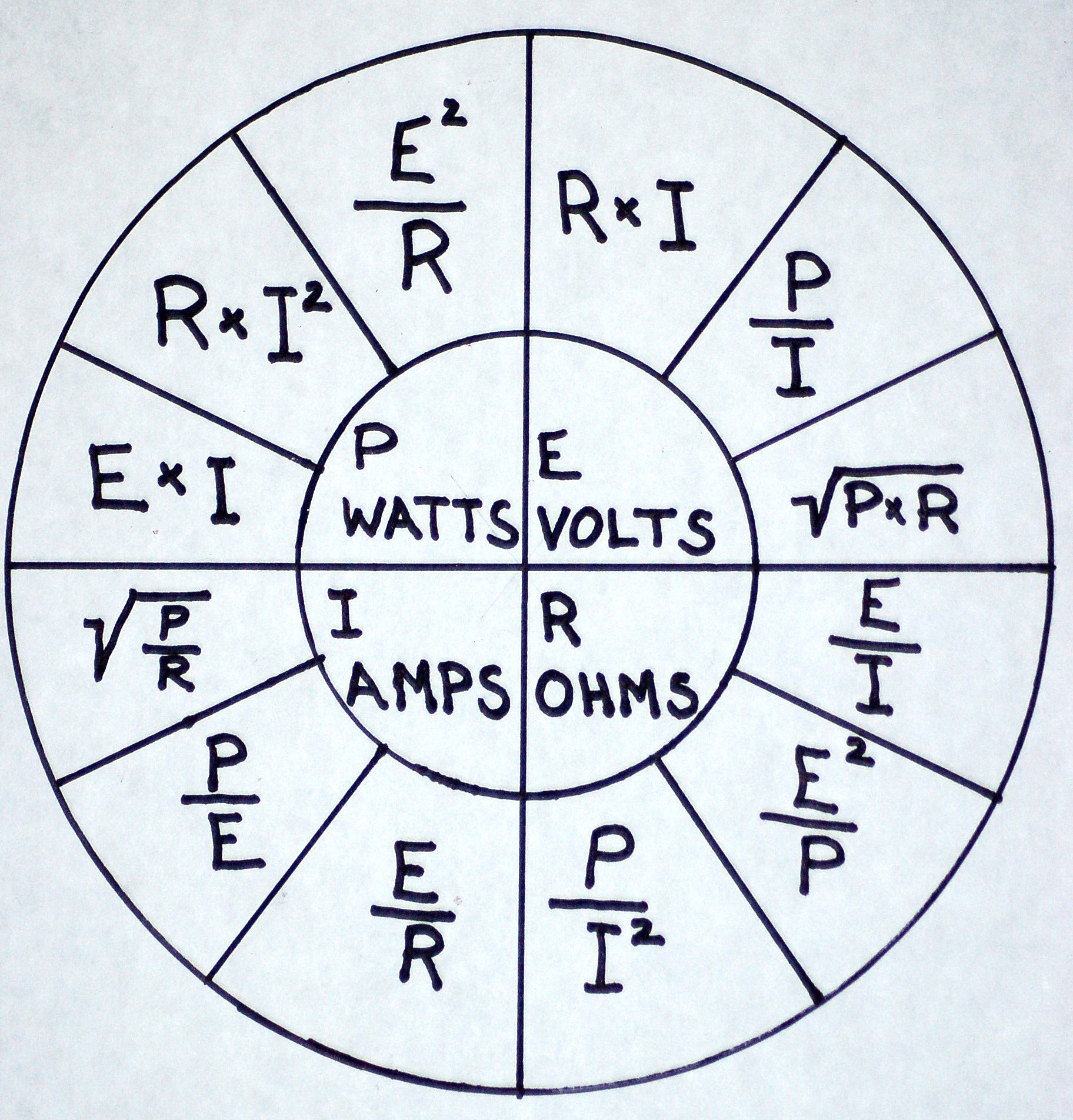
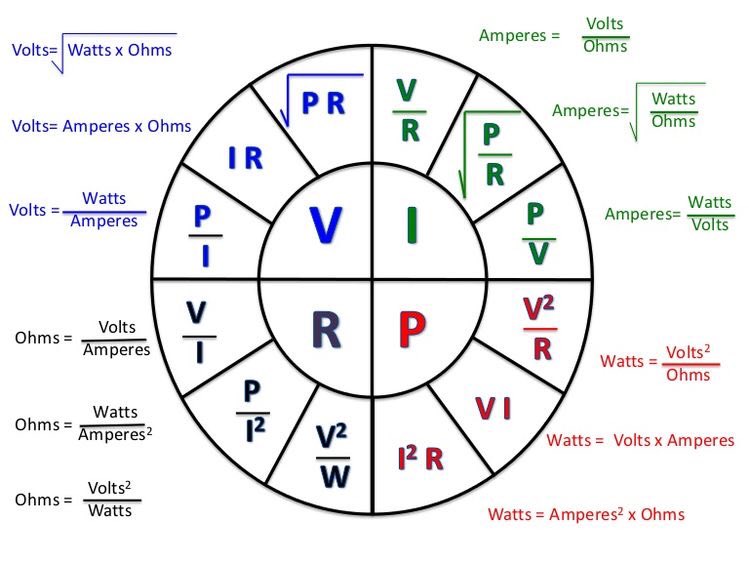
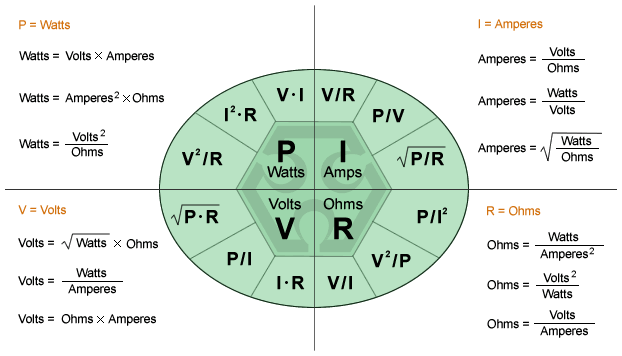 Просто измените пирамиду следующим образом:
Просто измените пирамиду следующим образом: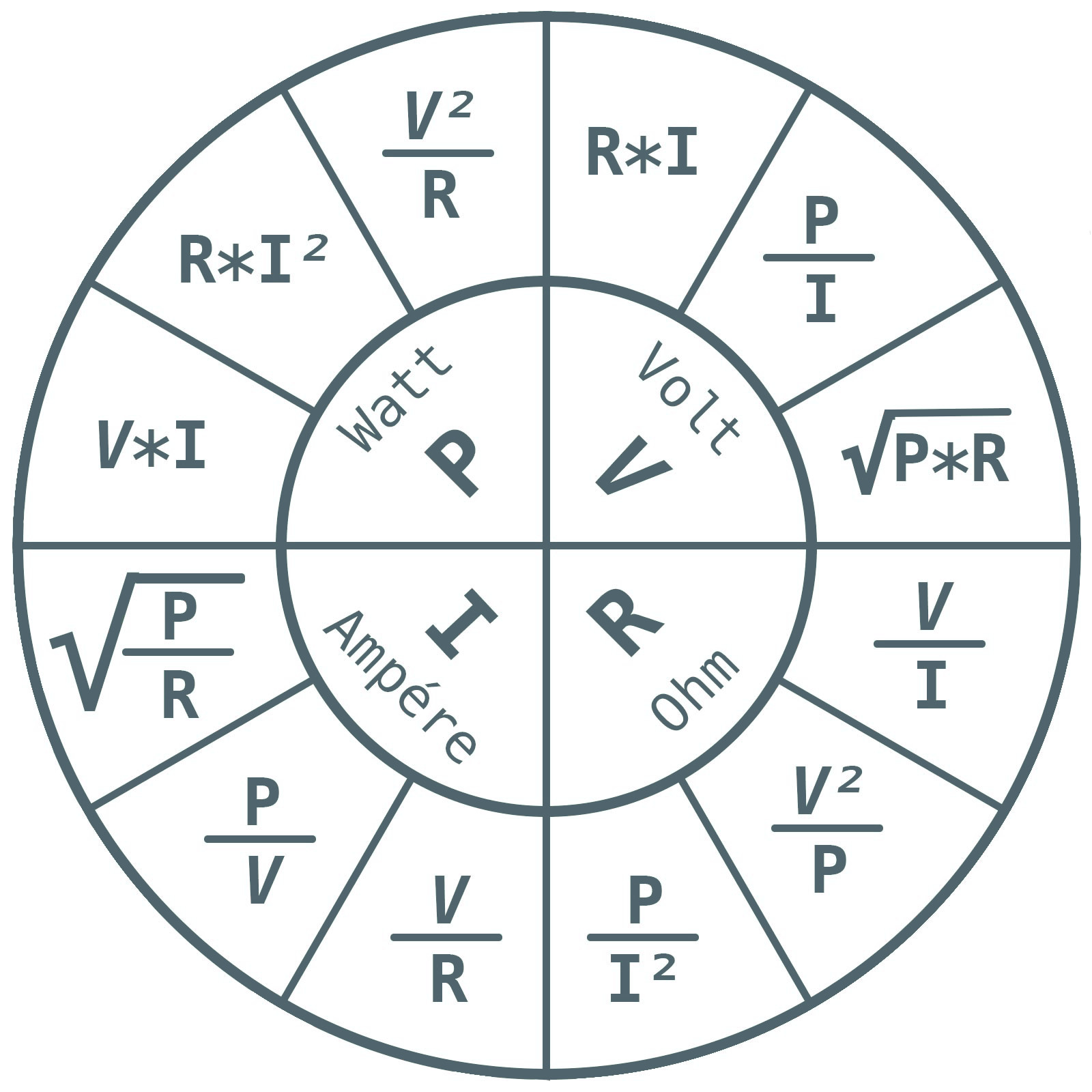 В каждом примере известны два значения. Используйте закон Ома, чтобы вычислить третий.
В каждом примере известны два значения. Используйте закон Ома, чтобы вычислить третий.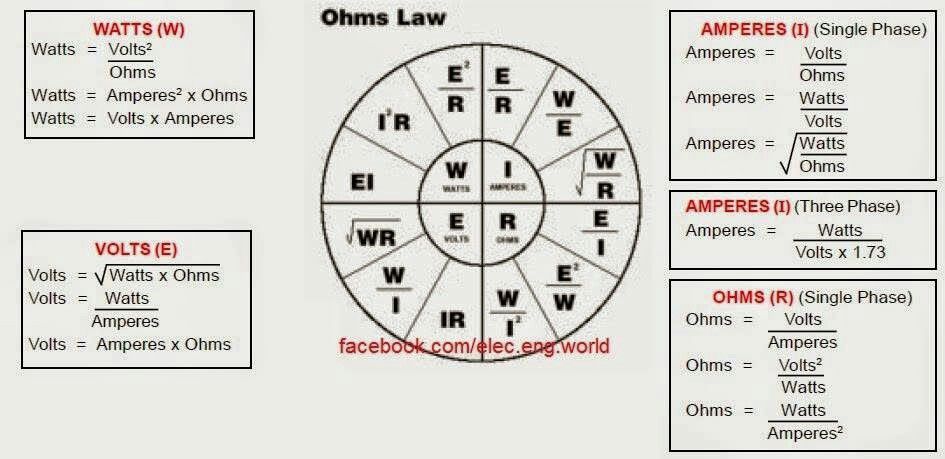 Если, например, контрольно-измерительный прибор обнаруживает измеренный ток выше нормального, это может означать, что сопротивление уменьшилось или напряжение увеличилось, что привело к возникновению ситуации с высоким напряжением. Это может указывать на проблему с питанием или цепью.
Если, например, контрольно-измерительный прибор обнаруживает измеренный ток выше нормального, это может означать, что сопротивление уменьшилось или напряжение увеличилось, что привело к возникновению ситуации с высоким напряжением. Это может указывать на проблему с питанием или цепью.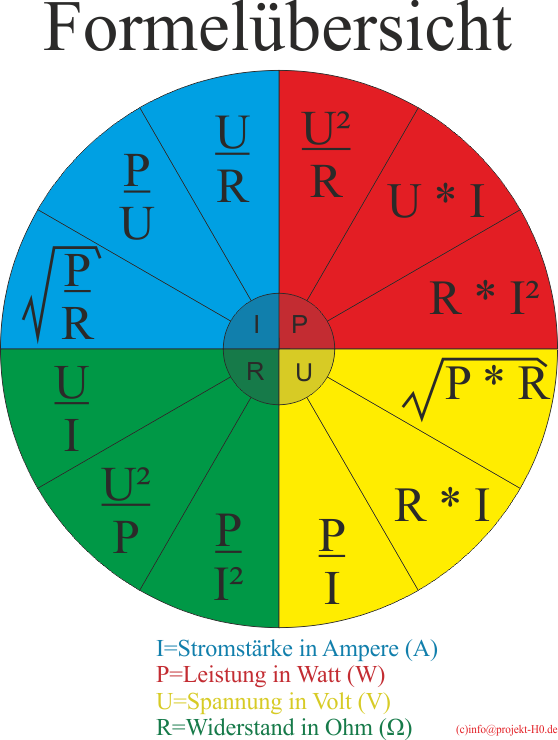 Если во время тестирования техники обнаруживают, что обычные значения не регистрируются на их цифровых мультиметрах или токоизмерительных клещах, они могут использовать закон Ома, чтобы определить, какая часть цепи дает сбой, и исходя из этого определить, в чем может заключаться проблема.
Если во время тестирования техники обнаруживают, что обычные значения не регистрируются на их цифровых мультиметрах или токоизмерительных клещах, они могут использовать закон Ома, чтобы определить, какая часть цепи дает сбой, и исходя из этого определить, в чем может заключаться проблема.

 с.) = P (Вт) / 746
с.) = P (Вт) / 746
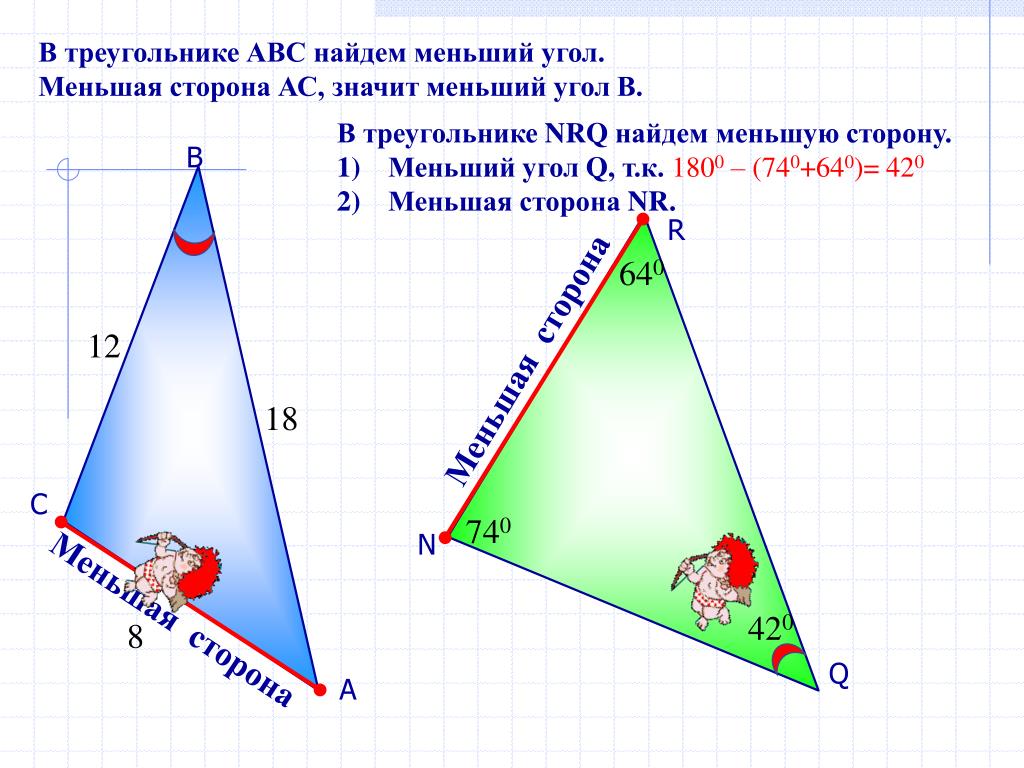
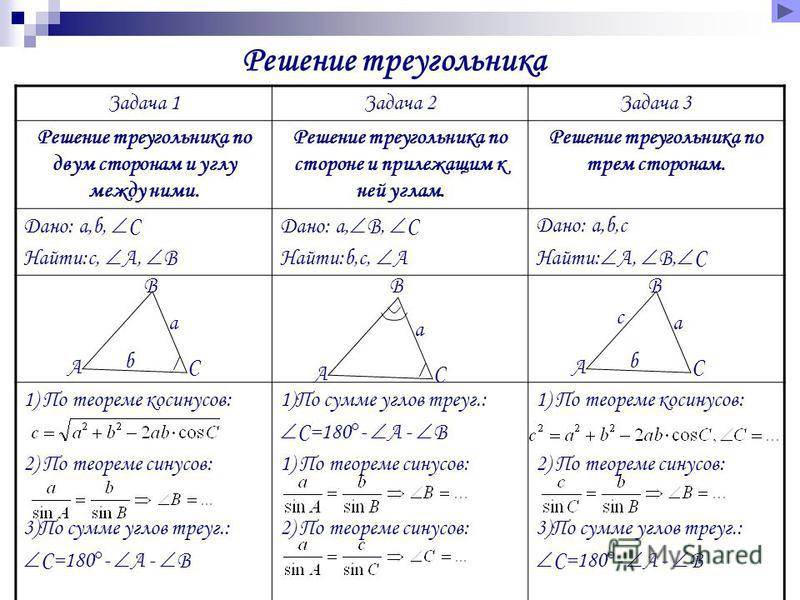 Остается поэтому лишь одно предположение, что AB = BC, которое и должно быть верно, так как иных сделать нельзя. Поэтому имеем:
Остается поэтому лишь одно предположение, что AB = BC, которое и должно быть верно, так как иных сделать нельзя. Поэтому имеем: В двух предыдущих пп. мы имели дело с двумя положениями: 1) против большей стороны лежит больший угол и 2) против большего угла лежит большая сторона. Мы нашли, что эти мысли справедливы для одного треугольника. Возникает вопрос, справедливы ли они для двух треугольников? Несомненно справедливы для двух равных треугольников, так как равные треугольники можно наложением слить в один треугольник. Но, вообще говоря, к двум различным (не равным) треугольникам эти положения не могут быть применимы: мы можем построить два таких треугольника ∆ABC и ∆A’B’C’ (чер. 94), чтобы ∠B был > ∠B’, но AC была бы < A’C’. Чертеж пояснений не требует. Но есть один случай, когда указанные мысли применимы и к двум различным треугольникам).
В двух предыдущих пп. мы имели дело с двумя положениями: 1) против большей стороны лежит больший угол и 2) против большего угла лежит большая сторона. Мы нашли, что эти мысли справедливы для одного треугольника. Возникает вопрос, справедливы ли они для двух треугольников? Несомненно справедливы для двух равных треугольников, так как равные треугольники можно наложением слить в один треугольник. Но, вообще говоря, к двум различным (не равным) треугольникам эти положения не могут быть применимы: мы можем построить два таких треугольника ∆ABC и ∆A’B’C’ (чер. 94), чтобы ∠B был > ∠B’, но AC была бы < A’C’. Чертеж пояснений не требует. Но есть один случай, когда указанные мысли применимы и к двум различным треугольникам). Обратим внимание, что точками A и C определяется еще отрезок AC, на чертеже не изображенный. При вышеуказанном вращении точка C меняет свое место и нам ясно, что этот отрезок AC, не изображенный на чертеже, должен увеличиваться (напр. AC’ > AC), т. е., если 2 стороны треугольника не изменяются, а угол между ними увеличивается, то третья сторона так же увеличивается. В тексте этот случай выяснен без помощи такого наглядного представления.
Обратим внимание, что точками A и C определяется еще отрезок AC, на чертеже не изображенный. При вышеуказанном вращении точка C меняет свое место и нам ясно, что этот отрезок AC, не изображенный на чертеже, должен увеличиваться (напр. AC’ > AC), т. е., если 2 стороны треугольника не изменяются, а угол между ними увеличивается, то третья сторона так же увеличивается. В тексте этот случай выяснен без помощи такого наглядного представления. Разберем эти три случая отдельно.
Разберем эти три случая отдельно.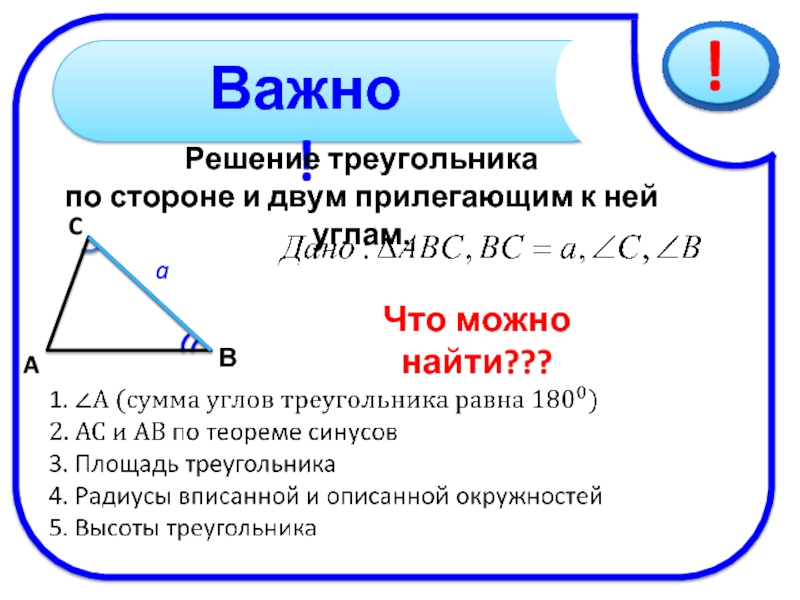 Поэтому на основании п. 86 (применяя его к ∆ACD) имеем AC > AD, но AD есть сторона A’C’, перенесенная в другое место, – следовательно, AC > A’C’.
Поэтому на основании п. 86 (применяя его к ∆ACD) имеем AC > AD, но AD есть сторона A’C’, перенесенная в другое место, – следовательно, AC > A’C’.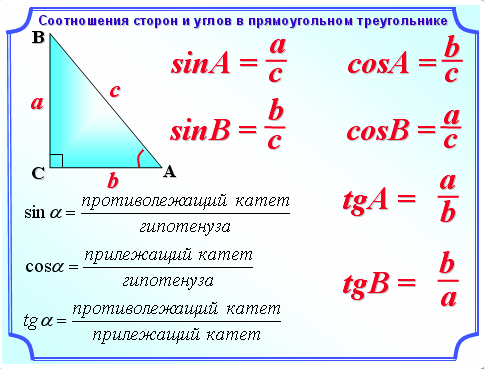





 Самаров
Самаров еще)
еще)  $$ \angle $$ HOP равен 64°, а m$$ \angle $$ HPO равен 26°.
$$ \angle $$ HOP равен 64°, а m$$ \angle $$ HPO равен 26°.  Тем не менее, принцип, изложенный выше, остается в силе.
истинный. !)
Тем не менее, принцип, изложенный выше, остается в силе.
истинный. !)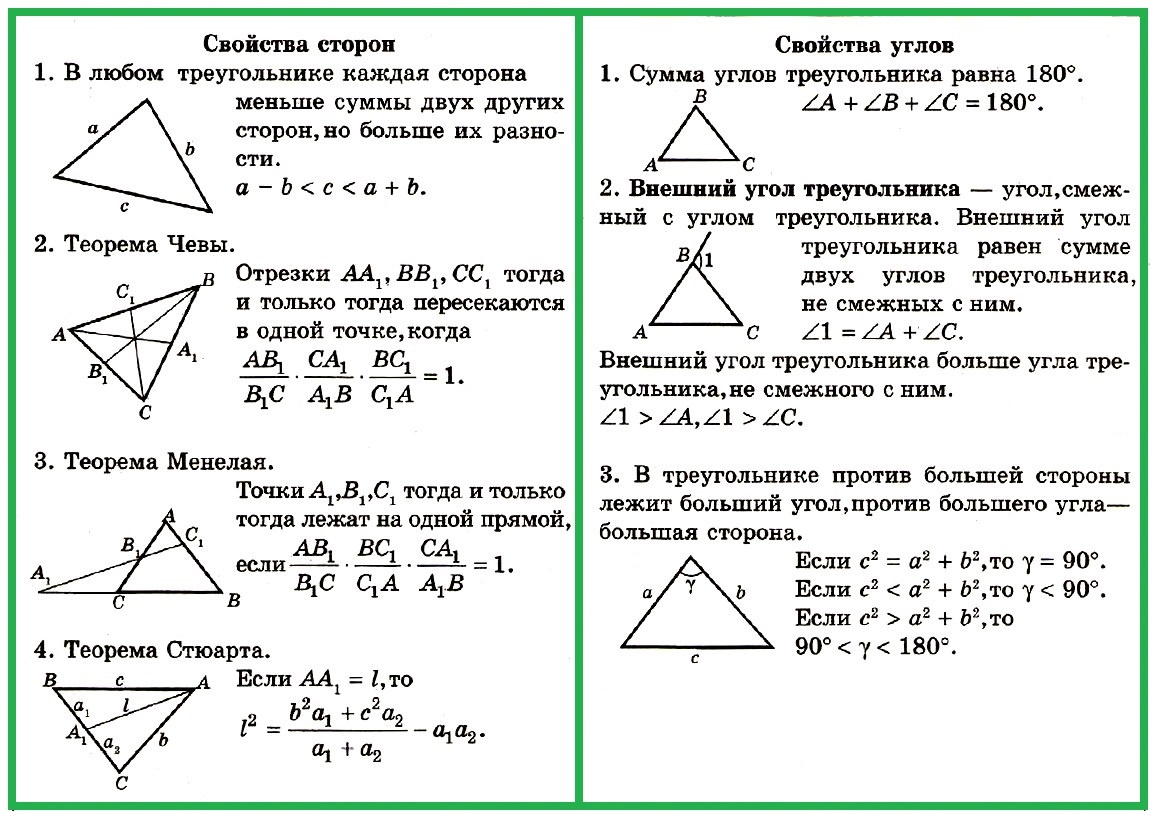

 2
2
 И это если у нас есть 𝑥 в степени 𝑎 в степени 𝑏, это равно 𝑥 в степени 𝑎𝑏. Итак, мы умножаем наши показатели. Итак, мы получим восемь в степени девять на два минус восемь в степени четыре. И это потому, что у нас есть отрицательная единица, умноженная на отрицательную четыре, что дает нам четыре, затем все делится на восемь в степени пять на два минус восемь в квадрате.
И это если у нас есть 𝑥 в степени 𝑎 в степени 𝑏, это равно 𝑥 в степени 𝑎𝑏. Итак, мы умножаем наши показатели. Итак, мы получим восемь в степени девять на два минус восемь в степени четыре. И это потому, что у нас есть отрицательная единица, умноженная на отрицательную четыре, что дает нам четыре, затем все делится на восемь в степени пять на два минус восемь в квадрате. Что ж, девять больше двух плюс минус один больше двух дает нам восемь больше двух, что равно четырем, что у нас было в числителе ранее.
Что ж, девять больше двух плюс минус один больше двух дает нам восемь больше двух, что равно четырем, что у нас было в числителе ранее.

 ВНП обычно рассчитывают за год.
ВНП обычно рассчитывают за год.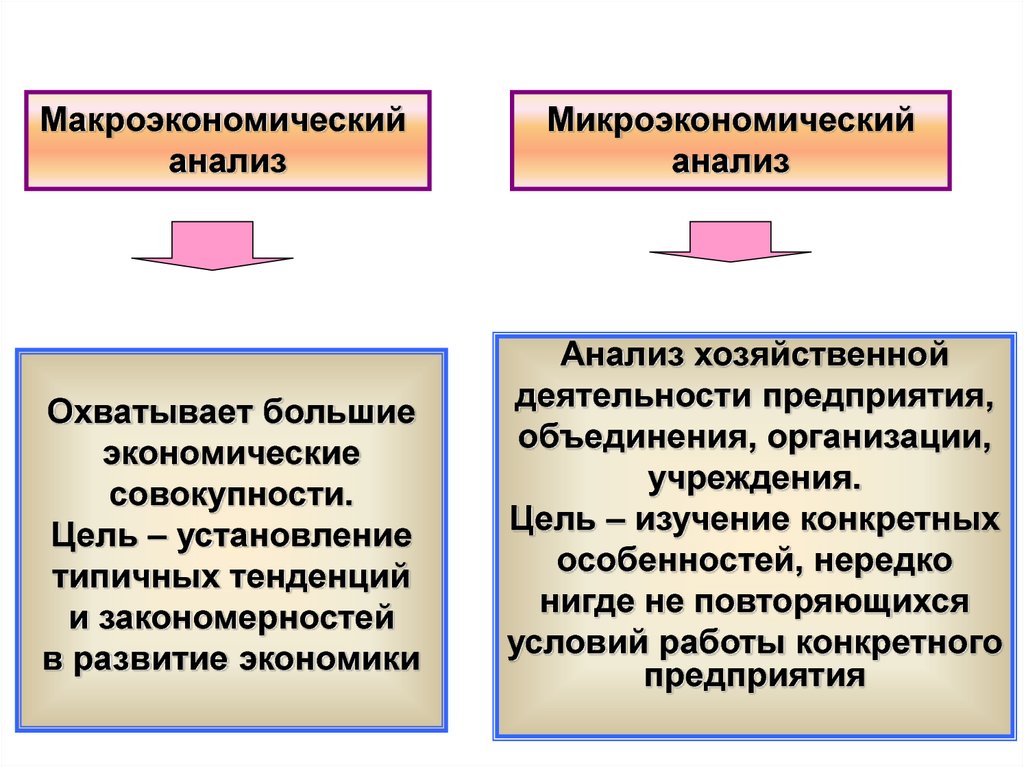
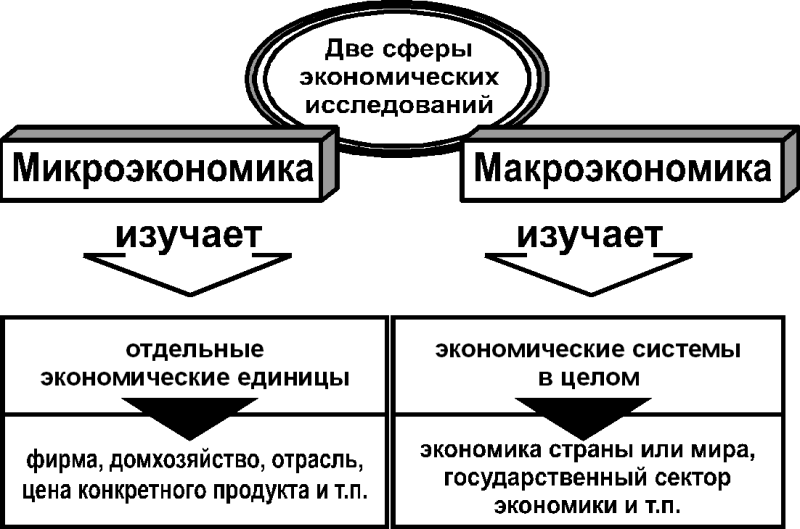
 д., то есть отдельных экономических субъектов:
д., то есть отдельных экономических субъектов: При этом теряется возможность реализации альтернатив.
При этом теряется возможность реализации альтернатив.


 В основе понимания макропроцессов лежит анализ поведения отдельных хозяйственных единиц.
В основе понимания макропроцессов лежит анализ поведения отдельных хозяйственных единиц.
 Домохозяйства предоставляют ресурсы фирмам с целью удовлетворения собственных потребностей.
Домохозяйства предоставляют ресурсы фирмам с целью удовлетворения собственных потребностей.
 Для макроэкономики важны изменения абсолютных цен — то есть изменения общего уровня цен, что позволяет проанализировать проблему инфляции.
Для макроэкономики важны изменения абсолютных цен — то есть изменения общего уровня цен, что позволяет проанализировать проблему инфляции. От того, насколько хорошо организована хозяйственная жизнь станы, зависят остальные области человеческой деятельности. Узнаем, что такое макроэкономика и микроэкономика, чем они отличаются.
От того, насколько хорошо организована хозяйственная жизнь станы, зависят остальные области человеческой деятельности. Узнаем, что такое макроэкономика и микроэкономика, чем они отличаются.


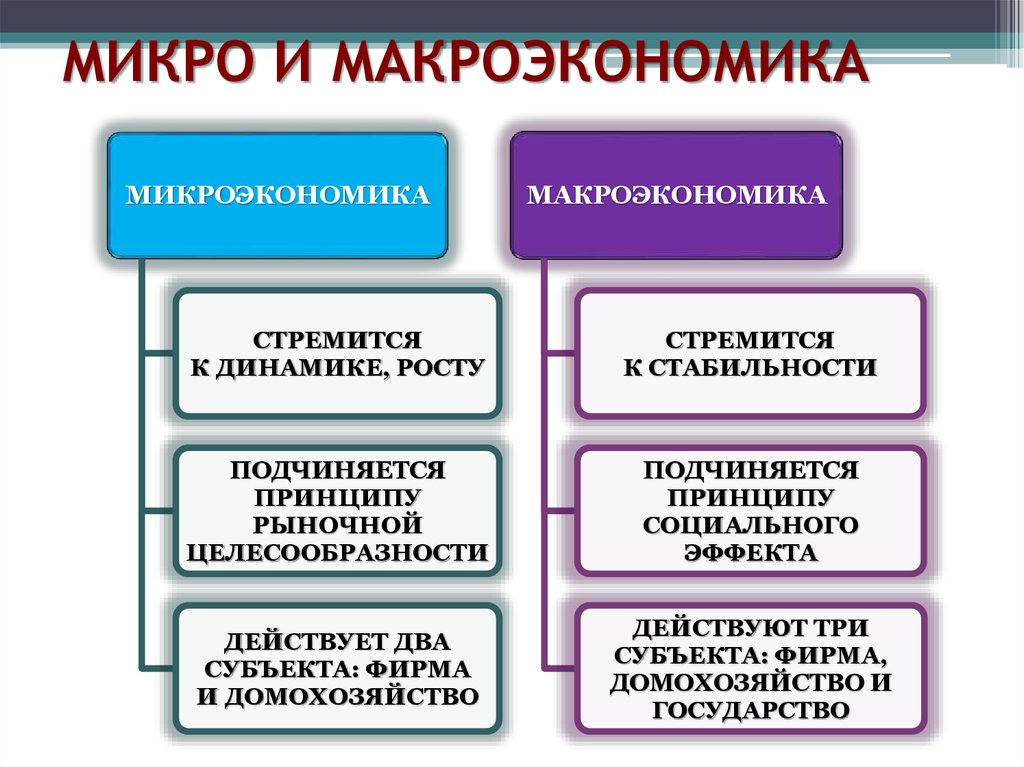
 Как правило, микроэкономика обеспечивает более точное и детальное понимание, чем макроэкономика.
Как правило, микроэкономика обеспечивает более точное и детальное понимание, чем макроэкономика.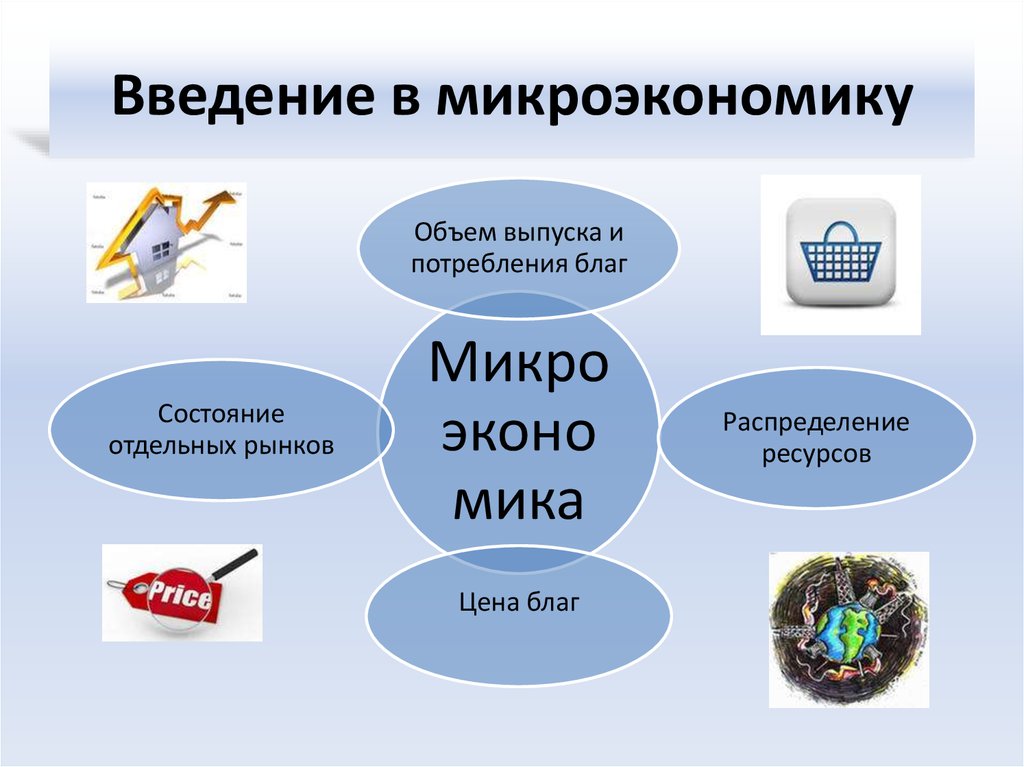
 Эти факторы позволяют производственному предприятию генерировать больше продаж или более высокую прибыль по сравнению с его рыночными конкурентами». Таким образом, конкурентное преимущество, пример микроэкономики, представляет собой бизнес-атрибут, который дает хозяйствующему субъекту свободу действий, чтобы превзойти своих конкурентов.
Эти факторы позволяют производственному предприятию генерировать больше продаж или более высокую прибыль по сравнению с его рыночными конкурентами». Таким образом, конкурентное преимущество, пример микроэкономики, представляет собой бизнес-атрибут, который дает хозяйствующему субъекту свободу действий, чтобы превзойти своих конкурентов.
 Например, фонд развития сообщества (CDF) Замбии предназначен для оказания помощи почти всем жителям избирательного округа.
Например, фонд развития сообщества (CDF) Замбии предназначен для оказания помощи почти всем жителям избирательного округа.

 Микроэкономика показывает, как и почему разные товары имеют разную стоимость, как люди и предприятия ведут себя и извлекают выгоду из эффективного производства и обмена, а также как люди лучше всего координируют свои действия и сотрудничают друг с другом. Вообще говоря, микроэкономика дает более полное и детальное понимание, чем макроэкономика.
Микроэкономика показывает, как и почему разные товары имеют разную стоимость, как люди и предприятия ведут себя и извлекают выгоду из эффективного производства и обмена, а также как люди лучше всего координируют свои действия и сотрудничают друг с другом. Вообще говоря, микроэкономика дает более полное и детальное понимание, чем макроэкономика. Отдельные участники часто группируются в микроэкономические подгруппы, такие как покупатели, продавцы и владельцы бизнеса. Эти группы создают спрос и предложение на ресурсы, используя деньги и процентные ставки в качестве механизма ценообразования для координации.
Отдельные участники часто группируются в микроэкономические подгруппы, такие как покупатели, продавцы и владельцы бизнеса. Эти группы создают спрос и предложение на ресурсы, используя деньги и процентные ставки в качестве механизма ценообразования для координации.
 Неоклассическая экономика фокусируется на том, как потребители и производители делают рациональный выбор, чтобы максимизировать свое экономическое благосостояние, с учетом ограничений, связанных с тем, какой доход и ресурсы у них есть. Экономисты-неоклассики делают упрощающие предположения о рынках, такие как совершенное знание, бесконечное число покупателей и продавцов, однородные товары или статические переменные отношения, чтобы построить математические модели экономического поведения.
Неоклассическая экономика фокусируется на том, как потребители и производители делают рациональный выбор, чтобы максимизировать свое экономическое благосостояние, с учетом ограничений, связанных с тем, какой доход и ресурсы у них есть. Экономисты-неоклассики делают упрощающие предположения о рынках, такие как совершенное знание, бесконечное число покупателей и продавцов, однородные товары или статические переменные отношения, чтобы построить математические модели экономического поведения.
 ..
..
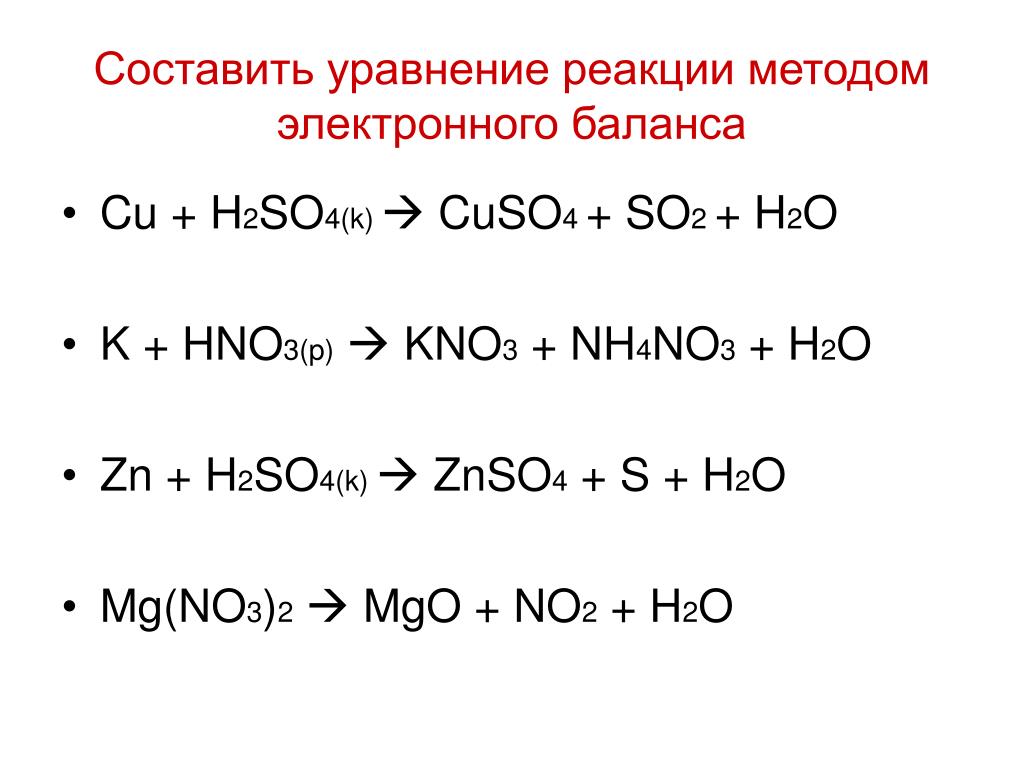
 Между исходными веществами ставим «+», а затем знак «=».
Между исходными веществами ставим «+», а затем знак «=».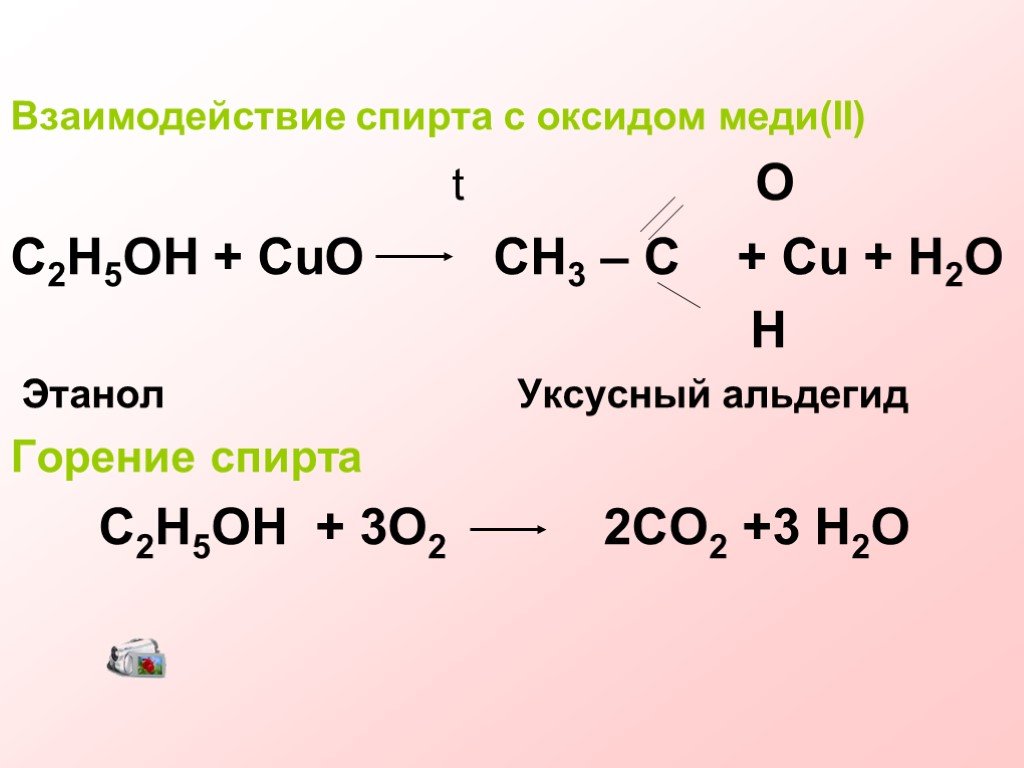








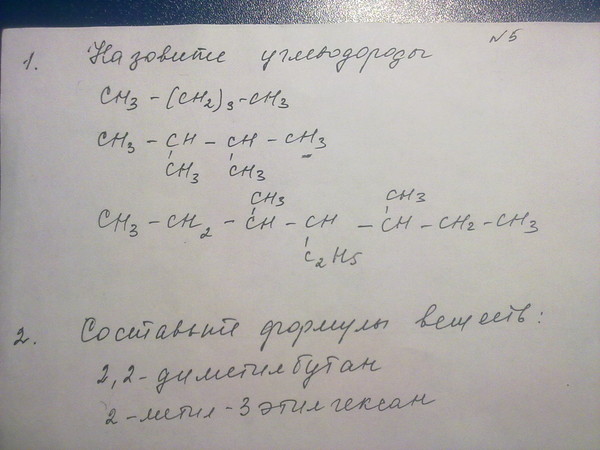 В химической реакции реагенты (то, что вы начинаете) превращаются в продукты (то, чем вы заканчиваете). Реагенты, показанные в левой части уравнения, и продукты, показанные в правой, разделены стрелкой. Уравнение ниже представляет собой реакцию углерода с газообразным кислородом с образованием двуокиси углерода.
В химической реакции реагенты (то, что вы начинаете) превращаются в продукты (то, чем вы заканчиваете). Реагенты, показанные в левой части уравнения, и продукты, показанные в правой, разделены стрелкой. Уравнение ниже представляет собой реакцию углерода с газообразным кислородом с образованием двуокиси углерода.
 Если вещество растворено в воде, используется (aq), что означает водный. Добавляя эти символы, уравнение принимает вид:
Если вещество растворено в воде, используется (aq), что означает водный. Добавляя эти символы, уравнение принимает вид: nasa.gov/topics/technology/features/atomic_oxygen.html, относительно атомарного кислорода:
nasa.gov/topics/technology/features/atomic_oxygen.html, относительно атомарного кислорода:



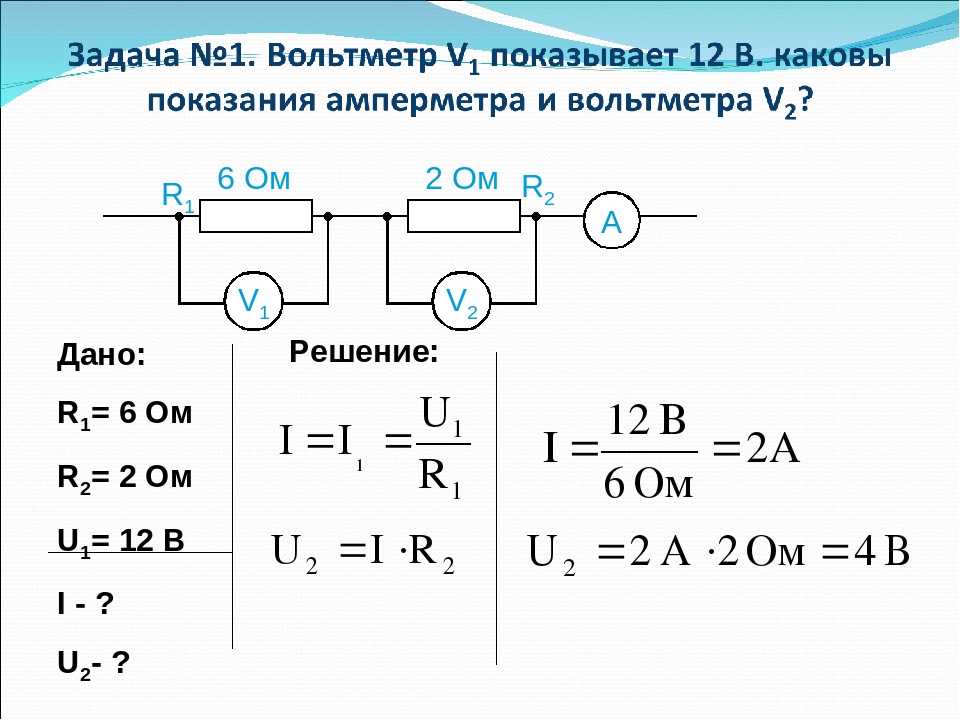 нашли 17 слитков серебра общей массой 3,5 кг при температуре 5 °С. Какова удельная теплота плавления серебра, если для переплавки потребовалось 254 г газа удельной теплотой сгорания 45 МДж/кг? Потерями пренебречь.
нашли 17 слитков серебра общей массой 3,5 кг при температуре 5 °С. Какова удельная теплота плавления серебра, если для переплавки потребовалось 254 г газа удельной теплотой сгорания 45 МДж/кг? Потерями пренебречь.

 Он считается самым крупным, из сохранившихся в мире. На сколько градусов он нагреется, если получит 18 720 Дж тепла? Удельная теплоемкость золота 0,13 кДж/(кг • К).
Он считается самым крупным, из сохранившихся в мире. На сколько градусов он нагреется, если получит 18 720 Дж тепла? Удельная теплоемкость золота 0,13 кДж/(кг • К). При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока.
При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока. 3}$.
3}$.

 3$
3$ 3 \frac{Дж}{\degree C}} \approx 22.3 \degree C$.
3 \frac{Дж}{\degree C}} \approx 22.3 \degree C$. Эти энергии будут численно равны друг другу, но противоположны по знаку:
Эти энергии будут численно равны друг другу, но противоположны по знаку:
 Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды.
Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды. Остывание происходит за $9 \space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 \space мин$ будет равно:
Остывание происходит за $9 \space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 \space мин$ будет равно: е., в окружающую среду рассеивается $\frac{1}{4}$ часть энергии, сообщаемая воде в чайнике.
е., в окружающую среду рассеивается $\frac{1}{4}$ часть энергии, сообщаемая воде в чайнике. Вам предлагается прочитать каждую задачу и попрактиковаться в использовании стратегии при решении задачи. Затем нажмите кнопку, чтобы проверить ответ, или воспользуйтесь ссылкой для просмотра решения.
Вам предлагается прочитать каждую задачу и попрактиковаться в использовании стратегии при решении задачи. Затем нажмите кнопку, чтобы проверить ответ, или воспользуйтесь ссылкой для просмотра решения.  Определите время падения пера на поверхность Луны.
Определите время падения пера на поверхность Луны.
 Пуля проникает на расстояние 0,0621 м. Определить ускорение пули при движении в глину. (Предположим, что ускорение равномерное.)
Пуля проникает на расстояние 0,0621 м. Определить ускорение пули при движении в глину. (Предположим, что ускорение равномерное.)

 )
) )
) Недавно мы переработали и улучшили Калькулятор. Версия 2 теперь ЖИВАЯ! Мы увеличили количество задач более чем в три раза, разбили каждую часть на несколько небольших однотематических наборов задач и использовали генератор случайных чисел для предоставления числовой информации по каждой задаче. Ответы учащихся оцениваются автоматически, а обратная связь осуществляется мгновенно. И мы сохранили такое же обязательство предоставлять помощь через ссылки на существующие ресурсы. В то время как БЕСПЛАТНАЯ версия делает все вышеперечисленное, учителя с подпиской на Task Tracker могут пойти еще дальше. Они могут модифицировать наши готовые наборы задач, писать свои собственные задачи с помощью нашего простого в использовании Конструктора задач и использовать планшет для разработки собственной программы, выражающей их акцент на использовании математики в физике.
Недавно мы переработали и улучшили Калькулятор. Версия 2 теперь ЖИВАЯ! Мы увеличили количество задач более чем в три раза, разбили каждую часть на несколько небольших однотематических наборов задач и использовали генератор случайных чисел для предоставления числовой информации по каждой задаче. Ответы учащихся оцениваются автоматически, а обратная связь осуществляется мгновенно. И мы сохранили такое же обязательство предоставлять помощь через ссылки на существующие ресурсы. В то время как БЕСПЛАТНАЯ версия делает все вышеперечисленное, учителя с подпиской на Task Tracker могут пойти еще дальше. Они могут модифицировать наши готовые наборы задач, писать свои собственные задачи с помощью нашего простого в использовании Конструктора задач и использовать планшет для разработки собственной программы, выражающей их акцент на использовании математики в физике.
 Определить работу, совершенную Ламаром при подъеме становой тяги 300 кг на высоту 0,90 м над землей.
Определить работу, совершенную Ламаром при подъеме становой тяги 300 кг на высоту 0,90 м над землей.
 Один из буксирных тросов приводится в действие двигателем мощностью 22 кВт, который тянет лыжников по обледенелому склону 14° с постоянной скоростью. Предположим, что 18 лыжников со средней массой 48 кг держатся за веревку и предположим, что мотор работает на полную мощность.
Один из буксирных тросов приводится в действие двигателем мощностью 22 кВт, который тянет лыжников по обледенелому склону 14° с постоянной скоростью. Предположим, что 18 лыжников со средней массой 48 кг держатся за веревку и предположим, что мотор работает на полную мощность. Какой кинетической энергией был бы велосипед, если бы он имел …
Какой кинетической энергией был бы велосипед, если бы он имел … Он движется со скоростью 23,4 м/с на высоте 44,6 метра над землей. Определить полную механическую энергию Ли Бен Фардеста.
Он движется со скоростью 23,4 м/с на высоте 44,6 метра над землей. Определить полную механическую энергию Ли Бен Фардеста. Примите пренебрежимо малое сопротивление воздуха во время движения. Используйте эту информацию для заполнения таблицы.
Примите пренебрежимо малое сопротивление воздуха во время движения. Используйте эту информацию для заполнения таблицы. Она движется со скоростью 16 м/с по гребню лыжной горки, расположенной на высоте 34 м над уровнем земли в конце трассы.
Она движется со скоростью 16 м/с по гребню лыжной горки, расположенной на высоте 34 м над уровнем земли в конце трассы. Определите потенциальную энергию Николаса в верхней части слайда.
Определите потенциальную энергию Николаса в верхней части слайда.  Определите потенциальную энергию Имы в верхней части петли.
Определите потенциальную энергию Имы в верхней части петли.  Он наполняет кувшин колой, ставит его на прилавок и толкает кувшин весом 2,6 кг вперед с усилием 8,8 Н на расстояние 48 см, чтобы отправить его покупателю в конце прилавка. Коэффициент трения между кувшином и столешницей равен 0,28.
Он наполняет кувшин колой, ставит его на прилавок и толкает кувшин весом 2,6 кг вперед с усилием 8,8 Н на расстояние 48 см, чтобы отправить его покупателю в конце прилавка. Коэффициент трения между кувшином и столешницей равен 0,28. Он садится в машину, пристегивается ремнями и готовится к волнениям дня. Какова кинетическая энергия Джерома до периода ускорения?
Он садится в машину, пристегивается ремнями и готовится к волнениям дня. Какова кинетическая энергия Джерома до периода ускорения?  Пейдж бросает мяч, совершая над ним работу 9,89 Дж.
Пейдж бросает мяч, совершая над ним работу 9,89 Дж. Вместо этого он потерял равновесие, кувыркнулся и кувыркнулся со склона в плотную толпу. В течение почти 30 лет после этого кадры этого события были включены во вступление к печально известному спортивному шоу ABC, и Винко стал известен как 9-й.1808 агония поражения икона.
Вместо этого он потерял равновесие, кувыркнулся и кувыркнулся со склона в плотную толпу. В течение почти 30 лет после этого кадры этого события были включены во вступление к печально известному спортивному шоу ABC, и Винко стал известен как 9-й.1808 агония поражения икона. Если бы такая подача была направлена вертикально вверх с той же скоростью, то на какой высоте оно путешествовало?
Если бы такая подача была направлена вертикально вверх с той же скоростью, то на какой высоте оно путешествовало? Тормозная система резко разгоняет 328-килограммовый автомобиль (включая массу гонщика) до скорости 2,9 м/с на дистанции 5,55 метра. Определите тормозную силу, действующую на автомобиль Диззи.
Тормозная система резко разгоняет 328-килограммовый автомобиль (включая массу гонщика) до скорости 2,9 м/с на дистанции 5,55 метра. Определите тормозную силу, действующую на автомобиль Диззи. Она берет 3-летнюю Эллисон в соседний парк и усаживает ее на детские качели. Гвен тянет 1,8-метровую цепь назад, образуя угол 26° с вертикалью, и отпускает 14-килограммовую Эллисон (включая поворотный груз). Предполагая, что трение и сопротивление воздуха пренебрежимо малы, определите скорость Эллисон в самой нижней точке траектории.
Она берет 3-летнюю Эллисон в соседний парк и усаживает ее на детские качели. Гвен тянет 1,8-метровую цепь назад, образуя угол 26° с вертикалью, и отпускает 14-килограммовую Эллисон (включая поворотный груз). Предполагая, что трение и сопротивление воздуха пренебрежимо малы, определите скорость Эллисон в самой нижней точке траектории.

 02.2023, 14:18
02.2023, 14:18  Оно и убило (почти) десятичные логарифмы.
Оно и убило (почти) десятичные логарифмы. Я только неделю назад вообще узнал о таком пособии.
Я только неделю назад вообще узнал о таком пособии.
 И обращён материал к её слушателям, практикам. скажем. офицерам-расчётчикам, а не математикам. восхищающимся изяществом формулы. По ней надо получить конкретное значение. Для тех лет, когда создавалось пособие — у расчётчика была логарифмическая линейка, а на ней шкала десятичных логарифмов. Сейчас есть калькулятор, где тоже есть десятичные логарифмы, есть натуральные. А по произвольному основанию нет, по нему надо считать по приведенной ею формуле, или по аналогичной, с заменой lg на ln.
И обращён материал к её слушателям, практикам. скажем. офицерам-расчётчикам, а не математикам. восхищающимся изяществом формулы. По ней надо получить конкретное значение. Для тех лет, когда создавалось пособие — у расчётчика была логарифмическая линейка, а на ней шкала десятичных логарифмов. Сейчас есть калькулятор, где тоже есть десятичные логарифмы, есть натуральные. А по произвольному основанию нет, по нему надо считать по приведенной ею формуле, или по аналогичной, с заменой lg на ln. Грекова. Лишь гораздо позже узнал, что это псевдоним, и что её настоящее имя — Елена Сергеевна Вентцель. (Более того, думал, что она Ирина Грекова; на самом деле псевдоним образован от «игрек».)
Грекова. Лишь гораздо позже узнал, что это псевдоним, и что её настоящее имя — Елена Сергеевна Вентцель. (Более того, думал, что она Ирина Грекова; на самом деле псевдоним образован от «игрек».) С. Элементарный курс теории вероятностей в применении к задачам стрельбы и бомбометания. — М.: Военная Воздушная Краснознамённая ордена Ленина академия им. Жуковского, 1945.
С. Элементарный курс теории вероятностей в применении к задачам стрельбы и бомбометания. — М.: Военная Воздушная Краснознамённая ордена Ленина академия им. Жуковского, 1945. С. Элементарный курс теории вероятностей в применении к задачам стрельбы и бомбометания. — М.: Военная Воздушная Краснознамённая ордена Ленина академия им. Жуковского, 1945.
С. Элементарный курс теории вероятностей в применении к задачам стрельбы и бомбометания. — М.: Военная Воздушная Краснознамённая ордена Ленина академия им. Жуковского, 1945.
 — Когда ему попадалась особенно интересная математическая задача, бывало, что он не спал и не ел, пока не находил ее решения». Он является первым изобретателем логарифмической линейки.
— Когда ему попадалась особенно интересная математическая задача, бывало, что он не спал и не ел, пока не находил ее решения». Он является первым изобретателем логарифмической линейки. ..», их использование он считал допустимым только после овладения этим искусством. Однако ученик настоял на публикации, и в 1632 году Отред написал (на латыни), а Форстер перевел на английский брошюру «Круги пропорций и горизонтальный инструмент», где была описана логарифмическая линейка.
..», их использование он считал допустимым только после овладения этим искусством. Однако ученик настоял на публикации, и в 1632 году Отред написал (на латыни), а Форстер перевел на английский брошюру «Круги пропорций и горизонтальный инструмент», где была описана логарифмическая линейка. В XX веке до появления калькуляторов и компьютеров логарифмическая линейка была таким же символом инженерных специальностей, каким для врачей является фонендоскоп.
В XX веке до появления калькуляторов и компьютеров логарифмическая линейка была таким же символом инженерных специальностей, каким для врачей является фонендоскоп. Взяв две линейки с логарифмическими шкалами, увидим, что сложение значений lg2 и lg3 дает в результате lg6, то есть произведение 2 на 3.
Взяв две линейки с логарифмическими шкалами, увидим, что сложение значений lg2 и lg3 дает в результате lg6, то есть произведение 2 на 3. Результат определяется на основной шкале корпуса напротив начала или конца движка.
Результат определяется на основной шкале корпуса напротив начала или конца движка. Как правило, мы пишем
Как правило, мы пишем  03.2008 13:01
03.2008 13:01 Не говоря уже о том, что вы склонны к
делать ошибки.
Не говоря уже о том, что вы склонны к
делать ошибки. 





 Вы делаете а не нужно брать 10 как основание для ввода показателя степени. Ты можешь взять любой номер .
Вы делаете а не нужно брать 10 как основание для ввода показателя степени. Ты можешь взять любой номер .


 На словах:
вторая производная определяемой функции y равна
сама функция, умноженная на некоторую константу А . Вы можете понять, что это было бы
полезно знать функцию y(x) , которая совпадает со своей производной, или dy(x)/dx = y(x) .
На словах:
вторая производная определяемой функции y равна
сама функция, умноженная на некоторую константу А . Вы можете понять, что это было бы
полезно знать функцию y(x) , которая совпадает со своей производной, или dy(x)/dx = y(x) . 
 Приз, который нужно заплатить, заключается в том, что теперь вы должны работать с
комплексные числа с вида с = с’ + ic» с i = воображаемая единица, обычно, хотя и несколько ошибочно, называемая «квадратом».
корень минус -1″. Правильно это: i 2 = 1 . И нет, это не то же самое.
Приз, который нужно заплатить, заключается в том, что теперь вы должны работать с
комплексные числа с вида с = с’ + ic» с i = воображаемая единица, обычно, хотя и несколько ошибочно, называемая «квадратом».
корень минус -1″. Правильно это: i 2 = 1 . И нет, это не то же самое. 
 х + пер. у
х + пер. у Если вы хотите рассчитать
числовое значение e , просто возьмите x = 1 .
Если вы хотите рассчитать
числовое значение e , просто возьмите x = 1 . .
. 

 Как найти длину окружности: через диаметр и радиус
Как найти длину окружности: через диаметр и радиус Найти радиус окружности, длина которой равна 7,85 м.
Найти радиус окружности, длина которой равна 7,85 м. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр: В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса. 2»).
2»). 2 / 4 + 20*10/2», а нажать клавишу Enter.
2 / 4 + 20*10/2», а нажать клавишу Enter.


 Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.
Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360. 14
14 Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
 Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной. Радиус в дюймах в 36 раз больше этого.
Радиус в дюймах в 36 раз больше этого.
 Наконец, мы делим обе части на 6,28, чтобы получить 4,70 = r. (Информация о 22 унциях бесполезна)
Наконец, мы делим обе части на 6,28, чтобы получить 4,70 = r. (Информация о 22 унциях бесполезна) Хорда не проходит через центр окружности.
Хорда не проходит через центр окружности.
 Следовательно, мы должны установить 49 π равным этой формуле, чтобы найти радиус круга.
Следовательно, мы должны установить 49 π равным этой формуле, чтобы найти радиус круга.
 Ее также называют секущей окружности.
Ее также называют секущей окружности.
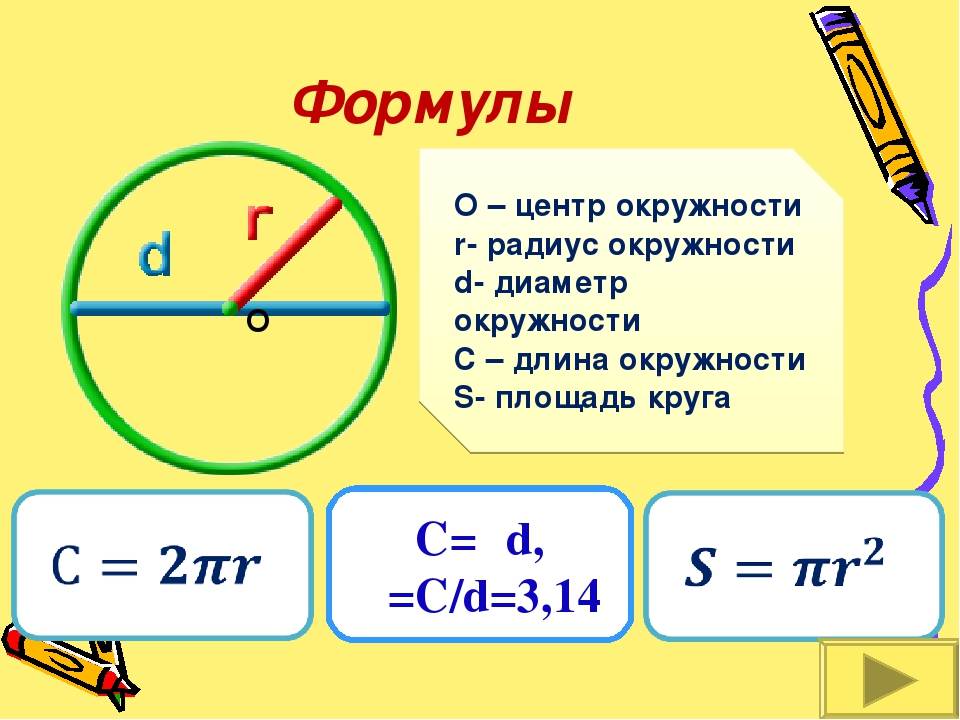 Здесь r представляет радиус, а константа π равна 3,14159.. Формула радиуса с использованием длины окружности выглядит следующим образом:
Здесь r представляет радиус, а константа π равна 3,14159.. Формула радиуса с использованием длины окружности выглядит следующим образом: Радиус сферы — это расстояние между ее центром и любой точкой на ее поверхности. Радиус сферы легко вычислить, если задан объем сферы или площадь поверхности сферы.
Радиус сферы — это расстояние между ее центром и любой точкой на ее поверхности. Радиус сферы легко вычислить, если задан объем сферы или площадь поверхности сферы. Если начало координат (0,0) становится центром окружности, то ее уравнение задается как x 2 + у 2 = г 2 . Для нахождения радиуса окружности используется следующая формула:
Если начало координат (0,0) становится центром окружности, то ее уравнение задается как x 2 + у 2 = г 2 . Для нахождения радиуса окружности используется следующая формула:


