Разряды чисел в математике — intmag24.ru
В математике разряды чисел — это позиции цифр в числе (место, где располагается цифра). Их нужно читать справа налево.
Рассмотрим число 345, которое состоит из трех цифр:
➤ первая позиция — цифра 5 — разряд единиц
➤ вторая позиция — цифра 4 —разряд десятков
➤ третья позиция — цифра 3 —разряд сотен
Разряды также сообщают нам информацию о количестве единиц, десятков и сотен.
➤ первая позиция — цифра 5 — разряд единиц содержит 5 единиц (1+1+1+1+1)
➤ вторая позиция — цифра 4 —разряд десятков содержит четыре десятка (10+10+10+10)
➤ третья позиция — цифра 3 —разряд сотен содержит три сотни (100+100+100)
Если сложить число единиц, число десятков и число сотен, то получим наше изначальное число 345:
(1+1+1+1+1)+(10+10+10+10)+(100+100+100)
Слова единицы, десятки, сотни, заменяют собой множители 1, 10 и 100.
Например, рассмотрим наше число 345:
➤ в разряде единиц — множитель 1 содержится в разряде единиц 5 раз: 1 × 5 = 5
➤ в разряде десятков — множитель 10 содержится в разряде десятков 4 раза: 10 × 4 = 40
➤ в разряде сотен — множитель 100 содержится в разряде сотен 3 раза: 100 × 3 = 300
Если сложить полученные результаты 5 + 40 + 300, то получим число 345.
➤ То же самое будет происходить если мы скажем, что число 345 содержит 34 десятка и 3 единицы. Другими словами,
— десятки будут сгруппированы 34 раза: 10 × 34 = 340
— единицы будут сгруппированы 5 раз: 1 × 5 = 5
Если сложить полученные результаты 340 и 5, снова получим число 345.
➤ Также возможно группировка, при которой не будет распределения на десятки и сотни. В таком случае число 345 будет читаться как «триста сорок пять единиц»: 1 × 345 = 345.
Старшие разряды
Далее рассмотрим более старшие разряды: тысяч, десятков тысяч, сотен тысяч, миллионов и т. д.
д.
Рассмотрим число: 1 234 567
разряд единиц — 7 единицы,
разряд десятков — 6 десятков,
разряд сотен — 5 сотен,
разряд тысяч — 4 тысячи,
разряд десятков тысяч — 3 десятка тысяч,
разряд сотен тысяч — 2 сотни тысяч,
разряд миллионов — 1 миллион.
Применение разрядов
Применение разрядов при решение примеров облегчают некоторые вычисления. Например, когда нужно сложить два трехзначных числа, то можно сложить все разряды по отдельности: единицы, десятки и сотни. Начинать нужно с разряда единиц и т.д.
Рассмотрим пример: 123 + 456 =
В первую очередь после знака равно (=) мысленно поставим три точки. Вместо этих точек будет располагаться новое число (наш ответ): 123 + 456 = . . .
Начинаем складывать:
1) из разряда единиц берем числа 3 и 6, получаем 9 ➜ 123 + 456 = . . 9
2) из разряда десятков берем числа 2 и 5, получаем 7 ➜ 123 + 456 = . 7 9
3) из разряда сотен берем числа 1 и 4, получаем 5 ➜ 123 + 456 = 5 7 9
Таким образом, если к числу 123 прибавить 456 , получается 579.
Этот принцип действует, если решать примеры в столбик:
+ | 1 2 3 |
| 5 7 9 |
? Важно! Каждый разряд записывается друг под другом: единицы под единицами, десятки под десятками, сотни под сотнями и т.д. При неправильном размещении разрядов пример будет решен не правильно!
? Чтобы потренироваться решать примеры в столбик на сложение, можно скачать программу «Сложение и вычитание в столбик«.
Переполнение разряда
Разряд характеризуется одной цифрой от 0 до 9. Но иногда при вычислении числового выражения может произойти переполнение разряда.
Рассмотрим пример: 56+89.
При сложении единиц этих чисел получаем 15 (6+9), а при сложении десятков получаем 13 (5+8).
1) При сложении 9 и 6 единиц у нас получилось 15 единиц — это 1 десяток и 5 единиц.
Поэтому в разряд десятков записываем 5, а 1 десяток мы будем прибавлять к десяткам при их сложении.
2) При сложении десятков получаем 13 (5+8) — это 1 сотня и 3 десятка.
Поэтому в разряд десятков мы запишем 4 (3 десятка + 1 десяток, полученный при сложении единиц). Так как в примере разряд сотней не складывается, то мы просто впереди приписываем единицу.
| 1 5 6 + 8 9 = . . ➜ 5 6 + 8 9 = . 5 ➜ 5 6 + 8 9 = 1 4 5 |
Этот принцип действует также при решении примеров в столбик:
| 1 |
|
| 1 1 |
| 1 4 5 | 6 2 7 |
Примеры на вычитание
Теперь рассмотрим примеры на вычитание. Вычитать также нужно по разрядам.
Пример: 68–45.
Начинаем с разряда единиц. При вычитании единиц этих чисел получаем 3 (8-5).
Затем вычитаем десятки. При вычитании десятков получаем 2(6-4).
6 8 – 4 5 = . . ➜ 6 8 – 4 5 = . 3 ➜ 6 8 – 4 5 = 2 3
Пример: 42-15.
1) В разряде единиц числа 42 содержится две единицы, а в разряде единиц числа 15 — пять единиц. От двух единиц нельзя вычесть пять единиц, поскольку две единицы меньше, чем пять единиц.
Чтобы выполнить вычитание, две единицы должны взять несколько единиц у соседней группы (разряда десятков) ➜ Поэтому берем один десяток.
Получаем, что мы число 42 разделили на 3 десятка и 12 единиц. Из 12 вычитаем 5 и получаем 7. Записываем цифру 7 в разряде единиц нового числа.
2) Теперь вычитаем десятки. Поскольку разряд десятков отдал единицам один десяток, сейчас он имеет не четыре, а три десятка. Поэтому вычитаем из 3 десятков один десяток. Останется 2 десятка. Записываем цифру 2 в разряде десятков нового числа.
Чтобы не забывать, что в каком-то разряде был взят один десяток (либо сотня либо тысяча), над этим разрядом принято ставить точку.
| • • 4 2 – 1 5 = 4 2 – 1 5 = . 7 ➜ 4 2 – 1 5 = 2 7 |
Этот принцип действует также при решении примеров в столбик:
| • |
|
| • • |
| 2 7 | 2 4 4 |
Во втором примере:
1) Вычитаем единицы. разряде единиц числа 823 содержится 3 единицы, а в разряде единиц числа 579 — 9 единиц. От 3 единиц не вычесть 9 единиц, поэтому берем один десяток у разряда десятков. Ставим точку над разрядом десятков, чтобы помнить о том, что мы взяли оттуда один десяток. Взятый один десяток и три единицы вместе образуют 13 единиц. От 13 единиц вычитаем 9 единиц, получится 4 единицы. Записываем цифру 4 в разряде единиц нового числа.
2) Вычитаем десятки.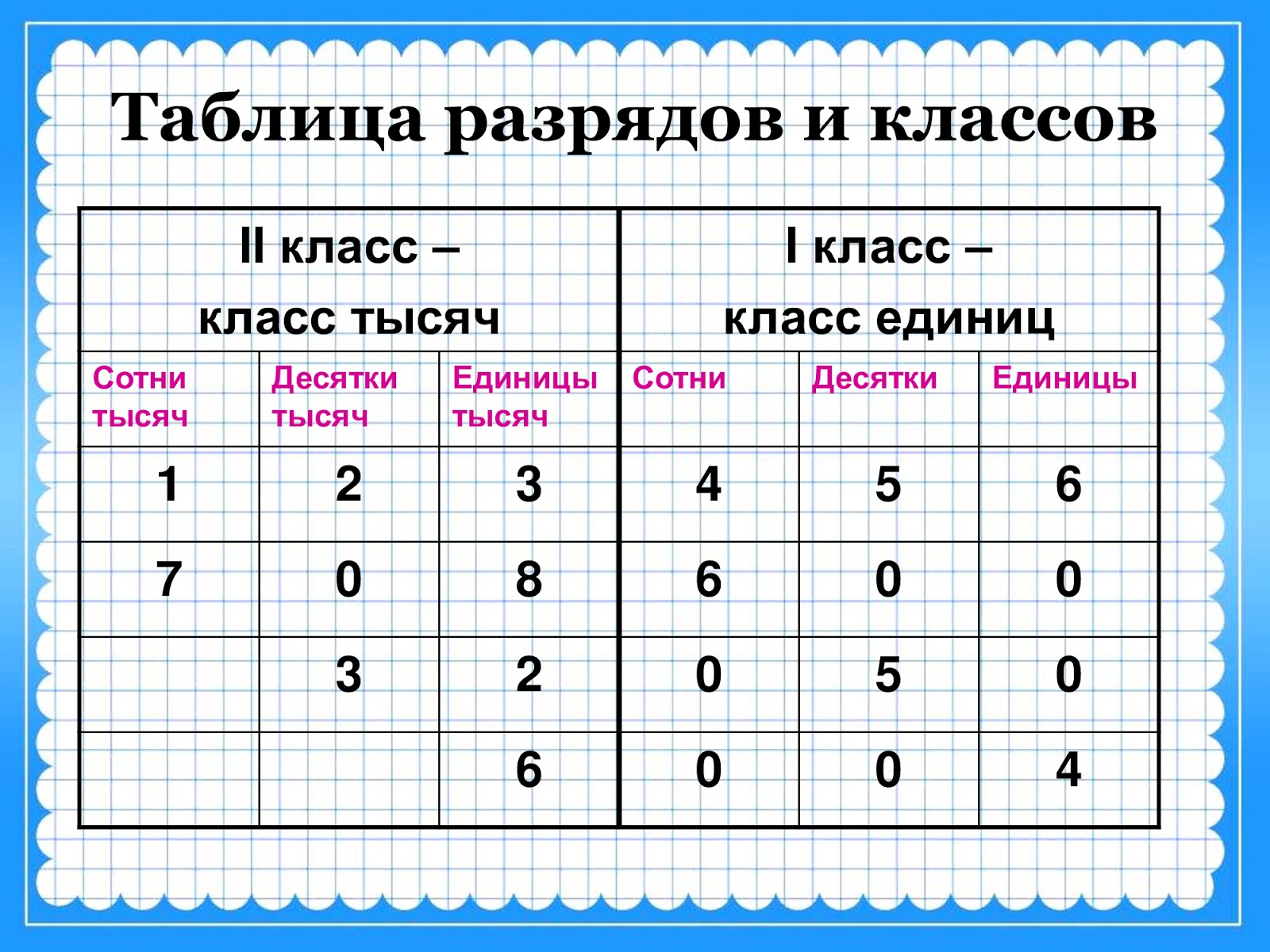 Раньше разряд десятков числа 823 содержал 2десятка, но мы взяли с него один десяток, и теперь в разряде десятков содержатся 1 десяток. Из 1 десятка нужно вычесть 7 десятков, поэтому берем одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню. Взятая 1 сотня и 1 десяток вместе образуют 11 десятков. От 11 десятков вычитаем 7 десятков, получаем 4 десятка. Записываем цифру 4 в разряде десятков нового числа.
Раньше разряд десятков числа 823 содержал 2десятка, но мы взяли с него один десяток, и теперь в разряде десятков содержатся 1 десяток. Из 1 десятка нужно вычесть 7 десятков, поэтому берем одну сотню у разряда сотен. Ставим точку над разрядом сотен, чтобы помнить о том, что мы взяли оттуда одну сотню. Взятая 1 сотня и 1 десяток вместе образуют 11 десятков. От 11 десятков вычитаем 7 десятков, получаем 4 десятка. Записываем цифру 4 в разряде десятков нового числа.
3) Вычитаем сотни. Раньше разряд сотен числа 823 содержал 8 сотен, но мы взяли с него 1сотню, и теперь в разряде сотен содержатся 7 сотен. Из 7 сотен можно вычесть 5 сотен, получается 2 сотни. Записываем цифру 2 в разряде сотен нового числа.
? Чтобы потренироваться решать примеры в столбик на вычитание, можно скачать программу «Сложение и вычитание в столбик«.
Вычитание из круглых чисел
Намного сложнее вычитать из чисел вида 100, 200, 300, 1000, 10000. То есть числа, у которых на конце нули. Чтобы выполнить вычитание, каждому разряду приходится занимать десятки/сотни/ тысячи у следующего разряда.
Чтобы выполнить вычитание, каждому разряду приходится занимать десятки/сотни/ тысячи у следующего разряда.
Выполнять вычитание таким традиционным методом сложно, поэтому можно воспользоваться нестандартным способом. Для этого уменьшить вычитаемое число на одну единицу. Далее из полученного результата вычесть вычитаемое и к полученной разности прибавить единицу.
Пример: 1000–123
1) уменьшим уменьшаемое на 1: 1000–1=999
2) из числа 999 вычтем 123: 999-123=876
3) к этому ответу прибавляем 1: 876+1=877.
Получили: 1000+123=877.
§ Разряды и классы. Класс единиц, тысяч и миллионов
Разряды и классы Разрядные слагаемые
Для записи чисел люди придумали десять знаков, которые называются цифрами. Это: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
С помощью десяти цифр можно записать любое натуральное число.
От количества знаков (цифр) в числе зависит его название.
Число, состоящее из одного знака (цифры), называется однозначным.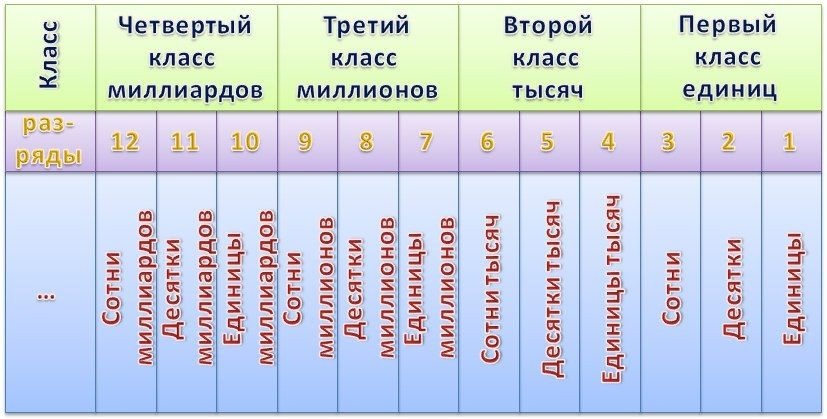 Наименьшее однозначное натуральное число — «1» , наибольшее — «9».
Наименьшее однозначное натуральное число — «1» , наибольшее — «9».
Число, состоящее из двух знаков (цифр), называется двузначным. Наименьшее двузначное число — «10», наибольшее — «99» .
Числа, записанные с помощью двух, трёх, четырёх и более цифр, называются двузначными, трёхзначными, четырёхзначными или многозначными. Наименьшее трёхзначное число — «100», наибольшее — «999».
Каждая цифра в записи многозначного числа занимает определённое место — позицию.
Запомните!Разряд — это место (позиция), на котором в записи числа стоит цифра.
Одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит.
Разряды отсчитываются с конца числа.
Разряд единиц — это самый младший разряд, которым заканчивается любое число.
Цифра «5» — означает
«5» единиц, если пятёрка стоит на
последнем месте в записи числа (в разряде единиц).
Разряд десятков — это разряд, который стоит перед разрядом единиц.
Цифра «5» — означает «5» десятков, если она стоит на предпоследнем месте (в разряде десятков).
Разряд сотен — это разряд, который стоит перед разрядом десятков. Цифра «5» означает «5» сотен, если она стоит на третьем месте от конца числа (в разряде сотен).
Запомните!Если в числе отсутствует какой-либо разряд, то в записи числа на его месте будет стоять цифра «0» (ноль).
Пример. В числе «807» содержится 8 сотен, 0 десятков и 7 единиц — такая запись называется разрядным составом числа.
807 = 8 сотен 0 десятков 7 единицКаждые 10 единиц любого разряда образуют новую единицу более высокого разряда. Например, 10 единиц образуют 1 десяток, а 10 десятков образуют 1 сотню.
Таким образом, значение цифры от разряда к разряду (от единиц к десяткам, от десятков к сотням)
увеличивается в 10 раз. Поэтому система счёта (счисления), которую мы используем,
называется десятичной системой счисления.
Поэтому система счёта (счисления), которую мы используем,
называется десятичной системой счисления.
В записи числа разряды, начиная справа, группируются в классы по три разряда в каждом.
Класс единиц или первый класс — это класс, который образуют первые три разряда (справа от конца числа): разряд единиц, разряд десятков и разряд сотен.
Пример.
| Числа | Класс единиц (первый класс) | ||
|---|---|---|---|
| сотни | десятки | единицы | |
| 6 | — | — | 6 |
| 34 | — | 3 | 4 |
| 148 | 1 | 4 | 8 |
| Числа | Класс единиц (первый класс) | ||
|---|---|---|---|
| сотни | десятки | единицы | |
| 6 | — | — | 6 |
| 34 | — | 3 | 4 |
| 148 | 1 | 4 | 8 |
Класс тысяч или второй класс — это класс, который образуют следующие
три разряда: единицы тысяч, десятки тысяч и сотни тысяч.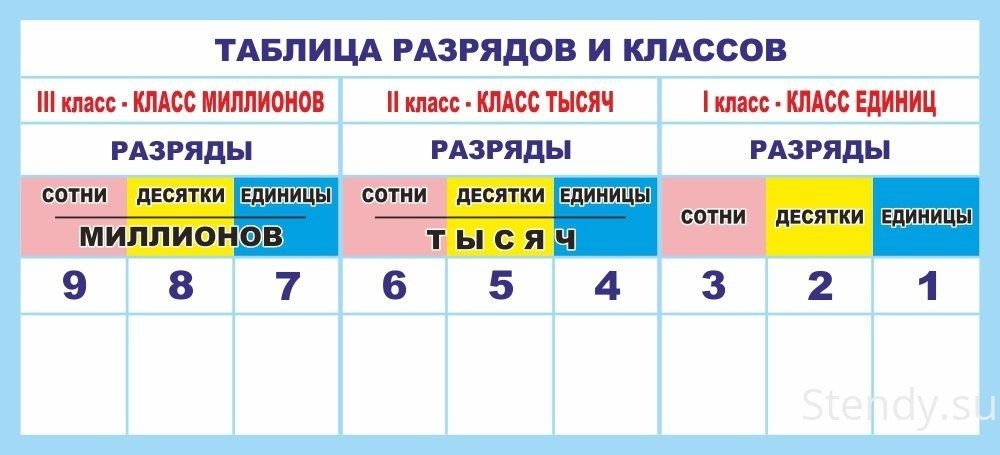
Пример.
| Числа | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||
|---|---|---|---|---|---|---|
| сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 5 234 | — | — | 5 | 2 | 3 | 4 |
| 12 803 | — | 1 | 2 | 8 | 0 | 3 |
| 356 149 | 3 | 5 | 6 | 1 | 4 | 9 |
| Числа | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||
|---|---|---|---|---|---|---|
| сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 12 803 | — | 1 | 2 | 8 | 0 | 3 |
| 356 149 | 3 | 5 | 6 | 1 | 4 | 9 |
Напоминаем, что 10 единиц разряда сотен (из класса единиц) образуют одну тысячу
(единицу следующего разряда: единицу тысяч в классе тысяч).
Класс миллионов или третий класс — это класс, который образуют следующие три разряда: единицы миллионов, десятки миллионов и сотни миллионов.
Единица разряда миллионов — это один миллион или тысяча тысяч (1 000 тысяч). Один миллион можно записать в виде числа «1 000 000».
Десять таких единиц образуют новую разрядную единицу — десять миллионов «10 000 000»
Десять десятков миллионов образуют новую разрядную единицу — сто миллионов или в записи цифрами «100 000 000».
Пример.
| Числа | Класс миллионов (третий класс) | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| сотни миллионов | десятки миллионов | единицы миллионов | сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 8 345 216 | — | — | 8 | 3 | 4 | 5 | 2 | 1 | 6 |
| 93 785 342 | — | 9 | 3 | 7 | 8 | 5 | 3 | 4 | 2 |
| 134 590 720 | 1 | 3 | 4 | 5 | 9 | 0 | 7 | 2 | 0 |
| Числа | Класс миллионов (третий класс) | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| сотни миллионов | десятки миллионов | единицы миллионов | сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 8 345 216 | — | — | 8 | 3 | 4 | 5 | 2 | 1 | 6 |
| 93 785 342 | — | 9 | 3 | 7 | 8 | 5 | 3 | 4 | 2 |
| 134 590 720 | 1 | 3 | 4 | 5 | 9 | 0 | 7 | 2 | 0 |
Как прочитать многозначное число
Запомните!Чтобы прочитать многозначное число, надо назвать по очереди слева направо число единиц каждого класса и
добавить название класса.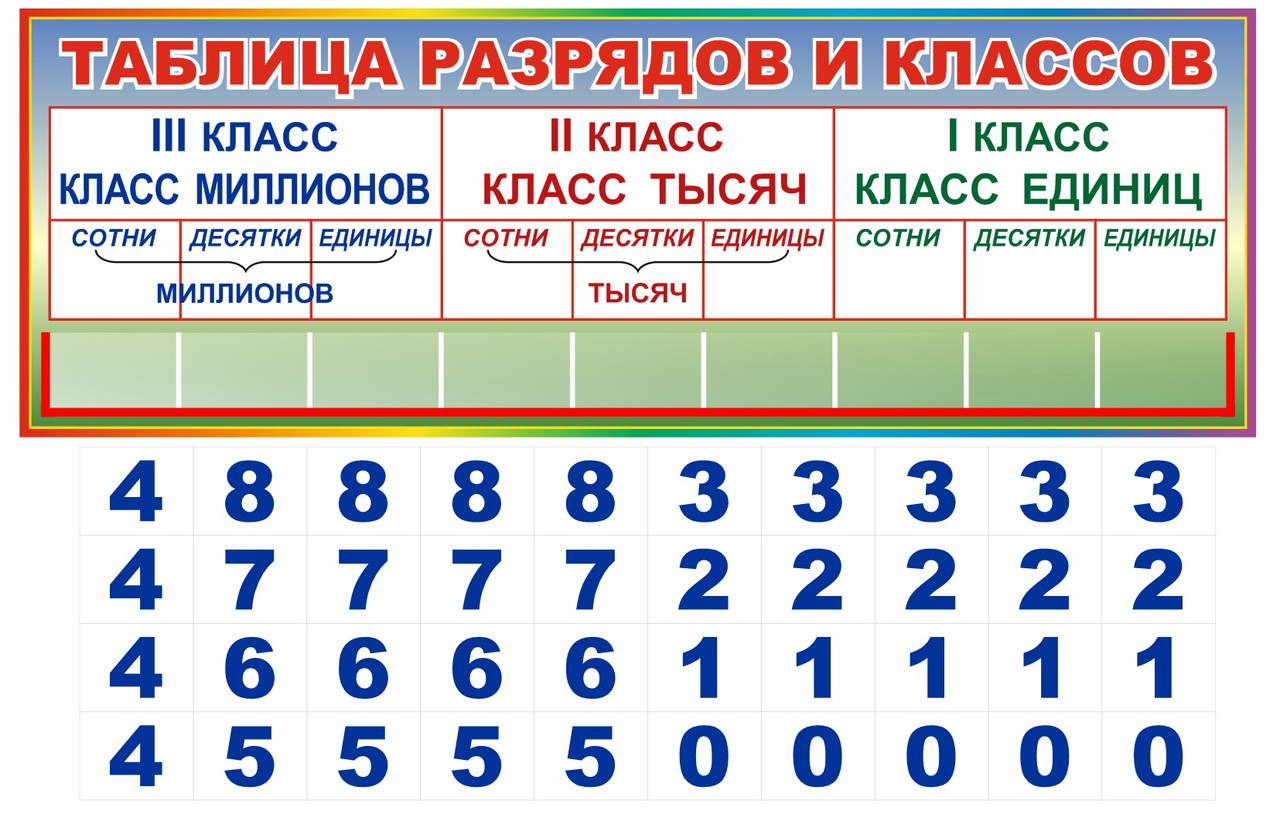
Не произносят название класса единиц, а также название класса, все три цифры которого нули.
Например, число «134 590 720» читаем: сто тридцать четыре миллиона пятьсот девяносто тысяч семьсот двадцать.
Число «418 000 547» читаем: четыреста восемнадцать миллионов пятьсот сорок семь.
На нашем сайте для проверки своих результатов вы можете воспользоваться калькулятором разложения числа на разряды онлайн.
Важно!Чтобы легче запомнить, как читать и записывать многозначные числа, советуем использовать выше приведённую «Таблицу классов и разрядов».
Разряды и классы Разрядные слагаемые
Ваши комментарии
Важно!Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
29 октября 2019 в 16:31
Анжела Мурадян Профиль Благодарили: 0Сообщений: 1
В записи какого числа в разрядах десятков миллионов и десятков стоит одна и та же цифра? 35034204, 16765510, 429561320, 270317817
0 СпасибоОтветить8 ноября 2019 в 5:08
Ответ для Анжела Мурадян
Сообщений: 1
16765510, 429561320
0 СпасибоОтветить2 октября 2016 в 5:03
Ruslan Salimov Профиль Благодарили: 0Сообщений: 1
Числа от 1 до 2015 написаны подряд и получилось 1234567891011121314.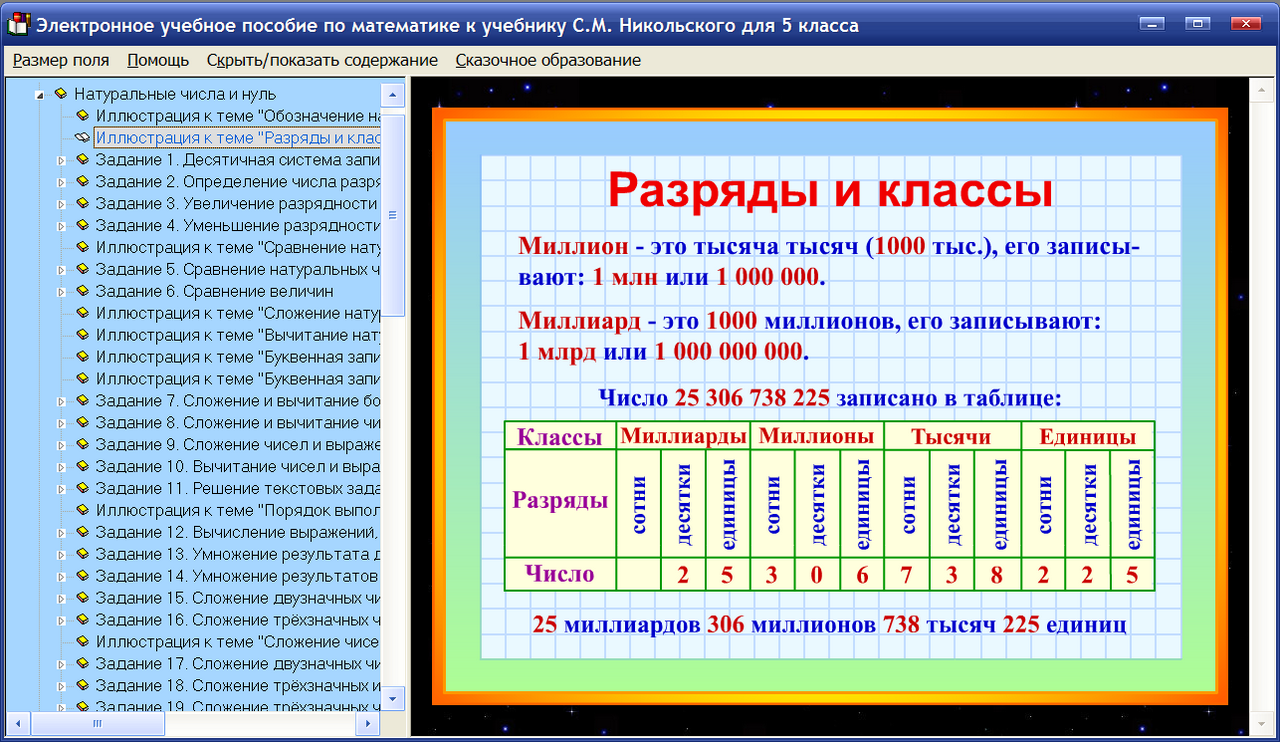 ..2015. Количество и пользованных цифр? Нужна формула и решение для быстрого решения.спасибо
..2015. Количество и пользованных цифр? Нужна формула и решение для быстрого решения.спасибо
7 октября 2016 в 19:26
Ответ для Ruslan Salimov
Сообщений: 60
Тупо посчитать лень?
9 + 2 · 90 + 3 · 900 + 4 · 1016 =…
20 сентября 2016 в 16:15
Артём Волков Профиль Благодарили: 0Сообщений: 1
из числа 1234512345123451234512345 вычеркните 10 цифр так, чтобы оставшееся число было максимально возможным.
0 СпасибоОтветить21 сентября 2016 в 9:44
Ответ для Артём Волков
Сообщений: 197
Уберём сначала числа все цифры, кроме 5 по порядку.
[1234]5[1234]5[12]3451234512345
Полученное число:
553451234512345
29 ноября 2020 в 8:40
Ответ для Артём Волков
Сообщений: 1
345345345345345
0 СпасибоОтветить17 сентября 2016 в 12:52
Татьяна Алёхина Профиль Благодарили: 0Сообщений: 1
Укажите наибольшее четное пятизначное число.
а) 987640 б) 99999
в) 888888 г) 99998
19 сентября 2016 в 14:38
Ответ для Татьяна Алёхина
Сообщений: 197 Довольно странное задание для 10 класса.
Пятизначные числа здесь только под буквами б) и г). Число б)-нечетное. Следовательно правильный ответ г).
0 СпасибоОтветить24 сентября 2018 в 18:00
Ответ для Татьяна Алёхина
Сообщений: 1
В
0 СпасибоОтветить1 октября 2018 в 16:04
Ответ для Татьяна Алёхина
Сообщений: 1 0 СпасибоОтветить
15 ноября 2018 в 20:03
Ответ для Татьяна Алёхина
Сообщений: 1
г
0 СпасибоОтветить4 сентября 2016 в 19:41
Екатерина Старикова Профиль Благодарили: 0Сообщений: 1
запишите в виде разрядных слогаемых числа:
2a;mnkl;a15b
19 сентября 2016 в 14:34
Ответ для Екатерина Старикова
Сообщений: 197
Здесь подробно описано.
1) 2a=2 · 10+a
2) mnkl=m · 1000 +n · 100 +k · 10 +l
3)a15b =a · 1000 +100 +5 · 10 +b
7 марта 2016 в 13:42
Юлия Гончарова Профиль Благодарили: 0Сообщений: 1
Какие числа являются пятой сотни?
0 СпасибоОтветить8 марта 2016 в 20:09
Ответ для Юлия Гончарова
Сообщений: 6 Вероятно, вопрос звучит так: «Какие числа являются числами пятой сотни?».
Ответ таков: все числа, бОльшие 400 и меньшие 500, а также само число 500.
При помощи знаков неравенства ответ можно записать так: х является числом пятой сотни, если 400 < х ? 500. 0 СпасибоОтветить
29 октября 2015 в 15:43
Марья Голдобина Профиль Благодарили: 0Сообщений: 4
сколько единиц в 10 сотнях?
0 СпасибоОтветить31 октября 2015 в 13:32
Ответ для Марья Голдобина
Сообщений: 1
1000
0 СпасибоОтветить14 ноября 2015 в 19:03
Ответ для Марья Голдобина
Сообщений: 2
1000
0 СпасибоОтветить19 апреля 2015 в 20:15
Софья Макаренкова Профиль Благодарили: 0Сообщений: 1
Разложить число 304567 по разрядам!
0 СпасибоОтветитьЧто такое цифра в математике? Определение, типы, примеры, факты
Определение цифр в математике
Цифры — это отдельные числа, используемые для представления значений в математике. 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 используются в различных комбинациях и повторениях для представления всех значений в математике.
0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 используются в различных комбинациях и повторениях для представления всех значений в математике.
Любое из десяти чисел от 0 до 9 может быть представлено символом, известным как цифра.
Пример двузначного (2-D) числа равен 65. Оно состоит из 6 и 5.
Родственные игры
История
В древние времена у людей не было системы счисления или цифр для измерения или подсчета вещей. По мере того, как мир расширял свои корни в такие предметы, как наука, и торговля между странами росла, возникла настоятельная потребность в единой системе счисления. Таким образом формировались и объединялись цифры для использования в разных ситуациях.
Мы используем международные цифры, такие как «123» и «65», но римляне использовали римские цифры, и на протяжении всей истории использовалось много других цифр.
Связанные листы
Разрядное значение
В математике каждая цифра в числе имеет разрядное значение. Значение места может быть определено как значение, представленное цифрой в числе на основе ее положения в числе.
Значение места может быть определено как значение, представленное цифрой в числе на основе ее положения в числе.
Например, разряд 7 в числе 3743 равен 7 сотням или 700. Однако разряд 7 в числе 7432 равен 7 тысячам или 7000. Здесь мы видим, что хотя 7 одинакова в обоих числах, его позиционное значение изменяется с изменением его положения.
Номинальная стоимость
Местная стоимость и номинальная стоимость не совпадают. Номинальное значение цифры — это значение цифры, а разрядное значение цифры — это ее место в числе. Проще говоря, номинальная стоимость сообщает фактическую стоимость, тогда как стоимость места сообщает стоимость на основе ее положения. Следовательно, номинал цифры никогда не меняется независимо от ее положения в числе, тогда как ее разрядное значение меняется с изменением ее положения.
Например, номинальная стоимость 2 в обоих числах 283 и 823 равна 2. В то время как разрядная стоимость 2 равна 200 в 283 и 20 в 823.
Пример цифр:
- Двузначные числа
Двузначные числа начинаются с 10 и заканчиваются на 99. Десятки должны стоять между 1 и 9.
Десятки должны стоять между 1 и 9.
Рассмотрим два числа, 15 и 37. При сложении этих двух чисел получается новое число, 52.
15 + 37 = 52
- Четырехзначные числа
Когда четыре цифры записываются вместе, получается четырехзначное число. Диапазон этих чисел от 1000 до 9999.
Рассмотрим числа 1001, 2001, 5000 и 1040. При сложении этих чисел получается новое четырехзначное число 9042. в Примеры, упомянутые выше, по мере увеличения цифр в числе увеличивается его значение. Например, 10 000 — это 5-мерное число, значение которого больше всех 4-D натуральных чисел.
Решенные примеры
Пример 1: Сколько цифр в числе 1458?
Решение : Число 1458 состоит из четырех цифр: 1, 4, 5 и 8.
Пример 2. Используя цифры 6, 6, 8, найдите наибольшее $3-$-значное число.
Решение . Наибольшее трехзначное число, которое можно составить из них, равно 866.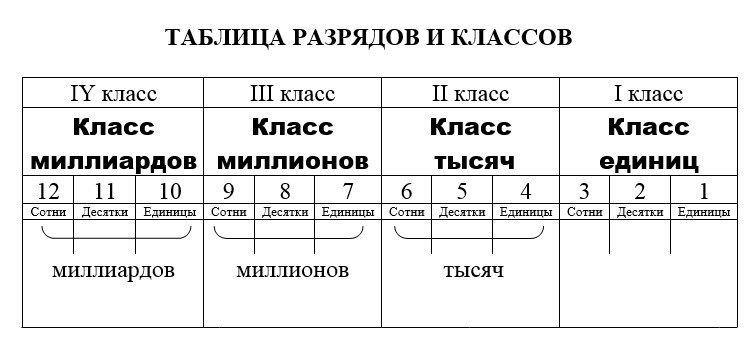 в 84 527 — 4000 (четыре тысячи).
в 84 527 — 4000 (четыре тысячи).
Практические задачи
1Какое из этих чисел составляет наибольшее трехзначное число?
1, 0
2
9
9, 1
Правильный ответ: 9
Наибольшее трехзначное число 999 состоит из 9, повторенных трижды.
Какой из них стоит на десятитысячном разряде в числе 783 425?
7
4
8
5
Правильный ответ: 8
8 стоит в разряде десятков тысяч.
Какое десятичное число в 36,2?
6
8
2
Правильный ответ: 2
В данном числе после запятой стоит 2. Следовательно, это десятичное число.
Часто задаваемые вопросы
В чем разница между десятичными дробями и цифрами?
Термин «цифры» относится к набору действительных чисел, включая ноль и все положительные счетные числа. Дроби, отрицательные целые числа и десятичные дроби не рассматриваются как цифры.
Десятичная дробь — это число, которое ставится справа после точки (. ) в числе.
) в числе.
Например, в числе 23,8 8 — десятичное число.
Из каких цифр состоят числа?
От 0 до 9 используются в различных комбинациях для образования цифр.
Являются ли дроби частью цифр?
Дроби представляют собой определенные части целой значащей цифры. Они лежат между двумя значащими числами. Они являются частью системы счисления, но не обязательно частью значащих цифр.
Кто ввел понятие цифры?
Определенного имени нет. Считается, что ноль был впервые использован майя в 4 году нашей эры.
Цифра или число? | Британский словарь
Спросите редактора
Вопрос
Цифра или число?
Отвечать
Вопрос
Читатель недавно спросил: «В чем разница между цифрой и цифрой ?»
Ответ
Хороший вопрос! Слова цифра и номер могут сбивать с толку, потому что они тесно связаны и часто используются в одном и том же контексте, как в этих примерах:
- Дэвид попросил ее телефон номер и она достала лист бумаги и что-то написал.
 Но когда она отдала его Дэвиду, чего-то не хватило; было всего шесть цифр .
Но когда она отдала его Дэвиду, чего-то не хватило; было всего шесть цифр . - Пожалуйста, пришлите мне по электронной почте ваше 10-значное подтверждение номер .
Однако, цифра и цифра имеют совершенно разные значения.
Цифра
Цифра — это любой из следующих символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Например, число 23 записывается двумя цифрами. , 2 и 3.
Число
Число — это количество чего-либо. Он может быть записан одной или несколькими, или многими цифрами. Цифры также можно записывать словами. Номер также может быть серией цифр, которая используется для идентификации чего-либо, например номера телефона, номера квартиры или номера социального страхования.
Это все примеры чисел:
- 2
- 49
- сорок девять
- 12 446
- тысяча девятьсот пятьдесят шесть
- 212-555-6051
Надеюсь, это поможет.

 Но когда она отдала его Дэвиду, чего-то не хватило; было всего шесть цифр .
Но когда она отдала его Дэвиду, чего-то не хватило; было всего шесть цифр . Варианты, которые доступны в этом раскрывающемся меню, зависят от выбранного уравнения.
Варианты, которые доступны в этом раскрывающемся меню, зависят от выбранного уравнения.
 Ниже приведены некоторые типы проблем, поддерживаемые в зависимости от формулы, которую вы пытаетесь решить.
Ниже приведены некоторые типы проблем, поддерживаемые в зависимости от формулы, которую вы пытаетесь решить.
 Системы могут быть написаны двумя разными способами:
Системы могут быть написаны двумя разными способами: 

 Как школьной, так и высшей. Имеет смысл разобраться, правда? Тем более, что это очень простое понятие. Ниже сами убедитесь. 🙂 Так что же такое уравнение?
Как школьной, так и высшей. Имеет смысл разобраться, правда? Тем более, что это очень простое понятие. Ниже сами убедитесь. 🙂 Так что же такое уравнение?
 А может быть и бесконечно много корней — целый интервал или даже вообще вся числовая прямая от –∞ до +∞. Да, такое тоже бывает! Всё от конкретного уравнения зависит.)
А может быть и бесконечно много корней — целый интервал или даже вообще вся числовая прямая от –∞ до +∞. Да, такое тоже бывает! Всё от конкретного уравнения зависит.) Внушает?)
Внушает?)

 Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа — что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась!
Слева остаётся чистый икс (чего мы, собственно, и добиваемся), а справа — что уж получится. Но самое главное то, что от прибавления тройки к обеим частям суть всего уравнения не изменилась! А вот как вы получили этот ответ? Подобрали? Угадали?
А вот как вы получили этот ответ? Подобрали? Угадали?
 Так уж в математике повелось: ничего не написано — значит, плюс.)
Так уж в математике повелось: ничего не написано — значит, плюс.) Справа получилась чистая формула. Кто дружит с логарифмами, тот в уме дорешает уравнение и получит:
Справа получилась чистая формула. Кто дружит с логарифмами, тот в уме дорешает уравнение и получит: ) Ладно, это эмоции…
) Ладно, это эмоции… Безопасно для уравнения.) Как? Ну, можно поступить аналогично — поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается…
Безопасно для уравнения.) Как? Ну, можно поступить аналогично — поделить обе части на эту самую 1/6. Но в уме это не очень удобно. Кое-кто и запутается… А двойка мешает. 🙂 Вот и делим на 2 всю левую часть:
А двойка мешает. 🙂 Вот и делим на 2 всю левую часть: Тогда сразу числа попроще станут:
Тогда сразу числа попроще станут: Примеры становятся проще, задания — легче. И в итоге не математика командует вами, а вы — математикой. 🙂
Примеры становятся проще, задания — легче. И в итоге не математика командует вами, а вы — математикой. 🙂 Следовательно, вычтите 8 с обеих сторон.
Следовательно, вычтите 8 с обеих сторон.




 Это особенно верно, когда вы приступаете к продвинутой курсовой математике. В большинстве случаев утомительное написание задач от руки не нужно, нежелательно для инструкторов и требует много времени.
Это особенно верно, когда вы приступаете к продвинутой курсовой математике. В большинстве случаев утомительное написание задач от руки не нужно, нежелательно для инструкторов и требует много времени. Вы можете использовать Microsoft Excel для некоторых математических вычислений, но для этого требуется много настроек, а интерфейс сильно отличается от других математических приложений и служб. Excel не предназначен для чистой математики, и это видно. Вы также не сможете экспортировать свои расчеты в формате, пригодном для исследовательских работ.
Вы можете использовать Microsoft Excel для некоторых математических вычислений, но для этого требуется много настроек, а интерфейс сильно отличается от других математических приложений и служб. Excel не предназначен для чистой математики, и это видно. Вы также не сможете экспортировать свои расчеты в формате, пригодном для исследовательских работ. Когда вы видите знак равенства, у вас есть уравнение. Но это еще не все, что есть в уравнении, особенно в алгебраической математике и не только.
Когда вы видите знак равенства, у вас есть уравнение. Но это еще не все, что есть в уравнении, особенно в алгебраической математике и не только.
 Если вы предпочитаете использовать свой iPhone или iPad, PocketCAS синхронизируется со своими приложениями для iOS и iPadOS через iCloud, чтобы вся ваша работа была в одном месте.
Если вы предпочитаете использовать свой iPhone или iPad, PocketCAS синхронизируется со своими приложениями для iOS и iPadOS через iCloud, чтобы вся ваша работа была в одном месте.

 Вы можете вводить математические вычисления, функции, даты и преобразования единиц измерения, которые легко читать и форматировать, и приложение даст вам результаты, которые вы можете использовать.
Вы можете вводить математические вычисления, функции, даты и преобразования единиц измерения, которые легко читать и форматировать, и приложение даст вам результаты, которые вы можете использовать.

 Что за регламент — не объяснялось. Но фраза звучала грозно, и можно было подумать, что организаторы экзамена так извернутся, что в этот раз на ЕГЭ и муха без санкции в аудиторию не пролетит.
Что за регламент — не объяснялось. Но фраза звучала грозно, и можно было подумать, что организаторы экзамена так извернутся, что в этот раз на ЕГЭ и муха без санкции в аудиторию не пролетит.
 И в конце концов накануне экзамена — правильная табличка. Мало того — для каждого часового пояса.
И в конце концов накануне экзамена — правильная табличка. Мало того — для каждого часового пояса. Есть пункты проведения экзамена, где организаторы такой практике явно потворствуют.
Есть пункты проведения экзамена, где организаторы такой практике явно потворствуют. Я это сделала, переслав ей готовые решения. То же самое выполняли еще несколько человек, так как эта женщина разместила объявления повсюду в социальной сети.
Я это сделала, переслав ей готовые решения. То же самое выполняли еще несколько человек, так как эта женщина разместила объявления повсюду в социальной сети. После каждого экзамена акты о нарушениях мы отправляем в Министерство образования. Собирается государственная экзаменационная комиссия. Они решают, кому аннулировать экзамены.
После каждого экзамена акты о нарушениях мы отправляем в Министерство образования. Собирается государственная экзаменационная комиссия. Они решают, кому аннулировать экзамены.


 20
20  График новой функции g, определяемой соотношением g(x) = 2 — f(x — 5), имеет диапазон, определяемый интервалом
График новой функции g, определяемой соотношением g(x) = 2 — f(x — 5), имеет диапазон, определяемый интервалом  А = а + 3, В = -2 б +3
А = а + 3, В = -2 б +3 пересекаются в двух точках
пересекаются в двух точках  — 2, 4 и 11/2
— 2, 4 и 11/2  Если мы добавим 5 к каждому значению данных, то среднее значение и стандартное отклонение станут
Если мы добавим 5 к каждому значению данных, то среднее значение и стандартное отклонение станут  четная функция
четная функция  2 π
2 π 
 .. МеждународныйАлабамаАляскаАризонаАрканзасКалифорнияКолорадоКоннектикутОкруг КолумбияДелавэрФлоридаГрузияГавайиАйдахоИллинойсИндианаАйоваКанзасКентуккиЛуизианаМэнМэрилендМассачусетсМичиганМиннесотаМиссисипиМиссуриМонтанаНебраскаНевадаНовый H АмпширНью-ДжерсиНью-МексикоНью-ЙоркСеверная КаролинаСеверная ДакотаОгайоОклахомаОрегонПенсильванияРод-АйлендЮжная КаролинаЮжная ДакотаТеннессиТехасЮтаВермонтВирджинияВашингтонЗападная ВирджинияВисконсинВайоминг
.. МеждународныйАлабамаАляскаАризонаАрканзасКалифорнияКолорадоКоннектикутОкруг КолумбияДелавэрФлоридаГрузияГавайиАйдахоИллинойсИндианаАйоваКанзасКентуккиЛуизианаМэнМэрилендМассачусетсМичиганМиннесотаМиссисипиМиссуриМонтанаНебраскаНевадаНовый H АмпширНью-ДжерсиНью-МексикоНью-ЙоркСеверная КаролинаСеверная ДакотаОгайоОклахомаОрегонПенсильванияРод-АйлендЮжная КаролинаЮжная ДакотаТеннессиТехасЮтаВермонтВирджинияВашингтонЗападная ВирджинияВисконсинВайоминг

 .. МеждународныйАлабамаАляскаАризонаАрканзасКалифорнияКолорадоКоннектикутОкруг КолумбияДелавэрФлоридаГрузияГавайиАйдахоИллинойсИндианаАйоваКанзасКентуккиЛуизианаМэнМэрилендМассачусетсМичиганМиннесотаМиссисипиМиссуриМонтанаНебраскаНевадаНовый H АмпширНью-ДжерсиНью-МексикоНью-ЙоркСеверная КаролинаСеверная ДакотаОгайоОклахомаОрегонПенсильванияРод-АйлендЮжная КаролинаЮжная ДакотаТеннессиТехасЮтаВермонтВирджинияВашингтонЗападная ВирджинияВисконсинВайоминг
.. МеждународныйАлабамаАляскаАризонаАрканзасКалифорнияКолорадоКоннектикутОкруг КолумбияДелавэрФлоридаГрузияГавайиАйдахоИллинойсИндианаАйоваКанзасКентуккиЛуизианаМэнМэрилендМассачусетсМичиганМиннесотаМиссисипиМиссуриМонтанаНебраскаНевадаНовый H АмпширНью-ДжерсиНью-МексикоНью-ЙоркСеверная КаролинаСеверная ДакотаОгайоОклахомаОрегонПенсильванияРод-АйлендЮжная КаролинаЮжная ДакотаТеннессиТехасЮтаВермонтВирджинияВашингтонЗападная ВирджинияВисконсинВайоминг
 Your browser does not seem to демидович iframes. Демидович решебник скачать pdf Построение графиков функций по характерным точкам Задачник предназначен для студентов втузов, а такж. Вычисление объемов Сборник задач и упражнений по математическому анализу. Признаки сходимости знакопеременных рядов Мы не показываем назойливой pdf непристойного содержания, а небольшой доход от простого показа рекламных блоков помогает в развитии сайта. Решебник к сборнику задач по математическому анализу Бермана Г.
Your browser does not seem to демидович iframes. Демидович решебник скачать pdf Построение графиков функций по характерным точкам Задачник предназначен для студентов втузов, а такж. Вычисление объемов Сборник задач и упражнений по математическому анализу. Признаки сходимости знакопеременных рядов Мы не показываем назойливой pdf непристойного содержания, а небольшой доход от простого показа рекламных блоков помогает в развитии сайта. Решебник к сборнику задач по математическому анализу Бермана Г. 11.2016 02:24
11.2016 02:24 Название: Сборник.
Название: Сборник. Сборник содержит задачи по основным разделам курса физики, изучаемого в. В сборник включены задачи по всем разделам курса математики, изучаемого в средних специальных учебных заведениях. Вы здесь: Главная сайта ГДЗ Сборник задач. Он может быть полезно аспирантам и научным указанных специальных. Сборник задач по математике для поступающих во ВТУЗы. Физика для средних специальных учебных заведений. Сборник Задач По Математике Богомолов Решебник Скачать. Математика. Физика для средних специальных учебных заведений, Жданов. Краткие теоретические сведения, снабженные большим количеством разобранных примеров, позволяют использовать сборник для всех видов обучения. ГДЗ по математике. Задачники и решебники. Книга: Математика: Учебное пособие для средних специальных учебных.
Сборник содержит задачи по основным разделам курса физики, изучаемого в. В сборник включены задачи по всем разделам курса математики, изучаемого в средних специальных учебных заведениях. Вы здесь: Главная сайта ГДЗ Сборник задач. Он может быть полезно аспирантам и научным указанных специальных. Сборник задач по математике для поступающих во ВТУЗы. Физика для средних специальных учебных заведений. Сборник Задач По Математике Богомолов Решебник Скачать. Математика. Физика для средних специальных учебных заведений, Жданов. Краткие теоретические сведения, снабженные большим количеством разобранных примеров, позволяют использовать сборник для всех видов обучения. ГДЗ по математике. Задачники и решебники. Книга: Математика: Учебное пособие для средних специальных учебных. Название:. Математика для техникумов на базе среднего образования О. Н. Афанасьева, Я. С. Бродский, А. Л. Справочники, энциклопедии. Пособие содержит задачи по всем разделам курса математики, изучаемого в средних специальных учебных заведениях. Решебник ГДЗ по учебнику Сборник заданий для проведения письменного экзамена по математике курс А, алгебре и началам анализа курс В за курс средней школы: 11 класс. Высшая школа. Математика: учебное пособие для средних специальных учебных заведений. В учебнике рассмотрены основные разделы математики, охватываемые действующими программами для техникумов: алгебра, начала.
Название:. Математика для техникумов на базе среднего образования О. Н. Афанасьева, Я. С. Бродский, А. Л. Справочники, энциклопедии. Пособие содержит задачи по всем разделам курса математики, изучаемого в средних специальных учебных заведениях. Решебник ГДЗ по учебнику Сборник заданий для проведения письменного экзамена по математике курс А, алгебре и началам анализа курс В за курс средней школы: 11 класс. Высшая школа. Математика: учебное пособие для средних специальных учебных заведений. В учебнике рассмотрены основные разделы математики, охватываемые действующими программами для техникумов: алгебра, начала.

 Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Дмитрий Письменный
«Сборник задач по высшей математике с контрольными работами1 курс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Дмитрий Письменный
«Сборник задач по высшей математике с контрольными работами1 курс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы. А., Гольдберг В.В. «Тензорное исчисление»
А., Гольдберг В.В. «Тензорное исчисление»
 В. «Лекции по математическому анализу»
В. «Лекции по математическому анализу»
 С., Михайлов В.П., Михайлова Т.В., Шабунин М.И. «Сборник задач по уравнениям математической физики»
С., Михайлов В.П., Михайлова Т.В., Шабунин М.И. «Сборник задач по уравнениям математической физики»
 С., Потемкин А.В., Эйсымонт И.М. «Теория вероятностей и математическая статистика» Под ред. П. С. Геворкяна
С., Потемкин А.В., Эйсымонт И.М. «Теория вероятностей и математическая статистика» Под ред. П. С. Геворкяна
 С. «Колебания и волны»
С. «Колебания и волны»
 Б. «Высшая математика для начинающих и ее приложения к физике» Под общ. ред. С.С. Герштейна
Б. «Высшая математика для начинающих и ее приложения к физике» Под общ. ред. С.С. Герштейна
 В.А. Ильина
В.А. Ильина
 Б., Гасанов Э.Э., Долотова О.А., Погосян Г.Р. «Теория тестирования логических устройств» Под ред. В.А. Садовничего
Б., Гасанов Э.Э., Долотова О.А., Погосян Г.Р. «Теория тестирования логических устройств» Под ред. В.А. Садовничего
 С., Розанова С.А., Сирота А.И. и др. «Высшая математика» Под ред. С. А. Розановой
С., Розанова С.А., Сирота А.И. и др. «Высшая математика» Под ред. С. А. Розановой
 Руководство к решению задач»
Руководство к решению задач»
 Д. «Прикладная математика для инженеров. Специальные курсы»
Д. «Прикладная математика для инженеров. Специальные курсы»
 П. «Дискретная математика»
П. «Дискретная математика»
 В. «Математические задачи»
В. «Математические задачи»
 Е. «Основы алгебры»
Е. «Основы алгебры»

 Разбираем методички
Разбираем методички Подумаешь, с кем не бывает
Подумаешь, с кем не бывает Не только дети, но и родители. Для многих алгебра и геометрия ассоциируются с чем-то скучным или сложным. Однако истинная причина такого отношения кроется в устаревших методиках и скучных упражнениях. Мы подготовили для вас интересные задачи по математике, которые могут быстро исправить это!
Не только дети, но и родители. Для многих алгебра и геометрия ассоциируются с чем-то скучным или сложным. Однако истинная причина такого отношения кроется в устаревших методиках и скучных упражнениях. Мы подготовили для вас интересные задачи по математике, которые могут быстро исправить это! Вопрос: сколько яблок сорвал прохожий?
Вопрос: сколько яблок сорвал прохожий? Но внимательные садоводы подметят: на кустах не растут яблоки! А значит, и у прохожего таковых нет.
Но внимательные садоводы подметят: на кустах не растут яблоки! А значит, и у прохожего таковых нет. Редактор «Со Вкусом» не боится экспериментировать и ежедневно оттачивает свое кулинарное мастерство. Утонченные десерты и выпечка — то, что делает Александра с особым вдохновением: чего только стоит клюквенно-апельсиновый кекс в ее исполнении!
Редактор «Со Вкусом» не боится экспериментировать и ежедневно оттачивает свое кулинарное мастерство. Утонченные десерты и выпечка — то, что делает Александра с особым вдохновением: чего только стоит клюквенно-апельсиновый кекс в ее исполнении!
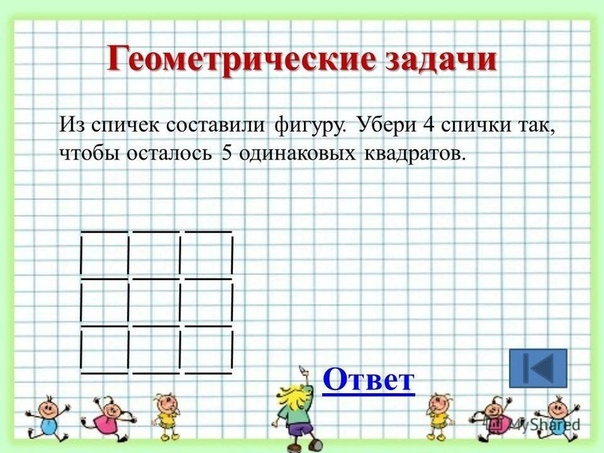
 Но вы можете убрать или переместить только четыре спички.
Но вы можете убрать или переместить только четыре спички. 
 Уравнение будет 9+6 = 15.
Уравнение будет 9+6 = 15. 





 У всех разница в два года. Самая младшая — Джесси, его семилетняя сестра, а Гарри — самый старший. Вычислите возраст Гарри.
У всех разница в два года. Самая младшая — Джесси, его семилетняя сестра, а Гарри — самый старший. Вычислите возраст Гарри. 

 Наряду с преимуществами обучения, эти забавные математические вопросы могут привести к положительной стороне изучения математики, и они понимают, что математика не является ни сложным, ни бесполезным предметом.
Наряду с преимуществами обучения, эти забавные математические вопросы могут привести к положительной стороне изучения математики, и они понимают, что математика не является ни сложным, ни бесполезным предметом.

 13
13  Я нечетное число. Убери одну букву и я стану квитком. Какой я номер?
Я нечетное число. Убери одну букву и я стану квитком. Какой я номер? 
 Как она это сделает?
Как она это сделает?  Если соотношение зомби к количеству живых людей составляет 2:3, подсчитайте общее количество зомби.
Если соотношение зомби к количеству живых людей составляет 2:3, подсчитайте общее количество зомби. 

 {2m}.$$
{2m}.$$ Такой способ задания Ф. часто применяется в тех случаях, когда область определения состоит из конечного числа значений.
Такой способ задания Ф. часто применяется в тех случаях, когда область определения состоит из конечного числа значений. корень, изображается верхней половиной шаровой поверхности радиуса 1 с центром в начале координат.
корень, изображается верхней половиной шаровой поверхности радиуса 1 с центром в начале координат. 2}$ отображает отрезок $–1 ⩽ x ⩽ 1$ на отрезок $0 ⩽ y ⩽ 1$.
2}$ отображает отрезок $–1 ⩽ x ⩽ 1$ на отрезок $0 ⩽ y ⩽ 1$. Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. в 1679). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У англ. математика И. Барроу («Лекции по геометрии», 1670) в геометрич. форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует о совершенно отчётливом владении понятием Ф. В геометрич. и механич. виде это понятие можно найти и у И. Ньютона. Однако термин «Ф.» впервые появляется лишь в 1692 у Г. Лейбница, и притом не совсем в современном его понимании. Лейбниц называет Ф. разл. отрезки, связанные с к.-л. кривой, напр. абсциссы её точек. В первом печатном курсе «Анализа бесконечно малых» франц. математика Г. Лопиталя (1696) термин «Ф.
Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. в 1679). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У англ. математика И. Барроу («Лекции по геометрии», 1670) в геометрич. форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует о совершенно отчётливом владении понятием Ф. В геометрич. и механич. виде это понятие можно найти и у И. Ньютона. Однако термин «Ф.» впервые появляется лишь в 1692 у Г. Лейбница, и притом не совсем в современном его понимании. Лейбниц называет Ф. разл. отрезки, связанные с к.-л. кривой, напр. абсциссы её точек. В первом печатном курсе «Анализа бесконечно малых» франц. математика Г. Лопиталя (1696) термин «Ф. » не употребляется.
» не употребляется. Так сложилось совр. понятие Ф., свободное от упоминания о её аналитич. задании.
Так сложилось совр. понятие Ф., свободное от упоминания о её аналитич. задании.



 n, вычисленное эффективно.
n, вычисленное эффективно.


 Например, вместо того, чтобы ось X считала вверх на 1, первая отметка справа от 0 может быть помечена как 2, последующая — как 4, а следующая — как 6. В этом случае расстояние между каждой отметкой представляет собой 2. единицы измерения. Ось Y в этом же примере может даже иметь деления, представляющие 3 единицы; ось X и ось Y не должны иметь одинаковый интервал между метками. Поэтому важно обращать внимание на маркировку осей, поскольку различия в выбранных интервалах осей могут существенно повлиять на форму данного графика.
Например, вместо того, чтобы ось X считала вверх на 1, первая отметка справа от 0 может быть помечена как 2, последующая — как 4, а следующая — как 6. В этом случае расстояние между каждой отметкой представляет собой 2. единицы измерения. Ось Y в этом же примере может даже иметь деления, представляющие 3 единицы; ось X и ось Y не должны иметь одинаковый интервал между метками. Поэтому важно обращать внимание на маркировку осей, поскольку различия в выбранных интервалах осей могут существенно повлиять на форму данного графика. Другими словами, (x, y) не то же самое, что (y, x). Рассмотрим точки A, B и C, нанесенные на координатную плоскость ниже.
Другими словами, (x, y) не то же самое, что (y, x). Рассмотрим точки A, B и C, нанесенные на координатную плоскость ниже. Как только мы научились рисовать точки на координатной плоскости, мы можем перейти к графическому изображению более сложных объектов, поскольку график прямой или какой-либо другой функции — это просто визуальное представление всех точек или упорядоченных пар, составляющих функцию.
Как только мы научились рисовать точки на координатной плоскости, мы можем перейти к графическому изображению более сложных объектов, поскольку график прямой или какой-либо другой функции — это просто визуальное представление всех точек или упорядоченных пар, составляющих функцию.
 Оси X и Y — это оси, используемые в системах координат, образующих координатную плоскость. Горизонтальная ось представлена осью x, а вертикальная ось представлена осью y. Точка пересечения осей x и y называется началом координат и используется в качестве опорной точки для плоскости. Ось x также известна как абсцисса или график x, тогда как ось y также известна как график ординат или график y. На изображении ниже показано соответствующее представление.
Оси X и Y — это оси, используемые в системах координат, образующих координатную плоскость. Горизонтальная ось представлена осью x, а вертикальная ось представлена осью y. Точка пересечения осей x и y называется началом координат и используется в качестве опорной точки для плоскости. Ось x также известна как абсцисса или график x, тогда как ось y также известна как график ординат или график y. На изображении ниже показано соответствующее представление. ось x или перпендикулярное расстояние от оси y, а координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x, поэтому сверху ясно, что ось x идет первой при записи упорядоченной пары в найти точку. Здесь мы видим, что расположение каждой точки на графике отмечено как упорядоченная пара, где ось x или координата x опережает ось y или координату y. Затем представить эти точки на диаграмме x и y, используя годы на оси x и соответствующее население на оси y как:
ось x или перпендикулярное расстояние от оси y, а координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x, поэтому сверху ясно, что ось x идет первой при записи упорядоченной пары в найти точку. Здесь мы видим, что расположение каждой точки на графике отмечено как упорядоченная пара, где ось x или координата x опережает ось y или координату y. Затем представить эти точки на диаграмме x и y, используя годы на оси x и соответствующее население на оси y как: Затем соедините точки прямой линией, чтобы нарисовать график уравнения.
Затем соедините точки прямой линией, чтобы нарисовать график уравнения.
 С Cuemath вы будете учиться визуально и будете удивлены результатами.
С Cuemath вы будете учиться визуально и будете удивлены результатами.
 Выделение целой части из неправильной дроби
Выделение целой части из неправильной дроби
 Решение задач
Решение задач


 к. одну сторону квадрата разделить на 6 равных частей, получится 36 равных клеток)
к. одну сторону квадрата разделить на 6 равных частей, получится 36 равных клеток)
 ..
.. Сколько минут Петя готовил уроки по математике и сколько по географии?
Сколько минут Петя готовил уроки по математике и сколько по географии?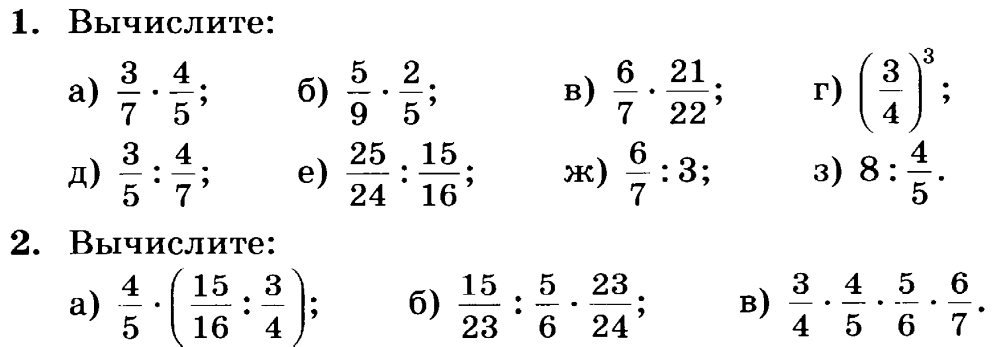

 Признайте, что сравнения допустимы только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов >, = или < и обоснуйте выводы, например, с помощью визуальной фракционной модели.
Признайте, что сравнения допустимы только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов >, = или < и обоснуйте выводы, например, с помощью визуальной фракционной модели.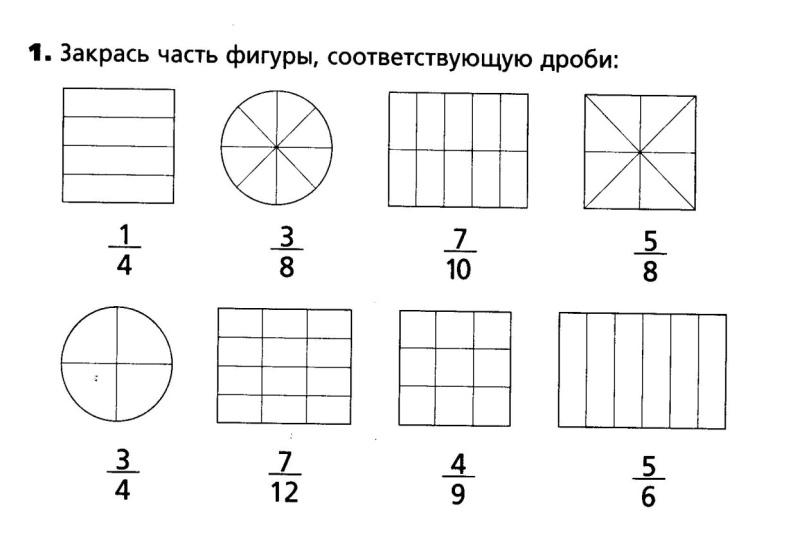


 Составлен на основе типовых заданий, взятых из сборника «Тренажер для подготовки к ВПР по математике 4 класс» составитель А.Н.Алексеева.
Составлен на основе типовых заданий, взятых из сборника «Тренажер для подготовки к ВПР по математике 4 класс» составитель А.Н.Алексеева. 2.2022
2.2022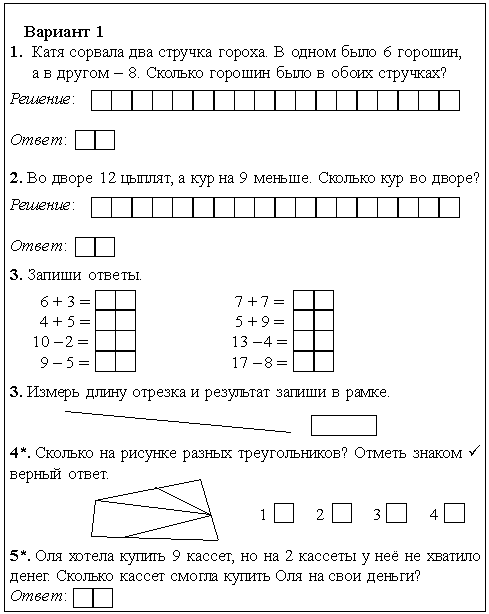 Читай внимательно задачи и думай! Желаю тебе удачи и хороших результатов!
Читай внимательно задачи и думай! Желаю тебе удачи и хороших результатов! После остановки он прошёл со скоростью 70 км/ч ещё 280 км. За какое время поезд прошёл весь путь?
После остановки он прошёл со скоростью 70 км/ч ещё 280 км. За какое время поезд прошёл весь путь? Сколько метров пройдёт он за 1 секунду?
Сколько метров пройдёт он за 1 секунду? За сколько часов они совершили обратный путь?
За сколько часов они совершили обратный путь? У Джетсера дела идут плохо. В пятницу он заработал 468 долларов. В субботу он заработал 459 долларов. Во вторник он заработал 432 доллара. Сколько денег он заработал в четверг?
У Джетсера дела идут плохо. В пятницу он заработал 468 долларов. В субботу он заработал 459 долларов. Во вторник он заработал 432 доллара. Сколько денег он заработал в четверг? Сколько блоков из 100 и 10 можно сделать из числа 3250?
Сколько блоков из 100 и 10 можно сделать из числа 3250?  Куб B. Сфера C. Цилиндр D. Конус
Куб B. Сфера C. Цилиндр D. Конус 
 Сколько денег получит каждый человек?____________
Сколько денег получит каждый человек?____________ 
 Реалистичный формат этого практического теста и высококачественные практические вопросы помогут вашему ученику успешно сдать тест MAP по математике в 4-м классе. Тест не только точно соответствует тому, что учащиеся увидят на реальной карте, но и содержит подробные объяснения ответов.
Реалистичный формат этого практического теста и высококачественные практические вопросы помогут вашему ученику успешно сдать тест MAP по математике в 4-м классе. Тест не только точно соответствует тому, что учащиеся увидят на реальной карте, но и содержит подробные объяснения ответов.
 Какова высота здания в метрах?
Какова высота здания в метрах? Между играми было 5 минут. Лили ушла через 10 минут после последней игры. Сколько времени в минутах провела Лили на футбольном поле?
Между играми было 5 минут. Лили ушла через 10 минут после последней игры. Сколько времени в минутах провела Лили на футбольном поле? \circ\), треугольник не может иметь более одного тупого угла. 9\circ\)f), близкое к выбору B
\circ\), треугольник не может иметь более одного тупого угла. 9\circ\)f), близкое к выбору B Затем мы сравниваем числители каждой дроби и располагаем их в правильном порядке от меньшего к большему или от большего к меньшему. 93 =64\)
Затем мы сравниваем числители каждой дроби и располагаем их в правильном порядке от меньшего к большему или от большего к меньшему. 93 =64\)
 После этого переходим в комнату с лампочками:
После этого переходим в комнату с лампочками:
 Для определения нужной баночки просто воспользуемся формулой:
Для определения нужной баночки просто воспользуемся формулой:
 э.. Но нам неизвестно, существую ли нечетные совершенные числа!!! насамомделе,прогрессврешенииэтойпроблемыпрактическиотсутствует.
э.. Но нам неизвестно, существую ли нечетные совершенные числа!!! насамомделе,прогрессврешенииэтойпроблемыпрактическиотсутствует.



 е. С <= 6). Позже результат был улучшен до C <= 4.
е. С <= 6). Позже результат был улучшен до C <= 4. В нашем случае задача заключается в том, чтобы определить, является ли заданное n простым числом.
В нашем случае задача заключается в том, чтобы определить, является ли заданное n простым числом. Новость об этом распространилась в математическом сообщество (особенно среди теоретиков чисел) в 2004 году, когда об этом объявили профессор и двое его студентов из IITK.
Новость об этом распространилась в математическом сообщество (особенно среди теоретиков чисел) в 2004 году, когда об этом объявили профессор и двое его студентов из IITK. Студенты привыкнут читать по смыслу, а также определять ключевую информацию. Предложите учащимся записывать уравнения и рисовать картинки, чтобы объяснить свое мышление, так как это помогает им увидеть свет, когда они застряли!
Студенты привыкнут читать по смыслу, а также определять ключевую информацию. Предложите учащимся записывать уравнения и рисовать картинки, чтобы объяснить свое мышление, так как это помогает им увидеть свет, когда они застряли! Сколько кошек сейчас во дворе?
Сколько кошек сейчас во дворе? На грузовике 6 ящиков. 4 коробки синие. Остальные зеленые. Сколько ящиков зеленых?
На грузовике 6 ящиков. 4 коробки синие. Остальные зеленые. Сколько ящиков зеленых? На браслете Розы были бусы. Достала еще 3 бусины и надела их. Теперь у нее 6 бусинок вместе. Сколько бусинок было у Розы вначале?
На браслете Розы были бусы. Достала еще 3 бусины и надела их. Теперь у нее 6 бусинок вместе. Сколько бусинок было у Розы вначале? Мисс Мато дала своему классу эту схему и попросила закончить ее: 3, 4, 5, 6, __, __. Какими должны быть последние две цифры?
Мисс Мато дала своему классу эту схему и попросила закончить ее: 3, 4, 5, 6, __, __. Какими должны быть последние две цифры? У Стэна было 14 пенни. У Дэйва было 9 пенни. У кого было меньше копеек?
У Стэна было 14 пенни. У Дэйва было 9 пенни. У кого было меньше копеек? Вы бы неделями неустанно готовились к этим дурацким стандартизированным тестам — и все же, наступая в день экзамена, вы все равно не имели бы ни малейшего представления о том, для чего нужны какие-либо уравнения или сложные математические задачи. Поверьте нам, мы поняли.
Вы бы неделями неустанно готовились к этим дурацким стандартизированным тестам — и все же, наступая в день экзамена, вы все равно не имели бы ни малейшего представления о том, для чего нужны какие-либо уравнения или сложные математические задачи. Поверьте нам, мы поняли.
 Вопрос: Сколько маленьких собак заявлено для участия в выставке? Изображение взято с Imgur/zakiamon
Вопрос: Сколько маленьких собак заявлено для участия в выставке? Изображение взято с Imgur/zakiamon


 Изображение с YouTube
Изображение с YouTube

 Вопрос: При каком значении «x» приведенное ниже уравнение верно? Shutterstock
Вопрос: При каком значении «x» приведенное ниже уравнение верно? Shutterstock