как найти, примеры и задачи с решением — OneKu
Содержание статьи:
- Как сформулировать признак делимости на 15
- Как узнать, что число делится на 3
- Когда число делится на 5
- Примеры с решением
Зачастую при решении задач нужно узнать, делится ли то или иное число на заданную цифру без остатка. Но каждый раз делить его очень долго. К тому же велика вероятность допустить ошибку в расчетах и уйти от правильного ответа. Для того чтобы избежать этой проблемы, были найдены признаки делимости на основные простые или однозначные числа: 2, 3, 9, 11. Но что делать, если нужно произвести деление на другую, большую цифру? Например, как рассчитать признак делимости на 15? Ответ на этот вопрос мы постараемся найти в данной статье.
Как сформулировать признак делимости на 15?
Вам будет интересно:Тангенциальное, или касательное ускорение
Если для простых чисел признаки делимости хорошо известны, то что делать с остальными?
Если число не является простым, то его можно разложить на множители. Например, 33 – это произведение 3 и 11, а 45 – 9 и 5. Существует свойство, согласно которому число делится на данное без остатка в случае, если его можно разделить и на тот, и на другой множитель. Это значит, что любое большое число можно представить в виде простых, и уже исходя из них, формулировать признак делимости.
Например, 33 – это произведение 3 и 11, а 45 – 9 и 5. Существует свойство, согласно которому число делится на данное без остатка в случае, если его можно разделить и на тот, и на другой множитель. Это значит, что любое большое число можно представить в виде простых, и уже исходя из них, формулировать признак делимости.
Итак, нам нужно узнать, можно ли разделить данное число на 15. Для этого рассмотрим его подробнее. Число 15 можно представить, как произведение 3 и 5. Значит, чтобы число делилось на 15, оно должно быть кратно одновременно 3 и 5. Это и есть признак делимости на 15. В дальнейшем мы рассмотрим его подробнее и сформулируем точнее.
Как узнать, что число делится на 3?
Вспомним признак делимости на 3.
Число делится на 3, если сумма его цифр (количество единиц, десятков, сотен и так далее) делится на 3.
Так, например, необходимо узнать, какие из этих чисел можно разделить на 3 без остатка: 76348, 24606, 1128904, 540813.
Конечно, можно просто разделить данные числа в столбец, но это займет немало времени. Поэтому мы воспользуемся признаком делимости на 3.
Поэтому мы воспользуемся признаком делимости на 3.
- 7 + 6 + 3 + 4 + 8 = 28. Число 28 не делится на 3, значит и 76348 не делится на 3.
- 2 + 4 + 6 + 0 + 6 = 18. Число 18 можно разделить на 3 — значит, и данное число делится на 3 без остатка. Действительно, 24 606 : 3 = 8 202.
Таким же образом проанализируем остальные числа:
- 1 + 1 + 2 + 8 + 9 + 4 = 25. Число 25 не делится на 3. Значит, 1 128 904 не делится на 3.
- 5 + 4 + 0 + 8 + 1 + 3 = 21. Число 21 делится на 3, а это значит, что 540 813 делится на 3. (540 813 : 3 = 180 271)
Ответ: 24 606 и 540 813.
Когда число делится на 5?
Однако признак делимости числа на 15 также включает в себя не только делимость на 3, но и кратность пяти.
Признак делимости на 5 таков: число делится на 5, если оно оканчивается на 5 или на 0.
Например, нужно найти числа кратные 5: 11 467, 909, 670, 840 435, 67 900
Числа 11 467 и 909 не делятся на 5.
Числа 670, 840 435 и 67 900 оканчиваются на 0 или 5, а значит, кратны 5.
Примеры с решением
Итак, теперь мы можем полноценно сформулировать признак делимости на 15: число делится на 15 тогда, когда сумма его цифр кратна 3, а последней цифрой является или 5, или 0. Важно отметить, что оба этих условия должны выполняться одновременно. Иначе мы получим число кратное не 15, а только 3 или 5.
Признак делимости чисел на 15 очень часто нужен для решения контрольных и экзаменационных заданий. Например, зачастую в базовом уровне ЕГЭ по математике встречаются задачи, основанные на понимании именно этой темы. Рассмотрим некоторые их решения на практике.
Задача 1.
Среди чисел найдите те, которые делятся на 15.
9 085 475; 78 545; 531; 12 000; 90 952
Итак, для начала отбросим те числа, которые очевидно не удовлетворяют нашим критериям. Это 531 и 90 952. Несмотря на то, что сумма 5+3+1 = 9 делится на 3, число оканчивается на единицу, а значит, не подходит. То же самое касается 90 952, которое оканчивается на 2.
9 085 475, 78 545 и 12 000 удовлетворяют первому критерию, теперь проверим их на соответствие второму.
9+0+8+5+4+7+5 = 38, 38 не делится на 3. Значит, это число является лишним в нашем ряду.
7+8+5+4+5 = 29. 29 не кратно 3, не удовлетворяет условиям.
А вот 1+2 = 3, 3 делится на 3 нацело, это значит, что именно это число и является ответом.
Ответ: 12 000
Задача 2.
Трехзначное число С больше 700 и делится на 15. Запишите наименьшее такое число.
Итак, по признаку делимости на 15 данное число должно заканчиваться на 5 или 0. Так как на нужно самое маленькое из возможных, возьмем 0 – это будет последней цифрой.
Так как число больше 700, то первой может быть цифра 7 или больше. Помня, что нам следует найти наименьшее значение, выбираем 7.
Чтобы число делилось на 15, должно выполняться условие 7+х+0 = число, кратное 3, где х – количество десятков.
Итак, 7+х+0 = 9
Х = 9 -7
Х = 2
Число 720 – искомое.
Ответ: 720
Задача 3.
Вычеркните из числа 3426578 любые три цифры так, чтобы получившееся число было кратно 15.
Во-первых, искомое число должно оканчиваться на цифру 5 или 0. Значит, последние две цифры – 7 и 8 нужно вычеркнуть сразу.
Остается 34265.
3+4+2+6+5 = 20, 20 не делится на 3. Ближайшее кратное 3 число – это 18. Для того, чтобы получить его, нужно отнять 2. Вычеркиваем цифру 2.
Получается 3465. Проверим свой ответ, 3465 : 15 = 231.
Ответ: 3465
В данной статье были рассмотрены основные признаки делимости на 15 с примерами. Этот материал должен помочь ученикам с решением заданий такого типа и подобных им, а также понять алгоритм работы с ними.
как найти, примеры и задачи с решением
Зачастую при решении задач нужно узнать, делится ли то или иное число на заданную цифру без остатка. Но каждый раз делить его очень долго. К тому же велика вероятность допустить ошибку в расчетах и уйти от правильного ответа. Для того чтобы избежать этой проблемы, были найдены признаки делимости на основные простые или однозначные числа: 2, 3, 9, 11. Но что делать, если нужно произвести деление на другую, большую цифру? Например, как рассчитать признак делимости на 15? Ответ на этот вопрос мы постараемся найти в данной статье.
Как сформулировать признак делимости на 15?
Если для простых чисел признаки делимости хорошо известны, то что делать с остальными?
Если число не является простым, то его можно разложить на множители. Например, 33 – это произведение 3 и 11, а 45 – 9 и 5. Существует свойство, согласно которому число делится на данное без остатка в случае, если его можно разделить и на тот, и на другой множитель. Это значит, что любое большое число можно представить в виде простых, и уже исходя из них, формулировать признак делимости.
Итак, нам нужно узнать, можно ли разделить данное число на 15. Для этого рассмотрим его подробнее. Число 15 можно представить, как произведение 3 и 5. Значит, чтобы число делилось на 15, оно должно быть кратно одновременно 3 и 5. Это и есть признак делимости на 15. В дальнейшем мы рассмотрим его подробнее и сформулируем точнее.
Как узнать, что число делится на 3?
Вспомним признак делимости на 3.
Число делится на 3, если сумма его цифр (количество единиц, десятков, сотен и так далее) делится на 3.
Так, например, необходимо узнать, какие из этих чисел можно разделить на 3 без остатка: 76348, 24606, 1128904, 540813.
Конечно, можно просто разделить данные числа в столбец, но это займет немало времени. Поэтому мы воспользуемся признаком делимости на 3.
- 7 + 6 + 3 + 4 + 8 = 28. Число 28 не делится на 3, значит и 76348 не делится на 3.
- 2 + 4 + 6 + 0 + 6 = 18. Число 18 можно разделить на 3 — значит, и данное число делится на 3 без остатка. Действительно, 24 606 : 3 = 8 202.
Таким же образом проанализируем остальные числа:
- 1 + 1 + 2 + 8 + 9 + 4 = 25. Число 25 не делится на 3. Значит, 1 128 904 не делится на 3.
- 5 + 4 + 0 + 8 + 1 + 3 = 21. Число 21 делится на 3, а это значит, что 540 813 делится на 3. (540 813 : 3 = 180 271)
Ответ: 24 606 и 540 813.
Когда число делится на 5?
Однако признак делимости числа на 15 также включает в себя не только делимость на 3, но и кратность пяти.
Признак делимости на 5 таков: число делится на 5, если оно оканчивается на 5 или на 0.
Например, нужно найти числа кратные 5: 11 467, 909, 670, 840 435, 67 900
Числа 11 467 и 909 не делятся на 5.
Числа 670, 840 435 и 67 900 оканчиваются на 0 или 5, а значит, кратны 5.
Примеры с решением
Итак, теперь мы можем полноценно сформулировать признак делимости на 15: число делится на 15 тогда, когда сумма его цифр кратна 3, а последней цифрой является или 5, или 0. Важно отметить, что оба этих условия должны выполняться одновременно. Иначе мы получим число кратное не 15, а только 3 или 5.
Признак делимости чисел на 15 очень часто нужен для решения контрольных и экзаменационных заданий. Например, зачастую в базовом уровне ЕГЭ по математике встречаются задачи, основанные на понимании именно этой темы. Рассмотрим некоторые их решения на практике.
Задача 1.
Среди чисел найдите те, которые делятся на 15.
9 085 475; 78 545; 531; 12 000; 90 952
Итак, для начала отбросим те числа, которые очевидно не удовлетворяют нашим критериям. Это 531 и 90 952. Несмотря на то, что сумма 5+3+1 = 9 делится на 3, число оканчивается на единицу, а значит, не подходит. То же самое касается 90 952, которое оканчивается на 2.
Это 531 и 90 952. Несмотря на то, что сумма 5+3+1 = 9 делится на 3, число оканчивается на единицу, а значит, не подходит. То же самое касается 90 952, которое оканчивается на 2.
9 085 475, 78 545 и 12 000 удовлетворяют первому критерию, теперь проверим их на соответствие второму.
9+0+8+5+4+7+5 = 38, 38 не делится на 3. Значит, это число является лишним в нашем ряду.
7+8+5+4+5 = 29. 29 не кратно 3, не удовлетворяет условиям.
А вот 1+2 = 3, 3 делится на 3 нацело, это значит, что именно это число и является ответом.
Ответ: 12 000
Задача 2.
Трехзначное число С больше 700 и делится на 15. Запишите наименьшее такое число.
Итак, по признаку делимости на 15 данное число должно заканчиваться на 5 или 0. Так как на нужно самое маленькое из возможных, возьмем 0 – это будет последней цифрой.
Так как число больше 700, то первой может быть цифра 7 или больше. Помня, что нам следует найти наименьшее значение, выбираем 7.
Чтобы число делилось на 15, должно выполняться условие 7+х+0 = число, кратное 3, где х – количество десятков.
Итак, 7+х+0 = 9
Х = 9 -7
Х = 2
Число 720 – искомое.
Ответ: 720
Задача 3.
Вычеркните из числа 3426578 любые три цифры так, чтобы получившееся число было кратно 15.
Во-первых, искомое число должно оканчиваться на цифру 5 или 0. Значит, последние две цифры – 7 и 8 нужно вычеркнуть сразу.
Остается 34265.
3+4+2+6+5 = 20, 20 не делится на 3. Ближайшее кратное 3 число – это 18. Для того, чтобы получить его, нужно отнять 2. Вычеркиваем цифру 2.
Получается 3465. Проверим свой ответ, 3465 : 15 = 231.
Ответ: 3465
В данной статье были рассмотрены основные признаки делимости на 15 с примерами. Этот материал должен помочь ученикам с решением заданий такого типа и подобных им, а также понять алгоритм работы с ними.
Какое из следующих чисел делится на 15? числа делится на 15. Для этого воспользуемся понятием правила делимости на 15 и проверим каждый из заданных вариантов один за другим.
Полный пошаговый ответ :
Согласно правилу делимости 15, число делится на 15, если оно делится и на 3, и на 5. Итак, нам нужно проверить делимость числа на 5 и 3.
Итак, нам нужно проверить делимость числа на 5 и 3.
Согласно правилу делимости на 5 число делится на 5, если оно оканчивается либо на 0, либо на 5.
Согласно правилу делимости на 3 число делится на 3, если сумма цифр числа делится на 3.
Теперь нам нужно проверить варианты один за другим на делимость на 3 и 5.
A.30560
Поскольку число заканчивается на 0, мы можем сказать, что число делится на 5.
Сумма цифр числа 30560 такова: $ 3+0+5+6+0=14 $ и 14 не делится на 3, значит, данное число не делится на 3 и, следовательно, не делится и на 15.
B.29515
Поскольку число оканчивается на 5, мы можем сказать, что число делится на 5.
Сумма цифр числа 29515 равна $ 2+9+5+1+5=22 $ и 22 не делится на 3, значит, данное число не делится на 3 и, следовательно, не делится на 15.
C.23755
Поскольку число оканчивается на 5, мы можем сказать, что число делится на 5.
Сумма цифр числа 23755 равна $ 2+3+7+5+5=22 $ и 22 не делится на 3, значит, данное число не делится на 3 и, следовательно, не делится на 15.
D.17325
Поскольку число оканчивается на 5, мы можем сказать, что число делится на 5.
Сумма цифр числа 17325 равна $ 1+7+3+2+5=18 $ и 18 делится на 3, значит, данное число также делится на 3 и, следовательно, 17325 также делится на 15.
Значит, 17325 делится на 15.
Вариант D верен.
Итак, правильный ответ «Вариант D».
Примечание : Правило делимости чисел играет важную роль, чтобы решить, делится данное число или нет. Однако этот тип вопросов также можно решить с помощью метода деления в длину, если остаток от деления членов равен нулю, то мы можем сказать, что число делится.
Недавно обновленные страницы
Если ab и c единичные векторы, то left ab2 right+bc2+ca2 математика класса 12 JEE_Main
Стержень AB длиной 4 единицы перемещается горизонтально, когда математика класса 11 JEE_Main
Вычислить значение intlimits0 cos 3xdx A 0 B 1 class 12 maths JEE_Main
Что из следующего верно0002 Координаты точек A и B равны a0 и a0 математическому классу 11 JEE_Main
Если ab и c единичные векторы, то влево ab2 right+bc2+ca2 математическому классу 12 JEE_Main
Стержень AB длиной 4 единицы движется горизонтально, когда class 11 maths JEE_Main
Оценить значение intlimits0pi cos 3xdx A 0 B 1 class 12 maths JEE_Main
Что из следующего верно 1 nleft S cup T right class 10 maths JEE_Main
Какова площадь треугольника с вершинами Левый класс 11 математика JEE_Main
Координаты точек A и B равны a0 и a0 класс 11 математики JEE_Main
Сомнения в тренде
цифровая логика — проверить, делится ли беззнаковое двоичное число на 15 \$\начало группы\$
Я изучаю информатику и несколько часов застрял на этом вопросе.
У нас есть двоичное беззнаковое число X, представленное 12 битами. Мы хотели бы построить систему с 1-битным выходом — Y, который будет ‘1’, если X делится на 15 без остатка. 9i % 15 для 0<=i<=11 (поскольку это 12 бит), тогда для я получу последовательность 1248 1248 1248.
И если у меня есть 0001 1110 1111, то я могу просто умножить все цифры, суммировать их , и проверьте, делится ли мое число на 15.
0 + 0 + 0 + 8 + 1 + 2 + 4 + 0 + 1 + 2 + 4 + 8 = 30
Проблема в том, что я понятия не имею, как реализовать его, и если это даже эффективно.
Мне бы не помешала помощь.
- цифровая логика
- логические элементы
- сумматор
- двоичный код
- домашнее задание
\$\конечная группа\$
2
\$\начало группы\$
Знаете ли вы, как проверить делимость на 9 по основанию 10?
Сложите все цифры, используя арифметику с основанием 10. Если результат содержит несколько цифр, повторите процесс. Остановитесь, когда у вас будет одна цифра. Если цифра равна 9, исходное число делилось на 9. Это работает, потому что проверяемый делитель имеет основание 1. Например, 45 делится на 9., а сумма цифр равна 9, для двух цифр требуется только один сумматор. 999 тоже, для трех цифр нужны два сумматора.
Если результат содержит несколько цифр, повторите процесс. Остановитесь, когда у вас будет одна цифра. Если цифра равна 9, исходное число делилось на 9. Это работает, потому что проверяемый делитель имеет основание 1. Например, 45 делится на 9., а сумма цифр равна 9, для двух цифр требуется только один сумматор. 999 тоже, для трех цифр нужны два сумматора.
Итак, теперь вы знаете, как проверить делимость на 15, когда у вас есть под рукой арифметические средства с основанием 16?
\$\конечная группа\$
3
\$\начало группы\$
Техника похожа на то, что вы сделали бы, чтобы проверить, делится ли число на 9в десятичной системе. Нам нужно разбить число на четыре бита, а затем многократно складывать цифры, пока у нас не останется одна цифра.
Назовем цифры X Y Z
c1,r1 = X + Y c2,r2 = Z + r1 + c1 с3,г3 = г2 + 1
ЕСЛИ X,Y,Z делится на 15, то c2,r2 также делится на 15. Кроме того, c2,r2 меньше 0x1e. Итак, если r=15, то исходное число делилось на 15. Мы проверяем, равно ли r 15, добавляя единицу и глядя на полученный флаг переноса.
Кроме того, c2,r2 меньше 0x1e. Итак, если r=15, то исходное число делилось на 15. Мы проверяем, равно ли r 15, добавляя единицу и глядя на полученный флаг переноса.
Что меня озадачивает, так это то, для чего должны быть ворота Нор.
\$\конечная группа\$
1
\$\начало группы\$
Полный ответ:
Как сказал @Neil_UK, у меня есть 12 бит, и если я хочу проверить, делится ли это число на 15, я возьму 12 бит и рассмотрю их как 3 числа в базе 16.
Я складываю три числа вместе, всегда добавляя перенос к следующему сумматору.
Сложив их все, я получу в результате некоторое число. Как я уже сказал, мы хотим увидеть, делится ли число на 15, а поскольку числа находятся в основе 16, поэтому, если результат равен 15, число делится на 15.
Если это число 15, в двоичном формате 1111 , поэтому, если я добавлю 1 к 1111 , я получу перенос 1 и 0000 .

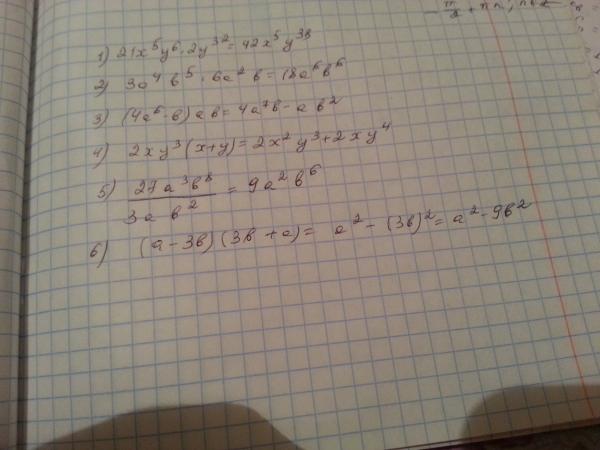
 Возможно, вам придется изучить это. Тест Хи-квадрат на независимость (ассоциацию) потребует от вас разбить данные на логические группы.
Возможно, вам придется изучить это. Тест Хи-квадрат на независимость (ассоциацию) потребует от вас разбить данные на логические группы. test <- таблица (train $ SalePrice, train $ LotArea)
chisq.test(chi.test)
test <- таблица (train $ SalePrice, train $ LotArea)
chisq.test(chi.test)  1 кв. Медиана Среднее 3-е кв. Максимум.
## 34900 129975 163000 180921 214000 755000
1 кв. Медиана Среднее 3-е кв. Максимум.
## 34900 129975 163000 180921 214000 755000  median, col = "зеленый", lwd = 1) +
geom_density (настройка = 5, col = 'темно-синий') +
labs(title="Плотность и медиана для LotArea") +
лаборатории(x="LotArea", y="")
median, col = "зеленый", lwd = 1) +
geom_density (настройка = 5, col = 'темно-синий') +
labs(title="Плотность и медиана для LotArea") +
лаборатории(x="LotArea", y="")  LotArea и trans.SalePrice
## t = 16,14, df = 1458, значение p < 2,2e-16
## альтернативная гипотеза: истинная корреляция не равна 0
## 99-процентный доверительный интервал:
## 0,3306244 0,4450358
## примерные оценки:
## кор
## 0.3893308
LotArea и trans.SalePrice
## t = 16,14, df = 1458, значение p < 2,2e-16
## альтернативная гипотеза: истинная корреляция не равна 0
## 99-процентный доверительный интервал:
## 0,3306244 0,4450358
## примерные оценки:
## кор
## 0.3893308  ) Умножьте матрицу корреляции на матрицу точности, а затем умножьте матрицу точности на матрицу корреляции.
) Умножьте матрицу корреляции на матрицу точности, а затем умножьте матрицу точности на матрицу корреляции. na (y) == T)))
NA_Count <- data.frame (Item = colnames (df), Count = Num_NA)
col_rm <- NA_Count$Count> 1500
# удаляем переменные с большими отсутствующими значениями выше 1500
дф <- дф[ !col_rm]
# числовые переменные и передача дамм
isnum <- sapply (df, is.numeric)
dfnum <- df[ isnum]
тусклый (dfnum)
na (y) == T)))
NA_Count <- data.frame (Item = colnames (df), Count = Num_NA)
col_rm <- NA_Count$Count> 1500
# удаляем переменные с большими отсутствующими значениями выше 1500
дф <- дф[ !col_rm]
# числовые переменные и передача дамм
isnum <- sapply (df, is.numeric)
dfnum <- df[ isnum]
тусклый (dfnum)  tri(descrCor2)])
tri(descrCor2)])  packages('Boruta')
packages('Boruta')  numeric)
lm_model <- lm(SalePrice ~ ., data = train)
резюме (lm_model)
numeric)
lm_model <- lm(SalePrice ~ ., data = train)
резюме (lm_model)  20e+03 2.60e+03 0,85 0,3966
## BedroomAbvGr -4,29e+03 1,70e+03 -2,52 0,0117 *
## KitchenAbvGr -1,53e+04 5,10e+03 -3,01 0,0027 **
## TotRmsAbvGrd 3.19e+03 1.19e+03 2.68 0.0074 **
## Камины 1.17e+04 2.66e+03 4.38 1.3e-05 ***
## GarageYrBlt 1.36e-01 5.93e+00 0,02 0,9817
## GarageArea 3.27e+01 6.69e+00 4.89 1.2e-06 ***
## WoodDeckSF 2.08e+01 7.54e+00 2,76 0,0059**
## OpenPorchSF -1.21e+01 1.46e+01 -0.83 0.4049
## MSZoning -1.01e+03 1.53e+03 -0.66 0.5110
## LotShape -1.33e+03 6.81e+02 -1.96 0.0504 .
## Окрестности 2.51e+02 1.61e+02 1.56 0.1190
## Условие1 -2.10e+02 1.03e+03 -0.20 0.8393
## Тип здания -2,26e+03 1,51e+03 -1,50 0,1336
## HouseStyle -1,42e+03 6,58e+02 -2,15 0,0315 *
## RoofStyle 2.35e+03 1.15e+03 2.05 0.0409*
## Внешний 1-й -7,77e+02 5,35e+02 -1,45 0,1465
## Внешний 2-й 1,77e+02 4,85e+02 0,37 0,7150
## MasVnrType 3.35e+03 1.52e+03 2.21 0.0275 *
## ExterQual -8.16e+03 1.98e+03 -4.12 4.1e-05 ***
## Фундамент -4,45e+02 1,71e+03 -0,26 0,7955
## BsmtQual -6,58e+03 1,33e+03 -4,94 9,0e-07 ***
## BsmtCond 4.
20e+03 2.60e+03 0,85 0,3966
## BedroomAbvGr -4,29e+03 1,70e+03 -2,52 0,0117 *
## KitchenAbvGr -1,53e+04 5,10e+03 -3,01 0,0027 **
## TotRmsAbvGrd 3.19e+03 1.19e+03 2.68 0.0074 **
## Камины 1.17e+04 2.66e+03 4.38 1.3e-05 ***
## GarageYrBlt 1.36e-01 5.93e+00 0,02 0,9817
## GarageArea 3.27e+01 6.69e+00 4.89 1.2e-06 ***
## WoodDeckSF 2.08e+01 7.54e+00 2,76 0,0059**
## OpenPorchSF -1.21e+01 1.46e+01 -0.83 0.4049
## MSZoning -1.01e+03 1.53e+03 -0.66 0.5110
## LotShape -1.33e+03 6.81e+02 -1.96 0.0504 .
## Окрестности 2.51e+02 1.61e+02 1.56 0.1190
## Условие1 -2.10e+02 1.03e+03 -0.20 0.8393
## Тип здания -2,26e+03 1,51e+03 -1,50 0,1336
## HouseStyle -1,42e+03 6,58e+02 -2,15 0,0315 *
## RoofStyle 2.35e+03 1.15e+03 2.05 0.0409*
## Внешний 1-й -7,77e+02 5,35e+02 -1,45 0,1465
## Внешний 2-й 1,77e+02 4,85e+02 0,37 0,7150
## MasVnrType 3.35e+03 1.52e+03 2.21 0.0275 *
## ExterQual -8.16e+03 1.98e+03 -4.12 4.1e-05 ***
## Фундамент -4,45e+02 1,71e+03 -0,26 0,7955
## BsmtQual -6,58e+03 1,33e+03 -4,94 9,0e-07 ***
## BsmtCond 4. 19e+03 1.28e+03 3.27 0.0011 **
## BsmtExposure -3.48e+03 8.86e+02 -3.93 9.0e-05 ***
## BsmtFinType1 -6.07e+02 6.35e+02 -0.96 0,3393
## BsmtFinType2 1.14e+03 1.00e+03 1.14 0.2562
## ОтоплениеQC -4,63e+02 6,27e+02 -0,74 0,4599
## ЦентралЭйр 2.33e+03 4.37e+03 0,53 0,5947
## Электрический -4,35e+02 9,33e+02 -0,47 0,6411
## KitchenQual -7.90e+03 1.49e+03 -5.30 1.3e-07 ***
## КаминQu -1,84e+03 8,09e+02 -2,28 0,0230 *
## GarageType 1.27e+01 6.53e+02 0,02 0,9845
## GarageFinish -1.80e+03 1.52e+03 -1.18 0.2371
## GarageQual -6,77e+02 1,82e+03 -0,37 0,7100
## GarageCond 4.45e+01 2.06e+03 0,02 0,9828
## PavedDrive 2,75e+03 2,13e+03 1,29 0,1969
## ---
## Значение. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1
##
## Остаточная стандартная ошибка: 32900 на 1410 степенях свободы
## Множественный R-квадрат: 0,834, скорректированный R-квадрат: 0,828
## F-статистика: 144 на 49 и 1410 DF, значение p: <2e-16
19e+03 1.28e+03 3.27 0.0011 **
## BsmtExposure -3.48e+03 8.86e+02 -3.93 9.0e-05 ***
## BsmtFinType1 -6.07e+02 6.35e+02 -0.96 0,3393
## BsmtFinType2 1.14e+03 1.00e+03 1.14 0.2562
## ОтоплениеQC -4,63e+02 6,27e+02 -0,74 0,4599
## ЦентралЭйр 2.33e+03 4.37e+03 0,53 0,5947
## Электрический -4,35e+02 9,33e+02 -0,47 0,6411
## KitchenQual -7.90e+03 1.49e+03 -5.30 1.3e-07 ***
## КаминQu -1,84e+03 8,09e+02 -2,28 0,0230 *
## GarageType 1.27e+01 6.53e+02 0,02 0,9845
## GarageFinish -1.80e+03 1.52e+03 -1.18 0.2371
## GarageQual -6,77e+02 1,82e+03 -0,37 0,7100
## GarageCond 4.45e+01 2.06e+03 0,02 0,9828
## PavedDrive 2,75e+03 2,13e+03 1,29 0,1969
## ---
## Значение. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1
##
## Остаточная стандартная ошибка: 32900 на 1410 степенях свободы
## Множественный R-квадрат: 0,834, скорректированный R-квадрат: 0,828
## F-статистика: 144 на 49 и 1410 DF, значение p: <2e-16  54e+10 3.54e+11 5.47e+12 7.37e+08 8.37e+10
## град. свободы 1 1 1 1 1
## YearRemodAdd MasVnrArea BsmtFinSF1 BsmtUnfSF X2ndFlrSF
## Сумма квадратов 2.30e+10 2.46e+11 2.40e+11 4.95е+10 3,57е+11
## град. свободы 1 1 1 1 1
## GrLivArea BsmtFullBath FullBath HalfBath BedroomAbvGr
## Сумма квадратов 3.68e+11 2.64e+10 9.54e+08 4.82e+07 4.17e+10
## град. свободы 1 1 1 1 1
## KitchenAbvGr TotRmsAbvGrd Камины GarageYrBlt
## Сумма квадратов 4.88e+09 2.43e+10 1.55e+10 1.34e+08
## град. свободы 1 1 1 1
## GarageArea WoodDeckSF OpenPorchSF MSЗонирование LotShape
## Сумма квадратов 4.98e+10 1.34e+10 2.88e+08 1.73e+09 6.12e+09
## град. свободы 1 1 1 1 1
## Соседство Condition1 BldgType HouseStyle RoofStyle
## Сумма квадратов 2.83e+09 9.15e+07 1.03e+09 6.63e+09 6.14e+09
## град. свободы 1 1 1 1 1
## Exterior1st Exterior2nd MasVnrType ExterQual Foundation
## Сумма квадратов 4.84e+09 4.57e+08 2.20e+10 7.03e+10 1.57e+09## град. свободы 1 1 1 1 1
## BsmtQual BsmtCond BsmtExposure BsmtFinType1 BsmtFinType2
## Сумма квадратов 3.
54e+10 3.54e+11 5.47e+12 7.37e+08 8.37e+10
## град. свободы 1 1 1 1 1
## YearRemodAdd MasVnrArea BsmtFinSF1 BsmtUnfSF X2ndFlrSF
## Сумма квадратов 2.30e+10 2.46e+11 2.40e+11 4.95е+10 3,57е+11
## град. свободы 1 1 1 1 1
## GrLivArea BsmtFullBath FullBath HalfBath BedroomAbvGr
## Сумма квадратов 3.68e+11 2.64e+10 9.54e+08 4.82e+07 4.17e+10
## град. свободы 1 1 1 1 1
## KitchenAbvGr TotRmsAbvGrd Камины GarageYrBlt
## Сумма квадратов 4.88e+09 2.43e+10 1.55e+10 1.34e+08
## град. свободы 1 1 1 1
## GarageArea WoodDeckSF OpenPorchSF MSЗонирование LotShape
## Сумма квадратов 4.98e+10 1.34e+10 2.88e+08 1.73e+09 6.12e+09
## град. свободы 1 1 1 1 1
## Соседство Condition1 BldgType HouseStyle RoofStyle
## Сумма квадратов 2.83e+09 9.15e+07 1.03e+09 6.63e+09 6.14e+09
## град. свободы 1 1 1 1 1
## Exterior1st Exterior2nd MasVnrType ExterQual Foundation
## Сумма квадратов 4.84e+09 4.57e+08 2.20e+10 7.03e+10 1.57e+09## град. свободы 1 1 1 1 1
## BsmtQual BsmtCond BsmtExposure BsmtFinType1 BsmtFinType2
## Сумма квадратов 3. 84e+10 1.20e+10 1.77e+10 6.03e+08 1.40e+09
## град. свободы 1 1 1 1 1
## ОтоплениеQC CentralAir Electric KitchenQual FireplaceQu
## Сумма квадратов 1.90e+09 6.30e+06 9.84e+08 3.39e+10 5.20e+09
## град. свободы 1 1 1 1 1
## GarageType GarageFinish GarageQual GarageCond PavedDrive
## Сумма квадратов 6.14e+07 1.37e+091.34e+08 1.44e+07 1.81e+09
## град. свободы 1 1 1 1 1
## Остатки
## Сумма квадратов 1.53e+12
## град. Свободы 1410
##
## Остаточная стандартная ошибка: 32944
## Оценочные эффекты могут быть несбалансированными
84e+10 1.20e+10 1.77e+10 6.03e+08 1.40e+09
## град. свободы 1 1 1 1 1
## ОтоплениеQC CentralAir Electric KitchenQual FireplaceQu
## Сумма квадратов 1.90e+09 6.30e+06 9.84e+08 3.39e+10 5.20e+09
## град. свободы 1 1 1 1 1
## GarageType GarageFinish GarageQual GarageCond PavedDrive
## Сумма квадратов 6.14e+07 1.37e+091.34e+08 1.44e+07 1.81e+09
## град. свободы 1 1 1 1 1
## Остатки
## Сумма квадратов 1.53e+12
## град. Свободы 1410
##
## Остаточная стандартная ошибка: 32944
## Оценочные эффекты могут быть несбалансированными 
 Однако в эпоху компьютеров и компьютерных сетей перестает быть проблемой. Синхронизация в блокчейне настолько же быстрая, насколько быстро открывается веб-страница в гугле.
Однако в эпоху компьютеров и компьютерных сетей перестает быть проблемой. Синхронизация в блокчейне настолько же быстрая, насколько быстро открывается веб-страница в гугле.
 А на какой номер отправить деньги в блокчейне? Снова на помощь приходит математика.
А на какой номер отправить деньги в блокчейне? Снова на помощь приходит математика. Public keys:
Public keys: Разница между кодированием, шифрованием и хешированием
Разница между кодированием, шифрованием и хешированием 2
2

 Ведь вам нужно лишь навести камеру на этот QR-код, и по несложному алгоритму вы получаете уже что-то доступное человеческому восприятию.
Ведь вам нужно лишь навести камеру на этот QR-код, и по несложному алгоритму вы получаете уже что-то доступное человеческому восприятию.
 Бдительность и безопасность превыше всего!
Бдительность и безопасность превыше всего! Это очень важный этап, позволяющий исключить вероятность того, что вашими деньгами воспользуются другие люди.
Это очень важный этап, позволяющий исключить вероятность того, что вашими деньгами воспользуются другие люди. Но слишком заморачиваться с размером комиссий на самом деле не приходится – кошельки с которых вы будете переводить средства всегда подскажут вам хорошую комиссию, а с сайтов криптобирж так и вовсе за вас размер комиссии выставит сама биржа в принудительном порядке. Такие вот абьюзеры. Что поделать, биржи крайне удобны для пользования.
Но слишком заморачиваться с размером комиссий на самом деле не приходится – кошельки с которых вы будете переводить средства всегда подскажут вам хорошую комиссию, а с сайтов криптобирж так и вовсе за вас размер комиссии выставит сама биржа в принудительном порядке. Такие вот абьюзеры. Что поделать, биржи крайне удобны для пользования.
 Баланс не может быть отрицательным
Баланс не может быть отрицательным
 Рис. 9). . Полезный факт, не обязательный к изучению.
Рис. 9). . Полезный факт, не обязательный к изучению.
 com/watch?v=Zw9Vm3gDOno
com/watch?v=Zw9Vm3gDOno
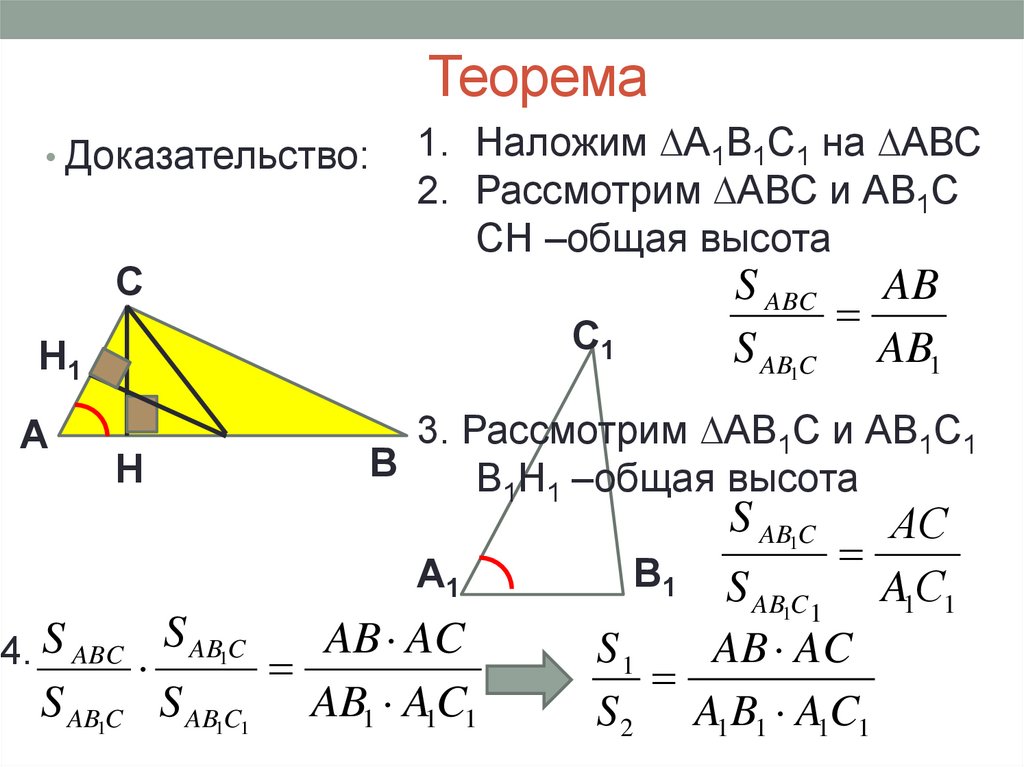 Их определение.
Их определение. 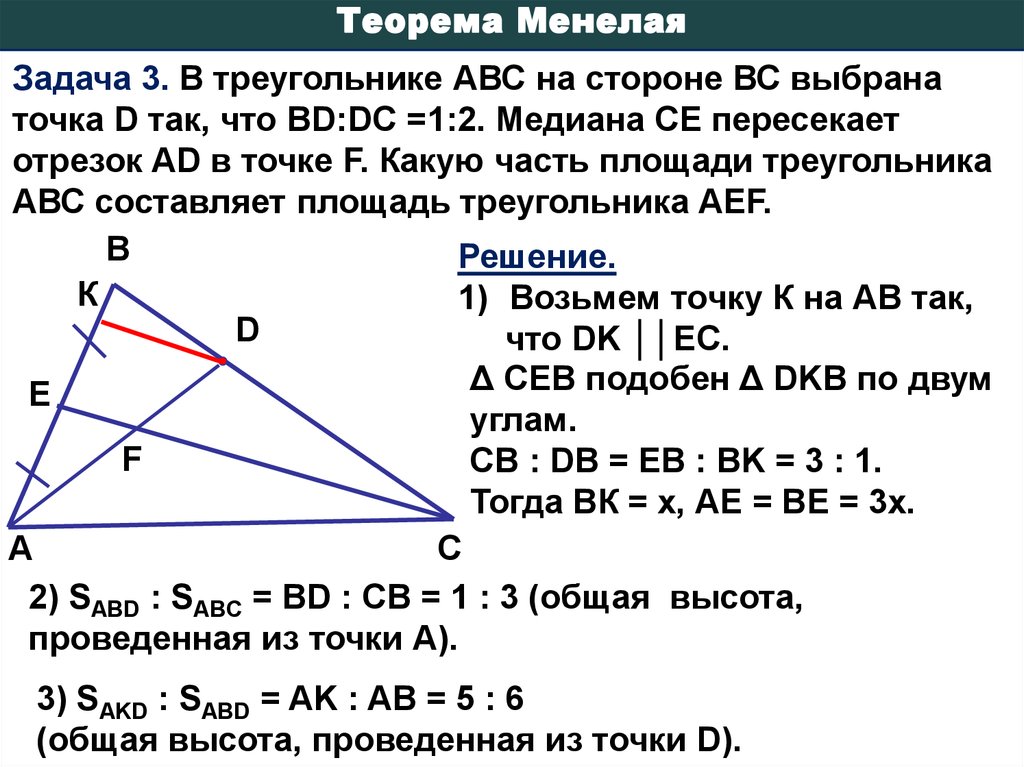 (Обучение талантливых и одаренных детей, управление и лидерство в обучении).
(Обучение талантливых и одаренных детей, управление и лидерство в обучении).
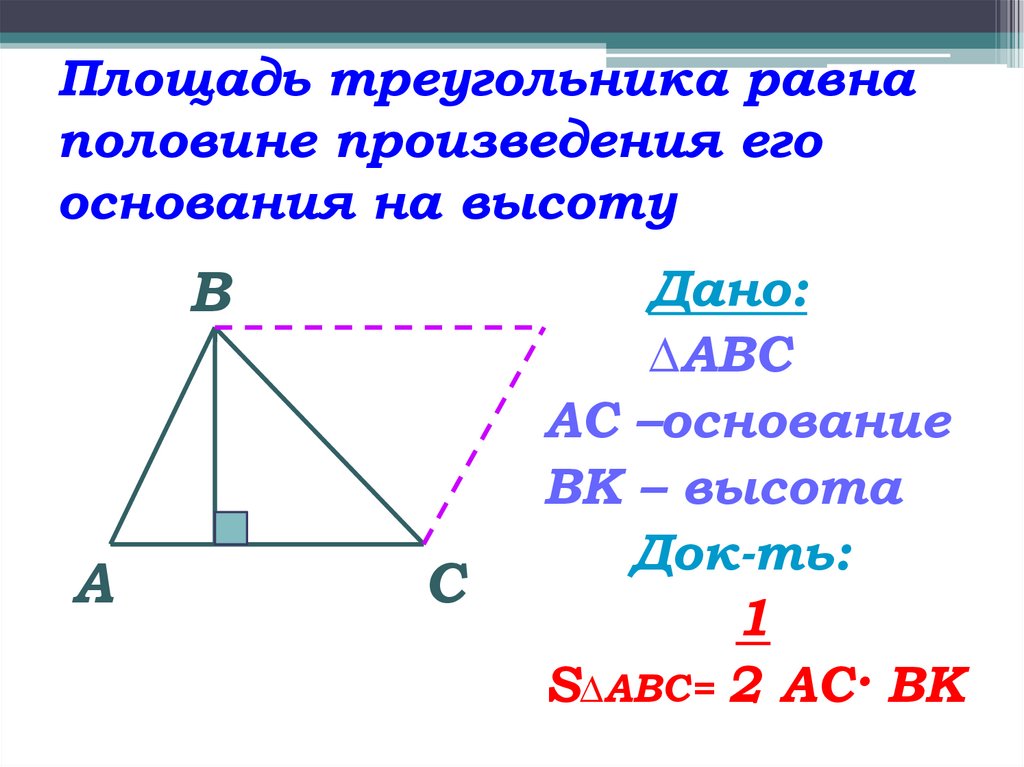
 АС=9см, АВ=7см, СВ=8см.
АС=9см, АВ=7см, СВ=8см.
 S∆.= 1/2 * 34,5*12,6 = 217,35 дм2 . Ответ: 217,35 дм2.
S∆.= 1/2 * 34,5*12,6 = 217,35 дм2 . Ответ: 217,35 дм2.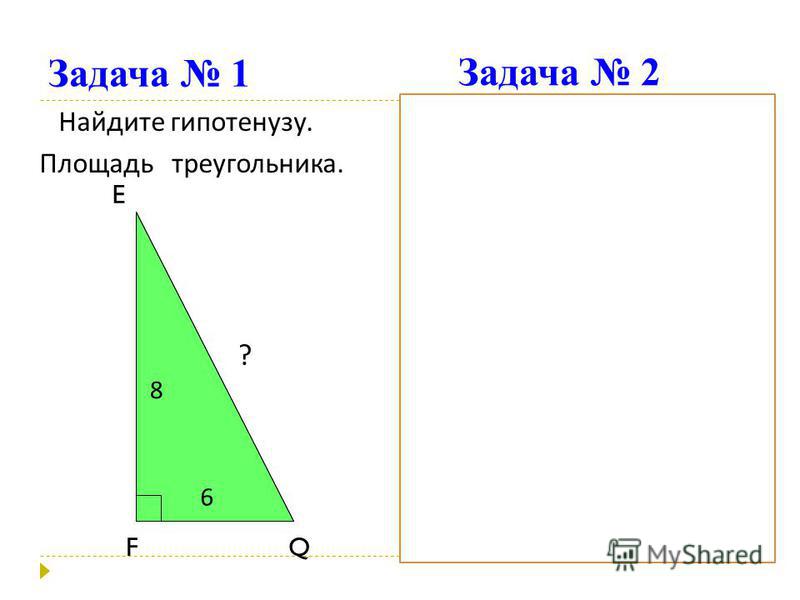 Оценить свою работу и выставить себе за работу оценку в оценочный лист.
Оценить свою работу и выставить себе за работу оценку в оценочный лист.
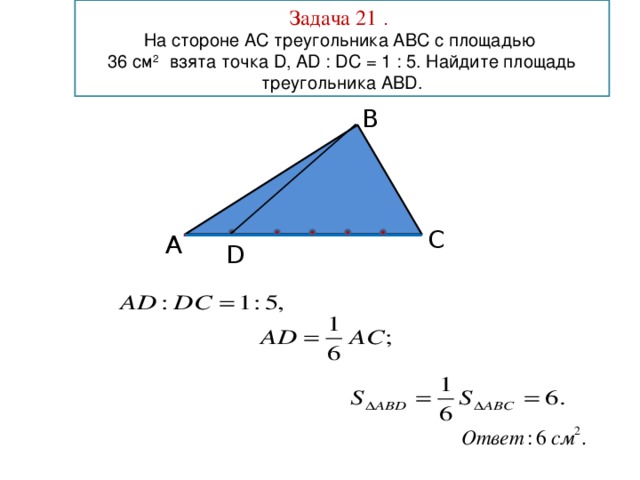
 Проверка решения домашней задачи по готовому чертежу.
Проверка решения домашней задачи по готовому чертежу. 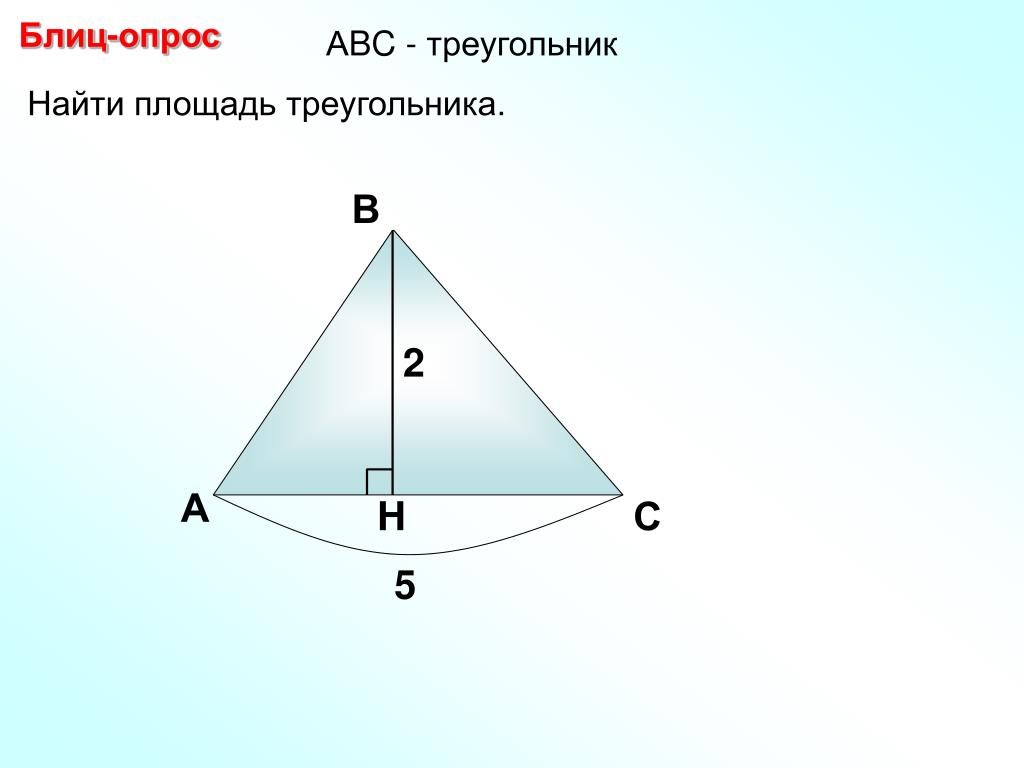


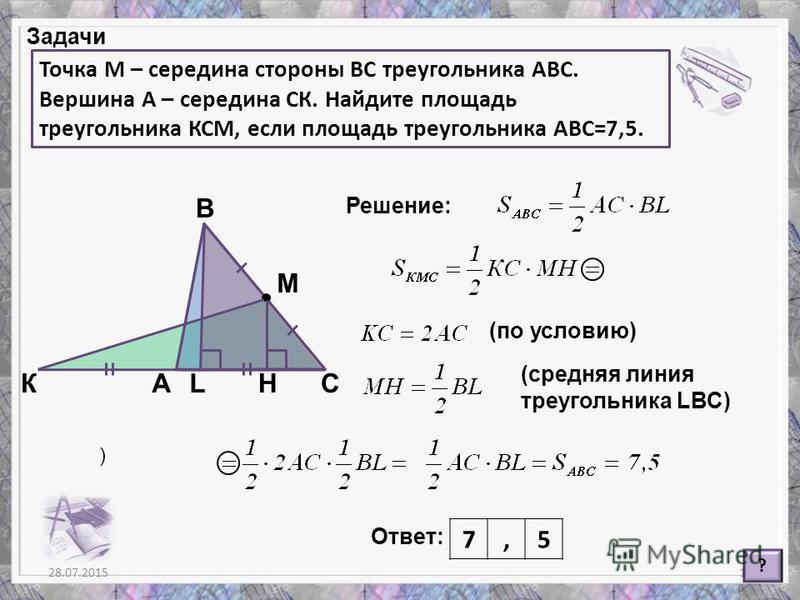
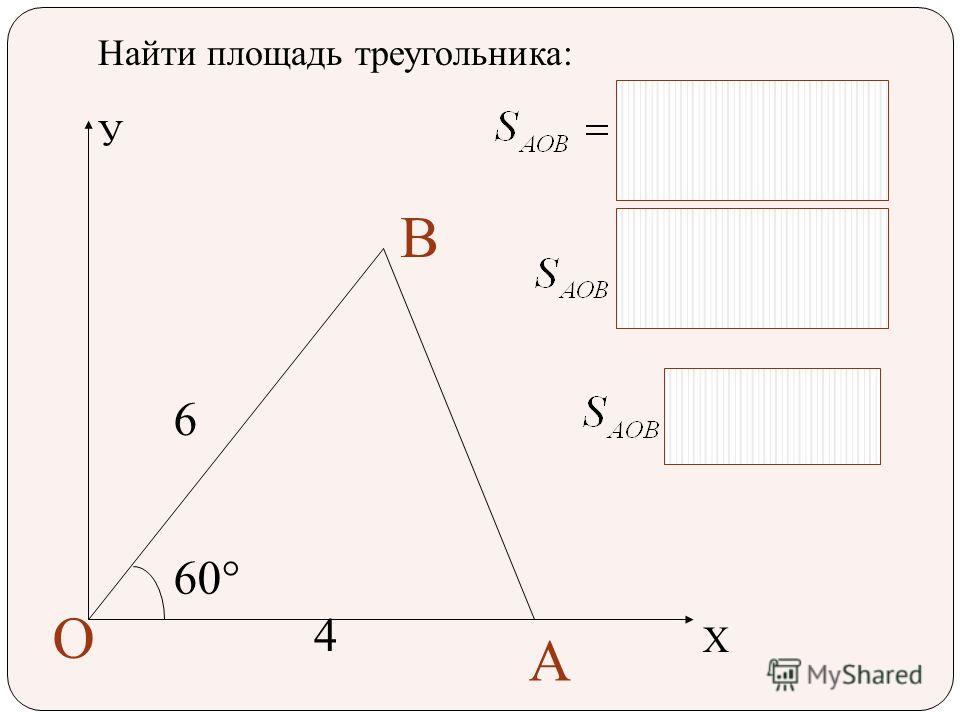
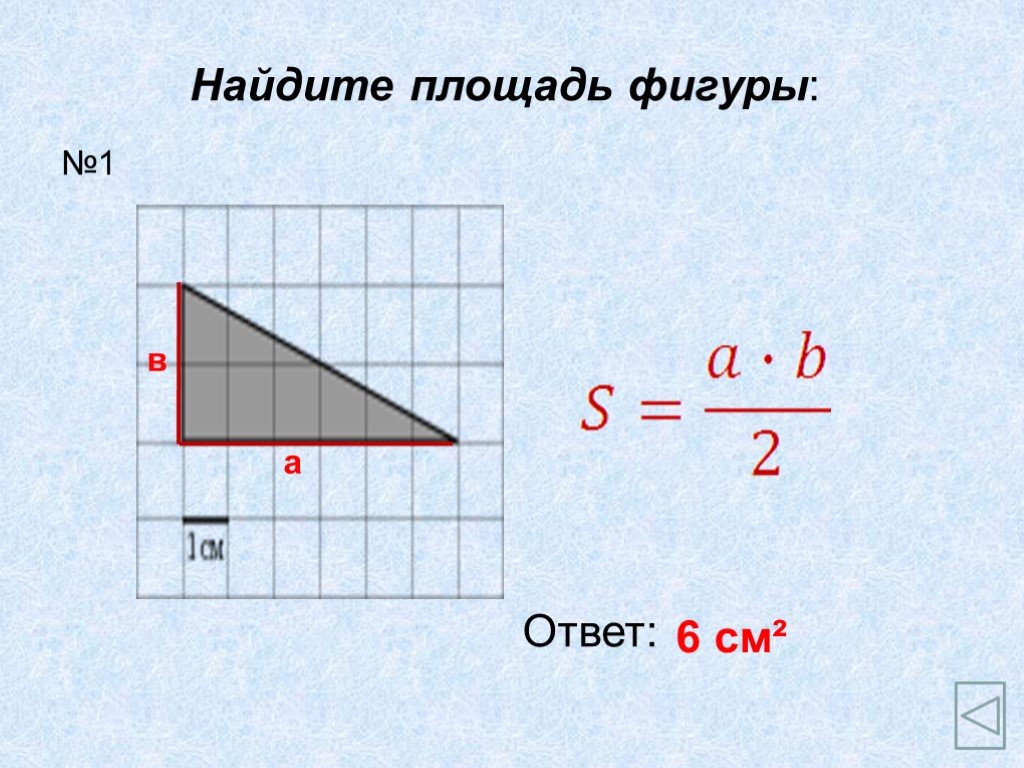

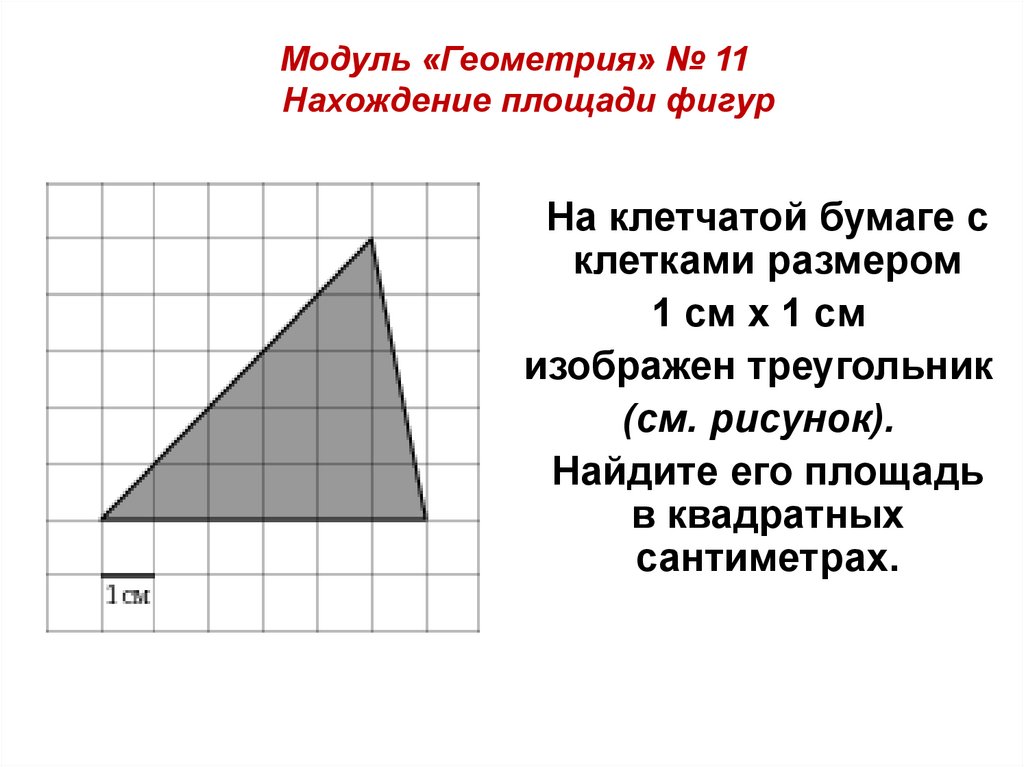
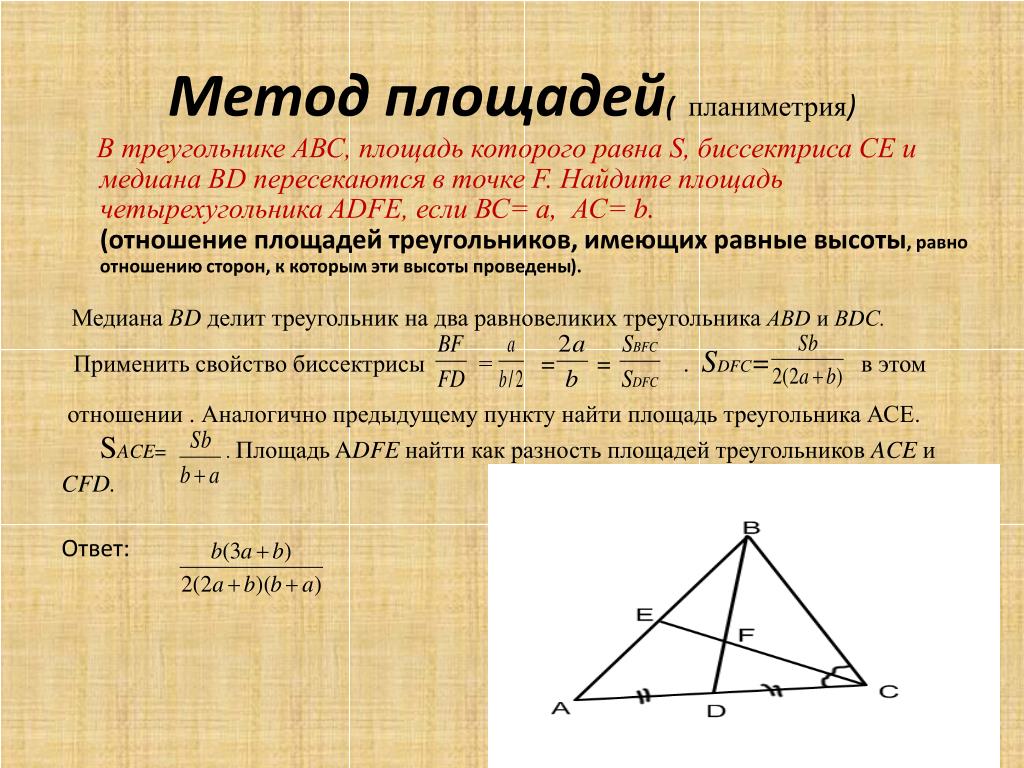

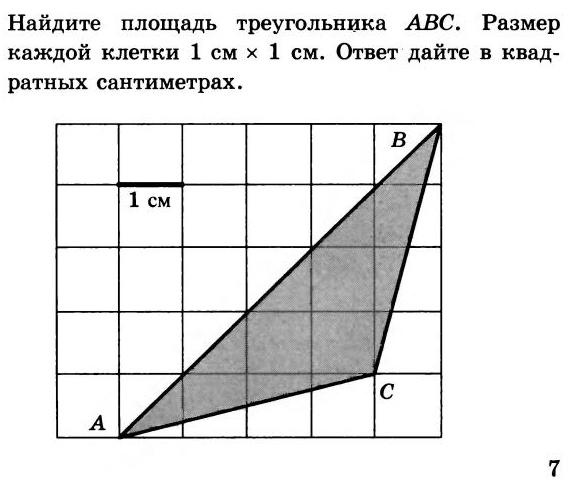
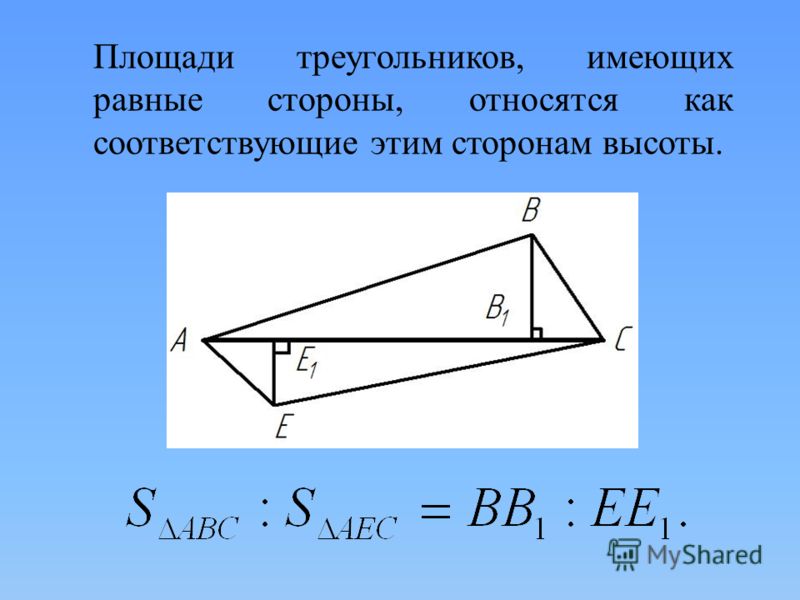 Если основание стены 8 футов, а треугольник покрывает 40 квадратных футов стены, какова высота треугольника?
Если основание стены 8 футов, а треугольник покрывает 40 квадратных футов стены, какова высота треугольника?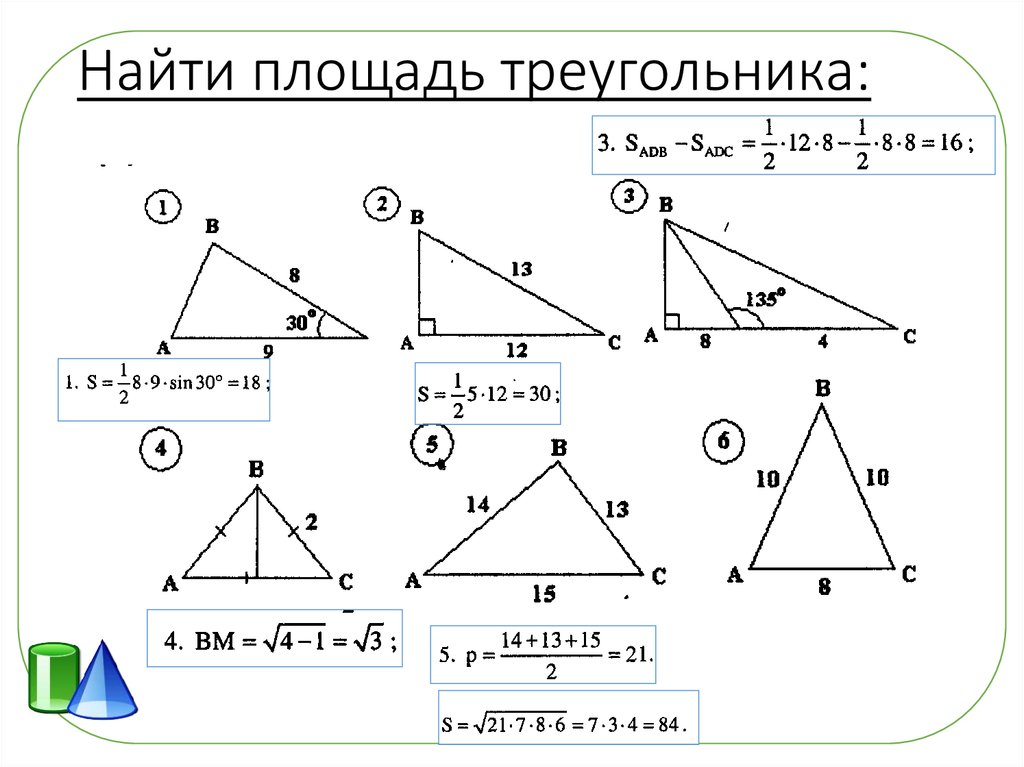 Чему равна площадь треугольника в квадратных дюймах?
Чему равна площадь треугольника в квадратных дюймах? В данном случае основание равно 11, а высота 9. Таким образом, мы умножаем
В данном случае основание равно 11, а высота 9. Таким образом, мы умножаем


 Округлите каждый ответ до ближайшей десятой единицы.
Округлите каждый ответ до ближайшей десятой единицы.
 5)
\\ = 15 \text{ дюймов в квадрате}
$$
5)
\\ = 15 \text{ дюймов в квадрате}
$$
 4)
\\ = 73,7 \text{дюймы в квадрате}
$$
4)
\\ = 73,7 \text{дюймы в квадрате}
$$ Только помните, что основание и высота перпендикулярны. Следовательно, основание равно «4», поскольку оно перпендикулярно высоте 17,7.
Только помните, что основание и высота перпендикулярны. Следовательно, основание равно «4», поскольку оно перпендикулярно высоте 17,7.



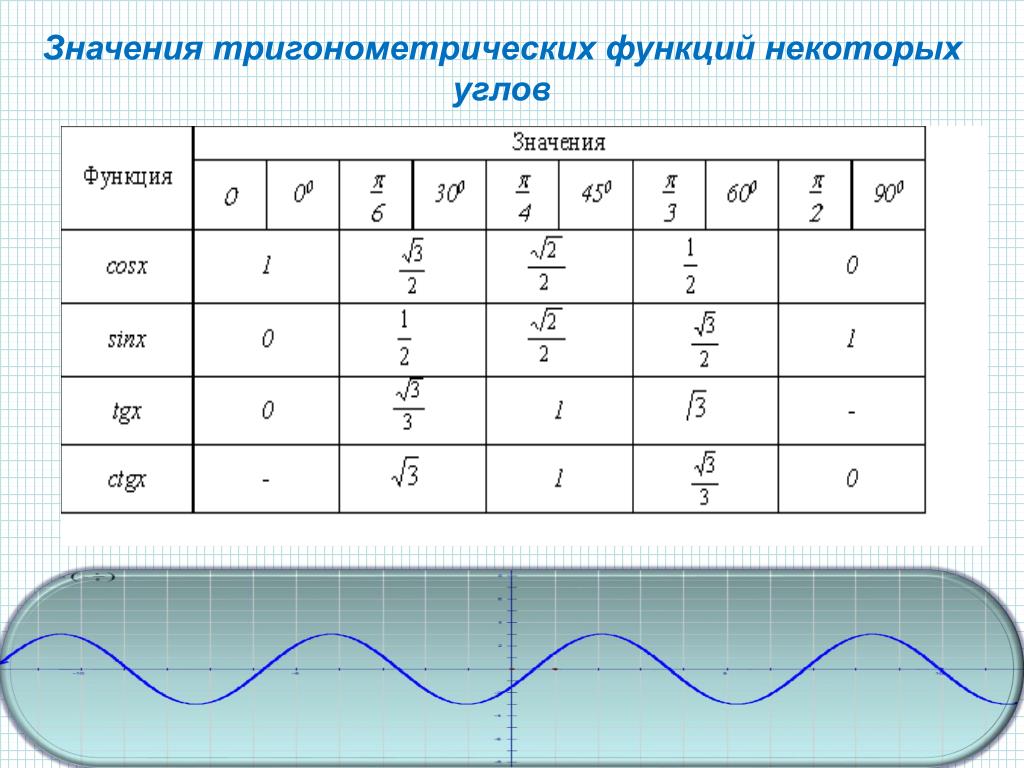 Примером может служить парабола.
Примером может служить парабола.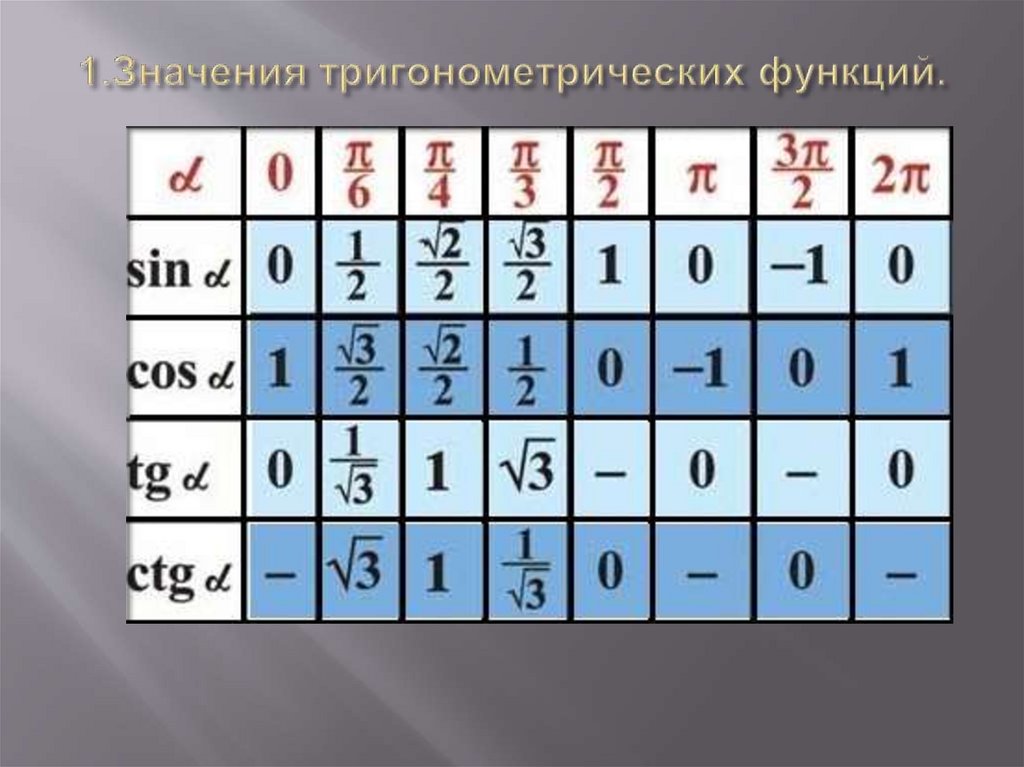 Однако чаще всего лишь наименьшее из всех таких чисел Т положительное, называют наименьшим периодом функции.
Однако чаще всего лишь наименьшее из всех таких чисел Т положительное, называют наименьшим периодом функции. Получаем:
Получаем: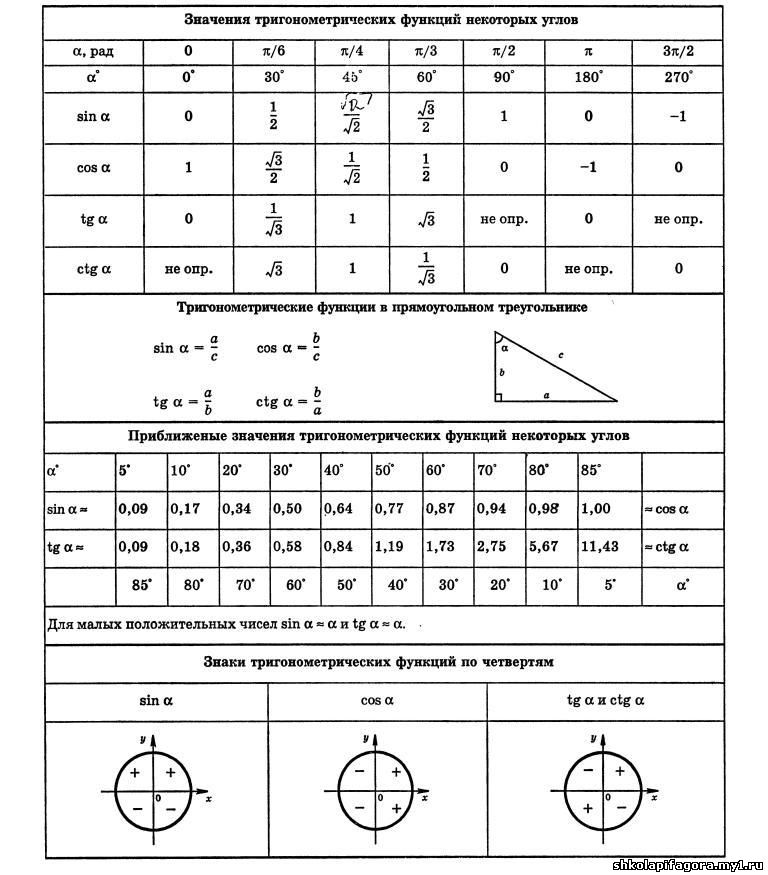
 Мы начнем с рассмотрения
квадрат со стороной 2,
Мы начнем с рассмотрения
квадрат со стороной 2, Обозначение сторон треугольника по отношению к их положению относительно нижнего левого угла 45∘,
получаем следующее.
Обозначение сторон треугольника по отношению к их положению относительно нижнего левого угла 45∘,
получаем следующее.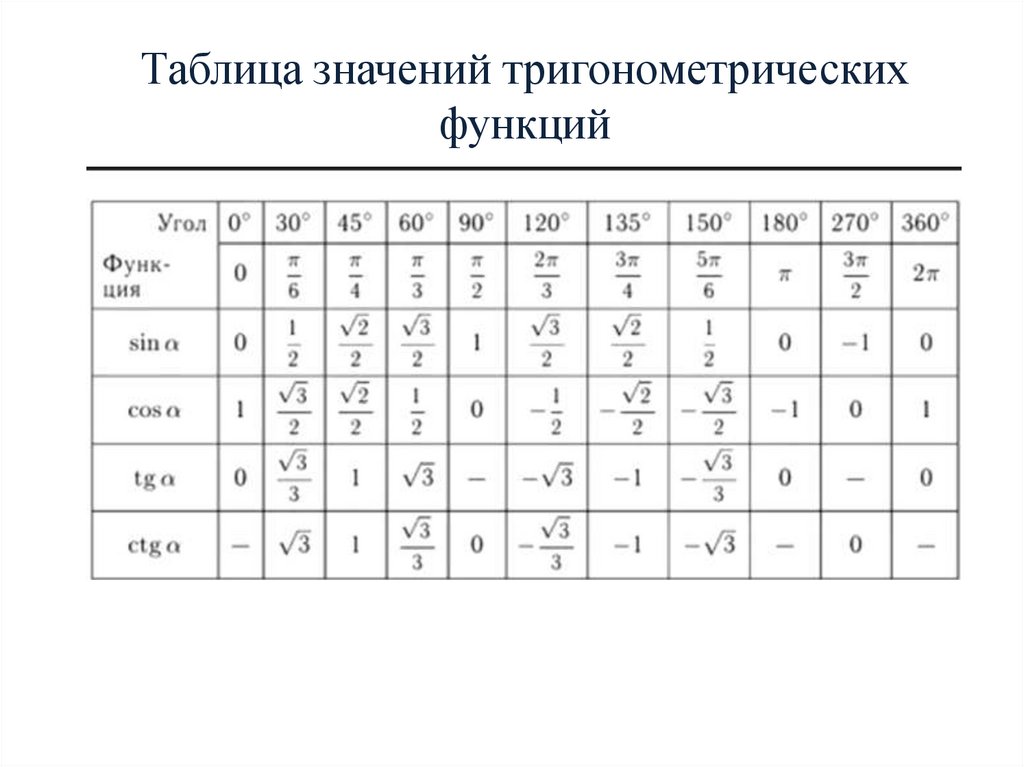



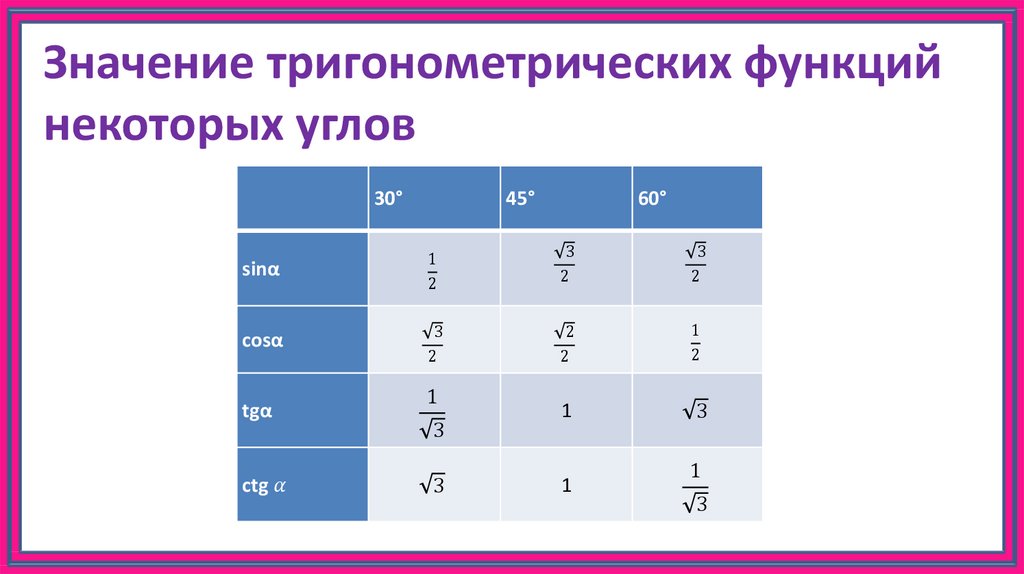
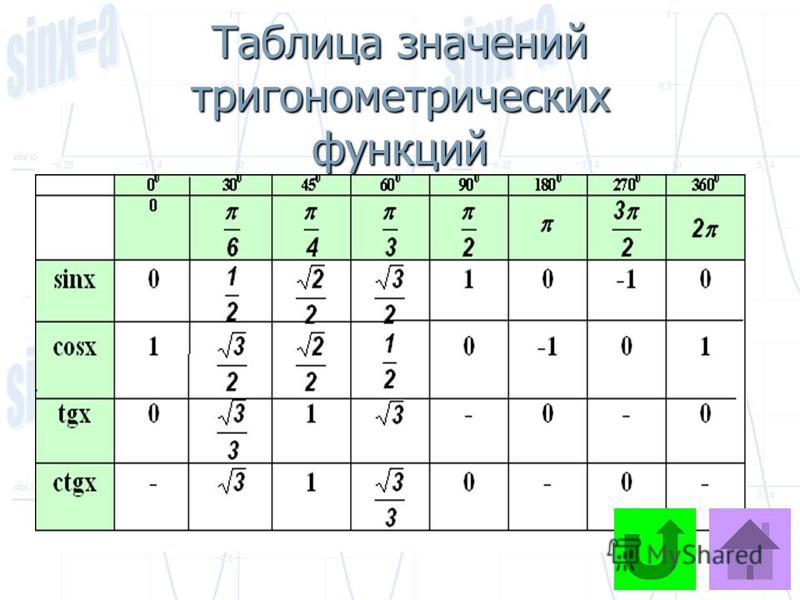
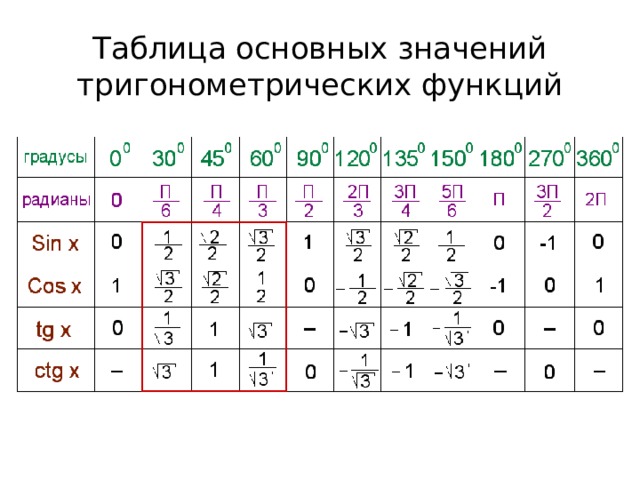
 Тем не менее, это полезный навык, чтобы уметь оценивать тригонометрические
работает под углами 30∘,
45∘ и 60∘ без
калькулятор, поэтому ответим на этот вопрос без калькулятора.
Тем не менее, это полезный навык, чтобы уметь оценивать тригонометрические
работает под углами 30∘,
45∘ и 60∘ без
калькулятор, поэтому ответим на этот вопрос без калькулятора.

 Мы знаем это
tan45=1∘ и что 45∘
возможный угол прямоугольного треугольника, так как он острый. Итак, мы можем просто заключить, что 𝜃 равно 45∘.
используя наши знания о том, что tan45=1∘.
Мы знаем это
tan45=1∘ и что 45∘
возможный угол прямоугольного треугольника, так как он острый. Итак, мы можем просто заключить, что 𝜃 равно 45∘.
используя наши знания о том, что tan45=1∘.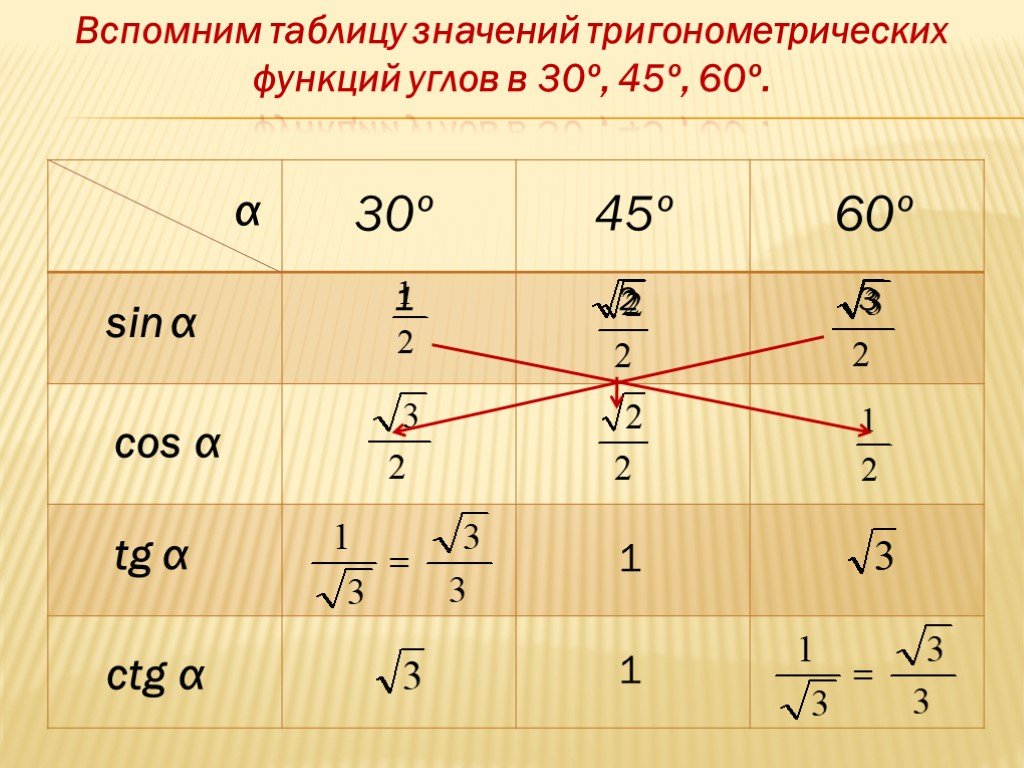
 cos
cos Так как острое решение
уникален, мы должны иметь, что 𝑥=30∘.
Так как острое решение
уникален, мы должны иметь, что 𝑥=30∘.


 Что означает термин «Философия»?
Что означает термин «Философия»? В каком веке до н.э. берет свое начало греческая философия?
В каком веке до н.э. берет свое начало греческая философия? Где родился Жан Жак Руссо?
Где родился Жан Жак Руссо?








 После каждого ответа указывается ожидаемый класс эссе на этом уровне вместе с кратким обоснованием. Они должны дать вам некоторое представление о том, что ожидают увидеть экзаменаторы.
После каждого ответа указывается ожидаемый класс эссе на этом уровне вместе с кратким обоснованием. Они должны дать вам некоторое представление о том, что ожидают увидеть экзаменаторы.

 А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию. Решение тригонометрического уравнения в конечном итоге сводится к решению четырех основных тригонометрических уравнений.
Решение тригонометрического уравнения в конечном итоге сводится к решению четырех основных тригонометрических уравнений. Единичная окружность дает еще один ответ: -2π/3.
Единичная окружность дает еще один ответ: -2π/3. Это можно сделать при помощи таблицы преобразования или калькулятора.
Это можно сделать при помощи таблицы преобразования или калькулятора.
 2 — 1) = 0. Теперь найдите t, а затем найдите х для t = tg х.
2 — 1) = 0. Теперь найдите t, а затем найдите х для t = tg х.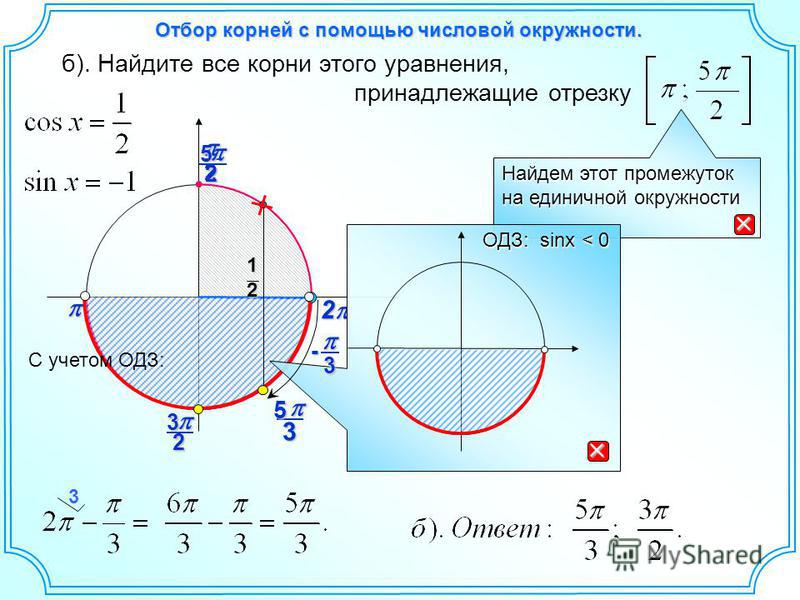 n – минус один в степени n.
n – минус один в степени n.

 Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде
Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде

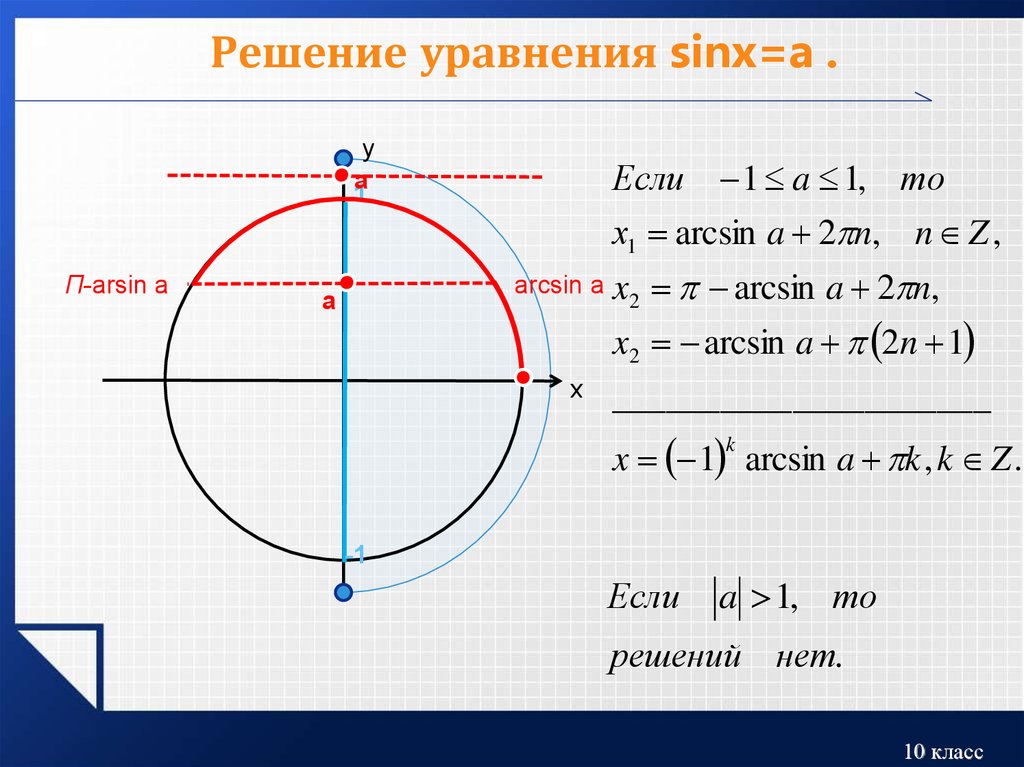 Для решения однородного уравнения, поступают следующим образом:
Для решения однородного уравнения, поступают следующим образом:
 )/3
)/3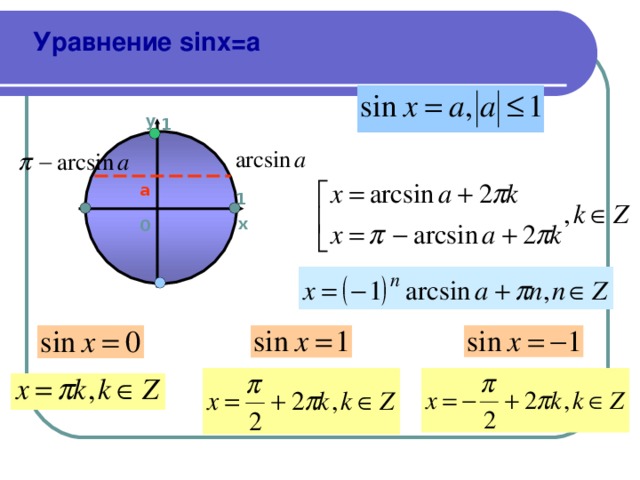
 -1, то можно вынести -1 за скобки по аналогии с предыдущим свойством.
-1, то можно вынести -1 за скобки по аналогии с предыдущим свойством.

 2}x+log_{a}x+c=0$</b>.
2}x+log_{a}x+c=0$</b>. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.) На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
На рисунке 3 показаны величины тригонометрических функций для единичной окружности. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов). Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:
Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов: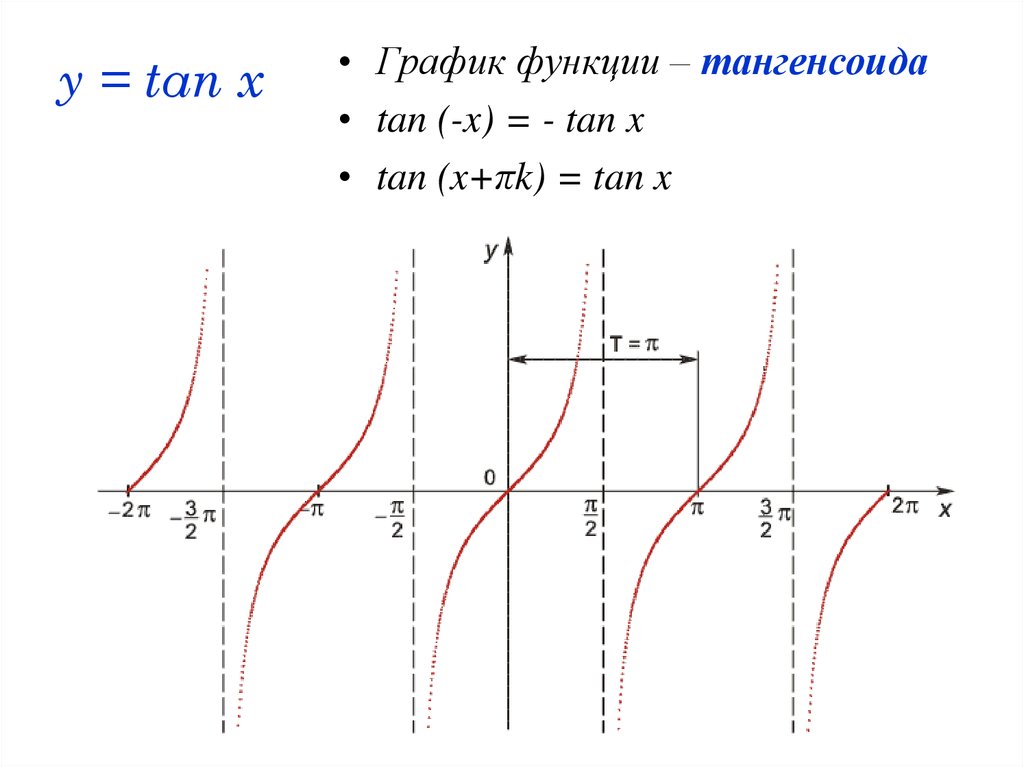 Остальные четыре функции — нечётные, то есть:
Остальные четыре функции — нечётные, то есть:
 При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
 4 = 0,75
4 = 0,75

 Предварительно такой интеграл приводят к интегралам группы (4).
Для этого в знаменателе подынтегральной функции выделяют полный квадрат (это делается при помощи формул
сокращённого умножения и ) и представляют его в одном из следующих видов:
Предварительно такой интеграл приводят к интегралам группы (4).
Для этого в знаменателе подынтегральной функции выделяют полный квадрат (это делается при помощи формул
сокращённого умножения и ) и представляют его в одном из следующих видов: В результате этого:
В результате этого:

 Это может быть актуально, если вы используете свой телефон, проходите тест, в котором ваш учитель предоставляет только простые калькуляторы, или проходите стандартизированный онлайн-тест, такой как GRE, где у вас есть только простой калькулятор на экране.
Это может быть актуально, если вы используете свой телефон, проходите тест, в котором ваш учитель предоставляет только простые калькуляторы, или проходите стандартизированный онлайн-тест, такой как GRE, где у вас есть только простой калькулятор на экране.
 Многие будут следовать порядку операций, но другие просто дадут вам немедленный результат вашей первой операции. Например, чтобы найти 47-19/4 вам нужно сначала выполнить 47–19 и отдельно, а затем разделить этот ответ на 4.
Многие будут следовать порядку операций, но другие просто дадут вам немедленный результат вашей первой операции. Например, чтобы найти 47-19/4 вам нужно сначала выполнить 47–19 и отдельно, а затем разделить этот ответ на 4. Однако, скорее всего, это не тот ответ, который нам нужен, поскольку это не дробная часть и не полное число.
Однако, скорее всего, это не тот ответ, который нам нужен, поскольку это не дробная часть и не полное число. Делая это, мы можем, по сути, проверить наши ответы, чтобы убедиться, что они верны. Завершите операцию дроби вручную и найдите ответ в виде дроби. Затем преобразуйте его в десятичное число в калькуляторе и найдите десятичное число, используя только калькулятор, и сравните ответы. Если они не совпадают, вы, вероятно, допустили ошибку в операциях с дробями.
Делая это, мы можем, по сути, проверить наши ответы, чтобы убедиться, что они верны. Завершите операцию дроби вручную и найдите ответ в виде дроби. Затем преобразуйте его в десятичное число в калькуляторе и найдите десятичное число, используя только калькулятор, и сравните ответы. Если они не совпадают, вы, вероятно, допустили ошибку в операциях с дробями. 0,5 мы могли бы записать как 5/10. 0,14 мы могли бы записать как 14/100. А 0,027 мы могли бы записать как 27/1000. Следуя этой тенденции, мы могли бы записать 0,248 как 248/1000. Это дробь, которую мы затем можем уменьшить, чтобы получить простейший ответ: 31/125 после деления верхней и нижней части на 8.
0,5 мы могли бы записать как 5/10. 0,14 мы могли бы записать как 14/100. А 0,027 мы могли бы записать как 27/1000. Следуя этой тенденции, мы могли бы записать 0,248 как 248/1000. Это дробь, которую мы затем можем уменьшить, чтобы получить простейший ответ: 31/125 после деления верхней и нижней части на 8.
 Для деления используйте «%», например «3/4 % 89/11». Используйте этот решатель только для работы дробей .
Для деления используйте «%», например «3/4 % 89/11». Используйте этот решатель только для работы дробей . В этом случае общий знаменатель равен 12. Идея состоит в том, чтобы переписать каждую дробь так, чтобы они обе имели один и тот же знаменатель, и это достигается путем увеличения дробей, чтобы у каждой дроби был один и тот же знаменатель. В этом примере общий знаменатель равен 12, поэтому мы проводим следующие усиления:
В этом случае общий знаменатель равен 12. Идея состоит в том, чтобы переписать каждую дробь так, чтобы они обе имели один и тот же знаменатель, и это достигается путем увеличения дробей, чтобы у каждой дроби был один и тот же знаменатель. В этом примере общий знаменатель равен 12, поэтому мы проводим следующие усиления: