Таблица менделеева — Электронный учебник K-tree
Электронный учебник
Периодический закон, открытый Д. И. Менделеевым был выражен в таблице. Периодическая таблица химических элементов, или таблица менделеева.
1
H
1.008
2
He
4.003
3
Li
6.938
4
Be
9.012
5
B
10.806
6
C
12.01
7
N
14.006
8
O
15.999
9
F
18.998
10
Ne
20.18
11
Na
22.99
12
Mg
24.304
13
Al
26.982
14
Si
28.084
15
P
30.974
16
S
32.059
17
Cl
35.446
18
Ar
39.948
19
K
39.098
20
Ca
40.078
21
Sc
44.956
22
Ti
47.867
23
V
50.942
24
Cr
51. 996
996
25
Mn
54.938
26
Fe
55.845
27
Co
58.933
28
Ni
58.693
29
Cu
63.546
30
Zn
65.38
31
Ga
69.723
32
Ge
72.63
33
As
74.922
34
Se
78.971
35
Br
79.901
36
Kr
83.798
37
Rb
85.468
38
Sr
87.62
39
Y
88.906
40
Zr
91.224
41
Nb
92.906
42
Mo
95.95
44
Ru
101.07
45
Rh
102.906
46
Pd
106.42
47
Ag
107.868
48
Cd
112.414
49
In
114.818
50
Sn
118.71
51
Sb
121.76
52
Te
127.6
53
I
126.904
54
Xe
131.293
55
Cs
132.905
56
Ba
137.327
57
La
138.905
72
Hf
178. 49
49
73
Ta
180.948
74
W
183.84
75
Re
186.207
76
Os
190.23
77
Ir
192.217
78
Pt
195.084
79
Au
196.967
80
Hg
200.592
81
Tl
204.382
82
Pb
207.2
83
Bi
208.98
58
Ce
140.116
59
Pr
140.908
60
Nd
144.242
62
Sm
150.36
63
Eu
151.964
64
Gd
157.25
65
Tb
158.925
66
Dy
162.5
67
Ho
164.93
68
Er
167.259
69
Tm
168.934
70
Yb
173.045
71
Lu
174.967
90
Th
232.038
91
Pa
231.036
92
U
238.029
В таблице менделеева колонки называются группами, строки называются периодами. Элементы в группах как правило имеют
одинаковые электронные конфигурации внешних оболочек, например, благородные газы — последняя группа, имеют законченную
электронную конфигурацию.
Как заполняется электронная конфигурация элементов подробно описано в статье
Скачать таблицу менделеева в хорошем качестве
© 2015-2022 — K-Tree.ru • Электронный учебник
По любым вопросам Вы можете связаться по почте [email protected]
Копия материалов, размещённых на данном сайте, допускается только по письменному разрешению владельцев сайта.
Степень окисления. Большая российская энциклопедия
Химические величины
- Области знаний:
- Основные понятия и законы
- Другие наименования:
- Окислительное число
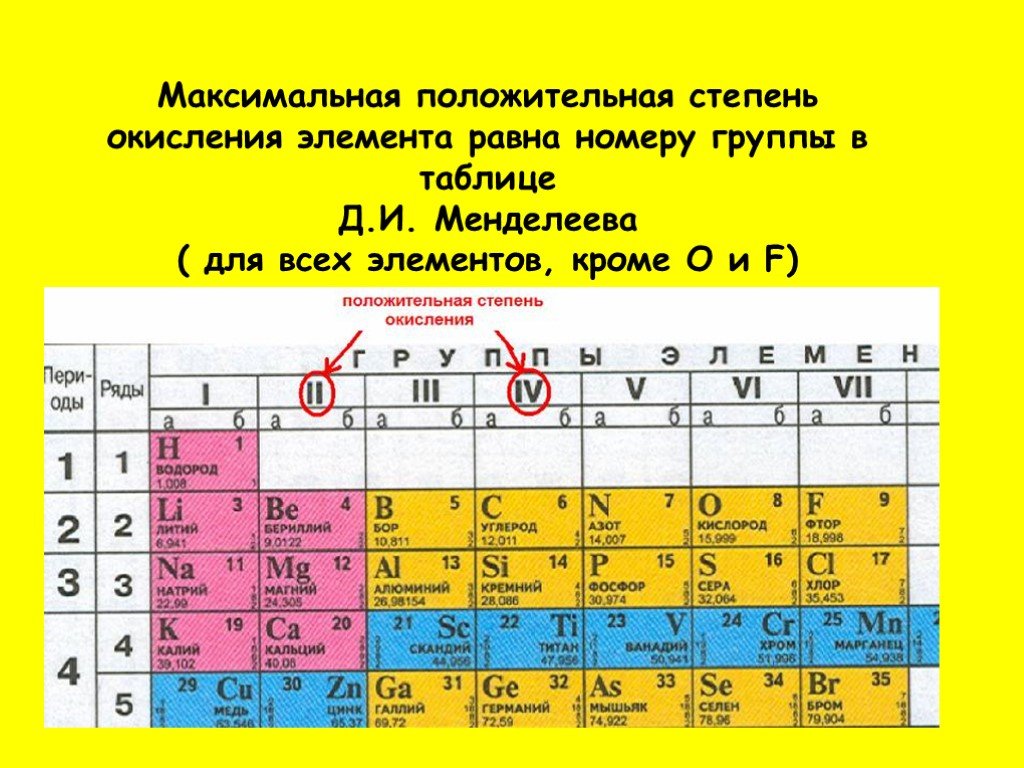
Сте́пень окисле́ния (окислительное число), формальный заряд атома в молекуле в предположении, что все электронные пары, осуществляющие химическую связь, полностью смещены в сторону более электроотрицательного элемента. Степень окисления химических элементов обозначают римской или арабской цифрой с предшествующим знаком (в отличие от заряда иона, где знак ставится после числа). Степень окисления атома в простом веществе равна нулю. Алгебраическая сумма степеней окисления атомов в молекуле равна нулю. Алгебраическая сумма степеней окисления атомов в многозарядном ионе равна заряду иона. Значение степени окисления обычно является целочисленным и может изменяться от –4 до +8.
Степень окисления химических элементов обозначают римской или арабской цифрой с предшествующим знаком (в отличие от заряда иона, где знак ставится после числа). Степень окисления атома в простом веществе равна нулю. Алгебраическая сумма степеней окисления атомов в молекуле равна нулю. Алгебраическая сумма степеней окисления атомов в многозарядном ионе равна заряду иона. Значение степени окисления обычно является целочисленным и может изменяться от –4 до +8.
Cтепень окисления водорода в большинстве его соединений (кроме гидридов металлов) принимают равной +1, степень окисления кислорода в большинстве соединений – равной –2. Исключениями являются пероксиды со связями О−О (степень окисления равна –1) и О−О−О (степень окисления дробная) и фториды кислорода (OF, O2F, O2F2, O3F2 и др.), у которых степень окисления атома О имеет положительные (+1, +2) или дробные значения.
Наиболее высокие положительные значения степени окисления металлов проявляются во фторидах (ReF7, OsF7), оксифторидах (Os+8O3F2), перманганатах (KMn+7O4), оксидах Ru+8O4, Os+8O4, Ir+8O4, Hs+8O4, Xe+8O4 и некоторых комплексах Pu. Наиболее высокие положительные значения степени окисления неметаллов свойственны S, Se, Te и Po (наибольшие значения +6), Cl, Br и I в галогенфторидах (ClF5, Br+7O3F, I+7O2F3) и их производных, а также Хе в XeF6 и его соединениях. Значение степени окисления –4 проявляют химические элементы подгруппы углерода. Дробные значения степени окисления имеют металлы в оксидах вида Fe3O4.
Наиболее высокие положительные значения степени окисления неметаллов свойственны S, Se, Te и Po (наибольшие значения +6), Cl, Br и I в галогенфторидах (ClF5, Br+7O3F, I+7O2F3) и их производных, а также Хе в XeF6 и его соединениях. Значение степени окисления –4 проявляют химические элементы подгруппы углерода. Дробные значения степени окисления имеют металлы в оксидах вида Fe3O4.
Степень окисления F, Cl, Br и I в ионных веществах равна –1, однако степени окисления Cl, Br и I в некоторых кислотах и солях могут иметь положительные значения: HCl+7O4, KCl+7O4. Cтепень окисления щелочных металлов принимают равной +1, щёлочноземельных металлов – +2, металлов 3-й группы (короткой формы периодической системы) – +3, высшие степени окисления элементов 4-й, 5-й, 6-й и частично 7-й и 8-й групп составляют соответственно +4, +5, +6, +7 и +8. Графическая зависимость высшей степени окисления от порядкового номера химического элемента имеет поэтому вид нерегулярной пилообразной кривой с максимумами у N (+5), Cl (+7), Mn (+7), Br (+7), Ru (+8), I (+7), Pr (+5), Os (+8) и минимумами у С, Si и Ge (по –4), а также у Sb (–3). При этом химические элементы, имеющие высокие степени окисления, проявляют и более низкие их значения.
При этом химические элементы, имеющие высокие степени окисления, проявляют и более низкие их значения.
Имеются публикации об обнаружении в твёрдом состоянии соединений Ag+4, Ca+1, Mg+1, Al+2, Ga+2, In+2, Tl+2, Dy+4, Tm+4, Fe+7, Fe+8, Rn+4, Rn+6, Pu+8, Am+7, Db+5, Sg+7, Bh+7, Hs+8 и других химических элементов с необычными значениями степени окисления. Длительное время публиковавшиеся сообщения о соединении XeF8 не подтвердились.
В ряде случаев степень окисления элемента не совпадает с его валентностью даже при совпадении абсолютных значений. Так, для органических соединений степень окисления углерода может составлять –4 (СН4), –3 (С2Н6), –2 (СH3Cl), –1 (C2H2), 0 (СН2Cl2), +1 (CHCl2 CHCl2), +2 (CHCl3), +4 (CCl4). У координационных соединений степень окисления центрального атома определяется при условном удалении всех лигандов вместе с электронными парами, связанными с центральным атомом.
У координационных соединений степень окисления центрального атома определяется при условном удалении всех лигандов вместе с электронными парами, связанными с центральным атомом.
Экспериментально определяемые истинные заряды атомов в соединениях отличаются от степеней окисления этих элементов. Понятие «степень окисления» используется при составлении уравнений окислительно-восстановительных реакций.
Раков Эдуард Григорьевич. Первая публикация: Большая российская энциклопедия, 2016.Дата публикации: 17 января 2023 г. в 00:28 (GMT+3)
19.1: Определение степени окисления углерода
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 225880
- В связи C-H H рассматривается так, как если бы он имел степень окисления +1.
 Это означает, что каждая связь C-H будет уменьшить степень окисления углерода на 1.
Это означает, что каждая связь C-H будет уменьшить степень окисления углерода на 1. - Для углерода, связанного с более электроотрицательным неметаллом X, таким как азот, кислород, сера или галогены, каждая связь C-X будет увеличивать степень окисления углерода на 1. (Некоторые неметаллы менее электроотрицательны, чем углерод , такие как фосфор, кремний или бор, но связи углерода с этими элементами встречаются гораздо реже.)
- Для углерода, связанного с другим углеродом, степень окисления не изменяется. Таким образом, углерод, присоединенный к 4 атомам углерода, имеет нулевую степень окисления.
Таким образом, в отличие от металлов, которые почти всегда находятся в положительной степени окисления, степень окисления углерода может варьироваться в широких пределах, от -4 (в Ch5) до +4 (например, в CO2). Вот некоторые примеры.
(Не забывайте, что это называется «формализм» по какой-то причине. Заряд углерода не равен на самом деле +4 или –4. Но формализм степени окисления помогает нам отслеживать, куда движутся электроны, что очень скоро пригодится).
Заряд углерода не равен на самом деле +4 или –4. Но формализм степени окисления помогает нам отслеживать, куда движутся электроны, что очень скоро пригодится).
Поняв, как рассчитать степени окисления углерода, мы готовы к следующему шагу: пониманию изменяет в степени окисления углерода посредством реакций, известных как окисления (когда степень окисления увеличивается) и восстановления (когда степень окисления уменьшается). Подробнее об этом в следующий раз.
Лестница окисления
Каталожные номера
- http://www.masterorganicchemistry.co…e-of-a-carbon/
Авторы
- Джеймс Эшенхерст (MasterOrganicChemistry.com)
Вы, несомненно, уже знакомы с общей идеей окисления и восстановления: из общей химии вы узнали, что при окислении соединение или атом теряет электроны, а при восстановлении приобретает электроны. Вы также знаете, что реакции окисления и восстановления протекают парами: если один вид окисляется, другой должен одновременно восстанавливаться — отсюда и термин «окислительно-восстановительная реакция». поток электронов от одного металла к другому, например, реакция между ионом меди в растворе и металлическим цинком: 9{+2}_{(aq)} \tag{16.1.1}\]
Вы также знаете, что реакции окисления и восстановления протекают парами: если один вид окисляется, другой должен одновременно восстанавливаться — отсюда и термин «окислительно-восстановительная реакция». поток электронов от одного металла к другому, например, реакция между ионом меди в растворе и металлическим цинком: 9{+2}_{(aq)} \tag{16.1.1}\]
В органической химии окислительно-восстановительные реакции выглядят несколько иначе. Электроны в органической окислительно-восстановительной реакции часто передаются в виде гидрид-иона – протона и двух электронов. Поскольку они происходят вместе с переносом протона, их обычно называют реакциями гидрирования и дегидрирования : гидрид плюс протон образуют молекулу водорода (H 2 ). Будьте осторожны – не перепутайте термины hyd водород ионизация и дегидрирование дроген ионизация с гидратацией и дегидратацией – последние относятся к приросту и отщеплению молекулы воды (и являются , а не окислительно-восстановительными реакциями), в то время как первые относятся к приросту и потеря молекулы водорода .
Когда атом углерода в органическом соединении теряет связь с водородом и приобретает новую связь с гетероатомом (или с другим углеродом), мы говорим, что соединение дегидрировано или окислено. Очень распространенным биохимическим примером является окисление спирта в кетон или альдегид:
Когда атом углерода теряет связь с водородом и приобретает связь с гетероатомом (или с другим атомом углерода), это считается окислительным процессом, поскольку водород из всех элементов является наименее электроотрицательным. Таким образом, в процессе дегидрирования атом углерода претерпевает общую потерю электронной плотности – а потеря электронов есть окисление.
И наоборот, когда атом углерода в органическом соединении получает связь с водородом и теряет связь с гетероатомом (или с другим атомом углерода), мы говорим, что соединение гидрировано или восстановлено. Гидрирование кетона в спирт, например, в целом является обратным дегидрированию спирта, показанному выше. Ниже проиллюстрирована другая распространенная возможность — гидрирование (восстановление) алкена до алкана.
Гидрирование приводит к более высокой электронной плотности на атоме(ах) углерода, и, таким образом, мы считаем процесс восстановлением органической молекулы.
Обратите внимание, что ни гидрирование, ни дегидрирование не связаны с приобретением или потерей атома кислорода . Реакции, которые — включают приобретение или потерю одного или нескольких атомов кислорода, обычно называют «оксигеназными» и «редуктазными» реакциями.
По большей части, говоря об окислительно-восстановительных реакциях в органической химии, мы имеем дело с небольшим набором хорошо узнаваемых превращений функциональных групп. Поэтому очень полезно ознакомиться с идеей «степеней окисления» применительно к органическим функциональным группам. Сравнивая относительное количество связей с атомами водорода, мы можем упорядочить знакомые функциональные группы по степени окисления. В качестве примера возьмем ряд одноуглеродных соединений. Метан с четырьмя углеродно-водородными связями сильно восстановлен.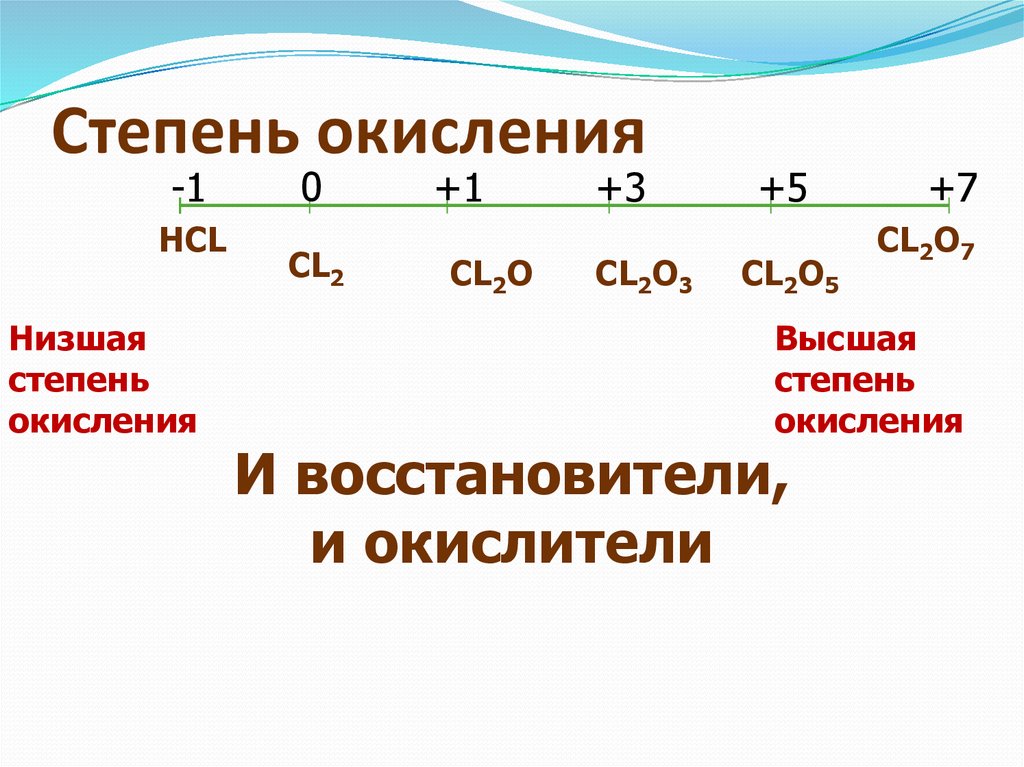 Далее в ряду идет метанол (на одну связь углерод-водород меньше, на одну связь углерод-кислород больше), за ним следуют формальдегид, формиат и, наконец, диоксид углерода на сильно окисленном конце группы.
Далее в ряду идет метанол (на одну связь углерод-водород меньше, на одну связь углерод-кислород больше), за ним следуют формальдегид, формиат и, наконец, диоксид углерода на сильно окисленном конце группы.
Эта закономерность верна для соответствующих функциональных групп органических молекул с двумя или более атомами углерода:
Алканы сильно восстановлены, в то время как спирты, а также алкены, простые эфиры, амины, сульфиды и сложные эфиры фосфорной кислоты – на одну ступень выше по шкале окисления, за которыми следуют альдегиды/кетоны/имины и эпоксиды, и, наконец, производные карбоновых кислот (диоксид углерода в верхней части списка окисления специфичен для одного углеродного ряда).
Обратите внимание, что в приведенном выше ряду двухуглеродных соединений этанол и этен считаются находящимися в одной и той же степени окисления. Вы уже знаете, что спирты и алкены взаимопревращаются путем присоединения или отщепления воды (например, в разделе 10.4.). Когда спирт дегидратируется с образованием алкена, один из двух атомов углерода теряет связь С-Н и приобретает связь С-С и, таким образом, окисляется. Однако другой углерод теряет связь С-О и приобретает связь С-С и, таким образом, считается восстановленным. Таким образом, в целом степень окисления атомов углерода, рассматриваемых вместе, не меняется.
Однако другой углерод теряет связь С-О и приобретает связь С-С и, таким образом, считается восстановленным. Таким образом, в целом степень окисления атомов углерода, рассматриваемых вместе, не меняется.
Вы должны научиться распознавать, когда реакция включает изменение степени окисления атомов углерода в органическом реагенте. Глядя, например, на следующее превращение, вы сможете быстро распознать, что это окисление: функциональная группа спирта превращается в кетон, что является одной ступенью вверх по лестнице окисления.
Аналогично, следующая реакция включает превращение производного карбоновой кислоты (тиоэфира) сначала в альдегид, а затем в спирт: это двойное восстановление , так как субстрат теряет две связи с гетероатомами и приобретает две связи с атомами водорода.
Реакция переноса ацила (например, превращение ацилфосфата в амид) не считается окислительно-восстановительной реакцией – степень окисления органической молекулы не изменяется по мере превращения субстрата в продукт, потому что связь с одним гетероатомом (кислородом) была просто обменена на связь с другим гетероатомом (азот).
Важно уметь распознавать, когда органическая молекула окисляется или восстанавливается, потому что эта информация говорит вам искать участие соответствующего окислительно-восстановительного агента, который восстанавливается или окисляется — помните, окисление и восстановление всегда происходят в тандем! Вскоре мы подробно узнаем о наиболее важных биохимических и лабораторных окислительно-восстановительных агентах.
- Органическая химия с акцентом на биологию Тим Содерберг (Университет Миннесоты, Моррис)
Элемент YouTube был исключен из этой версии текста. Вы можете просмотреть его онлайн здесь: http://pb.libretexts.org/ochem2walker/?p=116
Контент по лицензии CC, ранее опубликованный
- Статусы окисления органических молекул. Автор : Джеймс Эшенхерст. Расположен по адресу : https://www.masterorganicchemistry.com/. Лицензия : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
- Органическая химия с биологическим акцентом.
 Автор : Тим Содерберг. Расположен по адресу : https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Book%3A_Organic_Chemistry_with_a_Biological_Emphasis_(Soderberg). Проект : Химия LibreTexts. Лицензия : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
Автор : Тим Содерберг. Расположен по адресу : https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Book%3A_Organic_Chemistry_with_a_Biological_Emphasis_(Soderberg). Проект : Химия LibreTexts. Лицензия : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Теги
19.1. Определение степени окисления углерода
- В связи C-H H рассматривается так, как если бы он имел степень окисления +1.
 Это означает, что каждая связь C-H будет уменьшать степень окисления углерода на 1.
Это означает, что каждая связь C-H будет уменьшать степень окисления углерода на 1. - Для углерода, связанного с более электроотрицательным неметаллом X, таким как азот, кислород, сера или галогены, каждая связь C-X будет увеличивать степень окисления углерода на 1. (Некоторые неметаллы менее электроотрицательны, чем углерод , такие как фосфор, кремний или бор, но связи углерода с этими элементами встречаются гораздо реже.)
- Для углерода, связанного с другим углеродом, степень окисления не изменяется. Таким образом, углерод, присоединенный к 4 атомам углерода, имеет нулевую степень окисления.
Таким образом, в отличие от металлов, которые почти всегда находятся в положительной степени окисления, степень окисления углерода может варьироваться в широких пределах, от -4 (в Ch5) до +4 (например, в CO2). Вот некоторые примеры.
(Не забывайте, что это называется «формализм» по какой-то причине. Заряд углерода не равен на самом деле +4 или –4. Но формализм степени окисления помогает нам отслеживать, куда движутся электроны, что очень скоро пригодится).
Но формализм степени окисления помогает нам отслеживать, куда движутся электроны, что очень скоро пригодится).
Поняв, как рассчитать степени окисления углерода, мы готовы к следующему шагу: пониманию изменений в степени окисления углерода посредством реакций, известных как окисления (где степень окисления увеличивается), и редукции (где степень окисления снижена). Подробнее об этом в следующий раз.
Дополнительная литература
Лестница окисления
Ссылки
- http://www.masterorganicchemistry.co…e-of-a-carbon/
Авторы
- Джеймс Эшенхерст (MasterOrganicChemistry.com)
Окисление и восстановление органических соединений – обзор
Вы, несомненно, уже знакомы с общей идеей окисления и восстановления: из общей химии вы узнали, что при окислении соединение или атом теряет электроны, а при восстановлении приобретает электроны. Вы также знаете, что реакции окисления и восстановления протекают парами: если один вид окисляется, другой должен одновременно восстанавливаться — отсюда и термин «окислительно-восстановительная реакция». поток электронов от одного металла к другому, например, реакция между ионом меди в растворе и металлическим цинком: 9{+2}_{(водн.)} \tag{16.1.1}\]
Вы также знаете, что реакции окисления и восстановления протекают парами: если один вид окисляется, другой должен одновременно восстанавливаться — отсюда и термин «окислительно-восстановительная реакция». поток электронов от одного металла к другому, например, реакция между ионом меди в растворе и металлическим цинком: 9{+2}_{(водн.)} \tag{16.1.1}\]
В органической химии окислительно-восстановительные реакции выглядят несколько иначе. Электроны в органической окислительно-восстановительной реакции часто передаются в виде гидрид-иона – протона и двух электронов. Поскольку они происходят вместе с переносом протона, их обычно называют реакциями гидрирования и дегидрирования : гидрид плюс протон образуют молекулу водорода (H 2 ). Будьте осторожны – не перепутайте термины hyd водород ионизация и дегидрирование дроген ионизация с гидратацией и дегидратацией – последние относятся к приросту и отщеплению молекулы воды (и являются , а не окислительно-восстановительными реакциями), в то время как первые относятся к приросту и потеря молекулы водорода .
Когда атом углерода в органическом соединении теряет связь с водородом и приобретает новую связь с гетероатомом (или с другим углеродом), мы говорим, что соединение дегидрировано или окислено. Очень распространенным биохимическим примером является окисление спирта в кетон или альдегид:
Когда атом углерода теряет связь с водородом и приобретает связь с гетероатомом (или с другим атомом углерода), это считается окислительным процессом, поскольку водород из всех элементов является наименее электроотрицательным. Таким образом, в процессе дегидрирования атом углерода претерпевает общую потерю электронной плотности – а потеря электронов есть окисление.
И наоборот, когда атом углерода в органическом соединении получает связь с водородом и теряет связь с гетероатомом (или с другим атомом углерода), мы говорим, что соединение гидрировано или восстановлено. Гидрирование кетона в спирт, например, в целом является обратным дегидрированию спирта, показанному выше. Ниже проиллюстрирована другая распространенная возможность — гидрирование (восстановление) алкена до алкана.
Гидрогенизация приводит к более высокой электронной плотности на атоме(ах) углерода, и, таким образом, мы считаем процесс восстановлением органической молекулы.
Обратите внимание, что ни гидрирование, ни дегидрирование не связаны с приобретением или потерей атома кислорода . Реакции, которые — включают приобретение или потерю одного или нескольких атомов кислорода, обычно называют «оксигеназными» и «редуктазными» реакциями.
По большей части, говоря об окислительно-восстановительных реакциях в органической химии, мы имеем дело с небольшим набором хорошо узнаваемых превращений функциональных групп. Поэтому очень полезно ознакомиться с идеей «степеней окисления» применительно к органическим функциональным группам. Сравнивая относительное количество связей с атомами водорода, мы можем упорядочить знакомые функциональные группы по степени окисления. В качестве примера возьмем ряд одноуглеродных соединений. Метан с четырьмя углеродно-водородными связями сильно восстановлен. Далее в ряду идет метанол (на одну связь углерод-водород меньше, на одну связь углерод-кислород больше), за ним следуют формальдегид, формиат и, наконец, диоксид углерода на сильно окисленном конце группы.
Далее в ряду идет метанол (на одну связь углерод-водород меньше, на одну связь углерод-кислород больше), за ним следуют формальдегид, формиат и, наконец, диоксид углерода на сильно окисленном конце группы.
Эта закономерность справедлива для соответствующих функциональных групп органических молекул с двумя или более атомами углерода:
Алканы сильно восстанавливаются, в то время как спирты, а также алкены, простые эфиры, амины, сульфиды и эфиры фосфорной кислоты находятся на одну ступень выше по шкале окисления, за ними следуют альдегиды/кетоны/имины и эпоксиды и, наконец, производные карбоновых кислот ( двуокись углерода, находящаяся в верхней части списка окисления, характерна для одного ряда углерода).
Обратите внимание, что в приведенном выше ряду двухуглеродных соединений этанол и этен считаются находящимися в одной и той же степени окисления. Вы уже знаете, что спирты и алкены взаимопревращаются путем присоединения или отщепления воды (например, в разделе 10. 4.). Когда спирт дегидратируется с образованием алкена, один из двух атомов углерода теряет связь С-Н и приобретает связь С-С и, таким образом, окисляется. Однако другой углерод теряет связь С-О и приобретает связь С-С и, таким образом, считается восстановленным. Таким образом, в целом степень окисления атомов углерода, рассматриваемых вместе, не меняется.
4.). Когда спирт дегидратируется с образованием алкена, один из двух атомов углерода теряет связь С-Н и приобретает связь С-С и, таким образом, окисляется. Однако другой углерод теряет связь С-О и приобретает связь С-С и, таким образом, считается восстановленным. Таким образом, в целом степень окисления атомов углерода, рассматриваемых вместе, не меняется.
Вы должны научиться распознавать, когда реакция включает изменение степени окисления атомов углерода в органическом реагенте. Глядя, например, на следующее превращение, вы сможете быстро распознать, что это окисление: функциональная группа спирта превращается в кетон, что является одной ступенью вверх по лестнице окисления.
Аналогично, следующая реакция включает превращение производного карбоновой кислоты (тиоэфира) сначала в альдегид, а затем в спирт: это двойное восстановление , так как субстрат теряет две связи с гетероатомами и приобретает две связи с атомами водорода.
Реакция переноса ацила (например, превращение ацилфосфата в амид) , а не считается окислительно-восстановительной реакцией – степень окисления органической молекулы не изменяется по мере превращения субстрата в продукт, потому что связь к одному гетероатому (кислороду) просто обменяли на связь с другим гетероатомом (азот).

 Это означает, что каждая связь C-H будет уменьшить степень окисления углерода на 1.
Это означает, что каждая связь C-H будет уменьшить степень окисления углерода на 1.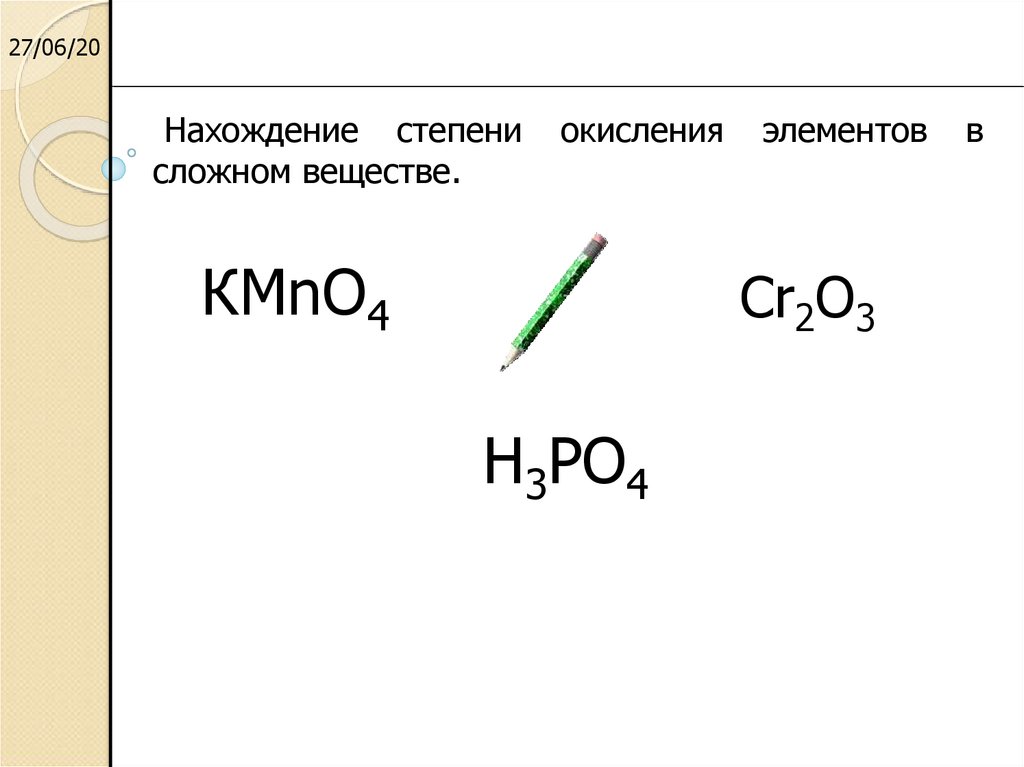 Автор : Тим Содерберг. Расположен по адресу : https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Book%3A_Organic_Chemistry_with_a_Biological_Emphasis_(Soderberg). Проект : Химия LibreTexts. Лицензия : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
Автор : Тим Содерберг. Расположен по адресу : https://chem.libretexts.org/Textbook_Maps/Organic_Chemistry/Book%3A_Organic_Chemistry_with_a_Biological_Emphasis_(Soderberg). Проект : Химия LibreTexts. Лицензия : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike  Это означает, что каждая связь C-H будет уменьшать степень окисления углерода на 1.
Это означает, что каждая связь C-H будет уменьшать степень окисления углерода на 1.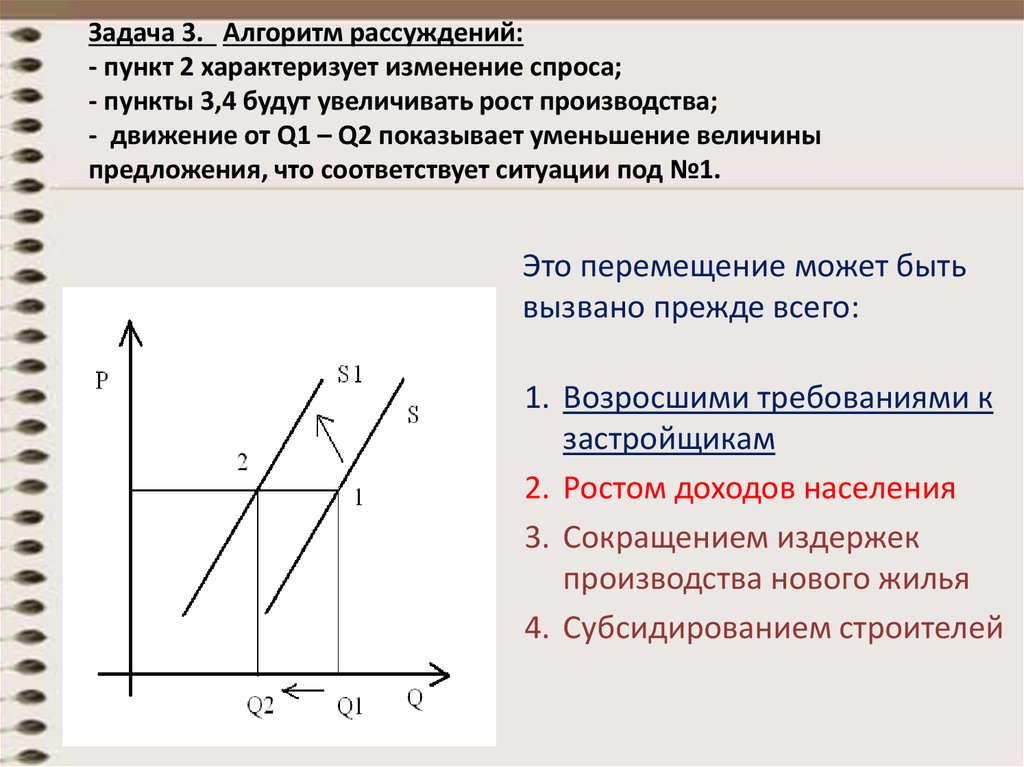 ; 1143 шт.
; 1143 шт.
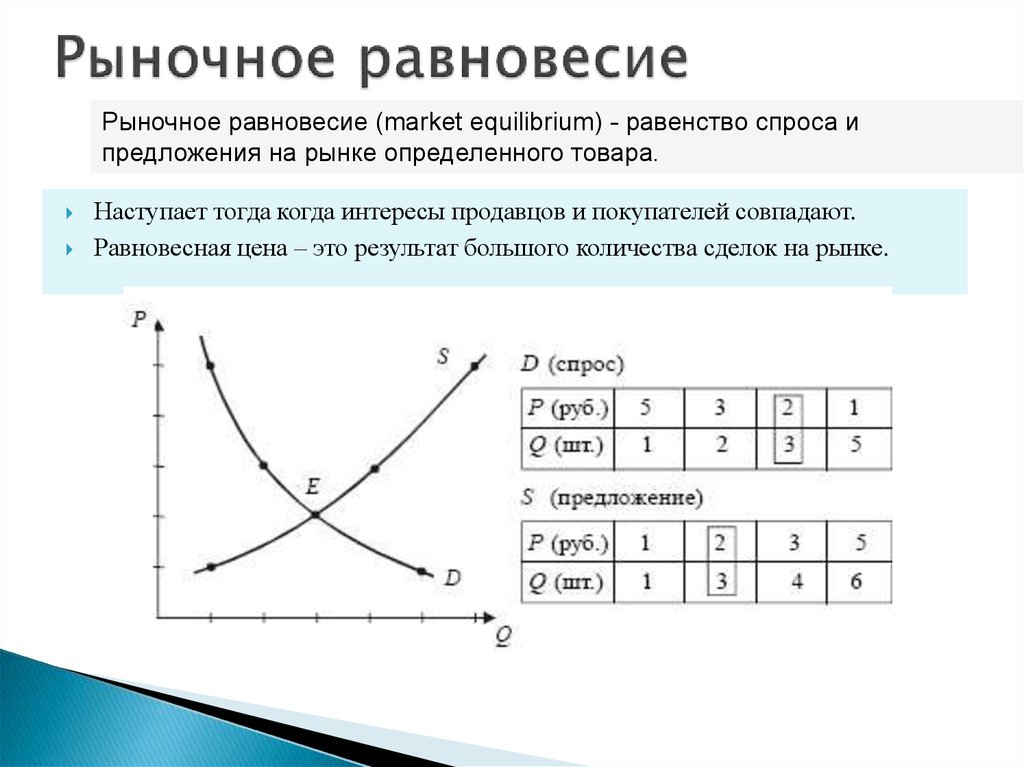
 Как изменится величина спроса,
если цена возрастет на 2,5%.
Как изменится величина спроса,
если цена возрастет на 2,5%. ед. за литр – цена
при которой молокозавод будет получать
максимальную выручку.
ед. за литр – цена
при которой молокозавод будет получать
максимальную выручку.
 Следовательно, число
дополнительных работников, которые, в
случае принятия закона, обратятся за
помощью в агентство, составляет около
21 945 человек.
Следовательно, число
дополнительных работников, которые, в
случае принятия закона, обратятся за
помощью в агентство, составляет около
21 945 человек.

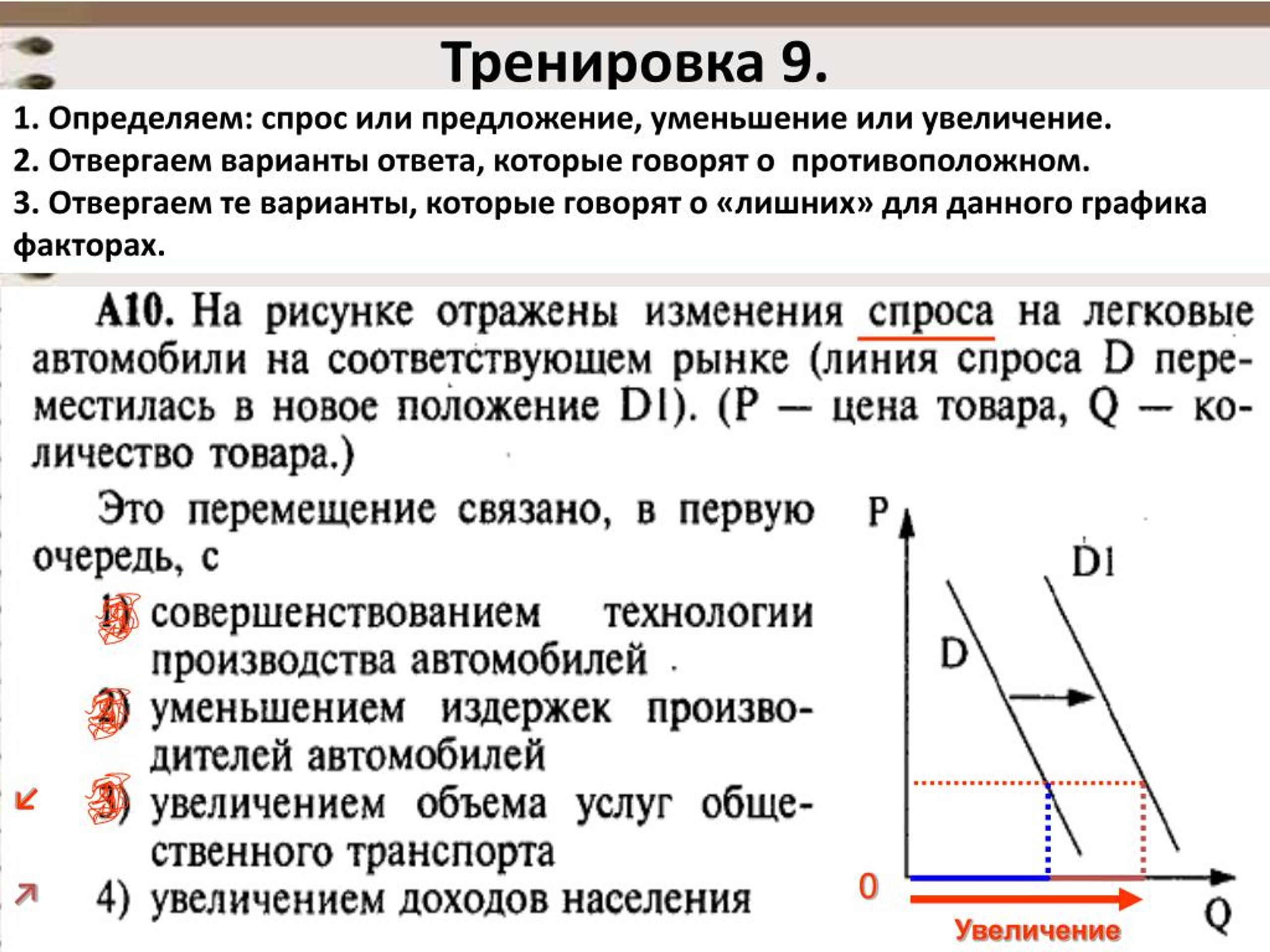
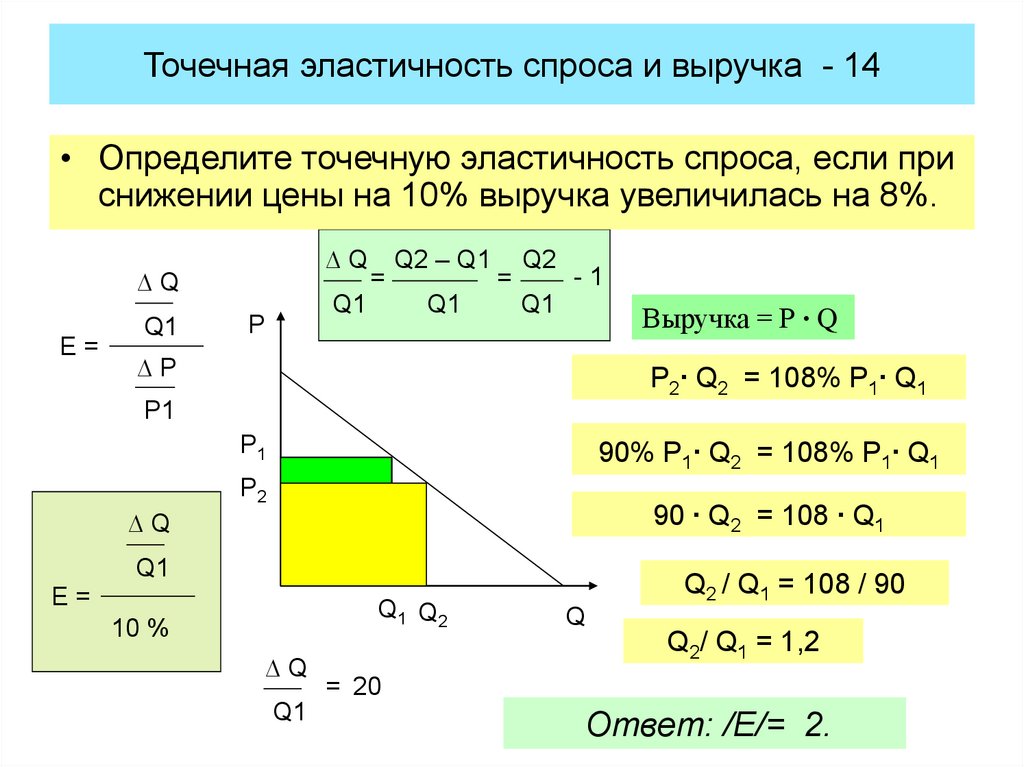
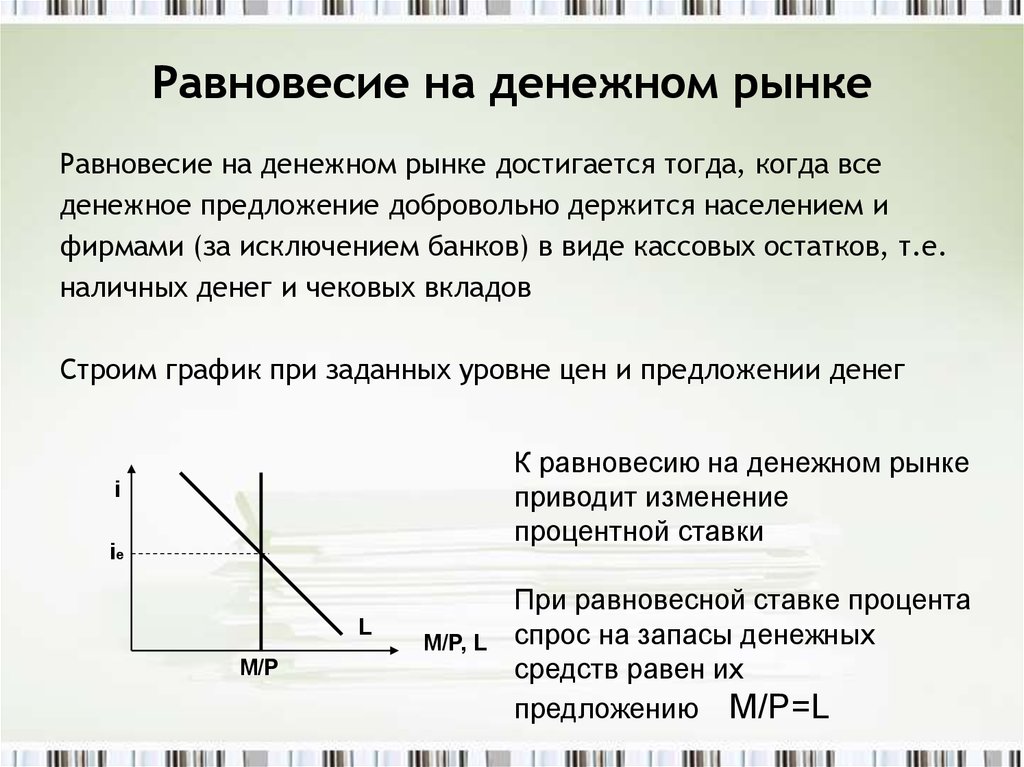
 При том же значении P будет предложено больше — мы имеем увеличение предложения на .
При том же значении P будет предложено больше — мы имеем увеличение предложения на . 



 0006
0006
 Следовательно, при любой заданной цене производители готовы и могут поставлять больше гамбургеров. Это приводит к сдвигу кривой предложения вправо.
Следовательно, при любой заданной цене производители готовы и могут поставлять больше гамбургеров. Это приводит к сдвигу кривой предложения вправо. 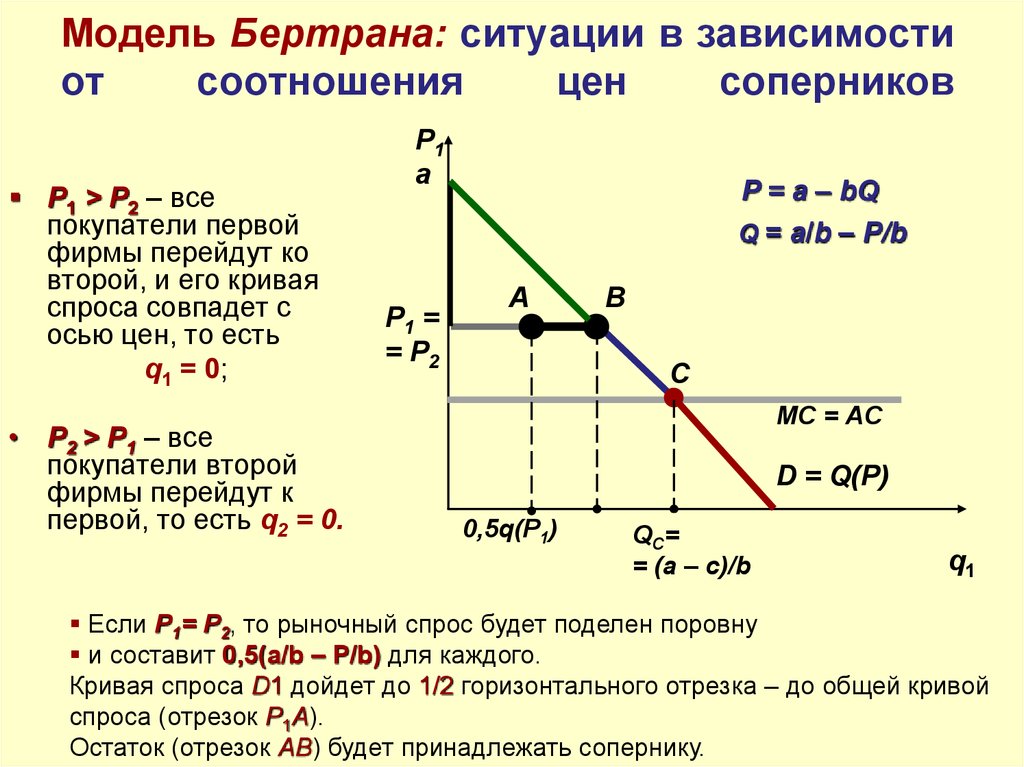

 04.2009, 08:32
04.2009, 08:32 
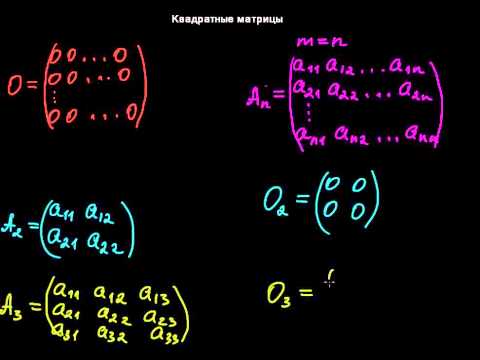 Математики обычно тоже не в курсе. Поэтому эта информация может быть полезна.
Математики обычно тоже не в курсе. Поэтому эта информация может быть полезна. Так что теперь тему можно каталогизировать.
Так что теперь тему можно каталогизировать. Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…
Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…
 Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…
Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё… Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…
Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё… Поэтому естественно в качестве значения функции при принять значение , где — такой многочлен, что разность делится на характеристический многочлен матрицы. В качестве можно взят интерполяционный многочлен Лагранжа, если корни хар. многочлена простые. Если же корни кратные, то надо еще потребовать, чтобы на корнях совпадали еще и значения производных и до порядка кратности корня. Это называется интерполяционный многочлен Лагранжа-Сильвестра.
Поэтому естественно в качестве значения функции при принять значение , где — такой многочлен, что разность делится на характеристический многочлен матрицы. В качестве можно взят интерполяционный многочлен Лагранжа, если корни хар. многочлена простые. Если же корни кратные, то надо еще потребовать, чтобы на корнях совпадали еще и значения производных и до порядка кратности корня. Это называется интерполяционный многочлен Лагранжа-Сильвестра.
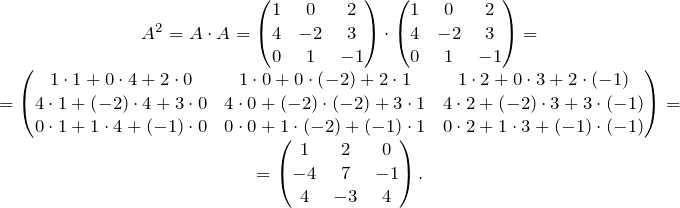 Нет просто точки опоры. Нет никакого универсального критерия того, что разумно считать функцией от матрицы.
Нет просто точки опоры. Нет никакого универсального критерия того, что разумно считать функцией от матрицы. Разумный вопрос, всплывший в комментариях, был: «зачем это может пригодиться на практике». Само по себе вычисление N-ого числа фибоначи может и не очень интересно, однако подход с матрицами, использованный в статье, на практике может применяться для гораздо более широкого круга задач.
Разумный вопрос, всплывший в комментариях, был: «зачем это может пригодиться на практике». Само по себе вычисление N-ого числа фибоначи может и не очень интересно, однако подход с матрицами, использованный в статье, на практике может применяться для гораздо более широкого круга задач.
 Это можно претставить в виде следующей матрицы:
Это можно претставить в виде следующей матрицы: Умножение вектора текущего состояния на такую матрицу эквивалентно выполнению команды
Умножение вектора текущего состояния на такую матрицу эквивалентно выполнению команды 3
3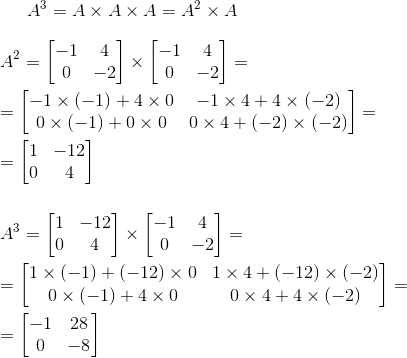
 stdin.readline().lower()
tokens = line.split()
if tokens[0] == 'loop':
# тут будет код для циклов
elif tokens[0] == 'end':
return mat
else:
r1 = reg_names.index(tokens[0])
try:
r2 = reg_names.index(tokens[2])
except:
r2 = -1
if tokens[1] == '+=':
if r2 == -1: cur = addval(r1, long(tokens[2]))
else: cur = addreg(r1, r2)
elif tokens[1] == '-=':
....
mat = matmul(mat, cur)
stdin.readline().lower()
tokens = line.split()
if tokens[0] == 'loop':
# тут будет код для циклов
elif tokens[0] == 'end':
return mat
else:
r1 = reg_names.index(tokens[0])
try:
r2 = reg_names.index(tokens[2])
except:
r2 = -1
if tokens[1] == '+=':
if r2 == -1: cur = addval(r1, long(tokens[2]))
else: cur = addreg(r1, r2)
elif tokens[1] == '-=':
....
mat = matmul(mat, cur) 2N, и вернуть полученную матрицу, умноженную на M.
2N, и вернуть полученную матрицу, умноженную на M. Выполнение такой программы в лоб заняло бы гораздо больше, потому что программе приходится оперировать многотысячезначными числами. Если написать код, которому не приходится оперировать большими числами, например код для вычисления суммы арифметической прогрессии, приведенный в начале статьи, то количество итераций может уходить за рамки разумного, но код будет выполняться за доли секунды
Выполнение такой программы в лоб заняло бы гораздо больше, потому что программе приходится оперировать многотысячезначными числами. Если написать код, которому не приходится оперировать большими числами, например код для вычисления суммы арифметической прогрессии, приведенный в начале статьи, то количество итераций может уходить за рамки разумного, но код будет выполняться за доли секунды Мощность матрицы заключается в возведении матрицы в степень (умножении на себя).
Мощность матрицы заключается в возведении матрицы в степень (умножении на себя). д.) и загрузка всех данных, скрипт, или доступ к API для «Matrix Power» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
д.) и загрузка всех данных, скрипт, или доступ к API для «Matrix Power» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android! 




 Он может проверить номер IBAN, проверив все элементы, такие как код банка, код филиала, номер счета и определенные контрольные цифры для каждой страны.
Он может проверить номер IBAN, проверив все элементы, такие как код банка, код филиала, номер счета и определенные контрольные цифры для каждой страны.



 Формат IBAN состоит из двухзначного кода страны, двух контрольных номеров, четырехзначного кода банка, шестизначного кода отделения банка и восьмизначного номера банковского счета.
Формат IBAN состоит из двухзначного кода страны, двух контрольных номеров, четырехзначного кода банка, шестизначного кода отделения банка и восьмизначного номера банковского счета.
 Помимо онлайн-конвертера валют XE, компания также предлагает современный калькулятор IBAN. Используя реестр SWIFT IBAN, этот калькулятор IBAN прост в использовании, а XE предоставляет две возможности: проверить формат IBAN или просмотреть пример формата IBAN по стране.
Помимо онлайн-конвертера валют XE, компания также предлагает современный калькулятор IBAN. Используя реестр SWIFT IBAN, этот калькулятор IBAN прост в использовании, а XE предоставляет две возможности: проверить формат IBAN или просмотреть пример формата IBAN по стране.

 Есть разница между требованиями к
главному бухгалтеру компании и, например, бухгалтеру-кассиру, поскольку зоны
ответственности значительно отличаются. Так или иначе такие тесты не только
помогают продемонстрировать нанимателям компетенции специалиста, но и
рассказывают о предстоящем объеме и характере работ соискателю.
Есть разница между требованиями к
главному бухгалтеру компании и, например, бухгалтеру-кассиру, поскольку зоны
ответственности значительно отличаются. Так или иначе такие тесты не только
помогают продемонстрировать нанимателям компетенции специалиста, но и
рассказывают о предстоящем объеме и характере работ соискателю.




 » data-question-id=»%4_jz!!v&qji» data-test-id=»1402″ data-post-id=»5765″ data-answer-count=»0″> Стоящим
» data-question-id=»%4_jz!!v&qji» data-test-id=»1402″ data-post-id=»5765″ data-answer-count=»0″> Стоящим Довольны ли вы результатами?
Довольны ли вы результатами?
 Бухгалтеры несут ответственность за бухгалтерский учет, который включает в себя отслеживание расходов и доходов, начисление заработной платы и счета. Они готовят финансовые отчеты и анализируют тенденции, чтобы делать прогнозы, которые могут определять общие решения компании. Они также несут ответственность за обеспечение надлежащего соблюдения юридическими и физическими лицами налогового законодательства. Бухгалтеры ежедневно работают с числами, что обязательно требует от них хорошего понимания математики в сочетании с аналитическим складом ума. Это также требует, чтобы бухгалтеры были критичными мыслителями, ориентированными на детали, которым нравится решать проблемы.
Бухгалтеры несут ответственность за бухгалтерский учет, который включает в себя отслеживание расходов и доходов, начисление заработной платы и счета. Они готовят финансовые отчеты и анализируют тенденции, чтобы делать прогнозы, которые могут определять общие решения компании. Они также несут ответственность за обеспечение надлежащего соблюдения юридическими и физическими лицами налогового законодательства. Бухгалтеры ежедневно работают с числами, что обязательно требует от них хорошего понимания математики в сочетании с аналитическим складом ума. Это также требует, чтобы бухгалтеры были критичными мыслителями, ориентированными на детали, которым нравится решать проблемы. Некоторые бухгалтеры становятся дипломированными бухгалтерами (CPA), сдав экзамен на получение лицензии. Советы штатов обычно требуют 150 семестровых кредитов в аккредитованном университете, степень бакалавра и определенное количество курсов по бухгалтерскому учету и бизнесу, прежде чем бухгалтер получит право сдавать экзамен CPA. В сфере бухгалтерского учета существует несколько различных типов должностей, в том числе финансовые аналитики, личные финансовые консультанты, налоговые инспекторы, кредитные специалисты, бюджетные аналитики, аудиторы и другие.
Некоторые бухгалтеры становятся дипломированными бухгалтерами (CPA), сдав экзамен на получение лицензии. Советы штатов обычно требуют 150 семестровых кредитов в аккредитованном университете, степень бакалавра и определенное количество курсов по бухгалтерскому учету и бизнесу, прежде чем бухгалтер получит право сдавать экзамен CPA. В сфере бухгалтерского учета существует несколько различных типов должностей, в том числе финансовые аналитики, личные финансовые консультанты, налоговые инспекторы, кредитные специалисты, бюджетные аналитики, аудиторы и другие. Работодатели также могут захотеть администрировать профиль личности сотрудника (EPP), личностный тест, который может оценить, насколько кандидат будет доволен работой в области бухгалтерского учета с точки зрения соответствия должности. Определенные черты личности, такие как добросовестность, связаны с успехом в бухгалтерском учете, и ПОП может дать рекомендации относительно того, насколько хорошо кандидат подходит для этой конкретной должности.
Работодатели также могут захотеть администрировать профиль личности сотрудника (EPP), личностный тест, который может оценить, насколько кандидат будет доволен работой в области бухгалтерского учета с точки зрения соответствия должности. Определенные черты личности, такие как добросовестность, связаны с успехом в бухгалтерском учете, и ПОП может дать рекомендации относительно того, насколько хорошо кандидат подходит для этой конкретной должности. Часто бухгалтерским компаниям особенно сложно нанять и удержать талантливого и надежного вспомогательного персонала. Вот почему многие бухгалтерские фирмы полагаются на тесты Criteria при приеме на работу секретарей, административных помощников и канцелярского персонала. Тестирование перед приемом на работу позволяет работодателям фильтровать большие группы кандидатов и сокращать время найма, одновременно улучшая общее качество найма.
Часто бухгалтерским компаниям особенно сложно нанять и удержать талантливого и надежного вспомогательного персонала. Вот почему многие бухгалтерские фирмы полагаются на тесты Criteria при приеме на работу секретарей, административных помощников и канцелярского персонала. Тестирование перед приемом на работу позволяет работодателям фильтровать большие группы кандидатов и сокращать время найма, одновременно улучшая общее качество найма.


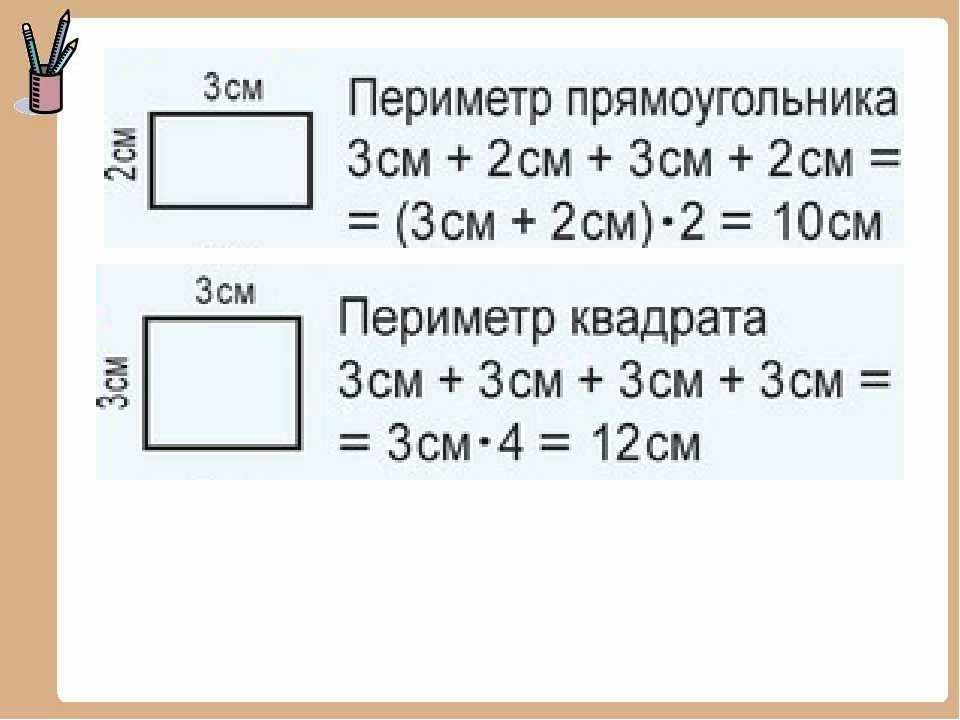 В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.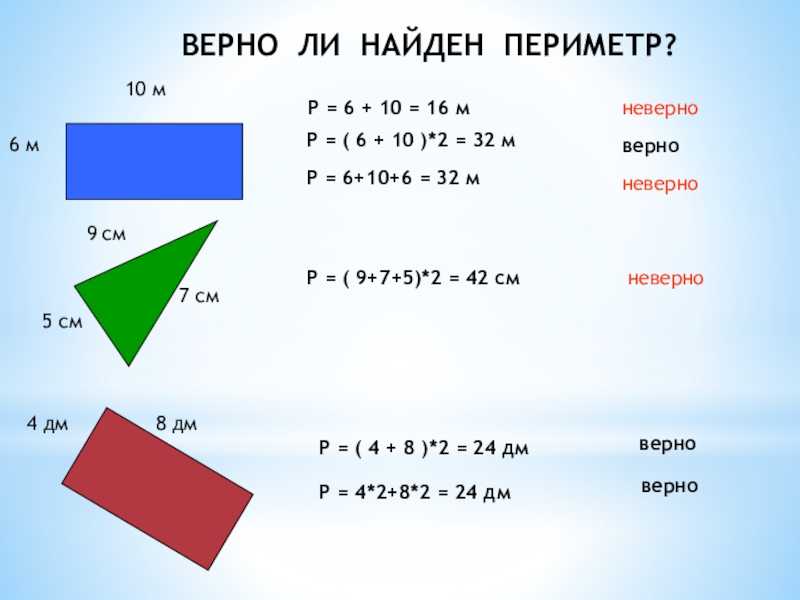
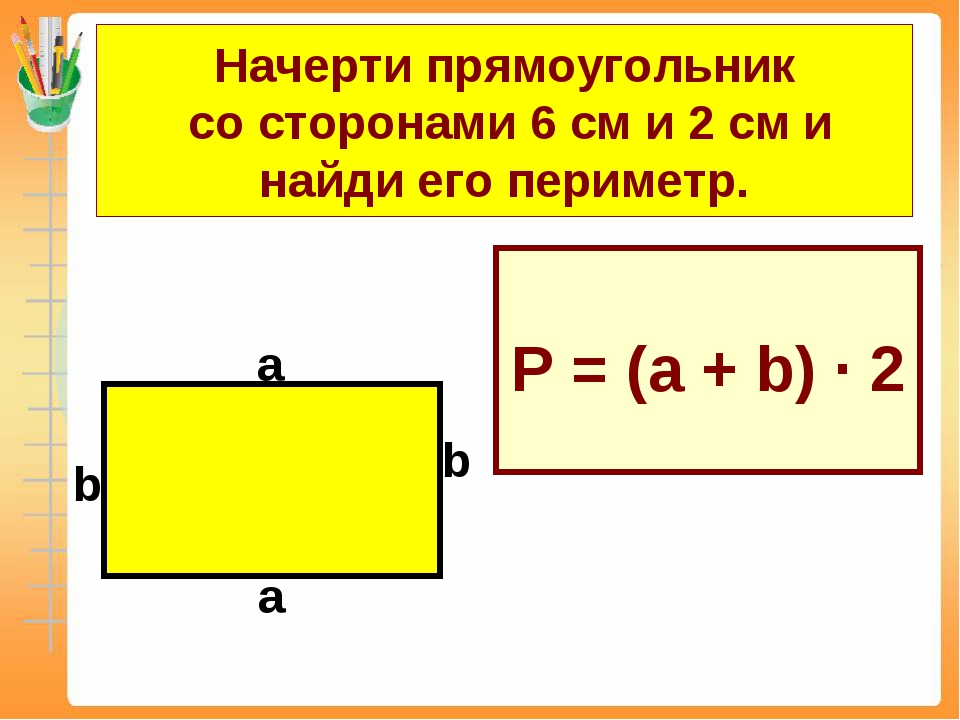


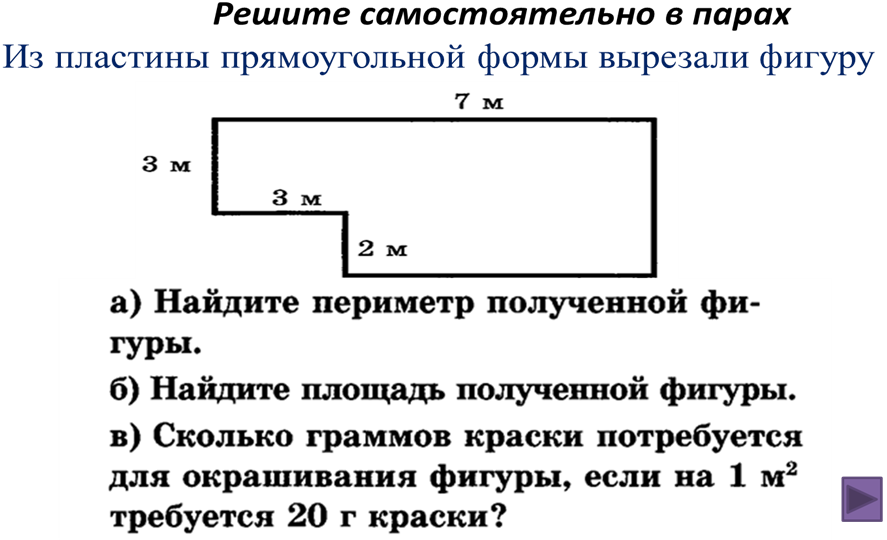 , а длина – 6.
, а длина – 6.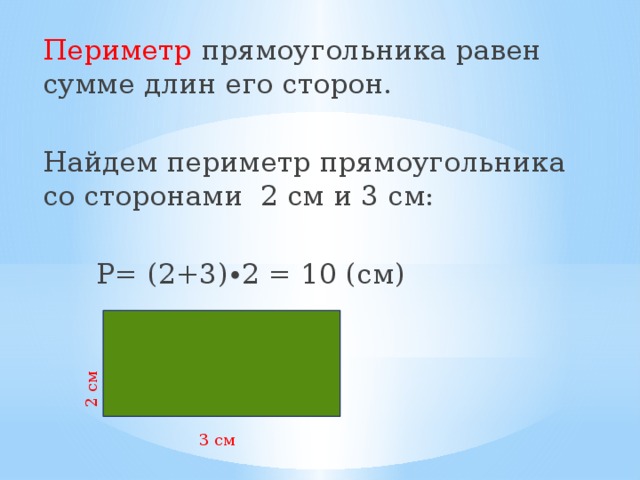

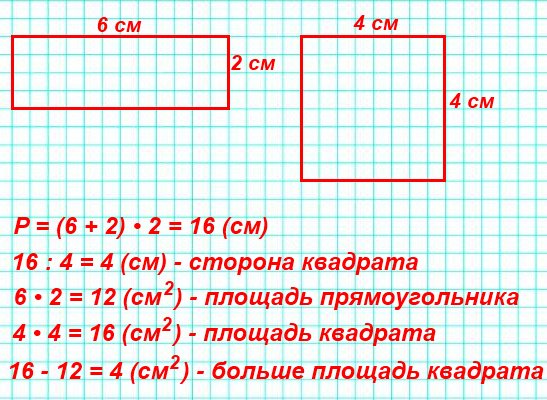 Чему равны остальные стороны прямоугольника?
Чему равны остальные стороны прямоугольника?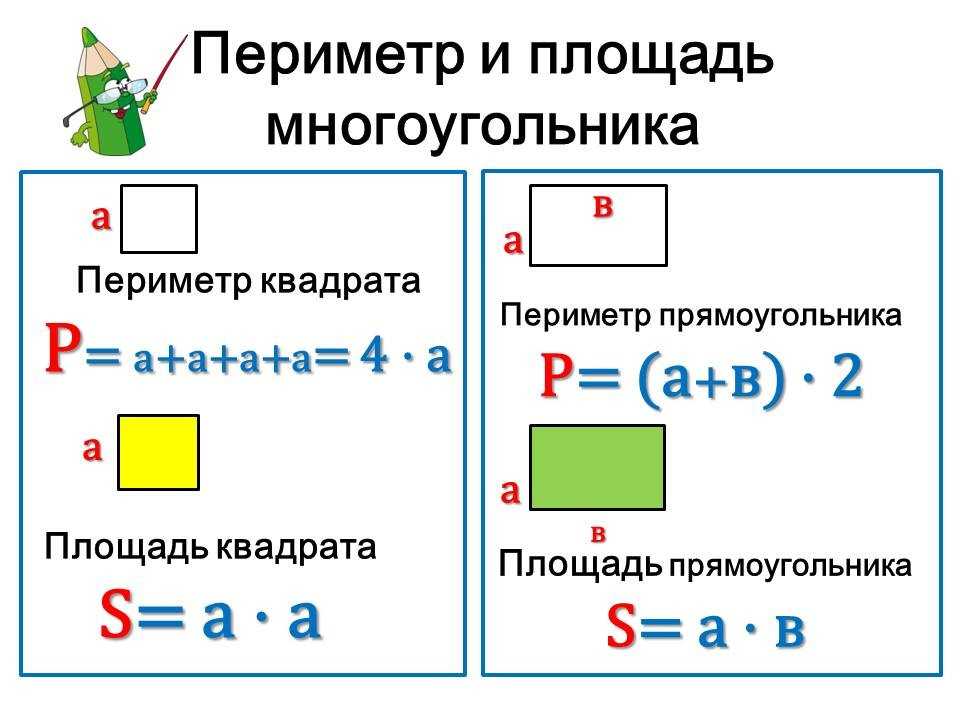
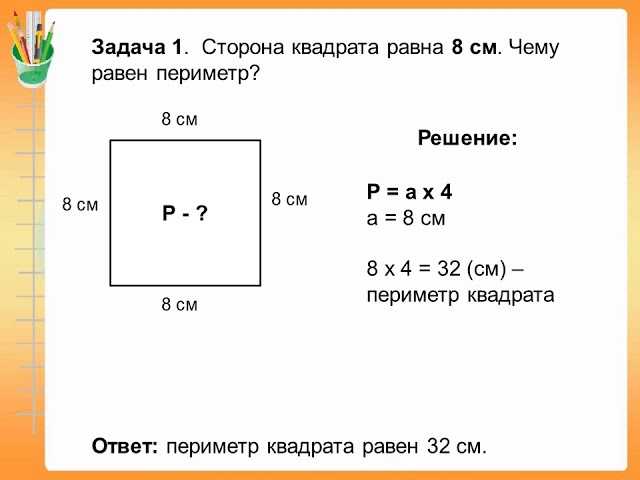
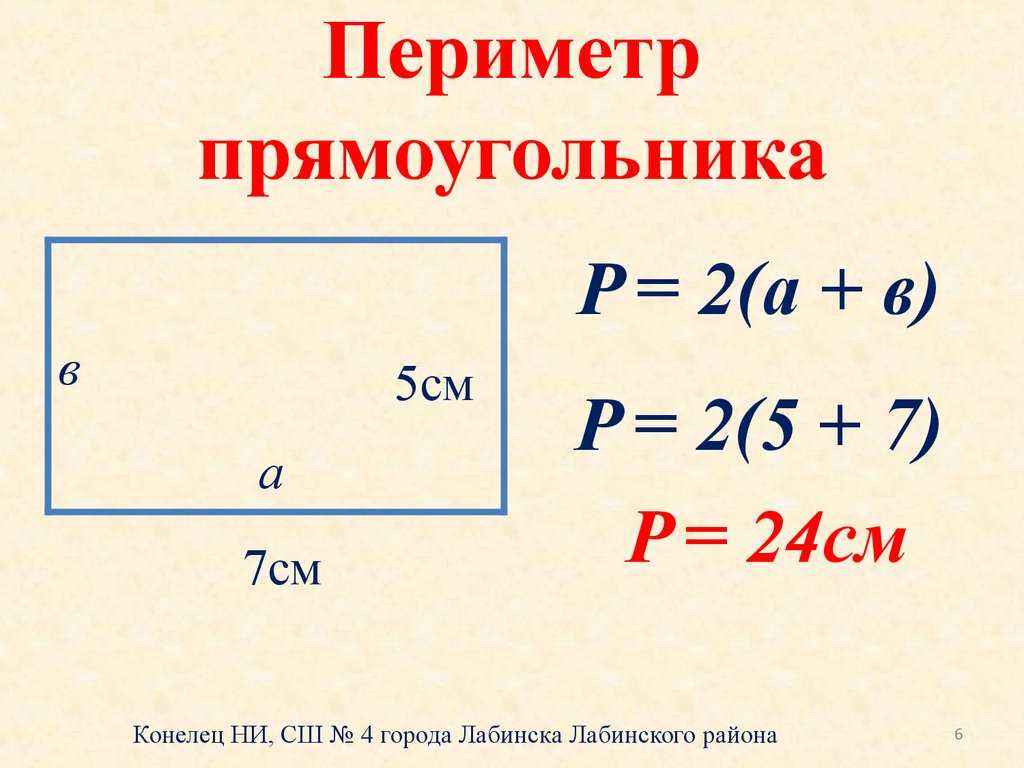 Поэтому принимаем следующее целое число. Это шесть.
Поэтому принимаем следующее целое число. Это шесть.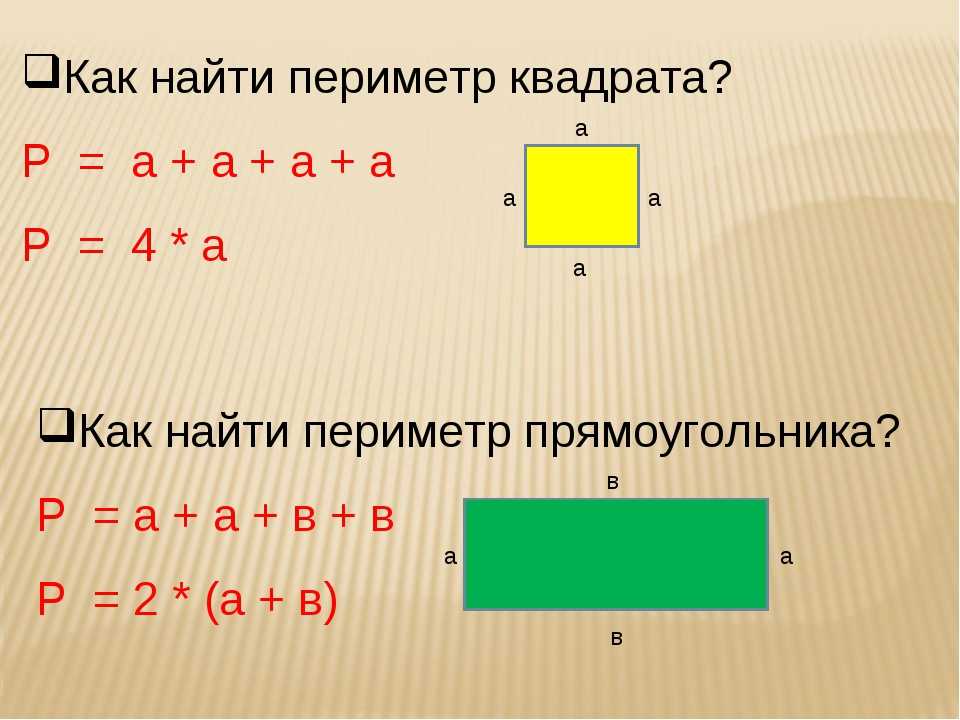
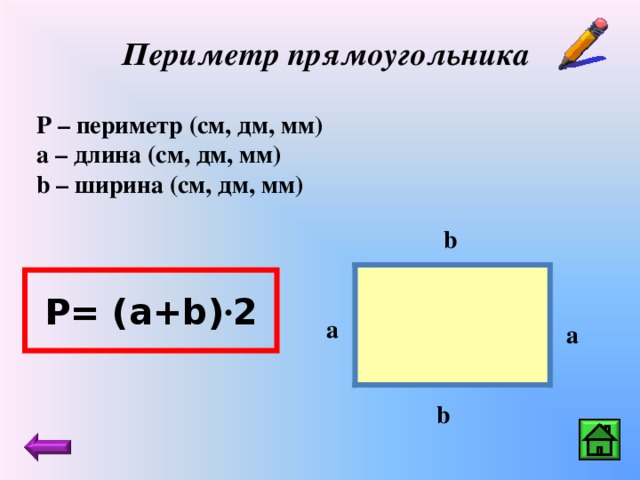
 Поскольку противоположные стороны прямоугольника равны, периметр равен удвоенной длине плюс удвоенной ширине прямоугольника, обозначаемому буквой «P».
Поскольку противоположные стороны прямоугольника равны, периметр равен удвоенной длине плюс удвоенной ширине прямоугольника, обозначаемому буквой «P».



 Расстояние, которое потребуется, чтобы обойти фигуру один раз вдоль ее края. В качестве альтернативы периметр фигуры можно определить как сумму длин всех ее сторон.
Расстояние, которое потребуется, чтобы обойти фигуру один раз вдоль ее края. В качестве альтернативы периметр фигуры можно определить как сумму длин всех ее сторон.
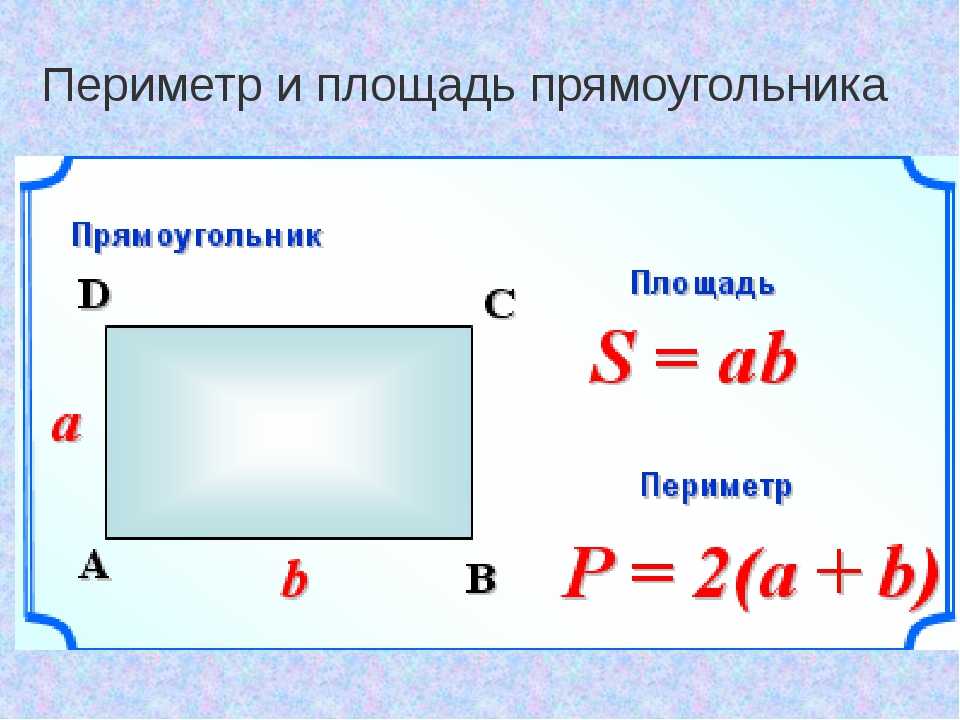 Как найти периметр треугольника с двумя равными сторонами?
Как найти периметр треугольника с двумя равными сторонами?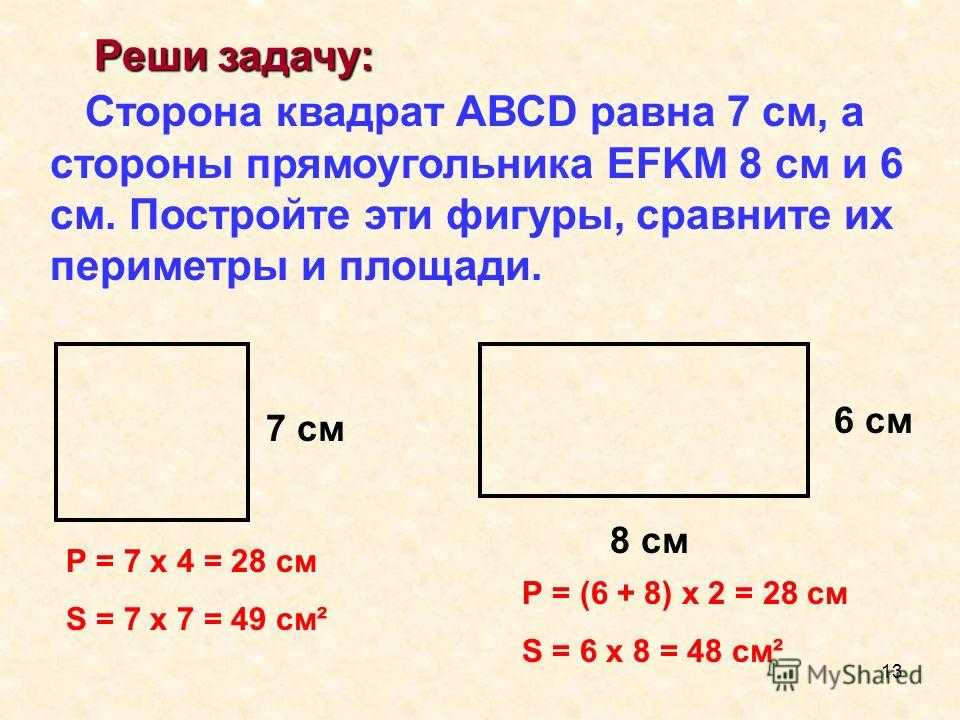 Периметр прямоугольника можно найти, вычислив сумму длин его четырех сторон. Иногда вы увидите формулу периметра как
Периметр прямоугольника можно найти, вычислив сумму длин его четырех сторон. Иногда вы увидите формулу периметра как

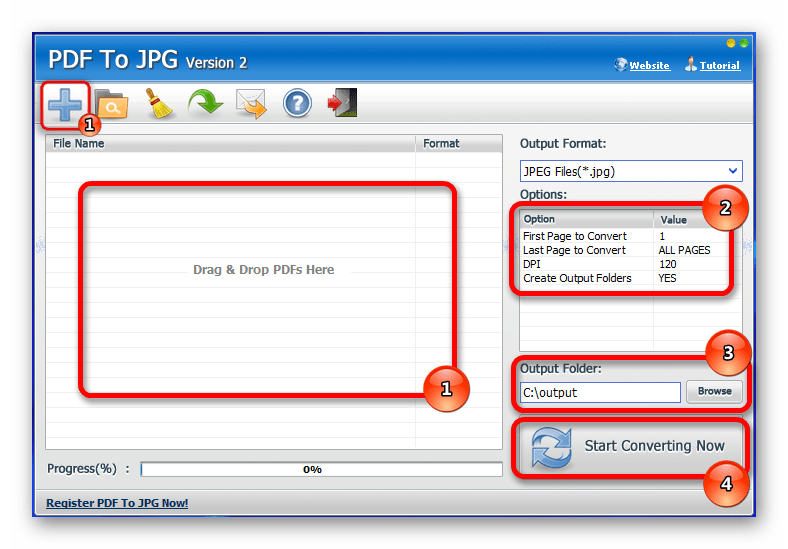 Для перевода ПДФ в JPG с ее помощью следует:
Для перевода ПДФ в JPG с ее помощью следует: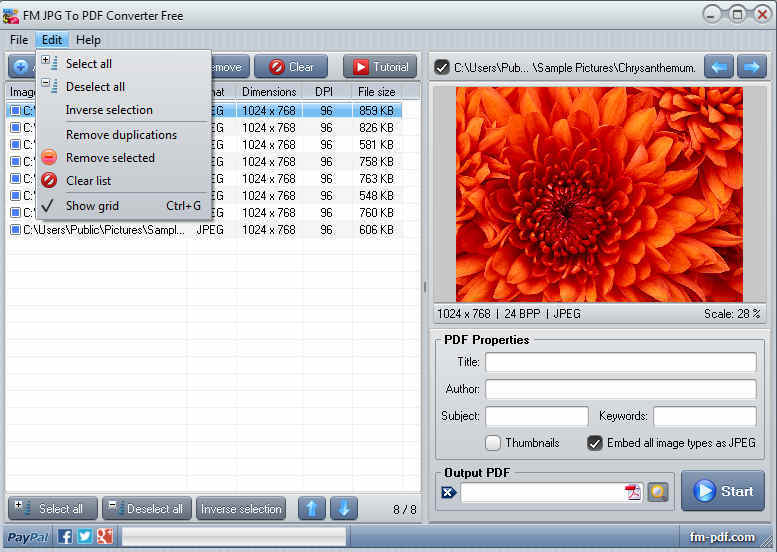 Также к преимуществам утилиты стоит отнести:
Также к преимуществам утилиты стоит отнести: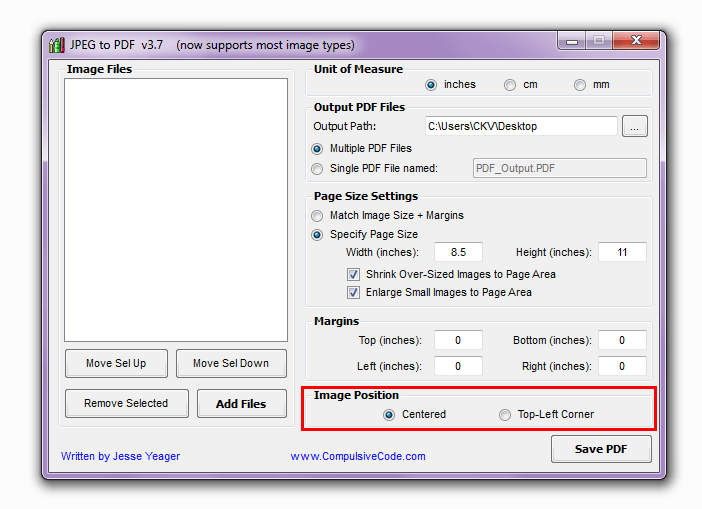
 Кроме того, файлы XCF сохраняют все изображения и уровни обработки и, таким образом, позволяют манипулировать изображением, или исходное изображение можно восстановить из них. Только по этой причине стоит конвертировать XCF в jpg. Кроме того, формат JPG является общим стандартом для изображений в сети. Это позволяет не только легко загружать файлы, но и удобно открывать их на смартфоне, особенно там, где доступная память и возможности открытия файлов наиболее ограничены. Но даже на ПК с Windows и Mac очень немногие пользователи имеют бесплатную альтернативу Photoshop GIMP. Загрузка немного запутана из-за большого количества версий, и даже в GIMP XCF придется конвертировать в jpg, если вы не хотите каждый раз открывать программу редактирования изображений для просмотра. Даже если вы работаете с GIMP, стоит не переводить вашу работу с обработки изображений, а конвертировать ее в формат jpg с помощью конвертера. Другая причина конвертировать XCF в jpg — уменьшить размер файла. Поскольку вся рабочая информация и уровни хранятся в XCF, файлы соответственно большие и громоздкие.
Кроме того, файлы XCF сохраняют все изображения и уровни обработки и, таким образом, позволяют манипулировать изображением, или исходное изображение можно восстановить из них. Только по этой причине стоит конвертировать XCF в jpg. Кроме того, формат JPG является общим стандартом для изображений в сети. Это позволяет не только легко загружать файлы, но и удобно открывать их на смартфоне, особенно там, где доступная память и возможности открытия файлов наиболее ограничены. Но даже на ПК с Windows и Mac очень немногие пользователи имеют бесплатную альтернативу Photoshop GIMP. Загрузка немного запутана из-за большого количества версий, и даже в GIMP XCF придется конвертировать в jpg, если вы не хотите каждый раз открывать программу редактирования изображений для просмотра. Даже если вы работаете с GIMP, стоит не переводить вашу работу с обработки изображений, а конвертировать ее в формат jpg с помощью конвертера. Другая причина конвертировать XCF в jpg — уменьшить размер файла. Поскольку вся рабочая информация и уровни хранятся в XCF, файлы соответственно большие и громоздкие.
 Если вы хотите быть уверены, что вы можете открыть формат файла в любое время и оптимизировать файлы для удобной отправки, вам просто нужно конвертировать XCF в jpg. Это повышает удобочитаемость файлов и в то же время предотвращает неправильное использование вашей работы.
Если вы хотите быть уверены, что вы можете открыть формат файла в любое время и оптимизировать файлы для удобной отправки, вам просто нужно конвертировать XCF в jpg. Это повышает удобочитаемость файлов и в то же время предотвращает неправильное использование вашей работы.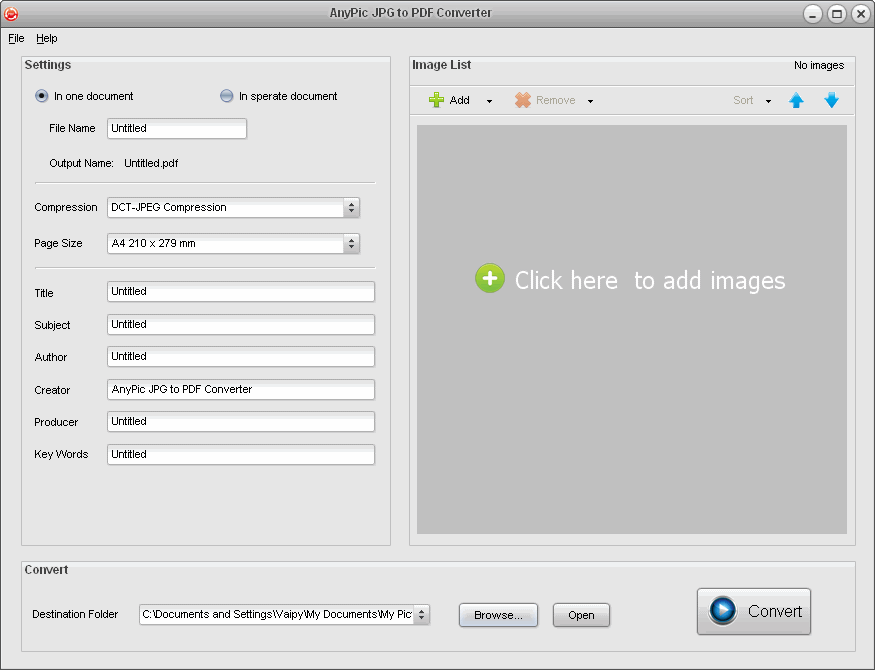 Результат будет всегда одинаково высокого качества, без водяных знаков.
Результат будет всегда одинаково высокого качества, без водяных знаков.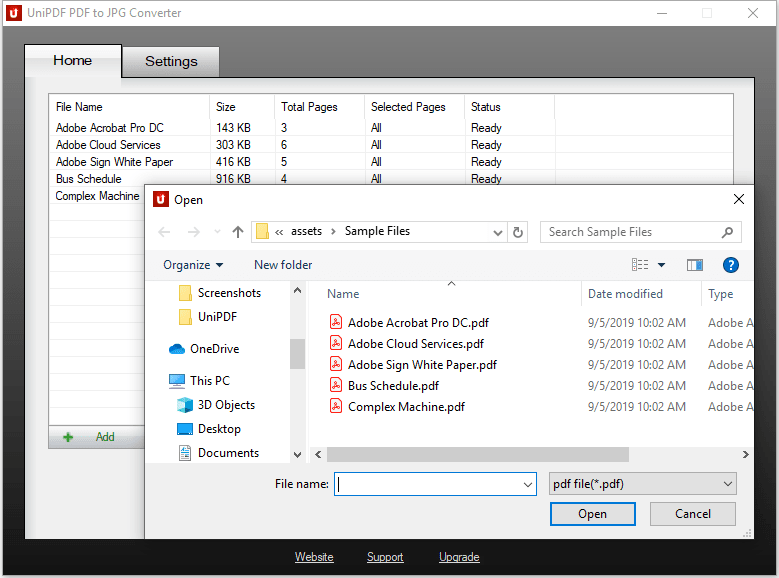

 Отличный!
Отличный! д. и перевести его на английский, арабский, чешский, немецкий, испанский, французский, итальянский, японский, португальский, русский, турецкий или китайский язык.
д. и перевести его на английский, арабский, чешский, немецкий, испанский, французский, итальянский, японский, португальский, русский, турецкий или китайский язык. Выберите целевой язык
Выберите целевой язык  Мы также можем принять цифровые фотографии вашего документа при условии, что весь документ виден и разборчив.
Мы также можем принять цифровые фотографии вашего документа при условии, что весь документ виден и разборчив.

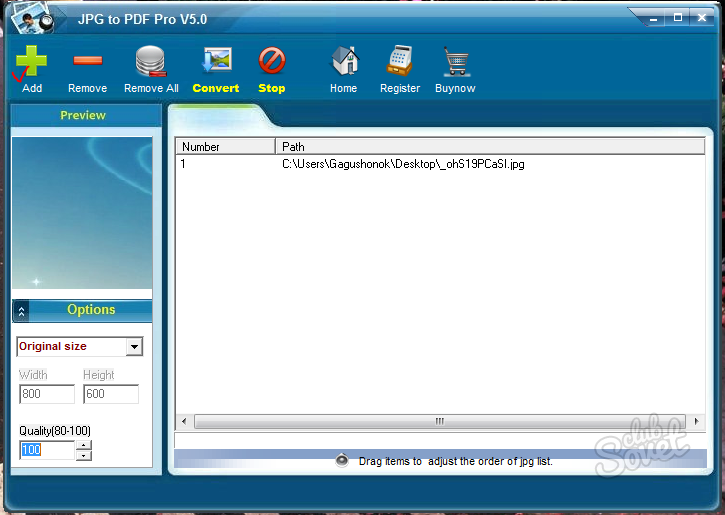
 Кроме того, вы можете использовать приложение для редактирования изображений, которые вы создаете , поворачивая и комбинируя их. Другими приложениями, которые позволяют конвертировать файлы и которые стоит попробовать, являются Free PDF to JPG Converter, JPG to PDF Converter, JPG to PDF Pro Converter.
Кроме того, вы можете использовать приложение для редактирования изображений, которые вы создаете , поворачивая и комбинируя их. Другими приложениями, которые позволяют конвертировать файлы и которые стоит попробовать, являются Free PDF to JPG Converter, JPG to PDF Converter, JPG to PDF Pro Converter. После преобразования вы можете поворачивать или комбинировать файлы изображений любым удобным для вас способом. Вы также можете персонализировать эти изображения, добавив верхний или нижний колонтитул. И последнее, но не менее важное: вы можете использовать конвертер PDF в JPG в для преобразования нескольких страниц вместо всего файла .
После преобразования вы можете поворачивать или комбинировать файлы изображений любым удобным для вас способом. Вы также можете персонализировать эти изображения, добавив верхний или нижний колонтитул. И последнее, но не менее важное: вы можете использовать конвертер PDF в JPG в для преобразования нескольких страниц вместо всего файла .

 7
7 5
5 9
9 5
5 7
7 8
8 3
3
 Наиболее популярные конвертеры — ODS в PDF (альтернатива OpenOffice для MS Excel) и ODT в PDF (альтернатива OpenOffice для MS Word).
Наиболее популярные конвертеры — ODS в PDF (альтернатива OpenOffice для MS Excel) и ODT в PDF (альтернатива OpenOffice для MS Word).

 Рабочая группа OpenOffice XML, основанная OASIS в 2002 году, программировала ODF на основе XML. В 2006 году ODF был официально представлен в качестве международного стандарта ISO/IEC 26300.
Рабочая группа OpenOffice XML, основанная OASIS в 2002 году, программировала ODF на основе XML. В 2006 году ODF был официально представлен в качестве международного стандарта ISO/IEC 26300. е. платных) приложениях.
е. платных) приложениях.
 Вы можете загружать файлы ODT размером до 15 мегабайт в программу просмотра, открывать их в Интернете, переносить в PDF и сохранять на своем устройстве.
Вы можете загружать файлы ODT размером до 15 мегабайт в программу просмотра, открывать их в Интернете, переносить в PDF и сохранять на своем устройстве. Однако оптимальное использование приложения возможно только с помощью Bluetooth-мыши, клавиатуры или планшета.
Однако оптимальное использование приложения возможно только с помощью Bluetooth-мыши, клавиатуры или планшета. № 4.28. ГДЗ Алгебра 9 класс ОГЭ Кузнецова. Помогите задать аналитически функцию.
№ 4.28. ГДЗ Алгебра 9 класс ОГЭ Кузнецова. Помогите задать аналитически функцию. (Подробнее…)
(Подробнее…) 0007 n + 1 в числителе. Все эти формы эквивалентны, и приведенная выше формулировка может быть получена из полиномиального длинного деления.
0007 n + 1 в числителе. Все эти формы эквивалентны, и приведенная выше формулировка может быть получена из полиномиального длинного деления. …
… Вместо этого мой ответ:
Вместо этого мой ответ: Подключив к формуле суммы геометрического ряда, я получаю:
Подключив к формуле суммы геометрического ряда, я получаю: Эту расширенно-десятичную форму можно записать в дробной форме, а затем преобразовать в форму геометрического ряда:
Эту расширенно-десятичную форму можно записать в дробной форме, а затем преобразовать в форму геометрического ряда: ..
.. Среднее геометрическое
Среднее геометрическое n + 93.
n + 93.
 39 MB
39 MB 61 MB
61 MB

 Как мы получаем значение 14 дней? Предполагать
почва может удерживать 2,5 дюйма доступной влаги на фут, а активная корневая зона составляет 3,3 дюйма.
ноги. Это означает, что почва сразу после полива может обеспечить 8,25 дюйма воды (2,5 дюйма на фут).
х 3,3′ корневой зоны). Но рекомендуемый уровень влажности почвы составляет 65% от нормы.
доступной влаги, которая оставляет 2,9дюймов воды для растения. Если мы используем это
значения и разделить на 0,28″/день, чистый результат для этой конкретной почвы составляет около 10 дней.
Суть такова: для максимизации выхода и производства сахара требуется довольно частая
орошение.
Как мы получаем значение 14 дней? Предполагать
почва может удерживать 2,5 дюйма доступной влаги на фут, а активная корневая зона составляет 3,3 дюйма.
ноги. Это означает, что почва сразу после полива может обеспечить 8,25 дюйма воды (2,5 дюйма на фут).
х 3,3′ корневой зоны). Но рекомендуемый уровень влажности почвы составляет 65% от нормы.
доступной влаги, которая оставляет 2,9дюймов воды для растения. Если мы используем это
значения и разделить на 0,28″/день, чистый результат для этой конкретной почвы составляет около 10 дней.
Суть такова: для максимизации выхода и производства сахара требуется довольно частая
орошение. урожая сахарной свеклы по сравнению с свеклой, выращиваемой после таких культур, как люцерна или подсолнечник.
Культуры, предпочитаемые в краткосрочном севообороте с сахарной свеклой, включают фасоль, донник,
кукуруза, крупы, горох, картофель, и если вы склонны попробовать что-то другое,
помидоры. Люцерна является подходящей культурой в долгосрочном севообороте с сахарной свеклой.
другой фактор, который, по-видимому, играет значительную роль в отношении болезней сахарной свеклы.
это возникновение деятельности, которая ранит корни. Это делает корни более уязвимыми.
к атакам бактерий и грибков.
урожая сахарной свеклы по сравнению с свеклой, выращиваемой после таких культур, как люцерна или подсолнечник.
Культуры, предпочитаемые в краткосрочном севообороте с сахарной свеклой, включают фасоль, донник,
кукуруза, крупы, горох, картофель, и если вы склонны попробовать что-то другое,
помидоры. Люцерна является подходящей культурой в долгосрочном севообороте с сахарной свеклой.
другой фактор, который, по-видимому, играет значительную роль в отношении болезней сахарной свеклы.
это возникновение деятельности, которая ранит корни. Это делает корни более уязвимыми.
к атакам бактерий и грибков. до сбора урожая. Исследования показали, что если содержание нитратов в сахарной свекле
превышает 1000 частей на миллион в течение 6 недель после сбора урожая, содержание сахара будет снижено.
Слишком большое количество азота приводит к высокой урожайности корнеплодов, сопровождающейся низким содержанием сахарозы и высоким содержанием азота.
концентрации примесей, особенно натрия и амино-н. Высокие концентрации
примесей снижают процент экстрагируемой сахарозы. Слишком мало N приводит к
высокий выход сахарозы и хорошее качество за счет выхода корней.
до сбора урожая. Исследования показали, что если содержание нитратов в сахарной свекле
превышает 1000 частей на миллион в течение 6 недель после сбора урожая, содержание сахара будет снижено.
Слишком большое количество азота приводит к высокой урожайности корнеплодов, сопровождающейся низким содержанием сахарозы и высоким содержанием азота.
концентрации примесей, особенно натрия и амино-н. Высокие концентрации
примесей снижают процент экстрагируемой сахарозы. Слишком мало N приводит к
высокий выход сахарозы и хорошее качество за счет выхода корней.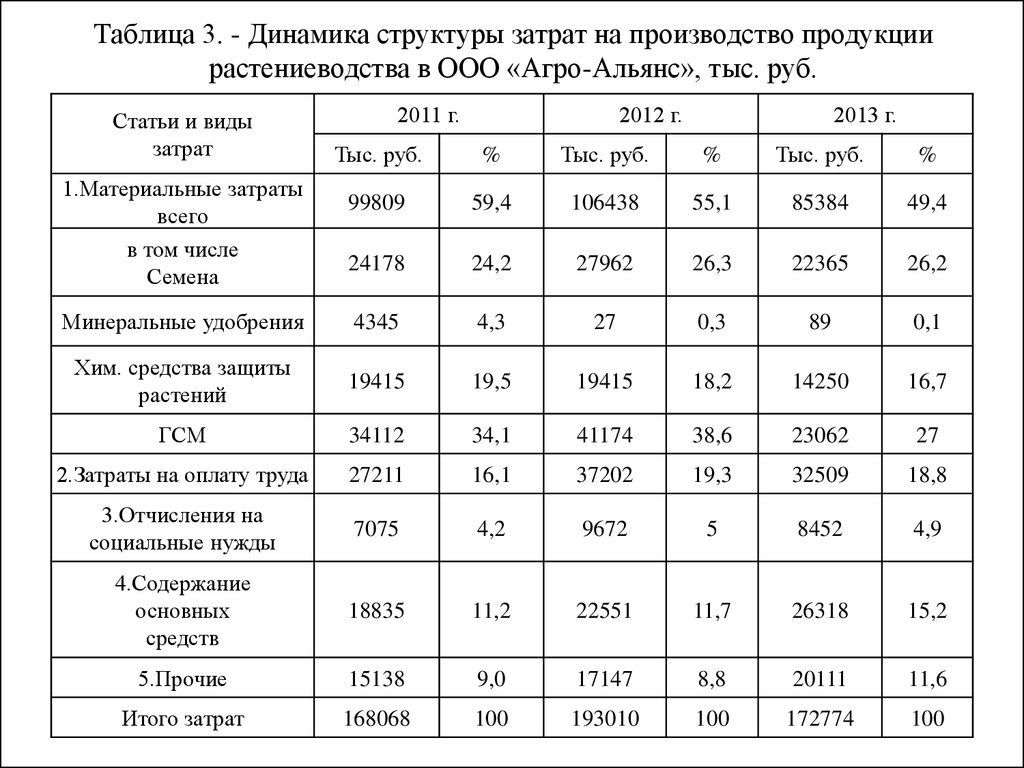 Пониженная норма азота подходит для раннего контрактного сахара
свекла. Норма азота выше рекомендуемой нормы не увеличивает выход сахарозы или валовой
доходы от сахарной свеклы, собранной в конце сезона.
Пониженная норма азота подходит для раннего контрактного сахара
свекла. Норма азота выше рекомендуемой нормы не увеличивает выход сахарозы или валовой
доходы от сахарной свеклы, собранной в конце сезона.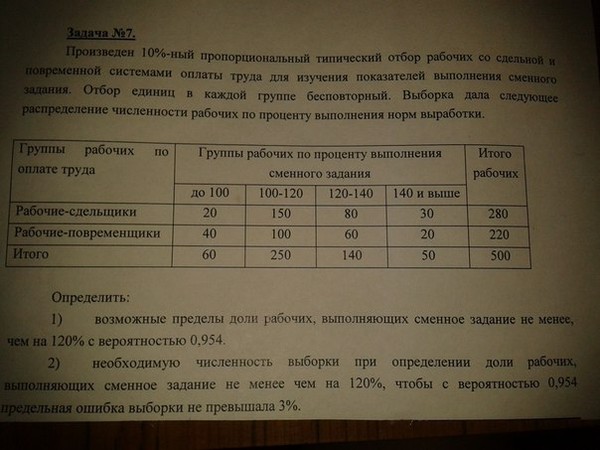 Тем не менее, время от времени оглядываться по сторонам не помешает.
В следующей таблице показаны результаты исследования, проведенного на экспериментальной станции Malheur.
в Онтарио, штат Орегон. Свекла выращивалась с междурядьями 11 дюймов и 22 дюйма с различными растениями.
интервалы внутри рядов. Результаты показали увеличение выхода, содержания сахара и экстракции.
для свеклы, выращенной в 11-дюймовых рядах, по сравнению со свеклой, выращенной в 22-дюймовых рядах. Отсюда следует, что растет
сахарной свеклы на более узких рядах может увеличить общее производство сахара.
Помимо потенциально более высоких урожаев, узкорядная сахарная свекла образует навес над
почву в начале сезона, что, возможно, делает их более конкурентоспособными с сорняками, чем
сахарной свеклы в 22-дюймовых рядах.
Тем не менее, время от времени оглядываться по сторонам не помешает.
В следующей таблице показаны результаты исследования, проведенного на экспериментальной станции Malheur.
в Онтарио, штат Орегон. Свекла выращивалась с междурядьями 11 дюймов и 22 дюйма с различными растениями.
интервалы внутри рядов. Результаты показали увеличение выхода, содержания сахара и экстракции.
для свеклы, выращенной в 11-дюймовых рядах, по сравнению со свеклой, выращенной в 22-дюймовых рядах. Отсюда следует, что растет
сахарной свеклы на более узких рядах может увеличить общее производство сахара.
Помимо потенциально более высоких урожаев, узкорядная сахарная свекла образует навес над
почву в начале сезона, что, возможно, делает их более конкурентоспособными с сорняками, чем
сахарной свеклы в 22-дюймовых рядах.
 agric.gov.ab.ca/irrigate/sugarbeet.html
agric.gov.ab.ca/irrigate/sugarbeet.html Цель статьи — выяснить причины снижения рыночной цены на продукты переработки сахарной свеклы, в частности на белый сахар, а также разработать рекомендации по оптимизации производства и реализации сахарной свеклы. Новизна исследования заключается в выявлении тенденций развития рынка сырья для производства сахара из сахарной свеклы на региональном уровне и обосновании необходимых первоочередных мер по повышению экономической эффективности в свекловодческой отрасли. В статье представлены результаты анализа уровня развития товарного рынка производителей сахара. Определены приоритетные направления увеличения объемов производства и повышения эффективности производства сахарной свеклы как основного сырья для производства белого сахара и сахара-песка; даны рекомендации по обеспечению устойчивого роста доходов от реализации корнеплодов сахарной свеклы. Практическая значимость результатов исследований заключается в возможности их использования при разработке программ развития региональных продовольственных рынков, организационно-экономических, технологических мероприятий по повышению эффективности свеклопроизводства в отдельных муниципальных районах для достижения высоких целевых показателей.
Цель статьи — выяснить причины снижения рыночной цены на продукты переработки сахарной свеклы, в частности на белый сахар, а также разработать рекомендации по оптимизации производства и реализации сахарной свеклы. Новизна исследования заключается в выявлении тенденций развития рынка сырья для производства сахара из сахарной свеклы на региональном уровне и обосновании необходимых первоочередных мер по повышению экономической эффективности в свекловодческой отрасли. В статье представлены результаты анализа уровня развития товарного рынка производителей сахара. Определены приоритетные направления увеличения объемов производства и повышения эффективности производства сахарной свеклы как основного сырья для производства белого сахара и сахара-песка; даны рекомендации по обеспечению устойчивого роста доходов от реализации корнеплодов сахарной свеклы. Практическая значимость результатов исследований заключается в возможности их использования при разработке программ развития региональных продовольственных рынков, организационно-экономических, технологических мероприятий по повышению эффективности свеклопроизводства в отдельных муниципальных районах для достижения высоких целевых показателей.
 По мнению экспертов, с учетом этой тенденции, а также растущей производительности свеклосахарной отрасли обеспечить Россию сахаром можно будет с каждым годом все меньшими урожаями сахарной свеклы. По оценкам, для обеспечения внутренних потребностей в ближайшие годы достаточно возделывания сахарной свеклы на площади 1−1,05 млн га.
По мнению экспертов, с учетом этой тенденции, а также растущей производительности свеклосахарной отрасли обеспечить Россию сахаром можно будет с каждым годом все меньшими урожаями сахарной свеклы. По оценкам, для обеспечения внутренних потребностей в ближайшие годы достаточно возделывания сахарной свеклы на площади 1−1,05 млн га. НДС (19.25 руб./кг вкл. НДС) Большинство производителей сырья и готовой продукции еще не осознали тенденции развития сегмента и продолжают наращивать объемы, рассчитывая при этом на прежнюю рентабельность производства, но ожидать этого в ближайшее время не следует. Таким образом, перед производителями сахарной свеклы-сырца стоит задача повышения эффективности отрасли в условиях негативной динамики спроса и отпускных цен на готовую продукцию.
НДС (19.25 руб./кг вкл. НДС) Большинство производителей сырья и готовой продукции еще не осознали тенденции развития сегмента и продолжают наращивать объемы, рассчитывая при этом на прежнюю рентабельность производства, но ожидать этого в ближайшее время не следует. Таким образом, перед производителями сахарной свеклы-сырца стоит задача повышения эффективности отрасли в условиях негативной динамики спроса и отпускных цен на готовую продукцию.
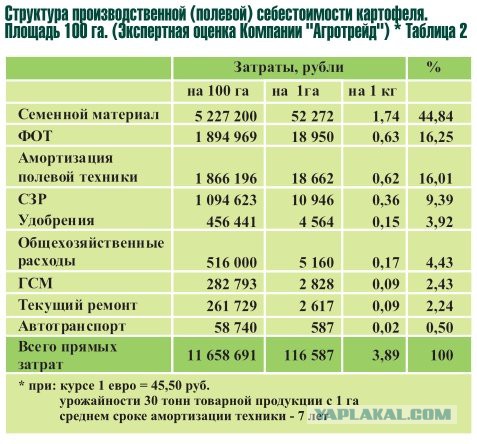 Перепроизводство сахара в стране уже привело к падению цен на сахар в 2019 г. К середине июля оптовые цены снизились до 26,6 руб./кг (Краснодар с НДС) против 32 руб./кг на начало октября 2018 г. когда был зафиксирован максимум сезона (2018/19). За период 2017–2020 гг. средние цены производителей на сахар свекловичный или тростниковый и сахарозу химически чистую в твердом состоянии без вкусоароматических и красящих добавок снизились на 35,9 %, с 28 999,8 руб./т до 18 572,0 руб./т. Наибольшее падение средних цен производителей произошло в 2020 году, тогда темп роста составил минус 29,3 %.
Перепроизводство сахара в стране уже привело к падению цен на сахар в 2019 г. К середине июля оптовые цены снизились до 26,6 руб./кг (Краснодар с НДС) против 32 руб./кг на начало октября 2018 г. когда был зафиксирован максимум сезона (2018/19). За период 2017–2020 гг. средние цены производителей на сахар свекловичный или тростниковый и сахарозу химически чистую в твердом состоянии без вкусоароматических и красящих добавок снизились на 35,9 %, с 28 999,8 руб./т до 18 572,0 руб./т. Наибольшее падение средних цен производителей произошло в 2020 году, тогда темп роста составил минус 29,3 %.
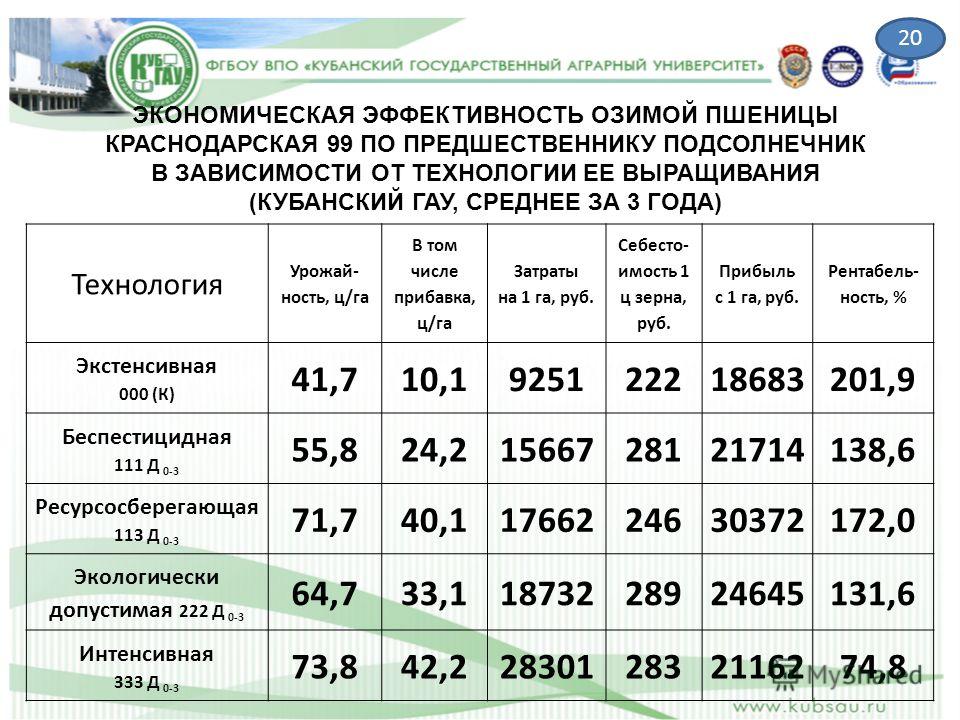 В то же время в ряде районов удалось производить сахарную свеклу при снижении затрат на единицу продукции [7, 8]. Например, в Апастовском районе себестоимость корнеплодов сахарной свеклы снизилась на 12,8 %, в Кайбитском и Нижнекамском районах на 35,5–35,1 %. В 2019 г. в 7 из 12 муниципальных районов себестоимость единицы продукции была ниже по сравнению с 2015 г. (табл. 2).
В то же время в ряде районов удалось производить сахарную свеклу при снижении затрат на единицу продукции [7, 8]. Например, в Апастовском районе себестоимость корнеплодов сахарной свеклы снизилась на 12,8 %, в Кайбитском и Нижнекамском районах на 35,5–35,1 %. В 2019 г. в 7 из 12 муниципальных районов себестоимость единицы продукции была ниже по сравнению с 2015 г. (табл. 2). д.).
д.).
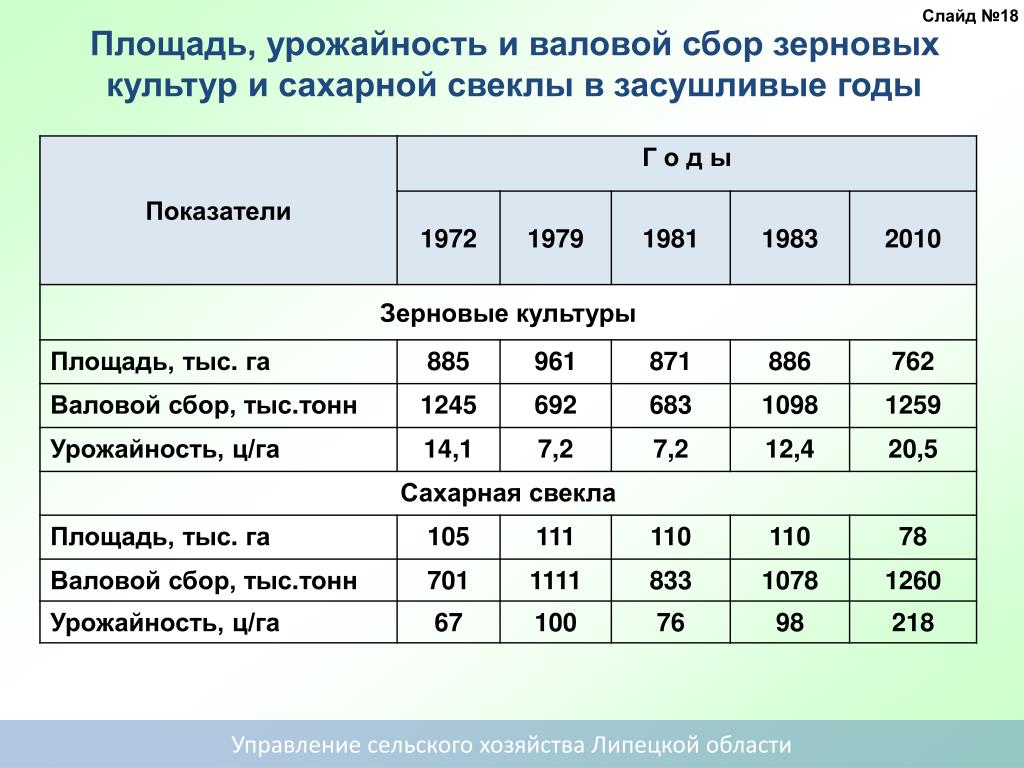
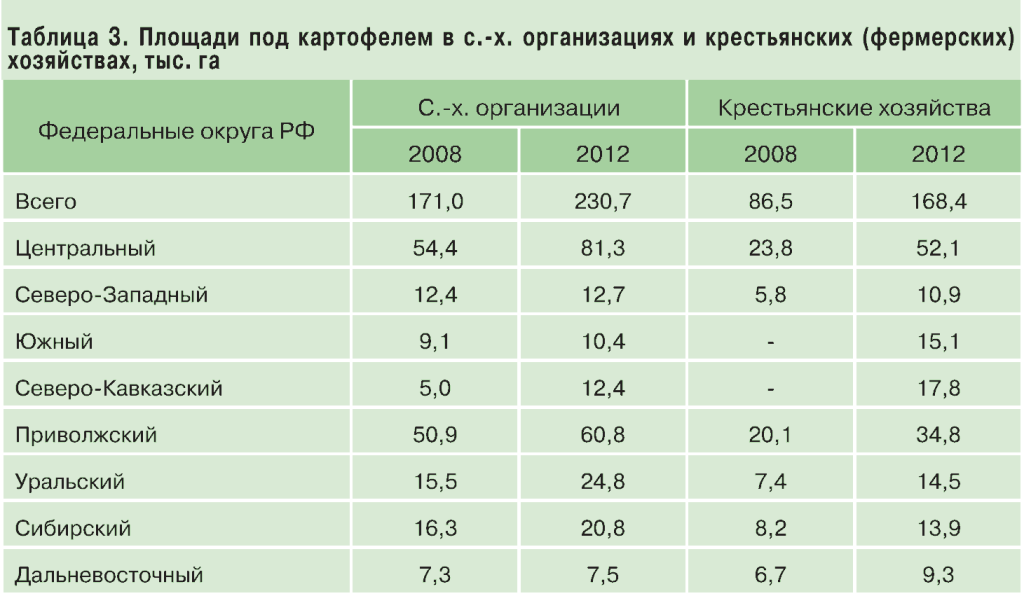 Одни страны (Ирландия) в целом полностью сокращают посевные площади сахарной свеклы, а ряд других (Италия, Испания, Греция, Чехия и Дания) значительно сокращают посевные площади сахарной свеклы.
Одни страны (Ирландия) в целом полностью сокращают посевные площади сахарной свеклы, а ряд других (Италия, Испания, Греция, Чехия и Дания) значительно сокращают посевные площади сахарной свеклы.

 Ситдикова, И. Гайнутдинов, Д. Файзрахманов, Ф. Мухаметгалиев, Бюлл. Казанского государственного аграрного фонда. ун-т, 10(3(37)), 46–51 (2015) [Перекрестная ссылка]
[Google Scholar]
Ситдикова, И. Гайнутдинов, Д. Файзрахманов, Ф. Мухаметгалиев, Бюлл. Казанского государственного аграрного фонда. ун-т, 10(3(37)), 46–51 (2015) [Перекрестная ссылка]
[Google Scholar] Михайлова, А. Николаев, Актуальные научно-технические средства и проблемы сельского хозяйства: Матер. III Национальной науч. и Практ. конф. (Кемерово, 30 декабря 2019 г.)
[Google Scholar]
Михайлова, А. Николаев, Актуальные научно-технические средства и проблемы сельского хозяйства: Матер. III Национальной науч. и Практ. конф. (Кемерово, 30 декабря 2019 г.)
[Google Scholar] Авхадиев, Бюлл. Казанского государственного аграрного фонда. ун-т, 6(1(19)), 5–7 (2011)
[Google Scholar]
Авхадиев, Бюлл. Казанского государственного аграрного фонда. ун-т, 6(1(19)), 5–7 (2011)
[Google Scholar]