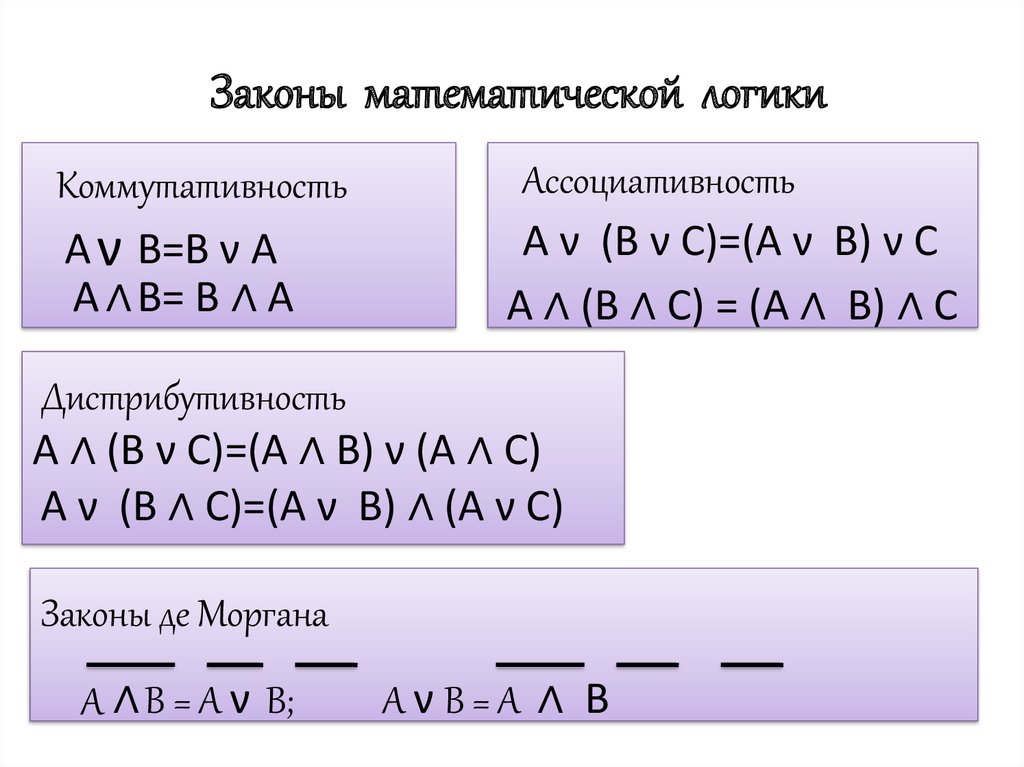
Онлайн калькулятор: Объем геометрических фигур
УчебаМатематикаГеометрия
Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид).
Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.
Объем куба
Размеры куба
Формула:
Объем куба
Сторона (H)
Длина ребра куба (H)
Точность вычисления
Знаков после запятой: 5
Объем
Объем прямоугольной призмы
Размеры прямоугольной призмы
Формула:
Объем прямоугольной призмы
Ширина (W)
Высота (H)
Высота (H)
Длина (L)
Точность вычисления
Знаков после запятой: 5
Объем
Объем пирамиды
Размеры пирамиды
Формула:
Объем пирамиды
Площадь основания (Sb)
Площадь основания
Высота (H)
Высота (H)
Точность вычисления
Знаков после запятой: 5
Объем
Объем усеченной пирамиды
Размеры усеченной пирамиды
Формула:
Объем усеченной пирамиды
Площадь первого основания (Sb1)
Площадь второго основания (Sb2)
Высота (H)
Высота (H)
Точность вычисления
Знаков после запятой: 5
Объем
Объем конуса
Размеры конуса
Формула:
Объем конуса
Радиус (R)
Высота (H)
Высота (H)
Точность вычисления
Знаков после запятой: 5
Объем
Объем цилиндра
Размеры цилиндра
Formula:
Объем цилиндра
Высота (H)
Высота (H)
Радиус (R)
Точность вычисления
Знаков после запятой: 5
Объем
Объем сферы
Размеры сферы
Формула:
Объем сферы
Радиус (R)
Точность вычисления
Знаков после запятой: 5
Объем
Объем эллипсоида
Размеры эллипсоида
Формула:
Объем эллипсоида
Радиус 1 (R1)
Радиус 2 (R2)
Радиус (R3)
Точность вычисления
Знаков после запятой: 5
Объем
Объем тороида
Размеры тороида
Формула:
Объем тора
Радиус 1 (R1)
Радиус 2 (R2)
Точность вычисления
Знаков после запятой: 5
Объем
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Куб
- • Конус
- • Тор
- • Объем сегмента цилиндра
- • Объем жидкости в прямоугольном баке под наклоном
- • Раздел: Геометрия ( 97 калькуляторов )
#геометрия #объем Геометрия Инженерные конус куб Математика объем пирамида прямоугольная призма сфера тор тороид усеченная пирамида цилиндр эллипсоид
PLANETCALC, Объем геометрических фигур
Anton2020-11-03 14:19:26
по 4 сторонам и тд
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
В публикации представлены онлайн-калькуляторы и формулы для расчета площади трапеции по разным исходным данным: через длины оснований и высоту, по всем сторонам, через диагонали и угол между ними.
- Расчет площади
- 1. Через основания и высоту
- 2. По 4 сторонам (формула Герона)
- 3. Через диагонали и угол между ними
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через основания и высоту
Формула расчета
2. По 4 сторонам (формула Герона)
Формула расчета
p – полупериметр трапеции, считается так:
3. Через диагонали и угол между ними
Формулы расчета
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Калькулятор объема трапециевидной призмы
Создано Wei Bin Loo
Отредактировано Анна Щепанек, доктор философии и Стивен Вудинг
Последнее обновление: 09 февраля 2023 г.
- Что такое объем трехмерного объекта?
- Как найти объем трапециевидной призмы?
- Часто задаваемые вопросы
С помощью этого калькулятора объема трапециевидной призмы мы стремимся помочь вам рассчитать объем трапециевидной призмы . Вы можете проверить наш калькулятор трапеции и калькулятор площади трапеции, чтобы понять больше по этой теме.
Мы написали эту статью, чтобы помочь вам понять что такое объем трапециевидной призмы и как найти объем трапециевидной призмы . Мы также продемонстрируем несколько примеров, которые помогут вам понять формулу объема трапециевидной призмы.
Что такое объем трехмерного объекта?
Объем 3D-объекта – это объем пространства, занимаемый 3D-объектом. Чем больше объем, тем больше места занимает объект. Одним из способов измерения объема является измерение количества воды, которое вытесняет объект, когда его опускают в воду.
Пожалуйста, ознакомьтесь с нашим калькулятором объема, чтобы лучше понять эту тему.
Как найти объем трапециевидной призмы?
Трапециевидная призмаЧтобы понять формулу объема трапециевидной призмы, рассмотрим пример ниже:
- Длина короткого основания (b): 5 м
- Длина длинной базы (B): 5 м
- Длина (ℓ): 5 м
- Высота (в): 3 м
Определите длину короткой базы (b).
Первым шагом является определение длины короткого основания b трапециевидной призмы. Для нашего примера b равно 5 м .
Определите длину длинной базы (B).
Следующим шагом является определение длины длинного основания B трапециевидной призмы. Для нашего примера b равно 5 м .
Рассчитать длину (ℓ).
Теперь вам нужно вычислить длину ℓ трапециевидной призмы.
 л этой трапециевидной призмы составляет 5 м .
л этой трапециевидной призмы составляет 5 м .Определить высоту (h).
Кроме того, высота h трапециевидной призмы равна 3 м .
Вычислите объем трапециевидной призмы.
Последним шагом является расчет объема трапециевидной призмы по формуле:
((б + В) / 2) × ч × л
Таким образом, объем трапециевидной призмы равен ((5 м + 5 м)/2) × 5 м × 3 м = 75 м³ .
Часто задаваемые вопросы
Может ли громкость быть отрицательной?
Нет , объем не может быть отрицательным. Это потому, что нулевого и отрицательного объема просто не существует. Объект не может иметь нулевой или отрицательный объем.
Каков объем трапециевидной призмы со всеми сторонами 1 м?
Объем этой трапециевидной призмы будет 1 м³ . Вы можете рассчитать его по следующей формуле:
Вы можете рассчитать его по следующей формуле:
объем = ((длина короткого основания + длина длинного основания) / 2) × высота × длина .
Как рассчитать объем трапециевидной призмы?
Объем трапециевидной призмы можно рассчитать за пять шагов:
Определить длину короткой базы (b)
Определить длину длинной базы (B)
Рассчитать длину (ℓ)
Определить высоту (h)
Примените формулу объема трапециевидной призмы :
((б + В) / 2) × ч × л
Что такое боковая область для трехмерного объекта?
Боковая площадь трехмерного объекта представляет собой сумму площадей всех сторон трехмерного объекта, кроме основания и вершины .
Вэй Бин Лоо
Высота
Длина
Длинная база (B)
Короткая база (b)
Объем
Посмотреть 23 похожих калькулятора 3d геометрии
Объем трапециевидной призмы
LearnPracticeDownload
Объем трапециевидной призмы — это емкость призмы. Его также можно определить как пространство внутри трапециевидной призмы. Призма имеет конгруэнтные многоугольники на верхней и нижней гранях, а основания одинаковы. Боковые грани призмы представляют собой параллелограммы, которые называются боковыми гранями. Призму можно назвать по форме двух одинаковых граней на ее конце. Трапециевидная призма представляет собой трехмерное тело, имеющее два основания трапеции/трапеции внизу и вверху. Форма боковых граней/боковых граней трапециевидной призмы – параллелограмм.
Его также можно определить как пространство внутри трапециевидной призмы. Призма имеет конгруэнтные многоугольники на верхней и нижней гранях, а основания одинаковы. Боковые грани призмы представляют собой параллелограммы, которые называются боковыми гранями. Призму можно назвать по форме двух одинаковых граней на ее конце. Трапециевидная призма представляет собой трехмерное тело, имеющее два основания трапеции/трапеции внизу и вверху. Форма боковых граней/боковых граней трапециевидной призмы – параллелограмм.
| 1. | Каков объем трапециевидной призмы? |
| 2. | Объем трапециевидной призмы Формула |
| 3. | Как рассчитать объем трапециевидной призмы? |
| 4. | Часто задаваемые вопросы об объеме трапециевидной призмы |
Каков объем трапециевидной призмы?
Объем трапециевидной призмы – это пространство внутри нее. Трапециевидная призма представляет собой трехмерную фигуру с двумя трапециевидными основаниями и четырьмя гранями в виде параллелограмма. Призма представляет собой многогранник с равными многоугольниками на верхней и нижней гранях и имеет одинаковые основания. Трапециевидные призмы бывают двух видов: косые и прямые. У косой трапециевидной призмы боковые грани — параллелограммы, а у правильной трапециевидной призмы — прямоугольники. В общем случае трапециевидная призма означает правильную трапециевидную призму. Следовательно, боковые грани прямоугольники. Таким образом, у трапециевидной призмы всего 6 граней, 12 ребер и 8 вершин. Два основания имеют форму трапеции или трапеции, которые конгруэнтны друг другу. Он имеет
Трапециевидная призма представляет собой трехмерную фигуру с двумя трапециевидными основаниями и четырьмя гранями в виде параллелограмма. Призма представляет собой многогранник с равными многоугольниками на верхней и нижней гранях и имеет одинаковые основания. Трапециевидные призмы бывают двух видов: косые и прямые. У косой трапециевидной призмы боковые грани — параллелограммы, а у правильной трапециевидной призмы — прямоугольники. В общем случае трапециевидная призма означает правильную трапециевидную призму. Следовательно, боковые грани прямоугольники. Таким образом, у трапециевидной призмы всего 6 граней, 12 ребер и 8 вершин. Два основания имеют форму трапеции или трапеции, которые конгруэнтны друг другу. Он имеет
- 6 сторон
- 12 кромок
- 8 вершин
- 4 стороны: прямоугольник
- Трапеция/трапеция в качестве основания снизу и сверху
Объем трапециевидной призмы Формула
Объем трапециевидной призмы — вместимость призмы (или) объем трапециевидной призмы — пространство внутри нее. Измеряется в кубических единицах, таких как мм 3 , см 3 , 3 и т. д. Мы увидим формулы для расчета объема трапециевидной призмы. Объем призмы можно получить, умножив площадь ее основания на общую высоту призмы. т. е. объем призмы = площадь основания × высота призмы. Мы также будем использовать эту формулу для расчета объема трапециевидной призмы. Рассмотрим трапециевидную призму, две параллельные стороны основания которой равны \(b_1\) и \(b_2\), высота равна ‘h’, а длина призмы равна L. Мы знаем, что основание трапециевидная призма — это трапеция/трапеция. Таким образом,
Измеряется в кубических единицах, таких как мм 3 , см 3 , 3 и т. д. Мы увидим формулы для расчета объема трапециевидной призмы. Объем призмы можно получить, умножив площадь ее основания на общую высоту призмы. т. е. объем призмы = площадь основания × высота призмы. Мы также будем использовать эту формулу для расчета объема трапециевидной призмы. Рассмотрим трапециевидную призму, две параллельные стороны основания которой равны \(b_1\) и \(b_2\), высота равна ‘h’, а длина призмы равна L. Мы знаем, что основание трапециевидная призма — это трапеция/трапеция. Таким образом,
Площадь основания (площадь трапеции) = \(\dfrac{1}{2}{(b_{1} + b_{2})× h }\)
Теперь, используя объем призмы формула (как указано выше),
Объем трапециевидной призмы = площадь основания × длина = \(\dfrac{1}{2}{(b_{1} + b_{2})×h}×L\)
Как рассчитать объем трапециевидной призмы?
Ниже приведены шаги для расчета объема трапециевидной призмы. Убедитесь, что все измерения выполнены в одних и тех же единицах. Обратитесь к следующему примеру.
Убедитесь, что все измерения выполнены в одних и тех же единицах. Обратитесь к следующему примеру.
- Шаг 1: Определите, что параллельные стороны основания (трапеции) равны \(b_1\) и \(b_2\), а перпендикулярное расстояние между ними равно \(h\), и найдите площадь трапеции, используя формула:
Площадь трапеции = \(\dfrac{1}{2}{(b_{1} + b_{2})× h}\) - Шаг 2: Определите его высоту/длину призмы (расстояние по вертикали между двумя основаниями).
- Шаг 3: Умножьте площадь основания, полученную на шаге 1, и высоту, полученную на шаге 2, чтобы найти объем.
Примеры объема трапециевидной призмы
Пример 1: Найдите объем трапециевидной призмы заданных размеров.
Решение:
На приведенном выше рисунке, Учитывая, что
Основание 1 (\(b_1\)) = 6 дюймов, основание (\(b_2\)) = 20 дюймов
Высота основания трапеции = 12 в
Длина трапеции = 17 в
Площадь трапеции/трапеции = \(\dfrac{1}{2}{(b_{1} + b_{2})× h}\)
⇒ A = \(\dfrac{1}{2}\) (6 + 20) × 12
⇒ А = 13 × 12
⇒ a = 156 в 2Как мы знаем, объем трапециевидной призмы = область × общая длина трапеции
⇒ 156 × 17
⇒ 2652 в 3
.
 трапецеидальная призма равна 2652 в 3 .
трапецеидальная призма равна 2652 в 3 .Пример 2: Рассчитайте объем трапециевидной призмы, учитывая, что высота основания трапеции 5 см, а длины ее параллельных сторон 14 см и 10 см, длина призмы 6 см.
Решение:
На приведенном выше рисунке Учитывая, что
Основание 1 (\(b_1\)) = 14 см, основание (\(b_2\)) = 10 см
Высота основания трапеции (h ) = 5 см
Общая длина трапеции = 6 см
Площадь трапеции/трапеции = \(\dfrac{1}{2}{(b_{1} + b_{2})× h }\)
⇒ А = (1/2) (14 + 10 ) × 5
⇒ А = 12 × 5
⇒ A = 60 см 2Как мы знаем, объем трапециевидной призмы = площадь × длина трапеции
объем = 60 × 6 = 360 см 3
Ответ : Объем трапециевидной призмы равен 360 см 3 .
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
С Cuemath вы будете учиться визуально и будете удивлены результатами.
Запись на бесплатный пробный урок
Практические вопросы по объему трапециевидной призмы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об объеме трапециевидной призмы
Имеет ли трапециевидная призма объем?
Призма представляет собой трехмерное твердое тело. Трехмерное твердое тело имеет внутри себя пространство. Объем объясняется как пространство внутри объекта. Таким образом, трапециевидная призма имеет объем, поскольку представляет собой трехмерную форму и измеряется в кубических единицах.
Что вы подразумеваете под объемом трапециевидной призмы?
Объем трапециевидной призмы — вместимость призмы. Формула объема трапециевидной призмы представляет собой площадь основания × высоту призмы в кубических единицах.
По какой формуле найти объем трапециевидной призмы?
Объем трапециевидной призмы равен произведению площади основания на высоту призмы в кубических единицах.

 л этой трапециевидной призмы составляет 5 м .
л этой трапециевидной призмы составляет 5 м . трапецеидальная призма равна 2652 в 3 .
трапецеидальная призма равна 2652 в 3 . Например, возьмём любых два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а, число 3 место b
Например, возьмём любых два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а, число 3 место b
 Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом:
Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом: Найти значение выражения 1 × 2 × 3 × 4
Найти значение выражения 1 × 2 × 3 × 4 Начало у него выглядит так: (a + b) × c.
Начало у него выглядит так: (a + b) × c. 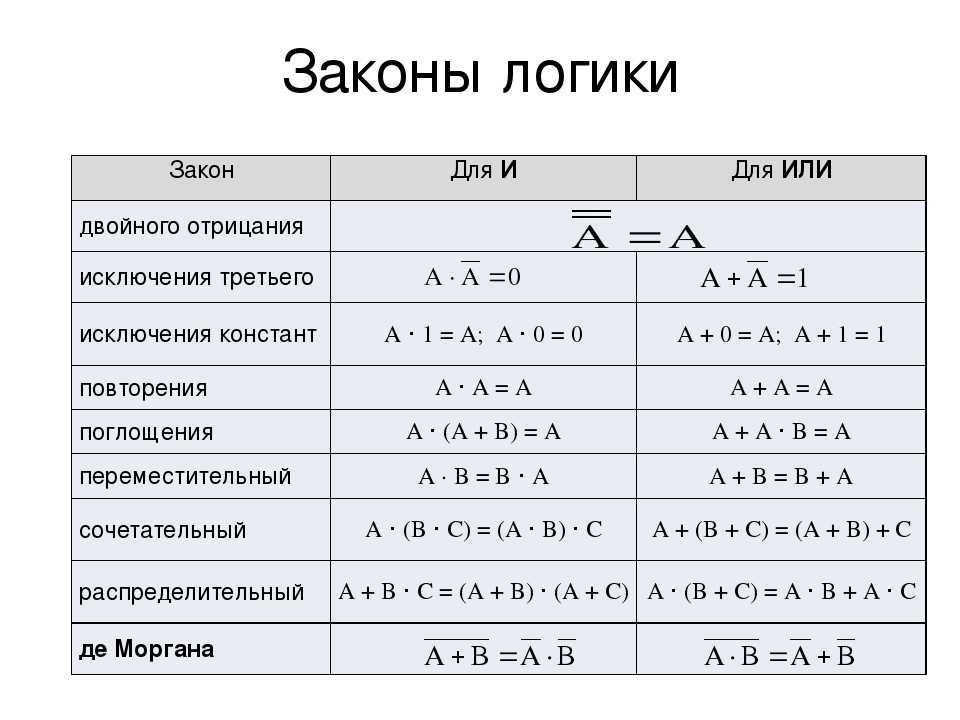 Найти значение выражения 6 × (5 + 2)
Найти значение выражения 6 × (5 + 2)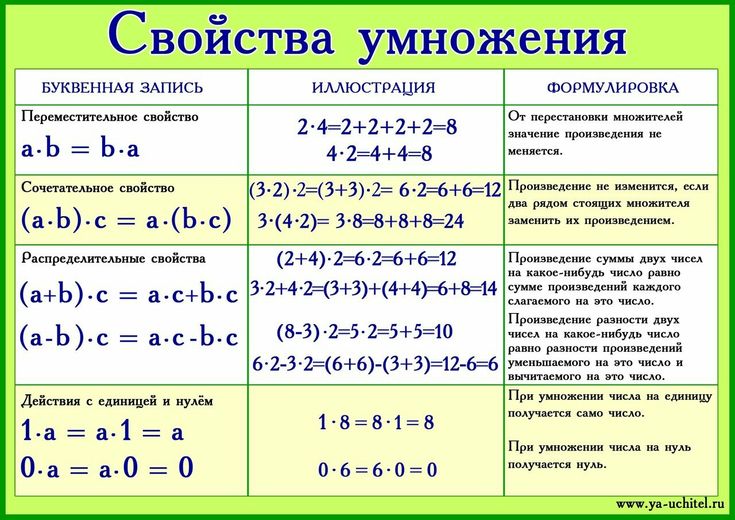 Найдите значение выражения, используя распределительный закон умножения:
Найдите значение выражения, используя распределительный закон умножения: ru
ru


 Таким образом, если множимое (a + b) и множитель c поменять местами, то получим выражение c×(a+b).
Таким образом, если множимое (a + b) и множитель c поменять местами, то получим выражение c×(a+b).  Их нам хватит для дальнейшего изучения математики.
Их нам хватит для дальнейшего изучения математики. Например, возьмем любые два числа. Пусть a = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3. Эти значения войдут в основное выражение a + b = b + a и подставят там, где это необходимо. Номер 2 будет заменен на a, номер 3 будет заменен на b
Например, возьмем любые два числа. Пусть a = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3. Эти значения войдут в основное выражение a + b = b + a и подставят там, где это необходимо. Номер 2 будет заменен на a, номер 3 будет заменен на b
 Найдите значение выражения 1 × 2 × 3 × 4
Найдите значение выражения 1 × 2 × 3 × 4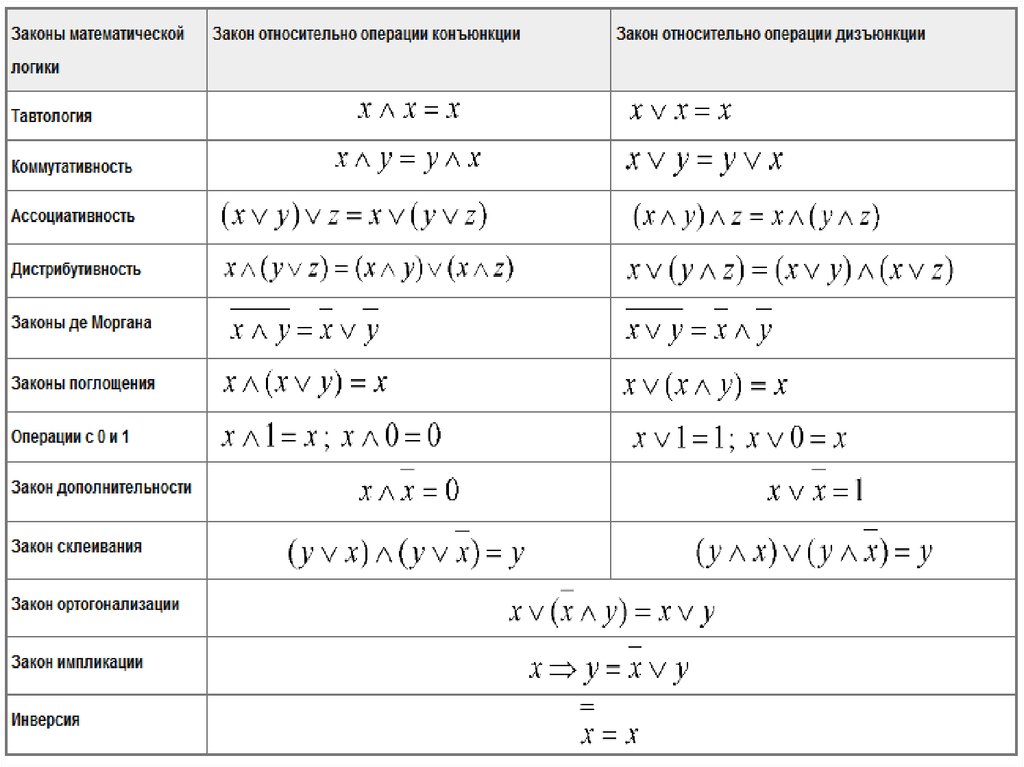 Для этого умножьте каждое слагаемое в скобках на 2, затем сложите результаты:
Для этого умножьте каждое слагаемое в скобках на 2, затем сложите результаты: Затем мы умножаем переменную c на сумму (a + b). Чтобы сделать это умножение, мы применяем распределительный закон умножения. В этом случае переменная c должна быть умножена на каждое слагаемое в скобках:
Затем мы умножаем переменную c на сумму (a + b). Чтобы сделать это умножение, мы применяем распределительный закон умножения. В этом случае переменная c должна быть умножена на каждое слагаемое в скобках: Вычислите 7 × (3 — 2)
Вычислите 7 × (3 — 2) Найдите значение выражения, используя распределительный закон умножения:
Найдите значение выражения, используя распределительный закон умножения: .. ?
.. ?


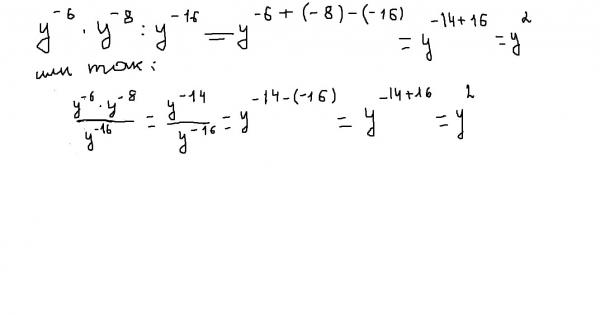
 2
2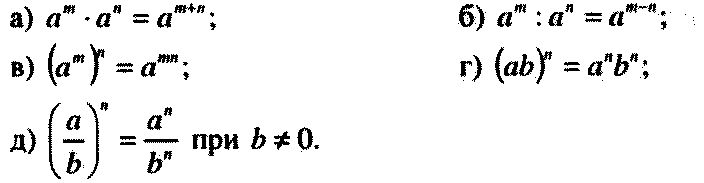
 Найдите его объем.
Найдите его объем.

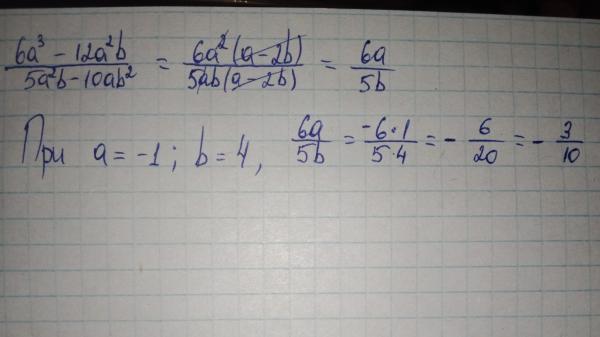 Алгебраические функции — это функции, которые
могут быть выражены с помощью арифметических операций и значения которых либо рациональны, либо являются корнем
Рациональное число. Теперь мы будем иметь дело с трансцендентными функциями. трансцендентный
функции возвращают значения, которые не могут быть выражены в виде рациональных чисел или корней рациональных чисел.
числа.
Алгебраические функции — это функции, которые
могут быть выражены с помощью арифметических операций и значения которых либо рациональны, либо являются корнем
Рациональное число. Теперь мы будем иметь дело с трансцендентными функциями. трансцендентный
функции возвращают значения, которые не могут быть выражены в виде рациональных чисел или корней рациональных чисел.
числа. Если а=1,
то независимо от того, что такое x, значение f(x) равно 1. Это довольно скучная функция, и она определенно
не один в один.
Если а=1,
то независимо от того, что такое x, значение f(x) равно 1. Это довольно скучная функция, и она определенно
не один в один. Мы также
известно, что когда мы возводим основание в отрицательную степень,
один результат состоит в том, что берется обратное число. Так,
если бы мы построили график y=2 -x , график будет
отражение относительно оси Y y = 2 x , и функция будет
быть эквивалентным y=(1/2) x .
Мы также
известно, что когда мы возводим основание в отрицательную степень,
один результат состоит в том, что берется обратное число. Так,
если бы мы построили график y=2 -x , график будет
отражение относительно оси Y y = 2 x , и функция будет
быть эквивалентным y=(1/2) x .
 Исчисление — это алгебра с понятием предела. Люди всегда
есть этот страх исчисления, что я не могу понять. Сам расчет несложный. Причина
люди не преуспевают в вычислениях не из-за вычислений, а потому что они плохие
по алгебре.
Исчисление — это алгебра с понятием предела. Люди всегда
есть этот страх исчисления, что я не могу понять. Сам расчет несложный. Причина
люди не преуспевают в вычислениях не из-за вычислений, а потому что они плохие
по алгебре.
 Формула
Показанная мной выше формула немного отличается от формулы в книге, но согласуется
с формулой, которую вы будете использовать, если пойдете
к конечной математике (Math 160). В конечной математике есть
целую главу о финансах и соответствующих формулах.
Формула
Показанная мной выше формула немного отличается от формулы в книге, но согласуется
с формулой, которую вы будете использовать, если пойдете
к конечной математике (Math 160). В конечной математике есть
целую главу о финансах и соответствующих формулах.

 420.1-19.
420.1-19.
 Для обеспечения лёгкости подъёмных работ и переноса изделия снабжаются строповочными отверстиями или монтажными петлями. Каждое изделие из номенклатурного ряда обладает своими характеристиками, однако общим для всех них является предел огнестойкости, равный трём часам.
Для обеспечения лёгкости подъёмных работ и переноса изделия снабжаются строповочными отверстиями или монтажными петлями. Каждое изделие из номенклатурного ряда обладает своими характеристиками, однако общим для всех них является предел огнестойкости, равный трём часам.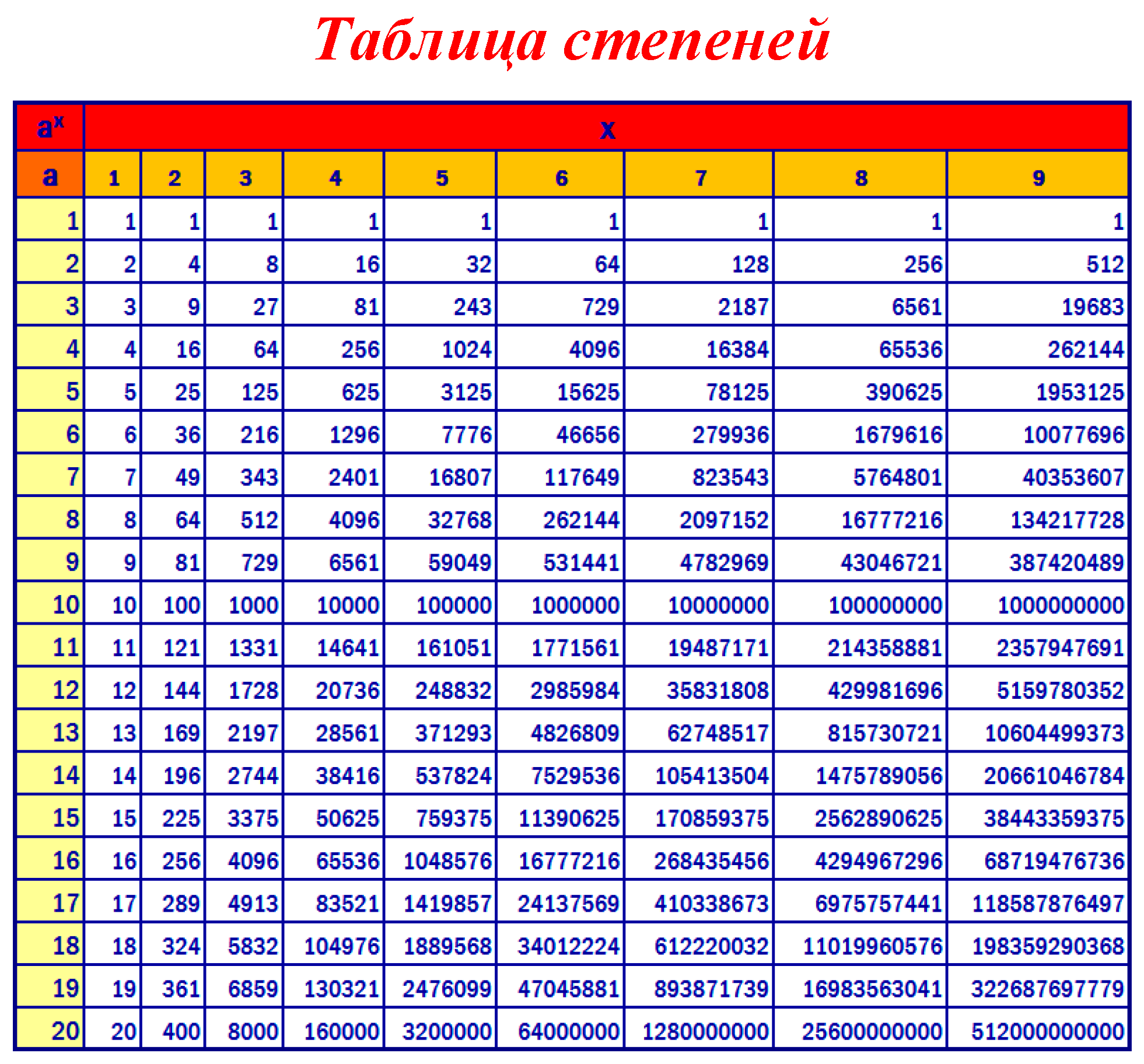 Маркировка всегда должна свободно просматриваться.
Маркировка всегда должна свободно просматриваться. Это выражение можно прочитать как «b в степени n». Термин мощность может также относиться к результату выражения.
Это выражение можно прочитать как «b в степени n». Термин мощность может также относиться к результату выражения.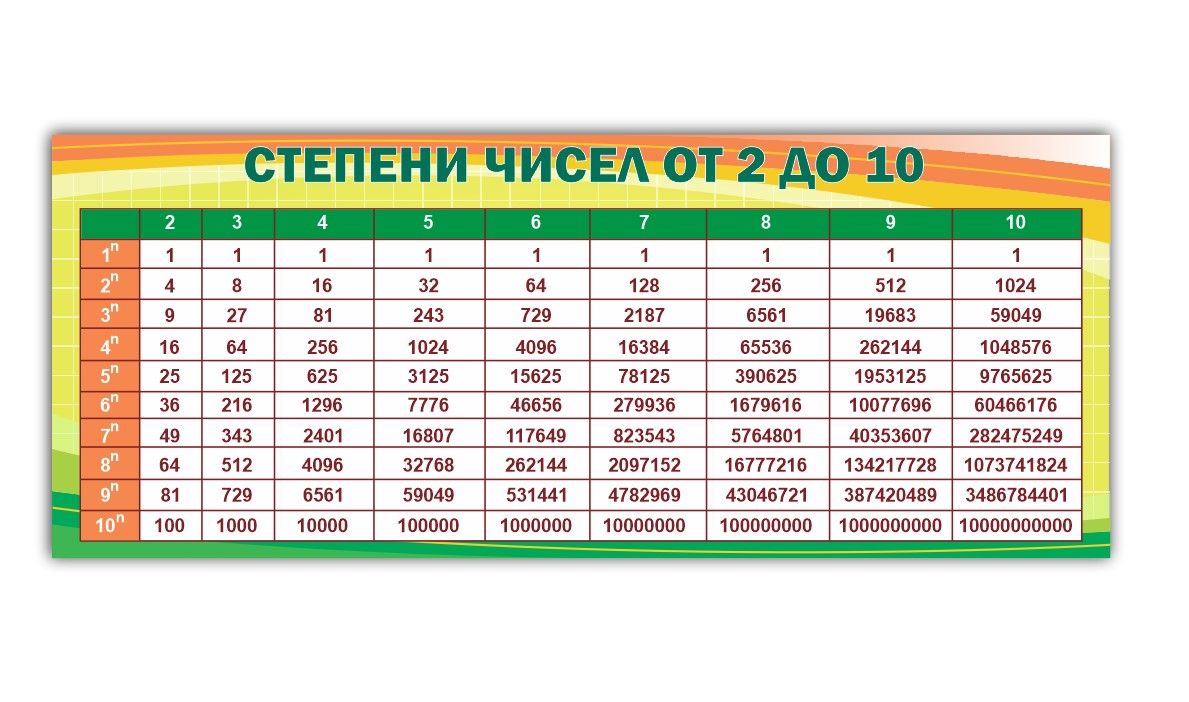 Это верно и для алгебраических выражений.
Это верно и для алгебраических выражений.

 Остальные участвуют в выборе
рационального метода решения неравенства. Записывают решение в тетрадь.
Остальные участвуют в выборе
рационального метода решения неравенства. Записывают решение в тетрадь.








 Проверить знания, умения их применять для выполнения учащимися:
Проверить знания, умения их применять для выполнения учащимися:  Решите рациональное неравенство: а) 2х2 – 3х – 9 ;
Решите рациональное неравенство: а) 2х2 – 3х – 9 ;
 предварительный просмотр
предварительный просмотр  Множественный выбор
Множественный выбор Множественный выбор
Множественный выбор Множественный выбор
Множественный выбор 2+3}{x-2}x+x−210=x−2×2+3 92+3}{x-2}x+x−210=x−2×2+3
2+3}{x-2}x+x−210=x−2×2+3 92+3}{x-2}x+x−210=x−2×2+3  Если они начнут работать в 10 утра, когда они закончат?
Если они начнут работать в 10 утра, когда они закончат? {2}+bх+с=0[/латекс], где 9{2}+x — 6=0[/latex] имеет стандартную форму.
{2}+bх+с=0[/латекс], где 9{2}+x — 6=0[/latex] имеет стандартную форму. Используйте числа именно так, как они есть. Другими словами, если эти два числа равны 1 и [латекс]-2[/латекс], множители будут [латекс]\влево(х+1\вправо)\влево(х — 2\вправо)[/латекс]. 9{2}+bx+c=0[/latex], умножьте [latex]a\cdot c[/latex].
Используйте числа именно так, как они есть. Другими словами, если эти два числа равны 1 и [латекс]-2[/латекс], множители будут [латекс]\влево(х+1\вправо)\влево(х — 2\вправо)[/латекс]. 9{2}+bx+c=0[/latex], умножьте [latex]a\cdot c[/latex]. Однако не все квадратные уравнения могут быть факторизованы. В этом разделе вы будете использовать квадратные корни, чтобы изучить другой способ решения квадратных уравнений, и этот метод будет работать с 9{2}=a[/latex], затем [latex] x=\sqrt{a}[/latex] или [latex] -\sqrt{a}[/latex].
Однако не все квадратные уравнения могут быть факторизованы. В этом разделе вы будете использовать квадратные корни, чтобы изучить другой способ решения квадратных уравнений, и этот метод будет работать с 9{2}=a[/latex], затем [latex] x=\sqrt{a}[/latex] или [latex] -\sqrt{a}[/latex]. {2}[/латекс].
{2}[/латекс]. Если вы не начинаете с идеального квадратного трехчлена, вы можете завершить квадрат, чтобы превратить то, что у вас есть, в один.
Если вы не начинаете с идеального квадратного трехчлена, вы можете завершить квадрат, чтобы превратить то, что у вас есть, в один. {2}}-4ac}}{2a}[/latex]. Это уравнение известно как квадратичная формула. 9{2}+bx+c=0[/latex] называется стандартной формой квадратного уравнения. Прежде чем решать квадратное уравнение с помощью квадратной формулы, важно убедиться, что уравнение имеет именно такую форму. В противном случае вы можете использовать неправильные значения для [латекс]а[/латекс], [латекс]b[/латекс] или [латекс]с[/латекс], и тогда формула будет давать неверные решения.
{2}}-4ac}}{2a}[/latex]. Это уравнение известно как квадратичная формула. 9{2}+bx+c=0[/latex] называется стандартной формой квадратного уравнения. Прежде чем решать квадратное уравнение с помощью квадратной формулы, важно убедиться, что уравнение имеет именно такую форму. В противном случае вы можете использовать неправильные значения для [латекс]а[/латекс], [латекс]b[/латекс] или [латекс]с[/латекс], и тогда формула будет давать неверные решения. Чтобы избежать ненужных ошибок, используйте круглые скобки вокруг каждого числа, введенного в формулу.
Чтобы избежать ненужных ошибок, используйте круглые скобки вокруг каждого числа, введенного в формулу.
 Следующий пример немного отличается.
Следующий пример немного отличается.
 Вычисление площадей поверхностей с
помощью двойного интеграла.
Вычисление площадей поверхностей с
помощью двойного интеграла.



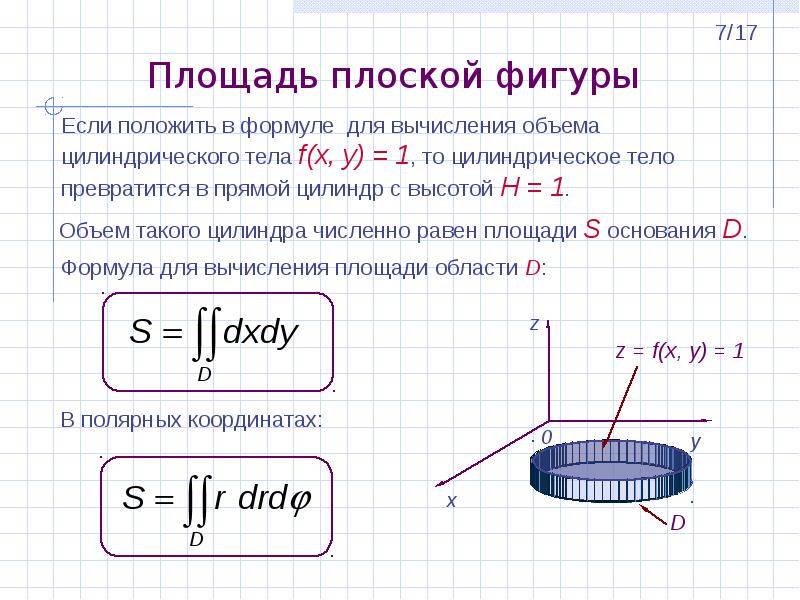 1)
1)
 Тогда объем поверхности равен двойным интегралам:
Тогда объем поверхности равен двойным интегралам: д.) дает
д.) дает Подставляем
Подставляем Двойной интеграл действует как сумма, а сумма есть
область. Это приводит нас к следующему определению.
Двойной интеграл действует как сумма, а сумма есть
область. Это приводит нас к следующему определению.

 Г.
Г. Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.
Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.  Хотя также вы можете смотреть видео уроки чтобы убедиться что вы все сделали правильно!
Хотя также вы можете смотреть видео уроки чтобы убедиться что вы все сделали правильно! Прочтите задачу. Вы понимаете все слова?
Прочтите задачу. Вы понимаете все слова? Это проверяет.
Это проверяет. Может показаться заманчивым назвать их все разными переменными, но до сих пор мы решали уравнения только с одной переменной. Определим числа через ту же переменную. Обязательно внимательно прочитайте задачу, чтобы узнать, как все числа соотносятся друг с другом.
Может показаться заманчивым назвать их все разными переменными, но до сих пор мы решали уравнения только с одной переменной. Определим числа через ту же переменную. Обязательно внимательно прочитайте задачу, чтобы узнать, как все числа соотносятся друг с другом.
 Итак, если мы определим первое целое число как [latex]n[/latex], следующее последовательное целое число будет [latex]n+1[/latex]. Следующий после этого на единицу больше, чем [latex]n+1[/latex], поэтому это [latex]n+1+1[/latex] или [latex]n+2[/latex].
Итак, если мы определим первое целое число как [latex]n[/latex], следующее последовательное целое число будет [latex]n+1[/latex]. Следующий после этого на единицу больше, чем [latex]n+1[/latex], поэтому это [latex]n+1+1[/latex] или [latex]n+2[/latex]. Перевести. Переформулировать одним предложением.
Перевести. Переформулировать одним предложением. Ответьте на вопрос.
Ответьте на вопрос. В числовых задачах вам даются некоторые подсказки об одном или нескольких числах, и вы используете эти подсказки для построения уравнения. Проблемы с числами обычно не возникают каждый день, но они являются хорошим введением в практику стратегии решения проблем. Не забывайте искать ключевые слова, такие как разница , , и .
В числовых задачах вам даются некоторые подсказки об одном или нескольких числах, и вы используете эти подсказки для построения уравнения. Проблемы с числами обычно не возникают каждый день, но они являются хорошим введением в практику стратегии решения проблем. Не забывайте искать ключевые слова, такие как разница , , и .
 Проверка: является суммой удвоенных
Проверка: является суммой удвоенных
 Решите уравнение.
Решите уравнение. Ответьте на вопрос.
Ответьте на вопрос. Решите уравнение.
Решите уравнение. {\text{nd}}\text{число}2x+10=2-е число
{\text{nd}}\text{число}2x+10=2-е число Проверка.
Проверка.  ..\text{…}-10,-9,-8,-7\text{,…}…− 10,−9,−8,−7,…
..\text{…}-10,-9,-8,-7\text{,…}…− 10,−9,−8,−7,… Найдите числа.
Найдите числа.

 Решите уравнение.
Решите уравнение.
 ..)
..) Они расположены по линии
Они расположены по линии

 ответил 28.03.21
ответил 28.03.21
 Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Никаких пакетов или подписок, платите только за то время, которое вам нужно.




 Пам’ятай про круглi дужки!)
Пам’ятай про круглi дужки!)
 З
ескізу довільного многокутника (малюнок
1) очевидно, що з однієї вершини n
– кутника виходить (n
– 3) діагоналі.
З
ескізу довільного многокутника (малюнок
1) очевидно, що з однієї вершини n
– кутника виходить (n
– 3) діагоналі. Пірамідку
з K кілець,
що
лежать на найбільшому
k+
1-м
кільці,
ми
можемо згідно припущенню
перемістити
на будь-який стрижень.
Зробимо
це,
перекладемо
її на третій стрижень.
Нерухоме
k +
1-е
кільце
не буде нам заважати провести алгоритм
переміщення,
так
як воно найбільше.
Після
переміщення K кілець
перемістимо k +
1-е
кільце,
яке залишилось,
на
другий стрижень.
Ми
можемо це зробити, так як другий стрижень
вільний.
Тепер
звернемо увагу,
той
факт,
що
другий стрижень не пустий,
не
заважає перекладати на нього будь-які
кільця, так як кільце на ньому найбільше
(,
будь-яке
кільце можна покласти на більше за
умовою задачі)і потім знов застосуємо
відомий нам по припущенню алгоритм
переміщення k кілець
і перемістимо їх
на
другий стрижень,
стрижень,
на якому внизу лежить
k +
1-е
кільце.
Таким
чином,
якщо
ми вміємо переміщувати пірамідки
з k кільцями,
то
вміємо переміщувати пірамідки і з k +
1кільцем.
Пірамідку
з K кілець,
що
лежать на найбільшому
k+
1-м
кільці,
ми
можемо згідно припущенню
перемістити
на будь-який стрижень.
Зробимо
це,
перекладемо
її на третій стрижень.
Нерухоме
k +
1-е
кільце
не буде нам заважати провести алгоритм
переміщення,
так
як воно найбільше.
Після
переміщення K кілець
перемістимо k +
1-е
кільце,
яке залишилось,
на
другий стрижень.
Ми
можемо це зробити, так як другий стрижень
вільний.
Тепер
звернемо увагу,
той
факт,
що
другий стрижень не пустий,
не
заважає перекладати на нього будь-які
кільця, так як кільце на ньому найбільше
(,
будь-яке
кільце можна покласти на більше за
умовою задачі)і потім знов застосуємо
відомий нам по припущенню алгоритм
переміщення k кілець
і перемістимо їх
на
другий стрижень,
стрижень,
на якому внизу лежить
k +
1-е
кільце.
Таким
чином,
якщо
ми вміємо переміщувати пірамідки
з k кільцями,
то
вміємо переміщувати пірамідки і з k +
1кільцем.
 /
8
/
8 Довести,
що для будь – яких значень n
справедливе твердження:
Довести,
що для будь – яких значень n
справедливе твердження: / 27
/ 27 / 3
/ 3 Первые 9 0007 домино падает
Первые 9 0007 домино падает
 ..
.. .. + (2k−1) = k 2 верно
.. + (2k−1) = k 2 верно 


 В качестве альтернативы, если целое число 1 принадлежит классу F и F является наследственным, то каждое положительное целое число принадлежит F . Принцип формулируется иногда в одной форме, иногда в другой. Поскольку любая форма принципа легко доказывается как следствие другой, нет необходимости проводить различие между ними.
В качестве альтернативы, если целое число 1 принадлежит классу F и F является наследственным, то каждое положительное целое число принадлежит F . Принцип формулируется иногда в одной форме, иногда в другой. Поскольку любая форма принципа легко доказывается как следствие другой, нет необходимости проводить различие между ними. ) 1 + 3 + 5 +⋯+ (2 n − 1) = n 2 для каждого положительного целого числа n . Пусть F будет классом целых чисел, для которых выполняется уравнение (1.) ; тогда целое число 1 принадлежит F , так как 1 = 1 2 . Если любое целое число x принадлежит F , то (2.) 1 + 3 + 5 +⋯+ (2 х — 1) = х 2 .
Следующее нечетное целое число после 2 x — 1 равно 2 x + 1, и, если прибавить его к обеим частям уравнения (2.) , получится (3.) 1 + 3 + 5 +⋯+ (2 x + 1) = x 2 + 2 x + 1 = ( x + 1) 2 Уравнение (2.) называется гипотезой индукции и утверждает, что уравнение (1.) выполняется, когда n равно x , а уравнение (3.
) 1 + 3 + 5 +⋯+ (2 n − 1) = n 2 для каждого положительного целого числа n . Пусть F будет классом целых чисел, для которых выполняется уравнение (1.) ; тогда целое число 1 принадлежит F , так как 1 = 1 2 . Если любое целое число x принадлежит F , то (2.) 1 + 3 + 5 +⋯+ (2 х — 1) = х 2 .
Следующее нечетное целое число после 2 x — 1 равно 2 x + 1, и, если прибавить его к обеим частям уравнения (2.) , получится (3.) 1 + 3 + 5 +⋯+ (2 x + 1) = x 2 + 2 x + 1 = ( x + 1) 2 Уравнение (2.) называется гипотезой индукции и утверждает, что уравнение (1.) выполняется, когда n равно x , а уравнение (3. ) утверждает, что уравнение (1.) выполняется, когда n + равно 9064 уравнение 44 ( 3.) было доказано как следствие уравнения (2.) , было доказано, что каждый раз, когда x принадлежит F , преемник x принадлежит F . Следовательно, по принципу математической индукции все натуральные числа принадлежат Ф .
) утверждает, что уравнение (1.) выполняется, когда n + равно 9064 уравнение 44 ( 3.) было доказано как следствие уравнения (2.) , было доказано, что каждый раз, когда x принадлежит F , преемник x принадлежит F . Следовательно, по принципу математической индукции все натуральные числа принадлежат Ф .
 В этой доктрине за Пуанкаре последовала школа математического интуитивизма, которая рассматривает математическую индукцию как высшую основу математического мышления, несводимую ни к чему предшествующему и априорно синтетическую в смысле Иммануила Канта.
В этой доктрине за Пуанкаре последовала школа математического интуитивизма, которая рассматривает математическую индукцию как высшую основу математического мышления, несводимую ни к чему предшествующему и априорно синтетическую в смысле Иммануила Канта. ни один элемент не предшествует себя в порядке; 2. если x предшествует y по порядку, и y предшествует z , то x предшествует z ; 3. в каждом непустом подклассе D есть первый элемент (тот, который предшествует всем остальным элементам в подклассе). От 3. следует, в частности, что сам домен D , если он не пустой, имеет первый элемент.
ни один элемент не предшествует себя в порядке; 2. если x предшествует y по порядку, и y предшествует z , то x предшествует z ; 3. в каждом непустом подклассе D есть первый элемент (тот, который предшествует всем остальным элементам в подклассе). От 3. следует, в частности, что сам домен D , если он не пустой, имеет первый элемент. Класс F элементов D называется наследственным, если всякий раз, когда все члены класса E элементов D принадлежат F , преемник E , если таковой имеется, также принадлежит до F (и, следовательно, в частности, всякий раз, когда элемент x из D принадлежит F , преемник x , если таковой имеется, также принадлежит F ). Доказательство с помощью трансфинитной индукции тогда зависит от принципа, что если первый элемент хорошо упорядоченной области D принадлежит наследственному классу F , то все элементы D принадлежат F .
Класс F элементов D называется наследственным, если всякий раз, когда все члены класса E элементов D принадлежат F , преемник E , если таковой имеется, также принадлежит до F (и, следовательно, в частности, всякий раз, когда элемент x из D принадлежит F , преемник x , если таковой имеется, также принадлежит F ). Доказательство с помощью трансфинитной индукции тогда зависит от принципа, что если первый элемент хорошо упорядоченной области D принадлежит наследственному классу F , то все элементы D принадлежат F .