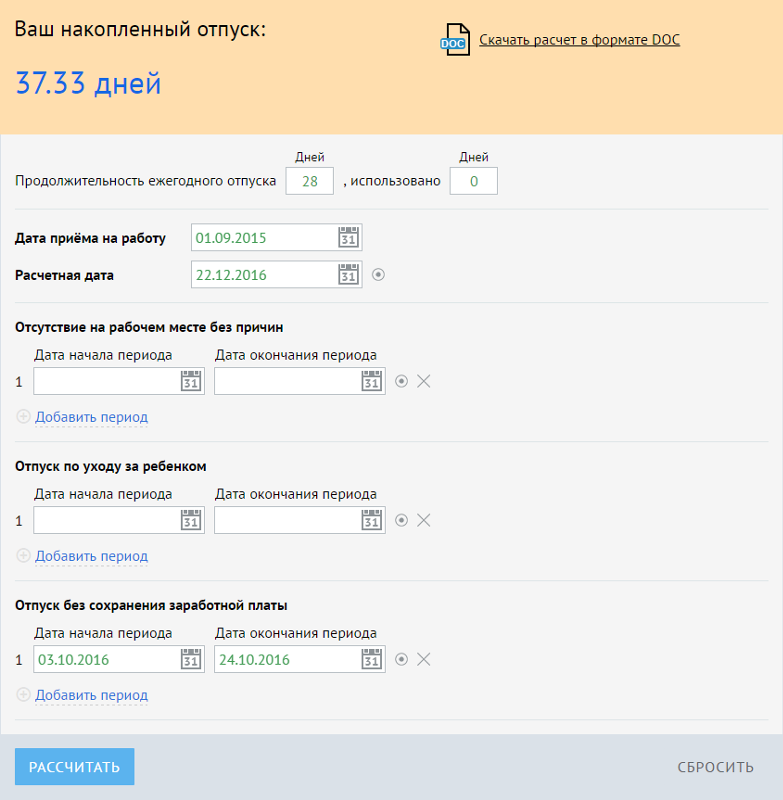
Карта Карно для:
2 переменных
3 переменных
переменных
Определяем формат минимизации функции:
ДНФ (дизъюнктивная нормальная форма) использовать 1 для обводки контура
или
КНФ (конъюнктивная нормальная форма) использовать 0 для обводки контура
Выделяем контуры (обводим клетки количество которых равно 20 или 21 или 22 или …) на карте Кано
Пример для ДНФ:
Для каждого контура выделяем области:
Смотрим на значения каждого х, на выбранной области, и записываем х, если значения равны только 1 и ¬х если значения равны только 0, а если значения равны 0 и 1, то данный х не записываем. (для ДНФ)
Между х в одном контуре ставиться ⋅ (умножение или И)
Между контурами ставиться + (сложение или ИЛИ)
Смотрим
на значения каждого х, на выбранной
области, и записываем х, если значения
равны только 0 и ¬х
если значения равны только 1, а если
значения равны 0 и 1, то данный х не
записываем. n
клеток. Каждой клетке диаграммы ставится
в соответствие двоичный n-мерный набор.
Взаимно однозначное соответствие между
двоичными наборами и клетками диаграммы
устанавливается разметкой последней.
n
клеток. Каждой клетке диаграммы ставится
в соответствие двоичный n-мерный набор.
Взаимно однозначное соответствие между
двоичными наборами и клетками диаграммы
устанавливается разметкой последней.
Рекомендации по минимизации булевых функций с использованием диаграмм Вейча:
1. Рассматриваются поочередно клетки, содержащие единицы, и анализируются всевозможные варианты склеивания. При этом сначала склеивание выполняется только для тех клеток (единиц), для которых вариант склеивания единственный. В результате будут выделены обязательные (или существенные) простые импликанты.
2. Оставшиеся несклеенные клетки (единицы) необходимо склеивать таким образом, чтобы образовать минимальное число групп с максимальным числом клеток в каждой группе.
3.
Каждой группе объединенных клеток в
минимальной ДНФ будет соответствовать
простая импликанта, определяемая как
конъюнкция только тех переменных,
значения которых постоянны для всех
наборов, задающих клетки данной группы.
Советую посмотреть ролик на 9 мин. https://www.youtube.com/watch?v=42o6pFXCtnQ, но вот небольшая инструкция по тому как пользоваться диаграммой Вейча.
Заполняем значения функции в диаграмму по следующей схеме
Определяем формат минимизации функции:
ДНФ (дизъюнктивная нормальная форма) использовать 1 для обводки контура
или
КНФ (конъюнктивная нормальная форма) использовать 0 для обводки контура
Выделяем контуры (обводим клетки количество которых равно 20 или 21 или 22 или …) как на карте Карно
Пример для ДНФ:
Смотрим на каждый из контуров и записываем х если он полность входит в эту область, если контур полностью не входит в область, то записываем ¬х, если контур входит частично в область, то эту область (х) не записываем.
 (для
ДНФ)
(для
ДНФ)
Между х в одном контуре ставится ⋅ (умножение или И)
Между контурами ставится + (сложение или ИЛИ)
Смотрим на каждый из контуров и записываем х если он полность входит в эту область, если контур полностью не входит в область, то записываем ¬х, если контур входит частично в область, то эту область (х) не записываем. (для КНФ)
Между х в одном контуре ставится + (сложение или ИЛИ)
Между контурами ставится ⋅ (умножение или И)
Для примера из 3) была бы СДНФ (совершенная дизъюнктивная нормальная форма) такая:
F = х1⋅х2⋅¬х4 + ¬х1⋅х3⋅х4
Карты Карно для 4-х переменных — Студопедия
Поделись с друзьями:
Как и в обычных таблицах соответствия клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписываются, им соответствуют пустые клетки).
Например, на рис. показана карта Карно для функции, отображение которой дано на 4-х-мерном кубе (см. рис.).
Для упрощения строки и столбцы, соответствующие значениям “1” для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.
Рис. а) отображение функции четырех переменных;
б) отображение ее минимального покрытия.
Между отображениями функции на n -мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно S -кубу соответствует совокупность 2-х соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике. Поэтому все положения, изложенные ранее, справедливы и для карт Карно. Так на рис. б) показано покрытие единиц карты, соответствующее минимальной дизъюнктивной форме
у = , рассматриваемой функции.
Считывание минитермов с карты Карно осуществляется по простому правилу. Клетки, образующие S -куб, дают минитерм (n-S)-го ранга, в который входят те (n-S)-переменные, которые сохраняют одинаковые значения на этом S -кубе, причем значениям “1” соответствуют сами переменные, а значениям “0” их отрицание.
Переменные, которые не сохраняют свои значения на S -кубе, в минитерме отсутствуют. Различные способы считывания приводят к различным представлениям функции в ДНФ.
у = у =
у =
Использование карт Карно требует более простых построений по сравнению с отображением на n -мерном кубе, особенно в случае 4-х переменных.
Для отображения функций 5-ти переменных используют две карты Карно на 4-ре переменные, а для функции 6-ти переменных — четыре таких карты.
При дальнейшем увеличении числа переменных карты Карно становятся практически непригодны.
Метод Мак-Класски (алгебраический метод)
Алгебраический метод известен как метод Мак-Класски, модифицировавшего в 1956 году метод Квайна. Базируется данный метод на следующей теореме.
Теорема. Если в СДНФ функции алгебры логики произвести всевозможные операции неполного склеивания, а затем всевозможные операции элементарного поглощения, то полученная форма функции будет сокращенной.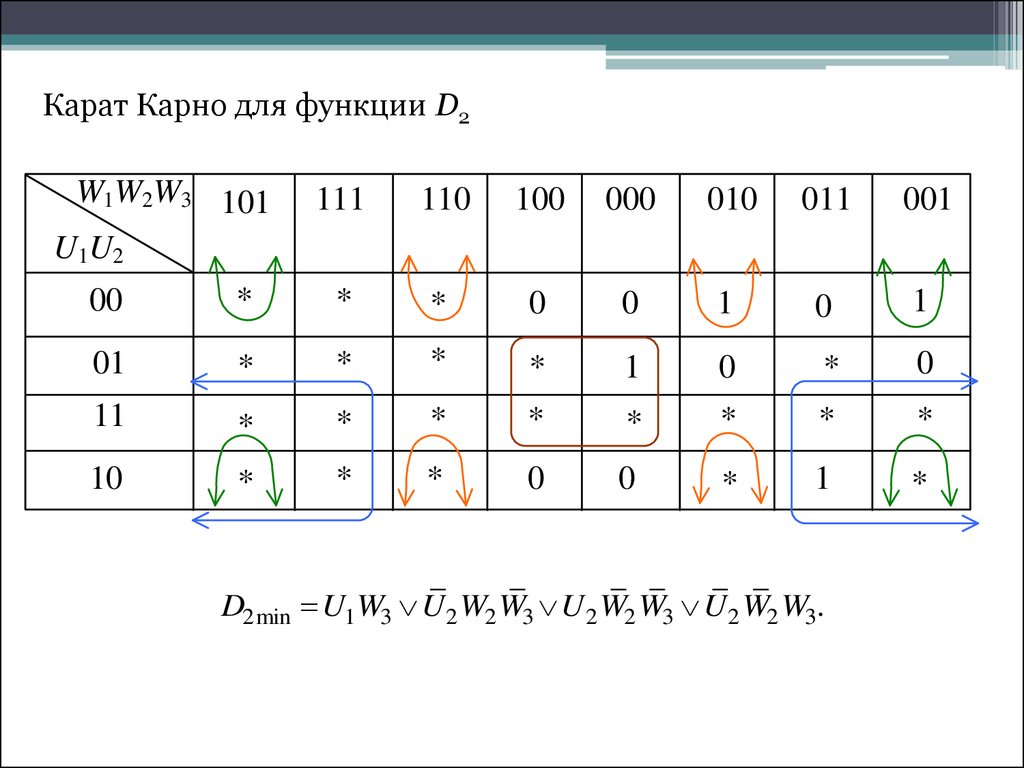
Элементарную конъюнкцию ранга n будем называть минитермом ранга n.
Элементарная конъюнкция называется импликантой булевой функции , если , то есть булева функция на данном наборе является константной и равна 1.
Минимизация булевой функции по методу Мак-Класски осуществляется согласно следующей последовательности действий:
1. Записать минитермы в виде их двоичных кодов и разбить их на непересекающиеся группы по числу единиц в этих группах. В i-ю группу войдут только те кодовые комбинации, которые в своей двоичной записи содержат ровно i единиц. Группы располагаются по мере роста i.
2. Попарное сравнение минитермов.
2.1. Произвести попарное сравнение двоичных номеров всех членов группы с индексом i с членами только группы с индексом (i+1).
2.2. Если некоторые два минитерма имеют вид axi и , то выписывают конъюнкцию а, которая является минитермом ранга (n-1), то есть если сравниваемы двоичные коды различаются только в одном разряде, то в столбец остатков записывается двоичный код с прочерком “-” на месте этого разряда (этот код соответствует минитерму (n-1)-го ранга.
2.3. Все двоичные коды номеров, участвующих в операции сравнения при условии их склеивания, отмечаются знаком “*”.
2.4. Пункты 2.1-2.3. повторяются для всех групп последовательно в порядке возрастания i. Двоичные коды, не отмеченные знаком “*”, соответствуют простым импликантам.
2.5. После построения всех минитермов (n-1) ранга по пунктам 2.1-2.3, они также сравниваются между собой и получают минитермы ранга (n-2) и т.д. Работа по первому этапу продолжается до тех пор, пока среди двоичных кодов можно будет обнаружить сравнимые, то есть такие укороченные коды, которые содержат прочерки в одних и тех же разрядах и различаются значением одного разряда.
Все неотмеченные минитермы называются первичными или простыми импликантами.
3. Построение импликантной таблицы. Строится таблица, в которой число строк равно числу полученных первичных импликант минимизируемой функции, а число столбцов равно числу минитермов исходной СДНФ. Если в некоторый минитерм исходной СДНФ входит первичная импликанта, то на пересечении строки и столбца ставится метка. Данные импликантной таблицы позволяют определить импликанты, отбросив которые, истинность функции не изменится.
Данные импликантной таблицы позволяют определить импликанты, отбросив которые, истинность функции не изменится.
4. Нахождение существенных импликант. Если в каком-либо из столбцов полученной таблицы имеется только одна метка, то первичная импликанта, стоящая в соответствующей строке, называется существенной. Существенная импликанта включается в минимальную ДНФ, а из таблицы исключаются строки, соответствующие существенным импликантам, а также столбцы минитермов, покрываемые этими существенными импликантами. Если в таблице нет столбцов, содержащих только одну метку, то переход на п.7.
5. Вычеркивание лишних столбцов. Если в таблице после четвертого этапа есть два столбца, в которых стоят метки в одинаковых строках, то один из них вычеркивают, так как покрытие оставшегося столбца будет осуществлять покрытие исключенного минитерма.
6. Вычеркивание лишних первичных импликант. Если на пятом этапе появляются строки, в которых нет меток, то первичная импликанта исключается из дальнейшего рассмотрения.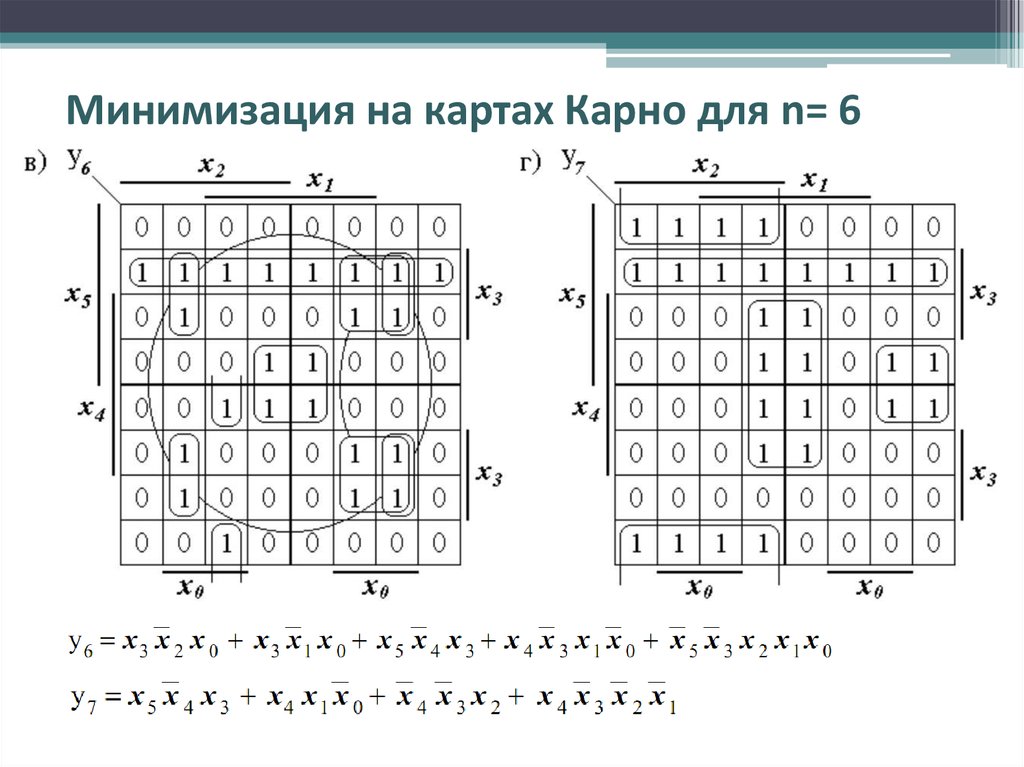
7. Выбор минимального покрытия. Выбирают наименьшее число строк таких, чтобы для каждого столбца из данной таблицы и каждой метки в этом столбце нашлась бы по крайней мере одна строка из множества выбранных строк, которая содержит эту метку.
Дизъюнкция всех простых импликантов покрытия, в том числе и существенных, образует тупиковую форму функции. Из найденных тупиковых форм выбирают минимальную по наименьшему числу дизъюнкций и элементов переменных.
Пример.
.
1) Получение групп кодовых комбинаций. 0011 0100 0101 0111 1001 1011 1100 1101
1 гр. 0100 2 гр. 0011 3 гр. 0111
0101 1011
1001 1101
2) Попарное сравнение минитермов.
Минитермы 3-го ранга: 010-*, -100, 0-11, -011, -101, 10-1, 1-01, 110-*
Минитермы 2-го ранга: -10-.
3) Построение импликантной таблицы и расстановка меток
| -100 | * | * | ||||||
| 0-11 | * | * | ||||||
| -011 | * | * | ||||||
| -101 | * | * | ||||||
| 10-1 | * | * | ||||||
| 1-01 | * | * | ||||||
| -10- | * | * | * | * |
4) Нахождение существенных импликант. Столбец, соответствующий кодовой комбинации 0111 содержит единственную метку. Соответствующая этой метке импликанта является существенной, поэтому включаем ее в минимальную ДНФ , а из таблицы согласно п.4 исключаем столбцы и строку, после чего получаем следующую таблицу:
Столбец, соответствующий кодовой комбинации 0111 содержит единственную метку. Соответствующая этой метке импликанта является существенной, поэтому включаем ее в минимальную ДНФ , а из таблицы согласно п.4 исключаем столбцы и строку, после чего получаем следующую таблицу:
| -100 | * | * | ||||
| -011 | * | |||||
| -101 | * | * | ||||
| 10-1 | * | * | ||||
| 1-01 | * | * | ||||
| -10- | * | * | * | * |
5) и 6) В полученной таблице нет столбцов, в которых стоят метки в одинаковых строках и нет строк, в которых нет меток, поэтому переходим к п. 7.
7.
7) Выбор минимального покрытия. Минимальному покрытию соответствует выбор строк -10- и 10-1. Тогда минимизированная ДНФ запишется как .
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Введение K-Map (Карта Карно)
Во многих цифровых схемах и практических задачах нам нужно найти выражение с минимальным количеством переменных. Мы можем очень легко минимизировать булевы выражения с 3, 4 переменными, используя K-карту, не используя никаких теорем булевой алгебры. K-map может принимать две формы: сумма продукта (SOP) и продукт суммы (POS) в зависимости от необходимости проблемы. K-map представляет собой табличное представление, но дает больше информации, чем TRUTH TABLE. Мы заполняем сетку K-карты нулями и единицами, а затем решаем ее, создавая группы.
Шаги для решения выражения с использованием K-карты-
- Выберите K-карту в соответствии с количеством переменных.

- Определите minterms или maxterms, указанные в задаче.
- Для SOP поставьте 1 в блоках K-map, соответствующих minterms (0 в других местах).
- Для POS поместите 0 в блоки K-карты, соответствующие maxterms (1 в других местах).
- Составьте прямоугольные группы, содержащие суммы членов в степени двойки, например 2,4,8 ..(кроме 1), и постарайтесь охватить как можно больше элементов в одной группе.
- Из групп, созданных на шаге 5, найдите условия продукта и суммируйте их для формы СОП.
ФОРМА СОП:
1. К-карта с 3 переменными –
К-карта СОП с 3 переменными 9000 3
Z= ∑A,B,C(1,3, 6,7)
Из группы красный получаем товарный термин—
A'C
Из зеленый группа получаем товарный термин—
AB
Суммируя эти условия продукта, мы получаем- Окончательное выражение (A’C+AB)
2.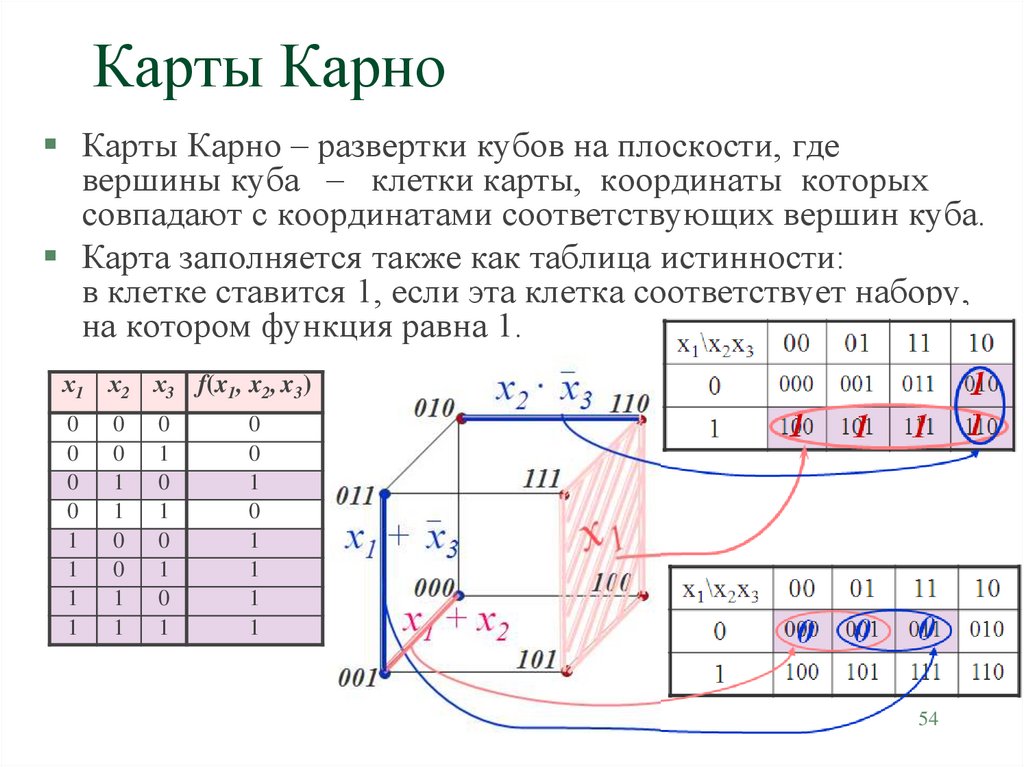 К-карта для 4-х переменных –
К-карта для 4-х переменных –
К-карта 4-х переменных СОП форма
F(P,Q,R,S)= ∑ (0,2,5,7,8,10,13,15)
Из группы красный получаем товарный термин –
QS
Из зеленый группы получаем товарный термин –
9 0038 вопросСуммируя эти условия продукта, мы получаем- Окончательное выражение (QS+Q’S’)
ФОРМА POS:
1. К-карта 3 переменных –
3,6, 7)
Из группы красный находим термы
A B
Дополняя эти два
A' B'
Теперь суммируйте
(A' + B')
Из группы коричневый находим термины
B C
Дополняя эти два термина
B' C'
Теперь суммируем их
(B'+C')
Из группы желтый находим термины
A' B' C'
Взятие дополнение этих двух
A B C
Теперь суммируем
(A + B + C)
Возьмем произведение этих трех членов: Окончательное выражение –
90 005 (А'+В') (B' + C') (A + B + C)
2.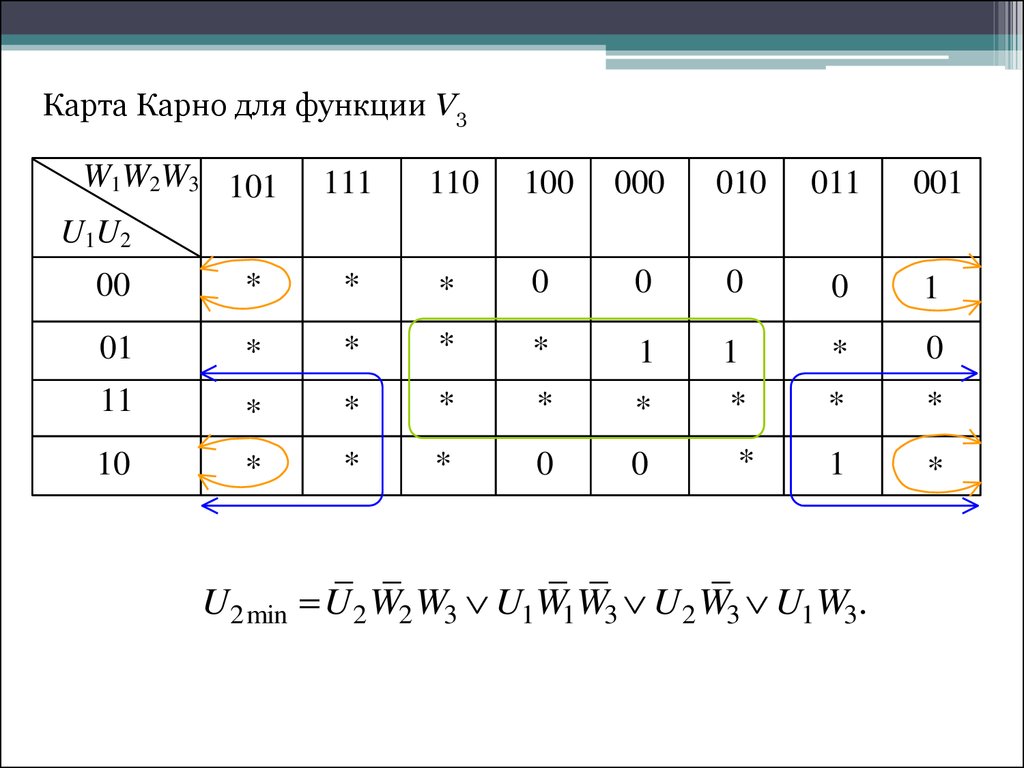 K-карта 4 переменных –
K-карта 4 переменных –
K-карта 4 переменных Форма POS
F(A,B,C,D)=π(3,5,7,8,10,11,12 ,13)
Из группы зеленых находим члены
C' D B
Взяв их дополнение и просуммировав их
(C+D' +B')
Из группы красный мы найти термины
C D A'
Взять их дополнение и суммировать их
(C'+D'+A)
Из синий группа находим термины
A C' D'
Взяв их дополнение и просуммировав их
(A'+C+D)
Из коричневый группа находим термины
9 0038 А В’ СБеря их дополнение и суммируя их
(A'+B+C')
Наконец, мы выражаем их как произведение –
(C+D'+B').(C'+D'+A).( A'+C+D).(A'+B+C')
PITFALL – * Всегда помните POS ≠ (SOP)’
*Правильная форма: ( POS of F)=(SOP of F’)’
Викторина по K-MAP
Эта статья написана Ануджем Бхатамом. Пожалуйста, пишите комментарии, если вы обнаружите что-то неверное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше
Пожалуйста, пишите комментарии, если вы обнаружите что-то неверное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше
Цикл Карно — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1962
В начале 19 века паровые машины стали играть все более важную роль в промышленности и на транспорте. Однако систематический набор теорий преобразования тепловой энергии в движущую силу паровыми двигателями еще не был разработан. Николя Леонар Сади Карно (1796-1832), французский военный инженер, опубликовал в 1824 году «Размышления о движущей силе огня ». известный как цикл Карно. Карно разработал основу второго закона термодинамики, и его часто называют «отцом термодинамики».
Цикл Карно
Цикл Карно состоит из следующих четырех процессов:
- Процесс обратимого изотермического расширения газа. В этом процессе идеальный газ в системе поглощает количество тепла \(q_{in}\) от источника тепла при высокой температуре \(T_{high}\), расширяется и совершает работу с окружающей средой.
- Процесс обратимого адиабатического расширения газа. При этом система теплоизолируется. Газ продолжает расширяться и совершать работу с окружающей средой, что приводит к охлаждению системы до более низкой температуры, \(T_{low}\).
- Процесс обратимого изотермического сжатия газа. В этом процессе окружающая среда совершает работу с газом при \(T_{low}\) и вызывает потерю тепла, \(q_{out}\).
- Процесс обратимого адиабатического сжатия газа. При этом система теплоизолируется. Окружающая среда продолжает совершать работу с газом, из-за чего температура снова поднимается до \(T_{high}\).
 (CC BY 4.0; XiSen Hou через Hope College)
(CC BY 4.0; XiSen Hou через Hope College)Диаграмма P-V
Диаграмма P-V цикла Карно показана на рисунке \(\PageIndex{2}\). В изотермических процессах I и III ∆U=0, так как ∆T=0. В адиабатических процессах II и IV q=0. Работа, теплота, ∆U и ∆H каждого процесса в цикле Карно суммированы в таблице \(\PageIndex{1}\).
Рисунок \(\PageIndex{2}\): PV-диаграмма цикла Карно.| Процесс | ш | q | ΔU | ΔH |
|---|---|---|---|---|
| я | \(-nRT_{высокий}\ln\left(\dfrac{V_{2}}{V_{1}}\right)\) | \(nRT_{high}\ln\left(\dfrac{V_{2}}{V_{1}}\right)\) | 0 | 0 |
| II | \(n\bar{C_{v}}(T_{низкий}-T_{высокий})\) | 0 | \(n\bar{C_{v}}(T_{низкий}-T_{высокий})\) | \(n\bar{C_{p}}(T_{низкий}-T_{высокий})\) |
| III | \(-nRT_{low}\ln\left(\dfrac{V_{4}}{V_{3}}\right)\) | \(nRT_{low}\ln\left(\dfrac{V_{4}}{V_{3}}\right)\) | 0 | 0 |
| IV | \(n\bar{C_{v}}(T_{высокий}-T_{низкий})\) | 0 | \(n\bar{C_{v}}(T_{высокий}-T_{низкий})\) | \(n\bar{C_{p}}(T_{высокий}-T_{низкий})\) |
| Полный цикл | \(-nRT_{высокий}\ln\left(\dfrac{V_{2}}{V_{1}}\right)-nRT_{low}\ln\left(\dfrac{V_{4}}{V_ {3}}\справа)\) | \(nRT_{высокий}\ln\left(\dfrac{V_{2}}{V_{1}}\right)+nRT_{low}\ln\left(\dfrac{V_{4}}{V_{ 3}}\справа)\) | 0 | 0 |
Диаграмма T-S
Диаграмма T-S цикла Карно показана на рисунке \(\PageIndex{3}\).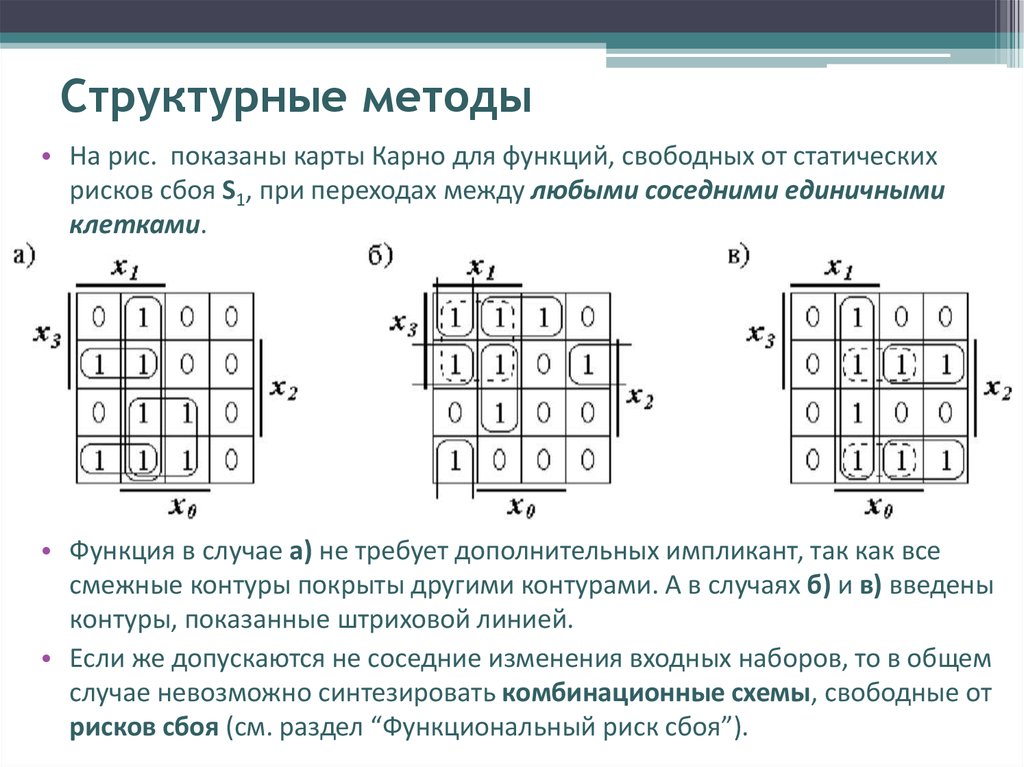 В изотермических процессах I и III ∆T=0. В адиабатических процессах II и IV ∆S=0, так как dq=0. ∆T и ∆S каждого процесса в цикле Карно показаны в таблице \(\PageIndex{2}\).
В изотермических процессах I и III ∆T=0. В адиабатических процессах II и IV ∆S=0, так как dq=0. ∆T и ∆S каждого процесса в цикле Карно показаны в таблице \(\PageIndex{2}\).
| Процесс | ΔT | ΔS |
|---|---|---|
| я | 0 | \(-nR\ln\left(\dfrac{V_{2}}{V_{1}}\right)\) |
| II | \(T_{низкий}-T_{высокий}\) | 0 |
| III | 0 | \(-nR\ln\left(\dfrac{V_{4}}{V_{3}}\right)\) |
| IV | \(T_{высокий}-T_{низкий}\) | 0 |
| Полный цикл | 0 | 0 |
Эффективность
Цикл Карно является наиболее эффективным из возможных двигателей, основанным на допущении об отсутствии случайных расточительных процессов, таких как трение, и допущении об отсутствии теплопроводности между различными частями двигателя при разных температурах.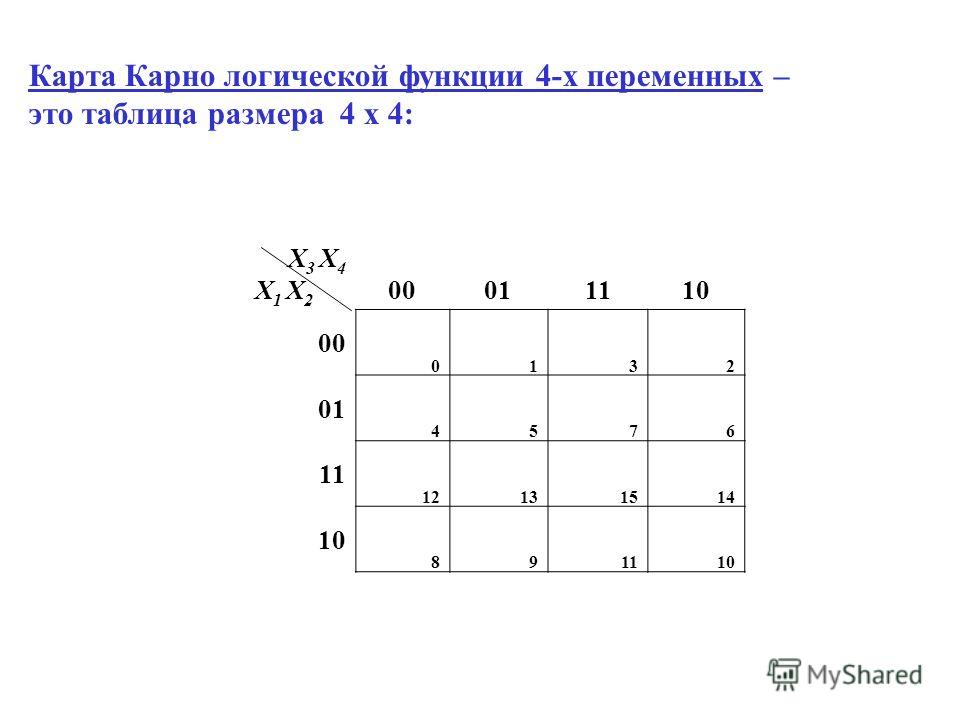 КПД двигателя Карно определяется как отношение выходной энергии к подводимой энергии. 9{C_{V}/R}=\dfrac{V_{4}}{V_{1}}\]
КПД двигателя Карно определяется как отношение выходной энергии к подводимой энергии. 9{C_{V}/R}=\dfrac{V_{4}}{V_{1}}\]
И с T 1 = T 2 и T 3 90 465 = T 4 ,
\[\dfrac{V_{3}}{V_{4}}=\dfrac{V_{2}}{V_{1}}\]
Следовательно,
\[ \text{эффективность}=\dfrac{nRT_{высокий}\ln\left(\dfrac{V_{2}}{V_{1}}\right)-nRT_{low}\ln\left(\dfrac{V_{ 2}}{V_{1}}\right)}{nRT_{high}\ln\left(\dfrac{V_{2}}{V_{1}}\right)}\]
\[\boxed{ \text{эффективность}=\dfrac{T_{высокий}-T_{низкий}}{T_{высокий}}}\]
Резюме
Цикл Карно имеет максимально возможный КПД двигателя (хотя другие циклы имеют такой же КПД) на основе предположения об отсутствии побочных расточительных процессов, таких как трение, и предположения об отсутствии теплопроводности между различными частей двигателя при различных температурах.
Проблемы
- Сейчас вы работаете с двигателем Карно с КПД 40%, который отводит тепло в радиатор при температуре 298 К.
 Если вы хотите увеличить КПД двигателя до 65%, до какой температуры вам придется поднять резервуар для тепла?
Если вы хотите увеличить КПД двигателя до 65%, до какой температуры вам придется поднять резервуар для тепла? - Двигатель Карно поглощал 1,0 кДж тепла при температуре 300 К и выделял 400 Дж тепла в конце цикла. Какая температура в конце цикла?
- Внутренний обогреватель, работающий по циклу Карно, нагревает дом со скоростью 30 кДж/с, чтобы поддерживать внутреннюю температуру на уровне 72 ºF. Какова мощность нагревателя, если температура наружного воздуха 30 ºF?
Ссылки
- Goldstein, M. J. Chem. Образовательный , 1980 , 57, 114-116
- Bader, M. J. Chem. Образовательный , 1973 , 50 , 834
- В. Ф. Людер. J. Chem. Образовательный , 1944 , 21 , 600-601
- Salter, C. J. Chem. Образовательный , 2000 , 77, 1027-1030
Цикл Карно распространяется под лицензией CC BY 4.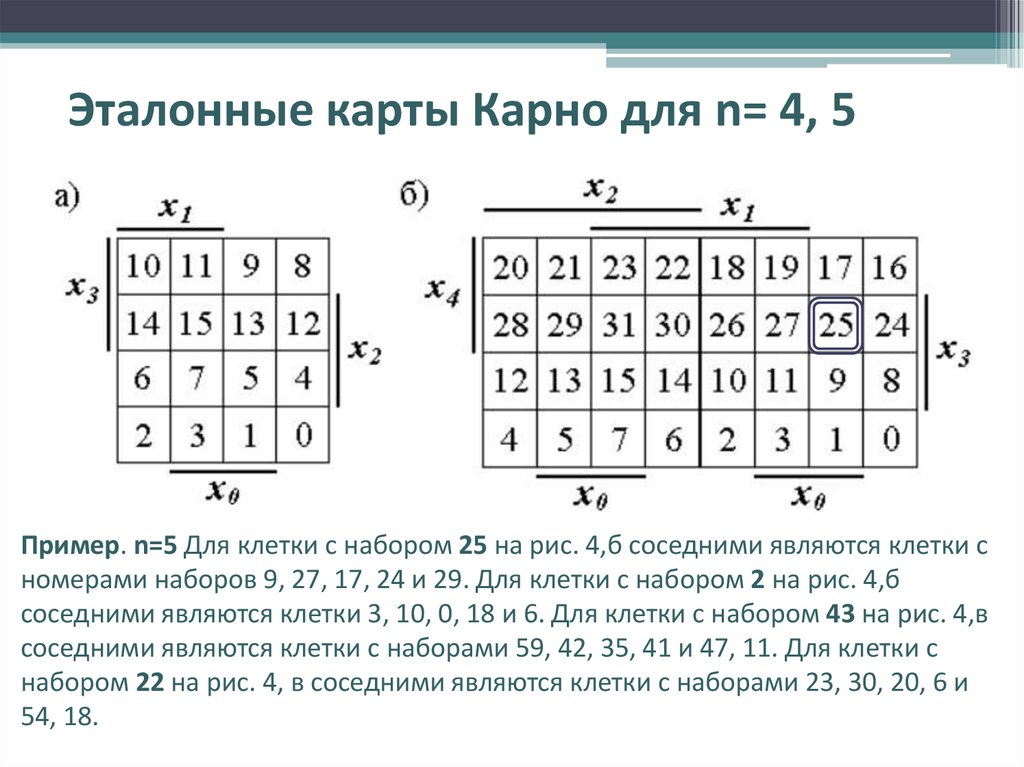

 (для
ДНФ)
(для
ДНФ)
 Если вы хотите увеличить КПД двигателя до 65%, до какой температуры вам придется поднять резервуар для тепла?
Если вы хотите увеличить КПД двигателя до 65%, до какой температуры вам придется поднять резервуар для тепла?


 Выполните сложение (3 – i) + (-1 + 2i) .
Выполните сложение (3 – i) + (-1 + 2i) . Дистрибутивность умножения относительно сложения:
Дистрибутивность умножения относительно сложения:

 Операции
с комплексными
Операции
с комплексными 
 Разностью двух комплексных чисел a
+
bi (уменьшаемое) и c
+
di (вычитаемое) называется комплексное число ( a
–
c ) + (b
–
d ) i
.
Разностью двух комплексных чисел a
+
bi (уменьшаемое) и c
+
di (вычитаемое) называется комплексное число ( a
–
c ) + (b
–
d ) i
. 
 Модуль комплексного числа a
+
bi обозначается | a
+
bi | или буквой r
Модуль комплексного числа a
+
bi обозначается | a
+
bi | или буквой r 









 Они имеют широкий спектр потенциальных применений в реальной жизни, особенно в области электроники и электромагнетизма.
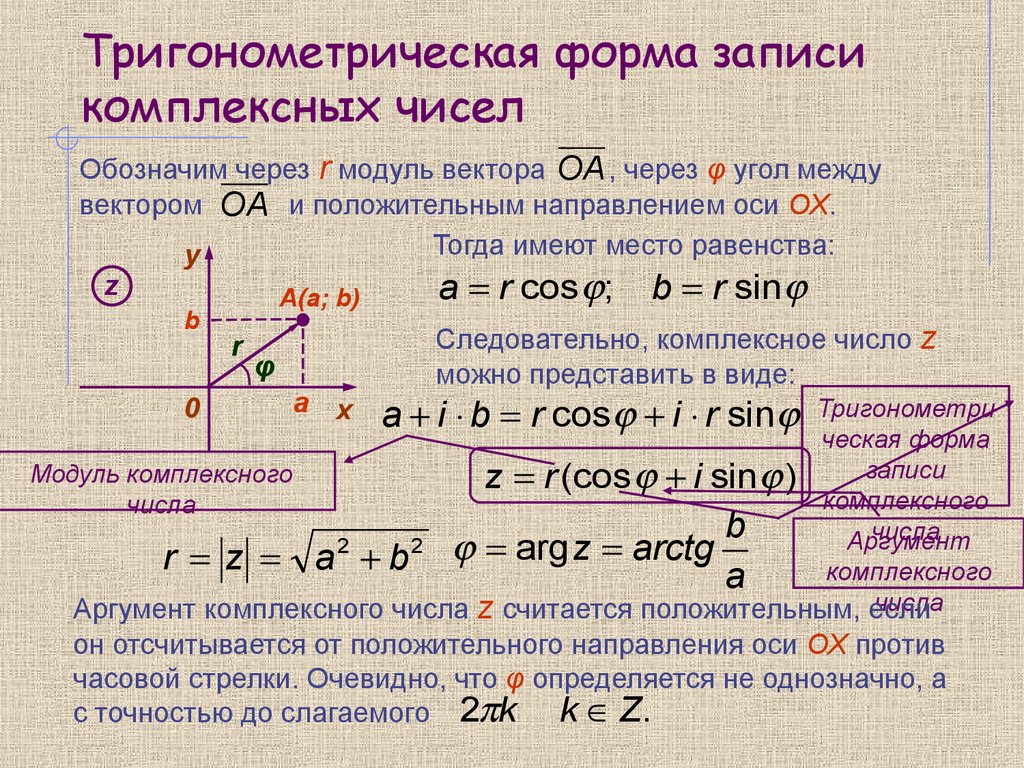
Они имеют широкий спектр потенциальных применений в реальной жизни, особенно в области электроники и электромагнетизма. Мы видим, что корень три 𝑖 будет лежать где-то на этой вертикальной оси, тогда как общее комплексное число в нашей алгебраической форме с положительными значениями 𝑎 и 𝑏 будет лежать где-то в этом первом квадранте.
Мы видим, что корень три 𝑖 будет лежать где-то на этой вертикальной оси, тогда как общее комплексное число в нашей алгебраической форме с положительными значениями 𝑎 и 𝑏 будет лежать где-то в этом первом квадранте. И мы можем решить это уравнение для 𝜃, найдя обратный тангенс или 𝑟 арктангенс обеих сторон. Таким образом, 𝜃 равно арктангенсу 𝑏 над 𝑎. И теперь у нас есть две формулы преобразования, которые мы можем использовать для выражения комплексного числа в прямоугольной форме в тригонометрической форме.
И мы можем решить это уравнение для 𝜃, найдя обратный тангенс или 𝑟 арктангенс обеих сторон. Таким образом, 𝜃 равно арктангенсу 𝑏 над 𝑎. И теперь у нас есть две формулы преобразования, которые мы можем использовать для выражения комплексного числа в прямоугольной форме в тригонометрической форме.
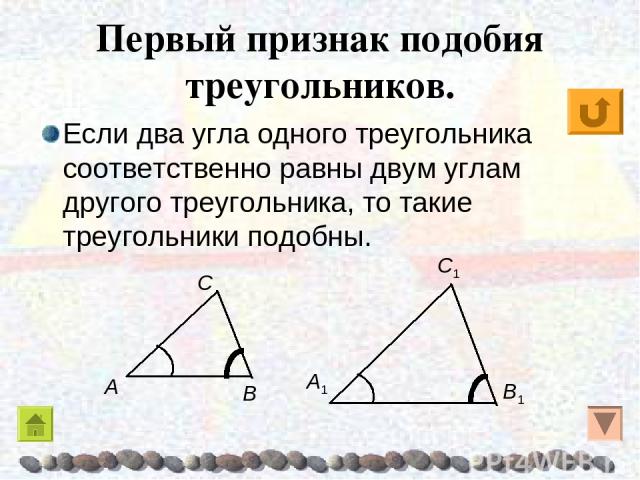
 Укажите номера верных утверждений.
Укажите номера верных утверждений.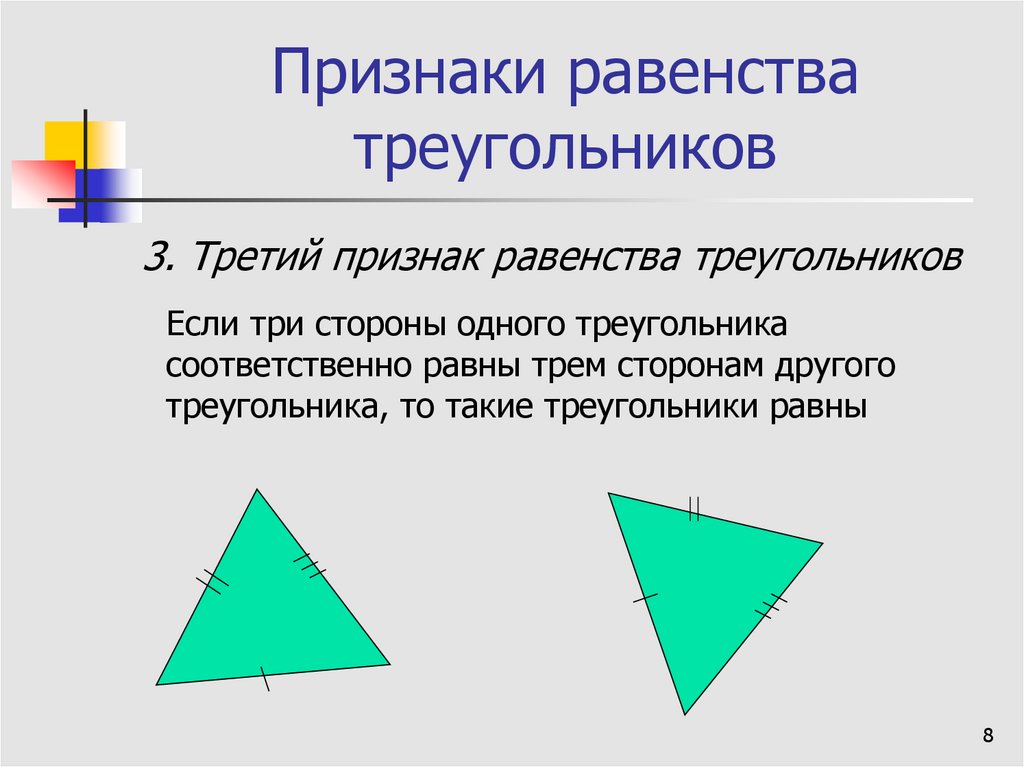


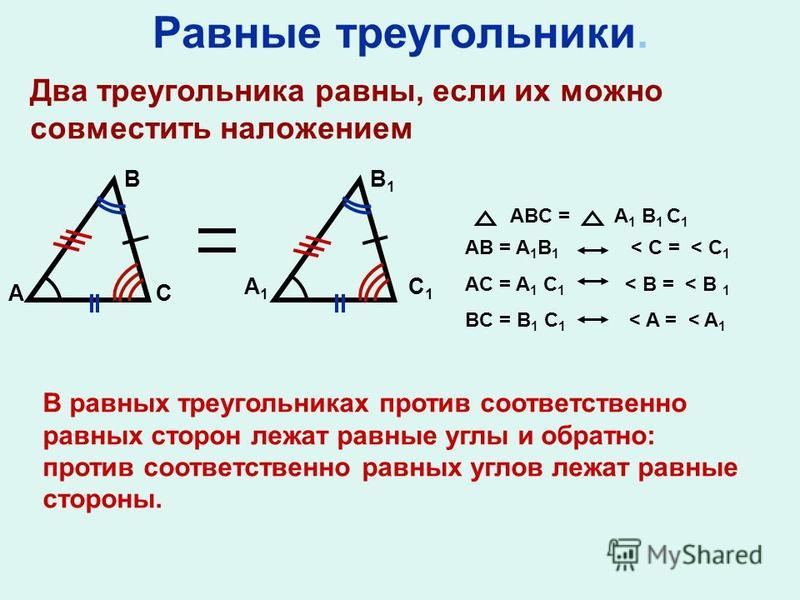

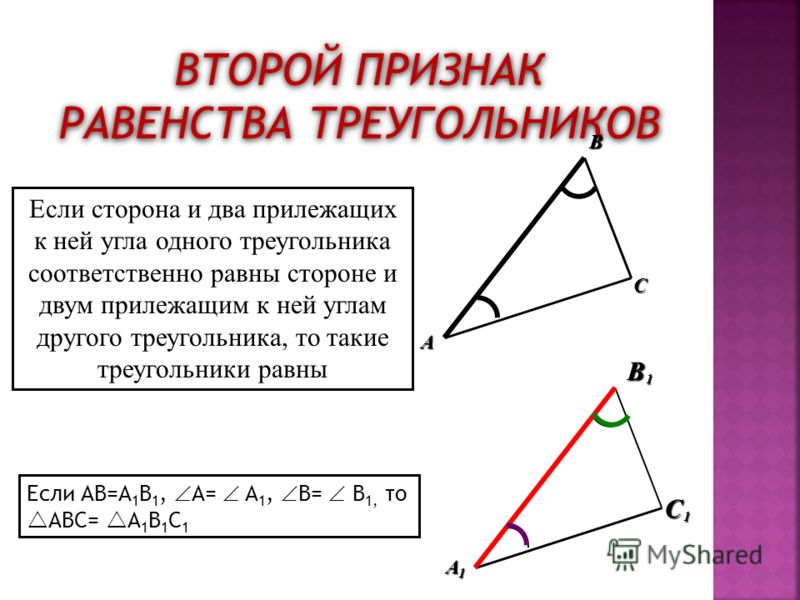



 Укажите номера верных утверждений.
Укажите номера верных утверждений.
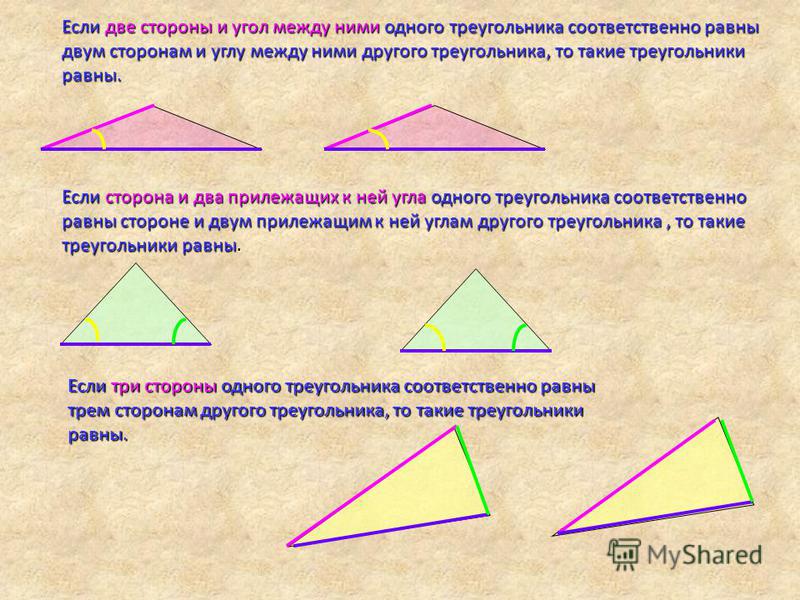

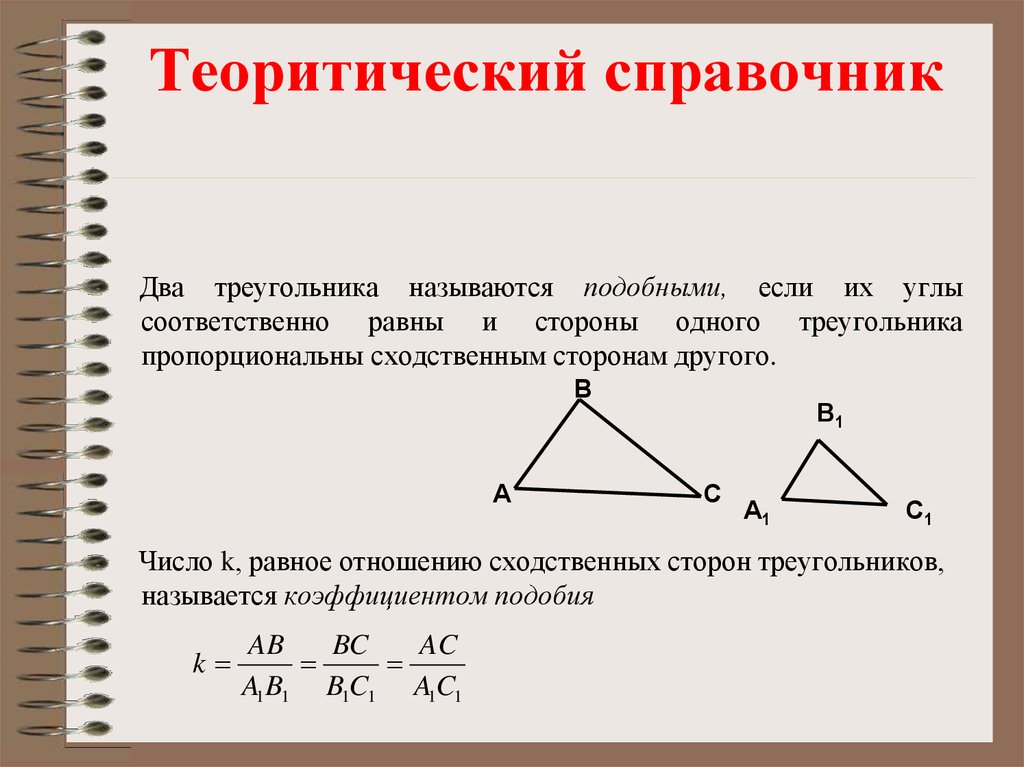
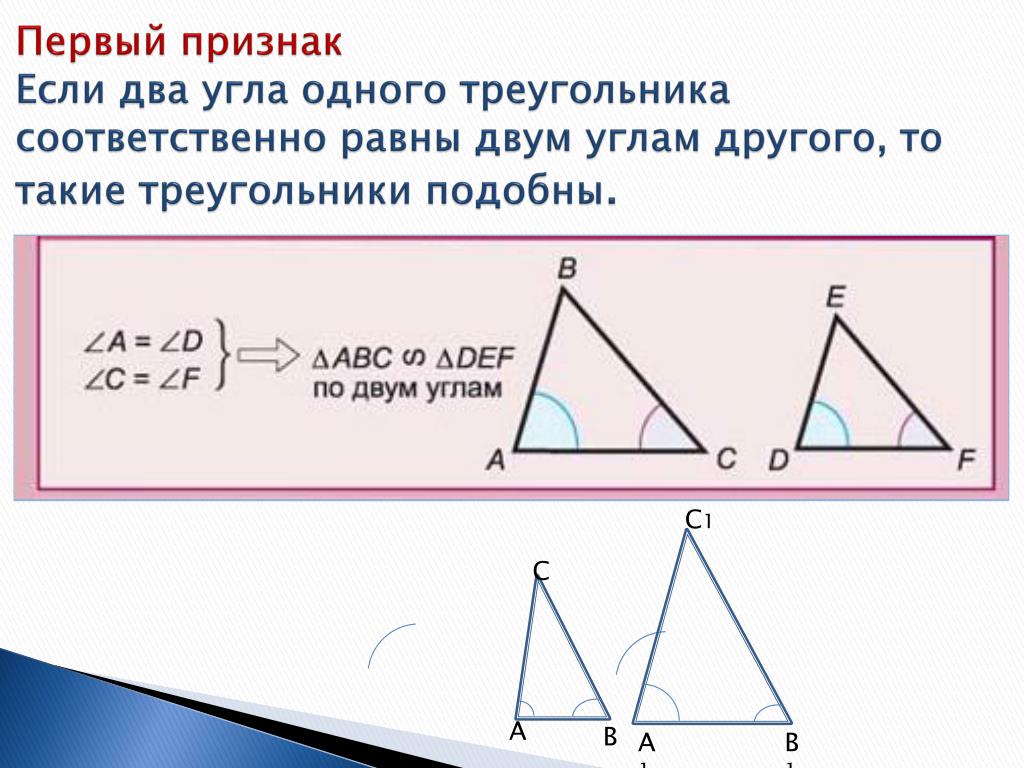




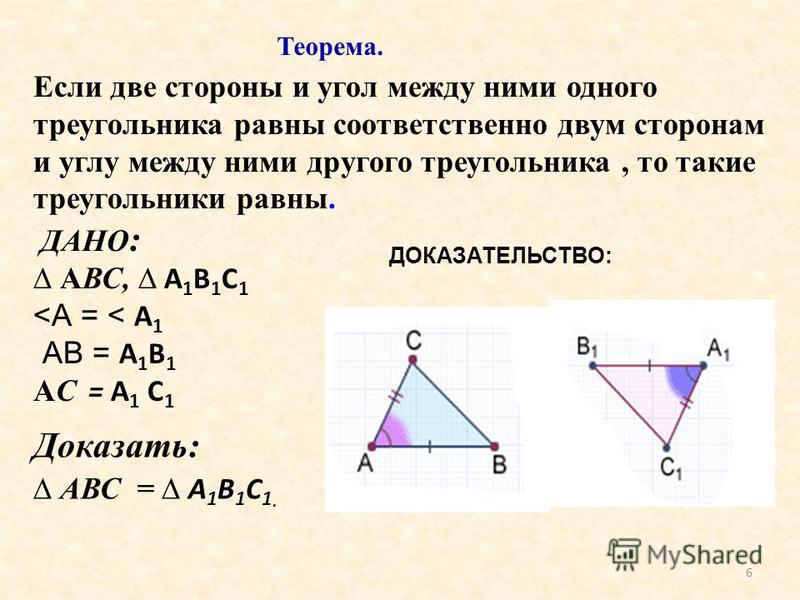
 У подобных треугольников углы равны, но стороны разной длины. Конгруэнтные треугольники будут иметь полностью совпадающие углы и стороны. Их внутренние углы и стороны будут равны. Проверка конгруэнтности треугольников включает три постулата, сокращенно 9.0382 SAS , ASA и SSS .
У подобных треугольников углы равны, но стороны разной длины. Конгруэнтные треугольники будут иметь полностью совпадающие углы и стороны. Их внутренние углы и стороны будут равны. Проверка конгруэнтности треугольников включает три постулата, сокращенно 9.0382 SAS , ASA и SSS . Это не очень полезно и портит ваш учебник. Если вы работаете с онлайн-учебником, вы не сможете сделать даже , что .
Это не очень полезно и портит ваш учебник. Если вы работаете с онлайн-учебником, вы не сможете сделать даже , что .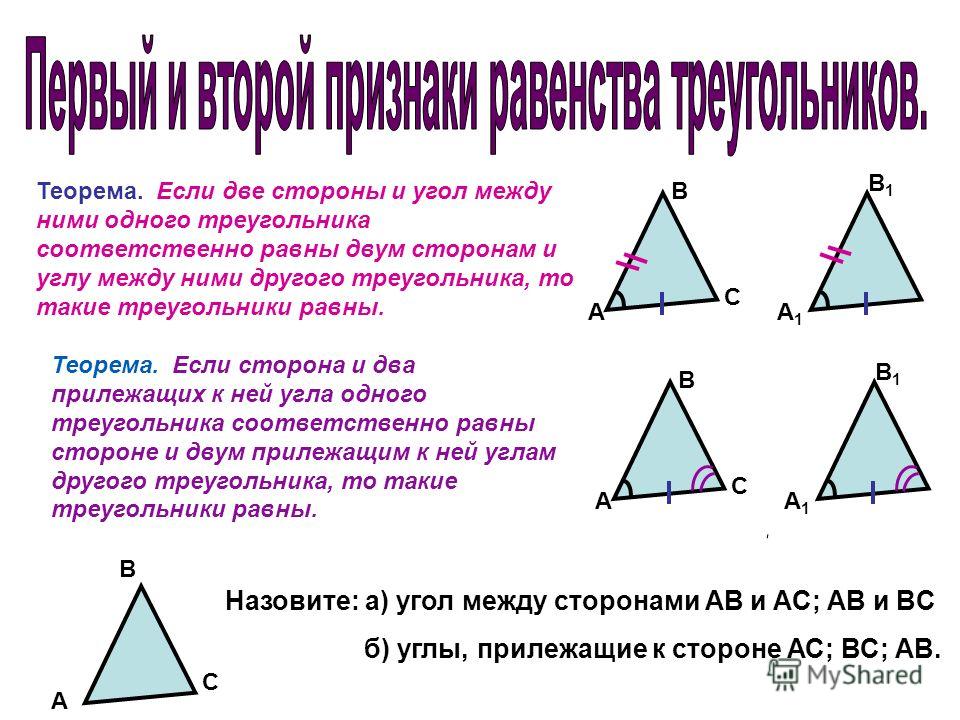

 Здесь вместо выбора двух углов мы выбираем сторону и соответствующую ей сторону двух треугольников.
Здесь вместо выбора двух углов мы выбираем сторону и соответствующую ей сторону двух треугольников. .
.
 0.
0. io/ru/number/least-common-multiple-lcm-of/42—98
io/ru/number/least-common-multiple-lcm-of/42—98 E. Paul BIYA, reçu en Audience, le mercredi 29 mars 2023 au… Lire la suite…
E. Paul BIYA, reçu en Audience, le mercredi 29 mars 2023 au… Lire la suite… ..
.. ..
.. ..
..
 .. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
.. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30. Пожалуйста помогите!! Электромагнитные колебания и волны
Пожалуйста помогите!! Электромагнитные колебания и волны у)
у) Найдите вводные слова и вводныепредложения, обозначьте их. Спишите, расставляя знаки препинания.1) Эта фраза пожалуй была сказана между прочим хотя её содержаниенапомнило мне между прочим одну двусмысле..ую шутку.2) У Татьяны Андреевны к сож..лению замёрзли ресницы и (по)этомуей к..залось что от звезды падают на дорогу ломкие полосысвета. (К.Г.Паустовский)3) Письмо должно быть срочно доставле..о адресату потому чтокажется мы и так опаздываем с доставкой.4) А впрочем судьба наша кажет..ся одинакова и родились мы(по)вид..мому под еди..ым созвездием. (А. Пушкин)5) Почти (на)против его подвала прост..рался огромный пустырьгородской земли словом те..итория была внушительной. 6) После (не)состоявш..йся встречи с дядей к сожалениюпр..мешивалось ещё и чувство разоч..рования и это к сожалению мешалососредоточит..ся на серьёзных размышлениях.7) Книги брош..ры газеты словом все виды журнальной продукции во-первых валялись на полу во-вторых были (по)вид..мому в таком состоянииуже давно о чём свидетельствовал (в)час.
Найдите вводные слова и вводныепредложения, обозначьте их. Спишите, расставляя знаки препинания.1) Эта фраза пожалуй была сказана между прочим хотя её содержаниенапомнило мне между прочим одну двусмысле..ую шутку.2) У Татьяны Андреевны к сож..лению замёрзли ресницы и (по)этомуей к..залось что от звезды падают на дорогу ломкие полосысвета. (К.Г.Паустовский)3) Письмо должно быть срочно доставле..о адресату потому чтокажется мы и так опаздываем с доставкой.4) А впрочем судьба наша кажет..ся одинакова и родились мы(по)вид..мому под еди..ым созвездием. (А. Пушкин)5) Почти (на)против его подвала прост..рался огромный пустырьгородской земли словом те..итория была внушительной. 6) После (не)состоявш..йся встречи с дядей к сожалениюпр..мешивалось ещё и чувство разоч..рования и это к сожалению мешалососредоточит..ся на серьёзных размышлениях.7) Книги брош..ры газеты словом все виды журнальной продукции во-первых валялись на полу во-вторых были (по)вид..мому в таком состоянииуже давно о чём свидетельствовал (в)час. .ности слой пыли на них но этооднако не помешало нашему ра..ледованию.8) Потом (в)прочем он говорил что наверное (не)стоило горячит..ся(не)много поостыть и действовать уже (на)верняка (по)тому(что) по егомнению ситуация (до)конца (не)была проясне..а и у пр..сутствующих всё(же)ост..вались наверное вопросы.9) Увы он счастия не ищ..т и не от счастия бежит. (М.Ю. Лермонтов)10) Вронский к ужасу своему почувствовал что сделал скверноенепростительное движение. (Л.Н. Толстой)ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО
.ности слой пыли на них но этооднако не помешало нашему ра..ледованию.8) Потом (в)прочем он говорил что наверное (не)стоило горячит..ся(не)много поостыть и действовать уже (на)верняка (по)тому(что) по егомнению ситуация (до)конца (не)была проясне..а и у пр..сутствующих всё(же)ост..вались наверное вопросы.9) Увы он счастия не ищ..т и не от счастия бежит. (М.Ю. Лермонтов)10) Вронский к ужасу своему почувствовал что сделал скверноенепростительное движение. (Л.Н. Толстой)ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО  Оберіть правильну відповідь. На яку висоту піднявся літак, якщо за бортом температура повітря становить –30оС, в той час, як біля поверхні землі +24оС? Розв’язок: 1) +24oC-(-30oC )= 54 oC 2) 54oC : 6оС = Виберіть одну відповідь: 7 км 9 км 10 км 8 км
Оберіть правильну відповідь. На яку висоту піднявся літак, якщо за бортом температура повітря становить –30оС, в той час, як біля поверхні землі +24оС? Розв’язок: 1) +24oC-(-30oC )= 54 oC 2) 54oC : 6оС = Виберіть одну відповідь: 7 км 9 км 10 км 8 км філолог. фотограф.будь ласочка
філолог. фотограф.будь ласочка См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя. 7320006
7320006 472
472 745
745 000
000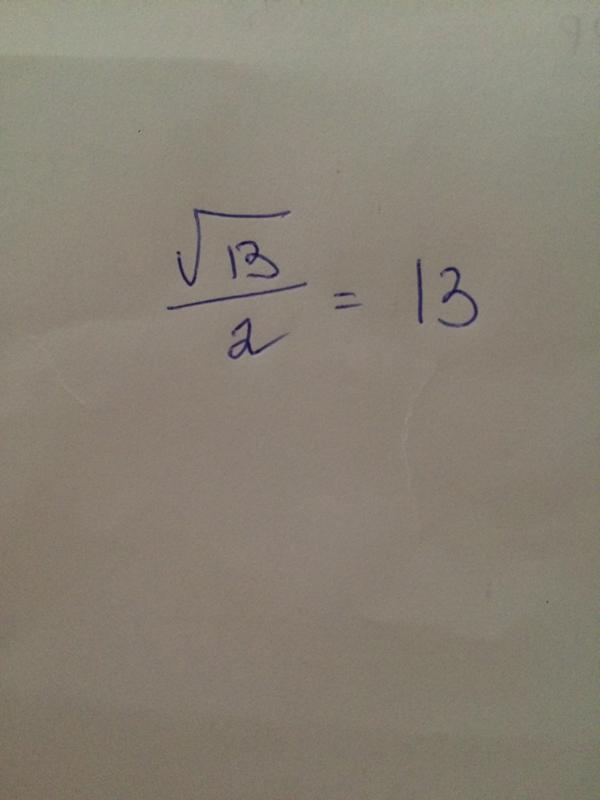 937
937 718
718 539
539 Математически квадратный корень из 13 может быть выражен как в радикальной, так и в экспоненциальной форме: 9(0.5)
Математически квадратный корень из 13 может быть выражен как в радикальной, так и в экспоненциальной форме: 9(0.5) 
 Однако такие числа, как -5, 7,025 или 5 ½, не считаются целыми числами.
Однако такие числа, как -5, 7,025 или 5 ½, не считаются целыми числами.  Важно отметить, что символ √ используется для обозначения главного (положительного) квадратного корня числа.
Важно отметить, что символ √ используется для обозначения главного (положительного) квадратного корня числа. 
 {\circ}=\left(\frac{\pi}{180}\right) \cdot 60 \text { радиан }=1 \text { рад } \]
{\circ}=\left(\frac{\pi}{180}\right) \cdot 60 \text { радиан }=1 \text { рад } \] )
) )
) )
) )
) )
) )
) )
) )
) )
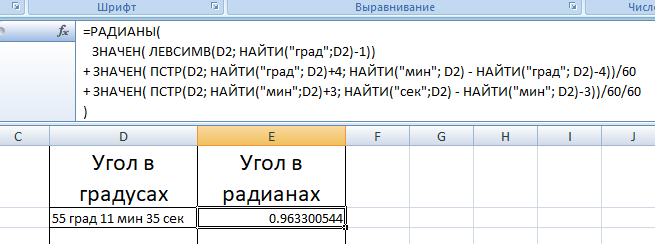
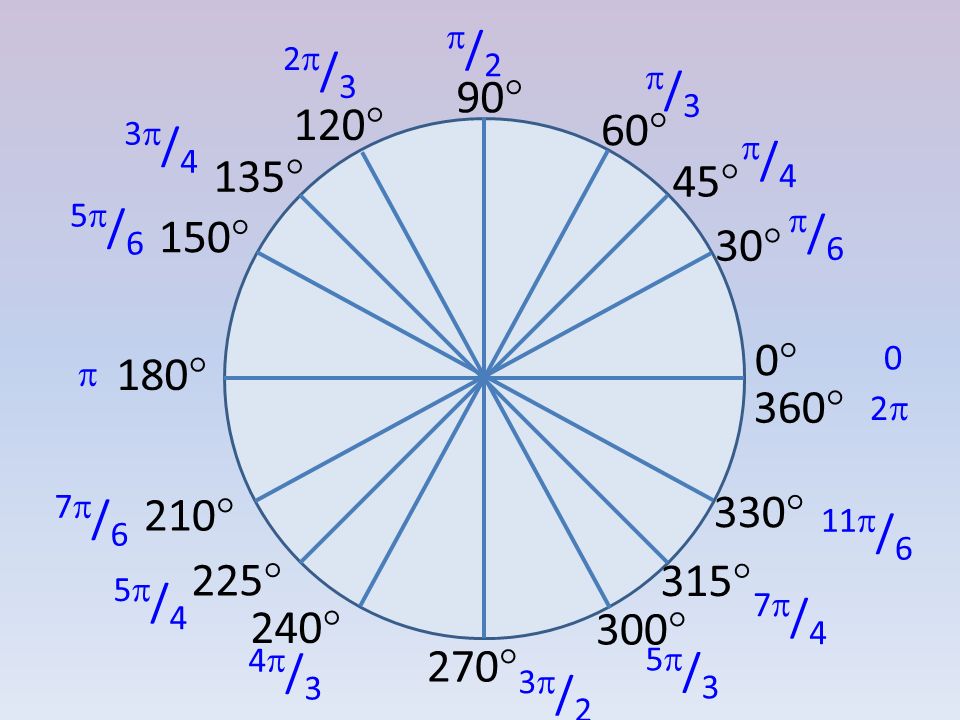
) Двумя единицами измерения угла являются радианы и градусы. Единица радианы используется в основном в концепции тригонометрии. Меру углов можно преобразовать из радианов в градусы с помощью формулы. Чтобы понять эту формулу и преобразование радианов в градусы, мы поймем значение каждой единицы угла. В этой статье мы также увидим таблицу преобразования радианов в градусы.
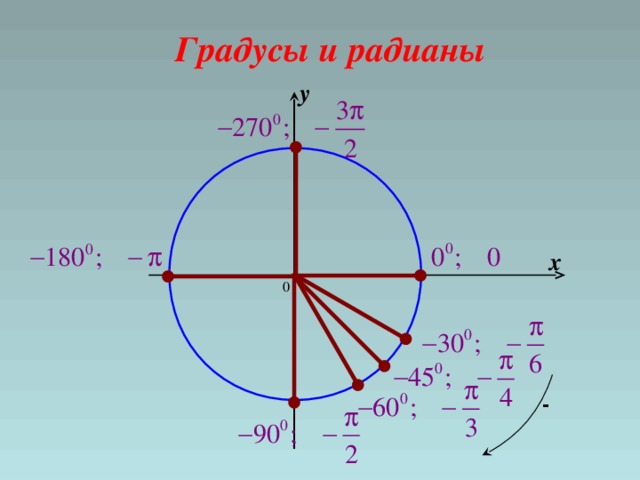
Двумя единицами измерения угла являются радианы и градусы. Единица радианы используется в основном в концепции тригонометрии. Меру углов можно преобразовать из радианов в градусы с помощью формулы. Чтобы понять эту формулу и преобразование радианов в градусы, мы поймем значение каждой единицы угла. В этой статье мы также увидим таблицу преобразования радианов в градусы. Когда мы берем радиус круга и вращаем его, мы начинаем строить угол, который можно измерить в радианах или градусах. Давайте посмотрим, что означает каждая единица угла и как измерить угол.
Когда мы берем радиус круга и вращаем его, мы начинаем строить угол, который можно измерить в радианах или градусах. Давайте посмотрим, что означает каждая единица угла и как измерить угол.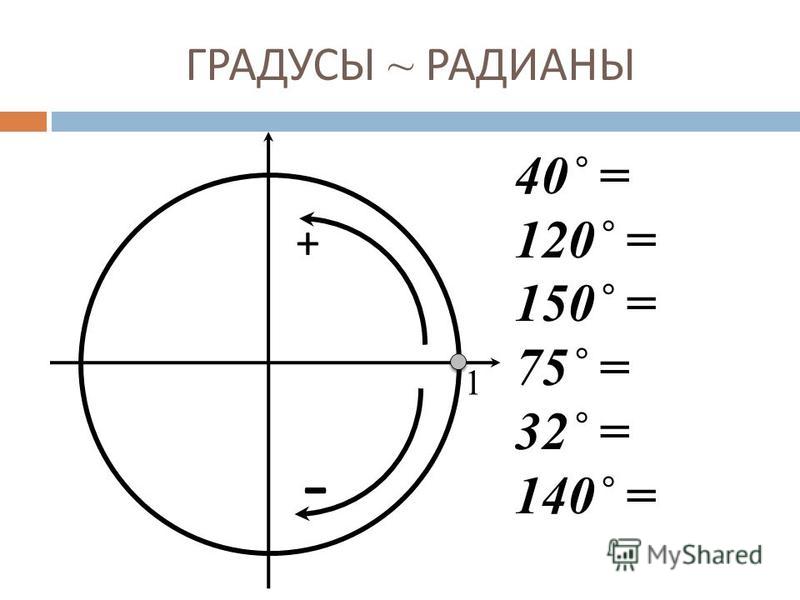 Следовательно, при решении задач предпочтительно переводить единицу измерения угла из радианов в градусы, чтобы лучше понять ее. Инструментом для измерения угла в градусах является транспортир.
Следовательно, при решении задач предпочтительно переводить единицу измерения угла из радианов в градусы, чтобы лучше понять ее. Инструментом для измерения угла в градусах является транспортир. Формула для преобразования угла в радианах в градусы:
Формула для преобразования угла в радианах в градусы: 2π радиан эквивалентны 360°, полученным после одного полного оборота окружности. Преобразование радианов в градусы можно выполнить по формуле «Угол в радианах × 180°/π = угол в градусах». Любой угол, указанный в радианах, можно преобразовать в градусы, используя следующие шаги:
2π радиан эквивалентны 360°, полученным после одного полного оборота окружности. Преобразование радианов в градусы можно выполнить по формуле «Угол в радианах × 180°/π = угол в градусах». Любой угол, указанный в радианах, можно преобразовать в градусы, используя следующие шаги: В приведенной ниже таблице показаны значения радиана для соответствующих мер угла в градусах:
В приведенной ниже таблице показаны значения радиана для соответствующих мер угла в градусах:
 ∠AOB имеет меру π/4 рад. Преобразование меры угла ∠AOB из радианов в градусы.
∠AOB имеет меру π/4 рад. Преобразование меры угла ∠AOB из радианов в градусы.
 Например, рассмотрим угол π/9 рад. Теперь, используя формулу преобразования радианов в градусы, мы имеем π/9 рад × 180°/π = (угол в градусах).
Например, рассмотрим угол π/9 рад. Теперь, используя формулу преобразования радианов в градусы, мы имеем π/9 рад × 180°/π = (угол в градусах).  Это поможет вам преобразовать радианы в градусы за несколько секунд. Чтобы преобразовать угол, указанный в радианах, в градусы, нам просто нужно умножить угол на 180 ° / π.
Это поможет вам преобразовать радианы в градусы за несколько секунд. Чтобы преобразовать угол, указанный в радианах, в градусы, нам просто нужно умножить угол на 180 ° / π.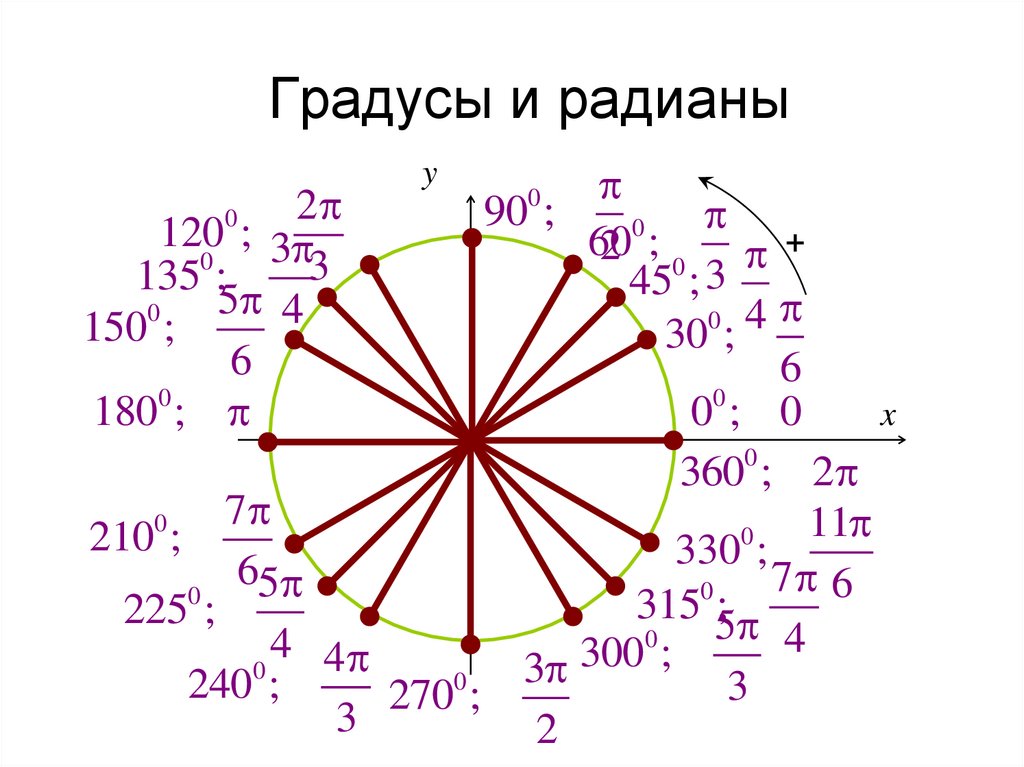 Формула градусы = радианы × 180 / π, и ее можно использовать как для положительных, так и для отрицательных значений.
Формула градусы = радианы × 180 / π, и ее можно использовать как для положительных, так и для отрицательных значений. Различные типы углов измеряются в радианах, а затем преобразуются в градусы по формуле. Эта формула обсуждается ниже.
Различные типы углов измеряются в радианах, а затем преобразуются в градусы по формуле. Эта формула обсуждается ниже.





 Пусть нужно сложить два вектора: a(3; 5) и b(4; 3). Произведем вычисления:
Пусть нужно сложить два вектора: a(3; 5) и b(4; 3). Произведем вычисления: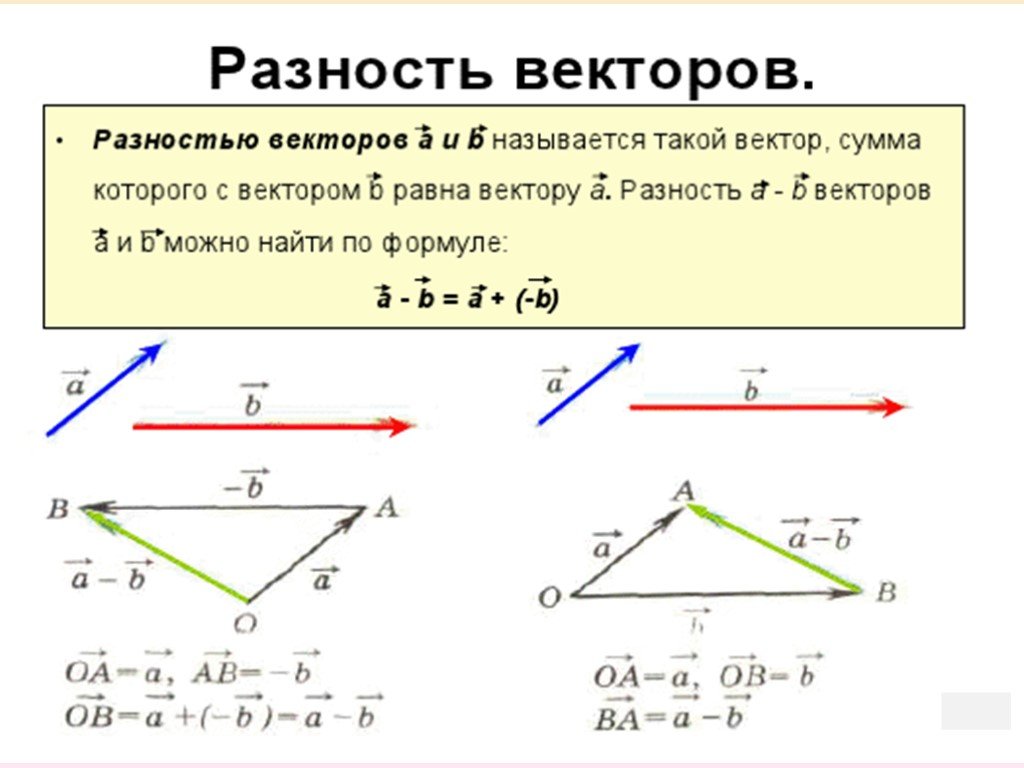 Параллельно перенести векторы a и b, так чтобы начало одного из векторов совпадало с концом другого.
Параллельно перенести векторы a и b, так чтобы начало одного из векторов совпадало с концом другого.
 Координаты обоих векторов заданны точками:
Координаты обоих векторов заданны точками: Найдем разность векторов пространства. Координаты обоих векторов заданны точками.
Найдем разность векторов пространства. Координаты обоих векторов заданны точками. 2 ; -75.75}
2 ; -75.75} .
.
 векторные калькуляторы
векторные калькуляторы 
 Один множимый, второй множитель. Результат их умножения называется произведением.
Один множимый, второй множитель. Результат их умножения называется произведением. Это значит, что для любых отрицательных чисел -a, -b верно равенство:
Это значит, что для любых отрицательных чисел -a, -b верно равенство:
 Вычислить произведение: 5∗(-5) и 12∗(-8)
Вычислить произведение: 5∗(-5) и 12∗(-8) 6K
6K



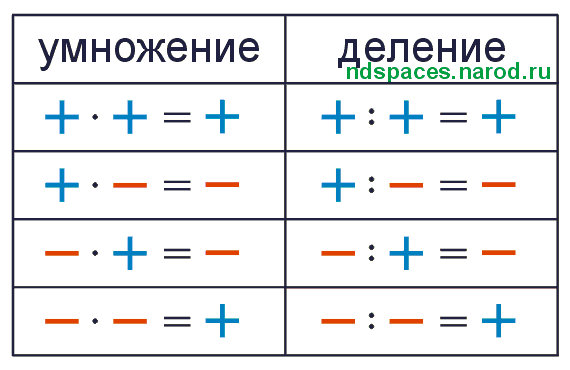
 Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.
Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.
 Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение.
Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение. По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению.
По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению. Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например:
Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например: В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.
В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.


 ..
..






 Когда вы открываете Калькулятор дня, дата автоматически устанавливается на сегодняшнюю дату. Поскольку калькулятор берет сегодняшнюю дату с ваших системных часов, важно убедиться, что ваша системная дата установлена правильно, чтобы эта функция работала должным образом.
Когда вы открываете Калькулятор дня, дата автоматически устанавливается на сегодняшнюю дату. Поскольку калькулятор берет сегодняшнюю дату с ваших системных часов, важно убедиться, что ваша системная дата установлена правильно, чтобы эта функция работала должным образом. Страницу лучше всего просматривать при разрешении 800 x 600 или выше.
Страницу лучше всего просматривать при разрешении 800 x 600 или выше. Пожалуйста, напишите нам по электронной почте. Спасибо.
Пожалуйста, напишите нам по электронной почте. Спасибо.