Векторы на плоскости и в пространстве: основные определения
Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Определение 1Вектор – это направленный отрезок прямой.
Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a→. Если известны граничные точки вектора – его начало и конец, к примеру A и B, то вектор обозначается так AB→.
Нулевой вектор
Определение 2Под нулевым вектором 0→ будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Длина вектора
Определение 3Под длиной вектора AB→ понимается число, большее либо равное 0, и равное длине отрезка АВ.
Длину вектораAB→ принято обозначать так AB→.
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Коллинеарность векторов
Определение 4Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Определение 5Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.
Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.
Направление векторов
Определение 6Сонаправленными векторами называют два коллинеарных вектора a→ и b→, у которых направления совпадают, такие векторы обозначаются так a→↑↑b→.
Определение 7Противоположно направленными векторами называются два коллинеарных вектора a→ и b→, у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a→↑↓b→.
Считается, что нулевой вектор является сонаправленым к любым другим векторам.
Равные и противоположные векторы
Определение 8Равными называются сонаправленные вектора, у которых длины равны.
Определение 9Противопожными называются противоположно направленные вектора, у которых их длины равны.
Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Пусть заданы два произвольных вектора на плоскости или в пространстве a→ и b→. Отложим от некоторой точки O плоскости или пространства векторы OA→=a→ и OB→=b→. Лучи OA и OB образуют угол ∠AOB=φ.
Углы между векторами
Определение 9Угол φ=∠AOB называется углом между векторами a→=OA→ и b→=OB→.
Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.
Определение 10Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π2 радиан).
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
Навигация по статьям
Предыдущая статья
Координаты вектора в ДСК
Следующая статья
Длина вектора
- Векторное произведение
- Векторное пространство
- Геометрическая фигура угол
- Деление отрезка в заданном соотношении
- Длина вектора
- Все темы по математике
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Все предметы
Узнать подробнее
электрические аппараты
Вид работы:
Контрольная работа
Выполнена:
5 марта 2023 г.

Стоимость:
1 700 руб
Математические фокусы
Вид работы:
Школьный проект
Выполнена:
24 февраля 2023 г.

Стоимость:
1 000 руб
Создание сайта предмет основы разработки интернет систем
Вид работы:
Контрольная работа
Выполнена:
10 февраля 2023 г.

Стоимость:
3 600 руб
сдать онлайн экзамен на системного администратора Windows
Заказать такую же работуМатематические предметы
Заказать такую же работуПриветствую Тема любой сервисный центр Интерфейс
Вид работы:
Лабораторная работа
Выполнена:
14 октября 2022 г.

Стоимость:
8 000 руб
Смотреть все работы по электронике
Векторы в пространстве — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Направленный
отрезок АВ
А – начало вектора
В – конец вектора
a
А
В
Обозначения:
AB a
2. ВЕКТОР ЗАДАЕТСЯ КООРДИНАТАМИ
aВ
А
А a1 , a 2 , a3
В b1 , b2 , b3
Вычисление координат вектора:
a AB b1 a1 ; b2 a2 ; b3 a3
x
y
z
3. МОДУЛЬ ВЕКТОРА
Известны координаты вектораa AB x; y; z
Длина вектора (модуль)
2
2
2
| a | x y z
Нулевой вектор:
Равные векторы:
AB 0 0
a b 1) a b;
2)
a b
4. ДЕЙСТВИЯ НАД ВЕКТОРАМИ
1. Сложениеa
b
( x1, y1, z1 )
x2 , y 2 , z 2
Правило
треугольника
b
a
c
параллелограмма
a
c
b
c a b ( x1 x 2 ; y1 y 2 ; z1 z 2 )
5. СЛОЖЕНИЕ ВЕКТОРОВ
Правиломногоугольника
a1
a2
c
an
c a1 a 2 .
-1651486231984584979626fae17bc7ab.jpg) .. a n
.. a n6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ
2. Вычитаниеa
a
b
( x1( x,1,yy11,,zz11) )
d
a
b
x2 , y 2 , z 2
d a b x1 x 2 ; y1 y 2 ; z1 z 2
7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ
3. Умножение вектора на число ( )a AB x; y; z
0
a
a b
a b
Векторы сонаправленые
(одинаково направленные)
a x; y; z
0
a
a b
a b
Векторы противоположно
направленные
8. ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ СООТНОШЕНИИ НА ПЛОСКОСТИ
Отрезок АВ разделен точкой С в отношенииА
С
Если
AC : CB ,
В
то координаты точки С находятся по
формулам:
y
y
x
A xB
A
B
;
y
xC 1
C
1
1, то отрезок АВ разделен точкой С пополам.
Координаты середины находят по формулам:
y
x
y
z
x
z
x 2 ; y 2 ;z 2
A
C
B
A
C
B
A
C
B
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
ВЕКТОРОВ
a
b
a
b
Скалярным
произведением двух
векторов называется
произведение их длин на
косинус угла между ними:
a b a b cos
10.
 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВСкалярное произведение векторов
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВСкалярное произведение векторовa x1; y1; z1 ; b x2 ; y2 ; z2
выражается формулой:
a b x1 x2 y1 y2 z1 z2
Косинус угла между ненулевыми
векторами:
cos
a b
a b
x1 x2 y1 y2 z1 z2
x12 y12 z12 x22 y22 z22
11. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
13. Свойства скалярного произведения
14. КОЛЛИНЕАРНОСТЬ ВЕКТОРОВ
Векторы лежат на одной прямойили параллельных прямых
a
c
b
d
Обозначают:
a || b
15. КОМЛАНАРНОСТЬ ВЕКТОРОВ
Векторы называются компланарными,если отложены из одной точки и
лежат в одной плоскости
b
a
c
O
a, b, c
— компланарны
c xa yb
, где x и y – некоторые
числа.
16. ПРАВИЛО ПАРАЛЛЕЛЕПИПЕДА
Любой вектор можно разложить по тремданным некомпланарным векторам:
d a b c
d
b
a
c
English Русский Правила
компонентов вектора
Горячая математика В двумерной системе координат любой
вектор
можно разбить на
Икс
-компонент и
у
-компонент.
в → «=» 〈 в Икс , в у 〉
Например, на рисунке ниже вектор в → распадается на две составляющие, в Икс и в у . Пусть угол между вектором и его Икс -компонент быть θ .
Вектор и его компоненты образуют прямоугольный треугольник, как показано ниже.
На приведенном выше рисунке компоненты можно быстро прочитать. Вектор в компонентной форме равен в → «=» 〈 4 , 5 〉 .
тригонометрические отношения дать отношение между величина вектора и компоненты вектора.
потому что θ «=» Соседняя сторона Гипотенуза «=» в Икс в
грех θ «=» Обратная сторона Гипотенуза «=» в у в
в Икс «=» в потому что θ
в у «=» в грех θ
Используя Теорема Пифагора в прямоугольном треугольнике с длинами в Икс и в у :
| в | «=» в Икс 2 + в у 2
Здесь показанные числа являются величинами векторов.
Дело 1: По данным компонентам вектора найдите модуль и направление вектора.
В этом случае используйте следующие формулы.
Величина вектора | в | «=» в Икс 2 + в у 2 .
Чтобы найти направление вектора, решите загар θ «=» в у в Икс для θ .
Случай 2: Зная величину и направление вектора, найдите компоненты вектора.
В этом случае используйте следующие формулы.
в Икс «=» в потому что θ
в у «=» в грех θ
Пример:
Величина вектора
Ф
→
является
10
единицы, а направление вектора равно
60
°
с горизонталью. Найдите компоненты вектора.
Найдите компоненты вектора.
Ф Икс «=» Ф потому что 60 ° «=» 10 ⋅ 1 2 «=» 5
Ф у «=» Ф грех 60 ° «=» 10 ⋅ 3 2 «=» 5 3
Итак, вектор
Ф
→
является
〈
5
,
5
3
〉
.
Перекрестное произведение двух векторов
Перекрестное произведение двух векторов — это метод умножения двух векторов. Перекрестное произведение обозначается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, определенная в трехмерной системе. Перекрестное произведение двух векторов — это третий вектор, перпендикулярный двум исходным векторам. Его величина определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. Перекрестное произведение двух векторов также известно как векторное произведение, поскольку результирующая перекрестного произведения векторов является векторной величиной. Здесь мы узнаем больше о векторном произведении двух векторов.
| 1. | Перекрестное произведение двух векторов |
| 2. | Формула перекрестного произведения |
3. | Правило правой руки перекрестного произведения |
| 4. | Свойства перекрестного произведения |
| 5. | Продукт тройного креста |
| 6. | Пример перекрестного произведения |
| 7. | Часто задаваемые вопросы о векторном произведении двух векторов |
Перекрестное произведение двух векторов
Перекрестное произведение — это форма умножения векторов, выполняемая между двумя векторами разной природы или вида. Вектор имеет как величину, так и направление. Мы можем умножать два или более векторов на перекрестное произведение и скалярное произведение. Когда два вектора перемножаются друг с другом и произведение векторов также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.
Определение векторного произведения
Если A и B — два независимых вектора, то результат векторного произведения этих двух векторов (Ax B) перпендикулярен обоим векторам и нормален к плоскости, содержащей оба вектора. Он представлен:
А х В = |А| |Б| sin θ
Мы можем понять это на примере, что если у нас есть два вектора, лежащих в плоскости X-Y, то их векторное произведение даст результирующий вектор в направлении оси Z, которая перпендикулярна плоскости XY . Символ × используется между исходными векторами. Векторное произведение или перекрестное произведение двух векторов показано как:
\(\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}\)
Где
- \(\overrightarrow{a}\) и \(\overrightarrow{b}\) два вектора.
- \(\overrightarrow{c}\) — результирующий вектор.
Перекрестное произведение двух векторов Значение
Используйте изображение, показанное ниже, и обратите внимание на углы между векторами \(\overrightarrow{a}\) и \(\overrightarrow{c}\) и углы между векторами \(\ overrightarrow{b}\) и \(\overrightarrow{c}\). 9\circ\).т. е. \(\overrightarrow{b}\) и \(\overrightarrow{c}\) являются ортогональными векторами.
9\circ\).т. е. \(\overrightarrow{b}\) и \(\overrightarrow{c}\) являются ортогональными векторами.
Формула перекрестного произведения
Формула перекрестного произведения между любыми двумя векторами дает площадь между этими векторами. Формула векторного произведения дает величину результирующего вектора, который представляет собой площадь параллелограмма, натянутого на два вектора.
Формула перекрестного произведения
Рассмотрим два вектора \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \шляпа i+b_2 \шляпа j+b_3 \шляпа k\). Пусть θ — угол, образованный между \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а \(\hat n\) — единичный вектор, перпендикулярный плоскости, содержащей обе \(\overrightarrow{a }\) и \(\overrightarrow{b}\). Перекрестное произведение двух векторов определяется формулой:
Перекрестное произведение двух векторов определяется формулой:
\(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)
Где
- \(\mid \overrightarrow a \mid\ ) — величина вектора a или длина \(\overrightarrow{a}\), 90 141
- \(\mid \overrightarrow b \mid\) — величина вектора b или длина \(\overrightarrow{b}\).
Предположим, что \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — два вектора, такие что \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \ hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \hat i+b_2 \hat j+b_3 \hat k\), то с помощью определителей мы могли бы найти векторное произведение и запишите результат в виде формулы перекрестного произведения, используя матричную запись.
Перекрестное произведение двух векторов также представляется с помощью формулы перекрестного произведения как: j (a_1b_3-a_3b_1)\\+ \hat k (a_1b_2-a_2b_1)\)
Примечание: \( \hat i, \hat j, \text{ и } \hat k \) — единичные векторы в направлении оси x, оси y и оси z соответственно.
Правило правой руки — векторное произведение двух векторов
Мы можем узнать направление вектора, который получается при перекрестном произведении двух векторов по правилу правой руки. Мы следуем следующей процедуре, чтобы узнать направление результата перекрестного произведения двух векторов:
- Направьте указательный палец в направлении первого вектора (\(\overrightarrow{A}\)).
- Выровняйте средний палец в направлении второго вектора \(\overrightarrow{B}\).
- Теперь большой палец указывает в направлении векторного произведения двух векторов.
Посмотрите на изображение ниже, чтобы лучше понять это.
Свойства перекрестного произведения двух векторов
Свойства перекрестного произведения помогают ясно понять умножение векторов и помогают легко решать все проблемы векторных вычислений. Свойства векторного произведения двух векторов следующие:
- Длина векторного произведения двух векторов \(= \overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta)\).

- Антикоммутативное свойство: \(\overrightarrow{a} \times \overrightarrow{b} = — \overrightarrow{b} \times \overrightarrow{a}\)
- Распределительное свойство: \(\overrightarrow{a} \times (\overrightarrow{b} + \overrightarrow{c}) = (\overrightarrow{a}\times \overrightarrow{b} )+ (\overrightarrow{a}\times \overrightarrow{с})\)
- Перемножение нулевого вектора: \(\overrightarrow{a}\times \overrightarrow{0} = \overrightarrow{0}\)
- Перемножение вектора с самим собой: \(\overrightarrow{a}\times \overrightarrow{a} = \overrightarrow{0}\)
- Умножить на скалярную величину: \(\overrightarrow{c}(\overrightarrow{a}\times \overrightarrow{b}) = c\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{a}\times c\overrightarrow{b}\)
- Перекрестное произведение единичных векторов: \(\overrightarrow{i}\times \overrightarrow{i} =\overrightarrow{j}\times \overrightarrow{j} = \overrightarrow{k}\times \overrightarrow{k} = 0\)
- \(\overrightarrow{i}\times \overrightarrow{j} = \overrightarrow{k}\\ \overrightarrow{j}\times \overrightarrow{k}= \overrightarrow{i}\\\overrightarrow{k}\times \overrightarrow{i} = \overrightarrow{j}\)
- \(\overrightarrow{j}\times \overrightarrow{i} = \overrightarrow{-k}\\ \overrightarrow{k}\times \overrightarrow{j}= \overrightarrow{-i}\\ \overrightarrow{i} \times \overrightarrow{k} = \overrightarrow{-j}\)
Тройное перекрестное произведение
Перекрестное произведение вектора на перекрестное произведение двух других векторов представляет собой тройное перекрестное произведение векторов. Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:
Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:
\((\overrightarrow{a}\times \overrightarrow{b}) \times \overrightarrow{c} = (\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b} -(\overrightarrow{b}\cdot \overrightarrow{c}) \overrightarrow{a}\)
Перекрестное произведение двух векторов Пример
Перекрестное произведение играет решающую роль в нескольких областях науки и техники. Два очень простых примера показаны ниже.
Пример 1: Открытие крана: Мы прикладываем равные и противоположные силы к двум диаметрально противоположным концам крана. В этом случае применяется крутящий момент. В векторной форме крутящий момент представляет собой векторное произведение радиус-вектора (от оси вращения до точки приложения силы) и вектора силы.
т. е. \(\overrightarrow{T} = \overrightarrow{r} \times \overrightarrow{F}\)
Пример 2: Скручивание болта гаечным ключом: длина гаечного ключа равна одному вектору. Здесь направление, в котором мы прикладываем усилие к гаечному ключу (чтобы затянуть или ослабить болт), является другим вектором. Результирующее направление закручивания перпендикулярно обоим векторам.
Важные примечания
- В результате перекрестного произведения двух векторов получается вектор, ортогональный двум заданным векторам.
- Направление векторного произведения двух векторов определяется правилом большого пальца правой руки, а величина определяется площадью параллелограмма, образованного исходными двумя векторами \(\overrightarrow{a}\) и \(\overrightarrow {б}\).
- Перекрестное произведение двух линейных векторов или параллельных векторов является нулевым вектором.
☛ Также проверьте:
- Типы векторов
- Векторные формулы
- Компоненты вектора
- Калькулятор перекрестного произведения
- Добавление векторов
Примеры перекрестного произведения двух векторов
Пример 1: Два вектора имеют скалярную величину как ∣a∣=2√3 и ∣b∣ = 4, а угол между двумя векторами равен 60 ∘ .

Вычислить векторное произведение двух векторов.
Решение:
Мы знаем, что sin60° = √3/2
Перекрестное произведение двух векторов определяется выражением \(\overrightarrow{a} \times \overrightarrow{b} \) = |a ||b|sin(θ)\( \шляпа n \) = 2√3×4×√3/2 = 12\( \шляпа n \)
Ответ: перекрестное произведение равно 12n.
Вопрос 2: Найдите векторное произведение двух векторов \(\overrightarrow{a}\) = (3,4,5) и \(\overrightarrow{b}\) = (7,8,9)
Решение:
Перекрестное произведение задается как
\(\begin{align}a \times b &=\begin{matrix} \hat i & \hat j & \hat k\\ 3 & 4 & 5\\ 7 & 8 & 9 \end{matrix}\end{align}\)
= [(4×9)−(5×8)] \( \шляпа {i}\) −[(3×9)−(5×7)]\( \шляпа {j} \)+[(3×8)−(4 ×7)] \( \hat {k}\)
= (36−40)\( \hat i\) − (27−35)\( \hat j\) +(24−28) \( \ шляпа k\) = −4\( \hat i\) + 8\( \hat j\) −4\( \hat k\)
Ответ: ∴ \(\overrightarrow{a} \times \overrightarrow{ b} \) = −4\( \hat i\) + 8\( \hat j\) −4\( \hat k\)
Пример 3: Если \(\overrightarrow{a}\) = (2, -4, 4) и \(\overrightarrow{b}\) = (4, 0,3), найдите угол между ними.

Решение
\(\overrightarrow{a}\) = 2i — 4j + 4k
\(\overrightarrow{b}\) = 4i + 0j +3k
Величина \(\overrightarrow{a }\) равно
∣a∣=√(2 2 +4 2 +4 2 ) = √36 = 6
Величина \(\overrightarrow{b}\) равна
∣ b∣=√(4 2 +0 2 +3 2 ) = √25 = 5
Согласно формуле перекрестного произведения, мы имеем\(\begin{align}\overrightarrow{a}\times \overrightarrow{b} &= \begin{matrix} \hat i & \hat j & \hat k\\ 2 & -4 & 4\\ 4 & 0 & 3 \end{matrix}\\\\&=[(-4\times3) — (4\times0)]\hat i \\ — &[(3\times 2) — (4\times 4)] \hat j \\\\ + &[(2\times 0) -(-4\times 4)]\hat k \\\\&= -12\hat i + 10 \hat j +16 \hat k \\ \overrightarrow{a}\times \overrightarrow{b} &= (-12, 10, 16) \end{align}\)
Длина \(\overrightarrow{c}\) равна
∣c∣=√(−(12) 2 +10 2 +16 2 )
= √(144+100 +256)
=√500
=10√5
\(\begin{align}\overrightarrow{a}\times \overrightarrow{b} &= \mid a \mid \mid b \mid \sin\ тета\\\sin\theta &= \dfrac{\overrightarrow{a}\times \overrightarrow{b}}{\mid a \mid \mid b \mid}\end{align}\)
sinθ = 10√ 5/(5×6)
sinθ = √5/3
θ = sin −1 (√5/3)
θ = sin −1 (0,74)
θ = 48 ∘
Ответ: Угол между векторами равен 4 8 ∘ .

перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по векторному произведению двух векторов
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о перекрестном произведении двух векторов
Что такое векторное произведение двух векторов?
В результате перекрестного произведения двух векторов при умножении третий вектор перпендикулярен двум исходным векторам. Величина результирующего вектора определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. a × b = c, где c — векторное произведение двух векторов a и b.
Каков результат векторного перекрестного произведения?
Когда мы находим векторное произведение двух векторов, мы получаем другой вектор, выровненный перпендикулярно плоскости, содержащей два вектора. Величина результирующего вектора является произведением греха угла между векторами и величиной двух векторов. а × б = | а | |б| грех θ.
Величина результирующего вектора является произведением греха угла между векторами и величиной двух векторов. а × б = | а | |б| грех θ.
Что такое скалярное произведение и векторное произведение двух векторов?
Векторы можно умножать двумя разными способами, т. е. скалярным произведением и перекрестным произведением. Результаты обоих этих умножений векторов различны. В результате скалярное произведение дает скалярную величину, тогда как векторное произведение дает векторную величину. Скалярное произведение — это скалярное произведение двух векторов, а перекрестное произведение двух векторов — это векторное произведение двух векторов. Скалярное произведение также известно как скалярное произведение, а перекрестное произведение также известно как векторное произведение. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\)
\overrightarrow{b} = |a| |b| \cos(\theta)\)
Как найти векторное произведение двух векторов?
Перекрестное произведение двух векторов определяется по формуле: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)
Где
- |\(\overrightarrow a\)| величина или длина \(\overrightarrow{a}\),
- |\(\overrightarrow b\)| является величиной или длиной \(\overrightarrow{b}\)
Почему перекрестное произведение является синусоидальным?
Поскольку θ — это угол между двумя исходными векторами, используется sin θ, поскольку площадь параллелограмма получается путем перекрестного произведения двух векторов.
Всегда ли положительное произведение двух векторов?
Когда угол между двумя исходными векторами изменяется от 180° до 360°, векторное произведение становится отрицательным. Это связано с тем, что sin θ отрицателен для 180°< θ <360°.
В чем разница между скалярным произведением и перекрестным произведением двух векторов?
При умножении векторов скалярное произведение исходных векторов дает скалярную величину, тогда как перекрестное произведение двух векторов дает векторную величину. Скалярное произведение — это произведение величины векторов и cos угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
Скалярное произведение — это произведение величины векторов и cos угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
Что такое формула векторного произведения для двух векторов?
Формула векторного произведения определяет векторное произведение для любых двух заданных векторов, задавая площадь между этими векторами. Формула перекрестного произведения имеет вид \(\overrightarrow{A} × \overrightarrow{B} =|A||B| sinθ\), где |A| = величина вектора A, |B| = величина вектора B, а θ = угол между векторами A и B.
Как найти величину векторного произведения двух векторов?
Перекрестное произведение двух векторов — это еще один вектор, величина которого определяется выражением \(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3-a_3b_1) \\+ \шляпа k (a_1b_2-a_2b_1)\)
Что такое формула перекрестного произведения с использованием матричной записи?
Для двух заданных векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) мы можем найти векторное произведение, используя определители. Например, \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \hat i+b_2 \hat j+b_3 \hat k\), то мы можем записать результат как \(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3- a_3b_1)\\+ \шляпа k (a_1b_2-a_2b_1)\)
Например, \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \hat i+b_2 \hat j+b_3 \hat k\), то мы можем записать результат как \(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3- a_3b_1)\\+ \шляпа k (a_1b_2-a_2b_1)\)
Как использовать формулу перекрестного произведения?
Рассмотрим заданные векторы.
- Шаг 1: Проверьте компоненты векторов |A| = величина вектора A, |B| = модуль вектора B и θ = угол между векторами A и B.
- Шаг 2: Подставьте значения в формулу векторного произведения: \ ((\vec {A × B})=|A||B|\text{Sin}\vec{θ_n}\)
Например, если \(\vec {A}=a\hat{i} + b\hat{j}+c\hat{k}\) и \( \vec{B}=d\hat{i } + e\hat{j}+f\hat{k}\), затем \({\vec{A × B}} = \begin{matrix} \hat{i} & \hat{j} & \hat{ k} \\ a & b & c \\ d & e & f \end{matrix}\)
\({\vec{A × B}} = \шляпа{i}(bf-ce) — \шляпа{j}(af-cd) + \шляпа{k}(ae-bd)\)
Что такое правило большого пальца правой руки для перекрестного произведения двух векторов?
Правило правой руки для векторного произведения двух векторов помогает определить направление результирующего вектора.










 0.0 \(Windows\))
/ModDate (D:20100514103350+03’00’)
/Company
/SourceModified (D:20100511092740)
/Title
>>
endobj
2 0 obj
>
endobj
3 0 obj
>
stream
Acrobat Distiller 8.0.0 (Windows) БНТУ, ФИТР, ВМ1, БалашоваD:20100511092740Acrobat PDFMaker 8.0 для Word2010-05-14T10:33:50+03:002010-05-11T12:28:20+03:002010-05-14T10:33:50+03:00uuid:f1030f28-16f4-4873-8896-dc039de0187buuid:18e3f8c1-f77e-44ac-8460-29f12b077eca
0.0 \(Windows\))
/ModDate (D:20100514103350+03’00’)
/Company
/SourceModified (D:20100511092740)
/Title
>>
endobj
2 0 obj
>
endobj
3 0 obj
>
stream
Acrobat Distiller 8.0.0 (Windows) БНТУ, ФИТР, ВМ1, БалашоваD:20100511092740Acrobat PDFMaker 8.0 для Word2010-05-14T10:33:50+03:002010-05-11T12:28:20+03:002010-05-14T10:33:50+03:00uuid:f1030f28-16f4-4873-8896-dc039de0187buuid:18e3f8c1-f77e-44ac-8460-29f12b077eca Упражнения
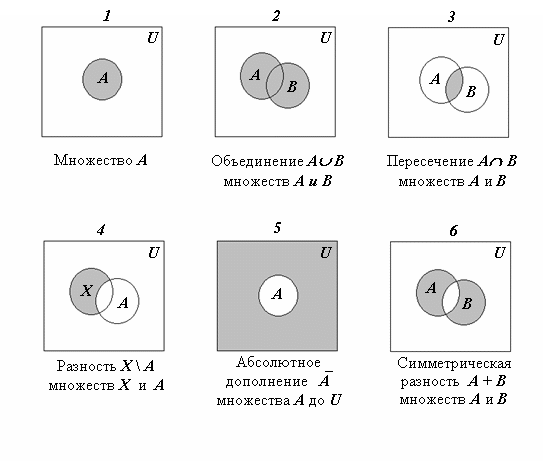
Упражнения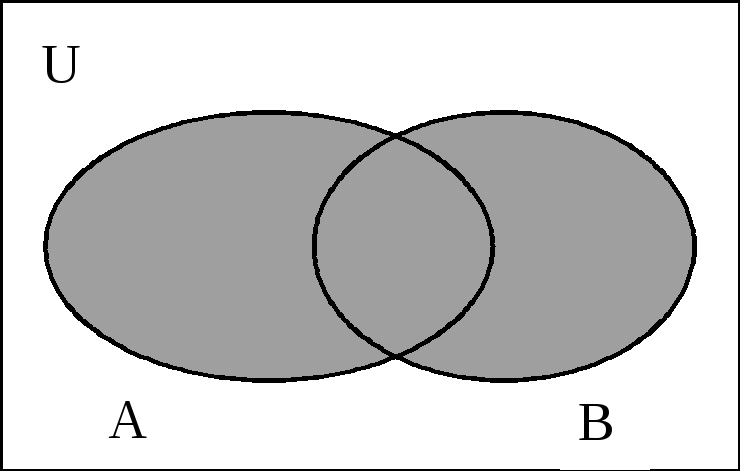 Поскольку «объединение» означает «все в любом из наборов», все кружки заштрихованы. (Если вам не ясна логика записи набора, просмотрите запись набора, прежде чем двигаться дальше.)
Поскольку «объединение» означает «все в любом из наборов», все кружки заштрихованы. (Если вам не ясна логика записи набора, просмотрите запись набора, прежде чем двигаться дальше.) Тильда в контексте отношения множества говорит, что теперь я хочу найти дополнение (в некотором смысле противоположное) тому, что отрицается или «выбрасывается»; в данном случае это множество A. Тип дополнения, который мы видим в этом упражнении, дополнение «не», означает «выбросить все, что у вас есть сейчас (в данном случае, множество A), и вместо этого взять все остальное во вселенной». «.
Тильда в контексте отношения множества говорит, что теперь я хочу найти дополнение (в некотором смысле противоположное) тому, что отрицается или «выбрасывается»; в данном случае это множество A. Тип дополнения, который мы видим в этом упражнении, дополнение «не», означает «выбросить все, что у вас есть сейчас (в данном случае, множество A), и вместо этого взять все остальное во вселенной». «. . Некоторые из приведенных выше примеров демонстрируют более одного способа форматирования (и произношения) одного и того же. В разных текстах используются разные наборы обозначений, поэтому не стоит удивляться, если в вашем тексте используются еще и другие символы, чем те, что использовались выше. Но хотя обозначения могут отличаться, концепции будут одинаковыми.
. Некоторые из приведенных выше примеров демонстрируют более одного способа форматирования (и произношения) одного и того же. В разных текстах используются разные наборы обозначений, поэтому не стоит удивляться, если в вашем тексте используются еще и другие символы, чем те, что использовались выше. Но хотя обозначения могут отличаться, концепции будут одинаковыми.
 Диаграммы Венна также называются логическими или диаграммами множеств и широко используются в теории множеств, логике, математике, бизнесе, обучении, информатике и статистике.
Диаграммы Венна также называются логическими или диаграммами множеств и широко используются в теории множеств, логике, математике, бизнесе, обучении, информатике и статистике. Диаграмма Венна обычно использует пересекающиеся и непересекающиеся круги (хотя могут использоваться и другие замкнутые фигуры, такие как квадраты) для обозначения отношений между множествами.
Диаграмма Венна обычно использует пересекающиеся и непересекающиеся круги (хотя могут использоваться и другие замкнутые фигуры, такие как квадраты) для обозначения отношений между множествами. Всякий раз, когда мы рисуем диаграмму Венна:
Всякий раз, когда мы рисуем диаграмму Венна: Рассмотрим примеры двух множеств A и B на приведенном ниже рисунке. Здесь A является подмножеством B. Окружность A полностью содержится внутри окружности B. Кроме того, все элементы A являются элементами множества B.
Рассмотрим примеры двух множеств A и B на приведенном ниже рисунке. Здесь A является подмножеством B. Окружность A полностью содержится внутри окружности B. Кроме того, все элементы A являются элементами множества B.

 Суммарная площадь обеих окружностей вместе обозначает объединение множеств A и B.
Суммарная площадь обеих окружностей вместе обозначает объединение множеств A и B. Область, покрываемая множеством A, исключая область, общую для множества B, дает разницу множеств A и B.
Область, покрываемая множеством A, исключая область, общую для множества B, дает разницу множеств A и B. Поскольку число больше трех становится очень сложным, мы обычно будем рассматривать только два или три круга на диаграмме Венна. Вот 4 простых шага, чтобы нарисовать диаграмму Венна:
Поскольку число больше трех становится очень сложным, мы обычно будем рассматривать только два или три круга на диаграмме Венна. Вот 4 простых шага, чтобы нарисовать диаграмму Венна: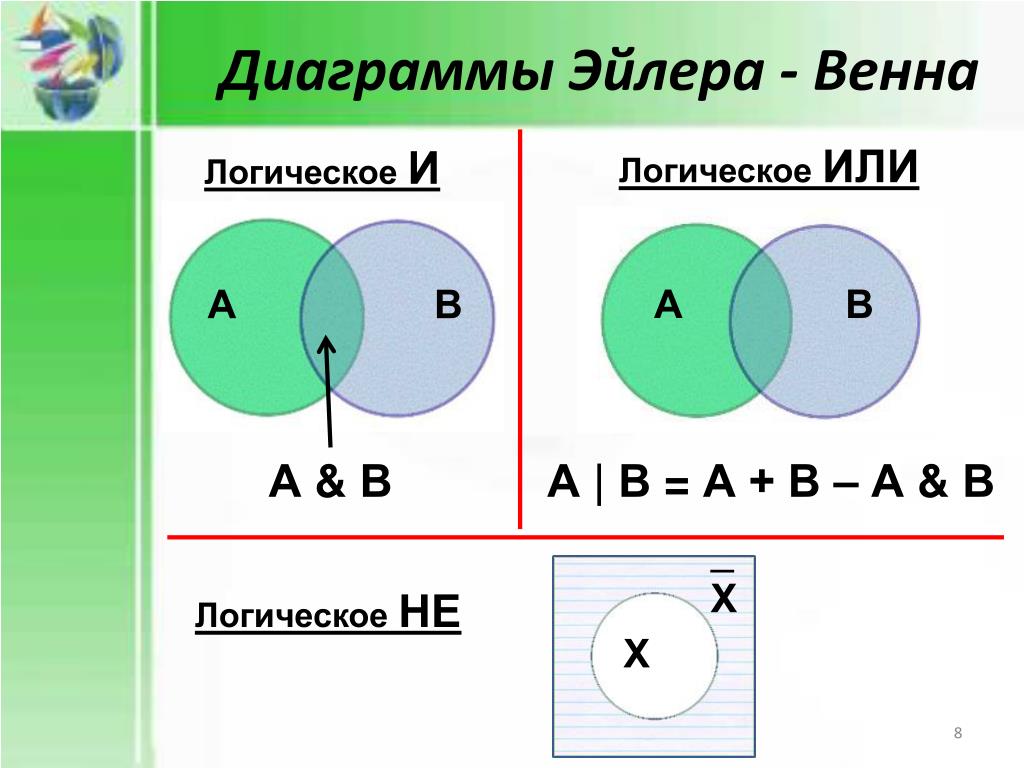 Обе категории (открытая и закрытая): Кролики и Рыбы.
Обе категории (открытая и закрытая): Кролики и Рыбы.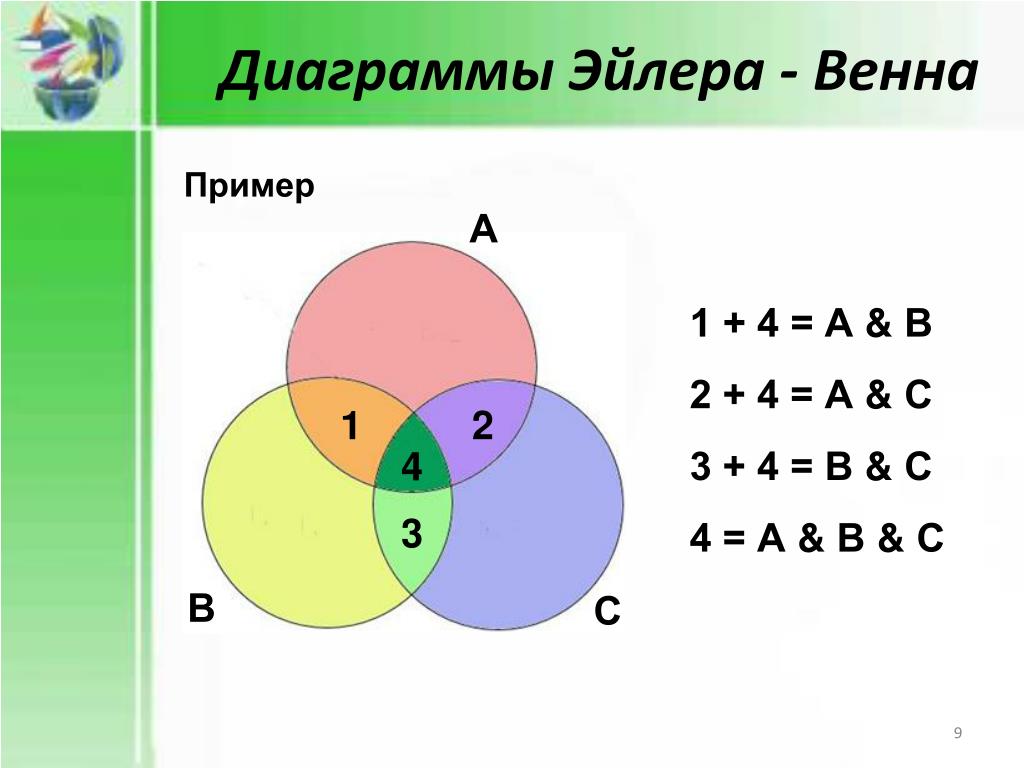
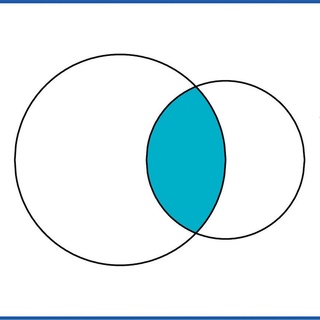 Тогда
Тогда
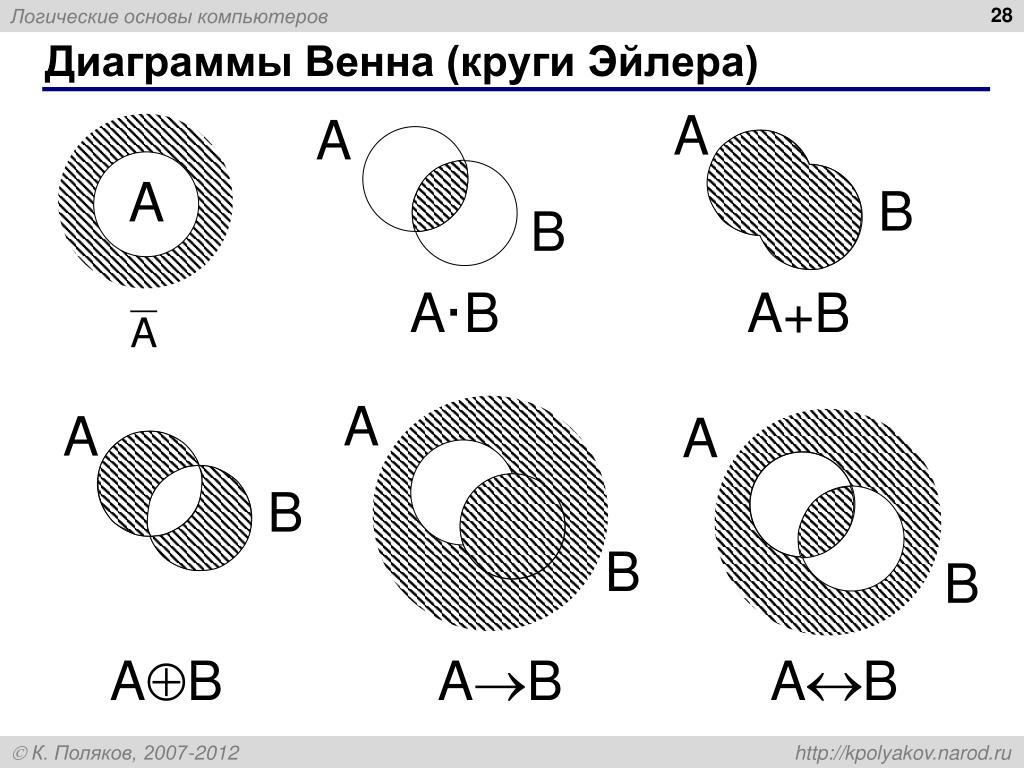


 Все остальные наборы представлены кружками или замкнутыми фигурами внутри этого большего прямоугольника, представляющего универсальный набор.
Все остальные наборы представлены кружками или замкнутыми фигурами внутри этого большего прямоугольника, представляющего универсальный набор.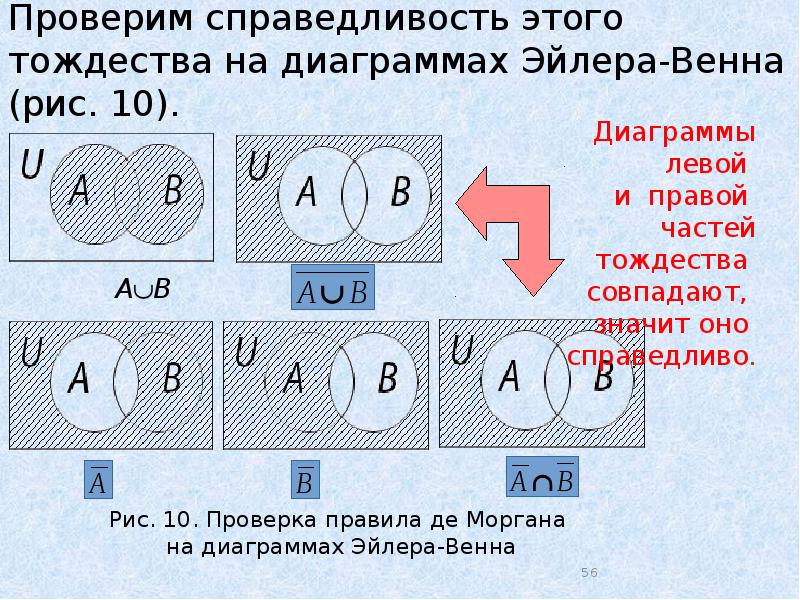


 2 \) равен:
2 \) равен:
 2-xy \) равен:
2-xy \) равен:
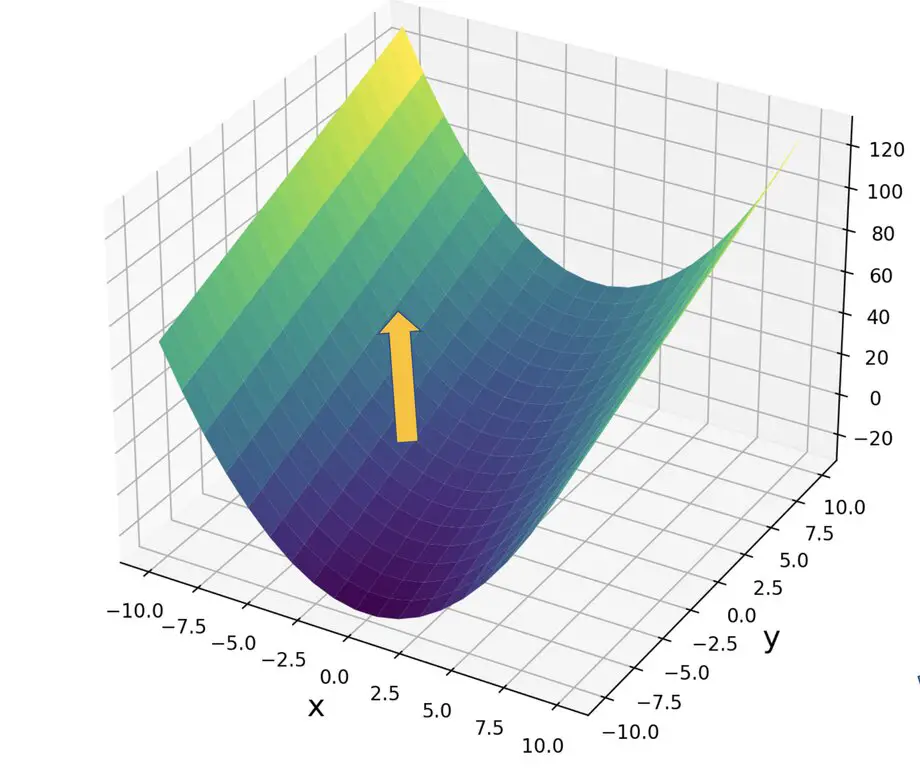 Таким образом,
Правило цепи
,
Правило Продукта
а также
правило квоты
также будет работать для многомерной функции, учитывая правильные размеры.
Таким образом,
Правило цепи
,
Правило Продукта
а также
правило квоты
также будет работать для многомерной функции, учитывая правильные размеры.
 Данный показатель используется при диагностике источника гипоксемии.
Данный показатель используется при диагностике источника гипоксемии. Обычно градиент A-a увеличивается с возрастом. Считается, что за каждое десятилетие жизни человека градиент увеличивается на 1 мм рт.ст.
Обычно градиент A-a увеличивается с возрастом. Считается, что за каждое десятилетие жизни человека градиент увеличивается на 1 мм рт.ст. 4)
4)





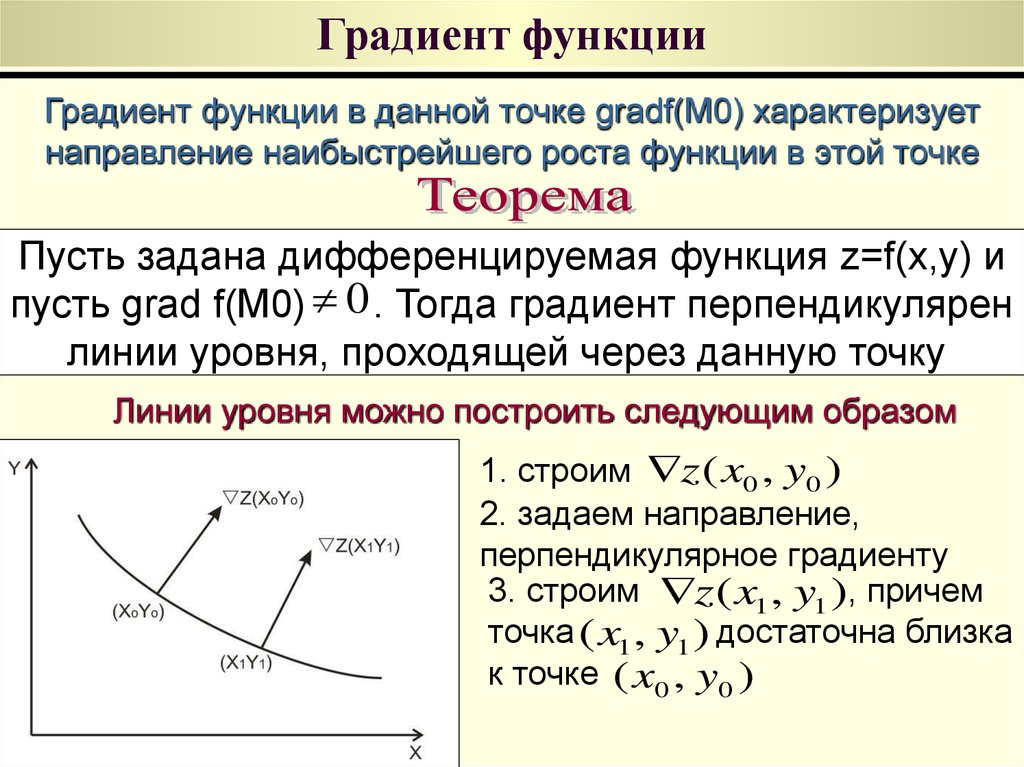 « Что такое градиент? » спросите вы. Ну, вы когда-нибудь смотрели на гору и говорили себе: « Ого, эта гора довольно крутая, но не такая крутая, как близлежащая! »? И если такого рода вопрос заставил вас задаться вопросом, как сравнить их крутизну, вы попали в нужное место ! Продолжайте читать, чтобы узнать определение градиента.
« Что такое градиент? » спросите вы. Ну, вы когда-нибудь смотрели на гору и говорили себе: « Ого, эта гора довольно крутая, но не такая крутая, как близлежащая! »? И если такого рода вопрос заставил вас задаться вопросом, как сравнить их крутизну, вы попали в нужное место ! Продолжайте читать, чтобы узнать определение градиента. .. ну центр , то есть точку (x₁,y₁) = (0,0) на плоскости.
.. ну центр , то есть точку (x₁,y₁) = (0,0) на плоскости. Они заслуживают столько же.
Они заслуживают столько же. Следовательно, в данном случае градиент не определен .
Следовательно, в данном случае градиент не определен .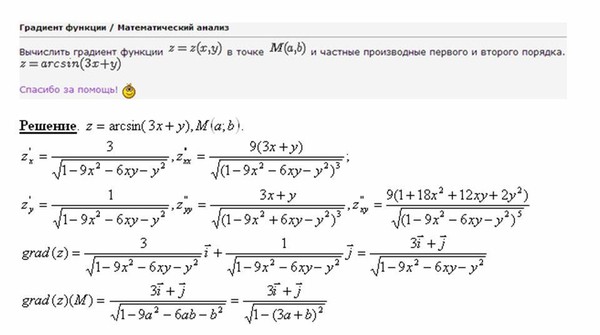 Допустим, мы хотим вычислить градиент линии, проходящей через точки (-2,1) и (3,11) .
Допустим, мы хотим вычислить градиент линии, проходящей через точки (-2,1) и (3,11) .



 С помощью Microsoft Word вы можете составить такие документы как:
С помощью Microsoft Word вы можете составить такие документы как:
 Физкультминутка.
Физкультминутка. д. По умолчанию, для абзаца в Word 2016 задается режим выравнивания текста по левой границе.
д. По умолчанию, для абзаца в Word 2016 задается режим выравнивания текста по левой границе.


 docx
docx docx
docx д. Учащиеся могут Подробнее…
д. Учащиеся могут Подробнее…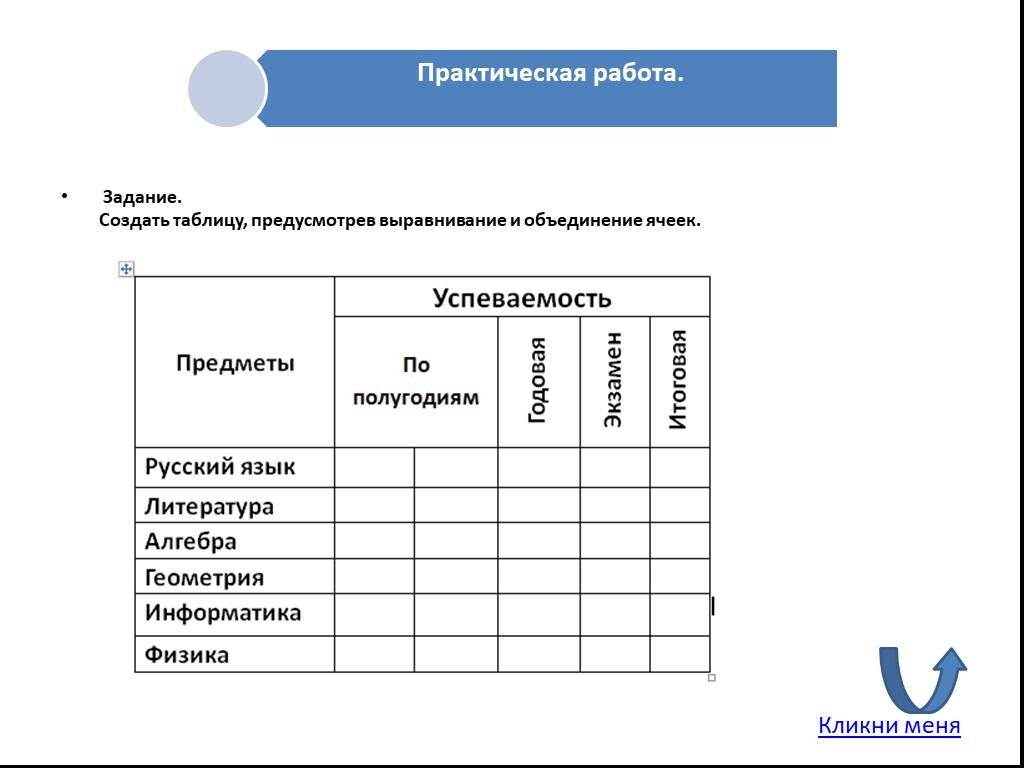 ..
.. Это включает в себя план с несколькими Подробнее…
Это включает в себя план с несколькими Подробнее… ..
.. ..
.. Читать далее…
Читать далее…


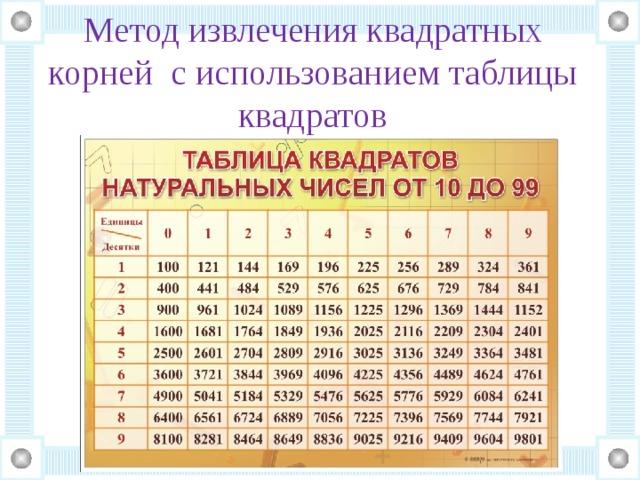 Просто и ясно.
Просто и ясно.
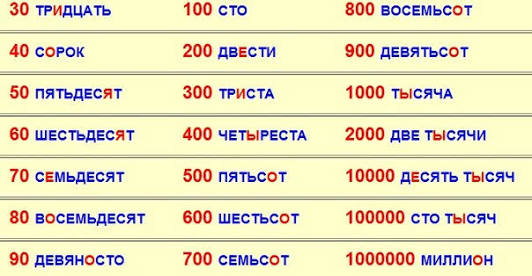
 д. Эти числительные могут быть представлены в состоянии реальностей, а также термины должным образом. Например, такие целые числа, как 20 и 25, показанные при формировании цифр, также могут быть представлены как двадцать и двадцать пять. Система счисления или система счисления описывается как несложная/простая система для отображения цифр и образований. Это уникальная форма отображения цифр в математической и арифметической формах.
д. Эти числительные могут быть представлены в состоянии реальностей, а также термины должным образом. Например, такие целые числа, как 20 и 25, показанные при формировании цифр, также могут быть представлены как двадцать и двадцать пять. Система счисления или система счисления описывается как несложная/простая система для отображения цифр и образований. Это уникальная форма отображения цифр в математической и арифметической формах. Он образован такими цифрами, как 4, 5, 78 и т. д.
Он образован такими цифрами, как 4, 5, 78 и т. д.


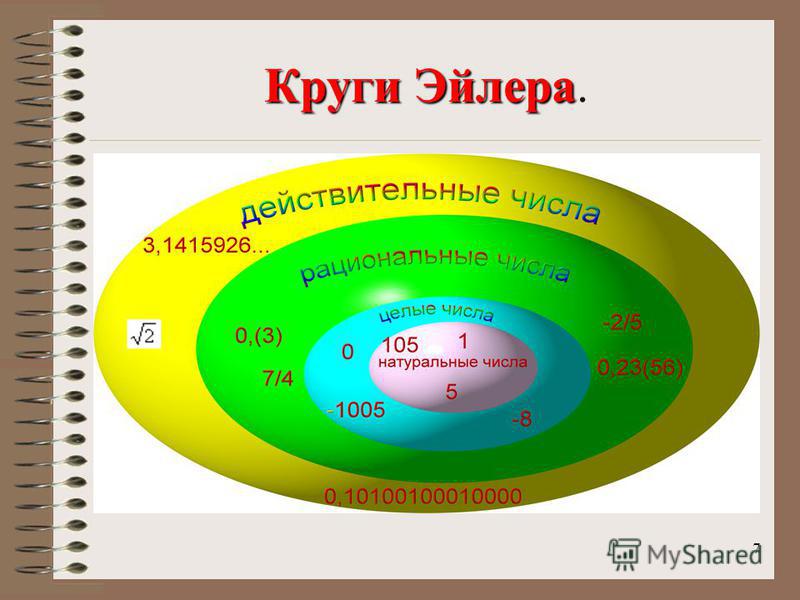 Преобразование выражений, содержащих переменную под знаком логарифма
Преобразование выражений, содержащих переменную под знаком логарифма Аксиомы стереометрии и некоторые следствия из них
Аксиомы стереометрии и некоторые следствия из них {-2}\). Поскольку целая часть у нормализованного представления числа всегда (кроме числа 0) равна 1, то целая часть не хранится, а хранится только дробная часть мантиссы. Количество значащих знаков мантиcсы, которое хранится, может быть различным для различных способов представления действительных чисел. Например, в типе данных двойной точности, который в языке Python соответствует типу float, в языке C — типу double, в языке Pascal — типу double, хранится 52 бита дробной части мантиcсы.
{-2}\). Поскольку целая часть у нормализованного представления числа всегда (кроме числа 0) равна 1, то целая часть не хранится, а хранится только дробная часть мантиссы. Количество значащих знаков мантиcсы, которое хранится, может быть различным для различных способов представления действительных чисел. Например, в типе данных двойной точности, который в языке Python соответствует типу float, в языке C — типу double, в языке Pascal — типу double, хранится 52 бита дробной части мантиcсы.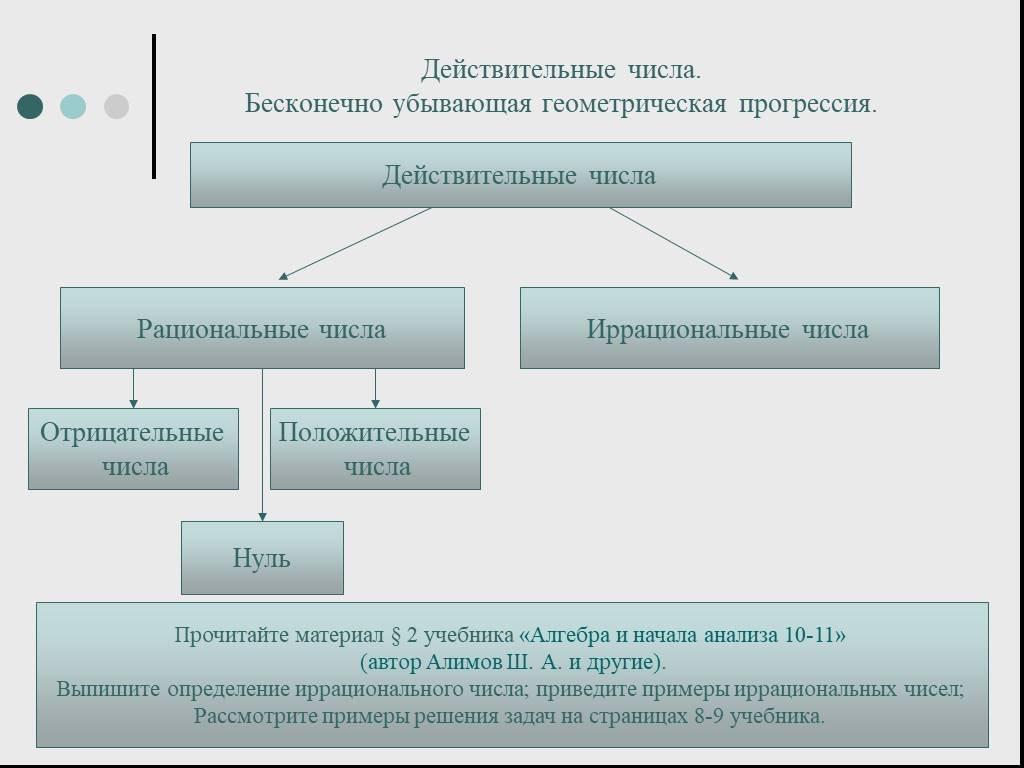 {-2}\) и хранятся только 52 цифры дробной части мантиссы числа. Дальнейшие цифры отбрасываются, поэтому вместо числа \(\frac{1}{3}\), которое непредставимо в действительных типах данных, хранится другое ближайшее к нему представимое число. В случае с числом \(\frac{1}{3}\) записывается меньшее число, также меньшее число записывается и при записи в переменную двойной точности значений \(\frac{1}{10}\) и \(\frac{2}{10}\), а вот вместо числа \(\frac{3}{10}\) уже будет записано большее представимое число. Поэтому если записать в две переменные значения \(0{.}1\) и \(0{.}2\) (десятичные), а в третью переменную записать их сумму, то результат окажется меньше, чем
\(\frac{3}{10}\), в то время как при записи в переменную значения \(\frac{3}{10}\) явно в виде \(0{.}3\), получится результат, больший чем \(\frac{3}{10}\). То есть при вычислении суммы чисел \(0{.}1\) и \(0{.}2\) результат получится отличным от значения \(0{.}3\), записанного в переменную явно, то есть с точки зрения компьютерной арифметики
\(0{.
{-2}\) и хранятся только 52 цифры дробной части мантиссы числа. Дальнейшие цифры отбрасываются, поэтому вместо числа \(\frac{1}{3}\), которое непредставимо в действительных типах данных, хранится другое ближайшее к нему представимое число. В случае с числом \(\frac{1}{3}\) записывается меньшее число, также меньшее число записывается и при записи в переменную двойной точности значений \(\frac{1}{10}\) и \(\frac{2}{10}\), а вот вместо числа \(\frac{3}{10}\) уже будет записано большее представимое число. Поэтому если записать в две переменные значения \(0{.}1\) и \(0{.}2\) (десятичные), а в третью переменную записать их сумму, то результат окажется меньше, чем
\(\frac{3}{10}\), в то время как при записи в переменную значения \(\frac{3}{10}\) явно в виде \(0{.}3\), получится результат, больший чем \(\frac{3}{10}\). То есть при вычислении суммы чисел \(0{.}1\) и \(0{.}2\) результат получится отличным от значения \(0{.}3\), записанного в переменную явно, то есть с точки зрения компьютерной арифметики
\(0{. }1 + 0{.}2 \ne 0{.}3\). Эту проблему (неточное представление действительных чисел и выполнение арифметических операций с действительными числами) всегда следует иметь в виду.
}1 + 0{.}2 \ne 0{.}3\). Эту проблему (неточное представление действительных чисел и выполнение арифметических операций с действительными числами) всегда следует иметь в виду.
 Примеры операций, дающих в результате nan:
Примеры операций, дающих в результате nan: Числа 3,5, -0,003, 2/3, π и √2 — все действительные числа.
Числа 3,5, -0,003, 2/3, π и √2 — все действительные числа. 1. Представьте, что ноги равны одной единице длины.
1. Представьте, что ноги равны одной единице длины. Множество натуральных чисел равно исчисляемое , потому что обычный процесс счета, если он продолжается достаточно долго, приведет к единице к любому конкретному числу в наборе. Однако в случае с иррациональными числами их так много, что при любом мыслимом их перечислении по крайней мере одно из них будет упущено.
Множество натуральных чисел равно исчисляемое , потому что обычный процесс счета, если он продолжается достаточно долго, приведет к единице к любому конкретному числу в наборе. Однако в случае с иррациональными числами их так много, что при любом мыслимом их перечислении по крайней мере одно из них будет упущено. Результат никогда не бывает точным. Однако всегда можно подобраться к точному вещественному ответу сколь угодно близко. Если Рисунок 1. Иллюстрация Hans & Cassidy. Предоставлено Гейл Групп.
Результат никогда не бывает точным. Однако всегда можно подобраться к точному вещественному ответу сколь угодно близко. Если Рисунок 1. Иллюстрация Hans & Cassidy. Предоставлено Гейл Групп.
 852299546353
852299546353
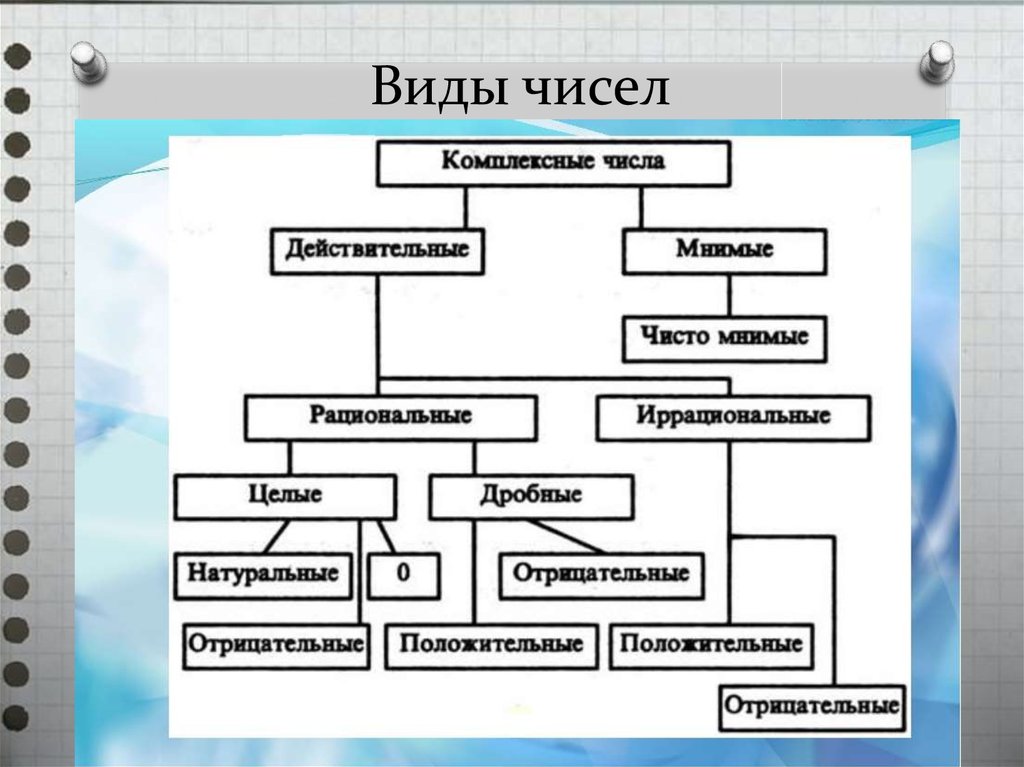
 Всего в русском языке существует шесть падежей, каждый из которых имеет свой вспомогательный вопрос.
Всего в русском языке существует шесть падежей, каждый из которых имеет свой вспомогательный вопрос. У числительных на -десят два окончания, так как изменяются обе части: пятидесяти, пятьюдесятью.
У числительных на -десят два окончания, так как изменяются обе части: пятидесяти, пятьюдесятью.

 J.P. / ОТРИЦАТЕЛЬНОЕ МЕСТО: / РОЛЛ 0203 КАДР 2 / ТАКЖЕ СМОТРИ:»
J.P. / ОТРИЦАТЕЛЬНОЕ МЕСТО: / РОЛЛ 0203 КАДР 2 / ТАКЖЕ СМОТРИ:» J.P.
J.P. J.P.
J.P. Пустая строка в середине чека предназначена для записи
количество долларов и центов прописью, например «Сто тридцать пять и 50/100». Поле справа от этого
строка, в которой вы пишете числовое значение платежа, в данном случае «135,50».
Пустая строка в середине чека предназначена для записи
количество долларов и центов прописью, например «Сто тридцать пять и 50/100». Поле справа от этого
строка, в которой вы пишете числовое значение платежа, в данном случае «135,50».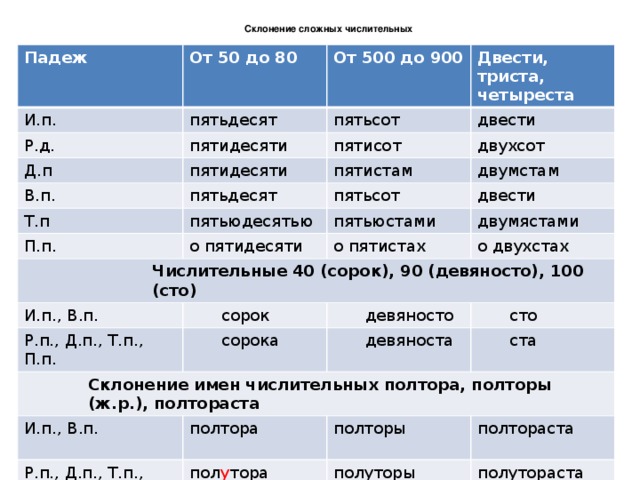
 Вам понадобятся оба, если вы планируете настроить прямой депозит или электронные платежи, а также номер чека, который будет отображаться в выписке по вашему счету.
Вам понадобятся оба, если вы планируете настроить прямой депозит или электронные платежи, а также номер чека, который будет отображаться в выписке по вашему счету.
 Процентное изменение числа (появляется после длительного нажатия на кнопку 1/x)
Процентное изменение числа (появляется после длительного нажатия на кнопку 1/x) Угол (x) может быть задан в градусах или радианах
Угол (x) может быть задан в градусах или радианах
 Устройство могло также выполнять сложение, вычитание, деление.
Устройство могло также выполнять сложение, вычитание, деление.
 п.). Применяется в области инженерии и науки. Используется инженерами, научными работниками, учащимися технических профессий.
п.). Применяется в области инженерии и науки. Используется инженерами, научными работниками, учащимися технических профессий.

 Геометрический способ решения.
Геометрический способ решения.


 Матричный метод. Матрица парных коэффициентов корреляции
Матричный метод. Матрица парных коэффициентов корреляции
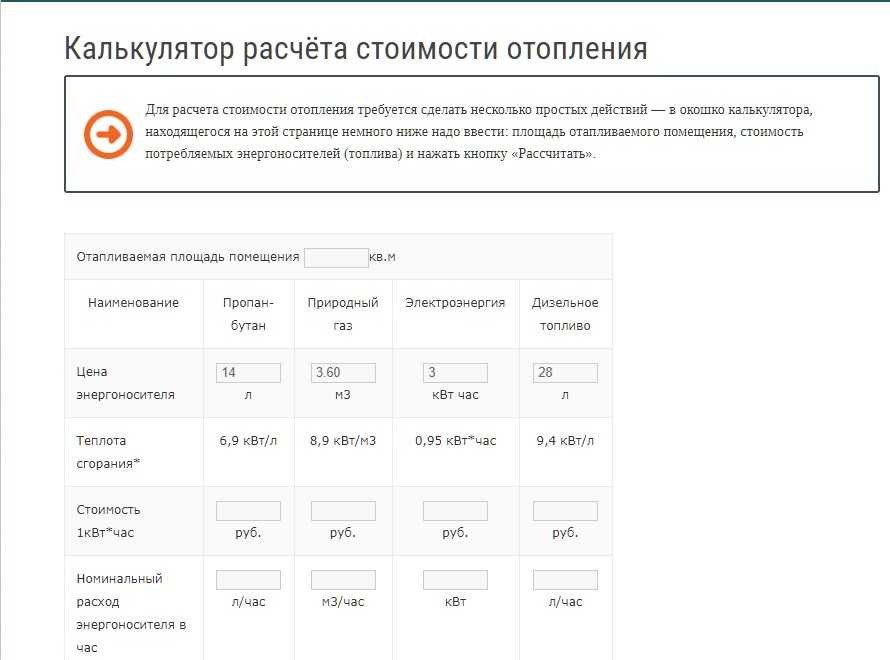
 Как выполнять повторяющиеся операции, высшие степени и корни, память и четкие функции для этого стандартного калькулятора объясняются ниже.
Как выполнять повторяющиеся операции, высшие степени и корни, память и четкие функции для этого стандартного калькулятора объясняются ниже. Следуйте инструкциям для ввода чисел и символов и выполнения расчетов с помощью кнопок оператора. На примерах показано, как выполнять простые математические операции, а также как вычислять проценты на калькуляторе. Вы также можете узнать, как рассчитать текущую и будущую стоимость на калькуляторе.
Следуйте инструкциям для ввода чисел и символов и выполнения расчетов с помощью кнопок оператора. На примерах показано, как выполнять простые математические операции, а также как вычислять проценты на калькуляторе. Вы также можете узнать, как рассчитать текущую и будущую стоимость на калькуляторе. 25
− 10,75
=
25
− 10,75
=
 26548246
26548246
 00 — 10.00 = 30.00
00 — 10.00 = 30.00 766
назад назад назад 55
=
766
назад назад назад 55
= Использовать CE для удаления самой последней записи. Обратите внимание, что если ключ AC не виден, нажмите CE , а затем AC , чтобы очистить ваш расчет.
Использовать CE для удаления самой последней записи. Обратите внимание, что если ключ AC не виден, нажмите CE , а затем AC , чтобы очистить ваш расчет. Интерактивные типы контента, такие как калькуляторы, делают именно это. Они предлагают персонализированные решения, основанные на уникальных потребностях пользователей. Интерактивные калькуляторы для веб-сайтов действуют как фантастические лид-магниты, поскольку они предлагают ценность для потенциальных клиентов.
Интерактивные типы контента, такие как калькуляторы, делают именно это. Они предлагают персонализированные решения, основанные на уникальных потребностях пользователей. Интерактивные калькуляторы для веб-сайтов действуют как фантастические лид-магниты, поскольку они предлагают ценность для потенциальных клиентов.
 Все базовые расчеты и функции проектирования, которые вам нужны, встроены в панель управления. Следовательно, вы можете просто перетащить все элементы или настроить существующий шаблон всего несколькими щелчками мыши.
Все базовые расчеты и функции проектирования, которые вам нужны, встроены в панель управления. Следовательно, вы можете просто перетащить все элементы или настроить существующий шаблон всего несколькими щелчками мыши.
 К ним относятся ипотечные калькуляторы, калькуляторы личных финансов и калькуляторы погашения кредита, и это лишь некоторые из них. Ниже приведен список интерактивных калькуляторов и вариантов их использования для разных предприятий в разных отраслях.
К ним относятся ипотечные калькуляторы, калькуляторы личных финансов и калькуляторы погашения кредита, и это лишь некоторые из них. Ниже приведен список интерактивных калькуляторов и вариантов их использования для разных предприятий в разных отраслях. Они также помогут вам собрать информацию о лидах, которую вы сможете использовать для запуска целевых кампаний в будущем.
Они также помогут вам собрать информацию о лидах, которую вы сможете использовать для запуска целевых кампаний в будущем. Outgrow
Outgrow  Внешние API-интеграции, включая курсы обмена валют.
Внешние API-интеграции, включая курсы обмена валют. В конструкторе перетаскивания Bubble вы можете редактировать пользовательский интерфейс и настраивать пользовательский интерфейс, что позволяет вам вносить изменения в каждую деталь макета.
В конструкторе перетаскивания Bubble вы можете редактировать пользовательский интерфейс и настраивать пользовательский интерфейс, что позволяет вам вносить изменения в каждую деталь макета.
 Несколько плагинов и интеграций, включая Math.js, Moment.js и Lo-Dash.js
Несколько плагинов и интеграций, включая Math.js, Moment.js и Lo-Dash.js Возможность установить единицы измерения по умолчанию как британские или метрические единицы.
Возможность установить единицы измерения по умолчанию как британские или метрические единицы. д. .
д. . 
 Кроме того, вы можете настроить шаблоны в соответствии с вашим брендом и добавить несколько типов вопросов.
Кроме того, вы можете настроить шаблоны в соответствии с вашим брендом и добавить несколько типов вопросов. Проверьте их и расскажите нам, как они вам понравились. В заключение, как насчет интерактивных калькуляторов Outgrow? Они очень любимы малым и крупным бизнесом. Создайте свой первый калькулятор бесплатно!
Проверьте их и расскажите нам, как они вам понравились. В заключение, как насчет интерактивных калькуляторов Outgrow? Они очень любимы малым и крупным бизнесом. Создайте свой первый калькулятор бесплатно!
 Например, при масштабе 75 %, скопированные с него объекты могут отображаться больше, так как они вкоплены в реальный размер.
Например, при масштабе 75 %, скопированные с него объекты могут отображаться больше, так как они вкоплены в реальный размер.






 5),
5),

 (-2;-10), (-1;-10), (-1;-11), (-2;-13), (0;-15), (2;-11), (2;-9) и глазки (0;-2) и (4;-2)
(-2;-10), (-1;-10), (-1;-11), (-2;-13), (0;-15), (2;-11), (2;-9) и глазки (0;-2) и (4;-2)
 Правые лапки: (-4;-1), (-6;-2), (-8;-2),
Правые лапки: (-4;-1), (-6;-2), (-8;-2),


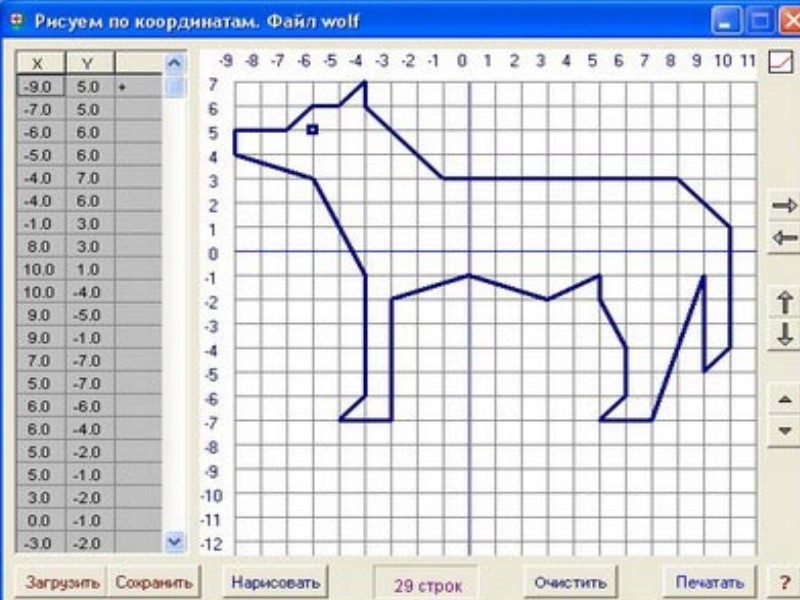 Shapes.AddPolyline sngArr
Конец суб
Shapes.AddPolyline sngArr
Конец суб 





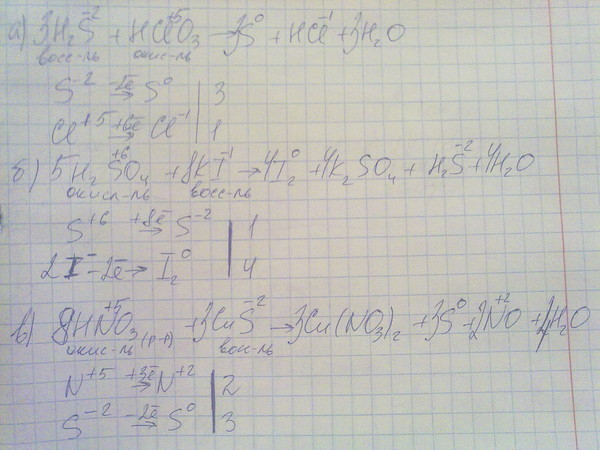


 Перекись водорода имеет
свойства восстановителя.
Перекись водорода имеет
свойства восстановителя. ОВ реакции сопровождаются
переходом электронов от одних атомов
или ионов к другим. Восстановителями
называют вещества, атомы или ионы которых
отдают электроны, а окислителями —
вещества, атомы или ионы которых принимают
электроны. Коэффициенты в ОВР реакциях
можно вычислить составлением схем
перехода электронов на основе изменения
степени окисления атомов или ионов,
методом электронно-ионных уравнений
ОВ реакций и алгебраическим методом
расчета коэффициентов.
ОВ реакции сопровождаются
переходом электронов от одних атомов
или ионов к другим. Восстановителями
называют вещества, атомы или ионы которых
отдают электроны, а окислителями —
вещества, атомы или ионы которых принимают
электроны. Коэффициенты в ОВР реакциях
можно вычислить составлением схем
перехода электронов на основе изменения
степени окисления атомов или ионов,
методом электронно-ионных уравнений
ОВ реакций и алгебраическим методом
расчета коэффициентов. Реагенты в этой реакции отдают и забирают определенное количество электронов, чтобы получить некоторый продукт. Здесь в этой химической реакции основную роль играют KMnO4 и h3O2, так как они обмениваются электронами. С другой стороны, серная кислота (h3SO4) создает подходящую реакционную среду. Поскольку происходит электронный обмен, мы можем понять, что степень окисления реагентов должна измениться. Следовательно, рассматриваемое уравнение реакции представляет собой уравнение реакции окисления-восстановления.
Реагенты в этой реакции отдают и забирают определенное количество электронов, чтобы получить некоторый продукт. Здесь в этой химической реакции основную роль играют KMnO4 и h3O2, так как они обмениваются электронами. С другой стороны, серная кислота (h3SO4) создает подходящую реакционную среду. Поскольку происходит электронный обмен, мы можем понять, что степень окисления реагентов должна измениться. Следовательно, рассматриваемое уравнение реакции представляет собой уравнение реакции окисления-восстановления.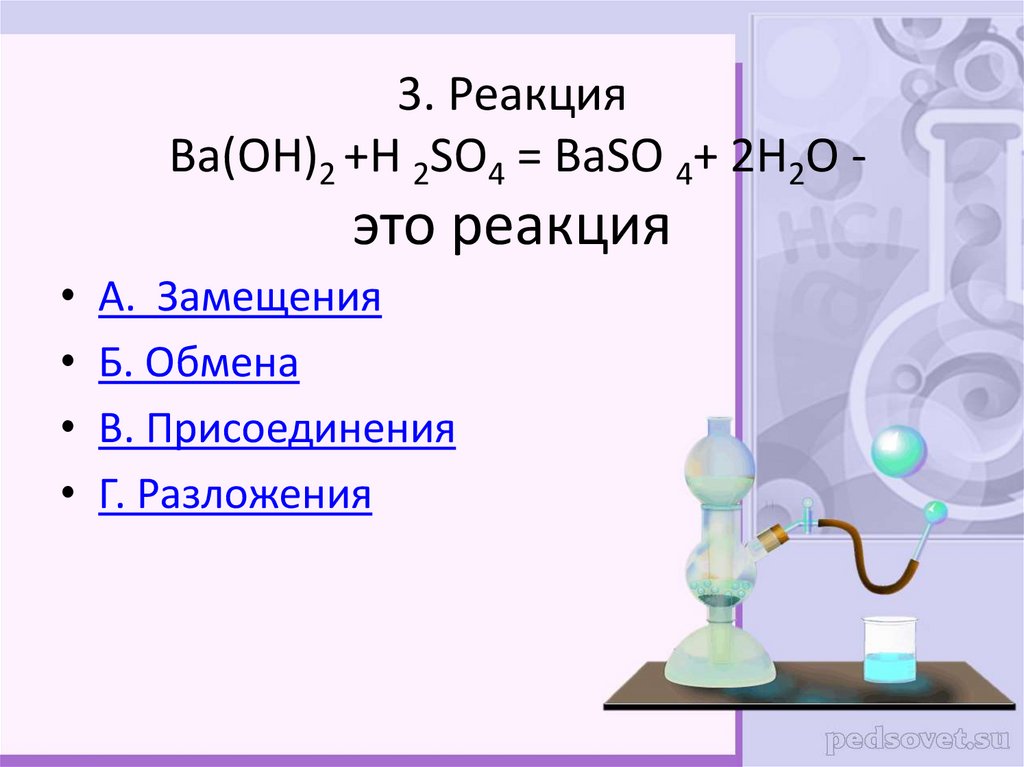
 После принятия электронов окислителем KMnO 4 восстанавливается восстановителем, H 2 O 2 .
После принятия электронов окислителем KMnO 4 восстанавливается восстановителем, H 2 O 2 .
 Это один из самых популярных агентов на рынке с глубокими последствиями. Превосходные дезинфицирующие и отбеливающие свойства перекиси водорода не имеют себе равных.
Это один из самых популярных агентов на рынке с глубокими последствиями. Превосходные дезинфицирующие и отбеливающие свойства перекиси водорода не имеют себе равных.
 Как и во многих других реакциях, один субстрат действует как окислитель, а другой — как восстановитель. Такие типы реакций называются окислительно-восстановительными реакциями.
Как и во многих других реакциях, один субстрат действует как окислитель, а другой — как восстановитель. Такие типы реакций называются окислительно-восстановительными реакциями.
 Однако при правильном обращении его можно использовать в качестве окислителя.
Однако при правильном обращении его можно использовать в качестве окислителя. Вы сразу начнете замечать явление пузырения. Это кислород, высвобождающийся в результате реакции двух химических веществ. Затем начните смешивать химикаты с помощью мешалки и обратите внимание, как фиолетовый цвет начинает разбавляться.
Вы сразу начнете замечать явление пузырения. Это кислород, высвобождающийся в результате реакции двух химических веществ. Затем начните смешивать химикаты с помощью мешалки и обратите внимание, как фиолетовый цвет начинает разбавляться. Во-первых, вы не можете использовать сильнодействующий окислитель на коже. Мягкий окислитель также неэффективен в промышленных условиях. Поэтому при объявлении окислителя «лучшим» следует сначала уточнить ситуацию.
Во-первых, вы не можете использовать сильнодействующий окислитель на коже. Мягкий окислитель также неэффективен в промышленных условиях. Поэтому при объявлении окислителя «лучшим» следует сначала уточнить ситуацию.
 Атопический и контактный дерматит возникают как аллергическая реакция на чужеродные раздражители, тогда как себорейный дерматит относится к перхоти и шелушащимся пятнам на коже головы.
Атопический и контактный дерматит возникают как аллергическая реакция на чужеродные раздражители, тогда как себорейный дерматит относится к перхоти и шелушащимся пятнам на коже головы. Кислород — одно из самых необычных лекарственных средств, которыми мы располагаем. Он может окислять клеточную стенку бактерий, которая в основном состоит из простых жирных кислот и липидов. Это изменение состава клеточной стенки позволяет кислороду без разбора убивать практически все виды бактерий и патогенов.
Кислород — одно из самых необычных лекарственных средств, которыми мы располагаем. Он может окислять клеточную стенку бактерий, которая в основном состоит из простых жирных кислот и липидов. Это изменение состава клеточной стенки позволяет кислороду без разбора убивать практически все виды бактерий и патогенов. Это явление в основном наблюдается в недавнем коронавирусе, который может сохраняться на поверхности до 3 дней!
Это явление в основном наблюдается в недавнем коронавирусе, который может сохраняться на поверхности до 3 дней! Однако окислительные свойства перекиси водорода и перманганата калия могут предложить гораздо больше!
Однако окислительные свойства перекиси водорода и перманганата калия могут предложить гораздо больше! Таким образом, перекись водорода и перманганат калия являются выбором для многих отраслей промышленности, поскольку они быстро высвобождают необходимый кислород.
Таким образом, перекись водорода и перманганат калия являются выбором для многих отраслей промышленности, поскольку они быстро высвобождают необходимый кислород.

 И вы должны убедиться, что оборудование полностью очищено от микробов.
И вы должны убедиться, что оборудование полностью очищено от микробов.