Сложение и вычитание одночленов. Подобные одночлены
- Подобные одночлены
- Сложение одночленов
- Вычитание одночленов
Сложить одночлены или вычесть один одночлен из другого можно только в том случае, если одночлены являются подобными. Если одночлены не подобные, в этом случае сложение одночленов можно записать в виде суммы, а вычитание в виде разности.
Подобные одночлены
Подобные одночлены — одночлены, которые состоят из одних и тех же букв, но могут иметь разные или одинаковые коэффициенты (числовые множители). Одинаковые буквы в подобных одночленах должны иметь одинаковые показатели степени. Если у одной и той же буквы в разных одночленах степени не совпадают, то такие одночлены нельзя назвать подобными:
5ab2 и -7ab2 — подобные одночлены;
5a2b и 5ab — не подобные одночлены.
Обратите внимание, что последовательность букв в подобных одночленах может не совпадать. Также одночлены могут быть представлены в виде выражения, которое можно упростить. Поэтому, прежде чем приступать к определению, подобны ли данные одночлены, или нет, стоит привести одночлены к стандартному виду. Например, возьмём два одночлена:
Также одночлены могут быть представлены в виде выражения, которое можно упростить. Поэтому, прежде чем приступать к определению, подобны ли данные одночлены, или нет, стоит привести одночлены к стандартному виду. Например, возьмём два одночлена:
5abb и -7b2a.
Оба одночлена находятся в нестандартном виде, поэтому будет нелегко определить, являются ли они подобными. Чтобы это узнать, приведём одночлены к стандартному виду:
5ab2 и -7ab2.
Теперь сразу видно, что данные одночлены являются подобными.
Два подобных одночлена, отличающиеся только знаком, называются противоположными. Например:
5a2bc и -5a2bc — противоположные одночлены.
Приведение подобных одночленов — это упрощение выражения, содержащего подобные одночлены, путём их сложения. Сложение подобных одночленов производится по правилам приведения подобных слагаемых.
Сложение одночленов
Чтобы сложить одночлены, надо:
- Составить сумму, записав все слагаемые одно за другим.
- Привести все одночлены к стандартному виду.
- Раскрыть скобки, если они есть в выражении.
- Привести подобные слагаемые. Для этого нужно:
- сложить их численные множители;
- после получившегося коэффициента дописать буквенные множители без изменений.
Пример 1. Сложить одночлены 12ab, -4a2b и -5ab.
Решение: Составим сумму одночленов:
12ab + (-4a2b) + (-5ab).
Все одночлены находятся в стандартном виде. Значит, можно приступить к раскрытию скобок. Правила раскрытия скобок смотрите тут.
12ab — 4a2b — 5ab.
Теперь надо определить, есть ли среди слагаемых подобные одночлены и, если они есть, сделать приведение:
12ab — 4a2b — 5ab = (12 + (-5))ab — 4a2b = 7ab — 4a2b.
Пример 2. Сложить одночлены 5a2bc и -5a2bc.
Решение: Составим сумму одночленов:
5a2bc + (-5a2bc).
Раскроем скобки:
5a2bc — 5a2bc.
Эти два одночлена являются противоположными, то есть, отличаются только знаком. Значит, если мы сложим их численные множители, то получим нуль:
5a2bc — 5a2bc = (5 — 5)a2bc = 0a2bc = 0.
Следовательно, при сложении противоположных одночленов в результате получается нуль.
Общее правило сложения одночленов:
Чтобы сложить несколько одночленов, следует записать все слагаемые одно за другим с сохранением их знаков, отрицательные одночлены надо заключить в скобки и сделать приведение подобных слагаемых (подобных одночленов).
Вычитание одночленов
Чтобы произвести вычитание одночленов, надо:
- Составить разность, записав все одночлены один за другим, разделяя их знаком
—
(минус). - Привести все одночлены к стандартному виду.
- Раскрыть скобки, если они есть в выражении.
- Сделать приведение подобных одночленов, то есть:
- сложить их численные множители,
- после получившегося коэффициента дописать буквенные множители без изменений.
Пример. Найти разность одночленов 8ab2, -5a2b и —ab2.
Решение: Составим разность одночленов:
8ab2 — (-5a2b) — (-ab2).
Все одночлены находятся в стандартном виде. Значит, можно приступить к раскрытию скобок. Правила раскрытия скобок смотрите тут.
8ab2 + 5a2b + ab2.
Теперь надо определить, есть ли среди одночленов подобные и, если они есть, сделать приведение:
8ab2 + 5a2b + ab2 = (8 + 1)ab2 + 5a2b = 9ab2 + 5a2b.
Общее правило вычитания одночленов:
Для вычитания одного одночлена из другого следует к уменьшаемому одночлену приписать вычитаемый одночлен с противоположным знаком и сделать приведение подобных одночленов.
Арифметические операции | Основы Python
Для перемещения по курсу нужно зарегистрироваться
1. Введение ↳ теория
2. Hello, World! ↳ теория / тесты / упражнение
3. Инструкции ↳ теория / тесты / упражнение
4. Арифметические операции ↳ теория / тесты / упражнение
5. Ошибки оформления — синтаксис и линтер ↳ теория / тесты / упражнение
6. Строки ↳ теория / тесты / упражнение
7. Переменные ↳ теория / тесты / упражнение
8. Выражения в определениях
↳
теория
/
тесты
/
упражнение
Выражения в определениях
↳
теория
/
тесты
/
упражнение
9. Именование ↳ теория / тесты / упражнение
10. Интерполяция ↳ теория / тесты / упражнение
11. Извлечение символов из строки ↳ теория / тесты / упражнение
12. Срезы строк ↳ теория / тесты / упражнение
13. Типы данных ↳ теория / тесты / упражнение
14. Неизменяемость и примитивные типы ↳ теория / тесты / упражнение
15. Функции и их вызов ↳ теория / тесты / упражнение
16. Сигнатура функции ↳ теория / тесты / упражнение
17. Вызов функции — выражение ↳ теория / тесты / упражнение
18. Детерминированность ↳ теория / тесты / упражнение
19. Стандартная библиотека ↳ теория / тесты / упражнение
20. Свойства и методы ↳ теория / тесты / упражнение
21. Цепочка методов ↳ теория / тесты / упражнение
22. Определение функций ↳ теория / тесты / упражнение
23. Возврат значений ↳ теория / тесты / упражнение
24. Параметры функций ↳ теория / тесты / упражнение
25. Необязательные параметры функций
↳
теория
/
тесты
/
упражнение
Необязательные параметры функций
↳
теория
/
тесты
/
упражнение
26. Именованные аргументы ↳ теория / тесты / упражнение
27. Окружение ↳ теория / тесты / упражнение
28. Логика ↳ теория / тесты / упражнение
29. Логические операторы ↳ теория / тесты / упражнение
30. Результат логических операций ↳ теория / тесты / упражнение
31. Условные конструкции ↳ теория / тесты / упражнение
32. Оператор Match ↳ теория / тесты / упражнение
33. Цикл while ↳ теория / тесты / упражнение
34. Агрегация данных ↳ теория / тесты / упражнение
35. Обход строк ↳ теория / тесты / упражнение
36. Условия внутри тела цикла ↳ теория / тесты / упражнение
37. Цикл for ↳ теория / тесты / упражнение
38. Отладка ↳ теория / тесты / упражнение
39. Модули ↳ теория / тесты / упражнение
40. Модули поглубже ↳ теория / тесты / упражнение
41. Пакеты ↳ теория / тесты / упражнение
42. Модуль random ↳ теория / тесты / упражнение
43. Кортежи
↳
теория
/
тесты
/
упражнение
Кортежи
↳
теория
/
тесты
/
упражнение
44. История развития языка Python ↳ теория / тесты
Испытания
1. Фибоначчи
2. Сумма двоичных чисел
3. Физзбазз
4. Классификация отрезков
5. Вращение троек
6. Разница углов
7. Степени тройки
8. Фасад
9. Счастливый билет
10. Идеальные числа
11. Инвертированный регистр
12. Счастливые числа
13. Шифрование
Порой обучение продвигается с трудом. Сложная теория, непонятные задания… Хочется бросить. Не сдавайтесь, все сложности можно преодолеть. Рассказываем, как
Не понятна формулировка, нашли опечатку?
Выделите текст, нажмите ctrl + enter и опишите проблему, затем отправьте нам. В течение нескольких дней мы улучшим формулировку или исправим опечатку
Что-то не получается в уроке?
Загляните в раздел «Обсуждение»:
- Изучите вопросы, которые задавали по уроку другие студенты — возможно, ответ на ваш уже есть
- Если вопросы остались, задайте свой.
 Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов
Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов - Мы отвечаем на сообщения в течение 2-3 дней. К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!
Подробнее о том, как задавать вопросы по уроку
Как добавить символ градуса в Microsoft Word тремя способами
- Вы можете добавить символ градуса в Word, используя сочетание клавиш Alt+0176.
- При желании вы можете добавить символ градуса с помощью инструмента «Символ» на вкладке «Вставка» на ленте.
- Вы также можете использовать утилиту «Карта символов» в Windows, которая позволяет вставлять символ в любую программу.
Microsoft Word имеет бесчисленное количество символов для обозначения математики, естественных наук, бухгалтерского учета и других областей, но один из наиболее часто используемых символов — это символ для ученых степеней.
Символ степени легко вставить всего несколькими щелчками мыши, и на самом деле есть несколько способов сделать это. Выберите самый простой метод или самый простой для запоминания.
Как добавить символ градуса в Word с помощью сочетания клавиш
Это удобный способ, если вам нравятся сочетания клавиш и вы легко запоминаете числа. Кроме того, это будет работать, только если ваша клавиатура имеет цифровую клавиатуру. Если нет, вам нужно будет использовать один из других методов.
1. Поместите курсор туда, где вы хотите, чтобы в документе отображался символ градуса.
2. На клавиатуре нажмите Alt + 0176, где «0176» вводится с помощью цифровой клавиатуры клавиатуры.
Вам нужна цифровая клавиатура, чтобы использовать сочетание клавиш для символа градуса. Дэйв Джонсон/ИнсайдерКак вставить символ градуса в Word с помощью ленты
Это не самый удобный способ при первом использовании, потому что вам придется искать символ градуса. Однако после того, как вы сделали это один раз, это простой метод, потому что символ степени появится в списке недавно использованных символов.
Однако после того, как вы сделали это один раз, это простой метод, потому что символ степени появится в списке недавно использованных символов.
1. Поместите курсор туда, где вы хотите, чтобы в документе появился символ градуса.
2. В верхней части экрана щелкните вкладку «Вставка» на ленте.
3. На ленте нажмите «Символ». Он, наверное, крайний справа. В раскрывающемся меню выберите «Дополнительные символы…». Если вы используете веб-приложение Office 365 Word, символ градуса уже должен быть доступен в раскрывающемся меню.
Выберите «Дополнительные символы» в инструменте «Символы» на ленте. Дэйв Джонсон/Инсайдер 4. В раскрывающемся списке «Шрифт» выберите текущий шрифт документа.
В раскрывающемся списке «Шрифт» выберите текущий шрифт документа.
5. В раскрывающемся списке «Подмножество» справа выберите «Дополнение Latin-1».
6. Теперь прокрутите список символов и найдите символ градуса. Есть несколько кругов, которые выглядят так, как будто они могут быть символами градусов, поэтому проверьте метку в нижней части окна. Щелкните его и нажмите «Вставить». Если вы уже использовали этот метод ранее, вы, вероятно, сможете найти символ в списке «Недавно использованные символы».
Самая сложная часть этого процесса — найти символ степени в первый раз. Дэйв Джонсон/ИнсайдерКак вставить символ степени в Word с помощью карты символов
Преимущество этого метода в том, что он работает в любой программе — вы скопируете символ из карты символов (утилита, входящая в состав Windows), а затем вставите его в Word. После копирования, конечно, вы можете вставить его в любую программу.
После копирования, конечно, вы можете вставить его в любую программу.
1. В поле поиска кнопки «Пуск» введите «Персонаж» и выберите «Карта символов» в результатах поиска.
2. В нижней части окна «Карта символов» установите флажок «Расширенный вид», если он еще не выбран.
3. В поле «Искать» введите «степень» и нажмите «Ввод». Вы должны увидеть символ градуса.
4. Дважды щелкните символ и нажмите «Копировать». Теперь вернитесь в Word и вставьте символ туда, где он вам нужен.
Вы можете использовать утилиту «Карта символов», чтобы вставить символ градуса в любом месте. Дэйв Джонсон/ИнсайдерДэйв Джонсон
Внештатный писатель
Дэйв Джонсон — технический журналист, который пишет о потребительских технологиях и о том, как индустрия трансформирует спекулятивный мир научной фантастики в современную реальную жизнь. Дэйв вырос в Нью-Джерси, прежде чем поступить в ВВС, чтобы управлять спутниками, преподавать космические операции и планировать космические запуски. Затем он провел восемь лет в качестве руководителя отдела контента в группе Windows в Microsoft. Как фотограф Дэйв фотографировал волков в их естественной среде обитания; он также инструктор по подводному плаванию и соведущий нескольких подкастов. Дэйв является автором более двух десятков книг и участвовал во многих сайтах и публикациях, включая CNET, Forbes, PC World, How To Geek и Insider.
Дэйв вырос в Нью-Джерси, прежде чем поступить в ВВС, чтобы управлять спутниками, преподавать космические операции и планировать космические запуски. Затем он провел восемь лет в качестве руководителя отдела контента в группе Windows в Microsoft. Как фотограф Дэйв фотографировал волков в их естественной среде обитания; он также инструктор по подводному плаванию и соведущий нескольких подкастов. Дэйв является автором более двух десятков книг и участвовал во многих сайтах и публикациях, включая CNET, Forbes, PC World, How To Geek и Insider.
ПодробнееПодробнее
Как ввести символ градуса на клавиатуре
- Вы можете ввести символ градуса на клавиатуре, используя комбинации клавиш на компьютере или меню цифровой клавиатуры на телефоне или планшете.
- Например, на ПК вы можете использовать код цифровой клавиатуры Alt + 0176; на Mac используйте Shift + Option + 8.

- Вы также можете использовать сторонние приложения для переназначения клавиатуры, что может упростить ввод символа градуса.
На столько клавиш, сколько удерживает ваша клавиатура, всегда остаются сотни дополнительных символов, которые не учитываются. Одним из них является знак степени.
К счастью, символ градуса есть на вашей клавиатуре — он просто спрятан за специальным кодом или действием. Вот как ввести символ градуса на клавиатуре, независимо от того, используете ли вы компьютер или телефон.
Как ввести символ градуса на ПК с WindowsНа ПК у вас есть несколько вариантов.
Альтернативные коды Если вы используете полноразмерную клавиатуру с цифровой панелью (или «цифровой панелью») справа, вы можете ввести символ градуса с альтернативным кодом. Эти коды требуют, чтобы вы удерживали клавишу Alt и вводили ряд цифр на цифровой клавиатуре.
Код символа градуса: Alt + 0176 . Как только вы отпустите клавишу Alt, символ должен появиться.
Использование альтернативного кода — самый быстрый способ вставить знак градуса. Уильям Антонелли/Инсайдер Меню эмодзиВ Windows 10 есть скрытое меню эмодзи, которое позволяет легко вставлять в текст любой эмодзи или специальный символ.
1. Пока вы можете печатать, нажмите клавишу Windows + . (точка) , чтобы открыть меню эмодзи.
2. В верхней части меню щелкните символ омега (Ω), чтобы просмотреть список всех специальных символов.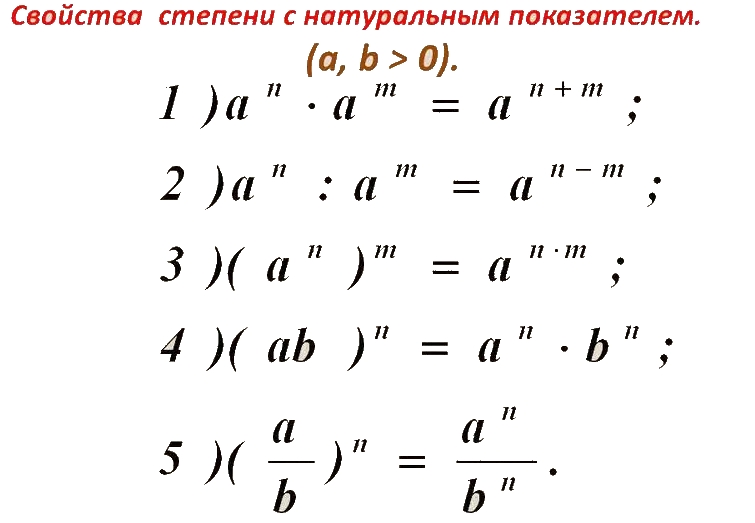
3. Прокрутите список вниз, пока не найдете символ градуса, и щелкните его, чтобы добавить в текст.
Меню эмодзи позволяет вводить эмодзи или специальные символы. Уильям Антонелли/Инсайдер Сторонние программы переназначения клавиатурыПереназначение — это процесс изменения функций, выполняемых определенной кнопкой или клавишей. Вы можете загружать приложения и настраивать клавиатуру таким образом, чтобы при нажатии определенной клавиши или вводе сочетания клавиш отображался символ градуса.
Есть несколько приложений, которые позволяют создавать собственные сочетания клавиш, но лучше всего для создания сочетаний клавиш со специальными символами (например, для символа степени), вероятно, CatchChar. Требуется немного повозиться, но вы сможете вставить любой специальный символ с помощью быстрого сочетания клавиш.
Требуется немного повозиться, но вы сможете вставить любой специальный символ с помощью быстрого сочетания клавиш.
Чтобы ввести символ градуса на Mac, нажмите Shift + Option + 8 .
Вы будете нажимать три клавиши одновременно, чтобы сделать символ градуса. Уильям Антонелли/Инсайдер Либо нажмите Control + Command + Space , чтобы открыть меню «Эмодзи и символы», а затем нажмите Пунктуация на левой боковой панели. В этом списке вы найдете символ градуса — дважды щелкните его, чтобы добавить в текст.
Примечание: Если все, что вы видите, — это небольшое всплывающее окно, заполненное смайликами, щелкните значок крошечной коробки в правом верхнем углу, чтобы развернуть меню до полного размера.
Как ввести символ градуса на ChromebookПоначалу метод на Chromebook может показаться немного запутанным, но как только вы сделаете это один раз, все станет ясно.
1. Пока вы можете печатать, нажмите Ctrl + Shift + U . Буква u с линией под ней появится там, где вы набрали.
Буква u с линией под ней появится там, где вы набрали.
2. Не щелкая мышью, введите OOBA и нажмите Введите .
Подчеркнутая буква u превратится в символ градуса.
Вам нужно будет использовать Unicode-код знака градуса, OOBA. Уильям Антонелли/Инсайдер Как ввести символ градуса на iPhone или iPad1. Коснитесь места, которое вы можете ввести, чтобы появилась клавиатура.
2. Нажмите значок 123 в левом нижнем углу клавиатуры, а затем нажмите и удерживайте палец на клавише нуля (0) .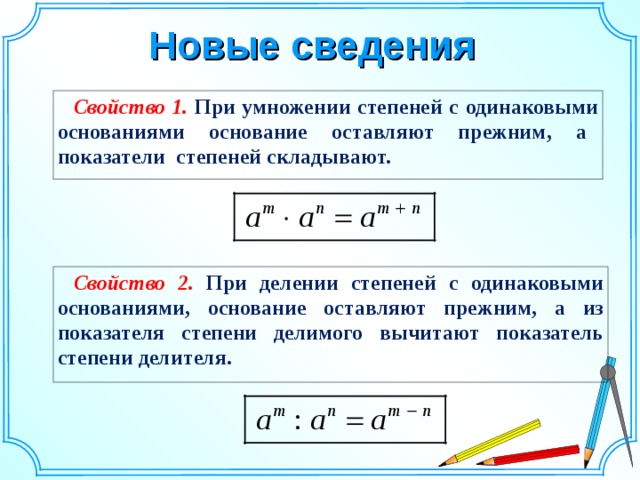
3. Через некоторое время появится небольшое всплывающее окно с символом градуса в нем. Перетащите к нему палец и отпустите.
Символ градуса скрыт за нулевой клавишей. Уильям Антонелли/Инсайдер Как ввести символ градуса на Android1. Коснитесь места, которое вы можете ввести, чтобы появилась клавиатура.
2. Нажмите значок ?123 в левом нижнем углу, а затем значок =\< над ним.
3. На этой странице будет символ градуса. Коснитесь его, чтобы ввести.
Символ градуса нетрудно найти на Android. Уильям Антонелли/Инсайдер
Уильям Антонелли/ИнсайдерУильям Антонелли
Технический репортер для Insider Reviews
Уильям Антонелли (он/она/они) — писатель, редактор и организатор из Нью-Йорка. Как один из основателей команды Reference, он помог вырастить Tech Reference (теперь часть Insider Reviews) из скромных начинаний в гигантскую силу, которая привлекает более 20 миллионов посещений в месяц.
Помимо Insider, его тексты публиковались в таких изданиях, как Polygon, The Outline, Kotaku и других. Он также является источником технического анализа на таких каналах, как Newsy, Cheddar и NewsNation.

 Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов
Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов
 Подставляя полученное выражение для C(x), окончательно получаем решение исходного линейного уравнения
Подставляя полученное выражение для C(x), окончательно получаем решение исходного линейного уравнения
 В этом решении y1(x) = 2x-1 — движение
объекта под действием силы b(x) = 4x, y2(x) = C1e-2x -собственное движение объекта.
В этом решении y1(x) = 2x-1 — движение
объекта под действием силы b(x) = 4x, y2(x) = C1e-2x -собственное движение объекта.
 Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?
Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать? Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.
Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.

 В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»:
В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему «Как решать дифференциальные уравнения»: д.
д. д дх = ты дв дх + в дю дх
д дх = ты дв дх + в дю дх 


 д дх = ты дв дх + в дю дх
д дх = ты дв дх + в дю дх  .. мы можем интегрировать по частям… что говорит:
.. мы можем интегрировать по частям… что говорит:
 е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Ниже приведен список тем, обсуждаемых в этой главе.
Ниже приведен список тем, обсуждаемых в этой главе. В частности, мы обсудим использование решений для решения дифференциальных уравнений вида \(y’ = F(\frac{y}{x})\) и \(y’ = G(ax + by)\).
В частности, мы обсудим использование решений для решения дифференциальных уравнений вида \(y’ = F(\frac{y}{x})\) и \(y’ = G(ax + by)\).
 Значение постоянной определяем из условия нормировки
Значение постоянной определяем из условия нормировки Если известна точка пересечения прямой с осью ординат , то уравнение прямой которая через эту точку проходит следующее
Если известна точка пересечения прямой с осью ординат , то уравнение прямой которая через эту точку проходит следующее



 Функция плотности вероятности не может принимать отрицательные значения:
Функция плотности вероятности не может принимать отрицательные значения:
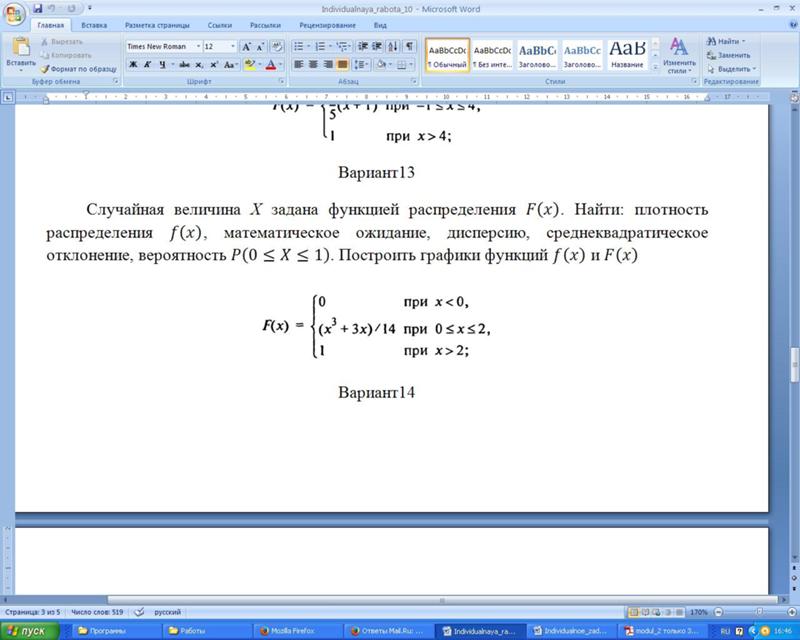
 Найти функцию F(x)
распределения вероятностей непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что
непрерывная случайная величина примет какое-либо значение в интервале от 0 до 5:
.
Найти функцию F(x)
распределения вероятностей непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что
непрерывная случайная величина примет какое-либо значение в интервале от 0 до 5:
.

 Итак, функция распределения данной непрерывной случайной величины имеет вид:
Итак, функция распределения данной непрерывной случайной величины имеет вид: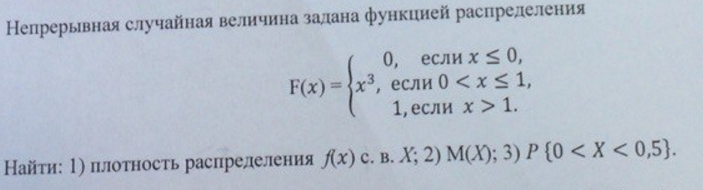
 Для
непрерывные случайные величины, CDF четко определен, поэтому мы можем предоставить CDF. Тем не менее, PMF делает
не работают для непрерывных случайных величин, потому что для непрерывной случайной величины $P(X=x)=0$ для всех
$x \in \mathbb{R}$. Вместо этого мы обычно можем определить функцию плотности вероятности (PDF) 9+} \frac{P(x
Для
непрерывные случайные величины, CDF четко определен, поэтому мы можем предоставить CDF. Тем не менее, PMF делает
не работают для непрерывных случайных величин, потому что для непрерывной случайной величины $P(X=x)=0$ для всех
$x \in \mathbb{R}$. Вместо этого мы обычно можем определить функцию плотности вероятности (PDF) 9+} \frac{P(x
 $$
Кроме того, у нас есть
$$P(а
9{-x} & \quad x \geq 0\\
0 & \quad \text{иначе}
\end{массив} \right.
\end{уравнение}
где $c$ — положительная константа.
$$
Кроме того, у нас есть
$$P(а
9{-x} & \quad x \geq 0\\
0 & \quad \text{иначе}
\end{массив} \right.
\end{уравнение}
где $c$ — положительная константа.
 2
2 3
3 14159..
14159..




 Двутавровые балки выдерживают даже прямоугольные отверстия.
Двутавровые балки выдерживают даже прямоугольные отверстия.


 Созданный с учетом простоты, этот инструмент предлагает самые низкие цены на Земле, начиная с 0,001 доллара США за слово. Это в 60 раз дешевле самой конкурентоспособной цены, которую предлагают люди, живущие в самой малоизвестной и дешевой части мира.
Созданный с учетом простоты, этот инструмент предлагает самые низкие цены на Земле, начиная с 0,001 доллара США за слово. Это в 60 раз дешевле самой конкурентоспособной цены, которую предлагают люди, живущие в самой малоизвестной и дешевой части мира. Нет больше хлопот, конвертировать txt в редактируемый pdf всего за несколько шагов. Узнайте, как конвертировать txt в pdf с PDFsun.com, следуя инструкциям выше.
Нет больше хлопот, конвертировать txt в редактируемый pdf всего за несколько шагов. Узнайте, как конвертировать txt в pdf с PDFsun.com, следуя инструкциям выше. Поскольку текстовые файлы очень просты, их часто используют для хранения данных.
Поскольку текстовые файлы очень просты, их часто используют для хранения данных. Если вам интересно, как бесплатно сменить txt на pdf, важно отметить, что качество получаемого pdf также важно, а не только стоимость. Хотя существует несколько бесплатных конвертеров txt в pdf, большинство из них недостаточно поддерживают исходное форматирование и интервал файла. Наш инструмент конвертации обеспечивает результат, который выглядит как ваш оригинальный файл txt.
Если вам интересно, как бесплатно сменить txt на pdf, важно отметить, что качество получаемого pdf также важно, а не только стоимость. Хотя существует несколько бесплатных конвертеров txt в pdf, большинство из них недостаточно поддерживают исходное форматирование и интервал файла. Наш инструмент конвертации обеспечивает результат, который выглядит как ваш оригинальный файл txt. Выберите файлы для конвертации
Выберите файлы для конвертации Мы обеспечиваем безопасность ваших файлов и данных и предлагаем выбор и контроль над удалением файлов.
Мы обеспечиваем безопасность ваших файлов и данных и предлагаем выбор и контроль над удалением файлов.
 Поскольку Word Perfect практически мертв, я решил конвертировать все ее файлы. Преобразователь Замзара был идеальным.
Поскольку Word Perfect практически мертв, я решил конвертировать все ее файлы. Преобразователь Замзара был идеальным. Помимо нашей онлайн-службы преобразования файлов, мы также предлагаем настольное приложение для преобразования файлов прямо с вашего рабочего стола и API для автоматического преобразования файлов для разработчиков. Какой инструмент вы используете, зависит от вас!
Помимо нашей онлайн-службы преобразования файлов, мы также предлагаем настольное приложение для преобразования файлов прямо с вашего рабочего стола и API для автоматического преобразования файлов для разработчиков. Какой инструмент вы используете, зависит от вас! ..
..
 Microsoft и Apple имеют встроенные приложения для текстового редактора, называемые Notepad и TextEdit соответственно, и часто используются для создания файлов TXT. Они широко используются не только обычным уличным пользователем, который может решить вести протоколы совещаний, заметки и т. п., но и более технически подкованными ИТ-специалистами, которые могут использовать их при кодировании.
Microsoft и Apple имеют встроенные приложения для текстового редактора, называемые Notepad и TextEdit соответственно, и часто используются для создания файлов TXT. Они широко используются не только обычным уличным пользователем, который может решить вести протоколы совещаний, заметки и т. п., но и более технически подкованными ИТ-специалистами, которые могут использовать их при кодировании. Он был разработан Adobe, чтобы люди могли обмениваться документами независимо от того, какое устройство, операционную систему или программное обеспечение они используют, сохраняя при этом содержимое и форматирование. Формат эволюционировал, чтобы разрешить редактирование и интерактивные элементы, такие как электронные подписи или кнопки. Формат PDF теперь является стандартным открытым форматом, доступным не только в Adobe Acrobat. Он поддерживается Международной организацией по стандартизации (ISO).
Он был разработан Adobe, чтобы люди могли обмениваться документами независимо от того, какое устройство, операционную систему или программное обеспечение они используют, сохраняя при этом содержимое и форматирование. Формат эволюционировал, чтобы разрешить редактирование и интерактивные элементы, такие как электронные подписи или кнопки. Формат PDF теперь является стандартным открытым форматом, доступным не только в Adobe Acrobat. Он поддерживается Международной организацией по стандартизации (ISO).
 ZIP в TXT
PDB в TXT
PDF в ТХТ
PML в TXT
PPS в TXT
PPSX в TXT
PPT в TXT
PPTX в TXT
PRC в TXT
PUB в TXT
РБ в TXT
TCR в TXT
WPD в TXT
WPS в TXT
XLS в TXT
XLSX в TXT
ZIP в TXT
PDB в TXT
PDF в ТХТ
PML в TXT
PPS в TXT
PPSX в TXT
PPT в TXT
PPTX в TXT
PRC в TXT
PUB в TXT
РБ в TXT
TCR в TXT
WPD в TXT
WPS в TXT
XLS в TXT
XLSX в TXT
 Файлы PDF открываются на большинстве устройств, а также сохраняют текст документа для совместного использования.
Файлы PDF открываются на большинстве устройств, а также сохраняют текст документа для совместного использования. Форма отчета
Форма отчета Форматы документов PDF и TXT в некоторых случаях дополняют друг друга и поэтому тесно связаны в современной офисной работе. Довольно часто мы хотим преобразовать редактируемый документ TXT в неизменяемый файл PDF. Это может быть контракт или какие-то финансовые данные, которые не следует изменять.
Форматы документов PDF и TXT в некоторых случаях дополняют друг друга и поэтому тесно связаны в современной офисной работе. Довольно часто мы хотим преобразовать редактируемый документ TXT в неизменяемый файл PDF. Это может быть контракт или какие-то финансовые данные, которые не следует изменять.


 {2}+2 x-3}
{2}+2 x-3}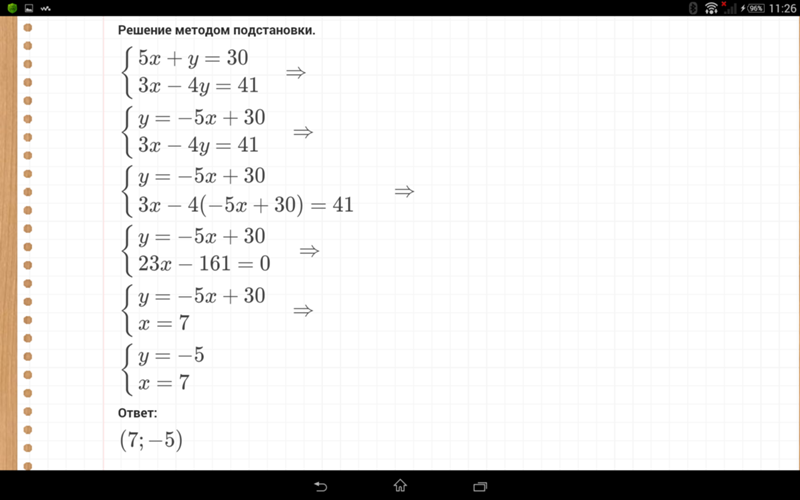 \begin{array} { c } { 4 x + 3 y = 1 } \\ { 16 x — 5 y = 21 } \end{array} \right.
\begin{array} { c } { 4 x + 3 y = 1 } \\ { 16 x — 5 y = 21 } \end{array} \right.




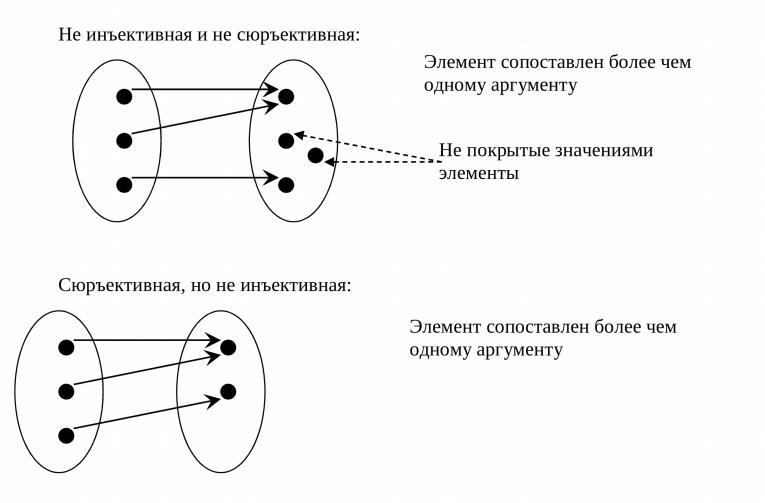
 Очевидно, что функция / биективна тогда и только тогда, когда она одновременно инъективна и сюръективна. В этом случае стрелки (рис. 2.4) соединяют попарно каждый элемент из X с каждым элементом из У.
Очевидно, что функция / биективна тогда и только тогда, когда она одновременно инъективна и сюръективна. В этом случае стрелки (рис. 2.4) соединяют попарно каждый элемент из X с каждым элементом из У.
 комсество действительных чисел.
комсество действительных чисел.
 Числа х и у называют координатами точки М ( в выбранной системе координат), причем х называют абсциссой точки М, а у — ординатой этой точки.
Числа х и у называют координатами точки М ( в выбранной системе координат), причем х называют абсциссой точки М, а у — ординатой этой точки.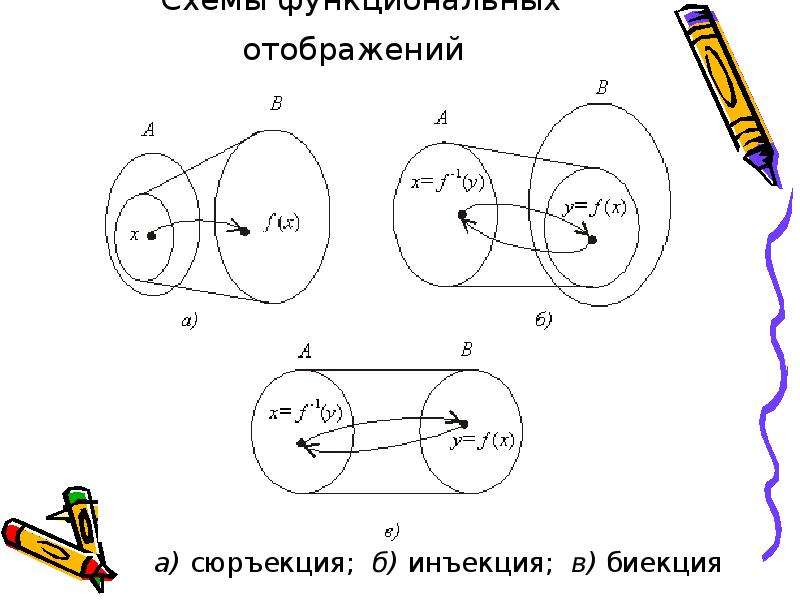 Определение 2.2.
Определение 2.2. Аналогично определению 2.2 можно ввести понятие произведения более чем двух множеств. Множества (А х В) х С и А*х (В х С) отождествляют и обозначают просто А х В х С, так что . Произведения Ах Ау Ах Ах А и т.д. обозначают, как правило, через А2 , А3 и т.д. Очевидно, плоскость R2 можно рассматривать как произведение R х R двух экземпляров множества действительных чисел (отсюда и происходит обозначение множества точек плоскости как произведения двух множеств точек числовой прямой). Множеству точек геометрического (трехмерного) пространства соответствует произведение R х R х R трех экземпляров множества точек числовой прямой, обозначаемое R3.
Аналогично определению 2.2 можно ввести понятие произведения более чем двух множеств. Множества (А х В) х С и А*х (В х С) отождествляют и обозначают просто А х В х С, так что . Произведения Ах Ау Ах Ах А и т.д. обозначают, как правило, через А2 , А3 и т.д. Очевидно, плоскость R2 можно рассматривать как произведение R х R двух экземпляров множества действительных чисел (отсюда и происходит обозначение множества точек плоскости как произведения двух множеств точек числовой прямой). Множеству точек геометрического (трехмерного) пространства соответствует произведение R х R х R трех экземпляров множества точек числовой прямой, обозначаемое R3. Для таких наборов употребляют названия кортеж или n-ка (произносят „энка»). Пример 2.3. Пусть А = { 1, 2} и В = {1, 2}. Тогда , и множество А х В можно отождествить с четырьмя точками плоскости R2, координаты которых указаны при перечислении элементов этого множества. Если С={ 1,2} и D={3,4}, то . Пример 2.4. Пусть Тогда Геометрическая интерпретация множеств Е х F и F х Е представлена на рис. 2.8. # Для отображения /: X можно составить множество упорядоченных пар (г, у), которое является подмножеством прямого произведения X х У.
Для таких наборов употребляют названия кортеж или n-ка (произносят „энка»). Пример 2.3. Пусть А = { 1, 2} и В = {1, 2}. Тогда , и множество А х В можно отождествить с четырьмя точками плоскости R2, координаты которых указаны при перечислении элементов этого множества. Если С={ 1,2} и D={3,4}, то . Пример 2.4. Пусть Тогда Геометрическая интерпретация множеств Е х F и F х Е представлена на рис. 2.8. # Для отображения /: X можно составить множество упорядоченных пар (г, у), которое является подмножеством прямого произведения X х У. 2.11). # Все упомянутые примеры графиков функции являются важнейшими объектами математического анализа, и в дальнейшем они будут подробно рассмотрены.
2.11). # Все упомянутые примеры графиков функции являются важнейшими объектами математического анализа, и в дальнейшем они будут подробно рассмотрены.
 9).
9).
 Для отношения порядка на
произвольном множестве часто используют
символ <=, соответственно для строгого
порядка можно использовать символ ≺
Для отношения порядка на
произвольном множестве часто используют
символ <=, соответственно для строгого
порядка можно использовать символ ≺

 Теорема об
альтернативности АТ.
Теорема об
альтернативности АТ. е. позволяет найти копию $A$ внутри $B$.
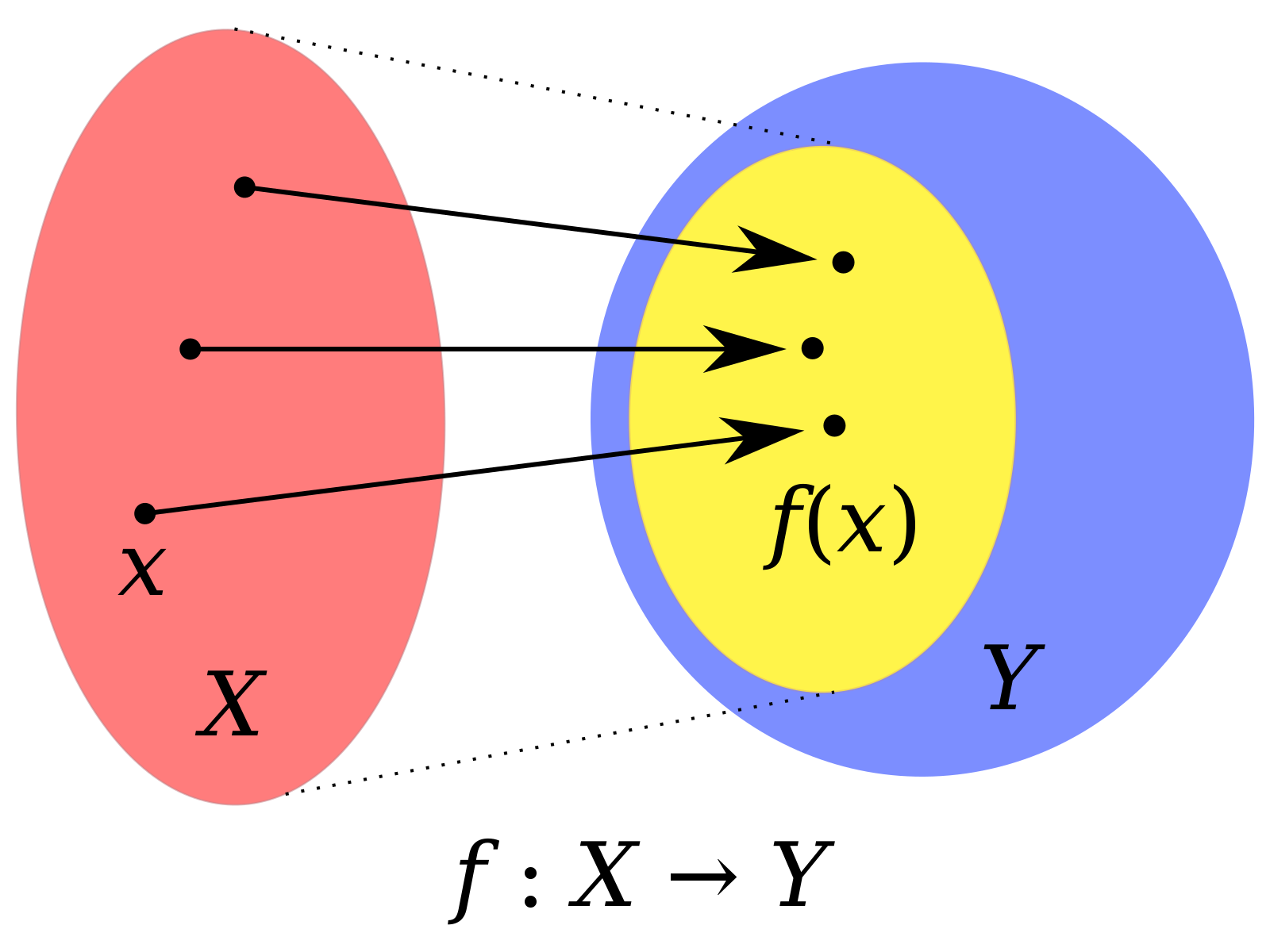
е. позволяет найти копию $A$ внутри $B$.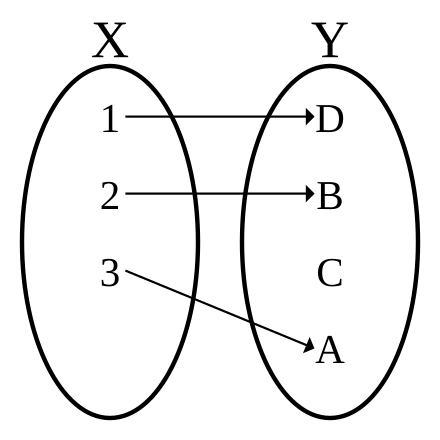 {-1}(f(x) = f( y)) \ подразумевает x = y$
{-1}(f(x) = f( y)) \ подразумевает x = y$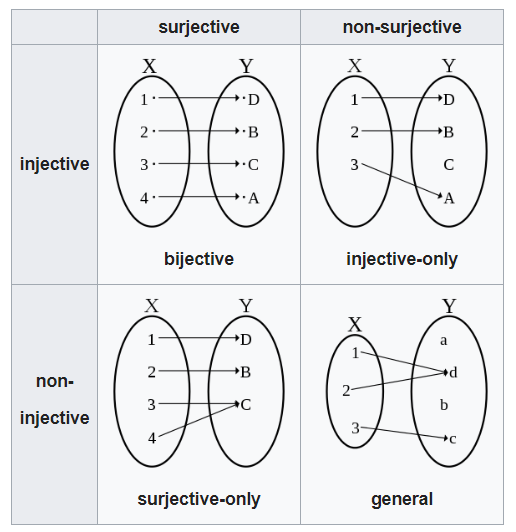



 Таким образом, генератор паролей ESET позволяет создавать большое количество сложных комбинаций.
Таким образом, генератор паролей ESET позволяет создавать большое количество сложных комбинаций.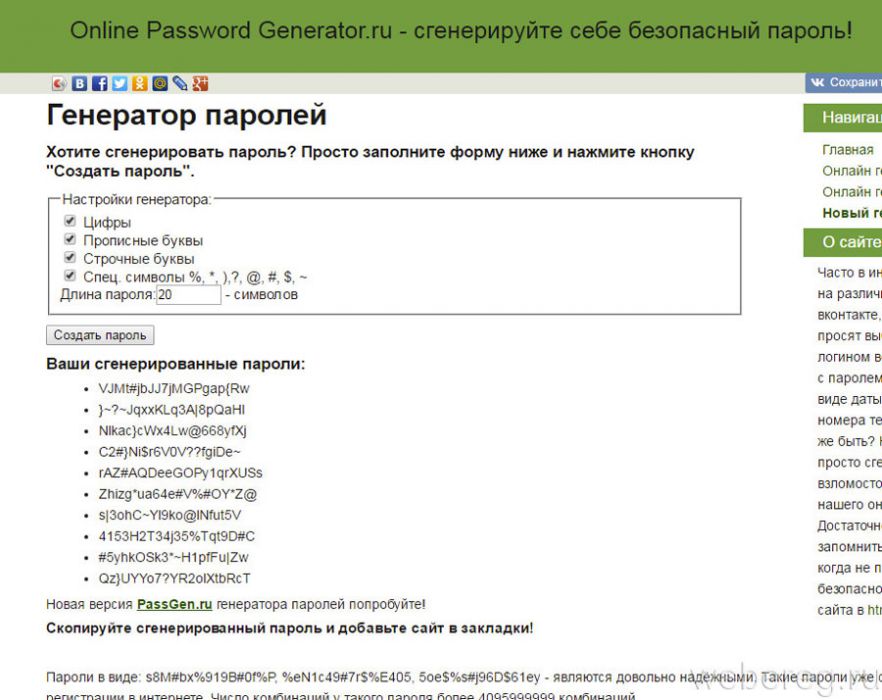 Однако, как подтверждают сотни миллионов паролей в ежегодных утечках данных, большинство пользователей предпочитают легкие для запоминания фразы.
Однако, как подтверждают сотни миллионов паролей в ежегодных утечках данных, большинство пользователей предпочитают легкие для запоминания фразы. Знак препинания в конце затрудняет перебор символьных комбинаций.
Знак препинания в конце затрудняет перебор символьных комбинаций.


 Например:
Например:
 или четыре). Вы чувствуете себя хорошо — в конце концов, никто не может угадать этот пароль! Но уверены ли вы, что пароль достаточно надежен для защиты вашей личной информации?
или четыре). Вы чувствуете себя хорошо — в конце концов, никто не может угадать этот пароль! Но уверены ли вы, что пароль достаточно надежен для защиты вашей личной информации?
 Менеджер паролей позволяет легко защитить себя и свои онлайн-данные. Это позволяет вам генерировать и хранить длинные сложные пароли для каждого сайта, при этом вам нужно помнить только один мастер-пароль (тот, который разблокирует вашу учетную запись менеджера паролей).
Менеджер паролей позволяет легко защитить себя и свои онлайн-данные. Это позволяет вам генерировать и хранить длинные сложные пароли для каждого сайта, при этом вам нужно помнить только один мастер-пароль (тот, который разблокирует вашу учетную запись менеджера паролей). Создайте новую учетную запись и не забудьте сохранить мастер-пароль в надежном месте .
Создайте новую учетную запись и не забудьте сохранить мастер-пароль в надежном месте . Если вы использовали один и тот же пароль для 14 разных учетных записей, вы сильно упрощаете работу злоумышленника. Вы можете защитить себя, используя генератор для создания уникальных паролей, которые легко запомнить.
Если вы использовали один и тот же пароль для 14 разных учетных записей, вы сильно упрощаете работу злоумышленника. Вы можете защитить себя, используя генератор для создания уникальных паролей, которые легко запомнить.
 Вы можете быть удивлены тем, как много этой информации можно найти в Интернете. Те три контрольных вопроса, которые ваш банк требует от вас, чтобы войти в систему? Не отвечайте на них. Вместо этого используйте Генератор надежных паролей, чтобы генерировать случайные уникальные ответы на эти вопросы. Сохраните ответы в своем хранилище 1Password, как обычный пароль, и все готово.
Вы можете быть удивлены тем, как много этой информации можно найти в Интернете. Те три контрольных вопроса, которые ваш банк требует от вас, чтобы войти в систему? Не отвечайте на них. Вместо этого используйте Генератор надежных паролей, чтобы генерировать случайные уникальные ответы на эти вопросы. Сохраните ответы в своем хранилище 1Password, как обычный пароль, и все готово. Например, 12-символьный пароль, состоящий только из букв, всего в восемь раз сложнее взломать, чем 12-символьный пароль с цифрами. Но 16-символьный пароль, состоящий только из букв, угадать в восемь миллионов раз труднее, чем 12-символьный.
Например, 12-символьный пароль, состоящий только из букв, всего в восемь раз сложнее взломать, чем 12-символьный пароль с цифрами. Но 16-символьный пароль, состоящий только из букв, угадать в восемь миллионов раз труднее, чем 12-символьный. Для этого требуется дополнительная форма проверки помимо вашего имени пользователя и пароля — обычно это код, срок действия которого истекает через короткий промежуток времени. Наш менеджер паролей может действовать как стороннее приложение для проверки подлинности для хранения и доставки этих кодов, блокируя любого злоумышленника, который знает только ваше имя пользователя и пароль.
Для этого требуется дополнительная форма проверки помимо вашего имени пользователя и пароля — обычно это код, срок действия которого истекает через короткий промежуток времени. Наш менеджер паролей может действовать как стороннее приложение для проверки подлинности для хранения и доставки этих кодов, блокируя любого злоумышленника, который знает только ваше имя пользователя и пароль.
 (Подробнее…)
(Подробнее…) Найди значение выражения:
Найди значение выражения: Найди значение выражения:
Найди значение выражения:


 продали 1/5 часть этого куска. Сколько метров ткани осталось в куске?
продали 1/5 часть этого куска. Сколько метров ткани осталось в куске? Сколько лет живёт берёза?
Сколько лет живёт берёза?

 …… (Утверждение 1)
…… (Утверждение 1) 


 Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х1 не будут иметь коэффициент 0.
Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х1 не будут иметь коэффициент 0. Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
 Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок: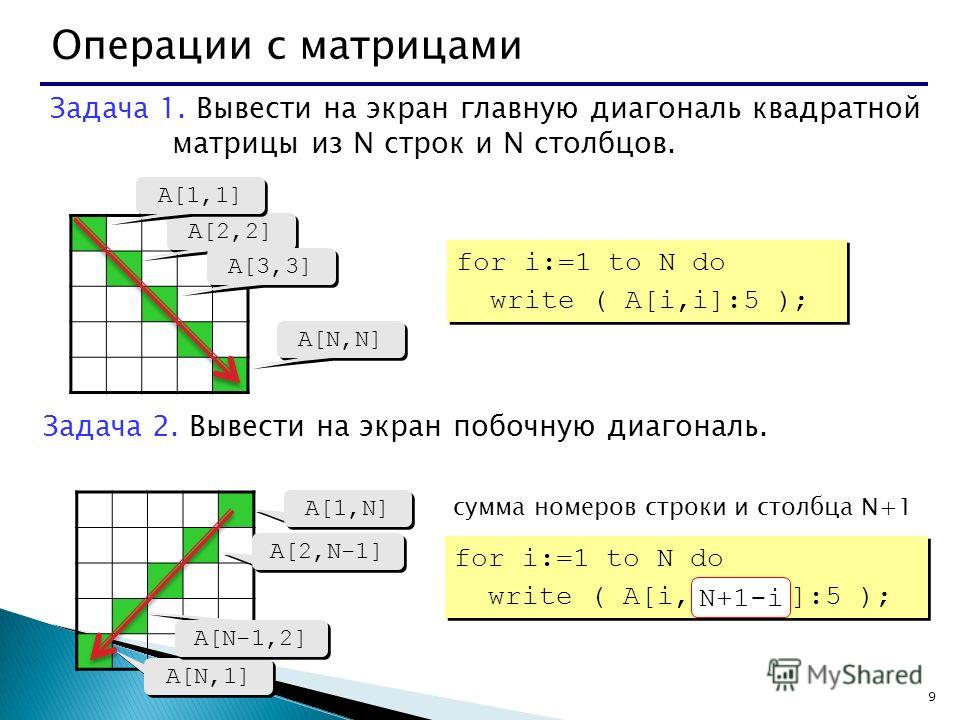 6875 –1.5625
6875 –1.5625
 Проведём его для
определителя второго порядка.
Проведём его для
определителя второго порядка.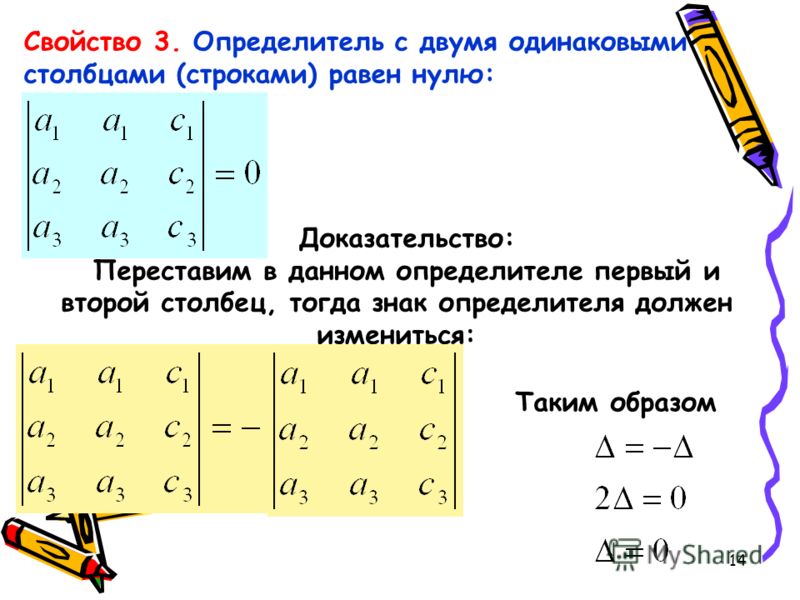

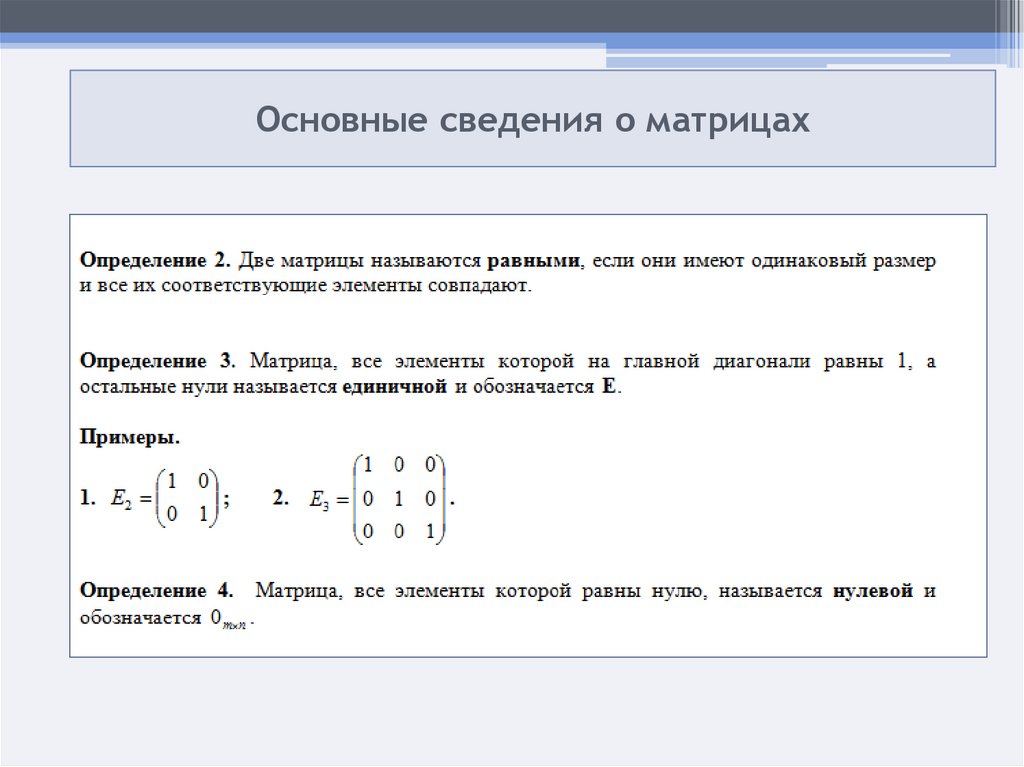
 Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой
строки.
Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой
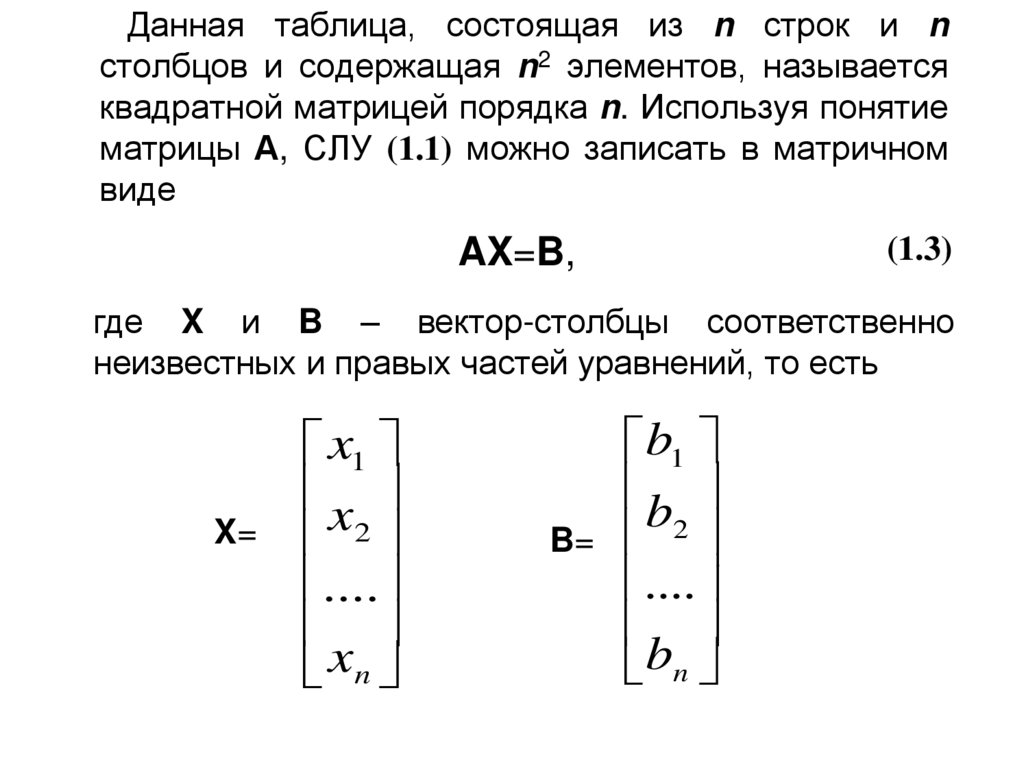
строки. В
данном случае удобно рассмотреть 4-й столбец или 4-ю строку:
В
данном случае удобно рассмотреть 4-й столбец или 4-ю строку:

 Вы можете использовать
Вы можете использовать 
 Это можно сделать, выполнив операцию
Это можно сделать, выполнив операцию  Поскольку многие из этих свойств связаны с операциями со строками, которые обсуждались в главе 1, мы сейчас вспомним это определение.
Поскольку многие из этих свойств связаны с операциями со строками, которые обсуждались в главе 1, мы сейчас вспомним это определение. \) Тогда \(\det \left( B\right) = — \det \left( A\right).\)
\) Тогда \(\det \left( B\right) = — \det \left( A\right).\) Тогда \(\det \left( B\right) = k \det \left( A\right)\).
Тогда \(\det \left( B\right) = k \det \left( A\right)\). \)
\)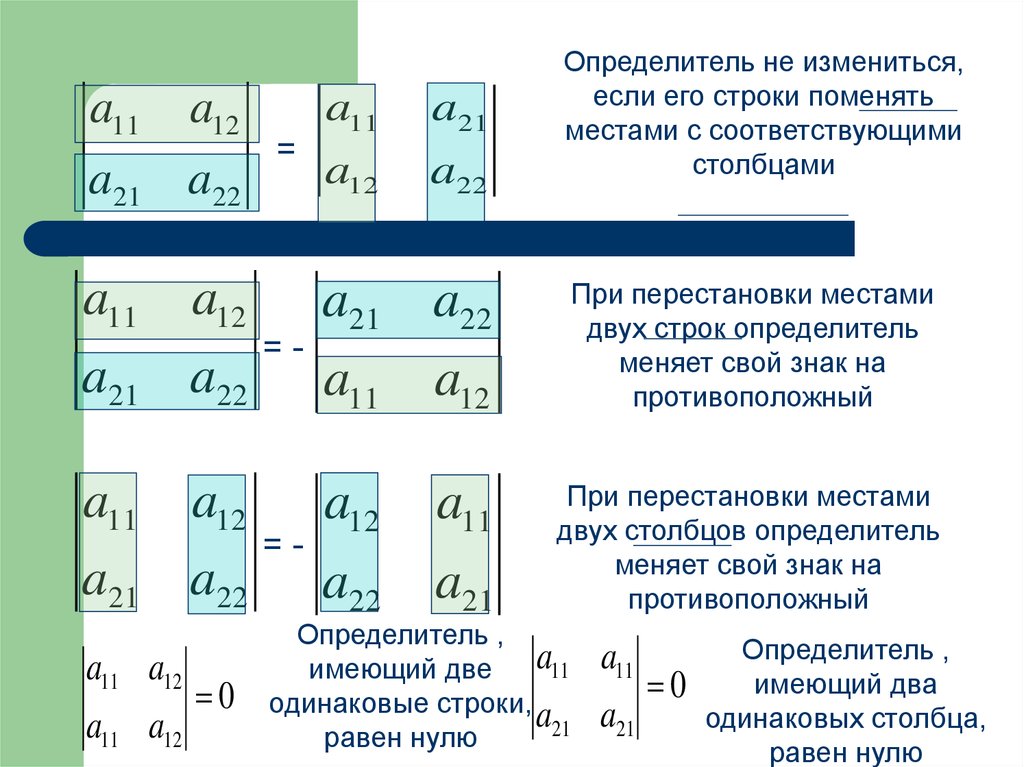
 Тогда по приведенному выше обсуждению в соответствии с теоремой \(\PageIndex{4}\) определитель будет равен \(0\).
Тогда по приведенному выше обсуждению в соответствии с теоремой \(\PageIndex{4}\) определитель будет равен \(0\).

 Тогда \(\det E_{ik}=k\). 9Т\).
Тогда \(\det E_{ik}=k\). 9Т\).

 9n a_{1,l} \mathrm{cof}(A)_{1,l}\\ &=\sum_{l\neq i} a_{1,l}(\mathrm{cof}(B)_{ 1,l}+\mathrm{cof}(C)_{1,l})+ (b_{1,i}+c_{1,i})\mathrm{cof}(A)_{1,i} \\ &= \det B+\det C\end{aligned}\] Это доказывает, что утверждение верно для всех \(n\), и завершает доказательство.
9n a_{1,l} \mathrm{cof}(A)_{1,l}\\ &=\sum_{l\neq i} a_{1,l}(\mathrm{cof}(B)_{ 1,l}+\mathrm{cof}(C)_{1,l})+ (b_{1,i}+c_{1,i})\mathrm{cof}(A)_{1,i} \\ &= \det B+\det C\end{aligned}\] Это доказывает, что утверждение верно для всех \(n\), и завершает доказательство. n b_{1l} B_{1l} =\det B.\nonumber \]
n b_{1l} B_{1l} =\det B.\nonumber \] Поэтому \(\mathrm{cof}(A)_{1l}=k\mathrm{cof}(B)_{1l}\) для \(l\neq i\), и для всех \(l\) мы имеют \(a_{1l} \mathrm{cof}(A)_{1l}=k b_{1l}\mathrm{cof}(B)_{1l}\). По \(\eqref{E1}\) имеем \(\det A=k\det B\).
Поэтому \(\mathrm{cof}(A)_{1l}=k\mathrm{cof}(B)_{1l}\) для \(l\neq i\), и для всех \(l\) мы имеют \(a_{1l} \mathrm{cof}(A)_{1l}=k b_{1l}\mathrm{cof}(B)_{1l}\). По \(\eqref{E1}\) имеем \(\det A=k\det B\). Но \(i\)-я и \(j\)-я строки \(C\) пропорциональны. Если \(D\) получается умножением \(j\)-й строки \(C\) на \(\frac 1k\), то по (2) имеем \(\det C=\frac 1k\det D\) (напомним, что \(k\neq 0\)!). Но \(i\)-я и \(j\)-я строки \(D\) идентичны, поэтому по (3) мы имеем \(\det D=0\) и, следовательно, \(\det C=0\ ).
Но \(i\)-я и \(j\)-я строки \(C\) пропорциональны. Если \(D\) получается умножением \(j\)-й строки \(C\) на \(\frac 1k\), то по (2) имеем \(\det C=\frac 1k\det D\) (напомним, что \(k\neq 0\)!). Но \(i\)-я и \(j\)-я строки \(D\) идентичны, поэтому по (3) мы имеем \(\det D=0\) и, следовательно, \(\det C=0\ ).
