Таблица степеней 🆕
Поможем понять и полюбить математику
Начать учиться
141.6K
После изучения арифметических основ в виде сложения, вычитания, деления и умножения, открывается математика и ее большой мир. В этом материале рассмотрим такое понятие, как степень.
Основные понятия
Степень числа с натуральным показателем — это результат многократного умножения числа на себя. Само число называют основанием степени, а количество операций умножения — показателем степени.
- an = a × a × … × a, где a — основание степени,
- n — натуральный показатель степени.
Запись читается, как «a» в степени «n».
Вот пример для наглядности:
- 35 = 3 × 3 × 3 × 3 × 3 = 243
Эту запись можно прочитать тремя способами:
- 3 в 5 степени;
- пятая степень числа три;
- возвести число три в пятую степень.

Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства степеней
Свойства степеней обычно используют, чтобы сократить или упростить сложные примеры. Удобно использовать вместе с таблицей степеней и таблицей умножения.
a1 = а a0 = 1 (a ≠ 0) a−n = 1 : an am × an = am+n am : an = am-n (a × b)n = an × bn (am)n = am×n (a : b)n = an : bn |
Подготовка к ЕГЭ по математике онлайн поможет снять стресс перед экзаменом и повысит шансы на высокий балл.
Таблица степеней от 1 до 10
Таблица степеней — это перечень чисел от 1 до 10, возведенных в степень от 1 до 10. Ниже приведены два вида таблиц: выберите ту, которая удобнее для вас, скачайте на телефон или распечатайте и положите в учебник.
Как найти необходимые значения в этой таблице:
- В первом столбце находим число, которое обозначает степень. Запомним номер этой строки.
- В первой строке находим показатель степени. Запомним найденный столбец.
- На пересечении строки и столбца находится ответ.
В этой табличке мы просто ищем нужное нам число в степени и получаем ответ.
А если ответ нужно получить как можно быстрее, можно использовать онлайн-калькулятор степеней.
Решение задач
Задание 1. Упростить и решить выражение 52 × 53.
Как решаем:
52 × 53 = 52+3 = 55 = 3125
Задание 2. Упростить и решить выражение 24 × 33 × 25.
Как решаем:
24 × 33 × 25 = 24+5 × 33 = 29 × 33 = 512 × 27 = 13 824
Задание 3. Найти 364.
Как решаем:
При условии, что у нас есть только таблица до 10, разложим основание степени на множители:
364 = 64 × 64 = 1296 × 1296 = 1 679 616
364 = 64 × 64 = 68 = 1 679 616
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
282. 6K
6K
Как решать систему уравнений
К следующей статье
414.2K
Сокращенное умножение: правила, формулы
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т. е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example | |
|---|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 | |
| — | знак минус | вычитание | 1 1/2 — 2/3 | |
| * | asterisk | multiplication | 2/3 * 3/4 | |
| × | times sign | multiplication | 2 /3 × 5/6 | |
| : | division sign | division | 1/2 : 3 | |
| / | division slash | division | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
|
Как привести дробные числа к общему знаменателю. Записи с меткой «наименьший общий знаменатель»
Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Примеры. Привести следующие дроби к наименьшему общему знаменателю.
Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20: 5=4). Для 2-й дроби дополнительный множитель равен 5 (20: 4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8: 4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8 ).
Данные дроби не являются несократимыми.
Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. (см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей
). Находим НОК(16; 20)=2 4 · 5=16· 5=80. Дополнительный множитель для 1-й дроби равен 5 (80: 16=5). Дополнительный множитель для 2-й дроби равен 4 (80: 20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80 ).
Находим наименьший общий знаменатель НОЗ(5; 6 и 15)=НОК(5; 6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30: 5=6), дополнительный множитель ко 2-й дроби равен 5 (30: 6=5), дополнительный множитель к 3-ей дроби равен 2 (30: 15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30 ).
Страница 1 из 1 1
Для решения примеров с дробями необходимо уметь находить наименьший общий знаменатель. Ниже приведена подробная инструкция.
Как найти наименьший общий знаменатель – понятие
Наименьший общий знаменатель (НОЗ) простыми словами – это минимальное число, которое делится на знаменатели всех дробей данного примера. Другими словами его называют Наименьшим Общим Кратным (НОК). НОЗ используют только в том случае, если знаменатели у дробей различны.
Как найти наименьший общий знаменатель – примеры
Рассмотрим примеры нахождения НОЗ.
Вычислить: 3/5 + 2/15.
Решение (Последовательность действий):
- Смотрим на знаменатели дробей, убеждаемся, что они разные и выражения максимально сокращены.
- Находим наименьшее число, которое делится и на 5, и на 15. Таким числом будет 15. Таким образом, 3/5 + 2/15 = ?/15.
- Со знаменателем разобрались. Что будет в числителе? Помочь выяснить это нам поможет дополнительный множитель. Дополнительный множитель – это число, получившееся при делении НОЗ на знаменатель конкретной дроби. Для 3/5 дополнительный множитель равен 3, так как 15/5 = 3. Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.
- Выяснив дополнительный множитель, умножаем его на числители дробей и складываем получившиеся значения. 3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.
Ответ: 3/5 + 2/15 = 11/15.
Если в примере складываются или вычитаются не 2, а 3 или больше дробей, то НОЗ нужно искать уже для стольких дробей, сколько дано.
Вычислить: 1/2 – 5/12 + 3/6
Решение (последовательность действий):
- Находим наименьший общий знаменатель. Минимальным числом, делящимся на 2, 12 и 6 будет 12.
- Получим: 1/2 – 5/12 + 3/6 = ?/12.
- Ищем дополнительные множители. Для 1/2 – 6; для 5/12 – 1; для 3/6 – 2.
- Умножаем на числители и приписываем соответствующие знаки: 1/2 – 5/12 + 3/6 = (1*6 – 5*1 + 2*3)/12 = 7/12.
Ответ: 1/2 – 5/12 + 3/6 = 7/12.
Знаменателем арифметической дроби a / b называют число b, показывающее размеры долей единицы, из которых составлена дробь. Знаменателем алгебраической дроби A / B называют алгебраическое выражение B. Для выполнения арифметических действий с дробями их необходимо привести к наименьшему общему знаменателю.
Вам понадобится
- Для работы с алгебраическими дробями при нахождении наименьшего общего знаменателя необходимо знать методы разложения многочленов на множители.
Инструкция
Рассмотрим приведение к наименьшему общему знаменателю двух арифметических дробей n/m и s/t, где n, m, s, t – целые числа. 2. Для
2. Для
Поделиться с друзьями:
КалькуляторLCM — CalcuNation.com Калькулятор
LCM — CalcuNation.comНайдите наименьшее общее кратное (НОК) двух чисел с помощью этого калькулятора НОК.
Первое число:
Второе число:
Вычислить наименьшее общее кратное двух чисел.
Что такое наименьшее общее кратное?
Наименьшее общее кратное (НОК) между двумя числами — это наименьшее целое число, которое делится на оба числа. Иногда наименьшее общее кратное называют наименьшим общим кратным или наименьшим общим знаменателем.
Например, найдите НОК двух чисел 12 и 16:
Число кратное 12 равно 12, 24, 36, 48, 60, 72, 84, 96 и т. д.
Число кратное 16 равно 16, 32, 48, 64, 80 и т. д.
Два числа (12 и 16) имеют много общих кратных, если вы продолжаете расширять списки кратных. Но из сравнения двух списков мы видим, что 48 — это самый низкий или наименее распространенный множитель.
Но из сравнения двух списков мы видим, что 48 — это самый низкий или наименее распространенный множитель.
Уравнение наименьшего общего кратного
НОК = (a*b) / GCF(a и b)
Используйте этот калькулятор GCF, чтобы помочь с этой формулой
Найдите НОК, наименьшее общее кратное с использованием наибольшего общего делителя
Чтобы понять, как использовать этот метод, может быть важно ознакомиться с тем, как найти наибольший общий множитель.
Наибольший общий множитель двух чисел — это наибольший множитель, на который делятся оба числа. Иногда наибольший общий делитель также называют наибольшим общим делителем (НОД). или наивысший общий множитель (hcf).
Например, найдите НОК двух чисел 12 и 16:
Множители для 12 равны 1, 2, 3, 4, 6 и 12. Это множители 12, потому что
12 делится на все эти числа.
Делители числа 16: 1, 2, 4, 8, 16.
Два числа (12 и 16) имеют общие делители (1, 2, 4).
Наибольшее из них равно 4, и это наибольший общий множитель.
Если использовать уравнение LCM = (a * b) / GCF (a и b).
Давайте использовать числа 8 и 12, где 8 является переменной (a), а 12 — переменной (b). Используя калькулятор GCF CalcuNation, мы знаем, что GCF 8 и 12 равен 4. Таким образом, наше уравнение выходит на LCM = (8 * 12) / 4. Это вычисляется как LCM = 24,
Другие методы LCM
Существуют и другие методы нахождения наименьшего общего кратного. Хотя в этом калькуляторе используется наибольший общий множитель, вы также можете использовать метод множителей листинга.
Метод Listing Multiples может занять много времени. Вы буквально перечисляете все числа, кратные каждому числу, пока не найдете подходящее число. Наименьшее число, совпадающее в списке кратных является наименьшим общим кратным.
Существует также метод простой факторизации. С помощью этого метода вы перечисляете все простые множители для каждого числа. Затем перечислите все простые множители столько раз, сколько раз они встречаются для любого заданного числа. Затем
умножьте список факторов вместе, чтобы найти LCM.
Затем
умножьте список факторов вместе, чтобы найти LCM.
LCM также можно найти с помощью метода диаграммы Венна, метода пирога/лестницы или метода деления.
Дополнительные ссылки
- Наименее распространенное множественное видео
- Наименее распространенные множественные игры
- Наименее распространенное множественное руководство
Связанные калькуляторы
LCM Калькулятор для вычисления наименьшего общего кратного 12, 16
Создано: Джитендер Кумар
Просмотрено: Phani Ponnapalli, Rajasekhar Valipishetty
Последнее обновление: 06 апреля 2023 г.
Бесплатный калькулятор LCM определяет наименьшее общее кратное (НОК) между 12 и 16 — наименьшее целое число, равное 48, которое делится на оба числа.
Наименьшее общее кратное (НОК) чисел 12 и 16 равно 48 .
LCM(12,16) = 48
Наименьшее общее кратное или наименьший общий знаменатель (LCD) можно вычислить тремя способами;
- Наименьшее общее кратное 12 и 16 методом простых чисел
- Наименьшее общее кратное 12 и 16 с помощью формулы GCF
Имя пользователя
LCM:
100004 и4 5 сообщите об этом объявлении
Наименее распространенное кратное может быть найдено путем умножения самых высоких показателей степени простых делителей 12 и 16. Сначала мы вычислим простых делителей 12 и 16 .
Сначала мы вычислим простых делителей 12 и 16 .
Факторизация числа 12
| 2 | 12 |
| 2 | 6 |
| 3 | 1 |
Простые делители числа 12 равны 2,3. Простая факторизация 12 в экспоненциальной форме:
12 = 2 2 × 3 1
Простая факторизация 16
12 2900
0
Простые множители числа 16 равны 2. Разложение числа 16 в экспоненциальной форме на простые множители:
16 = 2 4
Теперь умножаем самые высокие простые множители степени, чтобы вычислить LCM 12 и 16 .
НОК(12,16) = 2 4 ×3 1
НОК(12,16) = 48
Делители числа 12
Список натуральных делителей числа 12, на которое 12 делится без остатка.
1, 2, 3, 4, 6, 12
Делители 16
Список положительных целых множителей числа 16, на которое 16 делится без остатка.
1, 2, 4, 8, 16
Формула LCM : LCM(a,b) = (a × b) / GCF(a,b).
Нам нужно рассчитать наибольший общий делитель 12 и 16, а затем применить в уравнении НОК.
GCF(12,16) = 4
НОК(12,16) = ( 12 × 16) / 4
НОК(12,16) = 192 / 4
НОК(12,16) = 48
(i) НОК 16 и 12 ассоциативна
LCM из 12 и 16 = LCM из 16 и 12
- LCM из 12 и 16
- LCM из 12 и 17
- LCM из 12 и 18
- LCM из 12 и 19 LCM
- LCM 16 и 20
- LCM 16 и 21
- LCM 16 и 22
- LCM 16 и 23
- LCM 16 и 24
1. Что такое LCM 12 и 16?
Ответ: НОК 12 и 16 равно 48.
2. Каковы множители числа 12?
Ответ: Делители 12 равны 1, 2, 3, 4, 6, 12. Есть 6 целых чисел, которые являются делителями 12. Калькулятор «Конвертер обыкновенных дробей в десятичные» Ответ: Дробь 3/7 в десятичном виде это 0,428571428571… или 0,(428571) =0,428571428571… = 0,(428571) Для того, чтобы перевести дробь 3/7 в десятичный формат необходимо разделить числитель 3 на знаменатель 7. Результат деления: 3 ÷ 7 = 0,428571428571… Как можно заметить, наша десятичная дробь имеет повторяющуюся группу цифр (428571) после запятой, длиною в 6 цифру. Это значит, что мы имеем периодическую десятичную дробь, которую можно записать следующим образом: 0,(428571) число в скобках (428571) обозначает группу цифр, повторяющихся бесконечно Смотрите также: Сократить дробь 3/7 Поделитесь текущим расчетом Печать https://calculat. <a href=»https://calculat.io/ru/number/fraction-as-a-decimal/0—3—7″>Дробь 3/7 в виде десятичной дроби — Calculatio</a> Данный онлайн-конвертер обыкновенных дробей в десятичные является полезным инструментом, предназначенным для легкого преобразовывания любой дроби в ее эквивалентную десятичную форму. Например, он может помочь узнать как записать 3/7 в виде десятичной дроби? Независимо от того, являетесь ли вы учеником, студентом или профессионалом, этот конвертер может сэкономить ваше время и усилия при выполнении ручных вычислений. Чтобы использовать этот конвертер, просто введите дробь, которую вы хотите преобразовать, в соответствующие поля. Вам необходимо ввести целую часть (если есть), числитель и знаменатель дроби. Например, если вы хотите преобразовать 3/7 в его десятичный эквивалент, вы введете ‘0’ как целую часть, ‘3’ как числитель и ‘7’ как знаменатель. После того, как вы ввели дробь, нажмите кнопку ‘Конвертировать’, чтобы получить результаты. Конвертер отобразит десятичный эквивалент дроби, который в нашем случае равен 0,428571428571…. Кроме того, он предоставит пошаговое объяснение процесса преобразования, чтобы вы могли понять, как был получен десятичный эквивалент дроби. Если результат является периодической десятичной дробью, конвертер отобразит повторяющийся шаблон, используя скобки для обозначения повторяющихся цифр. Одной из ключевых особенностей этого конвертера является его способность выводить периодические десятичные дроби. В математике периодическая десятичная дробь — это десятичная дробь, в которой есть повторяющийся шаблон цифр, например, 0,33333… или 0,142857142857… Это отличает такие дроби от непериодических десятичных дробей, которые заканчиваются после определенного числа цифр, например, 0,5 или 0,75. Использование этого онлайн-конвертера дробей в десятичные является быстрым и простым способом преобразования любой дроби в ее десятичный эквивалент. Вы хотите вычислить, как упростить дробь 3/7? В этом действительно простом руководстве мы научим вас, как именно упростить 3/7 и преобразовать его в низшую форму (иногда это называется сокращением дроби до низших членов). Начнем с того, что число над чертой (3) в дроби называется числителем, а число под чертой (7) называется знаменателем. Итак, что мы хотим здесь сделать, так это упростить числитель и знаменатель в 3/7 до наименьших возможных значений, сохранив фактическую дробь прежней. Для этого мы используем то, что называется наибольшим общим делителем . Он также известен как наибольший общий делитель и, проще говоря, это наибольшее число, которое делится точно на два или более чисел. Хотите быстро узнать или освежить в памяти способы упрощения дробей? Посмотрите это быстрое и информативное видео прямо сейчас! В нашем случае с 3/7 наибольший общий множитель равен 1. Получив это, мы можем разделить на него и числитель, и знаменатель, и вуаля, дробь упрощается: 3/1 = 3 7/1 = 7 3
/
7 Как видите, 3/7 нельзя упростить дальше, поэтому результат тот же, с которого мы начали. Не очень интересно, я знаю, но, надеюсь, вы, по крайней мере, поняли, почему это нельзя упростить дальше! Вот оно! Теперь вы точно знаете, как упростить 3/7 до минимума. 3/7 Вот небольшой бонусный расчет, который поможет вам легко определить десятичный формат дроби, которую мы рассчитали. Все, что вам нужно сделать, это разделить числитель на знаменатель, и вы можете преобразовать любую дробь в десятичную: 3
/
7
«=»
0.4286 Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку! «Что такое упрощенное 3/7?». VisualFractions.com . Говорят, что целое число a делится на натуральное число b, если существует такое целое число c, что выполняется равенство \(a = bc\). В этом случае число b называют делителем числа a, а число a — кратным числу b. Если числа \(a\) делится на b, то пишут \(a \vdots b\). Например, \(95 \vdots 5\), так как \(95 = 5 \bullet 19\) СВОЙСТВА ДЕЛИМОСТИ 1. Если a делится на b, то для любого числа k число ka делится на b. \(a \vdots b \rightarrow ak \vdots b\) 2. Если a делится на c и b делится на c, то сумма, разность и произведение чисел a и b делится на c. \(\ \left\{ \begin{matrix} a \vdots c \\ b \vdots c \\ \end{matrix} \rightarrow \left\lbrack \begin{matrix} \left( a + b \right) \vdots c \\ \left( a — b \right) \vdots c \\ (a \bullet b) \vdots c \\ \end{matrix} \right.\ \right.\ \) 3. Если a делится на b и b делится на c, то a делится на c. \(\left\{ \begin{matrix} a \vdots b \\ b \vdots c \\ \end{matrix} \rightarrow \right. 4. Если a делится на b и c делится на d, то ac делится на bd. \(\left\{ \begin{matrix} a \vdots b \\ c \vdots d \\ \end{matrix} \right.\ \rightarrow ac \vdots bd\) ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА Число \(p\ (p \geq 2)\) называется простым, если оно делится только на себя и на единицу. Составными числами называются целые числа, имеющие больше двух различных делителей. Например, Число 17 простое. Делители \(17:\ 1,\ 17\). Число 9 составное. Делители \(9:\ 1,\ 3,\ 9\). Единица не является ни простым, ни составным числом. Два числа, наибольший делитель которых, равен 1, называются взаимно простыми. ПРИЗНАКИ ДЕЛИМОСТИ Число делится на 2 тогда и только тогда, когда последняя цифра числа делится на 2 (последняя цифра – четная). Число делится на 4 тогда и только тогда, когда последние две цифры числа делятся на 4. Число делится на 8 тогда и только тогда, когда последние три цифры числа делятся на 8. Число делится на 3 тогда и только тогда, когда сумма цифр делится на 3. Число делится на 9 тогда и только тогда, когда сумма цифр делится на 9. Число делится на 5 тогда и только тогда, когда последняя цифра числа делится на 5 (последняя цифра 0 или 5). Число делится на 25 тогда и только тогда, когда последние две цифры числа делятся на 25. Число делится на 11 тогда и только тогда, когда разность суммы цифр, стоящих на нечетных местах, и суммы цифр, стоящих на четных местах, делится на 11. Пример №1: \(123456789\) делится на 3, так как \(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45\), а 45 делится на 3. Пример №2: 1452 делится на 11, так как \((1 + 5)\ –\ (4 + 2)\) делится на 11. ДЕЛЕНИЕ С ОСТАТКОМ Пусть \(a\ и\ b \neq 0\) – два целых числа. \(\left\{ \begin{matrix} a = \text{bc} + d \\ 0 \leq d < |b| \\ \end{matrix} \right.\ \) От деления на b могут быть только остатки\(:\ 0,\ 1,\ 2,\ 3\ldots,\ |b| — 1\). Пример №3: \(19\ :\ 7\ = \ 2\ (ост.\ 5)\) \(19\ = \ 7\ \bullet \ 2\ + \ 5\ \) Пример №4: \(22\ :\ ( — 3)\ = \ — 7\ (ост.\ 1).\) \(22\ = \ — 3\ \bullet \ ( — 7)\ + \ 1\) Пример №5: \(- 22\ :\ 3\ = \ — 8\ (ост.\ 2)\) \(- 22\ = \ 3\ \bullet \ ( — 8)\ + \ 2\) ТЕОРЕМЫ Сумма чисел a и b даёт тот же остаток при делении на число m, что и сумма остатков чисел a и b при делении на число m. Например, \(\left\{ \begin{matrix} 15:2 = 7\left( ост.\ 1 \right) \\ 16:2 = 8(ост.\ 0) \\ \end{matrix} \right.\ \rightarrow \left( 15 + 16 \right):2 = 15\left( ост. Произведение чисел a и b даёт тот же остаток при делении на число m, что и произведение остатков чисел a и b при делении на число m. Например, \(\left\{ \begin{matrix} 13:3 = 4\left( ост.\ 1 \right) \\ 20:3 = 6(ост.\ 2) \\ \end{matrix} \right.\ \rightarrow \left( 13 \bullet 20 \right):3 = 86\left( ост.\ \mathbf{2} \right)\text{\ \ \ \ \ }\left( 1 \bullet 2 \right):3 = 0(ост.\ \mathbf{2})\) Оглавление Время чтения:
7 минут 451 Определение 1 Деление — одна из четырех основных операций, которая делит число на равные части. Это математический метод, при котором число делится на более мелкие группы, или метод распределения количества на равные части. Обозначается несколькими символами: косой чертой, горизонтальной чертой и знаком деления. Определение 2 Как следует из названия, правила делимости— это процедуры, используемые для проверки того, делится ли число на другое число, без обязательного фактического деления. Число делится на другое число, если результат или частное является целым числом, а остаток равен нулю. По сути, это алгоритм, позволяющий быстро определить, делится ли число на заданное число. В случае если признак делимости позволяет узнать и остальное распределение, его называют признаком компетентности. Эта статья демонстрирует смысл признака делимости на 6. Его формулировка представлена с примерами решения. Ниже мы приводим доказательство признака делимости на 6 на примере некоторых выражений. Говорят, что целое число делится на 6, если оно удовлетворяет двум условиям, приведенным ниже. Оба условия должны применяться к числу при выполнении теста на делимость 6. Если число не удовлетворяет ни одному из данных условий или обоим, то мы можем сказать, что число не делится на 6. Другими словами, мы можем сказать, что все четные числа в таблице умножения 3 делятся на 6. Давайте разберемся с правилом делимости на 6 на примерах. Правило делимости 6 одинаково для всех чисел, будь то меньшее число или большое число. Большое число делится на 6, если оно делится и на 2, и на 3. Большое число должно удовлетворять обоим условиям признака делимости числа 6. Следуйте инструкциям, чтобы проверить, делится ли большое число на 6 или нет. Например, 145962 Примеры 1 — 3 Узнать, делятся ли данные числа на 6 или нет, используя признак делимости на 6. а) 80 б) 264 а) Поскольку 80 — четное число, оно делится на 2, но сумма цифр, то есть 8 + 0 = 8, не делится на 3, поэтому 80 не делится на 3. Таким образом, число 80 не делится на 3. делится на 6, потому что делится на 2, но не делится на 3. б) Поскольку 264 является четным числом, оно делится на 2. Кроме того, сумма цифр, то есть 2 + 6 + 4 = 12, делится на 3, поэтому 264 также делится на 3. Таким образом, число 264 делится на 6, потому что делится и на 2, и на 3. Используя правило делимости на 6, узнайте, делится ли число 4578 на 6 или нет. Решение: Поскольку 4578 — четное число, оно делится на 2. Кроме того, сумма цифр 4+ 5+ 7 + 8 = 24 делится на 3, или мы можем добавить цифры 24, чтобы упростить 2 +4 = 6 делится на 3, следовательно, 4578 также делится на 3. Следовательно, число 4578 делится на 6, потому что оно делится на 2 и 3 (4578 ÷ 6 = 763). Проверьте, делится ли заданное большое число 433788 на 6 или нет, используя правило делимости на 6. Рассмотрим доказательство признака делимости на 6 с необходимыми и достаточными условиями. Теорема 1 Для того чтобы целое число, а делилось на 6, необходимо и достаточно, чтобы это число делилось на 2 и 3. Доказательство Сначала нужно доказать, что делимость числа a на 6 делает его делящимся на два и три. Используя свойство делимости: если целое число делится на b, то произведение ba на целое число b также делится на b. Отсюда следует, что при делении a на 6 можно использовать свойство делимости, чтобы представить равенство как a = 6 ⋅ q a=6 q, где q — целое число. Такое обозначение произведения говорит о том, что наличие множителя дает гарантию деления на 2 и на 3. Необходимость доказана. Чтобы полностью доказать делимость на 6, нужно доказать достаточность. Для этого нужно доказать, что если число делится и на 2, и на 3, то оно делится и на 6 без остатка. Нет времени решать самому? Наши эксперты помогут! Контрольная | от 300 ₽ | Реферат | от 500 ₽ | Курсовая | от 1 000 ₽ | В этом разделе мы рассмотрим способы доказательства делимости на 6 с использованием переменных. В этих случаях (когда целое число явно не указано) прямое деление и применение признака делимости на 6 зачастую невозможно, поэтому необходим другой подход к решению. Оценить статью (85 оценок): Поделиться Задавать вопрос спросил Изменено
7 лет, 6 месяцев назад Просмотрено
39 тысяч раз
9я\эквив1\пмод 3$. Утверждение является непосредственным следствием этого соответствия. Я не понимаю последнее утверждение. $\endgroup$ 3 $\begingroup$ Простой способ увидеть это (который на самом деле хорошо обобщает маленькую теорему Ферма): $$10 — 1 = 92 + 1 \times 10 + 7 \\ &= 4\times 9999 + 3 \times 999 + 6 \times 99 + 1 \times 9 + (4 + 3 + 6 + 1 + 7) \end{align}$$ Каждый член справа, кроме суммы цифр, делится на $3$. Таким образом, остаток при делении исходного числа на $3$ и суммы цифр на $3$ должен быть одинаковым. $\endgroup$ 4 $\begingroup$ n = $a_0$ + …. + $a_n$ mod (3) означает, что n и сумма цифр будут эквивалентны одному и тому же числу по модулю 3. Если это число равно 0, то n и сумма обе цифры будут делиться на 3. Другими словами, остаток от деления $n$ на $3$ такой же, как остаток деления суммы его цифр на $3$. В случае нулевой невязки получаем искомое утверждение: $n$ делится на $3$ тогда и только тогда, когда сумма его цифр делится на $3$. $\endgroup$ Найдите число, которое при делении на 28 дает отношение 606, а остаток 23. Нашли ошибку или неточность? Не стесняйтесь . Спасибо! Советы для связанных онлайн-калькуляторов Вы хотите выполнить деление натуральных чисел — найти частное и остаток? Правильные ответы выделены курсивом и + 1. Управление – это:
+ процесс планирования, организации, мотивации и контроля, необходимые для того, чтобы сформулировать и достичь целей;
— особый вид деятельности, превращающий неорганизованную толпу в эффективно и целенаправленно работающую производственную группу;
— эффективное и производительное достижение целей предприятия посредством планирования, организации и лидерства руководителя.
2. Менеджмент – это:
— процесс планирования, организации, мотивации и контроля, необходимые для того, чтобы сформулировать и достичь целей;
— особый вид деятельности, превращающий неорганизованную толпу в эффективно и целенаправленно работающую производственную группу;
+ эффективное и производительное достижение целей предприятия посредством планирования, организации и лидерства руководителя. 3. Кто является родоначальником классической школы менеджмента: — Ч. Бебидж;
— М. Вебер;
+ Ф. Тейлор.
4. Первый учебник по управлению был написан английским предпринимателем М. Веберов в:
— 1850;
-1790;
+ 1832;
5. Кто автор этих слов: «Управление – это искусство знать точно, что предстоит сделать и как это сделать самым дешевым и наилучшим способом»?
— Ч. Бебидж;
— М. Вебер;
+ Ф. Тейлор.
6. Какие бывают виды разделения труда менеджеров?
— функциональное;
+ горизонтальное;
+ вертикальное;
-прямое.
7. Сколько существует иерархических уровней менеджмента?
— 5;
+3;
-9.
8. Кто относится к среднему уровню менеджеров?
— заместители;
+ руководители подразделений;
— руководители групп. 9. Функции менеджмента бывают:
— общие, индивидуальные;
— групповые, специфические;
— конкретные, расширенные;
— правильного ответа нет.
10. Выберите правильные функции менеджмента:
+ планирование;
+ коодинирование;
— распределение;
— стимулирование;
— все ответы верны.
1. Планирование – это:
+ управленческая деятельность, отраженная в планах и фиксирующая будущее состояние менеджмента в текущее время;
— перспективная ориентация в рамках распознавания проблем развития;
— обеспечение целенаправленного развития организации в целом и всех её подразделений.
2. Сформулируйте задачи планирования:
+ перспективная ориентация в рамках распознавания проблем развития;
— обеспечение целенаправленного развития организации в целом и всех её подразделений. — создание базы для эффективного контроля путем сравнения показателей.
3. По форме планирование бывает:
— тактическое;
— конкретное;
+ перспективное.
4. Необходимость планирования заключается в определении:
+ конечных и промежуточных целей;
+ задач, решение которых необходимо для достижения целей;
+ средств и способов решения задач;
— правильного ответа нет.
5. При какой форме планирования осуществляется выбор средств для выполнения целей на период от 1 года до 5 лет?
— перспективное;
+ среднесрочное;
— оперативное.
6. При какой форме планирования осуществляется определение целей деятельности на срок больше 5 лет:
+ перспективное;
— среднесрочное;
— оперативное.
7. Организация – это:
— процесс планирования, организации, мотивации и контроля, необходимые для того, чтобы сформулировать и достичь целей;
— особый вид деятельности, превращающий неорганизованную толпу в эффективно и целенаправленно работающую производственную группу;
+ это управленческая деятельность, посредством которой система управления приспосабливается для выполнения задач, поставленных на этапе планирования. 8. Установление постоянных и временных связей между всеми подразделениями организации осуществляет функция:
— планирования;
+ организации;
— контроля.
9. Выберите основные принципы организации менеджмента:
— непрерывность;
— ритмичность;
— надежность;
+ все ответы верны.
10. Функции административно-оперативного управления:
+ определение структуры предприятий;
— периодическое или непрерывное сравнение;
+ установление ответственности.
Тесты по менеджменту 3-ий вариант 1. Регулирование – это:
+ управленческая деятельность, направленная на ликвидацию отклонений от заданного режима управления;
— процесс выработки корректируемых мер и реализации принятых технологий;
+ функция менеджмента.
2. + рациональность;
— ритмичность;
— надежность;
+ достоверность.
3. Задача регулирования:
— обновление планируемых заданий;
+ обеспечение своевременного эффективного достижения организацией своих целей;
— корректировка результатов деятельности;
4. Виды регулирования:
+ реактивное;
-операционное;
+ упреждающее.
5. При каком виде регулирования проблема рассматривается как потенциальная возможность:
— реактивное;
— операционное;
+ упреждающее.
6. Назовите этапы регулирования:
+ информационная подготовка для принятия решений;
+ разработка и принятие решений;
— определение структуры предприятия.
7. Дайте правильное определение функции координации:
+ управленческая деятельность, обеспечивающая согласованность работы рабочих подразделений;
— управленческая деятельность, направленная на ликвидацию отклонений от заданного режима управления;
— это управленческая деятельность, посредством которой система управления приспосабливается для выполнения задач, поставленных на этапе планирования. 8. Назовите функции менеджмента:
— ритмичность;
+ мотивация;
— законность;
9. Тип власти, который может использовать менеджер:
— экспертная;
— эталонная;
— законная;
+ все ответы верны.
10. Влияние – это:
+ поведение одного человека, которое вносит изменение в поведение другого человека;
— волевое отношение между людьми, основанное на силе;
— убеждение человека в чем-либо.
Тесты по теория менеджмента тесты с ответами вариант 4 1. Назовите форму влияния, которая может побудить человека к более тесному сотрудничеству:
+ убеждение;
-принуждение;
+ участие сотрудников в управлении.
2. Задачи контроля:
— сбор и систематизация информации о фактическом состоянии деятельности;
+ оценка состояния и значимости полученных результатов;
— разработка и принятие решений. 3. Анализ – это:
+ это управленческая деятельность, обеспечивающая выявление причин отклонения желаемого состояния системы от фактического и осуществляющая разработку мер по устранению выявленных недостатков;
— управленческая деятельность, направленная на ликвидацию отклонений от заданного режима управления;
— это управленческая деятельность, посредством которой система управления приспосабливается для выполнения задач, поставленных на этапе планирования.
4. Кто является продолжателем теоретической работы Тейлора о менеджменте:
— А. Файолль;
— Ч. Бебидж;
+ М. Вебер.
5. Назовите психологические методы управления:
+ метод профессионального отбора;
— метод социального нормирования;
+ метод гуманизации труда.
6. Какие приемы используются при психологических методах управления?
+ интервью;
+ беседы;
+ тесты;
— наблюдения. 7. Назовите социальные методы управления:
— метод профессионального отбора;
+метод социального нормирования;
— метод гуманизации труда.
8. Управление – это:
— эффективное и производительное достижение целей предприятия посредством планирования, организации и лидерства руководителя.
+ процесс планирования, организации, мотивации и контроля, необходимые для того, чтобы сформулировать и достичь целей;
— особый вид деятельности, превращающий неорганизованную толпу в эффективно и целенаправленно работающую производственную группу;
9. Назовите этапы регулирования:
— определение структуры предприятия;
+ информационная подготовка для принятия решений;
+ разработка и принятие решений;
10. Социальные методы управления:
— метод управления группами;
— метод ролевых изменений;
— метод управления групповыми явлениями;
+ все ответы верны.
1 Тест. Что такое менеджмент?
1. Разновидность науки управления.
2. Группа руководителей.
3. Разновидность управленческой деятельности.
4. Это отношение, складывается в процессе управленческой деятельности.
+ 5. Совокупность принципов, методов, форм и средств управления, особый вид деятельности, связанный с руководством людьми, умелым использованием их труда и знаний.
2. Задачами менеджмента являются:
1. Тактическая.
2. Стратегическая
3. Оперативная
+ 4. Поддержание устойчивости фирмы и всех ее элементов и ее развитие.
5. Контроль результатов деятельности и внесение коррективов.
3. Функции менеджмента – это …
1. Виды управленческой деятельности, которые обеспечивают формирование управленческого влияния. + 2. Отдельные виды управленческой деятельности, которые увеличивают эффективность руководства.
3. Отдельные управленческие процессы, направленные на увеличение продуктивности труда подчиненных.
Тест № 4. Функции менеджмента
1. Инновационный менеджмент.
2. Оптимальное сочетание централизованного регулирования и самоуправления.
+ 3. Организация, планирование, контроль, мотивация.
4. Перевод фирмы в качественно новое состояние.
5. Целенаправленность.
5. Тест. Процесс менеджменту – это …
1. Последовательное выполнение функций менеджмента, конкретно: планирование, организация, мотивация, контроль и регулирование.
2. Последовательность определенных оконченных этапов, выполнение которых способствует обеспечению: управленческого влияния руководящей системы на руководимую для достижения целей организации.
3. Последовательное выполнение функций и методов менеджмента. + 4. Правильные ответы 1 и 3.
6. Выберите понятие, относящиеся к принципам менеджмента.
+ 1. Единоначалия и коллегиальность.
2. Организация.
3. Достижение цели.
4. Планирование.
7. Среди условий, что перечислены ниже, выберите такие, которые определяют успех организации.
1. Наличие формальных и неформальных организаций.
2. Выход на внешний рынок.
3. Способность к выживанию, результативности, практической реализации.
+ 4. Наличие современных технологий.
8. В чем состоит основное отличие формальных и неформальных организаций.
1. В количестве членов организаций.
2. В контактах с внешней средой.
+ 3. В способе возникновения.
4. В связях между членами организации.
9. Организация – это:
1. Группа людей, которые владеют определенными ресурсами. + 2. Группа людей, которые владеют определенными ресурсами, имеют общее руководство и общие цели.
3. Группа людей, деятельность которых сознательно, направленно или спонтанно координируется для достижения определенной цели.
4. Группа лиц, которые имеют общее руководство.
10. Какие из нижеприведенных понятий относятся к целям по содержанию.
1. Долгосрочные.
2. Общие.
3. Территориальные.
+ 4. Экономические
11. Выберите правильные ответы:
1. Организация
А – процесс установления пропорций и согласование действий в системе управления.
2. Мотивация
Б – процесс приобщения рабочих до высокопроизводительности труда.
3. Координация
В – процесс формирования структуры управления и создания определенного порядка в работе. 4. Контроль
Г – система наблюдения и проверки функционирования предприятия.
1-В; 2-Б; 3-А; 4-Г
12. Функция организации базируется на таких категориях:
1. Полномочие, ответственность, стимулирование, делегирование.
2. Полномочие, ответственность.
+ 3. Полномочие, ответственность, делегирование.
13. Полномочия – это:
+ 1. Возложена на должностное лицо обязанность выполнять постановленные задания и обеспечивать их позитивное решение.
2. Ограниченное право использовать ресурсы предупреждения и направлять усилия подчиненных на выполнения задания.
3. Передача заданий и полномочий лицу, что берет на себя ответственность за их выполнение.
14. Ответственность – это:
1. Возложенная на должностное лицо обязанность выполнить поставленные задачи, обеспечить их позитивное решение. + 2. Ограничения права использовать ресурсы предприятия и направлять усилия подчиненных на выполнение задания.
3. Передача заданий и полномочий лицу, что берет на себя ответственность за их выполнение.
15. Делегирование – это:
1. Возложенная на должностное лицо обязанность выполнить поставленные задачи, обеспечить их позитивное решение.
2. Ограничения права использовать ресурсы предприятия и направлять усилия подчиненных на выполнение задания.
+ 3. Передача заданий и полномочий лицу, что берет на себя ответственность за их выполнение.
17. Управленческое решение это:
1. Формы влияния на исполнителей.
2. Организационный инструмент в руках работников управления.
+ 3. Творческая деятельность по анализу проблемной ситуации, выбор средств от разрешения.
4. Разрешение.
18. Дайте определение понятий:
1. А – поведение руководителя, что меняет отношение подчиненных к нему.
2. Влияние
Б – способность вести за собой.
3. Лидерство
В – способность и возможность менеджера влиять на деятельность и поведение рабочих.
4. Обычаи
Г – общепринятые повторяющиеся социальные действия, что становятся обычными.
1 – В; 2 – А; 3 – Ь; 4 – Г.
Тест № 19. Какие качества должны быть присущи менеджеру?
1. Знание по специальности.
+ 2. Практичность ума.
3. Спонсорство.
4. Любовь к чтению художественной литературы.
20. Что Вы понимаете под словом «группа».
1. Количество людей, едущих в одном автобусе. 2. Личности, имеющие одинаковые наклонности к какому-то процессу.
+ 3. Две и больше личности, что взаимодействуют одна с одной.
4. Четко определенное количество людей.
21. Кто такой формальный лидер:
1. Один из членов группы, что владеет силой личного влияния на других.
+ 2. Руководитель коллектива, который пользуется данной ему служебной властью.
3. Целеустремленный менеджер.
4. Главный специалист.
22. Группы работников делят на такие категории:
+ 1. Формальные и неформальные.
2. Простые и сложные.
3. Открытые и закрытые.
23. Отметьте какие из нижеперечисленных предложений не являются признаками коллектива.
1. Наличие непосредственных производственных связей.
+ 2. Наличие высокой активности.
3. Психологический климат.
4. Общность целей и задач. 24. Назовите причины конфликтов:
1. Психологическая совместимость
2. Конкуренция.
+ 3. Режимы труда и отдыха.
4. Сотрудничество.
25. Путь разрешения конфликтов:
1. Премирование.
+ 2. Компромисс.
3. Поездка на природу.
4. Гласное обсуждение.
26. Стресс – это:
1. Перегрузка нервной системы.
2. Рассеянность.
+ 3. Вегетативно-психологическое состояние.
4. Увольнение с работы.
27. Руководитель авторитарного стиля руководства:
+ 1. Много работает, требует этого от других.
2. Много работаем сам.
3. Делится властью с подчиненными.
4. Ценить подчиненных.
28 — Тест. Руководитель демократического стиля руководства.
1. Не терпит критики.
2. Ждет указаний сверху. 3. Избегает конфликтов.
+ 4. Коллегиально решает проблемы коллектива.
29. Технология принятия управленческих решений в порядке их разрешения.
+ 1. Одобрение.
+ 2. Реализация.
+ 3. Подготовка.
30. Что относится к методам принятия управленческих решений:
+ 1. Мозговая атака.
2. Организация.
3. Формулировка.
4. Форма контроля. Главная / Ответы на новые тесты / Теория менеджмента / Страница 1 Упражнение 32553: Номер Ответ:  Слоун А.   Тейлор Ф.   Файоль А.  Форд Г.  Упражнение 32554: Номер Ответ:  введена в научный оборот концепция «человека экономического»   переосмыслена правильность концепции Ф.Тейлора и его теории «кнута и пряника»   разработаны методы анализа работы и рабочего места   создана теоретическая база для построения автоматизированных систем управления  Упражнение 32555: Номер Ответ:  введена в научный оборот концепция «человека экономического»   переосмыслена правильность концепции Ф.  разработаны методы анализа работы и рабочего места   создана теоретическая база для построения автоматизированных систем управления  Упражнение 32556: Номер Ответ:  организация   связующий процесс   ситуация   управленческая задача  Упражнение 32557: Номер Ответ:  всегда конкретна и должна осуществляться в рамках, прописанных в инструкциях   носит индивидуальный характер, именно поэтому управление это и наука и искусство   однотипна и не зависит от особенностей технологического процесса   определяется конкретными особенностями данной организации, поэтому так важен опыт  Упражнение 32558: Номер Ответ:  отдельных исполнителей   подчиненного   подчиненного и руководителя   руководителя  Упражнение 32559: Номер Ответ:  возможно шире, поскольку специальные термины точнее отражают тонкости явления   избирательно, среди посвященных   не использовать в устной речи, но активно применять в специальных документах   только в узко профессиональной среде, где все понимают термины однозначно  Упражнение 32560: Номер Ответ:  2   3   4   5  Упражнение 32561: Номер Ответ:  вербальный и невербальный   деловой и общепринятый   жестов и мимики   официальный и просторечный  Упражнение 32562: Номер Ответ:  основные приемы формализации управленческих задач   основные теории мотивации   принципы определения нормы управляемости   рамки ответственности мастера и рабочего  Упражнение 32563: Номер Ответ:  основные приемы формализации управленческих задач   основные теории мотивации   принципы нормирования труда   принципы определения нормы управляемости  Упражнение 32564: Номер Ответ:  основные приемы формализации управленческих задач   основные теории мотивации   принципы нормирования труда   принципы определения нормы управляемости  Упражнение 32565: Номер Ответ:  ответственность   скорость   эффект масштаба   эффект синергии  Упражнение 32566: Номер Ответ:  внутреннее и внешнее   материальное и моральное   официальное и неофициальное   текущее и ожидаемое  Упражнение 32567: Номер Ответ:  документальное оформление общих целей организации   определение действий специализированных звеньев   определение цели и способа ее достижения   получение прибыли  Упражнение 32568: Номер Ответ:  возможно только в исключительных ситуациях   возможно, но всегда носит разовый характер   возможно и активно используется подчиненными   невозможно  Упражнение 32569: Номер Ответ:  быструю разработку новых изделий для производства   гибкость в использовании высококвалифицированных специалистов   ориентацию основных производственных единиц на рынок   полную прозрачность в распределении обязанностей  Упражнение 32570: Номер Ответ:  выбор системы поощрения   жесткость и неотвратимость наказания   разработку стандарта исполнения   соблюдение правил и норм  Упражнение 32571: Номер Ответ:  воспитательные и организационные   межличностные и организационные   структурные и воспитательные   структурные и межличностные  Упражнение 32572: Номер Ответ:  информационная обеспеченность   ответственность   проявление эффекта эмпатии   скорость  Упражнение 32573: Номер Ответ:  выделять те проблемы, которые надо обсудить в коллективе   высвечивать те места в организации, где старое пришло в несоответствие с новым   определить направление будущих изменений   понять, от каких организационных составляющих следует отказаться  Упражнение 32574: Номер Ответ:  возможность быстрой реструктуризации   ясность в распределении полномочий и ответственности   хорошие условия для внедрения внутриорганизационного хозрасчета   возможность адекватного учета региональных условий бизнеса  Упражнение 32575: Номер Ответ:  двух факторов   ожидания   Портера-Лоулера   справедливости  Упражнение 32576: Номер Ответ:  стандартами, принятыми в отрасли   экономичностью организационной структуры   ценой продукции или услуг   реакцией потребителей  Упражнение 32577: Номер Ответ:  не допустить простоев оборудования   обеспечить наиболее экономичное использование имеющихся ресурсов   обеспечить своевременность изменений   объединить цели разных уровней управления  Упражнение 32578: Номер Ответ:  трудовая норма   управленческая задача   функция   человеческий фактор  Упражнение 32579: Номер Ответ:  Трудовая норма   Управленческая задача   Функция   Человеческий фактор  Упражнение 32580: Номер Ответ:  независимой   парной   специфической   универсальной  Упражнение 32581: Номер Ответ:  индивида   индивида и группы   индивида, группы и организации   индивида, группы, комитета, организации  Упражнение 32582: Номер Ответ:  инцидента   объекта   проблемы   реципиента  Упражнение 32583: Номер Ответ:  быстрое прохождение информации сверху вниз   быструю разработку новых изделий   контроль снижения издержек   четкость и ясность в распределении обязанностей  Упражнение 32584: Номер Ответ:  каждый делает свое дело и потому независим   мы делаем общее дело, поэтому решаем вместе   я больше знаю, я советую   подчинение нижестоящих уровней вышестоящим уровням  Упражнение 32585: Номер Ответ:  дивизиональная   матричная   проектная   традиционная  Упражнение 32586: Номер Ответ:  дивизиональная   матричная   проектная   линейно-функциональная  Упражнение 32587: Номер Ответ:  быструю разработку новых изделий для производства   гибкость в использовании линейных руководителей   ориентацию основных производственных единиц на рынок   полную прозрачность в распределении обязанностей  Упражнение 32588: Номер Ответ:  владельцы организации   должностные лица, имеющие полномочия по распоряжению ресурсами организации   должностные лица, осуществляющие контакты с внешней средой организации   должностные лица, имеющие подчиненных  Упражнение 32589: Номер Ответ:  временную   закрытую   открытую   постоянную  Упражнение 32590: Номер Ответ:  взаимосвязанной со всеми функциями цикла   основной в цикле   особой, независимой   парной функцией  Упражнение 32591: Номер Ответ:  воображаемой   пунктирной   сплошной   цветной  Упражнение 32592: Номер Ответ:  не отражаются, но подразумеваются   отражаются только на уровне производственных единиц   отражаются сплошной линией   отражаются только на очень подробных схемах  Упражнение 32593: Номер Ответ:  краха эпохи «свободного предпринимательства»   перехода к фабричному производству   роста активности трудящихся, расцвета профсоюзного движения   становления крупного бизнеса  Упражнение 32594: Номер Ответ:  исключительно редко, поэтому не важно кто их принимает   подчиненными и руководителями в зависимости от ситуации   только подчиненными   только руководителями  Упражнение 32595: Номер Ответ:  В. Врум   Г. Минцберг   Г. Саймон   Н. Винер  Упражнение 32596: Номер Ответ:  вида организации (производственная, коммерческая и т.  типа производства (серийное, массовое, единичное)   уровня иерархии   числа подчиненных  Упражнение 32597: Номер Ответ:  не для каждого уровня иерархии следует рассчитывать свою норму   чем больше норма, тем экономически выгоднее система управления   чем больше уровней иерархии, тем разнообразнее норма   чем ниже уровень иерархии, тем больше норма  Упражнение 32598: Номер Ответ:  Законы взаимодействия объекта и субъекта управления   Отдельная управленческая задача   Процесс управления   Рабочее место и выполняемая на нем работа  Упражнение 32599: Номер Ответ:  организация и ее устройство   процесс управления как массовое явление   руководитель и его работа   управленческий цикл и его составляющие  Упражнение 32600: Номер Ответ:  1) цели и задачи   2) пути и средства   3) ресурсы, необходимые для выполнения поставленных задач   4) пропорции   5) организация выполнения плана и контроль  Упражнение 32601: Номер Ответ:  1) выработка ясной и сжатой формулировки цели   2) разработка планов ее достижения   3) систематический контроль и измерение качества работы и результатов   4) принятие корректирующих мер для достижения планируемых результатов  Упражнение 32602: Номер Ответ:  1) предварительный   2) формирование   3) брожение   4) нормирование   5) деятельность  Главная / Тесты 2 / Теория менеджмента / Страница 1 PMP®, или Project Management Professional, — это экзамен, проводимый Project Management Institute (PMI)®, всемирно признанной сертификацией. Ожидаемое контролируемое значение (EMV) рассчитывается как EMV = Вероятность × Воздействие. Вычислить как положительные, так и отрицательные значения, а затем сложить их: 0,6 × 100 000 долл. США = 60 000 долл. США 0,4 × 100 000 долл. США = 40 000 долл. США EMV = 60 000 долл. США — 40 000 долл. США = 20 000 долл. США прибыли Оценка с наименьшим диапазоном менее рискованна. Диаграмма RACI является примером матрицы распределения ответственности (RAM), которая показывает взаимосвязь между действиями и членами команды. В данной ситуации существует конфликт интересов. Вы должны сообщить своему боссу об этих отношениях. EMV = 0,9 X 10 000 долл. Отчет о состоянии проекта может использоваться для управления рисками. Однако при первом завершении управления рисками у вас еще не будет отчета о состоянии проекта. Таким образом, отчет о состоянии проекта не всегда является исходной информацией для управления рисками. Если вы знаете терпимость заинтересованных сторон, вы можете предсказать, как они могут реагировать на различные ситуации и события риска. Эта информация может помочь определить уровни риска для каждого действия рабочего пакета. Если вы не можете точно определить влияние затрат на событие, используйте качественные оценки, такие как Низкий, Средний и Высокий. Техника Delphi обычно используется для получения экспертных заключений по техническим вопросам, необходимому проекту или объему продукта. Найдите наш тренинг PMP в лучших городах Перенос — это стратегия реагирования на риски. Закрытие не является группой процессов. Результатом процесса мониторинга и контроля является план управления проектом. Вводом в процесс разработки плана управления проектом является реестр заинтересованных сторон. Входными данными для процесса контроллинга является план управления проектом. Результатом процесса закрытия является план управления проектом. 45 миллионов долларов. Стоимость невыбранной альтернативы называется альтернативной стоимостью. Инициирование. Новый проект или новая фаза существующего проекта определяется группой инициирующих процессов. Определение заинтересованных сторон После разработки и утверждения устава проекта следует процесс определения заинтересованных сторон. Держите спонсора довольным Матрица прослеживаемости требований Ознакомьтесь с уставом проекта, чтобы получить общую информацию о проекте Избыточные запасы. Процесс, который определяет, как будет подготовлено описание содержания проекта Проведение фактического сравнения эффективности проекта с планом управления проектом Любая заинтересованная сторона См. договор Выполнение процесса определения заинтересованных сторон проекта Деловые документы для получения информации о заинтересованных лицах Запланировать фокус-группу Проведение анализа требований к связи Консультации с сертифицированным экспертом «Черного пояса шести сигм» Внесение изменений в план управления ресурсами Словарь WBS Передача готовой сборочной линии в эксплуатацию Запустить симуляцию Монте-Карло Проверенный результат Ежедневные стендапы. Оценка организационной культуры и готовности к преобразованиям Создание отчета о рисках 14 Отправить список вопросов участникам накануне творческой сессии Регистр связи 0774 Мэтт Вера BSN, Р.Н. Это ваш обзор NCLEX и практические вопросы для руководства и управления в сестринском деле. В этом банке сестринских тестов проверьте свои знания концепций, лежащих в основе лидерства и управления сестринским делом, с помощью этих 80 практических вопросов. Лидерство – это способность направлять или мотивировать человека или группу для достижения поставленных целей. Тесты, включенные в это руководство: УВЕДОМЛЕНИЕ ДЛЯ ВСЕХ ПОЛЬЗОВАТЕЛЕЙ 9078 2 Имейте в виду, что наши тестовые банки ВСЕГДА БЕСПЛАТНО, и РЕГИСТРАЦИЯ НЕ ТРЕБУЕТСЯ . У Nurseslabs НЕТ и НИКОГДА НЕ БУДЕТ ЗАПРОСИТЬ у данные вашей кредитной карты или какую-либо личную информацию, чтобы получить доступ к нашим практическим вопросам. Правила викторины: Рекомендуемые книги и ресурсы для вашего успеха NCLEX: Раскрытие информации: Ниже приведены партнерские ссылки от Amazon без каких-либо дополнительных затрат с вашей стороны. Мы можем получить небольшую комиссию от вашей покупки. Для получения дополнительной информации ознакомьтесь с нашей политикой конфиденциальности. Всеобъемлющий обзор Saunders для экзамена NCLEX-RN Стратегии успешного прохождения учащимися тестовых заданий следующего поколения NCLEX® (NGN) Обзор вопросов и ответов Сондерса для экзамена NCLEX-RN® NCLEX-RN Prep Plus от Kaplan Иллюстрированное учебное пособие для экзамена NCLEX-RN® Карточки для подготовки к экзамену NCLEX RN (издание 2023 г.) Как найти объем полушария с высотой? Ревекка, высота полушария — это его радиус. Объем шара равен 4/3 π r3. Итак, объем полушария вдвое меньше: V = (2/3) π r3. Что такое площадь полушария? Общая площадь поверхности полушария = площадь плоской поверхности + площадь криволинейной поверхности. Мы знаем, что площадь криволинейной поверхности полушария = 2πr2, а площадь плоской поверхности = πr2. ∴ Общая площадь поверхности полушария =2πr2+πr2=3πr2. Во-вторых, сколько будет объем полушария, если радиус 3.5 метра? 0 0 тогда каков радиус полушария? Поскольку последний равен 4πr2, площадь криволинейной поверхности полусферы радиуса r равна 2πr2. и, следовательно, общая площадь поверхности полушария равна 2πr2+πr2=3πr2. Следовательно, радиус полушария равен 4 см. Чему равен объем полусферы радиусом 2.6 м, округленный до десятых долей кубического метра? Чему равен объем полусферы радиусом 2. Радиус и высота полушария равный. Одинаков ли радиус полушария? По высоте и радиусу цилиндра, конуса и полушарие такое же. … А их радиус равен r единиц. Что такое полушарие и его формула? Поскольку полушарие является половиной сферы, площадь изогнутой поверхности также составляет половину площади сферы. Площадь искривленной поверхности полушария = 1/2 ( 4π г2) = 2 π г2. Как найти радиус полушария? Как рассчитать радиус полушария? Вы должны знать другую информацию. Если, например, вы знаете площадь поверхности (А) полушария, разделите ее на 2π, а затем найдите квадратный корень из этого числа. Таким образом, г = √ (А / 2π). Формула для расчета объема полусферы имеет следующий вид: Объем полусферы = 2πr3/3, где r — радиус полусферы. Чему равен объем полушария радиусом 7 см? Следовательно, объем полушария радиусом 7 см равен 718.66 куб. См. Каков объем 20 шариков радиусом 3.5 мм? да объем 1 шара 179.5. Как найти радиус с площадью полушария? Уравнения, используемые калькулятором этой площади полушария, следующие: Дан радиус: А = 3 * π * r² , Заданный диаметр: A = 3/4 * π * d² , Заданный объем: A = ³√[243/4 * π * V²] 1 ответ эксперта поэтому объем шара (4/3)π(22.85 метра)3, что составляет 49974.35787 метра в кубе. Поскольку мы на самом деле ищем полушарие, мы можем разделить этот объем пополам, чтобы получить объем полушария как 24987.17894 метра в кубе. Как найти объем полушария по радиусу? Формула объема полушария Объем полусферы некоторого радиуса можно легко узнать, вычислив всего лишь половину объема сферы того же радиуса. Объем полусферы = 2πr3/3, где r — радиус полусферы. Чему равен объем полушария радиусом 26.7 м, округленному до десятых долей кубического метра? Это 4 6 или 2/3. Итак, объем полушария 2/3 фута в кубе. Итак, воспользуйтесь калькулятором, умножив две трети на High, умножив на радиус 26.7 в кубе. 39865 0.1 39 865 0.1. Объем шара равен площади поверхности? Ответ на вопрос: объем шара численно равна площади поверхности сферы. Что такое форма полушария? Определение полушария Таким образом, полусфера представляет собой трехмерную геометрическую фигуру, половина сферы с одной плоской стороной, а другая сторона в виде круглой чаши. Он образуется, когда сфера разрезается точно по центру по ее диаметру, оставляя после себя две равные полусферы. ✖Радиус полушария — это расстояние между центром и любой точкой на окружности полушария. створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр +10% -10%
✖Объем Полушария – это общее количество трехмерного пространства, заключенного на поверхности Полушария.
Акр-футАкр-фут (исследование США)Акко-дюймовыйБочка (масло)Бочка (UK)Ствол (США)Ванна (библейский)Совет для ногКабина (библейский)СантилитрКентум кубический футКор (библейский)шнурКубический Ангстремкубический сантиметркубический дециметркубический футкубический дюймКилометры CubicКубический метрКубический Mileкубический миллиметркубический ярдКубок (метрический)Кубок (Великобритания)Кубок (США)ДекалитрДецилитрДестистерДекастерДесертная ложка (Великобритания)Десертная ложка (США)драхмаКапляFemtoliterЖидкость Унция (Великобритания)Жидкость Унция (США)Галлон (Великобритания)Галлона (США)гигалитрГилл (Великобритания)Гилл (США)ГектолитрHin (библейский)хогсхедГомер (библейский)Сто кубический футкилолитрЛитрLog (библейский)мегалитрМикролитрМиллилитрMinim (Великобритания)Minim (США)нанолитрPetaliterпиколитрПинта (Великобритания)Пинта (США)Кварта (Великобритания)Quart (США)StereСтоловая ложка (метрическая)Столовая ложка (Великобритания)Столовая ложка (США)Таза (испанский)Чайная ложка (метрическая)Чайная ложка (Великобритания)Чайная ложка (США)тералитрTon РегистрацияТунОбъем Земли
⎘ копия
👎
Формула
сбросить
👍
ШАГ 0: Сводка предварительного расчета ШАГ 1.
Сфера определяется как набор точек в трех измерениях, и все точки, лежащие на поверхности, равноудалены от центра. Когда плоскость пересекает сферу в центре или на равных частях, она образует полушарие. Можно сказать, что полушарие — это ровно половина сферы.
Share
Copied!
объем полушария – это пространство, занимаемое полушарием. Объект большего объема занимает больше места. Полушарие — это трехмерный объект, который составляет половину полной сферы, например чаши, наушники, иглу, купола в архитектуре и т. д. Следовательно, объем полусферы составляет половину объема сферы. Давайте научимся находить объем полушария с помощью нескольких решенных примеров и практических вопросов. Полушарие — это трехмерная фигура (3D-форма), которая составляет половину сферы. Когда сфера разрезается плоскостью, проходящей через ее центр, форма, которую мы получаем, называется полусферой. Полусфера имеет криволинейную поверхность и одно плоское круглое основание. Объем полушария — это количество единичных кубов, которые могут в него поместиться. Единицей объема являются кубические единицы, следовательно, объем полушария можно выразить как м 3 , см 3 , в 3 и так далее. Давайте узнаем больше о формуле объема полушария. Объем полушария составляет половину объема сферы, поэтому он выражается как Объем полушария = 2πr 3 /3, где r — радиус полушария. Посмотрим, как выводится формула объема полушария. Поскольку полушарие является половиной сферы, мы можем разделить объем сферы на 2, чтобы получить объем ее полусферы. Теперь, учитывая, что радиус сферы равен r. Объем сферы можно рассчитать по формуле Объем сферы = 4πr 3 /3. Итак, объем полушария = 1/2 от 4πr 3 /3 = 1/2 × 4πr 3 /3 = 2πr 3 /3 Объем полушария рассчитывается по формуле Объем полушария = 2πr 3 /3. Итак, найдем объем полушария, радиус которого равен 7 единицам. ☛ Статьи по теме Пример 1: Найдите объем полусферы с радиусом, равным 9 единицам. (Возьмем π = 3,14) Решение: Дано, что радиус (r) полушария = 9 единиц Подставляя r вместо 9, получаем Объем полушария = (2π × 9 3 )/3 Объем полушария = (2 × 3,14 × 9 3 )/3 Следовательно, объем полушария равен 1526,04 единицы 3 . Пример 2: Радиус полусферы равен 3 дюймам. Каков объем полушария? (Возьмите пи = 3,14) Решение: Объем полусферы равен половине объема сферы. Итак, объем полушария вычисляется по формуле Объем полушария = 2πr 3 /3 После подстановки значения r = 3 получаем, Объем полушария = 2πr 3 /3 = = (2 × 3,14 × (3) 3 )/3 = 56,57 кубических дюймов. Следовательно, объем полусферы равен 56,57 кубических дюймов. Пример 3: Сфера радиусом 4 м разрезана на две равные половины. Найдите объем каждого образованного полушария. Решение: Радиус полученной полусферы равен Радиус полусферы, r = 4 м Мы знаем, что Объем полусферы = 2πr 3 )/3 = 133,9 м 3 . Следовательно, объем каждой полусферы = 133,9 м 3 перейти к слайдуперейти к слайдуперейти к слайду Разбивайте сложные концепции с помощью простых визуальных средств. Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций. Записаться на бесплатный пробный урок перейти к слайдуперейти к слайду Объем полусферы определяется как общее пространство, занимаемое трехмерной формой в трехмерной плоскости. Объем полушария выражается в кубических единицах, см 3 , м 3 , фут 3 и т. д. Полусфера — это трехмерная фигура, которая составляет половину сферы. Когда мы разрезаем шар на две половины, то форма, которую мы получаем, называется полушарием. Объем полушария можно рассчитать по формуле Объем полушария = 2πr 3 /3; где «r» — радиус сферы. Формула, используемая для расчета объема полушария, выражается следующим образом: Объем полушария = 2πr 3 /3, где r — радиус полушария. Объем полушария выражается в квадратных единицах. В метрической системе измерения наиболее распространенными единицами объема полушария являются кубические метры, кубические дюймы, миллилитры и литры. Для определения объема сферы используется следующая формула: Объем сферы = 4πr 3 /3, где r — радиус сферы. Если диаметр полушария равен 12,6 единиц, его радиус будет равен 12,6 ÷ 2 = 6,3, потому что диаметр = 2 × радиус. Теперь мы можем применить формулу: объем полушария = 2πr 3 /3. После подстановки значения r = 6,3 получаем, объем полушария = 2πr 3 /3 = (2 × 3,14 × 6,3 3 )/3 = 523,4 кубических единиц. Скачать БЕСПЛАТНЫЕ учебные материалы Рабочий лист Создано Домиником Черня, доктором философии Этот калькулятор объема полушария быстро находит объем полушария с шесть различных уравнений . Вам интересно, какие принципы лежат в основе нашего инструмента? В следующем тексте вы узнаете больше о свойствах полушария и узнаете, какие формулы объема полушария мы использовали. Во всех случаях вам понадобится только один из следующих количеств: ррр – Радиус полушария; ddd – Диаметр полусферы; ВВВ – Объем полушария; ААА – общая площадь поверхности полушария; AbAbAb – площадь базовой поверхности полушария; AcAcAc – площадь поверхности крышки полусферы; и A/VA/VA/V – отношение поверхности к объему полусферы. Как следует из названия, полушарие — это часть сферы, разделенная на две равные половины. Если вы уже закончили расчеты, связанные с полушарием, вас может заинтересовать наш калькулятор сферы для анализа всей сферы. 93
\конец{выравнивание*}
VV=2Vsphere=32πr3 Немного сложнее обстоит дело с площадью поверхности. Если вы хотите определить разницу между площадями сферы и полушария, перейдите к калькулятору площади полушария. Короче говоря, у полушария есть дополнительной базовой площади , которую вы должны учитывать. С нашим калькулятором объема полушария вы можете выполнять расчеты в многих различных единицах (включая SI и имперские единицы). Не медлите и ознакомьтесь с нашим инструментом преобразования объема, чтобы узнать больше о различных преобразованиях единиц измерения! Как найти объем полусферы, если радиус не известен? Это зависит от того, что вы знаете о конкретном полушарии. Диаметр полушария: d=2rd = 2rd=2r. 93В=243π/4(А/В)3. Вы можете найти полушария во многих аспектах нашей жизни. Многие окружающие объекты имеют форму половины сферы. В географии и физике часто говорят, что Земля разделена на полушария: северное и южное. Знаете ли вы, что когда вы путешествуете на самолете, на вас действует «невидимая» сила, сбивающая вас с курса? Этот эффект называется эффектом Кориолиса, и он по-разному проявляется в северном и южном полушариях Земли. Посетите калькулятор эффекта Кориолиса, чтобы узнать больше об этом! Полусфера. Это слово происходит от греческого слова «hemi», что означает «половина», и латинского слова «shaera», что означает «шар». Для расчета площади поверхности полушария: Математически это Полусфера имеет одну грань , которая является плоским основанием. Купольная часть классифицируется как криволинейная поверхность. Полусфера также имеет одно ребро окружности и не имеет вершин. Если вы знаете диаметр полушария, вот как вычислить его объем: Математика 12.11.21 7 мин. При упрощении выражений необходимо знать некоторые особенности или правила с примерами. Признаки делимости на 4 вызывают сложности у учеников в 5 классе. Для изучения этой темы специалисты предлагают использовать научный подход, который основан на психофизиологических особенностях работы головного мозга. Он включает ознакомление с основными элементами теории и алгоритмом. Оглавление: Деление — арифметическая операция, позволяющая найти один из множителей при их произведении. Иными словами, деление является обратным действием относительно умножения. Записывается оно следующим образом: U/T=V. Далее следует подробно разобрать каждый из элементов операции: Если провести аналогию с умножением, то компоненты можно назвать по-другому: U — произведение, T и V — I и II множители соответственно. Следует отметить, что операция деления проверяется при помощи произведения. Например, нужно поделить 12 на 4. Записывать действие необходимо в виде математического числового выражения, т. е. 12/4. Результат эквивалентен значению 3. Чтобы проверить правильность нахождения частного, необходимо осуществить произведение «4*3». По таблице Пифагора результат равен числу 12. Так выглядит доказательство того, что деление — обратная операция умножению. Можно придумать любой пример для закрепления материала. Следует помнить, что теория должна всегда подтверждаться практикой. Следует отметить, что деление бывает двух видов: целочисленным и с остатком. Если величина не делится нацело на определенное число, то образуется дробь. Последняя бывает обыкновенной или десятичной. При сокращении выражений следует подбирать делитель только для целочисленной операции. Например, для дроби 24/32 общим делителем является 8, поскольку 8*3=24 и 8*4=32. Математическая запись имеет такой вид: 24/32=(8*3)/(8*4)=(8/8)*(¾)=¾. Специалисты рекомендуют всегда подбирать делитель, чтобы при сокращении получалось целая величина. Если этого принципа не придерживаться, то вычисления существенно усложняться. Далее необходимо разобрать критерии деления числа на четверку, поскольку эта тема является очень сложной для некоторых учеников. Для деления искомого числа на четверку нацело специалисты разработали специальный алгоритм. Исходя из методики, можно сформулировать такое свойство, позволяющее узнать, делится ли исходное значение на 4: величина на четверку делится в том случае, когда является четной и число, образованное разрядами десятков и единиц, можно поделить на это значение без остатка. Для реализации методики необходимо доказать кратность числа 213 четверке. Это осуществляется таким образом: Далее необходимо разобрать другой пример деления 212 на 4. Если выполнить операцию «212/4» при помощи калькулятора, то можно получить целочисленное значение, которое равно 53. Чтобы понять принцип действия алгоритма, нужно придумать любое число, и попытаться поделить его на четверку. Например, нужно разделить 4325624 на 4. Для этого требуется сначала выяснить кратность искомого числа четырем. Решать задачу нужно таким образом: Далее требуется на калькуляторе или в столбик осуществить операцию деления, результатом которой будет число «1081406». Таким образом, чтобы поделить любое числовое значение на четверку нужно проверить его четность, а также целочисленное деление на искомый делитель величины, образованной двумя последними цифрами.
* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности
Ей присвоен номер 0000. Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам. Приступим к рассмотрению темы «Признак делимости на 4». Приведем здесь формулировку признака, проведем его доказательство, рассмотрим основные примеры задач. В конце раздела мы собрали сведения о подходах, которые можно применять в тех случаях, когда нам нужно доказать делимость чисел на 4, заданных буквенным выражением. Мы можем пойти простым путем и поделить однозначное натуральное число на 4 для того, чтобы проверить, делится ли это число на 4 без остатка. Так же можно поступить с двузначными, трехзначными и проч. Гораздо проще становится использовать признак делимости на 4. Он предполагает проведение проверки делимости одной или двух последних цифр целого числа на 4. Что это значит? Это значит, что некоторое число a делится на 4 в том случае, если одна или две крайние правые цифры в записи числа a делятся на 4. Если число, составленное из двух крайних правых цифр в записи числа a не делятся на 4 без остатка, то и число a не делится на 4 без остатка. Какие из чисел 98 028, 7 612 и 999 888 777 делятся на 4? Решение Крайние правые цифры чисел − 98 028, 7 612 составляют числа 28 и 12, которые делятся на 4 без остатка. Это значит, что и целые числа − 98 028, 7 612 делятся на 4 без остатка. Последние две цифры в записи числа 999 888 777 образуют число 77, которое не делится на 4 без остатка. Ответ: −98 028 и 7 612. Если предпоследней цифрой в записи числа является 0, то нам необходимо этот ноль отбросить и смотреть на оставшуюся крайнюю правую цифру в записи. Получается, что две цифры 01 мы заменяем 1. И уже по одной оставшейся цифре мы делаем вывод о том, делится ли исходное число на 4. Делится ли числа 75 003 и −88 108 на 4? Решение Две последние цифры числа 75 003 — видим 03. Если отбросить ноль, то у нас остается цифра 3, которая на 4 без остатка не делится. Это значит, что исходное число 75 003 на 4 без остатка не делится. Теперь возьмем две последние цифры числа −88 108. Это 08, из которых мы должны оставить лишь последнюю цифру 8. 8 делится на 4 без остатка. Это значит, что и исходное число −88 108 мы можем поделить на 4 без остатка. Ответ: 75 003 не делится на 4, а −88 108 – делится. Числа, у которых в конце записи идет сразу два нуля, также делятся на 4 без остатка. Например, 100 делится на 4, получается 25. Доказать правдивость этого утверждения нам позволяет правило умножения числа на 100. Представим произвольно выбранное многозначное число a, запись которого справа заканчивается двумя нулями, как произведение a1·100, где число a1 получается из числа a, если в его записи справа отбросить два нуля. Например, 486700=4867·100. Произведение a1·100 содержит множитель 100, который делится на 4. Это значит, что все приведенное произведение делится на 4. Представим любое натуральное число a в виде равенства a=a1·100+a0, в котором число a1 – это число a, из записи которого убрали две последние цифры, а число a0 – это две крайние правые цифры из записи числа a. Если использовать конкретные натуральные числа, то равенство будет иметь вид undefined. Теперь обратимся к свойствам делимости: Теперь, освежив в памяти необходимые свойства делимости, переформулируем доказательство признака делимости на 4 в виде необходимого и достаточного условия делимости на 4. Деление двух последних цифр в записи числа a на 4 – это необходимое и достаточное условие для делимости целого числа a на 4. Если предположить, что a=0, то теорема в доказательстве не нуждается. Для всех остальных целых чисел a мы будем использовать модуль числа a, который является числом положительным:a=a1·100+a0 С учетом того, что произведение a1·100всегда делится на 4, а также с учетом свойств делимости, которые мы привели выше, мы можем сделать следующее утверждение: если число a делится на 4, то и модуль числа a делится на 4, тогда из равенства a=a1·100+a0 следует, что a0 делится на 4. Из равенства a=a1·100+a0 следует, что модуль a делится на 4. Это значит, что и само число a делится на 4. Так мы доказали достаточность. Рассмотрим случаи, когда нам нужно установить делимость на 4 целого числа, заданного некоторым выражением, значение которого надо вычислить. Для этого мы можем пойти следующим путем: Помочь в решении задачи часто помогает формула бинома Ньютона. Делится ли на 4 значение выражения 9n-12n+7 при некотором натуральном n? Решение Мы можем представить 9 в виде суммы 8+1. Это дает нам возможность применить формулу бинома Ньютона: 9n-12n+7=8+1n-12n+7==Cn0·8n+Cn1·8n-1·1+…+Cnn-2·82·1n-2+Cnn-1·8·1n-1+Cnn·1n—12n+7==8n+Cn1·8n-1·1+. Произведение, которое мы получили в ходе преобразований, содержит множитель 4, а выражение в скобках представляет собой натуральное число. Это значит, что это произведение можно разделить на 4 без остатка. Мы можем утверждать, что исходное выражение 9n-12n+7 делится на 4 при любом натуральном n. Ответ: Да. Также мы можем применить к решению задачи метод математической индукции. Чтобы не отвлекать ваше внимание на второстепенные детали разбора решения, возьмем прежний пример. Докажите, что 9n-12n+7 делится на 4 при любом натуральном n. Решение Начнем с установления того, что при значении n=1 значение выражения 9n-12n+7 Получаем: 91-12·1+7=4. 4 делится на 4 без остатка. Теперь мы можем предположить, что при значении n=k значение выражения Нам необходимо доказать, что 9n-12n+7 при n=k+1будет делиться на 4 с учетом того, что 9k-12k+7 делится на 4: 9k+1-12(k+1)+7=9·9k-12k-5=9·9k-12k+7+96k-68==9·9k-12k+7+4·24k-17 Мы получили сумму, в которой первое слагаемое 9·9k-12k+7 делится на 4 в связи с нашим предположением о том, что 9k-12k+7 делится на 4, а второе слагаемое 4·24k-17 содержит множитель 4, в связи с чем также делится на 4. Это значит, что вся сумма делится на 4. Ответ: мы доказали, что 9n-12n+7 делится на 4 при любом натуральном значении n методом математической индукции. Мы можем использовать еще один подход для того, чтобы доказать делимость некоторого выражения на 4. Этот подход предполагает: Докажите, что значение выражения n·n2+1·n+3·n2+4 при любом целом nделится на 4. Решение Если предположить, что n=4·m, получаем: 4m·4m2+1·4m+3·4m2+4=4m·16m2+1·4m+3·4·4m2+1 Полученное произведение содержит множитель 4, все остальные множители представлены целыми числами. Это дает нам основание предполагать, что все произведение делится на 4. Если предположить, что n=4·m+1, получаем: 4m+1·4m+12+1·4m+1+3·4m+12+4==(4m·1)+4m+12+1·4m+1·4m+12+4 И опять в произведении, которое мы получили в ходе преобразований, Это значит, что выражение делится на 4. Если предположить, что n=4·m+2, то: 4m+2·4m+22+1·4m+2+3·4m+22+4==2·2m+1·16m2+16m+5·(4m+5)·8·(2m2+2m+1) Здесь в произведении мы получили множитель 8, который можно без остатка поделить на 4. Это значит, что все произведение делится на 4. Если предположить, что n=4·m+3, получаем: 4m+3·4m+32+1·4m+3+3·4m+32+4==4m+3·2·8m2+12m+5·2·2m+3·16m2+24m+13==4·4m+3·8m2+12m+5·16m2+24m+13 Произведение содержит множитель 4, значит делится на 4 без остатка. Ответ: мы доказали, что исходное выражение делится на 4 при любом n. Согласно правилу делимости на 4, целое число считается делящимся на 4, если оно удовлетворяет одному из двух условий: Правило делимости на 4 можно понять с помощью следующих примеров. Пример: Проверить делимость следующих чисел на 4. а.) 1124 б.) 1171 в.) 1300 г.) 500 9 0005 Решение: а. ) В 1124 последние две цифры в данном числе образуют число 24, которое делится на 4 (24 ÷ 4 = 6) b.) В 1171 последние две цифры в данном числе образуют число 71, которое не делится полностью на 4 (71÷4 = 17 — частное, а 3 — остаток) в.) В числе 1300 последние две цифры в данном числе — нули. Это означает, что 1300 полностью делится на 4. г) В числе 500 последние две цифры данного числа — нули. Это означает, что 500 полностью делится на 4. Правила делимости помогают решать задачи без процесса деления. Правило делимости на 4 гласит, что если число имеет два нуля в конце или две последние цифры образуют число, которое точно делится на 4, то данное число также делится на 4. Следовательно, для любых больших чисел мы проверяем последние две цифры и применяем правило делимости на 4 и можем узнать, делится ли большое число на 4 или нет. Пример 1: в 238900 последние две цифры в разряде десятков и разряде единиц равны нулю. Это означает, что 238900 делится на 4. Пример 2: В числе 148936 две последние цифры десятков и единиц образуют число 36, которое делится на 4 (36 ÷ 4 = 9). Правила делимости на 4 и 6 совершенно разные. В правиле делимости 4, если последние две цифры являются нулями или число, образованное двумя последними цифрами, точно делится на 4, то мы можем сказать, что число делится на 4. Однако, согласно правилу делимости 6 , говорят, что число делится на 6 только в том случае, если оно делится и на 2, и на 3. В тесте на делимость 4 мы проверяем две последние цифры, а в тесте на делимость 6 мы проверяем, все ли число делится на 2 и 3 или нет. Например, давайте проверим, если 936 делится на 6. Поскольку последняя цифра числа 936 четное число, можно сказать, что 936 делится на 2. Теперь проверим его делимость на 3. Сумма цифр равна 9 + 3 + 6 = 18, что делится на 3. Это означает, что 936 тоже делится на 3. Признаки делимости 4 и 8 немного похожи. В тесте на делимость 4 мы проверяем две последние цифры, если последние две цифры — нули или число, образованное двумя последними цифрами числа, точно делится на 4, то исходное число также делится на 4. В тесте тест делимости 8, мы проверяем последние три цифры, если последние три цифры нули или число, образованное последними тремя цифрами числа, точно делится на 8, то исходное число также делится на 8. Например, пусть мы проверим, делится ли 61816 на 8. Если мы проверим последние 3 цифры, они образуют число 816, которое делится на 8. Следовательно, можно сказать, что 61816 делится на 8. ☛ Похожие темы Пример 1: Узнать, делятся ли данные числа на 4 или нет, используя признак делимости на 4. а.) 380 Решение: а) В числе 380 последние две цифры образуют число 80, которое делится на 4. Следовательно, 380 делится на 4 (380 ÷ 4 = 95). б) В числе 549 последние две цифры образуют число 49, которое не делится на 4. Следовательно, 549 не делится на 4. в) В числе 740 последние две цифры образуют число 40, которое делится на 4. Следовательно, 740 делится на 4 (740 ÷ 4 = 185). Пример 2: Определите, делится ли наименьшее 6-значное число на 4 или нет, используя правило делимости на 4. Решение: последние две цифры наименьшего шестизначного числа — два нуля. Пример 3: Проверить, делится ли заданное большое число 434788 на 4, используя правило делимости на 4. Решение: В 434788 последние две цифры образуют число 88, а 88 делится на 4 точно, следовательно, число 434788 делится на 4. перейти к слайду перейти к слайду перейти к слайду Отличное обучение в старшей школе с использованием простых подсказок Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами. Записаться на бесплатный пробный урок перейти к слайдуперейти к слайду Правило делимости числа 4 гласит, что число считается делящимся на 4, если две последние цифры числа равны нулю или образуют число, которое делится на 4. Например, 2300 делится на 4, потому что два нуля в конце числа. Точно так же 488 также делится на 4, потому что последние две цифры 88 делятся на 4. Сначала нам нужно проверить, делится ли число, состоящее из двух последних цифр заданного числа, на 4 или нет. В данном числе 14540 число, образованное двумя последними цифрами, равно 40, а 40 делится на 4. Таким образом, 14540 делится на 4. Правила делимости на 4 и 8 немного похожи. В правиле делимости на 4 мы ориентируемся на две последние цифры числа. Если последние две цифры нули или число, образованное двумя последними цифрами числа, точно делится на 4, то можно сказать, что данное число также делится на 4. Например, 800, 900 и 348 делятся на 4, поскольку они удовлетворяют условию правила делимости на 4. В правиле делимости на 8 мы фокусируемся на трех последних цифрах числа. Если последние три цифры — нули или число, образованное последними тремя цифрами числа, точно делится на 8, то мы можем сказать, что исходное число также делится на 8. Например, 8000, 9000 и 3896 делятся. на 8, поскольку они удовлетворяют условию правила делимости на 8. Согласно правилу делимости на 4 любое большое число делится на 4 точно, если число, состоящее из цифр, стоящих на десятках и единицах, делится на 4 точно. Например, число 2 146 484 делится на 4 точно, потому что число 84 (последние две цифры) делится на 4. Согласно правилу делимости на 4, если последние две цифры данного числа равны нулю или образуют число, которое полностью делится на 4, то говорят, что данное число делится на 4. Например, 412, 532, 700 и т. д. — это несколько чисел, которые делятся на 4, потому что они удовлетворяют критерию делимости на 4. Скачать БЕСПЛАТНЫЕ учебные материалы Рабочий лист правил делимости Предоставление учащимся инструментов для решения деления с помощью этих ярлыков не только делает деление менее сложным, но и превращает его в забавную головоломку. Приступая к разделу о делении, обязательно поделитесь этими правилами с классом и обсудите их во время выступления по математике: Число, которое делится на 2, называется четным. Когда последняя цифра в числе равна 0 или даже четной, то есть 2, 4, 6 или 8, то число делится на 2. Например, 20 оканчивается на 0, поэтому оно делится на 2. Число 936 заканчивается в 6, а 6 четно. Значит, 936 делится на 2,9.0005 Число делится на 3, если сумма цифр делится на 3. Чтобы использовать этот прием, учащиеся должны уметь делить, но проверка меньших чисел менее сложна, чем проверка больших. 1 + 6 + 8 = 15 15/3 = 5 Следовательно, 168 делится на 3. Если последние две цифры числа делятся на 4, то делится и все число. Например, в 1012 12 делится на 4. Однако в 1013 13 не делится. Следовательно, 1012 делится на 4, а 1013 — нет. Когда последняя цифра числа 0 или 5, число можно разделить на 5 без остатка. Таким образом, 5, 10, 15, 20, 25 и так далее можно разделить на 5. Учащиеся могут посмотреть на большие числа и сразу сказать, можно ли их поровну разделить на пять частей. Числа, которые делятся на 6, также могут делиться на как на 3, так и на 2. Учащиеся должны проверить число с обоими правилами для 3 и 2. Если число проходит оба теста, его можно разделить на 6. Если он провалит хотя бы один тест, он не сможет. Например: 308 оканчивается на четную цифру, поэтому оно делится на 2. Большое число делится на 8, если последние три цифры также делятся на 8 или равны 000. В числе 7120 120 можно разделить на 8 без остатка, поэтому 7120 также делится на 8. Правило делимости 9 такое же, как и 3. Если сумма цифр числа делится на 9, так же как и весь номер. Например: В числе 549 5 + 4 + 9 = 18 18/9 = 2 Итак, 549 делится на 9. Если последняя цифра 0, число может быть разделить поровну на 10. Эти правила позволяют учащимся рассматривать большие числа в менее сложном контексте. Правила делимости также позволяют им многое узнать о числе, просто взглянув на его цифры. Таким образом, вы должны поощрять учащихся использовать все правила при изучении числа. Преобразование двоичных градусов в градусов значения в шкале угловых единиц. ПЕРЕКЛЮЧЕНИЕ : из градусов в двоичные наоборот. ПРЕОБРАЗОВАТЬ: между другими единицами измерения угла — полный список. Сколько градусов в 1 двоичной степени? Ответ: 1 бред равен 1,41 ° Число градусов 1,41° преобразуется в 1 брад, один двоичный градус. Это РАВНОЕ значение угла 1 двоичному градусу, но в альтернативной единице измерения угла в градусах. 1 Двоичная степень до градусов = 1,41 ° 2 Бинарные градусы. 5 бинарных градусов в градусы = 7,03 ° 6 бинарных градусов в градусы = 8,44 ° 7 бинарных градусов в градусы = 9,84 ° 8 бинарных градусов в градусы = 11,25 ° 9 двоичных градусов в градусы = 12,66 ° 10 двоичных градусов в градусы = 14,06 ° 11 двоичных градусов в градусы = 15,47 ° 14 двоичных градусов в градусы = 19,69 ° 15 двоичных градусов в градусы = 21,09 ° Категория : главное меню • меню угла • Двоичные градусы0061 и градусов (°) единиц в обратном порядке из градусов в двоичные градусы. Этот калькулятор основан на преобразовании двух угловых единиц. Угол состоит из двух лучей (как стороны угла, имеющие общую вершину или иначе называемые конечной точкой). Некоторые относятся к измерениям вращения — сферические углы измеряются длинами дуг, указывающими из центра, плюс радиус. Чтобы получить полный набор единиц измерения угла на одной странице, попробуйте конвертер Multiunit, в который встроены все варианты единиц измерения угла. Первая единица измерения: двоичный градус (брад) используется для измерения угла. ВОПРОС : ОТВЕТ : Аббревиатура или префикс для двоичной степени: Благодаря вышеупомянутой услуге расчета двух единиц, которую он предоставляет, этот угловой преобразователь оказался полезным также в качестве учебного пособия: Чтобы связать этот онлайн-конвертер угла двоичных градусов в градусов, просто вырежьте и вставьте следующее. Ссылка: онлайн-конвертер угла из двоичных градусов ( brad ) в градусы ( ° ) Я сделал все возможное, чтобы создать этот сайт для вас. Пожалуйста, отправьте отзыв, чтобы сообщить мне, как вам понравилось его посещение. by My Teaching Pal 12,50 $ 8,00 $ Bundle Предложите своим ученикам попрактиковаться во всем, что связано с алфавитом, с помощью этого ОГРОМНОГО комплекта рабочих листов по алфавиту. Студенты будут работать над идентификацией букв, начальными звуками, формированием букв, различением строчных и прописных букв и многим другим. В этот пакет включены 4 различных типа рабочих листов, которые охватывают каждую букву алфавита. Subjects: English Language Arts, Phonics, Writing Grades: PreK — K Types: Activities, Printables, Worksheets by My Nerdy Teacher by Alina V $100.00 $19.00 ⭐⭐⭐ СРОЧНАЯ РАСПРОДАЖА ⭐⭐⭐Получите Мега-набор Decodable Readers Passages всего за 19 долларов! Спешите, время истекает! Ваши ученики могут практиковаться в чтении в увлекательной игровой форме, используя эти декодируемые тексты. Наука чтения AlignedLow Требуется подготовка. Просто распечатайте и идите. Эти декодируемые отрывки помогут вашим ученикам практиковать фонетические модели, которым вы их учите. Идеально подходит для центров, домашних заданий, утренней работы и многого другого. Печатные и цифровые (Google Slides™) Идеально подходит для дошкольного детского сада, 1-й класс Предметы: Акустика, Чтение, Письмо Классы: К — 2-й Виды: Занятия, Центры, Печатные издания CCSS, RFd. by My Nerdy Teacher by Alina V $100.00 $19.00 ⭐⭐⭐ FLASH SALE ВСЕГО 19 долларов! (СТОИМОСТЬ 100 долл. США) Вы ищете веселые и увлекательные занятия по интервенции при чтении, связанные с наукой о чтении? Получите МЕГА-НАБОР Ultimate Phonics Reading Intervention всего за 19 долларов США.! Спешите, время истекает! Ваши студенты станут бегло читать, используя эти забавные действия. Требуется низкая подготовка. Просто распечатайте и приступайте к работе. Эти занятия помогут вашим ученикам практиковать фонетические модели, которые вы преподаете Предметы: Акустика, чтение, письмо Классы: PreK — 1st Типы: Занятия, центры, печатные формы CCSS: RF.K.1, RF.K.1a, RF.K.1b, RF.K.1c, RF.K.1d… по Мой друг-преподаватель Этот пакет набит рабочими листами, чтобы помочь вашим ученикам практиковать диграфы. Subjects: English Language Arts, Phonics, Reading Grades: K — 2nd Types: Centers, Printables, Worksheets by Aimee’s Edventures LLC $10.75 $5.50 It У меня разрывалось сердце, когда я смотрел, как мои ученики бродят по комнате, пытаясь не заплакать, когда я сказал: «Пожалуйста, найдите партнера». Вот я и создал эти открытки! Теперь их любят тысячи учителей, которые преследуют одну и ту же цель — включить всех учащихся в свой класс. Объекты: Back to School, Classroom Community, Classroom Management . Little Learners 128,00 $ 34,99 $ Это годовой набор из 576 дифференцированных отрывков и вопросов для понимания прочитанного для 2-го класса на трех разных уровнях. Эти отрывки для беглого чтения меняют правила игры! Цифровые отрывки и вопросы для понимания прочитанного во 2-м классе также включены! ⭐️Загрузите файл предварительного просмотра, чтобы увидеть каждый заголовок! ⭐️Хотите улучшить беглость чтения? Каждый отрывок для понимания прочитанного во 2-м классе включает подсчет слов и трекер беглости. Идеально подходит для повторного чтения и практики беглости чтения. Предметы: Английский язык, чтение, стратегии чтения Классы: Типы: Оценка, печатные формы CCSS: , RL. by My Nerdy Teacher by Alina V Вы ищете веселые и увлекательные рабочие листы по алфавиту от А до Я для своих учеников? Этот пакет идеально подходит для тех, кто рано заканчивает работу, утренней работы, домашних заданий и многого другого. Каждый рабочий лист включает 5 различных упражнений, которые ваши ученики могут использовать, чтобы узнать все о прописных и строчных буквах. — — — — — — — — — > Проверьте наш БЕСКОНЕЧНЫЙ НАБОР АЛФАВИТА и получите этот ресурс с огромной скидкой!! <- - - - - - - - -ВКЛЮЧЕННЫЕ МЕРОПРИЯТИЯ: • Произнеси по буквам! Напишите буквы в коробках • Раскрасьте! Цвет Предметы: Акустика, Изобразительное искусство Классы: PreK — K Типы: Занятия, Печатные формы, Рабочие листы CCSS, Также включено в: Рабочий лист «Начало звуков». Буквенная практика. Бесплатные карточки с алфавитом. Subjects: English Language Arts, Reading, Reading Strategies Grades: K — 1st Types: Centers, Printables, Worksheets by My Teaching Pal $13.75 $10.00 Набор В этом наборе множество занимательных математических заданий для учащихся детского сада. Он идеально подходит для общеклассных занятий, математических станций, быстрых финишеров, домашних заданий и повторения. Объекты: Основные операции, математика, номера Оценки: Prek — 1st Типы: Центры, печатные изготовления, рабочие листы . Этот комплект содержит ОГРОМНЫЕ 263 математических листа для первого класса! Рабочие листы охватывают сложение и вычитание, числа и разрядность, 2D и 3D фигуры, данные и графики, дроби и разбиение на части и время. Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для общеклассных занятий, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D Subjects: Basic Operations, Math, Numbers Grades: Types: Printables, Workbooks, Worksheets by Teaching With a Mountain View $22. $15.99 Bundle This discounted НАБОР из трех ресурсов включает 90 печатных (и ЦИФРОВЫХ!) страниц для обучения, повторения и применения навыков чтения и письма! В комплект включены следующие ресурсы: Использование иллюстраций для обучения навыкам чтения 40 страниц, обучающих 8 основным навыкам чтения. Каждому навыку чтения посвящено пять страниц! Использование иллюстраций для обзора смешанных навыков чтения20 страниц, посвященных основным навыкам чтения. На каждой странице рассматриваются различные навыки чтения. Использование иллюстраций для обучения изобразительному языку15, стр. Объекты: Английский язык искусства, чтение, стратегии чтения Оценки: 3 -е — 5 -е Типы: Центры, печатные изделия . отрывки по беглости чтения и пониманию содержат 30 готовых к печати отрывков (15 художественных и 15 научно-популярных). Каждый уровневый отрывок находится в диапазоне 520L и 830L и содержит от 196 до 222 слов. Предметы: Чтение Классы: Типы: Деятельность, Оценка CCSS: RF.3.4, RF.3.4a, RF.004b, RF.014c Также включено 9 в: RF.0014c НАБОР «Отрывки для понимания прочитанного» и «Отрывки для беглости чтения» — СКИДКА 30% на Teaching Trove 242,00 $ 20,00 $ Этот массивный набор из 123 первоклассных и второстепенных центров обучения грамоте обеспечивает идеальный способ обеспечить увлекательное, в течение года. Все центры имеют аналогичный формат, что делает их идеальными для самостоятельной практики, оставляя вам больше времени для обучения с меньшим количеством перерывов! Отлично подходит для центров или быстрых финишеров, с этим пакетом вы сможете легко дифференцировать потребности всем вашим ученикам с огромным выбором игр на выбор. Предметы: Английский язык, акустика, правописание Классы: 1-2 CCSS: RF.1.1a, RF.1.2, RF.1.2a, RF.1.2b, RF.1.2b, RF.1.2b c… by Обучение с видом на горы 27,54 $ 19,99 $ Bundle Читать и понимать художественную литературу и информационные тексты с помощью идеального комплекта для чтения и повторения. Это лучший набор для проверки навыков чтения на ВЕСЬ ГОД. «Быстрое чтение и повторение» — идеальный способ вовлечь учащихся в актуальную и тщательную проверку навыков чтения! Этот набор обзоров — идеальный способ поддерживать навыки чтения у ваших учеников ИЛИ помочь вам обучить их навыкам. Его можно использовать в центрах, небольших группах, всем классом или в качестве домашнего задания для повторения основного информационного текста com Объекты: Краткое чтение, английский язык, стратегии чтения Оценки: 4 -й — 5th Типы: , Центры CCSS: RL. by Kaitlynn Albani Внутри вы найдете 6 забавных и уникальных шрифтов в ZIP-файле! Большинство символов ударения включено во все шрифты. Пожалуйста, проверьте предварительный просмотр, чтобы увидеть все шрифты, включенные в этот набор! Примечания. Включено 5 шрифтов + 1 шрифт для каракулей. Все шрифты с заглавными буквами Elementary. Проверьте предварительный просмотр, чтобы увидеть все шрифты в действии! $ СЭКОНОМЬТЕ ДЕНЬГИ $ БОЛЕЕ 400 ШРИФТОВ + КАЖДЫЙ НОВЫЙ ШРИФТ БЕСПЛАТНО! ПРОВЕРЬТЕ РАСТУЩИЙ НАБОР ШРИФТОВ ЗДЕСЬУсловия использования * Шрифты Предметы: Для всех предметов, Товары для продавцов ТРТ, Специальность Классы: ПреК — 12-е, Высшее образование, Обучение взрослых, Персонал Типы: По ТРТ Продавцы для ТРТ 900, Арт 900, 4 по Магазин «Маленькая божья коровка» 10,95 $ 6,95 $ Развивайте своих читателей с помощью этого замечательного набора отрывков и вопросов для понимания прочитанного для 3–5 классов (теперь доступны цифровые варианты)! Пакет «Отрывки для чтения» включает в себя 20 недель еженедельной практики, идеально подходящей для: разминки, работы с колокольчиками, домашних заданий или быстрой оценки. Объекты: закрыть чтение, ELA Test Prep, стратегии чтения Оценки: 3 -е — 5th Типы: , печатные издания CCS: RL.3.1, RL.3.2, RL.3.4. , Rl.4.1, rl.4.2… также включен в: Отрывные поэзии по поэзии по поэзии и вопросы 3 -й 4 -й класс по Dots Polka Please $ 14.00 $ 10.00 Bundle Объекты: Фоника, чтение, стратегии чтения Оценки: Prek — 3 -й Типы: Флэш -карты, печатные изделия, Word Walls By Что я выучил . не повезло ирландцам в этот День Святого Патрика? Подарите им свой собственный четырехлистный клевер, полный волшебства и очарования, с этим веселым мастерством ко Дню Святого Патрика! С помощью этого клевера учащиеся будут размышлять о том, как им «везет» в жизни. Это также отлично подходит для SEL или социально-эмоционального обучения! Проведите мозговой штурм со своими учениками, составьте список «счастливых» вещей до занятия и позвольте им выбрать четыре, которые наполнят их жизнь волшебством. Это мастерство ко Дню Святого Патрика в Предметы: Для всех предметных областей, День Святого Патрика Классы: 1–4 Типы: Мероприятия, Доска объявлений Идеи Тематическая доска объявлений на Ким Миллер Эти ПРОСТЫЕ шаблоны информационных бюллетеней для занятий без суеты идеально подходят для использования в течение всего года и облегчают общение с родителями! Держите родителей в курсе того, что происходит в вашем классе в течение года. Объекты: Вернуться в школу, для всех предметных областей, для всех предметов Оценки: Prek — 5th Типы: Формы класса, для родителей от , что Kind.kindermama . — это четырехнедельный блок иллюстраций, который поможет писателям детского сада/первоклассника стать уверенными в своих навыках рисования и раскрашивания. Учащиеся начальных классов научатся рисовать фигуры и людей с разными выражениями лица, прическами и оттенками кожи. Это иллюстративное исследование настраивает учащихся детского сада на успех до конца года во время писательского семинара. Предметы: Искусство и музыка, Снова в школу, Письмо Классы: PreK — 1st Типы: Уроки, Печатные формы Также включены в: LEGROWND Writing Units | Мастерская писателей by Pocket of Preschool Помощники сообщества Центры математики и грамотности заполнены увлекательными практическими занятиями на школьную тематику, которые помогут вашим учащимся усвоить математические концепции и грамотность! Теперь включает в себя два занятия по мелкой моторике, один центр письма, шесть заданий по обучению грамоте и восемь заданий по математике. Охватываемые навыки грамотности включают определение букв, начальные звуки, почерк, написание дружеских писем, группы рифм/слов, слоги, построение словарного запаса слов, слов, виденных, и письмо / ведение журнала. Предметы: Английский язык, математика Классы: PreK — K Типы: Мероприятия, центры Также включены в: Тематические центры математики и грамотности, TK-K, BUNDLE for Preschool & Kindergarten by Учительница с обсыпанным верхом $18,00 Рукописный ввод должен быть интересным и для старших школьников! Это набор ежедневных листов для практики письма, которые ученики действительно будут просить! Этот набор для рукописного ввода отлично подходит для учащихся, которые уже знают, как составлять буквы, но просто не могут замедлить темп и писать аккуратно! Практика письма для всех возрастов! ВКЛЮЧЕННЫЕ ЗАНЯТИЯ: 26 страниц глупых предложений с алфавитом, 20 страниц положительных утверждений, 20 страниц потрясающих фактов о животных, 20 страниц общих фактов, 20 страниц удивительных математических фактов, 20 страниц Space 9.0014 Предметы: Английский язык, правописание, письмо Классы: 1–6 Типы: Упражнения, оценка Также включено в: Рабочие листы для рукописного ввода | CURSIVE PRINT D’NEALIAN BUNDLE для старшеклассников by Преподавание во втором классе Сложение двух цифр с перегруппировкой — Нужна ли вашим учащимся дополнительная практика сложения и вычитания двух цифр? Тогда эти рабочие листы именно то, что вам нужно. Субъекты: Арифметика, базовые операции, математика Оценки: 1 -й — 3 -е Типы: Мероприятия, печатные изделия, рабочие листы CCSS: 2.NBT.A.2, 2.NBT. B.5, 2.NBT.B.6, 2.OA.A.1 Также включено в: Рабочие листы для сложения и вычитания двух- и трехзначных чисел для 1-го, 2-го и 3-го классов by The Moffatt Girls Определение времени может быть сложной концепцией для многих видов, но этот пакет NO PREP наполнен практическими здесь, увлекательными и забавными ресурсами, которые помогут детям освоить эту концепцию. Тип урока: урок –открытие нового знани я Форма урока: урок-исследование Цель Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными 7 класс Что называют системой уравнений? Рассмотрим два линейных уравнения: 1) y – 2 x = – 3 2) x + y = 3 Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. y – 2 x = – 3 x + y = 3 Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Решить систему уравнений — значит найти все её решения или установить, что их нет. Способы решения систем уравнений Алгоритм решения системы уравнений графическим способом 1. Приводим оба уравнения к виду линейной функции y = k x + m. 2. Составляем расчётные таблицы для каждой функции. 3. Строим графики функций в одной координатной плоскости. 4. Определяем число решений: 5. Записываем ответ. Решение системы графическим способом Выразим у через х у – х = 2, у + х = 10; y y=x+2 10 у = х + 2, у = 10 – х ; Построим график первого уравнения 6 у = х + 2 y=10 — x х 0 -2 у 2 2 0 1 Построим график второго уравнения 1 0 -2 x 4 10 у = 10 – х х 0 10 Ответ: (4; 6) у 10 0 Графический метод решения системы x + y = 3 y – 2 x = – 3 у = 3 – x x y A(0;3) D(3;3) 3 0 0 3 M(2;1) у =1 B(3;0) X=2 у = 2x – 3 y x 0 – 3 C(0; – 3) 3 3 Ответ: (2; 1) Y=0,5x+2 x y B(2;3) 0 2 2 A(0;2) 3 D(2;0) C(0;-1) Y=0,5x-1 Графики функций параллельны и не пересекаются. y x 0 -1 0 2 Говорят, что система несовместна. Решим систему уравнений : Y= 0 ,5 x+2 Y= 0,5x-1 Ответ: Система не имеет решений. Y=x+3 D( 1 ; 4 ) y x Система Y=x+3 Y=x+3 A(0;3) 0 3 C( -1 ; 2 ) 0 — 3 B( — 3;0) Y=x + 3 Графики функций совпадают. y x 4 1 2 -1 Говорят, что система неопределенна Ответ: система имеет бесконечное множество решений Если система уравнений не имеет решений, то она называется несовместной. Достоинство графического способа – наглядность. Недостаток графического способа– приближённые значения переменных. Проверим, что у нас получилось ! Зарядка для глаз Частные случаи пересечения графиков линейных функций (памятка) Решите систему уравнений графическим способом (памятка) у = 3 х + 4 у = 3 х — 2 у = 3 х + 4 х у 0 -2 у = 3 х — 2 Х У 0 2 Самостоятельная работа Решите систему уравнений графическим способом у = 2 х — 3 у = 3 х — 4 у = — х + 3 у = 0,5 х + 1 У = 2х — 3 У = — х + 3 У = 0,5 х + 1 У = 3 х — 4 Проверим, что у нас получилось ! у у . . . . . . В(2;2) . А(2;1) . х х . . Ответ: В ( 2; 2) Ответ: А ( 2; 1) вывод: 1) угловые коэффициенты не равны , 2) прямые пересекаются. Найдём координаты точек пересечения графиков 2х – 3 = — х + 3, 2х + х = 3 + 3, 3х = 6, х = 2, у = 2 • 2 — 3, у = 1. 3х – 4 = 0,5х + 1, 3х – 0,5х = 1 + 4, 2,5х = 5, х = 2, у = 3 • 2 – 4, у = 2. Ответ: В ( 2; 2). Ответ: А ( 2; 1). Решите систему уравнений графическим способом у = 2х — 4 у = — 3х + 6 у = 2х — 4 х у 0 3 У = — 3х + 6 х у 0 1 Работа с учебником: № 1010, 1012, 1016, 1018. С п а с и б о за у р о к Б ы л о п р и я т н о с В а м и р а б о т а т ь! Основные
понятия Уравнение — это равенство, содержащее в себе переменную, значение
которой требуется найти. Системами
уравнений называют записи, представляющие собой
расположенные друг под другом уравнения, объединенные слева фигурной скобкой,
которые обозначают множество всех решений уравнений, одновременно являющихся
решениями каждого уравнения системы. Решить уравнение означает найти его корни или доказать, что корней
нет. Корень или решение уравнения — это значение переменной, при котором уравнение
обращается в верное числовое равенство. Решить
систему уравнений – значит найти все ее решения или доказать, что решений нет. Линейное уравнение с одной
переменной — это уравнение вида ax=b, где a и b — числа, x — переменная. Квадратное уравнение — это уравнение вида ax2 + bx + c =
0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0 Рациональные уравнения – это уравнения, в которых и левая, и
правая части рациональные выражения. Линейные уравнения Линейное
уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная. Алгоритм
решения уравнений, сводящихся к линейным. 1-й
шаг. Если выражения, стоящие в левой или правой части уравнения,
содержат скобки, то раскрываем их по правилам. 2-й
шаг. Переносим слагаемые с переменными в левую часть уравнения, а без
переменных в правую. 3-й
шаг. Приводим подобные слагаемые в обеих частях уравнения, приводя
его к виду ax = b. 4-й
шаг. Решаем получившееся линейное уравнение, равносильное исходному,
в зависимости от значений коэффициентов a и b. ax = b,
где х – переменная, a, b – любое
число. Если a ≠
0, то x = b/a ; Если а = 0 и b = 0, то х – любое; Если а = 0 и b ≠
0, то нет корней. Образцы решения линейных уравнений Квадратное
уравнение Квадратное уравнение — это уравнение вида ax2 + bx + c =
0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0. Способы
решений квадратного уравнения Решение
квадратных уравнений по формуле Умножим
обе части уравнения ах2 + bх
+ с = 0, а ≠ 0 на 4а
и последовательно имеем: 4а2х2 +
4аbх + 4ас = 0, ((2ах)2 +
2ах • b + b2)
— b2 +
4ac = 0, (2ax
+ b)2 = b2 —
4ac, 2ax +
b = ± √ b2 —
4ac, 2ax =
— b ± √ b2 —
4ac, а) Решим
уравнение: 4х2 + 7х + 3 = 0. а = 4, b =
7, с = 3, D = b2 —
4ac = 72 — 4 • 4 • 3 = 49 — 48 = 1, D >0, два
разных корня; b б) Решим
уравнение: 4х2 — 4х + 1 = 0, а
= 4, b = — 4, с = 1, D = b2 —
4ac = (-4)2 — 4 • 4 • 1= 16 — 16 = 0, D =
0, один корень; в) Решим
уравнение: 2х2 + 3х + 4 = 0, а =
2, b = 3, с = 4, D = b2 —
4ac = 32 — 4 • 2 • 4 = 9 — 32 = — 13 , D<0. Данное
уравнение корней не имеет. Решение
уравнений с использованием теоремы Виета Как известно,
приведенное квадратное уравнение имеет вид х2 + px + c = 0. Его корни удовлетворяют
теореме Виета, которая при а =1 имеет вид x1 x2 = q, x1 + x2 = — p Отсюда можно
сделать следующие выводы (по коэффициентам p и q можно предсказать знаки
корней). а) Если
свободный член q приведенного уравнения (1) положителен (q 0), то уравнение имеет два одинаковых по
знаку корня и это зависти от второго коэффициента p. Если р , то оба корня отрицательны, если р , то оба корня положительны. Например, x2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 и p = — 3 x2 + 8x + 7 = 0; x1 = — 7 и x2 = — 1, так как q = 7
0 и p= 8 0. б) Если
свободный член q приведенного уравнения (1) отрицателен (q ), то уравнение имеет два различных по
знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p 0 . Например, x2 + 4x – 5 = 0; x1 = —
5 и x2 = 1, так как q=
— 5 и p = 4; x2 – 8x – 9 = 0; x1 = 9 и x2 = — 1, так как q = —
9 и p = — 8 Решение уравнений с использованием теоремы Виета (обратной) Справедлива теорема, обратная теореме Виета: Если числа х1 и х2 таковы, что х1+х2 = -р, х1х2 = q, то х1 и х2 – корни квадратного уравнения х2 +рх + q = 0. Эта теорема
позволяет в ряде случаев находить корни квадратного уравнения без использования
формулы корней. 1. Решить
уравнение х2 +3х –
28 = 0 Попробуем
найти два числа х1 и х2 , такие, что х1 +х2 = — 3 и х1х2 = — 28 Нетрудно
заметить, что такими числами будут – 7 и 4. Они и являются корнями уравнения. Разложение
левой части уравнения на множители Решим
уравнение х2 — 2х — 8 = 0. Разложим левую часть на множители: х2 — 2х — 8 = х2 — 4х +2х -8 = х(х
-4 ) + 2(х -4) = (х + 2)(х -42). Следовательно,
уравнение можно переписать так: (х + 2)(х -4)=0. Так
как произведение равно нулю, то, по крайней мере, один из его множителей равен
нулю. Поэтому левая часть уравнения обращается в нуль при х = -2, а
также при х = 4. Это означает, что число — 2 и 4
являются корнями уравнения х2 — 2х — 8 = 0. Метод
выделения полного квадрата Решим
уравнение х2 + 6х — 7 = 0. Выделим в левой части
полный квадрат. Для
этого запишем выражение х2 + 6х в следующем виде: х2 +
6х = х2 + 2• х • 3. В
полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное
произведение х на 3. Поэтому чтобы получить полный квадрат, нужно прибавить 32,
так как х2 + 2• х • 3 + 32 = (х + 3)2. Преобразуем
теперь левую часть уравнения х2 +
6х — 7 = 0, прибавляя к ней и вычитая 32. Имеем: х2 +
6х — 7 = х2 + 2• х • 3 + 32 —
32 — 7 = (х + 3)2 — 9 — 7 = (х + 3)2 —
16. Таким
образом, данное уравнение можно записать так: (х +
3)2 — 16 =0, (х + 3)2 = 16. Следовательно, х
+ 3 — 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7. Свойства
коэффициентов квадратного уравнения. А. Пусть дано квадратное уравнение ах2 + bх + с = 0, где а ≠ 0. 1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1, х2 = с/а. Пример. Решим
уравнение 132х2 – 247х + 115 = 0. Решение. Так как а + b + с
= 0 (132 – 247 + 115 = 0), то х1 = 1, х2 = c/a =
115/132. Ответ: 1;
115/132. Б. Если второй коэффициент b = 2k –
четное число, то формулу корней Пример. Решим
уравнение 3х2 -14х + 16 = 0. Решение.
Имеем: а = 3, b =
— 14, с = 16, k = — 7; D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D >0, два
различных корня; Ответ: 2; 8/3 В. Приведенное уравнение х2 + рх + q=
0 совпадает с
уравнением общего вида, в котором а = 1, b = р и с = q. принимает
вид: Данную
формулу особенно удобно использовать, когда р — четное число. Пример. Решим уравнениех2 – 14х – 15 = 0. Решение. Имеем: х1,2 =7±Ö 49+15 =7±Ö64=7±8 Ответ: х1 = 15; х2 = -1. Графическое
решение квадратного уравнения Если в
уравнении х2 + px + q = 0 перенести
второй и третий члены в правую часть, то получим х2 = — px -q. Построим
графики зависимости у = х2 и у = — px — q. График первой
зависимости — парабола, проходящая через начало координат. График второй
зависимости — прямая (рис.1). Возможны следующие случаи: — прямая и парабола могут пересекаться в двух точках,
абсциссы точек пересечения являются корнями квадратного уравнения; — прямая и парабола могут касаться (одна общая точка), т. — прямая и парабола не имеют общих точек, т.е. квадратное
уравнение не имеет корней. Примеры. 1) Решим графически уравнение х2 — 3х — 4 = 0 (рис. 2). Решение. Запишем уравнение в виде х2 = 3х + 4. Построим
параболу у = х2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13). Прямая и парабола пересекаются в
двух точках А и В с абсциссами х1 = — 1 и х2 = 4. Ответ: х1 = — 1; х2 = 4. 2) Решим графически уравнение (рис. 3) х2 — 2х + 1 = 0. Решение. Запишем уравнение в виде х2 = 2х — 1. Построим
параболу у = х2 и прямую у = 2х — 1. Прямую у = 2х — 1 построим по двум точкам М (0; — 1)и N(1/2; 0). Прямая и парабола пересекаются
в точке А с абсциссой х = 1. Ответ: х = 1. 3) Решим графически уравнение х2 — 2х + 5 = 0 (рис. Решение. Запишем уравнение в виде х2 = 5х — 5. Построим параболу у = х2 и прямую у = 2х -5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5;
0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней
не имеет. Ответ. Уравнение х2 — 2х + 5 = 0 корней не имеет. Рациональные уравнения Рациональные уравнения – это уравнения, в которых и левая, и правая
части рациональные выражения. Алгоритм решения рационального
уравнения 1.
Перенести все слагаемые в левую часть, чтобы в правой части получился 0. 2.
Преобразовать и упростить левую часть, привести все дроби к общему знаменателю. 3. Полученную дробь приравнять к
0, по следующему алгоритму: 4.
Записать те корни, которые получились в первом уравнении и удовлетворяют
второму неравенству, в ответ. Пример Решить уравнение: Решение В
самом начале перенесем все слагаемые в левую сторону, чтобы справа остался 0. Теперь
приведем левую часть уравнения к общему знаменателю: Данное
уравнение эквивалентно системе: Первое
уравнение системы – это квадратное уравнение. Коэффициенты
данного уравнения: .
Вычисляем дискриминант: Далее,
по формуле корней квадратного уравнения находим: Получаем два корня: Теперь
решим второе неравенство: произведение множителей не равно 0 тогда и только
тогда, когда ни один из множителей не равен 0. Необходимо, чтобы выполнялись два
условия: Получаем,
что из двух корней первого уравнения подходит только один – 3. Системы
уравнений Способы решения
систем уравнений 1. Решение методом подстановки Нужно в одном из уравнений выразить одну переменную через другие,
а затем полученное выражение подставить в остальные уравнения вместо этой
переменной, повторять подобную процедуру пока не будут найдены все переменные. 2. Решение графическим методом Если
построить графики для каждого уравнения в одной системе координат, решениями
системы уравнений будут точки пересечения графиков. Графический
метод – самый неточный. Практически его можно применять только для систем линейных уравнений
(вида ), графиками которых
являются прямые. Если же хотя бы одно из уравнений имеет более сложный вид
(содержит квадрат, корень, логарифм и т.д.), то не рекомендуется использовать
графический метод (только для иллюстраций). 3. Решение методом сложения Метод сложения основан на следующем: если сложить левые части двух
(или больше) уравнений, полученное выражение будет равно сложенным правым
частям этих же уравнений. Новосибирская
область Барабинский
район МКОУ
Новониколаевская СОШ Работу
выполнила: ученица
9 класса Мельникова
Анастасия Руководитель: Моисеенко
Р. 2019-2020
уч. год Цель проекта: создание
брошюры по подготовке к ГИА по теме «Уравнения и
системы уравнений» Задачи: — определить основные понятия по данной
теме; — выяснить в каких типовых заданиях в ОГЭ
встречается тема «Уравнения и системы уравнений»; — сделать подборку заданий с образцами
решений и необходимой теорией; — оформить брошюру. Актуальность
проекта. В современном мире сдача государственной
итоговой аттестации по математике обязательна для всех учащихся. Подготовка к
экзаменам это ответственное и трудоемкое дело, а задания по теме «Уравнения и
системы уравнений» включены в экзаменационную работу. Гипотеза:
использование подготовленной брошюры поможет учащимся в подготовке к ГИА по
математике. Свою
работу я начала с того, что нашла и систематизировала основные определения по
теме «Уравнения и системы уравнений». Основные
понятия: уравнение, система уравнений, корень уравнения, решить уравнение,
решить систему уравнений, линейное уравнение, квадратное уравнение,
рациональное уравнение. Все данные понятия представлены в брошюре в первом
разделе. Уравнение — это равенство, содержащее в себе переменную,
значение которой требуется найти. Системами уравнений называют записи, представляющие собой
расположенные друг под другом уравнения, объединенные слева фигурной скобкой,
которые обозначают множество всех решений уравнений, одновременно являющихся
решениями каждого уравнения системы. Решить уравнение означает найти его корни или
доказать, что корней нет. Корень или решение уравнения — это значение переменной, при котором
уравнение обращается в верное числовое равенство. Решить систему уравнений – значит найти все ее решения или доказать, что решений нет. Линейное
уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная. Квадратное
уравнение — это
уравнение вида ax2 + bx + c =
0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0 Рациональные уравнения – это уравнения, в которых и левая, и
правая части рациональные выражения. На
втором этапе работы, мною были изучены разные варианты экзаменационных работ,
для определения в каких типовых заданиях встречаются темы «Уравнения», «Системы
уравнений». И выяснила, что это задания № 9 в первой части, № 21 во второй
части. Они могут быть сформулированы следующим образом: —
найти корень уравнения; -решите
систему уравнений; -решите
уравнение. Далее,
к каждому виду заданий, я оформила в виде образца алгоритм решения уравнения и
системы уравнений. Добавила необходимый теоретический материал по данной
тематике. Изучив разную литературу и интернет-ресурсы, сделала выборку
подходящих уравнений и систем уравнений. Оформила все это, в виде брошюры. В
данной брошюре рассмотрены: —
линейные уравнения; —
квадратные уравнения; —
рациональные уравнения; —
системы уравнений. Данная брошюра будет находиться в кабинете
математики. Её могут использовать одноклассники и другие учащиеся не только для
подготовки к экзаменам, но и при изучении темы «Уравнения и системы уравнений». Работая над
проектом, я систематизировала и улучшила свои знания по теме «Уравнения и
системы уравнений». И посоветую всем у кого проблемы с уравнениями
воспользоваться данной брошюрой. спросил Изменено
1 год, 4 месяца назад Просмотрено
1к раз У меня вопрос по фигурным скобкам в тексте. У меня есть следующие формулы: Теперь я хочу, чтобы f(x) и g(x) были заключены в фигурные скобки с правой стороны, и я хочу написать что-то за фигурной скобкой. И мне также нужна фигурная скобка за h(x), k(x) и l(x). Как я могу это сделать, а также убедиться, что все пять уравнений выровнены по знаку «=»? Я только что попытался поместить формулы в \begin{rcases} … \end{rcases}, но тогда формулы больше не выравниваются. Заранее большое спасибо! С уважением! 1 Вы можете использовать Странная настройка Спецификации для столбцов являются обычными для имитации Пара прогонов LaTeX необходима для стабилизации выходных данных, поскольку украшения устанавливаются последовательными шагами после измерения объекта. 2 Один из способов — определить новый тип столбца для выравнивания по адресу Я не уверен, правильно ли я понял ваш вопрос. Насколько я понимаю, следующее должно помочь Получение Если правая часть всех уравнений имеет одинаковую длину, внутренние выравнивания &, к счастью, дадут желаемое выравнивание. Зарегистрироваться через Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Требуется, но никогда не отображается Электронная почта Требуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Дробь 3 7: 3,7 это сколько в дроби ?
Дробь 3/7 в виде десятичной дроби
Как записать 3/7 в виде десятичной дроби?
Объяснение конвертации дроби 3/7 в десятичную
 io/ru/number/fraction-as-a-decimal/0—3—7
io/ru/number/fraction-as-a-decimal/0—3—7О калькуляторе «Конвертер обыкновенных дробей в десятичные»

 Он может быть особенно полезен тем, кто испытывает трудности с ручными вычислениями или кто часто выполняет преобразования.
Он может быть особенно полезен тем, кто испытывает трудности с ручными вычислениями или кто часто выполняет преобразования.Калькулятор «Конвертер обыкновенных дробей в десятичные»
Таблица конвертации обыкновенных дробей в десятичные
Дробь Десятичная 3/1 3 3/2 1,5 3/3 1 3/4 0,75 3/5 0,6 3/6 0,5 3/7 0,(428571) 3/8 0,375 3/9 0,(3) 3/10 0,3 3/11 0,(27) 3/12 0,25 3/13 0,(230769) 3/14 0,2(142857) 3/15 0,2 3/16 0,1875 3/17 0,(1764705882352941) 3/18 0,1(6) 3/19 0,(157894736842105263) 3/20 0,15 3/21 0,(142857) 3/22 0,1(36) 3/23 0,(1304347826086956521739) 3/24 0,125 3/25 0,12 3/26 0,1(153846) 3/27 0,(1) 3/28 0,10(714285) 3/29 0,(1034482758620689655172413793) 3/30 0,1 Mathway | Популярные задачи
1 Множитель x^2-4 2 Множитель 4x^2+20x+16 3 График y=-x^2 4 Вычислить 2+2 5 Множитель x^2-25 6 Множитель x^2+5x+6 7 Множитель x^2-9 8 Множитель x^3-8 9 Вычислить квадратный корень из 12 10 Вычислить квадратный корень из 20 11 Вычислить квадратный корень из 50 12 Множитель x^2-16 13 Вычислить квадратный корень из 75 14 Множитель x^2-1 15 Множитель x^3+8 16 Вычислить -2^2 17 Вычислить квадратный корень из (-3)^4 18 Вычислить квадратный корень из 45 19 Вычислить квадратный корень из 32 20 Вычислить квадратный корень из 18 21 Множитель x^4-16 22 Вычислить квадратный корень из 48 23 Вычислить квадратный корень из 72 24 Вычислить квадратный корень из (-2)^4 25 Множитель x^3-27 26 Вычислить -3^2 27 Множитель x^4-1 28 Множитель x^2+x-6 29 Множитель x^3+27 30 Множитель x^2-5x+6 31 Вычислить квадратный корень из 24 32 Множитель x^2-36 33 Множитель x^2-4x+4 34 Вычислить -4^2 35 Множитель x^2-x-6 36 Множитель x^4-81 37 Множитель x^3-64 38 Вычислить 4^3 39 Множитель x^3-1 40 График y=x^2 41 Вычислить 2^3 42 Вычислить (-12+ квадратный корень из -18)/60 43 Множитель x^2-6x+9 44 Множитель x^2-64 45 График y=2x 46 Множитель x^3+64 47 Вычислить (-8+ квадратный корень из -12)/40 48 Множитель x^2-8x+16 49 Вычислить 3^4 50 Вычислить -5^2 51 Множитель x^2-49 52 Вычислить (-20+ квадратный корень из -75)/40 53 Множитель x^2+6x+9 54 Множитель 4x^2-25 55 Вычислить квадратный корень из 28 56 Множитель x^2-81 57 Вычислить 2^5 58 Вычислить -8^2 59 Вычислить 2^4 60 Множитель 4x^2-9 61 Вычислить (-20+ квадратный корень из -50)/60 62 Вычислить (-8+ квадратный корень из -20)/24 63 Множитель x^2+4x+4 64 Множитель x^2-10x+25 65 Вычислить квадратный корень из -16 66 Множитель x^2-2x+1 67 Вычислить -7^2 68 График f(x)=2^x 69 Вычислить 2^-2 70 Вычислить квадратный корень из 27 71 Вычислить квадратный корень из 80 72 Множитель x^3+125 73 Вычислить -9^2 74 Множитель 2x^2-5x-3 75 Вычислить квадратный корень из 40 76 Множитель x^2+2x+1 77 Множитель x^2+8x+16 78 График y=3x 79 Множитель x^2+10x+25 80 Вычислить 3^3 81 Вычислить 5^-2 82 График f(x)=x^2 83 Вычислить квадратный корень из 54 84 Вычислить (-12+ квадратный корень из -45)/24 85 Множитель x^2+x-2 86 Вычислить (-3)^3 87 Множитель x^2-12x+36 88 Множитель x^2+4 89 Вычислить квадратный корень из (-8)^2 90 Множитель x^2+7x+12 91 Вычислить квадратный корень из -25 92 Множитель x^2-x-20 93 Вычислить 5^3 94 Множитель x^2+8x+15 95 Множитель x^2+7x+10 96 Множитель 2x^2+5x-3 97 Вычислить квадратный корень квадратный корень из 116 98 Множитель x^2-x-12 99 Множитель x^2-x-2 100 Вычислить 2^2 Что такое 3/7 упрощенное? Сократите дробь 3/7 до наименьшего члена

 Надеюсь, вы поняли процесс и можете использовать те же методы для самостоятельного упрощения других дробей. Полный ответ ниже:
Надеюсь, вы поняли процесс и можете использовать те же методы для самостоятельного упрощения других дробей. Полный ответ ниже: Преобразование 3/7 в десятичную
Процитируйте, дайте ссылку или ссылку на эту страницу

Натуральное число делится на 3 если: § Признак делимости на 3. Признак делимости на 9
Делимость — что это, определение и ответ
 \ a \vdots c\)
\ a \vdots c\)
 Разделить число a на число b с остатком – это значит найти такие числа c и d, что выполнены следующие условия:
Разделить число a на число b с остатком – это значит найти такие числа c и d, что выполнены следующие условия: \ \mathbf{1} \right)\text{\ \ \ \ \ }\left( 1 + 0 \right):2 = 0(ост.\ \mathbf{1})\)
\ \mathbf{1} \right)\text{\ \ \ \ \ }\left( 1 + 0 \right):2 = 0(ост.\ \mathbf{1})\)Признак делимости на 6 в математике
Деление — это операция, обратная умножению. Например, умножение 5 на 2 дает 10. Вы можете получить любой из множителей 2 и 5, разделив 10 на любое из чисел.
Например, умножение 5 на 2 дает 10. Вы можете получить любой из множителей 2 и 5, разделив 10 на любое из чисел.Что такое признаки делимости?
Признаки делимости на 6, примеры

Первое условие: число должно делиться на 2 ⇒ 9156 оканчивается на четное число (6). Оно делится на 2 [9156 ÷ 2 = 4578].
Условие второе: число должно делиться на 3. Сумма цифр числа 9156 равна 21 (9 + 1 + 5 + 6 = 21). Сумма 21 делится на 3. Число 9156 делится на 3.
Таким образом, 9156 делится и на 2, и на 3. Следовательно, оно делится на 6.
Следовательно, оно делится на 6.
Условие первое: число должно делиться на 2 ⇒ 825 оканчивается на нечетное число (5). Оно НЕ делится на 2.
Второе условие: число должно делиться на 3. Сумма цифр числа 825 равна 15 (8+ 2 + 5 = 15). Сумма 15 делится на 3. Число 825 делится на 3 (825 ÷ 3 = 275).
Мы видим, что 825 НЕ делится на 2 и делится на 3. Поскольку число не удовлетворяет одному условию, следовательно, 825 НЕ делится на 6.Правило делимости на 6 для больших чисел


Решение: Поскольку заданное большое число 433788 является четным числом (цифра разряда единиц четна), оно делится на 2. Кроме того, сумма цифр, равная 4 + 3 + 3 + 7 + 8 + 8 = 33, делится. на 3, или мы можем добавить цифры 33, чтобы упростить 3 +3 = 6 делится на 3, таким образом, 433788 также делится на 3. Следовательно, число 433788 делится на 6, потому что оно делится на оба числа 2 и 3. (433788 ÷ 6 = 72298).
Следовательно, число 433788 делится на 6, потому что оно делится на оба числа 2 и 3. (433788 ÷ 6 = 72298).Доказательство признака делимости на 6
 Необходимо применить основную теорему арифметики. Если произведение нескольких положительных целых множителей, отличных от единицы, делится на простое число p, то хотя бы один множитель делится на p. Имеем, что целое число a делится на 2, тогда существует такое число q, когда a = 2 ⋅ q a = 2 q. Это же выражение делится на 3, где 2 ⋅ q 2 q делится на 3. Очевидно, 2 не делится на 3. Из теоремы следует, что q должно делиться на 3. Отсюда получаем, что существует целое число q1, где q = 3 ⋅ q 1 q = 3 q1. Отсюда полученное неравенство вида a = 2 ⋅ q = 2 ⋅ 3 ⋅ q 1 = 6 ⋅ q 1 a = 2 q = 2 3 q1 = 6 q1 говорит о том, что число a будет делиться на 6. Доказывается достаточность.
Необходимо применить основную теорему арифметики. Если произведение нескольких положительных целых множителей, отличных от единицы, делится на простое число p, то хотя бы один множитель делится на p. Имеем, что целое число a делится на 2, тогда существует такое число q, когда a = 2 ⋅ q a = 2 q. Это же выражение делится на 3, где 2 ⋅ q 2 q делится на 3. Очевидно, 2 не делится на 3. Из теоремы следует, что q должно делиться на 3. Отсюда получаем, что существует целое число q1, где q = 3 ⋅ q 1 q = 3 q1. Отсюда полученное неравенство вида a = 2 ⋅ q = 2 ⋅ 3 ⋅ q 1 = 6 ⋅ q 1 a = 2 q = 2 3 q1 = 6 q1 говорит о том, что число a будет делиться на 6. Доказывается достаточность.Другие случаи делимости на 6
 {2}+5\right)\]
{2}+5\right)\]
Полученное произведение содержит множитель 6, поэтому оно делится на 6 для любого целого числа b.
Правила деления на числа от 1 до 10, а также на 11 и 25 были выведены для упрощения процесса деления натуральных чисел. Оканчивающиеся на 2, 4, 6, 8, 0 считаются четными. сравнений — Докажите, что число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3
 Почему оно следует из этого соответствия?
Почему оно следует из этого соответствия? Если число не равно 0 (или любому другому кратному 3), ни n, ни сумма цифр не будут делиться на 3. 9k\equiv a_k+a_{k-1}+a_{k-2}+\cdots+a_0\pmod3.$$
Если число не равно 0 (или любому другому кратному 3), ни n, ни сумма цифр не будут делиться на 3. 9k\equiv a_k+a_{k-1}+a_{k-2}+\cdots+a_0\pmod3.$$ Математическая задача: остаток 33031 — математическая задача, натуральные числа
Правильный ответ:
Для решения этой математической задачи вам необходимо знать следующие знания:
Уровень задачи:
Найдите наибольшее трехзначное число, которое дает остаток 1 при делении на три, дает остаток 2 при делении на четыре, дает остаток 3 при делении на пять и дает остаток 4 при делении на шесть.
Число X — наименьшее натуральное число, половина которого делится на три, треть делится на четыре, четверть делится на одиннадцать, а его половина дает остаток 5 при делении на семь. Найдите это число.
Определите наименьшее целое число, которое при делении на 11 дает остаток 4. При делении 15 дает остаток 10, а при делении на 19 дает остаток 16. при делении на 5 n дает остаток 4 при делении на 5. Докажите непосредственно
Вычислите целое число, деленное на 34, дает 10, а остальные 25.
Мое 4-значное число есть палиндром; у него есть остаток 21, когда вы делите его на 100. какое у меня число? Палиндром — это число, которое не изменится, если его записать в обратном порядке.
Есть тысяча однозначного числа, которое состоит из повторяющихся цифр 123412341234. Какой остаток дает это число при делении на девять?
A — произвольное целое число, дающее остаток 1 при делении на 6. B — случайное целое число, дающее остаток при делении на два. Что дает остаток от деления на три произведения чисел А х В?
B — случайное целое число, дающее остаток при делении на два. Что дает остаток от деления на три произведения чисел А х В?
После деления неизвестного числа на число 23 получается частное 11 и остаток четыре. Найдите неизвестный номер.
A. Найдите наибольшее натуральное число, на которое можно разделить числа 54 и 72 (120, 60 и 42) B. Найдите наименьшее натуральное число, на которое можно разделить каждое из чисел 36 и 48 ( 24,18 и 16)
Найдите x в уравнении по модулю: 47x = 4 (mod 9) Подсказка – прочитайте, какое число 47x разделить на 9 (по модулю 9) дает остаток 4.
Сумма число равно 878. Если мы разделим большее число на меньшее, мы получим отношение 6 к остатку 17. Что это за числа?
Найдите остаток после деления суммы на 1! +2! +3! +. … . +300! число 13.
Какой остаток при делении 10 на 9 до 47 — 111?
Четырехзначное число, разделенное на 2020, дает результат 1, **.
Тест по менеджменту 1 курс с ответами: Тесты с ответами по менеджменту
Тесты с ответами по менеджменту


Тесты по менеджменту с ответами 2-ой вариант


 Принципы регулирования:
Принципы регулирования:




Итоговое тестирование по менеджменту с ответами:





 Власть
Власть



Теория менеджмента — ответы часть 1
«При правильной организации собственной работы каждый руководитель может добиться успеха». Так считал:
  
 Благодаря разработкам научной школы управления ...
Благодаря разработке школы человеческих отношений была:
 Тейлора и его теории «кнута и пряника» 
Тейлора и его теории «кнута и пряника» В качестве объекта рассмотрения при системном подходе выступает:
В основе концепции классической школы управления лежит следующее утверждение: «Работа любого руководителя ...»
В процессе делегирования психологические проблемы возникают у .
 ..
..В процессе коммуникации профессионализмы следует использовать ...
В процессе коммуникации теория выделяет следующее число базовых элементов:
В процессе межличностного общения менеджер использует язык .
 ..
..В рамках классической школы управления были разработаны:
В рамках научной школы управления были разработаны ...
В рамках школы человеческих отношений были разработаны:
Важным достоинством группового решения является .
 ..
..Вознаграждение принято делить на ...
Главной целью осуществления функции планирования является ...
Делегирование вышестоящему начальнику .
 ..
..Дивизиональная структура позволяет обеспечить ...
Для правильной организации функции контроля важно обеспечить .
 ..
..Для целей управления конфликтом используют методы ...
Достоинством группового решения является ...
Индикативная функция организационного конфликта проявляется в том, что он помогает .
 ..
..К преимуществам функциональной структуры управления относится:
К содержательным относится теория мотивации .
 ..
..Качество продукции или услуг определяется:
Ключевая задача оперативного плана состоит в том, чтобы ...
Ключевое понятие классической школы:
Ключевое понятие школы науки управления:
Контроль является функцией .
 ..
..Конфликт может разворачиваться на уровне ...
Конфликт отличается от конфликтной ситуации наличием ...
Линейно-функциональная структура не может обеспечить .
 ..
..Линейные полномочия строятся по принципу ...
Лучший результат в условиях управления диверсифицированной фирмой дает .
 .. структура.
.. структура.Лучший результат в условиях централизованного управления дает ... структура .
Матричная структура позволяет обеспечить ...
Менеджерами называются:
Модель «черный ящик» рассматривает организацию как систему:
Мотивация является функцией .
 ..
..На структурных схемах линейные полномочия отражаются ... линией.
На структурных схемах функциональные полномочия ...
Наука «менеджмент» возникла в условиях:
Непрограммируемые (слабоструктурированные) решения принимаются .
 ..
..Нобелевской премии за вклад в развитие теории принятия решений был удостоен ...
Норма управляемости зависит от ...
 д.) 
д.) Норма управляемости определяется по следующему закону:
Объект изучения в школе человеческих отношений:
Объектом изучения в курсе «менеджмент» является:
Определите последовательность действий по реализации плана, как системы взаимосвязанных решений, направленных на достижение поставленного результата:
Определите последовательность действий по целевому управлению:
Определите последовательность процесса формирования и развития группы:
Бесплатный экзамен Top 50+ PMP Вопросы и ответы на 2023 год
 Экзамен состоит из 200 вопросов с несколькими вариантами ответов, описывающих пять групп процессов (Инициация, Планирование, Выполнение, Мониторинг и контроль и Закрытие) и девять областей знаний (Интеграция, Объем, Время, Стоимость, Качество, Человеческие ресурсы, Коммуникация, Риск). и Закупки).
Экзамен состоит из 200 вопросов с несколькими вариантами ответов, описывающих пять групп процессов (Инициация, Планирование, Выполнение, Мониторинг и контроль и Закрытие) и девять областей знаний (Интеграция, Объем, Время, Стоимость, Качество, Человеческие ресурсы, Коммуникация, Риск). и Закупки). 1. Проект имеет 60-процентную вероятность получения прибыли в размере 100 000 долларов США и 40 процентов убытка в размере 100 000 долларов США. Ожидаемая денежная стоимость проекта:
2. Предполагая, что концы диапазона оценок составляют +/- 3 сигмы от среднего значения, какая из следующих оценок диапазона связана с НАИМЕНЬШИМ риском?

3. Если риск имеет 20-процентную вероятность возникновения в данном месяце, и ожидается, что проект продлится пять месяцев, какова вероятность того, что рисковое событие произойдет в течение четвертого месяца проекта?
4. Принятый срок для проектных подходов. Однако руководитель проекта понимает, что выполнено только 75% работы. Затем менеджер проекта выдает запрос на изменение. Что должен разрешать запрос на изменение?
5. В ходе какого(их) процесса(ов) управления рисками будет выявлен риск?
Ссылка: Руководство PMBOK®, 5-е издание, стр.  312, рис. 11.1
312, рис. 11.1 6. Что подразумевается под RACI?
7. Какое из следующих утверждений о программе верно?
Ссылка: Руководство PMBOK®, 5-е издание, стр. 9 8. Руководитель проекта встречается с проектной группой для обсуждения уроков, извлеченных из предыдущих проектов.
 В какой деятельности участвует команда?
В какой деятельности участвует команда? 9. Во время конференции участников торгов вы видите, что один из участников торгов является вашим близким другом. Каким должен быть ваш следующий шаг?
10. Если событие риска имеет 90-процентную вероятность возникновения, а последствия будут составлять 10 000 долларов США, что представляют собой 9 000 долларов США?
 США = 9 000 долл. США
США = 9 000 долл. США 11. Землетрясение повредило вашу стройку. Ваш подрядчик говорит, что он не может выполнить условия контракта из-за определенного пункта, который вы оба подписали. Он имеет в виду:
12. Все перечисленное ВСЕГДА является входными данными для процесса управления рисками, КРОМЕ:
13. При расчете времени на деятельность руководитель проекта должен:
14.
 Толерантность к риску определяется, чтобы помочь:
Толерантность к риску определяется, чтобы помочь: 15. Вы выполняете проект по разработке и внедрению набора бизнес-процессов и программного решения для управления взаимоотношениями с клиентами. В проекте участвует большое количество организаций―крупная корпорация и множество поставщиков разного масштаба. В ходе проекта вы наблюдаете влияние различий между корпоративными культурами компаний. Это приводит к различным ожиданиям в отношении того, как следует вести проект, а также к частым недопониманиям между заинтересованными сторонами.
 Другим следствием является растущая степень недоверия и скептицизма. Что вы должны попробовать в первую очередь, чтобы интегрировать различные группы заинтересованных сторон?
Другим следствием является растущая степень недоверия и скептицизма. Что вы должны попробовать в первую очередь, чтобы интегрировать различные группы заинтересованных сторон? Ссылка: PMBOK® Guide 5th Edition, page 194 (последний абзац). 16. Вам трудно оценить точное влияние риска на стоимость. Вы должны оценить на (n) :

17. Менеджер проекта оценивает риск своего проекта. Несколько ее экспертов находятся за пределами офиса, но хотят, чтобы их включили. Как это может быть сделано?
18. Будучи назначенным руководителем проекта, вы заметили в процессе выполнения проекта, что в команде возникают конфликты как на техническом, так и на межличностном уровне. Как правильно разрешать конфликты?

19. В ходе какого процесса управления рисками принимается решение о передаче риска?
20. При использовании контрольных карт выбросами являются:

21. Что из перечисленного не является группой процессов?
22. Каков результат процесса мониторинга и контроля?
23. Что из следующего не является входом в процесс разработки плана управления проектом?
24. Что из следующего не является входом в процесс контроля?

25. Что из следующего не является результатом процесса закрытия?
26. Альфа и Бета — два проекта, рассматриваемых компанией. Ожидается чистая прибыль в размере $50 млн от «Альфы» и $45 млн от «Беты». Оба являются прибыльными и полезными проектами, но компания может инвестировать только в один из них. Если выбрана Альфа, рассчитайте альтернативную стоимость?
27. Вы руководитель проекта по строительству пяти мостов.
 Проект состоит из пяти последовательных этапов, на каждом из которых завершается один мост. После завершения первой фазы проекта, какая группа процессов второй фазы должна следовать?
Проект состоит из пяти последовательных этапов, на каждом из которых завершается один мост. После завершения первой фазы проекта, какая группа процессов второй фазы должна следовать? 28. Целью проекта является исследование технической, экономической и социальной осуществимости строительства плотины гидроэлектростанции. Устав проекта утверждается спонсором проекта. Какой следующий шаг необходимо выполнить?

29. Управляя проектом по обновлению программного обеспечения для вашей компании, вы понимаете, что ваш спонсор имеет большие полномочия в принятии решений, но низкий интерес. Какую стратегию управления заинтересованными сторонами вы должны использовать, чтобы обеспечить постоянную поддержку спонсора?
30. Спонсор проекта запрашивает копию документа, содержащего описание, владельца, источник, приоритет и статус требований к продукту. О каком проектном документе идет речь?
31.
 Разработка является важнейшим аспектом в проекте большого размера, с соблюдением нормативных и экологических требований. Что вы должны сделать в первую очередь в качестве отправной точки для начального планирования проекта?
Разработка является важнейшим аспектом в проекте большого размера, с соблюдением нормативных и экологических требований. Что вы должны сделать в первую очередь в качестве отправной точки для начального планирования проекта? 32. При мониторинге базовой стоимости проекта было отмечено, что на данный момент расходы по проекту выше ожидаемых. Какова наиболее вероятная причина этого?
 Неспособность эффективно управлять ресурсами и контролировать их может стать источником увеличения затрат в проекте.
Неспособность эффективно управлять ресурсами и контролировать их может стать источником увеличения затрат в проекте. 33. Недавно вы назначили своего звездного программиста Пэм руководителем группы гибкой разработки. Пэм была фантастическим программистом, и вы думали, что повышение будет означать, что теперь она сможет делиться своим опытом с другими членами команды разработчиков. Но вы замечаете, что работа Пэм в ее новой роли не впечатляет и не соответствует вашим ожиданиям. Какое эмпирическое правило вы проигнорировали или забыли при рассмотрении вопроса о повышении Пэм?
Гало эффект 34. Просматривая план управления требованиями проекта, вы заметили, что один из компонентов ему не принадлежит. Какой из них лишний?
35.
 В рамках проекта по совершенствованию производственного процесса проект и команда выполняют процесс мониторинга и контроля работы по проекту. Что из нижеперечисленного выполняется в ходе этого процесса?
В рамках проекта по совершенствованию производственного процесса проект и команда выполняют процесс мониторинга и контроля работы по проекту. Что из нижеперечисленного выполняется в ходе этого процесса? 36. Компания создает совет по контролю за изменениями (CCB), предназначенный для рассмотрения и оценки изменений, представляемых для всех проектов. Что из следующего лучше всего описывает человека или группу, которые могут запросить изменение проекта в ситуации, когда спонсор проекта является членом CCB?
37.
 Вы хотите заменить подрядчика, потому что он не выполняет согласованные стандарты, и нанять другого подрядчика для выполнения той же работы. Вам необходимо определить конкретный юридический порядок досрочного расторжения договора. Что вы должны сделать?
Вы хотите заменить подрядчика, потому что он не выполняет согласованные стандарты, и нанять другого подрядчика для выполнения той же работы. Вам необходимо определить конкретный юридический порядок досрочного расторжения договора. Что вы должны сделать? 38. В проекте, последовательно разделенном на четыре фазы, что должен делать менеджер проекта, когда вторая фаза завершена и вот-вот начнется третья?
39.
 Офис управления проектами (ОУП) организации обеспечивает соответствие всех процессов управления проектами и всех соответствующих проектных документов установленным передовым методам. Что в первую очередь должен рассмотреть руководитель проекта, чтобы определить заинтересованные стороны для нового проекта?
Офис управления проектами (ОУП) организации обеспечивает соответствие всех процессов управления проектами и всех соответствующих проектных документов установленным передовым методам. Что в первую очередь должен рассмотреть руководитель проекта, чтобы определить заинтересованные стороны для нового проекта? 40. Используя гибкую структуру, вы должны возглавить проект по разработке продукта.
 Вы хотите собрать вместе заинтересованные стороны и МСП для обсуждения рисков, критериев успеха и других тем. Каков наилучший способ для достижения этой цели?
Вы хотите собрать вместе заинтересованные стороны и МСП для обсуждения рисков, критериев успеха и других тем. Каков наилучший способ для достижения этой цели? 41. В рамках подготовки плана управления коммуникациями для проекта в стадии строительства вы хотите определить потребности заинтересованных сторон проекта в отношении информации. Ваше внимание сосредоточено на типе и формате информации, необходимой для передачи им. Каков ваш лучший план действий?
42.
 Для снижения уровня брака в производственном процессе выполняется проект. Команда проекта проводит мероприятия по обеспечению качества для анализа и улучшения процесса. Что из следующего было бы наиболее полезным для этого проекта?
Для снижения уровня брака в производственном процессе выполняется проект. Команда проекта проводит мероприятия по обеспечению качества для анализа и улучшения процесса. Что из следующего было бы наиболее полезным для этого проекта? 43. Вы руководитель проекта по разработке программного обеспечения, в котором задействованные разработчики работают в арендованном офисе. Написание кода занимает больше времени, чем предполагалось. Вы попросили арендодателя арендовать офис еще на неделю. К сожалению, арендодатель сообщает вам, что офис на этот период забронирован.
 Вы фиксируете проблему в документах проекта. Что делать дальше?
Вы фиксируете проблему в документах проекта. Что делать дальше? 44. Вы являетесь частью проектной группы, разрабатывающей новый тип транспортного средства. Вы готовы приступить к работе над набором задач (рабочим пакетом) для тормозной системы автомобиля. Вы хотели бы оценить критерии приемлемости перед началом работы. Где искать, чтобы найти эту информацию?
45. Почти завершен проект по строительству сборочной линии.
 Менеджер проекта закрыл закупки, представил окончательный отчет по проекту, обновил реестр извлеченных уроков и получил отзывы от соответствующих заинтересованных сторон. Каким должен быть следующий шаг менеджера проекта?
Менеджер проекта закрыл закупки, представил окончательный отчет по проекту, обновил реестр извлеченных уроков и получил отзывы от соответствующих заинтересованных сторон. Каким должен быть следующий шаг менеджера проекта? 46. Команда проекта взвешивает два варианта реагирования на риски для включения в реестр рисков. Первая реакция на риск должна соответствовать двум критериям и стоит 5000 долларов. Вторая реакция на риск должна соответствовать четырем критериям, но стоит всего 2000 долларов. Какое действие с наименьшей вероятностью будет предпринято проектной группой для выбора наилучшего ответа на риск?
47.
 Члены вашей проектной группы пишут код парами и оценивают работу друг друга, чтобы проверить и определить, соответствует ли код требованиям документации. Какой из следующих результатов будет получен в результате этого процесса?
Члены вашей проектной группы пишут код парами и оценивают работу друг друга, чтобы проверить и определить, соответствует ли код требованиям документации. Какой из следующих результатов будет получен в результате этого процесса? 48. На строительном объекте ежедневно присутствует много людей и специализированных бригад. Частая и бесперебойная коммуникация между руководителями команд жизненно важна для обеспечения безопасного и эффективного прогресса. Какую гибкую церемонию можно включить в этот проект, чтобы повысить своевременную межфункциональную коммуникацию?
 Ежедневные стендапы — это ограниченные по времени встречи, которые посещают команда проекта и соответствующие заинтересованные стороны.
Ежедневные стендапы — это ограниченные по времени встречи, которые посещают команда проекта и соответствующие заинтересованные стороны. 49. Руководство организации хочет включить в свои проекты более гибкие методологии. Что нужно сделать в первую очередь, прежде чем начать применять agile-подходы в проекте?
50. Вам необходимо установить относительные приоритеты рисков, признанных в проекте. Какая из следующих задач, скорее всего, не повлияет на эту расстановку приоритетов?
51.
 Следующая таблица представляет собой список действий, который включает продолжительность и предшествующие серии действий проекта. Какова продолжительность критического пути?
Следующая таблица представляет собой список действий, который включает продолжительность и предшествующие серии действий проекта. Какова продолжительность критического пути? 52. Менеджер проекта при составлении реестра заинтересованных сторон составляет список потенциальных заинтересованных сторон и выбирает метод сбора данных, известный как мозговое письмо. Что нужно сделать в первую очередь при использовании этого метода?
53.
 Менеджер проекта в основном общается по электронной почте с членами своей команды, внутренними и внешними заинтересованными сторонами проекта. Определенные методы включены, чтобы гарантировать отсутствие недоразумений. Что из следующего не считается одним из этих методов?
Менеджер проекта в основном общается по электронной почте с членами своей команды, внутренними и внешними заинтересованными сторонами проекта. Определенные методы включены, чтобы гарантировать отсутствие недоразумений. Что из следующего не считается одним из этих методов? Управление должно планировать, организовывать, направлять и контролировать имеющиеся человеческие, материальные и финансовые ресурсы для оказания качественной помощи пациентам и их семьям. Этот раздел включает практические вопросы, связанные с лидерством и управлением. Этот набор включает 80 практических вопросов, разделенных на две части.
Управление должно планировать, организовывать, направлять и контролировать имеющиеся человеческие, материальные и финансовые ресурсы для оказания качественной помощи пациентам и их семьям. Этот раздел включает практические вопросы, связанные с лидерством и управлением. Этот набор включает 80 практических вопросов, разделенных на две части. Nurseslabs стремится сделать эту услугу БЕСПЛАТНОЙ И ДОСТУПНОЙ ДЛЯ ВСЕХ , которые хотят продвинуться по карьерной лестнице, особенно для студентов и медсестер.
Nurseslabs стремится сделать эту услугу БЕСПЛАТНОЙ И ДОСТУПНОЙ ДЛЯ ВСЕХ , которые хотят продвинуться по карьерной лестнице, особенно для студентов и медсестер.
Лидерство и управление в сестринском деле Практика NCLEX | Викторина № 1: 40 вопросов 
Комплексный обзор Saunders для экзамена NCLEX-RN часто упоминается как лучший сборник обзоров экзаменов по сестринскому делу. В тексте доступно более 5700 практических вопросов. Подробные стратегии прохождения теста предоставляются для каждого вопроса с подсказками для анализа и выявления правильного варианта ответа.
Практические вопросы всех типов в стиле NCLEX® нового поколения проиллюстрированы в виде отдельных тематических исследований и развернутых тематических исследований. Модель измерения клинических суждений NCSBN (NCJMM) включена в сценарии клинических случаев, которые объединяют шесть когнитивных навыков клинического суждения.
Это издание содержит более 6000 практических вопросов, каждый из которых содержит стратегию прохождения теста и обоснования правильных и неправильных ответов для улучшения обзора. Вопросы организованы в соответствии с последним планом тестирования NCLEX-RN «Потребности клиентов и интегрированные процессы». Вопросы написаны на более высоких когнитивных уровнях (применение, анализ, синтез, оценка и создание), чем вопросы самого теста.
NCLEX-RN Prep Plus от Kaplan использует экспертные методы критического мышления и целевые примеры вопросов. В этом издании определены семь типов вопросов по СПП и подробно объясняется, как подойти к каждому типу и ответить на него. Кроме того, он предоставляет 10 путей критического мышления для анализа экзаменационных вопросов.
В этом издании определены семь типов вопросов по СПП и подробно объясняется, как подойти к каждому типу и ответить на него. Кроме того, он предоставляет 10 путей критического мышления для анализа экзаменационных вопросов.
10-е издание Иллюстрированного учебного пособия для экзамена NCLEX-RN, 10-е издание. Это учебное пособие дает вам надежный, наглядный и менее пугающий способ запомнить ключевые факты. На сопутствующем веб-сайте Evolve теперь размещено 2500 контрольных вопросов. 25 дополнительных иллюстраций и мнемоники делают книгу еще более привлекательной.
Карточки для обзора экзамена NCLEX RN Учебное пособие с практическими вопросами к экзамену [полноцветные карточки] из книг для подготовки к экзамену. Эти карточки готовы к использованию, что позволяет вам сразу приступить к обучению. Каждая флэш-карта имеет цветовую маркировку для легкой идентификации объекта.
Формула объема полусферы: Как найти объем полусферы и конуса? – Обзоры Вики
Чему равен объем полусферы, если радиус основания равен 3.5 м?
 6 м, округленный до десятых долей кубического метра? Отвечать: m3 Отправить попытку ответа 1 из 4 Политики конфиденциальности Условия обслуживания.
6 м, округленный до десятых долей кубического метра? Отвечать: m3 Отправить попытку ответа 1 из 4 Политики конфиденциальности Условия обслуживания.Радиус полушария равен его высоте?
Чему равен объем полушария, если радиус?

Каков объем полушария диаметром 45.7 м, округленного до десятых долей кубического метра?
 Теперь, учитывая, что радиус сферы равен r.
Теперь, учитывая, что радиус сферы равен r.Как найти глубину полушария?
Объем полушария Калькулятор | Вычислить Объем полушария
 ⓘ Радиус полушария [r]
ⓘ Радиус полушария [r]
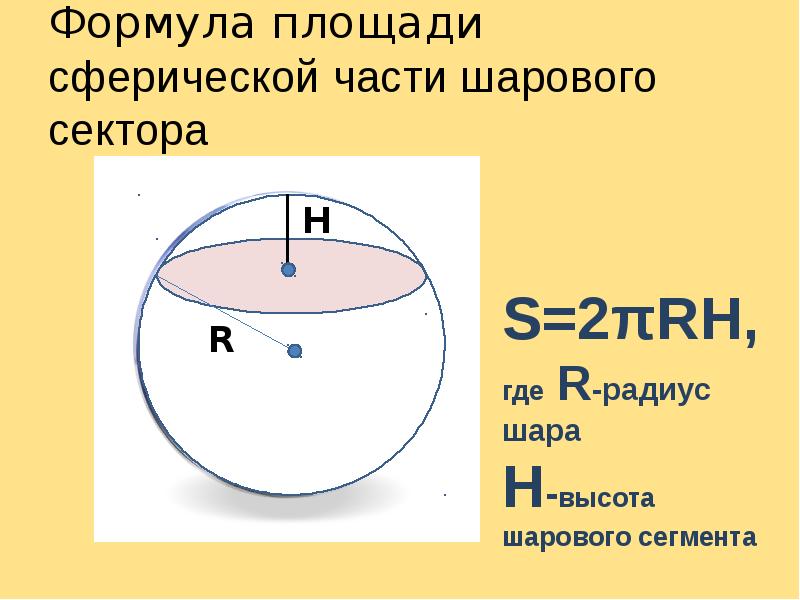 ⓘ Объем полушария [V]
ⓘ Объем полушария [V]
Объем полушария Решение
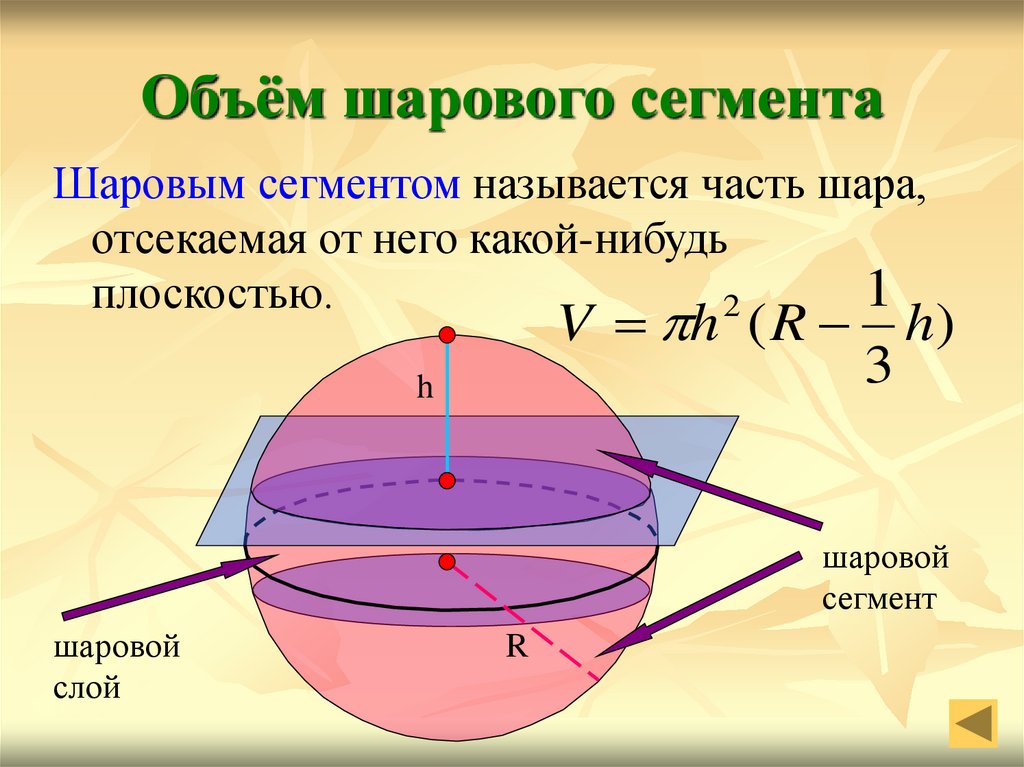 3
3
Что такое полушарие?
Объем полушария – формула, определение, примеры
1. 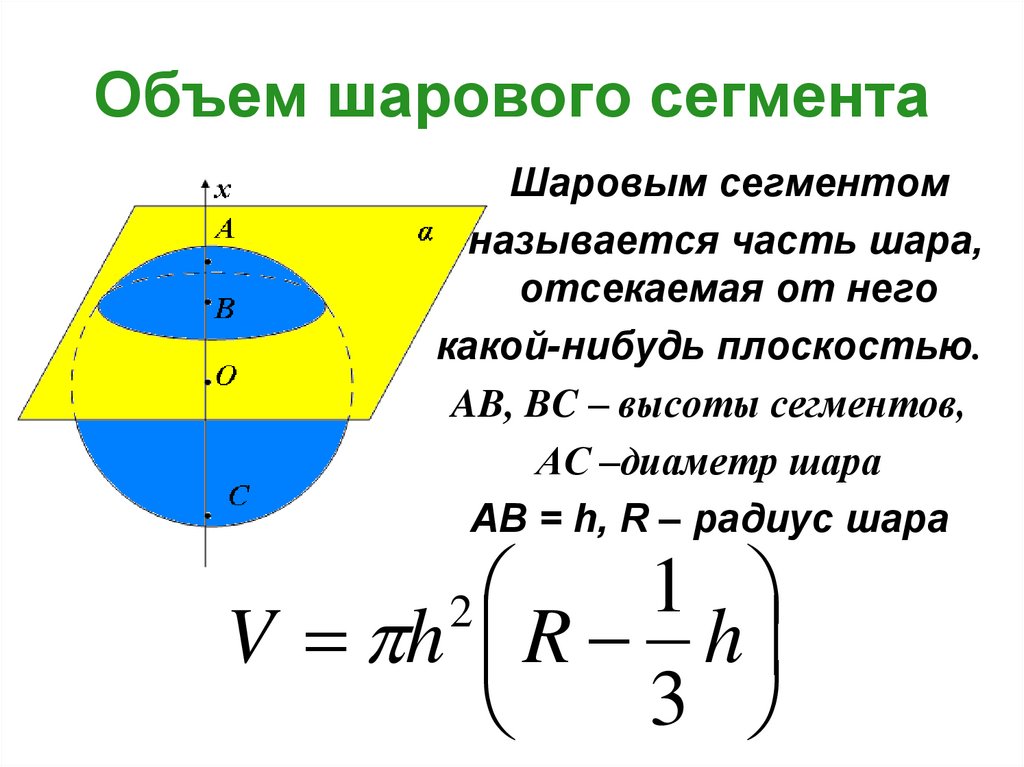
Каков объем полушария? 2. Объем полушария Формула 3. Как найти объем полушария? 4. Часто задаваемые вопросы об объеме полушария Каков объем полушария?
Объем полушария Формула

Как найти объем полушария?
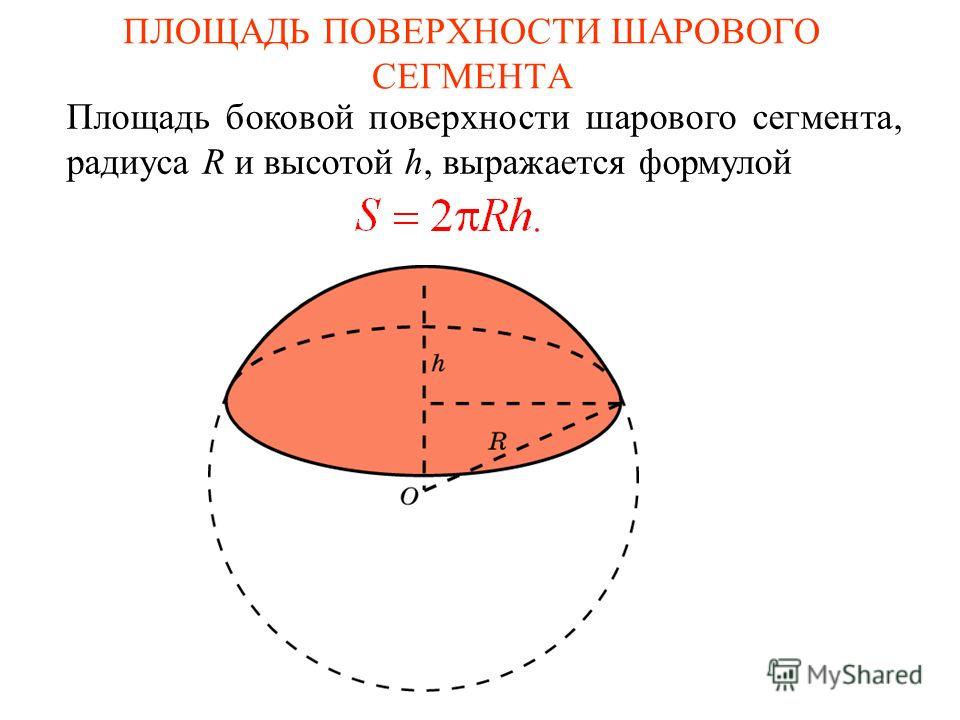
Примеры объема полушария
Объем полушария = 2πr 3 /3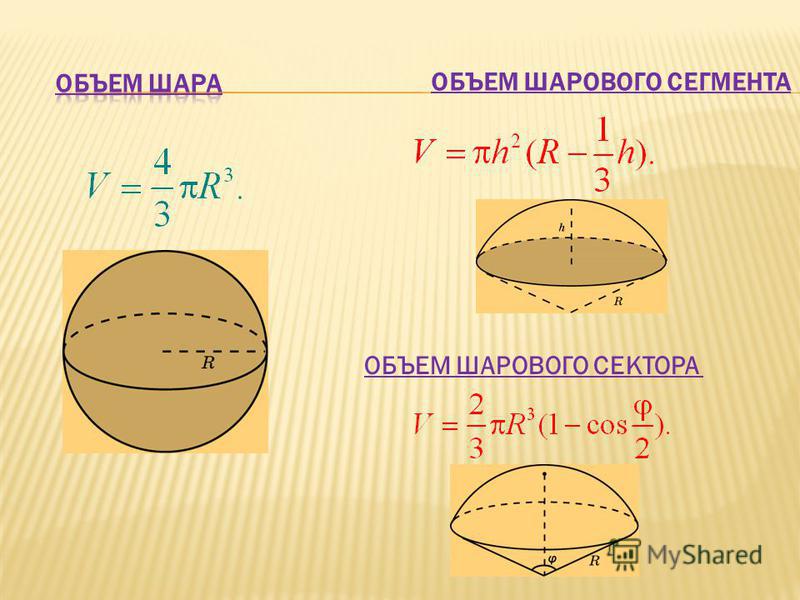

Практические вопросы по объему полушария
Часто задаваемые вопросы об объеме полушария
Каков объем полушария?
Что такое полушарие?
Как найти объем полушария?
Какова формула объема полушария?

В каких единицах измеряется объем полушария?
Как найти объем шара?
Каков объем полушария, имеющего диаметр 12,6 единиц?
Калькулятор объема полушария
 Вам нужно решить конкретную задачу, но вы не знаете, как найти объем полушария? Попробуйте ввести один из параметров и посмотрите, как просто работает этот калькулятор.
Вам нужно решить конкретную задачу, но вы не знаете, как найти объем полушария? Попробуйте ввести один из параметров и посмотрите, как просто работает этот калькулятор. Общая площадь поверхности каждого полушария состоит из площади основания (круг) и площади крышки . С одной стороны, сумма площадей двух полушарий не равна площади поверхности полной сферы, а с другой стороны, сумма объемов двух полушарий равна объему полной сферы.
Общая площадь поверхности каждого полушария состоит из площади основания (круг) и площади крышки . С одной стороны, сумма площадей двух полушарий не равна площади поверхности полной сферы, а с другой стороны, сумма объемов двух полушарий равна объему полной сферы. Какова формула объема полушария?
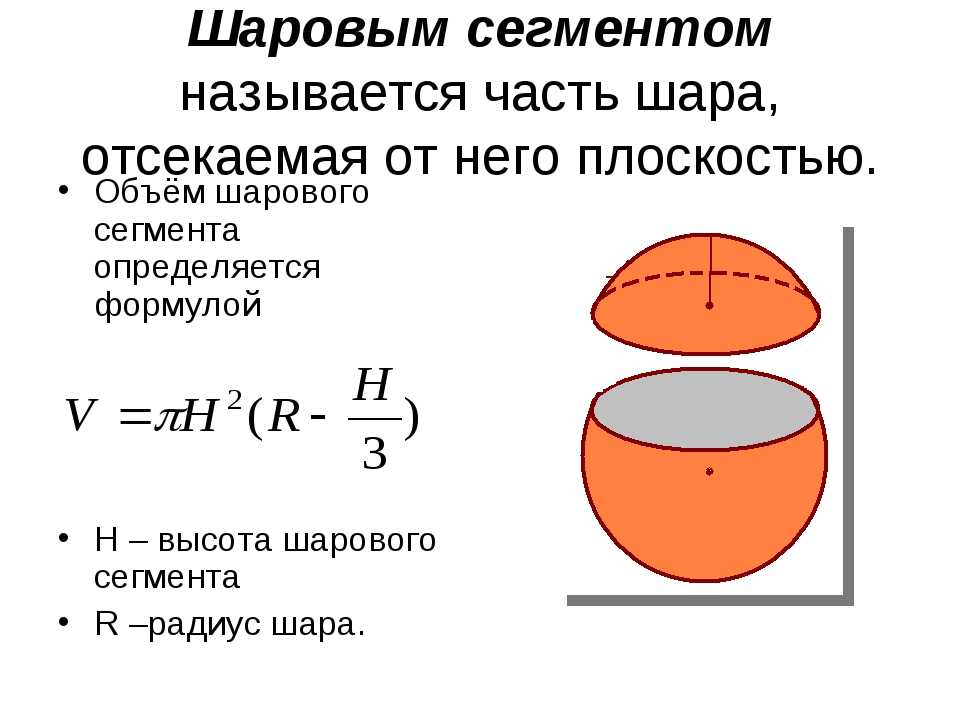 Наш калькулятор объема полушария может рассчитать из одного выбранного параметра все остальные величины полушария. Чтобы объяснить это, давайте начнем с перечисления некоторых основных уравнений, описывающих свойства полушария:
Наш калькулятор объема полушария может рассчитать из одного выбранного параметра все остальные величины полушария. Чтобы объяснить это, давайте начнем с перечисления некоторых основных уравнений, описывающих свойства полушария: Часто задаваемые вопросы
Как называется половина сферы?
 Вот почему мы разделили Землю на полушария, северное и южное, а также восточное и западное.
Вот почему мы разделили Землю на полушария, северное и южное, а также восточное и западное. Как рассчитать площадь поверхности полушария?
A = 3𝜋r² . Сколько граней на полушарии?
Как рассчитать объем полушария, зная его диаметр?

Правила деления на 4: § Признак делимости на 2, 4 и 8
правило и примеры нахождения частного двух чисел без остатка
Общие сведения

Классификация деления
 Первое осуществляется без остатка, и его результатом всегда является целое число. Об этом говорят, что исходное значение кратно делителю.
Первое осуществляется без остатка, и его результатом всегда является целое число. Об этом говорят, что исходное значение кратно делителю.Признаки делимости на 4
 Он позволяет быстро определить, какое число делится на 4. Он имеет следующий вид:
Он позволяет быстро определить, какое число делится на 4. Он имеет следующий вид:Пример реализации
 Проверка кратности осуществляется следующим образом:
Проверка кратности осуществляется следующим образом:
Не успеваете написать работу?
Заполните форму и узнайте стоимость
Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертацияКонтактные данные — строго конфиденциальны!
Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.
Подтверждение
Ваша заявка принята.

Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.Ошибка оформления заказа
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.Признак делимости на 4: примеры, доказательство
Признак делимости на 4, примеры
 числами. Однако, чем больше становятся числа, тем сложнее проводить с ними действия с целью проверки делимости их на 4.
числами. Однако, чем больше становятся числа, тем сложнее проводить с ними действия с целью проверки делимости их на 4. Это значит, что и исходное число на 4 без остатка не делится.
Это значит, что и исходное число на 4 без остатка не делится.
Доказательство признака делимости на 4
 Для одно- и двузначных чисел a=a0.
Для одно- и двузначных чисел a=a0. Так мы доказали необходимость.
Так мы доказали необходимость.Другие случаи делимости на 4
4.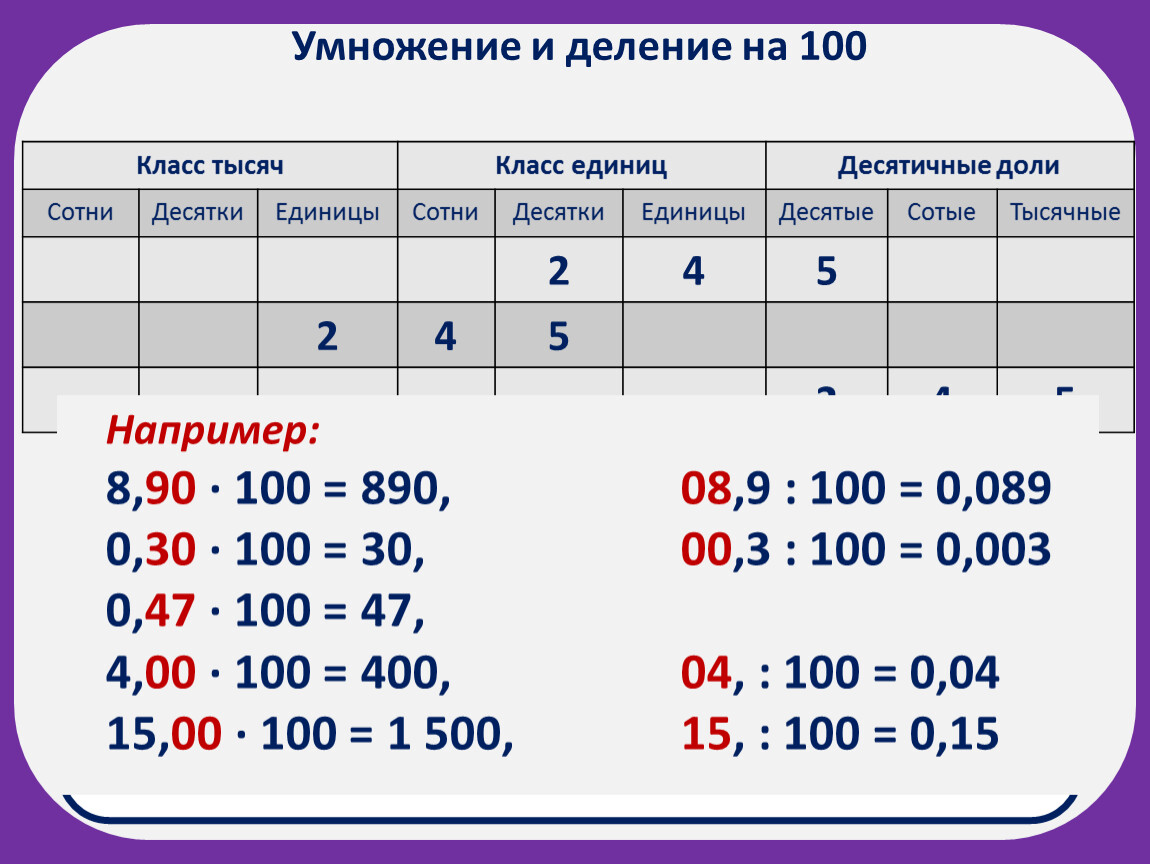 ..+Cnn-2·82+n·8+1—12n+7==8n+Cn1·8n-1·1+…+Cnn-2·82-4n+8==4·2·8n-1+2·Cn1·8n-2+…+2·Cnn-2·81-n+2
..+Cnn-2·82+n·8+1—12n+7==8n+Cn1·8n-1·1+…+Cnn-2·82-4n+8==4·2·8n-1+2·Cn1·8n-2+…+2·Cnn-2·81-n+2
можно будет разделить на 4 без остатка.
9n-12n+7 будет делиться на 4. Фактически, мы будем работать с выражением 9k-12k+7, которое должно делиться на 4.
Фактически, мы будем работать с выражением 9k-12k+7, которое должно делиться на 4.
Пример 5
содержится множитель 4.
Правило делимости на 4 — Методы, примеры также известен как тест на делимость на 4. Правило делимости на 4 помогает узнать, делится ли число на 4 или нет без выполнения деления. Первые четыре целых числа, которые делятся на 4, — это 0, 4, 8, 12 и 16. Все они кратны 4, и каждое кратное 4 полностью делится на 4.
1. Что такое правило делимости на 4? 2. Правило делимости на 4 для больших чисел 3. Правило делимости на 4 и 6 4. Признак делимости на 4 и 8 5. Часто задаваемые вопросы о правиле делимости числа 4 Что такое правило делимости на 4?
 Это означает, что число имеет нули в разряде десятков и разряде единиц. Например, в числе 300 последние две цифры 00, следовательно, 300 делится на 4.
Это означает, что число имеет нули в разряде десятков и разряде единиц. Например, в числе 300 последние две цифры 00, следовательно, 300 делится на 4. Правило делимости на 4 с примерами
Таким образом, 1124 делится на 4. Это можно проверить следующим образом: 1124 ÷ 4 = 281
Таким образом, 1171 не делится на 4.
1300 ÷ 4 = 325
Таким образом, 1300 делится на 4.
500 ÷ 4 = 125
Таким образом, 500 делится на 4. Правило делимости на 4 для больших чисел
238900 ÷ 4 = 59725
Таким образом, 238900 делится на 4.
148936 ÷ 4 = 37234
Таким образом, 148936 делится на 4. Правило делимости на 4 и 6
 Следовательно, можно сказать, что число 936 полностью делится на 6.
Следовательно, можно сказать, что число 936 полностью делится на 6. Признак делимости на 4 и 8
Правило делимости на 4 примера

б.) 549
в) 740
(100000 ÷ 4 = 25000)
(434788 ÷ 4 = 108697) Практические вопросы по правилу делимости 4
Часто задаваемые вопросы о правиле делимости числа 4
Что такое правило делимости на 4?
Используя правило делимости на 4, проверьте, делится ли 14540 на 4.

Каково правило делимости 4 и 8?

Как узнать, делится ли большое число на 4?
Используя правило делимости 4, проверьте, делится ли 19500 на 4. нули в конце или две последние цифры образуют число, которое точно делится на 4, тогда это число также делится на 4.
Какие числа делятся на 4?
Правила деления в математике
 Для многих наличие четкого набора правил и структуры помогает прояснить концепцию и помогает учащимся решать уравнения и манипулировать выражениями. Возможность проверки делимости может помочь во многих математических настройках, таких как возможность проверить решение, уменьшить дроби или проверить правильность расчета.
Для многих наличие четкого набора правил и структуры помогает прояснить концепцию и помогает учащимся решать уравнения и манипулировать выражениями. Возможность проверки делимости может помочь во многих математических настройках, таких как возможность проверить решение, уменьшить дроби или проверить правильность расчета. Каковы правила разделения?
ДЕЛИМОСТЬ НА 2
 . Например, если вы спросите учащихся, делится ли 168 на 3, они должны ответить следующим образом:
. Например, если вы спросите учащихся, делится ли 168 на 3, они должны ответить следующим образом: ДЕЛИМОСТЬ НА 4
ДЕЛИМОСТЬ НА 6
 Однако 3 + 0 + 8 = 11, что не может делиться на 3 без остатка. Таким образом, 308 не делится на 6.
Однако 3 + 0 + 8 = 11, что не может делиться на 3 без остатка. Таким образом, 308 не делится на 6. ДЕЛИМОСТЬ НА 9
ДЕЛИМОСТЬ НА 10

Перевод числа в градусы: Онлайн калькулятор: Перевод градусов в радианы
Перевести брэды в ° | двоичные градусы в градусы
Сумма: 1 двоичный градус (брад) угла
Равно: 1,41 градуса (°) по углу 1,41° преобразуется в 1 чего?
Брэд/° Угол Результат Из Символ .0032 ° Диаграмма конверсии —
Двоичные градусы до градусов  4 бинарных градуса в градусы = 5,63 °
4 бинарных градуса в градусы = 5,63 ° Углы
 Страница с отдельными угловыми единицами.
Страница с отдельными угловыми единицами.
Секунды: градус (°) является единицей измерения угла.
15 бред = ? °
15 брэд = 21,09 °
брэд
Аббревиатура для градуса:
° Другие приложения для этого углового калькулятора …
1. в практике бинарных степеней и степеней (брэд против °) измеряет обмен.
2. для коэффициентов пересчета между парами единиц.
3. работа со значениями и свойствами угла.
Ссылка на этот инструмент будет выглядеть так: преобразование угла из двоичных градусов (брад) в градусы (°).
Рабочие листы | TPT
 Всего включено 104 рабочих листа. Что включено: ♥ Рабочие листы по алфавиту — Работа с буквами ♥ Рабочие листы для начальных звуков — цвет по моему звуку ♥ Алфавит M
Всего включено 104 рабочих листа. Что включено: ♥ Рабочие листы по алфавиту — Работа с буквами ♥ Рабочие листы для начальных звуков — цвет по моему звуку ♥ Алфавит M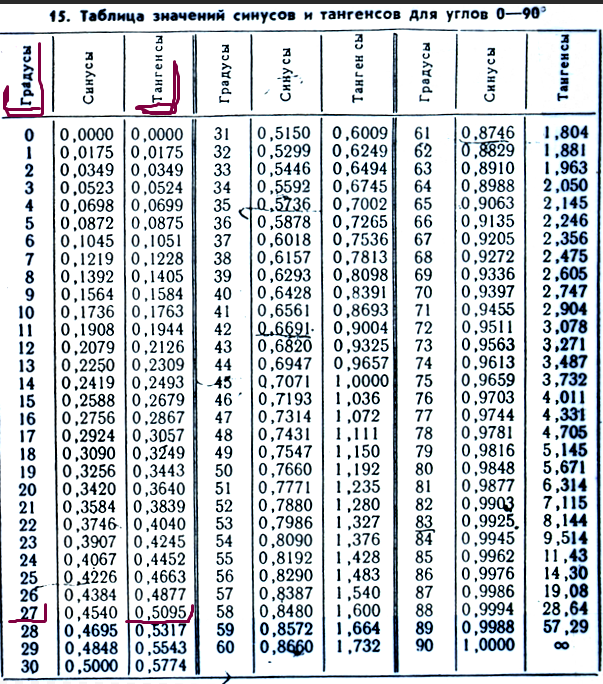 3.K. .K.3c, RF.1.2c, RF.1.2d…
3.K. .K.3c, RF.1.2c, RF.1.2d… Он включает рабочие листы для орграфов ch, sh, th, ph и wh. Бонусное включение диграфов ph и wh идеально подходит для того, чтобы бросить вызов вашим ученикам с более высокими способностями. Пакет включает в себя 42 увлекательных рабочих листа, которые позволяют учащимся практиковаться в написании диграфов, чтении диграфов, определении звуков диграфов и многому другому! Он идеально подходит для общеклассных занятий, математических станций, быстрых финишеров, домашних заданий и
Он включает рабочие листы для орграфов ch, sh, th, ph и wh. Бонусное включение диграфов ph и wh идеально подходит для того, чтобы бросить вызов вашим ученикам с более высокими способностями. Пакет включает в себя 42 увлекательных рабочих листа, которые позволяют учащимся практиковаться в написании диграфов, чтении диграфов, определении звуков диграфов и многому другому! Он идеально подходит для общеклассных занятий, математических станций, быстрых финишеров, домашних заданий и Эти партнерские карточки позволяют быстро и легко организовать дифференцированную работу в малых группах и идеально подходят для детей с любым уровнем способностей. Самое приятное то, что им не нужно угадывать, кто их партнер, это прямо на карте (whi
Эти партнерские карточки позволяют быстро и легко организовать дифференцированную работу в малых группах и идеально подходят для детей с любым уровнем способностей. Самое приятное то, что им не нужно угадывать, кто их партнер, это прямо на карте (whi 2.1, RL.2.2 .2.5…
2.1, RL.2.2 .2.5… RF.Ka, RF.Ka, RF.Ka, RF.Ka, RF.Ka. K.1b, RF.K.1c, RF.K.1d…
 Эти отрывки отлично подходят для детей младшего возраста, а также подойдут для первоклассников или первоклассников, в зависимости от того, как вы их используете. В комплекте много разнообразия. Пожалуйста, проверьте изображения и предварительный просмотр, чтобы увидеть, подойдут ли эти отрывки для ваших учеников. Отрывки разбиты на три категории… Первые 20 отрывков: Основная история с 3 вопросами. Студентам дается два ответа на выбор на каждый вопрос. Вторые 20 отрывков: Базовый
Эти отрывки отлично подходят для детей младшего возраста, а также подойдут для первоклассников или первоклассников, в зависимости от того, как вы их используете. В комплекте много разнообразия. Пожалуйста, проверьте изображения и предварительный просмотр, чтобы увидеть, подойдут ли эти отрывки для ваших учеников. Отрывки разбиты на три категории… Первые 20 отрывков: Основная история с 3 вопросами. Студентам дается два ответа на выбор на каждый вопрос. Вторые 20 отрывков: Базовый Рабочие листы охватывают сложение и вычитание до 10, разрядное значение, 2D и 3D-фигуры и числа до 20. Всего включено 126 рабочих листов, которые отлично подходят для использования круглый год. Этот комплект состоит из следующих пакетов: Рабочие листы для детского сада на сложение и вычитание. Детский сад Числа до 20. Работа 9.0014
Рабочие листы охватывают сложение и вычитание до 10, разрядное значение, 2D и 3D-фигуры и числа до 20. Всего включено 126 рабочих листов, которые отлично подходят для использования круглый год. Этот комплект состоит из следующих пакетов: Рабочие листы для детского сада на сложение и вычитание. Детский сад Числа до 20. Работа 9.0014 96
96 Используйте вопросы на понимание, чтобы оценить понимание после того, как учащиеся прочитают текст! *ОБНОВЛЕНИЕ* Теперь вы можете поделиться этим со своими учениками в цифровом виде! Этот ресурс был создан с помощью Google Forms. Для использования у вас должна быть электронная почта Google. Каждому проходу можно присвоить в Google Classr
Используйте вопросы на понимание, чтобы оценить понимание после того, как учащиеся прочитают текст! *ОБНОВЛЕНИЕ* Теперь вы можете поделиться этим со своими учениками в цифровом виде! Этот ресурс был создан с помощью Google Forms. Для использования у вас должна быть электронная почта Google. Каждому проходу можно присвоить в Google Classr Каждое общее ядро соответствует
Каждое общее ядро соответствует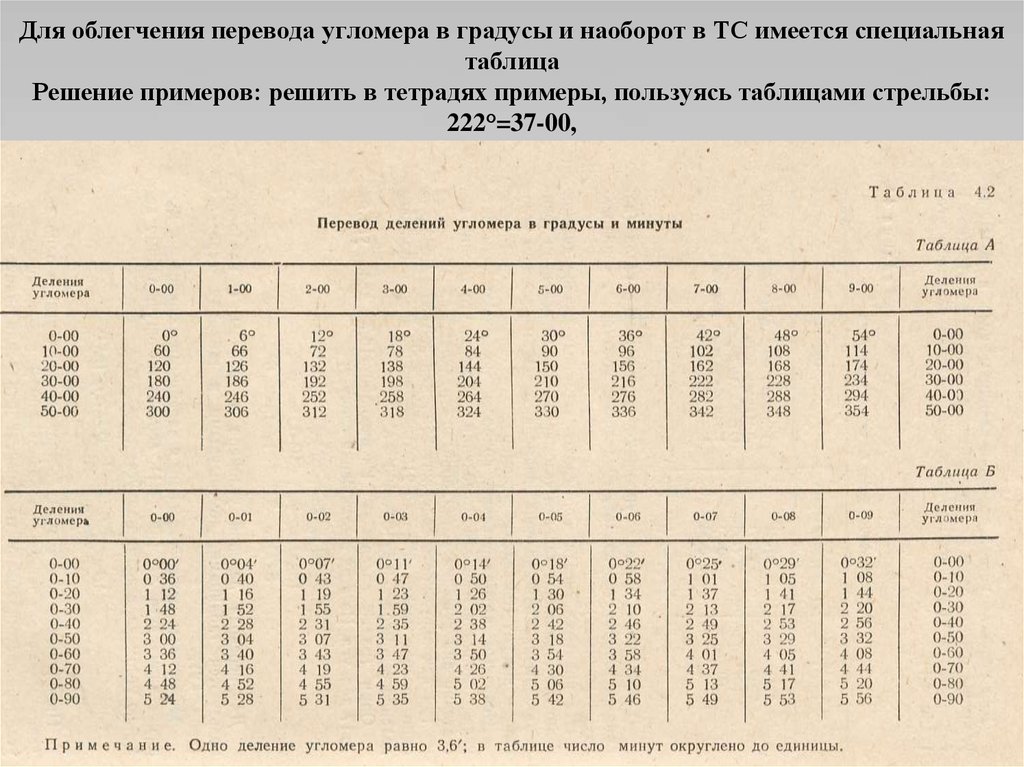 4.1, RL.4.2, RL.4. , RL.4.4, RL.4.5…
4.1, RL.4.2, RL.4. , RL.4.4, RL.4.5…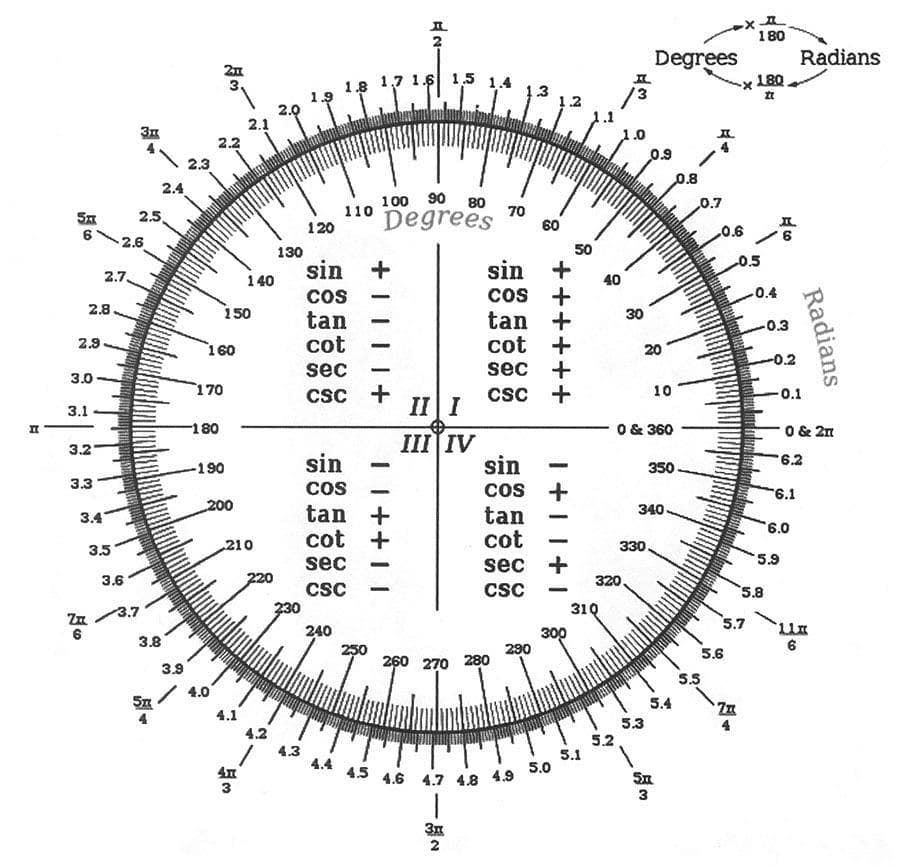 Учащиеся могут использовать эти наборы самостоятельно, в группах по обучению грамоте, в группах по чтению с гидом для выполнения домашних заданий или в качестве замены. Эти занятия проверяют навыки учащихся без утомительной болтовни, а также позволяют научить их
Учащиеся могут использовать эти наборы самостоятельно, в группах по обучению грамоте, в группах по чтению с гидом для выполнения домашних заданий или в качестве замены. Эти занятия проверяют навыки учащихся без утомительной болтовни, а также позволяют научить их Нажмите на предварительный просмотр, чтобы увидеть, что делает эти карточки такими особенными! Исследование чтения поддерживает изучение новых слов в предложении. Что включено? 400 карточек со словами с расшифровкой
Нажмите на предварительный просмотр, чтобы увидеть, что делает эти карточки такими особенными! Исследование чтения поддерживает изучение новых слов в предложении. Что включено? 400 карточек со словами с расшифровкой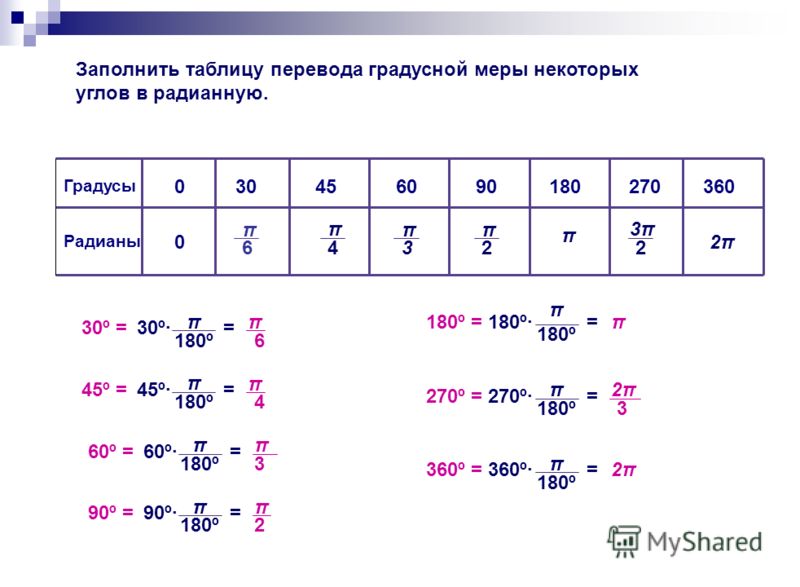 Независимо от того, отправляете ли вы информационный бюллетень домой еженедельно или ежемесячно, эти шаблоны облегчат вам задачу, а редактировать их очень просто! В эту загрузку включены: 24 различных ЦВЕТНЫХ шаблона информационного бюллетеня (цветной и черно-белый) 24 различных ЧЕРНО-БЕЛЫХ шаблона информационного бюллетеня шаблоны информационных бюллетеней
Независимо от того, отправляете ли вы информационный бюллетень домой еженедельно или ежемесячно, эти шаблоны облегчат вам задачу, а редактировать их очень просто! В эту загрузку включены: 24 различных ЦВЕТНЫХ шаблона информационного бюллетеня (цветной и черно-белый) 24 различных ЧЕРНО-БЕЛЫХ шаблона информационного бюллетеня шаблоны информационных бюллетеней Учащиеся могут обращаться к своей тетради для направленного рисования в течение года, если они забывают, как рисовать объект, который они уже выучили
Учащиеся могут обращаться к своей тетради для направленного рисования в течение года, если они забывают, как рисовать объект, который они уже выучили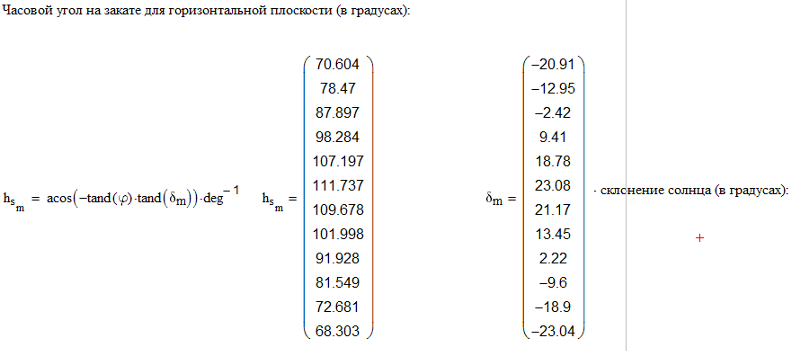 Охватываемые математические навыки от одного до
Охватываемые математические навыки от одного до Полностью пересмотрено! Теперь включает ключ ответа. Включены: * 5 страниц сложения 2 цифр (без перегруппировки) * 5 страниц сложения 2 цифр (перегруппировка) * 3 страниц сложения 2 цифр (с перегруппировкой и без нее) * 5 страниц вычитания 2 цифр (без перегруппировки)*5 страниц двухзначного вычитания (перегруппировка)*3 страницы двухзначного вычитания (с и с
Полностью пересмотрено! Теперь включает ключ ответа. Включены: * 5 страниц сложения 2 цифр (без перегруппировки) * 5 страниц сложения 2 цифр (перегруппировка) * 3 страниц сложения 2 цифр (с перегруппировкой и без нее) * 5 страниц вычитания 2 цифр (без перегруппировки)*5 страниц двухзначного вычитания (перегруппировка)*3 страницы двухзначного вычитания (с и с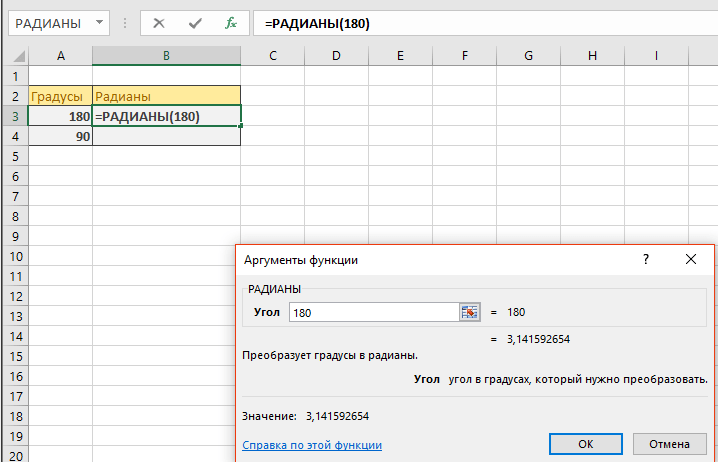
Уравнения с фигурной скобкой как решать: Решение систем уравнений — метод как решить систему линейных уравнений
Графический способ решения систем уравнений
 Фигурная скобка означает, что все уравнения должны выполняться одновременно.
Фигурная скобка означает, что все уравнения должны выполняться одновременно.

 Если система уравнений имеет бесконечно много решений, то она называется неопределённой.
Если система уравнений имеет бесконечно много решений, то она называется неопределённой.

Проект по математике «Уравнения и системы уравнений в ОГЭ»








 Поэтому для приведенного квадратного
уравнения формула корней
Поэтому для приведенного квадратного
уравнения формула корней е.
уравнение имеет одно решение;
е.
уравнение имеет одно решение; 4).
4). Получаем:
Получаем:
 Ф.
Ф.


Фигурная скобка над кратным уравнением — TeX
 Пока не нашел хорошего решения задачи:
Пока не нашел хорошего решения задачи: \начало{уравнение}
\begin{выровнено}
f (х) &= х + 1 \\
г (х) &= х + 2 \\
ч (х) &= х + 3 \\
к (х) &= х + 4 \\
л(х) &= х + 5
\end{выровнено}
\end{уравнение}
nicematrix и его мощные методы. \documentclass{статья}
\usepackage{аммат}
\usepackage{nicematrix}
\AtBeginEnvironment{NiceArray}{\tracinglostchars=0 }
\начать{документ}
\[
\renewcommand{\arraystretch}{1. 2}
\begin{NiceArray}{ @{} r @{} >{{}}c<{{}} @{} l l}
f(x) &=& x + 1 & \Block{2-1}{\text{независимо}}\\
г(х) &=& х + 2 \\
h(x) &=& x + 3 & \Block{3-1}{\text{что-то еще}}\\
к(х) &=& х + 4 \\
л(х) &=& х + 5 \\
\CodeAfter
\Подматрица.{1-3}{2-3}\}
\Подматрица.{3-3}{5-3}\}
\end{NiceArray}
\]
\конец{документ}
2}
\begin{NiceArray}{ @{} r @{} >{{}}c<{{}} @{} l l}
f(x) &=& x + 1 & \Block{2-1}{\text{независимо}}\\
г(х) &=& х + 2 \\
h(x) &=& x + 3 & \Block{3-1}{\text{что-то еще}}\\
к(х) &=& х + 4 \\
л(х) &=& х + 5 \\
\CodeAfter
\Подматрица.{1-3}{2-3}\}
\Подматрица.{3-3}{5-3}\}
\end{NiceArray}
\]
\конец{документ}
\tracinglostchars заключается в том, чтобы избежать ложных предупреждений (но они заслуживают некоторого изучения)., выровненных по , включая настройку \arraystretch . Мы строим две «подматрицы» с пустым разделителем слева и фигурными скобками справа, а также два блока, охватывающих две и три строки соответственно. = следующим образом: \newcolumntype{e}{@{{{$\mspace{\thinmuskip}$}}c@{{}} }
NiceArray from nicematrix хорошо подходит для таких целей \documentclass[11pt, a4paper]{article}
\usepackage{nicematrix}
\newcolumntype{e}{@{{$\mspace{\thinmuskip}$}}c@{{}}}
\начать{документ}
\begin{уравнение*}
\everymath{\displaystyle}
\begin{NiceArray}[cell-space-limits=3. 7pt]{r e @{\quad}l}
f(x) &= x + 1 & \Block[l]{2-1}{\text{Текст для $f(x)$} \\ \text{и $g(x)$}}
\\
г(х) &= х + 2 &
\\
h(x) &= x + 3 & \Block[l]{3-1}{\text{Текст для $h(x)$,} \\ \text{$k(x)$, и $k( х)$}}
\\
к (х) &= х + 4 &
\\
л(х) &= х + 5 &
\CodeAfter
\SubMatrix{.}{1-1}{2-2}{\}}[extra-height=-1.1pt]
\SubMatrix{.}{3-2}{5-2}{\}}[extra-height=-1.1pt]
\end{NiceArray}
\end{уравнение*}
\конец{документ}
7pt]{r e @{\quad}l}
f(x) &= x + 1 & \Block[l]{2-1}{\text{Текст для $f(x)$} \\ \text{и $g(x)$}}
\\
г(х) &= х + 2 &
\\
h(x) &= x + 3 & \Block[l]{3-1}{\text{Текст для $h(x)$,} \\ \text{$k(x)$, и $k( х)$}}
\\
к (х) &= х + 4 &
\\
л(х) &= х + 5 &
\CodeAfter
\SubMatrix{.}{1-1}{2-2}{\}}[extra-height=-1.1pt]
\SubMatrix{.}{3-2}{5-2}{\}}[extra-height=-1.1pt]
\end{NiceArray}
\end{уравнение*}
\конец{документ}
\documentclass{article}
\usepackage{аммат}
\начать{документ}
\begin{уравнение}
\begin{выровнено}
&\left.\begin{выровнено}
f (х) &= х + 1 \\
г (х) &= х + 2 \\
\end{выровнено}\right\}\hspace{0,5 см}\text{кое-что}\\
&\left.\begin{выровнено}
ч (х) &= х + 3 \\
к (х) &= х + 4 \\
л(х) &= х + 5
\конец{выровнено}\справа\}
\end{выровнено}
\end{уравнение}
\конец{документ}
 Однако, если вы действительно хотите принудительно выполнить выравнивание, решение менее простое, и я предлагаю вам взглянуть на следующий вопрос: ЗДЕСЬ
Однако, если вы действительно хотите принудительно выполнить выравнивание, решение менее простое, и я предлагаю вам взглянуть на следующий вопрос: ЗДЕСЬ Зарегистрируйтесь или войдите
Опубликовать как гость
Опубликовать как гость


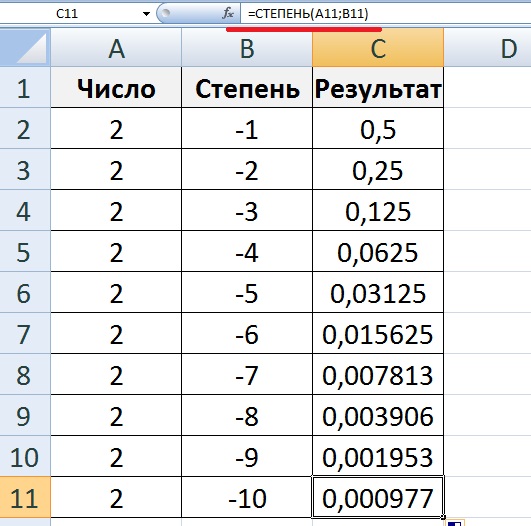 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  1/6 рядов — морковь. Остальное петрушка. Сколько рядов засажено петрушкой?
1/6 рядов — морковь. Остальное петрушка. Сколько рядов засажено петрушкой?



 Учитывал контекст, который задаёт этот термин всему смыслу блога.
Учитывал контекст, который задаёт этот термин всему смыслу блога. Не описывают задачу, как сущность, которую нужно опознать и отсортировать от других сущностей. Которой можно оперировать.
Не описывают задачу, как сущность, которую нужно опознать и отсортировать от других сущностей. Которой можно оперировать. Из которого получается, что это проблемы. Тогда опять же выходит смешение двух понятий, говорится, что задача – это проблема. По сути, выходит, это одно и то же.
Из которого получается, что это проблемы. Тогда опять же выходит смешение двух понятий, говорится, что задача – это проблема. По сути, выходит, это одно и то же.

 Воздействие всегда объектно. То есть воздействовать надо на что-либо или в отношении чего-либо. Нет объекта воздействия, не на что и воздействовать, а соответственно нет задачи.
Воздействие всегда объектно. То есть воздействовать надо на что-либо или в отношении чего-либо. Нет объекта воздействия, не на что и воздействовать, а соответственно нет задачи. В тексте блога я буду везде применять слово «декомпозиция», означающее разложение чего-то большого на более мелкие части.
В тексте блога я буду везде применять слово «декомпозиция», означающее разложение чего-то большого на более мелкие части. В названии задачи должен применяться глагол, нацеливающий на активные действия, а не на пассивное ожидание или вялотекущий процесс.
В названии задачи должен применяться глагол, нацеливающий на активные действия, а не на пассивное ожидание или вялотекущий процесс. Формулировка наименования задачи всегда начинается с глагола, нацеливающего на активные действия, отражающего вашу амбицию.
Формулировка наименования задачи всегда начинается с глагола, нацеливающего на активные действия, отражающего вашу амбицию.
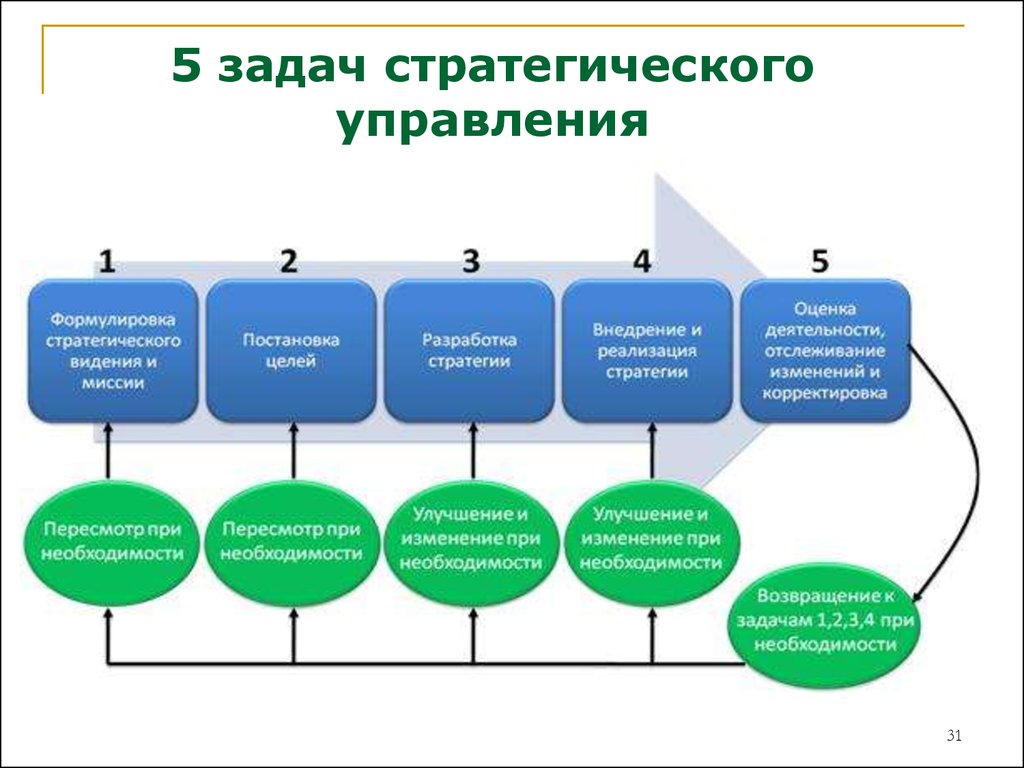
 д.
д. С другой стороны, управление задачами включает в себя микрофокус на достижении только выполнения задачи. Как управление проектами, так и управление задачами требуют участия команды и управления, чтобы убедиться, что ресурсы могут оптимально совмещать несколько рабочих элементов.
С другой стороны, управление задачами включает в себя микрофокус на достижении только выполнения задачи. Как управление проектами, так и управление задачами требуют участия команды и управления, чтобы убедиться, что ресурсы могут оптимально совмещать несколько рабочих элементов.
 Программное обеспечение для управления задачами для команд может помочь вам поддерживать связь между вашей командой.
Программное обеспечение для управления задачами для команд может помочь вам поддерживать связь между вашей командой.
 Скажите это всему, что не поможет в достижении вашей цели.
Скажите это всему, что не поможет в достижении вашей цели. При планировании оставьте место для неожиданного, но в остальном не позволяйте этому повлиять на вашу работу.
При планировании оставьте место для неожиданного, но в остальном не позволяйте этому повлиять на вашу работу. Возможность отслеживать ваши задачи, сроки, встречи и обязанности в команде делает программное обеспечение для управления задачами важным инструментом для ваших бизнес-потребностей. Если возникают какие-либо проблемы, достаточно одного щелчка мыши, чтобы понять точный источник проблемы, немедленно взять на себя управление и внести изменения, чтобы успешно улучшить рабочий процесс. Дополнительные функции для совместной работы, такие как чат, форумы и панель мониторинга, помогут всей вашей команде оставаться на связи и быть в курсе последних событий.
Возможность отслеживать ваши задачи, сроки, встречи и обязанности в команде делает программное обеспечение для управления задачами важным инструментом для ваших бизнес-потребностей. Если возникают какие-либо проблемы, достаточно одного щелчка мыши, чтобы понять точный источник проблемы, немедленно взять на себя управление и внести изменения, чтобы успешно улучшить рабочий процесс. Дополнительные функции для совместной работы, такие как чат, форумы и панель мониторинга, помогут всей вашей команде оставаться на связи и быть в курсе последних событий. От простых контрольных списков, которые могут даже не требовать подключения к Интернету, до полноценного программного обеспечения для управления задачами проекта, возможности разнообразны. Существуют также варианты программного обеспечения, которые подходят для конкретных отраслей, таких как строительство, ИТ или образование, или для конкретных функций, таких как управление задачами crm.
От простых контрольных списков, которые могут даже не требовать подключения к Интернету, до полноценного программного обеспечения для управления задачами проекта, возможности разнообразны. Существуют также варианты программного обеспечения, которые подходят для конкретных отраслей, таких как строительство, ИТ или образование, или для конкретных функций, таких как управление задачами crm.


 Менеджеры в то же время должны гарантировать, что компания сохранит текущий уровень успеха и подготовиться к внедрению изменений, которые принесут успех в будущем.
Менеджеры в то же время должны гарантировать, что компания сохранит текущий уровень успеха и подготовиться к внедрению изменений, которые принесут успех в будущем. Итак, создание и распространение мотивации — еще одна управленческая задача.
Итак, создание и распространение мотивации — еще одна управленческая задача.
