Таблица менделеева — Электронный учебник K-tree
Электронный учебник
Периодический закон, открытый Д. И. Менделеевым был выражен в таблице. Периодическая таблица химических элементов, или таблица менделеева.
1
H
1.008
2
He
4.003
3
Li
6.938
4
Be
9.012
5
B
10.806
6
C
12.01
7
N
14.006
8
O
15.999
9
F
18.998
10
Ne
20.18
11
Na
22.99
12
Mg
24.304
13
Al
26.982
14
Si
28.084
15
P
30.974
16
S
32.059
17
Cl
35.446
18
Ar
39.948
19
K
39.098
20
Ca
40.078
21
Sc
44.956
22
Ti
47.867
23
V
50.942
24
Cr
51. 996
996
25
Mn
54.938
26
Fe
55.845
27
Co
58.933
28
Ni
58.693
29
Cu
63.546
30
Zn
65.38
31
Ga
69.723
32
Ge
72.63
33
As
74.922
34
Se
78.971
35
Br
79.901
36
Kr
83.798
37
Rb
85.468
38
Sr
87.62
39
Y
88.906
40
Zr
91.224
41
Nb
92.906
42
Mo
95.95
44
Ru
101.07
45
Rh
102.906
46
Pd
106.42
47
Ag
107.868
48
Cd
112.414
49
In
114.818
50
Sn
118.71
51
Sb
121.76
52
Te
127.6
53
I
126.904
54
Xe
131.293
55
Cs
132.905
56
Ba
137.327
57
La
138.905
72
Hf
178. 49
49
73
Ta
180.948
74
W
183.84
75
Re
186.207
76
Os
190.23
77
Ir
192.217
78
Pt
195.084
79
Au
196.967
80
Hg
200.592
81
Tl
204.382
82
Pb
207.2
83
Bi
208.98
58
Ce
140.116
59
Pr
140.908
60
Nd
144.242
62
Sm
150.36
63
Eu
151.964
64
Gd
157.25
65
Tb
158.925
66
Dy
162.5
67
Ho
164.93
68
Er
167.259
69
Tm
168.934
70
Yb
173.045
71
Lu
174.967
90
Th
232.038
91
Pa
231.036
92
U
238.029
В таблице менделеева колонки называются группами, строки называются периодами. Элементы в группах как правило имеют
одинаковые электронные конфигурации внешних оболочек, например, благородные газы — последняя группа, имеют законченную
электронную конфигурацию.
Как заполняется электронная конфигурация элементов подробно описано в статье
Скачать таблицу менделеева в хорошем качестве
© 2015-2022 — K-Tree.ru • Электронный учебник
По любым вопросам Вы можете связаться по почте [email protected]
Копия материалов, размещённых на данном сайте, допускается только по письменному разрешению владельцев сайта.
AL-AL2O3-ALCL3-AL (OH)3-AL2O3-AL (NO3)3ПОМОГИТЕ ПОЖАЛУЙСТА!!! — Знания.site
Последние вопросы
Русский язык
1 минута назад
Прочитайте предложения. Найдите вводные слова и вводныепредложения, обозначьте их. Спишите, расставляя знаки препинания.1) Эта фраза пожалуй была сказана между прочим хотя её содержаниенапомнило мне между прочим одну двусмысле. .ую шутку.2) У Татьяны Андреевны к сож..лению замёрзли ресницы и (по)этомуей к..залось что от звезды падают на дорогу ломкие полосысвета. (К.Г.Паустовский)3) Письмо должно быть срочно доставле..о адресату потому чтокажется мы и так опаздываем с доставкой.4) А впрочем судьба наша кажет..ся одинакова и родились мы(по)вид..мому под еди..ым созвездием. (А. Пушкин)5) Почти (на)против его подвала прост..рался огромный пустырьгородской земли словом те..итория была внушительной. 6) После (не)состоявш..йся встречи с дядей к сожалениюпр..мешивалось ещё и чувство разоч..рования и это к сожалению мешалососредоточит..ся на серьёзных размышлениях.7) Книги брош..ры газеты словом все виды журнальной продукции во-первых валялись на полу во-вторых были (по)вид..мому в таком состоянииуже давно о чём свидетельствовал (в)час..ности слой пыли на них но этооднако не помешало нашему ра..ледованию.8) Потом (в)прочем он говорил что наверное (не)стоило горячит..ся(не)много поостыть и действовать уже (на)верняка (по)тому(что) по егомнению ситуация (до)конца (не)была проясне.
.ую шутку.2) У Татьяны Андреевны к сож..лению замёрзли ресницы и (по)этомуей к..залось что от звезды падают на дорогу ломкие полосысвета. (К.Г.Паустовский)3) Письмо должно быть срочно доставле..о адресату потому чтокажется мы и так опаздываем с доставкой.4) А впрочем судьба наша кажет..ся одинакова и родились мы(по)вид..мому под еди..ым созвездием. (А. Пушкин)5) Почти (на)против его подвала прост..рался огромный пустырьгородской земли словом те..итория была внушительной. 6) После (не)состоявш..йся встречи с дядей к сожалениюпр..мешивалось ещё и чувство разоч..рования и это к сожалению мешалососредоточит..ся на серьёзных размышлениях.7) Книги брош..ры газеты словом все виды журнальной продукции во-первых валялись на полу во-вторых были (по)вид..мому в таком состоянииуже давно о чём свидетельствовал (в)час..ности слой пыли на них но этооднако не помешало нашему ра..ледованию.8) Потом (в)прочем он говорил что наверное (не)стоило горячит..ся(не)много поостыть и действовать уже (на)верняка (по)тому(что) по егомнению ситуация (до)конца (не)была проясне. .а и у пр..сутствующих всё(же)ост..вались наверное вопросы.9) Увы он счастия не ищ..т и не от счастия бежит. (М.Ю. Лермонтов)10) Вронский к ужасу своему почувствовал что сделал скверноенепростительное движение. (Л.Н. Толстой)ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО
.а и у пр..сутствующих всё(же)ост..вались наверное вопросы.9) Увы он счастия не ищ..т и не от счастия бежит. (М.Ю. Лермонтов)10) Вронский к ужасу своему почувствовал что сделал скверноенепростительное движение. (Л.Н. Толстой)ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО Українська мова
1 минута назад
Згрупуйте спільнокореневі слова і запишіть. Яке явище відбувасться в поланих словах? — газ, газета, газівник, газетяр, газетка, газосховище, газетний; — хороший, хор, хорошенький, хорист, хоровод, хоровий; — вода, водити, водіння, підводнии, водичка, переводити, воджу.будь ласочкаГеография
1 минута назад
Розгляньте задачу з поясненням розв’язку. Оберіть правильну відповідь. На яку висоту піднявся літак, якщо за бортом температура повітря становить –30оС, в той час, як біля поверхні землі +24оС? Розв’язок: 1) +24oC-(-30oC )= 54 oC 2) 54oC : 6оС = Виберіть одну відповідь: 7 км 9 км 10 км 8 кмГеография
1 минута назад
доповіді про заповідники та національні парки України. Написати про один.
Написати про один.Українська мова
1 минута назад
За допомогою суфіксів -к-, -иц-. -ин-, -ес- від іменників чоловічого роду утворіть іменники на означення осто жіночо статі фемінтиви): Агент. автор. архітектор, кравець, філолог, диякон, депутат. виконавець. директор. доцент. етнограф, кравець, математик, шмець, педагог, президент продавець. полтик, служоовець, творець. філолог. фотограф.будь ласочкаУкраїнська мова
1 минута назад
виправте речення Я рахую, що до інтерв’ю треба готуватися дуже старательно. Правий журналіст, який задає самі важливі питання. До слідуючого запитання можна переходити, почувши відповідь на попереднє. Велике спасибі телебаченню за гарні взірці інтерв’ю. Упевнений, що подавляючі оцінки нашої
праці будуть положительні.
Упевнений, що подавляючі оцінки нашої
праці будуть положительні.Биология
1 минута назад
Вкажіть рослину на нижній поверхні листка якої розиіщуються спориМатематика
6 минут назад
Теория вероятностей. Помогите пожалуйстаДругие предметы
6 минут назад
Что означает местоимение «оно»? По отношению к кому его используют?Алгебра
6 минут назад
Помогите пожалуйста с алгебройЛитература
6 минут назад
Напишете пожалуйста сочинение по плану: «. ..что это было: любовь или сумасшествие?» (По рассказу А. Куприна «Гранатовый браслет»)
План
І. Тема любви в творчестве писателей и поэтов.
ІІ. Что это было: любовь или сумасшествие?
Глубина чувств Желткова.
Последнее письмо Желткова.
Отношение мужа Веры к чувствам и письмам Желткова.
ІІІ. Почему и в наши дни история Желткова волнует читателя? Какие чувства эта история пробудила во мне?
..что это было: любовь или сумасшествие?» (По рассказу А. Куприна «Гранатовый браслет»)
План
І. Тема любви в творчестве писателей и поэтов.
ІІ. Что это было: любовь или сумасшествие?
Глубина чувств Желткова.
Последнее письмо Желткова.
Отношение мужа Веры к чувствам и письмам Желткова.
ІІІ. Почему и в наши дни история Желткова волнует читателя? Какие чувства эта история пробудила во мне?История
6 минут назад
1. Який хрестовий похід(1-8) показав справжню суть хрестових походів? Чому? 2. Доведіть, що Франція, Англія та Іспанія були станово — представницькими монархіями. 3. Чому Генуя, Флоренція та Венеція були республіками? Помогите очень срочноМатематика
6 минут назад
2.Петя идет от дома до школы 40 минут, а его сестра – 60 минут. Через сколько минут Петя догонит сестру, если он вышел из дома через 10 минут после её ухода?
Через сколько минут Петя догонит сестру, если он вышел из дома через 10 минут после её ухода?Алгебра
6 минут назад
Проведите полное исследование функции y = 12x — x³ и постройте её графикФизика
11 минут назад
Пуля массой 10 г выпущенная под углом 60 к горизонту в верхней точке имеет кинетическую энергию равную 800 дж
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
Оксид алюминия | Свойства материала Al2O3
Глинозем является одним из
самый экономичный и широко используемый материал в семействе машиностроения
керамика. Сырье, из которого изготовлен этот высокоэффективный технический сорт
Керамика легкодоступна и доступна по разумной цене, что приводит к хорошему
значение стоимости изготовленных форм из оксида алюминия. С отличным сочетанием
свойств и привлекательной цене, неудивительно, что мелкое зерно
Технический глинозем имеет очень широкую область применения.
Сырье, из которого изготовлен этот высокоэффективный технический сорт
Керамика легкодоступна и доступна по разумной цене, что приводит к хорошему
значение стоимости изготовленных форм из оксида алюминия. С отличным сочетанием
свойств и привлекательной цене, неудивительно, что мелкое зерно
Технический глинозем имеет очень широкую область применения.
| . Ключ Свойства | |
| Твердый, износостойкий | |
| Отличные диэлектрические свойства в диапазоне частот от постоянного тока до ГГц | |
| Устойчив к воздействию сильных кислот и щелочей при повышенных температурах | |
| Хорошая теплопроводность | |
| Отличные размеры и форма | |
| Высокая прочность и жесткость | |
Доступен в диапазоне чистоты от 94%, легко металлизуемый состав, до
99,8% для самых требовательных высокотемпературных применений. | |
| . Типичное использование | |
| Газовые лазерные трубки | |
| Изнашиваемые накладки | |
| Уплотнительные кольца | |
| Изоляторы электрические высокотемпературные | |
| Изоляторы высокого напряжения | |
| Трубы футеровки печи | |
| Направляющие нити и проволоки | |
| Электронные подложки | |
| Баллистическая броня | |
| Абразивостойкие вкладыши для труб и колен | |
| Датчики термометрии | |
| Лабораторные пробирки и держатели образцов | |
| Детали приборов для машин для испытания тепловых свойств | |
| Мелющие тела | |
Оксид алюминия, обычно называемый глиноземом, обладает сильным ионным
межатомные связи, приводящие к желаемым характеристикам материала. Это
может существовать в нескольких кристаллических фазах, которые все возвращаются к наиболее стабильной
гексагональная альфа-фаза при повышенных температурах. Это фаза особого
интерес к структурным применениям и материалу, доступному от Accuratus.
Это
может существовать в нескольких кристаллических фазах, которые все возвращаются к наиболее стабильной
гексагональная альфа-фаза при повышенных температурах. Это фаза особого
интерес к структурным применениям и материалу, доступному от Accuratus.
Альфа-фаза глинозема самая прочная и жесткая из оксидной керамики. Его высокая твердость, превосходная диэлектрические свойства, огнеупорность и хорошие тепловые свойства делают его Материал выбора для широкого спектра применений.
Глинозем высокой чистоты
может использоваться как в окислительной, так и в восстановительной атмосфере до 1925°C. Потеря веса в
диапазон вакуума от 10 до 7 до 10 –6 г/см 2 мкс в диапазоне температур от 1700° до
2000°С. Он устойчив к воздействию всех газов, кроме влажного фтора, и устойчив к
все обычные реагенты, кроме плавиковой кислоты и фосфорной кислоты. Повышенный
температурная коррозия происходит в присутствии паров щелочных металлов, особенно при
более низкий уровень чистоты.
Состав керамическое тело может быть изменено, чтобы улучшить конкретный желаемый материал характеристики. Примером могут служить добавки оксида хрома или марганца. оксид для улучшения твердости и изменения цвета. Другие дополнения могут быть сделаны в улучшить легкость и консистенцию металлических пленок, обожженных на керамику для последующая сборка пайкой и пайкой.
Скачать техпаспорт 94% глинозема |
| 94% Оксид алюминия | |||
| Механический | Единицы Мера | СИ/Метрика | (Империал) |
| Плотность | г/куб. | 3,69 | (230,4) |
| Пористость | % (%) | 0 | (0) |
| Цвет | — | белый | — |
| Прочность на изгиб | МПа (фунт/дюйм 2 x10 3 ) | 330 | (47) |
| Модуль упругости | ГПа (фунт/дюйм 2 x10 6 ) | 300 | (43,5) |
| Модуль сдвига | ГПа (фунт/дюйм 2 x10 6 ) | 124 | (18) |
| Объемный модуль | ГПа (фунт/дюйм 2 x10 6 ) | 165 | (24) |
| Коэффициент Пуассона | — | 0,21 | (0,21) |
| Прочность на сжатие | МПа (фунт/дюйм 2 x10 3 ) | 2100 | (304,5) |
| Твердость | кг/мм 2 | 1175 | — |
| Прочность на излом K IC | МПа•м 1/2 | 3,5 | — |
| Максимальная рабочая температура (без нагрузки) | °С (°Ф) | 1700 | (3090) |
| Термический | | | |
| Теплопроводность | Вт/м•°К (БТЕ•дюйм/фут 2 •час•°F) | 18 | (125) |
| Коэффициент теплового расширения | 10 –6 /°С (10 –6 /°F) | 8. | (4,5) |
| Удельная теплоемкость | Дж/кг•°К (БТЕ/фунт•°F) | 880 | (0,21) |
| Электрика | | | |
| Диэлектрическая прочность | ак-кв/мм (вольт/мил) | 16,7 | (418) |
| Диэлектрическая проницаемость | @ 1 МГц | 9. | (9.1) |
| Коэффициент рассеяния | при 1 кГц | 0,0007 | (0,0007) |
| Тангенс потерь | при 1 кГц | — | — |
| Объемное удельное сопротивление | Ом•см | >10 14 | — |
Скачать техпаспорт 96% глинозема |
| 96% Оксид алюминия | |||
| Механический | Единицы Мера | СИ/Метрика | (Империал) |
| Плотность | г/куб. | 3,72 | (232,2) |
| Пористость | % (%) | 0 | (0) |
| Цвет | — | белый | — |
| Прочность на изгиб | МПа (фунт/дюйм 2 x10 3 ) | 345 | (50) |
| Модуль упругости | ГПа (фунт/дюйм 2 x10 6 ) | 300 | (43,5) |
| Модуль сдвига | ГПа (фунт/дюйм 2 x10 6 ) | 124 | (18) |
| Объемный модуль | ГПа (фунт/дюйм 2 x10 6 ) | 172 | (25) |
| Коэффициент Пуассона | — | 0,21 | (0,21) |
| Прочность на сжатие | МПа (фунт/дюйм 2 x10 3 ) | 2100 | (304,5) |
| Твердость | кг/мм 2 | 1100 | — |
| Прочность на излом K IC | МПа•м 1/2 | 3,5 | — |
| Максимальная рабочая температура (без нагрузки) | °С (°Ф) | 1700 | (3090) |
| Термический | | | |
| Теплопроводность | Вт/м•°К (БТЕ•дюйм/фут 2 •час•°F) | 25 | (174) |
| Коэффициент теплового расширения | 10 –6 /°С (10 –6 /°F) | 8. | (4,6) |
| Удельная теплоемкость | Дж/кг•°К (БТЕ/фунт•°F) | 880 | (0,21) |
| Электрика | | | |
| Диэлектрическая прочность | ак-кв/мм (вольт/мил) | 14,6 | (365) |
| Диэлектрическая проницаемость | @ 1 МГц | 9,0 | (9. |
| Коэффициент рассеяния | при 1 кГц | 0,0011 | (0,0011) |
| Тангенс потерь | при 1 кГц | — | — |
| Объемное удельное сопротивление | Ом•см | >10 14 | — |
Скачать техническое описание 99,5% глинозема |
| 99,5% Оксид алюминия | |||
| Механический | Единицы Мера | СИ/Метрика | (Империал) |
| Плотность | г/куб. | 3,89 | (242,8) |
| Пористость | % (%) | 0 | (0) |
| Цвет | — | слоновая кость | — |
| Прочность на изгиб | МПа (фунт/дюйм 2 x10 3 ) | 379 | (55) |
| Модуль упругости | ГПа (фунт/дюйм 2 x10 6 ) | 375 | (54,4) |
| Модуль сдвига | ГПа (фунт/дюйм 2 x10 6 ) | 152 | (22) |
| Объемный модуль | ГПа (фунт/дюйм 2 x10 6 ) | 228 | (33) |
| Коэффициент Пуассона | — | 0,22 | (0,22) |
| Прочность на сжатие | МПа (фунт/дюйм 2 x10 3 ) | 2600 | (377) |
| Твердость | кг/мм 2 | 1440 | — |
| Прочность на излом K IC | МПа•м 1/2 | 4 | — |
| Максимальная рабочая температура (без нагрузки) | °С (°Ф) | 1750 | (3180) |
| Термический | | | |
| Теплопроводность | Вт/м°К (БТЕ•дюйм/фут 2 •час•°F) | 35 | (243) |
| Коэффициент теплового расширения | 10 –6 /°С (10 –6 /°F) | 8. | (4.7) |
| Удельная теплоемкость | Дж/кг•°К (БТЕ/фунт•°F) | 880 | (0,21) |
| Электрика | | | |
| Диэлектрическая прочность | ак-кв/мм (вольт/мил) | 16,9 | (420) |
| Диэлектрическая проницаемость | @ 1 МГц | 9,8 | (9,8) |
| Коэффициент рассеяния | при 1 кГц | 0,0002 | (0,0002) |
| Тангенс потерь | при 1 кГц | — | — |
| Объемное удельное сопротивление | Ом•см | >10 14 | — |
*Все объекты являются комнатами
значения температуры, если не указано иное.
Представленные данные типичны для имеющегося в продаже материала и предлагаются
только для сравнительных целей. Информация не должна интерпретироваться как
абсолютные свойства материала, а также не является заявлением или гарантией
за что мы берем на себя юридическую ответственность. Пользователь должен определить пригодность
материал для использования по назначению и принимает на себя все риски и ответственность, какие бы
связь с ним.
См. также:
Керамический стержень и трубка
См. также: Керамический стержень и трубка > Доступный оксид алюминия
Размеры
Вернуться к началу
Стандартные продукты | Индивидуальные продукты и услуги
| Тематические исследования | Материалы
Примечания по дизайну
| Работаем вместе | Зрение
| Свяжитесь с нами | Карта сайта
1-908-213-7070
© 2013 Аккурат
Дизайн площадки М. Адамс
Материалы Данные по AlO3 по проекту материалов (набор данных)
Материалы Данные по AlO3 по проекту материалов (набор данных) | Исследователь данных Министерства энергетики США- Набор данных
- Другие связанные исследования
AlO3 имеет структуру, подобную альфа-триоксиду рения, и кристаллизуется в тригональной пространственной группе R-3c. Структура трехмерная. Al связан с шестью эквивалентными атомами O, образуя октаэдры AlO6 с общими углами. Углы наклона октаэдра с общим углом равны 9°. Все длины связи Al–O равны 1,86 Å. O связан в линейной геометрии с двумя эквивалентными атомами Al.
Структура трехмерная. Al связан с шестью эквивалентными атомами O, образуя октаэдры AlO6 с общими углами. Углы наклона октаэдра с общим углом равны 9°. Все длины связи Al–O равны 1,86 Å. O связан в линейной геометрии с двумя эквивалентными атомами Al.
- Авторов:
- Проект материалов
- Дата публикации:
- Другие номера:
- мп-35200
- Номер контракта Министерства энергетики:
- АЦ02-05Ч21231; EDCBEE
- Исследовательская организация:
- Национальная лаборатория Лоуренса Беркли. (LBNL), Беркли, Калифорния (США). Материалы LBNL Проект
- Организация-спонсор:
- Департамент науки Министерства энергетики США (SC), Базовые энергетические науки (BES)
- Сотрудничество:
- Массачусетский технологический институт; Калифорнийский университет в Беркли; герцог; У Лувен
- Тема:
- 36 МАТЕРИАЛОВЕДЕНИЕ
- Ключевые слова: кристаллическая структура
- ; AlO3; Ал-О
- Идентификатор ОСТИ:
- 1206950
- DOI:
- https://doi.
 org/10.17188/1206950
org/10.17188/1206950
Форматы цитирования
- MLA
- АПА
- Чикаго
- БибТекс
Проект материалов. Материалы Данные по AlO3 по материалам Проект . США: Н. П., 2020.
Веб. дои: 10.17188/1206950.
Копировать в буфер обмена
Проект материалов. Материалы Данные по AlO3 по материалам Проект . Соединенные Штаты. Дои: https://doi.org/10.17188/1206950
Копировать в буфер обмена
Проект материалов. 2020.
«Материальные данные по AlO3 по проекту материалов». Соединенные Штаты. дои: https://doi.org/10.17188/1206950. https://www.osti.gov/servlets/purl/1206950. Дата публикации: четверг, 23 июля, 00:00:00 по восточному поясному времени 2020
Копировать в буфер обмена
@article{osti_1206950,
title = {Данные материалов по AlO3 по проекту материалов},
автор = {Проект материалов},
abstractNote = {AlO3 имеет структуру, подобную альфа-триоксиду рения, и кристаллизуется в тригональной пространственной группе R-3c.

 .ую шутку.2) У Татьяны Андреевны к сож..лению замёрзли ресницы и (по)этомуей к..залось что от звезды падают на дорогу ломкие полосысвета. (К.Г.Паустовский)3) Письмо должно быть срочно доставле..о адресату потому чтокажется мы и так опаздываем с доставкой.4) А впрочем судьба наша кажет..ся одинакова и родились мы(по)вид..мому под еди..ым созвездием. (А. Пушкин)5) Почти (на)против его подвала прост..рался огромный пустырьгородской земли словом те..итория была внушительной. 6) После (не)состоявш..йся встречи с дядей к сожалениюпр..мешивалось ещё и чувство разоч..рования и это к сожалению мешалососредоточит..ся на серьёзных размышлениях.7) Книги брош..ры газеты словом все виды журнальной продукции во-первых валялись на полу во-вторых были (по)вид..мому в таком состоянииуже давно о чём свидетельствовал (в)час..ности слой пыли на них но этооднако не помешало нашему ра..ледованию.8) Потом (в)прочем он говорил что наверное (не)стоило горячит..ся(не)много поостыть и действовать уже (на)верняка (по)тому(что) по егомнению ситуация (до)конца (не)была проясне.
.ую шутку.2) У Татьяны Андреевны к сож..лению замёрзли ресницы и (по)этомуей к..залось что от звезды падают на дорогу ломкие полосысвета. (К.Г.Паустовский)3) Письмо должно быть срочно доставле..о адресату потому чтокажется мы и так опаздываем с доставкой.4) А впрочем судьба наша кажет..ся одинакова и родились мы(по)вид..мому под еди..ым созвездием. (А. Пушкин)5) Почти (на)против его подвала прост..рался огромный пустырьгородской земли словом те..итория была внушительной. 6) После (не)состоявш..йся встречи с дядей к сожалениюпр..мешивалось ещё и чувство разоч..рования и это к сожалению мешалососредоточит..ся на серьёзных размышлениях.7) Книги брош..ры газеты словом все виды журнальной продукции во-первых валялись на полу во-вторых были (по)вид..мому в таком состоянииуже давно о чём свидетельствовал (в)час..ности слой пыли на них но этооднако не помешало нашему ра..ледованию.8) Потом (в)прочем он говорил что наверное (не)стоило горячит..ся(не)много поостыть и действовать уже (на)верняка (по)тому(что) по егомнению ситуация (до)конца (не)была проясне. .а и у пр..сутствующих всё(же)ост..вались наверное вопросы.9) Увы он счастия не ищ..т и не от счастия бежит. (М.Ю. Лермонтов)10) Вронский к ужасу своему почувствовал что сделал скверноенепростительное движение. (Л.Н. Толстой)ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО
.а и у пр..сутствующих всё(же)ост..вались наверное вопросы.9) Увы он счастия не ищ..т и не от счастия бежит. (М.Ю. Лермонтов)10) Вронский к ужасу своему почувствовал что сделал скверноенепростительное движение. (Л.Н. Толстой)ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО  Написати про один.
Написати про один. Упевнений, що подавляючі оцінки нашої
праці будуть положительні.
Упевнений, що подавляючі оцінки нашої
праці будуть положительні. ..что это было: любовь или сумасшествие?» (По рассказу А. Куприна «Гранатовый браслет»)
План
І. Тема любви в творчестве писателей и поэтов.
ІІ. Что это было: любовь или сумасшествие?
Глубина чувств Желткова.
Последнее письмо Желткова.
Отношение мужа Веры к чувствам и письмам Желткова.
ІІІ. Почему и в наши дни история Желткова волнует читателя? Какие чувства эта история пробудила во мне?
..что это было: любовь или сумасшествие?» (По рассказу А. Куприна «Гранатовый браслет»)
План
І. Тема любви в творчестве писателей и поэтов.
ІІ. Что это было: любовь или сумасшествие?
Глубина чувств Желткова.
Последнее письмо Желткова.
Отношение мужа Веры к чувствам и письмам Желткова.
ІІІ. Почему и в наши дни история Желткова волнует читателя? Какие чувства эта история пробудила во мне? Через сколько минут Петя догонит сестру, если он вышел из дома через 10 минут после её ухода?
Через сколько минут Петя догонит сестру, если он вышел из дома через 10 минут после её ухода? см
(фунт/фут 3 )
см
(фунт/фут 3 ) 1
1 1
1 см
(фунт/фут 3 )
см
(фунт/фут 3 ) 2
2 0)
0) см
(фунт/фут 3 )
см
(фунт/фут 3 ) 4
4 org/10.17188/1206950
org/10.17188/1206950 ), квадратный корень (√), скобки и π (число пи), уже поддерживаются на настоящий момент.
), квадратный корень (√), скобки и π (число пи), уже поддерживаются на настоящий момент. Как вариант, преобразуемое значение можно ввести следующим образом: ’34 мА в А‘ или ’68 мА сколько А‘ или ’20 миллиампер -> ампер‘ или ’60 мА = А‘ или ’36 миллиампер в А‘ или ’47 мА в ампер‘ или ’54 миллиампер сколько ампер‘. В этом случае калькулятор также сразу поймет, в какую единицу измерения нужно преобразовать исходное значение. Независимо от того, какой из этих вариантов используется, исключается необходимость сложного поиска нужного значения в длинных списках выбора с бесчисленными категориями и бесчисленным количеством поддерживаемых единиц измерения. Все это за нас делает калькулятор, который справляется со своей задачей за доли секунды.
Как вариант, преобразуемое значение можно ввести следующим образом: ’34 мА в А‘ или ’68 мА сколько А‘ или ’20 миллиампер -> ампер‘ или ’60 мА = А‘ или ’36 миллиампер в А‘ или ’47 мА в ампер‘ или ’54 миллиампер сколько ампер‘. В этом случае калькулятор также сразу поймет, в какую единицу измерения нужно преобразовать исходное значение. Независимо от того, какой из этих вариантов используется, исключается необходимость сложного поиска нужного значения в длинных списках выбора с бесчисленными категориями и бесчисленным количеством поддерживаемых единиц измерения. Все это за нас делает калькулятор, который справляется со своей задачей за доли секунды. 3′. Объединенные таким образом единицы измерения, естественно, должны соответствовать друг другу и иметь смысл в заданной комбинации.
3′. Объединенные таким образом единицы измерения, естественно, должны соответствовать друг другу и иметь смысл в заданной комбинации. Такой точности должно хватить для большинства целей.
Такой точности должно хватить для большинства целей.
 2}=\left|а-2\right|+\left|а-4\right|\)
2}=\left|а-2\right|+\left|а-4\right|\) Большинство других программ просто дают вам ответ, который не помог мне, когда дело дошло до времени тестирования, Algebrator помог мне шаг за шагом решить каждую проблему. Спасибо!
Большинство других программ просто дают вам ответ, который не помог мне, когда дело дошло до времени тестирования, Algebrator помог мне шаг за шагом решить каждую проблему. Спасибо!  com
com также: Кубический корень — калькулятор
также: Кубический корень — калькулятор




 {\prime}=x+0=f(x)$
{\prime}=x+0=f(x)$
 е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Сначала важно помнить, что на самом деле мы просто спрашиваем, что мы дифференцировали, чтобы получить данную функцию.
Сначала важно помнить, что на самом деле мы просто спрашиваем, что мы дифференцировали, чтобы получить данную функцию. 25in}\,\,\,\,c{\mbox{ произвольная константа}}\]
25in}\,\,\,\,c{\mbox{ произвольная константа}}\] Это необходимо! Думайте о знаке интеграла и dx как о наборе скобок. Вы уже знаете и, вероятно, вполне довольны идеей, что каждый раз, когда вы открываете скобку, вы должны ее закрывать. В интегралах думайте о знаке интеграла как о «открытой скобке», а 95} + c + 3x — 9\end{выравнивание*}\]
Это необходимо! Думайте о знаке интеграла и dx как о наборе скобок. Вы уже знаете и, вероятно, вполне довольны идеей, что каждый раз, когда вы открываете скобку, вы должны ее закрывать. В интегралах думайте о знаке интеграла как о «открытой скобке», а 95} + c + 3x — 9\end{выравнивание*}\]
 Однако, если вы находитесь на пути к получению степени, который приведет вас к исчислению с несколькими переменными, это будет очень важно на этом этапе, поскольку в задаче будет более одной переменной. Вам нужно выработать привычку записывать правильный дифференциал в конце интеграла, чтобы, когда он станет важным в этих классах, вы уже привыкли записывать его. 92} + с\]
Однако, если вы находитесь на пути к получению степени, который приведет вас к исчислению с несколькими переменными, это будет очень важно на этом этапе, поскольку в задаче будет более одной переменной. Вам нужно выработать привычку записывать правильный дифференциал в конце интеграла, чтобы, когда он станет важным в этих классах, вы уже привыкли записывать его. 92} + с\]

 92} — 9х + с\]
92} — 9х + с\]
 Если мы начнем с определения ff как локально интегрируемой функции? на отрезке II, содержащем аа, то полуопределенный интеграл также будет иметь областью определения II. 9х f(t) \,\mathrm{d}t .
Если мы начнем с определения ff как локально интегрируемой функции? на отрезке II, содержащем аа, то полуопределенный интеграл также будет иметь областью определения II. 9х f(t) \,\mathrm{d}t . \forall\, x \in \dom F,\; f(x) = F'(x) .
\forall\, x \in \dom F,\; f(x) = F'(x) . Для различных определений интеграла можно доказать, что каждый полуопределенный интеграл или вообще любой неопределенный интеграл в смысле определения является первообразной; и что каждая первообразная или, вообще говоря, каждая почти первообразная является неопределенным интегралом; возможно, с техническими условиями (в зависимости от типа рассматриваемого интеграла), такими как дифференцируемость или абсолютная непрерывность. Подробнее см. в этой статье.
Для различных определений интеграла можно доказать, что каждый полуопределенный интеграл или вообще любой неопределенный интеграл в смысле определения является первообразной; и что каждая первообразная или, вообще говоря, каждая почти первообразная является неопределенным интегралом; возможно, с техническими условиями (в зависимости от типа рассматриваемого интеграла), такими как дифференцируемость или абсолютная непрерывность. Подробнее см. в этой статье. Тогда, когда PP является точкой в SS (или, возможно, ее замыканием), мы можем определить значение полуопределенного интеграла от ω\omega с начальной точкой PP как интеграл от ω\omega вдоль отрезка прямой от PP; домен представляет собой звездно-выпуклое множество? исходящие из ПП и содержащиеся в (замыкании) СС. Если мы определим неопределенный интеграл как полуопределенный интеграл плюс постоянное начальное значение, то каждая первообразная ω \ omega на звездно-выпуклом множестве является неопределенным интегралом. Обратно, всякий неопределенный интеграл является первообразной, если ω\omega замкнута. Если ω \ omega не замкнута, то у нее все еще есть неопределенные интегралы (пока они непрерывны или иным образом локально интегрируемы), но они больше не являются первообразными (чего никогда не бывает у незамкнутых форм).
Тогда, когда PP является точкой в SS (или, возможно, ее замыканием), мы можем определить значение полуопределенного интеграла от ω\omega с начальной точкой PP как интеграл от ω\omega вдоль отрезка прямой от PP; домен представляет собой звездно-выпуклое множество? исходящие из ПП и содержащиеся в (замыкании) СС. Если мы определим неопределенный интеграл как полуопределенный интеграл плюс постоянное начальное значение, то каждая первообразная ω \ omega на звездно-выпуклом множестве является неопределенным интегралом. Обратно, всякий неопределенный интеграл является первообразной, если ω\omega замкнута. Если ω \ omega не замкнута, то у нее все еще есть неопределенные интегралы (пока они непрерывны или иным образом локально интегрируемы), но они больше не являются первообразными (чего никогда не бывает у незамкнутых форм). (Например, на сфере, пока ω\omega интегрируема, мы можем определить таким образом неопределенный интеграл в любой точке, кроме той, которая находится прямо напротив начальной точки.)
(Например, на сфере, пока ω\omega интегрируема, мы можем определить таким образом неопределенный интеграл в любой точке, кроме той, которая находится прямо напротив начальной точки.)
 Расчет данной системы происходит в определенной экспресс-ставке, после будут складываться все числа и в результате появляется выигрыш. Притом букмекер может выставлять ограничения на определенные ставки в системе. Представлены они на огромное количество исходов, и могут насчитываться в объеме 12-20. Минимальное число событий, начинается от трех и более.
Расчет данной системы происходит в определенной экспресс-ставке, после будут складываться все числа и в результате появляется выигрыш. Притом букмекер может выставлять ограничения на определенные ставки в системе. Представлены они на огромное количество исходов, и могут насчитываться в объеме 12-20. Минимальное число событий, начинается от трех и более. Ставки в объеме 1000 гривен можно поделить на четыре позиций, получаем по 250 гривен на каждую. К примеру, победителями оказываются выборы 1,3,4, это значит, что в системе выигрывает одна комбинация, которая состоит с данных выборов. Считать коэффициент можно следующим образом:
Ставки в объеме 1000 гривен можно поделить на четыре позиций, получаем по 250 гривен на каждую. К примеру, победителями оказываются выборы 1,3,4, это значит, что в системе выигрывает одна комбинация, которая состоит с данных выборов. Считать коэффициент можно следующим образом: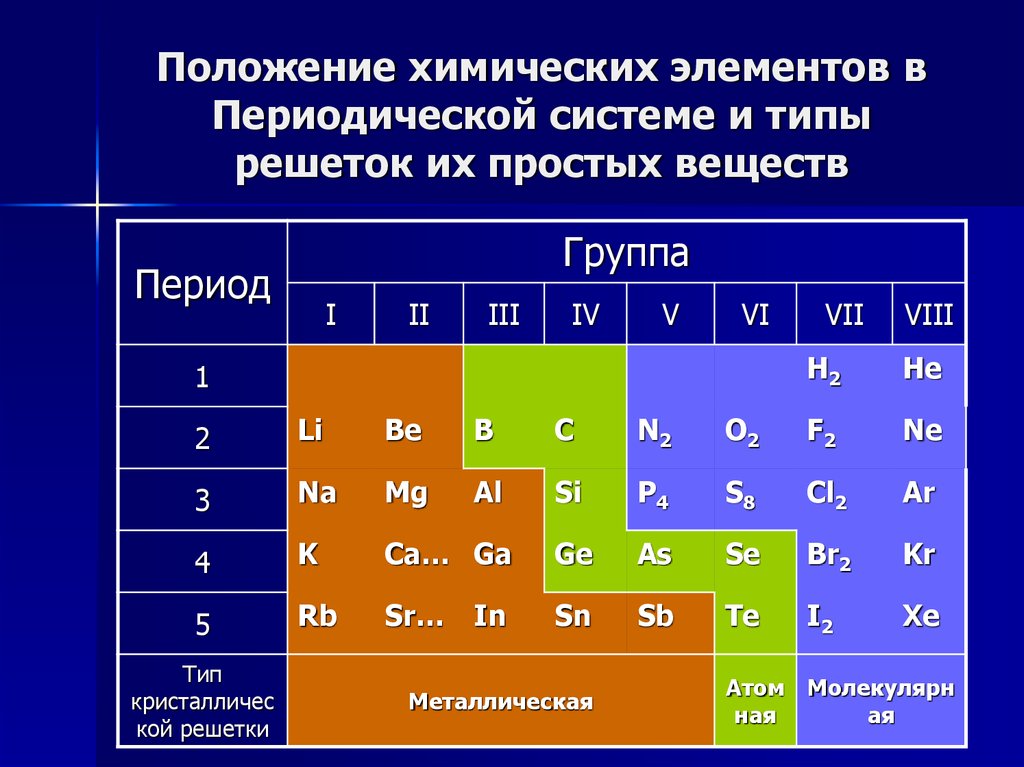
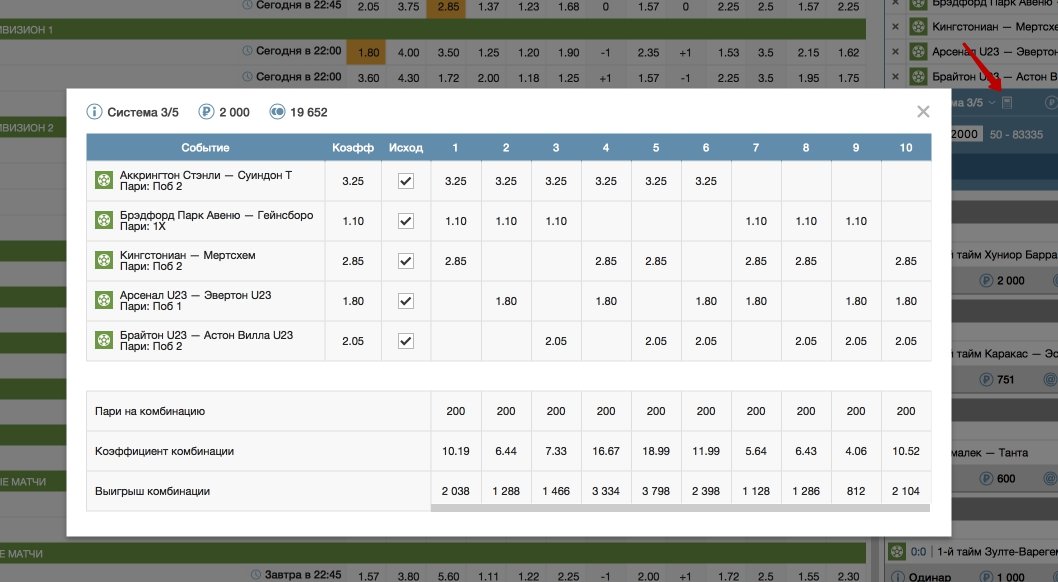
 Возможно, ими могут стать:
Возможно, ими могут стать: Соответственно особенностью букмекера перед бетторами заметно возрастет. Система практически ничем не отличается от экспресс-ставок.
Соответственно особенностью букмекера перед бетторами заметно возрастет. Система практически ничем не отличается от экспресс-ставок. Отличительными свойствами по сравнению с экспрессами – является то, что даже при проигрыше определенных событий пользователи могут начать получать доход. Расчет системы будет зависеть только от определенного коэффициента, сыгравших при событиях, которые были заданы по размерности ставок.
Отличительными свойствами по сравнению с экспрессами – является то, что даже при проигрыше определенных событий пользователи могут начать получать доход. Расчет системы будет зависеть только от определенного коэффициента, сыгравших при событиях, которые были заданы по размерности ставок. Ставки по системе «2 с 3» — как понять?
Ставки по системе «2 с 3» — как понять?
 2(a) Система 8 на выбор из восьми (8) номеров . Система 9 для выбора из девяти (9) номеров . Система 10 на выбор из десяти (10) номера . Система 11 на выбор из одиннадцати (11) номеров . Система 12 на выбор …
2(a) Система 8 на выбор из восьми (8) номеров . Система 9 для выбора из девяти (9) номеров . Система 10 на выбор из десяти (10) номера . Система 11 на выбор из одиннадцати (11) номеров . Система 12 на выбор … com
com Шанс 83 816. Кроме того, как работает Toto ?
Шанс 83 816. Кроме того, как работает Toto ?
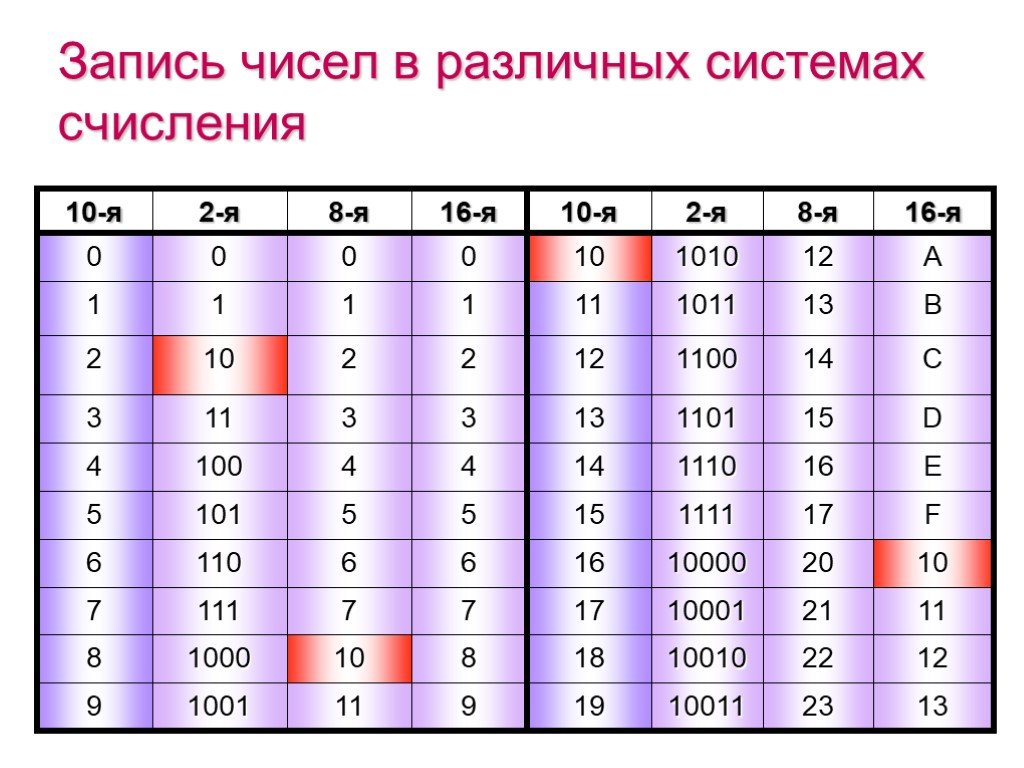 В этой таблице рассказывается о каждой Системе , о том, сколько комбинаций вы можете иметь и о том, сколько сколько стоит играть. Стоимость комбинации 1 руб.
В этой таблице рассказывается о каждой Системе , о том, сколько комбинаций вы можете иметь и о том, сколько сколько стоит играть. Стоимость комбинации 1 руб. Это обойдется вам в 10 раз больше вашей ставки.
Это обойдется вам в 10 раз больше вашей ставки.
 2
2 3
3 14159..
14159.. )/3
)/3
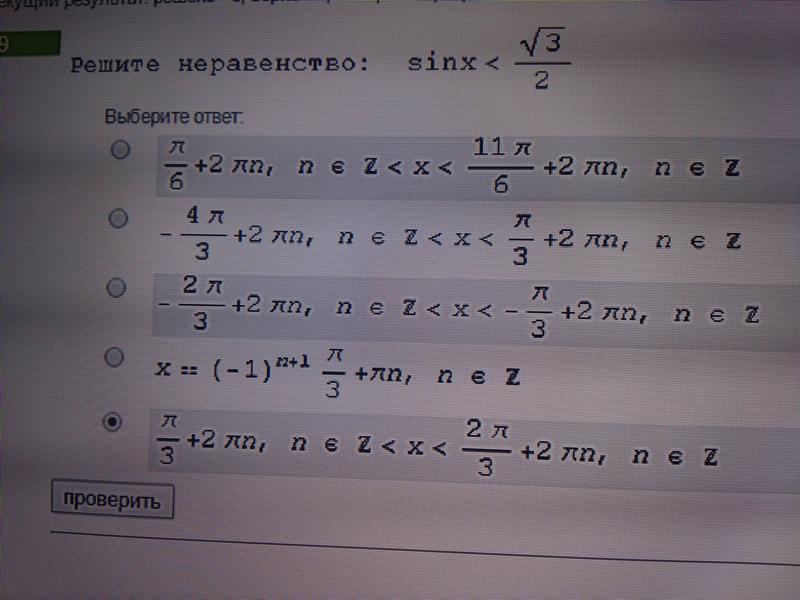 2 интегрирование DX на cos x минус 5 на 3 равно cos x минус 5 на 3 единицы на cos theta в это равно 1 при 2 интегрировании сек x минус 5 на
2 интегрирование DX на cos x минус 5 на 3 равно cos x минус 5 на 3 единицы на cos theta в это равно 1 при 2 интегрировании сек x минус 5 на
 14159..
14159.. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.
3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.  Частотные характеристики САР
Частотные характеристики САР рисунок 6.4.3:
рисунок 6.4.3: Обозначим изменение фазы как
Обозначим изменение фазы как Преобразуем скобку
Преобразуем скобку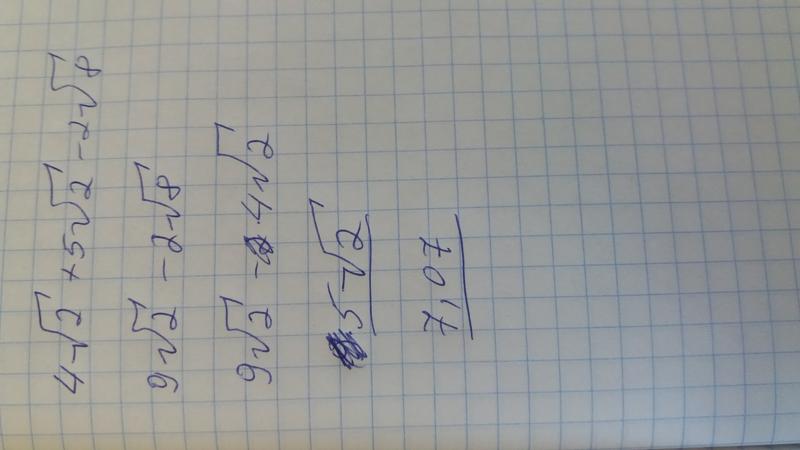
 рисунок 6.4.12):
рисунок 6.4.12): 4.15.
4.15.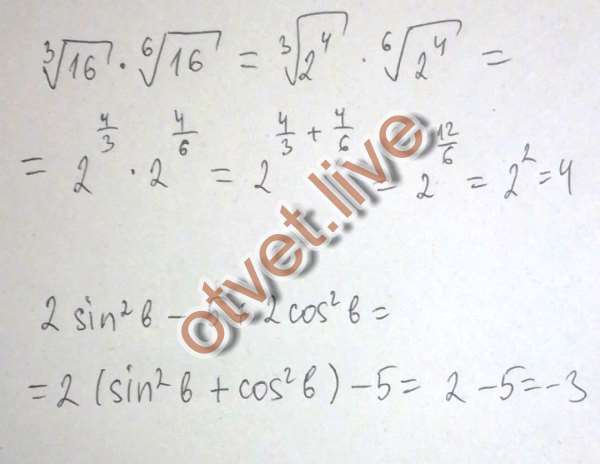

 Параллелограмм и его свойства.
Параллелограмм и его свойства.





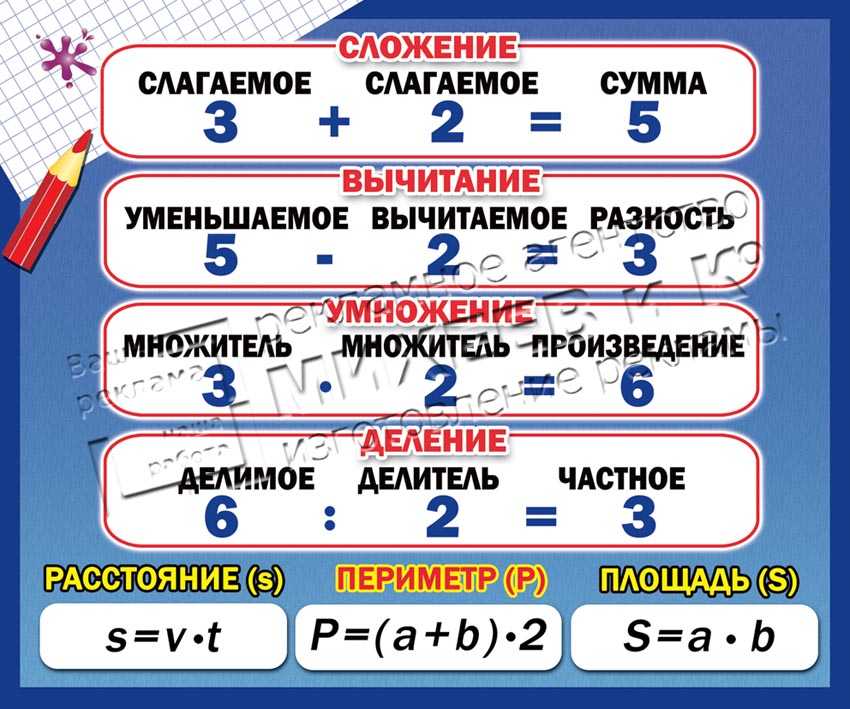
 Если делитель умножить на частное, то получится делимое.
Если делитель умножить на частное, то получится делимое. Если нет, вы можете рассчитать дивиденды, используя баланс и отчет о прибылях и убытках. Вы найдете их в годовом отчете компании 10-K.
Если нет, вы можете рассчитать дивиденды, используя баланс и отчет о прибылях и убытках. Вы найдете их в годовом отчете компании 10-K. Эта цифра помогает установить, каким было бы изменение нераспределенной прибыли, если бы компания решила не выплачивать 90 005 дивидендов в размере 90 006 в течение данного года.
Эта цифра помогает установить, каким было бы изменение нераспределенной прибыли, если бы компания решила не выплачивать 90 005 дивидендов в размере 90 006 в течение данного года.

 Эти изменения могут повлиять на точность этого расчета.
Эти изменения могут повлиять на точность этого расчета. Какие здесь лучшие акции?
Какие здесь лучшие акции?




 Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.
Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах. Выполним несколько несложных заданий.
Выполним несколько несложных заданий.
 В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?
В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное? Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.
Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.
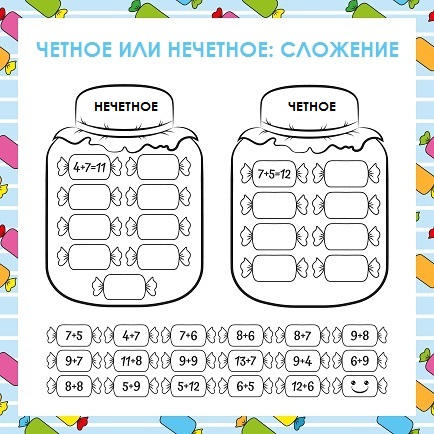

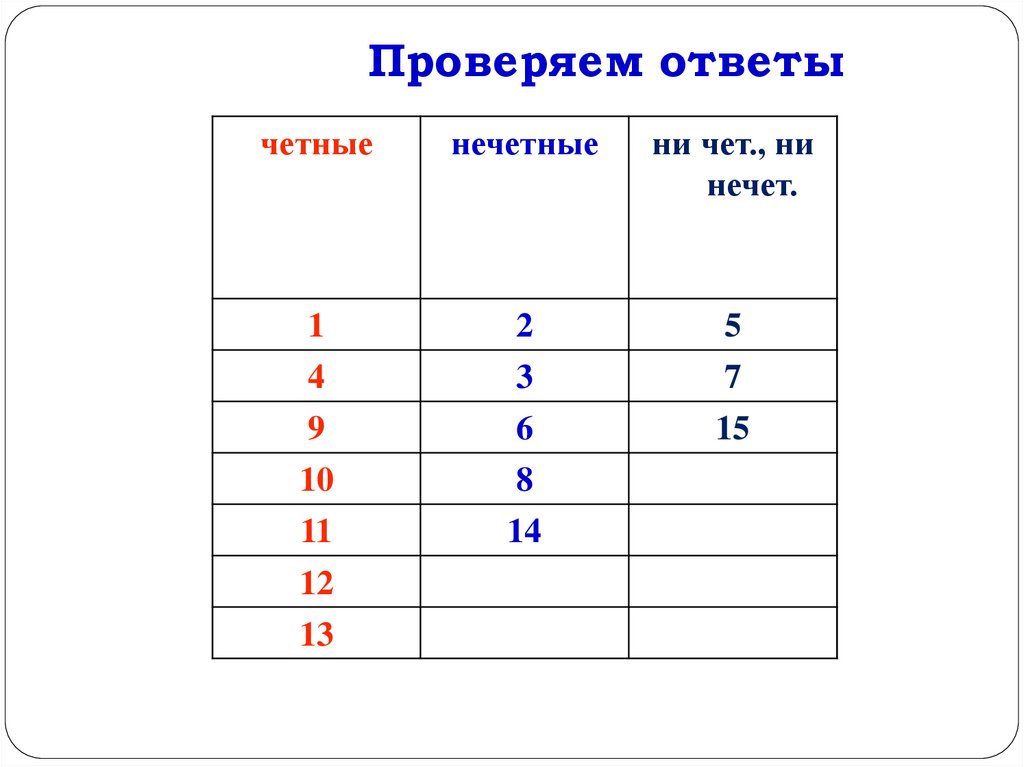

 Остаток в случае нечетного числа всегда равен «1». 11 — нечетное число.
Остаток в случае нечетного числа всегда равен «1». 11 — нечетное число.
 Является ли 29510 четным числом?
Является ли 29510 четным числом? 


 .+(2n) ……. (1)
.+(2n) ……. (1)
 По определению четных чисел к четным числам от 51 до 100 относятся 52, 54, 56, 58, 60, 62, 64, 66, 68, 70,72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100. Таким образом, всего 25 четных чисел от 51 до 100.
По определению четных чисел к четным числам от 51 до 100 относятся 52, 54, 56, 58, 60, 62, 64, 66, 68, 70,72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100. Таким образом, всего 25 четных чисел от 51 до 100.
 Молекула углекислого
газа состоит из атома углерода и двух атомов
кислорода. Напишите ее формулу и
рассчитайте относительную молекулярную
массу.
Молекула углекислого
газа состоит из атома углерода и двух атомов
кислорода. Напишите ее формулу и
рассчитайте относительную молекулярную
массу. Соотнесите:
Соотнесите: Выберите формулы веществ, относительная
молекулярная масса которых равна 98:
Выберите формулы веществ, относительная
молекулярная масса которых равна 98: Рассчитайте относительные молекулярные
массы веществ и поставьте знаки
равенства, «больше» или «меньше» в
следующих записях (место знака отмечено
звездочкой, формулы переставлять
нельзя):
Рассчитайте относительные молекулярные
массы веществ и поставьте знаки
равенства, «больше» или «меньше» в
следующих записях (место знака отмечено
звездочкой, формулы переставлять
нельзя):

 При пожаре выделяет раздражающие или токсичные пары (или газы).
При пожаре выделяет раздражающие или токсичные пары (или газы). 



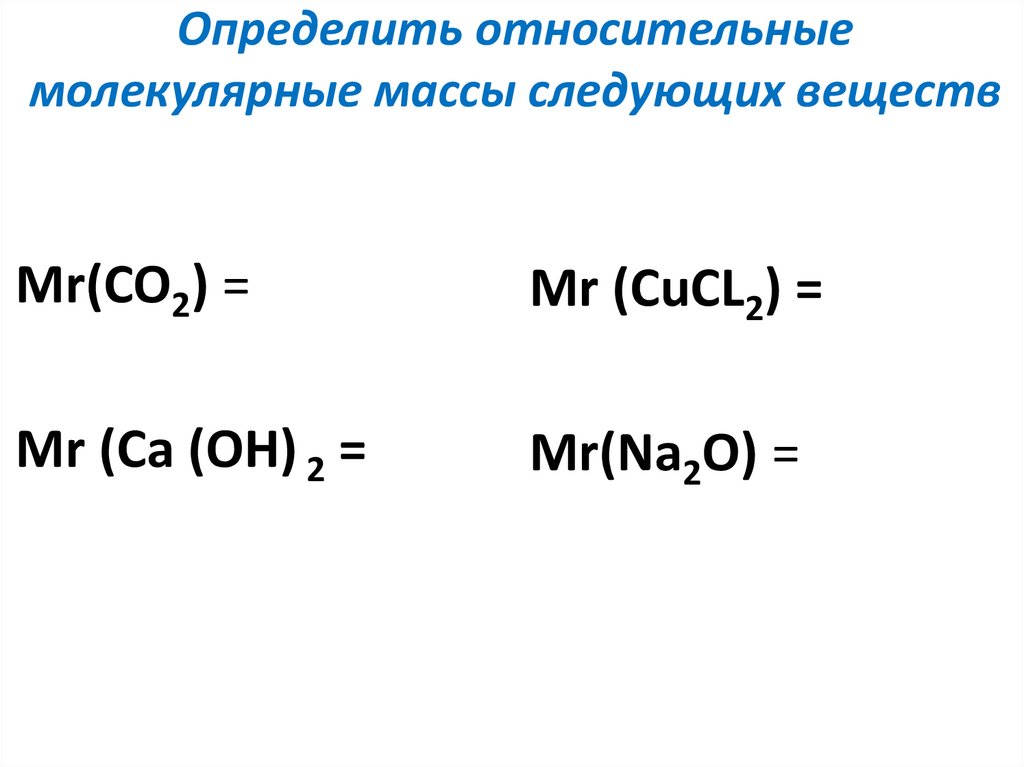 Поэтому мы предпочитаем использовать средние массы атомов и молекул. Таким образом, $\dfrac{1}{12}\text{th}$
Поэтому мы предпочитаем использовать средние массы атомов и молекул. Таким образом, $\dfrac{1}{12}\text{th}$  Таким образом,
Таким образом,  Молярная масса кислорода 16
граммов на моль, натрия — 23 грамма на моль, а серы — 32 грамма на моль.
Молярная масса кислорода 16
граммов на моль, натрия — 23 грамма на моль, а серы — 32 грамма на моль. Мы можем использовать уравнение 𝑛 равно
нижний регистр 𝑚 разделить на заглавную 𝑀, чтобы преобразовать массу в граммах в количество в
родинки. В этом уравнении 𝑛 представляет собой количество
в молях, строчная 𝑚 — масса в граммах, а заглавная 𝑀 — молярная масса в
грамм на моль. Мы знаем массу, но у нас нет
дана молярная масса сульфата натрия. Нам дали среднее
молярная масса кислорода, натрия и серы. Мы можем использовать эти значения для
рассчитать молярную массу сульфата натрия.
Мы можем использовать уравнение 𝑛 равно
нижний регистр 𝑚 разделить на заглавную 𝑀, чтобы преобразовать массу в граммах в количество в
родинки. В этом уравнении 𝑛 представляет собой количество
в молях, строчная 𝑚 — масса в граммах, а заглавная 𝑀 — молярная масса в
грамм на моль. Мы знаем массу, но у нас нет
дана молярная масса сульфата натрия. Нам дали среднее
молярная масса кислорода, натрия и серы. Мы можем использовать эти значения для
рассчитать молярную массу сульфата натрия. Один атом кислорода имеет в среднем
молярная масса 16 грамм на моль, поэтому четыре атома кислорода будут иметь среднюю молярную массу.
масса 64 грамма на моль. Складывая эти молярные массы вместе
дает нам молярную массу сульфата натрия, 142 грамма на моль.
Один атом кислорода имеет в среднем
молярная масса 16 грамм на моль, поэтому четыре атома кислорода будут иметь среднюю молярную массу.
масса 64 грамма на моль. Складывая эти молярные массы вместе
дает нам молярную массу сульфата натрия, 142 грамма на моль.
 Известны следующие кислоты в свободном состоянии: HClO4, HIO3, H5IO6. Соли кислот стабильнее самих кислот. Кислоты и их соли являются сильными окислителями, особенно в кислой среде.
Известны следующие кислоты в свободном состоянии: HClO4, HIO3, H5IO6. Соли кислот стабильнее самих кислот. Кислоты и их соли являются сильными окислителями, особенно в кислой среде.


 HClO — хлорноватистая кислота.
HClO — хлорноватистая кислота.
 Катализаторы — это вещества, которые ускоряют темп (скорость) химической реакции, не потребляясь и не становясь частью конечного продукта.
Катализаторы не влияют на равновесные ситуации.
Катализаторы — это вещества, которые ускоряют темп (скорость) химической реакции, не потребляясь и не становясь частью конечного продукта.
Катализаторы не влияют на равновесные ситуации.