Доклад «Признаки делимости» | Образовательная социальная сеть
VI ГОРОДСКАЯ МЕЖШКОЛЬНАЯ КОНФЕРЕНЦИЯ
«Я — исследователь»
Секция «Математика»
Тема: «Признаки делимости чисел»
Выполнил:
ученик 6 «А» класса
МБОУ школы № 132 Ленинского района
Жулябин Дмитрий Алексеевич
Научный руководитель:
Климанова Наталья Николаевна
учитель математики
Самара, 2015 г.
Содержание
I. Введение ………………………………………………………………………..3
II. Делимость чисел ………………………………………………………………5
1. Понятие делимости чисел…………………………………………………5
2. Свойства делимости……..…………………………………………………6
3. Признаки делимости чисел, изучаемые в школе на 2, 3, 5, 9, 10………7
Признаки делимости чисел, изучаемые в школе на 2, 3, 5, 9, 10………7
4. Признаки делимости чисел, не изучаемые в школе
(на 4, 11, 25, 6, 12, 15, 13)…………………………..…………………………..10
III . Задачи для самостоятельного решения……………………………………12
IV. Заключение………………………………………………………………….14
V. Приложение. Таблица «Признаки делимости чисел»……………………..15
VI. Список литературы…………………………………………………..………16
I. Введение.
Жалок тот ученик, который
не превосходит своего учителя.
Леонардо да Винчи
Математика — самая древняя наука, она была и остаётся необходимой людям. Слово математика греческого происхождения. Оно означает «наука», «размышление».
Вопросами делимости чисел люди интересовались очень и очень давно. Благодаря многолетнему труду математиков над проблемами делимости чисел были разгаданы многие ее тайны, но и сейчас в этом разделе математики остается еще много неясного.
Решая задачи и выполняя действия на деления, не всегда удается число разделить нацело. Возникает необходимость предсказать – делится число нацело или нет. Поэтому в математике исследуются условия делимости, выводятся определенные правила и признаки, по которым можно определить делится ли натуральное число на другое натуральное число или нет.
Возникает необходимость предсказать – делится число нацело или нет. Поэтому в математике исследуются условия делимости, выводятся определенные правила и признаки, по которым можно определить делится ли натуральное число на другое натуральное число или нет.
Чтобы ответить на вопрос о том, делится ли целое число a на целое число b, можно произвести деление этих чисел. Но при решении некоторых задач это может оказаться очень трудоёмким делом. Поэтому удобно знать некоторые признаки, которые позволяют без выполнения деления определять, делится одно целое число на другое или нет.
Изучая в курсе математики признаки делимости натуральных чисел на 2, на 3, на 5, на 9, на 10, у меня возник вопрос: «Нельзя ли, не прибегая к непосредственному делению числа, установить его делимость на другое натуральное число?». Именно поэтому для творческой работы мной выбрана тема «Признаки делимости чисел».
Актуальность выбранной темы заключается в том, что знание признаков делимости чисел поможет учащимся более быстро выполнять сокращения дробей, нахождения и вынесения общего множителя за скобки, при упрощении выражений.
Цель исследовательской работы: осветить признаки делимости чисел на 2, 3, 4, 5, 6, 9, 10, 11, 12, 13, 15, 25.
В связи с этим, при написании данной работы я ставлю перед собой следующие задачи:
- Изучить научную литературу по теме «Признаки делимости чисел», расширить и углубить свои знания по этой теме.
- Овладеть в совершенстве признаками делимости чисел, изучаемых на уроках математики и вне школьной программы.
- Рассмотреть решения задач на применение признаков делимости чисел, подобрать серию задач, связанных с признаками делимости чисел для самостоятельного решения.
- Разработать мини-справочник «Признаки делимости чисел».
Объект исследования: признаки делимости чисел.
Предмет исследования: изучение правил и методов делимости чисел.
II. Делимость чисел.
Признак делимости – это правило, позволяющее сравнительно быстро определить, является ли число кратным заранее заданному числу без необходимости выполнять фактическое деление.
Признаки делимости на 2, 5, 10, 3 и 9 были известны с давних времен. Так, например, признак делимости на 2 знали древние египтяне за две тысячи лет до нашей эры, а признаки делимости на 2, 3, и 5 были обстоятельно изложены итальянским математиком Леонардо Фибоначчи (1170-1228).
Мы знаем, что в результате сложения, вычитания или умножения целых чисел всегда получается число целое. А вот деление натуральных чисел нацело не всегда возможно. Для того чтобы узнать, делится ли натуральное число а на натуральное число b нацело, надо предварительно выяснить некоторые общие свойства делимости чисел.
1. Понятие делимости чисел.
Разделить число а на число b – это значит найти такое число q, при умножении которого на b получается а, т.е. b∙q = а. Если для целых чисел а и b такое число q существует, то говорят, что а делится на b.
Целое число а делится на целое число b, не равное нулю, если существует целое число q, такое, что а = b∙q.
В том случае, когда а делится нацело на b, число а называется кратным числу b, а число b называется делителем числа а.
Например, число 45 делится нацело на число 9, так как существует натуральное число 5, такое, что выполняется равенство 9 ∙ 5 = 45. Число 73 не делится на 9, так как не существует такое целое число q, при котором выполняется равенство 9 ∙ q = 73.
При определении делимости мы исключили случай, когда b = 0. В том случае, когда а = 0 и b = 0, любое число может выступать в роли частного, т.е. частное становится неопределенным. Если а ≠ 0 и b = 0, то равенство а = 0∙q не будет верным ни при каком значении q.
2. Свойства делимости.
Чтобы узнать, делится ли одно число на другое нацело, можно просто разделить первое число на второе. Если при делении остатка не будет, значит, числа делятся нацело. Если же при делении получится остаток, не равный нулю, значит, эти числа нацело не делятся. Можно ли, не производя самого деления, установить, делится ли одно число на другое нацело?
Можно, так как делимость одних чисел связана с делимостью других. Поэтому надо найти такие свойства делимости, при помощи которых было бы возможно, не производя деления, установить, является ли данное число кратным другому.
Делимость суммы.
Если каждое слагаемое суммы делится на одно и то же число, то и сумма делится на это число.
Например, числа 180 и 210 делятся на 3. Разделится ли сумма этих чисел на 3?
180 + 210 = 10∙18 + 10 ∙21 = 10∙ (18 + 21) = 10∙39
39 делится на 3. А это значит, что сумма чисел 180 и 210 делится на 3.
Делимость разности.
Если уменьшаемое и вычитаемое делятся на одно и то же число, то и разность делится на это число.
Например, числа 180 и 210 делятся на 3. Разделится ли разность этих чисел на 3?
210 — 180 = 10∙21 — 10 ∙18 = 10∙ (21 -18) = 10∙3
Значит, разность 210 и 180 делится на 3.
Делимость произведения.
Если в произведении нескольких натуральных чисел хотя бы один из сомножителей делится на какое-то число, то и всё произведение делится на это число.
Например, известно, что число 147 делится на 49. А 49 делится на 7. Делится ли 147 на 7?
147 = 49∙3 = (7∙7) ∙3 = 7∙(7∙3) = 7 ∙ 21
Полученное равенство показывает, что число 147 делится на 7.
3. Признаки делимости чисел, изучаемые в школе.
Рассмотрим сначала признаки делимости чисел на 2, 3, 5, 9, 10.
Признак делимости на 2: если число оканчивается одной из цифр 0, 2, 4, 6, 8, то оно делится на 2.
Оканчи-вается | Пример | Представили в виде суммы слагаемых | Вывод |
0 | 2210 | 1000∙2 + 100∙2 + 10∙1 + 0 | Каждое из слагаемых делится на 2, значит и число делится на 2 |
2 | 2212 | 1000∙2 + 100∙2 + 10∙1 + 2 | Каждое из слагаемых делится на 2, значит и число делится на 2 |
4 | 2214 | 1000∙2 + 100∙2 + 10∙1 + 4 | Каждое из слагаемых делится на 2, значит и число делится на 2 |
6 | 2216 | 1000∙2 + 100∙2 + 10∙1 + 6 | Каждое из слагаемых делится на 2, значит и число делится на 2 |
8 | 2218 | 1000∙2 + 100∙2 + 10∙1 + 8 | Каждое из слагаемых делится на 2, значит и число делится на 2 |
Например, число 2472 делится на 2, т. к. 2472 = 1000∙2 + 100∙4 + 10∙7 + 2. Все четыре слагаемых делятся на 2. Значит, число 2472 делится на 2.
к. 2472 = 1000∙2 + 100∙4 + 10∙7 + 2. Все четыре слагаемых делятся на 2. Значит, число 2472 делится на 2.
Число 2477 не делится на 2, т.к. 2477 = 1000∙2 + 100∙4 + 10∙7 +7. Первые три слагаемых делятся на 2, а четвёртое слагаемое не делится на 2. Значит, число 2477 не делится на 2.
Числа, делящиеся на 2, называют чётными. Числа, не делящиеся на 2, называют нечётными.
Признак делимости на 3: если сумма цифр числа делится на 3, то и само число делится на 3.
Делится ли число на 3 | Сумма цифр | Вывод |
270 | 2 + 7 + 0 = 9. | число 9 делится на 3. Значит 270 делится на 3 |
541 | 5+4 +1 = 10. | число 10 не делится на 3. Значит 541 не делится на 3 |
Признак делимости на 5: если число оканчивается одной из цифр 0 или 5, то оно делится на 5.
Делится ли число на 5 | Представим в виде | Вывод |
2570 | 2570 = 257 ∙ 10. | Второй множитель 10 делится на 5, значит, число 2570 делится на 5. |
645 | 645= 100∙6 + 10∙4 + 5. | Все слагаемые делятся на 5, значит, число 645 делится на 5. |
643 | 643= 100∙6 + 10∙4 + 3. | Первое и второе слагаемые делятся на 5, третье слагаемое не делится на 5. Значит число 643 не делится на 5. |
Признак делимости на 9: если сумма цифр числа делится на 9, то и само число делится на 9.
Делится ли число на 9 | Сумма цифр | Вывод |
576 | 5 + 7 + 6 = 18. | число 18 делится на 9. Значит 576 делится на 9 |
535 | 5+3 +5 = 13. | число 13 на 9 не делится. Значит 535 не делится на 9 |
Признак делимости на 10: если число оканчивается цифрой 0, то оно делится на 10.
Делится ли число на 10 | Представим в виде | Вывод |
4370 | 4370 = 437 ∙ 10. | Один из множителей делится на 10, значит, число 4370 делится на 10. |
2378 | 2378= 1000 ∙2 + 100 ∙3+ +10∙7 +8. | Первое, второе, третье слагаемые делятся на 10, а четвертое слагаемое не делится на 10. Значит число 2378 не делится на 10. |
4. Признаки делимости чисел, не изучаемые в школе.
Признак делимости на 4: число делится на 4 тогда, когда две последние цифры этого числа представляют собой число, делящееся на 4.
Делится ли число на 4 | Представим в виде | Вывод |
664 | 664 = 600 + 60 + 4 = =100∙6 + 10∙6 + 4 = =100∙6 + (10∙6 + 4) | (10∙6 + 4) представляет собой число 64, а это число делится на 4. |
433 | 433= 100∙4 + (10∙3 + 3). | (10∙3 + 3) представляет собой число 33, а это число не делится на 4. Значит, число 433 не делится на 4. |
Признак делимости на 11: число делится на 11 тогда, когда разность между суммой цифр, стоящих на чётных местах, и суммой цифр, стоящих на нечётных местах, делится на 11.
Делится ли число на 11 | Запишем по правилу | Вывод |
4939. | (9 +9) — (4 + 3) = 18-7=11. | Полученное число11 делится на 11, значит, число 4939 делится на 11. |
1534 | (5 +4) — (1 +3) =9 – 4= 5. | Полученное число 6 не делится на 11, значит, число 1534 не делится на 11. |
Признак делимости на 25: число делится на 25 тогда, когда две последние цифры этого числа представляют собой число, делящееся на 25.
Делится ли число на 25 | Запишем по правилу | Вывод |
875 | 875= 800 + 70 + 5 = = 100∙8 + 10∙7 + 5 = =100∙8 + (10∙7 + 5) | (10∙7 + 5) представляет собой число 75, а это число делится на 25. Значит, и число 875 делится на 25. |
427 | 427 = 100∙4 + (10∙2 + 7). | (10∙2 + 7) представляет собой число 27, а это число не делится на 25. |
Сформулируем ещё несколько признаков делимости чисел.
Признак делимости на 6: для того чтобы число делилось на 6, необходимо и достаточно, чтобы оно делилось на 2 и на 3, т.е. чтобы его последняя цифра была четной и, кроме того, сумма его цифр делилась на 3.
234:2=117 2+3+4=9:3, значит 234 делится на 6 |
Признак делимости на 12: для того чтобы число делилось на 12, необходимо и достаточно, чтобы оно делилось на 4 и на 3.
108:4=27 108:3= 1+0+8= 9:3, значит 108:12=9 |
Признак делимости на 15: для того чтобы число делилось на 15, необходимо и достаточно, чтобы оно делилось на 5 и на 3, т.е. чтобы оно оканчивалось нулем или пятеркой и, кроме того, сумма его цифр делилась на 3.
Признак делимости на 13: число делится на 13 тогда и только тогда, когда результат вычитания последней цифры умноженной на 9 из этого числа без последней цифры делится на 13.
858 делится на 13, так как 85 — 9·8 = 13 делится на 13. |
III. Задачи для самостоятельного решения.
- Делится ли на 9 тридцатизначное число, у которого первая цифра 8, последняя 1, а остальные цифры равны нулю?
РЕШЕНИЕ: 8000….1. Найдем сумму цифр 8+0+0+…+0+1=9, сумма цифр делится на 9, значит и само число делится на 9
- Делится ли на 81 число, записанное 81 единицей?
РЕШЕНИЕ:
- При делении на 2 число дает в остатке 1, а при делении на 3 – остаток 2. Какой остаток дает число при делении на 6?
РЕШЕНИЕ:
- Цифры трехзначного числа записали в обратном порядке и из большего вычли меньшее.
 Докажите, что разность делится на 9 и на 11.
Докажите, что разность делится на 9 и на 11.
РЕШЕНИЕ:
- Выписали подряд все цифры от 1 до 9 включительно, а затем от 9 до 1. Будет ли полученное число делиться на 9?
РЕШЕНИЕ:
- Выписали подряд натуральные числа, начиная с 1 и заканчивая числом 11. будет ли полученное число кратно 9?
РЕШЕНИЕ:
- К числу 43 припишите справа и слева по одной цифре так, чтобы полученное число делилось на 45.
РЕШЕНИЕ:
- Какие из данных чисел 384123, 108675, 138963, 903150 делятся на: 3; на 4; на 9; на 25?
РЕШЕНИЕ:
- Сократите дробь:
РЕШЕНИЕ:
- Вместо звёздочек поставьте некоторые числа так, чтобы число 5*4* делилось на 9 и на 4. Найдите все возможные решения.
РЕШЕНИЕ:
- Какие из данных чисел 7194, 18456, 36735, 17214, 781120 делятся: на 6; на 15; на 12?
РЕШЕНИЕ:
IV. Заключение.
Заключение.
В данной работе мной рассмотрено понятие делимости чисел, некоторых его свойств, признаков делимости и задачи, решение которых связано с ними.
При написании данной творческой работы я изучил большое количество дополнительной научной литературы по теме «Признаки делимости», расширил и углубил свои знания по данному вопросу, овладел простейшими и более сложными признаками делимости чисел.
Рассмотрев различные признаки делимости чисел, я убедился, что знание этих признаков существенно поможет при вынесении общего множителя за скобки, упрощении выражений, сокращении дробей, а так же значительно сэкономит время в получении ответа на вопрос, об определении делимости числа, не прибегая к самому действию деления.
Работа имеет практическое применение. Ее могут использовать учителя, как при проведении уроков по математике, так и на факультативных курсах и дополнительных занятиях на повторение. Данная работа будет полезна и для учащихся при самостоятельной подготовке к экзаменам по математике и для учеников, целью которых стали высокие места на олимпиадах.
V. Приложение. Таблица «Признаки делимости чисел»
на 2 | На 2 делятся те, и только те натуральные числа, запись которых оканчивается на четные цифры (0,2,4, 6,8) |
на 3 | На 3 делятся те, и только те натуральные числа, сумма цифр которых делится на 3 |
на 4 | На 4 делятся те, и только те натуральные числа, в записи которых последние две цифры образуют число, делящееся на 4 |
на 5 | На 5 делятся те, и только те натуральные числа, запись которых оканчивается на 0 или на 5. |
на 6 | На 6 делятся те, и только те натуральные числа, которые оканчиваются чётной цифрой, и сумма цифр делится на 3 |
на 8 | На 8 делятся те, и только те натуральные числа, в записи которых три последние цифры образуют число, делящееся на 8 |
на 9 | На 9 делятся те, и только те натуральные числа, сумма цифр которых делится на 9 |
на 10 | На 10 делятся те, и только те натуральные числа, запись которых оканчивается на 0 |
на 11 | На 11 делится то число, когда разность между суммой цифр, стоящих на чётных местах, и суммой цифр, стоящих на нечётных местах, делится на 11. |
на 12 | На 12 делятся те, и только те натуральные числа, в записи которых две последние цифры образуют число, делящееся на 4 и сумма цифр числа делится на 3. |
на 13 | Число делится на 13 тогда и только тогда, когда результат вычитания последней цифры умноженной на 9 из этого числа без последней цифры делится на 13. |
на 15 | На 15 делятся те, и только те натуральные числа, запись которых оканчивается на 0 или на 5 и сумма цифр делится на 3 |
на 25. | Для того чтобы натуральное число содержащее не менее трёх цифр, делилось на 25 необходимо и достаточно, чтобы делилось на 25 число, образованное двумя последними |
VI. Список литературы
Список литературы
- Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений. – М.: Мнемозина, 2008.
- Воробьев Н.Н. Признаки делимости.- 4-е изд., испр.- М.: Наука, 2008.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М.: Просвещение, 2006.
- Макарычев Ю.Н., Миндюк Н.Г. Алгебра: дополнительные главы к школьному учебнику 8 класс. Учебное пособие для учащихся школ и классов с углубленным изучением математики. – М.: Просвещение, 2007.
- Никольский С.М. Арифметика 5 класс: учебник для общеобразовательных школ. — М.: издат. отдел УНЦ ДО МГУ, 2003.
- Фридман Л.М. Изучаем математику. Кн. для учащихся 5-6 кл. — М.: Просвещение, 2005.
Признаки делимости
В этой статье мы поговорим о таком понятии, как признаки делимости. Это определенные действия, с помощью которых можно узнать, делится ли целое число a на другое число b, которое в данном случае будет целым положительным. При это само деление не проводится. Очевидно, что для изучения данных признаков необходимо иметь общее представление о делимости чисел.
При это само деление не проводится. Очевидно, что для изучения данных признаков необходимо иметь общее представление о делимости чисел.
Когда мы говорим о признаках делимости, чаще всего нам приходится иметь дело не с самим числом, а с цифрами, из которых оно состоит.
С помощью определенных признаков делимости можно заключить, что некое число a можно разделить на другое число. Для одних нам будет нужна последняя цифра в записи: так можно сделать вывод о делимости на 2, 5 и 10. Сформулируем эти признаки.
Определение 1Те числа, в конце которых стоят цифры 0, 2, 4, 6, делятся на 2.
Определение 2На 5 можно разделить те числа, которые заканчиваются на 5 и 0.
Определение 3Все числа, заканчивающиеся на 0, можно разделить на 10.
Приведем примеры.
Пример 1Например, число 34 564 обладает делимостью на 2, поскольку в конце у него стоит 4. Число 567 разделить на 5 нельзя, потому что последняя цифра в нем не удовлетворяет нужным условиям. Число 89 120 мы можем разделить на 10, потому что оно заканчивается нулем.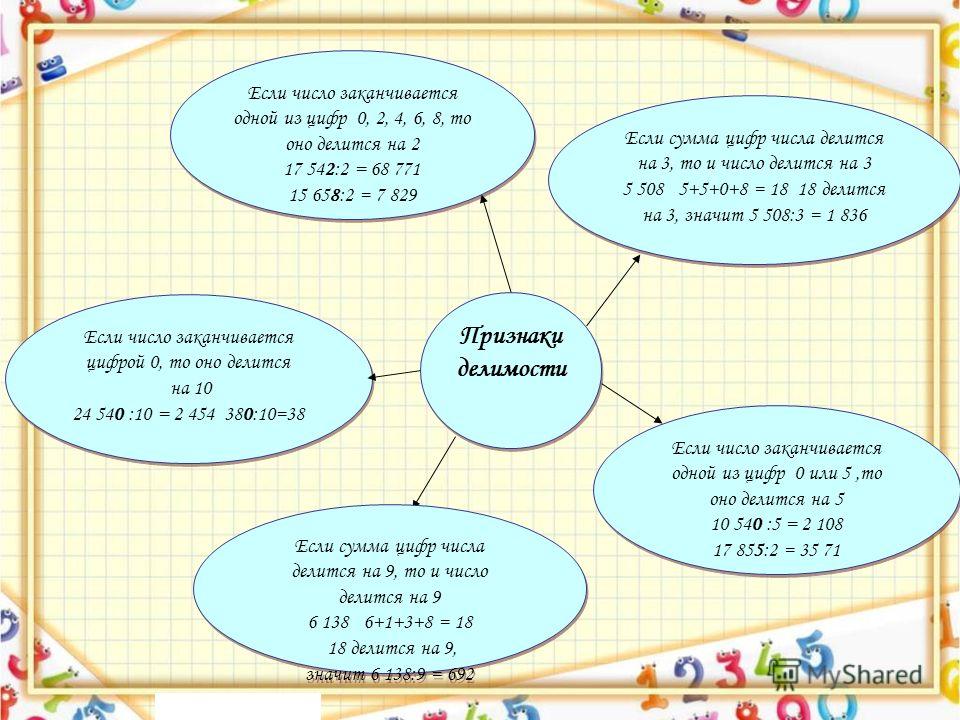
Другие признаки делимости требуют предварительного анализа не одной, а нескольких последний цифр числа.
Признак делимости на 4 выглядит так:
Определение 4Число можно разделить на 4, если двузначное число, образованное двумя последними цифрами в нем, делится на 4.
Определение 5О признаке делимости на 8 мы говорим, когда число из трех последних цифр можно разделить на 8.
Пример 2Вот примеры таких расчетов: 99 769 775 012 делится на 4, так как в конце у него стоит 12, а 45 907 нельзя разделить на 8: берем три последние цифры, убираем из них 0 и получаем 97. Без остатка на 8 это число разделить нельзя, значит, и 45 907 делимостью на 8 не обладает.
Остальные признаки делимости требуют анализа сразу всех цифр в числе.
Определение 6Число можно разделить на 3 или 9, если сумма всех цифр в нем делится на 3 или 9 соответственно.
После вычисления суммы цифр, возможно, придется использовать указанные признаки делимости еще раз. Вот примеры таких вычислений.
Проверим, делится ли 1 001 103. Подсчитаем сумму цифр: 1+0+0+1+1+0+3=6. Шестерка делится на 3, значит, и все число тоже можно разделить на 3.
Пример 4Число 65 051 991 можно разделить на 9, потому что суммой его цифр является 36: 6+5+0+5+1+9+9+1=36, а его можно разделить на 9.
А вот пример последовательного применения признаков.
Пример 5Проверим, можно ли разделить 879 901 831 799 782 на 3. Считаем сумму цифр и получаем 114. Для проверки делимости этого числа на 3 складываем цифры уже этого числа и получаем 6. Шесть можно разделить на 3, значит, 114 делится на 3 и 879 901 831 799 782 998 тоже делится на 3.
В целом можно сказать, что с помощью признаков делимости можно перейти от анализа исходного числа к анализу меньшего числа, причем второе число мы проверяем, используя тот же самый признак делимости. Иначе говоря, в случае с длинными числами признаки нужно применять циклически для получения нужного результата.
Есть и другие признаки делимости, которые объединяют в себе несколько других.
Чтобы узнать, делится ли число на 6, нужно объединить два признака делимости – на 2 и на 3.
Определение 8Признаком делимости на 12 является соответствие двум другим признакам делимости – на 3 и 4.
Пример 6К примеру, 78 804 заканчивается на 4, следовательно, его можно разделить на 2. Считаем сумму цифр и получаем 27. Это число можно разделить на 3, получается, что это можно сделать и с исходным числом. В итоге заключаем, что 78 804 делится без остатка на 6.
Пример 7Число 208 436 316 можно разделить на 12, поскольку его цифры в сумме дают 33, что делится на 3, и две последние цифры образуют число 16, которое можно разделить на 4.
Отметим, что иногда для проверки делимости требуется значительная вычислительная работа, что в некоторых случаях нецелесообразно. Иногда проще выполнить непосредственное деление, чтобы ответить на вопрос, делится ли это число на другое или нет.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
Навигация по статьям
Предыдущая статья
Делители и кратные числа
Следующая статья
Признак делимости на 2
- Взаимно простые числа
- Делители и кратные числа
- Линейные дифференциальные уравнения второго порядка
- Наибольший общий делитель (НОД)
- Наименьшее общее кратное (НОК)
- Все темы по математике
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Все предметы
Узнать подробнее
теста по предмету анализ данных
Вид работы:
Тест
Выполнена:
5 февраля 2023 г.

Стоимость:
3 800 руб
Заказать такую же работу
Автоматизация документооборота на примере ООО Биверс
Вид работы:
Кейс
Выполнена:
20 января 2023 г.

Стоимость:
3 200 руб
Заказать такую же работу
Строймех выполнить задачу
Вид работы:
Решение задач
Выполнена:
17 декабря 2022 г.

Стоимость:
1 900 руб
Заказать такую же работу
Задачи с параметром от руки можно
Вид работы:
Контрольная работа
Выполнена:
25 ноября 2022 г.

Стоимость:
1 000 руб
Заказать такую же работу
Решение задач Желательно автору из
Вид работы:
Решение задач
Выполнена:
19 ноября 2022 г.

Стоимость:
1 300 руб
Заказать такую же работу
Техникоэкономическое сравнение ветрогенератора и солнечных батарей
Вид работы:
Домашняя работа
Выполнена:
18 октября 2022 г.

Стоимость:
2 000 руб
Заказать такую же работу
Смотреть все работы по статистике
Таблицы правил делимости для бесплатной печати по математике
Нужен ли вашему ребенку инструмент для изучения правил делимости? Эти распечатанные таблицы правил делимости являются идеальным учебным пособием, которое поможет детям легче освоить деление!
Правила делимости — это экономящие время уловки, помогающие определить, делится ли число на определенное число. Они действительно могут помочь вам, когда вам не обязательно знать ответ на задачу о делении, а только в том случае, если МОЖНО разделить поровну.
Они действительно могут помочь вам, когда вам не обязательно знать ответ на задачу о делении, а только в том случае, если МОЖНО разделить поровну.
** Этот сайт содержит партнерские ссылки. Если вы совершите покупку по одной из этих ссылок, я могу получить комиссию. Пожалуйста, нажмите здесь для получения дополнительной информации о собранных файлах cookie и нашей политике конфиденциальности **.
Эти правила помогут сэкономить время на выполнении домашних заданий по математике, стандартных тестов и т. д.
Эти бесплатные образовательные таблицы правил делимости — именно то, что вам нужно, чтобы помочь вашему ребенку запомнить и усвоить правила делимости!
Как использовать таблицы правил делимости для печати
Мой любимый способ использования этих таблиц — поместить их на защитную пленку (или заламинировать) и повесить на видное место на стене или в школьной папке вашего ребенка. ссылаться всякий раз, когда им нужно.
Это может показаться жульничеством, но даже если им придется искать ответы на задачи во время работы, это поможет им запомнить информацию.
Если вы ищете дополнительные математические инструменты для печати, они также могут стать отличным справочным пособием:
- Таблица сотен для печати
- Пропуск таблиц подсчета
- Числовые строки для печати
- Таблицы стоимости места для печати
- Полоски фракций для свободной печати
Используйте эти таблицы, чтобы помочь детям запомнить правила делимости.
Эти диаграммы легко загрузить и распечатать, и их можно бесплатно использовать в личных целях или в классе.
Для загрузки просто щелкните ссылку под нужной диаграммой.
Таблица правил делимости черно-белых чисел
Эта таблица включает правила делимости чисел от 2 до 10 (число 7 пропущено).
Это наиболее часто используемые и простые правила делимости.
Загрузить таблицу правил делимости сейчас
Или загрузить ту же таблицу в цвете:
Загрузить таблицу правил делимости сейчас
Таблица правил делимости с примерами
Эта таблица включает правила делимости чисел 2, 3, 4, 5, 6, 9 и 10.
Она также включает примеры чисел, иллюстрирующие правила делимости.
Загрузить таблицу правил делимости сейчас
Или загрузить ту же таблицу в цвете:
Загрузить таблицу правил делимости сейчас
Таблица правил делимости с ячейками
Эта диаграмма находится в коробке формат вместо вертикальной диаграммы.
Включает правила делимости чисел 2, 3, 4, 5, 6, 8, 9 и 10.
Сохранить, поделиться!
3 акции
Признаки делимости: история и руководство пользователя. Начало делимости
Автор(ы):
Эрик Л. Макдауэлл (Берри Колледж)
Макдауэлл (Берри Колледж)
Самый ранний из известных нам признаков делимости взят из Вавилонского Талмуда . Он использовался для расчета данного года в рамках творческого отпуска; то есть он дает остаток, полученный при делении целого числа \(N\) на \(7\):
… отложите сотни как юбилейные циклы и преобразуйте остаток в субботние циклы [по семь лет каждый] после добавления к ним двух лет за каждое полное столетие; то, что осталось, даст ему номер данного года в текущем субботнем цикле [1].
В переводе на язык математики отрывок подразумевает, что для целых чисел \(N,\) \(a,\) и \(b\) с \(N=100a+b,\) мы имеем
\ [100a+b\экв 2a+b\,\,({\rm{mod}}\,\,7).\]
Другими словами, \(100a+b\) и \(2a+b\) дают один и тот же остаток при делении на \(7.\) Например, \(1866=100(18)+66\экв 2( 18)+66 = 102\,\,({\rm{mod}}\,\,7),\) и \(102\экв 2(1)+2=4\,\,({\rm{ mod}}\,\,7).\) Следовательно, \(1866\equiv4\,\,({\rm{mod}}\,\,7).\) Следовательно, поскольку \(4\) не делится на \(7,\) и не является \(1866.




 Значит, и число 664 делится на 4.
Значит, и число 664 делится на 4.
 Значит, число 427 не делится на 25.
Значит, число 427 не делится на 25. Докажите, что разность делится на 9 и на 11.
Докажите, что разность делится на 9 и на 11.






 )
) )
) )
) )
) )
) )
) )
) )
) )
) Он также известен как арктан (x). У нас есть 6 обратных тригонометрических функций, которые соответствуют шести тригонометрическим функциям. Функция обратного загара является одной из них.
Он также известен как арктан (x). У нас есть 6 обратных тригонометрических функций, которые соответствуют шести тригонометрическим функциям. Функция обратного загара является одной из них. Она также известна как функция арктангенса, которая произносится как «арктангенс». Математически это записывается как «атан х» (или) «тан -1 x» или «arctan x». Мы читаем «tan -1 x» как «tan inverse x». Если две функции f и f -1 являются обратными друг другу, то когда f(x ) = y , имеем x = f -1 (y).Таким образом, tan x = y ⇒ x = tan -1 (y) , т. е. когда «tan» перемещается с одной стороны на другую
Она также известна как функция арктангенса, которая произносится как «арктангенс». Математически это записывается как «атан х» (или) «тан -1 x» или «arctan x». Мы читаем «tan -1 x» как «tan inverse x». Если две функции f и f -1 являются обратными друг другу, то когда f(x ) = y , имеем x = f -1 (y).Таким образом, tan x = y ⇒ x = tan -1 (y) , т. е. когда «tan» перемещается с одной стороны на другую
 т. е. tan x : (-π/2, π/2) → R.
т. е. tan x : (-π/2, π/2) → R.
 Вы можете попробовать использовать этот калькулятор.
Вы можете попробовать использовать этот калькулятор.


 Например, тангенс -1 (1/√3) = π/6, поскольку тангенс π/6 = 1/√3. Но убедитесь, что угол лежит в интервале (-π/2, π/2).
Например, тангенс -1 (1/√3) = π/6, поскольку тангенс π/6 = 1/√3. Но убедитесь, что угол лежит в интервале (-π/2, π/2).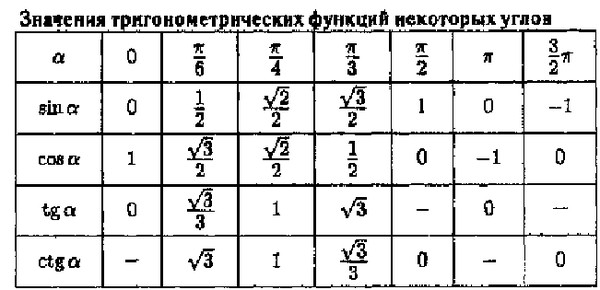 т. е. угол = тангенс -1 (противоположная сторона/прилегающая сторона).
т. е. угол = тангенс -1 (противоположная сторона/прилегающая сторона).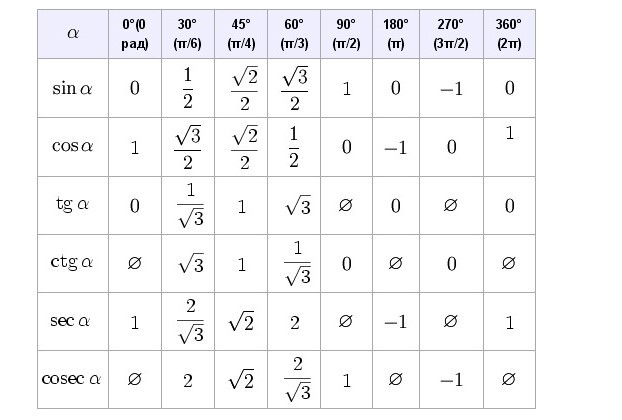 )/3
)/3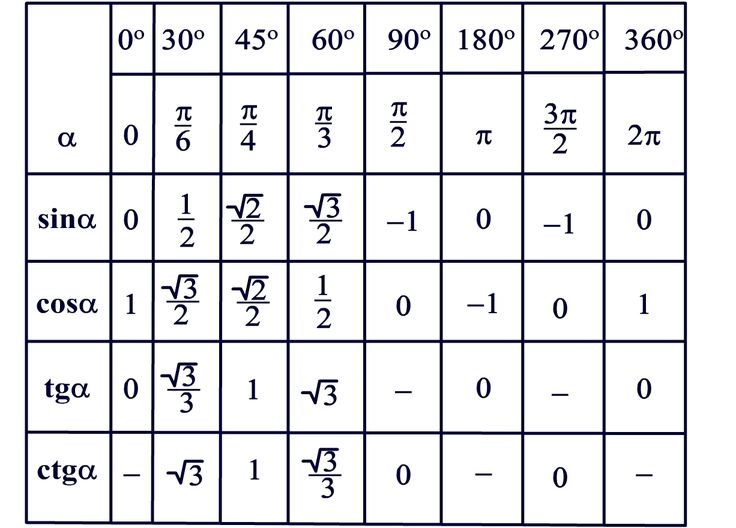
 8″1/2.7″1/2.5″1/2″1/1.8″
8″1/2.7″1/2.5″1/2″1/1.8″ 0
0 Характеристическое уравнение – это уравнение, полученное приравниванием характеристического многочлена к нулю. Таким образом, этот калькулятор сначала получает характеристическое уравнение с помощью калькулятора характеристического полинома, а затем решает его аналитически для получения собственных значений (действительных или комплексных). Это происходит только для матриц 2×2, 3×3 и 4×4 с использованием калькуляторов решения квадратного уравнения, кубического уравнения и решения уравнения четвертой степени. Таким образом, он может найти собственные значения квадратной матрицы до четвертой степени.
Характеристическое уравнение – это уравнение, полученное приравниванием характеристического многочлена к нулю. Таким образом, этот калькулятор сначала получает характеристическое уравнение с помощью калькулятора характеристического полинома, а затем решает его аналитически для получения собственных значений (действительных или комплексных). Это происходит только для матриц 2×2, 3×3 и 4×4 с использованием калькуляторов решения квадратного уравнения, кубического уравнения и решения уравнения четвертой степени. Таким образом, он может найти собственные значения квадратной матрицы до четвертой степени. Больше теории можно найти под калькулятором.
Больше теории можно найти под калькулятором. .
. И здесь вы можете найти отличное введение о том, почему мы вообще должны заботиться о поиске собственных значений и собственных векторов, и почему они являются очень важными понятиями в линейной алгебре.
И здесь вы можете найти отличное введение о том, почему мы вообще должны заботиться о поиске собственных значений и собственных векторов, и почему они являются очень важными понятиями в линейной алгебре.
 То есть ядро (или нулевое пространство) $ M — I \lambda_i $.
То есть ядро (или нулевое пространство) $ M — I \lambda_i $. Векторное пространство записывается $ \text{Vect} \left\{ \begin{pmatrix} -1 \\ 1 \end{pmatrix} \right\} $
Векторное пространство записывается $ \text{Vect} \left\{ \begin{pmatrix} -1 \\ 1 \end{pmatrix} \right\} $

 95 МБ, 845793.rar Автор: Ковалева Инга Михайловна, 1 Апр 2015
95 МБ, 845793.rar Автор: Ковалева Инга Михайловна, 1 Апр 2015 Алгебра 8 класс
Алгебра 8 класс

 PowerPoint 2007 Диск
PowerPoint 2007 Диск 32 варианта.
32 варианта. Пропорции». ГИА-9
Пропорции». ГИА-9 То есть, чтобы разделить рациональное выражение на другое рациональное выражение, умножить первое рациональное выражение на
взаимный
второго рационального выражения.
То есть, чтобы разделить рациональное выражение на другое рациональное выражение, умножить первое рациональное выражение на
взаимный
второго рационального выражения.

 4 Сложение и вычитание рациональных выражений — Алгебра среднего уровня
4 Сложение и вычитание рациональных выражений — Алгебра среднего уровня
 Точка касания
делит большую боковую сторону на отрезки длиной 4 см и 9 см. Найдите площадь трапеции.
Точка касания
делит большую боковую сторону на отрезки длиной 4 см и 9 см. Найдите площадь трапеции.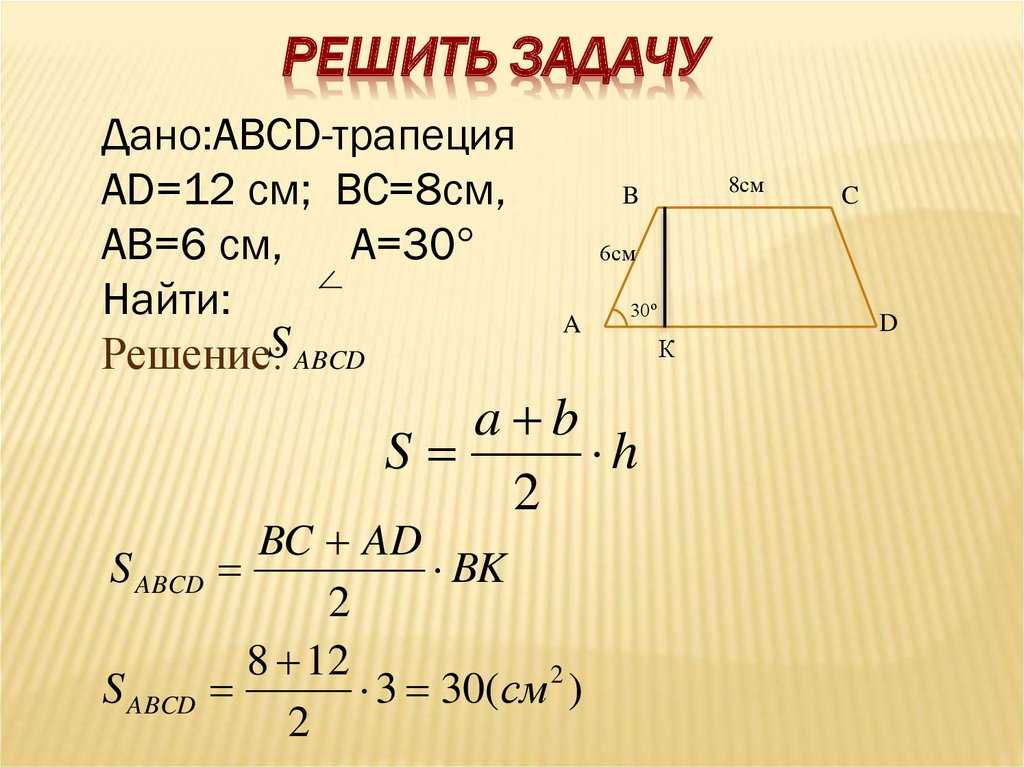

 Из
равенств (1) и (2) получим, что ∠ СDВ = ∠ ВDА. Поэтому, DВ –
биссектриса ∠ СDА трапеции.
Из
равенств (1) и (2) получим, что ∠ СDВ = ∠ ВDА. Поэтому, DВ –
биссектриса ∠ СDА трапеции.

 ru
ru Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
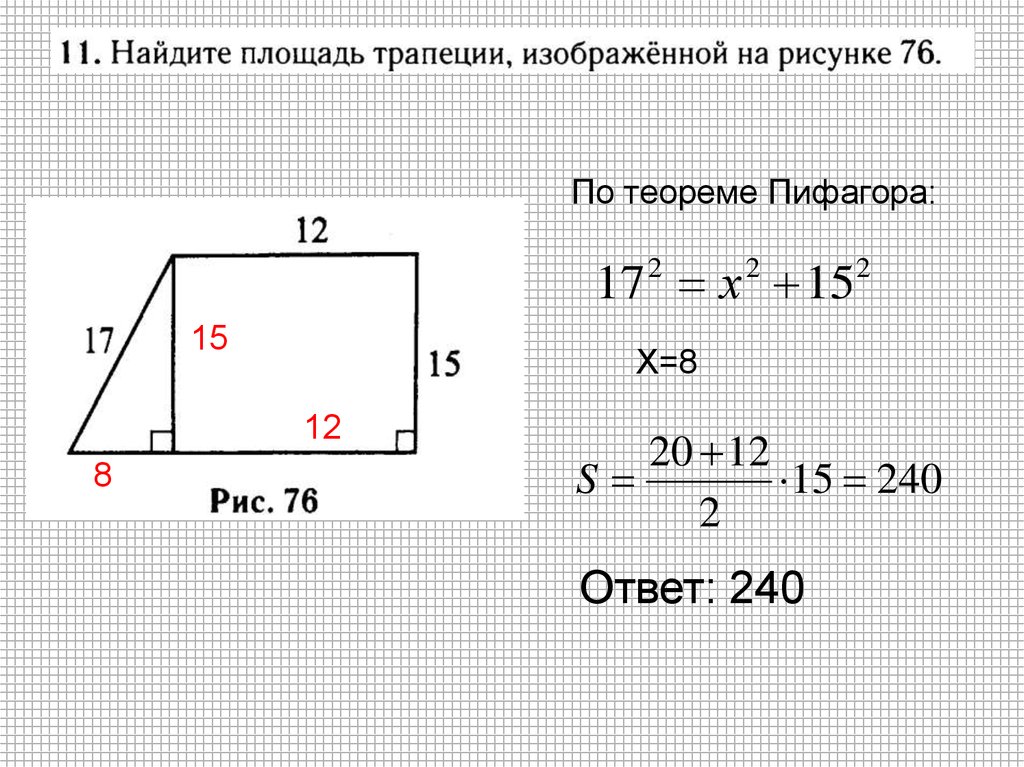

 Объединив эти уравнения, можно сосчитать оба основания:
Объединив эти уравнения, можно сосчитать оба основания: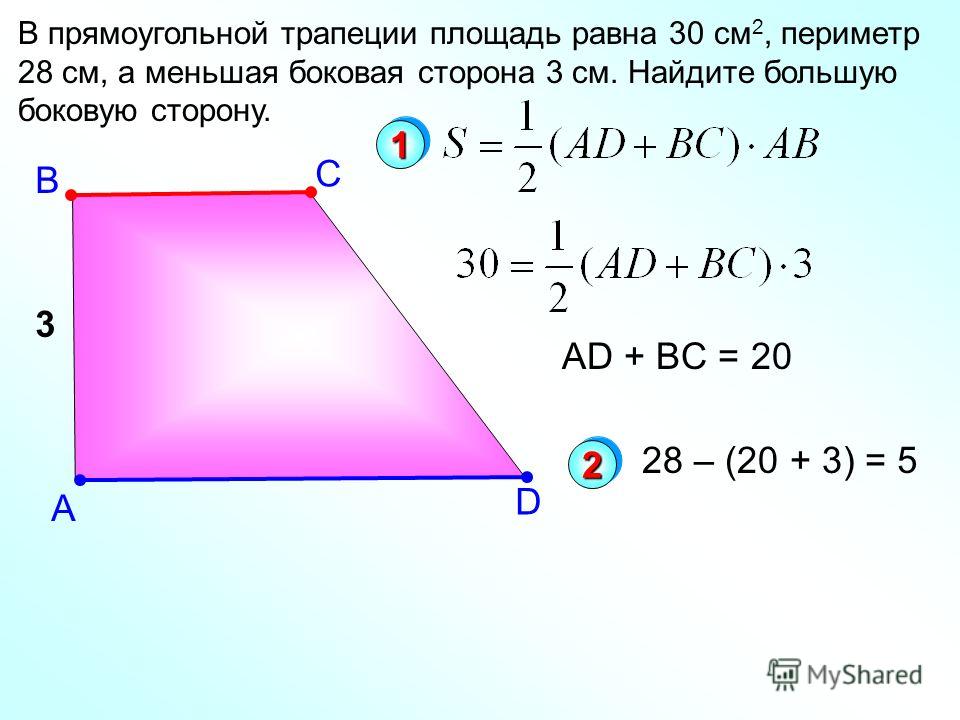 Получится: d2 = с2 + (a – b)2 или (a + b)2 = с2 + (a – b)2.
Получится: d2 = с2 + (a – b)2 или (a + b)2 = с2 + (a – b)2. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
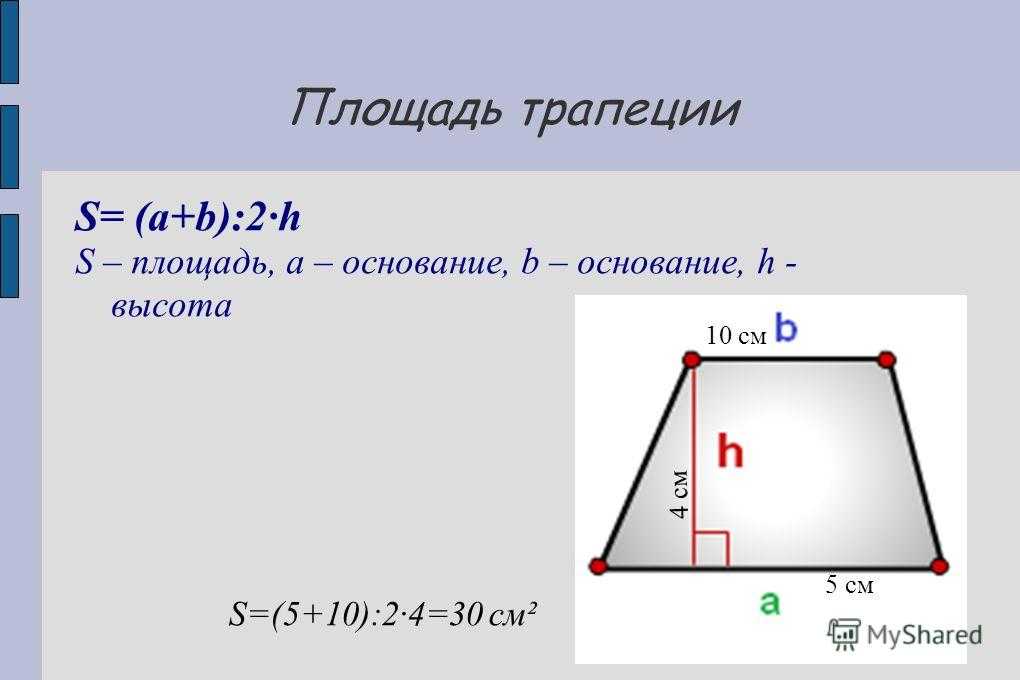
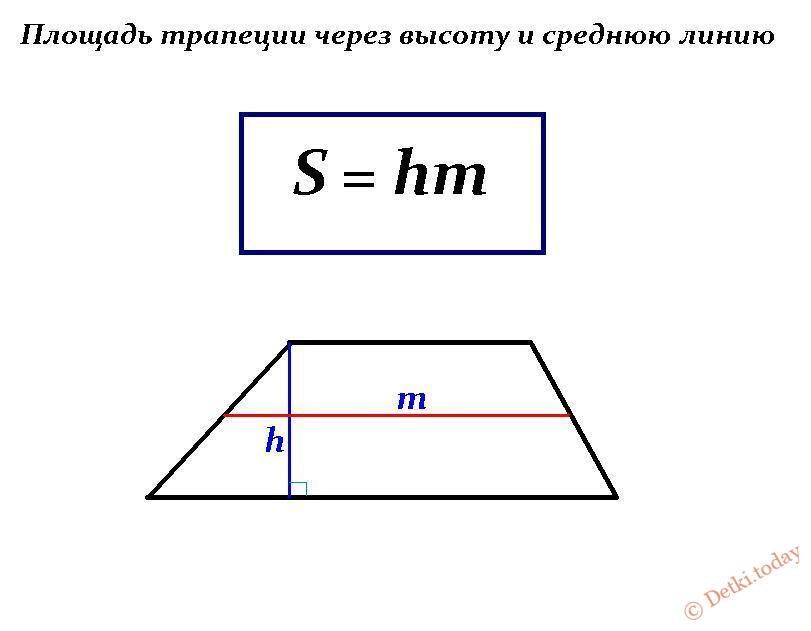
 Площадь трапеции равна половине суммы длин оснований, умноженных на высоту или высоту трапеции.
Площадь трапеции равна половине суммы длин оснований, умноженных на высоту или высоту трапеции. Как найти площадь? Вам нужно сделать прямоугольник и треугольник с трапецией.
Как найти площадь? Вам нужно сделать прямоугольник и треугольник с трапецией.
 Ноуууу, тогда у вас есть несколько вопросов о количественных показателях, в частности, о вопросе 3 раздела 4 практического теста 1. Эти четырехсторонние вопросы могут быть довольно сложными, но не бойтесь, PrepScholar прикроет вашу спину!
Ноуууу, тогда у вас есть несколько вопросов о количественных показателях, в частности, о вопросе 3 раздела 4 практического теста 1. Эти четырехсторонние вопросы могут быть довольно сложными, но не бойтесь, PrepScholar прикроет вашу спину!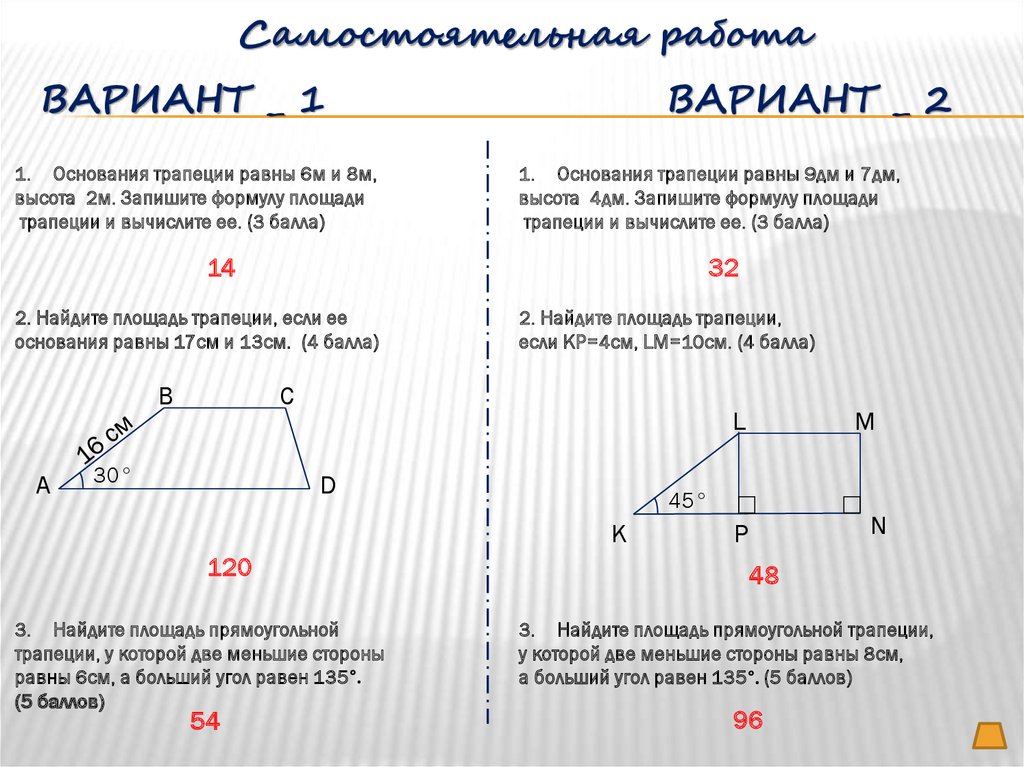

 В этом случае можно говорить, что навык счета доведен до автоматизма.
В этом случае можно говорить, что навык счета доведен до автоматизма. 
 Но мы, взрослые, знаем, если скорость решения примеров высока, значит ребёнок таблицу запомнил.
Но мы, взрослые, знаем, если скорость решения примеров высока, значит ребёнок таблицу запомнил.
 Все вопросы сопровождаются иллюстрациями.
Все вопросы сопровождаются иллюстрациями.  Дана иллюстрированная поддержка.
Дана иллюстрированная поддержка. 

 Это также может быть полезно, если им дают число и спрашивают, кратно ли оно 3 или нет.
Это также может быть полезно, если им дают число и спрашивают, кратно ли оно 3 или нет.

 ад ки рукаават ке!
ад ки рукаават ке!
 000 переведенные страницы
000 переведенные страницы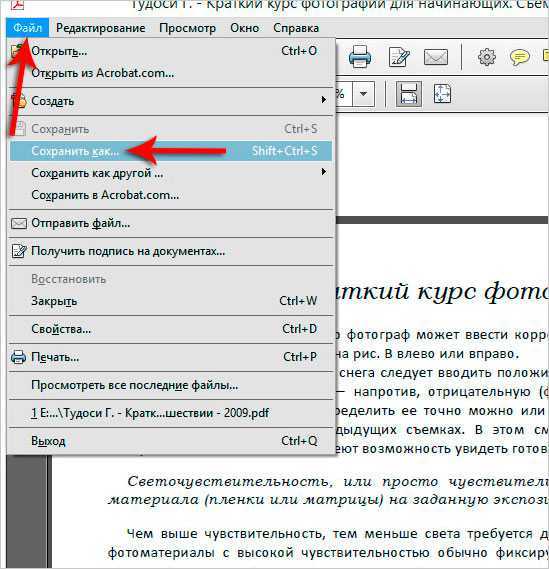 После обработки файлы будут безвозвратно удалены.
После обработки файлы будут безвозвратно удалены. Процесс
Процесс 3 / 5 — 3577 votes
5
1
3 / 5 — 3577 votes
5
1 Форма отчета
Форма отчета
 Форматы документов ПДФ и текст в некоторых случаях дополняют друг друга и тесно связываются в современной офисной работе. Довольно часто мы хотим преобразовать редактируемый текст документ в неизменяемый ПДФ файл. Это может быть контракт или какие-то финансовые данные, которые не следует изменять.
Форматы документов ПДФ и текст в некоторых случаях дополняют друг друга и тесно связываются в современной офисной работе. Довольно часто мы хотим преобразовать редактируемый текст документ в неизменяемый ПДФ файл. Это может быть контракт или какие-то финансовые данные, которые не следует изменять.
 По истечении этого времени они автоматически удаляются.
По истечении этого времени они автоматически удаляются. Неважно, какую платформу вы используете, например, для создания PDF-файла, потому что он будет работать и выглядеть одинаково на любой другой платформе. Эта универсальность сделала PDF форматом по умолчанию для обмена документами в Интернете.
Неважно, какую платформу вы используете, например, для создания PDF-файла, потому что он будет работать и выглядеть одинаково на любой другой платформе. Эта универсальность сделала PDF форматом по умолчанию для обмена документами в Интернете.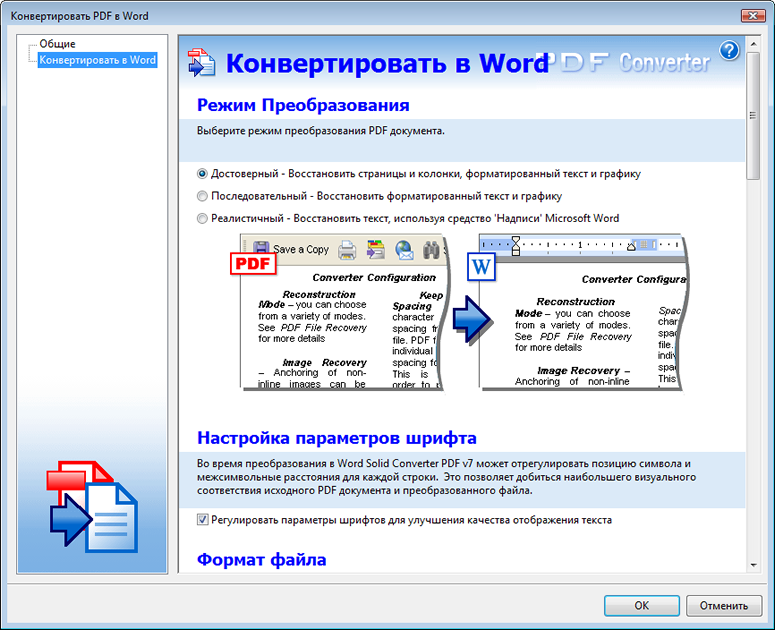 Однако, если вы конвертируете этот PDF в текст, это будет очень просто. Это наиболее распространенная причина преобразования PDF в текст!
Однако, если вы конвертируете этот PDF в текст, это будет очень просто. Это наиболее распространенная причина преобразования PDF в текст!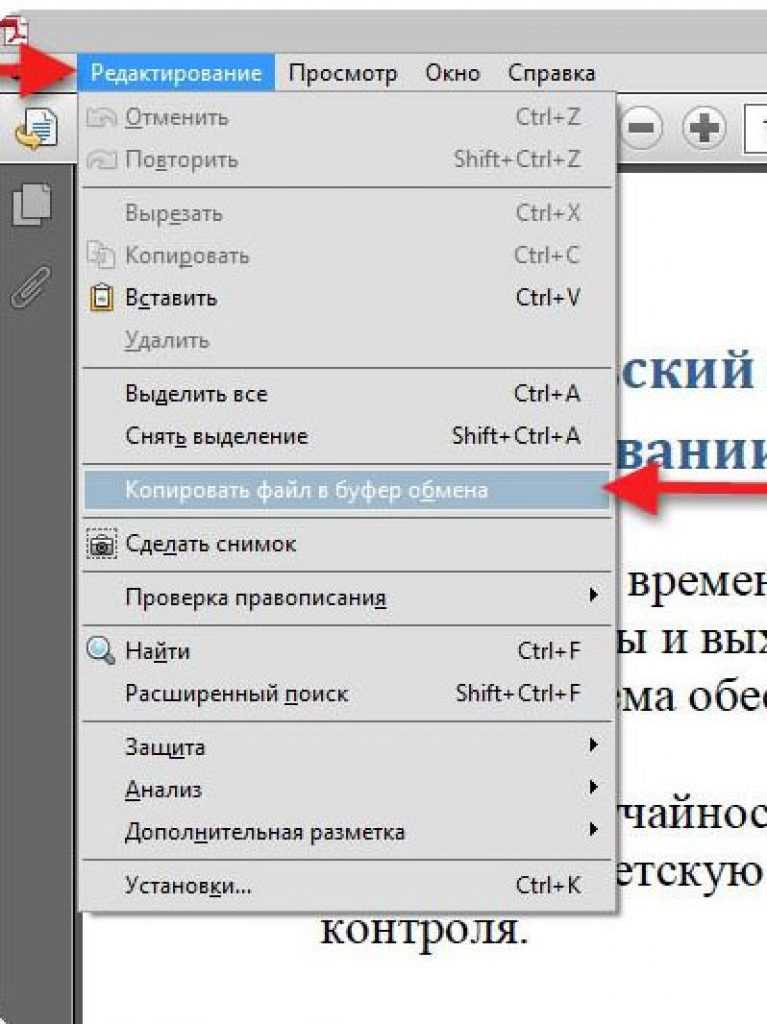 Если у вас более 20 файлов, не беспокойтесь — вы сможете повторить эти шаги столько раз, сколько вам нужно.
Если у вас более 20 файлов, не беспокойтесь — вы сможете повторить эти шаги столько раз, сколько вам нужно.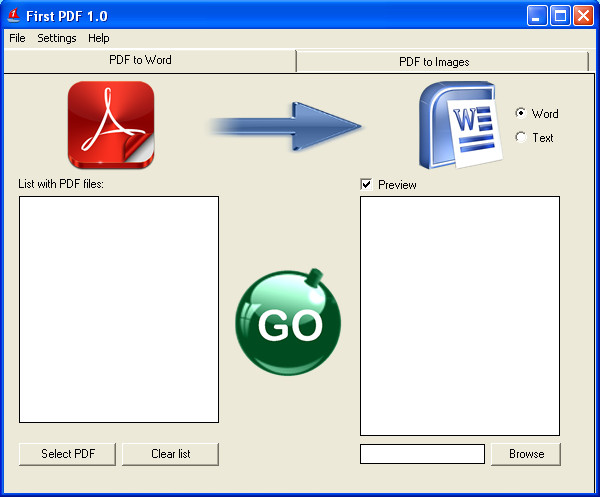 Наш инструмент копирует ваши PDF-файлы, когда вы их загружаете, а затем конвертирует эти копии. Ваши основные PDF-файлы всегда будут в безопасности на вашем устройстве, если они вам снова понадобятся.
Наш инструмент копирует ваши PDF-файлы, когда вы их загружаете, а затем конвертирует эти копии. Ваши основные PDF-файлы всегда будут в безопасности на вашем устройстве, если они вам снова понадобятся.
 Когда процесс перевода будет завершен, преобразованный текст будет доступен на новой вкладке в вашем браузере.
Когда процесс перевода будет завершен, преобразованный текст будет доступен на новой вкладке в вашем браузере. Результаты будут сгенерированы в новом файле PDF с включением как исходной, так и переведенной версий.
Результаты будут сгенерированы в новом файле PDF с включением как исходной, так и переведенной версий.

 ..
.. Игра с числами
>
Упражнение 3.1
>
Вопрос 2
Игра с числами
>
Упражнение 3.1
>
Вопрос 2 Итак, это ваш ответ. Спасибо вам, ребята. Если у вас есть какие-либо сомнения, пожалуйста, дайте мне знать в комментариях ниже. Я свяжусь с вами как можно скорее. Большое спасибо.
Итак, это ваш ответ. Спасибо вам, ребята. Если у вас есть какие-либо сомнения, пожалуйста, дайте мне знать в комментариях ниже. Я свяжусь с вами как можно скорее. Большое спасибо.
 5, не 7,5
5, не 7,5 Дифференциалы имеют символы dy и dx. Вторая производная также известна как двойное дифференцирование, потому что это производная от производной функции.
Дифференциалы имеют символы dy и dx. Вторая производная также известна как двойное дифференцирование, потому что это производная от производной функции. {(\frac{1}{3})} \right) \;=\; \left[ — \frac{2}{9{\frac{5}{3}}} \right] $$
{(\frac{1}{3})} \right) \;=\; \left[ — \frac{2}{9{\frac{5}{3}}} \right] $$ Он также отображает все пошаговые расчеты конкретной функции.
Он также отображает все пошаговые расчеты конкретной функции. Калькулятор теста второй производной расскажет нам, как увеличивается или уменьшается мгновенная скорость изменения на граничном интервале. 9{3x} \; sin2x $$
Калькулятор теста второй производной расскажет нам, как увеличивается или уменьшается мгновенная скорость изменения на граничном интервале. 9{3x} \; sin2x $$

 2 x $$
2 x $$ 92} $$
92} $$



