4. Логические выражения и таблицы истинности
13
4.1.Логические выражения
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание
«(2·2=5 или 2·2=4) и (2·2≠5 или 2·2≠4)».
Проанализируем составное высказывание. Оно содержит два простых высказывания:
А = «2•2=5»—ложно (0), В = «2•2=4»—истинно (1).
Тогда составное высказывание можно записать в следующей форме: «(А или В) и (Ā или В)».
Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:
инверсия, конъюнкция, дизъюнкция.
Для изменения указанного порядка могут использоваться скобки:
F = (A v В) & (Ā v В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F = (A v В) & (Ā v В) = (0 v 1) & (1 v 0) = 1 & 1 = 1.
14
4.2.Таблицы истинности
Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.
Простые высказывания обозначаются переменными (например, A и B).
При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:
1) необходимо определить количество строк в таблице истинности.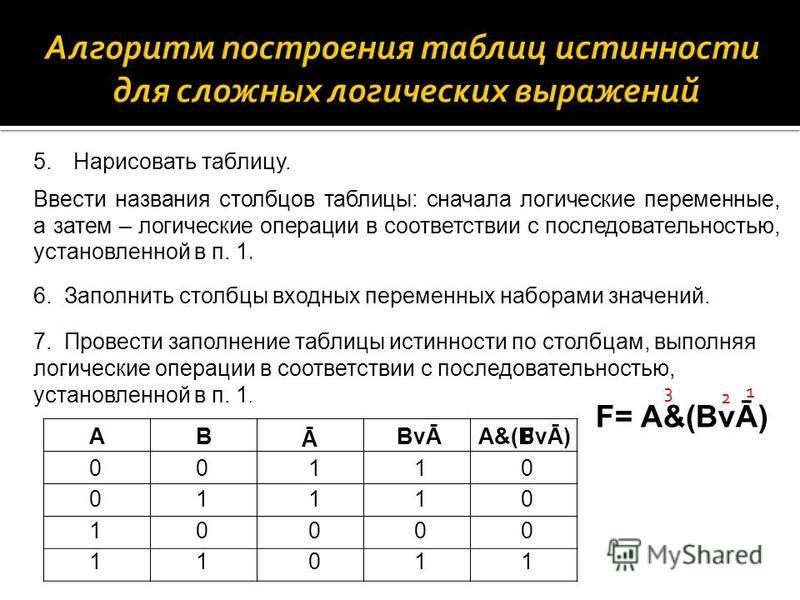 Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
В нашем случае логическая функция имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;
2)необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;
3)необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;
4)необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.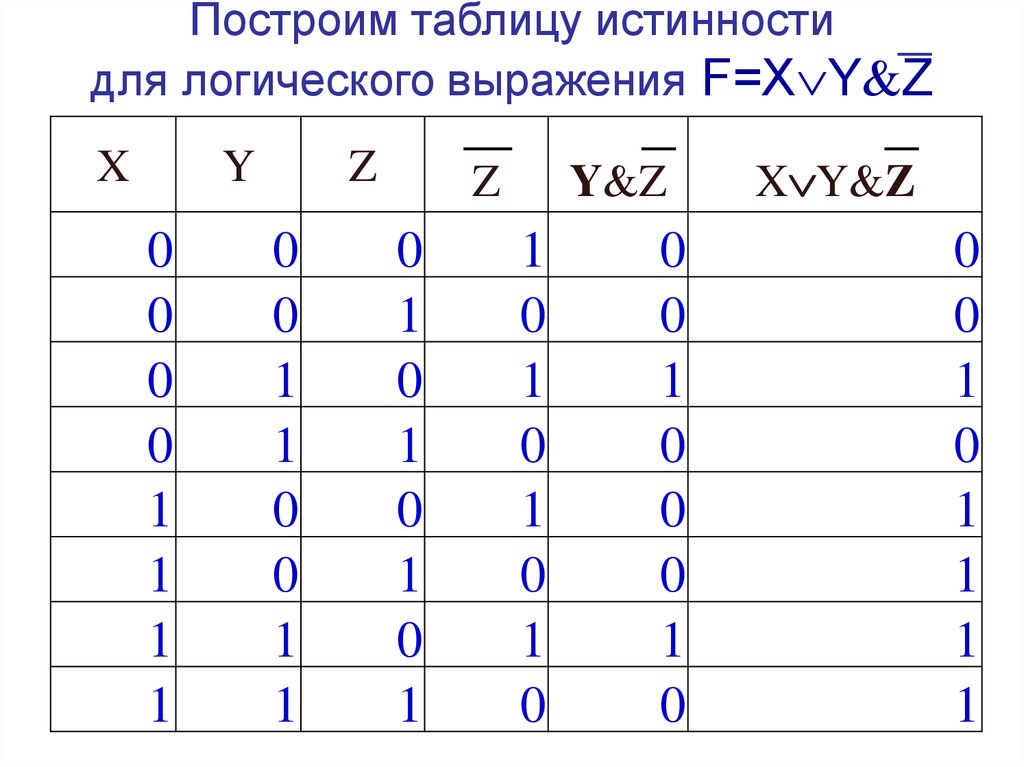
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
15
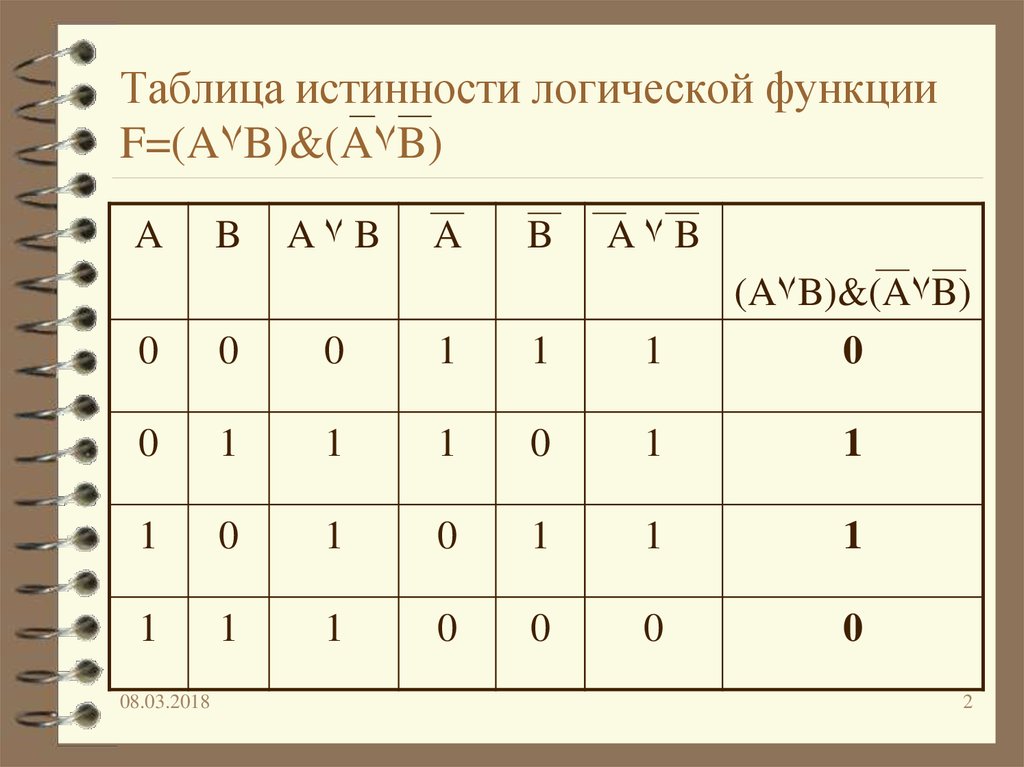
Таблица 8 – Таблица истинности логической функции
4.3.Равносильные логические выражения
Логические выражения, у которых последние столбцы таблиц истинности сов-
падают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Докажем, что логические выражения равносильны. Построим сначала таблицу истинности логического выражения (табли-
ца 9).
Таблица 9 – Таблица истинности логического выражения
А | В |
|
|
|
|
|
|
|
|
0 | 0 | 1 | 1 | 1 |
|
|
|
|
|
0 | 1 | 1 | 0 | 0 |
|
|
|
|
|
1 | 0 | 0 | 1 | 0 |
|
|
|
|
|
1 | 1 | 0 | 0 | 0 |
|
|
|
|
|
Теперь построим таблицу истинности логического выражения (таблица 10).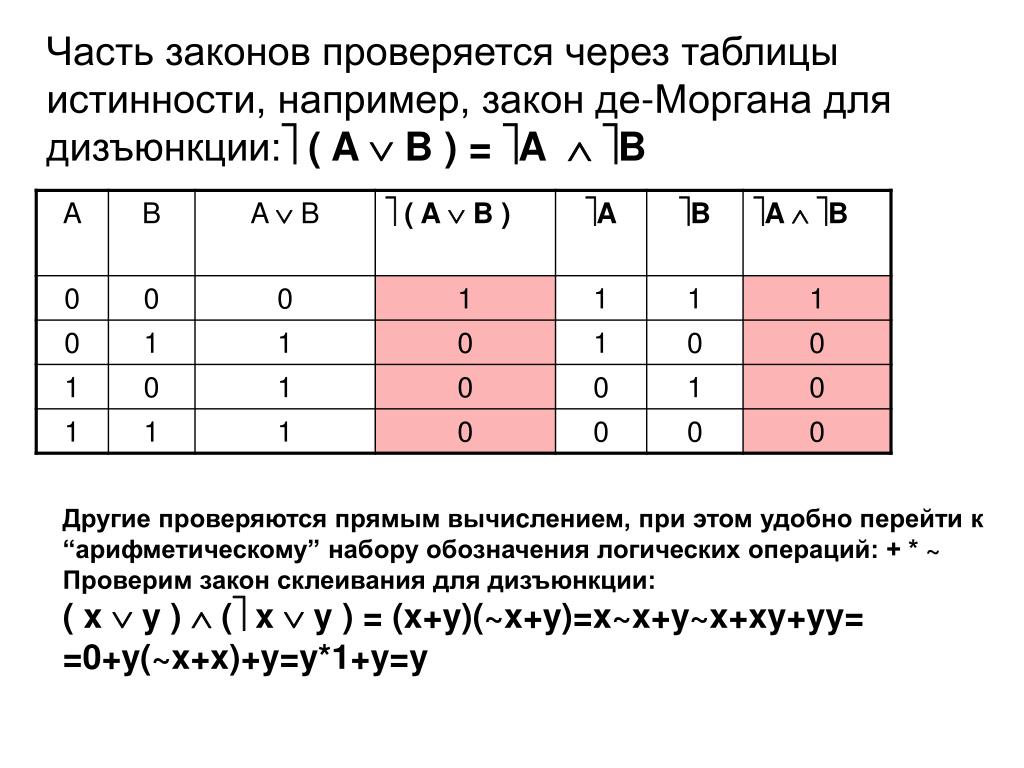
Таблица 10 – Таблица истинности логического выражения
А | В | А v В |
|
|
|
|
|
0 | 0 | 0 | 1 |
|
|
|
|
0 | 1 | 1 | 0 |
|
|
|
|
1 | 0 | 1 | 0 |
|
|
|
|
1 | 1 | 1 | 0 |
|
|
|
|
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:
=.
16
5. Построение таблиц истинности для сложных выражений
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений
переменных всего четыре: |
| ||
(0, 0), | (0, 1), | (1, 0), | (1, 1). |
Если формула содержит три переменные, то возможных наборов значений
переменных восемь: |
|
|
|
|
|
| |
(0, 0, 0), | (0, 0, 1), | (0, 1, 0), | (0, 1, 1), | (1, 0, 0), | (1, 0, 1), | (1, 1, 0), | (1, 1, 1). |
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Пример 1 1. Составим таблицу истинности для формулы, которая содержит две пере-
менные X и Y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 11:
Таблица 11 – Таблица истинности для формулы с переменными Х и У
Пример 2
Cоставить таблицу истинности сложного логического выражения: D = неA & (B+C).
А, В, С – три простых высказывания, поэтому:
количество строк = 23 +2 = 10 (n=3, т.к. на входе три элемента А, В, С) количество столбцов (таблица 12):
1)А,
2)В,
Урок по теме: Логические выражения и таблицы истинности | План-конспект урока по информатике и икт (9 класс) по теме:
Урок по информатике: Логические выражения и таблицы истинности
Цели: построение таблиц истинности логических выражений.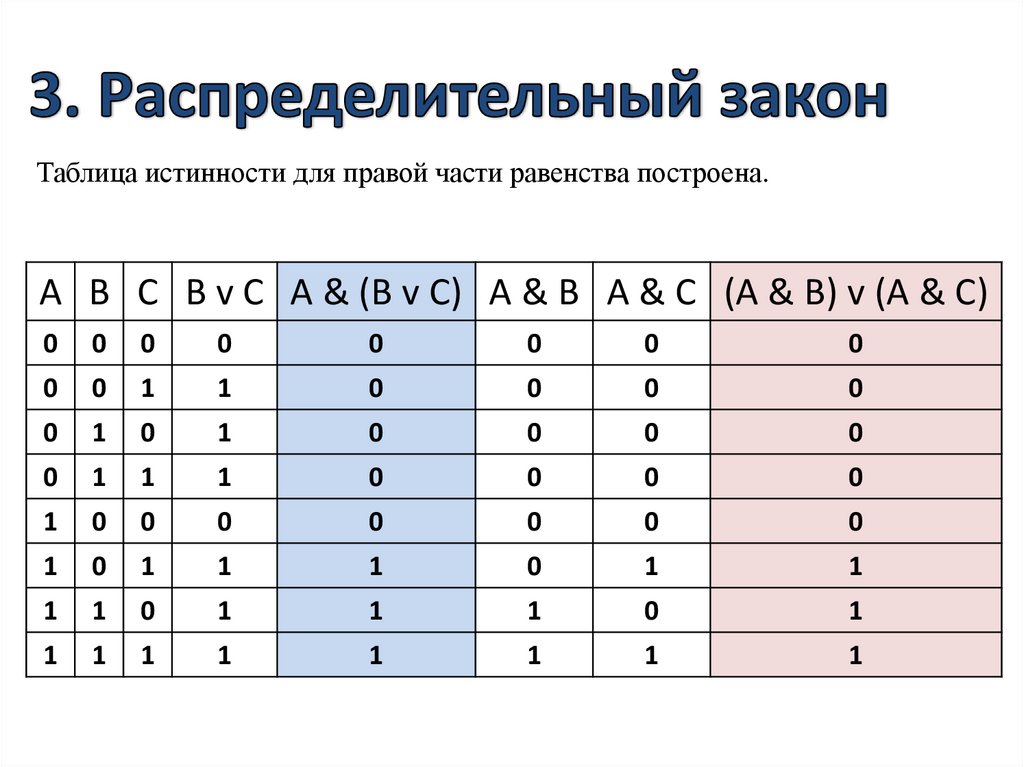
Задачи:
- Научить составлять логические выражения из высказываний;
- Ввести понятие “таблица истинности логического выражения”;
- Изучить последовательность действий построения таблиц истинности;
- Научить находить значение логических выражений посредством построения таблиц истинности;
- Ввести понятие равносильности логических выражений;
- Научить доказывать равносильность логических выражений, используя таблицы истинности;
- Закрепить навыки нахождения значений логических выражений посредством построения таблиц истинности.
Ожидаемые результаты обучения:
Учащиеся должны знать:
- таблицы истинности логических операций;
- этапы составления таблиц истинности логических выражений;
- понятие равносильные логические выражения.
Учащиеся должны уметь:
- строить и заполнять таблицу истинности логического выражения;
- находить значение логических выражений посредством построения таблиц истинности;
- доказывать равносильность логических выражений, используя таблицы истинности.

Ход урока
I. Оргмомент.
Здравствуйте, ребята. Мы продолжаем изучать основы логики и тема нашего сегодняшнего урока «Составление логических выражений. Таблицы истинности». Изучив данную тему, вы научитесь, как из высказываний составляются логические формы, и определять их истинность посредством составления таблиц истинности.
II. Проверка домашнего задания.
III. Изложение нового материала.
1. Построение таблиц истинности.
Мы уже несколько уроков используем понятие “таблица истинности”, определим же его.
Опр.1 Таблица истинности — это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций.
При построении таблиц истинности есть определенная последовательность действий:
- Необходимо определить количество строк в таблице истинности: количество строк равно 2n, где n — количество логических переменных.
- Необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.

- Необходимо построить таблицу истинности с указанным количеством строк и столбцов, ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
- Заполнить столбцы входных переменных наборами значений;
- Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
Пример. Построить таблицу истинности для составного высказывания:
1). Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.
Количество строк в таблице истинности должно быть равно 22=4.
2). Определяем количество столбцов. Это количество логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум, а количество логических операции — пяти, то есть количество столбцов таблицы истинности равно семи.
3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.
Можно сначала выполнить логическое отрицание или найти значение сначала в первой скобке, затем инверсию и значение во второй скобке, затем значение между этими скобками.
A | B | |||||
0 | 0 | 0 | 1 | 1 | 1 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 0 | 0 |
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
2. Равносильные логические выражения.
Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак “ = “.
Пример. Докажем, что логические выражения и равносильны.
Построим сначала таблицу истинности логического выражения:
1). Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.
Количество строк в таблице истинности должно быть равно 22=4.
2). Определяем количество столбцов. Это количество логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум, а количество логических операции — трем, то есть количество столбцов таблицы истинности равно пяти.
3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.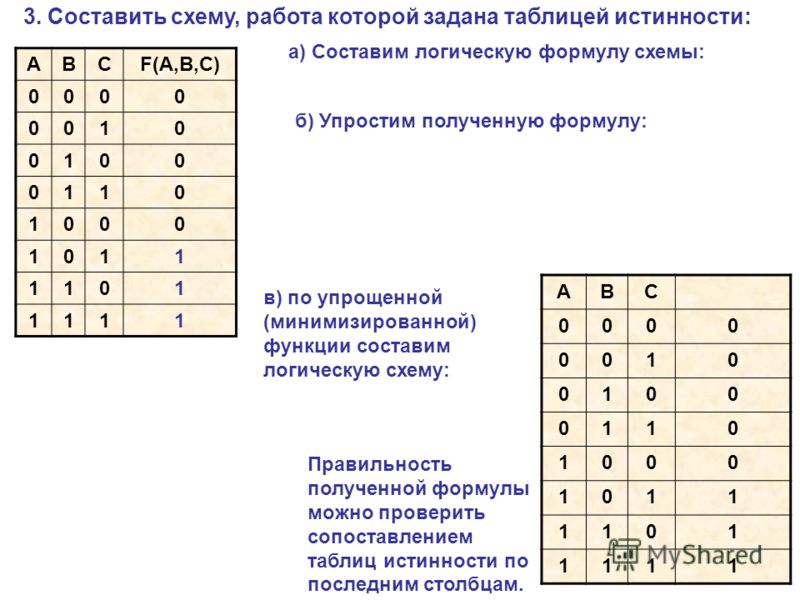
Сначала необходимо выполнить логическое отрицание А, а затем логическое отрицание В. Последним действием выполним логическое сложение.
A | B | |||
0 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 0 |
1 | 0 | 0 | 1 | 0 |
1 | 1 | 0 | 0 | 0 |
Теперь построим таблицу истинности логического выражения:
1). Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.
Количество строк в таблице истинности должно быть равно 22=4.
2). Определяем количество столбцов. В нашем случае количество переменных равно двум, а количество логических операции — двум, то есть количество столбцов таблицы истинности равно четырем.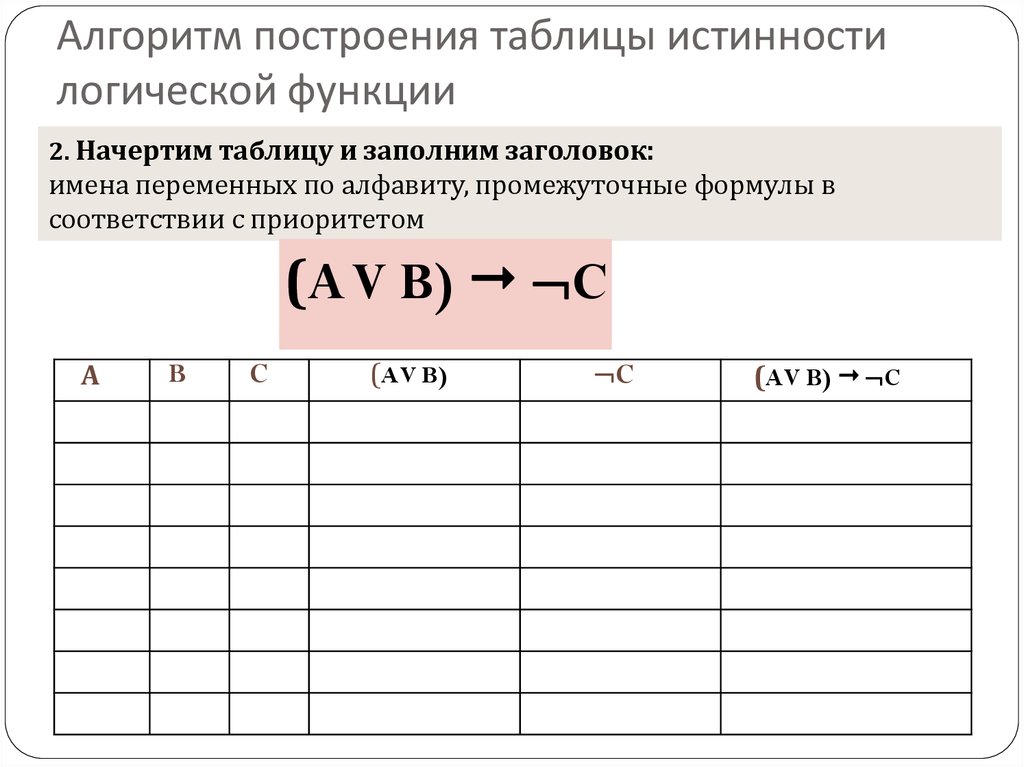
3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.
Сначала необходимо выполнить действие в скобках, а затем логическое отрицание.
A | B | ||
0 | 0 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 1 | 0 |
Построили таблицы. Теперь давайте, сравним значения в последних столбцах таблиц истинности, т.к. именно последние столбцы являются результирующими:
=
IV. Закрепление изученного материала.
1. Построить таблицу истинности для формулы: .
1).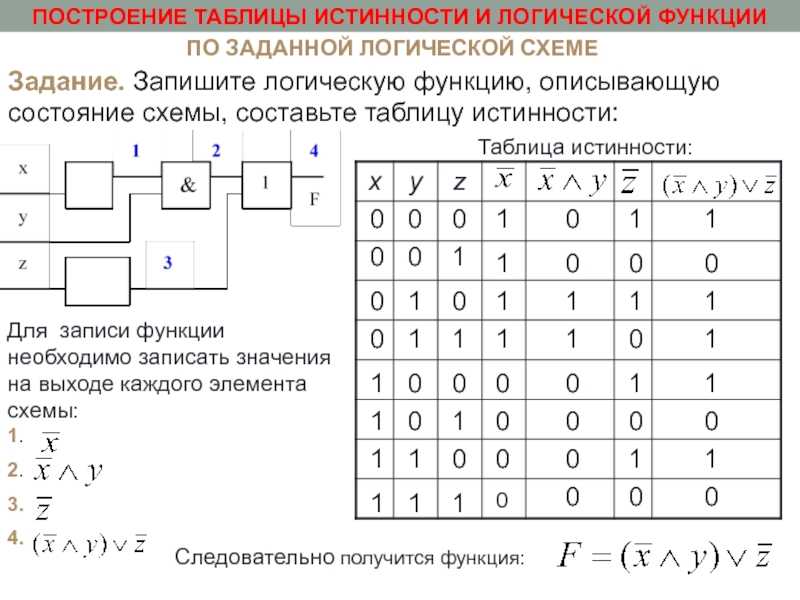 Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 3переменные: А, В и С.
Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 3переменные: А, В и С.
Количество строк в таблице истинности должно быть равно 23=8.
2). Определяем количество столбцов. В нашем случае количество переменных равно трем, а количество логических операции — пяти, то есть количество столбцов таблицы истинности равно восьми.
3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.
Последовательность операций: инверсия, операции в скобках, операция за скобкой.
A | B | C | |||||
0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
2. Докажите с помощью таблиц истинности равносильность следующих логических выражений: и .
Докажите с помощью таблиц истинности равносильность следующих логических выражений: и .
Построим сначала таблицу истинности логического выражения: .
1). Определим количество строк в таблице: 22=4.
2). Определяем количество столбцов: 2+1=3.
3). Строим таблицу с указанным количеством строк и столбцов.
A | B | |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 0 |
1 | 1 | 1 |
Построим таблицу истинности логического выражения: .
1). Определим количество строк в таблице: 22=4.
2). Определяем количество столбцов: 2+2=4.
3). Строим таблицу с указанным количеством строк и столбцов.
A | B | ||
0 | 0 | 1 | 1 |
0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
Вывод: данные логические выражения не равносильны.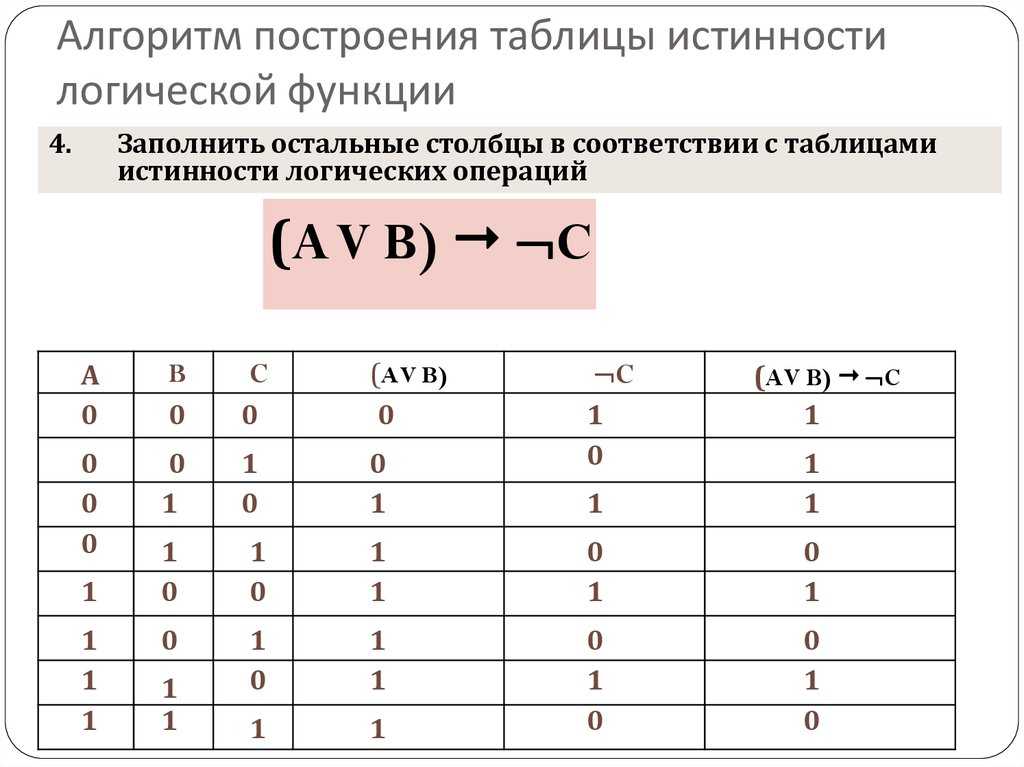
V. Итог урока.
Обобщить пройденный материал, оценить работу активных учеников.
VI. Домашнее задание.
- Доказать, используя таблицы истинности, что логические выражения и равносильны.
Построить таблицу истинности для формулы:
Примечания к таблице истинности и логическим утверждениям
Таблица истинности логической функции содержит списки всех возможных значений, которые функция может получить для данного входа. Таблица истинности состоит из множества строк и столбцов, причем верхняя строка указывает логические переменные и их комбинации, а нижняя строка показывает конечную функцию с возрастающей сложностью. Таблица истинности логической системы представляет выходные данные системы для данного входа в виде строк и столбцов. Чтобы назвать столбцы таблицы истинности, используются входы и выходы со строками, представляющими все потенциальные входы и выходы схемы.
Что такое логические операторы? Логическое утверждение — это утверждение, которое возвращает либо истину, либо ложь, т. е. 0 или 1. Если оно возвращает истину, оно позволяет нам получить известный набор фактов или получить из них новый факт. Пример: Диагонали прямоугольника имеют одинаковую длину.
е. 0 или 1. Если оно возвращает истину, оно позволяет нам получить известный набор фактов или получить из них новый факт. Пример: Диагонали прямоугольника имеют одинаковую длину.
Здесь он вернет либо истину, либо ложь в зависимости от оператора. Это декларативный тип оператора, который возвращает true или false.
Некоторые примеры логических утверждений:Примеры предложений, которые являются (или содержат) истинными утверждениями:
- «Том Круз — мужчина».
- «У треугольника три стороны».
- «Милан — столица Италии».
Примеры ложных предложений:
- «Все кулеры сделаны из чистого золота».
- «Два плюс два равно девять».
Примеры предложений, которые не являются (или не составляют) утверждениями: Эмоции, чувства, вопросы и т. д. не могут быть включены в логические утверждения.
- «Кто ты?»
- «Беги!»
- «Королева Англии мудра».
- «Пегас существует».

В логической функции есть три основные операции НЕ, ИЛИ и И:
- НЕ: Это также называется инверсией или отрицанием. Обозначается -. Это означает прямо противоположное или отрицательное значение.
- ИЛИ: Это также называется дизъюнкцией или сложением. Обозначается +. Это похоже на простое добавление значений. Функция возвращает истину, если хотя бы одно из ее значений истинно.
- И: Это также называется соединением или умножением. Он обозначается *. Это похоже на износ умножения для функции, возвращающей истину, оба значения должны быть истинными.
Унарные логические операторы содержат только один логический оператор. Это может быть либо Логическая Истина, либо Логическая Ложь.
Таблица истинности для логической истины: для каждого логического входа возвращается истинное значение.
Вход | Output |
T | T |
F | T |
Truth Table for Logical false: For each logical input, it returns a false Значение
Вход | Выход | |
T | F | |
F 9003 | ||
| 9192 F | ||
| 1912 F 9003 | ||
| 91111003 | ||
| 191219 9003 | ||
. 0074 0074 | F |
Таблица истинности для комплимента: возвращает значение, прямо противоположное логическому входу.
Input | Output(~) |
T | F |
F | T |
В двоичных операциях есть два логических входа. Над этими операторами выполняются операции И, ИЛИ и НЕ.
Таблица истинности для операции ИЛИ: Возвращает истину, если любой из входных данных верен, и ложь, если оба входа ложны.
A | B | A OR B |
T | T | T |
T | F | Т |
Ф | T | T |
F | F | F |
Tall Table For For For For For Empormance: It True On True On True Tons Thes This This This This This This This This This This This This This False Thes This False Tons On True Tons Thes Thes Thes This.
A | B | A AND B |
T | T | T |
T | F | F |
F | T | F |
F | F | F |
Значения функций могут быть 0 или 1. Где логический 0 означает ложь, а логическая 1 означает истину. Таким образом, применяются следующие правила:
Если A = 0, то -A = 1
Если A = 1, то -A = 0
A+B = 0, если A = 0 и B = 0
A+B = 1, за исключением случаев, когда A = 0 и B = 0
A*B = 1 если A = 1 и B = 1
A*B = 0, за исключением случаев, когда A = 1 и B = 1
Как оценить значения логической функции: Пример: показать процесс оценки значений логическая функция -(A+B) * -(A*B).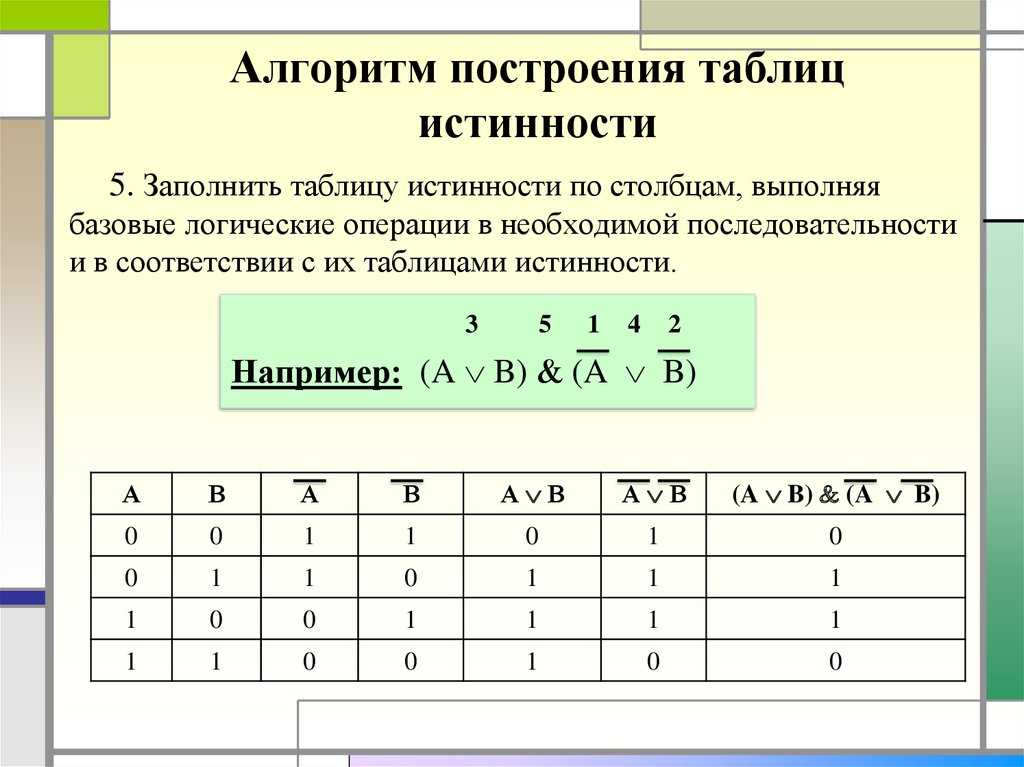
Определяется путем разбиения на более мелкие составные функции и вычисления их значений для достижения последнего шага. Это последовательный процесс. Необходимо выполнить следующие шаги:-
- Две логические переменные, A и B, перечислены вверху первых двух столбцов. Все возможные комбинации значений для A и B перечислены в этих столбцах путем подсчета двоичными числами: 00, 01, 10, 11.
- В третьем столбце значение (A+B) вычисляется с помощью операции ИЛИ. .
- В четвертом столбце минус (дополнение) третьего столбца берется, чтобы найти значения, связанные с функцией -(A+B)
- В пятом столбце мы вычисляем значения (A*B) с помощью AND операция.
- Мы находим отрицательное значение (A*B), чтобы вычислить значение -(A*B)
- В седьмом столбце мы находим И значений в четвертом столбце и шестом столбце, чтобы получить значение -(A+B )*-(A*B)
Таким же образом мы вычисляем таблицу истинности и значения для всех функций. Ниже приведена таблица выражения для -(A+B) * -(A*B).
Ниже приведена таблица выражения для -(A+B) * -(A*B).
А | В | (А+В) | -(А+В) | (A*B) | -(A*B) | -(A+B) * -(A*B) |
0 | 0 | 0 | 1 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 0 | 1 | 0 |
1 | 0 | 1 | 0 | 0 | 1 | 0 |
1 | 1 | 1 | 0 | 1 | 0 | 0 |
Крайний правый (седьмой) столбец содержит последнюю функцию, которая должна быть оценена.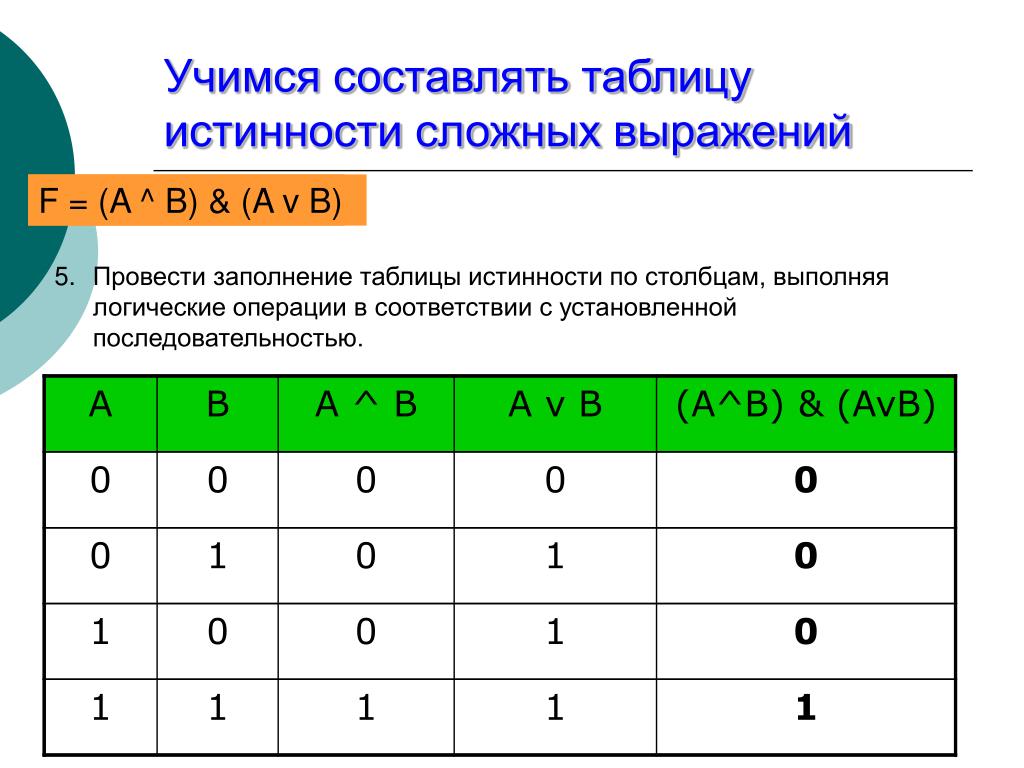 Другие значения в других столбцах (3-й-6-й) определяются путем определения сложения и умножения, а затем отрицания значений.
Другие значения в других столбцах (3-й-6-й) определяются путем определения сложения и умножения, а затем отрицания значений.
Для все более сложных логических функций компьютеры используются для построения таблиц истинности. Некоторые функции имеют большое количество входных переменных и состоят из нескольких составляющих функций; может получиться таблица с сотнями строк и столбцов.
Мы можем использовать таблицы истинности, чтобы определить, правильна ли структура логического аргумента. Они широко используются в логике запросов к базе данных, а также в их оптимизации. Кроме того, для приложений, связанных с общей логикой, таких как экспертные системы. Любой анализ, вероятно, должен реализовать их в той или иной форме. Кроме того, они используются в структурах базовых решений (IF, Case/Switch, IIF и т. д.). Вы можете построить любое количество логических слоев, и было бы полезно их использовать. Они там на фоне системы.
Использование булевых теорем является альтернативой таблице истинности. Этот процесс используется для определения простейшей схемы, которая будет выполнять необходимую логическую функцию. Это уменьшает количество операций, необходимых для выполнения данной задачи, и, следовательно, повышает эффективность системы.
Создание таблиц истинности — обучающиеся машины
Короткий на сегодня: в этом посте мы узнаем, как легко создавать таблицы истинности с помощью R, и внесем наш код в растущий репозиторий Код Розетты . Я надеюсь, что вы узнаете несколько трюков по пути, так что читайте дальше!
Мы рассмотрели фрагменты кода, которые я добавлял в Rosetta Code в этом блоге ранее (см. Категорию: Rosetta Code). На этот раз мы хотим решить следующую задачу:
Таблица истинности
Таблица истинности представляет собой отображение входных и выходных данных булевой функции, организованной в виде таблицы, где каждая строка содержит одну комбинацию входных значений и соответствующее значение функции.Задача
- Введите логическую функцию от пользователя в виде строки, затем вычислите и распечатайте форматированную таблицу истинности для данной функции.
(Можно предположить, что ввод пользователя правильный).- Распечатать и показать вывод для логических функций с двумя и тремя входными переменными, но ни одна программа не должна ограничиваться таким количеством переменных в функции.
- Разрешены выражения как с обратной шлифовкой, так и с инфиксной нотацией.
Ядром таблицы истинности является перестановка всех утверждений TRUE и FALSE для всех переменных (= букв), которые мы извлекаем из булевой функции x . К счастью, несколько сообщений назад мы создали такую функцию перестановки (см. Изучение R: перестановки и комбинации с базой R), так что мы можем адаптировать ее соответствующим образом: expand.grid(rep(list(c(FALSE, TRUE)), длина(вары))) .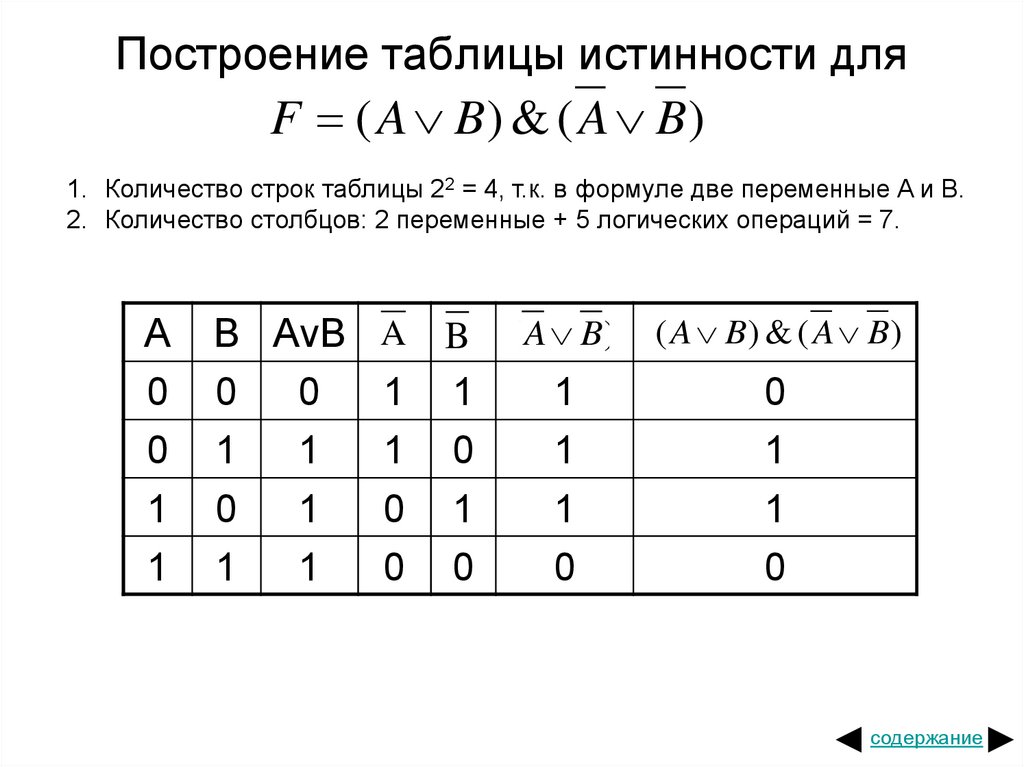




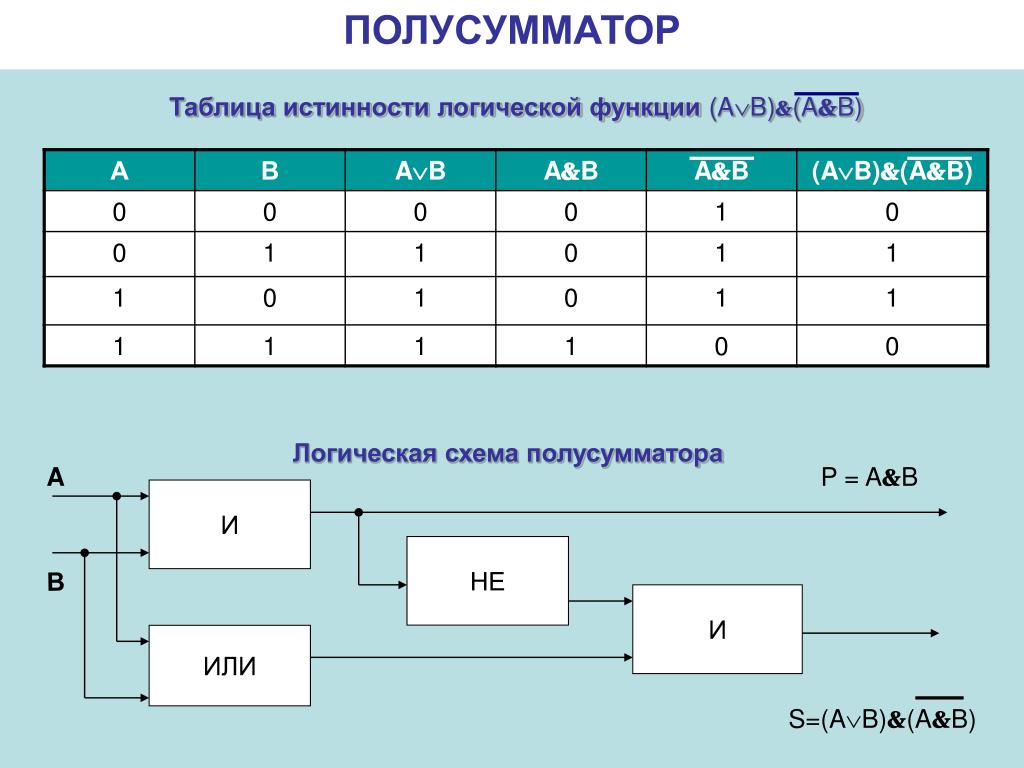
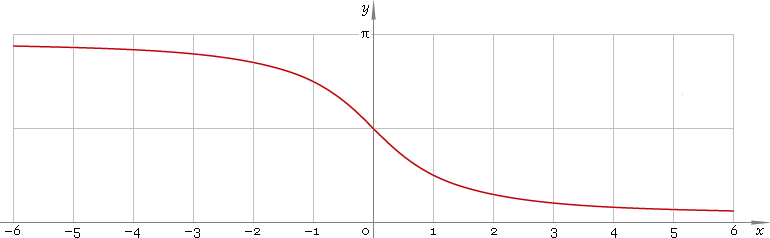
 Итак, функция y = arcsin x определена на отрезке [-1,+1], является монотонно возрастающей, и ее значения заполняют отрезок [-π/2, +π/2]. График функции показан на рис. 2.
Итак, функция y = arcsin x определена на отрезке [-1,+1], является монотонно возрастающей, и ее значения заполняют отрезок [-π/2, +π/2]. График функции показан на рис. 2. 3.
3.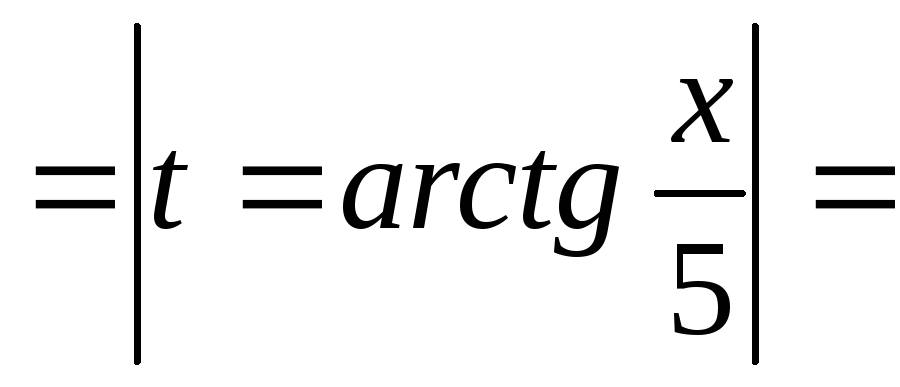
-and-arctan(x).gif)

 )/3
)/3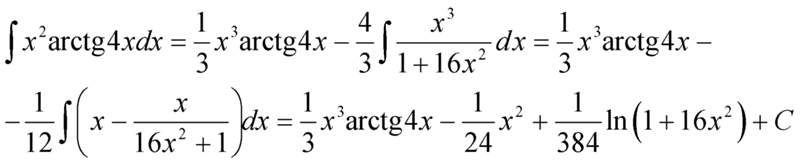
 ) = \ frac {\ pi {2} — \ arctan \ left ( {\ frac {1} {2}} \ right) + \ frac {\ pi {2} — \ arctan \ left ( {\ frac { 1}{3}} \справа)\) (M1)
) = \ frac {\ pi {2} — \ arctan \ left ( {\ frac {1} {2}} \ right) + \ frac {\ pi {2} — \ arctan \ left ( {\ frac { 1}{3}} \справа)\) (M1) 


 [3]
[3]

 Давайте посчитаем в шестнадцатиричной:
Давайте посчитаем в шестнадцатиричной:
 Количество конфет не поменялось, мы просто считали их по-разному!
Количество конфет не поменялось, мы просто считали их по-разному! Число в степени – это число, сколько-то раз умноженное на само себя. То есть 53=5*5*5 (пять в третьей степени – это пять, три раза умноженная сама на себя: 5*5*5), или 85=8*8*8*8*8 (восемь в пятой степени – это восемь, пять раз умноженная на саму себя: 8*8*8*8*8).
Число в степени – это число, сколько-то раз умноженное на само себя. То есть 53=5*5*5 (пять в третьей степени – это пять, три раза умноженная сама на себя: 5*5*5), или 85=8*8*8*8*8 (восемь в пятой степени – это восемь, пять раз умноженная на саму себя: 8*8*8*8*8). Просто так поделить это число на коробочки по 2 оказалось затруднительным. Но если вспомнить про наши сотни-тысячи, можно задуматься: а ведь в двоичной 100=2*2, 1000=2*2*2, 10 000=2*2*2*2 и так далее.
Просто так поделить это число на коробочки по 2 оказалось затруднительным. Но если вспомнить про наши сотни-тысячи, можно задуматься: а ведь в двоичной 100=2*2, 1000=2*2*2, 10 000=2*2*2*2 и так далее. Получается, что это 8, то есть 23, то есть 2*2*2.
Получается, что это 8, то есть 23, то есть 2*2*2.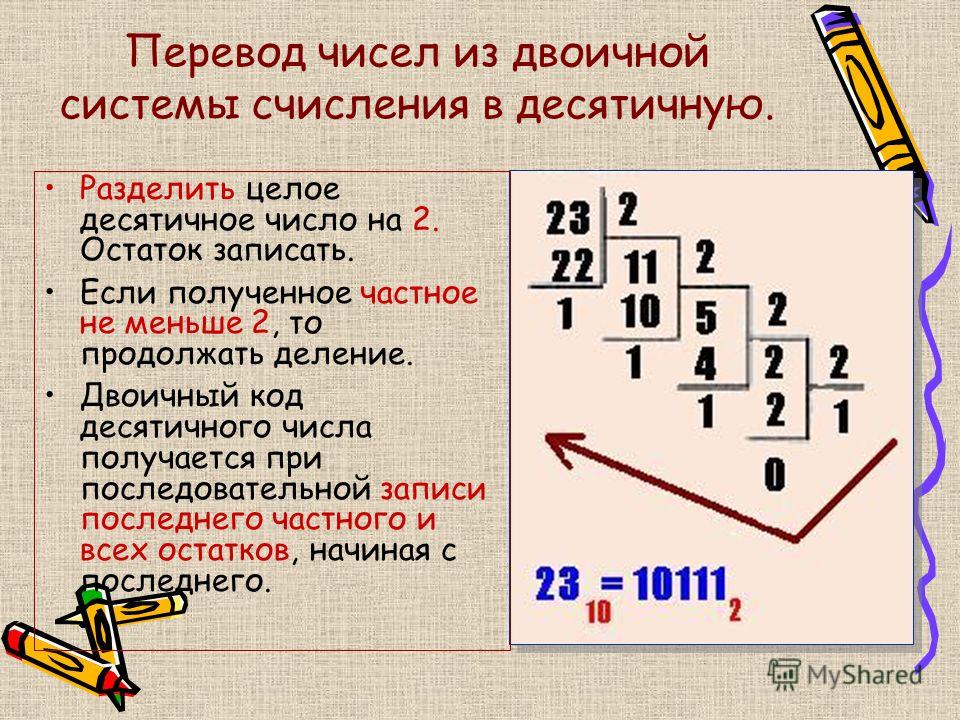 И запутаться во всём этом в первый раз – нормально. И во второй, и в третий. Просто попробуйте сделать это ещё и ещё раз – по шагам, как написано выше, и всё получится.
И запутаться во всём этом в первый раз – нормально. И во второй, и в третий. Просто попробуйте сделать это ещё и ещё раз – по шагам, как написано выше, и всё получится.
 Как это делается? Так же, как и в десятичной, но надо помнить, что десяток в восьмеричной системе – это восемь, а не десять, и что 8 и 9 в ней не существует.
Как это делается? Так же, как и в десятичной, но надо помнить, что десяток в восьмеричной системе – это восемь, а не десять, и что 8 и 9 в ней не существует. В восьмеричной, как вы, наверное, уже догадались, число 258 – это две восьмерки и пять единиц. То есть 258=2*8+5=2110.
В восьмеричной, как вы, наверное, уже догадались, число 258 – это две восьмерки и пять единиц. То есть 258=2*8+5=2110. Мы используем слова, из слов делаем предложения, из предложений – текст, рассказ, диалог. Но чтобы сделать слово, мы используем буквы, которых всего-навсего 33 штуки!
Мы используем слова, из слов делаем предложения, из предложений – текст, рассказ, диалог. Но чтобы сделать слово, мы используем буквы, которых всего-навсего 33 штуки! Это, примерно, как если бы мы букву А записали как 1, Б как 2, В как 3, и так далее.
Это, примерно, как если бы мы букву А записали как 1, Б как 2, В как 3, и так далее.
 И получилось это из-за того, что таблица для шифровки и таблица для дешифровки не совпали.
И получилось это из-за того, что таблица для шифровки и таблица для дешифровки не совпали. Например, весь вай-фай в мире работает примерно одинаково, поэтому почти любой телефон может подключиться почти к любой точке вай-фай.
Например, весь вай-фай в мире работает примерно одинаково, поэтому почти любой телефон может подключиться почти к любой точке вай-фай.

 У этой науки есть множество простых практических точек приложения, и если ребёнок знаком с её концепциями, то многое, что может испугать, сбить с толку и привести в отчаяние, для него будет просто задачей, к которой надо найти правильное решение.
У этой науки есть множество простых практических точек приложения, и если ребёнок знаком с её концепциями, то многое, что может испугать, сбить с толку и привести в отчаяние, для него будет просто задачей, к которой надо найти правильное решение.
 В итоге древними египтянами были впервые придуманы знаки, обозначающие 1, 5 и 10.
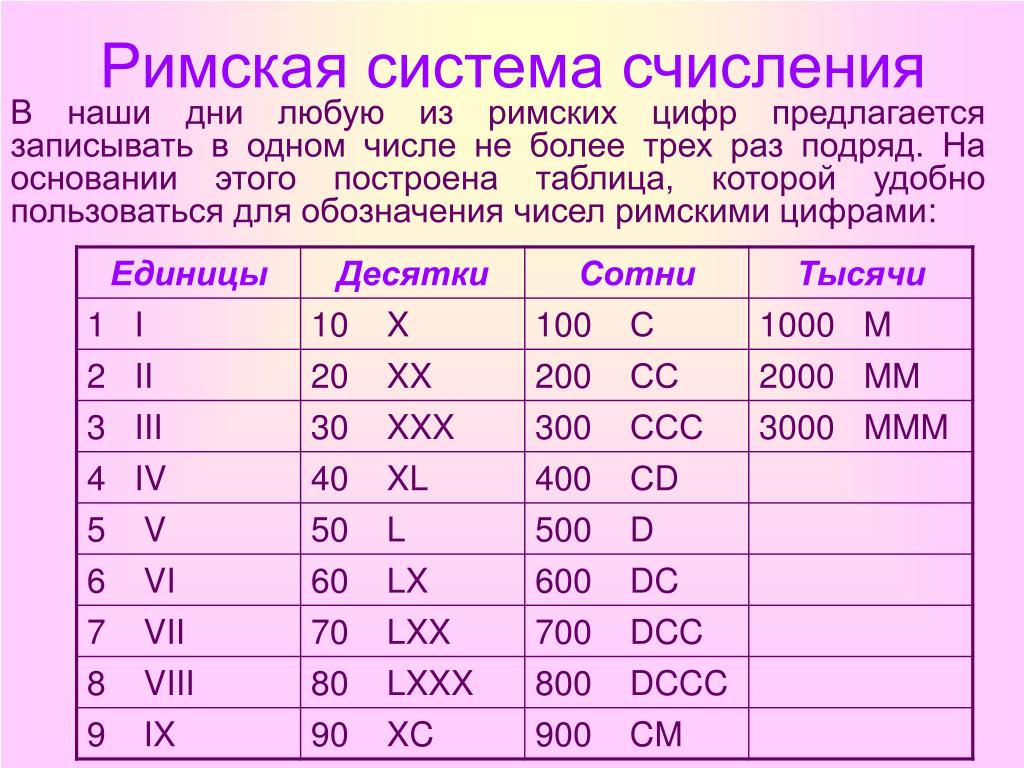
В итоге древними египтянами были впервые придуманы знаки, обозначающие 1, 5 и 10. Наиболее показательным представителем данной группы является римская система счисления. Здесь имеется еще одна отличительная особенность. Для записи очень больших чисел необязательно использовать весь набор знаков — на такие случаи существуют функции сложения и вычитания.
Наиболее показательным представителем данной группы является римская система счисления. Здесь имеется еще одна отличительная особенность. Для записи очень больших чисел необязательно использовать весь набор знаков — на такие случаи существуют функции сложения и вычитания.
 Эта схема может пребывать в одном из двух состояний — «ноль» или «единица».
Эта схема может пребывать в одном из двух состояний — «ноль» или «единица».

 После 1 ставится так называемая двоичная точка.
После 1 ставится так называемая двоичная точка.
 Это делается в два подэтапа:
Это делается в два подэтапа: На самом деле двоичная арифметика предельно логична и понятна. Пользование таблицами сложения и умножения не представляет сложности, если в них разобраться.
На самом деле двоичная арифметика предельно логична и понятна. Пользование таблицами сложения и умножения не представляет сложности, если в них разобраться.

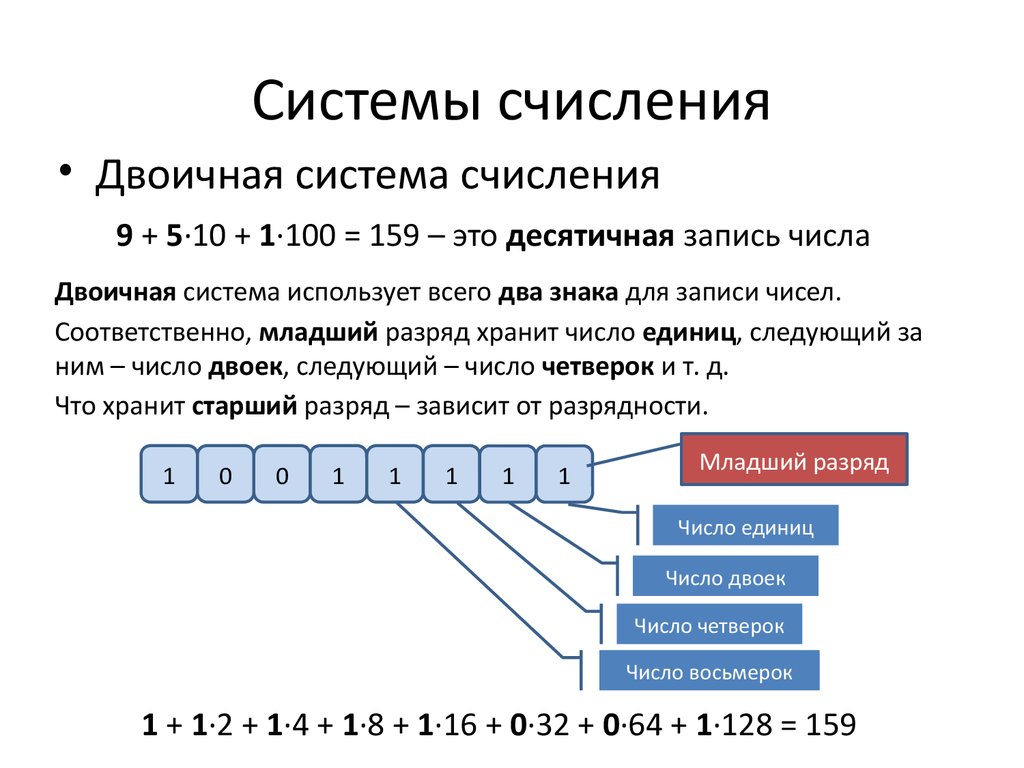
 Например, десятичная система , которую мы используем чаще всего в повседневной жизни, использует число 10 в качестве основы и состоит из 10 различных чисел, с помощью которых вы можете представить все остальные: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Это позиционная система и поэтому значение каждого числа меняется в зависимости от его положения (единицы, десятки, сотни и т.д.).
Например, десятичная система , которую мы используем чаще всего в повседневной жизни, использует число 10 в качестве основы и состоит из 10 различных чисел, с помощью которых вы можете представить все остальные: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Это позиционная система и поэтому значение каждого числа меняется в зависимости от его положения (единицы, десятки, сотни и т.д.). система, которую мы используем каждый день для измерения времени (один час равен 60 минутам, а каждая минута равна 60 секундам).
система, которую мы используем каждый день для измерения времени (один час равен 60 минутам, а каждая минута равна 60 секундам). В 1703 году Лейбниц опубликовал статью « Explication de l’Arithmétique Binaire », в которой объяснялось, как числа могут быть представлены с помощью цифр 0 и 1. В то время его исследования не отвечали какой-либо конкретной цели, но с появление первых компьютеров в начале 20-го века, почти 300 лет спустя, можно было понять, как все, что объяснил Лейбниц в своей статье, применялось первыми программистами компьютеров.
В 1703 году Лейбниц опубликовал статью « Explication de l’Arithmétique Binaire », в которой объяснялось, как числа могут быть представлены с помощью цифр 0 и 1. В то время его исследования не отвечали какой-либо конкретной цели, но с появление первых компьютеров в начале 20-го века, почти 300 лет спустя, можно было понять, как все, что объяснил Лейбниц в своей статье, применялось первыми программистами компьютеров. Если у нас есть двоичное число 10111101 и мы хотим преобразовать его в десятичное число, мы должны сначала разложить его на множители, используя число 2 и возведя его в степень, соответствующую каждой цифре, в соответствии с положением, которое она занимает в ряду чисел. В качестве показателей степени мы будем использовать 0, 1, 2, 3… пока не достигнем 7, и мы начнем факторизовать в порядке слева направо, начиная с наибольшей степени. Наконец, мы вычислим сложение и найдем эквивалентное десятичное число, которое в данном случае равно 189.:
Если у нас есть двоичное число 10111101 и мы хотим преобразовать его в десятичное число, мы должны сначала разложить его на множители, используя число 2 и возведя его в степень, соответствующую каждой цифре, в соответствии с положением, которое она занимает в ряду чисел. В качестве показателей степени мы будем использовать 0, 1, 2, 3… пока не достигнем 7, и мы начнем факторизовать в порядке слева направо, начиная с наибольшей степени. Наконец, мы вычислим сложение и найдем эквивалентное десятичное число, которое в данном случае равно 189.:


 Конечно, готов кратко
рассказать про решения таких задач,
если спросите.
Конечно, готов кратко
рассказать про решения таких задач,
если спросите.




 + xnan.
+ xnan.


 Например, 64·4 + 81·(-3) = 13.
Например, 64·4 + 81·(-3) = 13. Поэтому и делится на
.
Поэтому и делится на
.
 node.js:96:31)
в Workflow.runNode (/usr/local/lib/node_modules/n8n/node_modules/n8n-workflow/dist/src/Workflow.js:594:51)
в /usr/local/lib/node_modules/n8n/node_modules/n8n-core/dist/src/WorkflowExecute.js:537:64
node.js:96:31)
в Workflow.runNode (/usr/local/lib/node_modules/n8n/node_modules/n8n-workflow/dist/src/Workflow.js:594:51)
в /usr/local/lib/node_modules/n8n/node_modules/n8n-core/dist/src/WorkflowExecute.js:537:64  NET, React JS, JavaScript, TypeScript, Azure Data Factory, Vue.js, Avanade, Go,Microsoft,YouTube,Facebook,Instagram,Dynamics 365,Microsoft Dynamics 365,Microsoft Dynamics,Microsoft Azure,Sitecore,Angular,Kubernetes,React,Gulp,Npm,SCSS,Webpack,Netcore,API REST,Azure Functions,Azure Pipelines, Git, Kafka, NoSQL, React Native, ASP.NET MVC, Azure PaaS, Excel, SAP",
"company_labels": "ИИ, SaaS",
"company_follower_count": 362629,
"адрес_компании": "ххххх",
"фирма_специальности": [
"ИТ-услуги",
«Майкрософт Динамика»,
"Майкрософт",
"Шарпойнт",
"CRM",
"Облачные вычисления",
«Динамика 365»,
«Технологическая инфраструктура»,
"Разработка приложения",
"ЕРП",
«Цифровая трансформация»,
"Безопасность",
"Опыт клиентов",
"Управление цепочками поставок",
«Устойчивость»,
«Инновация»,
"Технологии",
«Майкрософт Азур»,
«Платформа Microsoft Power»,
«Облака Microsoft Industry»,
«Быстрая доставка»,
«Команды Майкрософт»,
"Виндовс 10",
«Аналитика и ИИ»,
"Бизнес-консультирование",
«Современное рабочее место»,
"Управляемые службы",
"Исследовать",
"Консультативный"
],
"company_tagline": "ххххх",
"company_hashtags": [
"хххх",
"хххх"
],
"company_description": "ххххх",
"matched_job_offers_company_count": 1,
"Предложения о работе": [
{
"job_id": "b335522558808c-2148-4b65-b97b-54fffbc34724",
"имя_работы": "хххх",
"job_contract": "Полная работа",
"job_location": "ххххх",
"job_categories": "Бизнес",
"job_level": "Индивидуальный участник",
"job_published_at": "2022-08-01T00:00:00.
NET, React JS, JavaScript, TypeScript, Azure Data Factory, Vue.js, Avanade, Go,Microsoft,YouTube,Facebook,Instagram,Dynamics 365,Microsoft Dynamics 365,Microsoft Dynamics,Microsoft Azure,Sitecore,Angular,Kubernetes,React,Gulp,Npm,SCSS,Webpack,Netcore,API REST,Azure Functions,Azure Pipelines, Git, Kafka, NoSQL, React Native, ASP.NET MVC, Azure PaaS, Excel, SAP",
"company_labels": "ИИ, SaaS",
"company_follower_count": 362629,
"адрес_компании": "ххххх",
"фирма_специальности": [
"ИТ-услуги",
«Майкрософт Динамика»,
"Майкрософт",
"Шарпойнт",
"CRM",
"Облачные вычисления",
«Динамика 365»,
«Технологическая инфраструктура»,
"Разработка приложения",
"ЕРП",
«Цифровая трансформация»,
"Безопасность",
"Опыт клиентов",
"Управление цепочками поставок",
«Устойчивость»,
«Инновация»,
"Технологии",
«Майкрософт Азур»,
«Платформа Microsoft Power»,
«Облака Microsoft Industry»,
«Быстрая доставка»,
«Команды Майкрософт»,
"Виндовс 10",
«Аналитика и ИИ»,
"Бизнес-консультирование",
«Современное рабочее место»,
"Управляемые службы",
"Исследовать",
"Консультативный"
],
"company_tagline": "ххххх",
"company_hashtags": [
"хххх",
"хххх"
],
"company_description": "ххххх",
"matched_job_offers_company_count": 1,
"Предложения о работе": [
{
"job_id": "b335522558808c-2148-4b65-b97b-54fffbc34724",
"имя_работы": "хххх",
"job_contract": "Полная работа",
"job_location": "ххххх",
"job_categories": "Бизнес",
"job_level": "Индивидуальный участник",
"job_published_at": "2022-08-01T00:00:00. 000Z",
"job_description": "хххх",
"workflow_keywords": ""
}
],
"people_first_name": "ххххх",
"people_last_name": "ххххх",
"people_full_name": "ххххх",
"people_current_position": "Старший директор по продажам и альянсам",
"people_linkedin_url": "xxxxxx",
"люди_компания_домен": "xxx",
"people_company_name": "xxxx",
"people_buying_signals_id": "c258808c-2148-4b65-b97b-54fffbc34724",
"people_buying_signals_title": "Специалист по развитию продаж",
"источник": "ххх",
"рабочий процесс": "00327f3d-806d-4eed-9c75-e5253df3b252"
}
000Z",
"job_description": "хххх",
"workflow_keywords": ""
}
],
"people_first_name": "ххххх",
"people_last_name": "ххххх",
"people_full_name": "ххххх",
"people_current_position": "Старший директор по продажам и альянсам",
"people_linkedin_url": "xxxxxx",
"люди_компания_домен": "xxx",
"people_company_name": "xxxx",
"people_buying_signals_id": "c258808c-2148-4b65-b97b-54fffbc34724",
"people_buying_signals_title": "Специалист по развитию продаж",
"источник": "ххх",
"рабочий процесс": "00327f3d-806d-4eed-9c75-e5253df3b252"
}


 % 210 выводов, 0,000 ЦП за 0,000 секунды (98% ЦП, 4100201 губ)
ЛОЖЬ.
?- T = узел( 2 , ноль, узел( 1 , ноль, узел(3, ноль, узел(4, ноль, узел(5, ноль, узел)(6, ноль, узел(7, ноль, узел(8, ноль, узел(9, ноль, узел(10, ноль, узел(11, ноль, узел(12, ноль), узел(13, ноль, узел(14, ноль, узел(15, ноль, узел)( 16, ноль, узел(17, ноль, узел(18, ноль, узел(19), ноль, узел(20, ноль, узел(21, ноль, узел(22, ноль, узел(23, ноль), узел(24, ноль, узел(25, ноль, узел(26, ноль), узел(27, ноль) , узел(28, ноль, узел(29, ноль, узел(30, ноль, узел(31, ноль), узел(32, ноль, узел(33, ноль, узел(34, ноль), узел(35, ноль, узел (36, ноль, узел (37, ноль, узел (38, ноль, узел (39), ноль, узел (40, ноль, узел (41, ноль, узел (42), ноль, узел (43, ноль, узел (44) , ноль, узел(45, ноль, узел(46, ноль, узел(47, ноль, узел(48, ноль), узел(49, ноль, узел(50, ноль, узел(51, ноль, узел(52, ноль) , узел(53, ноль, узел(54, ноль, узел(55, ноль, узел(56), ноль, узел(57, ноль, узел(58, ноль, узел(59), ноль, узел(60, ноль, узел(61, ноль, узел(62, ноль, узел(63, ноль), узел(64, ноль, узел(65, ноль, узел(66, ноль, узел(67, ноль) , узел(68, ноль, узел(69, ноль, узел(70, ноль, узел(71), ноль, узел(72, ноль, узел(73, ноль, узел(74, ноль), узел(75, ноль, узел (76, ноль, узел (77, ноль, узел (78, ноль, узел (79), ноль, узел (80, ноль, узел (81, ноль, узел (82), ноль, узел (83, ноль, узел (84) , ноль, узел(85, ноль, узел(86, ноль, узел(87, ноль, узел(88, ноль), узел(89, ноль, узел(90, ноль, узел(91, ноль, узел(92, ноль) , узел (93, ноль, узел (94, ноль, узел (9)5, ноль, узел(96, ноль, узел(97, ноль, узел(98, ноль, узел(99, ноль, узел(100, ноль, ноль))))))))))))))) )))))))))))))))))))))))))))))))))))))))))))))))))))) ))))))))))))))))))))))))))))))))))),
time(( lazy _chain(Zs,#<),phrase(in_order(T),Zs))).
% 210 выводов, 0,000 ЦП за 0,000 секунды (98% ЦП, 4100201 губ)
ЛОЖЬ.
?- T = узел( 2 , ноль, узел( 1 , ноль, узел(3, ноль, узел(4, ноль, узел(5, ноль, узел)(6, ноль, узел(7, ноль, узел(8, ноль, узел(9, ноль, узел(10, ноль, узел(11, ноль, узел(12, ноль), узел(13, ноль, узел(14, ноль, узел(15, ноль, узел)( 16, ноль, узел(17, ноль, узел(18, ноль, узел(19), ноль, узел(20, ноль, узел(21, ноль, узел(22, ноль, узел(23, ноль), узел(24, ноль, узел(25, ноль, узел(26, ноль), узел(27, ноль) , узел(28, ноль, узел(29, ноль, узел(30, ноль, узел(31, ноль), узел(32, ноль, узел(33, ноль, узел(34, ноль), узел(35, ноль, узел (36, ноль, узел (37, ноль, узел (38, ноль, узел (39), ноль, узел (40, ноль, узел (41, ноль, узел (42), ноль, узел (43, ноль, узел (44) , ноль, узел(45, ноль, узел(46, ноль, узел(47, ноль, узел(48, ноль), узел(49, ноль, узел(50, ноль, узел(51, ноль, узел(52, ноль) , узел(53, ноль, узел(54, ноль, узел(55, ноль, узел(56), ноль, узел(57, ноль, узел(58, ноль, узел(59), ноль, узел(60, ноль, узел(61, ноль, узел(62, ноль, узел(63, ноль), узел(64, ноль, узел(65, ноль, узел(66, ноль, узел(67, ноль) , узел(68, ноль, узел(69, ноль, узел(70, ноль, узел(71), ноль, узел(72, ноль, узел(73, ноль, узел(74, ноль), узел(75, ноль, узел (76, ноль, узел (77, ноль, узел (78, ноль, узел (79), ноль, узел (80, ноль, узел (81, ноль, узел (82), ноль, узел (83, ноль, узел (84) , ноль, узел(85, ноль, узел(86, ноль, узел(87, ноль, узел(88, ноль), узел(89, ноль, узел(90, ноль, узел(91, ноль, узел(92, ноль) , узел (93, ноль, узел (94, ноль, узел (9)5, ноль, узел(96, ноль, узел(97, ноль, узел(98, ноль, узел(99, ноль, узел(100, ноль, ноль))))))))))))))) )))))))))))))))))))))))))))))))))))))))))))))))))))) ))))))))))))))))))))))))))))))))))),
time(( lazy _chain(Zs,#<),phrase(in_order(T),Zs))).

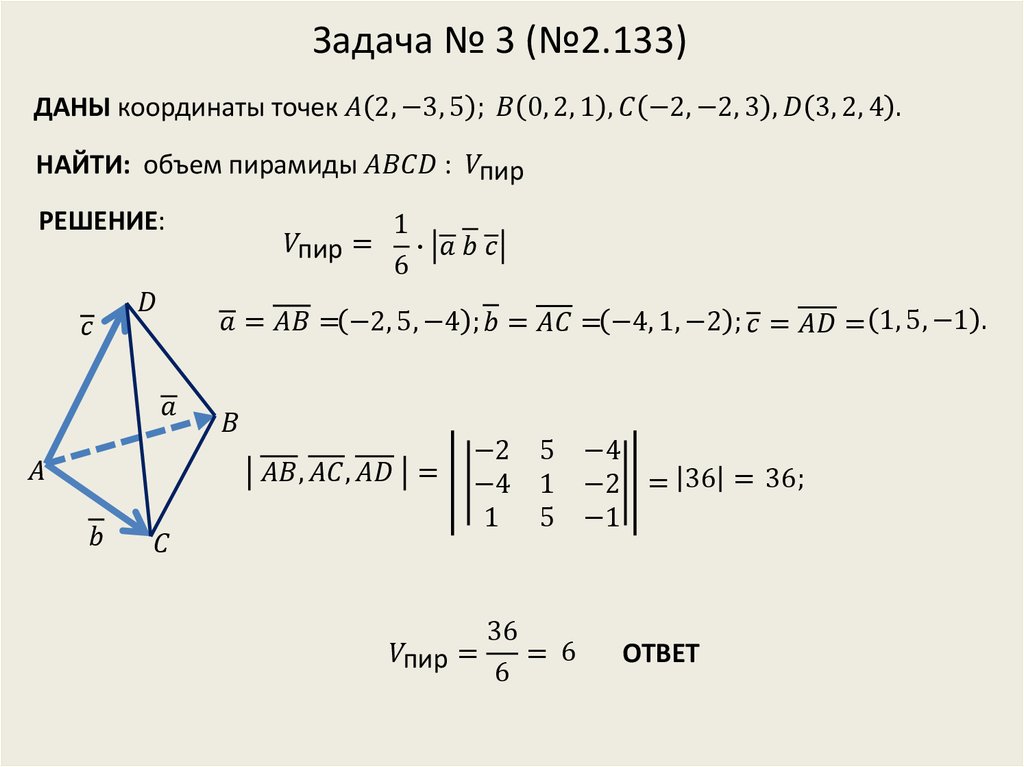 Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку




 д., чтобы ответить на этот вопрос, но мое решение не включает никаких векторов и в значительной степени геометрическое. Ответ не совпадает.
д., чтобы ответить на этот вопрос, но мое решение не включает никаких векторов и в значительной степени геометрическое. Ответ не совпадает.  2$$
Подставляя предыдущие значения для $\alpha$ и $\beta$, получаем $$\gamma=x\sqrt\frac{2}{3}$$
2$$
Подставляя предыдущие значения для $\alpha$ и $\beta$, получаем $$\gamma=x\sqrt\frac{2}{3}$$ 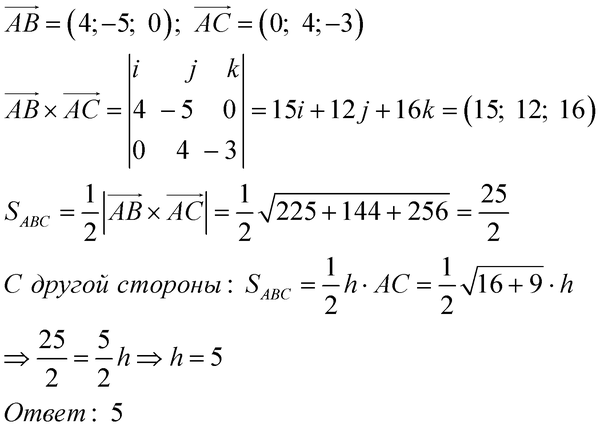 Таким образом, ваш ответ $\sqrt{2/3}$
Таким образом, ваш ответ $\sqrt{2/3}$ 
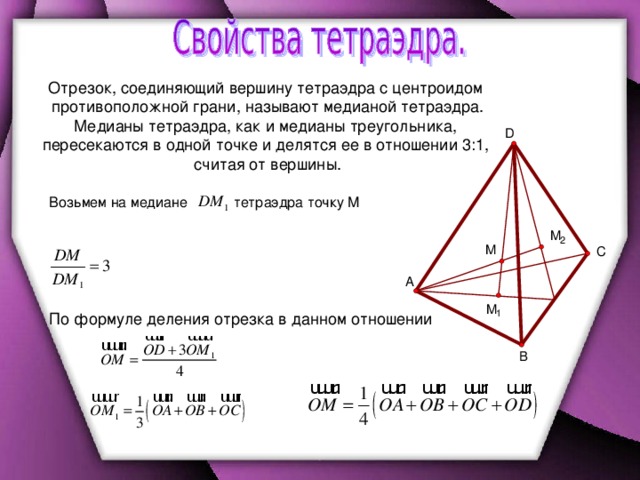 Этот треугольник, как показано ниже, равнобедренный:
Этот треугольник, как показано ниже, равнобедренный:  Этот треугольник, как показано ниже, является равнобедренным (рисунок не в масштабе):
Этот треугольник, как показано ниже, является равнобедренным (рисунок не в масштабе): 
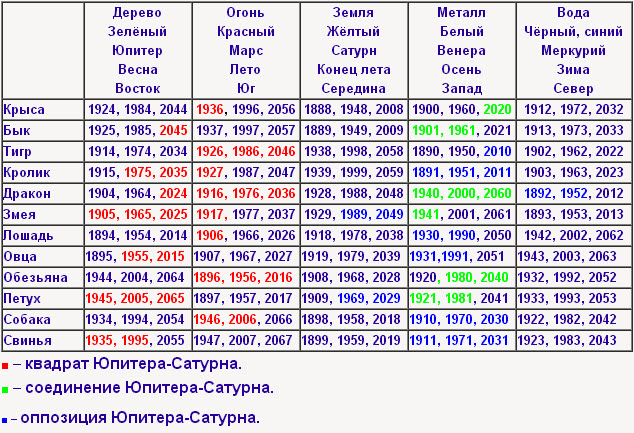 Поля Start Date и End Date (Дата начала и Дата окончания) в этой формуле — это параметры из первых двух шагов выше.
Поля Start Date и End Date (Дата начала и Дата окончания) в этой формуле — это параметры из первых двух шагов выше. Вот как выглядит линейный график с Sales на Rows Shelf (полке строк), наше вычисляемое поле Automated Date Part на Columns Shelf (полке колонок) и вычисляемое поле Date Filter (фильтр даты) на Filters Shelf (полке фильтров). Также указаны элементы управления параметрами Start Date и End Date.
Вот как выглядит линейный график с Sales на Rows Shelf (полке строк), наше вычисляемое поле Automated Date Part на Columns Shelf (полке колонок) и вычисляемое поле Date Filter (фильтр даты) на Filters Shelf (полке фильтров). Также указаны элементы управления параметрами Start Date и End Date. com
com Вы можете отслеживать все события и встречи в одном календаре, но дополнительные календари также легко настроить и удобно использовать.
Вы можете отслеживать все события и встречи в одном календаре, но дополнительные календари также легко настроить и удобно использовать.

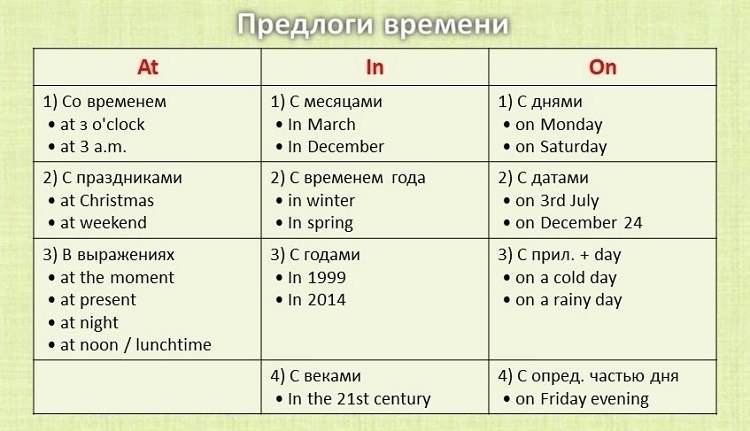
 Это ваша дата начала или окончания.
Это ваша дата начала или окончания.
 Время обычно представляется в виде лет, месяцев, недель и дней. Лучший подход при добавлении или вычитании дат — сначала суммировать годы, затем месяцы, затем недели и, наконец, дни. Каждая сумма времени должна рассчитываться отдельно и прибавляться к дате отдельно.
Время обычно представляется в виде лет, месяцев, недель и дней. Лучший подход при добавлении или вычитании дат — сначала суммировать годы, затем месяцы, затем недели и, наконец, дни. Каждая сумма времени должна рассчитываться отдельно и прибавляться к дате отдельно. 
 В этом случае вы узнаете, как преуспеть в добавлении дней к дате с помощью трех эффективных методов. Таким образом, вы выполните эту цель манипулирования Excel как профессионал и позволите себе выделиться на работе. Однако, чтобы научиться добавлять дни к дате Mac, удобно выполнить несколько основных шагов. Вы можете узнать, как превзойти ….
В этом случае вы узнаете, как преуспеть в добавлении дней к дате с помощью трех эффективных методов. Таким образом, вы выполните эту цель манипулирования Excel как профессионал и позволите себе выделиться на работе. Однако, чтобы научиться добавлять дни к дате Mac, удобно выполнить несколько основных шагов. Вы можете узнать, как превзойти ….
 Если вы являетесь HR компании, вы можете использовать функцию «Сегодня», чтобы рассчитать оставшееся время каждого сотрудника'.;s контрактный период, когда вы управляете контрактным периодом ваших сотрудников. Он может четко показать вам сотрудников, чьи контракты нарушаются….
Если вы являетесь HR компании, вы можете использовать функцию «Сегодня», чтобы рассчитать оставшееся время каждого сотрудника'.;s контрактный период, когда вы управляете контрактным периодом ваших сотрудников. Он может четко показать вам сотрудников, чьи контракты нарушаются….
 Мы можем сначала щелкнуть ячейку C2, а затем нажать «Вставить функцию». Вставьте DATEDIF в поле «Поиск функции» диалогового окна. Нажмите кнопку «ОК», после чего появится диалоговое окно «Аргументы функции».
Мы можем сначала щелкнуть ячейку C2, а затем нажать «Вставить функцию». Вставьте DATEDIF в поле «Поиск функции» диалогового окна. Нажмите кнопку «ОК», после чего появится диалоговое окно «Аргументы функции».
 просмотров
просмотров  Как правильно выразить время и дату в формуле функции2. Поделитесь формулой функции для извлечения года, месяца, дня и часа, минуты и секунды3. Реальный случай: как использовать функцию ДАТЕСЛИ для расчета стажа сотрудников4. Как преобразовать разные единицы времени друг в друга
Как правильно выразить время и дату в формуле функции2. Поделитесь формулой функции для извлечения года, месяца, дня и часа, минуты и секунды3. Реальный случай: как использовать функцию ДАТЕСЛИ для расчета стажа сотрудников4. Как преобразовать разные единицы времени друг в друга

 Правила вычитания обратны правилам сложения (см. таблицу выше).
Правила вычитания обратны правилам сложения (см. таблицу выше). также
также …
… 


 com — это сайт, поддерживаемый рекламой. Рекомендуемые или доверенные партнерские программы, а также все результаты поиска, поиска или подбора школ предназначены для школ, которые выплачивают нам компенсацию. Эта компенсация не влияет на рейтинги наших школ, справочники ресурсов или другую независимую от редакции информацию, опубликованную на этом сайте.
от наших партнеров.
com — это сайт, поддерживаемый рекламой. Рекомендуемые или доверенные партнерские программы, а также все результаты поиска, поиска или подбора школ предназначены для школ, которые выплачивают нам компенсацию. Эта компенсация не влияет на рейтинги наших школ, справочники ресурсов или другую независимую от редакции информацию, опубликованную на этом сайте.
от наших партнеров.
 Вы также можете пройти стажировку, чтобы удовлетворить выборные требования.
Вы также можете пройти стажировку, чтобы удовлетворить выборные требования.  Стоимость кредита
Стоимость кредита  Подходящие кандидаты должны иметь средний балл не менее 2,75.
Подходящие кандидаты должны иметь средний балл не менее 2,75.  Это дает вам возможность ускорить получение степени за один год или учиться на неполный рабочий день и получить высшее образование через 2-4 года.
Это дает вам возможность ускорить получение степени за один год или учиться на неполный рабочий день и получить высшее образование через 2-4 года.  Стоимость кредита
Стоимость кредита  США
США 
 Эта компенсация не влияет на рейтинги наших школ, справочники ресурсов или другую независимую от редакции информацию, опубликованную на этом сайте.
Эта компенсация не влияет на рейтинги наших школ, справочники ресурсов или другую независимую от редакции информацию, опубликованную на этом сайте.  Чтобы получить степень магистра информатики в области здравоохранения, требуется 33 кредита, включая завершающий проект. Учебная программа объединяет статистические методы, интеллектуальный анализ данных, визуализацию данных и методы исследования. Вы также изучите управление проектами в области здравоохранения.
Чтобы получить степень магистра информатики в области здравоохранения, требуется 33 кредита, включая завершающий проект. Учебная программа объединяет статистические методы, интеллектуальный анализ данных, визуализацию данных и методы исследования. Вы также изучите управление проектами в области здравоохранения.  Стоимость кредита
Стоимость кредита  0, резюме, личное заявление и три рекомендательных письма.
0, резюме, личное заявление и три рекомендательных письма. 
 Стоимость кредита
Стоимость кредита  Процент онлайн-регистрации
Процент онлайн-регистрации  А некоторые онлайн-школы предлагают ускоренные программы, чтобы вы могли раньше финишировать.
А некоторые онлайн-школы предлагают ускоренные программы, чтобы вы могли раньше финишировать.  BLS прогнозирует рост числа профессий в сфере здравоохранения на 13% в течение следующих десяти лет, что намного быстрее, чем в среднем по всем профессиям.
BLS прогнозирует рост числа профессий в сфере здравоохранения на 13% в течение следующих десяти лет, что намного быстрее, чем в среднем по всем профессиям. 
 Кроме того, прогнозируется, что карьера в области компьютерных и информационных технологий вырастет на 15% за тот же период.
Кроме того, прогнозируется, что карьера в области компьютерных и информационных технологий вырастет на 15% за тот же период.  Получив эту степень в области информатики для медсестер, вы приобретете навыки, которые позволят вам делать выводы и влиять на политику и процедуры, которые будут спасать жизни и улучшать результаты лечения пациентов.
Получив эту степень в области информатики для медсестер, вы приобретете навыки, которые позволят вам делать выводы и влиять на политику и процедуры, которые будут спасать жизни и улучшать результаты лечения пациентов. 
 Студенты учатся применять стратегии системного мышления и овладевают навыками преобразования данных в мудрость, которая лучше отвечает потребностям здравоохранения различных групп населения. Мы берем науку об успехе и объединяем ее с искусством ухода, чтобы вы были готовы к этой увлекательной профессии в области здравоохранения.
Студенты учатся применять стратегии системного мышления и овладевают навыками преобразования данных в мудрость, которая лучше отвечает потребностям здравоохранения различных групп населения. Мы берем науку об успехе и объединяем ее с искусством ухода, чтобы вы были готовы к этой увлекательной профессии в области здравоохранения.  Вы будете работать над каждым курсом так быстро, как сможете изучать и усваивать материал. Как только вы будете готовы, вы пройдете оценку, закончите курс и двинетесь дальше. Это означает, что вы можете пройти столько курсов, сколько сможете, за семестр без каких-либо дополнительных затрат.
Вы будете работать над каждым курсом так быстро, как сможете изучать и усваивать материал. Как только вы будете готовы, вы пройдете оценку, закончите курс и двинетесь дальше. Это означает, что вы можете пройти столько курсов, сколько сможете, за семестр без каких-либо дополнительных затрат.  Обращается внимание на важность эффективного взаимодействия, функциональности, доступа к данным и удовлетворенности пользователей. Студент будет анализировать отчеты и интегрировать федеральные нормативные акты, принципы исследований и принципы гигиены окружающей среды в построение реального системного анализа и проектного проекта. Этот курс будет непосредственно применим к учреждениям здравоохранения, поскольку управление электронными записями стало обязательным для поставщиков медицинских услуг. Вся информация в этом курсе будет напрямую связана с предоставлением качественного ухода за пациентами и их безопасностью. Основы в области информатики сестринского дела рекомендуется в качестве предварительного условия.
Обращается внимание на важность эффективного взаимодействия, функциональности, доступа к данным и удовлетворенности пользователей. Студент будет анализировать отчеты и интегрировать федеральные нормативные акты, принципы исследований и принципы гигиены окружающей среды в построение реального системного анализа и проектного проекта. Этот курс будет непосредственно применим к учреждениям здравоохранения, поскольку управление электронными записями стало обязательным для поставщиков медицинских услуг. Вся информация в этом курсе будет напрямую связана с предоставлением качественного ухода за пациентами и их безопасностью. Основы в области информатики сестринского дела рекомендуется в качестве предварительного условия.  Темы включают анализ данных; Управление базой данных; выводная и описательная статистика; статистические выводы; и улучшение процесса.
Темы включают анализ данных; Управление базой данных; выводная и описательная статистика; статистические выводы; и улучшение процесса.  Все курсы MSN Core и Specialty, за исключением курса Capstone, являются предварительными условиями для этого курса и должны быть пройдены до прохождения этого курса.
Этот курс имеет право на получение оценки In Progress. Пожалуйста, ознакомьтесь с Политикой шкалы оценок для получения дополнительной информации.
Все курсы MSN Core и Specialty, за исключением курса Capstone, являются предварительными условиями для этого курса и должны быть пройдены до прохождения этого курса.
Этот курс имеет право на получение оценки In Progress. Пожалуйста, ознакомьтесь с Политикой шкалы оценок для получения дополнительной информации.  Это завершающий курс, который дает студентам возможность продемонстрировать компетенции, приобретенные в ходе этой программы. Все базовые и специальные курсы MSN, включая курс «Полевой опыт», являются предварительными условиями для этого курса и должны быть пройдены до прохождения этого курса.
Этот курс имеет право на получение оценки In Progress. Пожалуйста, ознакомьтесь с Политикой шкалы оценок для получения дополнительной информации.
Это завершающий курс, который дает студентам возможность продемонстрировать компетенции, приобретенные в ходе этой программы. Все базовые и специальные курсы MSN, включая курс «Полевой опыт», являются предварительными условиями для этого курса и должны быть пройдены до прохождения этого курса.
Этот курс имеет право на получение оценки In Progress. Пожалуйста, ознакомьтесь с Политикой шкалы оценок для получения дополнительной информации.  Характеристики присутствия, которые включают целостность, близость, чувствительность и адаптивность, создают повышенное чувство осознания, которое способствует терапевтическим отношениям между медсестрой и пациентом. Развитие внимательного, подлинного присутствия занимает центральное место в оздоровительных и духовных практиках в нескольких культурах и является важным элементом лидерства. Студенты намеренно разработают целенаправленную практику осознанности, которая повлияет на результаты лечения пациентов и создаст условия, приносящие радость на рабочем месте.
Характеристики присутствия, которые включают целостность, близость, чувствительность и адаптивность, создают повышенное чувство осознания, которое способствует терапевтическим отношениям между медсестрой и пациентом. Развитие внимательного, подлинного присутствия занимает центральное место в оздоровительных и духовных практиках в нескольких культурах и является важным элементом лидерства. Студенты намеренно разработают целенаправленную практику осознанности, которая повлияет на результаты лечения пациентов и создаст условия, приносящие радость на рабочем месте.  Учащиеся изучат роль медсестер в пропаганде изменений у постели больного, а также возглавят группы, выступающие за реформу политики здравоохранения. Учащиеся будут собирать и анализировать данные для выявления пациентов и групп риска и рекомендовать изменение политики для улучшения результатов в отношении здоровья в сообществе.
Учащиеся изучат роль медсестер в пропаганде изменений у постели больного, а также возглавят группы, выступающие за реформу политики здравоохранения. Учащиеся будут собирать и анализировать данные для выявления пациентов и групп риска и рекомендовать изменение политики для улучшения результатов в отношении здоровья в сообществе.  Особое внимание уделяется методам повышения производительности и качества, лежащим в основе сестринского ухода, основанного на ценностях. Медсестра передовой практики сегодня должна служить примером стандартов качества и безопасности и быть готовой возглавить оказание ориентированной на пациента помощи, основанной на ценностях.
Особое внимание уделяется методам повышения производительности и качества, лежащим в основе сестринского ухода, основанного на ценностях. Медсестра передовой практики сегодня должна служить примером стандартов качества и безопасности и быть готовой возглавить оказание ориентированной на пациента помощи, основанной на ценностях.  Этот курс подчеркивает использование комплексной модели укрепления здоровья, профилактики заболеваний и восстановления здоровья для решения проблем со здоровьем у пациентов и сообществ. Студенты получат расширенные знания и навыки оценки для клинического опроса, целенаправленного сбора анамнеза, критического диагностического рассуждения и принятия клинических решений с использованием ориентированной на проблему структуры, которая объединяет подлинный опыт с практическими знаниями о моделях здоровья пациентов и сообществ. Для этого курса нет предварительных условий.
Этот курс подчеркивает использование комплексной модели укрепления здоровья, профилактики заболеваний и восстановления здоровья для решения проблем со здоровьем у пациентов и сообществ. Студенты получат расширенные знания и навыки оценки для клинического опроса, целенаправленного сбора анамнеза, критического диагностического рассуждения и принятия клинических решений с использованием ориентированной на проблему структуры, которая объединяет подлинный опыт с практическими знаниями о моделях здоровья пациентов и сообществ. Для этого курса нет предварительных условий.  Он предназначен для повышения компетентности в использовании приложений для пациентов и населения, которые информируют и поддерживают преобразование оказания сестринской помощи в сторону будущего качественного сестринского ухода, основанного на ценности, который улучшает результаты для здоровья. Этот курс согласовывает теоретические концепции с практическим применением информатики и согласуется с функциональными областями и обязанностями медсестер по информатике, как это определено Американской ассоциацией медсестер. Область применения и стандарты для сестринской информатики.
Он предназначен для повышения компетентности в использовании приложений для пациентов и населения, которые информируют и поддерживают преобразование оказания сестринской помощи в сторону будущего качественного сестринского ухода, основанного на ценности, который улучшает результаты для здоровья. Этот курс согласовывает теоретические концепции с практическим применением информатики и согласуется с функциональными областями и обязанностями медсестер по информатике, как это определено Американской ассоциацией медсестер. Область применения и стандарты для сестринской информатики.  Кроме того, студенты приобретают знания и навыки, чтобы стать полноправными партнерами с другими специалистами в области здравоохранения, демонстрируя вклад медсестер в обеспечение высококачественного ухода за пациентами и населением, работая в сотрудничестве с межпрофессиональными командами. Для этого курса нет предварительных условий.
Кроме того, студенты приобретают знания и навыки, чтобы стать полноправными партнерами с другими специалистами в области здравоохранения, демонстрируя вклад медсестер в обеспечение высококачественного ухода за пациентами и населением, работая в сотрудничестве с межпрофессиональными командами. Для этого курса нет предварительных условий.  Студенты получат опыт создания сообществ практиков для совместной разработки инновационных практик и политик, направленных на улучшение здоровья населения и повышение качества обслуживания пациентов.
Студенты получат опыт создания сообществ практиков для совместной разработки инновационных практик и политик, направленных на улучшение здоровья населения и повышение качества обслуживания пациентов. 
 Это означает, что если вы хотите быстрее пройти эту программу информатики для медсестер, вы будете платить меньше.
Это означает, что если вы хотите быстрее пройти эту программу информатики для медсестер, вы будете платить меньше. 

 В первом задании обаятельного волка из всеми известного мультика «Ну погоди!» нужно привести к зайцу . Волк в этом задании настроен очень дружелюбно и совершенно не хочет конфликтовать с зайцем, поэтому идет к нему с цветами. Чтобы волк смог дойти, ему нужно проложить путь с помощью кружочков с числами.
В первом задании обаятельного волка из всеми известного мультика «Ну погоди!» нужно привести к зайцу . Волк в этом задании настроен очень дружелюбно и совершенно не хочет конфликтовать с зайцем, поэтому идет к нему с цветами. Чтобы волк смог дойти, ему нужно проложить путь с помощью кружочков с числами.  Если четное — продукты поделятся поровну, если нечетное — то нет. Во втором задании нужно посчитать, сколько на картинке: солнечных лучиков, тучек, яблок, грибов, птичек, зверят, деревьев, цветов. А затем ответить, чего или кого получилось четное количество?
Если четное — продукты поделятся поровну, если нечетное — то нет. Во втором задании нужно посчитать, сколько на картинке: солнечных лучиков, тучек, яблок, грибов, птичек, зверят, деревьев, цветов. А затем ответить, чего или кого получилось четное количество?
 В китайской космологии и натурософии чётные числа соответствуют понятию «инь», а нечётные — «ян»[1].
В китайской космологии и натурософии чётные числа соответствуют понятию «инь», а нечётные — «ян»[1].
 Если ответ никогда не может быть целым числом, запишите это как ответ.
Если ответ никогда не может быть целым числом, запишите это как ответ. Результат n/m не говорит нам, четный результат или нечетный. И приведенные выше примеры подтверждают, что результат может быть любым.
Результат n/m не говорит нам, четный результат или нечетный. И приведенные выше примеры подтверждают, что результат может быть любым.


 LGD vs Outsiders From CN
LGD vs Outsiders From CN
 В
В
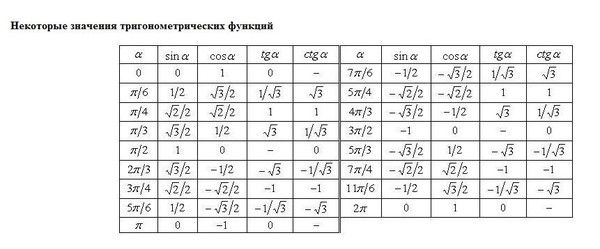 Далее стороны еще раз обмениваются блокировками в том же порядке, после чего переходят к выбору персонажей. Тут начинают Dire, выбирающие первого героя, а затем пик доходит до Radiant, которые выбирают 2 персонажей. Закрывает стадию пик Dire.
Далее стороны еще раз обмениваются блокировками в том же порядке, после чего переходят к выбору персонажей. Тут начинают Dire, выбирающие первого героя, а затем пик доходит до Radiant, которые выбирают 2 персонажей. Закрывает стадию пик Dire.
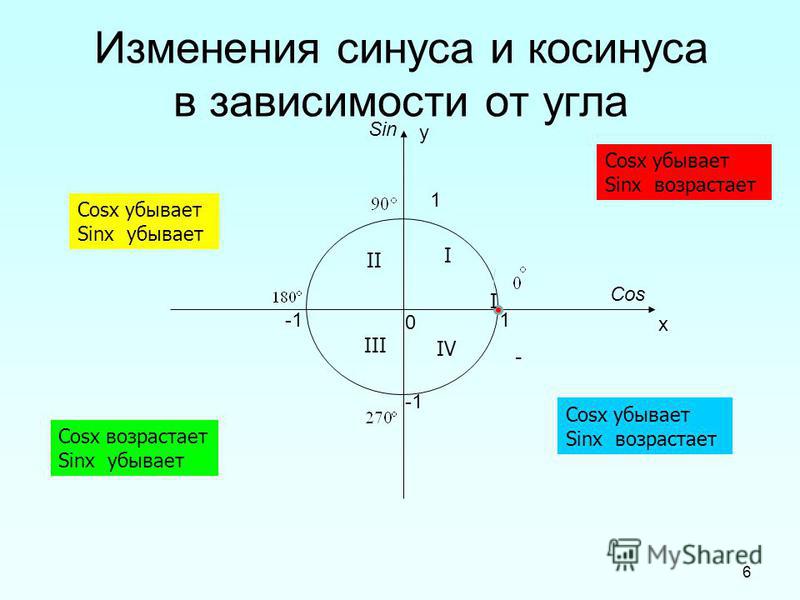
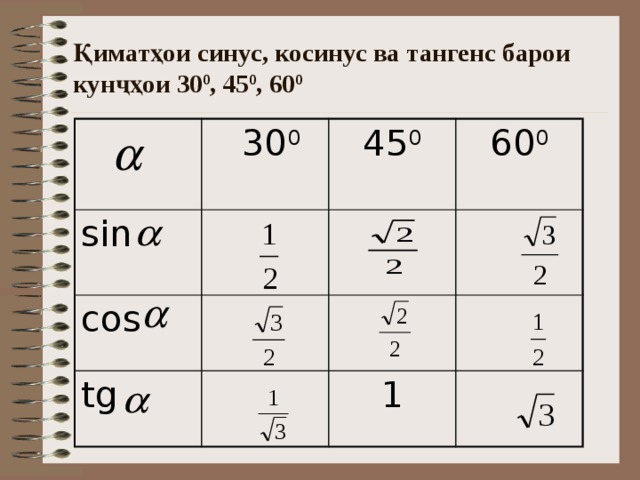 Чтобы прояснить эту концепцию, мы предоставили подробную информацию о Sin 0. Функция синуса показывает отношение между перпендикуляром и гипотенузой. В треугольнике, где одна сторона образует угол 90 градусов, называется прямоугольным треугольником. Сторона, расположенная перед углом 90 градусов, называется стороной гипотенузы. Синус тета равен отношению перпендикуляров к гипотенузе прямоугольного треугольника.
Чтобы прояснить эту концепцию, мы предоставили подробную информацию о Sin 0. Функция синуса показывает отношение между перпендикуляром и гипотенузой. В треугольнике, где одна сторона образует угол 90 градусов, называется прямоугольным треугольником. Сторона, расположенная перед углом 90 градусов, называется стороной гипотенузы. Синус тета равен отношению перпендикуляров к гипотенузе прямоугольного треугольника.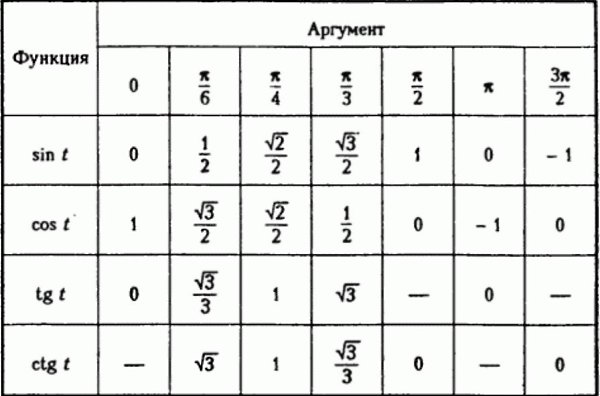
 Найдите значение 2Sin 90 +2 sin 30
Найдите значение 2Sin 90 +2 sin 30  Найдите значение 10 sin 270+ 20 sin 90
Найдите значение 10 sin 270+ 20 sin 90  е. (x,y) равно (1,0). То есть перпендикуляр имеет значение 0, а гипотенуза имеет значение 1. Если мы положим эти значения в тету синуса, равную отношению перпендикуляра и гипотенузы, мы получим ноль.
е. (x,y) равно (1,0). То есть перпендикуляр имеет значение 0, а гипотенуза имеет значение 1. Если мы положим эти значения в тету синуса, равную отношению перпендикуляра и гипотенузы, мы получим ноль.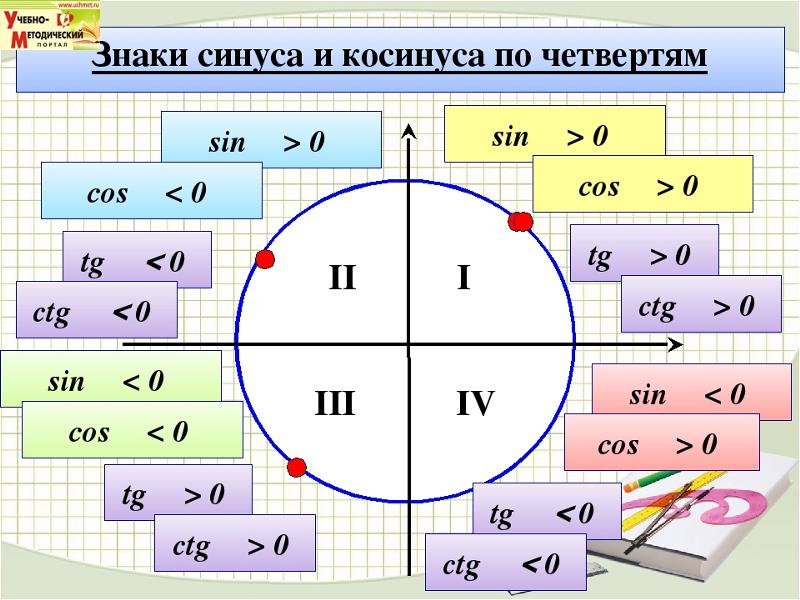 Мы могли бы назвать его координаты 𝑥,
𝑦. Но что, если мы затем добавим
прямоугольный треугольник к нашей диаграмме и определить угол здесь. Это называется включенным углом,
и мы собираемся назвать это 𝜃.
Мы могли бы назвать его координаты 𝑥,
𝑦. Но что, если мы затем добавим
прямоугольный треугольник к нашей диаграмме и определить угол здесь. Это называется включенным углом,
и мы собираемся назвать это 𝜃. Это потому, что 𝜃 находится рядом с
гипотенуза.
Это потому, что 𝜃 находится рядом с
гипотенуза.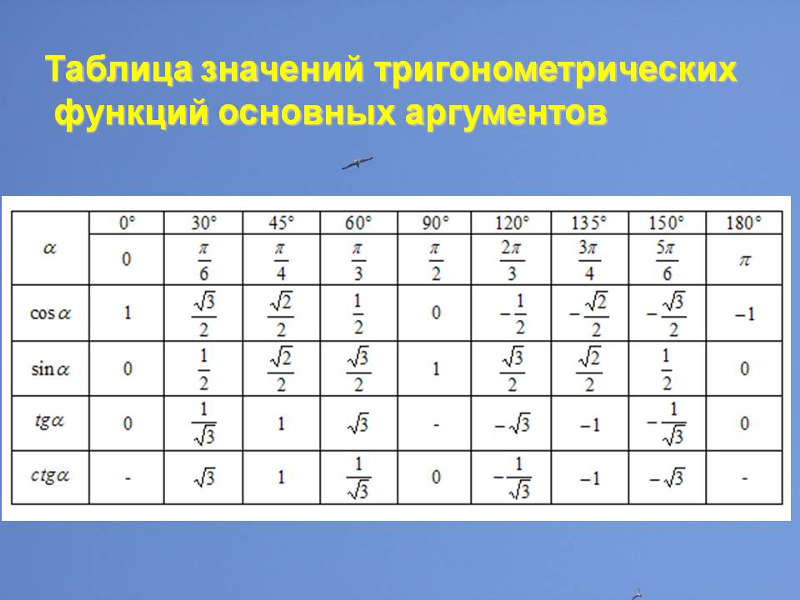 Когда 𝜃 равно нулю, мы видим, что
cos 𝜃, который представляет 𝑥, равен единице. грех 𝜃, который представляет 𝑦, равен нулю. Теперь мы повторим этот процесс
здесь. На этот раз 𝜃 равно 45
градусов. И мы можем добавить прямоугольный
треугольника и мы видим, что гипотенуза равна одной единице. Однако, поскольку это
прямоугольный треугольник с одним углом 45 градусов, мы знаем, что на самом деле это
равнобедренный треугольник. И так, можно сказать, что это другое
две стороны равны 𝑎 единиц.
Когда 𝜃 равно нулю, мы видим, что
cos 𝜃, который представляет 𝑥, равен единице. грех 𝜃, который представляет 𝑦, равен нулю. Теперь мы повторим этот процесс
здесь. На этот раз 𝜃 равно 45
градусов. И мы можем добавить прямоугольный
треугольника и мы видим, что гипотенуза равна одной единице. Однако, поскольку это
прямоугольный треугольник с одним углом 45 градусов, мы знаем, что на самом деле это
равнобедренный треугольник. И так, можно сказать, что это другое
две стороны равны 𝑎 единиц.
 А все остальные слушания и вынесение приговора прошли в Нюрнберге.
А все остальные слушания и вынесение приговора прошли в Нюрнберге.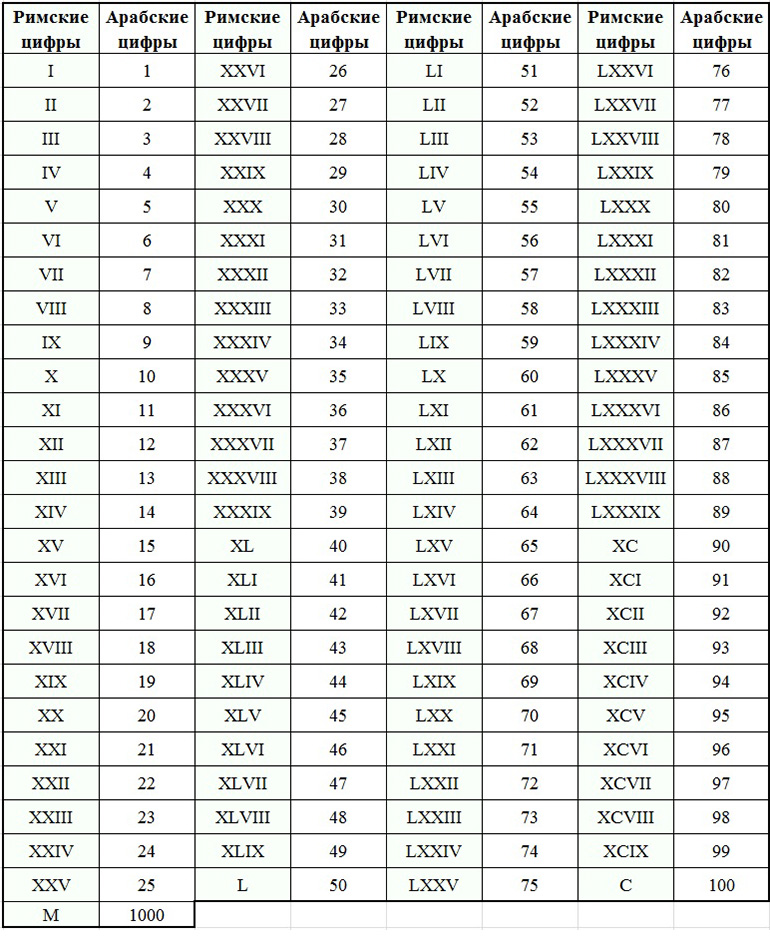
 Здесь с мая по август 1945 года содержались и регулярно подвергались допросам 86 высокопоставленных германских военнопленных, в том числе Герман Геринг и Карл Дениц. В период подготовки Нюрнбергского трибунала всех его подсудимых перевели в тюрьму, соединенную подземным ходом с Дворцом правосудия: они оставались там до вынесения приговора и приведения его в исполнение. Круглосуточную охрану в тюрьме несли военнослужащие роты «Дельта» 26 полка 1-й пехотной дивизии армии США. Они же осуществляли доставку подсудимых в зал суда и обратно, охраняли их во время заседаний.
Здесь с мая по август 1945 года содержались и регулярно подвергались допросам 86 высокопоставленных германских военнопленных, в том числе Герман Геринг и Карл Дениц. В период подготовки Нюрнбергского трибунала всех его подсудимых перевели в тюрьму, соединенную подземным ходом с Дворцом правосудия: они оставались там до вынесения приговора и приведения его в исполнение. Круглосуточную охрану в тюрьме несли военнослужащие роты «Дельта» 26 полка 1-й пехотной дивизии армии США. Они же осуществляли доставку подсудимых в зал суда и обратно, охраняли их во время заседаний.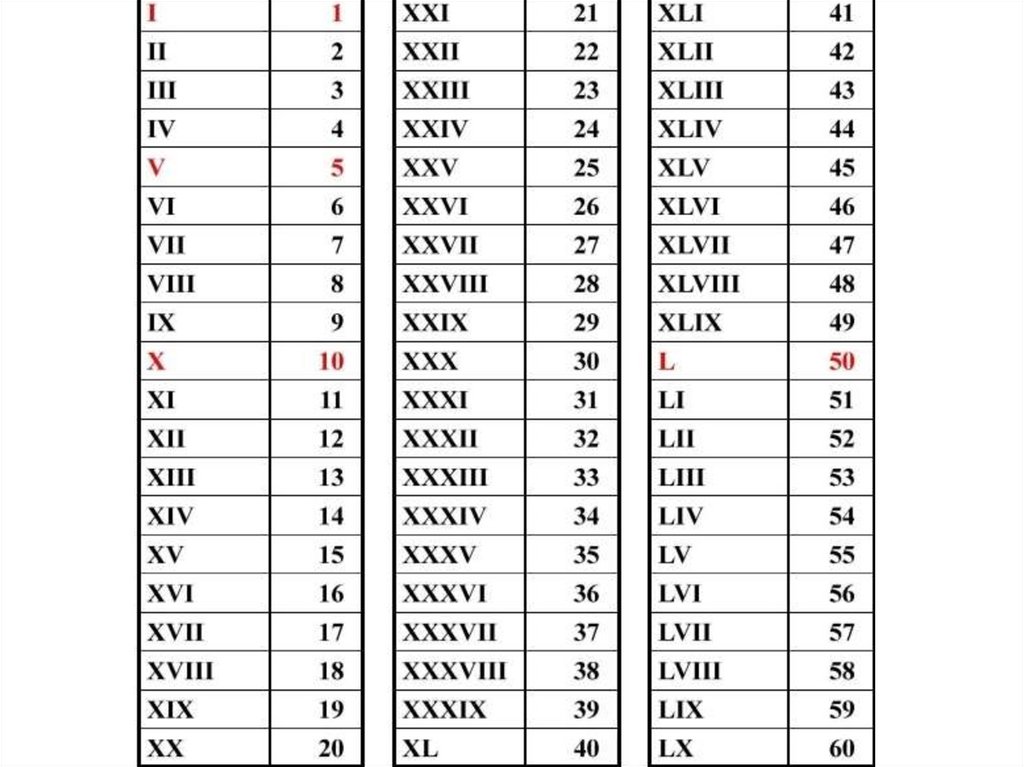
 Многие осужденные ходатайствовали о замене ее на расстрел, но им в этом было отказано. Три человека получили пожизненное заключение, два человека были приговорены к 20 годам тюрьмы, один — к 15 годам и один — к 10 годам. Еще троих подсудимых в конечном счете оправдали, хоть представители Советского Союза и пытались опротестовать это решение трибунала. Глава Германского трудового фронта Роберт Лей не дожил до приговора: он покончил с собой меньше чем за месяц до начала процесса. А промышленник Густав Крупп был признан неизлечимо больным, в связи с чем его дело было приостановлено, а затем и прекращено из-за смерти обвиняемого. Кроме того, СС, СД и гестапо, а также руководящий состав НСДАП были признаны виновными в преступной деятельности, а вот кабинет министров и военное командование Германии — нет (что тоже вызвало протест со стороны СССР).
Многие осужденные ходатайствовали о замене ее на расстрел, но им в этом было отказано. Три человека получили пожизненное заключение, два человека были приговорены к 20 годам тюрьмы, один — к 15 годам и один — к 10 годам. Еще троих подсудимых в конечном счете оправдали, хоть представители Советского Союза и пытались опротестовать это решение трибунала. Глава Германского трудового фронта Роберт Лей не дожил до приговора: он покончил с собой меньше чем за месяц до начала процесса. А промышленник Густав Крупп был признан неизлечимо больным, в связи с чем его дело было приостановлено, а затем и прекращено из-за смерти обвиняемого. Кроме того, СС, СД и гестапо, а также руководящий состав НСДАП были признаны виновными в преступной деятельности, а вот кабинет министров и военное командование Германии — нет (что тоже вызвало протест со стороны СССР).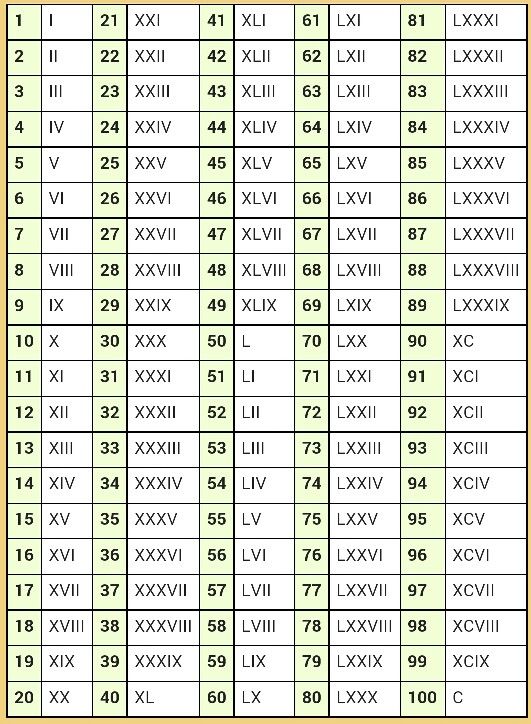 За три часа до казни Герман Геринг успел покончить с собой, приняв цианистый калий. Остальных по одному приводили в спортивный зал тюрьмы при Дворце правосудия, где на помостах были установлены виселицы. Казнили приговоренных два американских военнослужащих: сержант Джон Вудз, являвшийся профессиональным палачом с 1920 года, и добровольно вызвавшийся помогать ему военный полицейский Джозеф Малта. Казнь была закончена в течение двух часов, после чего тела казненных и тело Геринга увезли в мюнхенский крематорий, а пепел двое суток спустя высыпали в реку Изар.
За три часа до казни Герман Геринг успел покончить с собой, приняв цианистый калий. Остальных по одному приводили в спортивный зал тюрьмы при Дворце правосудия, где на помостах были установлены виселицы. Казнили приговоренных два американских военнослужащих: сержант Джон Вудз, являвшийся профессиональным палачом с 1920 года, и добровольно вызвавшийся помогать ему военный полицейский Джозеф Малта. Казнь была закончена в течение двух часов, после чего тела казненных и тело Геринга увезли в мюнхенский крематорий, а пепел двое суток спустя высыпали в реку Изар. В итоге этих слушаний 24 человека были приговорены к смертной казни, 118 — к тюремному заключению, а 35 подсудимых — оправданы.
В итоге этих слушаний 24 человека были приговорены к смертной казни, 118 — к тюремному заключению, а 35 подсудимых — оправданы. В Стокгольме впервые вручают Нобелевскую премию. Студент Петр Карпович стреляет в министра просвещения России. В Лондоне проходит первое соревнование по бодибилдингу.
В Стокгольме впервые вручают Нобелевскую премию. Студент Петр Карпович стреляет в министра просвещения России. В Лондоне проходит первое соревнование по бодибилдингу. Конец Русско-японской войны. Эсер Каляев убивает великого князя Сергея Александровича. Роберт Кох получает Нобелевскую премию «за исследования и открытия, касающиеся лечения туберкулеза».
Конец Русско-японской войны. Эсер Каляев убивает великого князя Сергея Александровича. Роберт Кох получает Нобелевскую премию «за исследования и открытия, касающиеся лечения туберкулеза». Создана компания Audi. Открыт возбудитель полиомиелита.
Создана компания Audi. Открыт возбудитель полиомиелита.
 Москва становится столицей Советского государства. Фанни Каплан стреляет в Ленина. В Советской России вводят григорианский календарь: после 31 января сразу наступает 14 февраля. Расстрел царской семьи.
Москва становится столицей Советского государства. Фанни Каплан стреляет в Ленина. В Советской России вводят григорианский календарь: после 31 января сразу наступает 14 февраля. Расстрел царской семьи. Прорыв в лечении сахарного диабета — получен гормон инсулин. Обнаружена гробница Тутанхамона. Троцкий разрабатывает план расправы над руководством Православной церкви. Создана Всесоюзная пионерская организация.
Прорыв в лечении сахарного диабета — получен гормон инсулин. Обнаружена гробница Тутанхамона. Троцкий разрабатывает план расправы над руководством Православной церкви. Создана Всесоюзная пионерская организация.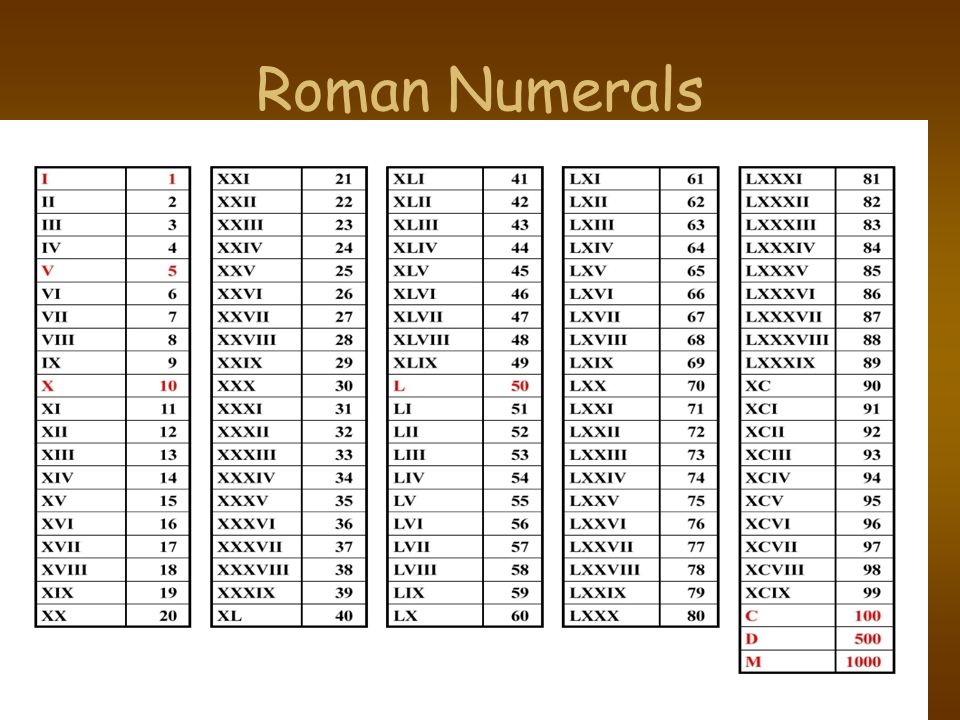 Троцкий и Каменев исключены из Политбюро. В Лондоне выходит книга А. А. Милна «Винни‑Пух».
Троцкий и Каменев исключены из Политбюро. В Лондоне выходит книга А. А. Милна «Винни‑Пух».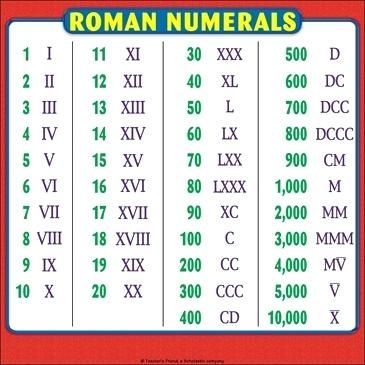 В США выходит фильм «Дракула».
В США выходит фильм «Дракула». Выходит настольная игра «Монополия».
Выходит настольная игра «Монополия».
 Япония и США заявляют о нейтралитете. СССР исключен из Лиги Наций за нападение на Финляндию. Иосиф Сталин — человек года по версии журнала Time.
Япония и США заявляют о нейтралитете. СССР исключен из Лиги Наций за нападение на Финляндию. Иосиф Сталин — человек года по версии журнала Time. Великобритания и США объединяют усилия в создании атомного оружия. В Ленинграде исполняется Седьмая симфония Шостаковича.
Великобритания и США объединяют усилия в создании атомного оружия. В Ленинграде исполняется Седьмая симфония Шостаковича.
 Создан Совет Европы. В СССР проходят испытания атомной бомбы. Иерусалим провозглашен столицей Израиля. В США впервые вручают телевизионную премию «Эмми».
Создан Совет Европы. В СССР проходят испытания атомной бомбы. Иерусалим провозглашен столицей Израиля. В США впервые вручают телевизионную премию «Эмми». Записан «Rock Around the Clock» — один из самых продаваемых рок-н-ролльных синглов в истории. Компания IBM выпускает первый массовый калькулятор. Нобелевскую премию по литературе получает Эрнест Хемингуэй «за повествовательное мастерство, в очередной раз продемонстрированное в „Старике и море“».
Записан «Rock Around the Clock» — один из самых продаваемых рок-н-ролльных синглов в истории. Компания IBM выпускает первый массовый калькулятор. Нобелевскую премию по литературе получает Эрнест Хемингуэй «за повествовательное мастерство, в очередной раз продемонстрированное в „Старике и море“».
 Ядерная гонка: СССР возобновляет ядерные испытания. Учреждена премия «Грэмми».
Ядерная гонка: СССР возобновляет ядерные испытания. Учреждена премия «Грэмми». Убит Джон Кеннеди. В Стэнфордском университете изобретают компьютерную мышь.
Убит Джон Кеннеди. В Стэнфордском университете изобретают компьютерную мышь.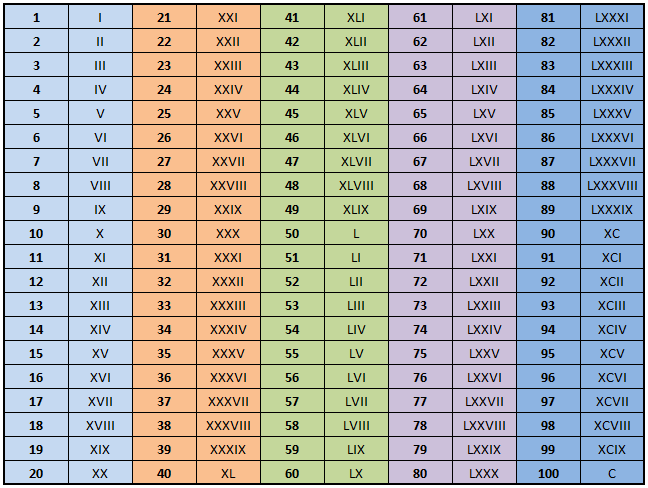
 Убит Харви Милк, первый открыто гомосексуальный политик в США.
Убит Харви Милк, первый открыто гомосексуальный политик в США.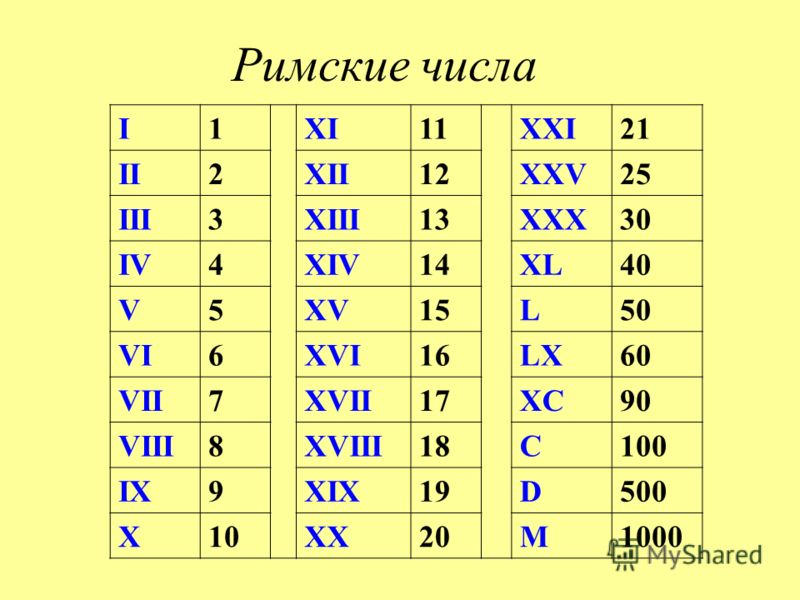 В Токио открыт первый Диснейленд за пределами США. Появляется первая коммерческая сотовая сеть.
В Токио открыт первый Диснейленд за пределами США. Появляется первая коммерческая сотовая сеть. Картина Ван Гога «Подсолнухи» продана за $ 39,9 млн.
Картина Ван Гога «Подсолнухи» продана за $ 39,9 млн. 03.2023
03.2023
 Давайте посмотрим на некоторые примеры.
Давайте посмотрим на некоторые примеры.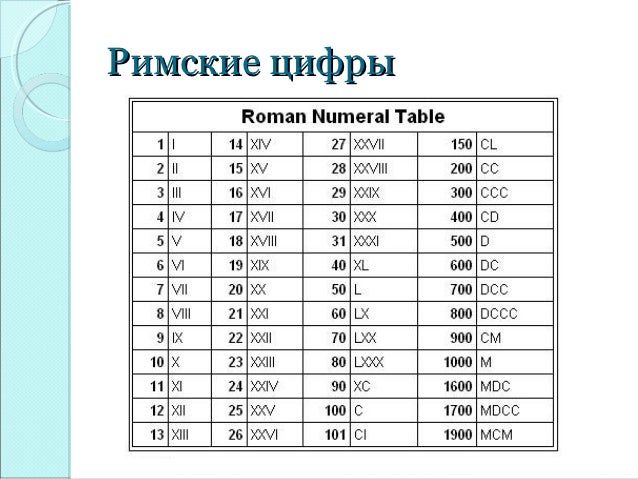 Исаак Пераль изобрел подводную лодку в 19 веке.
Исаак Пераль изобрел подводную лодку в 19 веке. 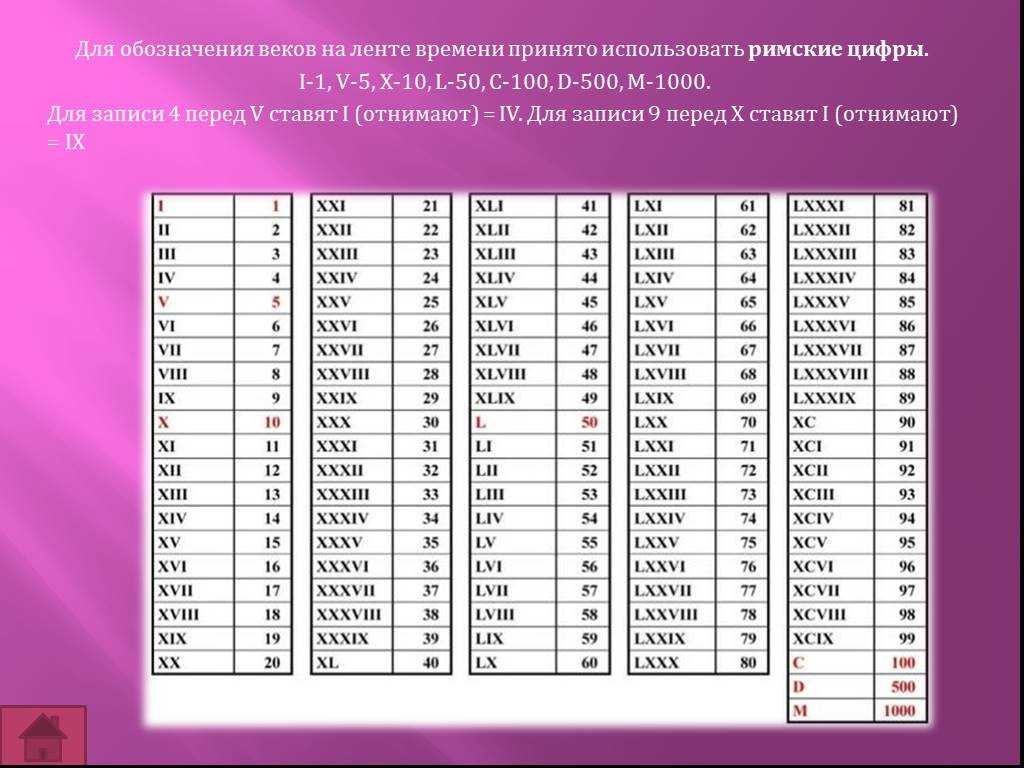 Например: «сигло xxi » вместо использования заглавных букв обычного размера: «siglo XXI «. буквы проще вводить.
Например: «сигло xxi » вместо использования заглавных букв обычного размера: «siglo XXI «. буквы проще вводить.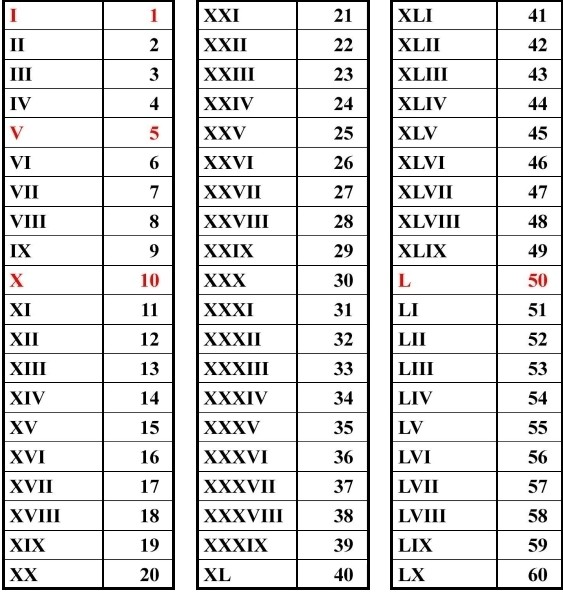
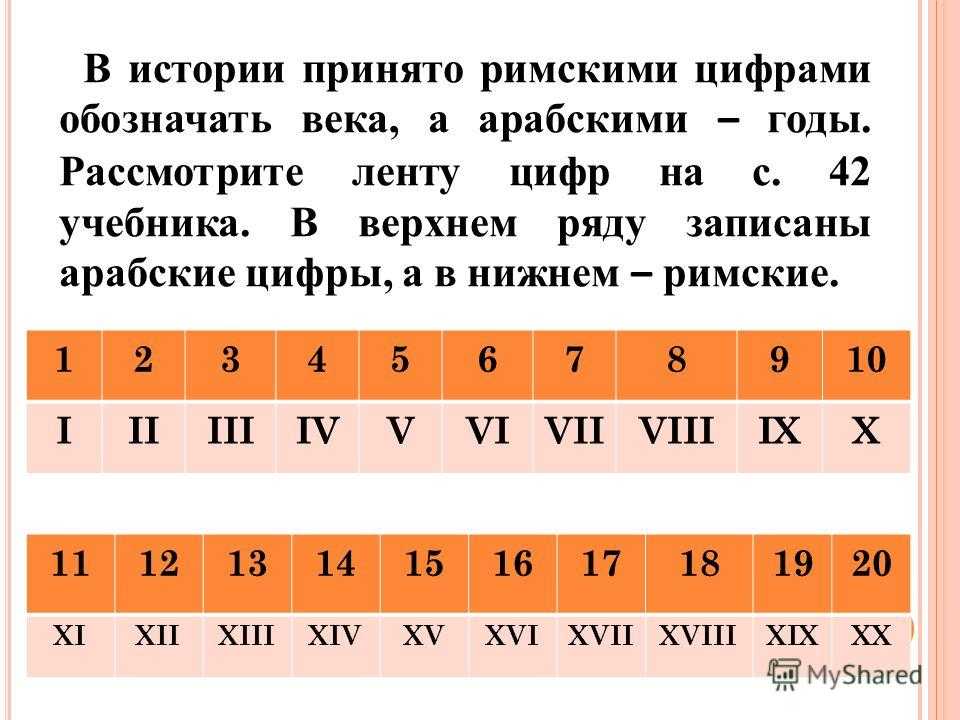 Обратите внимание, что в британском английском даты пишутся в порядке день-месяц-год без внутренней пунктуации.
Обратите внимание, что в британском английском даты пишутся в порядке день-месяц-год без внутренней пунктуации.
 Не добавляйте апостроф перед множественным числом s .
Не добавляйте апостроф перед множественным числом s .