Минус на плюс что дает?
Автор Admin На чтение 6 мин Просмотров 1.3к. Опубликовано
Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных чисел придумали всё те же математики. Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.
Запомнить правила умножения или деления положительных и отрицательных чисел очень просто.
Если два числа имеют разные знаки, в результате всегда будет знак минус.
Если два числа имеют одинаковые знаки, в результате всегда будет плюс.
Рассмотрим все возможные варианты. Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус.
| Минус на плюс, плюс на минус. |
Как вы видите, все варианты умножения и деления положительных и отрицательных чисел исчерпаны, но знак плюс у нас так и не появился. Это мы сформулировали правило для себя, чтобы запомнить. Что говорить математикам? При умножении или делении положительных и отрицательных чисел в результате получается отрицательное число. Всегда.
Что дает минус на минус? Всегда будет получаться плюс, если мы выполняем умножение или деление. Что дает плюс на плюс? Здесь совсем просто. Умножение или деление плюса на плюс дает всегда плюс.
| Минус на минус, плюс на плюс. |
Надеюсь, это вы запомнили: минус на минус дает плюс, плюс на плюс дает минус. Что говорить математикам? При умножении и делении положительных или отрицательных чисел в результате получается положительное число.
Если с умножением и делением двух плюсов всё понятно (в результате получается такой же плюс), то с двумя минусами ничего не понятно. По логике, если два плюса дают плюс, то два минуса должны давать минус. Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс?
Могу вас заверить, что интуитивно математики правильно решили задачу на умножение и деление плюсов и минусов. Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.
Давайте попробуем применить правило умножениея и деления положительных и отрицательных чисел на практике. Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд — это положительные числа, а дёготь — это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила.
Если в бочку дёгтя добавить ложку мёда, получится бочка дёгтя.
Если в бочку мёда добавить ложку дёгтя, получится бочка дёгтя.
Если в бочку дёгтя добавить ложку дёгтя, получится бочка мёда.
Если в бочку мёда добавить ложку мёда, получится бочка мёда.
Первых два примера с натяжкой можно принять. Последний пример вообще не вызывает вопросов. А вот с предпоследним примером возникают очень большие проблемы — в жизни такого не бывает.
Здесь возможны два варианта:
1. Математики не правильно записали свое правило.
2. Мы не правильно применяем математическое правило.
Лично я за второй вариант. Объясню почему. Математику не только нужно знать, но нею ещё нужно уметь пользоваться.
Приведу пример из собственного опыта. Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат. Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?
Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат. Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?
Но вернемся к нашим бочкам. Кстати, говорят, именно с бочек с вином математики срисовали знак «минус». Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».
Так что же не так с мёдом и дёгтем в бочках? Мои четыре примера описывают действие сложения — ведь мы прибавляем одно к другому, а математические правила мы рассматриваем для деления и умножения. Это абсолютно разные вещи, сколько бы математики не повторяли, что умножение это и есть сложение. Сложение — это изменение количества. Умножение — это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. Мы просто получаем бочку испорченного мёда. Точно так же и дёготь, добавленный в бочку дёгтя, не превращает всё в мёд. При сложении и вычитании положительных и отрицательных чисел действуют совсем другие правила знаков.
Сложение — это изменение количества. Умножение — это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь. Мы просто получаем бочку испорченного мёда. Точно так же и дёготь, добавленный в бочку дёгтя, не превращает всё в мёд. При сложении и вычитании положительных и отрицательных чисел действуют совсем другие правила знаков.
В чем же отличие качественных изменений от количественных? В единицах измерения, которые в математике предпочитают игнорировать. Вот смотрите. Если мы к метрам длины прибавим метры ширины, мы получим метры периметра. А если мы умножим метры длины на метры ширины, то в результате будут метры квадратные площади. Теперь вопрос к математикам: сколько метров длины или ширины нужно сложить, чтобы получить один метр квадратный площади? Или вопрос к вам: сколько метров ниток вам нужно намотать на себя, чтобы одеться? Ведь ткань — это те же самые нитки, только в совершенно другом качестве. Ну и наглядный пример из алгебры:
2а+2а=4а
2а*2а=4а^2
В этом примере буква а выполняет роль единицы измерения. Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число?
Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число?
(-2)+(-2)=-4
(-2)*(-2)=+4
Так что же такое знаки «плюс» и «минус» в математике? Существуют ли отрицательные числа? Об этом мы поговорим как-нибудь в другой раз.
Узнаем как понять, почему «плюс» на «минус» дает «минус» ?
Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.
Законы математики
Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель…
А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель…
Дальнозоркость — это плюс или минус? Причины…
В данной статье рассматривается принцип функционирования зрительной системы человека, а также…
Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.
Аксиома кольца
Существует несколько математических законов.
- Первый из них переместительный, согласно ему, C + V = V + C.
- Второй называется сочетательным (V + C) + D = V + (C + D).
Им же подчиняется и умножение (V х C) х D = V х (C х D).
Никто не отменял и правил, по которым открываются скобки (V + C) х D = V х D + C х D, также верно, что C х (V + D) = C х V + C х D.
Кроме того, установлено, что в кольцо можно ввести специальный, нейтральный по сложению элемент, при использовании которого будет верно следующее: C + 0 = C. Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.
Координатная прямая. Точки на координатной прямой. Узнаем…
Чтобы допускать меньше ошибок по невнимательности, следует использовать в расчётах графики,…
Выведение аксиом для отрицательных чисел
Приняв приведенные выше утверждения, можно ответить на вопрос: «»Плюс» на «минус» дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.
А также, что верно такое равенство: (-(-C)) = C.
Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа — V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.
Газовое оборудование на автомобиль: цена и отзывы. Газовое…
В последнее время все больше автолюбителей стали задумываться о переоборудовании своих…
Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.
Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.
Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.
Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V. Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).
Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.
Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.
Умножение и деление двух чисел со знаком «-»
Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.
Допустим, что C — (-V) = D, исходя из этого, C = D + (-V), то есть C = D — V. Переносим V и получаем, что C + V = D. То есть C + V = C — (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.
Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.
(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) — (C х V) = D.
Вспомная о правилах работы со скобками, получаем:
1) (-C) х (-V) + (C х V) + (-C) х V = D;
2) (-C) х ((-V) + V) + C х V = D;
3) (-C) х 0 + C х V = D;
4) C х V = D.
Из этого следует, что C х V = (-C) х (-V).
Аналогично можно доказать, что и в результате деления двух отрицательных чисел выйдет положительное.
Общие математические правила
Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья. Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.
Почему отрицательное время является отрицательным положительным? – The Reflective Educator
Возможны разные ответы на этот вопрос, в зависимости от необходимого стандарта доказательства и исходных знаний, которые человек привносит в вопрос.
Математическая согласованность и закономерности
Попробуйте решить каждую из этих задач, обращая внимание на предыдущий набор задач. Ищите закономерности, чтобы упростить решение задач.
3 × 3 = ?
3 × 2 = ?
3 × 1 = ?
3 × 0 = ?
3 × -1 = ?
3 × -2 = ?
3 × -3 = ?
2 × -3 = ?
1 × -3 = ?
0 × -3 = ?
-1 × -3 = ?
-2 × -3 = ?
-3 × -3 = ?
Ответы на эти задачи приведены ниже, но я настоятельно рекомендую сначала самостоятельно решить приведенные выше задачи, чтобы вы поняли, как учащиеся могут продумать этот набор задач.
3 × 3 = 9
3 × 2 = 6
3 × 1 = 3
3 × 0 = 0
На этом этапе многие люди заметят, что ответы каждый раз становятся на 3 меньше, а число, умножаемое на 3, каждый раз уменьшается на единицу, поэтому они продолжают использовать эту схему, чтобы ответить на следующие вопросы.
3 × -1 = -3
3 × -2 = -6
3 × -3 = -9
Теперь уменьшим первое число в шаблоне на 3, и нужно сделать некоторые выводы о том, что ответ должно быть.
2 × -3 = -6
1 × -3 = -3
0 × -3 = 0
Теперь можно заметить, что ответы увеличиваются на 3 каждый раз, когда мы увеличиваем первое число, и поэтому разумно продолжать эту схему.
-1 × -3 = 3
-2 × -3 = 6
-3 × -3 = 9
Хотя для некоторых эта закономерность может показаться очевидной, когда кто-то еще находится в середине изучения этой концепции, у них есть меньше когнитивных способностей, доступных для выполнения поставленной задачи (умножения чисел) и выполнения дополнительной задачи по поиску закономерностей в их ответах, так что именно здесь кто-то еще побудит их остановиться и поискать закономерности в их работе до сих пор будет очень полезный.
Необходимые знания : Нужно знать, что означают эти символы, что подразумевается под нахождением одного числа, умноженного на другое, и как работают отрицательные числа с точки зрения обратного отсчета и вычитания.
Математическая непротиворечивость и математические свойства
Давайте рассмотрим задачу, которую мы можем решить несколькими способами, заимствованными из Академии Хана.
5 × (3 + -3) = ?
Если мы сначала добавим числа в скобках, то это будет 5 умножить на 0, что равно 0, так как 3 + -3 = 0,
5 × (3 + -3) = 0
Но что, если мы сначала распределим 5 через оба слагаемых?
5 × 3 + 5 × -3 = ?
Так как распределение 5 по сложению не меняет значения выражения, мы знаем, что оно по-прежнему равно 0.
5 × 3 + 5 × -3 = 0
Но это означает, что 5 × 3 и 5 × -3 противоположные знаки, так как 5 × 3 = 15, то 5 × -3 равно -15. Давайте посмотрим на другой пример.
-5 × (3 + -3) = ?
Мы знаем, что это то же самое, что -5 умножить на 0, так что это значение равно 0,
-5 × (3 + -3) = 0
Как и раньше, мы распределяем -5 через оба слагаемых.
-5 × 3 + -5 × -3 = ?
Опять же, распределение членов не меняет значения выражения в левой части уравнения, поэтому результат по-прежнему равен 0.
-5 × 3 + -5 × -3 = 0
Мы заранее известно, что -5 × 3 равно -15, поэтому мы можем заменить это значение на -5 × 3 в левой части уравнения.
-15 + -5 × -3 = 0
Следовательно, -15 и -5 × -3 являются противоположностями, поскольку они добавляют к 0, поэтому -5 × -3 должно быть положительным.
Ничто в том, что мы сделали для двух приведенных выше примеров, не относится к значению 5 × 3, поэтому мы можем повторить этот аргумент для любого другого факта умножения, который мы хотим вывести, так что эти две идеи можно обобщить.
Необходимые знания : Нужно знать, что означают эти символы, что подразумевается под нахождением одного числа, умноженного на другое, как работает распределительное свойство и как отрицательные числа могут быть определены как противоположные положительным числам.
Представление на числовой прямой
Представьте, что мы представляем умножение в виде скачков на числовой прямой.
3 раза по 3 на числовой прямой Для 3 × 3 мы рисуем 3 группы по 3, двигаясь вправо. Как количество групп, так и направление каждой группы указаны справа.
А как насчет 3 × -3? Теперь у нас есть еще 3 группы числа, но число отрицательное.
3 раза -3 на числовой прямойЕсли мы находим -3 × 3, размер и направление умножаемого числа те же, но теперь мы находим -3 группы этого числа. Один из способов подумать об этом — подумать об удалении 3 групп числа. Другой вариант — рассматривать число, умноженное на -3, как отражение 3-кратного одного и того же числа.
-3 умножить на 3 на числовой прямойТаким образом, -3 × -3 является отражением 3 × -3 на числовой прямой.
-3 умножить на -3 на числовой прямойОднако в некотором смысле этот визуальный аргумент является просто математической последовательностью, представленной с помощью числовой прямой. Если умножение на отрицательное число является отражением через 0 на числовой прямой, а мы думаем об отрицательных числах как отражение через 0 на числовой прямой, то умножение отрицательного числа на отрицательное число является двойным отражением.
Контекст
У Карен Лью есть аналогия.
Умножение на минус — это повторное вычитание. Когда мы умножаем отрицательное число на отрицательное число, мы получаем меньше отрицательного числа.
Эта аналогия между умножением, сложением и вычитанием помогает учащимся красиво связать эти два понятия.
Джозеф Рурк поделился этим контекстом.
Игрок проигрывает 10 долларов в день. Насколько больше денег у них было 5 дней назад?
Здесь убыток за день — это одно отрицательное значение, а движение назад во времени — другое.
@M_Teacher_w_T поделился этой аналогией:
«Враг моего врага — мой друг».
Это направлено не на алгебраические или арифметические свойства чисел, а скорее на противоположность отрицательных чисел.
Необходимые знания: Все контексты, формирующие новое понимание, требуют, чтобы учащиеся достаточно хорошо понимали части контекста, поэтому особенно важно выяснить, как учащиеся понимают идею, когда она представлена в контексте.
Алгебраическое доказательство из первых принципов
От доктора Алекса Юстиса мы получили это алгебраическое доказательство того, что отрицание, умноженное на отрицательное, является положительным.
Во-первых, он формулирует набор аксиом, применимых к любому кольцу с единицей. Кольцо — это, по сути, система счисления с двумя операциями. Каждая операция является закрытой, что означает, что использование этих операций (таких как сложение и умножение действительных чисел) приводит к другому числу в системе счисления. Каждая операция также имеет элемент идентичности или элемент, который не изменяет другой элемент в системе при применении к ней. Например, при добавлении 0 является аддитивной идентичностью. При умножении 1 является мультипликативным тождеством. Полный набор необходимых аксиом приведен ниже.
| Аксиома 1 : a + b = b + a | (аддитивная коммутативность) 9018 6 |
| Аксиома 2 : ( a + b ) + c = a + ( b + c ) | (Аддитивная ассоциативность) |
| Аксиома 3 : 0 + 900 54 a = a | (Аддитивная идентичность) |
| Аксиома 4 : Существует − a , удовлетворяющее a + (− a ) = 0 | (аддитивная обратная) |
| Аксиома 5 : 1 × a = a × 1 = a | (множительное тождество) |
| Аксиома 6 : ( a × b ) × c = a × ( b × c ) | (Мультипликативный ассоциативность) |
| Аксиома 7 : a × ( b + c ) = a × b + a × 9005 4 c | (Левое мультипликативное распределение) |
| Аксиома 8 (R распределения умножения) |
Из этих аксиом мы можем доказать, что отрицательный раз отрицательный является положительным. Ниже я воспроизведу доказательство доктора Юстиса и включу ссылку на использованные аксиомы. Сначала докажем, что a = -(- a ).
Ниже я воспроизведу доказательство доктора Юстиса и включу ссылку на использованные аксиомы. Сначала докажем, что a = -(- a ).
| a = a + 0 | style=»text-align: right»>(Аксиома 3 и Аксиома 1) 901 86 |
| а = а + (− a + −(− a )) | (аксиома 4 применяется к − a ) |
| a = ( a + (- a )) + (-( − a )) | (Аксиома 2 – свойство ассоциативности) |
| a = 0 + (−(− a )) | (аксиома 4) |
| a = −(− 90 054 а ) | (Аксиома 3) |
Итак, теперь мы знаем, что если ввести отрицательные числа , то будет равно −(−?).
Следствие 2| 0 = a + (− a ) | (аксиома 4) | 0 = (0 + 1) × a + (− a ) | (Аксиома 3 и Аксиома 5) |
| 0 = 0 × a + 1 × a + (− a ) | (Аксиома 8) |
| 0 = 0 × a + ( a + (− a )) | (Аксиома 5 и Аксиома 2) |
| 0 = 0 × a + 0 | (Аксиома 4 ) |
| 0 = 0 × a | (аксиома 3 и аксиома 1) |
Доказательство того, что 0 = 0 × a — это до боли очевидная идея, которая едва ли требует доказательств, но она устанавливает связь между умножением и аддитивной идентичностью в действительных числах. , который еще не включен в приведенные выше аксиомы.
, который еще не включен в приведенные выше аксиомы.
Далее докажем, что (−1) × a = − a .
Следствие 3| − a = − a + 0 × a | (Следствие 2 и аксиома 3) |
| − a = − a + (1 + (−1)) × a | (аксиома 4) |
| − a = − a + 1 × a + (−1) × a | (Аксиома 8) |
| − a = (− a + a ) + (−1) × a | (аксиома 5 и 2) |
| (аксиома 4) | |
| − a = 0 + (−1) × a | (аксиома 3) | 901 89
Теперь, наконец, мы можем доказать, что (− a ) × (− b ) = ab .
| (− a ) × (− b ) = ( a × (−1)) × (− b ) | (Следствие 3) |
| (− a ) × (− b ) = a × (( −1) × (− b )) | (аксиома 6) |
| (− a ) × (− b ) = a × (−(− 900 54 б )) | (Следствие 3) |
| (− a ) × (− b ) = a × b | (Следствие 1) |
Это последнее «доказательство» вряд ли оправдывает тот факт, что отрицательное значение, умноженное на отрицательное, является положительным для любого студента. Это то, что является необходимым уровнем обоснования для математика, заинтересованного в строгом доказательстве, который, вероятно, счел бы другие обоснования «шаблонными» и недостаточными.
Это то, что является необходимым уровнем обоснования для математика, заинтересованного в строгом доказательстве, который, вероятно, счел бы другие обоснования «шаблонными» и недостаточными.
Критическая идея доказательства, однако, заключается в том, что целевая аудитория доказательства остается убежденной в том, что идея верна, и поэтому я утверждаю, что представленное здесь алгебраическое «доказательство» вообще не является доказательством почти для всех.
Предварительные знания : Пока я прорабатывал и добавлял обоснование для каждого отсутствующего шага доказательства, мне нужно было достаточно бегло обращаться с первоначальным набором аксиом. Мне также нужно было не упускать из виду общую цель и уметь распознавать структуру каждой части аргумента и сопоставлять эту структуру с аксиомами.
Более простое алгебраическое доказательство
Это алгебраическое доказательство Бенджамина Дикмана намного проще, чем возвращение к доказательству, основанному на аксиомах арифметики.
a + (− a ) = 0
a × b + (− a ) × b = 0 × b
от + (- от ) = 0
Отсюда мы можем показать, что ab и – ab имеют противоположные знаки и, следовательно, положительное произведение на отрицательное является отрицательным. Используя факт, умножение коммутативно, отрицательное произведение, умноженное на положительное, также является отрицательным.
Точно так же мы можем доказать, что отрицательное произведение, умноженное на отрицательное, является положительным.
a + (− a ) = 0
a × (− b ) + (− a ) × (− b ) = 0 × (− б )
− ab + (− a ) × (− b ) = 0
Поскольку мы знаем, что − ab отрицательно, а сумма этих двух членов равна 0, поэтому (− a ) × (− b ) положительный.
Предварительные знания : Предварительные знания для этого доказательства намного меньше, чем для другого, но оно предполагает достаточное владение алгебраическими структурами.
Вывод:
Учитывая, что цель аргумента в пользу истинности чего-либо состоит в том, чтобы убедить другого человека в истинности аргумента, всякий раз, когда кто-либо использует какое-либо обоснование, репрезентацию или доказательство, следует убедиться, что аудитория убеждена.
1.5 Почему NEGATIVE TIMES NEGATIVE POSITIVE?
Когда мы обнаруживаем отрицательные числа, мы естественно, даже без сомнения, предполагаем, что они подчиняются тем же законам арифметики, что и обычные положительные счетные числа. То есть нам нравится верить, что основные законы, такие как \(a\times b=b\times a\) и (a\times 1=a\) и \(a \times 0=0\) выполняются для всех числа, как положительные, так и отрицательные, и что мы можем раскрывать скобки даже с отрицательными значениями и так далее. Конечно, эти правила предполагают, что мы знаем априори умеют умножать отрицательные числа.
УМНОЖЕНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
В начальной учебной программе умножение вводится в контексте целых счетных чисел и определяется там как многократное сложение. Например, \(4 \times 5\) читается как «четыре группы по пять» и вычисляется следующим образом: \(4 \times 5 = 5 + 5 + 5 + 5 = 20\).
Например, \(4 \times 5\) читается как «четыре группы по пять» и вычисляется следующим образом: \(4 \times 5 = 5 + 5 + 5 + 5 = 20\).
На самом деле довольно удивительно, что \(5 х 4\), «пять групп по четыре» дает тот же числовой ответ, что и четыре группы по пять. Расчет совсем другой, когда числа 5 и 4 поменялись ролями.
Вопрос: Как бы вы убедили молодого студента в том, что 193 группы по 307 обязательно будут иметь такое же значение, как 307 групп по 193? Почему мы хотим верить, что \(a \times b = b \times a\) для подсчета чисел? (СОВЕТ: расставьте точки прямоугольными рядами.)
Повторное сложение позволяет нам умножать положительное число и отрицательное число. Например, \(2 \times \left(-3\right)\) может быть прочитано как «две группы отрицательных трех» и поэтому вычисляется как \(2 \times \left(-3\right)=-3 +\;-3=-6\). С помощью свай и отверстий это выглядит так:
Интерпретация отрицательного числа, умноженного на положительное, и отрицательного, умноженного на отрицательное путем многократного сложения, однако, проблематична.
Что может означать \(\left(-2\right) \times 3\) ? «Отрицательные две группы по три» не имеет смысла.
И \(\left(-2\right) \times \left(-3\right)\) одинаково странно: «отрицательные две группы отрицательных трех».
Правда в том, что умножение здесь не имеет смысла в контексте многократного сложения. Мы вступили на новую территорию, и если мы хотим открыть наш мир новым типам чисел, неудивительно, что ранее конкретные, буквальные определения начинают колебаться. Таким образом, мы должны осуществить изощренный сдвиг мышления, отпустив вопрос 9.0054 Что такое умножение? , чтобы вместо этого спросить:
Как бы мы хотели, чтобы вело себя умножение?
Комментарий: Позвольте мне подчеркнуть этот момент. Вопрос «Что означает умножение отрицательных чисел?» — вводящий в заблуждение вопрос, и это не тот вопрос, который стоит задавать на данном этапе нашей работы: мы все еще пытаемся решить вопрос о том, чем может быть умножение в мире отрицательных чисел. Чтобы подойти к этому, мы сначала должны четко определить, какие особенности арифметики, по нашему мнению, должны оставаться верными.
Чтобы подойти к этому, мы сначала должны четко определить, какие особенности арифметики, по нашему мнению, должны оставаться верными.
ДУМАЕМ ЧЕРЕЗ ВЕЩИ
Положительное время Отрицательное : Кажется убедительным придерживаться понятия «повторяющегося сложения» для произведения отрицательного и положительного:
900 02 \(2\раз \left(-3\right)=\) две группы отрицательных троек \(=-3+-3=-6\).Большинство людей согласны с тем, что мы должны придерживаться этой идеи.
Отрицательное время Положительное : Это проблематично: \(\left(-2\right)\times 3=?\)
Но кажется убедительным утверждение, что коммутативный закон \(a \times b = b\times a\) должен выполняться для всех типов чисел, включая отрицательные числа. В этом случае мы можем написать:
\(\left(-2\right)\times 3 =3\times \left(-2\right)\) три группы отрицательных двойок \(=-2+-2+ -2=-6\).
Отрицательное время Отрицательное : Как мы должны вычислить \(\влево(-2\вправо) \умножить на \влево(-3\вправо)\)?
Применение коммутативного закона и представление об этом как \(\left(-3\right) \times \left(-2\right)\) в этом случае не помогает. Итак, какая математика могла бы направить нас в нашем мышлении здесь?
Итак, какая математика могла бы направить нас в нашем мышлении здесь?
Мы говорили, что нам нравится верить, что все обычные законы арифметики ( \(a\times b=b\times a\), \(a \times 1=a\) , \(a \times 0= 0\), раскрывающиеся скобки и т. д.) должны выполняться для всех типов чисел. Поскольку модель площади — это просто представление нашей веры в расширение скобок, модель площади должна работать и для отрицательных чисел!
КЛЮЧЕВОЙ ПРИМЕР: Вот три способа вычислить \(17\умножить на 18\), представляя \(17\) либо как \(10+7\), либо как \(20+\влево(-3\вправо). )\) и \(18\) как \(10+8\) или \(20 + \влево(-2\вправо)\). Хотя с геометрической точки зрения нет смысла иметь отрицательную длину стороны геометрической фигуры, мы видим, что математика, которую представляет каждая диаграмма, по-прежнему является правильной математикой.
Но есть и четвертая возможная картинка!
Математика раскрывающихся скобок предполагает, что правильное значение \(\left(-2\right)\times\left(-3\right)\) равно \(+6\).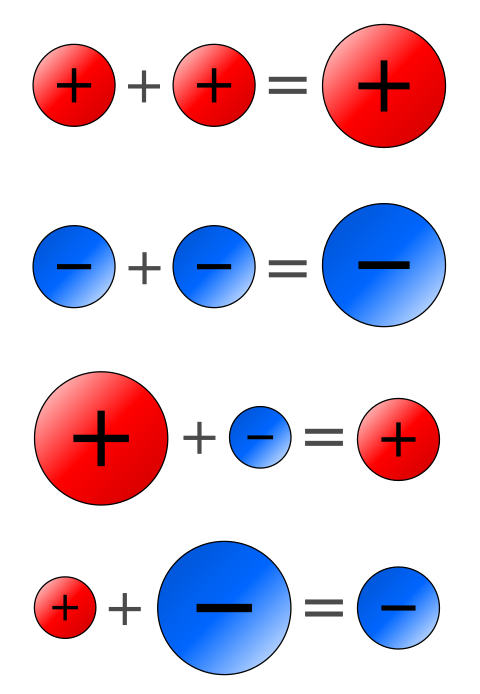 (В произведении по-прежнему должен быть ответ \(306\).)
(В произведении по-прежнему должен быть ответ \(306\).)
УПРАЖНЕНИЕ: Нарисуйте четыре диаграммы, представляющие \(26\x 35\), и используйте последнюю, чтобы продемонстрировать, почему мы должны установить \(\ влево(-4\вправо)\раз\влево(-5\вправо)=+20\).
ТОЧНЫЙ ЛОГИЧЕСКИЙ АРГУМЕНТ, ПОЧЕМУ ОТРИЦАТЕЛЬНОЕ ВРЕМЯ ОТРИЦАТЕЛЬНОЕ ДОЛЖНО БЫТЬ ПОЛОЖИТЕЛЬНЫМ )=-6\) (через многократное добавление ) и \(\left(-3\right)\times 2=-6\) (через веру в коммутативность), что отрицательное, умноженное на отрицательное, является положительным, является вынужденным логическим следствием следующих двух основных убеждений арифметики: \( a\times 0 = 0\) и \(a\left(b+c\right)=ab+ac\). Вот почему:
Докажем \(\влево(-2\вправо)\раз\влево(-3\вправо)=+6\).
По первому из правил мы должны сказать: \(\left(-2\right)\times 0 = 0\).
Переписав первый ноль, мы должны договориться, что: \(\влево(-2\вправо)\times \влево(3+\влево(-3\вправо)\вправо) = 0\).
При распределении мы также должны согласиться с тем, что: \(\влево(-2\вправо)\умножить на 3 + \влево(-2\направо)\раз\влево(-3\направо)=0\).
Это выглядит так: \(-6 + \влево(-2\вправо)\times\влево(-3\вправо)=0\).
Отсюда следует, что \(\влево(-2\вправо)\times\влево(-3\вправо)\) должно быть \(+6\).
УПРАЖНЕНИЕ: Создайте аналогичный аргумент, чтобы установить, что \(\left(-4\right)\times\left(-5\right)=+20\).
Итак… ЧТО ТАКОЕ УМНОЖЕНИЕ?
В контексте положительных целых чисел повторяется сложение.
В контексте положительных и отрицательных целых чисел я лично не знаю, что это такое, кроме математически согласованного набора операций, так что если \(a\) и \(b\) — положительные целые числа, тогда \(a\times \left(-b\right)=-ab\) и с логическими последствиями \(\left(-a\right)\times b = b \times \left(-a\right) =-ab\) и \(\left(-a\right)\times\left(-b\right) = ab\).
Люди пытаются придать всему этому конкретный смысл с моделями солдат, марширующих по числовым линиям, поворачивающих в разные стороны, системами прибыли и долга, работающими при плюсовых и минусовых температурах и так далее. Каждая модель хороша для иллюстрации НЕКОТОРЫХ аспектов арифметики отрицательных чисел, но не всех. Например, идея «убрать пять градусов холода — это то же самое, что добавить пять градусов тепла» может помочь некоторым объяснить, почему \(-\left(-5\right)\) должно равняться \(5\) , но само по себе это не объясняет, почему отрицательное, умноженное на отрицательное, называется положительным.
С педагогической точки зрения нам нужно отойти от того, чтобы ученик начал думать об умножении отрицательных чисел с помощью моделей, которые пытаются, но должны в какой-то момент потерпеть неудачу, «объяснить», что такое умножение отрицательных чисел. Вместо этого мы должны начать с обсуждения того, что, по нашему мнению, должно быть верным в отношении умножения в целом и как оно ведет себя.

 Если PDF содержит редактируемый текст, выберите «Преобразовать». Если вы хотите извлечь текст из отсканированного документа, выберите «Преобразовать с OCR». Чтобы оптимизировать результаты распознавания, укажите язык исходного файла.
Если PDF содержит редактируемый текст, выберите «Преобразовать». Если вы хотите извлечь текст из отсканированного документа, выберите «Преобразовать с OCR». Чтобы оптимизировать результаты распознавания, укажите язык исходного файла. 1 / 5
1 / 5 You can also drag and drop the PDF file. Uploading a file from the Internet (Enter URL) or cloud storage services (Google Drive, Dropbox) is also possible.
You can also drag and drop the PDF file. Uploading a file from the Internet (Enter URL) or cloud storage services (Google Drive, Dropbox) is also possible. 6 / 5
6 / 5
 Есть несколько способов добиться этого. В этой статье мы опишем три способа преобразования ваших документов с помощью Google Docs, Microsoft Office и нашего бесплатного конвертера PDF!
Есть несколько способов добиться этого. В этой статье мы опишем три способа преобразования ваших документов с помощью Google Docs, Microsoft Office и нашего бесплатного конвертера PDF! Выберите файл OpenOffice.
Выберите файл OpenOffice.
 Загружайте любой файл на любую ОС, настольный компьютер или мобильное устройство и быстро получайте результаты. Преобразование .ODT или .ODS в PDF еще никогда не было таким простым!
Загружайте любой файл на любую ОС, настольный компьютер или мобильное устройство и быстро получайте результаты. Преобразование .ODT или .ODS в PDF еще никогда не было таким простым! Быстрый и простой способ для любой ситуации.
Быстрый и простой способ для любой ситуации. Бесплатные пользователи могут конвертировать до двух файлов в день.
Бесплатные пользователи могут конвертировать до двух файлов в день.
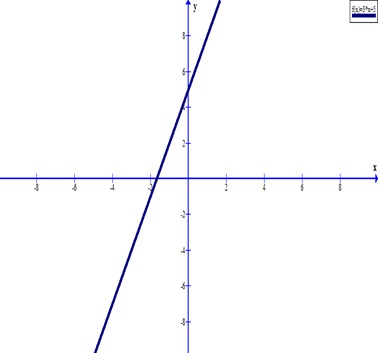 Известно, что среди любых 11 грибов имеется хотя бы один рыжик ,а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине?
Известно, что среди любых 11 грибов имеется хотя бы один рыжик ,а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине?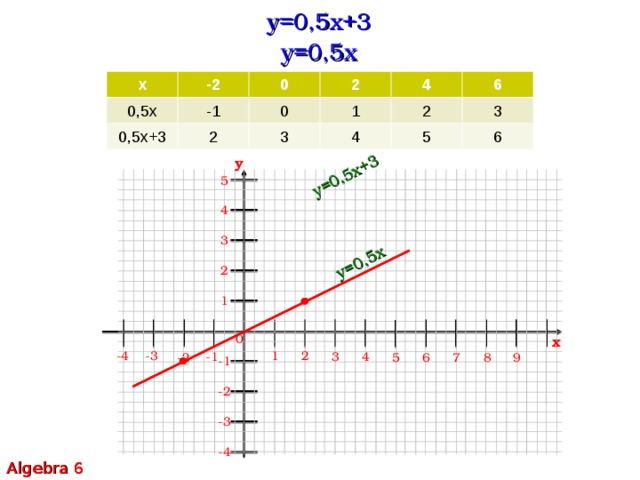
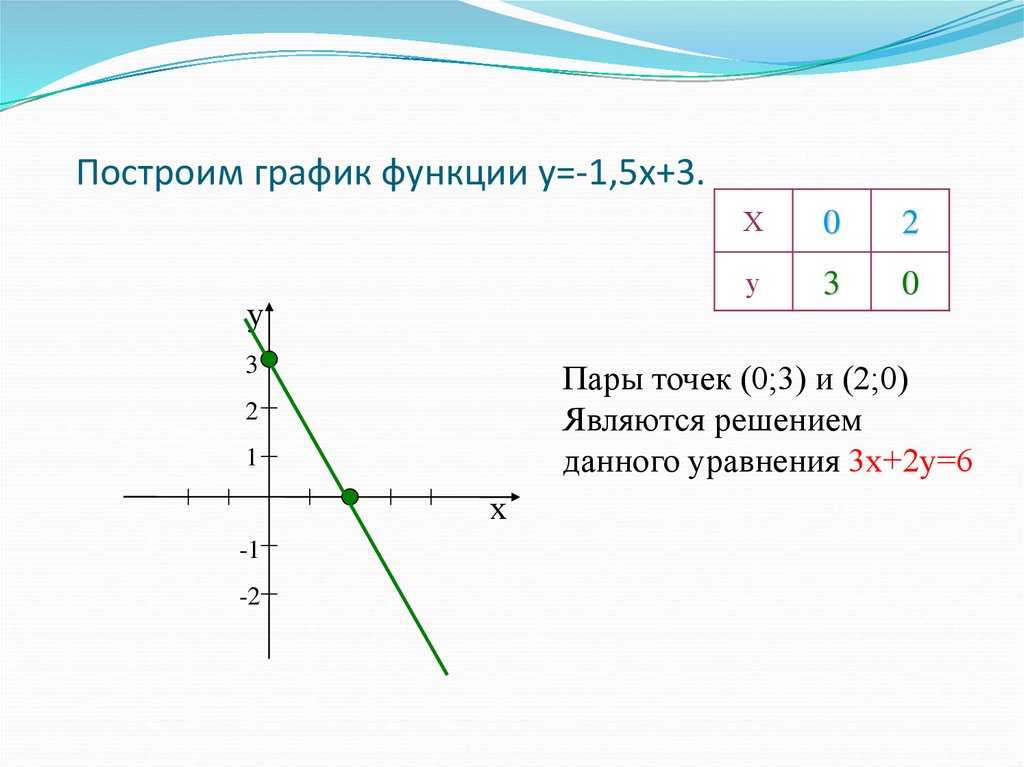 Số các cặp số nguyên (x,y) thoả mãn x+y+xy=3 là …..
Số các cặp số nguyên (x,y) thoả mãn x+y+xy=3 là ….. 2=2 \). Chứng minh rằng \(\sqrt{1+xy}\) là một số hữu tỉ.
2=2 \). Chứng minh rằng \(\sqrt{1+xy}\) là một số hữu tỉ.
 Вам необходимо ввести целую часть (если есть), числитель и знаменатель дроби. Например, если вы хотите преобразовать 5 3/12 в его десятичный эквивалент, вы введете ‘5’ как целую часть, ‘3’ как числитель и ’12’ как знаменатель.
Вам необходимо ввести целую часть (если есть), числитель и знаменатель дроби. Например, если вы хотите преобразовать 5 3/12 в его десятичный эквивалент, вы введете ‘5’ как целую часть, ‘3’ как числитель и ’12’ как знаменатель. , https://www.enotes.com/homework-help/what-change-this-imporper-fraction-mixed-number-5-112985 .
По состоянию на 14 марта 2023 г.
, https://www.enotes.com/homework-help/what-change-this-imporper-fraction-mixed-number-5-112985 .
По состоянию на 14 марта 2023 г.
 в 20:13:27.
в 20:13:27. укажите это f и a. lim h->0 [(4-й корень из)(16+h)-2]/h a=? ф=?
укажите это f и a. lim h->0 [(4-й корень из)(16+h)-2]/h a=? ф=?
 Все, что нам нужно сделать, это взять новый числитель и поместить его над исходным знаменателем, поставив перед ним целое число:
Все, что нам нужно сделать, это взять новый числитель и поместить его над исходным знаменателем, поставив перед ним целое число:
 При преобразовании файлов PDF с помощью Acrobat форматирование исходного документа сохраняется.
При преобразовании файлов PDF с помощью Acrobat форматирование исходного документа сохраняется. Формат Простой способ распространять документы, чтобы все стороны могли получить к ним доступ и увидеть их одинаково на любом экране. это просто Создать файл PDF Из документа Word, Excel или PowerPoint или из изображения.
Формат Простой способ распространять документы, чтобы все стороны могли получить к ним доступ и увидеть их одинаково на любом экране. это просто Создать файл PDF Из документа Word, Excel или PowerPoint или из изображения.
 Ваш документ Word будет напечатан в формате PDF, что означает, что распечатка будет создана как файл PDF. Назовите свой документ, выберите место для его сохранения, а затем сохраните документ PDF.
Ваш документ Word будет напечатан в формате PDF, что означает, что распечатка будет создана как файл PDF. Назовите свой документ, выберите место для его сохранения, а затем сохраните документ PDF.



 Этот инструмент преобразования Word в книгу возьмет ваш документ Microsoft Word и преобразует его в готовый к печати файл PDF. После того, как вы закончите вносить изменения в свою рукопись, вы можете загрузить файл Word на наш защищенный сервер, и наше программное обеспечение преобразует ваш документ Word в PDF.
Этот инструмент преобразования Word в книгу возьмет ваш документ Microsoft Word и преобразует его в готовый к печати файл PDF. После того, как вы закончите вносить изменения в свою рукопись, вы можете загрузить файл Word на наш защищенный сервер, и наше программное обеспечение преобразует ваш документ Word в PDF.

 Это доказательство в формате PDF покажет вам, правильно ли центрированы поля для левой и правой страниц. Вы хотите убедиться, что ваш текст не попадает в переплет книги, так как это затруднит чтение копии.
Это доказательство в формате PDF покажет вам, правильно ли центрированы поля для левой и правой страниц. Вы хотите убедиться, что ваш текст не попадает в переплет книги, так как это затруднит чтение копии. Обслуживание клиентов также было очень полезным. В целом я был очень доволен, а человек, получивший книги в подарок, был в восторге.»
Обслуживание клиентов также было очень полезным. В целом я был очень доволен, а человек, получивший книги в подарок, был в восторге.» 0
0
 Мы работаем над улучшением производительности.
Мы работаем над улучшением производительности. 0
0 Adobe представила текстовые документы, которые содержат форматированный текст и изображения.
Adobe представила текстовые документы, которые содержат форматированный текст и изображения. 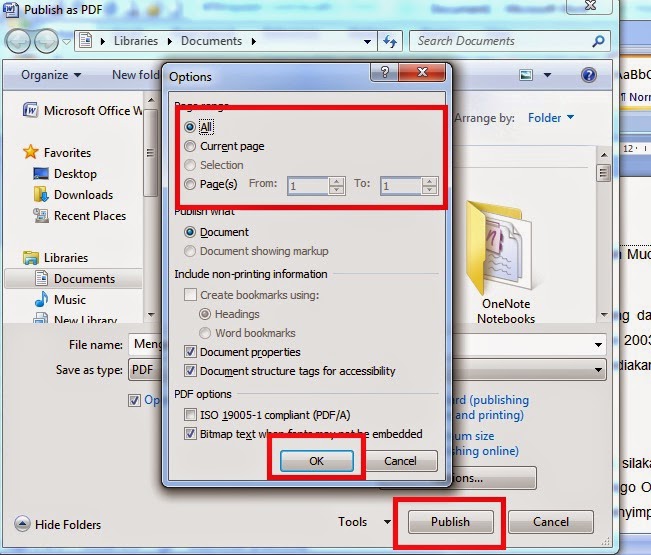
 В большой турке не получится выварить кофе, он скорее будет недоэкстрагированным (с травянистыми и
овощными оттенками во вкусе). Выбирайте джезву под объем вашей чашки.
В большой турке не получится выварить кофе, он скорее будет недоэкстрагированным (с травянистыми и
овощными оттенками во вкусе). Выбирайте джезву под объем вашей чашки.

 Смело меняйте их по вкусу!
Смело меняйте их по вкусу! Чем больше кофе по отношению к воде
– тем насыщеннее и ярче будет напиток, но важно не переусердствовать, чтобы не получить горькую
чашку»..
При расчете, ориентируйтесь на объём вашей турки, заполняйте её до точки сужения.
Чем больше кофе по отношению к воде
– тем насыщеннее и ярче будет напиток, но важно не переусердствовать, чтобы не получить горькую
чашку»..
При расчете, ориентируйтесь на объём вашей турки, заполняйте её до точки сужения. Если кофе начнет выбегать из-под шапки тонкой струйкой, аккуратнее: он вот-вот сбежит!
Если кофе начнет выбегать из-под шапки тонкой струйкой, аккуратнее: он вот-вот сбежит! В принципе, сироп можно не использовать, так как кофе сухой обработки сладкий сам по себе.
Засыпьте кофе в турку, добавьте воду, предварительно размешав в ней сироп палочкой корицы.
Сварите напиток так, как вы обычно это делаете, но перед тем, как разлить по чашкам,
размешайте кофейную шапку не ложкой, а палочкой корицы. Тонкий пряный оттенок во вкусе
удивительным образом будет дополнять сладость, характерную для сухой обработки.
В принципе, сироп можно не использовать, так как кофе сухой обработки сладкий сам по себе.
Засыпьте кофе в турку, добавьте воду, предварительно размешав в ней сироп палочкой корицы.
Сварите напиток так, как вы обычно это делаете, но перед тем, как разлить по чашкам,
размешайте кофейную шапку не ложкой, а палочкой корицы. Тонкий пряный оттенок во вкусе
удивительным образом будет дополнять сладость, характерную для сухой обработки.
 У некоторых может быть только легкая боль при выполнении определенных видов деятельности, особенно при выполнение бега или прыжков. У других же боль может быть постоянной и изнурительной. Как правило, болезнь Осгуда-Шлаттера развивается только в одном колене, но иногда может иметь место в обоих коленях. Дискомфорт может быть длительностью от нескольких недель до нескольких месяцев и может повторяться, пока ребенок не перестает расти.
У некоторых может быть только легкая боль при выполнении определенных видов деятельности, особенно при выполнение бега или прыжков. У других же боль может быть постоянной и изнурительной. Как правило, болезнь Осгуда-Шлаттера развивается только в одном колене, но иногда может иметь место в обоих коленях. Дискомфорт может быть длительностью от нескольких недель до нескольких месяцев и может повторяться, пока ребенок не перестает расти. В некоторых случаях организм ребенка пытается закрыть этот дефект ростом костной ткани, что приводит к образованию костной шишки.
В некоторых случаях организм ребенка пытается закрыть этот дефект ростом костной ткани, что приводит к образованию костной шишки. Заболевание возникает в основном при занятиях такими видами спорта, где требуется много прыжков бег изменения траектории движения. Это, например:
Заболевание возникает в основном при занятиях такими видами спорта, где требуется много прыжков бег изменения траектории движения. Это, например:
 Упражнения на усиление мышц бедра помогают также стабилизировать коленный сустав.
Упражнения на усиление мышц бедра помогают также стабилизировать коленный сустав.
 Существует множество различных эталонных объемов, называемых бочками, в зависимости от характера содержимого.
Существует множество различных эталонных объемов, называемых бочками, в зависимости от характера содержимого. [2]
[2]  2020-04-17. Проверено 25 сентября 2020 г. .
2020-04-17. Проверено 25 сентября 2020 г. .  Эта чашка измеряет объем в чашках, жидких унциях и миллилитрах.
Эта чашка измеряет объем в чашках, жидких унциях и миллилитрах.
 svg|thumb|220px|Измерения объема из справочника новичка 1914 года]].
svg|thumb|220px|Измерения объема из справочника новичка 1914 года]]. 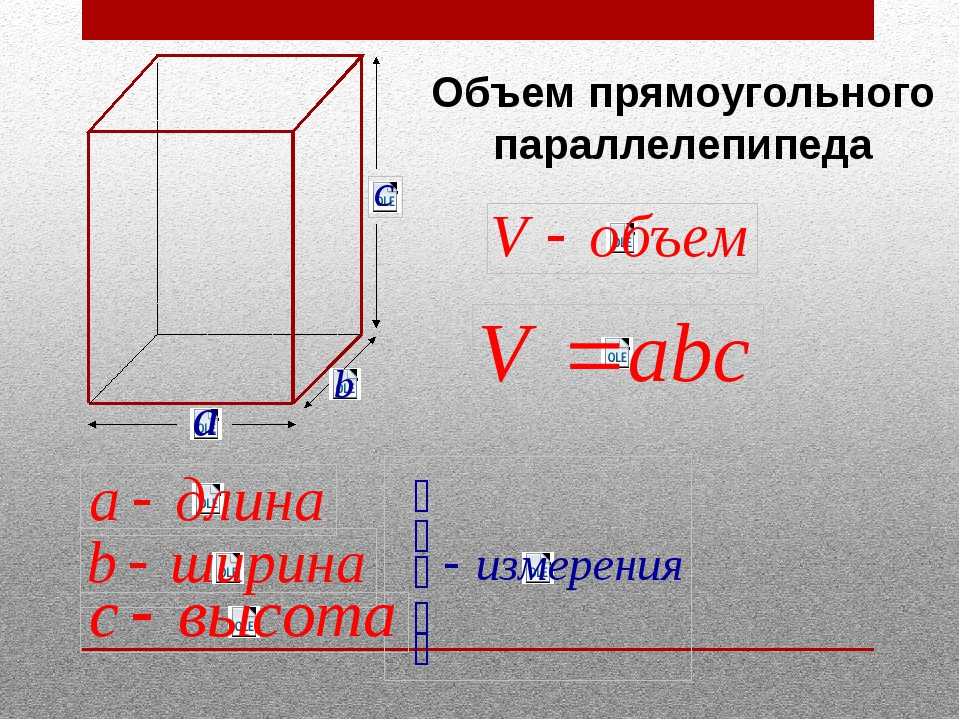
 a и b — пределы интегрирования для объемной развертки.
a и b — пределы интегрирования для объемной развертки.  {2}}.
9{3}.}
{2}}.
9{3}.}


 За неприличное или неспортивное поведение спортсмен может быть отстранён от текущих соревнований, и к нему могут даже применить дисциплинарные санкции.
За неприличное или неспортивное поведение спортсмен может быть отстранён от текущих соревнований, и к нему могут даже применить дисциплинарные санкции.

 С записанным треком гонки проблема устранения ошибки оборудования решится быстро.
С записанным треком гонки проблема устранения ошибки оборудования решится быстро.


 Если– список всех максимальных интервалов
подмножества,
то нетрудно видеть, что.
Если– список всех максимальных интервалов
подмножества,
то нетрудно видеть, что.

 Отметим, что клетки,
расположенные по краям таблицы, также
считаются соседними. Покажем работу
этого метода на следующем примере.
Отметим, что клетки,
расположенные по краям таблицы, также
считаются соседними. Покажем работу
этого метода на следующем примере.

 Поэтому в конъюнкциюмогли бы входить лишь буквы,
причем не все. Но тогда.
Получили противоречие с максимальностью
интервала.
Следовательно, для любого максимального
интерваласуществует вершина куба,
которая покрывается только этим
интервалом. Поэтому из покрытиясоответствующего сокращенной ДНФ,
нельзя удалить ни один из интервалов.
Теперь, применяя предыдущую теорему,
получаем требуемый результат.
Поэтому в конъюнкциюмогли бы входить лишь буквы,
причем не все. Но тогда.
Получили противоречие с максимальностью
интервала.
Следовательно, для любого максимального
интерваласуществует вершина куба,
которая покрывается только этим
интервалом. Поэтому из покрытиясоответствующего сокращенной ДНФ,
нельзя удалить ни один из интервалов.
Теперь, применяя предыдущую теорему,
получаем требуемый результат.
 1)
1) Для этого составим КНФ данной функции
.
Для этого составим КНФ данной функции
. ..
..
 Это преемник и замена менеджера пакетов Yum, который был представлен в Fedora 18 и с тех пор стал менеджером пакетов по умолчанию для Fedora и CentOS/RHEL 8, включая Almalinux, Rocky и другие подобные дистрибутивы. DNF был создан для устранения некоторых недостатков Yum, таких как низкая производительность и ограниченные возможности разрешения зависимостей. Использование и синтаксис команд DNF точно такие же, как у YUM, поэтому у новых пользователей не возникнет никаких проблем.
Это преемник и замена менеджера пакетов Yum, который был представлен в Fedora 18 и с тех пор стал менеджером пакетов по умолчанию для Fedora и CentOS/RHEL 8, включая Almalinux, Rocky и другие подобные дистрибутивы. DNF был создан для устранения некоторых недостатков Yum, таких как низкая производительность и ограниченные возможности разрешения зависимостей. Использование и синтаксис команд DNF точно такие же, как у YUM, поэтому у новых пользователей не возникнет никаких проблем.



 После этого RHEL 8 и другие системы перешли на диспетчер пакетов DNF для обновления, установки, удаления и управления системными пакетами.
После этого RHEL 8 и другие системы перешли на диспетчер пакетов DNF для обновления, установки, удаления и управления системными пакетами.

 Действительно,
Действительно, 2) .
2) .
 Помогает. Иногда.
Помогает. Иногда.

 2 + 2n + 1
2 + 2n + 1 Попадаются и задачи, где база дана в рекурсивной форме.
Попадаются и задачи, где база дана в рекурсивной форме. Вы учитесь распознавать всякого рода паттерны.
Вы учитесь распознавать всякого рода паттерны.


 То есть утверждение верно для n=1.
То есть утверждение верно для n=1.
 На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и график дифференциального уравнения онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь (например, диф уравнения онлайн).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и график дифференциального уравнения онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь (например, диф уравнения онлайн).



 В результате получим дифференциальное уравнение с разделенными переменными
В результате получим дифференциальное уравнение с разделенными переменными



 Он может решать обычные линейные дифференциальные уравнения первого порядка, линейные …
Он может решать обычные линейные дифференциальные уравнения первого порядка, линейные … Решайте ОДУ, линейные, нелинейные, обыкновенные и численные дифференциальные уравнения, функции Бесселя, …
Решайте ОДУ, линейные, нелинейные, обыкновенные и численные дифференциальные уравнения, функции Бесселя, …
 также
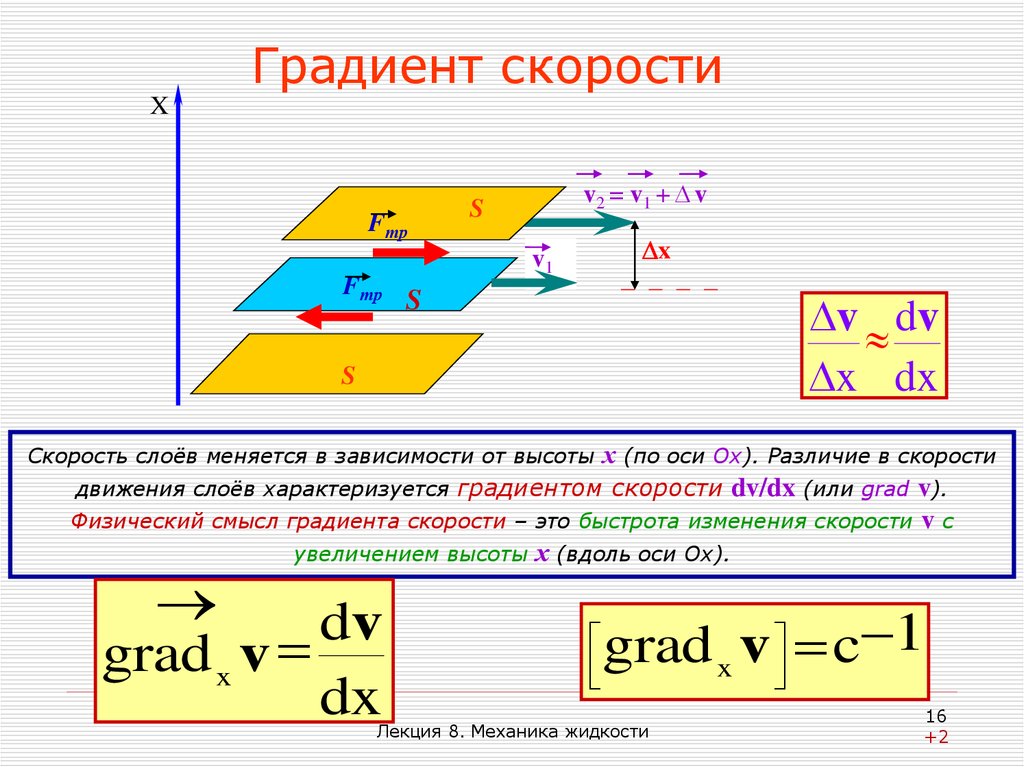
также Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:
Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:
 д.
д.
 : Градиент (компьютерная графика).
: Градиент (компьютерная графика).

 Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:
Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:
 д.
д.
 запись класса 2 смысл переходный 2) подъем или спуск : наклон
запись класса 2 смысл переходный 2) подъем или спуск : наклон
 — Даниэль Бошов, Anchorage Daily News , 6 апреля 2023 г.
Бивер-Крик Этот тихий и пологий приток Уайт-Ривер отлично подходит для длительных экскурсий благодаря своим пологим и постоянным градиент .
— Элизабет Роудс, Travel + Leisure , 16 марта 2023 г.
Море пенилось и бушевало, как обезумевший зверь во время шторма, над головой пузырились и пенились облака, сливаясь вместе, образуя серый градиент .
— Джори Макдональд, EW.com , 23 августа 2022 г.
Сапфиры шести градиентов оттенков синего выражают переход от дня к ночи.
— Джастин Феннер, 9 лет.0011 Отчет Робба , 27 марта 2023 г.
Или, возможно, обновление с яркой линзой или градиентом ?
— Сара Клаусинг, Men’s Health , 27 марта 2023 г.
— Даниэль Бошов, Anchorage Daily News , 6 апреля 2023 г.
Бивер-Крик Этот тихий и пологий приток Уайт-Ривер отлично подходит для длительных экскурсий благодаря своим пологим и постоянным градиент .
— Элизабет Роудс, Travel + Leisure , 16 марта 2023 г.
Море пенилось и бушевало, как обезумевший зверь во время шторма, над головой пузырились и пенились облака, сливаясь вместе, образуя серый градиент .
— Джори Макдональд, EW.com , 23 августа 2022 г.
Сапфиры шести градиентов оттенков синего выражают переход от дня к ночи.
— Джастин Феннер, 9 лет.0011 Отчет Робба , 27 марта 2023 г.
Или, возможно, обновление с яркой линзой или градиентом ?
— Сара Клаусинг, Men’s Health , 27 марта 2023 г. Доступны новые функции редактирования макетов, слоев, стилей и градиентов , чтобы оживить ваши проекты, а замещающий текст теперь можно создавать для изображений непосредственно в Canva.
— Джесс Уэзербед, 9 лет.0011 Грань , 23 марта 2023 г.
Специальное издание также имеет градиентную окраску , переходя от серебристого к черному, с желтой окантовкой.
— Калеб Миллер, Автомобиль и водитель , 21 марта 2023 г.
Шелковистая модель отличалась многослойным верхом, похожим на накидку, и эффектом омбре с градиентом , переходящим от водолазки к расклешенным брюкам.
— Роза Санчес, 9 лет.0011 Harper’s BAZAAR , 10 февраля 2023 г.
Узнать больше
Доступны новые функции редактирования макетов, слоев, стилей и градиентов , чтобы оживить ваши проекты, а замещающий текст теперь можно создавать для изображений непосредственно в Canva.
— Джесс Уэзербед, 9 лет.0011 Грань , 23 марта 2023 г.
Специальное издание также имеет градиентную окраску , переходя от серебристого к черному, с желтой окантовкой.
— Калеб Миллер, Автомобиль и водитель , 21 марта 2023 г.
Шелковистая модель отличалась многослойным верхом, похожим на накидку, и эффектом омбре с градиентом , переходящим от водолазки к расклешенным брюкам.
— Роза Санчес, 9 лет.0011 Harper’s BAZAAR , 10 февраля 2023 г.
Узнать больше Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.
Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах. Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/gradient. По состоянию на 24 апреля 2023 г.
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/gradient. По состоянию на 24 апреля 2023 г. Определения и примеры »
Определения и примеры »
 com Unabridged
Основано на словаре Random House Unabridged Dictionary, © Random House, Inc., 2023
com Unabridged
Основано на словаре Random House Unabridged Dictionary, © Random House, Inc., 2023 |Новости науки для студентов
|Новости науки для студентов
