Обыкновенные дроби и действия с ними — что это, определение и ответ
Доля – это часть от целого.
Например, пирог разделили на 8 частей, значит каждый кусочек пирога равен одной восьмой доле пирога или просто одной восьмой пирога. Записать такую долю можно в виде дроби\(\ = \frac{1}{8}\).
Если из полученных кусочков забрать три и оставить пять, получится, что забрали три восьмые\(\ –\ \frac{3}{8}\ \)пирога и оставили пять восьмых \(–\ \frac{5}{8}.\)
Число выше черты дроби называется числителем, число ниже черты – знаменателем, а запись вида \(\frac{5}{8}\) – обыкновенной дробью.
Дробь \(\frac{1}{2}\) называется половиной, \(\frac{1}{3}\) – третью, а \(\frac{1}{4}\) – четвертью.
ОСНОВНОЕ СВОЙСТВО ДРОБЕЙ:
Если мы представим пирог, который разделили на четыре части и забрали две из них (\(\frac{2}{4}\)), мы увидим, что забрали ровно половину пирога, то есть \(\frac{1}{2}\).
Значит \(\frac{2}{4} = \frac{1}{2}\). Так получается, потому что дроби можно сокращать (делить) и расширять (умножать). Если числитель и знаменатель дроби умножить или разделить на одно число, то дробь останется такой же.
Например:
\(\frac{1}{2} = \frac{1 \bullet 2}{2 \bullet 2} = \frac{2}{4}\)
\(\frac{28}{77} = \frac{28 : 7}{77 : 7} = \frac{4}{11}\)
\(\frac{5}{12} = \frac{5 \bullet 4}{12 \bullet 4} = \frac{20}{48}\)
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ:
Можно складывать и вычитать только те дроби, у которых одинаковый знаменатель. Тогда знаменатель суммы или разности будет такой же, как и у слагаемых, а числители складываются или вычитаются.
\(\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)
Например:
\(\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}\)
\(\frac{8}{9}\ –\ \frac{3}{9} = \frac{8\ –\ 3}{9} = \frac{5}{9}\)
Если у дробей разные знаменатели, то нужно привести их к общему знаменателю.

Приведем дробь \(\frac{5}{6}\ \)к знаменателю 42. Чтобы это сделать, нужно знаменатель 6 умножить на \(42 : 6 = 7\), значит и числительно тоже нужно умножить на 7:
\(\frac{5}{7} = \frac{5 \bullet 7}{6 \bullet 7} = \frac{35}{42}\)
Таким образом, мы пришли к новому знаменателю 42 с помощью дополнительного множителя 7.
Общим знаменателем является общее кратное исходных знаменателей. Обычно дроби приводят к наименьшему общему знаменателю. А уже дроби с общим знаменателем можно складывать и вычитать.
АЛГОРИТМ СЛОЖЕНИЯ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ:
Найти наименьшее общее кратное знаменателей дробей. Оно и будет новым знаменателем суммы.
Разделить найденный наименьший общий знаменатель на знаменатели слагаемых. Это будут дополнительные множители для дробей.
Умножить и числитель, и знаменатель каждой дроби на её дополнительный множитель. Получим сумму дробей с одинаковым знаменателем.

Складывать или вычитать дроби как обыкновенные дроби с одинаковыми знаменателями.
Например:
\(\frac{3}{4} + \frac{5}{6} = \frac{3 \bullet 3}{4 \bullet 3} + \frac{5 \bullet 2}{6 \bullet 2} = \frac{9}{12} + \frac{10}{12} = \frac{9 + 10}{12} = \frac{19}{12}\)
УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ:
Обратные числа:
Любая дробь – это действие деления. Один пирог разделили на восемь частей – получили одну восьмую пирога. Если мы видим дробь с единицей в знаменателе, то эту дробь можно представить числом:
\(\frac{a}{1} = a : 1 = a\)
Например: \(\frac{4}{1} = 4\), \(\frac{27}{1} = 27\).
Если дробь «перевернуть», то есть поменять местами числитель и знаменатель, тогда получится число обратное исходному. Например, числа \(\frac{4}{11}\) и \(\frac{11}{4}\) или \(19\) и \(\frac{1}{19}\) – обратные друг другу.
Умножение дробей:
Представим умножение дроби на число как сумму дробей:
\(\frac{3}{5} \bullet 3 = \frac{3}{5} + \frac{3}{5} + \frac{3}{5} = \frac{3 + 3 + 3}{5} = \frac{3 \bullet 3}{5} = \frac{9}{5}\)
Видим, что таким образом при умножении дроби на число перемножается число и числитель без изменения знаменателя:
\(\frac{a}{c} \bullet b = \frac{a}{c} \bullet \frac{b}{1} = \frac{a \bullet b}{c \bullet 1}\)
Деление дробей:
Чтобы разделить дробь на число, представим это число как дробь с единицей в знаменателе. Тогда мы делим дробь на дробь.
Тогда мы делим дробь на дробь.
Чтобы разделить дробь на дробь, нужно вторую дробь перевернуть и перемножить соответственно числители и знаменатели получившихся дробей:
\(\frac{a}{c} : b = \frac{a}{c} : \frac{b}{1} = \frac{a}{c} \bullet \frac{1}{b} = \frac{a}{c \bullet b}\)
Таким же образом делят дроби на дроби:
\(\frac{a}{c} : \frac{b}{d} = \frac{a}{c} \bullet \frac{d}{b} = \frac{a \bullet d}{c \bullet b} = \frac{\text{ad}}{\text{cb}}\)
Как решать дроби на деление. Деление дроби на натуральное число
Для решения различных заданий из курса математики, физики приходится производить деление дробей. Это сделать очень легко, если знать определенные правила выполнения этого математического действия.
Прежде чем перейти к формулированию правило том, как делить дроби, давайте вспомним некоторые математические термины:
- Верхняя часть дроби называется числителем, а нижняя – знаменателем.
- При делении числа называются так: делимое: делитель = частное
Как делить дроби: простые дроби
Для выполнения деления двух простых дробей следует умножить делимое на дробь, обратную делителю. Эту дробь по-другому называют еще перевернутой, потому что она получается в результате замены местами числителя и знаменателя. Например:
Эту дробь по-другому называют еще перевернутой, потому что она получается в результате замены местами числителя и знаменателя. Например:
3/77: 1/11 = 3 /77 * 11 /1 = 3/7
Как делить дроби: смешанные дроби
Если нам предстоит разделить смешанные дроби, то здесь тоже все достаточно просто и понятно. Сначала переводим смешанную дробь в обычную неправильную дробь. Для этого умножаем знаменатель такой дроби на целое число и числитель прибавляем к полученному произведению. В итоге мы получили новый числитель смешанной дроби, а знаменатель ее останется без изменения. Дальше деление дробей будет осуществляться точно так же, как и деление простых дробей. Например:
10 2/3: 4/15 = 32/3: 4/15 = 32/3 * 15 /4 = 40/1 = 40
Как делить дробь на число
Для того чтобы разделить простую дробь на число, последнее следует написать в виде дроби (неправильной). Это сделать очень легко: на месте числителя пишется это число, а знаменатель такой дроби равен единице. Дальше деление выполняется обычным способом. Рассмотрим это на примере:
Рассмотрим это на примере:
5/11: 7 = 5/11: 7/1 = 5/11 * 1/7 = 5/77
Как делить десятичные дроби
Нередко взрослый человек испытывает затруднения при необходимости без помощи калькулятора разделить целое число или десятичную дробь на десятичную дробь.
Итак, чтобы выполнить деление десятичных дробей, нужно в делителе просто зачеркнуть запятую и перестать обращать на нее внимание. В делимом запятую нужно передвинуть вправо ровно на столько знаков, сколько было в дробной части делителя, при необходимости дописывая нули. И дальше производят обычное деление на целое число. Чтобы это стало более понятно, приведем следующий пример.
С дробями можно выполнять все действия, в том числе и деление. Данная статья показывает деление обыкновенных дробей. Будут даны определения, рассмотрены примеры. Подробно остановимся на делении дробей на натуральные числа и наоборот. Будет рассмотрено деление обыкновенной дроби на смешанное число.
Деление обыкновенных дробей
Деления является обратным умножению. При делении неизвестный множитель находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.
При делении неизвестный множитель находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.
Если необходимо произвести деление обыкновенной дроби a b на c d , тогда для определения такого числа нужно произвести умножение на делитель c d , это даст в итоге делимое a b . Получим число и запишем его a b · d c , где d c является обратным c d числу. Равенства можно записать при помощи свойств умножения, а именно: a b · d c · c d = a b · d c · c d = a b · 1 = a b , где выражение a b · d c является частным от деления a b на c d .
Отсюда получим и сформулируем правило деления обыкновенных дробей:
Определение 1
Чтобы разделить обыкновенную дробь a b на c d , необходимо делимое умножить на число, обратное делителю.
Запишем правило в виде выражения: a b: c d = a b · d c
Правила деления сводятся к умножению. Чтобы придерживаться его, нужно хорошо разбираться в выполнении умножения обыкновенных дробей.
Перейдем к рассмотрению деления обыкновенных дробей.
Пример 1
Выполнить деление 9 7 на 5 3 . Результат записать в виде дроби.
Решение
Число 5 3 – это обратная дробь 3 5 . Необходимо использовать правило деления обыкновенных дробей. Это выражение запишем так: 9 7: 5 3 = 9 7 · 3 5 = 9 · 3 7 · 5 = 27 35 .
Ответ: 9 7: 5 3 = 27 35 .
При сокращении дробей следует выделять целую часть, если числитель больше знаменателя.
Пример 2
Разделить 8 15: 24 65 . Ответ записать в виде дроби.
Решение
Для решения нужно перейти от деления к умножению. Запишем это в такой форме: 8 15: 24 65 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Необходимо произвести сокращение, а это выполняется следующим образом: 8 · 65 15 · 24 = 2 · 2 · 2 · 5 · 13 3 · 5 · 2 · 2 · 2 · 3 = 13 3 · 3 = 13 9
Выделяем целую часть и получаем 13 9 = 1 4 9 .
Ответ: 8 15: 24 65 = 1 4 9 .
Деление необыкновенной дроби на натуральное число
Используем правило деления дроби на натуральное число:чтобы разделить a b на натуральное число n , необходимо умножить только знаменатель на n . Отсюда получим выражение: a b: n = a b · n .
Отсюда получим выражение: a b: n = a b · n .
Правило деления является следствием правила умножения. Поэтому представление натурального числа в виде дроби даст равенство такого типа: a b: n = a b: n 1 = a b · 1 n = a b · n .
Рассмотрим данное деление дроби на число.
Пример 3
Произвести деление дроби 16 45 на число 12 .
Решение
Применим правило деления дроби на число. Получим выражение вида 16 45: 12 = 16 45 · 12 .
Произведем сокращение дроби. Получим 16 45 · 12 = 2 · 2 · 2 · 2 (3 · 3 · 5) · (2 · 2 · 3) = 2 · 2 3 · 3 · 3 · 5 = 4 135 .
Ответ: 16 45: 12 = 4 135 .
Деление натурального числа на обыкновенную дробь
Правило деления аналогично правилу деления натурального числа на обыкновенную дробь: чтобы разделить натуральное число n на обыкновенную a b , необходимо произвести умножение числа n на обратное дроби a b .
Исходя из правила, имеем n: a b = n · b a , а благодаря правилу умножения натурального числа на обыкновенную дробь, получим наше выражение в виде n: a b = n · b a . Необходимо рассмотреть данное деление на примере.
Необходимо рассмотреть данное деление на примере.
Пример 4
Делить 25 на 15 28 .
Решение
Нам необходимо переходить от деления к умножению. Запишем в виде выражения 25: 15 28 = 25 · 28 15 = 25 · 28 15 . Сократим дробь и получим результат в виде дроби 46 2 3 .
Ответ: 25: 15 28 = 46 2 3 .
Деление обыкновенной дроби на смешанное число
При делении обыкновенной дроби на смешанное числолегко можно свети к делению обыкновенных дробей. Нужно совершить перевод смешанного числа в неправильную дробь.
Пример 5
Разделить дробь 35 16 на 3 1 8 .
Решение
Так как 3 1 8 — смешанное число, представим его в виде неправильной дроби. Тогда получим 3 1 8 = 3 · 8 + 1 8 = 25 8 . Теперь произведем деление дробей. Получим 35 16: 3 1 8 = 35 16: 25 8 = 35 16 · 8 25 = 35 · 8 16 · 25 = 5 · 7 · 2 · 2 · 2 2 · 2 · 2 · 2 · (5 · 5) = 7 10
Ответ: 35 16: 3 1 8 = 7 10 .
Деление смешанного числа производится таким же образом, как и обыкновенных.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут.
 В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
В крайнем случае, один минус может выжить — тот, которому не нашлось пары; - Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
Дробь – это одна или более долей целого, за которое обычно принимается единица (1). Как и с натуральными числами, с дробями можно выполнять все основные арифметические действия (сложение, вычитание, деление, умножения), для этого нужно знать особенности работы с дробями и различать их виды. Существует несколько видов дробей: десятичные и обыкновенные, или простые. Своя специфика есть у каждого вида дробей, но, обстоятельно разобравшись один раз, как с ними обращаться, вы сможете решать любые примеры с дробями, поскольку будете знать основные принципы выполнения арифметических вычислений с дробями. Рассмотрим на примерах как разделить дробь на целое число, используя разные виды дробей.
Существует несколько видов дробей: десятичные и обыкновенные, или простые. Своя специфика есть у каждого вида дробей, но, обстоятельно разобравшись один раз, как с ними обращаться, вы сможете решать любые примеры с дробями, поскольку будете знать основные принципы выполнения арифметических вычислений с дробями. Рассмотрим на примерах как разделить дробь на целое число, используя разные виды дробей.
Как разделить простую дробь на натуральное число?
Обыкновенными или простыми называют дроби, записывающиеся в виде такого отношения чисел, при котором вверху дроби указывается делимое (числитель), а внизу – делитель (знаменатель) дроби. Как разделить такую дробь на целое число? Рассмотрим на примере! Допустим, нам нужно разделить 8/12 на 2.
Для этого мы должны выполнить ряд действий:
Таким образом, если перед нами стоит задача разделить дробь на целое число, схема решения будет выглядеть примерно так:
Подобным образом можно разделить любую обыкновенную (простую) дробь на целое число.
Как разделить десятичную дробь на целое число?
Десятичная дробь — это такая дробь, которая получается вследствие деления единицы на десять, тысячу и так далее частей. Арифметические действия с десятичными дробями выполняются довольно просто.
Рассмотрим на примере как разделить дробь на целое число. Допустим, нам нужно поделить десятичную дробь 0,925 на натуральное число 5.
Подводя итоги, остановимся на двух основных моментах, которые важны при выполнении операции деления десятичных дробей на целое число:
- для разделения десятичной дроби на натуральное число применяют деление в столбик;
- запятая ставится в частном тогда, когда закончено деление целой части делимого.
Применяя эти простые правила, всегда можно без особого труда разделить любую десятичную или простую дроби на целое число.
Деление дробей с помощью полосок дробей
Деление дробей может быть очень сложным для многих учащихся. Трудно представить разделение одной фракции на группы других фракций. Чтобы разделить дроби, многие студенты запоминают алгоритм «сохранить-изменить-перевернуть», не зная, почему он работает.
Трудно представить разделение одной фракции на группы других фракций. Чтобы разделить дроби, многие студенты запоминают алгоритм «сохранить-изменить-перевернуть», не зная, почему он работает.
Без концептуального понимания деления дробей учащиеся, как правило, застревают, когда сталкиваются с задачами (особенно со словами), где им нужно делить на неединичные дроби, такие как 2/3 или 3/4, или задачами, где делитель больше, чем дивиденд.
К шестому классу, когда учащиеся должны разделить смешанные числа, они часто полагаются на многоэтапный метод «сохранить-изменить-перевернуть», который трудно запомнить и понять.
Вы можете помочь своим учащимся понять, как делить дроби, используя полоски дробей, которые они могут перемещать. Манипуляции и визуальные представления — это основанные на фактических данных стратегии, которые поддерживают изучение новых математических концепций. Полоски дробей могут помочь учащимся не только понять концепцию деления дробей, но и буквально увидеть, как решать эти задачи без каких-либо вычислений.
Загрузить: Полосы дробей для печати
Полосы дробей PDF
Прочитать: Как использовать эту стратегию
Цель: Учащиеся будут использовать две полосы дробей, чтобы показать и решить.
Изучение тем, выбранных нашими экспертами
Математика
Школа поддерживает
Стратегии и советы
- 5 (Common Core 5.NF.B.7: Применение и расширение предыдущего понимания деления для деления дробей на целые числа и целых чисел на дроби)
- 5 (Common Core 5.NF.B.7) .B: Интерпретация деления целого числа на единичную дробь и вычисление таких частных)
- 6 (Common Core 6.NS.A.1: Интерпретация и вычисление частных дробей, а также решение текстовых задач, связанных с делением дробей на дроби , например, используя визуальные дробные модели и уравнения для представления проблемы)
- 5–6 (Common Core Math Practice MP1: понять проблемы и настойчиво решать их; Common Core Math Practice MP5: стратегически использовать соответствующие инструменты)
Лучше всего использовать для обучения с:
Как подготовиться:
Соберите и изучите материалы. Дайте каждому учащемуся или паре учащихся набор полосок с дробями. Попросите учащихся разрезать каждую полоску на части (с числителем 1). Учащимся, у которых проблемы с мелкой моторикой, можно заранее вырезать несколько комплектов. Вы также можете сделать несколько ламинированных или картонных наборов для студентов.
Дайте каждому учащемуся или паре учащихся набор полосок с дробями. Попросите учащихся разрезать каждую полоску на части (с числителем 1). Учащимся, у которых проблемы с мелкой моторикой, можно заранее вырезать несколько комплектов. Вы также можете сделать несколько ламинированных или картонных наборов для студентов.
После того, как вы разрежете каждую полоску на части, попросите учеников собрать каждую из полосок, чтобы у них был полный набор, соответствующий тому, что напечатано. Дайте учащимся копию печатной формы или спроецируйте изображение печатной формы, чтобы у них была визуальная модель, к которой можно обратиться.
После того, как учащиеся разложат все полоски, снова познакомьте их с понятием целого. Напомните учащимся, что визуальное представление 1 и слово «целое» часто взаимозаменяемы, когда мы говорим о дробях. Скажите: «В верхней части нашего набора у нас есть 1 целая деталь». Затем спросите учащихся, что они замечают в полосках под всем произведением. Смоделируйте пример. Вы можете сказать: «Я заметил, что каждый ряд полосок дробей имеет одинаковый размер». Предложите учащимся поделиться тем, что они заметили, с партнером. Затем попросите нескольких студентов поделиться со всем классом. Напомните учащимся о предыдущих уроках, где они работали над делением целых чисел на дроби.
Смоделируйте пример. Вы можете сказать: «Я заметил, что каждый ряд полосок дробей имеет одинаковый размер». Предложите учащимся поделиться тем, что они заметили, с партнером. Затем попросите нескольких студентов поделиться со всем классом. Напомните учащимся о предыдущих уроках, где они работали над делением целых чисел на дроби.
Как учить:
1. Повторить деление целого числа на дробь. Попросите учащихся положить 1 полоску целиком на верх парты. Под этой полоской попросите учащихся поместить столько полосок 1/4, сколько необходимо, чтобы они соответствовали размеру 1 целой. Напишите на доске уравнение 1 ÷ 1/4 = 4 и спросите учащихся, откуда они знают, что это верно. Учащиеся должны обратиться к полоскам перед собой, чтобы объяснить ответ.
Просмотрите все распространенные способы, которыми учащиеся могут объяснить свои ответы, приведя следующие примеры как визуально, так и устно:
- «1/4 укладывается в 1 целое 4 раза»
- «Есть 4 группы 1/4 в 1 целом»
- «1 делится на группы по 1/4 равно 4»
- «4 раза 1/ 4 равно 1 дюйму
2. Объясните, как использовать полоски дробей для деления дроби на дробь. Используйте модель «Я делаю, мы делаем, вы делаете» (также известную как модель обучения с постепенным выпуском), чтобы направлять учащихся в процессе использования полосок.
Объясните, как использовать полоски дробей для деления дроби на дробь. Используйте модель «Я делаю, мы делаем, вы делаете» (также известную как модель обучения с постепенным выпуском), чтобы направлять учащихся в процессе использования полосок.
Делаю: Объясните и смоделируйте с помощью полосок. Скажите: «Теперь мы можем использовать аналогичную стратегию для решения задач на деление с двумя дробями в них. Давайте посмотрим на 1/2 ÷ 1/6. Я начну с размещения 1/2 полосы вверху вот так. Затем под ним я положу столько полосок 1/6, сколько смогу, чтобы они соответствовали полоске 1/2. Мы видим, что требуется одна, две, три полоски 1/6, чтобы соответствовать полоске 1/2. Таким образом, я могу заключить, что 1/2 ÷ 1/6 = 3, или 1/6 вписывается в 1/2 трижды».
Мы делаем: Помогите учащимся попробовать это вместе с вами. Скажите: «А теперь давай попробуем это вместе. Начните с 1/2 снова. Я поставлю 1/2 вверху. Ты делаешь тоже самое.» Смоделируйте размещение 1/2 полосы вверху. «На этот раз разделите 1/2 на 1/8. Давайте разместим как можно больше полос 1/8, чтобы они соответствовали полосе 1/2». Смоделируйте его, а затем пройдитесь, чтобы помочь учащимся, которым может понадобиться поддержка. Учащимся, умеющим ее правильно составить, предложите выписать задачу на деление с решением.
«На этот раз разделите 1/2 на 1/8. Давайте разместим как можно больше полос 1/8, чтобы они соответствовали полосе 1/2». Смоделируйте его, а затем пройдитесь, чтобы помочь учащимся, которым может понадобиться поддержка. Учащимся, умеющим ее правильно составить, предложите выписать задачу на деление с решением.
Когда все закончат, обсудите ответ всем классом. Напишите предложение с номером дивизии для учащихся, которые, возможно, не дали правильный ответ. Опишите решение несколькими способами.
Вы делаете: Выберите три задачи на деление, используя единичные дроби как для делителя, так и для делимого. Скажите учащимся, что они будут выполнять их самостоятельно. Скажите: «Попробуйте решить следующие несколько задач самостоятельно или с партнером. Обязательно напишите предложение о делении вместе с вашим решением, как только вы настроите его, используя полоски дробей». Обеспечьте руководство по мере необходимости. При регистрации попросите учащихся объяснить свои решения, используя язык, который обсуждался в начале урока, например: «____ группы ____ подходят к ____».
Совет преподавателям: Многим учащимся, в том числе изучающим английский язык (ELL) и учащимся, у которых проблемы с выразительной речью, полезно иметь на своих партах рамки предложений. Распечатайте набор рамок и положите их в кармашки для сухого стирания, чтобы учащиеся каждый раз могли записывать свои ответы.
3. Перейдите к более сложным задачам. Снова следуйте модели «Я делаю, мы делаем, вы делаете».
Делаю: Скажем, «Давайте попробуем решить несколько более сложных задач. На этот раз начните с 2/3». Модель для них. Учащиеся должны поместить две полоски шириной 1/3 в верхней части парты. «Я хочу, чтобы вы разделили 2/3 на 1/6». Покажите, как выстроить 1/6 полоски ниже 2/3, пока не сопоставите все. Подсчитайте количество полосок, которые вы использовали вслух, указывая на них. «Итак, 2/3 ÷ 1/6 = 4».
Мы делаем: «Теперь давайте сделаем это вместе. Давайте попробуем 3/4 ÷ 1/8. Я собираюсь показать 3/4 вверху, используя три полоски 1/4. Ты делаешь тоже самое.» Модель размещает 3/4 вверху. «На этот раз разделите 3/4 на 1/8. Давайте разместим как можно больше полос 1/8, чтобы они соответствовали полосе 3/4». Смоделируйте его, а затем пройдитесь, чтобы помочь учащимся, которым может понадобиться поддержка. Учащимся, умеющим ее правильно составить, предложите выписать задачу на деление с решением.
Я собираюсь показать 3/4 вверху, используя три полоски 1/4. Ты делаешь тоже самое.» Модель размещает 3/4 вверху. «На этот раз разделите 3/4 на 1/8. Давайте разместим как можно больше полос 1/8, чтобы они соответствовали полосе 3/4». Смоделируйте его, а затем пройдитесь, чтобы помочь учащимся, которым может понадобиться поддержка. Учащимся, умеющим ее правильно составить, предложите выписать задачу на деление с решением.
Когда все закончат, обсудите ответ всем классом. Напишите предложение с номером дивизии для учащихся, которые, возможно, не дали правильный ответ. Опишите решение несколькими способами.
Вы делаете: Предложите учащимся несколько практических задач, чтобы они могли решить их самостоятельно. Зайдите, чтобы увидеть, как учащиеся используют полоски с дробями. Некоторые учащиеся к этому моменту, возможно, поняли, как решать задачи без использования полосок. Поговорите с этими студентами о том, какую процедуру они используют. Если вы чувствуете, что к концу урока класс готов, попросите этих учащихся продемонстрировать алгоритм «сохраняй-меняй-переворачивай». Это поможет начать переход к использованию алгоритма над полосами дробей.
Это поможет начать переход к использованию алгоритма над полосами дробей.
4. Продолжайте тренироваться. Некоторые учащиеся могут начать решать без полос дробей. Другие продолжат их использовать. Пока все практикуются, предложите учащимся, использующим полоски, вместо этого нарисовать модели для каждой задачи на деление. Они могут ссылаться на полоски в качестве эталона, но рисование собственных версий полосок поможет перейти от конкретных полосок к абстрактным числам.
Поймите: почему полоски дробей работают
Дробные полоски (или дробные столбцы или плитки) помогают учащимся увидеть, что одно и то же «целое» можно разбить на разные части одинакового размера. Когда учащиеся перемещают полоски и кладут их рядом, они могут визуализировать дробные суммы. Они также могут сравнивать дроби и выполнять сложение, вычитание, умножение и деление дробей.
Учащиеся, испытывающие трудности с математикой, особенно с дробями, часто не могут связать значения чисел и символов в алгоритме. Полоски дробей дают учащимся концептуальное представление проблемы. Они могут использовать полосы для создания как делимого, так и делителя, чтобы они могли видеть и то, и другое как дробные части целого. Студенты также могут подсчитать количество групп (частное), полученных путем деления.
Полоски дробей дают учащимся концептуальное представление проблемы. Они могут использовать полосы для создания как делимого, так и делителя, чтобы они могли видеть и то, и другое как дробные части целого. Студенты также могут подсчитать количество групп (частное), полученных путем деления.
С этой стратегией вы используете явные инструкции в модели «Я делаю, мы делаем, вы делаете». Показывая учащимся, как использовать полоски дробей, а затем позволяя им практиковаться как с учителем, так и с поддержкой сверстников, эта стратегия предоставляет множество возможностей для обучения.
Использование этой стратегии перед тем, как перейти к делителям, которые не являются единичными дробями, поможет учащимся лучше понять почему работает алгоритм, а не только как он работает.
После того, как учащиеся освоят использование полосок с дробями, отправьте домой новую страницу с полосками с дробями или уже вырезанный набор. Семьи могут помочь закрепить использование полосок с дробями дома, когда учащиеся работают над своей домашней работой.
Если вы обнаружите, что домашняя работа вызывает у семьи затруднения, рассмотрите возможность отправки этого ресурса, чтобы помочь родителям и опекунам понять, почему математика сейчас преподается не так, как в школе.
Исследования, лежащие в основе этой стратегии
«Конкретно-репрезентативно-абстрактный подход для учащихся с трудностями в обучении: синтез доказательной практики», из Корректирующее и специальное образование
«Явное обучение математике: что учителя могут сделать для обучения учащихся с трудностями в математике, ” из Вмешательство в школу и поликлинику
Похожие темы
Математика
Поддержка школы
Стратегии и советы
Численность, математика и статистика — Набор академических навыков
Дроби и проценты (психология)
ContentsToggle Главное меню 3.3 Использование процентного изменения для расчета новых сумм: 3. 4 Важное примечание 4 Примеры работы 5 Проверь себя 6 Внешние ресурсы
4 Важное примечание 4 Примеры работы 5 Проверь себя 6 Внешние ресурсы
Введение
A дробь — это пропорция, а не целое число. Дробь имеет вид $\bigg(\dfrac{\text{числитель}}{\text{знаменатель}}\bigg)$. Дроби и проценты полезны в психологии для отображения данных и используются при анализе данных.
Для упрощения дробей нужно найти общий множитель числителя и знаменателя и разделить оба на этот множитель. Повторяйте этот процесс до тех пор, пока у них не останется общих делителей (тогда говорят, что они взаимно просты 9).0205). Например, чтобы упростить $\frac{48}{18}$, мы видим, что $48$ и $18$ имеют общий делитель $6$, поэтому разделите на $6$, чтобы получить упрощенную дробь $\frac{8}{3}. $.
См. также дроби.
Процент — это доля суммы, группы или набора, превышающая 100 долларов США. Другой способ представить это как дробь от 100$. Таким образом, если бы у вас был показатель успеха в размере 80 долларов США, это означало бы, что на каждые 100 долларов США попыток 80 долларов из них будут успешными.
См. также проценты
Преобразование дробей в проценты
Чтобы преобразовать дроби в проценты, разделите числитель (число вверху) на знаменатель (число внизу) и умножьте на $100$. Это даст вам дробь в процентах.
Рабочий пример
Преобразование $\dfrac{17}{20}$ в проценты.
Расчет процентных изменений
Вы рассчитываете процентное изменение , когда изменяется количество чего-то, что у вас есть. Используйте следующие методы, если вы знаете исходное значение и новое значение и хотите рассчитать процентное изменение.
Например, можно рассчитать процентное изменение числа детей с диагнозом СДВГ в школе за определенный период времени.
Увеличение в процентах:
Если сумма у вас увеличивается, мы используем формулу:
\begin{equation} \frac{\text{(новое значение} — \text{исходное значение)}}{\text{исходное значение значение}}\times100 = \text{ Увеличение в процентах}. \end{equation}
Процентное уменьшение:
Если сумма, которую вы имеете, уменьшается, мы манипулируем приведенной выше формулой, чтобы она не была отрицательной, путем замены двух значений в числителе дроби:
\begin{уравнение} \frac{\text{(исходное значение} — \text{новое значение)}}{\text{исходное значение}}\times100 = \text {Уменьшение в процентах}. \end{equation}
\end{equation}
Использование процентного изменения для расчета новых сумм:
Этот метод используется, когда вы знаете процентное изменение и исходное значение и хотите рассчитать, сколько у вас сейчас есть. Для этого используйте формулу:
\begin{equation} \frac{\text{(новый процент)}}{100}\times\text{(исходное значение)} = \text{Новая сумма}. \end{уравнение}
‘ Примечание: ‘ Эти формулы могут быть изменены в соответствии с различными вопросами.
Важное примечание
Примеры, приведенные на этой странице, являются чисто гипотетическими, и любые результаты или данные не взяты из реальных случаев. Их цель — продемонстрировать, как использовать различные математические методы, описанные в этом разделе.
Примеры работы
Для каждого из приведенных выше случаев мы будем работать с примером.
Решение
Сначала подсчитайте средний балл теста по каждому столбцу. Вы делаете это, используя среднее значение данных.
Среднее значение тестов до введения «активного обучения»: $13$.
Среднее значение тестов после введения «активного обучения»: $17,3$.
Результаты тестов увеличились, теперь для расчета процентного увеличения мы используем приведенную выше формулу:
\[\bigg(\dfrac{~\text{новое значение — исходное значение}~}{~\text{ исходное значение}~}\bigg)\times 100\]
, чтобы получить:
\[\bigg(\dfrac{17.3 — 13}{13}\bigg)\times100 \примерно 33,1\%.\] Итак, вот — это процентное увеличение результатов тестов на 33,1$\%$.
Рабочий пример — процентное снижение
Ниже представлена таблица мужчин и женщин с диагнозом депрессия за последние 6 месяцев. Если число женщин с диагнозом депрессия продолжает уменьшаться с той же процентной скоростью с июня по июль и с июля по август, как и с мая по июнь, сколько случаев депрессии у женщин, по вашему мнению, будет диагностировано в августе? ?
Пол | Январь | фев | март | Апрель | май | Июн |
|---|---|---|---|---|---|---|
Мужской | 50 | 52 | 61 | 54 | 49 | 47 |
Женщина | 61 | 72 | 75 | 68 | 67 | 59 |
Решение
Во-первых, определите процентное уменьшение с мая по июнь. Из приведенной выше формулы это:
Из приведенной выше формулы это:
$\dfrac{67 — 59}{67}\times100 = 11,94$% Таким образом, с мая по июнь наблюдается снижение диагностированных случаев депрессии у женщин на $11,94$%. Таким образом, количество женщин с диагнозом депрессия в июне составляет 100-11,94 = 88,06% от числа женщин с диагнозом в мае.
Есть два способа подсчитать, сколько случаев депрессии у женщин будет диагностировано как депрессия к августу:
1. Вы можете рассчитать 88,06$% от 59$, чтобы получить ожидаемое число за июль, а затем повторите эту операцию над ожидаемым числом за июль, чтобы получить ожидаемое количество случаев депрессии в августе. 92$, чтобы получить количество женщин, которым, как ожидается, будет поставлен диагноз в августе. Примечание: вы берете $0,8806$ в степени 2, так как есть еще два периода этой скорости убывания.
Оба метода эквивалентны.
Метод 1: $59 \times \dfrac{88.06}{100} = 52$ случаев (округлено до ближайшего целого числа) в июле.



 В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
В крайнем случае, один минус может выжить — тот, которому не нашлось пары; Страдательный залог глагола ‘to repair’ в группе ‘continuous’ :
To be repaired = Быть исправленным.
The road is being repaired = Дорогу чинят.
The road is not being repaired = Дорогу не чинят.
Is the road being repaired? = Чинят ли дорогу?
The road was being repaired = Дорогу чинили.
The road was not being repaired = Дорогу не чинили.
Was the road being repaired? = Чинили ли дорогу?
Страдательный …
Страдательный залог глагола ‘to repair’ в группе ‘continuous’ :
To be repaired = Быть исправленным.
The road is being repaired = Дорогу чинят.
The road is not being repaired = Дорогу не чинят.
Is the road being repaired? = Чинят ли дорогу?
The road was being repaired = Дорогу чинили.
The road was not being repaired = Дорогу не чинили.
Was the road being repaired? = Чинили ли дорогу?
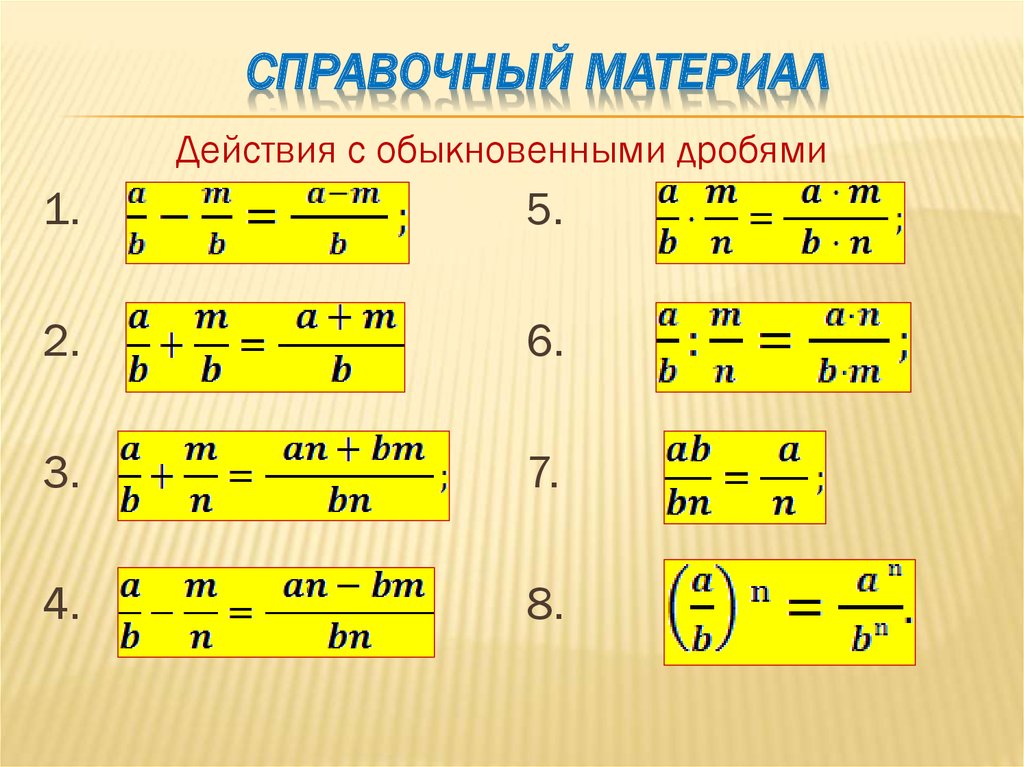
Страдательный …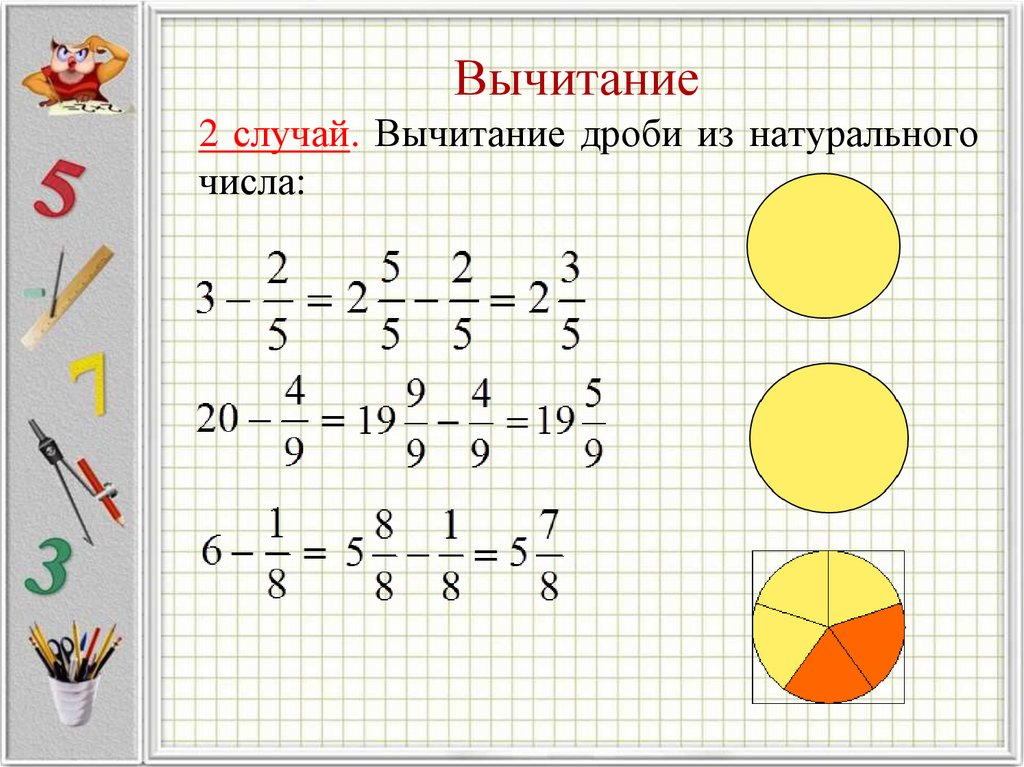 М(СхНу)=12х +у
3.
Приравнять найденное в общем виде значение молярной массы к данному в …
М(СхНу)=12х +у
3.
Приравнять найденное в общем виде значение молярной массы к данному в … А. 1
А. 1
 Горизонтальная или косая линия в дроби обозначает деление. Черта наклонная называется — «солидус», а горизонтальная – «винкулум».
Горизонтальная или косая линия в дроби обозначает деление. Черта наклонная называется — «солидус», а горизонтальная – «винкулум».


 Вавилонская математика оказала влияние на греческую математику. Следы вавилонской шестидесятеричной системы счисления удержались в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60 мин., минуты на 60 с, окружности на 360˚, градуса на 60 мин., минуты на 60с.
Вавилонская математика оказала влияние на греческую математику. Следы вавилонской шестидесятеричной системы счисления удержались в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60 мин., минуты на 60 с, окружности на 360˚, градуса на 60 мин., минуты на 60с.
 Она окончательно вытеснила славянскую нумерацию при Петре I.
Она окончательно вытеснила славянскую нумерацию при Петре I. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.
Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики. Учащиеся музыкальной школы знакомятся с дробями раньше, чем в общеобразовательной школе. С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Древнегреческий философ Пифагор (570 г. до н. э.), один из самых первых установил связь музыки и математики. Он создал учение о звуке. Пифагор связал длительность звучания нот с дробями.
Учащиеся музыкальной школы знакомятся с дробями раньше, чем в общеобразовательной школе. С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Древнегреческий философ Пифагор (570 г. до н. э.), один из самых первых установил связь музыки и математики. Он создал учение о звуке. Пифагор связал длительность звучания нот с дробями.
 Всё тщательно перемешиваем и печем пряники.
Всё тщательно перемешиваем и печем пряники. Знание понятия математическая дробь очень важно!
Знание понятия математическая дробь очень важно!
 Простая фракция — это число, чье число и деноминатор являются оба цифровые цифры. , десятичные точки, запятые или разделительные пробелы, а дробная черта которого проведена между двумя вертикально или почти вертикально расположенными цифрами. Числовой индикатор используется с числителем, за которым следует строка простой числовой дроби и число знаменателя. Строка простой числовой дроби продолжает числовой режим, поэтому числовой показатель не повторяется со знаменателем в простой дроби. Строка простой числовой дроби образована точками три четыре.
Простая фракция — это число, чье число и деноминатор являются оба цифровые цифры. , десятичные точки, запятые или разделительные пробелы, а дробная черта которого проведена между двумя вертикально или почти вертикально расположенными цифрами. Числовой индикатор используется с числителем, за которым следует строка простой числовой дроби и число знаменателя. Строка простой числовой дроби продолжает числовой режим, поэтому числовой показатель не повторяется со знаменателем в простой дроби. Строка простой числовой дроби образована точками три четыре. Режим уровня 1 задается индикатором символа уровня 1, числовым индикатором и индикаторами слов или отрывков уровня 1. Все выражение должно быть оценено для выбора индикаторов.
Режим уровня 1 задается индикатором символа уровня 1, числовым индикатором и индикаторами слов или отрывков уровня 1. Все выражение должно быть оценено для выбора индикаторов. Индикаторы общих фракций должны быть в режиме 1 класса. Индикатор символа степени 1 включает степень 1 для индикатора начальной дроби. Цифровой индикатор переводит индикатор закрывающей дроби в режим 1-й степени.
Индикаторы общих фракций должны быть в режиме 1 класса. Индикатор символа степени 1 включает степень 1 для индикатора начальной дроби. Цифровой индикатор переводит индикатор закрывающей дроби в режим 1-й степени.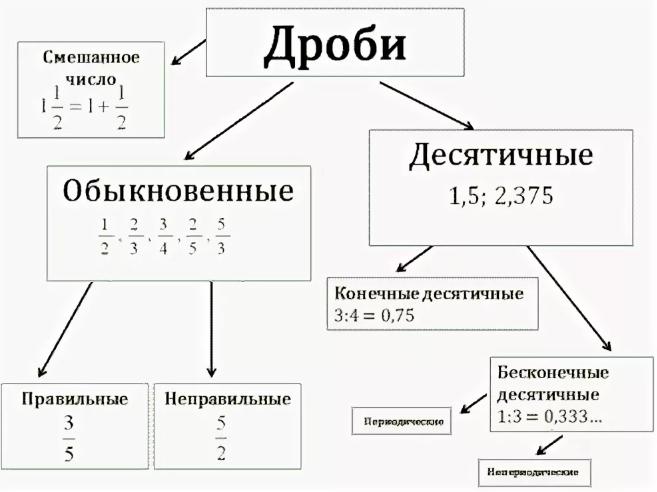
 T=\det A.$
T=\det A.$ $
$ {3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$
{3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$ 2.$
2.$ Но такую большую матрицу он считает очень долго, несколько часов…
Но такую большую матрицу он считает очень долго, несколько часов… random.rand(20, 20)
In [34]: res = np.linalg.det(a)
In [35]: res
Out[35]: 0.09252260373277807
random.rand(20, 20)
In [34]: res = np.linalg.det(a)
In [35]: res
Out[35]: 0.09252260373277807
 4 — Определитель квадратной матрицы
4 — Определитель квадратной матрицы Это произведение элементов главной диагонали на минус
произведение элементов вне главной диагонали.
Это произведение элементов главной диагонали на минус
произведение элементов вне главной диагонали.
 Это означает, что мы должны удалить
строку 2 и столбец 1, а затем найти определитель.
Это означает, что мы должны удалить
строку 2 и столбец 1, а затем найти определитель.
 Здесь
определитель.
Здесь
определитель. Опять же, вам не нужно ставить ярлыки
для строки и столбцов там, но это может вам помочь.
Опять же, вам не нужно ставить ярлыки
для строки и столбцов там, но это может вам помочь. Если ряд и
столбец элемента в сумме должен быть четным числом, тогда кофактор — это
то же, что минор. Если строка и столбец элемента в сумме являются нечетными
число, то кофактор
напротив минора.
Если ряд и
столбец элемента в сумме должен быть четным числом, тогда кофактор — это
то же, что минор. Если строка и столбец элемента в сумме являются нечетными
число, то кофактор
напротив минора.


 На самом деле, если элемент равен нулю, вы не
нужно найти даже несовершеннолетнего
или кофактор.
На самом деле, если элемент равен нулю, вы не
нужно найти даже несовершеннолетнего
или кофактор.
 то есть ряды
стать столбцами и
столбцы становятся строками. Транспонирование матрицы можно найти с помощью TI-82.
или калькулятор ТИ-83, введя название матрицы и выбрав Матрица,
Математика, а затем вариант 2, буква T с надстрочным индексом, например [A] Т .
то есть ряды
стать столбцами и
столбцы становятся строками. Транспонирование матрицы можно найти с помощью TI-82.
или калькулятор ТИ-83, введя название матрицы и выбрав Матрица,
Математика, а затем вариант 2, буква T с надстрочным индексом, например [A] Т . Не пытайтесь это сделать на своем
калькулятор, так как калькулятор не позволит вам разделить матрицу на
скаляр. Вместо этого вам придется умножать на обратный определитель.
Не пытайтесь это сделать на своем
калькулятор, так как калькулятор не позволит вам разделить матрицу на
скаляр. Вместо этого вам придется умножать на обратный определитель. В данном случае это
второй столбец.
В данном случае это
второй столбец. На самом деле, вы могли бы так же легко
пропустить их.
На самом деле, вы могли бы так же легко
пропустить их. В этой строке стоит 0
1 и столбец 2. Любой из них был бы хорошим выбором для расширения, но
поскольку в строке 1 числа немного больше, мы будем расширяться по первой строке.
В этой строке стоит 0
1 и столбец 2. Любой из них был бы хорошим выбором для расширения, но
поскольку в строке 1 числа немного больше, мы будем расширяться по первой строке. Первый был -2, а второй +2.
Первый был -2, а второй +2. Затем введите имя матрицы, которую вы используете.
Затем введите имя матрицы, которую вы используете.


 1628 определитель . Определитель полезен для решения линейных уравнений, определения того, как линейное преобразование изменяет площадь или объем, а также для изменения переменных в интегралах.
1628 определитель . Определитель полезен для решения линейных уравнений, определения того, как линейное преобразование изменяет площадь или объем, а также для изменения переменных в интегралах. Мы продолжаем
по первой строке, начиная с левого верхнего компонента $a$. Мы
умножить компоненту $a$ на определитель «подматрицы»
формируется путем игнорирования строки и столбца $a$. В этом случае эта подматрица
матрица $1 \times 1$, состоящая из $d$, и ее определитель просто
$д$. Таким образом, первый член определителя равен $ad$.
Мы продолжаем
по первой строке, начиная с левого верхнего компонента $a$. Мы
умножить компоненту $a$ на определитель «подматрицы»
формируется путем игнорирования строки и столбца $a$. В этом случае эта подматрица
матрица $1 \times 1$, состоящая из $d$, и ее определитель просто
$д$. Таким образом, первый член определителя равен $ad$. Причина прохождения этого процесса
должен был упростить вычисление определителя $3 \times 3$ (и больше).
Причина прохождения этого процесса
должен был упростить вычисление определителя $3 \times 3$ (и больше). \times 3$ определитель. Но я предпочел бы использовать синаптическую связь моего мозга
связи, чтобы сделать что-то более полезное. На самом деле, я боюсь, если я
пытался запомнить это, я мог забыть что-то еще важное, например
как сочетать одинаковые термины в алгебре.
\times 3$ определитель. Но я предпочел бы использовать синаптическую связь моего мозга
связи, чтобы сделать что-то более полезное. На самом деле, я боюсь, если я
пытался запомнить это, я мог забыть что-то еще важное, например
как сочетать одинаковые термины в алгебре.
 А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
 д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов. : Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7



 5.Формулы
суммы и разности
5.Формулы
суммы и разности
 Решение
уравнения sinx=a.
Решение
уравнения sinx=a. Решение
уравнения cosx=a
Решение
уравнения cosx=a Решение
уравнения tgx=a.
Решение
уравнения tgx=a. Решение
уравнения ctg=a.
Решение
уравнения ctg=a.
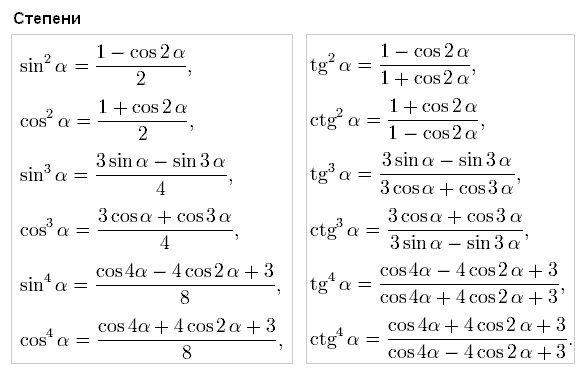 07:30
07:30
 DX
DX
 Подробнее …
Подробнее … Решить уравнение 2x3 — x2 — 8x + 4 = 0.
Решить уравнение 2x3 — x2 — 8x + 4 = 0.

 Получим
Получим



 Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену У уравнения (13) других вещественных корней нет.
У уравнения (13) других вещественных корней нет. Алгебраическое уравнение — это уравнение, имеющее вид ax n + bx n-1 + cx n-2 +… + 1 = 0. Например, 2x-5 = 0 является примером алгебраического уравнения, где (2x-5) является полиномом. Существуют различные типы алгебраических уравнений в зависимости от высшей степени переменной, такие как линейное уравнение, квадратное уравнение, кубическое уравнение, уравнение и т. д.
Алгебраическое уравнение — это уравнение, имеющее вид ax n + bx n-1 + cx n-2 +… + 1 = 0. Например, 2x-5 = 0 является примером алгебраического уравнения, где (2x-5) является полиномом. Существуют различные типы алгебраических уравнений в зависимости от высшей степени переменной, такие как линейное уравнение, квадратное уравнение, кубическое уравнение, уравнение и т. д. Подобно тому, как квадратное уравнение имеет два корня, кубическое уравнение имеет три корня. Кубическое уравнение может иметь три действительных корня или действительный корень и два мнимых корня. Любое уравнение, в том числе и кубическое, всегда должно быть сначала приведено в стандартную форму.
Подобно тому, как квадратное уравнение имеет два корня, кубическое уравнение имеет три корня. Кубическое уравнение может иметь три действительных корня или действительный корень и два мнимых корня. Любое уравнение, в том числе и кубическое, всегда должно быть сначала приведено в стандартную форму.


 Решение:
Решение: 
 Его можно было бы легко упомянуть в
многие математические курсы бакалавриата, хотя это не кажется
появляться в большинстве учебников, используемых для этих курсов.
Ни один из этих материалов не был обнаружен мной. —
ЕС
Его можно было бы легко упомянуть в
многие математические курсы бакалавриата, хотя это не кажется
появляться в большинстве учебников, используемых для этих курсов.
Ни один из этих материалов не был обнаружен мной. —
ЕС
 (Подсказка: один из корней
маленькое положительное целое число; Теперь ты можешь найти все
три корня?)
Но если мы применим к этому примеру формулу Кардано,
мы используем a=1, b=0, c=-15, d=-4 и находим, что
нам нужно извлечь квадратный корень из -109в
полученный расчет. В конечном счете,
квадратные корни отрицательных чисел сокращаются
позже в вычислении, но это вычисление
не может быть понят студентом, изучающим математику, без
дополнительное обсуждение комплексных чисел.
(Подсказка: один из корней
маленькое положительное целое число; Теперь ты можешь найти все
три корня?)
Но если мы применим к этому примеру формулу Кардано,
мы используем a=1, b=0, c=-15, d=-4 и находим, что
нам нужно извлечь квадратный корень из -109в
полученный расчет. В конечном счете,
квадратные корни отрицательных чисел сокращаются
позже в вычислении, но это вычисление
не может быть понят студентом, изучающим математику, без
дополнительное обсуждение комплексных чисел.
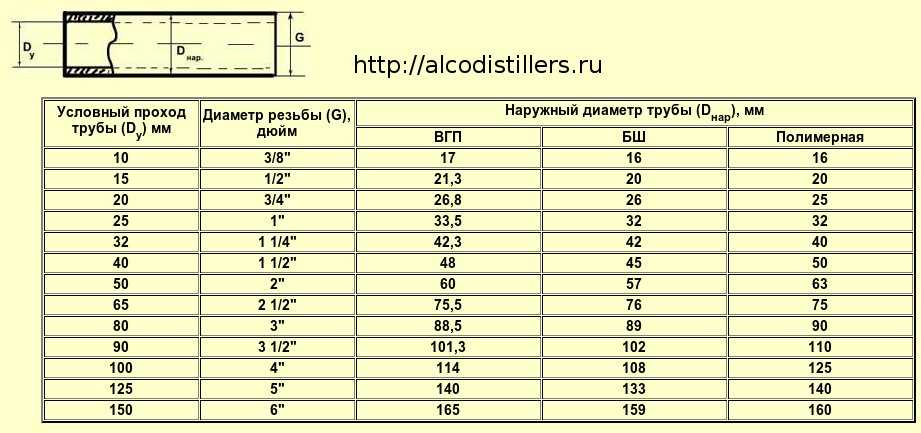 5 м, 7 мкм, полиэтиленовая Matrix
5 м, 7 мкм, полиэтиленовая Matrix 07
07
 В этой статье мы расскажем об основных способах нахождения этой величины и подберем формулы, подходящие для решения заданий из школьной программы.
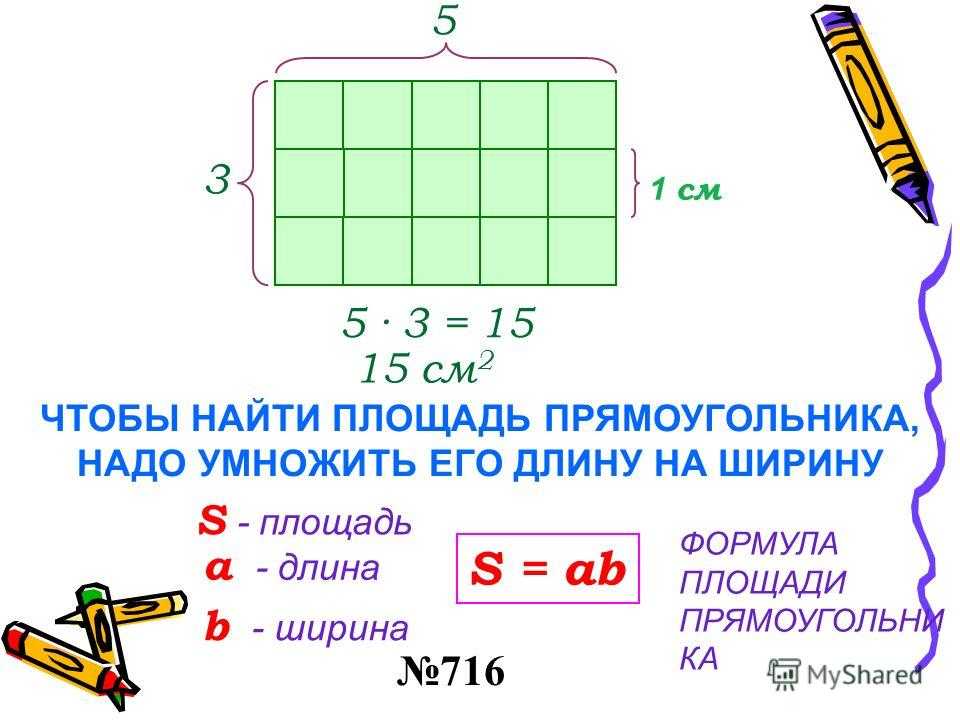
В этой статье мы расскажем об основных способах нахождения этой величины и подберем формулы, подходящие для решения заданий из школьной программы. 1): S= (a*b)/2. Прямоугольный треугольник — это половина прямоугольника. А площадь прямоугольника как раз и находится произведением S= (a*b)
1): S= (a*b)/2. Прямоугольный треугольник — это половина прямоугольника. А площадь прямоугольника как раз и находится произведением S= (a*b)
 Две противоположные стороны прямоугольника равны и параллельны друг другу. Какова площадь прямоугольника? Это пространство, охватываемое фигурой, или пространство внутри периметра прямоугольника. Альтернативно, пространство внутри периметра прямоугольника является площадью прямоугольника.
Две противоположные стороны прямоугольника равны и параллельны друг другу. Какова площадь прямоугольника? Это пространство, охватываемое фигурой, или пространство внутри периметра прямоугольника. Альтернативно, пространство внутри периметра прямоугольника является площадью прямоугольника. Как найти площадь прямоугольника, используя единичные квадраты?
Как найти площадь прямоугольника, используя единичные квадраты?
 Например, в данном прямоугольнике ABCD проведена диагональ из вершины A в C.
Например, в данном прямоугольнике ABCD проведена диагональ из вершины A в C. В современной математике эти понятия используются при составлении карт, топографической съемке, моделировании объектов и т. д.
В современной математике эти понятия используются при составлении карт, топографической съемке, моделировании объектов и т. д.
 Размер блоков $2 \text{m} \times 1 \text{m}$. Найдите общее количество блоков, необходимых для полного покрытия стены. 92$
Размер блоков $2 \text{m} \times 1 \text{m}$. Найдите общее количество блоков, необходимых для полного покрытия стены. 92$ Длина прямоугольника $= \frac{Area}{Width}$
Длина прямоугольника $= \frac{Area}{Width}$
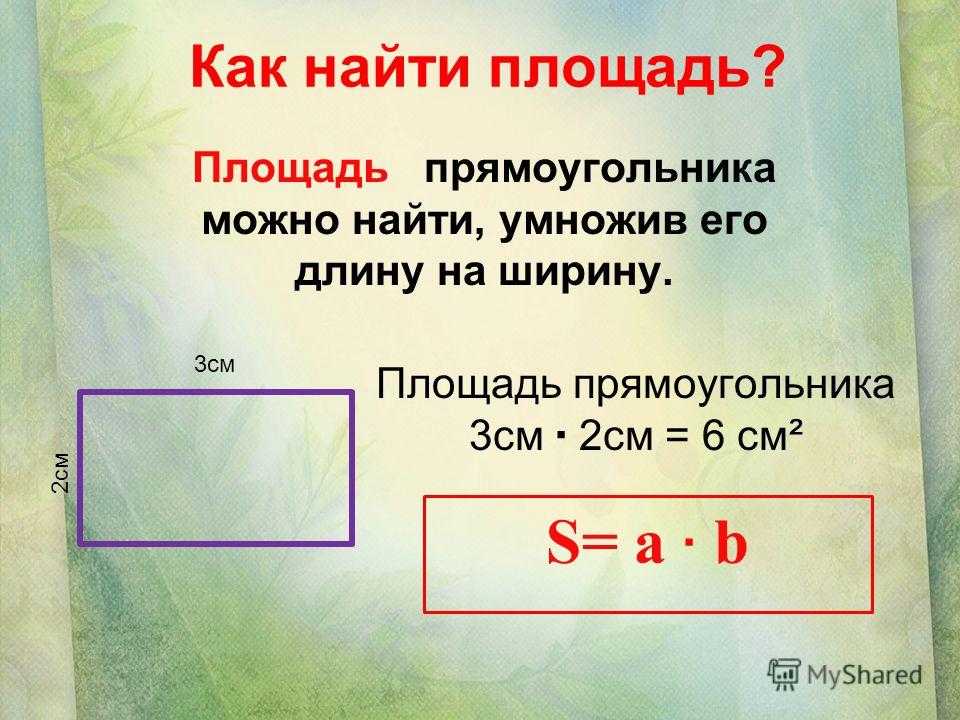 Д. Площадь прямоугольника можно рассчитать, используя формулу площади прямоугольника, чтобы найти пространство, занимаемое этими объектами.
Д. Площадь прямоугольника можно рассчитать, используя формулу площади прямоугольника, чтобы найти пространство, занимаемое этими объектами.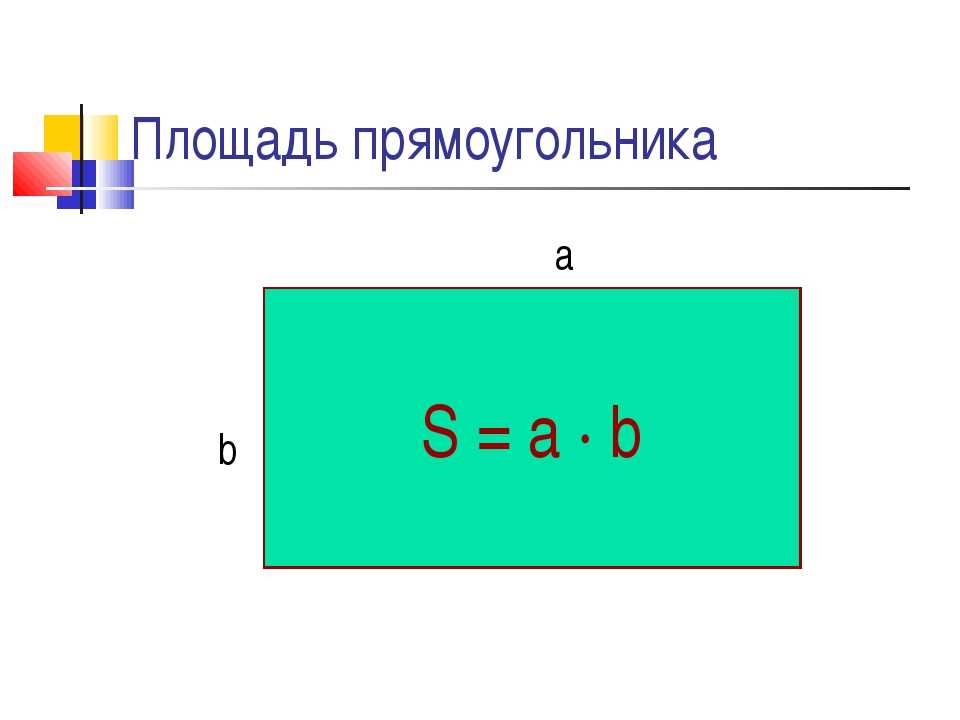


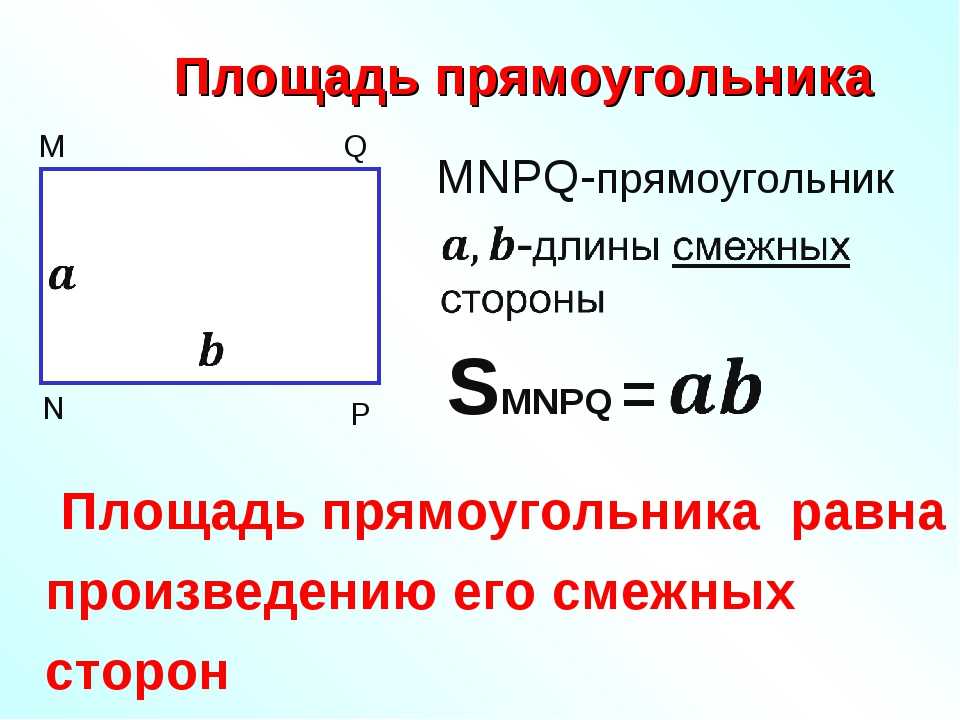 Итак, площадь прямоугольника = l × w. В этом случае
Итак, площадь прямоугольника = l × w. В этом случае Теперь, если мы заменим приведенную выше формулу длины формулой площади прямоугольника, то формула площади прямоугольника может быть выражена следующим образом: Площадь прямоугольника = ⎷[(Диагональ) 2 — (Ширина) 2 ] × Ширина
Теперь, если мы заменим приведенную выше формулу длины формулой площади прямоугольника, то формула площади прямоугольника может быть выражена следующим образом: Площадь прямоугольника = ⎷[(Диагональ) 2 — (Ширина) 2 ] × Ширина С помощью периметра мы можем найти неизвестную сторону, а затем вычислить площадь по той же формуле: площадь прямоугольника = длина × ширина. Давайте разберемся в этом с помощью примера.
С помощью периметра мы можем найти неизвестную сторону, а затем вычислить площадь по той же формуле: площадь прямоугольника = длина × ширина. Давайте разберемся в этом с помощью примера.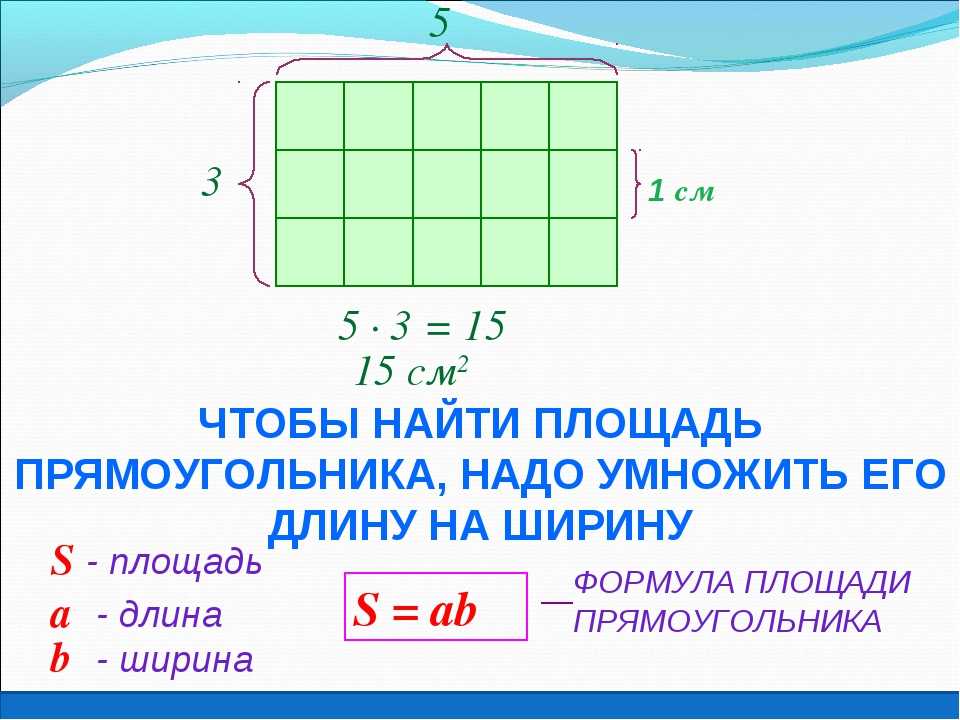 Площадь прямоугольника равна сумме площадей этих двух треугольников.
Площадь прямоугольника равна сумме площадей этих двух треугольников.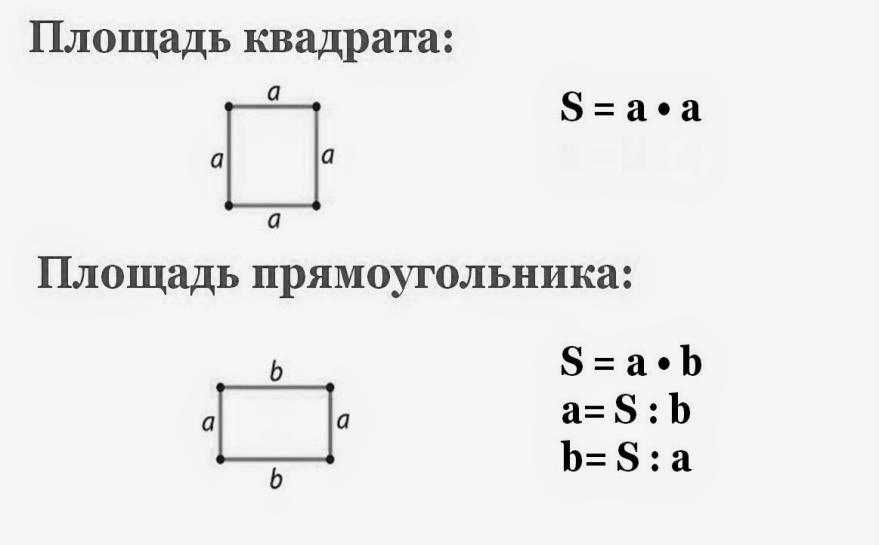 Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

 Мы можем найти значение недостающей стороны, используя теорему Пифагора, а затем найти площадь. Например, давайте найдем площадь прямоугольника, диагональ которого равна 10 единицам, а длина — 8 единицам, используя следующие шаги.
Мы можем найти значение недостающей стороны, используя теорему Пифагора, а затем найти площадь. Например, давайте найдем площадь прямоугольника, диагональ которого равна 10 единицам, а длина — 8 единицам, используя следующие шаги.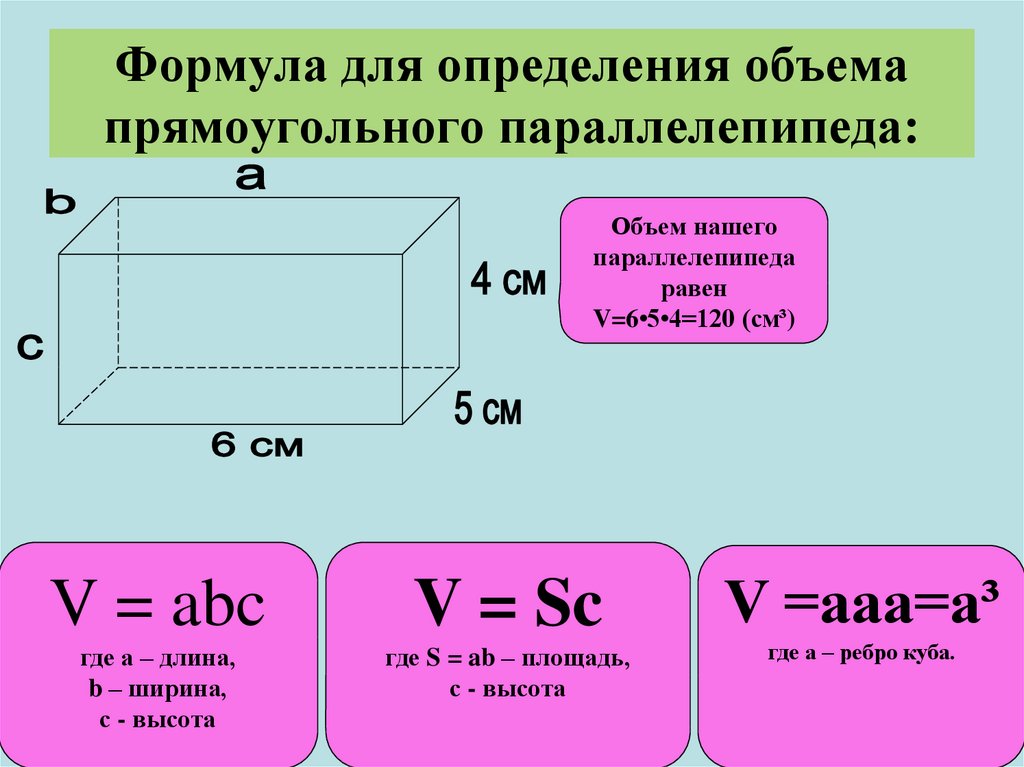 Нам просто нужно упростить дроби, используя их правила упрощения. Если у нас есть правильные дроби, мы можем просто использовать формулу площади прямоугольника и умножить длину и ширину. Однако, если у нас есть размеры, данные в смешанных дробях, нам нужно преобразовать их в неправильные дроби, а затем упростить, используя та же формула. Например, давайте найдем площадь прямоугольника, в котором длина задана как \(2\dfrac{1}{3}\) единиц, а ширина задана как \(1\dfrac{1}{3}\) единиц, теперь мы преобразуем смешанные дроби в неправильные дроби, и мы получим длину как 7/3, а ширину как 4/3. Теперь мы можем найти площадь, Площадь прямоугольника = 7/3 × 4/3 = 28/9= \(3\dfrac{1}{9}\) квадратных единиц.
Нам просто нужно упростить дроби, используя их правила упрощения. Если у нас есть правильные дроби, мы можем просто использовать формулу площади прямоугольника и умножить длину и ширину. Однако, если у нас есть размеры, данные в смешанных дробях, нам нужно преобразовать их в неправильные дроби, а затем упростить, используя та же формула. Например, давайте найдем площадь прямоугольника, в котором длина задана как \(2\dfrac{1}{3}\) единиц, а ширина задана как \(1\dfrac{1}{3}\) единиц, теперь мы преобразуем смешанные дроби в неправильные дроби, и мы получим длину как 7/3, а ширину как 4/3. Теперь мы можем найти площадь, Площадь прямоугольника = 7/3 × 4/3 = 28/9= \(3\dfrac{1}{9}\) квадратных единиц.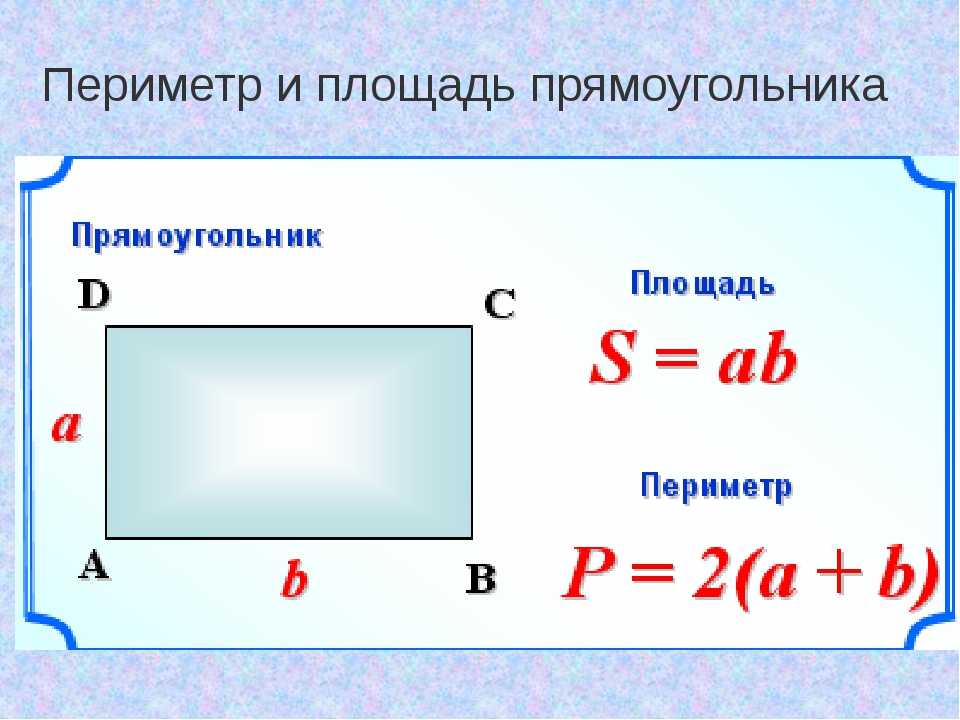
 4. Плотность распределения
4. Плотность распределения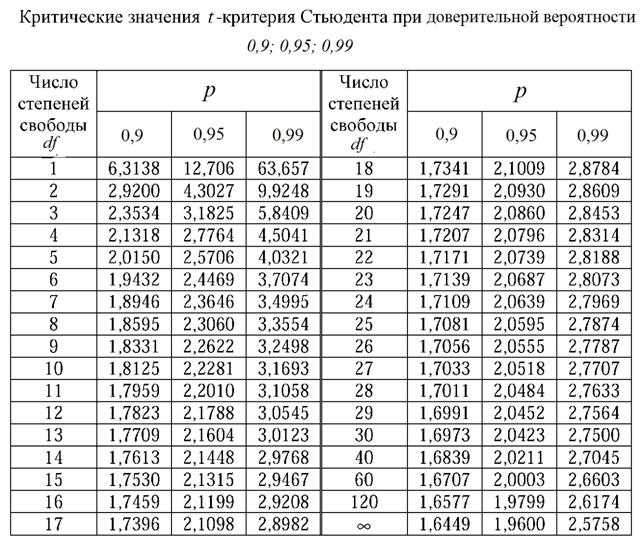 Системы случайных величин
Системы случайных величин Общая запись нормального закона для системы произвольного числа случайных величин
Общая запись нормального закона для системы произвольного числа случайных величин Композиция законов распределения
Композиция законов распределения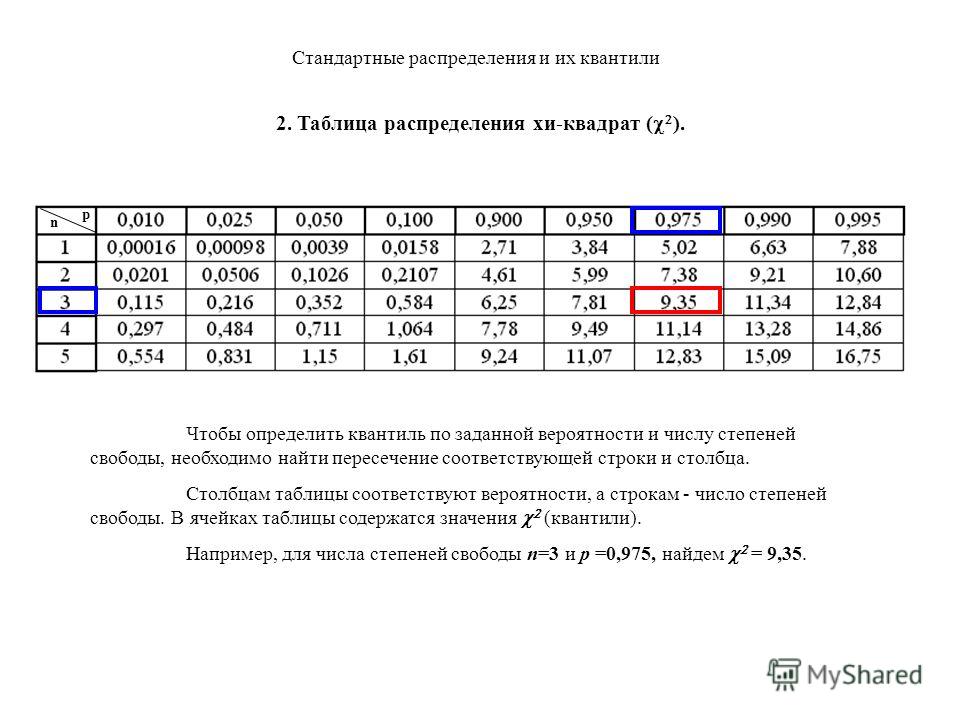 3. Доверительный интервал. Доверительная вероятность
3. Доверительный интервал. Доверительная вероятность 7.2. Производная от случайной функции
7.2. Производная от случайной функции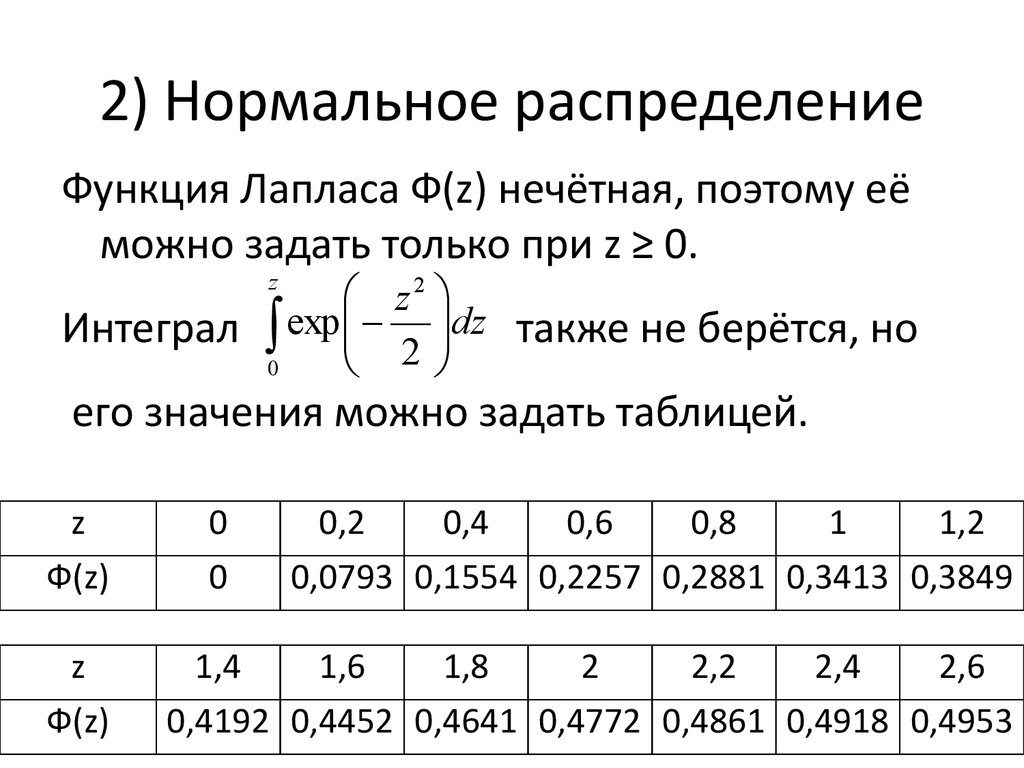 7. Эргодическое свойство стационарных случайных функций
7. Эргодическое свойство стационарных случайных функций 3. Поток событий. Простейший поток и его свойства
3. Поток событий. Простейший поток и его свойства




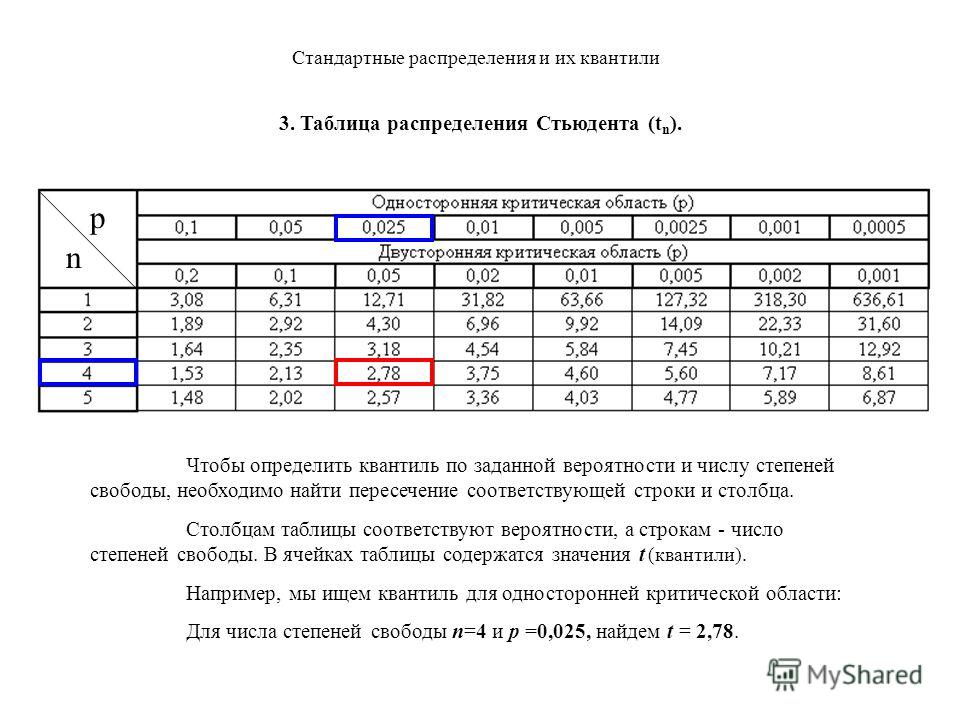 Например, ваше сердцебиение составляет 72 удара в минуту в нормальных условиях. Частота соответствует числу появлений значения.
Например, ваше сердцебиение составляет 72 удара в минуту в нормальных условиях. Частота соответствует числу появлений значения.

 е. для одного класса.
е. для одного класса. Таблица, которую мы получим, будет довольно длинной, а данные будут запутанными.
Таблица, которую мы получим, будет довольно длинной, а данные будут запутанными.
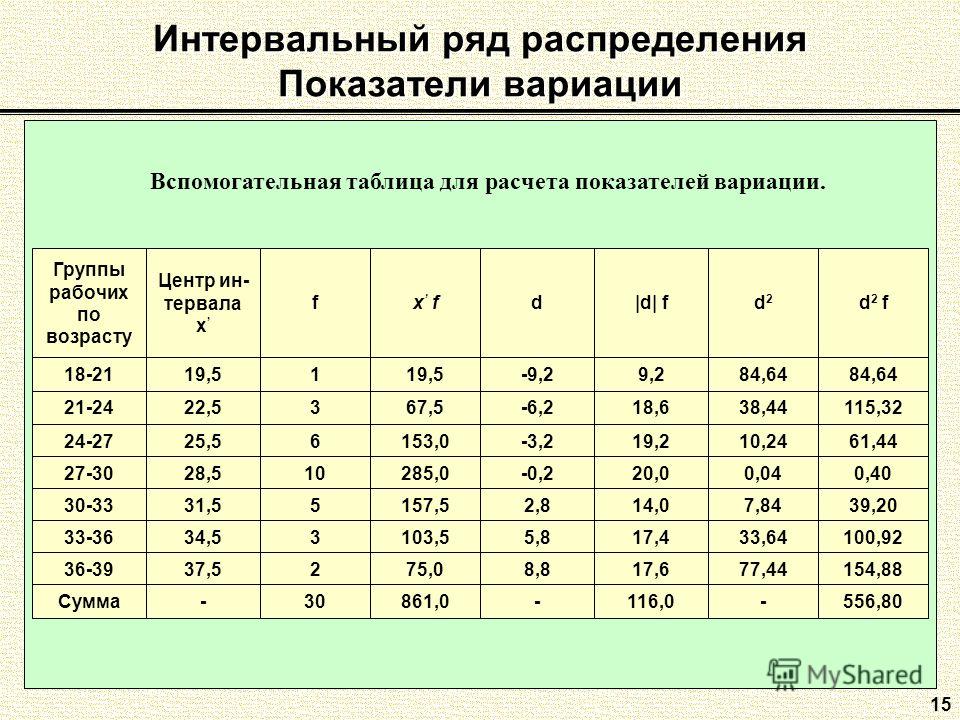 Он основан на частотах интервалов классов. Как уже обсуждалось выше, в этой таблице все категории данных разбиты на разные классовые интервалы одинаковой ширины, например, 0-10, 10-20, 20-30 и т.д. интервал класса отмечен против каждого интервала. Посмотрите на пример таблицы распределения частот для сгруппированных данных, приведенный на изображении ниже.
Он основан на частотах интервалов классов. Как уже обсуждалось выше, в этой таблице все категории данных разбиты на разные классовые интервалы одинаковой ширины, например, 0-10, 10-20, 20-30 и т.д. интервал класса отмечен против каждого интервала. Посмотрите на пример таблицы распределения частот для сгруппированных данных, приведенный на изображении ниже.
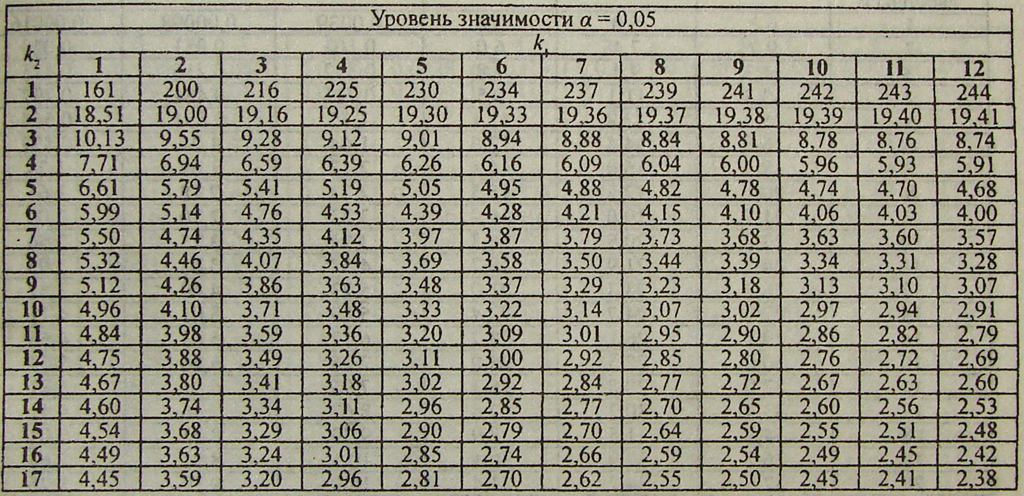 Кроме того, таблица частотного распределения полезна для представления данных в аккуратном и легком для понимания виде.
Кроме того, таблица частотного распределения полезна для представления данных в аккуратном и легком для понимания виде.
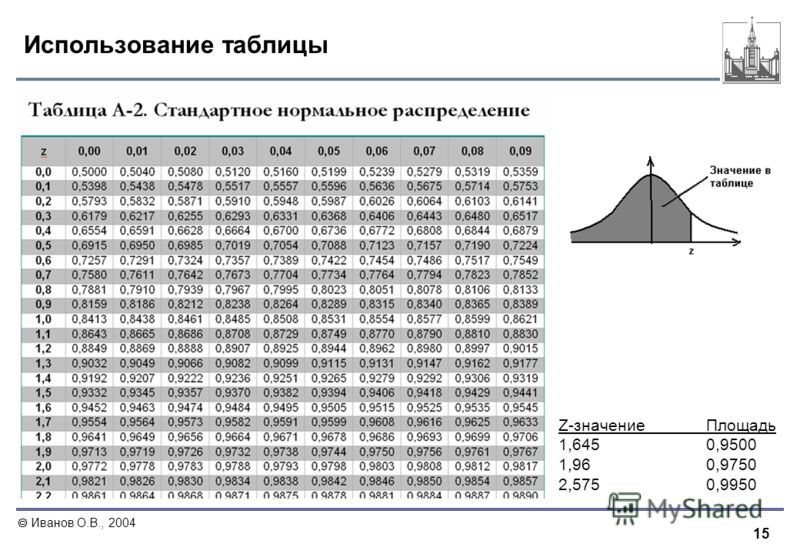 Сначала выявляем все категории или интервалы классов, затем записываем их отдельными строками в столбец 1. После этого фокусируемся на каждой категории по очереди и подсчитываем их частоты. Мы пишем их соответствующую частоту в третьем столбце. Вот как мы можем нарисовать таблицу частотного распределения.
Сначала выявляем все категории или интервалы классов, затем записываем их отдельными строками в столбец 1. После этого фокусируемся на каждой категории по очереди и подсчитываем их частоты. Мы пишем их соответствующую частоту в третьем столбце. Вот как мы можем нарисовать таблицу частотного распределения.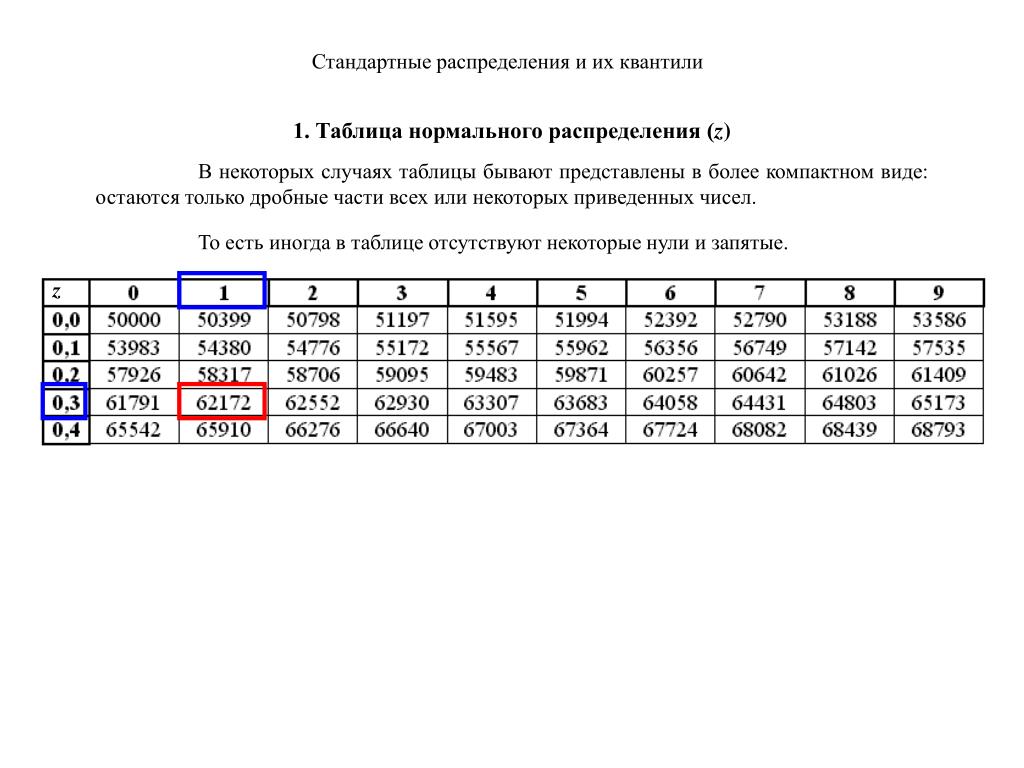 3 Распределение частот
3 Распределение частот В последнем случае распределение называется относительное частотное распределение .
В последнем случае распределение называется относительное частотное распределение .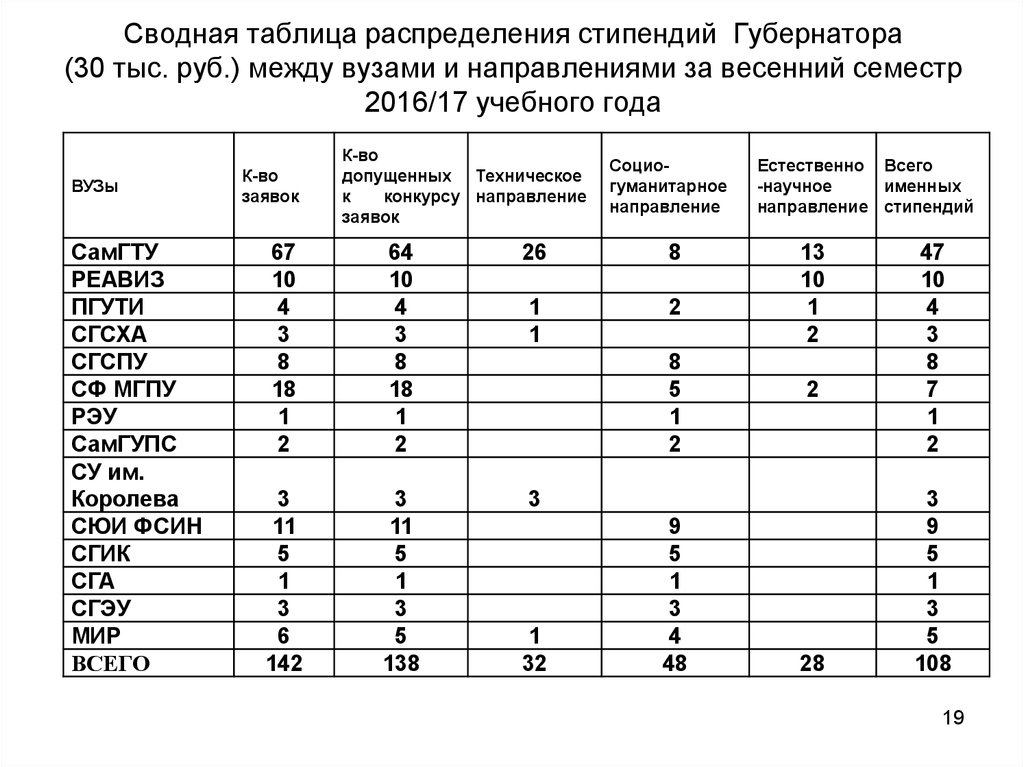 В этом случае интервалами будут количество домохозяйств без машины (0), одна машина (1), две машины (2) и так далее.
В этом случае интервалами будут количество домохозяйств без машины (0), одна машина (1), две машины (2) и так далее.
 д.
д.
 Непрерывные переменные с большей вероятностью будут представлены в интервалах классов, в то время как дискретные переменные могут быть сгруппированы в интервалы классов или нет.
Непрерывные переменные с большей вероятностью будут представлены в интервалах классов, в то время как дискретные переменные могут быть сгруппированы в интервалы классов или нет.
 2-1)≥0\\x<3\end{cases}\)
2-1)≥0\\x<3\end{cases}\)
 2\)
2\)
 2-28x+196\\(x-5)(x-50)≥0\\x>14\end{cases}\)
2-28x+196\\(x-5)(x-50)≥0\\x>14\end{cases}\)

 Оба являются $\leq 0$ в некотором интервале $[x_1, x_2]$, где это действительные корни соответствующей параболы (если, конечно, существуют действительные корни, мы хотим, чтобы они существовали, даже если они совпадают, отсюда и ограничения, которые вы найдено для $\alpha$ гарантирует это, ОК).
Оба являются $\leq 0$ в некотором интервале $[x_1, x_2]$, где это действительные корни соответствующей параболы (если, конечно, существуют действительные корни, мы хотим, чтобы они существовали, даже если они совпадают, отсюда и ограничения, которые вы найдено для $\alpha$ гарантирует это, ОК).