тригонометрической, множество функций, порядок нахождения
Содержание:
- Что такое функция в алгебре
-
Виды функций
- Линейная
- Обратная пропорциональность
- Квадратичная (квадратная)
- Степенная
- Показательная
- Логарифмическая
- Тригонометрические
-
Типы функций
- Важные свойства
-
Методы нахождения
- Перебор значений
- Графический метод
- Учет непрерывности и монотонности
- Производная, min и max
- Пример решения
Содержание
- Что такое функция в алгебре
-
Виды функций
- Линейная
- Обратная пропорциональность
- Квадратичная (квадратная)
- Степенная
- Показательная
- Логарифмическая
- Тригонометрические
-
Типы функций
- Важные свойства
-
Методы нахождения
- Перебор значений
- Графический метод
- Учет непрерывности и монотонности
- Производная, min и max
- Пример решения
Что такое функция в алгебре
Определение
Функция в алгебре — некое математическое выражение y=f(x), где каждому значению переменной x соответствует одно значение переменной y.
Из этого следует, что решений у функции может быть много. Для обозначения совокупностей таких решений вводятся особые термины.
Определние
Множество значений функции y=f(x) — совокупность значений переменной y, которые она принимает при переборе всех значений переменной x на заданном отрезке X.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Областью значений функции y=f(x) называется такое множество значений, которые функция y принимает при переборе всех значений аргумента x из области определения. Область значений обозначается как E(f).
Определение
Область допустимых значений (область определения) функции — такое множество всех значений переменных, при которых функция имеет смысл, то есть решается. {\mathrm x}\)
{\mathrm x}\)
Для показательной функции существует одно определяющее условие: \(\mathrm a>0\). В связи с этим область ее значений включает в себя все положительные числа:
\(\mathrm E(\mathrm f)=(0;\;+\infty) \)
Логарифмическая
\(\mathrm y=\log_{\mathrm a}\left(\mathrm x\right)\)
По своим свойствам логарифмическая функция обратна показательной. Для данных функций область определения и область значений меняются местами соответственно. ОЗ логарифмической функции включает в себя все действительные числа:
\(\mathrm E(\mathrm f)=(-\infty;\;+\infty)\)
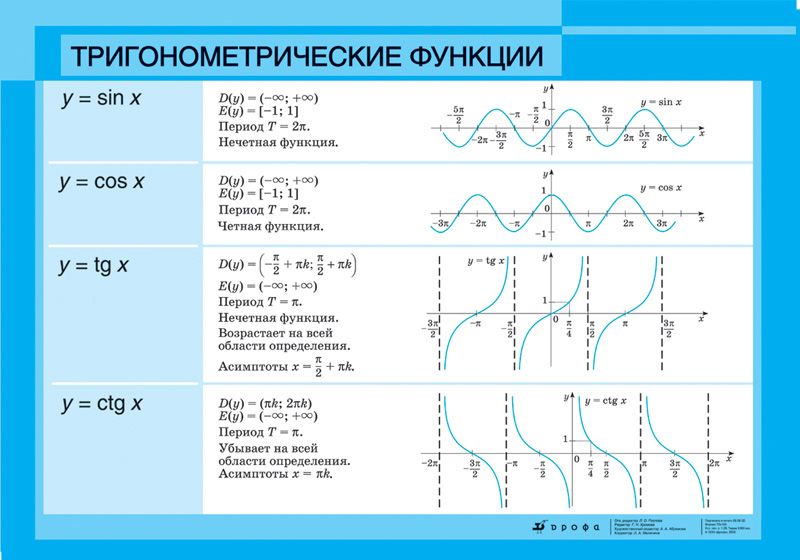
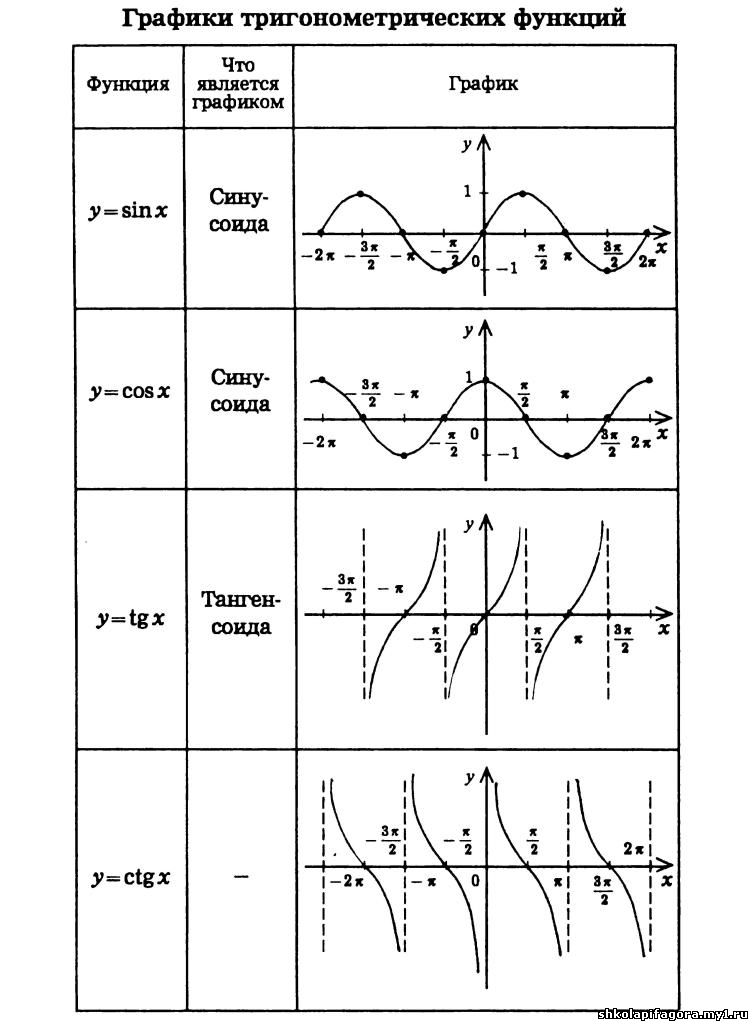
Тригонометрические
Рассмотрим четыре базовые тригонометрические функции:
- синус;
- косинус;
- тангенс;
- котангенс.
Первые две периодически повторяются в промежутке между -1 и 1:
\(\mathrm E(\mathrm f)=(-1;\;1)\)
Область значения тангенса и котангенса включает в себя все действительные числа:
\(\mathrm E(\mathrm f)=(-\infty;\;+\infty)\)
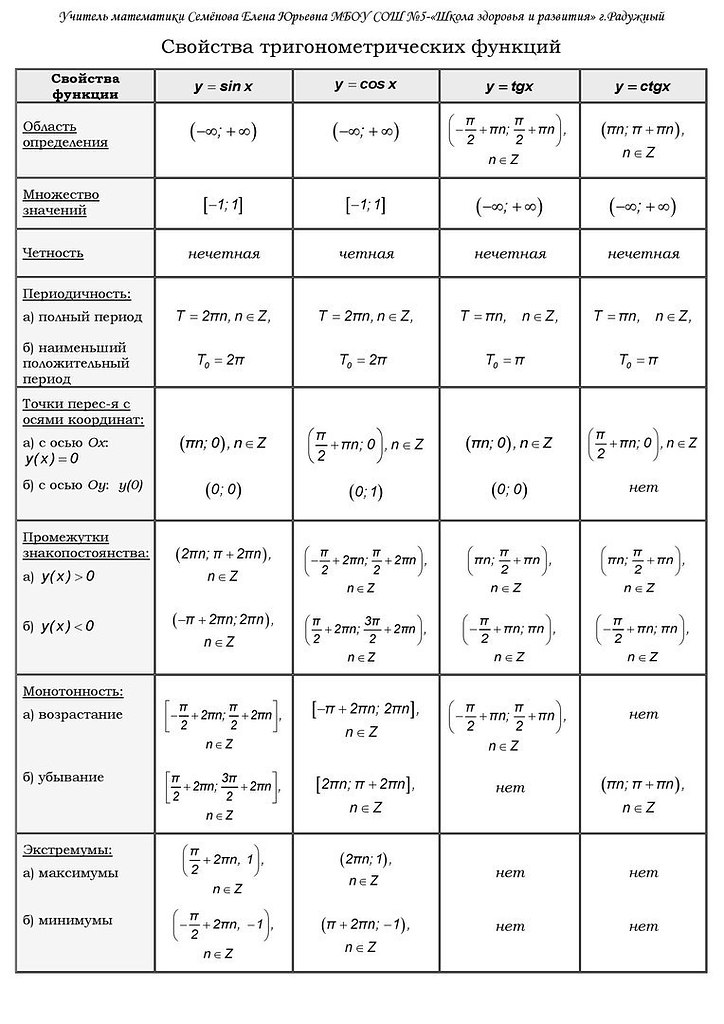
Типы функций
При определении области значений функции необходимо учитывать ее фундаментальные особенности. Обозначенная выше классификация — не единственная. У математических функций есть некоторые параметры, которые влияют как на саму область значений, так и на выбор методики ее нахождения.
Обозначенная выше классификация — не единственная. У математических функций есть некоторые параметры, которые влияют как на саму область значений, так и на выбор методики ее нахождения.
Важные свойства
К наиболее важным для поиска области значений функции относят следующие ее свойства:
- Непрерывность. Непрерывной называется функция, на графике которой нет «точек разрыва». Таким точкам соответствуют значения переменной, при которых функция не имеет смысла, то есть — исключенные из области определения.
- Монотонность. Монотонной называется функция, которая не возрастает или не убывает на всей области определения.
- Четность. Четной называется функция, не меняющая своего значения при смене знака переменной. То есть, f(-x)=f(x). Соответственно, нечетная функция меняет значение. Выделяют также функции общего вида, которые не симметричны относительно центра или оси координат.

- Периодичность. Периодическая функция повторяет свои значения через определенные равные интервалы значений переменной.
Методы нахождения
Поиск области значений функции несколько сложнее, чем определение ОДЗ. В зависимости от вида и типа функции, а также условий задачи для этого могут применяться различные методы.
Перебор значений
Самый простой и ограниченный способ. При его помощи можно находить область значений на небольшом промежутке целых чисел \(x\in(a;\;b)\). В таком случае заданные значения переменной поочередно подставляются в уравнение и вычисляются значения функции, соответствующие им.
Графический метод
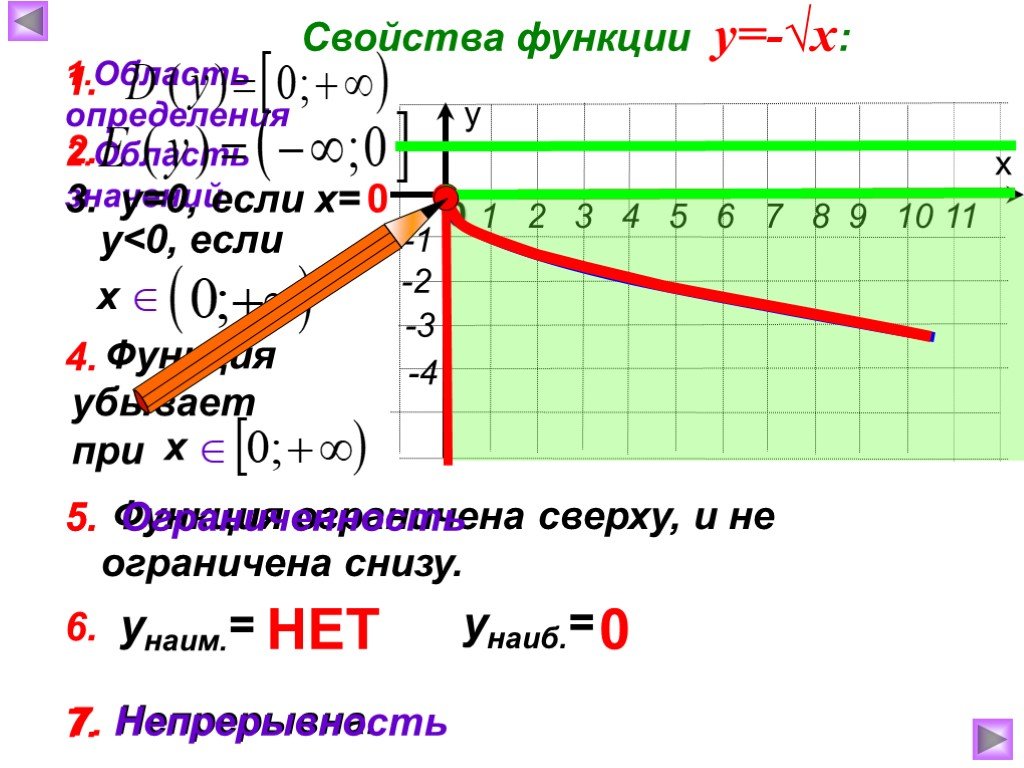
Как ясно из названия способа, для его реализации необходимо построить график исследуемой функции. По внешнему виду кривой уже можно делать некоторые выводы. Если линия графика соответствует одному из видов элементарных функций, например, является параболой, то в качестве области значений берется промежуток, соответствующий данному графику. 2 имеет вид параболы с точкой перегиба с координатами (0, 0). Кривая непрерывна, то есть не имеет разрывов в области определения. Для того, чтобы определить область значений данной функции, достаточно построить ее график на ограниченном промежутке. Для примера возьмем \(x\in\lbrack-4;\;4\rbrack\):
2 имеет вид параболы с точкой перегиба с координатами (0, 0). Кривая непрерывна, то есть не имеет разрывов в области определения. Для того, чтобы определить область значений данной функции, достаточно построить ее график на ограниченном промежутке. Для примера возьмем \(x\in\lbrack-4;\;4\rbrack\):
Рисунок 1. Значение непрерывности и монотонности функции для области определения
На графике видно, что функция монотонно убывает на промежутке \(\lbrack-4;\;0\rbrack\) и монотонно возрастает на промежутке\( \lbrack0;\;4\rbrack\). Исходя из этого и непрерывности функции, можно экстраполировать данную закономерность на всю область определения. Так как минимальное значение данной функции равняется нулю, область значений будет следующей:
\(\mathrm E(\mathrm f)=\lbrack0;\;+\infty)\)
Производная, min и max
Описанные выше способы подходят не для всех ситуаций. В общем случае, задача по определению области значений функции всегда сводится к нахождению ее минимального и максимального значения или точек экстремума.
Определение
Согласно теореме Ферма, в точках локального экстремума производная исследуемой функции равняется нулю.
Важно понимать, что сами локальный экстремум не обязательно является максимумом или минимумом для функции в целом. Такие точки называются критическими или стационарными. Поэтому, кроме самих точек необходимо определять промежутки возрастания и убывания:
- если при переходе через критическую точку производная функции меняет знак с (+) на (-), то эта точка является максимумом;
- если при переходе через критическую точку производная меняет знак с (-) на (+), то такая точка является минимумом;
- если при переходе знак производной не меняется, то экстремума в данной точке нет.
Кроме того, экстремумы функции можно определять по второй производной. Предположим, при исследовании функции обнаружилась некая критическая точка x_1. Для нее справедливы следующие неравенства:
Если \(f»(x_1)>0\), то \(x_1\) — точка минимума. 2-5\) следующая:
2-5\) следующая:
\(E(y)=\lbrack-6;\;+\infty).\)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Поиск по содержимому
Область определения и область значений функции. | Презентация к уроку по алгебре (9 класс) на тему:
Слайд 1
функция. Область определения функции. Область значений функции. Алгебра 9 класс
Слайд 2
Давайте вспомним: Какую зависимость называют функцией? Как читают запись y = f(x) ? Что называют аргументом функции? Что такое область определения функции? Что называют значением функции? Как читают запись f(2) = 6 и что она означает? Что называют областью значений функции?
Слайд 3
Определение функции. Обозначение функции. у( х ) — функция х — аргумент зависимая переменная независимая переменная
Слайд 4
Область определения функции. Область определения функции у(х) это все значения аргумента — Х Обозначение области определения — D( у )
Слайд 5
Область значений функции. Область значений функции у(х) это все значения — У _ Обозначение области значений — Е ( у )
Область значений функции у(х) это все значения — У _ Обозначение области значений — Е ( у )
Слайд 6
x — 4 — 3 — 2 — 1 0 1 2 3 y -8 — 6 — 4 — 2 0 2 4 6
Слайд 8
g(2) = g(- 2) = g(x) = 0 при x = g(x) = 1 при х = или х = D(g) = E(g) =
Слайд 9
f(-3) = f(- 1) = f(x) = — 1,5 при x = f(x) = 2 при х = х = , x = D(f) = E(f) =
Слайд 10
а) f(2) = ? б) D(f) = ? Решение: а) f( 16 ) = ? б) D(f) = ? Решение:
Слайд 11
График функции (х; у)- координаты точки в плоскости у( х )- функция х — аргумент у – ордината точки (координата оси ОУ ) х – абсцисса точки (координата оси ОХ )
Слайд 12
Область определения линейной функции y( х) = k x + b , k≠0 y x k > 0 y x k 0 х > 0 I ч. III ч. II ч. IV ч.
Слайд 13
Область значений линейной функции y( х ) = k x + b , k≠0 y x k > 0 y x k 0 у > 0 I ч. III ч. II ч. IV ч.
Слайд 14
Область определения линейной функции y( х) = k x + b , k= 0 y x y( х) = b y x y( х) = -b D( у ) = (-∞ ; + ∞) х Є (-∞ ; + ∞) -∞ + ∞ -∞ + ∞ О О х 0 х > 0 I ч.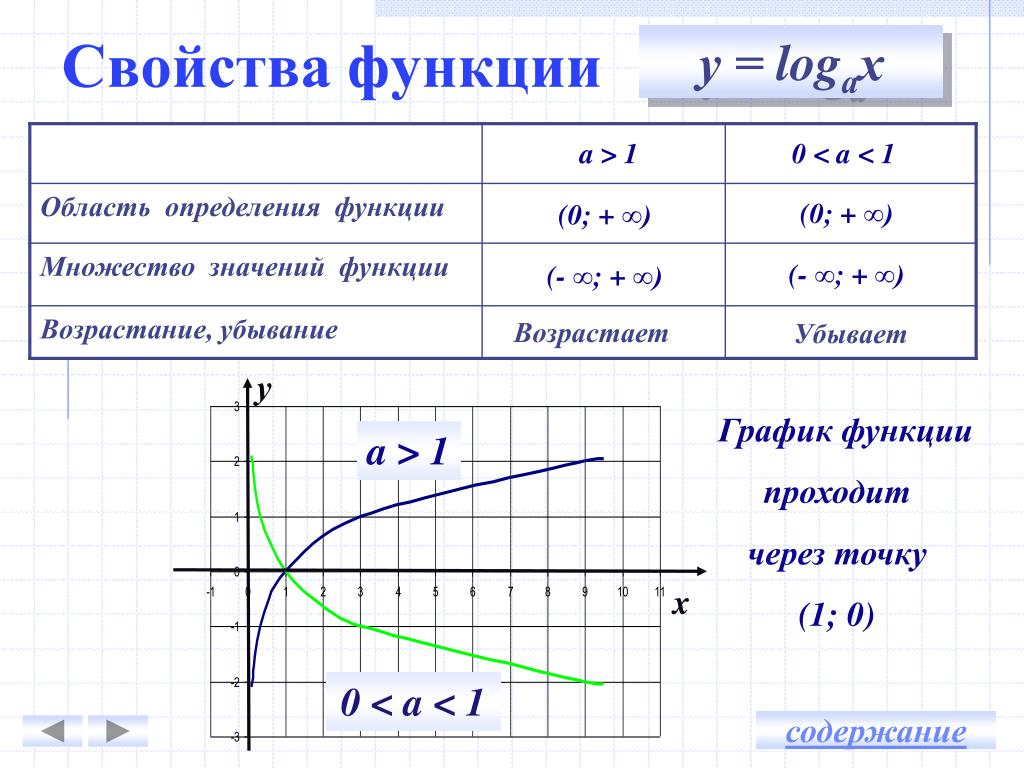 II ч. III ч. IV ч.
II ч. III ч. IV ч.
Слайд 15
Область значений линейной функции y( х) = k x + b , k= 0 y x y( х) = b y x y( х) = -b Е ( у ) = b -∞ + ∞ -∞ + ∞ О О I ч. II ч. III ч. IV ч. Е ( у ) = — b b -b
Слайд 16
Область определения прямой пропорциональности y( х) = k x y x k > 0 y x k 0 х > 0 I ч. III ч. II ч. IV ч.
Слайд 17
Область значений прамой пропорциональности y( х ) = k x y x k > 0 y x k 0 у > 0 I ч. III ч. II ч. IV ч.
Слайд 18
Область определения обратной пропорциональности , х≠0 y x k > 0 y x k 0 х > 0 I ч. III ч. II ч. IV ч.
Слайд 19
Область значений обратной пропорциональности , х≠0 y x k > 0 y x k 0 y > 0 I ч. III ч. II ч. IV ч.
Слайд 20
Область определения квадратичной функции , а≠0 y x а > 0 y x а 0 х > 0 I ч. III ч. II ч. IV ч.
Слайд 21
Область значений квадратичной функции , а≠0 y x а > 0 y x а 0 y
Слайд 22
Область определения функции , х ≥ 0 y x D( у ) = [0; + ∞) ; х Є [0; + ∞) + ∞ О х ≥ 0 I ч.
Слайд 23
Область значений функции , х ≥ 0 y x Е ( у ) = [0; + ∞) ; у(х) Є [0; + ∞) + ∞ О у ≥ 0 I ч.
Слайд 24
Область определения функции у = l х l _ y x D( у ) = (- ∞ ; + ∞) ; х Є (- ∞ ; + ∞) + ∞ О х
Слайд 25
Область значений функции у = l х l _ y x Е ( у ) = [ 0 ; + ∞) ; у(х) Є [ 0 ; + ∞) + ∞ О I ч. у ≥ 0 II ч.
Слайд 26
Область определения функции у = х³ y x D( у ) = (-∞ ; + ∞) ; х Є (-∞ ; + ∞) + ∞ О х ≥ 0 I ч. III ч. х
Слайд 27
Область значений функции у = х³ y x D( у ) = (-∞ ; + ∞) ; у(х) Є (-∞ ; + ∞) + ∞ О у ≥ 0 I ч. III ч. у
Слайд 28
Найдите по графику область определения функции — D( у ) -5 4 D( у )= [ -5 ; 4,5 ]
Слайд 29
Найдите по графику область значений функции — Е ( у ) -2 5 Е ( у )= [ -2 ; 5 ]
Слайд 30
По графику определите промежуток на котором определена данная функция -6 3 D( у )= [ -6 ; 3,5 ]
Слайд 31
По графику определите промежуток на котором определена данная функция -2 4 Е ( у )= [ -2 ; 4 ]
Слайд 32
Найдите по графику область определения функции -5 5 D( у )= [ -5 ; 5 ]
Слайд 33
Найдите по графику область определения функции -2 6 Е ( у )= [ -2 ; 6 ]
Слайд 34
Найдите область определения и значений функции -4 4 [ -4 ; 4) 3 ( — 1;3] а) б) в) г) д)
Слайд 35
Найдите область определения и значений функции 5 ( -1 ; 5 ] -3 4 [ — 3;4) а) б) в) г) д)
Слайд 36
Найдите область определения и значений функции -2 4 [ — 2;4) 4 [ — 1;4] а) б) в) г) д)
Слайд 37
Найдите область определения и значений функции б) в) г) — 4 2 [ -4 ; 2 ] 2 [ -1 ; 2 ] д) а)
Объяснение всех 4 областей действия JavaScript
Если вы написали хотя бы одну строку кода JavaScript, значит, вы использовали одну из четырех областей действия JavaScript, даже не подозревая об этом. Эти различные уровни области действия определяют, как будет работать ваш код, насколько легко ваш код будет писать/изменяться, а также многие другие факторы вашего кода, поэтому крайне важно знать все нюансы каждой отдельной области. В этой короткой статье я расскажу вам, что такое каждый уровень области видимости, как они взаимодействуют с вашим кодом и что вы можете сделать с этими знаниями, чтобы писать более чистый код.
Эти различные уровни области действия определяют, как будет работать ваш код, насколько легко ваш код будет писать/изменяться, а также многие другие факторы вашего кода, поэтому крайне важно знать все нюансы каждой отдельной области. В этой короткой статье я расскажу вам, что такое каждый уровень области видимости, как они взаимодействуют с вашим кодом и что вы можете сделать с этими знаниями, чтобы писать более чистый код.
Если вы предпочитаете учиться визуально, посмотрите видеоверсию этой статьи.
Что такое объем?
Первый вопрос, который нам нужно решить, это что такое масштаб. В JavaScript и практически в любом другом языке программирования ваш код выполняется в рамках заданной области. Эта область определяет, к каким переменным имеет доступ ваш код, как новые переменные будут взаимодействовать с остальной частью вашего кода и некоторые другие вещи. Лучший способ представить область действия — это раздел, который поможет вам отделить разные части кода друг от друга.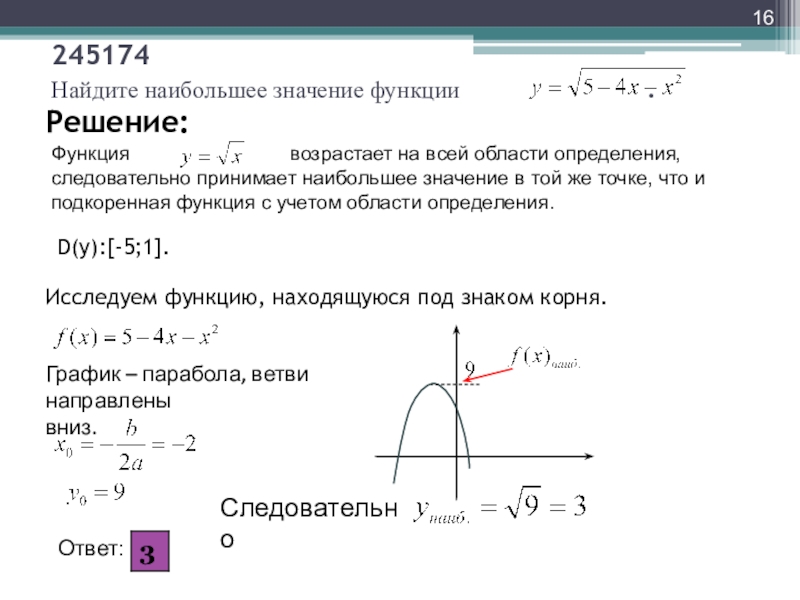
В приведенном выше примере у нас есть простой код, который определяет переменную вне функции и внутри функции. Затем мы записываем обе переменные в консоль как внутри, так и вне функции. Это прекрасно работает внутри функции, но вне функции наш журнал выдает ошибку, поскольку у нас нет доступа к внутренней переменной вне области действия функции.
В этом примере используются две из четырех областей видимости в JavaScript для разделения нашего кода таким образом, чтобы только определенные части кода имели доступ к определенным переменным. Это основная причина существования разных уровней охвата, поэтому давайте сейчас рассмотрим эти разные охваты.
Уровни охвата
Четыре различных уровня охвата:
- Глобальный охват
- Объем модуля
- Блочный прицел
- Область действия
Может показаться, что это слишком много для отслеживания, но на самом деле вы, вероятно, будете использовать область модуля и блока для 95% всего кода, который вы пишете, поэтому отслеживать его немного легче. Однако это не означает, что вы должны игнорировать другие области видимости, так как важно понимать, как они работают.
Однако это не означает, что вы должны игнорировать другие области видимости, так как важно понимать, как они работают.
Глобальная область действия
Для начала мы поговорим о самой простой области действия, чтобы понять, какую область действия большинство разработчиков используют для всего своего кода, поскольку она просто игнорирует все ограничения, налагаемые другими областями. Чтобы понять глобальную область видимости, представьте, что у меня есть следующий HTML/JS.
Этот простой пример использует глобальную область видимости для определения своих переменных. Глобальная область действия работает так: каждый раз, когда вы определяете переменную на верхнем уровне файла (вне любой функции/фигурных скобок), она считается глобальной областью действия и к ней можно получить доступ ВЕЗДЕ во всем приложении. Этот глобальный доступ поначалу упрощает написание кода, поскольку вам не нужно беспокоиться о том, что переменные блокируются разными областями, но по мере того, как вы начинаете писать более сложный код, управлять этим быстро становится сложно. Эта проблема еще хуже, когда у вас есть несколько файлов.
Эта проблема еще хуже, когда у вас есть несколько файлов.
Как вы можете видеть в приведенном выше примере, мы определили переменную в script-1.js и можем использовать эту переменную в script-2.js . Это потому, что переменная из script-1.js определяется глобально и может использоваться ВСЕГДА в вашем коде. Из-за этой особенности глобальной области видимости я стараюсь никогда не использовать глобальную область видимости ни в одном из своих приложений. Невероятно сложно отслеживать глобальную область действия по мере роста вашего приложения, поэтому я предпочитаю область действия модуля.
Область действия модуля
Область действия модуля очень похожа на глобальную область действия, но с одним небольшим отличием. Второстепенные переменные области доступны только в файле, в котором вы их определяете. Это означает, что их нельзя использовать в других файлах, что идеально, когда вы пытаетесь мысленно отслеживать все. Чтобы войти в область модуля, вам нужно использовать
Чтобы войти в область модуля, вам нужно использовать type="module" в тегах скрипта. Это гораздо больше, чем просто изменение области действия, поэтому, если вы не знакомы с модулями ES, вам следует ознакомиться с моим полным руководством по модулям ES.
С помощью этого единственного изменения мы устранили самую большую проблему, связанную с глобальной областью действия переменных, доступной в каждом файле, сохранив при этом преимущества возможности использования переменной в любом месте файла, в котором она определена. Из-за того, что область действия этого модуля является одной из двух областей видимости, которые я использую постоянно.
Область блока
Другая основная область, которую я постоянно использую, — это блочная область. Область блока — одна из самых простых для понимания областей, поскольку она соответствует фигурной скобке {} . По сути, каждый раз, когда у вас есть код внутри фигурных скобок, он считается собственной областью действия блока.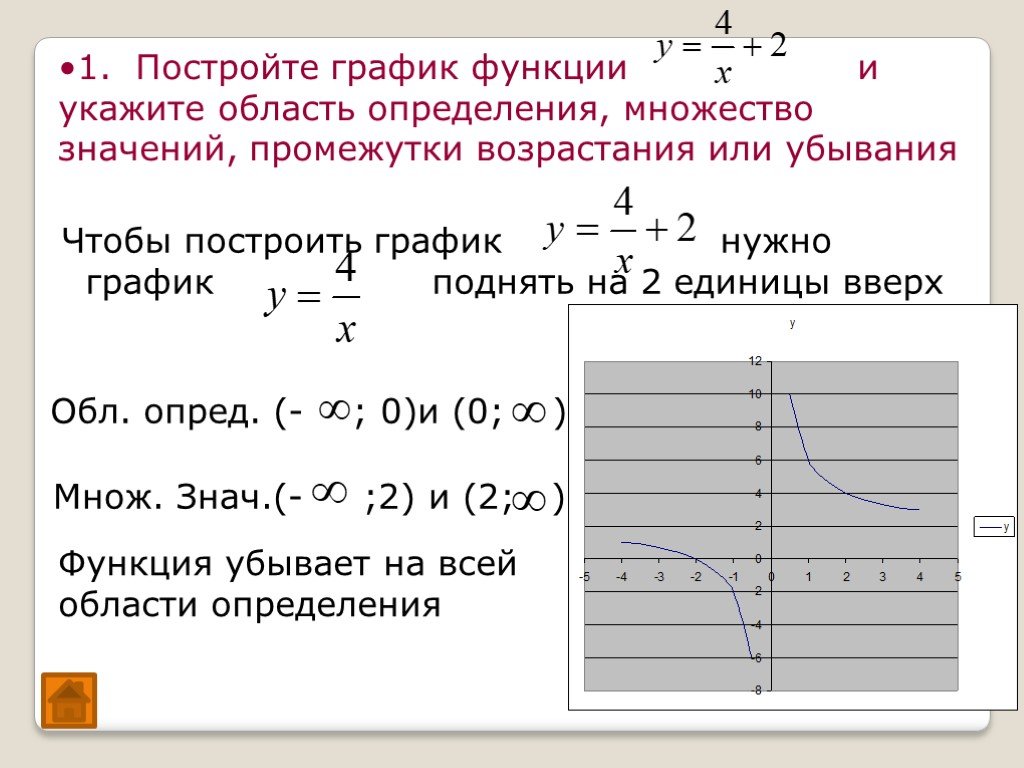 Это означает, что такие вещи, как функции, операторы if, циклы for и т. д., создают собственную область действия блока.
Это означает, что такие вещи, как функции, операторы if, циклы for и т. д., создают собственную область действия блока.
В этом примере определяются две отдельные области блока. Каждая область блока определяется как код между фигурными скобками, и каждый блок имеет доступ ко всем переменным, которые находятся между фигурными скобками, кроме 9.0037 NOT в другом наборе фигурных скобок, а также во всех переменных его родительской области.
В нашем случае у нас есть два блока: функция test и оператор if . Наша область test имеет доступ ко всем переменным в функции test , которые не вложены в другой набор фигурных скобок, что означает, что у нее есть доступ к переменной funcVar . Наша тестовая область также будет иметь доступ к любым глобальным/модульным переменным уровня области, поскольку они являются родителями тест прицел.
Наша вторая область — это оператор if , и эта область имеет доступ к ifVar , а также ко всему, к чему имеет доступ область test , поскольку область test является родительской областью области if .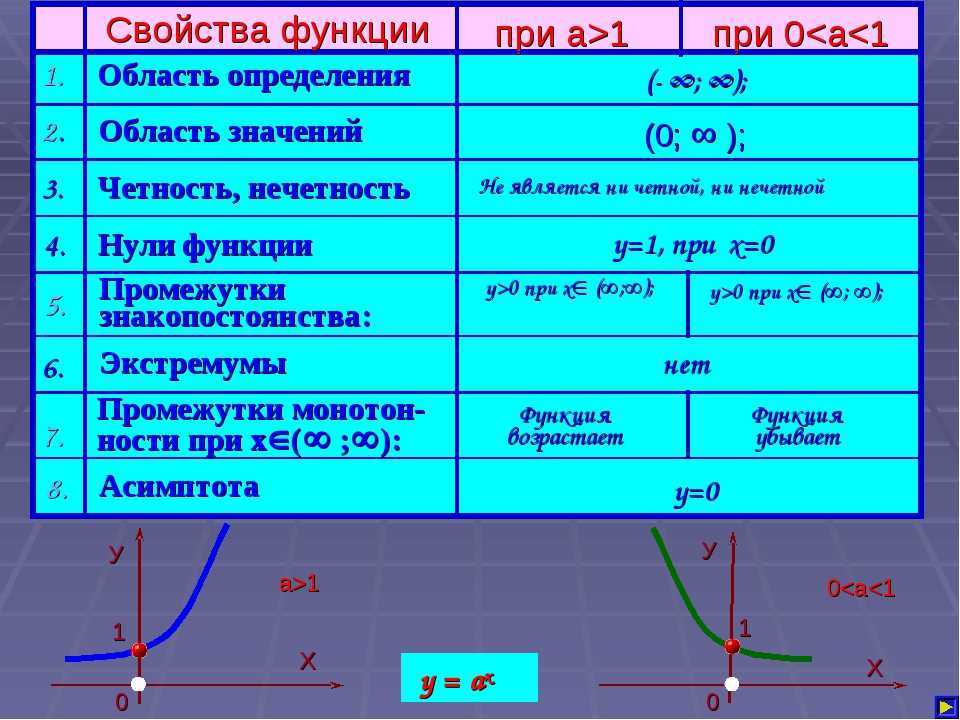
Важный вывод о блочной области: каждый раз, когда у вас есть фигурные скобки, вы создаете новую блочную область, которая имеет доступ ко всем областям, внутри которых она находится, но ни к одной из областей внутри нее. Это внутреннее/внешнее правило на самом деле верно для всех областей. Любая область будет иметь доступ к областям, в которых она находится, но у нее не будет доступа к областям внутри нее.
Вы даже можете добавить фигурные скобки в любом месте вашего кода, чтобы создать область видимости. Это не то, что я делаю часто, но это может быть полезно.
Область действия функции
Последняя область действия — это область действия функции, и мы надеемся, что вам никогда не придется об этом беспокоиться, поскольку она относится к ключевому слову var . Переменные, определенные с помощью ключевого слова var , имеют область действия на уровне функции, а не на уровне блока, что означает, что они заботятся только о фигурных скобках функции.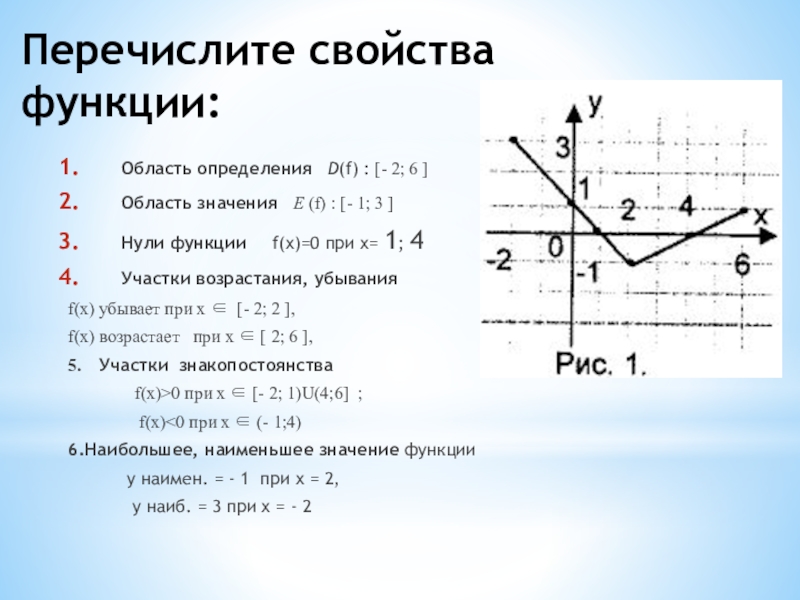
Этот код точно такой же, как код из примера уровня блока, но мы используем var вместо const для определения наших переменных. Вы увидите, что в этом примере наш код будет работать просто отлично, потому что ключевое слово var игнорирует область уровня блока, поэтому даже если ifVar определено в нашем блоке if , это не имеет значения для области действия функции.
Честно говоря, это довольно неинтуитивно, а var как ключевое слово вообще сложно использовать, поэтому я рекомендую никогда не использовать вар . Если вы хотите узнать больше о том, почему мне не нравится var и о различиях между var , let и const , ознакомьтесь с моим полным руководством var vs let vs const.
Несколько переменных с одним и тем же именем
Одна важная вещь, которую нужно понять об этой области видимости, — это то, как она работает, когда у вас есть несколько переменных с одним и тем же именем.
В этом примере у нас есть переменная a , определенная как внутри нашего проверить функцию и внутри нашего блока if . Когда мы выходим из системы и в блоке , если , мы получаем значение и из области , если , а когда мы регистрируем и вне блока , если , мы получаем значение и из области видимости , если . тест прицел.
Основной вывод из этого кода заключается в том, что когда у вас есть две переменные с одинаковыми именами, которые находятся в разных областях, они на самом деле являются двумя совершенно отдельными переменными. Они не имеют ничего общего друг с другом, они никогда не перезаписывают значения друг друга и работают точно так же, как две переменные с разными именами. Единственная разница в том, что если они имеют одно и то же имя, теперь невозможно получить доступ к значению переменной внешней области видимости после доступа к и всегда будут обращаться к самой доступной внутренней переменной области видимости.
Обычно я стараюсь не использовать одинаковые имена переменных при написании кода, но в некоторых случаях это может упростить написание кода, поэтому иногда это необходимо.
Заключение
Хотя наличие четырех разных областей видимости в JavaScript может показаться запутанным, на самом деле все немного проще, поскольку нас интересуют только две из четырех областей видимости. Понимание того, как работают эти области видимости, также имеет решающее значение для написания хорошего чистого кода.
Никто не говорил мне, что Scope и Scope Chain в JavaScript так легко понять | by Divyojyoti Ghosh
Изображение выше создано Divyojyoti Ghosh(me) на сайте www.canva.com с использованием различных элементов, доступных для создания дизайнов. В области компьютерного программирования область видимости имеет дело с организацией переменных (где находится переменная?) и их присоединением (откуда можно получить доступ к переменной? ).
JavaScript имеет лексическую область видимости , что означает, что размещение блоков и функций в коде управляет областью видимости.
Перед тем, как начать с области действия и цепочки областей действия, нам нужно понять, что область действия и область действия переменной — это разные вещи в JavaScript. Итак, в чем именно разница? Область — это пространство или среда в коде, где была объявлена конкретная переменная. Напротив, область действия переменной — это область в коде, где можно получить доступ к конкретной переменной.
Знание различных прицелов поможет нам лучше понять сам прицел. Есть три типа прицелов —
- Глобальная область действия
- Область действия функции
- Область действия блока
Глобальная область действия
Область действия переменных, объявленных вне какой-либо функции или блока, является глобальной, т. е. к ним можно получить доступ в любом месте кода.
Все три переменные student_name , age и Minimum_marks имеют глобальную область действия и могут быть доступны в любом месте кода, поскольку все они объявлены вне какой-либо функции или блока.
Область действия
Все переменные, объявленные внутри функции, имеют область действия функции, т. е. к ним нельзя получить доступ где-либо за пределами функции. Все переменные, определенные в функции, объявлены ли они с использованием var , const или let , имеют область действия.
В приведенном выше фрагменте кода переменные minimum_marks , min_age_of_senior и max_marks имеют область действия функции, т. е. к ним можно получить доступ только внутри функции.
Область действия блока
Переменные, объявленные с помощью let или const в фигурных скобках { } (кроме функции), имеют область действия блока, т. е. доступ к этим переменным вне блока невозможен. Переменные, объявленные с помощью var в фигурных скобках, не могут быть блочными, т. е. к ним можно получить доступ и за пределами блока.
е. доступ к этим переменным вне блока невозможен. Переменные, объявленные с помощью var в фигурных скобках, не могут быть блочными, т. е. к ним можно получить доступ и за пределами блока.
В приведенном выше фрагменте кода minimum_marks , определенные с помощью var в блоке if, доступны из любого места в коде, кроме maximal_marks , который определен с помощью let, заблокирован, поэтому он выдает ReferenceError, когда он вызывается вне блока.
В строгом режиме функции, объявленные с помощью let или const внутри блока, также являются заблокированными, даже именованные функции (не объявленные с использованием var, let или const) также являются заблокированными в строгом режиме.
В Javascript каждая область действия имеет доступ к переменным и функциям всех предковых/родительских областей. Во время выполнения, если JS-движок сталкивается с переменной, для доступа к переменной и ее значению он сначала ищет в локальной области видимости, если он не находит переменную в локальной области видимости, он ищет переменную в области своего родителя.
Поиск продолжается от одной области до ее родительской области до родительской области своего родителя, пока не будет найдена переменная. Вся эта концепция поиска переменной из внутренней области во внешнюю область известна как цепочка областей видимости. Последняя и самая внешняя область — это глобальная область, которая является конечной родительской областью.
Если переменная не найдена во всей этой цепочке областей видимости, механизм JS выдает ошибку ссылки и объявляет переменную не определенной.
В приведенном выше фрагменте кода последняя строка из Функция getGradYear() выдает ошибку ссылки, так как у функции нет доступа к переменной totalFees . Переменная totalfees отсутствует в локальной области действия функции или в какой-либо родительской функции функции getGradYear() , переменная определяется с помощью let в блоке if и, следовательно, ее область действия заблокирована.
Область блока if и область действия функции getGradYear являются дочерними элементами getDetailsOfStudent() область действия функции.


 Поэтому во многих случаях мы можем с достаточной степенью точности использовать модель периодически повторяющегося процесса и решать с помощью этой модели различные задачи.
Поэтому во многих случаях мы можем с достаточной степенью точности использовать модель периодически повторяющегося процесса и решать с помощью этой модели различные задачи.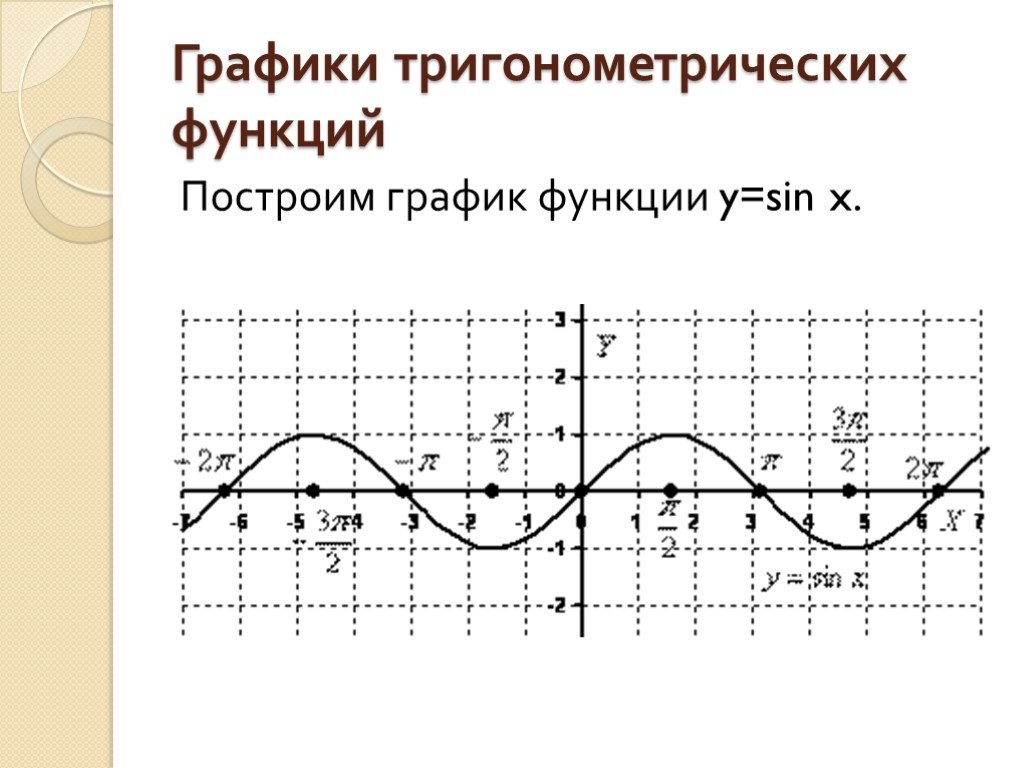 1. Единичная окружность
1. Единичная окружность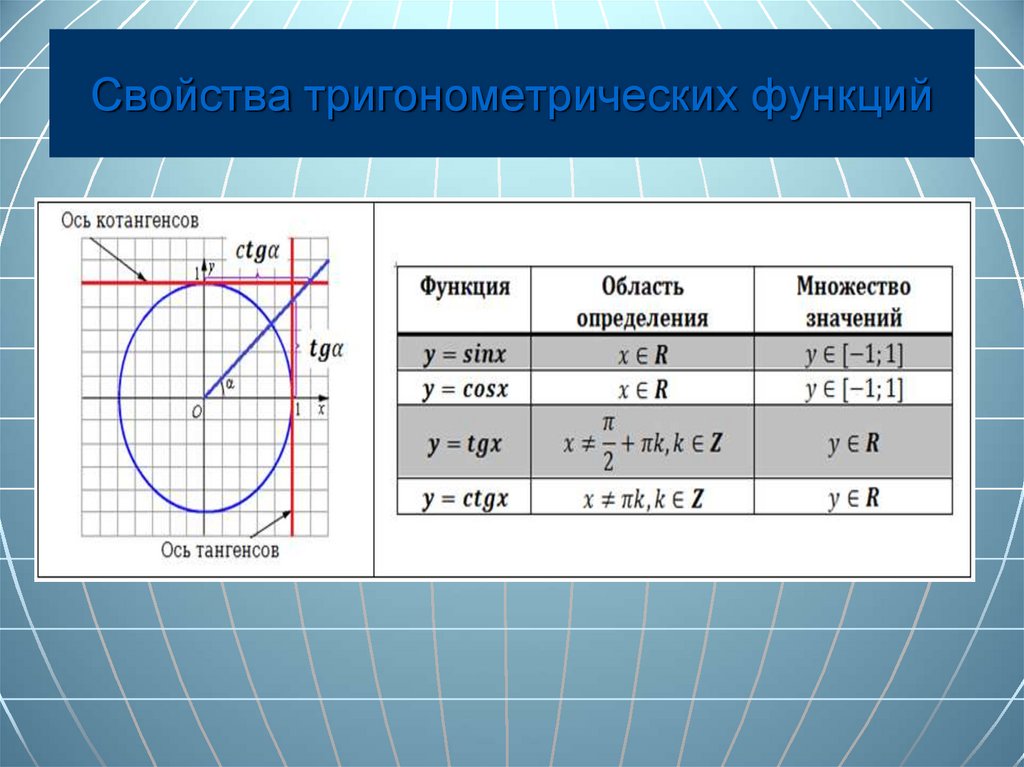 В тригонометрических же функциях мы говорили, что углу ставится в соответствие число. Разрешить эту ситуацию просто: будем брать величину угла, выраженную в радианах. Под записью будем понимать, что числу ставится в соответствие число . Причем так, что значение равно синусу радиан. Например,
В тригонометрических же функциях мы говорили, что углу ставится в соответствие число. Разрешить эту ситуацию просто: будем брать величину угла, выраженную в радианах. Под записью будем понимать, что числу ставится в соответствие число . Причем так, что значение равно синусу радиан. Например, Соответственно, функция является четной функцией; – нечетной.
Соответственно, функция является четной функцией; – нечетной. Помним, что числовой аргумент функции – это величина угла в радианах. Поэтому получаем следующую таблицу:
Помним, что числовой аргумент функции – это величина угла в радианах. Поэтому получаем следующую таблицу: рис. 4).
рис. 4). С решениями уравнений подробнее вы познакомитесь на следующем уроке. А пока можем воспользоваться графиком. Нули функции: . В общем виде это можно записать так: , где – целое число.
С решениями уравнений подробнее вы познакомитесь на следующем уроке. А пока можем воспользоваться графиком. Нули функции: . В общем виде это можно записать так: , где – целое число.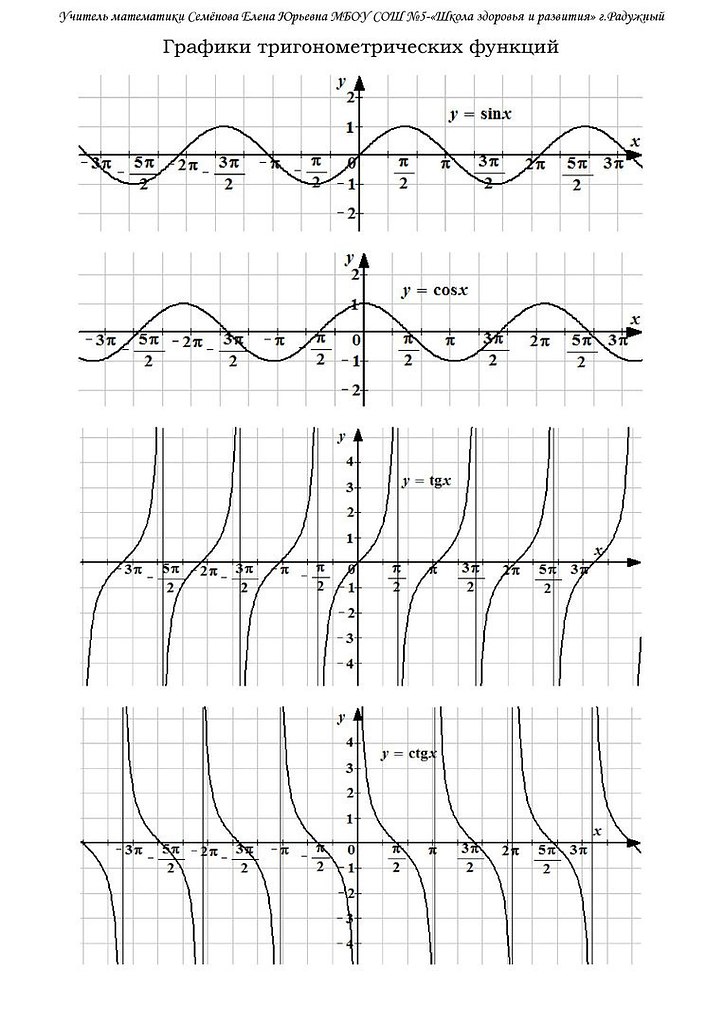 Вот и получили график косинуса (см. рис. 6).
Вот и получили график косинуса (см. рис. 6). Что же делать? Соединим уже имеющиеся точки и посмотрим, что будет происходить с графиком по мере приближения аргумента к (см. рис. 7).
Что же делать? Соединим уже имеющиеся точки и посмотрим, что будет происходить с графиком по мере приближения аргумента к (см. рис. 7).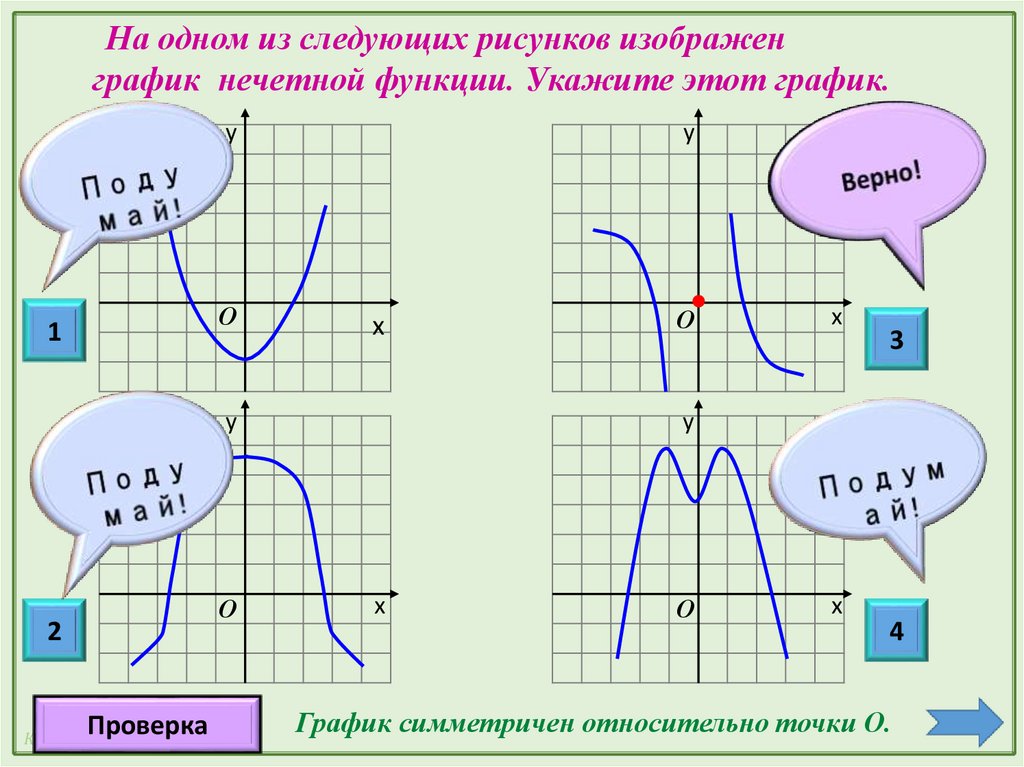 Получили график функции (см. рис. 9).
Получили график функции (см. рис. 9).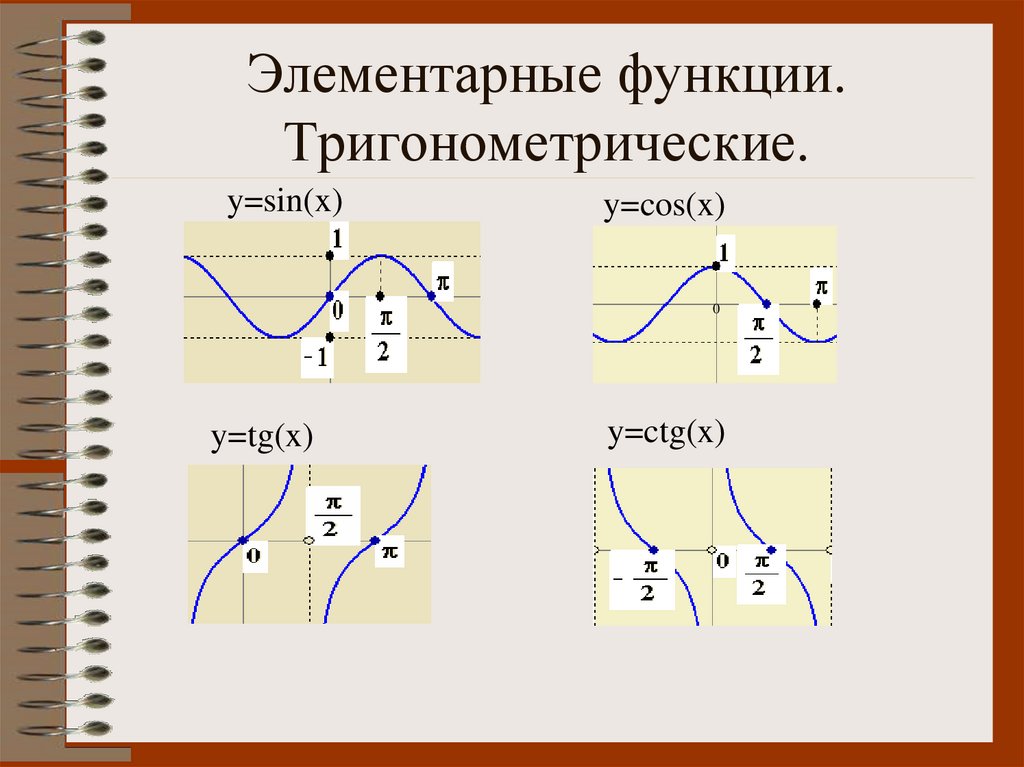 Т. е. значение уменьшается.
Т. е. значение уменьшается.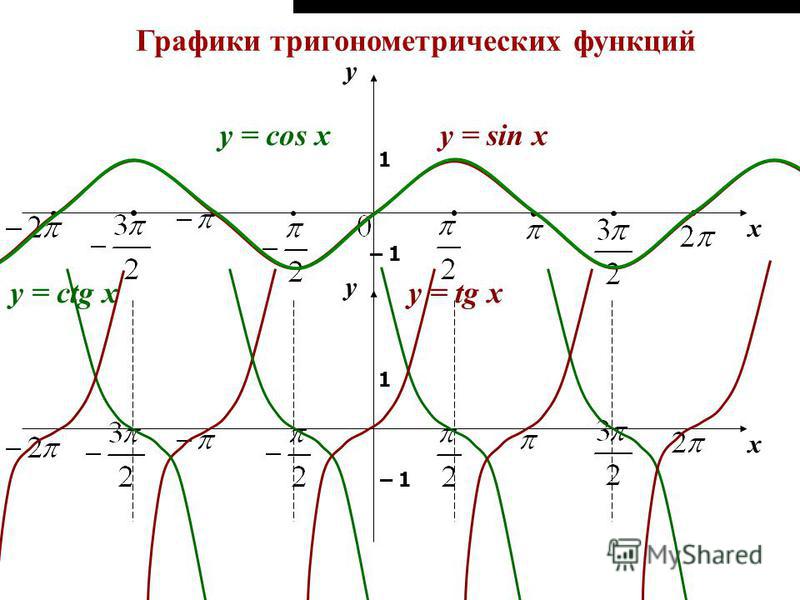 Вспомним эти преобразования (можете пересмотреть соответствующие уроки «Повторение и систематизация курса алгебры 7-9 класса. Функции», «Преобразование графиков функций»).
Вспомним эти преобразования (можете пересмотреть соответствующие уроки «Повторение и систематизация курса алгебры 7-9 класса. Функции», «Преобразование графиков функций»).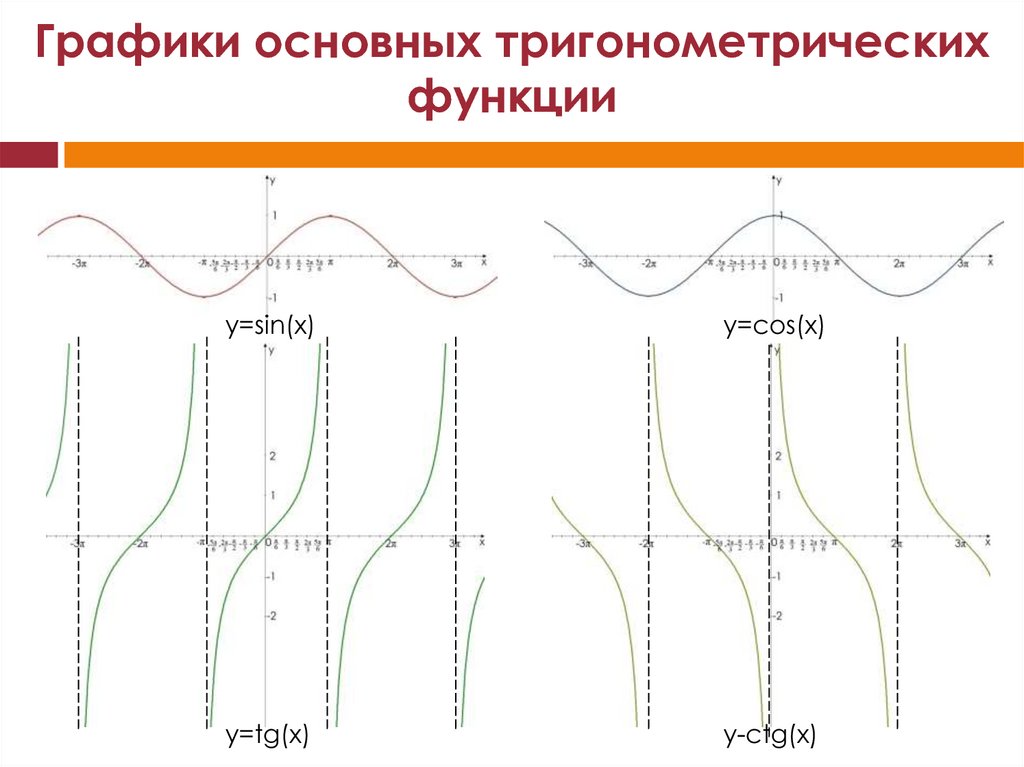 В итоге получим график функции (см. рис. 14).
В итоге получим график функции (см. рис. 14). Но в математической модели могут встретиться и другие тригонометрические выражения. Например, при колебаниях математического маятника зависимость его скорости от времени выглядит следующим образом:
Но в математической модели могут встретиться и другие тригонометрические выражения. Например, при колебаниях математического маятника зависимость его скорости от времени выглядит следующим образом: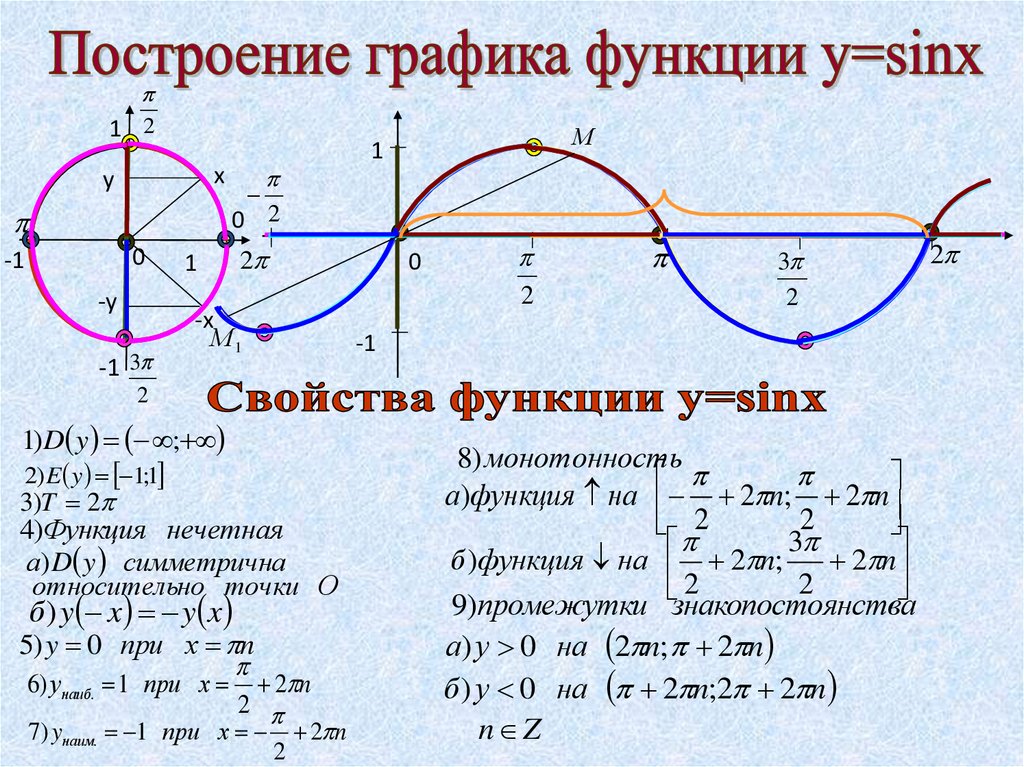 рис. 16).
рис. 16). Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.
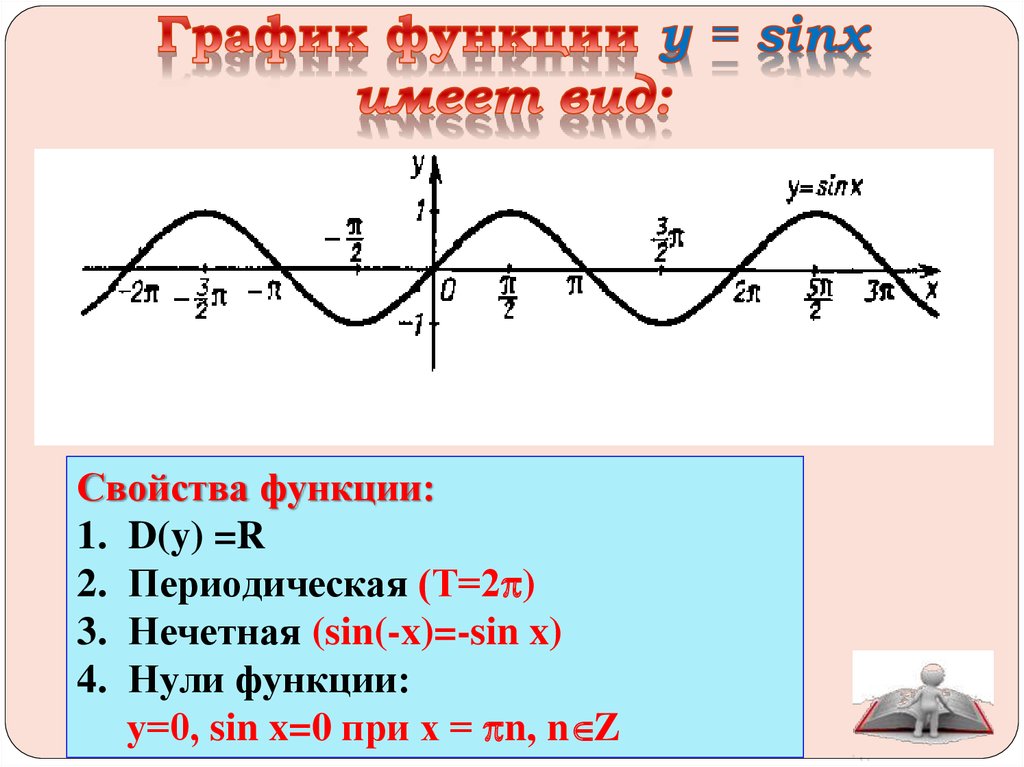
Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.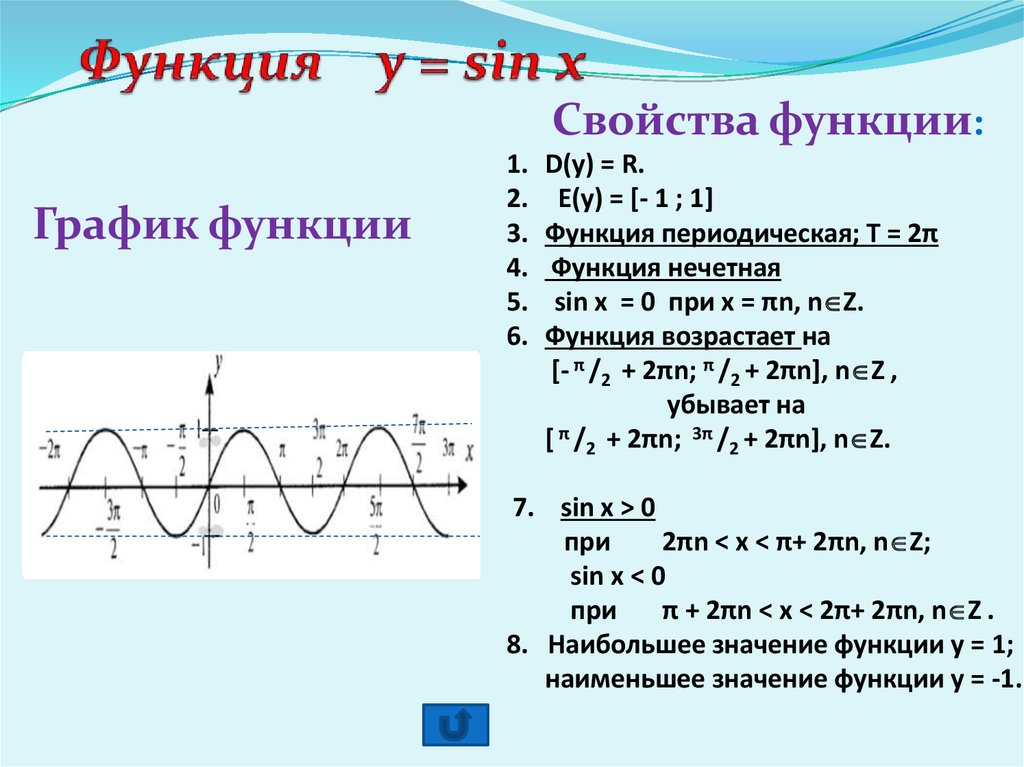 Также для каждой тригонометрической
функции мы укажем значения аргумента,
при которых соответствующая функция
обращается в ноль.
Также для каждой тригонометрической
функции мы укажем значения аргумента,
при которых соответствующая функция
обращается в ноль.

 1 мы видели, как графики тригонометрических функций повторяются через каждые \(2\pi \) радиан. В этом разделе мы обсудим это и другие свойства графиков, особенно для синусоидальных функций (синуса и косинуса).
1 мы видели, как графики тригонометрических функций повторяются через каждые \(2\pi \) радиан. В этом разделе мы обсудим это и другие свойства графиков, особенно для синусоидальных функций (синуса и косинуса).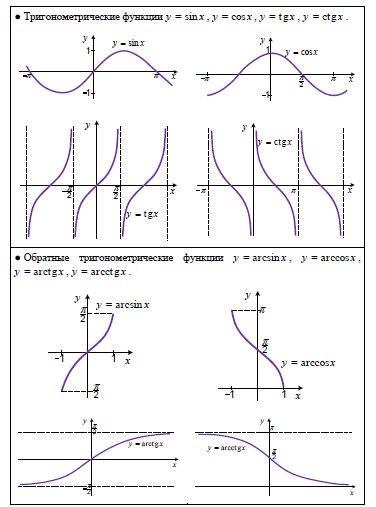
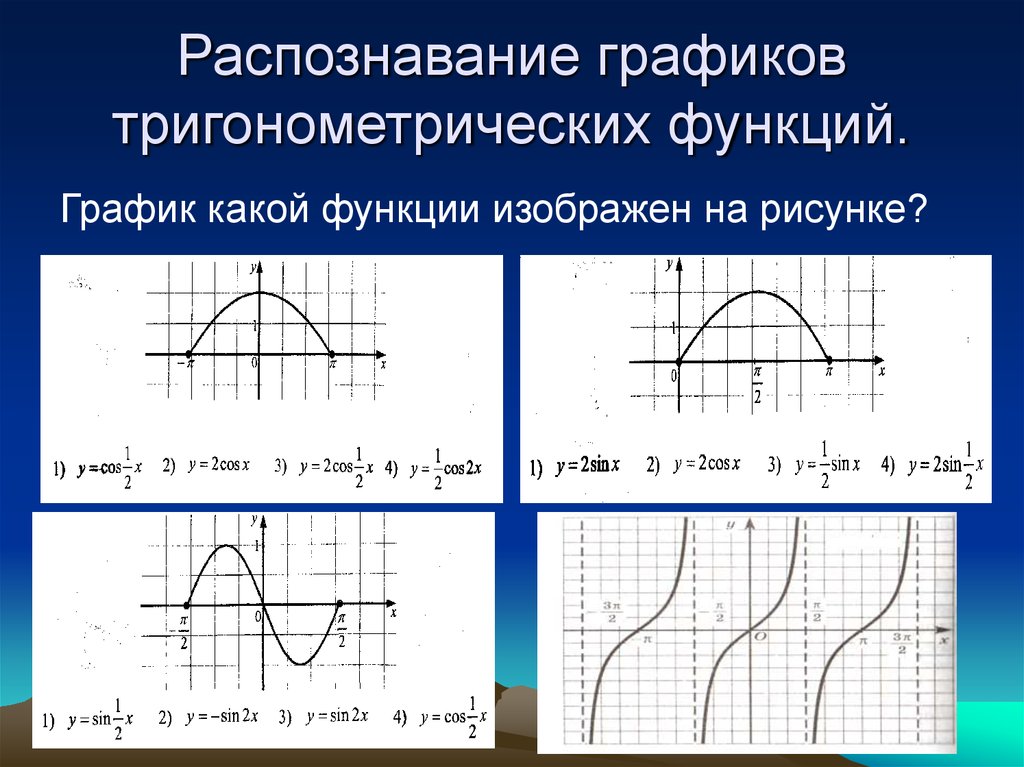 Обратите внимание, что \(\sin\;2x \) «работает в два раза быстрее», чем \(\sin\;x \).
Обратите внимание, что \(\sin\;2x \) «работает в два раза быстрее», чем \(\sin\;x \).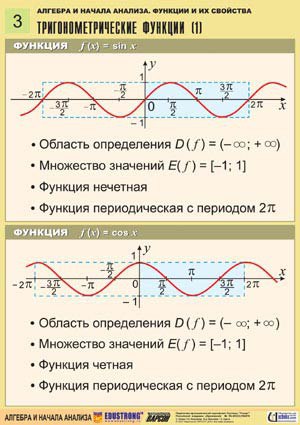 Затем
Затем е. \(u = 2(u/2)\)), это означает, что \(\sin\;u = \sin\;(u+2p)\) для всех действительных чисел \(u\), и, следовательно, период \(\sin\;x \) максимально равен \(2p \). Это противоречие. Почему? Потому что период \(\sin\;x\) равен \(2\pi > 2p\). Следовательно, период \(p \) функции \(\sin\;2x \) не может быть меньше \(\pi \), поэтому период должен быть равен \(\pi \).
е. \(u = 2(u/2)\)), это означает, что \(\sin\;u = \sin\;(u+2p)\) для всех действительных чисел \(u\), и, следовательно, период \(\sin\;x \) максимально равен \(2p \). Это противоречие. Почему? Потому что период \(\sin\;x\) равен \(2\pi > 2p\). Следовательно, период \(p \) функции \(\sin\;2x \) не может быть меньше \(\pi \), поэтому период должен быть равен \(\pi \).
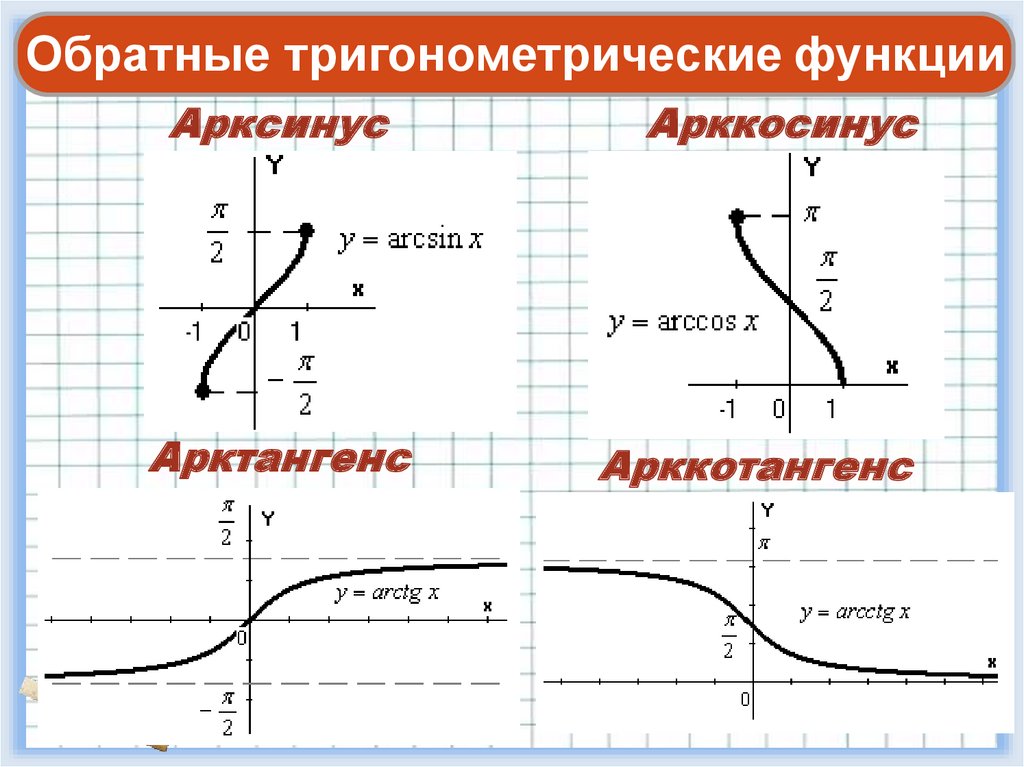 5.2.3.
5.2.3.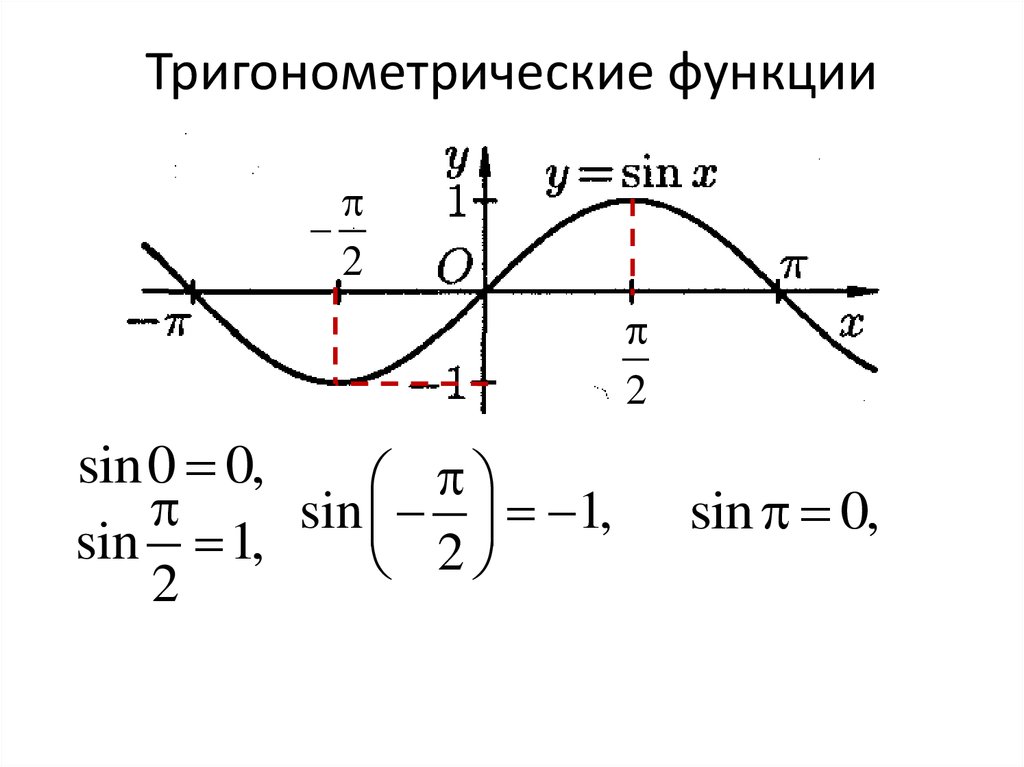 Он просто сдвигает весь график вверх на \(2\). Итак, в данном случае у нас 92 ) \) достигает максимального значения \(2\) и минимального значения \(-2\). Таким образом, амплитуда действительно равна \(2\).
Он просто сдвигает весь график вверх на \(2\). Итак, в данном случае у нас 92 ) \) достигает максимального значения \(2\) и минимального значения \(-2\). Таким образом, амплитуда действительно равна \(2\).  Мы можем видеть это на графике, показанном на рисунке 5.2.7:
Мы можем видеть это на графике, показанном на рисунке 5.2.7: 2.8
2.8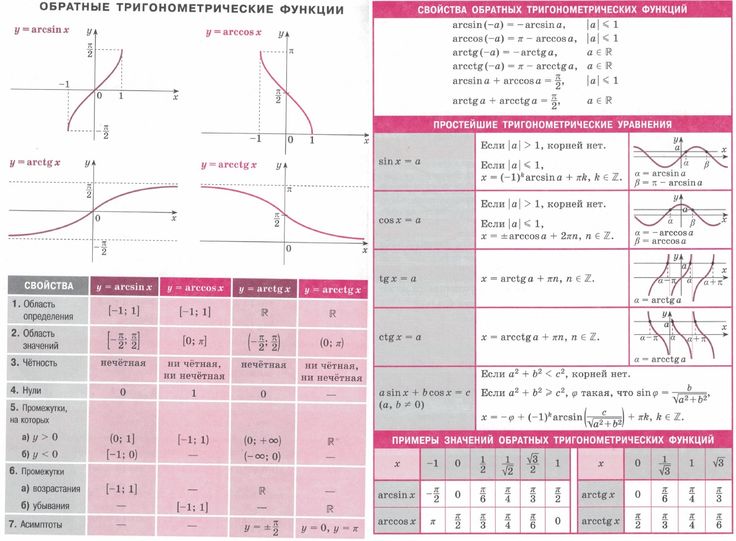 Это видно из его графика на рис. 5.2.9.:
Это видно из его графика на рис. 5.2.9.: Тогда амплитуда равна \(A \), а период равен \(\frac{2\pi}{\omega} \). График показан на рисунке 5.2.10.
Тогда амплитуда равна \(A \), а период равен \(\frac{2\pi}{\omega} \). График показан на рисунке 5.2.10.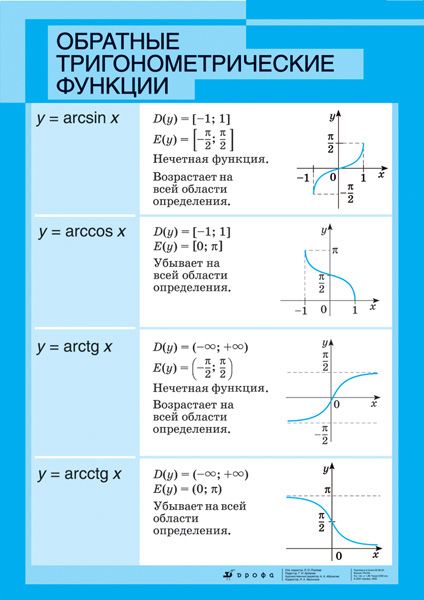 5.2.11. График сдвигается вправо, когда \(\phi >0 \), и влево, когда \(\phi <0 \). Величина \(\frac{\phi}{\omega} \) сдвига называется фазовый сдвиг графика.
5.2.11. График сдвигается вправо, когда \(\phi >0 \), и влево, когда \(\phi <0 \). Величина \(\frac{\phi}{\omega} \) сдвига называется фазовый сдвиг графика.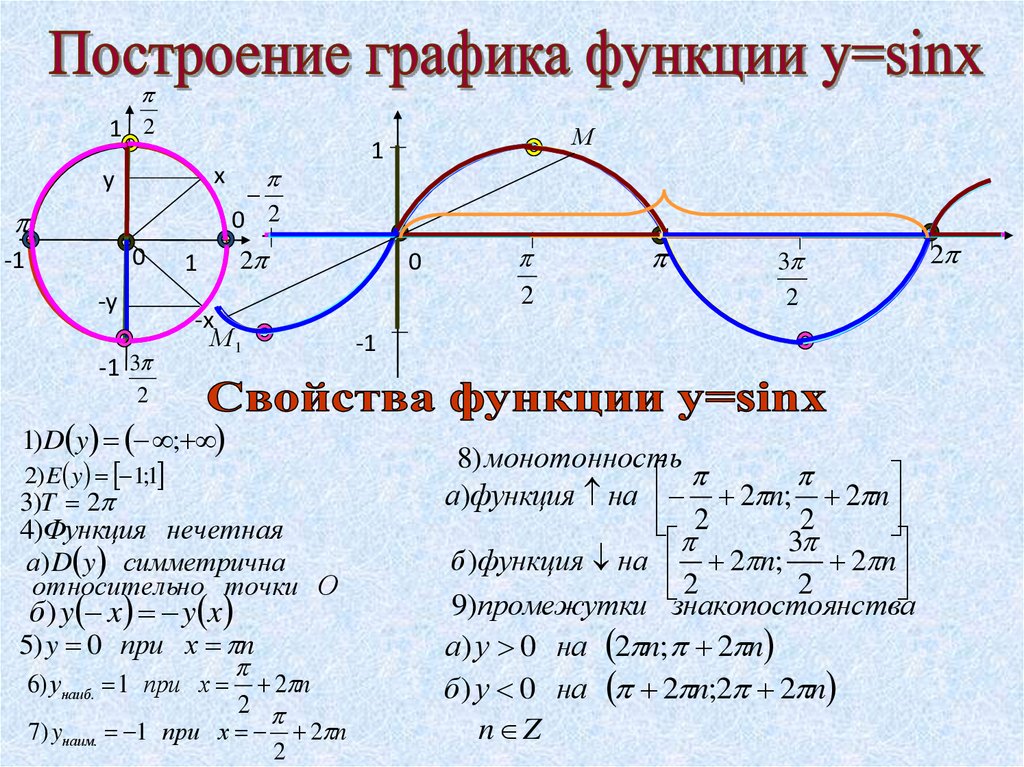 Обратите внимание на отрицательный знак фазового сдвига, поскольку \(3x+\pi=3x-(-\pi)\) имеет вид \(\omega x — \phi\). График показан на рисунке 5.2.13: 9\circ\)) не совпадает по фазе, и \(\sin\;x \) можно сказать, что отстает от \(\sin\;\left( x — \frac{\pi}{6} \right) \ ) на \(\frac{\pi}{6} \) радиан, а \(\sin\;\left( x — \frac{\pi}{6} \right) \) отведения \( \sin \;x \) на \(\frac{\pi}{6} \) радиан. Периодические функции с одинаковым периодом и одинаковым фазовым сдвигом равны в фазе .
Обратите внимание на отрицательный знак фазового сдвига, поскольку \(3x+\pi=3x-(-\pi)\) имеет вид \(\omega x — \phi\). График показан на рисунке 5.2.13: 9\circ\)) не совпадает по фазе, и \(\sin\;x \) можно сказать, что отстает от \(\sin\;\left( x — \frac{\pi}{6} \right) \ ) на \(\frac{\pi}{6} \) радиан, а \(\sin\;\left( x — \frac{\pi}{6} \right) \) отведения \( \sin \;x \) на \(\frac{\pi}{6} \) радиан. Периодические функции с одинаковым периодом и одинаковым фазовым сдвигом равны в фазе . 2: Свойства графиков тригонометрических функций распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
2: Свойства графиков тригонометрических функций распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу. mecmath.net/trig/index.html
mecmath.net/trig/index.html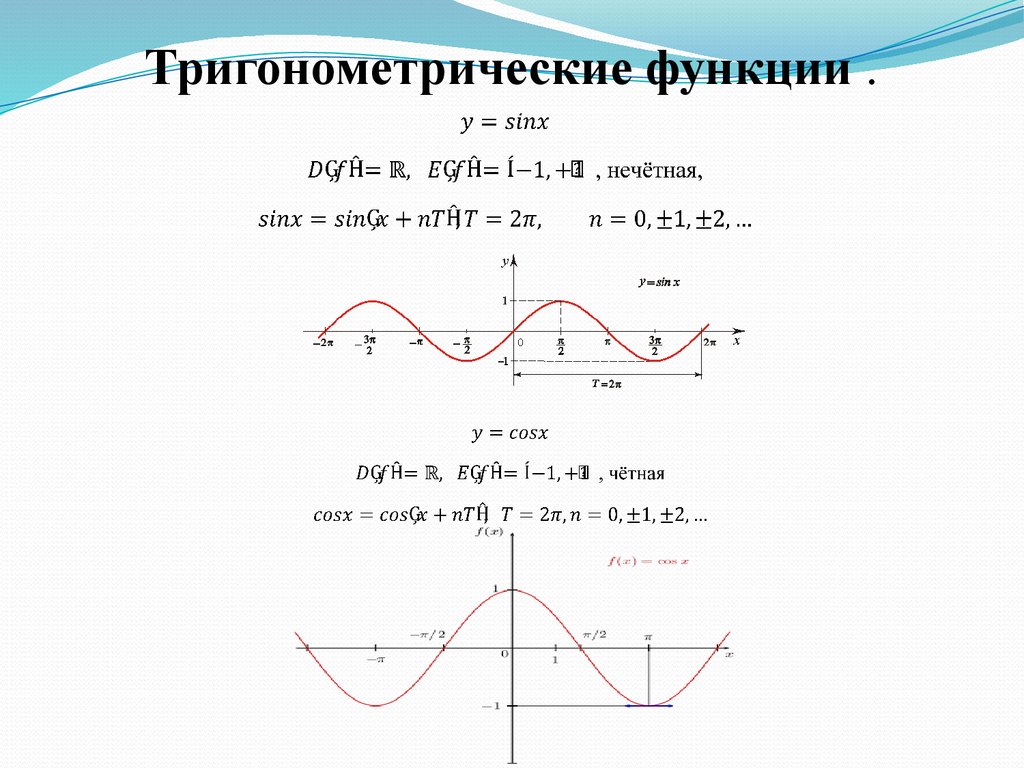 Например, диапазон f ( x ) = sin x представляет собой набор всех действительных чисел между -1 и 1 (т.е. интервал [-1,1]), тогда как диапазон f ( x ) = tan x — это множество всех действительных чисел, как видно из их графиков.
Например, диапазон f ( x ) = sin x представляет собой набор всех действительных чисел между -1 и 1 (т.е. интервал [-1,1]), тогда как диапазон f ( x ) = tan x — это множество всех действительных чисел, как видно из их графиков. Таким образом, функции tan x и cot x имеют период π радиан.
Таким образом, функции tan x и cot x имеют период π радиан.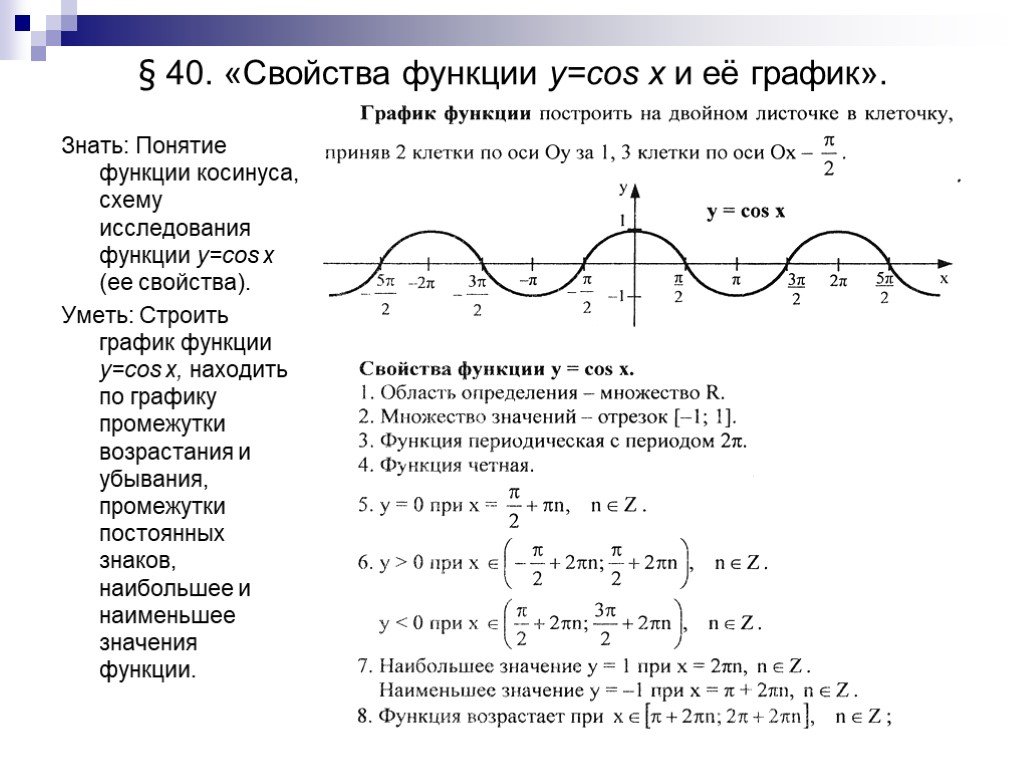 Поскольку sin x имеет период 2 π ,1 мы знаем, что sin ( x +2 π ) = sin x для всех x . Поскольку 2 x является числом для всех x , это означает, в частности, что sin (2 x +2 π = sin 2 x для всех x . Теперь определим f (3 ) = sin 2 x . Тогда
Поскольку sin x имеет период 2 π ,1 мы знаем, что sin ( x +2 π ) = sin x для всех x . Поскольку 2 x является числом для всех x , это означает, в частности, что sin (2 x +2 π = sin 2 x для всех x . Теперь определим f (3 ) = sin 2 x . Тогда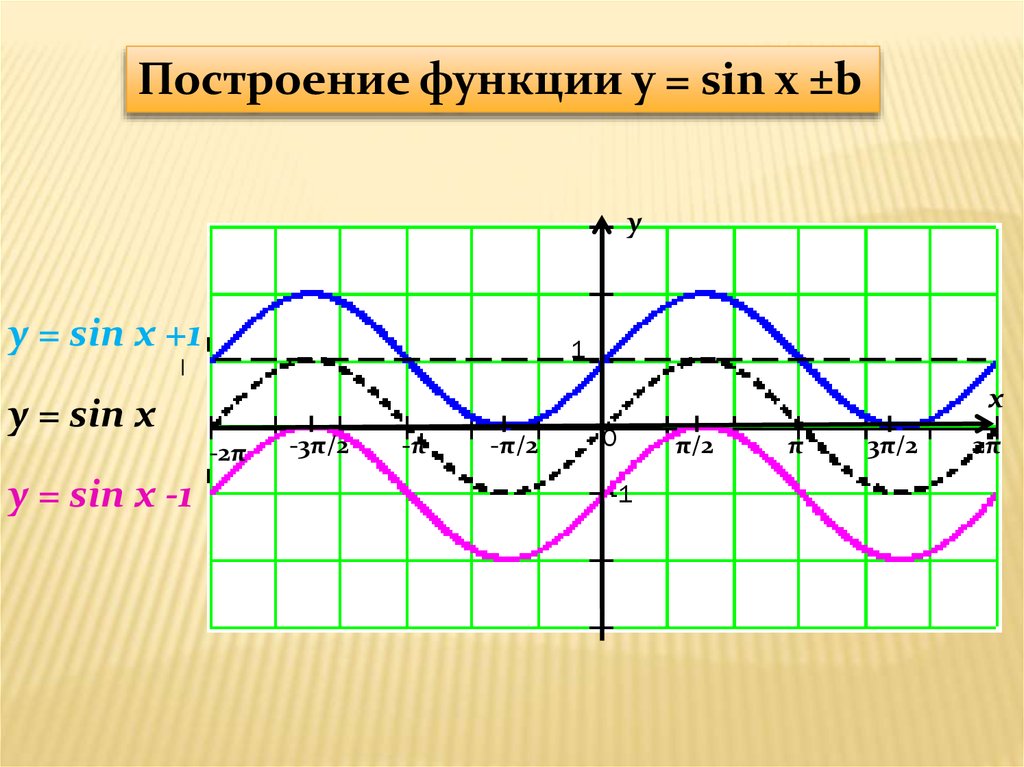 Тогда 0 < 2 p < 2 π , и, следовательно,
Тогда 0 < 2 p < 2 π , и, следовательно, И этот аргумент работает и для других тригонометрических функций. Таким образом, получаем:
И этот аргумент работает и для других тригонометрических функций. Таким образом, получаем: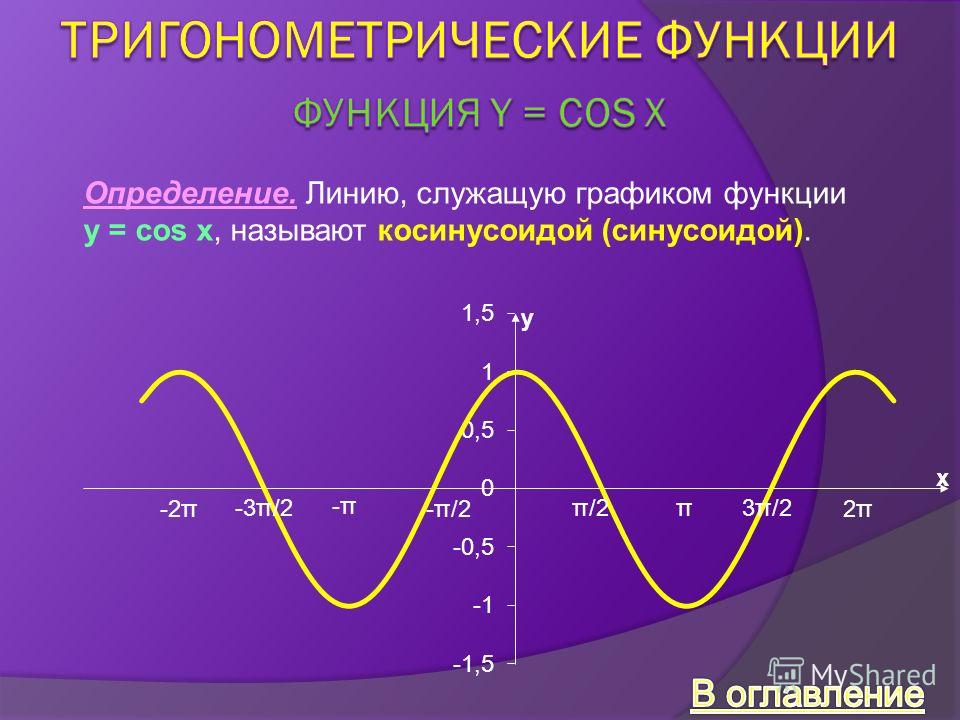 Таким образом, для константы A \(\ne\) 0,
Таким образом, для константы A \(\ne\) 0,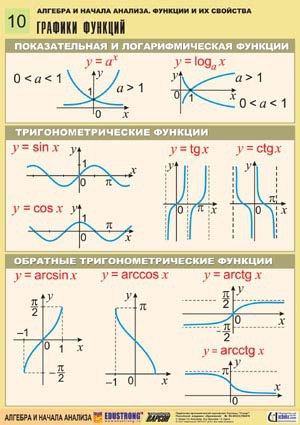 Точно так же cot x , csc x и sec x не имеют амплитуды. Поскольку амплитуда включает вертикальные расстояния, она не влияет на период функции, и наоборот.
Точно так же cot x , csc x и sec x не имеют амплитуды. Поскольку амплитуда включает вертикальные расстояния, она не влияет на период функции, и наоборот. График показан на рисунке 5:
График показан на рисунке 5:
 (почему?).
(почему?).
 В этом случае из графика видно, что максимум близок к 2, а минимум близок к -2.
В этом случае из графика видно, что максимум близок к 2, а минимум близок к -2.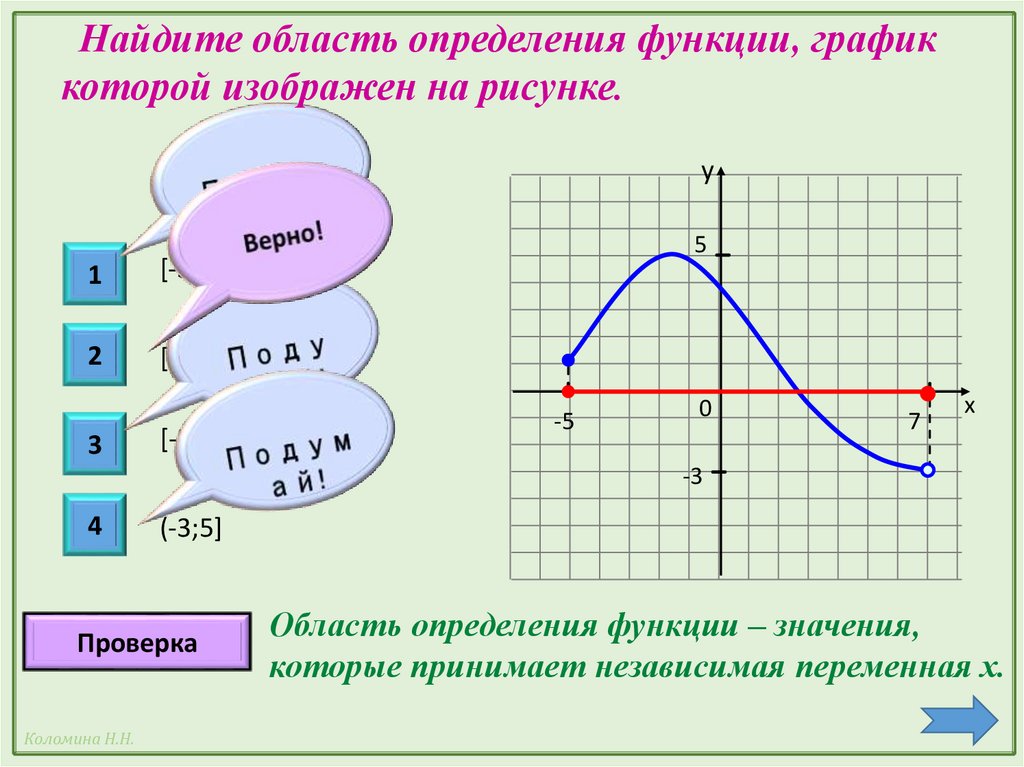 Кроме того, мы знаем, что синусоидальная функция проходит полный цикл, когда ее угол изменяется от 0 до 2 № . Здесь мы берем синус угла ωx − φ . Таким образом, при переходе ωx − φ от 0 до 2 π будет прослеживаться полный цикл функции y = A sin ( ωx − φ ). Этот цикл начинается, когда
Кроме того, мы знаем, что синусоидальная функция проходит полный цикл, когда ее угол изменяется от 0 до 2 № . Здесь мы берем синус угла ωx − φ . Таким образом, при переходе ωx − φ от 0 до 2 π будет прослеживаться полный цикл функции y = A sin ( ωx − φ ). Этот цикл начинается, когда





 к. на экзамене никто не предложит выбор правильного ответа из уже представленных ответов, а также задания будут сложнее, чем данные тесты
к. на экзамене никто не предложит выбор правильного ответа из уже представленных ответов, а также задания будут сложнее, чем данные тесты Будьте практикующим профессором! Решайте задачи!
Будьте практикующим профессором! Решайте задачи!
 ОДДС не выносится на экзамен.
ОДДС не выносится на экзамен.
 Поэтому сумма на конец периода всегда включает сумму на начало периода и за период.
Поэтому сумма на конец периода всегда включает сумму на начало периода и за период. А далее задолженность погашается денежными средствами.
А далее задолженность погашается денежными средствами. Поэтому % расходы отражаются в ОПУ по статей «Финансовые расходы».
Поэтому % расходы отражаются в ОПУ по статей «Финансовые расходы». Только через ОИК!
Только через ОИК! Этот отборочный тест перед приемом на работу поможет вам нанять экспертов с практическими навыками финансового учета.
Этот отборочный тест перед приемом на работу поможет вам нанять экспертов с практическими навыками финансового учета.

 Наши механизмы обратной связи и уникальные алгоритмы позволяют нашим профильным экспертам постоянно улучшать свои тесты.
Наши механизмы обратной связи и уникальные алгоритмы позволяют нашим профильным экспертам постоянно улучшать свои тесты. Мне нравится разнообразие тестов, которые мы использовали для найма разработчиков программного обеспечения и специалистов по данным. Платформа проста в использовании и легко подключается к другому программному обеспечению, которое мы используем.
Мне нравится разнообразие тестов, которые мы использовали для найма разработчиков программного обеспечения и специалистов по данным. Платформа проста в использовании и легко подключается к другому программному обеспечению, которое мы используем.
 Когда вы нанимаете бухгалтера для отслеживания ваших доходов и расходов, тест по финансовому учету (МСФО) — лучший способ гарантировать, что вы получите найм самого высокого качества. Но сначала давайте посмотрим, почему финансовый учет важен в современной бизнес-среде.
Когда вы нанимаете бухгалтера для отслеживания ваших доходов и расходов, тест по финансовому учету (МСФО) — лучший способ гарантировать, что вы получите найм самого высокого качества. Но сначала давайте посмотрим, почему финансовый учет важен в современной бизнес-среде. Таким образом, компаниям будет сложно отслеживать балансовые отчеты в соответствии с различными национальными стандартами, и даже небольшая ошибка может поставить под угрозу точность их отчетов.
Таким образом, компаниям будет сложно отслеживать балансовые отчеты в соответствии с различными национальными стандартами, и даже небольшая ошибка может поставить под угрозу точность их отчетов. МСФО достигли этого, установив единый язык бухгалтерского учета, который снижает затраты на международную отчетность и обеспечивает понимание отчетов всеми инвесторами.
МСФО достигли этого, установив единый язык бухгалтерского учета, который снижает затраты на международную отчетность и обеспечивает понимание отчетов всеми инвесторами.




 Множественный выбор позволяет вашим кандидатам выбирать из списка ответов, которые вы предоставляете, кодирование позволяет вам создать задачу кодирования для их решения, загрузка файла позволяет вашим кандидатам загружать файл, который вы запрашиваете (например, резюме или портфолио), и Эссе позволяет дать открытый текстовый ответ на ваш вопрос. Вы можете узнать больше о различных типах настраиваемых вопросов здесь.
Множественный выбор позволяет вашим кандидатам выбирать из списка ответов, которые вы предоставляете, кодирование позволяет вам создать задачу кодирования для их решения, загрузка файла позволяет вашим кандидатам загружать файл, который вы запрашиваете (например, резюме или портфолио), и Эссе позволяет дать открытый текстовый ответ на ваш вопрос. Вы можете узнать больше о различных типах настраиваемых вопросов здесь. Мы также предлагаем подробные руководства в нашем обширном Центре справки и вдохновения.
Мы также предлагаем подробные руководства в нашем обширном Центре справки и вдохновения. е., из которых: 30 000 д.е. выплачивается авансом до того, как мы въехали; и 30 000 д.е. выплачивается в начале 4-го…
е., из которых: 30 000 д.е. выплачивается авансом до того, как мы въехали; и 30 000 д.е. выплачивается в начале 4-го… Являются ли эти предоплаты по налогу на финансовые активы? Должны ли мы включать их в расчет ожидаемых кредитных убытков? Если нет, то какой стандарт мы должны применять? Ответ Нет,…
Являются ли эти предоплаты по налогу на финансовые активы? Должны ли мы включать их в расчет ожидаемых кредитных убытков? Если нет, то какой стандарт мы должны применять? Ответ Нет,… Согласно МСФО мы должны проверять гудвил на предмет обесценения не реже одного раза в год. Как мы можем сделать это? Деловая репутация не имеет справедливой стоимости и ее невозможно определить…
Согласно МСФО мы должны проверять гудвил на предмет обесценения не реже одного раза в год. Как мы можем сделать это? Деловая репутация не имеет справедливой стоимости и ее невозможно определить…




 В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².
В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с². Известны лишь величины их сторон.
Известны лишь величины их сторон. 2\right)\]
2\right)\] В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².
В виде выражения данное правило записывается следующим образом: (а + с)² = a² + 2ас + с².
 Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).
Таким образом, разность кубов — формула, равная произведению разности данных чисел на их неполный квадрат суммы. В виде разность кубов выглядит следующим образом: а 3 — с 3 = (а — с)(а 2 + ас + с 2).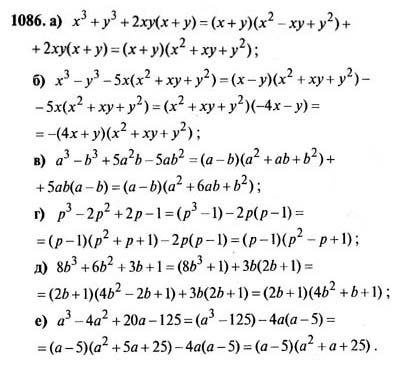 Для лучшего запоминания выпишите все
формулы сокращённого умножения себе на небольшую
шпаргалку .
Для лучшего запоминания выпишите все
формулы сокращённого умножения себе на небольшую
шпаргалку .
 Формулы сокращенного умножения нужно знать наизусть .
Формулы сокращенного умножения нужно знать наизусть .
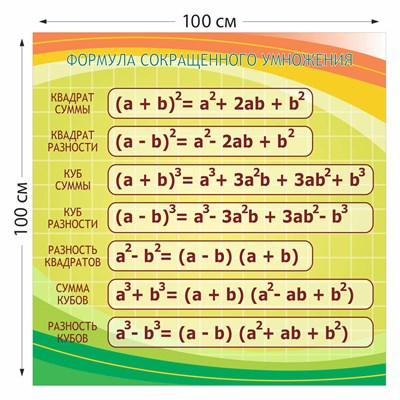 Формулы сокращенного умножения
Формулы сокращенного умножения



 В этом уроке следующий мощный способ: формулы сокращенного умножения … Короче — пох.
В этом уроке следующий мощный способ: формулы сокращенного умножения … Короче — пох. Мы просто умножаем скобки и даем похожие. Вот и получается всех формул сокращенного умножения. Сокращенное умножение связано с тем, что в самих формулах нет умножения скобок и слепка однотипных. Сокращено.) Сразу выдается результат.
Мы просто умножаем скобки и даем похожие. Вот и получается всех формул сокращенного умножения. Сокращенное умножение связано с тем, что в самих формулах нет умножения скобок и слепка однотипных. Сокращено.) Сразу выдается результат. .. По определению степени выражение ( a + b a 8 8 + б )( а + б ). Следовательно, из квадрата суммы можно сделать вывод, что
.. По определению степени выражение ( a + b a 8 8 + б )( а + б ). Следовательно, из квадрата суммы можно сделать вывод, что
 .. Выражение ( a — b ) 2 есть произведение двух полиномов ( a — b ) 9017 б )( а — б ). Следовательно, из квадрата разности можно сделать вывод, что
.. Выражение ( a — b ) 2 есть произведение двух полиномов ( a — b ) 9017 б )( а — б ). Следовательно, из квадрата разности можно сделать вывод, что





 А это значит, что будет очень полезно понять, как они получаются, для чего нужны, а главное, как их запомнить, а затем применить. Затем применяя формулы сокращенного умножения на практике, самое сложное будет посмотреть что такое NS и что у вас есть. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
А это значит, что будет очень полезно понять, как они получаются, для чего нужны, а главное, как их запомнить, а затем применить. Затем применяя формулы сокращенного умножения на практике, самое сложное будет посмотреть что такое NS и что у вас есть. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.

 2$ 92\справа)\]
2$ 92\справа)\] В виде выражения это правило записывается так: (a + c)² = a² + 2ac + c².
В виде выражения это правило записывается так: (a + c)² = a² + 2ac + c². В виде выражения это правило выглядит так: а³ + с³ = (а + с) (а² — ас + с²).
В виде выражения это правило выглядит так: а³ + с³ = (а + с) (а² — ас + с²). В виде разность кубов выглядит так: а 3 — с 3 = (а — с) (а 2 + ас + с 2).
В виде разность кубов выглядит так: а 3 — с 3 = (а — с) (а 2 + ас + с 2).

 Тогда:
Тогда:


 Получаем:
Получаем:
 3 Kb.
3 Kb. к.
к.
 В этом посте мы покажем вам методы, которые вы должны знать для решения подобных задач.
В этом посте мы покажем вам методы, которые вы должны знать для решения подобных задач.
 Достаточно было простой техники «Подстановки».
Достаточно было простой техники «Подстановки».  . .
. .
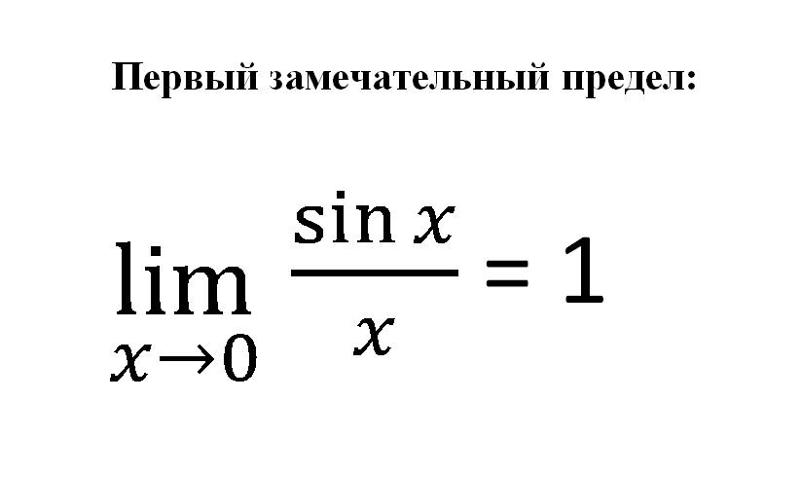
 Пример 4 иллюстрирует.
Пример 4 иллюстрирует.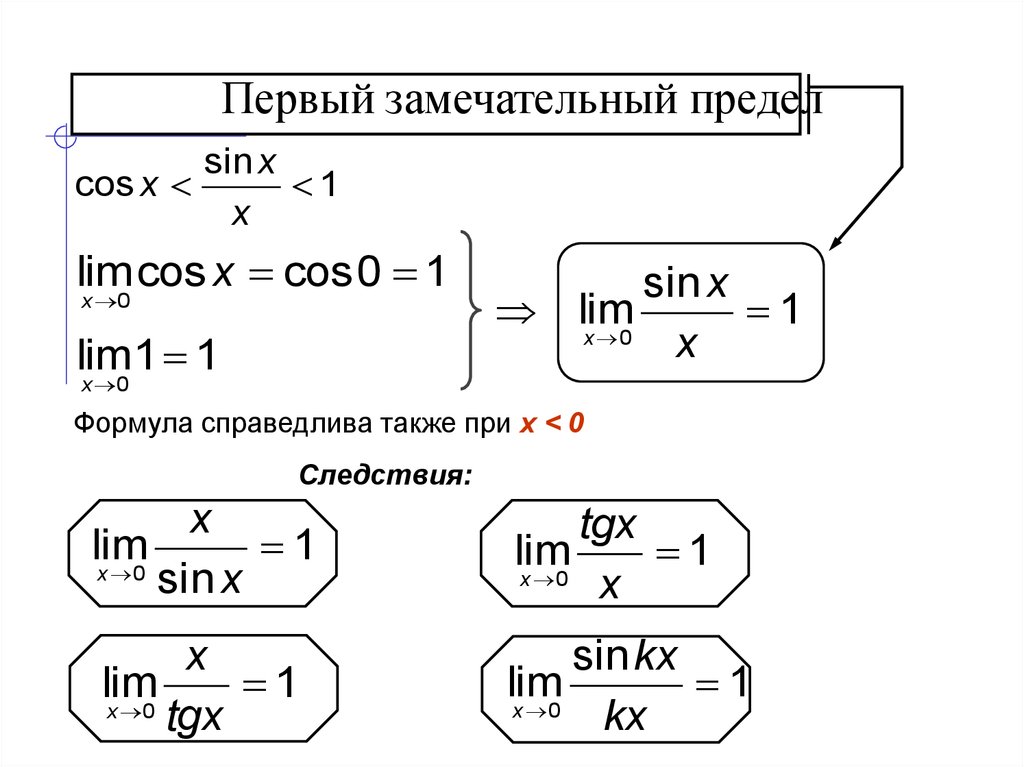 Мы показали это на параллельных графиках ниже. Следовательно, их пределы такие же, как $x \to 0$, и поэтому $\displaystyle{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} = \ lim_{x \to 0}\dfrac{1}{\sqrt{x+5} + \sqrt{5}} = \dfrac{1}{2\sqrt{5}} }$.
Мы показали это на параллельных графиках ниже. Следовательно, их пределы такие же, как $x \to 0$, и поэтому $\displaystyle{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} = \ lim_{x \to 0}\dfrac{1}{\sqrt{x+5} + \sqrt{5}} = \dfrac{1}{2\sqrt{5}} }$. Итак, давайте умножим числитель и знаменатель на сопряженное значение знаменателя, $3+\sqrt{x}$:
Итак, давайте умножим числитель и знаменатель на сопряженное значение знаменателя, $3+\sqrt{x}$: 
 Мы потратили тысячи часов на создание всего, что здесь есть, и с вашей помощью мы можем продолжать расти и предлагать больше!
Мы потратили тысячи часов на создание всего, что здесь есть, и с вашей помощью мы можем продолжать расти и предлагать больше! Я создаю эту вики-сообщество, так как это не совсем ответ на вопрос.
Я создаю эту вики-сообщество, так как это не совсем ответ на вопрос.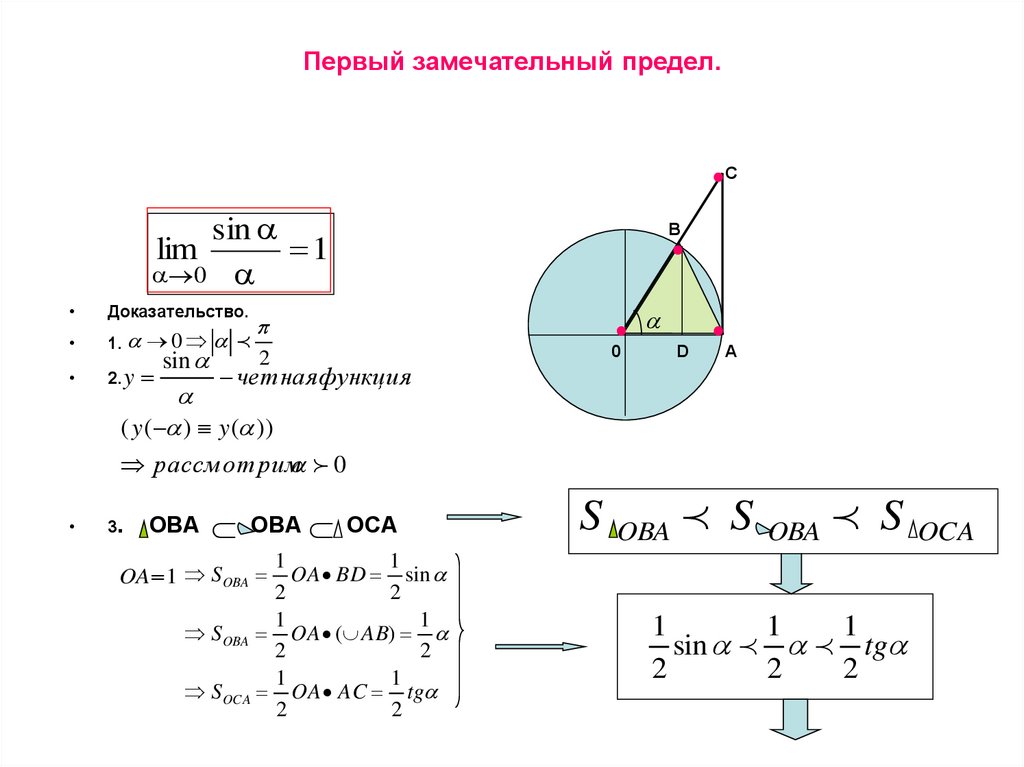 Rawsthorne , Wheaton, Maryland, который в том же разделе того же номера (стр. 42) предложил более сложную задачу *1185 . Звездочка означает, что он предложил задачу, не предлагая решения самостоятельно.
Rawsthorne , Wheaton, Maryland, который в том же разделе того же номера (стр. 42) предложил более сложную задачу *1185 . Звездочка означает, что он предложил задачу, не предлагая решения самостоятельно.
 3=1000. Ваш кодовый замок имеет 1000 комбинаций паролей.
3=1000. Ваш кодовый замок имеет 1000 комбинаций паролей.



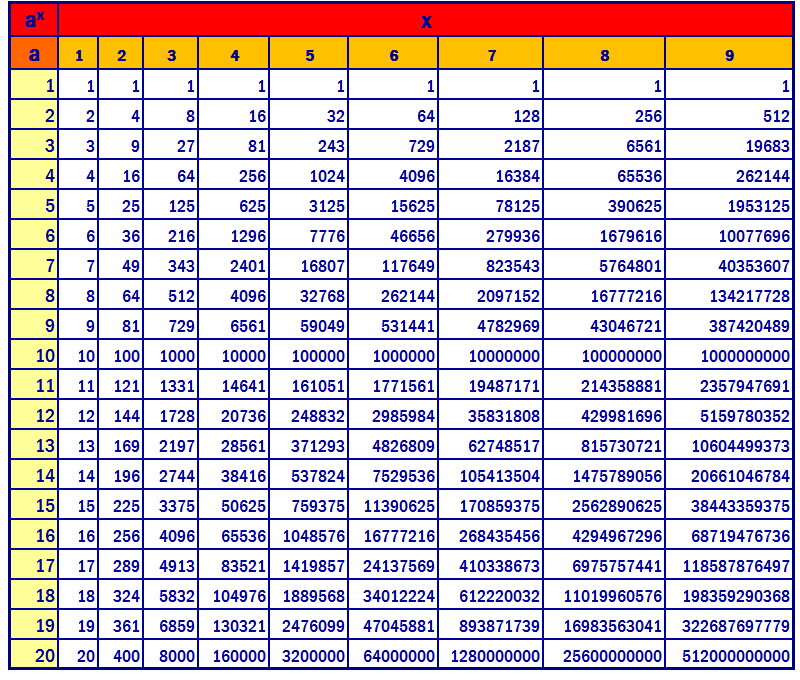
 е. указанных чисел будет:
е. указанных чисел будет:
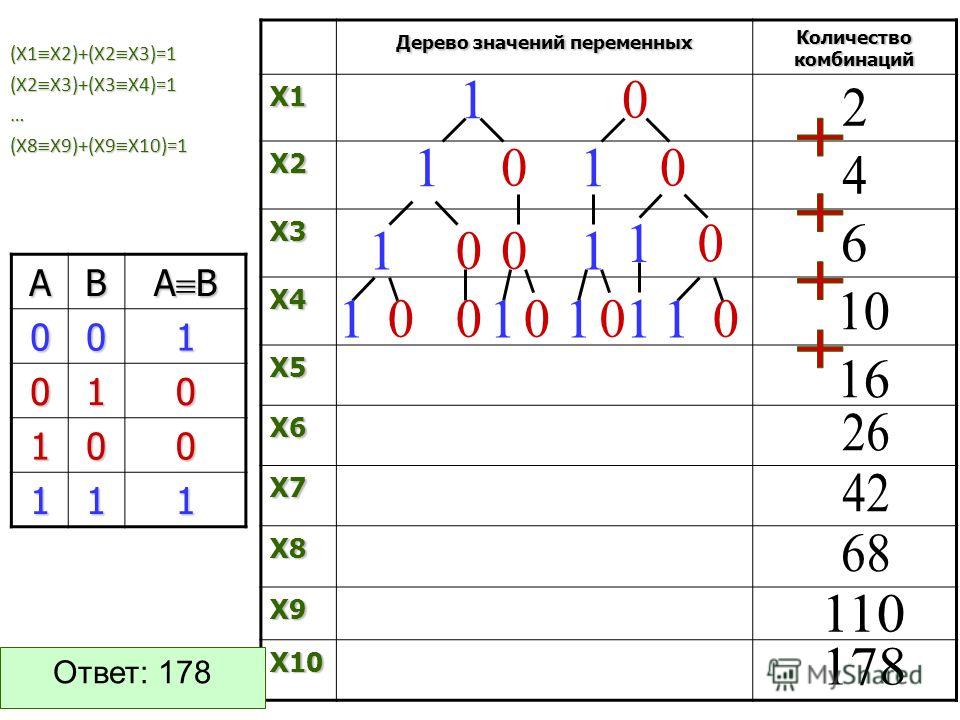 Поясним последний фактор на
следующем примере.
Поясним последний фактор на
следующем примере.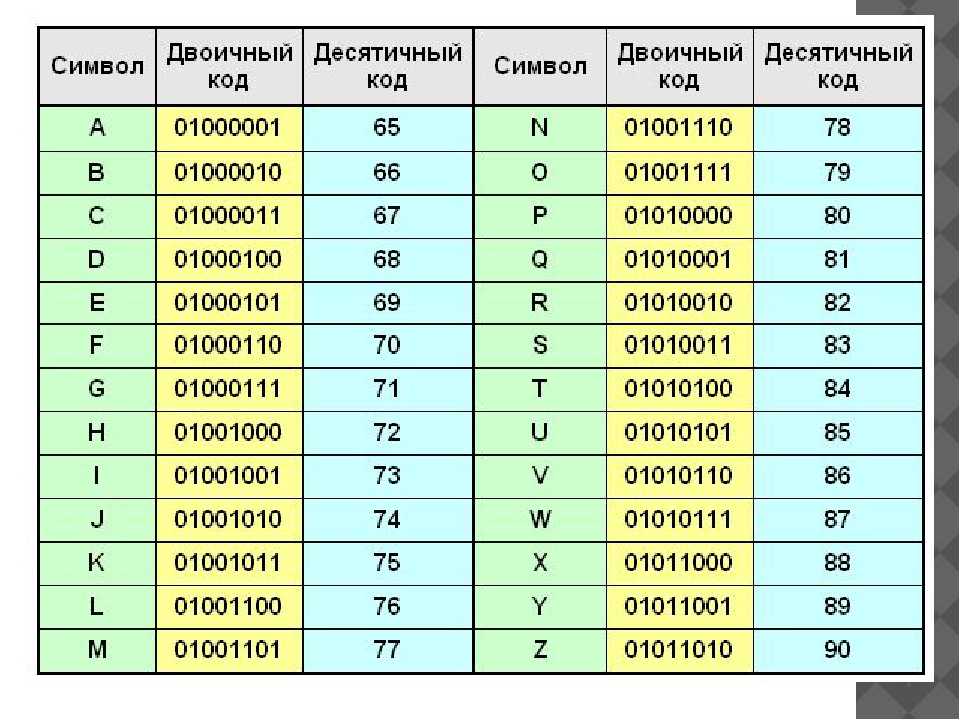 к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168.
к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168. д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
д. n = 8! = 1*2*3*4*5*6*7*8 = 40320. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.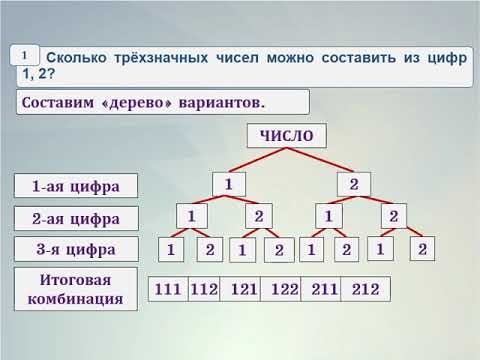 Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?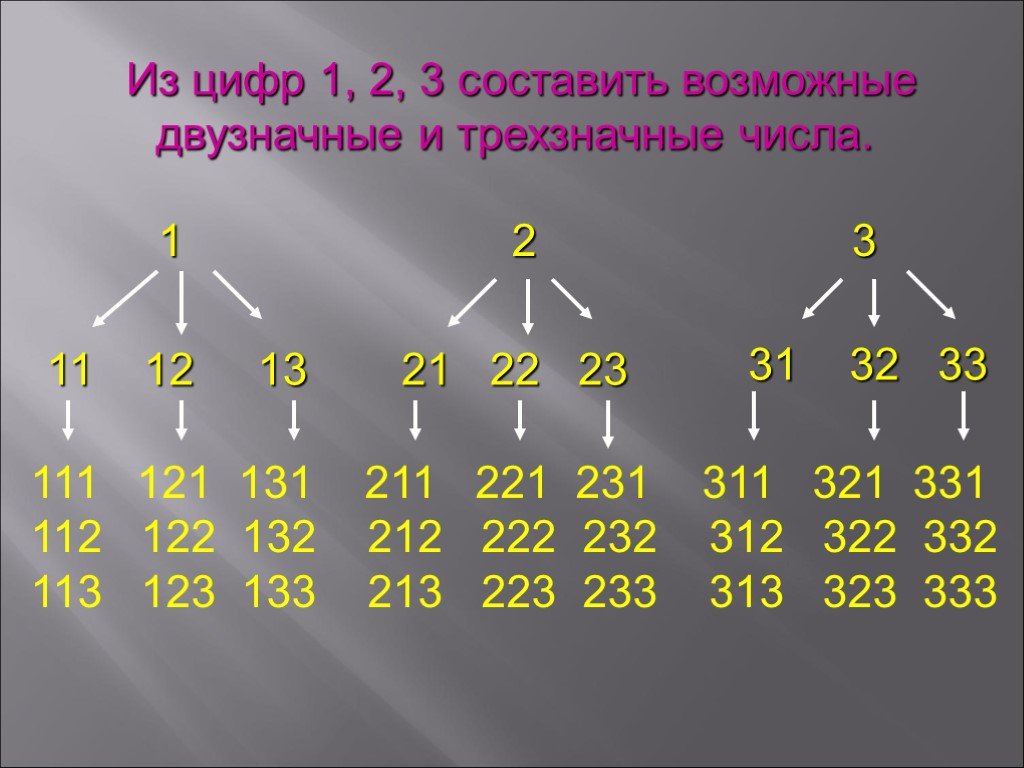 Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну? Перестановки, размещения, сочетания.
Перестановки, размещения, сочетания.
 Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
 06
06 40
40




 Сколько различных пятизначных номеров может составить мальчик?
Сколько различных пятизначных номеров может составить мальчик?
 Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).
Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»). Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
 При расчете вам необходимо рассмотреть все возможные способы заполнения этих пустых мест (здесь вы упустили возможность $(2)$). Надеюсь, вы получили ответ.
При расчете вам необходимо рассмотреть все возможные способы заполнения этих пустых мест (здесь вы упустили возможность $(2)$). Надеюсь, вы получили ответ. Мы должны разместить все цифры $3$ в каждой комбинации. Таким образом, это можно сделать только способом $1$.
Мы должны разместить все цифры $3$ в каждой комбинации. Таким образом, это можно сделать только способом $1$. Порядок не имеет значения — он должен зависеть исключительно от различных полученных чисел.
Порядок не имеет значения — он должен зависеть исключительно от различных полученных чисел.
 ..
.. Онлайн вариант факт…
Онлайн вариант факт… Данная игра включает все специфические шахматные правила.
Играть можно без регистрации (без испытательного периода) и оплаты полностью бесплатно.
Ваш веб обозреватель, браузер должен включать поддержку flash.
Браузерная игра — это значит, что играть можно прямо в вашем web просмотрщике (броузере),
без необходимости загрузки
дистрибутива программы на диск ПК.
Ход делается за два клика мышки: первым кликом вы указываете на фигуру, вторым нажатием мышки фигура ходит.
Данная игра включает все специфические шахматные правила.
Играть можно без регистрации (без испытательного периода) и оплаты полностью бесплатно.
Ваш веб обозреватель, браузер должен включать поддержку flash.
Браузерная игра — это значит, что играть можно прямо в вашем web просмотрщике (броузере),
без необходимости загрузки
дистрибутива программы на диск ПК.
Ход делается за два клика мышки: первым кликом вы указываете на фигуру, вторым нажатием мышки фигура ходит. ActionScript компилируется в байткод, который включается в SWF-файл.
ActionScript компилируется в байткод, который включается в SWF-файл. С одной стороны, в игре имеется очень много различных настроек внешнего вида фигур и шахматной доски, с другой стороны — игра Chess3D позволяет тщательно анализировать каждую партию, сохранять игры и загружать их в любое время. Различные уровни сложности удовлетворят каждого игрока, так как здесь себе найдет достойного противника абсолютно каждый!
С одной стороны, в игре имеется очень много различных настроек внешнего вида фигур и шахматной доски, с другой стороны — игра Chess3D позволяет тщательно анализировать каждую партию, сохранять игры и загружать их в любое время. Различные уровни сложности удовлетворят каждого игрока, так как здесь себе найдет достойного противника абсолютно каждый! Из особенностей игры стоит отметить весьма низкий уровень графики и ограниченное количество настроек, которые, якобы, позволяют менять внешний вид, хотя на самом деле изменяется лишь фоновый рисунок, а сама шахматная доска и фигуры остаются такими же. Музыкальное сопровождение Falco Chess немного резкое, и отвлекает от процесса игры. Никакой статистики и отчетности игрока в данной игре нет, поэтому, делаем вывод, что она предназначена исключительно новичков, которые хотят скоротать время, но никак не повысить уровень свой игры.
Из особенностей игры стоит отметить весьма низкий уровень графики и ограниченное количество настроек, которые, якобы, позволяют менять внешний вид, хотя на самом деле изменяется лишь фоновый рисунок, а сама шахматная доска и фигуры остаются такими же. Музыкальное сопровождение Falco Chess немного резкое, и отвлекает от процесса игры. Никакой статистики и отчетности игрока в данной игре нет, поэтому, делаем вывод, что она предназначена исключительно новичков, которые хотят скоротать время, но никак не повысить уровень свой игры. рф — магазин шахмат
рф — магазин шахмат
 Именно это умение позволяло сохранять тысячи жизней и получать такие желанные триумфы. Все это со временем обрело игровую форму, два противника встречались у шахматной доски, где и вершился исход битвы, битвы разума.
Именно это умение позволяло сохранять тысячи жизней и получать такие желанные триумфы. Все это со временем обрело игровую форму, два противника встречались у шахматной доски, где и вершился исход битвы, битвы разума. Сражение может завлечь вас на целый часы! Игрок, находящийся по ту сторону экрана, возможно будет находиться за тысячи километров от вас, однако это не столь важно, поскольку наличие Интернета стирает все грани расстояния.
Сражение может завлечь вас на целый часы! Игрок, находящийся по ту сторону экрана, возможно будет находиться за тысячи километров от вас, однако это не столь важно, поскольку наличие Интернета стирает все грани расстояния. Эта флеш реализация популярнейшей игры не содержит ничего лишнего. Только доска и фигуры. Так просто и гениально, что невольно вспоминаются слова Остапа про Межпланетный Васюкинский Шахматный Турнир… Все просто и без наворотов. Играть нужно вдвоем, думать эту игру не научили разработчики. Тем лучше, ничего не будет тормозить. Берите друга в охапку и проведите время с пользой. Может вспомните какие-нибудь дебюты, защиту Алехина, например?
Эта флеш реализация популярнейшей игры не содержит ничего лишнего. Только доска и фигуры. Так просто и гениально, что невольно вспоминаются слова Остапа про Межпланетный Васюкинский Шахматный Турнир… Все просто и без наворотов. Играть нужно вдвоем, думать эту игру не научили разработчики. Тем лучше, ничего не будет тормозить. Берите друга в охапку и проведите время с пользой. Может вспомните какие-нибудь дебюты, защиту Алехина, например? Если возможности электронного рабочего стола позволяют, можно развернуть сюжет ШАХМАТЫ 2 ИГРОКА во весь экрани усилить эффект от прохождения сценариев. Многие вещи действительно имеет смысл рассмотреть детальнее.
Если возможности электронного рабочего стола позволяют, можно развернуть сюжет ШАХМАТЫ 2 ИГРОКА во весь экрани усилить эффект от прохождения сценариев. Многие вещи действительно имеет смысл рассмотреть детальнее.


 Основные функции: — Получить игр … и полную графику … все игр
Основные функции: — Получить игр … и полную графику … все игр  ..онлайн шахматы игра
..онлайн шахматы игра  Они никогда не могут двигаться или захватывать назад. Если прямо перед пешкой есть другая фигура, он не может пройти мимо или взять эту фигуру.
Они никогда не могут двигаться или захватывать назад. Если прямо перед пешкой есть другая фигура, он не может пройти мимо или взять эту фигуру.

 Если A3 содержит значение, не равное нулю, производится расчет дискриминанта по известной формуле. Иначе будет выведена текстовая строка «NaN», то есть, уравнение не является квадратным, вычислить значение дискриминанта невозможно.
Если A3 содержит значение, не равное нулю, производится расчет дискриминанта по известной формуле. Иначе будет выведена текстовая строка «NaN», то есть, уравнение не является квадратным, вычислить значение дискриминанта невозможно. Также изменена формула расчета второго корня уравнения.
Также изменена формула расчета второго корня уравнения. 0,5».
0,5».


 04.2023
04.2023 04.2023
04.2023 2023
2023 leag)морская миля (naut.mi)кабельтов (cbl)фатом, морская сажень (fath)морская миля СШАкабельтов СШАфатом США (fath)Адмиралтейская миляАдмиралтейский кабельтовквадра Аргентиныквадра Боливииквадра Чиликвадра Колумбииквадра Эквадораквадра Нигарагуаквадра Парагваяквадра Уругваявара Аргентинывара Бразилиивара Чиливара Колумбиивара Коста Рикивара Кубывара Доминиканской республикивара Эквадоравара Эль Сальвадоравара Гватемалывара Гондурасавара Мексикивара Никарагуавара Панамывара Парагваявара Перу (перуанская)вара Перу (испанская)вара Уругваявара Сан-Томе и Принсипивара Венесуэлыри (里)тё (町)дзё (丈)хиро (尋)кэн (間)сяку (尺)сун (寸)бу (分)рин (厘)мо (毛, 毫)ли (市里)уин (引)жанг (市丈)чи (市尺)кан (市寸)фен (市分)ли малое (釐 или 厘)хао (毫)сы (丝)ху (忽)ли (里)инь (引)чжан (丈)бу (步)чи (尺)цунь (寸)фень (分)ли малое (釐 или 厘)хао (毫)сы (丝)ху (忽)чи (尺)цунь (寸)фэнь (分)йот (โยชน์, лига)сен (เส้น, канат)ва (วา, сажень)сок (ศอก, локоть)кып (คืบ, ладонь)ниу (นิ้ว, сиамский дюйм)крабиат (กระเบียด четверть дюйма)диоптриягеографическая миляюнит (U)горизонтальный шаг (HP)пикапика пункт (пт)пункт (пт)пиксель (px)твип (twip)цицеропункт (пт)штрих (парижская точка)красное смещение (z)парсек (пк)световой годастрономическая единица (а.
leag)морская миля (naut.mi)кабельтов (cbl)фатом, морская сажень (fath)морская миля СШАкабельтов СШАфатом США (fath)Адмиралтейская миляАдмиралтейский кабельтовквадра Аргентиныквадра Боливииквадра Чиликвадра Колумбииквадра Эквадораквадра Нигарагуаквадра Парагваяквадра Уругваявара Аргентинывара Бразилиивара Чиливара Колумбиивара Коста Рикивара Кубывара Доминиканской республикивара Эквадоравара Эль Сальвадоравара Гватемалывара Гондурасавара Мексикивара Никарагуавара Панамывара Парагваявара Перу (перуанская)вара Перу (испанская)вара Уругваявара Сан-Томе и Принсипивара Венесуэлыри (里)тё (町)дзё (丈)хиро (尋)кэн (間)сяку (尺)сун (寸)бу (分)рин (厘)мо (毛, 毫)ли (市里)уин (引)жанг (市丈)чи (市尺)кан (市寸)фен (市分)ли малое (釐 или 厘)хао (毫)сы (丝)ху (忽)ли (里)инь (引)чжан (丈)бу (步)чи (尺)цунь (寸)фень (分)ли малое (釐 или 厘)хао (毫)сы (丝)ху (忽)чи (尺)цунь (寸)фэнь (分)йот (โยชน์, лига)сен (เส้น, канат)ва (วา, сажень)сок (ศอก, локоть)кып (คืบ, ладонь)ниу (นิ้ว, сиамский дюйм)крабиат (กระเบียด четверть дюйма)диоптриягеографическая миляюнит (U)горизонтальный шаг (HP)пикапика пункт (пт)пункт (пт)пиксель (px)твип (twip)цицеропункт (пт)штрих (парижская точка)красное смещение (z)парсек (пк)световой годастрономическая единица (а.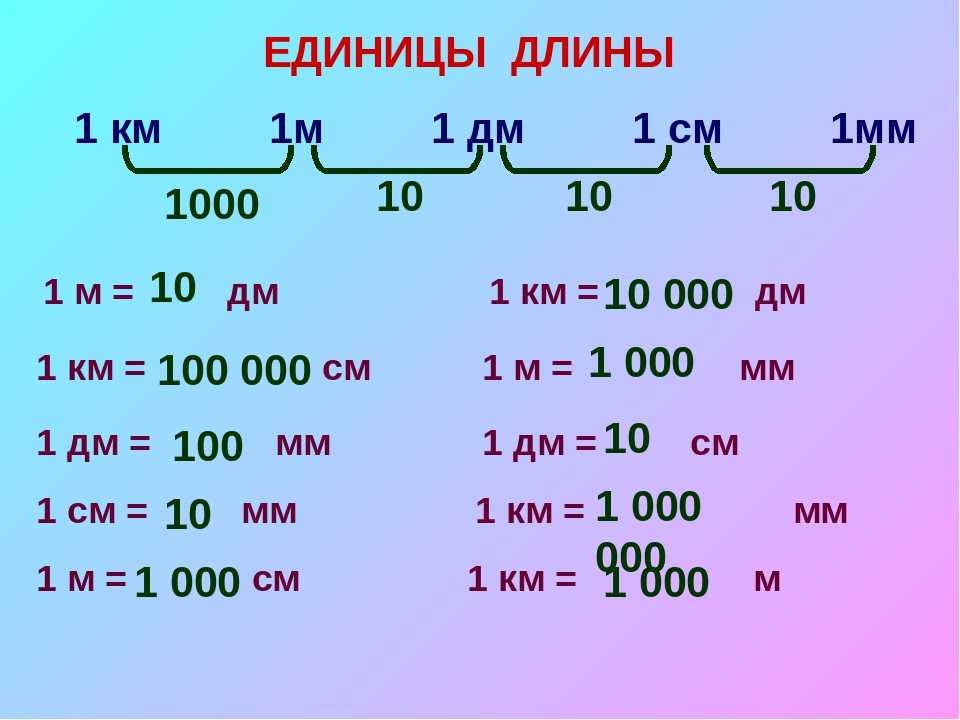 е.)световая минутасветовая секундасветовая микросекундасветовая наносекундасветовая пикосекундапланковская длина (L)Всё
е.)световая минутасветовая секундасветовая микросекундасветовая наносекундасветовая пикосекундапланковская длина (L)Всё е.)световая минутасветовая секундасветовая микросекундасветовая наносекундасветовая пикосекундапланковская длина (L)Всё
е.)световая минутасветовая секундасветовая микросекундасветовая наносекундасветовая пикосекундапланковская длина (L)Всё , что примерно эквивалентно 39,37 дюймам.
, что примерно эквивалентно 39,37 дюймам.