Задание 7 ОГЭ по математике. Числовые неравенства, координатная прямая.
Задание 7 ОГЭ по математике – это решение неравенств, а также выбор верного или неверного утверждения. Тема задания — расположение чисел на координатной прямой.
При выполнении задания 7 ОГЭ по математике необходимо уметь сравнивать числа, включая обыкновенные и десятичные дроби, а также расставлять их на числовой прямой.
Приступим к решению задач.
Пример 1. Какое из следующих чисел заключено между числами и ?
| 1) 0,4 | 2) 0,5 | 3) 0,6 | 4) 0,7 |
Решение. Чтобы ответить на вопрос задачи, преобразуем дроби к виду десятичных:
Между числами 0,58 и 0,625 находится число 0,6. Но в ответ здесь указывается не само число, а номер, под которым оно записано.
Ответ: 3.
Пример 2. Одно из чисел отмечено на прямой точкой. Укажите это число.
В ответе укажите номер правильного варианта.
| 2) | 3) | 4) |
Решение. Выделим целую часть в каждой неправильной дроби:
Отметим на числовой прямой числа 2, 3, 4, 5.
Точка, показанная на рисунке, соответствует числу, которое меньше, чем 5, но больше, чем 4,5. Значит, подходит .
Ответ: 1.
Пример 3. Какому промежутку принадлежит число?
В ответе укажите номер правильного варианта.
| 1) [4; 5] | 2) [5; 6] | 3) [6; 7] | 4) [7; 8] |
Решение. Составим двойное неравенство:
Ответ очевиден.
Ответ: 4.
Пример 4. На координатной прямой отмечены числа а, b и c.
Из следующих утверждений выберите верное. В ответе укажите номер правильного варианта.
| 1) | 2) | 3) | 4) |
Решение. Заметим, что Проанализируем предложенные утверждения:
1) Неверно. Из меньшего вычитается большее, разность меньше нуля.
2) Неверно. Из большего вычитается меньшее, разность больше нуля.
3) Верно. Из меньшего вычитается большее, разность меньше нуля.
4) Неверно. Из меньшего вычитается большее, разность меньше нуля.
Верно только утверждение 3.
Ответ: 3.
Пример 5. На координатной прямой отмечены числа а и х.
Какое из следующих чисел наименьшее? В ответе укажите номер правильного варианта.
| 2) | 3) -a | 4) a-x |
Решение. Можно решить эту задачу строго математическими рассуждениями. А мы пойдём другим, более наглядным путём. Позволим себе такую вольность, т. к. от нас требуется только правильный ответ. Выберем условную единицу на числовой прямой и оценим приблизительно числа а и х.
Позволим себе такую вольность, т. к. от нас требуется только правильный ответ. Выберем условную единицу на числовой прямой и оценим приблизительно числа а и х.
Итак, предположим, что Тогда рассчитаем предложенные варианты и выберем наименьшее значение:
1) – наименьшее из всех чисел
2)
3)
4)
Ответ: 1.
Замечание. Условную величину -1 можно было отметить в другом месте числовой прямой. Результат вычислений при этом не изменится. Проверьте сами на следующем рисунке:
Пример 6. Известно, что число отрицательное. На каком из рисунков точки с координатами расположены на координатной прямой в правильном порядке?
В ответе укажите номер правильного варианта.
Решение. Используем сначала наглядно-вычислительный способ. Пусть , тогда , . Отсюда понятно, что . Такой ситуации соответствует рисунок под цифрой 2.
Ответ: 2.
Замечание. Значение буквенной переменной выбиралось произвольно. Подставив любое другое отрицательное число, мы придём к тем же самым выводам.
Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Задание 7 ОГЭ по математике. Числовые неравенства, координатная прямая.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 08.05.2023
ГДЗ Алгебра 7 класс | Топ 2023
Поскольку не все школьники прилежно выполняли домашние и классные задания по математике с первого по шестой класс включительно, алгебра в ряде случаев вызывает серьезную обеспокоенность у семиклассников. Чтобы наверстать упущенное и приобрести глубокие и полные знания по дисциплине в настоящем, создать задел на будущее, потребуется ответственная и скрупулезная подготовка. Для её организации гдз по алгебре за 7 класс – понятный и доступный практически каждому школьнику инструмент.
Чтобы наверстать упущенное и приобрести глубокие и полные знания по дисциплине в настоящем, создать задел на будущее, потребуется ответственная и скрупулезная подготовка. Для её организации гдз по алгебре за 7 класс – понятный и доступный практически каждому школьнику инструмент.
Чтобы результат подготовки оправдал ожидания, а в идеале – превзошел их, необходимо:
- Провести эффективное планирование подготовительных занятий. Оно должно учитывать базовый уровень математических знаний семиклассника, его заинтересованность, степень ответственности.
- Грамотно и четко распределить временной ресурс. Слишком малое количество времени не позволит качественно проработать все темы. Желательно выделять на работу минимум час ежедневно. В том случае, если математических навыков недостаточно, рекомендуется увеличить время подготовки до полутора-двух. Если такой режим занятий невозможен, специалисты рекомендуют в качестве альтернативы трехразовые недельные занятия по два часа.

- Периодически проверять достигнутый результат. Используя справочные материалы по алгебре, сделать это значительно проще. В сборниках все решения и ответы приведены в соответствии с образовательными стандартами, в которых регламентированы:
- принципы правильной записи условия: дано, чертежей, схем, формулирования вопросов;
- алгоритм получения правильного ответа, последовательность рассмотрения вариантов решения заданий;
- логика выбора и фиксирования верного результата.
Очевидные преимущества применения онлайн помощников
Самопроверка – результативная и полезная методика проверки собственных знаний, а также динамики подготовительных работ. Она не подразумевает финансовых вложений, то есть поможет экономить семейный бюджет, что актуально для многих семей, в которых есть дети-школьники. Помимо экономической выгоды, самоконтроль с привлечением онлайн ответов по алгебре в 7 классе позволяет выработать важный навык работы с математической информацией:
- её выбором, сбором всех необходимых данных;
- анализом, сравнением;
- поиском актуальных решений;
- технологией верной записи результатов.

Ряд школьных педагогов считают такую подготовку интересным и полезным решением не только для тех школьников, кто по тем или иным причинам не получает регулярного объяснения материала от учителя. Но и для тех, кто учится в традиционной школе, в офлайновом режиме. Многие современные учителя признали, что семиклассники используют решебники не только для простого списывания готовых ответов, а и для того, чтобы более внимательно, в спокойной домашней обстановке, проанализировать и понять даже самые сложные темы, параграфы, задания. Но даже переписывание ответов из еуроки ГДЗ – полезная идея с точки зрения запоминания техники их отображения. Это пригодится при написании самостоятельных, контрольных, ВПР по дисциплине.
Критерии выбора качественного ресурса со справочной информацией
В поиске наиболее эффективного ресурса со сборниками решебников семиклассники обращают внимание на такие важные моменты:
- наличие достаточного количества учебного материала на сайте и подробных решений по алгебре 7 класс к нему.
 Случаи, когда начав заниматься по решебникам с целью улучшить оценку, углубить знания, школьники переходили на более серьезный уровень подготовки, например, олимпиадный, встречаются в практике;
Случаи, когда начав заниматься по решебникам с целью улучшить оценку, углубить знания, школьники переходили на более серьезный уровень подготовки, например, олимпиадный, встречаются в практике; - наглядность и удобство интерфейса, эффективно организованный поиск. Чаще всего решения необходимы в условиях ограниченного времени. И возможность найти нужное задание и ответ к нему в минимально короткие сроки крайне важна. Поэтому к наиболее актуальным ресурсам относятся те, на которых поиск быстрых ответов по алгебре за 7 класс организован не только по автору и названию пособия, но и по теме, разделу, номерам страниц.
Еще один важный запрос – наличие четкой и качественной фотографии обложки учебного пособия на странице поиска. У учащихся неплохо развита зрительная память и наличие такой «подсказки» – идеальное решение, чтобы быстро найти нужный вопрос и ответ на него.
Кто чаще всего использует гдз по алгебре к школьным учебникам
По мнению педагогов и экспертов, хотя бы раз за весь учебный год решебниками воспользовался практически каждый семиклассник. Например, перед ответственной контрольной или не успевая выполнить домашнюю работу. Но есть и такие категории пользователей, которые применяют сборники готовых ответов регулярно или постоянно. К ним относятся:
Например, перед ответственной контрольной или не успевая выполнить домашнюю работу. Но есть и такие категории пользователей, которые применяют сборники готовых ответов регулярно или постоянно. К ним относятся:
Репетиторы и руководители математических кружков и курсов для учеников средней школы, которые сами не являются школьными учителями. Для них решебники становятся актуальной и готовой методической разработкой, по которой можно изучить, как следует:
- объяснять те или иные темы в соответствии с действующим ФГОСом;
- записывать условие и решение;
- отображать ответ.
Семиклассники, находящиеся на семейной или домашней форме обучения. Им пособия-решебники позволяют понять, как применять на практике полученные теоретические алгебраические знания. В большинстве случаев этим школьникам сборники готовых ответов эффективно заменяют объяснение учителя.
Ученики, часто пропускающие занятия в классе по уважительным причинам.
 Например, часто болеющие или профессионально занимающиеся творчеством, спортом и по этой причине уезжающие на спортивные сборы, соревнования, конкурсы. В этом случае по решебникам разбираются пропущенные темы, определяются пути и методы решения практических заданий по ним.
Например, часто болеющие или профессионально занимающиеся творчеством, спортом и по этой причине уезжающие на спортивные сборы, соревнования, конкурсы. В этом случае по решебникам разбираются пропущенные темы, определяются пути и методы решения практических заданий по ним.
В связи с переводом на дистанционную форму обучения всех школьников в период осуществления карантинных мероприятий, онлайн справочники стали еще более востребованы и популярны у всех без исключения семиклассников. Количество часов на дисциплину значительно сократилось, и сами уроки тоже стали короче – их продолжительность уменьшилась с традиционных 45 до 30 минут соответственно. Поскольку объем материала, который необходимо освоить в 7-м классе по алгебре меньше не стал, как не снизились и требования к качеству знаний, семиклассники и их родители, учителя стали искать альтернативные формы и инструменты обучения. В их числе и сборники с готовыми решениями – как наглядный и понятный, доступный каждому семикласснику, материал.
Порядок работы с гдз по алгебре в 7 классе – стандартная и альтернативная формы
Традиционно готовое решение переписывается из сборника во время занятий или подготовки домашней работы – в том случае, если сам семиклассник затрудняется или не может дать верный ответ. Или если сомневается в его правильности, но желает получить высокую отметку.
Помимо этого способа, одобряемого далеко не всеми педагогами-предметниками, есть и другой, альтернативный. Он предполагает применение решебников для серьезной и вдумчивой проработки материала. Схема применения сборников в этом случае будет такой:
- Самостоятельное прочтение теоретического материла в учебнике или повторение пройденного в школе.
- Решение задач, примеров, уравнений, построение графиков функций и выполнение иных заданий, предложенных после соответствующего параграфа или заданных учителем.
- Сверка полученного собственного ответа с эталонным, представленным в сборнике-решебнике.
- При выявлении расхождений – оценка факторов, повлиявших на них, причин, которые привели к получению такого результата.

- Самостоятельное выполнение заданий другого аналогичного варианта, представленных в том же или ином сборнике по этой же теме по алгебре для семиклассников и проверка правильности решения по готовым домашним заданиям.
- Выполнение пункта 5 до тех пор, пока расхождения не будут выявляться и пока тема не будет понята полностью.
Самостоятельная работа с ответами по алгебре в 7 классе разовьет навык работы с математической информацией, который будет полезен не только в седьмом классе, но и впоследствии, в том числе – после окончания школы.
Решения NCERT для математики 7-го класса (обновлено для 2020 г.
Если вы ищете Решения NCERT для математики 7-го класса, , вы попали в нужное место. Опытные учителя LearnCBSE.in создали подробные решения CBSE по математике для 7-го класса. Мы предоставляем точную и абсолютно безошибочную информацию. Математические решения NCERT для класса 7 включают в себя все вопросы, представленные в соответствии с новой пересмотренной программой в учебнике по математике NCERT для класса 7. Решения NCERT по математике для класса 7 в формате pdf можно скачать в один клик без ВХОДА , Вы также можете попрактиковаться в дополнительных вопросах по математике для 7 класса на сайте LearnCBSE.in 9.0005
Решения NCERT по математике для класса 7 в формате pdf можно скачать в один клик без ВХОДА , Вы также можете попрактиковаться в дополнительных вопросах по математике для 7 класса на сайте LearnCBSE.in 9.0005
Подробные решения NCERT по математике для класса 7 приведены ниже.
Вы также можете бесплатно скачать PDF-файл «Решения NCERT для математики для 7-го класса, все главы» или сохранить изображения решений и распечатать их, чтобы они всегда были под рукой при подготовке к экзамену.
Решения NCERT для математики класса 7, глава 1, целые числа
- Целые числа, математика класса 7, упражнение 1.1
- Математические упражнения с целыми числами для 7 класса 1.2
- Класс 7 Целые числа, упражнение 1.3
- Класс 7 Целые числа по математике. Упражнение 1.4
- Дополнительные вопросы класса 7 для целых чисел
Решения NCERT для класса 7. Математика, глава 2. Дроби и десятичные числа
- Математика, класс 7.
 Дроби и десятичные числа. Упражнение 2.1
Дроби и десятичные числа. Упражнение 2.1 - Класс 7. Математические дроби и десятичные числа. Упражнение 2.2
- Класс 7. Математические дроби и десятичные числа. Упражнение 2.3
- Класс 7. Математические дроби и десятичные числа. Упражнение 2.4
- Класс 7. Математические дроби и десятичные числа. Упражнение 2.5
- Класс 7. Математические дроби и десятичные числа. Упражнение 2.6
- Класс 7. Математические дроби и десятичные числа. Упражнение 2.7
- Дроби и десятичные дроби Класс 7 Дополнительные вопросы
Решения NCERT для математических вычислений класса 7. Глава 3. Обработка данных
- Упражнение 3.1 по обработке математических данных класса 7
- Класс 7. Упражнение по обработке математических данных 3.2
- Упражнение по обработке математических данных для класса 7 3.3
- Класс 7. Упражнение по обработке математических данных 3.4
- Дополнительные вопросы класса 7 по обработке данных
Решения NCERT для математики класса 7.
 Глава 4. Простые уравнения
Глава 4. Простые уравнения- Математика класса 7. Простые уравнения. Упражнение 4.1
- Простые уравнения по математике для 7 класса. Упражнение 4.2
- Класс 7. Простые уравнения по математике. Упражнение 4.3
- Класс 7. Простые уравнения по математике. Упражнение 4.4
- Дополнительные вопросы по простым уравнениям, класс 7
Решения NCERT для математики класса 7 Глава 5 Линии и углы
- Класс 7. Математические линии и углы. Упражнение 5.1
- Класс 7. Математические линии и углы. Упражнение 5.2
- Линии и углы Класс 7 Дополнительные вопросы
Решения NCERT для математики класса 7 Глава 6 Треугольники и их свойства
- Математика класса 7 Треугольник и его свойства Упражнение 6.1
- Математика для 7 класса Треугольник и его свойства Упражнение 6.2
- Математика для 7 класса Треугольник и его свойства Упражнение 6.3
- Математика для 7 класса Треугольник и его свойства Упражнение 6.
 4
4 - Математика для 7 класса Треугольник и его свойства Упражнение 6.5
- Треугольники и их свойства Класс 7 Дополнительные вопросы
Решения NCERT для класса 7 по математике, глава 7. Конгруэнтность треугольников
- Математика, класс 7. Упражнение на конгруэнтность треугольников 7.1
- Класс 7 Математические упражнения на сходство треугольников 7.2
- Конгруэнтность треугольников Класс 7 Дополнительные вопросы
Решения NCERT для математики класса 7 Глава 8 Сравнение величин
- Математика класса 7 Сравнение величин Упражнение 8.1
- Математическое сравнение величин, класс 7. Упражнение 8.2
- Математическое сравнение величин, класс 7. Упражнение 8.3
- Дополнительные вопросы по сравнению классов 7
Решения NCERT для математики класса 7. Глава 9. Рациональные числа
- Математика класса 7. Рациональные числа. Упражнение 9.1
- Класс 7 Рациональные числа по математике Упражнение 9.
 2
2 - Дополнительные вопросы по рациональным числам, класс 7
Решения NCERT для 7-го класса по математике, глава 10. Практическая геометрия
- Математика для 7-го класса, практическое упражнение по геометрии 10.1
- Практическое упражнение по геометрии по математике для 7 класса 10.2
- Практическое упражнение по геометрии по математике для 7 класса 10.3
- Практическое упражнение по геометрии по математике для 7 класса 10.4
- Практическое упражнение по геометрии по математике для 7 класса 10.5
- Практическая геометрия Класс 7 Дополнительные вопросы
Решения NCERT для класса 7 по математике Глава 11 Периметр и площадь
- Математика для класса 7 Периметр и площадь. Упражнение 11.1
- Класс 7. Математическое упражнение по периметру и площади 11.2
- Класс 7. Математическое упражнение по периметру и площади 11.3
- Класс 7. Математическое упражнение по периметру и площади 11.
 4
4 - Дополнительные вопросы по периметру и площади 7 класса
Решения NCERT для математики класса 7 Глава 12 Алгебраические выражения
- Математика класса 7 Алгебраические выражения Упражнение 12.1
- Упражнение по математическим алгебраическим выражениям для 7 класса 12.2
- Класс 7 Математические алгебраические выражения Упражнение 12.3
- Класс 7 Математические алгебраические выражения Упражнение 12.4
- Дополнительные вопросы по алгебраическим выражениям, класс 7
Решения NCERT для математики класса 7 Глава 13 Показатели и степени
- Математика класса 7. Показатели и степени Упражнение 13.1
- Класс 7. Математические упражнения в степени и степени 13.2
- Класс 7. Математические упражнения в показателях и степенях 13.3
- Экспоненты и полномочия Класс 7 Дополнительные вопросы
Решения NCERT для математики класса 7, глава 14, симметрия
- Математика, симметрия класса 7, упражнение 14.
 1
1 - Упражнение на симметрию по математике для 7 класса 14.2
- Упражнение на симметрию по математике для 7 класса 14.3
- Дополнительные вопросы по классу симметрии 7
Решения NCERT для математики класса 7 Глава 15 Визуализация объемных фигур
- Математика класса 7 Визуализация объемных фигур Упражнение 15.1
- Математика, класс 7. Визуализация объемных фигур. Упражнение 15.2
- Математика, класс 7. Визуализация объемных фигур. Упражнение 15.3
- Математика, класс 7. Визуализация объемных фигур. Упражнение 15.4
- Визуализация твердых фигур Дополнительные вопросы для класса 7
Решения NCERT для математики 7 класса (скачать PDF)
Математические решения NCERT
Математические формулы для 7 класса Решения были подготовлены профильными экспертами.

Мы стараемся помогать учащимся всеми возможными способами, включая предоставление решений по каждому предмету. Учебники NCERT зарекомендовали себя как лучшие учебники для школьного образования, и мы делаем решения компетентными для книг.
Математика представляет собой довольно неприятный предмет для большинства учащихся в школе, и мы считаем, что небольшая практика может решить эту проблему. проблема.
Просматривайте все решения Class 7 Maths NCERT на своем планшете, компьютере или мобильном телефоне и получайте больше баллов на выпускных экзаменах. Вы также можете воспользоваться решениями RD Sharma Class 7 и RS Aggarwal Class 7 Solutions, которые помогут вам в дополнительной практике и на экзаменах.
Вот список основных тем из учебника NCERT по математике для 7-го класса:
Математика для 7-го класса, глава 1, целые числа
учащиеся чувствуют действительные числа. Эта глава дает учащимся новый взгляд на свойства и важность целых чисел. Упражнения составлены таким образом, чтобы учащиеся полностью усвоили всю концепцию.
- 1.1 Введение
- 1.2 Отзыв
- 1.3 Свойства сложения и вычитания целых чисел
- 1.4 Умножение целых чисел
- 1.5 Свойства умножения целых чисел
- 1.6 Деление целых чисел
- 1.7 Свойства деления целых чисел
Класс 7 Математика Глава 2 Дроби и десятичные числа
Это не совсем новая концепция, а скорее дальнейшее исследование старых концепций. В главе рассматриваются свойства дробей и десятичных дробей, а также действия над ними. Они также имеют дело с изображением дробей и десятичных знаков на числовой прямой, их разложением и вычитанием.
- 2.
 1 Введение
1 Введение - 2.2 Насколько хорошо вы узнали о дробях?
- 2.3 Умножение дробей
- 2.4 Деление дробей
- 2.5 Насколько хорошо вы знаете десятичные числа
- 2.6 Умножение десятичных чисел
- 2.7 Деление десятичных чисел
Класс 7 Математика Глава 3 Обработка данных
Эту главу можно рассматривать как первый шаг к статистике, поскольку она посвящена накоплению данных, интерпретации данных и построению графиков с использованием примеров из реальной жизни. В главах также рассказывается, как сделать несколько выводов из накопленных данных. Упражнения очень близки к примерам из реальной жизни, и, таким образом, выполнение одних и тех же упражнений дает лучшее ощущение того же самого.
- 3.1 Введение
- 3.2 Сбор данных
- 3.3 Организация данных
- 3.4 Репрезентативные значения
- 3,5 Среднее арифметическое
- 3.6 Режим
- 3,7 Медиана
- 3.8 Использование гистограмм с другим назначением
- 3.
 9 Шанс и вероятность
9 Шанс и вероятность
Класс 7 Математика Глава 4 Простые уравнения
Как следует из названия, эта глава посвящена формулированию и применению простых уравнений. В этой главе подробно исследуется теория уравнений, от составления простых уравнений до их решения. Проблемы широко обсуждались в решениях.
- 4.1 Игра в чтение мыслей!
- 4.2 Составление уравнения.
- 4.3 Обзор того, что мы знаем.
- 4.4 Что такое уравнение?
- 4.5 Дополнительные уравнения.
- 4.6 От решения к уравнению.
- 4.7 Применение простых уравнений к практическим ситуациям.
Математика для 7 класса Глава 5 Линии и углы
Первая глава геометрии в 7 классе, линии и углы начинается с основных определений линии и угла. В этой главе мы рассмотрим концепции параллельных линий и связанных с ними углов, таких как чередующиеся внутренние углы, соответствующие углы, вертикально противоположные углы. Эта довольно простая глава становится еще интереснее с помощью упражнений, а решения эффективно оправдывают ее.
- 5.1 Введение.
- 5.2 Связанные углы.
- 5.3 Пары линий.
- 5.4 Проверка параллельных линий.
Класс 7 Математика Глава 6 Треугольник и его свойства
Вторая глава геометрии посвящена треугольникам и их свойствам. В этой главе рассказывается о типах треугольников, свойстве суммы углов, медианах и высотах, а также о теореме Пифагора. В этой главе учащиеся получат представление о том, что такое треугольники вообще, и о конкретных применениях теоремы Пифагора.
- 6.1 Введение.
- 6.2 Медианы треугольника.
- 6.3 Высота треугольника.
- 6.4 Внешний угол треугольника и его свойства.
- 6.5 Свойство суммы углов треугольника.
- 6.6 Два особых треугольника: равносторонний и равнобедренный.
- 6.7 Сумма длин двух сторон треугольника.
- 6.8 Прямоугольные треугольники и свойство Пифагора.
Класс 7 Математика Глава 7 Конгруэнтность треугольников
После общего введения треугольников в главе 6 в седьмой главе рассматривается особое свойство конгруэнтности треугольников. В главе рассматриваются все критерии конгруэнтности и рассматриваются различные виды проблем. В решениях широко обсуждаются критерии конгруэнтности, где возможно используется альтернативный подход.
В главе рассматриваются все критерии конгруэнтности и рассматриваются различные виды проблем. В решениях широко обсуждаются критерии конгруэнтности, где возможно используется альтернативный подход.
- 7.1 Введение.
- 7.2 Конгруэнтность плоских фигур.
- 7.3 Конгруэнтность отрезков.
- 7.4 Конгруэнтность углов.
- 7.5 Конгруэнтность треугольников.
- 7.6 Критерии равенства треугольников.
- 7.7 Конгруэнтность прямоугольных треугольников.
Математика для 7 класса Глава 8 Сравнение величин
Эту главу можно смело считать одной из наиболее прикладных глав во всей программе математики для 7 класса. Как следует из названия, в этой главе дается инструмент для измерения и сравнения величин. Основными инструментами являются проценты, коэффициенты, прибыли и убытки и проценты. Эта глава пригодится во всех сферах жизни, поскольку расчеты, изученные здесь, чаще всего используются в реальном мире.
- 8.
 1 Введение.
1 Введение. - 8.2 Эквивалентные соотношения.
- 8.3 Процент – еще один способ сравнения величин.
- 8.4 Использование процентов.
- 8.5 Цены, связанные с товаром или покупкой и продажей.
- 8.6 Плата за заемные деньги или простые проценты.
Математика для 7 класса Глава 9 Рациональные числа
После подробного обсуждения целых чисел в первой главе эта глава возвращается к числам, а именно к рациональным числам. В главе рассматриваются определения и свойства рациональных чисел.
- 9.1 Введение
- 9.2 Потребность в рациональных числах.
- 9.3 Что такое рациональные числа?
- 9.4 Положительные и отрицательные рациональные числа.
- 9.5 Рациональные числа на числовой прямой.
- 9.6 Рациональные числа в стандартной форме.
- 9.7 Сравнение рациональных чисел.
- 9.8 Рациональные числа между двумя рациональными числами.
- 9.9 Операции над рациональными числами.

Класс 7 Математика Глава 10 Практическая геометрия
В этой главе рассматривается изображение геометрии на бумаге с точки зрения построения линий и углов. Это довольно простая глава, которая требует только соблюдения установленной процедуры при построении.
- 10.1 Введение
- 10.2 Построение прямой, параллельной данной прямой, через точку, не лежащую на этой прямой.
- 10.3 Построение треугольников.
- 10.4 Построение треугольника по известным длинам трех его сторон (критерий SSS)
- 10.5 Построение треугольника по известным длинам двух сторон и величине угла между ними. (Критерий SAS)
- 10.6 Построение треугольника, если известны меры двух его углов и длина стороны, заключенной между ними. (Критерий ASA)
- 10.7 Построение прямоугольного треугольника по заданным длине катета и его гипотенузе (критерий RHS).
Математика для 7 класса Глава 11 Периметр и площадь
В этой главе представлена часть программы, посвященная измерениям. Он имеет дело с площадями и периметрами всех важных фигур в математике. Глава очень простая, без введения каких-либо сложных форм.
Он имеет дело с площадями и периметрами всех важных фигур в математике. Глава очень простая, без введения каких-либо сложных форм.
- 11.1 Введение.
- 11.2 Квадраты и прямоугольники.
- 11.3 Площадь параллелограмма.
- 11.4 Площадь треугольника.
- 11,5 Круги.
- 11.6 Преобразование единиц.
- 11.7 Приложения.
Класс 7 Математика Глава 12 Алгебраические уравнения
В этой главе рассматривается преобразование простых математических выражений в алгебраические уравнения и их использование для решения определенных задач с использованием принципов алгебры. Математические утверждения тесно связаны с некоторыми примерами из реальной жизни, где можно использовать алгебру. Упражнения удваивают удовольствие.
- 12.1 Введение.
- 12.2 Как формируются выражения?
- 12.3 Условия выражения.
- 12.4 Подобие и отличие терминов.
- 12.5 Одночлены, двучлены, трехчлены и многочлены.

- 12.6 Сложение и вычитание алгебраических выражений.
- 12.7 Нахождение значения выражения.
- 12.8 Использование алгебраических выражений – формулы и правила.
Класс 7 Математика Глава 13 Показатель степени и степени
В этой главе рассматриваются введение в показатели степени, правила умножения и деления показателей степени, степень степени, десятичная система и выражение очень больших чисел в стандартной форме или научной нотации.
- 13.1 Введение.
- 13.2 Экспоненты.
- 13.3 Законы экспоненты.
- 13.4 Разные примеры с использованием законов экспонент.
- 13.5 Десятичная система счисления.
- 13.6 Представление больших чисел в стандартной форме.
Математика для 7 класса Глава 14 Симметрия
В этой главе учащиеся получают представление о симметричных формах. Симметрия широко используется мастерами и дизайнерами для планирования сложных шаблонов дизайна. Эта глава о симметрии должна дать учащимся общее представление о симметрии в мире.
Эта глава о симметрии должна дать учащимся общее представление о симметрии в мире.
- 14.1 Введение: Симметрия
- 14.2 Линии симметрии для правильных многоугольников.
- 14.3 Вращательная симметрия.
- 14.4 Линейная симметрия и вращательная симметрия.
Математика для 7 класса Глава 15 Визуализация объемных фигур
В этой главе рассматривается визуализация геометрии путем объяснения различных геометрических форм, используемых при проектировании повседневных предметов вокруг нас. В этой главе рассматриваются как плоские фигуры, так и объемные формы.
- 15.1 Введение: плоские фигуры и объемные формы.
- 15.2 Грани, ребра и вершины.
- 15.3 Сети для построения трехмерных фигур.
- 15.4 Рисование тел на плоской поверхности.
- 15.5 Просмотр различных сечений твердого тела.
Часто задаваемые вопросы о решениях NCERT для математики 7-го класса
1. Как получить хорошие оценки по математике в 7-м классе?
Тщательно изучите концепции и подготовьтесь в соответствии с темами, используя решения NCERT. Убедитесь, что вы разработали правильную стратегию подготовки, чтобы с легкостью сдать экзамен класса 7.
Убедитесь, что вы разработали правильную стратегию подготовки, чтобы с легкостью сдать экзамен класса 7.
2. Какой лучший справочник по математике для 7 класса?
Для основ учебников NCERT, предписанных Советом CBSE, более чем достаточно, чтобы получить более высокие оценки на экзамене по математике в классе 7.
3. Почему важны решения NCERT для математики класса 7?
Решения NCERT по математике для класса 7 готовятся экспертами и дают вам пошаговые решения для лучшего понимания задач. Они могут оказаться весьма полезными во время подготовки.
4. Как скачать решения NCERT для класса 7 бесплатно?
Соискатели могут бесплатно загрузить решения NCERT для класса 7 с нашего сайта. Используйте их в качестве справочного материала и помогите в подготовке.
5. Какие главы содержатся в решениях NCERT для математики класса 7?
Вы можете просмотреть список глав математических решений NCERT класса 7, обратившись к нашей странице. Обратитесь к темам в каждой главе и соответствующим образом спланируйте свою подготовку.
Обратитесь к темам в каждой главе и соответствующим образом спланируйте свою подготовку.
6. Где я могу получить решения NCERT для математики 7-го класса?
Вы можете получить решения NCERT для математики 7-го класса, обратившись к нашей странице. Получите доступ к прямым ссылкам для просмотра или загрузки и используйте их в качестве справочного материала во время подготовки.
Мы надеемся, что вы получите большой опыт при использовании решений. Скачать решения можно по ссылкам выше в описании.
Решения NCERT для класса 7 по математике Глава 3 Обработка данных Ex 3.3
by phani
- Упражнение 3.1 по математической обработке данных для класса 7
- Класс 7. Упражнение по обработке математических данных 3.2
- Упражнение по обработке математических данных для класса 7 3.3
- Класс 7. Упражнение по обработке математических данных 3.4
Решения NCERT для математики класса 7. Глава 3. Обработка данных. Упражнение 3.3
Глава 3. Обработка данных. Упражнение 3.3
Пример 3.3. Математика класса 7. Вопрос 1.
Используйте гистограмму, чтобы ответить на следующие вопросы.
(а) Какое домашнее животное самое популярное?
(b) У скольких учащихся есть собака в качестве домашнего питомца?
Решение:
Из данной гистограммы на рисунке мы имеем
(a) Кошки являются самыми популярными домашними животными среди учащихся.
(b) 8 учащихся держат собаку в качестве домашнего животного.
Упр. 3.3 Класс 7 Математика Вопрос 2.
Прочтите гистограмму, показывающую количество книг, проданных книжным магазином за пять лет подряд, и ответьте на следующие вопросы:
(i) Сколько книг было продано в 1989, 1990, 1992 годах?
(ii) В каком году было продано около 475 книг? Продано около 225 книг?
(iii) В каком году было продано менее 250 книг?
(iv) Можете ли вы объяснить, как бы вы оценили количество книг, проданных в 1989 году?
Решение:
Из данной гистограммы мы имеем
(i) Количество книг, проданных в 19 году89 — около 180, в 1990 г.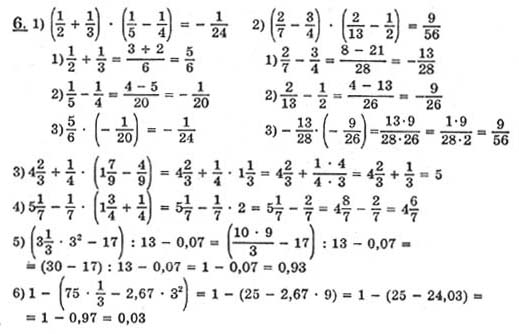 — около 490, а в 1992 г. — около 295.
— около 490, а в 1992 г. — около 295.
(ii) В 1990 г. было продано около 475 книг. В 1992 г. было продано около 225 книг. 1989 и 1992 годы.
(iv) По оси Y линия разделена на 10 небольших частей по 10 книг в каждой. Таким образом, мы можем оценить количество книг, проданных в 1989 году, примерно в 180.
Пример 3.3 Математика для 7 класса Вопрос 3.
Количество детей в шести разных классах указано ниже. Представьте данные на гистограмме.
| Класс | Количество детей |
| Пятый | 135 |
| Шестой | 120 |
| Седьмой | 95 |
| Восьмой | 100 |
| Девятый | 90 |
| Десятый | 80 |
(a) Как бы вы выбрали шкалу?
(b) Ответьте на следующие вопросы:
- В каком классе больше всего детей? А минимум?
- Найдите соотношение учащихся шестого класса к числу учащихся восьмого класса.

Решение:
(a) Шкала по оси Y: 1 см = 10 учеников
(b)
- В пятом классе максимальное количество детей, т.е. 135.
В десятом классе минимальное количество детей, т.е. 80. - Количество детей в восьмом классе = 100
∴ Отношение учащихся шестого класса к числу учащихся 9-го класса0213
Упр. 3.3 Класс 7 Математика Вопрос 4.
Дана успеваемость учащегося за 1-й и 2-й семестр. Нарисуйте двойную гистограмму, выбрав соответствующий масштаб, и ответьте на следующие вопросы:
| Тема | 1 семестр (М.М. 100) | 2-й срок (М.М. 100) |
| Английский | 67 | 70 |
| Хинди | 72 | 65 |
| Математика | 88 | 95 |
| Наука | 81 | 85 |
| С. Наука | 73 | 75 |
(i) По какому предмету ребенок улучшил свои результаты больше всего?
(ii) По какому предмету улучшение наименьшее?
(iii) Ухудшилась ли успеваемость по какому-либо предмету?
Решение:
(i) По математике успеваемость учащихся улучшилась больше всего.
(ii) В области социальных наук успеваемость учащихся улучшилась меньше всего.
(iii) Да, по хинди успеваемость учащихся снизилась.
Пример 3.3 Математика для класса 7 Вопрос 5.
Рассмотрим эти данные, полученные в результате обследования колонии.
| Любимый вид спорта | Просмотр | Участие |
| Крикет | 1240 | 620 |
| Баскетбольный мяч | 470 | 320 |
| Плавание | 510 | 320 |
| Хоккей | 430 | 250 |
| Легкая атлетика | 250 | 105 |
(i) Нарисуйте двойную гистограмму, выбрав соответствующий масштаб. Что вы делаете из гистограммы?
(ii) Какой вид спорта наиболее популярен?
(iii) Что предпочтительнее: смотреть или участвовать в спортивных состязаниях?
Решение:
(i) На приведенной выше гистограмме показано количество людей, которые смотрят и участвуют в спортивных состязаниях.
(ii) Крикет является самым популярным видом спорта.
(iii) Люди предпочитают смотреть спортивные состязания.
Пример 3.3 Класс 7 Математика Вопрос 6.
Возьмите данные о минимальной и максимальной температуре в различных городах, приведенные в начале этой главы. Постройте двойную гистограмму, используя данные, и ответьте на следующие вопросы:
(i) В каком городе самая большая разница в минимальной и максимальной температуре в указанную дату?
(ii) Какой город самый жаркий, а какой самый холодный?
(iii) Назовите два города, максимальная температура в одном из которых была ниже минимальной температуры в другом.
(iv) Назовите город с наименьшей разницей между минимальной и максимальной температурой.
| Температура городов на 20.06.2006 | ||
| Город | Макс. | Мин. |
| Ахмадабад | 38°С | 29°С |
| Амритсар | 37°С | 26°С |
| Бангалор | 28°С | 21°С |
| Ченнаи | 36°С | 27°С |
| Дели | 38°С | 28°С |
| Джайпур | 39°С | 29°С |
| Джамму | 41°С | 26°С |
| Мумбаи | 32°С | 27°С |
Решение:
Двойная гистограмма:
(i) В Джамму самая большая разница между максимальной и минимальной температурой, т.



 Случаи, когда начав заниматься по решебникам с целью улучшить оценку, углубить знания, школьники переходили на более серьезный уровень подготовки, например, олимпиадный, встречаются в практике;
Случаи, когда начав заниматься по решебникам с целью улучшить оценку, углубить знания, школьники переходили на более серьезный уровень подготовки, например, олимпиадный, встречаются в практике; Например, часто болеющие или профессионально занимающиеся творчеством, спортом и по этой причине уезжающие на спортивные сборы, соревнования, конкурсы. В этом случае по решебникам разбираются пропущенные темы, определяются пути и методы решения практических заданий по ним.
Например, часто болеющие или профессионально занимающиеся творчеством, спортом и по этой причине уезжающие на спортивные сборы, соревнования, конкурсы. В этом случае по решебникам разбираются пропущенные темы, определяются пути и методы решения практических заданий по ним.
 Дроби и десятичные числа. Упражнение 2.1
Дроби и десятичные числа. Упражнение 2.1  4
4 2
2 4
4 1
1  1 Введение
1 Введение 9 Шанс и вероятность
9 Шанс и вероятность 1 Введение.
1 Введение.


 Найти кинетическую энергию и скорость тела на высоте 6 м (посередине) . Найти кинетическую энергию и скорость тела в момент удара о Землю.
Найти кинетическую энергию и скорость тела на высоте 6 м (посередине) . Найти кинетическую энергию и скорость тела в момент удара о Землю. В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура
В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура Сколько всего книг было в магазине?
Сколько всего книг было в магазине?
 Чему равна постоянная дифракционной решётки, если при освещении её
Чему равна постоянная дифракционной решётки, если при освещении её Нужно к среде (3 мая) ЗАДАНИЯ ВНИЗУ!!!!
Нужно к среде (3 мая) ЗАДАНИЯ ВНИЗУ!!!! В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура
В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура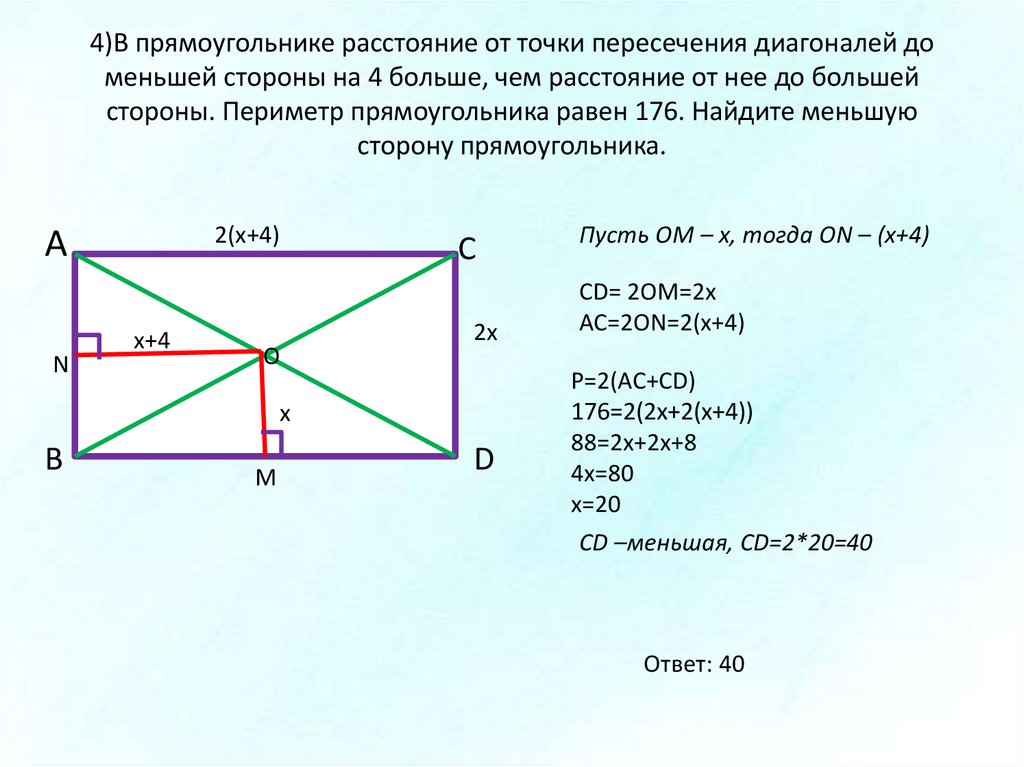 Сколько всего книг было в магазине?
Сколько всего книг было в магазине?
 В квадрате весь интерьер
углы тоже будут 90 градусов. Если нам известна длина стороны
квадрат, назовем его 𝑙, тогда мы знаем, что каждая сторона также будет стороной
длина 𝑙.
В квадрате весь интерьер
углы тоже будут 90 градусов. Если нам известна длина стороны
квадрат, назовем его 𝑙, тогда мы знаем, что каждая сторона также будет стороной
длина 𝑙. Эта теорема применима к правому
только треугольники. И это говорит о том, что площадь
гипотенуза равна сумме квадратов двух других сторон.
Эта теорема применима к правому
только треугольники. И это говорит о том, что площадь
гипотенуза равна сумме квадратов двух других сторон.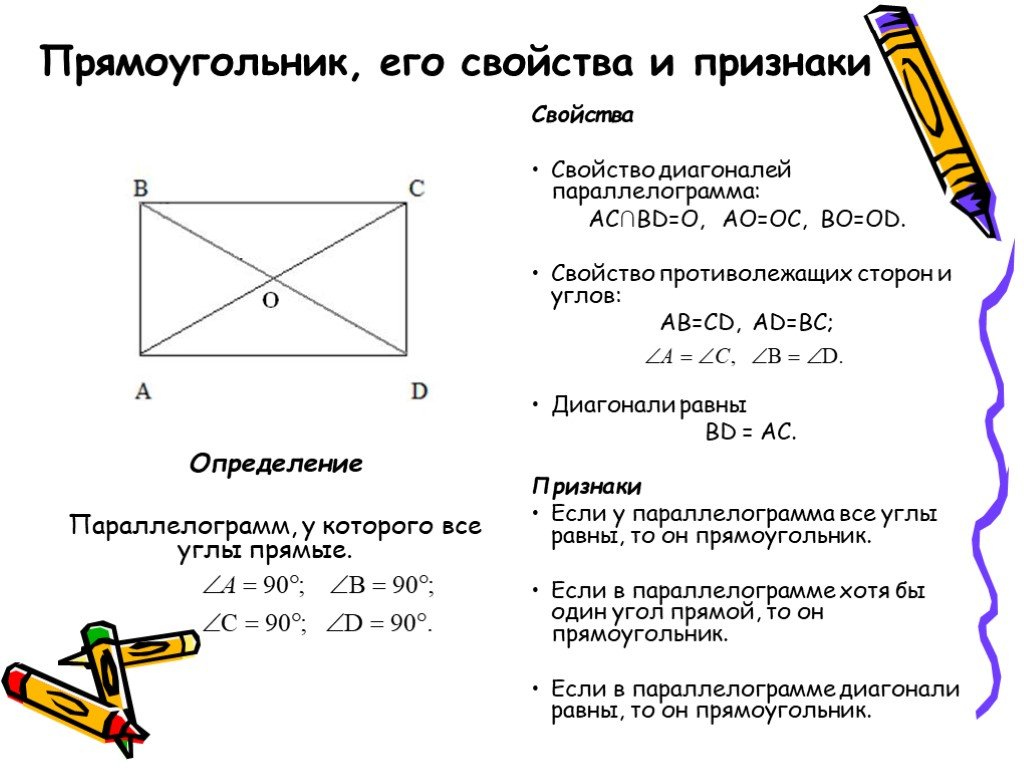 Мы возьмем нашу формулу и заполним
в значениях для 𝑙, чтобы дать нам, что площадь квадрата равна квадрату
корень из 𝑑 в квадрате, умноженный на квадратный корень из 𝑑 в квадрате
два.
Мы возьмем нашу формулу и заполним
в значениях для 𝑙, чтобы дать нам, что площадь квадрата равна квадрату
корень из 𝑑 в квадрате, умноженный на квадратный корень из 𝑑 в квадрате
два. Мы знаем, что у него будет четыре
равные стороны и четыре угла по 90 градусов. Мы можем вспомнить, что легко
найдите площадь квадрата, если известна длина одной из сторон. Однако здесь нам дается
длина диагонали. Итак, нам нужно запомнить
другая формула, то есть площадь квадрата равна 𝑑 в квадрате над
два, где 𝑑 — длина диагонали.
Мы знаем, что у него будет четыре
равные стороны и четыре угла по 90 градусов. Мы можем вспомнить, что легко
найдите площадь квадрата, если известна длина одной из сторон. Однако здесь нам дается
длина диагонали. Итак, нам нужно запомнить
другая формула, то есть площадь квадрата равна 𝑑 в квадрате над
два, где 𝑑 — длина диагонали.
 Это также подтвердит, что мы делаем
действительно есть квадратная шахматная доска. Поскольку у нас есть восемь квадратов в каждом
ряд и восемь в каждом столбце, то общее количество квадратов будет 64
квадраты. Чтобы найти общую площадь всех
этих квадратов, мы знаем, что есть 64 квадрата, и каждый из них будет иметь площадь 81
квадратных сантиметров. Оценка этого даст нам
общая площадь 5184 квадратных сантиметра.
Это также подтвердит, что мы делаем
действительно есть квадратная шахматная доска. Поскольку у нас есть восемь квадратов в каждом
ряд и восемь в каждом столбце, то общее количество квадратов будет 64
квадраты. Чтобы найти общую площадь всех
этих квадратов, мы знаем, что есть 64 квадрата, и каждый из них будет иметь площадь 81
квадратных сантиметров. Оценка этого даст нам
общая площадь 5184 квадратных сантиметра. Мы можем заполнить значение, которое
площадь 𝐴 равна 5184 в нашей формуле, учитывая, что квадратный корень также
включает в себя это значение площади, а не только два. Мы можем упростить это, чтобы получить 𝑑
равен квадратному корню из 10368.
Мы можем заполнить значение, которое
площадь 𝐴 равна 5184 в нашей формуле, учитывая, что квадратный корень также
включает в себя это значение площади, а не только два. Мы можем упростить это, чтобы получить 𝑑
равен квадратному корню из 10368. А единицами будут сантиметры
поскольку мы работаем с длиной, а не с площадью.
А единицами будут сантиметры
поскольку мы работаем с длиной, а не с площадью. Итак, площадь нашего квадрата будет
также быть 350 квадратных сантиметров. Нам нужно запомнить формулу
которая соединяет площадь квадрата с его диагональю. Площадь квадрата равна
диагональ 𝑑 в квадрате над двумя. Так как мы хотим найти диагональ
учитывая площадь, то мы можем использовать переставленную форму этой формулы, чтобы получить, что
𝑑 равно квадратному корню из двух 𝐴, где 𝐴 — площадь квадрата.
Итак, площадь нашего квадрата будет
также быть 350 квадратных сантиметров. Нам нужно запомнить формулу
которая соединяет площадь квадрата с его диагональю. Площадь квадрата равна
диагональ 𝑑 в квадрате над двумя. Так как мы хотим найти диагональ
учитывая площадь, то мы можем использовать переставленную форму этой формулы, чтобы получить, что
𝑑 равно квадратному корню из двух 𝐴, где 𝐴 — площадь квадрата. Поскольку 𝑑 — длина диагонали, то
мы можем дать окончательный ответ из 10 корней из семи сантиметров.
Поскольку 𝑑 — длина диагонали, то
мы можем дать окончательный ответ из 10 корней из семи сантиметров. На самом деле, нам нужно отработать
разница между областями. Но давайте для начала подумаем, как мы
найти площадь каждого квадрата. В первом квадрате у нас есть
длина стороны, так что давайте вспомним нашу первую формулу. Площадь квадрата равна
длина, умноженная на длину, или, альтернативно, длина в квадрате. Мы можем заполнить длину стороны 𝑙
в нашу формулу, поэтому мы будем вычислять 17, умноженное на 17. Используя любое умножение
метод, мы получим ответ 289. И поскольку это область, мы будем
имеют единицы площади квадратные сантиметры.
На самом деле, нам нужно отработать
разница между областями. Но давайте для начала подумаем, как мы
найти площадь каждого квадрата. В первом квадрате у нас есть
длина стороны, так что давайте вспомним нашу первую формулу. Площадь квадрата равна
длина, умноженная на длину, или, альтернативно, длина в квадрате. Мы можем заполнить длину стороны 𝑙
в нашу формулу, поэтому мы будем вычислять 17, умноженное на 17. Используя любое умножение
метод, мы получим ответ 289. И поскольку это область, мы будем
имеют единицы площади квадратные сантиметры. Подставляем длину диагонали 𝑑
как 20 сантиметров, у нас есть формула, что площадь равна 20 в квадрате над
два. 20 умножить на 20 даст нам
400 и деление на два дает нам площадь 200 квадратных сантиметров.
Подставляем длину диагонали 𝑑
как 20 сантиметров, у нас есть формула, что площадь равна 20 в квадрате над
два. 20 умножить на 20 даст нам
400 и деление на два дает нам площадь 200 квадратных сантиметров. Затем мы увидели, как мы можем переставить
что формула 𝐴, площадь, равна 𝑑 в квадрате над двумя, что дает нам формулу 𝑑
равно квадратному корню из двух 𝐴. Эта формула позволяет нам более
быстро найти длину диагонали, зная площадь квадрата.
Затем мы увидели, как мы можем переставить
что формула 𝐴, площадь, равна 𝑑 в квадрате над двумя, что дает нам формулу 𝑑
равно квадратному корню из двух 𝐴. Эта формула позволяет нам более
быстро найти длину диагонали, зная площадь квадрата.
 Длина диагонали «d» квадрата со стороной «а» вычисляется по теореме Пифагора. Обратите внимание на следующий квадрат, чтобы увидеть, что длина диагонали обозначена буквой «d», а длина стороны обозначена буквой «a».
Длина диагонали «d» квадрата со стороной «а» вычисляется по теореме Пифагора. Обратите внимание на следующий квадрат, чтобы увидеть, что длина диагонали обозначена буквой «d», а длина стороны обозначена буквой «a».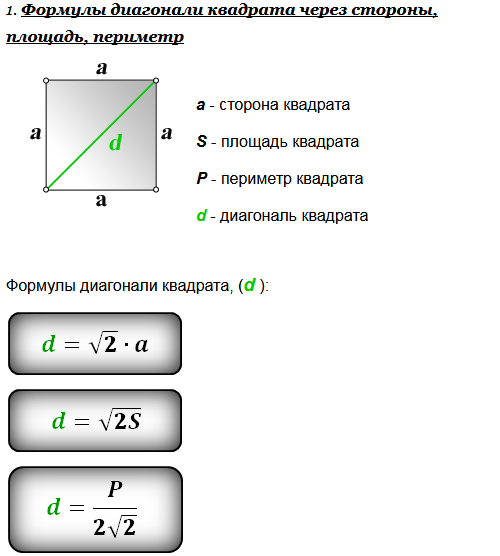 Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Свойства диагоналей квадрата следующие:
Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Свойства диагоналей квадрата следующие:
 Затем значение длины стороны можно использовать для нахождения диагонали квадрата с помощью формулы d = a√2. Например, если площадь квадрата составляет 81 кв. Сначала найдем длину его стороны, так как мы знаем, что площадь квадрата = a 2 . Следовательно, сторона «а» = √81 = 9 единиц. Теперь мы будем использовать это значение в формуле d = a√2, d = 9√2 = 12,72 единицы.
Затем значение длины стороны можно использовать для нахождения диагонали квадрата с помощью формулы d = a√2. Например, если площадь квадрата составляет 81 кв. Сначала найдем длину его стороны, так как мы знаем, что площадь квадрата = a 2 . Следовательно, сторона «а» = √81 = 9 единиц. Теперь мы будем использовать это значение в формуле d = a√2, d = 9√2 = 12,72 единицы.
 Смотрите подробный материал о развитии логики у детей.
Смотрите подробный материал о развитии логики у детей.
 Всего стало 33 стержня.
Всего стало 33 стержня.







 Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.
Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.
 Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.
Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении. У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?
У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?
 15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
 Соревнование длилось ровно 45 минут. За это время все соревнующиеся в сумме съели 179 пирожков.
Соревнование длилось ровно 45 минут. За это время все соревнующиеся в сумме съели 179 пирожков. Значит, Ква-Квариус и Грамотигр вместе съели 69 пирожков.
Значит, Ква-Квариус и Грамотигр вместе съели 69 пирожков.

 Владелец магазина предоставил скидку в размере 5 рупий на общую покупку 3 игрушек за 30 рупий. Затем среди 5 рупий каждый человек взял 1 рупию, а оставшиеся 2 рупии отдали нищему возле магазина.
Владелец магазина предоставил скидку в размере 5 рупий на общую покупку 3 игрушек за 30 рупий. Затем среди 5 рупий каждый человек взял 1 рупию, а оставшиеся 2 рупии отдали нищему возле магазина. Теперь вы хотите получить 100 фруктов за 100 рупий. Итак, сколько бананов, манго и яблок вы купите ??
Теперь вы хотите получить 100 фруктов за 100 рупий. Итак, сколько бананов, манго и яблок вы купите ??
 Запишите каждое из следующих предложений в символьной форме, используя переменные операторов p и q .
Запишите каждое из следующих предложений в символьной форме, используя переменные операторов p и q .  Запишите обратное, обратное и контрапозитивное значение каждого из следующих импликаций.
Запишите обратное, обратное и контрапозитивное значение каждого из следующих импликаций.  Покажите, что (i) ¬( p ∧ q ) ≡ ¬ p ∨¬ q (ii) ¬( p → 90 263 q ) ≡ p ∧¬ q .
Покажите, что (i) ¬( p ∧ q ) ≡ ¬ p ∨¬ q (ii) ¬( p → 90 263 q ) ≡ p ∧¬ q . 

 Если бесплатное бронирование и осмотр закончились, а вы ещё не уехали — минуты простоя тарифицируются по опции «Парковка».
Если бесплатное бронирование и осмотр закончились, а вы ещё не уехали — минуты простоя тарифицируются по опции «Парковка».
 От качества данных процессов существенно зависит развитие будущего плода.
От качества данных процессов существенно зависит развитие будущего плода. С первого дня цикла и слизистая матки начинает готовиться к вероятной беременности. Для имплантации, т. е. внедрения образовавшегося зародыша в стенку матки, создается оптимальная среда. Для этого вследствие влияния гормонов происходит утолщение эндометрия, он покрывается сетью сосудов и накапливает необходимые для будущего зародыша питательные вещества.
С первого дня цикла и слизистая матки начинает готовиться к вероятной беременности. Для имплантации, т. е. внедрения образовавшегося зародыша в стенку матки, создается оптимальная среда. Для этого вследствие влияния гормонов происходит утолщение эндометрия, он покрывается сетью сосудов и накапливает необходимые для будущего зародыша питательные вещества.

 Если сперматозоиды находят яйцеклетку, они начинают выделять специальные ферменты, способные разрыхлить ее оболочку. Как только один из сперматозоидов проникает внутрь яйцеклетки, другие этого уже сделать не могут вследствие восстановления плотности ее оболочки. Таким образом, одна яйцеклетка может быть оплодотворена только одним сперматозоидом.
Если сперматозоиды находят яйцеклетку, они начинают выделять специальные ферменты, способные разрыхлить ее оболочку. Как только один из сперматозоидов проникает внутрь яйцеклетки, другие этого уже сделать не могут вследствие восстановления плотности ее оболочки. Таким образом, одна яйцеклетка может быть оплодотворена только одним сперматозоидом. Женский организм создает все необходимые условия для безопасного развития плода.
Женский организм создает все необходимые условия для безопасного развития плода. Термин имплантация обозначает процесс внедрения эмбриона в слой эндометрия.
Термин имплантация обозначает процесс внедрения эмбриона в слой эндометрия. Происходит сплетение кровеносными сосудами эмбриона с организмом мамы, что позволяет ему сразу же начать добывать полезные и нужные для развития вещества. Это жизненно необходимо, поскольку к данному времени запас, который несла в себе зрелая яйцеклетка, оказывается исчерпанным.
Происходит сплетение кровеносными сосудами эмбриона с организмом мамы, что позволяет ему сразу же начать добывать полезные и нужные для развития вещества. Это жизненно необходимо, поскольку к данному времени запас, который несла в себе зрелая яйцеклетка, оказывается исчерпанным. После первого дня задержки менструации при ее регулярном цикле уже возможно определить беременность с помощью теста самостоятельно.
После первого дня задержки менструации при ее регулярном цикле уже возможно определить беременность с помощью теста самостоятельно.

 В этом случае просто сделайте «математику» ниже:
В этом случае просто сделайте «математику» ниже:

 12
12 01
01
 Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала.
Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала.
 График функции
График функции Окружность
Окружность Разложение вектора на составляющие по осям координат
Разложение вектора на составляющие по осям координат Уравнение плоскости, проходящей через данную точку
Уравнение плоскости, проходящей через данную точку Предел функции при х->х0
Предел функции при х->х0 Геометрический смысл производной
Геометрический смысл производной Дифференцирование функций, заданных параметрически
Дифференцирование функций, заданных параметрически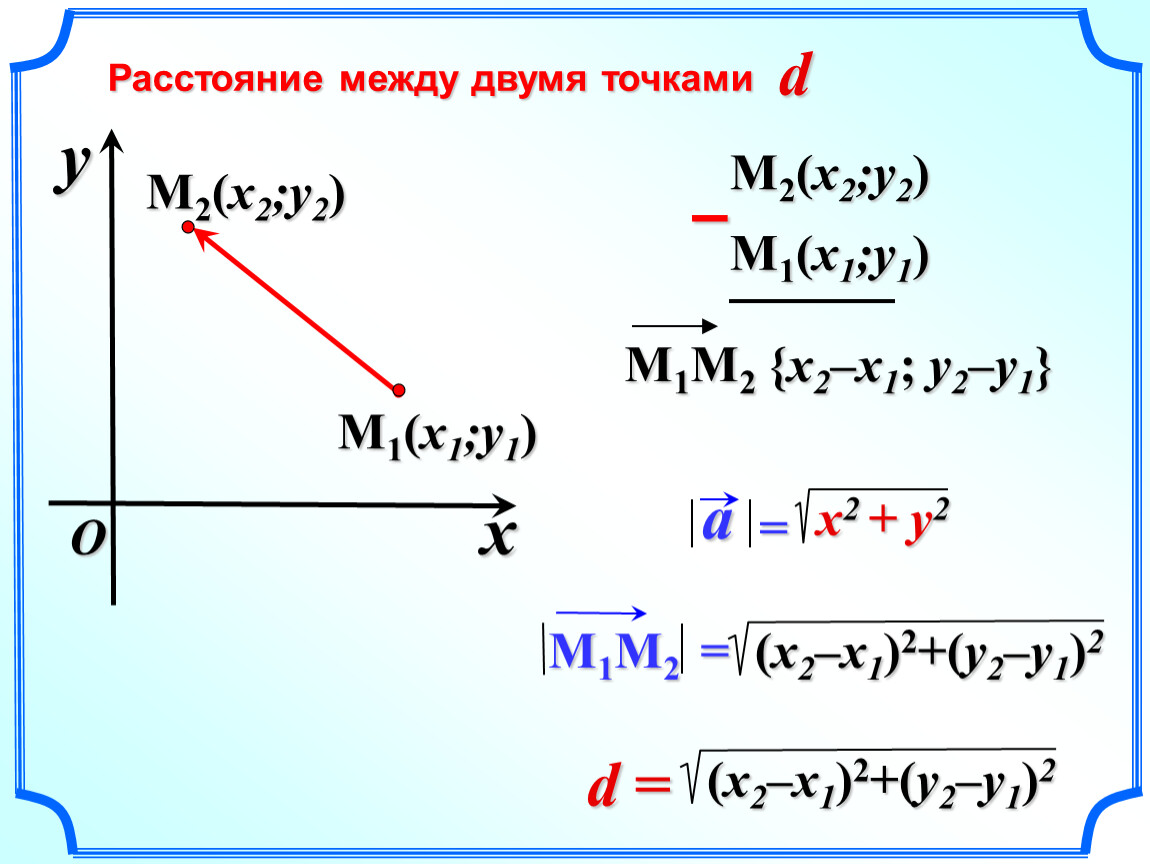 ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА Понятие об интегралах, не берущихся в элементарных функциях
Понятие об интегралах, не берущихся в элементарных функциях Интегралы от разрывных функций
Интегралы от разрывных функций Инвариантность формы полного дифференциала
Инвариантность формы полного дифференциала Вычисление криволинейного интеграла
Вычисление криволинейного интеграла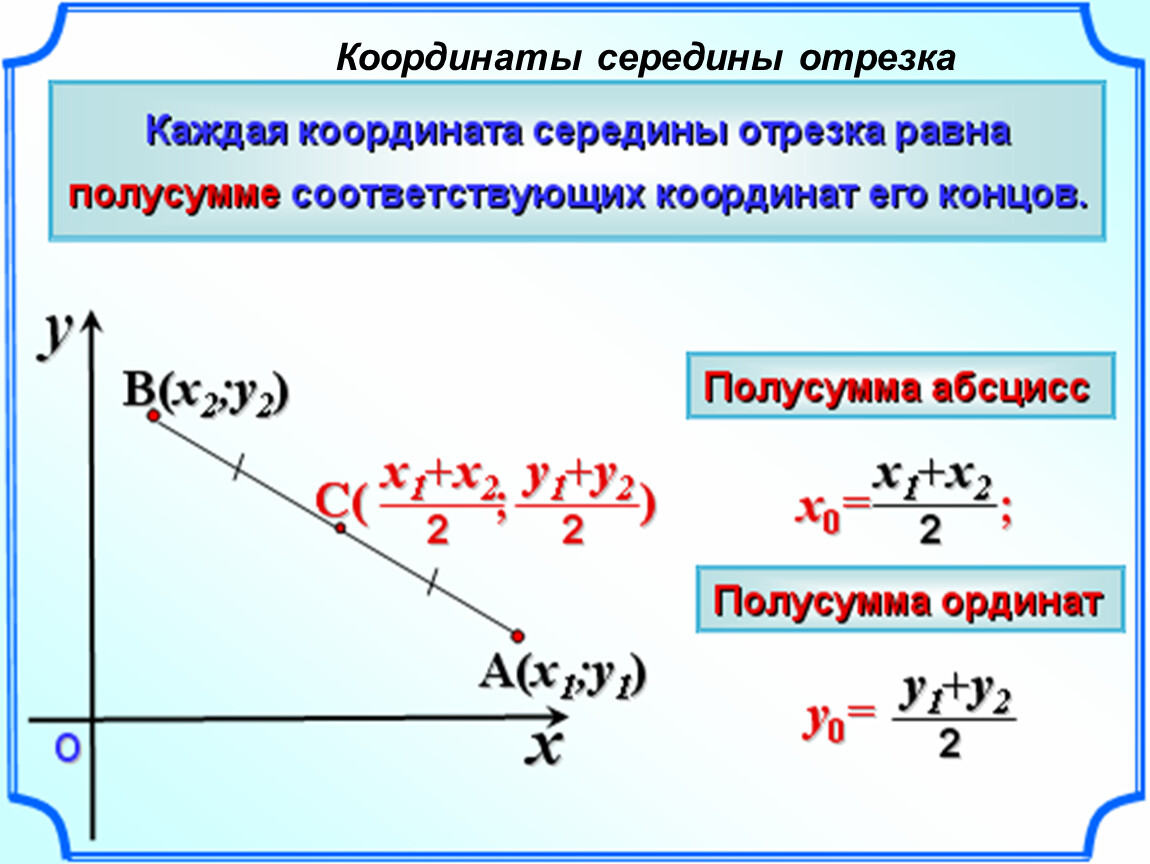 Числовые ряды с комплексными членами
Числовые ряды с комплексными членами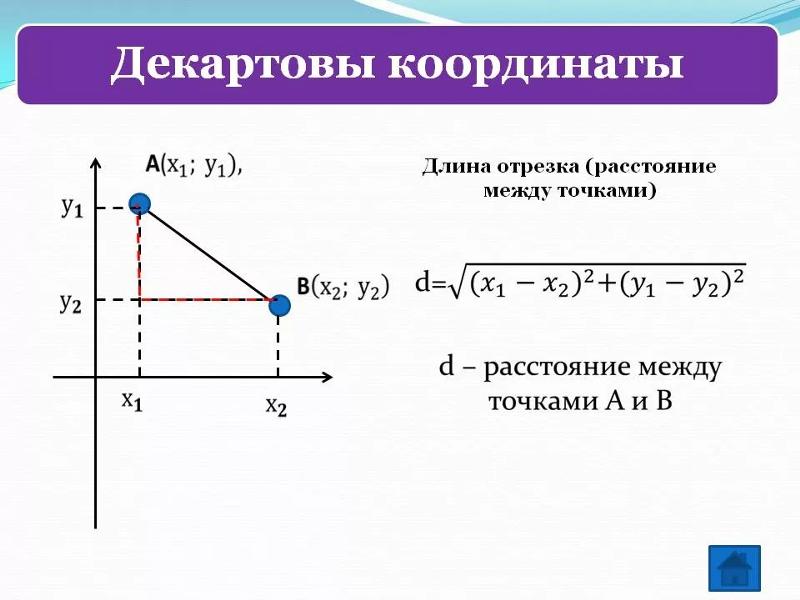 Метод вариации произвольных постоянных
Метод вариации произвольных постоянных Расстояние между двумя точками в координатной геометрии можно рассчитать, найдя длину отрезка, соединяющего заданные координаты.
Расстояние между двумя точками в координатной геометрии можно рассчитать, найдя длину отрезка, соединяющего заданные координаты.




 Рассмотрим два комплексных числа z 1 = a + ib и z 2 = c + id. Напомним, что каждому комплексному числу на комплексной плоскости соответствует точка на координатной плоскости. Тогда расстояние между двумя комплексными числами z 1 и z 2 это:
Рассмотрим два комплексных числа z 1 = a + ib и z 2 = c + id. Напомним, что каждому комплексному числу на комплексной плоскости соответствует точка на координатной плоскости. Тогда расстояние между двумя комплексными числами z 1 и z 2 это: То же самое работает и с y-координатами. Таким образом, расстояние между двумя точками также можно записать как √[(x 1 — х 2 ) 2 + (у 1 — у 2 ) 2 ].
То же самое работает и с y-координатами. Таким образом, расстояние между двумя точками также можно записать как √[(x 1 — х 2 ) 2 + (у 1 — у 2 ) 2 ].





 Очень хорошо получается. . . Я думаю, что программное обеспечение прекрасно помогает студентам в течение всего года, дополняя любые материалы, которые они получают в обычном классе.
Очень хорошо получается. . . Я думаю, что программное обеспечение прекрасно помогает студентам в течение всего года, дополняя любые материалы, которые они получают в обычном классе.  Отличная программа!
Отличная программа! 
 Восклицательное предложение находится:
Восклицательное предложение находится:  23 молекуласының (қж) алатын көлемін есепте.
23 молекуласының (қж) алатын көлемін есепте. 23=11.2 л
23=11.2 л 02.2023
Химия
сұрақ қойды
02.2023
Химия
сұрақ қойды Концентрированная солнечная энергия служит источником высокотемпературного технологического тепла. Теоретическая чистая потребность в энергии оценивается в 2,5 МДж/моль CO 9 .0008 2 захвачено.
Концентрированная солнечная энергия служит источником высокотемпературного технологического тепла. Теоретическая чистая потребность в энергии оценивается в 2,5 МДж/моль CO 9 .0008 2 захвачено.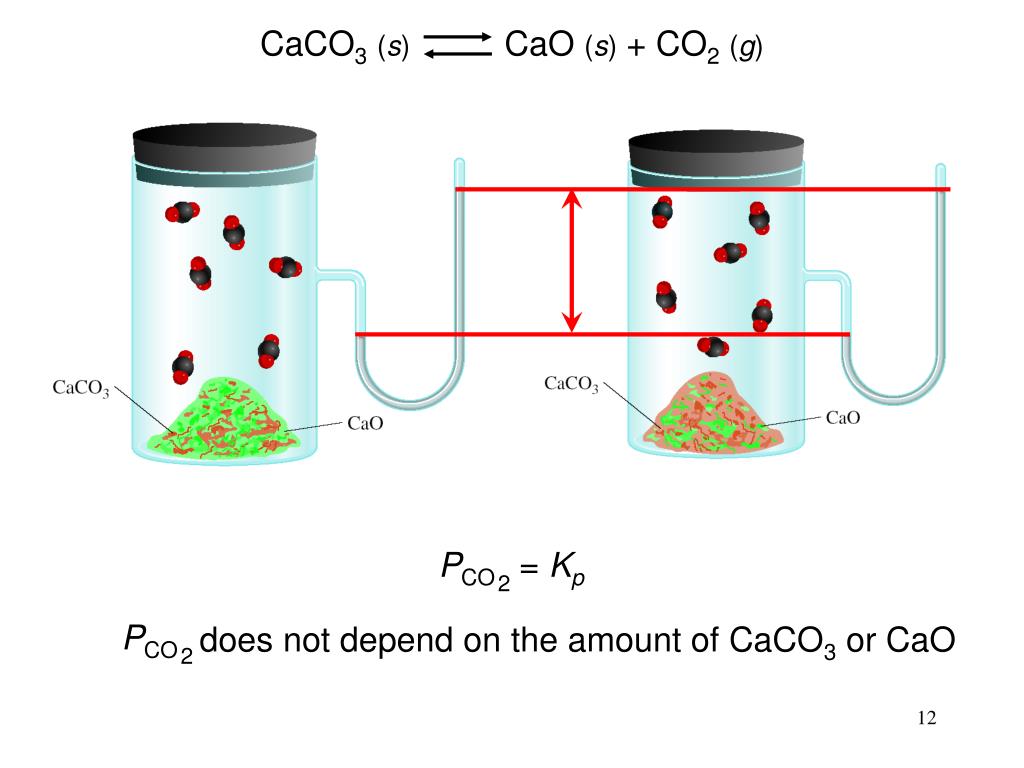 2. Схема солнечного реактора с псевдоожиженным слоем для последовательного проведения циклов карбонизации-прокаливания с использованием солнечной энергии
2. Схема солнечного реактора с псевдоожиженным слоем для последовательного проведения циклов карбонизации-прокаливания с использованием солнечной энергии



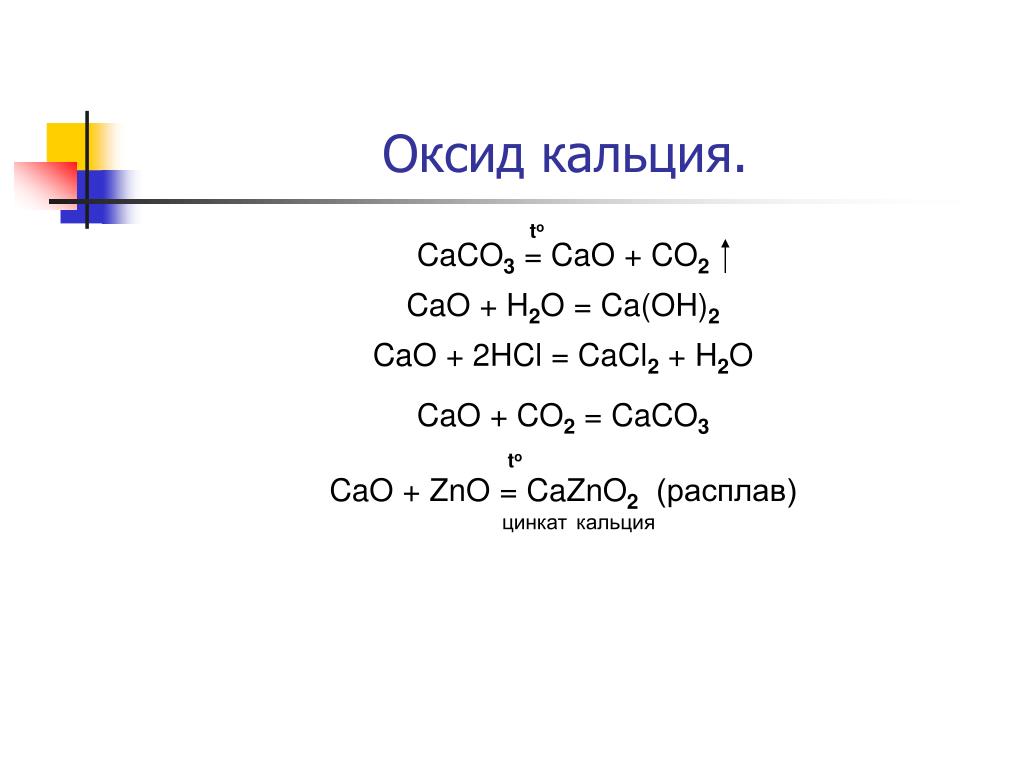

 Вот как это работает:
Вот как это работает:
 В любом случае, теперь я могу прочитать требуемые значения из уравнения:
В любом случае, теперь я могу прочитать требуемые значения из уравнения:
 14159..
14159.. 03.15
03.15 Одновременно с ним из пункта А вышел катер.Дойдя до В,катер сразу же…
Одновременно с ним из пункта А вышел катер.Дойдя до В,катер сразу же… 1 Разложение на множители 2x 2 -3x-20
1 Разложение на множители 2x 2 -3x-20 1 Произведение нескольких членов равно нулю.
1 Произведение нескольких членов равно нулю. давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу точка, называемая вершиной . Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, 2 , положителен (больше нуля).
давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу точка, называемая вершиной . Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, 2 , положителен (больше нуля). В нашем случае координата x равна 0,7500
В нашем случае координата x равна 0,7500  Так как
Так как  3 Решение 2x 2 -3x-20 = 0 с помощью квадратной формулы .
3 Решение 2x 2 -3x-20 = 0 с помощью квадратной формулы .