Калькулятор интерполяции — Найти точку интерполяции
Онлайн-калькулятор интерполяции помогает найти интерполированные значения для точек данных на линии или кривой. Калькулятор отображает интерполированную точку на линии и показывает пошаговое решение с использованием формулы линейной интерполяции.
Просто прочтите контекст, чтобы получить общее представление о том, как выполнять интерполяцию, ее формулу и некоторые стандартные термины, которые помогают понять интерполяцию.
Что такое линейная интерполяция в математике?
интерполяция калькулятор – это метод создания новых точек данных в уже известном дискретном наборе точек данных. В этой математической процедуре некоторые исходные точки данных могут быть интерполированы для создания простой и новой функции, которая будет близка к исходным данным. Эта интеграция нового значения называется интерполяцией. Другими словами, мы также можем сказать, что линейный интерполянт – это прямая линия, которая существует между двумя распознанными координатными точками (x0, y0) и (x1, y1). Вы можете легко найти значение интерполяции между двумя координатами на прямой с помощью калькулятор интерполяции.
Вы можете легко найти значение интерполяции между двумя координатами на прямой с помощью калькулятор интерполяции.
Формула линейной интерполяции:
Формула линейной интерполяции:
$$ y = y1 + ((x – x1) / (x2 – x1)) * (y2 – y1) $$
В этом уравнении интерполяции:
- X = известное значение,
- y = неизвестное значение,
- x1 и y1 = координаты, которые ниже известного значения x
- x2 и y2 = координаты выше значения x.
Кроме того, интерполяция онлайн калькулятор уклона помогает найти точки уклона или уклона A (x1, y1) и B (y1, y2) в декартовой координатной плоскости.
Пример1:
Если заданными точками данных являются (2, 4) и (6, 8), как вы рассчитаете значение y, когда x = 2.
На первом этапе мы извлечем координаты заданных точек данных.
$$ x1 = 2 $$
$$ y1 = 4 $$
$$ x2 = 6 $$
$$ y2 = 8 $$
На втором этапе мы возьмем следующие уравнения, чтобы получить значения m, а затем y
- \ (m = y2 – y1 / x2 − x1 \) = уравнение 1
- \ (y = y1 + m * (x – x1) \) = уравнение 2
- Чтобы вычислить значение m, поместите значения в уравнение 1, \ (= m = 8−4 / 6−2 = 1 \)
- Теперь у нас есть значение m, поэтому мы воспользуемся уравнением 2, чтобы найти значение y.
 2 \) в заданной строке, пока заданные данные
2 \) в заданной строке, пока заданные данные«$$ x1 = 4, y1 = 6, x2 = 8, x3 = 12, y3 = 14 $$».
Решение:
Поскольку у нас есть линейное интерполяционное уравнение:
$$ y_2 = (x_2 – x_1) x (y_3- y_1) / (x_3 – x_1) + y_1 $$
Пошаговое решение для нахождения y2 будет таким, как если бы вышеприведенное уравнение было следующим:
$$ y_2 = (x_3 − x_2) x (y_3 − y_1) / (x_3 − x_2) + y_3 $$
$$ y_2 = (12−8) x (14−6) / (12−8) + 14 $$
$$ y_2 = (4) x (8) / (4) + 14 $$
$$ y_2 = (32) / (4) + 14 $$
$$ y_2 = 8 + 14 $$
$$ y_2 = 22 $$
Как работает калькулятор интерполяции линейной?
Вот как работает онлайн-калькулятор для вычисления линейных интерполированных значений.
Вход:
- Введите 5 различных точек данных, чтобы найти линейное интерполированное значение конкретной точки и выполнить интерполяцию.
- Нажмите кнопку “Рассчитать”
Выход:
Онлайн-калькулятор интерполяции предоставит вам следующие результаты:
- Новое интерполированное значение будет отображаться в той точке, где мы хотим провести интерполяцию.

- Этот интерполятор нанесет точку интерполяции на линию.
- Точки входных данных и формула линейной интерполяции
- Это даст вам подробное пошаговое решение для вычисленного интерполированного значения.
Часто задаваемые вопросы (FAQ):
Какой метод можно использовать в любом вопросе интерполяции?
Обычно мы используем метод интерполяции калькулятор полиномов. Причины использования полиномов:
- Их легко оценить
- Дифференциация и интеграция просты.
Это называется полиномиальной интерполяцией.
Когда следует использовать интерполяцию?
Как мы уже знаем, с помощью интерполяции мы можем найти неизвестные точки, поэтому ее можно использовать всякий раз, когда нам нужно предсказать неизвестные значения для любых данных географических точек. Это полезно для прогнозирования осадков, полученных в результате концентраций химических веществ, оценки уровней шума и т. Д.
Какой метод интерполяции лучший?
Интерполяция с обратным взвешиванием по расстоянию (IDW) считается одним из лучших методов для достижения лучших результатов, чем любой другой метод интерполяции калькулятор.

Кригинг – это точная интерполяция?
Методика интерполяция калькулятор обычно связана с точной интерполяцией. Все предсказания Кригинга могут постепенно меняться в космосе. Они будут меняться после того, как попадут в место, где были собраны данные. В этот момент происходит «скачок» прогноза к наиболее точному значению, которое было измерено первым. Однако для быстрых и точных прогнозов можно использовать интерполятор.
интерполяция онлайн калькулятор момент:
Благодаря калькулятор интерполяции линейной для поиска неизвестной точки данных для заданных координат и построения точки на графиках. Кроме того, этот инструмент показывает формулу, которая используется для выполнения требований, с пошаговыми расчетами для облегчения конечных пользователей в кратчайшие сроки. Он обеспечивает бесплатную поддержку в учебных и образовательных целях. Поэтому давайте интерполяция калькулятор найти ответ, поместив известную точку данных в этот интерполятор!
Other Languages: Linear Interpolation Calculator, Kalkulator Interpolasi, Interpolacja Kalkulator, Interpolation Rechner, Interpolasyon Hesaplama, 補間計算, Calculadora De Interpolação, Calcul Interpolation Linéaire, Interpolar Calculadora, Calcolo Interpolazione Lineare, Lineární Interpolace Výpočet, حاسبة الاستيفاء, Interpolointi Laskin.

соединяем точки так, чтобы было красиво / Хабр
Как построить график по n точкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:Немного матчасти
Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек P1 … Pn, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти n – 1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:
На основе этого и может быть построен график:Функции fi могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками Pi) называется сплайном.
В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.
Ставим опыты
Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
Давайте добавим немного конкретики. Вот набор точек (взяты почти с потолка):0 0 20 0 45 -47 53 335 57 26 62 387 74 104 89 0 95 100 100 0
Результат линейной интерполяции этих точек выглядит так:Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.

Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [a; b], это означает, что на [a; b] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз Pi, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:
Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа.
 Это полиномы степени n – 1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Это полиномы степени n – 1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Но вот что получается:Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.
В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k + 1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные k – 1 точек играют роль своего рода «гравитационных центров», притягивающих к себе кривую.
Вот пример кубической кривой Безье:Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k = 1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k – 1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k = 3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (Pi), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
Вот что получится на нашем тестовом наборе:Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.

Думаем и экспериментируем
Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:В качестве прямых, на которых лежат точки Ci – 1(2), Pi и Ci(1), целесообразно взять касательные к графику интерполируемой функции в точках Pi. Это гарантирует отсутствие ложных экстремумов, так как кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).
Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:
Эвристика 1
Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки C1(1) и Cn – 1(2) совпадают с точками P1 и Pn соответственно).
В этом случае получается вот такая кривая:Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.
К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки Pi до точек Ci – 1(2) и Ci(1), но при этом сохраняем их все лежащими на одной прямой:Эвристика для вычисления расстояний будет такой:
Эвристика 2Расчёт l1 и l2 такой же, как в «эвристике 1».
Результат получается такой:
При этом, однако, стоит ещё проверять, не совпали ли точки Pi и Pi + 1 по ординате, и, если совпали, полагать l1 = l2 = 0. Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).
Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:
Эвристика 3Если абсцисса точки пересечения касательных в точках Pi(xi, yi) и Pi + 1(xi + 1, yi + 1) лежит в отрезке [xi; xi + 1], то l1 либо l2 полагаем равным нулю. В том случае, если касательная в точке Pi направлена вверх, нулю полагаем максимальное из l1 и l2, если вниз — минимальное.
Результат следующий:
На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.А как люди-то делают?
Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.MS Excel
Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.
LibreOffice Calc
В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.

Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат 🙂
Highcharts, одна из самых популярных JS-библиотек для построения диаграмм
Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).
amCharts, ещё одна популярная JS-библиотека
Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.
Coreplot, самая популярная библиотека построения графиков для iOS и OS X
Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.aChartEngine, вроде как самая популярная библиотека построения графиков для Android
Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line».
 Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.
Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.Вместо заключения
В конечном счёте получается, что из «больших ребят» лучше всех проблему решили Highcharts. Но метод, описанный в этой статье, обеспечивает ещё меньшую ошибку относительно линейной интерполяции.
Вообще, заняться этим пришлось по просьбе покупателей, которые зарепортили нам «острые углы» в качестве бага в нашем движке диаграмм. Будем рады, если описанный опыт кому-то пригодится.Калькулятор формулы уравнения линейной интерполяции
Инженерное дело — формула интерполяции
Чтобы интерполировать значение y 2 :
x 1 , x 3 , y 1 и y 3 необходимо ввести/скопировать из таблицы.
x 2 определяет точку для выполнения интерполяции.
y 2 — интерполированное значение и решение.х 1 у 1 x 2 y 2 x 9000 6 3 y 3 Ввод:
Решение:
y 2
= НЕ РАСЧЕТНО
Изменить уравнение или формулу
Выберите для решения другого неизвестноголинейная интерполяция
одиночный интерполяторбилинейная интерполяция
двойная интерполяцияЧто такое линейная интерполяция?
Линейная интерполяция — это математический метод, используемый для оценки неизвестного значения между двумя известными точками данных на прямой линии, при условии постоянной скорости изменения между точками и линейной функции, соединяющей их.

Аппроксимация кривой, с другой стороны, представляет собой более широкий процесс построения кривой или математической функции, которая наилучшим образом соответствует ряду точек данных. Например, линейную интерполяцию можно рассматривать как простую форму подбора кривой, когда кривая представляет собой прямую линию.
Почему это необходимо?
Линейная интерполяция и подгонка кривых необходимы, поскольку они обеспечивают эффективные способы оценки значений в наборе данных, когда точные данные недоступны, анализа тенденций данных и создания графических представлений данных. Эти методы имеют решающее значение для аппроксимации, анализа данных и визуализации.
Уравнение линейной интерполяции
Уравнение линейной интерполяции определяется как:
y = y1 + (x — x1) * ((y2 — y1) / (x2 — x1))
где (x1, y1) и (x2, y2) — известные точки данных, x — значение x неизвестной точки, а y — значение y неизвестной точки.
Как решить:
Чтобы найти y с помощью линейной интерполяции, выполните следующие действия:
- Определите две известные точки данных (x1, y1) и (x2, y2), окружающие значение x, для которых вы хотите оценить значение y.

- Подставить известные значения в уравнение линейной интерполяции.
- Решите для y.
Распространенные ошибки:
- Экстраполяция за пределы известных точек данных может привести к неточным оценкам.
- Использование линейной интерполяции для нелинейных наборов данных приводит к плохим приближениям.
- Непроверка допущений о постоянной скорости изменения и линейности.
- Использование только интерполяции при наличии более точных методов или данных.
- Неверная интерпретация результатов, например предположение, что интерполированное значение равно точному значению.
- Чувствительность к выбросам и экстремальным значениям в наборе данных.
Области применения:
- Компьютерная графика и обработка изображений
- Финансы (например, расчет процентных ставок)
- Инжиниринг (например, оценка температуры и давления)
- Географические информационные системы (ГИС) и картография
- Медицинская визуализация
- Разработка видеоигр
- Прогноз погоды
- Обработка аудиосигнала
- Компьютерное проектирование (САПР)
- Наука о данных и аналитика
Другие типы интерполяции:
- Полиномиальная интерполяция
- Сплайн-интерполяция (например, кубический и B-сплайн)
- Интерполяция Hermite
- Рациональная интерполяция
- Интерполяция ближайшего соседа
Калькулятор интерполяции — Примеры, онлайн-калькулятор интерполяции
Калькулятор интерполяции помогает вычислить интерполированное значение для заданных координат.
 Интерполяция — это процесс поиска нового значения функции, когда мы уже знаем любые два значения.
Интерполяция — это процесс поиска нового значения функции, когда мы уже знаем любые два значения.Что такое интерполяционный калькулятор?
Калькулятор интерполяции — это онлайн-инструмент, который помогает вычислить интерполированное значение y для линейной функции, когда нам заданы определенные координаты. Формула линейной интерполяции используется для нахождения нового значения функции. Чтобы использовать калькулятор интерполяции введите значения в поля ввода.
Калькулятор интерполяции
ПРИМЕЧАНИЕ. Введите значения не более двух цифр.
Как пользоваться калькулятором интерполяции?
Чтобы найти значение интерполяции с помощью онлайн-калькулятора интерполяции, следуйте инструкциям ниже:
- Шаг 1: Перейдите к онлайн-калькулятору интерполяции Cuemath.
- Шаг 2: Введите координаты в указанные поля ввода.
- Шаг 3: Нажмите «Рассчитать» , чтобы найти интерполированное значение для заданных координат.

- Шаг 4: Нажмите «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор интерполяции?
Когда мы хотим оценить значение функции между любыми двумя точками, мы используем метод интерполяции. Интерполяция – это метод, который используется для поиска нового значения между двумя точками на кривой заданной функции. Предположим, нам известны координаты двух точек (\(x_{1}\), \(y_{1}\)) и (\(x_{2}\), \(y_{2}\)). Мы также знаем точку, в которой должна быть выполнена интерполяция. Это обозначается х. Тогда формула для линейной интерполяции задается следующим образом:
Линейная интерполяция(y) = \(y_{1} + (x — x_{1})\frac{(y_{2}-y_{1})}{x_{2}-x_{1}}\ )
Здесь y — интерполированное значение. Мы можем подставить данные значения в вышеупомянутое уравнение, чтобы определить интерполированное значение y.
Линейная интерполяция используется для прогнозирования данных, предсказания фондового рынка и многих других научных приложений.
 Линейная интерполяция — это метод подгонки кривой при работе с линейными полиномами. Его можно использовать для построения новых точек данных в пределах некоторых известных точек данных.
Линейная интерполяция — это метод подгонки кривой при работе с линейными полиномами. Его можно использовать для построения новых точек данных в пределах некоторых известных точек данных.Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запись на бесплатный пробный урок
Решенные примеры на калькуляторе интерполяции
Пример 1:
Найдите интерполированное значение y при x = 2, если задано некоторое множество значений (-2, 3), (4, 6). Проверьте это с помощью онлайн-калькулятора интерполяции.
Решение:
Используя формулу интерполяции, \(y_{1} + (x — x_{1})\frac{(y_{2}-y_{1})}{x_{2}-x_{ 1}}\)
Дано: x = 2, x 1 = -2, y 1 = 3, x 2 = 4 , y 2 = 6
9000 2 у = 3 + (2 — (-2)) (6 — 3) / (4 — (-2))y = 3 + 4 × (-3 /-6)
y = 5
Пример 2:
Найдите интерполированное значение y при x = -3, если задан некоторый набор значений (5, 3,5), (10, 6).


 2 \) в заданной строке, пока заданные данные
2 \) в заданной строке, пока заданные данные


 На основе этого и может быть построен график:
На основе этого и может быть построен график:

 Это полиномы степени n – 1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.
Это полиномы степени n – 1, принимающие заданные значения в заданных точках. То есть членения на сегменты здесь не происходит, вся последовательность описывается одним полиномом.


 Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).
Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).

 Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.
Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.

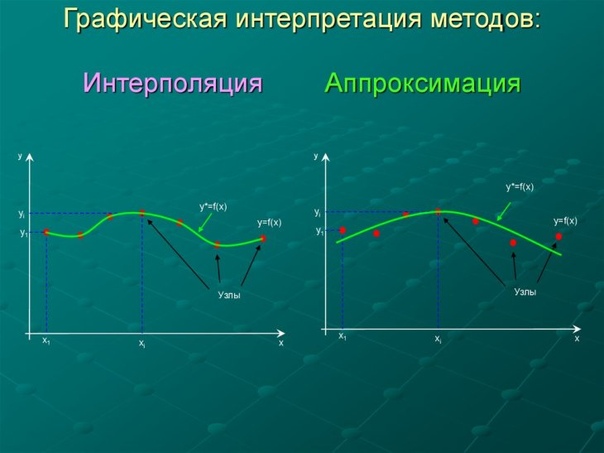 Интерполяция — это процесс поиска нового значения функции, когда мы уже знаем любые два значения.
Интерполяция — это процесс поиска нового значения функции, когда мы уже знаем любые два значения.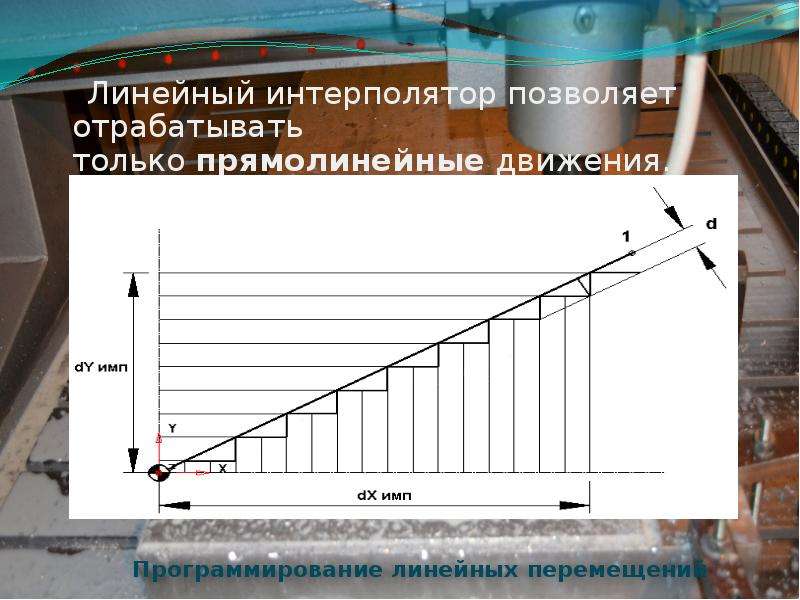
 Линейная интерполяция — это метод подгонки кривой при работе с линейными полиномами. Его можно использовать для построения новых точек данных в пределах некоторых известных точек данных.
Линейная интерполяция — это метод подгонки кривой при работе с линейными полиномами. Его можно использовать для построения новых точек данных в пределах некоторых известных точек данных.



 2+3x-4>0 \) D<0 -2<0 и у неравенства опять нет решений.
2+3x-4>0 \) D<0 -2<0 и у неравенства опять нет решений.
 )
)

 Стандартная форма: ax² + bx + c = 0 с a , b и c — константы или числовые коэффициенты, а x — неизвестная переменная. Продолжайте читать примеры квадратных уравнений в стандартных и нестандартных формах, а также список членов квадратных уравнений.
Стандартная форма: ax² + bx + c = 0 с a , b и c — константы или числовые коэффициенты, а x — неизвестная переменная. Продолжайте читать примеры квадратных уравнений в стандартных и нестандартных формах, а также список членов квадратных уравнений. Ознакомьтесь с примерами нескольких различных экземпляров нестандартных квадратных уравнений.
Ознакомьтесь с примерами нескольких различных экземпляров нестандартных квадратных уравнений.
 Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить?
Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить? 2 … …)на месте точек должны быть цифры или знаки + и —
2 … …)на месте точек должны быть цифры или знаки + и — Источник : https://www.mathworks.com/help/wireless-hdl/ref/dvbs2ldpcde…
Источник : https://www.mathworks.com/help/wireless-hdl/ref/dvbs2ldpcde… 04.2023
04.2023 04.2023
04.2023 ..
.. то есть он развернут на одной ПЭВМ, а мне нужно подключится с другой ПЭВМ, но не к виндоус чер…
то есть он развернут на одной ПЭВМ, а мне нужно подключится с другой ПЭВМ, но не к виндоус чер… рис. 1).
рис. 1). 0003
0003
 е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
 9{ — 1}} \ влево ( {\ гидроразрыва {1} {2}} \ вправо) \)
9{ — 1}} \ влево ( {\ гидроразрыва {1} {2}} \ вправо) \) { — 1}}\left({\cos x} \ справа) = х\]
9{ — 1}}x\hspace{0,5 дюйма} \Leftrightarrow \hspace{0,5 дюйма}\tan y = x\hspace{0,25 дюйма}{\mbox{for}}\,\,\,\,\,\, \,\,\, — \frac{\pi }{2} < y <\frac{\pi }{2}\]
{ — 1}}\left({\cos x} \ справа) = х\]
9{ — 1}}x\hspace{0,5 дюйма} \Leftrightarrow \hspace{0,5 дюйма}\tan y = x\hspace{0,25 дюйма}{\mbox{for}}\,\,\,\,\,\, \,\,\, — \frac{\pi }{2} < y <\frac{\pi }{2}\]
 е. между кусочками функции нет разрыва.
е. между кусочками функции нет разрыва. y = 0,5x, при x < –2.
y = 0,5x, при x < –2.
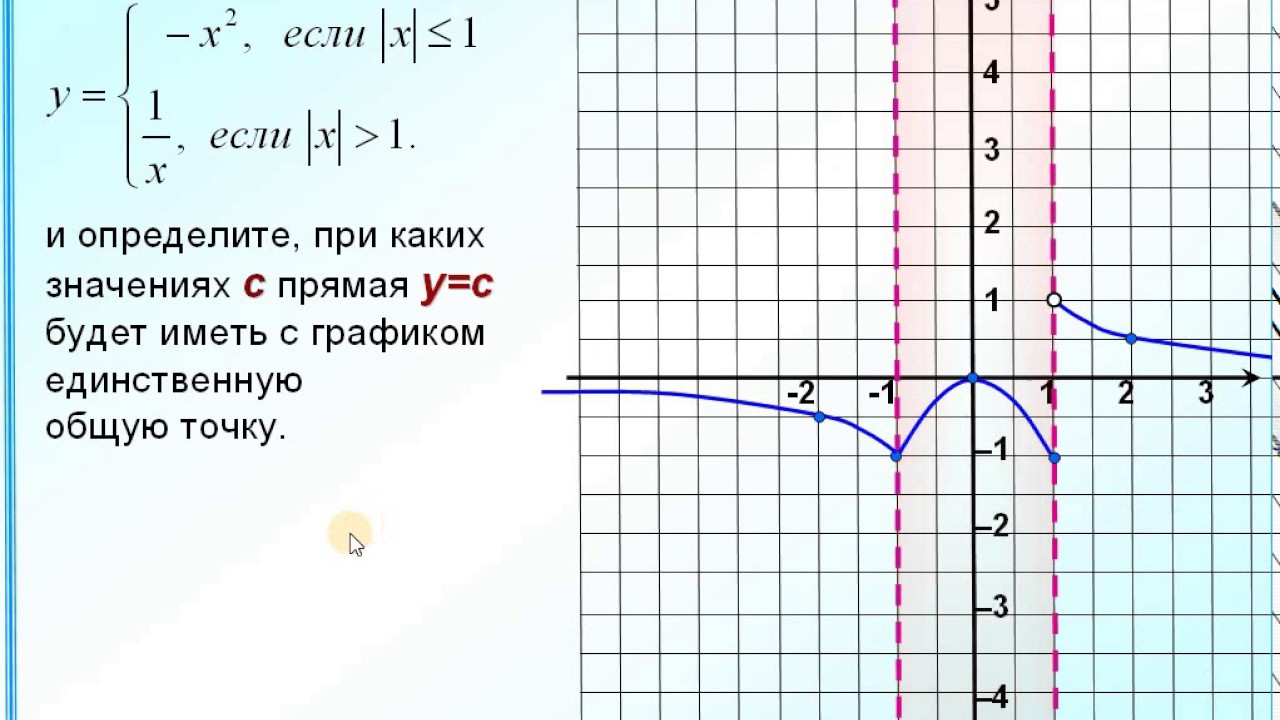
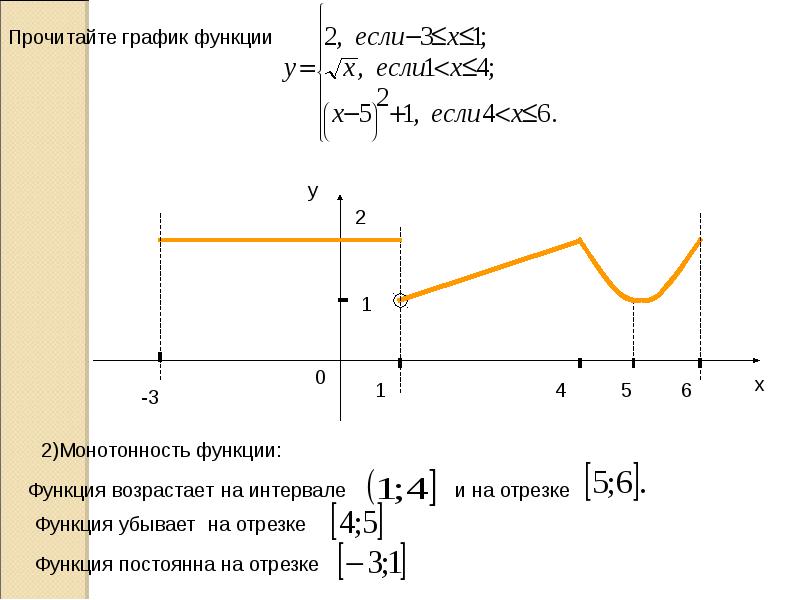 (слайд 20 — 24)
(слайд 20 — 24) В.
В.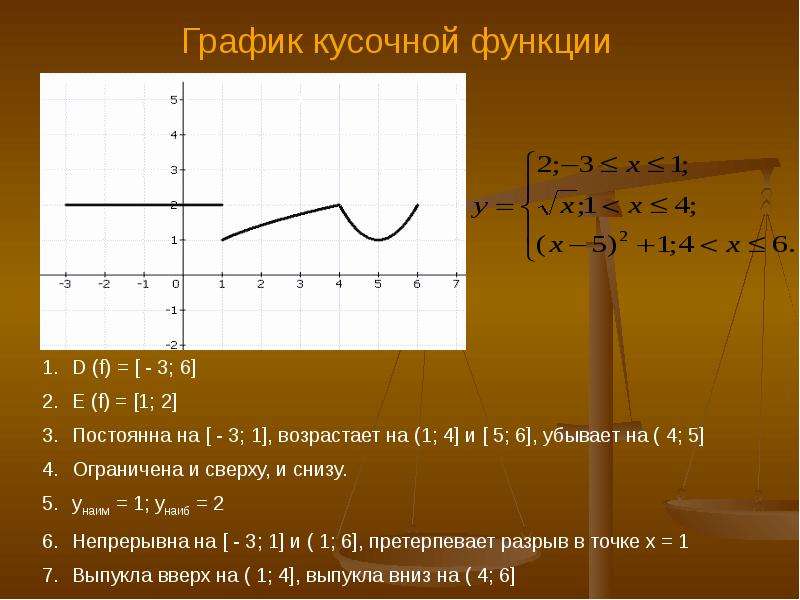
 Его график выглядит следующим образом:
Его график выглядит следующим образом:
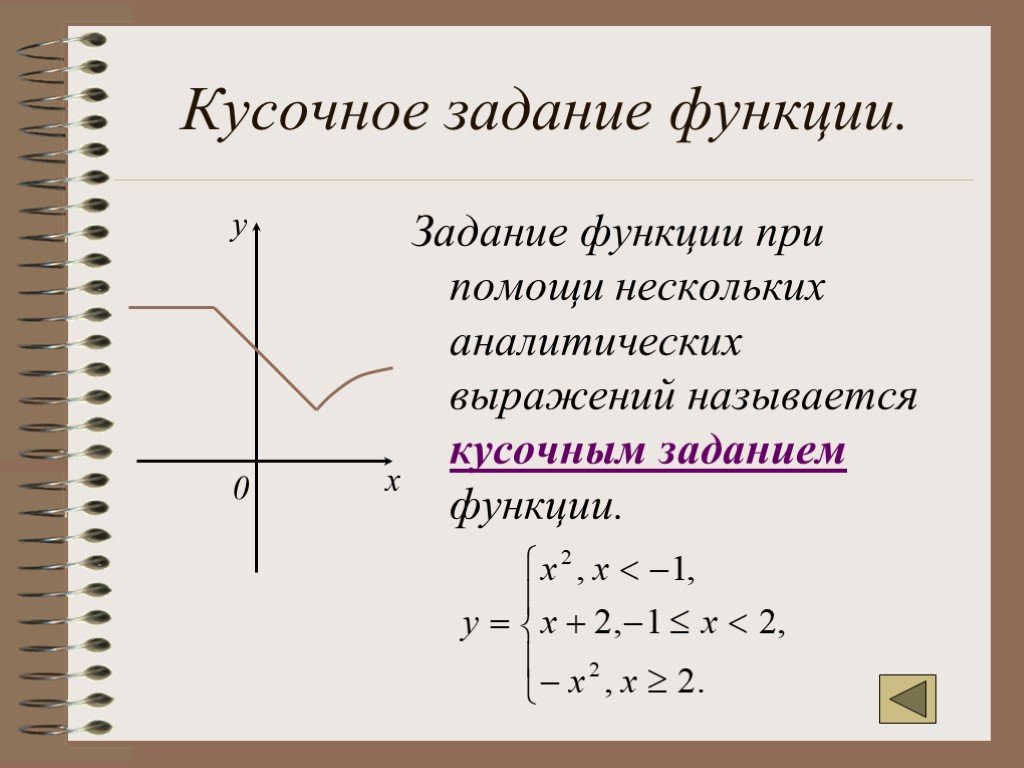 Обратите внимание, что мы должны поставить открытые точки в (-2, -0,25) (первая таблица) и (0, 2) (последняя таблица), поскольку их соответствующие координаты x исключены из интервала. Кроме того, расширьте график в соответствующих интервалах за пределы точек, показанных в таблицах, где это необходимо.
Обратите внимание, что мы должны поставить открытые точки в (-2, -0,25) (первая таблица) и (0, 2) (последняя таблица), поскольку их соответствующие координаты x исключены из интервала. Кроме того, расширьте график в соответствующих интервалах за пределы точек, показанных в таблицах, где это необходимо. Таким образом, область определения f(x) (в приведенном выше примере) равна R.
Таким образом, область определения f(x) (в приведенном выше примере) равна R. \) .
\) .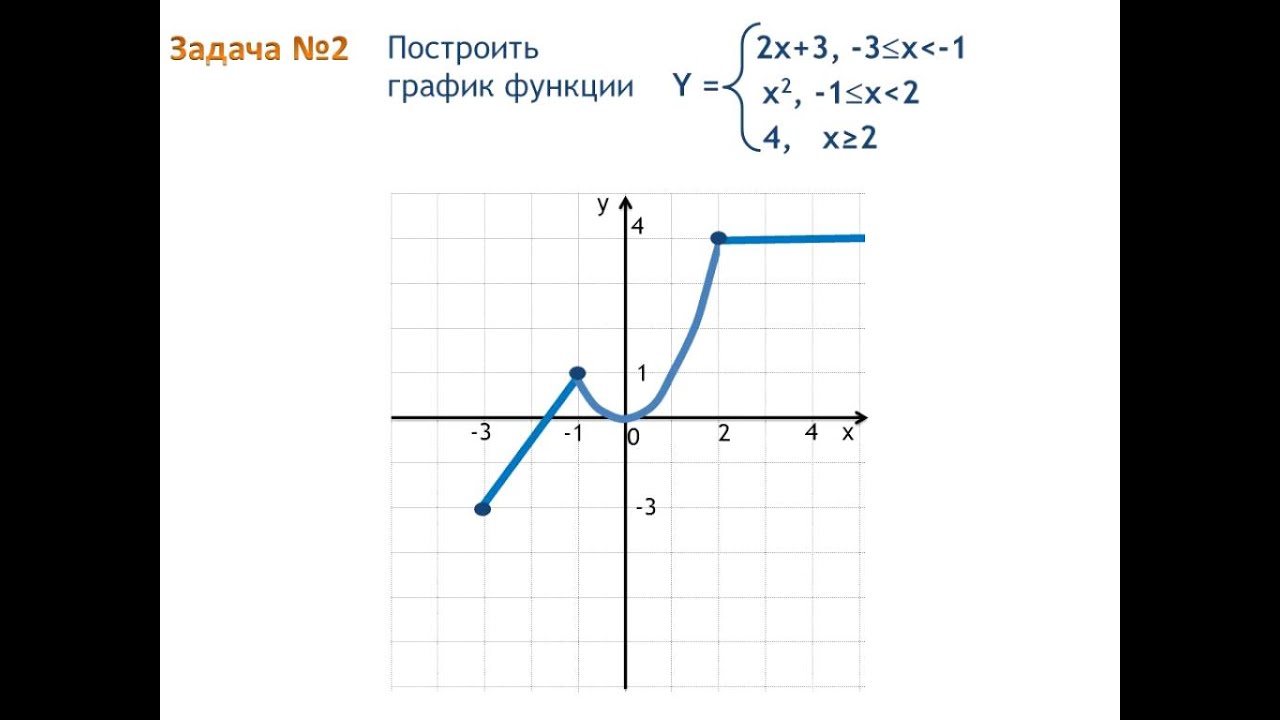 Открытая точка в точке означает, что конкретная точка НЕ является частью функции.
Открытая точка в точке означает, что конкретная точка НЕ является частью функции.
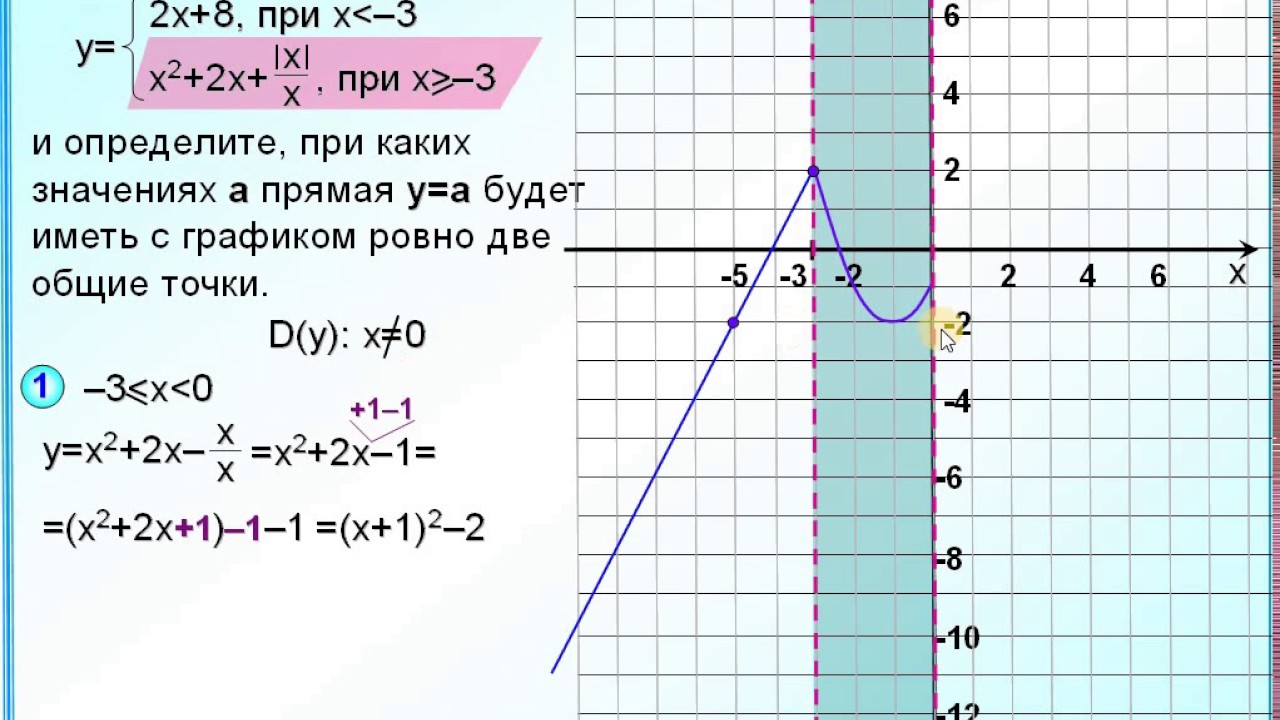

 м ла&
м ла& ru. Хотите тоже свой сайт?
ru. Хотите тоже свой сайт? Глава I . Пределы Пособие «Кузнецов Л .А . Сборник заданий по высшей математике (типовые расчеты)» содержит индивидуальные . .
Глава I . Пределы Пособие «Кузнецов Л .А . Сборник заданий по высшей математике (типовые расчеты)» содержит индивидуальные . .  .
.  .
.  Решебник к сборнику заданий по высшей математике Л .А . Кузнецова . Пределы . 19 .01 .15 .05 .2020 . Глава I . Пределы Пособие «Кузнецов Л .А . Сборник заданий по высшей математике (типовые расчеты)» содержит индивидуальные . .
Решебник к сборнику заданий по высшей математике Л .А . Кузнецова . Пределы . 19 .01 .15 .05 .2020 . Глава I . Пределы Пособие «Кузнецов Л .А . Сборник заданий по высшей математике (типовые расчеты)» содержит индивидуальные . .  .
.  .
.  Эта экспозиция может помочь учащемуся определиться с второстепенным в науках, но несовершеннолетние не ограничиваются науками. Несовершеннолетние выпускники математики включают авиацию, биологию, деловое администрирование, информатику, английский язык, финансы и физику. Для студентов, интересующихся инженерией, мы предлагаем инженерную концентрацию вместо несовершеннолетней, а для студентов, которые хотят сосредоточиться исключительно на математике, мы предлагаем концентрацию по математике и статистике. Поскольку математика так тесно связана с инженерией и естественными науками, специалисты по математике нередко получают степень в одной из этих областей в дополнение к своей математической степени. Гибкость математики отражена в учебной программе, которая, помимо основных занятий по линейной алгебре, логике и теории множеств, абстрактной алгебре и анализу, полностью состоит из факультативов; студенты могут адаптировать свою учебную программу к своим интересам.
Эта экспозиция может помочь учащемуся определиться с второстепенным в науках, но несовершеннолетние не ограничиваются науками. Несовершеннолетние выпускники математики включают авиацию, биологию, деловое администрирование, информатику, английский язык, финансы и физику. Для студентов, интересующихся инженерией, мы предлагаем инженерную концентрацию вместо несовершеннолетней, а для студентов, которые хотят сосредоточиться исключительно на математике, мы предлагаем концентрацию по математике и статистике. Поскольку математика так тесно связана с инженерией и естественными науками, специалисты по математике нередко получают степень в одной из этих областей в дополнение к своей математической степени. Гибкость математики отражена в учебной программе, которая, помимо основных занятий по линейной алгебре, логике и теории множеств, абстрактной алгебре и анализу, полностью состоит из факультативов; студенты могут адаптировать свою учебную программу к своим интересам. ..
.. и Статистика 200 (кроме STAT 402). В статистике может находиться не более 6 семестровых часов. Все курсы, применяемые к несовершеннолетнему, должны быть завершены с оценкой «С» или выше.
и Статистика 200 (кроме STAT 402). В статистике может находиться не более 6 семестровых часов. Все курсы, применяемые к несовершеннолетнему, должны быть завершены с оценкой «С» или выше. Для студентов, изучающих математику, которые хотят получить дополнительное образование в области естественных наук, МАТЕМАТИКА 315, STAT 405 и девять часов МАТЕМАТИЧЕСКОГО 490, использованные для дополнительного актуарного обучения, не могут засчитываться в счет их основных требований; вместо INEN 301 для выполнения основного требования необходимо использовать курс математики уровня 300 или выше.
Для студентов, изучающих математику, которые хотят получить дополнительное образование в области естественных наук, МАТЕМАТИКА 315, STAT 405 и девять часов МАТЕМАТИЧЕСКОГО 490, использованные для дополнительного актуарного обучения, не могут засчитываться в счет их основных требований; вместо INEN 301 для выполнения основного требования необходимо использовать курс математики уровня 300 или выше. Некоторые преподаватели также консультируют аспирантов по программе «Вычислительный анализ и моделирование», Междисциплинарный кандидат наук. Программа вычислительного анализа и моделирования .
Некоторые преподаватели также консультируют аспирантов по программе «Вычислительный анализ и моделирование», Междисциплинарный кандидат наук. Программа вычислительного анализа и моделирования . Следующее ближайшее учреждение, ориентированное на STEM, было примерно в два раза дальше.
Следующее ближайшее учреждение, ориентированное на STEM, было примерно в два раза дальше. Преподаватели, отделы и администраторы Технологического института были хорошими образцами для подражания в создании эффективной и доброжелательной среды и программ для студентов.
Преподаватели, отделы и администраторы Технологического института были хорошими образцами для подражания в создании эффективной и доброжелательной среды и программ для студентов. Я не чувствовал, что очень хорошо понял материал, поэтому очень нервничал перед первым тестом. Мне стало очень плохо, пока я сдавала анализ, но я его закончила и потом пошла к врачу, где узнала, что у меня ходячая пневмония. Я был очень удивлен, когда получил свой тест и получил пятерку!
Я не чувствовал, что очень хорошо понял материал, поэтому очень нервничал перед первым тестом. Мне стало очень плохо, пока я сдавала анализ, но я его закончила и потом пошла к врачу, где узнала, что у меня ходячая пневмония. Я был очень удивлен, когда получил свой тест и получил пятерку! Кроме того, в Технологическом институте Луизианы есть отличные возможности для получения стипендии, которые позволили мне получить высшее образование, когда в противном случае это было бы трудно себе позволить.
Кроме того, в Технологическом институте Луизианы есть отличные возможности для получения стипендии, которые позволили мне получить высшее образование, когда в противном случае это было бы трудно себе позволить. В Технологическом институте Луизианы также есть много прекрасных возможностей для профессионального роста. В выпускном классе я посетил ярмарку вакансий, чтобы узнать, какие есть возможности трудоустройства; несмотря на то, что я не нашел работу, я научился писать резюме и взаимодействовать с потенциальными работодателями.
В Технологическом институте Луизианы также есть много прекрасных возможностей для профессионального роста. В выпускном классе я посетил ярмарку вакансий, чтобы узнать, какие есть возможности трудоустройства; несмотря на то, что я не нашел работу, я научился писать резюме и взаимодействовать с потенциальными работодателями.
 Кроме того, я действительно не знал, что могу специализироваться на математике. В первой четверти я переключился на математику, потому что это мне очень нравилось. На самом деле у меня не было плана, чем бы я хотел заниматься после колледжа, но я понял это по ходу дела.
Кроме того, я действительно не знал, что могу специализироваться на математике. В первой четверти я переключился на математику, потому что это мне очень нравилось. На самом деле у меня не было плана, чем бы я хотел заниматься после колледжа, но я понял это по ходу дела.
 М. Обыкновенные дифференциальные уравнения – СПб: Специальная Литература, 1996.
М. Обыкновенные дифференциальные уравнения – СПб: Специальная Литература, 1996.
 03.01 Информатика и вычислительная техника
03.01 Информатика и вычислительная техника 


 Применим подстановку y = x· u, y’ = u + x· u’.
Применим подстановку y = x· u, y’ = u + x· u’. Сделаем замену
Сделаем замену 3).
3). 6) или использовать прием Бернулли.
6) или использовать прием Бернулли. Проинтегрировав его, получим следующее
Проинтегрировав его, получим следующее
 Дифференциальные уравнения включают много типов: линейные уравнения против нелинейных уравнений, обыкновенные дифференциальные уравнения против уравнений в частных производных и, наконец, однородные уравнения против неоднородных уравнений. Общие решения или исследование зависят от расшифровки типа уравнения.
Дифференциальные уравнения включают много типов: линейные уравнения против нелинейных уравнений, обыкновенные дифференциальные уравнения против уравнений в частных производных и, наконец, однородные уравнения против неоднородных уравнений. Общие решения или исследование зависят от расшифровки типа уравнения. Вы научитесь решать уравнения первого порядка, автономные уравнения и нелинейные дифференциальные уравнения. Вы будете применять эти знания, используя такие вещи, как волновые уравнения и другие численные методы. Вы можете расширить эти знания с помощью курса 2×2 Systems Массачусетского технологического института, предназначенного для введения связанных дифференциальных уравнений. Вы поймете, как решать скорости изменения с помощью дифференциальных уравнений первого порядка и линейных дифференциальных уравнений. Вы можете продолжить изучение всей серии X, изучая все более и более сложные уравнения, включая дифференциальные уравнения второго порядка и частные производные. Оттуда вы можете пройти практические курсы, предназначенные для интеграции использования дифференциальных уравнений в практические приложения. МИСиС предлагает курс «Комплексный анализ с физическими приложениями», призванный дать вам возможность исследовать мир сложных уравнений. Или вы можете применить эти знания к творческим занятиям, используя эти уравнения для CGI с Мичиганским университетом.
Вы научитесь решать уравнения первого порядка, автономные уравнения и нелинейные дифференциальные уравнения. Вы будете применять эти знания, используя такие вещи, как волновые уравнения и другие численные методы. Вы можете расширить эти знания с помощью курса 2×2 Systems Массачусетского технологического института, предназначенного для введения связанных дифференциальных уравнений. Вы поймете, как решать скорости изменения с помощью дифференциальных уравнений первого порядка и линейных дифференциальных уравнений. Вы можете продолжить изучение всей серии X, изучая все более и более сложные уравнения, включая дифференциальные уравнения второго порядка и частные производные. Оттуда вы можете пройти практические курсы, предназначенные для интеграции использования дифференциальных уравнений в практические приложения. МИСиС предлагает курс «Комплексный анализ с физическими приложениями», призванный дать вам возможность исследовать мир сложных уравнений. Или вы можете применить эти знания к творческим занятиям, используя эти уравнения для CGI с Мичиганским университетом.
 Вы тоже можете.
Вы тоже можете.

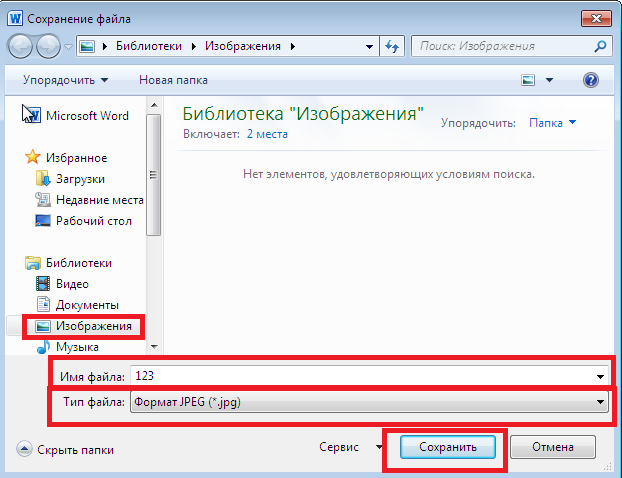




 При использовании этих способов, каждая страница документа Word сохраняется в виде отдельного графического файла в формате «.jpg» или «.jpeg». У пользователя есть возможности для сохранения на компьютере отдельных изображений, находящихся на страницах документа Word.
При использовании этих способов, каждая страница документа Word сохраняется в виде отдельного графического файла в формате «.jpg» или «.jpeg». У пользователя есть возможности для сохранения на компьютере отдельных изображений, находящихся на страницах документа Word. Все они бесплатны и просты, поэтому вы можете использовать любой, который вам наиболее удобен.
Все они бесплатны и просты, поэтому вы можете использовать любой, который вам наиболее удобен. Вы также можете щелкнуть выбранный контент правой кнопкой мыши и выбрать Копировать.
Вы также можете щелкнуть выбранный контент правой кнопкой мыши и выбрать Копировать.

 Ограничение состоит в том, что нет поддержки сохранения в GIF или других форматах изображений. Кроме того, вы не можете настроить качество изображений.
Ограничение состоит в том, что нет поддержки сохранения в GIF или других форматах изображений. Кроме того, вы не можете настроить качество изображений.
 Вы можете выбрать до 20 документов Word для преобразования. Общий размер файла не может превышать 50 МБ.
Вы можете выбрать до 20 документов Word для преобразования. Общий размер файла не может превышать 50 МБ.

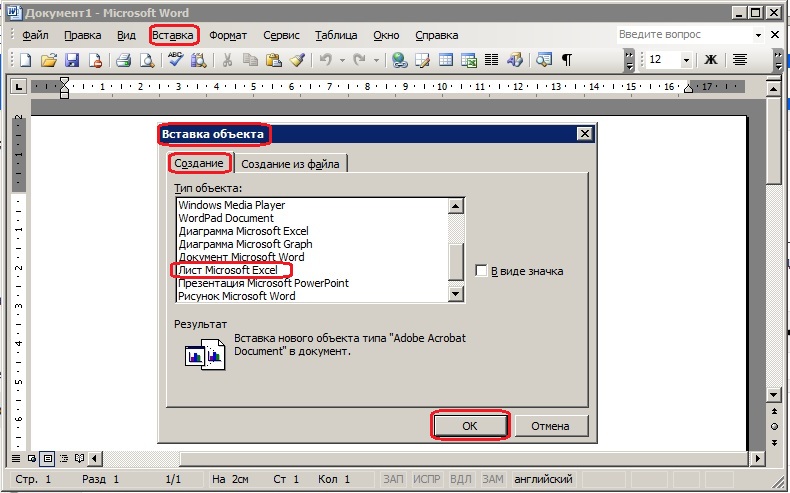 Используя эти шаги, вы также можете сохранить документ Word в формате PNG или TIFF.
Используя эти шаги, вы также можете сохранить документ Word в формате PNG или TIFF.
 Вам нечего терять, кроме файлов, которые вы продолжаете сохранять!
Вам нечего терять, кроме файлов, которые вы продолжаете сохранять! Если обучение редактированию в выбранном вами программном обеспечении занимает больше времени, чем само редактирование, значит, вы еще не нашли подходящий инструмент. С DocHub вы легко получите все необходимые функции, даже если вы используете их впервые.
Если обучение редактированию в выбранном вами программном обеспечении занимает больше времени, чем само редактирование, значит, вы еще не нашли подходящий инструмент. С DocHub вы легко получите все необходимые функции, даже если вы используете их впервые.
 Нет растеризованного текста или удаленных полей. Используйте онлайн-редактор PDF, чтобы получить идеальный документ за считанные минуты.
Нет растеризованного текста или удаленных полей. Используйте онлайн-редактор PDF, чтобы получить идеальный документ за считанные минуты.

 Если вы не можете найти ответ на свой вопрос, пожалуйста, не стесняйтесь обращаться к нам.
Если вы не можете найти ответ на свой вопрос, пожалуйста, не стесняйтесь обращаться к нам. MoreFile выберите переносимую сеть графика из выпадающего меню, чтобы получить jpg.
MoreFile выберите переносимую сеть графика из выпадающего меню, чтобы получить jpg.
 Цены на доставку вы можете рассчитать онлайн.
Цены на доставку вы можете рассчитать онлайн.

 Целое число не может содержать дроби или десятичные дроби.
Целое число не может содержать дроби или десятичные дроби.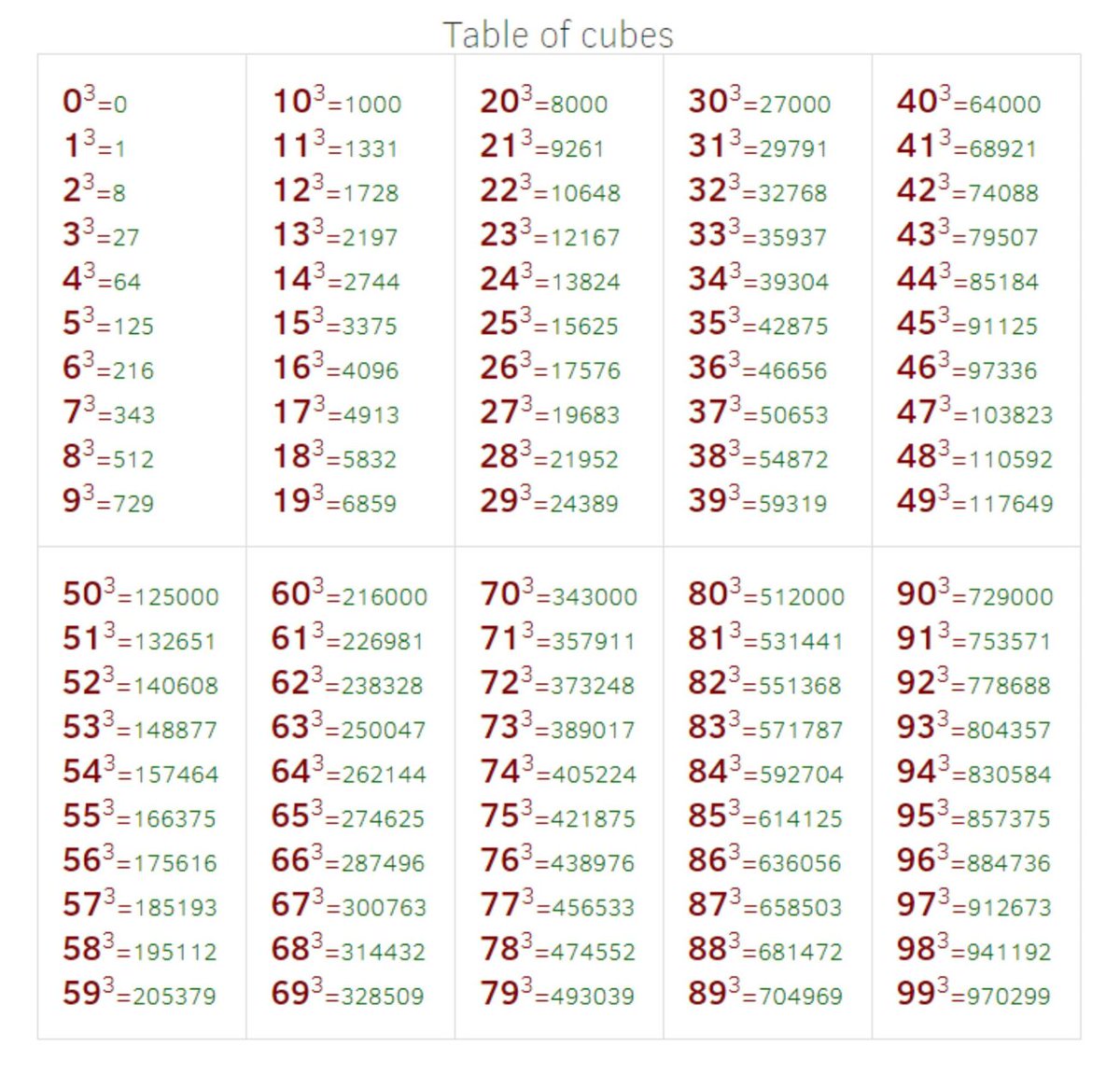 Не стесняйтесь вводить целых уравнений ; попробуйте умножение (5*67), деление (3/675), сложение (1+1) или вычитание (1,56-0,86).
Не стесняйтесь вводить целых уравнений ; попробуйте умножение (5*67), деление (3/675), сложение (1+1) или вычитание (1,56-0,86).
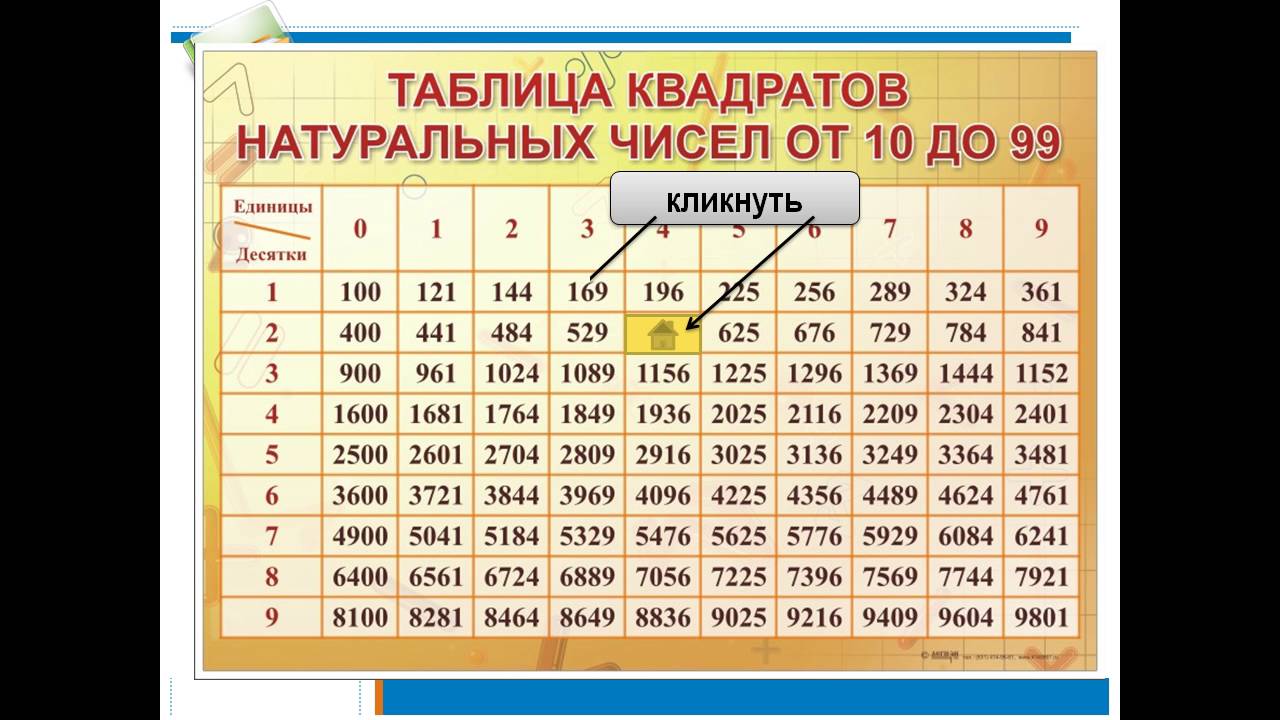
 Если вычисленный цифровой корень не является одним из упомянутых значений, ваше число не может быть идеальным квадратом.
Если вычисленный цифровой корень не является одним из упомянутых значений, ваше число не может быть идеальным квадратом. Наше число не может быть полным квадратом.
Наше число не может быть полным квадратом. Он обладает множеством встроенных библиотек, которые помогут вам выполнять несколько операций, таких как возведение числа в квадрат. В этой статье мы узнаем обо всех методах возведения в квадрат числа в Python с различными вариантами использования. Итак, приступим!
Он обладает множеством встроенных библиотек, которые помогут вам выполнять несколько операций, таких как возведение числа в квадрат. В этой статье мы узнаем обо всех методах возведения в квадрат числа в Python с различными вариантами использования. Итак, приступим! Он представлен «**» . При применении этого метода оператор экспоненты возвращает экспоненциальную степень, в результате чего получается квадрат числа. Обратите внимание, что выражение «a**b» будет определено как «a в степени b».
Он представлен «**» . При применении этого метода оператор экспоненты возвращает экспоненциальную степень, в результате чего получается квадрат числа. Обратите внимание, что выражение «a**b» будет определено как «a в степени b».
 Следовательно, мы будем находить квадрат числа с помощью цикла while, пока условие не станет ложным.
Следовательно, мы будем находить квадрат числа с помощью цикла while, пока условие не станет ложным.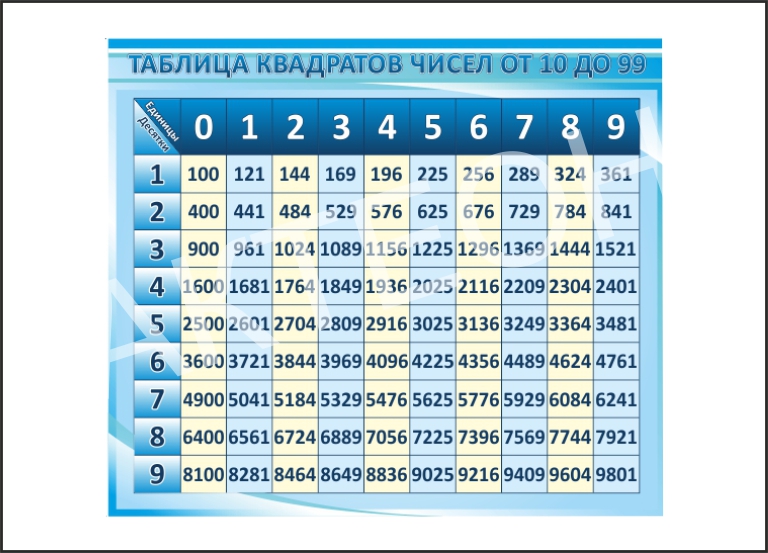 square(arr))
square(arr))

 Подставляем
Подставляем При x > 0 имеем:
При x > 0 имеем:





 Вычислить интеграл
Вычислить интеграл 7
7
 \]
\]
 {2}+C \), где \(C \) — любая константа (при условии, что это действительное число).
{2}+C \), где \(C \) — любая константа (при условии, что это действительное число). \]Это означает, что \( F(x) \pm G(x) \) является первообразной \( f(x) \pm g(x) \), так что \[ \int (f(x) \pm g(x)) ~\mathrm{d}x = F(x) \pm G(x) + C. \]
\]Это означает, что \( F(x) \pm G(x) \) является первообразной \( f(x) \pm g(x) \), так что \[ \int (f(x) \pm g(x)) ~\mathrm{d}x = F(x) \pm G(x) + C. \] Теперь предположим, что вы хотите обратить этот процесс вспять, и спросите себя: какая функция (функции) могла бы иметь производную \(f(x) = 0 \)? Очевидно, \( F(x) = 3 \) — один ответ. Вы говорите, что \(F(x) = 3\) является первообразной \(f(x) = 0\).
Теперь предположим, что вы хотите обратить этот процесс вспять, и спросите себя: какая функция (функции) могла бы иметь производную \(f(x) = 0 \)? Очевидно, \( F(x) = 3 \) — один ответ. Вы говорите, что \(F(x) = 3\) является первообразной \(f(x) = 0\). Другими словами, так же, как и с производными:
Другими словами, так же, как и с производными: 9{2}} ~\mathrm{d}x \]
9{2}} ~\mathrm{d}x \]



 Интеграция есть процесс, обратный дифференциации. Вместо дифференцирования функции нам дается производная функции и требуется вычислить функцию по производной. Этот процесс называется интеграцией или антидифференциацией. Рассмотрим функцию f(x) = sin(x), производную этой функции, если f'(x) = cos(x). Итак, интегрирование f'(x) должно вернуть функцию f(x). Обратите внимание, что для каждой функции f(x) = sin(x) + C производная одинакова, потому что после дифференцирования константа становится равной нулю. Таким образом, первообразные не уникальны, для каждой функции ее первообразные бесконечны.
Интеграция есть процесс, обратный дифференциации. Вместо дифференцирования функции нам дается производная функции и требуется вычислить функцию по производной. Этот процесс называется интеграцией или антидифференциацией. Рассмотрим функцию f(x) = sin(x), производную этой функции, если f'(x) = cos(x). Итак, интегрирование f'(x) должно вернуть функцию f(x). Обратите внимание, что для каждой функции f(x) = sin(x) + C производная одинакова, потому что после дифференцирования константа становится равной нулю. Таким образом, первообразные не уникальны, для каждой функции ее первообразные бесконечны. Правило обратной степени — это одно из правил, которые помогают нам интегрировать многочлены и другие функции. Правило обратной мощности
Правило обратной степени — это одно из правил, которые помогают нам интегрировать многочлены и другие функции. Правило обратной мощности  Интегралы можно понять через графики. Ясно, что интегралы есть не что иное, как антипроизводные. Рассмотрим функцию f(x) и скажем, что она является антипроизводной, если задана F(x). В этом случае F'(x) = f(x). Рассматривайте приведенный ниже график как график функции f(x), это означает, что график производных функции F(x) задан и целью является определение интегральной функции F(x).
Интегралы можно понять через графики. Ясно, что интегралы есть не что иное, как антипроизводные. Рассмотрим функцию f(x) и скажем, что она является антипроизводной, если задана F(x). В этом случае F'(x) = f(x). Рассматривайте приведенный ниже график как график функции f(x), это означает, что график производных функции F(x) задан и целью является определение интегральной функции F(x). Подынтегральные выражения есть не что иное, как производные от интегралов. Они дают информацию о скорости увеличения/уменьшения и максимумах и минимумах интегралов. Рассмотрим график функции f(x),
Подынтегральные выражения есть не что иное, как производные от интегралов. Они дают информацию о скорости увеличения/уменьшения и максимумах и минимумах интегралов. Рассмотрим график функции f(x),
 е. не имеет ни нижнего предела, ни верхнего предела. В то время как определенные интегралы дают значение функции в пределе. т. е. определенные интегралы интегрируются по определенному интервалу. Неопределенные интегралы имеют постоянную интегрирования, тогда как определенный интеграл не имеет постоянной интегрирования.
е. не имеет ни нижнего предела, ни верхнего предела. В то время как определенные интегралы дают значение функции в пределе. т. е. определенные интегралы интегрируются по определенному интервалу. Неопределенные интегралы имеют постоянную интегрирования, тогда как определенный интеграл не имеет постоянной интегрирования. 0003
0003


 Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,2. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Вероятность того, что это вопрос по теме «Внешние углы», равна 0,2. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
 Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежат 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежат 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.


 Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
 Найдите вероятность
Найдите вероятность Какова вероятность, что доклад профессора
Какова вероятность, что доклад профессора

 Найдите вероятность того, что А.
Найдите вероятность того, что А.


 Это независимые события, вероятность их
Это независимые события, вероятность их Брать
один из наших многочисленных практических тестов по теории вероятностей для прогона часто задаваемых вопросов. Ты
получите невероятно подробные результаты оценки в конце практического теста по теории вероятностей, чтобы
помочь вам определить свои сильные и слабые стороны. Выберите один из наших практических тестов по теории вероятностей прямо сейчас
и начать!
Брать
один из наших многочисленных практических тестов по теории вероятностей для прогона часто задаваемых вопросов. Ты
получите невероятно подробные результаты оценки в конце практического теста по теории вероятностей, чтобы
помочь вам определить свои сильные и слабые стороны. Выберите один из наших практических тестов по теории вероятностей прямо сейчас
и начать!
 edu
edu  Основной принцип подсчета и примеры.
Основной принцип подсчета и примеры. 



 Решение здесь.
Решение здесь. 