Деление многочленов
Продолжаем изучать многочлены. В данном уроке мы научимся их делить.
Деление многочлена на одночлен
Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.
Например, разделим многочлен 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Запишем это деление в виде дроби:
Теперь делим каждый член многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Получающиеся частные будем складывать:
Получили привычное для нас деление одночленов. Выполним это деление:
Таким образом, при делении многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy получается многочлен 15xy2 + 10y + 5y2.
При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.
В нашем примере произведение полученного многочлена 15xy2 + 10y + 5y2 и делителя xy должно быть равно многочлену 15x2y3 + 10xy2 + 5xy3, то есть исходному делимому. Проверим так ли это:
(15xy2 + 10y + 5y2)xy = 15x2y3 + 10xy2 + 5xy3
Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.
Например, чтобы сложить дроби , и нужно записать следующее выражение:
Если мы вычислим выражение , то получим дробь , значение которой равно 1,5.
При этом выражение мы можем вернуть в исходное состояние , и вычислить по отдельности каждую дробь, затем сложить полученные частные. Результат по прежнему будет равен 1,5
Тоже самое происходит при делении многочлена на одночлен. Одночлен берёт на себя роль общего знаменателя для всех членов многочлена. Например, при делении многочлена ax + bx + cx на многочлен x, образуется три дроби с общим знаменателем x
Вычисление каждой дроби даст в результате многочлен a + b + c
Пример 2. Разделить многочлен 8m3n + 24m2n2 на одночлен 8m2n
Пример 3. Разделить многочлен 4c2d − 12c4d3 на одночлен −4c2d
Деление одночлена на многочлен
Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.
Допустим, мы захотели разделить одночлен 2xy на многочлен 5x + 3y + 5.
Результатом этого деления должен быть многочлен, перемножение которого с многочленом 5x + 3y + 5 даёт одночлен 2xy. Но не существует многочлена, перемножение которого с многочленом 5x + 3y + 5 давало бы в результате одночлен 2xy, поскольку перемножение многочленов даёт в результате многочлен, а не одночлен.
Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.
Например, найдём значение выражения при x = 2.
Выражение представляет собой деление одночлена на многочлен. В данном случае мы не сможем выполнить какие-либо преобразования. Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:
Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:
Деление многочлена на многочлен
Если первый многочлен умножить на второй многочлен, получается третий многочлен. Например, если умножить многочлен x + 5 на многочлен x + 3, получается многочлен x2 + 8x + 15
(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15
(x + 5)(x + 3) = x2 + 8x + 15
Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.
Тогда согласно этому правилу, деление полученного нами многочлена x2 + 8x + 15 на многочлен x + 3 должно давать в результате многочлен x + 5.
Деление многочлена на многочлен выполняется уголком. Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.
Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.
Выполним уголком деление многочлена x2 + 8x + 15 на многочлен x + 3. Так мы поэтапно увидим, как получается многочлен x + 5.
В данном случае результат нам известен заранее. Это будет многочлен x + 5. Но чаще всего результат бывает неизвестным. Поэтому решение будем комментировать так, будто результат нам неизвестен.
Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.
Сейчас наша задача найти первый член нового многочлена. Как это сделать?
Когда мы изначально перемножали многочлены x + 5 и x + 3, мы сначала умножили первый член первого многочлена на первый член второго многочлена. Тем самым мы получили первый член третьего многочлена:
Если мы обратно разделим первый член третьего многочлена на первый член второго многочлена, то получим первый член первого многочлена. А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5.
А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5.
Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.
Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.
Если первый член делимого (в нашем случае это x2) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:
Теперь, как и при делении обычных чисел, умножаем x на делитель x + 3. На этом этапе нужно суметь умножить одночлен на многочлен. При умножении x на x + 3, получается x2 + 3x. Записываем этот многочлен под делимым x2+ 8x+ 15 так, чтобы подобные члены располагались друг под другом:
Теперь из делимого x2 + 8x + 15 вычитаем x2 + 3x. Подобные члены вычитаем из подобных им членов. Если из x2 вычесть x2, получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x
Подобные члены вычитаем из подобных им членов. Если из x2 вычесть x2, получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x
Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:
Теперь делим многочлен 5x + 15 на x + 3. Для этого нужно найти второй член нового многочлена. Чтобы его найти, нужно первый член делимого (сейчас это член 5x) разделить на первый член делителя (это член x). Если 5x разделить на x, получится 5. То есть вторым членом нового многочлена является 5. Записываем его под правым углом, вместе со своим знаком (член 5 в данном случае положителен)
Теперь умножаем 5 на делитель x + 3. При умножении 5 на x + 3, получается 5x + 15. Записываем этот многочлен под делимым 5x + 15
Записываем этот многочлен под делимым 5x + 15
Теперь из делимого 5x + 15 вычитаем 5x + 15. Если из 5x + 15 вычесть 5x + 15 получится 0.
На этом деление завершено.
После выполнения деления можно выполнить проверку, умножив частное на делитель. В нашем случае, если частное x + 5 умножить на делитель x + 3, должен получаться многочлен x2 + 8x + 15
(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15
Пример 2. Разделить многочлен x2 − 8x + 7 на многочлен x − 7
Записываем уголком данное деление:
Находим первый член частного. Разделим первый член делимого на первый член делителя, получим x. Записываем x под правым углом:
Умножаем x на x − 7, получаем x2 − 7x. Записываем этот многочлен под делимым x2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:
Записываем этот многочлен под делимым x2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:
Вычитаем из x2 − 8x + 7 многочлен x2 − 7x. При вычитании x2 из x2 получается 0. Ноль не записываем. А при вычитании −7x из −8x получается −x, поскольку −8x − (−7x) = −8x + 7x = −x. Записываем −x под членами −7x и −8x. Далее сносим следующий член 7
Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:
Давайте воспользуемся этим методом:
Вернёмся к нашей задаче. Разделим многочлен −x + 7 на x − 7. Для этого нужно найти второй член частного. Чтобы его найти, нужно первый член делимого (сейчас это член −x) разделить на первый член делителя (это член x). Если −x разделить на x, получится −1. Записываем −1 под правым углом вместе со своим знаком:
Умножаем −1 на x − 7, получаем −x + 7. Записываем этот многочлен под делимым −x + 7
Теперь из −x + 7 вычитаем −x + 7. Если из −x + 7 вычесть −x + 7 получится 0
Деление завершено. Таким образом, частное от деления многочлена x2 − 8x + 7 на многочлен x − 7 равно x − 1
Выполним проверку. Умножим частное x − 1 на делитель x − 7. У нас должен получиться многочлен x2 − 8x + 7
(x − 1)(x − 7) = x2 − x − 7x + 7 = x2 − 8x + 7
Пример 3. Разделить многочлен x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3
Разделить многочлен x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3
Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x4
Умножаем x4 на делитель x2 + x3 и полученный результат записываем под делимым. Если x4 умножить на x2 + x3 получится x6 + x7. Члены этого многочлена записываем под делимым так, чтобы подобные члены располагались друг под другом:
Теперь из делимого вычитаем многочлен x6 + x7. Вычитание x6 из x6 даст в результате 0. Вычитание x7 из x7 тоже даст в результате 0. Оставшиеся члены 2x4 и 2x5 снесём:
Получилось новое делимое 2x4 + 2x5. Это же делимое можно было получить, выписав отдельно многочлен x6 + 2x4 + x7 + 2x5 и вычтя из него многочлен x6 + x7
Это же делимое можно было получить, выписав отдельно многочлен x6 + 2x4 + x7 + 2x5 и вычтя из него многочлен x6 + x7
Разделим многочлен 2x4 + 2x5 на делитель x2 + x3. Как и раньше сначала делим первый член делимого на первый член делителя, получим 2x2. Записываем этот член в частном:
Умножаем 2x2 на делитель x2 + x3 и полученный результат записываем под делимым. Если 2x2 умножить на x2 + x3 получится 2x4 + 2x5. Записываем члены этого многочлена под делимым так, чтобы подобные члены располагались друг под другом. Затем выполним вычитание:
Вычитание многочлена 2x4 + 2x5 из многочлена 2x4 + 2x5 дало в результате 0, поэтому деление успешно завершилось.
В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.
Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.
Решим предыдущий пример, упорядочив члены исходных многочленов в порядке убывания степеней. Если члены многочлена x6 + 2x4 + x7 + 2x5 упорядочить в порядке убывания степеней, то получим многочлен x7 + x6 + 2x5 + 2x4. А если члены многочлена x2 + x3 упорядочить в порядке убывания степеней, то получим многочлен x3 + x2
Тогда деление уголком многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 примет следующий вид:
Деление завершено. Таким образом, частное от деления многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 равно x4 + 2x2
Таким образом, частное от деления многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 равно x4 + 2x2
Выполним проверку. Умножим частное x4 + 2x2 на делитель x2 + x3. У нас должен получиться многочлен x6 + 2x4 + x7 + 2x5
(x4 + 2x2)(x2 + x3) = x4 (x2 + x3) + 2x2(x2 + x3) = x6 + 2x4 + x7 + 2x5
При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.
Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.
Перепишем умножение (x4 + 2x2)(x2 + x3) упорядочив члены многочленов в порядке убывания степеней.
(x4 + 2x2)(x3 + x2) = x4(x3 + x2) + 2x2(x3 + x2) = x7 + x6 + 2x5 + 2x4
Пример 4. Разделить многочлен 17x2 − 6x4 + 5x3 − 23x + 7 на многочлен 7 − 3x2 − 2x
Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:
Значит,
Пример 5. Разделить многочлен 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2
Разделить многочлен 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 4a2. Записываем 4a2 в частном:
Умножим 4a2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 4a4 − 12a3b − 36a2b2
Теперь делим −2a3b + 12a2b2 − 54b4 на делитель a2 − 3ab − 9b2. Разделим первый член делимого на первый член делителя, получим −2ab. Записываем −2ab в частном:
Записываем −2ab в частном:
Умножим −2ab на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым −2a3b + 12a2b2 − 54b4
Вычтем из многочлена −2a3b + 12a2b2 − 54b4 многочлен −2a3b + 12a2b2 − 18ab3. При вычитании подобных членов обнаруживаем, что члены −54b4 и 18ab3 не являются подобными, а значит их вычитание не даст никакого преобразования. В этом случае выполняем вычитание там где это можно, а именно вычтем −2a3b из −2a3b и 6a2b2 из 12a2b2, а вычитание 18ab3 из −54b4 запишем в виде разности −54b4 − (+18ab3) или −54b4 − 18ab3
Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:
Вернёмся к нашей задаче. Разделим 6a2b2 − 54b4 − 18ab3 на делитель a2 − 3ab − 9b2. Делим первый член делимого на первый член делителя, получим 6b2. Записываем 6b2 в частном:
Разделим 6a2b2 − 54b4 − 18ab3 на делитель a2 − 3ab − 9b2. Делим первый член делимого на первый член делителя, получим 6b2. Записываем 6b2 в частном:
Умножим 6b2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым 6a2b2 − 54b4 − 18ab3. Сразу вычтем этот полученный результат из делимого 6a2b2 − 54b4 − 18ab3
Деление завершено. Таким образом, частное от деления многочлена 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2 равно 4a2 − 2ab + 6b2.
Выполним проверку. Умножим частное 4a2 − 2ab + 6b2 на делитель a2 − 3ab − 9b2. У нас должен получиться многочлен 4a4 − 14a3b − 24a2b2 − 54b4
Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.
Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:
То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:
Рациональное число читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.
Например, если при делении многочлена a на многочлен b получится частное c, да еще останется остаток q, то ответ будет записан так:
Например, разделим многочлен 2x3 − x2 − 5x + 4 на многочлен x − 3
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2x2. Записываем 2x2 в частном:
Разделим первый член делимого на первый член делителя, получим 2x2. Записываем 2x2 в частном:
Умножим 2x2 на делитель x − 3 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 2x3 − 6x2
Теперь делим 5x2 − 5x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 5x. Записываем 5x в частном:
Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x2 − 5x + 4
Вычтем из многочлена 5x2 − 5x + 4 многочлен 5x2 − 15x
Теперь делим 10x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 10. Записываем 10 в частном:
Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4. Сразу вычтем этот полученный результат из делимого 10x + 4
Сразу вычтем этот полученный результат из делимого 10x + 4
Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4, является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34.
Поэтому при делении многочлена 2x3 − 2x2 − 5x + 4 на многочлен x − 3 получается 2x2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:
Когда деление многочленов невозможно
Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.
Например, нельзя разделить многочлен x3 + x на многочлен x4 + x2, поскольку делимое является многочленом третьей степени, а делитель — многочленом четвёртой степени.
Вопреки этому запрету можно попробовать разделить многочлен x3 + x на многочлен x4 + x2, и даже получить частное x−1, которое при перемножении с делителем будет давать делимое:
Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x−1 многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x−1 это дробь , которая не является произведением.
Пусть имеется прямоугольник со сторонами 4 и 2
Площадь этого прямоугольника будет равна 4 × 2 = 8 кв.ед.
Увеличим длину и ширину этого прямоугольника на x
Достроим отсутствующие стороны:
Теперь прямоугольник имеет длину x + 4 и ширину x + 2. Площадь этого прямоугольника будет равна произведению (x + 4)(x + 2) и выражаться многочленом x2 + 6x + 8
(x + 4)(x + 2) = x2 + 4x + 2x + 8 = x2 + 6x + 8
При этом мы можем выполнить обратную операцию, а именно разделить площадь x2 + 6x + 8 на ширину x + 2 и получить длину x + 4.
Степень многочлена x2 + 6x + 8 равна сумме степеней многочленов-сомножителей x + 4 и x + 2, а значит ни одна из степеней многочленов-сомножителей не может превосходить степень многочлена-произведения. Следовательно, чтобы обратное деление было возможным, степень делителя должна быть меньше степени делимого.
Задания для самостоятельного решения
Задание 1. Выполните деление:
Решение:
Показать решение
Задание 2. Выполните деление:
Решение:
Показать решение
Задание 3. Выполните деление:
Решение:
Показать решение
Задание 4. Выполните деление:
Решение:
Показать решение
Задание 5. Выполните деление:
Решение:
Показать решение
Задание 6. Выполните деление:
Решение:
Показать решение
Задание 7. Выполните деление:
Решение:
Показать решение
Задание 8. Выполните деление:
Решение:
Показать решение
Задание 9. Выполните деление:
Выполните деление:
Решение:
Показать решение
Задание 10. Выполните деление:
Решение:
Показать решение
Задание 11. Выполните деление:
Решение:
Показать решение
Задание 12. Выполните деление:
Решение:
Показать решение
Задание 13. Выполните деление:
Решение:
Показать решение
Задание 14. Выполните деление:
Решение:
Показать решение
Задание 15. Выполните деление:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
| 1 | Оценка с использованием заданного значения | квадратный корень из 50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Оценка с использованием заданного значения | квадратный корень из 45 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Оценить | 5+5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Оценить | 7*7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Найти простую факторизацию | 24 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Преобразование в смешанный номер | 52/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Преобразование в смешанный номер | 93/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Преобразование в смешанный номер | 34/5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | График | у=х+1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Оценка с использованием заданного значения | квадратный корень из 128 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Найдите площадь поверхности | сфера (3) | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Оценить | 54-6÷2+6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | График | г=-2x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Оценить | 8*8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Преобразование в десятичное число | 5/9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Оценка с использованием заданного значения | квадратный корень из 180 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | График | у=2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Преобразование в смешанный номер | 7/8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Оценить | 9*9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Решите для C | С=5/9*(Ф-32) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Упростить | 1/3+1 1/12 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | График | у=х+4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | График | г=-3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | График | х+у=3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | График | х=5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | Оценить | 6*6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | Оценить | 2*2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | Оценить | 4*4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | Оценить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | Оценить | 1/3+13/12 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | Оценка | 5*5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | Решить для d | 2д=5в(о)-вр | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | Преобразование в смешанный номер | 3/7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | График | г=-2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | Найдите склон | у=6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | Преобразование в проценты | 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | График | у=2х+2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | 92+5х+6=0|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | Преобразование в смешанный номер | 1/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | Преобразование в десятичное число | 9% | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | Найти n | 12н-24=14н+28 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | Оценить | 16*4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | Упростить | кубический корень из 125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | Преобразование в упрощенную дробь | 43% | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | График | х=1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | График | у=6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 | График | г=-7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 | График | у=4х+2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51 | Найдите склон | у=7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 | График | у=3х+4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 | График | у=х+5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54 | График | 92-9=0||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 | Оценка с использованием заданного значения | квадратный корень из 192 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 | Оценка с использованием заданного значения | квадратный корень из 25/36 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | Найти простую факторизацию | 14 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 61 | Преобразование в смешанный номер | 7/10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | Решите для | (-5а)/2=75 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 | Упростить | х | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 | Оценить | 6*4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | Оценить | 6+6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | Оценить | -3-5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | Оценить | -2-2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | Упростить | квадратный корень из 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 | Упростить | квадратный корень из 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | Найди обратное | 1/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | Преобразование в смешанный номер | 20. 11. 11. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | Преобразование в смешанный номер | 7/9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 | Найти LCM | 11, 13, 5, 15, 14 | , , , , | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76 | График | 3x+4y=12 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 77 | График | 3x-2y=6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 78 | График | у=-х-2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 79 | График | у=3х+7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 | Определить, является ли многочлен | 2x+2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 81 | График | у=2х-6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 | График | у=2х-7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 83 | График | у=2х-2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 | График | у=-2х+1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 | График | у=-3х+4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 | График | у=-3х+2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | График | у=х-4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | Оценить | (4/3)÷(7/2) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89 | График | 2x-3y=6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | График | х+2у=4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 91 | График | х=7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92 | График | х-у=5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 93 | Решение с использованием свойства квадратного корня 92-2x-3=0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 95 | Найдите площадь поверхности | конус (12)(9) | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 96 | Преобразование в смешанный номер | 3/10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 97 | Преобразование в смешанный номер | 7/20 | 92+9b+6+((2b+4)/(3b-2)) Tiger Algebra Solver|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -2 | + | -1 | = | -3 | ||
| -1 9000 5 | + | -2 | = | -3 | ||
| 1 | 900 04 +2 | = | 3 | Вот и все |
1 и 2
b 2 + 1b + 2b + 2
Шаг 4. Сложите первые два члена, вытащив одинаковые множители :
b • (b+1)
Сложите два последних условия, выделив общие множители :
2 • (b+1)
Шаг 5 : Сложите четыре члена шага 4 : это желаемая факторизация
Сложение дробей, имеющих общий знаменатель:
5. 3 Сложение двух эквивалентных дробей
3 Сложение двух эквивалентных дробей
Сложите две эквивалентные дроби, которые теперь имеют общий знаменатель
Объедините числители вместе, подставьте сумму или разность к общему знаменателю, затем приведите к наименьшему члену, если возможно:
3 • (b+2) • (b+1 ) • (3b-2) + 2 • (b+2) 9b 3 + 21b 2 + 2b - 8
"=" ————————
1 • (3б-2) 1 • (3б — 2)
Проверка идеального куба:
5.4 9b 3 + 21b 2 + 2b — 8 не является идеальным кубом
Попытка разложить на множители путем вытягивания :
5.5 Разложение на множители: 9b 909 25 3 + 21b 2 + 2b — 8
Вдумчиво разбейте имеющееся выражение на группы, в каждой группе по два члена:
Группа 1: 2b — 8
Группа 2: 9b 3 + 21b 2
Вытяните из каждой группы отдельно:
9091 7 Группа 1: (б — 4) • (2)Группа 2: (3б + 7) • (3б 2 )
Плохие новости !! Разложение на множители путем вытягивания не удается:
Группы не имеют общего множителя и не могут быть сложены для образования умножения.
Калькулятор корней многочленов :
5.6 Найти корни (нули) : F(b) = 9b 3 + 21b 2 + 2b — 8
Вычисление корней многочленов ulator — это набор методов, предназначенных для нахождения значений b для который F(b)=0
Rational Roots Test является одним из вышеупомянутых инструментов. Он найдет только рациональные корни, то есть числа b, которые можно выразить как частное двух целых чисел 9.0918
Теорема о рациональном корне утверждает, что если многочлен равен нулю для рационального числа P/Q , то P является множителем замыкающей константы, а Q является множителем старшего коэффициента
В этом случае старший коэффициент равен 9, а Константа трейлинга: -8.
Коэффициент(ы):
ведущего коэффициента: 1,3 ,9
константы замыкания: 1 ,2 ,4 ,8
Проверим ….
| стр. | Q | P/Q | F(P/Q) | Делитель | |||||
|---|---|---|---|---|---|---|---|---|---|
| -1 | 1 | -1,00 | 9000 4 2. 00 00 | ||||||
| -1 | 3 | 90 005 | -0,33 | -6,67 | |||||
| -1 | 9 | -0,11 | 900 04-7,98 | ||||||
| -2 | 1 | -2,00 | 0.00 | b + 2 | |||||
| -2 | 3 | -0,67 | -2,67 |
Примечание. Для аккуратности печать 19 чеков, не обнаруживших корня, была подавлена
Факторная теорема утверждает, что если P/Q является корнем многочлена, то этот многочлен может делится на q*x-p Обратите внимание, что q и p происходят из P/Q, приведенного к наименьшему члену
. В нашем случае это означает, что
В нашем случае это означает, что
9b 3 + 21b 2 + 2b — 8
можно разделить на b + 2
Длинный полином :
5.7 Длинный полином
Деление : 9b 3 + 21b 2 + 2b — 8
(«Дивиденд»)
By : b + 2 («Делитель»)
| делимое | 9b 3 | + | 21b 2 | + 900 05 | 2b | — | 8 | ||
| — делитель | * 9b 2 | 9b 3 | + | 18b 2 9092 6 | |||||
| остаток | 900 05 | 3b 2 | + | 2b | — | 8 | |||
| — делитель | * 3b 1 | 3b 2 | + | 6b | |||||
| остаток | — | 4b | — | 8 | — делитель | * -4b 0 | — | 4b | — 900 05 | 8 |
| остаток | 0 |
Частное: 9b 2 +3b-4 Остаток: 0
Попытка факторизовать путем разделения среднего члена
5. Круглая труба
Марка:
российская / АSТМO3Х17Н14М2 / 316LO3Х17Н14М3 / 316LO3Х18Н11 / 304LO4Х18Н10O6ХН28МДТO6Х18Н11 / 305O7Х16Н6 / 30108Х1308Х17Т08Х20Н14С208Х18Н10 / 304/304H08Х18Н10Т / 32108Х18Н12Т08Х18Н12Б / 34708Х17Н15М3Т08Х17Н13М2Т / 316Ti06Х22Н6Т08Х18Н12Б10Х17Н13М2Т10Х23Н18 / 310S12Х13 / 41012Х17 / 43012Х18Н10Т12Х18Н10E / 30320Х13 / 42020Х23h28 / 309S30Х13 / 42012Х18Н12Т12Х18Н915Х25Т17Х18Н9- / 416- / 201- / 202- / 316- / 904L
Стенка (мм):
Диаметр (мм):
Длина (мм):
Масса 1 метра (кг): 0. Рассчетная масса (кг): 0.00 Квадратная труба
Марка:
российская / АSТМO3Х17Н14М2 / 316LO3Х17Н14М3 / 316LO3Х18Н11 / 304LO4Х18Н10O6ХН28МДТO6Х18Н11 / 305O7Х16Н6 / 30108Х1308Х17Т08Х20Н14С208Х18Н10 / 304/304H08Х18Н10Т / 32108Х18Н12Т08Х18Н12Б / 34708Х17Н15М3Т08Х17Н13М2Т / 316Ti06Х22Н6Т08Х18Н12Б10Х17Н13М2Т10Х23Н18 / 310S12Х13 / 41012Х17 / 43012Х18Н10Т12Х18Н10E / 30320Х13 / 42020Х23h28 / 309S30Х13 / 42012Х18Н12Т12Х18Н915Х25Т17Х18Н9- / 416- / 201- / 202- / 316- / 904L
Стенка (мм):
Размер A (мм):
Длина (мм):
Масса 1 метра (кг): 0.00 Рассчетная масса (кг): 0.00 Прямоугольная труба
Марка:
российская / АSТМO3Х17Н14М2 / 316LO3Х17Н14М3 / 316LO3Х18Н11 / 304LO4Х18Н10O6ХН28МДТO6Х18Н11 / 305O7Х16Н6 / 30108Х1308Х17Т08Х20Н14С208Х18Н10 / 304/304H08Х18Н10Т / 32108Х18Н12Т08Х18Н12Б / 34708Х17Н15М3Т08Х17Н13М2Т / 316Ti06Х22Н6Т08Х18Н12Б10Х17Н13М2Т10Х23Н18 / 310S12Х13 / 41012Х17 / 43012Х18Н10Т12Х18Н10E / 30320Х13 / 42020Х23h28 / 309S30Х13 / 42012Х18Н12Т12Х18Н915Х25Т17Х18Н9- / 416- / 201- / 202- / 316- / 904L
Стенка (мм):
Размер A (мм):
Длина (мм):
Размер B (мм):
Масса 1 метра (кг): 0. Рассчетная масса (кг): 0.00 Вводите требуемые значения,
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
тонны
метры
длина 1 шт.
кол-во шт.
Быстрая навигация: Расчет веса любого вида металлопродукции: балки, профили различные типы, стержни, трубы, трубы, листы и т. В приведенном выше калькуляторе веса металла мы предварительно ввели плотности многих широко используемых металлов, таких как углеродистая сталь, нержавеющая сталь, железо, медь, никель, алюминий, а также металлических сплавов, таких как бронза, алюминий и никелевые сплавы: Никель 200, Monel 400, Inconel 600, Inconel 625, Inconel 718, Inconel X-750, Incoloy 800. Выбор материала из списка автоматически заполнит его плотность в поле «плотность». Однако вы всегда можете ввести пользовательскую плотность, если она вам известна и калькулятор будет использовать ее вместо нее. Распространенная ошибка — перепутал «сталь» с «металлом» . Это не синонимы! На самом деле сталь технически является не металлом, а металлическим сплавом, поскольку изготавливается из смеси железа, углерода и других элементов в очень малых количествах. Калькулятор имеет набор различных типов продуктов на выбор, и для каждого из них требуется ввести свой набор измерений, чтобы рассчитать его объем. Наш калькулятор веса стали поддерживает различные типы продуктов, как описано ниже. Если вы хотите рассчитать более сложный продукт, вы можете либо разбить его на более простые компоненты, которые затем можно рассчитать по отдельности, либо использовать более сложное программное обеспечение. Круглый металлический стержень является одним из самых простых для расчета, так как уравнение веса требует знания только двух измерений: диаметра и длины стержня. Например, рассчитаем вес стального прутка длиной 1 метр и диаметром 20 мм. Объем стального стержня представляет собой произведение площади поперечного сечения на длину: π x r 2 x l = 3,1416 x 10 2 x 1000 = 314 160 мм 3 = 314,16 см 3 (r = 1/2 x диаметр, l = 1 м = 1000 мм). Для расчета веса квадратного металлического стержня вам нужно знать только одну сторону его поперечного сечения и его длину, но вам все равно нужно будет ввести две стороны, так как наша Инструмент также поддерживает прямоугольные стержни, у которых вторая сторона может отличаться. Формула тогда состоит в том, чтобы умножить три вместе: ширина x высота x длина, а затем умножить на плотность, чтобы получить вес. Например, для алюминиевого прямоугольного бруска сечением 20 мм на 30 мм и длиной 2 метра нам необходимо рассчитать объем как 20 х 30 х 2000 = 1 200 000 кубических миллиметров или 1 200 кубических сантиметров. При плотности 2,72 мы получаем произведение 2,72 х 1200 = 3264 г или 3,264 кг. В качестве входных данных для калькулятора веса металла для шестиугольного стержня необходимы два измерения: длина и ширина, где ширина — это расстояние между любыми двумя его противоположными сторонами. Металлический лист ничем не отличается от прямоугольного стержня, он в калькуляторе веса стали в основном для вашего удобства. Формула, используемая для расчета веса, точно такая же. Вес металлической трубы вычислить немного сложнее, чем вес круглого металлического стержня, так как нам нужно знать либо внутренний и внешний диаметры, либо один из диаметров и толщина трубки. Мы решили указать внешний диаметр и толщину, так как их обычно проще всего измерить (и если у вас есть планы перед вами, в любом случае будет легко получить любые два числа). Прямоугольные металлические профили очень часто используются в строительстве благодаря их хорошей способности противостоять силам со всех направлений. L-образный (маленький L) профиль представляет собой две металлические планки, соединенные или отлитые вместе под углом 90 градусов. Это в основном основание и фланец только с одной стороны. Мы поддерживаем расчет веса металла для металлических уголков с равными или неравными плечами. Расчеты веса этих металлических профилей требуют большого количества измерений из-за их сложной формы. U-образный профиль, также известный как U-образный профиль в Европе и C-образный профиль в США, показан ниже: U-образный профиль имеет основание и два параллельных фланца: по одному с каждой стороны от него. Их также называют U-каналами, и многие из них стандартизированы. Ниже вы видите иллюстрацию каналов UPN и UPE, которые по общей форме эквивалентны C-каналам и BC-каналам соответственно. Стальные профили UPN широко используются во многих отраслях промышленности и машиностроения. C-каналы являются их американским стандартизированным эквивалентом. Профили UPE имеют меньшую толщину, но несколько более широкие полки, чем профили UPN, и сопоставимые статические характеристики. Использование профилей UPE потенциально может привести к снижению веса до 30% практически без каких-либо потерь в статических условиях. BC — это сокращение от «Швеллерная секция с параллельными полками». Его полки и стенки имеют одинаковую толщину по определению, и они часто используются в качестве недорогой альтернативы более тяжелым профилям для широкого спектра применений, поскольку значение удельного веса на метр относительно низкое. Каналы IPE и BC значительно проще в сборке, так как нет необходимости в конических плоских шайбах для компенсации естественной конусности фланцев каналов C-Channel / UPN. Двутавровый профиль, также известный как двутавровая балка, двутавровый профиль и двутавровая балка, представляет собой два U-образных профиля, расположенных спиной к спине. Он имеет два фланца и перегородку между ними. Существует два типа формы поперечного сечения двутавровой балки. У W-образной формы полки имеют примерно одинаковую толщину от края до края, а у S-образной формы полки значительно тоньше у краев. Оба используются в качестве опорных балок для строительства, объектов и машиностроения, заводских цехов, складов и каркаса кузова грузовика. Наш онлайн-инструмент поддерживает расчет веса двутавровых профилей любых размеров. Слишком много стандартов таких профилей, как IPE, IPN, HD, HE, HL, HP, S и так далее. Т-образный так и звучит: он похож на букву Т. Он может быть составным — если он сварной или болтовой, или теплым — когда он горячекатаный или экструдированные. Как и в случае с другими профилями и балками, горизонтальная часть поперечного сечения называется «полкой», а вертикальная часть — «стенкой». Наш калькулятор поддерживает расчеты веса металла для всех типов нестандартных тавровых балок. Стальной мост [1] Институт никеля. «Свойства некоторых металлов и сплавов» (1982 г.) [онлайн]. Стандартные переводные коэффициенты 1) МЯГКИЙ СТАЛЬ (MS) КВАДРАТ MS MS КРУГЛЫЙ SS / MS CIRCLE Лист из нержавеющей стали S. ЛИСТ ЛАТУННЫЙ ЛАТУННАЯ / МЕДНАЯ ТРУБА АЛЮМИНИЕВЫЙ ЛИСТ АЛЮМИНИЕВАЯ ТРУБА Рекламные объявления Мы очень благодарны Er.
Данный сервис содержит ряд онлайн-калькулятор по экономическим направлениям. Результат работы каждого калькулятора — это отчет в формате Word и Excel, в котором приведены все расчетные формулы и выводы.
Метод абсолютных разниц
Анализ затрат на рубль произведенной продукции и Анализ материалоемкости
Анализ производительности труда и анализ трудоемкости
Другие калькуляторы
Другие калькуляторы
Инвестиционные показатели ценных бумаг: балансовая стоимость облигации и акции, дивиденд и прибыль на одну акцию, покрытие процента по облигациям.
Общий индекс затрат на производство продукции (общий индекс товарооборота). Индекс переменного состава, Индексы с постоянными и переменными весами
Анализ сезонных колебаний
Группировка статистических данных
Все сервисы
Все сервисы
Все сервисы
Калькулятор расчета окупаемости Timetta. Сотрудники, непосредственно оказывающие услуги клиентам и внутренним заказчикам, например: консультанты, юристы, инженеры, аудиторы, архитекторы и так далее. Мы продаем услуги клиентам (есть коммерческие проекты/работы) тыс. ₽ Есть проекты с повременной (T&M) оплатой Итоговые показатели сильно зависят от зрелости компании, рынка на котором она работает и готовности руководства к изменениям. Мы выбрали самые важные факторы, которые помогут сделать оценку более точной. 0 — учёта рабочего времени нет, никакие KPI не учитываются, у всех оклады, никакого управления проектами нет, целей сотрудникам никто не ставит. 5 — примерно ясно, кто чем занимается, учитываются базовые KPI (например, рентабельность в целом, сроки работ и т.д.), мотивация как-то учитывает результативность работ. 10 — есть интегрированная бизнес модель управления, по каждому проекту в каждый момент времени известна рентабельность, по каждому сотруднику известна эффективность (утилизация), в компании есть реально работающая сбалансированная модель показателей. 0 — из автоматизации электронная почта и мессенджер. 5 — пользуемся общими электронными таблицами (например, для учёта рабочего времени), есть реестр проектов в котором иногда вручную обновляем показатели. 10 — есть интегрированное бизнес-решение для учёта рабочего времени, управления экономикой проектов и управления эффективностью ресурсов, все KPI считаются автоматически. 0 — поставим ПО и посмотрим — «взлетит» само или нет. 5 — возможность изменений ограничена, но доступен контроль/мотивация сотрудников в части учёта рабочего времени, учёта проектов с плановыми показателями и т.д. 10 — готовы ввести мотивацию сотрудников на утилизацию и рентабельность проектов, готовы не продлевать контракты сотрудникам с низкой утилизацией, готовы искать более дешевые ресурсы, если это позволяют проекты и так далее. Добавить в расходы внедрение (нет опыта/времени/людей для самостоятельного внедрения) Добавить в расходы расширенную поддержку (нужна постоянная вторая линия поддержки с консультациями) Пессимист.
Базовый
Оптимист. Учёт времени занимает в среднем 1-2% рабочего времени сотрудника. Так же требуется время сотрудников на ввод и актуализацию сведения о проектах, клиентах и т.д. Эффект достигается не мгновенно. Расчет предполагает, что в течение 6 месяцев показатели плавно выходят на плановые значения: Мы отправим письмо со ссылкой на расчет. Ссылка на расчет отправлена на указанный адрес. Начните бесплатный 14-дневный пробный период и попробуйте все возможности Timetta самостоятельно. Авторское право (с)
1999-2000 гг. Количество * Из чего *
километр (км)метр (м)дециметр (дм)сантиметр (см)миллиметр (мм)микрометр (микрон)нанометр (нм)ангстрем (А)лига, льемиля (mi)лэндфурлонгболтчейнпольрод (rd)перчярд (yd)фут (ft)футы и дюймы (x’y»)спанхенддюйм (in)лайнмилмикродюймлига, льемиля (mi)лэндскейнболтшакльфурлонгчейнроуппольгоадэл (локоть)ярд (yd)пейскубит (cu)фут (ft)спан (sp)нейлшафтментхенд (рука) (hd)палм (ладонь) (plm)дюйм (in)фингер (палец)диждитбарлейкорнпопписидлайн (линия)баттонкалибртоу (th)мильфурлонгЧейн Рамсдена (инженерный) (ch)Чейн Гунтера (межевой) (ch)Чейн Гурлея (ch)Поль Гунтера (межевой)Ярд Гунтера (межевой)Линк Рамсдена (инженерный)Линк Гунтера (межевой)Линк ГурлеяФут Гунтера (межевой), surveyors’ foot (ft)морская лига (naut.leag)морская миля (naut.mi)кабельтов (cbl)фатом, морская сажень (fath)морская миля СШАкабельтов СШАфатом США (fath)Адмиралтейская миляАдмиралтейский кабельтовквадра Аргентиныквадра Боливииквадра Чиликвадра Колумбииквадра Эквадораквадра Нигарагуаквадра Парагваяквадра Уругваявара Аргентинывара Бразилиивара Чиливара Колумбиивара Коста Рикивара Кубывара Доминиканской республикивара Эквадоравара Эль Сальвадоравара Гватемалывара Гондурасавара Мексикивара Никарагуавара Панамывара Парагваявара Перу (перуанская)вара Перу (испанская)вара Уругваявара Сан-Томе и Принсипивара Венесуэлыри (里)тё (町)дзё (丈)хиро (尋)кэн (間)сяку (尺)сун (寸)бу (分)рин (厘)мо (毛, 毫)ли (市里)уин (引)жанг (市丈)чи (市尺)кан (市寸)фен (市分)ли малое (釐 или 厘)хао (毫)сы (丝)ху (忽)ли (里)инь (引)чжан (丈)бу (步)чи (尺)цунь (寸)фень (分)ли малое (釐 или 厘)хао (毫)сы (丝)ху (忽)чи (尺)цунь (寸)фэнь (分)йот (โยชน์, лига)сен (เส้น, канат)ва (วา, сажень)сок (ศอก, локоть)кып (คืบ, ладонь)ниу (นิ้ว, сиамский дюйм)крабиат (กระเบียด четверть дюйма)диоптриягеографическая миляюнит (U)горизонтальный шаг (HP)пикапика пункт (пт)пункт (пт)пиксель (px)твип (twip)цицеропункт (пт)штрих (парижская точка)красное смещение (z)парсек (пк)световой годастрономическая единица (а. Во что *
километр (км)метр (м)дециметр (дм)сантиметр (см)миллиметр (мм)микрометр (микрон)нанометр (нм)ангстрем (А)лига, льемиля (mi)лэндфурлонгболтчейнпольрод (rd)перчярд (yd)фут (ft)футы и дюймы (x’y»)спанхенддюйм (in)лайнмилмикродюймлига, льемиля (mi)лэндскейнболтшакльфурлонгчейнроуппольгоадэл (локоть)ярд (yd)пейскубит (cu)фут (ft)спан (sp)нейлшафтментхенд (рука) (hd)палм (ладонь) (plm)дюйм (in)фингер (палец)диждитбарлейкорнпопписидлайн (линия)баттонкалибртоу (th)мильфурлонгЧейн Рамсдена (инженерный) (ch)Чейн Гунтера (межевой) (ch)Чейн Гурлея (ch)Поль Гунтера (межевой)Ярд Гунтера (межевой)Линк Рамсдена (инженерный)Линк Гунтера (межевой)Линк ГурлеяФут Гунтера (межевой), surveyors’ foot (ft)морская лига (naut.leag)морская миля (naut.mi)кабельтов (cbl)фатом, морская сажень (fath)морская миля СШАкабельтов СШАфатом США (fath)Адмиралтейская миляАдмиралтейский кабельтовквадра Аргентиныквадра Боливииквадра Чиликвадра Колумбииквадра Эквадораквадра Нигарагуаквадра Парагваяквадра Уругваявара Аргентинывара Бразилиивара Чиливара Колумбиивара Коста Рикивара Кубывара Доминиканской республикивара Эквадоравара Эль Сальвадоравара Гватемалывара Гондурасавара Мексикивара Никарагуавара Панамывара Парагваявара Перу (перуанская)вара Перу (испанская)вара Уругваявара Сан-Томе и Принсипивара Венесуэлыри (里)тё (町)дзё (丈)хиро (尋)кэн (間)сяку (尺)сун (寸)бу (分)рин (厘)мо (毛, 毫)ли (市里)уин (引)жанг (市丈)чи (市尺)кан (市寸)фен (市分)ли малое (釐 или 厘)хао (毫)сы (丝)ху (忽)ли (里)инь (引)чжан (丈)бу (步)чи (尺)цунь (寸)фень (分)ли малое (釐 или 厘)хао (毫)сы (丝)ху (忽)чи (尺)цунь (寸)фэнь (分)йот (โยชน์, лига)сен (เส้น, канат)ва (วา, сажень)сок (ศอก, локоть)кып (คืบ, ладонь)ниу (นิ้ว, сиамский дюйм)крабиат (กระเบียด четверть дюйма)диоптриягеографическая миляюнит (U)горизонтальный шаг (HP)пикапика пункт (пт)пункт (пт)пиксель (px)твип (twip)цицеропункт (пт)штрих (парижская точка)красное смещение (z)парсек (пк)световой годастрономическая единица (а. * — обязательно заполнить 1200 км равно 1200000 метров
Вес трубы стальной онлайн калькулятор: Трубный калькулятор
Калькулятор веса нержавеющей трубы | Компания «Пассат»
НаверхКалькулятор
 00
00 00
00Вес трубы ВГП – вес метра, расчет веса, таблица веса.
остальные поля пересчитаются автоматически
6х1.8
Размеры
6х2
Размеры
6х2.
 5
5
Размеры
8х2
Размеры
8х2.2
Размеры
8х2.
 8
8
Размеры
10х2
Размеры
10х2.2
Размеры
10х2.
 8
8
Размеры
Цены
15х2.35
Размеры
Цены
15х2.5
Размеры
Цены
15х2.8
Размеры
Цены
15х3.2
Размеры
Цены
20х2.
 35
35
Размеры
Цены
20х2.5
Размеры
Цены
20х2.8

Размеры
Цены
20х3.2
Размеры
Цены
25х2.8
Размеры
Цены
25х3.
 2
2
Размеры
Цены
25х4
Размеры
Цены
32х2.8
Размеры
Цены
32х3.2
Размеры
Цены
32х4
Размеры
Цены
40х3
Размеры
Цены
40х3.5
Размеры
Цены
40х4
Размеры
Цены
50х3
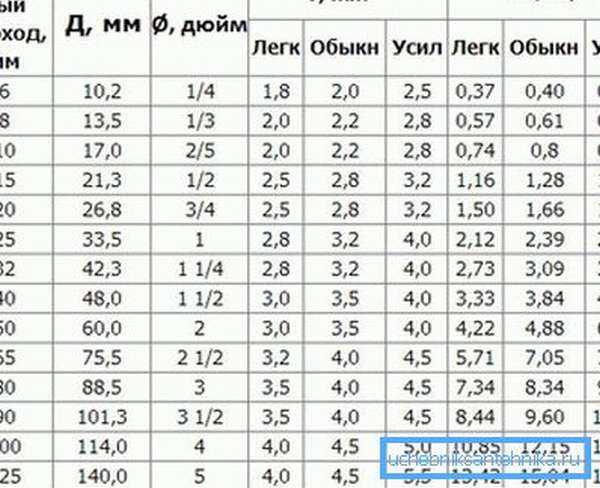
Размеры
Цены
50х3.5
Размеры
Цены
50х4
Цены
65х3.
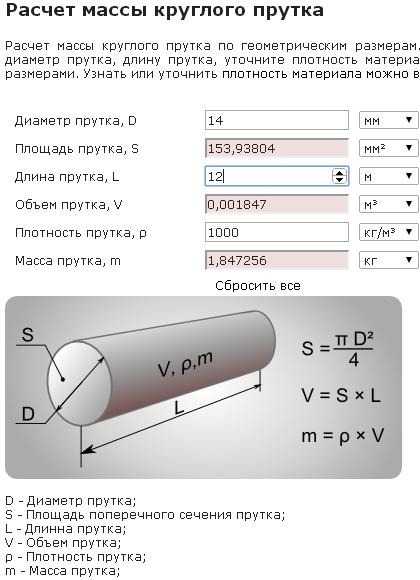 2
2
Размеры
Цены
65х4
Размеры
Цены
65х4.5

Размеры
Цены
80х3.5
Размеры
Цены
80х4
Размеры
Цены
80х4.
 5
5
Размеры
Цены
90х3.5
Размеры
90х4
Размеры
90х4.
 5
5
Размеры
100х4
Размеры
Цены
100х4.5
Размеры
Цены
100х5

Размеры
Цены
125х4
Размеры
125х4.5
Размеры
125х5.
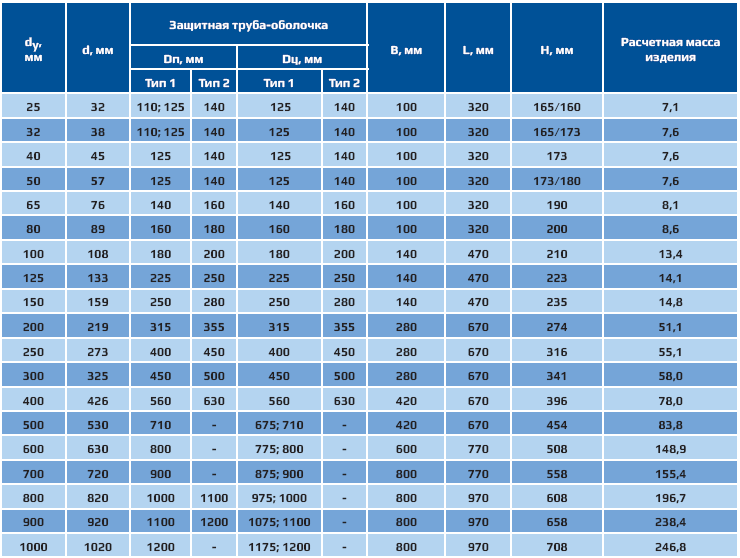 5
5
Размеры
150х4
Размеры
150х4.5
Размеры
150х5.
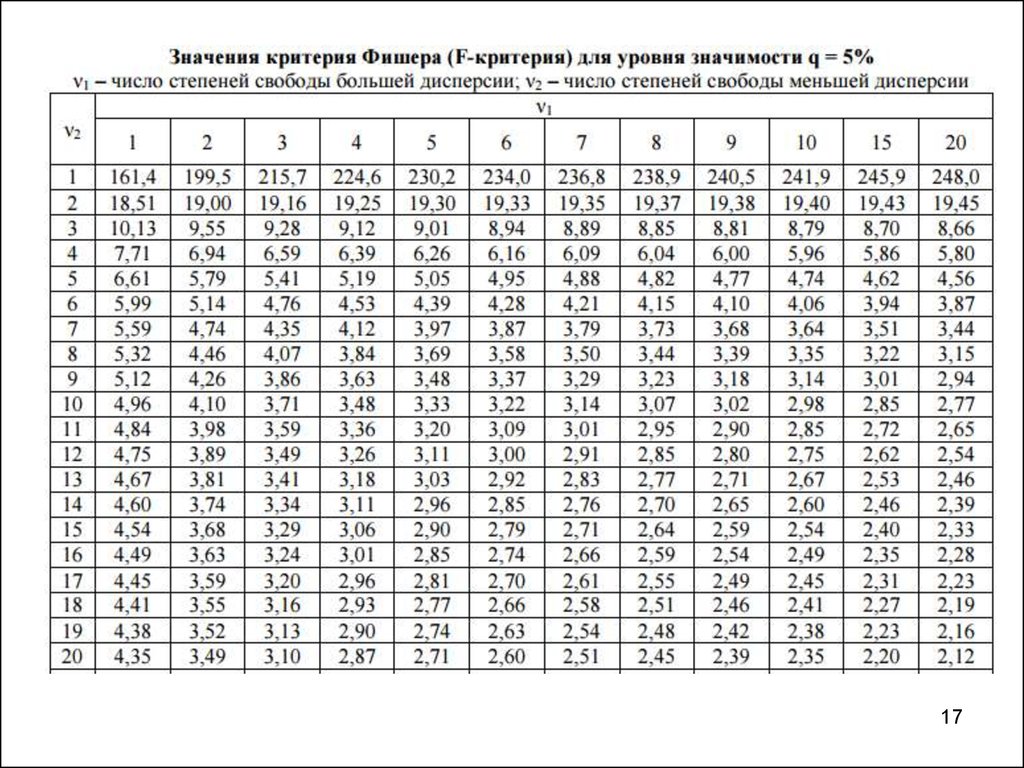 5
5
Размеры
Калькулятор веса металла — Калькулятор веса стали
Расчет веса металла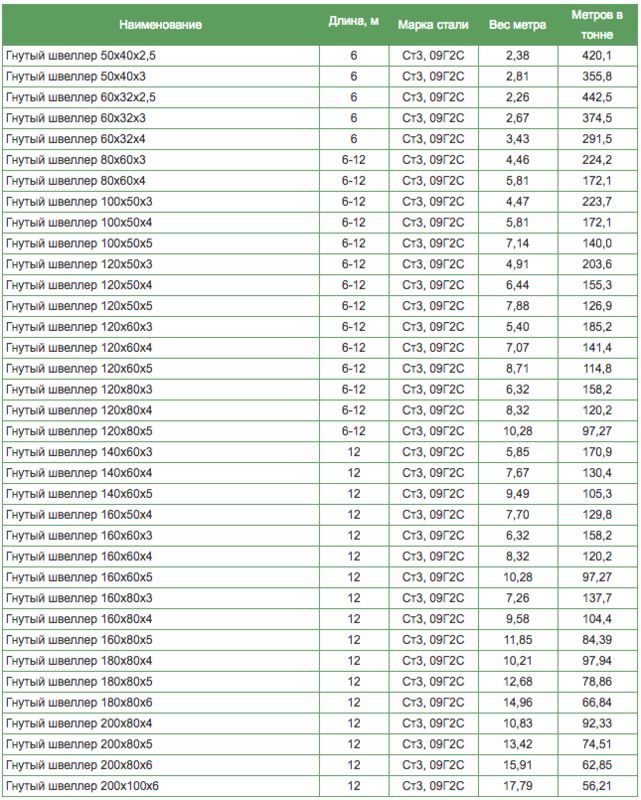 д. аналогичны материалам любого другого типа. Нам нужно знать объем металла (куб.дюйм, куб.мм, куб.см и т.д.) и его плотность (обычно в г/см 3 , унций/дюйм 3 ). Умножение двух дает нам результирующий вес металла.
д. аналогичны материалам любого другого типа. Нам нужно знать объем металла (куб.дюйм, куб.мм, куб.см и т.д.) и его плотность (обычно в г/см 3 , унций/дюйм 3 ). Умножение двух дает нам результирующий вес металла.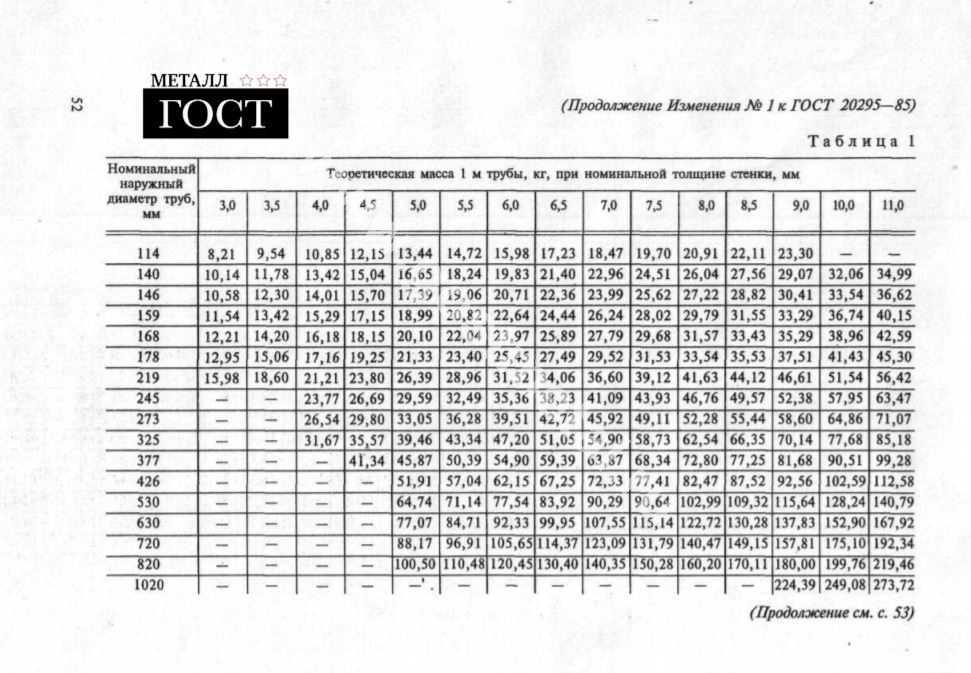
Круглый металлический стержень
 При использовании углеродистой стали плотностью 7,95 г/см 3 нам потребуется произведение 7,95 и 314,16, что равно 2497,572 г или ~2,498 кг.
При использовании углеродистой стали плотностью 7,95 г/см 3 нам потребуется произведение 7,95 и 314,16, что равно 2497,572 г или ~2,498 кг. Прямоугольный или квадратный металлический стержень
Шестигранный металлический стержень
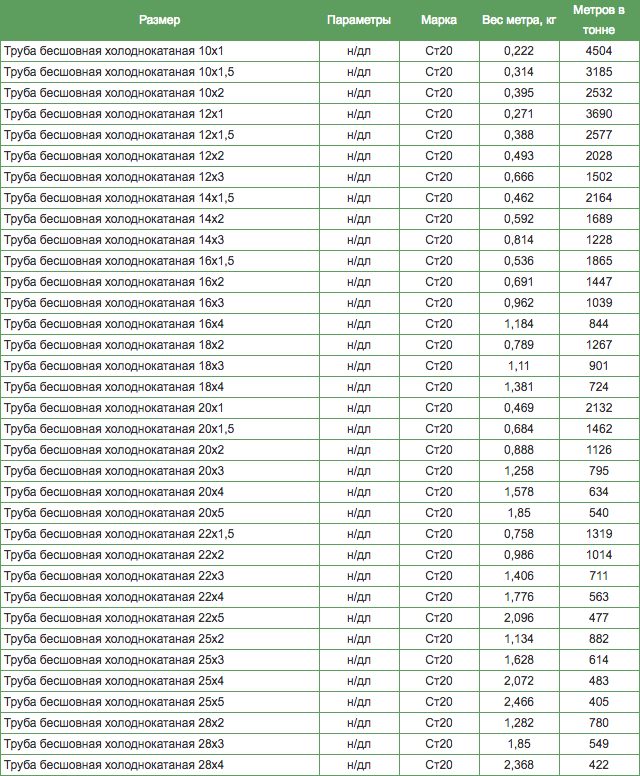 На данный момент мы поддерживаем только правильные шестиугольники. Зная ширину, мы можем легко вычислить площадь поперечного сечения шестиугольника, а оттуда — общий объем и вес стержня.
На данный момент мы поддерживаем только правильные шестиугольники. Зная ширину, мы можем легко вычислить площадь поперечного сечения шестиугольника, а оттуда — общий объем и вес стержня. Металлический лист
Металлическая труба
Прямоугольный металлический профиль
 В настоящее время мы поддерживаем только прямоугольные профили только с прямыми углами. Дополнительным размером по сравнению с прямоугольным стержнем является толщина профиля. Вес металла снова равен объему, умноженному на плотность металла.
В настоящее время мы поддерживаем только прямоугольные профили только с прямыми углами. Дополнительным размером по сравнению с прямоугольным стержнем является толщина профиля. Вес металла снова равен объему, умноженному на плотность металла. L-образный профиль
U-образный профиль (U-образный профиль, C-образный профиль)
 В нашем калькуляторе стали есть множество стандартных профилей — UPN и UPE ЕС, каналы C и BC США, так что вы можете просто выбрать их, и мы будем использовать их данные автоматически. В противном случае вы можете указать пользовательский профиль.
В нашем калькуляторе стали есть множество стандартных профилей — UPN и UPE ЕС, каналы C и BC США, так что вы можете просто выбрать их, и мы будем использовать их данные автоматически. В противном случае вы можете указать пользовательский профиль.
Двутавровый профиль (двутавровый профиль, двутавровая балка или двутавровая балка)
 Из-за огромного количества стандартов у нас нет автоматического заполнения для этих типов, вам нужно будет вводить числа в калькулятор самостоятельно, а расчеты для S-образных балок, вероятно, будут менее точными, чем для W-образных балок. те.
Из-за огромного количества стандартов у нас нет автоматического заполнения для этих типов, вам нужно будет вводить числа в калькулятор самостоятельно, а расчеты для S-образных балок, вероятно, будут менее точными, чем для W-образных балок. те. Т-образный металлический
Калькулятор веса — Портал гражданского строительства
ДЮЙМЫ = 25,4 МИЛЛИМЕТРА
ФУТ = 0,3048 МЕТРА
ДВОР = 0,9144 МЕТРА
МИЛЬ = 1,6093 КИЛОМЕТРА
АКР = 0,4047 ГА
ФУНТА = 0,4536 КИЛОГРАММА
ГРАДУСОВ ПО ФАРЕНГЕЙТАм X 5/9 – 32 = ГРАДУС ЦЕЛЬСИЯ
МИЛЛИМЕТРОВ = 0,09ME 80394 ДЮЙМА 9018 167 МЕТРОВ = 1,0936 ярдов
ЛИСТ
ВЕС (КГС) = ДЛИНА (ММ) X ШИРИНА (ММ) X 0.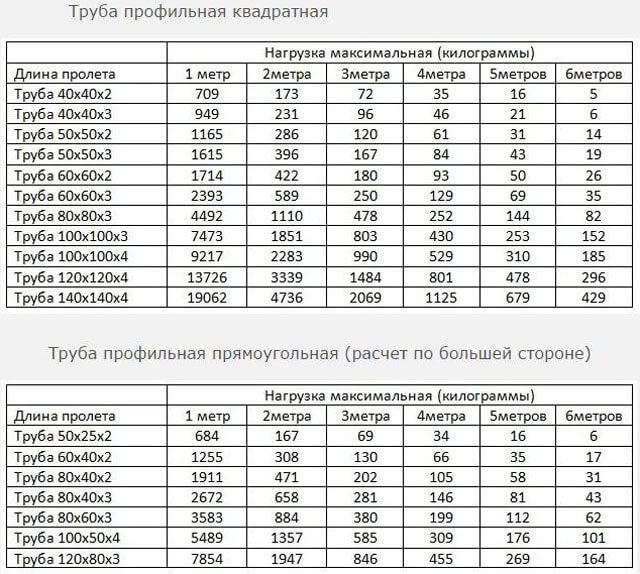 00000785 X ТОЛЩИНА
00000785 X ТОЛЩИНА
2500 мм X 1250 мм X 0,00000785 X 1 = 24,53 кг/ЛИСТ
ПРОКАТНЫЕ СТАЛЬНЫЕ КАНАЛЫ
ВЕС (КГС) = ШИРИНА X ШИРИНА X 0,00000785 X ДЛИНА.
Пример: Квадрат размером 25 мм и длиной 1 метр, тогда вес должен быть.
25x25X 0,00000785 X 1000 мм = 4,90 кг/метр
ВЕС (КГС) = 3,14 X 0,00000785 X ((диаметр / 2) X (диаметр / 2)) X ДЛИНА.
Пример: Круг диаметром 20 мм и длиной 1 метр, тогда вес должен быть равен.
3,14 X 0,00000785 X ((20/2) X (20/2)) X 1000 мм = 2,46 кг/метр METER
SS / MS Труба
Наружный диаметр (мм) – ШТтолщина (мм) X Ширина (мм) X 0,0248 = Вес на метр
Наружный диаметр (мм) – Ширина (мм) X Ширина (мм) X 0,00756 = Вес на фут
ДИАМ. (мм) X ДИАМ. (мм) X ТОЛЩИНА (мм) 0,0000063 = кг на штуку
Длина (метры) X Ширина (метры) X Толщина (мм) X 8 = Вес за штуку
Длина (футы) X Ширина (футы) X Толщина (дюймы) X 3/4 = Вес за штуку S ШЕСТИУГОЛЬНИК
S ШЕСТИУГОЛЬНИК
ДИАМ. (мм) X ДИАМ. (мм) X 0,00680 = ВЕС. PER Mtr
Диаметр (мм) X Диаметр (мм) X 0,002072 = Вес. За фут.
ВЕС (КГС) = ДЛИНА (ММ) X ШИРИНА (ММ) X 0. 0000085 X ТОЛЩИНА
Пример. Вес латунного листа толщиной 1 мм, длиной 1220 мм и шириной 355 мм должен быть равен
1220 X355X 0,0000085 X 1 = 3,68 кг/лист за лист толщина 1 мм, длина 1220 мм и ширина 355 мм должны быть
1220X355 X 0,0000087 X 1 = 3,76 кг/лист
Внешний диаметр (мм) – ТОЛЩИНА (мм) X ТОЛЩИНА 6 НА ВЕС (мм) X 0,02 МЕТР
ВЕС (КГС) = ДЛИНА (ММ) X ШИРИНА (ММ) X 0. 00000026 X ТОЛЩИНА
Пример. Вес алюминиевого листа толщиной 1 мм, длиной 2500 мм и шириной 1250 мм должен составлять
2500x1250X 0,0000026 X 1 = 8,12. кг/лист
Внешний диаметр (мм) – ТОЛСТАЯ (мм) X ТОЛЩИНА (мм) X0,0083 = ВЕС НА МЕТР
Экономический калькулятор: Онлайн-калькулятор по экономике
Онлайн-калькулятор по экономике
Метод цепных подстановок
Способ относительных разниц (метод индексных разниц)
Интегральный метод факторного анализа
Баланс движения основных фондов. Определение среднегодовой стоимости основных фондов.

Показатели движения трудовых ресурсов
Анализ динамики выпуска продукции
Анализ технического состояния производства (интенсивность и экстенсивность производства)
Факторный анализ фондоотдачи
Анализ фонда заработной платы и Факторный анализ фонда заработной платы
Анализ платежеспособности (ликвидности), Анализ финансовой устойчивости.
Анализ финансового состояния, Анализ собственного и заемного капитала.
Анализ прибыли предприятия
Анализ финансового левериджа
Эффект финансового рычага: оценка предпринимательского риска, анализ чувствительности прибыли, анализ безубыточности.
Показатели эффективности инвестиционного проекта: чистая текущая стоимость (NРV), индекс рентабельности (IR) и внутренняя норма доходности (IRR).
Текущая рыночная доходность
Индикатор уровней Мюррея
Мультипликативная индексная двухфакторная модель.
Аддитивная модель временного ряда
Мультипликативная модель временного ряда
Выявление тренда методом аналитического выравнивания, сглаживание временного ряда экспоненциальным методом и методом скользящей средней
 Параметры равновесия на рынке: равновесный объем, коэффициент эластичности, излишки продавца и покупателя
Параметры равновесия на рынке: равновесный объем, коэффициент эластичности, излишки продавца и покупателя
Расчет оптимального заказа. Формула Вильсона
Функция спроса: задача потребительского выбора (функция полезности, предельные полезности)
Производственная функция Кобба-Дугласа: средняя фондоотдача и средняя производительность труда, предельная фондоотдача, эластичность продукта и эластичность масштаба производства.
Кривая Лоренца. Индекс Джини
Расчет ВНП по потоку доходов и расходов
Система национальных счетов: расчет ВВП и построение счетов
Денежные агрегаты: M0, M1, M2, M3, M4
Индекс Херфиндаля-Хиршмана: оценка степени монополизации отрасли
Экономически активное население: расчет коэффициентов экономической активности населения, занятости и безработицы.
Статистика населения: расчет коэффициентов рождаемости, смертности, естественного прироста, интенсивности миграционного оборота.
Анализ сетевого графика
Кластерный анализ: Метод К-среднихКалькулятор ROI – расчет экономической эффективности бизнеса
Калькулятор ROI – расчет экономической эффективности бизнеса | Timetta1. Сведения о работниках
Зарплата сотрудника (на руки в месяц): +НДФЛ 13%: +Страховые взносы (в среднем по году): Полная зарплата на сотрудника в месяц: Фонд оплаты труда в месяц: 2.
 Сведения о проектах
Сведения о проектах3. Оценка бизнеса

4.
 Расчет
РасчетОжидаемые улучшения
Повышение утилизации сотрудников (п.п.) Снижение себестоимости Повышение рентабельности проектов Снижение утечек выручки по T&M проектам Повышение достоверности и точности сведений о структуре рабочего времени Улучшения в денежном выражении в месяц
Повышение утилизации сотрудников Снижение себестоимости Повышение рентабельности проектов Снижение утечек выручки по T&M проектам Итого: Структура выгод
Стоимость владения
Подписка Timetta, в год Поддержка, в год *Себестоимость работ, необходимых для учёта рабочего времени, администрирования решения и пр.  , в месяц
, в месяцРазовая инвестиция
Внедрение Выгода по месяцам накопленным итогом
Финансовые показатели
Дополнительный доход в первый год Дополнительные расходы в первый год Финансовый результат в первый год ROI в первый год ROI за три года NPV за три года (при ставке дисконтирования 17%) 5.
 Получить расчет на почту
Получить расчет на почтуПопробовать бесплатно
Экономические калькуляторы — Капитан Калькулятор
Экономические калькуляторы — Капитан Калькулятор
Перейти к содержимому Макроэкономика


Микроэкономика


Инженерно-экономический калькулятор
Инженерно-экономический калькулятор Проблемы Формулы Решения Курсы Публикации Исследования Дом Звенья 
1200 км в м: Mathway | Популярные задачи
Mathway | Популярные задачи
1 Оценить с использованием заданного значения квадратный корень из 50 2 Оценить с использованием заданного значения квадратный корень из 45 3 Вычислить 5+5 4 Вычислить 7*7 5 Разложить на простые множители 24 6 Преобразовать в смешанную дробь 52/6 7 Преобразовать в смешанную дробь 93/8 8 Преобразовать в смешанную дробь 34/5 9 График y=x+1 10 Оценить с использованием заданного значения квадратный корень из 128 11 Найти площадь поверхности сфера (3) 12 Вычислить 54-6÷2+6 13 График y=-2x 14 Вычислить 8*8 15 Преобразовать в десятичную форму 5/9 16 Оценить с использованием заданного значения квадратный корень из 180 17 График y=2 18 Преобразовать в смешанную дробь 7/8 19 Вычислить 9*9 20 Risolvere per C C=5/9*(F-32) 21 Упростить 1/3+1 1/12 22 График y=x+4 23 График y=-3 24 График x+y=3 25 График x=5 26 Вычислить 6*6 27 Вычислить 2*2 28 Вычислить 4*4 29 Вычислить 1/2+(2/3)÷(3/4)-(4/5*5/6) 30 Вычислить 1/3+13/12 31 Вычислить 5*5 32 Risolvere per d 2d=5v(o)-vr 33 Преобразовать в смешанную дробь 3/7 34 График y=-2 35 Определить наклон y=6 36 Перевести в процентное соотношение 9 37 График y=2x+2 38 График y=2x-4 39 График x=-3 40 Решить, используя свойство квадратного корня x^2+5x+6=0 41 Преобразовать в смешанную дробь 1/6 42 Преобразовать в десятичную форму 9% 43 Risolvere per n 12n-24=14n+28 44 Вычислить 16*4 45 Упростить кубический корень из 125 46 Преобразовать в упрощенную дробь 43% 47 График x=1 48 График y=6 49 График y=-7 50 График y=4x+2 51 Определить наклон y=7 52 График y=3x+4 53 График y=x+5 54 График 3x+2y=6 55 Решить, используя свойство квадратного корня x^2-5x+6=0 56 Решить, используя свойство квадратного корня x^2-6x+5=0 57 Решить, используя свойство квадратного корня x^2-9=0 58 Оценить с использованием заданного значения квадратный корень из 192 59 Оценить с использованием заданного значения квадратный корень из 25/36 60 Разложить на простые множители 14 61 Преобразовать в смешанную дробь 7/10 62 Risolvere per a (-5a)/2=75 63 Упростить x 64 Вычислить 6*4 65 Вычислить 6+6 66 Вычислить -3-5 67 Вычислить -2-2 68 Упростить квадратный корень из 1 69 Упростить квадратный корень из 4 70 Найти обратную величину 1/3 71 Преобразовать в смешанную дробь 11/20 72 Преобразовать в смешанную дробь 7/9 73 Найти НОК 11 , 13 , 5 , 15 , 14 , , , , 74 Решить, используя свойство квадратного корня x^2-3x-10=0 75 Решить, используя свойство квадратного корня x^2+2x-8=0 76 График 3x+4y=12 77 График 3x-2y=6 78 График y=-x-2 79 График y=3x+7 80 Определить, является ли полиномом 2x+2 81 График y=2x-6 82 График y=2x-7 83 График y=2x-2 84 График y=-2x+1 85 График y=-3x+4 86 График y=-3x+2 87 График y=x-4 88 Вычислить (4/3)÷(7/2) 89 График 2x-3y=6 90 График x+2y=4 91 График x=7 92 График x-y=5 93 Решить, используя свойство квадратного корня x^2+3x-10=0 94 Решить, используя свойство квадратного корня x^2-2x-3=0 95 Найти площадь поверхности конус (12)(9) 96 Преобразовать в смешанную дробь 3/10 97 Преобразовать в смешанную дробь 7/20 98 Преобразовать в смешанную дробь 2/8 99 Risolvere per w V=lwh 100 Упростить 6/(5m)+3/(7m^2) 1200 километров (км) в метрах (м), сантиметрах (см), милях (mi), ярдах (yd), футах (ft), дюймах (in).
 .. Конвертер, онлайн калькулятор.
.. Конвертер, онлайн калькулятор. е.)световая минутасветовая секундасветовая микросекундасветовая наносекундасветовая пикосекундапланковская длина (L)Всё
е.)световая минутасветовая секундасветовая микросекундасветовая наносекундасветовая пикосекундапланковская длина (L)Всё е.)световая минутасветовая секундасветовая микросекундасветовая наносекундасветовая пикосекундапланковская длина (L)Всё
е.)световая минутасветовая секундасветовая микросекундасветовая наносекундасветовая пикосекундапланковская длина (L)Всё 1200 км в метры
Пожалуйста, выберите физическую величину, две единицы, затем введите значение в любое из полей выше.
Чтобы вычислить значение километра до соответствующего значения в метрах, просто умножьте количество в километрах на 1000 (коэффициент пересчета). Вот 9формула 0035 :
Значение в метрах = значение в км × 1000
Предположим, вы хотите преобразовать 1200 км в метры. Используя приведенную выше формулу преобразования, вы получите:
Значение в метрах = 1200 × 1000 = 1200000 метров
Определение километра
Километр (км) – десятичная единица, кратная метру. Международная стандартная единица длины, приблизительно эквивалентно 39,37 дюйма. Километр в настоящее время официально используется для выражения расстояний между географическими точками на суше в большинстве стран мира, за исключением США и Великобритании.
Километр в настоящее время официально используется для выражения расстояний между географическими точками на суше в большинстве стран мира, за исключением США и Великобритании.
Определение метра
Метр (м) — основная единица длины в Международной системе единиц (СИ). Он определяется как длина пути, пройденного светом в вакууме за промежуток времени 1/299 792 458 секунды.
Этот конвертер поможет вам получить ответы на такие вопросы, как:
- Сколько километров в 1200 метрах?
- 1200 км равны скольким метрам?
- Сколько будет 1200 км в метрах?
- Как перевести км в метры?
- Какой коэффициент пересчета из километров в метры?
- Как перевести км в метры?
- Какая формула для перевода километров в метры? Среди прочих.
Таблица перевода километров в метры около 1200 км
| Таблица перевода километров в метры | ||
|---|---|---|
| 500 км | = | 500000 метров |
| 600 км | = | 600000 метров |
| 700 км | = | 700000 метров |
| 800 км | = | 800000 метров 9001 2 |
| 900 км | = | 0 метров |
| 1000 км | = | 1000000 метров |
| 1100 км | = | 1100000 метров |
| 1200 км | = | 1 200000 метров |
| Таблица перевода километров в метры | ||||
|---|---|---|---|---|
| 1200 км | = | 1200000 метров 2 | = | 1300000 метров |
| 1400 км | = | 1400000 метров | ||
| 1500 км | = | 1500000 метров | ||
| 1600 км | = | 1600000 метров | ||
| 1700 км | = | 1700000 метров | ||
| 1800 км | = | 1800000 метров | ||
| 1900 км | 9 0015 = 10 метров | |||
Примечание: некоторые значения могут быть округлены.
Другие преобразователи длины и расстояния
Отказ от ответственности
Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
1200 км в мили
1200 км равно 745.645 миль
Пожалуйста, выберите физическую величину, две единицы, затем введите значение в любое из полей выше.
Чтобы вычислить значение километра до соответствующего значения в милях, просто умножьте количество в км на 0,62137119223733 (коэффициент пересчета). Вот формула :
Значение в милях = значение в км × 0,62137119223733
Предположим, вы хотите преобразовать 1200 км в мили. Используя приведенную выше формулу преобразования, вы получите:
Используя приведенную выше формулу преобразования, вы получите:
Значение в милях = 1200 × 0,62137119223733 = 745,645 миль
Определение километра
Километр (км) – это десятичное число, кратное метру. Международная стандартная единица длины, приблизительно эквивалентно 39,37 дюйма. Километр в настоящее время официально используется для выражения расстояний между географическими точками на суше в большинстве стран мира, за исключением США и Великобритании.
Определение мили
Миля – это единица измерения длины в американских и британских имперских единицах измерения. Чаще всего она равна 5280 футам (1760 ярдов, или около 1609 метров).
Этот конвертер поможет вам получить ответы на такие вопросы, как:
- Сколько километров в 1200 милях?
- 1200 км равны скольким милям?
- Сколько 1200 км в милях?
- Как перевести км в мили?
- Какой коэффициент преобразования км в мили?
- Как перевести км в мили?
- Какова формула перевода километров в мили? Среди прочих.


 1 Вытягивание одинаковых множителей :
1 Вытягивание одинаковых множителей : 2 Разложение на множители b 2 + 3b + 2
2 Разложение на множители b 2 + 3b + 2 
 Изображения товара актуальные и полностью совпадают с 3D-моделью. После оплаты Вы получите e-mail с ссылкой на скачивание модели. Вы всегда можете скачать 3D-модель в личном кабинете на нашем сайте.
Изображения товара актуальные и полностью совпадают с 3D-моделью. После оплаты Вы получите e-mail с ссылкой на скачивание модели. Вы всегда можете скачать 3D-модель в личном кабинете на нашем сайте. В заключение хочется отметить, что используя наши модели, вы не столкнетесь с проблемами полигональной сетки или аналогичными проблемами.
В заключение хочется отметить, что используя наши модели, вы не столкнетесь с проблемами полигональной сетки или аналогичными проблемами.


 Разница между ними в том, что у куба грани квадратные, а у кубоида — прямоугольные.
Разница между ними в том, что у куба грани квадратные, а у кубоида — прямоугольные. Ниже показаны названия нескольких 3D-форм и их сетей:
Ниже показаны названия нескольких 3D-форм и их сетей: Трехмерные формы также называют объемными формами.
Трехмерные формы также называют объемными формами.



 Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны. Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников). Многогранники также могут быть вогнутыми или выпуклыми.
Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников). Многогранники также могут быть вогнутыми или выпуклыми.
 Кроме того, пирамида может иметь вершину прямо в центре основания, т.0005 Правая пирамида
Кроме того, пирамида может иметь вершину прямо в центре основания, т.0005 Правая пирамида  В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора). Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы.
Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
 Возможно, вам придется измерить стороны по отдельности.
Возможно, вам придется измерить стороны по отдельности.

 Расчет одинаков для каждой части.
Расчет одинаков для каждой части.
 По теореме Коши имеется точка \(\xi\in (a,x)\), такая, что:
По теореме Коши имеется точка \(\xi\in (a,x)\), такая, что:
 {-1} < A+\frac{\varepsilon}{2}\)
{-1} < A+\frac{\varepsilon}{2}\) {\infty}\) нередко удается преобразить в неопределенности типа \(\displaystyle \frac{0}{0}\) или \(\displaystyle \frac{\infty}{\infty}\), используя при этом различные преобразования.
{\infty}\) нередко удается преобразить в неопределенности типа \(\displaystyle \frac{0}{0}\) или \(\displaystyle \frac{\infty}{\infty}\), используя при этом различные преобразования. {5x}+1}{x-\cos x+1} = -3\)
Источник: fbto.psuti.ru
{5x}+1}{x-\cos x+1} = -3\)
Источник: fbto.psuti.ru
 Мотивация. (3 минуты)
Мотивация. (3 минуты)
 Предельный анализ в экономике исследует изменяющиеся величины затрат или
результатов при изменении объемов производства или потребления на основе
анализа их предельных значений. Задачи на темы: рост вклада, рост населения
страны, распад радиоактивного вещества, размножение бактерий решаются с помощью
второго замечательного предела.
Предельный анализ в экономике исследует изменяющиеся величины затрат или
результатов при изменении объемов производства или потребления на основе
анализа их предельных значений. Задачи на темы: рост вклада, рост населения
страны, распад радиоактивного вещества, размножение бактерий решаются с помощью
второго замечательного предела.

 Для того чтобы раскрыть эту неопределенность, разложим
числитель и знаменатель дроби на множители и до перехода к пределу сократим
дробь на множитель х-2. В результате получим
Для того чтобы раскрыть эту неопределенность, разложим
числитель и знаменатель дроби на множители и до перехода к пределу сократим
дробь на множитель х-2. В результате получим Знаменатель уже
является простейшим множителем, и упростить его никак нельзя.
Знаменатель уже
является простейшим множителем, и упростить его никак нельзя.
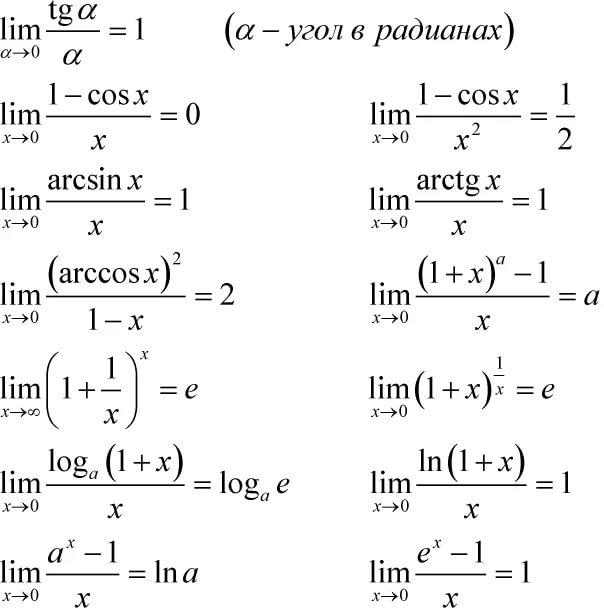

 все
пределы на бесконечности
все
пределы на бесконечности При стремлении аргумента x
к бесконечности имеем неопределенность вида ∞/∞. Чтобы раскрыть ее, разделим
числитель и знаменатель дроби на x. Тогда получим
При стремлении аргумента x
к бесконечности имеем неопределенность вида ∞/∞. Чтобы раскрыть ее, разделим
числитель и знаменатель дроби на x. Тогда получим Произведем подстановку
kx=y. Отсюда следует, что при , а
x=y/k. Тогда получим
Произведем подстановку
kx=y. Отсюда следует, что при , а
x=y/k. Тогда получим
 Запишем основание степени
в виде , а
показатель степени – в виде .
Следовательно,
Запишем основание степени
в виде , а
показатель степени – в виде .
Следовательно, Повторение
основных понятий.
Повторение
основных понятий. П
П Р
Р Выражение,
значение которого не определено, — это неопределенность;
Выражение,
значение которого не определено, — это неопределенность;
 а) б)
а) б) Лицензия на использование CPT для любого использования, не разрешенного здесь, должна быть получена через AMA, Службу интеллектуальной собственности CPT, 515 N. State Street, Chicago, IL 60610. Заявки доступны на веб-сайте AMA.
Лицензия на использование CPT для любого использования, не разрешенного здесь, должна быть получена через AMA, Службу интеллектуальной собственности CPT, 515 N. State Street, Chicago, IL 60610. Заявки доступны на веб-сайте AMA. 7202-1(a) (июнь 1995 г.) и DFARS 227.7202-3(a) июнь 1995 г.), применимыми к закупкам Министерства обороны США, и ограниченными правами FAR 52.227- 14 (июнь 1987 г.) и/или в соответствии с положениями об ограничении прав FAR 52.227-14 (июнь 1987 г.) и FAR 52.227-19 (июнь 1987 г.), в зависимости от обстоятельств, и любыми применимыми дополнениями FAR агентства для закупок вне федерального ведомства.
7202-1(a) (июнь 1995 г.) и DFARS 227.7202-3(a) июнь 1995 г.), применимыми к закупкам Министерства обороны США, и ограниченными правами FAR 52.227- 14 (июнь 1987 г.) и/или в соответствии с положениями об ограничении прав FAR 52.227-14 (июнь 1987 г.) и FAR 52.227-19 (июнь 1987 г.), в зависимости от обстоятельств, и любыми применимыми дополнениями FAR агентства для закупок вне федерального ведомства. AMA прямо или косвенно не занимается медицинской практикой и не оказывает медицинские услуги. Ответственность за содержание этого файла/продукта лежит на CGS или CMS, и AMA не намерено или подразумевает никакого одобрения. AMA отказывается от ответственности за любые последствия или ответственность, связанные с любым использованием, неиспользованием или интерпретацией информации, содержащейся или не содержащейся в этом файле/продукте. Настоящее Соглашение будет расторгнуто после уведомления, если вы нарушите его условия. AMA является бенефициаром третьей стороны по настоящему Соглашению.
AMA прямо или косвенно не занимается медицинской практикой и не оказывает медицинские услуги. Ответственность за содержание этого файла/продукта лежит на CGS или CMS, и AMA не намерено или подразумевает никакого одобрения. AMA отказывается от ответственности за любые последствия или ответственность, связанные с любым использованием, неиспользованием или интерпретацией информации, содержащейся или не содержащейся в этом файле/продукте. Настоящее Соглашение будет расторгнуто после уведомления, если вы нарушите его условия. AMA является бенефициаром третьей стороны по настоящему Соглашению. Ни при каких обстоятельствах CMS не несет ответственности за прямой, косвенный, специальный, случайный или последующий ущерб, возникающий в результате использования такой информации или материалов.
Ни при каких обстоятельствах CMS не несет ответственности за прямой, косвенный, специальный, случайный или последующий ущерб, возникающий в результате использования такой информации или материалов.
 Вы не должны удалять, изменять или скрывать какие-либо уведомления об авторских правах ADA или другие уведомления о правах собственности, включенные в материалы.
Вы не должны удалять, изменять или скрывать какие-либо уведомления об авторских правах ADA или другие уведомления о правах собственности, включенные в материалы. Щелкните здесь, чтобы ознакомиться со всеми положениями о правах правительства США.
Щелкните здесь, чтобы ознакомиться со всеми положениями о правах правительства США. Настоящее Соглашение прекратит свое действие после уведомления вас, если вы нарушите условия настоящего Соглашения. ADA является сторонним бенефициаром по настоящему Соглашению.
Настоящее Соглашение прекратит свое действие после уведомления вас, если вы нарушите условия настоящего Соглашения. ADA является сторонним бенефициаром по настоящему Соглашению. Если вышеуказанные условия приемлемы для вас, пожалуйста, подтвердите свое согласие, нажав кнопку ниже с надписью «Я ПРИНИМАЮ». Если вы не согласны с условиями, вы не можете получить доступ к программному обеспечению или использовать его. Вместо этого вы должны нажать ниже на кнопку с надписью «Я НЕ ПРИНИМАЮ» и выйти из этого экрана компьютера.
Если вышеуказанные условия приемлемы для вас, пожалуйста, подтвердите свое согласие, нажав кнопку ниже с надписью «Я ПРИНИМАЮ». Если вы не согласны с условиями, вы не можете получить доступ к программному обеспечению или использовать его. Вместо этого вы должны нажать ниже на кнопку с надписью «Я НЕ ПРИНИМАЮ» и выйти из этого экрана компьютера.


 Вам нужно определиться с поставщиком, который будет создавать визуальные и видеоматериалы для дизайна. Сейчас на выбор у вас есть три дизайнерских агентства, однако у каждого из них есть свои преимущества и недостатки.
Вам нужно определиться с поставщиком, который будет создавать визуальные и видеоматериалы для дизайна. Сейчас на выбор у вас есть три дизайнерских агентства, однако у каждого из них есть свои преимущества и недостатки.
 У его сотрудников довольно хороший опыт, и оно получает отличные отзывы от клиентов, однако коммуникации оставляют желать лучшего.
У его сотрудников довольно хороший опыт, и оно получает отличные отзывы от клиентов, однако коммуникации оставляют желать лучшего. Отзывы клиентов также важны, так как дают базовое представление об эффективности того или иного агентства в прошлом.
Отзывы клиентов также важны, так как дают базовое представление об эффективности того или иного агентства в прошлом.

 Постарайтесь по возможности делегировать эту работу.
Постарайтесь по возможности делегировать эту работу.



 При возникновении экстремальных погодных явлений, эпидемически неблагополучных ситуаций и угроз безопасности вашего персонала, незамедлительно предпринятые нами действия, обеспечат непрерывность бизнес процессов вашей организации. Основанная в 1985 году, группа компаний International SOS заслужила доверие 11,000 организаций, включая более половины компаний, включённых в список Fortune Global 500, многонациональных корпораций и предприятий среднего бизнеса, представителей правительств, образовательных учреждений и частных компаний. 11,000 специалистов в области медицины, безопасности и организации перевозок обеспечивают помощь и поддержку в более чем 1000 локаций в 90 странах мира 365 дней в неделю в круглосуточном режиме. Для обеспечения необходимой защиты ваших сотрудников, посетите www.internationalsos.com
При возникновении экстремальных погодных явлений, эпидемически неблагополучных ситуаций и угроз безопасности вашего персонала, незамедлительно предпринятые нами действия, обеспечат непрерывность бизнес процессов вашей организации. Основанная в 1985 году, группа компаний International SOS заслужила доверие 11,000 организаций, включая более половины компаний, включённых в список Fortune Global 500, многонациональных корпораций и предприятий среднего бизнеса, представителей правительств, образовательных учреждений и частных компаний. 11,000 специалистов в области медицины, безопасности и организации перевозок обеспечивают помощь и поддержку в более чем 1000 локаций в 90 странах мира 365 дней в неделю в круглосуточном режиме. Для обеспечения необходимой защиты ваших сотрудников, посетите www.internationalsos.com
 Чтобы добавить две матрицы одного порядка, добавьте соответствующий элемент первой матрицы к соответствующему элементу второй матрицы.
Чтобы добавить две матрицы одного порядка, добавьте соответствующий элемент первой матрицы к соответствующему элементу второй матрицы. 

 Однако вот метод умножения двух матриц.
Однако вот метод умножения двух матриц. 





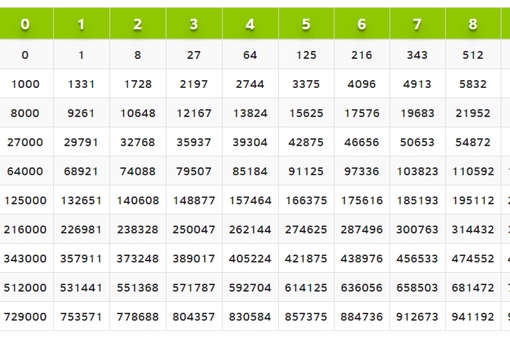
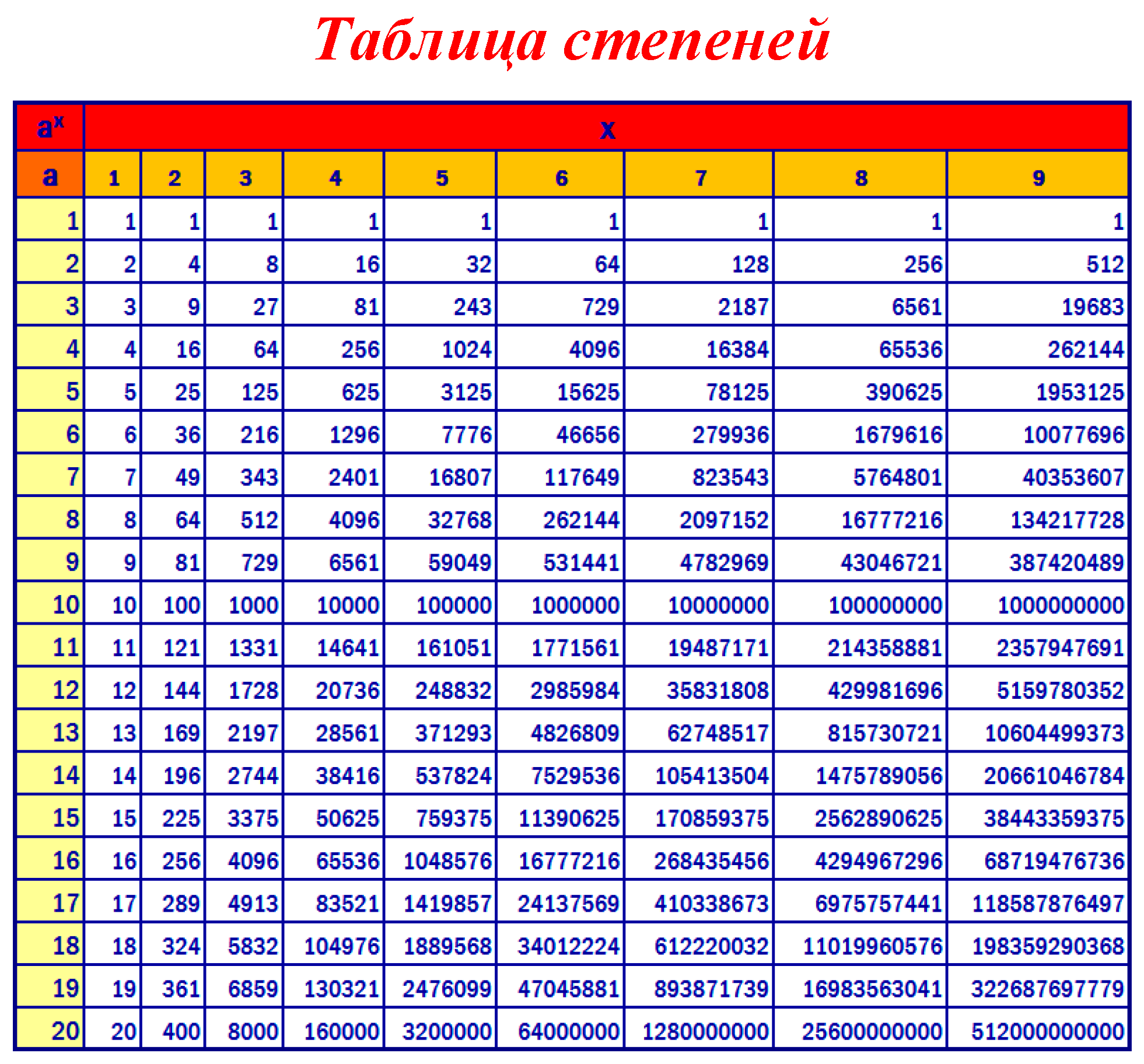
 Давайте посмотрим на это более наглядно:
Давайте посмотрим на это более наглядно:


 {\prime}=\frac{1}{\sin x} \cdot \cos x=\operatorname{ctg} x
\]
{\prime}=\frac{1}{\sin x} \cdot \cos x=\operatorname{ctg} x
\] Интегрирование — действие, обратное дифференцированию, а именно, восстановление
функции по известной производной этой функции. Восстановленная таким образом функция F(x) называется первообразной для функции f(x).
Интегрирование — действие, обратное дифференцированию, а именно, восстановление
функции по известной производной этой функции. Восстановленная таким образом функция F(x) называется первообразной для функции f(x). При этом употребляется запись
При этом употребляется запись Подобно тому, как дверь сделана
из дерева при помощи некоторых инструментов, производная функции «сделана» из первообразной функции
при помощи формулы, которую мы узнали, изучая производную.
Подобно тому, как дверь сделана
из дерева при помощи некоторых инструментов, производная функции «сделана» из первообразной функции
при помощи формулы, которую мы узнали, изучая производную. Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку
первообразная может быть функцией, например, 5x³+4 или 5x³+3
и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.
Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку
первообразная может быть функцией, например, 5x³+4 или 5x³+3
и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль. е.
е.
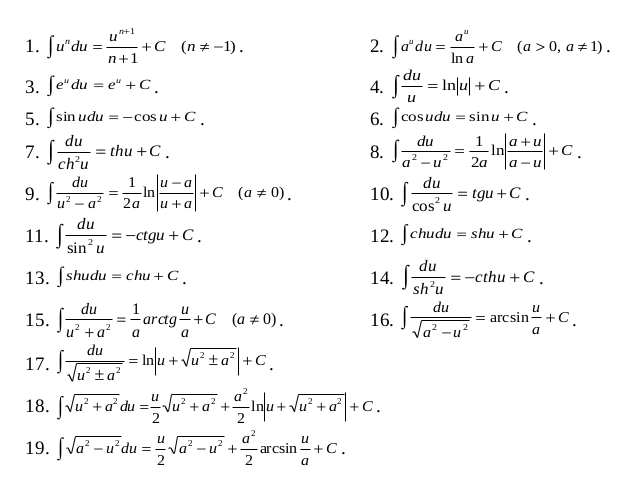
 Значит, нужно найти такую функцию F(x), для которой F'(x)=f(x). Требуемая в задаче функция F(x) является первообразной от f(x). Условию задачи удовлетворяет не одна
кривая, а семейство кривых. y=F(x) — одна из таких кривых, а всякая другая кривая может быть получена
из неё параллельным переносом вдоль оси Oy.
Значит, нужно найти такую функцию F(x), для которой F'(x)=f(x). Требуемая в задаче функция F(x) является первообразной от f(x). Условию задачи удовлетворяет не одна
кривая, а семейство кривых. y=F(x) — одна из таких кривых, а всякая другая кривая может быть получена
из неё параллельным переносом вдоль оси Oy.

 Расчет, том 1
Расчет, том 1 ∫cos2udu=12u+14sin2u+C∫cos2udu=12u+14sin2u+C
∫cos2udu=12u+14sin2u+C∫cos2udu=12u+14sin2u+C ∫cscnudu=−1n−1cotucscn−2u+n−2n−1∫cscn−2udu∫cscnudu=−1n−1cotucscn−2u+n−2n−1∫cscn−2udu
∫cscnudu=−1n−1cotucscn−2u+n−2n−1∫cscn−2udu∫cscnudu=−1n−1cotucscn−2u+n−2n−1∫cscn−2udu ∫eaucosbudu=eaua2+b2(acosbu+bsinbu)+C∫eaucosbudu=eaua2+b2(acosbu+bsinbu)+C
∫eaucosbudu=eaua2+b2(acosbu+bsinbu)+C∫eaucosbudu=eaua2+b2(acosbu+bsinbu)+C ∫tan−1udu=utan−1u−12ln(1+u2)+C∫tan−1udu=utan−1u−12ln(1+u2)+C
∫tan−1udu=utan−1u−12ln(1+u2)+C∫tan−1udu=utan−1u−12ln(1+u2)+C ∫a2+u2u2du=−a2+u2u+ln(u+a2+u2)+C∫a2+u2u2du=−a2+u2u+ln(u+a2+u2)+C
∫a2+u2u2du=−a2+u2u+ln(u+a2+u2)+C∫a2+u2u2du=−a2+u2u+ln(u+a2+u2)+C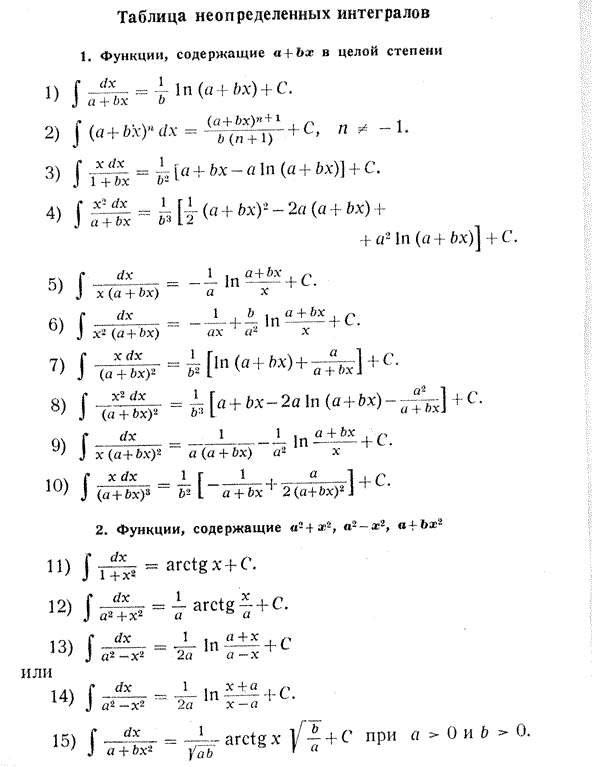 ∫u2duu2−a2=u2u2−a2+a22ln|u+u2−a2|+C∫u2duu2−a2=u2u2−a2+a22ln|u+u2−a2|+C
∫u2duu2−a2=u2u2−a2+a22ln|u+u2−a2|+C∫u2duu2−a2=u2u2−a2+a22ln|u+u2−a2|+C ∫du(a2−u2)3/2=ua2a2−u2+C∫du(a2−u2)3/2=ua2a2−u2+C
∫du(a2−u2)3/2=ua2a2−u2+C∫du(a2−u2)3/2=ua2a2−u2+C ∫duu2(a+bu)=−1au+ba2ln|a+buu|+C∫duu2(a+bu)=−1au+ba2ln|a+buu|+C
∫duu2(a+bu)=−1au+ba2ln|a+buu|+C∫duu2(a+bu)=−1au+ba2ln|a+buu|+C ∫duuna+bu=−a+bua(n−1)un−1−b(2n−3)2a(n−1)∫duun−1a+bu∫duuna+bu=−a+bua(n −1)un−1−b(2n−3)2a(n−1)∫duun−1a+bu
∫duuna+bu=−a+bua(n−1)un−1−b(2n−3)2a(n−1)∫duun−1a+bu∫duuna+bu=−a+bua(n −1)un−1−b(2n−3)2a(n−1)∫duun−1a+bu 9{n−2}u\,du\)
9{n−2}u\,du\)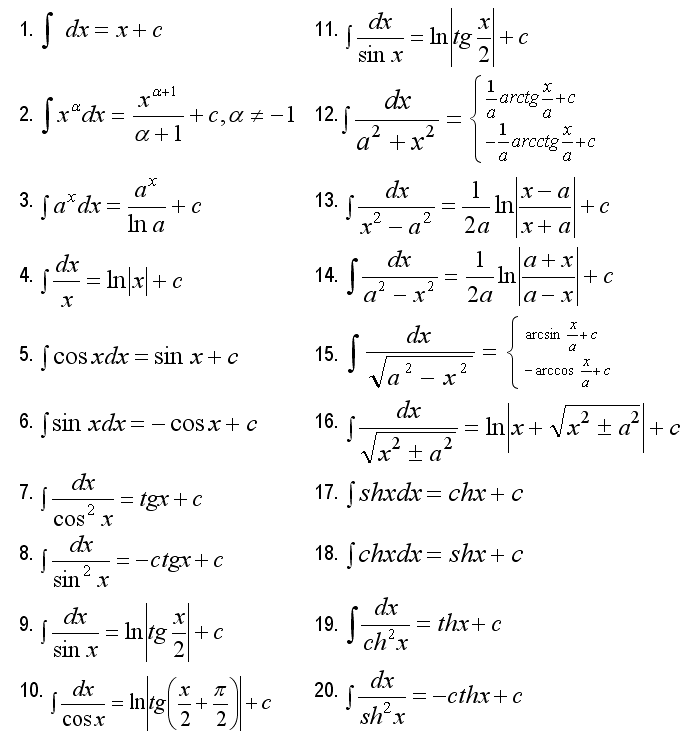
 Свойства логарифмов — презентация онлайн
Свойства логарифмов — презентация онлайн Вычислите:log4 7
Вычислите:log4 7 е. логарифм произведения равен сумме
е. логарифм произведения равен сумме Свойства логарифмовlog 113 log 3 11 1
Свойства логарифмовlog 113 log 3 11 1
 Число 2 0 = 1, 2 1 = 2, 2 2 = 4, 2 3 = 8, 2 4 = 16, но если у нас есть 2 х = 25 и нам нужно чтобы найти значение x, мы можем сначала записать его как логарифмическую базу 2 или \(log_225 = x\) и найти значение x. Логарифмическая база 2 помогает найти экспоненциальное значение 2.
Число 2 0 = 1, 2 1 = 2, 2 2 = 4, 2 3 = 8, 2 4 = 16, но если у нас есть 2 х = 25 и нам нужно чтобы найти значение x, мы можем сначала записать его как логарифмическую базу 2 или \(log_225 = x\) и найти значение x. Логарифмическая база 2 помогает найти экспоненциальное значение 2.
 Давайте поймем это с помощью простой формулы. Для натурального числа N его логарифм по основанию 2 равен k и записывается как \(log_2N = k\), что может быть записано в экспоненциальной форме как 2 k = N.
Давайте поймем это с помощью простой формулы. Для натурального числа N его логарифм по основанию 2 равен k и записывается как \(log_2N = k\), что может быть записано в экспоненциальной форме как 2 k = N. \(log_2a + log_2b = log_2ab\).
\(log_2a + log_2b = log_2ab\). = 64
= 64