Калькулятор уравнения четвертой степени
Уравнения четвертой степени имеет вид ах4; + bх3 + сх2 + ах + е = 0. Общее уравнение четвертой степени (также называемый биквадратным) является четвертой степени полиномиального уравнения. Бесплатный онлайн калькулятор расчета уравнения четвертой степени, используемый для нахождения корней уравнения.
Вычисление корней:
Например, Введите a=3, b=6, c=-123, d=-126 и e=1080
Формула уравнения четвертой степени:
ax4 + bx3 + cx2 + dx + e = 0
- Примечание : Допустим что p и q квадратные корни из 2 ненулевых корней.
- p = sqrt(y1)
- q = sqrt(y3)
- r = -g / (8pq)
- s = b / (4a)
- x1 = p + q + r — s
- x2 = p — q — r — s
- x3> = -p + q — r — s
- x4 = -p — q + r — s
Уравнением четвертой степени называется полиномиальное уравнение четвертого порядка вида, ax4+ bx3 + cx2 + dx + e = 0:
Формула уравнения четвертой степени:
ax4 + bx3+ cx2 + dx + e = 0
где,
- a = коэффициент для x4
- b = коэффициент для x3
- c = коэффициент для x2
- d = коэффициент для x
- e = константа.

Решение уравнения четвертой степени:
- x1 = p + q + r — s
- x2 = p — q — r — s
- x3 = -p + q — r — s
- x4 = -p — q + r — s
Пример 1:
Вычислить корни (x1, x2, x3, x4) уравнения четвертой степени, 3X4 + 6X3 — 123X2 — 126X + 1080 = 0
Шаг 1:
Из приведенного выше уравнения, значения a=3, b=6, c=-123, d=-126, e=1080.
Шаг 2:
Найдем x : Подставьте значения в приведенных ниже формул.
- f = c — ( 3b ² / 8 )
- g = d + ( b ³ / 8 ) — ( b x c / 2 )
- h = e — ( 3 x b4 / 256 ) + ( b ² x c / 16 ) — ( b x d / 4 )
Шаг 3:
Представим как уравнение третьей степени : y ³ + ( f / 2 ) y ² + (( f ² — 4 x h ) / 16 ) y — g ² / 64 = 0
где,
- a = коэффициент для y ³
- b = коэффициент для y²
- c = коэффициент для y
- d = константа
Шаг 4:
Из приведенного выше уравнения, значения:
- a = 1,
- b = f/2,
- c = (( f ² — 4 x h ) / 16 ),
- d = — g² / 64.

Шаг 5:
Найдем y: Подставьте значения в формулу, чтобы найти корни.
дискриминант (Δ) = q3 + r2
- q = (3c — b2) / 9
- r = -27d + b(9c — 2b2)
- s = r +√ (дискриминант)
- t = r — √(дискриминант)
- term1 = √(3.0) * ((-t + s) / 2)
- r13 = 2 * √(q)
- y1 = (- term1 + r13*cos(q3/3) )
- y2 = (- term1 + r13*cos(q3+(2∏)/3) )
- y3 = (- term1 + r13*cos(q3+(4∏)/3) )
Шаг 6:
Получим корни, y1 = 20.25 , y2 = 0 и y3 = 1.
Шаг 7:
После решения уравнения третьей степени решим уравнение четвертой степени.
Подставим y1, y2, y3 в p, q, r, s.
Примечание : Пусть p и q квадратные корни 2 ненулевых корней.
- p = sqrt(y1) = 4.5
- q = sqrt(y3) = 1
- r = -g / (8pq) = 0
- s = b / (4a) = 0.
 5
5
Шаг 8:
Мы получили корни, x1 = 5, x2 = 3, x3 = -4 и x4 = -6.
Практический пример решения уравнения четвертой степени.
людей нашли эту статью полезной. А Вы?
Решение уравнений 3 и 4 степени
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Исследовательская работа по теме: «Решение уравнений 3-ей и 4-ой степени»
Выполнил:ученик 9 класса
Кравченко Виталий
Руководитель:
учитель математики
Нечаева
Елена Николаевна
© Фокина Лидия Петровна
2.
 Основные методы решения уравнений высших порядков1. Метод разложения на множители
Основные методы решения уравнений высших порядков1. Метод разложения на множителилевой части уравнения.
2.Метод введения новой переменной.
3.Функционально-графический метод
© Фокина Лидия Петровна
3. Уравнения вида ax3 + bx2 + cx + d = 0, где a ≠ 0, называются уравнениями 3-ей степени
Уравнение видаx 3 + px + q = 0
называется приведённым
кубическим уравнением
Известные формулы Кардано для решения уравнений этого типа
очень сложны и почти не применяются на практике.
© Фокина Лидия Петровна
4. Решу уравнение х3 -7х+6=0 разными способами
1. Разложение на множителих3 -7х + 6 =0
х3 — х2 + х2 – х — 6х + 6=0
х2 (х-1)+ х(х-1)-6(х-1)=0
(х-1)(х2 + х — 6) = 0
х-1=0 или х2 + х – 6 = 0
х1 =1
х2 =-3 х3 = 2
Ответ: 1; 2; -3
© Фокина Лидия Петровна
5. 2.Метод деления на многочлен
х3 -7х+6 = 0 делители 6: ±1; ±2; ±3; ±61³-7+6=0
3-7х+6 =(х-1)(х2 +х-6)=0
х
x³-0х2-7x+6 x-1
2 +х-6=0
х-1=0
или
х
x³-x²
x²+x-6
х1 =1
х2 =-3 х3 = 2
x²-7x
x²-x
-6x+6
-6x+6
0
© Фокина Лидия Петровна
Ответ: 1; 2; -3
6.
 3.Функционально-графический метод х3 -7х+6 = 0у = х3 и у = 7х-6
3.Функционально-графический метод х3 -7х+6 = 0у = х3 и у = 7х-6Ответ:1;2;-3
© Фокина Лидия Петровна
7. Уравнение четвертой степени общего вида ax4 + bx3 + cx2 + dx + e = 0 где а ≠ 0
Уравнение четвертой степени общего видаax4 + bx3 + cx2 + dx + e = 0 где а ≠ 0
1.Разложение на множители
x4 + 2×3 + 5×2 + 4x – 12 = 0
x4 + 2×3 + 5×2 + 10x – 6x – 12 = 0
(x4 + 2×3) + (5×2 + 10x) – (6x + 12 ) = 0
x3 (x+2) +5х (х+2) – 6 (х+2) =0
(x + 2) (x3 + 5x – 6) = 0
(x + 2)(x – 1)(x2 + x + 6) = 0
x1 = -2, x2 = 1.
Ответ: -2 ; 1
© Фокина Лидия Петровна
8. 2.Деление на многочлен Х4 — Х3-13 Х -15=0 -1 делитель числа -15 (1+1+13-15=0) Х4 — Х3-13 Х -15 = (Х+1)(Х-3)(Х2 +Х +5) = 0 Х+1
=0 или Х-3=0 или Х2 +Х +5 =0 (Д<0)Х1=-1 Х 2=3
Ответ: -1; 3
© Фокина Лидия Петровна
9. Биквадратное уравнение вида ax4 + bx2 + с = 0. 3.Метод: введение новой переменной
Биквадратное уравнение вида ax4 + bx2 + с = 0.3.Метод: введение новой переменной
x4 + 5×2 – 36 = 0.

Замена y = x2.
У2+ 5У-36=0
У1*У2 =-36= -9*4
У1=-9
У1 + У1 =-5= -9+4
У2 =4
X2 =-9
x2 =4
Корней нет
х1 =2 х2 =-2
Ответ: 2; -2
© Фокина Лидия Петровна
10. Задание:Решите уравнение Х3+2Х2- 5Х — 6 = 0
Делители -6: ±1; ±2; ±3; ±6-1 корень уравнения (-1+2+5-6=0)
Х3+2Х2- 5Х — 6 = (Х+1)(Х2+Х -6) = 0
Х+1= 0 или Х2+Х -6=0
Х1 =-1
Х2 =-3 Х3 = 2
Ответ: -1; -3; 2
© Фокина Лидия Петровна
English Русский Правила
Калькулятор уравнения 4-й степени | Калькулятор уравнения четвертой степени
Калькулятор уравнения четвертой степени, также известный как Калькулятор уравнения четвертой степени, позволяет вычислять корни уравнения четвертой степени. Эта страница содержит онлайн-калькулятор уравнения 4-й степени, который вы можете использовать на своем мобильном телефоне, устройстве, настольном компьютере или планшете, а также содержит вспомогательное руководство и инструкции по использованию калькулятора.
| ax 4 | ||
| + | xb 3 | |
| + | ||
| + | дх | |
| + | е |
| x 1 : | + | i | ||
| + | i | |||
| x 3 : | + | i | ||
| x 4 +2 12 | i |
Если вам пригодился калькулятор уравнений четвертой степени, он было бы здорово, если бы вы любезно дали оценку калькулятору и, если у вас есть время, поделитесь им в своей любимой социальной сети. Это помогает нам сосредоточить наши ресурсы и поддерживать существующие калькуляторы, а также разрабатывать новые математические калькуляторы для поддержки нашего глобального сообщества.
★ ★ ★ ★ ★ [ 5 голосов ]
Чем мне полезен этот калькулятор?
Калькулятор уравнений 4-й степени Это математический онлайн-калькулятор, разработанный калькулятором для помощи в развитии ваших математических знаний. Вы можете использовать его для проверки домашних заданий и помощи в расчетах уравнений четвертой степени. Это особенно полезно, если вы новичок в уравнениях четвертой степени или вам нужно освежить свои математические знания, поскольку калькулятор уравнений 4-й степени точно вычислит расчет, чтобы вы могли проверить свои собственные математические вычисления вручную.
Как вычислить корень четвертой степени?
Вы можете вычислить корень четвертой степени вручную, используя приведенное ниже уравнение четвертой степени, или вы можете использовать калькулятор уравнения четвертой степени и сэкономить время и нервы, связанные с математическими расчетами вручную. Вы также можете использовать калькулятор для проверки собственных математических расчетов вручную, чтобы убедиться, что ваши расчеты верны, и чтобы вы могли проверить любые ошибки в расчетах уравнения четвертой степени.
Уравнение четвертой степени Формула:
ax 4 + bx 3 + cx 2 + dx + e = 0
p = sqrt(y1)
q = sqrt(y3)7
r = — g /(8pq)
s = b /(4a)
x1 = p + q + r — s
x2 = p — q — r — s
x3 = -p + q — r — s
x4 = -p — q + r — s
Как вычислить корень четвертой степени с помощью калькулятора уравнений 4-й степени?
Для тех, кто уже знает, как рассчитать уравнение четвертой степени и хочет сэкономить время или проверить свои результаты, вы можете использовать калькулятор уравнения четвертой степени, выполнив следующие действия:
- Введите значение для ax 4
- Введите значение для xb 3
- Введите значение для cx 2
- Введите значение для 1 dx 8
- 4-я степень Калькулятор уравнений рассчитает корни уравнения 4-й степени, которое вы ввели
История уравнения 4-й степени
Формула уравнения четвертой степени была впервые открыта Лодовико Феррари в 1540 году, хотя утверждалось, что в 1486 году испанский математик якобы был Томас де Торквемада, главный инквизитор испанской инквизиции, сказал, что «это была воля бога, чтобы такое решение было недоступно человеческому пониманию», в результате чего математика сожгли на костре.
Несмотря на то, что Лодовико обнаружил решение квартики в 1540 году, оно не было опубликовано до 1545 года, поскольку решение также требовало решения куба, которое было обнаружено и опубликовано вместе с решением квартики наставником Лодовико Джероламо Кардано в книге Ars Magna.
Как эта формула применяется в жизни?
Уравнения четвертой степени довольно распространены в вычислительной геометрии и используются в таких областях, как компьютерная графика, оптика, проектирование и производство. Они также могут быть полезны для расчета коэффициентов.
Например, в автоматизированном производстве фреза концевой фрезы, если она часто ассоциируется с формой тора, требует решения четвертой степени для расчета ее положения относительно треугольной поверхности.
Quartic Equation Solver
Полиномы четвертой степени, уравнения вида
Ax 4 + Bx 3 + C4 10 + C4 2 9011 9011 Дх + Е = 0
где А не равно нулю, называются уравнениями четвертой степени. Если разделить обе части уравнения на A можно упростить уравнение до
Если разделить обе части уравнения на A можно упростить уравнение до
x 4 + bx 3 + cx 2 + 9 e0 = 90 0 0 + 4x 0.0 + 4 dx 0.0
Уравнение четвертой степени с действительными коэффициентами может иметь четыре действительных корня, два действительных корня и два комплексных корня или четыре комплексных корня. Сложные корни встречаются сопряженными парами. Чтобы решить общее уравнение четвертой степени, вам необходимо решить связанные кубические и квадратные уравнения в многоэтапном процессе. Некоторые специальные квартики можно решить более простыми методами.
Вы можете применить формулу четвертой степени, следуя приведенным ниже инструкциям, или воспользоваться калькулятором решения уравнения четвертой степени слева.
Формула четвертой степени
Учитывая общее уравнение четвертой степени переставить члены, чтобы сформировать уравнение
x 4 + bx 3 = — cx 2 — дх — эл.
Теперь добавьте выражение ( b 2 /4 + 2 p ) x 2 + bpx + p 20 с обеих сторон: 0 20
х 4 + bx 3 + ( b 2 /4 + 2 p ) x 2 + bpx 909104 + p 0011 = ( б 2 /4 + 2 р — с ) х 2 + ( п.н. — d ) х + р 2 — е .
Левая сторона теперь представляет собой идеальный квадрат: ( x 2 + ( b /2) x + p ) 2 . Вы хотите найти действительное число p такое, что правая часть тоже является квадратом. Чтобы правая часть была квадратным квадратом, дискриминант должен быть равен нулю. То есть
( п.н. — d ) 2 — 4( b 2 /4 + 2 p — c )( p 2 — e ) = 0,
-8 р 3 + 4 кп 2 + (8 е — 2 бд ) р + д 90 4 1 900 03 се + б 2 e = 0.
Поскольку каждое кубическое уравнение имеет хотя бы один действительный корень, вы можете найти подходящее значение p для разрешения квартики. После того, как вы подставите значение p , вы возьмете квадратный корень из обеих частей, чтобы создать два квадратных уравнения. Это дает вам в общей сложности четыре решения
Пример: Решите уравнение четвертой степени x 4 — 4 x 3 + 5 x 1 — 4 9001 . 3 х 4 — 4 х 3 = -5 х 2 + 4х — 4
x 4 — 4 x 3 + (4 + 2 p ) x 2 — 4 px +
Теперь решим куб. 0 3 + 20 р 2 = 0. Решения: p = 0, 0, 5/2. Вы можете использовать любое реальное значение р для подключения к квартике. В этом примере мы будем использовать 0, так как с ним проще работать.
В этом примере мы будем использовать 0, так как с ним проще работать.
х 4 — 4 х 3 + 4 х 2 = — х 1 0 3 х 1 0 3 х 90910 2 4 — 4 x 90 — 2 х = ± i ( x — 2) Это дает два квадратных уравнения с комплексными коэффициентами: 0 Используя квадратное уравнение, корни первого уравнения равны 2 и — i , а корни второго вторые 2 и я . Эти четыре корня являются корнями исходной квартики. Уравнения квартик, которые принимают одну из этих четырех форм, могут быть решены с использованием только квадратного уравнения, без необходимости применения более сложных формул, приведенных выше.
кв.( x 4 — 4 x 3 + 4 x 2 ) = sqrt(- x 2 + 4 x — 4)
x 2 + (-2 — i ) x + 2 i = 0 Особые случаи квартик




 5
5 2 = 6$$
2 = 6$$ k, где N — количество возможных комбинаций, m — количество разрешенных символов для каждого знака пароля, k — длина пароля.
k, где N — количество возможных комбинаций, m — количество разрешенных символов для каждого знака пароля, k — длина пароля.
 3=1000. Ваш кодовый замок имеет 1000 комбинаций паролей.
3=1000. Ваш кодовый замок имеет 1000 комбинаций паролей.
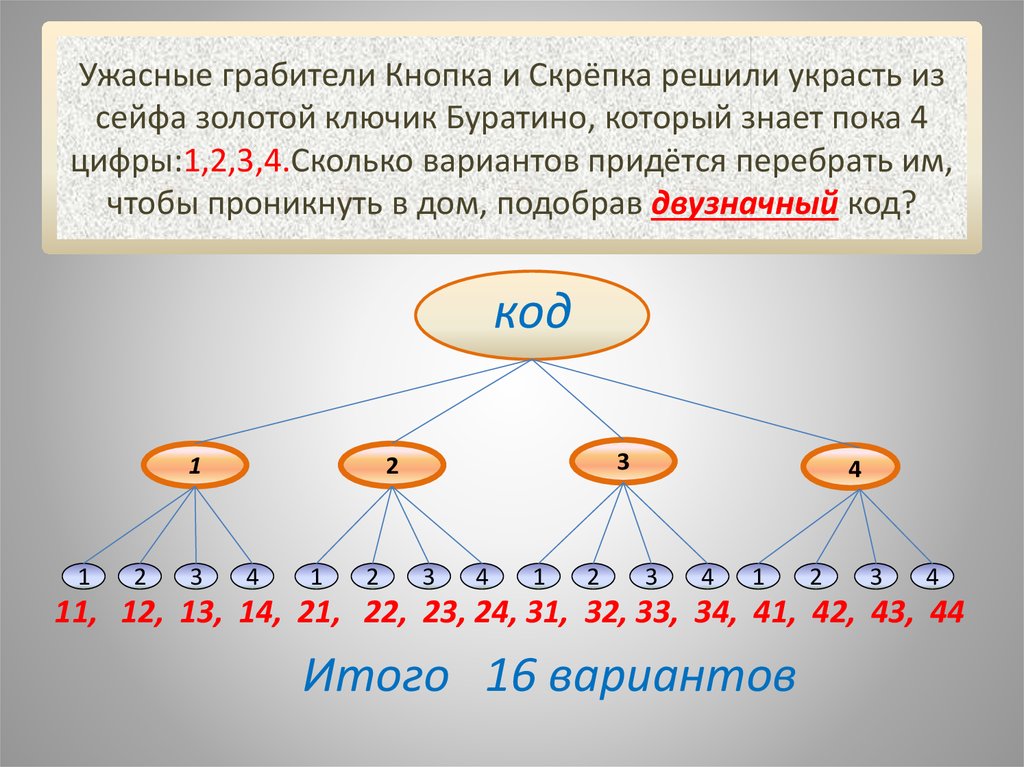
 это все комбинации.
это все комбинации.
 Если вы забыли свой новый код, вы должны открыть сейф, взломав его. Очень важно защитить код вашего сейфа, особенно если его можно сбросить, поскольку производитель не может предоставить вам новый код.
Если вы забыли свой новый код, вы должны открыть сейф, взломав его. Очень важно защитить код вашего сейфа, особенно если его можно сбросить, поскольку производитель не может предоставить вам новый код. После этого ящик с замком автоматически откроется. Если вы хотите узнать больше, вы также можете посмотреть это видео об открытии и закрытии сейфа MasterLock.
После этого ящик с замком автоматически откроется. Если вы хотите узнать больше, вы также можете посмотреть это видео об открытии и закрытии сейфа MasterLock.

 2743
2743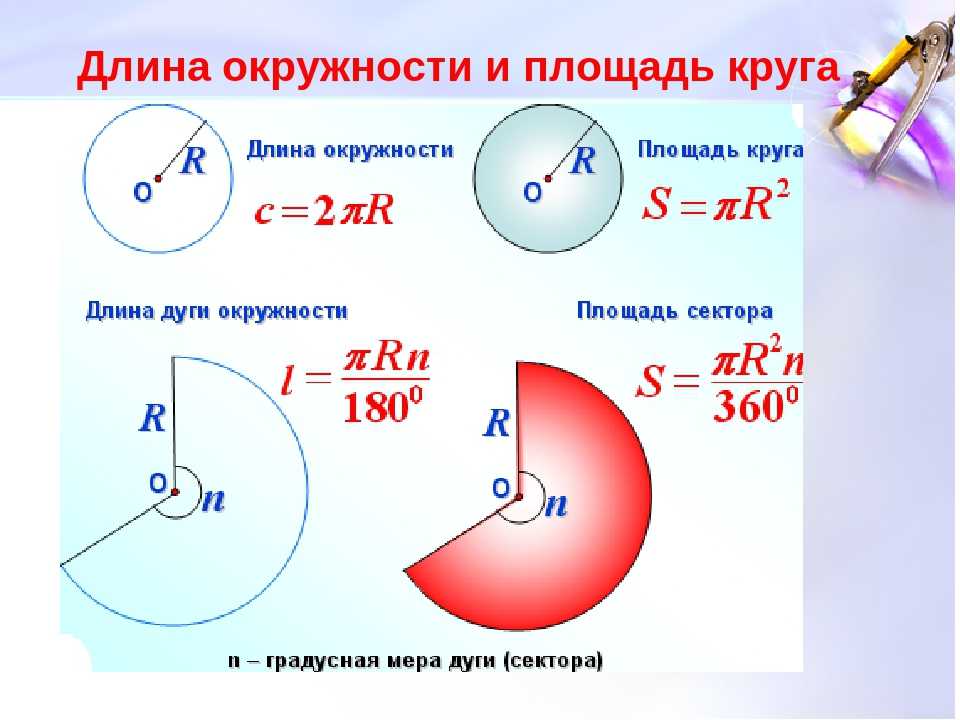
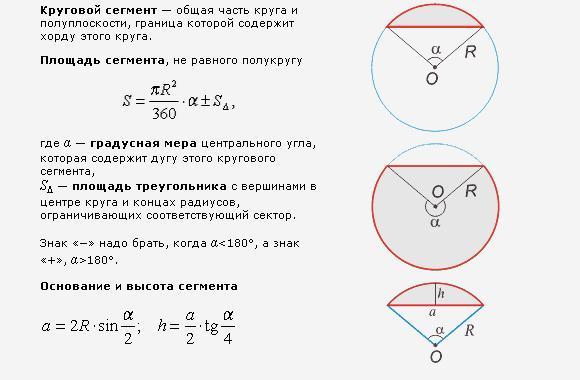

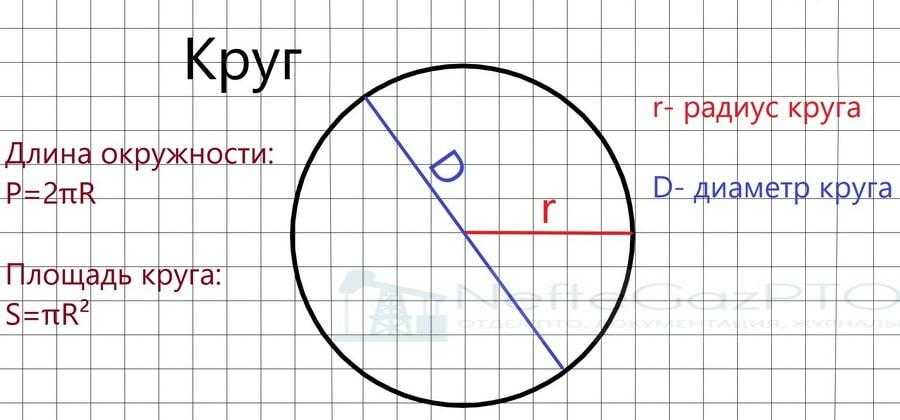 ..
.. 14)
14) Калькулятор прост в использовании и может быть использован для любого круга или единиц. Обратите внимание, что при использовании онлайн-калькулятора полученные значения не зависят от применяемых единиц.
Калькулятор прост в использовании и может быть использован для любого круга или единиц. Обратите внимание, что при использовании онлайн-калькулятора полученные значения не зависят от применяемых единиц.

 Составлен на основе типовых заданий, взятых из сборника «Тренажер для подготовки к ВПР по математике 4 класс» составитель А.Н.Алексеева.
Составлен на основе типовых заданий, взятых из сборника «Тренажер для подготовки к ВПР по математике 4 класс» составитель А.Н.Алексеева. 2.2022
2.2022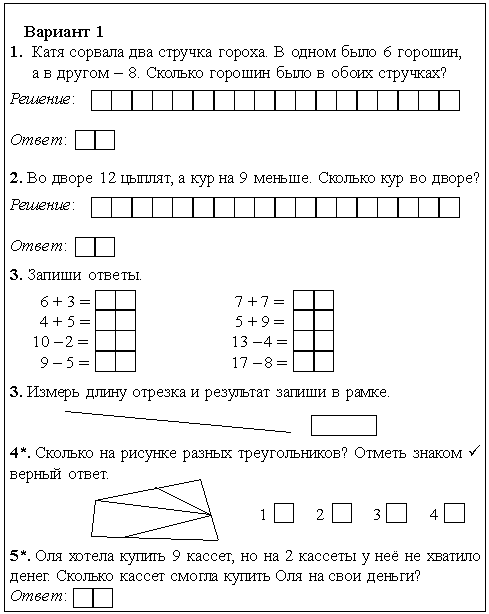 Читай внимательно задачи и думай! Желаю тебе удачи и хороших результатов!
Читай внимательно задачи и думай! Желаю тебе удачи и хороших результатов! После остановки он прошёл со скоростью 70 км/ч ещё 280 км. За какое время поезд прошёл весь путь?
После остановки он прошёл со скоростью 70 км/ч ещё 280 км. За какое время поезд прошёл весь путь? Сколько метров пройдёт он за 1 секунду?
Сколько метров пройдёт он за 1 секунду? За сколько часов они совершили обратный путь?
За сколько часов они совершили обратный путь? У Джетсера дела идут плохо. В пятницу он заработал 468 долларов. В субботу он заработал 459 долларов. Во вторник он заработал 432 доллара. Сколько денег он заработал в четверг?
У Джетсера дела идут плохо. В пятницу он заработал 468 долларов. В субботу он заработал 459 долларов. Во вторник он заработал 432 доллара. Сколько денег он заработал в четверг? Сколько блоков из 100 и 10 можно сделать из числа 3250?
Сколько блоков из 100 и 10 можно сделать из числа 3250?  Куб B. Сфера C. Цилиндр D. Конус
Куб B. Сфера C. Цилиндр D. Конус 
 Сколько денег получит каждый человек?____________
Сколько денег получит каждый человек?____________ 
 Реалистичный формат этого практического теста и высококачественные практические вопросы помогут вашему ученику успешно сдать тест MAP по математике в 4-м классе. Тест не только точно соответствует тому, что учащиеся увидят на реальной карте, но и содержит подробные объяснения ответов.
Реалистичный формат этого практического теста и высококачественные практические вопросы помогут вашему ученику успешно сдать тест MAP по математике в 4-м классе. Тест не только точно соответствует тому, что учащиеся увидят на реальной карте, но и содержит подробные объяснения ответов.
 Какова высота здания в метрах?
Какова высота здания в метрах? Между играми было 5 минут. Лили ушла через 10 минут после последней игры. Сколько времени в минутах провела Лили на футбольном поле?
Между играми было 5 минут. Лили ушла через 10 минут после последней игры. Сколько времени в минутах провела Лили на футбольном поле? \circ\), треугольник не может иметь более одного тупого угла. 9\circ\)f), близкое к выбору B
\circ\), треугольник не может иметь более одного тупого угла. 9\circ\)f), близкое к выбору B Затем мы сравниваем числители каждой дроби и располагаем их в правильном порядке от меньшего к большему или от большего к меньшему. 93 =64\)
Затем мы сравниваем числители каждой дроби и располагаем их в правильном порядке от меньшего к большему или от большего к меньшему. 93 =64\)


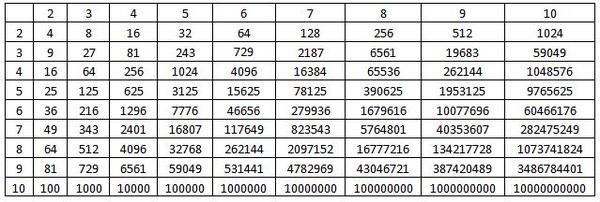
 Градус также имеет свои составные части, которые представляют собой минуты и секунды. Это преобразование играет важную роль в приложениях тригонометрии. В этой статье мы узнаем, как преобразовать градусы в радианы, градусы в формулу радианов и рассмотрим некоторые решенные примеры, основанные на том, как преобразовать градусы в формулу радианов. Давайте сначала посмотрим на преобразование градусов в радианы.
Градус также имеет свои составные части, которые представляют собой минуты и секунды. Это преобразование играет важную роль в приложениях тригонометрии. В этой статье мы узнаем, как преобразовать градусы в радианы, градусы в формулу радианов и рассмотрим некоторые решенные примеры, основанные на том, как преобразовать градусы в формулу радианов. Давайте сначала посмотрим на преобразование градусов в радианы.
 Последний шаг — упростить. Теперь вам нужно поставить каждую дробь в наименьшее значение, чтобы получить окончательный ответ. Найдите наибольшее число, которое можно без остатка разделить на числитель и знаменатель каждой дроби, и используйте его для упрощения каждой дроби.
Последний шаг — упростить. Теперь вам нужно поставить каждую дробь в наименьшее значение, чтобы получить окончательный ответ. Найдите наибольшее число, которое можно без остатка разделить на числитель и знаменатель каждой дроби, и используйте его для упрощения каждой дроби.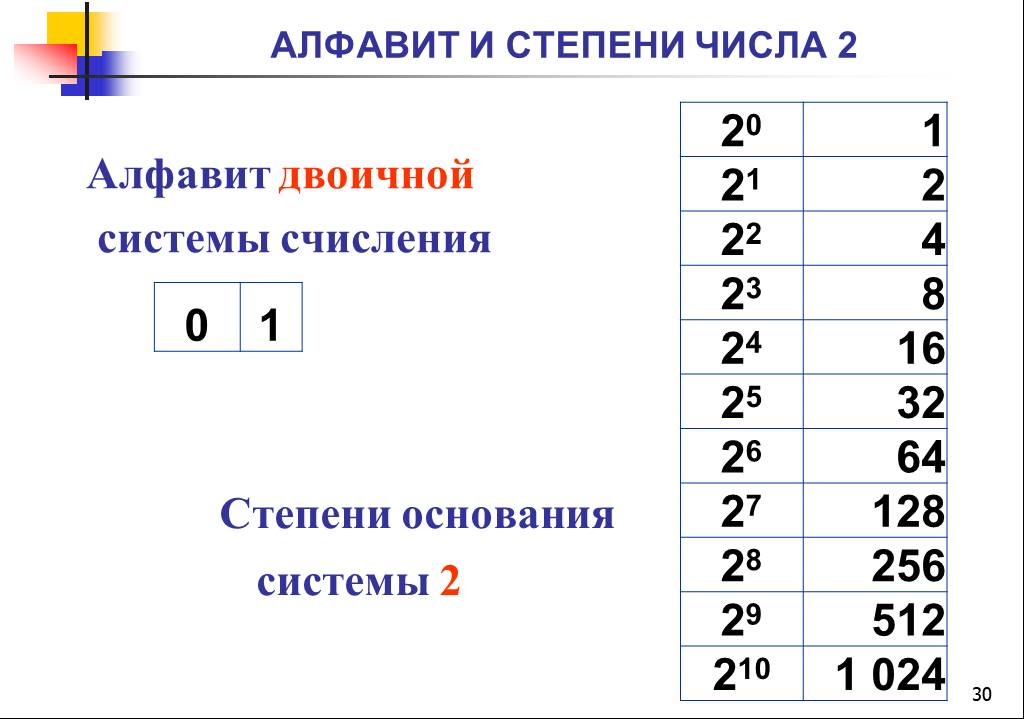
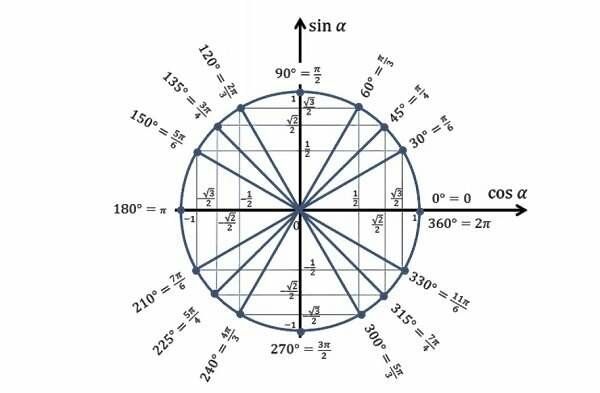
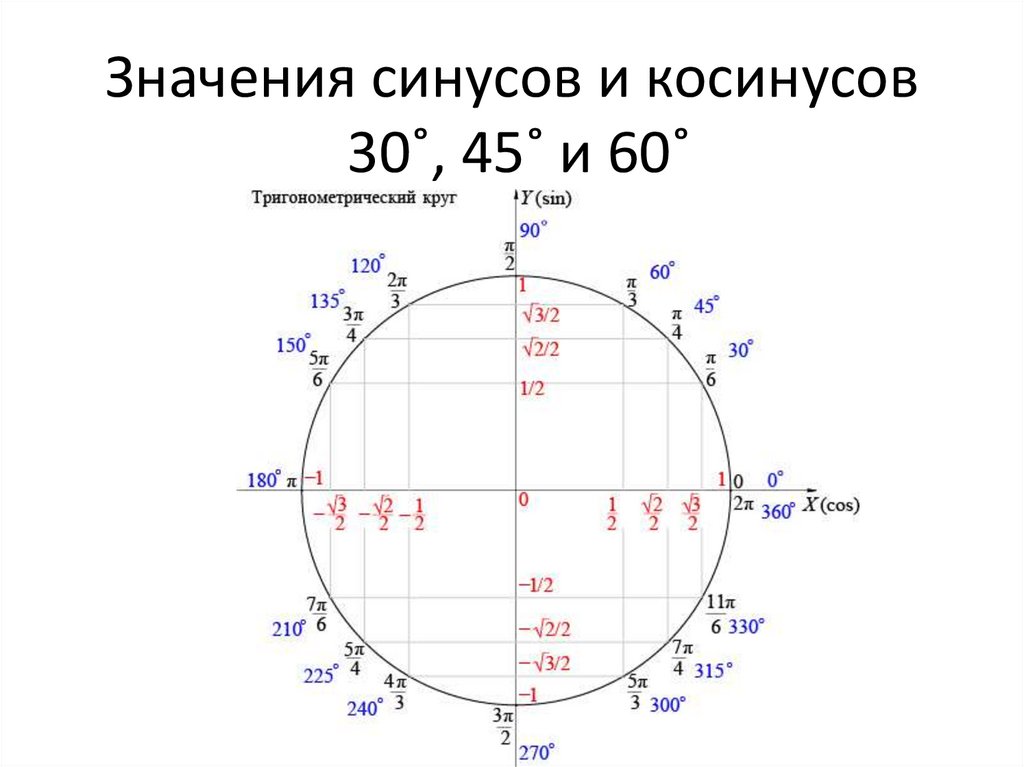
 Умножьте данное значение в градусах на \[\frac{\pi}{180}\]. Это простой шаг, и учащиеся могут использовать его, чтобы найти меру в радианах. Однако в таблице, приведенной выше, указаны радианы и приблизительные значения радианов для наиболее распространенных углов. Студенты могут использовать эту таблицу для более простых и быстрых вычислений. Например, если учащийся хочет вычислить в радианах 30°, 60° и 90°, он или она может обратиться к таблице. Радианные меры следующих мер в градусах будут \[\frac{\pi}{6}\], \[\frac{\pi}{3}\] и \[\frac{\pi}{2} \] и значения в радианах будут 0,524, 1,047 и 1,571 соответственно.
Умножьте данное значение в градусах на \[\frac{\pi}{180}\]. Это простой шаг, и учащиеся могут использовать его, чтобы найти меру в радианах. Однако в таблице, приведенной выше, указаны радианы и приблизительные значения радианов для наиболее распространенных углов. Студенты могут использовать эту таблицу для более простых и быстрых вычислений. Например, если учащийся хочет вычислить в радианах 30°, 60° и 90°, он или она может обратиться к таблице. Радианные меры следующих мер в градусах будут \[\frac{\pi}{6}\], \[\frac{\pi}{3}\] и \[\frac{\pi}{2} \] и значения в радианах будут 0,524, 1,047 и 1,571 соответственно. Угол, написанный без единицы измерения, означает, что он записан в радианах. Некоторые примеры: 4 рад, \[\frac{\pi}{2}\] или 90°
Угол, написанный без единицы измерения, означает, что он записан в радианах. Некоторые примеры: 4 рад, \[\frac{\pi}{2}\] или 90° 



 При замене переменной в неопределённом интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от x.
При замене переменной в неопределённом интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от x.

 Положим ,
откуда , .
Положим ,
откуда , .
 Этот интеграл калькулятора помогает вычислить площадь под кривой. Этот калькулятор может работать с помощью нескольких простых кликов. Интегральная функция очень проста в использовании и ее легко понять. Шаги, упомянутые здесь, очень понятны.
Этот интеграл калькулятора помогает вычислить площадь под кривой. Этот калькулятор может работать с помощью нескольких простых кликов. Интегральная функция очень проста в использовании и ее легко понять. Шаги, упомянутые здесь, очень понятны. Он вычисляет интегральную функцию , чтобы быстро и точно предоставить вам результаты. Выполняя несколько умных кликов, можно получить требуемые результаты. Он также обозначает число функции, которая известна как интеграл.
Он вычисляет интегральную функцию , чтобы быстро и точно предоставить вам результаты. Выполняя несколько умных кликов, можно получить требуемые результаты. Он также обозначает число функции, которая известна как интеграл. 93}{3} \;+\; 9x \;+\; C $$
93}{3} \;+\; 9x \;+\; C $$ В частности, интеграция занимает так много времени и полна ошибок. Таким образом, для оценки различных методов исчисления существуют специально разработанные калькуляторы, такие как интегральный калькулятор с делением на длинное деление и многие другие.
В частности, интеграция занимает так много времени и полна ошибок. Таким образом, для оценки различных методов исчисления существуют специально разработанные калькуляторы, такие как интегральный калькулятор с делением на длинное деление и многие другие. Этот инструмент также предлагает опцию «Примеры» . Вы можете получить пример для расчета интеграла с пошаговыми подробными решениями.
Этот инструмент также предлагает опцию «Примеры» . Вы можете получить пример для расчета интеграла с пошаговыми подробными решениями.


 Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT(n, k) или SLTn (k).
Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT(n, k) или SLTn (k).

 Аналогичное утверждение справедливо для нижнетреугольных матриц.
Аналогичное утверждение справедливо для нижнетреугольных матриц.



 Ниже приведен пример нижней треугольной матрицы:
Ниже приведен пример нижней треугольной матрицы: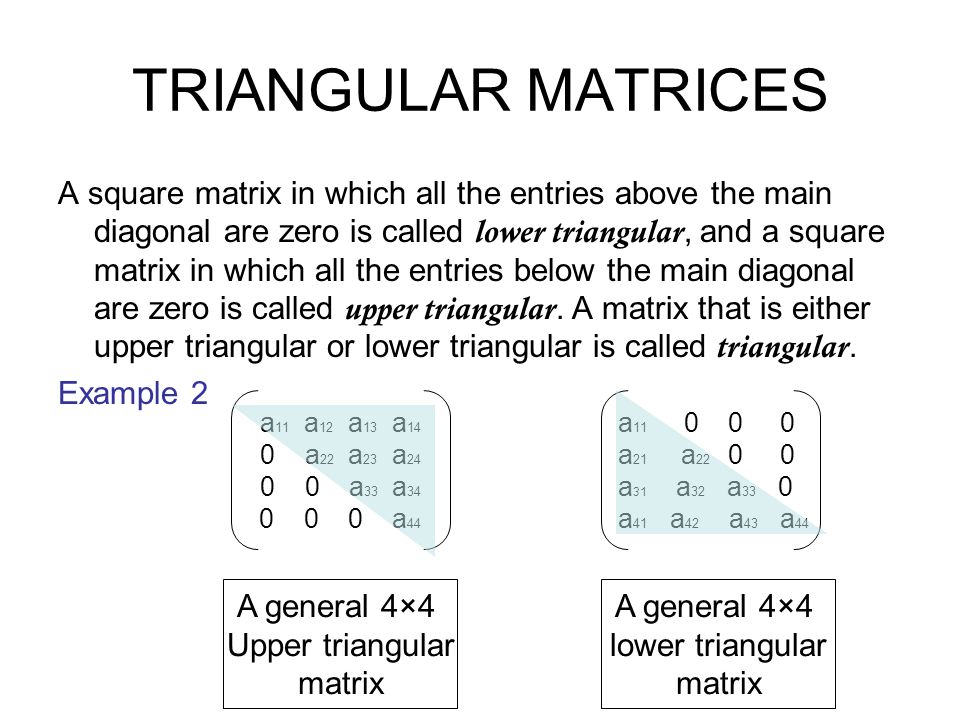 Это также известно как разложение LU.
Это также известно как разложение LU.
 Узнайте, почему математика стоит за нашими сертифицированными экспертами.
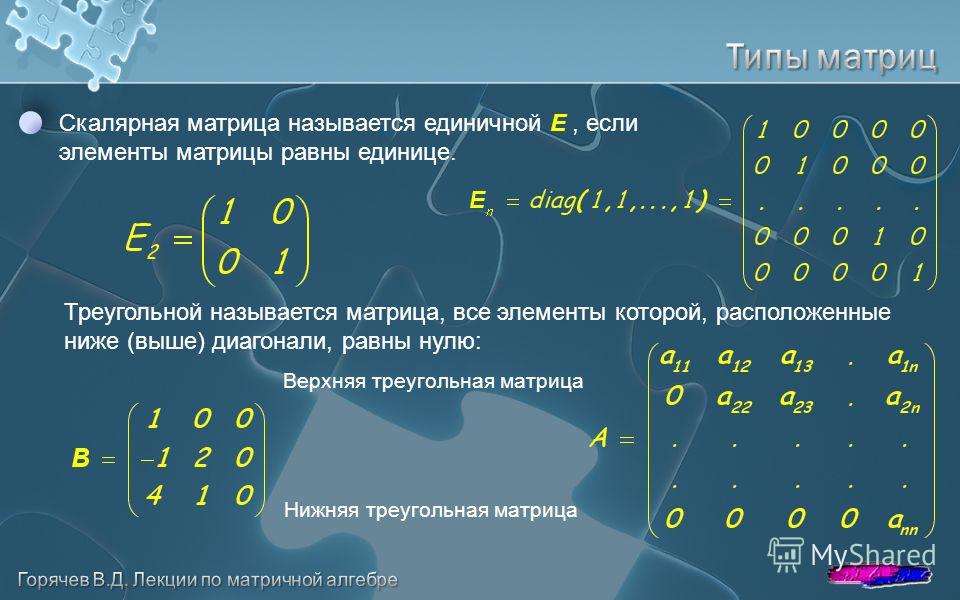
Узнайте, почему математика стоит за нашими сертифицированными экспертами. В этом случае она называется диагональной матрицей.
В этом случае она называется диагональной матрицей.
 Матрицы на изображении, приведенном ниже, являются верхней треугольной и нижней треугольной матрицами порядка «4 × 4».
Матрицы на изображении, приведенном ниже, являются верхней треугольной и нижней треугольной матрицами порядка «4 × 4».
 Квадратная матрица «A = [a ij ]» называется верхней треугольной матрицей, когда ij = 0 для всех i > j.
Квадратная матрица «A = [a ij ]» называется верхней треугольной матрицей, когда ij = 0 для всех i > j.
 , а транспонированием нижней треугольной матрицы является верхняя треугольная матрица, т. е. L T = U.
, а транспонированием нижней треугольной матрицы является верхняя треугольная матрица, т. е. L T = U. Вычисление определителя матрицы нижеприведенный.
Вычисление определителя матрицы нижеприведенный. 

 В биохимии, растительные сапонины имеют широкий спектр действий, включая понижение холестерина в крови, замедляют рост раковых клеток, и входят в состав противогрибковых и антибактериальных препаратов. Фитохимики сообщают, что сапонины могут вступать в реакцию с желчными кислотами и холестерином. Таким образом, они «чистят» организм от жировых бляшек, шлаков, понижая уровень холестерина в крови.
В биохимии, растительные сапонины имеют широкий спектр действий, включая понижение холестерина в крови, замедляют рост раковых клеток, и входят в состав противогрибковых и антибактериальных препаратов. Фитохимики сообщают, что сапонины могут вступать в реакцию с желчными кислотами и холестерином. Таким образом, они «чистят» организм от жировых бляшек, шлаков, понижая уровень холестерина в крови.
 Мы знаем, что 20 × 20 = 400. Таким образом, длина сторон сарая равна 20 ярдам.
Мы знаем, что 20 × 20 = 400. Таким образом, длина сторон сарая равна 20 ярдам.
 Таким образом, квадратный корень из 200 равен 20.
Таким образом, квадратный корень из 200 равен 20. Таким образом, частное 20 — это квадратный корень из 400.
Таким образом, частное 20 — это квадратный корень из 400. Площадь его двора составляет 400 квадратных футов. Какой длины проволока для ограждения понадобится Марку?
Площадь его двора составляет 400 квадратных футов. Какой длины проволока для ограждения понадобится Марку?

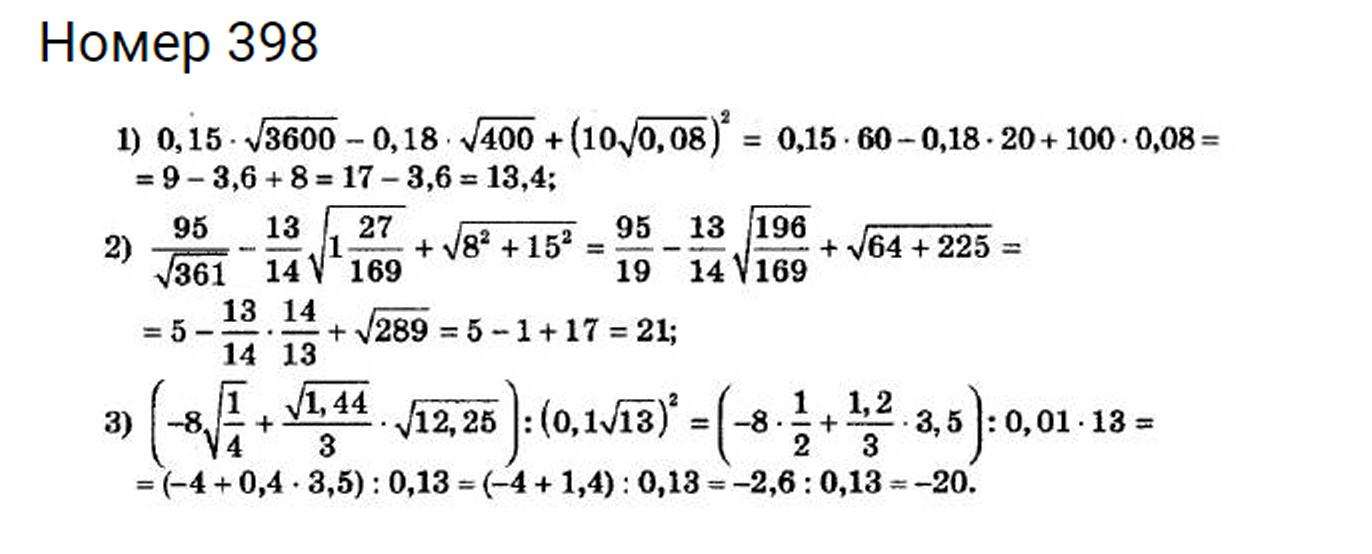 Например, 20 — это квадратный корень из 400, потому что 20 2 = 20•20 = 400, -20 — это квадратный корень из 400, потому что (-20) 2 = (-20)•(-20) = 400. При написании математических выражений люди часто используют sqrt(x) для обозначения квадратного корня из x. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
Например, 20 — это квадратный корень из 400, потому что 20 2 = 20•20 = 400, -20 — это квадратный корень из 400, потому что (-20) 2 = (-20)•(-20) = 400. При написании математических выражений люди часто используют sqrt(x) для обозначения квадратного корня из x. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram 449
449 899
899 000
000 062
062 110
110
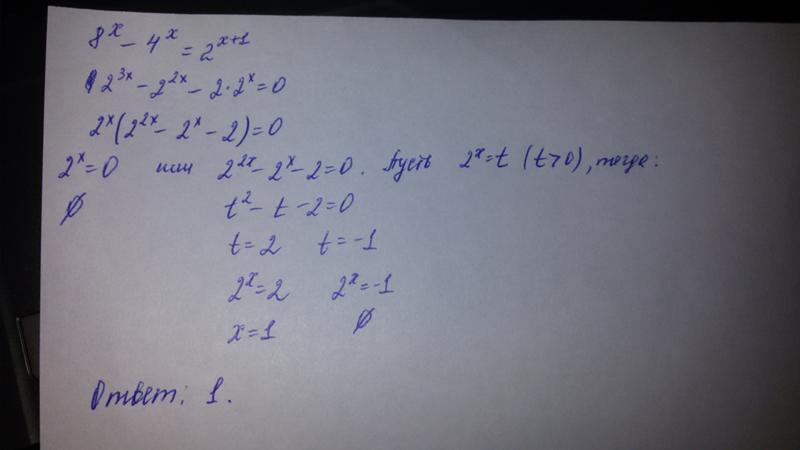

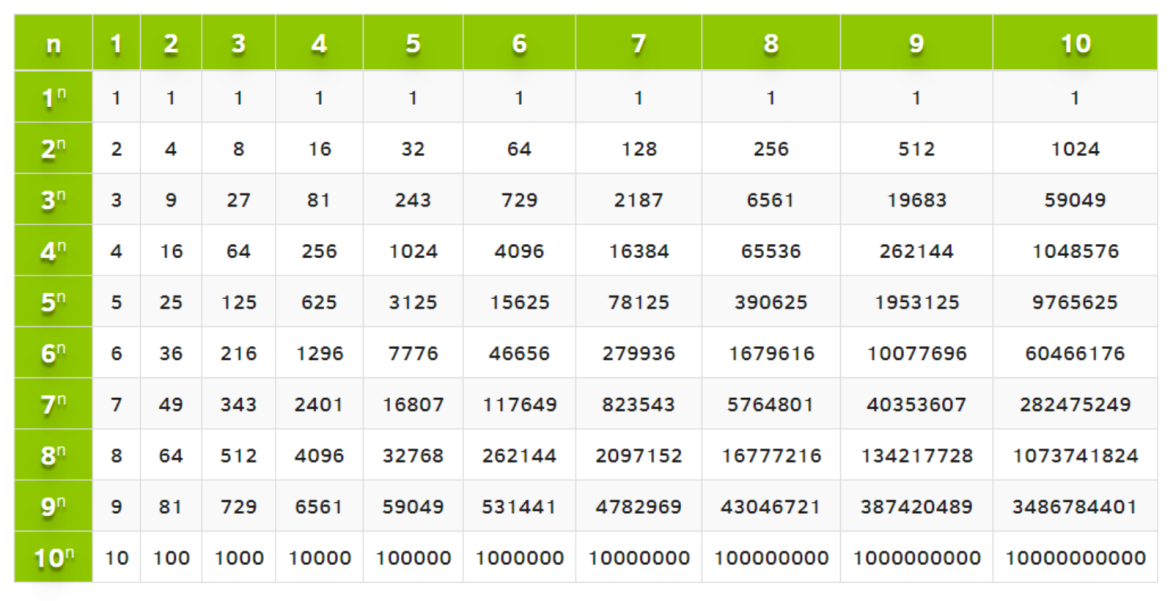
 Результаты возведения
в степень данных выражений будут разные.
Результаты возведения
в степень данных выражений будут разные. Это действие третьей ступени.
Это действие третьей ступени.
 Их поражение — отдельный критерий для оценки риска.
Их поражение — отдельный критерий для оценки риска. Избежать этого можно лишь одним способом: контролировать состояние своей сердечно-сосудистой системы и регулярно проходить обследование.
Избежать этого можно лишь одним способом: контролировать состояние своей сердечно-сосудистой системы и регулярно проходить обследование.
 Это может быть стабильная стенокардия, коронарная реваскуляризация (аортокоронарное шунтирование и другие процедуры реваскуляризации артерий), инсульт и транзиторные ишемические атаки, ранее перенесенный острый коронарный синдром (инфаркт или нестабильная стенокардия), а также заболевание периферических артерий. Обязательно учитываются результаты визуализирующих исследований, значимые для прогноза клинических событий: значительный объем бляшек на коронарных ангиограммах или сканах компьютерной томографии (многососудистое поражение коронарных артерий со стенозом двух основных эпикардиальных артерий более чем на 50 %) или по результатам УЗИ сонных артерий.
Это может быть стабильная стенокардия, коронарная реваскуляризация (аортокоронарное шунтирование и другие процедуры реваскуляризации артерий), инсульт и транзиторные ишемические атаки, ранее перенесенный острый коронарный синдром (инфаркт или нестабильная стенокардия), а также заболевание периферических артерий. Обязательно учитываются результаты визуализирующих исследований, значимые для прогноза клинических событий: значительный объем бляшек на коронарных ангиограммах или сканах компьютерной томографии (многососудистое поражение коронарных артерий со стенозом двух основных эпикардиальных артерий более чем на 50 %) или по результатам УЗИ сонных артерий.


 {0}$, что тогда, не будет ли это $1 + 1$, поскольку все, что имеет степень $0 = 1$? Может быть я неправильно понял, но это то, что я получил. 90 = 1 $$
{0}$, что тогда, не будет ли это $1 + 1$, поскольку все, что имеет степень $0 = 1$? Может быть я неправильно понял, но это то, что я получил. 90 = 1 $$ ниже), но как насчет формата уравнения?
ниже), но как насчет формата уравнения? 9y$ не является непрерывным в $(0,0)$.
9y$ не является непрерывным в $(0,0)$.
 90$ должен быть равен $1$, чтобы биномиальная теорема была верна. Даже эти странно выглядящие числа $\binom{n}{k}$ можно определить с помощью конечных множеств: если у вас есть $N$ игрушек и $K$ детей, $\binom{N}{K}$ — это множество способы, которыми вы можете выбрать достаточное количество игрушек, чтобы иметь по одной для каждого ребенка. (Обратите внимание, что вы не даете каждую игрушку конкретному ребенку: вы просто хотите, чтобы количество детей и игрушек было одинаковым.) Если вы достанете свой набор красок $C$ и еще один набор красок $D$ и начните раскрашивать различное количество детей и раздавать игрушки в зависимости от количества цветов детей, вы должны как-то быть в состоянии убедить себя в том, что биномиальная теорема верна, даже если в $C$ нет красок. Вот почему Андре Николя придумал те же правила для нулевых экспонент, что и мы. 90=1$$
90$ должен быть равен $1$, чтобы биномиальная теорема была верна. Даже эти странно выглядящие числа $\binom{n}{k}$ можно определить с помощью конечных множеств: если у вас есть $N$ игрушек и $K$ детей, $\binom{N}{K}$ — это множество способы, которыми вы можете выбрать достаточное количество игрушек, чтобы иметь по одной для каждого ребенка. (Обратите внимание, что вы не даете каждую игрушку конкретному ребенку: вы просто хотите, чтобы количество детей и игрушек было одинаковым.) Если вы достанете свой набор красок $C$ и еще один набор красок $D$ и начните раскрашивать различное количество детей и раздавать игрушки в зависимости от количества цветов детей, вы должны как-то быть в состоянии убедить себя в том, что биномиальная теорема верна, даже если в $C$ нет красок. Вот почему Андре Николя придумал те же правила для нулевых экспонент, что и мы. 90=1$$ ..
.. n\,\Rightarrow\, a = b\,$ для целых чисел $a,b,\,$ Такие расширения до более богатых структур с $0$ и инверсии позволяют нам работать с объектами в более простых формах, которые лучше подчеркивают фундаментальную алгебраическую структуру (здесь циклические группы или главные идеалы)
n\,\Rightarrow\, a = b\,$ для целых чисел $a,b,\,$ Такие расширения до более богатых структур с $0$ и инверсии позволяют нам работать с объектами в более простых формах, которые лучше подчеркивают фундаментальную алгебраическую структуру (здесь циклические группы или главные идеалы)
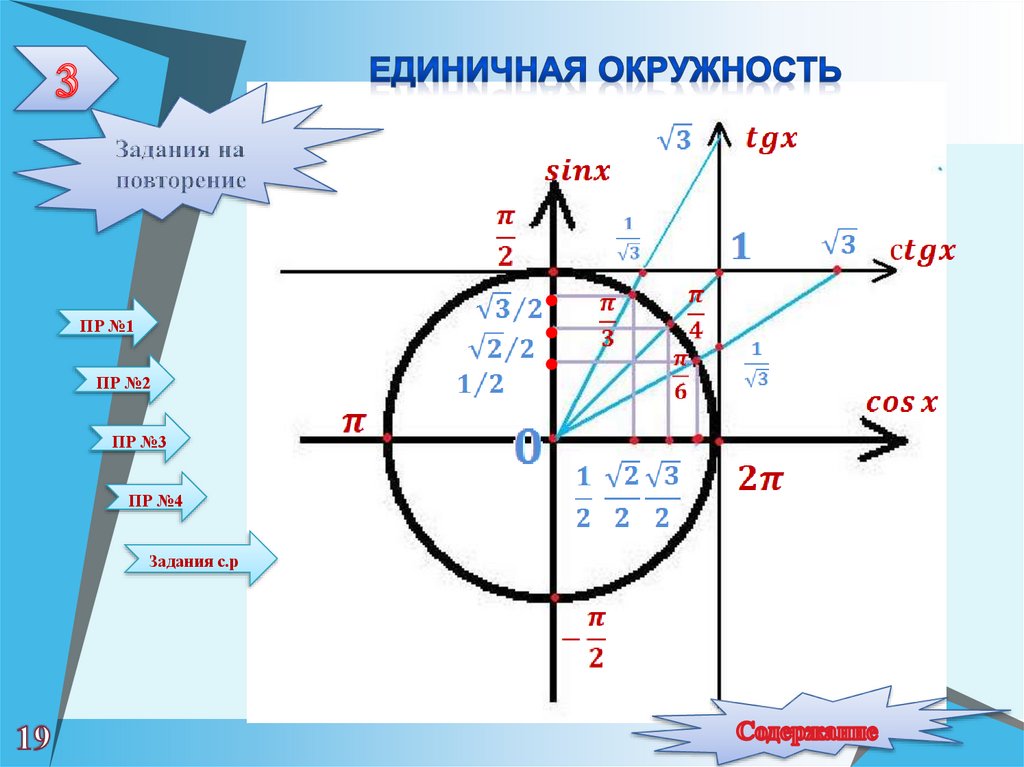
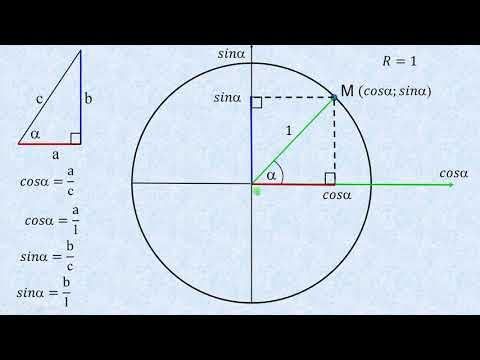
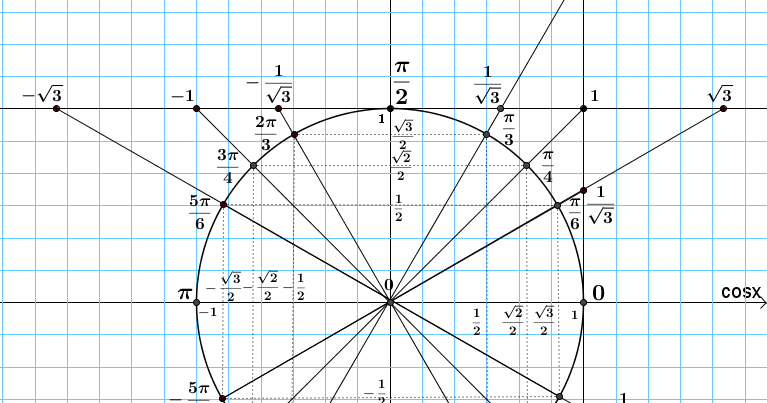
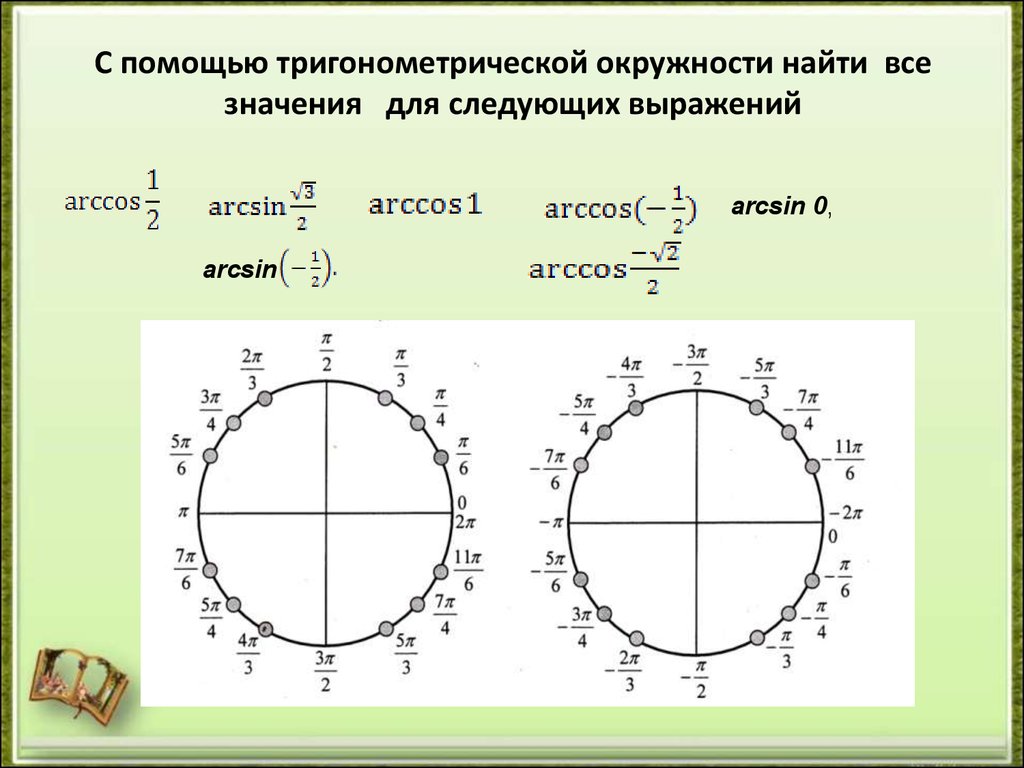
 Касательная
к окружности в точке (0;1) называется осью
котангенса. Для того чтобы графически
определить чему равен котангенс,
необходимо провести луч через начало
координат и точку, соответствующую
данному углу, до пересечения с осью
котангенса. X
– координата точки пересечения и будет
являться значением котангенса.
Касательная
к окружности в точке (0;1) называется осью
котангенса. Для того чтобы графически
определить чему равен котангенс,
необходимо провести луч через начало
координат и точку, соответствующую
данному углу, до пересечения с осью
котангенса. X
– координата точки пересечения и будет
являться значением котангенса.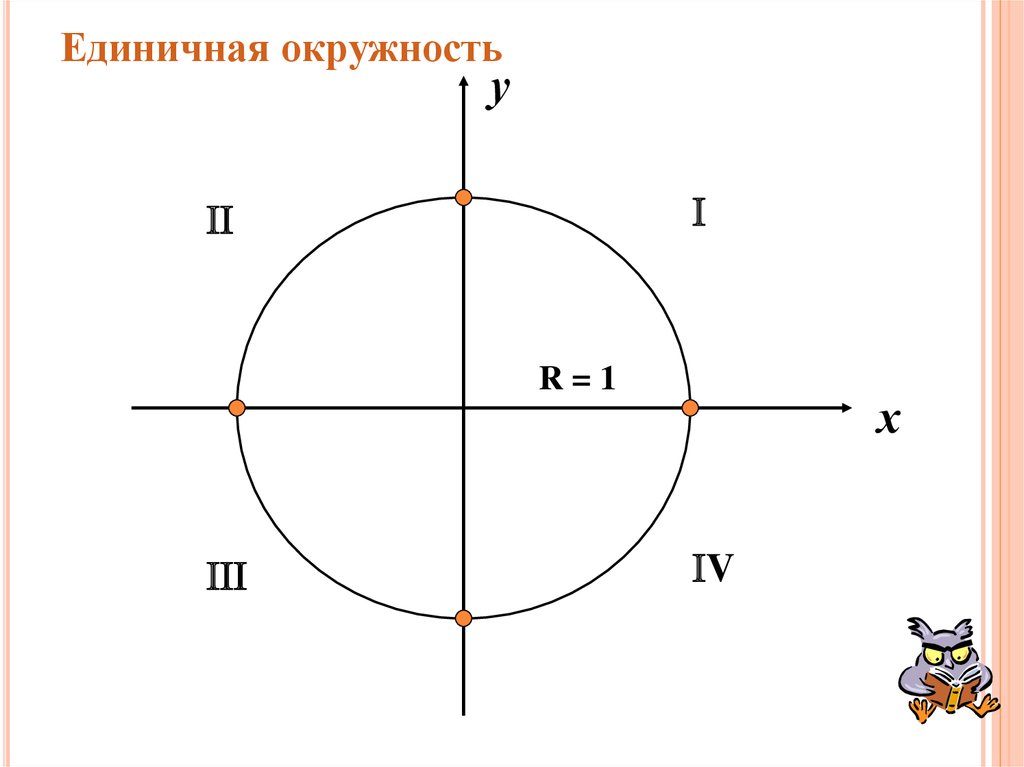 )
)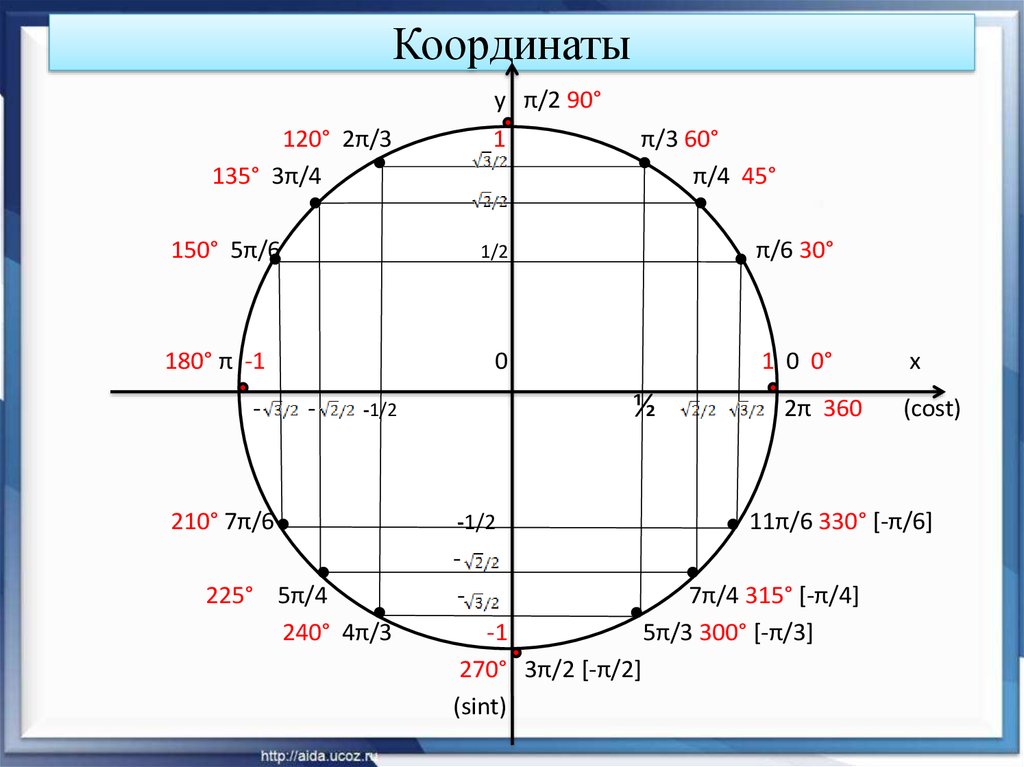 )
) )
) )
) )
) )
) )
) )
) )
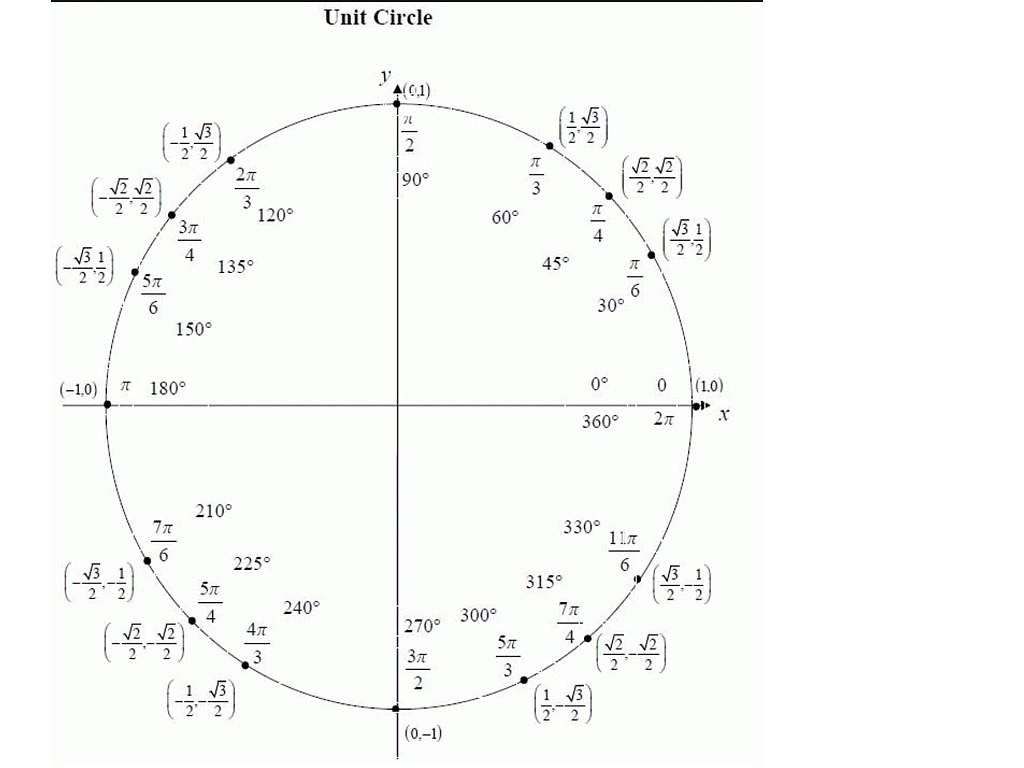
) Для любой точки (𝑥,𝑦) на единичной окружности можно построить прямоугольный треугольник, как показано на следующей диаграмме. Гипотенуза этого прямоугольного треугольника образует угол 𝜃 с положительной осью 𝑥.
Для любой точки (𝑥,𝑦) на единичной окружности можно построить прямоугольный треугольник, как показано на следующей диаграмме. Гипотенуза этого прямоугольного треугольника образует угол 𝜃 с положительной осью 𝑥.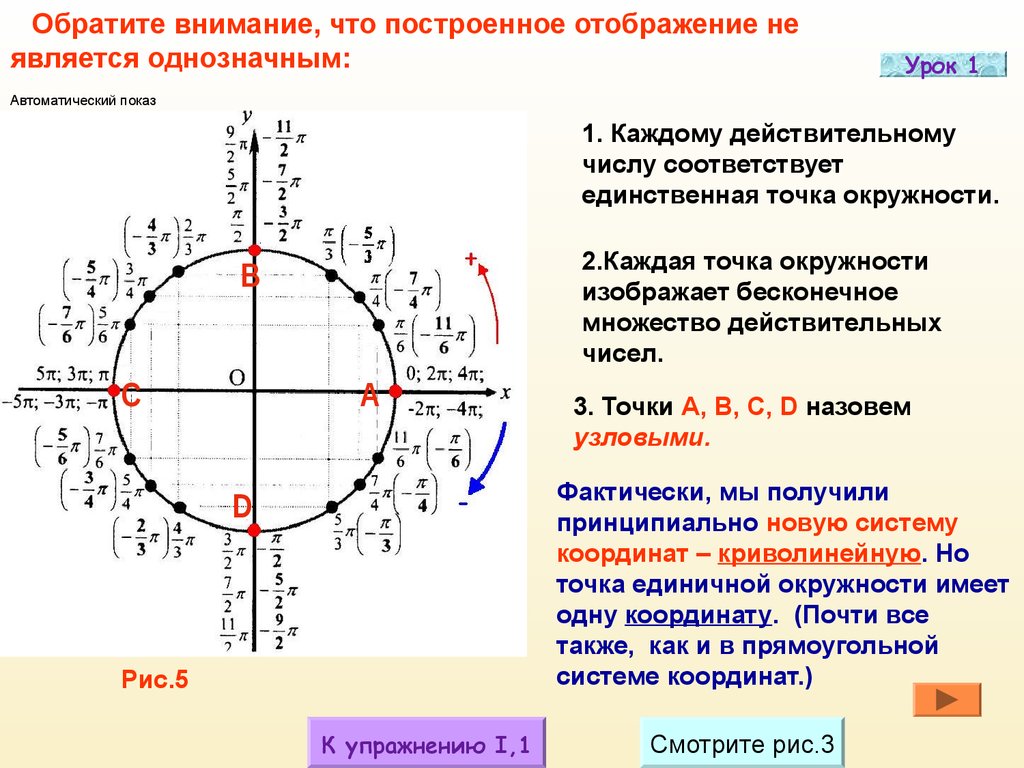
 То есть давайте еще раз рассмотрим точку (𝑥,𝑦) на единичной окружности,
под углом 𝜃 к положительной 𝑥-оси.
То есть давайте еще раз рассмотрим точку (𝑥,𝑦) на единичной окружности,
под углом 𝜃 к положительной 𝑥-оси. Для этого рассмотрим прямоугольный треугольник со сторонами 45 единиц и 35
единицы, как показано ниже.
Для этого рассмотрим прямоугольный треугольник со сторонами 45 единиц и 35
единицы, как показано ниже.
 Поскольку и 𝑥-, и 𝑦-координаты этой точки отрицательны, мы определим ее как 𝑃(−𝑎,−𝑏) для некоторых положительных констант 𝑎 и 𝑏.
Поскольку и 𝑥-, и 𝑦-координаты этой точки отрицательны, мы определим ее как 𝑃(−𝑎,−𝑏) для некоторых положительных констант 𝑎 и 𝑏.
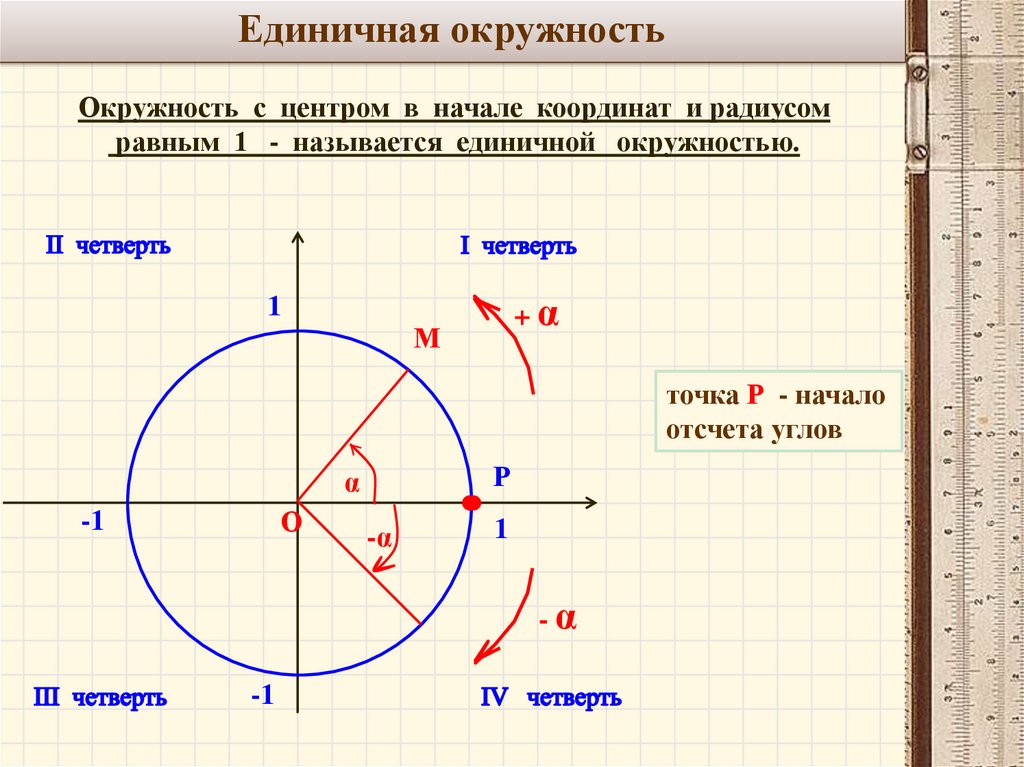
 Например, для любой точки на конце окружности угла в стандартном положении значение свойства синуса такого угла эквивалентно координате y точки. Кроме того, косинус такого угла эквивалентен координате x этой точки соответственно.
Например, для любой точки на конце окружности угла в стандартном положении значение свойства синуса такого угла эквивалентно координате y точки. Кроме того, косинус такого угла эквивалентен координате x этой точки соответственно. Кроме того, координаты конечных точек радиус-вектора равны (x, y) соответственно.
Кроме того, координаты конечных точек радиус-вектора равны (x, y) соответственно.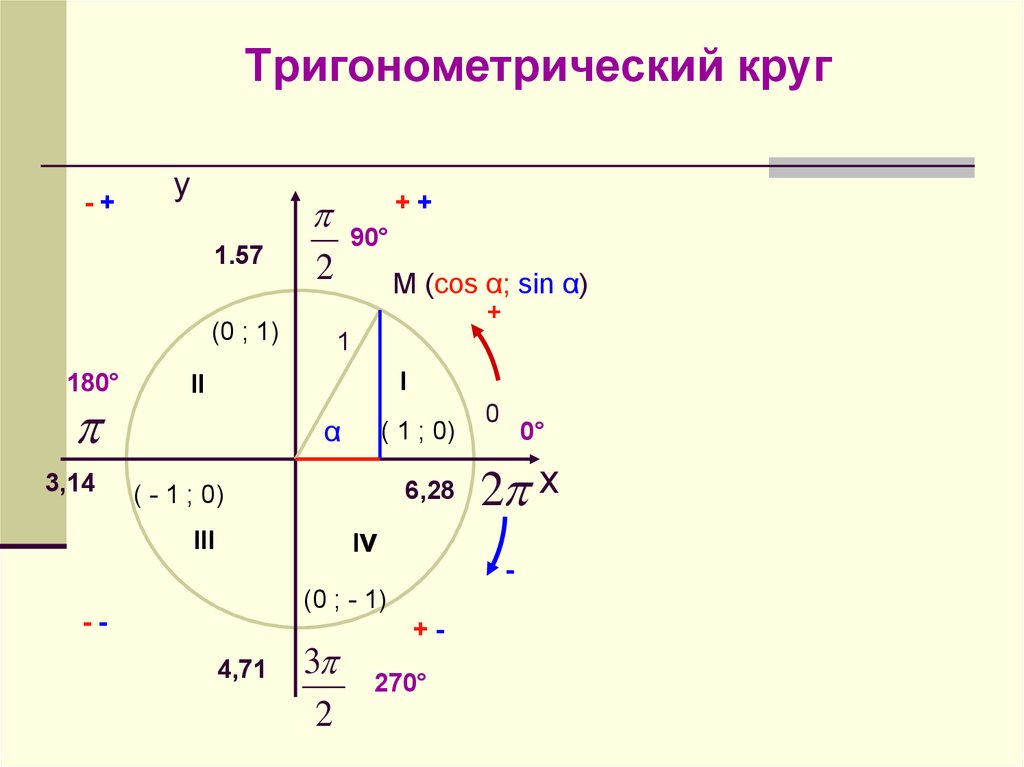 Значения радиуса находятся в диапазоне от -1 до 1 соответственно. Кроме того, значения sinθ и cosθ лежат между 1 и -1 соответственно.
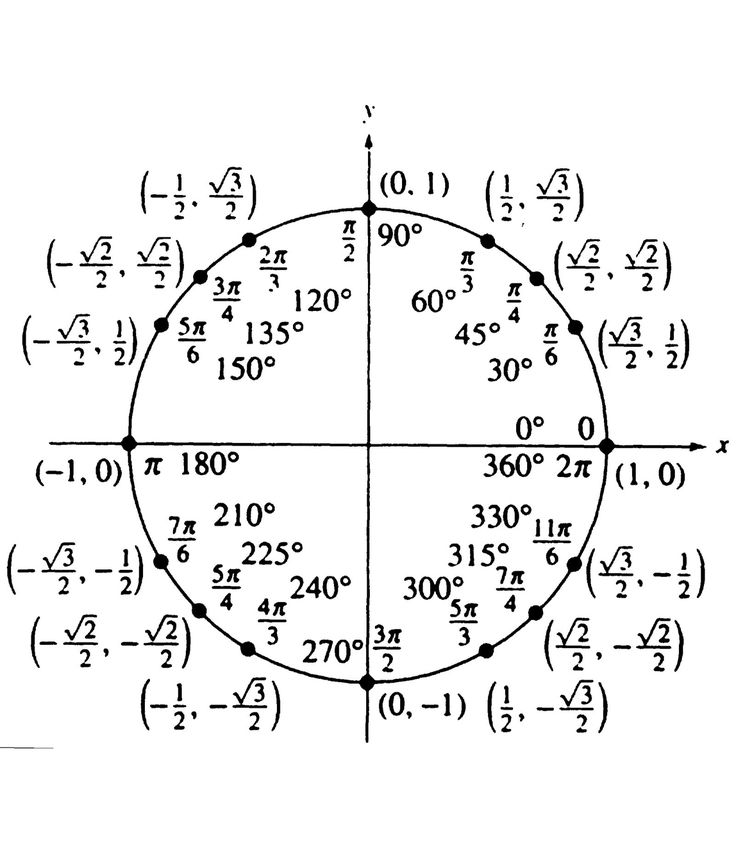
Значения радиуса находятся в диапазоне от -1 до 1 соответственно. Кроме того, значения sinθ и cosθ лежат между 1 и -1 соответственно. Точно так же мы можем расширить и найти радианы для всех квадрантов единичной окружности. Числа 1/2, 1/√2, √3/2, 0 и 1 повторяются вместе со знаком во всех 4 квадрантах.
Точно так же мы можем расширить и найти радианы для всех квадрантов единичной окружности. Числа 1/2, 1/√2, √3/2, 0 и 1 повторяются вместе со знаком во всех 4 квадрантах. Проверить, лежит ли точка P(2/3, 3/2) на единичной окружности.
Проверить, лежит ли точка P(2/3, 3/2) на единичной окружности.