Предмет и задачи экономики труда, возникновение экономики труда
Предмет и задачи экономики труда
ОпределениеЭкономика труда – это система знаний о труде, которая сформировалась на стыке различных областей знаний: политической экономики, социологии, акмеологии, психологии, менеджмента и пр.
Труд является основным предметом изучения и анализа, а все иные факторы производства выступают в качестве предпосылок, которые объединены объективными условиями его осуществления и развития. Одновременно с этим труд можно рассматривать как наиболее важный фактор производства, при анализе которого требуется разработка особых методологических подходов. Это можно объяснить при помощи того, что человеческие ресурсы, которые представляют собой не только фактор экономического развития, но и саму его цель, занимают ключевое место в структуре производительных сил общества во всех высокоразвитых странах мира. Их изучение требует специфических подходов.
Пример 1Лауреат Нобелевской премии по экономике Р. Солоу в своём труде «Рынок труда как социальный институт» утверждал, что занятость и доход, который она приносит, не является простым эквивалентом, который соответствует набору потребительских товаров, из чего следует, что их анализ должен производиться иным путём.
Солоу в своём труде «Рынок труда как социальный институт» утверждал, что занятость и доход, который она приносит, не является простым эквивалентом, который соответствует набору потребительских товаров, из чего следует, что их анализ должен производиться иным путём.
Таким образом, можно говорить о том, что процесс управления трудом имеет особое, отличное от управления всеми иными факторами производства, значение. Оно должно принимать во внимание как основную роль труда в процессе экономического развития, так и уникальные характеристики носителей способности к труду, которые своим существованием преобразуют процесс управления трудом в многокритериальную творческую деятельность.
Возникновение экономики труда
Экономика труда появилась в начале прошлого века в качестве методологического направления в науке о труде как ответ на социальную потребность практики, развития и усложнения производства, что стало определяющим фактором места и роли всего курса в системе социально-экономических наук.
В будущем данное направление смогло получить приоритетное развитие.
Это происходит потому, что экономика труда выступает в качестве теоретической основы для всех других наук о труде. Годовая подшивка журнала «Journal of labor economics» является прямым отражением неоклассических подходов к изучению труда, чтобы в полной мере осознать, что здесь рассматриваются самые важные аспекты трудовой деятельности, но исключительно на теоретико-методологическом уровне.
Кроме того, экономика труда представляет собой самую чистую экономико-трудовую науку. Поведение предприятий и индивидов всегда рассматривается в ней в контексте экономического поведения, которое определяется как соотношение выгод и потерь, а не существующими нормами и традициями. Все иные виды науки о труде содержат существенную неэкономическую составляющую.
Пример 2Один из разделов выдержавшего несколько изданий английского учебника «Управление человеческими ресурсами» содержит данные только из области социологии и психологии.
Также стоит отметить, что экономика труда нацелена на исследование проблем труда в границах предприятия и его непосредственного окружения, т.к. в любых социально-экономических условиях реальная трудовая деятельность происходит именно на предприятиях, в этой связи процессы, происходящие на более высоком уровне, в любом случае определяются ими.
В итоге большая часть разделов экономики труда представляет собой основу других социальных и экономико-трудовых дисциплин. Одновременно с этим самыми сложными, которые имеют принципиальное значение, проблемами этих наук становятся предметом изучения в экономике труда.
Основные направления экономики труда
Выделяют несколько основных направлений экономики труда, они следующие:
- Оценка самых важных качественных и количественных параметров трудовой деятельности и факторов их образования.
- Установление самых приоритетных тенденций в сфере труда.
- Изучение с последующим прогнозированием различных процессов в сфере труда.

- Исследование ключевых особенностей мобильности работников.
- Рассмотрение процессов управления трудом и их регулирование на уровне предприятия.
- Исследование механизмов проведения в жизнь государственной политики, в том числе оценка её внедрения в сферу труда.
Общим с управлением человеческими ресурсами и экономикой трудовых ресурсов можно определить исследование рынка труда и связанных с ним социально-экономическими отношениями по поводу воспроизводства рабочей силы. Оценка привлечённых предприятием трудовых ресурсов тоже выступает как совокупный предмет исследования этих дисциплин.
Взаимодействие экономики труда и социологии труда можно рассмотреть в общности объекта исследования – человека труда, познании закономерностей социальной жизни, поведении и мотивов, выработке рекомендаций, которые сконцентрированы на увеличение эффективности управления социальными процессами.
Взаимосвязь экономики труда и управления персонала проявляется на уровне предприятия, где, собственно, и осуществляется трудовая деятельность. Важно отметить, что методологические подходы и принципы, метода и рекомендации по эффективной организации трудовой деятельности, планированию и оплате труда являются достаточно серьёзными вопросами.
Важно отметить, что методологические подходы и принципы, метода и рекомендации по эффективной организации трудовой деятельности, планированию и оплате труда являются достаточно серьёзными вопросами.
Трудовое право и экономика труда связаны общей законодательно-нормативной базой регулирования социально-трудовых отношений. Развитие трудового законодательства способствует углублению в проблемы управления человеческими ресурсами с точки зрения существующих в обществе трудовых правоотношений.
Экономика труда и экономика народонаселения связаны между собой общей информационной базой о воспроизводстве населения, его экономической активности и миграционных процессах.
В статистике и в экономике труда используются одни и те же приёмы и методы количественного и качественного анализа процессов в сфере труда, использования рабочего времени, различных видов вознаграждения и пр.
Подводя итог, можно сказать, что экономика труда в качестве научной дисциплины, не подменяет собственный предмет изучения, при этом используется весь спектр смежных наук как собственного инструмента.
Более того, важно отметить, что экономика труда как основная экономика-трудовая дисциплина имеет прямое отношений к другим социально-экономическим дисциплинам, в первую очередь, к экономической теории, которая, в свою очередь, выступает в качестве основы экономических знаний, дающих представление о факторах производства, действии законов рыночной экономики, механизме и границах государственного регулирования в условиях рынка.
Замечание 2Эти знания нужны для правильного восприятия законов функционирования рынка труда, механизма установления цены труда – заработной платы, источников образования доходов населения.
Правильное восприятие и усвоение экономики труда подразумевает ознакомление с историей экономических учений, в первую очередь, с той её областью, которая рассказывает о разделении науки о труде на две принципиально разные ветви: трудовую теорию стоимости, в завершённом виде которую сформулировал К. Маркс, а также теорию факторов производства, основоположником которой был Ж. Б. Сэй и в дальнейшем развивал И. Шумпетер.
Б. Сэй и в дальнейшем развивал И. Шумпетер.
Марксистская интерпретация теории стоимости привела к всеобъемлющей идеологизации данной науки, но при этом она сама оказалась ошибочной и стала причиной того, что большое количество людей стали жертвами во имя реализации утопической идеи построения коммунистического общества. Здесь можно смело говорить о том, что знание истории науки о труде способствует критическому пониманию реальной отечественной истории и осознанному применению в практической работе современных знаний относительно природы труда, заработной платы и доходов.
Вопросы управления трудом, которые рассматриваются в данной статье, образуют собой часть проблем общего менеджмента, в котором внимание сконцентрировано на методологических основах менеджмента, моделировании ситуаций и разработке управленческих решений на перспективу, связи планирования с прогнозированием, региональной экономике с макростратегическими программами углубления экономических реформ.
Замечание 3Вместе с тем экономика труда рассматривает вопросы организации, оплаты и нормирования труда, текущего и перспективного планирования трудовых показателей, которые представляют собой частное по сравнению с общими вопросами управления организацией, изучаемых общим менеджментом.
Экономика труда и бухгалтерский учёт связаны между собой посредством учёта, которому они подлежат вместе с иными элементами производства, затратами труда, средствами на оплату и материальное стимулирование труда.
Для наиболее точного проведения анализа трудовых показателей и моделирования трудовых процессов экономики труда используются приёмы и методы, которые глубоко исследуются наукой эконометрика.
Пример 3Исследование источников и механизмов формирования трудового потенциала предприятия, а также мобильности рабочей силы происходит одновременно с исследованием рынка труда.
В этой связи взаимодействие экономики труда с другими науками способствует её развитию, обогащает различными научными инструментами для проведения исследований и способствует установлению всего многообразия социально-экономических проблем и связей.
Объект исследования экономики труда
В первую очередь, необходимо отметить, что всеобщим объектом исследования, который имеется во всех отраслях и сферах экономики и исследуется вышеперечисленными научными направлениями, является труд. Отличие этих наук одна от одной только в предмете исследования, в силу того, какую сторону и какие свойства объекта исследования они изучают.
Отличие этих наук одна от одной только в предмете исследования, в силу того, какую сторону и какие свойства объекта исследования они изучают.
Предмет экономики труда изучает экономические закономерности построения и осуществления трудовых процессов, факторы и условия их эффективности, а также социально-трудовые отношения, которые возникают между субъектами по поводу пользования труда.
Говоря об отечественной экономике, следует отметить, что новая российская экономика нуждается в реализации реструктуризации системы управления производством на научной основе. Ключевое место в данной системе отводится системе управления трудом на уровне предприятия. Основной наукой, которая исследует её функционирование, является экономика труда. Логично, что работа предприятия напрямую зависит от того, как им управляют. Сегодня возросло время влияния деструктивных факторов на деятельность предприятий, которые вынуждены постоянно приспосабливаться к трудностям, опасностям и вызовам внешней и внутренней среды. Такое динамическое развитие и весьма жёсткие требования рынка становятся причиной потребности в выработке целого перечня антикризисных мер, глубокой реструктуризации всего производственного аппарата. Данные меры выступают как реальные, а не как интуитивные и тем более импульсивными действиями руководителей предприятий.
Такое динамическое развитие и весьма жёсткие требования рынка становятся причиной потребности в выработке целого перечня антикризисных мер, глубокой реструктуризации всего производственного аппарата. Данные меры выступают как реальные, а не как интуитивные и тем более импульсивными действиями руководителей предприятий.
Исследование науки экономики труда даёт возможность осознать с точки зрения системности позиции методологических и методических основ системы управления трудом на предприятиях различных форм собственности.
На данной основе можно сформулировать ключевые задачи курса экономики труда как науки:
- Определить общее представление об экономико-трудовых проблемах мировой и российской экономики и ключевых путях их решения.
- Установить главные свойства труда, которые влияют на уровень его эффективности.
- Раскрыть ключевые закономерности функционирования внешнего и внутреннего рынков труда.
- Описать систему управления трудом на предприятии, которая соответствует условиям современной российской действительности, происходящей в экономике.

- Установить базу для формирования систем трудового вознаграждения применительно к различным категориям.
- Определить факторы, которые оказывают влияние на динамику системы управления трудом в пределах стратегического управления предприятием.
- Уточнить содержание мероприятий, связанных со структуризацией и реинжинирингом занятости на предприятии, в том числе методы оценки результативности этих мероприятий с учётом финансового положения предприятия.
- Определить методологический аппарат организации мониторинга трудовых показателей и осуществлению их всестороннего анализа.
- Описать порядок проведения исследований экономико-трудовых процессов в ходе решения комплекса стратегических задач и тактического плана, который ставится перед предприятием.
Основные задачи экономики труда
К слову, среди основных задач экономики труда как науки выделяют выработку стратегического, вариантного мышления в сфере управления трудом на предприятии. Это происходит по той причине, что в настоящее время всё больше конкретных проблем имеют различные, иногда противоположные способы решения. Важно, правильно и грамотно сформулировать данные задачи, установить противоречия интересов различных экономических субъектов, поменять характер взаимодействия предприятия и внешней среды. Справедливо заметить, что перечисленные задача весьма сложные, поскольку в большинстве своём они требуют нестандартного решения или творческого подхода. Таким образом, можно говорить о том, что более важное значение приобретает обеспечение должной информационной базой осуществляемых мероприятий.
Важно, правильно и грамотно сформулировать данные задачи, установить противоречия интересов различных экономических субъектов, поменять характер взаимодействия предприятия и внешней среды. Справедливо заметить, что перечисленные задача весьма сложные, поскольку в большинстве своём они требуют нестандартного решения или творческого подхода. Таким образом, можно говорить о том, что более важное значение приобретает обеспечение должной информационной базой осуществляемых мероприятий.
В результате, выбор мероприятий в сфере управления трудом осуществляется на основе системы показателей. Аналитическая работа множества периферийных служб предприятия в первую очередь нацелена на повышение эффективности его работы. Но при этом оценка имеющегося и перспективного уровней эффективности зачастую не представляет собой одномоментный процесс, а требует проведения последовательных расчётов. При этом каждый субъект хозяйственной деятельности имеет собственную систему приоритетов, характер согласования которых в серьёзной степени воздействует на итоговые результаты в целом.
Кроме того, очень важно в данном контексте говорить о требованиях учёта состояния внешней среды. Изменение её состояния способно привести к существенной переоценки ключевых направлений политики предприятия в сфере труда и занятости. В некоторых ситуациях трансформация окружения предприятия может стать причиной возобновления интереса к жизни ранее отвергнутых решений. В другом случае оказывается необходимым предложить новые, но не рассматриваемые в прошлом варианты действия.
В конечном итоге, достаточно важные экономико-трудовые проблемы для своего решения требуют использования так называемого междисциплинарного подхода. Однако, в современных российских условиях при установлении междисциплинарного подхода. При этом, важно понимать, что в современных условиях в РФ при установлении механизма разрешения возникающих в трудовой сфере противоречий ключевая роль отходит экономике труда как науке, которая способна обеспечить формирование единых принципов и механизмов согласования различного рода интересов участников хозяйственной деятельности. В этой связи можно говорить о том, что изучению экономики труда отводится важное место в ходе подготовки высококвалифицированных экономистов, которые должны:
В этой связи можно говорить о том, что изучению экономики труда отводится важное место в ходе подготовки высококвалифицированных экономистов, которые должны:
- Знать сущность и порядок, которые регулируют трудовые отношения, механизм прогнозирования, планирования и управления человеческими ресурсами; методы и приёмы анализа экономических показателей по труду и заработной плате; резервы роста производительности и эффективности труда; методы экономико-математического моделирования и оптимизации трудовых показателей с использованием ЭВМ и персональных компьютеров; методы анализа, прогнозирования и регулирования рынка труда и занятости.
- Владеть умением принимать профессиональные решения в области управления трудом, учитывая при этом экономические и социальные последствия; формировать и реализовывать кадровую политику предприятия; заниматься исследованиями эффективности применяемых тарифов, форм и систем заработной платы; разрабатывать и реализовывать мероприятия по их совершенствованию, сопоставлять проекты положений, связанных со стимулированием труда; устанавливать и объяснять размеры доплаты, надбавок, премий к тарифной части заработной платы; разрабатывать штатные расписания и осуществлять контроль за их соблюдение, за расходованием фондов заработной платы и материального вознаграждения; заниматься тарификацией работ и рабочих, аттестацию работников; устанавливать потребность предприятий в рабочей силе, устанавливать источники её пополнения и развития; разрабатывать проекты коллективных договоров на предприятиях и следить за выполнением принятых правил и норм.

- В совершенстве владеть методами научной организации труда, нормирования трудовых процессов, оценки уровня и факторов повышения производительности труда, а также регулирование и контроль внутрифирменного рынка труда и управления человеческими ресурсами на конкретном предприятии.
СОДЕРЖАНИЕ ГЛАВНАЯ Глава 1. Основные понятия экономики Глава 2. Рынок, конкуренция: смотри главу 2 сайта d-66-2007.ru/ Глава 3. Спрос, предложение, эластичность: смотри главу 3 сайта d-66-2007.ru/ Глава 4. Товар, цена, деньги, кредит Глава 5. Виды рынков Глава 6. Математические приложения Использованные источники | Глава
5. Задача 1. Определить, какие из описанных ниже явлений относятся к таким факторам дифференциации заработной платы: а)наличие неконкурентных групп; б) разные условия труда; в) ограниченность мобильности рабочей силы.
Ответ. а: 1),4) б: 3), 5) в: 2. Задача 2. Почасовая оплата труда служащего равна 1,5 ден.ед. Экономист Савченко отработал 22 рабочих дня по 8 часов. Какую заработную плату он получит в конце месяца? Ответ. 1,5*8=12 ден. 12*22=264 ден.ед за месяц. Задача 3. Предложение труда определённой отрасли описывается уравнением LS=200w, а отраслевой спрос на услуги труда описывает уравнение LD=1200-100w, где w– это дневная ставка заработной платы, а L– количество работников.
Ответ.
200w=1200-100w 300w=1200 w = 4 ден.ед за день Lравн=200*4=800 чел
LS=200*6=1200 LD=1200-100*6=600 1200-600=600 возникнет
безработица. Задача 4. В 2005 году на заводе ввели новую технологическую линию. Объём продукции при той же самой численности работающих увеличился так, как приведено в таблице:
Ответ. Индекс (І) – относительная величина, которая характеризует изменение явления со временем, в пространстве, или по сравнению с планом (нормою, стандартом). Измеряется в частях или процентах.
— выросла в 2005 по сравнению с 2004 на 44%; — выросла в 2006 по сравнению с 2005 на 4%; — не изменилась в 2007 по
сравнению с 2006.
— формула для нахождения среднего геометрического трёх чисел. В нашем случае:
в 2007 году продуктивность труда равна 1,5 от уровня 2004 года, или – увеличилась на 50%. Задача 5. Завод выпускает 100 телевизоров за день. После реконструкции продуктивность труда одного работника выросла на 10%. А в следующем году продуктивность труда одного работника равна 0,26 телевизоров за день. Определить:
Ответ. Запишем условие задачи в виде таблицы:
ПТ1 =1,1х ПТ0 = 0,275 шт/раб, С формулы ПТ = Q:L находим Q= ПТх L Q1=
0,275х400 = 110 шт. Q2= 0,26х400 = 104 шт.
1,1 -1 = 0,1 продуктивность труда увеличилась на 10%.
Задача 6. Маслозавод выпускает 60 тыс. тонн масла в месяц по цене 4 ден.ед. за килограмм. После повышения цены до 6 ден.ед за 1 кг завод стал изготавливать 80 тыс. тонн масла в месяц. На сколько процентов увеличилась продуктивность труда, если численность работающих не изменялась. Ответ. ПТ = Q:L I ПТ1/0= ПТ0 : ПТ1=, L0= L1, значит I ПТ1/0=ю Продуктивность труда выросла на 3,33% Задача 7. Как изменилась продуктивность труда, если за первый год она выросла на 15%, за второй – на 10%, а за третий год уменьшилась на 9%? Ответ. ПТ0 =1, ПТ1 = 1,15ПТ0, ПТ2 = 1,1ПТ1, ПТ3 = 0,91ПТ2, I ПТ3/0 = 1,15х1,1х0,91х1=1,02465. Тоже самое можно записать по другому: I ПТ3/0 = I ПТ1/0 х I ПТ2/1 х I ПТ3/2 = 1,15х1,1х1,91=1,151. Продуктивность выросла ≈ на 15,1% Задача 8. При условии сохранения численности работающих, объём продукции изменялся по годам таким образом:
Оценить изменение продуктивности труда при фиксированных
ценах: продукт А – 5 ден. Ответ. Находим валовый выпуск продукции в каждом году: Так как численность работающих не изменялась, то I ПТ2000/2001 = Продуктивность уменьшилась на 4,5%. Задача 9. Выпуск продукции в натуральном виде вырос на 25%, а численность работающих увеличилась на 10%. На сколько процентов изменилась продуктивность труда? Ответ. IQ = 1,15, IL = 1,1, I ПТ= Или по другому: Q1=1,15 Q0, L0 = 1, L1= 1,1 L0 , I ПТ= Задача 10. Стоимость товаров и услуг, которые изготовляет компания за день, выросла в конце года в 3 раза. Цены за год выросли в 2 раза, численность работающих каждый день увеличивалась в 1,5 раза. Как изменилась продуктивность труда? Ответ. IPQ = 3,
IP = 2, IL =1,5. однако, чтобы избавиться от влияния цен нужно из этого выражения удалить цены. Получим индекс изменения продуктивности труда в натуральном выражении.
Продуктивность труда не изменилась. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Джунгли вакансий: игра на рынке труда*
*Авторское право © 2001 Raymond P.H. Фише – используется с разрешения. Фонд преподавания экономики. Разрешено полное или частичное копирование только для некоммерческого использования в образовательных целях.
Загрузить руководство по работе с Job Jungle (включает раздаточные материалы, наглядные материалы, руководство для учителей)
Демонстрация видео:
Участники:- Рабочие: T goty или более студентов, чтобы действовать в качестве рабочих в поисках работы.

- Работодатели : От четырех до шести студентов (или 8-12 студентов в парах) для работы в качестве работодателей в кайт-индустрии.
- Преподаватель: 1 или 2 студента (или классных помощников), которые могут повысить квалификацию работников на рынке труда.
Рабочие: Цель каждого работника — получить наибольший общий доход. Работники получают доход, находя работодателя, который будет нанимать их за взаимоприемлемую заработную плату, или оставаясь безработными и получая государственную помощь. Победивший рабочий получает 5 долларов.
Работодатели: Целью каждого работодателя является получение наибольшей общей прибыли. Прибыль равна разнице между выручкой и затратами на производство. Работодатели должны нанимать рабочих для производства воздушных змеев, которые приносят доход. Издержки производства определяются заработной платой, согласованной между рабочими и работодателями. Работодатели пытаются договориться об относительно низкой заработной плате, чтобы увеличить прибыль, в то время как рабочие стремятся к относительно высокой заработной плате, чтобы максимизировать общий доход. Победивший работодатель получает 5 долларов.
Работодатели пытаются договориться об относительно низкой заработной плате, чтобы увеличить прибыль, в то время как рабочие стремятся к относительно высокой заработной плате, чтобы максимизировать общий доход. Победивший работодатель получает 5 долларов.
Навыки и ресурсы:
Низкоквалифицированные рабочие: ( желтая каталожная карточка 3×5) Все рабочие начинают первый раунд как НИЗКОквалифицированные. Эти работники имеют желтую карточку, которая идентифицирует их для работодателей как НИЗКОквалифицированных. На обратной стороне желтых карточек написано случайное богатство в размере 4, 5 или 6 долларов, поэтому все рабочие начинают с некоторыми ресурсами.
Высококвалифицированные рабочие: (карточка розового цвета 3×5 или любого цвета, отличного от низкоквалифицированного, кроме зеленого. «Зеленая карточка» вносит ненужное усложнение в деятельность.) В конце любого раунда рабочий может стать ВЫСОКОЙ квалификацией, получив образование у педагога. За это образование работник платит 25 долларов из общего дохода. Воспитатель дает работнику розовую карточку и забирает у работника желтую карточку, вычитая «плату за обучение» из общей суммы работника. (Примечание: займы не допускаются; работники должны иметь общий доход не менее 25 долларов США, чтобы получить ВЫСОКИЙ уровень квалификации.)
За это образование работник платит 25 долларов из общего дохода. Воспитатель дает работнику розовую карточку и забирает у работника желтую карточку, вычитая «плату за обучение» из общей суммы работника. (Примечание: займы не допускаются; работники должны иметь общий доход не менее 25 долларов США, чтобы получить ВЫСОКИЙ уровень квалификации.)
1. Обсудите со студентами спрос на рабочую силу и ее предложение. Инструкторы должны подготовить участников к этому упражнению, обсудив производный спрос и предложение рабочей силы. Обсуждение со стороны спроса должно объяснить, почему работодатели, стремящиеся к максимизации прибыли, не будут предлагать больше, чем стоимость предельного продукта работника. Обсуждение со стороны предложения должно подчеркивать альтернативные издержки, с которыми сталкивается работник при рассмотрении вопроса о том, принимать ли предложение о заработной плате. Это голая дискуссия. Другие вопросы, такие как условия труда, страхование по безработице или экономические колебания, на данном этапе не важны.
2. Раздайте игровые фишки. Все рабочие получают карты низкого навыка для начала игры. Каждый работодатель получает график производства и предельных продуктов и цветную ручку. Дайте каждому преподавателю карточки с высокими навыками и ручку разного цвета.
3. Рыночная цена и государственная помощь. Попросите работодателей и их консультантов распределиться по комнате; они могут передвигаться позже, если захотят.
- Объявите работодателям, что конкурентная рыночная цена воздушных змеев составляет 10 долларов. (Вы можете менять цену от раунда к раунду, в зависимости от того, насколько сложной вы хотите сделать игру.)
- ( Вариант ) Объявите работникам с желтой карточкой, что, если они не найдут приемлемого предложения о работе, они получат доход в размере 15 долларов США за раунд в рамках программ государственной помощи. В более поздних раундах объявите работникам с розовой картой, что они получают 35 долларов за раунд дохода от программ социальной помощи, если они не примут предложение о работе.

4. Повторить цели работников и работодателей.
- Обратите внимание, что общий доход и общая прибыль суммируются. Рабочие прибавляют свои первоначальные пожертвования к доходу, полученному во всех раундах, а затем вычитают любые расходы на образование, чтобы вычислить общий доход. Работодатели суммируют прибыль, полученную во всех раундах, для расчета общей прибыли.
- Еще раз объявить награды для победителей.
5. Объясните процесс найма.
- Работа длится только один раунд . (Убедитесь, что рабочие и работодатели знают, что они торгуются по поводу заработной платы в каждом раунде. Напомните работодателям, что стоимость предельного продукта меняется с каждым новым нанятым работником!)
- Когда работодатель и работник договариваются о заработной плате, работодатель записывает заработную плату и свое имя или удостоверение личности на карточке работника цветной ручкой. Это гарантирует, что работники не будут пытаться продать свои услуги дважды в одном и том же раунде, потому что они нашли более выгодное предложение.

- Однажды заключенная сделка не может быть нарушена ни работодателем, ни работником.
- Работодатели также регистрируют выплаченную заработную плату в своих графиках производства и предельного продукта.
6. Объясните, как рабочие приобретают навыки.
- В конце любого раунда работники могут выбрать ВЫСОКУЮ квалификацию, заплатив 25 долларов преподавателю. Педагог вычитает 25 долларов из общего дохода, указанного на желтой карточке работника, и записывает новую сумму на розовой карточке работника. Желтые карточки рабочие не хранят!
- После того, как они инвестировали в образование, они не могут отменить эти инвестиции.
7. Сыграйте в первый раунд. Первый раунд может длиться 6-8 минут, поскольку работники ищут лучшие предложения о работе.
- Лучше установить ограничение по времени для каждого раунда и объявлять оставшееся время, когда приближается конец.
- Попросите всех рабочих сесть, когда раунд закончится.

- Убедитесь, что работодатели/консультанты своевременно ведут записи по каждому раунду.
8. Конец игры. Игра может быть остановлена после двух или трех раундов.
- Если будет сыграно больше раундов, следует использовать некоторые из обсуждаемых ниже вариантов, чтобы поддерживать интерес участников.
- После определения потенциальных победителей обязательно проверьте их расчеты. Ошибки часто допускают работодатели.
- В случае ничьей для определения победителя используется жеребьевка.
Экономические колебания: Эффекты экономического расширения и сокращения могут быть добавлены путем изменения цены выпуска воздушных змеев. Выходная цена в 6 долларов снижает равновесную занятость на одного работника с желтой и одной розовой карточкой на каждого работодателя. Точно так же цена выпуска в 20 долларов увеличивает занятость каждого типа на одного рабочего.
Государственная помощь: Влияние программ государственной помощи можно проиллюстрировать изменением суммы помощи, выплачиваемой каждому типу работников. Если высококвалифицированные работники получают 15 долларов во время безработицы, например, более высококвалифицированные работники будут наняты при новой равновесной заработной плате в 20 долларов.
Если высококвалифицированные работники получают 15 долларов во время безработицы, например, более высококвалифицированные работники будут наняты при новой равновесной заработной плате в 20 долларов.
Новые работодатели или вступление: Влияние вступления на прибыль можно показать, позволив работникам, заработавшим 100 долларов, стать работодателями. Новые участники получают прибыль, близкую к нулю, если игра ведется в несколько раундов.
Высококвалифицированные работники: Разрешить высококвалифицированным карточным работникам выполнять низкоквалифицированную работу. Это поможет уравнять заработную плату работников с желтой и розовой карточками.
Новый способ измерения концентрации на рынке труда
Степень влияния работодателей на установление заработной платы на рынках труда (также известная как власть монопсонии) является ключевым эмпирическим вопросом, имеющим широкий спектр последствий для работников, фирм и рабочей силы. регулирование рынка. Это связано с тем, что фирмы, обладающие монопсонической властью, могут устанавливать как заработную плату, так и занятость ниже уровней, которые преобладали бы, если бы рынок был совершенно конкурентным. Таким образом, степень и размах монопсонической власти на рынках труда влияют на распределение доходов и неравенство. Например, власть монопсонии в определенных профессиях является одним из объяснений выводов о том, что минимальная заработная плата не снижает занятость, а тот факт, что мужчины и женщины распределяются по профессиям, характеризующимся разной степенью концентрации, является одним из объяснений того, почему гендерный разрыв в оплате труда может быть таким большим. настойчивый. Поскольку власть монопсонии имеет такие широкие последствия для работников, государственные регулирующие органы часто рассматривают вопрос о том, как слияния и поглощения повлияют на рыночную власть пострадавшей фирмы. Неверная характеристика степени монопсонической власти в результате слияния или поглощения может привести к тому, что слияние, в противном случае повышающее эффективность, не произойдет, или может привести к слиянию, которое нанесет ущерб работникам.
регулирование рынка. Это связано с тем, что фирмы, обладающие монопсонической властью, могут устанавливать как заработную плату, так и занятость ниже уровней, которые преобладали бы, если бы рынок был совершенно конкурентным. Таким образом, степень и размах монопсонической власти на рынках труда влияют на распределение доходов и неравенство. Например, власть монопсонии в определенных профессиях является одним из объяснений выводов о том, что минимальная заработная плата не снижает занятость, а тот факт, что мужчины и женщины распределяются по профессиям, характеризующимся разной степенью концентрации, является одним из объяснений того, почему гендерный разрыв в оплате труда может быть таким большим. настойчивый. Поскольку власть монопсонии имеет такие широкие последствия для работников, государственные регулирующие органы часто рассматривают вопрос о том, как слияния и поглощения повлияют на рыночную власть пострадавшей фирмы. Неверная характеристика степени монопсонической власти в результате слияния или поглощения может привести к тому, что слияние, в противном случае повышающее эффективность, не произойдет, или может привести к слиянию, которое нанесет ущерб работникам. Таким образом, правильное измерение степени рыночной власти фирм имеет критически важные последствия для фирм, работников и экономики в целом.
Таким образом, правильное измерение степени рыночной власти фирм имеет критически важные последствия для фирм, работников и экономики в целом.
Подход к измерению концентрации на основе задач
Экономисты использовали несколько различных подходов к измерению рыночной власти работодателя, которые обычно основаны на экономических моделях рынков труда. Как правило, эти методы вынуждают исследователей сосредотачиваться на одной профессии, например учителях или медсестрах, и не позволяют более широко исследовать власть монопсонии.
В последнее время появилось большое количество работ, в которых используется более прямой показатель рыночной власти работодателя: концентрация работников среди работодателей. Рынки труда являются концентрированными, если работники данного типа сосредоточены в небольшом числе фирм на местном рынке труда. Каноническим примером монопсониста является одиночная горнодобывающая компания в маленьком городке, где все горнодобывающие рабочие сосредоточены в одной фирме. Исследователи измеряют эту концентрацию, рассчитывая индекс Хиршмана-Херфиндаля (HHI), который представляет собой квадрат доли занятости работников данного типа в фирмах на местном рынке труда.
Исследователи измеряют эту концентрацию, рассчитывая индекс Хиршмана-Херфиндаля (HHI), который представляет собой квадрат доли занятости работников данного типа в фирмах на местном рынке труда.
Основная проблема при измерении концентрации рынка труда заключается в том, как классифицировать работников по сходным «типам». Существующие исследования характеризовали работников, использующих профессию или отрасль, где концентрация основана на доле местного рынка труда в каждой профессии или отрасли, занятой конкретными фирмами (например, Azar et al. 2020a, 2020b, Azar et al. 2019, Benmelech et al. , 2018 г., Маринеску и др. 2019 г., Цю и Соджорнер 2019 г., Ринц 2018 г.).
Недостатком таких подходов является то, что работники могут переходить из одной профессии в другую, особенно если в экономике есть рабочие места, требующие аналогичных навыков. То есть рабочие задачи взаимозаменяемы в разных профессиях и отраслях. Например, помощник по административным вопросам в одной отрасли может выполнять эту работу в другой отрасли. Его навыки, связанные с задачами, также могут быть использованы в других профессиях, например, в бухгалтерии. Проще говоря, основной проблемой измерения власти монопсонии является группировка профессий таким образом, чтобы отразить концентрацию спроса на рабочие задачи среди фирм на рынке труда. В нашей недавней статье мы расширяем литературу по монопсонии и концентрации на рынке труда, используя подход, основанный на задачах, для оценки причинно-следственного влияния власти монопсонии на результаты на рынке труда (Dodini et al. 2022). Мы утверждаем, что концентрация спроса на конкретные рабочие задачи является более подходящим показателем концентрации рынка труда, чем тот, который использовался в предыдущей работе, потому что он допускает взаимозаменяемость работников в тесно связанных отраслях и профессиях.
Его навыки, связанные с задачами, также могут быть использованы в других профессиях, например, в бухгалтерии. Проще говоря, основной проблемой измерения власти монопсонии является группировка профессий таким образом, чтобы отразить концентрацию спроса на рабочие задачи среди фирм на рынке труда. В нашей недавней статье мы расширяем литературу по монопсонии и концентрации на рынке труда, используя подход, основанный на задачах, для оценки причинно-следственного влияния власти монопсонии на результаты на рынке труда (Dodini et al. 2022). Мы утверждаем, что концентрация спроса на конкретные рабочие задачи является более подходящим показателем концентрации рынка труда, чем тот, который использовался в предыдущей работе, потому что он допускает взаимозаменяемость работников в тесно связанных отраслях и профессиях.
Измерение концентрации рынка труда на основе задач
Используя обширные данные норвежского реестра со связями между отдельными работниками, профессиями и фирмами, которые недоступны в США, мы оцениваем прямую, основанную на задачах меру внешних возможностей работников ( то есть другие рабочие места в их местной экономике, которые требуют аналогичного набора задач). Мы делаем это, объединяя данные регистра с информацией о содержании задач профессий из O*NET. Затем мы используем технику машинного обучения без присмотра и позволяем данным сообщать нам, как сгруппировать работников на основе содержания задач их текущей работы. Это позволяет нам группировать работников на основе навыков, основанных на задачах, без необходимости навязывать какие-либо строгие предположения о взаимосвязи между профессиями, отраслями и местной занятостью.
Мы делаем это, объединяя данные регистра с информацией о содержании задач профессий из O*NET. Затем мы используем технику машинного обучения без присмотра и позволяем данным сообщать нам, как сгруппировать работников на основе содержания задач их текущей работы. Это позволяет нам группировать работников на основе навыков, основанных на задачах, без необходимости навязывать какие-либо строгие предположения о взаимосвязи между профессиями, отраслями и местной занятостью.
Панель А на Рисунке 1 показывает, что существуют значительные различия в концентрации спроса на навыки, основанные на задачах, между рынками труда и внутри них в Норвегии. Мы сравниваем общую метрику концентрации (HHI), используя кластеры на основе задач, занятия (панель B), отрасли (панель C) и образование (панель D). Результаты показывают, что, особенно для малых и средних рынков труда, наша мера, основанная на задачах, демонстрирует более низкий уровень концентрации. Это важно, потому что измерение, основанное на задачах, допускает замену отраслями и профессиями с аналогичными требованиями к задачам, чего нельзя сделать с помощью показателей, основанных на отрасли и роде занятий. Это имеет важные политические последствия, если регулирующие органы используют профессиональные или отраслевые показатели для оценки последствий слияния или поглощения.
Это имеет важные политические последствия, если регулирующие органы используют профессиональные или отраслевые показатели для оценки последствий слияния или поглощения.
Рисунок 1 Индексы Херфиндаля-Хиршмана по местному рынку труда
Наши данные позволяют нам также изучить различия по полу. На Рисунке 2 показано, что женщины, как правило, относятся к группам навыков, основанных на задачах, которые гораздо более сконцентрированы, чем мужчины. Эту разницу можно объяснить неодинаковой сортировкой мужчин и женщин в государственном и частном секторах. Женщины гораздо чаще работают в государственном секторе, который характеризуется более высоким уровнем концентрации. Внутри сектора гендерные различия невелики.
Рисунок 2 Индексы Херфиндаля-Хиршмана, основанные на навыках, в разбивке по местному рынку труда и полу
Причинный эффект концентрации на рынке труда
мер, мы используем нашу новую меру для изучения причинно-следственного воздействия концентрации рынка труда на работников. Мысленный эксперимент, лежащий в основе нашего подхода, заключается в том, чтобы рассмотреть работников, которые невольно отделены от своих рабочих мест на рынках труда, которые различаются по уровню их концентрации. Затем этим работникам необходимо искать новую работу на рынках с разной концентрацией. Предложения по заработной плате, которые они получат, будут определяться набором имеющихся у них внешних возможностей, который определяется концентрацией. Их чувствительность к предложениям заработной платы определяется наклоном кривой предложения труда на местном рынке труда. Концентрированный рынок связан с более крутой кривой, что приводит к более низкой заработной плате после увольнения с текущей работы. Мы аппроксимируем этот мысленный эксперимент, стимулируя поиск работы посредством массовых увольнений и закрытия фирм среди людей, которые внешне похожи, но находятся на рынках с разной концентрацией.
Мысленный эксперимент, лежащий в основе нашего подхода, заключается в том, чтобы рассмотреть работников, которые невольно отделены от своих рабочих мест на рынках труда, которые различаются по уровню их концентрации. Затем этим работникам необходимо искать новую работу на рынках с разной концентрацией. Предложения по заработной плате, которые они получат, будут определяться набором имеющихся у них внешних возможностей, который определяется концентрацией. Их чувствительность к предложениям заработной платы определяется наклоном кривой предложения труда на местном рынке труда. Концентрированный рынок связан с более крутой кривой, что приводит к более низкой заработной плате после увольнения с текущей работы. Мы аппроксимируем этот мысленный эксперимент, стимулируя поиск работы посредством массовых увольнений и закрытия фирм среди людей, которые внешне похожи, но находятся на рынках с разной концентрацией.
Результаты нашего эмпирического анализа показывают, что работники, сталкивающиеся с аналогичными случаями увольнения, имеют худшие последующие результаты на рынке труда, когда они выполняют более концентрированные кластеры задач. У работника с HHI на 0,10 выше (примерно одно стандартное отклонение в наших данных), который сталкивается с массовым увольнением или закрытием предприятия, годовой заработок после этого события на 9 120 норвежских крон ниже, что составляет 1,78% по сравнению со средним значением. Мы обнаруживаем положительные, но не статистически или экономически значимые эффекты на выход из состава рабочей силы и на занятость, предполагая, что эффекты заработной платы обусловлены преимущественно заработной платой, которую люди получают при повторном приеме на работу, а не тем, получают ли они работу вообще. В соответствии с важностью реакции на заработную плату увеличение HHI на 0,1 пункта приводит к увеличению на один процентный пункт вероятности работы неполный рабочий день после увольнения. Кроме того, наши результаты указывают на снижение повышения квалификации и увеличение понижения квалификации в более высоких кластерах HHI после разделения. Это означает, что те, кто находится на более концентрированных рынках труда, с большей вероятностью будут работать на должностях с более низким средним уровнем образования по сравнению с работой, с которой они были уволены.
У работника с HHI на 0,10 выше (примерно одно стандартное отклонение в наших данных), который сталкивается с массовым увольнением или закрытием предприятия, годовой заработок после этого события на 9 120 норвежских крон ниже, что составляет 1,78% по сравнению со средним значением. Мы обнаруживаем положительные, но не статистически или экономически значимые эффекты на выход из состава рабочей силы и на занятость, предполагая, что эффекты заработной платы обусловлены преимущественно заработной платой, которую люди получают при повторном приеме на работу, а не тем, получают ли они работу вообще. В соответствии с важностью реакции на заработную плату увеличение HHI на 0,1 пункта приводит к увеличению на один процентный пункт вероятности работы неполный рабочий день после увольнения. Кроме того, наши результаты указывают на снижение повышения квалификации и увеличение понижения квалификации в более высоких кластерах HHI после разделения. Это означает, что те, кто находится на более концентрированных рынках труда, с большей вероятностью будут работать на должностях с более низким средним уровнем образования по сравнению с работой, с которой они были уволены.
Мы также оцениваем нашу модель отдельно для мужчин и женщин. Результаты показывают, что влияние монопсонии на заработок после увольнения больше для мужчин, чем для женщин: заработная плата мужчин снижается на 11 890 норвежских крон (или 2,04%), а заработная плата женщин снижается на 4 812 норвежских крон (1,13%). Эта разница почти полностью обусловлена разным эффектом концентрации в государственном и частном секторах. Влияние на заработок мужчин и женщин велико в частном секторе и более скромно в государственном секторе. Женщины чаще работают в государственном секторе, что подвергает их более высокой концентрации, но смягчает влияние концентрации на результаты рынка труда.
Актуальность политики и заключительные замечания
Мы расширяем наше понимание монопсонии и концентрации на рынке труда, применяя подход, основанный на задачах, для оценки причинно-следственного влияния монопсонии на результаты рынка труда. Наш методологический вклад и эмпирические результаты имеют важное значение для политики, поскольку точное измерение власти монопсонии необходимо для надлежащего регулирования рынка труда. Предложения Конгрессу США поддерживают предоставление Министерству юстиции полномочий регулировать влияние предполагаемых слияний и поглощений на концентрацию рынка труда, аналогично тому, как в настоящее время изучается концентрация рынка товаров. Существенной частью этих предложений является использование показателей концентрации рынка труда, которые рассчитываются в рамках профессии или отрасли. Эти меры могут преувеличивать эффективную концентрацию рынка, опуская внешние возможности работников. Без корректировки соответствующих нормативных порогов регулирующие органы могут наложить слишком жесткие ограничения на действия фирм, которые в противном случае не представляли бы угрозы для конкуренции на рынке труда, или могут предотвратить слияния, которые в противном случае могли бы привести к росту доходов работников и владельцев. В то же время наши результаты показывают, что концентрация рынка труда создает реальные риски для благополучия работников, которые должны учитываться регулирующими органами.
Предложения Конгрессу США поддерживают предоставление Министерству юстиции полномочий регулировать влияние предполагаемых слияний и поглощений на концентрацию рынка труда, аналогично тому, как в настоящее время изучается концентрация рынка товаров. Существенной частью этих предложений является использование показателей концентрации рынка труда, которые рассчитываются в рамках профессии или отрасли. Эти меры могут преувеличивать эффективную концентрацию рынка, опуская внешние возможности работников. Без корректировки соответствующих нормативных порогов регулирующие органы могут наложить слишком жесткие ограничения на действия фирм, которые в противном случае не представляли бы угрозы для конкуренции на рынке труда, или могут предотвратить слияния, которые в противном случае могли бы привести к росту доходов работников и владельцев. В то же время наши результаты показывают, что концентрация рынка труда создает реальные риски для благополучия работников, которые должны учитываться регулирующими органами.
Ссылки
Азар, Дж., И. Маринеску и М. Стейнбаум (2020a), «Концентрация рынка труда». Журнал управления персоналом 1218–9914R1.
Азар, Дж., И. Маринеску, М. Стейнбаум и Б. Таска (2020b), «Концентрация на рынках труда США: данные по онлайн-данным о вакансиях», Экономика труда 66.
Азар, Дж., С. Берри и И. Э. Маринеску ( 2019 г.), «Оценка влияния на рынке труда», доступно по адресу SSRN 3456277.
Бенмелех, Э., Бергман Н. и Ким Х. (2018 г.), «Сильные работодатели и слабые работники: как концентрация работодателей влияет на заработную плату?», Технический отчет, Национальный Бюро экономических исследований.
Додини, С., М. Ловенхайм, К. Сальванес и А. Виллен (2022 г.), «Монопсония, должностные обязанности и концентрация рынка труда», рабочий документ NBER № 30823
Маринеску, И. Э., И. Усс и Л.-Д. Папе (2019 г.) , «Заработная плата, наем и концентрация рынка труда», доступно по адресу SSRN 3453855.
Qiu, Y and A Sojourner (2019), «Концентрация рынка труда и оплата труда», доступно по адресу SSRN 3312197.




 Виды рынков
Виды рынков ед за один день.
ед за один день.
 Проанализировать полученные данные;
Проанализировать полученные данные;



 ед., продукт В – 20 ден.ед., продукт С – 10 ден.ед.
ед., продукт В – 20 ден.ед., продукт С – 10 ден.ед.




 05
05 833
833 532
532 369
369 317
317 243
243 Кот, доктор философии; Рупа Г. Гордон, доктор философии; Крислин Э. Рэнделл, доктор философии; Джуди Шмитт; и Хелена Марвин находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, если не указано иное.
Кот, доктор философии; Рупа Г. Гордон, доктор философии; Крислин Э. Рэнделл, доктор философии; Джуди Шмитт; и Хелена Марвин находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, если не указано иное.
 В частности, он описывает силу и направление линейной зависимости между двумя количественными переменными.
В частности, он описывает силу и направление линейной зависимости между двумя количественными переменными.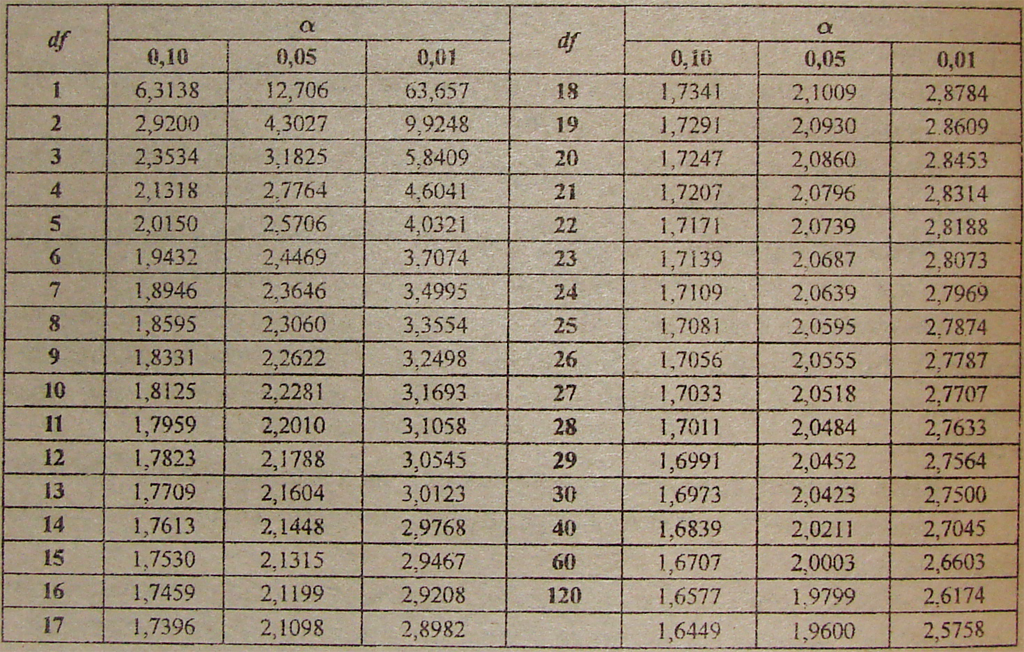 В частности, мы можем проверить, существует ли значительная связь между двумя переменными.
В частности, мы можем проверить, существует ли значительная связь между двумя переменными.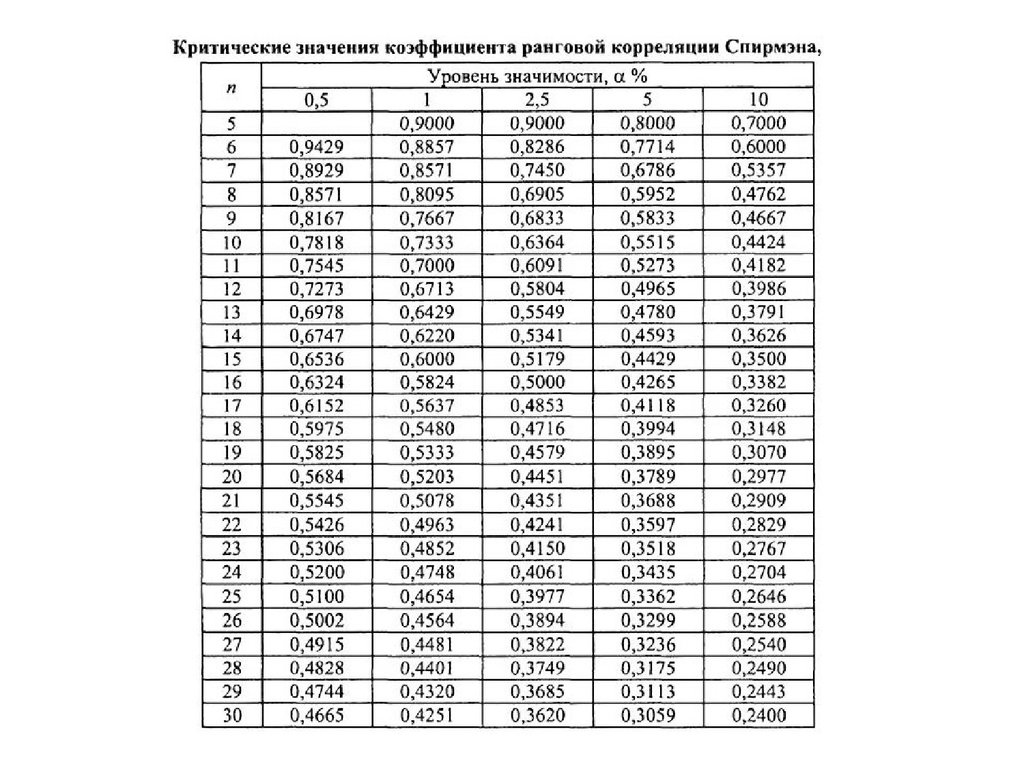 Коэффициент корреляции Пирсона является хорошим выбором, когда все из следующего верны:
Коэффициент корреляции Пирсона является хорошим выбором, когда все из следующего верны: Вы можете использовать диаграмму рассеяния, чтобы проверить, является ли связь между двумя переменными линейной.
Вы можете использовать диаграмму рассеяния, чтобы проверить, является ли связь между двумя переменными линейной.
 Неважно, какая переменная называется x , а какая y — формула в любом случае даст один и тот же ответ.
Неважно, какая переменная называется x , а какая y — формула в любом случае даст один и тот же ответ.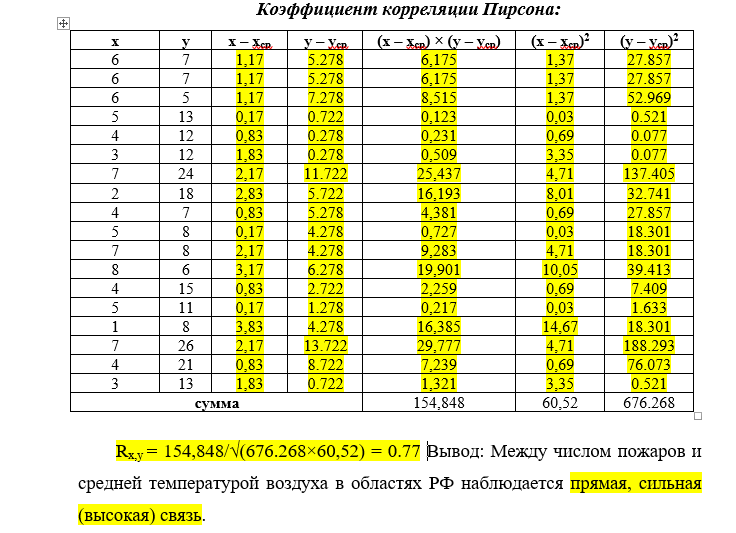 12
12
 18
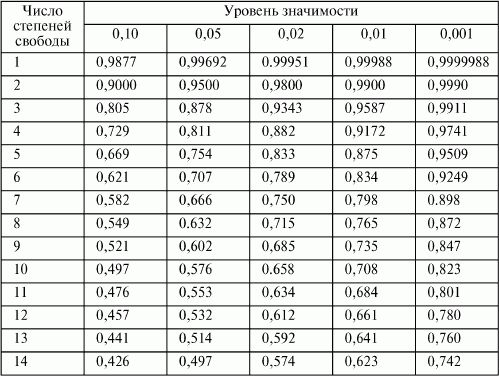
18 Это оценка ро ( ρ ), корреляции Пирсона населения. Зная r и n (размер выборки), мы можем сделать вывод, значительно ли ρ отличается от 0,9.0017
Это оценка ро ( ρ ), корреляции Пирсона населения. Зная r и n (размер выборки), мы можем сделать вывод, значительно ли ρ отличается от 0,9.0017 Чтобы пользоваться таблицей, нужно знать три вещи:
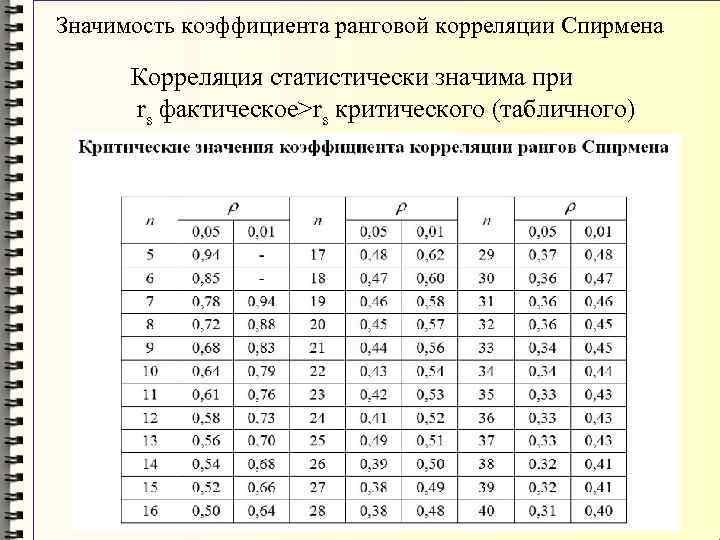
Чтобы пользоваться таблицей, нужно знать три вещи: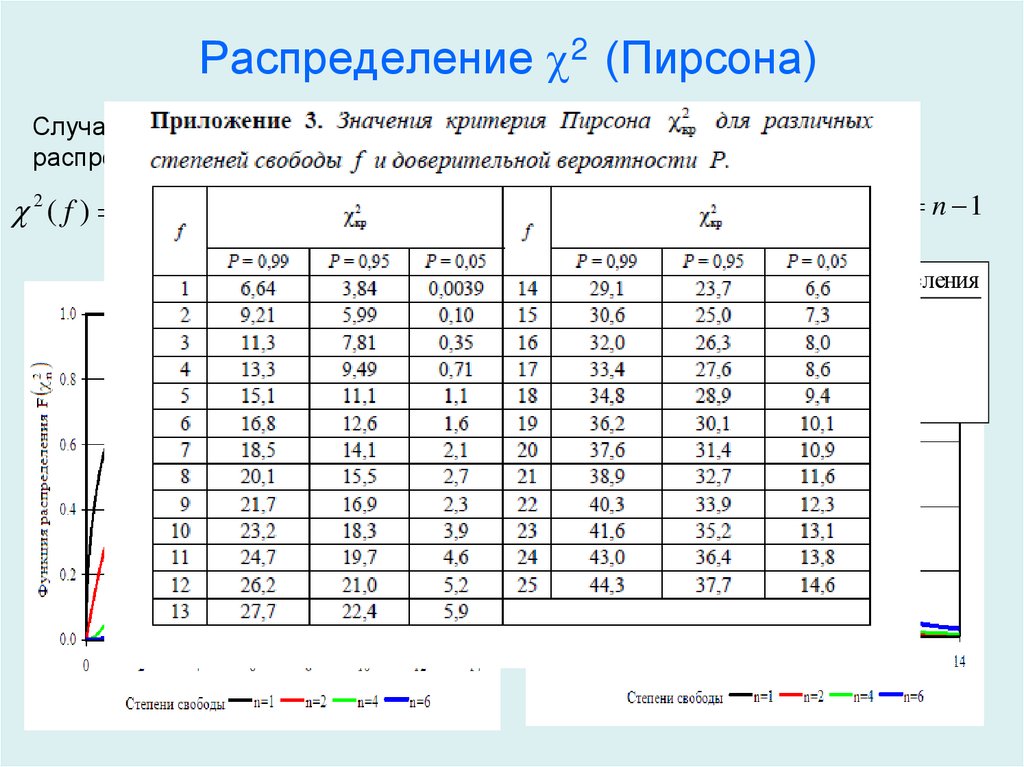

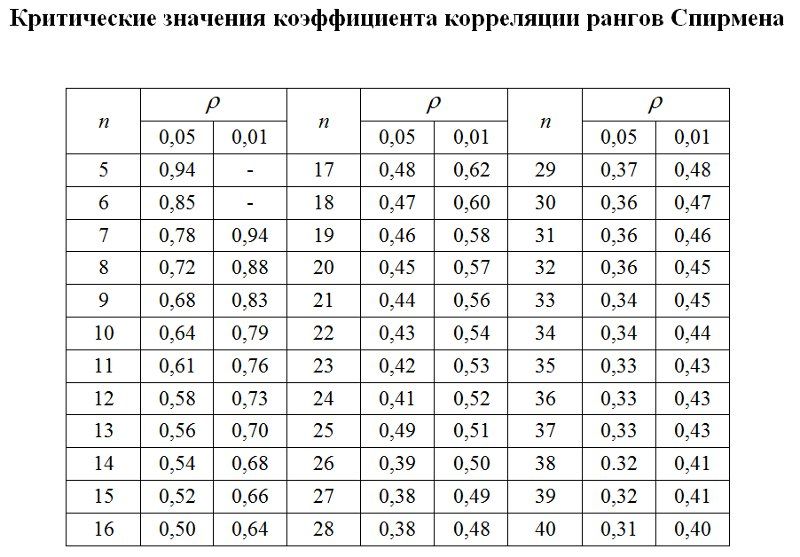 Степени свободы указаны в скобках рядом с r .
Степени свободы указаны в скобках рядом с r .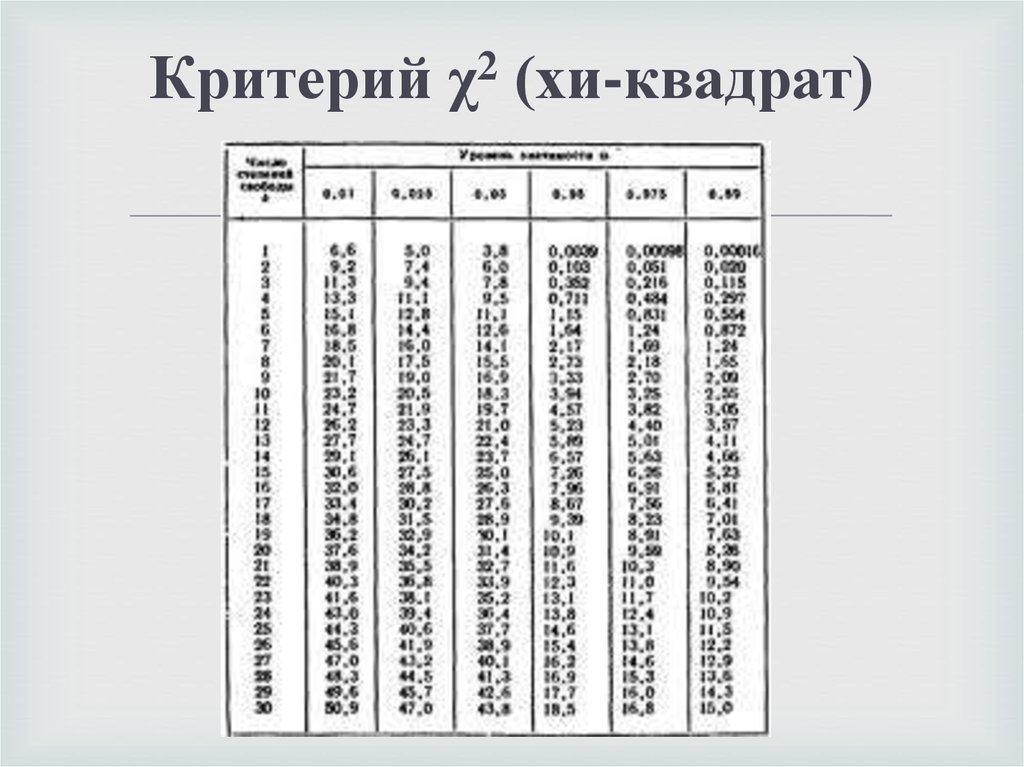
 Англия
стала конституционной монархией согласно …
Англия
стала конституционной монархией согласно … мировым лидером в экономике была …
мировым лидером в экономике была … ..,
содействовали консервации феодальной раздробленности, по существу затормозили
поступательное развитие русских земель»
..,
содействовали консервации феодальной раздробленности, по существу затормозили
поступательное развитие русских земель»  В
съезд Коммунистической партии Советского Союза (КПСС) состоялся в …
В
съезд Коммунистической партии Советского Союза (КПСС) состоялся в … Восточные
славяне языческого периода поклонялись богам:
Восточные
славяне языческого периода поклонялись богам: Древнейший
свод законов, датируемый xviii в. до н.э., связан с именем вавилонского царя:
Древнейший
свод законов, датируемый xviii в. до н.э., связан с именем вавилонского царя: .. четко выполнял свои обязательства в рамках
Священного союза, за что получил прозвище «жандарм Европы»
.. четко выполнял свои обязательства в рамках
Священного союза, за что получил прозвище «жандарм Европы» Энгельс предложили …
Энгельс предложили … Летопись, повествующая о жизни восточных славян, называлась…
Летопись, повествующая о жизни восточных славян, называлась… Новая экономическая
политика (нэп) привела к …
Новая экономическая
политика (нэп) привела к … Окончательный распад древней руси на отдельные самостоятельные
территории произошел после смерти князя …
Окончательный распад древней руси на отдельные самостоятельные
территории произошел после смерти князя … Отношения киевского князя и дружины на раннем этапе развития
государства можно охарактеризовать как … 164.
Патриархат характерен для эпохи …
Отношения киевского князя и дружины на раннем этапе развития
государства можно охарактеризовать как … 164.
Патриархат характерен для эпохи … Петербург стал столицей россии в …
Петербург стал столицей россии в …  шуйского в 1610
г., называлось … 189. Правление
Петра I называют …
шуйского в 1610
г., называлось … 189. Правление
Петра I называют … Расцвет и укрепление киевского государства начался с эпохи
княжения …
Расцвет и укрепление киевского государства начался с эпохи
княжения … Самодержавный характер российской государственной власти
зарождается в период правления …
Самодержавный характер российской государственной власти
зарождается в период правления … Среди
главных вопросов, обсуждаемых в тайных декабристских организациях, были вопросы
…
Среди
главных вопросов, обсуждаемых в тайных декабристских организациях, были вопросы
… .. 240. Судебник 1550 г. — это …
источник 241. Теория
неоконсерватизма …
.. 240. Судебник 1550 г. — это …
источник 241. Теория
неоконсерватизма … Человек умелый (homo habilis) появился в эпоху:
Человек умелый (homo habilis) появился в эпоху:  «Просвещенный абсолютизм» -это политика, характерная для правления …
«Просвещенный абсолютизм» -это политика, характерная для правления …  Основопологающие вопросы общественной жизни России после Февральской революции предполагалось вынести на решение …
Основопологающие вопросы общественной жизни России после Февральской революции предполагалось вынести на решение …  М. Соловьев
М. Соловьев  М. Кирова
М. Кирова  Среди реформ государственного управления, осуществленных в период правления Александра I, можно выделить …Отметьте правильный вариант ответа:
Среди реформ государственного управления, осуществленных в период правления Александра I, можно выделить …Отметьте правильный вариант ответа: 
 Н. Милюков
Н. Милюков 
 Cреди причин, вызвавших кризис Российской государственности на рубеже XVI-XVII веке, можно назвать …
Cреди причин, вызвавших кризис Российской государственности на рубеже XVI-XVII веке, можно назвать …  И. Глинка, М. П. Мусоргский, Н. А. Римский-Корсаков
И. Глинка, М. П. Мусоргский, Н. А. Римский-Корсаков  Победа большевиков в России осенью 1917 года явилась следствием ряда факторов, среди которых …Отметьте правильный вариант ответа:
Победа большевиков в России осенью 1917 года явилась следствием ряда факторов, среди которых …Отметьте правильный вариант ответа:  Хрущева в СШАB-Создание Организации Варшавского Договора
Хрущева в СШАB-Создание Организации Варшавского Договора 
 (Рейтер) — Дмитрий Медведев видно, как он обменивается доверительными улыбками с Бараком Обамой под зловещую музыку. Труп союзника России Муаммара Каддафи, отстраненного от власти Западом, валяется в грязи. Камера фиксирует вспотевшего премьер-министра, который беспокойно ерзает в кресле.
(Рейтер) — Дмитрий Медведев видно, как он обменивается доверительными улыбками с Бараком Обамой под зловещую музыку. Труп союзника России Муаммара Каддафи, отстраненного от власти Западом, валяется в грязи. Камера фиксирует вспотевшего премьер-министра, который беспокойно ерзает в кресле. Совсем недавно министр обороны Анатолий Сердюков был уволен из-за многомиллионного коррупционного скандала.
Совсем недавно министр обороны Анатолий Сердюков был уволен из-за многомиллионного коррупционного скандала.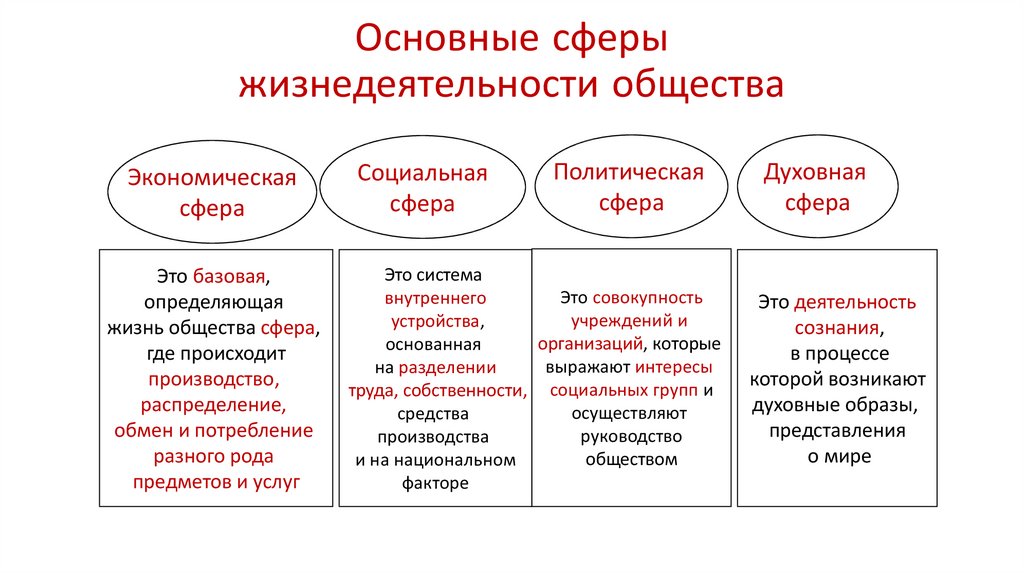


 2147/CMAR.S165228. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
2147/CMAR.S165228. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] ПЛОС ОДИН. 2016;11:e0153274. doi: 10.1371/journal.pone.0153274. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
ПЛОС ОДИН. 2016;11:e0153274. doi: 10.1371/journal.pone.0153274. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] Междунар. Дж. Мол. науч. 2020;21:222. дои: 10.3390/ijms21010222. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Междунар. Дж. Мол. науч. 2020;21:222. дои: 10.3390/ijms21010222. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] , Arbyn M. Цитология в сравнении с тестированием на ВПЧ для скрининга рака шейки матки у населения в целом . Кокрановская система баз данных. Ред. 2017; 8:CD008587. doi: 10.1002/14651858.CD008587.pub2. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
, Arbyn M. Цитология в сравнении с тестированием на ВПЧ для скрининга рака шейки матки у населения в целом . Кокрановская система баз данных. Ред. 2017; 8:CD008587. doi: 10.1002/14651858.CD008587.pub2. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] doi: 10.1007/s10096-019-03538-7. [PubMed] [CrossRef] [Академия Google]
doi: 10.1007/s10096-019-03538-7. [PubMed] [CrossRef] [Академия Google] Передний. микробиол. 2017;8:1162. дои: 10.3389/fmicb.2017.01162. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Передний. микробиол. 2017;8:1162. дои: 10.3389/fmicb.2017.01162. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
[Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] doi: 10.1038/nrmicro.2017.157. [PubMed] [CrossRef] [Google Scholar]
doi: 10.1038/nrmicro.2017.157. [PubMed] [CrossRef] [Google Scholar] БМК Рак. 2018;18:696. doi: 10.1186/s12885-018-4590-4. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
БМК Рак. 2018;18:696. doi: 10.1186/s12885-018-4590-4. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] Микробиом. 2013;1:29. дои: 10.1186/2049-2618-1-29. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Микробиом. 2013;1:29. дои: 10.1186/2049-2618-1-29. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] Женское здоровье BMC. 2019;19:30. doi: 10.1186/s12905-019-0727-0. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Женское здоровье BMC. 2019;19:30. doi: 10.1186/s12905-019-0727-0. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
[Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] Zhang Y., Xu X., Yu L., Shi X., Min M., Xiong L., Pan J., Zhang Y., Liu P., Wu G., et al. Изменения вагинальной микробиоты, вызванные инфекцией ВПЧ у китайских женщин. Передний. Клетка. Заразить. микробиол. 2022;12:814668. doi: 10.3389/fcimb.2022.814668. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Zhang Y., Xu X., Yu L., Shi X., Min M., Xiong L., Pan J., Zhang Y., Liu P., Wu G., et al. Изменения вагинальной микробиоты, вызванные инфекцией ВПЧ у китайских женщин. Передний. Клетка. Заразить. микробиол. 2022;12:814668. doi: 10.3389/fcimb.2022.814668. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] Ou Y.-C., Fu H.-C., Tseng C.-W., Wu C.-H., Tsai C. -C., Lin H. Влияние пробиотиков на клиренс вируса папилломы человека высокого риска и качество цервикального мазка: рандомизированное плацебо-контролируемое исследование. Женское здоровье BMC. 2019;19:103. doi: 10.1186/s12905-019-0798-y. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Ou Y.-C., Fu H.-C., Tseng C.-W., Wu C.-H., Tsai C. -C., Lin H. Влияние пробиотиков на клиренс вируса папилломы человека высокого риска и качество цервикального мазка: рандомизированное плацебо-контролируемое исследование. Женское здоровье BMC. 2019;19:103. doi: 10.1186/s12905-019-0798-y. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] [PMC free article] [PubMed] [CrossRef] [Google Scholar]
[PMC free article] [PubMed] [CrossRef] [Google Scholar] [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
[Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

 Многие из них составлены по принципу «один курс — один год школьной программы», но есть и такие, что покрывают сразу все главные темы в одном из разделов математики. Например, общий курс алгебры начинается с простых линейных уравнений и заканчивается тригонометрическими функциями.
Многие из них составлены по принципу «один курс — один год школьной программы», но есть и такие, что покрывают сразу все главные темы в одном из разделов математики. Например, общий курс алгебры начинается с простых линейных уравнений и заканчивается тригонометрическими функциями. Пользователь управляет синей плиткой: цель игры — довести ее до пункта назначения, совершив по пути нужные арифметические операции. Головоломки разделены по темам: например, в приложении можно отработать задачи с положительными и отрицательными числами, неравенствами, степенями, логарифмами и модульными функциями.
Пользователь управляет синей плиткой: цель игры — довести ее до пункта назначения, совершив по пути нужные арифметические операции. Головоломки разделены по темам: например, в приложении можно отработать задачи с положительными и отрицательными числами, неравенствами, степенями, логарифмами и модульными функциями. Например, можно соединить две точки прямыми, очертить окружность или провести перпендикуляр: чем выше сложность, тем больше инструментарий. Чтобы получить высшую оценку, нужно справиться с заданием за минимальное количество ходов.
Например, можно соединить две точки прямыми, очертить окружность или провести перпендикуляр: чем выше сложность, тем больше инструментарий. Чтобы получить высшую оценку, нужно справиться с заданием за минимальное количество ходов. Задача пользователя — решить за отведенное время максимальное количество примеров, сложность которых растет с каждым правильным ответом.
Задача пользователя — решить за отведенное время максимальное количество примеров, сложность которых растет с каждым правильным ответом. В школе нас учили решать задачи по готовым формулам и алгоритмам, а Девлин рассказывает об университетском подходе к математике, который основывается на умениях рассуждать о проблеме, самостоятельно разрабатывать пути ее решения и предоставлять стройные доказательства в защиту своих утверждений.
В школе нас учили решать задачи по готовым формулам и алгоритмам, а Девлин рассказывает об университетском подходе к математике, который основывается на умениях рассуждать о проблеме, самостоятельно разрабатывать пути ее решения и предоставлять стройные доказательства в защиту своих утверждений. Объяснение:
Объяснение: Например:
Например:
 Университет Клемсона, магистр наук, вычислительная…
Университет Клемсона, магистр наук, вычислительная…



 2)
2) Начальному условию У(0)=1 оно не удовлетворяет, поэтому решением данной задачи Коши не является.
Начальному условию У(0)=1 оно не удовлетворяет, поэтому решением данной задачи Коши не является. В итоге для определения функции Получаем задачу Коши:
В итоге для определения функции Получаем задачу Коши: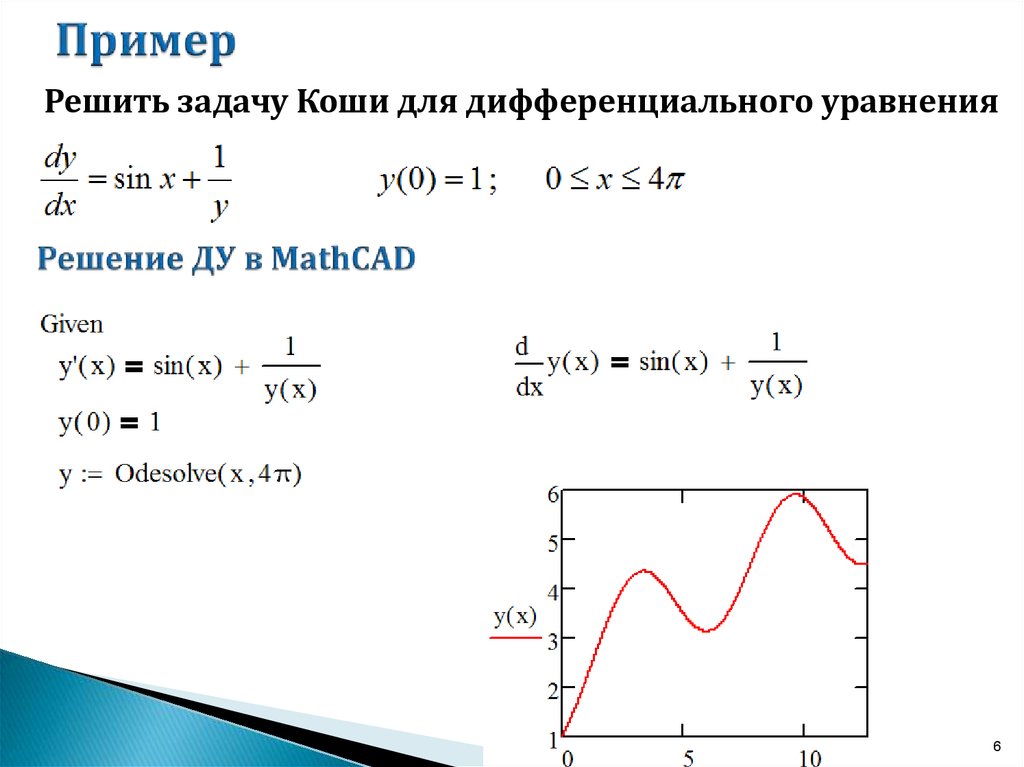
 Тогда общее изменение численности населения за время найдется по формуле:
Тогда общее изменение численности населения за время найдется по формуле:
 Но это, как известно, не так: с течением времени, в силу разных причин, ситуация и со смертностью, и с рождаемостью может существенно измениться. Поэтому полученную формулу при конкретном числовом значении оправданно применять лишь на протяжении достаточно ограниченного периода времени. В другой период времени тоже можно применять эту формулу, но уже при другом значении .
Но это, как известно, не так: с течением времени, в силу разных причин, ситуация и со смертностью, и с рождаемостью может существенно измениться. Поэтому полученную формулу при конкретном числовом значении оправданно применять лишь на протяжении достаточно ограниченного периода времени. В другой период времени тоже можно применять эту формулу, но уже при другом значении . То есть объем инвестиций составит:
То есть объем инвестиций составит: пример 3). Значит, у них полностью совпадают и решения:
пример 3). Значит, у них полностью совпадают и решения:
 04.2023
04.2023 Результат этого проектирования, временные диаг…
Результат этого проектирования, временные диаг… 04.2023
04.2023
 ..
.. оптический волновод , входные параметры, законы геометрической оптики , построение мод (волн) учитывая вышеперечисленные параметры,…
оптический волновод , входные параметры, законы геометрической оптики , построение мод (волн) учитывая вышеперечисленные параметры,… Задачи Коши отличаются от краевых задач тем, что область, в которой должно быть определено искомое решение, не указывается заранее. Тем не менее задачи Коши, как и краевые задачи, определяются наложением предельных условий для решения на (части) границы области определения.
Задачи Коши отличаются от краевых задач тем, что область, в которой должно быть определено искомое решение, не указывается заранее. Тем не менее задачи Коши, как и краевые задачи, определяются наложением предельных условий для решения на (части) границы области определения. $$
$$ теорему Пеано), но оно не обязательно должно быть уникальным. Решение не обязательно должно существовать во всех точках области определения $f$.
9{( п — 1) } ,
$$
Стандартным устройством
теорему Пеано), но оно не обязательно должно быть уникальным. Решение не обязательно должно существовать во всех точках области определения $f$.
9{( п — 1) } ,
$$
Стандартным устройством Основным источником трудностей является тот факт, что пространство независимых переменных является многомерным, что приводит к проблемам (алгебраической) разрешимости. Например, рассмотрим задачу Коши для системы уравнений в полных дифференциалах,
9\альфа}
«=»
ж (х)
$$
Основным источником трудностей является тот факт, что пространство независимых переменных является многомерным, что приводит к проблемам (алгебраической) разрешимости. Например, рассмотрим задачу Коши для системы уравнений в полных дифференциалах,
9\альфа}
«=»
ж (х)
$$ е. когда условие (5) выполняется для всех $ x _ {0} \in S $.
е. когда условие (5) выполняется для всех $ x _ {0} \in S $. {k}$
метрика) по этим функциям. Для случаев $ n = 1, 2 $
и $n = 3$,
явный вид решения задается формулами Даламбера, Пуассона и Кирхгофа соответственно:
9{2} } }
,
$$
{k}$
метрика) по этим функциям. Для случаев $ n = 1, 2 $
и $n = 3$,
явный вид решения задается формулами Даламбера, Пуассона и Кирхгофа соответственно:
9{2} } }
,
$$


 3} $$ Одна критическая точка 2-го порядка \(x=\frac12\)
3} $$ Одна критическая точка 2-го порядка \(x=\frac12\) е. $$ \begin{cases} 0\lt x\lt 1\\ 0\lt x\lt\frac12 \end{cases} \Rightarrow 0\lt x\lt\frac12 $$ Решение совокупности – это объединение полученных решений систем: $$ 0\lt x\lt\frac12\cup x\gt 1 $$ Ответ: \(x\in\left(0;\frac12\right)\cup (1;+\infty)\)
е. $$ \begin{cases} 0\lt x\lt 1\\ 0\lt x\lt\frac12 \end{cases} \Rightarrow 0\lt x\lt\frac12 $$ Решение совокупности – это объединение полученных решений систем: $$ 0\lt x\lt\frac12\cup x\gt 1 $$ Ответ: \(x\in\left(0;\frac12\right)\cup (1;+\infty)\)

 Все корни мнимые
причем все эти корни имеют один и тот
же модуль. .
Покажем, что мнимые: ,u—0.,v—0.=-,p—3.>0(т.к
дескрименант меньше 0). Таким образом,
равенство модулей и положительное
действительное число произведение,
возможно только для комплексных
сопряжённых
Все корни мнимые
причем все эти корни имеют один и тот
же модуль. .
Покажем, что мнимые: ,u—0.,v—0.=-,p—3.>0(т.к
дескрименант меньше 0). Таким образом,
равенство модулей и положительное
действительное число произведение,
возможно только для комплексных
сопряжённых  .-2.+,2a—2.,x—2.x+,,a—2.-4.,x—2.=,,a—2.-4.,x—2.-b,x—2.-cx-d
.-2.+,2a—2.,x—2.x+,,a—2.-4.,x—2.=,,a—2.-4.,x—2.-b,x—2.-cx-d x+,,,t—2.-4.-d.
x+,,,t—2.-4.-d.
 2-6x+9
2-6x+9 Затем используйте правило степени для производных, чтобы найти f’(x) = (1/2)*x -1/2 . Затем упростите до вида 1/2√ x. Мы также можем использовать цепное правило, чтобы найти производную функции композиции квадратного корня.
Затем используйте правило степени для производных, чтобы найти f’(x) = (1/2)*x -1/2 . Затем упростите до вида 1/2√ x. Мы также можем использовать цепное правило, чтобы найти производную функции композиции квадратного корня. 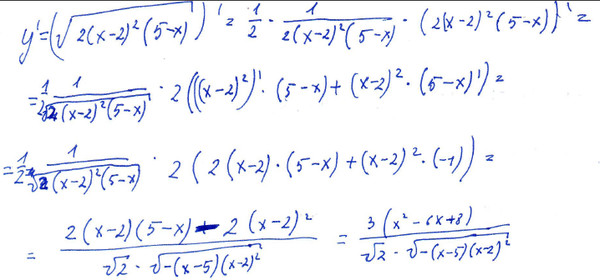
 д.:
д.:

 Затем вы можете использовать правило степени для производных (и, если необходимо, цепное правило), чтобы найти производную.
Затем вы можете использовать правило степени для производных (и, если необходимо, цепное правило), чтобы найти производную.
 Его график показан ниже.
Его график показан ниже.

 Это график функции f'(x) = -0,25/x 5/4 .
Это график функции f'(x) = -0,25/x 5/4 .




 Использование учебного пособия с пояснениями позволяет родителям сэкономить деньги. Ученикам не нужно тратить дополнительное время на дорогу к репетитору и обратно домой. В любой момент школьник может самостоятельно проверить себя, открыть подробные пояснения, чтобы разобраться в трудном материале. Теперь ему можно не переживать, если он пропустил занятия, был невнимательным на уроке при объяснении новой темы.
Использование учебного пособия с пояснениями позволяет родителям сэкономить деньги. Ученикам не нужно тратить дополнительное время на дорогу к репетитору и обратно домой. В любой момент школьник может самостоятельно проверить себя, открыть подробные пояснения, чтобы разобраться в трудном материале. Теперь ему можно не переживать, если он пропустил занятия, был невнимательным на уроке при объяснении новой темы.
 Ознакомьтесь с кратким вариантом ответа, который откроется на новой странице. Если вы хотите увидеть подробный алгоритм решения задачи с разными вариантами – зарегистрируйтесь на нашем сайте.
Ознакомьтесь с кратким вариантом ответа, который откроется на новой странице. Если вы хотите увидеть подробный алгоритм решения задачи с разными вариантами – зарегистрируйтесь на нашем сайте.
 К каждой теме помимо теории есть практические упражнения. Для коллективного решения предусмотрены «задачи-исследования» и задания для работы в парах. В конце каждого параграфа, для закрепления изученного материала размещены контрольные вопросы. По уровню подготовки среди упражнений есть обязательные, а также повышенной сложности, которые выполняют на добровольной основе.
К каждой теме помимо теории есть практические упражнения. Для коллективного решения предусмотрены «задачи-исследования» и задания для работы в парах. В конце каждого параграфа, для закрепления изученного материала размещены контрольные вопросы. По уровню подготовки среди упражнений есть обязательные, а также повышенной сложности, которые выполняют на добровольной основе. Умножение одночленов, одночлена на многочлен, многочлена на многочлен. Возведение одночлена в степень. Сложение и вычитание многочленов. Преобразование целого выражения в многочлен. Разложение многочлена на множители.
Умножение одночленов, одночлена на многочлен, многочлена на многочлен. Возведение одночлена в степень. Сложение и вычитание многочленов. Преобразование целого выражения в многочлен. Разложение многочлена на множители.

 В том случае, когда надо наверстывать упущенное и интенсивно не просто повторять, а заново проходить некоторые параграфы и темы курса, необходимо минимум два часа ответственных занятий ежедневно.
В том случае, когда надо наверстывать упущенное и интенсивно не просто повторять, а заново проходить некоторые параграфы и темы курса, необходимо минимум два часа ответственных занятий ежедневно. Такая экономия без потери качества крайне важна многим семьям.
Такая экономия без потери качества крайне важна многим семьям. Но так однозначно оценивать эту работу можно лишь на первый и довольно предвзятый взгляд. На самом деле – польза такого подхода очевидна:
Но так однозначно оценивать эту работу можно лишь на первый и довольно предвзятый взгляд. На самом деле – польза такого подхода очевидна:
/Tablitsy%20s%20formulami/%D0%A1%D1%82%D0%B5%D0%BF%D0%B5%D0%BD%D0%B8%20%D0%BA%D0%BE%D1%80%D0%BD%D0%B8%20%D0%B4%D0%B8%D1%81%D0%BA%D1%80%D0%B8%D0%BC%D0%B8%D0%BD%D0%B0%D0%BD%D1%82.jpg) Такой навык пригодится не только в школьные годы, но и впоследствии, в том числе — в деловой и профессиональной сфере.
Такой навык пригодится не только в школьные годы, но и впоследствии, в том числе — в деловой и профессиональной сфере.
 Например, заболевшие, находящиеся на конкурсах, спортивных сборах и пр. Для них решебники станут альтернативой объяснения учителя, позволят проработать на практике материал пропущенных уроков.
Например, заболевшие, находящиеся на конкурсах, спортивных сборах и пр. Для них решебники станут альтернативой объяснения учителя, позволят проработать на практике материал пропущенных уроков. С их помощью они освоили материал, на который не хватило времени на уроках – ведь количество последних, а также их продолжительность, значительно сократились.
С их помощью они освоили материал, на который не хватило времени на уроках – ведь количество последних, а также их продолжительность, значительно сократились.

 Кроме того, научитесь решать, заполнив квадрат.
Кроме того, научитесь решать, заполнив квадрат.
 Выполняйте арифметические операции, такие как сложение, вычитание, умножение и деление над абсолютным значением действительных чисел.
Выполняйте арифметические операции, такие как сложение, вычитание, умножение и деление над абсолютным значением действительных чисел.

 Закончите все эти бесплатные рабочие листы, и вы будете на пути к тому, чтобы стать экспертом в решении алгебры.
Закончите все эти бесплатные рабочие листы, и вы будете на пути к тому, чтобы стать экспертом в решении алгебры. Заполните рабочие листы по алгебре онлайн с помощью iPad или современного браузера Мы только что добавили еще одно измерение в наши бесплатные рабочие листы по алгебре. Теперь вы можете выполнять их без использования принтера. Все наши рабочие листы имеют две версии. Первый — это печатный рабочий лист по алгебре, оптимизированный для печати. Вторая версия представляет собой онлайн-рабочий лист по алгебре. Онлайн-версия позволяет вам использовать iPad или другие планшетные устройства для заполнения рабочих листов. Наша передовая технология использует функцию мультитач мобильных устройств. Пишите числа пальцами прямо на листах по алгебре. Онлайн-рабочие листы по алгебре также можно выполнять на настольных и портативных компьютерах при использовании современных браузеров, таких как Chrome, Safari и Firefox. Практика по алгебре 1, алгебре 2, элементарной алгебре, предварительной алгебре, средней алгебре и задачам по алгебре Какой студент не получил бы удовольствия от работы с полиномами, терминами, уравнениями и алгебраическими структурами? Я не знаю многих, кто думал бы, что алгебра может быть интересной, когда они только начинают.
Заполните рабочие листы по алгебре онлайн с помощью iPad или современного браузера Мы только что добавили еще одно измерение в наши бесплатные рабочие листы по алгебре. Теперь вы можете выполнять их без использования принтера. Все наши рабочие листы имеют две версии. Первый — это печатный рабочий лист по алгебре, оптимизированный для печати. Вторая версия представляет собой онлайн-рабочий лист по алгебре. Онлайн-версия позволяет вам использовать iPad или другие планшетные устройства для заполнения рабочих листов. Наша передовая технология использует функцию мультитач мобильных устройств. Пишите числа пальцами прямо на листах по алгебре. Онлайн-рабочие листы по алгебре также можно выполнять на настольных и портативных компьютерах при использовании современных браузеров, таких как Chrome, Safari и Firefox. Практика по алгебре 1, алгебре 2, элементарной алгебре, предварительной алгебре, средней алгебре и задачам по алгебре Какой студент не получил бы удовольствия от работы с полиномами, терминами, уравнениями и алгебраическими структурами? Я не знаю многих, кто думал бы, что алгебра может быть интересной, когда они только начинают. Опытные студенты, изучающие алгебру, обнаружат, что решение задач — это интересно. Так как же дойти до того, что алгебра будет интересной? Тебе нужно потренироваться. К счастью, у нас есть множество рабочих листов по алгебре , на которых вы можете попрактиковаться. Рабочие листы охватывают различные уровни алгебры. Существуют рабочие листы по элементарной алгебре, предварительные рабочие листы по алгебре, рабочие листы по алгебре 1, рабочие листы по алгебре 2, рабочие листы по алгебре со словами и рабочие листы по промежуточной алгебре. У меня также есть алгебраический калькулятор, который вы можете использовать, когда будете решать задачи по алгебре. Вы ищете что-то более продвинутое? Вы можете попробовать онлайн-курс «Введение в линейные модели и матричную алгебру» Гарвардского университета. Ответы предоставляются Все рабочие листы по алгебре на этом веб-сайте имеют дополнительный PDF-файл с ответами. Это позволяет учащимся проверить свою работу.
Опытные студенты, изучающие алгебру, обнаружат, что решение задач — это интересно. Так как же дойти до того, что алгебра будет интересной? Тебе нужно потренироваться. К счастью, у нас есть множество рабочих листов по алгебре , на которых вы можете попрактиковаться. Рабочие листы охватывают различные уровни алгебры. Существуют рабочие листы по элементарной алгебре, предварительные рабочие листы по алгебре, рабочие листы по алгебре 1, рабочие листы по алгебре 2, рабочие листы по алгебре со словами и рабочие листы по промежуточной алгебре. У меня также есть алгебраический калькулятор, который вы можете использовать, когда будете решать задачи по алгебре. Вы ищете что-то более продвинутое? Вы можете попробовать онлайн-курс «Введение в линейные модели и матричную алгебру» Гарвардского университета. Ответы предоставляются Все рабочие листы по алгебре на этом веб-сайте имеют дополнительный PDF-файл с ответами. Это позволяет учащимся проверить свою работу. Это также полезно для учителей, у которых мало времени, поскольку они могут упростить процесс выставления оценок.
Это также полезно для учителей, у которых мало времени, поскольку они могут упростить процесс выставления оценок. 
 (1/5)-1
(1/5)-1
 Или можно нажать кнопку Назад в меню браузера.
Или можно нажать кнопку Назад в меню браузера.
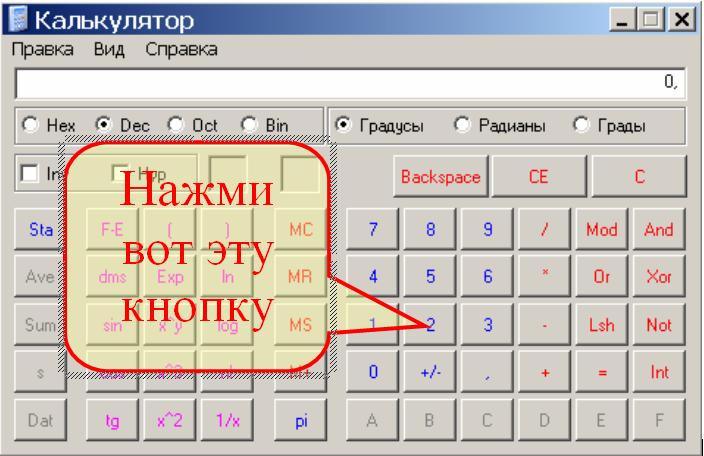 Кроме того, с помощью функции «Автоумма» можно быстро свести ряд значений, не вводя их в формулу вручную. Создав формулу, вы можете скопировать ее в смежные ячейки, не создав одну и ту же формулу раз за разом.
Кроме того, с помощью функции «Автоумма» можно быстро свести ряд значений, не вводя их в формулу вручную. Создав формулу, вы можете скопировать ее в смежные ячейки, не создав одну и ту же формулу раз за разом.
 Она также работает и по горизонтали, если вы выберете ячейку справа или слева от суммируемого диапазона.
Она также работает и по горизонтали, если вы выберете ячейку справа или слева от суммируемого диапазона.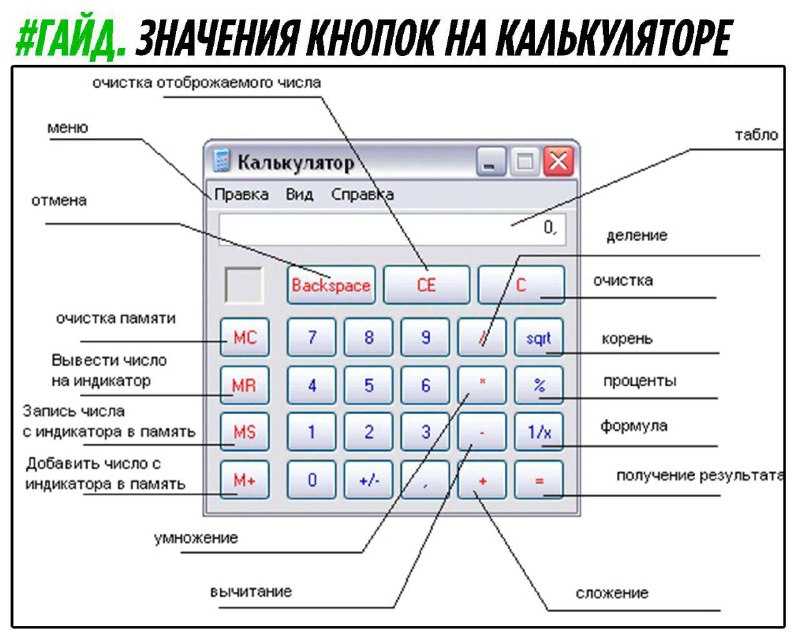 ..) Плавающий тег под функцией — это руководство Intellisense. Если щелкнуть имя функции или СУММ, изменится синяя гиперссылка на раздел справки для этой функции. Если щелкнуть отдельные элементы функции, их представительные части в формуле будут выделены. В этом случае будет выделен только B2:B5, поскольку в этой формуле есть только одна ссылка на число. Тег Intellisense будет отображаться для любой функции.
..) Плавающий тег под функцией — это руководство Intellisense. Если щелкнуть имя функции или СУММ, изменится синяя гиперссылка на раздел справки для этой функции. Если щелкнуть отдельные элементы функции, их представительные части в формуле будут выделены. В этом случае будет выделен только B2:B5, поскольку в этой формуле есть только одна ссылка на число. Тег Intellisense будет отображаться для любой функции.
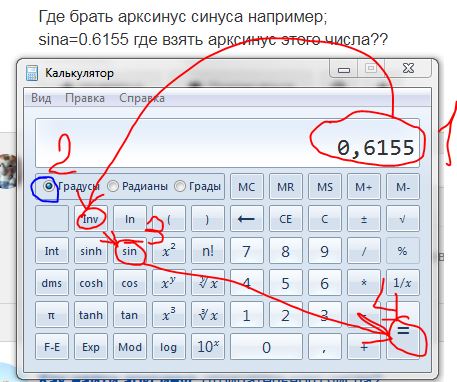 Пример: =4+6+2
Пример: =4+6+2 Пример: =8*3
Пример: =8*3 Пример: =15%*20
Пример: =15%*20
 Обратитесь к Свойству 1, упомянутому ниже, для получения дополнительных разъяснений по этому вопросу.
Обратитесь к Свойству 1, упомянутому ниже, для получения дополнительных разъяснений по этому вопросу.
 Цифровым корнем полного квадрата будет одна из четырех цифр 1, 4, 7, 9.только. Следовательно, если мы найдем любую другую цифру в качестве цифровой суммы, число точно не будет идеальным квадратом.
Цифровым корнем полного квадрата будет одна из четырех цифр 1, 4, 7, 9.только. Следовательно, если мы найдем любую другую цифру в качестве цифровой суммы, число точно не будет идеальным квадратом.
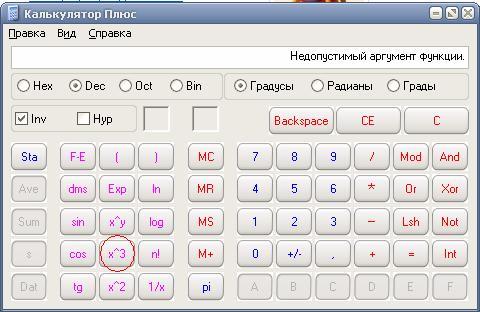
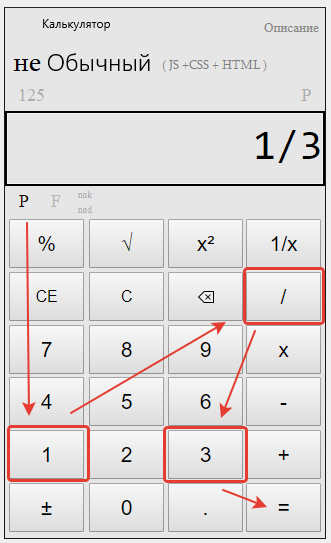
 Затем вы разделите 10 на 2, что даст вам 5. Затем вы добавите следующую цифру (0) и получите 50. Затем вы разделите 50 на 20, что даст вам 2,5. Вы продолжаете этот процесс, пока не достигнете желаемого уровня точности. Конечно, всегда достаточно просто ввести числа в онлайн-калькулятор квадратного корня выше и нажать «Рассчитать».
Затем вы разделите 10 на 2, что даст вам 5. Затем вы добавите следующую цифру (0) и получите 50. Затем вы разделите 50 на 20, что даст вам 2,5. Вы продолжаете этот процесс, пока не достигнете желаемого уровня точности. Конечно, всегда достаточно просто ввести числа в онлайн-калькулятор квадратного корня выше и нажать «Рассчитать».


 Вас ждёт курс
развития мышления, онлайн-тренажер, обучающий думать и рассуждать.
Вас ждёт курс
развития мышления, онлайн-тренажер, обучающий думать и рассуждать.

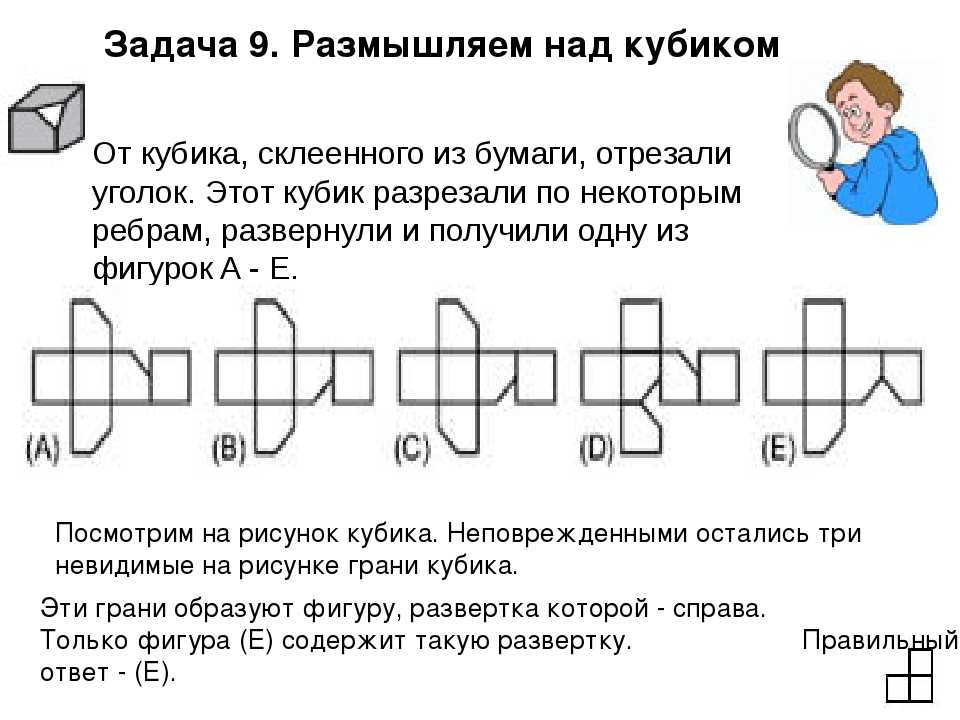
 Знакомимся
с высказываниями
Знакомимся
с высказываниями

 Значит, рыжего кота
брать не будут.
Значит, рыжего кота
брать не будут.

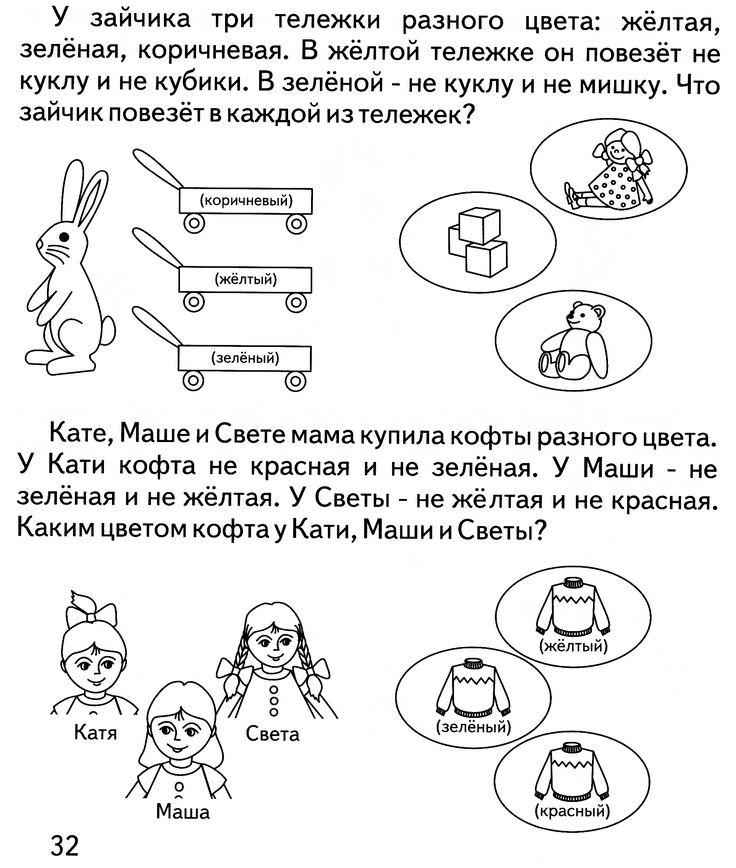 Повышаем
познавательный интерес и уверенность в себе.
Повышаем
познавательный интерес и уверенность в себе.
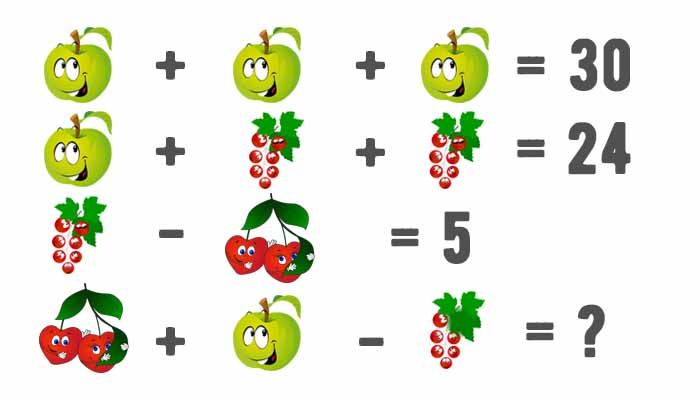

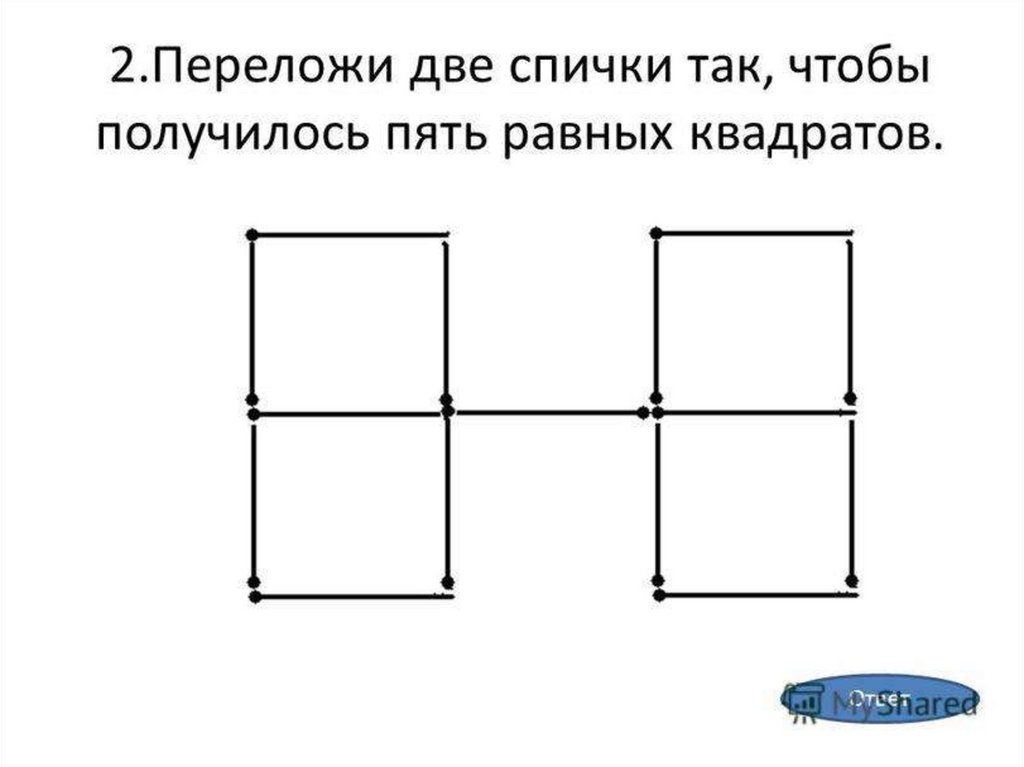
 Группировка объектов
Группировка объектов
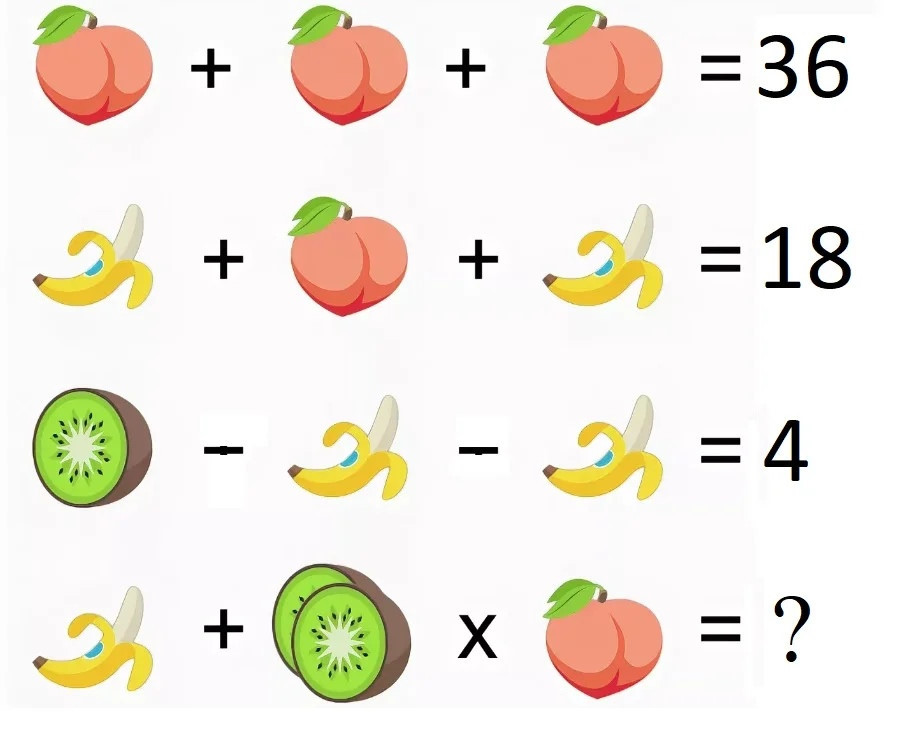

 Разбираем, рассуждаем
Разбираем, рассуждаем


 Поэтому время прокачать мозг: проверьте свои способности. Вам под силу эти логические задачи?
Поэтому время прокачать мозг: проверьте свои способности. Вам под силу эти логические задачи? Три первые из них ничем не наполнены, а три следующие – с водой. Как добиться чередования пустых чашек и чашек с водой? Касаться разрешается только одной чашки. При этом толкать чашку чашкой запрещается.
Три первые из них ничем не наполнены, а три следующие – с водой. Как добиться чередования пустых чашек и чашек с водой? Касаться разрешается только одной чашки. При этом толкать чашку чашкой запрещается. д.).
д.).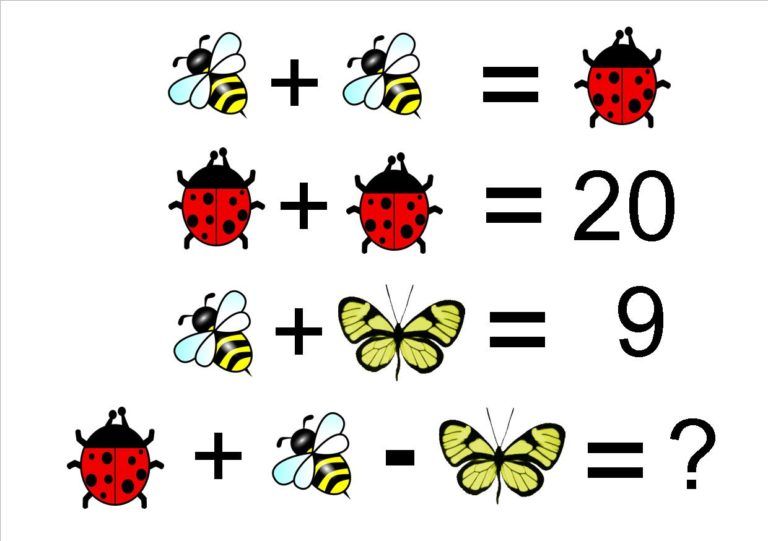 Султан приказал отправить смельчака в темницу, где вместе с ним беспрерывно будут рядом два надзирателя. Один стражник исключительно правдив в разговоре, а второй лжёт. Внутри темницы оказались два закрытых входа. Войдёшь в один – выберешь «неволю навсегда», а в другой – «освобождение». Султан предложил воину избрать один вход: если это окажется «освобождение», то пленник свободен.
Султан приказал отправить смельчака в темницу, где вместе с ним беспрерывно будут рядом два надзирателя. Один стражник исключительно правдив в разговоре, а второй лжёт. Внутри темницы оказались два закрытых входа. Войдёшь в один – выберешь «неволю навсегда», а в другой – «освобождение». Султан предложил воину избрать один вход: если это окажется «освобождение», то пленник свободен. Мёртвая вода из родников с первого по девятый доступна каждому, а десятый родник во власти Кощея в пещере, в которую он никого не впускает. По вкусу и цвету мёртвую воду не отличить от обыкновенной, однако глоток воды из родника означает смерть. Спасёт только вода из родника с номером выше. Поэтому того, кто изначально выпьет десятую воду, ничего не спасёт.
Мёртвая вода из родников с первого по девятый доступна каждому, а десятый родник во власти Кощея в пещере, в которую он никого не впускает. По вкусу и цвету мёртвую воду не отличить от обыкновенной, однако глоток воды из родника означает смерть. Спасёт только вода из родника с номером выше. Поэтому того, кто изначально выпьет десятую воду, ничего не спасёт. Вышло, что он запил яд Кощеевым десятым, что привело к нейтрализации яда.
Вышло, что он запил яд Кощеевым десятым, что привело к нейтрализации яда.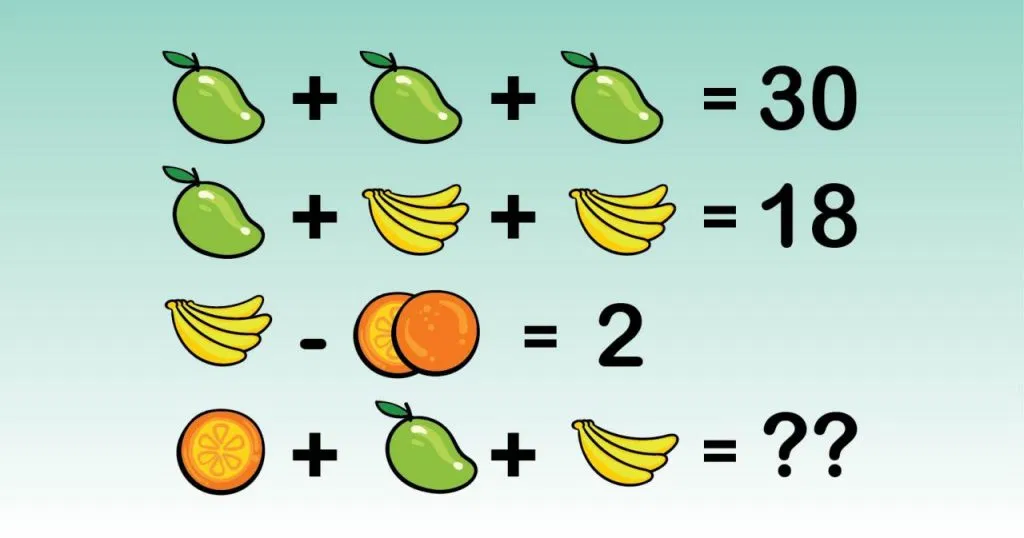 Вождь посчитал, что исключительно правильным исходом будет подарить свободу страннику.
Вождь посчитал, что исключительно правильным исходом будет подарить свободу страннику.



 Они способствуют абстрактному мышлению и побуждают учащихся критически относиться к стоящим перед ними задачам. В качестве дополнительного бонуса учащиеся, страдающие от математической тревожности, могут обнадежить отсутствие сложных уравнений и с большей готовностью попытаются найти решение.
Они способствуют абстрактному мышлению и побуждают учащихся критически относиться к стоящим перед ними задачам. В качестве дополнительного бонуса учащиеся, страдающие от математической тревожности, могут обнадежить отсутствие сложных уравнений и с большей готовностью попытаются найти решение.
 Используя переработанные крышки от бутылок, пометьте каждую цифрой от одного до девяти. Попросите учащихся расположить их в виде квадрата три на три так, чтобы сумма любых трех заглавных букв в строке (по горизонтали, вертикали и диагонали) равнялась 15.
Используя переработанные крышки от бутылок, пометьте каждую цифрой от одного до девяти. Попросите учащихся расположить их в виде квадрата три на три так, чтобы сумма любых трех заглавных букв в строке (по горизонтали, вертикали и диагонали) равнялась 15.
 (Подсказка: это требует некоторого «нестандартного» мышления.)
(Подсказка: это требует некоторого «нестандартного» мышления.)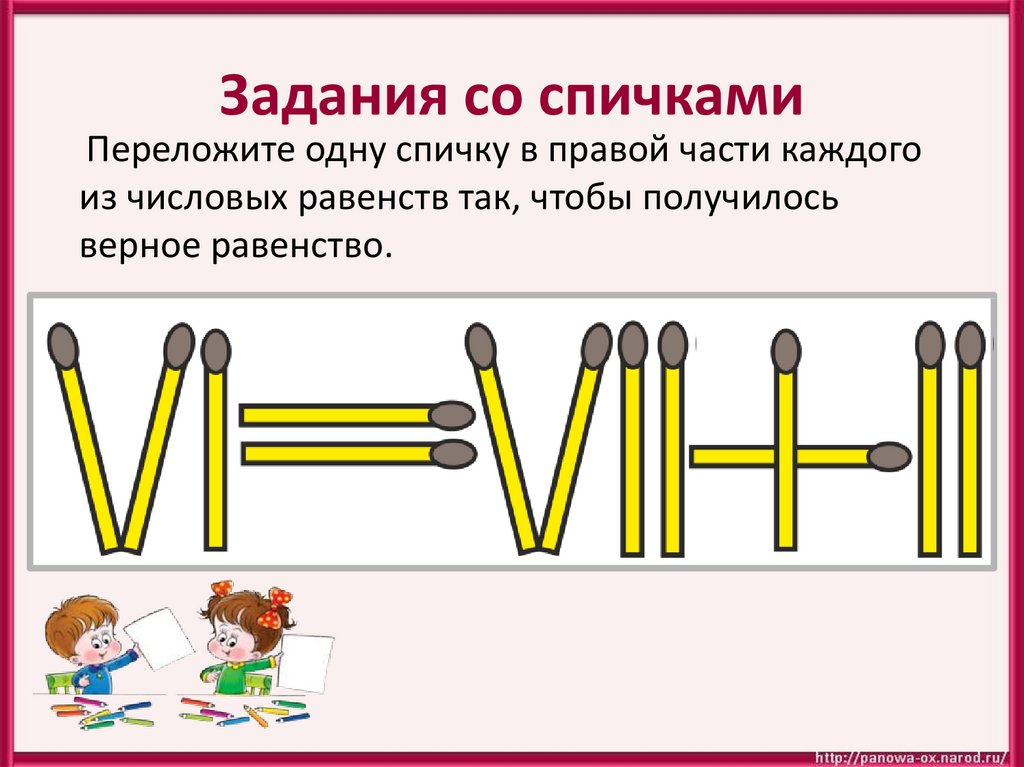
 Числа могут быть последовательными, но могут появляться в любом порядке. Например, строка может быть заполнена 5, 7, 4, 6 и 8 . Эта головоломка больше подходит для учащихся старшего возраста, и ее можно использовать в качестве задания до или после урока, чтобы укрепить основные логические навыки.
Числа могут быть последовательными, но могут появляться в любом порядке. Например, строка может быть заполнена 5, 7, 4, 6 и 8 . Эта головоломка больше подходит для учащихся старшего возраста, и ее можно использовать в качестве задания до или после урока, чтобы укрепить основные логические навыки.


 Вместо этого используйте их, чтобы закрепить понятия, которые они уже изучили.
Вместо этого используйте их, чтобы закрепить понятия, которые они уже изучили.
 Рассмотрите возможность создания еженедельной таблицы лидеров в своем классе для учеников, которые решают больше всего головоломок, или проработайте несколько вместе с классом, прежде чем отправлять учеников самостоятельно.
Рассмотрите возможность создания еженедельной таблицы лидеров в своем классе для учеников, которые решают больше всего головоломок, или проработайте несколько вместе с классом, прежде чем отправлять учеников самостоятельно.



 Можно подождать, пока вы не найдете ответ на каждую проблему, прежде чем прокрутить вниз, чтобы увидеть ответы ниже.
Можно подождать, пока вы не найдете ответ на каждую проблему, прежде чем прокрутить вниз, чтобы увидеть ответы ниже. Вы можете получить свой сегодня, нажав здесь.
Вы можете получить свой сегодня, нажав здесь.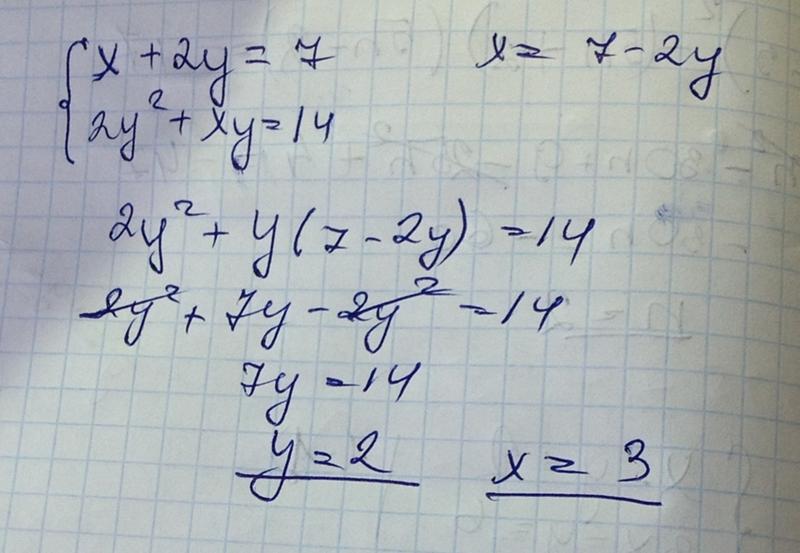 3
3 14159..
14159.. Влияние ДМСО на каталитическую активность цитохрома P450 BM3 было ранее исследовано, и была определена важность Phe87 в его устойчивости к органическим сорастворителям…
Влияние ДМСО на каталитическую активность цитохрома P450 BM3 было ранее исследовано, и была определена важность Phe87 в его устойчивости к органическим сорастворителям… Ориентация молекулы ДМСО указывает на процесс динамической координации, который конкурирует с молекулой воды в активном центре. Способность молекулы ДМСО координировать железо гема, вероятно, является основной причиной, по которой P450 BM3 инактивируется при повышенных концентрациях ДМСО. Данные позволили провести интересное сравнение со структурами дикого типа, о которых сообщалось ранее. Молекула ДМСО была обнаружена, когда белок дикого типа был помещен в 28% (об./об.) ДМСО, в котором молекула ДМСО координировала железо гема непосредственно через его атом S. Интересно, что молекулы ДМСО не наблюдали при 14% (об./об.) ДМСО для структуры дикого типа. Эти результаты свидетельствуют о том, что объемная фенильная боковая цепь Phe87 защищает гем от доступа молекулы ДМСО и объясняет более высокую толерантность фермента дикого типа к органическим сорастворителям по сравнению с его вариантом F87A.
Ориентация молекулы ДМСО указывает на процесс динамической координации, который конкурирует с молекулой воды в активном центре. Способность молекулы ДМСО координировать железо гема, вероятно, является основной причиной, по которой P450 BM3 инактивируется при повышенных концентрациях ДМСО. Данные позволили провести интересное сравнение со структурами дикого типа, о которых сообщалось ранее. Молекула ДМСО была обнаружена, когда белок дикого типа был помещен в 28% (об./об.) ДМСО, в котором молекула ДМСО координировала железо гема непосредственно через его атом S. Интересно, что молекулы ДМСО не наблюдали при 14% (об./об.) ДМСО для структуры дикого типа. Эти результаты свидетельствуют о том, что объемная фенильная боковая цепь Phe87 защищает гем от доступа молекулы ДМСО и объясняет более высокую толерантность фермента дикого типа к органическим сорастворителям по сравнению с его вариантом F87A.
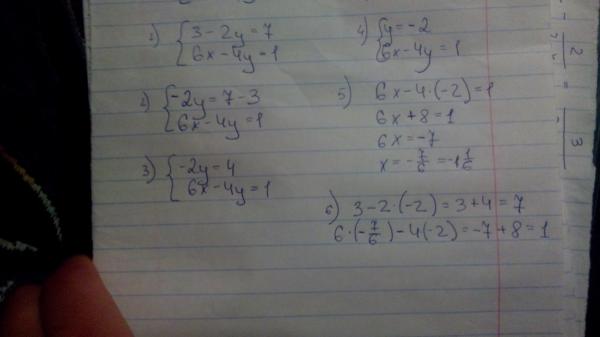 11.
11.