Базовые алгоритмы нахождения кратчайших путей во взвешенных графах / Хабр
Наверняка многим из гейм-девелоперов (или просто людям, увлекающимися програмировагнием) будет интересно услышать эти четыре важнейших алгоритма, решающих задачи о кратчайших путях.
Сформулируем определения и задачу.
Графом будем называть несколько точек (вершин), некоторые пары которых соединены отрезками (рёбрами). Граф связный, если от каждой вершины можно дойти до любой другой по этим отрезкам. Циклом назовём какой-то путь по рёбрам графа, начинающегося и заканчивающегося в одной и той же вершине. И ещё граф называется взвешенным, если каждому ребру соответствует какое-то число (вес). Не может быть двух рёбер, соединяющих одни и те же вершины.
Каждый из алгоритмов будет решать какую-то задачу о кратчайших путях на взвешенном связном. Кратчайший путь из одной вершины в другую — это такой путь по рёбрам, что сумма весов рёбер, по которым мы прошли будет минимальна. 3 операций.
3 операций.
Псевдокод:
прочитать g // g[0 ... n - 1][0 ... n - 1] - массив, в котором хранятся веса рёбер, g[i][j] = 2000000000, если ребра между i и j нет
d = g
for i = 1 ... n + 1
for j = 0 ... n - 1
for k = 0 ... n - 1
if d[j][k] > d[j][i - 1] + d[i - 1][k]
d[j][k] = d[j][i - 1] + d[i - 1][k]
вывести d
Алгоритм Форда-Беллмана
Находит расстояние от одной вершины (дадим ей номер 0) до всех остальных за количество операций порядка n * m. Аналогично предыдущему алгоритму, веса могут быть отрицательными, но у нас не может быть циклов с отрицательной суммой весов рёбер.
Заведём массив d[0… n — 1], в котором на i-ой итерации будем хранить ответ на исходную задачу с ограничением на то, что в путь должно входить строго меньше i рёбер. Если таких путей до вершины j нет, то d[j] = 2000000000 (это должна быть какая-то недостижимая константа, «бесконечность»).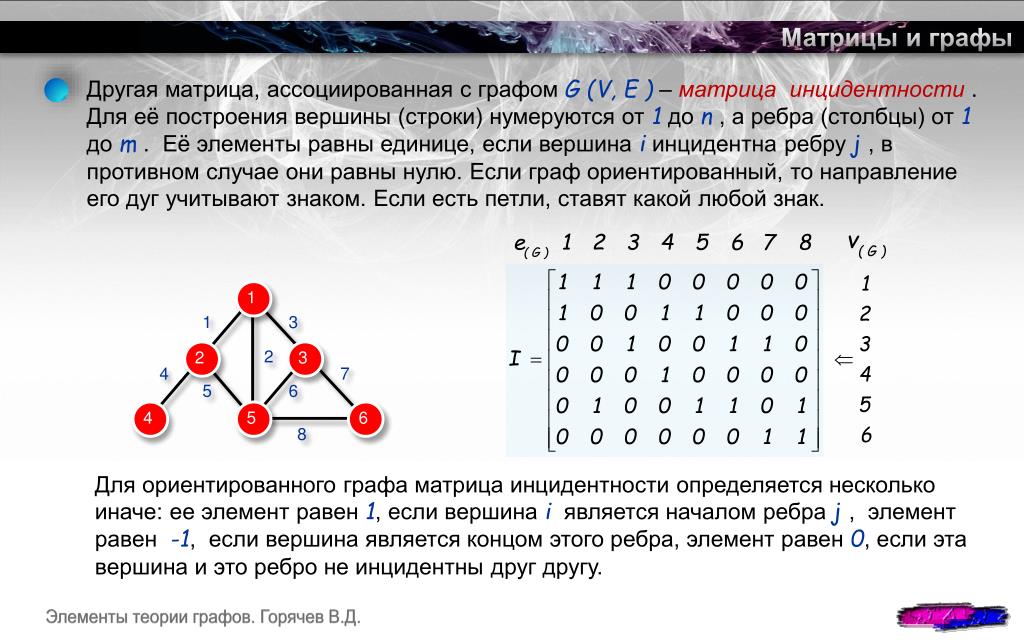 В самом начале d заполнен 2000000000. Чтобы обновлять на i-ой итерации массив, надо просто пройти по каждому ребру и попробовать улучшить расстояние до вершин, которые оно соединяет. Кратчайшие пути не содержат циклов, так как все циклы неотрицательны, и мы можем убрать цикл из путя, при этом длина пути не ухудшится (хочется также отметить, что именно так можно найти отрицательные циклы в графе: надо сделать ещё одну итерацию и посмотреть, не улучшилось ли расстояние до какой-нибудь вершины). Поэтому длина кратчайшего пути не больше n — 1, значит, после n-ой итерации d будет ответом на задачу.
В самом начале d заполнен 2000000000. Чтобы обновлять на i-ой итерации массив, надо просто пройти по каждому ребру и попробовать улучшить расстояние до вершин, которые оно соединяет. Кратчайшие пути не содержат циклов, так как все циклы неотрицательны, и мы можем убрать цикл из путя, при этом длина пути не ухудшится (хочется также отметить, что именно так можно найти отрицательные циклы в графе: надо сделать ещё одну итерацию и посмотреть, не улучшилось ли расстояние до какой-нибудь вершины). Поэтому длина кратчайшего пути не больше n — 1, значит, после n-ой итерации d будет ответом на задачу.
n итераций по m итераций, итого порядка n * m операций.
Псевдокод:
прочитать e // e[0 ... m - 1] - массив, в котором хранятся рёбра и их веса (first, second - вершины, соединяемые ребром, value - вес ребра)
for i = 0 ... n - 1
d[i] = 2000000000
d[0] = 0
for i = 1 ... n
for j = 0 ... m - 1
if d[e[j].second] > d[e[j].first] + e[j].value
d[e[j]. 2. Все веса неотрицательны.
2. Все веса неотрицательны.
На каждой итерации какие-то вершины будут помечены, а какие-то нет. Заведём два массива: mark[0… n — 1] — True, если вершина помечена, False иначе, d[0… n — 1] — для каждой вершины будет храниться длина кратчайшего пути, проходящего только по помеченным вершинам в качестве «пересадочных». Также поддерживается инвариант того, что для помеченных вершин длина, указанная в d, и есть ответ. Сначала помечена только вершина 0, а g[i] равно x, если 0 и i соединяет ребро весом x, равно 2000000000, если их не соединяет ребро, и равно 0, если i = 0.
На каждой итерации мы находим вершину, с наименьшим значением в d среди непомеченных, пусть это вершина v. Тогда значение d[v] является ответом для v. Докажем. Пусть, кратчайший путь до v из 0 проходит не только по помеченным вершинам в качестве «пересадочных», и при этом он короче d[v]. Возьмём первую встретившуюся непомеченную вершину на этом пути, назовём её u. Длина пройденной части пути (от 0 до u) — d[u]. 2, то есть эта вариация алгоритма Дейкстры не всегда быстрее классической, а только при маленьких m.
2, то есть эта вариация алгоритма Дейкстры не всегда быстрее классической, а только при маленьких m.
Что нам нужно в алгоритме Дейкстры? Нам нужно уметь находить по значению d минимальную вершину и уметь обновлять значение d в какой-то вершине. В классической реализации мы пользуемся простым массивом, находить минимальную по d вершину мы можем за порядка n операций, а обновлять — за 1 операцию. Воспользуемся двоичной кучей (во многих объектно-ориентированных языках она встроена). Куча поддерживает операции: добавить в кучу элемент (за порядка log(n) операций), найти минимальный элемент (за 1 операцию), удалить минимальный элемент (за порядка log(n) операций), где n — количество элементов в куче.
Создадим массив d[0… n — 1] (его значение то же самое, что и раньше) и кучу q. В куче будем хранить пары из номера вершины v и d[v] (сравниваться пары должны по d[v]). Также в куче могут быть фиктивные элементы. Так происходит, потому что значение d[v] обновляется, но мы не можем изменить его в куче. Поэтому в куче могут быть несколько элементов с одинаковым номером вершины, но с разным значением d (но всего вершин в куче будет не более m, я гарантирую это). Когда мы берём минимальное значение в куче, надо проверить, является ли этот элемент фиктивным. Для этого достаточно сравнить значение d в куче и реальное его значение. А ещё для записи графа вместо двоичного массива используем массив списков.
Поэтому в куче могут быть несколько элементов с одинаковым номером вершины, но с разным значением d (но всего вершин в куче будет не более m, я гарантирую это). Когда мы берём минимальное значение в куче, надо проверить, является ли этот элемент фиктивным. Для этого достаточно сравнить значение d в куче и реальное его значение. А ещё для записи графа вместо двоичного массива используем массив списков.
m раз добавляем элемент в кучу, получаем порядка m * log(n) операций.
Псевдокод:прочитать g // g[0 ... n - 1] - массив списков, в i-ом списке хранятся пары: first - вершина, соединённая с i-ой вершиной ребром, second - вес этого ребра
d[0] = 0
for i = 0 ... n - 1
d[i] = 2000000000
for i in g[0] // python style
d[i.first] = i.second
q.add(pair(i.second, i.first))
for i = 1 ... n - 1
v = -1
while (v = -1) or (d[v] != val)
v = q.top.second
val = q.top.first
q.removeTop
mark[v] = true
for i in g[v]
if d[i.first] > d[v] + i. second
d[i.first] = d[v] + i.second
q.add(pair(d[i.first], i.first))
вывести d
second
d[i.first] = d[v] + i.second
q.add(pair(d[i.first], i.first))
вывести d
Алгоритм Дейкстры - поиск кратчайшего пути в графе
Алгоритм Дейкстры — это метод, который находит кратчайший путь от одной вершины графа к другой. Граф — структура из точек-вершин, соединенных ребрами-отрезками. Его можно представить как схему дорог или как компьютерную сеть. Ребра — это связи, по ним можно двигаться от одной вершины к другой.
Графы используют для моделирования реальных объектов, а алгоритмы поиска пути — при их изучении, а также решении практических задач. Алгоритм Дейкстры работает для графов, у которых нет ребер с отрицательным весом, т.е. таких, при прохождении через которые длина пути как бы уменьшается.
В отличие от похожих методов, алгоритм Дейкстры ищет оптимальный маршрут от одной заданной вершины ко всем остальным. Попутно он высчитывает длину пути — суммарный вес ребер, по которым проходит при этом маршруте.
Кто пользуется алгоритмом Дейкстры
- Математики и другие ученые, которые пользуются графами как абстрактными единицами.
 Задача поиска маршрута в науке может быть и чисто фундаментальной, и прикладной.
Задача поиска маршрута в науке может быть и чисто фундаментальной, и прикладной. - Дата-сайентисты. В этой области много математики, в том числе активно используется теория графов.
- Сетевые инженеры, так как алгоритм Дейкстры лежит в основе работы нескольких протоколов маршрутизации. Сама по себе компьютерная сеть представляет собой граф, поэтому специалисты по сетям должны знать, что это такое.
Зачем нужен алгоритм Дейкстры
Основная задача — поиск кратчайшего пути по схеме, где множество точек соединено между собой отрезками. В виде такой схемы можно представить многие объекты реального мира, поэтому практических примеров использования алгоритма много:
- автоматическое построение маршрута на онлайн-карте;
- поиск системой бронирования наиболее быстрых или дешевых билетов, в том числе с возможными пересадками;
- моделирование движения робота, который перемещается по местности;
- разработка поведения неигровых персонажей, создание игрового ИИ в геймдеве;
- автоматическая обработка транспортных потоков;
- маршрутизация движения данных в компьютерной сети;
- расчет движения тока по электрическим цепям.

Как работает алгоритм
Алгоритм Дейкстры пошаговый. Сначала выбирается точка, от которой будут отсчитываться пути. Затем алгоритм поочередно ищет самые короткие маршруты из исходной точки в другие. Вершины, где он уже побывал, отмечает посещенными. Алгоритм использует посещенные вершины, когда рассчитывает пути для непосещенных.
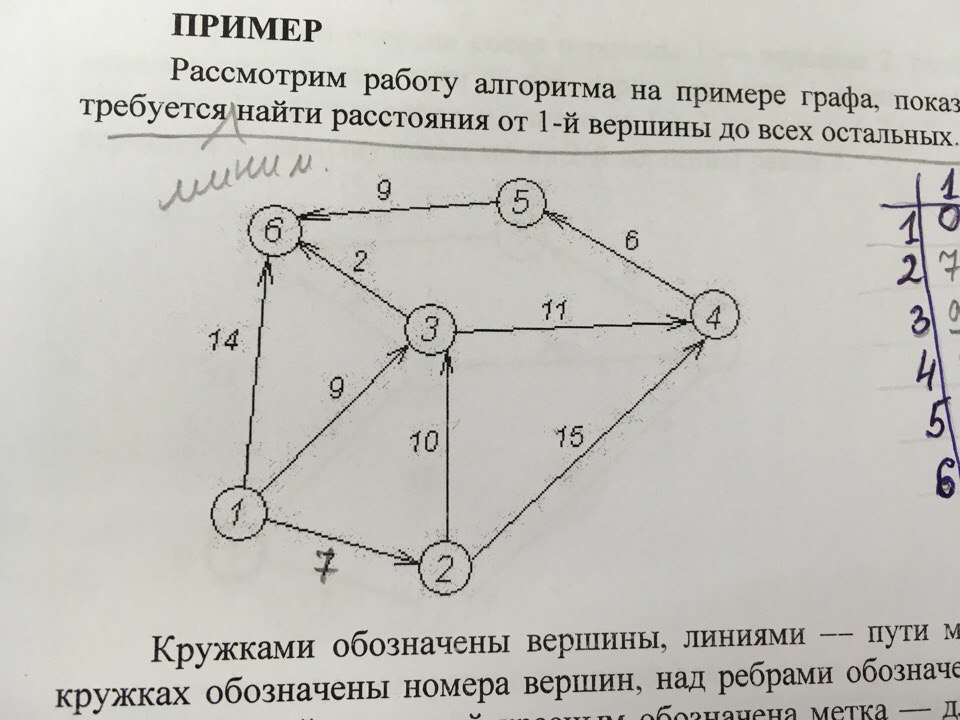
Это может звучать сложно, поэтому мы хотим показать вам, как это выглядит на примере. Возьмем такой граф: цифрами в кружках обозначены вершины, а числа возле ребер — это вес путей между ними.
Инициализация. Пусть вершиной, из которой мы будем считать маршруты, будет 0. Расстояние до самой себя у этой вершины логично равно нулю. Остальные мы пока не знаем, поэтому отметим символом бесконечности.
Расстояние от 0 до 0 помечаем равным нулю, а саму вершину — посещенной.
Первый шаг алгоритма. Мы выбираем еще не посещенную вершину с самой маленькой меткой относительно исходной — то есть такую, которая находится ближе всех. На первом шаге это одна из соседних вершин — та, которая соединена с исходной самым «маленьким» ребром.
На первом шаге это одна из соседних вершин — та, которая соединена с исходной самым «маленьким» ребром.
Для графа, который мы рассматриваем, это точка 2. Мы выбираем ее, «переходим» в нее и смотрим уже на ее соседей.
Дальнейшие шаги алгоритма. Для выбранной точки нужно осмотреть соседей и записать длину пути до них с учетом пройденного пути. А потом выбрать ближнюю точку. Но есть нюанс: нужно учитывать точки, которые мы уже использовали в прошлый раз. Если они дают более «выгодный» путь, лучше воспользоваться ими.
Например, на выбранном графе есть точка 1. В нее можно перейти из точки 2, где мы находимся. Но этот путь будет длиннее, чем при переходе напрямую из точки 0, а ведь она для нас исходная. Поэтому «короткий путь» для точки 1 — это маршрут 0–1. Отмечаем вершину посещенной.
Шаги повторяются, пока на графе есть непосещенные точки. Если вершину не посетили, она не участвует в расчетах. Если после ее «открытия» появился новый, более короткий путь к какой-либо точке, то минимальное расстояние для нее перезаписывается.
Конец алгоритма. Когда непосещенные вершины заканчиваются, алгоритм прекращает работу. Результат его действия — список кратчайших маршрутов до каждой точки из исходной. Для каждого маршрута указана его длина.
Мы говорим «длина», но это условно. Например, при поиске билетов в роли веса ребра может выступать их цена, а при организации электрической цепи — расход электроэнергии.
Теория графов — обширная отрасль дискретной математики. Ее используют во множестве сфер, от химии до разработки. В профильных университетах теорию графов изучают на курсе дискретной математики. Также получить базу знаний и решать практические задачи под контролем наставника можно на курсах SkillFactory.
Кратчайший путь | Математика для гуманитарных наук
Результаты обучения
- Определение вершин, ребер и петель графа
- Определить степень вершины
- Определить и нарисовать как путь, так и цепь через граф
- Определить, подключен граф или нет
- Найдите кратчайший путь через граф с помощью алгоритма Дейкстры
Когда вы посещаете веб-сайт, такой как Google Maps, или используете свой смартфон, чтобы узнать дорогу от дома до дома вашей тети в Пасадене, вы обычно ищете кратчайший путь между двумя точками. Эти компьютерные приложения используют представления карт улиц в виде графиков с расчетным временем в пути в качестве весовых коэффициентов.
Эти компьютерные приложения используют представления карт улиц в виде графиков с расчетным временем в пути в качестве весовых коэффициентов.
Хотя часто можно найти кратчайший путь на небольшом графе методом угадывания и проверки, наша цель в этой главе — разработать методы для систематического решения сложных задач, следуя алгоритмам . Алгоритм — это пошаговая процедура решения проблемы. Алгоритм Дейкстры (произносится как дайк-стра) найдет кратчайший путь между двумя вершинами.
Алгоритм Дейкстры
1. Отметьте конечную вершину нулевым расстоянием. Назовите эту вершину текущей.
2. Найти все вершины, ведущие к текущей вершине. Вычислите их расстояния до конца. Поскольку мы уже знаем, на каком расстоянии от конца находится текущая вершина, потребуется просто добавить самое последнее ребро. Не записывайте это расстояние, если оно больше, чем ранее записанное расстояние.
3. Отметить текущую вершину как посещенную. Мы больше никогда не будем смотреть на эту вершину.
Мы больше никогда не будем смотреть на эту вершину.
4. Отметьте вершину с наименьшим расстоянием как текущую и повторите действия, начиная с шага 2.
ПРИМЕР
Предположим, вам нужно проехать из Такомы, штат Вашингтон (вершина T), в Якима, штат Вашингтон (вершина Y). Глядя на карту, кажется, что ехать через Оберн (A), а затем через Маунт-Рейнир (MR) может быть кратчайшим, но это не совсем ясно, поскольку эта дорога, вероятно, медленнее, чем ехать по главному шоссе через Норт-Бенд (NB). Ниже показан график времени в пути в минутах. Также показан альтернативный маршрут через Итонвилль (E) и Паквуд (P).
Шаг 1: Отметьте конечную вершину нулевым расстоянием. Расстояния будут записаны в [скобках] после имени вершины
Шаг 2: Для каждой вершины, ведущей к Y, мы вычисляем расстояние до конца. Например, NB — это расстояние 104 от конца, а MR — 96 от конца. Помните, что расстояния в данном случае относятся к времени в пути в минутах.
Шаг 3 и 4: Мы отмечаем Y как посещенную и отмечаем вершину с наименьшим записанным расстоянием как текущую. В этот момент P будет обозначаться текущим. Вернемся к шагу 2.
В этот момент P будет обозначаться текущим. Вернемся к шагу 2.
Шаг 2 (#2): Для каждой вершины, ведущей в P (и не ведущей в посещенную вершину), мы находим расстояние от конца. Так как Е равно 96 минут от P, и мы уже подсчитали, что P составляет 76 минут от Y, мы можем вычислить, что E составляет 96+76 = 172 минуты от Y. и обозначим вершину с наименьшим зарегистрированным расстоянием как текущую: MR. Вернемся к шагу 2.
Шаг 2 (#3): Для каждой вершины, ведущей в MR (и не ведущей в посещенную вершину), мы находим расстояние до конца. Единственная рассматриваемая вершина — это A, так как мы уже посетили Y и P. Добавление расстояния MR 96 к длине от A до MR дает расстояние 96+79 = 175 минут от A до Y.
Шаги 3 и 4 (#3): Мы помечаем MR как посещенную и обозначаем вершину с наименьшим зарегистрированным расстоянием как текущую: NB. Вернемся к шагу 2.
Шаг 2 (№4): Для каждой вершины, ведущей к NB, мы находим расстояние до конца. Мы знаем, что кратчайшее расстояние от NB до Y равно 104, а расстояние от A до NB равно 36, поэтому расстояние от A до Y через NB равно 104+36 = 140. Так как это расстояние короче рассчитанного ранее расстояния от Y до А через MR, заменяем.
Так как это расстояние короче рассчитанного ранее расстояния от Y до А через MR, заменяем.
Шаги 3 и 4 (#4): Мы помечаем NB как посещенный и обозначаем A как текущий, так как теперь он имеет кратчайшее расстояние.
Шаг 2 (#5): T — единственная непосещаемая вершина, ведущая к A, поэтому мы вычисляем расстояние от T до Y через A: 20+140 = 160 минут.
Шаг 3 и 4 (#5): Мы помечаем A как посещенный, а E — как текущий.
Шаг 2 (#6): Единственная непосещаемая вершина, ведущая к E, — это T. Вычисляя расстояние от T до Y через E, мы вычисляем 172+57 = 229минут. Поскольку это больше, чем существующее отмеченное время, мы не заменяем его.
Шаг 3 (#6): Мы отмечаем E как посещенный. Поскольку все вершины были посещены, мы закончили.
Отсюда мы знаем, что кратчайший путь от Такомы до Якимы займет 160 минут. Отслеживая, какая последовательность ребер дала 160 минут, мы видим, что кратчайший путь — это T-A-NB-Y.
Алгоритм Дейкстры является оптимальным алгоритмом , а это означает, что он всегда выдает фактический кратчайший путь, а не просто довольно короткий путь, если он существует.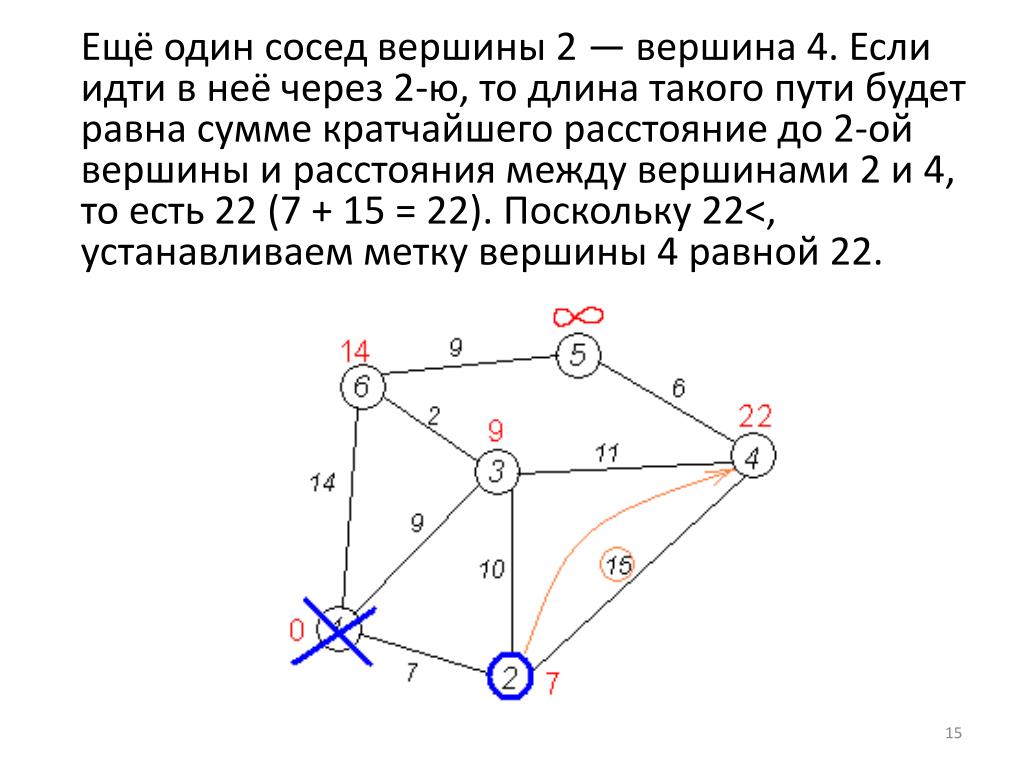 Этот алгоритм тоже эффективен , что означает, что его можно реализовать за разумное время. Алгоритм Дейкстры требует около V2 вычислений, где V — количество вершин в графе[1]. Граф со 100 вершинами потребует около 10 000 вычислений. В то время как это было бы много, чтобы сделать вручную, это не так уж много для компьютера. Именно благодаря этой эффективности GPS-устройство вашего автомобиля может вычислить направление движения всего за несколько секунд.
Этот алгоритм тоже эффективен , что означает, что его можно реализовать за разумное время. Алгоритм Дейкстры требует около V2 вычислений, где V — количество вершин в графе[1]. Граф со 100 вершинами потребует около 10 000 вычислений. В то время как это было бы много, чтобы сделать вручную, это не так уж много для компьютера. Именно благодаря этой эффективности GPS-устройство вашего автомобиля может вычислить направление движения всего за несколько секунд.
[1] Его можно ускорить за счет различных оптимизаций реализации.
Напротив, неэффективный алгоритм может попытаться перечислить все возможные пути, а затем вычислить длину каждого пути. Попытка перечислить все возможные пути может легко потребовать 1025 вычислений для вычисления кратчайшего пути всего с 25 вершинами; это 1 с 25 нулями после нее! Для сравнения, самый быстрый компьютер в мире все равно потратил бы более 1000 лет на анализ всех этих путей.
ПРИМЕР
Транспортной компании необходимо направить посылку из Вашингтона, округ Колумбия, в Сан-Диего, Калифорния. Чтобы свести к минимуму затраты, посылка сначала будет отправлена в их центр обработки в Балтиморе, штат Мэриленд, а затем отправлена в рамках массовых поставок между их различными центрами обработки и в конечном итоге окажется в их центре обработки в Бейкерсфилде, Калифорния. Оттуда он будет доставлен на небольшом грузовике в Сан-Диего.
Чтобы свести к минимуму затраты, посылка сначала будет отправлена в их центр обработки в Балтиморе, штат Мэриленд, а затем отправлена в рамках массовых поставок между их различными центрами обработки и в конечном итоге окажется в их центре обработки в Бейкерсфилде, Калифорния. Оттуда он будет доставлен на небольшом грузовике в Сан-Диего.
Время в пути в часах между их центрами обработки показано в таблице ниже. К каждому времени в пути было добавлено три часа для обработки. Найдите кратчайший путь из Балтимора в Бейкерсфилд.
| Балтимор | Денвер | Даллас | Чикаго | Атланта | Бейкерсфилд | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Хотя мы могли бы нарисовать график, мы также можем работать непосредственно с таблицей.
Шаг 1: Конечная вершина Бейкерсфилд помечается как текущая.
Шаг 2: Все города, связанные с Бейкерсфилдом, в данном случае Денвер и Даллас, рассчитываются по расстоянию; мы отметим эти расстояния в заголовках столбцов.
Шаг 3 и 4: Отметьте Бейкерсфилд как посещенный. Здесь мы делаем это, затеняя соответствующую строку и столбец таблицы. Мы помечаем Денвер как текущий, выделенный жирным шрифтом, так как это вершина с кратчайшим расстоянием.
| Балтимор
| Денвер [19] | Даллас [25] | Чикаго | Атланта | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#2): Для городов, связанных с Денвером, рассчитайте расстояние до конца. Например, Чикаго находится в 18 часах от Денвера, а Денвер — в 19 часах от конца, расстояние от Чикаго до конца составляет 18+19 = 37 (от Чикаго до Денвера до Бейкерсфилда). Атланта находится в 24 часах от Денвера, поэтому расстояние до конца равно 24+19 = 43 (от Атланты до Денвера до Бейкерсфилда).
Например, Чикаго находится в 18 часах от Денвера, а Денвер — в 19 часах от конца, расстояние от Чикаго до конца составляет 18+19 = 37 (от Чикаго до Денвера до Бейкерсфилда). Атланта находится в 24 часах от Денвера, поэтому расстояние до конца равно 24+19 = 43 (от Атланты до Денвера до Бейкерсфилда).
Шаг 3 и 4 (#2): Мы отмечаем Денвер как посещенный и помечаем Даллас как текущий.
| Балтимор
| Денвер [19] | Даллас [25] | Чикаго [37] | Атланта [43] | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#3): Для городов, связанных с Далласом, рассчитайте расстояние до конца. Для Чикаго расстояние от Чикаго до Далласа равно 18, а от Далласа до конца — 25, поэтому расстояние от Чикаго до конца через Даллас будет 18 + 25 = 43. Поскольку это больше, чем отмеченное в настоящее время расстояние для Чикаго, мы не заменяем его. Для Атланты мы вычисляем 15+25 = 40. Так как это меньше, чем текущее отмеченное расстояние для Атланты, мы заменяем существующее расстояние.
Для Чикаго расстояние от Чикаго до Далласа равно 18, а от Далласа до конца — 25, поэтому расстояние от Чикаго до конца через Даллас будет 18 + 25 = 43. Поскольку это больше, чем отмеченное в настоящее время расстояние для Чикаго, мы не заменяем его. Для Атланты мы вычисляем 15+25 = 40. Так как это меньше, чем текущее отмеченное расстояние для Атланты, мы заменяем существующее расстояние.
Шаг 3 и 4 (#3): Мы отмечаем Даллас как посещенный, а Чикаго как текущий.
| Балтимор
| Денвер [19] | Даллас [25] | Чикаго [37] | Атланта [40] | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#4): Балтимор и Атланта — единственные непосещаемые города, связанные с Чикаго. Для Балтимора мы вычисляем 15+37 = 52 и отмечаем это расстояние. Для Атланты мы вычисляем 14+37 = 51. Поскольку это больше, чем существующее расстояние 40 для Атланты, мы не заменяем это расстояние.
Для Балтимора мы вычисляем 15+37 = 52 и отмечаем это расстояние. Для Атланты мы вычисляем 14+37 = 51. Поскольку это больше, чем существующее расстояние 40 для Атланты, мы не заменяем это расстояние.
Шаг 3 и 4 (#4): Отметьте Чикаго как посещенный, а Атланту как текущий.
| Балтимор [52] | Денвер [19] | Даллас [25] | Чикаго [37] | Атланта [40] | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#5): Расстояние от Атланты до Балтимора равно 14. Прибавив это к расстоянию, уже рассчитанному для Атланты, мы получим общее расстояние 14+40 = 54 часа от Балтимора до Бейкерсфилда через Атланту. Так как это больше рассчитываемого в настоящее время расстояния, мы не заменяем расстояние для Балтимора.
Прибавив это к расстоянию, уже рассчитанному для Атланты, мы получим общее расстояние 14+40 = 54 часа от Балтимора до Бейкерсфилда через Атланту. Так как это больше рассчитываемого в настоящее время расстояния, мы не заменяем расстояние для Балтимора.
Шаг 3 и 4 (#5): Мы отмечаем Атланту как посещенную. Все города были посещены, и мы закончили.
Самый короткий маршрут из Балтимора в Бейкерсфилд займет 52 часа и пройдет через Чикаго и Денвер.
Попробуйте
- Найдите кратчайший путь между вершинами A и G на приведенном ниже графике.
В следующем видео обобщены темы, затронутые на этой странице.
Введение в графики | Типы графиков
Введение
«В графиках есть магия. Профиль кривой мгновенно раскрывает всю ситуацию — историю жизни эпохи процветания.
Кривая информирует ум, пробуждает воображение, убеждает».
– Генри Д. Хаббард
Визуализация — это мощный способ упростить и интерпретировать лежащие в основе шаблоны данных. Первое, что я делаю, когда работаю над новым набором данных, — это исследую его с помощью визуализации. И этот подход хорошо сработал для меня. К сожалению, я не вижу, чтобы многие люди так активно использовали визуализацию. Вот почему я подумал, что поделюсь с миром частью своего «секретного соуса»!
Использование графиков является одним из таких методов визуализации. Это невероятно полезно и помогает компаниям принимать более обоснованные решения на основе данных. Но чтобы детально понять концепции графов, мы должны сначала понять их основу — теорию графов.
В этой статье мы будем изучать концепции графов и теории графов. Мы также рассмотрим основы и основные свойства графов, а также различные типы графов.
Затем мы будем работать над конкретным примером, чтобы решить часто встречающуюся проблему в авиационной отрасли, применяя концепции теории графов с использованием Python.
Начнем!
Содержание
- Знакомство с графиками
- Почему графики?
- Происхождение теории графов: семь мостов Кенигсберга
- Основы графиков
- Основные свойства и терминология, относящиеся к графикам
- Типы графиков
- Продолжение задачи о семи мостах Кенигсберга
- Знакомство с деревьями
- Обход графа
- Реализация концепций теории графов для решения задачи авиакомпаний
Введение в графики 907:10
Рассмотрим график, показанный ниже:
Это хорошая визуализация продаж определенного товара в магазине. Но это не график, это график. Теперь вам может быть интересно, почему это диаграмма, а не график, верно?
Диаграмма представляет собой график функции. Позвольте мне объяснить это, расширив приведенный выше пример.
Из общего количества единиц определенного товара 15,1% продается в магазине А, 15,4% — в магазине Б и так далее. Мы можем представить это с помощью таблицы:
Мы можем представить это с помощью таблицы:
Каждому магазину соответствует его вклад (в %) в общий объем продаж. На приведенной выше диаграмме мы сопоставили магазин A с вкладом 15,1%, магазин B с 15,4% и т. д. и т. д. Наконец, мы визуализировали это с помощью круговой диаграммы. Но тогда в чем разница между этой диаграммой и графиком?
Чтобы ответить на этот вопрос, рассмотрите изображение, показанное ниже:
Точки на изображении выше представляют персонажей Игры престолов, а линии, соединяющие эти точки, представляют собой связь между ними. У Джона Сноу есть связи с несколькими персонажами, и то же самое касается Тириона, Серсеи, Джейми и т. д.
А вот так выглядит график. Одна точка может иметь соединения с несколькими точками или даже с одной точкой. Обычно граф представляет собой комбинацию вершин (узлов) и ребер. В представленном выше GOT-визуале все символы являются вершинами, а соединения между ними — ребрами.
Теперь у нас есть представление о том, что такое графы, но зачем нам вообще нужны графы? Мы рассмотрим этот актуальный вопрос в следующем разделе.
Почему графики? 907:10
Предположим, вы заказали такси Uber. Одна из самых важных вещей, которая имеет решающее значение для функционирования Uber, — это его способность эффективно подбирать водителей с пассажирами. Учтите, что есть 6 возможных аттракционов, с которыми вы можете совпасть. Итак, как Uber выделяет вам поездку? Мы можем использовать графики, чтобы визуализировать процесс распределения поездок:
Как вы понимаете, существует 6 возможных аттракционов (Поездка 1, Поездка 2, …. Поездка 6), с которыми может сочетаться всадник. Представление этого в виде графика упрощает визуализацию и, наконец, достижение нашей цели, то есть сопоставление ближайшей поездки к пользователю. Числа на приведенном выше графике представляют собой расстояние (в километрах) между гонщиком и его/ее соответствующей поездкой. Мы (и, конечно же, Uber) можем ясно представить, что Ride 3 — ближайший вариант.
Примечание. Для простоты я использовал только показатель расстояния, чтобы решить, какая поездка будет назначена гонщику. В то время как в реальном сценарии существует несколько показателей, по которым определяется распределение поездки, например, , например, , рейтинг гонщика и водителя, трафик между разными маршрутами, время, в течение которого гонщик простаивает, и т. д.
В то время как в реальном сценарии существует несколько показателей, по которым определяется распределение поездки, например, , например, , рейтинг гонщика и водителя, трафик между разными маршрутами, время, в течение которого гонщик простаивает, и т. д.
Точно так же агрегаторы онлайн-доставки еды, такие как Zomato, могут выбрать водителя, который заберет наши заказы из соответствующего ресторана и доставит их нам. Это один из многих вариантов использования графов, с помощью которого мы можем решить множество задач. Графики упрощают визуализацию и делают ее более интерпретируемой.
Чтобы понять концепцию графов в деталях, мы должны сначала понять теорию графов.
Происхождение теории графов: семь мостов Кенигсберга
Сначала мы обсудим истоки теории графов, чтобы получить интуитивное представление о графах. За его происхождением стоит интересная история, и я стремлюсь сделать его еще более интригующим, используя сюжеты и визуализации.
Все началось с семи мостов Кенигсберга. Задача (или просто головоломка) с мостами Кенигсберга заключалась в том, чтобы пройти через весь город, перейдя все семь мостов только один раз. Давайте сначала визуализируем его, чтобы иметь четкое представление о проблеме:
Попробуйте и посмотрите, сможете ли вы пройтись по городу с этим ограничением. Вы должны помнить о двух вещах, пытаясь решить вышеупомянутую проблему (или я должен сказать загадку?):
- Вы не можете перейти ни один мост
- Каждый мост нельзя пересекать более одного раза
Вы можете пробовать любое количество комбинаций, но взломать ее по-прежнему невозможно. Невозможно пройти через город, пройдя каждый мост только один раз. Леонард Эйлер углубился в эту загадку, чтобы понять, почему это такая невыполнимая задача. Давайте проанализируем, как он это сделал:
На изображении выше есть четыре разных места: два острова (B и D), две части материка (A и C) и всего семь мостов.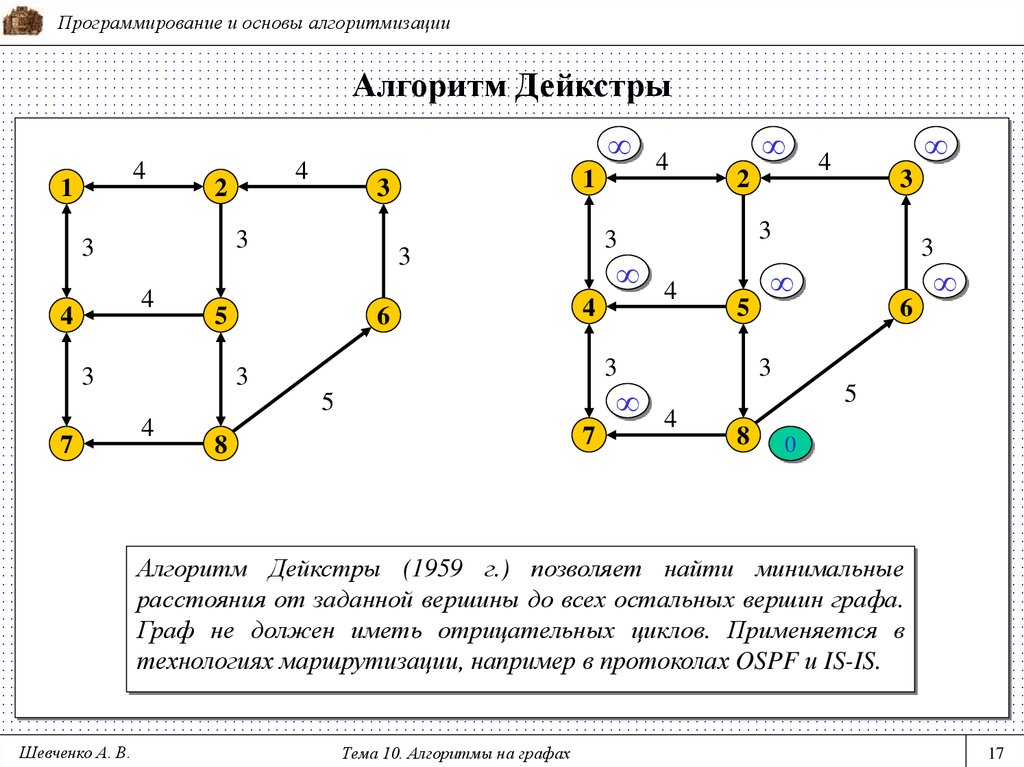 Давайте сначала посмотрим на каждую землю отдельно и попробуем найти закономерности (если они вообще существуют):
Давайте сначала посмотрим на каждую землю отдельно и попробуем найти закономерности (если они вообще существуют):
Один из выводов из приведенного выше изображения заключается в том, что каждая земля связана с нечетным количеством мостов. Если вы хотите пересечь каждый мост только один раз, то вы можете войти и покинуть землю, только если она соединена с четным числом мостов. Другими словами, мы можем обобщить, что если есть четное количество мостов, то можно покинуть землю, а с нечетным - нельзя.
Давайте попробуем добавить еще один мост к текущей проблеме и посмотрим, сможет ли он решить эту проблему:
Теперь у нас есть 2 земли, соединенные четным числом мостов, и 2 земли, соединенные нечетным числом мостов. Нарисуем новый маршрут после добавления нового моста:
Добавление одного моста решило проблему! Вам может быть интересно, сыграло ли количество мостов значительную роль в решении этой проблемы? Должно ли оно быть ровным все время? Ну, это не всегда так. Эйлер объяснил, что наряду с количеством мостов имеет значение и количество участков земли с нечетным числом соединенных между собой мостов. Эйлер преобразовал эту задачу от земли и мостов к графам, где он представил землю как вершины, а мосты как ребра:
Эйлер объяснил, что наряду с количеством мостов имеет значение и количество участков земли с нечетным числом соединенных между собой мостов. Эйлер преобразовал эту задачу от земли и мостов к графам, где он представил землю как вершины, а мосты как ребра:
Здесь визуализация проста и кристально ясна. Прежде чем мы двинемся дальше и углубимся в эту проблему, давайте сначала разберемся с основами и основными свойствами графа.
Основы графов
Есть много ключевых моментов и ключевых слов, которые мы должны иметь в виду, когда имеем дело с графиками. В этом разделе мы подробно обсудим все эти ключевые слова.
- Вершина : это точка, где сходятся несколько линий. Он также известен как узел .
Вершина обычно обозначается алфавитом, как показано выше. - Край : Это линия, соединяющая две вершины.
- Граф : Как обсуждалось в предыдущем разделе, граф представляет собой комбинацию вершин (узлов) и ребер.
 G = (V, E), где V представляет набор всех вершин, а E представляет набор всех ребер графа.
G = (V, E), где V представляет набор всех вершин, а E представляет набор всех ребер графа. - Степень вершины : Степень вершины – это количество соединенных с ней ребер. В приведенном ниже примере степень вершины A, deg(A) = 3, степень вершины B, deg(B) = 2.
- Параллельное ребро : Если две вершины соединены более чем одним ребром, то эти ребра называются параллельными ребрами.
- Multi Graph : Это графы с параллельными ребрами:
Вот некоторые основные принципы, которые вы должны помнить при работе с графиками. Теперь о понимании основных свойств графа.
Основные свойства и терминология, относящиеся к графам
До сих пор мы видели, как выглядит граф и его различные компоненты. Теперь мы сосредоточимся на некоторых основных свойствах и терминах, связанных с графом. Мы будем использовать приведенный ниже график (обозначенный как G) и понимать каждую терминологию, используя одно и то же:
Найдите минутку и подумайте о возможных решениях следующих вопросов:
- Как далеко вершина от других вершин графа?
- Каково максимальное расстояние между вершиной и всеми остальными вершинами?
- Существует ли вершина, ближайшая ко всем остальным вершинам? Если да, то каково это кратчайшее расстояние?
- Что является центральной точкой графика?
Я попытаюсь ответить на все эти вопросы, используя базовую терминологию графов:
- Расстояние между двумя вершинами : это количество ребер на кратчайшем пути между двумя вершинами.
 Попробуем вычислить расстояние между вершинами A и D:
Попробуем вычислить расстояние между вершинами A и D:
Возможные пути между A и D:
AB -> BC -> CD
AD
AB -> BD
Из этих трех путей AD является кратчайшим, имеющим только один край. Следовательно, расстояние между A и D равно 1.
Точно так же мы можем вычислить расстояние между каждой парой вершин. Итак, это ответило на наш первый вопрос об определении расстояния между любой парой вершин.
- Эксцентриситет вершины : Максимальное расстояние между вершиной и всеми другими вершинами. Чтобы вычислить эксцентриситет любой вершины, мы должны знать расстояние между этой вершиной и всеми другими вершинами. Вычислим эксцентриситет для вершины A. Итак, расстояния равны:
Расстояние между A и B – 1
Расстояние между A и C – 2
Расстояние между A и D – 1
Максимум всех этих расстояний – эксцентриситет вершины .
Эксцентриситет A, e(A) = 2
: Когда эксцентриситет вершины высок, это означает, что есть вершины, которые находятся далеко от этой вершины. Это отвечает на наш второй вопрос, где мы стремились вычислить максимальное расстояние между вершиной и всеми другими вершинами.
Это отвечает на наш второй вопрос, где мы стремились вычислить максимальное расстояние между вершиной и всеми другими вершинами.
- Радиус связного графа : Минимальный эксцентриситет всех вершин графа называется радиусом этого графа. Сначала мы должны вычислить эксцентриситет для каждой вершины. Попробуйте рассчитать эксцентриситет самостоятельно, и если у вас возникнут трудности с вычислениями, не стесняйтесь спрашивать в разделе комментариев. Эксцентриситет для всех вершин:
e(A) = 2
e(B) = 1
e(C) = 2
e(D) = 1
Минимальное значение эксцентриситета для всех вершин равно радиусу этого графа. В нашем случае минимальный эксцентриситет равен 1, и, следовательно, радиус графика равен:
r(G) = 1
Он говорит нам о расстоянии вершины, которая является ближайшей ко всем остальным вершинам.
- Диаметр связного графа : Радиус графа — это минимальное значение эксцентриситета для всех вершин, аналогично, Диаметр графа — это максимальное значение эксцентриситета для всех вершин.
 В нашем случае Диаметр графика равен:
В нашем случае Диаметр графика равен:
d(G) = 2
- Центральная точка графика : Вершина, эксцентриситет которой равен радиусу графика, называется центральной точкой графика. Граф также может иметь более одной центральной точки. В нашем случае радиус графа равен 1, а вершины с эксцентриситетом, равным 1, — это B и D. Следовательно, «B» и «D» — центральные точки графа G.
Это отвечает на наш последний вопрос об определении центральной точки. графика. Рассмотрим пример графа связности аэропорта. Таким образом, аэропорт, который соединен с большинством других аэропортов, может считаться центральным аэропортом.
Вот некоторые из терминов, связанных с графиками. Далее мы обсудим различные типы графиков.
Типы графиков
Существуют различные типы графиков. В этом разделе мы обсудим некоторые из наиболее часто используемых.
- Нулевой граф: Это графы, которые не содержат ребер.

Нет связи между вершинами.
- Неориентированный граф: Это графы, которые имеют ребра, но эти ребра не имеют определенного направления.
- Направленный граф : Когда ребра графа имеют определенное направление, они называются ориентированными графами.
Рассмотрим пример соединений Facebook и Twitter. Когда вы добавляете кого-то в свой список друзей на Facebook, вы также будете добавлены в его список друзей. Это двусторонняя связь, и этот граф соединений будет ненаправленным. Принимая во внимание, что если вы подписаны на человека в Твиттере, этот человек может не подписаться на вас в ответ. Это ориентированный граф.
- Связный граф : Когда нет недостижимой вершины, т. е. существует путь между каждой парой вершин, такие графы называются связными графами.
- Несвязный граф : это те графы, которые имеют недостижимую вершину (вершины), т.
 Е. Между каждой парой вершин не существует пути.
Е. Между каждой парой вершин не существует пути.
Если граф связен, то всегда существует путь от каждой вершины ко всем остальным вершинам этого графа. А если граф несвязный, то всегда найдется хотя бы одна вершина, не имеющая связи со всеми остальными вершинами графа. Это может помочь авиакомпаниям решить, все ли аэропорты подключены или нет. Они могут визуализировать стыковки, и, если есть какой-либо несвязанный аэропорт, могут быть введены новые рейсы, чтобы улучшить существующую ситуацию.
- Обычный граф : Когда все вершины в графе имеют одинаковую степень, такие графы называются k-регулярными графами (где k — степень любой вершины). Рассмотрим два графика, показанные ниже:
- Для графа-1 степень каждой вершины равна 2, следовательно, граф-1 является обычным графом. Граф-2 не является регулярным графом, так как степень каждой вершины неодинакова (для A и D степень равна 3, а для B и D — 2).
Теперь, когда у нас есть представление о различных типах графов, их компонентах и некоторых основных терминах, связанных с графами, давайте вернемся к проблеме, которую мы пытались решить, то есть к семи мостам Кенигсберга. Мы еще более подробно рассмотрим, как Леонард Эйлер подошел к своим рассуждениям и объяснил их.
Мы еще более подробно рассмотрим, как Леонард Эйлер подошел к своим рассуждениям и объяснил их.
Продолжение задачи о семи мостах Кенигсберга
Ранее мы видели, что Эйлер преобразовал эту задачу с помощью графов:
Здесь A, B, C и D обозначают землю, а соединяющие их линии — мосты. Мы можем вычислить степень каждой вершины.
град(В) = 5
град(А) = град(С) = град(D) = 3
Эйлер показал, что возможность обхода графа (города) по каждому ребру (мосту) только один раз строго зависит от степени вершин (земли). И такой путь, который содержит каждое ребро графа только один раз, называется путем Эйлера.
Можете ли вы вычислить путь Эйлера для нашей задачи? Давай попробуем!
Вот как можно решить классическую задачу «Семь мостов Кенигсберга» с помощью графов и пути Эйлера. И это в основном происхождение теории графов. Спасибо Леонарду Эйлеру!
Деревья — один из самых мощных и эффективных способов представления графа. В этом разделе мы узнаем, что такое бинарные деревья поиска, как они работают и как они делают визуализацию более интерпретируемой. Но прежде чем все это, найдите минутку, чтобы понять, что на самом деле представляют собой деревья в этом контексте.
В этом разделе мы узнаем, что такое бинарные деревья поиска, как они работают и как они делают визуализацию более интерпретируемой. Но прежде чем все это, найдите минутку, чтобы понять, что на самом деле представляют собой деревья в этом контексте.
Деревья — это графы, не содержащие ни одного цикла:
В приведенном выше примере первый граф не имеет цикла (он же дерево), а второй граф имеет цикл (A-B-E-C-A, следовательно, это не дерево).
Элементы дерева называются узлами. (A, B, C, D и E) — это узлы в приведенном выше дереве. Первый узел (или самый верхний узел) дерева известен как корневой узел, а последний узел (узел C, D и E в приведенном выше примере) известен как конечный узел. Все остальные узлы известны как дочерние узлы (узел B в нашем случае).
Пришло время перейти к одной из самых важных тем теории графов, а именно к обходу графа.
Обход графа
Предположим, мы хотим определить положение определенного узла в графе. Какое возможное решение для идентификации узлов графа? Как начать? Что должно быть отправной точкой? Как только мы узнаем начальную точку, как двигаться дальше? Я постараюсь ответить на все эти вопросы в этом разделе, объясняя концепции обхода графа.
Какое возможное решение для идентификации узлов графа? Как начать? Что должно быть отправной точкой? Как только мы узнаем начальную точку, как двигаться дальше? Я постараюсь ответить на все эти вопросы в этом разделе, объясняя концепции обхода графа.
Обход графа означает посещение каждой вершины и ребра графа ровно один раз в строго определенном порядке. Поскольку цель обхода состоит в том, чтобы посетить каждую вершину только один раз, мы отслеживаем пройденные вершины, чтобы не покрывать одну и ту же вершину дважды. Существуют различные методы обхода графа, и мы обсудим некоторые из известных методов:
- Поиск в ширину
Мы начинаем с исходного узла (корневого узла) и проходим по графу по слоям. Шаги для поиска в ширину:
- Сначала переместитесь по горизонтали и посетите все узлы текущего слоя.
- Перейдите на следующий слой и повторите шаги, сделанные выше.
Позвольте мне объяснить это визуализацией:
Итак, при поиске в ширину мы начинаем с исходного узла (в нашем случае A) и двигаемся вниз к первому слою, т. е. к слою 1. Мы покрываем все узлы этого слоя, перемещаясь по горизонтали (B -> C). Затем переходим к следующему слою, т.е. Layer 2 и повторяем тот же шаг (движемся от D -> E -> F). Мы продолжаем этот шаг, пока все слои и вершины не будут покрыты.
е. к слою 1. Мы покрываем все узлы этого слоя, перемещаясь по горизонтали (B -> C). Затем переходим к следующему слою, т.е. Layer 2 и повторяем тот же шаг (движемся от D -> E -> F). Мы продолжаем этот шаг, пока все слои и вершины не будут покрыты.
Ключевое преимущество такого подхода в том, что мы всегда найдем кратчайший путь к цели. Это подходит для небольших графов и деревьев, но для более сложных и больших графов его производительность очень низкая, а также требуется много памяти. Мы рассмотрим другой подход обхода, который занимает меньше места в памяти по сравнению с BFS.
- Поиск в глубину
Давайте сначала рассмотрим шаги, связанные с этим подходом:
- Сначала мы выбираем исходный узел и сохраняем все его соседние узлы.
- Затем мы выбираем узел из сохраненных узлов и сохраняем все его соседние узлы.
- Этот процесс повторяется до тех пор, пока ни один узел не станет доступным.
Последовательность поиска в глубину для приведенного выше примера будет следующей:
А -> В -> Г -> Е -> С -> F
После того, как путь был полностью исследован, его можно удалить из памяти, поэтому DFS нужно сохранить только корневой узел, все дочерние элементы корневого узла и его текущее местоположение. Следовательно, он преодолевает проблему памяти BFS.
Следовательно, он преодолевает проблему памяти BFS.
- Двоичное дерево поиска
В этом подходе все узлы дерева располагаются в отсортированном порядке. Давайте посмотрим на пример двоичного дерева поиска:
.Как упоминалось ранее, все узлы в приведенном выше дереве упорядочены на основе условия. Предположим, мы хотим получить доступ к узлу со значением 45. Если бы мы следовали BFS или DFS, нам потребовалось бы много вычислительного времени, чтобы добраться до него. Теперь давайте посмотрим, как двоичное дерево поиска поможет нам добраться до нужного узла, используя наименьшее количество шагов. Шагов для достижения узла со значением 45 с помощью двоичного дерева поиска:
- Начинаем с корневого узла, т.е. 50.
- Теперь 45 меньше 50 (45 < 50), поэтому мы движемся влево от корневого узла.
- Затем мы сравниваем значения. Как оказалось, 45 больше 40 (45 > 40), поэтому мы двигаемся вправо от этого узла.

- Здесь мы находимся в узле со значением 45.
Этот подход очень быстрый и требует очень меньше памяти. Были рассмотрены большинство концепций теории графов. Далее мы попытаемся реализовать эти концепции для решения реальной проблемы с помощью Python.
Реализация теории графов на Python для решения задачи авиакомпании
И, наконец, мы приступаем к работе с данными в Python! В этом наборе данных у нас есть записи о более чем 7 миллионах рейсов из США. Были предоставлены следующие переменные:
- Пункт отправления и назначения
- Запланированное время прибытия и отправления
- Фактическое время прибытия и отправления
- Дата поездки
- Расстояние между источником и получателем
- Общее эфирное время рейса
Это гигантский набор данных, и я взял из него только образец для этой статьи. Идея состоит в том, чтобы дать вам понимание концепций, используя этот образец набора данных, и затем вы можете применить их ко всему набору данных. Загрузите набор данных, который мы будем использовать для тематического исследования, отсюда . Сначала мы импортируем обычные библиотеки и считываем набор данных, который предоставляется в формате .csv:
Загрузите набор данных, который мы будем использовать для тематического исследования, отсюда . Сначала мы импортируем обычные библиотеки и считываем набор данных, который предоставляется в формате .csv:
импортировать панд как pd
импортировать numpy как np
данные = pd.read_csv('data.csv') Давайте посмотрим на первые несколько строк набора данных, используя функцию head() :
data.head()
Здесь CRSDepTime , CRSArrTime , DepTime и ArrTime представляют запланированное время отправления, запланированное время прибытия, фактическое время отправления и фактическое время прибытия соответственно. Пункт отправления и пункт назначения являются пунктом отправления и пунктом назначения путешествия.
Часто может быть несколько путей из одного аэропорта в другой, и цель состоит в том, чтобы найти кратчайший путь между всеми аэропортами.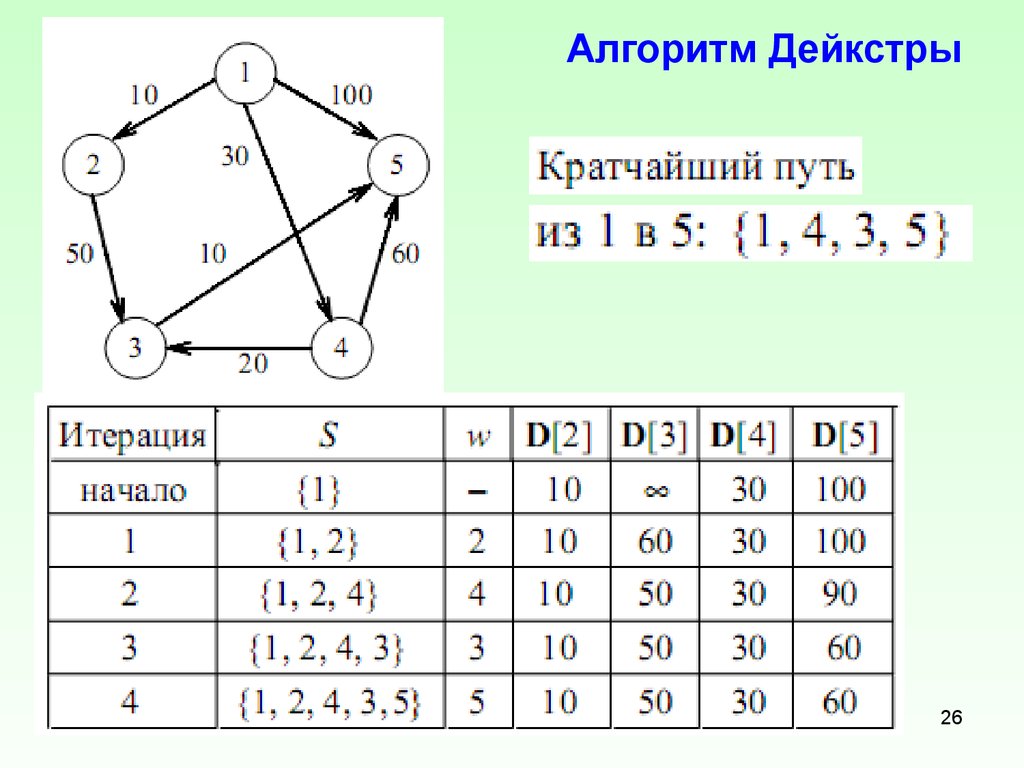 Есть два способа определить путь как кратчайший:
Есть два способа определить путь как кратчайший:
- По расстоянию
- По эфиру
Мы можем решать такие задачи, используя концепции теории графов, которые мы уже изучили. Можете ли вы вспомнить, что нам нужно сделать, чтобы построить график?
Ответ заключается в определении вершин и ребер! Мы можем преобразовать задачу в граф, представив все аэропорты в виде вершин, а маршрут между ними — в виде ребер. Мы будем использовать NetworkX для создания и визуализации графиков. NetworkX — это пакет Python для создания, управления и изучения структуры, динамики и функций сложных сетей. Вы можете обратиться к документации NetworkX здесь.
После установки NetworkX мы создадим ребра и вершины для нашего графа, используя набор данных:
импортировать networkx как nx df = nx.from_pandas_edgelist(data, source='Origin', target='Dest', edge_attr=True)
Он автоматически сохранит вершины и ребра. Взгляните на ребра и вершины графа, который мы создали:
Взгляните на ребра и вершины графа, который мы создали:
df.nodes()
дф.края()
Давайте построим и визуализируем график, используя функции matplotlib и draw_networkx() networkx.
импортировать matplotlib.pyplot как plt % matplotlib встроенный plt.figure(figsize=(12,8)) nx.draw_networkx(df, with_labels=Истина)
Вышеупомянутая удивительная визуализация представляет различные маршруты полета. Предположим, пассажир хочет выбрать кратчайший маршрут от AMA до PBI . Теория графов снова приходит на помощь!
Попробуем рассчитать кратчайший путь, исходя из эфирного времени между аэропортами AMA и PBI. Мы будем использовать алгоритм кратчайшего пути Дейкстры . Этот алгоритм находит кратчайший путь от исходной вершины ко всем вершинам данного графа. Позвольте мне дать вам краткий обзор шагов, которым следует этот алгоритм:
- Создает набор sptSet (набор деревьев кратчайших путей), который отслеживает вершины, включенные в дерево кратчайших путей, т.
 е. минимальное расстояние от исходной вершины вычисляется и завершается. Изначально это множество пусто.
е. минимальное расстояние от исходной вершины вычисляется и завершается. Изначально это множество пусто. - Присвоить значение расстояния всем вершинам входного графа. Мы присваиваем значение 0 исходной вершине и значение INFINITE всем остальным вершинам.
- Пока sptSet не включает все вершины, мы выполняем следующие подэтапы:
- Выберите вершину, не входящую в sptSet и ближайшую к исходной вершине
- Включить эту вершину в sptSet
- Обновить расстояния до всех соседних вершин
Давайте рассмотрим пример, чтобы лучше понять этот алгоритм:
Здесь исходной вершиной является A. Числа обозначают расстояние между вершинами. Изначально sptSet пуст, поэтому мы назначим расстояния для всех вершин. Дистанции:
{0, INF, INF, INF, INF, INF}, где INF представляет БЕСКОНЕЧНОЕ.
Теперь мы выберем вершину с минимальным расстоянием, т. е. A, и она будет включена в sptSet. Итак, новый sptSet — это {A}. Следующим шагом является выбор вершины, которая не входит в sptSet и находится ближе всего к исходной вершине. В нашем случае это B со значением расстояния 2. Так что это будет добавлено в sptSet.
Следующим шагом является выбор вершины, которая не входит в sptSet и находится ближе всего к исходной вершине. В нашем случае это B со значением расстояния 2. Так что это будет добавлено в sptSet.
sptSet = {A,B}
Теперь обновим расстояния вершин, прилегающих к вершине B:
Значение расстояния вершины F становится равным 6. Мы снова выберем вершину с минимальным значением расстояния, которая еще не включена в SPT (C со значением расстояния 4).
sptSet = {A,B,C}
Мы будем следовать аналогичным шагам, пока все вершины не будут включены в sptSet. Давайте реализуем этот алгоритм и попробуем вычислить кратчайшее расстояние между аэропортами. Для этого мы воспользуемся функцией dijkstra_path() networkx:
shortest_path_distance = nx.dijkstra_path(df, source='AMA', target='PBI', weight='Distance') Shortest_path_distance
Это кратчайший путь между двумя аэропортами, исходя из расстояния между ними. Мы также можем рассчитать кратчайший путь на основе эфирного времени, просто изменив гиперпараметр weight='AirTime' :
Мы также можем рассчитать кратчайший путь на основе эфирного времени, просто изменив гиперпараметр weight='AirTime' :
shortest_path_airtime = nx.dijkstra_path(df, source='AMA', target='PBI', weight='AirTime') Shortest_path_airtime
Это кратчайший путь, основанный на эфирном времени. Интуитивно понятный и простой для понимания, это все о теории графов!
Конечные примечания
Это лишь одно из многих приложений теории графов. Мы можем применить его практически к любой проблеме и получить решения и визуализации. Некоторые из приложений теории графов, о которых я могу думать, это:
- Поиск наилучшего маршрута доставки почты
- Представление сетей связи. Например, ссылочную структуру веб-сайта можно представить с помощью ориентированных графов.
- Определение социального поведения человека по графу его социальных связей
- Планирование поездок, как обсуждалось в тематическом исследовании авиакомпаний
Вот некоторые из приложений.

 2. Все веса неотрицательны.
2. Все веса неотрицательны. 2, то есть эта вариация алгоритма Дейкстры не всегда быстрее классической, а только при маленьких m.
2, то есть эта вариация алгоритма Дейкстры не всегда быстрее классической, а только при маленьких m. Поэтому в куче могут быть несколько элементов с одинаковым номером вершины, но с разным значением d (но всего вершин в куче будет не более m, я гарантирую это). Когда мы берём минимальное значение в куче, надо проверить, является ли этот элемент фиктивным. Для этого достаточно сравнить значение d в куче и реальное его значение. А ещё для записи графа вместо двоичного массива используем массив списков.
Поэтому в куче могут быть несколько элементов с одинаковым номером вершины, но с разным значением d (но всего вершин в куче будет не более m, я гарантирую это). Когда мы берём минимальное значение в куче, надо проверить, является ли этот элемент фиктивным. Для этого достаточно сравнить значение d в куче и реальное его значение. А ещё для записи графа вместо двоичного массива используем массив списков. second
d[i.first] = d[v] + i.second
q.add(pair(d[i.first], i.first))
вывести d
second
d[i.first] = d[v] + i.second
q.add(pair(d[i.first], i.first))
вывести d
 Задача поиска маршрута в науке может быть и чисто фундаментальной, и прикладной.
Задача поиска маршрута в науке может быть и чисто фундаментальной, и прикладной.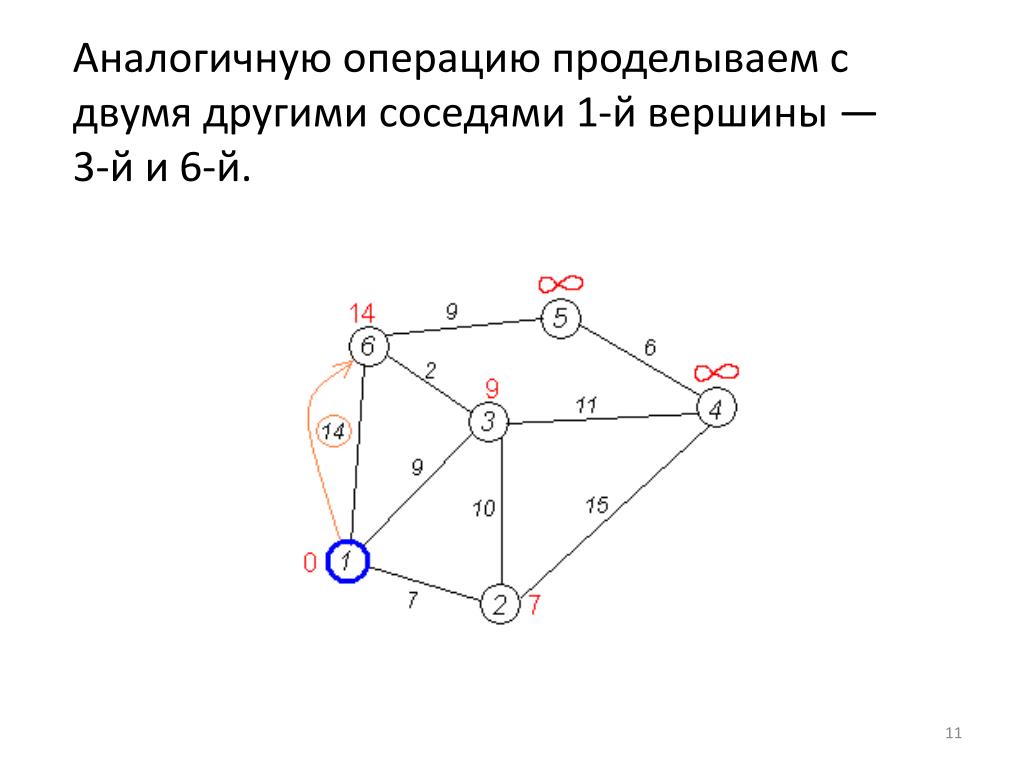
 Кривая информирует ум, пробуждает воображение, убеждает».
Кривая информирует ум, пробуждает воображение, убеждает». G = (V, E), где V представляет набор всех вершин, а E представляет набор всех ребер графа.
G = (V, E), где V представляет набор всех вершин, а E представляет набор всех ребер графа.  Попробуем вычислить расстояние между вершинами A и D:
Попробуем вычислить расстояние между вершинами A и D: 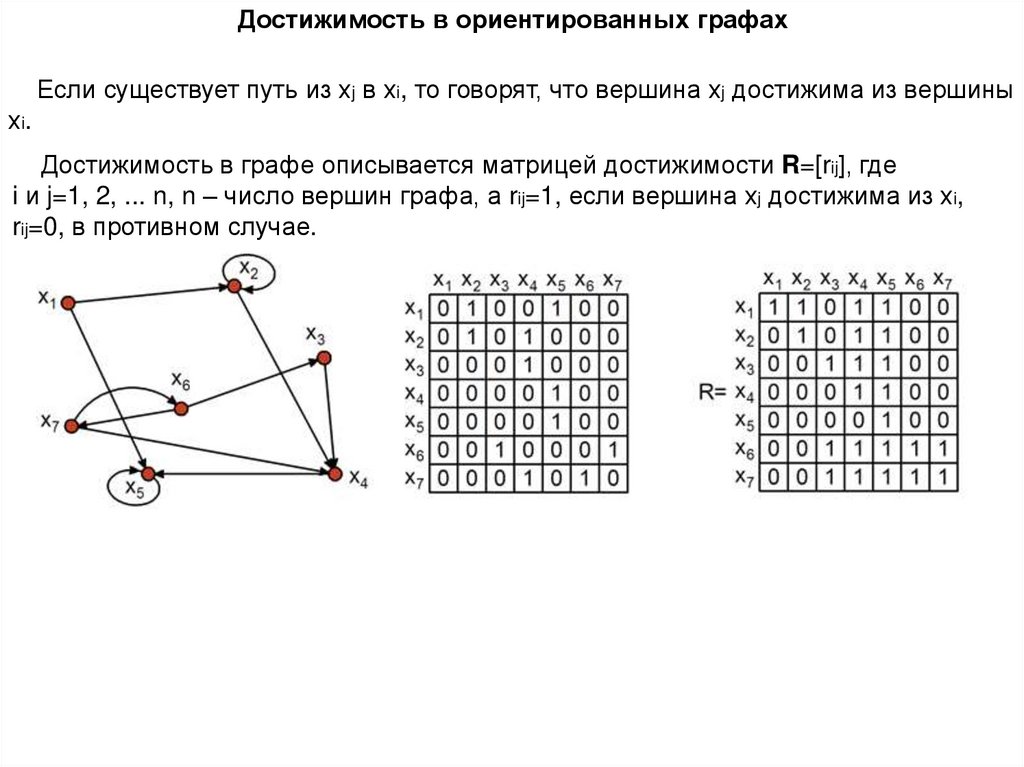 Это отвечает на наш второй вопрос, где мы стремились вычислить максимальное расстояние между вершиной и всеми другими вершинами.
Это отвечает на наш второй вопрос, где мы стремились вычислить максимальное расстояние между вершиной и всеми другими вершинами. В нашем случае Диаметр графика равен:
В нашем случае Диаметр графика равен: 
 Е. Между каждой парой вершин не существует пути.
Е. Между каждой парой вершин не существует пути. 
 е. минимальное расстояние от исходной вершины вычисляется и завершается. Изначально это множество пусто.
е. минимальное расстояние от исходной вершины вычисляется и завершается. Изначально это множество пусто.
 Методом Бернулли. Ищем решение в виде произведения двух функций y = u ⋅ v. Подставив
его и y‘ = u‘v + uv‘
в данное дифференциальное уравнение, получим
Методом Бернулли. Ищем решение в виде произведения двух функций y = u ⋅ v. Подставив
его и y‘ = u‘v + uv‘
в данное дифференциальное уравнение, получим

 Первый:
Первый:

 Будет ли сложной схема Бернулли для линейных уравнений зависит от Вашего уровня подготовки. Разберите внимательно приведенные ответы и сделайте выводы, что и как Вам нужно углубленно изучить.
Будет ли сложной схема Бернулли для линейных уравнений зависит от Вашего уровня подготовки. Разберите внимательно приведенные ответы и сделайте выводы, что и как Вам нужно углубленно изучить. уравнения v’+p(x)*v=0 и за произвольную постоянную интегрирования берем ноль (С=0). Данное уравнение является дифференциальным уравнением с разделяющимися переменными.
уравнения v’+p(x)*v=0 и за произвольную постоянную интегрирования берем ноль (С=0). Данное уравнение является дифференциальным уравнением с разделяющимися переменными.
 уравнения, хотя мало кто из Вас увидит эту подсказку
уравнения, хотя мало кто из Вас увидит эту подсказку 
 Используйте алгоритм решения уравнения Бернулли ко всем подобным дифференциальным уравнениям.
Используйте алгоритм решения уравнения Бернулли ко всем подобным дифференциальным уравнениям.
 Предположим, что жидкость находится под давлением 1000 Па , на высоте 3 метра и течет при 2 метра в секунду .
Предположим, что жидкость находится под давлением 1000 Па , на высоте 3 метра и течет при 2 метра в секунду . Расход показывает, сколько кубических метров (в случае объемного расхода) или сколько килограммов (в случае массового расхода) проходит через одну точку на линии тока в течение одного часа.
Расход показывает, сколько кубических метров (в случае объемного расхода) или сколько килограммов (в случае массового расхода) проходит через одну точку на линии тока в течение одного часа.
 4}\ln x\end{align*}\]
4}\ln x\end{align*}\]

 Ученый-математик Колмогоров А.Н. говорил: «Без знаний математики нельзя понять ни основ современной техники, ни того, как ученые изучают природные и социальные явления», поэтому математика связана с будущей специальностью. В результате изучения темы научимся решать задачи прикладного характера для профессиональной деятельности.
Ученый-математик Колмогоров А.Н. говорил: «Без знаний математики нельзя понять ни основ современной техники, ни того, как ученые изучают природные и социальные явления», поэтому математика связана с будущей специальностью. В результате изучения темы научимся решать задачи прикладного характера для профессиональной деятельности.


 В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: a) в минувшем году; б) в этом году?
В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: a) в минувшем году; б) в этом году? Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.
Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой. en.edu.ru
en.edu.ru


 Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.






 Лицензия : CC BY: Атрибуция
Лицензия : CC BY: Атрибуция  Следующий,
умножьте числа на трех нисходящих диагоналях и добавьте эти
продукты вместе. Умножьте числа на восходящих диагоналях, и
добавить эти продуктов вместе. Затем вычтите сумму из
произведения восходящих диагоналей из суммы произведений
диагоналей вниз (отнять второе число от первого
число):
Следующий,
умножьте числа на трех нисходящих диагоналях и добавьте эти
продукты вместе. Умножьте числа на восходящих диагоналях, и
добавить эти продуктов вместе. Затем вычтите сумму из
произведения восходящих диагоналей из суммы произведений
диагоналей вниз (отнять второе число от первого
число):




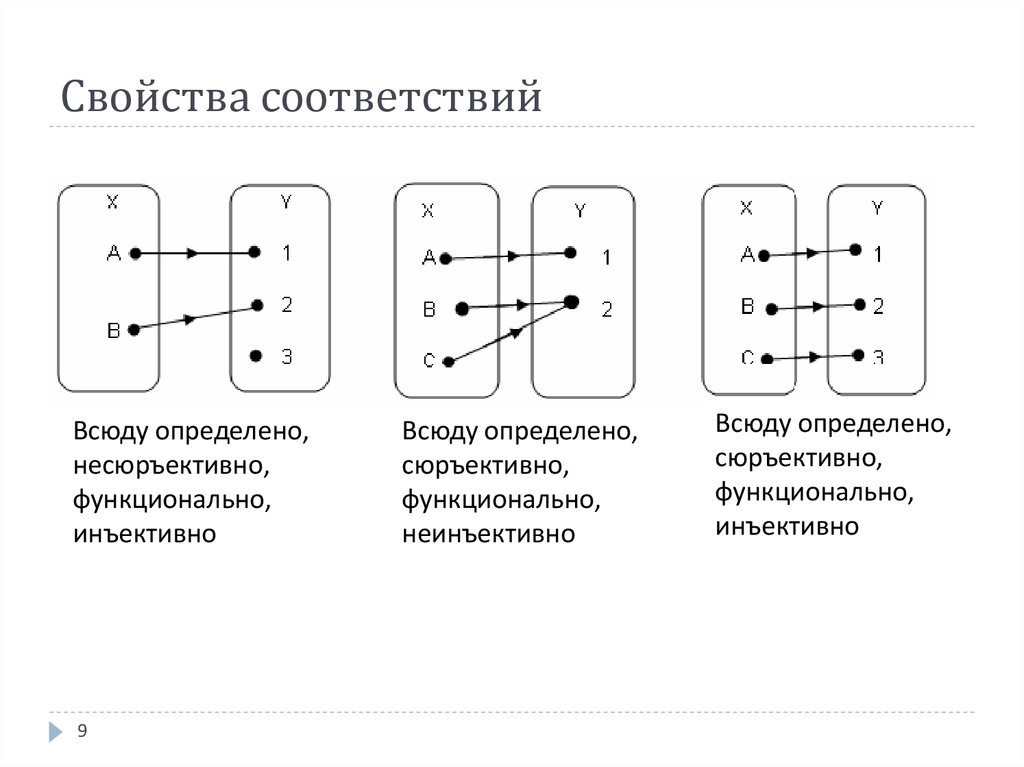 Кроме того, функции можно использовать для наложения математических структур на множества.
Кроме того, функции можно использовать для наложения математических структур на множества. Если для всех x и y в A функция называется инъективной.
Если для всех x и y в A функция называется инъективной. Чтобы продемонстрировать, что данная функция сюръективна, мы должны установить, что Б Р; поэтому R = B будет истинным.
Чтобы продемонстрировать, что данная функция сюръективна, мы должны установить, что Б Р; поэтому R = B будет истинным.
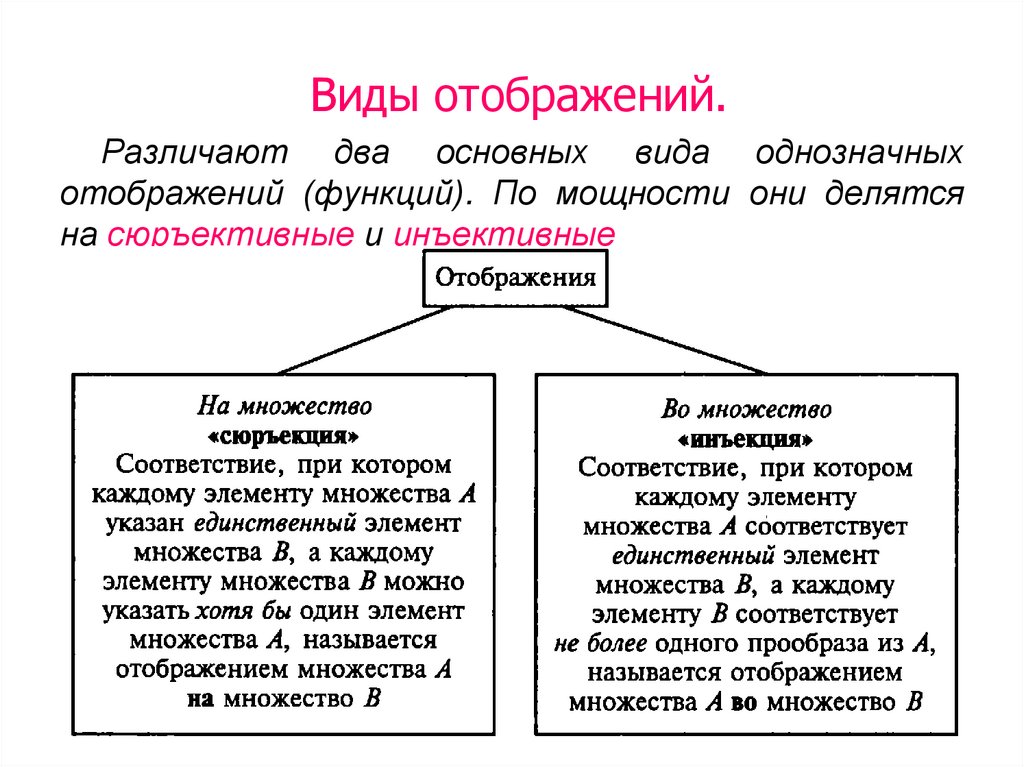 Сюръективный означает, что для каждого «В» есть по крайней мере одно «А», которое ему соответствует, если не больше. У нас не будет двух или более «А», указывающих на одно и то же «В», потому что это инъективно. Сюръективность означает, что для каждого «В» есть по крайней мере одно соответствие «А». (может быть больше одного). Неформально инъекция имеет не более одного входа, отображаемого на каждый выход, сюръекция имеет полный возможный диапазон на выходе, а биекция имеет оба критерия истинны.
Сюръективный означает, что для каждого «В» есть по крайней мере одно «А», которое ему соответствует, если не больше. У нас не будет двух или более «А», указывающих на одно и то же «В», потому что это инъективно. Сюръективность означает, что для каждого «В» есть по крайней мере одно соответствие «А». (может быть больше одного). Неформально инъекция имеет не более одного входа, отображаемого на каждый выход, сюръекция имеет полный возможный диапазон на выходе, а биекция имеет оба критерия истинны.
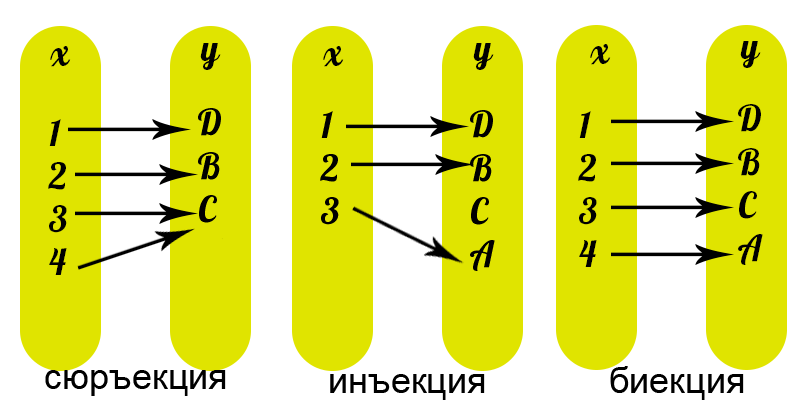
 В оставшейся части этого урока пусть («пусть f будет функцией от множества A до множества B). Во-первых, вспомним, что f может отправить два разных элемента из A в один и тот же элемент из B. Например, если и , то функция, определяемая как , является совершенно хорошей функцией, несмотря на то, что и кошка, и собака отправляются к сыру. Предположим, однако, что f — функция, которая не не обладает этим свойством ни для каких элементов в A. А именно, предположим, что f не переводит никакие два различных элемента в A в один и тот же элемент B. Тогда мы назвали бы эту функцию инъективной . Давайте посмотрим пример.
В оставшейся части этого урока пусть («пусть f будет функцией от множества A до множества B). Во-первых, вспомним, что f может отправить два разных элемента из A в один и тот же элемент из B. Например, если и , то функция, определяемая как , является совершенно хорошей функцией, несмотря на то, что и кошка, и собака отправляются к сыру. Предположим, однако, что f — функция, которая не не обладает этим свойством ни для каких элементов в A. А именно, предположим, что f не переводит никакие два различных элемента в A в один и тот же элемент B. Тогда мы назвали бы эту функцию инъективной . Давайте посмотрим пример. Но предположим, что каждому мальчику было назначено разных девушек, чтобы ни одна девушка не танцевала более чем с одним мальчиком. Тогда эта функция была бы инъективной.
Но предположим, что каждому мальчику было назначено разных девушек, чтобы ни одна девушка не танцевала более чем с одним мальчиком. Тогда эта функция была бы инъективной.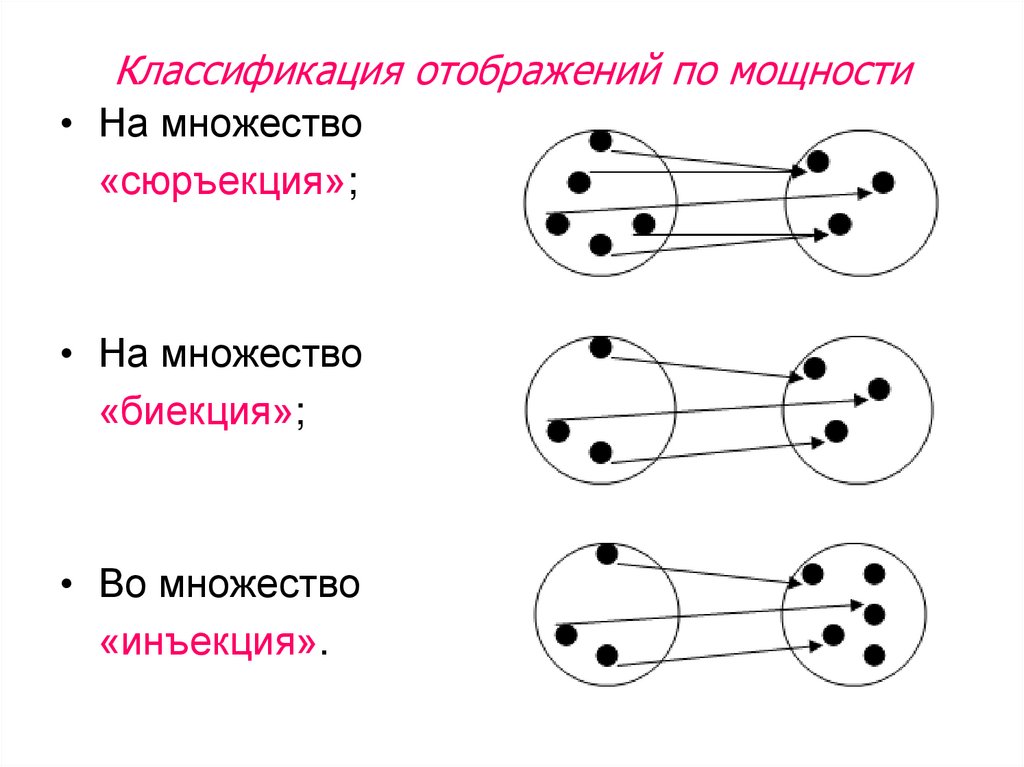 1 Пусть будет функция из множества A в множество B. Тогда f равно инъективный если для любых элементов a и b в A следует, что . //
1 Пусть будет функция из множества A в множество B. Тогда f равно инъективный если для любых элементов a и b в A следует, что . // Это все еще не обязательно означает, что у каждой девочки будет партнер по танцу, потому что мы могли бы, например, назначить всем мальчикам танцевать с одной и той же девочкой (оставив всех остальных без партнеров). Если, однако, мы распределили мальчиков таким образом, что каждая девочка имела партнера по танцу (возможно, более одного), то функция называется сюръективной .
Это все еще не обязательно означает, что у каждой девочки будет партнер по танцу, потому что мы могли бы, например, назначить всем мальчикам танцевать с одной и той же девочкой (оставив всех остальных без партнеров). Если, однако, мы распределили мальчиков таким образом, что каждая девочка имела партнера по танцу (возможно, более одного), то функция называется сюръективной .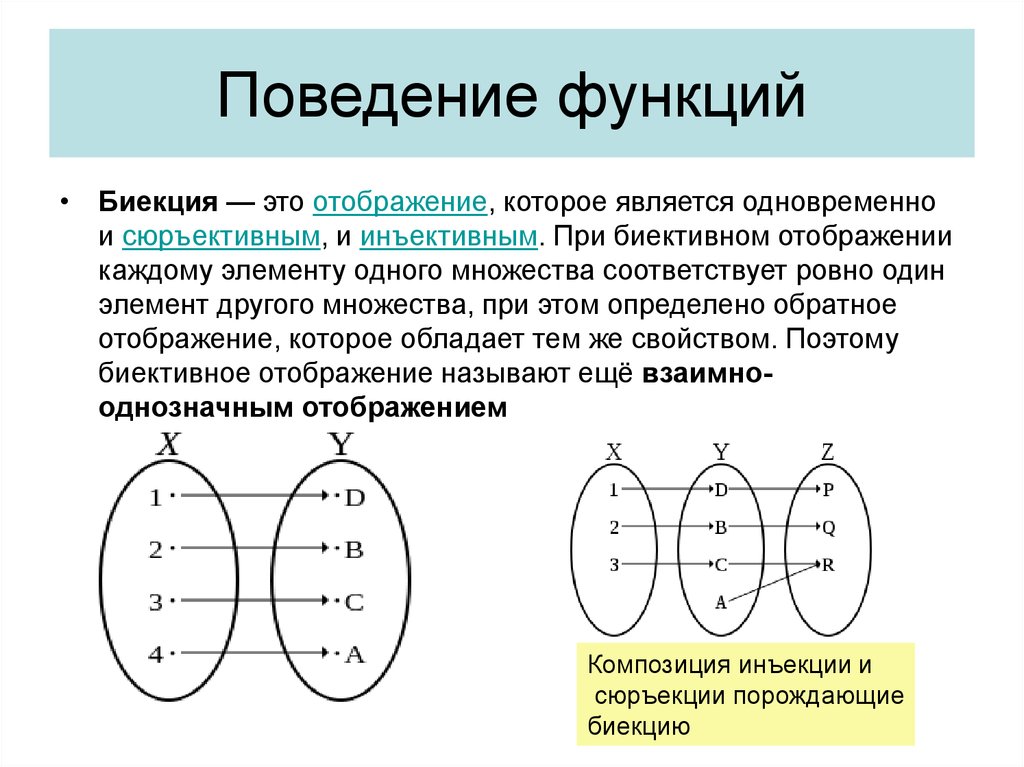 2 Пусть . Тогда f называется сюръективным , если для каждого элемента b в B существует некоторый элемент a в A такой, что . //
2 Пусть . Тогда f называется сюръективным , если для каждого элемента b в B существует некоторый элемент a в A такой, что . // Другими словами, мы видели, что у нас могут быть функции, которые являются инъективными и не сюръективными (если девочек больше, чем мальчиков), и у нас могут быть функции, которые являются сюръективными, но не инъективными (если мальчиков больше, чем девочек, то мы должны были отправить более одного мальчика хотя бы к одной из девочек). Таким образом, мы дополнительно ограничиваемся рассмотрением биективных функций. То есть класс биективных функций «меньше» класса инъективных функций, а также он меньше класса сюръективных. Более того, класс инъективных функций и класс сюръективных функций меньше, чем класс всех общих функций. Таким образом, мы потеряли некоторую общность, говоря, скажем, об инъективных функциях, но получили возможность описывать более подробную структуру внутри этих функций. Это окажется очень плодотворным в следующих уроках (по мере того, как мы продвигаемся к пониманию того, что существует более одного типа бесконечности).
Другими словами, мы видели, что у нас могут быть функции, которые являются инъективными и не сюръективными (если девочек больше, чем мальчиков), и у нас могут быть функции, которые являются сюръективными, но не инъективными (если мальчиков больше, чем девочек, то мы должны были отправить более одного мальчика хотя бы к одной из девочек). Таким образом, мы дополнительно ограничиваемся рассмотрением биективных функций. То есть класс биективных функций «меньше» класса инъективных функций, а также он меньше класса сюръективных. Более того, класс инъективных функций и класс сюръективных функций меньше, чем класс всех общих функций. Таким образом, мы потеряли некоторую общность, говоря, скажем, об инъективных функциях, но получили возможность описывать более подробную структуру внутри этих функций. Это окажется очень плодотворным в следующих уроках (по мере того, как мы продвигаемся к пониманию того, что существует более одного типа бесконечности).
 Если отнестись к этому как к развлечению, то с каким результатом пришли к финишу не имеет значение. Вы познакомились с новыми фактами, о которых не знали ранее. Пополнили багаж знаний. И это здорово.
Пишите в комментариях, какие темы получили отклик. Прочитав ваше мнение, легче подобрать интересные факты. На какое количество вопросов в тесте по географии комфортно отвечать? Блиц-тест или объемный? Пишите. Для нас это действительно важно.
Желаем вам интересных тестов по географии и 100%-результатов!
Если отнестись к этому как к развлечению, то с каким результатом пришли к финишу не имеет значение. Вы познакомились с новыми фактами, о которых не знали ранее. Пополнили багаж знаний. И это здорово.
Пишите в комментариях, какие темы получили отклик. Прочитав ваше мнение, легче подобрать интересные факты. На какое количество вопросов в тесте по географии комфортно отвечать? Блиц-тест или объемный? Пишите. Для нас это действительно важно.
Желаем вам интересных тестов по географии и 100%-результатов! Вы также узнаете о различных типах доступных тестов по географии и о том, как использовать пробные экзамены и практические тесты в рамках подготовки к экзамену. С этим руководством у вас будут все инструменты, необходимые для успешной сдачи экзамена по географии.
Вы также узнаете о различных типах доступных тестов по географии и о том, как использовать пробные экзамены и практические тесты в рамках подготовки к экзамену. С этим руководством у вас будут все инструменты, необходимые для успешной сдачи экзамена по географии.
 Эти тесты обычно включают вопросы, связанные с анализом карт, анализом диаграмм, анализом населения и анализом атласа. Каждый тип вопросов требует от учащегося демонстрации своего понимания физических особенностей мира и того, как они взаимодействуют друг с другом. Имея возможность эффективно отвечать на эти типы вопросов, учащиеся могут продемонстрировать глубокое понимание географии.
Эти тесты обычно включают вопросы, связанные с анализом карт, анализом диаграмм, анализом населения и анализом атласа. Каждый тип вопросов требует от учащегося демонстрации своего понимания физических особенностей мира и того, как они взаимодействуют друг с другом. Имея возможность эффективно отвечать на эти типы вопросов, учащиеся могут продемонстрировать глубокое понимание географии. Кроме того, мы дадим советы о том, как использовать эти ресурсы, чтобы убедиться, что вы хорошо подготовлены, когда придет время сдавать экзамен.
Кроме того, мы дадим советы о том, как использовать эти ресурсы, чтобы убедиться, что вы хорошо подготовлены, когда придет время сдавать экзамен. Люди на улице действительно так отвечали на эти вопросы. Мы лишь собрали вместе самые популярные варианты и предлагаем тебе их отгадать. Удачи!
Люди на улице действительно так отвечали на эти вопросы. Мы лишь собрали вместе самые популярные варианты и предлагаем тебе их отгадать. Удачи!
 В одном только Нью-Йорке насчитывается 300 тысяч мастеров кисти. Даже если вы не являетесь почитателем этого вида искусства и частым посетителем выставок, вы просто обязаны знать эти мировые шедевры живописи и их авторов. Проверьте, насколько вы эрудированны в этой области и попробуйте набрать максимальный балл.
В одном только Нью-Йорке насчитывается 300 тысяч мастеров кисти. Даже если вы не являетесь почитателем этого вида искусства и частым посетителем выставок, вы просто обязаны знать эти мировые шедевры живописи и их авторов. Проверьте, насколько вы эрудированны в этой области и попробуйте набрать максимальный балл. верхний правый столбец этой страницы), поэтому качество нашего контента не имеет себе равных. Если вы сравниваете наш пробный экзамен с экзаменом другой компании, знаете ли вы, кто написал их материал?
верхний правый столбец этой страницы), поэтому качество нашего контента не имеет себе равных. Если вы сравниваете наш пробный экзамен с экзаменом другой компании, знаете ли вы, кто написал их материал?

 Формат вашего онлайн-аккаунта отображает один вопрос за раз. См. Пример.
Формат вашего онлайн-аккаунта отображает один вопрос за раз. См. Пример.




 Мы считаем, что студенты имеют право на самую последнюю информацию при покупке подготовительного курса.
Мы считаем, что студенты имеют право на самую последнюю информацию при покупке подготовительного курса. Мы достигаем этого:
Мы достигаем этого: …
…
 Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ.
Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы.
Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
 Найти решение матричного уравнения
Найти решение матричного уравнения  Калькулятор напишет вам подробное решение дробей и выдаст удобную для копирования картинку .
Калькулятор напишет вам подробное решение дробей и выдаст удобную для копирования картинку . Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу.
При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную.
Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу.
При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную. Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ.
Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

 Например:
Например: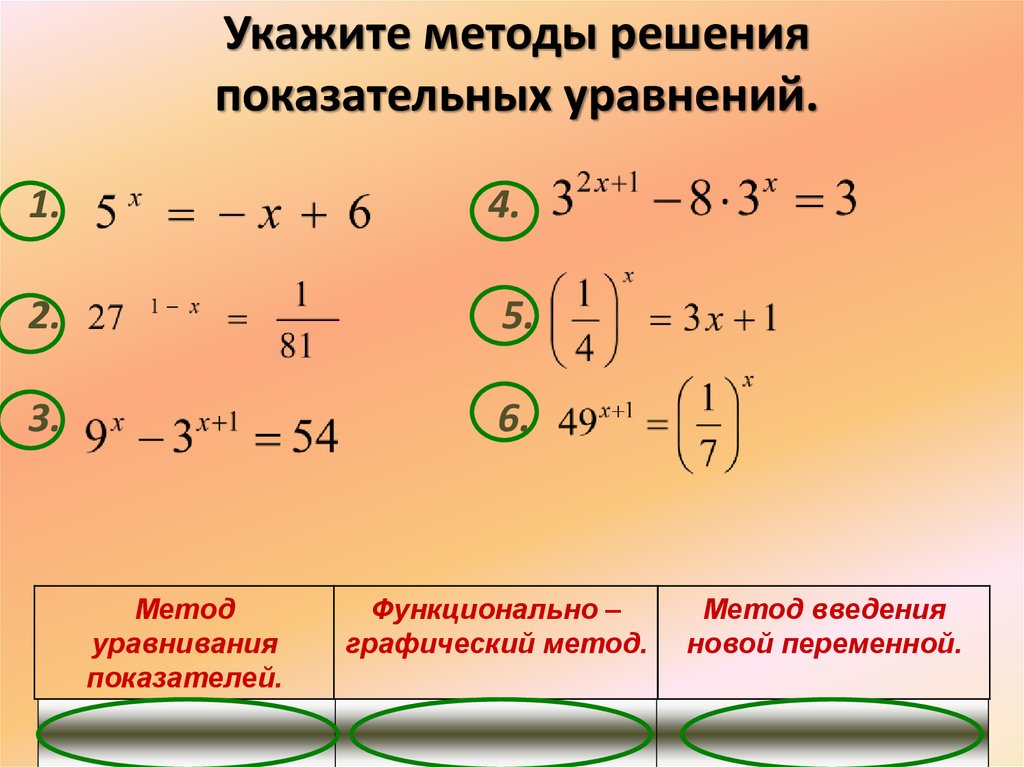 Формула дана выше;
Формула дана выше;


 Это уравнение, в котором показатели степени являются $$ \red{ переменными}$$.
Это уравнение, в котором показатели степени являются $$ \red{ переменными}$$. Сделайте это, спросив себя:
Сделайте это, спросив себя: Спроси себя :
Спроси себя :
 Изолируйте экспоненциальное выражение следующим образом:
Изолируйте экспоненциальное выражение следующим образом: {(3x -4)} = 125
$$
93
$$
{(3x -4)} = 125
$$
93
$$

 Чем больше n , тем больше , но даже если n = бесконечность , значение последовательности не равно числу Эйлера.
Чем больше n , тем больше , но даже если n = бесконечность , значение последовательности не равно числу Эйлера.


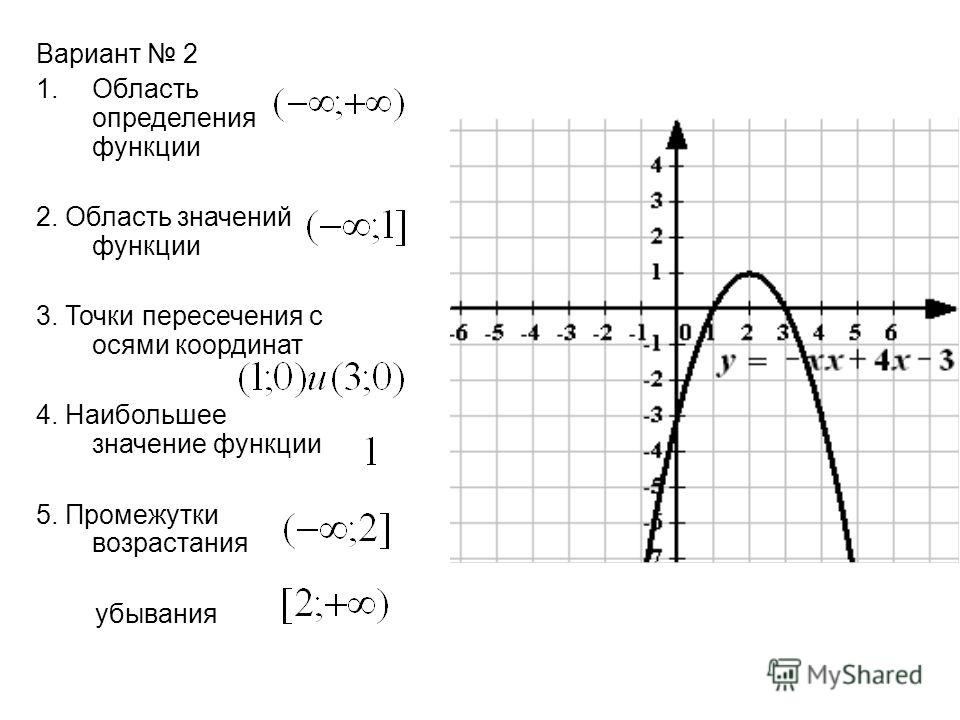 Если нет графического калькулятора,
постройте приблизительный график, подставив в функцию несколько значений х и, вычислив
соответствующие значения у,
нанесите найденные точки на координатную плоскость, чтобы получить общее
представление о форме графика.
Если нет графического калькулятора,
постройте приблизительный график, подставив в функцию несколько значений х и, вычислив
соответствующие значения у,
нанесите найденные точки на координатную плоскость, чтобы получить общее
представление о форме графика.
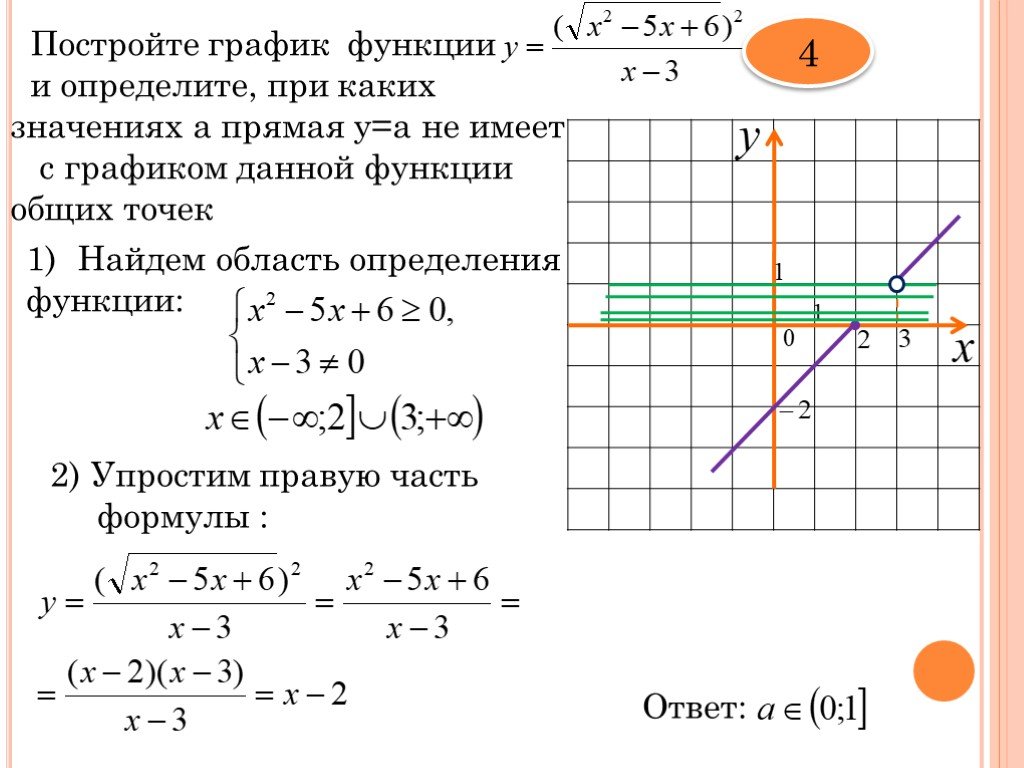
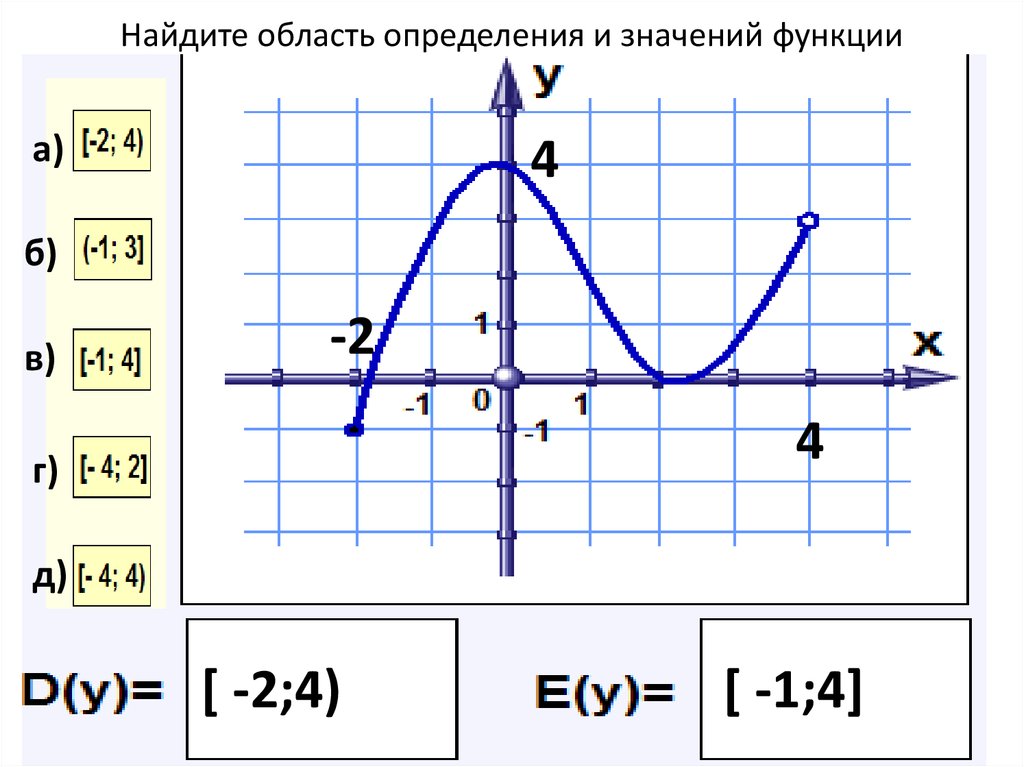 Если выражение f(x) находится под квадратным корнем, область определения можно узнать из неравенства f(x)≥0.
Если выражение f(x) находится под квадратным корнем, область определения можно узнать из неравенства f(x)≥0.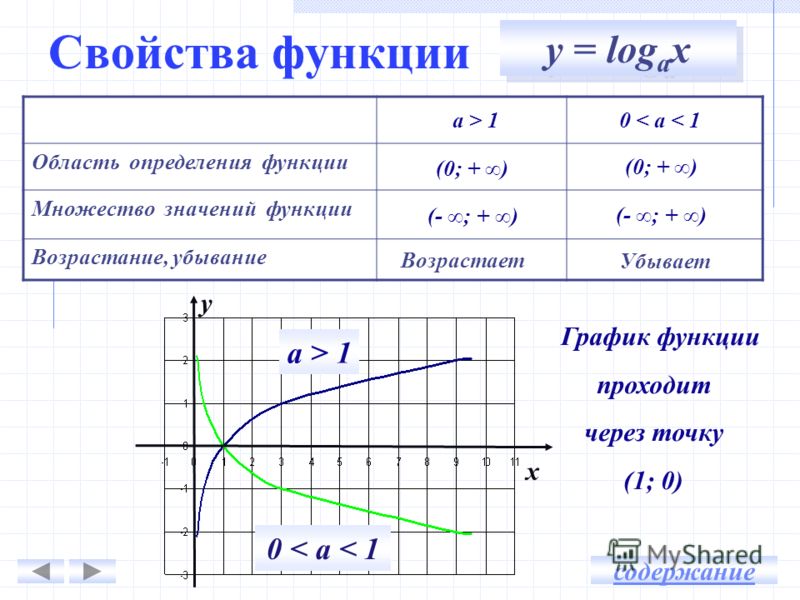
 Выражение под знаком квадратного корня всегда положительно, то есть x≥0, и область определения D(f(x))=[0; +∞). Теперь построим график функции.
Выражение под знаком квадратного корня всегда положительно, то есть x≥0, и область определения D(f(x))=[0; +∞). Теперь построим график функции.
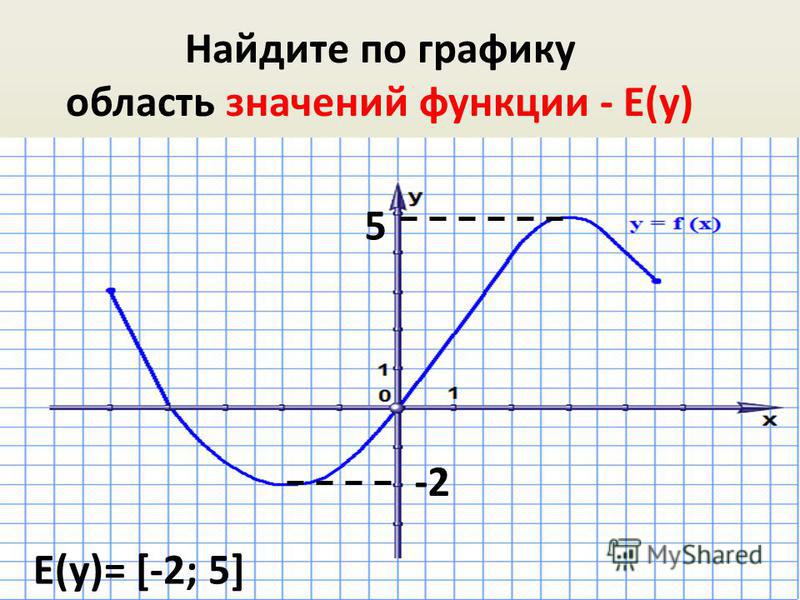
 Машина не даст вам никакого вкуса газировки, если вы введете пенни. Следовательно, домен представляет входные данные, которые мы можем здесь иметь, то есть монеты в четвертаке и однодолларовые купюры.
Машина не даст вам никакого вкуса газировки, если вы введете пенни. Следовательно, домен представляет входные данные, которые мы можем здесь иметь, то есть монеты в четвертаке и однодолларовые купюры.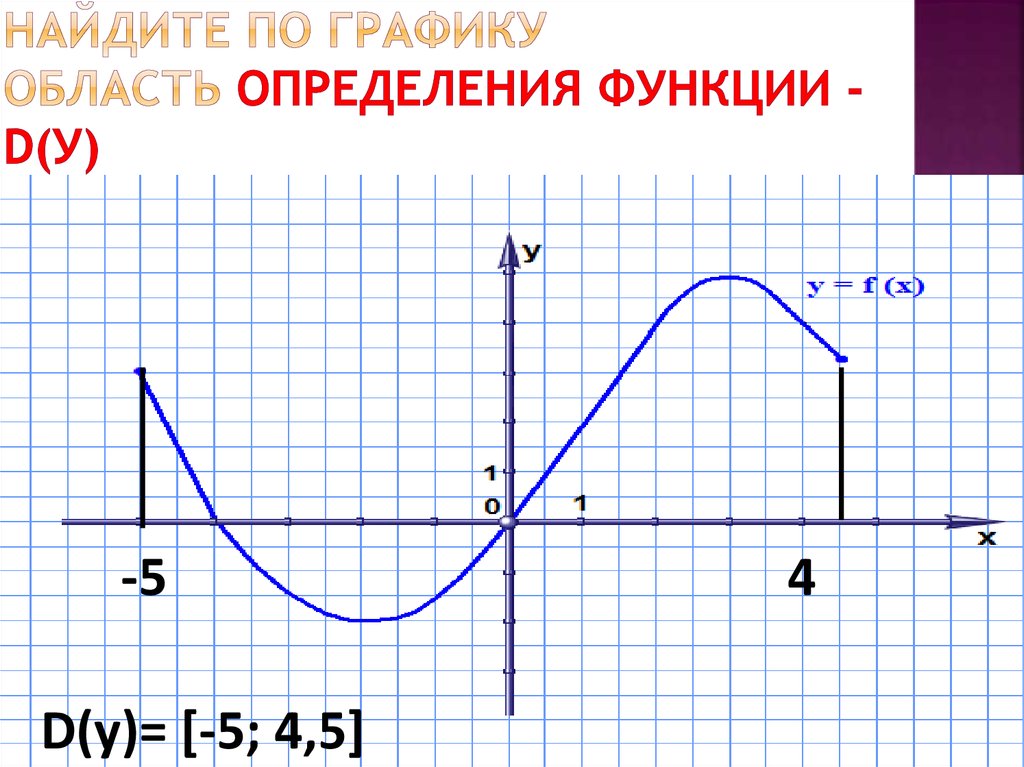
 Домен → Функция → Диапазон. Если существует функция f: A → B такая, что каждый элемент множества A отображается в элементы множества B, то A является доменом, а B — со-областью. Образ элемента ‘a’ при отношении R задается как ‘b’, где (a,b) ∈ R. Областью значений функции является множество изображений. Область определения и область значений функции обозначаются в общем случае следующим образом: область определения (f) = {x ∈ R : условие} и область значений (f) = {f (x) : x ∈ область значений (f)}
Домен → Функция → Диапазон. Если существует функция f: A → B такая, что каждый элемент множества A отображается в элементы множества B, то A является доменом, а B — со-областью. Образ элемента ‘a’ при отношении R задается как ‘b’, где (a,b) ∈ R. Областью значений функции является множество изображений. Область определения и область значений функции обозначаются в общем случае следующим образом: область определения (f) = {x ∈ R : условие} и область значений (f) = {f (x) : x ∈ область значений (f)}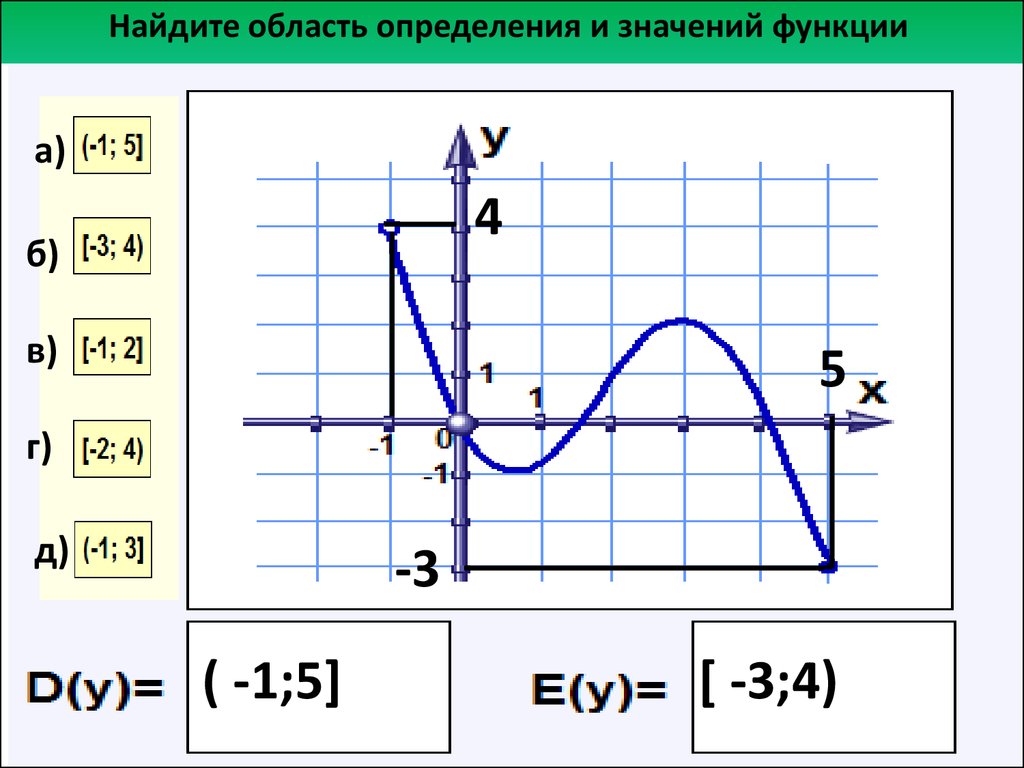 При вводе значений x = {1,2,3,4,…} область определения представляет собой просто набор натуральных чисел. Но в общем случае (если область определения не указана как натуральные числа), f (x) = 2x определено для всех действительных значений x, и, следовательно, его областью определения является множество всех действительных чисел, которое обозначается (-∞, ∞) . Вот общие формулы, используемые для нахождения области определения различных типов функций. Здесь R — множество всех действительных чисел.
При вводе значений x = {1,2,3,4,…} область определения представляет собой просто набор натуральных чисел. Но в общем случае (если область определения не указана как натуральные числа), f (x) = 2x определено для всех действительных значений x, и, следовательно, его областью определения является множество всех действительных чисел, которое обозначается (-∞, ∞) . Вот общие формулы, используемые для нахождения области определения различных типов функций. Здесь R — множество всех действительных чисел.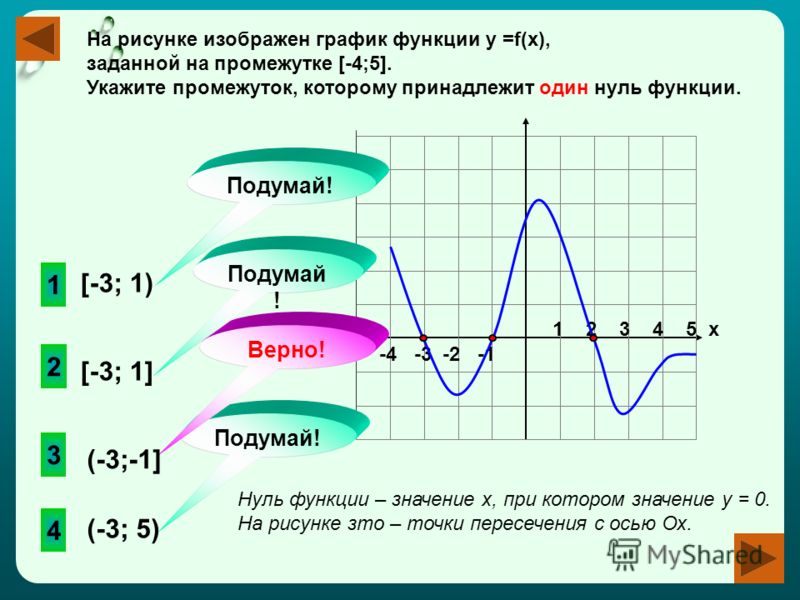
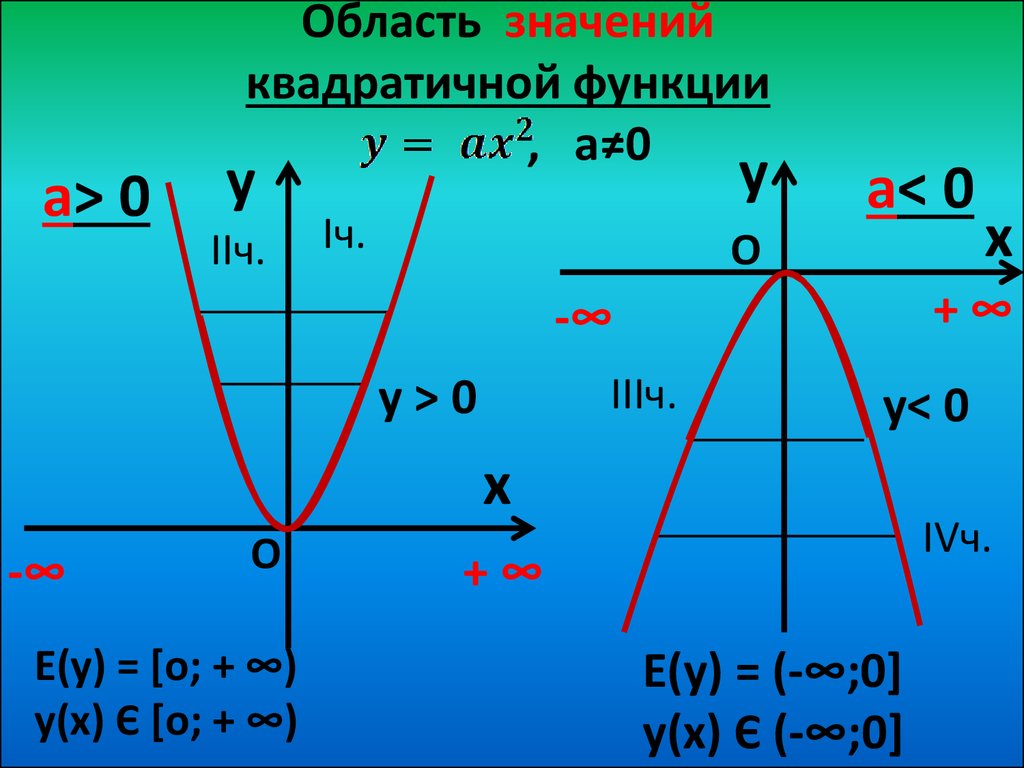 Здесь мы говорим, что А — домен, а В — содомен. Затем выход этой функции становится диапазоном. Диапазон = {множество четных натуральных чисел}. Элементы домена называются прообразами, а отображаемые элементы содомена называются изображениями. Здесь областью значений функции f является множество всех изображений элементов области (или) множество всех выходов функции.
Здесь мы говорим, что А — домен, а В — содомен. Затем выход этой функции становится диапазоном. Диапазон = {множество четных натуральных чисел}. Элементы домена называются прообразами, а отображаемые элементы содомена называются изображениями. Здесь областью значений функции f является множество всех изображений элементов области (или) множество всех выходов функции.
 Рассмотрим функцию f: X → Y, где R = {(x,y) : y = x+1}.
Рассмотрим функцию f: X → Y, где R = {(x,y) : y = x+1}. Область определения и диапазон экспоненциальных функций задаются следующим образом:
Область определения и диапазон экспоненциальных функций задаются следующим образом: Итак, область определения функции абсолютного значения — это множество всех действительных чисел. Абсолютное значение числа всегда дает неотрицательное значение. Таким образом, диапазон функции абсолютного значения вида y= |ax+b| есть {y ∈ ℝ | у ≥ 0}. Область определения и диапазон функции абсолютного значения задаются следующим образом
Итак, область определения функции абсолютного значения — это множество всех действительных чисел. Абсолютное значение числа всегда дает неотрицательное значение. Таким образом, диапазон функции абсолютного значения вида y= |ax+b| есть {y ∈ ℝ | у ≥ 0}. Область определения и диапазон функции абсолютного значения задаются следующим образом Мы знаем, что квадратный корень всегда дает неотрицательное значение. Таким образом, областью действия функции квадратного корня является множество всех неотрицательных действительных чисел. Следовательно, область определения и область значений функции квадратного корня задаются следующим образом: Область определения = [-b/a, ∞), Область значений = [0, ∞)
Мы знаем, что квадратный корень всегда дает неотрицательное значение. Таким образом, областью действия функции квадратного корня является множество всех неотрицательных действительных чисел. Следовательно, область определения и область значений функции квадратного корня задаются следующим образом: Область определения = [-b/a, ∞), Область значений = [0, ∞)

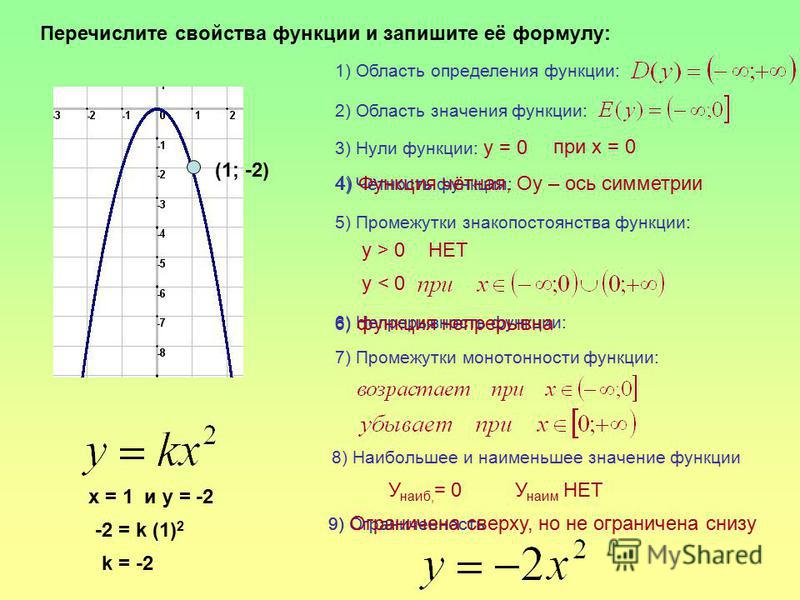 Самый простой способ найти область значений функции — построить ее график.
Самый простой способ найти область значений функции — построить ее график.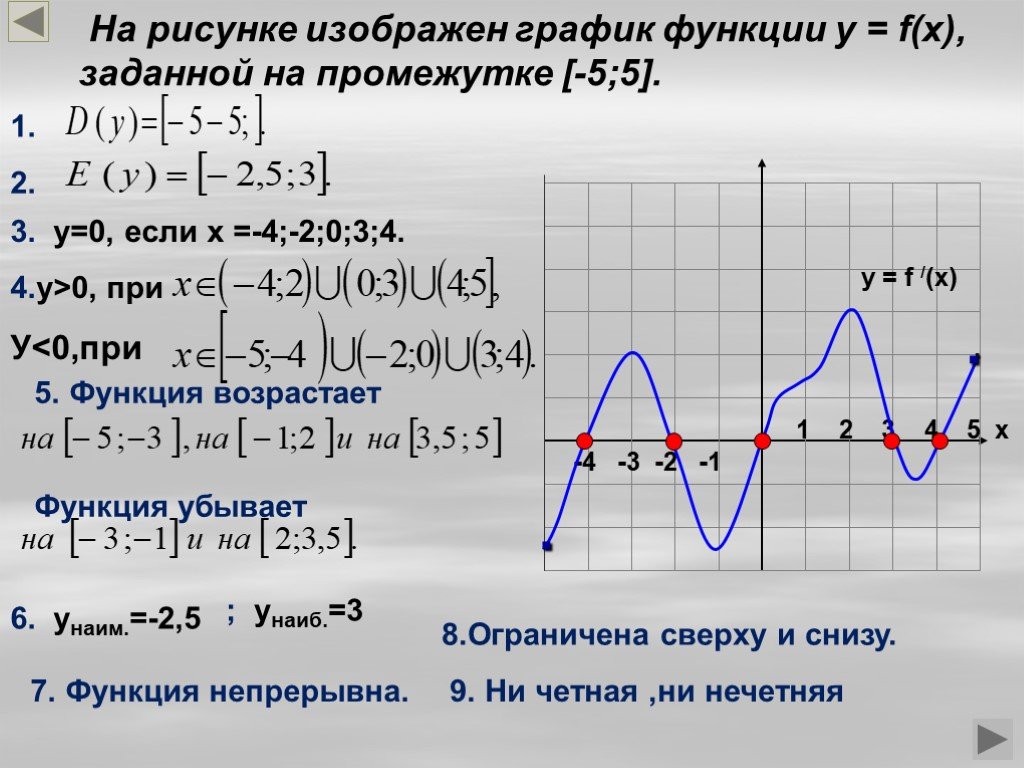 Домен и диапазон в обозначении интервала включают в себя открытые и квадратные скобки.
Домен и диапазон в обозначении интервала включают в себя открытые и квадратные скобки.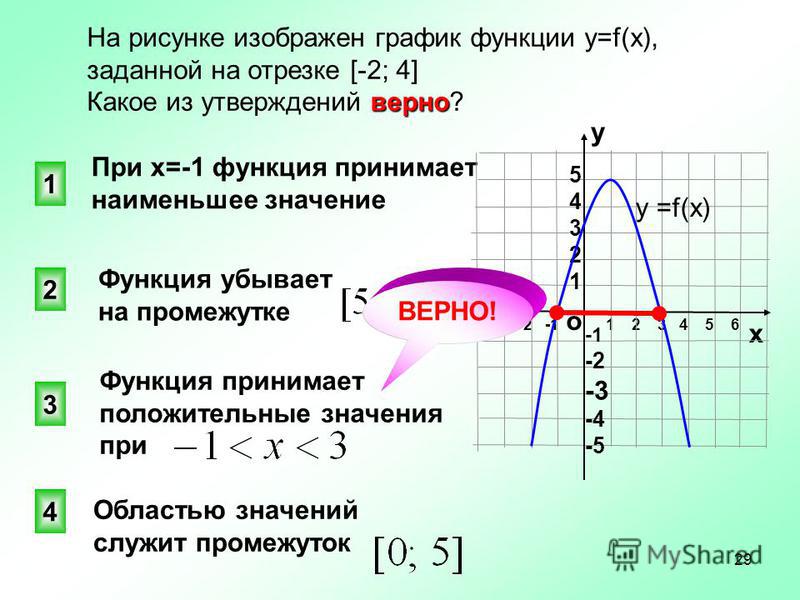
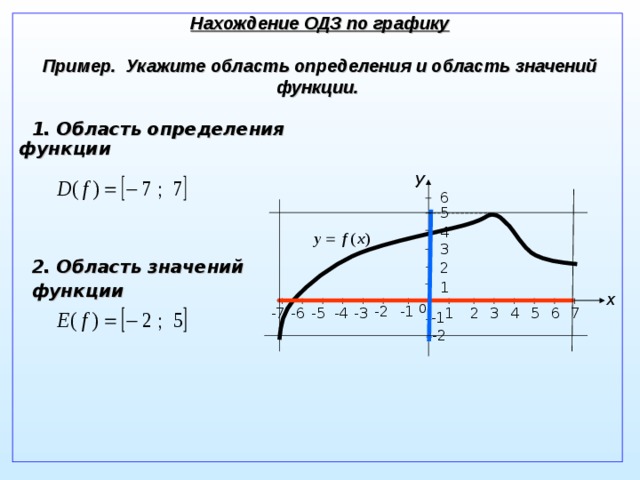 Чтобы вычислить диапазон функции, мы просто выражаем уравнение как x = g (y), а затем находим область определения g (y).
Чтобы вычислить диапазон функции, мы просто выражаем уравнение как x = g (y), а затем находим область определения g (y).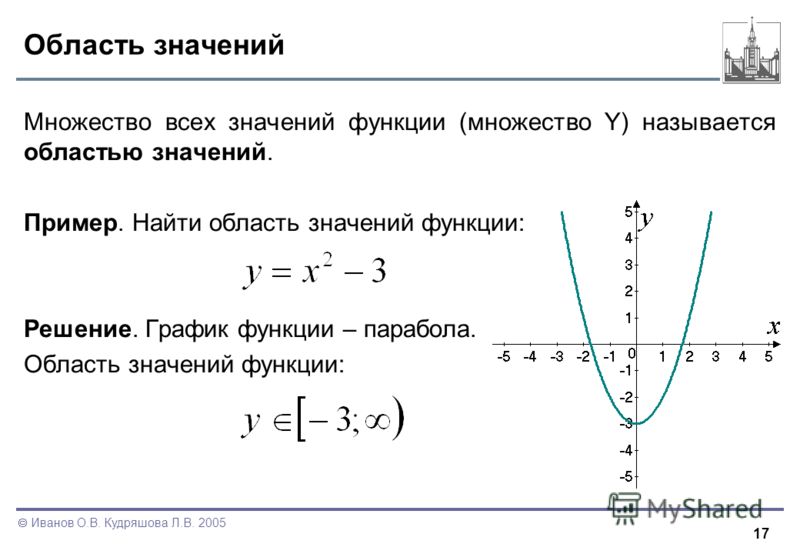
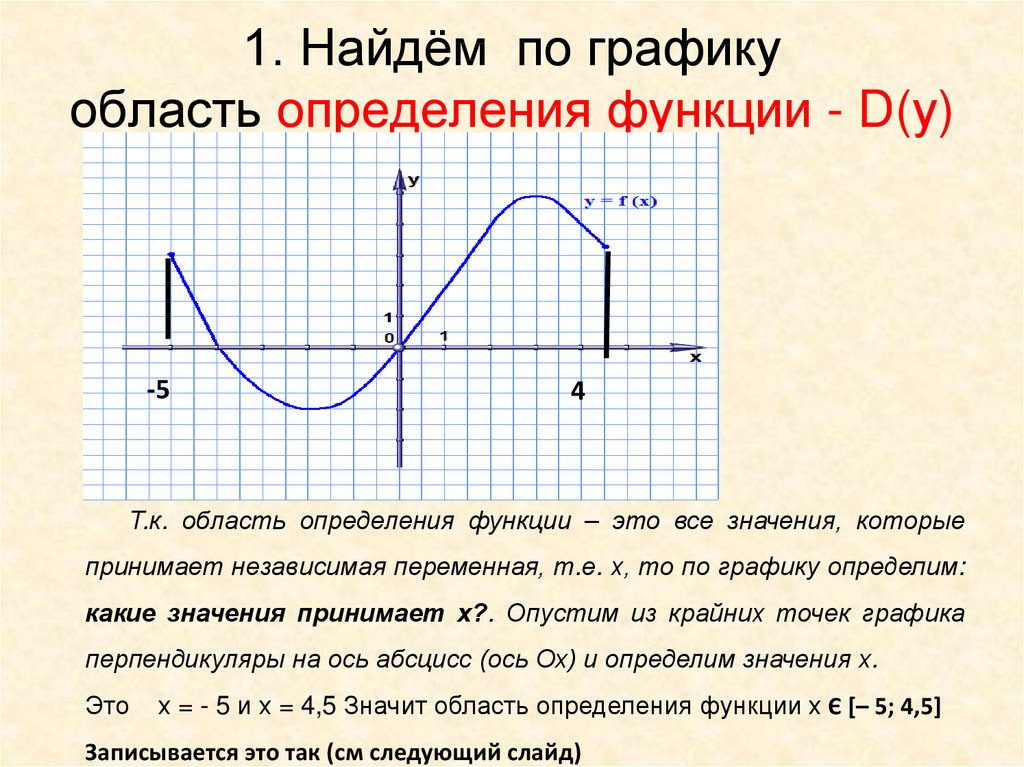 Таким образом, чтобы найти диапазон графика, посмотрите на значения y, охватываемые графиком. Самые высокие и самые низкие значения графиков полезны при записи диапазона графика.
Таким образом, чтобы найти диапазон графика, посмотрите на значения y, охватываемые графиком. Самые высокие и самые низкие значения графиков полезны при записи диапазона графика. Вертикальный экстент графика — это все значения диапазона
Вертикальный экстент графика — это все значения диапазона




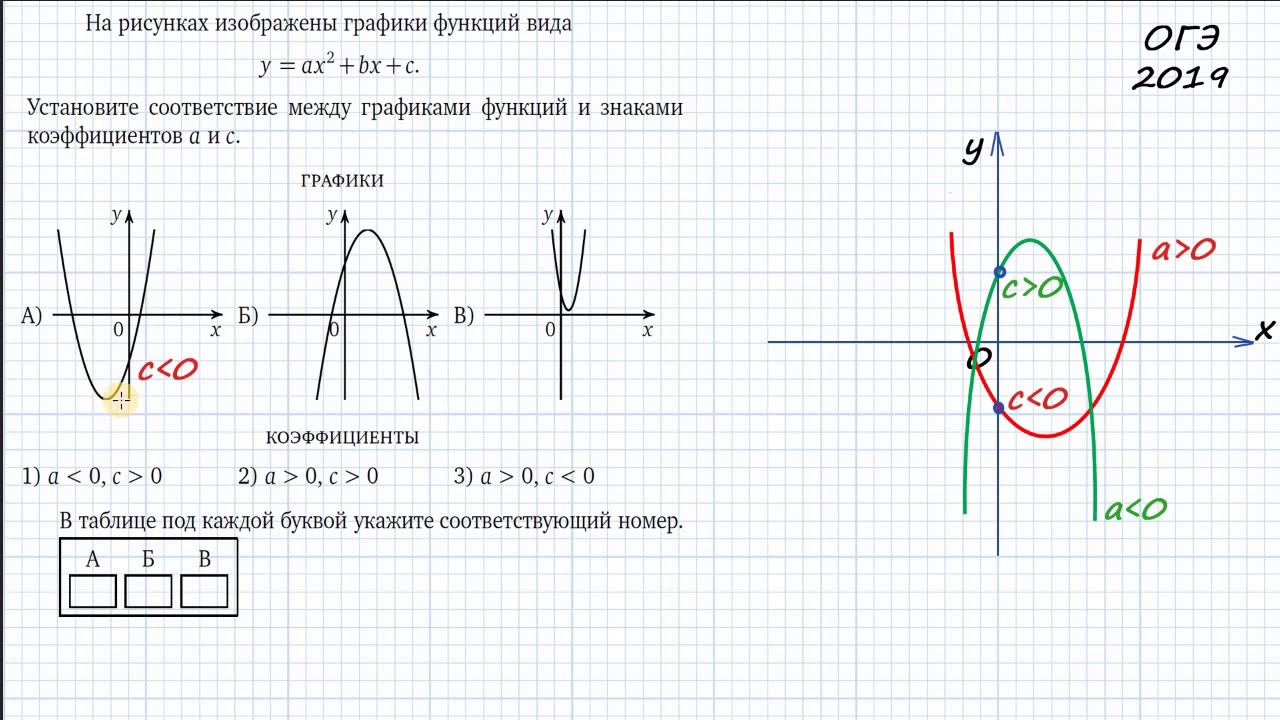
 В библиотеке доступно более 70 различных типов диаграмм.
В библиотеке доступно более 70 различных типов диаграмм. 
 В результате получается сгруппированная информативная схема.
В результате получается сгруппированная информативная схема.
 Программа доступна на Windows, Unix/Linux и Mac.
Программа доступна на Windows, Unix/Linux и Mac.
 Также в программе есть калькулятор, с помощью которого можно решать разнообразные уравнения за несколько секунд.
Также в программе есть калькулятор, с помощью которого можно решать разнообразные уравнения за несколько секунд.

 На сайте 4000 схем с выгрузкой прямо в PowerPoint. Удобный выбор нужной визуализации: тип схемы — 2D/3D (правильный ответ 2D) число элементов цвет. Бесплатно через регистрацию.
На сайте 4000 схем с выгрузкой прямо в PowerPoint. Удобный выбор нужной визуализации: тип схемы — 2D/3D (правильный ответ 2D) число элементов цвет. Бесплатно через регистрацию.
 Профессиональная версия даёт возможность работать со слоями, экспортировать графики в SVG и создавать схемы с помощью клавиатуры. Стандартная версия стоит $ 149,99, профессиональная — $ 249,99. Работает на Mac и iOS.
Профессиональная версия даёт возможность работать со слоями, экспортировать графики в SVG и создавать схемы с помощью клавиатуры. Стандартная версия стоит $ 149,99, профессиональная — $ 249,99. Работает на Mac и iOS. Профессиональная версия за $ 19 в месяц даёт возможность создавать до 100 диаграмм в месяц, версия «Business» за $ 67 — 1000.
Профессиональная версия за $ 19 в месяц даёт возможность создавать до 100 диаграмм в месяц, версия «Business» за $ 67 — 1000.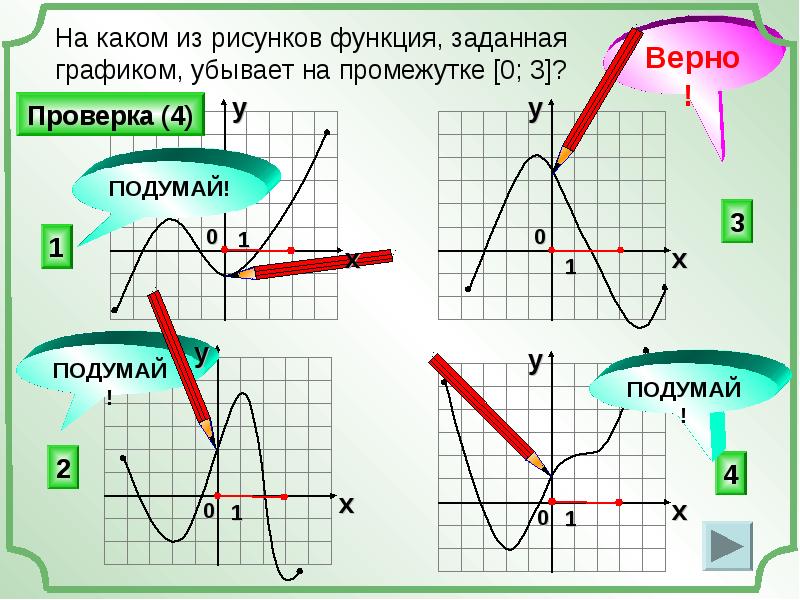 Можно легко добавлять фото, видео, менять стили и шрифты, есть интеграция с Google таблицами и другими сервисами.
Можно легко добавлять фото, видео, менять стили и шрифты, есть интеграция с Google таблицами и другими сервисами. Это похоже на Adobe Illustrator или CorelDraw, но работает на холсте html5 с Google Диском. Таким образом, нет необходимости загружать программное обеспечение, и вы можете получить доступ к своей работе в любое время и в любом месте. Внезапно ваш творческий потенциал высвобождается!
Независимо от того, начинаете ли вы или уже являетесь опытным дизайнером, онлайн-инструмент Drawing — это мощное решение для векторного графического дизайна в Интернете. С онлайн-графическим дизайном в различных средах у вас есть все, что вам нужно, чтобы выразить свой стиль и творчество.
Это похоже на Adobe Illustrator или CorelDraw, но работает на холсте html5 с Google Диском. Таким образом, нет необходимости загружать программное обеспечение, и вы можете получить доступ к своей работе в любое время и в любом месте. Внезапно ваш творческий потенциал высвобождается!
Независимо от того, начинаете ли вы или уже являетесь опытным дизайнером, онлайн-инструмент Drawing — это мощное решение для векторного графического дизайна в Интернете. С онлайн-графическим дизайном в различных средах у вас есть все, что вам нужно, чтобы выразить свой стиль и творчество. Вы можете открыть шаблон и отредактировать его, а затем экспортировать на локальный диск или сохранить на Google Диске.
Вы можете открыть шаблон и отредактировать его, а затем экспортировать на локальный диск или сохранить на Google Диске. Вы можете найти настройки освещения на последней вкладке эффектов фильтра, вы можете установить 3 разных источника света на свои элементы, чтобы получить более удивительный художественный эффект.
Вы можете найти настройки освещения на последней вкладке эффектов фильтра, вы можете установить 3 разных источника света на свои элементы, чтобы получить более удивительный художественный эффект.
 Введение — Образовательная инфографика […]
Введение — Образовательная инфографика […] Идеи дизайна инфографики из этого списка 10 лучших вдохновят […]
Идеи дизайна инфографики из этого списка 10 лучших вдохновят […]
 Во-первых, […]
Во-первых, […]

 2n+B=0 >>
2n+B=0 >>
 Настройка.
Настройка. 3.$
3.$ Например, уравнение x 2 + 1 = 0 не имеет действительных решений. Если вы запишете это как x 2 = –1 и попытаетесь извлечь квадратный корень из каждой стороны, у вас возникнут проблемы.
Например, уравнение x 2 + 1 = 0 не имеет действительных решений. Если вы запишете это как x 2 = –1 и попытаетесь извлечь квадратный корень из каждой стороны, у вас возникнут проблемы. Сначала разложите уравнение на множители, чтобы получить x 2 ( x – 2) + 25 ( x – 2) = ( x – 2)( x 2) + 25) = 0 Используя свойство умножения нуля, вы определяете, что x – 2 = 0 и x = 2. Вы также получаете x 2 + 25 = 0 и x . 2 = –25. Возьмите квадратный корень из каждой стороны и
Сначала разложите уравнение на множители, чтобы получить x 2 ( x – 2) + 25 ( x – 2) = ( x – 2)( x 2) + 25) = 0 Используя свойство умножения нуля, вы определяете, что x – 2 = 0 и x = 2. Вы также получаете x 2 + 25 = 0 и x . 2 = –25. Возьмите квадратный корень из каждой стороны и



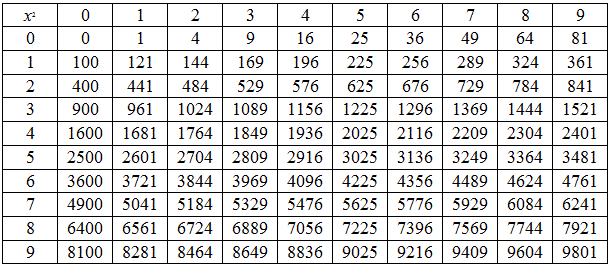
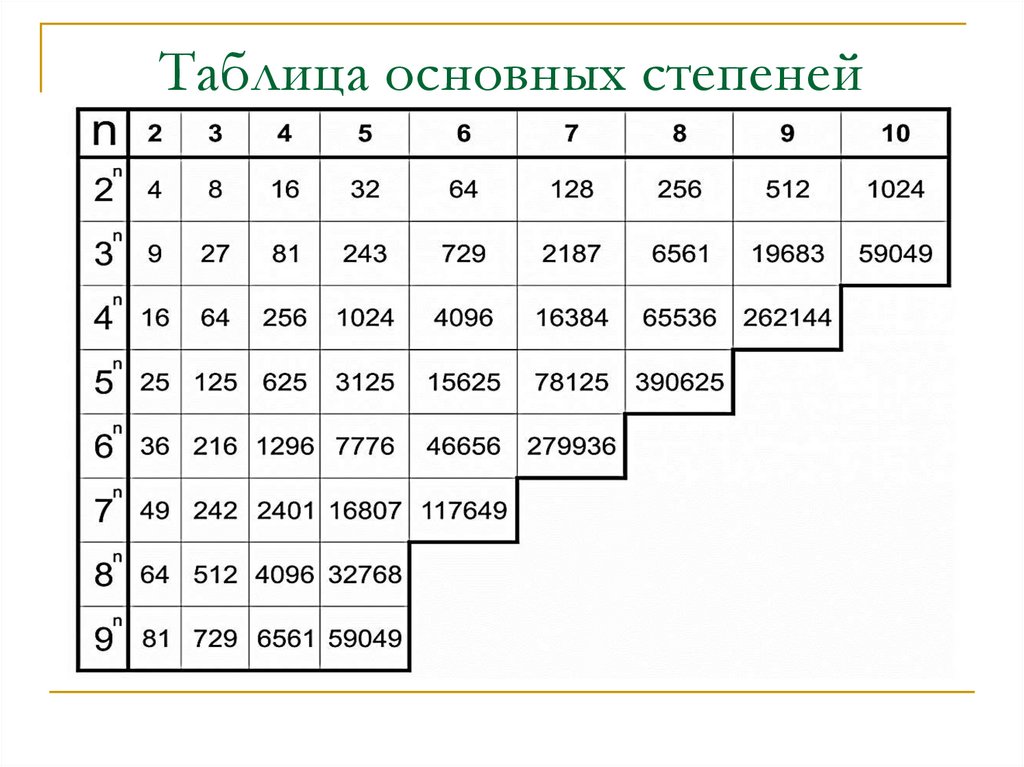 – Только 10 минут, у нас еще есть время.
– Только 10 минут, у нас еще есть время.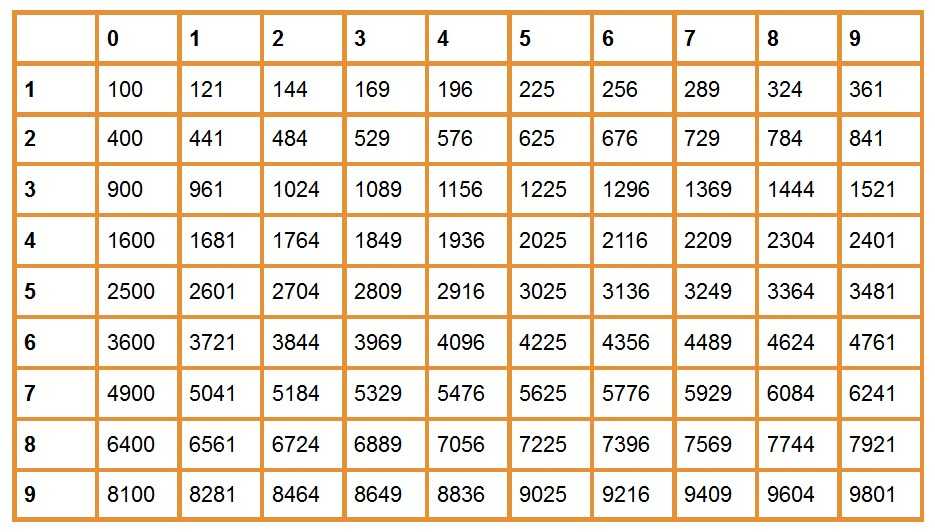 – Да, одна синяя ручка и одна красная ручка.
– Да, одна синяя ручка и одна красная ручка. «). Но могут писаться и буквами: erste, zweite, dritte, neunte, dreizehnte, …
«). Но могут писаться и буквами: erste, zweite, dritte, neunte, dreizehnte, …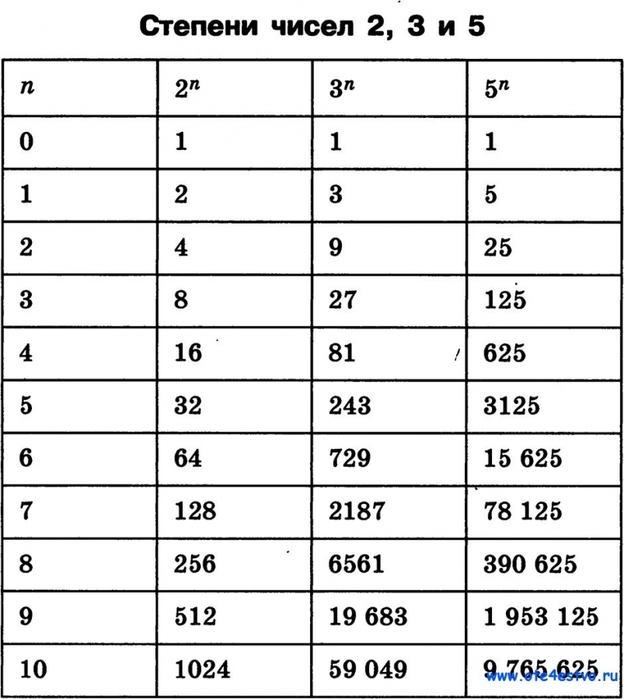 – В девятом выпуске этого журнала Вы найдете сообщение о кругосветном путешествии Михаэля Брауна.
– В девятом выпуске этого журнала Вы найдете сообщение о кругосветном путешествии Михаэля Брауна.  – 30,12% суммы уже потрачено.
– 30,12% суммы уже потрачено. – Новая машина BMW может ехать быстрее 200 км/ч.
– Новая машина BMW может ехать быстрее 200 км/ч. На томограммах — множественных сканах дыхательного органа в трех плоскостях — визуализируются нефункциональные участки уплотнения или инфильтрации легочной ткани.
На томограммах — множественных сканах дыхательного органа в трех плоскостях — визуализируются нефункциональные участки уплотнения или инфильтрации легочной ткани.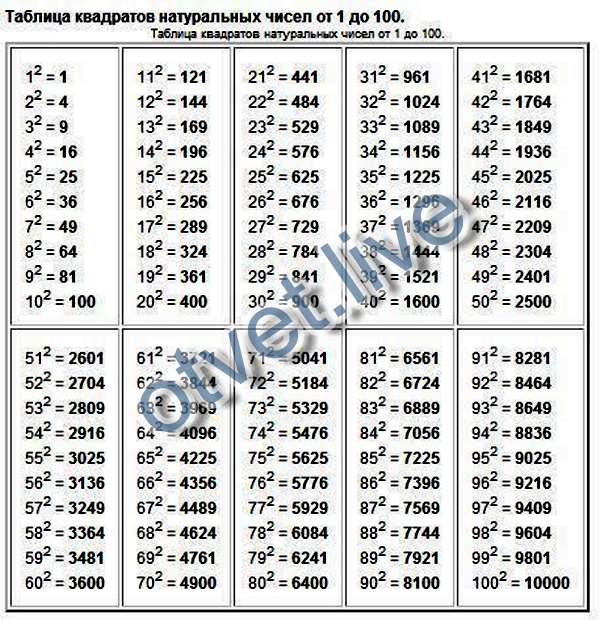
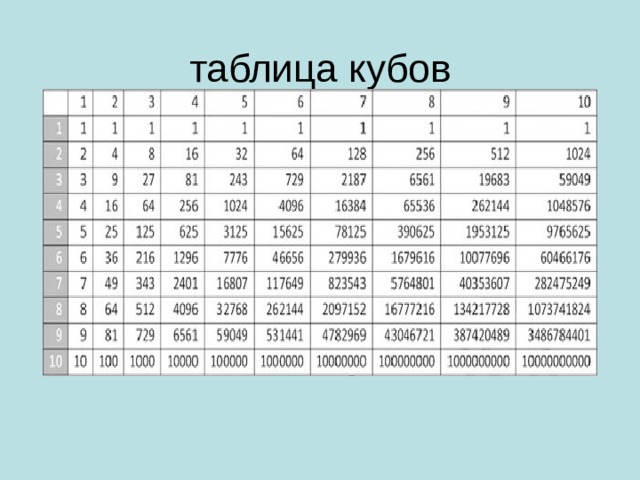
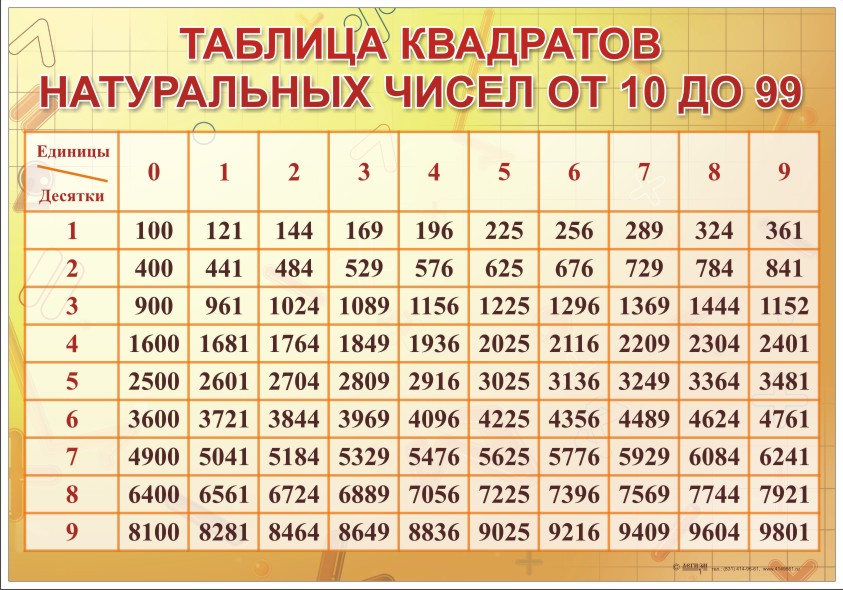 Ее ввели специалисты из Центра диагностики и телемедицины США, изучив КТ-исследования 13 003 человек, которые составили основную выборку.
Ее ввели специалисты из Центра диагностики и телемедицины США, изучив КТ-исследования 13 003 человек, которые составили основную выборку.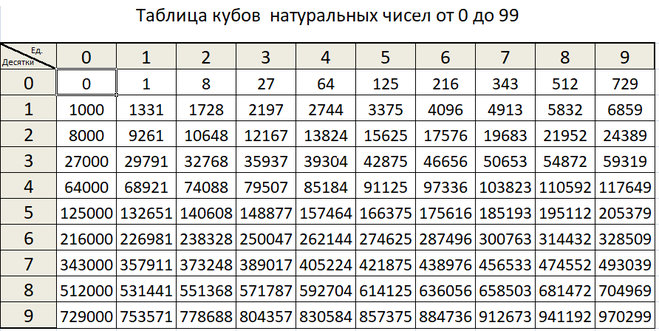 При определении степени тяжести воспаления легких учитываются и другие признаки воспаления легких:
При определении степени тяжести воспаления легких учитываются и другие признаки воспаления легких:
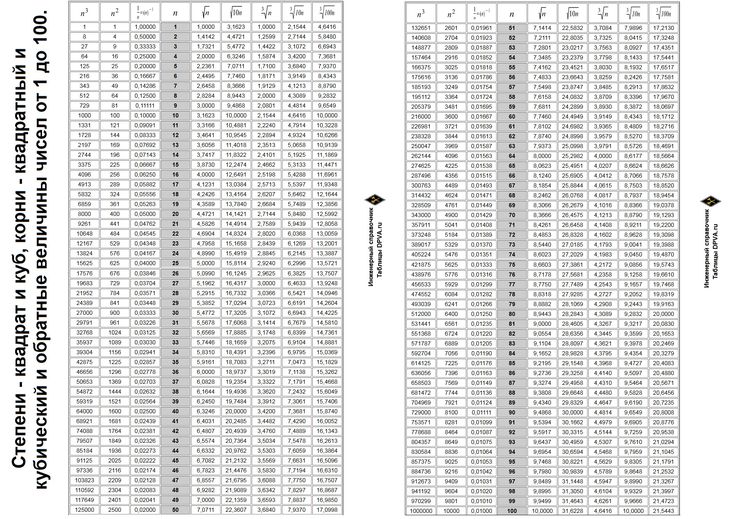 Если лечение не помогает, и становится хуже, рекомендовано сделать повторное КТ легких, чтобы оценить динамику и скорректировать лечение. Поскольку у пациента с умеренной пневмонией КТ2 может быть поражено до 50% легких, после основного лечения необходима реабилитация.
Если лечение не помогает, и становится хуже, рекомендовано сделать повторное КТ легких, чтобы оценить динамику и скорректировать лечение. Поскольку у пациента с умеренной пневмонией КТ2 может быть поражено до 50% легких, после основного лечения необходима реабилитация.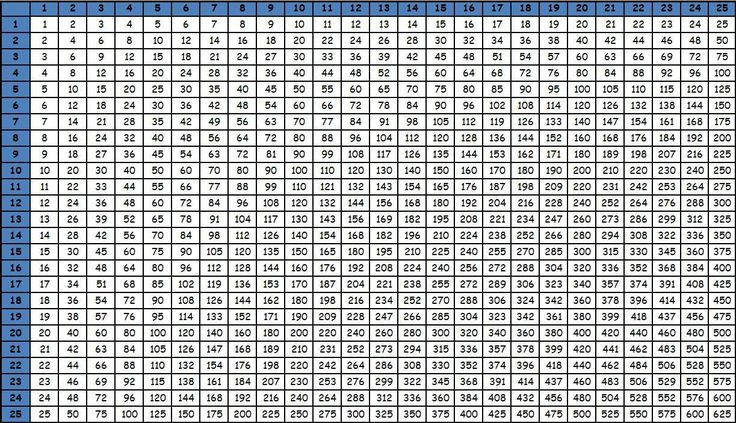 Пациент может нуждаться в реанимации с искусственной вентиляцией легких (ИВЛ).
Пациент может нуждаться в реанимации с искусственной вентиляцией легких (ИВЛ).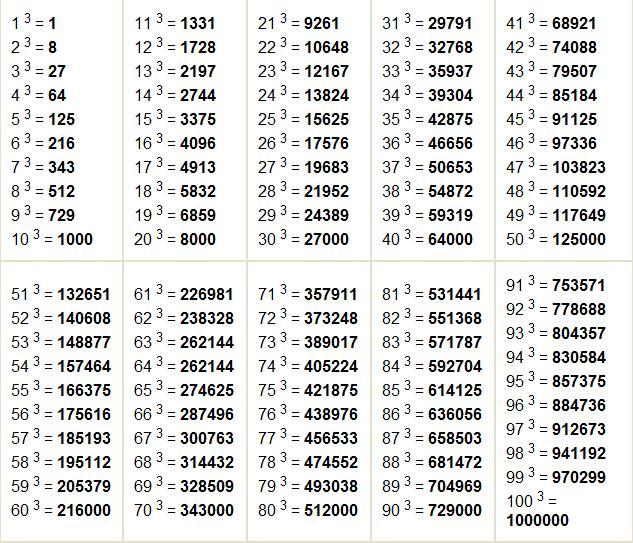 Давайте посмотрим на это более наглядно:
Давайте посмотрим на это более наглядно: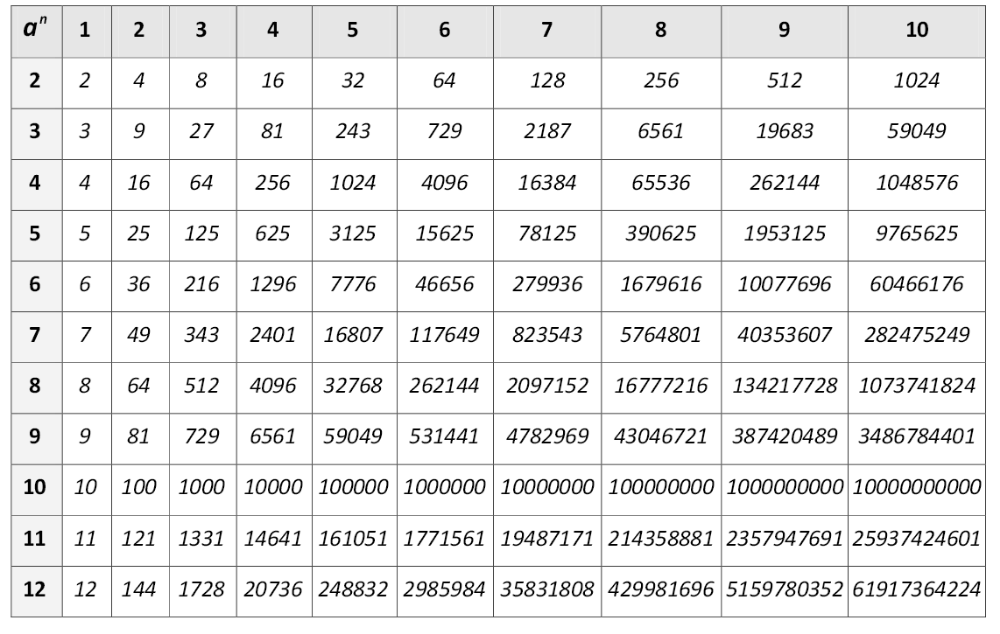

 Число Поднятый силой Равно
Число Поднятый силой Равно