Решение уравнений | Онлайн калькулятор
Уравнение представляет собой буквенное равенство, которое справедливо только при некоторых значениях букв, которые в него входят. Эти буквы получили название неизвестных. А корнями уравнения называют значения неизвестных, при которых уравнение становится тождеством. Решить уравнение означает найти все его корни. Если два или несколько уравнений имеют одни и те же корни, их называют равносильными.
Специально для решения самых разнообразных уравнений на нашем сайте создан онлайн калькулятор, позволяющий сделать расчеты более легкими и быстрыми. Можно решить логарифмические, алгебраические, линейные, нелинейные, квадратные, тригонометрические уравнения и многие другие.
Загляните на наш сайт, воспользуйтесь лучшим способом решений уравнений и убедитесь, насколько это быстро и удобно.
Калькуляторы для решения уравнений, онлайн
и как найти корни | вычислить корни |
любые показательные уравнения онлайн | и график в координатной плоскости |
построить график функции и нормали в системе координат | любого типа и порядка |
линейных, квадратных, кубических, тригонометрических и тд | с ходом действий |
калькулятор | через дискриминант |
по методу Виета Кардано | онлайн |
до 10 степени | онлайн калькулятор |
2 порядка многочлена | найти значение всех его корней |
рассчитать | нахождения корней уравнения |
алгебраические и трансцендентные | онлайн калькулятор |
онлайн расчет |
Select rating12345
Рейтинг: 3. 2 (Голосов 5)
2 (Голосов 5)
Сообщить об ошибке
Вам помог этот калькулятор?
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
НЕТ
Смотрите также
| Операции с матрицами | Действия с векторами | Решение СЛУ | Ранг матрицы | Минор матрицы |
| Решение матриц | Геометрия | Математический анализ | Аналитическая геометрия | Арифметика |
Проект «Решение систем линейных уравнений различными методами» • Наука и образование ONLINE
Главная Работы на конкурс Предметное образование Физико-математические дисциплины Проект «Решение систем линейных уравнений различными методами»
Автор: Пономарева Софья Сергеевна
Место работы/учебы (аффилиация): МАОУ «Лицей №15 им. Н.Н. Макаренко», г.Кызыл, Республика Тыва, 10 класс
Н.Н. Макаренко», г.Кызыл, Республика Тыва, 10 класс
Научный руководитель: Яговдик Надежда Васильевна
В работе рассмотрены различные математические методы решения систем линейных уравнений, показаны алгоритмы и примеры решения линейных алгебраических уравнений различными методами. Дается краткая историческая справка о жизни ученых, занимавшихся данной проблемой. Приводятся примеры использования СЛАУ. Данная тема способствует формированию математической интуиции, которая поможет ориентироваться в способах решения систем.
Целью работы является оценка различных методов решения систем линейных уравнений с точки зрения вычислительной сложности.
Задачи:
- обобщение методов решения СЛАУ, знакомых с 7 класса;
- знакомство с новыми методами решения СЛАУ;
- изучение истории вопроса (развития теории, имена ученых, их достижения).
При работе над данным проектом прослежено развитие алгебры на протяжении 2,5 тысяч лет, накоплен банк задач, решенных разными методами. Исследованы методы решения систем уравнений. Например, графический метод решения более удобен для системы из двух линейных уравнений (наглядно и быстро), а метод Гаусса для этой цели менее пригоден. Он проигрывает с точки зрения наглядности. Однако, именно метод Гаусса и метод Крамера являются наиболее универсальными для решения систем уравнений с большим количеством уравнений и переменных.
Исследованы методы решения систем уравнений. Например, графический метод решения более удобен для системы из двух линейных уравнений (наглядно и быстро), а метод Гаусса для этой цели менее пригоден. Он проигрывает с точки зрения наглядности. Однако, именно метод Гаусса и метод Крамера являются наиболее универсальными для решения систем уравнений с большим количеством уравнений и переменных.
Работа на выбранную тему является актуальной в связи с тем, что она систематизирует знания и позволяет учащимся лучше понять данную тему, т.к. способы решения систем линейных уравнений собраны в единое пособие.
Загрузка…
Исследовательский проект «Последовательность Фибоначчи в трейдинге»
Доступна к просмотру полнотекстовая версия работы
Обоснование выбора темы. В последние годы интерес к инвестициям в России постоянно растёт. Инвестирование в ценные бумаги стало более выгодной альтернативой хранению сбережений дома или на банковском депозите. Что общего между Московской фондовой бир…
Что общего между Московской фондовой бир…
Посмотреть работу
Исследовательский проект «Уравнения в целых числах»
Доступна к просмотру полнотекстовая версия работы
Исследование диофантовых уравнений — уравнений в целых числах — интересовало математиков с древних времен до современности. Общего подхода к решению таких уравнений открыть не удалось, не зря их называют неопределенными. Решение таких уравнений рассм…
Посмотреть работу
Проект «Алгебра в экономике (бизнес планирование)»
В экономической науке широко используется методы анализа, синтеза, индукции, научного абстрагирования, а также математический инструментарий. Гипотеза: Математические законы и понятия, которыми мы владеем, используются ли в экономике. Цель работы: По…
Посмотреть работу
4″>Проектная работа «Нестандартные способы умножения»Тема очень актуальна, поскольку простое умножение — это долгое и скучное занятие, а вот с нестандартными способами это занятие становиться весёлым и быстрым. Цель: подробно рассмотреть несколько нестандартных способов умножения и выявить самый удобны…
Посмотреть работу
Исследовательская работа «Многоугольники на целочисленной решетке»
Мы часто предпочитаем рисовать и чертить на клетчатой бумаге. И даже не задумываемся о том, что она (а точнее – узлы клетчатой бумаги) являются одним из важнейших примеров точечной решетки на плоскости. Решетки на плоскости позволяют переводить на ге…
Посмотреть работу
Мероприятие завершено
Выберите подписку
Все планы включают калькулятор алгебры, уроки, практику и отсутствие рекламы.
Ежемесячно
$9,99 /месяцКупить
Скидка 50%!
Ежегодно
4,99 доллара США /месяцКупить
(59,88 долларов США в год)
Пошаговые пояснения к домашним заданиям
Получите мгновенную непрерывную помощь с простыми для понимания объяснениями при решении сложных уравнений.
Просто введите уравнение, и оно рассчитает ответ. Мало того, это приложение также дает вам пошаговое объяснение того, как найти ответ! Чрезвычайно полезно …
A.J.B
Премиум-уроки по алгебре
Исследуйте интерактивные уроки, смотрите видео и читайте дальше, чтобы лучше понять математическую задачу, над которой вы работаете.
Основы алгебры еще никогда не были для меня такими понятными. Ваш метод сработал как никто другой.
Дон Д.
Непрерывный доступ к бесконечным практическим задачам
Оттачивайте свои навыки с помощью наших автоматически создаваемых практических задач. Практикуйтесь столько, сколько хотите по каждой теме.
Мне 79 лет, и я нахожу это отличным упражнением для мозга. В школе я очень плохо учился по алгебре.
Чарльз Дж.
Не позволяйте алгебре стоять у вас на пути. Сокруши его с MathPapa!
Премиальный план Алгебра калькулятор
Практические задачи
Уроки
Нет рекламы
Общие вопросы
900Улучшу ли я алгебру?
Мы максимально упрощаем понимание алгебры быстро. Практика, уроки, видео и многое другое предоставят вам инструменты для самостоятельного изучения алгебры или помощи вашему ученику. Если вы только начинаете или повторяете свои знания по алгебре, ваше членство поможет вам перейти на следующий уровень.
Практика, уроки, видео и многое другое предоставят вам инструменты для самостоятельного изучения алгебры или помощи вашему ученику. Если вы только начинаете или повторяете свои знания по алгебре, ваше членство поможет вам перейти на следующий уровень.
Что, если я передумаю?
Без проблем. Вы можете получить полный возврат средств без вопросов в течение 7 дней с момента первоначальной покупки, связавшись с нами напрямую. И вы всегда можете отменить подписку в настройках своей учетной записи. Итак, получите премиум сегодня!
Будет ли мое приложение для iOS или Android также обновлено?
Да, вы можете войти в мобильное приложение с помощью своей обновленной веб-учетной записи, чтобы получить доступ к премиум-приложению.
Больше вопросов?
Свяжитесь с нами
Решатель математических уравнений | Порядок операций
Использование калькулятора
Решайте математические задачи, используя порядок операций, такой как PEMDAS, BEDMAS, BODMAS, GEMDAS и MDAS. (Предостережение PEMDAS) Этот калькулятор решает математические уравнения, которые складывают, вычитают, умножают и делят положительные и отрицательные числа и экспоненциальные числа. Вы также можете включать в уравнения скобки и числа с показателями степени или корнями.
95 это 2 в степени 5)
(Предостережение PEMDAS) Этот калькулятор решает математические уравнения, которые складывают, вычитают, умножают и делят положительные и отрицательные числа и экспоненциальные числа. Вы также можете включать в уравнения скобки и числа с показателями степени или корнями.
95 это 2 в степени 5)
r Корни (2r3 — корень 3-й степени из 2)
() [] {} Скобки или группировка
Вы можете попытаться скопировать уравнения из других печатных источников и вставить их сюда, и, если они используют ÷ для деления и × для умножения, этот калькулятор уравнений попытается преобразовать их в / и * соответственно, но в некоторых случаях вам может понадобиться повторно введите скопированные и вставленные символы или даже полные уравнения. 9(2/3) равно 5, увеличенному до 2/3
Ввод дробей
Если вы хотите, чтобы запись, такая как 1/2, рассматривалась как дробь, введите ее как (1/2). Например, в уравнении 4 разделить на ½ вы должны ввести его как 4/(1/2). Тогда первым выполняется деление 1/2 = 0,5, а последним — 4/0,5 = 8. Если вы неправильно введете его как 4/1/2, то сначала будет решено 4/1 = 4, а затем 4/2 = 2. 2 неправильный ответ. 8 был правильным ответом.
Например, в уравнении 4 разделить на ½ вы должны ввести его как 4/(1/2). Тогда первым выполняется деление 1/2 = 0,5, а последним — 4/0,5 = 8. Если вы неправильно введете его как 4/1/2, то сначала будет решено 4/1 = 4, а затем 4/2 = 2. 2 неправильный ответ. 8 был правильным ответом.
Математический порядок операций — PEMDAS, BEDMAS, BODMAS, GEMDAS, MDAS
PEMDAS — это аббревиатура, которая может помочь вам запомнить порядок операций при решении математических уравнений. PEMDAS обычно расширяется до фразы «Пожалуйста, извините, моя дорогая тетя Салли». Первая буква каждого слова во фразе образует аббревиатуру PEMDAS. Решайте математические задачи со стандартным математическим порядком операций, работая слева направо:
- Скобки, Скобки, Группировка — работая слева направо в уравнении, сначала найдите и решите выражения в скобках; если у вас есть вложенные скобки, работайте от самых внутренних до самых внешних
- Экспоненты и корни — работая слева направо в уравнении, вычислить все экспоненциальные и корневые выражения второй
- Умножение и деление — затем решите выражения умножения И деления по мере их появления, работая слева направо в уравнении.
 Для правила MDAS вы начнете с этого шага.
Для правила MDAS вы начнете с этого шага. - Сложение и вычитание — затем решите оба выражения сложения и вычитания по мере их появления, работая слева направо в уравнении 9.0140
PEMDAS Caution
Умножение НЕ всегда выполняется перед делением. Умножение и деление выполняются по мере их появления в уравнении, слева направо.
Сложение НЕ всегда выполняется перед вычитанием. Сложение и вычитание выполняются по мере их появления в уравнении, слева направо.
Порядок «MD» (DM в BEDMAS) иногда путают, чтобы означать, что Умножение происходит перед Делением (или наоборот). Однако умножение и деление имеют одинаковый приоритет. Другими словами, умножение и деление выполняются на одном шаге слева направо. Например, 4/2*2 = 4, а 4/2*2 не равно 1.
Такая же путаница может произойти и с «AS», однако сложение и вычитание также имеют одинаковый приоритет и выполняются на одном и том же шаге слева направо. Например, 5 — 3 + 2 = 4 и 5 — 3 + 2 не равно 0.
Чтобы запомнить это, можно записать PEMDAS как PE(MD)(AS) или BEDMAS как BE(DM)(AS). ).
Порядок операций Акронимы
Акронимы для порядка операций означают, что вы должны решать уравнения в этом порядке, всегда работая слева направо в вашем уравнении.
PEMDAS означает » P арены, E экспоненты, M умножение и D ivision, A дополнение и S вычитание»
Вы также можете увидеть BEDMAS, BODMAS и GEMDAS как аббревиатуры порядка операций. В этих аббревиатурах «квадратные скобки» совпадают со скобками, а «порядок» совпадает с показателями степени. GEMDAS, «группировка» похожа на скобки или квадратные скобки.
BEDMAS означает » B ракетки, E экспоненты, D ivision и M умножение, A дополнение и S «вычитание»
BEDMAS аналогичен BODMAS. D ivision и M умножение, A дополнение и S вычитание»
D ivision и M умножение, A дополнение и S вычитание»
GEMDAS означает » G нарезка, E экспоненты, D ivision и M умножение, A дополнение и S вычитание»
MDAS является подмножеством приведенных выше аббревиатур. Он означает « M умножение, и D ivision, A сложение и S вычитание»
Ассоциативность операторов
Умножение, деление, сложение и вычитание являются левоассоциативными. Это означает, что при решении выражений умножения и деления вы исходите из левой части уравнения.
Примеры левой ассоциативности:
- a / b * c = (a / b) * c 9(4/5))
Для вложенных скобок или квадратных скобок сначала решите самые внутренние скобки или скобочные выражения, а затем работайте с самыми внешними скобками. Для каждого выражения в круглых скобках следуйте остальной части порядка PEMDAS: сначала вычислите показатели степени и радикалы, затем умножение и деление и, наконец, сложение и вычитание.
Для каждого выражения в круглых скобках следуйте остальной части порядка PEMDAS: сначала вычислите показатели степени и радикалы, затем умножение и деление и, наконец, сложение и вычитание.
Умножение и деление можно решать на одном и том же шаге математической задачи: после решения скобок, показателей степени и радикалов и перед сложением и вычитанием. Продолжайте слева направо для умножения и деления. Решайте сложение и вычитание в последнюю очередь после скобок, показателей степени, корней и умножения/деления. Снова действуйте слева направо для сложения и вычитания.
Сложение, вычитание, умножение и деление положительных и отрицательных чисел
Этот калькулятор использует стандартные правила для решения уравнений.
Правила операций сложения (+)
Если знаки совпадают, сохраняем знак и добавляем числа.
-21 + -9 = — 30
(+7) + (+13) = (+20)
Если знаки разные, то из большего числа вычесть меньшее и сохранить знак большего числа.
(-13) + (+5) = (-8)
(-7) + (+9) = (+2)
Правила операций вычитания (-)
Сохранить знак первого числа. Замените все следующие знаки вычитания на знаки сложения. Измените знак каждого следующего числа так, чтобы положительное стало отрицательным, а отрицательное стало положительным, затем следуйте правилам для задач на сложение.
(-15) — (-7) =
(-5) — (+6) =
(+4) — (-3) =
(-15) + (+7) = (- 8)
(-5) + (-6) = (-11)
(+4) + (+3) = (+7)
Правила операций умножения (* или ×)
Умножение отрицательного значения на отрицательное или положительного на положительное дает положительный результат. Умножение положительного на отрицательное или отрицательного на положительное дает отрицательный результат.
-10 * -2 = 20
10 * 2 = 20
10 * -2 = -20
-10 * 2 = -20
-10 × -2 = 20
10 × 2 = 20
10 × -2 = -20
-10 × 2 = -20
Правила операций деления (/ или ÷)
Аналогично умножению, деление отрицательного числа на отрицательное или положительное положительным дает положительный результат.

 Для правила MDAS вы начнете с этого шага.
Для правила MDAS вы начнете с этого шага. ..
.. Са (ОН)2 легко взаимодействует с кислотами из-за своей основной природы.
Са (ОН)2 легко взаимодействует с кислотами из-за своей основной природы. 

 Следовательно, полное ионное уравнение –
Следовательно, полное ионное уравнение – Это связано с тем, что HI является полярной молекулой.
Это связано с тем, что HI является полярной молекулой.
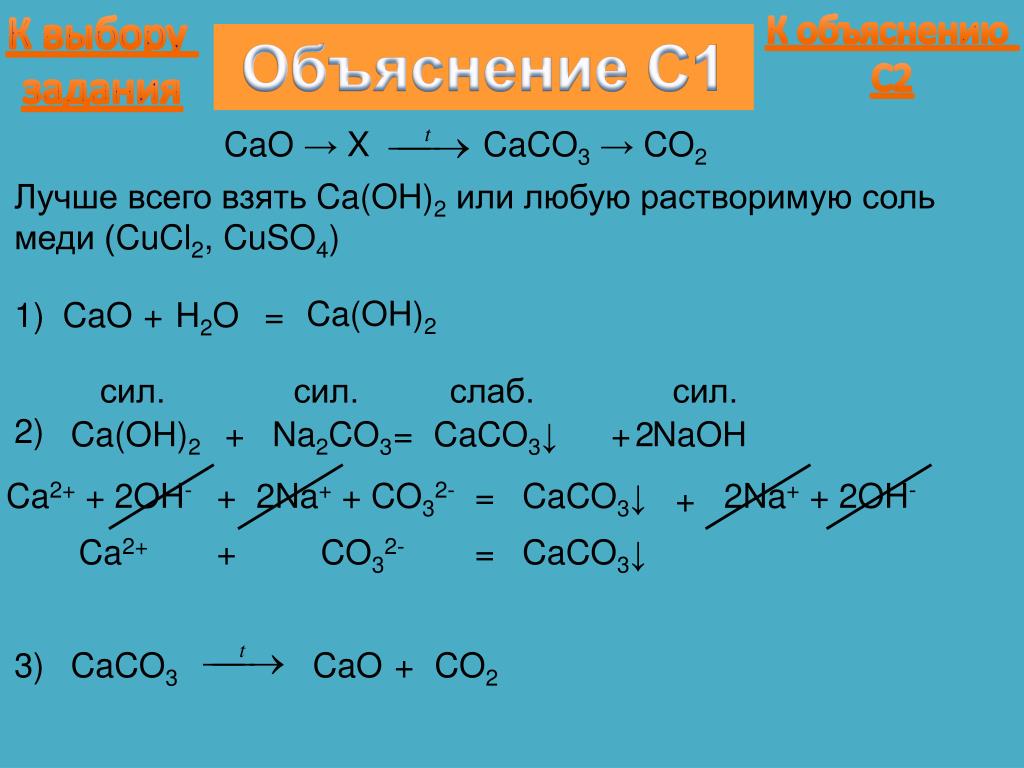



 Раствор фильтруют, и для нейтрализации образца объемом 25,00 мл требуется 22,50 мл 0,0250 М HCl. Рассчитайте значение для K sp Ca(OH) 2 по этим данным.
Раствор фильтруют, и для нейтрализации образца объемом 25,00 мл требуется 22,50 мл 0,0250 М HCl. Рассчитайте значение для K sp Ca(OH) 2 по этим данным.
 )
)
 Вы можете с легкостью заблокировать веб-сайты с неподходящим для детей контентом
и запретить определенным устройствам доступ в интернет одним касанием экрана вашего смартфона5.
Вы можете с легкостью заблокировать веб-сайты с неподходящим для детей контентом
и запретить определенным устройствам доступ в интернет одним касанием экрана вашего смартфона5.

 2, её график и свойства»
2, её график и свойства» Соответственно,
график может иметь 2 точки пересечения с осью х, 1 точку пересечения с
осью х или не пересекать её. Понятно, что нулями квадратичной функции
являются корни соответствующего квадратного уравнения. По графику удобно
находить промежутки знакопостоянства и промежутки
монотонности функции.
Соответственно,
график может иметь 2 точки пересечения с осью х, 1 точку пересечения с
осью х или не пересекать её. Понятно, что нулями квадратичной функции
являются корни соответствующего квадратного уравнения. По графику удобно
находить промежутки знакопостоянства и промежутки
монотонности функции. Возможны два случая изображения графика.
Возможны два случая изображения графика.
 . На борту орбитальной лаборатории многонациональная команда из четырех человек будет проводить обширные исследования, исследовать новые технологии и общаться с аудиторией по всему миру как поборники науки, технологий, инженерии, искусства и математики. Их усилия будут продолжать закладывать основу и создавать ключевые возможности, необходимые для создания и эксплуатации станции «Аксиом», первой в мире коммерческой космической станции.
. На борту орбитальной лаборатории многонациональная команда из четырех человек будет проводить обширные исследования, исследовать новые технологии и общаться с аудиторией по всему миру как поборники науки, технологий, инженерии, искусства и математики. Их усилия будут продолжать закладывать основу и создавать ключевые возможности, необходимые для создания и эксплуатации станции «Аксиом», первой в мире коммерческой космической станции. МКС.
МКС.

 com
com Станция, которая поддержит человеческий рост за пределами планеты и принесет неисчислимые преимущества дома.
Станция, которая поддержит человеческий рост за пределами планеты и принесет неисчислимые преимущества дома. Однако всего через два дня мы получили его.
Однако всего через два дня мы получили его. Барнауи и Аль-Карни являются членами первого класса астронавтов Саудовской Аравии. Они станут первыми жителями королевства, посетившими МКС, а Барнауи станет первой женщиной из Саудовской Аравии, достигшей последнего рубежа.
Барнауи и Аль-Карни являются членами первого класса астронавтов Саудовской Аравии. Они станут первыми жителями королевства, посетившими МКС, а Барнауи станет первой женщиной из Саудовской Аравии, достигшей последнего рубежа. Следите за нами в Твиттере @Spacedotcom (открывается в новой вкладке) или на Facebook (открывается в новой вкладке) .
Следите за нами в Твиттере @Spacedotcom (открывается в новой вкладке) или на Facebook (открывается в новой вкладке) . 


 Вам просто нужно указать метод для получения удаленного потока документов, а затем передать его классу Converter в качестве конструктора.
Вам просто нужно указать метод для получения удаленного потока документов, а затем передать его классу Converter в качестве конструктора. NET CLI.
NET CLI. Total для .NET поддерживает пакетное преобразование документов DOC, что позволяет разработчикам конвертировать несколько файлов одновременно.
Total для .NET поддерживает пакетное преобразование документов DOC, что позволяет разработчикам конвертировать несколько файлов одновременно.
 innerHTML = »
innerHTML = »

 Кроме того, вы можете хранить их в онлайн-хранилище документов Smallpdf, если зарегистрируете бесплатную учетную запись.
Кроме того, вы можете хранить их в онлайн-хранилище документов Smallpdf, если зарегистрируете бесплатную учетную запись.
 Не требуется регистрация или загрузка.
Не требуется регистрация или загрузка.
 Conversion Cloud в свое приложение Python, используя следующую команду в консоль:
Conversion Cloud в свое приложение Python, используя следующую команду в консоль:
 Вы можете загрузить его, используя следующий пример кода:
Вы можете загрузить его, используя следующий пример кода: приведено ниже:
приведено ниже:


 Теперь вы можете заново вырастить все существо из этого крошечного образца.
Теперь вы можете заново вырастить все существо из этого крошечного образца.
 Делая это, мы получаем:
Делая это, мы получаем: Это почти слишком удобно.
Это почти слишком удобно. Вместо нашего обычного плана мы используем:
Вместо нашего обычного плана мы используем:
 x$: 9x$ имеет положительные члены, а синус и косинус чередуют знаки. Как мы можем связать их вместе?
x$: 9x$ имеет положительные члены, а синус и косинус чередуют знаки. Как мы можем связать их вместе?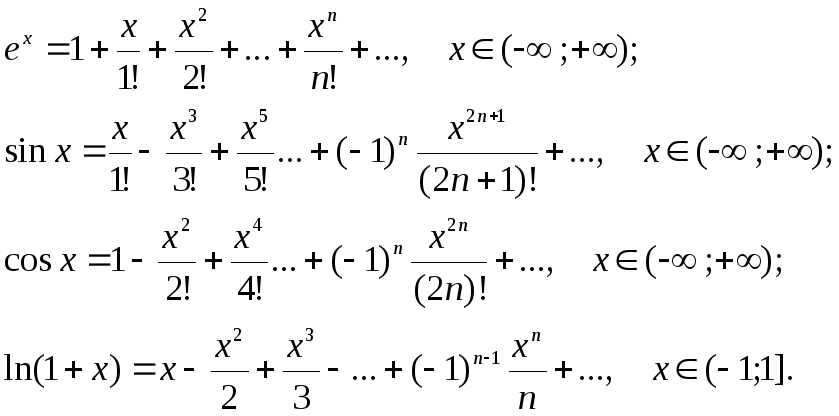 93$ взрываются по мере роста $x$. Чтобы иметь медленную, постепенную кривую, вам нужна армия полиномиальных членов, сражающихся за нее, и один победитель едва ли появится. Если вы остановите поезд слишком рано, приближение снова взорвется.
93$ взрываются по мере роста $x$. Чтобы иметь медленную, постепенную кривую, вам нужна армия полиномиальных членов, сражающихся за нее, и один победитель едва ли появится. Если вы остановите поезд слишком рано, приближение снова взорвется. 93 + \точки $. Мы перешли от словесного описания к уравнению.
93 + \точки $. Мы перешли от словесного описания к уравнению. д. Таким образом, формула ряда Тейлора помогает в математическом представлении ряда Тейлора. Давайте изучим формулу ряда Тейлора, используя несколько решенных примеров в конце страницы. 9n \)
д. Таким образом, формула ряда Тейлора помогает в математическом представлении ряда Тейлора. Давайте изучим формулу ряда Тейлора, используя несколько решенных примеров в конце страницы. 9n \)


 ..
..
 Методы решения уравнений математической физики зависят от типа к которому принадлежит рассматриваемое уравнение. Выделяют три основных типа дифференциальных уравнений с частными производными второго порядка, поиск решения которых имеют качественные различия: уравнения параболического, гиперболического и эллиптического типов.
Методы решения уравнений математической физики зависят от типа к которому принадлежит рассматриваемое уравнение. Выделяют три основных типа дифференциальных уравнений с частными производными второго порядка, поиск решения которых имеют качественные различия: уравнения параболического, гиперболического и эллиптического типов. Левая часть уравнения (8) полностью совпадает с частью волнового уравнения.
Левая часть уравнения (8) полностью совпадает с частью волнового уравнения. В которой, требуется найти функцию w, удовлетворяющую уравнению (13) (при -эвклидово пространство) и начальном условии w=f(x) при t=0 и граничному условию:
В которой, требуется найти функцию w, удовлетворяющую уравнению (13) (при -эвклидово пространство) и начальном условии w=f(x) при t=0 и граничному условию: Уравнение (18) называется однородным, если
Уравнение (18) называется однородным, если

 Когда объект с моментом инерции I (угловой эквивалент массы) имеет угловое ускорение α , тогда возникает чистый крутящий момент Στ.
Когда объект с моментом инерции I (угловой эквивалент массы) имеет угловое ускорение α , тогда возникает чистый крутящий момент Στ.  Сила, F , по площади, A , вызывает давление, P . Давление жидкости на глубине ч зависит от плотности и гравитационной постоянной, г . Объекты, погруженные в жидкость, создающие массу веса, Вт вода вытесненные , создают направленную вверх выталкивающую силу, F плавучесть . Из-за сохранения массы объемный расход жидкости, движущейся со скоростью v , через площадь поперечного сечения A , является постоянным. Уравнение Бернулли связывает давление и скорость жидкости.
Сила, F , по площади, A , вызывает давление, P . Давление жидкости на глубине ч зависит от плотности и гравитационной постоянной, г . Объекты, погруженные в жидкость, создающие массу веса, Вт вода вытесненные , создают направленную вверх выталкивающую силу, F плавучесть . Из-за сохранения массы объемный расход жидкости, движущейся со скоростью v , через площадь поперечного сечения A , является постоянным. Уравнение Бернулли связывает давление и скорость жидкости. Две массы, M 1 и M 2 , разделенные на расстояние, R , притягивает друг друга гравитационной силой, приведенным следующим уравнением, в продовольственных гравитационная постоянная Г :
Две массы, M 1 и M 2 , разделенные на расстояние, R , притягивает друг друга гравитационной силой, приведенным следующим уравнением, в продовольственных гравитационная постоянная Г :  Одним из примеров такой силы является пружина с жесткостью k . Положение x , скорость v и ускорение a, объекта, совершающего простое гармоническое движение, могут быть выражены синусом и косинусом.
Одним из примеров такой силы является пружина с жесткостью k . Положение x , скорость v и ускорение a, объекта, совершающего простое гармоническое движение, могут быть выражены синусом и косинусом. В стержне из материала с площадью поперечного сечения A , длиной L и разностью температур на концах ΔT существует тепловой поток за время t , , определяемый выражением эти формулы:
В стержне из материала с площадью поперечного сечения A , длиной L и разностью температур на концах ΔT существует тепловой поток за время t , , определяемый выражением эти формулы:





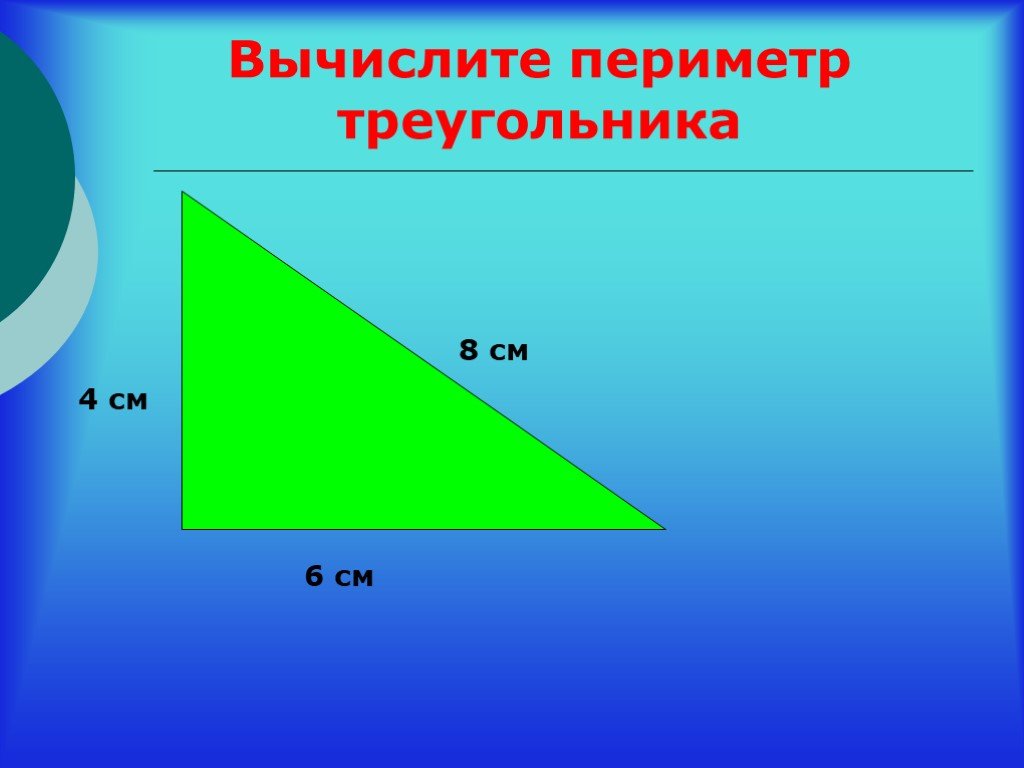 Найдём периметр:
Найдём периметр: Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если р = 72, b = 26.
Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если р = 72, b = 26.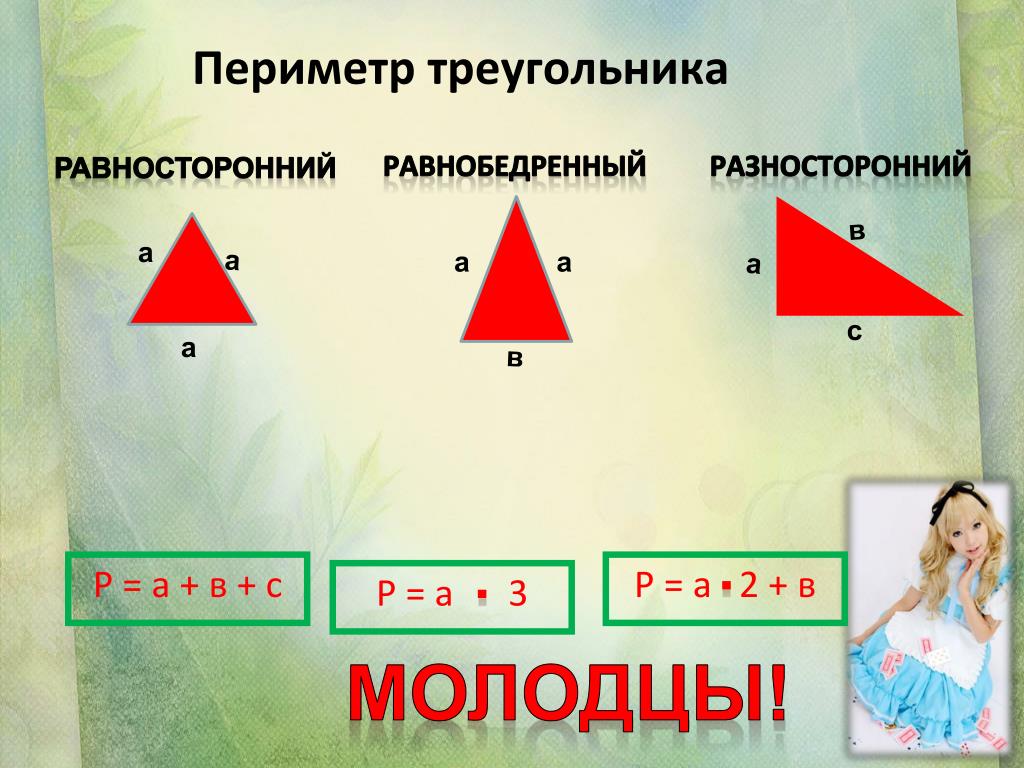

 Миша делал домашнее задание по математике с 16 ч 48 мин до 17 ч 16 мин, а Дима — с 17 ч 53 мин до 18 ч 20 мин. Кто из мальчиков дольше делал задание и на сколько минут?
Миша делал домашнее задание по математике с 16 ч 48 мин до 17 ч 16 мин, а Дима — с 17 ч 53 мин до 18 ч 20 мин. Кто из мальчиков дольше делал задание и на сколько минут?
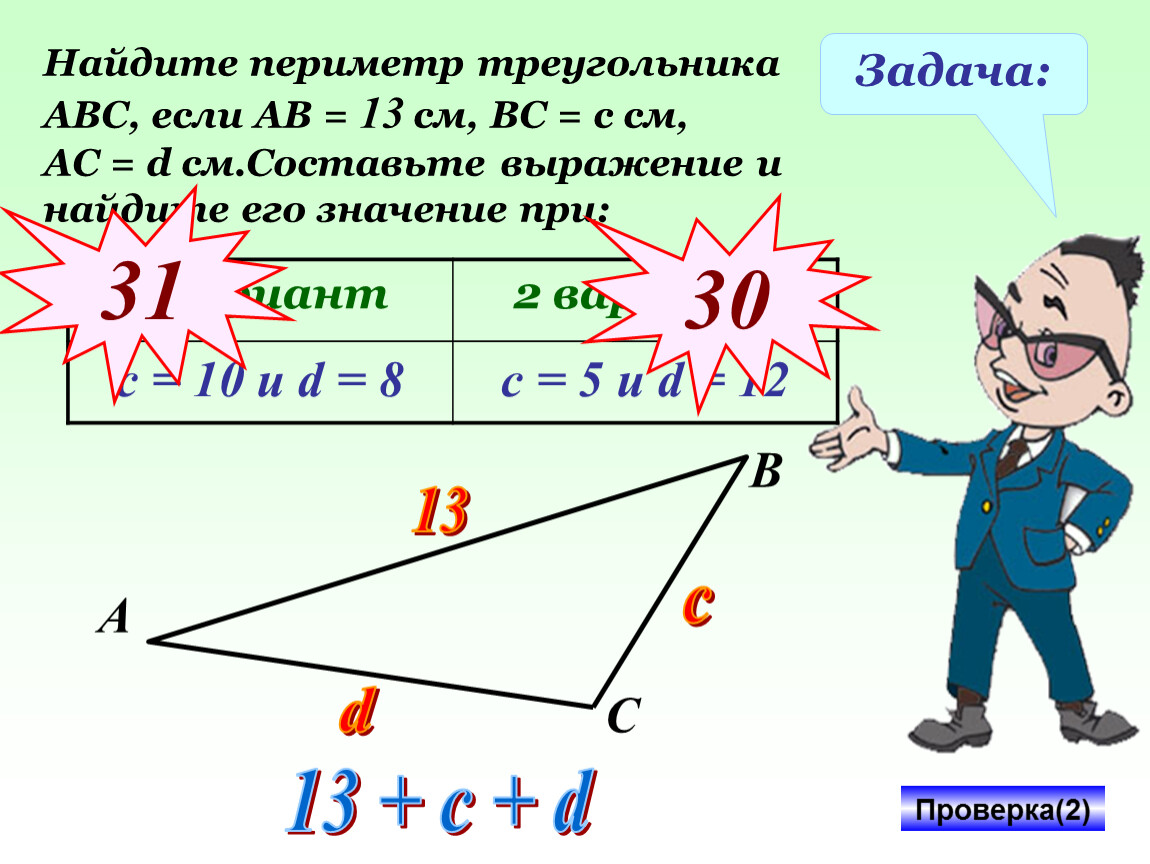 Сколько треугольников вы видите? устно № 1 Часто знает и дошкольник, Что такое треугольник, А уж вам-то как не знать! Но совсем другое дело – Быстро, точно и умело Треугольники считать. Например, на картинке этой Сколько разных? Рассмотри! Все внимательно исследуй И по краю, и внутри! На рисунке изображено 13 треугольников .
Сколько треугольников вы видите? устно № 1 Часто знает и дошкольник, Что такое треугольник, А уж вам-то как не знать! Но совсем другое дело – Быстро, точно и умело Треугольники считать. Например, на картинке этой Сколько разных? Рассмотри! Все внимательно исследуй И по краю, и внутри! На рисунке изображено 13 треугольников . Наши итоги 1 2 3 3 12 4 6 5 Характерные ошибки… Как исправить… Над чем поработать дома с родителями…
Наши итоги 1 2 3 3 12 4 6 5 Характерные ошибки… Как исправить… Над чем поработать дома с родителями…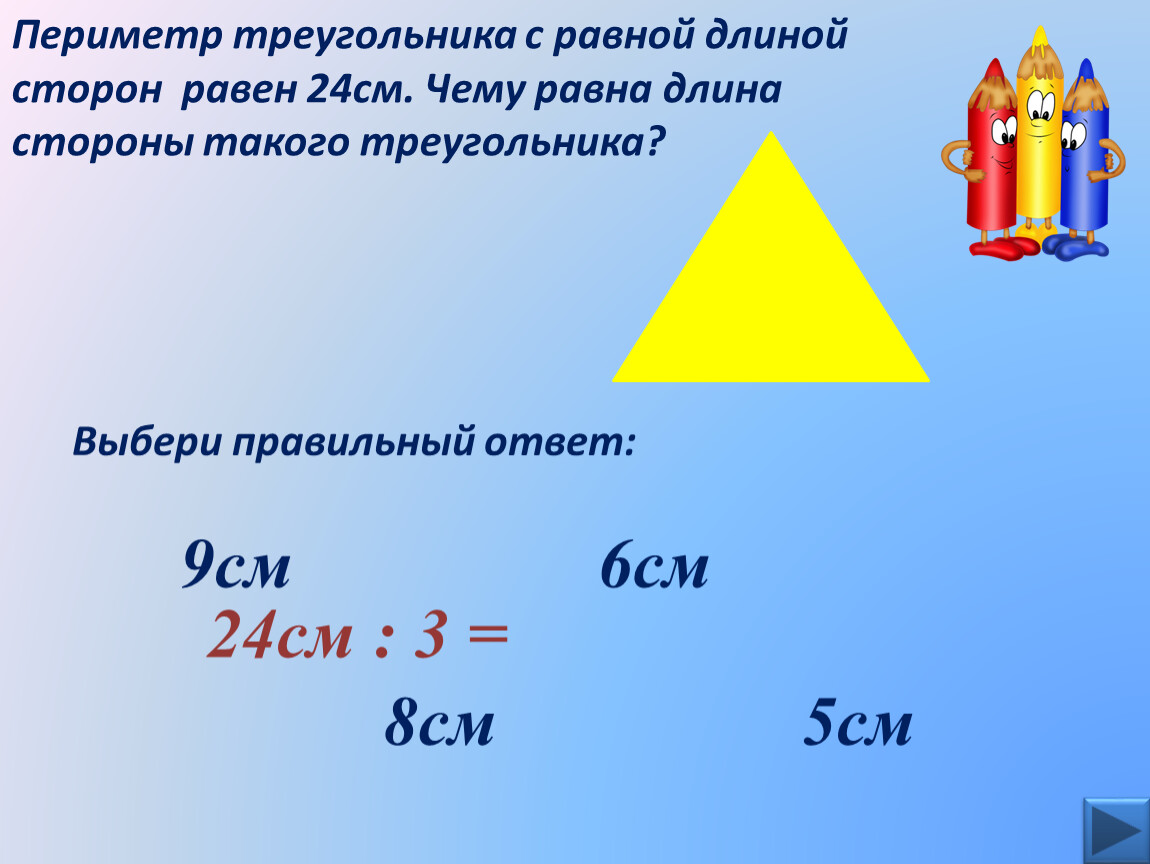 Обозначьте его. Измерьте сторону, противолежащую прямому углу. УЧЕБНИК № 4 10 построение АВ = 5 см А В С 4 см 3 см 5 см
Обозначьте его. Измерьте сторону, противолежащую прямому углу. УЧЕБНИК № 4 10 построение АВ = 5 см А В С 4 см 3 см 5 см Ч то вы можете сказать об этом треугольнике? УЧЕБНИК № 4 16 ? Равнобедренный, т.к. 17 – (5 + 6) = 6 (см). Вычислите периметр равностороннего треугольника со стороной 8 см. УЧЕБНИК № 4 1 7 ? Р = 8 + 8 + 8 = 24 (см) б) В равнобедренном треугольнике периметр равен 21 см, а боковая сторона равна 6 см. найдите длину основания. УЧЕБНИК № 4 1 8 ? 2 ∙ 6 = 12 (см) 21 – 12= 9(см)
Ч то вы можете сказать об этом треугольнике? УЧЕБНИК № 4 16 ? Равнобедренный, т.к. 17 – (5 + 6) = 6 (см). Вычислите периметр равностороннего треугольника со стороной 8 см. УЧЕБНИК № 4 1 7 ? Р = 8 + 8 + 8 = 24 (см) б) В равнобедренном треугольнике периметр равен 21 см, а боковая сторона равна 6 см. найдите длину основания. УЧЕБНИК № 4 1 8 ? 2 ∙ 6 = 12 (см) 21 – 12= 9(см)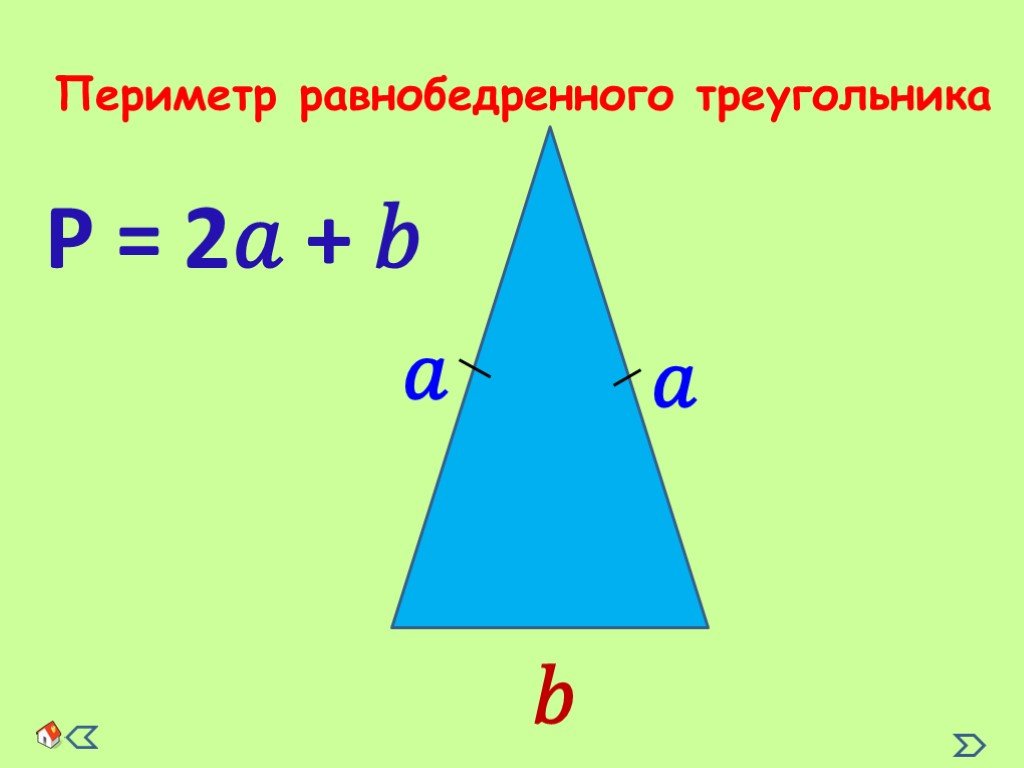 Задачное множество Домашнее задание п.7.1, №п.7.1, №523, 534, выполнить задания на сайте » Учи.ру » — ГЕОМЕТРИЯ. Треугольники
Задачное множество Домашнее задание п.7.1, №п.7.1, №523, 534, выполнить задания на сайте » Учи.ру » — ГЕОМЕТРИЯ. Треугольники
 Как мы это делаем? Необходимую длину забора можно рассчитать, найдя общую длину границы (периметра) треугольника.
Как мы это делаем? Необходимую длину забора можно рассчитать, найдя общую длину границы (периметра) треугольника. Каково значение x, если периметр треугольника PQR равен 40 единицам? Также найдите длину трех сторон.
Каково значение x, если периметр треугольника PQR равен 40 единицам? Также найдите длину трех сторон.  Если две стороны равны 12 футам и 7 футам, то чему равна третья сторона?
Если две стороны равны 12 футам и 7 футам, то чему равна третья сторона?
 Эта фундаментальная концепция важна для понимания учащимися, поскольку она закладывает основу для более сложных математических тем. Итак, без лишних слов, давайте отправимся в приключение в царство периметров треугольников и откроем секреты этого геометрического чуда!
Эта фундаментальная концепция важна для понимания учащимися, поскольку она закладывает основу для более сложных математических тем. Итак, без лишних слов, давайте отправимся в приключение в царство периметров треугольников и откроем секреты этого геометрического чуда! Однако, если вам не хватает некоторых длин сторон, вам может понадобиться использовать другую информацию о треугольнике, чтобы найти недостающие значения. Например, вы можете использовать теорему Пифагора для прямоугольных треугольников или применить свойства равнобедренных и равносторонних треугольников. Ниже мы обсудим формулы для нахождения периметра различных типов треугольников.
Однако, если вам не хватает некоторых длин сторон, вам может понадобиться использовать другую информацию о треугольнике, чтобы найти недостающие значения. Например, вы можете использовать теорему Пифагора для прямоугольных треугольников или применить свойства равнобедренных и равносторонних треугольников. Ниже мы обсудим формулы для нахождения периметра различных типов треугольников. Поскольку две стороны равны, формула для его периметра:
Поскольку две стороны равны, формула для его периметра: Поскольку к прямому углу примыкают равные стороны, можно воспользоваться теоремой Пифагора, чтобы найти гипотенузу:
Поскольку к прямому углу примыкают равные стороны, можно воспользоваться теоремой Пифагора, чтобы найти гипотенузу: Каков его периметр?
Каков его периметр? Периметр является важным понятием в геометрии и используется для измерения границ любой формы. В случае треугольников периметр помогает нам понять размер и масштаб треугольника на основе длин его сторон.
Периметр является важным понятием в геометрии и используется для измерения границ любой формы. В случае треугольников периметр помогает нам понять размер и масштаб треугольника на основе длин его сторон.
 В пособие собрана большая подборка заданий по темам курса алгебры 7 класса для отработки навыка решения тематических задач.
В пособие собрана большая подборка заданий по темам курса алгебры 7 класса для отработки навыка решения тематических задач.
 Часть 1-я — теоретический материал (учебник). Часть 2-я — практический материал (задачник).
Часть 1-я — теоретический материал (учебник). Часть 2-я — практический материал (задачник). Основное свойство алгебраической дроби. Упр. 2.1 — 2.48
Основное свойство алгебраической дроби. Упр. 2.1 — 2.48  СВОЙСТВА КВАДРАТНОГО КОРНЯ
СВОЙСТВА КВАДРАТНОГО КОРНЯ 2 + bх + с, её свойства и график. Упр. 24.1 — 24.55
2 + bх + с, её свойства и график. Упр. 24.1 — 24.55  24
24  В 2 ч. Ч. 2 / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — перераб. — М.: Мнемозина (новый учебник, года выпуска: 2018-2020). Алгебра 8 Мордкович ЗАДАЧНИК 2020 ответами и решениями
В 2 ч. Ч. 2 / [А. Г. Мордкович и др.]; под ред. А. Г. Мордковича. — перераб. — М.: Мнемозина (новый учебник, года выпуска: 2018-2020). Алгебра 8 Мордкович ЗАДАЧНИК 2020 ответами и решениями
 7.2 Промежуточный уровень
7.2 Промежуточный уровень Это написано членом сообщества AoPS cargeek9., в настоящее время младший в средней школе. Он охватывает основы алгебры, геометрии, комбинаторики и теории чисел, а также наборы сопутствующих практических задач в конце каждого раздела.
Это написано членом сообщества AoPS cargeek9., в настоящее время младший в средней школе. Он охватывает основы алгебры, геометрии, комбинаторики и теории чисел, а также наборы сопутствующих практических задач в конце каждого раздела.





 М. Гельфанда и Марка Сола.
М. Гельфанда и Марка Сола.


 Учащиеся узнают, как интерпретировать и решать задачи в том виде, в каком они обычно представлены на курсах алгебры, и подготовятся к решению тех задач, которые никогда не обсуждались в классе, но всегда появляются на экзаменах.
Учащиеся узнают, как интерпретировать и решать задачи в том виде, в каком они обычно представлены на курсах алгебры, и подготовятся к решению тех задач, которые никогда не обсуждались в классе, но всегда появляются на экзаменах. Я знаю, о чем вы думаете….
Я знаю, о чем вы думаете….  Тем не менее, весьма озадачивает, почему автор (имеющий довольно много книг по математике) не предоставил для них опечатки. Тем более, что у него есть веб-страница, посвященная этим книгам.
Тем не менее, весьма озадачивает, почему автор (имеющий довольно много книг по математике) не предоставил для них опечатки. Тем более, что у него есть веб-страница, посвященная этим книгам.

 В этом случае вам придется выполнить конвертацию заново.
В этом случае вам придется выполнить конвертацию заново. Чем выше качество, тем больше весит файл. И наоборот, чем ниже качество, тем меньше размер файла.
Чем выше качество, тем больше весит файл. И наоборот, чем ниже качество, тем меньше размер файла. Они очень похожи тем, что оба содержат данные изображений, например фотографии. Однако каждый из них имеет свою индивидуальность.
Они очень похожи тем, что оба содержат данные изображений, например фотографии. Однако каждый из них имеет свою индивидуальность. Например, вы не можете напечатать его профессионально. Поскольку файлы PNG не содержат информацию о цвете CMYK, профессиональная полиграфическая компания не примет их.
Например, вы не можете напечатать его профессионально. Поскольку файлы PNG не содержат информацию о цвете CMYK, профессиональная полиграфическая компания не примет их. Перейдите к файлам, которые вы хотите преобразовать. И наоборот, вы также можете перетаскивать файлы, которые хотите загрузить. Вы можете загрузить до 20 одновременно.
Перейдите к файлам, которые вы хотите преобразовать. И наоборот, вы также можете перетаскивать файлы, которые хотите загрузить. Вы можете загрузить до 20 одновременно. Это означает, что сжатие изображения несколько снизило его общее качество. Когда вы создаете JPG, вы можете выбрать, насколько он будет с потерями. Как правило, чем выше качество изображения, тем больше его размер, поэтому сжатие изображения может помочь ему занимать меньше места на жестком диске.
Это означает, что сжатие изображения несколько снизило его общее качество. Когда вы создаете JPG, вы можете выбрать, насколько он будет с потерями. Как правило, чем выше качество изображения, тем больше его размер, поэтому сжатие изображения может помочь ему занимать меньше места на жестком диске. JPG должны иметь информацию о цвете в каждом пикселе, поэтому пустые пиксели обычно заполняются черным или белым цветом.
JPG должны иметь информацию о цвете в каждом пикселе, поэтому пустые пиксели обычно заполняются черным или белым цветом.



 Домашнее задание:Расставьте коэффициенты в
Домашнее задание:Расставьте коэффициенты в

 Азот в этой степени окисления может как принимать, так и отдавать электроны, т.е. может являться как окислителем, так восстановителем.
Азот в этой степени окисления может как принимать, так и отдавать электроны, т.е. может являться как окислителем, так восстановителем. Определите степени окисления всех компонентов, входящих в состав следующих соединений: HСl, Cl2, HClO2 , HClO3 , Cl2O7 . Какие из веществ являются только окислителями, только восстановителями, и окислителями и восстановителями? Расставьте коэффициенты в уравнении реакции:
Определите степени окисления всех компонентов, входящих в состав следующих соединений: HСl, Cl2, HClO2 , HClO3 , Cl2O7 . Какие из веществ являются только окислителями, только восстановителями, и окислителями и восстановителями? Расставьте коэффициенты в уравнении реакции: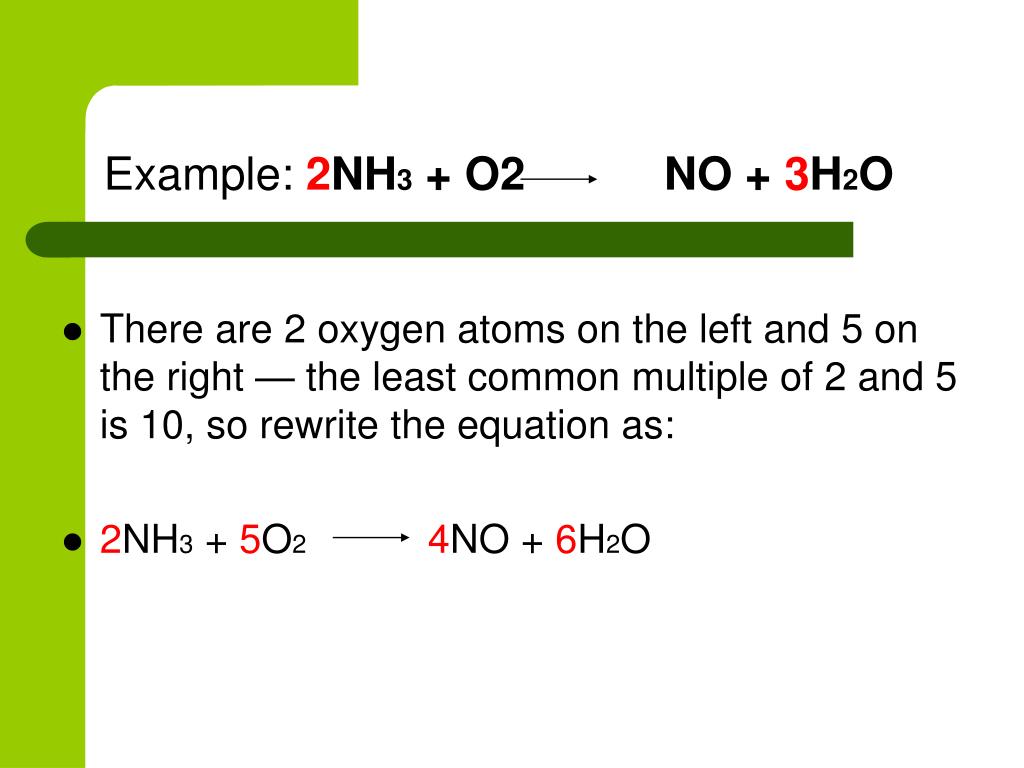 е. могут отдавать, так и принимать электроны.
е. могут отдавать, так и принимать электроны.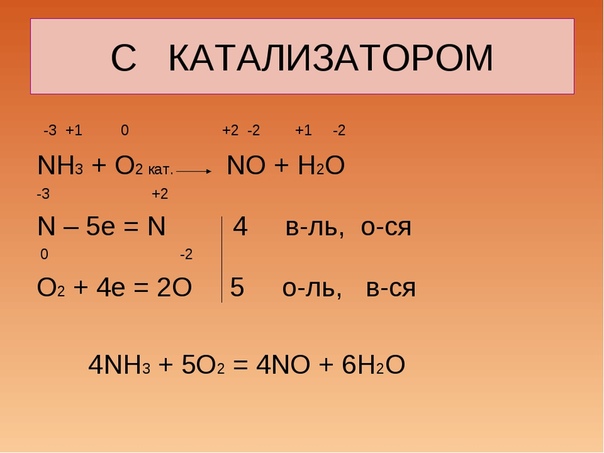
 Какие ОВР относятся к реакциям диспропорционирования? Расставьте коэффициенты в реакциях:
Какие ОВР относятся к реакциям диспропорционирования? Расставьте коэффициенты в реакциях: Составьте электронные уравнения и подберите коэффициенты ионно-электронным методом в реакции
Составьте электронные уравнения и подберите коэффициенты ионно-электронным методом в реакции Определите методом электронного баланса коэффициенты в уравнениях окислительно-восстановительных реакций:
Определите методом электронного баланса коэффициенты в уравнениях окислительно-восстановительных реакций: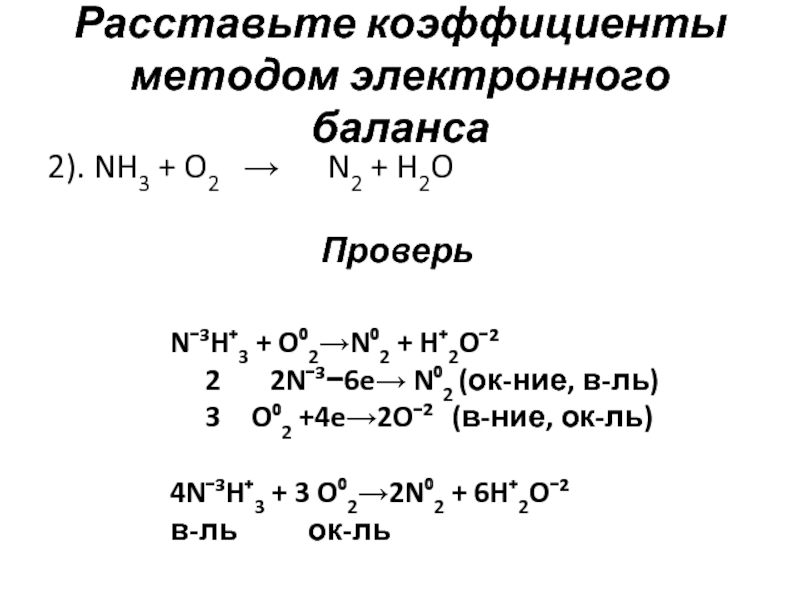 Можно ли в качестве окислителя в кислой среде использовать K2Cr2O7 в следующих процессах при стандартных условиях:
Можно ли в качестве окислителя в кислой среде использовать K2Cr2O7 в следующих процессах при стандартных условиях: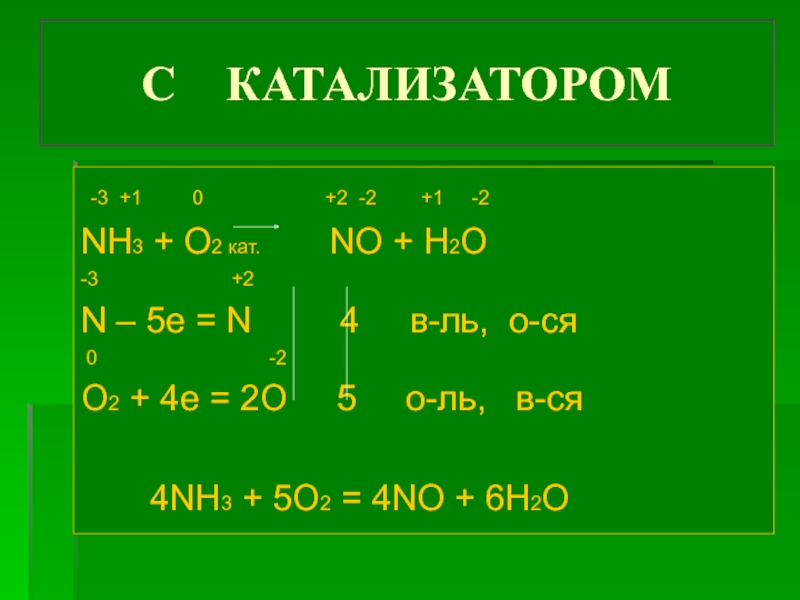

 Kc=[Nh4]4[O2]5[NO]4[h3O]6 న రసాయన సమీకరణం రాయండి.
Kc=[Nh4]4[O2]5[NO]4[h3O]6 న రసాయన సమీకరణం రాయండి. ..
.. Для балансировки этих реакций используется метод полууравнения.
Для балансировки этих реакций используется метод полууравнения.

