Переход между плоскими прямоугольными координатами Гаусса и географическими координатами и обратно
Учеба
Страница содержит онлайн калькуляторы для перехода от географических координат к плоским прямоугольным координатам Гаусса и обратно (используются формулы для референц-эллипсоида Красовского).
Плоские прямоугольные координаты Гаусса х и у связаны с географическими координатами φ (широта) и λ (долгота) точек земной поверхности довольно сложными формулами (ключами перехода). Ниже представлены два калькулятора, которые осуществляют переход от одних координат к другим.
Данные калькуляторы используют ключи перехода, рассчитанные для референц-эллипсоида Красовского, или системы координат СК-42. Использование СК-42 допускается только до 1 января 2021 года, так что эти калькуляторы представляют, скорее, исторический интерес.
Переход от географических координат к плоским прямоугольным координатам Гаусса-Крюгера
Широта
Долгота
Точность вычисления
Знаков после запятой: 3
Переход от плоских прямоугольных координат Гаусса-Крюгера к географическим координатам
Широта
Долгота
Зональная система плоских прямоугольных координат Гаусса
В топографии и геодезии широко распространено использование прямоугольных координат. Просто потому, что километрами и метрами пользоваться проще чем градусами, минутами и секундами. В качестве системы плоских прямоугольных координат обычно используют систему плоских прямоугольных координат Гаусса, основанную на проекции Гаусса-Крюгера (в 1825-1830 годах Гаусс разработал поперечно-цилиндрическую конформную (равноугольную) проекцию эллипсоида на плоскость, а Крюгер в 1912 году вывел для нее рабочие формулы вычислений).
Просто потому, что километрами и метрами пользоваться проще чем градусами, минутами и секундами. В качестве системы плоских прямоугольных координат обычно используют систему плоских прямоугольных координат Гаусса, основанную на проекции Гаусса-Крюгера (в 1825-1830 годах Гаусс разработал поперечно-цилиндрическую конформную (равноугольную) проекцию эллипсоида на плоскость, а Крюгер в 1912 году вывел для нее рабочие формулы вычислений).
Суть, если вкратце в том, что земной эллипсоид разбивают меридианами на сферические двуугольники – зоны. Затем каждую зону проектируют на внутреннюю боковую поверхность цилиндра, развернув который,
получают проекцию поверхности Земли. Ширина зоны — 6 градусов, то есть всего существует 60 зон. В России зоны отсчитываются от нулевого меридиана (осевой меридиан первой зоны — 3 градуса восточной долготы). Внутри каждой зоны действует своя система координат, включающая номер зоны. Ширина любой координатной зоны составляет на экваторе примерно 670 км, на широте 40° — 510 км, на широте 50° — 430 км. Координата x, направленная вдоль меридиана в северном полушарии всегда положительна, чтобы сделать и координату y положительной, начало координат смещают на 500 км левее осевого меридиана. См. иллюстрацию ниже (оригинальный источник изображения неизвестен).
Координата x, направленная вдоль меридиана в северном полушарии всегда положительна, чтобы сделать и координату y положительной, начало координат смещают на 500 км левее осевого меридиана. См. иллюстрацию ниже (оригинальный источник изображения неизвестен).
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Прямоугольная и полярная система координат на плоскости
- • Расстояние между двумя координатами
- • Радиус Земли по широте (WGS 84)
- • Системы координат в пространстве
- • Расстояние между двумя координатами сквозь Землю
- • Раздел: Учеба ( 411 калькуляторов )
географические координаты геодезия долгота конвертер осевой меридиан плоские прямоугольные координаты проекция Гаусса-Крюгера референц-эллипсоид Красовского топография Учеба широта
PLANETCALC, Переход между плоскими прямоугольными координатами Гаусса и географическими координатами и обратно
Timur2020-11-03 14:19:40
Калькулятор географических координат
|
|
|
||||||||||||||||||||||||||||||||
Расчет с географическими координатами
Anzeige
Преобразование географических координат | Средние значения | Пакетная обработка | Направления | Самая высокая солнечная высота | Позиция
Калькуляторы для преобразования географических координат, предоставленных инструментом GPS, для расстояния до двух точек и для пеленга. Три полезных инструмента, например. для геокэшинга. Географические координаты описывают точное положение точки на земле с точки зрения широты и долготы.
Три полезных инструмента, например. для геокэшинга. Географические координаты описывают точное положение точки на земле с точки зрения широты и долготы.
Преобразование географических координат
Распространенными форматами географических координат являются (градусы°, минуты′, секунды″), (десятичные градусы) и (градусы, десятичные минуты). Порядок: широта (N), долгота (E). Различные инструменты GPS предоставляют разные форматы, которые можно конвертировать здесь. Пожалуйста, введите полное и правильное выражение (включая градусы) в одно поле и нажмите «Рассчитать».
| Градусы, минуты, секунды | Десятичные градусы | Градусы, десятичные минуты | например. N52° 31′ 14,941″ E13° 24′ 34,020″ | напр. 52.520817 13.40945 | напр. N52° 31,249 E13° 24,567 |
|---|---|---|
Anzeige
Расстояние между двумя точками
Вставьте обе точки в десятичных градусов . Расчет является оценочным, который дает неплохие результаты до нескольких сотен километров. Это не может быть точным, потому что Земля не является идеальной сферой. Расстояние север-юг игнорирует долготу, расстояние восток-запад рассчитывается посередине двух широт. ↵ переносит десятичные градусы сверху.
Расчет является оценочным, который дает неплохие результаты до нескольких сотен километров. Это не может быть точным, потому что Земля не является идеальной сферой. Расстояние север-юг игнорирует долготу, расстояние восток-запад рассчитывается посередине двух широт. ↵ переносит десятичные градусы сверху.
Точка 1: Точка 2:
Расстояние между двумя точками: м = км
Расстояние с севера на юг: м = км
Расстояние с востока на запад: м = км
Угол пеленга от точки 1 до точки 2: °
Используйте этот сайт для перевода расстояния в другие единицы измерения.
Anzeige
Подшипник
Bearig означает отмерять от начальной точки под определенным углом и на определенном расстоянии до конечной точки. Угол начинается на севере с 0° и оттуда движется по часовой стрелке. Пожалуйста, введите начальную точку и угол в десятичных градусов . ↵ передает десятичные градусы из верхнего калькулятора, ↑ передает точку назначения в верхний калькулятор, ↖ переводит точку назначения в начальную точку.
Расчет производится с радиусом Земли на заданной широте. Азимут обеспечивает хорошие значения для расстояний до нескольких сотен метров или нескольких километров.
| Начальная точка: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Подшипник: | ° | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Расстояние: | м | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Пункт назначения: | Ответственность за нет правильность расчетов и информации. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дили – дон, дили – дон,
| Наклоны из стороны в сторону руки на поясе.
|
Строят гномы новый дом, | Стучат кулаком об кулак |
Красят стены, красят пол, | Руками «красят» сбоку, снизу. |
Прибирают всё кругом | «метут» |
К гномам в гости мы идём | Шаги на месте |
И подарки им несём | Руки вперёд |
На пол – мягкую дорожку,
| Наклоны вперёд, руками «расстилают» дорожку |
Расстелив её к порожку | Шаги назад |
Две подушки на диван, | Руки под щёку |
Мёду липового жбан | Руки округляют и вытягивают перед собой |
8. Первичное закрепление.
Первичное закрепление.
Гномик Среда приготовил для вас задание по учебнику на странице 108 №2 Слайд 16
Проверка в парах по таблице умножения Слайд 17
3*2=6 3*7=21 3*9=27
3*6=18 3*4=12 3*5=15
Оцените себя и своего товарища.
9. Продолжение работы над темой урока. Треть числа.
Продолжаем нашу работу.
Гномики у нас трудолюбивые. И надеются, что вы тоже будите трудиться.
Слайд 18
Вот гномик Четверг решил затопить печь и стал пилить дрова. У него получилось 18 поленьев. Третью из них он решил затопить печь для гостей.
Как узнать, сколько нужно поленьев для гостей, чтобы затопить печь?
Давайте,
ребята, посмотрим на экран, и прочитаем, какой нам совет даст Белоснежка,
чтобы решить эту задачу.
Совет от Белоснежки: Слайд 19
Если разделить число на 3, то можно найти его часть – треть числа.
Чтобы найти треть какого – нибудь числа, надо это число разделить на 3.
Какое запишем решение?
На доске: Слайд 20
18:3=6 (п.)
Треть числа 18 равно 6.
Сколько же нужно затопить поленьев для гостей?
Ответ: 6 поленьев.
10. Закрепление изученного материала.
Слайд 21
Весёлый Пятница просит вас решить задачу на странице 11 № 21.
Разбор задачи:
О ком говорится в задаче?
В задаче говорится о Маше.
Что нашла Маша?
Маша нашла грибы.
Сколько грибов она нашла?
Она
нашла 27 грибов.
Сколько грибов составляет подосиновики?
Треть грибов – подосиновики.
Прочитайте вопрос задачи. Что нужно узнать?
Сколько подосиновиков нашла Маша?
Как узнать, сколько подосиновиков нашла Маша. Каким действием?
Решите задачу.
1 учащийся с обратной стороны доски. Оцените себя.
На доске запись:
27:3= 9 (г.).
Ответ: 9 подосиновиков нашла Маша.
Самостоятельная работа. Слайд 22
Карточка 2
А теперь пора убедится, что вы в гостях у гномов узнали нового!
Гном Суббота принёс вам задания на карточках.
3*2= 3*5= 3*9= 3*4=
3*7= 3*8= 3*1= 3*7=
Взаимопроверка.
Молодцы. Вы
справились с этой работой.
11. Рефлексия.
Проанализируйте наш урок. Удалось ли нам добиться поставленных целей?
В каких Заданиях испытывали трудности?
12. Домашнее задание.
Домашнее задание выполните от гномика Воскресенье. Слайд 23
Он просит, чтобы вы выучили таблицу умножения и деления на 3,
Выполнили задание на странице 109 №14, и решили задачу на странице 111 №23.
Спасибо за урок. Все свободны. Слайд 24
Конспект урока «Деление на 3» 2 класс «Школа России» | План-конспект урока по математике (2 класс):
Дата: 24.04.2020 Школа: МКОУ СОШ №2 Класс: 2 «А» Урок: 2 | Учитель: Давыдова Н.К. Студент: Камаева А. Методист: Шакирова О.Г |
Конспект урока по математике
Тема: «Деление на 3»
Цели деятельности учителя: закрепление умения выполнять деление на 3, используя соответствующие случаи умножения
Планируемые результаты:
Предметные:
- знать: табличные случаи умножения с числом 3;
- уметь: использовать взаимосвязь умножения и деления при делении на3; решать задачи изученных видов.
Личностные:
- принимать и осваивать социальную роль обучающегося;
- проявлять мотивы к учебной деятельности, навыки сотрудничества со взрослыми и сверстниками в разных социальных ситуациях;
- осознавать личностный смысл учения.
Тип урока: систематизация знаний
Оборудование: программа: «Школа России»; учебник: Моро М.И. Математика. 2 класс (2 часть), рабочие тетради, раздаточный материал (карточки), презентация
Челябинск,2020
м
ЭТАПЫ УРОКА Методы и приемы | Хронометраж | СОДЕРЖАНИЕ УРОКА | ФОРМИРУЕМЫЕ УУД | |
| ДЕЯТЕЛЬНОСТЬ УЧАЩИХСЯ | |||
1. Словесный: слово учителя | 1 мин | — Здравствуйте ребята! Садитесь. | Приветствуют учителя, показывают настрой на предстоящую совместную деятельность, показывают готовность к уроку. | Р:саморегуляция как способность к мобилизации сил и энергии, к волевому усилию и преодолению препятствий |
2.Актуализация знаний и мотивация Словесный: учебный диалог | 4 мин | — Давайте вспомним таблицы умножения на 2 и 3. — Вы получили карточки с цифрами от 2,3,4,6,8,10.12,14,15,16,18,21,24,27. Читаю примеры — Ответьте на вопросы: — Какое свойство умножения использовали? — Назовите компоненты умножения. — Какая операция обратная операции умножения? — Как связаны между собой умножение и деление? — Назовите компоненты деления. — Давайте вспомним таблицу деления на 3. По цепочки проверяем таблицу. — Сегодня мы продолжим тему деление на 3 и выполним задания для закрепления. | — 3х2,2×7,2×4,3×5,7×3,2×8, 9×3,2×2,8×3,2×6,4×3,2×5,3×6,9×2,3×3 — Переместительное — Первый множитель, второй множитель, произведение — Деление — Если произведение разделить на один из множителей, то получим другой множитель — Делимое, делитель, частное Рассказывают таблицу деления на 3. | П: построение логической цепочки рассуждений |
3.Постановка учебной задачи Словесный: учебный диалог Практический: работа у доски | 3 мин | — Как вы думаете, какая сегодня будет тема? — Мы с вами проходили данную тему и сегодня продолжим ее. Какие цели мы можем поставить на урок? — Давайте составим план на урок: | — «Деление на 3» — Закрепим умение выполнять деление на 3 — План: 1. 2. Выполним упражнения на закрепление | П: построение логической цепочки рассуждений К: умение с достаточной полнотой и точностью выражать свои мысли Р: целеполагание |
7.Включение в систему знаний, повторение Словесный: учебный диалог Практический: выполнение упражнения | 25 мин | — Посмотрите на № 1. Найдите верные равенства. — Прочитайте задачу №3. — Что нам известно? — Что нам нужно найти? — Как мы найдем, сколько рабочих дней в 2-х неделях? — Как мы найдем, сколько рабочих дней в 3-х неделях? — Запишите задачу в тетрадь. — Прочитайте задачу под №5. — Что нам известно? — Чего не хватает в задаче? — Составьте вопрос к задаче. Кто составил, прочитайте свой вопрос. — Что нам не известно? — Как мы можем это узнать? — Что теперь мы можем узнать? — Как мы это узнаем? — На странице 94 устно по цепочке решим № 1. — Выполняем подготовку к контрольной работе. — Как всегда 2 варианта. 1 вариант – стр. 93 № 4, № 6 — 1 строчка, стр. 94 № 2 — под цифрой 1. 2 вариант – стр. 93 № под ?, № 6 – 2 строчка, стр. 94 № 2 – под цифрой 2. — Обменяйтесь тетрадями с соседом по парте. — Посмотрите на слайд, на правильные ответы. Проверьте друг друга. За каждое правильно выполненное задание ставите знак «+». Если не верно, подчеркните карандашом. | 3*5+3=3*6 3*8-3=3*7 2*6-2=2*5 — Что в неделе 5 рабочих дней — Сколько рабочих дней в 2-х неделях и в 3-х неделях — Нужно рабочие дни умножить на 2 недели 5*2=10 (д.) – рабочих дней в 2-х неделях. — Нужно рабочие дни умножить на 3 недели 5*3=15 (д.) – рабочих дней в 3-х неделях. Ответ: 10 д., 15 д.
— Что задание по математике Коля выполнил за 15 минут, по РЯ за 10, а по чтению на 15 минут больше, чем по РЯ — Вопроса — Сколько времени Коля потратил на выполнение домашнего задания? — Сколько времени он потратил на выполнение задания по чтению — Сказано, что на него он потратил на 15 минут больше, чем на русский, РЯ он выполнил за 10 минут, значит 1) 10+15=25 (мин. — Сколько всего он потратил времени на выполнение ДЗ — Нужно сложить все время 15+10+25=50 (мин.) – всего Ответ: 50 минут. Выполняют устный счет. Выполняют задания для подготовке к КР. Взаимопроверка. | П: смысловое чтение как осмысление цели чтения П: построение логической цепочки рассуждений П: поиск и выделение необходимой информации П: поиск и выделение необходимой информации П: осознанное построение речевого высказывания К: умение полно и точно выражать мысли |
8.Рефлексия деятельности Словесный: учебный диалог | 4 мин | — Как звучала тема нашего урока? таблицу деления? — Какие цели мы ставил на урок? — Реализовали ли мы их? — Спасибо за урок! Мне было приятно с вами работать. | — Деление на 3 — Закрепляли умение делить на 3 — Да | К: умение с достаточной полнотой и точностью выражать свои мысли П: рефлексия способов и условий действия |
Задания ля дистанционного обучения:
- Выполнить стр.
 93 № 3, 4, 5, стр. 94 № 2.
93 № 3, 4, 5, стр. 94 № 2.
Шаблон умножения и деления опасности
2-й класс: Шаблон умножения и деления опасностиУмножение
Деление
Умножение
Деление
Умножение
100
5×7
Ответ: 35!
100
4×3=___
Ответ: 12!
100
36 разделить на 4= _____
Ответ: 9, потому что 4 умножить на 9 равно 36
100
21 разделить на 3=_____
Ответ: 7 потому что… 3 умножить на 7 равно 21
100
100 разделить на 10=_____
Ответ: 10 потому что 10 умножить на 10 равно 100
200
Какие два других способа сказать 3 умножить на 6 ?
3 группы по 6 и 6+6+6
200
Разделите 10 кукол на группы по 2 человека. Сколько групп?
Всего 5 групп, потому что 10 разделить на 2 равно 5.
200
Сэм читал по 6 страниц каждый день в течение 4 дней. Сколько всего страниц он прочитал?
Ответ: Всего он прочитал 24 страницы, потому что 4 умножить на 6 равно 24.
200
20 конфет делятся поровну между 5 детьми. Сколько конфет получил каждый ребенок?
Ответ: Каждый ребенок получает 4 конфеты, потому что 20 разделить на 5 равно 4.
200
Тим собирал 5 марок в месяц. Сколько марок он собрал через 6 месяцев?
Ответ: Он собрал 30 марок, потому что 5 умножить на 6 равно 30.
300
Есть 3 шкафа. В каждом шкафу по 7 тарелок. Сколько блюд?
Ответ: Всего 21 блюдо, потому что 3 умножить на 7 равно 21.
300
Миссис Артур поделила 14 блинов поровну между 7 детьми. Сколько блинов она дала каждому ребенку?
Ответ: Она дала каждому ребенку по 2 блина, потому что 14 разделить на 7 равно 2.
300
На каждой книге по 4 наклейки. Если есть 7 книг, сколько всего наклеек?
Ответ: всего 28 наклеек, потому что 4 умножить на 7 равно 28.
300
Есть 16 серег. 2 серьги составляют одну пару. Сколько пар сережек?
Ответ: Есть 8 пар серег, потому что 16 разделить на 2 равно 8.
300
Превратите эту задачу на умножение в задачу на деление: 6х5=30 А) 30 разделить на 5=6 Б) 6 разделить на 5=30 C) 5 разделить на 30=6 D) 5 разделить на 6=30
A) 30 разделить на 5=6 потому что 30-5-5-5-5-5-5=0. Сколько раз мы вычли на 5? 6!
400
Есть 3 картины. На каждой картине по 5 животных. Сколько здесь животных?
Ответ: Животных 15, потому что 3 умножить на 5 будет 15.
400
На 6 платьях 18 лент. Каждое платье имеет равное количество лент. Сколько лент на каждом платье?
Ответ: На каждом платье 3 ленточки, потому что 18 разделить на 6 равно 3.
400
Есть 2 вазы. В каждой вазе по 9 цветов. Сколько всего цветов?
Ответ: всего 18 цветов, потому что 2 умножить на 9 равно 18.
400
У Тима 16 книг. Он ставит равное количество книг на 4 полки. Сколько книг на каждой полке?
Ответ: На каждой полке 4 книги, потому что 16 разделить на 4 равно 4.
400
Есть 3 пенала. В каждом пенале по 4 карандаша. Сколько всего карандашей?
В каждом пенале по 4 карандаша. Сколько всего карандашей?
Ответ: всего 12 карандашей, потому что 3 умножить на 4 равно 12.
500
Пятеро детей. Каждый ребенок получает по 8 печений. Сколько файлов cookie всего?
Ответ: всего 40 печенек, потому что 5 умножить на 8 равно 40.
500
У мистера Тана 16 булочек. Он делит их поровну между двумя детьми. Сколько булочек получил каждый ребенок?
Ответ: Каждый ребенок получает по 8 булочек, потому что 16 разделить на 2 равно 8.
500
Есть 3 часа. У каждых часов 2 стрелки. Сколько рук?
Ответ: 6 рук, потому что 3 умножить на 2 равно 6.
500
Разделите 9 шаров на группы по 3. Сколько групп?
Ответ: Есть 3 группы, потому что 9 разделить на 3 равно 3.
500
Шерман построит 4 карточные башни. В каждой башне было по 8 карт. Сколько карт он использовал?
Ответ: Он использовал 32 карты, потому что 4 умножить на 8 равно 32.
Нажмите, чтобы увеличить
Нет команд1 команда2 команды3 команды4 команды5 команд6 команд7 команд8 команд9 команд10 командПользовательский
Магия математики 2 класса.
 Часть 9: Умножение и деление
Часть 9: Умножение и деление- Описание
- Отзывы (0)
Магия математики Раздел 9 для ВТОРОГО КЛАССА фокусируется на:
Неделя 1: Ситуации умножения – равные группы и повторяющиеся сложения
Неделя 2: Ситуации умножения – массивы
901 75 Неделя 3: Подразделение
Неделя 4: Задачи на умножение и деление
Вот что входит в этот двухнедельный модуль для 2-го класса:
— Ежедневные планы уроков на 20 дней
— В соответствии с Common Core 2-го класса и TEKS
— 20 словесных задач на каждый день, которые дополняют навыки
— Интерактивные распечатки для записных книжек
— Игры, занятия и поделки для улучшения обучения
— Мини-уроки с идеями о том, как обучать навыкам, а также с необходимыми материалами
— Словарные карточки
— Утверждения «Я могу»
— Оценки
— Опорная таблица и материалы для карманных диаграмм
Хотите узнать поближе? Вот некоторые (не все!) мероприятия:
— Таблица с повторным добавлением
— Scoot с повторным добавлением
— Перевороты с повторным добавлением
— Активность с повторным добавлением
— Игра с динозаврами с повторным добавлением
— Таблица с равными группами
— Буклет с равными группами 6 – Равные группы Повязка на голову монстра
– Равные группы Monster Mash Game
– Сопоставление равных групп
– Создание модели – накормите собак
– Равные группы Откидные створки: вращение и создание равных групп
– Оценка умножения
— Таблица массивов
— Буклет по созданию массивов
— Блокноты Array Interactive
— Вращение массива
— Массивы на сетках
— Рабочие станции массивов: 16 станций для создания массивов
– Массив Sunshine Craft
– Оценка массива
– Разделение с обручами
– Карманный справочник разделения
– Маркировка уравнения деления
– День отряда Safari
– Деятельность Jurassic Safari EggSpert – Разделение яиц динозавров по гнездам
– Загон животных с разделением
– Загон для коров, разделяющий животных
– Тракторный буксир Разделение Интерактивная тетрадь.
– Построение массивов для решения уравнений деления
– Разрушители делений
– Разрыв над делением
– Оценка деления
– Задачи на умножение слов
– Поделка «Морская звезда» со словесными задачами
– Задания на деление слов
– Определение ключевых слов
– Словесные задачи БИНГО
– Стратегии словесных задач
– Шаги словесных задач PSA
– Быстрая оценка текстовых задач
– В чем магия математики?
«Магия математики» — это серия планов уроков математики и заданий, которые можно использовать в качестве учебной программы по математике или в качестве дополнения к программе, которую вы уже используете. Мы предоставляем ежедневные планы уроков, текстовые задачи, мини-уроки, задания и записи в интерактивной тетради. Если у вас нет времени на все это, это тоже нормально! Вы можете просто выбрать части, которые вы хотите включить в свой математический блок!
-Эти действия повторяются из других ваших устройств?
Абсолютно НЕТ! Мы создаем все новые действия для каждого модуля Magic of Math. Все они уникальны для этой покупки и не копируются/вставляются из вещей, которые мы сделали ранее.
Все они уникальны для этой покупки и не копируются/вставляются из вещей, которые мы сделали ранее.
-Чем отличается Magic of Math от других ваших юнитов?
Магия математики организована в виде ежедневных планов уроков со всем необходимым, а не просто упражнениями.
— ЧЕМ ЭТО НЕ ЯВЛЯЕТСЯ:
Это НЕ набор рабочих листов. В этой серии вы не найдете рабочих листов. Вместо этого мы используем игры, практические занятия, увлекательные мини-уроки и интерактивные тетради для построения нашей учебной программы. Мы стараемся учитывать объем подготовки, связанный с уроками, но некоторые вещи нужно будет распечатать, вырезать и собрать, чтобы использовать в классе.
-Хотите узнать больше о магии математики? Вы можете найти запись в блоге об этом ЗДЕСЬ!
Ознакомьтесь с другими нашими модулями:
2-й класс Магия математики НАБОР
Модуль 1: Размещение значения
Модуль 2: Сложение и вычитание
Модуль 3: Геометрия и дроби
Модуль 4: Перегруппировка 2 и 3 цифр
Блок 5.
Конвертировать из odt в doc: Конвертировать ODT в DOC (WORD) онлайн — Convertio
Конвертировать Openoffice В DOC Бесплатно
ODT в DOC
Разработано на базе программных решений от aspose.com а также aspose.cloud
Выберите OpenOffice файлы или перетащите OpenOffice файлы мышью
Google Drive Dropbox
Использовать пароль
Этот пароль будет применяться ко всем документам
Использовать распознавание текста Использовать распознавание текста
АнглийскийАрабскийИспанскийИтальянскийКитайский упрощенныйНемецкийПерсидскийПольскийПортугальскийРусскийФранцузский «/>
Загружая свои файлы или используя наш сервис, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности.
Сохранить как
DOCDOCXTXTDOTDOCMDOTXDOTMRTFODTOTT
КОНВЕРТИРОВАТЬ
Ваши файлы были успешно сконвертированы
СКАЧАТЬ
Загрузить в Google Загрузить в Dropbox
Конвертация других документов
Отправить на электронную почту
Отправьте нам свой отзыв
Хотите сообщить об этой ошибке на форуме Aspose, чтобы мы могли изучить и решить проблему? Когда ошибка будет исправлена, вы получите уведомление на email. Форма отчета
Google Sheets
Mail Merge
Облачный API
Конвертировать ODT в DOC онлайн
Используйте конвертер ODT в DOC для экспорта файлов ODT в DOC формат онлайн. Наш конвертер файлов проанализирует содержимое исходного ODT файла до мельчайших деталей и воссоздаст содержимое в целевом DOC формате.
Наш конвертер файлов проанализирует содержимое исходного ODT файла до мельчайших деталей и воссоздаст содержимое в целевом DOC формате.
Вы можете использовать конвертер из ODT в DOC совершенно бесплатно, в любое время и с любого устройства.
Онлайн Конвертер ODT в DOC
Конвертация ODT файлов в DOC формат — одна из самых распространенных операций. Нам часто нужны обе функции, предоставляемые форматами ODT и DOC. ODT и DOC в определённых случаях дополняют друг друга.
Конвертировать файл ODT в DOC онлайн
Чтобы конвертировать ODT в DOC формат, просто перетащите ODT файл в область загрузки данных, укажите параметры преобразования, нажмите кнопку ‘Конвертировать’ и получите выходной DOC файл за считанные секунды.
Бесплатный онлайн конвертер ODT в DOC основан на продуктах компании Aspose, которые широко используются во всем мире для программной обработки ODT и DOC с высокой скоростью и профессиональным качеством результата.
Как преобразовать ODT в DOC
- Загрузите ODT файлы, чтобы преобразовать их в DOC формат онлайн.

- Укажите параметры преобразования ODT в DOC.
- Нажмите кнопку, чтобы конвертировать ODT в DOC онлайн.
- Загрузите результат в DOC формате для просмотра.
- Вы можете отправить ссылку для скачивания по электронной почте, если хотите получить результаты позже.
Вопросы-Ответы
Как конвертировать ODT в DOC бесплатно?
Просто используйте наш ODT в DOC Converter. Вы получите выходные файлы DOC одним кликом мыши.
Сколько ODT файлов я могу конвертировать в DOC формат за раз?
Вы можете конвертировать до 10 ODT файлов за раз.
Каков максимально допустимый размер ODT файла?
Размер каждого ODT файла не должен превышать 10 МБ.
Какие есть способы получить результат в DOC формате?
После завершения преобразования ODT в DOC вы получите ссылку для скачивания. Вы можете скачать результат сразу или отправить ссылку на скачивание DOC на свой e-mail позже.
Как долго мои файлы будут храниться на ваших серверах?
Все пользовательские файлы хранятся на серверах Aspose в течение 24 часов. По истечении этого времени они автоматически удаляются.
Можете ли вы гарантировать сохранность моих файлов? Все безопасно?
Aspose уделяет первостепенное внимание безопасности и защите пользовательских данных. Будьте уверены, что ваши файлы хранятся на надежных серверах и защищены от любого несанкционированного доступа.
Почему конвертация ODT в DOC занимает немного больше времени, чем я ожидал?
Конвертация больших ODT файлов в DOC формат может занять некоторое время, поскольку эта операция включает перекодирование и повторное сжатие данных.
Конвертировать Openoffice В ВОРД Бесплатно
ODT в Ворд
Разработано на базе программных решений от aspose.com а также aspose.cloud
Выберите OpenOffice файлы или перетащите OpenOffice файлы мышью
Google Drive Dropbox
Использовать пароль
Этот пароль будет применяться ко всем документам
Использовать распознавание текста Использовать распознавание текста
АнглийскийАрабскийИспанскийИтальянскийКитайский упрощенныйНемецкийПерсидскийПольскийПортугальскийРусскийФранцузский Для корректной работы алгоритма OCR текст и таблицы не должны быть повернуты вниз или вбок.»/>
Если вам нужно преобразовать несколько ODT в один Ворд, используйте Merger
Загружая свои файлы или используя наш сервис, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности.
Сохранить как
DOCXTXTDOCDOTDOCMDOTXDOTMRTFODTOTT
КОНВЕРТИРОВАТЬ
Ваши файлы были успешно сконвертированы
СКАЧАТЬ
Загрузить в Google Загрузить в Dropbox
Конвертация других документов
Отправить на электронную почту
Отправьте нам свой отзыв
Хотите сообщить об этой ошибке на форуме Aspose, чтобы мы могли изучить и решить проблему? Когда ошибка будет исправлена, вы получите уведомление на email. Форма отчета
Форма отчета
Google Sheets
Mail Merge
Облачный API
Конвертировать ODT в Ворд онлайн
Используйте конвертер ODT в Ворд для экспорта файлов ODT в Ворд формат онлайн. Наш конвертер файлов проанализирует содержимое исходного ODT файла до мельчайших деталей и воссоздаст содержимое в целевом Ворд формате.
Вы можете использовать конвертер из ODT в Ворд совершенно бесплатно, в любое время и с любого устройства.
Онлайн Конвертер ODT в Ворд
Конвертация ODT файлов в Ворд формат — одна из самых распространенных операций. Нам часто нужны обе функции, предоставляемые форматами ODT и Ворд. ODT и Ворд в определённых случаях дополняют друг друга.
Конвертировать файл ODT в Ворд онлайн
Чтобы конвертировать ODT в Ворд формат, просто перетащите ODT файл в область загрузки данных, укажите параметры преобразования, нажмите кнопку ‘Конвертировать’ и получите выходной Ворд файл за считанные секунды.
Бесплатный онлайн конвертер ODT в Ворд основан на продуктах компании Aspose, которые широко используются во всем мире для программной обработки ODT и Ворд с высокой скоростью и профессиональным качеством результата.
Как преобразовать ODT в Ворд
- Загрузите ODT файлы, чтобы преобразовать их в Ворд формат онлайн.
- Укажите параметры преобразования ODT в Ворд.
- Нажмите кнопку, чтобы конвертировать ODT в Ворд онлайн.
- Загрузите результат в Ворд формате для просмотра.
- Вы можете отправить ссылку для скачивания по электронной почте, если хотите получить результаты позже.
Вопросы-Ответы
Как конвертировать ODT в Ворд бесплатно?
Просто используйте наш ODT в Ворд Converter. Вы получите выходные файлы Ворд одним кликом мыши.
Сколько ODT файлов я могу конвертировать в Ворд формат за раз?
Вы можете конвертировать до 10 ODT файлов за раз.
Каков максимально допустимый размер ODT файла?
Размер каждого ODT файла не должен превышать 10 МБ.
Какие есть способы получить результат в Ворд формате?
После завершения преобразования ODT в Ворд вы получите ссылку для скачивания. Вы можете скачать результат сразу или отправить ссылку на скачивание Ворд на свой e-mail позже.
Вы можете скачать результат сразу или отправить ссылку на скачивание Ворд на свой e-mail позже.
Как долго мои файлы будут храниться на ваших серверах?
Все пользовательские файлы хранятся на серверах Aspose в течение 24 часов. По истечении этого времени они автоматически удаляются.
Можете ли вы гарантировать сохранность моих файлов? Все безопасно?
Aspose уделяет первостепенное внимание безопасности и защите пользовательских данных. Будьте уверены, что ваши файлы хранятся на надежных серверах и защищены от любого несанкционированного доступа.
Почему конвертация ODT в Ворд занимает немного больше времени, чем я ожидал?
Конвертация больших ODT файлов в Ворд формат может занять некоторое время, поскольку эта операция включает перекодирование и повторное сжатие данных.
Как легко преобразовать файл ODT в Word
OpenOffice — это
бесплатный программный пакет с открытым исходным кодом, который включает в себя Writer, альтернативу
Microsoft Word. Хотя Writer работает невероятно хорошо, он сохраняет файлы в
Формат OpenDocument Text (.ODT). Это не должно быть проблемой, за исключением случаев, когда вам нужно
для открытия файлов в Microsoft Word.
Хотя Writer работает невероятно хорошо, он сохраняет файлы в
Формат OpenDocument Text (.ODT). Это не должно быть проблемой, за исключением случаев, когда вам нужно
для открытия файлов в Microsoft Word.
Если у вас Word 2010 или более поздней версии, файл .ODT будет открываться автоматически при двойном щелчке. Но как насчет тех, кто использует более старые версии Word или не установил Word?
Содержание
Не волнуйтесь. Хорошо показать вам, как конвертировать .ODT в документ Word. Попробуйте один из следующих способов перечислено ниже.
Использование WordPad
Первый способ использует WordPad для преобразования файлов .ODT в файлы .DOC, формат файла Word. Найдите файл .ODT, который вы хотите открыть. Щелкните файл правой кнопкой мыши и выберите Открыть с помощью .
Это подскажет Windows, чтобы показать вам все совместимые приложения. Выберите WordPad из списка и нажмите ОК .
Файл будет
открыть как документ WordPad. Перейти к файлу > Сохранить как > Документ Office Open XML .
Перейти к файлу > Сохранить как > Документ Office Open XML .
Переименуйте файл при необходимости нажмите Сохранить в продолжать. Это создаст версию исходного файла в формате .DOC. Вы должны сейчас получить доступ к документу в MS Word.
Преобразование файлов онлайн
Существует множество сторонних сайтов, которые позволяют пользователям преобразовывать файлы .ODT в .DOC. Эти сайты обычно имеют один и тот же процесс. Пользователи загружают файл, который хотят преобразовать, выбирают формат для преобразования, а затем загружают результат. В некоторых случаях пользователям по электронной почте отправляется ссылка, сообщающая им, где скачать файл.
Перед преобразованием файлы в Интернете, убедитесь, что вы используете надежный сервис.
Перейти на Google Диск
Знаете ли вы, что вы
можно использовать Google Диск для преобразования файлов? Google Диск бесплатен. Все, что вам нужно, это
учетная запись Google.
Перейдите на Google Диск и Войдите в систему . На панели инструментов перейдите к Новый > Загрузка файла . Выберите файл, который хотите преобразовать, и нажмите Открыть .
В качестве альтернативы, вы можете перетащить файл на Google Диск.
После загрузки дважды щелкните документ. Нажмите Открыть С Документами Google .
Этот процесс позволяет пользователям редактировать файлы через Google Docs, веб-приложение для редактирования документов. Файлы .ODT, которые открываются через приложение, автоматически конвертируются в .DOC. формат.
Чтобы скачать документ, перейдите к Файл > Загрузить как > Microsoft Word .
Перейти к расположение загрузки Chrome по умолчанию (обычно это папка «Загрузки»). Ты найдешь копия файла .DOC. Откройте в Word и редактируйте как обычно.
Примечание: То же
Метод можно использовать для сохранения файлов в формате PDF.
Почему я не могу открыть файлы ODT?
Что произойдет, если вы не можете открыть файлы .ODT ни одним из вышеперечисленных способов? Если это так, есть вероятность, что то, что у вас есть, не является файлом .ODT с самого начала. Некоторый файлы имеют расширения файлов, которые кажутся .ODT, но на самом деле таковыми не являются.
Файл .ADT для Например, это формат файла, используемый в продукте под названием ACT. Расширение .ODM может легко спутать с .ODT. Однако этот формат используется компанией OverDrive. для сохранения медиафайлов.
Заключение
Вам необходимо конвертировать файлы .ODT в формат Word, чтобы открывать их в Word. Из всех методов обсуждалось, использование WordPad было бы самым простым и безопасным вариантом.
Использование Google Диск работает так же хорошо, но для этого вам нужно быть в сети.
Некоторые сторонние
Преобразователи OpenOffice в Microsoft Word работают. Но некоторые из них не так безопасны, как
другие. Вам нужно будет провести некоторое исследование, чтобы проверить, какой документ .ODT в Word
конвертеры нормальные.
Вам нужно будет провести некоторое исследование, чтобы проверить, какой документ .ODT в Word
конвертеры нормальные.
Кристофер Ян Бенитес (Christopher Jan Benitez) — наемный писатель-фрилансер, который предоставляет действенный и полезный веб-контент для малого бизнеса и стартапов. В свободное время он неукоснительно смотрит профессиональный рестлинг и находит утешение в прослушивании спид-метала 80-х. Прочитать полную биографию Кристофера
Подписывайтесь на YouTube!
Вам понравился этот совет? Если это так, загляните на наш канал YouTube на нашем родственном сайте Online Tech Tips. Мы охватываем Windows, Mac, программное обеспечение и приложения, а также предлагаем множество советов по устранению неполадок и обучающих видеороликов. Нажмите на кнопку ниже, чтобы подписаться!
Подписаться
Конвертер Openoffice в DOC Бесплатно. Openoffice в DOC онлайн.
ODT в DOC
Питаться от
aspose. com
и
aspose.cloud
com
и
aspose.cloud
Выберите файлы OpenOffice или перетащите файлы OpenOffice
Google Диск Дропбокс
Использовать пароль
Этот пароль будет применяться ко всем документам
Использовать распознавание текста Использовать распознавание текста
АрабскийКитайский упрощенныйАнглийскийФранцузскийНемецкийИтальянскийПерсидскийПольскийПортугальскийРусскийИспанский
Загружая свои файлы или используя наш сервис, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности
Сохранить как
DOCDOCXTXTDOTDOCMDOTXDOTMRTFODTOTT
КОНВЕРТИРОВАТЬ
Ваши файлы были успешно преобразованы
СКАЧАТЬ
Загрузить в Google Загрузить в Дропбокс
Преобразование других документов Отправить по электронной почте
Ответьте на наш опрос
Вы хотите сообщить об этой ошибке на форум Aspose, чтобы мы могли изучить и решить проблему? Вы получите уведомление по электронной почте, когда ошибка будет исправлена. Форма отчета
Форма отчета
Google Таблицы
Слияние почты Облачный API
Преобразование ODT в DOC Online
Используйте конвертер ODT в DOC для экспорта файлов ODT в формат DOC онлайн. Наша бесплатная служба преобразования проанализирует содержимое исходного файла ODT до мельчайших деталей и воссоздаст содержимое в целевом формате DOC.
Вы можете использовать конвертер ODT в DOC совершенно бесплатно, в любое время и с любого устройства.
Конвертер ODT в DOC Online
Преобразование из формата ODT в DOC является одной из наиболее распространенных операций. Нам часто нужны обе функции, предоставляемые форматами ODT и DOC. Форматы ODT и DOC в некоторых случаях дополняют друг друга.
Преобразование файла ODT в DOC Online
Чтобы преобразовать файл ODT в формат DOC, просто перетащите файл ODT в область загрузки данных, укажите параметры преобразования, нажмите кнопку «Преобразовать» и получите выходной файл DOC за считанные секунды. .
.
Free ODT to DOC Converter основан на программных продуктах Aspose, которые широко используются во всем мире для программной обработки файлов ODT и DOC с высокой скоростью и профессиональным качеством результата.
Как преобразовать ODT в DOC
- Загрузите файлы ODT, чтобы преобразовать их в формат DOC онлайн.
- Укажите параметры преобразования ODT в DOC.
- Нажмите кнопку, чтобы преобразовать ODT в DOC онлайн.
- Скачать результат в формате DOC для просмотра.
- Вы можете отправить ссылку на скачивание по электронной почте, если хотите получить результаты позже.
FAQ
Как бесплатно конвертировать ODT в DOC?
Просто воспользуйтесь нашим конвертером ODT в DOC. Вы получите выходные файлы DOC одним щелчком мыши.
Сколько файлов ODT я могу конвертировать в формат DOC одновременно?
Одновременно можно конвертировать до 10 файлов ODT.
Каков максимально допустимый размер файла ODT?
Размер каждого файла ODT не должен превышать 10 МБ.
35 разделить на 7: Если 35 разделить на 7 то полученное число будет на 15 меньше задуманного числа. Задуманное число-?
| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | Найти объем | сфера (4) | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | 2 1/2÷22000000 | |
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | Перевести в процентное соотношение | 3/9 | |
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Страница 35 — ГДЗ Русский язык 1 класс Канакина, Горецкий учебник
Вернуться к содержанию учебника
Слово и слог
Вопрос
7. Прочитай. Назови сказку.
Прочитай. Назови сказку.
Посадил дед репку. Выросла репка большая-пребольшая. Стал дед репку из земли тащить. Тянет-потянет, вытянуть не может.
- Спиши первые два предложения.
- Разыграйте сценку вместе с друзьями. Покажите с помощью жестов, как дед тянет репку. Сопровождайте свои действия словами последнего предложения. Как вы будете проговаривать слова?
Ответ
Вариант ответа #1:
Сказка «Репка».
Посадил дед репку. Выросла репка большая-пребольшая.
Проговаривать слова из последнего предложения следует медленно, по слогам, протягивая гласные звуки.
Вариант ответа #2:
Это сказка «Репка».
Посадил дед репку. Выросла репка большая-пребольшая.
Слова надо проговаривать с выражением.
Вопрос
Проверь себя 1. Скажи, как узнать, сколько в слове слогов?
Ответ
В слове столько слогов, сколько гласных звуков.
Вопрос
Вариант вопроса #1:
Проверь себя 2. Прочитай. Раздели слова на слоги.
Слива, радуга, лилия.
Вариант вопроса #2:
Проверь себя 2. Какое слово нельзя разделить на слоги?
Слива, дождь, радуга.
Ответ
Вариант ответа #1:
Сли|ва, ра|ду|га, ли|ли|я.
Вариант ответа #2:
Слово дождь нельзя разделить на слоги, потому что в нём один гласный звук, значит один слог.
Вопрос
Проверь себя 3. Прочитай. Запиши слова в порядке увеличения в них количества слогов.
Утюг, лист, осина.
Ответ
Вариант ответа #1:
Лист, утюг, осина.
Вариант ответа #2:
Лист, у|тюг, о|си|на.
Вернуться к содержанию учебника
Сколько 35 разделить на 7 с использованием длинного деления?
Запутались в длинном делении? К концу этой статьи вы сможете разделить 35 на 7, используя деление в длинную сторону, и сможете применить ту же технику к любой другой задаче на деление в длинную сторону! Давайте взглянем.
Хотите быстро научиться или показать учащимся, как решить деление 35 на 7 с помощью деления в большую сторону? Включи это очень быстрое и веселое видео прямо сейчас!
Итак, первое, что нам нужно сделать, это уточнить термины, чтобы вы знали, что представляет собой каждая часть деления:
- Первое число, 35, называется делимым.
- Второе число 7 называется делителем.
Здесь мы разберем каждый шаг процесса длинного деления на 35, разделенного на 7, и объясним каждый из них, чтобы вы точно поняли, что происходит.
35 разделить на 7 пошаговое руководство
Шаг 1
Первый шаг — поставить задачу деления с делителем слева и делимым справа, как показано ниже:
Шаг 2
Мы можем выяснить, что делитель (7) входит в первую цифру делимого (3), 0 раз. Теперь, когда мы это знаем, мы можем поставить 0 вверху:
Теперь, когда мы это знаем, мы можем поставить 0 вверху:
Шаг 3
Если мы умножим делитель на результат предыдущего шага (7 x 0 = 0), то теперь мы можем добавить этот ответ под делимым:
Шаг 4
Далее из второй цифры делимого (3 — 0 = 3) вычтем результат предыдущего шага и запишем этот ответ ниже:
| 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 3 | 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 3 | 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 5 | ||||
| 7 | 3 900 39 | 5 | |||
| — | 0 | ||||
| 3 | 5 |
Шаг 7
Если мы умножим делитель на результат предыдущего шага (7 x 5 = 35), то теперь мы можем добавить этот ответ под делимым:
| 9003 6 | 0 | 5 | ||
| 7 | 3 | 5 | ||
| — | 9003 8 0||||
| 3 | 5 | |||
| 3 | 5 |
Шаг 8
Далее вычтем результат предыдущего шага из третьей цифры делимого (35 — 35 = 0) и запишем этот ответ ниже:
| 0 | 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 3 | 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 900 38 — | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | 3 | 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Символ | Название символа | Символ Значение | Пример | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | плюс | сложение | 1/2 + 1/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | минус | вычитание | 90 548 1 1/2 — 2/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | звездочка | умножение | 2/3 * 3/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | знак умножения | умножение | 2/3 × 5/6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | знак деления | деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .  Наиболее распространенные мнемоники для запоминания этого порядка операций: Наиболее распространенные мнемоники для запоминания этого порядка операций: PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание. BEDMAS — скобки, экспоненты, деление, умножение, сложение, вычитание BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание. GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание. MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS. Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Как находить ноз дробей примеры. Как найти наименьшее общее кратное чисел
Общее кратное для двух целых чисел — это такое целое число, которое делится нацело без остатка на оба заданных числа.Наименьшее общее кратное для двух целых чисел — это наименьшее из всех целых чисел, которое делится нацело и без остатка на оба заданных числа.
Способ 1 . Найти НОК можно, по очереди, для каждого из заданных чисел, выписывая в порядке возрастания все числа, которые получаются путем их умножения на 1, 2, 3, 4 и так далее.
Пример для чисел 6 и 9.
Умножаем число 6, последовательно, на 1, 2, 3, 4, 5.
Получаем: 6, 12, 18 , 24, 30
Умножаем число 9, последовательно, на 1, 2, 3, 4, 5.
Получаем: 9, 18 , 27, 36, 45
Как видно, НОК для чисел 6 и 9 будет равно 18.
Данный способ удобен, когда оба числа небольшие и их несложно умножать на последовательность целых чисел. Однако, бывают случаи, когда нужно найти НОК для двузначных или трехзначных чисел, а также, когда исходных чисел три или даже больше.
Способ 2 . Найти НОК можно, разложив исходные числа на простые множители.
После разложения необходимо вычеркнуть из получившихся рядов простых множителей одинаковые числа. Оставшиеся числа первого числа будут множителем для второго, а оставшиеся числа второго — множителем для первого.
Пример для числе 75 и 60.
Наименьшее общее кратное чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители:
75 = 3 * 5 * 5, а
60 = 2 * 2 * 3 * 5 .
Как видно, множители 3 и 5 встречаются в обоих строках. Мысленно их «зачеркиваем».
Выпишем оставшиеся множители, входящие в разложение каждого из этих чисел. При разложении числа 75 у нас осталось число 5, а при разложении числа 60 — остались 2 * 2
Значит, чтобы определить НОК для чисел 75 и 60, нам нужно оставшиеся числа от разложения 75 (это 5) умножить на 60, а числа, оставшиеся от разложения числа 60 (это 2 * 2) умножить на 75. То есть, для простоты понимания, мы говорим, что умножаем «накрест».
То есть, для простоты понимания, мы говорим, что умножаем «накрест».
75 * 2 * 2 = 300
60 * 5 = 300
Таким образом мы и нашли НОК для чисел 60 и 75. Это — число 300.
Пример . Определить НОК для чисел 12, 16, 24
В данном случае, наши действия будут несколько сложнее. Но, сначала, как всегда, разложим все числа на простые множители
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Чтобы правильно определить НОК, выбираем наименьшее из всех чисел (это число 12) и последовательно проходим по его множителям, вычеркивая их, если хотя бы в одном из других рядов чисел встретился такой же, еще не зачеркнутый множитель.
Шаг 1 . Мы видим, что 2 * 2 встречаются во всех рядах чисел. Зачеркиваем их.
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Шаг 2. В простых множителях числа 12 осталось только число 3. Но оно присутствует в простых множителях числа 24. Вычеркиваем число 3 из обоих рядов, при этом для числа 16 никаких действий не предполагается.
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Как видим, при разложении числа 12 мы «вычеркнули» все числа. Значит нахождение НОК завершено. Осталось только вычислить его значение.
Для числа 12 берем оставшиеся множители у числа 16 (ближайшего по возрастанию)
12 * 2 * 2 = 48
Это и есть НОК
Как видим, в данном случае, нахождение НОК было несколько сложнее, но когда нужно его найти для трех и более чисел, данный способ позволяет сделать это быстрее. Впрочем, оба способа нахождения НОК являются правильными.
Кратное число – это число, которое делится на данное число без остатка. Наименьшее общее кратное (НОК) группы чисел – это наименьшее число, которое делится без остатка на каждое число группы. Чтобы найти наименьшее общее кратное, нужно найти простые множители данных чисел. Также НОК можно вычислить с помощью ряда других методов, которые применимы к группам из двух и более чисел.
Шаги
Ряд кратных чисел
Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых меньше 10. Если даны большие числа, воспользуйтесь другим методом.
- Например, найдите наименьшее общее кратное чисел 5 и 8. Это небольшие числа, поэтому можно использовать данный метод.
Кратное число – это число, которое делится на данное число без остатка. Кратные числа можно посмотреть в таблице умножения..
- Например, числами, которые кратны 5, являются: 5, 10, 15, 20, 25, 30, 35, 40.
Запишите ряд чисел, которые кратны первому числу. Сделайте это под кратными числами первого числа, чтобы сравнить два ряда чисел.
- Например, числами, которые кратны 8, являются: 8, 16, 24, 32, 40, 48, 56, и 64.
Найдите наименьшее число, которое присутствует в обоих рядах кратных чисел. Возможно, вам придется написать длинные ряды кратных чисел, чтобы найти общее число. Наименьшее число, которое присутствует в обоих рядах кратных чисел, является наименьшим общим кратным.
Наименьшее число, которое присутствует в обоих рядах кратных чисел, является наименьшим общим кратным.
- Например, наименьшим числом, которое присутствует в рядах кратных чисел 5 и 8, является число 40. Поэтому 40 – это наименьшее общее кратное чисел 5 и 8.
Разложение на простые множители
Посмотрите на данные числа. Описанный здесь метод лучше применять, когда даны два числа, каждое из которых больше 10. Если даны меньшие числа, воспользуйтесь другим методом.
- Например, найдите наименьшее общее кратное чисел 20 и 84. Каждое из чисел больше 10, поэтому можно использовать данный метод.
Разложите на простые множители первое число. То есть нужно найти такие простые числа, при перемножении которых получится данное число. Найдя простые множители, запишите их в виде равенства.
- Например, 2 × 10 = 20 {\displaystyle {\mathbf {2} }\times 10=20}
и 2 × 5 = 10 {\displaystyle {\mathbf {2} }\times {\mathbf {5} }=10}
.
 Таким образом, простыми множителями числа 20 являются числа 2, 2 и 5. Запишите их в виде выражения: .
Таким образом, простыми множителями числа 20 являются числа 2, 2 и 5. Запишите их в виде выражения: .
- Например, 2 × 10 = 20 {\displaystyle {\mathbf {2} }\times 10=20}
и 2 × 5 = 10 {\displaystyle {\mathbf {2} }\times {\mathbf {5} }=10}
.
Разложите на простые множители второе число. Сделайте это так же, как вы раскладывали на множители первое число, то есть найдите такие простые числа, при перемножении которых получится данное число.
- Например, 2 × 42 = 84 {\displaystyle {\mathbf {2} }\times 42=84} , 7 × 6 = 42 {\displaystyle {\mathbf {7} }\times 6=42} и 3 × 2 = 6 {\displaystyle {\mathbf {3} }\times {\mathbf {2} }=6} . Таким образом, простыми множителями числа 84 являются числа 2, 7, 3 и 2. Запишите их в виде выражения: .
Запишите множители, общие для обоих чисел. Запишите такие множители в виде операции умножения. По мере записи каждого множителя зачеркивайте его в обоих выражениях (выражения, которые описывают разложения чисел на простые множители).
- Например, общим для обоих чисел является множитель 2, поэтому напишите 2 × {\displaystyle 2\times }
и зачеркните 2 в обоих выражениях.

- Общим для обоих чисел является еще один множитель 2, поэтому напишите 2 × 2 {\displaystyle 2\times 2} и зачеркните вторую 2 в обоих выражениях.
- Например, общим для обоих чисел является множитель 2, поэтому напишите 2 × {\displaystyle 2\times }
и зачеркните 2 в обоих выражениях.
К операции умножения добавьте оставшиеся множители. Это множители, которые не зачеркнуты в обоих выражениях, то есть множители, не являющиеся общими для обоих чисел.
- Например, в выражении 20 = 2 × 2 × 5 {\displaystyle 20=2\times 2\times 5} зачеркнуты обе двойки (2), потому что они являются общими множителями. Не зачеркнут множитель 5, поэтому операцию умножения запишите так: 2 × 2 × 5 {\displaystyle 2\times 2\times 5}
- В выражении 84 = 2 × 7 × 3 × 2 {\displaystyle 84=2\times 7\times 3\times 2} также зачеркнуты обе двойки (2). Не зачеркнуты множители 7 и 3, поэтому операцию умножения запишите так: 2 × 2 × 5 × 7 × 3 {\displaystyle 2\times 2\times 5\times 7\times 3} .
Вычислите наименьшее общее кратное. Для этого перемножьте числа в записанной операции умножения.

- Например, 2 × 2 × 5 × 7 × 3 = 420 {\displaystyle 2\times 2\times 5\times 7\times 3=420} . Таким образом, наименьшее общее кратное 20 и 84 равно 420.
Нахождение общих делителей
Нарисуйте сетку как для игры в крестики-нолики. Такая сетка представляет собой две параллельные прямые, которые пересекаются (под прямым углом) с другими двумя параллельными прямыми. Таким образом, получатся три строки и три столбца (сетка очень похожа на значок #). Первое число напишите в первой строке и втором столбце. Второе число напишите в первой строке и третьем столбце.
- Например, найдите наименьшее общее кратное чисел 18 и 30. Число 18 напишите в первой строке и втором столбце, а число 30 напишите в первой строке и третьем столбце.
Найдите делитель, общий для обоих чисел. Запишите его в первой строке и первом столбце. Лучше искать простые делители, но это не является обязательным условием.
- Например, 18 и 30 – это четные числа, поэтому их общим делителем будет число 2.
 Таким образом, напишите 2 в первой строке и первом столбце.
Таким образом, напишите 2 в первой строке и первом столбце.
- Например, 18 и 30 – это четные числа, поэтому их общим делителем будет число 2.
Разделите каждое число на первый делитель. Каждое частное запишите под соответствующим числом. Частное – это результат деления двух чисел.
- Например, 18 ÷ 2 = 9 {\displaystyle 18\div 2=9} , поэтому запишите 9 под 18.
- 30 ÷ 2 = 15 {\displaystyle 30\div 2=15} , поэтому запишите 15 под 30.
Найдите делитель, общий для обоих частных. Если такого делителя нет, пропустите два следующих шага. В противном случае делитель запишите во второй строке и первом столбце.
- Например, 9 и 15 делятся на 3, поэтому запишите 3 во второй строке и первом столбце.
Разделите каждое частное на второй делитель. Каждый результат деления запишите под соответствующим частным.
- Например, 9 ÷ 3 = 3 {\displaystyle 9\div 3=3} , поэтому запишите 3 под 9.
- 15 ÷ 3 = 5 {\displaystyle 15\div 3=5}
, поэтому запишите 5 под 15.

Если нужно, дополните сетку дополнительными ячейками. Повторяйте описанные действия до тех пор, пока у частных не будет общего делителя.
Обведите кружками числа в первом столбце и последней строке сетки. Затем выделенные числа запишите в виде операции умножения.
- Например, числа 2 и 3 находятся в первом столбце, а числа 3 и 5 находятся в последней строке, поэтому операцию умножения запишите так: 2 × 3 × 3 × 5 {\displaystyle 2\times 3\times 3\times 5} .
Найдите результат умножения чисел. Так вы вычислите наименьшее общее кратное двух данных чисел.
- Например, 2 × 3 × 3 × 5 = 90 {\displaystyle 2\times 3\times 3\times 5=90} . Таким образом, наименьшее общее кратное 18 и 30 равно 90.
Алгоритм Евклида
Запомните терминологию, связанную с операцией деления. Делимое – это число, которое делят. Делитель – это число, на которое делят.
 Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.
Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.- Например, в выражении 15 ÷ 6 = 2 {\displaystyle 15\div 6=2}
ост. 3:
15 – это делимое
6 – это делитель
2 – это частное
3 – это остаток.
- Например, в выражении 15 ÷ 6 = 2 {\displaystyle 15\div 6=2}
ост. 3:
В реальной жизни нам необходимо оперировать обыкновенными дробями. Однако чтобы сложить или вычесть дроби с разными знаменателями, например, 2/3 и 5/7, нам потребуется найти общий знаменатель. Приведя дроби к общему знаменателю, мы сможем легко осуществить операции сложения или вычитания.
Определение
Дроби — одна из самых сложных тем в начальной арифметике, и рациональные числа пугают школьников, которые встречаются с ними впервые. Мы привыкли оперировать с числами, записанными в десятичном формате. Куда проще сходу сложить 0,71 и 0,44, чем суммировать 5/7 и 4/9. Ведь для суммирования дробей их необходимо привести к общему знаменателю. Однако дроби куда точнее представляют значение величин, чем их десятичные эквиваленты, а в математике представление рядов или иррациональных чисел в виде дроби становится приоритетной задачей. Такая задача носит название «приведение выражения к замкнутому виду».
Такая задача носит название «приведение выражения к замкнутому виду».
Если и числитель, и знаменатель дроби умножить или разделить на один и тот же коэффициент, то значение дроби не изменится. Это одно из самых важных свойств дробных чисел. К примеру, дробь 3/4 в десятичной форме записывается как 0,75. Если умножить числитель и знаменатель на 3, то получим дробь 9/12, что точно также равняется 0,75. Благодаря этому свойству мы можем умножать разные дроби таким образом, чтобы они все имели одинаковые знаменатели. Как это сделать?
Поиск общего знаменателя
Наименьший общий знаменатель (НОЗ) — это наименьшее общее кратное для всех знаменателей выражения. Найти такое число мы можем тремя способами.
Использование максимального знаменателя
Это один из самых простых, но трудоемких методов поиска НОЗ. Вначале из знаменателей всех дробей выписываем самое большое число и проверяем его делимость на меньшие числа. Если делится, то наибольший знаменатель и есть НОЗ.
Если в предыдущей операции числа делятся с остатком, то необходимо самое большое из них умножить на 2 и повторить проверку на делимость. Если оно делится без остатка, то новый коэффициент становится НОЗ.
Если нет, то самый большой знаменатель умножается на 3, 4 , 5 и так далее, пока не будет найдено наименьшее общее кратное для нижних частей всех дробей. На практике это выглядит так.
Пусть у нас есть дроби 1/5, 1/8 и 1/20. Проверяем 20 на делимость 5 и 8. 20 не делится на 8. Умножаем 20 на 2. Проверяем 40 на делимость 5 и 8. Числа делятся без остатка, следовательно, НОЗ (1/5, 1/8 и 1/20) = 40, а дроби превращаются в 8/40, 5/40 и 2/40.
Последовательный перебор кратных
Второй способ — это простой перебор кратных и выбор из них наименьшего. Для поиска кратных мы умножаем число на 2, 3, 4 и так далее, поэтому количество кратных устремляется в бесконечность. Ограничить эту последовательность можно пределом, которое представляет собой произведение заданных чисел. К примеру, для чисел 12 и 20 НОК находится следующим образом:
К примеру, для чисел 12 и 20 НОК находится следующим образом:
- выписываем числа, кратные 12 — 24, 48, 60, 72, 84, 96, 108, 120;
- выписываем числа, кратные 20 — 40, 60, 80, 100, 120;
- определяем общие кратные — 60, 120;
- выбираем наименьшее из них — 60.
Таким образом, для 1/12 и 1/20 общим знаменателем будет 60, а дроби преобразуются в 5/60 и 3/60.
Разложение на простые множители
Этот способ нахождения НОК наиболее актуален. Данный метод подразумевает разложение всех чисел из нижних частей дробей на неделимые множители. После этого составляется число, которое содержит множители всех знаменателей. На практике это работает так. Найдем НОК для той же пары 12 и 20:
- раскладываем на множители 12 — 2 × 2 × 3;
- раскладываем 20 — 2 × 2 × 5;
- объединяем множители таким образом, чтобы они содержали в себе числа и 12, и 20 — 2 × 2 × 3 × 5;
- перемножаем неделимые и получаем результат — 60.
В третьем пункте мы объединяем множители без повторов, то есть двух двоек достаточно для формирования 12 в комбинации с тройкой и 20 — с пятеркой.
Наш калькулятор позволяет определить НОЗ для произвольного количества дробей, записанных как в обыкновенной, так и в десятичной форме. Для поиска НОЗ вам достаточно ввести значения через табуляцию или запятую, после чего программа вычислит общий знаменатель и выведет на экран преобразованные дроби.
Пример из реальной жизни
Сложение дробей
Пусть в задаче по арифметике нам необходимо сложить пять дробей:
0,75 + 1/5 + 0,875 + 1/4 + 1/20
Решение вручную производилось бы следующим способом. Для начала нам необходимо представить числа в одной форме записи:
- 0,75 = 75/100 = 3/4;
- 0,875 = 875/1000 = 35/40 = 7/8.
Теперь у нас есть ряд обыкновенных дробей, которые необходимо привести к одинаковому знаменателю:
3/4 + 1/5 + 7/8 + 1/4 + 1/20
Так как у нас 5 слагаемых, проще всего использовать способ поиска НОЗ по наибольшему числу. Проверяем 20 на делимость остальными числами. 20 не делится на 8 без остатка. Умножаем 20 на 2, проверим 40 на делимость — все числа делят 40 нацело. Это и есть наш общий знаменатель. Теперь для суммирования рациональных чисел нам необходимо определить дополнительные множители для каждой дроби, которые определяются как соотношение НОК к знаменателю. Дополнительные множители буду выглядеть так:
Это и есть наш общий знаменатель. Теперь для суммирования рациональных чисел нам необходимо определить дополнительные множители для каждой дроби, которые определяются как соотношение НОК к знаменателю. Дополнительные множители буду выглядеть так:
- 40/4 = 10;
- 40/5 = 8;
- 40/8 = 5;
- 40/4 = 10;
- 40/20 = 2.
Теперь умножим числитель и знаменатель дробей на соответствующие дополнительные множители:
30/40 + 8/40 + 35/40 + 10/40 + 2/40
Для такого выражения мы можем легко определить сумму, равную 85/40 или 2 целых и 1/8. Это громоздкие вычисления, поэтому вы можете просто ввести данные задачи в форму калькулятора и сразу получить ответ.
Заключение
Арифметические операции с дробями — не слишком удобная вещь, ведь для поиска ответа приходится осуществлять множество промежуточных вычислений. Используйте наш онлайн-калькулятор для приведения дробей к общему знаменателю и быстрого решения школьных задач.
Для решения примеров с дробями необходимо уметь находить наименьший общий знаменатель. Ниже приведена подробная инструкция.
Ниже приведена подробная инструкция.
Как найти наименьший общий знаменатель – понятие
Наименьший общий знаменатель (НОЗ) простыми словами – это минимальное число, которое делится на знаменатели всех дробей данного примера. Другими словами его называют Наименьшим Общим Кратным (НОК). НОЗ используют только в том случае, если знаменатели у дробей различны.
Как найти наименьший общий знаменатель – примеры
Рассмотрим примеры нахождения НОЗ.
Вычислить: 3/5 + 2/15.
Решение (Последовательность действий):
- Смотрим на знаменатели дробей, убеждаемся, что они разные и выражения максимально сокращены.
- Находим наименьшее число, которое делится и на 5, и на 15. Таким числом будет 15. Таким образом, 3/5 + 2/15 = ?/15.
- Со знаменателем разобрались. Что будет в числителе? Помочь выяснить это нам поможет дополнительный множитель. Дополнительный множитель – это число, получившееся при делении НОЗ на знаменатель конкретной дроби. Для 3/5 дополнительный множитель равен 3, так как 15/5 = 3.
 Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.
Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1. - Выяснив дополнительный множитель, умножаем его на числители дробей и складываем получившиеся значения. 3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.
Ответ: 3/5 + 2/15 = 11/15.
Если в примере складываются или вычитаются не 2, а 3 или больше дробей, то НОЗ нужно искать уже для стольких дробей, сколько дано.
Вычислить: 1/2 – 5/12 + 3/6
Решение (последовательность действий):
- Находим наименьший общий знаменатель. Минимальным числом, делящимся на 2, 12 и 6 будет 12.
- Получим: 1/2 – 5/12 + 3/6 = ?/12.
- Ищем дополнительные множители. Для 1/2 – 6; для 5/12 – 1; для 3/6 – 2.
- Умножаем на числители и приписываем соответствующие знаки: 1/2 – 5/12 + 3/6 = (1*6 – 5*1 + 2*3)/12 = 7/12.
Ответ: 1/2 – 5/12 + 3/6 = 7/12.
Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.
В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.
Yandex.RTB R-A-339285-1
Вычисление наименьшего общего кратного (НОК) через НОД
Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.
Определение 1
Найти наименьшее общее кратное через наибольший общий делитель можно по формуле НОК (a , b) = a · b: НОД (a , b) .
Пример 1
Необходимо найти НОК чисел 126 и 70 .
Решение
Примем a = 126 , b = 70 . Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК (a , b) = a · b: НОД (a , b) .
Найдет НОД чисел 70 и 126 . Для этого нам понадобится алгоритм Евклида: 126 = 70 · 1 + 56 , 70 = 56 · 1 + 14 , 56 = 14 · 4 , следовательно, НОД (126 , 70) = 14 .
Вычислим НОК: НОК (126 , 70) = 126 · 70: НОД (126 , 70) = 126 · 70: 14 = 630 .
Ответ: НОК (126 , 70) = 630 .
Пример 2
Найдите нок чисел 68 и 34 .
Решение
НОД в данном случае нейти несложно, так как 68 делится на 34 . Вычислим наименьшее общее кратное по формуле: НОК (68 , 34) = 68 · 34: НОД (68 , 34) = 68 · 34: 34 = 68 .
Ответ: НОК (68 , 34) = 68 .
В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.
Нахождение НОК с помощью разложения чисел на простые множители
Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.
Определение 2
Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:
- составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
- исключаем их полученных произведений все простые множители;
- полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК (a , b) = a · b: НОД (a , b) . Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.
Пример 3
У нас есть два числе 75 и 210 . Мы можем разложить их на множители следующим образом: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . Если составить произведение всех множителей двух исходных чисел, то получится: 2 · 3 · 3 · 5 · 5 · 5 · 7 .
Если исключить общие для обоих чисел множители 3 и 5 , мы получим произведение следующего вида: 2 · 3 · 5 · 5 · 7 = 1050 . Это произведение и будет нашим НОК для чисел 75 и 210 .
Пример 4
Найдите НОК чисел 441 и 700 , разложив оба числа на простые множители.
Решение
Найдем все простые множители чисел, данных в условии:
441 147 49 7 1 3 3 7 7
700 350 175 35 7 1 2 2 5 5 7
Получаем две цепочки чисел: 441 = 3 · 3 · 7 · 7 и 700 = 2 · 2 · 5 · 5 · 7 .
Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7 . Найдем общие множители. Это число 7 . Исключим его из общего произведения: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 . Получается, что НОК (441 , 700) = 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 = 44 100 .
Ответ: НОК (441 , 700) = 44 100 .
Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.
Определение 3
Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:
- разложим оба числа на простые множители:
- добавим к произведению простых множителей первого числа недостающие множители второго числа;
- получим произведение, которое и будет искомым НОК двух чисел.

Пример 5
Вернемся к числам 75 и 210 , для которых мы уже искали НОК в одном из прошлых примеров. Разложим их на простые множители: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . К произведению множителей 3 , 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210 . Получаем: 2 · 3 · 5 · 5 · 7 . Это и есть НОК чисел 75 и 210 .
Пример 6
Необходимо вычислить НОК чисел 84 и 648 .
Решение
Разложим числа из условия на простые множители: 84 = 2 · 2 · 3 · 7 и 648 = 2 · 2 · 2 · 3 · 3 · 3 · 3 . Добавим к произведению множителей 2 , 2 , 3 и 7 числа 84 недостающие множители 2 , 3 , 3 и
3 числа 648 . Получаем произведение 2 · 2 · 2 · 3 · 3 · 3 · 3 · 7 = 4536 . Это и есть наименьшее общее кратное чисел 84 и 648 .
Ответ: НОК (84 , 648) = 4 536 .
Нахождение НОК трех и большего количества чисел
Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.
На этот случай есть теорема.
Теорема 1
Предположим, что у нас есть целые числа a 1 , a 2 , … , a k . НОК m k этих чисел находится при последовательном вычислении m 2 = НОК (a 1 , a 2) , m 3 = НОК (m 2 , a 3) , … , m k = НОК (m k − 1 , a k) .
Теперь рассмотрим, как можно применять теорему для решения конкретных задач.
Пример 7
Необходимо вычислить наименьшее общее кратное четырех чисел 140 , 9 , 54 и 250 .
Решение
Введем обозначения: a 1 = 140 , a 2 = 9 , a 3 = 54 , a 4 = 250 .
Начнем с того, что вычислим m 2 = НОК (a 1 , a 2) = НОК (140 , 9) . Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140 = 9 · 15 + 5 , 9 = 5 · 1 + 4 , 5 = 4 · 1 + 1 , 4 = 1 · 4 . Получаем: НОД (140 , 9) = 1 , НОК (140 , 9) = 140 · 9: НОД (140 , 9) = 140 · 9: 1 = 1 260 . Следовательно, m 2 = 1 260 .
Теперь вычислим по тому е алгоритму m 3 = НОК (m 2 , a 3) = НОК (1 260 , 54) . В ходе вычислений получаем m 3 = 3 780 .
Нам осталось вычислить m 4 = НОК (m 3 , a 4) = НОК (3 780 , 250) . Действуем по тому же алгоритму. Получаем m 4 = 94 500 .
НОК четырех чисел из условия примера равно 94500 .
Ответ: НОК (140 , 9 , 54 , 250) = 94 500 .
Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.
Определение 4
Предлагаем вам следующий алгоритм действий:
- раскладываем все числа на простые множители;
- к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
- к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
- полученное произведение будет наименьшим общим кратным всех чисел из условия.
Пример 8
Необходимо найти НОК пяти чисел 84 , 6 , 48 , 7 , 143 .
Решение
Разложим все пять чисел на простые множители: 84 = 2 · 2 · 3 · 7 , 6 = 2 · 3 , 48 = 2 · 2 · 2 · 2 · 3 , 7 , 143 = 11 · 13 . Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.
Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.
Теперь возьмем произведение простых множителей 2 , 2 , 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3 . Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.
Продолжаем добавлять недостающие множители. Переходим к числу 48 , из произведения простых множителей которого берем 2 и 2 . Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 = 48 048 . Это и есть наименьшее общее кратное пяти исходных чисел.
Ответ: НОК (84 , 6 , 48 , 7 , 143) = 48 048 .
Нахождение наименьшего общего кратного отрицательных чисел
Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.
Пример 9
НОК (54 , − 34) = НОК (54 , 34) , а НОК (− 622 , − 46 , − 54 , − 888) = НОК (622 , 46 , 54 , 888) .
Такие действия допустимы в связи с тем, что если принять, что a и − a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа − a .
Пример 10
Необходимо вычислить НОК отрицательных чисел − 145 и − 45 .
Решение
Произведем замену чисел − 145 и − 45 на противоположные им числа 145 и 45 . Теперь по алгоритму вычислим НОК (145 , 45) = 145 · 45: НОД (145 , 45) = 145 · 45: 5 = 1 305 , предварительно определив НОД по алгоритму Евклида.
Получим, что НОК чисел − 145 и − 45 равно 1 305 .
Ответ: НОК (− 145 , − 45) = 1 305 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Вычисление наименьшего общего кратного
Введите цифры
- Три автобуса
Три автобуса общественного транспорта отправляются вместе с автовокзала утром. Первый автобус возвращается на станцию через 18 минут, второй – через 12 минут, а третий – через 24 минуты. Как долго снова будем вместе на вокзале? Пожалуйста, экспресс
Первый автобус возвращается на станцию через 18 минут, второй – через 12 минут, а третий – через 24 минуты. Как долго снова будем вместе на вокзале? Пожалуйста, экспресс - Портниха
Портниха оставила кусок холста короче 5 метров. Она решает, сшить ли ей юбку или платье. Холста было ровно столько, сколько они израсходовали, разрезав юбку до 120 см, или 180 сантиметров. Какой кусок холста оставил ей? - LCM двух чисел
Найдите наименьшее кратное 63 и 147 - Различные 6975
Три разных автобусных маршрута, 80, 81 и 82, отправляются с конечной станции в 5 ч 20 мин. Маршрут 80 отправляется каждые 30 минут, маршрут 81 — каждые 20 минут, а маршрут 82 — каждые 40 минут. Во сколько они снова уйдут? - Напоминание и частное
Даны числа A = 135, B = 315. Найдите наименьшее натуральное число R, большее единицы, чтобы отношения R:A, R:B были с остатком 1. - Бакалейная лавка
Сьюзен решила сделать продуктовые наборы для своего магазина. Оптовый торговец, у которого она покупает, продает сахар в упаковках по 20 штук в коробке, муку в упаковках по 12 штук в коробке и 15 мешков риса в коробке. Сколько штук каждого предмета она должна купить, чтобы их было одинаковое количество
Оптовый торговец, у которого она покупает, продает сахар в упаковках по 20 штук в коробке, муку в упаковках по 12 штук в коробке и 15 мешков риса в коробке. Сколько штук каждого предмета она должна купить, чтобы их было одинаковое количество - Вокруг клумбы
Вокруг прямоугольной клумбы размерами 5,25 м и 3,5 м нужно посадить розы через равные промежутки так, чтобы розы находились в каждом углу клумбы и потреблять как можно меньше. а) На каком расстоянии посажены розы? б) Сколько роз - Автобусы
На остановке в 10 часов встретились автобусы №2 и №9. Автобус №2 ходит с интервалом 4 минуты, а автобус №9 с интервалом 9 минут. Сколько раз автобус встречается в 18:00 по местному времени? - Зубчатая передача
Зубчатая передача состоит из двух колес. У одного 88, а у второго 56 зубов. Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо? - Автобусы 4
Интервалы: 1-й автобус 40 мин. 2-й автобус 2 часа 3-й бутон 20 минут Через какое время они встретятся — как можно скорее?
2-й автобус 2 часа 3-й бутон 20 минут Через какое время они встретятся — как можно скорее? - Четыре класса
Учащиеся всех 7, 8 и 9 классов одной школы могут занимать 4, 5, 6 и 7 ряд подряд, и никого не останется. Сколько в среднем учеников в одном классе, если в каждом классе всегда четыре класса? - Gcd и lcm
Вычислить наибольший общий делитель и наименьшее общее кратное чисел. a) 16 и 18 b) 24 и 22 c) 45 и 60 d) 36 и 30 - Вычислить 2976
Вычислить наименьшее общее кратное чисел 120, 660 и 210. - Уточните: 4001
Укажите: a = D (240,320) b = n (40,64) - Pardubická 4651
Йирка решил разделить выигрыш от пари в Velká Pardubická между собой и тремя своими младшими братьями по возрасту в соотношении 2:3:5:7. Каждую сумму они платили целыми кронами. Одна из сумм составила 679 чешских крон. Насколько велик был выигрыш? - Веревка
Пол может разрезать веревку на равные части, не оставив ни одной веревки. Длина может быть 15 см, 18 см или 25 см. Какова наименьшая возможная длина веревки?
Какова наименьшая возможная длина веревки?
другие математические задачи »
Наименьшие общие кратные (НОК)
А общее кратное из двух целые числа а и б это число с который а и б оба делятся на поровну.
Например, 48 является общим кратным 6 и 12 с
48 ÷ 6 «=» 8 и
48 ÷ 12 «=» 4 .
наименьший общий множитель это то, на что это похоже… наименьшее из всех общих кратных.
Пример 1:
Найдите наименьшее общее кратное 9 и 12 .
Для этого мы можем перечислить кратные:
9
:
9
,
18
,
27
,
36
_
,
45
,
54
,
63
,
72
,
. ..
12
:
12
,
24
,
36
_
,
48
,
60
,
72
,
…
..
12
:
12
,
24
,
36
_
,
48
,
60
,
72
,
…
36 первое число, встречающееся в обоих списках. Так 36 является ЛКМ.
Метод перечисления нецелесообразен для больших чисел. Другой способ найти НОК двух чисел — разделить их произведение на их наибольший общий делитель ( ЗКФ ).
Пример 2:
Найдите наименьшее общее кратное 18 и 20 .
Чтобы найти GCF 18 и 30 , вы можете написать их простые факторизации :
18 «=» 2 ⋅ 3 ⋅ 3 30 «=» 2 ⋅ 3 ⋅ 5
Общими факторами являются
2
и
3
. Итак, ГКФ
2
⋅
3
«=»
6
.
Итак, ГКФ
2
⋅
3
«=»
6
.
Теперь найдите LCM, умножив два числа и разделив на GCF. (Вы можете немного упростить этот расчет, убрав общий множитель.)
18 ⋅ 30 6 «=» 3 ⋅ 6 ⋅ 30 6 «=» 90
Когда GCF двух чисел 1 , НОК равен произведению двух чисел.
Пример 3:
Найдите наименьшее общее кратное 10 и 27 .
10 и 27 не имеют общих факторов, кроме 1 . Итак, ГКФ 1 .
Таким образом, LCM просто 10 ⋅ 27 «=» 270 .
Третий способ найти LCM состоит в том, чтобы перечислить все
главные факторы
каждого числа, а затем умножьте все факторы наибольшее количество раз, каждое из которых встречается в любом из списков. [Обратите внимание, что хотя предыдущий метод не всегда будет работать с более чем
2
номера, этот метод будет.]
[Обратите внимание, что хотя предыдущий метод не всегда будет работать с более чем
2
номера, этот метод будет.]
Пример 4:
Найдите LCM 16 , 25 и 60 .
16 «=» 2 ⋅ 2 ⋅ 2 ⋅ 2 25 «=» 5 ⋅ 5 60 «=» 2 ⋅ 2 ⋅ 3 ⋅ 5
Наибольшее число раз коэффициент 2 встречается четыре (в первом списке).
Наибольшее число раз коэффициент 3 встречается один (в третьем списке).
Наибольшее число раз коэффициент 5 встречается два (во втором списке).
Итак, умножаем четыре
2
с, один
3
, и два
5
с. Sign in Password recovery Восстановите свой пароль Ваш адрес электронной почты MicroExcel.ru Математика Геометрия Нахождение объема пирамиды: формула и задачи В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала. Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания. Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника): Подставляем данное выражение в формулу расчета объема фигуры и получаем: Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a2, где а – длина его стороны. Следовательно, формулу объема можно представить в виде: Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания): С учетом этого, объем фигуры считается так: Задание 1 Решение: Задание 2 Решение: Таблица знаков зодиака Нахождение площади трапеции: формула и примеры Нахождение длины окружности: формула и задачи Римские цифры: таблицы Таблица синусов Тригонометрическая функция: Тангенс угла (tg) Нахождение площади ромба: формула и примеры Нахождение объема цилиндра: формула и задачи Тригонометрическая функция: Синус угла (sin) Геометрическая фигура: треугольник Нахождение объема шара: формула и задачи Тригонометрическая функция: Косинус угла (cos) Нахождение объема конуса: формула и задачи Таблица сложения чисел Нахождение площади квадрата: формула и примеры Что такое тетраэдр: определение, виды, формулы площади и объема Нахождение объема пирамиды: формула и задачи Признаки подобия треугольников Нахождение периметра прямоугольника: формула и задачи Формула Герона для треугольника Что такое средняя линия треугольника Нахождение площади треугольника: формула и примеры Нахождение площади поверхности конуса: формула и задачи Что такое прямоугольник: определение, свойства, признаки, формулы Разность кубов: формула и примеры Степени натуральных чисел Нахождение площади правильного шестиугольника: формула и примеры Тригонометрические значения углов: sin, cos, tg, ctg Нахождение периметра квадрата: формула и задачи Теорема Фалеса: формулировка и пример решения задачи Сумма кубов: формула и примеры Нахождение объема куба: формула и задачи Куб разности: формула и примеры Нахождение площади шарового сегмента Что такое окружность: определение, свойства, формулы На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
{V= \dfrac{1}{3} S \cdot h}
S — площадь основания пирамиды h — высота пирамиды Правильная треугольная пирамида — пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками. Ответ: 0.25 см³ Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ. Введение Каков объем треугольной призмы? Как рассчитать объем треугольной призмы Рабочий лист объема треугольной призмы Расчет недостающей длины Как вычислить недостающую длину, учитывая объем Распространенные заблуждения Похожие уроки Практика объем треугольной призмы вопросы Объем треугольной призмы Вопросы GCSE Контрольный список обучения Следующие уроки Все еще застряли? Индивидуальные занятия по математике, созданные для успеха KS4 Еженедельные онлайн-уроки повторения математики GCSE теперь доступны Узнать больше Введение Каков объем треугольной призмы? Как рассчитать объем треугольной призмы Рабочий лист объема треугольной призмы Расчет недостающей длины Как вычислить недостающую длину, учитывая объем Распространенные заблуждения Похожие уроки Практика объем треугольной призмы вопросы Объем треугольной призмы Вопросы GCSE Контрольный список обучения Следующие уроки Все еще застряли? Здесь мы узнаем об объеме треугольной призмы, в том числе о том, как вычислить объем и как найти недостающую длину, зная объем. Существуют также листы с объемом и площадью поверхности треугольной призмы, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли. Объем треугольной призмы — это количество пространства внутри треугольной призмы. Треугольная призма представляет собой многогранник (3D-форма, состоящая из многоугольников) с двумя конгруэнтными треугольными концами, соединенными тремя прямоугольниками. Для этого найдем площадь треугольного сечения и умножим ее на длину. Объем треугольной призмы = площадь треугольного сечения x длина 93 и др.). Чтобы вычислить объем треугольной призмы: Получите свободный объем и площадь поверхности листа с треугольной призмой из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы. СКАЧАТЬ БЕСПЛАТНО Получите свой свободный объем и площадь поверхности треугольной призмы, рабочий лист из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы. СКАЧАТЬ БЕСПЛАТНО Определите объем этой треугольной призмы Объем треугольной призмы = площадь треугольного поперечного сечения x длина 92 . Определите объем этой треугольной призмы Запишите формулу. Объем треугольной призмы = Площадь треугольного сечения x длина Вычислите площадь треугольного сечения и подставьте значения. На этот раз треугольная призма направлена вверх, поэтому начнем с вычисления площади основания. Здесь есть некоторые измерения как в м, так и в см, поэтому нам нужно сделать единицы измерения одинаковыми, прежде чем мы начнем вычисления. В этом примере проще всего преобразовать 0,1 м в 10 см. \[\begin{массив}{l}
\text{Площадь треугольника }=\frac{1}{2} \times b \times h\\
\text{Площадь треугольника }=\frac{1}{2} \times 10 \times 10\\
\text{Площадь треугольника}=50
\end{array}\] Поскольку треугольная призма направлена вверх, длина, на которую нужно умножить, равна высоте призмы, 21 см . Объем треугольной призмы = площадь треугольного сечения x длина Объем треугольной призмы = 50 × 21 93 Иногда нам может быть известен объем и некоторые измерения треугольной призмы, и мы можем захотеть вычислить другие измерения. Запишите формулу. Объем треугольной призмы = площадь треугольного сечения x длина Вычислите площадь треугольного сечения и подставьте все в формулу объема треугольной призмы. \[\begin{массив}{l}
\text{Площадь треугольника }=\frac{1}{2} \times b \times h\\
\text{Площадь треугольника }=\frac{1}{2} \times 7 \times 6\\
\text{Площадь треугольника}=21
\end{массив}\] \[\begin{выровнено}
\text{Объем треугольной призмы } &= \text{ площадь треугольного сечения } \times { длина}\\
168&=21 х
\конец{выровнено}\] 93 . Определите высоту призмы. Запишите формулу. Объем треугольной призмы = площадь треугольного сечения x длина Вычислите площадь треугольного сечения и подставьте все в формулу объема треугольной призмы. \[\begin{массив}{l}
\text{Площадь треугольника }=\frac{1}{2} \times b \times h\\
\text{Площадь треугольника }=\frac{1}{2} \times 4 \times h\\
\text{Площадь треугольника}=2h
\конец{массив}\] \[\begin{выровнено}
\text{Объем треугольной призмы } &= \text{ площадь треугольного сечения } \times { длина}\\
80&=2ч \умножить на 16\\
80 &= 32ч
\end{align}\] Решите уравнение. \[\begin{выровнено}
\text{Объем треугольной призмы } &= \text{ площадь треугольного сечения } \times { длина}\\
440&=2г \умножить на 20\\
440 &= 40 лет
\end{align}\] Решите уравнение. \[\begin{выровнено}
40г&=440\\
у&=11
\end{aligned}\] Напишите ответ, включая единицы измерения. y=11 мм Перед расчетом объема необходимо убедиться, что все измерения указаны в одних и тех же единицах измерения. Будьте осторожны, чтобы применить правильную формулу, связанную с призмой, к правильному типу вопроса. Объем треугольной призмы является частью нашей серии уроков по повторению треугольной призмы. Возможно, вам будет полезно начать с основного урока по треугольной призме, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения более подробной информации по отдельным темам. Другие уроки в этой серии включают в себя: 9{2}
\end{выровнено} \begin{выровнено}
\text{Объем треугольной призмы }&=12 \times x\\
84 &= 12x\\
7&=х
\end{выровнено} Длина 7 см. \begin{выровнено}
\text{Площадь треугольника }&=\frac{1}{2} \times 6 \times h\\
&=3 часа
\end{выровнено} \begin{выровнено}
\text{Объем треугольной призмы }&=3h \times 15\\
405 &= 45ч\\
9&=ч
\end{выровнено} Высота 9м . 0,25 см 4050 см \begin{выровнено}
\text{Площадь треугольника }&=\frac{1}{2} \times 4 \times y\\
&=4 года
\end{выровнено} Обратите внимание, что высота треугольной призмы указана в миллиметрах, а объем — в см3. \begin{выровнено}
\text{Объем треугольной призмы }&=2y \times 4.5\\
45 &= 9{3}
\end{выровнено} (1) \begin{выровнено}
\text{Площадь треугольника B }&=\frac{1}{2} \times 4 \times h\\
&=2 часа
\end{выровнено} (1) 144 = 28,8 ч (1) ч = 5 см (1) 3. (a) Определите объем треугольной призмы. 9{3}
\end{выровнено} (1) Теперь вы научились: Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Узнайте больше о нашей программе обучения математике GCSE. Давайте представим, что вы делаете домашний шоколад и хотите придать ему форму, похожую на Toblerone. Вы идете на рынок и покупаете треугольную форму-пирамиду. Вам нужно будет вычислить объем треугольной формы в форме пирамиды, чтобы найти количество шоколада, которое нужно положить в нее. Итак, какая громкость? Объем определяется как пространство, занимаемое в границах объекта в трехмерном пространстве. Он также известен как мощность объекта. Объем треугольной пирамиды – это объем пирамиды с треугольным основанием. Треугольная пирамида представляет собой трехмерную фигуру с плоскими треугольными гранями, прямыми краями и острыми углами или вершинами. Если все четыре грани треугольной пирамиды являются равносторонними треугольниками, то она называется правильной треугольной пирамидой. Теперь, когда мы знаем, что такое треугольная пирамида, давайте посмотрим, как найти объем треугольной пирамиды. Объем треугольной пирамиды равен одной трети произведения площади основания треугольника на высоту пирамиды. Формула объема треугольной пирамиды равна 9.{3}}{6\sqrt{2}}$ кубических единиц Где V — объем правильной треугольной пирамиды, а a — сторона равностороннего треугольника. Теперь, когда мы знаем формулу, мы можем найти объем любой треугольной пирамиды. Во-первых, нам нужно знать, является ли данная треугольная пирамида правильной треугольной пирамидой или нет. $V = \frac{1}{3} \times Площадь основания \times h$ Площадь треугольника равна половине произведения основания треугольника на высоту треугольника. $A = \frac{1}{2} \times b \times h$ Здесь A — площадь треугольника, b — основание треугольника, h — площадь треугольника. высота треугольника. Если треугольник в основании равносторонний со стороной 9{3}}{6\sqrt{2}}$ Не забудьте указать единицу измерения! Объем измеряется в кубических единицах. Объем треугольной пирамиды является важным понятием для учащихся. Это можно лучше понять на практических примерах. Используя SplashLearn, учащиеся могут практиковать каждый пример с интерактивными онлайн-таблицами. Это игровое обучающее приложение превращает процесс обучения в увлекательное занятие и увлекает вашего ребенка. 1. Каков объем треугольной пирамиды, если площадь ее основания равна 19кв. дюймов, а его высота 1,5 дюйма? Решение: Известно, что площадь основания $B = 19$ квадратных дюймов, а высота пирамиды $= 1,5$ дюймов. Мы знаем Volume $= \frac{1}{3} \times B \times h$ Подставляя полученные значения, $Volume = \frac{1}{3} \times 19 \times 1. $Объем = 19 \х0,5$ $Объем = 9,5\; кубический\; дюймов $ 2. Найдите высоту треугольной пирамиды с площадью основания 175 кв. единиц и объемом 1050 куб. единиц. Решение: Дано, что B $= 175$ и V $= 1050$. Объем треугольной пирамиды $= \frac{1}{3} \times B \times h$ $1050 = \frac{1}{3} \times 175 \times h$ Переставляя полученные значения , $h = \frac{3 \times 1050}{175}$ $h = 18\; ед.$ Итак, высота пирамиды 18 единиц. 3. Каков объем правильной треугольной пирамиды со стороной 9{3}}{6\sqrt{2}}$ $V = \frac{9\sqrt{2} \times 9\sqrt{2} \times 9\sqrt{2}}{6\sqrt{2 }} = 243$ кубических единиц Итак, объем правильной треугольной пирамиды равен 243 кубических единиц. 4. Найдите высоту правильной треугольной пирамиды, имеющей объем $18\sqrt{2}$ кубических единиц. Решение: Известно, что объем правильной треугольной пирамиды, т. Мы знаем, что объем правильной треугольной пирамиды: 9{3} = 216$ Извлекая кубический корень с обеих сторон, получаем $a = 6$ единиц Итак, высота правильной треугольной пирамиды равна 6 единицам. 5. Найдите процентное изменение высоты треугольной пирамиды, если ее объем увеличить с 50 кубических футов до 75 кубических футов при неизменной площади основания. Решение: Пусть объем до увеличения высоты равен V1, а объем после увеличения высоты равен $V_{2}$ . 9{\frac{1}{3} \times B \times h_{1}}} = \frac{75}{50}$ $\frac{h_{2}}{h_{1}} = \frac {3}{2}$ Умножение обеих сторон на 100. $\frac{h_{2}}{h_{1}} \times 100 = \frac{3}{2} \times 100$ $\frac{h3}{h2} \times 100 = 1.5 \times 100 = 150\%$ Таким образом, процентное увеличение высоты составляет $150\%$. 1 $V = \frac{1}{6} \times B \times h$ $V = \frac{1}{3} \times B \times h$ $V = 3 \times B \ умножить на h$ $V = 6 \times B \times h$ Правильный ответ: $V = \frac{1}{3} \times B \times h$ 2 16 кв. дюймов 9{2}$ и высота 10 см. 125 куб.см 240 куб.см 254 куб.см 120 куб.см Правильный ответ: 120 куб.см 4 30,42 куб. дюйма 60,42 куб. дюйма 50,42 куб. дюйма 9{3}$. 15 м 24 м 25 м 12 м Правильный ответ: 15 м 
Как найти объем треугольника: Объем треугольника в м3 и литрах
формула для правильной треугольной и четырехугольной
Формула вычисления объема пирамиды
1. Общая формула

2. Объем правильной треугольной пирамиды
3. Объем правильной четырехугольной пирамиды
4. Объем правильной шестиугольной пирамиды
Примеры задач
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.
Воспользуемся соответствующей формулой, подставив в нее известные значения:
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.
Площадь квадрата, который является основанием пирамиды, равна 9 см2 (3 см ⋅ 3 см). Следовательно, объем равен:ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Все формулы объема пирамиды — калькулятор онлайн и примеры расчета
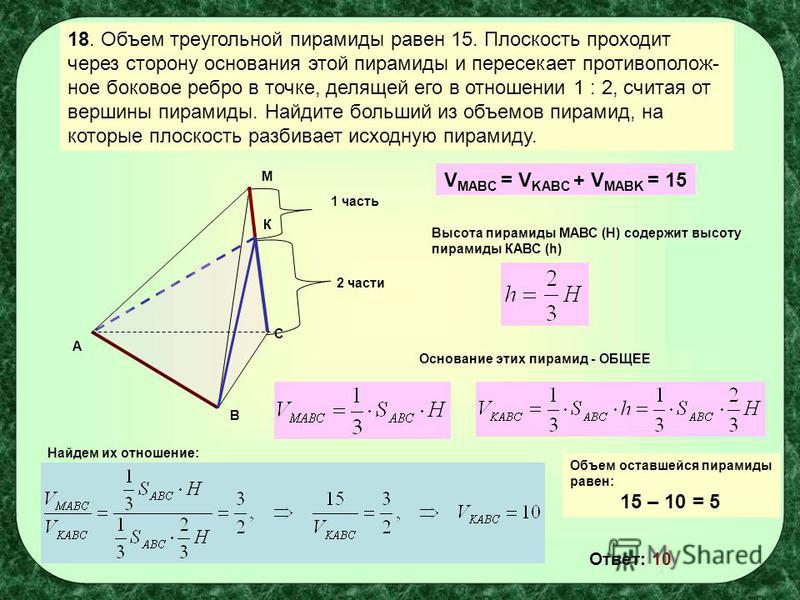 Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.
Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.Содержание:
Формула объема пирамиды
Формула объема правильной треугольной пирамиды
 3
3
Объем треугольной призмы — GCSE Maths

Каков объем треугольной призмы?
Каков объем треугольной призмы?
Как вычислить объем треугольной призмы
Объем треугольной призмы = Площадь треугольного сечения х длина 
Как рассчитать объем треугольной призмы
Объем и площадь поверхности листа с треугольной призмой
Объем и площадь поверхности треугольной призмы рабочий лист
Объем треугольной призмы примеры
Пример 1: объем треугольной призмы
 3. 93
3. 93 Пример 3: разные единицы измерения
Вычисление недостающей длины
 3 . Определите длину x треугольной призмы.
3 . Определите длину x треугольной призмы. 3. Поэтому нам нужно преобразовать 2 см в 20 мм.
3. Поэтому нам нужно преобразовать 2 см в 20 мм. Распространенные заблуждения
напр. у вас не может быть что-то в сантиметрах, а что-то в метрах
 Поэтому нам нужно изменить 45 мм на 4,5 см.
Поэтому нам нужно изменить 45 мм на 4,5 см.
\begin{выровнено}
\text{Объем треугольной призмы B}&=2h \times 14.4\\
\end{выровнено} Учебный контрольный список
Все еще зависает?
 Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики. Объем треугольной пирамиды Формула: определение, пример, факты
Каков объем треугольной пирамиды?
Родственные игры
Треугольная пирамида и ее части
 Он состоит из трех треугольных граней и треугольного основания. У него четыре грани, шесть ребер и четыре вершины.
Он состоит из трех треугольных граней и треугольного основания. У него четыре грани, шесть ребер и четыре вершины. Похожие рабочие листы
Формула объема треугольной пирамиды
Как найти объем треугольной пирамиды

Факты об объеме треугольной пирамиды
 д.
д.
Альтернативный текст изображения: Треугольная пирамида: пример из жизни Заключение
Решенные примеры объема треугольной пирамиды
 5$
5$ е. $V = 18\sqrt{2}$ кубических единиц.
е. $V = 18\sqrt{2}$ кубических единиц. Практические задачи на объем треугольной пирамиды
Выберите правильную формулу для определения объема треугольной пирамиды.

Формула объема треугольной пирамиды равно $V = \frac{1}{3} \times B \times h$. Найдите площадь основания треугольной пирамиды, высота которой 8 дюймов, а объем 256 кубических дюймов.
Объем треугольной пирамиды $= \frac{1}{3} \times B \times ч = \frac{1}{3} \times 36 \times 10 = 120$ кубических см. Каков объем правильной треугольной пирамиды, длина ребра одной из граней которой равна 7 дюймов?
Высота треугольной пирамиды $= \frac{V \times 3}{b} = \frac{600 \times 3}{120} = 15$ млн.
Постройте график функции y 4 x 2: Mathway | Популярные задачи
Мордкович алгебра 8 класс 18.7 Постройте график функции y=4\x – Рамблер/класс
Мордкович алгебра 8 класс 18.7 Постройте график функции y=4\x – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
18. 7. а) Постройте график функции y=4\x
7. а) Постройте график функции y=4\x
б) Найдите, при каких значениях аргумента значение
функции равно 2.
в) Выделите ту часть графика, которая соответствует
условию у > 2. При каких значениях х выполняется это
условие?
г) При каких значениях х выполняется условие у < 2?
ответы
держи график и ответ
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
ЕГЭ
10 класс
9 класс
похожие вопросы 5
Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра
10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее.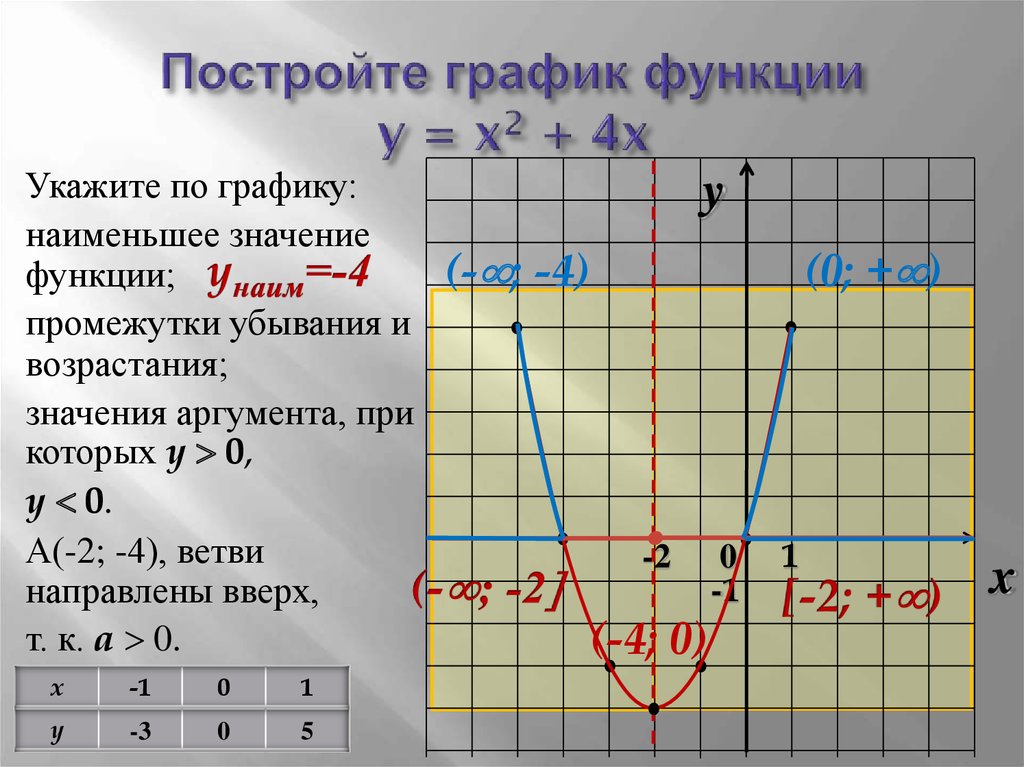 ..)
..)
ГДЗМордкович А.Г.Алгебра8 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
| 1 | Оценка с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценка с использованием заданного значения | квадратный корень из 45 | |
| 3 | Оценить | 5+5 | |
| 4 | Оценить | 7*7 | |
| 5 | Найти простую факторизацию | 24 | |
| 6 | Преобразование в смешанный номер | 52/6 | |
| 7 | Преобразование в смешанный номер | 93/8 | |
| 8 | Преобразование в смешанный номер | 34/5 | |
| 9 | График | у=х+1 | |
| 10 | Оценка с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найдите площадь поверхности | сфера (3) | |
| 12 | Оценить | 54-6÷2+6 | |
| 13 | График | г=-2x | |
| 14 | Оценить | 8*8 | |
| 15 | Преобразование в десятичное число | 5/9 | |
| 16 | Оценка с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | у=2 | |
| 18 | Преобразование в смешанный номер | 7/8 | |
| 19 | Оценить | 9*9 | |
| 20 | Решите для C | С=5/9*(Ф-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | у=х+4 | |
| 23 | График | г=-3 | |
| 24 | График | х+у=3 | |
| 25 | График | х=5 | |
| 26 | Оценить | 6*6 | |
| 27 | Оценить | 2*2 | |
| 28 | Оценить | 4*4 | |
| 29 | Оценить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Оценить | 1/3+13/12 | |
| 31 | Оценка | 5*5 | |
| 32 | Решить для d | 2д=5в(о)-вр | |
| 33 | Преобразование в смешанный номер | 3/7 | |
| 34 | График | г=-2 | |
| 35 | Найдите склон | у=6 | |
| 36 | Преобразование в проценты | 9 | |
| 37 | График | у=2х+2 | |
| 38 | 92+5х+6=0|||
| 41 | Преобразование в смешанный номер | 1/6 | |
| 42 | Преобразование в десятичное число | 9% | |
| 43 | Найти n | 12н-24=14н+28 | |
| 44 | Оценить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразование в упрощенную дробь | 43% | |
| 47 | График | х=1 | |
| 48 | График | у=6 | |
| 49 | График | г=-7 | |
| 50 | График | у=4х+2 | |
| 51 | Найдите склон | у=7 | |
| 52 | График | у=3х+4 | |
| 53 | График | у=х+5 | |
| 54 | График | 92-9=0||
| 58 | Оценка с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценка с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Найти простую факторизацию | 14 | |
| 61 | Преобразование в смешанный номер | 7/10 | |
| 62 | Решите для | (-5а)/2=75 | |
| 63 | Упростить | х | |
| 64 | Оценить | 6*4 | |
| 65 | Оценить | 6+6 | |
| 66 | Оценить | -3-5 | |
| 67 | Оценить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найди обратное | 1/3 | |
| 71 | Преобразование в смешанный номер | 20. Тесты по античной философии с ответами: Тест по философии Античная философияТест по философии Античная философияТест по философии Античная философия с ответами. Тест состоит из 22 заданий. 1. Укажите черты, присущие древнегреческой философии а) онтологизм 2. Назовите представителей философии Древней Греции: Лао-цзы, Платон, Конфуций, Будда, Сократ, Пифагор, Зенон, Берлин, Парменид, Гегель, Сенека. 3. Кого и почему считают первым философом Запада? а) Фалес 4. Установите соответствие между именами древнегреческих философов и их учениями: ФИЛОСОФЫ 1) Гераклит УЧЕНИЯ а) наивная стихийная диалектика 5. Соотнесите имена древнегреческих натурфилософов и выдвигаемые ими варианты первоначала мироздания: НАТУРФИЛОСОФЫ 1) Гераклит ВЫДВИГАЕМЫЕ ВАРИАНТЫ а) атомы 6. а) Фалес 7. Назовите мыслителя, которому принадлежит высказывание: «Все течет …» а) Фалес 8. Какое из философских учений наиболее полно разработано Парменидом? а) учение о бытии 9. Назовите древнегреческих философов, развивавших атомистическое учение а) Левкипп 10. Кого из древнегреческих философов называли «учителями мудрости»? а) софистов 11. Выделите имя древнегреческого философа, начиная с которого в западной традиции впервые четко обозначился интерес к человеку а) Платон 12. а) Аристотель 13. Выделите основные положения философии Платона а) наилучшая форма правления — это демократия 14. Назовите древнегреческого философа, которому принадлежит следующее определение человека: «Человек есть общественное животное» а) Сократ 15. Подчеркните суждения, которые правильно выражают учения Аристотеля а) Душа есть форма тела 16. Кому из античных мыслителей принадлежит следующее высказывание «Я знаю, что ничего не знаю»? а) Фалес 17. а) Аристотель 18. Выделите основные научно-философские достижения Аристотеля а) создал основу современной системы философских категорий 19. Назовите имя философа — автора философско-политической работы «Государство», в которой описывается представление об идеальном государстве а) К. Маркс 20. Назовите философские школы эпохи эллинизма а) рационализм 21. Как вы считаете, кто явился основателем неоплатонизма? а) Зенон 22. а) эпикуреизм Ответы на тест по философии Античная философия PDF версия Тест: Античная философия — ОРКСЭ 5 классТест: Античная философия — ОРКСЭ 5 классАнглийский язык Астрономия Белорусский язык Биология География ИЗО Информатика История Итальянский язык Краеведение Литература Математика Музыка Немецкий язык ОБЖ Обществознание Окружающий мир ОРКСЭ Русский язык Технология Физика Физкультура Химия Черчение Для учителей Дошкольникам VIP — доступ
Античная философия История Философии ОРКСЭ 5 класс | Автор: Мажиденова Р. Помещать страницу в закладки могут только зарегистрированные пользователи
Вопрос №
1
Кто является представителем объективного идеализма? А) Демокрит
Вопрос №
2
Концепция утверждающее «жить — значит наслаждаться» называется… А) Гедонизм
Вопрос №
3
Кто является представителем милетской школы в Древней Греции? А) Гераклит
Вопрос №
4
Кому принадлежит высказывание: «Платон мне друг, но истина дороже»? А) Аристотель
Вопрос №
5
Какое направление в философии развивали Левкипп, Демокрит, Лукреций Кар? A) Диалектику
Вопрос №
6
Кто из перечисленных древнегреческих философов принадлежит к элейской школе? А) Эпикур
Вопрос №
7
Какое высказывание принадлежит Гераклиту? А) «Судьба народов обуславливается, прежде всего, внешней средой их обитания»
Вопрос №
8
Основоположник античной диалектики: A) Фалес
Вопрос №
9
Какое высказывание принадлежит Демокриту? А) «Я знаю, что я ничего не знаю»
Вопрос №
10
Сократ призывал: А) Познавать и творить добро
Вопрос №
11
Основной проблемой милетской школы является поиск: А) Первоначала
Вопрос №
12
Звание «Первого Учителя» Аристотель получил за: А) Создание науки логики
Вопрос №
13
Кому принадлежат слова: «Начало всего — единица; из единицы исходят числа, из чисел фигуры…»: А) Платону
Вопрос №
14
Кто из древнегреческих философов первым поставил в центр своего учения не проблемы природы, а человека? А) Фалес
Вопрос №
15
Представителем милетского материализма является: А) Пифагор
Вопрос №
16
Греческим богам пришел конец с тех пор, как Фалес посмотрел на … A) Землю
Вопрос №
17
Кто считал, что мир произошел из идей: А) Пиррон
Вопрос №
18
«Государством должны управлять философы» — говорил: A) Анаксагор
Вопрос №
19
Основная проблема элейской школы: А) Проблема бытия
Вопрос №
20
Поворот к человеку в древнегреческой философии был осуществлен: А) Аристотелем Показать ответы Получение сертификата Доступно только зарегистрированным пользователям © TestEdu. E-mail администратора: [email protected] Final Exam Review — PHIL 305: Древнегреческая философия Essentials: экзамен состоится , четверг, 20 декабря, с 12:00 до 14:00. в нашем обычном номере. Это будет закрытая книга и закрытые заметки. Вам нужно будет принести большую экзаменационную тетрадь (также известную как «синяя книга») , чтобы сдать экзамен. Их можно купить в книжном магазине. Формат: Экзамен будет состоять из двух частей. Первая часть будет состоять из нескольких вопросов с краткими ответами, каждый из которых является одним из следующих вопросов (возможно, с небольшими изменениями в формулировках). Вторая часть будет состоять из меньшего количества, но более содержательных вопросов для эссе, каждый из которых будет состоять из некоторого количества следующих вопросов (возможно, с небольшими изменениями в формулировках). Таким образом, если вы сможете хорошо ответить на каждый из следующих вопросов, вы будете хорошо подготовлены к экзамену.
1. В категориях Аристотель использует отношение к и к . Сформулируйте различие между ними и определите, что вы считаете наиболее важным следствием этого различия. 2. В категориях Аристотель различает первичные и вторичные субстанции. Что это такое и как они связаны друг с другом? Сравните это описание с точкой зрения Платона. 3. В категориях Аристотель утверждает, что наиболее отличительной чертой субстанций является то, что они могут принимать противоположности. Представьте отчет об изменении, изложенный в Книге I Физики , и объясните загадку, которую он поднимает для аристотелевского взгляда на субстанцию. Как гиломорфизм должен помочь решить загадку? 4. В Physics II Аристотель проводит принципиальное различие между природными объектами и артефактами. Сформулируйте различие и кратко объясните, как оно фигурирует в его последующем описании субстанции. 5. В Physics II Аристотель развивает свое учение о четырех причинах. Проиллюстрируйте это описание, применив его к (а) артефакту, (б) неартефакту. 6. В Метафизике IV Аристотель говорит о «науке о бытии qua Бытия». Что именно эта наука берет в качестве объекта(ов) изучения и чем она отличается от других наук (например, физики или математики)? 7. В Metaphysics IV Аристотель говорит, что «о бытии говорят по-разному, но… не омонимично». Если не омонимично, то как? Почему это важно? 8. В Метафизике VII Аристотель выделяет два критерия субстанции. Кто они такие? Почему материя не удовлетворяет критериям? Как форма удовлетворяет их? 9. Зрелый гиломорфный взгляд Аристотеля развит в книгах VII и VIII Метафизики . Каково отношение между материей и формой, с этой точки зрения, и как Аристотель использует это отношение в последующих трактатах? 10. Укажите официальное определение Аристотеля psuchê , как он формулирует это в Книге II De Anima , и объясните роль каждой из частей определения. 11. В De Anima II Аристотель проводит сравнение между топором, глазом и животным. Как проходит сравнение и в чем его смысл? 12. Объясните, как понятие eudaimonia как разновидности деятельности связано с трактовкой Аристотелем psuchê в De Anima . 13. Объясните, как телеология фигурирует в (а) учении Аристотеля о четырех причинах; (b) его рассказ о psuchê ; и (c) его этическая теория. 14. В Никомаховой этике I Аристотель приходит к своему определению eudaimonia посредством функционального аргумента. Представьте аргумент и объясните, как он отражает психологию, развитую в De Anima . 15. Аристотель утверждает, что удовольствие, честь и добродетель достойны выбора сами по себе, и тем не менее мы также выбираем их ради эвдемония . Означает ли это, что удовольствие (и т. д.) служит средствами достижению eudaimonia ? Объяснять. 16. 17. Сформулируйте определение добродетелей характера, данное Аристотелем, обсудите психологическую основу определения и объясните, как это определение связано с интеллектуальной добродетелью. 18. В Этика VI.13, Аристотель говорит, что «мы не можем быть полностью хорошими [в характере] без разума или разумными без добродетели характера». Как может кто-либо когда-либо приобрести какую-либо черту, если каждая из них требует существования другой? 19. В Этике I.2 Аристотель определяет политическую науку как наиболее контролирующую науку ( architektonikês ), науку, которая заменяет все другие науки и та, чья задача состоит в том, чтобы обеспечить высшее человеческое благо для максимально возможной степени. Учитывая, как его взгляды на добродетель развиваются в последующих книгах Этика , зачем ему это говорить? 20. Философия и религия. Древняя история: ГрецияВся древняя история: ресурсы Греции2 диагностических теста 64 практических теста Вопрос дня Карточки Учитесь по концепции ← Предыдущая 1 2 Следующая → Древняя история: Греция Помощь » Классический период (480–323 гг. до н. э.) » Философия и религия Диоген Синопский продемонстрировал свое этическое неприятие греческого общества _______________. Возможные ответы: путешествие по сельской местности в качестве религиозного аскета чтение лекций и дискуссий в качестве члена платоновской академии написание давно забытых трактатов, которые легли в основу философии киников отказ от всего мирского имущества и жизнь в пустом ведре из-под вина Правильный ответ: отказ от всего мирского имущества и жизнь в пустом ведре из-под вина Пояснение: Диоген Синопский — известный циник, которого больше помнят за его выдающуюся роль в философии Фридриха Ницше и различные рассказы о нем, чем за его собственно перечисленные философские размышления. Это правда, что Диоген по своему выбору жил в пустом ведре из-под вина. Некоторое время его единственным имуществом была деревянная миска, которую он уничтожил, увидев, как крестьянский мальчик ест руками. Он также бродил среди бела дня по улицам с фонарем и кричал, что ищет праведника. Сообщить об ошибке Какое из приведенных утверждений точно описывает софистов как социальную группу? Возможные ответы: Ораторы, выступавшие от имени политиков Интеллектуалы, разработавшие принципы греческого права Учителя и философы, путешествовавшие по Греции, обучая богатых греков за плату Интеллектуалы, проводившие публичные дебаты на случайно выбранные темы Правильный ответ: Учителя и философы, путешествовавшие по Греции платное обучение состоятельных греков Объяснение: Софистика стала несколько уничижительным обозначением определенных видов философии и логики. Сообщить об ошибке Идея «Королей-философов» связана с __________. Возможные ответы: Сократ Драко Перикл Солон Платон 3Правильный ответ: 0008Пояснение: В своей самой известной работе Республика Платон представляет свою идею правительства, которым правят «цари-философы». Платон считал, что для того, чтобы обществом правили доброжелательно и наиболее эффективно, либо философы должны были править, либо короли должны были принять философию. Сообщить об ошибке Кто в древнегреческом пантеоне был Гермесом? Возможные ответы: Бог музыки и поэзии Бог-вестник Богиня охоты Богиня любви и красоты Бог смерти и подземного мира 04 Посланник Бога Пояснение: В древнегреческом пантеоне Гермес был богом-посланником. Сообщить об ошибке Кто из перечисленных ниже философов известен тем, что окончил академию Платона и обучал Александра Македонского? Возможные ответы: Archimedes Сократ Epicurus Aristotle Правильный ответ: Aristotle Пояснение: Аристотель был учеником Платона и посещал Академию в Афинах, а также обучал Александра Македонского, поэтому он был бы лучшим выбором. Сократ предшествовал Академии и сам обучал Платона, поэтому он не был бы хорошим выбором для этого вопроса. Эпикур был ребенком примерно в то время, когда к власти приходил Александр Македонский, а Архимед жил много лет спустя после него, поэтому ни один из них не был бы хорошим ответом. Сообщить об ошибке Кто из перечисленных ниже философов известен своей теорией мира форм и основанием Академии в Афинах? Возможные ответы: Архимед Платон Аристотель Сократ Эпикур Правильный ответ: 9004 Пояснение: Платон, пожалуй, наиболее известен благодаря Аллегории пещеры , в котором он описывает Мир Форм, и он основал Академию, так что он будет лучшим выбором. Сообщить об ошибке Деметра — греческая богиня __________. Возможные ответы: плодородие и урожай богатство и роскошь любовь и красота моряки, торговцы и воины мудрость и знание 5плодородие и урожай Пояснение: Деметра — греческая богиня плодородия и урожая. Она важна в греческой мифологии, потому что считается, что она познакомила доисторических греков с сельским хозяйством. Деметра почиталась в древнегреческом обществе и была предметом широко распространенного культового поклонения. Сообщить об ошибке Прометей был наказан Зевсом за __________. Возможные ответы: познакомить человечество с музыкой познакомить человечество с сельским хозяйством познакомить человечество с огнем открыть ящик Пандоры и выпустить грех на мир 2 вмешаться в повседневные дела людейПравильно ответ:огонь человечеству Объяснение: В греческой мифологии Прометей — трагическая фигура. Он знакомит человечество с огнем и тем самым значительно повышает уровень жизни. Но это, по-видимому, не входило в план Зевса, и Зевс осудил Прометея на вечные муки. Сообщить об ошибке В каком из следующих городов-государств жил Сократ? Возможные ответы: Аргос Спарта Македония Афины Коринф Правильный ответ: Афины Объяснение: Сократ был печально известен казнью по обвинению в «развращении афинской молодежи», и его интеллектуальный преемник Платон тоже жил и преподавал там, так что Афины были бы лучшим выбором. Сообщить об ошибке Платон, выдающийся греческий философ, классно рассуждал о надлежащей организации правительства и общества, в какой работе? Возможные ответы: Теократия Республика Горгий ДемоНи один из этих кратия Правильный ответ: Республика Объяснение: «Республика » — одно из наиболее известных произведений Платона, в котором он утверждает идеальную форму правления и классно исследует идею царя-философа, так что это был бы лучший выбор. |

 Часть вторая
Часть вторая Частное решение.
Частное решение.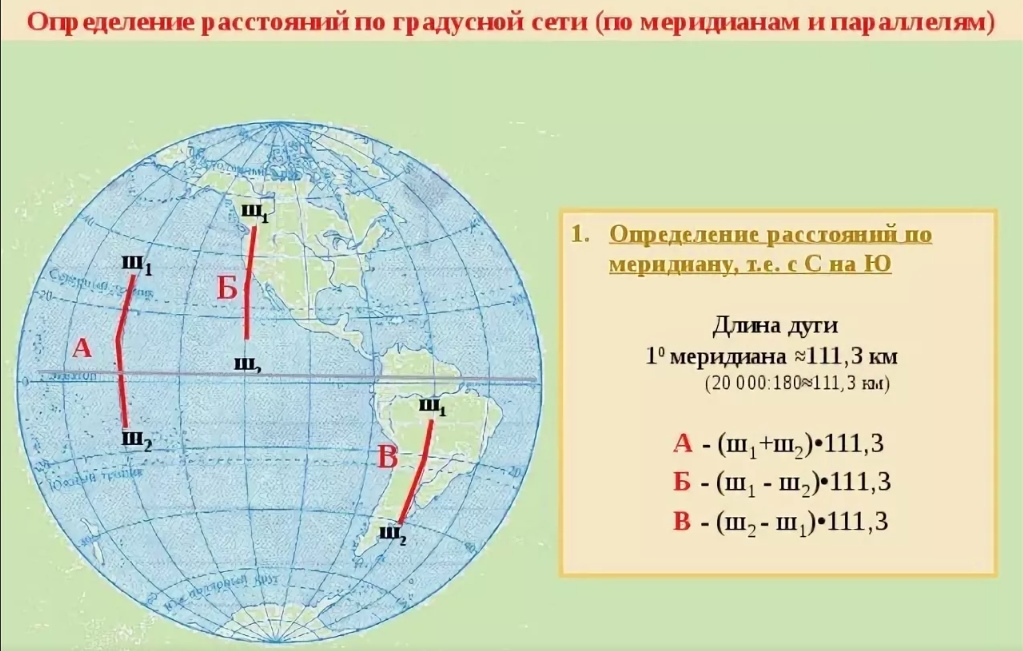
 Так как широты начинаются с числа 0 (это экватор) и заканчивая -90 градусов ( это Южный полюс) или +90 ( это Северный полюс)
Так как широты начинаются с числа 0 (это экватор) и заканчивая -90 градусов ( это Южный полюс) или +90 ( это Северный полюс)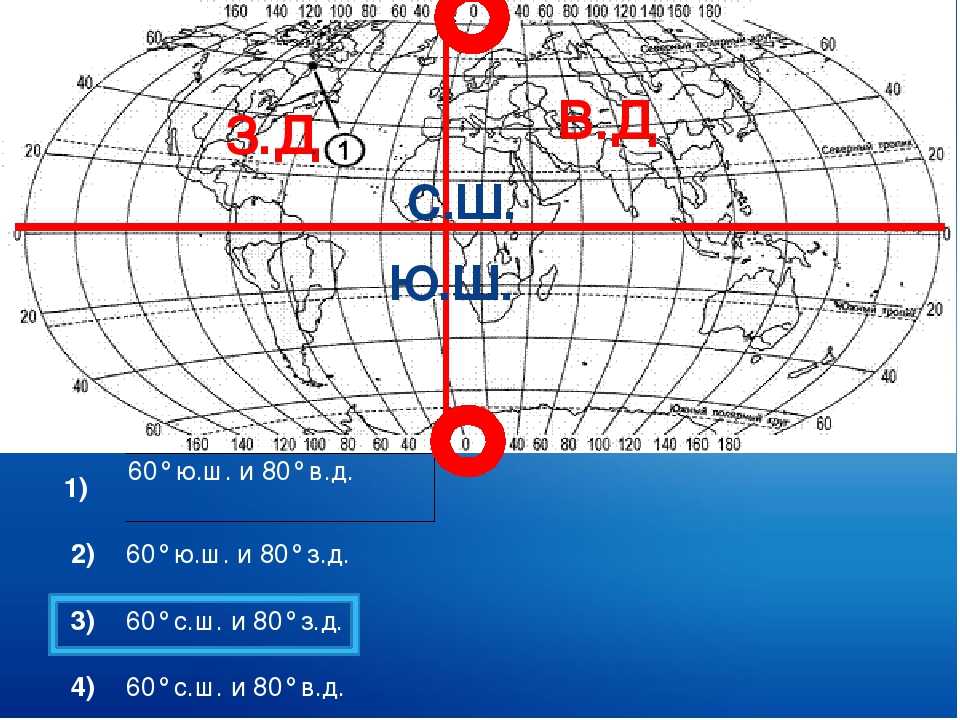

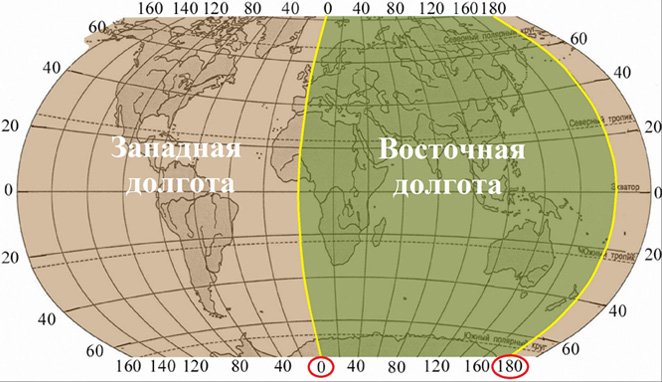 . Вы теряете размерность и в конечно итоге Вы получите какие фантастические а оттого неправильные результаты.
. Вы теряете размерность и в конечно итоге Вы получите какие фантастические а оттого неправильные результаты.
 002777777778
002777777778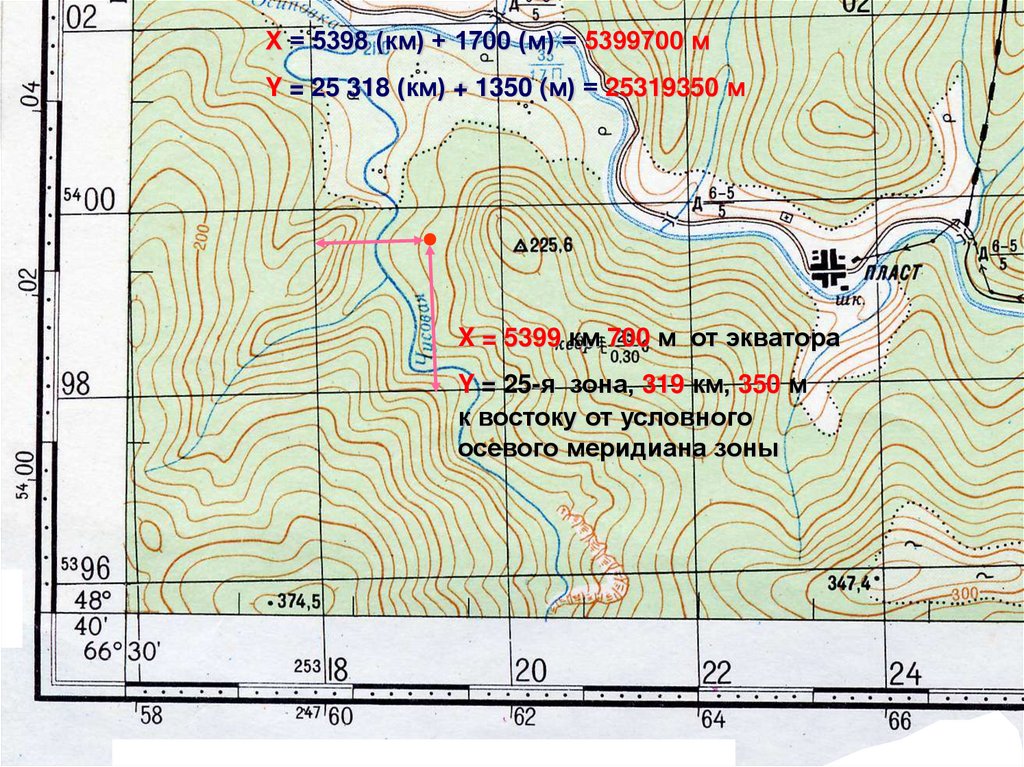 Настройка.
Настройка.
 KMZ в KML просто распакуйте файл KMZ с помощью WinRar, 7zip или аналогичного.
(Примечание: на данный момент локальные сетки коррекции не учитываются.)
Приложение находится в разработке, по ходу дела будут вноситься улучшения, рассчитываю на ваши отзывы.
KMZ в KML просто распакуйте файл KMZ с помощью WinRar, 7zip или аналогичного.
(Примечание: на данный момент локальные сетки коррекции не учитываются.)
Приложение находится в разработке, по ходу дела будут вноситься улучшения, рассчитываю на ваши отзывы.
 п.).
п.). Давайте ему в этом поможем.
Давайте ему в этом поможем. )
)
 А., 46 гр.
А., 46 гр. Этап самоопределения к деятельности
Этап самоопределения к деятельности
 Вспомним таблицу умножения и деления на 3
Вспомним таблицу умножения и деления на 3
 ) – потратится на выполнение чтения
) – потратится на выполнение чтения 93 № 3, 4, 5, стр. 94 № 2.
93 № 3, 4, 5, стр. 94 № 2.

 VisualFractions.com , http://visualfractions.com/calculator/long-division/what-is-35-divided-by-7-using-long-division/. По состоянию на 30 мая 2023 г.
VisualFractions.com , http://visualfractions.com/calculator/long-division/what-is-35-divided-by-7-using-long-division/. По состоянию на 30 мая 2023 г. Вот следующая задача, которую вам нужно решить:
Вот следующая задача, которую вам нужно решить: Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. е. 1,45 .
е. 1,45 . Шесть детей — девочки. Какую часть детей составляют девочки?
Шесть детей — девочки. Какую часть детей составляют девочки?
 16: Долговечность неподвижного объекта. 17: Температура 18: Интенсивность освещения 19: Использование энергии при движении 20: Использование энергии при неподвижном состоянии 21: Мощность 22: Потеря энергии 23: Потеря вещества 24: Потеря информации 25: Потери времени 26: Количество вещества/вещества 27: Надежность 28: Точность измерения 29: Точность изготовления 30: Вредное воздействие на объект 31: Вредное воздействие на объект 32: Простота изготовления 33: Простота изготовления эксплуатации 34: Простота ремонта 35: Приспособляемость или универсальность 36: Сложность устройства 37: Сложность обнаружения 38: Степень автоматизации 39: Производительность
16: Долговечность неподвижного объекта. 17: Температура 18: Интенсивность освещения 19: Использование энергии при движении 20: Использование энергии при неподвижном состоянии 21: Мощность 22: Потеря энергии 23: Потеря вещества 24: Потеря информации 25: Потери времени 26: Количество вещества/вещества 27: Надежность 28: Точность измерения 29: Точность изготовления 30: Вредное воздействие на объект 31: Вредное воздействие на объект 32: Простота изготовления 33: Простота изготовления эксплуатации 34: Простота ремонта 35: Приспособляемость или универсальность 36: Сложность устройства 37: Сложность обнаружения 38: Степень автоматизации 39: Производительность 
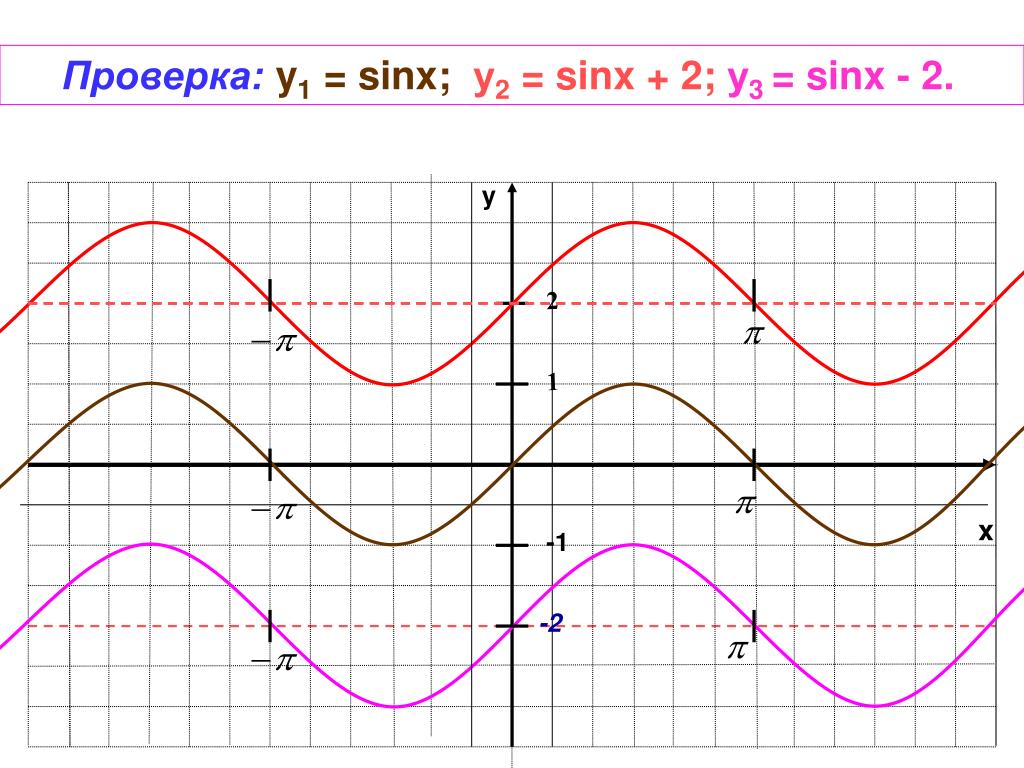 Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько
Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько site
site у.).
у.).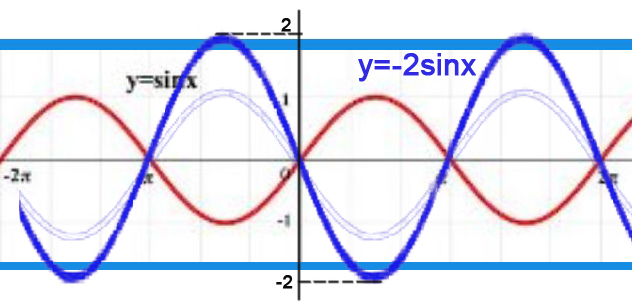 Choose the right form:
Choose the right form:

 6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.
6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.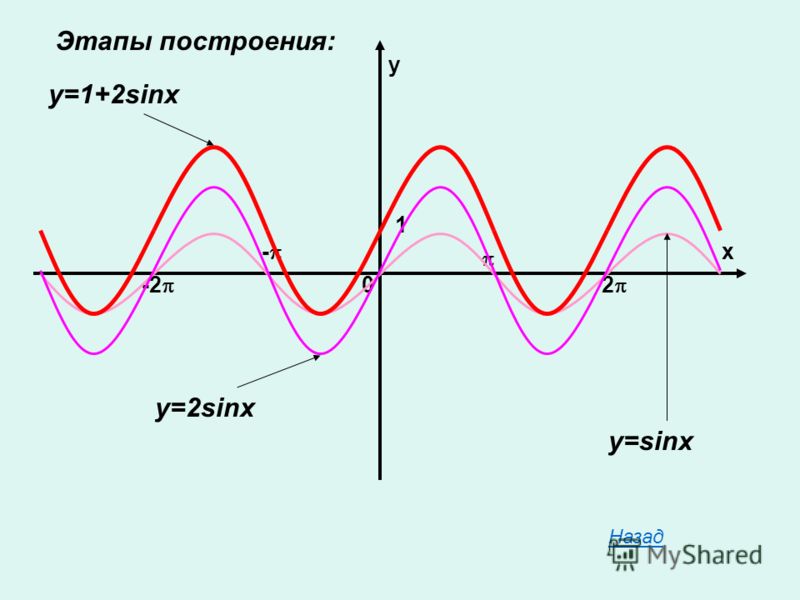
 )/3
)/3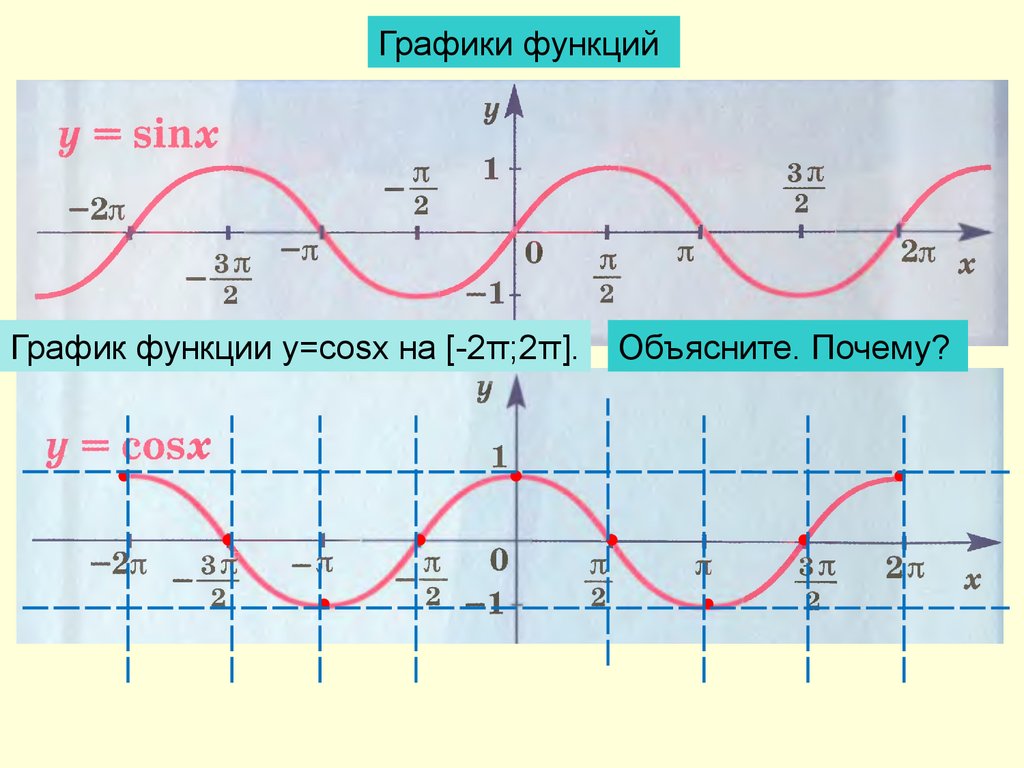 Какое из следующих уравнений
представляет график? (A) 𝑦 равно греху два 𝑥, (B) 𝑦
равно sin 𝑥 плюс два, (C) 𝑦 равно двум sin 𝑥, (D) 𝑦 равно sin 𝑥 минус два, или
(E) 𝑦 равно греху 𝑥 плюс два.
Какое из следующих уравнений
представляет график? (A) 𝑦 равно греху два 𝑥, (B) 𝑦
равно sin 𝑥 плюс два, (C) 𝑦 равно двум sin 𝑥, (D) 𝑦 равно sin 𝑥 минус два, или
(E) 𝑦 равно греху 𝑥 плюс два.
 Таким образом, простыми множителями числа 20 являются числа 2, 2 и 5. Запишите их в виде выражения: .
Таким образом, простыми множителями числа 20 являются числа 2, 2 и 5. Запишите их в виде выражения: .

 Таким образом, напишите 2 в первой строке и первом столбце.
Таким образом, напишите 2 в первой строке и первом столбце.
 Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел.
Частное – это результат деления двух чисел. Остаток – это число, оставшееся при делении двух чисел. Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.
Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.

 Первый автобус возвращается на станцию через 18 минут, второй – через 12 минут, а третий – через 24 минуты. Как долго снова будем вместе на вокзале? Пожалуйста, экспресс
Первый автобус возвращается на станцию через 18 минут, второй – через 12 минут, а третий – через 24 минуты. Как долго снова будем вместе на вокзале? Пожалуйста, экспресс Оптовый торговец, у которого она покупает, продает сахар в упаковках по 20 штук в коробке, муку в упаковках по 12 штук в коробке и 15 мешков риса в коробке. Сколько штук каждого предмета она должна купить, чтобы их было одинаковое количество
Оптовый торговец, у которого она покупает, продает сахар в упаковках по 20 штук в коробке, муку в упаковках по 12 штук в коробке и 15 мешков риса в коробке. Сколько штук каждого предмета она должна купить, чтобы их было одинаковое количество 2-й автобус 2 часа 3-й бутон 20 минут Через какое время они встретятся — как можно скорее?
2-й автобус 2 часа 3-й бутон 20 минут Через какое время они встретятся — как можно скорее? Какова наименьшая возможная длина веревки?
Какова наименьшая возможная длина веревки? Назовите автора тезиса: «Человек — мера всех вещей».
Назовите автора тезиса: «Человек — мера всех вещей». Кто из древнегреческих философов осуществил классификацию научно-философского знания?
Кто из древнегреческих философов осуществил классификацию научно-философского знания? В каком философском направлении поздней античности была предпринята попытка синтеза всей античной философии?
В каком философском направлении поздней античности была предпринята попытка синтеза всей античной философии? М., Мендыбаев С.К. | ID: 5326 | Дата: 26.6.2015
М., Мендыбаев С.К. | ID: 5326 | Дата: 26.6.2015 ru 2013-2022
ru 2013-2022 Там будет некоторая степень выбора относительно того, на какие вопросы вы отвечаете.
Там будет некоторая степень выбора относительно того, на какие вопросы вы отвечаете.

 Какой смысл можно придать утверждению, что Аристотеля не интересует прежде всего моральная уместность действий ?
Какой смысл можно придать утверждению, что Аристотеля не интересует прежде всего моральная уместность действий ? В Книге X Этики Аристотель утверждает, что «полное счастье человека [это созерцание], если он получает полную продолжительность жизни». Как это согласуется с остальной частью Этики ?
В Книге X Этики Аристотель утверждает, что «полное счастье человека [это созерцание], если он получает полную продолжительность жизни». Как это согласуется с остальной частью Этики ?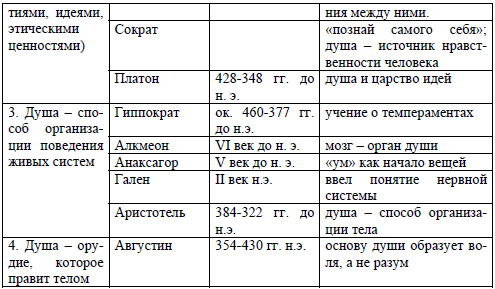 Диоген отказался от академической жизни и никогда не был членом Платоновской академии. Фактически, наиболее заметное взаимодействие Диогена с Платоном произошло, когда Диоген унизил Платона, опровергнув данное Платоном определение человека. Хотя Диоген скитался между городами, он не был религиозным аскетом.
Диоген отказался от академической жизни и никогда не был членом Платоновской академии. Фактически, наиболее заметное взаимодействие Диогена с Платоном произошло, когда Диоген унизил Платона, опровергнув данное Платоном определение человека. Хотя Диоген скитался между городами, он не был религиозным аскетом. Однако как социальная группа софисты были просто странствующими интеллектуалами, обучавшими богатую греческую молодежь за деньги.
Однако как социальная группа софисты были просто странствующими интеллектуалами, обучавшими богатую греческую молодежь за деньги. Гермес часто появляется в греческой мифологии как проводник героев и помогает им в их поисках.
Гермес часто появляется в греческой мифологии как проводник героев и помогает им в их поисках.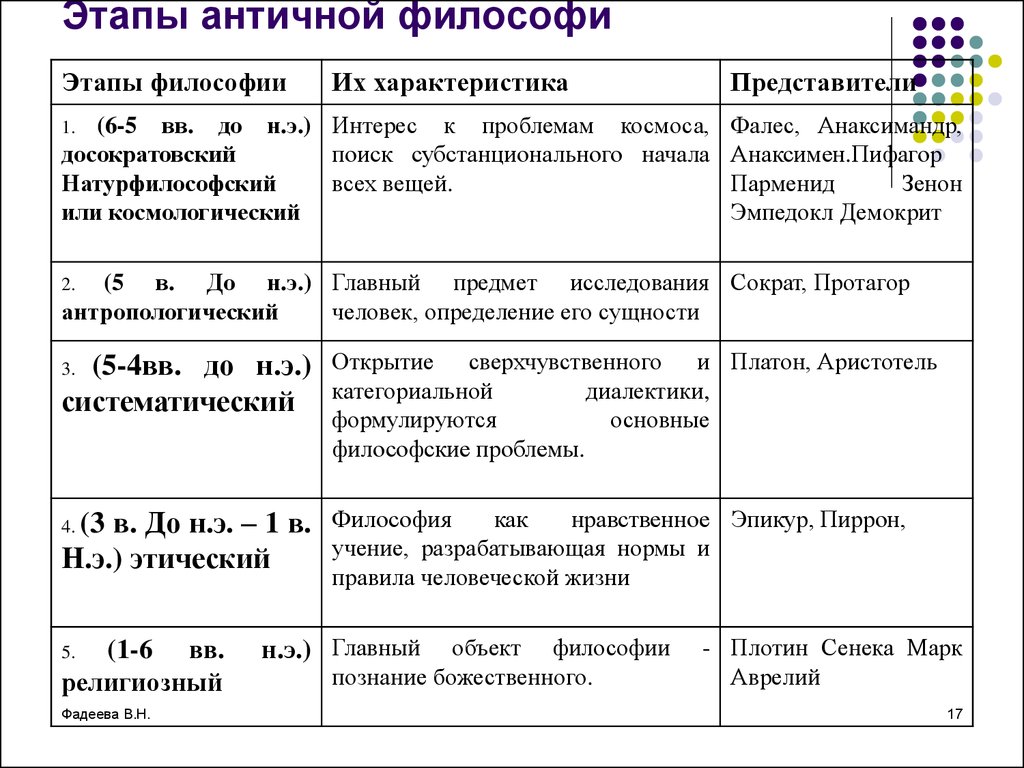 Сократ был учителем Платона, и у него не было понятия о Мире Форм, поэтому он не был бы хорошим ответом. Аристотеля учил Платон, и он сам посещал Академию, поэтому он был бы не лучшим выбором. Наконец, Эпикур и Архимед не представляли себе Мир Форм и не имели никаких связей с Академией, поэтому они не были бы хорошим выбором для этого вопроса.
Сократ был учителем Платона, и у него не было понятия о Мире Форм, поэтому он не был бы хорошим ответом. Аристотеля учил Платон, и он сам посещал Академию, поэтому он был бы не лучшим выбором. Наконец, Эпикур и Архимед не представляли себе Мир Форм и не имели никаких связей с Академией, поэтому они не были бы хорошим выбором для этого вопроса.
 Спарта не была известна своей философией или интеллектуальной жизнью, и Сократ там не жил, так что это не будет хорошим ответом. Аргос был городом-государством во времена Сократа, однако у него не было там связей, так что это тоже не лучший выбор. Коринф тоже был городом-государством, существовавшим в тот период, но не имевшим никаких связей с Сократом, так что это тоже не будет хорошим ответом. Наконец, Македония была более традиционным царством на материковой части Греции, поэтому, поскольку она вовсе не была городом-государством, это был бы не лучший выбор.
Спарта не была известна своей философией или интеллектуальной жизнью, и Сократ там не жил, так что это не будет хорошим ответом. Аргос был городом-государством во времена Сократа, однако у него не было там связей, так что это тоже не лучший выбор. Коринф тоже был городом-государством, существовавшим в тот период, но не имевшим никаких связей с Сократом, так что это тоже не будет хорошим ответом. Наконец, Македония была более традиционным царством на материковой части Греции, поэтому, поскольку она вовсе не была городом-государством, это был бы не лучший выбор.