Автор: 
Сложение и вычитание дробей
Навигация по странице:
- Сложение дробей
- Сложение дробей с одинаковыми знаменателями
- Сложение обыкновенных дробей
- Сложение смешаных чисел
- Вычитание дробей
- Вычитание дробей с одинаковыми знаменателями
- Вычитание обыкновенных дробей
- Вычитание смешаных чисел
Сложение дробей
Сложение дробей с одинаковыми знаменателями.
Определение.
Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:
| a | + | b | = | a + b |
| c | c | c |
Примеры сложения дробей с одинаковыми знаменателями
Пример 1.
Найти сумму двух дробей с одинаковыми знаменателями:
| 1 | + | 2 | = | 1 + 2 | = | 3 |
| 5 | 5 | 5 | 5 |
Пример 2.
Найти сумму двух дробей с одинаковыми знаменателями:
| 3 | + | 2 | = | 3 + 2 | = | 5 |
| 7 | 7 | 7 | 7 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание дробей с равными знаменателями
Сложение обыкновенных дробей.
Примеры сложения обыкновенных дробей
Пример 3.
Найти сумму двух дробей:
| 1 | + | 1 | = | 1·2 | + | 1 | = | 2 | + | 1 | = | 2 + 1 | = | 3 | = | 3 | = | 1 |
| 3 | 6 | 3·2 | 6 | 6 | 6 | 6 | 6 | 3·2 | 2 |
Пример 4.
Найти сумму двух дробей:
| 29 | + | 44 | = | 29·3 | + | 44·2 | = | 87 | + | 88 | = | 87 + 88 | = |
| 30 | 45 | 30·3 | 45·2 | 90 | 90 | 90 |
| = | 175 | = | 35·5 | = | 35 | = | 18 + 17 | = 1 | 17 |
| 90 | 18·5 | 18 | 18 | 18 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух обыкновенных дробей
Сложение смешанных чисел
Примеры сложения смешанных чисел
Пример 5.
Найти сумму двух смешанных чисел:
| 2 | + | 1 | 1 | = | 2·2 | + | 1 | 1·3 | = | 4 | + | 1 | 3 | = | 1 + | 4 + 3 | = |
| 3 | 2 | 3·2 | 2·3 | 6 | 6 | 6 |
| = | 1 + | 7 | = | 1 + | 6 + 1 | = | 1 + 1 | 1 | = 2 | 1 |
| 6 | 6 | 6 | 6 |
Пример 6.
Найти сумму двух смешанных чисел:
| 1 | 5 | + | 2 | 3 | = | 1 | 5·4 | + | 2 | 3·3 | = | 1 | 20 | + | 2 | 9 | = | 3 + | 20 + 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 | 24 |
| = | 3 + | 29 | = | 3 + | 24 + 5 | = | 3 + 1 | 5 | = 4 | 5 |
| 24 | 24 | 24 | 24 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух смешанных чисел
Вычитание дробей
Вычитание дробей с одинаковыми знаменателями.
Определение.
Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:
| a | — | b | = | a — b |
| c | c | c |
Примеры вычитания дробей с одинаковыми знаменателями
Пример 7.
Найти разность двух дробей с одинаковыми знаменателями:
| 3 | — | 1 | = | 3 — 1 | = | 2 |
| 5 | 5 | 5 | 5 |
Пример 8.
Найти разность двух дробей с одинаковыми знаменателями:
| 8 | — | 5 | = | 8 — 5 | = | 3 |
| 41 | 41 | 41 | 41 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание дробей с равными знаменателями
Вычитание обыкновенных дробей.
Примеры вычитания обыкновенных дробей
Пример 9.
Найти разность двух дробей:
| 5 | — | 1 | = | 5 | — | 1·3 | = | 5 | — | 3 | = | 5 — 3 | = | 2 | = | 2 | = | 1 |
| 6 | 2 | 6 | 2·3 | 6 | 6 | 6 | 6 | 2·3 | 3 |
Пример 10.
Найти разность двух дробей:
| 3 | — | 1 | = | 3·3 | — | 1·5 | = | 9 | — | 5 | = | 9 — 5 | = | 4 | = | 2·2 | = | 2 |
| 10 | 6 | 10·3 | 6·5 | 30 | 30 | 30 | 30 | 15·2 | 15 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух обыкновенных дробей
Вычитание смешанных чисел.
Примеры вычитания смешанных чисел
Пример 11.
Найти разность двух смешанных чисел:
| 2 | 1 | — | 1 | 1 | = | 2 | 1·3 | — | 1 | 1·2 | = | (2 — 1) | + | 3 | — | 2 | = |
| 2 | 3 | 2·3 | 3·2 | 6 | 6 |
| = | 1 | + | 3 -2 | = | 1 | + | 1 | = | 1 | 1 |
| 6 | 6 | 6 |
Пример 12.
Найти разность двух смешанных чисел:
| 3 | 1 | — | 1 | 3 | = | 3 | 1·4 | — | 1 | 3·3 | = | 3 | 4 | — | 1 | 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 |
| = | 2 | 24 + 4 | — | 1 | 9 | = | 1 + | 28 — 9 | = | 1 + | 19 | = 1 | 19 |
| 24 | 24 | 24 | 24 | 24 |
Пример 13.
Найти разность двух смешанных чисел:
| 1 | 1 | — | 3 | 2 | = | 1 | 1 | — | 3 | 2·2 | = | 1 | 1 | — | 3 | 4 | = | (1-3) | + | 1 — 4 | = |
| 6 | 3 | 6 | 3·2 | 6 | 6 | 6 |
| = -2 | — | 3 | = | -2 | — | 3 | = | -2 | — | 1 | = | -2 | 1 |
| 6 | 2·3 | 2 | 2 |
Онлайн калькулятор дробей
Упражнения на тему сложение и вычитание двух смешанных чисел
Дроби Виды дробей (обыкновенная правильная, неправильная, смешанная, десятичная) Основное свойство дроби Сокращение дроби Приведение дробей к общему знаменателю Преобразование неправильной дроби в смешанное число Преобразование смешанного числа в неправильную дробь Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичной дроби в обыкновенную дробь
Онлайн калькуляторы дробей
Онлайн упражнения с дробями
Дробь 2 9/2 в виде десятичной дроби
Калькулятор «Конвертер обыкновенных дробей в десятичные»
Как записать 2 целых 9/2 в виде десятичной дроби?
Ответ: Дробь 2 9/2 в десятичном виде это 6,5
Объяснение конвертации дроби 2 9/2 в десятичную
Для того, чтобы перевести дробь 2 9/2 в десятичный формат необходимо разделить числитель 9 на знаменатель 2.
Результат деления:
9 ÷ 2 = 6,5
и прибавить целую часть (2):
4.5 + 2 = 6,5
Другой способ перевод дроби 2 целых 9/2 в десятичный формат заключается в том, чтобы перевести эту смешанную дробь в неправильную дробь. Для этого необходимо сперва умножить целую часть (2) на знаменатель (2):
2 × 2 = 4
после чего прибавить результат к числителю (9):
4 + 9 = 13
и в конце разделить результат на числитель (2):
= 13 ÷ 2 =6,5
Поделитесь текущим расчетом
Печать
https://calculat.io/ru/number/fraction-as-a-decimal/2—9—2
<a href=»https://calculat.io/ru/number/fraction-as-a-decimal/2—9—2″>Дробь 2 9/2 в виде десятичной дроби — Calculatio</a>
О калькуляторе «Конвертер обыкновенных дробей в десятичные»
Данный онлайн-конвертер обыкновенных дробей в десятичные является полезным инструментом, предназначенным для легкого преобразовывания любой дроби в ее эквивалентную десятичную форму.
Например, он может помочь узнать как записать 2 целых 9/2 в виде десятичной дроби? Независимо от того, являетесь ли вы учеником, студентом или профессионалом, этот конвертер может сэкономить ваше время и усилия при выполнении ручных вычислений.
Чтобы использовать этот конвертер, просто введите дробь, которую вы хотите преобразовать, в соответствующие поля. Вам необходимо ввести целую часть (если есть), числитель и знаменатель дроби. Например, если вы хотите преобразовать 2 9/2 в его десятичный эквивалент, вы введете ‘2’ как целую часть, ‘9’ как числитель и ‘2’ как знаменатель.
После того, как вы ввели дробь, нажмите кнопку ‘Конвертировать’, чтобы получить результаты. Конвертер отобразит десятичный эквивалент дроби, который в нашем случае равен 6,5. Кроме того, он предоставит пошаговое объяснение процесса преобразования, чтобы вы могли понять, как был получен десятичный эквивалент дроби. Если результат является периодической десятичной дробью, конвертер отобразит повторяющийся шаблон, используя скобки для обозначения повторяющихся цифр.
Одной из ключевых особенностей этого конвертера является его способность выводить периодические десятичные дроби. В математике периодическая десятичная дробь — это десятичная дробь, в которой есть повторяющийся шаблон цифр, например, 0,33333… или 0,142857142857… Это отличает такие дроби от непериодических десятичных дробей, которые заканчиваются после определенного числа цифр, например, 0,5 или 0,75.
Использование этого онлайн-конвертера дробей в десятичные является быстрым и простым способом преобразования любой дроби в ее десятичный эквивалент. Он может быть особенно полезен тем, кто испытывает трудности с ручными вычислениями или кто часто выполняет преобразования.
Калькулятор «Конвертер обыкновенных дробей в десятичные»
Таблица конвертации обыкновенных дробей в десятичные
| Дробь | Десятичная |
|---|---|
| 2 9/1 | 11 |
| 2 9/2 | 6,5 |
| 2 9/3 | 5 |
| 2 9/4 | 4,25 |
| 2 9/5 | 3,8 |
| 2 9/6 | 3,5 |
| 2 9/7 | 3,(285714) |
| 2 9/8 | 3,125 |
| 2 9/9 | 3 |
| 2 9/10 | 2,9 |
| 2 9/11 | 2,(81) |
| 2 9/12 | 2,75 |
| 2 9/13 | 2,(692307) |
| 2 9/14 | 2,6(428571) |
| 2 9/15 | 2,6 |
| 2 9/16 | 2,5625 |
| 2 9/17 | 2,(5294117647058823) |
| 2 9/18 | 2,5 |
| 2 9/19 | 2,(473684210526315789) |
| 2 9/20 | 2,45 |
| 2 9/21 | 2,(428571) |
| 2 9/22 | 2,4(09) |
| 2 9/23 | 2,(3913043478260869565217) |
| 2 9/24 | 2,375 |
| 2 9/25 | 2,36 |
| 2 9/26 | 2,3(461538) |
| 2 9/27 | 2,(3) |
| 2 9/28 | 2,32(142857) |
| 2 9/29 | 2,(3103448275862068965517241379) |
| 2 9/30 | 2,3 |
Расчет промилле, калькулятор промилле, промилле, калькулятор промилле
Завершите предложение, описывающее вашу проблему.
Введите значения и нажмите Вычислить .
- Express 6027
Express снижение на 8 процентов на миллион. - Опрыскивание от насекомых
В 600 мл опрыскивания находится 5 мл действующего вещества. Сколько это за милю? - Рассчитайте 72994
Рассчитайте 50 промилле от 340. - Синдром Дауна
Синдром Дауна — одно из серьезных заболеваний, вызванных генной мутацией. Синдром Дауна встречается примерно у каждого 550 родившегося ребенка. Выразите заболеваемость синдромом Дауна у новорожденных в промилле. - Золотая монета
Золотая монета содержит 900 промилле чистого золота. Вес монеты 950 грамм. Сколько промилле золота? Сколько грамм золота? - Десятичный 26301
Запишите промилле в виде десятичного числа 2 ‰ 50 ‰ 2,5 ‰ 0,6 ‰ - Promile
Рассчитайте 4,6 ‰ от 199. - Штраф ежедневно
Джон должен был заплатить 1500 чешских крон. Если он не заплатит вовремя, с него будет начислен штраф в размере 0,5 промилле причитающейся суммы за каждый день просрочки.
Он вспомнит через 30 дней. Сколько стоит штраф? - Амфитеатр
Амфитеатр имеет форму полукруга, зрители сидят по периметру полукруга, а сцена образует диаметр полукруга. Кто из зрителей, P, Q, R, S, T, видит сцену под наибольшим углом обзора? - Неизвестно 73244
75 промилле неизвестного числа равно 60. Что такое неизвестное число? - Дивиденды
Трое друзей разделили выигрыш на вложенные деньги. Карлос получил три восьмых, Джон 320 пермиль, а остальные достались Мартину. Кто получил больше, а кто меньше? - Золотая монета
Золотая монета содержит чистое золото 962 промилле, что составляет 7,5 г. Каков вес монеты в граммах? - Пермилл
Сколько на мельницы будет 978 из 84370? - Автомобильная авария
После дорожно-транспортного происшествия полиция измерила 1,16 промилле алкоголя в крови водителя. В организме человека циркулирует около 5 кг крови. Какое количество алкоголя было у водителя в крови? - Железная дорога
Железнодорожная линия имеет уклон 12 промилле. На сколько метров он поднимется на расстояние 4 км по горизонтали? - AMSL и катание на лыжах
Томас идет на лыжах из точки A (3200 м над уровнем моря в точку B. Гора имеет уклон 20%. Горизонтальное расстояние между стартом и финишем 2,5 км. На какой высоте находится точка B? - Километры 81387
Рассчитайте уклон железнодорожной линии, высота которой составляет 22,5 метра на участке длиной 1,5 километра. Для железных дорог результат дается в ч (промилле).
Он вспомнит через 30 дней. Сколько стоит штраф?
На сколько метров он поднимется на расстояние 4 км по горизонтали?другие математические задачи »
Часто искомые расчеты промилле
- десятичные дроби
- дроби
- треугольник ΔABC
- проценты %
- промилле ‰
- простые множители
- комплексные числа
- LCM
- НОД
- LCD
- комбинаторика
- уравнения
- статистика
- … все математические калькуляторы
Калькулятор дробей: сложение и вычитание дробей
Как использовать калькулятор дробей: Введите значения числителя и знаменателя, выберите арифметический оператор, а калькулятор сделает все остальное.
Основное определение дроби
Дробь — это числовая величина, представляющая часть целого числа. В математических терминах дробь выражается делением одного целого числа (числителя) на другое целое число (знаменатель), например 1/3, 1/5, 2/7 и т. д.
На повседневном языке мы можем просто сказать, что дробь — это количество частей определенного размера, например одна восемь пятых.
Простые методы вычисления дробей
Простое сложение дробей
Ключевой момент для правильного сложения дробей — всегда помнить о самой важной части дроби, то есть о числе под чертой, известном как знаменатель. Если у нас есть ситуация, когда знаменатели в дробях, участвующих в процессе сложения, одинаковы, то мы просто складываем числа, которые находятся над разделительной чертой, или, как сказал бы математик, «складываем только числители». Мы можем посмотреть на пример сложения двух дробей, таких как 3/7 и 4/7. Выражение будет выглядеть так: 3/7 + 4/7 = 7/7. В случае, когда числитель равен знаменателю, как в предыдущем примере, его также можно приравнять к 1.
Однако это был один из самых простых примеров сложения дробей. Процесс может немного усложниться, если мы столкнемся с ситуацией, когда знаменатели дробей, участвующих в расчете, различны. Тем не менее, существует правило, которое позволяет нам эффективно выполнять этот тип расчета. Запомните первое: при сложении дробей знаменатели всегда должны быть одинаковыми, или, выражаясь языком математиков, у дробей должен быть общий знаменатель. Для этого нам нужно посмотреть на знаменатель, который у нас есть. Вот пример: 2⁄3 + 3⁄5. Так что общего знаменателя у нас пока нет. Поэтому воспользуемся таблицей умножения, чтобы найти число, которое является произведением 5 на 3. Это 15. Значит, общим знаменателем для этой дроби будет 15. Однако это еще не конец. Если мы разделим 15 на 3, то получим 5. Итак, теперь нам нужно умножить числитель первой дроби на 5, что даст нам 10 (2 х 5). Кроме того, мы умножаем числитель второй дроби на 3, потому что 15/5 = 3. Получаем 9(3 х 3 = 9). Теперь мы можем ввести все эти числа в выражение: 10/15 + 9/15 = 19/15.
Примечание. Если числитель больше знаменателя, мы делим его на последний.
Простое вычитание дробей
Для правильного вычитания дробей важно всегда помнить, что самой важной частью дроби является число под чертой, известное как знаменатель. Если у нас есть ситуация, когда знаменатели в дробях, участвующих в процессе вычитания, одинаковы, то мы просто вычитаем числа, которые находятся над разделительной линией или, как сказал бы математик: «вычитание только числителей». Мы можем посмотреть на пример вычитания двух дробей, таких как 3/7 и 4/7. Выражение будет выглядеть так: 4/7 — 3/7 = 1/7.
Однако это был один из самых простых примеров вычитания дробей. Процесс может немного усложниться, если мы столкнемся с ситуацией, когда знаменатели дробей, участвующих в расчете, различны. Тем не менее, существует правило, которое позволяет нам эффективно выполнять этот тип расчета. Запомните первое: при вычитании дробей знаменатели всегда должны быть одинаковыми, или, выражаясь языком математиков, у дробей должен быть общий знаменатель.
Такие изделия подходят для внутренней и воздушной прокладки питающего провода, но не могут использоваться как силовые.
): 0.07 l/min
)
)
Для получения дополнительной информации или оформления заказа обратитесь к нашим специалистам.
Связаться с нами
по настоящее время)
pdf)
) для Kinetic, Wolfpack
) B History, Camouflage and Markings
Первый полет F-5 состоялся 31 июля 1963 года на базе ВВС Эдвардс, Калифорния. Более 2600 самолетов было построено компанией Northrop Grumman в рамках соглашений о совместном производстве и лицензировании с Канадой, Китайской Республикой, Республикой Корея, Испанией и Швейцарией.
Оболочки.
.. 
5 — сумма цифр числа.
2 — количество делителей числа.
Обратное число для 5 — это 0.2. 
Смит (US-62 Восток) на I-40 Восток. Продолжайте движение по I-35 Север. Сверните на съезд № 211 / Fountain Road. Поверните направо на West Fountain Road. Поверните налево на шоссе США 77 (US-77). Продолжайте следовать по US-77. Поверните направо на Ист-Гранд-авеню. Поверните направо на NOC Drive. Поверните направо на Ист-Гранд-авеню. Прибытие в НОК.
Продолжайте движение по Ист-Оуэн К. Гэрриотт-роуд. Поверните направо на Лейквью Драйв. Поверните налево на Ист-Чероки-авеню. Поверните направо на Южной 20-й улице. Поверните направо на Ист-Мейн-стрит. Поверните налево на South University Avenue. Прибытие в НОК.
628.6900 
Поверните направо (восток) на улице Скотта. Знаки почасовой парковки направят вас в гараж. (Гараж находится менее чем в одном квартале к северо-востоку от колледжа Северной Оклахомы.)
1109/MDAT.2022.3203005
1109/MDAT.2022.3204201 | Презентация:
1109/MDAT.2022.3202994 | Презентация:
1109/MDAT.2022.3202996 | Презентация:
1109/MDAT.2022.3202998
1109/MDAT.2022.3202993 | Презентация:
Безопасность сети на кристалле: вызовы и меры противодействия». 
Она является членом IEEE и ACM и Золотым ядром.
член компьютерного общества IEEE. Она была избрана в Phi Beta Kappa и Tau Beta Pi. Она стала
фигурка 2018 года.
Эффективный NoC имеет решающее значение для
производительность и энергоэффективность современной цифровой системы. В этом докладе будут рассмотрены лучшие
способ построить NoC сегодня, учитывая наш 21-летний опыт. Все должно быть просто и быстро. К
свести к минимуму задержку и энергию, топология должна быть ячеистой, возможно, с диагоналями. чрезвычайно
простой самосинхронизирующийся маршрутизатор с задержкой 100 пс делает минимизацию количества переходов неактуальной. Задержка
сравнимы с выделенными проводами. Достаточно простого двухтактного управления потоком запросов-подтверждений. Есть
нет необходимости в виртуальных каналах для мультиплексирования проводов. Проводов полно. Оптимизированные схемы для привода
провода имеют решающее значение для энергоэффективности. Эффективные синхронизаторы имеют решающее значение для оптимизации
задержка.
Доклад завершится некоторыми будущими направлениями исследований NoCs/NoPs.
С 1983 по 1986 год он работал в Калифорнийском технологическом институте (CalTech), где он
разработал движок моделирования MOSSIM и чип Torus Routing, который стал пионером в маршрутизации «червоточины».
и управление потоком виртуального канала. Он является членом Национальной инженерной академии, членом
Американской академии искусств и наук, член IEEE и ACM, а также получил ACM
Премия Эккерта-Мочли, премия IEEE Сеймура Крея и премия Мориса Уилкса от ACM. У него есть
опубликовал более 250 статей, имеет более 120 выданных патентов и является автором четырех учебников. Далли
получил степень бакалавра электротехники в Технологическом институте Вирджинии, степень магистра электротехники
Инженер из Стэнфордского университета и доктор философии. в области компьютерных наук из Калифорнийского технологического института. Он был
соучредитель Velio Communications и Stream Processors.
1109/MDAT.2022.3203005
Найти:
Найти площадь параллелограмма,
построенного на векторах
и
и угол
.
Определить длины базисных векторов
и
и угол
.
Найти:
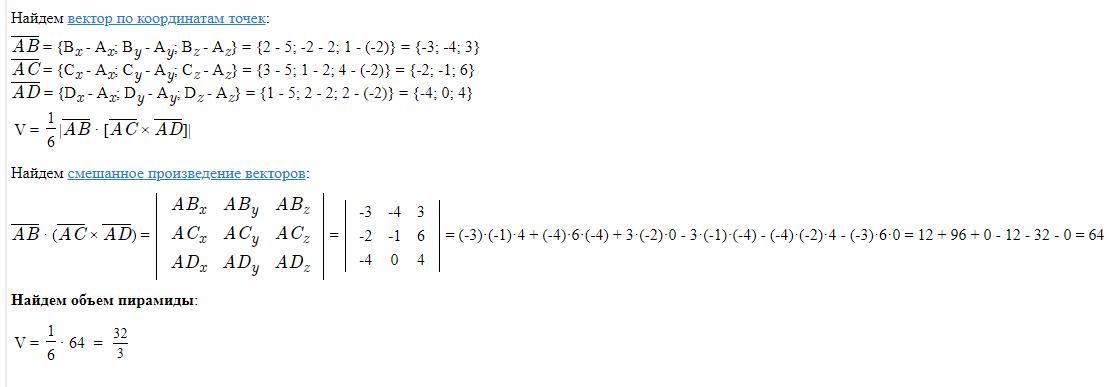Педагогический (научно-педагогический) состав
4
%
1 0 объект
>
/PageMode /UseOutlines
/Имена 2 0 Р
/Контуры 3 0 R
/Метаданные 4 0 R
/Страницы 5 0 Р
/PageLayout /Одностраничный
/OpenAction [6 0 R /FitH 850]
/Темы [7 0 R]
/Тип /Каталог
/Lang (ru)
/PageLabels 8 0 R
/OutputIntents [9 0 R]
>>
эндообъект
10 0 объект
/В ловушке /Ложь
>>
эндообъект
2 0 объект
>
эндообъект
3 0 объект
>
эндообъект
4 0 объект
>
транслировать
приложение/pdfdoi:10.1016/j.jmaa.2008.11.057
В ХVI веке появился глагол числити — «считать».
) При Петре I в России открыли цифирные школы — начальные государственные общеобразовательные учебные заведения для мальчиков. В них кроме других дисциплин детям преподавали цифирную науку — арифметику, математику.
.. – это имя поля, заключенного в ${}. А процессор Калькулятора полей ожидает, что поля будут определены только с помощью имени.
Для этого параметра отсутствует значение по умолчанию.
Для этого параметра отсутствует значение по умолчанию.
2 + {{Сумма}}/2 или 
04.2016
Если вы не хотите ограничивать верхнюю границу, то можете не указывать второй параметр, например 
Данная функция аналогична существующей в php, более подробно о ее возможностях вы можете прочитать здесь.
Полезна, когда нужно вывести в текст значения множественных переменных нестандартным разделителем (стандартный — просто запятая). Аналог implode в PHP. Возвращает строку, содержащую строковое представление всех элементов массива в указанном порядке, со значением glue между каждым элементом.
csv.
log7(x) — логарифм по основанию 7 
09.2021 12:29:40
Пример алгебраического выражения показан ниже.
9(3/2)». Наиболее
Важно помнить, что круглые скобки важны при вводе алгебраического выражения.
В частности, когда вам нужно разобраться с
упрощение выражений, хотя этот калькулятор даст вам окончательный ответ, без промежуточных шагов.
Получим: .
{n}=\underbrace{a \times a \times \ldots \times a}_{\text {п множсителей }}\]
{3}}=\frac{8}{125}\]
{n}=\underbrace{a \times a \times \ldots \times a}_{\text {п множсителей }}\]
{1 / 2}}=\frac{1}{\sqrt{49}}=\frac{1}{7}\]
{1,4142} \approx 2,66512\]
Но это боль, поэтому математики
разработали ярлыки, называемые ПРАВИЛАМИ, чтобы сделать расчеты быстрее и проще
написать.
Прежде чем мы углубимся в детали концепции, давайте вспомним значение силы и основания. Для выражения b x , b — это основание, а x — это степень (также называемая показателем степени), которая подразумевает, что b умножается на себя x раз. Теперь сила степенного правила используется для упрощения выражений вида (b x ) y что для упрощения записывается как b xy . Чтобы применить мощность к правилу мощности, мы умножаем две степени, сохраняя одно и то же основание.
Итак, если m > 0 и n > 0 и у нас отрицательные показатели, то, используя ту же формулу, что и выше, мы имеем
Вот некоторые из примеров рациональной мощности степенного правила:
Итак, мы умножаем две степени -5 и 9, чтобы получить результат и оставить основание x таким же.
Правило гласит: «Если основание, возведенное в степень, возводится в другую степень, то две степени перемножаются, а основание остается прежним».
Для примера, орбита планет вокруг звезды описывается эллипсом, так что вы можете себе представить, что это довольно важное применение.
2 \]
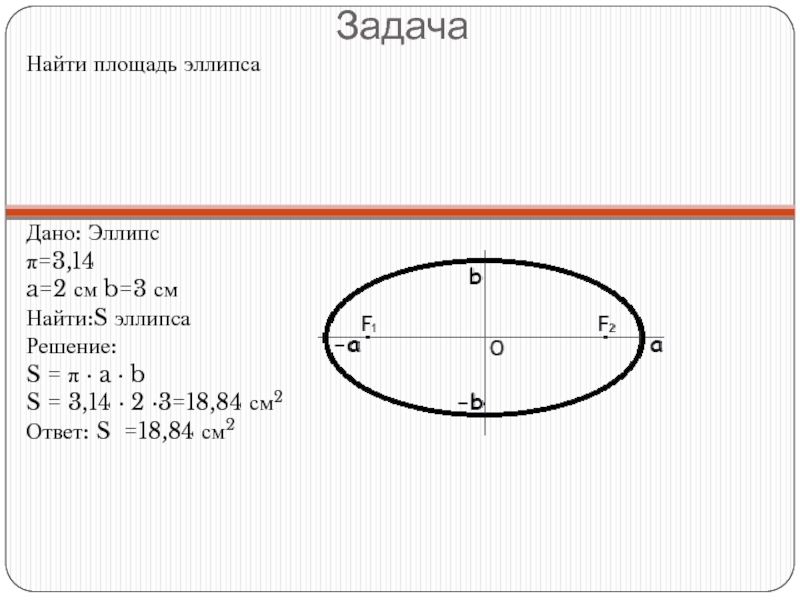Затем калькулятор выводит результаты в соответствующих выбранным единицам измерения.
Эллипс — это закругленная фигура, которая состоит из двух точек, называемых фокусами, и всех точек, для которых сумма расстояний до двух фокусов остается постоянной.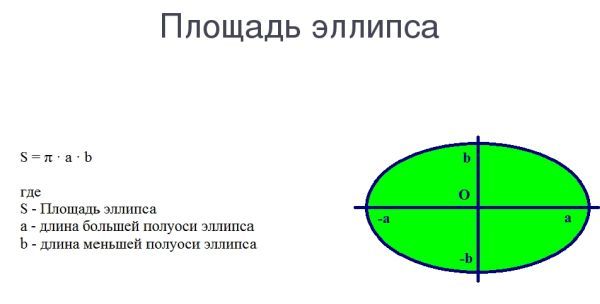
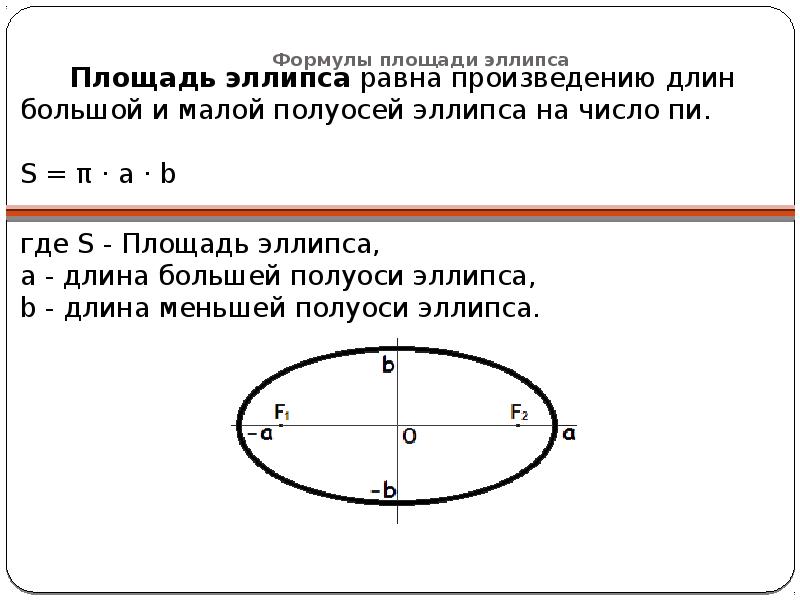
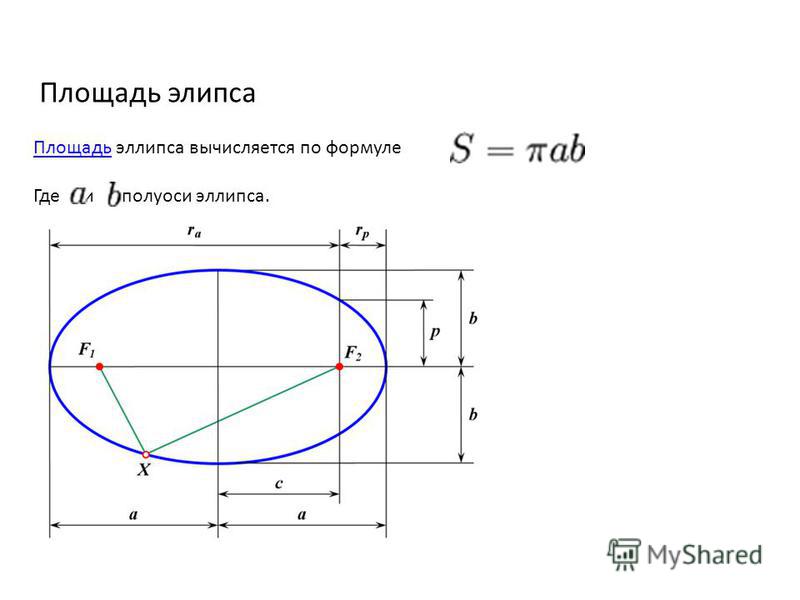
Их нужно определить, если вы хотите нарисовать овал. Фокусы в определении эллипса — это множество всех точек, для которых сумма расстояний до первого и второго фокусов равна постоянной величине.
Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник 
«/>
Без многослойности 
Допускаются значения от 0 до 255.»/>
PPT в .JPG
Выберите файлы для конвертации
Мы обеспечиваем безопасность ваших файлов и данных и предлагаем выбор и контроль над удалением файлов.
Вы имеете прямой доступ и даже можете оформить подписку всего на месяц.
Преобразователь Замзара был идеальным.
Какой инструмент вы используете, зависит от вас!
Благодаря более быстрой загрузке преобразованных файлов и дружелюбной и полезной поддержке, когда вам это нужно, у вас будет все необходимое для работы с вашими файлами.
С поддержкой более 1100 типов преобразования файлов, независимо от того, нужно ли вам конвертировать видео, аудио, документы или изображения, вы легко найдете то, что вам нужно, и вскоре ваши файлы будут в форматах и размерах, которые вам подходят.
JPG — это универсальный формат, который можно открыть почти во всех программах просмотра или редактирования изображений, в веб-браузерах и некоторых других приложениях, и они поддерживаются большинством устройств. JPG — это 2D-пиксельные «растровые» изображения, которые лучше подходят для фотографий или сканов, а не для цифровых иллюстраций, которые часто лучше подходят для «векторных» изображений. Многие камеры, смартфоны и базовые программы для работы с фотографиями или рисованием автоматически сохраняют изображения в формате JPG. Однако обычно вы можете настроить параметры для сохранения в других форматах, если это необходимо.
Выберите файл PPT, который вы хотите преобразовать.
ZIP в PPT
ODP в PPT
PDF в PPT
PPS в PPT
PPSX в PPT
PPTX в PPT
Также можно сохранить PowerPoint в формате PDF, а затем преобразовать этот файл в JPG. Однако вы должны получить изображение с более высоким разрешением и сэкономить время, преобразовав его напрямую с помощью Zamzar.
Он преобразует всю презентацию, поэтому вы получите файл JPG для каждого слайда и сможете сохранить те, которые вам нужны.
Вы получите отдельный JPG для каждого слайда PowerPoint, чтобы затем выбрать нужные изображения.
