Строки. Функции и методы строк
Итак, о работе со строками мы немного поговорили, теперь поговорим о функциях и методах строк.
Я постарался собрать здесь все строковые методы и функции, но если я что-то забыл — поправляйте.
Базовые операции
Конкатенация (сложение)
>>> S1 = 'spam' >>> S2 = 'eggs' >>> print(S1 + S2) 'spameggs'
Дублирование строки
>>> print('spam' * 3) spamspamspamДлина строки (функция len)
>>> len('spam') 4Доступ по индексу
>>> S = 'spam' >>> S[0] 's' >>> S[2] 'a' >>> S[-2] 'a'
Как видно из примера, в Python возможен и доступ по отрицательному индексу, при этом отсчет идет от конца строки.
Извлечение среза
Оператор извлечения среза: [X:Y]. X – начало среза, а Y – окончание;
символ с номером Y в срез не входит. По умолчанию первый индекс равен 0, а второй — длине строки.

>>> s = 'spameggs' >>> s[3:5] 'me' >>> s[2:-2] 'ameg' >>> s[:6] 'spameg' >>> s[1:] 'pameggs' >>> s[:] 'spameggs'
Кроме того, можно задать шаг, с которым нужно извлекать срез.
>>> s[::-1] 'sggemaps' >>> s[3:5:-1] '' >>> s[2::2] 'aeg'
Другие функции и методы строк
При вызове методов необходимо помнить, что строки в Python относятся к категории неизменяемых последовательностей, то есть все функции и методы могут лишь создавать новую строку.
>>> s = 'spam'
>>> s[1] = 'b'
Traceback (most recent call last):
File "", line 1, in
s[1] = 'b'
TypeError: 'str' object does not support item assignment
>>> s = s[0] + 'b' + s[2:]
>>> s
'sbam'Поэтому все строковые методы возвращают новую строку, которую потом следует присвоить переменной.
Таблица «Функции и методы строк»
| Функция или метод | Назначение |
|---|---|
| S = ‘str’; S = «str»; S = »’str»’; S = «»»str»»» | Литералы строк |
| S = «s\np\ta\nbbb» | Экранированные последовательности |
| S = r»C:\temp\new» | Неформатированные строки (подавляют экранирование) |
| S = b»byte» | Строка байтов |
| S1 + S2 | Конкатенация (сложение строк) |
| S1 * 3 | Повторение строки |
| S[i] | Обращение по индексу |
| S[i:j:step] | Извлечение среза |
| len(S) | Длина строки |
S. find(str, [start],[end]) find(str, [start],[end]) | Поиск подстроки в строке. Возвращает номер первого вхождения или -1 |
| S.rfind(str, [start],[end]) | Поиск подстроки в строке. Возвращает номер последнего вхождения или -1 |
| S.index(str, [start],[end]) | Поиск подстроки в строке. Возвращает номер первого вхождения или вызывает ValueError |
| S.rindex(str, [start],[end]) | Поиск подстроки в строке. Возвращает номер последнего вхождения или вызывает ValueError |
| S.replace(шаблон, замена[, maxcount]) | Замена шаблона на замену. maxcount ограничивает количество замен |
| S.split(символ) | Разбиение строки по разделителю |
| S.isdigit() | Состоит ли строка из цифр |
| S.isalpha() | Состоит ли строка из букв |
| S.isalnum() | Состоит ли строка из цифр или букв |
| S.islower() | Состоит ли строка из символов в нижнем регистре |
S. isupper() isupper() | Состоит ли строка из символов в верхнем регистре |
| S.isspace() | Состоит ли строка из неотображаемых символов (пробел, символ перевода страницы (‘\f’), «новая строка» (‘\n’), «перевод каретки» (‘\r’), «горизонтальная табуляция» (‘\t’) и «вертикальная табуляция» (‘\v’)) |
| S.istitle() | Начинаются ли слова в строке с заглавной буквы |
| S.upper() | Преобразование строки к верхнему регистру |
| S.lower() | Преобразование строки к нижнему регистру |
| S.startswith(str) | Начинается ли строка S с шаблона str |
| S.endswith(str) | Заканчивается ли строка S шаблоном str |
| S.join(список) | Сборка строки из списка с разделителем S |
| ord(символ) | Символ в его код ASCII |
| chr(число) | Код ASCII в символ |
| S.capitalize() | Переводит первый символ строки в верхний регистр, а все остальные в нижний |
S. center(width, [fill]) center(width, [fill]) | Возвращает отцентрованную строку, по краям которой стоит символ fill (пробел по умолчанию) |
| S.count(str, [start],[end]) | Возвращает количество непересекающихся вхождений подстроки в диапазоне [начало, конец] (0 и длина строки по умолчанию) |
| S.expandtabs([tabsize]) | Возвращает копию строки, в которой все символы табуляции заменяются одним или несколькими пробелами, в зависимости от текущего столбца. Если TabSize не указан, размер табуляции полагается равным 8 пробелам |
| S.lstrip([chars]) | Удаление пробельных символов в начале строки |
| S.rstrip([chars]) | Удаление пробельных символов в конце строки |
| S.strip([chars]) | Удаление пробельных символов в начале и в конце строки |
| S.partition(шаблон) | Возвращает кортеж, содержащий часть перед первым шаблоном, сам шаблон, и часть после шаблона. Если шаблон не найден, возвращается кортеж, содержащий саму строку, а затем две пустых строки Если шаблон не найден, возвращается кортеж, содержащий саму строку, а затем две пустых строки |
| S.rpartition(sep) | Возвращает кортеж, содержащий часть перед последним шаблоном, сам шаблон, и часть после шаблона. Если шаблон не найден, возвращается кортеж, содержащий две пустых строки, а затем саму строку |
| S.swapcase() | Переводит символы нижнего регистра в верхний, а верхнего – в нижний |
| S.title() | Первую букву каждого слова переводит в верхний регистр, а все остальные в нижний |
| S.zfill(width) | Делает длину строки не меньшей width, по необходимости заполняя первые символы нулями |
| S.ljust(width, fillchar=» «) | Делает длину строки не меньшей width, по необходимости заполняя последние символы символом fillchar |
| S.rjust(width, fillchar=» «) | Делает длину строки не меньшей width, по необходимости заполняя первые символы символом fillchar |
S.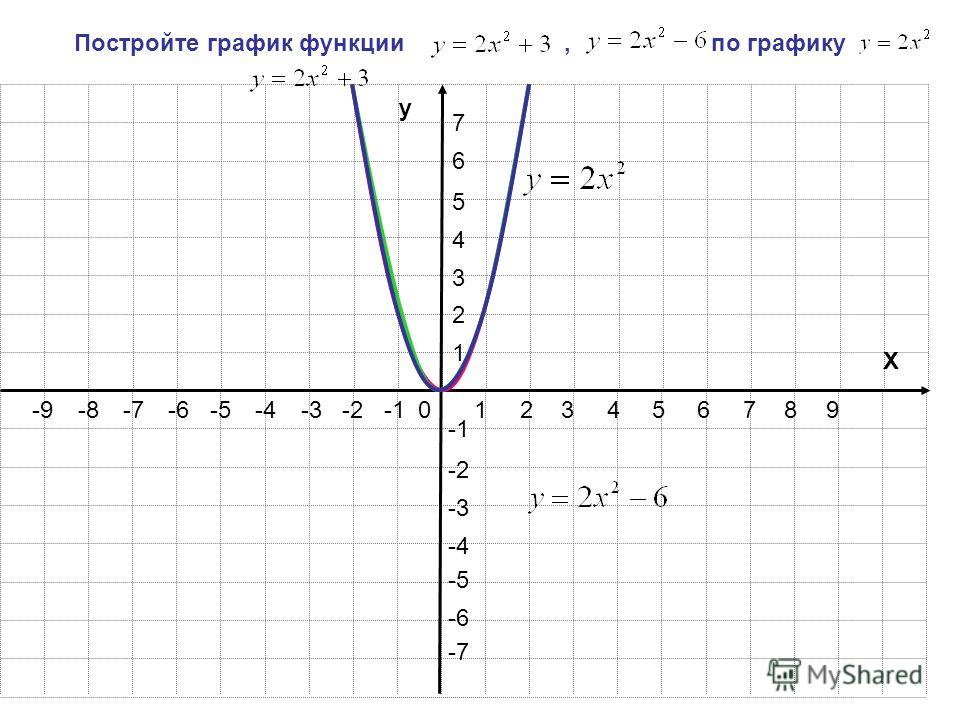 format(*args, **kwargs) format(*args, **kwargs) | Форматирование строки |
Для вставки кода на Python в комментарий заключайте его в теги <pre><code>Ваш код</code></pre>
Свежее
- Модуль csv — чтение и запись CSV файлов
- Создаём сайт на Django, используя хорошие практики. Часть 1: создаём проект
- Онлайн-обучение Python: сравнение популярных программ
Категории
- Книги о Python
- GUI (графический интерфейс пользователя)
- Курсы Python
- Модули
- Новости мира Python
- NumPy
- Обработка данных
- Основы программирования
- Примеры программ
- Типы данных в Python
- Видео
- Python для Web
- Работа для Python-программистов
Полезные материалы
- Сделай свой вклад в развитие сайта!
- Самоучитель Python
- Карта сайта
- Отзывы на книги по Python
- Реклама на сайте
Мы в соцсетях
Обратная функция y x 3.
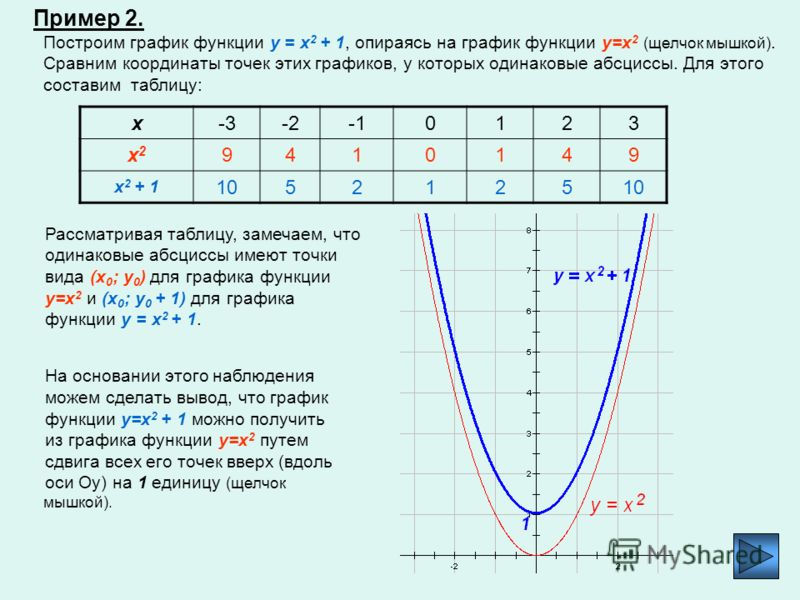 Обратные функции – определение и свойства
Обратные функции – определение и свойства1
Взаимно обратные функции Две функции f и g называются взаимно обратными, если формулы y=f(x) и x=g(y) выражают одну и ту же зависимость между переменными х и у, т.е. если равенство y=f(x) верно тогда и только тогда, когда верно равенство x=g(y): y=f(x) x=g(y) Если две функции f и g взаимно обратны, то g называют обратной функцией для f и, наоборот, f обратная функция для g. Например, у=10 х и х=lgy взаимно обратные функции. Условие существования взаимно обратной функции Функция f имеет обратную, если из соотношения y=f(x) переменную х можно однозначно выразить через у. Есть функции, для которых нельзя однозначно выразить аргумент через заданное значение функции. Например: 1. y= x. Для данного положительного числа у найдутся два значения аргумента х, такие, что x =у. Например, если у=2, то х=2 или х= — 2. Значит, выразить однозначно х через у нельзя. Следовательно, эта функция не имеет взаимно обратной. 2. у=х 2. х=, х= — 3. y=sinx. При заданном значении у (y 1) найдется бесконечно много значений х, таких, что y=sinx. Функция y=f(x) имеет обратную, если всякая прямая у=у 0 пересекает график функции y=f(x) не более чем в одной точке (она может совсем не пересекать график, если у 0 не принадлежит области значений функции f). Это условие можно сформулировать иначе: уравнение f(x)=y 0 при каждом у 0 имеет не более одного решения. Условие того, что функция имеет обратную, заведомо выполняется, если функция строго возрастает или строго убывает. Если f строго возрастает, то при двух различных значениях аргумента она принимает различные значения, так как большему значению аргумента соответствует большее значение функции. Следовательно, уравнение f(x)=y для строго монотонной функции имеет не более одного решения. Показательная функция у=а х строго монотонна, поэтому она имеет обратную логарифмическую функция. Многие функции не имеют обратных. Если при некотором b уравнение f(x)=b имеет более одного решения, то функция y=f(x) обратной не имеет.
При заданном значении у (y 1) найдется бесконечно много значений х, таких, что y=sinx. Функция y=f(x) имеет обратную, если всякая прямая у=у 0 пересекает график функции y=f(x) не более чем в одной точке (она может совсем не пересекать график, если у 0 не принадлежит области значений функции f). Это условие можно сформулировать иначе: уравнение f(x)=y 0 при каждом у 0 имеет не более одного решения. Условие того, что функция имеет обратную, заведомо выполняется, если функция строго возрастает или строго убывает. Если f строго возрастает, то при двух различных значениях аргумента она принимает различные значения, так как большему значению аргумента соответствует большее значение функции. Следовательно, уравнение f(x)=y для строго монотонной функции имеет не более одного решения. Показательная функция у=а х строго монотонна, поэтому она имеет обратную логарифмическую функция. Многие функции не имеют обратных. Если при некотором b уравнение f(x)=b имеет более одного решения, то функция y=f(x) обратной не имеет.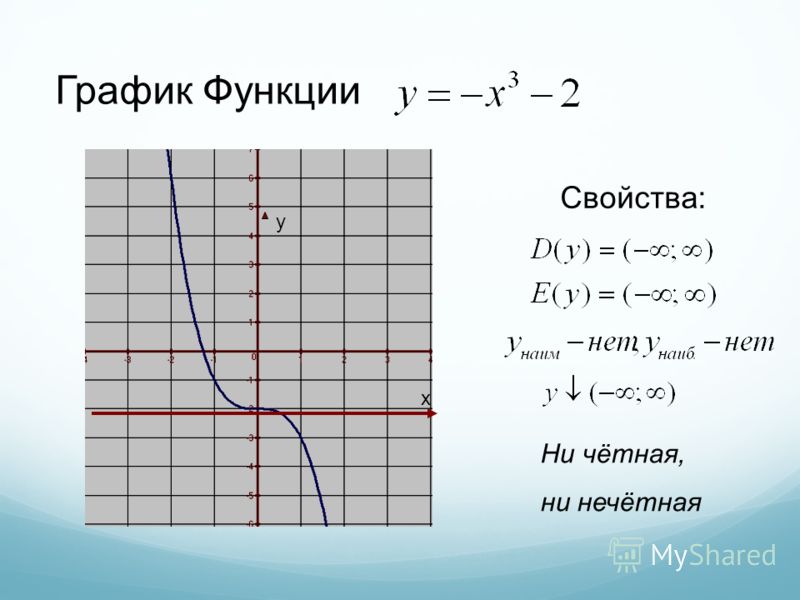 На графике это означает, что прямая y=b пересекает график функции более чем в одной точке. Например, у=х 2 ; y=sinx; у=tgx.
На графике это означает, что прямая y=b пересекает график функции более чем в одной точке. Например, у=х 2 ; y=sinx; у=tgx.
2
С неоднозначностью решения уравнения f(x)=b можно справиться, если уменьшить область определения функции f так, чтобы ее область значений не изменилась, но чтобы каждое свое значение она принимала один раз. Например, у=х 2, х 0; y=sinx, ; у=tgx,. Общее правило нахождения обратной функции для функции: 1. решая уравнение относительно х, находим; 2. меняя обозначения переменной х на у, а у на х, получаем функция обратную к данной. Свойства взаимно обратных функций Тождества Пусть f и g взаимно обратные функции. Это означает, что равенства y=f(x) и x=g(y) равносильны: f(g(y))=y и g(f(x))=x. Например, 1. Пусть f показательная, g логарифмическая функция. Получаем: и. 2. Функции у=х 2, х 0 и y= взаимно обратны. Имеем два тождества: и при х 0. Область определения Пусть f и g взаимно обратные функции. Область определения функции f совпадает с областью значений функции g, и, наоборот, область значений функции f совпадает с областью определения функции g. Пример. Область определения показательной функции вся числовая ось R, а ее область значений множество всех положительных чисел. У логарифмической функции наоборот: область определения множество всех положительных чисел, а область значений все множество R. Монотонность Если одна из взаимно обратных функций строго возрастает, то и другая строго возрастает. Доказательство. Пусть х 1 и х 2 два числа, лежащие в области определения функции g, причем x 1
Пример. Область определения показательной функции вся числовая ось R, а ее область значений множество всех положительных чисел. У логарифмической функции наоборот: область определения множество всех положительных чисел, а область значений все множество R. Монотонность Если одна из взаимно обратных функций строго возрастает, то и другая строго возрастает. Доказательство. Пусть х 1 и х 2 два числа, лежащие в области определения функции g, причем x 1
3
Графики взаимно обратных функций Теорема. Пусть f и g взаимно обратные функции. Графики функций y=f(x) и x=g(y) симметричны друг другу относительно биссектрисы угла хоу. Доказательство. По определению взаимно обратных функций формулы y=f(x) и x=g(y) выражают одну и ту же зависимость между переменными х и у, а значит, эта зависимость изображается одним и тем же графиком некоторой кривой С. Кривая С является графиком функции y=f(x). Возьмем произвольную точку Р(a; b) С. Это означает, что b=f(a) и одновременно a=g(b). Построим точку Q, симметричную точке Р относительно биссектрисы угла хоу. Точка Q будет иметь координаты (b; a). Так как a=g(b), то точка Q принадлежит графику функции y=g(x): действительно, при х=b значение у=а равно g(x). Таким образом, все точки, симметричные точкам кривой С относительно указанной прямой, лежат на графике функции у=g(x). Примеры функций графики которых взаимно обратны: у=е х и у=lnx; y=x 2 (x 0) и y= ; у=2x 4 и у= +2.
Точка Q будет иметь координаты (b; a). Так как a=g(b), то точка Q принадлежит графику функции y=g(x): действительно, при х=b значение у=а равно g(x). Таким образом, все точки, симметричные точкам кривой С относительно указанной прямой, лежат на графике функции у=g(x). Примеры функций графики которых взаимно обратны: у=е х и у=lnx; y=x 2 (x 0) и y= ; у=2x 4 и у= +2.
4
Производная обратной функции Пусть f и g взаимно обратные функции. Графики функций y=f(x) и x=g(y) симметричны друг другу относительно биссектрисы угла хоу. Возьмем точку х=а и вычислим значение одной из функций в этой точке: f(a)=b. Тогда по определению обратной функции g(b)=a. Точки (a; f(a))=(a; b) и (b; g(b))=(b; a) симметричны относительно прямой l. Так как кривые симметричны, то и касательные к ним симметричны относительно прямой l. Из симметрии угол одной из прямых с осью х равен углу другой прямой с осью у. Если прямая образует с осью х угол α, то ее угловой коэффициент равен k 1 =tgα; тогда вторая прямая имеет угловой коэффициент k 2 =tg(α)=ctgα=. Таким образом, угловые коэффициенты прямых, симметричных относительно прямой l, взаимно обратны, т.е. k 2 =, или k 1 k 2 =1. Переходя к производным и учитывая, что угловой коэффициент касательной является значением производной в точке касания делаем вывод: Значения производных взаимно обратных функций в соответствующих точках взаимно обратны, т.е.. Пример 1. Докажите, что функция f(x)=x 3, обратима. Решение. y=f(x)=x 3. Обратной функцией будет функция y=g(x)=. Найдем производную функции g:. Т.е. =. Задание 1. Докажите, что функция, заданная формулой, обратима 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Таким образом, угловые коэффициенты прямых, симметричных относительно прямой l, взаимно обратны, т.е. k 2 =, или k 1 k 2 =1. Переходя к производным и учитывая, что угловой коэффициент касательной является значением производной в точке касания делаем вывод: Значения производных взаимно обратных функций в соответствующих точках взаимно обратны, т.е.. Пример 1. Докажите, что функция f(x)=x 3, обратима. Решение. y=f(x)=x 3. Обратной функцией будет функция y=g(x)=. Найдем производную функции g:. Т.е. =. Задание 1. Докажите, что функция, заданная формулой, обратима 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
5 Пример 2. Найдите функцию, обратную функции у=2х+1. Решение. Функция у=2х+1 возрастающая, следовательно, она имеет обратную. Выразим х через у: получим.. Перейдя к общепринятым обозначениям, Ответ: Задание 2. Найдите обратные функции для данных функций 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Лекция 20 ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ. Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Последняя функция называется функцией от функции или сложной функцией.
Глава 9 Степени Степень с целым показателем. 0 = 0; 0 = ; 0 = 0. > 0 > 0 ; > >.. >. Если четно, то () (). Например, () = > = = (), так
Что будем изучать: Урок на тему: Исследование функции на монотонность. Убывающие и возрастающие функции. Связь производной и монотонности функции. Две важные теоремы о монотонности. Примеры. Ребята, мы
Линейное уравнение a x = b имеет: единственное решение, при a 0; бесконечное множество решений, при a = 0, b = 0; не имеет решений, при a = 0, b 0. Квадратное уравнение ax 2 + bx + c = 0 имеет: два различных
6 Задачи, приводящие к понятию производной Пусть материальная точка движется по прямой в одном направлении по закону s f (t), где t — время, а s — путь, проходимый точкой за время t Отметим некоторый момент
Банк заданий по теме «ПРОИЗВОДНАЯ» МАТЕМАТИКА 11 класс (база) Учащиеся должны знать/понимать: Понятие производной. Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Геометрический смысл производной Рассмотрим график функции y=f(x) и касательную в точке P 0 (x 0 ; f(x 0)). Найдем угловой коэффициент касательной к графику в этой точке. Угол наклона касательной Р 0
Квадратичная функция в различных задачах Дихтярь МБ Основные сведения Квадратичной функцией (квадратным трёхчленом) называется функция вида у ax bx c, где abc, заданные числа и Квадратичные функции у
ПОНЯТИЕ ПРОИЗВОДНОЙ ФУНКЦИИ Пусть имеем функцию определенную на множестве X и пусть точка X — внутренняя точка те точка для которой существует окрестность X Возьмем любую точку и обозначим через называется
Лекция 5 Производные основных элементарных функций Аннотация: Даются физическая и геометрическая интерпретации производной функции одной переменной Рассматриваются примеры дифференцирования функции и правила
1 СА Лавренченко Лекция 12 Обратные функции 1 Понятие обратной функции Определение 11 Функция называется взаимно-однозначной, если она не принимает никакое значение более одного раза, те из следует при
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Дифференциальное исчисление Составитель:
Глава 5 Исследование функций с помощью формулы Тейлора Локальный экстремум функции Определение Функция = f (достигает в точке с локального максимума (минимума), если можно указать такое δ >, что ее приращение
МОДУЛЬ «Применение непрерывности и производной. Применение производной к исследованию функций». Применение непрерывности.. Метод интервалов.. Касательная к графику. Формула Лагранжа. 4. Применение производной
Применение производной к исследованию функций». Применение непрерывности.. Метод интервалов.. Касательная к графику. Формула Лагранжа. 4. Применение производной
Лекция 9. Производные и дифференциалы высших порядков, их свойства. Точки экстремума функции. Теоремы Ферма и Ролля. Пусть функция y дифференцируема на некотором отрезке [b]. В таком случае ее производная
Кафедра математики и информатики Математический анализ Учебно-методический комплекс для студентов ВПО, обучающихся с применением дистанционных технологий Модуль 4 Приложения производной Составитель: доцент
Глава 1. Пределы и непрерывность 1. Числовые множества 1 0. Действительные числа Из школьной математики Вы знаете натуральные N целые Z рациональные Q и действительные R числа Натуральные и целые числа
Лекция 19 ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ. Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента xиз этого промежутка функция y=f(x)
Дифференциальное исчисление Основные понятия и формулы Определение 1 Производной функции в точке называется предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента
Тема 8.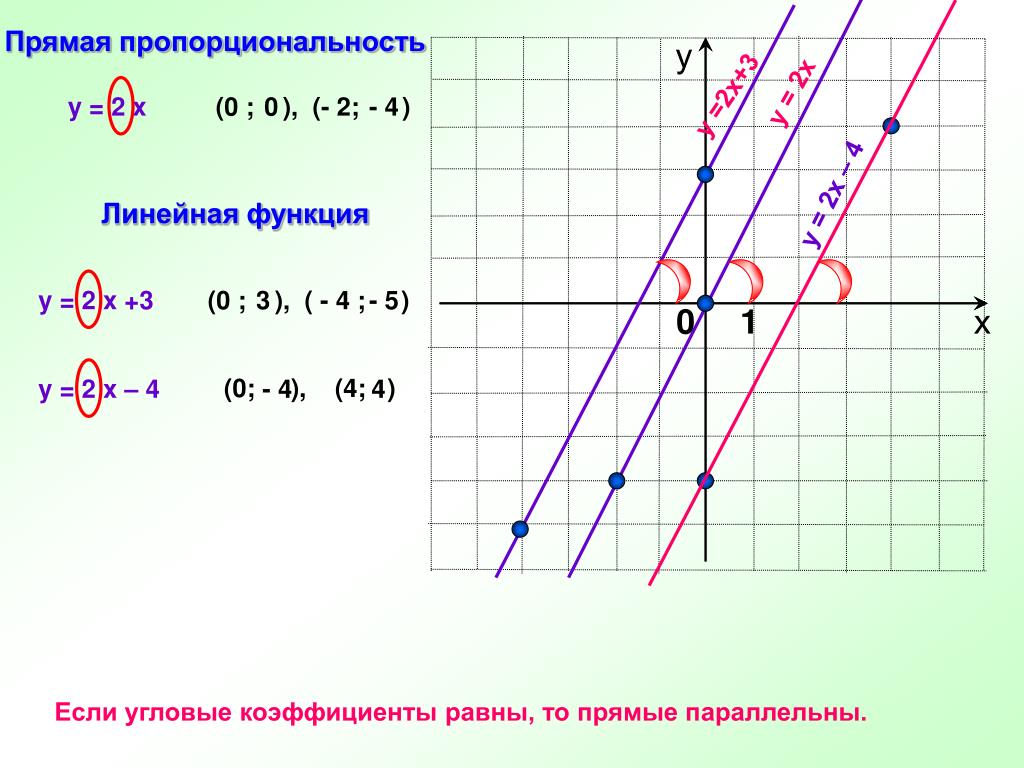 Показательная и логарифмическая функции. 1. Показательная функция, ее график и свойства В практике часто используются функции y=2 x,y=10 x,y=(1 2x),y=(0,1) x и т. д., т. е. функция вида y=a x,
Показательная и логарифмическая функции. 1. Показательная функция, ее график и свойства В практике часто используются функции y=2 x,y=10 x,y=(1 2x),y=(0,1) x и т. д., т. е. функция вида y=a x,
44 Пример Найти полную производную сложной функции = sin v cos w где v = ln + 1 w= 1 По формуле (9) d v w v w = v w d sin cos + cos cos + 1 sin sin 1 Найдем теперь полный дифференциал сложной функции f
Задания для самостоятельного решения. Найдите область определения функции 6x. Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через точку М (;) графика функции. Найдите тангенс угла
Тема Числовая функция, ее свойства и график Понятие числовой функции Область определения и множество значений функции Пусть задано числовое множество X Правило, сопоставляющее каждому числу X единственное
Лекция 23 ВЫПУКЛОСТЬ И ВОГНУТОСТЬ ГРАФИКА ФУНКЦИИ ТОЧКИ ПЕРЕГИБА График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале График
Тема Теория пределов Практическое занятие Числовые последовательности Определение числовой последовательности Ограниченные и неограниченные последовательности Монотонные последовательности Бесконечно малые
Числовые функции и числовые последовательности Д. В. Лыткина АЭС, I семестр Д. В. Лыткина (СибГУТИ) математический анализ АЭС, I семестр 1 / 35 Содержание 1 Числовая функция Понятие функции Числовые функции.
В. Лыткина АЭС, I семестр Д. В. Лыткина (СибГУТИ) математический анализ АЭС, I семестр 1 / 35 Содержание 1 Числовая функция Понятие функции Числовые функции.
Банк заданий по теме «ПРОИЗВОДНАЯ» МАТЕМАТИКА класс (профиль) Учащиеся должны знать/понимать: Понятие производной. Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Â. À. Äàëèíãåð ÌÀÒÅÌÀÒÈÊÀ: ÎÁÐÀÒÍÛÅ ÒÐÈÃÎÍÎÌÅÒÐÈ ÅÑÊÈÅ ÔÓÍÊÖÈÈ. ÐÅØÅÍÈÅ ÇÀÄÀ УЧЕБНОЕ ПОСОБИЕ ДЛЯ СПО -е издание, исправленное и дополненное Ðåêîìåíäîâàíî Ó åáíî-ìåòîäè åñêèì îòäåëîì ñðåäíåãî ïðîôåññèîíàëüíîãî
А.В. Землянко Математика. Алгебра и начала анализа Воронеж СОДЕРЖАНИЕ ТЕМА 1. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ… 6 1.1. Числовая функция… 6 1.2. График функции… 9 1.3. Преобразование графиков функции…
Тема. Функция. Способы задания. Неявная функция. Обратная функция. Классификация функций Элементы теории множеств. Основные понятия Одним из основных понятий современной математики является понятие множества.
Пусть задано числовое множество D R. Если каждому числу x D поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция: y = f (x), x D. Множество D, называется
Функции нескольких переменных 11. Определение функции нескольких переменных. Предел и непрерывность ФНП 1. Определение функции нескольких переменных ОПРЕДЕЛЕНИЕ. Пусть X = { 1 n i X i R } U R. Функция
МАТЕМАТИКА ДЛЯ ВСЕХ Ю.Л.Калиновский Contents 1 Графики функций. Часть I……………………………… 5 1.1 Введение 5 1.1.1 Понятие множества………………………………………. 5 1.1.
Практическая работа 6 Тема: «Полное исследование функций. Построение графиков» Цель работы: научиться исследовать функции по общей схеме и строить графики. В результате выполнения работы студент должен:
Глава 8 Функции и графики Переменные и зависимости между ними. Две величины и называются прямо пропорциональными, если их отношение постоянно, т. е. если =, где постоянное число, не меняющееся с изменением
е. если =, где постоянное число, не меняющееся с изменением
ЛЕКЦИЯ 2. Операции с подпространствами, число базисов число базисов и число подпространств размерности k. Основные результаты Лекции 2. 1) U V, U + V, dim(u + V). 2) Подсчет числа плоскостей в F 4 2.
Вопрос 5. Функция, способы задания. Примеры элементарных функций и их графики. Пусть даны два произвольных множества Х и Y. Функция это правило, по которому каждому элемента из множества X можно найти
Лекция 4 ЧИСЛОВЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ Понятие функции Способы задания функции Основные свойства функций Сложная функция 4 Обратная функция Понятие функции Способы задания функции Пусть D
Лекции Глава Функции нескольких переменных Основные понятия Некоторые функции многих переменных хорошо знакомы Приведем несколько примеров Для вычисления площади треугольника известна формула Герона S
Непрерывность функций Непрерывность функции в точке Односторонние пределы Определение Число A называется пределом функции f(x) слева при стремлении x к a, если для любого числа существует такое число
Научно-исследовательская работа Математика «Применение экстремальных свойств функции для решения уравнений» Выполнила: Гудкова Елена обучающаяся 11 класса «Г» МБОУ СОШ «Аннинский Лицей» п. г.т. Анна Руководитель:
г.т. Анна Руководитель:
Федеральное агентство по образованию —— САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АИ Сурыгин ЕФ Изотова ОА Новикова ТА Чайкина МАТЕМАТИКА Элементарные функции и их графики Учебное
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести
Функция Понятие функции Способы задания функции Характеристики функции Обратная функция Предел функции Предел функции в точке Односторонние пределы Предел функции при x Бесконечно большая функция 4 Лекция
Раздел Дифференциальное исчисление функции одной и нескольких переменных Функция действительного аргумента Действительные числа Целые положительные числа называются натуральными Добавим к натуральным
Сергей А Беляев стр 1 Математический минимум Часть 1 Теоретическая 1 Верно ли определение Наименьшим общим кратным двух целых чисел называется наименьшее число, которое делится на каждое из заданных чисел
Раздел 2 Теория пределов Тема Числовые последовательности Определение числовой последовательности 2 Ограниченные и неограниченные последовательности 3 Монотонные последовательности 4 Бесконечно малые и
Дифференцирование неявно заданной функции Рассмотрим функцию (,) = C (C = const) Это уравнение задает неявную функцию () Предположим, мы решили это уравнение и нашли явное выражение = () Теперь можно
Тестовые задания для подготовки к ЭКЗАМЕНУ по дисциплине «Математика» для студентов заочного отделения Производной функции y=f() называется: f A) B) f C) f f Если в некоторой окрестности точки функция
ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ В результате измерения физических величин (время, площадь, объем, масса, скорость и т. д.) определяются их числовые значения. Математика занимается величинами, отвлекаясь
д.) определяются их числовые значения. Математика занимается величинами, отвлекаясь
Математический анализ Раздел: Введение в анализ Тема: Понятие функции (основные определения, классификация, основные характеристики поведения) Лектор Рожкова С.В. 2012 г. Литература Пискунов Н.С. Дифференциальное
Занятие 7 Теоремы о среднем. Правило Лопиталя 7. Теоремы о среднем Теоремы о среднем это три теоремы: Ролля, Лагранжа и Коши, каждая следующая из которых обобщает предыдущую. Эти теоремы называют также
Лекция подготовлена доц Мусиной МВ Непрерывность функции Пусть функция y = f(x) определена в точке x и в некоторой окрестности этой точки Функция y = f(x) называется непрерывной в точке x, если существует
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ Понятие производной, ее геометрический и физический смысл Задачи, приводящие к понятию производной Определение Касательной S к линии y f (x) в точке A x ; f (
13. Частные производные высших порядков Пусть = имеет и определенные на D O. Функции и называют также частными производными первого порядка функции или первыми частными производными функции. и в общем
Функции и называют также частными производными первого порядка функции или первыми частными производными функции. и в общем
Министерство образования Республики Беларусь УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ ЯНКИ КУПАЛЫ» Ю.Ю. Гнездовский, В. Н. Горбузов, П.Ф. Проневич ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ
Лекция Глава Множества и операции над ними Понятие множества Понятие множество относится к наиболее первичным понятиям математики не определяемым через более простые Под множеством понимают совокупность
Лекция 8 Дифференцирование сложной функции Рассмотрим сложную функцию t t t f где ϕ t t t t t t t f t t t t t t t t t Теорема Пусть функции дифференцируемы в некоторой точке N t t t а функция f дифференцируема
Лекция 3 Экстремум функции нескольких переменных Пусть функция нескольких переменных u = f (x, x) определена в области D, и точка x (x, x) = принадлежит данной области Функция u = f (x, x) имеет
Вопрос. Неравенства, система линейных неравенств Рассмотрим выражения, которые содержат знак неравенства и переменную:. >, — +х -это линейные неравенств с одной переменной х.. 0 — квадратное неравенство.
Неравенства, система линейных неравенств Рассмотрим выражения, которые содержат знак неравенства и переменную:. >, — +х -это линейные неравенств с одной переменной х.. 0 — квадратное неравенство.
РАЗДЕЛ ЗАДАЧИ С ПАРАМЕТРАМИ Комментарий Задачи с параметрами традиционно являются сложными заданиями в структуре ЕГЭ, требующими от абитуриента не только владения всеми методами и приемам решения различных
2.2.7. Применение дифференциала к приближенным вычислениям. Дифференциал функции y = зависит от х и является главной частью приращения х. Также можно воспользоваться формулой: dy d Тогда абсолютная погрешность:
Глава 6 Дифференциальное исчисление функции одной переменной Задачи приводящие к понятию производной Задача о скорости неравномерного прямолинейного движения S — закон неравномерного прямолинейного движения
Прямая на плоскости Общее уравнение прямой. Прежде чем вводить общее уравнение прямой на плоскости введем общее определение линии. Определение. Уравнение вида F(x,y)=0 (1) называется уравнением линии L
Определение. Уравнение вида F(x,y)=0 (1) называется уравнением линии L
КОМИТЕТ ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ЛЕНИНГРАДСКОЙ ОБЛАСТИ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ЛЕНИНГРАДСКОЙ ОБЛАСТИ «ВОЛХОВСКИЙ АЛЮМИНИЕВЫЙ КОЛЛЕДЖ» Методическое
Производная и правила дифференцирования Пусть функция y = f получила приращение y f 0 f 0 соответствующее приращению аргумента 0 Определение Если существует предел отношения приращения функции y к вызвавшему
ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ Московский государственный технический университет имени Н.Э. Баумана Факультет «Фундаментальные науки» Кафедра «Математическое моделирование» À.Í. Êàíàòíèêîâ, À.Ï. Êðèùåíêî
ОБРАТНЫЕ ФУНКЦИИ Задачи, в которых участвуют обратные функции, встречаются в самых различных разделах математики и в ее приложениях Важную область математики составляют обратные задачи в теории интегральных
Система задач по теме «Уравнение касательной» Определите знак углового коэффициента касательной, проведенной к графику функции y f (), в точках с абсциссами a, b, c а) б) Укажите точки, в которых производная
Что такое обратная функция? Как найти функцию, обратную данной?
Определение
.
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо :
1) В формулу функции вместо y подставить x, вместо x — y:
2) Из полученного равенства выразить y через x:
Найти функцию, обратную функции y=2x-6.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — . Графиком линейной функции является . Для построения прямой берём две точки.
Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение.


 Решение уравнений с модулем. Математика 5 класса, повторение. Урок по математике для 6 класса. Определение модуля числа, примеры на модуль числа. Решить уравнение. Подготовка к контрольным, ЕГЭ. Форма заявки на участие. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен. Категория: Презентации по математике.
Решение уравнений с модулем. Математика 5 класса, повторение. Урок по математике для 6 класса. Определение модуля числа, примеры на модуль числа. Решить уравнение. Подготовка к контрольным, ЕГЭ. Форма заявки на участие. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен. Категория: Презентации по математике. т поглазова 3 класс
т поглазова 3 класс

 08.21, 3:18:11 по восточному поясному времени
08.21, 3:18:11 по восточному поясному времени Чтобы ввести , введите U.
Чтобы ввести , введите U.



 9{2}}\) = \(\sqrt{64}\)
9{2}}\) = \(\sqrt{64}\)  Когда число подставляется в уравнение и упрощается, левая часть уравнения и правая часть уравнения не равны; другими словами, это не истинное числовое предложение. Поскольку число 6 не удовлетворяет уравнению, оно не является решением уравнения.
Когда число подставляется в уравнение и упрощается, левая часть уравнения и правая часть уравнения не равны; другими словами, это не истинное числовое предложение. Поскольку число 6 не удовлетворяет уравнению, оно не является решением уравнения.
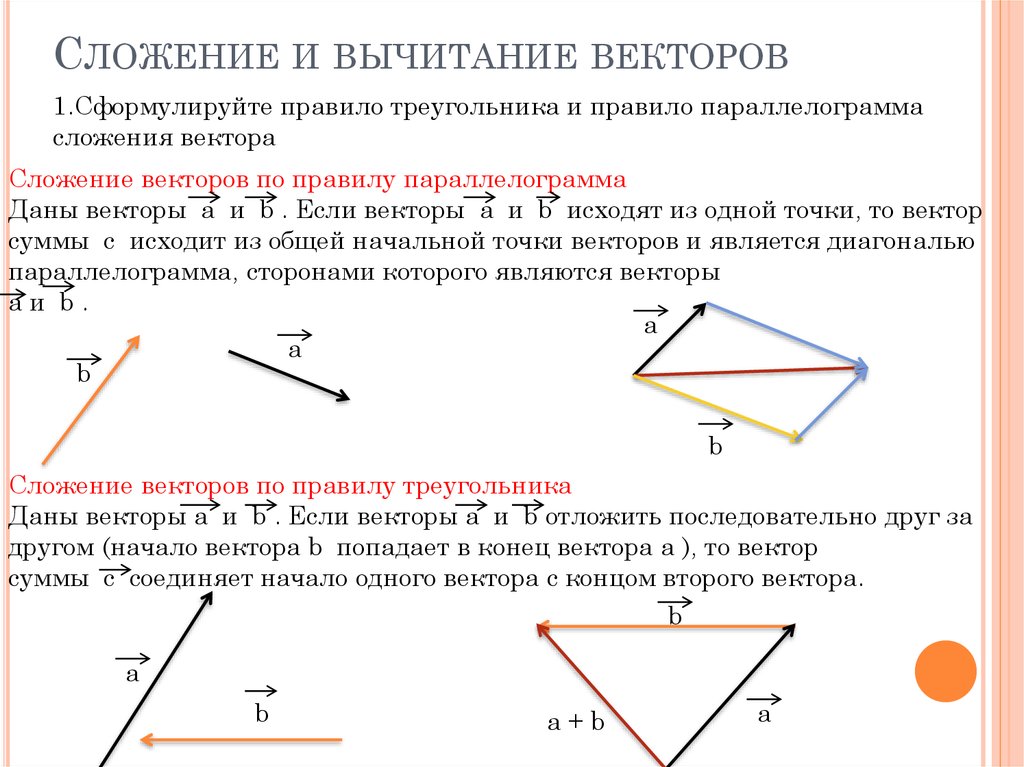 Таким образом, начальная точка вектора x+y будет точка A, а конечная точка — будет точка D’, которая вычисляется из выражения в (4).
Таким образом, начальная точка вектора x+y будет точка A, а конечная точка — будет точка D’, которая вычисляется из выражения в (4).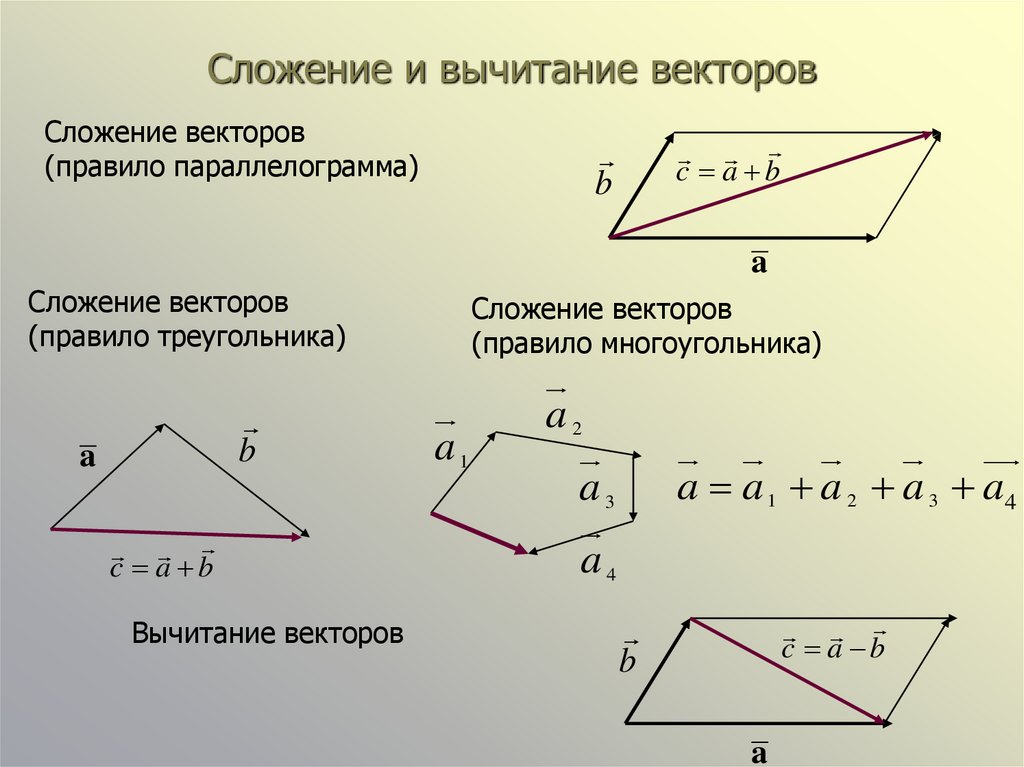
 Наряду с кольцами и полями, одним из важнейших понятий в математике, физике и технике является Вектор. Эволюция этого понятия — от Направленного отрезка до сложнейших Векторных пространств — история интересная и поучительная.
Наряду с кольцами и полями, одним из важнейших понятий в математике, физике и технике является Вектор. Эволюция этого понятия — от Направленного отрезка до сложнейших Векторных пространств — история интересная и поучительная. 35). При этом, каковы бы ни были векторы , , и числа K, I, всегда выполняются следующие равенства:
35). При этом, каковы бы ни были векторы , , и числа K, I, всегда выполняются следующие равенства: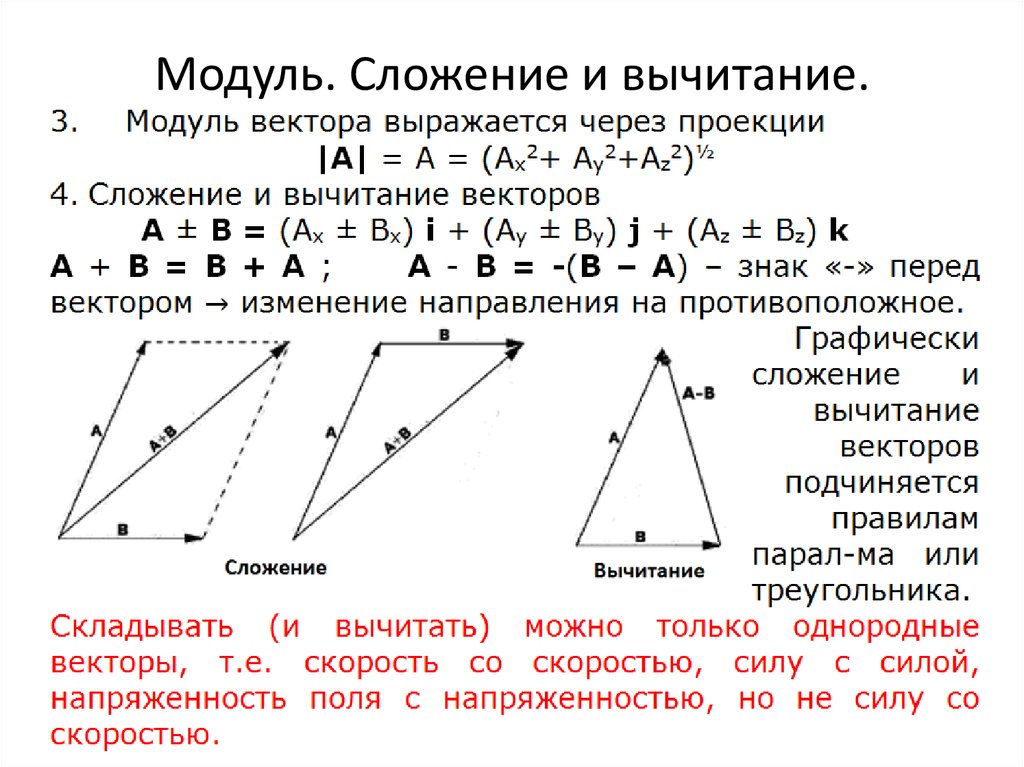
 Так мы приходим к Пространству событий — Одному из основных понятий современной физики. Другой пример. Всякий технологический процесс характеризуется набором различных параметров, которые фиксируются приборами, показывающими время, скорость процесса, давление, вязкость и т. п. Допустим, что таких параметров 10. Тогда состояние процесса определяется набором из десяти чисел, т. е. десятимерным вектором.
Так мы приходим к Пространству событий — Одному из основных понятий современной физики. Другой пример. Всякий технологический процесс характеризуется набором различных параметров, которые фиксируются приборами, показывающими время, скорость процесса, давление, вязкость и т. п. Допустим, что таких параметров 10. Тогда состояние процесса определяется набором из десяти чисел, т. е. десятимерным вектором. Термин «векторное поле» возник в физике, и его смысл вполне соответствует значению этого слова в обычном языке. Мы представляем себе поле как некоторый участок земли, засеянный, скажем, пшеницей. Теперь представим себе, что колос пшеницы — это вектор, и что колосья (векторы) растут в каждой точке участка. Это и будет векторное поле, причем не обязательно параллельное. Параллельное поле получается в случае, когда все «колоски» параллельны и имеют одинаковую длину.
Термин «векторное поле» возник в физике, и его смысл вполне соответствует значению этого слова в обычном языке. Мы представляем себе поле как некоторый участок земли, засеянный, скажем, пшеницей. Теперь представим себе, что колос пшеницы — это вектор, и что колосья (векторы) растут в каждой точке участка. Это и будет векторное поле, причем не обязательно параллельное. Параллельное поле получается в случае, когда все «колоски» параллельны и имеют одинаковую длину.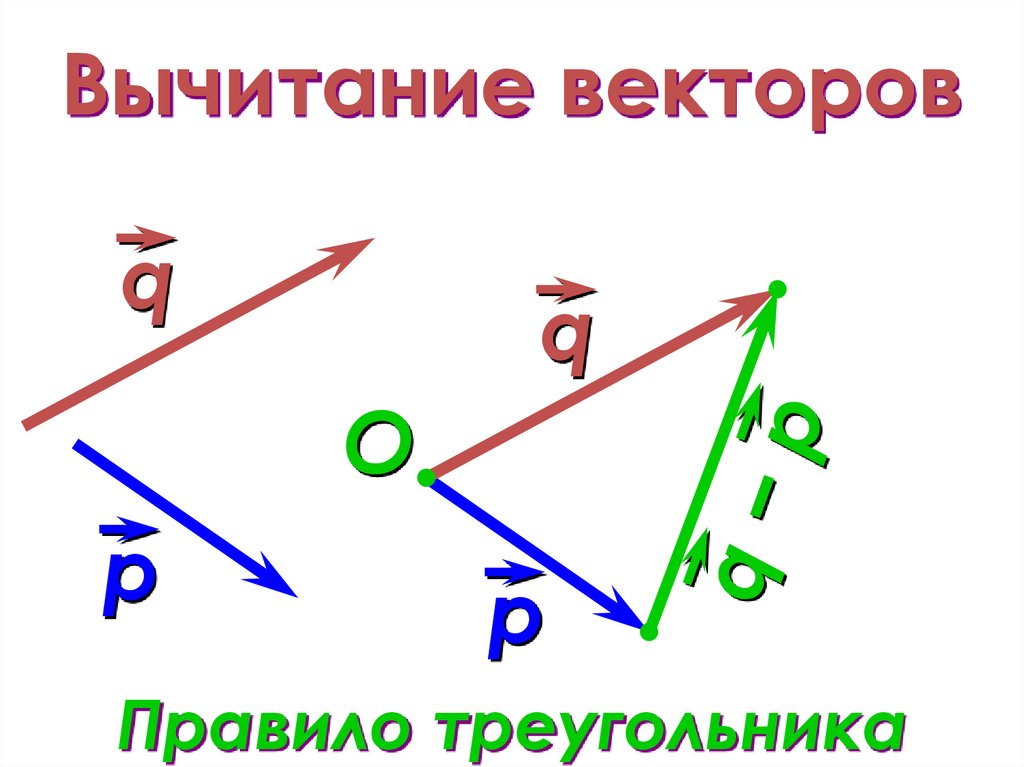
 Наконец, нарисуйте прямую линию от начала до начала последнего вектора в цепочке. Эта новая строка является векторным результатом сложения этих векторов.
Наконец, нарисуйте прямую линию от начала до начала последнего вектора в цепочке. Эта новая строка является векторным результатом сложения этих векторов.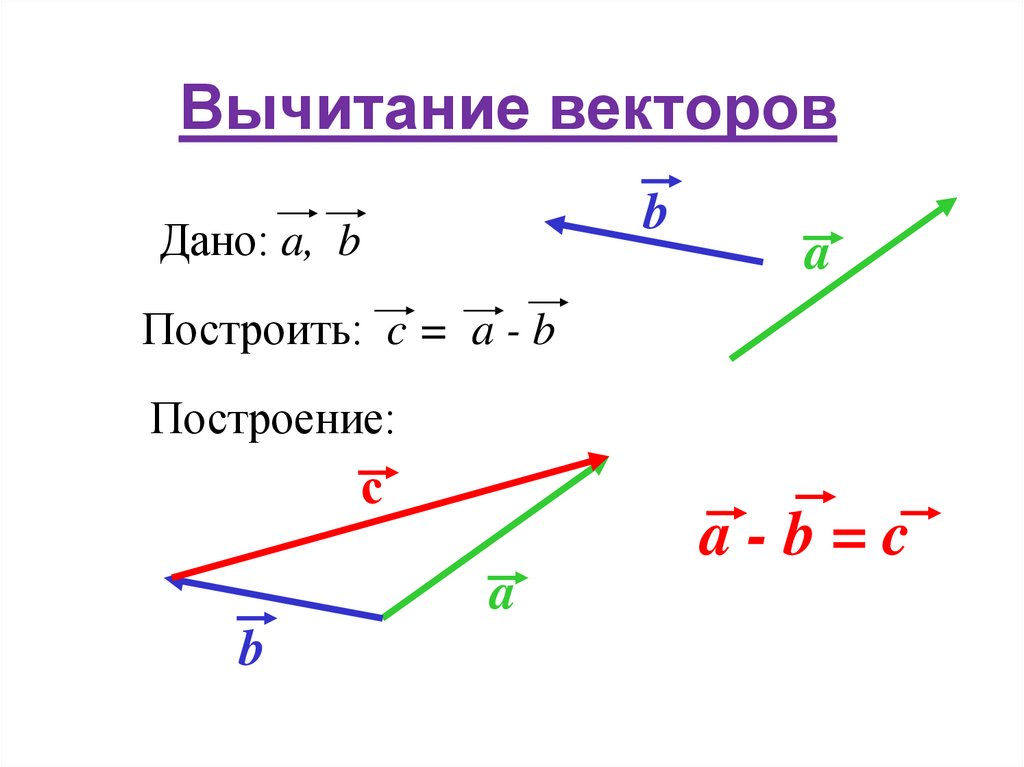

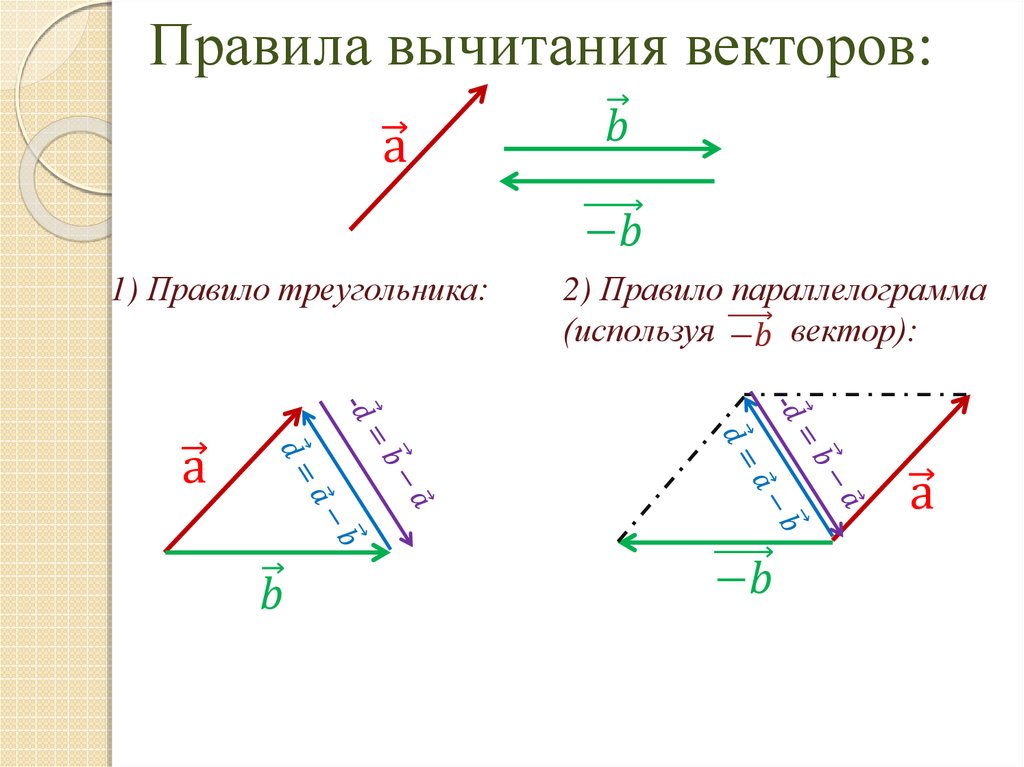
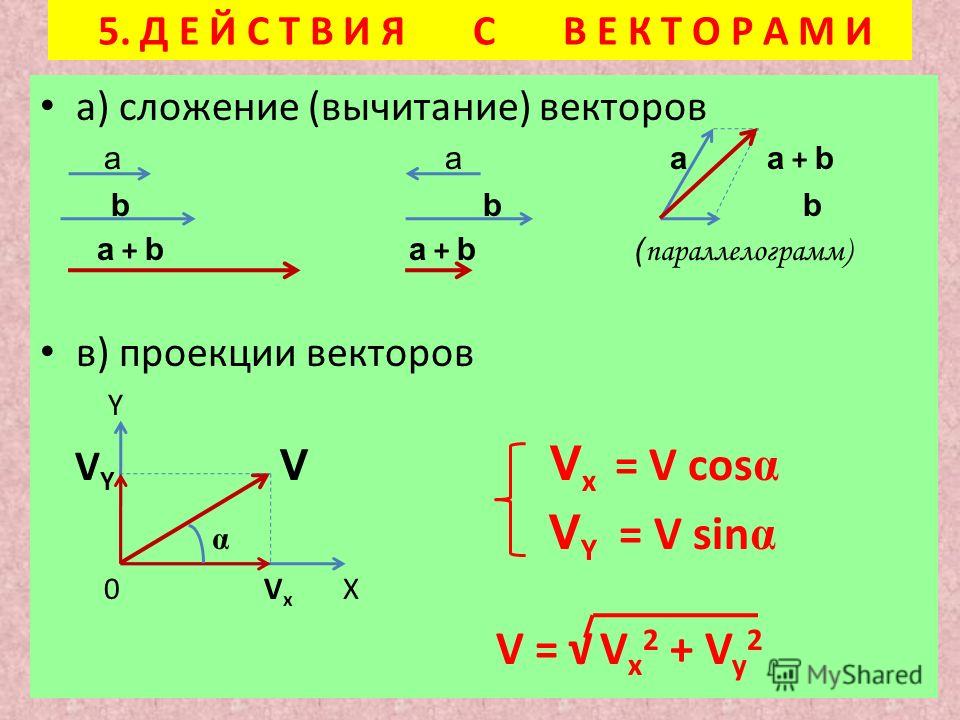 Мы произвольно присвоили отрицательное значение направлению, в котором двигался Синий № 5. Ответ был отрицательным, поэтому результирующая сила указывает в направлении, в котором пинал Синий № 5. Назовем это подальше от синего № 5.
Мы произвольно присвоили отрицательное значение направлению, в котором двигался Синий № 5. Ответ был отрицательным, поэтому результирующая сила указывает в направлении, в котором пинал Синий № 5. Назовем это подальше от синего № 5.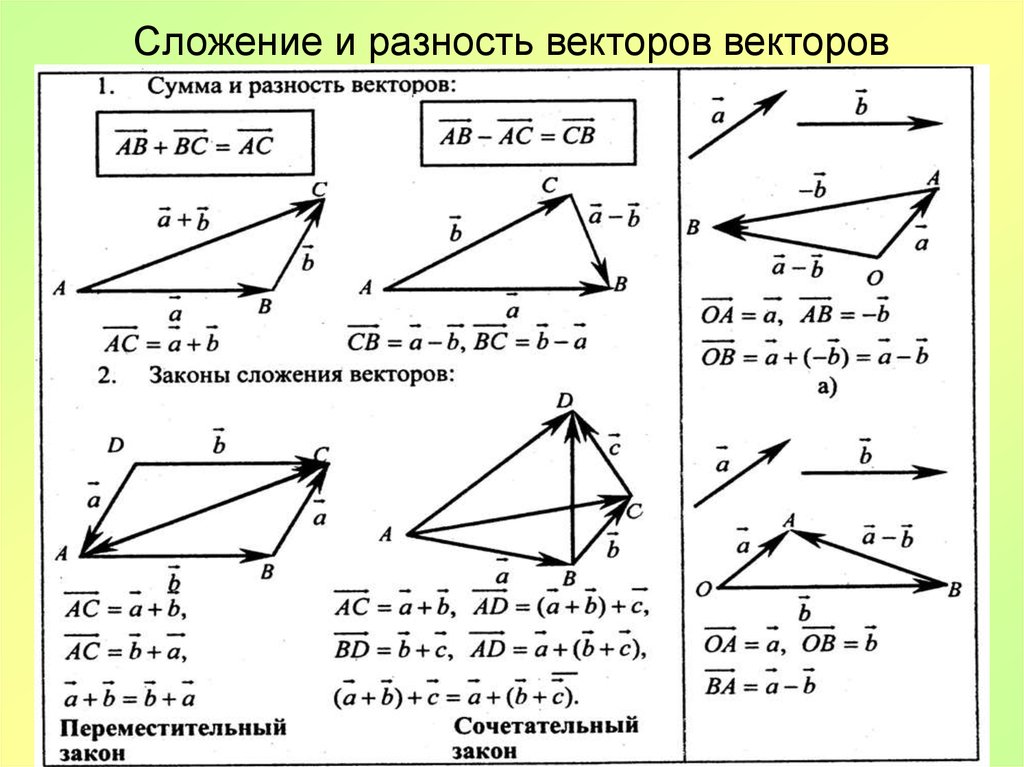
 1
1 8
8 3
3 19
19 14
14 Как получить доступ к AST вызываемых функций?
Как получить доступ к AST вызываемых функций?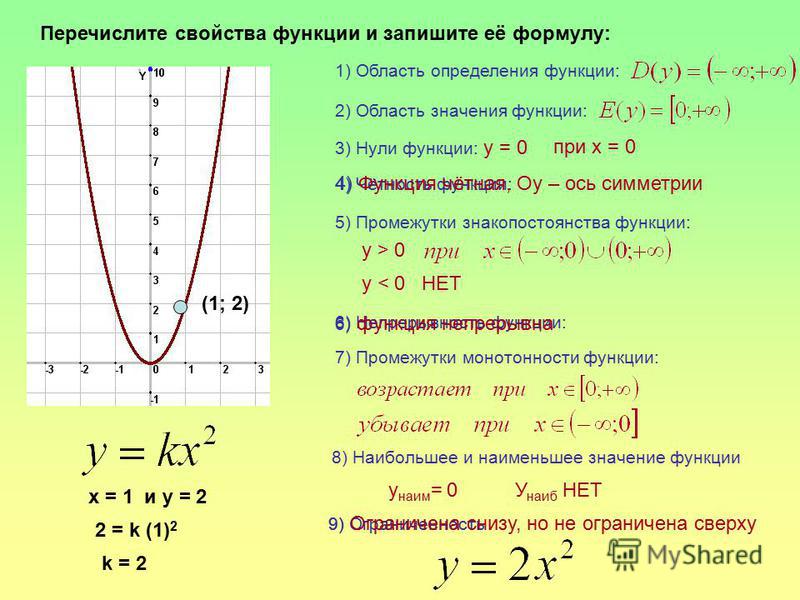
 Например, выполнение type(test.test_funt) вернет метод.
Например, выполнение type(test.test_funt) вернет метод.

 По правилу умножения получаем ответ: 9·10·2 = 180. (слайд
7)
По правилу умножения получаем ответ: 9·10·2 = 180. (слайд
7) Таким образом,
размещения отличаются друг от друга не только порядком расположения элементов,
но и тем, какие именно k элементов
выбраны в комбинацию. (слайд 11)
Таким образом,
размещения отличаются друг от друга не только порядком расположения элементов,
но и тем, какие именно k элементов
выбраны в комбинацию. (слайд 11)
 (слайд 15)Каждый
такой способ это перестановка из 10 элементов. Всего таких перестановок будет
(слайд 15)Каждый
такой способ это перестановка из 10 элементов. Всего таких перестановок будет Число всех перестановок из n элементов равно
Число всех перестановок из n элементов равно Если мальчики сядут на нечетные места, то существуют Р5 способов их расположения. Столькими же способами могут расположиться девочки на
четных местах. Каждому способу расположения мальчиков соответствует Р5 способов расположения девочек.
Если мальчики сядут на нечетные места, то существуют Р5 способов их расположения. Столькими же способами могут расположиться девочки на
четных местах. Каждому способу расположения мальчиков соответствует Р5 способов расположения девочек.
 (слайд 30)30 книг стоит на книжной полке, из них 27 различных книг и
одного автора три книги. Сколькими способами можно расставить эти книги на
полке так, чтобы книги одного автора стояли рядом?
(слайд 30)30 книг стоит на книжной полке, из них 27 различных книг и
одного автора три книги. Сколькими способами можно расставить эти книги на
полке так, чтобы книги одного автора стояли рядом? а) 90=2·5·9. Среди множителей числа 30! есть числа 2, 5 и 9. значит, число 30!
делится на 90.
а) 90=2·5·9. Среди множителей числа 30! есть числа 2, 5 и 9. значит, число 30!
делится на 90.
 Такие задачи не всегда являются полностью искусственными. Сайт tproger.ru рассказал, какие популярные учебные задания пригодятся в настоящей работе.
Такие задачи не всегда являются полностью искусственными. Сайт tproger.ru рассказал, какие популярные учебные задания пригодятся в настоящей работе.


 Сколько шариков у Стьюи?
Сколько шариков у Стьюи? Объяснение:
Объяснение:



 Words, затем передайте HTML любому из API-интерфейсов Aspose.Total, например Aspose.Cells, Aspose.PDF, Aspose.Email, Aspose.Slides, Aspose.Diagram, Aspose.Tasks, Aspose.3D, Aspose.HTML, чтобы экспортировать результат в более чем 100 популярных форматов файлов.
Words, затем передайте HTML любому из API-интерфейсов Aspose.Total, например Aspose.Cells, Aspose.PDF, Aspose.Email, Aspose.Slides, Aspose.Diagram, Aspose.Tasks, Aspose.3D, Aspose.HTML, чтобы экспортировать результат в более чем 100 популярных форматов файлов. Total REST?
Total REST? Total Cloud также доступен в виде контейнера Docker. Попробуйте использовать его с cURL, если требуемый SDK еще не доступен.
Total Cloud также доступен в виде контейнера Docker. Попробуйте использовать его с cURL, если требуемый SDK еще не доступен. Весит оно всего 30 килобайт и со своей единственной задачей справляется на ура.
Весит оно всего 30 килобайт и со своей единственной задачей справляется на ура.
 Так что, если вам важен 100% результат то он стоит того, что бы за него заплатить.
Так что, если вам важен 100% результат то он стоит того, что бы за него заплатить. Редактируйте, заполняйте, подписывайте и делитесь — на любом устройстве.
Редактируйте, заполняйте, подписывайте и делитесь — на любом устройстве. д.
д. Другими словами, результаты поиска Tropics будут отображаться в режиме полного слова, как и результаты поиска Wasp. Он включает в себя: — Функции обработки текста для преобразования документов JPG в Word — Предварительный просмотр и редактирование документа Word в конвертере JPG в Word — Копирование, вставка, перемещение, выбор, вырезание, вставка данных и вставка изображений в конвертере JPG в Word — Копирование , Вставка, Сохранить, Добавить в Microsoft Word и Копировать как текст с тегами — Перетащите, чтобы выбрать отдельные части JPG в документы Word — Простая в использовании панель инструментов с удобными параметрами
• Простой в использовании пользовательский интерфейс — это та часть, от которой вы зависите при преобразовании файлов .JPEG. • Преобразование текстовых файлов в форматы JPG и Word и сохранение в форматах JPG и Word.
• Преобразование документов Word в документы Word, сохранение в формате Word и сохранение в формате JPG.
• Преобразование файлов JPG в документы Word и сохранение в формате JPG.
Другими словами, результаты поиска Tropics будут отображаться в режиме полного слова, как и результаты поиска Wasp. Он включает в себя: — Функции обработки текста для преобразования документов JPG в Word — Предварительный просмотр и редактирование документа Word в конвертере JPG в Word — Копирование, вставка, перемещение, выбор, вырезание, вставка данных и вставка изображений в конвертере JPG в Word — Копирование , Вставка, Сохранить, Добавить в Microsoft Word и Копировать как текст с тегами — Перетащите, чтобы выбрать отдельные части JPG в документы Word — Простая в использовании панель инструментов с удобными параметрами
• Простой в использовании пользовательский интерфейс — это та часть, от которой вы зависите при преобразовании файлов .JPEG. • Преобразование текстовых файлов в форматы JPG и Word и сохранение в форматах JPG и Word.
• Преобразование документов Word в документы Word, сохранение в формате Word и сохранение в формате JPG.
• Преобразование файлов JPG в документы Word и сохранение в формате JPG. • Поддержка преобразования нескольких фотографий (несколько изображений) в Word.
• Поддержка нескольких папок для преобразования отдельных файлов и изображений .JPG.
• Совместимость с компьютерами Mac OSX и Microsoft Windows. Важно: Если у вас возникнут проблемы с преобразованием изображений, предоставьте нам информацию, которая поможет нам исправить проблему, на supportdilbertapps.com. — Доступ ко всем мощным функциям приложения через мощный редактор PDF. — Преобразование документов, которое позволяет преобразовывать ваши документы (или только определенные части) в другие форматы (например, — Интеллектуальное индексирование: автоматически генерирует, хранит и управляет структурированными индексными файлами для хранения и доступа к вашим данным, таким как списки и карточки, и создает мощные карты, списки и листы на основе карт для хранения данных с использованием нескольких стопок карт — Мощный поиск по ключевому слову, дате, автору и т. д. — Поддержка новейших форматов PDF (включая XPS, OLE и ZIP) и PDF-документов.
• Поддержка преобразования нескольких фотографий (несколько изображений) в Word.
• Поддержка нескольких папок для преобразования отдельных файлов и изображений .JPG.
• Совместимость с компьютерами Mac OSX и Microsoft Windows. Важно: Если у вас возникнут проблемы с преобразованием изображений, предоставьте нам информацию, которая поможет нам исправить проблему, на supportdilbertapps.com. — Доступ ко всем мощным функциям приложения через мощный редактор PDF. — Преобразование документов, которое позволяет преобразовывать ваши документы (или только определенные части) в другие форматы (например, — Интеллектуальное индексирование: автоматически генерирует, хранит и управляет структурированными индексными файлами для хранения и доступа к вашим данным, таким как списки и карточки, и создает мощные карты, списки и листы на основе карт для хранения данных с использованием нескольких стопок карт — Мощный поиск по ключевому слову, дате, автору и т. д. — Поддержка новейших форматов PDF (включая XPS, OLE и ZIP) и PDF-документов.

 В окне предварительного просмотра щелкните меню «Файл», а затем выберите команду «Экспорт». В появившемся окне выберите JPEG в качестве формата и с помощью ползунка «Качество» измените сжатие, используемое для сохранения изображения.
В окне предварительного просмотра щелкните меню «Файл», а затем выберите команду «Экспорт». В появившемся окне выберите JPEG в качестве формата и с помощью ползунка «Качество» измените сжатие, используемое для сохранения изображения. NET
NET NET Imaging SDK > VB.NET > Преобразование Word в JPEG
NET Imaging SDK > VB.NET > Преобразование Word в JPEG  net mvc pdf: ASP.NET MVC PDF Viewer & Editor: просмотр, аннотирование, редактирование, редактирование PDF-документа в C# ASP.NET MVC
net mvc pdf: ASP.NET MVC PDF Viewer & Editor: просмотр, аннотирование, редактирование, редактирование PDF-документа в C# ASP.NET MVC  net
net  Перейдите на соответствующие страницы, чтобы получить руководство и примеры кодов VB.NET, которые вам нужны:
Перейдите на соответствующие страницы, чтобы получить руководство и примеры кодов VB.NET, которые вам нужны: NET, такие как Windows Form, веб-приложение ASP.NET и библиотеку классов VB.NET. Пакет страниц Word в формате (форматах) изображения Jpeg с использованием кодировок VB.NET
NET, такие как Windows Form, веб-приложение ASP.NET и библиотеку классов VB.NET. Пакет страниц Word в формате (форматах) изображения Jpeg с использованием кодировок VB.NET NET для преобразования Word в Jpeg
NET для преобразования Word в Jpeg
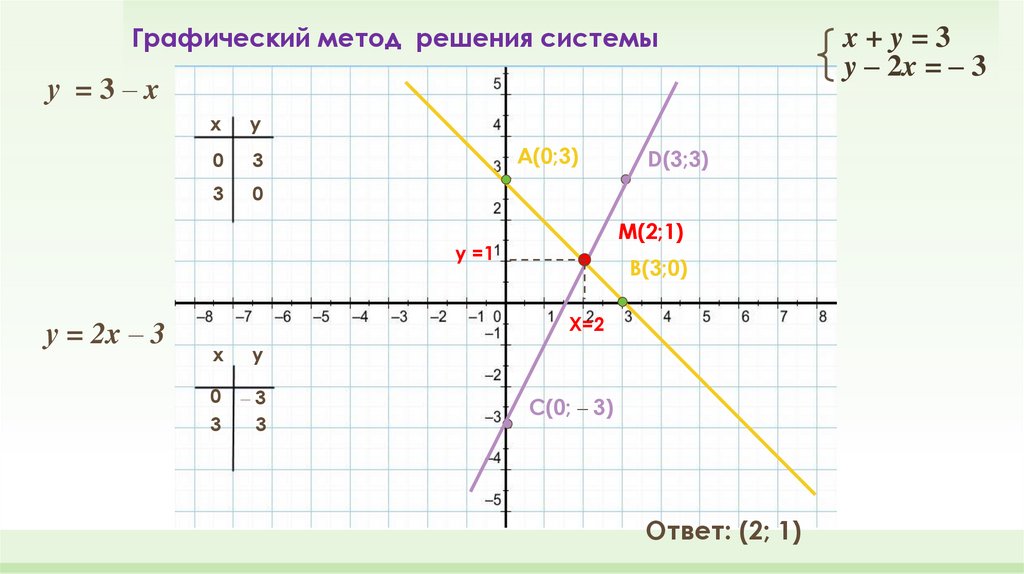 Решите графически задачу линейного программирования на максимум, если целевая функция Z(X) = 8x+9y, а
Решите графически задачу линейного программирования на максимум, если целевая функция Z(X) = 8x+9y, а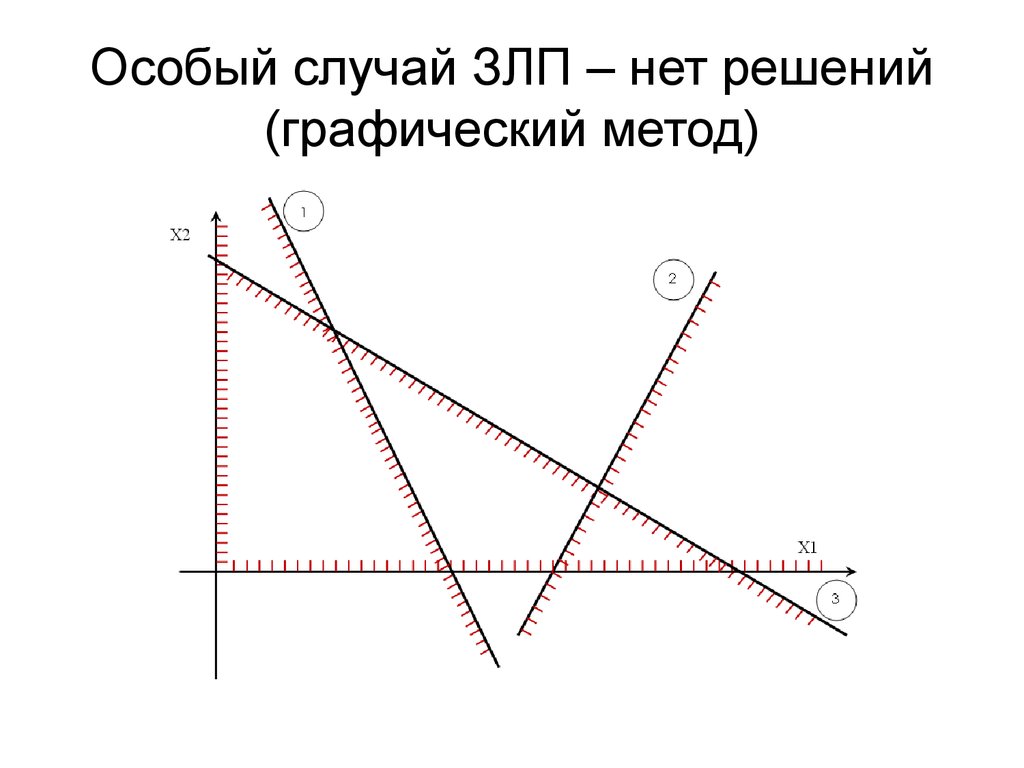
 Ограниченное
использование графического метода
обусловлено сложностью построения
многогранника решений в трехмерном
пространстве (для задач с тремя
переменными), а графическое изображение
задачи с количеством переменных больше
трех вообще невозможно. Однако графический
метод позволяет выработать у студентов
наглядные представления о линейном
программирование и подтвердить
справедливость некоторых его теорем.
В дальнейшем мы будем рассматривать и
решать задачи линейного программирования
графическим методом только в двумерном
пространстве.
Ограниченное
использование графического метода
обусловлено сложностью построения
многогранника решений в трехмерном
пространстве (для задач с тремя
переменными), а графическое изображение
задачи с количеством переменных больше
трех вообще невозможно. Однако графический
метод позволяет выработать у студентов
наглядные представления о линейном
программирование и подтвердить
справедливость некоторых его теорем.
В дальнейшем мы будем рассматривать и
решать задачи линейного программирования
графическим методом только в двумерном
пространстве. Условие неотрицательности переменных
означает, что область допустимых решений
задачи принадлежит первому квадранту
системы координат двумерного пространства.
Целевая функция геометрически
интерпретируется как семья параллельных
прямых .
Условие неотрицательности переменных
означает, что область допустимых решений
задачи принадлежит первому квадранту
системы координат двумерного пространства.
Целевая функция геометрически
интерпретируется как семья параллельных
прямых .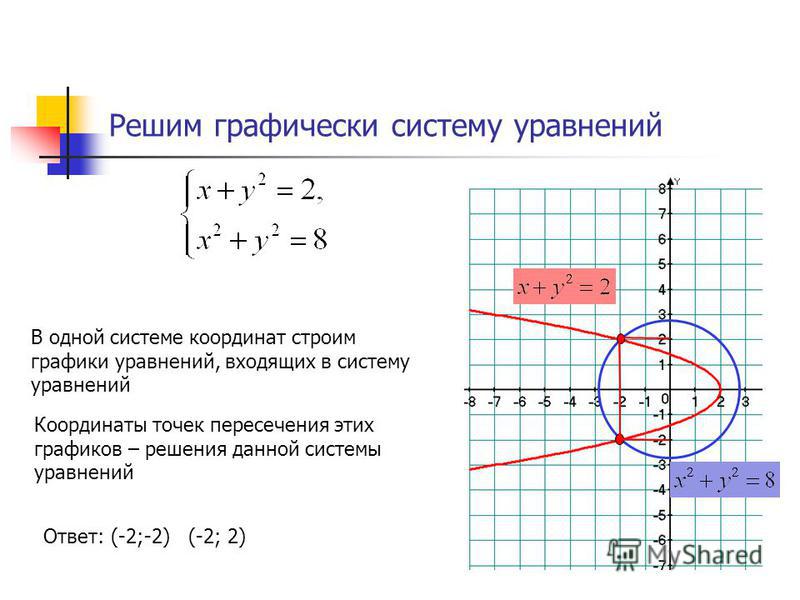 Аналогичным образом строим
полуплоскости для остальных неравенств
из системы ограничений задачи. В
результате пересечения этих полуплоскостей
получаем область допустимых решений –
многогранник ОABCD.
Аналогичным образом строим
полуплоскости для остальных неравенств
из системы ограничений задачи. В
результате пересечения этих полуплоскостей
получаем область допустимых решений –
многогранник ОABCD.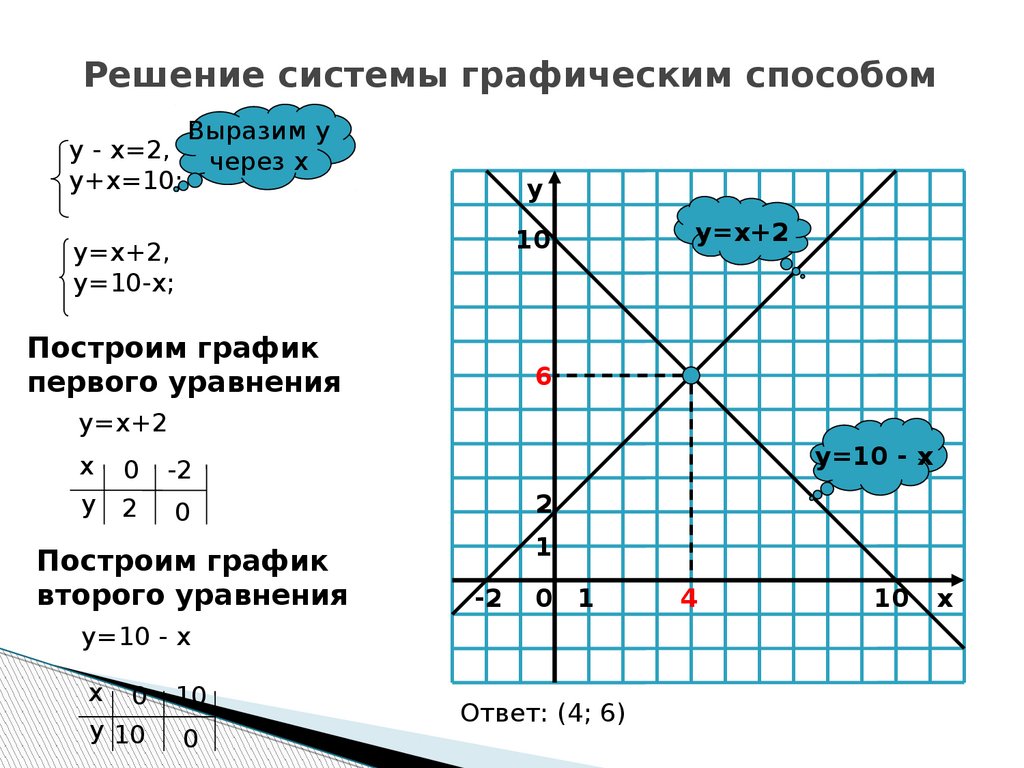 § 2.4)
допустимыми
базисными
решениями
данной задачи
являются
угловые
точки
многогранника
ОABCD,
а
по теореме
2
одна
(в отдельных случаях – две) из
этих точек
придает
максимального
значения
целевой
функции.
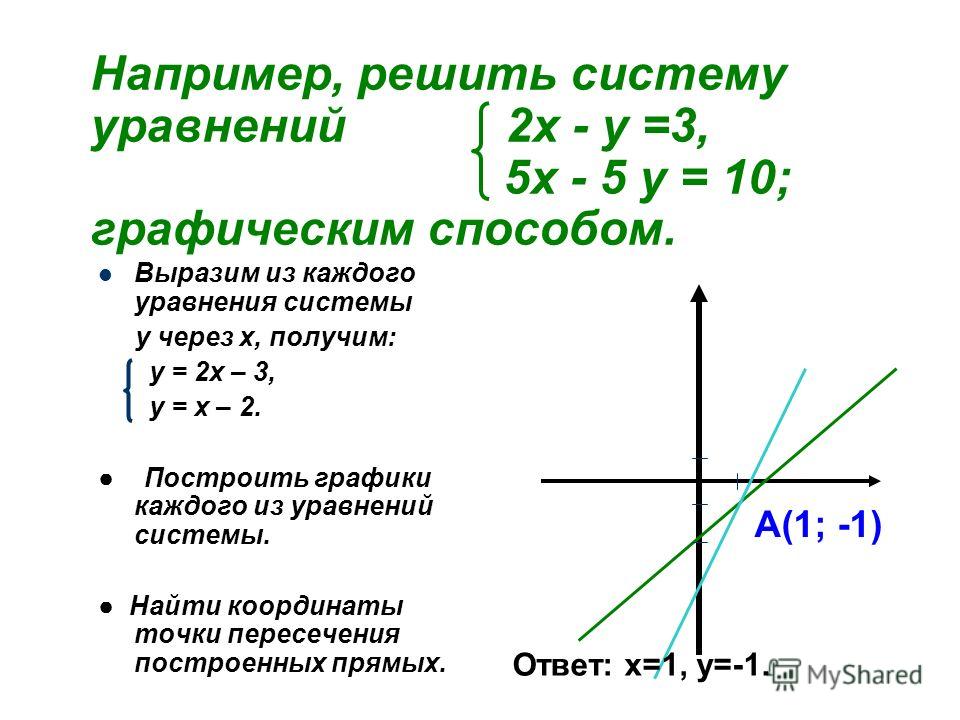
В
нашем примере максимального
значения целевая функция достигнет в точке
B,
т.е.
в
вершине многогранника
области
допустимых
решений, которая
является наиболее
отдаленной
от начала
координат,
если
двигаться
в направлении
вектора
.
§ 2.4)
допустимыми
базисными
решениями
данной задачи
являются
угловые
точки
многогранника
ОABCD,
а
по теореме
2
одна
(в отдельных случаях – две) из
этих точек
придает
максимального
значения
целевой
функции.
В
нашем примере максимального
значения целевая функция достигнет в точке
B,
т.е.
в
вершине многогранника
области
допустимых
решений, которая
является наиболее
отдаленной
от начала
координат,
если
двигаться
в направлении
вектора
.
 Однако в тех случаях, когда требуется большее количество переменных, можно использовать другие методы, такие как проецирование на плоскость.
Однако в тех случаях, когда требуется большее количество переменных, можно использовать другие методы, такие как проецирование на плоскость.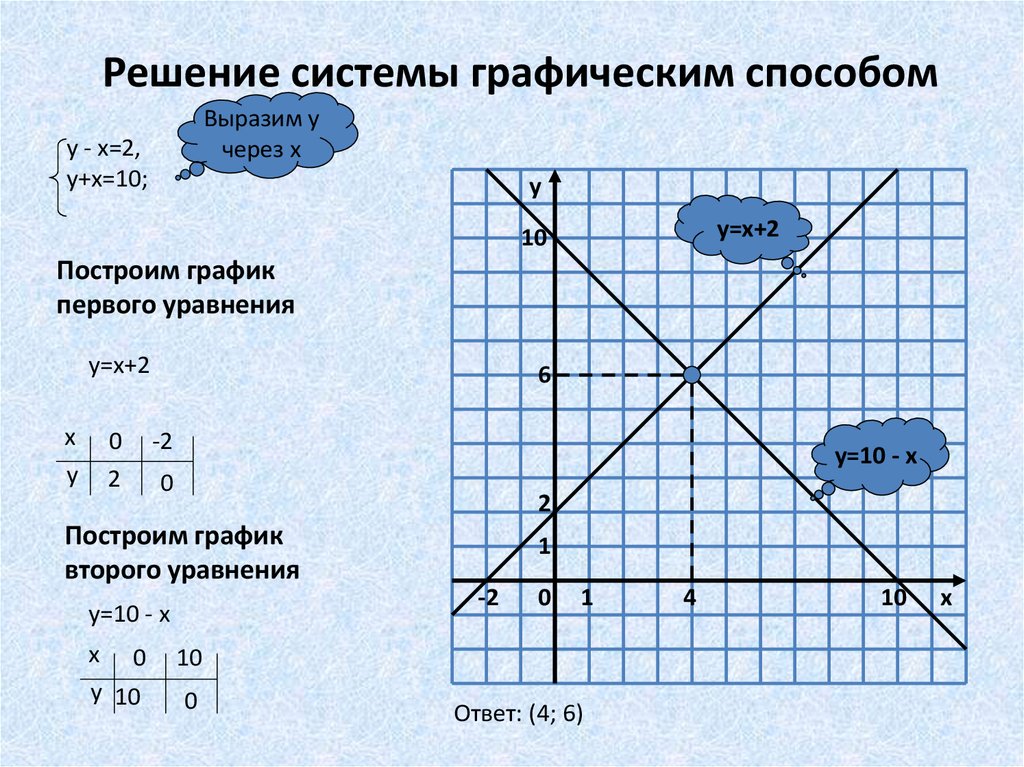
 Ткань Standard продается по цене 4000 долларов за метр, а ткань Premium — по 5000 долларов за метр. Если необходимо получить максимальную прибыль, сколько метров тканей Стандарт и Премиум необходимо произвести?
Ткань Standard продается по цене 4000 долларов за метр, а ткань Premium — по 5000 долларов за метр. Если необходимо получить максимальную прибыль, сколько метров тканей Стандарт и Премиум необходимо произвести?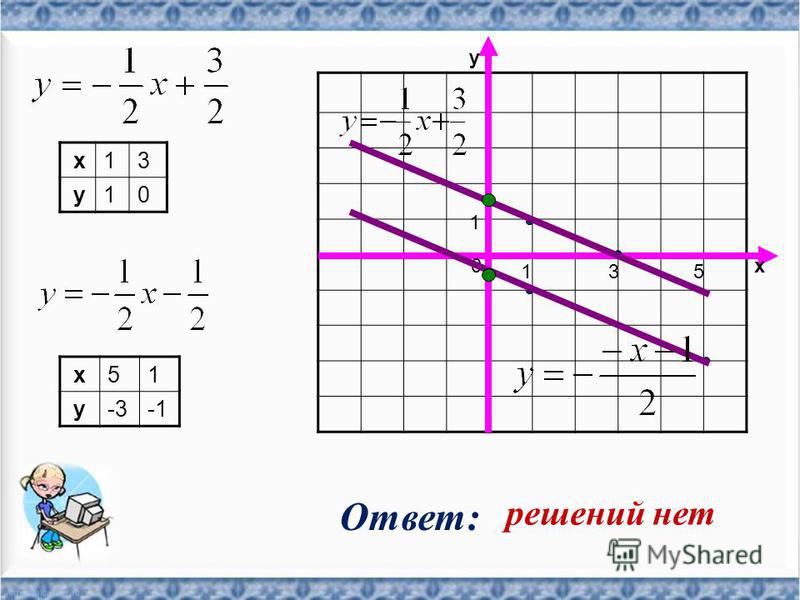
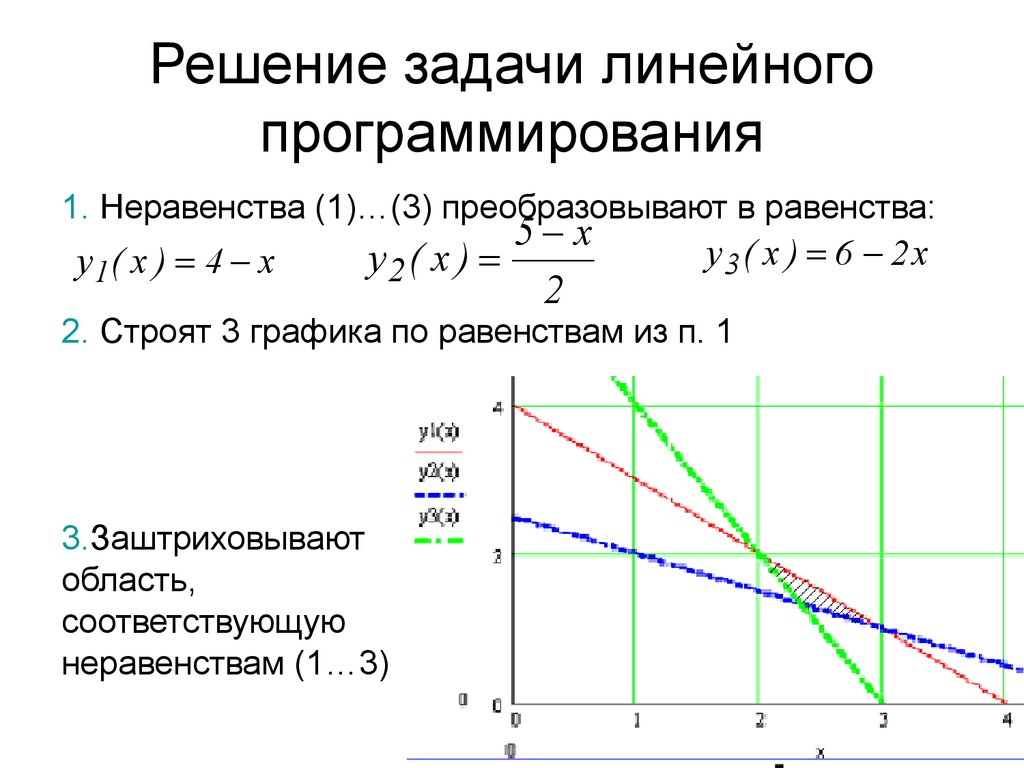 90 Constraint. Чтобы найти координаты, мы обычно устанавливаем одну из переменных в ноль, чтобы вторую было легче очистить.
90 Constraint. Чтобы найти координаты, мы обычно устанавливаем одну из переменных в ноль, чтобы вторую было легче очистить. y = 3000
y = 3000 /0,072
/0,072


 Во
избежание 4-х кратного повторения число
3999 записывается как MMMIM.
Во
избежание 4-х кратного повторения число
3999 записывается как MMMIM. д.
XX (20) — viginti (вигинти)
XXI (21) —
unus et viginti или viginti unus
XXII (22) — duo et viginti или
viginti duo и т.д.
XXVIII (28) — duodetriginta
(дуодэтригинта)
XXIX (29) — undetriginta
(ундэтригинта)
XXX (30) — triginta (тригинта)
XL
(40) — quadraginta (квадрагинта)
L (50) — quinquaginta
(квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX
(70) — septuaginta (сэптуагинта)
LXXX (80) — octoginta
(октогинтна)
XC (90) — nonaginta (нонагинта)
C
(100) — centum (центум)
CC (200) — ducenti (дуценти)
CCC
(300) — trecenti (трэценти)
CD (400) — quadrigenti
(квадригэнти)
D (500) — quingenti (квингэнти)
DC
(600) — sexcenti (сэксценти)
DCC (700) — septigenti
(сэптигэнти)
DCCC(800) — octingenti (октигенти)
CM
(DCCCC) (900) — nongenti (нонгэнти)
M (1000) — mille
(милле)
MM (2000) — duo milia (дуо милиа)
V (5000)
— quinque milia (квинквэ милиа)
X (10000) — decem
milia (дэцем милиа)
XX (20000) — viginti milia (вигинти
милиа)
C (1000000) — centum milia (центум милиа)
XI
(1000000) — decies centena milia (дэциэс центэна милиа)»
д.
XX (20) — viginti (вигинти)
XXI (21) —
unus et viginti или viginti unus
XXII (22) — duo et viginti или
viginti duo и т.д.
XXVIII (28) — duodetriginta
(дуодэтригинта)
XXIX (29) — undetriginta
(ундэтригинта)
XXX (30) — triginta (тригинта)
XL
(40) — quadraginta (квадрагинта)
L (50) — quinquaginta
(квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX
(70) — septuaginta (сэптуагинта)
LXXX (80) — octoginta
(октогинтна)
XC (90) — nonaginta (нонагинта)
C
(100) — centum (центум)
CC (200) — ducenti (дуценти)
CCC
(300) — trecenti (трэценти)
CD (400) — quadrigenti
(квадригэнти)
D (500) — quingenti (квингэнти)
DC
(600) — sexcenti (сэксценти)
DCC (700) — septigenti
(сэптигэнти)
DCCC(800) — octingenti (октигенти)
CM
(DCCCC) (900) — nongenti (нонгэнти)
M (1000) — mille
(милле)
MM (2000) — duo milia (дуо милиа)
V (5000)
— quinque milia (квинквэ милиа)
X (10000) — decem
milia (дэцем милиа)
XX (20000) — viginti milia (вигинти
милиа)
C (1000000) — centum milia (центум милиа)
XI
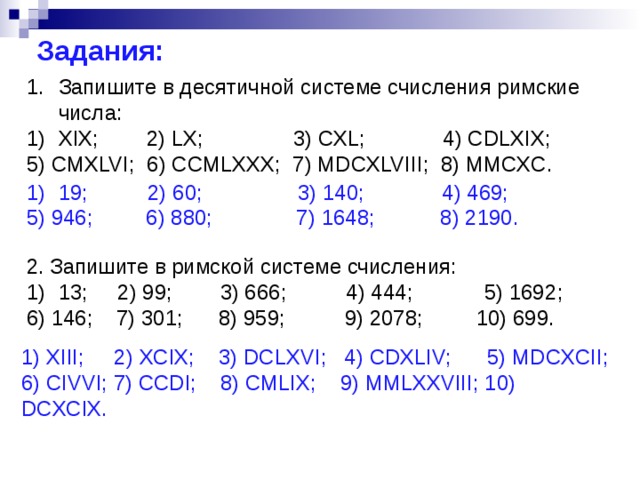
(1000000) — decies centena milia (дэциэс центэна милиа)» Они используются в исторических и военных дисциплинах, музыке, математике и других областях, где сложившиеся традиции и требования к оформлению материалов инспирируют применение римской числовой системы, в основном от 1 до 20. Потому для многих пользователей может возникнуть необходимость набрать какую-либо цифру в римском выражении, что может вызвать у некоторых людей определённые затруднения. В данном материале я постараюсь помочь таким пользователям и расскажу, как набрать римские цифры от 1 до 20, а также опишу особенности набора данных цифр в текстовом редакторе MS Word.
Они используются в исторических и военных дисциплинах, музыке, математике и других областях, где сложившиеся традиции и требования к оформлению материалов инспирируют применение римской числовой системы, в основном от 1 до 20. Потому для многих пользователей может возникнуть необходимость набрать какую-либо цифру в римском выражении, что может вызвать у некоторых людей определённые затруднения. В данном материале я постараюсь помочь таким пользователям и расскажу, как набрать римские цифры от 1 до 20, а также опишу особенности набора данных цифр в текстовом редакторе MS Word.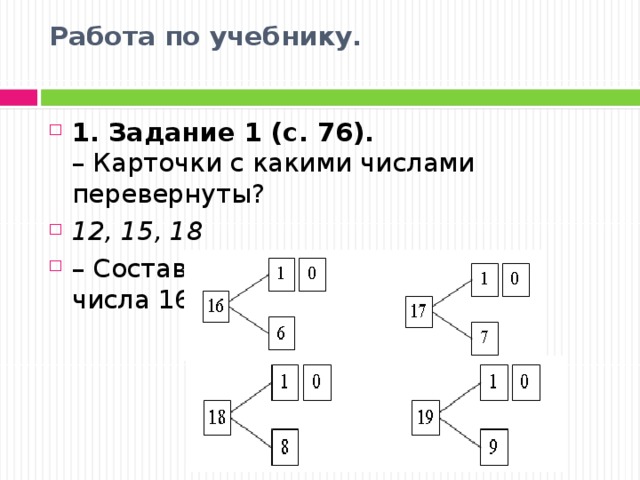
 Переключаемся на данную раскладку, жмём на «Caps Lock» слева для активации режима заглавных букв. Затем буквами набираем нужное нам число;
Переключаемся на данную раскладку, жмём на «Caps Lock» слева для активации режима заглавных букв. Затем буквами набираем нужное нам число;


 Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.
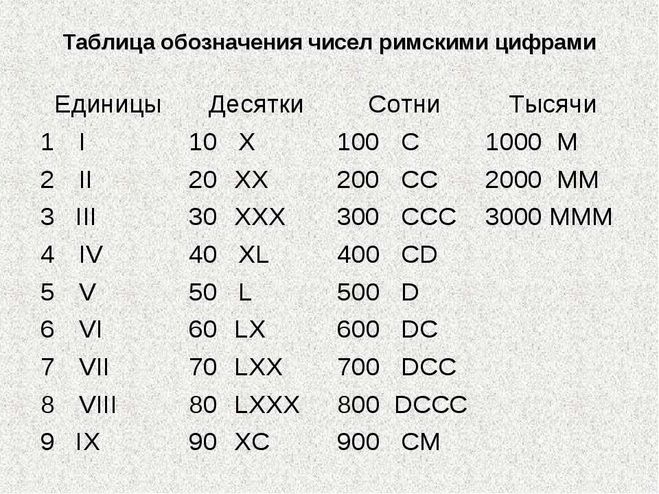
Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.  Это произошло потому, что римские цифры записать достаточно сложно, да и любые арифметические действия в римской системе выполнять гораздо сложнее, чем в арабской системе исчисления. Не смотря на то, что сегодня римская система не часто используется, это вовсе не значит, что она стала неактуальна. В большинстве случаев века римскими цифрами обозначают, а вот годы или точные даты принято писать арабскими цифрами.
Это произошло потому, что римские цифры записать достаточно сложно, да и любые арифметические действия в римской системе выполнять гораздо сложнее, чем в арабской системе исчисления. Не смотря на то, что сегодня римская система не часто используется, это вовсе не значит, что она стала неактуальна. В большинстве случаев века римскими цифрами обозначают, а вот годы или точные даты принято писать арабскими цифрами. Если меньшая цифра стоит перед большей, то используется принцип вычитания (меньшая цифра вычитается из большей).
Так, цифра 4 изображается как IV (то есть 5-1).
Если меньшая цифра стоит перед большей, то используется принцип вычитания (меньшая цифра вычитается из большей).
Так, цифра 4 изображается как IV (то есть 5-1).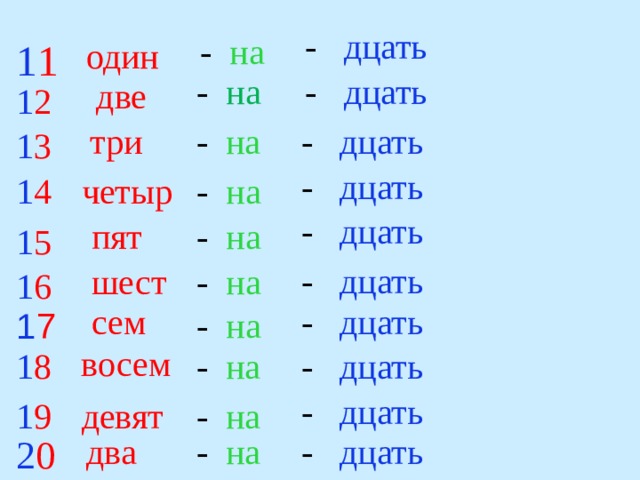 Цифры с одного до четырех напоминают вытянутые пальцы, цифру пять можно сравнить с раскрытой ладонью, где большой палец оттопырен. А цифра десять напоминает две скрещенные руки. В европейских странах при счете принято разгибать пальцы, а вот в России, наоборот, загибать.
Цифры с одного до четырех напоминают вытянутые пальцы, цифру пять можно сравнить с раскрытой ладонью, где большой палец оттопырен. А цифра десять напоминает две скрещенные руки. В европейских странах при счете принято разгибать пальцы, а вот в России, наоборот, загибать.

 В рамках форума также пройдут открытые лекции от экспертного сообщества, спортивные и культурно-массовые мероприятия.
В рамках форума также пройдут открытые лекции от экспертного сообщества, спортивные и культурно-массовые мероприятия.
 Поскольку в римской системе счисления нет нуля, час, минута и секунда в метках времени иногда становятся пустыми.
Поскольку в римской системе счисления нет нуля, час, минута и секунда в метках времени иногда становятся пустыми.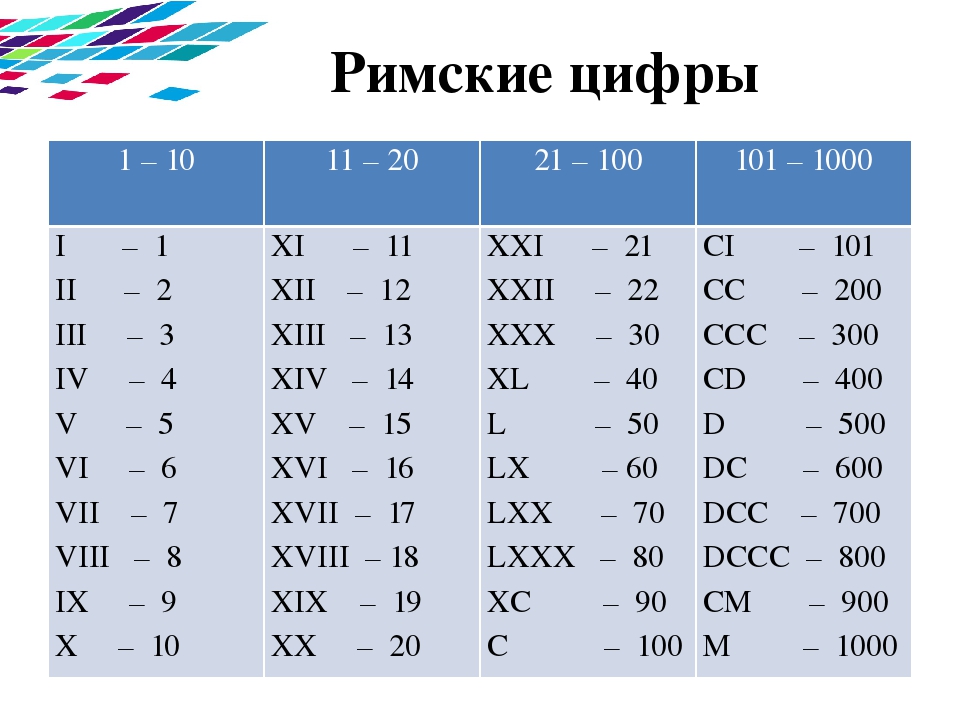 X
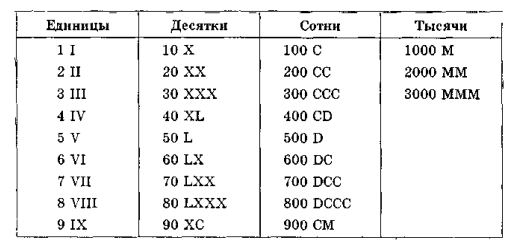
X Однако для чисел 4 и 9, вместо сложения используется вычитание, и меньшее число записывается перед большим числом: например, 14 записывается как XIV, т. е. 10 + 5 — 1, а 199 записывается как CXCIX, т. е. 100 + 100 — 10 + 10 — 1. Можно было бы возразить, что 199 было бы легче записать как CIC, но в соответствии с наиболее распространенным определения, вы можете вычесть только число, которое на один порядок меньше, чем числа, из которых вы вычитаете, а это означает, что IC для 99 неверен.
Однако для чисел 4 и 9, вместо сложения используется вычитание, и меньшее число записывается перед большим числом: например, 14 записывается как XIV, т. е. 10 + 5 — 1, а 199 записывается как CXCIX, т. е. 100 + 100 — 10 + 10 — 1. Можно было бы возразить, что 199 было бы легче записать как CIC, но в соответствии с наиболее распространенным определения, вы можете вычесть только число, которое на один порядок меньше, чем числа, из которых вы вычитаете, а это означает, что IC для 99 неверен.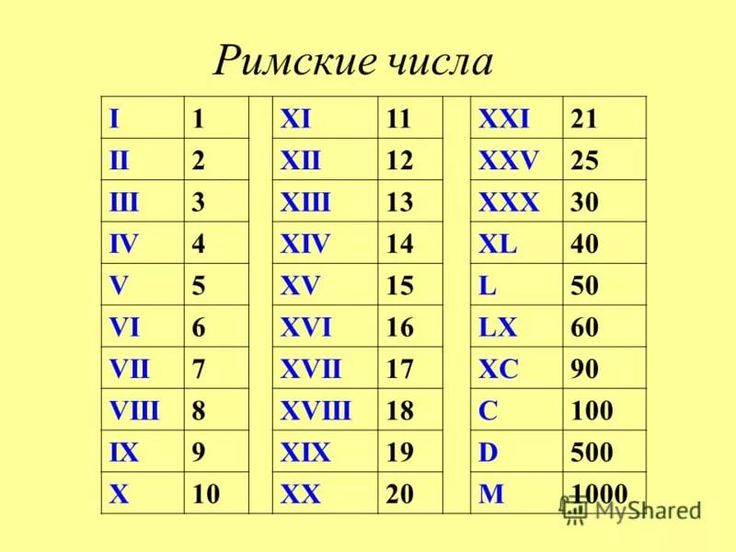
 Цены составляют долларов США долларов США.
Цены составляют долларов США долларов США.



 , , ,
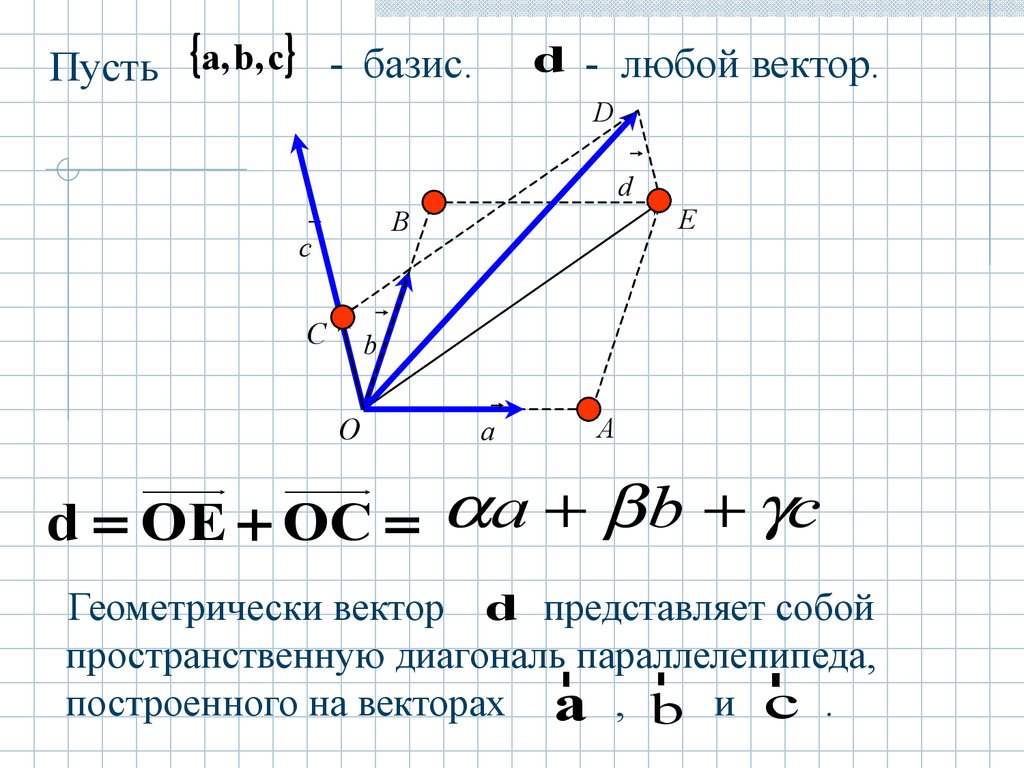
, , , Точка О — центр тяжести ABC.
Точка О — центр тяжести ABC. Т. е.,=++.
Т. е.,=++. 4) заданием базиса
,,и точкиО –
начала координат (affinis – смежный,
соседний).
4) заданием базиса
,,и точкиО –
начала координат (affinis – смежный,
соседний). Аффинная система координат на плоскости
определяет такое же соответствие между
точками и упорядоченными парами чисел.
Аффинная система координат на плоскости
определяет такое же соответствие между
точками и упорядоченными парами чисел. Эта длина берется со знаком плюс,
если направление от
ксовпадает с направлением осиl и минус в противном
случае (рис. 6). Аналогично определяется
проекция одного вектора на другой.
Эта длина берется со знаком плюс,
если направление от
ксовпадает с направлением осиl и минус в противном
случае (рис. 6). Аналогично определяется
проекция одного вектора на другой. 8
8 } = \alpha_k$$
} = \alpha_k$$ Если $e_k$ не ортонормированы, а только ортогональны, то: 92\\
\подразумевает a_k=\frac{a_k e_k\cdot e_k}{|e_k\cdot e_k|}\\
\подразумевает a_k=\frac{e_k\cdot v}{|e_k\cdot e_k|}
\end{выравнивание}
Если $e_k$ не ортонормированы, а только ортогональны, то: 92\\
\подразумевает a_k=\frac{a_k e_k\cdot e_k}{|e_k\cdot e_k|}\\
\подразумевает a_k=\frac{e_k\cdot v}{|e_k\cdot e_k|}
\end{выравнивание}
 50? Можно также сказать, что 1 единица на чертеже равна 100 единицам в реальной жизни. Итак, если бы мы рисовали стол шириной 100 см и длиной 200 см в масштабе 1:50, вы бы нарисовали стол шириной 2 см и длиной 4 см на листе бумаги. Это получается путем деления реального размера (100 см) на 50 (масштаб 1:50).
50? Можно также сказать, что 1 единица на чертеже равна 100 единицам в реальной жизни. Итак, если бы мы рисовали стол шириной 100 см и длиной 200 см в масштабе 1:50, вы бы нарисовали стол шириной 2 см и длиной 4 см на листе бумаги. Это получается путем деления реального размера (100 см) на 50 (масштаб 1:50).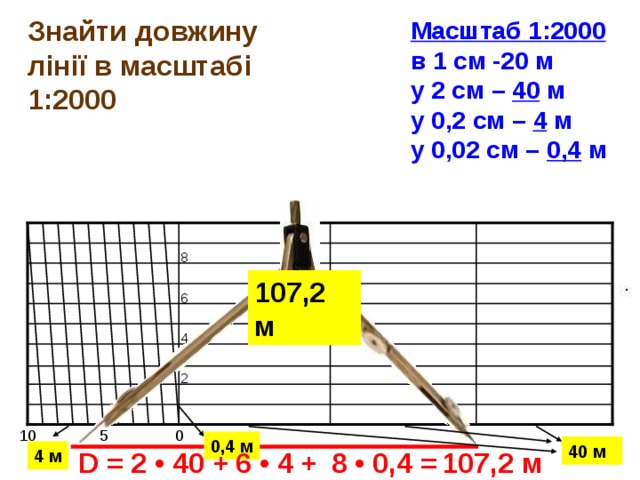 Умножение 16 на 0.5 дает 8, поэтому 8/16 равняется 0.5 дюйма.
Умножение 16 на 0.5 дает 8, поэтому 8/16 равняется 0.5 дюйма. Чтобы получить ответ, разделите цифру в сантиметрах на 2.54. Итак, 50 ÷ 2.54 = 19.685 дюйма.
Чтобы получить ответ, разделите цифру в сантиметрах на 2.54. Итак, 50 ÷ 2.54 = 19.685 дюйма.
 08.2022 21:16:50
08.2022 21:16:50 Diorama)11 декабря 2022 года, 17:33
Diorama)11 декабря 2022 года, 17:33 01.2023 09:26:04
01.2023 09:26:04 01.2023 17:15:16
01.2023 17:15:16 (Taiga13)15 мая 2021 года, 19:00
(Taiga13)15 мая 2021 года, 19:00 09.2022 21:24:02
09.2022 21:24:02 .. Кто во что, играется, делимся впечатлениями, колемся… (Михаил Кукота)31 августа 2022 года, 19:25
.. Кто во что, играется, делимся впечатлениями, колемся… (Михаил Кукота)31 августа 2022 года, 19:25 )3 августа 2022 года, 18:07
)3 августа 2022 года, 18:07 (BorisV)26 октября 2022 года, 7:52
(BorisV)26 октября 2022 года, 7:52

