Предел x ln x : Анализ-I
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| Aaron |
| ||
15/07/14 |
| ||
| |||
| Xaositect |
| |||
06/10/08 |
| |||
| ||||
| Aaron |
| ||
15/07/14 |
| ||
| |||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| Aaron |
| ||
15/07/14 |
| ||
| |||
| AV_77 |
| |||
11/11/07 |
| |||
| ||||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| Otta |
| |||
09/05/13 |
| |||
| ||||
| Aaron |
| ||
15/07/14 |
| ||
| |||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| ИСН |
| |||
18/05/06 |
| |||
| ||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Задавать вопрос
спросил
Изменено 8 лет, 10 месяцев назад
Просмотрено 242 раза
$\begingroup$
Я использовал правило произведения, чтобы получить $u=x$ и $v=e^{- \ln x}$. {- \ln x}$, и тогда это упростится до $dv= \ln x$? 9{-\ln(x)}=0$
{- \ln x}$, и тогда это упростится до $dv= \ln x$? 9{-\ln(x)}=0$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.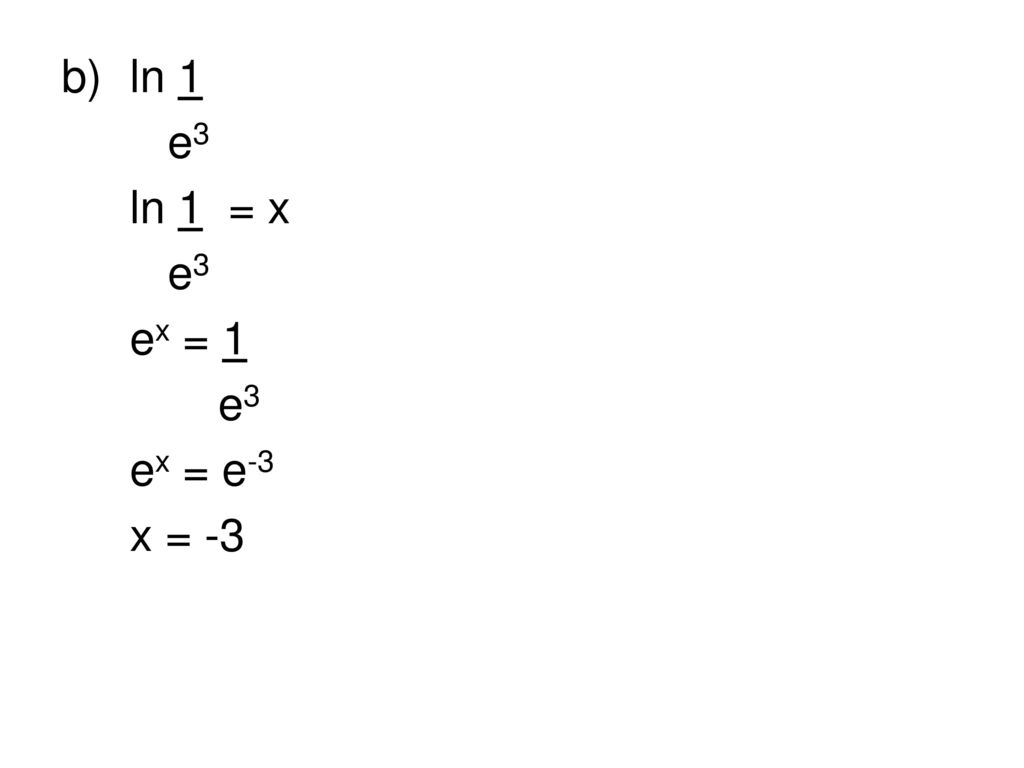
Вектор направления это: вектор направления | Перевод вектор направления?
Векторная Направленность Радиокомпонентов — Back To Music
Векторная Направленность — это эзотерическое ноу-хау, которое помогает создавать аудио системы с необычной ясностью и теплотой звучания и настраивать уже готовые системы в резонанс с вашим личным восприятием.
Антон Степичев
Термин «Направленность» возник в среде аудиофилов и меломанов в 1970х годах. Именно тогда люди впервые заговорили о том, что симметричные с точки зрения физики аудио кабели и провода оказывается вовсе не симметричны и каким-то образом изменяют звук аудио системы при смене направления их включения. Вплоть до середины 2000х считалось, что Направленность свойственна только электрическим проводникам. Большинство при этом было уверено, что направление проводников имеет значение только в сигнальных цепях, однако продвинутые аудиофилы ориентировали даже сетевые кабели, выбирая лучшее по звуку положение вилки в розетке, их считали сумасшедшими. Ориентация проводников в усилителях и пояснения причин выбора того или иного направления много лет были достаточно бессистемными, в 2005 году направленность проводников в сигнальных цепях и цепях питания усилителей наконец была систематизирована.
Систематизация направлений, наряду с отбором компонентов по специфическим критериям и выбором экстремально простой конструкции позволила создать необычный Тестовый Аудиотракт (ТА), благодаря которому появилась возможность определять музыкальные свойства отдельных радиодеталей и проводов с недостижимой до этого точностью. Довольно быстро выяснилось, что направление предпочтительного звучания компонентов практически никогда не совпадает с длинной стороной деталей. Даже у проводов, отношение длины к толщине у которых необычайно велико, наилучшее звучание всегда получалось при касании определенных точек на боковых поверхностях. Чтобы описать такое положение вещей был введен термин Векторная Направленность.
Термины:
Векторная Направленность — термин показывающий, что Направленность — это трехмерный, а не линейный (одномерный) феномен, как это считалось ранее.
Векторная Ориентация — соединение деталей аудиосистем с учетом направлений их векторов.
Внутренняя (Врожденная) Направленность (ВН) — это Направленность (Вектор), сформированный в процессе производства (металл, пластик) или рождения (дерево, камень) материала, из которого изготовлен компонент. см. Формирование Вектора.
Поверхностная Направленность (ПН) — это дополнительный к ВН Вектор меньшей силы и значительно меньшей устойчивости. ПН состоит из нескольких простых векторов последовательно возникающих при механической обработке, химических реакциях (окисление), окраске и лакировке поверхности.
Вектор — это отрезок прямой, проходящей сквозь тело компонента, начинающийся в определенной точке входа на поверхости компонента и заканчивающийся в определенной точке выхода. Вектор описывает трехмерное направление наиболее ясного звучания радиокомпонента (его входные и выходные точки) и ориентировочную выраженность (силу) его направленности. Общий Вектор компонента равен векторной сумме ВН и ПН и изменяется во времени всвязи с дрейфом силы и направления ПН.
Вектор Вращения (ВВ) — определяет поступательное и тангенциальное направление навивки проводника относительно продольного направления детали, на которую навивается проводник см. ниже.
Радиус Вектор — радиальная проекция Вектора, образующаяся в многослойных катушках индуктивности и рулонах конденсаторов, см. ниже. В природе присущ всем растениям (см. рис 4).
Вектор Фантом — Вектор \overline{AB}, пересекающий воздушное пространство, возникшее между точками A и B в процессе изменения формы детали. Подробнее здесь.
Векторные Потери — ухудшение ясности звучания аудиотракта, связанное с не точным соблюдением векторной направленности его компонентов при монтаже. Потери зависят от величины угла \beta рис.3 между вектором и линией, проведенной между точками соединения компонента в электрическую цепь.
Векторное Поле — поле неизвестной природы, формирующее векторную направленность у металлов и диэлектриков в момент их перехода из жидкого состояния в твердое. Наличие Векторного поля выведено гипотетически.
Наличие Векторного поля выведено гипотетически.
Ясность — везде, где не указано обратное имеется ввиду Музыкальная Ясность — субъективная (тонкая) характеристика звучания, тесно пересекающаяся с понятием Несомость звука — критерием из лексики скрипичных мастеров и специалистов по акустике помещений. Улучшение ясности часто воспринимается как появление «водуха», разборчивости звучания отдельных инструментов оркестра и точности в их интонациях. Экспериментально установлено, что потери ясности нарастают с добавлением каждого нового компонента, провода либо неточного соединения в тракте, поэтому ясность — это единственный устойчивый ориентир при выборе правильного направления компонента.
Определение направления вектора
Классический метод — тестируемый компонент включается в разрыв сигнальной цепи Тестового Аудиотракта (ТА) несколькими различными способами, изменения звучания тракта оцениваются на слух и выбирается наиболее ясный вариант. Замыкание сигнальной цепи через тестируемый компонент происходит с помощью длинных тестовых щупов J1 и J2 (см. схему рис.1), установленных в разрыве соединения между проволочным конденсатором WC2 и сеткой выходной лампы Siemens CA. Высокое входное сопротивление лампы СА позволяет тестировать не только провода, но и конденсаторы, индуктивности и даже диэлектрики, если их поверхность смочена водой. При этом небольшое усиление оконечного каскада позволяет использовать в качестве щупов длинные провода без экранов, ухудшающих ясность звучания системы.
Замыкание сигнальной цепи через тестируемый компонент происходит с помощью длинных тестовых щупов J1 и J2 (см. схему рис.1), установленных в разрыве соединения между проволочным конденсатором WC2 и сеткой выходной лампы Siemens CA. Высокое входное сопротивление лампы СА позволяет тестировать не только провода, но и конденсаторы, индуктивности и даже диэлектрики, если их поверхность смочена водой. При этом небольшое усиление оконечного каскада позволяет использовать в качестве щупов длинные провода без экранов, ухудшающих ясность звучания системы.
Вектор плоского проводника — определяется по двум ортогональным проекциям в два этапа. Сначала на поверхности исследуемого проводника (проекция \mathsf{X}\mathsf{Z} рис.2) определяется воображаемая окружность, щупы тестового аудиотракта устанавливаются в диаметрально противоположных точках \mathsf{А} и \mathsf{В} на этой воображаемой окружности и замыкают сигнальную цепь тестового тракта. Затем, оставаясь в диаметрально противоположных точках, оба щупа одновременно смещаются вдоль окружности без отрыва от поверхности и во время их перемещения оценивается изменения в звучании тестового тракта. По прошествии каждым из щупов полукруга, на поверхности фольги рисуется стрелка проекции \mathsf{XZ} вектора \overline{AB}, начало которой определят точка касания выходного щупа тестового тракта, а конец – точка касания входного щупа в тот момент, когда ясность звучания музыки оказывается наилучшей. На втором этапе определяется проекция вектора \mathsf{XY}, то-есть, определяется входная и выходная поверхности тестируемого проводника. Оцениваются два варианта \overline{AB} и \overline{A’B’}, из них выбирается наиболее ясный. По полученным двум проекциям строится результирующий, трехмерный вектор, деталь маркируется каким-либо удобным способом. Маркировка используется впоследствии при сборке электрических частей тракта в соответствии со схемой контуров или механических частей в соответствии со схемой корпуса АС, усилителя или других частей тракта.
По прошествии каждым из щупов полукруга, на поверхности фольги рисуется стрелка проекции \mathsf{XZ} вектора \overline{AB}, начало которой определят точка касания выходного щупа тестового тракта, а конец – точка касания входного щупа в тот момент, когда ясность звучания музыки оказывается наилучшей. На втором этапе определяется проекция вектора \mathsf{XY}, то-есть, определяется входная и выходная поверхности тестируемого проводника. Оцениваются два варианта \overline{AB} и \overline{A’B’}, из них выбирается наиболее ясный. По полученным двум проекциям строится результирующий, трехмерный вектор, деталь маркируется каким-либо удобным способом. Маркировка используется впоследствии при сборке электрических частей тракта в соответствии со схемой контуров или механических частей в соответствии со схемой корпуса АС, усилителя или других частей тракта.
Вектор проводника круглого сечения — один конец провода зажимается между щупами тестового тракта и медленно проворачивается на 360 градусов. Во время вращения проводника определяется такое его положение относительно щупов, когда ясность звучания тракта окажется наилучшей. Таким образом определяется поперечная проекция вектора одного конца провода (рис.3 Left Side View). Затем ту же операцию проделывают на другом конце провода. Затем определяется продольная направленность с касанием соответствующими щупами тестового тракта найденных боковых входных и выходных точек проводника (рис.3 Front View).
Во время вращения проводника определяется такое его положение относительно щупов, когда ясность звучания тракта окажется наилучшей. Таким образом определяется поперечная проекция вектора одного конца провода (рис.3 Left Side View). Затем ту же операцию проделывают на другом конце провода. Затем определяется продольная направленность с касанием соответствующими щупами тестового тракта найденных боковых входных и выходных точек проводника (рис.3 Front View).
На рис. 3 вектор \overline{AB}— это направление наилучшего звучания провода, определенное с помощью Тестового Аудиотракта. C, D, E, F — практически возможные точки электрического контакта провода с соседними компонентами. На практике наилучший реультат будет при контакте вдоль вектора \overline{CF}, наихудший — через \overline{FC}, варианты \overline{ED} и \overline{DE} — промежуточные. Не зная этих особенностей, можно легко ошибиться во время тестирования провода, поскольку хоть \overline{ED} и \overline{DE} по направлению почти противоположны, звучат они примерно одинаково тк оба находятся под большим углом к \overline{AB}. В случае тестирования провода через эти точки вероятность правильного определения направления провода близка к 50%. Интересно, что в длинном проводе угол a становится практически равным нулю, то-есть \overline{CF} становится практически равным \overline{ED}, а \overline{FC} — равным \overline{DE}, однако вышеперечисленные особенности звучания короткого отрезка провода так же хорошо проявляют себя и на длинном куске.
В случае тестирования провода через эти точки вероятность правильного определения направления провода близка к 50%. Интересно, что в длинном проводе угол a становится практически равным нулю, то-есть \overline{CF} становится практически равным \overline{ED}, а \overline{FC} — равным \overline{DE}, однако вышеперечисленные особенности звучания короткого отрезка провода так же хорошо проявляют себя и на длинном куске.
Вектор диэлектриков — определяется так же, как и у проводников, но после смачивания его поверхности водой (подробнее здесь).
* — Во избежание ошибок во время тестов необходимо учитывать направление вектора щупов Тестового Аудиотракта.
Экстрасенсорный (тактильный) вариант
Направленность — это феномен, не поддающийся привычному логическому анализу. Стороннему человеку вообще сложно поверить, что кто-то может чувствовать изменения в звучании, вносимые одним единственным проводом на фоне тысяч предположительно аналогичных по силе влияний, существующих в самом тракте и существовавших в процессе записи аудио носителя. Скептики справедливо обращают внимание на этот факт. На мой взгляд, аудиофильская сверхчувствительность сродни сверх обонянию некоторых животных, например самец бабочки Saturnia pavonia, ощущает запах феромона самки в радиусе 11 км. Если учесть, что концентрация вещества в воздухе с увеличением расстояния падает в кубе, то вероятность обнаружения хотя бы одной молекулы крохотного источника ферамона уверенно стремится к нулю. Однако самец как-то чувствует свою пару, точно так же, думаю, и меломаны остро чувствуют некие тонкие мелизмы, до которых обычным людям нет никакого дела. И судя по всему, механизмы этой чувствительности куда как тоньше тех, о которых нам рассказывают на уроках биологии.
Скептики справедливо обращают внимание на этот факт. На мой взгляд, аудиофильская сверхчувствительность сродни сверх обонянию некоторых животных, например самец бабочки Saturnia pavonia, ощущает запах феромона самки в радиусе 11 км. Если учесть, что концентрация вещества в воздухе с увеличением расстояния падает в кубе, то вероятность обнаружения хотя бы одной молекулы крохотного источника ферамона уверенно стремится к нулю. Однако самец как-то чувствует свою пару, точно так же, думаю, и меломаны остро чувствуют некие тонкие мелизмы, до которых обычным людям нет никакого дела. И судя по всему, механизмы этой чувствительности куда как тоньше тех, о которых нам рассказывают на уроках биологии.
Тонкость аудио-вибраций подтверждает интересный факт — качество Окраски и Направление компонента можно оценить не только на слух, но и с помощью осязания. В начале исследований для тестов использовался только Тестовый Аудиотракт, как описано выше, мне и в голову не могло прийти, что музыкальный потенциал деталей и проводов можно оценить как-то иначе, чем на слух. ТА исправно выполнял свои функции несколько лет, пока однажды во время сборки магнитопровода трансформатора не случился знаменательный инциндет — перед началом теста катушка была подпаяна к разъемам J1 и J2 (схема рис. 1), но выключатель SW2 остался замкнутым, то-есть сигнал проходил напрямую в сетку лампы минуя щупы. Работа проводилась как обычно: ш-пластина вставлялась в катушку четырьмя возможными способами, на слух выбиралось ее лучшее положение, затем процесс повторялся со следующей пластиной и так далее. Замкнутый выключатель был обнаружен только после окончания сборки: музыка продолжила играть когда выводы катушки были отпаяны от J1 и J2. Ситуация недвусмысленно намекала на то, что все обнаруженные различия были просто самовнушением и это был удар ниже пояса. Однако впечатления во время тестов были абсолютно реальны, в этом я мог поклясться и мне пришло в голову, что щупы соединенные с усилителем каким-то образом могли, например, играть роль антенны. Было решено перепроверить результат — пластины были помечены краской, затем магнитопровод разобран и собран в слепую по новой с разомкнутым SW2.
ТА исправно выполнял свои функции несколько лет, пока однажды во время сборки магнитопровода трансформатора не случился знаменательный инциндет — перед началом теста катушка была подпаяна к разъемам J1 и J2 (схема рис. 1), но выключатель SW2 остался замкнутым, то-есть сигнал проходил напрямую в сетку лампы минуя щупы. Работа проводилась как обычно: ш-пластина вставлялась в катушку четырьмя возможными способами, на слух выбиралось ее лучшее положение, затем процесс повторялся со следующей пластиной и так далее. Замкнутый выключатель был обнаружен только после окончания сборки: музыка продолжила играть когда выводы катушки были отпаяны от J1 и J2. Ситуация недвусмысленно намекала на то, что все обнаруженные различия были просто самовнушением и это был удар ниже пояса. Однако впечатления во время тестов были абсолютно реальны, в этом я мог поклясться и мне пришло в голову, что щупы соединенные с усилителем каким-то образом могли, например, играть роль антенны. Было решено перепроверить результат — пластины были помечены краской, затем магнитопровод разобран и собран в слепую по новой с разомкнутым SW2.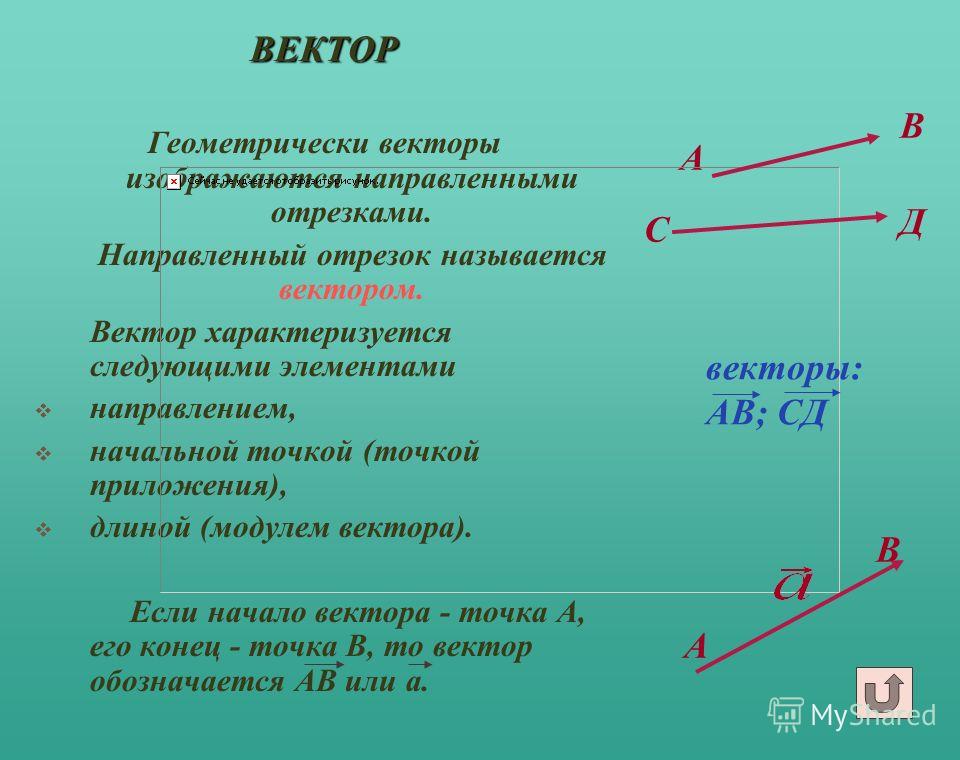 Новый результат на 80% совпал с предыдущим! Моему удивлению тогда не было конца, но это было только начало.
Новый результат на 80% совпал с предыдущим! Моему удивлению тогда не было конца, но это было только начало.
Следующий удивительный момент открылся в процессе поиска ответа на вопрос, каким образом в классическом тесте проводников с ТА могут возникать серийные ошибки. Например, при массовом тестировании с помощью ТА при перепроверке результатов 10 раз результат мог быть правильным, потом подряд могло быть 5 неправильных результатов потом опять шли правильные. После долгих мучений стало очевидно, что причиной большинства ошибок были мои руки, а именно каким образом удерживались щупы во время тестирования. Мои руки оказались энергетически несимметричными, левая рука была выраженным выходом, а правая — входом. Системные ошибки ушли в прошлое, когда выходной щуп J1 стал удерживаться в левой руке, а J2 — в правой.
Через какое-то время я столкнулся с совсем уж невероятным фактом — оказалось, что для определения направления щупы вообще не нужны — включив музыку можно было просто повертеть деталь в руках и найти ее наиболее естественное положение между ладонями или пальцами. Перепроверка на ТА показывала, что в этом случае со стороны левой руки располагалось начало компонента, а со стороны правой — конец. Это была эмоциональная встряска сокрушительной силы.
Перепроверка на ТА показывала, что в этом случае со стороны левой руки располагалось начало компонента, а со стороны правой — конец. Это была эмоциональная встряска сокрушительной силы.
Следущее открытие окончательно перевернуло все с ног на голову — во время очередных тактильных тестов я случайно обнаружил, что музыку при этом включать вообще не обязательно, направление и общий музыкальный потенциал детали так же уверенно можно было ощутить и в полной тишине. Шах и Мат материализму.
Свойства векторов
- Векторная направленность свойственна всем твердым предметам, как созданных человеком, так и необработанным, природным материалам.
- Направленность проявляет себя не только в аудио, но и в оптике.
- У растений вектор направлен в соответствии с изменениями их размеров во время их роста, то-есть — от корней к кроне и от сердцевины к поверхности (рис. 4).
- Совпадение направления вектора фабрично изготовленного компонента с его продольной осью – редкий, частный случай.
 Прямой связи вектора с геометрической формой фабричных компонентов не обнаружено.
Прямой связи вектора с геометрической формой фабричных компонентов не обнаружено. - При прочих равных, однонаправленные коллинеарные векторы звучат одинаково, таким образом, в каждом простом компоненте мы имеем бессчетное количество пар входных и выходных точек касания, с нулевыми векторными потерями. На рис. 5 \overline{AB} \equiv \overline{CD} \equiv \overline{EF} \equiv \overline{GH}
- При изгибе или скручивании моножильного провода, металлических пластин и т.п., их вектор изгибается и скручивается точно повторяя искаженную форму компонента (рис. 6), при этом, если затем восстановить форму компонента, направление его вектора так-же восстанавливается.
- Во направлениях, перпендикулярных вектору (см. рис. 2 нулевой вектор \overline{A3B4} ), направленность у компонента отсутствует, при этом звучание компонента становится усредненным по отношению к векторам \overline{AB} и \overline{BA} .
- Векторы не меняют свою ориентацию относительно геометрической формы радиокомпонентов, ни под действием постоянного электрического тока, ни под действием магнитного поля.

Данное утверждение базируется на тщательном исследовании старых, преимущественно довоенных радиодеталей: трансформаторов, кондесаторов, радиоламп, проводки электроприборов, как постоянного, так и переменного тока десятилетиями проработавших в одинаковых «электро-магнитных условиях». Проводники и диэлектрики из которых собраны бывшие в долгом употреблении радиокомпоненты, с точки зрения направленности, всегда были соединены без какой-либо системы, например: направление выводов трансформаторов практически никогда не совпадало с направлением их обмоток, а проводка, включая отрезки проводников из которых собраны радиолампы, резисторы и конденсаторы никогда не соответствовала Электрическим Контурам и содержала как прямые, так и встречные включения проводников.
- Механическая обработка поверхности компонентов (пиление, строгание, шлифовка, етс.) вызывает коррекцию направления и силы Поверхностной Направленности (ПН). На рис. 7 показана правильная ориентация доски и рубанка при строгании: рубанок, доска и правая (входная) рука, толкающая рубанок, должны быть сонаправлены, только в этом случае во время обработки не возникают векторные потери ясности.
 Так же механическая обработка оказывает значительное и устойчивое влияние на неполярные, тонкие свойства компонентов (подробнее здесь).
Так же механическая обработка оказывает значительное и устойчивое влияние на неполярные, тонкие свойства компонентов (подробнее здесь). - Направление и силу суммарного вектора группы компонентов можно оценить по математическим правилам сложения векторов отдельных компонентов, входящих в данную группу.
.
Вектор вращения
Вектор вращения (ВВ) определяет поступательное и тангенциальное направление навивки проводника относительно направления проводника и продольного направления детали, на которую навивается проводник. ВВ необходимо учитывать при намотке трансформаторов, катушек индуктивностей, проволочных резисторов, фольговых рулонных конденсаторов. Направление ВВ перпендикулярно плоскости вращения и связано с направлением вращения правилом правой руки.
«Если взять правой рукой каркас катушки индуктивности так, чтобы выпрямленный большой палец указывал в сторону продольной направленности каркаса, то провод должен навиваться на каркас в направлении, указанном обхватывающими каркас четырьмя пальцами. Начало провода должно быть расположено у мизинца, катушка мотается в направлении от мизинца к указательному пальцу»
Начало провода должно быть расположено у мизинца, катушка мотается в направлении от мизинца к указательному пальцу»
Радиус Вектор
Радиус Вектор (РВ) образуется в многослойных катушках индуктивности и рулонах конденсаторов, в природе присущ всем растениям и направлен от центра наружу (см. рис 4). Для достижения максимально ясного звучания системы, РВ индуктивностей и конденсаторов так-же должен быть направлен от центра наружу. Чтобы сформировать Вектор с таким направлением, надо перед намоткой компонента убедиться, что в катушке, с которой вы будете сматывать провод или фольгу, снаружи находится начало провода (фольги). Если это не так, то катушку — источник провода надо перемотать на пустую катушку и только потом мотать обмотку будущего трансформатора или обкладку конденсатора. У фольги дополнительно определяется входная и выходная поверхности ( см. рис 2 — вектор плоского проводника), при намотке входная поверхность фольги должна располагаться ближе к центру рулона. Правило Радиус Вектора:
Правило Радиус Вектора:
«Во всех моточных радиотехнических изделиях начало проводника должно быть у центра катушки, а конец находиться снаружи»
Формирование вектора с заданным направлением
В домашних условиях можно сформировать вектор у легкоплавких металлов (свинец, олово, алюминий), а так-же у диэлектриков (восках, смолах, лаках и красках). Так-же можно собрать из деталей с известной направленностью какой-либо предмет с необходимыми свойствами, например склеить корпус АС (рис. 8). На данный момент известно, что устойчивая, векторная направленность у металлов и диэлектриков формируется в момент их перехода из жидкого состояния в твердое, предположительно — под действием некого, направленного Векторного поля при этом компонент во время своего перехода из расплавленного состояния в твердое «запоминает» то состояние поля, которое его пересекало (окружало) в данный момент и «помнит» его до тех пор, пока его снова не расплавить. У человека (лично у меня) сильный и стабильный источник векторного поля — это руки. Степень влияния других частей тела варьируется под действием различных, плохо предсказуемых обстоятельств. Что-либо говорить о сознательном и целенаправленном применении тонких полей человека в аудио пока не представляется возможным, однако не подлежит сомнению, что человек оказывает ощутимое влияние на звучание конструкции, которую он изготавливает не зависимо от того, хочет он этого, или нет. Векторное поле каждого предмета, как и векторное поле человека, оказывает влияние на формирование направленности у находящихся рядом с ним предметов, которые в этот момент переходят из расплавленного состояния в твердое. Таким образом, можно говорить о наличии тонких, векторных полей разной силы и конфигурации у всех окружающих нас предметов. Влияние векторных полей предметов на формирование векторов у расположенных рядом с ними затвердевающих жидкостей, пропорционально их текущей силе и обратно пропорционально расстоянию между ними.
Степень влияния других частей тела варьируется под действием различных, плохо предсказуемых обстоятельств. Что-либо говорить о сознательном и целенаправленном применении тонких полей человека в аудио пока не представляется возможным, однако не подлежит сомнению, что человек оказывает ощутимое влияние на звучание конструкции, которую он изготавливает не зависимо от того, хочет он этого, или нет. Векторное поле каждого предмета, как и векторное поле человека, оказывает влияние на формирование направленности у находящихся рядом с ним предметов, которые в этот момент переходят из расплавленного состояния в твердое. Таким образом, можно говорить о наличии тонких, векторных полей разной силы и конфигурации у всех окружающих нас предметов. Влияние векторных полей предметов на формирование векторов у расположенных рядом с ними затвердевающих жидкостей, пропорционально их текущей силе и обратно пропорционально расстоянию между ними.
Существует, по крайней мере, один источник векторного поля, влияние которого не зависит от расстояния до какого либо объекта в помещении. Данное поле, в случае, когда ему не оказывает противодействие поля посторонних, близко расположенных предметов и/или человека, формирует у затвердевающих предметов устойчивый вектор с направлением «снизу-вверх». Наличие этого поля было выведено логически, когда стало ясно, что во время экспериментов по формированию направленности у радиокомпонентов, каждый раз отслеживается некая коррекция вектора в направлении «снизу-вверх». Скомпенсировать это влияние «снизу-вверх» (то-есть отклонить его в сторону или изменить на противоположное направление) можно только если припой застывает на массивной доске или куске металла вектор которых направлен вниз. Возможно, данное влияние «снизу-вверх» — это влияние векторного поля Земли. На рис. 9 и рис. 10 показано два варианта формирования вектора у капли припоя, застывающей на деревянной доске. Жирными красными стрелками показано поле Земли, обычными стрелками — векторы доски и припоя, после его застывания. Звук припоя на рис.10 получается не сформированным, мутноватым, правильное направление на нем определить сложно.
Данное поле, в случае, когда ему не оказывает противодействие поля посторонних, близко расположенных предметов и/или человека, формирует у затвердевающих предметов устойчивый вектор с направлением «снизу-вверх». Наличие этого поля было выведено логически, когда стало ясно, что во время экспериментов по формированию направленности у радиокомпонентов, каждый раз отслеживается некая коррекция вектора в направлении «снизу-вверх». Скомпенсировать это влияние «снизу-вверх» (то-есть отклонить его в сторону или изменить на противоположное направление) можно только если припой застывает на массивной доске или куске металла вектор которых направлен вниз. Возможно, данное влияние «снизу-вверх» — это влияние векторного поля Земли. На рис. 9 и рис. 10 показано два варианта формирования вектора у капли припоя, застывающей на деревянной доске. Жирными красными стрелками показано поле Земли, обычными стрелками — векторы доски и припоя, после его застывания. Звук припоя на рис.10 получается не сформированным, мутноватым, правильное направление на нем определить сложно.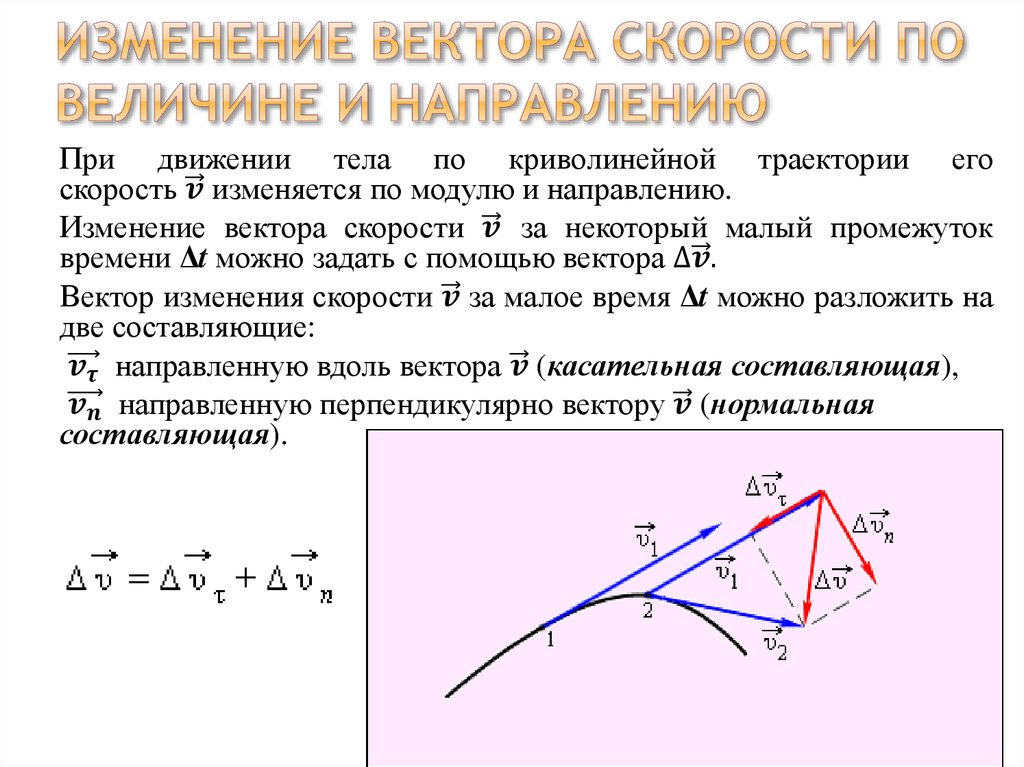 Чистое звучание у припоя получится только в случае, если вектор предмета на котором припой застыл примерно совпадал с направлением поля Земли (рис. 9).
Чистое звучание у припоя получится только в случае, если вектор предмета на котором припой застыл примерно совпадал с направлением поля Земли (рис. 9).
Вывод
Векторную Направленность можно смело назвать теорией, поскольку она объединяет разрозненные, субъективные факты (как слуховые, так и зрительные) в единую систему и объясняет плохую повторяемость многих субъективных экспериментов, позволяя сделать их более повторяемыми.
Антон Степичев, 2013 — 2021 гг.
Примечания
[1] — см. мое интернет сообщение от 7 марта 2006г, (Логин для входа — oldforum, пароль — 159357) Цитата:
…Правильное направление имеет три независимые координаты по отношению к продольной оси у ЛЮБОГО проводника т.е. у полоски фольги есть входная и выходная сторона а цилиндрический проводник необходимо соединять определенным боком. Таким образом Вектор правильного направления стал трехмерным и сейчас исследуются способы минимизации векторных потерь…
[2] — Ссылка на источник не найдена.
[3] — см. мое интернет сообщение от 6 декабря 2006г, (Логин для входа — oldforum, пароль — 159357) Цитата:
…Есть еще немаловажные тонкости. Эти, найденные мной эзотерические правила, действуют и в головках и в трансформаторах и в рулонах конденсаторов и в динамиках — в любых радиокомпонентах, где есть спирали:
Катушка должна быть расположена вертикально (отверстие смотрит вниз),
Провод, если смотреть на катушку сверху, намотан по часовой стрелке.
«начало» провода должно быть внутри и сверху катушки. Заземляется именно начало провода. Конец провода становится сигнальным и он должен выходить из катушки внизу…
Системно-векторная психология: типы личностей
Время чтения 8 минут
Современная психология и психиатрия уже давно не ограничиваются только классическими научными теориями. Споры и дискуссии об истинности и объективности популярных концепций ведутся столетиями, постоянно проводятся психологические исследования, цель которых – прийти к единственному верному итогу. Но помимо этого все чаще появляются новые альтернативные течения, общеизвестные теории видоизменяются, трансформируются учения мировых умов психологии и психиатрии, таких как профессионал психоанализа Зигмунд Фрейд или его не менее известный коллега Карл Густав Юнг.
Но помимо этого все чаще появляются новые альтернативные течения, общеизвестные теории видоизменяются, трансформируются учения мировых умов психологии и психиатрии, таких как профессионал психоанализа Зигмунд Фрейд или его не менее известный коллега Карл Густав Юнг.
В данной статье речь пойдет именно о подобном новом течении, которое произвело настоящую революцию в российской психологии носит название системно-векторная психология. Вы узнаете, что то это такое, какова основная идея этого направления, а также подробно сможете ознакомиться с каждым из 8 представленных векторов и даже самостоятельно определить свой собственный тип личности.
<<Оглавление>>
Идеи системно-векторной психологии
Для начала стоит сказать, что системно-векторная психология не является общепринятым направлением в современных научных кругах. Некоторые особо яростные приверженцы классических идей даже называют данное направление «сетевой псевдонаукой». Но, как и любая другая теория, психологическая концепция восьми векторов не только имеет возможность на существование, она даже успела приобрести свою армию приверженцев. Как сказал основатель системно-векторной теории В. К. Толкачев:
Но, как и любая другая теория, психологическая концепция восьми векторов не только имеет возможность на существование, она даже успела приобрести свою армию приверженцев. Как сказал основатель системно-векторной теории В. К. Толкачев:
Вселенная достаточно велика и неисчерпаема, что и позволяет найти в ней подтверждение любой теории. ©
Системно-векторная психология не возникла с нуля. За основу были взяты теории Зигмунда Фрейда, впоследствии доработанные Владимиром Ганзеном и законченные его учеником Виктором Толкачевым.
В 1908 году увидела мир статья психоаналитика Фрейда «Характер и анальная эротика», в которой психоаналитик делает умозаключение, что особенности характера напрямую связаны с эрогенными зонами человека. Публикация вызвала широкий резонанс, появились многочисленные последователи фрейдистской идеи. Одним из них в конце ХХ века стал Виктор Константинович Толкачев, психолог из Санкт-Петербурга. Он разработал типологию характеров, связанную с такими зонами, как глаза, рот, нос и уши. По словам В. К. Толкачева, на развитие и доработку теории Зигмунда Фрейда его вдохновила книга «Системные описания в психологии» академика Владимира Александровича Ганзена.
Он разработал типологию характеров, связанную с такими зонами, как глаза, рот, нос и уши. По словам В. К. Толкачева, на развитие и доработку теории Зигмунда Фрейда его вдохновила книга «Системные описания в психологии» академика Владимира Александровича Ганзена.
Зарождение и развитие учения Виктора Толкачева
В.К. Толкачев разработал целостную психологическую концепцию определения типа личности при помощи векторов. С помощью понятия «вектор» и подробного анализа 8 характерных типов на свет родилась теория под названием «Прикладной системно-векторный психоанализ». Толкачев более 30 лет проводил различные тренинги, семинары и лекции по данному вопросу. Благодаря одному из первых его учеников, Михаилу Бородянскому, был разработан специальный тест, оценивающий индивидуальный потенциал, имеющийся у каждого из векторов, и позволяющий определить личностный тип характера относительно системно–векторной психологии восьми векторов (тест Толкачева – Бородянского). Сейчас много последователей векторной системы, которые продолжают проводить психологические тренинги и семинары. Самым известным интернет-коучем в данной области является Юрий Бурлан.
Самым известным интернет-коучем в данной области является Юрий Бурлан.
В чем суть системно-векторной психологии
За время развития психологии, как науки, было разработано множество различных типологий личности. Это и типологии по Юнгу или по Ганнушкину, свою классификацию предлагал Эрих Фромм. Разработаны множественные тесты, определяющие психологический тип индивида, например, тест Сонди или распространенный 16Personalities. По сути, В.К. Толкачев, как и многие его предшественники, предложил свою собственную версию выявления типа личности.
Системно-векторная психология позиционируется не как отрасль классической психологии или определенное течение, а как отдельная наука изучения типологии личности. Вектор – это симбиоз физиологических и психологических качеств, таких как, например, характер, темперамент, здоровье, привычки индивида и другие подобные свойства. По сути, вектором является центр получения удовольствия. Векторы связаны с определенным отверстием на теле человека, являющимся одновременно эрогенной зоной. В каждой личности возможно наличие нескольких векторов (от 1 до 8, на практике самым большим количеством наличествующих векторов является число 5).
В каждой личности возможно наличие нескольких векторов (от 1 до 8, на практике самым большим количеством наличествующих векторов является число 5).
Наличием вектора определяется количество и степень человеческих стремлений и потребностей в самореализации, направленной на получение наслаждений. Неспособность реализовать существующий вектор, по мнению разработчиков теории, приводит к депрессии и чувству неудовлетворенности, что делает для человека невозможным достижение внутренней гармонии со своим «Я».
Системно-векторная психология выделяет 8 основных векторов в типологии личности. А именно: зрительный, кожный, звуковой, мышечный, оральный, обонятельный, уретральный и анальный векторы. Они располагаются в четырех основных квартелях (ступенях), формирующих жизненный уклад человека.
Принцип расположения векторов:
- Информационная ступень. Отвечают звуковой (внутренняя часть квартели) и зрительный (внешняя часть) векторы.
 На этой ступени происходит процесс развития и самопознания личности.
На этой ступени происходит процесс развития и самопознания личности. - Энергетическая ступень. Отвечают оральный (внешняя часть) и обонятельный (внутренняя часть) векторы. Цель этой ступени – предопределить место индивида в социальном строю, построение четкой иерархии.
- Временная ступень. Отвечают анальный (внутреннее пространство квартели) и уретральный (внешнее пространство) векторы. Временные разделения жизни на этапы: прошлое и будущее. На этой ступени происходит получение и обработка опыта от прошлых поколений, а также стремление к прогрессу и развитию общества.
- Пространственная ступень. Отвечают мышечный (внутренняя часть) и кожный (внешняя часть пространства квартели) векторы. Ступень, отвечающая за физическую оболочку – трудовая реализации человека, использование физической силы и т.п.
Характеристика векторов
Более детальная векторная характеристика выглядит так:
- Кожный вектор.
 Люди с ярким проявлением данного типа – ярко выраженные экстраверты. Реализуют себя на пространственной ступени. Основным направлением кожников является охрана территорий.
Люди с ярким проявлением данного типа – ярко выраженные экстраверты. Реализуют себя на пространственной ступени. Основным направлением кожников является охрана территорий. - Мышечный вектор. Интроверты. Тип мышления практический и наглядно-действенный. Основное направление – охота, участие в военных действиях.
- Анальный вектор. Интроверты с системным мышлением. Характерными занятиями для обладателей анального вектора является охрана домашнего очага, накопление и передача информации от предыдущих поколений.
- Уретральный вектор. Стопроцентные экстраверты. Обладают нестандартным мышлением. Прирожденные тактики. Жизненное предназначение людей с выраженным уретральным вектором — быть вождями, главнокомандующими, руководителями.
- Зрительный вектор. Экстраверты с образным типом интеллекта. Находятся на информационной ступени развития. Основное направление деятельности: охрана территорий (днем).

- Звуковой вектор. Абсолютные интроверты, обладающие абстрактным типом мышления. Деятельность: охрана территорий в темное время суток.
- Оральный вектор. Представители этого типа – в основном, экстраверты. Им присущий вербальный метод мышления. Основной род занятий: организация мероприятий (в мирное время), предупреждение об опасности (во время военных действий).
- Обонятельный вектор. Интроверты, отличающиеся интуитивным типом мышления, предпочитают невербальные способы передачи информации. Основное направление: разведка, составление стратегий.
Системно-векторная психология разделяет вектора на более важные, так сказать, основные, и те, которые имеют меньшую ценность в развитии личности. Обонятельный, уретральный и звуковой векторы являются главенствующими, они доминируют над остальными векторами. Эти три вектора не перекрываются другими имеющимися, а также не могут быть искоренены внешними социальными факторами, такими как воспитание или общественный строй.
Каждый индивид сам определяет, какие векторы являются основными в психотипе его личности. Для каждого вектора разработаны даже такие характеристики, как определенные внешние данные, особенности психики, присущие конкретному векторному архетипу. Каждому из восьми векторов присвоена определенная геометрическая форма и цвет.
Также вектора поделены на нижние (уретральный, анальный, мышечный и кожный) и верхние (зрительный, звуковой, обонятельный и оральный). Системно-векторная психология показывает то, что нижние векторы отвечают за либидо, сексуальные желания человека, в то время как верхние ищут сопряжение с духовным миром. Нижние вектора имеются в наличии абсолютно у каждого человека, в отличие от верхних, которыми наделены далеко не все личностные архетипы.
Системно-векторная психология: ее предназначение
Нет ни одного человека, способного отказаться от наслаждения; даже самой религии приходится обосновывать требование отказаться от удовольствий в ближайшее время обещанием несравненно больших и более ценных радостей в потустороннем мире.
© Зигмунд Фрейд
Для чего же нужна восьми векторная психология? Какая ее функция и польза для человека?
Основной целью векторной психологии является познание себя и получение наслаждений от жизни, используя свои внутренние векторы. Данная система направлена на самопознание индивида, определение его роли в обществе, с целью избежать морального неудовлетворения собой и своей жизнью. Если человек не может реализовать себя в социуме, не знает своих истинных потребностей и желаний, то постоянно ощущение неудовлетворения может привести к депрессивному состоянию.
Системно-векторная психология также направлена на раскрытие сексуальных желаний и потребностей человека. Может применяться в качестве профессионально ориентированных тестов.
Психологическая теория, разработанная Виктором Толкачевым на основе постулатов Фрейда, позволяет открывать тайны подсознания, осознавать, что именно является двигательной силой человека, первопричиной всех его действий и поступков. Польза изучения векторов системно-векторной психологии также в построении коммуникативных связей с окружающими людьми: сотрудниками, родственниками, друзьями. Если два человека обладают одинаковыми векторами, то зачастую это является залогом дружественных отношений. И наоборот – контрастность векторов объясняет несовместимость в парах и неприязнь отдельных личностей друг к другу. Говоря словами невольного основоположника данного учения Зигмунда Фрейда:
Польза изучения векторов системно-векторной психологии также в построении коммуникативных связей с окружающими людьми: сотрудниками, родственниками, друзьями. Если два человека обладают одинаковыми векторами, то зачастую это является залогом дружественных отношений. И наоборот – контрастность векторов объясняет несовместимость в парах и неприязнь отдельных личностей друг к другу. Говоря словами невольного основоположника данного учения Зигмунда Фрейда:
Мы выбираем не случайно друг друга… Мы встречаем только тех, кто уже существует в нашем подсознании. ©
Системно-векторная психология не является доказанной или абсолютно верной. Это всего лишь одна из методологий выявления определенного типа личности. Количество критики опытных специалистов относительно учений В. К. Толкачева доказывает не совершенность данной психологической концепции. Дискуссии и споры не утихают между приверженцами классической психологии и учениками Толкачева.
Первые склонны считать векторный подход определения личности сектантским и гипнотически-навязчивым (якобы, тренинги по обучению данной методике проводятся исключительно с коммерческими целями). Вторые же искренне верят в объективность системно-векторной психологии и доказывают ее пользу для отдельных индивидов и человечества в целом.
Чтобы подробнее ознакомиться с тезисами и понятиями данного учения, можно просмотреть видео вводных лекций Юрия Бурлуна относительно системы векторов. Только собрав воедино полную картину учения, каждый человек сможет самостоятельно сделать вывод об истинности выдвигаемых идей.
Тематика: Психология женщин, Психология мужчин, Личностный рост
Вектор направления можно определить по разнице положения двух векторов.
Задай вопрос
спросил
Изменено 3 года, 4 месяца назад
Просмотрено 276 раз
$\begingroup$
Я изучаю векторное уравнение, и у меня есть сомнения относительно этого утверждения:
Вектор направления можно определить по разности двух положение векторов.
Определенный вектор направления является исходным вектором направления или преобразованным вектором направления?
Под «транслированным вектором направления» я имею в виду: ( на двух изображениях красный сегмент — это вектор направления)
И под «вектором исходного направления» я подразумеваю:
И что является доказательством этого утверждения?
Приветствуются любые советы, чтобы лучше понять эту тему, заранее спасибо.
- векторов
$\endgroup$
$\begingroup$
Прямая параметризуется, зная некоторых точек на ней (заданных вектором $\vec x_0$ из начала координат) и вектором направления $\vec v$. Тогда вектор из начала координат в произвольную точку прямой можно записать в виде $$\vec x = \vec x_0 + t\vec v \quad\text{для некоторого значения скаляра } t.$$
Обратите внимание, что если вы знаете две точки на прямой, это соответствует таким выражениям для двух разных значений $t$, поэтому вы восстанавливаете вектор направления (или его ненулевое скалярное кратное) путем вычитания двух векторов: $\vec x_1 = \vec x_0 + t\vec v$ и $\vec x_2 = \vec x_0 + s\vec v$ (где $s$ и $t$ — разные скаляры), тогда
$$\vec x_2 — \vec x_1 = (\vec x_0 + s\vec v) — (\vec x_0 + t\vec v) = (s-t)\vec v,$$
по желанию.
$\endgroup$
3
$\begingroup$
Вы определяете исходный вектор направления. Для векторной алгебры важны только направление и величина, а не положение. Это связано с тем, что компоненты вектора не меняются при его переводе.
Полезно сначала взглянуть на это в одном измерении.
На вещественной прямой рассмотрим две точки. Скажем, $a=3$ и $b=5$.
Мы можем думать об этом как о векторах.
Величина $b-a$ представляет собой расстояние между $a$ и $b$.
Также вектор $b-a$ указывает от $a$ к $b$. Если $b-a$ положительное, то вектор указывает на положительную сторону, иначе он указывает на отрицательную сторону.
Точно так же вектор $a-b$ указывает от $b$ к $a$.
Затем вы можете экстраполировать это на $2D$.
Для векторов $a$ и $b$ вектор $b-a$ указывает от $a$ к $b$ :
Сложение векторов $a$ и $b-a$ дает вектор $b$.
Таким образом, чтобы получить любой вектор между $a$ и $b$, мы можем масштабировать $b-a$, а затем добавить его к $a$:
$$а + т(б-а)$$
$0\le t\le 1$.
$\endgroup$
1
Направление вектора Формула
Вектор образуется при соединении двух различных точек друг с другом. Точка, из которой проведена линия в другую точку, определяет направление этого вектора. Направление вектора — это угол, образованный вектором с горизонтальной осью, также известной как ось X. Это обеспечивается вращением против часовой стрелки угла вектора вокруг его хвоста строго на восток. Другими словами, ориентация вектора, то есть угол, который он образует с осью x, определяется как его направление.
Формула
Направление вектора обозначается символом θ. Его формула равна арктангенсу отношения расстояния, пройденного линией по оси y, к расстоянию, пройденному по оси x. Другими словами, это арктангенс наклона прямой.
Другими словами, это арктангенс наклона прямой.
θ = tan -1 (y/x)
где,
θ – направление вектора,
y – вертикальное смещение,
x — горизонтальное смещение.
Для векторной линии с начальной точкой (x 1 , y 1 ) и конечной точкой (x 2 , y 2 ) направление определяется выражением,
0 tan90 -1 ((Y 2 -Y 1 ) / (x 2 -x 1 ))
Проблемы с образцамиПроблема 1. Рассчитайте направление версии. смещение равно 5, а горизонтальное смещение равно 4,9.0024
Решение:
Мы имеем,
Y = 5
x = 4
, используя формулу, которую мы получаем,
θ = tan -1 (y/x)
= tan -1 (5/4)
= 51,34°
Задача 2. Вычислить направление вектора, если вертикальное смещение равно 7, а горизонтальное смещение равно 5.
Вычислить направление вектора, если вертикальное смещение равно 7, а горизонтальное смещение равно 5.
Решение:
6
у = 7
х = 5
Используя формулу, получаем
θ = tan -1 (y/x)
= tan -1 (7/5)
= 54,46°
2 Задача 3. Вычислить вертикаль смещение, если направление вектора равно 60°, а горизонтальное смещение равно 5.Решение:
Имеем,
θ = 60°
тангенс θ = y/x
=> y = x тангенс θ
= 5 tan 60°
= 8,66
Задача 4. Вычислить вертикальное смещение, если направление вектора равно 30°, а горизонтальное смещение равно 8.
Решение: 9023 ,
θ = 30 °
x = 8
с использованием формулы, которую мы получаем,
Tan θ = y/x
=> y = x tan θ
= 8 Tan 30 °
= 4,61
.
Задача 5. Вычислить горизонтальное смещение, если направление вектора равно 50°, а вертикальное смещение равно 4,
Решение:
Мы имеем,
θ = 50 °
x = 4
Используем формулу, которую мы получаем,
tan θ = y/x
=> y/y/tan θ
= 4/tan 50°
= 3,35
Задача 6. Вычислить горизонтальное смещение, если направление вектора равно 45°, а вертикальное смещение равно 9.
We есть,
θ = 45°
x = 9
Используя формулу, получаем направление вектора для начальной точки (8, 4) и конечной точки (10, 6).
Решение:
Мы имеем,
(x 1 , Y 1 ) = (8, 4)
(x 2 , Y 2 ) = (10, 6114 2 , Y 2 ) = (10, 61114 2 , у 2 ) = (10, 6 )
Найти вертикальное перемещение.
Cos 2 x первообразная: ПОМОГИТЕ ПОЖАЛУЙСТА.Нужно найти первообразную функции f(x)=1/cos^2x-cos(3x-1)
Тесты по теме Первообразная онлайн — АСТ партнер
Тест по теме первообразная
Тест предназначен на проверку знаний и умений учащихся по теме «Первообразная. Таблица первообразных.
Тест по теме: «Нахождение первообразных»
Данный тест поможет закрепить знания по теме: «Нахождение первообразных».
Первообразная. Нахождение первообразной.
Тест по алгебре и началам анализа для 11 класса. ТЕСТ НАПРВЛЕН НА ПРОВЕРКУ ПЕРВИЧНОГО УСВОЕЕНИЯ МАТЕРИАЛА
Определенный интеграл и его приложения
Тест предназначен для проверки знания физического и геометрического смысла определенного интеграла, формул первообразных элементарных функций, правил вычисления интеграла, формулы Ньютона-Лейбница, уения вычислять определенный интеграл, находить площади плоских фигур
Виртуальная образовательная среда
Данный тест предназначен для оценки знаний студентов Московского государственного областного университета по предмету «Виртуальная образовательная среда»
Первообразная и ее применение
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Первообразная» из раздела «Начала математического анализа». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 10 минут.
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 10 минут.
Тест по алгебре и началам анализа для 11 класса. ТЕСТ НАПРВЛЕН НА ПРОВЕРКУ ПЕРВИЧНОГО УСВОЕЕНИЯ МАТЕРИАЛА
Тест предназначен для проверки знания физического и геометрического смысла определенного интеграла, формул первообразных элементарных функций, правил вычисления интеграла, формулы Ньютона-Лейбница, уения вычислять определенный интеграл, находить площади плоских фигур
ТЕСТ НАПРВЛЕН НА ПРОВЕРКУ ПЕРВИЧНОГО УСВОЕЕНИЯ МАТЕРИАЛА.
Onlinetestpad. com
03.01.2019 6:36:55
2019-01-03 06:36:55
Источники:
Https://onlinetestpad. com/ru/tests/antiderivative
Тест по теме Первообразная » /> » /> .keyword { color: red; }
Тест по теме первообразная
Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.
Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.
Список вопросов теста
Вопрос 1
Найдите производную функции y=4cos2x в точке х 0 = — 3 π 4 .
Варианты ответов
Вопрос 2
Найдите промежутки возрастания функции у = х + 1 х — 1 .
Варианты ответов
Вопрос 3
Какая из данных функций является первоообразной для функциии у = 2 х 3 — 3 х 2 ?
Варианты ответов
F(x) = 0 , 5 х 4 — х 3 + 5
Вопрос 4
Какая из данных функций является первообразной для функции у = sin 2x?
Варианты ответов
F ( x ) = — 1 2 cos 2 x
F ( x ) = — cos 2 x
F ( x ) = — sin 2 x
Вопрос 5
На каком из указаанных промежутков функция F ( x ) = cos 2 x — 2 x + 1 является первообразной для f ( x ) = — 2 sin 2 x — 1 x?
Варианты ответов
Вопрос 6
Для функции у = — 1 — 2 х 2 найдите первообразную, график которой проходит через точку М(-3;12).
Варианты ответов
F ( x ) = — x — 2 3 x 3 — 2
F ( x ) = — x — 2 3 x 3 — 9
F ( x ) = 7 — x — 2 3 x 3
F ( x ) = — x — 2 3 x 3 + 9
Вопрос 7
Известно, что F1, F2, F3 — первообразные для f ( x ) = 4 x 3 — 3 x 2 на R, графики которых проходят через точки M(-1;2), N(1;4) и K(2;5) соответственно. Перечислите, в каком порядке (сверху вниз) графики этих функций пересекают ось ординат?
Перечислите, в каком порядке (сверху вниз) графики этих функций пересекают ось ординат?
Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.
Вопрос 1
Найдите производную функции y=4cos2x в точке х 0 = — 3 π 4 .
Варианты ответов
Вопрос 2
Найдите промежутки возрастания функции у = х + 1 х — 1 .
Варианты ответов
Вопрос 3
Какая из данных функций является первоообразной для функциии у = 2 х 3 — 3 х 2 ?
Варианты ответов
F(x) = 0 , 5 х 4 — х 3 + 5
Вопрос 4
Какая из данных функций является первообразной для функции у = sin 2x?
Варианты ответов
F ( x ) = — 1 2 cos 2 x
F ( x ) = — cos 2 x
F ( x ) = — sin 2 x
Вопрос 5
На каком из указаанных промежутков функция F ( x ) = cos 2 x — 2 x + 1 является первообразной для f ( x ) = — 2 sin 2 x — 1 x?
Варианты ответов
Вопрос 6
Для функции у = — 1 — 2 х 2 найдите первообразную, график которой проходит через точку М(-3;12).
Варианты ответов
F ( x ) = — x — 2 3 x 3 — 2
F ( x ) = — x — 2 3 x 3 — 9
F ( x ) = 7 — x — 2 3 x 3
F ( x ) = — x — 2 3 x 3 + 9
Вопрос 7
Известно, что F1, F2, F3 — первообразные для f ( x ) = 4 x 3 — 3 x 2 на R, графики которых проходят через точки M(-1;2), N(1;4) и K(2;5) соответственно. Перечислите, в каком порядке (сверху вниз) графики этих функций пересекают ось ординат?
Тест по теме Первообразная.
Multiurok. ru
11.10.2019 17:34:08
2019-10-11 17:34:08
Источники:
Https://multiurok. ru/tests/test-po-teme-pervoobraznaia. html
Тест по теме » Первообразная и интеграл» | Тест по алгебре (11 класс) по теме: | Образовательная социальная сеть » /> » /> .keyword { color: red; }
Тест по теме первообразная
Тест можно использовать на уроке при проверке знаний и умений по теме. Тест состоит из двух вариантов и содержит критерии оценки.
Скачать:
test_integrirovanie_na_sayt. pdf pdf | 199.51 КБ |
Подтяните оценки и знания с репетитором Учи. ру
За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Вводный урок бесплатно, онлайн, 30 минут
Предварительный просмотр:
По теме: методические разработки, презентации и конспекты
Программа элективного курса по математике для 9 класса «Интеграл»
Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельно.
Урок по теме «Вычисление площадей фигур с помощью определенного интеграла»
Урок изучения нового материала в 11 классе.
Интеграл
Вычисление интегралов по формуле прямоугольников.
Зачет по теме «Интеграл»
В старшей школе целесообразно проводить зачеты по основным темам курса математики. Предложенные мною билеты по теме «Интеграл» в 11 классах (профильном и общеобразовательном) – форма письм.
Предложенные мною билеты по теме «Интеграл» в 11 классах (профильном и общеобразовательном) – форма письм.
Научно практическая конференция «Интеграл и его применение»
Научно-практическая конференция «Интеграл и его применение» была разработана с акцентом на применение метода проектов. Во время подготовки.
Тест. Первообразная и интеграл (в 4-х вариантах).
Тест направлен на проверку знаний и умений учащихся по данной теме. Задачи теста позволяют эффективно подготовить учащихся к сдаче ЕГЭ по изученной теме. Задачи соответствуют программным требованиям. Д.
Тест можно использовать на уроке при проверке знаний и умений по теме. Тест состоит из двух вариантов и содержит критерии оценки.
| test_integrirovanie_na_sayt. pdf | 199.51 КБ |
Подтяните оценки и знания с репетитором Учи. ру
За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Вводный урок бесплатно, онлайн, 30 минут
Предварительный просмотр:
Предложенные мною билеты по теме Интеграл в 11 классах профильном и общеобразовательном форма письм.
Nsportal. ru
06.01.2020 8:11:13
2020-01-06 08:11:13
Источники:
Https://nsportal. ru/shkola/algebra/library/2013/02/17/test-po-teme-pervoobraznaya-i-integral
Неопределенный интеграл
Глава 5
Основной задачей дифференциального исчисления является отыскание производной заданной функции. Обратная задача — восстановление функции по известной производной, является основной задачей интегрального исчисления.
Всюду в этой главе функции рассматриваются на промежутках (конечных или бесконечных), расположенных в их области определения.
5.1 Первообразная функция и неопределенный интеграл
Определение 5.1.1. Пусть D — промежуток в R, конечный или бесконечный, f : D → R. Функция F : D → R называется первообразной функцией для функции f на D (или, проще и короче, первообразной функции f), если она дифференцируема на D и
Функция F : D → R называется первообразной функцией для функции f на D (или, проще и короче, первообразной функции f), если она дифференцируема на D и
F 0(x) = f(x), x D.
Очевидно, что если F — первообразная функции f на промежутке D, то F непрерывна на промежутке D, поскольку дифференцируема.
Например, функция F (x) = x является на R первообразная функции f(x) = 1, поскольку F (x) = x дифференцируема на R, и
F 0(x) = 1 = f(x), x R.
Аналогично, функция F (x) | = arcsin x — первообразная для функции | ||||||||
f(x) = | √ | 1 |
| на интервале (−1, 1), так как | |||||
1 − x | 2 | ||||||||
|
|
|
|
|
| 1 |
|
| |
|
|
|
| (arcsin x)0 | = | √ |
| , x (−1, 1). | |
|
|
|
| 1 − x | 2 | ||||
|
|
|
|
|
|
|
|
| |
В отличие от производной, первообразная функции не обладает свойством единственности. Например, для функции f(x) = −2 sin 2x, функции F (x) = cos 2x и Φ(x) = −2 sin2 x являются первообразными на R,
140
так как для всех x R
(cos 2x)0 = −2 sin 2x и (−2 sin2 x)0 = −4 sin x cos x = −2 sin 2x .
Естественно возникает вопрос об описании всех первообразных заданной функции.
Теорема 5.1. Пусть f : D → R. Если F(x) — первообразная на D для функции f(x), то множество всех ее первообразных на D совпадает с множеством {F (x) + C : C R}.
1). Обозначим через Jf множество всех первообразных функции f на D. Поскольку для любого числа C R функция F (x) + C дифференцируема на D и (F (x)+C)0 = f(x), x D, то функция F (x)+C, является первообразной функции f на D. Значит, {F (x) + C : C R} Jf .
Значит, {F (x) + C : C R} Jf .
2). Докажем обратное вложение, для чего рассмотрим функцию Φ(x) Jf . Введем функцию ϕ(x) = F (x) −Φ(x), x D. Тогда функция ϕ(x) дифференцируема на D и
ϕ0(x) = F 0(x) − Φ0(x) = f(x) − f(x) = 0, x D.
Откуда по критерию постоянства функции на промежутке (см. теорему 4.13) следует, что ϕ(x) ≡ C, x D, где C — некоторая постоянная. Таким оразом, F (x)−Φ(x) = C, x D, то есть Jf {F (x) + C : C R}.
Учитывая еще вложение, полученное в первой части доказательства, окончательно получаем, что Jf = {F (x) + C : C R} .
Определение 5.1.2. Пусть D — промежуток, функция f имеет на D первообразную. Совокупность всех первообразных функции f(x) на D называется неопределенным интегралом от функции f(x) на промежутке D и обозначается символом
Z
f(x) dx,
при этом x называется переменной интегрирования, f(x) — подынтегральной функцией, f(x) dx — подынтегральным выражением.
Таким образом, если F (x) — некоторая первообразная функции f(x)
на промежутке D, то | Z |
|
| f(x) dx = F (x) + C, |
где C — произвольная постоянная. Последнее равенство следует понимать как равенство двух множеств, состоящих из функций, определенных на промежутке D, причем слева — совокупность, образующая неопределенный интеграл от f(x), а справа — совокупность функций, отличающихся на D от F (x) на некоторую постоянную C.
Последнее равенство следует понимать как равенство двух множеств, состоящих из функций, определенных на промежутке D, причем слева — совокупность, образующая неопределенный интеграл от f(x), а справа — совокупность функций, отличающихся на D от F (x) на некоторую постоянную C.
141
Операция поиска неопределенного интеграла от заданной функции f(x) на промежутке D называется интегрированием.
Пример 5.1.1. Найти неопределенный интеграл функции f(x) = e|x| на всей числовой прямой.
При x > 0 e|x| = ex и для этой функции на интервале (0, +∞) ex является одной из ее первообразных. При x < 0 e|x| = e−x, и для этой функции на (−∞, 0) первообразной будет функция −e−x + C при любой постоянной C. Так как первообразная функции f(x) по определению 5.1.1 должна быть дифференцируемой на R, а, следовательно, непрерывной на R, то должно выполняться условие
lim ex = lim (−e−x + C),
x→+0 x→−0
то есть 1 = −1 + C, откуда C = 2. Итак, функция
F (x) = |
| ex, | ||
| 1, | |||
|
|
|
|
|
|
|
|
|
|
|
| −e− | x | + 2, |
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если x > 0, если x = 0, если x < 0
является непрерывной на R.
Докажем, что эта функция является на R первообразной функции f(x) = e|x|. Очевидно, что f0(x) = ex = e|x| для x > 0 и F 0(x) = e−x = e|x|
для x < 0. Покажем, что F 0(0) = e0 = 1: |
|
|
|
|
| ||||||||||
F 0(+0) = |
| lim | F (x) − F (0) | = | lim | ex − 1 | = 1, | ||||||||
|
|
| x→+0 | x |
|
|
|
| x→+0 | x | |||||
F 0( | 0) = lim | F (x) − F (0) | = lim | −e−x + 2 − 1 | = 1, | ||||||||||
− | x | →− | 0 |
| x |
|
| x | 0 |
| x | ||||
|
|
|
|
|
|
|
| →− |
|
|
| ||||
то есть F 0(+0) = F 0(−0) = F 0(0) = 1 = e|0|. | |||||||||||||||
e|x| dx = F (x) + C = |
| x |
|
|
|
| если x ≥ 0, | ||||||||
| ex | + C, | |||||||||||||
Z |
|
|
|
|
|
| e− | + 2 + C, | если x < 0. | ||||||
|
|
|
|
|
| − |
|
|
|
|
|
|
|
|
|
5.2 Основные свойства неопределенного интеграла
Теорема 5.2. Пусть функция f : D → R имеет первообразную на промежутке D, тогда на D
Z 0 Z
f(x) dx = f(x), x D, и d f(x) dx = f(x) dx, x D.
Действительно, если F (x) — некоторая первообразная функции f(x)
на D, то | Z |
|
f(x) dx = F (x) + C.
142
Тогда по определению 5.1.1 для всех x D |
|
| ||
| Z f(x) dx 0 | = (F (x) + C)0 = F (x)0 = f(x), | ||
d Z | f(x) dx = d(F (x) + C) = F 0(x)dx = Z | f(x) dx 0 | dx = f(x) dx. | |
Теорема 5.3. Если функция f(x) дифференцируема на промежут-
ке D, то | Z |
|
df(x) = f(x) + C.
Так как df(x) = f0(x)dx, то по определению 5. 1.2
1.2
ZZ
df(x) = f0(x) dx = f(x) + C.
Теорема 5.4. Если функции f(x) и g(x) имеют на промежутке D первообразные, то функция f(x) ± g(x) также имеет первообразную на D, причем
Z Z Z
(f(x) ± g(x)) dx = f(x) dx ± g(x) dx. (5.1)
Заметим, что равенство в формуле (5.1) следует понимать как совпадение двух множеcтв функций. Пусть F (x) и G(x) некоторые первообразные функций f(x) и g(x), соответственно, на промежутке D, то
есть Z Z
f(x) dx = F (x) + C1, g(x) dx = G(x) + C2.
Функция F (x) ± G(x) дифференцируема на D и
(F (x) ± G(x))0 = F 0(x) ± G0(x) = f(x) ± g(x), x D.
Последнее означает, что F (x) ± G(x) является первообразной функции f(x) ± g(x) на D, а поэтому
Z
(f(x) ± g(x)) dx = F (x) ± G(x) + C.
Левая часть формулы (5.1) — множество, состоящее из функций вида F (x) ±G(x) + C, а правая — из функций (F (x) + C1) ±(G(x) + C2). Ввиду произвольности постоянных C, C1, C2 эти множества совпадают, то есть справедливо равенство (5. 4).
4).
Теорема 5.5. Если функция f(x) имеет на промежутке D первообразную и λ — число, то функция λf(x) также имеет первообразную на D, причем при λ 6= 0
Z | Z | (5.2) |
λf(x) dx = λ | f(x) dx. |
143
3Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Тамара Дж. ответил 21.03.13
Репетитор
4.9(51)
Репетиторство по математике – алгебра и исчисление (все уровни)
См. таких репетиторов
Смотрите таких репетиторов
∫ COS 2 X · SIN 3 x DX = ∫ COS 2 X · SINX · SIN 2 X DX
Напомним: SIN 2 X + COS 2 X = 1 ==> sin 2 x = 1 — cos 2 x
∫ cos 2 x·sinx·(1 — cos 2 x) dx = ∫ (cos 2 x · sinx- cos 4 x · sinx) dx
= ∫ cos 2 x · sinx dx- ∫ cos 4 x · sinx dx
Использование u-substitution, пусть: u = cosx, так , du = -sinx dx
==> ∫ cos 2 x·sinx dx = ∫ -1·cos 2 x·(-1·sinx dx) = ∫ -(u) 2 · 900 ) = ∫ -u 2 DU
=-(U) 3 /3 =-(COSX) 3 /3 = -cos 3 x /3
==> ∫ cos x /3
==> ∫ Cos 4 x · sinx dx = ∫ -1 · cos 4 x · (-1 · sinx dx) = ∫ -(u) 4 · (du) = ∫ -u 4 DU
= — (U) 5 /5 =-(COSX) 5 /5 = -cos 5 x /5
∫ COS 2 X · SINX DX-COS 4 X · SINX DX = ( -cos 3 x/3)-(-cos 5 x/5)
= -cos 3 x/3+ cos 5 x/5 = cos 5 х/5 — cos 3 х/3
Голосовать за 0 голос против
Подробнее
Отчет
Джон М. ответил 20.03.13
ответил 20.03.13
Репетитор
4.9 (551)
Аналитическая помощь – Письмо, Математика и др.
См. таких репетиторов 94 x][sin x], при этом вы можете использовать правило сумм, u-подстановку и правило степени для решения каждого члена, что довольно просто. Не стесняйтесь писать по электронной почте или задавать дополнительный вопрос, если это не имеет смысла. Джон
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Как делать первообразные производные — синоним
МАРКИРОВКА САМУЭЛА
КЛАСС
… Jupiterimages/Photos.com/Getty Images
Исчисление — это раздел математики, изучающий изменение одной величины по отношению к другой. В исчислении есть два процесса — дифференцирование и интегрирование. Эти процессы противоположны друг другу, и поэтому результат интегрирования дает первообразную. Есть несколько способов интегрировать функцию для получения первообразной, и это зависит от конкретной функции.
Исследуйте эту статью
- Антидовитивные простые функции
- Антидовичение продуктов
- Антидовая по замене
- Антидервижение по тригонометрическим идентификациям
12012020202020202020202020202020202021
1.
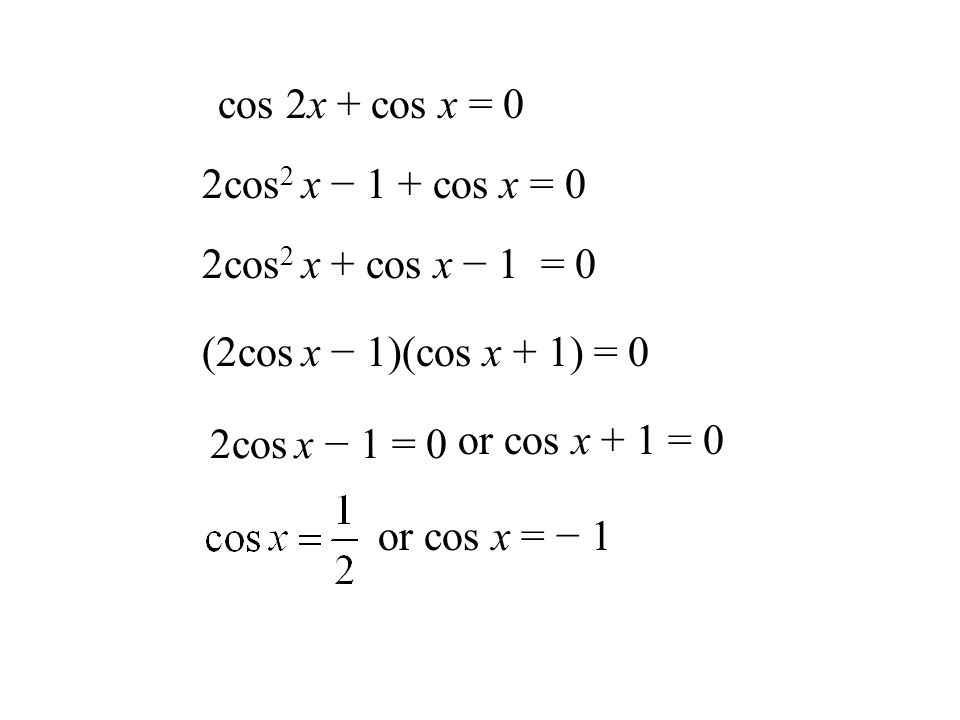 Если рассматриваемая функция проста, ее следует найти в таблице первообразных. Чтобы найти первообразную определенной функции, найдите функцию в левой части таблицы и соответствующую первообразную в правой части таблицы. Например, если требуется первообразная cos(x), таблица показывает, что первообразная равна sin(x) + c.
Если рассматриваемая функция проста, ее следует найти в таблице первообразных. Чтобы найти первообразную определенной функции, найдите функцию в левой части таблицы и соответствующую первообразную в правой части таблицы. Например, если требуется первообразная cos(x), таблица показывает, что первообразная равна sin(x) + c.2 Первообразная произведения
Иногда функция является произведением двух более простых функций. В этом случае таблица первообразных не даст результата. Вместо этого нужно будет выполнить некоторые простые математические действия. Метод нахождения первообразной произведения известен как интегрирование по частям. Чтобы выполнить интегрирование по частям, разделите исходное уравнение на два произведения. Например, если исходная функция y=x.cos(x), разбивается на u=x и dv/dx=cos(x). Следующим шагом будет использование таблицы первообразных для нахождения производной u и первообразной dv/dx:
u=x, поэтому производная du/dx=1
dv/dx=cos(x), следовательно, первообразная v=sin(x)
Следующее уравнение затем используется для вычисления первообразной:
Интеграл (u.
Квадратный корень посчитать онлайн: Калькулятор квадратных корней
Найти квадратный корень — формула и калькулятор квадратного корня с шагами
Предположим, вас попросили найти квадратный корень из числа. Но для этого нужно знать, что такое квадраты и квадратные корни. Значение числа, умножаемого само на себя, возвращает исходное заданное число, известное как его квадратный корень. Например, предположим, что у — квадратный корень из х, тогда у2 = х. Это уравнение также можно записать в виде y = √x. Квадратный корень числа представлен символом ‘√’ Всякий раз, когда мы умножаем число само на себя, мы получаем положительное значение, равное квадрату числа. Мы вернем исходное число, найдя квадратный корень из этого положительного значения.
Квадрат 4 равен 16 или 42 = 16 и √16 = 4. Легко найти квадратный корень из 16 или подобных чисел, потому что они являются полными квадратами. Но для таких чисел, как 10, 7, 20, 24 и многих других, это становится немного сложным и расчетливым. Не существует такой формулы для нахождения квадратного корня числа. Но есть различные методы и приемы, с помощью которых можно легко вычислить квадратный корень. В разных разделах мы узнаем о них.
Но есть различные методы и приемы, с помощью которых можно легко вычислить квадратный корень. В разных разделах мы узнаем о них.
Представление квадратных корней
Символ, используемый для представления квадратного корня, известен как радикальный символ. ‘√’ — это символ квадратного корня. Если x — это исходное число, то √x — это квадратный корень из числа. Здесь x также известен как подкоренное число. Радикал и квадратный корень представляют одно и то же. Формула квадратного корня может быть представлена следующим образом:
X = √Y, где X — квадратный корень из Y. С другой стороны, X2 = Y. Следовательно, где Y — квадрат X.
Свойства квадратов И Квадратные корни
В математике функция квадратного корня принимает положительное значение в качестве входных данных и возвращает квадратный корень входного значения в качестве выходных данных. Следовательно, говорят, что это функция один к одному. Например,
F(а) = √а.
Предположим, что если x = 25, то возвращаемое значение будет равно 5. Ниже приведены некоторые свойства квадратов и квадратных корней.
Число может иметь квадратный корень, если оно заканчивается четным числом нулей.
Число может быть полным квадратом. Тогда будет и идеальный квадратный корень.
Возможно умножение двух значений квадратного корня. Например, √2 × √3 = √6.
Если найти квадратный корень из отрицательного числа, в результате получится комплексное число. Совершенные квадраты никогда не бывают отрицательными.
Подкоренное число получается путем умножения двух одинаковых квадратных корней. Если вы умножите √7 × √7, вы получите 7, что является числом, не имеющим квадратного корня.

Числа, оканчивающиеся на 1, 4, 5 и 6, будут иметь квадратный корень.
Идеальный квадратный корень не существует для чисел, оканчивающихся на 2, 3, 7 и 8.
Простой способ найти квадратный корень из числа
Нам нужно найти квадратный корень из числа, будь то совершенный или несовершенный квадрат. Вы уже знаете, является ли это идеальным квадратом, тогда мы можем использовать метод простой факторизации, чтобы разложить на множители и легко найти квадратный корень. Для других чисел у нас есть метод деления.
Метод простой факторизации
Это один из самых простых способов найти квадратный корень из числа. Например, возьмем число 256. Теперь разобьем 256 на простые множители. Следовательно, 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2. Теперь нам нужно спарить одинаковые числа попарно и рассмотреть их только один раз, (2 × 2) × (2 × 2) × (2 × 2) × (2 × 2). Следовательно, √256 = (2 × 2 × 2 × 2) = 16,
Следовательно, √256 = (2 × 2 × 2 × 2) = 16,
Метод длинного деления
Это формула квадратного корня, используемая для неполных квадратов или больших чисел. Давайте рассмотрим число 3. Это не идеальное квадратное число. На этом примере мы проиллюстрировали метод длинного деления ниже.
Запись 3 с десятичной точкой и группами из двух нулей для десятичной точки. Помещаем все это под символ длинного квадратного корня (который выглядит как деление) и начинаем делить.
1√3.00 00 00 00 00
Подставить наибольшее число, квадрат которого меньше или равен 3 и больше 3. Возвести его в квадрат и вычесть из 3, что в данном случае равно 1.
Сведение пары нулей и умножение полученного результата на два. Следующая цифра в ответе будет помещена в конце удвоенного ответа и умножена на новую цифру. Произведение вычитается, и прибавляются еще два нуля. Мы должны продолжить этот процесс для стольких цифр точности, сколько мы хотим.
Квадратный корень из 3 дает 1,732.
Теперь рассмотрим число 24.
Решенные примеры
Приведите некоторые приложения формулы квадратного корня.
Ответ: Формула квадратного корня используется в геометрии, исчислении, алгебре, квадратных уравнениях, вычислениях и других математических приложениях.
Найдите квадратные корни из 5, 7, 9 и 11.
Ответ: Квадратные корни из 5, 7, 9 и 11 равны 2,236, 2,646, 3,0 и 3,317 соответственно.
Как найти квадратный корень из числа
Последнее обновление:
Операционное исчисление для чайников: Лямбда-исчисление: описание теоремы, особенности, примеры
Лямбда-исчисление: описание теоремы, особенности, примеры
Лямбда-исчисление — это формальная система в математической логике для выражения подсчетов на основе абстракции и применения функций с использованием привязки и подстановки переменных. Это универсальная модель, которую можно применять для проектирования любой машины Тьюринга. Впервые введена лямбда-исчисления Черчем, известным математиком, в 1930-х годах.
Система состоит из построения лямбда-членов и выполнения над ними операций сокращения.
Пояснения и приложения
Греческая буква lambda (λ) используется в лямбда-выражениях и лямбда-терминах для обозначения связывания переменной в функции.
Лямбда-исчисление может быть нетипизировано или типизировано. В первом варианте функции могут быть применены только в том случае, если они способны принимать данные этого типа. Типизированные лямбда-исчисления слабее, могут выражать меньшее значение. Но, с другой стороны, они позволяют доказывать больше вещей.
Одной из причин того, что существует много разных типов — это желание ученых сделать больше, не отказываясь от возможности доказывать сильные теоремы лямбда-исчислений.
Система находит применение во многих различных областях математики, философии, лингвистики, и компьютерных наук. В первую очередь, лямбда-исчисления — это расчет, который сыграл важную роль в развитии теории языков программирования. Именно стили функционального создания реализуют системы. Они также являются актуальной темой исследований в теории этих категорий.
Для чайников
Лямбда-исчисление была введена математиком Алонзо Черчем в 1930-х годах в рамках исследования основ науки. Первоначальная система была показана как логически несовместимая в 1935 году, когда Стивен Клин и Дж. Б. Россер разработали парадокс Клини-Россера.
В последствии, в 1936 году Черч выделил и опубликовал только ту часть, которая имеет отношение к расчетам, то, что сейчас называется нетипизированным лямбда-исчислением. В 1940 он также представил более слабую, но логически непротиворечивую теорию, известную как система простого типа. В свое работе он объясняет всю теорию простым языком, поэтому, можно сказать, что Черч опубликовал лямбду исчисления для чайников.
В 1940 он также представил более слабую, но логически непротиворечивую теорию, известную как система простого типа. В свое работе он объясняет всю теорию простым языком, поэтому, можно сказать, что Черч опубликовал лямбду исчисления для чайников.
До 1960-х годов, когда выяснилось его отношение к языкам программирования, λ стала лишь формализмом. Благодаря применениям Ричарда Монтегю и других лингвистов в семантике естественного языка, исчисление стало занимать почетное место как в лингвистике, так и в информатике.
Происхождение символа
Лямбда не обозначает слово или аббревиатуру, она возникла, благодаря ссылки в «Принципиальной математике» Рассела, за которой следуют два типографских изменения. Пример обозначения: для функции f с f (y) = 2y + 1 равно 2ŷ + 1. И здесь используется символ каретки («шляпа») над y для пометки входной переменной.
Церковь изначально намеревалась использовать аналогичные символы, но наборщики не смогли разместить символ «шляпа» над буквами. Поэтому вместо этого они напечатали его изначально как «/\y.2y+1». В следующем эпизоде редактирования наборщики заменили «/ \» на визуально похожий символ.
Поэтому вместо этого они напечатали его изначально как «/\y.2y+1». В следующем эпизоде редактирования наборщики заменили «/ \» на визуально похожий символ.
Введение в лямбда исчисление
Система состоит из языка терминов, которые выбираются определенным формальным синтаксисом, и набора правил преобразования, которые позволяют манипулировать ими. Последний пункт можно рассматривать как эквациональную теорию или как операционное определение.
Все функции в лямбда-исчислении являются анонимными, то есть не имеющими имен. Они принимают только одну входную переменную, при этом каррирование используется для реализации графиков с несколькими непостоянными.
Лямбда-термины
Синтаксис исчисления определяет некоторые выражения как допустимые, а другие — как недействительные. Также, как различные строки символов являются допустимыми программами на Си, а какие-то — нет. Действительное выражение лямбда-исчисления называется «лямбда-термином».
Следующие три правила дают индуктивное определение, которое можно применять для построения всех синтаксически допустимых понятий:
Переменная x сама по себе является действительным лямбда-термином:
- если T это ЛТ, и x непостоянная, то (lambda xt) называется абстракцией.

- если T, а также s понятия, то (TS) называется приложением.
Ничто другое не является лямбда-термином. Таким образом, понятие действительно тогда и только тогда, когда оно может быть получено повторным применением этих трех правил. Тем не менее некоторые скобки могут быть опущены в соответствии с другими критериями.
Определение
Лямбда-выражения состоят из:
- переменных v 1, v 2,…, v n,…
- символов абстракции ‘λ’ и точки ‘.’
- скобок ().
Множество Λ, может быть определено индуктивно:
- Если x переменная, то x ∈ Λ;
- x непостоянная и M ∈ Λ, то (λx.M) ∈ Λ;
- M, N ∈ Λ, то (MN) ∈ Λ.
Обозначение
Чтобы сохранить нотацию лямбда-выражений в незагроможденном виде, обычно применяются следующие соглашения:
- Внешние скобки опущены: MN вместо (MN).
- Предполагается, что приложения остаются ассоциативными: взамен ((MN) P) можно написать MNP.
- Тело абстракции простирается дальше вправо: λx.
 MN означает λx. (MN), а не (λx.M) N.
MN означает λx. (MN), а не (λx.M) N. - Сокращается последовательность абстракций: λx.λy.λz.N можно λxyz.N.
Свободные и связанные переменные
Оператор λ соединяет свою непостоянную, где бы он ни находился в теле абстракции. Переменные, попадающие в область, называются связанными. В выражении λ x. М, часть λ х часто называют связующим. Как бы намекая, что переменные становятся группой с добавлением Х х к М. Все остальные неустойчивые называются свободными.
Например, в выражении λ y. х х у, у — связанная непостоянная, а х — свободная. И также стоит обратить внимание, что переменная сгруппирована своей «ближайшей» абстракцией. В следующем примере решение лямбда-исчисления представлено единственным вхождением x, которое связано второй составляющей:
λ x. y (λ x. z x)
Множество свободных переменных M обозначается как FV (M) и определяется рекурсией по структуре терминов следующим образом:
- FV (x) = {x}, где x — переменная.
- FV (λx.M) = FV (M) \ {x}.

- FV (MN) = FV (M) ∪ FV (N).
Формула, которая не содержит свободных переменных, называется закрытой. Замкнутые лямбда-выражения также известны как комбинаторы и эквивалентны терминам в комбинаторной логике.
Сокращение
Значение лямбда-выражений определяется тем, как они могут быть сокращены.
Существует три вида урезания:
- α-преобразование: изменение связанных переменных (альфа).
- β-редукция: применение функций к своим аргументам (бета).
- η-преобразование: охватывает понятие экстенсиональности.
Здесь речь также идет о полученных эквивалентностях: два выражения являются β-эквивалентными, если они могут быть β-преобразованы в одно и то же составляющее, а α / η-эквивалентность определяется аналогично.
Термин redex, сокращение от приводимого оборота, относится к подтемам, которые могут быть сокращены одним из правил. Лямбда исчисление для чайников, примеры:
(λ x.M) N является бета-редексом в выражении замены N на x в M. Составляющее, к которому сводится редекс, называется его редуктом. Редукция (λ x.M) N есть M [x: = N].
Составляющее, к которому сводится редекс, называется его редуктом. Редукция (λ x.M) N есть M [x: = N].
Если x не является свободной в M, λ х. М х также ет-REDEX с регулятором М.
α-преобразование
Альфа-переименования позволяют изменять имена связанных переменных. Например, λ x. х может дать λ у. у. Термины, которые отличаются только альфа-преобразованием, называются α-эквивалентными. Часто при использовании лямбда-исчисления α-эквивалентные считаются взаимными.
Точные правила для альфа-преобразования не совсем тривиальны. Во-первых, при данной абстракции переименовываются только те переменные, которые связаны с одной и той же системой. Например, альфа-преобразование λ x.λ x. x может привести к λ y.λ x. х, но это может не ввергнуть к λy.λx.y Последний имеет иной смысл, чем оригинал. Это аналогично понятию программирования затенения переменных.
Во-вторых, альфа-преобразование невозможно, если оно приведет к захвату непостоянной другой абстракцией. Например, если заменить x на y в λ x.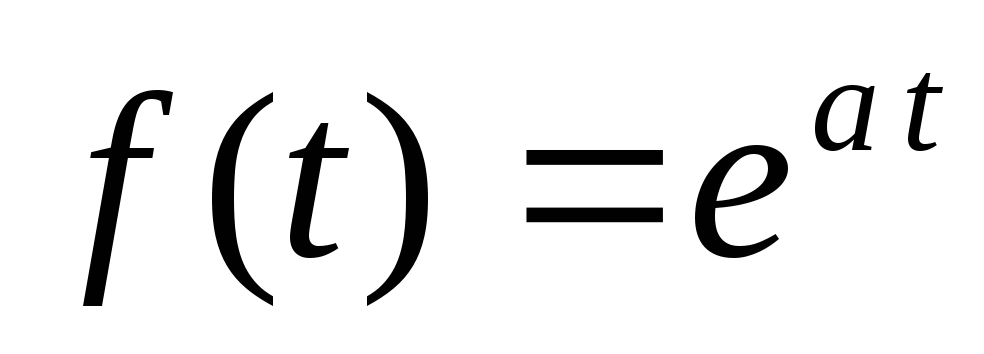 λ y. x, то можно получить λ y.λ y. у, что совсем не то же самое.
λ y. x, то можно получить λ y.λ y. у, что совсем не то же самое.
В языках программирования со статической областью видимости альфа-преобразование можно использовать для упрощения разрешения имен. При этом следя за тем, чтобы понятие переменной не маскировало обозначение в содержащей области.
В нотации индекса Де Брюйна любые два альфа-эквивалентных термина синтаксически идентичны.
Замена
Изменения, написанные Е [V: = R], представляют собой процесс замещения всех свободных вхождений переменной V в выражении Е с оборотом R. Подстановка в терминах λ определяется лямбдой исчисления рекурсии по структуре понятий следующим образом (примечание: x и y — только переменные, а M и N — любое λ-выражение).
x [x: = N] ≡ N
y [x: = N] ≡ y, если x ≠ y
(M 1 M 2) [x: = N] ≡ (M 1 [x: = N]) (M 2 [x: = N])
(λ x.M) [x: = N] ≡ λ x.M
(λ y.M) [x: = N] y λ y. (M [x: = N]), если x ≠ y, при условии, что y ∉ FV (N).
Для подстановки в лямбда-абстракцию иногда необходимо α-преобразовать выражение. Например, неверно, чтобы (λ x. Y) [y: = x] приводило к (λ x. X), потому что замещенный x должен был быть свободным, но в итоге был связанным. Правильная замена в этом случае (λ z. X) с точностью до α-эквивалентности. Стоит обратить внимание, что замещение определяется однозначно с верностью до лямбды.
Например, неверно, чтобы (λ x. Y) [y: = x] приводило к (λ x. X), потому что замещенный x должен был быть свободным, но в итоге был связанным. Правильная замена в этом случае (λ z. X) с точностью до α-эквивалентности. Стоит обратить внимание, что замещение определяется однозначно с верностью до лямбды.
β-редукция
Бета-редукция отражает идею применения функции. Бета-восстановительный определяется в терминах замещения: ((X V. E) Е ‘) является Е [V: = Е’].
Например, предполагая некоторое кодирование 2, 7, ×, имеется следующее β-уменьшение: ((λ n. N × 2) 7) → 7 × 2.
Бета-редукция может рассматриваться как то же самое, что и концепция локальной сводимости при естественной дедукции через изоморфизм Карри – Ховарда.
η-преобразование
Эта-конверсия выражает идею экстенсиональности, которая в этом контексте заключается в том, что две функции равны тогда, когда они дают одинаковый результат для всех аргументов. Эта конвертация обменивает между λ x. (F x) и f всякий раз, когда x не кажется свободным в f.
Данное действие может рассматриваться как то же самое, что и концепция локальной полноты в естественной дедукции через изоморфизм Карри – Ховарда.
Нормальные формы и слияние
Для нетипизированного лямбда-исчисления β-редукция как правило переписывания не является ни сильно нормализующей, ни слабо.
Тем не менее можно показать, что β-редукция сливается при работе до α-преобразования (т. е. можно считать две нормальные формы равными, если возможно α-преобразование одной в другую).
Поэтому и сильно нормализующие члены, и слабо налаживающие понятия имеют единственную нормальную форму. Для первых терминов любая стратегия сокращения гарантированно приведет к типичной конфигурации. Тогда как для слабо нормализующих условий некоторые стратегии сокращения могут не найти ее.
Дополнительные методы программирования
Существует большое количество идиом создания для лямбда-исчисления. Многие из них были первоначально разработаны в контексте использования систем в качестве основы для семантики языка программирования, эффективно применяя их в качестве создания низкого уровня. Поскольку некоторые стили включают лямбда-исчисление (или что-то очень похожее) в качестве фрагмента, эти методы также находят применение в практическом создании, но затем могут восприниматься как неясные или чужие.
Поскольку некоторые стили включают лямбда-исчисление (или что-то очень похожее) в качестве фрагмента, эти методы также находят применение в практическом создании, но затем могут восприниматься как неясные или чужие.
Именованные константы
В лямбда-исчислении библиотека принимает форму набора ранее определенных функций, в которой термины являются просто конкретными константами. Чистое исчисление не имеет понятия именованных неизменных, поскольку все атомные лямбда-термины являются переменными. Но их также можно имитировать, выделив непостоянную в качестве имени константы, используя лямбда-абстракцию для связывания этой изменчивой в основной части, и применить эту абстракцию к намеченному определению. Таким образом, если использовать f для обозначения M в N, можно сказать,
(λ ф. Н) М.
Авторы часто вводят синтаксическое понятие, такое как let, чтобы разрешить писать все в более интуитивном порядке.
f = M в N
Объединяя в цепочку такие определения, можно написать «программу» лямбда-исчисления как ноль или более дефиниций функций, за которыми следует один лямбда-член, используя те определения, которые составляют основную часть программы.
Заметным ограничением этого let является то, что имя f не определено в M, поскольку M находится вне области привязки лямбда-абстракции f. Это означает, что атрибут рекурсивной функции не может использоваться как M с let. Более продвинутая синтаксическая конструкция letrec, которая позволяет писать рекурсивные определения функций в этом стиле, вместо этого дополнительно использует комбинаторы с фиксированной точкой.
Печатные аналоги
Данный тип является типизированным формализмом, который использует символ для обозначения анонимной функции абстракция. В этом контексте типы обычно являются объектами синтаксической природы, которые присваиваются лямбда-терминам. Точная натура зависит от рассматриваемого исчисления. С определенной точки зрения, типизированные ЛИ можно рассматривать как уточнения нетипизированного ЛИ. Но с другой стороны, их также можно считать более фундаментальной теорией, а нетипизированное лямбда-исчисление — особым случаем только с одним типом.
Типизированные ЛИ являются основополагающими языками программирования и основой функциональных, таких как ML и Haskell. И, более косвенно, императивных стилей создания. Типизированные лямбда-исчисления играют важную роль в разработке систем типов для языков программирования. Здесь типизируемость обычно захватывает желательные свойства программы, например, она не вызовет нарушения доступа к памяти.
И, более косвенно, императивных стилей создания. Типизированные лямбда-исчисления играют важную роль в разработке систем типов для языков программирования. Здесь типизируемость обычно захватывает желательные свойства программы, например, она не вызовет нарушения доступа к памяти.
Типизированные лямбда-исчисления тесно связаны с математической логикой и теорией доказательств через изоморфизм Карри – Говарда, и их можно рассматривать как внутренний язык классов категорий, например, который просто является стилем декартовых замкнутых.
Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения
ОглавлениеПРЕДИСЛОВИЕГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 2. Дифференциальные уравнения первого порядка 2. Уравнения с разделяющимися переменными. 3. Однородные уравнения. 4. Линейные уравнения. 5. Уравнения в полных дифференциалах. 6. Интегрирующий множитель. 7. Уравнение Бернулли.  8. Уравнение Риккати. § 3. Линейные дифференциальные уравнения. Принцип суперпозиции 2. Принцип суперпозиции. § 4. Линейное уравнепие первого порядка с постоянными коэффициентами 2. Комплексные функции вещественного аргумента. Комплексная экспонента. § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами 2. Случай простых корней. 3. Случай кратных корней. 4. Уравнение Эйлера. 5. Выделение вещественных решений. § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами 2. Ангармонические колебания. § 7. Линейные уравнения с правой частью — квазимногочленом § 8. Линейные системы с постоянными коэффициентами. Случай простых корней § 9. Фазовая плоскость линейной системы 2. Комплексные корни. 3. Уравнение второго порядка. § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней § 11. Операционное исчисление § 12. Линейные разностные уравнения ГЛАВА 2.  ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ2. Доказательство основной теоремы при n = 1. 3. Теорема Коши. § 2. Линейные нормированные пространства § 3. Принцип сжатых отображений § 4. Лемма Адамара § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка 2. Дифференциальные уравнения n-го порядка. 3. Комментарии к основной теореме. 4. Продолжение решений. § 6. Гладкость решений § 7. Зависимость решений от параметров и начальных условий § 8. Обратные и неявные функции 2. Теорема о неявной функции. 3. Дифференцирование сложных функций. § 9. Зависимые и независимые функции. Криволинейные координаты 2. Кривые и поверхности. 3. Криволинейные координаты. § 10. Уравнения первого порядка, не разрешенные относительно производной 2. Особые решения. Огибающая. 3. Интегрирование уравнений вида (1). ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ 2. Доказательство теоремы.  3. Линейное уравнение n-го порядка. § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами 2. Вычисление матричной экспоненты. 3. Функции от матриц. 4. Малые колебания механических систем. § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского 2. Определитель Вронского. § 4. Формула Лиувилля § 5. Фундаментальные системы решений § 6. Неоднородные линейные системы с переменными коэффициентами § 7. Линейные дифференциальные уравнения n-го порядка 2. Уравнения второго порядка. § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений § 9. Нули решений однородных линейных уравнений второго порядка 2. Теорема сравнения. § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя 2. Регулярные особые точки. 3. Уравнение Бесселя. § 11. Уравнения с периодическими коэффициентами 2. Зоны устойчивости и неустойчивости. § 12.  Дельта-функция и ее применения Дельта-функция и ее применения2. Толчки. Принцип Дюамеля. 3. Периодические толчки в системах с трением. ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ 2. Векторные поля. Механическая интерпретация фазовых траекторий. § 2. Структура решений автономной системы в окрестности неособой точки § 3. Изменение фазового объема 2. Замечания о системах в трехмерном пространстве. § 4. Производная в силу системы. Первые интегралы 2. Первые интегралы. § 5. Одномерное движение частицы в потенциальном поле 2. Колебания маятника. 3. Эллиптические функции. 4. Движение частицы в поле с кубическим потенциалом. § 6. Устойчивость. Функция Ляпунова § 7. Устойчивость положения равновесия линейной системы § 8. Устойчивость по линейному приближению 2. Устойчивость по линейному приближению. 3. Неустойчивость по линейному приближению. 4. Устойчивость неавтономных систем. 5. Устойчивые многообразия решений (условная устойчивость). § 9.  Двумерные автономные системы (элементы качественной теории) Двумерные автономные системы (элементы качественной теории)2. Предельное поведение траекторий. 3. Функция последования. Автоколебания. ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА 2. Другие примеры. 3. Классификация уравнений с частными производными 1-го порядка. § 2. Интегрирование линейных и квазилинейных уравнений 2. Квазилинейные уравнения. 3. Характеристики и интегральные поверхности. § 3. Задача Коши для линейных и квазилинейных уравнений 2. Область зависимости от начальных данных. 3. Линейные уравнения со многими переменными. 4. Квазилинейные уравнения. § 4. Линейные и нелинейные волны § 5. Нелинейные уравнения 2. Задача Коши. ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ § 2. Функционалы в линейных нормированных пространствах 2. Линейные функционалы. 3. Первая вариация. 4. Необходимое условие экстремума. § 3. Простейшие задачи вариационного исчисления 2. Задача с одним закрепленным и с одним подвижным концом.  3. Примеры. § 4. Функционалы, зависящие от высших производных § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике 2. Принцип наименьшего действия. § 6. Условный экстремум § 7. Задача Лагранжа § 8. Функционалы от функций многих переменных 2. Уравнение колебаний мембраны. § 9. Достаточные условия слабого экстремума 2. Квадратичные функционалы. 3. Достаточные условия слабого экстремума. § 10. Дополнительные сведения из вариационного исчисления 2. Гамильтонова форма уравнений механики. 3. Задача с подвижными концами. § 11. Принцип максимума Понтрягина 2. Необходимые условия экстремума. ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 2. Основные оценки 2. Оценка решений. § 3. Асимптотика решений при больших значениях аргумента 2. Неосциллирующие решения. 3. Уравнения с комплексными коэффициентами. § 4. Асимптотика решений при больших значениях параметра 2.  Неосциллирующие решения. Неосциллирующие решения.3. Двойные асимптотики. 4. Асимптотические разложения решений. § 5. Элементы теории возмущений 2. Метод Линдштедта — Пуанкаре. 3. Метод Крылова — Боголюбова. 4. Метдд осреднения. 5. Пограничный слой и метод сращивания асимптотических разложений. 6. Метод ВКБ для нелинейных уравнений. СПИСОК ЛИТЕРАТУРЫ |
Математика | Бесплатный полнотекстовый | Оперативное исчисление для общих дробных производных произвольного порядка
1. Введение
Начиная с ранних фаз развития исчисления было предпринято несколько попыток интерпретации производных и интегралов как неких чисто алгебраических символов. Лейбниц, Эйлер, Лагранж и другие основатели исчисления ввели и использовали алгебраические правила для работы с интегральными и дифференциальными операторами. В большинстве случаев эти правила приводили к правильным результатам. Однако это были всего лишь формальные алгоритмы без строгой математической основы. Наиболее ярким примером этой процедуры были работы Оливера Хевисайда, который систематически использовал алгебраический подход к исследованию ряда практических проблем, включая дифференциальные уравнения электромагнетизма и теорию осцилляторов. Из-за важности подхода Хевисайда для инженеров математики начали задумываться о его строгом математическом обосновании. В работах Бромвича, Карсона, Ван дер Поля, Дётча и других математиков методы Хевисайда обосновывались в терминах преобразования Лапласа и его модификаций. Однако требование существования преобразования Лапласа приводило к некоторым условиям на поведение функций в бесконечности, что ограничивало применимость операционного исчисления Хевисайда.
Наиболее ярким примером этой процедуры были работы Оливера Хевисайда, который систематически использовал алгебраический подход к исследованию ряда практических проблем, включая дифференциальные уравнения электромагнетизма и теорию осцилляторов. Из-за важности подхода Хевисайда для инженеров математики начали задумываться о его строгом математическом обосновании. В работах Бромвича, Карсона, Ван дер Поля, Дётча и других математиков методы Хевисайда обосновывались в терминах преобразования Лапласа и его модификаций. Однако требование существования преобразования Лапласа приводило к некоторым условиям на поведение функций в бесконечности, что ограничивало применимость операционного исчисления Хевисайда.
В 1950-х годах в работах Яна Микусинского и его соавторов (см. [1] и ссылки в ней) был предложен кардинальный возврат к первоначальным идеям операционного исчисления, где операционное исчисление для производной первого порядка были разработаны и применены для ряда математических и реальных задач. Основными компонентами этого подхода являются интерпретация свертки Лапласа как умножения в кольце функций, непрерывных на вещественной положительной полуоси, и расширение этого кольца на поле отношений свертки. В дальнейшем схема Микусинского использовалась рядом математиков для разработки операционного исчисления некоторых специальных дифференциальных операторов с переменными коэффициентами (см., например, [2,3,4]), которые оказались частными случаями гипер- Дифференциальный оператор Бесселя в виде
Основными компонентами этого подхода являются интерпретация свертки Лапласа как умножения в кольце функций, непрерывных на вещественной положительной полуоси, и расширение этого кольца на поле отношений свертки. В дальнейшем схема Микусинского использовалась рядом математиков для разработки операционного исчисления некоторых специальных дифференциальных операторов с переменными коэффициентами (см., например, [2,3,4]), которые оказались частными случаями гипер- Дифференциальный оператор Бесселя в виде
Операционное исчисление типа Микусинского для дифференциального оператора гипербесселя (1) было построено Димовским в [5].
Новый этап в дальнейшем развитии операционного исчисления типа Микусинского был начат в работах Лучко и его соавторов, где были построены операционные исчисления для различных дробных производных и применены для вывода формул решения дробного интеграла в замкнутой форме и дифференциальные уравнения. Первое операционное исчисление для дробной производной было предложено в [6,7], где было разработано операционное исчисление типа Микусинского для кратной дробной производной Эрдейи-Кобера.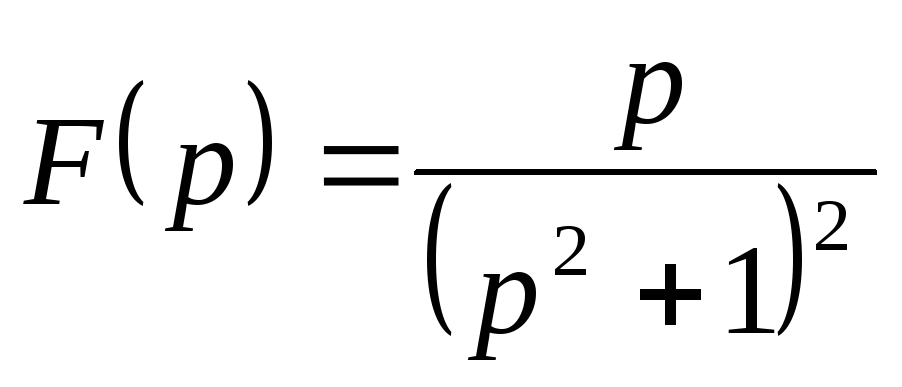 Двумя известными частными случаями этой дробной производной являются дифференциальный оператор гипер-Бесселя (1) и дробная производная Римана–Лиувилля. Расширенная версия операционного исчисления для дробной производной Римана–Лиувилля была предложена в [8,9].]. Операционное исчисление для другой основной дробной производной, производной Капуто, было разработано в [10]. Следует отметить, что в [10] это операционное исчисление было применено для вывода формул решений в замкнутой форме многочленных дробных дифференциальных уравнений, содержащих дробные производные Капуто соизмеримого и несоизмеримого порядков. В [11] разработано операционное исчисление типа Микусинского для дробной производной Гильфера. В [12] рассмотрен случай дробной производной Эрдейи-Кобера типа Капуто. В [13] было разработано операционное исчисление типа Микусинского для общей дробной производной (ОДП) «обобщенного порядка» из интервала (0,1) в смысле Капуто. Эта ОФД представляет собой композицию интеграла свертки Лапласа с ядром Сонина с интегрируемой особенностью типа степенной функции в нулевой точке и производной первого порядка.
Двумя известными частными случаями этой дробной производной являются дифференциальный оператор гипер-Бесселя (1) и дробная производная Римана–Лиувилля. Расширенная версия операционного исчисления для дробной производной Римана–Лиувилля была предложена в [8,9].]. Операционное исчисление для другой основной дробной производной, производной Капуто, было разработано в [10]. Следует отметить, что в [10] это операционное исчисление было применено для вывода формул решений в замкнутой форме многочленных дробных дифференциальных уравнений, содержащих дробные производные Капуто соизмеримого и несоизмеримого порядков. В [11] разработано операционное исчисление типа Микусинского для дробной производной Гильфера. В [12] рассмотрен случай дробной производной Эрдейи-Кобера типа Капуто. В [13] было разработано операционное исчисление типа Микусинского для общей дробной производной (ОДП) «обобщенного порядка» из интервала (0,1) в смысле Капуто. Эта ОФД представляет собой композицию интеграла свертки Лапласа с ядром Сонина с интегрируемой особенностью типа степенной функции в нулевой точке и производной первого порядка. В [13] это исчисление применялось для вывода формул решения в замкнутой форме начальных задач для многочленных дифференциальных уравнений дробного порядка с последовательными дробными производными этого типа. Случай GFD произвольного порядка в смысле Римана–Лиувилля был рассмотрен в совсем недавней работе [14], где соответствующее операционное исчисление применялось для решения многочленных дифференциальных уравнений дробного порядка с этими производными и соответствующим образом сформулированными начальными условиями . В [15,16] представлен обзор операционного исчисления для нескольких различных дробных производных.
В [13] это исчисление применялось для вывода формул решения в замкнутой форме начальных задач для многочленных дифференциальных уравнений дробного порядка с последовательными дробными производными этого типа. Случай GFD произвольного порядка в смысле Римана–Лиувилля был рассмотрен в совсем недавней работе [14], где соответствующее операционное исчисление применялось для решения многочленных дифференциальных уравнений дробного порядка с этими производными и соответствующим образом сформулированными начальными условиями . В [15,16] представлен обзор операционного исчисления для нескольких различных дробных производных.
Остальная часть этой статьи организована следующим образом: В разделе 2 мы представляем обзор некоторых важных свойств общих дробных интегралов (GFI) и GFD произвольного порядка. Затем мы вводим последовательные GFD, доказываем 1-ю и 2-ю фундаментальные теоремы дробного исчисления (FC) для этих производных и выводим явный вид для их проекторных операторов. Раздел 3 посвящен построению операционного исчисления типа Микусинского для GFD произвольного порядка. В частности, последовательные ОФД произвольного порядка представляются в виде умножения на некоторые элементы построенного поля сверточных отношений. Разработанное операционное исчисление может быть применено для вывода формул решений в замкнутой форме для обыкновенных дифференциальных уравнений и уравнений в частных дробях с последовательными ОФД произвольного порядка.
В частности, последовательные ОФД произвольного порядка представляются в виде умножения на некоторые элементы построенного поля сверточных отношений. Разработанное операционное исчисление может быть применено для вывода формул решений в замкнутой форме для обыкновенных дифференциальных уравнений и уравнений в частных дробях с последовательными ОФД произвольного порядка.
2. Общие дробные производные произвольного порядка
Первой публикацией, посвященной GFI и GFD, была статья [17] Сонина, опубликованная в 1884 г., даже если в ней не упоминались дробные интегралы и дробные производные. В [17] Сонин обобщил метод решения, использованный Абелем в [18,19] для интегро-дифференциального уравнения (в несколько иных обозначениях)
к случаю более общих интегральных уравнений. В своих выводах Абель существенно использовал соотношение
где hα обозначает степенную функцию
операция ∗ означает свертку Лапласа
а {1} — функция, тождественно равная 1 при t>0. Решение Абеля интегро-дифференциального уравнения (2) при условии g(0)=0 в настоящее время известно как дробный интеграл Римана–Лиувилля:
Решение Абеля интегро-дифференциального уравнения (2) при условии g(0)=0 в настоящее время известно как дробный интеграл Римана–Лиувилля:
Блестящая идея Сонина заключалась в том, чтобы заменить степенные функции hα и h2− α в соотношении (3) с произвольными функциями κ,k, удовлетворяющими тому же соотношению:
В настоящее время такие функции называются ядрами Сонина, а условие (7) — условием Сонина.
Используя метод Абеля, Сонин решил интегральное уравнение типа свертки
в явном виде:
если ядра κ,k удовлетворяют условию Сонина (7).
Следует отметить, что выводы как Абеля, так и Сонина не были строгими с современной точки зрения, поскольку не вводили подходящих пространств функций и не давали условий для корректности их формальных операций с интегралами и производными. Лишь недавно операторы (8) и (9) стали предметом активных исследований в ФК и в настоящее время интенсивно строится их математическая теория, см. [13,20,21,22,23,24,25,26,27,28].
[13,20,21,22,23,24,25,26,27,28].
В этой статье мы имеем дело с GFI и GFD произвольного порядка, впервые введенными в [24]. Хорошо известно, что дробный интеграл Римана–Лиувилля
и дробные производные Римана – Лиувилля и Капуто
определены корректно для любого порядка α>0.
Однако соотношение (3) справедливо только при ограничении 0<α<1. Аналогично операторы Сонина, определяемые правыми частями формул (8) и (9) (GFI и GFD в современных обозначениях FC) имеют «обобщенный порядок» между нулем и единицей из-за условия Сонина (7). Для определения ОГФ и GFD произвольного положительного порядка в [24] условие Сонина (7) было расширено и уточнено для ядер из некоторых подходящих пространств функций:
Для подробного рассмотрения случая n=1, т.е. , за теорией ОГФ и GFD с ядрами из L1 мы отсылаем к [23]. В этой статье мы сосредоточимся на случае n>1, даже если случай n=1 также будет включен во все формулировки и выводы.
Стоит отметить, что в определении 1 нельзя поменять местами ядра κ и k при n>1 из-за несимметричных включений κ∈C−1(0,+∞) и k∈C−1,0(0 ,+∞) (в случае n=1 определение 1 симметрично и ядра κ и k можно поменять местами). Однако ядро κ(t)=hα(t),α>0 интеграла Римана–Лиувилля (10) и ядро k(t)=hn−α(t) дробных производных Римана–Лиувилля и Капуто ( 11) и (12) порядка α,n−1<α Другие примеры ядер из Ln,n>1 и процедуры их построения, исходя из известных ядер Сонина из множества L1, см. в [24,28]. Теперь определим GFI и GFD произвольного порядка, представим их известные свойства и выведем некоторые новые. Как уже упоминалось, ядра дробного интеграла Римана–Лиувилля (10) и дробной производной Капуто (12) принадлежат множеству ядер Ln и, таким образом, эти операторы FC являются частными случаями ОГФ (16) и GFD ( 17) соответственно. Другой интересный частный случай GFI (16) и GFD (17) представлен в [24]. Пусть выполнено условие n−2<ν является частным случаем ОГФ (16) и соответствующая ОГФ произвольного порядка принимает следующий вид: где а функции Jν и Iν — соответственно функция Бесселя и модифицированная функция Бесселя. В этой статье мы исследуем ОГФ и GFD произвольного порядка на пространстве C−1(0,+∞), определяемом формулой (14), и его подпространствах. В частности, подпространства будет часто использоваться. Эти подпространства были введены и исследованы в [10] в связи с построением операционного исчисления типа Микусинского для дробной производной Капуто. Как отмечено в [24], при выполнении включения k∈C−1n−1(0,+∞) GFD (17) можно представить следующим образом: где D(k) определяется соотношением (18). который часто используется в случае ядра степенной зависимости k(τ)=hn−α(τ),n−1<α Основные свойства ОГФ (16) произвольного порядка на пространстве C−1(0,+∞) непосредственно следуют из известных свойств свертки Лапласа [23]: Отметим также следующие важные теорема: Кроме того, в [24] были доказаны две фундаментальные теоремы FC для GFI и GFD произвольного порядка. Формулировки этих теорем приведены ниже, доказательства см. в [24]. Стоит отметить, что результат теоремы 3 (2-я основная теорема ФК для GFD произвольного порядка) может быть переформулирован в терминах так называемого проекторного оператора P GFD (17): Вид оператора проектора P определяет естественные начальные условия для начальных задач для уравнений дробного порядка с GFD (17). Согласно представлению (29), они представляются через целочисленные производные f(j)(0),j=0,1,…,n−1 неизвестной функции, как это имеет место для обыкновенного дифференциала уравнений и для дробных дифференциальных уравнений с производными Капуто. В оставшейся части этого раздела мы определяем m-кратные последовательные ОГФ и GFD произвольного порядка с ядрами (κ,k)∈Ln,n∈N и исследуем их свойства. В случае n=1 m-кратные GFD и m-кратные последовательные GFD были введены и изучены в [25,29].]. В [14] рассмотрены m-кратные секвенциальные GFD по Риману–Лиувиллю с ядрами (κ,k)∈Ln на основе GFD произвольного порядка, определяемой в смысле Римана–Лиувилля формулой (18) . В данной работе мы рассматриваем случай GFD произвольного порядка в форме (17). Сначала определим степени свертки f По аналогии со случаем дробного интеграла Римана–Лиувилля и дробной производной Капуто операторы I(κ)< 0> и ∗D(k)<0> интерпретируются как тождественный оператор Id. В силу теоремы 1 ядро κ m-кратная секвенциальная GFD (32) произвольного порядка является прямым обобщением секвенциальной дробной производной в смысле Капуто на случай интегро-дифференциальных операторов с ядрами из Ln. Первая основная теорема ФК (теорема 2) для ОФП (16) и ОФД (17) произвольного порядка сразу приводит к следующему важному результату: Чтобы обобщить теорему 3 на случай m-кратных секвенциальных ОФД, сначала введем подходящие пространства функций в виде Для m=1 положим C−1,(k)n,1(0,+∞):=C−1n(0,+∞). Стоит отметить, что для любой функции f∈C−1,(k)n,m(0,+∞) ее образ Pmf оператором проектора принадлежит ядру m-кратной последовательной GFD: Отметим также включения которые непосредственно следуют из определения m-кратной последовательной GFD. Как уже упоминалось во введении, операционное исчисление типа Микусинского для GFD и GFD с ядрами (κ,k)∈L1 было построено в [13]. Этот случай соответствует GFI и GFD «обобщенного порядка» между нулем и единицей. Первым важным компонентом любого операционного исчисления типа Микусинского является подходящее кольцо функций. Для операционного исчисления для ОГФ и GFD с ядрами (κ,k)∈Ln это кольцо описано в теореме 1, утверждающей, что тройка R−1=(C−1(0,+∞),+,∗ ) с обычным сложением + и умножением ∗ в виде свертки Лапласа является коммутативным кольцом без делителей нуля. Кроме того, определение 1 гарантирует, что ядра κ и k из Ln являются элементами этого кольца: В частности, это означает, что ОФП с ядром κ сводится к обычному умножению на кольце R−1: Что касается GFD произвольного порядка, то его нельзя свести к алгебраическим операциям на кольце R−1. Причина в том, что GFD является левообратным оператором к GFI, а кольцо R−1 не имеет единичного элемента относительно умножения. Для демонстрации последнего утверждения предположим, что ОФД (17) произвольного порядка можно представить в виде свертки с некоторым элементом κ−1∈R−1: Согласно теореме 2 ОФД (17) произвольного порядка является левым обратным оператором к ОГФ (16). Комбинируя последнее уравнение с представлением (39), приходим к соотношению это противоречит тому, что кольцо R−1 не содержит единицы относительно умножения. Для решения упомянутой выше проблемы кольцо R−1 расширяется до поля сверточных отношений. Напомним, что R−1 не имеет делителей нуля (теорема 1), и поэтому это расширение следует стандартной процедуре, см., например, [10,13]. Во-первых, отношение эквивалентности на множестве вводится: Затем мы рассматриваем классы эквивалентностей C−12(0,+∞)/∼ и обозначаем их как частные: На пространстве C−12(0,+∞)/∼ обычные операции сложения и введено умножение: Эти операции определены корректно (не зависят от представителей классов эквивалентности). Как обычно, кольцо R−1 можно вложить в поле F−1: где κ — ядро ОГФ (16). Множество C−12(0,+∞)/∼ классов эквивалентности также является векторным пространством с упомянутой выше операцией сложения и умножения на скаляр λ∈R или λ∈C, определяемый следующим образом [10]: С другой стороны, постоянная функция {λ} (функция, принимающая значение λ при любом t≥0) принадлежит пространству C−1(0,+∞) и, следовательно, является элементом кольца R− 1. Согласно нашим определениям, умножение на {λ} в поле F−1 задается следующим выражением: Как видим, нужно различать умножение элемента из F−1 на скаляр λ и на постоянную функцию {λ}. Даже если кольцо R−1 вложено в поле F−1, некоторые элементы поля сверточных частных не сводятся к обычным функциям из кольца. По определению отношение верно, где I — единица поля F−1 относительно умножения. Затем, следуя [13], введем важное понятие алгебраической GFD произвольного порядка. Как видим, алгебраическая GFD произвольного порядка определена для любой функции f∈Cn−1[0,+∞). Однако GFD произвольного порядка, задаваемая формулой (17), очевидно, не всегда существует на пространстве Cn−1[0,+∞). Таким образом, алгебраическую GFD (43) можно интерпретировать как своего рода обобщенную производную, сопоставляющую любой функции f∈Cn−1[0,+∞) некоторый элемент поля F−1. Однако алгебраическое GFD (43) совпадает с GFD (17) на пространстве C−1n(0,+∞) (выполняется включение C−1n(0,+∞)⊂Cn−1[0,+∞) справедливо, см. Приведенные выше конструкции могут быть распространены на случай m-кратной последовательной GFD (32) произвольного порядка. Согласно формуле (37) корректно определена m-кратная секвенциальная алгебраическая GFD произвольного порядка для любой функции f, удовлетворяющей условиям ∗D(k)f∈Cn−1[0,+∞) , i=0,…,m−1. Эти условия, очевидно, не обеспечивают существование m-кратной секвенциальной GFD (32) произвольного порядка. Следовательно, m-кратную секвенциальную алгебраическую GFD произвольного порядка можно интерпретировать как своего рода обобщенную производную. Тем не менее, для функций из пространства C−1,(k)n,m(0,+∞), заданных формулой (35), теорема 5 и те же рассуждения, которые использовались в случае m=1 (теорема 7 и его доказательство) приводят к следующему важному результату: Согласно представлениям (44) и (47) (или (48)), ОФД (17) произвольного порядка и m-кратное последовательное ОФД (32) произвольного порядка могут быть представлены как алгебраические операции (умножения) на поле F−1 факторов свертки. Стоит отметить, что ряд сверток (51) является далеко идущим обобщением степенного ряда (50), который также является рядом сверток, порожденным ядром κ={1} (операционное исчисление Микусинского для производной первого порядка) . В качестве примера рассмотрим геометрический ряд Его радиус сходимости равен r=1/|λ|>0. Теорема 9 гарантирует, что ряд сверток есть функция, принадлежащая пространству C−1(0,+∞). В рамках операционного исчисления Микусинского для производной первого порядка использовалась функция ядра κ={1}. Легко проверить, что для этого ядра справедливо соотношение κ Другим важным примером является операционное исчисление типа Микусинского для дробной производной Капуто ([10]). В этом случае ядро κ является степенной функцией hα и справедлива формула κ где двухпараметрическая функция Миттаг–Леффлера Eα,β определяется следующим абсолютно сходящимся рядом: Некоторые другие частные случаи ряда свертки (54) представлены в [13]. Очень важное операциональное соотношение в терминах ряда свертки lκ,λ представлено в следующей теореме. В случае ядер (κ,k)∈L1 теорема (10) сформулирована и доказана в [13]. В качестве примера рассмотрим ядро κ={1} (операционное исчисление Микусинского для производной первого порядка). Согласно формуле (55) операционное соотношение (58) можно представить в известном виде: В случае ядра κ(t)=hα(t),t>0 (операционное исчисление для Дробная производная Капуто [10]), формула (56) приводит к следующему рабочему соотношению: где двухпараметрическая функция Миттаг–Леффлера Eα,β определяется соотношением (57). Это операциональное соотношение было выведено в [6] впервые. Другие частные случаи оперативного соотношения (58) представлены в [13]. Как уже упоминалось, операционное соотношение (58) можно использовать для вывода других полезных операционных соотношений. Представление степеней свертки lκ,λ В качестве примера рассмотрим ядро κ={1} (операционное исчисление Микусинского для производной первого порядка). Операционное соотношение (61) принимает известный вид [1]: В случае ядра κ(t)=hα(t),t>0 (операционное исчисление для дробной производной Капуто) получаем следующее рабочее соотношение [6,10]: где функция типа Миттаг–Леффлера Eα,βm определяется с помощью следующего сходящегося ряда: Комбинируя операторные соотношения (58) и (61), мы получаем еще одно важное операторное соотношение. Пусть R(Sκ)=Q(Sκ)/P(Sκ), где Q и P — многочлены и deg(Q) Тогда операциональное соотношение справедливо, где константы λj и mj, j=1,…,J однозначно определяются представлением рациональной функции R(Sκ) в виде суммы частных дробей в виде (64). Рабочее соотношение (65) является прямым следствием формулы (64) и рабочего соотношения (61). В этой статье мы впервые обсудили некоторые важные свойства общих интегралов дробного порядка (ОДД) и ООД произвольного порядка, введенные недавно в работах третьего названного соавтора. Новыми объектами, впервые определенными в этой статье, являются m-кратные GFD и последовательные GFD произвольного порядка. Для m-кратных ОГФ и секвенциальных ОГФ произвольного порядка доказаны 1-я и 2-я фундаментальные теоремы ФК и получен явный вид их оператора-проектора. Основным вкладом этой статьи является операционное исчисление типа Микусинского для GFD произвольного порядка. В заключение отметим, что построенное нами операционное исчисление для ОФД произвольного порядка может быть применено для вывода формул в замкнутой форме для решений обыкновенных уравнений и уравнений в частных дробях, содержащих m-кратные последовательные БГД. Эти вопросы будут обсуждаться в другом месте. Ошибка загрузки страницы. Издатель: OverDrive Чтение Электронная книга в формате PDF Овердрайв Чтение Английский Доступность может меняться в течение месяца в зависимости от бюджета библиотеки.
 Кроме того, при f∈C−1n(0,+∞) GFD (17) принимает вид
Кроме того, при f∈C−1n(0,+∞) GFD (17) принимает вид

3. Операционное исчисление для GFD произвольного порядка
 В настоящей работе мы распространяем конструкции, представленные в [13], на случай ядер (κ,k)∈Ln,n∈N, т.е. для ОГФ и GFD произвольного порядка.
В настоящей работе мы распространяем конструкции, представленные в [13], на случай ядер (κ,k)∈Ln,n∈N, т.е. для ОГФ и GFD произвольного порядка. Таким образом, в R−1 не существует элемента, обратного к κ∈R−1.
Таким образом, в R−1 не существует элемента, обратного к κ∈R−1. Теорема 1 и приведенные выше определения немедленно приводят к следующему важному результату:
Теорема 1 и приведенные выше определения немедленно приводят к следующему важному результату: Одним из них является единичный элемент I=κκ поля F−1 относительно умножения (см. [13]). Такие элементы можно интерпретировать как своего рода обобщенные функции (гиперфункции в терминологии [30]). Обратный элемент к ядру κ ИГФ (16) — еще одна важная гиперфункция.
Одним из них является единичный элемент I=κκ поля F−1 относительно умножения (см. [13]). Такие элементы можно интерпретировать как своего рода обобщенные функции (гиперфункции в терминологии [30]). Обратный элемент к ядру κ ИГФ (16) — еще одна важная гиперфункция. [10]).
[10]). Эти представления могут быть использованы для сведения начальных задач для дифференциальных уравнений дробного порядка с GFD произвольного порядка и m-кратных последовательных GFD произвольного порядка к некоторым алгебраическим уравнениям на поле F−1 факторов свертки. Решениями этих уравнений являются некоторые элементы F−1, которые в общем случае являются обобщенными функциями или гиперфункциями. Однако обычно решения ищут в виде обычных функций, скажем, из пространства C−1(0,+∞). Вот почему так называемые операционные отношения (представления некоторых элементов поля F−1 в виде обычных функций из кольца R−1) являются еще одним важным компонентом любого операционного исчисления типа Микусинского. В оставшейся части этого раздела мы приводим операторные соотношения для элементов поля F−1 в виде рациональных функций R(Sκ)=Q(Sκ)/P(Sκ) с deg(Q)
Эти представления могут быть использованы для сведения начальных задач для дифференциальных уравнений дробного порядка с GFD произвольного порядка и m-кратных последовательных GFD произвольного порядка к некоторым алгебраическим уравнениям на поле F−1 факторов свертки. Решениями этих уравнений являются некоторые элементы F−1, которые в общем случае являются обобщенными функциями или гиперфункциями. Однако обычно решения ищут в виде обычных функций, скажем, из пространства C−1(0,+∞). Вот почему так называемые операционные отношения (представления некоторых элементов поля F−1 в виде обычных функций из кольца R−1) являются еще одним важным компонентом любого операционного исчисления типа Микусинского. В оставшейся части этого раздела мы приводим операторные соотношения для элементов поля F−1 в виде рациональных функций R(Sκ)=Q(Sκ)/P(Sκ) с deg(Q)
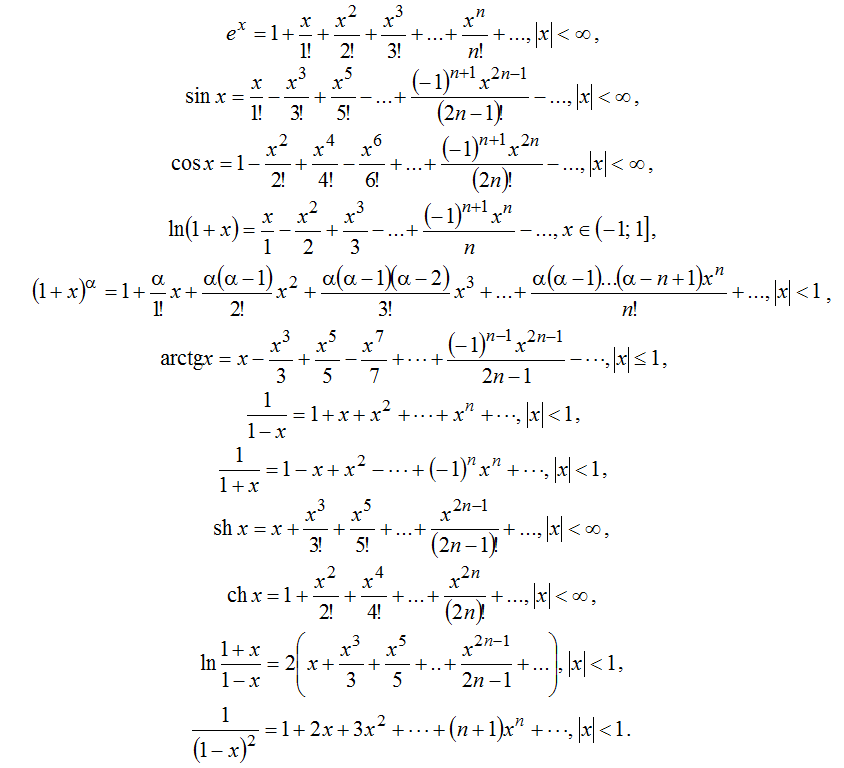
 Вложение кольца R−1 в поле F−1 означает, в частности, что свертка любых элементов кольца выполняется с умножением соответствующих элементов поля отношений свертки. Таким образом, получаем следующее операциональное соотношение:
Вложение кольца R−1 в поле F−1 означает, в частности, что свертка любых элементов кольца выполняется с умножением соответствующих элементов поля отношений свертки. Таким образом, получаем следующее операциональное соотношение: 4. Обсуждение
 В поле коэффициентов свертки GFD произвольного порядка и последовательные GFD произвольного порядка представляются как умножение на некоторые элементы поля. Мы также получили несколько важных операционных соотношений, которые обеспечивают полезное представление некоторых элементов поля в виде обычных функций, выраженных в терминах так называемого ряда свертки.
В поле коэффициентов свертки GFD произвольного порядка и последовательные GFD произвольного порядка представляются как умножение на некоторые элементы поля. Мы также получили несколько важных операционных соотношений, которые обеспечивают полезное представление некоторых элементов поля в виде обычных функций, выраженных в терминах так называемого ряда свертки. Введение в операционное исчисление — Публичная библиотека Гамильтона
Введение в операционное исчисление — Публичная библиотека Гамильтона — OverDrive
Попробуйте обновить страницу. Если это не сработает, возможно, возникла проблема с сетью, и вы можете использовать нашу страницу самопроверки, чтобы узнать, что мешает загрузке страницы.
Узнайте больше о возможных проблемах с сетью или обратитесь в службу поддержки за дополнительной помощью.
Поиск
Расширенный
«Введение в операционное исчисление» — это перевод книги «Einfuhrung in die Operatorenrechnung, второе издание».
Эта книга посвящена интерпретации Хевисайда, интегралу Лапласа и фундаментальному труду Яна Микусинки «Операционное исчисление». На протяжении всей книги основные алгебраические понятия появляются как вспомогательные средства для понимания некоторых важных моментов предмета. Важным направлением исследований в области анализа являются асимптотические свойства. В этом тексте также обсуждаются примеры, демонстрирующие возможности применения операционного исчисления, выходящие за рамки обыкновенных дифференциальных уравнений с постоянными коэффициентами. При использовании операционного исчисления для решения более сложных задач, чем задачи обыкновенных дифференциальных уравнений с постоянными коэффициентами, в области операторов значительную роль играет понятие сходимости. Эта книга также расширяет преобразование Лапласа и применяет его к нетрансформируемым функциям. В этом тексте также представлены три метода, с помощью которых операционное исчисление можно модифицировать и использовать при решении определенных задач. Эти методы относятся к конечному преобразованию Лапласа, уравнениям в частных производных, интегральным уравнениям Вольтерра и обыкновенным дифференциальным уравнениям с переменными коэффициентами.
Эта книга также расширяет преобразование Лапласа и применяет его к нетрансформируемым функциям. В этом тексте также представлены три метода, с помощью которых операционное исчисление можно модифицировать и использовать при решении определенных задач. Эти методы относятся к конечному преобразованию Лапласа, уравнениям в частных производных, интегральным уравнениям Вольтерра и обыкновенным дифференциальным уравнениям с переменными коэффициентами.
Эта книга может оказаться полезной для математиков, студентов и преподавателей исчисления и высшей математики.
Эльзевир Наука
ISBN: 9780323162456
Дата выпуска: 19 июля 2013 г.
ISBN: 9780323162456
Размер файла: 26238 КБ
Дата выпуска: 19 июля 2013 г.
Электронная книга в формате PDF 
Калькулятор для производных онлайн: Таблица производных
404 — Страница не найдена
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Производная калькулятор APK (Android App)
Математическое приложение «Калькулятор производных» позволяет легко вычислять производные на вашем устройстве. Он дает вам подробное решение всех производных формул с шагами и графиками, что позволяет вам понимать математические функции с помощью этого решателя производных исчисления.
Это небольшой и мощный калькулятор derive , который поможет вам решать производные по шагам. Этот калькулятор дифференциации подходит для студентов, изучающих математику и не умеющих находить производные решения. Потому что это математическое приложение предоставляет вам пошаговое решение для производных . Таким образом, вы можете познакомиться с каждым процессом решения математических функций от производных исчисления с помощью этого калькулятора.
Таким образом, вы можете познакомиться с каждым процессом решения математических функций от производных исчисления с помощью этого калькулятора.
С помощью этого математического калькулятора легко вставлять формулы или любые производные функции. Вы можете быстро вставить sin, tg, tan, cos, exp и другие функции производной с помощью этого калькулятора математических формул. Нажмите на кнопку решения, чтобы мгновенно получить решение вашего уравнения с помощью этого калькулятора производной .
Как решать производные
Эту производную решающую программу очень просто использовать. Просто откройте приложение и напишите желаемую математическую задачу с помощью гладкой клавиатуры калькулятора исчисления . Нажмите кнопку решения и получите подробный ответ с графиком, используя этот калькулятор производных с решением без каких-либо проблем.
Особенности математического приложения производного калькулятора
— Маленький размер.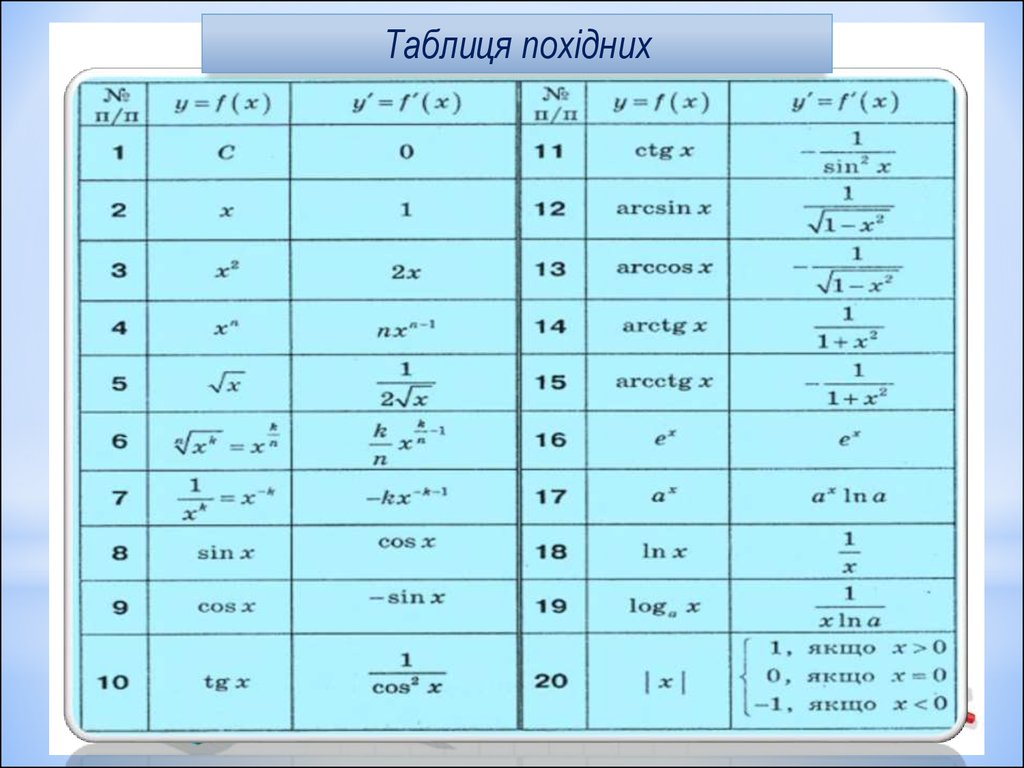
— Пошаговое решение производной.
— Классная цветовая гамма.
— Плавный расчет производных формул.
— Удобное приложение для математического калькулятора.
— Поддерживает все знаки и символы ctan, sin, tg, cos, tan, exp и другие.
— Точное решение математических функций и вывод.
— Легко копировать или распечатывать производные ответы с шагами.
Существует множество различных приложений-калькуляторов, которые позволяют решать производные задачи. Но это приложение уникально в своем роде, потому что этот калькулятор производных прост в использовании, позволяет легко вставлять уравнения и функции вывода и дифференцирования. Получите полное решение с помощью этого производного решателя .
Если вы ищете хороший калькулятор производной с решением и получаете полный ответ с шагами вывода. Этот калькулятор математических формул создан для вас. Как только вы начнете использовать это математическое приложение для производного калькулятора , оно вам понравится из-за его отличных функций производного решателя с решением и без проблем копируйте ответ в свой текстовый файл или файл документа с этим производным калькулятором с решением.
Подробнее…
Калькулятор производной онлайн
Калькулятор производной онлайн
Похожие темы:
Matlab Simultaneous Equations |
решатель сложения и вычитания радикалов |
сложные математические уравнения |
решить мою математику |
задачи по тригонометрии с ответами |
калькулятор для рациональных уравнений |
экзамен по математике 170 |
онлайн-учебник по алгебре 1 |
как решать уравнения по математике седьмой класс
| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
| CAH` Зарегистрирован: 26.10.2005 |
| ||||||
| Наверх | |||||||
| oc_rana Зарегистрирован: 08.03.2007 |
| ||||||
| Наверх | |||||||
| Вуз Зарегистрирован: 27.09.2001 |
| ||||||
| Наверх | |||||||
| THemg Зарегистрирован: 03.07.2004 |
| ||||||
| Наверх | |||||||
| Гулс Зарегистрирован: 01.12.2002 |
| ||||||
| Наверх | |||||||
| sxAoc Зарегистрирован: 16. |
| ||||||
| Наверх | |||||||
| Форум | |
|---|---|
калькулятор у. е. радикал е. радикал | |
| калькулятор алгебры — наименьшее общее кратное | |
| математические проекты со сложением, вычитанием и умножением дробей | |
| план урока +математика+7 класс | |
| как решить алгебраическое уравнение с дробями | |
| расчет разделительных радикалов | |
| математика | |
| решатель радикальных знаменателей | |
| 8 класс графические переводы вращения и отражения листы для печати | |
| нелинейное дифференциальное уравнение Matlab | |
| факторинг с дробными показателями | |
| бесплатные рабочие листы по алгебре для восьмого класса | |
| как преобразовать decmil в дробь с ti 83 plus | |
| бесплатная алгебра трехчленов | |
| решатель вершинных уравнений | |
| примеры гипербол | |
| формула для получения десятичных дробей | |
| математические листы сложения и вычитания отрицательных чисел | |
| математика + стихи + строка наилучшего соответствия | |
| бесплатный калькулятор скачать в С# | |
| помогите с d=rt алгеброй | |
| наименьшие общие знаменатели | |
| Рабочий лист точечной диаграммы для средней школы | |
| начальный 6 образец вопроса по геометрии и тригонометрии | |
| решение систем уравнений с 3 переменными история | |
| умножение и деление положительных и отрицательных дробей | |
| бесплатный тестовый онлайн-экзамен (по программному обеспечениюбесплатно) | |
| Техасский Ти-89 показывает рабочую алгебру | |
| стихи о том, как решать задачи по алгебре | |
| бесплатные математические листы по четырехугольникам для учащихся пятого класса | |
| lcm для идиотов | |
| решить квадратное уравнение в вершинной форме | |
| решатель математических задач | |
| выпуск по математике 8 | год|
| Рабочая тетрадь Аддисона-Уэсли по химии | |
| алгебратор скачать | |
| стандарты программного обеспечения для репетиторов по математике | |
| логическое упрощение ti89 | |
| комплексное число абсолютного значения | |
| как считать комбинации на графическом калькуляторе | |
| численно решать нелинейные уравнения maple | |
| сша 10 класс математика | |
| определение уровня точности в алгебре | |
| алгебра 2 книга ответы макдугал литтел | |
| бесплатные печатные дроби упражнения | |
| как решить матрицы с помощью javasript | |
| калькулятор рациональных выражений | |
как решать уравнения с более чем одной переменной с помощью графика. .. .. | |
| решить уравнение с рациональными показателями | |
| как решить сложное рациональное выражение | |
| специальные продукты и факторинговые биномы | |
| ошибка графического калькулятора ti-86 13 размер | |
| решить для перехвата y лист для печати | |
| ти-83 и гауссовская элиминация | |
| шаги для балансировки уравнения | |
| учебник по упрощению квадратных корней | |
| решатель экспоненциальных функций | |
| Рабочие листы балансировки химических уравнений | |
| кубический корень ти-83 плюс | |
| ks2 документы онлайн бесплатно | |
| бесплатное решение задач по алгебре в колледже | |
| бесплатный решатель алгебры | |
| решение одновременных уравнений ks3 | |
| помощь в построении графиков | |
| может ode45 решить оды второго порядка | |
| практические тесты на наименьшие и наибольшие общие делители | |
| логарифмические рабочие листы | |
| способы списывания на уроке математики с помощью ti-83 | |
| задачи на деление твердых дробей | |
| ошибка графического калькулятора | |
Калькулятор частных производных
Калькулятор частных производных
Калькулятор частных производных используется для определения дифференциала функций многих переменных относительно любой соответствующей переменной. Наш первый калькулятор частных производных несколько раз дифференцирует постоянные, линейные или полиномиальные функции по разным переменным.
Наш первый калькулятор частных производных несколько раз дифференцирует постоянные, линейные или полиномиальные функции по разным переменным.
Как работает этот калькулятор частичного дифференциала?
Выполните следующие действия, чтобы вычислить частичное дифференцирование любой функции.
- Ввод функции нескольких переменных f(x, y)
- Выберите переменную, т. е. x или y.
- Нажмите клавишу загрузки примеров , чтобы использовать образцы примеров.
- Нажмите кнопку вычислить , чтобы получить результат многомерной функции по отношению к одной переменной.
- Щелкните возможные промежуточные шаги, чтобы просмотреть пошаговое решение данной функции.
- Нажмите кнопку очистки для пересчета.
Что такое частная производная?
Функция нескольких переменных представляет собой мгновенную скорость изменения наклона функции в одном из координатных направлений, известную как частная производная. 2+2xy+z\) по x. 92+2xy+z\right)=2x\)
2+2xy+z\) по x. 92+2xy+z\right)=2x\)
Пример 2
Вычислить частную производную \(xsin\left(y\right)+cos\left(x\right)\) по x и у.
Решение
Шаг 1: Используйте обозначение частной производной.
\(\frac{\partial }{\partial x}\left(xsin\left(y\right)+cos\left(x\right)\right)\)
Шаг 2: Теперь продифференцируем заданная функция многих переменных относительно x.
\( \frac{\partial}{\partial x}\left(xsin\left(y\right)+cos\left(x\right)\right)=\frac{\partial}{\partial x} \left(xsin\left(y\right)\right)+\frac{\partial}{\partial x}\left(cos\left(x\right)\right)\)
\( \ гидроразрыва {\ парциальное} {\ парциальное х} \ влево (xsin \ влево (у \ вправо) + потому что \ влево (х \ вправо) \ вправо) = грех \ влево (у \ вправо) \ гидроразрыва { \ парциальное {\ парциальное х} \ влево (х \ вправо) + \ гидроразрыва {\ парциальное }{\ парциальное х} \ влево (потому что \ влево (х \ вправо) \ вправо) \)
\( \ гидроразрыва { \partial }{\partial x}\left(xsin\left(y\right)+cos\left(x\right)\right)=sin\left(y\right)\left(1\right)+\left (-sin\left(x\right)\right)\)
\( \frac{\partial}{\partial x}\left(xsin\left(y\right)+cos\left(x\right) \право)=грех\лево(у\право)-грех\лево(х\право)\)
Шаг 3: Теперь продифференцируем данную функцию многих переменных по y.
Когда пересекаются параллельные прямые: «В какой геометрии параллельные прямые пересекаются?» — Яндекс Кью
«В какой геометрии параллельные прямые пересекаются?» — Яндекс Кью
Популярное
Сообщества
МатематикаГеометрия
Vic Fowles
·
120,1 K
Ответить19УточнитьAndrei Novikov
Математика
2,3 K
кандидат физико-математических наук, математик, исследователь, data scientist, предпринима… · 4 февр 2021
Ни в какой. По определению прямые называются параллельными, если они не пересекаются. Точка. Если они пересекаются, то они не параллельные.
Заблуждение возникло в связи с пятвм постулатом, который дает возможность в евклидоаоц геометрии выделчть классы эквивалентномти параллельных прямых, потому что легко выводится, что если прямая l параллельна прямым m и n, то прямы m и n также параллельны. Это называется своймтвом транзитивность.
Это называется своймтвом транзитивность.
Так вот в геометрии Лобачевского если прямая l параллельна прямым m и n, то нет никакой гарантии, что сами m и n не пересекаются.
Виталий Авраменко
1 января
«Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной… Читать дальше
Комментировать ответ…Комментировать…
Максим Лапиков
Математика
2,1 K
математик-системный программист, асу тп для аэс. · 8 авг 2018
на память из неевклидовых помню римана и лобачевского, кроме чисто аксиоматических построений, как ни странно, они имеют реальные модели где применяются в пространствах определённой кривизны при проецировании плоскостей на сферы. у римана правда если я ничего не путаю просто все прямые пересекаются, а у лобачевского, что существуют пересекающиеся две прямые параллельные. .. Читать далее
.. Читать далее
Комментировать ответ…Комментировать…
Виталий Авраменко
-2
Психология, философия, религия, математика. · 4 янв
К вопросу к тому, что, и у кого, и где пересекается. Сфера Римана сама, хоть и, не имеет параллельных геодезических. Но построена через пересечение евклидовых прямых над комплексной плоскостью… Для начала, по факту введения бесконечно удалённой точки и прямые пересекаются в неизвестном месте. Но пересекаются… Вот вам чудеса проективной геометрии — по определению… Читать далее
Виталий Авраменко
18 января
А? Кому-то нужно описание в теоретико множественной интерпретации. Со стандартными и нестандартными множествами… Читать дальше
Комментировать ответ…Комментировать…
Kirill Stupakov
155
магистр математики; преподаватель математики в школе и на младших курсах · 18 авг 2018
Ни в какой. По определению, параллельные прямые не имеют точек пересечения.
Теперь давайте по геометриям и заблуждениям. Всюду будут рассматриваться «плоскости», чтобы это ни значило.
Геометрия Евклида. То, что учили в школе, то, что привычнее и почти точно выполняется в повседневной жизни. Выделю те два факта, что будут существенны потом. Первое: в этой геометрии есть… Читать далее
По определению, параллельные прямые не имеют точек пересечения.
Теперь давайте по геометриям и заблуждениям. Всюду будут рассматриваться «плоскости», чтобы это ни значило.
Геометрия Евклида. То, что учили в школе, то, что привычнее и почти точно выполняется в повседневной жизни. Выделю те два факта, что будут существенны потом. Первое: в этой геометрии есть… Читать далее
25,2 K
Последовательность Ч.
4 февраля 2019
Вы написали, что в геометрии Лобачевского бесконечное количество параллельных прямых через одну точку. Не могли бы… Читать дальше
Комментировать ответ…Комментировать…
Алексей В. Д. Старицкий
554
Православный, русский, радиоинженер. Интерес — жизнь. защищаю тех кого люблю, не жалея… · 10 нояб 2020
По здравому смыслу. Возьмите листок плоский бумаги и нарисуйте на ней две параллельные линии. Затем скомкайте лист бумаги произвольным образом. Если лист бумаги и линии условно будут бесконечными, то они могут пересечься между собой и сами с собой бессчётное количество раз. Теорема доказана. Это не совсем классическая геометрия, скорее схоластика.
Затем скомкайте лист бумаги произвольным образом. Если лист бумаги и линии условно будут бесконечными, то они могут пересечься между собой и сами с собой бессчётное количество раз. Теорема доказана. Это не совсем классическая геометрия, скорее схоластика.
1 эксперт не согласен
Andrei Novikov
возражает
4 февраля 2021
это не ответ по определению.
Комментировать ответ…Комментировать…
Первый
руслан б.
1
7 мар 2020
Здравствуйте . Не силён в геометрии и математике, но меня всегда смущало выражение » две параллельные прямые не пересекаются». Я считаю что зависит от обстоятельств . Например если проделать опыт : два столба стоят паралельно друг другу . Если их продолжить в обе стороны до бесконечности они ни когда не пересекутся , при условии что я стою и смотрю на них . Если взять… Читать далее
Если взять… Читать далее
1 эксперт не согласен
11,8 K
Andrei Novikov
возражает
4 февраля 2021
ответ не понятийный. Смешивает проективную геометрию в кучу с обычной.
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
2 ответа скрыто(Почему?)
Когда пересекаются параллельные линии? При каких условиях? — Спрашивалка
Виталька
Когда пересекаются параллельные линии? При каких условиях? условие линия
3809
457
2
Ответы
СМ
Санбай Манибай
Геометрия Лобачевского (или гиперболическая геометрия) основана на аксиомах групп I—IV абсолютной геометрии и на следующей аксиоме Лобачевского.
V*. Пусть а — произвольная прямая, а А — точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не менее двух прямых, проходящих через точку А и не пересекающих прямую а.
Ясно, что все определения и теоремы абсолютной геометрии имеют место и в геометрии Лобачевского. Из аксиомы V* непосредственно следует, что если даны произвольная прямая а и точка А, не лежащая на ней, то существует бесконечное множество прямых, проходящих через точку А и не пересекающих прямую а. В самом деле, по аксиоме V* существуют две прямые, которые обозначим через b и с, проходящие через точку А и не пересекающие прямую а (рис. 2-1). Прямые b и с образуют две пары вертикальных углов, которые на рисунке 2-1 обозначены цифрами 1, 2 и 3, 4. Прямая а не пересекает прямые b и с, поэтому все ее точки принадлежат внутренней области одного из четырех углов 1, 2, 3, 4, например внутренней области угла 1. Тогда, очевидно, любая прямая, проходящая через точку А и лежащая внутри вертикальных углов 3 и 4, не пересекает прямую а (например, прямые l и d на рис. 2-1).
2-1).
В отличие от определения параллельных прямых по Евклиду в геометрии Лобачевского параллельными к данной прямой называются (только некоторые прямые из тех, которые не пересекают данную прямую. Чтобы ввести это понятие, условимся считать, что все прямые, рассматриваемые нами, являются направленными прямыми. Поэтому мы их будем обозначать двумя буквами, например UV, считая, что точка U предшествует точке V. Предполагается также, что точки U и V выбраны так, что рассматриваемые нами точки на этой прямой лежат между точками U и V.
0
SF
Senior Full Stack Developer
Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений, при наличии других аксиом) может быть сформулирована следующим образом:
На плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
В геометрии Лобачевского вместо неё принимается следующая аксиома:
Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
Аксиома Лобачевского является точным отрицанием аксиомы Евклида (при выполнении всех остальных аксиом), так как случай, когда через точку, не лежащую на данной прямой, не проходят ни одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её, исключается в силу остальных аксиом (аксиомы абсолютной геометрии). Так, например, сферическая геометрия и геометрия Римана, в которых любые две прямые пересекаются, и следовательно, не выполнена ни аксиома о параллельных Евклида, ни аксиома Лобачевского, не совместимы с абсолютной геометрией.
0
To
Torkvemada
1
Александр Наумов
Тут, на просторах Спрашивалки, есть пользователь под кликухой Милан Холик.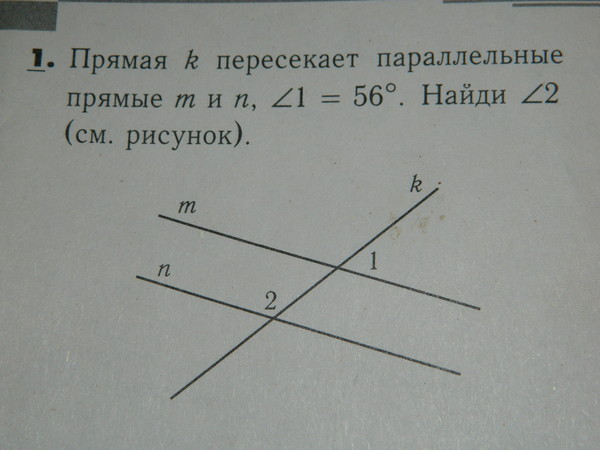 По его версии лучи от Солнца к Земле идут параллельно. Затем Солнце «как бы висит над облаками» и его лучи (через просветы туч) расходятся под углом в разные стороны. Если мысленно вернуть лучи в точку, откуда они исходят (солнце над облаками), то получается, что когда вышеупомянутый Милан Холик бредит, то параллельные линии пересекаются… на солнце. Слава Милан Холику! Слава! Слава! Аминь…. ШЮТКА
По его версии лучи от Солнца к Земле идут параллельно. Затем Солнце «как бы висит над облаками» и его лучи (через просветы туч) расходятся под углом в разные стороны. Если мысленно вернуть лучи в точку, откуда они исходят (солнце над облаками), то получается, что когда вышеупомянутый Милан Холик бредит, то параллельные линии пересекаются… на солнце. Слава Милан Холику! Слава! Слава! Аминь…. ШЮТКА
0
Viktor Piskov
Паралле́льные прямы́е (от греч. παράλληλος, буквально — «идущий рядом», «идущий вдоль другого») — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны. В стереометрии две прямые называются параллельными, если лежат в одной плоскости и не пересекаются.
0
Бактыбек Эркинбаев
. .,две линии пересекаются только при одном условии , если они будут проходит через одной точки…,!!.,параллельные , по теории они никогда не будут пересекаться , на то они и параллельные ..,!! .., параллельные линии пересекаются при условии , если хотя бы одному из них дано такое «право» ..,!!
.,две линии пересекаются только при одном условии , если они будут проходит через одной точки…,!!.,параллельные , по теории они никогда не будут пересекаться , на то они и параллельные ..,!! .., параллельные линии пересекаются при условии , если хотя бы одному из них дано такое «право» ..,!!
0
Glаdiator (Woodland, Са)
Такое возможно наблюдать только в проекции линий, находящихся в разных параллельных плоскостях и следующих в разных направлениях. Параллельные линии, находящиеся в одной плоскости никогда не пересекутся. Это следует из самого определения термина «параллельные линии».
0
…
При условии ,что они преломляются на закруглениях плоскости под определёнными углами они могут даже пересекаться. Например возьмите форму автомобильной покрышки и проведите две параллельные прямые перпендикулярно корду ,вот вы и получите результат вашего поиска.
Например возьмите форму автомобильной покрышки и проведите две параллельные прямые перпендикулярно корду ,вот вы и получите результат вашего поиска.
0
ВВ
Владимир Владимирович
Во-первых, параллельные прямые не могут пересекаться (ни в одной геометрии) по определению параллельности. Во-вторых, в геометрии Лобачевского как раз можно провести через точку, не лежащую на данной прямой, бесконечно много прямых, не пересекающихся с ней.
0
Виталька
Ну ну
1
ВВ
Владимир Владимирович
1
Tr
Traveler
Нельзя достоверно сказать, пересекаются параллельные прямые или нет, если дополнительно не указывать, какой из видов геометрии имеется в виду.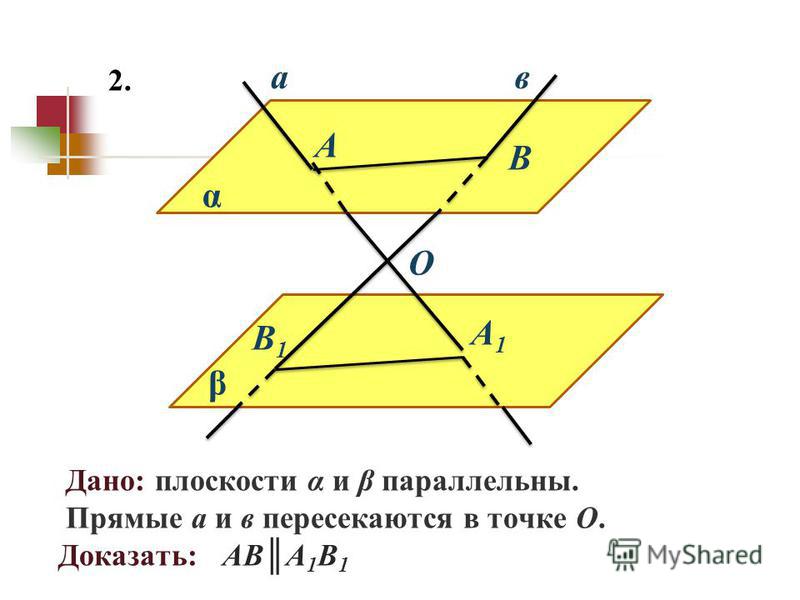 ..Эвклида,Лобачевского,Римана.
..Эвклида,Лобачевского,Римана.
0
Goldilocks
))) На всю жизнь запомнила ответ своей одноклассницы на уроке алгебры:
-Кристина, опиши признаки параллельности прямых?
-Если прямые пересекаются, то они параллельны.
0
Виталька
Напутала))))
1
Олег
Бывало еду я по прямой дороге, с двух сторон которой нарисованы параллельные полоски, смотрю вперед и вижу, о чудо! Параллельные прямые пересеклись на горизонте!
0
Виталька
))
1
Олег
Иногда я задаюсь вопросом. Неужели обычные слова и буквы нынче выходят из моды? А как же наш могучий и богатый….
Неужели обычные слова и буквы нынче выходят из моды? А как же наш могучий и богатый….
1
Наталья
У художника да:) если смотреть под другим углом зрения) а так они по определению не пересекаются, параллельные же. Если только рядышком скрещиваются
0
Виталька
))
1
Наталья
1
Виталька
Красотища!)))
1
Наталья
На параллельных плоскостях
1
Виталька
Возможно
1
Ал
Алиса
Не пересекаются в одной плоскости.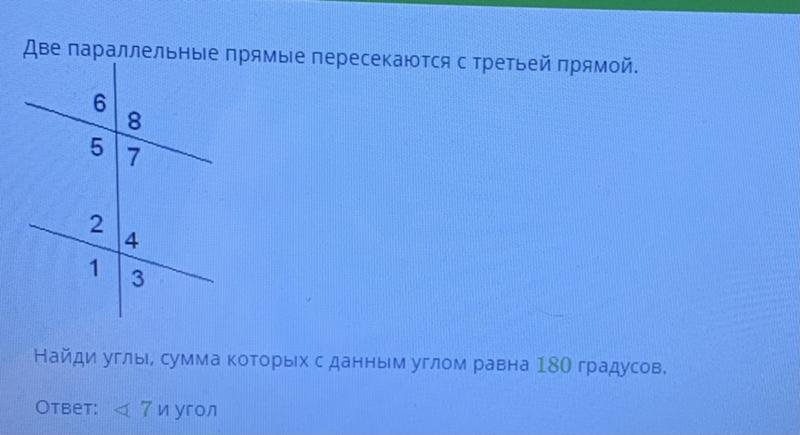 если менять плоскость наклонять, то визуально в начальной точке может казаться ,что они пересеклись ,но это иллюзия)
если менять плоскость наклонять, то визуально в начальной точке может казаться ,что они пересеклись ,но это иллюзия)
0
Виталька
Ок
1
Ал
Алиса
Без оков надо прочитал или молча или лайк
1
Виталька
Ага
1
ДД
Диво Дивное
но они же не могу пересекаться на то и параллельные прямые Разве что у Лобачевского-через одну точку Но это дебри науки, увы, не мое Я гуманитарий
0
Виталька
Ок
1
Егор🇷🇺
В Эвклидовой геометрии параллельные линии не пересекаются.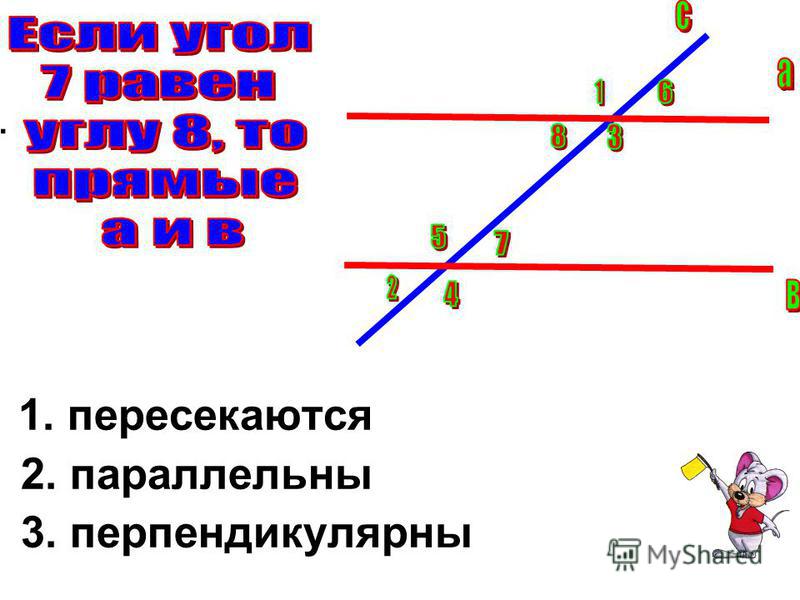 А в бесконечности при условии не абсолютной паралельности- возможна
А в бесконечности при условии не абсолютной паралельности- возможна
0
NP
N P
ну по теореме никогда, если не учитывать наличие аксиом, по которым все же возможно, и возможность пересечения в бесконечности
0
Виталька
Нееее
1
Снежана
По законам геометрии Лобачевского они могут встретиться в бесконечном пространстве, просто соединиться в общее кольцо
0
Виталька
)))
1
Николай В. Авантюрист
Авантюрист
линии пересекаються с озвездиях-во временах года каждое созездие имеет силуэто 100% я астролог -можешь мне не верить
0
АЛ
Алексей Лушин
Говорят, пространство искривляется. Если долго смотреть в сильный телескоп, увидишь свой затылок. Это я украл где-то.
0
Виталька
Прикольно
1
Володя
Википедия в помощь. Но это не в Эвкалиптовой геометрии, конечно, а в пространстве
Геометрия Лобачевского — Википедия
0
Виталька
Ок
1
Павел Казаков
по неевклидовой геометрии , они пересекаются в бесконечно удаленной точке, ну и .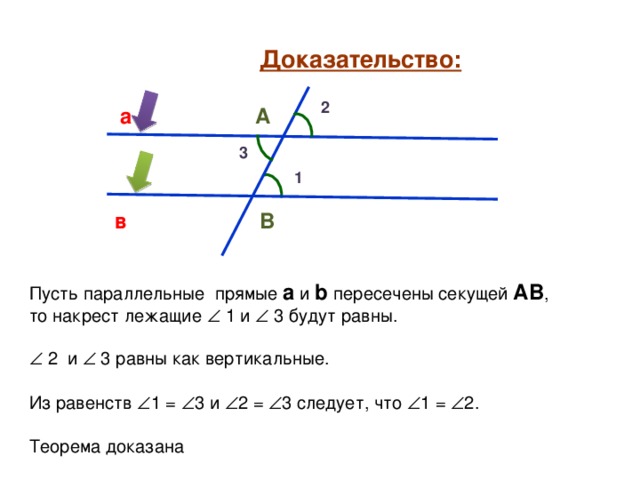 .. в случае искривления пространства
.. в случае искривления пространства
0
Пр
Пррпрполролпрорп
Если точка не лежит на данной прямой, через нее можно провести бесконечно много прямых, но не пересекающихся с ней.
0
Виталька
Ого
1
Ә(
Әруақ (Духи Предков) Ж.р.
Например Земля это сфера. А вернее овал сфера. Допустим мы провели две параллели. На такой форме они пересекутся.
0
Виталька
Агв
1
Ә(
Әруақ (Духи Предков) Ж.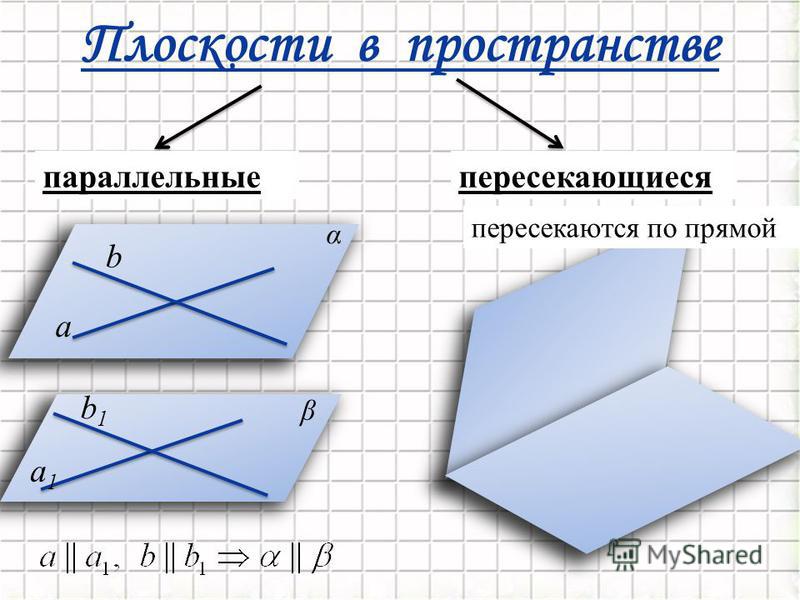 р.
р.
Все зависит от формы!
1
Виталька
Ок
1
Ә(
Әруақ (Духи Предков) Ж.р.
В природе нет параллелей
1
Виталька
Ок
1
Ә(
Әруақ (Духи Предков) Ж.р.
Вот у людей точно бывает параллельно.
1
Виталька
Ага. Душевно
1
Roman Balan
Если плоскость на которой они нарисованы скрутить в спираль! Визуально это будет похоже на двойную синусоиду!
0
Виталька
Ок
1
Ир
Ирина
А они могут пересекаться? Не хочу показаться невежественной, но они не могут пересечься даже в отношениях.
0
Виталька
Ни за что!
1
Ир
Ирина
Значит нет никакого мнения. Туман напустить каждый может.
1
Виталька
Да ну пряяяяям….
1
Ир
Ирина
Пустой разговор.
1
Виталька
Ок
1
Следующая страница
Другие вопросы
что такое креатин. Столько сайтов перечитала, никак не могу понять что именно делает креатин, и для чего он нужен?
Столько сайтов перечитала, никак не могу понять что именно делает креатин, и для чего он нужен?
Как вы думаете кто победит в ответном матче Бавария — Барселона? Пишите ваши прогнозы, очень интересно!
Если парень сменил узкие джинсы на спортивные штаны что это значит?
Помогите узнать имя певицы
Посоветуйте програму для харгэйнера
Как вернуть детей из детдома в семью, если органы опеки и сотрудники детдома всячески препятствуют этому?
Помогите! Может быть кто-то встречал такое платье или имеет представление каким оно должно быть спереди?
Есть ли смысл писать жалобу в управляющую компанию на соседей сверху?
Какая баня лучше всего?
на олимпиаде в беге, как измеряется время? электронный секундомер? а его нажимает судья? а его нажимает судья?
Букмекерские ставки. Объясните пожалуй что значит в букмекерских ставках Фора 0?
как правильнее распределить упражнения на разные группы мышц, какие упр делать в один день. Нужна программа на 4 дня.
мне 14 лет занимаюсь боксом нужно фирменные кросовки адидас около 5 тыщ рубле для тренеровок
Сгорела комната в квартире. Страховку оплачивалиежемесячно. Причина пожара-свечка. Что делать? Можно ли возместить что-
какой велик лучше купить???
геометрия — Как убедить кого-то, что параллельные линии могут соприкасаться/встречаться?
$\begingroup$
Говоря с кем-то, кто знает основы математики, но не очень глубоко, как бы вы объяснили, что параллельные линии могут соприкасаться?
Я имею в виду неевклидову/проективную геометрию.
Редактировать: Почему параллельные прямые на евклидовой плоскости (соответствующие прямым) пересекаются на проективной плоскости?
- геометрия
- проективная геометрия
- неевклидова геометрия
$\endgroup$
17
$\begingroup$
Прямые параллельны, если они лежат в одной плоскости и не пересекаются. В других геометриях параллельных линий может не быть, линии могут не иметь общей точки, но могут иметь общую предельную точку на бесконечности, или они могут просто не пересекаться.
В других геометриях параллельных линий может не быть, линии могут не иметь общей точки, но могут иметь общую предельную точку на бесконечности, или они могут просто не пересекаться.
Возможно, вы подумали о проективной геометрии, где «бесконечно удаленная точка» добавляется к каждому семейству параллельных прямых, а множество всех бесконечно удаленных точек называется «бесконечно удаленной линией».
Приложение
Обычно в формальной геометрии точки, линии и плоскости не определяются. Но постулаты определяют их «базовое» поведение. Постулат, который, по-видимому, согласуется с любой геометрией, гласит:
L1: Даны две различные точки на плоскости, и на этой плоскости имеется ровно одна линия, содержащая их.
«Двойственность» этого постулата равна
DL1: Даны две различные прямые на плоскости, и на этой плоскости есть ровно одна точка, принадлежащая обеим прямым.
Поскольку евклидова геометрия содержит параллельные линии, DL2 неверен. Но проективная геометрия принимает DL2 как постулат. Большой вопрос: «Существует ли геометрия, удовлетворяющая постулатам проективной геометрии?» Да есть.
Но проективная геометрия принимает DL2 как постулат. Большой вопрос: «Существует ли геометрия, удовлетворяющая постулатам проективной геометрии?» Да есть.
Создание такой геометрии действительно очень умно. Вы начинаете с евклидовой плоскости и добавляете к ней точки следующим образом. Выберите любую линию на плоскости. К этой линии и всем параллельным ей линиям вы добавляете одну дополнительную точку, точку в бесконечности. Это установленная вещь. Мы рассматриваем евклидову линию $l$ как набор точек и добавляем к этому набору неевклидову точку $p$, $l’ = l \cup \{p\}$. 92 — \{l\}$. Некоторые линии все равно будут пересекаться. Те, что пересекались в точке удаленной линии, теперь будут параллельны.
$\endgroup$
7
$\begingroup$
Я бы сказал, что если мы встанем рядом друг с другом и оба пойдем прямо на север, мы в конце концов столкнемся друг с другом возле северного полюса
Обратите внимание, как уже отмечалось, ваша предпосылка немного неверна.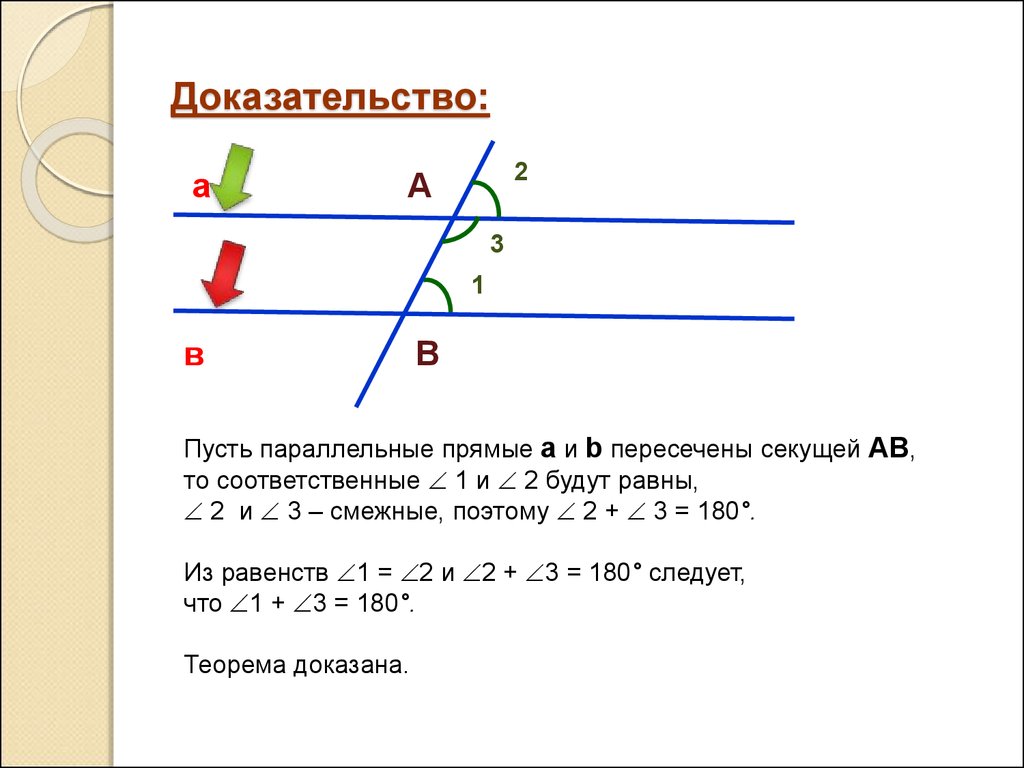 В чем вы можете убедить своего друга, так это в том, что любые две «прямые линии», то есть геодезические, пересекаются на сфере (не параллельные линии), тогда как на плоскости для любой линии существует особое семейство линий, которые никогда ее не касаются.
В чем вы можете убедить своего друга, так это в том, что любые две «прямые линии», то есть геодезические, пересекаются на сфере (не параллельные линии), тогда как на плоскости для любой линии существует особое семейство линий, которые никогда ее не касаются.
$\endgroup$
5
$\begingroup$
Как я уже говорил в комментариях, нельзя убедить кого-то тем, что не соответствует действительности.
ИМО, если кто-то знает основы геометрии, то он должен знать о том, что:
Этот раздел Википедии многого стоит здесь:
В геометрии параллельные линии — это линии на плоскости, которые не пересекаются; то есть две прямые на плоскости, которые не пересекаются и не касаются друг друга ни в одной точке, называются параллельными. В более широком смысле линия и плоскость или две плоскости в трехмерном евклидовом пространстве, которые не имеют общей точки, называются параллельными.
Хотя, если вы убеждаете/спорите с кем-то наивным в области геометрии, что Параллели не пересекаются, спросите его, почему люди называют его его/ее именем, а не Джастином Бибером/Селеной Гомес? Ожидаемый ответ: . Потому что это мое имя , и все. Вы получили его / ее. На самом деле параллельные линии не могут встречаться в точке или пересекаться, потому что они определены таким образом, если две линии пересекутся, то они не останутся параллельными линиями.
$\endgroup$
3
$\begingroup$
Когда мне было 16 или около того, мне было скучно решать домашнее задание по математике, поэтому я поиграл с увеличительным стеклом и заметил кое-что интересное:
Если вы посмотрите на бумагу с сеткой через увеличительное стекло, линии останутся параллельными ( это видно, когда они находятся более или менее на «верху стекла»), но все линии сходятся на краю стекла.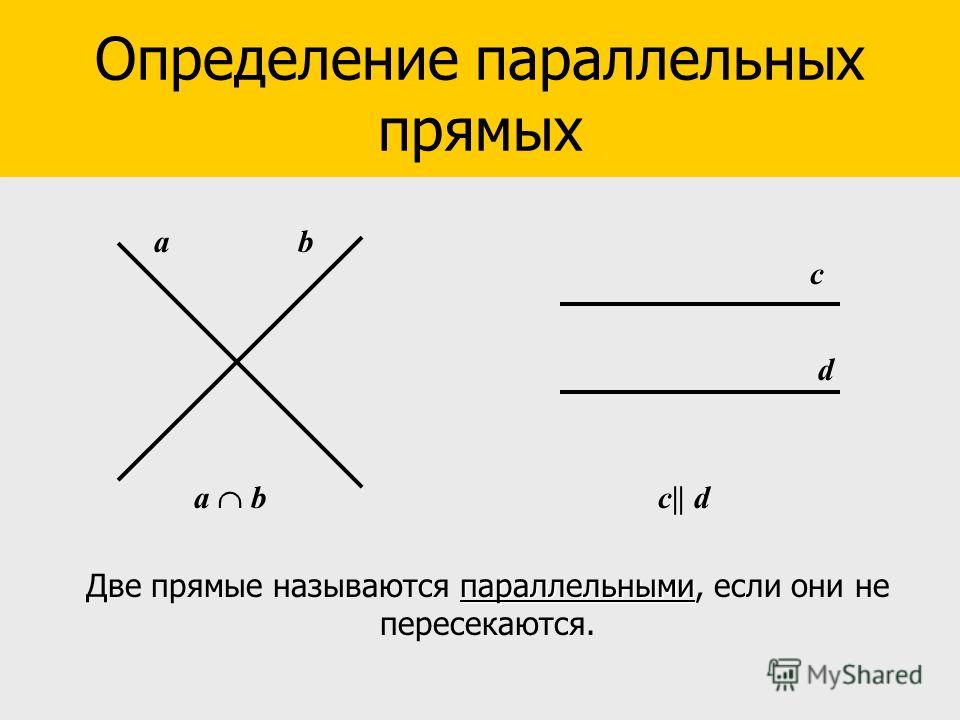
(Я пошел к своему старшему брату, который в то время был инженером-первокурсником, и сказал ему, что параллельные линии можно встретить ; но он ответил, что не могут, потому что это аксиома. Несколько лет спустя я узнал, что существует такая вещь, как неевклидова геометрия.)
Заметьте, кстати, что это может потребовать, чтобы вы думали о стакане как о бесконечности.
$\endgroup$
12
$\begingroup$
В своем комментарии @JackyChong обозначил предварительную проблему. Определение «параллели» ясно: линии, которые не пересекаются, значит, нет пересекающихся параллельных линий. Реальный вопрос заключается в определении «линии».
Геодезическая является наиболее естественной для геометрии на сфере. Тогда в этой геометрии нет параллельных прямых.
Для проективной геометрии одним из определений является добавление «бесконечно удаленной точки» к каждой линии, а затем преобразование добавленных точек в «бесконечно удаленную линию».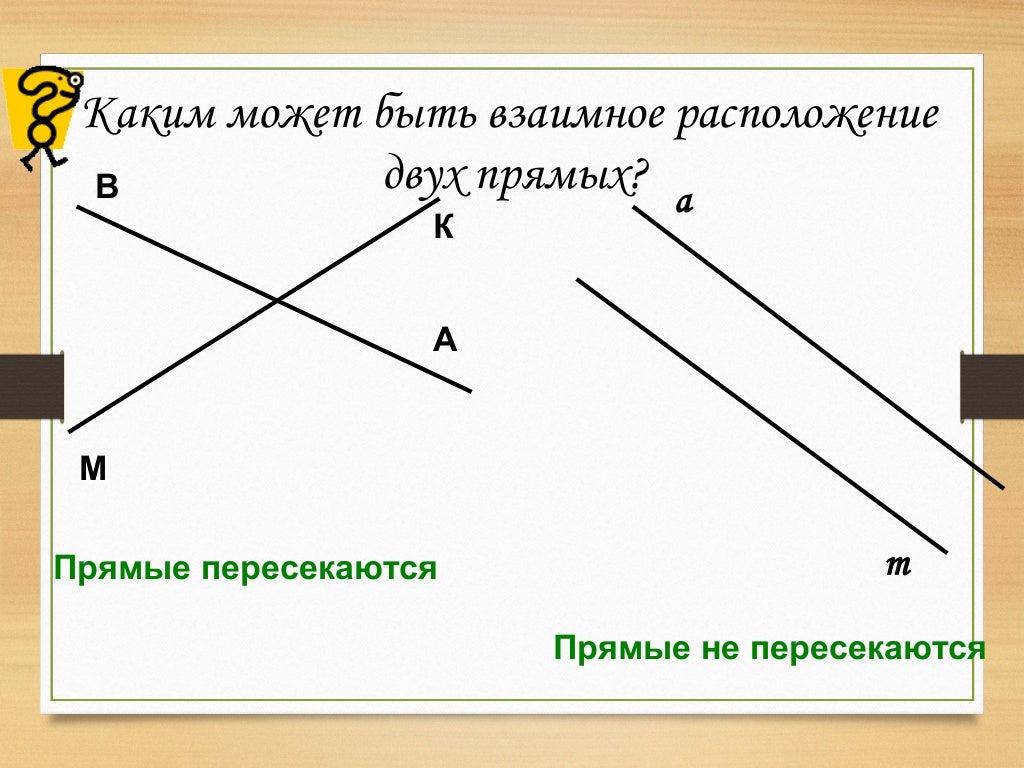 С этими дополнительными точками и линиями нет параллельных линий. Два, параллельные в евклидовой плоскости, имеют общую точку в бесконечности. Здесь помогает аналогия с железнодорожным полотном.
С этими дополнительными точками и линиями нет параллельных линий. Два, параллельные в евклидовой плоскости, имеют общую точку в бесконечности. Здесь помогает аналогия с железнодорожным полотном.
В гиперболической геометрии есть несколько прямых, параллельных заданной прямой, проходящих через точку, не принадлежащую этой прямой. Если вы зайдете так далеко с «человеком, который не знает математики», вы можете показать ему или ей модель Пуанкаре.
$\endgroup$
2
$\begingroup$
Я бы использовал два меридиана на Земле, которые касаются полюсов.
$\endgroup$
2
$\begingroup$
Это вопрос точки зрения 🙂
$\endgroup$
$\begingroup$
Вы можете говорить о поездах. Железнодорожные пути довольно наводящие на размышления.
Железнодорожные пути довольно наводящие на размышления.
$\endgroup$
4
$\begingroup$
Вы не сможете убедить ни одного математика, не говоря уже о своем друге, так как это ложь. Однако они могут столкнуться с идеей, что для чисто теоретических расчетов мы предполагаем, что две параллельные линии могут встретиться в точке в бесконечности. Если вы хотите отправиться в бесконечность, чтобы доказать это, пожалуйста, пришлите открытку, когда доберетесь туда.
$\endgroup$
$\begingroup$
Тот, кто знаком с основами математики, может легко понять это, поскольку согласно определению параллельных прямых
Параллельные прямые: Линии, расстояние между которыми постоянно, называются параллельными прямыми [см. самое верхнее определение]
самое верхнее определение]
Теперь, как мы знаем определение совпадающие прямые также параллельны, так как расстояние между ними является постоянным или $0$. Следовательно, поскольку совпадающие линии касаются друг друга, подразумевается, что параллельные линии также соприкасаются.
Смотрите видео здесь также
$\endgroup$
$\begingroup$
Я начертил бы две параллельные линии на листе бумаги. Затем я сводил все ребра вместе в одну точку и показывал, что параллельные прямые соприкасаются с этой точкой.
$\endgroup$
$\begingroup$
В детстве мама сказала мне фразу, которую я тогда не понял:
Параллельные прямые — это прямые, пересекающиеся в бесконечности.
Это утверждение и его объяснение с помощью искусства (как предложено Педро Тамароффом в комментариях) и демонстрации того, насколько упрощены многие утверждения и доказательства (если человек знает больше математики), является хорошим введением в идею того, что мышление на параллельных линиях как линии, пересекающиеся в бесконечности, имеют смысл и могут быть полезны.
В арте
Это, как вы также можете видеть в ответе Ива Дауста, можно увидеть всякий раз, когда вы смотрите на прямую дорогу, уходящую к горизонту. Например, см. источник на Wikimedia Commons,
Изображение выше показывает причину, по которой эта концепция изначально была концепцией, возникшей в искусстве, поскольку она была действительно полезна для представления того, как мы видим вещи. Поразительное применение этого можно увидеть в церкви Санта-Мария-прессо-Сан-Сатиро, где использовалась проективная геометрия, имитирующая отсутствующее пространство в церкви. Однако есть много других примеров.
В геометрии
В обычной геометрии (т.е. аффинной и евклидовой геометрии) приведенное выше определение или утверждение не имеет смысла, поскольку параллельные прямые не пересекаются. Это может быть определение на плоскости, но обычно (в более высоких измерениях) это результат, полученный из определения параллельных линий как линий с одинаковым направлением.
Однако причина, по которой мы все еще можем понять приведенное выше утверждение о пересечении в бесконечности, заключается в том, что аффинную геометрию можно поместить внутрь проективной геометрии. При этом точки вне аффинного пространства называются «точками на бесконечности», параллельные прямые пересекаются в них и становятся такими же, как пересекающиеся прямые, что упрощает огромное количество утверждений и доказательств, позволяя не различать случаи. Примером может служить теорема Паппа о шестиугольнике.
В заключение
В заключение: не пытайтесь убедить или показать, что параллельные линии соприкасаются. Просто попытайтесь объяснить полезность представления о параллельных линиях как о линиях, пересекающихся в бесконечности. В эпоху Возрождения у вас есть много примеров того, почему это утверждение полезно с точки зрения хорошего представления реальности и перспективы; в математике есть много примеров того, как это действительно полезно для упрощения утверждений и доказательств в геометрии.
$\endgroup$
1
$\begingroup$
В эллиптической геометрии предположение неверно.
В евклидовой геометрии параллельные линии «встречаются» и касаются друг друга на бесконечности, так как их наклон одинаков.
В плоской гиперболической геометрии параллельные линии также могут соприкасаться, но только в бесконечности.
В плоской модели диска Пуанкаре кругового сегмента геодезические параллели пересекаются по касательной только в бесконечно удаленных точках на границе «горизонта» или граничной окружности. Можно увидеть, как линии касаются и перемещаются по границе, указанной в ссылке Wiki.
Poincare Disk_MathWorld
Таким образом, полукруговые геодезические в полуплоскостной модели сходятся в точке $\infty$ на оси x. Анимация также может быть найдена в другом месте, где полукруги касаются оси X, изменяя размер полукруга во время движения.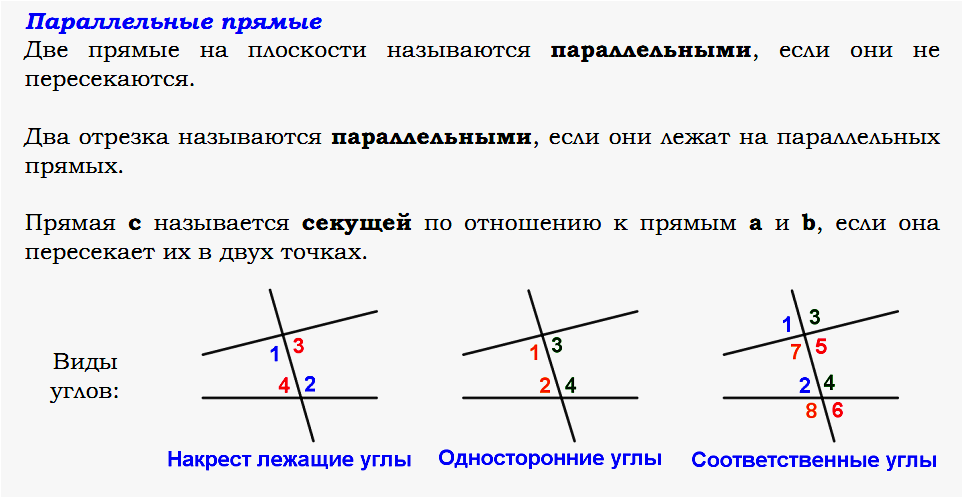
PoincareHalfPlane
Оба примера касаются параллельных линий, касаясь тангенциально/асимптотически в точке бесконечности.
http://math.etsu.edu/multicalc/prealpha/Chap3/Chap3-8/part4.htm
$\endgroup$
$\begingroup$
Один из способов объяснить это — думать о евклидовой плоскости как о изображении (части) объемлющего трехмерного мира. Это соответствует тому, как на самом деле работает наше зрение: свет из трехмерного мира проецируется через хрусталик глаза на поверхность позади нашего глаза.
Более подробно: поместите плоскость в любом месте трехмерного пространства (при условии, что она не проходит через начало координат). Назовите это «картинной плоскостью». Теперь любые 93$ пронзает плоскость изображения ровно в одной точке (при условии, что линия не параллельна плоскости изображения). Любая плоскость , проходящая через начало координат , проходит через плоскость изображения ровно по одной линии (опять же, если плоскость не параллельна плоскости изображения).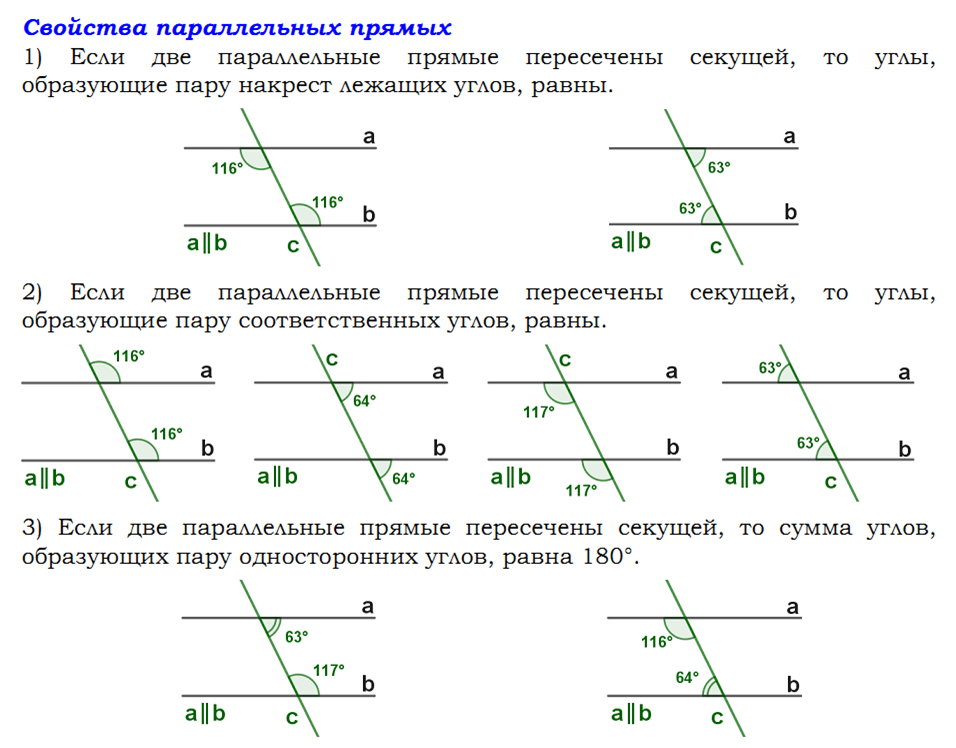 См. ниже (на котором картинная плоскость показана синим цветом).
См. ниже (на котором картинная плоскость показана синим цветом).
Теперь у нас есть словарь: $$\textrm{точка на картинной плоскости} \longleftrightarrow \textrm{линия, проходящая через начало координат в трехмерном пространстве}$$ $$\textrm{линия в картинной плоскости} \longleftrightarrow \textrm{плоскость, проходящая через начало координат в трехмерном пространстве}$$ 93$, которые параллельны картинной плоскости и, следовательно, не соответствуют никаким точкам или линиям на картинной плоскости. Это точки и эту линию можно считать «уходящей в бесконечность», но на самом деле все это означает, что они не имеют изображения в картинной плоскости.
Вы можете увидеть это визуально, держа палец на расстоянии вытянутой руки впереди и на несколько дюймов выше. По мере того, как вы приближаете руку (сохраняя ее высоту), положение кончика пальца кажется «выше» или «дальше» в вашем поле зрения, так как ваши глаза должны все больше и больше напрягаться, чтобы увидеть его.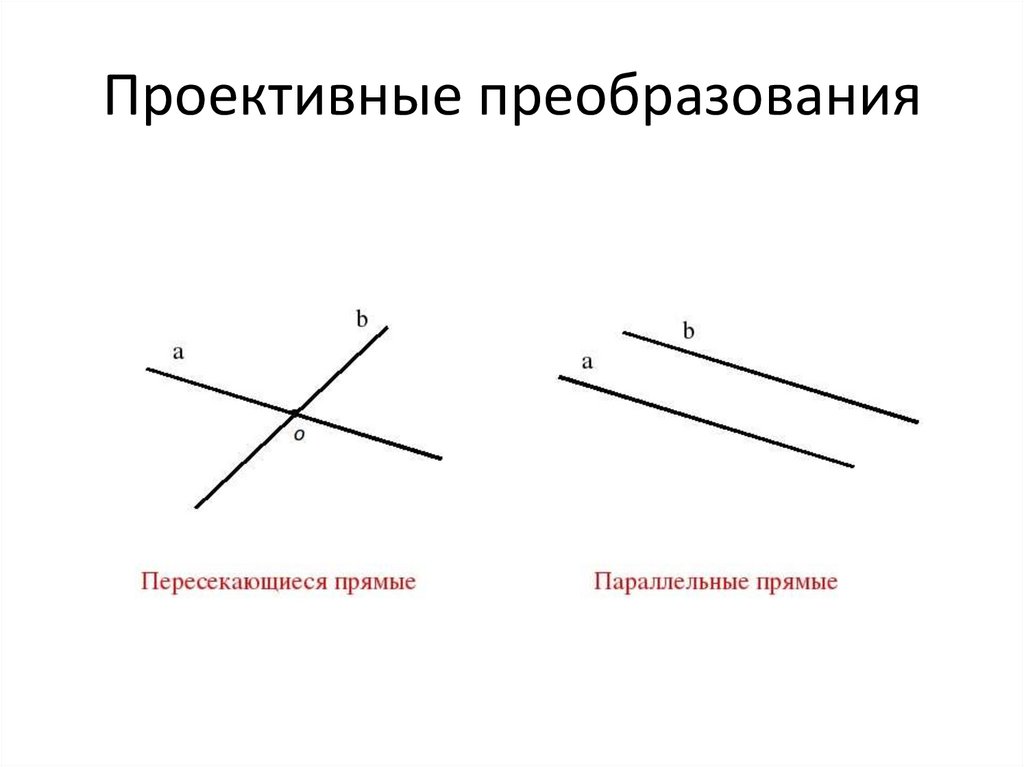 В конце концов, когда кончик пальца оказывается прямо над глазом, палец «исчезает». Конечно, на самом деле он не исчез, но «линия зрения» от кончика пальца до хрусталика вашего глаза параллельна сетчатке, так что кончик пальца не виден. С точки зрения восприятия кончик пальца отодвинулся «бесконечно далеко» в картинной плоскости, но на самом деле он находится всего в паре дюймов в трехмерном пространстве.
В конце концов, когда кончик пальца оказывается прямо над глазом, палец «исчезает». Конечно, на самом деле он не исчез, но «линия зрения» от кончика пальца до хрусталика вашего глаза параллельна сетчатке, так что кончик пальца не виден. С точки зрения восприятия кончик пальца отодвинулся «бесконечно далеко» в картинной плоскости, но на самом деле он находится всего в паре дюймов в трехмерном пространстве.
Однако , мы все знаем, что делать в таких случаях: повернуть голову! Это соответствует выбору новой плоскости изображения с другой ориентацией. Теперь точка, бывшая «в бесконечности», вырисовывается и раскрывается как обычная точка в новой картинной плоскости (и в то же время точки, которые были ранее в поле зрения , никуда не исчезли).
Обратите внимание, что оператор типа
для любых двух различных точек на картинной плоскости существует единственная линия на картинной плоскости, проходящая через данные точки
, который описывает истинный факт о геометрии картинной плоскости, соответствует в этом словаре
.3$. (Точнее, линии $f$ и $g$ «параллельны» в синей картинной плоскости и соответствуют оранжевой и желтой плоскостям через начало координат.) 93$ соответствует точке «на бесконечности».
Конечно, если вы выберете другую плоскость изображения, то линии больше не будут казаться параллельными, и их пересечение будет ясно видно как точка на новой плоскости изображения. Последнее изображение ниже показывает это. На этом изображении оранжевая и желтая плоскости такие же, как и раньше, но синяя плоскость изображения была перемещена и переориентирована; изображения двух плоскостей теперь состоят из непараллельных линий.
Итого:
- Если 2-мерную плоскость понимать как изображение объемлющего 3-мерного пространства, то «точка» — это просто изображение линии, проходящей через начало координат , а «линия» — это просто изображение плоскость через начало координат
- Некоторые «точки» (и «линия», содержащая эту точку) не будут иметь изображения в картинной плоскости, что мы описываем, говоря, что они находятся «в бесконечности»
- Однако нахождение «в бесконечности» является артефактом того, какую плоскость изображения мы используем; изменение плоскостей изображения меняет точки, находящиеся на бесконечности
- Кроме того, параллельность двух «линий» является артефактом плоскости изображения, которую мы используем для их просмотра; линии, которые кажутся параллельными с одной точки зрения, не параллельны с другой точки зрения
- Связь между двумя последними пунктами состоит в том, что «линии», кажущиеся параллельными в одной картинной плоскости , пересекаются с , но точкой пересечения является точка «в бесконечности» относительно картинной плоскости ; изменить перспективу, и точка больше не находится в бесконечности, и линии больше не параллельны.
- Все вышеперечисленное более или менее точно соответствует тому, как работает человеческий глаз, поэтому перспективное искусство может так хорошо обманывать глаз и создавать иллюзию глубины на плоской поверхности.
$\endgroup$
$\begingroup$
Визуально или концептуально параллельные линии сходятся на чрезвычайно большом расстоянии, они НИКОГДА не пересекаются. Меня не волнует, в скольких измерениях вы работаете или в каком геометрическом пространстве вы работаете, если у вас есть линии: L1 и L2, вы всегда можете абстрагировать соответствующий вектор от каждого L1:v1<> и L2:v2<> и если вы примените аркос угла косинуса между двумя векторами, где угол косинуса представляет собой скалярное произведение v1 и v2, деленное на произведение их величин, вы узнаете, параллельны они или нет.
v1<> v2<> mag1 mag2 // где mag1 и mag2 — величины v1 и v2 cosAngle = (v1 точка v2) / (mag1 * mag2) Определяющее значение = arcos(cosAngle) Если определяющее значение == 0, 180, 360, если в градусах или 0, PI или 2PI в радианах тогда векторы параллельны В противном случае они неРедактировать
То же самое можно сказать и об ARC, если две дуги принадлежат двум разным окружностям с разной длиной радиуса, где оба радиуса имеют одинаковое начальное положение; другими словами, концентрические круги, как в яблочко на доске для дартс или доске для стрельбы из лука, или если они разделены на расстоянии, превышающем сумму их радиусов, иначе, если любой из их радиусов имеет разную длину и не имеет одинаковая центральная точка то они могут иметь точку пересечения.
Могут быть случаи, когда они не имеют одной и той же центральной точки и по-прежнему не пересекаются.
Из следующих нескольких изображений параллельными будут считаться только концентрические окружности и эллипсы, остальные либо пересекаются, либо нет.
Они не пересекаются
Они пересекаются
Единственный из них, который можно считать параллельным, — это концентрические круги, поскольку каждая дуга имеет одинаковое расстояние от другого круга.
То же самое можно применить к эллипсам — За исключением того, что они имеют два радиуса разной величины, один для оси x и один для оси y.
Редактировать
Я заметил, что многие использовали терминологию или утверждение, говорящее: «Поместите точку в бесконечность» либо в своих комментариях, либо в своих ответах. Меня это беспокоит, и я удивлен этим. Почему? Я думаю, что невозможно поместить точку в бесконечность, потому что Бесконечность — это концепция, и по определению она считается НАН (не числом).
Это понятие бесконечности применяется в математике со свойствами функций и их пределами. Вот почему мы говорим, что такая функция или уравнение имеет предел, стремящийся к бесконечности.
Я думаю, что лучшим или правильным утверждением для этого предположения было бы: «Если поместить точку в точку Конвергенции». Я говорю это, потому что параллельные линии всегда будут параллельны и всегда будут иметь одинаковое расстояние в любой заданной точке этих линий. Теперь из-за того, как работают наши глаза и как мы интерпретируем световые сигналы, параллельные линии будут сходиться на чрезвычайно большом расстоянии. Если бы кто-то сказал поместить точку на линии в месте, приближающемся к Бесконечности, это было бы лучшим утверждением, чем поместить точку в бесконечность, но даже это все равно неверно. Почему?
Подумайте вот о чем: представьте себе, что вы находитесь на плоских равнинах Среднего Запада Соединенных Штатов с очень небольшими холмами, где вы можете практически видеть весь горизонт без помех: Теперь посмотрите вниз на железнодорожные пути, которые оказались практически прямыми с очень минимальные изгибы.
Нашими глазами в очень ясный день (меньше влаги в воздухе) мы можем видеть эти следы примерно на 20-40 миль. Точка конвергенции находится на уровне того, что мы видим как Горизонт, или совсем рядом с ним, но мы знаем, что эти следы могут простираться на сотни или даже тысячи миль. Это далеко не приближение бесконечности. Мы можем воспринимать мысль о сотнях тысяч миль, даже миллионах или миллиардах миль, и все же это всего лишь часть доли приближения к бесконечности.
$\endgroup$
7
геометрия — Что произойдет, если две бесконечные линии перестанут пересекаться и станут параллельными?
Один неупомянутый момент заключается в том, что есть способ уточнить ваше представление о параллельных прямых, пересекающихся под нулевым углом, но это не означает, что они пересекаются на конечном расстоянии. В этом суть ошибки рассуждения.
Stan Liou упомянул проективную плоскость в комментарии.
Это один из возможных способов рассматривать параллельные прямые как пересекающиеся. На проективной плоскости каждые две различные прямые пересекаются в единственной точке. Но мы не можем определить осмысленное понятие угла в проективной плоскости.
Существует еще один возможный вид, который может отразить понятие параллельных прямых, пересекающихся под углом $0$, а именно расширенная комплексная плоскость. Можно доказать, что каждая (обобщенная) окружность (включая прямые) отображается в окружность на сфере Римана. Каждая прямая проходит через $\infty$, которая определяется как точка, соответствующая северному полюсу, и, таким образом, каждые две различные прямые пересекаются в двух точках, дважды считая касание. Параллельные линии сопоставляются с окружностями, касающимися северного полюса, а непараллельные линии сопоставляются с окружностями, которые пересекаются под положительным углом на северном полюсе. Оказывается, угол можно определить естественным образом (угол на поверхности сферы), и он удивительным образом согласуется с углом на плоскости, когда пересечение не в $\infty$! [См.
ниже, если вас интересуют доказательства.]
Теперь мы можем рассмотреть, что происходит на сфере Римана, когда у вас есть две линии, как в вашем вопросе, одна из которых постепенно меняется, чтобы стать параллельной другой. Для простоты предположим, что одна из них — это прямая, проходящая через начало координат, так что она отображается в большой круг $C$ через $\infty$. Теперь, куда сопоставляется другая линия? Я выполнил поиск в Google по изображению и был приятно удивлен, обнаружив, что Али Чаглаян уже сделал это здесь.
Предположим, что черная линия — фиксированная, а синяя — та, которую мы меняем. Обратите внимание, что красный круг пересекает $C$ на северном полюсе и в какой-то другой точке $P$. Теперь представьте, что произойдет, если вы повернете синюю линию так, чтобы она стала параллельной черной линии. Красный кружок тоже как бы вращается, и $P$ движется вдоль $C$ все ближе и ближе к северному полюсу. Наконец, когда синяя линия параллельна черной линии, $P$ достигла северного полюса (соответствующего $\infty$) и угол между линиями равен $0$, но теперь оба их пересечения находятся в точке $\infty$.
. Вы можете видеть, что ключевая ошибка в ваших рассуждениях заключается в том, что пересечение между линиями находится в конечной точке. Конечно, технически ваши рассуждения ошибочны с самого начала, поскольку вы не можете просто утверждать, что параллельные прямые должны пересекаться (не говоря уже под нулевым углом) только потому, что они являются результатом какого-то ограничивающего процесса. Просто для ясности предположим, что $\frac1n \to 0$ при $n \to \infty$ и $\frac1n > 0$ для каждого положительного $n$. Нет причин ожидать, что $\lim_{n\to\infty} \frac1n > 0$. 9*}} )$, соответствует отражению $F$ на сфере Римана относительно плоскости экватора. Затем докажите (факт 2), что $f$ сохраняет углы между прямыми, которые не проходят через начало координат. Эти доказательства можно провести, используя только подобные треугольники. И обратите внимание (факт 3), что $p$ сохраняет углы между прямыми, проходящими через начало координат. Теперь возьмем любые две прямые $l,m$, пересекающиеся в точке $z\ne 0$ на плоскости, и пусть $l’,m’,z’$ — их образы при $p$.
Умножить матрицы: Онлайн калькулятор. Умножение матриц
Лекции по алгебре
Лекции по алгебре
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. ЦЕЛЫЕ ЧИСЛА § 1. Теория делимости целых чисел 2. Деление с остатком. 3. Наибольший общий делитель. 4. Алгоритм Евклида. 5. Взаимно простые числа. 6. Простые числа. § 2. Теория сравнений 2. Действия над классами. 3. Приведенная система вычетов и примитивные классы. § 3. Некоторые общие понятия алгебры 2. Кольца и поля. 3. Изоморфизм. ГЛАВА II. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Обоснование комплексных чисел 3. Свойства действий. 4. Возвращение к обычной форме записи. 5. Вычитание и деление комплексных чисел. § 2. Тригонометрическая форма комплексного числа 2. Модуль и аргумент комплексного числа. 3. Тригонометрическая запись комплексного числа. 4. Неравенства для модуля суммы и модуля разности двух комплексных чисел.  5. Умножение комплексных чисел в тригонометрической записи. 6. Возведение комплексного числа в степень с целым показателем и формула Муавра. 7. Применения формулы Муавра к преобразованиям тригонометрических выражений. § 3. Извлечение корня из комплексного числа 2. Исследование формулы извлечения корня. 3. Извлечение квадратного корня. § 4. Корни из единицы § 5. Показательная и логарифмическая функции комплексной переменной ГЛАВА III. ПРОСТЕЙШИЕ СВЕДЕНИЯ ОБ АЛГЕБРЕ ПОЛИНОМОВ § 1. Полиномы от одной буквы 2. Высший член и степень полинома. 3. Степени элемента в ассоциативном кольце. 4. Значение полинома. 5. Схема Хорнера и теорема Безу. 6. Число корней полинома в коммутативной области целостности. 7. Теорема о тождестве. § 2. Алгебраическое решение уравнений третьей и четвертой степени 2. Исследование формулы Кардано. 3. Решение уравнений четвертой степени. § 3. Полиномы от нескольких букв 3. Теорема о тождестве. 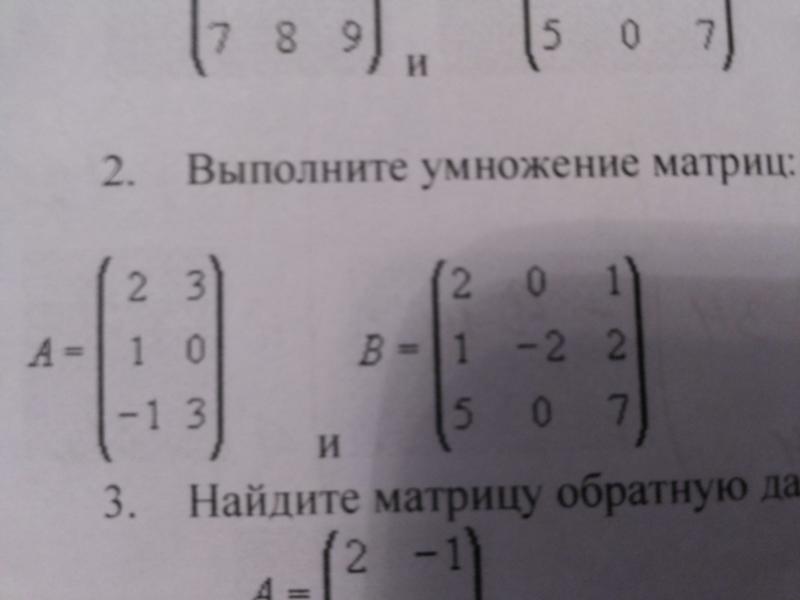 4. Теорема о несущественности алгебраических неравенств. ГЛАВА IV. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ § 1. Матрицы и действия над ними 2. Сложение матриц и умножение матрицы на число. 3. Умножение матриц. 4. Транспонирование матриц. 5. Обзор действий над матрицами. § 2. Теория определителей 2. Элементарные сведения теории перестановок. 3. Определитель порядка n. Определение. 4. Свойства определителя. 5. Алгебраические дополнения и миноры. 6. Вычисление определителей. 7. Определитель Вандермонда. 9. Некоторые следствия из теоремы Крамера. § 3. Линейная зависимость и линейная независимость строк (столбцов) 2. Линейные зависимости столбцов матрицы с линейно зависимыми строками. 3. Теорема о линейной зависимости линейных комбинаций. 4. Базис и ранг совокупности строк. 5. Линейно эквивалентные совокупности строк. 6. Ранг матрицы. 7. Условие линейной зависимости множества строк квадратной матрицы. 8. Ранг матрицы в терминах определителей.  9. Определение ранга матрицы при помощи элементарных преобразований. § 4. Системы линейных уравнений общего вида § 5. Дальнейшие свойства определителей 2. Умножение матриц, разбитых на клетки. 3. Умножение матрицы на вспомогательную матрицу как линейное преобразование строк (столбцов). 4. Определитель произведения двух квадратных матриц. 5. Примеры применения теоремы об определителе произведения квадратных матриц к вычислению определителей. 6. Теорема Бине — Коши. § 6. Обращение квадратных матриц § 7. Характеристический полином матрицы 2. Теорема Кэли—Гамильтона. ГЛАВА V. КВАДРАТИЧНЫЕ ФОРМЫ § 1. Преобразование квадратичной формы к каноническому виду линейной подстановкой букв § 2. Закон инерции квадратичных форм 2. Критерий Сильвестра положительности квадратичной формы. 3. Закон инерции квадратичных форм. § 3. Ортогональное преобразование квадратичной формы к каноническому виду 2. Собственные значения вещественной симметричной матрицы.  3. Построение ортогональных матриц. 4. Ортогональное преобразование квадратичной формы к каноническому виду. 5. Коэффициенты канонического вида квадратичной формы и столбцы преобразующей ортогональной матрицы. 6. Одновременные преобразования двух квадратичных форм к каноническому виду. § 4. Эрмитовы формы 2. Свойства эрмитовых форм. ГЛАВА VI. ПОЛИНОМЫ И ДРОБИ § 1. Теория делимости для полиномов от Одной буквы § 2. Производная 2. Разложение полинома по степеням линейного двучлена. 3. Разделение множителей различной кратности. § 3. Рациональные дроби 2. Поле частных. 3. Правильные рациональные дроби. 4. Разложение рациональной дроби на простейшие. 5. Разложение рациональной дроби на простейшие над полем С комплексных чисел. 6. Разложение рациональной дроби на простейшие над полем R вещественных чисел. 7. Разложение на простейшие правильной рациональной дроби, знаменатель которой разложен на попарно простые линейные множители.  § 4. Интерполяция 2. Интерполяционная формула Лагранжа. 3. Способ интерполяции Ньютона. 4. Приближенная интерполяция. ГЛАВА VII. СРАВНЕНИЯ В КОЛЬЦЕ ПОЛИНОМОВ И РАСШИРЕНИЯ ПОЛЕЙ § 1. Сравнения в кольце полиномов над полем § 2. Расширение полей 2. Конструирование простых расширений. ГЛАВА VIII. ПОЛИНОМЫ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ. ПОЛИНОМЫ НАД ФАКТОРИАЛЬНЫМИ КОЛЬЦАМИ § 1. Полиномы с целыми коэффициентами § 2. Полиномы от одной буквы над факториальным кольцом ГЛАВА IX. РАСПРЕДЕЛЕНИЕ КОРНЕЙ ПОЛИНОМА § 1. Существование корней в С § 2. Распределение корней на плоскости комплексной переменной 2. Принцип аргумента. 3. Теорема Руше. 4. Непрерывность корней полинома. § 3. Распределение вещественных корней полинома с вещественными коэффициентами 2. Теорема Штурма. 3. Построение ряда Штурма. § 4. Обобщенная теорема Штурма § 5. Приближенное вычисление корней полинома 2. Метод непрерывных дробей. ГЛАВА X. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП § 2.  Нормальные подгруппы и факторгруппы Нормальные подгруппы и факторгруппы§ 3. Гомоморфизм § 4. Прямое произведение групп § 5. Группы преобразований 2. Классы сопряженных элементов. 3. Строение однородных пространств. 4. К теории подстановок. 5. Примеры из геометрии. 6. Централизатор элемента и нормализатор подгруппы. 7. Центр p-группы. 8. Преобразования. 9. Автоморфизмы группы. § 6. Свободная группа § 7. Свободные произведения групп § 8. Конечные абелевы группы § 9. Конечно порожденные абелевы группы ГЛАВА XI. СИММЕТРИЧЕСКИЕ ПОЛИНОМЫ § 1. Выражение симметрических пэлииов через основные § 2. Значения симметрических полиномов от корней полинома 2. Степенные суммы. 3. Дискриминант полинома. 4. Алгебраическое решение уравнений третьей и четвертой степени в свете теории симметрических полиномов. § 3. Результант 2. Другой способ построения результанта. 3. Линейное представление результанта. 4. Применение результанта к исключению неизвестного из системы двух алгебраических уравнений с двумя неизвестными.  5. Связь дискриминанта полинома с результантом полинома и его производной. ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА 2. Линейные комбинации, линейная зависимость и линейная независимость. 3. Координаты вектора. 4. Замена базиса и преобразование координат. § 2. Подпространства 3. Прямая сумма подпространств. 4. Относительная линейная независимость и относительный базис. 5. Факторпространство. § 3. Линейные функции § 4. Линейные отображения векторных пространств § 5. Линейные операторы в векторном пространстве 2. Действия над операторами. 3. Инвариантные подпространства. 4. Циклическое подпространство и минимальный аннулятор вектора. 5. Матрица оператора на циклическом подпространстве и ее характеристический полином. 6. Минимальный полином оператора. 7. Разложение пространства с оператором в прямую сумму примарных подпространств. 8. Разложение примарного пространства в прямую сумму циклических примарных подпространств. 9.  Модули над кольцом главных идеалов. Модули над кольцом главных идеалов.10. Некоторые следствия. 11. Каноническая форма матрицы оператора. 12. Оператор проектирования. 13. Полуобратные линейные отображения. § 6. Операторы в векторных пространствах над полем С комплексных чисел 2. Корневые векторы. 3. Нильпотентный оператор. 4. Каноническая форма Жордана матрицы оператора. 5. Пример. § 7. Операторы в векторных пространствах над полем R вещественных чисел ГЛАВА XIII. ЕВКЛИДОВО И УНИТАРНОЕ ПРОСТРАНСТВА 1. Скалярное произведение. § 2. Подпространства унитарного (или евклидова) пространства § 3. Пространства, сопряженные с евклидовым и унитарным пространствами § 4. Операторы в унитарном пространстве § 5. Операторы в евклидовом пространстве § 6. Преобразование уравнения гиперповерхности второго порядка к каноническому виду § 7. Линейные отображения унитарного пространства в унитарное § 8. Объем параллелепипеда в евклидовом пространстве ГЛАВА XIV. ЭЛЕМЕНТЫ АЛГЕБРЫ ТЕНЗОРОВ § 2.  Действия над тензорами Действия над тензорами§ 3. Симметричные и антисимметричные тензоры § 4. Тензорные произведения векторных пространств ГЛАВА XV. АЛГЕБРЫ 1. Определение и простейшие свойства алгебр. 2. Структурные константы алгебры. 3. Некоторые классы алгебр. 4. Идеалы алгебры. 5. Присоединение единицы. 6. Вложение ассоциативной алгебры в алгебру матриц. § 2. Алгебра кватернионов § 3. Внешняя алгебра СПИСОК ЛИТЕРАТУРЫ |
Умножение матрицы на скаляр. Сложение и вычитание матриц. Умножение матриц. Транспонирование матриц
Другие предметы \ Радиотехника
Страницы работы
18 страниц (Word-файл)
Посмотреть все страницы
Скачать файл
Содержание работы
Содержание
Задание к курсовой работе
. …………………………2
…………………………2
Теоретическая часть :
1. Умножение матрицы на скаляр ……………………3
2. Сложение и вычитание матриц ……………………3
3. Умножение матриц ……………………………..4
4. Транспонирование матриц ……………………….5
5.Поиск максимального (минимального) элемента матрицы .6
6. Формирование вектора из элементов матрицы ……….7
Блок-схема алгоритма решения задачи …………………9
Программа решения задачи ………………………….13
Результаты вычисления по программе …………………16
Краткие выводы по решению задачи …………………..17
Список используемой литературы …………………….18
Задание к курсовой работе
Составить
программу вычисления и преобразования матрицы D=F(A,B,C), где F(A,B,C)
-матричное выражение А,В,С-исходные матрицы размер и значение элемнтов которых
выбираются произвально.
Выражение для расчёта матрицы D и действия по её преобразованию выбираются из таблицы № 1 и №2 в соответствии с номером варианта задания.
В программе предусмотреть вывод на печать всех исходных, промежуточных и разультирующих матриц, а также результатов преобразования
Таблица №1
D= (2*A*BT-С) T
Таблица №2
Определить количество элементов, удовлетворяющих условиям:
1) Pij>Q1 2)Pij<Q2 3)Q2<=Pij<=Q1.
Значения Q1 и Q2 выбрать произвольно
1. Умножение матрицы на скаляр
Чтобы умножить матрицу на скаляр, необходимо каждый элемент этой матрицы умножить на скаляр. Например, если требуется вычислить А=d*В, где А и В матрицы, d — скаляр, то каждый элемент матрицы А определяется по формуле аij = в*вij; i = 1, 2,…, n; j = 1, 2,…, m, (1)
где n, m — размеры матриц.
Алгоритмы
умножения матрицы на скаляр представлен на рис.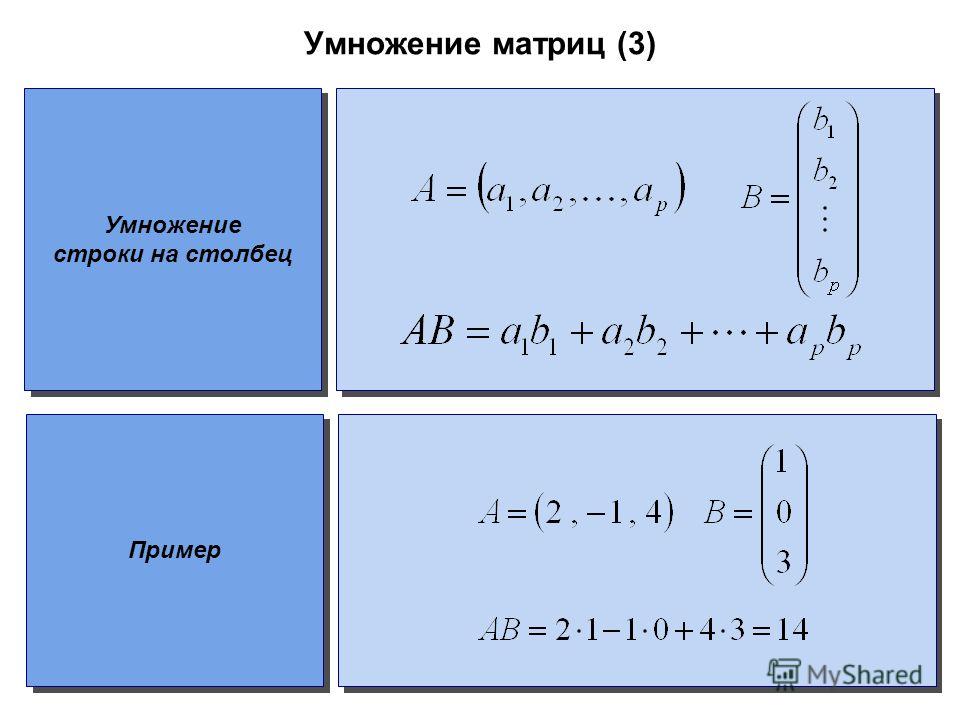 1. Здесь центральный оператор
вычисления очередного элемента матрицы-произведения (блок 4) является телом
двойного цикла по строкам (i) и столбцам (j).
1. Здесь центральный оператор
вычисления очередного элемента матрицы-произведения (блок 4) является телом
двойного цикла по строкам (i) и столбцам (j).
Рис. 1
Входные параметры матрица В(n,m) скаляр d
1
ВХОД
2
i=I,(1),n
3
j=I,(1),m
4
Aij =d*Bij
5
ВЫХОД
2. Сложение и вычитание матриц
Сложение и вычитание матриц
Чтобы сложить (вычесть) две матрицы, необходимо сложить (вычесть) соответствующие элементы этих матриц. Например, если требуется вычислить С = А+В, где А и В — матрицы, то каждый элемент матрицы С определяется по формуле сij = a ij = bij ; i = 1, 2,…, n ; j = 1, 2,…, m, (2)
где n, m — размеры матриц.
Из выражения (2) следует, что складывать (вычитать) можно только матрицы одинакового размера. Алгоритм сложения (вычитания) матриц будет таким же, как на рис. 1, если в блоке 4 вместо формулы (1) записать формулу (2). при этом соответственно изменятся и выходные параметры.
3. Умножение матриц
При перемножении матриц каждый элемент матрицы-произведения определяется как сумма произведений элементов строки матрицы-множителя [1]. Например, если требуется вычислить C = A*B, где A и B — матрицы, то каждый элемент матрицы С определяется по формуле
m
Сij = aik * bkj , i = 1, 2,. .., n ; j = 1, 2,…, m, (3)
.., n ; j = 1, 2,…, m, (3)
k=1 где n — число строк матрицы А;
i — число столбцов матрицы B;
m — число столбцов матрицы А или число строк матрицы В. Из (3) следует, что перемножать можно только такие матрицы, у которых число столбцов матрицы-множимого равно числу строк матрицы-множителя, т.е.
aij nm * bij nl = cij nl .
Блок-схема алгоритма перемножения матриц представлена на рис. 2. Здесь каждый элемент матрицы-произведения вычисляется в блоках 4-7 как сумма произведений. В блоке 4 сумма сбрасывается в ноль, в блоке 6 производится непосредственное суммирование произведений, в блоке 7 накопленная сумма записывается в выходной массив.
Рис. 2
Входные параметры матрица А(n,m), В(n,l)
1
ВХОД
2
i=I,(1),n
3
j=I,(1),m
4
S=0
5
Похожие материалы
Информация о работе
Скачать файл
Объяснение урока: Скалярное умножение матриц
В этом объяснении,
мы научимся умножать скаляр на матрицу и определять свойства
их размножения.
Матрица содержит массив чисел, упорядоченных по строкам и столбцам. До мы можем научиться использовать матрицы для практических приложений, мы должны сначала знать, как выполнять операции с матрицами. В этом объяснении мы сосредоточимся на скалярное умножение.
Скаляр относится к одному числу, например, −2 или 13. Как умножить матрицу, массив числа, на масштаб -2 или на 13? Давайте начнем с определение этой алгебраической операции для общих матриц.
Определение: скалярное умножение
Для матрицы порядка 𝑚×𝑛, определенной как 𝐴 = ⎛⎜⎜⎝𝑎𝑎 ⋯ 𝑎𝑎𝑎 ⋯ ⋮⋮ ⋱ ⋮ ⋮ 𝑎𝑎 ⋯ 𝑎⎞⎟⎟⎠, Мы можем завершить «скаляр умножение» на число 𝑘. Это требует умножения каждой записи 𝐴 по 𝑘: 𝑘𝐴 = ⎛⎜⎜⎜⎝𝑘 × 𝑎𝑘 × 𝑎 ⋯ 𝑘 × 𝑎𝑘 × 𝑎𝑘 × 𝑎… 𝑘 × 𝑎 ⋮⋮ ⋱ ⋮ 𝑘 × 𝑎𝑘 × 𝑎 ⋯ × 𝑎⎞⎟⎟⎟⎠. Эта операция часто называют «масштабированием» матрицы константой 𝑘.
Другими словами, мы можем умножить число (скаляр) на матрицу путем умножения
номер каждой записи в матрице.
Например, рассмотрим матрицу 𝐴=⎛⎜⎜⎝53−1−311061754−27−26−26−38⎞⎟⎟⎠.
Теперь предположим, что мы хотим масштабировать матрицу на константу −2. Затем мы умножаем каждую запись 𝐴 на −2, следовательно, находя, что )×1(−2)×0(−2)×6(−2)×1(−2)×7(−2)×5(−2)×4(−2)×(−2)(− 2)×7(−2)×(−2)(−2)×6(−2)×(−2)(−2)×6(−2)×(−3)(−2)×8⎞ ⎟⎟⎟⎠.
Завершение операции для каждой записи дает −2𝐴=⎛⎜⎜⎝−10−626−2−20−12−2−14−10−84−144−124−126−16⎞⎟⎟⎠.
Это не тот случай, когда мы ограничены масштабированием матрицы целым числом, и мы могли бы в равной степени выбрать масштабирование дробью, иррациональным числом,
или даже комплексное число, если мы чувствуем себя авантюрно. Хотя это не является строго необходимым, при масштабировании матрицы дробью обычно считается
хорошая практика для упрощения любых результирующих фракций до их простейшей формы. Например, мы определяем матрицу
𝐵=5−36488306−11−1
и решим масштабироваться на константу 13. Мы обнаружим, что
13𝐵=⎛⎜⎜⎜⎜⎝13×513×(−3)13×613×413×813×813×313×013×613×(−1)13×113×(−1)⎞⎟⎟⎟⎟⎠ .
Приведение как можно большего числа дробей к их низшей форме дает 13𝐵=⎛⎜⎜⎜⎜⎝53−12438383102−1313−13⎞⎟⎟⎟⎟⎠.
Скалярное умножение матрицы умножает константу на каждый элемент матрицы матрица, как мы видели. Исходя из этого определения, мы видим, что скалярное умножение на 1 сохраняет любую матрицу, а скалярное умножение на 0 превращает любую матрицу в нулевую матрицу.
Свойство: мультипликативное тождество и умножение на ноль в Скалярное умножение
Для любой матрицы 𝐴, 1𝐴=𝐴 и 0𝐴=𝑂, где 𝑂 — нулевая матрица в том же порядке, что и 𝐴.
Прежде чем обсуждать некоторые сложные проблемы, возникающие в связи с определением скалярного умножения, мы сначала попрактикуемся в одном вопросе.
Пример 1. Умножение матрицы на скаляр
Учитывая, что 𝐴=(−1−8), найти 3𝐴.
Ответ
Напомним, что число (скаляр) можно умножить на матрицу путем умножения
номер каждой записи в матрице.
Чтобы умножить 𝐴 на 3, мы умножаем каждую запись на это число, и поэтому мы имеем 3𝐴=(3×(−1)3×(−8))=(−3−24).
Один из ключевых принципов скалярного умножения заключается в том, что к каждой отдельной записи применяется один и тот же процесс, а именно, что каждая запись умножить на то же число. Скалярное умножение никогда не умножает разные записи на разные числа. Следующий вопрос дает пример того, как этот принцип может быть применен с точки зрения решения задач линейной алгебры.
Пример 2. Нахождение скалярного множителя матрицы
Учитывая, что 𝑥×−20−3−5=1402135, найдите значение 𝑥.
Ответ
Напомним, что число (скаляр) можно умножить на матрицу путем умножения номер каждой записи в матрице.
Умножая каждую запись на 𝑥 в левой матрице, мы ищем 𝑥, которая решает следующее уравнение:
𝑥×(−2)𝑥×0𝑥×(−3)𝑥×(−5)=1402135,
что эквивалентно можно записать как
−2𝑥0−3𝑥−5𝑥=1402135.
Напомним, что две матрицы равны, если они имеют одинаковый порядок и каждая пары записей из одной строки и столбца равны. Мы видим, что матрицы имеют одинаковый порядок, так как они обе имеют 2 строки и 2 столбцы. Поэтому мы должны соответствовать пары записей в одной и той же строке и столбце из двух матриц.
Получается система линейных уравнений −2𝑥=14,0=0,−3𝑥=21,−5𝑥=35.
Помимо тривиального второго уравнения, которое явно верно, мы видим, что каждое уравнение решается, полагая 𝑥=−7.
Часто при работе с интересующей матрицей мы предпочитаем выносить за скобки скалярное кратное от каждой записи, если это возможно. Например, если нам дана матрица 𝐴=36240−416−8−44−4, легко заметить, что это можно записать как 𝐴=4×(9)4×(6)4×(0)4×(−1)4×(4)4×(−2)4×(−1)4×(1)4×(− 1).
Таким образом, каждая запись имеет коэффициент 4, который можно удалить, получив таким образом
𝐴=4960−14−2−11−1.
В некоторых ситуациях может быть предпочтительнее определить новую матрицу 𝐵=960−14−2−11−1, что позволяет нам написать 𝐴=4𝐵.
Давайте рассмотрим пример, который включает факторизацию скаляра из матрицы.
Пример 3: скалярное умножение
Учитывая матрицу 𝐴=1−1652−4−3−174, какое наибольшее число 𝑘, для которого ни одна запись 𝑘𝐴 не больше 1?
Ответ
Напомним, что число (скаляр) можно умножить на матрицу путем умножения номер каждой записи в матрице.
Учитывая матрицу 𝐴, определенную выше, это означает 𝑘𝐴=𝑘−16𝑘5𝑘2𝑘−4𝑘−3𝑘−𝑘7𝑘4𝑘.
Если 𝑘=0, каждая запись будет нулевой (которая является нулевой матрицей), которая будет удовлетворять условию, что ни одна запись не больше 1. Поскольку мы ищем наибольшее число 𝑘, для которого выполняется это условие, мы можем сосредоточиться на поиске положительного числа 𝑘>0.
Проверка положительных записей,
у нас есть 𝑘, 2𝑘, 4𝑘,
5𝑘 и 7𝑘. Из них 7𝑘 должно быть самым большим входом, что означает
что данное условие будет выполнено, если 7𝑘≤1. Это приводит к 𝑘≤17. Поскольку это значение
𝑘 положительно, остальные значения
−𝑘, −3𝑘,
−4𝑘 и −16𝑘 все будут
отрицательно и, следовательно, меньше 1,
Из них 7𝑘 должно быть самым большим входом, что означает
что данное условие будет выполнено, если 7𝑘≤1. Это приводит к 𝑘≤17. Поскольку это значение
𝑘 положительно, остальные значения
−𝑘, −3𝑘,
−4𝑘 и −16𝑘 все будут
отрицательно и, следовательно, меньше 1,
Так как мы ищем верхний предел значения 𝑘, ответ 𝑘=17.
Скалярное умножение — это операция, регулярно встречающаяся в линейной алгебре. Наряду с сложением это, пожалуй, самая простая алгебраическая операция для понимания. Однако это не означает, что задачу линейной алгебры можно считать простой только потому, что она включает скалярное умножение. Следующие два вопроса проиллюстрируют, как скалярное умножение матриц может предоставить богатые и интересные примеры, которые позволят развить более высокий уровень понимания.
Пример 4. Решение уравнений, использующих скалярное умножение
Рассмотрим матричное уравнение
819−3=𝑚302−1+−1130.
Найдите значение 𝑚, которое решает это уравнение.
Ответ
Напомним, что число (скаляр) можно умножить на матрицу путем умножения номер каждой записи в матрице. Точно так же мы знаем, что можем добавить две матрицы одного порядка путем добавления пар элементов, соответствующих в одну и ту же строку и столбец из двух матриц.
Сначала мы перепишем уравнение после включения скалярного умножения на 𝑚: 819−3=3𝑚02𝑚−𝑚+−1130.
Завершаем сложение в правой части этого уравнения, работая запись за записью, чтобы найти 819−3=3𝑚−112𝑚+3−𝑚.
Напомним, что две матрицы равны, если они имеют одинаковый порядок и каждая пары записей из одной строки и столбца равны. Мы можем видеть, что матрицы имеют одинаковый порядок, так как они обе имеют 2 строки и 2 столбца.
Соответствие каждой паре записей в одной и той же строке и столбце из двух
матрицы, получаем
8=3𝑚−1,1=1,9=2𝑚+3,−3=−𝑚.
Окончательное уравнение дает 𝑚=3, и можно проверить, что все данные уравнения также верны, если 𝑚=3, значит, это и должен быть ответ. Это можно проверить, подставив 𝑚=3 обратно в исходную матрицу. уравнения, а затем наблюдая, что обе части уравнения совпадают.
В предыдущем примере мы нашли неизвестную константу в матричном уравнении. Если мы рассмотрим процесс ближе, мы можем заметить, что матричное уравнение приводит к одновременные уравнения. Следовательно, можно использовать матричное уравнение, чтобы найти больше чем одна неизвестная константа. В нашем последнем примере мы рассмотрим матрицу уравнение с тремя неизвестными константами.
Пример 5. Решение уравнений со скалярным умножением
Найдите числа 𝑎, 𝑏 и 𝑐 так, чтобы 𝑎110−1+𝑏1001+𝑐0−110=10−13.
Ответ
Напомним, что число (скаляр) можно умножить на матрицу путем умножения
номер каждой записи в матрице. Точно так же мы знаем, что можем добавить
две матрицы одного порядка путем добавления пар элементов, соответствующих
в одну и ту же строку и столбец из двух матриц.
Мы начинаем с включения скалярных членов в матрицы, давая 𝑎𝑎0−𝑎+𝑏00𝑏+0−𝑐𝑐0=10−13.
Поскольку добавление матрицы выполняется запись за записью, мы имеем 𝑎+𝑏𝑎−𝑐𝑐−𝑎+𝑏=10−13.
Напомним, что две матрицы равны, если они имеют одинаковый порядок и каждая пары записей из одной строки и столбца равны. Мы видим, что матрицы имеют одинаковый порядок, так как они обе имеют 2 строки и 2 столбцы.
Соответствие каждой паре записей в одной и той же строке и столбце из две матрицы, мы получаем одновременные уравнения 𝑎+𝑏=1,𝑎−𝑐=0,𝑐=−1,−𝑎+𝑏=3.
Третье уравнение дает 𝑐=−1, которое можно подставить во второе уравнение, чтобы показать, что 𝑎=−1. Затем подстановка значения 𝑎 либо в первое, либо в четвертое уравнение дает, что 𝑏=2.
Скалярное умножение имеет множество привлекательных свойств в сочетании с матричным
добавление. Если бы мы работали с обычной алгеброй, то мы знали бы, что
количества 𝑎, 𝑏 и 𝑐
всегда будет подчиняться правилу
𝑎×(𝑏+𝑐)=𝑎×𝑏+𝑎×𝑐,
которое известно как «распределительное свойство». Выясняется, что одно и то же свойство справедливо для сложения матриц и скалярного умножения.
Выясняется, что одно и то же свойство справедливо для сложения матриц и скалярного умножения.
Теорема: Распределительное свойство
Скалярное умножение является «дистрибутивным» в сочетании со сложением матриц. Другими словами, если предположить, что 𝑎 — скалярная константа, а 𝐵 и 𝐶 — матрицы одного порядка, то 𝑎(𝐵+𝐶)=𝑎𝐵+𝑎𝐶.
Продемонстрируем этот результат на примере. Положим 𝑎=3 и определим две матрицы 𝐵=−460872,𝐶=37−566−1.
Затем, 𝐵+𝐶=−460872+37−566−1=−113−514131; и поэтому 𝑎(𝐵+𝐶)=3−113−514131=−339−1542393.
Точно так же мы могли бы выбрать другой маршрут и сначала вычислить 𝑎𝐵=−1218024216,𝑎𝐶=921−151818−3.
Отсюда мы могли бы вычислить, что 𝑎𝐵+𝑎𝐶=−1218024216+921−151818−3=−339−1542393.
Таким образом, в этом примере мы показали, что
𝑎(𝐵+𝐶)=𝑎𝐵+𝑎𝐶. Естественно, что приведенную выше теорему можно доказать строго и без ссылки на какой-либо конкретный пример, хотя здесь мы дали лишь демонстрацию.
Хотя может показаться, что скалярное умножение — тривиальная матрица операции, способность свободно работать с этой концепцией часто является разница между коротким и простым решением проблемы и решение длинное и сложное. Изучая любую конкретную матрицу, обычно рекомендуется проверить, можно ли разложить на множители любое скалярное кратное со всех записей.
Давайте закончим повторением нескольких важных понятий из этого объяснения.
Ключевые точки
- Умножение матрицы 𝐴 на скаляр 𝑘 означает, что каждый элемент матрицы 𝐴 будет умножен на 𝑘.
- Когда каждый элемент матрицы имеет общий множитель, мы можем скаляр из матрицы путем обратного скалярного умножения.
- Скалярное умножение является дистрибутивным. Другими словами, если задан скаляр 𝑎 и матрицы 𝐵 и 𝐶 одного порядка, 𝑎(𝐵+𝐶)=𝑎𝐵+𝑎𝐶.
- Для любой матрицы 𝐴, 1𝐴=𝐴 и
0𝐴=𝑂, где 𝑂 — нулевая матрица
того же порядка, что и 𝐴.

матриц: умножение матриц | SparkNotes
Скалярное умножение
Чтобы умножить матрицу на скаляр, то есть на одну константу,
переменной или выражению, умножьте все элементы матрицы на
скаляр:
Например,
Скалярное умножение является распределительным: ± ( A + B ) = ± A + ± B . Например,
| 4( + ) = 4 +4 |
Умножение двух матриц
Чтобы умножить две матрицы, мы сначала должны знать, как умножить строку (а
матрица 1×p ) по столбцу (матрица p ×1). Умножить
строку на столбец, умножьте первую запись строки на первую
вход в столбец. Затем умножьте вторую запись строки на
вторая запись столбца и т. д., и добавить все результаты. ответ должен быть одним числом. Например,
ответ должен быть одним числом. Например,
| [ 8 –1 3 0 ] = 8(2) + (- 1)(6) + 3(- 4) + 0(- 2) = 16 — 6 — 12 + 0 = — 2 |
Строка может быть умножена на столбец тогда и только тогда, когда строка и столбец столбец имеет одинаковое количество записей. Точно так же две матрицы могут умножаться тогда и только тогда, когда первая матрица имеет одинаковое количество столбцы, так как вторая матрица имеет строки. То есть две матрицы могут перемножаться тогда и только тогда, когда они имеют размеры м × р и р × n . Ответом будет матрица с тем же количеством строк как первая матрица и такое же количество столбцов, как вторая матрица. Другими словами, она будет иметь размерность м × n .
ПУНКТ
Чтобы умножить две матрицы, умножьте каждую строку первой матрицы на каждую
столбец второй матрицы.
Приложения для решения примеров: 15 лучших приложений для безупречной учебы в школе / AdMe
15 лучших приложений для безупречной учебы в школе / AdMe
Знания усвоятся гораздо проще и легче, если с умом подойти в выбору помощников-приложений. Сейчас не нужно носить с собой кучу учебников и ночами корпеть над шпаргалками. Достаточно загрузить в смартфон эти программы — и всё в легкой и доступной форме само уложится в голове. Но их так много, что глаза разбегаются, и не знаешь, с чего начать.
Чтобы не дать вам утонуть в море информации, ADME отобрал только самые лучшие приложения для школьников и студентов.
МатематикаPhotoMath
PhotoMath — это калькулятор, использующий камеру смартфона — просто наведите камеру на математическую задачу, и PhotoMath сразу же выдаст ответ, с поэтапным решением задачи.
Платформа: Android | iOS
MalMath
Программа для решения математических задач с пошаговым описанием и графическим изображением. Генерирует случайные математические задачи в нескольких категориях и уровнях сложности. Работает автономно. Можно сохранить или поделиться решениями и графиками.
Работает автономно. Можно сохранить или поделиться решениями и графиками.
Платформа: Android
Решение уравнений по шагам
Калькулятор может решить все типы уравнений (кроме дифференциальных), исправляет ошибки в выражениях и предлагает для ввода свои варианты. Показывает подробное решение квадратных, простейших тригонометрических уравнений.
Платформа: Android
ФизикаЭто сборник всех формул физики, которые сортированы по разделам. Есть возможность поделится любой формулой со своими друзьями или одноклассниками простым свайпом влево и быстро искать формулы по их названию.
Платформа: iOS
Химия
Приложение решает химические уравнения реакций, поможет с органической и неорганической химией. Есть интерактивная таблица Менделеева и таблица растворимости веществ. Реакции отображены в обычном и ионном виде. И даже нарисованы формулы органической химии.
Платформа: Android | iOS
Химия X10
Химия X10 — это универсальный помощник по химии — решает задачи, содержит шпаргалки, расстанавливает коэффиценты в уравнениях.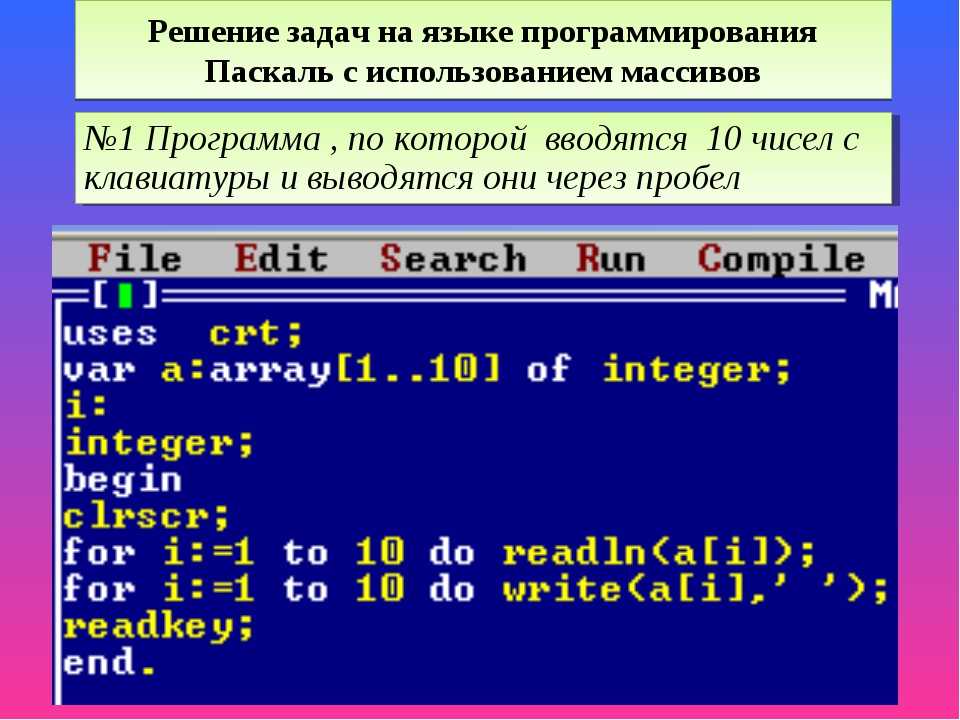 Здесь есть встроенный калькулятор молярных масс.
Здесь есть встроенный калькулятор молярных масс.
Платформа: Android | iOS
Иностранные языкиDuolingo: Учим языки бесплатно
Одно из лучших, полностью бесплатных приложений для изучения английского. Обучение проходит в игровой форме, незаметно и увлекательно. В случае неправильных ответов теряются жизни, а при усвоении небольших уроков вы продвигаетесь вперёд. Яркие трофеи отмечают этапы вашего прогресса.
Платформа: Android | iOS
English Grammar Test. 1200 заданий по английской грамматике
Приложение для проверки знаний английского языка. Здесь 60 тестов по 20 заданий. Каждый вопрос посвящен одной грамматической теме. Таким образом, пройдя один тест, вы сможете проверить свои знания сразу в 26 разделах английской грамматики.
Платформа: Android
Русский язык и литератураОрфография русского языка
«Орфография» — это и тест, и игра, и викторина. Слова, в которых вы делаете ошибки, будут появляться в последующих тестах для того, чтобы вы наверняка их запомнили. Проверка орфографии поможет с пользой провести время и улучшить правописание и грамотность. По нему можно готовиться к ЕГЭ по русскому языку.
Проверка орфографии поможет с пользой провести время и улучшить правописание и грамотность. По нему можно готовиться к ЕГЭ по русскому языку.
Платформа: Android
Грамматика русского языка
Приложение составлено в виде таблиц и схем и имеет, в основном, практическую направленность. Здесь в краткой и доступной форме систематически изложены основные правила грамматики русского языка в объеме средней школы. Работает в оффлайне.
Платформа: Android
Краткие содержания
30 произведений литературы с 9 по 11 класс в сокращенном виде. Работает без интернет-соединения.
Платформа: Android
Слово дня — толковый словарь
Каждый день приложение будет показывать новые актуальные слова и термины русского языка, значение которых многие не знают. Команда филологов изучает их определения в толковых словарях Даля и Ожегова и других авторитетных источниках. А потом адаптирует эту информацию в краткие определения для простоты понимания.
Платформа: Android | iOS
Универсальные помощникиФоксфорд Учебник
Это интерактивный справочник по школьной программе за 4–11 классы. В учебнике вы найдете теорию, отличные примеры и просто шпаргалки по разным предметам. Бонус — более 500 подробных видеоуроков с лучшими преподавателями страны.
Платформа: Android | iOS
Универсариум
Математика, химия, экономика, а, может быть, еще история искусства — изучайте столько предметов, сколько хотите и можете. Вы сами создаете свою программу. Основная часть обучения — это видеолекции. В конце каждого модуля следует проверочный тест.
Платформа: Android | iOS
Знания
Если не справляетесь с заданием, или нужна подсказка — задайте вопрос и в течение нескольких минут можете получить решение от пользователей.
Платформа: Android
Решаем примеры по фото — приложения для математиков
Приложения
Подобных приложений, которые решают примеры по фото, существует довольно много. Но мы выбрали три лучших приложения, которые вам точно понравятся!
Но мы выбрали три лучших приложения, которые вам точно понравятся!
Как же часто школьникам и студентам не удается решить сложные математические примеры! Даже если задания легкие, но их слишком много, хочется, чтобы их сделал кто-то другой. Решение существует! Решить примеры по фото — скачать приложения для решения математических заданий по фотографии.
Принцип их работы прост: фотографируете пример, загружаете фото в программу (чаще всего в подобных приложениях уже есть встроенная камера), и она решает пример по фото. Читайте до конца и узнавайте об этих программах, которые не только найдут правильное решение для всех примеров, но и научат вас делать то же самое!
Решаем примеры по фото: Photomath
Пожалуй, самым популярным и распространенным математическим приложением является Photomath. Приведем небольшую инструкцию по работе с этой программой:
- Photomath уже имеет встроенную камеру. Вы наводите ее на пример, и приложение начинает его анализ;
- если схемы решения данного задания уже заложены в «мозг» приложения, то оно выдает решение;
- решение разделено на несколько этапов, есть промежуточные результаты.
 Каждый шаг можно отдельно изучить;
Каждый шаг можно отдельно изучить; - немаловажный плюс — с построением графиков программа также справляется.
Скачать приложение можно на Android и на iOS.
Решаем примеры по фото: MalMath
Данное приложение, как и Photomath, способно выполнять построения графиков разной сложности. В MalMath заложены новейшие схемы решения уравнений, неравенств и прочих математических заданий.
Хотите потренироваться? Приложение выдаст случайные примеры любой сложности. При этом все решения можно сохранить в программе и продолжить работу позже.
Приложение можно скачать на Android.
Automath
Данное приложение, как и предыдущие, использует встроенную камеру и фокусируется на изображении примера. После непродолжительного анализа программа выдает поэтапно выстроенное решение. Удобный и качественный сервис помогает быстро сориентироваться на первоначальном этапе и вникнуть в принцип работы Automath.
Пользователи Android опять-таки могут воспользоваться предложенным математическим сервисом.
Подобных приложений, которые решают примеры по фото, существует довольно много. Но сервис и качество работы большинства из них крайне неудобны и малоэффективны.
Мы предлагаем вам воспользоваться тремя самыми способными программами, представленными выше. Пользуйтесь, решайте на отлично и учитесь на своих ошибках!
Поделитесь ссылкой на нашу статью — поддержите авторов!
Если вы нашли опечатку — выделите ее и нажмите Ctrl + Enter! Для связи с нами вы можете использовать [email protected].
Advertisement
15 лучших приложений, решающих повседневные проблемы
По данным Statista, Google Play предлагает 2,56 миллиона мобильных приложений для пользователей Android, а поклонники iOS имеют доступ к 1,85 миллионам приложений в App Store. Эти цифры означают широкий выбор для потребителей и высокую конкуренцию для владельцев бизнеса, борющихся за загрузки. Одна из проверенных стратегий для победы в этом соревновании за привлечение клиентов — превратить ваше приложение в решение.
Самые успешные продукты — очень эффективные обезболивающие. Чтобы придумать отличную бизнес-идею, сначала нужно найти проблему, которую стоит решить,
сказал Марк Макдональд, соучредитель Appster.
В этом руководстве рассматриваются приложения для решения повседневных задач, которые упростили жизнь пользователей и заняли достойное место в смартфонах.
1. Я не могу проснуться!: Трудное пробуждение
Большинство людей нажимают кнопку повтора, когда звонит будильник, чтобы получить дополнительные минуты сна. Это распространенная причина, по которой люди должны собираться в спешке и опаздывают. Это приложение решает проблемы тяжелых шпал. Чтобы отключить будильник, им нужно будет выполнить одно из 8 заданий, будь то математическая сумма, переписывание текста, поиск пары к слову и так далее — такая стимуляция гарантирует пробуждение мозга.
Я не могу проснуться! в App Store
Не могу проснуться! в Play Market
2.
 Лес: В центре внимания
Лес: В центре внимания60-80% сотрудников во время работы отвлекаются на социальные сети. Основатели Seekrtech решили нанять разработчиков приложений для iOS и инженеров Android, чтобы решить эти проблемы, отвлекающие внимание и прокрастинацию. Они создали приложение, в котором пользователи могут вырастить виртуальное дерево или даже целый лес. Для этого они должны держать приложение открытым и не переключаться на социальные сети. Их виртуальные монеты пожертвованы Trees в качестве фонда для посадки настоящих деревьев. Таким образом, пользователь сохраняет концентрацию на рабочем месте и вносит свой вклад в сохранение окружающей среды на планете.
Forest в App Store
Forest в Google Play
3. Вкладка: Разделение счета
Разделение счета в баре или кафе — одна из тех небольших проблем, с которыми сталкивается почти каждый.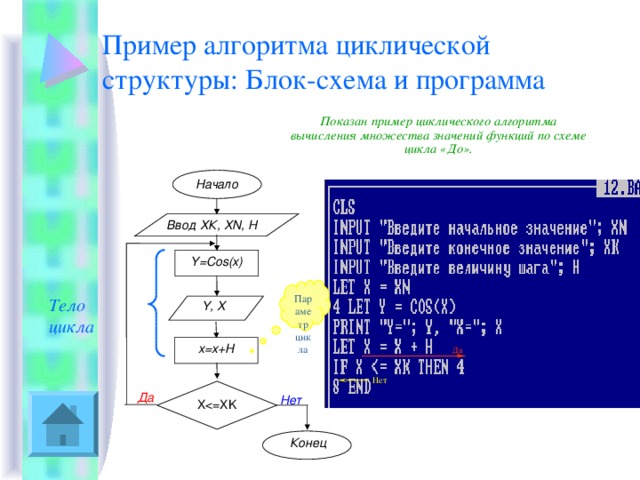 Tab – это инновационное решение. Теперь пользователи могут сфотографировать чек, и приложение прочитает его и отобразит все элементы на экране. После этого пользователю и его спутникам остается только выбрать заказанную еду и напитки. Tab автоматически рассчитает стоимость, налог и чаевые для каждого человека.
Tab – это инновационное решение. Теперь пользователи могут сфотографировать чек, и приложение прочитает его и отобразит все элементы на экране. После этого пользователю и его спутникам остается только выбрать заказанную еду и напитки. Tab автоматически рассчитает стоимость, налог и чаевые для каждого человека.
Вкладка в App Store
Вкладка в Google Play
4. Gratitude Journal: Борьба с депрессией и тревоги в повседневной жизни. Он предлагает пользователям делать заметки с благодарностью в онлайн-журнале и сосредотачиваться только на положительных аспектах каждого дня. Кроме того, пользователь получает ежедневные дзены, прививающие любовь к себе и мотивирующие не сдаваться, несмотря ни на какие сложности.
Журнал благодарности в App Store
Журнал благодарности в Google Play
Вас захватила идея? KeyUA поможет вам внедрить и улучшить его в вашем приложении. Сделайте шаг к решению проблемы вашей аудитории.
Сделайте шаг к решению проблемы вашей аудитории.
Свяжитесь с нами
5. Пьяный шкафчик: избегайте неловкости
Это приложение создано дальновидным и заботливым человеком, который нанял разработчиков приложений для Android, чтобы помочь людям избежать неловких ситуаций утром после вечеринки. Приложение позволяет пользователям блокировать все социальные сети, когда они немного навеселе. Это избавляет их от ненужных звонков, текстовых сообщений и публикации фотографий, которые могут подорвать их репутацию.
Drunk Locker в Google Play
6. Flush: Поиск туалетов
Это приложение решает проблему миллионов туристов и людей, оказавшихся в незнакомых местах. Им больше не нужно искать туалеты наугад или стесняться обращаться за помощью к незнакомцам. Теперь им достаточно открыть приложение и получить информацию обо всех туалетах поблизости, в том числе о тех, которые требуют ключ или плату за вход и подходят для людей с ограниченными возможностями.
Флеш в App Store
7. Пакт: Борьба с ленью
Если человек не может заставить себя вести здоровый образ жизни, это приложение решит эту проблему с помощью финансового поощрения. Пользователи составляют план тренировок и питания на неделю, указывают сумму, с которой они расстанутся в случае неудачи, подключаются к своему фитнес-трекеру или смарт-часам и делятся фотографиями своих приемов пищи и тренировок. Добросовестные пользователи могут получить деньги от тех, кто нарушает режим.
Pact в Google Play
8. Монитор счетов: просроченные счета
Это одно из приложений, которое решает проблемы забывчивых плательщиков. Он предлагает пользователям регистрировать свои счета, после чего они могут управлять календарем счетов, получать напоминания об оплате и отмечать частичные или полные платежи.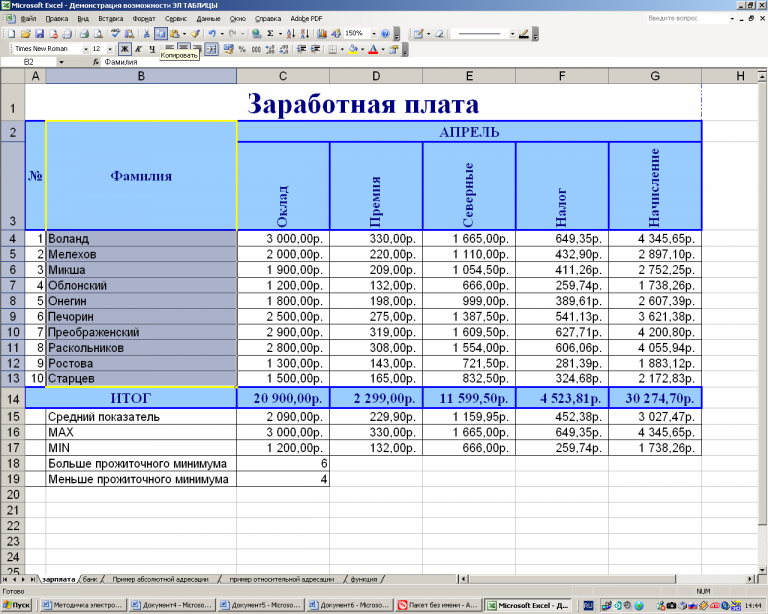 В качестве бонуса дизайн Bills Monitor включает значки для каждой категории счетов для удобства использования и управления.
В качестве бонуса дизайн Bills Monitor включает значки для каждой категории счетов для удобства использования и управления.
Монитор счетов в App Store
Разработчики KeyUA создают собственные приложения с широким функционалом и удобным интерфейсом. Таким образом, вы можете легко повторить и увеличить успех понравившегося приложения.
Свяжитесь с нами
9. Kwit: отказ от курения
Kwit относится к причудливым приложениям и вовлекает пользователя в решение проблем посредством игры. Каждый день без выкуривания сигарет выводит их на новый уровень и приносит дополнительные очки. Приложение помогает избежать рецидивов и предоставляет полезные советы и ободряющие сообщения. Для дополнительной мотивации Kwit подсчитывает, сколько денег вы сэкономили, сколько сигарет не выкурили и насколько продлили свою жизнь.
Kwit в App Store
Kwit в Google Play
10.
 LastPass: Потеря паролей
LastPass: Потеря паролейLastPass — это приложение, которое решает повседневные проблемы с запоминанием, поиском и угадыванием правильных паролей. Он хранит их все в одном зашифрованном хранилище и вводит их, как только вы пытаетесь войти в выбранную учетную запись. Вход в LastPass возможен через функцию Touch ID.
LastPass в App Store
LastPass в Google Play
Производители часто маркируют косметику и средства личной гигиены как органические или полностью натуральные, но на самом деле они могут содержать вредные или токсичные ингредиенты, оказывающие неблагоприятное воздействие на здоровье. Приложение Think Dirty позволяет пользователям сканировать штрих-код, получать подробную информацию о компонентах, узнавать об их безопасных альтернативах и делать потребление осознанным. Его база данных содержит более 850 000 товаров, но вы всегда можете добавить новые и внести свой вклад в борьбу с грязными товарами.

Think Dirty в App Store
Think Dirty в Google Play
Это приложение предоставляет информацию о дорожном движении, авариях и строительных работах, как только вы выбрали маршрут, и предлагает варианты объезда. При разработке пользовательского мобильного приложения создатели учли желание водителей слушать музыку в дороге и заправляться по пути. Поэтому Waze синхронизируется с вашим музыкальным приложением и подсказывает станции с самым дешевым бензином на вашем маршруте.
Waze в App Store
Waze в Google Play
Команда KeyUA учитывает все потребности пользователей при разработке приложения. Их удобство – залог вашего успеха на рынке.
Свяжитесь с нами
13. Убери мой дом: график уборки
Убери мой дом — отличный пример приложения, которое решает повседневные проблемы владельцев домов и квартир. Создает график уборки и распределяет задачи по дням. Благодаря этому пользователь не заваливается домашним заданием в выходной день. Приложение содержит категории в соответствии с комнатами в доме, позволяет добавлять задачи, отправляет напоминания и измеряет время, затраченное на каждое задание по уборке. Таким образом, пользователь рационально распределяет время и силы.
Создает график уборки и распределяет задачи по дням. Благодаря этому пользователь не заваливается домашним заданием в выходной день. Приложение содержит категории в соответствии с комнатами в доме, позволяет добавлять задачи, отправляет напоминания и измеряет время, затраченное на каждое задание по уборке. Таким образом, пользователь рационально распределяет время и силы.
Убери мой дом в Google Play
14. Medisafe: своевременные лекарства
Medisafe позволяет пользователям вручную вводить названия, графики и дозировки лекарств или импортировать рецепты своих больниц. После этого приложение составляет расписание на день и отправляет push-уведомления о каждом приеме лекарства. Пользователь может синхронизировать приложения с членами семьи, и они будут получать уведомления каждый раз, когда пациент забывает принять лекарство. Таким образом, Medisafe позволяет заботиться о близких даже на расстоянии. Также приложение формирует отчет о проделанной работе, который можно отправить непосредственно лечащему врачу в формате PDF.
Также приложение формирует отчет о проделанной работе, который можно отправить непосредственно лечащему врачу в формате PDF.
Medisafe в App Store. ездить на встречи. Doctor On Demand позволяет связаться с врачом, психологом или психиатром онлайн, чтобы обсудить симптомы, предоставить историю болезни, получить консультацию специалиста и план лечения. Все специалисты лицензированы и имеют высокий рейтинг пациентов. Услуги доступны со страховкой или без нее, а цена объявляется до того, как пользователи подтвердят прием.
Doctor On Demand в App Store
Doctor On Demand в Google Play
Заключение
Технологии призваны упростить жизнь, поэтому пользователи охотно скачивают приложения, решающие их конкретную проблему. Будьте внимательны к своим клиентам и понимайте их потребности, чтобы придумать стоящую идею. Заручитесь поддержкой профессиональной технической команды, чтобы это произошло.

Команда KeyUA объединяет только лучших разработчиков. Мы превратим любую идею в успешный продукт на рынке.
Свяжитесь с нами
Применение решения уравнений: решение текстовых задач
Стратегии решения текстовых задач с переменными
Часто текстовые задачи кажутся запутанными, и трудно понять, с чего начать. Вот несколько шагов, которые облегчат решение текстовых задач:
- Прочитайте задачу.
- Определить, что известно и что нужно найти (что неизвестно).
- Попробуйте несколько чисел, чтобы получить общее представление о возможном решении.
- Напишите уравнение.
- Решите уравнение с помощью обратных операций или путем подстановки значений.
- Проверьте свое решение — удовлетворяет ли оно уравнению? Имеет ли это смысл в контексте проблемы? (например, длина не должна быть отрицательной.)
Пример 1 : У Мэтта 12 пятицентовых монет. Все остальные его монеты — десять центов. У него достаточно денег, чтобы купить 2 куска пиццы по 95 центов каждый. Сколько у него копеек?
Все остальные его монеты — десять центов. У него достаточно денег, чтобы купить 2 куска пиццы по 95 центов каждый. Сколько у него копеек?- Прочитайте задачу.
- Что известно? У Мэтта 12 (5) = 60 центов в пятицентовых монетах. Всего у Мэтта 2(95) = 190 центов. Что нужно найти? Количество десятицентовиков, которое есть у Мэтта.
- Попробуйте ввести несколько номеров:
5 центов? 10(5) + 60 = 110. Слишком мало.
10 центов? 10(10) + 60 = 160. Слишком мало.
20 центов? 10(20) + 60 = 260. Слишком высокое.Итак, мы знаем, что ответ находится между 10 и 20.
- Напишите уравнение: 10 d + 60 = 190, где d — количество десятицентовиков, которое есть у Мэтта.
- Решить с помощью обратных операций:
10 д + 60 — 60 = 190 — 60
10 д = 130
=
д = 13 - Чек: 10(13) + 60 = 190? Да.
 Имеет ли смысл 13 десятицентовиков в контексте задачи? Да.
Имеет ли смысл 13 десятицентовиков в контексте задачи? Да.
Итак, у Мэтта 13 монет.
Пример 2 : Джен выполняет штрафные броски на баскетбольной площадке. Она делает 85% своих бросков. Если она сделает 51 выстрел, сколько она промахнется?- Прочитайте задачу.
- Что известно? Джен делает 85% своих снимков. Джен делает 51 выстрел. Что нужно найти? Количество бросков, которые Джен промахивается.
- Попробуйте несколько номеров:
5 выстрелов? знак равно Недостаточно промахов.
10 выстрелов? знак равно Слишком много промахов.
Итак, мы знаем, что ответ находится между 5 и 10. - Напишите уравнение: = где х — количество промахов.
- Решить с помощью обратных операций:
=
51() = 51()
51 + х = 60
51 + х — 51 = 60 — 51
х = 9 - Проверить: = ? Да.
 Имеет ли смысл 9 выстрелов в контексте задачи? Да.
Имеет ли смысл 9 выстрелов в контексте задачи? Да.
Таким образом, Джен промахивается 9 раз.
Диаграмма квадрата Пример 3 : Площадь этого квадрата в 2 раза больше его периметра. Какова длина стороны?
- Прочитайте задачу.
- Что известно? Площадь квадрата в 2 раза больше его периметра. Формула площади равна 9.0270 A = x 2 и формула для периметра: p = 4 x . Что нужно найти? Длина стороны.
- Попробуйте ввести несколько номеров:
х = 5? A = 5 2 = 25, p = 4(5) = 20. Площадь слишком мала.
х = 10? A = 10 2 = 100, p = 4(10) = 40. Слишком большая площадь.Итак, мы знаем, что ответ находится между 5 и 10.
- Напишите уравнение: х 2 = 2 (4 х ). х 2 = 8 х
- Решите, подставив значения —- или используя обратные операции:
=
х = 8 - Чек: 8 2 = 8(8) ? Да.

Задачи на точки экстремума тригонометрической функции: Тригонометрические функции. Задания ЕГЭ по математике (профильный уровень)
наименьшее значение на левом конце отрезка, то есть при x=-\frac{\pi}{4}. Наименьшее значение равно y\left(-\frac{\pi}{4}\right)= 32tg\left(-\frac{\pi}{4}\right)-32\cdot\left(-\frac{\pi}{4}\right)-8\pi+103= -32+103= 71.
Ответ
71
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите точку минимума функции y=(0,7-x)\cos x+\sin x+2, принадлежащую промежутку \left(0; \frac{\pi}{2}\right).
Показать решение
Решение
Найдём производную исходной функции: y’= (0,7-x)’ \cos x\,+ (0,7-x)(\cos x)’+(\sin x)’+(2)’ = -\cos x+(0,7-x)\cdot (- \sin x)+ \cos x= (x-0,7) \sin x. Найдём нули производной на интервале \left(0; \frac{\pi}{2}\right), учитывая, что на этом множестве \sin x>0.
Имеем (x-0,7) \sin x=0;
x-0,7=0;
x=0,7.
Значение x=0,7 принадлежит интервалу \left(0; \frac{\pi}{2}\right). При x \in (0; 0,7) выполняется неравенство y'(x)<0. При x \in \left(0,7; \frac{\pi}{2}\right) выполняется неравенство y'(x)>0.
Отсюда x=0,7 является единственной точкой минимума на рассматриваемом интервале.
Ответ
0,7
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наименьшее значение функции y=24+\frac{9\pi}{4}-9x-9\sqrt2\cos x на отрезке \left[0; \frac{\pi}{2}\right].
Показать решение
Решение
Найдём производную исходной функции: y’=-9+9\sqrt 2 \sin x. Вычислим нули производной: y’=0;
-9+9\sqrt 2\sin x=0;
\sin x=\frac{\sqrt2}{2}.
На отрезке \left[0; \frac{\pi}{2}\right] этому уравнению удовлетворяет только x=\frac{\pi}{4}. Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом отрезке.
Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом отрезке.
Из рисунка видно, что при x<\frac{\pi}{4} выполняется y'(x)<0 и исходная функция убывает. Аналогично, при x>\frac{\pi}{4} выполняется y'(x)>0 и исходная функция возрастает. Значит, наименьшее значение достигается при x=\frac{\pi}{4} и равно y\left(\frac{\pi}{4}\right)= 24+\frac{9\pi}{4}-9\cdot\frac{\pi}{4}-9\sqrt2\cos \frac{\pi}{4}= 24-9=15.
Ответ
15
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите точку максимума функции y=(4x-5)\cos x-4\sin x+12, принадлежащую промежутку \left ( 0; \frac{\pi}{2} \right ).
Показать решение
Решение
Найдём производную исходной функции: y’= (4x-5)’\cos x+(4x-5)(\cos x)’-4(\sin x)’+(12)’= 4\cos x+(4x-5)\cdot(-\sin x)-4\cos x= -(4x-5)\sin x.
Найдём нули производной на интервале \left ( 0; \frac{\pi}{2} \right ), учитывая, что на этом множестве \sin x>0.
Имеем -(4x-5)\sin x=0,
4x-5=0,
x=\frac54.
Значение x=\frac54 принадлежит интервалу \left ( 0; \frac{\pi}{2} \right ). При x\in\left ( 0; \frac54 \right ) выполняется неравенство y'(x)>0. При x\in\left ( \frac54; \frac{\pi}{2} \right ) выполняется неравенство y'(x)<0. Отсюда x=\frac54=1,25 является единственной точкой максимума на рассматриваемом интервале.
Ответ
1,25
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наибольшее значение функции y=18\cos x+9\sqrt3 x-3\sqrt3 \pi+16 на отрезке \left [ 0; \frac{\pi}{2} \right ].
Показать решение
Решение
Найдём производную исходной функции: y’=-18\sin x+9\sqrt3. Вычислим нули производной: y’=0.
Вычислим нули производной: y’=0.
-18\sin x+9\sqrt3=0,
\sin x=\frac{\sqrt3}{2}.
На отрезке \left [ 0; \frac{\pi}{2} \right ] этому уравнению удовлетворяет только x=\frac{\pi}{3}. Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом отрезке.
Из рисунка видно, что при x<\frac{\pi}{3} выполняется y'(x)>0 и исходная функция возрастает. Аналогично при x>\frac{\pi}{3} выполняется y'(x)<0 и исходная функция убывает. Значит, наибольшее значение достигается при x=\frac{\pi}{3} и равно y\left ( \frac{\pi}{3} \right )= 18\cos\frac{\pi}{3}+9\sqrt3\cdot\frac{\pi}{3}-3\sqrt3 \pi+16= 9+16=25.
Ответ
25
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наибольшее значение функции y=13tgx-13x+5 на отрезке \left [ -\frac{\pi}{4}; 0 \right ].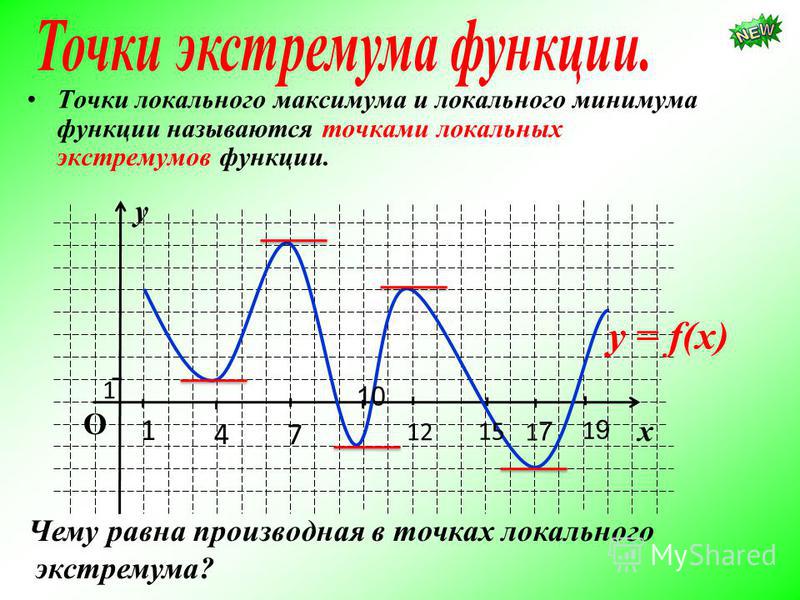 2x
2x
Производная функции на всем промежутке возрастает, значит наибольшее значение функции она достигает на правом конце отрезка. Вычислим значение функции в этой точке.
y(0)=13tg0-13\cdot0+5=5
Точка 5 – наибольшее значение функции.
Ответ
5
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите наименьшее значение функции y=8\cos x-17x+6 на отрезке \left [ -\frac{3\pi}{2}; 0 \right ].
Показать решение
Решение
Вычислим производную функции.
y’=-8\sin x-17
Так как выражение -8\sin x при любых значениях x всегда не больше чем 8, то полученная разность меньше нуля, а это говорит о том, что функция убывает. Следовательно наименьшее значение функция достигает на правом конце отрезка. Вычислим это значение.
y(0)=8\cos0-17\cdot0+6 = 8+6=14
Точка 14 – наименьшее значение функции.
Ответ
14
Тип задания: 12
Тема:
Тригонометрические функции
Условие
Найдите точку максимума функции y=(2x-3)\cos x-2\sin x+2 на промежутке \left ( 0; \frac{\pi}{2} \right ).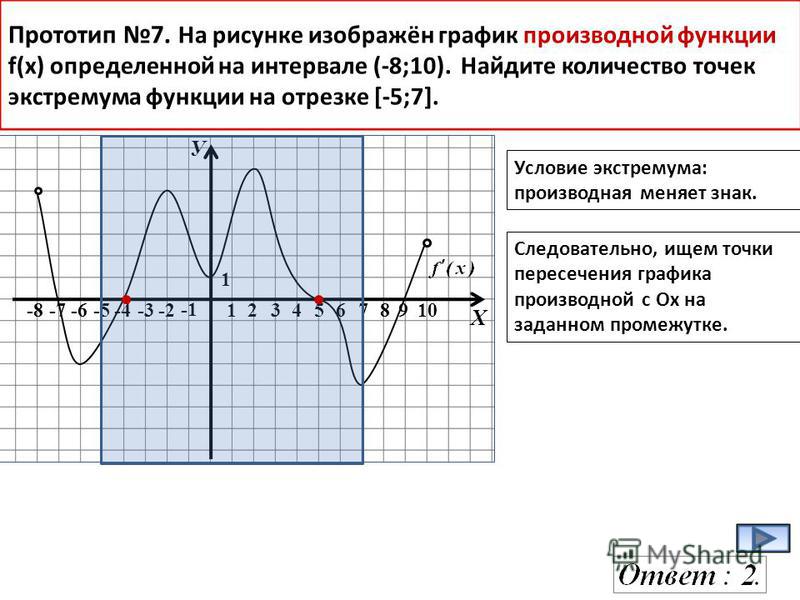
Показать решение
Решение
Вычислим производную функции.
y’=2\cos x-(2x-3)\sin x-2\cos x
y’=-(2x-3)\sin x
y’=(3-2x)\sin x
Найдем точки экстремума, в которых производная функции обращается в нуль.
(3-2x)\sin x=0
\left [\begin{array}{l} 3-2x=0 \\ \sin x=0 \end{array} \right .
\left [\begin{array}{l} x=1,5 \\ x=\pi n, n \in \mathbb{Z} \notin \left ( 0; \frac{\pi}{2} \right) \end{array} \right .
На числовой оси отложим граничные точки промежутка и точку экстремума и посмотрим как ведет себя функция.
При переходе через точку x = 1,5 производная меняет знак с плюса на минус. Значит x = 1,5 – точка максимума функции.
Ответ
1,5
Лучшие репетиторы для сдачи ЕГЭ
МатематикаРусский язык
История
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928 © 2016—2022
Все права защищены.
Служба поддержки портала
10 класс.
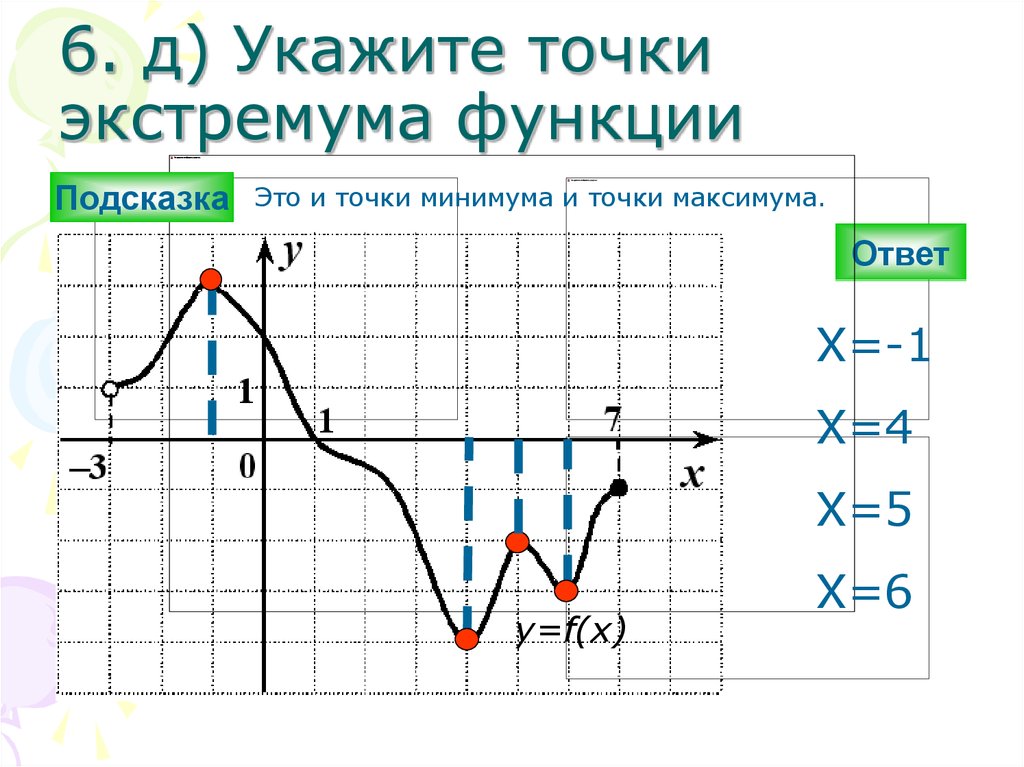 Алгебра. Производная. Применение производной в задачах на экстремум и при исследовании тригонометрических функций. — Типовые задачи на производную с тригонометрическими функциями. Функция f(x)=cos²x-cosx.Комментарии преподавателя
Алгебра. Производная. Применение производной в задачах на экстремум и при исследовании тригонометрических функций. — Типовые задачи на производную с тригонометрическими функциями. Функция f(x)=cos²x-cosx.Комментарии преподавателяФункция f(x)=cos2x-cosx
Тригонометрические функции имеют важную особенность – наличие периода. Всю методику, которую знаем для исследования функций без тригонометрических включений, используем, но надо учесть наличие периода.
Наличие периода дает возможность провести исследование функции и построение графика на отрезке длиной, равной периоду. Затем график функции периодически распространяется для всех значений аргумента из области определения функции.
Задача.
Построить график функции .
Преобразуем формулу: .
Найдем период данной функции. У функции наименьший период .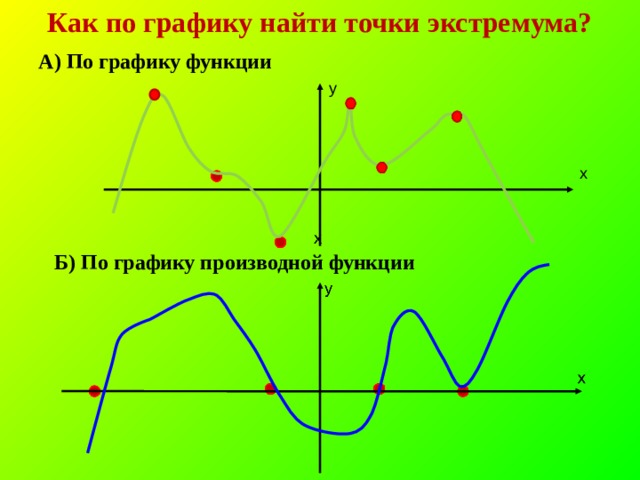 У функции , если понизить степень и выразить через — период . Итак,
У функции , если понизить степень и выразить через — период . Итак,
функция имеет наименьший период . Это означает, что график функции сначала можно построить на промежутке длиной , а потом продолжить по периодичности.
Функция четная, так как для всех из . График симметричный относительно оси .
Учитывая периодичность функции, можно построить график этой функции на любом промежутке, длиной . Свойство четности функции дает возможность задачу упростить, а именно, построить график на участке , а на участке — построить по симметрии.
Найдем интервалы знакопостоянства функции.
: .
, когда , отсюда или .
Знак функции на каждом интервале удобно определить с помощью единичной окружности (см. рис.1). Точки , , — точки, которые формируют интервалы знакопостоянства функции.
Рис. 1. Интервалы знакопостоянства функции на единичной окружности
Выясним знак функции на интервале . Для этого возьмем значение функции в какой-нибудь точке из этого интервала. Например,
Для этого возьмем значение функции в какой-нибудь точке из этого интервала. Например,
, значит, на этом интервале функция отрицательна. Дальше, на интервале функция меняет знак. В силу симметрии, на интервале — функция отрицательна, а на интервале — функция положительна (см. рис.2).
Рис. 2 Интервалы знакопостоянства функции
Построим график функции в окрестности каждого корня.
Точка — является точкой максимума, так как на промежутках и — функция отрицательна, кривая находится под осью , и только в точке она равна нулю. Значит, функция в окрестности корней ведет себя следующим образом (см. рис.3):
Рис. 3. График функции в окрестности каждого корня
Понятно, что на интервалах и – функция будет иметь точки экстремума.
Исследуем функцию с помощью производной:
Приравняем ее к нулю:
, отсюда .
Найдем критические точки:
— это все критические точки, которые имеет функция. Но нам нужны те, которые попадают в выбранный промежуток: , , . Вычислим значение функции в точках , и определим – это точки максимума или минимума.
Но нам нужны те, которые попадают в выбранный промежуток: , , . Вычислим значение функции в точках , и определим – это точки максимума или минимума.
Найдем интервалы знакопостоянства производной на единичной окружности (см. рис.4).
Рис. 4. Интервалы знакопостоянства производной
Найдем знак производной, в какой- либо точке из интервала :
. Таким образом, точка — точка минимума, а — точка максимума. Вычислим:
; .
Построим график функции (см. рис.5-6).
Рис. 5. График функции на
Рис. 6. График функции
Одна из типовых задач – нахождение множества значений функции.
Ответ: .
На уроке рассмотрены особенности исследования и построения графика тригонометрической функции. Все типовые задачи решаются аналогично задачам из предыдущих уроков.
ИСТОЧНИК
http://interneturok.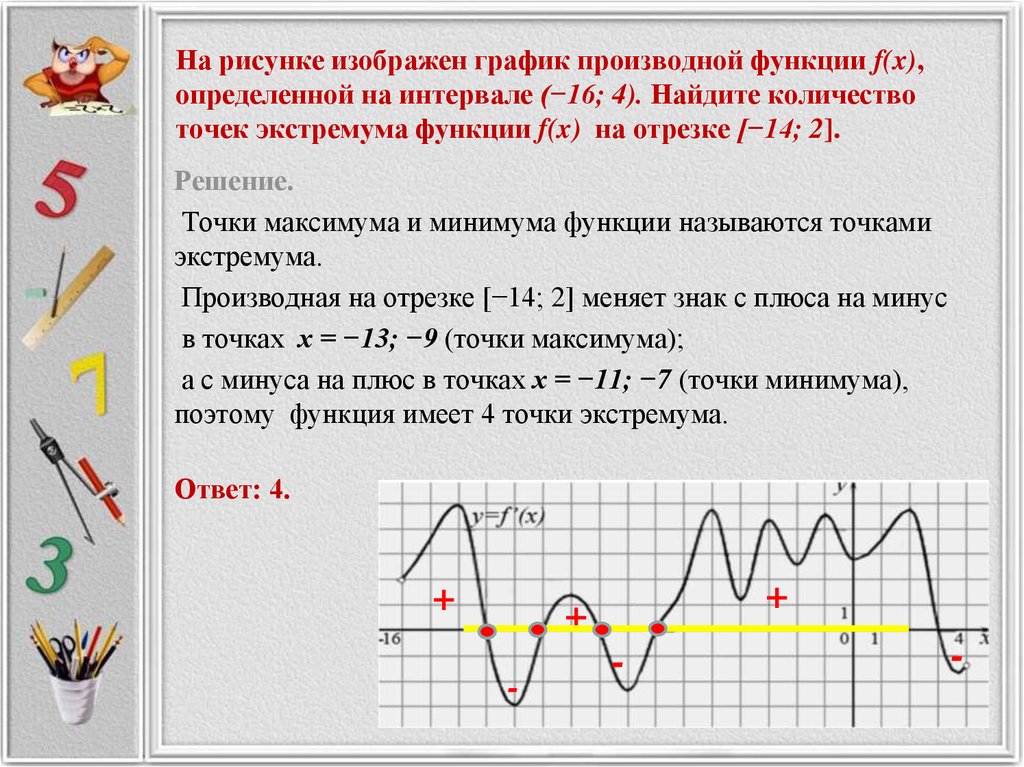 ru/ru/school/algebra/10-klass/proizvodnaya/issledovanie-trigonometricheskih-funktsiy-funktsiya-f-x-cos-sup-2-sup-x-cosx
ru/ru/school/algebra/10-klass/proizvodnaya/issledovanie-trigonometricheskih-funktsiy-funktsiya-f-x-cos-sup-2-sup-x-cosx
http://www.youtube.com/watch?v=sX-A2wpY5NE
https://downloader.disk.yandex.ru/disk/779ef72b0b73617de61c4dc2c21838459e86176ed8f801b37481d34346768467/56a16f54/KmTYbqVG3TgKGL9iUHPR0em0RlLtpxhP_BVgRtkosSgfwonkMOj8PI__aMfad3WZY71hHToni_M3mTC7aMwq3A%3D%3D?uid=0&filename=666.PDF&disposition=attachment&hash=RaLDsjqwggBTdSmademPwU40mOjt%2BFWdduHVDt9R80E%3D&limit=0&content_type=application%2Fpdf&fsize=8352787&hid=021760e85b03ef221c6c4091fc10c607&media_type=document&tknv=v2
http://matematikalegko.ru/issledovanie-funkcii-ege/trigonometricheskaya-funkciya-tochki-maksimuma-minimuma.html
http://www.berdov.com/ege/extremum/trigonometry/
исчисление — Проблема с нахождением критической точки триггерной функции
Задавать вопрос
спросил
Изменено 7 лет, 5 месяцев назад
Просмотрено 415 раз
$\begingroup$ 92(x/2)}=0,\стрелка вправо\sin(x/2)=\pm\frac1{\sqrt2}$$
Имеет только одно решение $x=\frac\pi2$ в $\left[\frac\pi3,\frac{2\pi}3\right]$.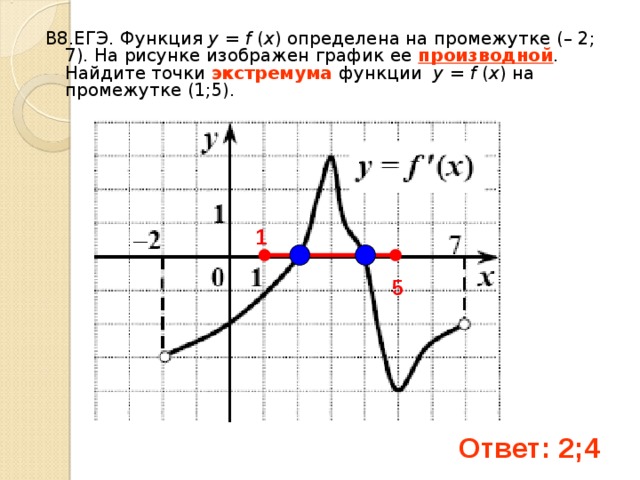 2 (х / 2)}
$$ 92(х/2).
$$
2 (х / 2)}
$$ 92(х/2).
$$
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
исчисление — Нахождение критических точек тригонометрической функции
Задавать вопрос
спросил
Изменено 6 лет, 1 месяц назад
Просмотрено 12 тысяч раз
$\begingroup$
Итак, мне нужны критические точки (и обратите внимание на интервалы возрастания и убывания функции) для:
$2cos\left(3x\right)$ на интервале $\left[-\pi ,\pi \right] $.
Честно говоря, самой сложной частью Calc I для меня пока является ВСЕ, связанное с тригонометрией. Я чувствую, что precalc был эоны лет назад, и я искренне задаюсь вопросом, изучал ли я его когда-либо должным образом. Взяв производную от f(x), я получаю:
Взяв производную от f(x), я получаю:
$-6sin\left(3x\right)$, которое я должен установить равным $0$.
Я знаю тригонометрические функции и единичный круг, но мне кажется, что все, что связано с тригонометрией, ведет себя совершенно иначе, чем все остальное в математике. Даже обозначения меня смущают. Как найти:
$-6sin\left(3x\right) = 0$? И когда у меня есть критические точки, как мне учесть $\left[-\pi ,\pi \right]$, отмечая, где эта функция увеличивается и уменьшается?
- исчисление
- тригонометрия
$\endgroup$
1
$\begingroup$
Если $\sin(3x)=0$, то $3x=k\pi$ для некоторого целого числа $k$. Следовательно, $x=k\pi/3$, и вам просто нужно определить все целые числа $k$ такие, что $k\pi/3\in[-\pi,\pi]$. В настоящее время
$$
-\pi\le \frac{k\pi}{3}\le \pi
$$
эквивалентно
$$
-3\ле к\ле 3
$$
Итак, у нас есть семь критических точек. Чтобы отличить точки максимума и минимума, проще всего посмотреть на вторую производную:
$$
f»(x)=-18\cos(3x)
$$
Чтобы отличить точки максимума и минимума, проще всего посмотреть на вторую производную:
$$
f»(x)=-18\cos(3x)
$$
Обратите внимание, что на самом деле нет проблем с точками $-\pi$ и $\pi$, находящимися на границах, потому что функция, которую вы имеете, является ограничением функции $x\maps на 2\cos(3x)$, определенное над реалами, которая везде явно гладкая.
Вот график функции:
Обратите внимание, что это функция косинуса, но растянутая по вертикали на коэффициент $2$ и «сжатая» по горизонтали на коэффициент $3$.
$\endgroup$
$\begingroup$
Помните:
$$\sin x=0\iff x=k\pi\;,\;\;k\in\Bbb Z=\{…-2,-1,0,1,2 ,…\}\;$$ и в вашем случае
$$\sin3x=0\iff 3x=k\pi\in(-\pi,\,\pi)\iff k=0\импульс x= 0$$
Теперь у вас также есть две крайние точки $\;\pm\pi\;$, которые не могут быть проверены описанным выше методом, так как функция там не дифференцируема (так как нам нужна полная окрестность точки где функция определена так, что даже есть шанс взять предел, определяющий производную.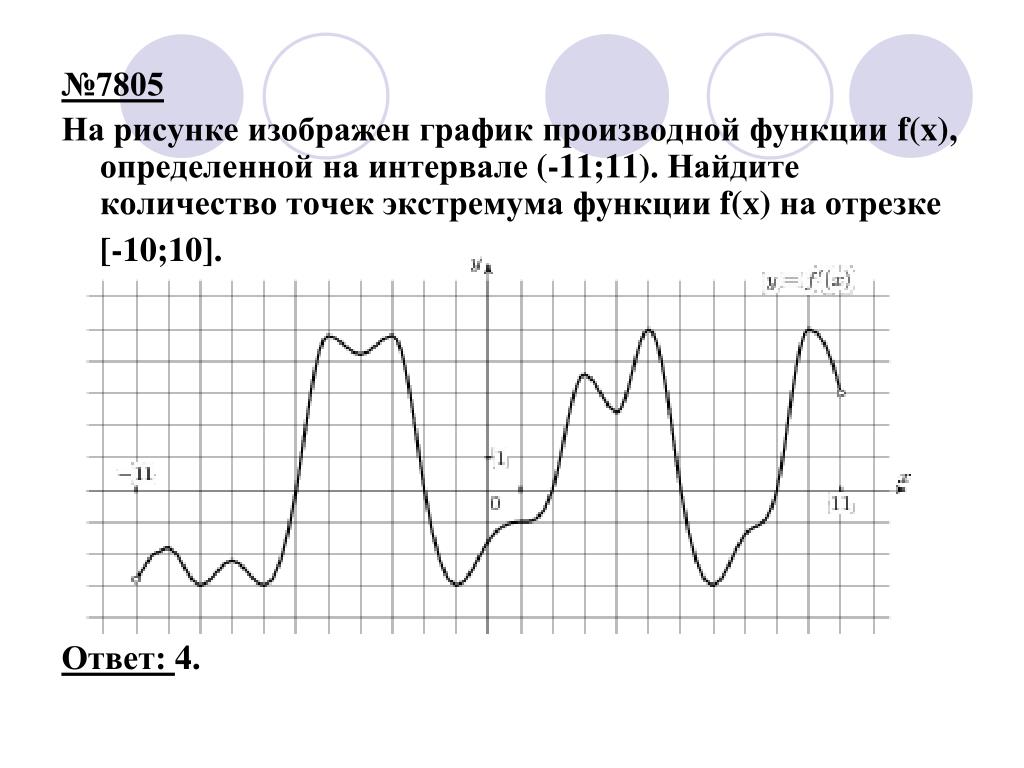

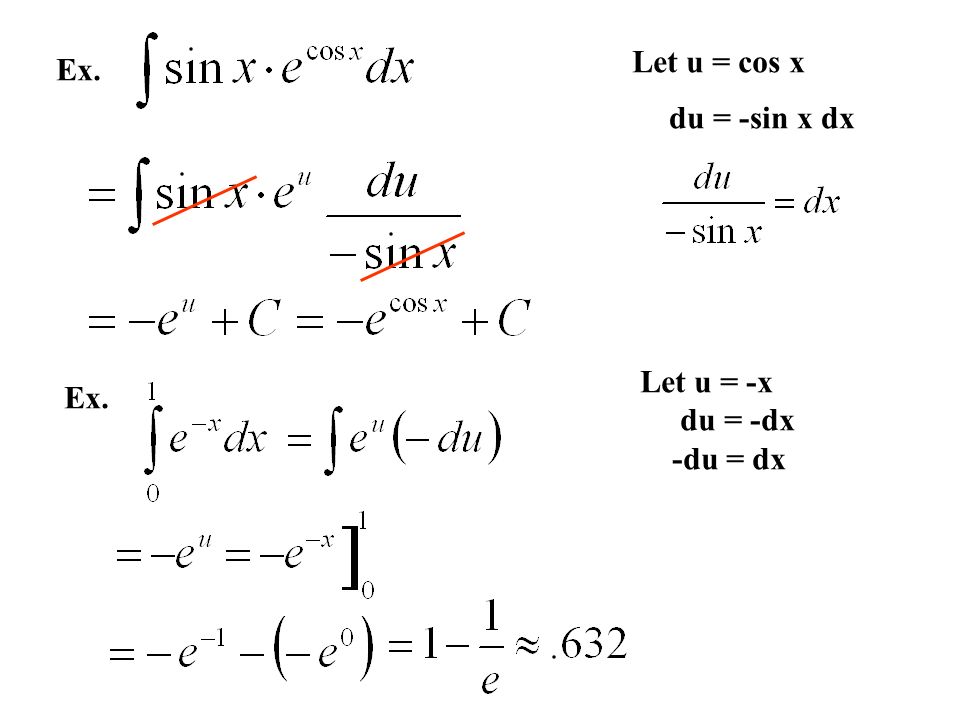 11.2014, 19:56
11.2014, 19:56  11.2014, 20:04
11.2014, 20:04  11.2014, 20:05
11.2014, 20:05 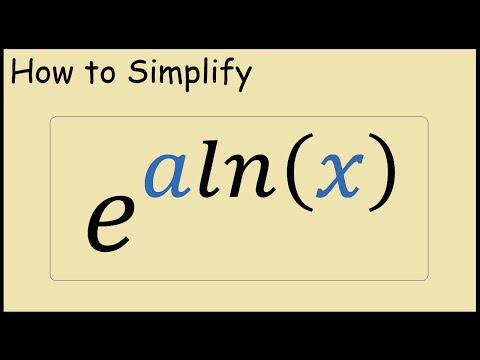 11.2014, 20:06
11.2014, 20:06 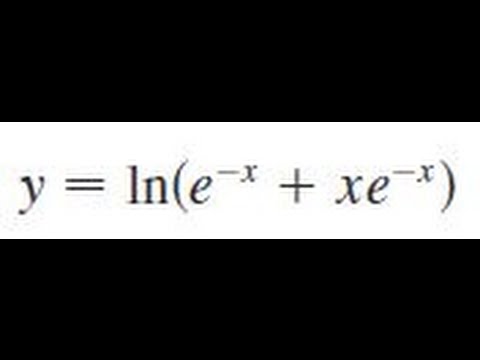 11.2014, 20:09
11.2014, 20:09  11.2014, 20:11
11.2014, 20:11  11.2014, 20:14
11.2014, 20:14  11.2014, 20:23
11.2014, 20:23  11.2014, 20:37
11.2014, 20:37  11.2014, 08:05
11.2014, 08:05  Прямой связи вектора с геометрической формой фабричных компонентов не обнаружено.
Прямой связи вектора с геометрической формой фабричных компонентов не обнаружено.
 Так же механическая обработка оказывает значительное и устойчивое влияние на неполярные, тонкие свойства компонентов (подробнее здесь).
Так же механическая обработка оказывает значительное и устойчивое влияние на неполярные, тонкие свойства компонентов (подробнее здесь).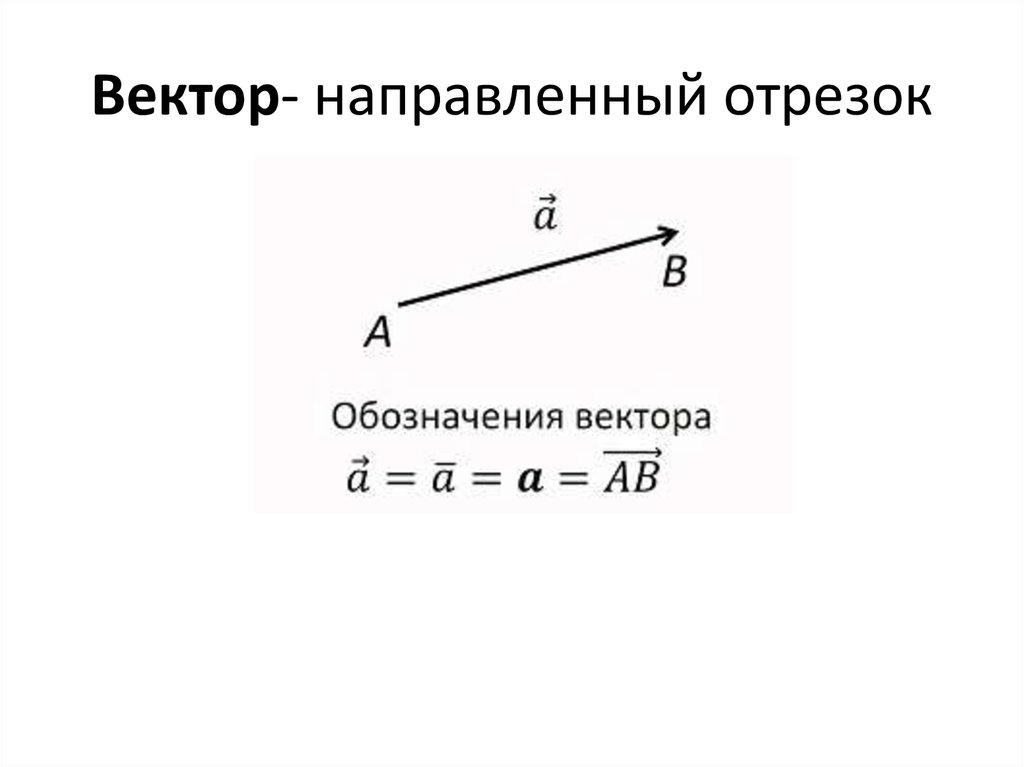 На этой ступени происходит процесс развития и самопознания личности.
На этой ступени происходит процесс развития и самопознания личности.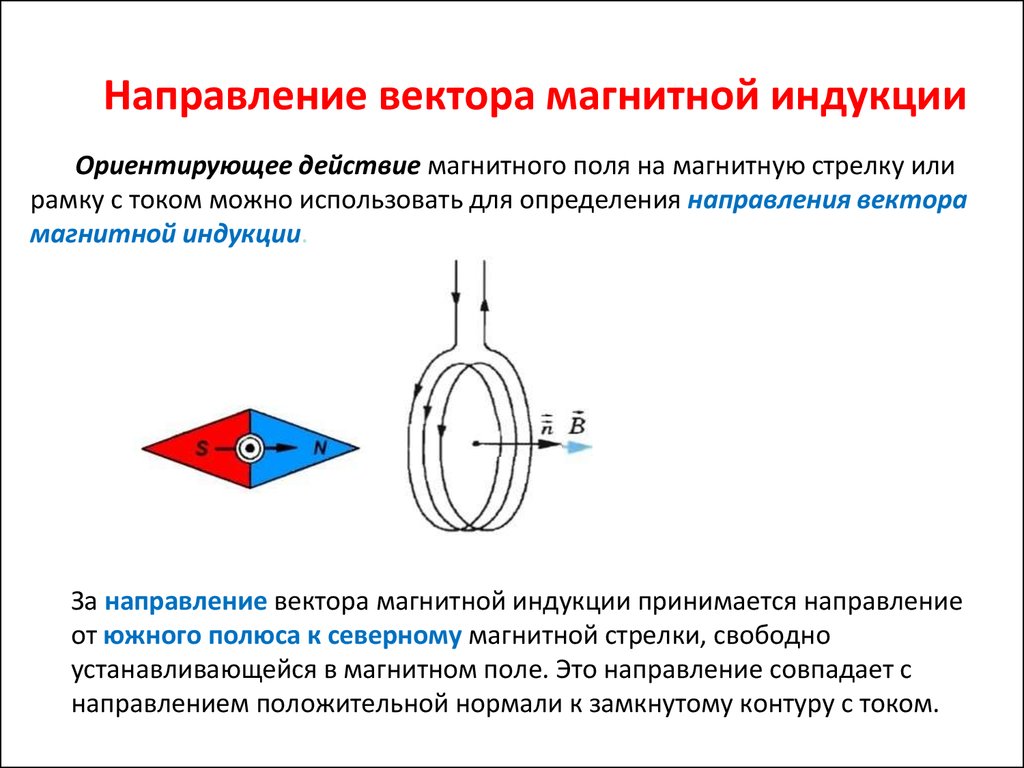 Люди с ярким проявлением данного типа – ярко выраженные экстраверты. Реализуют себя на пространственной ступени. Основным направлением кожников является охрана территорий.
Люди с ярким проявлением данного типа – ярко выраженные экстраверты. Реализуют себя на пространственной ступени. Основным направлением кожников является охрана территорий.
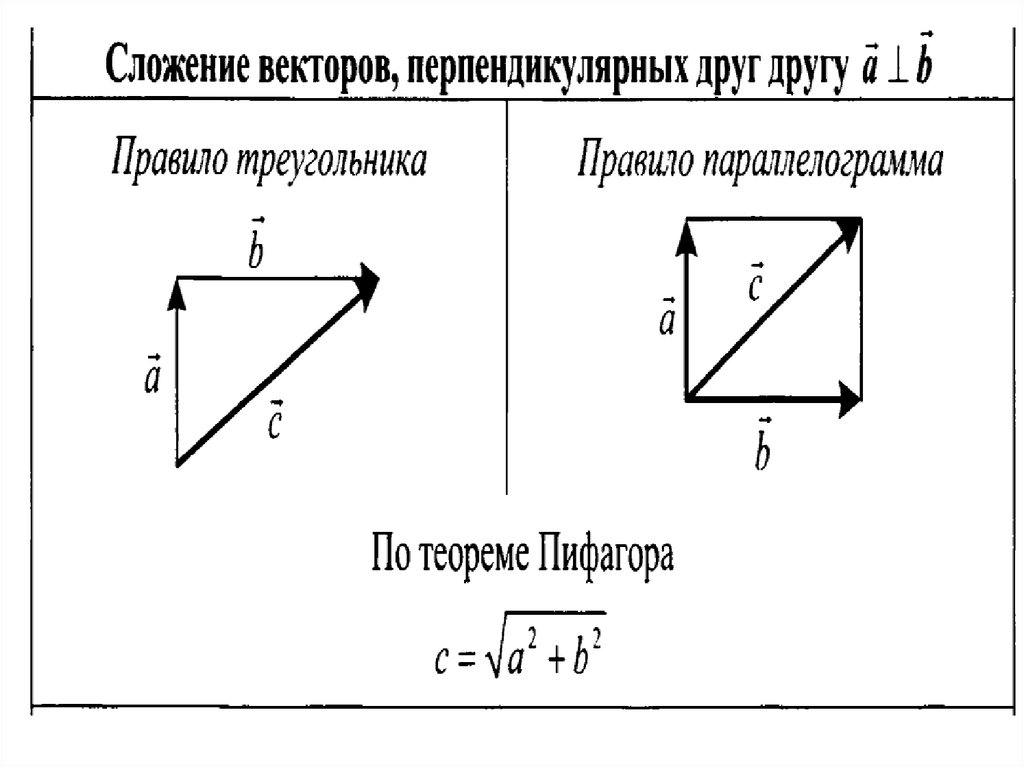 © Зигмунд Фрейд
© Зигмунд Фрейд
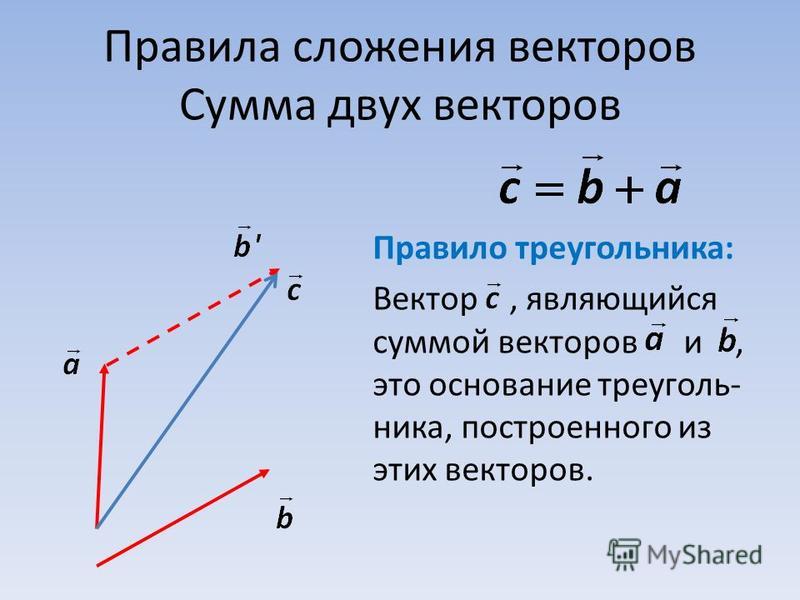

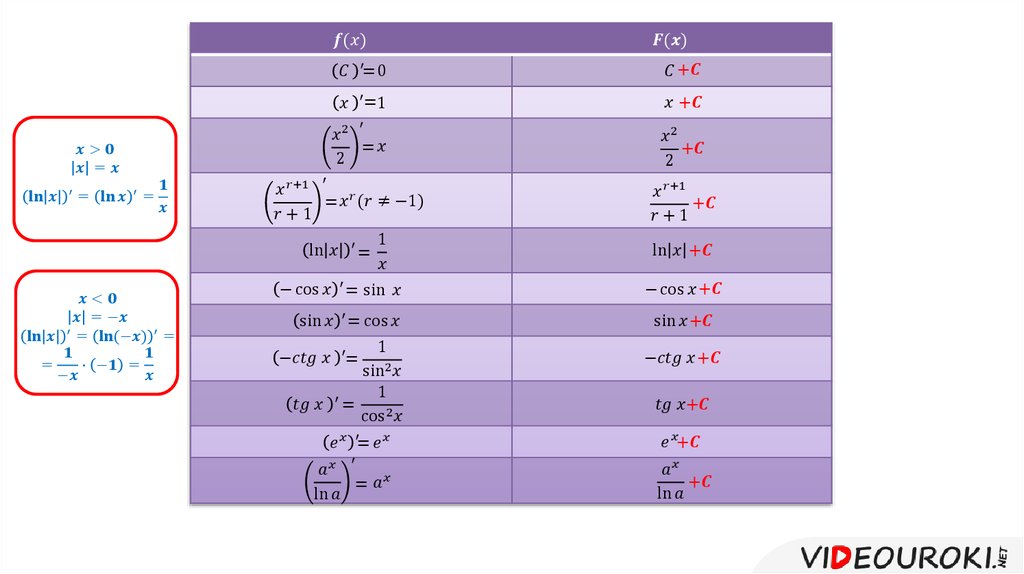 Следовательно,
Следовательно,

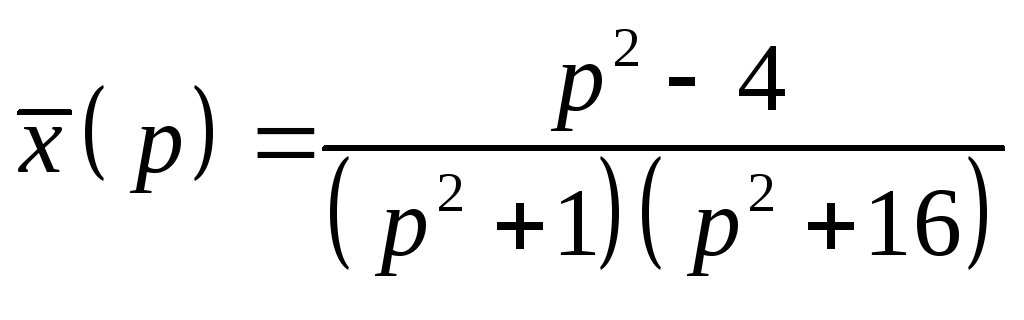 MN означает λx. (MN), а не (λx.M) N.
MN означает λx. (MN), а не (λx.M) N.
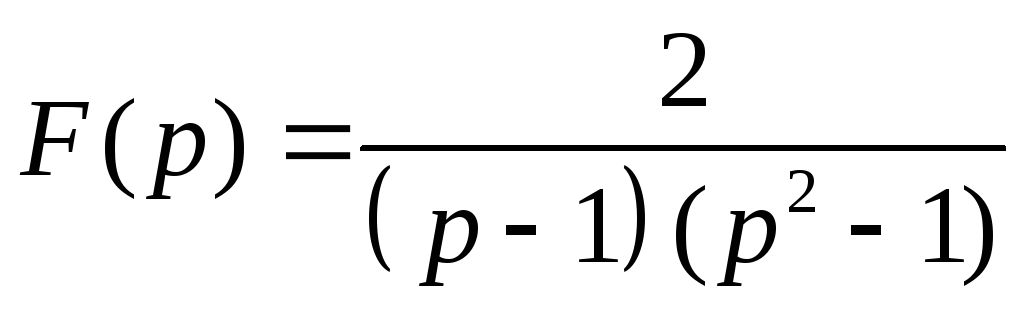 — 448 с.
— 448 с.
 05.13
05.13  by 2013-2016
by 2013-2016
 Я использую этот продукт уже несколько месяцев и могу откровенно сказать, что именно он помог мне сохранить свои оценки в этом семестре. Алгебратор предлагает удивительные способы решения сложных задач. Вам обязательно понравится, гарантирую.
Я использую этот продукт уже несколько месяцев и могу откровенно сказать, что именно он помог мне сохранить свои оценки в этом семестре. Алгебратор предлагает удивительные способы решения сложных задач. Вам обязательно понравится, гарантирую. Я получил Алгебратор с https://softmath.com/news.html. Давай, попробуй это и держи нас в курсе своего мнения. Я даже предложил Алгебратор в список своих школьных друзей.
Я получил Алгебратор с https://softmath.com/news.html. Давай, попробуй это и держи нас в курсе своего мнения. Я даже предложил Алгебратор в список своих школьных друзей.
 01.2002
01.2002 
 3$. (Точнее, линии $f$ и $g$ «параллельны» в синей картинной плоскости и соответствуют оранжевой и желтой плоскостям через начало координат.) 93$ соответствует точке «на бесконечности».
3$. (Точнее, линии $f$ и $g$ «параллельны» в синей картинной плоскости и соответствуют оранжевой и желтой плоскостям через начало координат.) 93$ соответствует точке «на бесконечности».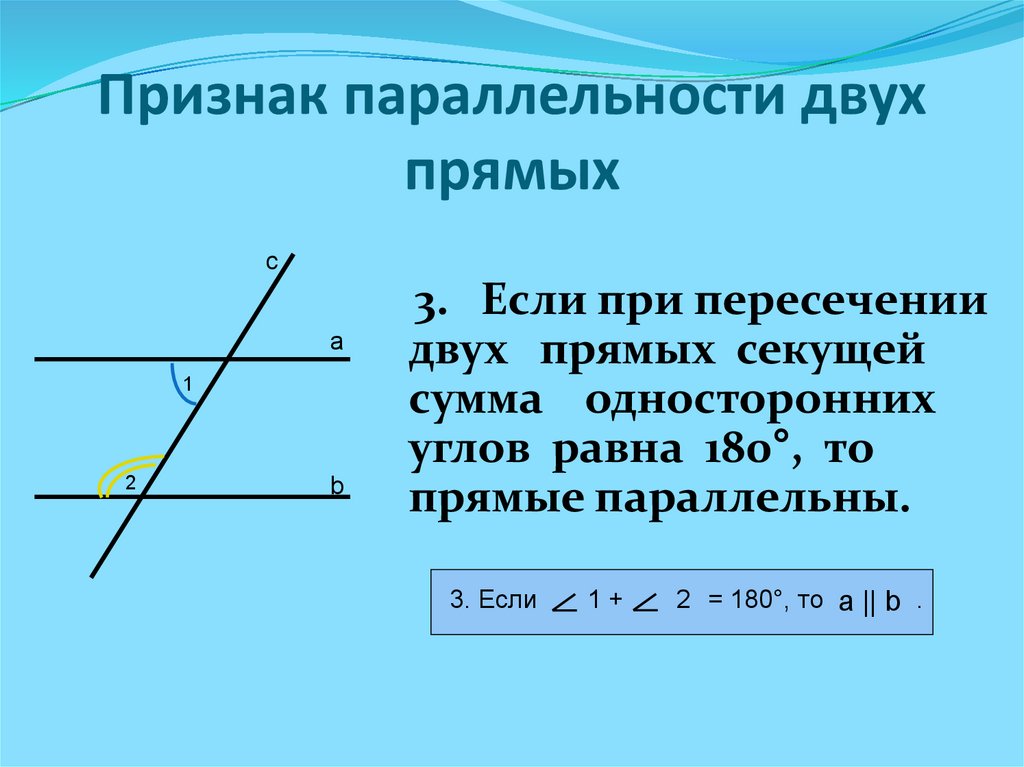
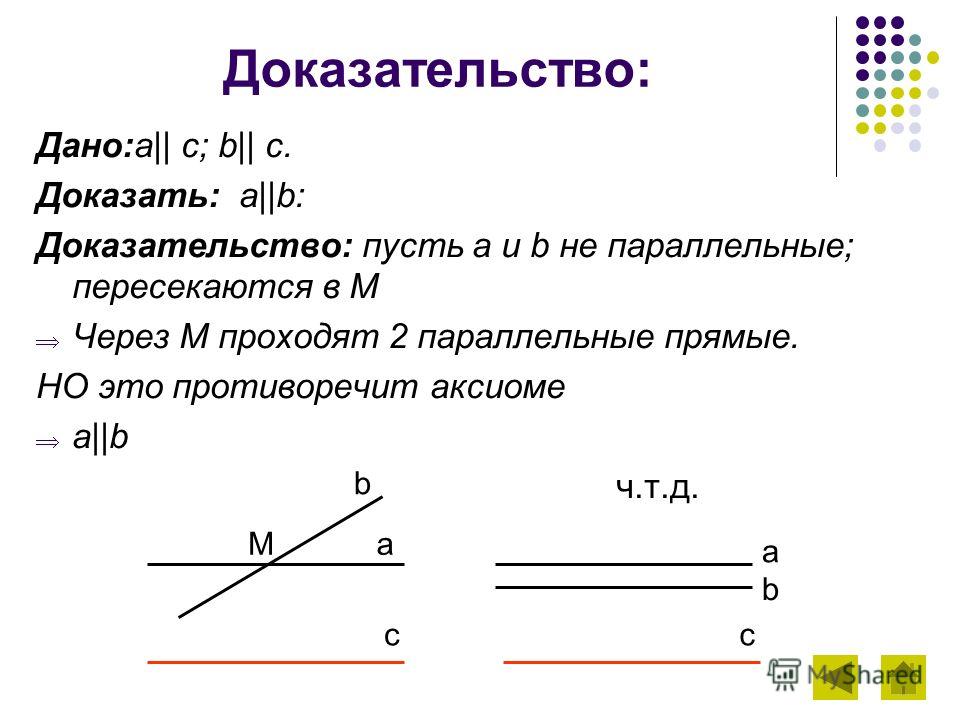 Могут быть случаи, когда они не имеют одной и той же центральной точки и по-прежнему не пересекаются.
Могут быть случаи, когда они не имеют одной и той же центральной точки и по-прежнему не пересекаются.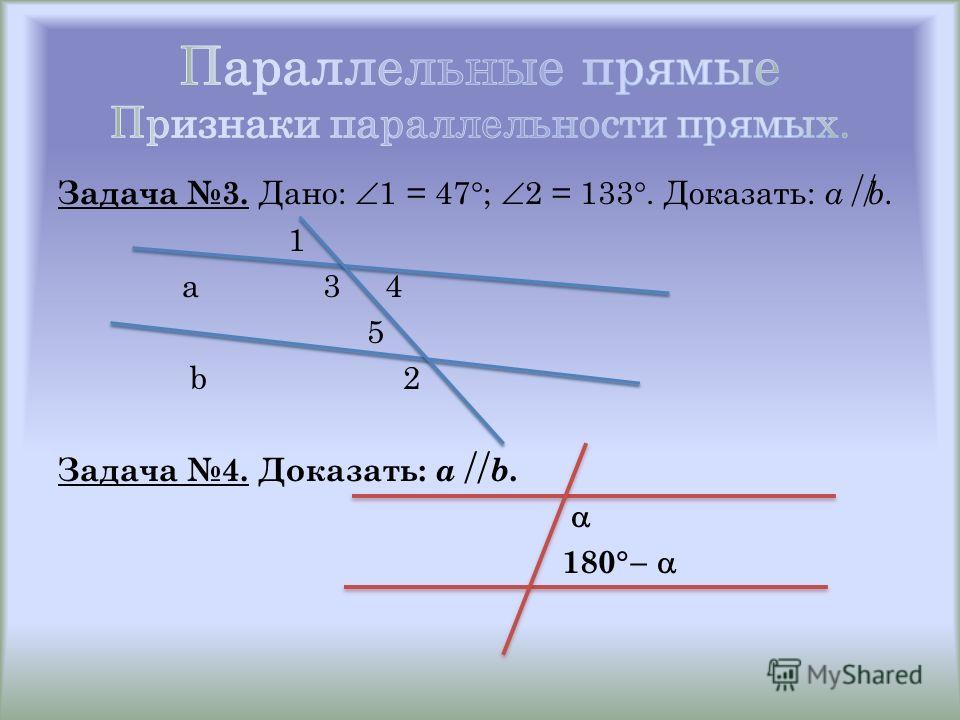 Это понятие бесконечности применяется в математике со свойствами функций и их пределами. Вот почему мы говорим, что такая функция или уравнение имеет предел, стремящийся к бесконечности.
Это понятие бесконечности применяется в математике со свойствами функций и их пределами. Вот почему мы говорим, что такая функция или уравнение имеет предел, стремящийся к бесконечности. Нашими глазами в очень ясный день (меньше влаги в воздухе) мы можем видеть эти следы примерно на 20-40 миль. Точка конвергенции находится на уровне того, что мы видим как Горизонт, или совсем рядом с ним, но мы знаем, что эти следы могут простираться на сотни или даже тысячи миль. Это далеко не приближение бесконечности. Мы можем воспринимать мысль о сотнях тысяч миль, даже миллионах или миллиардах миль, и все же это всего лишь часть доли приближения к бесконечности.
Нашими глазами в очень ясный день (меньше влаги в воздухе) мы можем видеть эти следы примерно на 20-40 миль. Точка конвергенции находится на уровне того, что мы видим как Горизонт, или совсем рядом с ним, но мы знаем, что эти следы могут простираться на сотни или даже тысячи миль. Это далеко не приближение бесконечности. Мы можем воспринимать мысль о сотнях тысяч миль, даже миллионах или миллиардах миль, и все же это всего лишь часть доли приближения к бесконечности. Это один из возможных способов рассматривать параллельные прямые как пересекающиеся. На проективной плоскости каждые две различные прямые пересекаются в единственной точке. Но мы не можем определить осмысленное понятие угла в проективной плоскости.
Это один из возможных способов рассматривать параллельные прямые как пересекающиеся. На проективной плоскости каждые две различные прямые пересекаются в единственной точке. Но мы не можем определить осмысленное понятие угла в проективной плоскости.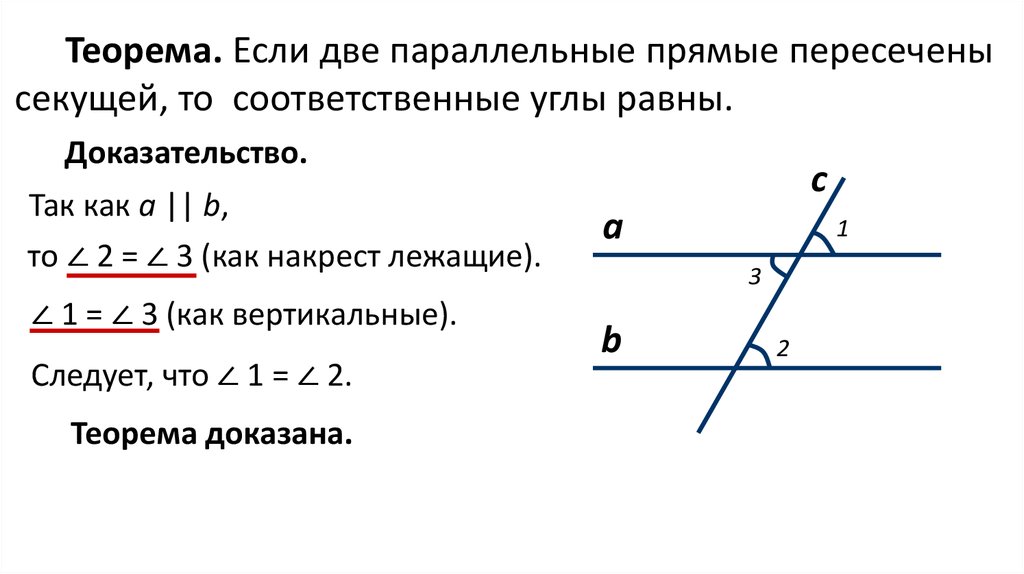 ниже, если вас интересуют доказательства.]
ниже, если вас интересуют доказательства.]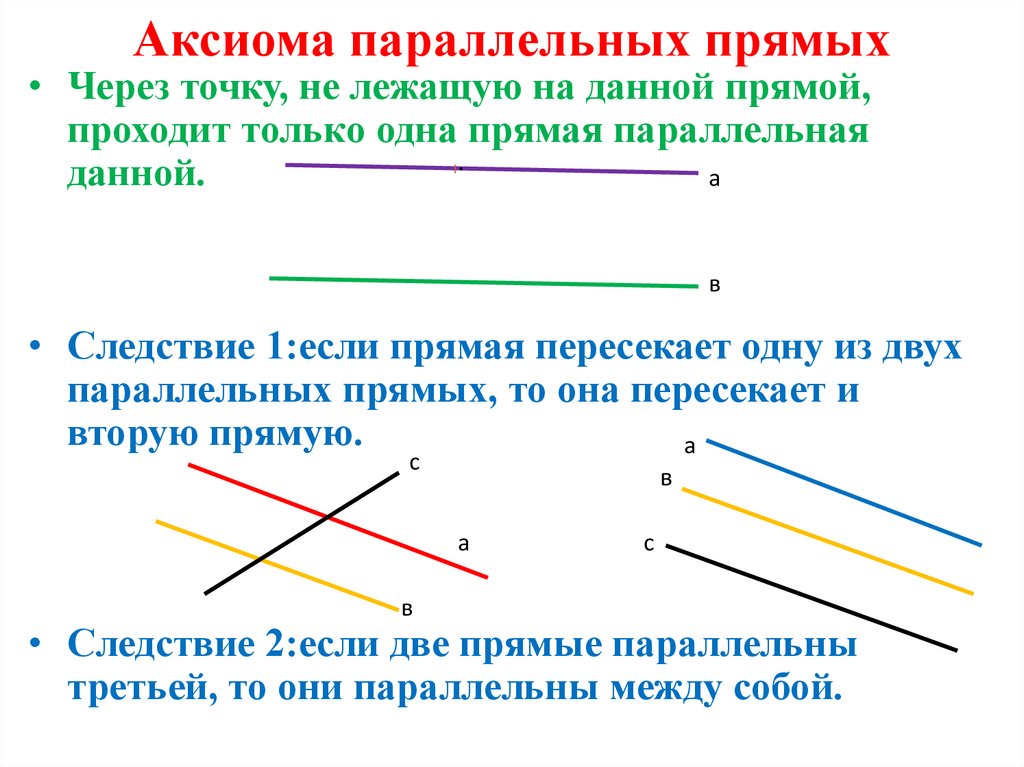 . Вы можете видеть, что ключевая ошибка в ваших рассуждениях заключается в том, что пересечение между линиями находится в конечной точке. Конечно, технически ваши рассуждения ошибочны с самого начала, поскольку вы не можете просто утверждать, что параллельные прямые должны пересекаться (не говоря уже под нулевым углом) только потому, что они являются результатом какого-то ограничивающего процесса. Просто для ясности предположим, что $\frac1n \to 0$ при $n \to \infty$ и $\frac1n > 0$ для каждого положительного $n$. Нет причин ожидать, что $\lim_{n\to\infty} \frac1n > 0$. 9*}} )$, соответствует отражению $F$ на сфере Римана относительно плоскости экватора. Затем докажите (факт 2), что $f$ сохраняет углы между прямыми, которые не проходят через начало координат. Эти доказательства можно провести, используя только подобные треугольники. И обратите внимание (факт 3), что $p$ сохраняет углы между прямыми, проходящими через начало координат. Теперь возьмем любые две прямые $l,m$, пересекающиеся в точке $z\ne 0$ на плоскости, и пусть $l’,m’,z’$ — их образы при $p$.
. Вы можете видеть, что ключевая ошибка в ваших рассуждениях заключается в том, что пересечение между линиями находится в конечной точке. Конечно, технически ваши рассуждения ошибочны с самого начала, поскольку вы не можете просто утверждать, что параллельные прямые должны пересекаться (не говоря уже под нулевым углом) только потому, что они являются результатом какого-то ограничивающего процесса. Просто для ясности предположим, что $\frac1n \to 0$ при $n \to \infty$ и $\frac1n > 0$ для каждого положительного $n$. Нет причин ожидать, что $\lim_{n\to\infty} \frac1n > 0$. 9*}} )$, соответствует отражению $F$ на сфере Римана относительно плоскости экватора. Затем докажите (факт 2), что $f$ сохраняет углы между прямыми, которые не проходят через начало координат. Эти доказательства можно провести, используя только подобные треугольники. И обратите внимание (факт 3), что $p$ сохраняет углы между прямыми, проходящими через начало координат. Теперь возьмем любые две прямые $l,m$, пересекающиеся в точке $z\ne 0$ на плоскости, и пусть $l’,m’,z’$ — их образы при $p$.

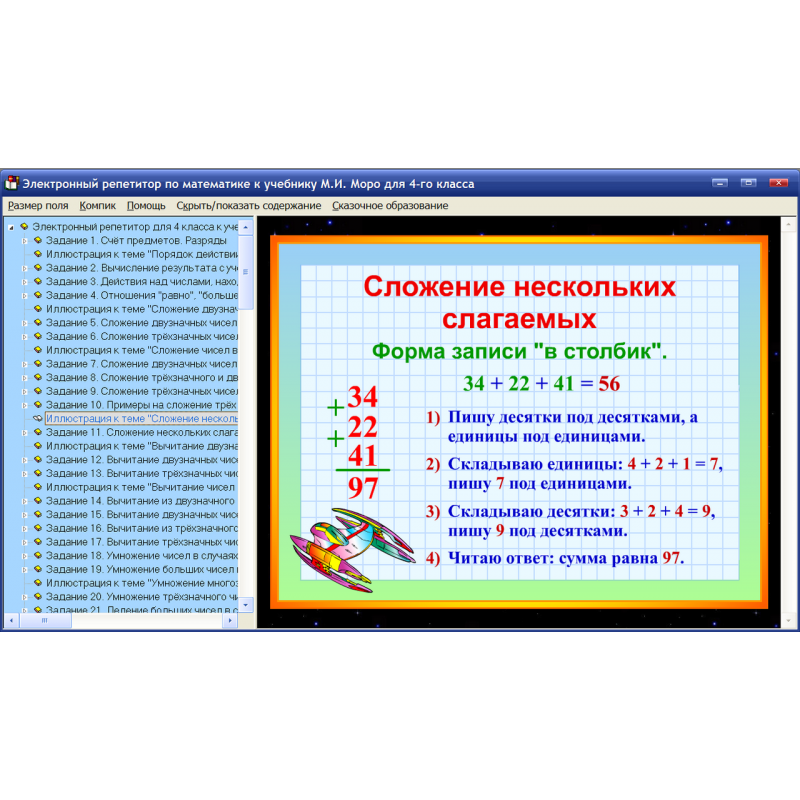 Каждый шаг можно отдельно изучить;
Каждый шаг можно отдельно изучить;
 Все остальные его монеты — десять центов. У него достаточно денег, чтобы купить 2 куска пиццы по 95 центов каждый. Сколько у него копеек?
Все остальные его монеты — десять центов. У него достаточно денег, чтобы купить 2 куска пиццы по 95 центов каждый. Сколько у него копеек? Имеет ли смысл 13 десятицентовиков в контексте задачи? Да.
Имеет ли смысл 13 десятицентовиков в контексте задачи? Да. Имеет ли смысл 9 выстрелов в контексте задачи? Да.
Имеет ли смысл 9 выстрелов в контексте задачи? Да.