Рубрика: Разное

Осмотическое давление | Задачи 463

 Задача 463. 
Чему равно осмотическое давление 0,5 М раствора глюкозы С₆Н₁₂О₆ при 25°С?
Решение:
Согласно уравнению Р = С_МRT, где С_М – молярная концентрация, R – газовая постоянная [8,314 Д ж/(моль ^. К)], T – температура.
Рассчитаем осмотическое давление:

                           Р = 0,5 .8,314 ^. 298 = 1238,786 кПа = 1,24 МПа.

Ответ: 1,24 МПа.

Задача 464.
Вычислить осмотическое давление раствора, содержащего 16 г сахарозы С₁₂Н₂₂О₁₁ в 350 г Н₂О при 293 К. Плотность раствора считать равной единице.
Решение:
M(С₁₂Н₂₂О₁₁) = 342 г/моль. Для расчётов используем  уравнение  Р = С_МRT,  С_М – молярная концентрация, R – газовая постоянная [8,314 Дж/(моль ^. К)] , T – температура. С_М можно выразить через массу растворённого вещества (m) и его мольную массу (М). Массу сахара, содержащегося в 1000 мл раствора, найдём из пропорции:

Отсюда

Ответ: 325 кПа.

Задача 465.
Сколько граммов глюкозы С₆Н₁₂О₆ должно находиться в 0,5 л раствора, чтобы его осмотическое давление (при той же температуре) было таким же, как раствора, в 1 л которого содержится 9,2 г глицерина  С₃Н₅(ОН)₃?
Решение:
М(С₆Н₁₂О₆)  = 180г/моль, М[С₃Н₅(ОН)_3] = 92г/моль. Осмотическое давление определяется по формуле: Р = С_MRT, где С_М – молярная концентрация, R – газовая постоянная [8,314 Дж/(моль ^. К)] , T – температура. Из данного уравнения вытекает, что осмотическое давление растворов зависит от концентрации и температуры.  

Таким образом, осмотическое давление двух растворов будет одинаковым, если концентрации растворённых веществ будут одинаковыми при одной и той же температуре. Поэтому справедливо равенство:

Р(С₆Н₁₂О₆) = Р[С₃Н₅(ОН)₃];  С_М(С₆Н₁₂О₆)RT = С_М[С₃Н₅(ОН)₃]RT

Находим молярную концентрацию глицерина: 

Теперь рассчитаем, сколько граммов глюкозы содержится в 0,5 л 0,1М раствора по формуле:

где С_М, m(B), M(B) и V(мл) соответственно молярная концентрация, масса, молярная масса растворённого вещества и объём раствора. 

Ответ: 9 г.

Задача 466.
К 100 мл 0,5М водного раствора сахарозы   добавлено 300 мл воды. Чему равно осмотическое давление полученного раствора при 25°С?  
Решение:
M(С₁₂Н₂₂О₁₁) = 342 г/моль.
Для расчёта массы С₁₂Н₂₂О₁₁ используем формулу:

Рассчитаем молярную концентрацию полученного раствора сахарозы, находим:

Осмотическое давление полученного раствора находим из формулы:  P = C_MRT, где С_М – молярная концентрация, R – газовая постоянная [8,314 Дж/(моль ^. К)], Т – температура.

Тогда

P = 0,125 ^. 8,314 ^.298 = 309,7 кПа.                      

Ответ: 309,7 кПа.

Расширенная номенклатура химических веществ

1,3-БУТИЛЕНГЛИКОЛЬ
Химическая формула: C4h20O2
Молярная масса: 90,12 г/моль

12-ГИДРОКСИСТЕАРИНОВАЯ КИСЛОТА
Химическая формула: C18h46O3
Молярная масса: 300,48 г/моль

DL-МЕТИОНИН
Химическая формула: C5h21NO2S
Молярная масса: 149.21134 г/моль

L-АСКОРБИНОВАЯ КИСЛОТА
Молярная масса: 176.13 г/моль

L-ТРИПТОФАН
Химическая формула: C11h22N2O2
Молярная масса: 204,23 г/моль

АДИПИНОВАЯ КИСЛОТА
Химическая формула: C6h20O4
Молярная масса: 146. 14 г/моль

АЗОТНАЯ КИСЛОТА 55%
Химическая формула: HNO3
Молярная масса: 63,01 г/моль

АЛКИЛ БЕНЗОЛ СУЛЬФОКИСЛОТЫ
Химическая формула: —
Молярная масса: — г/моль

АЛЛАНТОИН
Химическая формула: C4H6N4O3
Молярная масса: 158.11 г/моль

АЛЮМИНАТ НАТРИЯ РАСТВОР 27 %
Химическая формула: NaAlO2
Молярная масса: 81.97 г/моль

АЛЮМИНИЯ ГИДРОКСИД
Химическая формула: Al(OH)3
Молярная масса: 78 г/моль

АЛЮМИНИЯ СУЛЬФАТ
Химическая формула: Al2(SO4)3
Молярная масса: 342,15 г/моль

АЛЮМИНИЯ ХЛОРИД
Химическая формула: AlCl3
Молярная масса: 133,34 г/моль

АМИДОСУЛЬФОНОВАЯ КИСЛОТА
Химическая формула: h3NSO3H
Молярная масса: 97.09 г/моль

АММИАК, ВОДНЫЙ РАСТВОР 24%
Химическая формула: Nh4•h3O
Молярная масса: 35,0 г/моль

АММИАЧНАЯ СЕЛИТРА
Химическая формула: Nh5NO3
Молярная масса: 80.0434 г/моль

АММОНИЯ АЦЕТАТ
Химическая формула: Ch4COONh5
Молярная масса: 77,08 г/моль

XАММОНИЯ БИФТОРИД
Химическая формула: Nh5HF2
Молярная масса: 57,04 г/моль

АММОНИЯ ГИДРОКСИД
Химическая формула: Nh5HCO3
Молярная масса: 79. 06 г/моль

АММОНИЯ МОЛИБДАТ ТЕТРАГИДРАТ
Химическая формула: (Nh5)6Mo7O24•4h3O
Молярная масса: 1235,86 г/моль

АММОНИЯ ПЕРСУЛЬФАТ
Химическая формула: H8N2O8S2
Молярная масса: 228 г/моль

АММОНИЯ ПОЛИФОСФАТ
Химическая формула: [Nh5PO3]n
Молярная масса: —

АММОНИЯ СУЛЬФАТ
Химическая формула: (Nh5)2SO4
Молярная масса: — г/моль

АММОНИЯ ТИОСУЛЬФАТ
Химическая формула: (Nh5)2S2O3
Молярная масса: 148.20 г/моль

АММОНИЯ ТИОСУЛЬФАТА РАСТВОР
Химическая формула: (Nh5)2S2O3
Молярная масса: 148.20 г/моль

АММОНИЯ ХЛОРИД
Химическая формула: Nh5Cl
Молярная масса: 53,49 г/моль

АНОДЫ
Inne nazwy: —
Химическая формула: —

АРГАНОВОЕ МАСЛО
Химическая формула: —
Молярная масса: —

АСКОРБИЛПАЛЬМИТАТ
Химическая формула: C22h48O7
Молярная масса: 414,5 г/моль

АСПАРТАМ
Химическая формула: C14h28N2O5
Молярная масса: 294,3 г/моль

АЦЕСУЛЬФАМ К
Химическая формула: C4h5KNO4S
Молярная масса: 201,23 г/моль

АЦЕТИЛСАЛИЦИЛОВАЯ КИСЛОТА
Химическая формула: C9H8O4
Молярная масса: 180,16 г/моль

АЦЕТОН
Химическая формула: Ch4COCh4
Молярная масса: 58. 08 г/моль

БАРИЯ ГИДРОКСИД ОКТОГИДРАТ
Химическая формула: Ba(OH)2•8h3O
Молярная масса: 315,48 г/моль

БАРИЯ КАРБОНАТ
Химическая формула: BaCO3
Молярная масса: 197.34 г/моль

БАРИЯ СУЛЬФАТ
Химическая формула: BaSO4
Ciężar cząsteczkowy: 233,4 г/моль

БЕЛИЛО ТИТАНОВОЕ
Химическая формула: TiO2
Молярная масса: 79.87 г/моль

БЕНЗОЙНАЯ КИСЛОТА
Химическая формула: C6H5COOH
Молярная масса: 122.12 г/моль

БЕНЗОКАИН
Химическая формула: C9h21NO2
Молярная масса: 165,2 г/моль

БЕРОЛ
Химическая формула: —
Молярная масса: —

БЕТА-АЛАНИН
Химическая формула: C3H7NO2
Молярная масса: 89,09 г/моль

БЕТА-КАРОТИН
Химическая формула: C40H56
Молярная масса: 536,87 г/моль

БИС(2-ЭТИЛГЕКСИЛ)СЕБАЦАТ
Химическая формула: C26H50O4
Молярная масса: 426.67 г/моль

БОРНАЯ КИСЛОТА
Химическая формула: h4BO3
Молярная масса: 61,83 г/моль

БУРА ДЕКАГИДРАТ
Химическая формула: Na2B4O7•10h3O
Молярная масса: 381. 3 г/моль

БУРА ПЕНТАГИДРАТ
Химическая формула: Na2B4O7•5h3O
Молярная масса: 291.3 г/моль

БУРА БЕЗВОДНАЯ
Химическая формула: Na2B4O7
Молярная масса: 201.22 г/моль

БУТИЛГЛИКОЛЬ
Химическая формула: C6h24O2
Молярная масса: 118.17 г/моль

БУТИЛДИГЛИКОЛЬ
Химическая формула: C8h28O3
Молярная масса: 162.23 г/моль

ВАЗЕЛИН БЕЛЫЙ И ЖЁЛТЫЙ
Химическая формула: —
Молярная масса: —

ВАЗЕЛИНОВОЕ МАСЛО
Химическая формула: —
Молярная масса: —

ВИННАЯ КИСЛОТА
Химическая формула: C4H6O6
Молярная масса: 150.09 г/моль

ВИТАМИН А
Химическая формула: C20h40O
Молярная масса: 286,45 г/моль

ВИТАМИН Б1
Химическая формула: C12h27N4OS.NO3
Молярная масса: 327.36 г/моль

ВИТАМИН Е
токоферола ацетат
Химическая формула: C31h42O3
Молярная масса: 472,74 г/моль
токоферол
Химическая формула: C29H50O2
Молярная масса: 430,69 г/моль

ГИББЕРЕЛЛИНОВАЯ КИСЛОТА
Химическая формула: C19h32O6
Молярная масса: 346,37 г/моль

ГИДРОХИНОН
Химическая формула: C6h5(OH)2
Молярная масса: 110,11 г/моль

ГЛИКОЛЕВАЯ КИСЛОТА
Химическая формула: C2h5O3
Молярная масса: 76,05 г/моль

ГЛИЦЕРИЛ МОНОСТЕАРАТ
Химическая формула: C21h52O4
Молярная масса: 358,56 г/моль

ГЛИЦЕРИН РАСТИТЕЛЬНЫЙ
Химическая формула: C3H8O3
Молярная масса: 92,10 г/моль

ГЛИЦЕРОЛТРИАЦЕТАТ
Химическая формула: C9h24O6
Молярная масса: 218. 23 г/моль

ГЛИЦИН
Химическая формула: h3NCh3COOH
Молярная масса: 75.07 г/моль

ГЛУТАРАЛЬДЕГИД
Химическая формула: C5H8O2
Молярная масса: 100,12 г/моль

ГЛЮКОЗА
Химическая формула: C6h22O6
Молярная масса: 180,16 г/моль

ГРАФИТ
Химическая формула: (C)
Молярная масса: 12,01

ГУАРОВАЯ КАМЕДЬ
Химическая формула: —
Молярная масса: —

ДЕКСТРИН ЖЁЛТЫЙ
Химическая формула: —
Молярная масса: —

ДИАММОНИЙФОСФАТ
Химическая формула: (Nh5)2HPO4
Молярная масса: 132.1 г/моль

ДИБОРОНА ТРИОКСИД
Химическая формула: B2O3
Молярная масса: 69,6 г/моль

ДИГИДРОКСИАЦЕТОН
Химическая формула: C3H6O3
Молярная масса: 90,1 g/mol

ДИИЗОБУТИЛФТАЛАТ
Химическая формула: C16h32O4
Молярная масса: 278.34 г/моль

ДИКАЛИЙФОСФАТ
Химическая формула: K2HPO4
Молярная масса: 174.18 г/моль

ДИКАЛЬЦИЯ ФОСФАТ
Химическая формула: CaHO4P
Молярная масса: 136,06 г/моль

ДИМЕТИЛАМИНОПИРИДИН
Химическая формула: C7h20N2
Молярная масса: 122,17 г/моль

ДИМЕТИЛФОРМАМИД
Химическая формула: C3H7NO
Молярная масса: 73,09 г/моль

НАТРИЯ СУЛЬФИД
Химическая формула: Na2S•9h3O
Молярная масса: 240,18 г/моль

ДИНАТРИЯ ФОСФАТ БЕЗВОДНЫЙ
Химическая формула: Na2HPO4
Молярная масса: 141. 96 г/моль

ДИОКТИЛАДИПАТ
Химическая формула: C22h52O4
Молярная масса: 370,58 г/моль

ДИОКТИЛФТАЛАТ
Химическая формула: C6h5(COOC8h27)2
Молярная масса: 390.56 г/моль

ДИПРОПИЛЕНГЛИКОЛЬ
Химическая формула: C6h24O3
Молярная масса: 134.17 г/моль

ДИЭТАНОЛАМИН
Химическая формула: C4h21O2N
Молярная масса: 105,14 г/моль

ДИЭТИЛЕНГЛИКОЛЬ
Химическая формула: C4h20O3
Молярная масса: 106,12 г/моль

Д-ПАНТЕНОЛ
Химическая формула: C9h29NO4
Молярная масса: 205,25 г/моль

ДУКАНИТ®
Химическая формула: Cah5N4O9
Молярная масса: 244.13116 г/моль

ЖЕЛЕЗА ГЛИЦИНАТ
Химическая формула: —
Молярная масса: —

ЖЕЛЕЗА ОКСИД
Химическая формула: Fe2O3
Молярная масса: 159,69 г/моль

ЖЕЛЕЗА СУЛЬФАТ ГЕПТАГИДРАТ
Химическая формула: FeSO4•7h3O
Молярная масса: 278,02 г/моль

ЖЕЛЕЗА ХЕЛАТ ДТПА
Химическая формула: C14h28N3O10Fe(Nh5)2
Молярная масса: 80,23 г/моль

ЖЕЛЕЗА ХЕЛАТ ЭДТА
Химическая формула: C10h22FeN2O8•Na

ЖЕЛЕЗА ХЛОРИД РАСТВОР 40%
Химическая формула: FeCl3
Молярная масса: 162,2 г/моль

ЖИРНЫЕ КИСЛОТЫ
Химическая формула: —
Молярная масса: —

ИЗВЕСТЬ ГАШЕНАЯ
Химическая формула: CaO
Молярная масса: 56,08 г/моль

ИЗВЕСТЬ ХЛОРНАЯ
Химическая формула: Ca(ClO)2
Молярная масса: 142,98 г/моль

ИЗОМАСЛЯНАЯ КИСЛОТА
Химическая формула: (Ch4)2CHCOOH
Молярная масса: 88,11 г/моль

ИЗОПРОПИЛМИРИСТАТ
Химическая формула: C17h44O2
Молярная масса: 270. 46 г/моль

ИЗОПРОПИЛОВЫЙ СПИРТ
Химическая формула: Ch4CH(OH)Ch4
Молярная масса: 60,1 г/моль

ИЗОПРОПИЛПАЛЬМИТАТ
Химическая формула: C19h48O2
Молярная масса: 298.5 г/моль

ЙОД
Химическая формула: I2
Молярная масса: 253.8 г/моль

КАКАО-МАСЛО
Химическая формула: —
Молярная масса: —

КАЛИЯ АЦЕТАТ
Химическая формула: Ch4COOK
Молярная масса: 98,15 г/моль

КАЛИЯ БИХРОМАТ
Химическая формула: K2Cr2O7
Молярная масса: 294.18 г/моль

КАЛИЯ ГИДРОКСИД
Химическая формула: KOH
Молярная масса: 56,11 г/моль

КАЛИЯ ЙОДАТ
Химическая формула: KIO3
Молярная масса: 214,00 г/моль

КАЛИЯ ЙОДИД
Химическая формула: KI
Молярная масса: 166.01 г/моль

КАЛИЯ КАРБОНАТ БЕЗВОДНЫЙ
Химическая формула: K2CO3
Молярная масса: 138,21 г/моль

КАЛИЯ ЛАКТАТ
Химическая формула: C3H5KO3
Молярная масса: 128,17 г/моль

КАЛИЯ НИТРАТ
Химическая формула: K2SO4
Молярная масса: 174,27 г/моль

КАЛИЯ НИТРАТ
Химическая формула: KNO3
Молярная масса: 101,11 г/моль

КАЛИЯ ПЕРМАНГАНАТ (VII)
Химическая формула: KMnO4
Молярная масса: 158,04 г/моль

КАЛИЯ СОРБАТ
Химическая формула: C6H7KO2
Молярная масса: 150,22 г/моль

КАЛИЯ ФЕРРОЦИАНИД ТРИГИДРАТ
Химическая формула: K4[Fe(CN)6]•3h3O
Молярная масса: 422. 41 г/моль

КАЛИЯ ФОРМИАТ
Химическая формула: HCOOK
Молярная масса: 84.12 г/моль

КАЛИЯ ФОСФАТ ОДНОЗАМЕЩЕННЫЙ
Химическая формула: Kh3PO4
Молярная масса: 136.09 г/моль

КАЛИЯ ФТОРИД
Химическая формула: KF
Молярная масса: 58.1 г/моль

КАЛИЯ ХЛОРИД
Химическая формула: KCl
Молярная масса: 74.55 г/моль

КАЛИЯ-ХРОМА СУЛЬФАТ
Химическая формула: KCr(SO4)2•12h3O
Молярная масса: 499,41 г/моль

КАЛЬЦИЯ АЦЕТАТ МОНОГИДРАТ
Химическая формула: Ca(Ch4COO)2•h3O
Молярная масса: 176,17 г/моль

КАЛЬЦИЯ ГИДРОКСИД
Химическая формула: Ca(OH)2
Молярная масса: 74,09 г/моль

КАЛЬЦИЯ КАРБОНАТ БЕЗВОДНЫЙ
Химическая формула: CaCO3
Молярная масса: 100.08 г/моль

КАЛЬЦИЯ ЛАКТАТ ПЕНТАГИДРАТ
Химическая формула: C6h20CaO6•5h3O
Молярная масса: 308,3 г/моль

КАЛЬЦИЯ ПРОПИОНАТ
Химическая формула: (C3H5O2)2Ca
Молярная масса: 186,22 г/моль

КАЛЬЦИЯ СТЕАРАТ
Химическая формула: C36H70CaO4
Молярная масса: 607,02 г/моль

КАЛЬЦИЯ СУЛЬФАТ
Химическая формула: CaSO4
Молярная масса: 136,14 г/моль

КАЛЬЦИЯ ФОРМИАТ
Химическая формула: Ca(HCOO)2
Молярная масса: 130,11 г/моль

КАЛЬЦИЯ ХЛОРИД БЕЗВОДНЫЙ
Химическая формула: CaCl2
Молярная масса: 110,99 г/моль

КАЛЬЦИЯ ХЛОРИД ГЕКСАГИДРАТ
Химическая формула: CaCl2•6h3O
Молярная масса: 219. 07 г/моль

КАЛЬЦИЯ ХЛОРИД РАСТВОР 50%
Химическая формула: CaCl2
Молярная масса: 110,99 г/моль

КАЛЬЦИЯ ЦИТРАТ ТЕТРАГИДРАТА
Химическая формула: Ca3(C6H5O7)2•4h3O
Молярная масса: 570.49 г/моль

КАМЕДЬ РОЖКОВОГО ДЕРЕВА
Химическая формула: —
Молярная масса: —

КАРБОКСИМЕТИЛЦЕЛЛЮЛОЗА
Химическая формула: [C6H7O2(OH)3-X(OCh3COONa)X]n
Молярная масса: —

КАСТОРОВОЕ МАСЛО
Химическая формула: —
Молярная масса: —

КАУЧУК
Химическая формула: C9h20
Молярная масса: 118.18 г/моль

КОБАЛЬТА КАРБОНАТ
Химическая формула: CoCO3
Молярная масса: 118,94 г/моль

КОБАЛЬТА НИТРАТ
Numer indeksowy: 027-009-00-2
Химическая формула: Co(NO3)2•6h3O

КОБАЛЬТА СУЛЬФАТ
Химическая формула: CoSO4•7h3O
Молярная масса: 281,1 г/моль

КОКАМИД ДЭА
Химическая формула: Ch4(Ch3)nC(=O)N(Ch3Ch3OH)2
Молярная масса: —

КОКОСОВЫЙ БЕТАИН
Химическая формула: —
Молярная масса: —

КОФЕИН
Химическая формула: C8h20N4O2
Молярная масса: 194,19 г/моль

КРЕМНИЯ ПОРОШОК
Химическая формула: Si
Молярная масса: 28,09 г/моль

КСАНТАНОВАЯ КАМЕДЬ
Химическая формула: —
Молярная масса: —

КУКУРУЗНЫЙ КРАХМАЛ
Химическая формула: —
Молярная масса: —

ЛАКТОЗА
Химическая формула: C12h32O11
Молярная масса: 342,3 г/моль

ЛАНОЛИН
Химическая формула: —
Молярная масса: —

ЛАУРИНОВАЯ КИСЛОТА
Химическая формула: C12h34O2
Молярная масса: 200,32 г/моль

ЛИМОННАЯ КИСЛОТА БЕЗВОДНАЯ
Химическая формула: C6H8O7
Молярная масса: 192,12 г/моль

ЛИМОННАЯ КИСЛОТА МОНОГИДРАТ
Химическая формула: C6H8O7•h3O
Молярная масса: 210,14 г/моль

ЛИТИЯ ГИДРОКСИД МОНОГИДРАТ
Химическая формула: LiOH•h3O
Молярная масса: 41. 96 г/моль

ЛИТИЯ КАРБОНАТ
Химическая формула: Li2CO3
Молярная масса: 73.89 г/моль

МАГНИЯ КАРБОНАТ
Химическая формула: MgCO3
Молярная масса: 84,32 г/моль

МАГНИЯ НИТРАТ
Химическая формула: Mg(NO3)2•6h3O
Молярная масса: 256,41 г/моль

МАГНИЯ ОКСИД
Химическая формула: MgO
Молярная масса: 40,3 г/моль

МАГНИЯ СТЕАРАТ
Химическая формула: C36H70MgO4
Молярная масса: 591,24 г/моль

МАГНИЯ СУЛЬФАТ БЕЗВОДНЫЙ
Химическая формула: MgSO4
Ciężar cząsteczkowy: 120,37 г/моль

МАГНИЯ СУЛЬФАТ ГЕПТАГИДРАТ
Химическая формула: MgSO4•7h3O
Молярная масса: 246.48 г/моль

МАГНИЯ СУЛЬФАТ МОНОГИДРАТ
Химическая формула: MgSO4•1h3O
Молярная масса: 138,29 г/моль

МАГНИЯ ХЛОРИД ГЕКСАГИДРАТ
Химическая формула: MgCl2•6h3O
Молярная масса: 203,3 г/моль

МАЛАХИТОВЫЙ ЗЕЛЕНЫЙ
Химическая формула: C23h35ClN2
Молярная масса: 364,91 г/моль

МАЛЕИНОВЫЙ АНГИДРИД
Химическая формула: C4h3O3
Молярная масса: 98. 06 г/моль

МАЛЬТОДЕКСТРИН
Химическая формула: —
Молярная масса: —

МАРГАНЦА КАРБОНАТ
Химическая формула: MnCO3
Молярная масса: 114,95 г/моль

МАРГАНЦА ОКСИД
Химическая формула: MnO
Молярная масса: 70.94 г/моль

МАРГАНЦА СУЛЬФАТ МОНОГИДРАТ
Химическая формула: MnSO4•h3O
Молярная масса: 169.02 г/моль

МАРГАНЦА ХЕЛАТ 13 %
Химическая формула: C10h22MnN2O8•2Na
Молярная масса: 389.13 г/моль

МАРГАНЦА ХЛОРИД РАСТВОР 40%
Химическая формула: MnCl2
Молярная масса: 125,91 г/моль

МАРГАНЦА ХЛОРИД ТЕТРАГИДРАТ
Химическая формула: MnCl2•4h3O
Молярная масса: 197.91 г/моль

МАСЛО ОГУРЕЧНИКА
Химическая формула: —
Молярная масса: —

МАСЛО ПРИМУЛЫ ВЕЧЕРНЕЙ
Химическая формула: —
Молярная масса: —

МЕДИ (II) ХЛОРИД ДИГИДРАТ
Химическая формула: CuCl2•2h3O
Молярная масса: 170,45 г/моль

МЕДИ ГЛИЦИНАТ
Химическая формула: C4H8CuN204
Молярная масса: 211,66

МЕДИ КАРБОНАТ
Химическая формула: CuCO3
Молярная масса: 123,55 г/моль

XМЕДИ НИТРАТ
Химическая формула: Cu(NO3)2•3h3O
Молярная масса: 241,60 г/моль

МЕДИ ОКСИДН
Химическая формула: CuO
Молярная масса: 79. 55 г/моль

МЕДИ СУЛЬФАТ ПЕНТАГИДРАТ
Химическая формула: CuSO4•5h3O
Молярная масса: 249,68 г/моль

МЕДИ ХЕЛАТ 13 %
Химическая формула: C10h22CuN2O8•2Na
Молярная масса: 397,74 г/моль

МЕДИ ХЛОРИД РАСТВОР 40%
Химическая формула: CuCl2
Молярная масса: 134.45 г/моль

МЕДИ ХЛОРОКИСЬ
Химическая формула: Cu2(OH)3Cl
Молярная масса: 213,56 г/моль

МЕЛАМИН
Химическая формула: C6H6N6
Молярная масса: —

МЕЛАМИНА БОРАТ
Химическая формула: C3H6N6•xBh4O3
Молярная масса: 126,12 г/моль

МЕНТОЛ (L)
Химическая формула: C10h30O
Молярная масса: 156,27 г/моль

МЕТАНОЛ
Химическая формула: Ch4OH
Молярная масса: 32,04 г/моль

МЕТИЛЕНОВЫЙ СИНИЙ
Химическая формула: C16h28ClN3S
Молярная масса: 319,86 г/моль

МЕТИЛЕНХЛОРИД
Химическая формула: Ch3Cl2
Молярная масса: 119 г/моль

МЕТИЛИЗОБУТИЛКЕТОН
Химическая формула: C6h22O
Молярная масса: 100.16 г/моль

МЕТИЛЭТИЛКЕТОН
Химическая формула: C4H8O
Молярная масса: 72 г/моль

МИНДАЛЬНОЕ МАСЛО
Химическая формула: —
Молярная масса: —

МОЛИБДЕНА СУЛЬФИД
Химическая формула: MoS2
Молярная масса: 160,06 г/моль

МОЛОЧНАЯ КИСЛОТА 80 %
Химическая формула: C3H6O3
Молярная масса: 90. 08 г/моль

МОНОАММОНИЙФОСФАТ
Химическая формула: (Nh5)h3PO4
Молярная масса: 115,03 г/моль

XМОНОЭТИЛЕНГЛИКОЛЬ
Химическая формула: C2H6O2
Молярная масса: 62.07 г/моль

МОЧЕВИНА
Химическая формула: (Nh3)2CO
Молярная масса: 60.05 г/моль

МОЧЕВИНЫ ФОСФАТ
Химическая формула: Ch5N2O•h4O4P
Молярная масса: 158.05 г/моль

МУРАВЬИНАЯ КИСЛОТА 85 %
Химическая формула: HCOOH
Молярная масса: 46.03 г/моль

МЫЛЬНЫЕ ХЛОПЬЯ
Химическая формула: —
Молярная масса: —

НАТРИЯ АЦЕТАТ
Химическая формула: Ch4COONa
Молярная масса: 82,03 г/моль

НАТРИЯ БЕНЗОАТ
Химическая формула: C21h39N2O•C7H5O2
Молярная масса: 446,58 г/моль

XНАТРИЯ ГЕКСАМЕТАФОСФАТ
Химическая формула: Na6(PO3)6
Молярная масса: 611.77 г/моль

НАТРИЯ ГИДРОКСИД
Химическая формула: NaOH
Молярная масса: 40,00 г/моль

НАТРИЯ ГИДРОСУЛЬФИТ
Химическая формула: Na2S2O4
Молярная масса: 174.11 г/моль

НАТРИЯ ГИПОХЛОРИТ МИН. 13% CL
Химическая формула: NaOCl
Молярная масса: 74.44 г/моль

НАТРИЯ ГЛУТАМАТ
Химическая формула: C5H8NNaO4•h3O
Молярная масса: 187,13 г/моль

НАТРИЯ ГЛЮКОНАТ
Химическая формула: C6h21NaO7
Молярная масса: 218.14 г/моль

НАТРИЯ ДИАЦЕТАТ
Химическая формула: C4H7O4Na
Молярная масса: 142,1 г/моль

НАТРИЯ ДИХРОМАТ
Химическая формула: Na2Cr2O7
Молярная масса: 261,97 г/моль

НАТРИЯ КАРБОНАТ БЕЗВОДНЫЙ
Химическая формула: Na2CO3
Молярная масса: 105,99 г/моль

НАТРИЯ ЛАКТАТ
Химическая формула: C3H5NaO3
Молярная масса: 112 г/моль

НАТРИЯ МЕТАБИСУЛЬФИТ
Химическая формула: Na2S2O5
Молярная масса: 190.10 г/моль

XНАТРИЯ МЕТАСИЛИКАТ ПЕНТАГИДРАТ
Химическая формула: Na2SiO3•5h3O
Молярная масса: 212,06 г/моль

НАТРИЯ МОЛИБДАТ ДИГИДРАТ
Химическая формула: Na2MoO4•2 h3O
Молярная масса: 241.95 г/моль

НАТРИЯ НИТРАТ
Химическая формула: NaNO3
Молярная масса: 84,99 г/моль

НАТРИЯ НИТРИТ
Химическая формула: NaNO2
Молярная масса: 69,00 г/моль

НАТРИЯ ПЕРБОРАТ ТЕТРАГИДРАТ
Химическая формула: NaBO3•4h3O
Молярная масса: 153,9 г/моль

НАТРИЯ ПЕРСУЛЬФАТ
Химическая формула: Na2S2O8
Молярная масса: 238,1 г/моль

НАТРИЯ ПИРОФОСФАТ
Химическая формула: Na2h3P2O7
Молярная масса: 221. 94 г/моль

НАТРИЯ ПОЛИФОСФАТ
Химическая формула: (NaPO3)n
Молярная масса: —

НАТРИЯ ПРОПИОНАТ
Химическая формула: C3H5O2Na
Молярная масса: 96.07 г/моль

НАТРИЯ САЛИЦИЛАТ
Химическая формула: C7H5O3Na
Молярная масса: 160,11 г/моль

НАТРИЯ САХАРИН ДИГИДРАТ
Химическая формула: C7h5NNaO3S•2h3O
Молярная масса: 241,19 г/моль

НАТРИЯ СТАННАТ
Химическая формула: Na2Sn(OH)6
Молярная масса: 266,74 г/моль

НАТРИЯ СУЛЬФАТ
Химическая формула: Na2SO4•10h3O
Молярная масса: 322,2 г/моль

НАТРИЯ СУЛЬФАТ БЕЗВОДНЫЙ
Химическая формула: Na2SO4
Молярная масса: 142,04 г/моль

НАТРИЯ СУЛЬФИТ БЕЗВОДНЫЙ
Химическая формула: Na2SO3
Молярная масса: 126.04 г/моль

НАТРИЯ ТИОСУЛЬФАТ ПЕНТАГИДРАТ
Химическая формула: Na2S2O3•5h3O
Молярная масса: 248.21 г/моль

НАТРИЯ ТРИПОЛИФОСФАТ
Химическая формула: Na5P3O10
Молярная масса: 367.86 г/моль

НАТРИЯ ФОРМИАТ
Химическая формула: HCOONa
Молярная масса: 68,01 г/моль

НАТРИЯ ФОСФАТ ДОДЕКАГИДРАТ
Химическая формула: Na3PO4•12h3O
Молярная масса: 380. 18 г/моль

НАТРИЯ ФТОРИД
Химическая формула: FNa
Молярная масса: 41.99 г/моль

НАТРИЯ ФТОРСИЛИКАТ
Химическая формула: Na2SiF6
Молярная масса: 188.06 г/моль

НАТРИЯ ХЛОРИД
Химическая формула: NaCl
Молярная масса: 58.44 г/моль

XНАТРИЯ ЦИАНИД
Химическая формула: NaCN
Молярная масса: 49,02 г/моль

Н-БУТИЛАЦЕТАТ
Химическая формула: Ch4COOC4H9
Молярная масса: 116,16 г/моль

НЕОДЕКАНОВОЙ КИСЛОТЫ ВИНИЛОВЫЙ ЭФИР
Химическая формула: C12h32O2
Молярная масса: 198 г/моль

НИКЕЛЯ НИТРАТ
Химическая формула: Ni(NO3)2•6 h3O
Молярная масса: 290.81 г/моль

НИКЕЛЯ НИТРАТ ГЕКСАГИДРАТ
Химическая формула: NiSO4•6h3O
Молярная масса: 262,86 г/моль

НИКЕЛЯ ХЛОРИД ГЕКСАГИДРАТ
Химическая формула: NiCl2•6h3O
Молярная масса: 237,7 г/моль

НИКОТИНОВАЯ КИСЛОТА
Химическая формула: C6H5NO2
Молярная масса: 123,109 г/моль

НИТРОЭТАНОМ
Химическая формула: — C2H5NO2

Н-ПРОПИЛОВЫЙ СПИРТ
Химическая формула: C3H8O
Молярная масса: 60,1 г/моль

ОКСИБУТИРАТ НАТРИЯ
Химическая формула: C4H7O2Na
Молярная масса: 110,09 g/mol

ОЛЕИНОВАЯ КИСЛОТА
Химическая формула: C18h44O2
Молярная масса: 282. 46 г/моль

ОЛИВКОВОЕ МАСЛО
Химическая формула: C₄H₈O₃
Молярная масса: 104.10 г/моль

ОЛОВА СУЛЬФАТ
Химическая формула: SnSO4
Молярная масса: 214.77 г/моль

ПАРАФИН
Химическая формула: —
Молярная масса: —

ПАРАФИНОВОЕ МАСЛО
Химическая формула: —
Молярная масса: —

ПАРАФОРМАЛЬДЕГИД
Химическая формула: (Ch3O)n
Молярная масса: —

ПЕНТАНАТРИЙ ЭДТА
Химическая формула: C14h28N3O10Na5
Молярная масса: 503.1 г/моль

ПЕРЕКИСЬ ВОДОРОДА, РАСТВОР
Химическая формула: h3O2
Молярная масса: 34,02 г/моль

ПЕРКАРБОНАТ НАТРИЯ
Химическая формула: Na2CO3•1.5 h3O2
Молярная масса: 156,98 г/моль

ПОЛИЭТИЛЕНГЛИКОЛЬ 200
Химическая формула: HO(C2h5O)nH
Молярная масса: 190 — 210 г/моль

ПОЛИЭТИЛЕНГЛИКОЛЬ 300
Химическая формула: HO(C2h5O)nH
Молярная масса: 285 — 315 г/моль

ПОЛИЭТИЛЕНГЛИКОЛЬ 400
Химическая формула: HO(C2h5O)nH
Молярная масса: 380 — 420 г/моль

ПРОПИЛЕНГЛИКОЛЬ
Химическая формула: C3H8O2
Молярная масса: 76,10 г/моль

ПРОПИОНОВАЯ КИСЛОТА
Химическая формула: C3H6O2
Молярная масса: 74. 07 г/моль

РАСТВОР СЕЛИТРЫ И МОЧЕВИНЫ
Химическая формула: —
Молярная масса: —

САЛИЦИЛОВАЯ КИСЛОТА
Химическая формула: C7H6O3
Молярная масса: 138,12 г/моль

СВИНЦА НИТРАТ
Химическая формула: Pb(NO3)2
Молярная масса: 331,21 г/моль

СВИНЦА ОКСИД
Химическая формула: PbO
Молярная масса: 223,2 г/моль

СЕБАЦИНОВАЯ КИСЛОТА
Химическая формула: C10h28O4
Молярная масса: 202,25 г/моль

СЕРА
Химическая формула: S
Молярная масса: 32,07 г/моль

СЕРЕБРА НИТРАТ
Химическая формула: AgNO3
Молярная масса: 169,88 г/моль

СЕРЕБРА ЦИАНИД
Молярная масса: 133,89 г/моль
Химическая формула: AgCN

СЕРНАЯ КИСЛОТА МИН. 95%
Химическая формула: h3SO4
Молярная масса: 98.08 г/моль

СИЛИКАГЕЛЬ
Химическая формула: SiO2
Молярная масса: 60,08 г/моль

СИЛИКАТ ЦИРКОНИЯ
Химическая формула: ZrSiO4
Молярная масса: 183,31 г/моль

СИЛИКОНОВОЕ МАСЛО
Химическая формула: —
Молярная масса: —

СОЕВЫЙ ЛЕЦИТИН
Химическая формула: —
Молярная масса: —

СОЛЬ ДЛЯ ОБЕЗЖИРИВАНИЯ
Химическая формула: —
Молярная масса: —

СОЛЯНАЯ КИСЛОТА ~ 33%
Химическая формула: HCl
Молярная масса: 36,45 г/моль

СОРБИНОВАЯ КИСЛОТА
Химическая формула: C6H8O2
Молярная масса: 112,13 г/моль

СОРБИТОЛ 70%
Химическая формула: C6h24O6
Молярная масса: 182,17 г/моль

СТЕАРИНОВАЯ КИСЛОТА
Химическая формула: C18h46O2
Молярная масса: 284. 48 г/моль

12-ГИДРОКСИСТЕАРИНОВАЯ КИСЛОТА
Химическая формула: C18h46O3
Молярная масса: 300,48 г/моль

СТЕКЛО НАТРИЕВОЕ ЖИДКОЕ
Химическая формула: C2H6O2
Молярная масса: 62.07 г/моль

СТИРОЛ
Химическая формула: C8H8
Молярная масса: 104,15 г/моль

СУРЬМЫ ОКСИД
Химическая формула: Sb2O3
Молярная масса: 291,52 г/моль

СУРЬМЫ ТРЕХОКИСЬ
Химическая формула: Sb2O3
Молярная масса: 291.52 г/моль

ТАЛЬК
Химическая формула: 3MgO•4SiO2•h3O
Молярная масса: 379,34 г/моль

ТЕТРАГИДРОФУРАН
Химическая формула: Ch4CH(OH)Ch4
Молярная масса: 60,1 g/mol

ТЕТРАМЕТИЛТИУРАМСУЛЬФИД
Химическая формула: C6h22N2S4
Молярная масса: 240,4 г/моль

ТЕТРАФТОРОБОРАТ ВОДОРОДА 49 % – 51 %
Химическая формула: HBF4
Молярная масса: 87.81 г/моль

ТЕТРАХЛОРЭТИЛЕН
Химическая формула: C2Cl4
Молярная масса: 165.83 г/моль

ТЕТРАЭТИЛЕНПЕНТАМИН
Химическая формула: —
Молярная масса: —

ТИОМОЧЕВИНА
Химическая формула: Ch5N2S
Молярная масса: 76,12 г/моль

ТОЛУОЛ
Химическая формула: C7H8
Молярная масса: 92,14 г/моль

ТРИНАТРИЙЦИТРАТА ДИГИДРАТ
Химическая формула: C6H5Na3O7•2 h3O
Молярная масса: 294 г/моль

ТРИХЛОРЭТИЛЕН
Химическая формула: C2HCl3
Молярная масса: 131. 39 г/моль

ТРИЭТАНОЛАМИН
Химическая формула: (Ch3Ch3OH)3N
Молярная масса: 149.19 г/моль

ТРИЭТИЛЕНГЛИКОЛЬ
Химическая формула: C6h24O4
Молярная масса: 150,17 г/моль

УКСУСНАЯ КИСЛОТА 80 %
Химическая формула: Ch4COOH
Молярная масса: 60,05 г/моль

УМЯГЧИТЕЛЬ DOS
Химическая формула: C26H50O4
Молярная масса: 426.67 г/моль

УРОТРОПИН
Химическая формула: C6h22N4
Молярная масса: 140,20 г/моль

ФЕНОЛ
Химическая формула: C6H5OH
Молярная масса: 94.11 г/моль

ФЕНОЛФТАЛЕИН
Химическая формула: C20h24O4
Молярная масса: 318,33 г/моль

ФЛЮОРИТ
Химическая формула: CaF2
Молярная масса: 78.074 г/моль

ФОЛЬЦИСТЕИН
Химическая формула: C25h38N8O9S
Молярная масса: 616,60 г/моль

ФОРМАЛИН ТЕХНИЧЕСКИЙ 36-50 %
Химическая формула: HCHO
Молярная масса: 30.03 g/mol

ФОСФОРНАЯ КИСЛОТА 25, 30, 70
Химическая формула: h4PO4
Молярная масса: 97,995 г/моль

ФТАЛЕВЫЙ АНГИДРИД
Химическая формула: C8h5O3
Молярная масса: 148,1 г/моль

ФТОРОБОРНАЯ КИСЛОТА
Химическая формула: HF
Молярная масса: 20,01 г/моль

ФУМАРОВАЯ КИСЛОТА
Химическая формула: C4h5O4
Молярная масса: 116. 07 г/моль

ФУРФУРИЛОВЫЙ СПИРТ
Химическая формула: C5H6O2
Молярная масса: 98,10 г/моль

ФУРФУРОЛ
Химическая формула: C5h5O2
Молярная масса: 96,09 г/моль

ХЛОРОФОРМ
Химическая формула: CHCl3
Молярная масса: 119 г/моль

ХЛОРПАРАФИН
Химическая формула: —
Молярная масса: —

ХЛОРУКСУСНАЯ КИСЛОТА
Химическая формула: ClCh3COOH
Молярная масса: 94.49 г/моль

ХОЛЕСТЕРИН
Химическая формула: C27h56O
Молярная масса: 386,66 г/моль

ХОЛИНА ХЛОРИД 60%
Химическая формула: C5h24ClNO
Молярная масса: 139,62 г/моль

ХОЛИНА ХЛОРИДА РАСТВОР МИН. 75%
Химическая формула: C5h24ClNO
Молярная масса: 139,62 г/моль

ХРОМА ОКСИД (III)
Химическая формула: Cr2O3
Молярная масса: 151,99 г/моль

ХРОМОВЫЙ АНГИДРИД
Химическая формула: CrO3
Молярная масса: 99,99 г/моль

ЦЕРИЯ ОКСИД
Химическая формула: Na5P3O10
Молярная масса: 367.86 г/моль

ЦЕТИЛОВЫЙ СПИРТ
№ CAS: 36653-82-4
№ WE: 253-149-0
Химическая формула: C16h44O
Молярная масса: 242.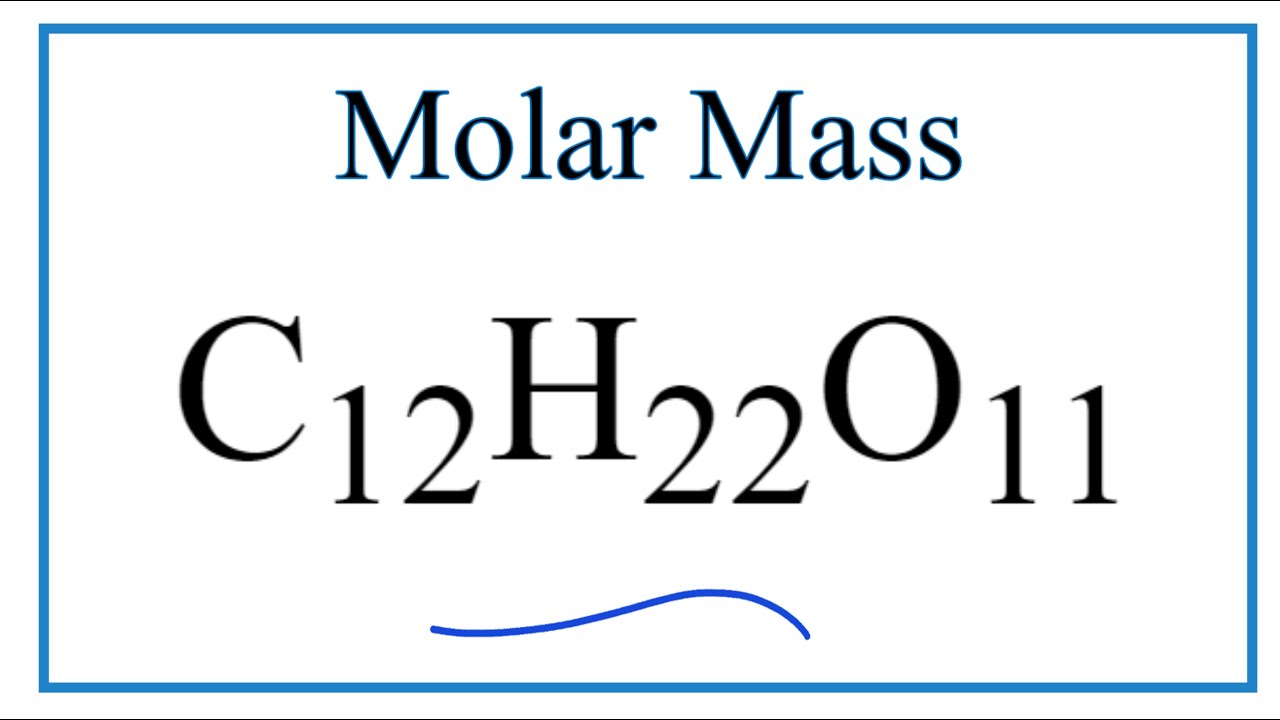 44 г/моль

ЦЕТОСТЕАРИЛОВЫЙ СПИРТ
Химическая формула: C34H72O2
Молярная масса: 512,93 г/моль

ЦИКЛОГЕКСАН
Химическая формула: C6h22
Молярная масса: 84,16 г/моль

ЦИНКА БОРАТ
Химическая формула: 2ZnO•3B2O3•3.5h3O
Молярная масса: —

ЦИНКА ДИГИДРОФОСФАТ
Химическая формула: Zn3( PO4)2•2h3O
Молярная масса: 422,11 г/моль

ЦИНКА ЛАКТАТ
Химическая формула: C6h20ZnO6
Молярная масса: 243,49 г/моль

ЦИНКА НИТРАТ ГЕКСАГИДРАТ
Химическая формула: Zn(NO3)2•6h3O
Молярная масса: 297.49 г/моль

ЦИНКА ОКСИД
Химическая формула: ZnO
Молярная масса: 81,37 г/моль

ЦИНКА СТЕАРАТ
Химическая формула: C36H70O4Zn
Молярная масса: 632,35 г/моль

ЦИНКА СУЛЬФАТ ГЕПТАГИДРАТ
Химическая формула: ZnSO4•7h3O
Молярная масса: 287,54 г/моль

ЦИНКА СУЛЬФАТ МОНОГИДРАТ
Химическая формула: ZnSO4•h3O
Ciężar cząsteczkowy: 179,45 г/моль

ЦИНКА ХЕЛАТ 13 %
Химическая формула: C10h22N2O8Zn•2Na
Молярная масса: 399. 58 г/моль

ЦИНКА ХЛОРИД
Химическая формула: ZnCl2
Молярная масса: 136,29 г/моль

ШЕЛУХА РИСА
Химическая формула: —
Молярная масса: —

ЩАВЕЛЕВАЯ КИСЛОТА ДИГИДРАТ
Химическая формула: C2h3O4•2h3O
Молярная масса: 126.07 г/моль

ЭДТА ДИНАТРИЕВАЯ
Химическая формула: C10h24N2Na2O8
Молярная масса: 336,21 г/моль

ЭДТА ТЕТРАНАТРИЕВАЯ
Химическая формула: C10h22N2O8Na4
Молярная масса: 380.2 г/моль

ЭДТА ТЕТРАНАТРИЕВОЙ РАСТВОР ОК. 39%
Химическая формула: C10h22N2O8Na4
Молярная масса: 380.2 г/моль

ЭКСТРАКТ ГОРЬКОГО АПЕЛЬСИНА
Химическая формула: —
Молярная масса: —

ЭКСТРАКТ ГРЕЧИХИ
Химическая формула: —
Молярная масса: —

ЭРБИЯ ОКСИД
Химическая формула: Er2O3
Молярная масса: 382,52 г/моль

XЭТАНОЛАМИН
Химическая формула: C2H7NO
Молярная масса: 61.08 г/моль

ЭТИЛАЦЕТАТ
Химическая формула: Ch4COOC2H5

ЭТИЛЕНДИАМИН
Химическая формула: C2H8N2
Молярная масса: 60. 10 г/моль

ЭТИЛЕНДИАМИНТЕТРАУКСУСНАЯ КИСЛОТА
Химическая формула: C10h26N2O8
Молярная масса: 292.25 г/моль

ЭТОКСИПРОПАНОЛ
Химическая формула: C5h22O2
Молярная масса: 104,15

ЯНТАРНАЯ КИСЛОТА Химическая формула: C4H6O4
Молярная масса: 118,09 г/моль

Стехиометрия

Атомная масса

Единицы, в которых выражается масса атома, равны 9.0030 атомный единицы массы . Когда-то самому легкому атому приписывали массу 1 а. е.м., а массу любого другого атома выражали в условия настоящего стандарта. Сегодня атомные единицы массы определяются в с точки зрения изотопа ¹² C, которому присвоена масса ровно 12.000… а.е.м.

Изотопы

Изотопы атомы одного и того же элемента с разными количество нейтронов, таких как ²⁰ Ne и ²² Не изотопы неона или ³⁵ Cl и ³⁷ Cl изотопы хлора.

Атомный вес

Атомный вес элемента является средневзвешенным атомных масс различных изотопов элемента. Природный углерод, например, представляет собой смесь двух изотопы ¹² С (98,89 %) и ¹³ С (1,11 %). Таким образом, отдельные атомы углерода имеют массу либо 12 000, либо 13.03354 а.е.м. Но средняя масса различных изотопов углерод составляет 12,011 а.е.м.

Молекулярная масса

Молекулярная масса соединения представляет собой сумму атомные массы атомов в молекулах, образующих эти соединения.

Пример: Молекулярная масса молекулы сахара, обнаруженная в тростниковый сахар представляет собой сумму атомных весов 12 атомов углерода. атомов, 22 атома водорода и 11 атомов кислорода в C ₁₂ H ₂₂ O ₁₁ молекула.

C ₁₂ H ₂₂ O ₁₁ имеет молекулярную вес 342,299 а.е.м. Моль C ₁₂ Н ₂₂ О ₁₁ будет иметь массу 342,299 грамма. Эта величина известна как молярных масса , термин, который часто используется вместо терминов атомный масса или молекулярная масса.

Крот

Термин крот буквально означает небольшую массу. Это используется как мост между химией на атомном и макроскопический масштаб. Если масса одного ¹² атом углерода 12.000 а.е.м., то один моль этих атомов будет иметь массу 12.000 грамм. По определению моль любого вещества содержит столько же элементарных частиц, сколько атомов ровно в 12 граммах ¹² C изотоп углерода.

Пример: Отдельный атом ¹² C имеет массу 12 а.е.м., и моль этих атомов будет иметь массу 12 граммов.

Моль любых атомов имеет массу в граммах равно атомному весу элемента. Термин родинка может быть применительно к любой частице: атомам, молю атомов, молю ионов, моль электронов или моль молекул. Каждый раз, когда мы используем термин, мы имеем в виду число частиц, равное числу атомов ровно в 12 граммах ¹² изотоп С углерод.

Постоянная Авогадро

Число Авогадро (или постоянная Авогадро) число элементарных частиц в моле любого вещества Для большинство расчетов, четыре значащие цифры для Авогадро констант достаточно: 6. 022 x 10 ²³ .

Моль любого вещества содержит Число элементарных частиц Авогадро. Это не имеет значения говорим ли мы о моле атомов, моле молекул, моль электронов или моль ионов. По определению, родинка всегда содержит 6,022 x 10 ²³ элементарных частиц.

Перевод граммов в Крот

Крот — мощный инструмент, позволяющий химикам, вооруженным не более чем таблица атомных весов и весы для определить количество атомов, ионов или молекул в образце.

Пример: Рассчитаем количество C ₁₂ H ₂₂ O ₁₁ молекул в фунте тростникового сахара.

Для этого вычисления нам нужны две части информации. Мы нужно знать количество граммов в фунте и молекулярную вес или молярная масса этого сахара. Фунт сахара имеет массу 453,6 г, а один моль этого сахара имеет массу 342,3 г. грамм.

Пара единичных факторов может быть построена из молекулярных веса или молярной массы.

Обращая внимание на единицы измерения во время расчета, легко выбрать правильный коэффициент единицы для преобразования граммов сахара в моли сахара.

Затем мы используем число Авогадро для определения числа C ₁₂ H ₂₂ O ₁₁ молекул в нашем образце.

Ответ: Какова молярная масса сахара…

ISBN: 978133739942 5

Автор: Стивен С. Зумдал, Дональд Дж. ДеКосте

Издатель: Cengage Learning

1 Химия: введение2 Измерения и расчеты3 Материя4 Химические основы: элементы, атомы и ионы5 Номенклатура6 Химические реакции: введение7 Реакции в водных растворах8 Химический состав9 Химические количества10 Энергия11 Современная атомная теория12 Химическая связь13 Газы14 Жидкости И твердые тела15 Растворы16 Кислоты и основания17 Равновесие18 Окислительно-восстановительные реакции и электрохимия19 Радиоактивность и ядерная энергия20 Органическая химия21 Биохимия expand_more

21.1 Белки 21.2 Первичная структура белков 21.3 Вторичная структура белков 21.4 Третичная структура белков 21.5 Функции белков 21.6 Ферменты 21.7 Углеводы 21.8 Нуклеиновые кислоты 21.9 Липиды Вопросы к главе expand_more

Проблема 1ALQ: различать первичную, вторичную и третичную структуру белков. Проблема 5QAPПроблема 6QAPПроблема 7QAPПроблема 8QAPПроблема 9QAPПроблема 10QAP: . Сколько уникальных аминокислотных последовательностей возможно для трипептида, содержащего только аминокислоты… Задача 11QAPЗадача 12QAPЗадача 13QAPЗадача 14QAPЗадача 15QAPЗадача 16QAPЗадача 17QAPЗадача 18QAPЗадача 19QAPЗадача 20QAP: . Какой белок отвечает за транспорт кислорода кровотоком? Задача 21QAPЗадача 22QAPЗадача 23QAPЗадача 24QAPЗадача 25QAP: . Чем отличается эффективность фермента от эффективности неорганических катализаторов? Ферментов больше или… Задача 26QAPЗадача 27QAPЗадача 28QAP: . Опишите модель «ключ-замок» для ферментов. Почему формы фермента и его субстрата… Задача 29QAPProblem 30QAPProblem 31QAPProblem 32QAPProblem 33QAPProblem 34QAPProblem 35QAPProblem 36QAPProblem 37QAPProblem 38QAPProblem 39QAPProblem 40QAPProblem 41QAPProblem 42QAPProblem 43QAPProblem 44QAP Проблема 45QAPПроблема 46QAPПроблема 47QAPПроблема 48QAPПроблема 49QAPПроблема 50QAPПроблема 51QAP: . Что такое стероид? Какая базовая кольцевая структура 15 является общей для всех стероидов? Нарисуйте пример задачи 52QAPProblem 53QAPProblem 54QAPProblem 55APProblem 56APProblem 57APProblem 58APProblem 59APProblem 60APProblem 61APProblem 62APProblem 63APProblem 64APProblem 65APProblem 66APProblem 67APPro проблема 68APпроблема 69APPProblem 70APProblem 71APProblem 72APProblem 73APProblem 74APProblem 75APProblem 76APProblem 77APProblem 78APProblem 79APProblem 80APProblem 81APProblem 82APProblem 83APProblem 84APProblem 85APProblem 86APProblem 87APПроблема 88APПроблема 89APПроблема 90APПроблема 91APПроблема 92APПроблема 93APПроблема 94APПроблема 95APПроблема 96APПроблема 97AP: .

Задачи по Python 3 для начинающих от Tproger и GeekBrains

Вместе с факультетом Python-разработки GeekUniversity собрали для вас несколько простых задач по Python для обучения и тренировки. Их можно решать в любом порядке.

Обратите внимание, что у любой задачи по программированию может быть несколько способов решения. Чтобы посмотреть добавленный нами вариант решения, кликните по соответствующей кнопке. Все приведённые варианты написаны на Python 3.

Задача 1

Есть список a = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89].

Выведите все элементы, которые меньше 5.

Вариант решения

Самый простой вариант, который первым приходит на ум — использовать цикл for:

for elem in a:
    if elem < 5:
        print(elem)

Также можно воспользоваться функцией filter, которая фильтрует элементы согласно заданному условию:

print(list(filter(lambda elem: elem < 5, a)))

И, вероятно, наиболее предпочтительный вариант решения этой задачи — списковое включение:

print([elem for elem in a if elem < 5])

Задача 2

Даны списки:

a = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89];

b = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13].

Нужно вернуть список, который состоит из элементов, общих для этих двух списков.

Вариант решения

Можем воспользоваться функцией filter:

result = list(filter(lambda elem: elem in b, a))

Или списковым включением:

result = [elem for elem in a if elem in b]

А можно привести оба списка к множествам и найти их пересечение:

result = list(set(a) & set(b))

Однако в таком случае каждый элемент встретится в результирующем списке лишь один раз, т.к. множество поддерживает уникальность входящих в него элементов. Первые два решения (с фильтрацией) оставят все дубли на своих местах.

Задача 3

Отсортируйте словарь по значению в порядке возрастания и убывания.

Вариант решения

Импортируем нужный модуль и объявляем словарь:

import operator 
d = {1: 2, 3: 4, 4: 3, 2: 1, 0: 0}

Сортируем в порядке возрастания:

result = dict(sorted(d.items(), key=operator. itemgetter(1)))

И в порядке убывания:

result = dict(sorted(d.items(), key=operator.itemgetter(1), reverse=True))

Задача 4

Напишите программу для слияния нескольких словарей в один.

Вариант решения

Допустим, вот наши словари:

dict_a = {1:10, 2:20}
dict_b = {3:30, 4:40}
dict_c = {5:50, 6:60}

Объединить их можно вот так:

result = {}
for d in (dict_a, dict_b, dict_c):
    result.update(d)

А можно с помощью «звёздочного» синтаксиса:

result = {**dict_a, **dict_b, **dict_c}

О звёздочном синтаксисе можно прочитать в нашей статье.

Задача 5

Найдите три ключа с самыми высокими значениями в словаре my_dict = {'a':500, 'b':5874, 'c': 560,'d':400, 'e':5874, 'f': 20}.

Вариант решения

Можно воспользоваться функцией sorted:

result = sorted(my_dict, key=my_dict.get, reverse=True)[:3]

Аналогичный результат можно получить с помощью функции nlargest из модуля heapq:

from heapq import nlargest
result = nlargest(3, my_dict, key=my_dict. get)

Читайте также: Всё о сортировке на Python

Задача 6

Напишите код, который переводит целое число в строку, при том что его можно применить в любой системе счисления.

Вариант решения

Второй аргумент функции int отвечает за указание основания системы счисления:

print(int('ABC', 16))

Задача 7

Нужно вывести первые n строк треугольника Паскаля. В этом треугольнике на вершине и по бокам стоят единицы, а каждое число внутри равно сумме двух расположенных над ним чисел.

Вариант решения

def pascal_triangle(n):
   row = [1]
   y = [0]
   for x in range(max(n, 0)):
      print(row)
      row = [left + right for left, right in zip(row + y, y + row)]
   
pascal_triangle(6) 

Задача 8

Напишите проверку на то, является ли строка палиндромом. Палиндром — это слово или фраза, которые одинаково читаются слева направо и справа налево.

Вариант решения

Тут всё просто, достаточно сравнить строку с её обратной версией, для чего можно использовать встроенную функцию reversed:

def is_palindrome(string):
    return string == ''. join(reversed(string))

print(is_palindrome('abba'))

Того же эффекта можно добиться с помощью срезов:

def is_palindrome(string):
    return string == string[::-1]

print(is_palindrome('abba'))

Задача 9

Сделайте так, чтобы число секунд отображалось в виде дни:часы:минуты:секунды.

Вариант решения

def convert(seconds):
    days = seconds // (24 * 3600)
    seconds %= 24 * 3600
    hours = seconds // 3600
    seconds %= 3600
    minutes = seconds // 60
    seconds %= 60
    print(f'{days}:{hours}:{minutes}:{seconds}')

convert(1234565)

Задача 10

Вы принимаете от пользователя последовательность чисел, разделённых запятой. Составьте список и кортеж с этими числами.

Вариант решения

values = input('Введите числа через запятую: ')
ints_as_strings = values.split(',')
ints = map(int, ints_as_strings)
lst = list(ints)
tup = tuple(lst)
print('Список:', lst)
print('Кортеж:', tup)

Задача 11

Выведите первый и последний элемент списка.

Вариант решения

lst = [1, 2, 3, 4, 5]
print(f'Первый: {lst[0]}; последний: {lst[-1]}')

Задача 12

Напишите программу, которая принимает имя файла и выводит его расширение. Если расширение у файла определить невозможно, выбросите исключение.

Вариант решения

def get_extension(filename):
    filename_parts = filename.split('.')
    if len(filename_parts) < 2:  # filename has no dots
        raise ValueError('the file has no extension')
    first, *middle, last = filename_parts
    if not last or not first and not middle:
        # example filenames: .filename, filename., file.name.
        raise ValueError('the file has no extension')
    return filename_parts[-1]

print(get_extension('abc.py'))
print(get_extension('abc'))  # raises ValueError
print(get_extension('.abc'))   # raises ValueError
print(get_extension('.abc.def.'))   # raises ValueError

Задача 13

При заданном целом числе n посчитайте n + nn + nnn.

Вариант решения

def solve(n):
    n1 = n
    n2 = int(str(n) * 2)
    n3 = int(str(n) * 3)
    print(n1 + n2 + n3)

solve(5)

Задача 14

Напишите программу, которая выводит чётные числа из заданного списка и останавливается, если встречает число 237.

Вариант решения

numbers = [    
    386, 462, 47, 418, 907, 344, 236, 375, 823, 566, 597, 978, 328, 615, 953, 345, 
    399, 162, 758, 219, 918, 237, 412, 566, 826, 248, 866, 950, 626, 949, 687, 217, 
]

for x in numbers:
    if x == 237:
        break
    elif x % 2 == 0:
        print(x)

Задача 15

Напишите программу, которая принимает два списка и выводит все элементы первого, которых нет во втором.

Вариант решения

set_1 = set(['White', 'Black', 'Red'])
set_2 = set(['Red', 'Green'])

print(set_1 - set_2)

Задача 16

Выведите список файлов в указанной директории.

Вариант решения

from os import listdir
from os.path import isfile, join
files = [f for f in listdir('/home') if isfile(join('/home', f))]
print(files)

Задача 17

Сложите цифры целого числа.

Вариант решения

def sum_digits(num):
    digits = [int(d) for d in str(num)]
    return sum(digits)

print(sum_digits(5245))

Задача 18

Посчитайте, сколько раз символ встречается в строке.

Вариант решения

string = 'Python Software Foundation'
string.count('o')

Задача 19

Поменяйте значения переменных местами.

Вариант решения

Можно написать монструозную конструкцию в стиле языка C:

x = 5
y = 10
temp = x
x = y
y = temp

Но в Python есть более удобный способ для решения этой задачи:

x = 5
y = 10
x, y = y, x

Задача 20

С помощью анонимной функции извлеките из списка числа, делимые на 15.

Вариант решения

nums = [45, 55, 60, 37, 100, 105, 220]
result = list(filter(lambda x: not x % 15, nums))

Задача 21

Нужно проверить, все ли числа в последовательности уникальны.

Вариант решения

def all_unique(numbers):
    return len(numbers) == len(set(numbers))

Задача 22

Напишите программу, которая принимает текст и выводит два слова: наиболее часто встречающееся и самое длинное.

Вариант решения

import collections

text = 'lorem ipsum dolor sit amet amet amet'
words = text.split()
counter = collections.Counter(words)
most_common, occurrences = counter.most_common()[0]

longest = max(words, key=len)

print(most_common, longest)

Хотите вырасти от новичка до профессионала? Факультет Python-разработки GeekUniversity даёт год опыта для вашего резюме. Обучайтесь на практических заданиях, по-настоящему освойте Python и станьте ближе к профессии мечты.

Узнать больше

Требования к Windows 11 — What’s new in Windows

Twitter LinkedIn Facebook Адрес электронной почты

• Статья
• 03/18/2023

Область применения

• Windows 11

В этой статье перечислены системные требования для Windows 11. Windows 11 также поддерживается на виртуальных машинах (ВМ).

Требования к оборудованию

Для установки или обновления до Windows 11 устройства должны соответствовать следующим минимальным требованиям к оборудованию:

• Процессор: 1 гигагерц (ГГц) или быстрее с двумя или более ядрами на совместимом 64-разрядном процессоре или системе на микросхеме (SoC).

• Память: 4 гигабайта (ГБ) или больше.

• Хранилище: 64 ГБ или больше свободного места на диске.

  Примечание.

  Со временем для обновлений может потребоваться больше требований к хранилищу, а также для включения определенных функций в ОС. Дополнительные сведения см. в статье Спецификации Windows 11.

• Графический карта: совместим с DirectX 12 или более поздней версии с драйвером WDDM 2.0.

• Встроенное ПО системы: UEFI, с поддержкой безопасной загрузки.

• TPM: доверенный платформенный модуль (TPM) версии 2. 0.

• Дисплей: дисплей с высоким разрешением (720p), монитор с разрешением 9 дюймов или более, 8 бит на цветовый канал.

• Подключение к Интернету. Подключение к Интернету необходимо для выполнения обновлений, а также для скачивания и использования некоторых функций.

  • Windows 11 Домашняя выпуск требует подключения к Интернету и учетной записи Майкрософт для завершения настройки устройства при первом использовании.

Дополнительные сведения см. в следующей записи блога программы предварительной оценки Windows: Обновление Windows 11 минимальных системных требований.

Дополнительные сведения о средствах оценки готовности см. в разделе Определение допустимости.

Требования к ОС

Подходящие устройства с Windows 10 должны использовать версию 2004 или более позднюю и содержать установленное обновление для системы безопасности от 14 сентября 2021 г. или более позднее, чтобы сразу перейти на Windows 11.

Примечание.

• S-режим поддерживается только в выпуске Windows 11 Домашняя.
• Если вы используете другой выпуск Windows в S-режиме, перед обновлением до Windows 11 сначала переключитесь из S-режима.
• Для переключения устройства из Windows 10 в S-режиме также требуется подключение к Интернету. При выходе из S-режима вы не сможете вернуться в S-режим позже.

Требования в зависимости от функций

Некоторые функции в Windows 11 имеют требования, превышающие минимальные требования к оборудованию.

• Поддержка 5G: требуется модем с поддержкой 5G.
• Автоматический HDR: требуется HDR-монитор.
• BitLocker to Go: требуется USB-накопитель. Эта функция доступна в выпусках Windows Профессиональный и выше.
• Клиент Hyper-V: требуется процессор с возможностями перевода адресов второго уровня (SLAT). Эта функция доступна в выпусках Windows Pro и более поздней версии.
• Кортана: требуется микрофон и динамики. В настоящее время доступна в Windows 11 для Австралии, Бразилии, Канады, Китая, Франции, Германии, Индии, Италии, Японии, Мексики, Испании, Соединенного Королевства и США.
• DirectStorage: требуется SSD с NVMe для хранения и запуска игр, который используют стандартный драйвер контроллера NVM Express, а также графический процессор с DirectX12 и поддержкой модели тендера 6.0.
• DirectX 12 Ultimate: доступно с поддерживаемыми играми и графическими микросхемами.
• Присутствие: требуется датчик, который может обнаруживать расстояние от человека от устройства или намерение взаимодействовать с устройством.
• Интеллектуальная видеоконференция: требуется видеокамера, микрофон и динамик (аудиовыпуск).
• Несколько голосовых помощников: требуется микрофон и динамик.
• Прикрепление: для раскладок из трех столбцов требуется экран шириной 1920 эффективных пикселей или больше.
• Отключить и включение звука: при использовании на панели задач требуется видеокамера, микрофон и динамик (аудиовывод). Приложение должно быть совместимо с функцией, чтобы включить глобальное отключение или включение звука.
• Пространственный звук: требуется поддерживающее функцию оборудование и программное обеспечение.
• Microsoft Teams: требуется видеокамера, микрофон и динамик (аудиовыход).
• Прикосновения: требуется экран или монитор, поддерживающий мультисенсорную технологию.
• Двухфакторная проверка подлинности: требуется использовать PIN-код, биометрию (сканер отпечатков пальцев или инфракрасную камеру) или телефон с поддержкой Wi-Fi или Bluetooth.
• Голосовой набор: требуется компьютер с микрофоном.
• Пробуждение по голосу: требуется модель питания «Современный режим ожидания» и микрофон в режиме ожидания.
• Wi-Fi 6E: требуется новое оборудование и драйвер WLAN IHV, а также точка доступа/маршрутизатор с функцией Wi-Fi 6E.
• Windows Hello: требуется камера, настроенная для создания инфракрасных изображений, или сканер отпечатков пальцев для биометрической проверки подлинности. Устройства без биометрических датчиков могут использовать Windows Hello с ПИН-кодом или переносным ключом безопасности, совместимым с продуктами Майкрософт. Дополнительные сведения см. в статье «ИТ-средства поддержки Windows 10 версии 21h2».
• Windows Projection: требуется видеоадаптер, который поддерживает модель драйверов дисплея Windows (WDDM) версии 2.0, а также адаптер Wi-Fi с поддержкой Wi-Fi Direct.
• Приложение Xbox: требуется учетная запись Xbox Live, доступная не во всех регионах. Перейдите на страницу «Страны и регионы Xbox Live», чтобы получить самую актуальную информацию о доступности. Для некоторых функций в приложении Xbox требуется активная подписка Xbox Game Pass .

Поддержка виртуальных машин

Для конфигурации всех виртуальных машин с Windows 11 действуют следующие требования:

• Поколение: 2

  Примечание.

  Существующие виртуальные машины 1-го поколения невозможно обновить на месте до Windows 11.

• Хранилище: 64 ГБ или больше места на диске.

• Безопасность:

• Память: 4 ГБ или больше.

• Процессор: два или более виртуальных процессоров.

  • Процессор узла виртуальной машины также должен соответствовать Windows 11 требованиям к процессору.

    Примечание.

    В некоторых случаях это требование к узлу виртуальной машины не применяется. Дополнительные сведения см. в разделе Параметры использования Windows 11 на компьютерах Mac.

  • Процедуры настройки необходимых параметров ВМ зависят от типа главного компьютера ВМ. Например, в BIOS должны быть включены узлы виртуальных машин под управлением Hyper-V, виртуализация (VT-x, VT-d). Виртуальный доверенный платформенный модуль (TPM) версии 2.0 эмулируется в гостевой ВМ вне зависимости от наличия и версии доверенного платформенного модуля в главном компьютере Hyper-V.

Дальнейшие действия

• Планирование Windows 11
• Подготовка к Windows 11

См. также

• Минимальные требования к оборудованию Windows
• Обзор новых возможностей Windows 11

элементарная теория множеств — Найдите область определения и область значений функции $f(x) = |x-1|$

спросил 3 года, 1 месяц назад

Изменено 3 года, 1 месяц назад

Просмотрено 1к раз

$\begingroup$

Я нашел домен $f$, который оказался $R$ (множество всех действительных чисел)

Но как найти диапазон функции?

• функции
• теория элементарных множеств

$\endgroup$

5

$\begingroup$

Вы видите, для каких значений $y$ уравнение $\lvert x-1\rvert=y$ имеет решение. Ясно, что она не имеет решения, если $y<0$. Если $y=0$, то она имеет одно решение: $x=1$. В противном случае их два: $y+1$ и $-y+1$.

Следовательно, диапазон равен $[0,\infty)$.

$\endgroup$

1

$\begingroup$

По определению абсолютного значения

$$|x-1|\ge0.$$ На данном этапе можно сказать, что $\text{range}(f)\subseteq\mathbb R_{\ge0}$, но не более того.

Теперь уравнение $$y=|x-1|$$ имеет хотя бы одно решение для каждого $y\ge0$, например $x=y+1$ (правда, что $y=|y+ 1-1|$, а $y+1$ всегда определено). Следовательно, диапазон действительно

$$\mathbb R_{\ge0}.$$

$\endgroup$

3

$\begingroup$

Домен не определен, так как символ $|\cdot|$ применяется к нескольким объектам. Это только набор действительных чисел, если $x$ предполагается действительным. В противном случае $x$ мог бы быть, например, некоторым бесконечномерным вектором.

Если вы установите $y=|x-1|,$, то увидите, что $y$ должно быть неотрицательным. Другими словами, диапазон содержится в наборе всех неотрицательных действительных чисел. Наконец, обратите внимание, что $y$ может стать сколь угодно большим, а также обращается в нуль (когда $x=1$), так что диапазон действительно представляет собой множество всех неотрицательных действительных чисел, поскольку функция непрерывна.

$\endgroup$

$\begingroup$

Как правило, мы знаем, что вычитание любого числа $k$ из входных данных функции приводит к смещению вправо по горизонтали на $k$ единиц.

Так, в частности, вычитание $1$ из входных данных функции $f(x)= |x|$ приводит к горизонтальному сдвигу этой функции (точнее, ее графика) вправо на $1$ единицу.

Тогда $g(x)= f(x-1)= |x-1|$ есть, так сказать, функция абсолютного значения, сдвинутая вправо на $1$ единицу.

Функция $g$ принимает на вход любое значение $x\in \mathbb R$ такое, что $(x-1)$ является возможным входом функции $f$, то есть такое, что $(x-1) $ принадлежит $\mathbb R$; для функции $f(x)=|x|$ определена на $\mathbb R$. Но $(x-1)$ принадлежит $\mathbb R$ для любого значения $x$. Итак, домен $\mathbb R$.

Поскольку смещение происходит только по горизонтали, а не по вертикали, диапазон не меняется: область определения функции $g$ совпадает с областью определения функции $f$, а именно положительная часть оси Y (точка $ (0,0)$ включено) или $\mathbb R_{+}$.

$\endgroup$

Функции: Домен, домен на диапазоне…🎶

Функции и отношения

Purplemath

Вернемся к теме доменов и диапазонов.

При первом знакомстве с функциями вам, вероятно, придется иметь дело с некоторыми упрощенными «функциями» и отношениями, обычно представляющими собой просто наборы точек. Это не будут очень полезные или интересные функции и отношения, но ваш текст хочет, чтобы вы получили представление о домене и диапазоне функции.

Содержание продолжается ниже

MathHelp.com

Домен и диапазон

Что такое домен и диапазон?

Область определения отношения (а значит, и функции) — это набор допустимых входных данных; это все значения x в точках ( x , y ), определяемые отношением. Диапазон отношения (и, следовательно, также функции) — это набор результирующих выходов; это все значения y в ( x , y ) точек, определяемых соотношением.

Есть ли музыкальный способ запомнить, где домен, а где диапазон?

Есть старая ковбойская песня, в которой начинается припев: «Домой, домом на пастбище / Где играют олени и антилопы»; вы, вероятно, слышите это в своей голове прямо сейчас. Вместо этого пойте припев как «Домен, домен в диапазоне», и это поможет вам понять, что есть что.

Представьте, что вы живете в маленькой усадьбе посреди большого открытого пространства. Ваш дом — это ваш домен; это место, где вы начинаете свой день. Как только вы встанете, вы берете лошадь и направляетесь в широкое открытое пространство, являющееся пастбищами равнин. Домен — это место, где начинаются отношения; диапазон, где он идет на работу.

(Эй, музыкальная штука может быть глупой, но она работает для некоторых из нас, хорошо?)

Небольшие наборы, содержащие всего несколько точек, обычно представляют собой самые простые виды отношений, поэтому ваша книга начинается с них.

Какой пример нахождения домена и диапазона набора точек?

{(2, −3), (4, 6), (3, −1), (6, 6), (2, 3)}

Приведенный выше список точек, являющийся отношением между определенными x и определенными и , это отношение. Домен — это все значения x , а диапазон — все значения y . Чтобы указать домен и диапазон, я просто перечисляю значения без дублирования:

домен: {2, 3, 4, 6}

диапазон: {−3, −1, 3, 6}

(обычно чтобы перечислить эти значения в числовом порядке, но требуется , а не . Наборы по определению являются *неупорядоченными* списками, поэтому вы можете перечислять числа в любом порядке, который вам нравится. нормально в наборах, но большинство инструкторов за это зачтут.)

Хотя данный набор точек действительно представляет отношение (поскольку x и y связаны друг с другом), набор, который мне дали, содержит две точки с одинаковыми x -значение: (2, −3) и (2, 3). Поскольку x  = 2 дает мне два возможных места назначения (то есть два возможных значения y ), то это отношение не может быть функцией.

И когда отношение, которое они мне дали, представляет собой набор точек, все, что мне нужно сделать, это проверить точки’ x — значения; если какое-либо x появляется более одного раза, то отношение не является функцией. Это отношение повторяется, так что оно есть:

не функция

Обратите внимание, что все, что мне нужно было сделать, чтобы проверить, является ли отношение функцией, это найти повторяющиеся значения x . Если вы найдете повторяющиеся значения x , то разные значения y означают, что у вас нет функции. Помните: чтобы отношение было функцией, каждое значение x должно соответствовать единице, и только одно значение , и .

{(-3, 5), (-2, 5), (-1, 5), (0, 5), (1, 5), (2, 5)}

Все, что мне нужно сделать для части домена и диапазона в этом упражнении, это перечислить значения x для домена и значения y для диапазона. Я не забываю использовать набор фигурных скобок для каждого:

домен: {−3, −2, −1, 0, 1, 2}

диапазон: {5}

Это еще один пример «скучного» как и в примере на предыдущей странице: каждые последние 9Значение 0091 x соответствует точно такому же значению y . Но каждое значение x отличается, поэтому, хотя и скучно,

это отношение действительно является функцией.

На самом деле эти точки лежат на горизонтальной линии y  = 5. «. Таким образом, диапазон также может быть указан как «одиночка из 5»

Есть еще один случай нахождения домена и диапазона функций. Вам дадут функцию и попросят найти домен (а может и диапазон тоже). На данном этапе вашей математической карьеры я видел (или даже могу думать) только о двух вещах, которые вам придется проверить, чтобы определить область определения функции, которую они вам дадут, и эти две вещи — знаменатели и квадратные корни.

Какой пример нахождения области определения и области значений рациональной функции?

Домен — это все значения, которые разрешено принимать x . Единственная проблема, с которой я столкнулся с этой функцией, заключается в том, что мне нужно быть осторожным, чтобы не делить на ноль. Таким образом, единственные значения, которые x не могут принимать, это те, которые вызвали бы деление на ноль. Поэтому я приравняю знаменатель к нулю и решу; мой домен будет всем остальным.

х ² − х — 2 = 0

( х — 2)( х + 1) = 0

х = 2 или х = -1

Диапазон немного сложнее, поэтому его могут и не попросить. В общем, однако, они захотят, чтобы вы построили график функции и нашли диапазон по картинке. В данном случае:

Как видно из моего рисунка, график «покрывает» все и -значения; то есть график будет идти так низко, как мне нравится, и также будет идти так высоко, как мне нравится. Для любой точки на и -оси, неважно, высоко вверх или низко, я могу пойти от этой точки вправо или влево и, в конце концов, пересечу график. Так как график в конечном итоге покроет все возможные значения y , то:

диапазон «все действительные числа».

Домен — это все значения, которые может принимать x . Единственная проблема, с которой я столкнулся с этой функцией, заключается в том, что у меня не может быть отрицательного значения внутри квадратного корня. Так что я установлю внутренности больше или равные нулю и решу. В результате будет мой домен:

−2 x + 3 ≥ 0
−2 x ≥ −3
2 х ≤ 3
x ≤ 3/2 = 1,5

Тогда домен «все x ≤ 3/2».

Для диапазона требуется график. Мне нужно быть осторожным при графическом отображении радикалов:

График начинается с y = 0 и идет вниз (направляясь влево) оттуда. Хотя график идет вниз очень медленно, я знаю, что, в конце концов, я могу опуститься так низко, как захочу (выбрав x , что достаточно много). Кроме того, из моего опыта построения графиков я знаю, что график никогда не начнет восстанавливаться. Тогда:

диапазон «все y ≤ 0″.

Это обычный многочлен. Здесь нет знаменателей (поэтому нет проблем с делением на ноль) и радикалов (поэтому нет проблем с извлечением квадратного корня из отрицательного). С многочленом проблем нет. Нет значений, которые я не могу использовать для х . Когда у меня есть многочлен, ответ для домена всегда :

домен «все x ».

Диапазон будет варьироваться от многочлена к многочлену, и они, вероятно, даже не спросят, но когда они это сделают, я смотрю на картинку:

График идет только до y = 4, но это будет так низко, как я хочу.

вычислить корень из 6+2 корня из 5

Кто не видел белого медведя? В зоопарках он – обычный гость. Нет нужды описывать, каков он на вид. Напомним лишь, что у него только нос черный, сам медведь белый и зимой, и летом (а не как, скажем, песец или заяц-беляк – те лишь зимой белые). Подошвы лап у белого медведя густой шерстью поросли, а пальцы примерно на половину своей длины соединены плавательными перепонками. 

Плавают и ныряют белые медведи отлично. Две минуты могут пробыть под водой, но погружаются в нее редко глубже двух метров. Далеко в открытом море не раз видели белых медведей, даже медведиц с медвежатами. Плывут со скоростью 5 километров в час, не беспокоясь, что ни земли, ни льдов нигде вблизи не видно.

Белый медведь и тюленей ловит не только на льду, украдкой к ним подползая. Обычный его прием, так сказать, атаки с моря такой: поблизости от лежбищ тюленей медведь осторожно, без плеска и шума, сползает в воду, плывет туда, где заметил тюленей. Затем он бесшумно ныряет и выныривает уже у самого лежбища, быстро карабкается на лед, отрезая тем самым тюленям путь к спасительной воде. По отвесным ледяным стенам медведь может прямо из воды выпрыгнуть на льдину, даже если высота ее над водой два метра.

Тюлени – главная охотничья добыча белого медведя весной. За год ловит и съедает он примерно 50 тюленей. Летом меню его более разнообразно. Ловит он рыбу на мелкой воде, на берегу – леммингов, песцов, лакомится яйцами птиц. Когда голоден, ест ягоды, водоросли, мхи, лишайник, грибы.

Белый медведь – самый могучий из сухопутных хищных зверей. Лев и тигр в сравнении с ним легковесы: средний вес медведиц 310 килограммов, медведей-самцов – 420 килограммов. Если медведь матерый и хорошо упитанный, то он может весить целую тонну!

Акимушкин И.И. Мир животных: Млекопитающие, или звери. – М., 1988 г

IV. Тест по русскому языку

1. В тексте про белых медведей больше всего предложений:

а) повествовательных; б) вопросительных

2. Восклицательное предложение находится: 

а) в начале текста; б) в конце текста

3. Вопросительное предложение находится 

а) в начале текста; б) в конце текста

4. Выпиши из второй части текста (из второго абзаца) первое предложение. Разбери его по членам предложения. Что ты можешь сказать о сказуемых? Они являются

а) родственными словами; б) однородными членами предложения 

5. Что можно сказать о глаголах, которыми выражены сказуемые? Эти глаголы:

а) I спряжения; б) II спряжения

6. Эти глаголы стоят в форме:

а) настоящего времени; б) будущего времени; в) прошедшего времени

7. Эти глаголы стоят в форме:

а) единственного числа; б) множественного числа

8. Эти глаголы стоят в форме:

а) 1-го лица;     б) 2-го лица;  в) 3-го лица;    г)нельзя определить лицо

9. Эти глаголы стоят в форме:

а) ж.р.; б) м.р.; в) ср.р.; г) нельзя определить род

10. Найди во второй части текста (во втором абзаце) все слова, которые являются родственными существительному, являющемуся подлежащим в первом предложении. Запиши их столбиком, поставив в начальную форму. У тебя получилось:

а) два слова; б) три слова  

11. Найди во второй части текста (во втором абзаце) другую форму слова, которое является подлежащим в первом предложении. Выпиши такое словосочетание с формой этого слова, из которого можно определить его падеж. Этот падеж: 

а) Р.п.; б) В.п.

• Курс
  • NCERT
    • Класс 12
    • Класс 11
    • Класс 10
    • Класс 9
    • Класс 8
    • Класс 7
    • Класс 6
  • IIT JEE

• Экзамен
  • JEE MAINS
  • JEE ADVANCED
  • X BOARDS
  • XII BOARDS
  • NEET
    • Neet Предыдущий год (по годам)
    • Физика Предыдущий год
    • Химия Предыдущий год
    • Биология Предыдущий год
    • Новый Все образцы работ
    • Образцы работ по биологии
    • Образцы работ по физике
    • Образцы работ по химии

• Загрузить PDF-файлы
  • Класс 12
  • Класс 11
  • Класс 10
  • Класс 9
  • Класс 8
  • Класс 7
  • Класс 6

• Экзаменационный уголок

• Онлайн класс
9 0925
• Викторина
• Задать вопрос в Whatsapp
• Поиск Doubtnut
• Английский словарь
9 0907 Toppers Talk
• Блог
• Скачать
• Получить приложение

Вопрос

Обновлено:26/04/2023

MTG IIT JEE FOUNDATION-КУБЫ И КУБИЧЕСКИЕ КОРНИ-Олимпиада/HOTS Corner

20 видео

РЕКЛАМА

Text Solution 9(log_(3)3)(sqrt((4+2sqrt(3)))-sqrt(4-2sqrt(3))) упрощается до

121783190

02:07

Упрощение:
(2+√ 3)6+(2−√3)6

234802262

04:07

সরল করো: 3√2√3+√6−4√3√6+√2+√6 √2+√3

5813

07:46

सरल कीजिए — 9√8÷9√6

643081922

01 :02

सरल करें : 6√12÷√33√2

643081923

04:25

Упростить: 7√48−√27−√3

643159102

03:31

(i) Упростить (223−2−23)(243+1+2−43)
(ii) [(6√7)2+(6√7)−2][(6√ 7)4−1+(6√7)−4]

645950539

06:18

Упрощенное значение 8 для [15-6+ ( 27-3) + 6-4] равно:

6466

02:50

Упрощенное значение 8 равно 15+ 6+ (27-3) + 6 + 4)

6467

02:15

Упрощенное значение 3√2√ 3+√6− 4√3√6+√2+√6√3+√2 равно

646927572

03:49

Наибольшее из √2, 3√3, 6√6, 5√5 равно

646927851

02:59

Какое из следующих чисел является самым большим?
√2,3√3,4√4,6√6

646927853

02:05

Наибольшее из
√2, 6√3, 3√4, 4√5 равно 9102 7

646927856

01 :08

Наибольшее из √3, 3√4, 4√6 и 6√8 равно

646927857

02:27

РЕКЛАМА

• MTG IIT JEE FOUNDATION-КУБЫ И КУБИЧЕСКИЕ КОРНИ-Олимпиада/ ГОРЯЧИЕ уголки

• 9(2)

  02:25

• На какое наименьшее число нужно умножить 3600, чтобы получить полный куб. ..

  01:39

• 25/(0,00005329))- root3(sqrt0.000064) is

  02:41

• Оценка: root3(-0.000008/(-0.000216))

  01:05

9090 7

Оценка: root3(0.008)-root3(-512) + root3(2.197)

01:40

• (3root3(13824))/(2root3(-15625))+(2root3(-13824))/root3(5832)=

  02:26

• Кубический корень числа при делении на наименьшее простое число дает …

  01:19

• его…

  01:25

• Что из перечисленного неверно?

  03:41

• root(3)(1- 127/343) के बराबर है?

  00:40

• Если root3(x/729)+root3((8x)/729)+root3((27x)/5832)=1 , то найти va… 9(n) — совершенный куб, n в N, тогда значение …

  03:15

• , если x=root3(2(93)/125), то значение x равно

  01: 14

• если sqrtroot3(x xx 0.000009)=0.3 , то значение sqrtx равно

  01:40

• root3(1.728)/root3(13.

Алгебра Первообразная

Материалы к уроку

Конспект урока

Первообразная

Остались вопросы по теме? Наши педагоги готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать педагогаОставить заявку на подбор

Мэтуэй | Популярные задачи

Математическая сцена — Производные, урок 5

Урок 5

Цепное правило

Пример 1

Дифференцировать f(x) = (х ³ +1) ² .

Единственный способ, который у нас есть делать это до сих пор, сначала умножая скобки, а затем дифференциация. Если мы сделаем это, мы получим

f(x) = x ⁶ + 2x ³ +1 и, следовательно, f(x) = 6x ⁵ +6x ² .

Это не проблема с простой пример, такой как приведенный выше, но что произойдет, если у нас, например, f(x) = (x ³ +1) ⁶ ?
В этом случае требуется слишком много усилий, чтобы умножить скобки перед дифференциация.

Чтобы различать составные функции, подобные этой, мы используем так называемое цепное правило. Делаем пример 1 еще раз, чтобы увидеть, как это работает.

f(x) является примером составная функция, представленная в функциях 2.
Его можно записать как f(u) = u ² , где u = x ³ +1, ты функция от x, то есть u(x) = x ³ +1.

Цепное правило гласит, что мы сначала продифференцируем f(u) относительно u как переменной и получим f(u) = 2u (точно так же, как (x ² ) = 2x)
Далее дифференцируем u и получаем u(x) = 3x ² . Наконец, мы умножаем два результата вместе и получите
е (х) = 2u3x ² . Возвращая значение u, получаем f(x) =2 ( х ³ +1)3х ² = 6x ⁵ +6x ²

^{Это дает нам правило называемое Цепным правилом, которое гласит, что}

Мы только указали правило здесь, но его легко доказать для всех непрерывных дифференцируемых функции.

Пример 2

Дифференцировать композит функция f(x) = sin ² х.

Обозначение грех ² х другой способ записи (sin x) ² так что квадрат — это внешняя функция, а sin x — внутренняя функция. Начать с мы разделим это на две части, но с практикой этого не будет необходимый.

ф(х) = (sin x) ² можно записать как f(u) = и ² где и = грех х.

 f(u) = 2u  и u= cos x , так что умножение вместе получаем

   f(x) = 2ucos x = 2 sin x cos x

Цепное правило гласит, что для дифференцируем составную функцию, мы дифференцируем внешнюю функцию и умножить на производную внутренней функции.

Пример 2 +

Дифференцируем f(x) = sin x ² . Это можно записать как f(u) = sin u, где ты = х ²

Таким образом, в этом случае синус является внешней функцией и квадрат является внутренним функция

   f(x) = cos x ² 2x

Пример 3

Мы можем использовать правила cos x = sin (/ ₂ x) и sin x = cos(/ ₂ x), чтобы найти производную от cos x.

cos x = f(x) = sin (/ ₂ x)

Производная синуса, внешняя функция является cos и производной от (/ ₂ x), внутренняя функция равна 1, поэтому мы получаем

   ф(х) = cos(/ ₂ х)(1)

= грех х (1)

= грех х

Пример 4

Найдите производную f(x) = sin ² x ² .

Это можно записать как f(x) = (sin x ² ) ² Итак, у нас есть тройная составная функция. Самая внешняя функция является квадратичной, затем синус и, наконец, еще один квадратичный.

Мы можем написать f = u ² , где u = sinv и v = х ² . Различение каждой функции и умножение дает нам 2 u cos v 2x, и сложив обратно значения u и v, получим результат:

Пример 5

Теперь мы хотим найти правило для дифференциации f(x) = lnx.

Мы используем метод под названием неявное дифференцирование , что означает дифференциацию обеих сторон уравнение.

Если f(x) = ln x, то e ^f(x) = х. Если мы продифференцируем обе части уравнения, мы получим следующее;

   e ^f(x) = х

   e ^f(x) ф(х) = 1 Использование цепного правила.

Решая f(x), мы получаем

   f(x) = 1/e ^f(x)

          = 1/x Помните, что x = e ^f(x) .

Теперь мы можем найти производную от другого логарифмические функции.

Найдите производную f(x) = log x.

Сначала мы должны напомнить себе о правила логарифмирования и соотношение между логарифмами с разным основанием. Этот нужное нам правило:

Таким образом, мы можем переписать любой логарифм как натуральный логарифм, ln x.

Логарифм ln 10 является константой, которая не влияет на производная, остальное просто.

Аналогичные расчеты работают для любой функции журнала, поэтому мы можем обобщить следующие три правила:

Пример 6

Дифференцируем f(x) = ln(x ² + 1).

Карточки «Сложение и вычитание в пределах 20» | Учебно-методическое пособие по математике (1 класс) на тему:

Опубликовано 30.03.2015 — 16:36 — Матвеева Анжелика Леонтьевна

Материал предназначен для отработки навыков сложения и вычитания в пределах 20.

Скачать:

Предварительный просмотр:

Сложение  и  вычитание  в  пределах  20.

Предварительный просмотр:

СЛОЖЕНИЕ  И  ВЫЧИТАНИЕ  В  ПРЕДЕЛАХ  20

По теме: методические разработки, презентации и конспекты

Урок математики в 1 классе на тему Закрепление случаев сложения и вычитания в пределах десяти.

ЦЕЛЬ: способствовать актуализации и закреплению полученных на предыдущих уроках знаний, упражнять в навыках счета. Задачи образовательные: 1. Закрепить и обобщить изученные приёмы сложения и вычита…

Урок математики в 1 классе на тему «Таблица сложения и вычитания в пределах 20. Состав чисел в пределах 10. Закрепление»

Урок  математики в 1 классе  на тему «Таблица сложения и вычитания в пределах 20. Состав чисел в пределах 10. Закрепление»…

Конспект урока по математике «Повторение пройденного. Нумерация чисел в пределах 100. Сложение и вычитание в пределах 100 »

Конспект урока по математике 2-й класс…

Урок по математике в 1 классе. Сложение и вычитание в пределах 10.Тема: «Счёт в пределах 10. Закрепление»

Данный урок был проведён по программе Школа России, на основе авторской программы М. И. Моро, М. А. Бантова » Математика 1 класс». Тип урока:Закрепление полученных знаний. Форма урока: Урок- путешеств. ..

Математические раскраски – сложение и вычитание с переходом через десяток, сложение и вычитание в пределах 100, таблица умножения и деления.

Математические раскраски – сложение и вычитание с переходом через десяток, сложение и вычитание в пределах 100, таблица умножения и деления….

Урок математики 1 класс по теме «Закрепление изученного. Решение текстовых задач, примеров на сложение и вычитание в пределах 10, сравнение чисел в пределах 10»

Учащиеся учатся решать задачи изученных видов; решать примеры на сложение и вычитание чисел 1,2,3; принимать и сохранять цели и задачи учебной деятельности; находить средства и способы её осуществлени…

Урок математики по теме:»Закрепление изученного по теме «Сложение однозначных чисел с переходом через разряд и соответствующие случаи вычитания (таблица сложения и вычитания в пределах 20)»

Закрепить знания о приеме сложения однозначных чисел с переходом через разряд…

Карточки для самостоятельной отработки вычислительных навыков на сложение и вычитание в пределах 20 с переходом через десяток (2 класс) | Картотека по математике (2 класс):

Опубликовано 05. 11.2020 — 9:11 — Тихонова Анна Михайловна

Карточки предназначены для отработки устных вычислительных навыков в пределах 20 с переходом через десяток. Данные карточки можно использовать как для самостоятельной работы на уроках, так и для работы дома. 

Скачать:

Предварительный просмотр:

Карточки для самостоятельной отработки вычислительных навыков на сложение и вычитание в пределах 20 с переходом через десяток

(2 класс)

ФИ_________________________________________________

Карточка №1

ФИ__________________________________________________

Карточка №2

ФИ_________________________________________________

Карточка №3

ФИ_____________________________________________

Карточка №4

ФИ__________________________________________________

Карточка №5

ФИ___________________________________________

Карточка №6

ФИ__________________________________________________

Карточка №7

ФИ____________________________________________

Карточка №8

ФИ__________________________________________________

Карточка №9

ФИ___________________________________________

Карточка №10

По теме: методические разработки, презентации и конспекты

Открытый урок по математике во 2 классе по теме: » Сложение и вычитание двузначных чисел с переходом через десяток.

Конспект открытого урока по математике во 2 классе по теме: » Сложение и вычитание двузначных чисел с переходом через десяток. Составление и решение задач»….

Урок математики в 1 классе: Сложение и вычитание двузначных чисел с переходом через десяток

Цели урока: 1.Повтороить приемы сложения и вычитания двузначных чисел с переходом через десяток  ( устные и письменные ) 2.Повторить приемы сложения, опираясь на переместительный закон сложения…

Контрольная работа по математике для 2 класса (УМК «Начальная школа XXI века») по теме: «Сложение и вычитание двузначных чисел с переходом через десяток».

Контрольная работа по математике для 2 класса (УМК «Начальная школа XXI века» ) по теме: » Сложение и вычитание двузначных чисел с переходом через десяток»….

2 класс математика Тема: ПИСЬМЕННОЕ СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДВУЗНАЧНЫХ ЧИСЕЛ БЕЗ ПЕРЕХОДА ЧЕРЕЗ ДЕСЯТОК

2 класс математикаТема: ПИСЬМЕННОЕ СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДВУЗНАЧНЫХ ЧИСЕЛБЕЗ ПЕРЕХОДА ЧЕРЕЗ ДЕСЯТОК. ..

Урок математики.1 класс. УМК » Школа России». Сложение и вычитание однозначных чисел с переходом через десяток»

Конспект урока по данной теме….

Математика во 2 классе. Тема. Закрепление письменных приемов сложения и вычитания двузначных чисел с переходом через десяток (с. 44-45, часть 2)

УМК «Школа России»…

Конспект урока по математике для 1 класса по теме: «Сложение и вычитание однозначных чисел с переходом через десяток»

Конспект предназначен для учителей начальной школы, работающих по УМК «Школа России»….

Печатные карточки с вычитанием 0-20 с бесплатным PDF 2 Когда вы вычитаете 0 из любого числа, результатом является само число. И когда вы вычитаете число из числа, результирующее значение равно нулю. Если подобные идеи очаровывают вас, но в то же время смущают, вы можете получить передышку в наших PDF-файлах с карточками для вычитания.

Мы разработали эти карточки для печати, чтобы вы могли практиковать вычитание до тех пор, пока не достигнете неоспоримого мастерства. Загрузите и сохраните или распечатайте эти карточки, чтобы сделать час обучения вычитанию веселым.

Бесплатные печатные карточки с вычитанием 0-20 [PDF] Скачать

Карточки могут облегчить процесс усвоения операций вычитания. Легкость припоминания укрепляет уверенность среди начинающих учащихся и позволяет свободно овладеть концепцией извлечения значения из другого, большего заданного значения. Вот несколько хорошо изученных способов использования карточек для обучения вычитанию:

• Учебный материал: Это не сильно поможет, если вы решите баловать детей книгами и рабочими листами только для освоения вычитания. Дети очарованы альтернативами книгам. Карточки легко переключают внимание с традиционных на нетрадиционные методы обучения. Таким образом, вы можете создавать множество действий, таких как заполнение диаграмм числовых связей, мысленное вычитание и т. д., используя карточки для вычитания.
• Элемент набора А: Как насчет того, чтобы дать тест детям на тему вычитания с помощью карточек? Сначала вы демонстрируете метод вычитания начинающим математикам. Затем, в зависимости от целей обучения, вы можете повторить одно и то же и, в конце концов, попросить детей решить вопросы самостоятельно. Это лучшая стратегия для ознакомления детей с основными математическими операциями, такими как вычитание. .
• Материалы для домашнего задания: Наши карточки с вычитанием могут стать отличным подспорьем для домашних заданий. При переводе на домашнее обучение опекуны могут помочь детям в эффективном процессе обучения, предоставив им карточки в качестве учебного материала.
• Помощь в обучении в дороге: Мы разработали карточки с вычитанием, чтобы продемонстрировать идею технологий в образовании. Используя их, вы можете легко вовлечь детей в значимую деятельность, например, в изучение концепций, когда вы находитесь в поездке. Кроме того, если тест готов и вы хотите в последнюю минуту освежить в памяти концепцию вычитания, вы можете извлечь эти удобные для устройства PDF-файлы из папки загрузок и удовлетворить потребность в быстром обучении.

Вычитание Флэш-карточки, которые можно распечатать в формате PDF, могут дать несколько преимуществ, ориентированных на обучение. Исследователи и специалисты в области образования из различных университетов мира также одобрили эти преимущества. Например,

• Избавление от беспокойства по поводу математики: Лучшее преимущество заключается в том, что PDF для печати с вычитанием снижает беспокойство по поводу математики. Поскольку ученикам не нужно иметь дело с книгами, они чувствуют необходимость практиковать эту концепцию.
• Быстрое запоминание понятий: Карточки эффективны для поощрения быстрого запоминания понятий. Программа AGILE, проводимая в Университете штата Мэн, делает упор на использование этих . Эти учебные материалы заслужили такую ​​репутацию благодаря своей роли в эффективном усвоении концепции учащимися.
• Сделайте самообучение интересным : Карточки для печати для изучения вычитания сделают самообучение легкой прогулкой. Учащиеся могут иметь свою личную коллекцию этих карточек и оживить свой математический час. Кроме того, при групповом обучении они могут служить ресурсом для быстрой викторины и формировать основу для содержательных дискуссий.

Попробуйте наши печатные карточки в формате PDF для вычитания, чтобы освоить эти основы. Поскольку эти операции полезны для различных жизненных действий, вы можете рассматривать эти учебные материалы не иначе как набор для выживания при подготовке к будущим обязанностям. Как продвинутый ученик, вы также можете вернуться к вычитанию, решая данные вопросы в уме. Поделитесь с нами, как эти печатные формы для вычитания улучшили вашу кривую обучения и помогли вам справиться с трудностями в обучении.

1-10 Дополнительные карточки — Совы (вертикально)

PDF | 61 страницы | Оценки: 1–2

Набор карточек для сложения в пределах 20.

Используйте этот ресурс, когда учащиеся изучают факты сложения в пределах 20.

Распечатайте карточки на картоне и вырежьте их. Храните их в закрывающемся пакете, чтобы использовать снова и снова.

Учащиеся сопоставят числовое предложение с правильным ответом. Для учащихся, нуждающихся в дополнительной поддержке, позвольте им использовать счетчики для определения ответа.

Этот ресурс хорошо работает при использовании в качестве занятия в математическом центре.

• учебное пособие

  Математические графические органайзеры — рабочие коврики для печати

  Попрактикуйтесь в работе над определенными математическими понятиями с помощью нашего набора из 5 математических графических органайзеров для печати.

  5 страниц Оценка с 1 — 5

• учебный ресурс

  Fact Family Math Blast Off — сложение и вычитание

  Продемонстрируйте понимание семейств фактов сложения и вычитания с помощью увлекательного занятия по вырезанию и сортировке.

  2 страницы Оценка с 1 — 2 Дифференцированный

• учебный ресурс

  Предложения с целыми числами — Головоломка Тарсия

  Потренируйтесь решать сложение и вычитание числовых предложений с целыми числами с помощью распечатываемой головоломки Tarsia!

  2 страницы Оценка с 6 — 7

• учебный ресурс

  Путь отсутствующей части — найдите рабочий лист пропущенного номера

  Попрактикуйтесь в использовании различных стратегий вычитания в забавном математическом лабиринте.

  2 страницы Оценка с 2 — 3

• учебный ресурс

  Сложение и вычитание десятичных знаков – Домино

  Используйте эту игру в домино, чтобы развить вычислительные навыки, добавляя и вычитая десятичные дроби до тысячных.

  6 страниц Оценка с 5 — 6

• учебный ресурс

  Часть-Часть-Целое — Презентация для обучения сложению и вычитанию

  Научите своих учащихся, как эффективно использовать линейчатую модель для решения фактов сложения и вычитания однозначных чисел, используя стратегию часть-часть-целое.

  1 страница Оценка с K — 1

• учебный ресурс

  Сложение в числовом ряду — слайд-колода «Стратегия прыжков»

  Научите своих учеников складывать двузначные числа, используя стратегию прыжка, с помощью обучающей презентации.

  1 страница Оценка с 2 — 3

• учебный ресурс

  Двухшаговые словесные задачи на числовой строке — задание «Поместите значение»

  Различайте концепции разряда для учащихся 1-го и 2-го классов с помощью пары наборов карточек с двузначными числами и строками.

  16 страниц Оценка с 1 — 3 Дифференцированный

• учебный ресурс

  Сложение и вычитание на числовой прямой — Супергеройская математическая деятельность

  Проведите сложение и вычитание в числовой строке с захватывающей карточкой-задачей «Герой числовой строки».

  11 страниц Оценка с К — 1 Дифференцированный

• учебный ресурс

  Bunny Number Lines — Карточки с заданиями на сложение и вычитание

  Прыгайте по числовой строке вместе с пасхальным кроликом, чтобы попрактиковаться в сложении и вычитании в числовой строке.

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

онлайн-тренажер, распечатать фото в хорошем качестве с крупными цифрами

Для учеников 2 и 3 классов мы подготовили таблицу умножения, чтобы было проще освоить это математическое действие. Ее можно распечатать в хорошем качестве и использовать при подготовке домашнего задания

Анастасия Краснослободская Учитель начальных классов Анна Стрельцова Автор КП

Содержание

1. Распечатать
2. Вариант таблицы умножения с ответами
3. Вариант таблицы умножения без ответов
4. Вопросы и ответы

Впервые ребенок сталкивается с таблицей умножения в начальной школе. До ее изучения он должен знать цифры, уметь складывать и вычитать. Ведь важно понимать, как именно получаются результаты в математических действиях. Ребенку необходимо объяснить, что умножение тесно связано со сложением: если складываем одинаковые числа, можем заменить сложение умножением.

Есть множество техник освоения таблицы умножения. Одна из самых простых — распечатать готовые и учить результаты вычислений по ним. Сначала придется частенько подглядывать, но со временем таблица умножения будет отскакивать от зубов.

Распечатать варианты таблиц умножения до 20

Вы можете воспользоваться нашей таблицей и распечатать ее, чтобы вместе с ребенком учить таблицу умножения. На первых этапах она будет служить хорошей шпаргалкой, а чуть позже — тренажером.

это интересно

Как быстро выучить таблицу умножения

5 легких способов от учителя математики

Подробнее

Вариант таблицы умножения с ответами

Готовая таблица умножения с ответами будет особенно полезна в самом начале изучения этого математического действия. Ребенку будет гораздо легче ориентироваться в числах, если он периодически будет смотреть на таблицу. Позже она понадобится и для повторения изученного.

Таблица умножения от 1 до 10

Таблица умножения от 11 до 20

Скачать таблицу умножения с вариантами ответов

Вариант таблицы умножения без ответов

Распечатанную таблицу умножения без ответов удобно использовать для практики: в пустые ячейки можно записывать результаты, а потом проверить себя.

Таблица умножения от 1 до 10

Таблица умножения от 11 до 20

Скачать таблицу умножения с вариантами ответов

Популярные вопросы и ответы

Отвечает Анастасия Краснослободская, учитель начальных классов в Домашней школе «ИнтернетУрок».

Кто придумал таблицу умножения?

— Существует множество версий появления таблицы умножения, но чаще всего создание таблицы умножения приписывают древнегреческому математику Пифагору. Поэтому таблицу умножения иногда называют таблицей Пифагора.

Как выучить таблицу умножения с помощью квадрата Пифагора?

— Таблица умножения Пифагора представляет собой квадрат, на левой и верхней сторонах которого расположены числа от 1 до 10, а ячейки содержат результат их перемножения. Лучше начать с запоминания столбиков на 1, 2, 5 и 10, так как это наиболее легкие и простые части таблицы.

Способов запомнить таблицу очень много, но выделю наиболее популярные.

1) Прибавлять нужное количество раз нужное число (2+2+2+2+2=10)
2) Отталкиваться от примера на умножение с одинаковыми числами (5х5, 6х6 и т. д). Например, нужно посчитать пример из таблицы на 5. Ребенок помнит, что 5 умножить на 5 равно 25, и затем, двигаясь по таблице методом прибавления и отнимания числа 5, доходит до необходмого результата.
3) Применять свойство умножения «от перемены мест множителей, произведение не меняется» для таблиц на 6-9.
4) Придумать с ребенком небольшие стишки (запоминалки) для наиболее сложных моментов.
5) Использовать лайфхаки (например, быстрый способ запоминания таблицы умножения на 9 при помощи пальцев рук).

Когда изучают таблицу умножения в школе?

— В начальных классах разных школ обучение происходит по своей программе. Обычно изучение понятия умножения и составление таблицы приходится на середину — конец второго года обучения. К середине третьего класса ребенок точно должен знать таблицу умножения и использовать ее в решении примеров.

Таблица умножения (примеры на умножение и деление)

75,00 ₽

Примеры на умножение и деление вразброс. Можно сформировать карточки только на умножение, деление или смешанные примеры. Для детей, которые уже знают таблицу умножения. Без ответов. Для печати А4.

Количество товара Таблица умножения (примеры на умножение и деление)

Артикул: i-1443 Категория: Для учебы Метки: Таблица умножения, 2 класс

• Описание
• Детали
• Отзывы (0)

Описание

Таблица умножения (примеры на умножение и деление)  — программа, которая представляет собой тренажер для счета. С помощью генератора примеров можно создать и распечатать готовые примеры на умножение и деление вразброс для детей 1-2 класса. Причем, в зависимости от потребности, можно сформировать карточки только на умножение, деление или смешанные примеры.

Программа написана в Excel с помощью макросов. Формируется примеры: 6 столбиков по 40 примеров на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено.

Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.

Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.
Чтобы выучить таблицу умножения, можно скачать карточку с примерами для заучивания и проверки своих знаний.

Данную программу также можно скачать в составе сборника заданий для 2 класса.

Для того, чтобы выучить таблицу умножения на каждое число в отдельности, скачайте программу «Таблица умножения для изучения (умножение и деление на каждое число и вразброс)«.

Для того, чтобы решать примеры в excel (без печати) с автоматической проверкой ответов, скачайте программы «Тренажер на таблицу умножения» или «Таблица умножения для изучения (с автопроверкой)«.

Другие программы, которые помогут закрепить навыки счета:

• • Таблица умножения — карточки
  • Игра «Крестики-нолики» на таблицу умножения
  • Игра «Найди примеры» на таблицу умножения
  • Математический лабиринт (таблица умножения)
  • Умножение и деление по типам (табличное, внетабличное, круглых чисел)
  • Головоломка «Квадрат множителей»

 Также есть программы, в которых можно выбрать уровень сложности. В них можно начать с решения легких примеров, а затем перейти к более сложным.

На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Вам также будет интересно…

• Таблица умножения для изучения (с автопроверкой)

  100,00 ₽В корзину

• Игра «Крестики-нолики» (таблица умножения)

  70,00 ₽В корзину

• Игра «Найди примеры на таблицу умножения»

  70,00 ₽В корзину

• Тренажер на таблицу умножения

  80,00 ₽В корзину

• Умножение и деление по типам (табличное, внетабличное, круглых чисел)

  120,00 ₽В корзину

• Таблица умножения для изучения (умножение и деление на каждое число и вразброс)

  Оценка 5.00 из 5

  90,00 ₽В корзину

• Головоломка «Математический лабиринт (таблица умножения)»

  95,00 ₽В корзину

• Квадрат множителей

  Оценка 5. 00 из 5

  75,00 ₽В корзину

• Математический кроссворд 2 (все действия)

  105,00 ₽В корзину

Таблицы умножения и таблицы умножения [Бесплатно и для печати!]

Распечатанные таблицы умножения для изучения или преподавания таблицы умножения

У нас есть две таблицы умножения для вашего класса — одна для справки и один пустой шаблон для самостоятельного заполнения учащимися.

Загрузите их здесь!

• Таблица умножения 1-12
• Пустая таблица умножения

Учащиеся постоянно изучают новый и сложный материал по мере своего обучения.

В раннем возрасте они знакомятся с умножением — тем, что используется в повседневной жизни, от простых математических навыков при покупке продуктов до сложных расчетов в налоговых формах.

Простой способ научить учащихся умножению — использовать таблицу умножения, также известную как таблица умножения или таблица умножения. Эти таблицы помогают учащимся запомнить различные уравнения умножения, чтобы они могли быстро и точно находить ответы.

Эта статья дает вам доступ к бесплатным распечатываемым таблицам умножения для вашего класса. Мы также объясним лучшие способы преподавания таблицы умножения вашим ученикам и покажем вам различные игры на умножение, чтобы помочь им запомнить эти таблицы как факты умножения.

Освойте умножение с Prodigy Math

Раскройте преимущества игрового обучения, чтобы помочь вашему ребенку или ученику освоить умножение с Prodigy Math.

Посмотрите, как это работает

Что такое умножение?

Освоив счет и сложение, учащиеся приступают к умножению.

Лучший способ научить умножению — это сказать « групп по » вместо « умножить на ». Объясните учащимся, что при умножении получается суммирование групп  чисел.

3 × 4 становится 3 группами по 4.

Или

4 + 4 + 4 = 12

Умножение — это быстрый способ сложения групп чисел вместе. Этот метод мышления помогает ученикам понять, почему они умножают, и как это работает.

Мы рассмотрим таблицу умножения на 1-12 и покажем вам лучшие советы для обучения ваших учеников.

Изучение таблиц умножения, как вы увидите, может быть очень простым для учащихся начальной школы и старше.

Советы для таблицы умножения 1

Все, что умножается на единицу, остается этим числом. Эти уравнения всегда означают, что существует только одна группа чисел.

Советы по таблице умножения на 2

Все, что умножается на два, равно удвоенному . Студенты также могут представить это как сложение двух одинаковых чисел.

 6 × 2 равно 6 + 6. 

Как запомнить таблицу умножения 1-12

Советы по таблице 3 умножения

Три не имеют правил, облегчающих запоминание таблицы умножения, но есть закономерность для каждых десяти кратных трем:

 3, 6, 9, 12, 15, 18, 21, 24, 27 , 30 

Последняя цифра этих кратных всегда повторяется, что означает, что учащиеся могут запомнить эти цифры, чтобы помочь им с тремя таблицами умножения.

Взгляните на следующие десять чисел, кратных трем:

 33, 36, 39, 42, 45, 48, 51, 54, 57, 60 

Последние цифры в обеих группах одинаковы: 3, 6, 9, 2, 5, 8, 1, 4, 7, 0 .

Если учащиеся смогут запомнить этот порядок, они, по крайней мере, будут знать, какая последняя цифра любого умножения на три. Например, числа, оканчивающиеся на девять , умноженные на три , станут числом, оканчивающимся на семь .

 9 × 3 = 27 19 × 3 = 57 159 × 3 = 477 1 428 659 × 3 = 4 285 977 

Научите своих учеников схеме таблицы умножения трех, как если бы это был номер телефона, (369) 258-1470 .

Советы по таблице умножения на 4

Когда число умножается на четыре, удвойте его, а затем еще раз удвойте. Это не самый умный трюк, но он работает!

 8 × 4 становится 8 + 8 = 16 → 16 +16 = 32. 

Советы по таблице умножения на 5

Пятерка — одна из самых простых для освоения таблиц умножения. Объясните учащимся, что таблица пятикратного умножения всегда оканчивается следующим образом:

 5, 0, 5, 0, 5, 0... 

Нечетные числа, умноженные на пять, оканчиваются на пять, а четные числа умножаются на на пять закончится нулем.

Советы по таблице умножения на 6

При умножении четного числа на шесть решение всегда заканчивается последней цифрой умножаемого числа.

 2 × 6 = 12         74 × 6 = 444         216 × 6 = 1 296         1 238 × 6 = 7 428 

К сожалению, этот трюк работает только для четных чисел, а не  для нечетных чисел.

Советы по таблице умножения на 7

Мы можем использовать наши предыдущие советы, чтобы вычислить первые несколько кратных семи:

• Умножение семи на два равносильно удвоению семи — 14
• Три раза по семь получается число, оканчивающееся на единицу — 21
• Умножение семи на четыре равносильно удвоению его дважды — 28
• Умножение нечетного числа на пять даст решение, оканчивающееся на пять — 35

Но как насчет запоминания более поздних чисел, кратных семи?

Вот удобный трюк на семь умножить на восемь. Решение для семи умножить на восемь похоже на счет вверх:

 5-6-7-8 

 7 × 8 = 56 

Теперь у ваших учеников есть еще один трюк с памятью, который поможет им справиться с таблицей умножения на семь.

Советы для таблицы умножения на 8

Удвоить, удвоить и еще раз удвоить!

 8 × 8 = 64 

 8 + 8 = 16 → 16 + 16 = 32 → 32 + 32 = 64 

Советы по таблице умножения на 9 что может сделать их простыми.

Умножение на девять аналогично умножению на десять с последующим вычитанием другого числа:

 9 × 5 = 45 

Или

 (10 × 5) - 5 = 50 - 5 = 45 

Второй совет работает для первых десяти кратных девяти. Каждый раз, когда учащиеся увеличивают число, на которое умножается девять, столбец десятков решения увеличивается на единицу, а столбец единиц уменьшается на единицу.

Авторы и права: VIRALNOVA

 10 × 4 = 40
10 × 7 = 70
10 × 11 = 110
10 × 123 = 1 230 

 12 × 6 = ?
(10 × 6) + (2 × 6) = ?
60 + 12 = 72 

Материалы Данные о Ba3(PO4)2 по материалам проекта (набор данных)

Материалы Данные о Ba3(PO4)2 по материалам проекта (набор данных) | Исследователь данных Министерства энергетики США

• Набор данных
• Другие связанные исследования

Ba3(PO4)2 кристаллизуется в тригональной пространственной группе R-3m. Структура трехмерная. имеются два неэквивалентных сайта Ba2+. В первом узле Ba2+ Ba2+ связан в 10-координатной геометрии с десятью атомами O2-. Расстояния связи Ba–O варьируются в пределах 2,67–2,99 Å. Во второй позиции Ba2+ Ba2+ связан с двенадцатью атомами O2-, образуя искаженные кубооктаэдры BaO12, которые имеют общие ребра с шестью эквивалентными кубооктаэдрами BaO12 и ребра с шестью эквивалентными тетраэдрами PO4. Существует шесть более коротких (2,78 Å) и шесть более длинных (3,28 Å) длин связи Ba–O. P5+ связан с четырьмя атомами O2-, образуя тетраэдры PO4, которые имеют общие ребра с тремя эквивалентными кубооктаэдрами BaO12. Имеется одна более короткая (1,55 Å) и три более длинные (1,57 Å) длины связи P–O. Имеются два неэквивалентных O2-сайта. В первом положении O2- O2- связан в искаженной геометрии одинарной связи с четырьмя атомами Ba2+ и одним атомом P5+. Во втором положении O2- O2- связан в искаженной геометрии одинарной связи с четырьмя атомами Ba2+ и одним атомом P5+.

Авторов:

Проект материалов

Дата публикации:

15.07.2020

Другие номера:

мп-3857

Номер контракта с Министерством энергетики:  

АЦ02-05Ч21231; EDCBEE

Исследовательская организация:

Национальная лаборатория Лоуренса Беркли. (LBNL), Беркли, Калифорния (США). Проект материалов LBNL

Организация-спонсор:

Департамент науки Министерства энергетики США (SC), Базовые энергетические науки (BES)

Сотрудничество:

Массачусетский технологический институт; Калифорнийский университет в Беркли; герцог; У Лувен

Тема:

36 МАТЕРИАЛОВЕДЕНИЕ

Ключевые слова:

кристаллическая структура

; Ba3(PO4)2; Ба-О-П

Идентификатор ОСТИ:

1207537

DOI:

https://doi.org/10.17188/1207537

---

Форматы цитирования

• MLA
• АПА
• Чикаго
• БибТекс

Проект материалов. Материалы Данные по Ba3(PO4)2 по материалам проекта . США: Н. П., 2020. Веб. дои: 10.17188/1207537.

Копировать в буфер обмена

Проект материалов. Материалы Данные по Ba3(PO4)2 по материалам проекта . Соединенные Штаты. Дои: https://doi.org/10.17188/1207537

Копировать в буфер обмена

Проект материалов. 2020. «Материальные данные по Ba3(PO4)2 по проекту материалов». Соединенные Штаты. дои: https://doi.org/10.17188/1207537. https://www.osti.gov/servlets/purl/1207537. Дата публикации: среда, 15 июля, 00:00:00 по восточному поясному времени 2020

Копировать в буфер обмена

@article{osti_1207537,
title = {Данные о материалах Ba3(PO4)2 по проекту материалов},
author = {Проект материалов},
abstractNote = {Ba3(PO4)2 кристаллизуется в тригональной пространственной группе R-3m. Структура трехмерная. имеются два неэквивалентных сайта Ba2+. В первом узле Ba2+ Ba2+ связан в 10-координатной геометрии с десятью атомами O2-. Расстояния связи Ba–O варьируются в пределах 2,67–2,9.9 Å. Во второй позиции Ba2+ Ba2+ связан с двенадцатью атомами O2-, образуя искаженные кубооктаэдры BaO12, которые имеют общие ребра с шестью эквивалентными кубооктаэдрами BaO12 и ребра с шестью эквивалентными тетраэдрами PO4. Существует шесть более коротких (2,78 Å) и шесть более длинных (3,28 Å) длин связи Ba–O. P5+ связан с четырьмя атомами O2-, образуя тетраэдры PO4, которые имеют общие ребра с тремя эквивалентными кубооктаэдрами BaO12. Имеется одна более короткая (1,55 Å) и три более длинные (1,57 Å) длины связи P–O. Имеются два неэквивалентных O2-сайта. В первом положении O2- O2- связан в искаженной геометрии одинарной связи с четырьмя атомами Ba2+ и одним атомом P5+. Во втором положении O2- O2- связан в искаженной геометрии одинарной связи с четырьмя атомами Ba2+ и одним атомом P5+.},
doi = {10. 17188/1207537},
журнал = {},
номер = ,
том = ,
место = {США},
год = {2020},
месяц = ​​{7}
}

Копировать в буфер обмена

---

Просмотреть набор данных

DOI: https://doi.org/10.17188/1207537

---

Экспорт Метаданные

Сохраните в мою библиотеку

Вы должны войти в систему или создать учетную запись, чтобы сохранить документы в вашу библиотеку.

Аналогичные записи в DOE Data Explorer и коллекции OSTI.GOV:

• Аналогичные записи

Свойства, химическая структура и применение

Формула фосфата бария

Фосфат бария Формула записывается как Ba3(PO4)2. Химическая и оптическая промышленность использует неорганическую соль, известную как фосфат бария, в качестве компонента при производстве очков и импульсных лазеров. Этот фосфат щелочноземельного металла обладает такими характеристиками, как низкая дисперсия, низкая температура плавления и низкая температура превращения в стекло, высокий показатель преломления, высокий коэффициент теплового расширения и хорошая прозрачность для УФ-излучения. Кроме того, по сравнению с другими щелочноземельными стеклами, стекла из фосфата бария демонстрируют большее разнообразие зон стеклообразования и большую однородность.

Формула фосфата бария

Формула фосфата бария записывается как Ba3(PO4)2 и имеет молекулярную массу 295,27 г/моль. Кроме того, два аниона фосфата PO43- и три катиона бария (Br2+) объединяются, образуя фосфат бария. Фосфат бария также встречается в форме гидрата Ba2 (P4O12). Ba3(P3O9)2 + 5h3O = 6h3O. Веб-сайт и мобильное приложение Extramarks предоставляют стандартное описание его химической формулы.

Свойства фосфата бария

Физические свойства фосфата бария:

Формула фосфата бария записывается как Ba3(PO4)2. Это бесцветное вещество в виде порошка со слабым вкусом уксусной кислоты. Кроме того, он имеет плотность 3,63 г/мл и температуру плавления 15600°C для фосфата бария. Он нерастворим в воде, но растворим в кислых водных растворах. Сложность фосфата бария составляет 36,8. Фосфат бария начинает разрушаться при нагревании.

Химические свойства фосфата бария:

Благодаря своему химическому составу можно создавать стекла с высокой температурой плавления и высоким коэффициентом теплового расширения. По этой причине он используется в нескольких промышленных процессах для создания специальных стекол, в которых фосфат бария используется в качестве исходного ингредиента. Формула фосфата бария записывается как Ba3(PO4)2.

Применение и меры безопасности фосфата бария

Формула фосфата бария записывается как Ba3(PO4)2.