письмо «Применение разложения на простые множители к сокращению дробей»
Письмо 4. Уроки № 6-7.
Инструкция. Как работать с письмом?
Прочитайте письмо от начала до конца «от корки до корки».
Возьмите карандаш и выделите карандашом те фрагменты, которые надо записать в классную тетрадь.
Приготовьте учебник, тетрадь, пенал.
Начинайте читать третий раз, выполняя записи и упражнения в тетради, соблюдая мои советы.
Прочитайте четвертый раз и выделите те моменты, которые вам не понятны. В эфире урока во вторник зададите свои вопросы.
Здравствуйте, ребята! Начинается новая неделя «на удаленке». Надеюсь, что вы немного привыкли обучаться самостоятельно. Рада, что многим из вас помогают родители: отправляют сообщения, держат связь с учителями. Это здорово! Большое им спасибо. На этой неделе мы работаем по предмету математика по следующему расписанию:
понедельник 13. 04.20 – вы получаете и изучаете письмо 4, выполняете задания, готовитесь обсудить со мной эту тему.
04.20 – вы получаете и изучаете письмо 4, выполняете задания, готовитесь обсудить со мной эту тему.
вторник 14.04.20 – эфир урока в Discord в 9.15
среда 15.04.20 – эфир урока в Discord в 12.00, получаете письмо 5.
четверг 16.04.20 – отправляете ответ на письмо 5 до 14.00.
На этой неделе у вас будет возможность получить оценки за устные ответы на уроках (во вторник и в среду).
Цель на неделю — узнать, для каких операций в математике можно применять разложение числа на простые множители.
Задача на неделю – научиться применять разложение на простые множители к сокращению дробей, к нахождению НОД и НОК.
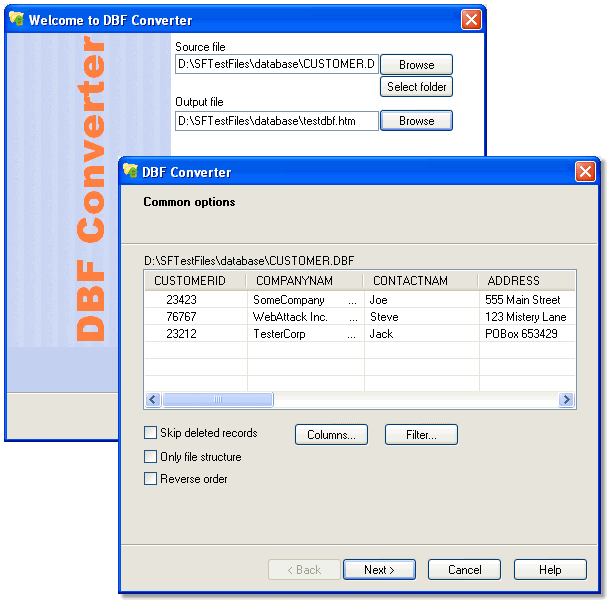
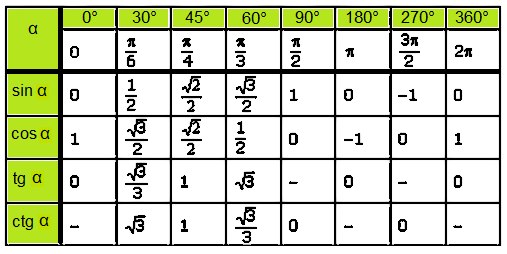
Но сначала проверим, как вы усвоили предыдущий урок. При проверке ваших работ я увидела, что не все следуют моему образцу оформления. Если надо разложить число на простые множители, то вы:
При проверке ваших работ я увидела, что не все следуют моему образцу оформления. Если надо разложить число на простые множители, то вы:
1) проводите разложение «столбиком» (как на рис.)
2) записывайте каноническое разложение .
Обратите внимание: всего два пункта.
Для тех, кто не смог справиться с этой темой – помните: наше дальнейшее продвижение будет зависеть от того, как вы научитесь выполнять разложение на простые множители.
Но большинство из вас получили хорошие и отличные оценки. Я рада и горжусь вашей работой. Надеюсь, что она честная!
Сегодня мы поговорим с вами о сокращении дробей. Кто-то возмутится!!!! Мы это уже изучали. Конечно, в 5 классе! Но тема «Разложение на простые множители» — настоящая Золушка в сокращении дробей (вам надо только аккуратно все записать, и ответ будет идеальным, т. е. Золушка за Вас всё сделает).
е. Золушка за Вас всё сделает).
Что же мы умеем делать? Как мы раньше сокращали дроби? Вспомним! Открывайте тетрадь и записывайте тему урока «СОКРАЩЕНИЕ ДРОБЕЙ С ПОМОЩЬЮ РАЗЛОЖЕНИЯ НА ПРОСТЫЕ МНОЖИТЕЛИ».
1 способ. Мы знаем основное свойство дроби. Если числитель и знаменатель дроби разделить на одно и то же число, то получится равная ей дробь. Т.е. выполняется равенство .
Например, . Такое преобразование мы называли с вами – сокращением дробей. Надеюсь, что вы записали это в тетрадь!
2 способ. Идем дальше, в этом году мы познакомились с признаками делимости и сокращали дроби последовательно. Например,
, т.е. сначала сократили на 3, потом 5, далее на 7. Так тоже – верно!
А сегодня мы попробуем выполнять сокращение с помощью разложения на простые множители. Откройте учебник стр. 197 №919. Посмотрите, какие «страшные» дроби! Но мы сначала выполним №918.
Разложим 350 и 756 на простые множители. Выполните самостоятельно по образцу (только пункт 1(разложение «столбиком»), без канонического разложения). А потом выпишите произведение простых множителей строчкой.
Если вы все сделали правильно, то у вас получились следующие ответы, проверьте: 350 = 2∙5∙5∙7 756 = 2∙2∙3∙3∙3∙7. А теперь вернемся к №919 (б). Необходимо сократить дробь . Заменим 350 и 756 на произведение множителей. (Запишите образец в тетрадь).
Образец записи.
. Все одинаковые множители сокращаем! Помните, я вам писала о Золушке, посмотрите, как и мы быстро справились с этим примером. После разложения нам осталось только вычеркнуть одинаковые множители и выполнить умножение. А ответ – НЕСОКРАТИМАЯ ДРОБЬ. Точно уже ошибок не будет! Преимущество этого способа, действительно в том, что всегда получается несократимая дробь.
Выполните тренировочные упражнения.
№1. Сократите дроби, предварительно разложив числитель и знаменатель на простые множители:
а) б) в)
Именно с этих примеров начнем завтрашний урок.
За окном – апрель, скоро окончание учебного года, значит, пора подводить итоги. А всё ли вы помните? Давайте проверим. Решайте самостоятельно!!!
№2. Решите уравнение
№3. Найдите значение числового выражения: (Подумайте, как лучше вычислить)
№4. Приведите пример двух чисел, сумма которых меньше их разности, а модуль каждого числа больше 5, но меньше 10.
САМОПРОВЕРКА.
Ответы к номерам:
№1. а) б) в) дробь несократимая
№2. х = — 2 (Помните: сначала раскрыть скобки, потом перенос слагаемых – и соблюдайте все правила)
№3. 1.
Если вы решили неверно, то находите ошибки, а не подгоняйте под ответ!
№4. Например, – 6 и 9. Модуль каждого числа больше 5, но меньше 10.
Например, – 6 и 9. Модуль каждого числа больше 5, но меньше 10.
Сумма чисел равна – 6+ 9 = 3. Разность чисел 9 – (– 6) = 15. Сумма 3 меньше разности 15.
Мой пример не записывать, воспользуйтесь объяснением и найдите свои примеры чисел.
Всего доброго. До свидания.
P.S. Надеюсь всё, что напечатано черным шрифтом в письме, у вас записано в тетради.
Сокращение дробей – примеры, правила, формулы (6 класс, математика)
4.6
Средняя оценка: 4.6
Всего получено оценок: 261.
4.6
Средняя оценка: 4.6
Всего получено оценок: 261.
Сокращение дробей тема достаточно трудная для математики 6 класса, поэтому разбирать ее стоит поэтапно. Чтобы не допускать ошибок, первые сокращения лучше делать так же, поэтапно. Приведем алгоритм, чтобы не допускать ошибок и научится быстро и просто сокращать любые дроби.
Алгоритм сокращения дробей.
Сначала нужно сказать, что само сокращение дробей возможно благодаря одному из определений дроби.
Дробь – это незавершенная операция деления. Имеется в виде, что всегда любую дробь можно заменить частным. Замена дробью нужна, чтобы сохранить точность вычислений.
Посмотрим, как выглядит подробное сокращение на примере:
$${25\over{40}}=25:40=(5*5):(5*8)=5:8 $$
Чтобы каждый раз не расписывать – это выражение, можно пользоваться правилом сокращения дробей: если умножить или разделить знаменатель на одно и тоже число, то значение дроби не измениться.
Теперь запишем сам алгоритм. Для того, чтобы сократить дробь нужно:
- Представить числитель и знаменатель в виде простых множителей.
- Сократить каждый из равных простых множителей.
- Перемножить оставшиеся числа и записать результат.
Вместо того, чтобы расписывать в качестве множителей числитель и знаменатель, можно просто найти НОД числителя и знаменателя. Это и будет максимально возможное число, на которое можно разделить оба значения.
Это и будет максимально возможное число, на которое можно разделить оба значения.
Специальной формулы для сокращения любой дроби не существует, зато можно использовать правила, приведенные в этом алгоритме.
Как найти НОД?
Вспомним, как находится НОД:
- Первый шаг это разложение числа на простые множители.
- В разложении ищутся общие простые числа и выписываются в отдельное выражение.
- Получившееся значение и есть НОД.
Приведем пример.
Необходимо найти НОД чисел 150 и 294.
150=2*3*5*5
98=2*3*7*7
НОД=2*3=6
Пример
Приведем пример сокращения дробей. Для этого упрости дробь ${513216\over{145152}}$. Для примера специально выбраны большие числа, чтобы показать, как самое большое число может стать маленьким в результате упрощения.
Мы не будем искать НОД, разложим числа на простые множители и найдем общие значения.
513216:2=256608 – в первую очередь число делится на 2. Чтобы число делилось на два, нужно, чтобы число единиц было четным.
Чтобы число делилось на два, нужно, чтобы число единиц было четным.
256608:2=128304 – деление на 2 продолжается вплоть до момента, когда последняя цифра числа перестанет быть четной. После этого пробуем делить число на 3 и другие простые числа. Все простые числа есть в таблице простых чисел.
128304:2=64152
64152:2=32076
32076:2=16038
16038:2=8019
8019:3=2673
2673:3=891
891:3=297
297:3=99
99:3=33
33:3=11
11:11=1
Запишем результат разложения: 513216=2*2*2*2*2*2*3*3*3*3*3*3*11 – всего получилось 6 чисел 3, 6 чисел 2 и число 11. Таким же образом разложим 145152.
145152:2=72576
72576:2=36288
36288:2=18144
18144:2=9072
9072:2=4536
4536:2=2268
2268:2=1134
1134:2=567
567:3=189
189:3=63
63:3=21
21:3=7
7:7=1
Запишем результаты:
145152=2*2*2*2*2*2*2*2*3*3*3*3*7 – всего 8 чисел 2, 4 числа 3 и одно число 7.
В обоих числах нужно сократить 6 чисел 2 и 4 числа 3. Запишем получившийся числитель. В нем останутся числа: 2 числа 3 и число 11
3*3*11=99
Запишем получившийся знаменатель. В нем останутся числа: 2 числа два и число 7
2*2*7=28
В результате сокращения получилась дробь:
${99\over{28}}$ – при желании можно выделить целую часть. Но, если этого не требуется в условии задачи, то допускается оставить ответ в таком виде.
Что мы узнали?
Мы поговорили о сокращении дробей. Узнали, почему сокращение возможно. Выяснили, как правильно производить сокращение. Привели алгоритм сокращения и два способа проведения операции. Рассмотрели пример сокращения дробей.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Олеся Смирнова
10/10
Елена Хромова
8/10
Саша Титаренко
10/10
Валентина Чалышева
10/10
Оценка статьи
4. 6
6
Средняя оценка: 4.6
Всего получено оценок: 261.
А какая ваша оценка?
Приведение дробей к наименьшим терминам — объяснение!
Смешанные и неправильные дробиУмножение и делениеСложение и вычитание полиномиальных дробей
Purplemath
В дальнейшем будет иногда полезно помнить, что дроби могут указывать на деление. Например, 1 / 3 может означать «один, разделенный на три», а также «одна часть из трех частей». На самом деле, давайте перейдем к делу; запомните это предложение: «Дроби — это деление».
Вы знаете, что любое число, деленное само на себя, равно 1. Вы используете этот факт, когда сокращаете дроби. Если вы можете преобразовать часть данной дроби в форму, умноженную на 1, то вы можете игнорировать эту часть, потому что умножение на 1 ничего не меняет.
Содержание продолжается ниже
MathHelp.com
Приведение дробей к наименьшим терминам
Например, вот как можно найти и использовать форму 1 для сокращения дроби 4 / 8 в наименьшем члене (то есть в простейшей форме):
Чтобы быть предельно ясным, смысл нахождения общего множителя (в данном случае 4-х) состоит в том, чтобы позволить вам преобразовать часть дроби в 1. Поскольку 4 / 4 = 1, то то, что я сделал выше, было следующим:
Поскольку 4 / 4 = 1, то то, что я сделал выше, было следующим:
Внимание: Обратите внимание, как я перешел от дроби с произведениями (в числителе и знаменателе):
.. .to произведение дробей:
Этот переключатель в порядке, пока вы умножаете:
…но это совсем НЕ, если вы добавляете. Например:
Левая часть выше, представляющая дробь, содержащую сложение, равна 5 / 6 , а правая часть выше, будучи сложением, содержащим дроби, равна 1 1 / 2 , так что эти два выражения не являются одним и тем же значением. Просто помните: дроби умножать намного проще, чем складывать. Теперь вернемся к делу…
В дополнение к методу отмены, который я использовал выше (с розовыми цифрами 1), вы, возможно, видели одно из следующих сокращений для отмены:
Любой из этих форматов подходит. Два метода стенографии, вероятно, являются самыми простыми для вашей рукописной домашней работы; формат, который я использовал выше, легче для набора текста.
Может ли мой калькулятор уменьшать для меня дроби?
Если у вас есть обычный (научный, деловой и т. д.) калькулятор, который может обрабатывать дроби, вы можете ввести дробь, а затем нажать кнопку «равно», чтобы получить уменьшенную дробь. Если у вас есть графический калькулятор с командой дроби, вы можете ввести дробь как деление (потому что 4 / 8 означает «четыре разделить на восемь»), а затем преобразовать в дробную форму. Подробности смотрите в руководстве пользователя вашего калькулятора.
Если ваш калькулятор не может работать с дробями или если знаменатель слишком велик для калькулятора, вам нужно будет выполнить сокращение вручную. (И вам понадобятся концепция и методология приведения дроби в более поздних курсах алгебры.)
Каковы шаги для приведения дроби к простейшей форме?
- Разложите числитель и знаменатель на множители.
- Отметьте все множители, которые являются общими для числителя и знаменателя.

- Отменить пары общих множителей.
- Умножьте все, что останется после отмены.
Помните, что если «все» сокращается, скажем, из числителя, то все равно остается множитель 1. Все всегда умножается на 1, но мы обычно этого не замечаем. Однако, если все нетривиальные множители (то есть все множители, не равные 1) сокращаются путем сопоставления множителей с другой стороны дробной линии, то у вас все еще есть эта 1; фракция не становится безголовой.
Что является примером сокращения дроби до наименьших членов?
- Привести к простейшей форме.
Я возьму свой калькулятор и лист бумаги и сомножу числитель (верхнее число) и знаменатель (нижнее число). Быстрая запись для получения простой факторизации каждого из этих чисел показана ниже, в суммированном делении (по простым числам) 2940:
Чтобы найти факторизацию, я просто прочитал простые множители снаружи верхней стороны. -нижнее деление. Из вышесказанного я вижу, что 2940 множителей как 2×2×3×5×7×7.
-нижнее деление. Из вышесказанного я вижу, что 2940 множителей как 2×2×3×5×7×7.
Далее я разложу на множители знаменатель, являющийся числом 3150:
Итак, 3150 делим как 2×3×3×5×5×7.
Теперь я могу сократить дробь, сократив общие множители:
Итак, после сокращения всех множителей, которые дублировались (то есть были общими) в числителе и знаменателе, моя упрощенная форма будет такой:
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в сокращении дробей. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. Или пропустите виджет и продолжите урок.)
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/fraction.htm 2Page 3Page 4Page 5
Как уменьшить дробь
Сокращение дроби — это процесс упрощения дроби путем деления числителя и знаменателя на одно и то же число. Это число обычно является множителем как числителя, так и знаменателя. Деление на общий множитель не изменит значение дроби, но может упростить работу с ней. Например, если у вас есть дробь ¾, вы можете уменьшить ее до 1/3, разделив числитель (3) и знаменатель (4) на 2. Есть несколько различных методов, которые вы можете использовать для сокращения дробей. В этом сообщении блога мы рассмотрим некоторые из этих методов и когда их следует использовать. Читайте дальше, чтобы узнать больше!
Это число обычно является множителем как числителя, так и знаменателя. Деление на общий множитель не изменит значение дроби, но может упростить работу с ней. Например, если у вас есть дробь ¾, вы можете уменьшить ее до 1/3, разделив числитель (3) и знаменатель (4) на 2. Есть несколько различных методов, которые вы можете использовать для сокращения дробей. В этом сообщении блога мы рассмотрим некоторые из этих методов и когда их следует использовать. Читайте дальше, чтобы узнать больше!
Как сократить дроби?
Чтобы сократить дробь, разделите числитель и знаменатель на наибольший общий делитель. Наибольший общий делитель — это наибольшее число, которое делится без остатка как на числитель, так и на знаменатель. Например, наибольший общий делитель 8 и 12 равен 4. Итак, чтобы уменьшить 8/12, мы должны разделить и 8, и 12 на 4, чтобы получить 2/3.
Методы сокращения дробей
Существует несколько методов сокращения дробей, которые вы можете использовать в зависимости от того, чего вы пытаетесь достичь. Самый распространенный способ сокращения дроби — разделить числитель и знаменатель на наибольший общий множитель (НОД). Это даст вам самые низкие условия для дроби.
Самый распространенный способ сокращения дроби — разделить числитель и знаменатель на наибольший общий множитель (НОД). Это даст вам самые низкие условия для дроби.
Если вы хотите просто уменьшить размер дроби, но не обязательно изменить ее значение, вы также можете разделить и числитель, и знаменатель на любое число. Например, если разделить на 2, дробь уменьшится пополам. Только будьте осторожны, чтобы случайно не изменить его значение!
Другой способ сокращения дробей — преобразование их в десятичные. Это можно сделать, разделив числитель на знаменатель. Это даст вам точное значение дроби, которое вы можете затем округлить по мере необходимости.
Наконец, если вы хотите превратить смешанную дробь (целое число и дробь) в неправильную дробь (просто числитель над знаменателем), то вы можете умножить целое число на знаменатель и добавить его к числителю. Это даст вам новую неправильную дробь в сокращенной форме.
Метод эквивалентных дробей
Сокращение дроби — это процесс нахождения более простой эквивалентной дроби. Самый простой способ сделать это — найти общий множитель между числителем и знаменателем и разделить их на это число. В результате получится дробь, равная исходной, но с меньшими числами.
Самый простой способ сделать это — найти общий множитель между числителем и знаменателем и разделить их на это число. В результате получится дробь, равная исходной, но с меньшими числами.
Например, если у нас есть дробь ¾, мы можем видеть, что число 3 является общим делителем между 3 и 4. Если мы разделим и 3, и 4 на 3, мы получим новую дробь 1/1, которая равна ¾.
Этот метод можно применить к любой дроби для упрощения. Просто не забудьте найти общий множитель между числителем и знаменателем, а затем разделить оба на это число!
Метод GCF
Метод GCF (Greatest Common Factor) — отличный способ уменьшить дроби. Этот метод также иногда называют методом наибольшего общего делителя (НОД). GCF двух или более чисел — это наибольшее число, которое делится на все числа без остатка. Чтобы использовать этот метод, начните с нахождения GCF числителя и знаменателя дроби, которую вы хотите уменьшить. Затем разделите числитель и знаменатель дроби на GCF. Это даст вам уменьшенную фракцию с эквивалентным значением.
Допустим, мы хотим уменьшить дробь ¾ . Мы начнем с нахождения GCF 3 и 4, который равен 1. Затем мы разделим и 3, и 4 на 1, чтобы получить 3 ÷ 1 = 3 и 4 ÷ 1 = 4. Итак, ¾ можно сократить до ? .
Метод простой факторизации
Чтобы найти простую факторизацию числа, начните с поиска наименьшего простого числа, которое делится на это число без остатка. Затем продолжайте делить на то же самое простое число, пока не перестанете делить без остатка. В этот момент перейдите к следующему наименьшему простому числу и повторите процесс. Продолжайте до тех пор, пока все множители не станут простыми числами.
Чтобы проиллюстрировать это, давайте посмотрим, как найти разложение 48 на простые множители. Наименьшее простое число, которое делится на 48 без остатка, равно 2, поэтому начнем с него:
48 ÷ 2 = 24
24 ÷ 2 = 12
12 ÷ 2 = 6
6 ÷ 2 = 3
3 ÷ 3 = 1
Как видите, как только мы дошли до коэффициента 3, мы больше не могли делить без остатка на 2. Итак, мы перешли к следующее наименьшее простое число (3) и продолжается до тех пор, пока все множители не станут простыми числами. В этом случае полная простая факторизация числа 48 равна: 2 × 2 × 2 × 2 × 3
Итак, мы перешли к следующее наименьшее простое число (3) и продолжается до тех пор, пока все множители не станут простыми числами. В этом случае полная простая факторизация числа 48 равна: 2 × 2 × 2 × 2 × 3
Дроби в числовой строке
Когда дело доходит до дробей, одним из самых полезных инструментов, который вы можете иметь, является числовая строка. Числовая линия может помочь вам визуализировать, что означает дробь, и может быть полезным инструментом, когда дело доходит до сокращения дробей.
Чтобы сократить дробь, нужно найти ее наибольший общий делитель и разделить числитель и знаменатель на это число. Например, если вы пытаетесь уменьшить дробь ¾, вам нужно найти наибольший общий делитель между 3 и 4. Наибольший общий делитель между 3 и 4 равен 1, поэтому вы должны разделить 3 на 1 и 4 на 1, чтобы получить уменьшенную дробь ½ .
Числовые линии могут быть полезным инструментом, когда дело доходит до нахождения наибольшего общего делителя между двумя числами. Для этого просто найдите два числа на числовой прямой и посчитайте, сколько пробелов между ними. В нашем примере выше есть четыре пробела между 3 и 4 на числовой прямой. Это означает, что наибольший общий делитель между этими двумя числами равен 4.
Для этого просто найдите два числа на числовой прямой и посчитайте, сколько пробелов между ними. В нашем примере выше есть четыре пробела между 3 и 4 на числовой прямой. Это означает, что наибольший общий делитель между этими двумя числами равен 4.
Если вам трудно представить себе этот процесс, попробуйте нарисовать числовую прямую на листе бумаги. Затем пометьте каждую точку дробями, с которыми вы работаете. После того, как вы это сделаете, вам будет легче понять, как работает нахождение наибольшего общего множителя на числовой прямой.
Плюсы и минусы сокращения дроби
Когда дело доходит до дробей, нет универсального ответа на вопрос, является ли сокращение дроби лучшим способом действий. Это зависит от конкретной ситуации и того, чего вы надеетесь достичь, сократив дробь. В некоторых случаях уменьшение дроби может помочь сделать расчеты проще и точнее. В других случаях сокращение дроби может усложнить задачу. Давайте подробнее рассмотрим плюсы и минусы сокращения дроби:
Основное преимущество сокращения дроби заключается в том, что это часто может упростить вычисления. Это потому, что когда вы уменьшаете дробь, вы, по сути, устраняете все ненужные факторы, которые в противном случае усложнили бы ваш расчет. Например, если вы добавляете две дроби и одну из них можно уменьшить, это часто значительно упрощает процесс сложения.
Это потому, что когда вы уменьшаете дробь, вы, по сути, устраняете все ненужные факторы, которые в противном случае усложнили бы ваш расчет. Например, если вы добавляете две дроби и одну из них можно уменьшить, это часто значительно упрощает процесс сложения.
Другим потенциальным преимуществом сокращения дроби является то, что иногда это может сделать результаты более точными. Это особенно верно в тех случаях, когда округление может быть проблемой. Если вы сократите дробь перед выполнением каких-либо вычислений, вы всегда получите максимально точный ответ.
С другой стороны, перед сокращением дроби следует принять во внимание некоторые недостатки. Одним из недостатков является то, что иногда это может сделать вещи более запутанными, особенно для новичков, которые все еще пытаются понять дроби в целом. Если вы сократите дробь перед тем, как работать с ней, может быть сложнее понять, что происходит в общем расчете.
Как сократить дроби с переменными?
Чтобы сократить дробь с переменными, сначала определите наибольший общий делитель числителя и знаменателя. Затем разделите числитель и знаменатель на наибольший общий множитель. Полученная фракция находится в наименьших условиях.
Затем разделите числитель и знаменатель на наибольший общий множитель. Полученная фракция находится в наименьших условиях.
Когда сокращать дробь
Чтобы сокращать дробь, разделите числитель и знаменатель на наибольший общий множитель. Наибольший общий множитель — это наибольшее число, которое делится без остатка как на числитель, так и на знаменатель. Чтобы найти наибольший общий делитель дроби, перечислите делители как числителя, так и знаменателя. Наибольший общий делитель будет наибольшим числом, которое появляется в обоих списках.
Например, чтобы уменьшить дробь ¾, перечислите множители 3 (3, 1) и перечислите множители 4 (4, 2, 1). Наибольший общий делитель равен 1, поэтому ¾ сводится к 1/1 или 1.
Вот еще несколько примеров:
Чтобы уменьшить 8/12, перечислите множители 8 (8, 4, 2, 1) и перечислите множители 12 (12, 6, 4, 3, 2, 1) . Наибольший общий делитель равен 4, поэтому 8/12 сводится к 2/3.
Чтобы уменьшить 15/25, перечислите множители 15 (15, 5, 3, 1) и перечислите множители 25 (25, 5, 5, 1). Наибольший общий делитель равен 5 , поэтому 15/25 сводится к 3/5 .
Наибольший общий делитель равен 5 , поэтому 15/25 сводится к 3/5 .
Советы и рекомендации по сокращению дробей
Чтобы сократить дробь, разделите числитель и знаменатель на наибольший общий множитель. Наибольший общий множитель — это наибольшее число, на которое без остатка делятся и числитель, и знаменатель. Чтобы найти наибольший общий множитель, перечислите множители каждого числа и найдите наибольшее число, которое встречается в обоих списках.
Например, чтобы уменьшить дробь ¾, перечислите множители 3 (3, 1) и множители 4 (4, 2, 1). Наибольший общий делитель равен 1, поэтому ¾ становится 1/1 или 1.
Вот несколько советов и приемов, которые помогут вам сокращать дроби:
-Начните с нахождения наибольшего общего делителя числителя и знаменателя. Вы можете сделать это, перечислив факторы каждого числа и найдя число, которое появляется в обоих списках.
-Найдя наибольший общий множитель, разделите числитель и знаменатель на это число. Это даст вам уменьшенную фракцию.
 Эта популярность основана на легко понять структуру и тот факт, что DBF был один из самых ранних файлов такого типа, который был адаптирован сообществом баз данных.
Эта популярность основана на легко понять структуру и тот факт, что DBF был один из самых ранних файлов такого типа, который был адаптирован сообществом баз данных. Таким образом, они могут быть открыты в Microsoft Excel, OpenOffice Calc и многих других программ.
Таким образом, они могут быть открыты в Microsoft Excel, OpenOffice Calc и многих других программ.
 Этот файл электронной таблицы поддерживается большинством открытого программного обеспечения или программного обеспечения для электронных таблиц.
Этот файл электронной таблицы поддерживается большинством открытого программного обеспечения или программного обеспечения для электронных таблиц. 99
99 99
99



 $ конвертировать DBF_INPUT_FILE —to xls
$ конвертировать DBF_INPUT_FILE —to xls ..
..

 99
99 99
99

 $ конвертировать DBF_INPUT_FILE —to xls
$ конвертировать DBF_INPUT_FILE —to xls При проверке ваших работ я увидела, что не все следуют моему образцу оформления. Если надо разложить число на простые множители, то вы:
При проверке ваших работ я увидела, что не все следуют моему образцу оформления. Если надо разложить число на простые множители, то вы: е. Золушка за Вас всё сделает).
е. Золушка за Вас всё сделает).

 Например, – 6 и 9. Модуль каждого числа больше 5, но меньше 10.
Например, – 6 и 9. Модуль каждого числа больше 5, но меньше 10.
 Это и будет максимально возможное число, на которое можно разделить оба значения.
Это и будет максимально возможное число, на которое можно разделить оба значения. Чтобы число делилось на два, нужно, чтобы число единиц было четным.
Чтобы число делилось на два, нужно, чтобы число единиц было четным.
 6
6 Поскольку 4 / 4 = 1, то то, что я сделал выше, было следующим:
Поскольку 4 / 4 = 1, то то, что я сделал выше, было следующим:

 -нижнее деление. Из вышесказанного я вижу, что 2940 множителей как 2×2×3×5×7×7.
-нижнее деление. Из вышесказанного я вижу, что 2940 множителей как 2×2×3×5×7×7. Это число обычно является множителем как числителя, так и знаменателя. Деление на общий множитель не изменит значение дроби, но может упростить работу с ней. Например, если у вас есть дробь ¾, вы можете уменьшить ее до 1/3, разделив числитель (3) и знаменатель (4) на 2. Есть несколько различных методов, которые вы можете использовать для сокращения дробей. В этом сообщении блога мы рассмотрим некоторые из этих методов и когда их следует использовать. Читайте дальше, чтобы узнать больше!
Это число обычно является множителем как числителя, так и знаменателя. Деление на общий множитель не изменит значение дроби, но может упростить работу с ней. Например, если у вас есть дробь ¾, вы можете уменьшить ее до 1/3, разделив числитель (3) и знаменатель (4) на 2. Есть несколько различных методов, которые вы можете использовать для сокращения дробей. В этом сообщении блога мы рассмотрим некоторые из этих методов и когда их следует использовать. Читайте дальше, чтобы узнать больше! Самый распространенный способ сокращения дроби — разделить числитель и знаменатель на наибольший общий множитель (НОД). Это даст вам самые низкие условия для дроби.
Самый распространенный способ сокращения дроби — разделить числитель и знаменатель на наибольший общий множитель (НОД). Это даст вам самые низкие условия для дроби. Самый простой способ сделать это — найти общий множитель между числителем и знаменателем и разделить их на это число. В результате получится дробь, равная исходной, но с меньшими числами.
Самый простой способ сделать это — найти общий множитель между числителем и знаменателем и разделить их на это число. В результате получится дробь, равная исходной, но с меньшими числами.
 Итак, мы перешли к следующее наименьшее простое число (3) и продолжается до тех пор, пока все множители не станут простыми числами. В этом случае полная простая факторизация числа 48 равна: 2 × 2 × 2 × 2 × 3
Итак, мы перешли к следующее наименьшее простое число (3) и продолжается до тех пор, пока все множители не станут простыми числами. В этом случае полная простая факторизация числа 48 равна: 2 × 2 × 2 × 2 × 3 Для этого просто найдите два числа на числовой прямой и посчитайте, сколько пробелов между ними. В нашем примере выше есть четыре пробела между 3 и 4 на числовой прямой. Это означает, что наибольший общий делитель между этими двумя числами равен 4.
Для этого просто найдите два числа на числовой прямой и посчитайте, сколько пробелов между ними. В нашем примере выше есть четыре пробела между 3 и 4 на числовой прямой. Это означает, что наибольший общий делитель между этими двумя числами равен 4. Это потому, что когда вы уменьшаете дробь, вы, по сути, устраняете все ненужные факторы, которые в противном случае усложнили бы ваш расчет. Например, если вы добавляете две дроби и одну из них можно уменьшить, это часто значительно упрощает процесс сложения.
Это потому, что когда вы уменьшаете дробь, вы, по сути, устраняете все ненужные факторы, которые в противном случае усложнили бы ваш расчет. Например, если вы добавляете две дроби и одну из них можно уменьшить, это часто значительно упрощает процесс сложения. Затем разделите числитель и знаменатель на наибольший общий множитель. Полученная фракция находится в наименьших условиях.
Затем разделите числитель и знаменатель на наибольший общий множитель. Полученная фракция находится в наименьших условиях. Наибольший общий делитель равен 5 , поэтому 15/25 сводится к 3/5 .
Наибольший общий делитель равен 5 , поэтому 15/25 сводится к 3/5 .
 2}{5}x+(i)=0\)
2}{5}x+(i)=0\) Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4-х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4-х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид xn+anxn-1+…+a1x+a0=0.
Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид xn+anxn-1+…+a1x+a0=0. Здесь Pn-m(x) является многочленом n-m-ной степени. Для подсчета удобно использовать схему Горнера.
Здесь Pn-m(x) является многочленом n-m-ной степени. Для подсчета удобно использовать схему Горнера.


 Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y=-2, y=3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x=y2=-22=-1 и x=y2=32.
Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y=-2, y=3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x=y2=-22=-1 и x=y2=32.



 Это первый семестр Integrated Math 3, он одобрен Калифорнийским университетом A-G как математика (категория C).
Это первый семестр Integrated Math 3, он одобрен Калифорнийским университетом A-G как математика (категория C).



 После факторизации мы можем приравнять множители к нулю и найти переменную.
После факторизации мы можем приравнять множители к нулю и найти переменную. 



 28675
28675 42447
42447 05030
05030 70463
70463 72654
72654 05241
05241 96569
96569 43005
43005 3138
3138 5399
5399 6494
6494 1763
1763 2309
2309 7002
7002 6003
6003 3138
3138 6713
6713 5399
5399 6745
6745 2126
2126 1944
1944 6494
6494 4826
4826 1446
1446 Женева: Всемирная организация здравоохранения; 2018.
Женева: Всемирная организация здравоохранения; 2018. 0 IGO (CC BY-NC-SA 3.0 IGO; https://creativecommons.org/licenses/by-nc-sa/3.0/igo).
0 IGO (CC BY-NC-SA 3.0 IGO; https://creativecommons.org/licenses/by-nc-sa/3.0/igo).
 занимается предоставлением решений в области информационных технологий и кадровых услуг. Услуги фирмы охватывают жизненный цикл бизнес-решения в области информационных технологий, включая этапы планирования, разработки, внедрения, управления и обслуживания решения в области информационных технологий. Он работает в следующих сегментах: ИТ-решения и услуги в Северной Америке, ИТ-решения и услуги в Европе и нестратегические технологические услуги. Сегменты ИТ-решений и услуг в Северной Америке и Европе предлагают решения для цифровой трансформации. Служба нестратегических технологий предоставляет кадровые услуги. Компания была основана Рэндольфом А. Марксом и Г. Дэвидом Бэром 11 марта 19 года.66 со штаб-квартирой в Буффало, штат Нью-Йорк.
занимается предоставлением решений в области информационных технологий и кадровых услуг. Услуги фирмы охватывают жизненный цикл бизнес-решения в области информационных технологий, включая этапы планирования, разработки, внедрения, управления и обслуживания решения в области информационных технологий. Он работает в следующих сегментах: ИТ-решения и услуги в Северной Америке, ИТ-решения и услуги в Европе и нестратегические технологические услуги. Сегменты ИТ-решений и услуг в Северной Америке и Европе предлагают решения для цифровой трансформации. Служба нестратегических технологий предоставляет кадровые услуги. Компания была основана Рэндольфом А. Марксом и Г. Дэвидом Бэром 11 марта 19 года.66 со штаб-квартирой в Буффало, штат Нью-Йорк.



 Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
 Найти решение уравнения 9x² + 4 = 0.
Найти решение уравнения 9x² + 4 = 0.

 Примеры и решение
Примеры и решение

 Решите уравнение:
Решите уравнение:
 Общий индекс тяжести (GSI, мера общего психологического дистресса) отрицательно, но слабо коррелировал с общим толстокишечным транзитом (r = -0,26, p <0,01). Ощущение анальной закупорки было единственным симптомом, связанным с дисфункцией тазового дна (при нормальных транзитных запорах). Только более регулярный характер дефекации, использование различных поз для дефекации и ощущение неполной эвакуации были связаны с медленным или нормальным транзиторным запором. Однако психологические или толстокишечные симптомы не были значимыми дискриминаторами в многомерном анализе. Время ректосигмовидного транзита при чувствительности 80% имело очень низкую специфичность для дифференциации дисфункции тазового дна от других подгрупп. Сделан вывод о том, что клинические симптомы, психологический дистресс и время ректосигмовидного транзита не могут быть использованы для выделения подгрупп пациентов с трудноизлечимыми запорами.
Общий индекс тяжести (GSI, мера общего психологического дистресса) отрицательно, но слабо коррелировал с общим толстокишечным транзитом (r = -0,26, p <0,01). Ощущение анальной закупорки было единственным симптомом, связанным с дисфункцией тазового дна (при нормальных транзитных запорах). Только более регулярный характер дефекации, использование различных поз для дефекации и ощущение неполной эвакуации были связаны с медленным или нормальным транзиторным запором. Однако психологические или толстокишечные симптомы не были значимыми дискриминаторами в многомерном анализе. Время ректосигмовидного транзита при чувствительности 80% имело очень низкую специфичность для дифференциации дисфункции тазового дна от других подгрупп. Сделан вывод о том, что клинические симптомы, психологический дистресс и время ректосигмовидного транзита не могут быть использованы для выделения подгрупп пациентов с трудноизлечимыми запорами. com
com

 0092 2 + bx + c = 0. Если правая часть не равна нулю, перенесите ее в левую часть и сделайте правую часть нулевой.
0092 2 + bx + c = 0. Если правая часть не равна нулю, перенесите ее в левую часть и сделайте правую часть нулевой. Если вы сделаете это, вы получите только одно решение уравнения (одно значение или один корень из x) и можете потерять другое решение (значение x).
Если вы сделаете это, вы получите только одно решение уравнения (одно значение или один корень из x) и можете потерять другое решение (значение x).

 Квадратичная формула вычисляет два значения x: x 1 и x 2 , где
Квадратичная формула вычисляет два значения x: x 1 и x 2 , где


 Как учить
Как учить Для начала ребенок должен хорошо уметь считать и понимать, например, что к 2 яблокам прибавить ещё 2 яблока будет 4. Важно, чтобы малыш правильно произносил цифры и не путал их. Только тогда можно приступить к изучению таблицы Пифагора.
Для начала ребенок должен хорошо уметь считать и понимать, например, что к 2 яблокам прибавить ещё 2 яблока будет 4. Важно, чтобы малыш правильно произносил цифры и не путал их. Только тогда можно приступить к изучению таблицы Пифагора. Этот метод следует применять тогда, когда ребенок «вызубрил» таблицу и имеет некоторые пробелы. Данный игровой метод представляет собой игру в фанты. Необходимо сделать заготовку карточек, на которых написать умножения на различные числа.
Этот метод следует применять тогда, когда ребенок «вызубрил» таблицу и имеет некоторые пробелы. Данный игровой метод представляет собой игру в фанты. Необходимо сделать заготовку карточек, на которых написать умножения на различные числа. В помощь ребенку сейчас имеется большой выбор различных товаров. Поэтому у родителей не должно возникнуть трудностей, при выборе таблице умножения.
В помощь ребенку сейчас имеется большой выбор различных товаров. Поэтому у родителей не должно возникнуть трудностей, при выборе таблице умножения. Здесь
список программ для печати таблицы умножения:
Здесь
список программ для печати таблицы умножения: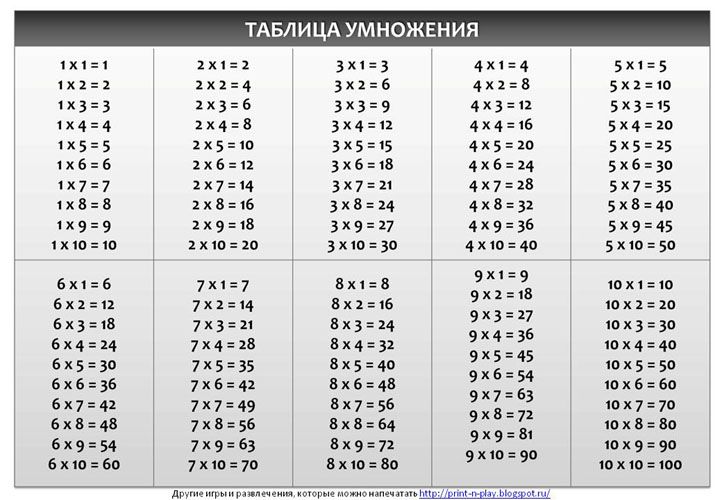 Не стесняйтесь посмотреть на все шаблоны, которые мы предлагаем ниже, и выбрать свой любимый!
Не стесняйтесь посмотреть на все шаблоны, которые мы предлагаем ниже, и выбрать свой любимый!  Чтобы сэкономить время, вы найдете в нашем Раздел таблиц All Times, PDF-файлы, включая все таблицы, окрашенные в радугу.
Чтобы сэкономить время, вы найдете в нашем Раздел таблиц All Times, PDF-файлы, включая все таблицы, окрашенные в радугу.
 Уясните, в чем состоит рассматриваемое в задаче испытание. Качественное описание случайных событий их вероятностей. Игральную кость бросают дважды. Последний пункт имеет практическое значение, так как показывает практическую пользу из подсчета вероятности. Элементарное введение в теорию вероятностей. Одна из таких перестановок может выглядеть так: 111110111001001111111110011. Аналогично определяется произвольное количество независимых величин. Сколько матчей играется в течение сезона. Найдите вероятность события AUB. Решение каждой задачи следует начинать с описания множества элементарных событий и благоприятствующих элементарных событий. Событию А благоприятствуют элементарные события 2, 4 и 6. Из 7 команд, участвующих в полуфинале, 3 команды разыграли медали: золотую, серебряную и бронзовую. Статистические характеристики вводятся для выборки, и после рассмотрения вопроса о распределении значений случайной величины. Перестановки без повторений В предыдущих параграфах комбинации отличались как составом предметов, так их порядком.
Уясните, в чем состоит рассматриваемое в задаче испытание. Качественное описание случайных событий их вероятностей. Игральную кость бросают дважды. Последний пункт имеет практическое значение, так как показывает практическую пользу из подсчета вероятности. Элементарное введение в теорию вероятностей. Одна из таких перестановок может выглядеть так: 111110111001001111111110011. Аналогично определяется произвольное количество независимых величин. Сколько матчей играется в течение сезона. Найдите вероятность события AUB. Решение каждой задачи следует начинать с описания множества элементарных событий и благоприятствующих элементарных событий. Событию А благоприятствуют элементарные события 2, 4 и 6. Из 7 команд, участвующих в полуфинале, 3 команды разыграли медали: золотую, серебряную и бронзовую. Статистические характеристики вводятся для выборки, и после рассмотрения вопроса о распределении значений случайной величины. Перестановки без повторений В предыдущих параграфах комбинации отличались как составом предметов, так их порядком.
 ru. Хотите тоже свой сайт?
ru. Хотите тоже свой сайт? Это обеспечит основу для понимания более сложных тем.
Это обеспечит основу для понимания более сложных тем.
 Случайная величина: Случайная величина — это величина, которая может случайным образом принимать различные значения. В науке о данных он используется для моделирования неопределенных результатов событий. Два типа случайных величин дискретные и непрерывные.
Случайная величина: Случайная величина — это величина, которая может случайным образом принимать различные значения. В науке о данных он используется для моделирования неопределенных результатов событий. Два типа случайных величин дискретные и непрерывные. В контексте науки о данных он используется для моделирования взаимосвязей между переменными, для прогнозирования на основе новых данных и понимания неопределенности, связанной с этими прогнозами.
В контексте науки о данных он используется для моделирования взаимосвязей между переменными, для прогнозирования на основе новых данных и понимания неопределенности, связанной с этими прогнозами. Вот несколько важных:
Вот несколько важных: В науке о данных декартово произведение используется для создания новых наборов данных путем объединения данных из нескольких источников.
В науке о данных декартово произведение используется для создания новых наборов данных путем объединения данных из нескольких источников. Она играет ключевую роль в следующих отношениях:
Она играет ключевую роль в следующих отношениях:
 Это мощный инструмент для проверки гипотез, построения моделей, оценки и принятия решений, что делает его важным компонентом науки о данных.
Это мощный инструмент для проверки гипотез, построения моделей, оценки и принятия решений, что делает его важным компонентом науки о данных. Оценка: Логическая статистика позволяет оценивать параметры совокупности на основе выборочных данных. Например, доверительные интервалы можно использовать для оценки диапазона значений, которые могут содержать истинный параметр совокупности, в то время как точечные оценки обеспечивают оценку одного значения параметра совокупности.
Оценка: Логическая статистика позволяет оценивать параметры совокупности на основе выборочных данных. Например, доверительные интервалы можно использовать для оценки диапазона значений, которые могут содержать истинный параметр совокупности, в то время как точечные оценки обеспечивают оценку одного значения параметра совокупности.

 Какую компоненту человеческого
бытия размывает возможность всегда
Какую компоненту человеческого
бытия размывает возможность всегда
 Концепция научно-исследовательских
программ принадлежит
Концепция научно-исследовательских
программ принадлежит Метод эмпирической индукции разработал
Метод эмпирической индукции разработал Один из типов умозаключения и метод
исследования, представляющий собой
вывод общего положения о классе в целом
на основе рассмотрения всех его элементов,
называется
Один из типов умозаключения и метод
исследования, представляющий собой
вывод общего положения о классе в целом
на основе рассмотрения всех его элементов,
называется Метод фальсификации для отделения
научного знания от ненаучного предложил
использовать
Метод фальсификации для отделения
научного знания от ненаучного предложил
использовать Книга, содержащая перечень определений
научных терминов, расположенных в
алфавитном порядке, называется
Книга, содержащая перечень определений
научных терминов, расположенных в
алфавитном порядке, называется Адекватное отражение объекта познающим
субъектом, воспроизведение его так, как
он существует сам по себе, вне и независимо
от человека и его сознания, называется
Адекватное отражение объекта познающим
субъектом, воспроизведение его так, как
он существует сам по себе, вне и независимо
от человека и его сознания, называется Метод познания, при котором все вещи,
их свойства и отношения, а также все
формы их отражения в сознании человека
рассматриваются во взаимной связи и
развитии, называется
Метод познания, при котором все вещи,
их свойства и отношения, а также все
формы их отражения в сознании человека
рассматриваются во взаимной связи и
развитии, называется Научное допущение или предположение,
истинное значение которого неопределенно,
называется
Научное допущение или предположение,
истинное значение которого неопределенно,
называется Предварительное и проблематичное
суждение называется
Предварительное и проблематичное
суждение называется Концепция научно-исследовательских
программ принадлежит
Концепция научно-исследовательских
программ принадлежит Революционный характер развития
науки в концепции Куна аналогичен
Революционный характер развития
науки в концепции Куна аналогичен  Инновации в науке определяются
Тулмином как
Инновации в науке определяются
Тулмином как В концепции Полани неявное, имплицитное
знание представлено как
В концепции Полани неявное, имплицитное
знание представлено как 04.2021
04.2021 К.Энгельмейер
К.Энгельмейер Цели и задачи модуля Целью изучения модуля «История и философия науки»
Цели и задачи модуля Целью изучения модуля «История и философия науки»
 Узнать больше
Узнать больше Множественный выбор
Множественный выбор Ставя под сомнение существующие идеи и гипотезы B. Отказываясь принимать объяснения без доказательств C. С вопросительным и сомнительным отношением .
Ставя под сомнение существующие идеи и гипотезы B. Отказываясь принимать объяснения без доказательств C. С вопросительным и сомнительным отношением .

 Это правда, что основатели новой социологии науки, такие как Дэвид Блур и Гарри Коллинз в 1970-х и 80-х годах, явно развивали свои собственные идеи, прямо противоречащие взглядам некоторых философов, в частности доктрине Поппера о фальсифицируемости. Но эти социологи также приняли философские идеи, подходящие для их целей: несоизмеримость, развитая Куном и Фейерабендом, и неопределенность теории Куайна наблюдением. Использование таких философских идей социологами науки хорошо задокументировано Джоном Заммито (2004). Как автор книги о Куне (2000), Фуллер, конечно, обсуждает влияние Куна на СС, но, как человек, «следящий [с] за развитием СС с большой высоты» (30), он не связывает влияет на конкретных членов сообщества СС. Что он в основном делает, так это рассматривает аспекты этих двух областей в социокультурных терминах, вдохновленных его участием в подходах к «общественному пониманию науки» и «научных войн», а также его собственным «проектом социальная эпистемология» (5). Его идея того, что он называет «вечной философией», применительно к СС — это вопрос: Что такое жизнь в СС? «как призвание, которое также является средством социальных преобразований» (5).
Это правда, что основатели новой социологии науки, такие как Дэвид Блур и Гарри Коллинз в 1970-х и 80-х годах, явно развивали свои собственные идеи, прямо противоречащие взглядам некоторых философов, в частности доктрине Поппера о фальсифицируемости. Но эти социологи также приняли философские идеи, подходящие для их целей: несоизмеримость, развитая Куном и Фейерабендом, и неопределенность теории Куайна наблюдением. Использование таких философских идей социологами науки хорошо задокументировано Джоном Заммито (2004). Как автор книги о Куне (2000), Фуллер, конечно, обсуждает влияние Куна на СС, но, как человек, «следящий [с] за развитием СС с большой высоты» (30), он не связывает влияет на конкретных членов сообщества СС. Что он в основном делает, так это рассматривает аспекты этих двух областей в социокультурных терминах, вдохновленных его участием в подходах к «общественному пониманию науки» и «научных войн», а также его собственным «проектом социальная эпистемология» (5). Его идея того, что он называет «вечной философией», применительно к СС — это вопрос: Что такое жизнь в СС? «как призвание, которое также является средством социальных преобразований» (5). Как бы трудно ни было писать эту книгу, ее еще труднее рецензировать. Те, кто знаком с несколькими работами Фуллера, знают, насколько широко Он легко скользит от Платона к Конту, к логическому позитивизму или от Французской революции к Первой мировой войне. … Решив, что тематически рассматривать эту книгу не в моих силах, я буду продвигаться вперед глава за главой, концентрируясь лишь на нескольких идеях или проблемах в каждой.0003
Как бы трудно ни было писать эту книгу, ее еще труднее рецензировать. Те, кто знаком с несколькими работами Фуллера, знают, насколько широко Он легко скользит от Платона к Конту, к логическому позитивизму или от Французской революции к Первой мировой войне. … Решив, что тематически рассматривать эту книгу не в моих силах, я буду продвигаться вперед глава за главой, концентрируясь лишь на нескольких идеях или проблемах в каждой.0003 0003
0003 Конструктивист, с другой стороны, только пытается продемонстрировать социальные и риторические стратегии, которые ученые используют для подтверждения своих претензий на объективное знание. Таким образом, утверждения ученых скорее разоблачаются, чем опровергаются. Ученые все еще могут претендовать на объективное знание, хотя объективность знания имеет другой источник, чем признает большинство ученых. Но принижается эпистемологический статус ученых. По Фуллеру, «социальная эпистемология науки должна задаться вопросом, как наука должна быть легитимирована после того, как социальные конструктивистские теории получили широкое признание. Может ли наука, как и религия, выжить в демистифицированной форме» (37)? Я бы сказал «да», но демистификация не должна заходить так далеко, как разоблачение.
Конструктивист, с другой стороны, только пытается продемонстрировать социальные и риторические стратегии, которые ученые используют для подтверждения своих претензий на объективное знание. Таким образом, утверждения ученых скорее разоблачаются, чем опровергаются. Ученые все еще могут претендовать на объективное знание, хотя объективность знания имеет другой источник, чем признает большинство ученых. Но принижается эпистемологический статус ученых. По Фуллеру, «социальная эпистемология науки должна задаться вопросом, как наука должна быть легитимирована после того, как социальные конструктивистские теории получили широкое признание. Может ли наука, как и религия, выжить в демистифицированной форме» (37)? Я бы сказал «да», но демистификация не должна заходить так далеко, как разоблачение. ). Он сетует на «крах философии науки как нормативного предприятия» (45). Философы науки, утверждает он, стали «младшими работниками», играя Локка в современной науке. Он особенно критически относится к попыткам историзации и натурализации философии науки. Здесь он критикует попытку Ларри Лаудана «проверить» методологические заявления философов на исторических и современных примерах (Донован, Лаудан и Лаудан 19).88) Его суровый вывод состоит в том, что
). Он сетует на «крах философии науки как нормативного предприятия» (45). Философы науки, утверждает он, стали «младшими работниками», играя Локка в современной науке. Он особенно критически относится к попыткам историзации и натурализации философии науки. Здесь он критикует попытку Ларри Лаудана «проверить» методологические заявления философов на исторических и современных примерах (Донован, Лаудан и Лаудан 19).88) Его суровый вывод состоит в том, что
 Шумиха в шведской прессе привела к тому, что Национальный совет Швеции по социальному здравоохранению отменил план по назначению нового лекарства от гиперактивности тысячам детей. Фуллер сетует на тот факт, что такие действия исследователя СС не получили особого признания со стороны истеблишмента СС в США, Великобритании или Франции.
Шумиха в шведской прессе привела к тому, что Национальный совет Швеции по социальному здравоохранению отменил план по назначению нового лекарства от гиперактивности тысячам детей. Фуллер сетует на тот факт, что такие действия исследователя СС не получили особого признания со стороны истеблишмента СС в США, Великобритании или Франции. ).
). Но тогда я, как и Фуллер, не историк.
Но тогда я, как и Фуллер, не историк.
 Научные пуритане, таким образом, поддерживают различие между научными фактами и социальными ценностями и не желают вмешиваться или вводить свою науку в вопросы, связанные с ценностями, за исключением, конечно, ценности занятия наукой. «По сути, — пишет Фуллер, — гностицизм — это пуританство, доведенное до его логической крайности» (128). Но отличия существенные. Для научных пуритан мир природы и сама наука «разочарованы». В мире природы нет ничего, что придавало бы ценность или смысл человеческому существованию. К сожалению, по словам Фуллера, мейнстримные СС демонстрируют пуританское отношение как к себе, так и к наукам, которые они изучают. Он хочет заново очаровать науку, но в скромном духе Просвещения, используя научные знания для улучшения человеческого благосостояния. Более того, он считает, что ученые должны отказаться от идеи «ценностного нейтралитета» для науки и активно поддерживать государственную политику, направленную на улучшение благосостояния и сокращение неравенства.
Научные пуритане, таким образом, поддерживают различие между научными фактами и социальными ценностями и не желают вмешиваться или вводить свою науку в вопросы, связанные с ценностями, за исключением, конечно, ценности занятия наукой. «По сути, — пишет Фуллер, — гностицизм — это пуританство, доведенное до его логической крайности» (128). Но отличия существенные. Для научных пуритан мир природы и сама наука «разочарованы». В мире природы нет ничего, что придавало бы ценность или смысл человеческому существованию. К сожалению, по словам Фуллера, мейнстримные СС демонстрируют пуританское отношение как к себе, так и к наукам, которые они изучают. Он хочет заново очаровать науку, но в скромном духе Просвещения, используя научные знания для улучшения человеческого благосостояния. Более того, он считает, что ученые должны отказаться от идеи «ценностного нейтралитета» для науки и активно поддерживать государственную политику, направленную на улучшение благосостояния и сокращение неравенства. В начале резюме своей главы он пишет:
В начале резюме своей главы он пишет: Присяжные выбираются из общей массы населения, как обычное жюри в США, чтобы гарантировать, что ни один из них не имеет прямой личной заинтересованности в исходе их обсуждения. Наконец, «результаты консенсусных конференций должны иметь обязательную силу для законодательства в области науки и техники» (169).). Фуллер признает, что существует множество препятствий для институционализации консенсусных конференций, и пытается преодолеть некоторые из них. Интересно, желательно ли вообще такое учреждение? Я разовью свое беспокойство в контексте преподавания «теории разумного замысла» (IDT), вопроса, который Фуллер поднимает несколько раз на протяжении всей книги, и, действительно, он «поддерживает преподавание и исследования теории разумного замысла в «основные университеты» (131).
Присяжные выбираются из общей массы населения, как обычное жюри в США, чтобы гарантировать, что ни один из них не имеет прямой личной заинтересованности в исходе их обсуждения. Наконец, «результаты консенсусных конференций должны иметь обязательную силу для законодательства в области науки и техники» (169).). Фуллер признает, что существует множество препятствий для институционализации консенсусных конференций, и пытается преодолеть некоторые из них. Интересно, желательно ли вообще такое учреждение? Я разовью свое беспокойство в контексте преподавания «теории разумного замысла» (IDT), вопроса, который Фуллер поднимает несколько раз на протяжении всей книги, и, действительно, он «поддерживает преподавание и исследования теории разумного замысла в «основные университеты» (131). Дело слушалось единоличным судьей, а не присяжных, но это дело все еще актуально здесь, потому что было бы трудно представить гражданское жюри, состоящее из граждан, столь же осведомленных, как Стив Фуллер. И что он сказал? Сообщалось, что он «сказал, что, по его мнению, эволюция предлагает лучшее объяснение биологического разнообразия, чем разумный замысел» (77). Хороший. Но также сообщается, что он сказал, что наличие «само собой разумеющихся теорий» в любой дисциплине — «плохая новость». Сообщается также, что он сказал, что «было бы интересно, если бы наука была« реконфигурирована так, чтобы понятие дизайна воспринималось как своего рода буквально объединяющая концепция »».
Дело слушалось единоличным судьей, а не присяжных, но это дело все еще актуально здесь, потому что было бы трудно представить гражданское жюри, состоящее из граждан, столь же осведомленных, как Стив Фуллер. И что он сказал? Сообщалось, что он «сказал, что, по его мнению, эволюция предлагает лучшее объяснение биологического разнообразия, чем разумный замысел» (77). Хороший. Но также сообщается, что он сказал, что наличие «само собой разумеющихся теорий» в любой дисциплине — «плохая новость». Сообщается также, что он сказал, что «было бы интересно, если бы наука была« реконфигурирована так, чтобы понятие дизайна воспринималось как своего рода буквально объединяющая концепция »». И это продукт лучших размышлений об органической жизни на Земле за последние 150 лет. Проблема, на мой взгляд, в том, что в наших государственных школах ET не уделяется должного внимания. Учителя биологии и издатели учебников по биологии были запуганы боязнью оскорбить религиозные чувства учащихся и, что более серьезно, их родителей. Прискорбно, что «свобода вероисповедания» понимается как означающая, что любые верования так же хороши, как и любые другие. На самом деле конституция США говорит лишь о том, что власть государства не может использоваться для навязывания каких-либо конкретных религиозных убеждений. Это не говорит о том, что учащихся не следует заставлять изучать ET в государственных школах. Я бы даже рекомендовал признать, что и ET, и IDT являются «теориями» происхождения человеческой жизни на Земле, а затем показать, почему ET заслуживает гораздо большего доверия, чем IDT. Это может способствовать пониманию науки и объединению демократических граждан не меньше, чем политически активная профессия СС или консенсусные конференции.
И это продукт лучших размышлений об органической жизни на Земле за последние 150 лет. Проблема, на мой взгляд, в том, что в наших государственных школах ET не уделяется должного внимания. Учителя биологии и издатели учебников по биологии были запуганы боязнью оскорбить религиозные чувства учащихся и, что более серьезно, их родителей. Прискорбно, что «свобода вероисповедания» понимается как означающая, что любые верования так же хороши, как и любые другие. На самом деле конституция США говорит лишь о том, что власть государства не может использоваться для навязывания каких-либо конкретных религиозных убеждений. Это не говорит о том, что учащихся не следует заставлять изучать ET в государственных школах. Я бы даже рекомендовал признать, что и ET, и IDT являются «теориями» происхождения человеческой жизни на Земле, а затем показать, почему ET заслуживает гораздо большего доверия, чем IDT. Это может способствовать пониманию науки и объединению демократических граждан не меньше, чем политически активная профессия СС или консенсусные конференции.




 Эти
числа являются
Эти
числа являются
 Используя нашу
замену, получим:
Используя нашу
замену, получим:
 Коэффициенты этих
уравнений обычно подобраны так, что искомый корень лежит среди небольших
целых чисел, таких как: 0,
±
1,
±
2,
±
3. Поэтому мы будем искать корень среди этих чисел и проверять его путём
подстановки в уравнение. Вероятность успеха
при
таком подходе очень высока. Предположим, что этот корень x 1 .
Коэффициенты этих
уравнений обычно подобраны так, что искомый корень лежит среди небольших
целых чисел, таких как: 0,
±
1,
±
2,
±
3. Поэтому мы будем искать корень среди этих чисел и проверять его путём
подстановки в уравнение. Вероятность успеха
при
таком подходе очень высока. Предположим, что этот корень x 1 .  Согласно теореме Безу (см. раздел «Деление многочлена на линейный
двучлен») это деление без остатка возможно, и мы получим в
результате многочлен второй степени, который надо приравнять к нулю. Решая
полученное квадратное уравнение, мы найдём (или нет!) оставшиеся два корня.
Согласно теореме Безу (см. раздел «Деление многочлена на линейный
двучлен») это деление без остатка возможно, и мы получим в
результате многочлен второй степени, который надо приравнять к нулю. Решая
полученное квадратное уравнение, мы найдём (или нет!) оставшиеся два корня. Ищем первый
корень перебором чисел: 0,
±
1,
±
2,
±
3
Ищем первый
корень перебором чисел: 0,
±
1,
±
2,
±
3



 Умышленно участвует в уничтожении заброшенного
здание, как оно определено в разделе одна тысяча девятьсот семьдесят один-а
права исков и процессуальных действий в отношении недвижимого имущества; или
3. По неосторожности наносит ущерб чужому имуществу на сумму
свыше двухсот пятидесяти долларов; или
4. С намерением воспрепятствовать тому, чтобы лицо сообщило запрос на
экстренная помощь, намеренно отключает или удаляет телефон, телетайп
или аналогичное оборудование для отправки сообщений, в то время как это лицо: (a) находится
пытается искать или занимается поиском чрезвычайной ситуации
помощь полиции, правоохранительных органов, пожарных или скорой медицинской помощи
обслуживающий персонал; или (b) пытается искать или участвует в
процесс обращения за экстренной помощью к другому физическому или юридическому лицу в
чтобы защитить себя, себя или третье лицо от неминуемой
телесное повреждение. Наличие у ответчика доли собственности
в таком оборудовании не является защитой от обвинения в соответствии с настоящим
подразделение.
Умышленно участвует в уничтожении заброшенного
здание, как оно определено в разделе одна тысяча девятьсот семьдесят один-а
права исков и процессуальных действий в отношении недвижимого имущества; или
3. По неосторожности наносит ущерб чужому имуществу на сумму
свыше двухсот пятидесяти долларов; или
4. С намерением воспрепятствовать тому, чтобы лицо сообщило запрос на
экстренная помощь, намеренно отключает или удаляет телефон, телетайп
или аналогичное оборудование для отправки сообщений, в то время как это лицо: (a) находится
пытается искать или занимается поиском чрезвычайной ситуации
помощь полиции, правоохранительных органов, пожарных или скорой медицинской помощи
обслуживающий персонал; или (b) пытается искать или участвует в
процесс обращения за экстренной помощью к другому физическому или юридическому лицу в
чтобы защитить себя, себя или третье лицо от неминуемой
телесное повреждение. Наличие у ответчика доли собственности
в таком оборудовании не является защитой от обвинения в соответствии с настоящим
подразделение. Преступное причинение вреда четвертой степени является мисдиминором класса А.
S 145.05 Преступное причинение вреда третьей степени.
Лицо виновно в преступном причинении вреда третьей степени, когда с
умысла на причинение вреда имуществу другого лица и не имеющего права совершать
поэтому нет никаких разумных оснований полагать, что он или она имеет такое право,
он или она:
1. повреждает автомобиль другого лица, взламывая такие
транспортное средство, когда оно заперто с целью кражи имущества, и
в течение предшествующего десятилетнего периода был судим три или более
раз, по отдельным уголовным делам, по которым было назначено наказание
в отдельных случаях за преступное причинение вреда четвертой степени, как
определено в разделе 145.00, преступное причинение вреда третьей степени как
определяемый в этом разделе, преступное причинение вреда второй степени как
определено в разделе 145.10, или преступное причинение вреда первой степени как
определено статьей 145.12 настоящей статьи; или
2.
Преступное причинение вреда четвертой степени является мисдиминором класса А.
S 145.05 Преступное причинение вреда третьей степени.
Лицо виновно в преступном причинении вреда третьей степени, когда с
умысла на причинение вреда имуществу другого лица и не имеющего права совершать
поэтому нет никаких разумных оснований полагать, что он или она имеет такое право,
он или она:
1. повреждает автомобиль другого лица, взламывая такие
транспортное средство, когда оно заперто с целью кражи имущества, и
в течение предшествующего десятилетнего периода был судим три или более
раз, по отдельным уголовным делам, по которым было назначено наказание
в отдельных случаях за преступное причинение вреда четвертой степени, как
определено в разделе 145.00, преступное причинение вреда третьей степени как
определяемый в этом разделе, преступное причинение вреда второй степени как
определено в разделе 145.10, или преступное причинение вреда первой степени как
определено статьей 145.12 настоящей статьи; или
2. причиняет ущерб имуществу другого лица на сумму, превышающую два
сто пятьдесят долларов.
Преступное причинение вреда третьей степени является фелонией класса Е.
S 145.10 Преступное причинение вреда второй степени.
Лицо виновно в преступном причинении вреда второй степени, когда с
умысла на причинение вреда имуществу другого лица и не имеющего права совершать
поэтому нет никаких разумных оснований полагать, что он имеет такое право, он
причиняет ущерб имуществу другого лица на сумму более тысячи
пятьсот долларов.
Преступное причинение вреда второй степени является тяжким преступлением класса D.
S 145.12 Преступное причинение вреда первой степени.
Лицо виновно в преступном причинении вреда первой степени, когда с
умысла на причинение вреда имуществу другого лица и не имеющего права совершать
поэтому нет никаких разумных оснований полагать, что он имеет такое право, он
наносит ущерб имуществу другого лица с помощью взрывчатого вещества.
Преступное причинение вреда первой степени является фелонией класса B.
причиняет ущерб имуществу другого лица на сумму, превышающую два
сто пятьдесят долларов.
Преступное причинение вреда третьей степени является фелонией класса Е.
S 145.10 Преступное причинение вреда второй степени.
Лицо виновно в преступном причинении вреда второй степени, когда с
умысла на причинение вреда имуществу другого лица и не имеющего права совершать
поэтому нет никаких разумных оснований полагать, что он имеет такое право, он
причиняет ущерб имуществу другого лица на сумму более тысячи
пятьсот долларов.
Преступное причинение вреда второй степени является тяжким преступлением класса D.
S 145.12 Преступное причинение вреда первой степени.
Лицо виновно в преступном причинении вреда первой степени, когда с
умысла на причинение вреда имуществу другого лица и не имеющего права совершать
поэтому нет никаких разумных оснований полагать, что он имеет такое право, он
наносит ущерб имуществу другого лица с помощью взрывчатого вещества.
Преступное причинение вреда первой степени является фелонией класса B. S 145.13 Определения.
Для целей разделов 145.00, 145.05, 145.10 и 145.12 настоящего
статья:
Имущество другого лица " включает все имущество, в котором находится другое
имеет право собственности, независимо от того, наносит ли лицо ущерб
такое имущество или любое другое лицо может также иметь интерес в таком
свойство.
S 145.14 Преступное вмешательство третьей степени.
Лицо виновно в преступном манипулировании третьей степенью, когда,
не имея на это ни права, ни разумных оснований полагать, что он
имеет такое право, он вмешивается в чужое имущество с умыслом
причинять существенные неудобства такому лицу или третьему лицу.
Преступное вмешательство третьей степени является мисдиминором класса B.
S 145.15 Преступное вмешательство второй степени.
Лицо виновно в преступном вторжении второй степени, когда,
не имея на это ни права, ни разумных оснований полагать, что он
имеет такое право, он или она вмешивается или устанавливает связь с собственностью
газовая, электрическая, канализационная, паровая или водопроводная корпорация, телефон или
телеграфная корпорация, обычный перевозчик, атомная электростанция
генерирующая установка или коммунальное предприятие, управляемое муниципалитетом или
округ; за исключением того, что в любом судебном преследовании в соответствии с этим разделом, это
утвердительная защита о том, что ответчик не участвовал в таком поведении
для воровства или иных незаконных или неправомерных целей.
S 145.13 Определения.
Для целей разделов 145.00, 145.05, 145.10 и 145.12 настоящего
статья:
Имущество другого лица " включает все имущество, в котором находится другое
имеет право собственности, независимо от того, наносит ли лицо ущерб
такое имущество или любое другое лицо может также иметь интерес в таком
свойство.
S 145.14 Преступное вмешательство третьей степени.
Лицо виновно в преступном манипулировании третьей степенью, когда,
не имея на это ни права, ни разумных оснований полагать, что он
имеет такое право, он вмешивается в чужое имущество с умыслом
причинять существенные неудобства такому лицу или третьему лицу.
Преступное вмешательство третьей степени является мисдиминором класса B.
S 145.15 Преступное вмешательство второй степени.
Лицо виновно в преступном вторжении второй степени, когда,
не имея на это ни права, ни разумных оснований полагать, что он
имеет такое право, он или она вмешивается или устанавливает связь с собственностью
газовая, электрическая, канализационная, паровая или водопроводная корпорация, телефон или
телеграфная корпорация, обычный перевозчик, атомная электростанция
генерирующая установка или коммунальное предприятие, управляемое муниципалитетом или
округ; за исключением того, что в любом судебном преследовании в соответствии с этим разделом, это
утвердительная защита о том, что ответчик не участвовал в таком поведении
для воровства или иных незаконных или неправомерных целей.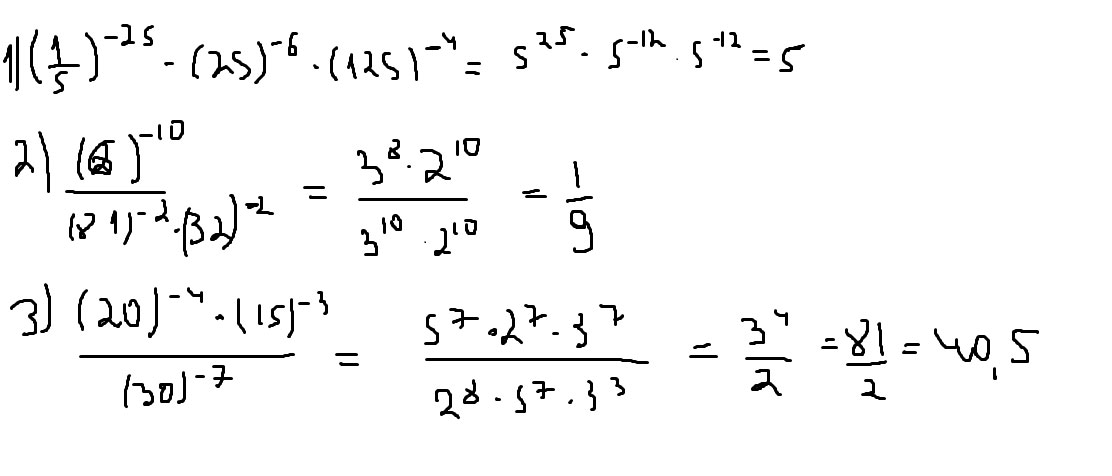 Преступное вмешательство второй степени является проступком класса А.
S 145.20 Преступное вмешательство первой степени.
Лицо виновно в преступном манипулировании первой степенью, когда,
с намерением вызвать существенное прерывание или нарушение
услугу, оказываемую обществу, и не имея на это ни права, ни какого-либо
разумные основания полагать, что он или она имеет такое право, он или она
повреждает или портит имущество газовой, электрической, канализационной, паровой или
водопроводная корпорация, телефонная или телеграфная корпорация, общее
перевозчик, атомная электростанция или коммунальное предприятие
управляется муниципалитетом или районом, и тем самым вызывает такие
существенное прерывание или ухудшение обслуживания.
Преступное вмешательство первой степени является тяжким преступлением класса D.
S 145.22 Осквернение кладбища второй степени.
Лицо виновно в осквернении кладбища второй степени, когда:
а) с намерением нанести ущерб имуществу другого лица и не имея
права на это и каких-либо разумных оснований полагать, что он имеет такое
правильно, он повреждает любое недвижимое или личное имущество, используемое в качестве кладбища.
Преступное вмешательство второй степени является проступком класса А.
S 145.20 Преступное вмешательство первой степени.
Лицо виновно в преступном манипулировании первой степенью, когда,
с намерением вызвать существенное прерывание или нарушение
услугу, оказываемую обществу, и не имея на это ни права, ни какого-либо
разумные основания полагать, что он или она имеет такое право, он или она
повреждает или портит имущество газовой, электрической, канализационной, паровой или
водопроводная корпорация, телефонная или телеграфная корпорация, общее
перевозчик, атомная электростанция или коммунальное предприятие
управляется муниципалитетом или районом, и тем самым вызывает такие
существенное прерывание или ухудшение обслуживания.
Преступное вмешательство первой степени является тяжким преступлением класса D.
S 145.22 Осквернение кладбища второй степени.
Лицо виновно в осквернении кладбища второй степени, когда:
а) с намерением нанести ущерб имуществу другого лица и не имея
права на это и каких-либо разумных оснований полагать, что он имеет такое
правильно, он повреждает любое недвижимое или личное имущество, используемое в качестве кладбища. участок, могила, место захоронения или иное место захоронения человеческих останков;
или
(b) с намерением украсть личное имущество, он крадет личное
имущество, находящееся на кладбищенском участке, могиле, месте захоронения или
другое место захоронения человеческих останков и имущество которого принадлежит
лицо или организация, которая содержит или владеет таким местом или
имущество, ближайшие родственники или представители умершего погребенного
там.
Осквернение кладбища второй степени является правонарушением класса А.
S 145.23 Осквернение кладбища первой степени.
Лицо виновно в осквернении кладбища первой степени, когда
с намерением причинить вред имуществу другого лица и не имея права
сделать это и нет никаких разумных оснований полагать, что он имеет такое право, он:
(a) повреждает любую недвижимую или личную собственность, используемую в качестве кладбища
участок, могила, место захоронения или иное место захоронения человеческих останков
на сумму, превышающую двести пятьдесят долларов; или
(b) с намерением украсть личное имущество, он крадет личное
имущество, стоимость которого превышает двести пятьдесят долларов, что
расположенных на кладбищенском участке, могиле, месте захоронения или другом месте
захоронение человеческих останков и какое имущество принадлежит лицу или
организация, которая содержит или владеет таким местом или имуществом,
близкие родственники или представители погребенного там умершего; или
(c) совершает преступление осквернения кладбища второй степени, как
определено статьей 145.
участок, могила, место захоронения или иное место захоронения человеческих останков;
или
(b) с намерением украсть личное имущество, он крадет личное
имущество, находящееся на кладбищенском участке, могиле, месте захоронения или
другое место захоронения человеческих останков и имущество которого принадлежит
лицо или организация, которая содержит или владеет таким местом или
имущество, ближайшие родственники или представители умершего погребенного
там.
Осквернение кладбища второй степени является правонарушением класса А.
S 145.23 Осквернение кладбища первой степени.
Лицо виновно в осквернении кладбища первой степени, когда
с намерением причинить вред имуществу другого лица и не имея права
сделать это и нет никаких разумных оснований полагать, что он имеет такое право, он:
(a) повреждает любую недвижимую или личную собственность, используемую в качестве кладбища
участок, могила, место захоронения или иное место захоронения человеческих останков
на сумму, превышающую двести пятьдесят долларов; или
(b) с намерением украсть личное имущество, он крадет личное
имущество, стоимость которого превышает двести пятьдесят долларов, что
расположенных на кладбищенском участке, могиле, месте захоронения или другом месте
захоронение человеческих останков и какое имущество принадлежит лицу или
организация, которая содержит или владеет таким местом или имуществом,
близкие родственники или представители погребенного там умершего; или
(c) совершает преступление осквернения кладбища второй степени, как
определено статьей 145. 22 настоящей статьи и ранее
осужден за преступление осквернения кладбища второй степени
в течение предшествующих пяти лет.
Осквернение кладбища первой степени является тяжким преступлением класса Е.
S 145.25 Безрассудная угроза имуществу.
Лицо виновно в неосторожном причинении вреда имуществу, когда оно
неосторожно совершает действия, которые создают значительный риск причинения ущерба
в собственность другого лица на сумму более двухсот
пятьдесят долларов.
Неосторожная угроза имуществу является правонарушением класса B.
S 145.26 Осквернение кладбища при отягчающих обстоятельствах второй степени.
Лицо виновно в осквернении кладбища с отягчающими обстоятельствами по второму
степени, когда, не имея на это права или каких-либо разумных оснований для
считает, что имеет такое право, открывает ларец, склеп,
или аналогичный сосуд, содержащий человеческое тело или человеческие останки,
был похоронен или иным образом предан земле на кладбище и незаконно удаляет
оттуда тело, часть тела, любые человеческие останки или любой предмет, содержащийся
в таком ларце, склепе или подобном сосуде с целью получения
незаконное владение таким телом, частью тела, человеческими останками или предметом
для такого лица или третьего лица.
22 настоящей статьи и ранее
осужден за преступление осквернения кладбища второй степени
в течение предшествующих пяти лет.
Осквернение кладбища первой степени является тяжким преступлением класса Е.
S 145.25 Безрассудная угроза имуществу.
Лицо виновно в неосторожном причинении вреда имуществу, когда оно
неосторожно совершает действия, которые создают значительный риск причинения ущерба
в собственность другого лица на сумму более двухсот
пятьдесят долларов.
Неосторожная угроза имуществу является правонарушением класса B.
S 145.26 Осквернение кладбища при отягчающих обстоятельствах второй степени.
Лицо виновно в осквернении кладбища с отягчающими обстоятельствами по второму
степени, когда, не имея на это права или каких-либо разумных оснований для
считает, что имеет такое право, открывает ларец, склеп,
или аналогичный сосуд, содержащий человеческое тело или человеческие останки,
был похоронен или иным образом предан земле на кладбище и незаконно удаляет
оттуда тело, часть тела, любые человеческие останки или любой предмет, содержащийся
в таком ларце, склепе или подобном сосуде с целью получения
незаконное владение таким телом, частью тела, человеческими останками или предметом
для такого лица или третьего лица. Осквернение кладбища второй степени при отягчающих обстоятельствах является тяжким преступлением класса Е.
S 145.27 Осквернение кладбища при отягчающих обстоятельствах первой степени.
Лицо виновно в осквернении кладбища с отягчающими обстоятельствами в первой
степень, когда такое лицо совершает преступление кладбища с отягчающими обстоятельствами
осквернение второй степени и ранее был судим
в течение последних пяти лет с момента совершения преступления осквернения кладбища в г.
второй степени, как это определено статьей 145.22 настоящей статьи, кладбище
осквернение первой степени, как это определено в статье 145.23 настоящего
осквернение кладбища второй степени с отягчающими обстоятельствами
определенных пунктом 145.26 настоящей статьи.
Осквернение кладбища с отягчающими обстоятельствами первой степени является тяжким преступлением класса D.
S 145.30 Незаконное размещение рекламы.
1. Лицо виновно в незаконном размещении рекламы, когда,
не имея на это ни права, ни разумных оснований полагать, что он
имеет такое право, он размещает, рисует или иным образом прикрепляет к имуществу
любое другое лицо любая реклама, плакат, уведомление или другой материал
направлено на получение выгоды от лица, не являющегося собственником имущества.
Осквернение кладбища второй степени при отягчающих обстоятельствах является тяжким преступлением класса Е.
S 145.27 Осквернение кладбища при отягчающих обстоятельствах первой степени.
Лицо виновно в осквернении кладбища с отягчающими обстоятельствами в первой
степень, когда такое лицо совершает преступление кладбища с отягчающими обстоятельствами
осквернение второй степени и ранее был судим
в течение последних пяти лет с момента совершения преступления осквернения кладбища в г.
второй степени, как это определено статьей 145.22 настоящей статьи, кладбище
осквернение первой степени, как это определено в статье 145.23 настоящего
осквернение кладбища второй степени с отягчающими обстоятельствами
определенных пунктом 145.26 настоящей статьи.
Осквернение кладбища с отягчающими обстоятельствами первой степени является тяжким преступлением класса D.
S 145.30 Незаконное размещение рекламы.
1. Лицо виновно в незаконном размещении рекламы, когда,
не имея на это ни права, ни разумных оснований полагать, что он
имеет такое право, он размещает, рисует или иным образом прикрепляет к имуществу
любое другое лицо любая реклама, плакат, уведомление или другой материал
направлено на получение выгоды от лица, не являющегося собственником имущества. 2. Если такой материал состоит из коммерческой рекламы, он
предполагается, что продавец указанного продукта, услуги или
развлечения – лицо, разместившее такую рекламу или побудившее ее
размещаться на имуществе.
Незаконное размещение рекламы является нарушением.
S 145.35 Фальсификация потребительского товара; потребительский продукт определен.
Для целей пунктов 145.40 и 145.45 настоящей статьи:
потребительский товар "означает любое лекарство, продукт питания, напиток или вещь, которая
выставлены или предложены для продажи публике, для введения в или
проглатывании человеком или для нанесения на любую внешнюю поверхность
будучи человеком.
S 145.40 Фальсификация потребительского товара второй степени.
Лицо виновно в фальсификации потребительского товара во второй
степени, когда, не имея на это права или каких-либо разумных оснований для
полагать, что он имеет такое право, и с намерением причинить телесные повреждения
другому или с намерением внушить другому страх, что он
нанести такие телесные повреждения, он изменяет, фальсифицирует или иным образом
загрязняет потребительский товар.
2. Если такой материал состоит из коммерческой рекламы, он
предполагается, что продавец указанного продукта, услуги или
развлечения – лицо, разместившее такую рекламу или побудившее ее
размещаться на имуществе.
Незаконное размещение рекламы является нарушением.
S 145.35 Фальсификация потребительского товара; потребительский продукт определен.
Для целей пунктов 145.40 и 145.45 настоящей статьи:
потребительский товар "означает любое лекарство, продукт питания, напиток или вещь, которая
выставлены или предложены для продажи публике, для введения в или
проглатывании человеком или для нанесения на любую внешнюю поверхность
будучи человеком.
S 145.40 Фальсификация потребительского товара второй степени.
Лицо виновно в фальсификации потребительского товара во второй
степени, когда, не имея на это права или каких-либо разумных оснований для
полагать, что он имеет такое право, и с намерением причинить телесные повреждения
другому или с намерением внушить другому страх, что он
нанести такие телесные повреждения, он изменяет, фальсифицирует или иным образом
загрязняет потребительский товар. Фальсификация потребительского товара второй степени
является правонарушением класса А.
S 145.45 Фальсификация потребительского товара первой степени.
Лицо виновно в фальсификации потребительского товара в первую очередь
степени, когда, не имея на это права или каких-либо разумных оснований для
полагать, что он имеет такое право, и с намерением причинить телесные повреждения
другому или с намерением внушить другому страх, что он
нанести такие телесные повреждения, он изменяет, фальсифицирует или иным образом
загрязняет потребительский товар и тем самым создает существенный риск
причинение тяжких телесных повреждений одному или нескольким лицам.
Фальсификация потребительского товара первой степени является уголовным преступлением класса Е.
S 145.50 Штрафы за мусор на железнодорожных путях и полосах отчуждения.
1. Никто не должен бросать, сбрасывать или заставлять бросать, сбрасывать,
сданы на хранение или размещены на железнодорожных путях или в пределах
полосе отчуждения любой железной дороги, любой мусор, хлам, отбросы, хлам,
мусор или любые тошнотворные или неприятные вещества.
Фальсификация потребительского товара второй степени
является правонарушением класса А.
S 145.45 Фальсификация потребительского товара первой степени.
Лицо виновно в фальсификации потребительского товара в первую очередь
степени, когда, не имея на это права или каких-либо разумных оснований для
полагать, что он имеет такое право, и с намерением причинить телесные повреждения
другому или с намерением внушить другому страх, что он
нанести такие телесные повреждения, он изменяет, фальсифицирует или иным образом
загрязняет потребительский товар и тем самым создает существенный риск
причинение тяжких телесных повреждений одному или нескольким лицам.
Фальсификация потребительского товара первой степени является уголовным преступлением класса Е.
S 145.50 Штрафы за мусор на железнодорожных путях и полосах отчуждения.
1. Никто не должен бросать, сбрасывать или заставлять бросать, сбрасывать,
сданы на хранение или размещены на железнодорожных путях или в пределах
полосе отчуждения любой железной дороги, любой мусор, хлам, отбросы, хлам,
мусор или любые тошнотворные или неприятные вещества. 2. Если шоссе или дорога полностью или частично проходят в пределах железной дороги.
право прохода, ничто в этом разделе не должно толковаться как запрещающее
разумное использование золы, песка, соли или других материалов
с целью уменьшения опасности или обеспечения тяги на
снег, лед или мокрый снег на таком шоссе или дороге.
3. Нарушение положений пункта первого настоящей статьи.
наказывается штрафом в размере до двухсот пятидесяти долларов
и/или требование оказывать услуги для общественных или некоммерческих
корпорации, ассоциации, учреждения или агентства не более восьми
часов, а за любое второе или последующее нарушение налагается штраф в размере не более
пятьсот долларов и/или требование об оказании услуг за
общественная или некоммерческая корпорация, ассоциация, учреждение или агентство
не более восьми часов.
4. Ничто в этом разделе не считается применимым к железной дороге или
его работники, когда предметы сбрасываются ими на железнодорожные пути или
право проезда осуществляется в соответствии с железнодорожными правилами, положениями или
процедуры.
2. Если шоссе или дорога полностью или частично проходят в пределах железной дороги.
право прохода, ничто в этом разделе не должно толковаться как запрещающее
разумное использование золы, песка, соли или других материалов
с целью уменьшения опасности или обеспечения тяги на
снег, лед или мокрый снег на таком шоссе или дороге.
3. Нарушение положений пункта первого настоящей статьи.
наказывается штрафом в размере до двухсот пятидесяти долларов
и/или требование оказывать услуги для общественных или некоммерческих
корпорации, ассоциации, учреждения или агентства не более восьми
часов, а за любое второе или последующее нарушение налагается штраф в размере не более
пятьсот долларов и/или требование об оказании услуг за
общественная или некоммерческая корпорация, ассоциация, учреждение или агентство
не более восьми часов.
4. Ничто в этом разделе не считается применимым к железной дороге или
его работники, когда предметы сбрасываются ими на железнодорожные пути или
право проезда осуществляется в соответствии с железнодорожными правилами, положениями или
процедуры. S 145.60 Создание граффити.
1. Для целей настоящего раздела термин " граффити "означает
травление, окраска, покрытие, нанесение рисунка или иное нанесение знака
на государственную или частную собственность с намерением нанести ущерб такой собственности.
2. Никто не может делать граффити любого типа на любом здании, общественном
или частное, или любое другое имущество, недвижимое или движимое, принадлежащее любому лицу,
фирма или корпорация или любое государственное учреждение или инструмент, без
прямое разрешение владельца или оператора указанного имущества.
Нанесение граффити является правонарушением класса А.
S 145.65 Владение граффити-инструментами.
Лицо виновно в хранении инструментов для граффити, когда оно
обладает любым инструментом, прибором, предметом, веществом, раствором или другим
соединение, разработанное или обычно используемое для травления, окрашивания, покрытия, рисования или
иным образом поставить отметку на объекте собственности, которым это лицо не владеет.
S 145.60 Создание граффити.
1. Для целей настоящего раздела термин " граффити "означает
травление, окраска, покрытие, нанесение рисунка или иное нанесение знака
на государственную или частную собственность с намерением нанести ущерб такой собственности.
2. Никто не может делать граффити любого типа на любом здании, общественном
или частное, или любое другое имущество, недвижимое или движимое, принадлежащее любому лицу,
фирма или корпорация или любое государственное учреждение или инструмент, без
прямое разрешение владельца или оператора указанного имущества.
Нанесение граффити является правонарушением класса А.
S 145.65 Владение граффити-инструментами.
Лицо виновно в хранении инструментов для граффити, когда оно
обладает любым инструментом, прибором, предметом, веществом, раствором или другим
соединение, разработанное или обычно используемое для травления, окрашивания, покрытия, рисования или
иным образом поставить отметку на объекте собственности, которым это лицо не владеет. разрешение или полномочия гравировать, рисовать, покрывать, рисовать или иным образом
товарный знак, при обстоятельствах, свидетельствующих о намерении использовать его для
повредить такое имущество.
Владение инструментами для граффити является правонарушением класса B.
S 145.70 Преступное владение ускорителем таксометра.
1. Для целей настоящего раздела a " таксометр "означает прибор или
устройство, которое автоматически рассчитывает и отображает заряд на
пассажир в транспортном средстве, имеющем лицензию на перевозку членов
общественность по найму в соответствии с местным законодательством.
2. Для целей настоящего раздела " устройство ускорения таксометра "
означает прибор или устройство, которое заставляет таксометр увеличивать
плата, отображаемая таким таксометром, на сумму, превышающую максимальную
суммы, разрешенной местным законодательством.
3. Лицо виновно в преступном хранении таксометра.
ускоряющее устройство, когда он сознательно владеет с намерением использовать
незаконно, ускоряющее устройство таксометра.
разрешение или полномочия гравировать, рисовать, покрывать, рисовать или иным образом
товарный знак, при обстоятельствах, свидетельствующих о намерении использовать его для
повредить такое имущество.
Владение инструментами для граффити является правонарушением класса B.
S 145.70 Преступное владение ускорителем таксометра.
1. Для целей настоящего раздела a " таксометр "означает прибор или
устройство, которое автоматически рассчитывает и отображает заряд на
пассажир в транспортном средстве, имеющем лицензию на перевозку членов
общественность по найму в соответствии с местным законодательством.
2. Для целей настоящего раздела " устройство ускорения таксометра "
означает прибор или устройство, которое заставляет таксометр увеличивать
плата, отображаемая таким таксометром, на сумму, превышающую максимальную
суммы, разрешенной местным законодательством.
3. Лицо виновно в преступном хранении таксометра.
ускоряющее устройство, когда он сознательно владеет с намерением использовать
незаконно, ускоряющее устройство таксометра. Если такое устройство
одержимым сознательно, существует опровержимая презумпция того, что оно
предназначены для незаконного использования.
Преступное хранение ускоряющего устройства таксометра
является правонарушением класса А.
Верх страницы
Если такое устройство
одержимым сознательно, существует опровержимая презумпция того, что оно
предназначены для незаконного использования.
Преступное хранение ускоряющего устройства таксометра
является правонарушением класса А.
Верх страницы



 {\prime}(x)=\frac{2 \ln x}{x}
\)
{\prime}(x)=\frac{2 \ln x}{x}
\) {-1}(y)\bigr)} .$$ 9n$
{-1}(y)\bigr)} .$$ 9n$ По этим причинам важно научиться находить производные логарифмических функций.
По этим причинам важно научиться находить производные логарифмических функций. Вместо этого вы можете использовать следующую формулу.
Вместо этого вы можете использовать следующую формулу. \]
\]
 \]
\] \]
\]