Равные треугольники – определение, свойства, признаки
4.5
Средняя оценка: 4.5
Всего получено оценок: 370.
4.5
Средняя оценка: 4.5
Всего получено оценок: 370.
Изучая тему треугольников, стоит обратить внимание на признаки равенства двух фигур. Их можно использовать во время решений различных заданий. О том, как определить признаки и свойства равенства треугольников – поговорим в этой статье.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение
Треугольники ABC и $A_1B_1C_1$ считаются равными в том случае, если их можно совместить наложением. При этом, все стороны и вершины фигур полностью наложатся друг на друга, а все соответствующие углы совместятся.
Исходя из определения равных треугольников, в равных треугольниках все соотвествующие стороны равны и все соответствующие углы равны. Используем это свойство для доказательства признаков равенства треугольников способом наложения.
Для обозначения равенства фигур используют знак “равно”, к примеру, $Δ ABC = Δ А_1В_1С_1$
Математик Фалес, чтобы вычесть расстояние от корабля до суши построил треугольник на суше равный треугольнику на «море». Он, таким образом, узнал точное расстояние.
Признаки равенства
Выделяют три признака равенства треугольников:
1. Если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу между ними другого треугольника, то такие фигуры равны.
Рис. 1. Первый признак равенства2. Если сторона и два прилегающих к ней угла одного треугольника равны соответствующей стороне и двум прилегающим к ней углам другого треугольника, то такие фигуры равны.
Рис. 2. Второй признак равенства3. Если три стороны в одном треугольнике равны трем сторонам в другом треугольнике, то такие треугольники равны.
Кроме того, стоит выделить некоторые свойства:
- Сумма двух внутренних углов треугольника будет всегда меньше 1800.

- Внешний угол треугольника всегда больше внутреннего, при условии, если угол не смежный с ним.
- Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Алгоритм доказательства равенства фигур
- Необходимо сориентироваться, для каких треугольников необходимо доказать равенство. Для удобства можно выделить их разными цветами.
- На рисунке отметить, все необходимые данные в условии задания.
- Проверить есть ли у двух треугольников общая сторона либо угол.
- Далее необходимо проанализировать, имеют ли треугольники по две пары равных сторон либо углов. А также необходимо поразмышлять, как можно доказать равенство третьей стороны, либо угла между ними.
- При недостатке данных необходимо выяснить: можно ли использовать равенство других треугольников, чтобы доказать равенство нужных по условию.
- При необходимости, можно сделать дополнительное построение.
Порядок названия вершин одного треугольника должен быть одинаковым с порядком названия вершин другого треугольника.
Стойки стремянки могут свободно раздвигаться, до того момента, когда их не зафиксировали перемычкой. Жесткость такой конструкции основывается на третьем признаке равенства фигур.
Пример
Задание:
Два отрезка пересекаются в точке О и делятся этой точкой пополам. Доказать, что $Δ ABO = Δ CDO$.
Решение:
Стоит обратить внимание на рисунок
В условии задания сказано, что $BO=OD$, $AO = OС$. А углы $AOB$ и $COD$ равны, так как они вертикальные. Поэтому $Δ ABO = Δ CDO$ по первому признаку равенства треугольников.
Что мы узнали?
Для того, чтобы доказать равенство фигур необходимо использовать один из трех признаков равенства треугольников. Треугольники могут быть равными по двум сторонами и углу между ними, по стороне и двум прилегающим к ней углам, а также по трем сторонам.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Анна Ножеева
5/5
Ярик Яраслав
5/5
Данила Салин
5/5
Никита Ушаков
5/5
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 370.
А какая ваша оценка?
Равенство треугольников. Признаки равенства треугольников – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Два треугольника называются равными, если их можно совместить наложением. Если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Признаки равенства прямоугольных треугольников
Два прямоугольных треугольника равны, если выполняется одно из следующих условий:
- равны их катеты;
- катет и гипотенуза одного треугольника равны катету и гипотенузе другого;
- гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;
- катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;
- катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Физика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Прикрепите скриншот
Объем файла не должен превышать 1МБ
Казахский
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
Стороны равной длины — определение, формы, примеры, факты
Стороны равной длины — введение
Математика — это не только числа, она также включает изучение различных форм, таких как круги, квадраты, овалы, цилиндры, треугольники, прямоугольники и многое другое.
Включает определение размеров сторон или точных углов фигур.
Сегодня мы обсудим фигуры, имеющие сторон одинаковой длины . Мы узнаем факторы, которые отличают их друг от друга, и их соответствующие названия. Давайте начнем!
Родственные игры
Что такое Стороны равной длины?
Стороны одинаковой длины означают, что их размеры одинаковы. Проще говоря, стороны фигуры, имеющие одинаковую длину, являются сторонами равной длины.
Проще говоря, стороны фигуры, имеющие одинаковую длину, являются сторонами равной длины.
Стороны, имеющие одинаковую длину, также называются конгруэнтными сторонами. Эти стороны могут быть частью одной формы или разных форм. Давайте посмотрим на несколько примеров фигур со сторонами одинаковой длины.
В прямоугольнике ниже противоположные стороны конгруэнтны друг другу.
В двух треугольниках ниже стороны конгруэнтны друг другу.
Связанные рабочие листы
Стороны равной длины в одной форме
Треугольники
В зависимости от длины сторон треугольники можно разделить на разносторонние, равнобедренные и равносторонние.
- Разносторонний треугольник:
Это треугольник, в котором каждая сторона имеет разную длину.
- Равнобедренный треугольник:
Это треугольник, в котором две стороны имеют одинаковую длину. Угол, падающий между равными сторонами, называется углом при вершине. Углы, противолежащие двум равным сторонам треугольника, всегда будут равны. Точно так же, если два угла треугольника равны, то их соответствующие противоположные стороны также будут иметь одинаковую длину.
Точно так же, если два угла треугольника равны, то их соответствующие противоположные стороны также будут иметь одинаковую длину.
- Равносторонний треугольник:
Это треугольник, в котором все три стороны имеют одинаковую длину. Каждый угол равностороннего треугольника равен 60°. Следовательно, его также называют равноугольным треугольником.
Итак, треугольники с равными сторонами могут быть либо равнобедренными, либо равносторонними.
Четырехугольники
Четырехугольники — это многоугольники с четырьмя сторонами. Они также могут иметь равные все или некоторые из сторон. Различные категории перечислены ниже:
- Все стороны равны
В этих четырехугольниках все четыре стороны равны. Их еще называют правильными четырехугольниками. Примерами правильных четырехугольников являются квадрат и ромб.
- Три равные стороны
В этих четырехугольниках три стороны равны.
- Одна пара равных сторон
В этих четырехугольниках есть одна пара равных сторон. Стороны могут быть как противоположными, так и примыкающими друг к другу.
Стороны могут быть как противоположными, так и примыкающими друг к другу.
- Противоположные стороны равны: Примером этого является равнобедренная трапеция
- Смежные стороны равны: Примером этого является неправильный четырехугольник, у которого две смежные стороны равны.
- Две пары равных сторон
- Равные стороны противоположны: Примеры: прямоугольник и параллелограмм.
- Равные стороны смежные: Пример — воздушный змей.
Многоугольники
Многоугольники — это двумерные замкнутые фигуры, состоящие только из прямых сторон. Многоугольники могут иметь любое количество сторон. Это означает, что треугольники и четырехугольники также являются многоугольниками. Многоугольники также могут иметь равные все или некоторые стороны.
- Правильные многоугольники:
Многоугольники, у которых все стороны и все внутренние углы равны, называются правильными многоугольниками. Все их углы также равны. Обратите внимание, что ромб не имеет равных сторон, а не является правильным многоугольником, потому что все его внутренние углы не равны.
Все их углы также равны. Обратите внимание, что ромб не имеет равных сторон, а не является правильным многоугольником, потому что все его внутренние углы не равны.
- Неправильные многоугольники:
Многоугольники, у которых все стороны не равны, называются правильными многоугольниками. У них могут быть некоторые стороны одинаковой длины, но не все. Таким образом, даже если прямоугольники и параллелограммы имеют равные противоположные стороны, они являются неправильными многоугольниками.
Стороны одинаковой длины в различных формах
При сравнении различных форм, если сторона одной формы равна стороне другой, говорят, что стороны равны.
Если все стороны одной фигуры равны всем сторонам другой фигуры и углы также одинаковы, то две фигуры называются конгруэнтными.
Например, два треугольника называются конгруэнтными, если все их соответствующие стороны и углы равны.
Критерии конгруэнтности треугольников
Нам не нужно измерять все стороны и углы двух треугольников, чтобы проверить, конгруэнтны они или нет. Если они соответствуют любому из заданных критериев, то они конгруэнтны.
Если они соответствуют любому из заданных критериев, то они конгруэнтны.
- Критерии SSS (сторона-сторона-сторона)
Два треугольника $\Delta\text{ABC}$ и $\Delta\text{PQR}$ называются конгруэнтными по критерию SSS, если их соответствующие стороны равны.
- AB $=$ PQ
- до н.э. $=$ QR
- AC $=$ PR
- Критерии SAS (сторона-угол-сторона)
Два треугольника $\Delta{ABC}$ и $\Delta{PQR}$ называются конгруэнтными по критериям SAS, если две их соответствующие стороны и угол между ними равны.
- AB $=$ PQ
- ∠A $=$ ∠P
- AC $=$ PR
- Критерии AAS (угол-угол-сторона)
Два треугольника $\Delta\text{ABC}$ и $\Delta\text{PQR}$ называются конгруэнтными по критериям ААС, если любые два их соответствующих угла и любая одна сторона равны.
- ∠A $=$ ∠P
- ∠С $=$ ∠Р
- AC $=$ PR
- RHS-критерий (правая сторона гипотенузы)
Два прямоугольных треугольника $\Delta\text{ABC}$ и $\Delta\text{XYZ}$ называются конгруэнтными по RHS-критерию, если их соответствующие гипотенуза и одна пара соответствующих сторон равны..jpg)
- ∠B $=$ ∠Y (прямой угол)
- AC $=$ XZ (гипотенуза)
- AB $=$ XY (сторона)
Заключение
У некоторых фигур все стороны равны, а у других ни одна из сторон не равна. Кроме того, есть фигуры, у которых только несколько равных сторон. Мы можем сравнивать стороны и углы различных фигур, чтобы найти конгруэнтные стороны и конгруэнтные формы.
Решенные примеры
1. Назовите три фигуры, все стороны которых имеют одинаковую длину.
Решение : Три фигуры, все стороны которых имеют одинаковую длину, это ромб, квадрат и равносторонний треугольник.
2. Найдите периметр правильного шестиугольника, если одна из его сторон равна 9 дм.
Решение: Правильный шестиугольник имеет 6 сторон одинаковой длины.
Поскольку сторона равна 9 дюймам, периметр будет:
6$\умножить на 9 = 54$ дюймов.
3. Если две стороны треугольника равны, какой это треугольник?
Решение : Это равнобедренный треугольник. У равнобедренного треугольника две равные стороны.
У равнобедренного треугольника две равные стороны.
4. Если одна сторона параллелограмма 10 дюймов, а другая сторона 6 дюймов, каков общий периметр?
Решение : В параллелограмме противоположные стороны равны друг другу.
Если одна сторона 10 дюймов, а другая сторона 6 дюймов, общий периметр будет:
10$ + 10 + 6 + 6 = 32$ дюймов.
Практические задачи
1
В $\Delta\text{ABC}$ ∠A $=$ 50°, ∠ B $=$ 80° и ∠ C $=$ 50°. Определите равные стороны.
AC $=$ BC
AB $=$ AC
AB $=$ BC
Стороны не равны
Правильный ответ: AB $=$ BC
Дано, что ∠A $=$∠ В $=$ 50°. Это означает, что стороны, противолежащие этим углам, также равны. То есть AB $=$ BC.
2
$\Delta\text{ABC}$ имеет стороны 6 дюймов, 8 дюймов и 10 дюймов. $\Delta\text{DEF}$ конгруэнтно $\Delta\text{ABC}$. Что за треугольник $\Delta\text{DEF}$?
Разносторонний
Равносторонний
Равнобедренный
Невозможно определить
Правильный ответ: Разносторонний
Если $\Delta\text{DEF}$ конгруэнтно $\Delta\text{ABC}$, стороны $\ Delta\text{DEF}$ также составляет 6 дюймов, 8 дюймов и 10 дюймов. Поскольку все три стороны $\Delta\text{DEF}$ имеют разную длину, это разносторонний треугольник.
Поскольку все три стороны $\Delta\text{DEF}$ имеют разную длину, это разносторонний треугольник.
3
Какие из следующих четырехугольников являются правильными многоугольниками?
Прямоугольник
Квадрат
Воздушный змей
Ромб
Правильный ответ: Квадрат
У правильного многоугольника все стороны равны и все углы равны. Квадрат – это единственный четырехугольник с равными сторонами и равными углами.
4
Определите фигуру, у которой не все стороны равны.
Равносторонний треугольник
Ромб
Прямоугольник
Правильный пятиугольник
Правильный ответ: Прямоугольник
В прямоугольнике смежные стороны имеют разную длину, а противоположные стороны равны.
Часто задаваемые вопросы
Возможны ли конгруэнтные формы с соответствующими сторонами разной длины?
Нет, конгруэнтные фигуры должны иметь стороны одинаковой длины.
Может ли быть неправильный многоугольник со сторонами одинаковой длины?
Да, если стороны равны, но углы разные, или равны только две или некоторые из сторон, то это будет неправильный многоугольник. Например, у ромба равные стороны, но разные углы.
Поскольку все углы равностороннего треугольника равны 60°, можем ли мы сказать, что все равносторонние треугольники конгруэнтны друг другу?
Нет, чтобы треугольники были равны, все их стороны и углы должны быть равны.
2.4: Доказательство равенства линий и углов
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 34127
- Генри Африк
- CUNY Технологический колледж Нью-Йорка через Технологический колледж Нью-Йорка в CUNY Академические работы
Мы можем доказать равенство прямых и углов, если мы можем показать, что они являются соответствующими частями конгруэнтных треугольников. Мы считаем удобным представить эти доказательства в форме в два столбца с утверждениями в левом столбце и причиной каждого утверждения в правом.
Мы считаем удобным представить эти доказательства в форме в два столбца с утверждениями в левом столбце и причиной каждого утверждения в правом.
Пример \(\PageIndex{1}\)
Дано \(AB || CD\) и \(AB = CD\) доказать \(AD = BC\)
Решение
| Причины | |
| 1. \(AB = CD\). | 1. Дано. |
| 2. \(\угол ABD = \угол CDB\). | 2. Альтернативные внутренние углы параллельных прямых \((AB || CD)\) равны. |
| 3. \(BD = DB\). | 3. Личность. |
| 4. \(\треугольник ABD \cong \треугольник CDB\) | 4. \(SAS = SAS\): \(AB, \угол B, BD\) из \(\треугольник ABD = CD\), \(\угол D\), \(DB\) из \(\ треугольник CDB\). |
| 5. \(АД = ВС\) | 5. Соответствующие стороны равных треугольников равны, |
Объяснение: Каждое из первых трех утверждений говорит о том, что сторона или угол \(\треугольника ABD\) равна соответствующей стороне или углу \(\треугольника CDB\). Чтобы получить эти утверждения, мы должны сначала написать конгруэнтность, используя методы предыдущих разделов. Затем мы выбираем три пары соответствующих сторон или углов, которые равны по одной из следующих причин:0005
Чтобы получить эти утверждения, мы должны сначала написать конгруэнтность, используя методы предыдущих разделов. Затем мы выбираем три пары соответствующих сторон или углов, которые равны по одной из следующих причин:0005
Причины равенства линий
- Дано. Это означает, что в начале упражнения нас просят предположить, что строки равны. Например, в задаче будет указано «дано \(AB = CD\)» или \(AB\) и \(CD\) будут отмечены так же на схеме.
- Личность. Это означает, что в обоих треугольниках появляется один и тот же отрезок прямой. Например, \(BD\) и \(DB\) представляют один и тот же отрезок прямой. Конечно, длина отрезка равна самой себе.
Причины равенства углов
- Дано.
- Личность.
- Альтернативные внутренние углы параллельных прямых равны. Чтобы применить эту причину, мы должны иметь в виду, что прямые параллельны.
- Соответствующие углы параллельных прямых равны.
- Вертикальные углы равны.

Это не единственные возможные причины, но это все, что мы будем использовать в первую очередь.
Мы также должны выбрать три пары равных сторон или углов, чтобы одну из причин \(SAS = SAS\), \(ASA = ASA\) или \(AAS = AAS\) можно было использовать для обоснования сравнения утверждение в утверждении 4. В разделах 2.6 и 2.7 мы приведем некоторые дополнительные причины конгруэнтности двух треугольников.
Мы хотим доказать утверждение 5. Причина в том, что соответствующие стороны (или углы) конгруэнтных треугольников равны. Мы можем использовать эту причину здесь, потому что конгруэнтность треугольников уже доказана в утверждении 4,
.Последнее замечание. Обратите внимание, что решение примера \(\PageIndex{1}\) согласуется с нашим первоначальным определением доказательства. Верность каждого нового утверждения подтверждается использованием предыдущих утверждений и уже установленных причин.
Приведем другой пример:
Пример \(\PageIndex{2}\)
Учитывая \(QP || ST\) и \(QR = TR\) докажите \(PR = SR\).
Решение
| Заявления | Причины |
| 1. \(QR = TR\) | 1. Дано. |
| 2. \(\угол Q = \угол T.\) | 2. Альтернативные внутренние углы параллельных прямых (\(QP || ST\)) равны. |
| 3. \(\угол PRQ = \угол SRT\). | 3. Вертикальные углы равны. |
| 4. \(\треугольник PQR \cong \треугольник STR\). | 4. \(ASA = ASA: \угол Q, QR, \угол R\) из \(\треугольник PQR = \угол T\), \(TR, \угол R\) из \(\треугольник STR\) . |
| 5. \(PR = SR\). | 5. Соответствующие стороны равных треугольников равны, |
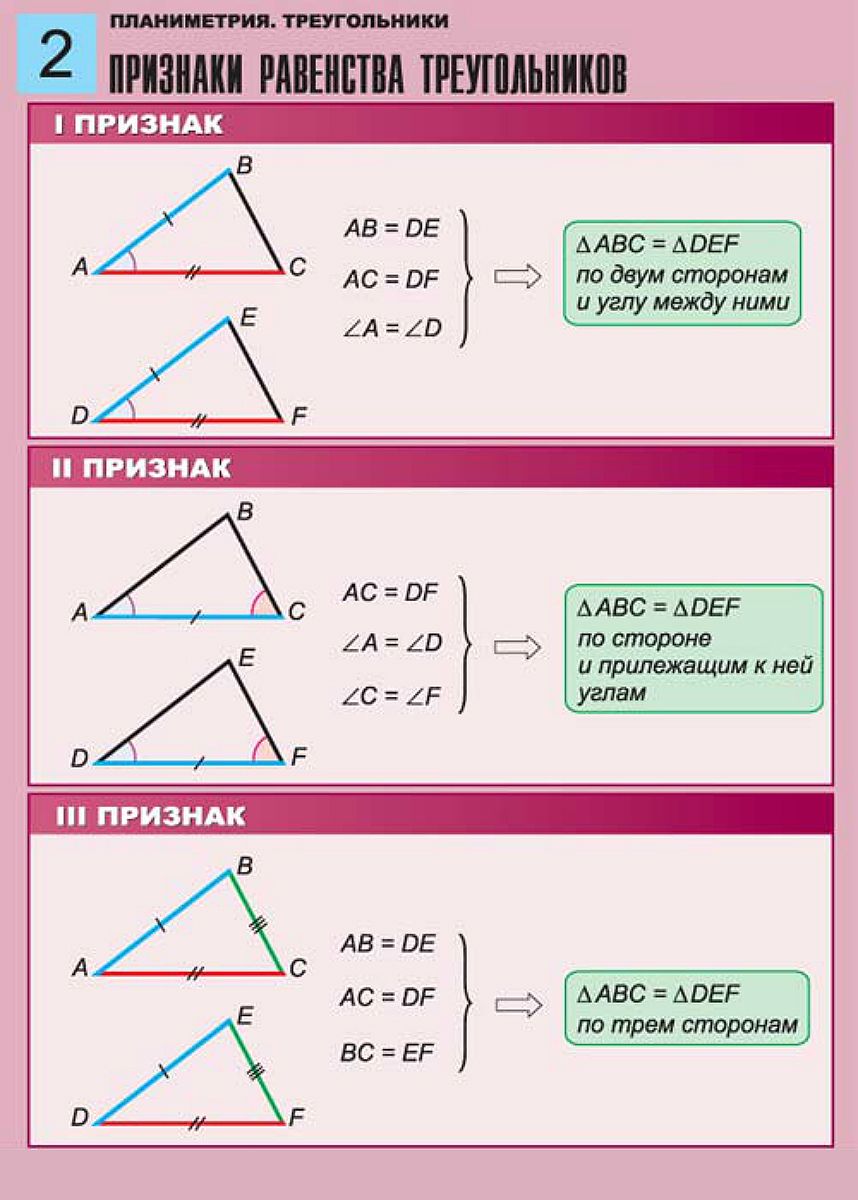
1. Даны \(\угол A = \угол D\), \(\угол B = \угол E\), \(AB = DE\). Докажите \(AC = DF\).
2. Даны \(AC=DF\), \(BC = EF\), \(\угол C = \угол F\).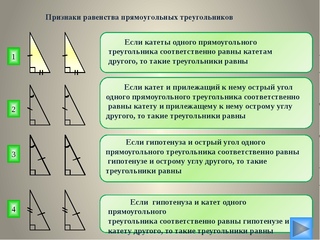 Докажите \(AB = DE\).
Докажите \(AB = DE\).
3. Даны \(AC = EC\) и \(BC = DC\). Докажите \(AB = ED\).
4. Даны \(AC = DC\), \(\угол A = \угол D\). Докажите \(BC = EC\).
5. Даны \(\угол ABD = \угол CDB\) и \(\угол ADB = \угол CBD\). Докажите \(AB = CD\).
6. Даны \(AB || CD\) и \(AD || CB\). Докажите \(AB = CD\).
7. Даны \(AC = BC\) и \(\угол ACD = \угол BCD\). Докажите \(\угол А = \угол В\).
8. Даны \(\угол A = \угол B\), \(\угол ACD = \угол BCD\). Докажите \(AC = BC\).
9. Даны \(AB || CD\) и \(AB = CD\). Докажите \(AE = CE\). (Подсказка: покажите \(\треугольник ABE \cong \треугольник CDE\))
10. Даны \(AE = CE\) и \(BE = DE\). Докажите \(\угол BAC = \угол CDB\).
11. Даны \(\угол A = \угол D\), \(AC = DE\), \(AB || DC\). Докажите \(BC = CE\).
12. Даны \(AB || DE\), \(AC || FE\) и \(DC = FE\). Докажите \(BE = EC\).
13.




 Взаимодействие азотной кислоты с металлами
Взаимодействие азотной кислоты с металлами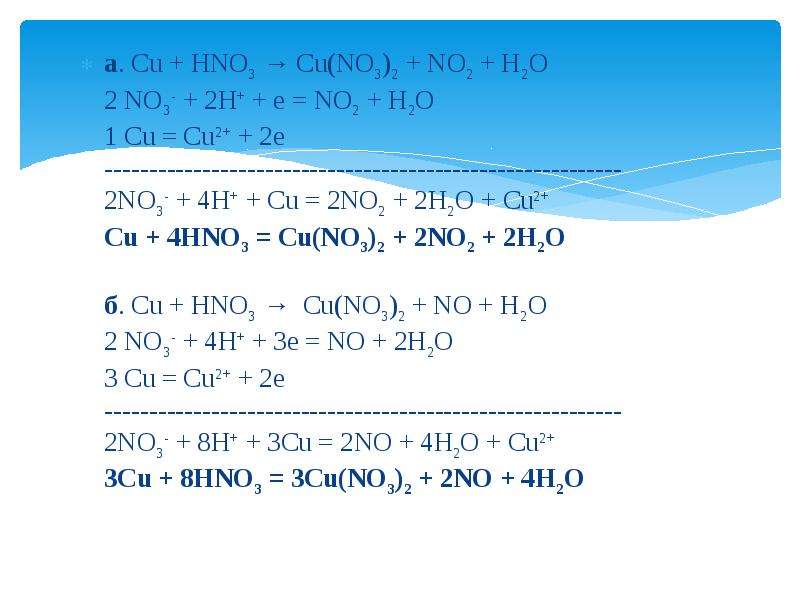 Ни
Ни кислоты
кислоты восстановления
восстановления Сильные электролиты, в
Сильные электролиты, в
 Запишите уравнение взаимодействия меди с концентрированной
Запишите уравнение взаимодействия меди с концентрированной При комнатной температуре
преобладает транс-изомер: эта структура
является более устойчивой. Так, для
цис-HNO2(г) ΔG°f = −42,59 кДж/моль, а для
транс-HNO2(г) ΔG°f = −44,65 кДж/моль. В водных
растворах существует равновесие: 2HNO2
↔ N2O3
+ h3O
↔ NO
+ NO2
+ h3O.
При нагревании раствора азотистая
кислота распадается с выделением NO и
образованием азотной кислоты: 3HNO2
↔ HNO3
+ 2 NO
+ h3O.
HNO2 является слабой кислотой. В водных
растворах диссоциирует (KD = 4,6⋅10−4),
немного сильнее уксусной кислоты. Легко
вытесняется более сильными кислотами
из солей: h3SO4 + 2 NaNO2 → Na2SO4 + 2HNO2. Азотистая
кислота проявляет как окислительные,
так и восстановительные свойства. При
действии более сильных окислителей
(пероксид водорода, хлор, перманганат
калия) окисляется в азотную кислоту:
HNO2 + h3O2 = HNO3 + h3O. HNO2
+ Cl2 + h3O = HNO3 + 2 HCl. 7HNO2 + 2 KMnO4 = 2 Mn(NO3)2 + 2 KNO3 +
3h3O + HNO3. В
то же время она способна окислять
вещества, обладающие восстановительными
свойствами: 2HNO2
+ 2 HI
= 2 NO
+ I2
+ 2 h3O.
При комнатной температуре
преобладает транс-изомер: эта структура
является более устойчивой. Так, для
цис-HNO2(г) ΔG°f = −42,59 кДж/моль, а для
транс-HNO2(г) ΔG°f = −44,65 кДж/моль. В водных
растворах существует равновесие: 2HNO2
↔ N2O3
+ h3O
↔ NO
+ NO2
+ h3O.
При нагревании раствора азотистая
кислота распадается с выделением NO и
образованием азотной кислоты: 3HNO2
↔ HNO3
+ 2 NO
+ h3O.
HNO2 является слабой кислотой. В водных
растворах диссоциирует (KD = 4,6⋅10−4),
немного сильнее уксусной кислоты. Легко
вытесняется более сильными кислотами
из солей: h3SO4 + 2 NaNO2 → Na2SO4 + 2HNO2. Азотистая
кислота проявляет как окислительные,
так и восстановительные свойства. При
действии более сильных окислителей
(пероксид водорода, хлор, перманганат
калия) окисляется в азотную кислоту:
HNO2 + h3O2 = HNO3 + h3O. HNO2
+ Cl2 + h3O = HNO3 + 2 HCl. 7HNO2 + 2 KMnO4 = 2 Mn(NO3)2 + 2 KNO3 +
3h3O + HNO3. В
то же время она способна окислять
вещества, обладающие восстановительными
свойствами: 2HNO2
+ 2 HI
= 2 NO
+ I2
+ 2 h3O. Азотистую кислоту можно получить при
растворении оксида азота (III) N2O3 в воде:
N2O3 + h3O = 2 HNO2. Также она получается при
растворении в воде оксида азота (IV) NO2:
2NO2
+ h3O
= HNO3
+ HNO2.
Азотистая кислота применяется для
диазотирования первичных ароматических
аминов и образования солей диазония.
Нитриты применяются в органическом
синтезе при производстве органических
красителей. Азотистая кислота (HNO2) весьма
токсична, причём обладает ярко выраженным
мутагенным действием, поскольку является
дезаминирующим агентом. Нитриты — соли азотистой кислоты HNO2, например,
нитрит натрия NaNO2, нитрит кальция
Ca(NO2)2. Известны нитриты щелочных,
щелочноземельных, 3d-металлов, а также
нитриты свинца и серебра. Кристаллическими
веществами являются только нитриты
калия, серебра, кальция и бария. Нитриты
калия, натрия и бария в воде хорошо
растворимы, малорастворимы нитриты
серебра, ртути (II), меди. С повышением
температуры растворимость нитритов
возрастает. В органических растворителях
нитриты растворяются плохо.
Азотистую кислоту можно получить при
растворении оксида азота (III) N2O3 в воде:
N2O3 + h3O = 2 HNO2. Также она получается при
растворении в воде оксида азота (IV) NO2:
2NO2
+ h3O
= HNO3
+ HNO2.
Азотистая кислота применяется для
диазотирования первичных ароматических
аминов и образования солей диазония.
Нитриты применяются в органическом
синтезе при производстве органических
красителей. Азотистая кислота (HNO2) весьма
токсична, причём обладает ярко выраженным
мутагенным действием, поскольку является
дезаминирующим агентом. Нитриты — соли азотистой кислоты HNO2, например,
нитрит натрия NaNO2, нитрит кальция
Ca(NO2)2. Известны нитриты щелочных,
щелочноземельных, 3d-металлов, а также
нитриты свинца и серебра. Кристаллическими
веществами являются только нитриты
калия, серебра, кальция и бария. Нитриты
калия, натрия и бария в воде хорошо
растворимы, малорастворимы нитриты
серебра, ртути (II), меди. С повышением
температуры растворимость нитритов
возрастает. В органических растворителях
нитриты растворяются плохо. Нитриты
являются термически малоустойчивыми
соединениями. Так, без разложения могут
плавиться только нитриты щелочных
металлов, остальные же начинают
разлагаться при 250—300 °C с выделением
металла либо его оксида, азота, оксидов
азота и кислорода. Нитриты реагируют с
солями меди, образуя комплексный
гексонитритокупрат-анион, придающий
раствору характерный зелёный цвет, что
можно использовать в лаборатории как
качественную реакцию. CuSO4 + 6NaNO2 = Na2SO4 +
Na4[Cu(NO2)6]. Нитриты медленно разлагаются
под действием кислот с выделением газа
(продуктов разложения азотистой кислоты).
2NaNO2 + h3SO4 = Na2SO4 + NO + NO2 +h3O. В горячей воде
те же вещества реагируют с образованием
оксида азота (II) и азотной кислоты: 6NaNO2
+ 3h3SO4 = 3Na2SO4 + 2HNO3 + 4NO + 4h3О. Нитриты могут
выступать как окислителями, так и
восстановителями — в кислой среде они
окисляются до нитратов, в щелочной
способны восстанавливаться до оксида
азота NO. В промышленности нитриты
получают поглощением нитрозного газа
(NO + NO2) растворами гидроксида или карбоната
натрия с образованием раствора нитрита
натрия, из которого кристаллизацией
получают сухой продукт.
Нитриты
являются термически малоустойчивыми
соединениями. Так, без разложения могут
плавиться только нитриты щелочных
металлов, остальные же начинают
разлагаться при 250—300 °C с выделением
металла либо его оксида, азота, оксидов
азота и кислорода. Нитриты реагируют с
солями меди, образуя комплексный
гексонитритокупрат-анион, придающий
раствору характерный зелёный цвет, что
можно использовать в лаборатории как
качественную реакцию. CuSO4 + 6NaNO2 = Na2SO4 +
Na4[Cu(NO2)6]. Нитриты медленно разлагаются
под действием кислот с выделением газа
(продуктов разложения азотистой кислоты).
2NaNO2 + h3SO4 = Na2SO4 + NO + NO2 +h3O. В горячей воде
те же вещества реагируют с образованием
оксида азота (II) и азотной кислоты: 6NaNO2
+ 3h3SO4 = 3Na2SO4 + 2HNO3 + 4NO + 4h3О. Нитриты могут
выступать как окислителями, так и
восстановителями — в кислой среде они
окисляются до нитратов, в щелочной
способны восстанавливаться до оксида
азота NO. В промышленности нитриты
получают поглощением нитрозного газа
(NO + NO2) растворами гидроксида или карбоната
натрия с образованием раствора нитрита
натрия, из которого кристаллизацией
получают сухой продукт. Нитриты других
металлов получают обменной реакцией с
нитритом натрия либо восстановлением
соответствующих нитратов. Нитриты
используются при получении азокрасителей,
для получения капролактама, как окисляющие
и восстанавливающие реагенты в
резинотехнической, текстильной и
металлообрабатывающей промышленности.
Нитрит натрия используется как консервант.
Нитриты других
металлов получают обменной реакцией с
нитритом натрия либо восстановлением
соответствующих нитратов. Нитриты
используются при получении азокрасителей,
для получения капролактама, как окисляющие
и восстанавливающие реагенты в
резинотехнической, текстильной и
металлообрабатывающей промышленности.
Нитрит натрия используется как консервант. Механические исследования
показывают, что образование опасных
нитросоединений (таких как нитрозамины)
ускоряется в присутствии компонентов
мяса и подавляется витамином С и другими
антиоксидантами и фитонутриентами из
растительных продуктов. Таким образом,
нитриты ведут себя неодинаково в
зависимости от того, из каких источников
они поступают в организм. Нитриты,
добавляемые в мясные продукты для их
консервации, преобразуются в нитрозамины.
Нитриты, преобразовавшиеся из нитратов
из овощей и фруктов, далее превращаются
в оксид азота (II), которые способствует
расширению кровеносных сосудов и
нормализации кровяного давления. При
нормальном физиологическом состоянии
и поступлении нитритов в организм не
более допустимой суточной дозы,
утверждённой Министерством здравоохранения
в 0,2 мг/кг массы тела (за исключением
детей грудного возраста), в организме
человека образуется примерно 2 %
метгемоглобина, поскольку редуктазы
эритроцитов взрослого человека обладают
способностью превращать образовавшийся
метгемоглобин обратно в гемоглобин.
Механические исследования
показывают, что образование опасных
нитросоединений (таких как нитрозамины)
ускоряется в присутствии компонентов
мяса и подавляется витамином С и другими
антиоксидантами и фитонутриентами из
растительных продуктов. Таким образом,
нитриты ведут себя неодинаково в
зависимости от того, из каких источников
они поступают в организм. Нитриты,
добавляемые в мясные продукты для их
консервации, преобразуются в нитрозамины.
Нитриты, преобразовавшиеся из нитратов
из овощей и фруктов, далее превращаются
в оксид азота (II), которые способствует
расширению кровеносных сосудов и
нормализации кровяного давления. При
нормальном физиологическом состоянии
и поступлении нитритов в организм не
более допустимой суточной дозы,
утверждённой Министерством здравоохранения
в 0,2 мг/кг массы тела (за исключением
детей грудного возраста), в организме
человека образуется примерно 2 %
метгемоглобина, поскольку редуктазы
эритроцитов взрослого человека обладают
способностью превращать образовавшийся
метгемоглобин обратно в гемоглобин. В
Европейском Союзе допустимая суточная
доза нитритов принята в 0.1 мг/кг массы
(в пересчете на нитрит натрия). Продажа
нитритов для пищевых применений разрешена
в Евросоюзе только в смеси с пищевой
солью, с содержанием нитритов около 0,6
%, для уменьшения риска превышения
суточных норм.
В
Европейском Союзе допустимая суточная
доза нитритов принята в 0.1 мг/кг массы
(в пересчете на нитрит натрия). Продажа
нитритов для пищевых применений разрешена
в Евросоюзе только в смеси с пищевой
солью, с содержанием нитритов около 0,6
%, для уменьшения риска превышения
суточных норм. Водород всегда имеет степень окисления $+1$, а кислород $-2$. Для нейтральных молекул (без заряда) сумма степеней окисления равна нулю. Поскольку все молекулы здесь нейтральны, сумма степеней окисления в этом случае всегда равна нулю.
Водород всегда имеет степень окисления $+1$, а кислород $-2$. Для нейтральных молекул (без заряда) сумма степеней окисления равна нулю. Поскольку все молекулы здесь нейтральны, сумма степеней окисления в этом случае всегда равна нулю. 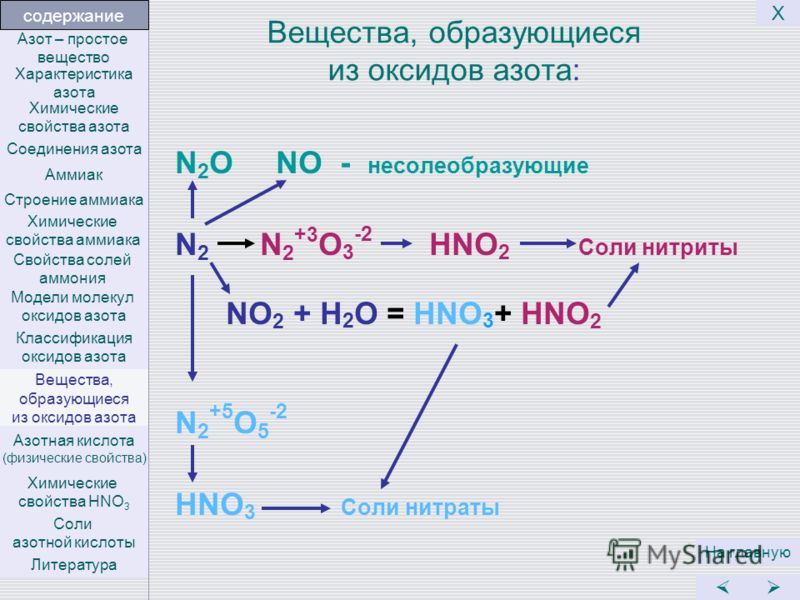 Это йод и азот. У обеих сторон есть по одному азоту, так что мы можем оставить это без внимания. В левой части находится только один йод, а в правой — два. Поэтому мы ставим $2$ рядом с $HI$:
Это йод и азот. У обеих сторон есть по одному азоту, так что мы можем оставить это без внимания. В левой части находится только один йод, а в правой — два. Поэтому мы ставим $2$ рядом с $HI$:  Отсюда умножаем молекулы процесса окисления ($HN{O_3}$ и $NO$) на $2$, так как $( + 3) \times 2 = 6$ и умножаем молекулы процесса окисления ($HI$ и ${I_2}$) с $3$, так как $( + 2) \times 3 = 6$ . Таким образом, мы получаем:
Отсюда умножаем молекулы процесса окисления ($HN{O_3}$ и $NO$) на $2$, так как $( + 3) \times 2 = 6$ и умножаем молекулы процесса окисления ($HI$ и ${I_2}$) с $3$, так как $( + 2) \times 3 = 6$ . Таким образом, мы получаем: 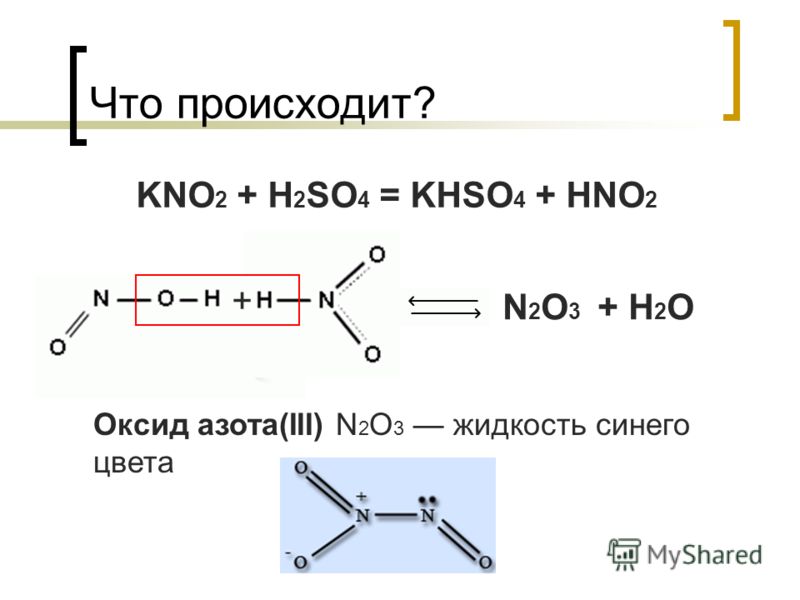
 АСИДО ДЕ
БРЕНСТЕД
БАЗА ДЕ БРЕНСТЕД АНФОТЕРО
h4O+ OH- h3O
Кh5+ Кh3- Кh4
HBr NO3-
HCN CO32-
El NO3- (нитратный анион) представляет собой соединение основания HNO3 без содержания
пропьедадес ацидо-основа.
АСИДО ДЕ
БРЕНСТЕД
БАЗА ДЕ БРЕНСТЕД АНФОТЕРО
h4O+ OH- h3O
Кh5+ Кh3- Кh4
HBr NO3-
HCN CO32-
El NO3- (нитратный анион) представляет собой соединение основания HNO3 без содержания
пропьедадес ацидо-основа. Расчет числа молей KOH на 5,50 мл при растворении KOH
0,360 M. ¿Cuál es el pOH de la disolución?
𝒏 ( 𝑶𝑯−) = [ 𝑂𝐻−] · 𝑉 ( 𝑂𝐻−) = 0,360
𝑚𝑜𝑙
𝐿
· 5,50 · 10−3
𝐿 = 𝟏, 𝟗𝟖 · 𝟏𝟎−𝟑
𝒎𝒐𝒍
𝒑𝑶𝑯 = − log [𝑂𝐻−] = − log [0,360 ] = 𝟎, 𝟒𝟒
Расчет числа молей KOH на 5,50 мл при растворении KOH
0,360 M. ¿Cuál es el pOH de la disolución?
𝒏 ( 𝑶𝑯−) = [ 𝑂𝐻−] · 𝑉 ( 𝑂𝐻−) = 0,360
𝑚𝑜𝑙
𝐿
· 5,50 · 10−3
𝐿 = 𝟏, 𝟗𝟖 · 𝟏𝟎−𝟑
𝒎𝒐𝒍
𝒑𝑶𝑯 = − log [𝑂𝐻−] = − log [0,360 ] = 𝟎, 𝟒𝟒 к.) + h3O (ж) Ch4COO- (а.к.) + h4O+ (а.к.)
0,40 м — —
0,40 — х х х
𝐾𝑎 =
[𝐶𝐻3 𝐶𝑂𝑂−] · [𝐻3 𝑂+
]
[𝐶𝐻3 𝐶𝑂𝑂𝐻]
1,58 · 10−5
«=»
𝑥2
0,40 − 𝑥
«=»
𝑥2
0,40
В равновесии:
[Ch4COOH) = 0,394 М; [Ch4COO-] = [h4O+] = 6,28·10-3 М
𝒑𝑯 = − log [𝐻3 𝑂+] = 𝟐, 𝟐𝟎
к.) + h3O (ж) Ch4COO- (а.к.) + h4O+ (а.к.)
0,40 м — —
0,40 — х х х
𝐾𝑎 =
[𝐶𝐻3 𝐶𝑂𝑂−] · [𝐻3 𝑂+
]
[𝐶𝐻3 𝐶𝑂𝑂𝐻]
1,58 · 10−5
«=»
𝑥2
0,40 − 𝑥
«=»
𝑥2
0,40
В равновесии:
[Ch4COOH) = 0,394 М; [Ch4COO-] = [h4O+] = 6,28·10-3 М
𝒑𝑯 = − log [𝐻3 𝑂+] = 𝟐, 𝟐𝟎 Ионизационный расчет растворения ацетилсалициловой кислоты
(аспирина) 0,20 М, как монопротез.
DATO: Ка (HA) = 3,0·10-4.
HA (а.с.) + h3O (ж) A- (а.с.) + h4O+ (а.с.)
0,20 м — —
0,20 · (1 – ) 0,20 · 0,20 ·
𝐾𝑎 =
[𝐴−] · [𝐻3 𝑂+
]
[𝐻𝐴]
3,0 · 10−4
«=»
0,202
· 𝛼2
0,20 · (1 − 𝛼)
𝜶 = 𝟎, 𝟎𝟑𝟖 (𝟑, 𝟖%)
Ионизационный расчет растворения ацетилсалициловой кислоты
(аспирина) 0,20 М, как монопротез.
DATO: Ка (HA) = 3,0·10-4.
HA (а.с.) + h3O (ж) A- (а.с.) + h4O+ (а.с.)
0,20 м — —
0,20 · (1 – ) 0,20 · 0,20 ·
𝐾𝑎 =
[𝐴−] · [𝐻3 𝑂+
]
[𝐻𝐴]
3,0 · 10−4
«=»
0,202
· 𝛼2
0,20 · (1 − 𝛼)
𝜶 = 𝟎, 𝟎𝟑𝟖 (𝟑, 𝟖%) с.) Na+ (а.с.) + OH- (а.с.)
𝑝𝑂𝐻 = − log [𝑂𝐻−] = 0,7
𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 𝟏𝟑, 𝟑
с.) Na+ (а.с.) + OH- (а.с.)
𝑝𝑂𝐻 = − log [𝑂𝐻−] = 0,7
𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 𝟏𝟑, 𝟑 Расторжение Nh4 0,080 M, ¿qué porcentaje Nh4 está presente como
Кh5+?
Nh4 (ач) + h3O (ж) Nh5+ (ач) + OH- (ач)
0,080 М — —
0,080 — х х х
1,8 · 10−5
«=»
𝑥2
0,080 — 𝑥
«=»
𝑥2
0,080
; 𝒙 = 𝟏, 𝟐 · 𝟏𝟎−𝟑
𝑴
𝜶 =
1,2 · 10−3
0,080
· 100 = 𝟏, 𝟓%
Расторжение Nh4 0,080 M, ¿qué porcentaje Nh4 está presente como
Кh5+?
Nh4 (ач) + h3O (ж) Nh5+ (ач) + OH- (ач)
0,080 М — —
0,080 — х х х
1,8 · 10−5
«=»
𝑥2
0,080 — 𝑥
«=»
𝑥2
0,080
; 𝒙 = 𝟏, 𝟐 · 𝟏𝟎−𝟑
𝑴
𝜶 =
1,2 · 10−3
0,080
· 100 = 𝟏, 𝟓%
 Таким образом, график функции игрек равно три икс квадрат можно получить из графика функции игрек равно икс квадрат растяжением от оси икс в три раза.
Таким образом, график функции игрек равно три икс квадрат можно получить из графика функции игрек равно икс квадрат растяжением от оси икс в три раза.
 График функции симметричен относительно оси игрек.
График функции симметричен относительно оси игрек.
 . и с помощью сжатия к оси х в единица деленная на а раз, если а больше нуля и меньше единицы.
. и с помощью сжатия к оси х в единица деленная на а раз, если а больше нуля и меньше единицы. 06.17
06.17 Найдите вероятность того, что ему попадется выученный билет
Найдите вероятность того, что ему попадется выученный билет Пожалуйста, обратитесь к приложенному графику.
Пожалуйста, обратитесь к приложенному графику. в 12:47:25.
в 12:47:25. . . вплоть до 100.
9(2)+х-2=0.
. . вплоть до 100.
9(2)+х-2=0.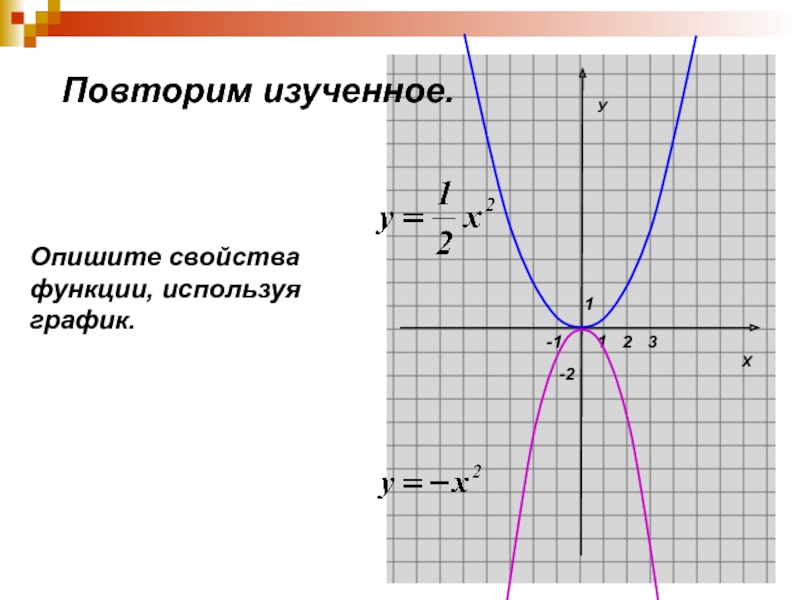


 Отсюда следует, что раскладывать их не будем на линейные множители.
Отсюда следует, что раскладывать их не будем на линейные множители. ..+a1x==x(anxn-1+an-1xn-2+…+a1)
..+a1x==x(anxn-1+an-1xn-2+…+a1)

 Получаем, что
Получаем, что Для этого необходимо пользоваться специальными способами для нахождения множителей. Но не все многочлены можно разложить или представить в виде произведения.
Для этого необходимо пользоваться специальными способами для нахождения множителей. Но не все многочлены можно разложить или представить в виде произведения. Для этого нам понадобится произвести разложение на множители. получаем, что
Для этого нам понадобится произвести разложение на множители. получаем, что После того, как были произведены преобразования, можно выстроить строчку, состоящую из треугольника Паскаля, иначе их называют биномом Ньютона.
После того, как были произведены преобразования, можно выстроить строчку, состоящую из треугольника Паскаля, иначе их называют биномом Ньютона. Получаем, что
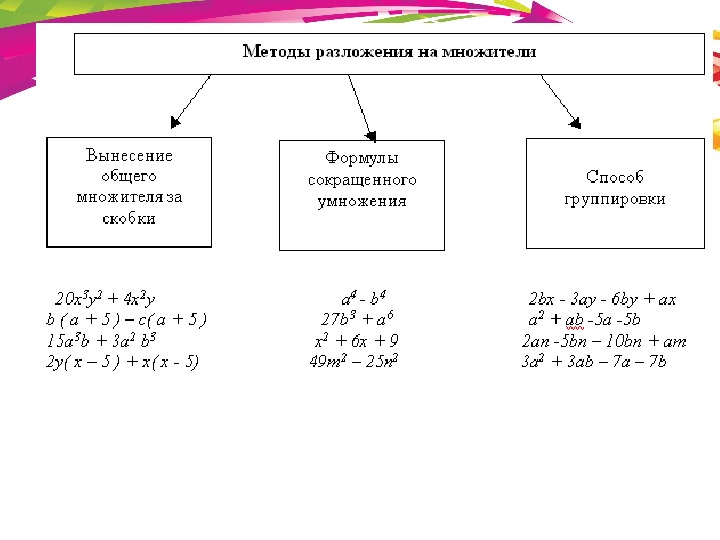
Получаем, что 2 = 0 \Rightarrow (x-1-10)(x-1+10) = 0 \Rightarrow \left[ \begin{array}{cc} x_1 = 11 \\ x_2 = -9 \end{array} \right. $$
2 = 0 \Rightarrow (x-1-10)(x-1+10) = 0 \Rightarrow \left[ \begin{array}{cc} x_1 = 11 \\ x_2 = -9 \end{array} \right. $$





 92-2аб\)
92-2аб\) Теперь мы можем разбить число 4 на 2×2. Точно так же мы можем разбить число 8 и представить его как 2x2x2. Итак, мы можем выразить 32 как результат 2x2x2x2x2. Этот процесс называется факторизацией простых чисел, когда мы находим простые числа, из которых состоит другое число.
Теперь мы можем разбить число 4 на 2×2. Точно так же мы можем разбить число 8 и представить его как 2x2x2. Итак, мы можем выразить 32 как результат 2x2x2x2x2. Этот процесс называется факторизацией простых чисел, когда мы находим простые числа, из которых состоит другое число. Включая вас, будет шесть человек. Вы проверяете свои формочки для маффинов и обнаруживаете, что можете испечь девять маффинов за раз. Значит, либо будет три лишних маффина, либо вы не сможете подарить всем своим друзьям по два маффина, если они попросят еще. Но что, если вы получите еще одну форму из девяти кексов? Тогда у вас получится 18 маффинов. Если разложить на множители 18, то получится 9.0003
Включая вас, будет шесть человек. Вы проверяете свои формочки для маффинов и обнаруживаете, что можете испечь девять маффинов за раз. Значит, либо будет три лишних маффина, либо вы не сможете подарить всем своим друзьям по два маффина, если они попросят еще. Но что, если вы получите еще одну форму из девяти кексов? Тогда у вас получится 18 маффинов. Если разложить на множители 18, то получится 9.0003
 Вы можете удовлетворить каждого ребенка с помощью факторизации.
Вы можете удовлетворить каждого ребенка с помощью факторизации. Итак, сколько еще вам нужно? Для начала у вас уже есть два фута, то есть 24 дюйма. Значит, нужно набрать еще 16 дюймов. Факторизуя 16, вы получаете-
Итак, сколько еще вам нужно? Для начала у вас уже есть два фута, то есть 24 дюйма. Значит, нужно набрать еще 16 дюймов. Факторизуя 16, вы получаете- Таким образом, если ваш врач дает вам таблетку для приема четыре раза в день, вам нужно будет разложить 24 часа на:
Таким образом, если ваш врач дает вам таблетку для приема четыре раза в день, вам нужно будет разложить 24 часа на:
 Таким образом, вы можете факторизовать их время и оценить, у кого сколько времени уйдет на то, чтобы закончить ту или иную часть кафе. Таким образом, вы сможете уложиться в срок и выполнить работу с умом. То, как вы выполняете математику, представляет собой не что иное, как простую факторизацию простых чисел и другие операции, такие как H.C.F. и Л.К.М.
Таким образом, вы можете факторизовать их время и оценить, у кого сколько времени уйдет на то, чтобы закончить ту или иную часть кафе. Таким образом, вы сможете уложиться в срок и выполнить работу с умом. То, как вы выполняете математику, представляет собой не что иное, как простую факторизацию простых чисел и другие операции, такие как H.C.F. и Л.К.М.
 14159..
14159.. Знак коэффициента a отвечает за направление ветвей. При a > 0 ветви направлены вверх, при a < 0 — вниз.
Знак коэффициента a отвечает за направление ветвей. При a > 0 ветви направлены вверх, при a < 0 — вниз. Если дискриминант равен нулю, то парабола касается оси X. Если дискриминант меньше нуля, то парабола не пересекает ось X.
Если дискриминант равен нулю, то парабола касается оси X. Если дискриминант меньше нуля, то парабола не пересекает ось X. Вот почему форма антенн — параболическая. И наоборот, если в фокусе параболы расположен источник света, то отражённые от зеркала лучи света будут параллельны. Поэтому карманный фонарик дает направленный луч света, хорошо видимый в темноте.
Вот почему форма антенн — параболическая. И наоборот, если в фокусе параболы расположен источник света, то отражённые от зеркала лучи света будут параллельны. Поэтому карманный фонарик дает направленный луч света, хорошо видимый в темноте.
 2 + c` (серая парабола), а значение `b` равно (2 a ), умноженное на длину пурпурного сегмента (расстояние от оси y до пересечения парабол). Чем больше значение b , тем дальше зеленая парабола движется вокруг серой.
2 + c` (серая парабола), а значение `b` равно (2 a ), умноженное на длину пурпурного сегмента (расстояние от оси y до пересечения парабол). Чем больше значение b , тем дальше зеленая парабола движется вокруг серой. Вершина находится в (0, 0) (если 92 + bx + c) из выражения трехчлена или значений a, b и c.
Вершина находится в (0, 0) (если 92 + bx + c) из выражения трехчлена или значений a, b и c. Это самый простой метод, и поэтому его чаще всего изучают. 92-4ac}}{2a} $$
Это самый простой метод, и поэтому его чаще всего изучают. 92-4ac}}{2a} $$



 е.
е.





 Элемент $x$ называется прообразом, а $y$ образом.
Элемент $x$ называется прообразом, а $y$ образом.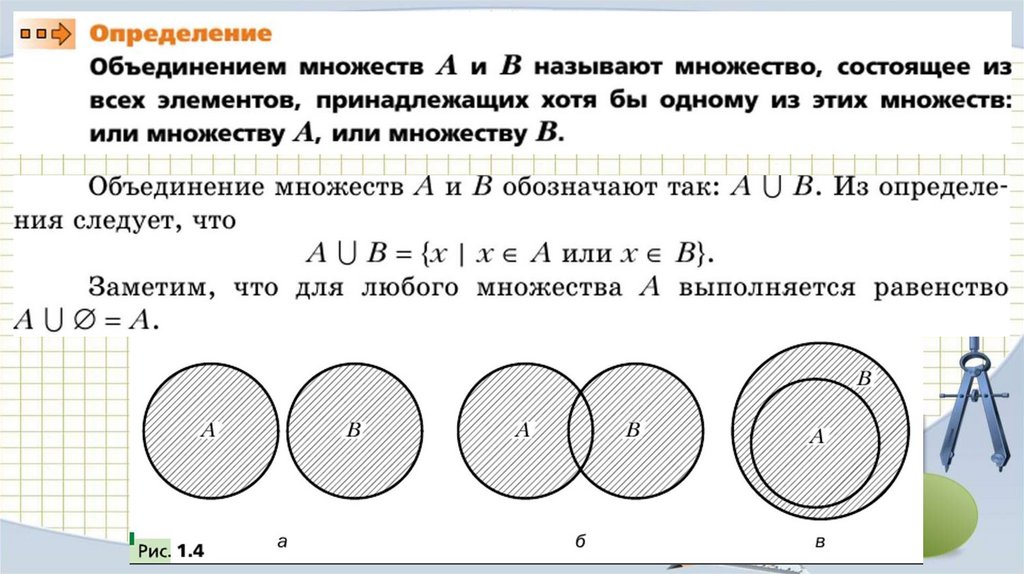

 хотите играть и решать, какую черту получить на какой части снаряжения. Оптимизация сетов в ESO — важная часть, и она может как улучшить сборку, так и разрушить ее.
хотите играть и решать, какую черту получить на какой части снаряжения. Оптимизация сетов в ESO — важная часть, и она может как улучшить сборку, так и разрушить ее.
 Они помогают конкретизировать роль и могут помочь с дефицитом, например, если у вас недостаточно магии, вы можете зачаровать свое снаряжение глифами магии. Они также бывают разного качества и могут быть найдены во всех видах контента. Однако создавать легендарные глифы могут только игроки.
Они помогают конкретизировать роль и могут помочь с дефицитом, например, если у вас недостаточно магии, вы можете зачаровать свое снаряжение глифами магии. Они также бывают разного качества и могут быть найдены во всех видах контента. Однако создавать легендарные глифы могут только игроки. Совершенные и несовершенные части являются частью одного и того же набора, но у идеальной версии есть дополнительная характеристика. Часто игроки в ESO переоценивают разницу в мощности идеальной и несовершенной версий, на самом деле разница незначительна, потому что увеличение мощности часто составляет всего около 1-2%.
Совершенные и несовершенные части являются частью одного и того же набора, но у идеальной версии есть дополнительная характеристика. Часто игроки в ESO переоценивают разницу в мощности идеальной и несовершенной версий, на самом деле разница незначительна, потому что увеличение мощности часто составляет всего около 1-2%. Тем не менее, это хорошо, потому что у вас уже может быть какое-то усовершенствованное снаряжение, но не все необходимые детали. Таким образом, вы можете смешивать наборы вместе, пока не сможете заменить несовершенные части шестерни улучшенной версией.
Тем не менее, это хорошо, потому что у вас уже может быть какое-то усовершенствованное снаряжение, но не все необходимые детали. Таким образом, вы можете смешивать наборы вместе, пока не сможете заменить несовершенные части шестерни улучшенной версией. Предметы, привязываемые при экипировке, навсегда привязываются к вашей учетной записи только тогда, когда вы их экипируете. Предметы из набора, привязываемые при получении, можно обменивать только в течение двух часов после получения предмета и только с другими членами группы в пределах инстанса, в котором вы его получили; после чего предмет навсегда привязывается к вашему аккаунту.
Предметы, привязываемые при экипировке, навсегда привязываются к вашей учетной записи только тогда, когда вы их экипируете. Предметы из набора, привязываемые при получении, можно обменивать только в течение двух часов после получения предмета и только с другими членами группы в пределах инстанса, в котором вы его получили; после чего предмет навсегда привязывается к вашему аккаунту. Сундуки с наградами дают эти наборы предметов после каждого раунда.
Сундуки с наградами дают эти наборы предметов после каждого раунда.
 Головные уборы выпадают из финального босса соответствующего группового подземелья ветеранского режима и, как и перечисленные выше наборы подземелий, могут быть обменены с вашей группой подземелий на короткое время, прежде чем они навсегда привяжутся к вашей учетной записи. Наплечники можно получить из сундуков, купленных за ключи у Неустрашимых ежедневных дарителей залога, и они привязываются при получении.
Головные уборы выпадают из финального босса соответствующего группового подземелья ветеранского режима и, как и перечисленные выше наборы подземелий, могут быть обменены с вашей группой подземелий на короткое время, прежде чем они навсегда привяжутся к вашей учетной записи. Наплечники можно получить из сундуков, купленных за ключи у Неустрашимых ежедневных дарителей залога, и они привязываются при получении.

 Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить?
Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить? 3 … u …
3 … u … Просвечивающая электронная микроскопия показала, что полученные частицы были сферическими. Метод позволял генерировать аэрозоль достаточной концентрации и размера для изучения физико-химических свойств и исследования гетерогенных реакций минерального аэрозоля.
Просвечивающая электронная микроскопия показала, что полученные частицы были сферическими. Метод позволял генерировать аэрозоль достаточной концентрации и размера для изучения физико-химических свойств и исследования гетерогенных реакций минерального аэрозоля. Это противоречило бы существующему мнению, что Ca(HCO 3 ) 2 (s) термодинамически нестабилен. Активность CCN аэрозоля Ca(HCO 3 ) 2 (s) (κ≈0,15) заметно выше, чем у аэрозоля CaCO 3 (κ=0,0019±0,0007), и меньше, чем у Ca(NO 3 ) 2 . Заметная, но ограниченная растворимость Ca(HCO 3 ) 2 ≈0,01 моль/л объясняет ограниченный гигроскопический рост и хорошую активность CCN.
Это противоречило бы существующему мнению, что Ca(HCO 3 ) 2 (s) термодинамически нестабилен. Активность CCN аэрозоля Ca(HCO 3 ) 2 (s) (κ≈0,15) заметно выше, чем у аэрозоля CaCO 3 (κ=0,0019±0,0007), и меньше, чем у Ca(NO 3 ) 2 . Заметная, но ограниченная растворимость Ca(HCO 3 ) 2 ≈0,01 моль/л объясняет ограниченный гигроскопический рост и хорошую активность CCN.
 Результаты показывают, что ни одна из реакций растворения не достигает термодинамического равновесия. Конгруэнтное растворение в растворах Ca(HCO3)2 либо достигает, либо близко приближается к стехиометрическому насыщению по отношению к растворяющемуся твердому веществу. В растворах Sr(HCO3)2 реакции обычно становятся неконгруэнтными, осаждая Sr-богатую фазу до достижения стехиометрического насыщения. Растворение механических смесей твердых веществ приближается к стехиометрическому насыщению по отношению к наименее стабильному твердому веществу в смеси. Поглощение поверхности из ненасыщенных объемных растворов наблюдалось в первые минуты растворения. Эта поверхностная фаза имеет толщину 0-10 атомных слоев в растворах Sr(HCO3)2 и 0-4 слоя в растворах Ca(HCO3)2, а затем растворяется и/или перекристаллизуется, обычно в течение 6 мин реакции. За начальным переходным процессом поверхностного осаждения (перекристаллизации) следует конгруэнтное растворение исходного твердого вещества, которое продолжается до стехиометрического насыщения или до осаждения более стабильного твердого вещества, богатого Sr.
Результаты показывают, что ни одна из реакций растворения не достигает термодинамического равновесия. Конгруэнтное растворение в растворах Ca(HCO3)2 либо достигает, либо близко приближается к стехиометрическому насыщению по отношению к растворяющемуся твердому веществу. В растворах Sr(HCO3)2 реакции обычно становятся неконгруэнтными, осаждая Sr-богатую фазу до достижения стехиометрического насыщения. Растворение механических смесей твердых веществ приближается к стехиометрическому насыщению по отношению к наименее стабильному твердому веществу в смеси. Поглощение поверхности из ненасыщенных объемных растворов наблюдалось в первые минуты растворения. Эта поверхностная фаза имеет толщину 0-10 атомных слоев в растворах Sr(HCO3)2 и 0-4 слоя в растворах Ca(HCO3)2, а затем растворяется и/или перекристаллизуется, обычно в течение 6 мин реакции. За начальным переходным процессом поверхностного осаждения (перекристаллизации) следует конгруэнтное растворение исходного твердого вещества, которое продолжается до стехиометрического насыщения или до осаждения более стабильного твердого вещества, богатого Sr. Составы вторичных выделений не соответствуют состояниям термодинамического равновесия или стехиометрического насыщения. Рентгенофотоэлектронная спектроскопия (РФЭС) свидетельствует об образовании твердых растворов на поверхности монокристаллов арагонита и стронцианита, погруженных в растворы Sr(HCO3)2 и Ca(HCO3)2 соответственно. В растворах Sr(HCO3)2 сигнал РФЭС снаружи ~ 60 А?? на арагоните указывает на состав 16 мол.% SrCO3 уже через 2 мин контакта и 14-18 мол.% SrCO3 через 3 недели контакта. Поверхность стронцианита составляет в среднем примерно 22 мол.% CaCO3 после 2 мин контакта с раствором Ca(HCO3)2 и составляет 34-39мол.% CaCO3 через 3 недели контакта. Анализ XPS предполагает, что состав поверхности зональный с несколько большим обогащением во внешнем ~ 25 A?? (до 26 мол. % SrCO3 на арагоните и 44 мол. % CaCO3 на стронцианите). Результаты указывают на быстрое образование поверхностной фазы твердого раствора из ненасыщенных водных растворов. Поверхностная фаза постоянно корректирует свой состав в ответ на изменения в составе основного флюида по мере того, как происходит чистое растворение.
Составы вторичных выделений не соответствуют состояниям термодинамического равновесия или стехиометрического насыщения. Рентгенофотоэлектронная спектроскопия (РФЭС) свидетельствует об образовании твердых растворов на поверхности монокристаллов арагонита и стронцианита, погруженных в растворы Sr(HCO3)2 и Ca(HCO3)2 соответственно. В растворах Sr(HCO3)2 сигнал РФЭС снаружи ~ 60 А?? на арагоните указывает на состав 16 мол.% SrCO3 уже через 2 мин контакта и 14-18 мол.% SrCO3 через 3 недели контакта. Поверхность стронцианита составляет в среднем примерно 22 мол.% CaCO3 после 2 мин контакта с раствором Ca(HCO3)2 и составляет 34-39мол.% CaCO3 через 3 недели контакта. Анализ XPS предполагает, что состав поверхности зональный с несколько большим обогащением во внешнем ~ 25 A?? (до 26 мол. % SrCO3 на арагоните и 44 мол. % CaCO3 на стронцианите). Результаты указывают на быстрое образование поверхностной фазы твердого раствора из ненасыщенных водных растворов. Поверхностная фаза постоянно корректирует свой состав в ответ на изменения в составе основного флюида по мере того, как происходит чистое растворение. Скорость растворения конечных элементов значительно снижается в нестехиометрических растворах по сравнению со скоростью растворения, наблюдаемой в стехиометрических растворах. Все твердые вещества растворяются медленнее в растворах с добавлением наименее растворимого компонента ((Sr(HCO3)2)), чем в растворах с добавлением более растворимого компонента (Ca(HCO3)2), и этот эффект становится все более значительным по мере приближения к стехиометрическому насыщению. . Предполагается, что образование нестехиометрической поверхностной реакционной зоны значительно снижает скорость растворения.
Скорость растворения конечных элементов значительно снижается в нестехиометрических растворах по сравнению со скоростью растворения, наблюдаемой в стехиометрических растворах. Все твердые вещества растворяются медленнее в растворах с добавлением наименее растворимого компонента ((Sr(HCO3)2)), чем в растворах с добавлением более растворимого компонента (Ca(HCO3)2), и этот эффект становится все более значительным по мере приближения к стехиометрическому насыщению. . Предполагается, что образование нестехиометрической поверхностной реакционной зоны значительно снижает скорость растворения.
 GE — მარტივად უყურეთ ან ჩამოქაჩეთ სასურველი ფილმი | Смотреть онлайн или скачать любимый фильм легко и просто!
GE — მარტივად უყურეთ ან ჩამოქაჩეთ სასურველი ფილმი | Смотреть онлайн или скачать любимый фильм легко и просто! Современное состояние теории при максимально доступном изложении. Рассматриваются математические методы и проблемы. Даны определения.
Современное состояние теории при максимально доступном изложении. Рассматриваются математические методы и проблемы. Даны определения. ru
ru 





 Выставленные учителем баллы отобразятся в вашей статистике.
Выставленные учителем баллы отобразятся в вашей статистике.
 com Скорость страницы
com Скорость страницы com
com onkinemschool.com
onkinemschool.com  on линдемшкола .com
on линдемшкола .com  com
com  com
com  onlinemschool.con
onlinemschool.con  i=1 в суммировании указывает начальный индекс, т. е. для набора данных 1, 3, 4, 7, 8, i=1 будет 1, i=2 будет 3 и т. д. . Следовательно, обозначение суммирования просто означает выполнение операции (x i — μ) 2 для каждого значения до N , что в данном случае равно 5, поскольку в этом наборе данных 5 значений.
i=1 в суммировании указывает начальный индекс, т. е. для набора данных 1, 3, 4, 7, 8, i=1 будет 1, i=2 будет 3 и т. д. . Следовательно, обозначение суммирования просто означает выполнение операции (x i — μ) 2 для каждого значения до N , что в данном случае равно 5, поскольку в этом наборе данных 5 значений. Стоит отметить, что существует множество различных уравнений для расчета стандартного отклонения выборки, поскольку, в отличие от среднего значения выборки, стандартное отклонение выборки не имеет какой-либо единственной оценки, которая была бы беспристрастной, эффективной и имела максимальную вероятность. Уравнение, представленное ниже, представляет собой «скорректированное стандартное отклонение выборки». Это скорректированная версия уравнения, полученная путем изменения уравнения стандартного отклонения совокупности с использованием размера выборки в качестве размера совокупности, что устраняет некоторую погрешность в уравнении. Однако беспристрастная оценка стандартного отклонения очень сложна и варьируется в зависимости от распределения. Таким образом, «скорректированное стандартное отклонение выборки» является наиболее часто используемой оценкой стандартного отклонения генеральной совокупности и обычно называется просто «стандартным отклонением выборки». Это намного лучшая оценка, чем ее нескорректированная версия, но все же она имеет значительную погрешность для малых размеров выборки (N
Стоит отметить, что существует множество различных уравнений для расчета стандартного отклонения выборки, поскольку, в отличие от среднего значения выборки, стандартное отклонение выборки не имеет какой-либо единственной оценки, которая была бы беспристрастной, эффективной и имела максимальную вероятность. Уравнение, представленное ниже, представляет собой «скорректированное стандартное отклонение выборки». Это скорректированная версия уравнения, полученная путем изменения уравнения стандартного отклонения совокупности с использованием размера выборки в качестве размера совокупности, что устраняет некоторую погрешность в уравнении. Однако беспристрастная оценка стандартного отклонения очень сложна и варьируется в зависимости от распределения. Таким образом, «скорректированное стандартное отклонение выборки» является наиболее часто используемой оценкой стандартного отклонения генеральной совокупности и обычно называется просто «стандартным отклонением выборки». Это намного лучшая оценка, чем ее нескорректированная версия, но все же она имеет значительную погрешность для малых размеров выборки (N в разделе «Стандартное отклонение генеральной совокупности». Уравнение по существу такое же, за исключением члена N-1 в уравнении скорректированного выборочного отклонения и использования выборочных значений.
в разделе «Стандартное отклонение генеральной совокупности». Уравнение по существу такое же, за исключением члена N-1 в уравнении скорректированного выборочного отклонения и использования выборочных значений. Хотя это может привести к убеждению, что температуры в этих двух городах практически одинаковы, реальность может быть замаскирована, если учитывать только среднее значение и игнорировать стандартное отклонение. Прибрежные города, как правило, имеют гораздо более стабильную температуру из-за регулирования большими водоемами, поскольку вода имеет более высокую теплоемкость, чем земля; по сути, это делает воду гораздо менее восприимчивой к изменениям температуры, а прибрежные районы остаются теплее зимой и прохладнее летом из-за количества энергии, необходимой для изменения температуры воды. Следовательно, в то время как прибрежный город может иметь диапазон температур от 60 ° F до 85 ° F в течение определенного периода времени, что приводит к среднему значению 75 ° F, внутренний город может иметь температуру от 30 ° F до 110 ° F. получается одно и то же среднее.
Хотя это может привести к убеждению, что температуры в этих двух городах практически одинаковы, реальность может быть замаскирована, если учитывать только среднее значение и игнорировать стандартное отклонение. Прибрежные города, как правило, имеют гораздо более стабильную температуру из-за регулирования большими водоемами, поскольку вода имеет более высокую теплоемкость, чем земля; по сути, это делает воду гораздо менее восприимчивой к изменениям температуры, а прибрежные районы остаются теплее зимой и прохладнее летом из-за количества энергии, необходимой для изменения температуры воды. Следовательно, в то время как прибрежный город может иметь диапазон температур от 60 ° F до 85 ° F в течение определенного периода времени, что приводит к среднему значению 75 ° F, внутренний город может иметь температуру от 30 ° F до 110 ° F. получается одно и то же среднее.