Калькулятор условной вероятности — MathCracker.com
Вероятность Решатели Статистика
Инструкции: Используйте этот калькулятор условной вероятности для вычисления условной вероятности \(\Pr(A | B)\). Пожалуйста, укажите вероятность \(\Pr(A \cap B)\) и \(\Pr(B)\) в форме ниже:
Концепция условной вероятности — одна из самых важных идей в теории вероятностей и статистики.
Идея простая: условная вероятность события \(A\)
данный
событие \(B\) — это вероятность того, что \(A\) произойдет в предположении, что также произойдет \(B\).
То есть мы ограничиваем пространство выборки выходными данными, в которых происходит \(B\), и ищем вероятность того, что \(A\) встречается в этом пространстве выборки подмножества.
Итак, какова формула условной вероятности?
С математической точки зрения условная вероятность \(\Pr(A|B)\) вычисляется по следующей формуле:
\[\Pr(A|B) = \displaystyle \frac{\Pr(A \cap B)}{\Pr(B)}\]
Вышеупомянутое выражение можно переписать, и оно также дает способ вычислить вероятность пересечения двух событий, когда известна условная вероятность:
\[ \Pr(A \cap B) = \Pr(A|B) \Pr(B) \]
Почему важна условная вероятность?
Концепция условной вероятности имеет решающее значение, потому что она отражает тот факт реальной жизни, что, когда мы знаем больше информации о каком-то событии, мы можем уточнить наше представление о вероятности события.
Идея вычисления вероятности при условии, что мы знаем, что определенное даже истинно, представляет собой представление о том, как работает наш мозг, и, следовательно, делает идею условной вероятности очень важной.
Кроме того, понятие условной вероятности и закон умножения играют решающую роль в строительстве Правило общей вероятности а также Теорема Байеса .
Базовый статистический пакет Правило Байеса Условные вероятности Калькулятор условной вероятности Калькулятор статистики Статистический решатель
Вероятность события Калькулятор | Вычислить Вероятность события
✖Число благоприятных исходов — это общее число исходов, благоприятствующих успешному завершению определенного события при данных обстоятельствах. | +10% -10% | ||
✖Общее количество исходов — это общее количество всех возможных исходов в случайном эксперименте.ⓘ Общее количество результатов [nTotal] | +10% -10% |
ⓘ Количество благоприятных исходов [nFavorable]|
✖Вероятность события — это доля шанса на успешное завершение определенного события в соответствии с заданными условиями и ограничениями.ⓘ Вероятность события [PEvent] |
⎘ копия |
👎
Формула
сбросить
👍
Вероятность события Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Преобразование входов в базовый блок
Количество благоприятных исходов: 3 —> Конверсия не требуется
Общее количество результатов: 10 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.3 —> Конверсия не требуется
< 6 Вероятность Калькуляторы
Вероятность события формула
Вероятность события = Количество благоприятных исходов/Общее количество результатов
PEvent = nFavorable/nTotal
Что такое вероятность в математике?
В математике теория вероятностей изучает шансы. В реальной жизни мы прогнозируем шансы в зависимости от ситуации. Но теория вероятностей подводит математическую основу концепции вероятности. Например, если в коробке 10 шаров, среди которых 7 черных и 3 красных шара, а также один случайно выбранный шар.
Тогда вероятность выпадения красного шара равна 3/10, а вероятность выпадения черного шара равна 7/10. Когда дело доходит до статистики, вероятность является ее основой. Он имеет широкое применение в принятии решений, науке о данных, исследованиях бизнес-тенденций и т. д.
Share
Copied!
вероятность калькулятора
, созданный Mateusz Muga и Wojciech SAS, PhD
, рассмотрено Bogna Szyk и Jack Bowater
Последнее обновление: 14 декабря 2022 г.
Содержание:- Как найти вероятность событий? – определение вероятности
- Как пользоваться калькулятором вероятности?
- Условная вероятность
- Формула условной вероятности
- Распределение вероятностей и кумулятивная функция распределения
- Теоретическая и экспериментальная вероятность
- Вероятность и статистика
- Статистика большой группы людей – вероятностная выборка
- Практическое применение теории вероятностей отдельные события .
Например, если вероятность того, что произойдет А, составляет 50%, и такая же вероятность для В, каковы шансы того, что произойдет и то, и другое, только одно, по крайней мере одно или ни одного события и так далее.Наш калькулятор вероятности дает вам шесть сценариев, плюс еще 4, когда вы вводите, сколько раз, так сказать, «бросается жребий». Если вы знаете, как найти вероятность отдельных событий, это сэкономит вам много времени.
Читая ниже, вы:
- узнаете, как правильно пользоваться калькулятором вероятностей;
- Проверить, как найти вероятность одиночных событий;
- Прочтите о нескольких примерах использования вероятности, включая формулы условной вероятности;
- Изучение разницы между теоретической и эмпирической вероятностью; и
- Расширьте свои знания о взаимосвязи между вероятностью и статистикой.
Вы пришли сюда специально, чтобы проверить свои шансы выиграть пари или сорвать джек-пот? Наш калькулятор шансов и лотерейный калькулятор помогут вам!
Как найти вероятность событий? – определение вероятности
Основное определение вероятности – это отношение всех благоприятных результатов к количеству всех возможных результатов.
Допустимые значения одной вероятности варьируются от 0 до 1 , поэтому также удобно записывать вероятности в процентах. Вероятность отдельного события может быть выражена следующим образом:
- Вероятность
A:P(A), - Вероятность
B:P(B), - Вероятность
+:P(+), - Вероятность
♥:P(♥)и т. д.
Давайте рассмотрим пример с разноцветными шарами. У нас есть мешок, наполненный оранжевыми, зелеными и желтыми шариками. Наше событие
Aравно выбору случайного шара из мешка . Мы можем определитьΩкак полный набор шаров. Вероятность событияΩ, означающего взятие любого шара, естественно равна 1. На самом деле сумма всех возможных событий в данном наборе всегда равна 1 .Теперь давайте посмотрим на кое-что посложнее — какова вероятность того, что выпадет оранжевый шар? Чтобы ответить на этот вопрос, вам нужно найти количество всех оранжевых шариков и разделить его на количество всех шариков в мешке.
Вы можете сделать это для любого цвета, например желтого, и вы, несомненно, заметите, что чем больше шариков определенного цвета, тем выше вероятность вытащить его из мешка, если процесс полностью случайный.Ознакомьтесь с нашим калькулятором вероятности 3 событий и калькулятором условной вероятности для определения шансов нескольких событий.
Мы можем определить дополнительное событие , записанное как
ÀилиA', что означает , а не A . В нашем примере вероятность выбора НЕ оранжевого шара оценивается как количество всех неоранжевых шаров, деленное на все шарики. СуммаP(A) + P(Ā)всегда равна 1, потому что нет другого варианта, как половинка шара или полуоранжевый.Теперь попробуйте найти вероятность выпадения синего шара. Как бы вы ни старались, у вас не получится, потому что в мешке нет ни одной, поэтому результат равен 0.
Мы все время используем интуитивные расчеты вероятности.
Знание того, как количественно определить вероятность, необходимо для статистического анализа. Это позволяет вам измерить туманную концепцию, называемую «вероятностью». Кроме того, при наличии дискретного набора данных относительная частота каждого значения является синонимом вероятности их появления.Вы ищете что-то немного другое? Взгляните на наш калькулятор вероятности после теста. 🎲
Как пользоваться калькулятором вероятности?
Чтобы максимально использовать наш калькулятор, вам необходимо выполнить следующие шаги:
1. Определите проблему, которую вы хотите решить.
Ваша проблема должна быть разделена на два отдельных события. Если вы хотите рассчитать вероятность события в эксперименте с несколькими равновозможными испытаниями, вы можете воспользоваться калькулятором z-score.
2. Найдите вероятность каждого события.
Теперь, когда вы знаете, как оценить вероятность отдельного события, вам нужно только выполнить задание и получить все необходимые значения.
3. Введите процентную вероятность каждого события в соответствующие поля.
Как только они появятся, калькулятор вероятности сразу же выдаст точную вероятность 6 различных сценариев:
- Произойдут оба события
- Произойдет хотя бы одно из событий
- Произойдет ровно одно из событий
- Ни одно из событий не произойдет
- Не произойдет только первое событие
- Только второе событие не произойдет
Калькулятор также покажет вероятность еще четырех сценариев при определенном количестве испытаний:
- Всегда встречающийся
- Никогда не встречающийся
- B встречается всегда
- B никогда не встречается
Вы можете изменить количество попыток и любое другое поле в калькуляторе, а остальные поля автоматически изменятся. Эта функция экономит массу времени, если вы хотите узнать, например, какой должна быть вероятность события
B, чтобы сделать вероятность того и другого события равной 50%.Если набор возможных вариантов чрезвычайно велик, а успешными являются лишь несколько исходов, результирующая вероятность мала, например,
P(A) = 0,0001. Удобно использовать экспоненциальную запись, чтобы не перепутать количество нулей.Условная вероятность
Одним из наиболее важных соображений в мире вероятностей является вопрос о том, являются ли события зависимыми или нет. Два события независимы, если появление первого не влияет на вероятность появления второго . Например, если мы бросаем идеально сбалансированный стандартный кубический кубик, вероятность выпадения двойки ⚁ равна 9.0062 1/6 (то же самое, что получить четыре ⚃ или любое другое число).
Допустим, у вас есть два броска костей, и вы получили пять ⚄ в первом. Если вы спросите себя, какова вероятность получить двойку ⚁ во второй ход, ответ снова будет
1/6из-за независимости событий.Способ мышления, а также расчеты меняются, если одно из событий прерывает работу всей системы.
На этот раз мы говорим о условной вероятности .Допустим, у нас есть
10бильярдных шара с разными номерами, от ➀ до ➉. Вы выбираете случайный шар, поэтому вероятность выпадения ➆ равна1/10. Предположим, вы выбрали три ➂ и удалили их из игры . Затем вы снова спрашиваете себя, каков шанс получить семерку ➆. Ситуация изменилась, потому что есть один шар с ➆ из девяти возможностей, что означает, что вероятность теперь составляет1/9. Другими словами, можно задать вопрос: «Какова вероятность выбора ➆, ЕСЛИ первый шар был ➂?»Давайте рассмотрим другой пример: представьте, что вы собираетесь сдавать экзамен по статистике. Вы знаете от своих старших коллег, что это сложно, и вероятность того, что вы сдадите первый семестр, составляет
0,5(18из36студентов, сдавших экзамен в прошлом году). Тогда давайте зададим себе вопрос: «Какова вероятность прохождения, ЕСЛИ вы уже изучили тему?»20человек признались, что просматривали свои записи хотя бы один раз перед экзаменом, и16из выпавших, значит, ответ на последний вопрос0,8. Этот результат указывает на то, что это дополнительное условие действительно имеет значение, если мы хотим выяснить, меняет ли обучение что-либо или нет.Если вы до сих пор не чувствуете понятие условной вероятности, давайте попробуем на другом примере: вам нужно проехать из города X в город Y на машине. Расстояние между ними составляет около 150 миль. На полном баке обычно можно проехать до 400 миль. Если вы не знаете уровень топлива, вы можете оценить вероятность успешного достижения пункта назначения без дозаправки. А что, если кто-то уже залил бак? Теперь вы почти уверены, что сможете это сделать, если этому не помешают другие проблемы.
Формула условной вероятности
Формальное выражение условной вероятности, которое может быть обозначено как
P(A|B),P(A/B)или P B (A) , может быть вычислено как:P(A|B) = P(A∩B) / P(B),, где
P(B)— вероятность событияB, аP(A∩ Б)является стыком обоих событий. С другой стороны, мы можем оценить пересечение двух событий, если нам известна одна из условных вероятностей:-
Р(А∩В) = Р(А|В) * Р(В)или -
P(A∩B) = P(B|A) * P(A).
Лучше понять концепцию формулы условной вероятности с древовидными диаграммами. Мы спрашиваем учащихся в классе, нравятся ли им математика и физика. Событие
Mобозначает процент увлеченных математикой, аPто же самое с физикой:Существует известная теорема, связывающая условные вероятности двух событий. Она называется теоремой Байеса 9.0032 , а формула выглядит следующим образом:
P(A|B) = P(B|A) * P(A) / P(B)Вы можете задать вопрос: «Какова вероятность того, что
AприB, если я знаю вероятностьBприA?». Эта теорема иногда дает удивительные и неинтуитивные результаты. Наиболее часто описываемыми примерами являются тестирование на наркотики и выявление заболеваний, что имеет много общего с относительным риском заболевания среди населения. Остановимся на втором. В группе 1000человек, из них10имеют редкое заболевание. У всех был тест, который показывает реальный результат в95%случаев. Итак, теперь мы хотим найти вероятность того, что человек болен, если результат его теста положительный.Не задумываясь, вы можете интуитивно предсказать, что результат должен быть примерно
90%, верно? Произведем некоторые расчеты и оценим правильный ответ.- Будем использовать обозначения:
H– здоров,I– заболел,+– положительный результат,-– отрицательный результат. - Перепишите информацию из текста выше в виде вероятностей: ) = 0,05 ,
P(+|H) = 0,05,P(-|H) = 0,95. - Определите общую вероятность положительного результата теста:
P(+) = P(+|I) * P(I) + P(+|H) * P(H) = 0,95 * 0,01 + 0,05 * 0,99 = 0,059. - Используйте теорему Байеса , чтобы найти условную вероятность
P(I|+) = P(+|I) * P(I) / P(+) = 0,95 * 0,01 / 0,059 = 0,161.
Хм… не так уж и много, не так ли? Оказывается, такого рода парадокс возникает при наличии значительного дисбаланса между числом здоровых и больных или вообще между двумя отдельными группами. Если результат положительный, всегда стоит повторить тест, чтобы поставить соответствующий диагноз.
Распределение вероятностей и кумулятивная функция распределения
Мы можем различать два вида распределения вероятностей в зависимости от того, являются ли случайные величины дискретными или непрерывными.
Дискретное распределение вероятностей описывает вероятность возникновения исчисляемых отдельных событий. Одним из примеров является биномиальная вероятность, которая учитывает вероятность какого-либо успеха в нескольких ходах, например, при подбрасывании монеты.
Напротив, в распределении Паскаля (также известном как отрицательное биномиальное) дается фиксированное количество успехов, и вы хотите оценить общее количество испытаний.Распределение Пуассона — это еще одно дискретное распределение вероятностей, которое на самом деле является частным случаем биномиального распределения, которое вы можете рассчитать с помощью нашего калькулятора распределения Пуассона. Функция массы вероятности может быть интерпретирована как другое определение дискретного распределения вероятностей – она присваивает заданное значение любому отдельному числу. Геометрическое распределение является прекрасным примером использования функции массы вероятности.
Непрерывное распределение вероятностей содержит информацию о неисчисляемых событиях. Невозможно предсказать вероятность отдельного события (как и дискретного), но мы можем найти событие в некотором диапазоне переменных. Нормальное распределение — одна из самых известных непрерывных функций распределения.
Он описывает набор свойств в любой популяции, например, рост взрослых людей или распространение IQ.
Если вы более продвинуты в теории вероятностей и расчетах, вам обязательно придется иметь дело с распределением SMp(x), которое учитывает комбинацию нескольких дискретных и непрерывных функций вероятности.
Для каждого распределения вероятностей мы можем построить кумулятивную функцию распределения (CDF) . Он говорит вам, какова вероятность того, что какая-то переменная примет значение, меньшее или равное заданному числу .
Допустим, вы участвуете в викторине по общим знаниям. Конкурс состоит из
100вопросов, и за правильный ответ вы получаете 1 балл, а за неправильный баллы не начисляются. Многие люди уже закончили, и из результатов мы можем получить распределение вероятностей. Правила гласят, что только20%лучших участника получают награды, так что вам интересно, сколько очков вы должны набрать, чтобы стать одним из победителей. Если вы посмотрите на график, вы можете разделить его так, чтобы 80%области ниже были слева, а20%результатов — справа от желаемого результата. То, что вы на самом деле ищете, — это левостороннее p-значение.Однако есть и другой способ найти его, если использовать кумулятивную функцию распределения — просто найти значение
80%на оси абсцисс и соответствующее количество точек, ничего не вычисляя!Теоретическая и экспериментальная вероятности
Почти каждый описанный выше пример учитывает теоретическую вероятность. Поэтому возникает вопрос: в чем разница между теоретической и экспериментальной (также известной как эмпирическая) вероятностью? Формальное определение теоретической вероятности: отношение числа благоприятных исходов к числу всех возможных исходов . Он опирается на предоставленную информацию, логические рассуждения и говорит нам, что мы следует ожидать от эксперимента .
Еще раз взгляните на мешочки с разноцветными шариками. Всего
42шариков, из них18оранжевых. Игра состоит в том, чтобы выбрать случайный шар из мешка и положить его обратно, так что внутри всегда будет42шара. Применяя определение вероятности, мы можем быстро оценить ее как18/42или, упростив дробь,3/7. Это значит, что если мы возьмем14шаров, то их должно быть 9.0062 6 оранжевые.С другой стороны, экспериментальная вероятность говорит нам точно о том, что произошло, когда мы проводим эксперимент , а не о том, что должно произойти. Он основан на соотношении числа успешных испытаний и числа всех испытаний . Возьмем тот же пример — вытащите случайный шарик из мешка и повторите процедуру
13еще раз. Предположим, вы получили8оранжевых шара за14попыток. Этот результат означает, что эмпирическая вероятность равна14/8или7/4.Как видите, ваш результат отличается от теоретического. В этом нет ничего странного, потому что, когда вы пытаетесь повторять эту игру снова и снова, иногда вы будете выбирать больше, а иногда меньше, а иногда выберете именно то число, которое теоретически предсказано. Если суммировать все результаты, то можно заметить, что общая вероятность становится все ближе и ближе к теоретической вероятности . Если нет, то мы можем заподозрить, что выбор мяча из мешка не совсем случайный, например, мячи разных цветов имеют неодинаковые размеры, поэтому их можно различить, не глядя.
Как статистика, так и вероятность являются разделами математики и имеют дело с взаимосвязью возникновения событий . Тем не менее, каждый должен знать о различиях, которые делают их двумя разными областями.
Вероятность, как правило, является теоретической областью математики, и она исследует следствия математических определений и теорем .
Напротив, статистика обычно представляет собой практическое применение математики в повседневных ситуациях и пытается0031 атрибут смысла и понимания наблюдений в реальном мире .Вероятность предсказывает возможность возникновения событий , тогда как статистика в основном анализирует частоту возникновения прошлых событий и создает модель на основе полученных знаний .
Представьте себе вероятностного игрока, играющего в карточную игру, которая основана на выборе случайной карты из всей колоды, зная, что выигрывают только пики с предопределенным соотношением шансов. Предполагая, что колода полная, а выбор полностью случайный и справедливый, они делают вывод, что вероятность равна 9.0062 = и можно делать ставки.
Статистик некоторое время понаблюдает за игрой, чтобы сначала проверить, действительно ли игра честная. Убедившись (с приемлемым приближением), что в игру стоит играть, он спросит у вероятностника, что ему следует сделать, чтобы выиграть больше всего.
Вы, несомненно, видели некоторые опросы о предпочтении на выборах и, возможно, задавались вопросом, как они могут быть настолько точными по сравнению с окончательными результатами, даже если количество опрошенных намного меньше, чем общая численность населения — это время, когда происходит вероятностная выборка .
Основное предположение, которое является основной идеей выборки, заключается в том, что добровольцы выбираются случайным образом с заранее определенной вероятностью. Мы можем различать несколько видов методов выборки:
- Простая случайная выборка
- Кластерная случайная выборка
- Систематический отбор проб
- Выборка, пропорциональная размеру вероятности
- Стратифицированная случайная выборка
- Минимаксный отбор проб
- Случайный отбор проб
- Выборка по квоте
- Добровольный отбор проб
- Панельный отбор проб
- Отбор проб снежного кома
- Выборка пересечения линии
- Теоретический отбор проб
Каждый из этих методов имеет свои преимущества и недостатки, но большинство из них удовлетворительны.
Существенными преимуществами вероятностной выборки являются экономия времени и рентабельность , поскольку необходимо обследовать ограниченное число людей. Простота этой процедуры не требует специальных знаний и может выполняться без какой-либо тщательной подготовки.Практическое применение теории вероятностей
Как вы уже поняли, есть много областей, где применима теория вероятностей. Большинство из них — это игры с высоким фактором случайности, такие как бросание костей или выбор одного цветного шара из
10разных цветов, или множество карточных игр. Лотереи и азартные игры — это виды игр, в которых широко используется концепция вероятности и общее отсутствие знаний о ней. Конечно, время от времени кто-то выигрывает, но Вероятность того, что этим человеком будете вы, крайне мала .Теория вероятностей также используется во многих различных типах задач. Особенно, когда речь идет об инвестициях, также стоит учитывать риск, чтобы выбрать наиболее подходящий вариант.
Наш калькулятор Белого Рождества использует исторические данные и знание вероятностей, чтобы предсказать появление снежного покрова во многих городах во время Рождества.
Часто задаваемые вопросы
Как рассчитать вероятность A и B?
Если A и B являются независимыми событиями , то вы можете перемножить их вероятности вместе, чтобы получить вероятность того, что A и B произойдут. Например, если вероятность события А составляет 20% (0,2) , а вероятность события В составляет 30% (0,3) , вероятность того, что произойдет то и другое, составляет
0,2 × 0,3 = 0,06 = 6%.Как рассчитать условную вероятность?
Для событий, которые происходят совершенно отдельно и не зависят друг от друга, можно просто умножить их индивидуальные вероятности вместе . Если исход события влияет на другое событие, то его вероятность необходимо будет пересчитать, прежде чем найти условную вероятность.
Какова вероятность того, что выпадут две шестерки?
Если вы используете игральные кости, вероятность выпадения двух шестерок составит
1/6 × 1/6 = 1/36 = 0,027 = 2,7%. Это означает, что требуется 36 бросков кубиков, чтобы ожидать выпадения двух шестерок хотя бы один раз, хотя нет никаких гарантий, когда дело доходит до вероятности.Каковы шансы выиграть в розыгрыше?
Это зависит от сколько билетов вы купите и общее количество билетов в розыгрыше. В качестве примера предположим, что вы принесли полосу из 5 билетов и знаете, что в розыгрыше 500 билетов. Это означает, что вероятность выиграть первый приз составляет
5/500 = 0,01 = 1%. Тогда вероятность второго приза равна4/499 = 0,008 = 0,8%и так далее. Вероятность того, что выиграет все призы есть сумма всех этих вероятностей:1% + 0,8% + 0,6% + 0,4% + 0,2% = 3%.Как преобразовать коэффициенты в проценты?
Преобразуйте шансы в десятичное число , затем умножьте на 100.
Например, если шансы равны 1 из 9, это 1/9 = 0,1111в десятичной форме. Затем умножьте на 100, чтобы получить 11,11% .Матеуш Муха и Войцех Сас, PhD
Вероятности отдельных событий
Вероятность A, P(A)
Вероятность B, P(B)
Какую вероятность вы хотите увидеть?
P(A∩B)
Вероятности серии событий
При попытке
раз… 🎲
Точность Теорема Байеса Парадокс дня рождения… 22 далее
Базовый калькулятор вероятности с шагами
В теории вероятности экспериментом называется любой процесс, приводящий к определенным результатам. Набор всех возможных результатов эксперимента называется пространством выборки, а каждый элемент пространства выборки известен как точка выборки. Поскольку пространство выборки состоит из результатов, точка выборки — это другое слово для обозначения результата. При расчете вероятности часто необходимо знать, сколько существует возможных исходов.
Иногда в эксперименте всего несколько исходов, поэтому легко подсчитать количество исходов. Когда в эксперименте может быть много возможных результатов, полезно использовать одно из правил подсчета.Эксперимент: Исходы: Подбросить монетку Голова, Хвост Бросьте кубик 1, 2, 3, 4, 5, 6 Играть в игру Победа, поражение, ничья Существует три разных правила подсчета, которые можно использовать для подсчета количества результатов в эксперименте. Если эксперимент состоит из нескольких более мелких экспериментов, используется правило подсчета для многошаговых экспериментов. В нем говорится, что когда в эксперименте есть k шагов, при n 1 исходов на первом шаге, n 2 на втором шаге и так далее, тогда общее количество исходов равно (n 1 )(n 2 )···(n k ).
Если эксперимент предполагает выбор n объектов из большего набора из N объектов, используется правило подсчета комбинаций. Если эксперимент включает выбор n объектов из большего набора из N объектов и порядок выбора имеет значение, используется правило подсчета перестановок.Комбинации 9N_n = \dfrac{N!}{(N-n)!} $Вероятность исхода можно определить несколькими способами. Если разумно полагать, что все исходы равновероятны, можно использовать классический метод. В нем говорится, что вероятность каждого исхода равна единице, деленной на количество возможных исходов. Если доступны исторические данные, в которых эксперимент повторялся несколько раз, можно использовать метод относительной частоты. В нем говорится, что вероятность каждого результата равна пропорции, если это произошло, или относительной частоте. Если исходы неравновероятны и исторических данных практически нет, мы должны полагаться на субъективный метод.
В нем говорится, что вероятность каждого исхода — это степень уверенности человека в том, что он произойдет.Метод: Вероятность исхода: Классический 1 / количество исходов Относительная частота доля раз Субъективный степень уверенности Независимо от того, какой метод используется для определения вероятности, важно, чтобы выполнялись два требования. Первое требование состоит в том, чтобы вероятность каждого исхода была между нулем и единицей. Второе требование состоит в том, чтобы сумма вероятностей равнялась единице. В теории вероятности термин «событие» имеет иное значение, чем в повседневной жизни. Событие определяется как набор точек выборки (результатов). Чтобы рассчитать вероятность события, просто просуммируйте вероятности исходов события.
Для данного события A дополнением к A, записанным A c , является событие, содержащее все точки выборки, не принадлежащие A. Отношения в вероятности можно проиллюстрировать на диаграмме Венна, как показано ниже. Прямоугольник представляет пространство выборки. Поскольку событие и его дополнение составляют все пространство выборки, их вероятности в сумме равны единице. То есть P(A) + P(A c ) = 1. Таким образом, учитывая вероятность дополнения события, мы можем вычислить вероятность события, используя P(A) = 1 — P(A с ). В качестве альтернативы, учитывая вероятность события, мы можем вычислить вероятность дополнения события, используя P(A c ) = 1 — P(A).
Для двух событий A и B объединение A и B, записанное как A∪B, является событием, содержащим все точки выборки в A, B или в обоих A и B. С другой стороны, пересечение A и B, записанное A ∩ B — это событие, содержащее все точки выборки как в A, так и в B. Закон сложения можно использовать для вычисления вероятности объединения двух событий.
Он говорит, что P(A∪B) = P(A) + P(B) — P(A∩B). Если события не имеют общих точек выборки, говорят, что они взаимоисключающие. Поскольку на пересечении не будет точек выборки, вероятность пересечения будет равна нулю. Таким образом, для взаимоисключающих событий закон сложения принимает вид P(A∪B) = P(A) + P(B).Иногда вероятность возникновения одного события зависит от возникновения другого события. Это известно как условная вероятность и записывается как P(A|B). Это можно интерпретировать как вероятность события А при условии, что произошло событие В, или просто вероятность события А при условии В. Если вероятность события А не зависит от события В, мы говорим, что А и В независимы. Для независимых событий формула условной вероятности такова: P(A|B) = P(A) или P(B|A) = P(B). Переставляя члены в формуле условной вероятности, мы можем вычислить вероятность пересечения: P(A∩B)=P(B)P(A|B) или P(A∩B)=P(A)P(B |А). Если A и B независимы, мы получаем P(A∩B)=P(A)P(B).
Условная вероятность $P(A \mid B) = \dfrac{P(A \cap B)}{P(B)}$ или $P(B \mid A) = \dfrac{P(A \cap B)}{P(\cancel{A})}$ Базовый калькулятор вероятности обрабатывает простейшие аспекты теории вероятностей.
Например, если вероятность того, что произойдет А, составляет 50%, и такая же вероятность для В, каковы шансы того, что произойдет и то, и другое, только одно, по крайней мере одно или ни одного события и так далее.
Вы можете сделать это для любого цвета, например желтого, и вы, несомненно, заметите, что чем больше шариков определенного цвета, тем выше вероятность вытащить его из мешка, если процесс полностью случайный.
Знание того, как количественно определить вероятность, необходимо для статистического анализа. Это позволяет вам измерить туманную концепцию, называемую «вероятностью». Кроме того, при наличии дискретного набора данных относительная частота каждого значения является синонимом вероятности их появления.
На этот раз мы говорим о условной вероятности .
Этот результат указывает на то, что это дополнительное условие действительно имеет значение, если мы хотим выяснить, меняет ли обучение что-либо или нет.
С другой стороны, мы можем оценить пересечение двух событий, если нам известна одна из условных вероятностей:
Остановимся на втором. В группе 
Напротив, в распределении Паскаля (также известном как отрицательное биномиальное) дается фиксированное количество успехов, и вы хотите оценить общее количество испытаний.
Он описывает набор свойств в любой популяции, например, рост взрослых людей или распространение IQ.
Если вы посмотрите на график, вы можете разделить его так, чтобы 
Напротив, статистика обычно представляет собой практическое применение математики в повседневных ситуациях и пытается0031 атрибут смысла и понимания наблюдений в реальном мире .
Существенными преимуществами вероятностной выборки являются экономия времени и рентабельность , поскольку необходимо обследовать ограниченное число людей. Простота этой процедуры не требует специальных знаний и может выполняться без какой-либо тщательной подготовки.
Например, если шансы равны 1 из 9, это 
Иногда в эксперименте всего несколько исходов, поэтому легко подсчитать количество исходов. Когда в эксперименте может быть много возможных результатов, полезно использовать одно из правил подсчета.
Если эксперимент предполагает выбор n объектов из большего набора из N объектов, используется правило подсчета комбинаций. Если эксперимент включает выбор n объектов из большего набора из N объектов и порядок выбора имеет значение, используется правило подсчета перестановок.
В нем говорится, что вероятность каждого исхода — это степень уверенности человека в том, что он произойдет.
Он говорит, что P(A∪B) = P(A) + P(B) — P(A∩B). Если события не имеют общих точек выборки, говорят, что они взаимоисключающие. Поскольку на пересечении не будет точек выборки, вероятность пересечения будет равна нулю. Таким образом, для взаимоисключающих событий закон сложения принимает вид P(A∪B) = P(A) + P(B).
)
)
)
)
)
)
)
)
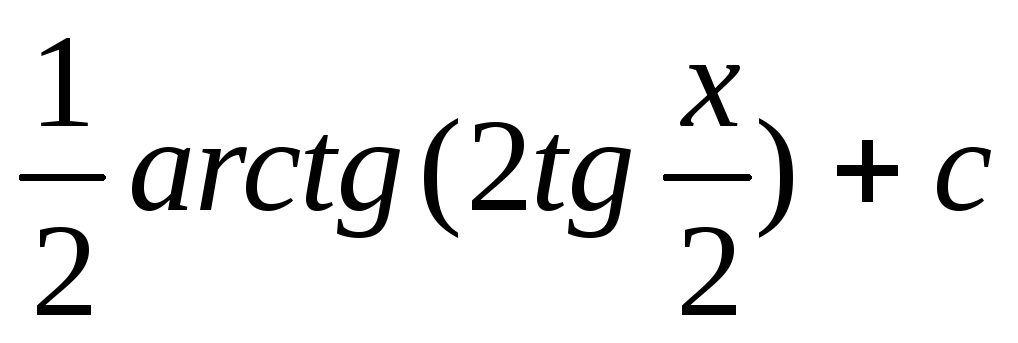10.20
Определите координаты точки D так, чтобы выполнялось равенство: 1) AB = CD 2)AB = DC
)/3
Вот что здесь происходит — atan возвращает значения между -pi/2 и pi/2 (см. документацию atan):
Она содержит большие библиотеки электронных компонентов с учётом требований ЕСКД и ГОСТов. Также можно загружать свои шаблоны элементов.
Для ознакомления с приложением предоставляется бесплатная демо-версия на 30 дней.
Их возможности уступают платным, но для выполнения отдельных работ вполне подходят.
Приложение имеет библиотеку готовых шаблонов популярных элементов, которые можно использовать при составлении схем. Однако более сложных и редко используемых элементов там нет. Также следует отметить особенность библиотек программы – каждый элемент расположен в отдельном файле.
Выбирайте для себя программу, в зависимости от выполняемых задач и выдвигаемых требований.
В Компасе существует собственная база данных, в которой хранятся наименования и номиналы всех наиболее популярных типов автоматики, релейной защиты, низковольтных установок и других элементов цепи. Помимо этого в базе данных заложены графические обозначения всех этих элементов, что позволит сделать понятную схему электроснабжения либо даже отдельного распределительного щита. ПО полностью на русском языке и к тому же можно скачать его бесплатно.
Недостаток данного программного пакета в том, что он официально не русифицирован, хотя если немного постараться, в интернете можно найти русификатор, что позволит без препятствий чертить электрические схемы квартир и домов.
д. Приятным дополнением в данном ПО является база данных с наклейками, которые можно распечатать и расклеить в собственном распределительном щитке для графического обозначения всех элементов цепи по госту.
д. «Эльф проектирование» полностью бесплатный программный пакет на русском языке.
Это один из самых простейших в использовании и к тому же многофункциональных программных пакетов для составления схем разводки электропроводки и трассировки электронных плат. Интерфейс удобный, на русском языке. В базе данных заложены все самые популярные графические элементы для черчения электросхем.
youtube.com/embed/eOG1lbxi8F0?feature=oembed&wmode=opaque» frameborder=»0″ allowfullscreen=»»> 
youtube.com/embed/8cy8N95DMzo?list=PLnpnrjTc9SIcc2Jv0UDxrdP0JDIip8wB1&rel=0″ frameborder=»0″ allowfullscreen=»allowfullscreen»> 
По сути, Maple фиксирует неотъемлемые предположения и мыслительный процесс, лежащие в основе анализа, а также расчетов.
МОП-транзисторы малой мощности имеют решающее значение для переключения в системах электропитания.
09.2010, 11:23 
09.2010, 11:34 
09.2010, 11:53 
09.2010, 11:58 
09.2010, 12:01 
09.2010, 12:21 
09.2010, 12:35 
09.2010, 12:49 
09.2010, 12:55 
3/3$ операций
..
Вывод такой, как я хочу, но мне нужно сделать его более читабельным, увеличив размер 
В моей серии «Исключение по Гауссу» мы исследовали, как можно решить квадратные обратимые матрицы методом исключения и замены строк, но мы никогда не углублялись в решение прямоугольных необратимых систем.
Если у вас есть квадратная и обратимая матрица (что часто бывает), используйте более простое исключение Гаусса . 
Затем мы умножаем первую строку на 2 и вычитаем из последней строки. Итак, теперь с нашими переменными b, как это выглядит?
Итак, наш окончательный ответ:
Эти числа так же условно относятся к дробям.
В 6 классе эта тема повторяется, но изучается более глубоко. А встречаться дроби и проценты продолжат вплоть до задач внешнего тестирования (ЗНО) для 11 класса.
3.
Мы можем найти одну пятую?
3.
Какую часть населения города составляют школьники?
Затем мы можем упростить полученную дробь, если это возможно. Например, 4/5 х 2/3 = (4 х 2) / (5 х 3) = 8/15.
Например, чтобы упростить 12/18, мы сначала находим наибольший общий делитель 12 и 18, который равен 6. Теперь разделим и числитель, и знаменатель на 6, чтобы получить упрощенную форму 12/18, которая равна 2/3.
Это дает нам продукт, и мы можем упростить продукт, если это необходимо.
Использование математических игр — эффективный способ для относительно сложных тем, подобных этим. Некоторые из математических игр, обсуждаемых ниже, могут улучшить понимание математических операций над дробями.
Далее детей нужно заставить построить дробь произведения аналогичным образом.
То есть 25 ÷ 6 или . Таким образом, дробь — это еще один способ представления деления. Записывается как деление числителя на знаменатель.
1
MD.C.4
24 КБ
08.2006 г. Зав. кафедрой Дорофиенко В. В. 181 стр. Введение. Логистика и факторы её развития. Концепция логистики. Информационная логистика. Закупочная логистика. Логистика производственных процессов. Сбытовая логистика. Логистика запасов. Логистика складирования и транспорта. Организация логистического управления. Литература.
54 МБ
Глобальная логистика. Управление запасами. Определение и оптимизация затрат. Организация логистического управления. Методы оптимизации материальных потоков. Применение методов прогнозирования в ло…
Интернет и сбытовая логистика. Интернет и транспортная логистика. Электронный документооборот через Интернет. Заключение
Tranquil — это надежное передовое решение ERP, развернутое в облаке, которое поможет вам максимально эффективно использовать свои запасы. Запланируйте демонстрацию с нами, чтобы узнать, как работает наше программное обеспечение и какую пользу оно может принести вашему бизнесу. 
Отсутствие централизованного центра инвентаризации 
Вопросы цепочки поставок 
Вместо этого будет создан пустой словарь:
Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за 
Или другими словами, пересечение этих множеств является пустым множеством.
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
Метод 
Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность 
, также существует два специальных метода – 
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
(См. также пример 10.)
Таким образом, пересечение с \(\overline{B}\) приводит к тому, что остаются только значения, не входящие в \(B\). То есть \(A\cap\overline{B}\) - это \(A\) со всеми удаленными значениями из \(B\). Таким образом, мы видим, что эти множества содержат одни и те же элементы. ∎
Например:
{n} S_i\,.\]
Студенты берут 92\,.\]
Множество, писал Кантор, есть совокупность определенных, различимых объектов восприятия или мысли, рассматриваемых как единое целое. Объекты называются элементами или членами множества.
Набор может быть определен правилом членства (формулой) или перечислением его членов в фигурных скобках. Например, множество, заданное правилом «простые числа меньше 10», также может быть задано как {2, 3, 5, 7}. В принципе, любое конечное множество может быть определено явным списком его элементов, но для определения бесконечных множеств требуется правило или шаблон для указания членства; например, многоточие в {0, 1, 2, 3, 4, 5, 6, 7, …} указывает, что список натуральных чисел ℕ можно продолжать бесконечно. Пустой (или недействительный, или нулевой) набор, обозначенный {} или Ø, вообще не содержит элементов. Тем не менее, он имеет статус набора.
Если
плоская кривая
определена уравнением
, причем перемещение от
точки
к точке
происходит при изменении
от
до
, то
Сделать чертеж.
Тогда криволинейный интеграл первого рода вдоль кривой вычисляется по формуле
интеграл и может быть определен в двух, трех и более измерениях.
Поясним, как это делается для кривых в R9.0044 2 .
Случай с R 3 аналогичен.
r ‘(t) = -x + 3xy + x + z = 3xy + z
r ‘(t)dt = Mdx + Ndy + Pdz
Линейные интегралы Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мы также рассмотрим одну из наиболее важных теорем, касающихся линейных интегралов, — теорему Грина.
Инвестиция ради процентов представляет собой краткосрочную стратегию, направленную на получение
4. АУДИТ НАЧИСЛЕННЫХ ПРОЦЕНТОВ
=>
Потребность в опоре на концепцию внешней
Практика, практика и еще раз практика
руб.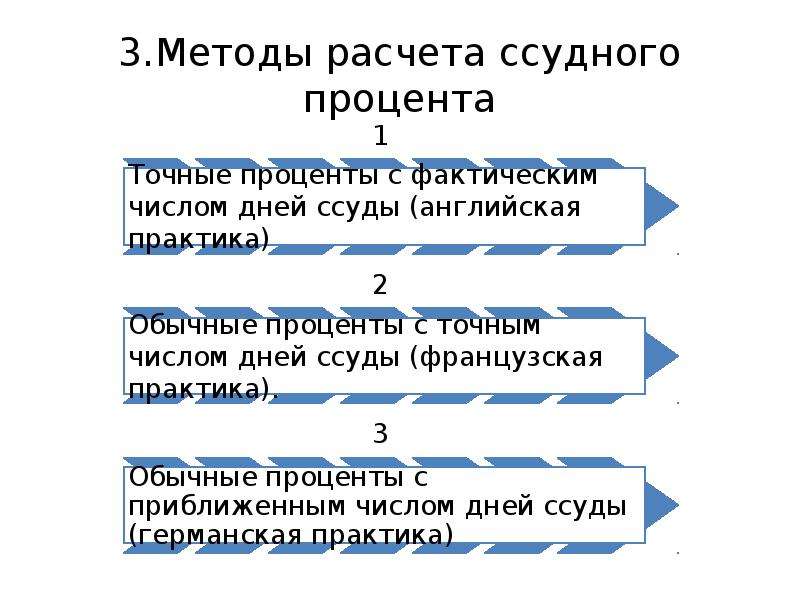
Основное
отличие сложных процентов от
простых процентов меняется от одного
расчетного периода к другому. 
При этом оговариваются годовая
номинальная ставка и
количество начислений за год. Фактически за базовый период
принимается часть
года со ставкой сложных
процентов , так что 
Эта плата называется процентом. Сумма процентов, которую нам придется платить, может варьироваться в зависимости от многих факторов, в том числе от того, сколько мы взяли взаймы, сколько времени нам потребуется, чтобы погасить их, а также от общей экономической ситуации в стране. Когда экономика в плохом состоянии, люди с меньшей вероятностью будут давать деньги взаймы, поэтому плата будет выше, и наоборот, когда экономика в порядке.
С другой стороны, сложные проценты зависят не только от основной суммы кредита, но и от процентов, которые накапливаются по нему в течение определенного периода времени. Расчет сложных процентов немного сложнее, чем расчет простых процентов.
Общая формула для расчета сложных процентов:
Сложные проценты = [P(1 + i) n ] — П. Здесь; P — основная сумма, I — процентная ставка, n — количество периодов начисления сложных процентов. Эти рабочие листы объясняют, как рассчитать простые проценты. Хотя это может показаться бесконечной задачей, она будет иметь большое значение в вашей будущей жизни при банковском обслуживании и покупке дома.
Решается примерная задача и предлагаются две практические задачи.
Дано десять задач. 
Предлагаются три задачи, а также место, где учащиеся могут скопировать правильный ответ, когда он будет дан. 
Это также тип процентов, которые банки выплачивают клиентам по их сберегательным счетам.
Обычно выражаемый в процентах, он представляет собой комиссию или сбор, который заемщик платит кредитору за финансируемую сумму. 
Сумма кредита составляет 18 000 долларов США. Годовая процентная ставка по кредиту составляет 6%. Срок кредита составляет три года.
Основные условия те же: кредит в размере 10 000 долларов, процентная ставка 5% и срок 5 лет.
Простые проценты, однако, не учитывают силу сложных процентов или процентов на проценты, где после первого года 1% фактически будет заработан на балансе в 101 доллар, что в сумме составит 1,01 доллара. В следующем году 1% будет заработан на 102,01 доллара, что составит 1,02 доллара. И так один.
Когда наступает срок погашения кредита, вместо 13 000 долларов вы в конечном итоге должны 13 310 долларов. Хотя вы можете не считать 310 долларов огромной разницей, этот пример — всего лишь трехлетняя ссуда; сложные проценты накапливаются и становятся угнетающими при более длительных сроках кредита.