110. Арифметическая прогрессия
Арифметическая прогрессия – это числовая последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и постоянного числа , где – это разность прогрессии: , .
Общий вид арифметической прогрессии:
; ; ; …; ; … .
Очевидно, что прогрессия является возрастающей, если , и убывающей, если .
Например, 2; 5; 8; 11; … () – возрастающая прогрессия;
12; 10; 8; 6; … () – убывающая прогрессия.
Если заданы первый член и разность , то —Й член прогрессии (любой член) Определяют по формуле:
.
Сумма первых членов Арифметической прогрессии вычисляется по формулам:
или ,
Где – количество членов прогрессии.
Свойства арифметической прогрессии.
1. Каждый средний член равен полусумме равноотстоящих от него членов: , ().
2. В конечной арифметической прогрессии суммы двух членов, равноотстоящих от ее концов, равны между собой и равны сумме крайних членов:
; ; ; . ..; ; … ; ; …; ; ; .
..; ; … ; ; …; ; ; .
Пример 1. Найдите семнадцатый член арифметической прогрессии:
3; 7; 11: 15; … .
Решение. Найдем разность прогрессии: . Тогда .
Ответ. .
Пример 2. Разность арифметической прогрессии равна 3, а сумма первых ее шести членов равна 57. Найдите , .
Решение. ; . Тогда
; .
Ответ. ; .
Пример 3. Третий член арифметической прогрессии равен 6, а седьмой 14. Сколько членов нужно взять, чтобы их сумма была равна 110?
Решение. ; . Запишем и , используя формулу и вычислим и :
; .
Подставим значения и в формулу и получим уравнение для вычисления :
; . Значение – не будет решением, так как .
Ответ. .
Пример 4. Найдите арифметическую прогрессию, если сумма ее первых членов .
Решение. По условию: ; .
можно найти также как сумму первого и второго членов арифметической прогрессии, тогда:.
Отсюда .
Ответ. , или .
Пример 5. Найдите арифметическую прогрессию, если сумма первых трех ее членов равна 15, сумма трех последних членов равна 39, а сумма всех членов равна 63.
Решение. (из условия).
Сложим равенства: . По второму свойству арифметической прогрессии суммы в скобках равны между собой: . Найдем число членов прогрессии, используя формулу: . Подставим значение в исходную систему, получим:
и . Запишем прогрессию, зная и .
Ответ. 3; 5; 7; 9; 11; 13; 15.
Пример 6. Между числами 1 и 25 напишите пять чисел, которые с данными числами составляют арифметическую прогрессию.
Решение. ; ; . Но, .
Ответ. 1; 5; 9; 13; 17; 21; 25; …
| < Предыдущая | Следующая > |
|---|
История- единое целое или арифметическая сумма цивилизаций | Материал для подготовки к ЕГЭ (ГИА) по истории (11 класс) по теме:
Эссе
История- единое целое или арифметическая сумма цивилизаций
Прошлое, настоящее и будущее… Связаны ли они между собой , или существуют сами по себе? Есть ли что-то общее между народами, их культурой, государственным строем и экономикой? Ответы на эти вопросы мы пытаемся найти в истории. А что же такое история в целом? На сегодняшний день на этот вопрос даётся два ответа.
А что же такое история в целом? На сегодняшний день на этот вопрос даётся два ответа.
Согласно первому — история представляет собой единое целое. Такое представление заключается во взгляде на всемирную историю как на единый процесс поступательного , восходящего развития человечества. Такое понимание истории предполагает существование стадий развития человечества в целом. Стадиальность –общее свойство процесса исторического развития на всех его уровнях: каждая последующая стадия вытекает из предыдущей, подготавливается предшествующим состоянием , поэтому представляет собой его продолжение , затем отрицание и , наконец, формирование нового. Такой взгляд на историю был характерен для представителей гуманизма, историков и философов Просвещения, утопического социализма, позитивизма, классической немецкой философии, марксизма, философии истории экзистенциализма, сторонников концепций индустриального и постиндустриального общества: К.Ясперса, Ф.Броделя, К.Маркса, Гегеля и др. По мнению этих историков и философов, подход «история- единое целое» единственно верный, потому что заключается 1.в единстве происхождения человека как вида, 2. в эволюции системы родства и семейно-брачных отношений. 3.в общности языков, 4. в сходной эволюции возникновения и развития религиозных верований, 5.в единой логике движения мировой истории и т.д.
По мнению этих историков и философов, подход «история- единое целое» единственно верный, потому что заключается 1.в единстве происхождения человека как вида, 2. в эволюции системы родства и семейно-брачных отношений. 3.в общности языков, 4. в сходной эволюции возникновения и развития религиозных верований, 5.в единой логике движения мировой истории и т.д.
Согласно второму подходу — история понимается как простая арифметическая сумма культур, стран, этносов, континентов, цивилизаций. Родоначальником этого подхода является российский историк Н.Я.Данилевский. Его теория культурно-исторических типов основана на отрицании всемирно-исторического процесса как целого и выделении в нем самостоятельных потоков — цивилизаций, создающихся ,прежде всего, по этническому признаку, с учетом социальных, территориальных и других факторов. Культурно-исторические типы, по мнению Н.Я.Данилевского, представляют собой живые организмы, они замкнуты, равноценны друг другу, обладают целостностью, не образуют общечеловеческую цивилизацию, являются единственными субъектами, носителями исторического действия.
Немецкий философ и историк, О. Шпенглер , выдвинул концепцию о культурах как множестве замкнутых организмов, выражающих коллективную душу народа. По его мнению, история — ничто иное , как сосуществование, параллельное развитие культур, каждая из которых возникает, развивается и гибнет подобно биологическому организму и существует независимо одна от другой. Идея единства всемирной истории, согласно О. Шпенглеру, совершенно неприемлема.
Теория локальных цивилизаций А.Тойнби — одна из самых известных. В ней выражается суть цивилизационного подхода к истории. Цивилизации — это носители исторического процесса, замкнутые или почти замкнутые общности. Цивилизация — область особенного , своеобразного, индивидуально- неповторимого. Любая цивилизация характеризуется, по
мнению историка, тремя факторами — культурным, политическим и экономическим — при решающем значении культурного фактора.
Мне кажется, что более верным является первый подход, потому что любой исторический феномен, любое историческое событие может быть понято и объяснено лишь как часть чего-то более общего во времени и в пространстве. Все исторические явления и процессы тесно взаимосвязаны и взаимообусловлены. Например, победа в битве на Куликовом поле 1380г. имела переломное значение в борьбе Руси с монгольским игом, а убийство Александра II в 1881 г. привело к остановке проведения реформ и т.д. и таких примеров можно привести много.
Все исторические явления и процессы тесно взаимосвязаны и взаимообусловлены. Например, победа в битве на Куликовом поле 1380г. имела переломное значение в борьбе Руси с монгольским игом, а убийство Александра II в 1881 г. привело к остановке проведения реформ и т.д. и таких примеров можно привести много.
Именно поэтому история не может быть простой арифметической суммой событий, её составляющих; не может иметь исключительно физиологический смысл: рождение, развитие, смерть; единство истории- это не внешний скреп, а внутренний стержень, вокруг которого формируется историческая реальность.
Сумма арифметической формулы последовательности
Последовательность — это расположение любых вещей или группы чисел в определенном порядке, которое следует правилу. По сути, это набор чисел (или элементов), которые следуют определенному образцу. Например, 5, 10, 15, 20…. представляет собой последовательность, поскольку каждый раз значение увеличивается на 5. Если элементы последовательности расположены в порядке возрастания, порядок последовательности является возрастающим. Если элементы последовательности расположены в порядке убывания, то порядок последовательности убывающий. Арифметическая последовательность, геометрическая последовательность, последовательность Фибоначчи, гармоническая последовательность, треугольная числовая последовательность, квадратная числовая последовательность и кубическая числовая последовательность — вот несколько примеров конкретных последовательностей.
Если элементы последовательности расположены в порядке убывания, то порядок последовательности убывающий. Арифметическая последовательность, геометрическая последовательность, последовательность Фибоначчи, гармоническая последовательность, треугольная числовая последовательность, квадратная числовая последовательность и кубическая числовая последовательность — вот несколько примеров конкретных последовательностей.
Арифметическая последовательность — это числовой ряд, в котором каждый последующий член представляет собой сумму предыдущего члена и постоянного целого числа. Это постоянное число называется общей разностью. В результате разность между каждыми двумя последовательными членами арифметического ряда одинакова.
Сумма арифметической прогрессииЕсли первым членом арифметической последовательности является а, а общая разность равна d, то члены арифметической последовательности имеют вид:
а, а+г, а+2д, а+ 3д, а+4д, ….

Предположим, что n — это общее количество элементов в последовательности.
Для n = 1 последовательность а.
Для n = 2 последовательность будет a, a + d.
Для n = 3 последовательность будет a, a + d, a + 2d.
Для n = 4 последовательность следующая: a, a + d, a + 2d, a + 3d.
Следовательно, общий член последовательности равен a n = a + (n – 1)d.
Формула для вычисления суммы всех членов арифметической последовательности определяется как сумма формулы арифметической последовательности. Если арифметическая последовательность записывается в виде сложения ее членов, таких как а + (а + d) + (а + 2d) + (а + 3d) + … .., то она называется арифметической последовательностью. Сумма первых n членов арифметического ряда, в котором n-й член неизвестен, определяется как:
S n = n/2 [2a + (n – 1)d]
где,
S n = сумма арифметической последовательности,
a = первый член последовательности,
d = разница между двумя последовательными членами,
n = количество членов в последовательности.
Если мы запишем 2a в формуле как (a + a), формула примет вид S n = n/2 [a + a + (n – 1)d]
Мы знаем, a + (n – 1)d обозначается n . Следовательно, формула принимает вид: S n = n/2 [a + a n ]
Вывод
Примеры вопросовПредположим, что первый член последовательности равен a, общая разность равна d, а количество членов равно n.
Мы знаем, что n -й член последовательности задается формулой
S n = a + (a + d) + (a + 2d) + (a + 3d) + …… + a + (n – 1)d …… (2)
Из (1) уравнение (2) также может быть выражено как
S n = a n + a n – d + a n – 2d + a n – 3d + …… + a n – (n – 1 )d …… (3 )
Складывая (2) и (3) получаем,
2 S n = [a + (a + d) + (a + 2d) + (a + 3d) + …… + a + (n – 1)d] + [a n + a n – d + a n – 2d + a n – 3d + …… + a n – (n – 1)d]
900 02 2 S n = (а + а + а + ….. n раз) + (а n + а n + a n + ….. n раз)
2 S n = n (a + a n )
S n = n/2 [а + а n ]
Выводит формулу суммы арифметической прогрессии.
Вопрос 1. Найдите сумму арифметической прогрессии: 4, 10, 16, 22, …… до 10 слагаемых.
Решение:
90 002 Вопрос 2. Найдите сумму арифметической прогрессии: 7, 9, 11, 13, …… до 15 членов.Имеем a = 4, d = 10 – 4 = 6 и n = 10,
Используйте формулу S n = n/2 [2a + (n – 1)d], чтобы найти нужную сумму.
S 10 = 10/2 [2(4) + (10 – 1)6]
= 5 (8 + 54)
= 5 (62)
= 310
Решение:
Мы имеем, a = 7, d = 9 — 7 = 2 и n = 15.
Используйте формулу S N = N/2 [2A + (N — 1) г] найти искомую сумму.
S 15 = 15/2 [2(7) + (15 – 1)2]
= 15/2 (14 + 28)
= 15/2 (42)
= 315
90 031Вопрос 3. Найдите первый член арифметической прогрессии, если она имеет сумму 240 для обычной разности 2 между 12 членами.
Решение:
Мы имеем, S = 200, D = 2 и N = 12.
Используйте формулу S N = N/2 [2A + (N — 1) D], чтобы найти требуемое значение.
=> 200 = 12/2 [2а + (12 – 1)2]
=> 240 = 6 (2а + 22)
=> 40 = 2а + 22
=> 2а = 18
=> а = 9
Вопрос 4. Найти общая разность арифметической прогрессии из 8 терминов, имеющих сумму 116, и первое термин как 4.
Решение:
Мы имеем, S = 116, A = 4, n = 8.
Используйте формулу S N = = n = 8.
. n/2 [2a + (n – 1)d], чтобы найти искомое значение.
=> 116 = 8/2 [2(4) + (8 – 1)d]
=> 116 = 4 (8 + 7d)
=> 29 = 8 + 7d
=> 7d = 21
=> d = 3
Вопрос 5.
Найдите сумму арифметической последовательности 8 терминов, первый и последний термины равны 4 и 10 соответственно.
Решение:
Имеем a = 4, n = 8 и a n = 10.
Используйте формулу S n = n/2 [a + a n ] до найти искомую сумму.
С 8 = 8/2 [4 + 10]
= 4 (14)
= 56
Вопрос 6. Найдите количество членов арифметической прогрессии, первый член, последний член и сумма которых равны 16, 12 и 140 соответственно.
Решение:
Имеем S = 140, a = 16 и a n = 12.
Используйте формулу S n = n/2 [ а + а n ] к найти нужное значение.
=> 140 = н/2 [16 + 12]
=> 140 = н/2 (28)
=> 14n = 140
=> n = 10
Вопрос 7. Найдите сумму арифметической прогрессии, у которой первый член, общая разность и последний член равны 8, 7 и 50 соответственно.

Решение:
Имеем a = 8, d = 7 и a n = 50.
Используйте формулу a n = a + (n – 1 )d, чтобы найти n.
=> 50 = 8 + (n – 1)7
=> 42 = 7 (n – 1)
=> n – 1 = 6
=> n = 7
Используйте формулу S n = n/2 [a + a n ], чтобы найти сумму последовательности.
S 7 = 7/2 (8 + 50)
= 7/2 (58)
= 203
Mathwords: Арифметический ряд
индекс: нажмите на букву индекс: предметные области
Арифметический ряд
А ряды типа 3+7+11+ 15 + ··· + 99 или 10 + 20 + 30 + ··· + 1000, что имеет постоянную разницу между терминами.
Первый член a 1 , общая разница это д , а количество терминов n . Сумма арифметический ряд получается путем умножения числа термины раз среднее значение первого и последнего членов.
Формула: или
Пример: 3 + 7 + 11 + 15 + ··· + 99 имеет a 1 = 3 и d = 4. Чтобы найти n , используйте явную формулу для арифметической прогрессии.
Решаем 3 + ( n – 1)·4 = 99, чтобы получить n = 25.
Считать дни онлайн: Сколько дней прошло между двумя датами?
Политика конфиденциальности
Представленная далее информация описывает все возможные виды персональных данных получаемых и собираемых на сайте planetcalc.ru, а также сведения о том как мы используем эти данные.
Мы собираем различную информацию у пользователей PLANETCALC. Вид собираемой информации зависит от уровня взаимодействия пользователя с сервисом. Мы различаем три уровня:
- Посетители Посетители просматривают материалы сайта без регистрации в системе. Это самая многочисленная группа Узнать больше
- Пользователи Любой Посетитель может стать Пользователем, заполнив форму регистрации или войдя через социальную сеть. Пользователи могут сохранять расчёты, оставлять комментарии, вставлять калькуляторы на свой сайт через виджет. Узнать больше
- Авторы Любой наш Пользователь может создать калькулятор, справочник или статью. Это делает его Автором. Материалы сайта публикуются Авторами под лицензией Creative Commons Attribution/Share-Alike.
Узнать больше
Посетители
Какую информацию мы собираем?
Мы автоматически собираем определенную информацию, когда Вы посещаете наш Сайт. Информация включает в себя: информация о Вашем веб-браузере, IP адрес, язык, настроенный в браузере и файлы cookie установленные в Вашем браузере. Кроме того мы запоминаем адреса индивидуальных веб-страниц на нашем сайте, которые вы посещали и критерии поиска, которые Вы вводили на Сайте. Далее мы будем называть, эту автоматически собранную информацию «Системной информацией».
Мы собираем системную информацию при помощи следующих технологий:
- Файлы Куки — данные, устанавливаемые на Ваше устройство или компьютер, чаще всего содержащие анонимный идентификатор. Больше информации о файлах куки вы можете узнать тут http://www.allaboutcookies.org.
- Журналы обращений — файлы, в которых хранятся действия, совершенные на Сайте, содержащие Ваш IP адрес, тип браузера, приблизительная геопозиция, полученная по IP адресу (например Ваша страна и город), страница обращения, дата и время обращения.
Как мы используем собранную информацию?
Мы используем системную информацию для предотвращения возможных неправомерных действий с нашим Сайтом, а также для улучшения и оптимизации нашего Сайта, путем создания аналитических отчетов о посещениях.
Данные в файлах журналов обращений обобщаются и анонимизируются. Мы можем передавать эту обобщенную и анонимизированную информацию третим лицам, например нашим рекламным партнерам. Исходные журналы обращений обрабатываются и удаляются по истечении 5 дней после их создания.
Информация, собираемая нашими партнерами
Мы размещаем на страницах нашего сайта рекламу от партнёров, которые также могут устанавливать файлы cookie. Куки позволяют серверу рекламодателя распознавать Ваш браузер всякий раз, когда они отображают Вам рекламу. Эта информация позвляет рекламным сетям отображать для Вас персонализированную рекламу, которая будет наиболее интересна именно Вам.
Некоторая часть рекламных объявлений может быть предоставлена компанией Yandex.
Изучить информацию о том, как Yandex использует cookie и другие Ваши данные, можно тут: https://yandex.com/legal/confidential/?lang=ru.
Пользователи
Какую информацию мы собираем?
Регистрация на сайте
Мы собираем и храним информацию, предоставляемую Вами при заполнении формы регистрации: Ваше имя, адрес электронной почты, по Вашему желанию мы сохраняем фото или картинку аватара.
Регистрация и вход через социальные медиа
Мы поддерживаем упрощенный доступ к персонализированным функциям сайта. Вы можете войти в персональный раздел, используя свой аккаунт Google, Facebook, Vkontakte или Twitter. При входе через эти сервисы по безопасному протоколу мы запрашиваем Ваше имя, адрес электронной почты и внутренний идентификатор в социальной сети.
Публичные действия
«Публичные действия» — действия, которые Вы совершаете на сайте, которые предназначены для просмотра другими посетителями, например:
- Данные справочников Некоторые калькуляторы используют публичные данные, собранные в специальных таблицах — справочниках, — например, географические координаты городов.
Пользователь может вносить свои записи в эти справочники.
- Сохраненные расчеты Пользователь может сохранить данные любого расчета, чтобы использовать его повторно или поделиться расчетом с друзьями. Мы допускаем, что расчет может содержать персональную информацию. Доступ к этим данным может получить Посетитель сайта, которому Пользователь отправит ссылку на сохраненный расчет.
- Комментарии Пользователь может оставить комментарий к материалам сайта.
Любая информация, которую Вы публикуете во время Публичных действий, а также Ваше имя и изображение становится публичной. Если вы собираетесь осуществлять вышеописанные публичные действия, Вы должны иметь в виду, что любая персональная информация, которую Вы отправляете может быть прочитана, собрана и использована другими посетителями Сайта. Мы не можем отвечать за персональную информацию, которую Вы решаете опубликовать в ходе Публичных действий. Мы не берем на себя обязательства редактировать и удалять такую информацию.
Куки
Наш Сайт применят файлы Куки для сохранения информации о Вашем сеансе взаимодействия с Сайтом после регистрации или входа. Вы можете отключить возможность сохранения и использования куки для сохранения информации о сеансе. Но если Вы примете такое решение, следует иметь в виду, что некоторые функции сайта, такие как персональный раздел или сохранение расчетов не будут работать.
Я согласен с правилами PLANETCALC и политикой использования личных данных и cookie для Пользователей.Дата и время получения согласия
Отмена данного разрешения не отменяет использование cookie нашими рекламными партнерами, отмена касается cookie, используемых PLANETCALC для Пользователей.
Как мы используем собранную информацию?
Данные, полученные нами при регистрации, а также сохраненные расчеты никогда не передаются третьим лицам.
Адрес электронной почты пользователя может использоваться PLANETCALC для отправки Вам уведомлений о новых комментариях и важных уведомлениях, касающихся работы сайта.
Посмотреть и изменить текущий список разрешенных Вами уведомлений о комментариях Вы можете в своем личном кабинете Мои подписки.
Как пользователи могут изменить или удалить собранную информацию?
Пользователь может отредактировать или удалить Данные справочника в редакторе данных справочника.
Любые сохраненные Пользователем расчеты могут быть удалены в персональном разделе, при этом пропадает доступ к этим расчетам, если кому-либо отправлялась ссылка на сохраненный расчет.
Пользователь может удалить любой свой комментарий на странице материала сайта.
Пользователь можете направить запрос на удаление своего аккаунта и всех связанных с ним данных. Данные будут удалены в течение 2-х недель.
Авторы
Какую информацию мы собираем?
Авторы могут публиковать на этом Сайте, созданные ими материалы. Материалы включают калькуляторы, статьи, справочники и переводы существующих материалов на другие языки, далее называемые Материалы. Материалы становятся публичными после их публикации и могут быть использованы на условиях лицензии Creative Commons Attribution/Share-Alike.
Следует иметь в виду, что любая информация размещенная Вами в Материалах, а также Ваше имя и изображение или фото переходят в публичный доступ. Любая персональная информация, включенная в контент может быть прочитана, собрана и использована другими посетителями Сайта. Мы не берем на себя обязательства редактировать и удалять такую информацию.
Как мы используем собранную информацию?
Мы можем использовать Ваши материалы на условиях лицензии Creative Commons Attribution/Share-Alike.
PLANETCALC имеет право по своему усмотрению отказать в публикации или удалить любой материал, нарушающий Условия использования или эту политику конфиденциальности.
Как авторы могут изменить или удалить собранную информацию?
Вы можете удалить любой Материал, созданный Вами в персональном разделе Сайта.
Соблюдение юридических требований
Мы можем передавать Вашу персональную информацию для соблюдения законов и правил, в ответ на требования суда, ордера на обыск и других юридических запросов запросов или иным образом защищать наши права.
Безопасность Ваших данных
PLANETCALC использует доступные технические и организационные меры безопасности для защиты личной информации, которая представляется нам через наш сайт.
Изменения
Мы можем изменять эту политику конфиденциальности время от времени, например, для того чтобы отразить изменения в нашем Сайте или по другим организационным или юридическим причинам.
Связаться с нами
Если у Вас остались вопросы, касательно нашей Политики Конфиденциальности пожалуйста свяжитесь с нами по электронной почте: [email protected].
Календарь овуляции. Рассчитать благоприятный для беременности период с помощью онлайн-калькулятора
Будни: 07:30 — 19:30 Вых: 08:00 — 15:00
+7 (4842) 279 800
Вызов на дом
Запись на прием
- Услуги
- Анализы
- Услуги
- Анализы
- О нас
- Врачи
- Программы
- Отзывы
- Блог
- Акции
- Терапия
- Акушерство и гинекология
- Дерматология
- Эндокринология
- Педиатрия
- Аллергология-иммунология
- Ударно-волновая терапия
- Кардиология
- Все услуги
- Панели тестов и алгоритмы обследования
- Наркотические вещества
- Лекарственный мониторинг
- Комплексные генетические исследования
- Исследование клеща
- Гистологические исследования
- Все анализы
- Главная страница
- Календарь овуляции и зачатия по дням
- Медицинский центр «Айболит»
- Информация для пациентов
- Услуги
- Программы медицинского центра «Айболит»
- Акции и специальные предложения медицинского центра «Айболит»
- Сдать анализы в медицинском центре «Айболит», Калуга
- Врачи медицинского центра «Айболит»
- Блог
- Отзывы
- Календарь овуляции и зачатия по дням
Спасибо за Ваши отзывы
Елена
20 мая 2023 г.
Посещаю клинику уже давно. Небольшая, но чистая и уютная, народа не много. Прием ведут по записи, приходишь к назначенному времени, без задержек. Грам …
Читать полностью
Елена
18 мая 2023 г.
Отличная клиника! Дружелюбный персонал, сервис всегда на высшем уровне, приятно посещать! Много грамотных специалистов.
Читать полностью
Елена Сергеевна
17 мая 2023 г.
Отличная клиника! Дружелюбный персонал, сервис всегда на высшем уровне, приятно посещать! Много грамотных специалистов
Читать полностью
Ольга Юрьевна
18 янв. 2023 г.
Отличная клиника, часто сдаём анализы и сама и ребенок, очень деликатный подход персонала, ребенок идёт с удовольствием и без страха. Отличный специал …
Читать полностью
Людмила
15 дек. 2022 г.
Спасибо за ваши советы. С наступающим Новым годом. Здоровья вам.
Читать полностью
Оставить отзыв медицинскому центру
Калькулятор дат — Дни между днями
Что такое Калькулятор дней между датами?
Наш калькулятор дней позволяет рассчитать количество дней между двумя датами.
Вы можете использовать его для просмотра количества дней, недель, месяцев и лет между двумя датами. Вы также можете использовать калькулятор даты, чтобы добавлять или вычитать дни, недели, месяцы или годы к дате и от нее.
Например, чтобы ответить на вопросы «Какое число будет через две недели?» или «Какое число было две недели назад?», вы можете использовать калькулятор дня, чтобы добавить дни к дате или вычесть дни из даты. Однако он не позволяет отслеживать время. Вы можете использовать онлайн-секундомер, онлайн-будильник и онлайн-таймер для этих задач.
Что делать с калькулятором календаря?
С помощью калькулятора календаря дней между датами вы можете:
- Рассчитать общее количество дней между двумя датами.
- Определите, сколько дней прошло с момента вашего рождения или какая-либо важная для вас историческая дата.
- Определите количество дней между двумя датами, включая или исключая дату окончания в расчете.
- Определите количество недель, месяцев или лет между двумя датами, включая или исключая последнюю дату.
- Вычитание лет, месяцев, недель или дней из заданной даты.
- Добавление лет, месяцев, недель или дней с заданной даты.
- Определите, какая дата будет с сегодняшнего дня, когда пройдет определенное количество времени, например, какая дата будет через 30 дней с сегодняшнего дня, через две недели с сегодняшнего дня или через 30 лет с сегодняшнего дня.
Как пользоваться калькулятором календаря дней между датами
Для расчета недель, месяцев или лет между двумя датами используйте Count Days вкладки. Для добавления или вычитания дней, недель, месяцев или лет из исторической даты используйте вкладку «Добавить/вычесть».
Подсчет дней между датами
Пользоваться калькулятором дат очень просто. Чтобы считать дни между датами , просто:
- Используйте вкладку Count Days .
- Выберите Начальную дату (день, месяц и год). Нажмите Сегодня , чтобы выбрать сегодняшнюю дату.
- Выберите дату окончания (день, месяц и год). Нажмите на Сегодня для выбора сегодняшней даты.
- Нажмите Рассчитать продолжительность , чтобы найти продолжительность между двумя заданными датами.
При расчете количества дней можно дополнительно указать дату окончания для расчета количества дней между датами, то есть добавляется один день.
Добавить дни
К добавить дни к датам , вы можете:
- Используйте вкладку Добавить дни .
- Введите года , месяца , недели или дня поля.
- Щелкните Рассчитать новую дату , чтобы найти новую дату.
Вычесть дни
Чтобы вычесть дни из дат , вы можете:
- Используйте вкладку Вычесть дни .
- Введите лет , месяцев , недель или дней .
- Щелкните Рассчитать новую дату , чтобы найти новую дату.
Зачем использовать калькулятор дней между двумя датами?
Хотя вы можете вручную подсчитать количество дней между двумя датами, калькулятор дней делает это легко и быстро. Если вы вручную рассчитываете продолжительность между двумя датами, вам необходимо учитывать високосные годы. Типичный год состоит из 365 дней, а високосный год состоит из 366 дней и бывает раз в четыре года. Использование калькулятора дней сэкономит время, потому что вам не нужно беспокоиться о сложностях григорианского календаря или вычислять количество дней в месяце (которое иногда составляет 28, 29)., 30 или 31).
С помощью этого счетчика дней вы можете быстро найти количество дней между двумя датами. Вы можете использовать этот калькулятор дней для:
- Организация мероприятий или встреч.
- Отпуск и планирование отпуска.
- Подарки.
- Расчет дня рождения и возраста.
Вы также можете использовать калькулятор дней с дат, чтобы решать личные задачи. Например, если вы хотите вернуть товар с 30-дневным окном возврата, вы можете использовать калькулятор дней с даты, чтобы определить, когда последний день, когда вы можете вернуть свой товар.
Сколько дней между двумя датами
Как работает калькулятор дней?
Чтобы использовать веб-приложение с обратным отсчетом дня до даты, вам необходимо сделать следующее:
- Исходная дата (год, месяц и время) — здесь дата обратного отсчета будет рассчитываться с
.- Конечная дата (год, месяц, день и время) — здесь остановится обратный отсчет до даты.
Введите обе даты в предоставленный интерфейс и нажмите зеленую кнопку «Рассчитать дни»
Автоматически будет рассчитан период времени между обоими пределами, и счетчик дней начнется со следующего загружаемого интерфейса.
Это калькулятор даты и времени с обратным отсчетом в режиме реального времени.
Так что не стесняйтесь использовать и ссылаться на друзей.
Сколько лет, дней, месяцев, минут и секунд находится между двумя датами?
Дата начала: Время начала: Дата окончания: Время окончания:Что такое калькулятор дня и даты?
Калькулятор дней — это период времени, определяемый конкретным началом (или началом) и остановкой (или окончанием). У него множество функций, но его основная функция — обеспечить ощущение меры в виде системы с временными рамками для любого объекта. деятельности, события или события. Калькулятор даты дней может быть ограничен годами, месяцами, днями, минутами или секундами в зависимости от ситуации, однако важно отметить, что калькулятор календарных дней лучше всего использовать, когда ограничения определенным, так как это даст четкую меру времени, которым нужно руководствоваться и наставлять.
Обычное использование счетчика дней
Применение калькулятора подсчета дней безгранично, если вы уверены, что используете его для измерения времени в заданных пределах.
Ежедневный калькулятор может использоваться кем угодно; пары ведут обратный отсчет до своего большого дня, студенты осторожно готовятся к датам испытаний и даже ждут мам, с тревогой наблюдая, как проходят секунды, прежде чем они встретят своего новорожденного. Дни, прошедшие с калькулятора, дают уникальное и интересное значение времени, особенно когда оно проходит.
Уникальность этого повседневного калькулятора
Мы рады приветствовать вас в нашем специальном веб-приложении счетчика часов на сегодняшний день. Мы еще больше рады поделиться с вами некоторыми причинами, по которым вам понравится использовать наше уникальное творение. Вот несколько преимуществ, которые вы получаете с нашим приложение калькулятора дней в месяцы;
- Простой в использовании калькулятор даты и времени
Наше тщательно просчитанное веб-приложение калькулятора дня и времени было создано, чтобы гарантировать беспрепятственное и быстрое использование платформы.
Мы избавим вас от всех препятствий и всех ненужных тестов, предоставив вам чистый и простой доступ к разделу ввода даты для подсчета, где вы можете определить пределы диапазона дат, который вы устанавливаете. Это буквально 1-минутный процесс, для которого вам не нужна помощь.
- Молниеносные результаты
С нашей превосходной платформой вы получаете калькулятор обратного отсчета дня за считанные секунды! Да! за исключением любых задержек сервера, которые, вероятно, могут зависеть от скорости вашего сетевого провайдера, ваши часы обратного отсчета на сегодняшний день вычисляются и запускаются немедленно
- Непревзойденное удобство
Сегодня мы предоставим вам простой счетчик дней для любого веб-приложения для дат, который обеспечивает непревзойденное удобство в использовании и исполнении. Наши системы оптимизированы для максимального удовольствия пользователей, что вы видите, то и получаете.
График y x sinx: Свойства функции y = sinx и её график — урок. Алгебра, 11 класс.
404 — Страница не найдена
Страницы
Партнеры сайта
_________________________________
404: Запрошенная страница с адресом [http://primer. by/algebra/funkcii/funkcija-ysinx] не найдена.
Если Вы уверены, что набрали ссылку корректно, напишите, пожалуйста, об этом на:
меню пользователя
Новости
30.11.16
17.03.15
25.03.14
29.08.13
05.
05.13
primer. by 2013-2016
Функции и Графики — сайт по математике и не только!!! Всё о Математических функциях и их графиках…
Функции и Графики — сайт по математике и не только!!! Всё о Математических функциях и их графиках…
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
ОПРЕДЕЛЕНИЕ ФУНКЦИИ СВОЙСТВА ФУНКЦИЙ ЛИНЕЙНАЯ КВАДРАТИЧНАЯ СТЕПЕННЫЕ ФУНКЦИИ ФУНКЦИИ y = ТРИГОНОМЕТРИЧЕСКИЕ ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ПОКАЗАТЕЛЬНАЯ ЛОГАРИФМИЧЕСКАЯ ГРАФИКИ ТЕСТЫ КОНТАКТЫ КАРТА САЙТА НА ГЛАВНУЮ ПРОГРАММИРОВАНИЕ TURBO PASCAL C++
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ y = sin xграфик — синусоида
Свойства функции
y = cos x
- Область определения: R
- Область значений: [-1; 1]
- Четность, нечетность: функция нечетная
- Период: 2
- Нули: sin x = 0 при x = n, n Z
- Промежутки знакопостоянства: sin x > 0 при x (2n; n + 2n), n Z sin x x (- + 2n; 2n), n Z
- Экстремумы: xmin = + 2 n, n Z; ymin = -1 xmax = + 2 n, n Z; ymin = 1
- Промежутки монотонности:
график — косинусоида
Свойства функции
- Область определения: R
- Область значений: [-1; 1]
- Четность, нечетность: функция четная
- Период: 2
- Нули:
- Промежутки знакопостоянства:
- Экстремумы: xmin = + 2 n, n Z; ymin = -1 xmax = 2n, n Z; ymin = 1
- Промежутки монотонности:
Преобразования графиков y = sinx и y = cosx : Графики функций y = sinx и y = cosx можно получить друг из друга путем параллельных переносов
y = tg x
вдоль оси x на /2:
график — тангенсоида
Свойства функции
y = ctg x
- Область определения: объединение интервалов
- Область значений: R
- Четность, нечетность: функция нечетная
- Период:
- Нули: y = 0 при x = n, n Z
- Промежутки знакопостоянства:
- Экстремумов нет
- Промежутки монотонности: функция возрастает на каждом интервале области определения
- Асимптоты: x = + n, n Z
график — катангенсоида
Свойства функции
- Область определения: объединение интервалов
- Область значений: R
- Четность, нечетность: функция нечетная
- Период:
- Нули:
- Промежутки знакопостоянства:
- Экстремумов нет
- Промежутки монотонности: функция убывает на каждом интервале области определения
- Асимптоты: x = n, n Z
Преобразования графика y = ctgx : График функци y = ctgx получается из графика y = tgx путем отражения относительно любой из координатныхосей и последующим параллельным переносом вдоль оси x на /2.

Используются технологии uCoz
Нарисовать график y = sin x
- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10
- Класс 9
9000 3 Класс 8- Класс 7
- Класс 6
- IIT JEE
- Exam
- JEE MAINS
- JEE ADVANCED
- ПЛАТЫ X
- ПЛАТЫ XII
- NEET 9004 0
- Новый предыдущий год (по годам)
- Физика Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Нет Все образцы работ
- Образцы работ Биология
- Образцы работ Физика
- Образцы работ Химия
- Скачать PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- Экзаменационный уголок
- Онлайн-класс
- Викторина
- Задать вопрос в Whatsapp
- Поиск Сомнения
900 03 Английский словарь
- Toppers Talk
- Блог
- О нас
- Карьера
- Скачать
- Получить приложение
Вопрос
Обновлено: 26/04/2023
Рекомендуемые вопросы
9 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Видео по теме
Нарисуйте график зависимости y=xsinx.
642540663
04:55
Нарисуйте график зависимости y=sinxx.
642540699
02:26
Нарисуйте график y=sin−1(sinx)
642542767
04:38
Нарисуйте график y=sinx и y=sin.x2.
644016228
01:37
Нарисуйте график зависимости y=sin|x| .
645278574
01:42
Нарисуйте график зависимости y = x sin x.
645279450
06:19
Нарисуйте график y = (sin x)/(x) .
645279486
01:42
Нарисуйте график зависимости y=sin|x| .
646278291
03:10
РЕКЛАМА
Рекомендуемые вопросы
Нарисуйте график y = sin x
04:34 9(-1)(sin x)
Текст Решение
y =sin x ग्राफ खींचिए|
02:42
Нарисуйте график зависимости y=sin x и y=sin . (х)/(2).
03:16
Нарисуйте график зависимости y=sin|x|.
02:19
- Ask Unlimited Doubts
- Видео решения на нескольких языках (включая хинди)
- Видео лекции экспертов
Doubtnut хочет отправлять вам уведомления.
Разрешите получать регулярные обновления!
Слушаю…
Тригонометрия — Интуитивное объяснение графика $y = \sin x$
спросил
Изменено 11 лет, 4 месяца назад
Просмотрено 2к раз
$\begingroup$
Возможный дубликат:
Intuition для построения графика синуса/косинусаМы все видели график $y = \sin x$
(я не могу опубликовать изображение из-за репутации, поэтому я разместил ссылку на график)Синусоидальный график Изображение
Сейчас выключено , единственные определения синуса, которые я понимаю, — это определение «отношения в треугольнике» и определение «единичного круга».
Поэтому я надеюсь, что можно ответить на мой вопрос, используя одно из этих определений.
Из этого определения легко понять, почему при ($0,5\pi$) радианах значение $y$ равно $1$, легко понять, почему при пи радианах значение $y$ равно $0$, и я, конечно, понимаю, почему функция повторяется каждые $2 \pi$ радиан, используя определение единичного круга.
Чего я не понимаю, так это почему он имеет именно такую форму, почему он выглядит так, как будто он находится между 0 и 0,5 Пи, почему он имеет именно такую вогнутость?
- У этого есть интуитивное объяснение?
- Как первые математики рисовали эту функцию, действительно ли они измеряли синус всех углов линейкой, а потом рисовали график?
- тригонометрия
- функции
- графические функции
$\endgroup$
1
$\begingroup$
Эта анимация скорее всего вам поможет! Ваше здоровье! 🙂
$\endgroup$
$\begingroup$
Вы спрашиваете, почему график $\sin$ выглядит именно так, как на $[0,\pi/2]$.
Вы можете легко (с помощью некоторых тригонометрических формул) вычислить значения $\sin x$ для $x=0,\pi/6,\pi/3,\pi/4,\pi/2, \pi/ 12,\пи/5$. Постройте эти значения.
Имейте в виду, что $\sin$ непрерывна как отношение двух непрерывных функций (противоположная сторона/гипотенуза). Он возрастает, так как при увеличении угла увеличивается и синус. Попробуйте сейчас и начертите $\sin$, зная только вышеупомянутые факты. Вы увидите, что это приближение графика похоже на приближение вогнутой функции. Конечно, вогнутость можно доказать с помощью тригонометрической формулы. Вы просили что-то более интуитивное.
[Могу я спросить, почему вы задали этот вопрос? Мне просто интересно. Не поймите неправильно, но спрашивать, почему $\sin$ вогнута между $0$ и $\pi/2$, все равно что спрашивать, почему буква $A$ выглядит именно так. Это один из элементарных блоков математики. Нет правильного ответа, почему график выглядит именно так. Это выглядит так из-за свойств функции $\sin$.]
$\endgroup$
3
$\begingroup$
Представьте себе точку, движущуюся по единичной окружности, начиная с $(1,0)$ и двигаясь против часовой стрелки.
Координата $y$ точки равна $\sin\theta$, где $\theta$ – угол между точкой, началом координат и точкой $(1,0)$ (и, конечно, измеренный положительный в направлении против часовой стрелки с положительной осью $x$, соответствующей $\theta=0$).
Теперь, когда точка перемещается из $(1,0)$ в $(0,1)$, что происходит с координатой точки $y$? Что ж, оно возрастает от 0 до 1. Итак, график $\sin\theta$ (с $\theta$ в качестве горизонтальной оси) возрастает по $[0,\pi/2]$ от 0 до 1.
Если вы представите точку, пересекающую всю единичную окружность, вы должны быть в состоянии убедить себя, что, по крайней мере, с точки зрения «возрастания или убывания» и с точки зрения того, где находятся нули и максимумы/минимумы, график $\sin$ как есть. 9\circ$, с помощью элементарной геометрии легко понять, почему значения синуса должны быть именно такими, какие они есть ($1/2$ и $\sqrt{3}/2$. Для других нужно действовать тоньше.
$\endgroup$
$\begingroup$
1.
Я изучил функцию sin как качающийся объект. Вы увидите $y$ как расстояние от центра и $x$ как прошедшее время. Обратите внимание, что качающийся объект дольше всего остается сбоку ($x = k*π$, $y = 0$) и быстро проходит через центр ($x = (k+1/2)*π$, $у = 1$).
Это также объясняет производную от $sin x$, которая равна $cos x$. Производная от позиции — это скорость, которая отображается на графике $cos x$. Объект проходит через центр с максимально возможной скоростью и останавливается на очень короткое время в самой удаленной от центра точке.
Попробуйте сами, просто качайте что-нибудь (например, часы на цепочке) и представьте себе функцию $sin x$.
2.
(Чисто предположение, у меня нет источника)
Лично я думаю, что ранние математики тянули «бумагу» под качающийся объект, оставляющий за собой след. Вы получите синусоидальную функцию, если будете тянуть бумагу с обычной скоростью. Может быть, у них не было ни бумаги, ни ручки, но это самый естественный способ нарисовать такой график.
$\endgroup$
$\begingroup$
Функции $\sin$ и $\cos$ являются результатом функции, которая экспоненциально проецирует прямую (числовую прямую $\mathbb{R}$) на окружность с радиусом $r=1$. Вот определение функции:
$E: \mathbb{R} \mapsto k$
для $t \in [0, 2\pi\rangle, E(t)=T$, так что $|IT|$( это арка )=t и эта арка $IT$ положительно ориентирована ( против часовой стрелки )
для $t \in \mathbb{R}\backslash [0, 2\pi\rangle, E(t)=E(t_0) $ где $t=t_0 +2k\pi,k\in \mathbb{Z},t_{0}=[0, 2\pi\rangle$
Точка I расположена на $(1,0)$. Из этого определения теперь ясно видно, что то, что вы в основном делаете, это, неформально говоря, «рисование» $\mathbb{R}$ в круг, а круг может иметь значения только в диапазоне $t[0, 2\pi \rangle$. Вот кое-что интересное происходит. Поскольку вы представляете числа на круге, вам легче определить, где находится $\pi$ (трансцендентное число), чем число $1$, например.
В 1000 м см: МСМ-1000 (Метилсульфонилметан) 120 капс. — купить в интернет-магазине Vitamina, цена, отзывы
Page not found — АгроВсесвіт
0.00грн Cart
0.00грн Cart
Схоже, що такої сторінки не існує
Можливо спробуєте пошукати?
Search
Каталог
Крапельна стрічка
Лей-флет
Фурнітура для стрічки
Плівка
Агроволокно
Фільтри
Туман та фурнітура
Інжектори, кульові крани, врізки
Набори для поливу
Трубка та фурнітура
Добрива
Скидка!
Kolla Tape Эмиттер 6-8 мил
Капельная лента Kolla Tape 6 мил Эмиттер 3000м(0.8-1.1-1.4 л/ч)
5,510.34грн КупитьСкидка!
Kolla Tape Эмиттер 6-8 мил
Капельная лента Kolla Tape 8 мил Эмиттер 1000м(0.8-1.1-1.4 л/ч)
2,111.40грн – 2,384.64грнКупитьСкидка!
Kolla Tape Эмиттер 6-8 мил
Капельная лента Kolla Tape 7 мил Эмиттер 1000м(0.
8-1.1-1.4 л/ч) 2,061.26грн – 2,324.84грнКупить
Скидка!
Kolla Tape Эмиттер 6-8 мил
Капельная лента Kolla Tape 6 мил Эмиттер 1000м(0.8-1.1-1.4 л/ч)
2,013.88грн Купить
Скидка!
Агроуспех 6 мил эмиттерная
Капельная лента АгроУспех 6 mil, Эмиттерная, шаг 20см, 1000 м 1,4 л/час
1,646.80грн КупитьСкидка!
AquaPlast 8 мил эмиттерная
Капельная лента AquaPlast 8 мил Эмиттерная, 1000 м 1,4л/час, шаг 20 см
1,889.68грн КупитьСкидка!
Agro way 8 мил эмиттерная
Капельная лента AgroWay 8 мил Эмиттерная, 1000 м 1,5л/час
2,208.00грн – 2,300.00грнКупить
Скидка!
OxiDrip эмиттерная 8 мил
Капельная лента OxiDrip 8 mil, Эмиттерная, 1000 м 1,38 л/час, шаг 20 см
2,124.97грн Купить
Скидка!
Inter Premium Drip 8 мил Корея
Капельная лента Inter Premium Drip 8 mil, Эмиттерная, 2500 м 1,4 л/час,
5,564.16грн КупитьСкидка!
OxiDrip эмиттерная 8 мил
Капельная лента OxiDrip 8 mil, Мягкий Эмиттер, 2500 м 1,38 л/час, шаг 10 см
5,544.38грн КупитьСкидка!
IRTECH эмиттерная 6, 8, 11 мил
Капельная лента IRTECH 6 мил, Эмиттерная, 3000 м 1.1 л/час
5,400.40грн КупитьСкидка!
IRTECH эмиттерная 6, 8, 11 мил
Капельная лента IRTECH 11 мил, Эмиттерная, 1000 м 1.4 л/час
3,795.00грн Купить
METHERPLAS эмиттерная 6-10 Мил
Капельная лента METZERPLAS 8mil, Эмиттерная, 1000м
2,702.04грн – 2,944.46грнКупитьMETHERPLAS эмиттерная 6-10 Мил
Капельная лента METZERPLAS 6mil, Эмиттерная, 1000м
2,277.00грн – 2,458.70грнКупитьMETHERPLAS эмиттерная 6-10 Мил
Капельная лента METZERPLAS 16mil, Эмиттерная, 1000м
3,824.44грн – 4,128.50грнКупитьMETHERPLAS эмиттерная 6-10 Мил
Капельная лента METZERPLAS 10mil, Эмиттерная, 1900м
5,652.48грн – 6,112.02грнКупить
Скидка!
Rosto 6, 7 мил Эмиттерная
Капельная лента Rosto 7 mil, Эмиттерная, 1000 м 1,4 л/час, шаг 20 см
1,932.00грн КупитьСкидка!
Rosto 6, 7 мил Эмиттерная
Капельная лента Rosto 6mil, Эмиттерная, 1000 м 1,4 л/час
1,800.44грн КупитьСкидка!
Santeh Plast эмиттерная 9 мил
Капельная лента SantehPlast 9mil, Эмиттерная, 1000 м 1.4 л/час 10cм
2,392.00грн КупитьSanteh Plast эмиттерная 9 мил
Капельная лента SantehPlast 9mil, Эмиттерная, 500 м 1.4 л/час
1,472.00грн – 1,932.00грнКупить
Скидка!
Kolla LFT Лейфлет Украина
Kolla Рукав Лей-флет d100 (4″) (100м) черный усиленный
5,950.56грн КупитьСкидка!
Kolla LFT Лейфлет Украина
Kolla Рукав Лей-флет d75 (3″) (100м) черный усиленный
4,186.00грн КупитьСкидка!
Kolla LFT Лейфлет Украина
Kolla Рукав Лей-флет d63 (21/2″) (100м) черный усиленный
3,381.00грн КупитьСкидка!
Kolla LFT Лейфлет Украина
Kolla Рукав Лей-флет d50 (2″) (100м) черный усиленный
3,059.00грн Купить
Скидка!
АгроУспех Лейфлет Корея
Шланг Агроуспех Лейфлет (Lay Flat) 4″ D 100 мм (100 м) Корея
8,740.00грн КупитьСкидка!
АгроУспех Лейфлет Корея
Шланг Агроуспех Лейфлет (Lay Flat) 3″ D 75 мм (100 м) Корея
5,740.80грн Купить
Скидка!
АгроУспех Лейфлет Корея
Шланг Агроуспех Лейфлет (Lay Flat) 2″ D 50 мм (100 м) Корея
4,416.00грн КупитьHeliflex Португалия
Гибкий шланг Heliflex Monoflat 6″(150mm), 3.5 бар, бухта 100 м
25,395.22грнКупить
Скидка!
Oxi LayFlat Корея
Шланг Лейфлет (Lay Flat) 6″ D 150 мм (100 м) Корея
15,640.00грн КупитьСкидка!
Oxi LayFlat Корея
Шланг Лейфлет (Lay Flat) 4″ D 100 мм (100 м) Корея
9,890.00грн КупитьСкидка!
Oxi LayFlat Корея
Шланг Лейфлет (Lay Flat) 3″ D 75 мм (100 м) Корея
6,210.00грн КупитьСкидка!
Oxi LayFlat Корея
Шланг Лейфлет (Lay Flat) 2″ D 50 мм (100 м) Корея
4,968.00грн Купить
Скидка!
Пленка для мульчирования
Пленка вторичная Прозрачная 30мкр 1000м
1,279.72грн – 3,447.70грнКупитьСкидка!
Пленка для мульчирования
Пленка вторичная Прозрачная 30мкр Украина ОПТ
69.00грн КупитьСкидка!
Пленка для мульчирования
Пленка вторичная Прозрачная Рукав (3м) Kolla Украина
1,491.78грн – 4,784.92грнКупитьСкидка!
Пленка для мульчирования
Пленка вторичная Прозрачная Kolla 30мкр 1000м Украина
1,434.28грн – 3,863.54грнКупить
Скидка!
Пленка для мульчирования
Пленка для мульчирования Черная 30мкр 1000м
1,490.40грн – 4,001.08грнКупитьСкидка!
Пленка для мульчирования
Пленка вторичная Черная 30мкр ОПТ Украина
84.00грн КупитьСкидка!
Пленка для мульчирования
Пленка для мульчирования Kolla вторичная Черная 40мкр 500м 36 мес. Украина
2,147.28грн – 3,105.92грнКупитьСкидка!
Пленка для мульчирования
Пленка для мульчирования Kolla вторичная Черная 30мкр 1000м Украина
1,594.36грн – 4,279.84грнКупить
Скидка!
Пленка для мульчирования
Пленка для мульчирования Черно-Серебристая Sotrafa Испания 1000м 25мкм (3 года)
9,200.00грн КупитьСкидка!
Пленка для мульчирования
Пленка для мульчирования Черная Sotrafa Испания 1000м 30мкм (3 года)
8,878.00грн КупитьПленка для мульчирования
Пленка для мульчирования Черная Sotrafa Испания 1000м 25мкм (3 года)
7,172.32грн – 8,238.14грнКупить
Скидка!
Агроволокно
Агроволокно Greentex 17г/м² 1.6м-15.8м x 100м Германия
660.10грн – 5,961.60грнКупитьСкидка!
Агроволокно
Агроволокно Greentex 19г/м² 1.6м-15.8м x 100м Германия
739.22грн – 6,641.48грнКупитьСкидка!
Агроволокно
Агроволокно Greentex 23г/м² 1.6м-15.8м x 100м Германия
923.68грн – 8,298.40грнКупить
Скидка!
Агроволокно
Агроволокно Greentex 30г/м² 1.6м-15.8м x 100м Германия
1,191.86грн – 10,695.00грнКупить
Скидка!
Агроволокно
Агроволокно Greentex 50г/м² 1.6м-15.8м x 100м Германия
2,123.82грн – 12,661.96грнКупитьСкидка!
Агроволокно
Агроволокно Черное Greentex 50г/м² 1.6м-15.8м x 100м Германия
1,471.08грн – 4,076.98грнКупитьСкидка!
Агроволокно
Агроволокно Черно-Белое Greentex 50г/м² 1.6м-15.8м x 100м Германия
1,591.60грн – 4,398.98грнКупить
Фильтры
Ручной фильтр сетка 2″ до 20 м3/ч, Irritec
911.26грнКупитьФильтры
Ручной фильтр диск 2″ 20 м3/ч, Irritec
1,260.40грнКупить
Фильтры
Ручной фильтр диск 3″ 50 м3/ч, Irritec
5,520.00грнКупить
Лента Туман
ТУМАН KOLLA SPRAY 25 100 м
814.66грнКупитьСкидка!
Лента Туман
ТУМАН KOLLA SPRAY 32 0.2мм 200 м
1,104.00грн КупитьСкидка!
Лента Туман
ТУМАН KOLLA SPRAY 50 0.35мм 100 м
1,288.00грн КупитьСкидка!
Лента Туман
ТУМАН KOLLA SPRAY 40 0.3мм 100 м
828.00грн Купить
Скидка!
Poly-Feed™
NPK удобрение Poly-Feed™ GG 11-44-11 + МЕ
4,416.00грн КупитьСкидка!
Haifa SOP™
Моно удобрение Haifa SOP™ 0-0-51 + 45SO3 – сульфат калия
2,484.00грн КупитьСкидка!
Poly-Feed™
NPK удобрение Poly-Feed™ GG 20-20-20 + МЕ
3,956.00грн КупитьСкидка!
Poly-Feed™
NPK удобрение Poly-Feed™ Drip 14-7-21 + 2MgО + МЕ
3,312.00грн Купить
Agroleaf Power
Минеральное удобрение Agroleaf Power Total (универсальный) 20-20-20 +МЕ, 15 кг
4,698.21грнКупитьAgroleaf Power
Минеральное удобрение Agroleaf Power High P (фосфорный) 12-52-5 +МЕ, 15 кг
6,011.28грнКупитьСкидка!
Solinure GT
NPK удобрение Solinure GT 1, 10-5-39 + 2МgО + ME
3,956.00грн КупитьСкидка!
Solinure GT
NPK удобрение Solinure GT 5, 20-20-20 + МЕ
3,956.00грн Купить
Terraflex (ICL)
Удобрения Террафлекс F – для цветочных культур
2,570.02грнКупитьTerraflex (ICL)
Удобрения Террафлекс S – для ягодных культур
2,595.78грнКупитьTerraflex (ICL)
Удобрения Террафлекс С – для огурцов, кабачков
2,502.86грнКупитьTerraflex (ICL)
Удобрения Террафлекс Т – для пасленовых культур
2,609.12грнКупитьПеревести 1000 метров в сантиметры
м см 1000 100 000 1 010 101 000 1 020 102 000 1 030 103 000 1 040 104 000 1 050 105 000 1 060 106 000 1 070 107 000 1 080 108 000 1 090 109 000 1 100 110 000 1 110 111 000 1 120 112 000 1 130 113 000 1 140 114 000 1 150 115 000 1 160 116 000 1 170 117 000 1 180 118 000 1 190 119 000 1 200 120 000 1 210 121 000 1 220 122 000 1 230 123 000 1 240 124 000
м см 1 250 125 000 1 260 126 000 1 270 127 000 1 280 128 000 1 290 129 000 1 300 130 000 1 310 131 000 1 320 132 000 1 330 133 000 1 340 134 000 1 350 135 000 1 360 136 000 1 370 137 000 1 380 138 000 1 390 139 000 1 400 140 000 1 410 141 000 1 420 142 000 1 430 143 000 1 440 144 000 1 450 145 000 1 460 146 000 1 470 147 000 1 480 148 000 1 490 149 000
м см 1 500 150 000 1 510 151 000 1 520 152 000 1 530 153 000 1 540 154 000 1 550 155 000 1 560 156 000 1 570 157 000 1 580 158 000 1 590 159 000 1 600 160 000 1 610 161 000 1 620 162 000 1 630 163 000 1 640 164 000 1 650 165 000 1 660 166 000 1 670 167 000 1 680 168 000 1 690 169 000 1 700 170 000 1 710 171 000 1 720 172 000 1 730 173 000 1 740 174 000
м см 1750 175 000 1 760 176 000 1 770 177 000 1 780 178 000 1 790 179 000 1 800 180 000 1 810 181 000 1 820 182 000 1 830 183 000 1 840 184 000 1 850 185 000 1 860 186 000 1 870 187 000 1 880 188 000 1 890 189 000 1 900 190 000 1 910 191 000 1 920 192 000 1 930 193 000 1 940 194 000 1 950 195 000 1 960 196 000 1 970 197 000 1 980 198 000 1 990 199,000 1000 Калькулятор преобразования метров в сантиметры
1000 метров (м)
1 м = 100 см
=
100 000 Сантиметры (см)
1 см = 1,0e-02 м
Преобразователь длины данных
Конвертировать:
(Пожалуйста, введите номер)
От: АнгстремАстрономические единицыЯчменьДлина кабеля (имперские)Длина кабеля (международная)Длина кабеля (США)КабелиСантиметрЦепьКубитДекаметрДециметрЭллЭмсFathomFingerFinger (ткань)FootFurlongGigameterHandHectometerInchKilofeetKilometerLeagueLeague (land)Light DayLight HourLight MinuteLight Second Световой ГодЛинияСсылкаМарафонМегаметрМетрМиккиМикродюймМикрометрМикронМилМиляМайл СШАМиллиметрМириаметрГвоздь (ткань)НанометрМорская ЛигаМорская МиляТемпPalmParsecPicaPicometerPointКварталРодВеревкаСкандинавская МиляShakuSmootSpanStepTerameterThouTwipЯрд
Кому: АнгстремАстрономические единицыЯчменьДлина кабеля (имперские)Длина кабеля (международная)Длина кабеля (США)КабелиСантиметрЦепьКубитДекаметрДециметрЭллЭмсFathomFingerFinger (ткань)FootFurlongGigameterHandHectometerInchKilofeetKilometerLeagueLeague (land)Light DayLight HourLight MinuteLight Second Световой ГодЛинияСсылкаМарафонМегаметрМетрМиккиМикродюймМикрометрМикронМилМиляМайл СШАМиллиметрМириаметрГвоздь (ткань)НанометрМорская ЛигаМорская МиляТемпPalmParsecPicaPicometerPointКварталРодВеревкаСкандинавская МиляShakuSmootSpanStepTerameterThouTwipЯрд
Дополнительная информация от конвертера величин
В: Сколько метров в сантиметре?
Ответ: 1.
Sin суммы двух углов: Синус суммы двух углов
вывод формул, примеры. Формулы суммы и разности синусов и косинусов
Данный электронный ресурс является отличным материалом для проведения интерактивного обучения в современных школах. Он составлен грамотно, обладает четкой структурой и соответствует школьному плану. Благодаря подробным объяснениям, тема, которая представлена в видеоуроке станет понятна как можно большему количеству учеников в классе. Учителя должны помнить, что не все ученики имеют одинаковую степень восприятия, быстроты понимания, базу. Справиться с трудностями и догнать своих сверстников, исправить успеваемость, помогут подобные материалы. С помощью них в домашней спокойной обстановке, самостоятельно либо вместе с репетитором, ученик может разобраться в той или иной теме, изучить теорию и просмотреть примеры практического применения той или иной формулы и т.д.
Данный видеоурок посвящен теме «Синус и косинус разности аргументов». Подразумевается, что ученики уже изучили основы тригонометрии, ознакомлены с основными функциями и их свойствами, формулами привидения и таблицами тригонометрических значений.
Также, до того, как перейти к изучению данной темы, необходимо иметь понятие о синусе и косинусе суммы аргументов, знать две основные формулы и уметь ими пользоваться.
Вначале видеоурока диктор напоминает школьникам эти две формулы. Далее демонстрируется первая формула — синус разности аргументов. Помимо того, как выводится сама формула, показывается каким образом она получается от другой. Таким образом, школьнику не придется зазубривать новую формулу без понимания, что является частой ошибкой. Это очень важно для учеников в этом классе. Нужно всегда помнить, что перед знаком минуса всего можно добавить знак +, а минуса на знак плюс в итоге превратится в минус. С помощью такого нехитрого шага, можно воспользоваться формулой синуса суммы и получить формулу синуса разности аргументов.
Аналогичным образом выводится формула косинуса разности из формулы косинуса суммы аргументов.
Диктор пошагово все объясняет, а в результате выводится общая формула косинуса суммы и разности аргументов и синуса, аналогично.
Первый пример из практической части данного видеоурока предлагает найти косинус Пи/12. Предлагается представить данное значение в виде некоторой разности, при котором уменьшаемое и вычитаемое будут являться табличными значениями. Далее применятся формула косинуса разности аргументов. Заменив выражение, можно подставить полученные значения и получить ответ. Диктор зачитывает ответ, который выводится в конце примера.
Второй пример представляет собой уравнение. И в правой, и в левой сторонах мы видим косинусы разностей аргументов. Диктор напоминает формулы приведений, которые используются для замены и упрощения этих выражения. Эти формулы записываются с правой стороны, чтобы школьники могли понять, откуда появляются те или иные изменения.
Еще один пример, третий, представляет собой некоторую дробь, где и в числителе и в знаменателе имеем тригонометрические выражения, а именно, разности произведений.
Здесь также при решении используются формулы приведений. Таким образом, школьники могут убедиться, что пропустив одну тему в тригонометрии, понять остальные будет все сложнее.
И, наконец, четвертый пример. Это также уравнение, при решении которых необходимо использовать новые изученные и старые формулы.
Примеры, которые приводятся в видеоуроке, можно рассмотреть более подробно и попробовать решить самостоятельно. Их можно задать в качестве домашнего задания школьникам.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тема занятия «Синус и косинус разности аргументов».
На предыдущем курсе мы познакомились с двумя тригонометрическими формулами синус и косинус суммы аргументов.
sin(x + y) = sin x cos y + cos x sin y,
cos (x + y) = cos x cos y — sin x sin y.
синус суммы двух углов равен сумме между произведением синуса первого угла и косинусом второго угла и произведением косинуса первого угла и синуса второго угла;
косинус суммы двух углов равен разности между произведением косинусов этих углов и произведением суммы этих углов.
При помощи этих формул выведем формулы Синус и косинус разности аргументов.
Синус разности аргументов sin(x- y)
Две формулы (синус суммы и синус разности) можно записать в виде:
sin(x y) = sin x cos y cos x sin y.

Аналогично выведем формулу косинуса разности:
Косинус разности аргументов перепишем в виде суммы и применим уже известную формулу косинуса суммы: cos (x + y) = cosxcosy — sinxsiny.
только для аргументов х и -y. Подставив данные аргументы в формулу, получим cosxcos(- y) — sinxsin(- y).
sin(- y)= — siny). и получим окончательное выражение cosxcosy + sinxsiny.
cos (x — y) = cos (x +(- y)) =cos xcos(- y) — sin x sin(- y)= cosx cos y + sin xsin y.
Значит, cos (x — y) = cosxcos y + sin xsin y.
косинус разности двух углов равен сумме между произведением косинусов этих углов и произведением синусов этих углов.
Объединяя две формулы (косинус суммы и косинус разности) в одну, запишем
cos (x y) = cosxcos y sin xsin y.
Запомним, что формулы на практике можно применять как слева направо, так и наоборот.
Рассмотрим примеры.
ПРИМЕР 1. Вычислить cos (косинус пи, деленное на двенадцать).
Решение. Запишем пи, деленное на двенадцать, как разность пи на три и пи, деленное на четыре: = — .
Подставим значения в формулу косинуса разности: cos (x — y) = cosxcosy + sinxsiny, таким образом cos = cos (-) = cos cos + sin sin
Нам известно, что cos = , cos = sin= , sin = . Показать таблицу значений.
Заменим значение синуса и косинуса числовыми значениями и получим ∙ + ∙ при умножении дробь на дробь числители и знаменатели перемножаем, получаем
cos = cos (-) = cos cos + sin sin = ∙ + ∙ = = =.
Ответ: cos =.
ПРИМЕР 2. Решить уравнение cos(2π — 5х) = cos(- 5х) (косинус два пи минус пять икс равно косинусу от пи на два минус пять икс).
Решение. К левой и правой частям уравнения применим формулы приведения cos(2π — cos (косинус два пи минус альфа равен косинусу альфа) и cos(- = sin (косинус пи на два минус альфа равно синусу альфа), получим cos 5х = sin 5х, приведем его к виду однородного уравнения первой степени и получим cos 5х — sin 5х = 0. Это однородное уравнение первой степени. Разделим почленно обе части уравнения на cos 5х. Имеем:
cos 5х: cos 5х — sin 5х: cos 5х = 0, т.
к. cos 5х: cos 5х =1, а sin 5х: cos 5х= tg 5x, то получим:
Так как мы уже знаем, что уравнение tgt = а имеет решение t = arctgа + πn, а так как у нас t=5х, а =1, то получим
5x = arctg 1 + πn,
а значение arctg 1, тогда tg 1= Показать таблицу
подставим значение в уравнение и решим его:
Ответ: х = + .
ПРИМЕР 3. Найти значение дроби. (в числителе разность произведения косинусов семидесяти пяти градусов и шестидесяти пяти градусов и произведения синусов семидесяти пяти градусов и шестидесяти пяти градусов, а в знаменателе разность произведения синуса восьмидесяти пяти градусов и косинуса тридцати пяти градусов и произведения косинуса восьмидесяти пяти градусов и синуса тридцати пяти градусов).
Решение. В числителе данной дроби разность можно «свернуть» в косинус суммы аргументов 75° и 65°, а в знаменателе — разность «свернем» в синус разности аргументов 85° и 35°. Получим
Ответ: — 1.
ПРИМЕР 4. Решить уравнение: cos(-х) + sin(-х) = 1(косинус разности пи на четыре и икс плюс синус разности пи на четыре и икс равно одному).
Решение. Применим формулы косинус разности и синус разности.
Показать общую формулу косинуса разности
Тогда cos (-х) = cos cos х + sinsinх
Показать общую формулу синуса разности
а sin (-х)= sin cosх — cos sinх
Подставим данные выражения в уравнение cos(-х) + sin(-х) = 1 и получим:
cos cos х + sinsin х + sin cos х — cos sin х = 1,
Так как cos= и sin= Показать таблицу значение синуса и косинуса
Получим ∙ cos х + ∙ sinх + ∙ cos х — ∙ sinх = 1,
второе и четвертое слагаемые противоположны, поэтому взаимно уничтожаются, остается:
∙ cos + ∙ cos = 1,
Решим данное уравнение и получим, что
2∙ ∙ cos x= 1,
Так ка мы уже знаем, что уравнение cos = а имеет решение t = arcos a + 2π k , а так как у нас t=x, а =, то получим
х = arccos + 2πn,
а так как значение arccos, тогда cos =
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 .
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Yandex.RTB R-A-339285-1
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.

Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению.
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
«Синус суммы и синус разности двух углов»
Формы организации познавательной деятельности обучающихся: коллективная, индивидуальная, парная.
Оборудование: компьютер, проектор, компьютерная презентация MS PowerPoint, раздаточный материал: карточка №1 «Вывод формул синус суммы и синус разности двух углов», карточка 2 «Самостоятельная работа», рефлексия.
Этапы урока
Деятельность учителя
Деятельность обучающихся
1. Организация начала урока, 1 мин
Здравствуйте, присаживайтесь. Какой раздел мы изучаем?
Занимают свои места.
Отвечают: тригонометрические формулы и функции.
2. Актуализация субъективного опыта. Постановка проблемы. 8 мин
Прежде чем приступить к изучению новой темы, давайте повторим ранее изученный материал.
Организует актуализация опорных знаний.
Какой знак имеет синус угла I, II координатной четверти? III и IV?
Какой знак имеет косинус угла I, IV координатной четверти? II и III?
Слайды 1-3
Замените тригонометрической функцией угла α:
=
=
=
Вычислите:
Вычислите:
1.
2.
3.
4.
5.
6.
7.
Отвечают на вопросы.
+, —
+,-
Выполняют устные задания
Целеполагание, 2 мин
Почему мы не можем вычислить задания 6,7?
Через какие известные нам значения мы могли бы выразить 105 градусов, 15 градусов?Какие формулы нужно знать, чтобы выполнить эти задания?
Давайте сформулируем тему и цель нашего урока.
Запишите тему в тетрадь.
Это не табличные углы
105=60+45
15=60-45
Чтобы вычислить sin 1050, надо применить формулу синус суммы, а sin 150 формулу синус разности.
Формулируют тему «Синус суммы и синус разности двух углов» и цель: вывести формулы и научиться применять их к преобразованию выражений. Записывают тему в тетрадь.
Открытие нового знания,7 мин
Вспомним правила парной работы.
Поработаем в парах.
Вывести формулы вам поможет карточка. Нужно заполнить пропуски, используя формулы для доп.углов и косинуса суммы и разности двух углов.
Контролирует работу, помогает, если возникают затруднения.
Проверьте вывод формул на стр. 264 в учебнике Можем ли мы теперь вычислить sin 1050 ,sin 150?
Сделайте это в своих тетрадях.
Проговаривают правила: работать тихо, работать вместе, помогать друг другу, уважать мнение друг друга.
Работают в парах с карточкой 4 минуты, записывают формулы в тетрадь.
Одна пара выходит и записывает полученные формулы на доске.
Остальной класс проверяет.
Да
Записывают:
Физкультминутка для глаз, 1 мин
Сложите руки перед лицом, двигайте их влево/вправо, вверх/вниз, по кругу. Следите глазами за своими руками
Выполняют упражнения для глаз
Первичное закрепление знаний, 10 минут
Научимся применять формулы синуса суммы и разности двух углов, выполняя упражнения № 9.28 (в,г), 9.27 (а,б) из учебника –самостоятельно, №9.29 а – 1 учащийся решает на доске, остальные – в тетради.
Составим алгоритм для решения № 9.31 а.
Контролирует работу пар, помогает, если возникают вопросы.
Выполняют № 9.28 (в,г), 9.27 (а,б) из учебника –самостоятельно, №9.
29 а – 1 учащийся решает на доске, остальные – в тетради.
Устно составляют алгоритм: 1. Вычислить недостающие значения синуса и косинуса, используя основное тригонометрическое тождество; 2. Применить формулу синуса суммы или синуса разности двух углов.
Решают пример 9.31 а по алгоритму в парах. Проверяют решение слайд 5
Самостоятельная работа
Организует разноуровневую самостоятельную работу.
Выбирают уровень. Выполняют с/р, сдают тетради.
Информация о домашнем задании 1 мин
Выучить формулы, выполнить № 9.26 г-е,9.27 в,г, 9.29 б, 9.31б
Записывают домашнее задание
Рефлексия 2 мин
Организует рефлексию.
Отвечают на вопросы анкеты, сдают анкету.
Итог урока 1 мин
Подведем итог урока.
Ответим на вопрос: достигли мы цели нашего урока?
Выставляет оценки за урок.
Отвечают на вопрос.
(раскройте скобки внутри аргумента) (сгруппируйте 1 и 2 слагаемые и примените формулу
тригонометрия — Доказательство идентичности синуса суммы для всех углов
спросил
Изменено 4 года, 1 месяц назад
Просмотрено 2к раз
$\begingroup$Кто-нибудь может представить доказательство идентичности синуса суммы для любой пары углов $a$, $b$?
$$\sin(a+b) = \sin(a) \cos(b) + \cos(a) \sin(b)$$
Большинство доказательств основано на геометрическом подходе (углы $<90 $ в этом случае). Но обратите внимание, что формула должна работать для любой пары углов.
Другой известный мне вывод использует формулу Эйлера, а именно этот.
Есть одна вещь, с которой я не чувствую себя комфортно: мы знаем, что при умножении двух комплексных чисел углы складываются. Это доказывается тождеством синусов суммы. Итак, сначала мы докажем, как работает умножение двух комплексных экспонент, используя тождество синуса суммы, а затем используем умножение комплексных экспонент, чтобы доказать тождество синуса суммы. Можете ли вы сказать мне, как это не циклический аргумент?
$\endgroup$ 5 $\begingroup$
- тригонометрия
вот геометрическое доказательство, которое я видел в старом американском ежемесячнике по математике, в котором используется единичный круг. сначала покажите, что квадрат хорды, соединяющей $(1,0)$ и $(\cos t, \sin t)$, равен $2(1-\cos t)$, используя формулу расстояния. теперь переинтерпретируйте $$\text{ длина хорды, образующей угол $t$ в центре, равна } 2 — 2\cos t $$
теперь вычислите квадрат длины между $\cos t, \sin t), (\cos s, \sin s)$ двумя разными способами:
(i) формула расстояния дает вам $2 — \cos t \cos s — \sin t \sin s$
(ii) хорда, образующая угол $t — s$ равна $2 — \cos(t-s)$
приравнивание двух дает $$\cos (t-s) = \cos t \ cos s + \sin t \sin s \tag 1$$
теперь используйте факт $\cos \pi/2$, чтобы вывести $\cos (\pi/2 — s) = \sin s$, положив $t = \pi/2$ в $(1)$
положить $t=0,$, чтобы получить $\cos$ — четная функция.
поставьте $t = -\pi/2,$, чтобы показать, что $\sin$ — нечетная функция. после всего этого вы получаете $$\sin(t-s) = \sin t \cos t — \cos t \sin s $$ и два для сумм. 9{ix}$.
Мы никогда не признавали существование идентичности суммы углов в этом доказательстве, следовательно, нет кругового рассуждения.
$\endgroup$ 0Тригонометрические функции суммы и разности двух углов
Тригонометрия — раздел математики, изучающий углы, длины и высоты треугольников и их соотношения. Это сыграло важную роль для вычисления сложных функций или больших расстояний, которые невозможно было вычислить без тригонометрии. При решении задач по тригонометрии мы сталкивались со многими ситуациями, когда приходится вычислять тригонометрические решения для суммы углов или разности углов. Например.
Здесь,
Это касательное тригонометрическое отношение с углом, противоположным BC.
tan(θ+Φ) =
Если θ = 30° и Φ = 45°.
Мы знаем тригонометрические углы 45° и 30°, но не знаем тригонометрический угол (45° + 30° = 75°). Таким образом, чтобы упростить эти типы проблем. Мы изучим тригонометрические формулы или тождества суммы и разности двух углов, что облегчит задачу.
Прежде чем двигаться дальше, сначала мы увидим знаки тригонометрических функций в четырех квадрантах. Эти знаки играют важную роль в тригонометрии.
Тригонометрические тождестваТеперь найдем тригонометрические тождества. Поскольку мы знаем, что
sin(-x) = – sin x
cos(-x) = cos x
Потому что только cos и sec положительны в четвертом квадранте. Итак, теперь мы докажем некоторые результаты относительно суммы и разности углов:
Рассмотрим единичный круг (радиус которого равен 1) с центром в начале координат. Пусть x будет ∠DOA, а y будет ∠AOB. Тогда (x + y) — это ∠DOB. Также пусть (– y) будет ∠DOC.
Следовательно, координаты A, B, C и D равны
A = (cos x, sin x)
B = [cos (x + y), sin (x + y)]
C = [ cos (– y), sin (– y)]
D = (1, 0).
As, ∠AOB = ∠COD
Складывая, ∠BOC обе стороны, получаем
∠AOB + ∠BOC = ∠COD + ∠BOC
∠AOC = ∠БПК
В △ AOC и △ БПК
OA = OB (радиус окружности)
∠AOC = ∠BOD (доказано ранее)
OC = OD (радиус окружности)
△ AOC ≅ △ БПК по конгруэнтности SAS.
Используя формулу расстояния, для
AC 2 = [cos x – cos (– y)] 2 + [sin x – sin(–y] 2
AC 2 90 155 = 2 – 2 (cos x cos y – sin x sin y) …………….(i)
И, теперь
Аналогично, используя формулу расстояния, получаем
BD 2 = [1 – cos (x + у)] 2 + [0 – sin (x + y)] 2
BD 2 = 2 – 2 cos (x + y) …………….(ii)
As, △ AOC ≅ △ БПК
AC = BD, поэтому AC 2 = BD 2
Из уравнения (i) и уравнения (ii) получаем
2 – 2 (cos x cos y – sin x sin y) = 2 – 2 cos (x + y)
Итак,
cos (x + y) = cos x cos y – sin x sin y
Возьмем y = -y, получим
cos (x + (-y)) = cos x cos (-y) – sin x sin (-y)
cos (x – y) = cos x cos y + sin x sin y
Сейчас , взяв
потому что (-(x + y)) = cos ((-x) – y) (cos (-θ) = sin θ)
sin(x – y) = sin x cos y – cos x sin y cos x sin (-y)
sin (x + y) = sin x cos y + cos x sin y
Полученные формулы для тригонометрических отношений составных углов следующие:
sin (A + B) = sin A cos B + cos A sin B ……………….
.(1)
sin (A – B) = sin A cos B – cos A sin B ………………..(2)
cos (A + B) = cos A cos B – sin A sin B .. ………………(3)
cos (A – B) = cos A cos B + sin A sin B ………………..(4)
Используя эти формулы, мы можем получить важную и наиболее часто используемую форму:
(1) Возьмем A =
В уравнении (1) и (3) мы получим
sin (+B) = cos B
cos (+B) = – sin A
(2 ) Возьмем, A = π
В уравнениях (1), (2), (3) и (4) мы получаем
sin (π + B) = – sin B
sin (π – B) = sin B
cos ( π ± B) = – cos B
(3) Возьмем A = 2π
В уравнении (2) и (4) получаем
sin (2π – B) = – sin B
cos (2π – B) = cos B
Аналогично для cot A, tan A, sec A и cosec A
(4)
Здесь A, B и (A + B) не являются нечетное число, кратное π/2, поэтому cosA, cosB и cos(A + B) отличны от нуля
tan(A + B) = sin(A + B)/cos(A + B)
Из уравнения (1) и (3) мы получаем
tan(A + B) = sin A cos B + cos A sin B/cos A cos B – sin A sin B
Теперь разделим числитель и знаменатель на cos A cos B, получим
tan(A + B) =
(5)
Так как мы знаем, что
Таким образом, полагая B = -B, мы получаем
(6)
Здесь A, B и (A + B) не кратно π, поэтому sinA, sinB и sin(A + B) отличны от нуля
cot(A + B) = cos(A + B)/sin(A + B)
Из уравнения (1) и (3) мы получаем
cot(A + B) = cos A cos B – sin A sin B/sin A cos B + cos A sin B
Теперь разделим числитель и знаменатель на sin A sin B, получим
cot(A + B) =
(7)
9 0118Поскольку мы знаем, что
Итак, поставив B = -B, мы получим
Здесь мы установим два набора формул преобразования: формулы факторизации и дефакторизации.
Формулы дефакторизации
В тригонометрии дефакторизация означает преобразование произведения в сумму или разность. Формулы с детокаторизацией:
(1) 2 sin a cos b = sin (a + b) + sin (a — b)
Доказательство:
Как мы знаем,
SIN (A + B) = sin A cos B + cos A sin B …………………………(1)
sin (A – B) = sin A cos B – cos A sin B ……………………… …(2)
Складывая уравнение (1) и (2), мы получаем
2 sin A cos B = sin (A + B) + sin (A – B)
(2) 2 cos A sin B = sin (A + B) – sin (A – B)
Доказательство:
Поскольку мы знаем, что
sin (A + B) = sin A cos B + cos A sin B …………………………(1)
sin (A – B) = sin A cos B – cos A sin B …………………………(2)
Вычитая уравнение (2) из (1), получаем
2 cos A sin B = sin (A + B) – sin (A – B)
(3) 2 cos A cos B = cos (A + B) + cos (A – B)
Доказательство:
Поскольку мы знаем, что
cos (A + B) = cos A cos B – sin A sin B …………………………(1)
cos (A – B) = cos A cos B + sin A sin B …………………………(2)
Складывая уравнения (1) и (2), мы получаем
2 cos A cos B = cos (A + B) + cos (A – B)
(4) 2 sin A sin B = cos (A – B) – cos (A + B)
Доказательство:
cos (A + B) = cos A cos B – sin A sin B ………………………(1)
cos (A – B) = cos A cos B + sin A sin B …………………………(2)
Вычитая уравнение (3) из (4), мы получаем
2 sin A sin B = cos (A – B) – cos (A + B)
Пример 1.
Преобразуйте каждое из следующих произведений в сумму или разность.
(i) 2 sin 40° cos 30°
(ii) 2 sin 75° sin 15°
(iii) cos 75° cos 15° 901 02
Решение:
(и) Дано: A = 40° и B = 30°
Теперь подставим все эти значения в формулу
2 sin A cos B = sin (A + B) + sin (A – B)
Получим
2 sin 40° cos 30° = sin (40 + 30) + sin (40 – 30)
= sin (70°) + sin (10°)
(ii) Дано: A = 75° и B = 15°
Теперь подставим все эти значения в формулу
2 sin A sin B = cos (A – B) – cos (A + B)
Получим
2 sin 75° sin 15° = cos (75-15) – cos (75+15)
= cos (60°) – cos (90°)
(iii) Дано: A = 75° и B = 15°
Теперь подставьте все эти значения в формулу
2 cos A cos B = cos (A + B) + cos (A – B)
Получаем
cos 75° cos 15° = 1/2(cos (75+15) + cos (75-15))
= 1/ 2 (cos (90°) + cos (60°))
Пример 2.
Найдите
Решение:
Используя формулу
2 cos A cos В = потому что (А + В) + cos (А – В)
=
=
=
Следовательно,
= 0
Формулы факторизации
В тригонометрии факторизация означает преобразование суммы или разности в произведение. Формулы факторизации:
(1) sin (C) + sin (D) = 2 sin cos
Доказательство:
Имеем
90 002 2 sin A cos B = sin (A + B) + sin (A – B) ………………………(1)Итак, теперь мы берем
A + B = C и A – B = D
Тогда A = и B =
Теперь поместите все эти значения в уравнение (1), мы получим
2 sin () cos () = sin (C ) + sin (D)
Или
sin (C) + sin (D) = 2 sin () cos ()
(2) sin (C) – sin (D) = 2 cos sin
Доказательство:
Имеем
2 cos A sin B = sin (A + B) – sin (A – B) ………………………(1)
Итак, теперь, мы берем
A + B = C и A – B = D
Тогда A = и B =
Теперь поместите все эти значения в уравнение (1), мы получим
2 cos () sin () = sin (C) – sin (D)
Или
sin ( C) – sin (D) = 2 cos () sin ()
(3) cos (C) + cos (D) = 2 cos cos
Доказательство:
901 18У нас есть
2 cos A cos B = cos (A + B) + cos (A – B) …………………………(1)
Итак, теперь мы берем
A + B = C и A – B = D
Тогда A = и B =
Теперь поместите все эти значения в уравнение (1), мы получим
2 cos () cos () = cos (C) + cos (D)
Или
cos (C) + cos (D) = 2 cos () cos ()
(4) cos (C) – cos (D) = 2 sin sin
Доказательство:
Имеем
2 sin A sin B = cos ( A – B) – cos (A + B) …………………………(1)
Итак, теперь мы берем
A + B = C и A – B = D
Тогда, А = и В =
Теперь поместите все эти значения в уравнение (1), мы получим
2 sin () sin () = cos (C) – cos (D)
Или
cos (C) – cos (D) = 2 sin () sin ()
Объясните 1.
Выразите каждое из следующих чисел в виде произведения
(i) sin 40° + sin 20°
(ii) sin 60° – sin 20° 901 02
(iii) cos 40° + cos 80°
Решение:
(i) Дано: C = 40° и D = 20°
Теперь подставим все эти значения в формулу,
sin (C) + sin (D) = 2 sin cos
Получим
sin 40° + sin 20° = 2 sin cos
= 2 sin cos 9000 5
= 2 sin 30° cos 10°
(ii) Дано: C = 60° и D = 20°
Теперь подставьте все эти значения в формулу
sin (C) – sin (D) = 2 cos sin
Получаем
sin 60° – sin 20° = 2 cos sin
= 2 cos sin
= 2 cos 40° sin 20°
(iii) Дано: C = 80° и D = 40°
Теперь подставим все эти значения в формулу
cos (C) + cos (D) = 2 cos cos
Получим
900 02 cos 40° + cos 80° = 2 cos cos= 2 cos cos
= 2 cos 60° cos 20°
Пример 2.
Докажите, что: 1 + cos 2x + cos 4x + cos 6x = 4 потому что x cos 2x cos 3x
Решение:
Возьмем LHS
1 + cos 2x + cos 4x + cos 6x
Здесь, cos 0x = 1
Итак,
(cos 0x + cos 2x) + (cos 4x + cos 6x)
Используя формулу
cos (C) + cos (D) = 2 cos cos
Получаем
(2 cos cos) + (2 cos cos)
(2 cos x cos x) + (2 cos 5x cos x)
Взяв 2 cos x общие, имеем
2 cos x (cos x + cos 5x)
Снова используя формулу
cos (C) + cos (D) = 2 cos cos
Получаем
2 cos x (2 cos cos)
2 cos x (2 cos 3x cos 2x)
4 cos x cos 2x cos 3x
LHS = RHS
Отсюда доказано
Тригонометрические отношения кратных углов (2A) через угол A 9010 3
Тригонометрические отношения угла в прямоугольном треугольнике определяют отношение между углом и длиной его сторон. sin 2x или cos 2x и т. д. также являются одной из таких тригонометрических формул, также известных как формула двойного угла, поскольку в ней есть двойной угол.
(1) sin 2A = 2 sin A cos A
Доказательство:
Поскольку мы знаем, что
sin (A + B) = sin A cos B + cos A sin B ………………..(1)
Теперь примем B = A , в уравнении (1) мы получаем
sin (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
(2) cos 2A = cos 2 (1) )
Теперь принимая B = A, в уравнении (1) мы получаем
cos (A + A) = cos A cos A + sin A sin A
cos 2A = cos 2 A – sin 2 A
(3) cos 2A = 2cos 2 A – 1
Доказательство:
Как мы знаем,
90 002 cos 2A = cos 2 A – sin 2 A ……… ………..(1)Мы также знаем, что
sin 2 A + cos 2 A = 1
Итак, sin 2 A = 1 – cos 2 A
Теперь подставим значение sin 2 A в уравнение (1), получим
cos 2A = cos 2 A – (1 – cos 9015 4 2 A)
cos 2A = cos 2 A – 1 + cos 2 A
cos 2A = 2cos 2 A – 1
(4) cos 2A = 1 – 2sin 2 A
Доказательство:
Поскольку мы знаем, что
cos 2A = 2cos 2 A – 1 ……………….
.(1)
Мы также знаем, что
sin 2 A + cos 2 A = 1
Итак, cos 2 A = 1 – sin 2 A
Теперь введите значение sin 2 A в уравнении (1) мы получаем
cos 2A = 2(1 – sin 2 A) – 1
cos 2A = 2 – 2sin 2 A) – 1
cos 2A = 1 – 2sin 9 0154 2 A
(5) cos 2A =
Доказательство:
Как мы знаем,
cos 2A = cos 2 A – sin 2 A
Итак, делим теперь на sin 2 A + cos 2 A = 1, получаем
900 02 cos 2A =Снова разделив числитель и знаменатель на cos 2 A, получаем
cos 2A =
cos 2A =
(6) sin 2A =
90 101 Доказательство:
Поскольку мы знаем, что
sin ( A + B) = sin A cos B + cos A sin B ……………….
.(1)
Теперь принимая B = A, в уравнении (1) мы получаем
sin (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
Поскольку мы также знаем, что sin 2 A + cos 2 A = 1
Итак, делим теперь на sin 2 A + cos 2 A = 1, получаем
sin 2A =
Теперь о делении числителя и знаменатель на cos 2 А, получаем
sin 2A =
(7) tan 2A =
Доказательство:
Поскольку мы знаем, что
………………..(1)
Теперь, взяв B = A, в уравнении (1) мы получим
tan(A + A) =
tan 2A =
Пример: Докажите, что
(i) = tan θ
(ii) 9010 2 = кроватка θ
(iii) cos 4x = 1 – 8 sin 2 x cos 2 x
Решение:
(i) sin 2θ = 2 sin θ cos θ ……….
.(из тождества 1)
и, 1 + cos 2θ = 2cos 2 θ ………..(из тождества 3)
=
= tan θ
Отсюда доказано 9000 5
(ii) sin 2θ = 2 sin θ cos θ ………..(из тождества 1)
и, 1 – cos 2θ = 2sin 2 θ ………..(из тождества 4)
=
= cot θ
Отсюда Доказано
(iii) cos 4x = cos 2(2x)
= 1 – 2sin 2 (2x) (с использованием 16)
= 1 – 2(sin(2x)) 2
= 1 – 2(2 sin x cos x) 2 (с использованием тождества 1)
= 1 – 2(4 sin 2 x cos 2 x)
cos 4x = 1 – 8 sin 2 x cos 2 x
Отсюда доказано
Тригонометрические отношения кратных углов (3A) через угол A
Тригонометрические отношения угла в прямоугольном треугольнике определяют соотношение между углом и длина его сторон. sin 3x или cos 3x и т. д. также являются одной из таких тригонометрических формул, также известных как формула тройного угла, поскольку в ней есть тройной угол.
(1) sin 3A = 3sin A – 4 sin 3 A
Доказательство:
Возьмем LHS
sin 3A = sin(2A + A)
Использование идентификатора
sin ( A + B) = sin A cos B + cos A sin B
Получаем
sin 3A = sin 2A cos A + cos 2A sin A
= 2sin A cos A cos A + (1 – 2 sin 2 А)sin А
= 2sin А(1 – sin 2 А) + sin А – 2 sin 3 А
= 2sin A – 2sin 3 A + sin A – 2 sin 3 A
sin 3A = 3sin A – 4 sin 3 A
902 23(2) cos 3A = 4 cos 3 A – 3cos A
Доказательство:
Возьмем LHS
sin 3A = sin(2A + A)
Используя тождество
900 02 cos (A + B) = cos A cos B – sin A sin BПолучаем
cos 3A = cos 2A cos A – sin 2A sin A
= (2cos 2 A – 1)cos A – 2sin A cos A sin A
= (2cos 2 A – 1)cos A – 2cos A(1 – cos 2 A)
= 2cos 3 A — потому что A – 2cos A + 2cos 3 A)
cos 3A = 4 cos 3 A – 3cos A
(3) tan 3A =
900 02 Доказательство:Возьмем LHS
tan 3A = tan(2A + A)
Используя идентификатор
Получаем
tan 3A =
=
=
=
Пример 1.
Формула x1 и x2 для квадратного уравнения: Квадратное уравнение: формула корней, как их решать и примеры
Квадратное уравнение: формула корней, как их решать и примеры
Квадратное уравнение — это уравнение вида ax² + bx + c, где a, b, c — некоторые числа (причём обязательно a ≠ 0),
В таком уравнении:
- x — переменная, которая присутствует в таком уравнении во второй степени,
- a — первый коэффициент,
- b — второй коэффициент,
- c — свободный член.
Ещё такое уравнение называется квадратный трёхчлен, т.к. самая большая степень в нём квадрат и он состоит из 3 одночленов.
Для решения таких уравнений сначала находится дискриминант по этой формуле:
Эту формулу нужно выучить наизусть.Если:
- D < 0 <=> корней не существует,
- D = 0 <=> есть один корень,
- D > 0 <=> есть два корня.
Пример: x² – x – 3 = 0; a = 1, b = –1, c = –3, D = (–1)² – 4×1×(–3) = 1 + 12 = 13, D > 0 <=> есть два корня.
Когда уже точно известно, что корни существуют, и известно количество этих корней, можно приступить к их поиску с помощью этой формулы:
Корни таких уравнений находят с помощью этой формулы.Пример: x² – x – 3 = 0; a = 1, b = –1, c = –3, D = 13.
X1,2 = ((–(–1)) ±√13)/(2×1) =>
x1 = (1 + √13)/2 ≈ (1 + 3,60555)/2 ≈ 2,302775
x2 = (1 – √13)/2 ≈ (1 – 3,60555)/2 ≈ -1,302775
Примеры
Пример 1
20x² – 15x – 10 = 0
Лучше сразу выписать так: a = 20, b = – 15, c = – 10.
1. Ищем дискриминант: формула D = b² – 4ac <=> D = (– 15)² – 4 × 20 × (– 10) = 225 + 800 = 1025; D > 0 <=> значит есть два корня.
2. Ищем эти корни: формула корней
2.1. Разбиваем формулу на две части, первый корень:
Уравнение 20x² – 15x – 10 = 0, где a = 20, b = – 15, c = – 10; D =1025.
x1 = ((–(–15)) + √ 1025)/(2×20) = (15 + 32,0156) / 40 ≈ 1,17539
2.2. Второй корень:
Уравнение 20x² – 15x – 10 = 0, где a = 20, b = – 15, c = – 10; D =1025.
x2 = ((–(–15)) – √ 1025)/(2×20) ≈ (15 – 32,0156) / 40 ≈ -0,42539
Пример 2
–x² +6x + 18 = 0
a = –1, b = 6, c = 18
Дискриминант D = b² – 4ac
D = 6² – 4×(–1)×(18) = 36 + 72 = 108, D > 0 <=> есть два корня
Ищем корни:
a = –1, b = 6, c = 18, D = 108
X1,2 = ((–6) ±√108)/(2×(–1)) =>
x1 = ((–6) +√108)/(–2) = ((–6) + 10,3923)/(–2) = – 2,19615
x2 = ((–6) –√108)/(–2) = ((–6) – 10,3923)/(–2) = 8,19615
Как разложить квадратный трёхчлен на множители?
Продолжим с примером уравнения 20x² – 15x – 10 = 0
Мы уже нашли корни
x1 ≈ 1,17539, x2 ≈ -0,42539
Выносим коэффициент x² за скобки, и оба корня ставятся с противоположными знаками таким образом:
20x² – 15x – 10 = 20 (x – 1,17539) (x+0,42539)
Хотите проверить? Открываем скобки и проверяем
20 (x – 1,17539) (x+0,42539) = 20 (x²–1,17539x + 0,42539x–0,42539×1,17539) = 20 (x²–0,75x – 0,4999991521) =
20 x²–15x–9,999983042
Погрешность в 0,000016958 должна быть из-за округления в предыдущих расчётах.
Виды квадратных уравнений
Полное и неполное квадратное уравнение
В полном уравнении присутствуют все три его члена (ax² + bx + c = 0). В противном случае уравнение неполное, например:
–x² – 9 = 0 (отсутствует bx)
x² + 16x = 0 (отсутствует с)
–5x² = 0 (отсутствуют bx и с)
Т.е. это когда коэффициент с = 0 или b = 0 (или оба одновременно равны нулю). Внимание: о том, что «a» может быть равно нулю, не говорится, т.к. таким образом уравнение станет линейным (ax + b = 0).
Как решать неполное квадратное уравнение?
Способ решения, когда b=0
5x² – 5 = 0
5x² = 5, делим всё на 5
x² = 1
x = ± √1 ⇔ x = 1 или x = –1
Первый способ решения, когда c=0 (это быстрый метод)
Пример:
x² + 16x = 0 (выносим x за скобки)
x (x + 16) = 0, таким образом, либо x = 0, либо то, что в скобках, равно нулю,
x = 0 или (x + 16)= 0
(x + 16)= 0 ⇔ x = – 16
Второй способ решения, когда c=0
Неполное уравнение (c=0, b=0 или когда оба равны нулю) можно решить по той же системе, как и полное, правильно выписав коэффициенты (но это долго и нерационально).
Например:
x² + 16x = 0
a = 1, b = 16, c = 0 (здесь отсутствует c, значит он равен нулю)
Дискриминант: D = b² – 4ac = 16² – 4×1×0 = 16² = 256 >0, есть два корня.
Ищем корни X1,2 = ((–b) ±√D)/(2×(a)) =>
X1,2 = ((–16) ± √256)/(2×(1)) =>
x1 = ((–16) + √256)/(2×(1)) = ((–16) + 16)/2 = 0
x2 = ((–16) – √256)/(2×(1)) = ((–16) – 16)/2 = –32/2 = – 16
Способ решения, когда b=0 и c=0
Например:
3x² = 0
Делим всё на 3
x² = 0
x = 0
Приведённое квадратное уравнение
Чтобы получить приведённое квадратное уравнение, нужно лишь разделить обе части уравнения на a:
x² + px + q = 0, где:
p = b/a
q = c/a
Примеры:
3x² – 6x = 0 (делим всё на 3) ⇔ x² – (6/3)x = 0 ⇔ x² – 2x = 0 (неполное приведённое)
2x² – 4x – 2 = 0 (делим всё на 2) ⇔ x² – (4/2)x – (2/2) = 0 ⇔ x² – 2x – 1 = 0 (полное приведённое)
Геометрический смысл решения корней квадратных уравнений
Корни квадратного уравнения ещё являются и нулями функции, т.
е. если вы ищете нули функции (в каких точках функция пересекает ось Ox), то вы их найдёте именно через этот процесс: поймёте, если они существуют, рассчитав дискриминант, затем найдёте их, используя формулу корней.
Вспомним наш пример уравнения 20x² – 15x – 10 = 0.
Мы сделали график 20x² – 15x – 10, на котором видно, что наши корни (x1 ≈ 1,17539, x2 ≈ -0,42539) являются нулями этой функции.Другой пример, в котором есть только один нуль, функция 3x². Здесь х = 0.Функция x² + 1 не имеет корней, это мы и видим на графике функции (она не пересекает ось Ox).Узнайте также, что такое Теорема Виета и Парабола.
Дискриминант для решения квадратных уравнений и нахождения корней
Главная » 8 класс. Алгебра. » Дискриминант — определение, свойства, геометрический смысл
Важная характеристика квадратных уравнений — их дискриминант. По значению этой величины определяют, сколько корней у данного уравнения и есть ли они.
В 8 классе по алгебре начинают изучать квадратные уравнения и самый популярный способ их решения — через дискриминант.
Формула вычисления дискриминанта известна
Дискриминант в математике используется чтобы определить сколько корней в уравнении — 1 корень, 2 корня или действительных корней нет. В этой статье определим, что такое дискриминант и выведем формулу дискриминанта.
Содержание
Определение
Определим что такое дискриминант и зачем он нужен в математике, а также как его рассчитать.
Дискриминантом называют число, описывающее свойство коэффициентов квадратного многочлена. Хотя есть дискриминанты и кубических многочленов.
По этому числу определяют характер корней уравнения, полученному если многочлен приравнять к нулю. Так, если дискриминант больше нуля, то уравнение будет иметь два корня, равен нулю, то 1 корень, а если будет меньше нуля, то корней не будет.
Дискриминант (определение) помогает определить наличие или отсутствие корней квадратного уравнения, не решая его.
Обозначается дискриминант квадратного уравнения буквой или знаком Δ.
2 — 4 \cdot 1 \cdot (-4)}}{2 \cdot 1} = $ 92-32$
$y=2(x-3)(x+5)$ y-точка пересечения с
$(0, -30)$вершина в
$(-1, -32)$x-отрезков на
$(3, 0)$ и $(-5, 0)$Парабола
График квадратного уравнения называется параболой .
Если a < 0, то его вершина направлена вверх: Если a = 0, то график представляет собой не параболу, а прямую линию.
Если a > 0, то его вершина указывает вниз:Вершина параболы $x = -\frac{b}{2a}$.
формулы Виета
Если x 1 и x 2 являются корнями квадратного уравнения ax 2 + bx + c = 0 тогда:
$x_1 + x_2 = -\frac{b}{a}$
$x_1x_2 = \frac{c}{a}$
Эти формулы называются формулами Виета .
Мы можем найти корни x 1 и x 2 квадратного уравнения, решив уравнения уравнений.Задачи на квадратные уравнения
Задача 1.
Решите уравнение:
x 2 — 4 = 0
Решение: x 2 — 4 = (x — 2)(x + 2)
(x — 2)(x + 2) = 0
x — 2 = 0 или x + 2 = 0
Корни x = 2 или x = -2Решение 2: a = 1, b = 0, c = -4
D = 0 2 — 4 ⋅ 1 ⋅ (-4) = 16
$x_1 = \frac{-b — \sqrt{D}}{2a} = \frac{- 0 — \sqrt{16}}{2 \cdot 1} = \frac{-4}{2} = -2$
$x_2 = \frac{-b + \sqrt{D}}{2a } = \frac{- 0 + \sqrt{16}}{2 \cdot 1} = \frac{4}{2} = 2$Задача 2. Решить уравнение:
3x 2 + 4x + 5 = 0
Решение: дискриминант D = 4 2 — 4⋅3⋅5 = 16 — 60 = -44 Таким образом, квадратное уравнение не имеет действительных корней.Задача 3. Решите уравнение:
х 2 + 4х — 5 = 0; х = ?
Решение: Дискриминант равен 4 2 — (-4⋅1⋅5) = 16 + 20 = 36 > 0
У уравнения два действительных корня: $\frac{-4 \pm \sqrt{36} {2}$
х = 1 или х = -5Задача 4.
Решить уравнение:
х 2 + 4х + 4 = 0; х = ?
Решение: Дискриминант равен 4 2 — (4⋅1⋅4) = 16 — 16 = 0
Таким образом, существует одно действительное решение: $x = \frac{-4}{2}$
x = -2Задача 5. Решить уравнение:
x 2 — 13x + 12 = 0
Корни: 1, 12Задача 6. Решить уравнение: 92 — 4ac}}{2a}$
Квадратные уравнения на нашем математическом форуме
Задачи на квадратные уравнения
Задачи по формулам Виета
Решение уравнений кубической и четвертой степени — 1Форумы, посвященные квадратным уравнениям
python — Квадратичная формула находит значение для x1 и x2 по уравнению
спросил
Изменено 7 лет, 3 месяца назад
Просмотрено 2к раз
Учитывая вложенный список
l, содержащий значения коэффициентов, я пытаюсь вычислить квадратичную формулу, чтобы найти нули x, обозначенные какx1,x2.У меня есть цикл for, который проходит через этот список и дает мне значение для a, b и c из вложенного списка:
import math as m l = [[1,2,1],[9,12,4],[1,-7,0],[1,2,-3]]#вложенный список для х в л: q = x[1]*x[1]-4*x[0]*x[2] #b*b - 4*a*c q_sr = m.sqrt(q)#корень из q x1 = (-x[1] + q_sr)/(2*x[0])#[1]=b и [0]=a x2 = (-x[1] - q_sr)/(2*x[0])#[1]=b и [0]=a eq = x[0]**2 + 2*x[1] + 1*x[2] #уравнение, которое я пытаюсь получить x1 и x2 print("вердье: ", x[0]) print("b verdier: ", x[1]) print("с Вердье: ", x[2]) print("x1 Вердье: ", x1) print("x2 Вердье: ", x2)Здесь x[0],x[1] и x[2] — соответствующие позиции в списке l, например, 0 = a, 1 = b и 2 = c. Все это работает, и я получаю правильные значения для x1 и x2.
У меня возникли проблемы с вычислением нулей (
x1, x2). Как рассчитать эти значения?3
- питон
- формула
- уравнение
- квадратичное
Сложный математический модуль отлично подходит для таких задач.
импорт cmath квадратичный по определению (а, б, с): d = число с плавающей запятой (b**2 - 4*a*c) x1 = ((-b)-cmath.sqrt(d))/(2*a) x2 = ((-b)+cmath.sqrt(d))/(2*a) вернуть [x.real if (x.imag == 0.0) else x вместо x в [x1, x2]]Для развлечения
Класс Квадратичный: def __init__(я, а, б, в): self.a, self.b, self.c = a, b, c self.d = float(self.b ** 2 - 4*self.a*self.c) self.x1 = ((-b)-cmath.sqrt(self.d))/(2*a) self.x2 = ((-b)+cmath.sqrt(self.d))/(2*a) @свойство определение решения (сам): вернуть [x.real, если x.imag == 0,0 иначе x вместо x в [self.x1, self.x2]] защита __str__(я): вернуть «X1 = {}, X2 = {}». формат (* self.solution) мойСписок = [[1, 2, 1], [92 + 2*х -3 для коэф в coef_list: a, b, c = coef # извлечь a, b и c из внутренних списков д = б**2 - 4*а*с # В случае q > 0 у вас есть два решения если д > 0: q_sqrt = sqrt(q) x1 = (-b + q_sqrt)/(2*a)#[1]=b и [0]=a x2 = (-b - q_sqrt)/(2*a)#[1]=b и [0]=a # В случае q = 0 у вас есть только одно решение Элиф д == 0: х1 = -b/(2*а) х2 = х1 # В случае q < 0 у вас нет реального решения еще: поднять ValueError ("q отрицательно") # печатать на всех итерациях цикла, чтобы иметь решения для каждой # уравнение, указанное в coef_list выведите "x1 = ", x1 напечатать "х2 = ", х2 выведите "a = ", a, ", b = ", b, "и c = ",c Распечатать "-----" # Вам не нужна следующая строка, так как уравнение, которое вы пытаетесь решить, # определяется в coef_list в строке 0 (т.Тоэ онлайн калькулятор: Решение задач по тоэ онлайн
Электротехника ТОЭ: Карта сайта
Электротехника ТОЭ: Карта сайтаКарта сайта
Теги details, summary, атрибут open Главная: О сайте toe1.ru Теория: Введение; 1. Основные понятия и законы линейных электрических цепей; 2. Методы преобразования электрических цепей; 3. Методы расчета электрических цепей 4. Цепи переменного синусоидального тока 5. Пассивные элементы в цепях переменного тока 6. Резонансные явления в электрических цепях 7. Комплексные частотные характеристики 8. Индуктивно связанные цепи 9. Четырехполюсники 10. Электрические фильтры 11. Переходные процессы в электрических цепях 12. Анализ электрических цепей при периодических несинусоидальных воздействиях 13. Анализ электрических цепей при непериодических воздействиях 14. Цепи с распределенными параметрами 15. Нелинейные электрические цепи 16. Магнитные цепи при постоянных магнитных потоках 17. Нелинейные цепи переменного тока Полезная литертура: Здесь собраны основные книги для студентов технических специальностей.База часто обновляется, добавляются новые материалы. Заказать решение: Тут можно заказать решение задачи, обратившись к автору, через ВКонтакте или через форму заполнения данных Познавательное: Статьи на тему «Электричество и магнетизм» Физика: Скачать мою тетрадь по физике Контакты: Контакты автора: ВКонтакте(личная страница), ВКонтакте(группа по ТОЭ), E-mail, Skype, YouTube канал по ТОЭ, WhatsApp. Готовые работы: Готовые задачи, курсовые, расчетные работы, тесты по Тоэ, схемотехнике и по другим техническим дисциплинам. Мы стараемся часто добавлять новые работы, которые у нас появились в эту базу. Цены: Цены могут меняться на плюс/минус (5-20)% в зависимости от ситуации: сезон заказов, условия задачи, сроков выполнения и др. Ниже приведены приблизительные расценки. Более точную информацию, уточняйте у автора в личных сообщениях ВКонтакте или на сайте в быстром чате(в нижнем правом углу). Вопрос-ответ: В данном разделе мы собрали часто задаваемые вопросы от наших пользователей Сайта, ВКонтакте и Ютуб канала по Электротехнике.
Если Вы не нашли ответ на свой вопрос, то задайте его нам любым удобным способом. Перед тем, как задать вопрос, убедитесь, что действительно нет ответа, который Вас интересует! Об авторе: Информация об авторе сайта Калькулятор комплексных чисел: Калькулятор перевода комплексных чисел из алгебраической формы в показательную и наоборот Популярные темы на сайте: Раздел с самыми популярными темами, которые читают посетители сайта Наша группа ВКонтакте по ТОЭ: Мы в соц. сетях Пройти тест по тоэ: Тесты по тоэ для новичков и не только Поделиться сайтом в соц сетях: Сайтом можно поделиться с друзьями в соц. сетях Подписывайтесь на наш канал: Наш Ютуб канал Статистика посещений: общее, сегодня: Статистика нашего сайта по посещениям
Главная страница
Электроемкость конденсатора — формула и определение
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.
Но прежде введём понятие электрической ёмкости.
Электроемкость проводников
Проводники умеют не только проводить через себя электрический ток, но и накапливать заряд. Эта способность характеризуется таким параметром, как электроемкость.
Особенность этой величины в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости. Самая популярная — формула электроемкости шара.
Электроемкость шара C = 4πεε0r
С — электроемкость [Ф]
ε — относительная диэлектрическая проницаемость среды [-]
ε0 — электрическая постоянная
ε0 = 8,85 × 10-12 Ф/м
r — радиус шара [м]
Заказать решение ТОЭ
- Метрология Электрические измерения
- Пигарев А.
Ю. РГЗ по электротехнике и электронике в Multisim
- Теория линейных электрических цепей ТЛЭЦ — Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте — Контрольная работа №1
- — Контрольная работа №2
Электротехника и основы электроники — Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил — Контрольная работа № 1 Электрические цепи
— Контрольная работа № 2 Трансформаторы и электрические машины — Контрольная работа № 3 Основы электроники Теоретические основы электротехники ТОЭ — Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009
— Переходные процессы Переходные процессы в электрических цепях — Теоретические основы электротехники Методические указания и контрольные задания для студентов технических специальностей вузов — Задание 1 Линейные электрические цепи постоянного и синусоидального тока — Задача 1. 1 Линейные электрические цепи постоянного тока
— Задача 1.2 Линейные электрические цепи синусоидального тока — Задание 2 Четырехполюсники, трехфазные цепи, периодические несинусоидальные токи, электрические фильтры, цепи с управляемыми источниками — Теоретические основы электротехники сб. заданий Р.Я. Сулейманов Т.А. Никитина Екатеринбург УрГУПС 2010 — Трехфазные цепи. Расчет трехфазных цепей — УГТУ-УПИ Решение ТОЭ Билеты по ТОЭ — Электромагнитное поле Электростатическое поле Электростатическое поле постоянного тока в проводящей среде Магнитное поле постоянного тока Конденсаторы
Способность накапливать заряд — полезная штука, поэтому люди придумали конденсаторы. Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.
Конденсатор состоит из двух проводящих пластин (обкладок), разделенных диэлектриком. Между проводящими пластинами образуется электрическое поле, все силовые линии которого идут от одной обкладки к другой.
Когда заряд накапливается на обкладках, происходит процесс под названием зарядка конденсатора. Заряды на разных обкладках равны по величине и противоположны по знаку.
Электроемкость конденсатора измеряется отношением заряда на одной из обкладок к разности потенциалов между обкладками:
Электроемкость конденсатора C = q/U
С — электроемкость [Ф]
q — электрический заряд [Кл]
U — напряжение (разность потенциалов) [В]
По закону сохранения заряда, если обкладки заряженного конденсатора соединить проводником, то заряды нейтрализуются, переходя с одной обкладки на другую. Так происходит разрядка конденсатора.
Любой конденсатор имеет предел напряжения. Если оно окажется слишком большим, то случится пробой диэлектрика, то есть разрядка произойдет прямо через диэлектрик. Такой конденсатор больше работать не будет.

Идея суперконденсатора
Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.
Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному. Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ.Основные недостатки аккумуляторов по сравнении и конденсаторами:
- непродолжительный жизненный цикл;
- невысокая удельная мощность;
- узкий диапазон температур зарядки и разрядки;
- неспособность быстро отдать весь запас энергии.
Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.
Крупнейшие коммерческие устройства обладают ёмкостью до нескольких тысяч фарад, но их возможности всё равно несопоставимы с аккумуляторами, поэтому подобные устройства используются для хранения зарядов в течение относительно короткого периода времени. Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.
Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками. Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.
Энергия конденсатора
У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.
Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор.
При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.
Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.
В случае с конденсатором d будет представлять собой расстояние между пластинами.
Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.
Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.
В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.
Тогда энергия конденсатора равна:
Wp = qEd/2
Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:
U = Ed
Поэтому:
Wp = qU/2
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.
Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:
Энергия конденсатора Wp = qU/2
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
U — напряжение на конденсаторе [В]
Энергия конденсатора Wp = CU2/2
Wp — энергия электростатического поля [Дж]
C — электроемкость конденсатора [Ф]
U — напряжение на конденсаторе [В]
Эти формулы справедливы для любого конденсатора.
Из истории
Первым конденсатором считается лейденская банка. Её разработали независимо сразу двое учёных:
- Эвальд Георг фон Клейст (11 октября 1745 года).
- Питер ван Мушенбрук (1745 – 1746 годы).
Двумя десятилетиями позже на свет появился электрофорус (1762 год), рассматриваемый как первый плоский конденсатор. Тогда не существовало терминов, вопросы накопления заряда мало интересовали. Учёные пока что развлекались получением статического заряда. К примеру, ван Мушенбрук испытывал лейденскую банку на слишком смелых студентах, когда сам оказался однажды полупарализован электрическим зарядом.
Наука не шла вперёд, хотя светила, включая Бенджамина Франклина, вовсю толкали паровоз. Современный этап развития физики начался с Алессандро Вольта. Учёный оказался привлечён конструкцией электрофоруса и заинтригован. Натёртая резина могла сколь угодно долго заряжать металлическую пластину. В то время предполагалось, что электричество переносится флюидами атмосферы, и Вольта считал аналогично. Узрев, что электрофорус способен запасать заряд, учёный решил посчитать и количество.
Применение конденсаторов
Конденсатор есть в каждом современном устройстве. Без него не будет работать ни один прибор.
Разберем два самых наглядных примера.
Пример раз — вспышка
Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.
Пример два — тачскрин
Тачскрин на телефоне работает по принципу, схожему с конденсатором. В самом смартфоне, конечно, тоже есть множество конденсаторов, но этот принцип куда интереснее.
Дело в том, что тело человека тоже умеет проводить электричество — у него даже есть сопротивление и электроемкость. Так что можно считать человеческий палец пластиной конденсатора — тело же проводник, почему бы и нет. Но если поднести палец к металлической пластине, получится плохой конденсатор.
В экран телефона встроена матрица из микроскопических пластинок.
Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.
Кстати, то же самое можно проделать, если взять обычную сосиску и поводить ей по экрану смартфона. Тачскрин будет реагировать на все контакты, как реагирует на человеческий палец.
Это не единственный вариант реализации тачскрина, но один из лучших на сегодняшний день. В айфоне используется именно он.
Активное и реактивное сопротивления
Хотя активное и реактивное сопротивления очень похожи. Даже значения обоих параметров измеряются в Омах, но они не совсем одинаковы. В результате этого невозможно сложить их вместе непосредственно.
Вместо этого их нужно суммировать «векторно». Другими словами, необходимо округлить каждое значение, а затем сложить их вместе и выделить квадратный корень из этого числа:
Xtot2 = Xc2 + R2
В данной статье были подробно описаны основные компоненты, устройство и принцип работы конденсаторов, а также приведены базовые формулы, предназначенные для того, чтобы посчитать полезный объём прибора. Для более глубокого ознакомления необходимо внимательно рассмотреть типы данных деталей и их практические особенности в различных схемах и устройствах.
Определение заряда
Определить, заряжен ли проводник, можно специальным измерительным прибором. К примеру, сделать это можно при помощи индикаторной отвертки. При разряде избыточные виды электронов, имеющих левую пластину, будут перемещены через некоторое время по проводам к правой части пластины, то есть они будут смещены к местам, где их недостаточно.
Обратите внимание! Когда число электронов будет одинаковым, то разряд прекратится и проводная энергия вместе с сопротивлением исчезнет.
Использование измерительного оборудования для определения конденсаторного заряда
Использование измерительного оборудования для определения конденсаторного зарядаФормула
Нахождение тока конденсаторного заряда происходит по формуле, представленной ниже. Измеряется он в фарадах, что равно кулону или вольту.
Формула нахождения заряда конденсатораВ целомэто элемент электросети, накапливающий и сохраняющий напряжение в ней. Бывает разного типа и размера, к примеру, электролитическим, керамическим и танталовым. Состоит, в основном, из нескольких токопроводящих обкладок с диэлектриком. Его емкость зависит от размеров диэлектрика и заполнителя между обкладками. Заряжается благодаря электричеству. Определить ток конденсаторного заряда можно измерительными приборами и формулой.
Значение диэлектрика
Кроме общего размера обкладок и расстояния между ними, существует ещё один параметр, влияющий на ёмкость — используемый тип изолятора. Фактор, по которому определяется способность диэлектрика повышать ёмкость конденсатора в сравнении с вакуумом, называется диэлектрической проницаемостью и описывается для разных материалов постоянной величиной от 1 и до бесконечности (теоретически):
- вакуум: 1,0000;
- воздух: 1,0006;
- бумага: 2,5—3,5;
- стекло: 3—10;
- оксиды металлов 6—20;
- электротехническая керамика: до 80.
Кроме конденсаторов с твёрдым диэлектриком (керамических, бумажных, плёночных) существуют также электролитические. В последних используют алюминиевые или танталовые пластины с оксидным изолирующим слоем в качестве одного электрода и раствор электролита в качестве другого.
Энергия, которую способны накопить большинство конденсаторов, обычно невелика — не больше сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому конденсаторы не могут заменить, например, аккумуляторные батареи в качестве источника питания. И хотя они способны эффективно выполнять только одну работу (сохранение заряда), их применение весьма многообразно в электрических цепях. Конденсаторы используются как фильтры, для сглаживания сетевого напряжения, в качестве устройств синхронизации и для других целей.
Практические измерения
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми.
Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат.
Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.
Синтаксис
Для пользователей XMPP клиентов, используется команда
fiz ключи
где ключи это известные параметры, параметра=значение, разделенные точкой с запятой
Обязателен ключ key=razryad при расчете разаряда конденсатора
и zaryad при расчете заряда
Так как при других параметрах ключах будут рассчитываться совершенно другие формулы. Например баллистического движения или давления над уровнем моря.
Заметьте, чем данный калькулятор отличается от других:
Во первых: данные можно вводить не переводя из наноФарад в Фарады, а килоОмы в Омы.
Если уж заданы параметры в единицах измерения то так и пишите. Если не напишите то считается что данные заданы в основным единицах СИ ( то есть метр, Фарад, Ом)
Во вторых: Расчет ведётся по тем параметрым которые можно рассчитать зная исходные.Это очень удобно, когда нужно рассчитать любой из параметров в формуле, когда известны все остальные. Другие известные калькуляторы могут рассчитывать только по определенному алгоритму и только в одну сторону.
RC Калькулятор вкладышей для таблеток
Калькулятор вкладышей для таблеток RC
Нужна помощь в понимании того, как на самом деле работают вкладыши для подвески? Используйте наш удобный калькулятор геометрии подвески, чтобы увидеть, что они делают и какое влияние на них окажут изменения.Калькулятор предназначен для вкладышей с 17 или 25 возможными положениями штифта — центральное положение с регулировкой 0,5 и 1,0 в каждом направлении. Эти вставки обеспечивают 9 возможных значений для схождения, антиприседания, ширины штифта и высоты штифта.
Мы не приводим фактические значения схождения или других параметров, поскольку они различаются в зависимости от автомобиля, но вы можете увидеть, какие из 9 параметровзначения для каждого используемого параметра. Важны относительные изменения.
Чтобы узнать, как схождение, антиприседание, ширина и высота штифта влияют на управляемость, ознакомьтесь с нашими советами по настройке внизу страницы.
Набор вкладышей для таблеток здесь
(передняя или задняя часть автомобиля)
Текущие передние вкладыши
Внутри
900 18
5″ data-x=»0.5″>
Вставка:
90 012 Текущие задние вставки
0 — центр
Внутри
5″>
9000 6
5″ data-y=»-1″>
900 06 Вставка:
0 — центральнаяНовые передние вставки
Внутри
900 18
90 006
5″ data-y=»0″>
9000 5
901 19
Вставка:
0 — центрНовые задние вставки
Внутри
9001 8
5″ data-x=»-1″>
9000 6
900 06
Вставка:
0 — центрСм.
геометрию и влияние изменений здесь
Схождение (сп) / Размах (фр)
-4
-3
-2
-1
0
900 06 12
3
4
+ схождение
+ стреловидность— схождение
— стреловидностьЗащита от приседаний (rr) / Защита от ныряния (fr)
-4
-3 9 0018
-2
-1
0
1
2
3
4
— защита от приседания (rr)
+ защита от погружения (fr)+ защита от приседания (rr)
— защита от пикирования (fr)Ширина поворота / дорожка
-4
-3
-2
-1
0
1
2
3
4
более узкий
Высота оси / центр ролика
-4
-3
-2
9000 6 -10
1
2
3
4
нижний
9000 6 выше
— центр ролика
+ центр кренаСоветы по настройке и определения
Схождение
Схождение измеряет угол наклона колеса по сравнению с движением прямо, если смотреть сверху.
Отрицательные углы схождения указывают на схождение (колеса смотрят внутрь), в то время как положительное схождение указывает на «схождение наружу» с колесами, направленными наружу.
Больше схождения передних колес
Больше рулевого управления с усилителем
Больше схождения передних колес
- Больше рулевого управления без усилителя
9065 9 Более плавный запуск- Более плавный запуск
Меньшее схождение задних колес
- Меньшее сцепление с дорогой
- Повышенная устойчивость на высоких скоростях
- Больше вращения в поворотах
- Обычно подходит для гусениц с высоким сцеплением
Больше заднего схождения
- Больше тяги вперед
- Меньше устойчивости на высоких скоростях
- Меньше вращения в поворотах
- Обычно подходит для гусениц с низким сцеплением ред в тылу.

Anti-squat
Anti-squat Angle (он же «anti-dive») — это угол, на который штифты подвески наклонены вверх спереди, если смотреть сбоку автомобиля. 0 градусов антиприседания указывает на то, что штифты параллельны шасси.
Больше антиприседаний
- Больше тяги вперед
- Меньше «приседания» (опускания задней части при ускорении)
- Меньше рулевого управления с усилителем
906 51Без защиты от приседаний
- Подробнее об усилителе рулевого управления
- Повышенная устойчивость в поворотах
Ширина шарнира
Ширина шарнира или ширина штифта — это расстояние между шарнирами нижних рычагов подвески в местах их крепления к переборке. Обычно он устанавливается с креплениями нижнего рычага подвески (часто известными как крепления C/D или крепления RF/RR).
Более узкие задние шарниры
Повышенная устойчивость под нагрузкой
Более широкие задние шарниры
- Подробнее об усилителе рулевого управления
- Подробнее устойчивость в поворотах
Ширина поворота также повлияет на ширину колеи , если только не используются более короткие рычаги или ступицы не сдвинуты внутрь.

Колея
Ширина колеи определяет общую ширину автомобиля. Обычно его регулируют, используя разные шестигранники колес или шайбы на оси, но использование рычагов подвески разной длины или изменение ширины шарниров подвески также влияет на ширину колеи. 9
- Медленная реакция на рулевое управление 659 Лучшее сцепление
- Быстрая реакция на рулевое управление
Более широкая задняя колея
- Большее сцепление сзади
- Более быстрое рулевое управление
- Уменьшение тягового крена
Более узкая задняя колея
- Больше сцепления в крутых поворотах
- Менее высокоскоростное рулевое управление
Высота поворота
Высота поворота описывает вертикальное положение внутренних, нижних штифтов рычага подвески.
Высота нижнего шарнира
- Нижний центр ролика
- Дополнительный ролик шасси
Высота большего шарнира
- Более высокий центр крена
- Меньший крен шасси
Центр крена
Вкратце, центр крена — это способ измерить, насколько охотно автомобиль наклоняется в поворотах.
Если вы понизите центр крена автомобиля, его шасси будет больше раскачиваться из стороны в сторону, и этот перенос веса на внешние колеса создает дополнительное сцепление с этой стороной.
Более низкий передний центр крена
- Больше кренов шасси в поворотах
- Больше бокового сцепления
- Больше рулевого управления с усилителем
- Обычно подходит для гусениц с низким сцеплением
Высокий передний центр крена
- Уменьшение крена шасси в поворотах
- Уменьшение бокового сцепления
- Уменьшение усилителя рулевого управления
- Уменьшение тягового крена
- Обычно подходит для гусениц с высоким сцеплением
Нижний задний центр крена
- Больше шасси крен в поворотах
- Больше бокового сцепления
- Больше сцепления с дорогой
- Меньше сцепления при торможении
- Обычно подходит для гусениц с низким сцеплением
Более высокий задний центр крена
- Уменьшение кренов шасси в поворотах
- Уменьшение бокового сцепления
- Уменьшение рулевого управления с усилителем
- Уменьшение тягового крена
- Обычно подходит для гусениц с высоким сцеплением
Изменения нижнего рычага подвески обычно имеют больший влияние, чем изменения в звене развала.

На центр крена влияет множество различных изменений подвески, включая длину тяги развала, расположение шаровых опор тяги развала, длину рычага, высоту пальца, высоту оси и другие.
Калькулятор максимального количества повторений — уровень силы
Рассчитайте свой одноповторный максимум (1ПМ) для любого подъема. Ваш одноповторный максимум — это максимальный вес, который вы можете поднять за одно повторение. повторение заданного упражнения.
Процент повторения 1 РМ
Повторы Процент от 1 ринггита 1 100% 2 97% 3 94% 4 92% 5 89% 6 86% 7 83% 8 81% 9 78% 10 75% 11 73% 12 71% 13 70% 14 68% 15 67% 16 65% 17 64% 18 63% 19 61% 20 60% 21 59% 22 58% 23 57% 24 56% 25 55% 26 54% 27 53% 28 52% 29 51% 30 50% Поднимите свою силу на новый уровень, следуйте проверенному плану тренировок
Бусткемп — это бесплатное фитнес-приложение с лучшими в мире программами тренировок, которые помогут вам нарастить силу и мышцы.
Сокращение дробей онлайн со степенями: Онлайн калькулятор для сокращения дробей
Возведение алгебраической дроби в степень 8 класс онлайн-подготовка на Ростелеком Лицей
Правила возведения дробей и целых выражений в натуральную степень с элементарными примерами
Правило возведения обыкновенных и алгебраических дробей в натуральную степень:
Можно провести аналогию со степенью целого выражения и вспомнить, что понимается под возведением его в степень:
Пример 1. .
Как видно из примера, возведение дроби в степень – это частный случай умножения дробей, что изучалось на предыдущем уроке.
Пример 2. а) , б) – минус уходит, т. к. мы возвели выражение в четную степень.
Ответ. ; .
Для удобства работы со степенями вспомним основные правила возведения в натуральную степень:
– произведение степеней;
– деление степеней;
– возведение степени в степень;
– степень произведения.
Пример 3. – это известно нам еще с темы «Возведение в степень целых выражений», кроме одного случая: не существует.
Простейшие примеры на возведение алгебраических дробей в натуральную степень
Далее рассмотрим примеры посложнее.
Пример 4. Возвести дробь в степень .
Решение. При возведении в четную степень минус уходит:
.
Ответ. .
Пример 5. Возвести дробь в степень .
Решение. Теперь пользуемся правилами возведения степени в степень сразу без отдельного расписывания:
.
Ответ..
Теперь рассмотрим комбинированные задачи, в которых нам будет необходимо и возводить дроби в степень, и умножать их, и делить.
Пример 6. Выполнить действия .
Решение. . Далее необходимо произвести сокращение. Распишем один раз подробно, как мы это будем делать, а затем будем указывать результат сразу по аналогии: . Аналогично (или по правилу деления степеней) . Имеем: .
Ответ. .
Пример 7. Выполнить действия .
Решение. . Сокращение осуществлено по аналогии с примером, разобранным ранее.
Ответ. .
Пример 8. Выполнить действия .
Решение. . В данном примере мы еще раз более подробно расписали процесс сокращения степеней в дробях, чтобы закрепить этот способ.
Ответ. .
Более сложные примеры на возведение алгебраических дробей в натуральную степень (с учетом знаков и со слагаемыми в скобках)
Пример 9. Выполнить действия .
Решение. В данном примере уже пропустим отдельное умножение дробей, а сразу воспользуемся правилом их умножения и запишем под один знаменатель. При этом следим за знаками – в указанном случае дроби возводятся в четные степени, поэтому минусы исчезают. В конце выполним сокращение.
.
Ответ..
Пример 10. Выполнить действия .
Решение. В данном примере присутствует деление дробей, вспомним, что при этом первая дробь умножается на вторую, но перевернутую.
.
Ответ. .
На данном уроке мы рассмотрели возведение дробей в натуральную степень. В дальнейшем умение это делать и осуществлять действия с дробями, изученными ранее, мы будем использовать для преобразования рациональных выражений.
Список литературы
1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Портал для всей семьи(Источник).
2. Старая школа (Источник).
Домашнее задание
1. №76. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
2. Возвести дроби в степень: а) , б) .
3. Возвести дроби в степень: а) , б) .
4. Возвести дроби в степень: а) , б) .
5. Выполнить действия: а) , б) .
Сокращение числитель 12 разделили. Онлайн калькулятор сокращения алгебраических дробей с подробным решением позволяет сократить дробь и перевести неправильную дробь в правильную дробь
В этой статье мы рассмотрим основные действия с алгебраическими дробями :
- сокращение дробей
- умножение дробей
- деление дробей
Начнем с сокращения алгебраических дробей .
Казалось бы, алгоритм очевиден.
Чтобы сократить алгебраические дроби , нужно
1. Разложить числитель и знаменатель дроби на множители.
2. Сократить одинаковые множители.
Однако, школьники часто делают ошибку, «сокращая» не множители, а слагаемые. Например, есть любители, которые в дроби «сокращают» на и получают в результате , что, разумеется, неверно.
Рассмотрим примеры:
1. Сократить дробь:
1. Разложим на множители числитель по формуле квадрата суммы, а знаменатель по формуле разности квадратов
2. Разделим числитель и знаменатель на
2. Сократить дробь:
1. Разложим на множители числитель. Так как числитель содержит четыре слагаемых, применим группировку.
2. Разложим на множители знаменатель. Так же применим группировку.
3. Запишем дробь, которая у нас получилась и сократим одинаковые множители:
Умножение алгебраических дробей.
При умножении алгебраических дробей мы числитель умножаем на числитель, а знаменатель умножаем на знаменатель.
Важно! Не нужно торопиться выполнять умножение в числителе и знаменателе дроби. После того, как мы записали в числителе произведение числителей дробей, а в знаменателе — произведение знаменателей, нужно разложить на множители каждый множитель и сократить дробь.Рассмотрим примеры:
3.
Упростите выражение:
1. Запишем произведение дробей: в числителе произведение числителей, а в знаменателе произведение знаменателей:
2. Разложим каждую скобку на множители:
Теперь нам нужно сократить одинаковые множители. Заметим, что выражения и отличаются только знаком: и в результате деления первого выражения на второе получим -1.
Итак,
Деление алгебраических дробей мы выполняем по такому правилу:
То есть чтобы разделить на дробь, нужно умножить на «перевернутую».Мы видим, что деление дробей сводится к умножению, а умножение, в конечном итоге, сводится к сокращению дробей.
Рассмотрим пример:
4. Упростите выражение:
Чтобы понять, как сокращать дроби, сначала рассмотрим один пример.
Сократить дробь — значит, разделить числитель и знаменатель на одно и то же . И 360, и 420 оканчиваются на цифру, поэтому можем сократить эту дробь на 2. В новой дроби и 180, и 210 тоже делятся на 2, сокращаем и эту дробь на 2.
В числах 90 и 105 сумма цифр делится на 3, поэтому оба эти числа делятся на 3, сокращаем дробь на 3. В новой дроби 30 и 35 оканчиваются на 0 и 5, значит, оба числа делятся на 5, поэтому сокращаем дробь на 5. Получившаяся дробь шесть седьмых — несократимая. Это — окончательный ответ.
К этому же ответу можем прийти другим путем.
И 360, и 420 оканчиваются нулем, значит, они делятся на 10. Сокращаем дробь на 10. В новой дроби и числитель 36, и знаменатель 42 делятся на 2. Сокращаем дробь на 2. В следующей дроби и числитель 18, и знаменатель 21 делятся на 3, значит, сокращаем дробь на 3. Пришли к результату — шесть седьмых.
И еще один вариант решения.
В следующий раз рассмотрим примеры сокращения дробей.
Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры.
Yandex.RTB R-A-339285-1
Смысл сокращения алгебраической дроби
В материалах об обыкновенной дроби мы рассматривали ее сокращение.
Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.
Сокращение алгебраической дроби представляет собой аналогичное действие.
Определение 1
Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число.
К примеру, алгебраическая дробь 3 · x 2 + 6 · x · y 6 · x 3 · y + 12 · x 2 · y 2 может быть сокращена на число 3 , в итоге получим: x 2 + 2 · x · y 6 · x 3 · y + 12 · x 2 · y 2 . Эту же дробь мы можем сократить на переменную х, и это даст нам выражение 3 · x + 6 · y 6 · x 2 · y + 12 · x · y 2 . Также заданную дробь возможно сократить на одночлен 3 · x или любой из многочленов x + 2 · y , 3 · x + 6 · y , x 2 + 2 · x · y или 3 · x 2 + 6 · x · y .

Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь.
Все ли алгебраические дроби подлежат сокращению?
Опять же из материалов об обыкновенных дробях мы знаем, что существуют сократимые и несократимые дроби. Несократимые – это дроби, не имеющие общих множителей числителя и знаменателя, отличных от 1 .
С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.
В общих случаях по заданному виду дроби довольно сложно понять, подлежит ли она сокращению. Конечно, в некоторых случаях наличие общего множителя числителя и знаменателя очевидно. Например, в алгебраической дроби 3 · x 2 3 · y совершенно понятно, что общим множителем является число 3 .
В дроби — x · y 5 · x · y · z 3 также мы сразу понимаем, что сократить ее возможно на х, или y , или на х · y .
И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует.
Например, дробь x 3 — 1 x 2 — 1 мы можем сократить на х — 1 , при этом указанный общий множитель в записи отсутствует. А вот дробь x 3 — x 2 + x — 1 x 3 + x 2 + 4 · x + 4 подвергнуть действию сокращения невозможно, поскольку числитель и знаменатель не имеют общего множителя.
Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.
Правило сокращения алгебраических дробей
Правило сокращения алгебраических дробей состоит из двух последовательных действий:
- нахождение общих множителей числителя и знаменателя;
- в случае нахождения таковых осуществление непосредственно действия сокращения дроби.
Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей.
Само действие сокращения алгебраической дроби базируется на основном свойстве алгебраической дроби, выражаемой равенством undefined , где a , b , c – некие многочлены, причем b и c – ненулевые. Первым шагом дробь приводится к виду a · c b · c , в котором мы сразу замечаем общий множитель c . Вторым шагом – выполняем сокращение, т.е. переход к дроби вида a b .
Характерные примеры
Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби:
5 5 = 1 ; — 2 3 — 2 3 = 1 ; x x = 1 ; — 3 , 2 · x 3 — 3 , 2 · x 3 = 1 ; 1 2 · x — x 2 · y 1 2 · x — x 2 · y ;
Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение.
Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).
К примеру, 24 1260 = 2 · 2 · 2 · 3 2 · 2 · 3 · 3 · 5 · 7 = 2 3 · 5 · 7 = 2 105
Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким:
24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 — 2 3 2 — 1 · 5 · 7 = 2 105
(числитель и знаменатель разделены на общий множитель 2 2 · 3 ). Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:
24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 2 2 · 3 3 2 · 1 5 · 7 = 2 1 · 1 3 · 1 35 = 2 105
По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами.
Пример 1
Задана алгебраическая дробь — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z .
Необходимо произвести ее сокращение.
Решение
Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение:
27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · c · z = = — 3 · 3 · a · a · a 2 · c · c · c · c · c · c = — 9 · a 3 2 · c 6
Однако, более рациональным способом будет запись решения в виде выражения со степенями:
27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = — 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = = — 3 3 — 1 2 · a 5 — 2 1 · 1 · 1 c 7 — 1 · 1 = · — 3 2 · a 3 2 · c 6 = · — 9 · a 3 2 · c 6 .
Ответ: — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 9 · a 3 2 · c 6
Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число.
Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).
Пример 2
Задана дробь 2 5 · x 0 , 3 · x 3 . Необходимо выполнить ее сокращение.
Решение
Возможно сократить дробь таким образом:
2 5 · x 0 , 3 · x 3 = 2 5 3 10 · x x 3 = 4 3 · 1 x 2 = 4 3 · x 2
Попробуем решить задачу иначе, предварительно избавившись от дробных коэффициентов – умножим числитель и знаменатель на наименьшее общее кратное знаменателей этих коэффициентов, т.е. на НОК (5 , 10) = 10 . Тогда получим:
2 5 · x 0 , 3 · x 3 = 10 · 2 5 · x 10 · 0 , 3 · x 3 = 4 · x 3 · x 3 = 4 3 · x 2 .
Ответ: 2 5 · x 0 , 3 · x 3 = 4 3 · x 2
Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует.
Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.
Пример 3
Задана рациональная дробь 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 . Необходимо ее сократить.
Решение
Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки:
2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · (a 2 + 14 · a + 49) b 3 · (a 2 — 49)
Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения:
2 · b 2 · (a 2 + 14 · a + 49) b 3 · (a 2 — 49) = 2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7)
Хорошо заметно, что возможно сократить дробь на общий множитель b 2 · (a + 7) . Произведем сокращение:
2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7) = 2 · (a + 7) b · (a — 7) = 2 · a + 14 a · b — 7 · b
Краткое решение без пояснений запишем как цепочку равенств:
2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · (a 2 + 14 a + 49) b 3 · (a 2 — 49) = = 2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7) = 2 · (a + 7) b · (a — 7) = 2 · a + 14 a · b — 7 · b
Ответ: 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · a + 14 a · b — 7 · b .
Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки.
Пример 4
Дана алгебраическая дробь 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 . Необходимо осуществить ее сокращение, если это возможно.
Решение
На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. Вынесем за скобки множитель х в числителе:
1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2
Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x 2 · y . Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов:
x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2 = x · — 2 7 · — 7 2 · 1 5 + x 2 · y 5 · x 2 · y — 1 5 · 3 1 2 = = — 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10
Теперь становится виден общий множитель, осуществляем сокращение:
2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10 = — 2 7 · x 5 = — 2 35 · x
Ответ: 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = — 2 35 · x .
Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В прошлый раз мы составили план, следуя которому, можно научиться быстро сокращать дроби. Теперь рассмотрим конкретные примеры сокращения дробей.
Примеры .
Проверяем, а не делится ли бо́льшее число на меньшее (числитель на знаменатель или знаменатель на числитель)? Да, во всех трех этих примерах бо́льшее число делится на меньшее. Таким образом, каждую дробь сокращаем на меньшее из чисел (на числитель либо на знаменатель). Имеем:
Проверяем, а не делится ли бо́льшее число на меньшее? Нет, не делится.
Тогда переходим к проверке следующего пункта: а не оканчивается ли запись и числителя, и знаменателя одним, двумя или несколькими нулями? В первом примере запись числителя и знаменателя оканчивается нулем, во втором — двумя нулями, в третьем — тремя нулями.
Значит, первую дробь сокращаем на 10, вторую — на 100, третью — на 1000:
Получили несократимые дроби.
Бо́льшее число на меньшее не делится, запись чисел нулями не оканчивается.
Теперь проверяем, а не стоят ли числитель и знаменатель в одном столбце в таблице умножения? 36 и 81 оба делятся на 9, 28 и 63 — на 7, а 32 и 40 — на 8 (они делятся еще и на 4, но если есть возможность выбора, всегда сокращать будем на бо́льшее). Таким образом, приходим к ответам:
Все полученные числа являются несократимыми дробями.
Бо́льшее число на меньшее не делится. А вот запись и числителя, и знаменателя оканчивается нулем. Значит, сокращаем дробь на 10:
Эту дробь еще можно сократить. Проверяем по таблице умножения: и 48, и 72 делятся на 8. Сокращаем дробь на 8:
Полученную дробь еще можем сократить на 3:
Эта дробь — несократимая.
Бо́льшее из чисел на меньшее не делится. Запись числителя и знаменателя оканчивается на нуль.Значит, сокращаем дробь на 10.
Полученные в числителе и знаменателе числа проверяем на и . Так как сумма цифр и 27, и 531 делятся на 3 и на 9, то эту дробь можно сократить как на 3, так и на 9. Выбираем большее и сокращаем на 9. Полученный результат — несократимая дробь.
На первый взгляд алгебраические дроби кажутся очень сложными, и неподготовленный учащийся может подумать, что с ними невозможно ничего сделать. Нагромождение переменных, чисел и даже степеней навевает страх. Тем не менее, для сокращения обычных (например, 15/25) и алгебраических дробей используются одни и те же правила.
Шаги
Сокращение дробей
Ознакомьтесь с действиями с простыми дробями. Операции с обычными и алгебраическими дробями аналогичны. К примеру, возьмем дробь 15/35. Чтобы упростить эту дробь, следует найти общий делитель . Оба числа делятся на пять, поэтому мы можем выделить 5 в числителе и знаменателе:
15→
5 * 335 → 5 * 7
Теперь можно сократить общие множители , то есть вычеркнуть 5 в числителе и знаменателе.
В результате получаем упрощенную дробь 3/7 . В алгебраических выражениях общие множители выделяются точно так же, как и в обычных. В предыдущем примере мы смогли легко выделить 5 из 15 — тот же принцип применим и к более сложным выражениям, таким как 15x – 5. Найдем общий множитель. В данном случае это будет 5, так как оба члена (15x и -5) делятся на 5. Как и ранее, выделим общий множитель и перенесем его влево .
15x – 5 = 5 * (3x – 1)
Чтобы проверить, все ли правильно, достаточно умножить на 5 стоящее в скобках выражение — в результате получатся те же числа, что были сначала. Сложные члены можно выделять точно так же, как и простые. Для алгебраических дробей применимы те же принципы, что и для обычных. Это наиболее простой способ сократить дробь. Рассмотрим следующую дробь:
(x+2)(x-3)(x+2)(x+10)
Отметим, что и в числителе (сверху), и в знаменателе (снизу) присутствует член (x+2), поэтому его можно сократить так же, как общий множитель 5 в дроби 15/35:
(x+2) (x-3)→
(x-3)(x+2) (x+10) → (x+10)
В результате получаем упрощенное выражение: (x-3)/(x+10)
Сокращение алгебраических дробей
Найдите общий множитель в числителе, то есть в верхней части дроби.
9x-3При сокращении алгебраической дроби первым делом следует упростить обе ее части. Начните с числителя и постарайтесь разложить его на как можно большее число множителей. Рассмотрим в данном разделе следующую дробь:
15x+6
Начнем с числителя: 9x – 3. Для 9x и -3 общим множителем является число 3. Вынесем 3 за скобки, как это делается с обычными числами: 3 * (3x-1). В результате данного преобразования получится следующая дробь:
3(3x-1)15x+6
Найдите общий множитель в числителе. Продолжим выполнение приведенного выше примера и выпишем знаменатель: 15x+6. Как и раньше, найдем, на какое число делятся обе части. И в этом случае общим множителем является 3, так что можно записать: 3 * (5x +2). Перепишем дробь в следующем виде:
3(3x-1)3(5x+2)
Сократите одинаковые члены. На этом шаге можно упростить дробь. Сократите одинаковые члены в числителе и знаменателе.
3 (3x-1)В нашем примере это число 3.
→
(3x-1)3 (5x+2) → (5x+2)
Определите, что дробь имеет простейший вид. Дробь полностью упрощена в том случае, когда в числителе и знаменателе не осталось общих множителей. Учтите, что нельзя сокращать те члены, которые стоят внутри скобок — в приведенном примере нет возможности выделить x из 3x и 5x, поскольку полными членами являются (3x -1) и (5x + 2). Таким образом, дробь не поддается дальнейшему упрощению, и окончательный ответ выглядит следующим образом:
(3x-1) (5x+2)
Потренируйтесь сокращать дроби самостоятельно. Лучший способ усвоить метод заключается в самостоятельном решении задач. Под примерами приведены правильные ответы.
4(x+2)(x-13)(4x+8)
Ответ: (x=13)
2x 2 -x5x
Ответ: (2x-1)/5
Специальные приемы
Вынесите отрицательный знак за пределы дроби.
3(x-4)Предположим, дана следующая дробь:
5(4-x)
Заметьте, что (x-4) и (4-x) “почти” идентичны, но их нельзя сократить сразу, поскольку они “перевернуты”. Тем не менее, (x — 4) можно записать как -1 * (4 — x), подобно тому как (4 + 2x) можно переписать в виде 2 * (2 + x). Это называется “переменой знака”.
-1 * 3(4-x)5(4-x)
Теперь можно сократить одинаковые члены (4-x):
-1 * 3 (4-x)5 (4-x)
Итак, получаем окончательный ответ: -3/5 . Научитесь распознавать разницу квадратов. Разница квадратов — это когда квадрат одного числа вычитается из квадрата другого числа, как в выражении (a 2 — b 2). Разницу полных квадратов всегда можно разложить на две части — сумму и разницу соответствующих квадратных корней. Тогда выражение примет следующий вид:
A 2 — b 2 = (a+b)(a-b)
Этот прием очень полезен при поиске общих членов в алгебраических дробях.
- Проверьте, правильно ли вы разложили то или иное выражение на множители. Для этого перемножьте множители — в результате должно получиться то же самое выражение.
- Чтобы полностью упростить дробь, всегда выделяйте наибольшие множители.
Калькулятор сокращающих дробей | Онлайн-калькулятор для упрощения дробей
Калькулятор сокращающих дробей: Калькулятор сокращающих дробей — это онлайн-инструмент, который отображает уменьшенную или упрощенную форму дроби. Все, что вам нужно сделать, это указать входное значение, то есть дробь, в поле ввода и нажать кнопку ввода, чтобы быстро отобразить вывод. Этот удобный инструмент ускоряет ваши расчеты и моментально отображает результат. Простой калькулятор сведет дроби, неправильные дроби к простейшей форме и даже шаг за шагом покажет выполняемую работу. Калькулятор разделит и числитель, и знаменатель на их наибольший общий делитель и сократит его до наименьшего члена.
Пример: Сокращающая дробь 25/10 (или) Сокращающая дробь 46/22 (или) Сокращающая дробь 57/15
Вот несколько примеров расчетов уменьшающих дробей.

- Редукционная фракция 812/14
- Редукционная фракция 794/38
- Редукционная фракция 230/20
- Редукционная фракция 194/22
- Редукционная фракция 7 88/54
- Редукционная дробь 472/50
- Редукционная фракция 664/56
- Редукционная фракция 110/28
- Редукционная фракция 100/90
- Редукционная фракция 558/36
- Редукционная фракция 842/72
- Редукционная фракция 778/48
9 0015 Редукционная дробь 480/80- Фракция редукционная 518/62
- Фракция редукционная 628/34
- Фракция редукционная 898/78
- Фракция редукционная 7254/90
- Фракция редукционная 4962/18 9001 6
- Уменьшающая дробь 6912/66
- Редукционная фракция 5640/51
- Редукционная фракция 9849/84
- Редукционная фракция 1587/21
- Редукционная фракция 8202/30
- Редукционная фракция 356 1/39
- Сокращающая дробь 5520/ 81
- Восстанавливающая фракция 7890/99
- Восстанавливающая фракция 8373/93
- Восстанавливающая фракция 6933/63
- Восстанавливающая фракция 6525/69
- Восстанавливающая фракция 6465/1 5
- Уменьшающая дробь 9792/60
- Редукционная дробь 3678/72
сообщите об этом объявлении фракция 9660/855
Редукционная фракция 7725/545 Восстанавливающая фракция 3035/495 Восстанавливающая фракция 5505/840 Восстанавливающая фракция 8695/380 Восстанавливающая фракция 1190/370 Восстанавливающая фракция 1910/ 175 Уменьшающая дробь 9340/985 Редукционная фракция 6075/570 Редукционная фракция 9995/565 Редукционная фракция 4615/515 Редукционная фракция 3430/120 Редукционная дробь 5515/585 Редукционная дробь 1235/ 450 сообщите об этом объявлении
Связанные калькуляторы:
- Не подходит для калькулятора смешанных чисел дробей
В математике дробь обычно определяет часть целого.
Дробь должна быть представлена в виде числителя и знаменателя. Дроби подразделяются на несколько типов, таких как похожие, непохожие, правильные, неправильные, смешанные и так далее. Если данная дробь представлена большим целочисленным значением, ее можно упростить, уменьшив ее до наименьшего целочисленного значения. Например, если числитель и знаменатель имеют общий множитель, исключите его.
Как упростить дроби?
Одним из самых простых способов сокращения дробей является использование Калькулятора сокращения на нашей странице. Если вы хотите уменьшить дроби вручную, есть несколько способов. Мы перечислили некоторые из них. Найдите тот, который наиболее подходит для вас, и легко сократите дроби.
Метод проб и ошибок
При использовании метода проб и ошибок для упрощения дробей вам просто нужно разделить числитель и знаменатель на наименьшее число, которое, по вашему мнению, является общим множителем для обоих. Продолжайте процесс и после каждого успешного сокращения нужно повторять процесс до тех пор, пока числитель и знаменатель не будут иметь больше общих множителей.
Метод наибольшего общего множителя
Чтобы использовать метод наибольшего общего множителя для упрощения дробей, вам необходимо вычислить НОД числителя и знаменателя. После этого разделите числитель и знаменатель на их наибольший общий делитель.
Независимо от того, какой метод упрощения дробей вы выберете, он может быть утомительным и трудоемким. Мы предлагаем вам использовать наш Калькулятор сокращения при работе с дробями.
Пример
Сократить дробь 36/45 до наименьшего члена?
Решение:
Для дроби 36/45 36 — числитель, а 45 — знаменатель
Первый шаг при сокращении дробей — найти НОД числителя и знаменателя
НОД 36, 4 5 это 9 наибольший общий делитель, который делит оба числа
36/45 = (36 ÷ 9)/(45÷ 9)
= 4/5
Следовательно, 36/45 можно свести к простейшим дробям как 4/5
Процедура использования калькулятора сокращающихся дробей приведена ниже.
- Введите числитель и знаменатель в поле ввода, предназначенное для калькулятора.
- После этого нажмите кнопку «Ввод» рядом с полем ввода или с клавиатуры.
- Наконец, вы получите вывод, то есть уменьшенную форму дробей, отображаемую на экране.
1. Как привести дробь к простейшей форме?
Вы можете привести дробь к простейшей форме, разделив числитель и знаменатель на их НОД.
2. Как быстро упростить большие дроби?
Вы можете использовать Калькулятор сокращающих дробей на нашей странице, чтобы слишком быстро и легко упростить большие дроби.
3. Какие есть два способа упростить дроби?
Два способа упрощения дробей: метод проб и ошибок и метод наибольшего общего множителя.
4. Где я могу получить примеры упрощения дробей шаг за шагом?
Вы можете найти примеры упрощения дробей шаг за шагом на нашей странице.
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами.Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
Символ Название символа Символ Значение Пример + плюс сложение 1/2 + 1/3 — минус вычитание 90 003 1 1/2 — 2/3 * звездочка умножение 2/3 * 3/4 × знак умножения умножение 2/3 × 5/6 : знак деления деление 91/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt(1/16)
• сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3Калькулятор следует известным правилам для порядка операций .
Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание
BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание.
GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
- Четверть
Четверть числа 72 это:- Дробь и десятичная дробь
Запишите дробь и десятичную дробь. Один и два плюс три и пять сотых- Энди получает
Энди ошибается на пять из 15 вопросов в своем тесте по математике.На какую часть вопроса Энди ответил правильно?
- Компания
Компания имеет 860 сотрудников, из которых 500 женщин. Напишите дробь, обозначающую сотрудниц компании.- Мэтью
У Мэтью восемь карандашей. У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце?- Значение Z
При x = -9, каково значение Z, где Z равно числителю дроби x минус 17 в знаменателе 6,5 конец дроби Дайте ответ с точностью до 2 знаков после запятой.- Коричневый или черный
У Макса 13 пар носков. Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?- Из 550 000,00
Из 550 000,00 было использовано 325 000,00. Какая часть от общей суммы была использована?- Класс А IV.А
В классе 15 девочек и 30 мальчиков. Какая часть класса представляет мальчиков?- Наименьшие члены 2
Мы можем записать выражение 4/12 в его наименьшем члене как 1/3.2 корень из х 3 корень из у: Mathway | Популярные задачи
Mathway | Популярные задачи
1 Найти точное значение sin(30) 2 Найти точное значение sin(45) 3 Найти точное значение sin(30 град. ) 4 Найти точное значение sin(60 град. ) 5 Найти точное значение tan(30 град. ) 6 Найти точное значение arcsin(-1) 7 Найти точное значение sin(pi/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение sin(45 град. )
10 Найти точное значение sin(pi/3) 11 Найти точное значение arctan(-1) 12 Найти точное значение cos(45 град. ) 13 Найти точное значение cos(30 град. ) 14 Найти точное значение tan(60) 15 Найти точное значение csc(45 град. ) 16 Найти точное значение tan(60 град. ) 17 Найти точное значение sec(30 град. )
18 Найти точное значение cos(60 град. ) 19 Найти точное значение cos(150) 20 Найти точное значение sin(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение tan(45 град. ) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 град. ) 25 Найти точное значение sec(45 град. )
26 Найти точное значение csc(30 град. ) 27 Найти точное значение sin(0) 28 Найти точное значение sin(120) 29 Найти точное значение cos(90) 30 Преобразовать из радианов в градусы pi/3 31 Найти точное значение tan(30) 32 Преобразовать из градусов в радианы 45 33 Найти точное значение cos(45) 34 Упростить sin(theta)^2+cos(theta)^2 35 Преобразовать из радианов в градусы pi/6 36 Найти точное значение cot(30 град. )
37 Найти точное значение arccos(-1) 38 Найти точное значение arctan(0) 39 Найти точное значение cot(60 град. ) 40 Преобразовать из градусов в радианы 30 41 Преобразовать из радианов в градусы (2pi)/3 42 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение tan(pi/2) 45 Найти точное значение sin(300) 46 Найти точное значение cos(30) 47 Найти точное значение cos(60) 48 Найти точное значение cos(0) 49 Найти точное значение cos(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение cos(210) 52 Найти точное значение sec(60 град. )
53 Найти точное значение sin(300 град. ) 54 Преобразовать из градусов в радианы 135 55 Преобразовать из градусов в радианы 150 56 Преобразовать из радианов в градусы (5pi)/6 57 Преобразовать из радианов в градусы (5pi)/3 58 Преобразовать из градусов в радианы 89 град. 59 Преобразовать из градусов в радианы 60 60 Найти точное значение sin(135 град. )
61 Найти точное значение sin(150) 62 Найти точное значение sin(240 град. ) 63 Найти точное значение cot(45 град. ) 64 Преобразовать из радианов в градусы (5pi)/4 65 Найти точное значение sin(225) 66 Найти точное значение sin(240) 67 Найти точное значение cos(150 град. ) 68 Найти точное значение tan(45) 69 Вычислить sin(30 град. )
70 Найти точное значение sec(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение csc(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение tan((5pi)/3) 75 Найти точное значение tan(0) 76 Вычислить sin(60 град. ) 77 Найти точное значение arctan(-( квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3pi)/4 79 Найти точное значение sin((7pi)/4) 80 Найти точное значение arcsin(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найти точное значение csc(45) 83 Упростить arctan( квадратный корень из 3) 84 Найти точное значение sin(135) 85 Найти точное значение sin(105) 86 Найти точное значение sin(150 град. )
87 Найти точное значение sin((2pi)/3) 88 Найти точное значение tan((2pi)/3) 89 Преобразовать из радианов в градусы pi/4 90 Найти точное значение sin(pi/2) 91 Найти точное значение sec(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение arcsin(0) 95 Найти точное значение sin(120 град. )
96 Найти точное значение tan((7pi)/6) 97 Найти точное значение cos(270) 98 Найти точное значение sin((7pi)/6) 99 Найти точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразовать из градусов в радианы 88 град. § 3. УРАВНЕНИЯ
Причина
При каких преобразованиях это может происходить
Пример неправильного (или неполного) решения
1.
Появление посторонних корней
в) применение к обеим частям уравнения функции, которая не является возрастающей или убывающей.
Возведение обеих частей уравнения в четную степень или применение к обеим частям уравнения тригонометрических функций (см. с. 272)
х — 1 = 2х + 1. Возведем обе части уравнения в квадрат:
(х — 1)2 = (2х + 1)2. Получим 3х2 + 6х = 0, х1 = 0, х2 = —2
2. Потеря корней
Явное или неявное сужение ОДЗ заданного уравнения, в частности выполнение преобразований, в ходе которых происходит неявное деление на нуль
1. Деление обеих частей уравнения на выражение с переменной
х2= х.

Поделив обе части уравнения на х, получим
х = 1
2. Сложение, вычитание, умножение или деление обеих частей уравнения на выражение, ОДЗ которого уже, чем ОДЗ заданного уравнения
х2 = 1.
Если к обеим частям уравнения прибавить , то получим уравнение
x2 + x = 1 + x, у которого только один корень х = 1
Где ошибка
Как получить правильное (или полное) решение
Пример правильного (или полного) решения
при решении уравнения
х1 = 0 не является корнем заданного уравнения
Выполнить проверку подстановкой корней в заданное уравнение
В данном уравнении не было необходимости возводить в квадрат.
х — 1 = 2х + 1.
►х — 2х = 1 + 1, х = —2.
Ответ: —2. <
Если применить возведение в квадрат, то проверка показывает, что х2 = —2 — корень, a х1 = 0 — посторонний корень
при решении уравнения
Потеряли корень х = 0, поскольку после деления на х фактически получили уравнение 2
ОДЗ которого: х( Ф)= 0, то есть сузили ОДЗ заданного уравнения.
Те значения, на которые сузилась ОДЗ, необходимо рассмотреть отдельно
► 1. При х = 0 получаем 02 = 0 — верное равенство, таким образом, х = 0 — корень.
2. При х Ф 0 получаем
2 х = 1
Ответ. 0; 1.
(Конечно, удобнее решать так: x2 — x = 0,
х (х — 1) = 0, х = 0 или х = 1.)
Потеряли корень х = —1, поскольку ОДЗ данного уравнения: х — любое число, а x существует только при х 1 0.
В данном уравнении не было необходимости прибавлять к обеим частям -\/x.
► х2 = 1, х = ±1.
Ответ: ±1.
(Если бы пришлось прибавить к обеим частям yfx, то при x < 0 данное уравнение необходимо рассмотреть отдельно, и тогда получим еще и корень х = —1.)
Объяснение и обоснование
1. Конечная ОДЗ. Напомним, что в случае, когда дано уравнение f (x) = g (x), общая область определения для функций f (x) и g (x) называется областью допустимых значений этого уравнения. Понятно, что каждый корень заданного уравнения принадлежит как области определения функции f (x), так и области определения функции g (x). Таким образом, каждый корень
уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет
в некоторых случаях за счет анализа ОДЗ получить решение уравнения.
Например, если дано уравнение л/x — 2 + V4 — 2x = 3x — 6, то его ОДЗ можно
[x — 210 Jx 12,
задать с помощью системы Решая эту систему, получаем —
{4 — 2x 10. {x < 2,
то есть х = 2. Таким образом, ОДЗ данного уравнения состоит только из одного значения х = 2. Но если только для одного числа необходимо выяснить, является ли оно корнем данного уравнения, то достаточно подставить это значение переменной в уравнение. В результате получаем верное числовое равенство (0 = 0). Следовательно, х = 2 — корень данного уравнения. Других корней у этого уравнения быть не может, поскольку все корни уравнения находятся в его ОДЗ, а там нет других значений, кроме х = 2.
Рассмотренный пример позволяет выделить о р и е н т и р для решения аналогичных уравнений:
Если f (x) > а, то равенство f (x) = g (x) не может выполняться, потому что g (x) < а, то есть при f (x) > а данное уравнение корней не имеет.
Остается только случай f (x) = a, но, учитывая необходимость выполнения равенства f (x) = g (x), имеем, что тогда и g (x) = а. Таким образом, мы обосновали, что выполнение равенства f (x) = g (x) (при условии f (x) 1 а и g (x) < а) гарантирует одновременное выполнение равенств f (x) = а и g (x) = а (и наоборот, если одновременно выполняются равенства f (x) = а и g (x) = а, то выполняется и равенство f (x) = g (x)). Как было показано в п. 3.1, это и
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 8.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения f1 (x) + f2 (x) + … + fn (x) = 0, в котором все функции- слагаемые неотрицательны (f1 (x) 1 0; f2 (x) 1 0; …; fn (x) 1 0).
• Если предположить, что f1 (x) > 0, то сумма всех функций, стоящих в левой части этого уравнения, может равняться нулю только тогда, когда сумма f2 (x) + .
.. + fn (x) будет отрицательной. Но это невозможно, поскольку по условию все функции неотрицательные. Таким образом, при f1 (x) > 0 данное уравнение не имеет корней. Эти же рассуждения можно повторить для любой другой функции-слагаемого. Остается единственная возможность — все функции-слагаемые равны нулю (очевидно, что в этом случае равенство f1 (x) + f2 (x) + … + fn (x) = 0 обязательно будет выполняться). Таким образом, сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.
Например, чтобы решить уравнение x4 + | x — 1 | = 2x2 — 1, достаточно перенести все члены в одну сторону, записать уравнение в виде (x2 — 1)2 + | x — 1 | = 0 и учесть, что функции (x2 — 1)2 и | x — 1 | неотрицательные. Таким образом, данное уравнение равносильно системе
Из второго уравнения получаем х = 1, что удовлетворяет и всей системе.
Следовательно, данное уравнение имеет единственный корень х = 1.
3. Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения. Полезно помнить специальные теоремы о корнях уравнения.
Теор ем а 1. Если в уравнении f (я) = а функция f (я) возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
Графически утверждение теоремы проиллюстрировано на рисунке 39. Прямая у = а пересекает график возрастающей на промежутке [а; в] функции у = f (x) только в одной точке. Это и означает, что уравнение f (x) = а не может иметь больше одного корня на промежутке [а; в]. Докажем это утверждение аналитически.
9 Если на промежутке [а; в] уравнение имеет корень x0, то f (x0) = а.
Других корней быть не может, поскольку для возрастающей функции f (x) при x > x0 получаем неравенство f (x) > f (x0) = а, а при x < x0 — неравенство f (x) < f (x0) = а. Таким образом, при x Ф x0 f (x) Ф а. Аналогично и для убывающей функции при x Ф x0 получаем f (x) Ф а.
Теор ема 2. Если в уравнении f (x) = g (x) функция f (x) возрастает на некотором промежутке, а функция g (x) убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более чем один корень на этом промежутке.
Графически утверждение теоремы проиллюстрировано на рисунке 40.
в Если на промежутке [а; в] уравнение имеет корень x0, то f (x0) = g (x0) = а. Других корней быть не может, поскольку, например, для возрастающей функции f (x) и убывающей функции g (x) при x > x0 имеем f (x) > а, a g (x) < а, таким образом, f (x) Ф g (x).
Аналогично и при x < x0 f (x) Ф g (x).
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение x3 + x = 10, достаточно заметить, что функция f (x) = x3 + x является возрастающей на всей числовой прямой (как сумма двух возрастающих функций) и что x = 2 — корень* этого уравнения (23 + 2 = 10; 10 = 10). Таким образом, данное уравнение f (x) = 10 имеет единственный корень x = 2.
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Решим с помощью теоремы 2 уравнение x + x = —.
► Сначала следует учесть его ОДЗ: x Ф 0 и вспомнить, что функция у = 2 на
всей области определения не является ни убывающей, ни возрастающей (с. 28), но она убывает на каждом из промежутков (—то; 0) и (0; +“). Поэтому рассмотрим каждый из этих промежутков отдельно.
1) При x > 0 данное уравнение имеет корень x = 1 (1 +1 = -,2 = 2).
Функция f (x) = x3 + x возрастает при x > 0 (как было показано выше, она
2
возрастает на множестве R), а функция g (x) = — убывает на промежутке
x
x > 0. Таким образом, данное уравнение f (x) = g (x) при x > 0 имеет единственный корень x = 1.
Комментарий
Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ (х Ф 0) x4 > 0, то в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2.
Задача 2 Решите систему уравнений
Рассмотрим функцию
Решение
Jx 10,
[у 10.f (t) = Vt +13. На своей области определения (t 1 0) эта функция является возрастающей (как сумма двух возрастающих функций).
Тогда первое уравнение заданной системы, которое имеет вид f (x) = f (у), равносильно уравнению x = у. Таким образом, на ОДЗ заданная система равносильна
Jx = у, системе —
[x2 + 3у2 = 36.
Подставляя x = у во второе уравнение системы, имеем 4у2 = 36, у2 = 9, у = ±3. Учитывая, что на ОДЗ у 1 0, получаем у = 3. Тогда x = у = 3. Ответ: (3; 3). <1
\4x-
-x2 + 3у2 = 36.
Комментарий
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство f (x) = f (у) для возрастающей функции возможно тогда и только тогда, когда х = у, поскольку возрастающая функция может принимать одинаковые значения только при одном значении аргумента.
а = в.
Вопросы для контроля
1. Объясните на примерах, как можно использовать свойства функций при решении уравнений.
2*. Обоснуйте правильность ориентиров по решению уравнений с использованием свойств функций, приведенных в таблице 8 (с. 60).
Мэтуэй | Популярные задачи
1 Найти точное значение грех(30) 2 Найти точное значение грех(45) 3 Найти точное значение грех(30 градусов) 4 Найти точное значение грех(60 градусов) 5 Найти точное значение загар (30 градусов) 6 Найти точное значение угловой синус(-1) 7 Найти точное значение грех(пи/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение грех(45 градусов) 10 Найти точное значение грех(пи/3) 11 Найти точное значение арктан(-1) 12 Найти точное значение cos(45 градусов) 13 Найти точное значение cos(30 градусов) 14 Найти точное значение желтовато-коричневый(60) 15 Найти точное значение csc(45 градусов) 16 Найти точное значение загар (60 градусов) 17 Найти точное значение сек(30 градусов) 18 Найти точное значение cos(60 градусов) 19 Найти точное значение cos(150) 20 Найти точное значение грех(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение загар (45 градусов) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 градусов) 25 Найти точное значение сек(45 градусов) 26 Найти точное значение csc(30 градусов) 27 Найти точное значение грех(0) 28 Найти точное значение грех(120) 29 Найти точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найти точное значение желтовато-коричневый(30) 32 9235 Преобразовать из радианов в градусы пи/6 36 Найти точное значение детская кроватка(30 градусов) 37 Найти точное значение арккос(-1) 38 Найти точное значение арктический(0) 39 Найти точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение тан(пи/2) 45 Найти точное значение грех(300) 46 Найти точное значение соз(30) 47 Найти точное значение соз(60) 48 Найти точное значение соз(0) 49 Найти точное значение соз(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение cos(210) 52 Найти точное значение сек(60 градусов) 53 Найти точное значение грех(300 градусов) 54 Преобразование градусов в радианы 135 55 Преобразование градусов в радианы 150 56 Преобразовать из радианов в градусы (5 дюймов)/6 57 Преобразовать из радианов в градусы (5 дюймов)/3 58 Преобразование градусов в радианы 89 градусов 59 Преобразование градусов в радианы 60 60 Найти точное значение грех(135 градусов) 61 Найти точное значение грех(150) 62 Найти точное значение грех(240 градусов) 63 Найти точное значение детская кроватка(45 градусов) 64 Преобразовать из радианов в градусы (5 дюймов)/4 65 Найти точное значение грех(225) 66 Найти точное значение грех(240) 67 Найти точное значение cos(150 градусов) 68 Найти точное значение желтовато-коричневый(45) 69 Оценить грех(30 градусов) 70 Найти точное значение сек(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение КСК(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение загар((5pi)/3) 75 Найти точное значение желтовато-коричневый(0) 76 Оценить грех(60 градусов) 77 Найти точное значение arctan(-( квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3 пи)/4 79 Найти точное значение sin((7pi)/4) 80 Найти точное значение угловой синус(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найти точное значение КСК(45) 83 Упростить арктан(квадратный корень из 3) 84 Найти точное значение грех(135) 85 Найти точное значение грех(105) 86 Найти точное значение грех(150 градусов) 87 Найти точное значение sin((2pi)/3) 88 Найти точное значение загар((2pi)/3) 89 Преобразовать из радианов в градусы пи/4 90 Найти точное значение грех(пи/2) 91 Найти точное значение сек(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение угловой синус(0) 95 Найти точное значение грех(120 градусов) 96 Найти точное значение желтовато-коричневый ((7pi)/6) 97 Найти точное значение соз(270) 98 Найти точное значение sin((7pi)/6) 99 Найти точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразование градусов в радианы 88 градусов Является ли кубический корень тем же самым, что и возведение в степень 1/3?
Недавно я столкнулся с интересным несоответствием, касающимся функции кубического корня.
Кубический корень
В Wolfram|Alpha (который использует систему компьютерной алгебры Mathematica в своей основе), если вы попросите его построить график, вы получите следующее, как и ожидалось:
[Источник изображения: Wolfram|Alpha]В поле поиска я ввел «кубический корень из x», и он указал, что «Результат» был правильно записан как .
Этот график является отражением графика y = х 3 в строке у = х . Это обратные функции.
Мы знаем, что этот кубический корень из отрицательного числа является отрицательным, поэтому, например, и мы можем видеть, что это имеет смысл на графике выше.
Wolfram|Alpha утверждает, что существует один корень ( x = 0), а домен и диапазон являются действительными числами, что согласуется с графиком выше.
ПРИМЕЧАНИЕ: Мелким шрифтом Wolfram|Alpha указано:
Предполагая, что «кубический корень из» является действительным корнем.
Есть возможность посмотреть «главный корень», но это дало тот же результат.
Возведение в степень 1/3
На раннем этапе изучения корней и дробных степеней мы узнаем, что можем записывать корни в терминах дробных показателей. В общем, это означает:
Таким образом, для квадратного корня мы имеем:
и для кубического корня:
.
Таким образом, мы ожидаем, что график для будет таким же, как и график для .
Но это не так. Вот что возвращает Wolfram|Alpha, когда я прошу его построить график:
[Источник изображения: Wolfram|Alpha]Синяя кривая помечена как «реальная часть», а красная — как «воображаемая часть».
Любопытно, что значение «Ввод» указано как: , но на самом деле это не то, что я ввел. Итак, часть ответа касается, а остальная часть ответа — нет.
Мы знаем из раздела о комплексных корнях (см. особенно Упражнение 4 в конце), что кубическое уравнение будет иметь 3 корня (точно так же, как квадратное уравнение имеет 2 корня).
Эти 3 корня могут быть действительными или смесью действительных и комплексных корней.
Wolfram|Alpha верно указывает, что есть мнимые части, но правилен ли их график? Ведь кубический корень из отрицательного числа должен быть отрицательным?
Пример: Чему равны все кубические корни из −8?
Я немного уменьшил масштаб, чтобы получить этот график, и добавил несколько направляющих сегментов (зеленые):
[Источник изображения: Wolfram|Alpha]Используя то же мышление, что и в упражнении 4, упомянутом ранее, комплексные решения для x 3 = −8 должны находиться на расстоянии 120° друг от друга, что дает (где):
x = −2
x = 1 + 1,73j
x = 1 − 1,73j
График выше дает нам одно из этих решений (среднее один, так как мы можем видеть действительная часть равна 1, а мнимая часть равна 1,73), но не дает двух других решений.
И снова страница сообщает нам, что предполагается «главный корень», и дает нам возможность выбрать «действительнозначный корень».
Если мы сделаем это на этот раз, мы получим настоящую версию только для root, выглядящую как график в верхней части страницы.
Ответ Scientific Notebook
Scientific Notebook дает следующие 2 графика, которые я наложил друг на друга.
Синий график — , и Scientific Notebook дает полное действительное решение (в первом и третьем квадрантах), а пурпурный (розовый) график — только в положительном квадранте.
Ответы Geogebra и Desmos
И Geogebra, и Desmos дают один и тот же график «полного реального значения» для обоих и .
Аналогично квадратному корню
Я уже писал о количестве решений для √16. Конечно, ответ есть одно решение, тогда как если вас попросят решить, вы получите 2 решения.
Wolfram|Alpha и Scientific Notebook признают, что есть разница между (каждый раз есть один «главный» ответ) и , где нам нужно помнить комплексные корни.
Заключение
Не верьте компьютеру на слово, когда он дает вам график или решение какого-то уравнения.
Cos 60 cos 30: Mathway | Популярные задачи
Mathway | Популярные задачи
1 Найти точное значение sin(30) 2 Найти точное значение sin(45) 3 Найти точное значение sin(30 град. ) 4 Найти точное значение sin(60 град. ) 5 Найти точное значение tan(30 град. ) 6 Найти точное значение arcsin(-1) 7 Найти точное значение sin(pi/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение sin(45 град. )
10 Найти точное значение sin(pi/3) 11 Найти точное значение arctan(-1) 12 Найти точное значение cos(45 град. ) 13 Найти точное значение cos(30 град. ) 14 Найти точное значение tan(60) 15 Найти точное значение csc(45 град. ) 16 Найти точное значение tan(60 град. ) 17 Найти точное значение sec(30 град. )
18 Найти точное значение cos(60 град. ) 19 Найти точное значение cos(150) 20 Найти точное значение sin(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение tan(45 град. ) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 град. ) 25 Найти точное значение sec(45 град. )
26 Найти точное значение csc(30 град. ) 27 Найти точное значение sin(0) 28 Найти точное значение sin(120) 29 Найти точное значение cos(90) 30 Преобразовать из радианов в градусы pi/3 31 Найти точное значение tan(30) 32 Преобразовать из градусов в радианы 45 33 Найти точное значение cos(45) 34 Упростить sin(theta)^2+cos(theta)^2 35 Преобразовать из радианов в градусы pi/6 36 Найти точное значение cot(30 град. )
37 Найти точное значение arccos(-1) 38 Найти точное значение arctan(0) 39 Найти точное значение cot(60 град. ) 40 Преобразовать из градусов в радианы 30 41 Преобразовать из радианов в градусы (2pi)/3 42 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение tan(pi/2) 45 Найти точное значение sin(300) 46 Найти точное значение cos(30) 47 Найти точное значение cos(60) 48 Найти точное значение cos(0) 49 Найти точное значение cos(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение cos(210) 52 Найти точное значение sec(60 град. )
53 Найти точное значение sin(300 град. ) 54 Преобразовать из градусов в радианы 135 55 Преобразовать из градусов в радианы 150 56 Преобразовать из радианов в градусы (5pi)/6 57 Преобразовать из радианов в градусы (5pi)/3 58 Преобразовать из градусов в радианы 89 град. 59 Преобразовать из градусов в радианы 60 60 Найти точное значение sin(135 град. )
61 Найти точное значение sin(150) 62 Найти точное значение sin(240 град. ) 63 Найти точное значение cot(45 град. ) 64 Преобразовать из радианов в градусы (5pi)/4 65 Найти точное значение sin(225) 66 Найти точное значение sin(240) 67 Найти точное значение cos(150 град. ) 68 Найти точное значение tan(45) 69 Вычислить sin(30 град. )
70 Найти точное значение sec(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение csc(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение tan((5pi)/3) 75 Найти точное значение tan(0) 76 Вычислить sin(60 град. ) 77 Найти точное значение arctan(-( квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3pi)/4 79 Найти точное значение sin((7pi)/4) 80 Найти точное значение arcsin(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найти точное значение csc(45) 83 Упростить arctan( квадратный корень из 3) 84 Найти точное значение sin(135) 85 Найти точное значение sin(105) 86 Найти точное значение sin(150 град. )
87 Найти точное значение sin((2pi)/3) 88 Найти точное значение tan((2pi)/3) 89 Преобразовать из радианов в градусы pi/4 90 Найти точное значение sin(pi/2) 91 Найти точное значение sec(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение arcsin(0) 95 Найти точное значение sin(120 град. )
96 Найти точное значение tan((7pi)/6) 97 Найти точное значение cos(270) 98 Найти точное значение sin((7pi)/6) 99 Найти точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразовать из градусов в радианы 88 град. Пять принципов тайм-менеджмента для тех, кому мало 24 часов в сутках
Время дороже денег, ведь, в отличие от денег, пополнить этот ресурс невозможно.
Однако, как утверждает популярный бизнес-коуч и мотивационный спикер Эд Майлетт, если подойти к вопросу правильно, можно сделать каждые сутки длиннее втрое и расширить свое субъективное время. Он объясняет, как двигаться со скоростью света, что поможет добиться приятного чувства выполненного долга и почему первые полчаса каждого дня имеют решающее значение
Мотивационный спикер Эд Майлетт вырос в неблагополучной семье, увлекся бейсболом — и именно он стал для Майлетта и карьерным лифтом, и безопасным пространством для развития самооценки. В итоге самооценка его выросла до такой степени, что Майлетт стал одним из самых востребованных в мире мотивационных спикеров — то есть теперь он своими выступлениями вдохновляет и мотивирует.
Он уверен, что наши мечты и цели ближе, чем нам кажется, и для того, чтобы их реализовать, часто нужен всего еще один шаг: еще одно решение, еще одна встреча, еще одна книга.
Свою новую книгу он назвал The Power of One More («Сила еще одного») и объединил в ней мотивирующие советы, примеры из жизни и научные исследования, чтобы показать, какие стратегии помогают выйти на новый уровень, и получить тот результат, который вам нужен, но который вы до сих пор считали невозможным.
Книга, которая в русском переводе называется «Не стойте в очереди за успехом», выходит в мае в издательстве «Манн, Иванов и Фербер». Forbes публикует отрывок.
Восприятие времени
Время — это константа. Но мы относимся к нему как к переменной. Часто ли вы слышите такие фразы? «Уф! Этот день длится бесконечно». «Месяц пролетел незаметно». И моя любимая: «Не могу поверить, что выходные уже закончились».
В зависимости от опыта, возраста, текущих обстоятельств, занятости и наличия свободного времени наше восприятие времени постоянно меняется.
Ученые называют это субъективным временем, и оно совершенно не похоже на время на часах. Это то, как воспринимается скорость течения времени, а время на часах — это постоянная хронология, измеряемая тикающими стрелками настенных часов.
Время — фундаментальный элемент нашего бытия и восприятия окружающего мира. Наше представление о том, кто мы, формируется в результате того, как мозг связывает воспоминания, ощущения в настоящем и ожидания от будущего. Нейробиологи, лингвисты, психологи и когнитивисты интенсивно изучают восприятие времени уже сотни лет. Помимо прочего, ученым известно, что воспринимаемая длительность у каждого человека своя и не фокусируется на какой-то одной сенсорной системе. Напротив, восприятие времени представляет собой смешанную систему распределения, включающую кору головного мозга, мозжечок и базальные ганглии.
Помните главное: как только вы поймете, что можете изменить свое восприятие времени, вы сможете начать искривлять его и использовать в своих интересах.

Материал по теме
Время — ваш самый ценный актив
Время дороже денег. Деньги — восполняемый ресурс. Вы всегда можете пополнить свой банковский счет, но нельзя добавить в свою жизнь лишние годы. Ваше время ограничено. Если вам 40, нельзя перелистать календарь обратно и снова стать 30-летним.
Писатели, художники, авторы песен и поэты испокон веков романтизировали время:
- «Два самых могущественных воина — это терпение и время». Лев Толстой
- « Самый мудрый человек тот, кого больше всего раздражает потеря времени». Данте Алигьери
Моя любимая цитата о времени, пожалуй, самая простая, ее приписывают Бенджамину Франклину: «Время — деньги».

Когда ваше время закончится, нельзя будет перемотать пленку назад. Вернуть время невозможно. Однако нашим самым ценным активом часто манипулируют.
Субъективное время — это воспринимаемое время, напрямую связанное с интерпретацией мозгом нескольких переменных. По мере того, как мы становимся старше, скорость обработки мысленных образов мозгом и скорость их восприятия снижаются. Это часть естественного процесса старения. Зрение и пластичность мозга ухудшаются, нервные пути, по которым передается информация, разрушаются, и все это приводит к тому, что в нашем восприятии время ускоряется. Даже если отдельное действие происходит за долю секунды, на его обработку требуется больше времени. И мы теряем эту долю секунды тысячи раз в день.
Материал по теме
Есть еще несколько переменных, которые мы тоже не способны контролировать.
Когда мы физически устаем, наш мозг не может с той же скоростью передавать и обрабатывать информацию. Он уже неоптимально видит и осмысливает данные от органов зрения, слуха и осязания. Реакции замедляются, и нам кажется, что время ускоряется. На самом деле это мы замедляемся по отношению к остальному миру.
Вот почему футболисты, которые плохо отдохнули, слабо играют. Их способность к обработке мяча снижается. Это нарушает их способность чувствовать время. Они не могут своевременно улавливать внутриигровые переменные и реагировать на них. Сильно влияют на изменение восприятия времени психологические травмы, употребление наркотиков, сильное чувство страха или шока, СДВГ, аутизм, депрессия, шизофрения и некоторые другие факторы.
Пять принципов тайм-менеджмента
За последние 20 лет я глубоко усвоил концепцию максимального использования времени ради достижения своих целей.
И на самых первых этапах я обнаружил, что нужно уважать природу времени. Все успешные люди, в том числе я, считают это основой своего успеха.
Как и любая другая переменная, ваше отношение ко времени может сильно повлиять на то, как далеко вы пойдете. Я перепробовал самые разные стратегии тайм-менеджмента. Я добавлял и убирал элементы разных философских подходов, которые созвучны моим взглядам. И в итоге разработал собственную систему, которую называю пятью принципами тайм-менеджмента. Если вы сможете адаптировать и освоить их, то добьетесь большего успеха, заработаете больше денег, станете более продуктивными, добавите больше удовольствия и построите жизнь, которой будете наслаждаться.
Рассмотрим эти пять принципов.
1. Добавьте к своему дню больше «дней»
Тот, кто живет по принципу «еще одного раза», должен забыть о том, что в сутках 24 часа.
День длиной в 24 часа подходил нам до того, как у нас появились интернет, смартфоны, беспроводные технологии, компьютеризированные автомобили, самолеты, спутники и другие инструменты, позволяющие расширить свое присутствие и двигаться со скоростью света.
Теперь мы можем отправить электронное письмо в любую точку мира в одно мгновение. Мы можем проводить телемост с десятками или сотнями человек круглосуточно. Вместо того, чтобы идти в библиотеку или копаться в энциклопедии, мы можем найти в поисковой системе что угодно и получить ответы за считаные секунды. Способность выполнять задачи растет в геометрической прогрессии. Доступ к информации, людям и локациям сегодня молниеносный. Вот почему, если вы хотите добиться высоких результатов, 24 часа в сутках — уже устаревшее понятие.
В моем мире и для всех приверженцев подхода «еще один раз» оно неприменимо. Сейчас мы за пять минут, час или день можем сделать больше, чем за целую неделю или месяц всего век назад.
Наша способность сжимать время — это способность изгибать его и манипулировать им себе во благо.
Угадайте, как это способствует достижению ваших целей? Вы видите их так отчетливо, как никогда раньше. И к цели, естественно, вы приближаетесь более стремительно.
Материал по теме
Этот подход вы можете применить на практике сегодня. Он эффективен. Я пользуюсь им уже более 20 лет, так что знаю: он работает.
Время от времени у вас будет один из тех дней, когда все идет своим чередом. Вы можете переделать кучу дел и быть продуктивнее за четыре-пять часов, чем за один из обычных полных дней. Или, может быть, у вас был день, когда вы сделали больше, чем за целый месяц. Что, если повторять этот порыв каждый день?
Вот как это сделать.
Вместо того чтобы считать свой день единым блоком времени, разделите часы бодрствования на три равные части — мини-дни. Для меня это означает, что «первый день» длится с 6 утра до полудня. «Второй день» — с полудня до 18:00, а «третий день» — с 18:00 до полуночи. Вы проживаете за неделю семь дней, а я — 21.
Создавая более короткие дни, мой мозг начинает больше ценить каждую минуту. Я не теряю времени зря, потому что мое чувство срочности гораздо острее. Я еще больше сосредотачиваюсь на том, что мне нужно сделать «сегодня». С помощью этой стратегии я укладываю работу, отношения, продуктивность, фитнес и развлечения в более короткие и интенсивные отрезки времени. Я передвигаю финишную черту, чтобы как можно больше моих занятий превратились в спринт.
Не забывайте при этом, что в вашей жизни по-прежнему должен присутствовать баланс. Вы по-прежнему должны находить время для всего.
Просто нужно выжимать бесполезный воздух из потраченных впустую отрезков дня. Сначала вам это может показаться пугающим. Но, попробовав, вы замените старые вредные привычки новыми, эффективными. Вы будете двигаться быстрее и лучше контролировать свое время.
А вот и кое-что приятное на случай, если вы усвоите этот образ мышления. Представьте совокупный эффект работы 21 день в неделю в течение месяца, года или десятилетия. Или на всю оставшуюся жизнь. Теперь сравните это с представлениями конкурентов, которые считают сутки единым 24-часовым блоком времени.
В своем сознании я проживаю более 1000 дней в том же годовом отрезке, в каком другие проживают 365 дней. У кого преимущество? Ответ вы знаете. Я живой пример того, что эта стратегия может принести вам, и на данный момент мои результаты меня вполне устраивают.
2.
Относитесь ко времени с более острым ощущением срочности
Немецкий философ Артур Шопенгауэр однажды сказал: «Обычный человек не беспокоится о том, что время проходит, а талантливого это стимулирует». Вы хотите быть обычным человеком или талантливым?
Главное здесь — безотлагательность. По моему опыту, есть прямая зависимость между тем, как быстро вы бежите, и тем, насколько приближаетесь к финишу.
Если вы наблюдаете за бегунами на длинные дистанции в гонке, то почему последний круг или этап гонки неизменно протекает быстрее остальных? В марафоне на 42 км темп равномерный. Но по мере того, как бегуны приближаются к финишу, адреналин зашкаливает, открывается второе дыхание. Они подстегивают себя, потому что приблизились к цели и финишной черте. Это вызывает выброс эндорфинов, и они чувствуют теплый позитивный прилив.

А теперь представьте стометровку. Это равномерный спринт от начала до конца. Вы максимально ускоряетесь. И для этого нужно другое мышление. Ваше тело и мозг реагируют на другие раздражители.
Материал по теме
Дело не в том, что люди чего-то не видят в жизни и поэтому терпят неудачу. Дело в определенном типе зрения, который они предпочитают в стремлении прийти к финишу. Ваше восприятие глубины влияет на вашу способность вызывать чувство безотлагательности, необходимое для более результативной работы. Когда цель далеко, вы бежите к ней трусцой. Когда она прямо перед вами, вы переходите на спринт.
Вот еще пример. Вы студент, которому в начале семестра назначен крупный проект с крайним сроком ближе к концу семестра. Сразу ли вы беретесь за него? Большинство ставят проект на круиз-контроль.
Они незаметно кладут его на верхнюю полку своей жизни, зная, что разберутся с ним позже. Ровно до тех пор, пока срок не подкрадется незаметно. В какой-то момент вас охватывают паника, страх, ужас, мысли вроде «я ненавижу колледж» и «пожалуй, пойду в бармены». Но если бы вы занялись проектом, вооружившись чувством безотлагательности, эта надвигающаяся тень, чудище, зверь, нависший над вами, были бы почти неощутимы.
Если вы будете применять этот подход ко всему, что делаете в течение дня, недели или года, то успеете больше и испытаете приятное чувство выполненного долга, о котором другие только мечтают.
3. Научитесь контролировать время, а не подчиняться ему
Если вы управляете своим временем с чувством безотлагательности, то становитесь хозяином, а не слугой. Двигаясь быстрее, вы чаще контролируете его.
У вас есть чувство срочности, и вы в большей степени сами решаете, что для вас важно. Это позволяет тратить больше времени на то, что действительно полезно.
Стремление контролировать свое время — настрой, который должен включаться сразу, как только мозг просыпается поутру. Если вы правильно настроитесь, контроль времени начнется еще до того, как ноги коснутся пола. Когда вы просыпаетесь, мозг уже планирует день. Обращаете ли вы внимание на эти первые мысли дня? Первые полчаса имеют решающее значение.
Вспомните своевременные слова британского государственного деятеля лорда Честерфилда: «Берегите минуты, а часы сами о себе позаботятся».
Материал по теме
Ваше отношение к первым 30 минутам своего дня задает тон всех последующих часов. Нужно держаться подальше от телефона, компьютера, телевизора и любых других устройств, способных отвлечь вас от важного.
Используйте эти полчаса, чтобы спланировать свой день; просмотрите список встреч, звонков и проектов; установите приоритеты, помедитируйте, помолитесь, сделайте растяжку, попрактикуйте самообладание, продумайте свои планки и уточните цели на день.
Прежде чем мозг загромоздят люди, события и информация, у него есть шанс сосредоточиться. Он получает сигнал о том, что вы контролируете ситуацию, а не она вас. Вы сможете эффективнее начать день, наполненный уверенностью и целями, которые вы сами задали.
Конечно, в течение дня обязательно случаются неожиданности, изменения и перераспределения. И вы реагируете соответственно. Но в отсутствие неожиданностей вы лучше контролируете ситуацию и работаете над достижением своих целей, а не реагируете на все подряд. Иными словами, диктуйте условия своему дню, или он будет диктовать условия вам.
4.
Часто измеряйте свою производительность
Продуктивность улучшается там, где ее можно измерить. Возможность измерений играет крайне важную роль. Каждый ведущий специалист по мотивации и организации, от Зига Зиглара до Питера Друкера, включает эту идею в свои основополагающие стратегии по простой причине.
Измерять производительность — это эффективно. По мере того как вы сокращаете временные рамки и увеличиваете срочность, также необходимо повышать частоту замеров своей производительности. Если вы не уделите время замерам, вам будет сложнее скорректировать эти рамки. А это ведет к неэффективности и потере времени.
Но проследите, чтобы измерялось то, что нужно. Четко определите цели, приоритеты и стандарты. Поймите, как они взаимодействуют друг с другом. Научитесь определять не только слабые стороны, но и их потенциальные причины.

Легендарный баскетбольный тренер Калифорнийского университета в Лос-Анджелесе Джон Вуден представил это в более широком контексте, сказав: «Если у вас нет времени, чтобы сделать все правильно, когда же вы найдете время, чтобы сделать это снова?» Вуден был сторонником того, чтобы все делать правильно, вплоть до того, как его игроки завязывают шнурки. Он годами оттачивал все техники и процессы в командах, признавая только один стандарт и почти ежедневно замеряя промежуточные этапы.
Если ваша цель в том, чтобы пробежать полтора километра за пять минут, или увеличить продажи на 50%, или повысить доход на $50 000, как вы узнаете, достигли ли вы этих целей, если не посмотрите на цифры? Если они меньше, то вы наобум бросаете дротики в надежде попасть в мишень.
В среднем люди оценивают себя один или два раза в год.
Но для того, кто живет по принципу «еще одного раза», одних новогодних обещаний недостаточно. Лучшие измеряют себя ежемесячно или еженедельно. Подводите ли вы итоги недели в пятницу вечером? Подводите ли итоги и составляете ли планы на предстоящую неделю в воскресенье вечером? Лучшие из лучших, мыслящие в парадигме «еще одного раза», проходят этот процесс ежедневно.
Материал по теме
Есть еще один уровень, выходящий за рамки ежедневных измерений. Некоторые измеряют себя ежечасно. У людей топ-уровня есть внутренний механизм, который срабатывает в экстренном порядке. Я приучил себя к этому, и я не лгу, когда говорю вам, что такая дисциплина сослужила мне хорошую службу, как бы тяжело это ни казалось. Задумайтесь на мгновение. Чей результат будет лучше? Того, кто сокращает интервал замеров, или того, кто редко измеряет свой прогресс? Ответ вы знаете.
5.
Сосредоточьтесь на будущем
Многие застряли в прошлом. Это убивает их продуктивность в настоящем и лишает возможности строить планы на будущее. Прошлое ушло навсегда, но, пока вы его не отпустите, оно крадет у вас способность мечтать и воображать. Вам нужно больше времени посвящать мыслям о будущем, ведь именно туда вы направляетесь. Кроме того, нельзя терять связь с настоящим, потому что именно так вы строите лучшее будущее.
Я выхожу из себя, когда вижу, сколько людей зациклились на том, как бы изменилась их жизнь сегодня, «если бы» что-то очень важное было не таким. Особенно склонны застревать в прошлом люди, находящиеся на стадии разрыва неудачных отношений или пытающиеся дистанцироваться от негативной ситуации в семье.
Это не значит, что вы не должны обращаться к своим прошлым травмам.
Нужно найти способ пережить их и двигаться вперед. Если вы не справляетесь, то причиняете боль себе и тем, кто вам небезразличен в данный момент. И наоборот, не попадайтесь в ловушку влюбленности в свое прошлое, если у вас получалось достичь чего-то выдающегося: получить высшее образование, повышение по службе, вступить в брак и т. д. Это все хорошо, но если вы будете почивать на лаврах, то все равно не будете жить настоящим и не построите лучшее будущее.
Те, кто живет по принципу «еще одного раза», обладают врожденной способностью проводить время в мечтах о своем будущем и предпринимают решительные действия в настоящем, чтобы сформировать это будущее.
Как изменить восприятие окружающих
Когда вы внедрите в свою жизнь пять принципов тайм-менеджмента, изменится и восприятие вас окружающими.
Когда люди видят, что вы больше не тратите время попусту, они тоже перестают расходовать ваше время. Они видят, что вы больше не уделяете слишком много минут и часов заботам о приоритетах других, потому что слишком сосредоточены на заботе о собственных.
На работе нужно относиться к этому разумно. Найдите способ сделать цели вашего работодателя своими и гармонично совместить их. Ваши друзья, родственники и коллеги поймут, что вы в режиме атаки, а не реагирования. Они будут относиться к вам с уважением, и ваши взаимодействия с ними тоже изменятся.
Это дополнительное преимущество, которое меняет вашу жизнь, потому что ваш новый способ управления временем — на самом деле новый способ управления жизнью. Кроме того, когда вы измените свое отношение ко времени, вы будете открыты для встречи с новыми единомышленниками, приступите к новым проектам и откроете новые горизонты, которые, возможно, прежде считали несбыточной мечтой.

Наконец, дарю вам цитату о времени от Чарльза Дарвина. «Человек, который осмеливается потратить впустую час, еще не осознал цену жизни». Перестаньте тратить время понапрасну и начните использовать его себе во благо, тратить его на действительно важные дела.
Мэтуэй | Популярные задачи
1 Найти точное значение грех(30) 2 Найти точное значение грех(45) 3 Найти точное значение грех(30 градусов) 4 Найти точное значение грех(60 градусов) 5 Найти точное значение загар (30 градусов) 6 Найти точное значение угловой синус(-1) 7 Найти точное значение грех(пи/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение грех(45 градусов) 10 Найти точное значение грех(пи/3) 11 Найти точное значение арктан(-1) 12 Найти точное значение cos(45 градусов) 13 Найти точное значение cos(30 градусов) 14 Найти точное значение желтовато-коричневый(60) 15 Найти точное значение csc(45 градусов) 16 Найти точное значение загар (60 градусов) 17 Найти точное значение сек(30 градусов) 18 Найти точное значение cos(60 градусов) 19 Найти точное значение cos(150) 20 Найти точное значение грех(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение загар (45 градусов) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 градусов) 25 Найти точное значение сек(45 градусов) 26 Найти точное значение csc(30 градусов) 27 Найти точное значение грех(0) 28 Найти точное значение грех(120) 29 Найти точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найти точное значение желтовато-коричневый(30) 32 9235 Преобразовать из радианов в градусы пи/6 36 Найти точное значение детская кроватка(30 градусов) 37 Найти точное значение арккос(-1) 38 Найти точное значение арктический(0) 39 Найти точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение тан(пи/2) 45 Найти точное значение грех(300) 46 Найти точное значение соз(30) 47 Найти точное значение соз(60) 48 Найти точное значение соз(0) 49 Найти точное значение соз(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение cos(210) 52 Найти точное значение сек(60 градусов) 53 Найти точное значение грех(300 градусов) 54 Преобразование градусов в радианы 135 55 Преобразование градусов в радианы 150 56 Преобразовать из радианов в градусы (5 дюймов)/6 57 Преобразовать из радианов в градусы (5 дюймов)/3 58 Преобразование градусов в радианы 89 градусов 59 Преобразование градусов в радианы 60 60 Найти точное значение грех(135 градусов) 61 Найти точное значение грех(150) 62 Найти точное значение грех(240 градусов) 63 Найти точное значение детская кроватка(45 градусов) 64 Преобразовать из радианов в градусы (5 дюймов)/4 65 Найти точное значение грех(225) 66 Найти точное значение грех(240) 67 Найти точное значение cos(150 градусов) 68 Найти точное значение желтовато-коричневый(45) 69 Оценить грех(30 градусов) 70 Найти точное значение сек(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение КСК(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение загар((5pi)/3) 75 Найти точное значение желтовато-коричневый(0) 76 Оценить грех(60 градусов) 77 Найти точное значение arctan(-( квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3 пи)/4 79 Найти точное значение sin((7pi)/4) 80 Найти точное значение угловой синус(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найти точное значение КСК(45) 83 Упростить арктан(квадратный корень из 3) 84 Найти точное значение грех(135) 85 Найти точное значение грех(105) 86 Найти точное значение грех(150 градусов) 87 Найти точное значение sin((2pi)/3) 88 Найти точное значение загар((2pi)/3) 89 Преобразовать из радианов в градусы пи/4 90 Найти точное значение грех(пи/2) 91 Найти точное значение сек(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение угловой синус(0) 95 Найти точное значение грех(120 градусов) 96 Найти точное значение желтовато-коричневый ((7pi)/6) 97 Найти точное значение соз(270) 98 Найти точное значение sin((7pi)/6) 99 Найти точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразование градусов в радианы 88 градусов
Мэтуэй | Популярные задачи
1 Найти точное значение грех(30) 2 Найти точное значение грех(45) 3 Найти точное значение грех(30 градусов) 4 Найти точное значение грех(60 градусов) 5 Найти точное значение загар (30 градусов) 6 Найти точное значение угловой синус(-1) 7 Найти точное значение грех(пи/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение грех(45 градусов) 10 Найти точное значение грех(пи/3) 11 Найти точное значение арктан(-1) 12 Найти точное значение cos(45 градусов) 13 Найти точное значение cos(30 градусов) 14 Найти точное значение желтовато-коричневый(60) 15 Найти точное значение csc(45 градусов) 16 Найти точное значение загар (60 градусов) 17 Найти точное значение сек(30 градусов) 18 Найти точное значение cos(60 градусов) 19 Найти точное значение соз(150) 20 Найти точное значение грех(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение загар (45 градусов) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 градусов) 25 Найти точное значение сек(45 градусов) 26 Найти точное значение csc(30 градусов) 27 Найти точное значение грех(0) 28 Найти точное значение грех(120) 29 Найти точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найти точное значение желтовато-коричневый(30) 32 Преобразование градусов в радианы 92 35 Преобразовать из радианов в градусы пи/6 36 Найти точное значение детская кроватка(30 градусов) 37 Найти точное значение арккос(-1) 38 Найти точное значение арктический(0) 39 Найти точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт.



 . n раз) + (а n + а n + a n + ….. n раз)
. n раз) + (а n + а n + a n + ….. n раз)
 Найдите сумму арифметической последовательности 8 терминов, первый и последний термины равны 4 и 10 соответственно.
Найдите сумму арифметической последовательности 8 терминов, первый и последний термины равны 4 и 10 соответственно. 
 Первый член a 1 , общая разница
это д ,
а количество терминов n . Сумма
арифметический ряд получается путем умножения числа
термины раз
среднее значение первого и последнего членов.
Первый член a 1 , общая разница
это д ,
а количество терминов n . Сумма
арифметический ряд получается путем умножения числа
термины раз
среднее значение первого и последнего членов.

 Изучить информацию о том, как Yandex использует cookie и другие Ваши данные, можно тут: https://yandex.com/legal/confidential/?lang=ru.
Изучить информацию о том, как Yandex использует cookie и другие Ваши данные, можно тут: https://yandex.com/legal/confidential/?lang=ru. Пользователь может вносить свои записи в эти справочники.
Пользователь может вносить свои записи в эти справочники.

.jpg)






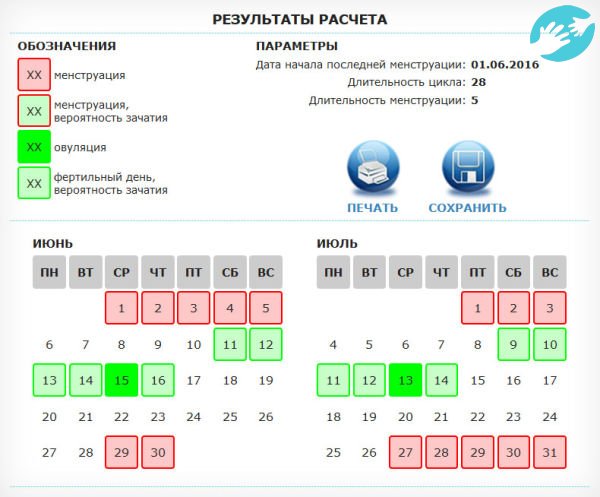
 Так что не стесняйтесь использовать и ссылаться на друзей.
Так что не стесняйтесь использовать и ссылаться на друзей. Ежедневный калькулятор может использоваться кем угодно; пары ведут обратный отсчет до своего большого дня, студенты осторожно
готовятся к датам испытаний и даже ждут мам, с тревогой наблюдая, как проходят секунды, прежде чем они встретят своего новорожденного. Дни, прошедшие с калькулятора, дают уникальное и интересное значение времени, особенно когда оно проходит.
Ежедневный калькулятор может использоваться кем угодно; пары ведут обратный отсчет до своего большого дня, студенты осторожно
готовятся к датам испытаний и даже ждут мам, с тревогой наблюдая, как проходят секунды, прежде чем они встретят своего новорожденного. Дни, прошедшие с калькулятора, дают уникальное и интересное значение времени, особенно когда оно проходит. Мы избавим вас от всех препятствий и всех ненужных тестов, предоставив вам чистый и простой
доступ к разделу ввода даты для подсчета, где вы можете определить пределы диапазона дат, который вы устанавливаете. Это буквально 1-минутный процесс, для которого вам не нужна помощь.
Мы избавим вас от всех препятствий и всех ненужных тестов, предоставив вам чистый и простой
доступ к разделу ввода даты для подсчета, где вы можете определить пределы диапазона дат, который вы устанавливаете. Это буквально 1-минутный процесс, для которого вам не нужна помощь.
 05.13
05.13  by 2013-2016
by 2013-2016

 Разрешите получать регулярные обновления!
Разрешите получать регулярные обновления! Поэтому я надеюсь, что можно ответить на мой вопрос, используя одно из этих определений.
Поэтому я надеюсь, что можно ответить на мой вопрос, используя одно из этих определений. Вы можете легко (с помощью некоторых тригонометрических формул) вычислить значения $\sin x$ для $x=0,\pi/6,\pi/3,\pi/4,\pi/2, \pi/ 12,\пи/5$. Постройте эти значения.
Вы можете легко (с помощью некоторых тригонометрических формул) вычислить значения $\sin x$ для $x=0,\pi/6,\pi/3,\pi/4,\pi/2, \pi/ 12,\пи/5$. Постройте эти значения.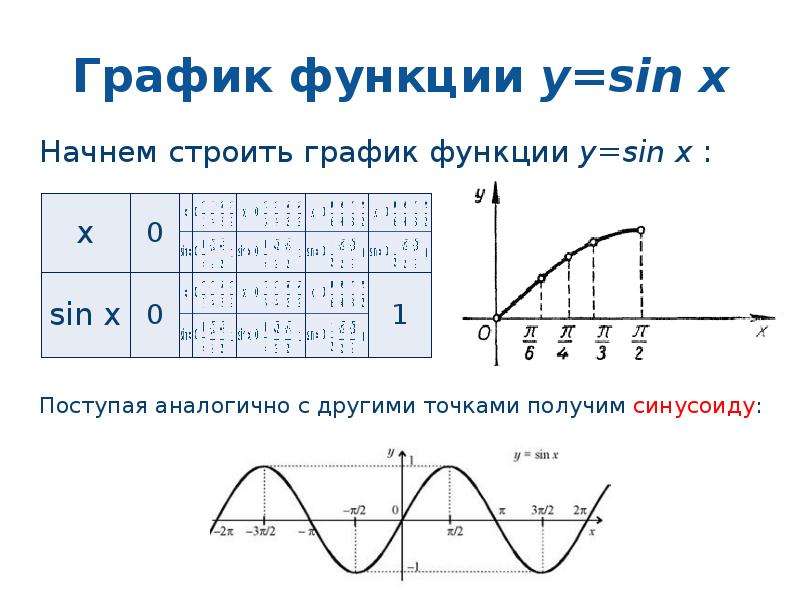 Координата $y$ точки равна $\sin\theta$, где $\theta$ – угол между точкой, началом координат и точкой $(1,0)$ (и, конечно, измеренный положительный в направлении против часовой стрелки с положительной осью $x$, соответствующей $\theta=0$).
Координата $y$ точки равна $\sin\theta$, где $\theta$ – угол между точкой, началом координат и точкой $(1,0)$ (и, конечно, измеренный положительный в направлении против часовой стрелки с положительной осью $x$, соответствующей $\theta=0$).


 00грн – 2,300.00грнКупить
00грн – 2,300.00грнКупить 00грн
00грн 00грн
00грн 00грн
00грн 80грн Купить
80грн Купить 50грн
50грн 28грн – 3,863.54грнКупить
28грн – 3,863.54грнКупить 20грн
20грн 68грн – 8,298.40грнКупить
68грн – 8,298.40грнКупить 40грнКупить
40грнКупить 00грн
00грн 00грн
00грн




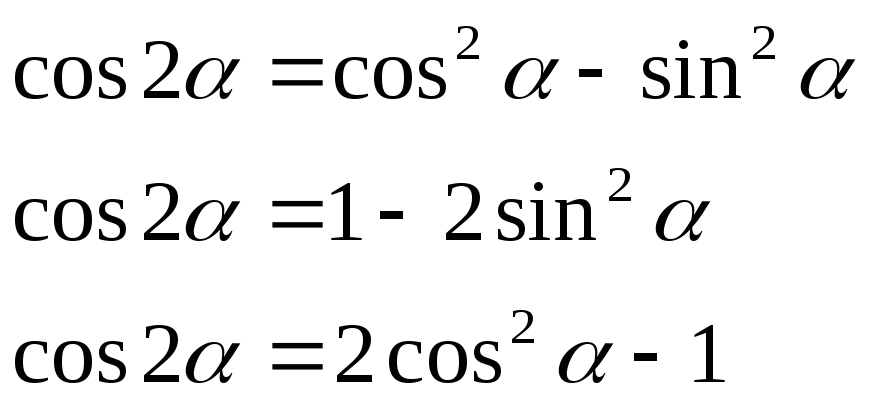 к. cos 5х: cos 5х =1, а sin 5х: cos 5х= tg 5x, то получим:
к. cos 5х: cos 5х =1, а sin 5х: cos 5х= tg 5x, то получим:
 Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.

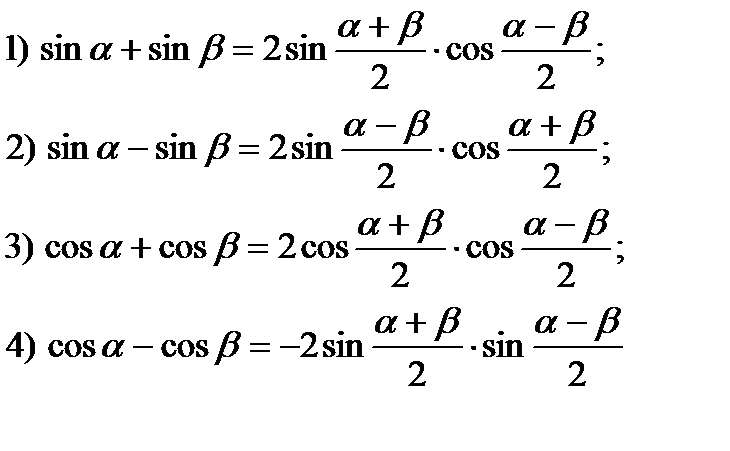 Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.


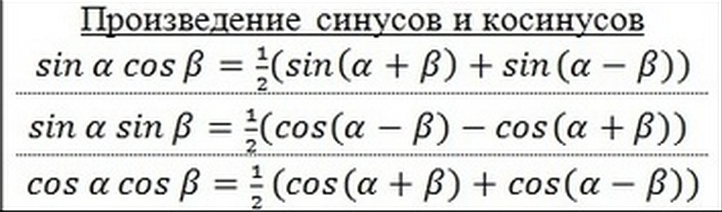 29 а – 1 учащийся решает на доске, остальные – в тетради.
29 а – 1 учащийся решает на доске, остальные – в тетради. Ответим на вопрос: достигли мы цели нашего урока?
Ответим на вопрос: достигли мы цели нашего урока?
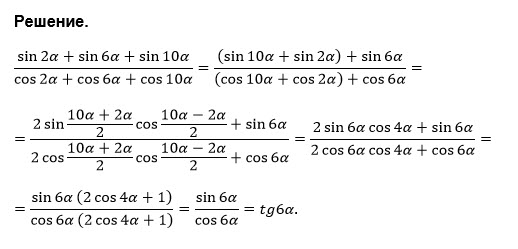 поставьте $t = -\pi/2,$, чтобы показать, что $\sin$ — нечетная функция. после всего этого вы получаете
$$\sin(t-s) = \sin t \cos t — \cos t \sin s $$ и два для сумм. 9{ix}$.
поставьте $t = -\pi/2,$, чтобы показать, что $\sin$ — нечетная функция. после всего этого вы получаете
$$\sin(t-s) = \sin t \cos t — \cos t \sin s $$ и два для сумм. 9{ix}$. Мы знаем тригонометрические углы 45° и 30°, но не знаем тригонометрический угол (45° + 30° = 75°). Таким образом, чтобы упростить эти типы проблем. Мы изучим тригонометрические формулы или тождества суммы и разности двух углов, что облегчит задачу.
Мы знаем тригонометрические углы 45° и 30°, но не знаем тригонометрический угол (45° + 30° = 75°). Таким образом, чтобы упростить эти типы проблем. Мы изучим тригонометрические формулы или тождества суммы и разности двух углов, что облегчит задачу.
 .(1)
.(1) 
 Преобразуйте каждое из следующих произведений в сумму или разность.
Преобразуйте каждое из следующих произведений в сумму или разность.  Найдите
Найдите  Выразите каждое из следующих чисел в виде произведения
Выразите каждое из следующих чисел в виде произведения  Докажите, что: 1 + cos 2x + cos 4x + cos 6x = 4 потому что x cos 2x cos 3x
Докажите, что: 1 + cos 2x + cos 4x + cos 6x = 4 потому что x cos 2x cos 3x 
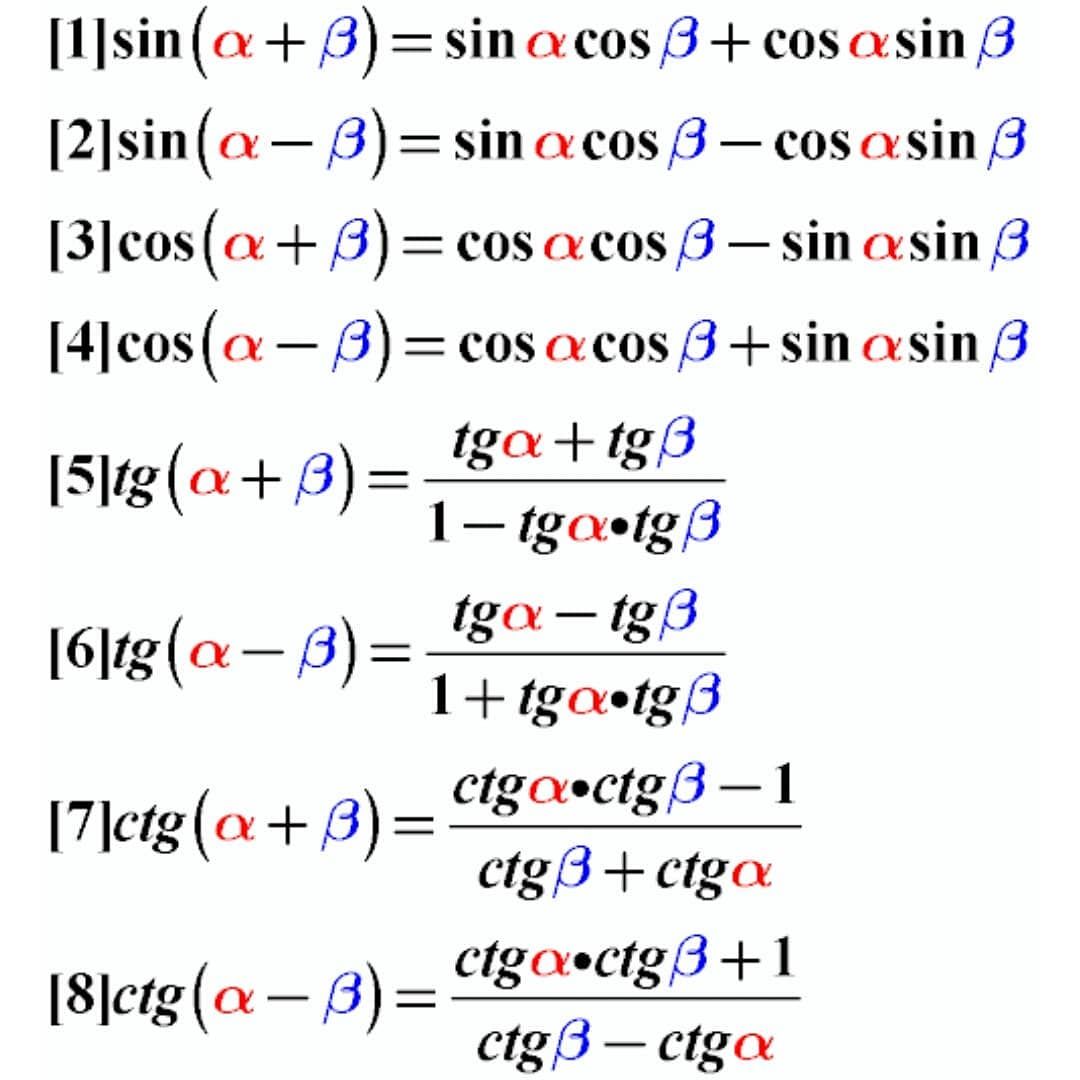 .(1)
.(1) .(1)
.(1) .(из тождества 1)
.(из тождества 1)



 е. если вы ищете нули функции (в каких точках функция пересекает ось Ox), то вы их найдёте именно через этот процесс: поймёте, если они существуют, рассчитав дискриминант, затем найдёте их, используя формулу корней.
е. если вы ищете нули функции (в каких точках функция пересекает ось Ox), то вы их найдёте именно через этот процесс: поймёте, если они существуют, рассчитав дискриминант, затем найдёте их, используя формулу корней. Формула вычисления дискриминанта известна
Формула вычисления дискриминанта известна 2 — 4 \cdot 1 \cdot (-4)}}{2 \cdot 1} = $ 92-32$
2 — 4 \cdot 1 \cdot (-4)}}{2 \cdot 1} = $ 92-32$ Решите уравнение:
Решите уравнение:  Решить уравнение:
Решить уравнение:  У меня есть цикл for, который проходит через этот список и дает мне значение для a, b и c из вложенного списка:
У меня есть цикл for, который проходит через этот список и дает мне значение для a, b и c из вложенного списка:

 Если Вы не нашли ответ на свой вопрос, то задайте его нам любым удобным способом. Перед тем, как задать вопрос, убедитесь, что действительно нет ответа, который Вас интересует!
Об авторе:
Информация об авторе сайта
Калькулятор комплексных чисел:
Калькулятор перевода комплексных чисел из алгебраической формы в показательную и наоборот
Популярные темы на сайте:
Раздел с самыми популярными темами, которые читают посетители сайта
Наша группа ВКонтакте по ТОЭ:
Мы в соц. сетях
Пройти тест по тоэ:
Тесты по тоэ для новичков и не только
Поделиться сайтом в соц сетях:
Сайтом можно поделиться с друзьями в соц. сетях
Подписывайтесь на наш канал:
Наш Ютуб канал
Статистика посещений: общее, сегодня:
Статистика нашего сайта по посещениям
Если Вы не нашли ответ на свой вопрос, то задайте его нам любым удобным способом. Перед тем, как задать вопрос, убедитесь, что действительно нет ответа, который Вас интересует!
Об авторе:
Информация об авторе сайта
Калькулятор комплексных чисел:
Калькулятор перевода комплексных чисел из алгебраической формы в показательную и наоборот
Популярные темы на сайте:
Раздел с самыми популярными темами, которые читают посетители сайта
Наша группа ВКонтакте по ТОЭ:
Мы в соц. сетях
Пройти тест по тоэ:
Тесты по тоэ для новичков и не только
Поделиться сайтом в соц сетях:
Сайтом можно поделиться с друзьями в соц. сетях
Подписывайтесь на наш канал:
Наш Ютуб канал
Статистика посещений: общее, сегодня:
Статистика нашего сайта по посещениям
 Ю. РГЗ по электротехнике и электронике в Multisim
Ю. РГЗ по электротехнике и электронике в Multisim 1 Линейные электрические цепи постоянного тока
1 Линейные электрические цепи постоянного тока

 Основные недостатки аккумуляторов по сравнении и конденсаторами:
Основные недостатки аккумуляторов по сравнении и конденсаторами: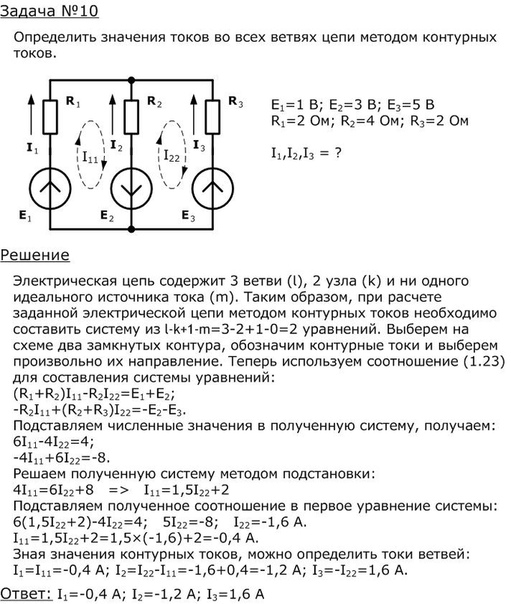
 При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.
При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.

 Разберем два самых наглядных примера.
Разберем два самых наглядных примера. Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.
Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать. Вместо этого их нужно суммировать «векторно». Другими словами, необходимо округлить каждое значение, а затем сложить их вместе и выделить квадратный корень из этого числа:
Вместо этого их нужно суммировать «векторно». Другими словами, необходимо округлить каждое значение, а затем сложить их вместе и выделить квадратный корень из этого числа: Использование измерительного оборудования для определения конденсаторного заряда
Использование измерительного оборудования для определения конденсаторного заряда
 Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин. Если уж заданы параметры в единицах измерения то так и пишите. Если не напишите то считается что данные заданы в основным единицах СИ ( то есть метр, Фарад, Ом)
Если уж заданы параметры в единицах измерения то так и пишите. Если не напишите то считается что данные заданы в основным единицах СИ ( то есть метр, Фарад, Ом) Мы не приводим фактические значения схождения или других параметров, поскольку они различаются в зависимости от автомобиля, но вы можете увидеть, какие из 9 параметровзначения для каждого используемого параметра. Важны относительные изменения.
Мы не приводим фактические значения схождения или других параметров, поскольку они различаются в зависимости от автомобиля, но вы можете увидеть, какие из 9 параметровзначения для каждого используемого параметра. Важны относительные изменения. геометрию и влияние изменений здесь
геометрию и влияние изменений здесь Отрицательные углы схождения указывают на схождение (колеса смотрят внутрь), в то время как положительное схождение указывает на «схождение наружу» с колесами, направленными наружу.
Отрицательные углы схождения указывают на схождение (колеса смотрят внутрь), в то время как положительное схождение указывает на «схождение наружу» с колесами, направленными наружу. 

 Если вы понизите центр крена автомобиля, его шасси будет больше раскачиваться из стороны в сторону, и этот перенос веса на внешние колеса создает дополнительное сцепление с этой стороной.
Если вы понизите центр крена автомобиля, его шасси будет больше раскачиваться из стороны в сторону, и этот перенос веса на внешние колеса создает дополнительное сцепление с этой стороной. 

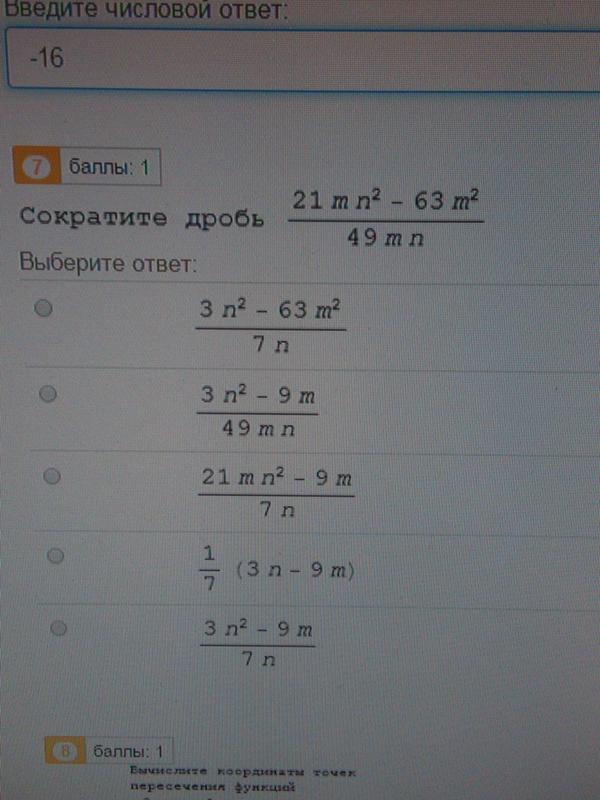



 Упростите выражение:
Упростите выражение: В числах 90 и 105 сумма цифр делится на 3, поэтому оба эти числа делятся на 3, сокращаем дробь на 3. В новой дроби 30 и 35 оканчиваются на 0 и 5, значит, оба числа делятся на 5, поэтому сокращаем дробь на 5. Получившаяся дробь шесть седьмых — несократимая. Это — окончательный ответ.
В числах 90 и 105 сумма цифр делится на 3, поэтому оба эти числа делятся на 3, сокращаем дробь на 3. В новой дроби 30 и 35 оканчиваются на 0 и 5, значит, оба числа делятся на 5, поэтому сокращаем дробь на 5. Получившаяся дробь шесть седьмых — несократимая. Это — окончательный ответ. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.
Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.
 И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует.
И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует.
 Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).
Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются). Необходимо произвести ее сокращение.
Необходимо произвести ее сокращение. Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).
Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»). Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.
Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.

 Значит, первую дробь сокращаем на 10, вторую — на 100, третью — на 1000:
Значит, первую дробь сокращаем на 10, вторую — на 100, третью — на 1000:/Dopolnitelnye%20zadaniya/8%20klass/Kontrolnye%20raboty%20ris/Kontrolnaya%20rabota%20(8kl)%201.jpg)
 В результате получаем упрощенную дробь 3/7 . В алгебраических выражениях общие множители выделяются точно так же, как и в обычных. В предыдущем примере мы смогли легко выделить 5 из 15 — тот же принцип применим и к более сложным выражениям, таким как 15x – 5. Найдем общий множитель. В данном случае это будет 5, так как оба члена (15x и -5) делятся на 5. Как и ранее, выделим общий множитель и перенесем его влево .
В результате получаем упрощенную дробь 3/7 . В алгебраических выражениях общие множители выделяются точно так же, как и в обычных. В предыдущем примере мы смогли легко выделить 5 из 15 — тот же принцип применим и к более сложным выражениям, таким как 15x – 5. Найдем общий множитель. В данном случае это будет 5, так как оба члена (15x и -5) делятся на 5. Как и ранее, выделим общий множитель и перенесем его влево . При сокращении алгебраической дроби первым делом следует упростить обе ее части. Начните с числителя и постарайтесь разложить его на как можно большее число множителей. Рассмотрим в данном разделе следующую дробь:
При сокращении алгебраической дроби первым делом следует упростить обе ее части. Начните с числителя и постарайтесь разложить его на как можно большее число множителей. Рассмотрим в данном разделе следующую дробь: В нашем примере это число 3.
В нашем примере это число 3. Предположим, дана следующая дробь:
Предположим, дана следующая дробь:

 Дробь должна быть представлена в виде числителя и знаменателя. Дроби подразделяются на несколько типов, таких как похожие, непохожие, правильные, неправильные, смешанные и так далее. Если данная дробь представлена большим целочисленным значением, ее можно упростить, уменьшив ее до наименьшего целочисленного значения. Например, если числитель и знаменатель имеют общий множитель, исключите его.
Дробь должна быть представлена в виде числителя и знаменателя. Дроби подразделяются на несколько типов, таких как похожие, непохожие, правильные, неправильные, смешанные и так далее. Если данная дробь представлена большим целочисленным значением, ее можно упростить, уменьшив ее до наименьшего целочисленного значения. Например, если числитель и знаменатель имеют общий множитель, исключите его.

 Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. е. 1,45 .
е. 1,45 . Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  На какую часть вопроса Энди ответил правильно?
На какую часть вопроса Энди ответил правильно?
 )
)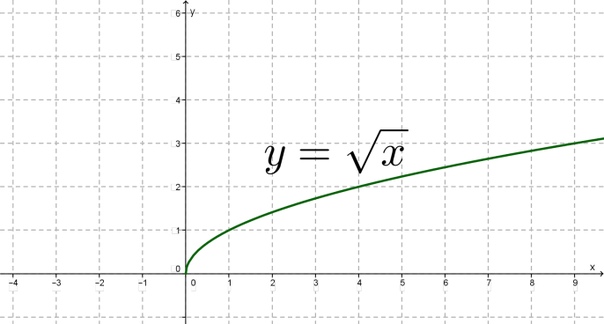 )
)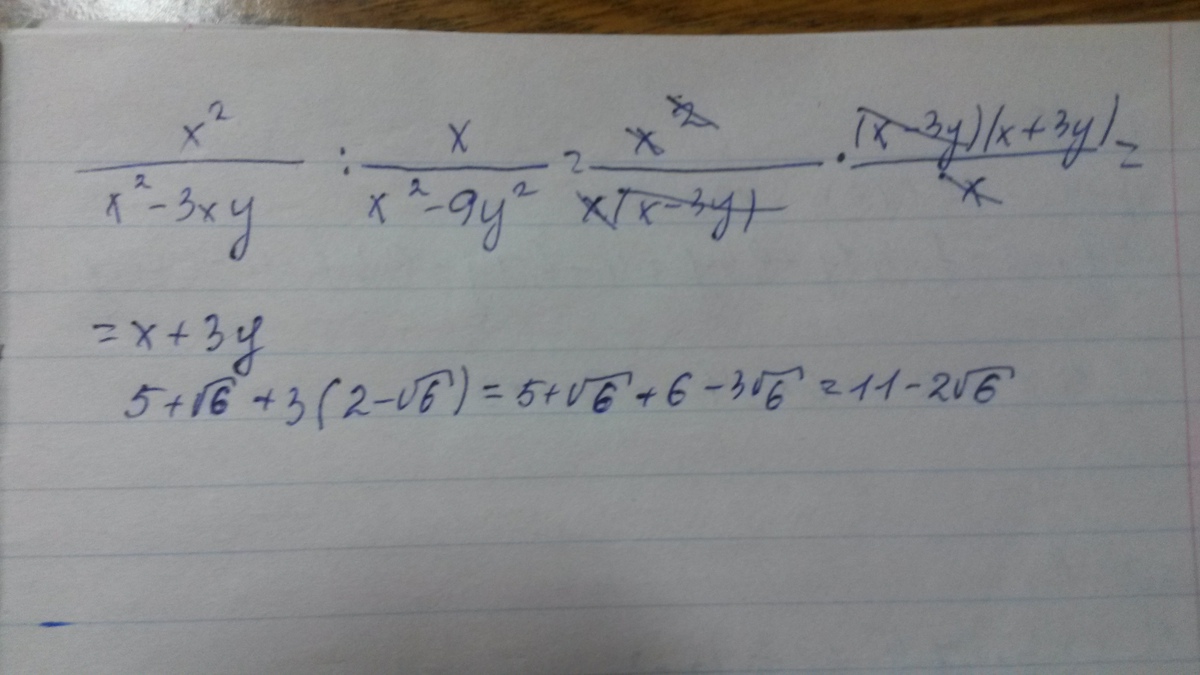 )
) )
) )
) )
) )
) )
) Появление посторонних корней
Появление посторонних корней
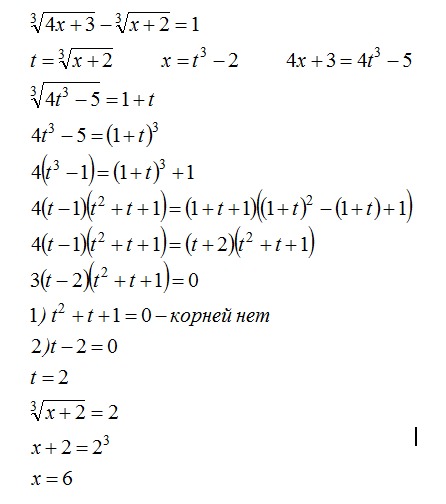


 Остается только случай f (x) = a, но, учитывая необходимость выполнения равенства f (x) = g (x), имеем, что тогда и g (x) = а. Таким образом, мы обосновали, что выполнение равенства f (x) = g (x) (при условии f (x) 1 а и g (x) < а) гарантирует одновременное выполнение равенств f (x) = а и g (x) = а (и наоборот, если одновременно выполняются равенства f (x) = а и g (x) = а, то выполняется и равенство f (x) = g (x)). Как было показано в п. 3.1, это и
Остается только случай f (x) = a, но, учитывая необходимость выполнения равенства f (x) = g (x), имеем, что тогда и g (x) = а. Таким образом, мы обосновали, что выполнение равенства f (x) = g (x) (при условии f (x) 1 а и g (x) < а) гарантирует одновременное выполнение равенств f (x) = а и g (x) = а (и наоборот, если одновременно выполняются равенства f (x) = а и g (x) = а, то выполняется и равенство f (x) = g (x)). Как было показано в п. 3.1, это и .. + fn (x) будет отрицательной. Но это невозможно, поскольку по условию все функции неотрицательные. Таким образом, при f1 (x) > 0 данное уравнение не имеет корней. Эти же рассуждения можно повторить для любой другой функции-слагаемого. Остается единственная возможность — все функции-слагаемые равны нулю (очевидно, что в этом случае равенство f1 (x) + f2 (x) + … + fn (x) = 0 обязательно будет выполняться). Таким образом, сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.
.. + fn (x) будет отрицательной. Но это невозможно, поскольку по условию все функции неотрицательные. Таким образом, при f1 (x) > 0 данное уравнение не имеет корней. Эти же рассуждения можно повторить для любой другой функции-слагаемого. Остается единственная возможность — все функции-слагаемые равны нулю (очевидно, что в этом случае равенство f1 (x) + f2 (x) + … + fn (x) = 0 обязательно будет выполняться). Таким образом, сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю. Следовательно, данное уравнение имеет единственный корень х = 1.
Следовательно, данное уравнение имеет единственный корень х = 1.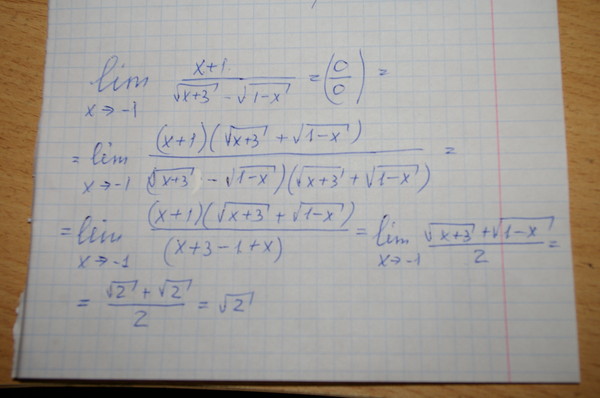 Других корней быть не может, поскольку для возрастающей функции f (x) при x > x0 получаем неравенство f (x) > f (x0) = а, а при x < x0 — неравенство f (x) < f (x0) = а. Таким образом, при x Ф x0 f (x) Ф а. Аналогично и для убывающей функции при x Ф x0 получаем f (x) Ф а.
Других корней быть не может, поскольку для возрастающей функции f (x) при x > x0 получаем неравенство f (x) > f (x0) = а, а при x < x0 — неравенство f (x) < f (x0) = а. Таким образом, при x Ф x0 f (x) Ф а. Аналогично и для убывающей функции при x Ф x0 получаем f (x) Ф а. Аналогично и при x < x0 f (x) Ф g (x).
Аналогично и при x < x0 f (x) Ф g (x).

 Тогда первое уравнение заданной системы, которое имеет вид f (x) = f (у), равносильно уравнению x = у. Таким образом, на ОДЗ заданная система равносильна
Тогда первое уравнение заданной системы, которое имеет вид f (x) = f (у), равносильно уравнению x = у. Таким образом, на ОДЗ заданная система равносильна а = в.
а = в. )/3
)/3

 Эти 3 корня могут быть действительными или смесью действительных и комплексных корней.
Эти 3 корня могут быть действительными или смесью действительных и комплексных корней. Если мы сделаем это на этот раз, мы получим настоящую версию только для root, выглядящую как график в верхней части страницы.
Если мы сделаем это на этот раз, мы получим настоящую версию только для root, выглядящую как график в верхней части страницы.
 )
) )
) )
)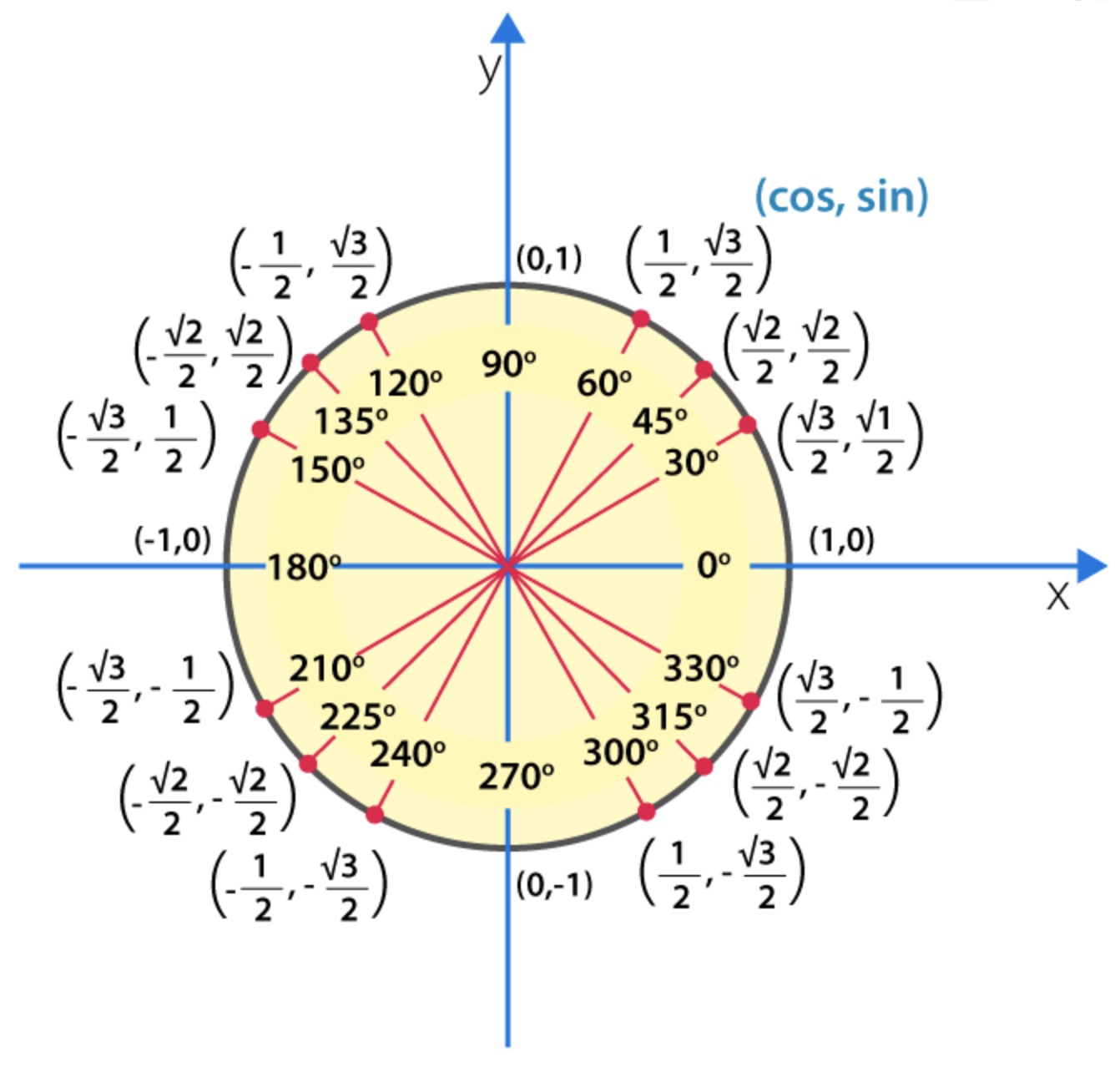 )
) )
) )
) )
) )
) Однако, как утверждает популярный бизнес-коуч и мотивационный спикер Эд Майлетт, если подойти к вопросу правильно, можно сделать каждые сутки длиннее втрое и расширить свое субъективное время. Он объясняет, как двигаться со скоростью света, что поможет добиться приятного чувства выполненного долга и почему первые полчаса каждого дня имеют решающее значение
Однако, как утверждает популярный бизнес-коуч и мотивационный спикер Эд Майлетт, если подойти к вопросу правильно, можно сделать каждые сутки длиннее втрое и расширить свое субъективное время. Он объясняет, как двигаться со скоростью света, что поможет добиться приятного чувства выполненного долга и почему первые полчаса каждого дня имеют решающее значение  Свою новую книгу он назвал The Power of One More («Сила еще одного») и объединил в ней мотивирующие советы, примеры из жизни и научные исследования, чтобы показать, какие стратегии помогают выйти на новый уровень, и получить тот результат, который вам нужен, но который вы до сих пор считали невозможным.
Свою новую книгу он назвал The Power of One More («Сила еще одного») и объединил в ней мотивирующие советы, примеры из жизни и научные исследования, чтобы показать, какие стратегии помогают выйти на новый уровень, и получить тот результат, который вам нужен, но который вы до сих пор считали невозможным.  Ученые называют это субъективным временем, и оно совершенно не похоже на время на часах. Это то, как воспринимается скорость течения времени, а время на часах — это постоянная хронология, измеряемая тикающими стрелками настенных часов.
Ученые называют это субъективным временем, и оно совершенно не похоже на время на часах. Это то, как воспринимается скорость течения времени, а время на часах — это постоянная хронология, измеряемая тикающими стрелками настенных часов. 

 Когда мы физически устаем, наш мозг не может с той же скоростью передавать и обрабатывать информацию. Он уже неоптимально видит и осмысливает данные от органов зрения, слуха и осязания. Реакции замедляются, и нам кажется, что время ускоряется. На самом деле это мы замедляемся по отношению к остальному миру.
Когда мы физически устаем, наш мозг не может с той же скоростью передавать и обрабатывать информацию. Он уже неоптимально видит и осмысливает данные от органов зрения, слуха и осязания. Реакции замедляются, и нам кажется, что время ускоряется. На самом деле это мы замедляемся по отношению к остальному миру.  И на самых первых этапах я обнаружил, что нужно уважать природу времени. Все успешные люди, в том числе я, считают это основой своего успеха.
И на самых первых этапах я обнаружил, что нужно уважать природу времени. Все успешные люди, в том числе я, считают это основой своего успеха.  День длиной в 24 часа подходил нам до того, как у нас появились интернет, смартфоны, беспроводные технологии, компьютеризированные автомобили, самолеты, спутники и другие инструменты, позволяющие расширить свое присутствие и двигаться со скоростью света.
День длиной в 24 часа подходил нам до того, как у нас появились интернет, смартфоны, беспроводные технологии, компьютеризированные автомобили, самолеты, спутники и другие инструменты, позволяющие расширить свое присутствие и двигаться со скоростью света.  Наша способность сжимать время — это способность изгибать его и манипулировать им себе во благо.
Наша способность сжимать время — это способность изгибать его и манипулировать им себе во благо.  Вместо того чтобы считать свой день единым блоком времени, разделите часы бодрствования на три равные части — мини-дни. Для меня это означает, что «первый день» длится с 6 утра до полудня. «Второй день» — с полудня до 18:00, а «третий день» — с 18:00 до полуночи. Вы проживаете за неделю семь дней, а я — 21.
Вместо того чтобы считать свой день единым блоком времени, разделите часы бодрствования на три равные части — мини-дни. Для меня это означает, что «первый день» длится с 6 утра до полудня. «Второй день» — с полудня до 18:00, а «третий день» — с 18:00 до полуночи. Вы проживаете за неделю семь дней, а я — 21.  Просто нужно выжимать бесполезный воздух из потраченных впустую отрезков дня. Сначала вам это может показаться пугающим. Но, попробовав, вы замените старые вредные привычки новыми, эффективными. Вы будете двигаться быстрее и лучше контролировать свое время.
Просто нужно выжимать бесполезный воздух из потраченных впустую отрезков дня. Сначала вам это может показаться пугающим. Но, попробовав, вы замените старые вредные привычки новыми, эффективными. Вы будете двигаться быстрее и лучше контролировать свое время.  Относитесь ко времени с более острым ощущением срочности
Относитесь ко времени с более острым ощущением срочности 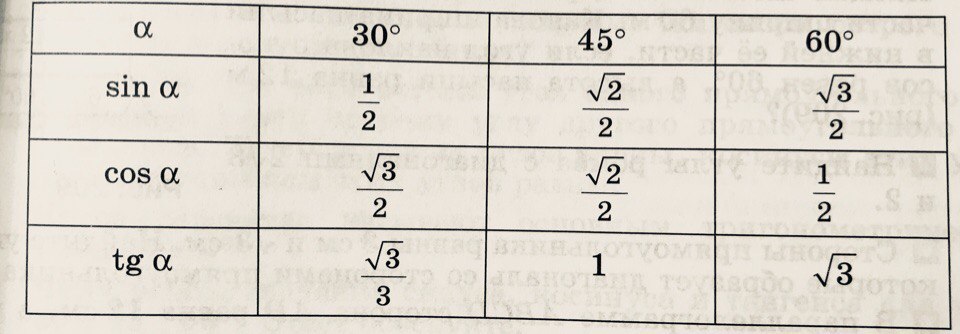
 Они незаметно кладут его на верхнюю полку своей жизни, зная, что разберутся с ним позже. Ровно до тех пор, пока срок не подкрадется незаметно. В какой-то момент вас охватывают паника, страх, ужас, мысли вроде «я ненавижу колледж» и «пожалуй, пойду в бармены». Но если бы вы занялись проектом, вооружившись чувством безотлагательности, эта надвигающаяся тень, чудище, зверь, нависший над вами, были бы почти неощутимы.
Они незаметно кладут его на верхнюю полку своей жизни, зная, что разберутся с ним позже. Ровно до тех пор, пока срок не подкрадется незаметно. В какой-то момент вас охватывают паника, страх, ужас, мысли вроде «я ненавижу колледж» и «пожалуй, пойду в бармены». Но если бы вы занялись проектом, вооружившись чувством безотлагательности, эта надвигающаяся тень, чудище, зверь, нависший над вами, были бы почти неощутимы.  У вас есть чувство срочности, и вы в большей степени сами решаете, что для вас важно. Это позволяет тратить больше времени на то, что действительно полезно.
У вас есть чувство срочности, и вы в большей степени сами решаете, что для вас важно. Это позволяет тратить больше времени на то, что действительно полезно. 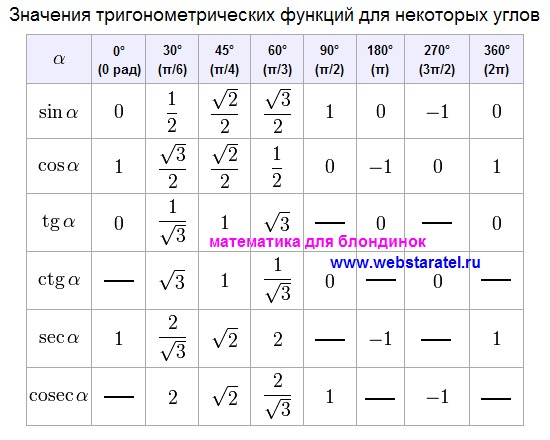 Используйте эти полчаса, чтобы спланировать свой день; просмотрите список встреч, звонков и проектов; установите приоритеты, помедитируйте, помолитесь, сделайте растяжку, попрактикуйте самообладание, продумайте свои планки и уточните цели на день.
Используйте эти полчаса, чтобы спланировать свой день; просмотрите список встреч, звонков и проектов; установите приоритеты, помедитируйте, помолитесь, сделайте растяжку, попрактикуйте самообладание, продумайте свои планки и уточните цели на день. Часто измеряйте свою производительность
Часто измеряйте свою производительность 
 Но для того, кто живет по принципу «еще одного раза», одних новогодних обещаний недостаточно. Лучшие измеряют себя ежемесячно или еженедельно. Подводите ли вы итоги недели в пятницу вечером? Подводите ли итоги и составляете ли планы на предстоящую неделю в воскресенье вечером? Лучшие из лучших, мыслящие в парадигме «еще одного раза», проходят этот процесс ежедневно.
Но для того, кто живет по принципу «еще одного раза», одних новогодних обещаний недостаточно. Лучшие измеряют себя ежемесячно или еженедельно. Подводите ли вы итоги недели в пятницу вечером? Подводите ли итоги и составляете ли планы на предстоящую неделю в воскресенье вечером? Лучшие из лучших, мыслящие в парадигме «еще одного раза», проходят этот процесс ежедневно.  Сосредоточьтесь на будущем
Сосредоточьтесь на будущем  Нужно найти способ пережить их и двигаться вперед. Если вы не справляетесь, то причиняете боль себе и тем, кто вам небезразличен в данный момент. И наоборот, не попадайтесь в ловушку влюбленности в свое прошлое, если у вас получалось достичь чего-то выдающегося: получить высшее образование, повышение по службе, вступить в брак и т. д. Это все хорошо, но если вы будете почивать на лаврах, то все равно не будете жить настоящим и не построите лучшее будущее.
Нужно найти способ пережить их и двигаться вперед. Если вы не справляетесь, то причиняете боль себе и тем, кто вам небезразличен в данный момент. И наоборот, не попадайтесь в ловушку влюбленности в свое прошлое, если у вас получалось достичь чего-то выдающегося: получить высшее образование, повышение по службе, вступить в брак и т. д. Это все хорошо, но если вы будете почивать на лаврах, то все равно не будете жить настоящим и не построите лучшее будущее. 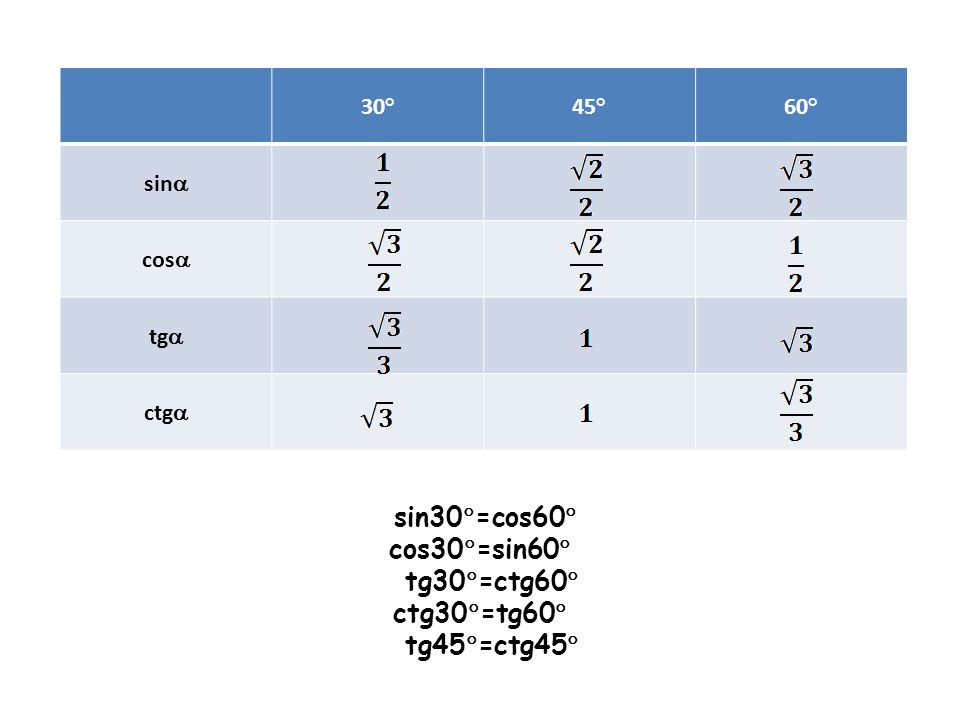 Когда люди видят, что вы больше не тратите время попусту, они тоже перестают расходовать ваше время. Они видят, что вы больше не уделяете слишком много минут и часов заботам о приоритетах других, потому что слишком сосредоточены на заботе о собственных.
Когда люди видят, что вы больше не тратите время попусту, они тоже перестают расходовать ваше время. Они видят, что вы больше не уделяете слишком много минут и часов заботам о приоритетах других, потому что слишком сосредоточены на заботе о собственных. 
 )/3
)/3