Рубрика: Разное

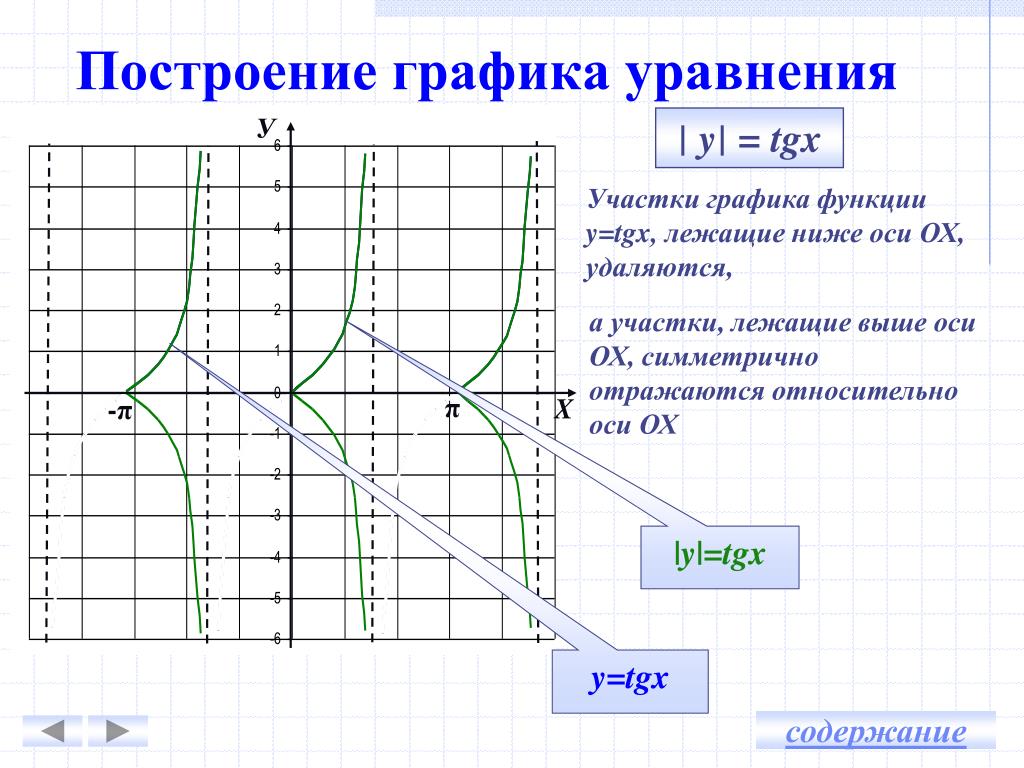
Примеры решения дифференциальных уравнений с ответами

Алгоритм решения

дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x, как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х), с помощью которой можно обратить уравнение в равенство.

Теорема

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Алгоритм

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Пример 1

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь 

   

переписываем дифференциальное уравнение, получаем

   

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей  по правилу пропорции получаем

   

Далее интегрируем полученное уравнение:

   

В данном случае интегралы берём из таблицы:

   

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

То есть,

   

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

y=Cx, где С=Const.

Пример 2

Задание

Найти частное решение дифференциального уравнения

   

.

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

   

   

   

   

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

   

   

Если  – это константа, то

   

– тоже некоторая константа, заменим её буквой С:

   

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

   

где С=const.

Ответ

   

где С=const.

Пример 3

Задание

Решить дифференциальное уравнение

   

Решение

В первую очередь необходимо переписать производную в необходимом виде:

   

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

   

   

После разделения переменных, интегрируем уравнение, как в примерах выше.

   

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

   

   

   

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

   

   

   

   

Приводим полученный общий интеграл к виду: F(x,y)=C:

   

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Общий интеграл:

   

где С=const.

Пример 4

Задание

Найти частное решение дифференциального уравнения

   

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

   

   

   

   

   

   

   

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

   

   

Получаем общее решение:

   

где С=const

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

   

   

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Частное решение:

   

.

Пример 5

Задание

Решить дифференциальное уравнение

   

.

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

   

   

   

   

   

В данном случае константу C считается  не обязательным определять под логарифм.

Ответ

Общий интеграл:

   

Пример 6

Задание

Найти частное решение дифференциального уравнения

   

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

   

   

Интегрируем:

   

   

   

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

   

Используя

   

можно выразить функцию в явном виде.

Общее решение:

   

где С=const.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

   

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Частное решение:

   

Проверка

Необходимо проверить, выполняется ли начальное условие:

   

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

   

дифференциальному уравнению. Для этого находим производную:

   

Подставим полученное частное решение

   

и найденную производную  в исходное уравнение

   

   

   

0=0

Получено верное равенство, значит, решение найдено правильно.

Пример 7

Задание

Найти общий интеграл уравнения

   

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

   

   

   

   

Ответ

Общий интеграл:

   

Пример 8

Задание

Найти частное решение ДУ.

   

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

   

   

   

Интегрируем:

   

   

Общий интеграл:

   

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

   

Подставляем в общее решение

   

   

   

   

Ответ

Частный интеграл:

   

Пример 9

Задание

Решить дифференциальное уравнение

   

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

   

   

Левую часть интегрируем по частям:

   

   

   

В интеграле правой части проведем замену:

   

   

   

Таким образом:

   

   

(здесь дробь раскладывается методом неопределенных коэффициентов)

   

Обратная замена:

   

   

   

Ответ

Общий интеграл:

   

где С=const.

Пример 10

Задание

Решить дифференциальное уравнение

   

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

   

   

   

   

   

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

   

   

   

   

   

   

   

   

   

   

   

Ответ

Общее решение:

   

где С=const.

Средняя оценка 2.5 / 5. Количество оценок: 13

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

52776

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

Полезно

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

2. Выбрать платежную систему.
3. Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
4. Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

---

Desertai be cukraus Vilniuje: tortai, pyragaičiai, saldainiai

интегрирование — Нахождение частичного решения дифференциального уравнения

спросил 8 лет, 2 месяца назад

Изменено 8 лет назад

Просмотрено 887 раз

$\begingroup$

Дано, $$\frac{dy}{dx} = yx \sin(x), \text{ при }y(0) = 1/4.$$ 9{С3}. $$ Здесь, поскольку отрицание не работает внутри ln(), я думаю, что с моим решением что-то не так. Может ли кто-нибудь помочь мне с тем, как мне подойти к этому вопросу?

Спасибо!

• интегрирование
• обыкновенные дифференциальные уравнения
• частные производные

$\endgroup$

1

$\begingroup$

В методе нет ничего плохого, вы просто напутали с возведением в степень. Когда сила — это сумма, вы получаете продукт, а не сумму! 9x t\sin t\,dt\Big)= \frac{1}{4}\exp\Big(-x\cos x+\sin x\Big). $$

$\endgroup$

Почему мы обычно не решаем уравнения в частных производных с суммами функций, а не произведениями?

Набор решений, которые вы найдете, предполагая отделимость, намного богаче, чем набор простых полиномиальных решений, которые вы найдете, взяв $u(x,t) = X(x) + T(t)$. В частности, взяв линейные комбинации разделимых решений, мы можем решить любую заданную начально-краевую задачу (НКЗ) для уравнения теплопроводности.

Я подробно покажу, как это работает. Следующий материал можно найти в учебниках PDE, таких как Boyce и DiPrima.

Например, рассмотрим следующую ОКЗ: Найдите непрерывную функцию $u: [0,1] \times [0,\infty)$ такую, что $u$ удовлетворяет уравнению теплопроводности $u_t = u_{xx}$ на $ \Omega = (0,1) \times (0,\infty)$, а также граничные условия $u(0,t) = u(1,t) = 0$ (для всех $t > 0$) и начальное условие $u(x,0) = f(x)$. Здесь $f:[0,1] \to \mathbb R$ — любая заданная непрерывная кусочно дифференцируемая функция, удовлетворяющая условию $f(0) = f(1) = 0$. (Возможны и другие предположения относительно $f$, но ограничения на $f$ всегда очень мягкие.)

Сначала найдем сепарабельные решения уравнения теплопроводности, удовлетворяющие заданным граничным условиям. Если сепарабельная функция $u(x,t) = X(x) T(t)$ удовлетворяет уравнению теплопроводности на $\Omega$, то должна существовать константа $\lambda$ такая, что $$ T'(t)/T(t) = X»(x)/X(x) = \lambda $$ для всех $(x,t) \in \Omega$. Если бы $\lambda$ было положительным, наши граничные условия не могли бы выполняться.

2

Как извлечь корень из 7. Как высчитать квадратный корень из числа без помощи калькулятора

Для вычисления квадратного корня без калькулятора существует несколько методов.

Как найти корень из числа – 1 способ

• Один из методов заключается в разложении на множители того числа, которое находится под корнем. Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем.
• Например, если взять число 1 600 и начать раскладывать его на множители, то рассуждение построится таким образом: данное число кратно 100, значит, его можно разделить на 25; так как корень из числа 25 извлекается, то число является квадратным и подходит для дальнейших вычислений; при делении получаем еще одно число – 64. Это число тоже квадратное, поэтому корень извлекается хорошо; после этих расчетов под корнем можно записать число 1600 в виде произведения 25 и 64.

• Одно из правил извлечения корня гласит, что корень из произведения множителей равен числу, которое получается при умножении корней из каждого множителя. Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
• Но бывает так, что число, находящееся под корнем, не раскладывается на два множителя, из которых извлекается целый корень. Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
• В таком случае можно высчитать только приблизительное значение. Поэтому нужно извлечь корень из множителя, который является квадратным числом. Это значение затем умножить на корень из второго числа, которое не является квадратным членом уравнения.
• Выглядит это таким образом, например, возьмем число 320. Его можно разложить на 64 и 5. Из 64 целый корень извлечь можно, а из 5 – нет. Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
• Если есть необходимость, то можно найти приблизительное значение этого результата, вычислив
  √5 ≈ 2,236, следовательно, √320 = 8 * 2,236 = 17,88 ≈ 18.
• Также число под корнем можно разложить на несколько простых множителей, а одинаковые можно вынести из-под него. Пример: √75 = √(5*5*3) = 5√3 ≈ 8,66 ≈ 9.

Как найти корень из числа – 2 способ

• Другой способ заключается в делении в столбик. Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
• В этом случае квадратное число пишем сверху и отнимаем его в левой части, а извлеченный корень снизу.
• Теперь второе значение нужно удвоить и записать снизу справа в виде: число_х_=. Пропуски необходимо заполнить числом, которое будет меньше или равно необходимому значению слева – все как в обычном делении.
• При необходимости этот результат снова вычитается слева. Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.

Рассмотрим этот алгоритм на примере. Найдем

1-й шаг. Число под корнем разбиваем на грани по две цифры (справа налево):

2-й шаг. Извлекаем квадратный корень из первой грани, т. е. из числа 65, получаем число 8. Под первой гранью пишем квадрат числа 8 и вычитаем. К остатку приписываем вторую грань (59):

(число 159 — первый остаток).

3-й шаг. Удваиваем найденный корень и пишем результат слева:

4-й шаг. Отделяем в остатке (159) одну цифру справа, слева получаем число десятков (оно равно 15). Затем делим 15 на удвоенную первую цифру корня, т. е. на 16, так как 15 на 16 не делится, то в частном получается нуль, который записываем как вторую цифру корня. Итак, в частном получили число 80, которое опять удваиваем, и сносим следующую грань

(число 15 901 — второй остаток).

5-й шаг. Отделяем во втором остатке одну цифру справа и полученное число 1590 делим на 160. Результат (цифру 9) записываем как третью цифру корня и приписываем к числу 160. Полученное число 1609 умножаем на 9 и находим следующий остаток (1420):

В дальнейшем действия выполняются в той последовательности, которая указана в алгоритме (корень можно извлекать с нужной степенью точности).

Замечание. Если подкоренное выражение — десятичная — дробь, то ее целую часть разбивают на грани по две цифры справа налево, дробную часть — по две цифры слева направо и извлекают корень по указанному алгоритму.

ДИДАКТИЧЕСКИЙ МАТЕРИАЛ

1. Извлеките квадратный корень из числа: а) 32; б) 32,45; в) 249,5; г) 0,9511.

Извлечение корня – обратная операция возведению степени. То есть Извлекая корень из числа Х, получим число, которое в квадрате даст то самое число Х.

Извлечение корня довольно-таки несложная операция. Таблица квадратов сможет облегчить работу по извлечению. Потому что, наизусть помнить все квадраты и корни невозможно, а числа могут встретиться большие.

Извлечение корня из числа

Извлечение квадратного корня из числа – просто. Тем более что это можно делать не сразу, а постепенно. Например, возьмем выражение √256. Изначально, незнающему человеку сложно дать ответ сразу. Тогда будем делать по шагам. Сначала разделим на просто число 4, из которого вынесем за корень выделенный квадрат.

Изобразим: √(644), тогда это будет равносильно 2√64. А как известно, по таблице умножения 64=8 8. Ответ будет 2*8=16.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Извлечение комплексного корня

Корень квадратный не может вычисляться из отрицательных чисел, потому что любое число в квадрате – положительное число!

Комплексное число – число i, которое в квадрате равно -1. То есть i2=-1.

В математике существует число, которое получается при извлечении корня из числа -1.

То есть есть возможность вычислить корень из отрицательного числа, но это уже относится к высшей математике, не школьной.

Рассмотрим пример такого извлечения корня: √(-49)=7*√(-1)=7i.

Калькулятор корня онлайн

С помощью нашего калькулятора, Вы сможете посчитать извлечение числа из квадратного корня:

Преобразование выражений, содержащих операцию извлечения корня

Суть преобразования подкоренных выражений в разложении подкоренного числа на более простые, из которых можно извлечь корень. Такие как 4, 9, 25 и так далее.

Приведем пример, √625. Поделим подкоренное выражение на число 5. Получим √(1255), повторим операцию √(25 25), но мы знаем, что 25 это 52. А значит ответом будет 5*5=25.

Но бывают числа, у которых корень таким методом не вычислить и просто нужно знать ответ или иметь таблицу квадратов под рукой.

√289=√(17*17)=17

Итог

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Вычисление (или извлечение) квадратного корня можно производить несколькими способами, но все они не сказать что уж очень просты. Проще, конечно, прибегнуть к помощи калькулятора. Но если такой возможности нет (или вы хотите понять суть квадратного корня), могу посоветовать пойти следующим путем, его алгоритм таков:

Если на такие длительные вычисления у вас нет сил, желания или терпения, можно прибегнуть к помощи грубого подбора, его плюс в том, что он невероятно быстрый и при должной смекалке точный. Пример:

Когда я учился в школе (в начале 60-х годов), нас учили извлекать квадратный корень из любого числа. Методика несложная, внешне похожа на деление столбиком, но излагать е здесь, это потребуется полчаса времени и 4-5 тысяч знаков текста. Но зачем это Вам? У вас есть телефон или иной гаджет, в нм есть калькулятор. Калькулятор есть и в любом компьютере. Лично я предпочитаю производить такого рода вычисления в Excel.

Зачастую в школе требуется находить квадратные корни разных чисел. Но если вот мы привыкли пользоваться постоянно для этого калькулятором, то на экзаменах такой возможности не будет, поэтому нужно учиться искать корень без помощи калькулятора. А сделать-то это в принципе возможно.

Алгоритм таков:

Смотрите сначала на последнюю цифру вашего числа:

Например,

Теперь требуется определить примерно значение для корня из самой левой группы

В случае когда число имеет больше двух групп, то находить корень надо так:

А вот следующая циферка должна быть именно наибольшей, подобрать е надо так:

Теперь надо образовать новое число А посредством добавления к остатку, который был получен выше, следующую группу.

В наших примерах:

Столбиком наджней, а когда нужно больше пятнадцати знаков, то компьютеры и телефоны с калькуляторами чаще всего отдыхают. Осталось проверить, займт ли описание методики 4-5 тыс. знаков.

Берм любое число, от запятой отсчитываем пары цифр вправо и влево

Например, 1234567890,098765432100

Пара цифр — это как бы двузначное число. Корень из двузначного — однозначное. Подбираем однозначное, квадрат которого меньше первой пары цифр. В нашем случае это 3.

Как при делении столбиком, под первой парой выписываем этот квадрат и из первой пары вычитаем. Результат сносим под подчерк. 12 — 9 = 3. Добавляем к этой разнице вторую пару цифр (будет 334). Слева от числа берм удвоенное значение той части результата, которую уже нашли о дополняем цифрой (у нас 2*6=6), такой, чтобы при умножении на не полученное число не превосходило число со второй парой цифр. Получаем, что найденная цифра — пятрка. Снова находим разность (9), сносим следующую пару цифр получая 956, снова выписываем удвоенную часть результата (70), снова е дополняем нужной цифрой и так далее до упора. Или до нужной точности вычислений.

Во-первых для того что бы вычислить квадратный корень надо хорошо знать таблицу умножения. Самые простые примеры — это 25 (5 на 5 = 25) и так далее. Если же брать числа посложнее, то можно использовать данную таблицу, где по горизонтали единицы, а по вертикале десятки.

Есть хороший способ как найти корень из числа без помощи калькуляторов. Для этого вам понадобится линейка и циркуль. Суть в том, что вы находите на линейке значение, которое у вас под корнем. Например, ставите отметку возле 9. Ваша задача — поделить это число на равное количество отрезков, то есть на два линии по 4,5 см, а на ровный отрезок. Несложно догадаться, что в итоге получится 3 отрезка по 3 сантиметра.

Способ нелегкий и для больших чисел не подойдет, но зато считается без калькулятора.

без помощи калькулятора способу извлечения корня квадратного учили в советские времена в школе в 8-м классе.

Для этого надо разбить многозначное число справа налево на грани по 2 цифры :

Первая цифра корня это целый корень из левой грани, в данном случае, 5.

Вычитаем 5 в квадрате из 31, 31-25=6 и к шестерке приписываем следующую грань, имеем 678.

Следующая цифра х подбирается к удвоенной пятерке так, чтобы

10х*х было максимально большим, но меньшим чем 678.

х=6, поскольку 106*6 = 636,

теперь вычисляем 678 — 636 = 42 и добавляем следующую грань 92, имеем 4292.

Снова ищем максимальный х, такой что 112х*х lt; 4292.

Ответ: корень равен 563

Так можно продолжать сколько требуется.

В некоторых случаях можно попытаться разложить подкоренное число на два или несколько квадратных множителей.

Также полезно запомнить таблицу (или хотя бы какую-то ее часть) — квадраты натуральных чисел от 10 до 99.

Предлагаю изобретенный мною вариант извлечения квадратного корня в столбик. Он отличается от общеизвестного, исключением подбора чисел. Но как выяснил позже, данный метод уже существовал за много лет до моего рождения. Описал его в своей книге Всеобщая арифметика или книга об арифметических синтезе и анализе великий Исаак Ньютон. Так что здесь излагаю свое видение и обоснование алгоритма метода по Ньютону. Запоминать алгоритм не стоит. Можно просто при необходимости пользоваться схемой на рисунке в качестве наглядного пособия.

С помощью таблиц можно не вычислить, а найти, корни квадратные толь из чисел которые есть в таблицах. Проще всего вычислять корни не только квадратные, но и других степеней, методом последовательных приближений. Например вычислим корень квадратный из 10739, заменяем три последние цифры нулями и извлечем корень из 10000 получим 100 с недостатком, поэтому берем число 102 возводим его в квадрат, получаем 10404, что тоже меньше заданного, берем 103*103=10609 опять с недостатком, берем 103,5*103,5=10712,25, берем ещ больше 103,6*103,6=10732, берем 103,7*103,7=10753,69, что уже с избытком. Можно принять корень из 10739 примерно равны 103,6. Более точно 10739=103,629… . . Аналогично вычисляем корень кубический сначала из 10000 получаем примерно 25*25*25=15625, что с избытком, берем 22*22*22=10,648, берем чуть больше 22,06*22,06*22,06=10735, что очень близко к заданному.

Квадратный корень из 7 — Как найти квадратный корень из 7?

ОБЕЩАНИЕ НА 30 ДНЕЙ | ПОЛУЧИТЕ 100% ВОЗВРАТ ДЕНЕГ*

*T&C Apply

LearnPracticeDownload

Квадратный корень из 7 выражается как √7 в радикальной форме и как (7) ^½ или (7) ^0,5 в экспоненте форма. Квадратный корень из 7, округленный до 8 знаков после запятой, равен 2,64575131. Это положительное решение уравнения x ² = 7.

• Корень квадратный из 7: 2,6457513110645907
• Квадратный корень из 7 в экспоненциальной форме: (7) ^½ или (7) ^0,5
• Квадратный корень из 7 в подкоренной форме: √7

В этом мини-уроке мы узнаем больше о том, как найти квадратный корень из 7.

1.	Что такое квадратный корень из 7?
2.	Является ли квадратный корень из 7 рациональным или иррациональным?
3.	Как найти квадратный корень из 7?
4.	Важные примечания по квадратному корню из 7
5.	Советы и рекомендации
6.	Часто задаваемые вопросы о квадратном корне из 7

Что такое квадратный корень из 7?

• Квадратный корень числа — это число, которое при умножении на себя дает исходное число как произведение.
• √7 = 2,645 х 2,645 или -2,645 х -2,645

Является ли квадратный корень из 7 рациональным или иррациональным?

• Рациональное число определяется как число, которое может быть выражено в виде частного или деления двух целых чисел, т. е. p/q, где q не равно 0.
• √7 = 2,645751311064591. Из-за того, что число √7 не имеет конца после запятой, оно не имеет конца.

Как найти квадратный корень из 7?

Квадратный корень из 7 можно вычислить, используя метод среднего или длинного деления. √7 нельзя еще больше упростить, поскольку оно простое. Радикальная форма квадратного корня из 7 – √7.

Квадратный корень из 7 методом усреднения

• Квадратный корень из 7 будет лежать между квадратными корнями двух полных квадратов ближе к 7.
• Сначала мы определим квадратный корень из 4 и квадратный корень из 9. √4 < √7 < √9.
• Таким образом, мы определяем, что квадратный корень из 7 лежит между 2 и 3. 2 < √7 < 3
• Используя метод среднего, найдите 7 ÷ 3 или 7 ÷ 2.
• 7 ÷ 3 = 2,33
• Найдите среднее значение полученного частного и 3. Среднее = (2,33 + 3) ÷ 2 = 5,33 ÷ 2 = 2,66
• Таким образом, √7 = 2,66 методом среднего.

Извлечение квадратного корня из 7 методом деления в длину

 

• Запишите 7 как 7,000000. Рассмотрим числа в парах справа. Так что 7 стоит особняком.
• Теперь разделите 7 на такое число, что число × число дает 7 или меньшее число. Определяем 2 × 2 = 4
• Завершить процесс деления. Получите 2 как частное и 3 как остаток. Снесите первую пару нулей.
• Удвойте полученное частное. Теперь 2 × 2 образует новый делитель в разряде десятков.
• Найдите число, которое в единицах ставится рядом с 40, дает произведение 300 или меньшее число.
• Мы находим, что 6 × 46 дает 276. Завершите деление и получите остаток как 24.
• Теперь наше частное равно 2,6. Удвойте это и получите 520 в качестве нашего нового делителя.
• Сбить следующую пару нулей. Найдите число, которое вместе с 520 дает 2400 или меньшее число.
• Делаем вывод 4 × 524 = 2096. Завершаем деление.
• Повторяем тот же процесс деления, пока не получим частное, округленное до 3 цифр.
• Таким образом, мы вычислили √7 = 2,645.

Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров.

• Квадратный корень из 5
• Квадратный корень из 8
• Квадратный корень из 9 
• Квадратный корень из 12
• Квадратный корень из 2

Важные примечания

• Квадратный корень из 7 выражается как √7 в радикальной форме и как 7 ^½ в экспоненциальной форме.
• Квадратный корень числа является как отрицательным, так и положительным для одного и того же числового значения, т. е. квадратный корень из 7 равен +2,645 или -2,645.

Советы и подсказки

• Квадратный корень из 7 лежит между полными квадратами, ближайшими к 7. Таким образом, √7 лежит между 2 и 3.
• Используйте метод среднего, чтобы определить приблизительное значение 7, и метод деления, чтобы определить точное значение √7.

 

1. Пример 1: Площадь пиццы, которую купил Майк, составляет 22 кв. Каков будет радиус пиццы?

   Решение:

   Площадь пиццы = π r ² квадратных единиц

   π r ² = 22

   r ² = 22 × 7 / 22

   r ² = 7. Отсюда следует r = √7

   Таким образом, радиус пиццы составляет 2,645 единицы.

2. Пример 2 : Если ²  = 0,07, найдите a.

   Решение:

   Учитывая ² = 0,07

   a ² = (7/100)

   a = √(7/100 )

   = √7/√100

   = √7 /10

   = 2,645/10

   Таким образом, a = 0,2645

3. Пример 3:  В прямоугольном треугольнике две стороны равны √3 и 2 соответственно. Чему равна гипотенуза?

   Решение:

   Согласно теореме Пифагора,

   Гипотенуза ² = катет1 ² + катет2 ²  

   Гипотенуза ^{2 9001 0 = ( √3) 2  + 2 2}

   Извлечение квадратного корня, получаем √Гипотенуза ²   =  √(( √3) ²  + 2 ²  )

   Гипотенуза = √(3+4) = √7 = 2,645

   Таким образом, гипотенуза равна 2,645.

перейти к слайдуперейти к слайдуперейти к слайду

 

Как ваш ребенок может освоить математические понятия?

Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о квадратном корне из 7

Каково значение квадратного корня из 7?

Квадратный корень из 7 равен 2,64575.

Почему квадратный корень из 7 является иррациональным числом?

Число 7 простое. Это означает, что число 7 не имеет пары и не находится в степени двойки. Следовательно, квадратный корень из 7 иррационален.

Является ли число 7 идеальным квадратом?

Число 7 простое. Это означает, что квадратный корень из 7 не может быть выражен как произведение двух равных целых чисел. Следовательно, число 7 не является полным квадратом.

Что такое квадратный корень из 7 в простейшей радикальной форме?

Число 7 — простое число. Это означает, что число 7 не имеет своей пары и не находится в степени 2. Следовательно, радикальная форма квадратного корня из 7 не может быть дополнительно упрощена.

Каково значение 20 квадратного корня из 7?

Квадратный корень из 7 равен 2,646. Следовательно, 20 √7 = 20 × 2,646 = 52,915.

Что такое квадратный корень из -7?

Квадратный корень из -7 является мнимым числом. Это можно записать как √-7 = √-1 × √7 = i √7 = 2,645i
где i = √-1 и называется мнимой единицей.

Рабочие листы по математике и
визуальные учебные программы

Квадратный корень из 7 | Thinkster Math

Методы

Что такое квадратный корень из 7?

Квадратный корень из числа — это значение, которое при умножении само на себя дает исходное число. Например, квадратный корень из 25 равен 5, потому что 5 x 5 = 25. Выражаясь в радикальной форме: √25 = 5. Следовательно, находя квадратный корень из 7, мы находим, что квадратный корень из 7 2,646 . Всегда помните: ваш ответ может быть как целым, так и десятичным числом.

Является ли квадратный корень из 7 иррациональным?

Числа можно разделить на подмножества, называемые рациональными и иррациональными числами. Примером иррациональных чисел являются десятичные дроби, которые не имеют конца или не заканчиваются. Распространенная путаница заключается в том, что, поскольку у десятичной дроби нет конца, это большое число, стремящееся к бесконечности, тогда как это неверно.

Взгляните на экспоненциальную константу e, e имеет значение 2,7182818… и является неограниченным, но не огромным значением, потому что в конце дня e никогда не будет больше 3. С другой стороны, рациональные числа — это десятичные дроби, которые можно записать в виде дробей, делящих два целых числа (если знаменатель не равен 0). Таким образом, для этой задачи, поскольку квадратный корень из 7 или 2,646 является неконечной десятичной дробью, квадратный корень из 7 иррационален.

Методы извлечения квадратного корня из 7

Начнем с того, что есть два способа вычисления квадратного корня числа: простая факторизация и длинное деление. Обычно простая факторизация используется для идеальных квадратов, а длинное деление используется, когда значение квадратного корня является десятичным.

Поскольку мы знаем, что 7 — десятичное число, мы знаем, что подходящим методом будет деление в длинную сторону. Этот метод работает очень похоже на обычное длинное деление, за исключением того, что в этом методе есть еще несколько правил, которые помогают нам получить ответ. Взгляните на этот пример, в котором подробно рассказывается о том, что представляет собой этот метод, как его использовать, а также приводится несколько решенных примеров. Таким образом, результат после использования метода деления в длинную сторону равен 2,646.

Нахождение квадратного корня из других чисел

Нахождение квадратного корня любого числа можно выполнить с помощью того же метода, который показан выше. Посмотрите, как найти квадратный корень из этих других конкретных примеров, нажав на любую из ссылок ниже:

Квадратный корень из 896

Квадратный корень из 56

Квадратный корень из 4806

Квадратный корень из 798

Квадратный корень из 2052

Загрузите БЕСПЛАТНЫЕ математические ресурсы

Воспользуйтесь нашими бесплатными загружаемыми ресурсами и учебными материалами для обучения дома.

{2}-4ac}}{2a}.

x=\frac{0±\sqrt{-4\left(-\frac{1}{15}\right)\times \frac{31}{600}}}{2\left(-\frac{1}{15}\right)}

Возведите 0 в квадрат.

x=\frac{0±\sqrt{\frac{4}{15}\times \frac{31}{600}}}{2\left(-\frac{1}{15}\right)}

Умножьте -4 на -\frac{1}{15}.

x=\frac{0±\sqrt{\frac{31}{2250}}}{2\left(-\frac{1}{15}\right)}

Умножьте \frac{4}{15} на \frac{31}{600}, перемножив числители и знаменатели. Затем, если это возможно, сократите дробь до младших членов.

x=\frac{0±\frac{\sqrt{310}}{150}}{2\left(-\frac{1}{15}\right)}

Извлеките квадратный корень из \frac{31}{2250}.

x=\frac{0±\frac{\sqrt{310}}{150}}{-\frac{2}{15}}

Умножьте 2 на -\frac{1}{15}.

x=-\frac{\sqrt{310}}{20}

Решите уравнение x=\frac{0±\frac{\sqrt{310}}{150}}{-\frac{2}{15}} при условии, что ± — плюс.

x=\frac{\sqrt{310}}{20}

Решите уравнение x=\frac{0±\frac{\sqrt{310}}{150}}{-\frac{2}{15}} при условии, что ± — минус.

x=-\frac{\sqrt{310}}{20} x=\frac{\sqrt{310}}{20}

Уравнение решено.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Квадратный корень из 5 — значение, метод расчета, примеры решений и часто задаваемые вопросы

Значение корня из 5, уменьшенное до 5 знаков после запятой, равно √5 = 2,23606. У него есть место с большим списком иррациональных алгебраических чисел. Он был отсортирован в свете из-за того, что квадратный корень из 5 не может быть описан как дробь и имеет бесконечное количество десятичных знаков. Кроме того, конкретное значение никогда не может быть найдено идеально. В математике квадратный корень из 5 представляется или записывается как √5. Это положительное число, а также значение √5 при умножении на себя дает простое число 5. Чтобы отличить себя от отрицательного числа с теми же свойствами, оно называется главным корнем из 5.

 

Как найти квадратный корень из 5?

Этот вопрос может беспокоить вас уже довольно давно. Самый простой способ найти квадратный корень из любого числа — использовать метод деления. Как найти значение корня 5? Выполните шаги, указанные ниже:

 

Шаг 1: Первый шаг — сгруппировать цифры парами по два. Вы начинаете с единицы, которая находится в месте единицы, и двигаетесь к левой стороне для числа до десятичной точки. Для числа после запятой вы группируете первые два числа и двигаетесь вправо.

5. 00 00 00 00

 

Шаг 2. На этом шаге вам нужно будет выбрать наибольшее квадратное число, которое равно или меньше первой пары чисел. Теперь возьмите это число в качестве делителя и также запишите частное.

 

Шаг 3: Теперь вы вычитаете конечный продукт частного и делителя и частного из пары чисел или числа. Далее вы сбиваете следующую пару чисел.

 

Шаг 4: Теперь вам нужно вычислить делитель. Для этого вам нужно будет умножить предыдущее частное на 2, а затем выбрать новое число таким образом, чтобы цифра и новый делитель были меньше или равны новому делимому 9.0907

 

Шаг 5. Повторяйте шаги 2, 3 и 4, пока не будут исчерпаны все пары чисел. Итак, найденное вами частное — это квадратный корень. В случае значения под root 5 это делается так.

 

(Изображение будет загружено в ближайшее время)

 

90 004

4452

	9 0906 2. 236
2 +2	5 . 00 00 00 4
42 + 2	1 00 — 84
443 + 3	16 00 — 13 29
4466 +    6	27100  —     26796
304

 

Следовательно, квадратный корень из 5 = 2,236

 

Чему равен квадратный корень из 5?

Значение корня 5, уменьшенное до 5 знаков после запятой, равно 2,23606, и это просто упрощенная версия значения. Кроме того, фактическое значение корня 5 может быть равно как минимум десяти миллиардам цифр.

 

Примеры вопросов

1. Используя метод деления, найдите квадратный корень из числа 784.

Решение:

 

900 04

  2

+2

	28
784 4
48 9 0005	384 — 384
	0

 

2. Методом деления найдите квадратный корень из значения 5329.

Решение:

 

	73
7 +7	53 29 49
143	4 29 —  4 29
	0

 

3. Найдите квадратный корень из 66049.

Решение:

 

	257
2 +2	6 60 49 4
9090 6   45 +  5	2 60 2 25
507	35 49 —  35 49
	0

 

Знаете ли вы?

• 5 не является полным квадратом, так как квадратный корень из 5 не является целым числом.

•  Квадратный корень из 5 в экспоненциальной форме можно записать как (5)½ или (5)0,5.

• При решении задачи на квадратный корень из 5 желательно брать значение до 3 знаков после запятой.

 

Является ли квадратный корень из числа 5 рациональным или иррациональным числом?

Сначала давайте разберемся, что такое рациональные и иррациональные числа. Рациональное число — это число, которое можно записать в виде отношения любых двух целых чисел. Например, квадратный корень из 9 равен 3, что также можно записать как 3/1.

 

Принимая во внимание, что иррациональное число — это число, которое нельзя записать в виде отношения любых двух целых чисел. Итак, квадратный корень из 5, который эквивалентен 2,23 с точностью до двух десятичных значений, что является иррациональным числом.

 

Решенные примеры

1. Предположим, что стороны квадратной фоторамки имеют длину 2,33 м. Узнайте площадь фоторамки и запишите ответ до ее ближайшего округления.

Ответ. Длина стороны фоторамки = 2,33 м

Площадь квадрата = (сторона)2

Подставляя значение длины в приведенное выше уравнение, получаем

Площадь фоторамки = (2,33)2= 5,4289 м2

Округлив, получим 5 м2

 

2. Площадь стены квадратной формы 25м2. Какова длина одной стороны стены? Чему равен периметр стены?

Ответ. Площадь квадрата = (сторона)2

Подставляя значение площади стены, получаем

25 = (сторона)2

√25 = сторона = 5 метров.

Периметр квадрата = 4 х сторона

= 4 х 5 = 20 метров.

 

3. Каково значение 15√5?

Ответ. 15√5 = 15 х 2,236 = 33,54101

 

4. Оцените следующие задачи:

1.

Построить график функции c помощью GeoGebra

Полином Чебышева с свободным членом Создать вектор(диофант) по матрице Египетские дроби. Часть вторая Египетские (аликвотные) дроби По сегменту определить радиус окружности Круг и площадь, отсекаемая перпендикулярами Деление треугольника на равные площади параллельными Определение основных параметров целого числа Свойства обратных тригонометрических функций Разделить шар на равные объемы параллельными плоскостями Взаимосвязь между организмами с различными типами обмена веществ Аутотрофные и миксотрофные организмы Рассечение круга прямыми на равные площади Период нечетной дроби онлайн. Первые полторы тысяч разложений. Представить дробь, как сумму её множителей Решение системы из двух однородных диофантовых уравнений Расчет основных параметров четырехполюсника Цепочка остатков от деления в кольце целого числа Система счисления на базе ряда Фибоначчи онлайн Уравнение пятой степени. Частное решение. Рассчитать площадь треугольника по трем сторонам онлайн Общее решение линейного диофантового неоднородного уравнения Частное решение диофантового уравнения с несколькими неизвестными Онлайн разложение дробно рациональной функции Корни характеристического уравнения

В поисках решения,  как же предложить всем желающим, создавать графики уравнения или строить произвольные графики функций, я перелопатил многое:   искал скрипты, писал сам и пытался изучить язык metapost и научить гостей сайта, но в к конечном  итоге я нашел ту «жемчужину» которая помогла мне. Речь идет о бесплаьной программе Geogebra, сайт которого размещен по адресу http://www.geogebra.org/ Программа написана на Java, поэтому является кроссплатформенным решением, то работает как на Linux-совместимых ( Ubuntu, Red Hat  и прочее), так и на Windows операционных системах. Рабочее окно GeoGebra выглядит вот так     Функционал  программы очень обширен,  но в основном на 100% процентов  эту программу будут использовать  преподаватели для создания учебных материалов, студенты для создания дипломных работ, и школьники  при защите курсовых или для понимания той или иной задачи. Программа может строить: — Многоугольники и рассчитывать  площади — Вектора и вычисления с ними — поворот точки или фигуры вокруг начала координат  или другой произвольной точки — зеркальное отображени фигуры. — биссектриссу угла — много другое, вплоть до анимационных картинок для  показания физических процессов.   Но самое главная возможность, на мой взгляд это  построение графика любого уравнения  от одного или двух переменных. Рассмотрим примеры Открываем GeoGebra  и внизу в поле Ввод пишем уравнение третьей степени и получаем следующее Поставив точку на пересечении графика уравнения и оси абсцисс  мы можем получить  координаты Точка А имеет координаты (-2.46:0) То есть один из корней уравнения третьей степени  будет иметь значение -2.46 и это легко проверяется подстановкой в исходное уравнение.   С помощью программы можно  создавать  более сложные графики как здесь   так и анимационные ролики, которые можно увидеть в форуме создателей GeoGebra. Программа GeoGebra почему то незаслуженно забыта на российских просторах,  и ни один из более менее популярных ресурсах, посвященных учебе, об этой программе не говорит. Хотя для возникновения интереса у школьников, для понимания геометрических а иногда и алгебраических задач это незаменимая программа.   Успехов в изучении программы!     Построить ненаправленный граф по матрице >> Поиск по сайту

Русский и английский алфавит в одну строку Часовая и минутная стрелка онлайн.Угол между ними. Массовая доля химического вещества онлайн Декoдировать текст \u0xxx онлайн Универсальный калькулятор комплексных чисел онлайн Перемешать буквы в тексте онлайн Частотный анализ текста онлайн Поворот точек на произвольный угол онлайн Обратный и дополнительный код числа онлайн Площадь многоугольника по координатам онлайн Остаток числа в степени по модулю Расчет пропорций и соотношений Как перевести градусы в минуты и секунды Расчет процентов онлайн Поиск объекта по географическим координатам Растворимость металлов в различных жидкостях DameWare Mini Control. Настройка. Время восхода и захода Солнца и Луны для местности Калькулятор географических координат Расчет значения функции Эйлера Теория графов. Матрица смежности онлайн Перевод числа в код Грея и обратно Произвольный треугольник по заданным параметрам НОД двух многочленов. Greatest Common Factor (GCF) Географические координаты любых городов мира Площадь пересечения окружностей на плоскости Непрерывные, цепные дроби онлайн Онлайн определение эквивалентного сопротивления Сообщество животных. Кто как называется? Проекция точки на плоскость онлайн Из показательной в алгебраическую. Подробно Калькулятор онлайн расчета количества рабочих дней Система комплексных линейных уравнений Расчет заряда и разряда конденсатора через сопротивление Расчет понижающего конденсатора Месторождения золота и его спутники Построить ненаправленный граф по матрице Определение формулы касательной к окружности Дата выхода на работу из отпуска, декрета онлайн Каноническое уравнение гиперболы по двум точкам Онлайн расчеты Подписаться письмом

Как построить график: 4 бесплатных приложения

4 бесплатных математических инструмента для создания графиков, которые позволяют создавать их, просто вводя функции, выражения и уравнения.  Эти инструменты включает в себя простой и удобный интерфейс, и, как предоставляется, красочный интерфейс, а также возможность вводить нужные функции или выражения. Кроме того, эти инструменты позволяют сохранять созданные графики в различных форматах: PNG, JPG, PDF — и многих другое. Эти инструменты подходят для преподавателей и студентов. Graph Graph представляет собой бесплатное программное обеспечение для создания графиков для Windows, позволяя рисовать графики в системе координат. Можно создать график с использованием часто используемых математических функций, линейных, тригонометрических и т.д. ПО включает регулируемый масштаб, с помощью которого можно легко настроить значение системы координат, как большие, так и малые. Есть возможность применять различные цвета для выделения разных участков графика. Можно рассчитать площадь и длину пути. Инструмент позволяет настроить функции, а также константы. Мало того, он позволяет добавлять текстовые метки, включающие различные шрифты, изображения и объекты.  График можно сохранить в различных форматах, таких как JPG, PNG, PDF, SVG, BMP, EMF, GIF. График можно распечатать. Лучшей частью этой бесплатной программы является то, что она позволяет создавать анимацию, с помощью которой можно показать изменения на графике при изменении значения. Скачать Graph Functy Functy — другое бесплатное обеспечение для создания математических графиков для Windows, которое позволяет создавать и визуализировать 3D декартовы и сферические математические функции в реальном масштабе времени. Оно позволяет вводить математические функции, мгновенно показывая вид на график и предоставляя вам возможность редактировать нанесенные диапазоны значений, используемых в функциях, X, Y или Z. Есть функция просмотра, где можно вращать, перемещать, масштабировать, а также оценить график. Это бесплатное программное обеспечение поддерживает анимированные функции с временной переменной. Можно сохранить и экспортировать созданный график в PLY-формат, так что он может использоваться в дальнейшем с другими приложениями по 3D моделированию. Скачать Functy Calc5 Calc5 является бесплатным онлайн-инструментом для создания математических графиков, который позволяет построить 2D и 3D графики, просто введя нужные математические функции. Он предоставляет современный математический калькулятор графиков и поддерживает вычислительные операции. Можно делать символьные вычисления: дифференцирование, интегрирование и многое другое. Есть опции масштабирования и панорамирования при создании 2D графика. Введите требуемую функцию, нажмите на OK, и график будет готов. Для сохранения созданного графика можно сделать скриншот экрана, поскольку инструмент не имеет функции сохранения графиков. Попробовать Calc5 Desmos Graphing Calculator Desmos Graphing Calculator — другой бесплатный онлайн-инструмент, позволяющий создавать простые и сложные графики, просто введя выражения и уравнения вручную или с помощью клавиатуры приложения. Интерфейс яркий и удобный, где можно нарисовать несколько графиков. Бесплатный инструмент позволяет настроить формат бумаги графика, в зависимости от ваших требований. Требуется зарегистрироваться на  бесплатном веб-сервисе, чтобы сохранять и делиться созданными графиками с друзьями и коллегами. Есть три способа сохранения графика: можно отправить по электронной почте, встроить или сохранить график в виде изображения в формате PNG. График можно и напечатать. Инструмент доступен как приложение для браузера Chrome. Попробовать Desmos Graphing Calculator  Поделиться:     Оставьте свой комментарий! Комментарий в ВКонтакте Tags: windows Добавить комментарий < Предыдущая   Следующая >

Создание пользовательских функций в Excel — надстройки Office

Редактировать

Твиттер LinkedIn Фейсбук Электронная почта

• Статья
• 28. 03.2023

Пользовательские функции позволяют разработчикам добавлять новые функции в Excel, определяя эти функции в JavaScript как часть надстройки. Пользователи в Excel могут получать доступ к пользовательским функциям точно так же, как и к любой встроенной функции в Excel, например СУММ() .

Примечание

Пользовательская функция — это общий термин, взаимозаменяемый с определяемой пользователем функцией . Оба термина применяются к надстройкам VBA, COM и Office.js. В документации надстроек Office используется термин пользовательская функция , когда речь идет о настраиваемых функциях, использующих API JavaScript для Office.

Важно

Обратите внимание, что пользовательские функции Excel доступны на следующих платформах.

• Офис в Windows
  • Подписка на Microsoft 365
  • бессрочная розничная версия Office 2016 и более поздних версий
• Офис на Mac
• Офис в Интернете

Пользовательские функции Excel в настоящее время не поддерживаются в следующих устройствах:

• Office на iPad
• бессрочные версии Office 2019 или более ранних версий с корпоративной лицензией

На следующем анимированном изображении показано, как ваша книга вызывает функцию, которую вы создали с помощью JavaScript или TypeScript. В этом примере пользовательская функция =MYFUNCTION.SPHEREVOLUME вычисляет объем сферы.

Следующий код определяет пользовательскую функцию =MYFUNCTION.SPHEREVOLUME .

 /**
 * Возвращает объем сферы.
 * @пользовательская функция
 * @param {число} радиус
 */
функцияsphereVolume(радиус) {
  вернуть Math.pow(радиус, 3) * 4 * Math.PI / 3;
}
 

Как пользовательская функция определяется в коде

Если вы используете генератор Yeoman для надстроек Office для создания проекта надстройки пользовательских функций Excel, он создает файлы, которые управляют вашими функциями и областью задач. Мы сосредоточимся на файлах, важных для пользовательских функций.

Файл	Формат файла	Описание
./src/functions/functions.js или ./src/functions/functions.ts	JavaScript или TypeScript	Содержит код, определяющий пользовательские функции.
./src/functions/functions.html	HTML	Предоставляет ссылку