Как доказать, что 1 градус равен 60 минутам? – Обзоры Вики
Как 1 градус равен 60 минутам?
- Ответ: Один градус делится на 60 угловых минут, а одна минута — на 60 угловых секунд. Использование градусов-минут-секунд также признано как обозначение DMS.
- Чтобы доказать. 1 градус = 60 минут.
- Доказательство. Мы знаем это. 1 минута = 60 секунд. 1 день = 24 часа.
Точно так же, как вы конвертируете десятичные градусы в градусы, минуты, секунды? Как преобразовать десятичные градусы в DMS
- Для градусов используйте целую часть десятичной дроби.
- Для минут умножьте оставшуюся десятичную дробь на 60. Используйте целую часть ответа как минуты.
- Для секунд умножьте новую оставшуюся десятичную дробь на 60.
Какой угол 1 градус? Градус (полностью, градус дуги, градус дуги или градус дуги), обычно обозначаемый градусом (символ градуса), представляет собой измерение плоского угла, в котором один полный оборот составляет 360 градусов. … Поскольку полный оборот равен 2π радиан, один градус эквивалентен π180 радиан.
… Поскольку полный оборот равен 2π радиан, один градус эквивалентен π180 радиан.
Что мы называем 1 минутами? При измерении углов минута составляет 60/1 градуса (и Второй составляет 1/60 минуты).
Во-вторых, почему степень делится на 60 минут? Нам известно, что Земля делает один оборот вокруг своей оси за 24 часа. Таким образом, простыми рассуждениями мы можем сказать, что 360 градусов долготы составляют разница во времени 24 часа = (24 * 60) минут = 1440 минут.
Как перевести десятичные градусы в градусы, минуты, секунды на научном калькуляторе?
то что такое обозначение минут градуса? Градусы, минуты и секунды обозначаются символами °, ‘, «. например, 10 ° 33 ’19 ″ означает угол в 10 градусов, 33 минуты и 19 секунд. Градус делится на 60 минут (дуговых), а каждая минута делится на 60 секунд (дуговых).
Почему 360 градусов?
Полный круг составляет 360 градусов, потому что вавилоняне использовали шестидесятеричную систему. Он также представляет количество дней в году, а также потому, что 360 очень сложен.
Какие есть 4 типа степеней? Степени колледжа обычно делятся на четыре категории: младший, бакалавр, магистр и докторантура. Каждый уровень степени колледжа различается по продолжительности, требованиям и результатам.
Кто изобрел 360 градусов?
Жители Месопотамии передали свою числовую систему с основанием 60 в древние египтяне, который использовал его, чтобы разделить круг на 360 градусов.
Что такое минутный и второй угол? Каждый градус делится на 60 частей, каждая из которых составляет 1/60 градуса. Эти части называются минутами. Каждая минута делится на 60 частей, каждая из которых равна 1/60 минуты. Эти части называются секундами. Величину угла можно определить так: 40 градусов, 20 минут, 50 секунд.
Эти части называются секундами. Величину угла можно определить так: 40 градусов, 20 минут, 50 секунд.
Почему градус делится на минуты?
Их астрономия быстро потребовала дальнейшего усовершенствования., поэтому они разделили каждый градус на 60-минутные части: минуты. Вскоре им потребовалась еще большая точность, поэтому они разделили каждую минуту на минуту второго порядка: секунду. Мы до сих пор используем вавилонскую тригонометрию!
Сколько градусов в процентах?
Круг имеет 360 градусов, поэтому, если вы хотите выразить угол в процентах, просто разделите значение угла (в градусах) на 360 и умножьте на 100. И наоборот, разделите процент на 100 и умножьте на 360.
Сколько км составляет градус? Приблизительные метрические эквиваленты градусов. На экваторе для долготы и для широты в любом месте действительны следующие приближения: 1 = 111 км (или 60 морских миль)
Сколько градусов составляет 100 баллов? Градиент равен 1/400 оборота или окружности или 9/10°. Град, или гон, более точно определяется как π/200, или 1.570796 × 10. – 2 радиан.
Град, или гон, более точно определяется как π/200, или 1.570796 × 10. – 2 радиан.
…
Градианы.
| Градианы | Степени |
|---|---|
| 100 град | 90° |
| 200 град | 180° |
| 300 град | 270° |
| 400 град | 360° |
Как перевести градусы десятичные минуты в десятичные градусы?
Десятичные градусы = Градусы + (Минуты / 60) + (Секунды / 3600)
- Сначала преобразуйте минуты и секунды в их эквиваленты в градусах и сложите результаты. 25 ‘/ 60 = 0.4167 ° 30 ″ / 3600 = 0083 °…
- Затем добавьте это число к количеству градусов. 39 ° + 0.425 ° = 39.425 °
- Итак, окончательный результат: 39 ° 25 ′ 30 ″ = 39.425 °.
Как написать минуты в сокращенной форме?
Один для «Минуты» ‘мин‘. Это единица измерения, которая имеет стандартные сокращения, не изменяется во множественном числе и не имеет конечной точки. Таким образом, правильное сокращение для минуты (минут) — «мин».
Это единица измерения, которая имеет стандартные сокращения, не изменяется во множественном числе и не имеет конечной точки. Таким образом, правильное сокращение для минуты (минут) — «мин».
Как записать минуты во время? Час представлен двузначным числом от 00 до 23 (или 24), а минуты представлены двузначное число от 00 до 59. Двоеточие используется как разделитель между часами и минутами: 00:15 (12:15, т. е. через 15 минут после полуночи).
Как перевести мой калькулятор в режим градусов?
Чтобы перевести большинство моделей научных калькуляторов в режим градусов, все, что вам нужно сделать, это нажмите «Режим», а затем посмотрите на цифры на экране рядом с пунктами меню.. Найдите число рядом с «Градусом» или «Градусами» и нажмите его, чтобы изменить режим вашего калькулятора.
Как определить угол наклона?
Как только вы определите второй угол, прибавь это число к 180. Результат — общее количество градусов угла. На рисунке 6 180 ° + 45 ° = 225 °.
Результат — общее количество градусов угла. На рисунке 6 180 ° + 45 ° = 225 °.
Mathway | Популярные задачи
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Мы не можем найти эту страницу
Онлайн приложение Compass Google Maps ЛогинРегистрацияМои маршрутыПожертвованияТемы справки
- Назначение сайта
- Функции компаса
- Меню компаса
- Компас или GPS – преимущества и недостатки
- Тест компаса
- Рисование одно- или многоэтапного маршрута
- Расширение стрелки направления движения компаса
- Ложные показания при использовании компаса
- Точная настройка компаса
- Начало работы с компасом
- Проекция Google Maps
- GPS или компас – плюсы и минусы для навигации
- Тест ссылок на сетку
- Как пользоваться компасом
- Импорт маршрутов Google Map
- Широта и долгота: градусы, минуты и секунды
- Магнитное склонение или вариация
- Регулировка магнитного склонения или вариации
- Расчет магнитного склонения или вариации
- Картографические проекции
- Чтение карты
- Тест на умение читать карту
- Меню
- Перемещение установленного компаса
- Мои маршруты Google Map Compass
- Отрицательное магнитное склонение или вариация
- Новые возможности
- Север: разные типы
- Север на Google Maps
- Компас для артиллерийских орудий
- Интеграция карт Ordnance Survey
- Картографическая проекция артиллерийского вооружения
- Символы карты артиллерийской службы
- Панорамирование и масштабирование с помощью Google Maps
- Положительное магнитное склонение или вариация
- Функция печати карты
- Чертеж маршрута
- Дисплей информации о маршруте
- Безопасность
- Сохранить и сохранить Установить компаса Google Map Routes
- Одноэтапные или многоэтапные маршруты?
- Проверьте свои навыки чтения компаса
- Советы
- Типы подшипников
- Обновления
- Руководство пользователя
- Часы как компас
- Что такое компас?
- Какой тип компаса используется на сайте?
- Масштабирование с помощью Google Maps
Ссылка, по которой вы щелкнули, или URL-адрес, который вы ввели в браузере,
не работал по какой-то причине. Вот несколько возможных причин:
Вот несколько возможных причин:
1. У нас есть «плохая» ссылка, и вы
не повезло щелкнуть по нему.
2. Возможно, вы неправильно ввели адрес страницы.
3. Наш обычно надежный веб-сервер ведет себя очень странно.
4. URL страницы:
Ну и что еще?
- Как насчет того, чтобы попробовать еще раз:
- Если у вас есть время, вы можете сообщить о неработающей ссылке на страницу по электронной почте, и мы отправить вам правильный URL страницы:
- Или вы можете сообщить о неработающей ссылке реферальной страницы анонимно:
Ваш адрес электронной почты, если он указан, будет использоваться только для отправки вам правильного ссылка на страницу. Мы никому и никогда не передаем адреса электронной почты .
Используйте кнопку «Назад» в браузере, чтобы вернуться на предыдущую страницу.
Copyright © 2009–2023 Все права защищены. Центр полевых исследований Барселоны S. L.
L.
1 градус равен скольким минутам
Введение
Один градус можно разделить на 60 угловых минут, а одна минута — на 60 угловых секунд. Градусы-минуты-секунды также называют нотацией DMS. Чтобы часы отработали 24 часа в круглосуточном режиме, им требуется дважды повернуться на 360 градусов. Градус представлен символом «∘», а минуты представлены символом «».
Один градус равен скольким минутам?
Один градус равен 60 минутам. Это означает, что если дать 25 градусов, можно сказать, что это равно 1500 минутам.
\begin{equation}
1 \text { градус }=60 \text { минуты }
\end{equation}
Преобразование 1 градуса в минуты
Как известно, 1 минута = 60 секундам
Кроме того, 1 день = 24 часа
И часовая стрелка совершает 360-градусную дугу два раза в день.
Следовательно,
\begin{equation}
\begin{aligned}
&2 \times 360=720 \text {степень} \\
&1 \text {степень} \frac{2 \times 360}{ 12}=60 \text {минуты}
\end{aligned}
\end{equation}
Отсюда можно сказать, что 1 градус = 60 минут.
Как перевести заданные градусы в минуты?
Чтобы перевести градусы в минуты,
Как мы знаем, 1 градус = 60 минут.
Итак, мы должны умножить данный градус на 60, чтобы получить желаемый результат в минутах.
Мы можем использовать формулу, указанную как
\begin{equation}
\text { Минуты = градус } \mathrm{\times} 60
\end{equation},
Где мы должны поместить заданную степень в приведенном выше уравнении, чтобы получить результат, преобразованный в минуты.
Таблица преобразования:
Используя формулу преобразования, мы можем создать таблицу, как показано ниже:
9{\prime}\end{equation}
Часто задаваемые вопросы (FAQ) — Сколько минут равно 1 градусу
Вопрос: Где широко используется градус?Ответ:
Градус широко используется для измерения углов.
Решение матрицы уравнение онлайн: Метод обратной матрицы онлайн
Системы линейных алгебраических уравнений — презентация онлайн
Похожие презентации:
Системы линейных уравнений
Матрицы. Определитель матрицы
Системы линейных алгебраических уравнений
Высшая математика. Лекция 2. Обратная матрица
Системы линейных уравнений
Решение систем линейных алгебраических уравнений по правилу Крамера, матричным методом, методом Гаусса
Элементы линейной алгебры
Матрицы и определители
Системы линейных алгебраических уравнений
Системы линейных уравнений
Системы линейных
алгебраических уравнений
(СЛАУ)
Система m линейных алгебраических уравнений c
n неизвестными имеет вид:
а11х1 + а12х2 + …..+ а1nхn = в1
а21х1 + а22х2 + ….+ а2nхn = в2
………………………………
аm1х1 + аm2х2 + ….+ аmnхn = вm
аij – коэффициенты, хj — неизвестные, bi свободные члены уравнений.
Опр. Решить систему означает найти все совокупности
значений неизвестных (х1, х2,. …хn), удовлетворяющих
…хn), удовлетворяющих
системе или показать, что система не имеет решений.
1.Если система не имеет решений, то она называется
несовместимой.
2. Если она имеет единственное решение –
определенной.
3. Если она имеет бесконечно много решений –
неопределенной.
Опр: Если хотя бы одно из чисел bi, отлично от нуля,
система называется неоднородной. Если все свободные
члены равны нулю, то система называется однородной.
Опр: Матрица составленная из коэффициентов
системы называется основной матрицей, если к
основной матрице приписать справа столбец
свободных членов, то получится расширенная
матрица системы.
5. Метод Крамера
По формулам Крамера решаются тольконеоднородные системы.
а11х1 а12 х2 а13 х3 в1
а21х1 а22 х2 а23 х3 в2
а х а х а х в
32 2
33 3
3
31 1
Опр: Определитель Δ основной матрицы
называется
главным
(основным)
определителем.
Δ=
а11 а12
а21 а22
а13
а23
а31 а32
а33
Опр: Дополнительным определителем
называется определитель полученный из
главного определителя путем замены j-го
столбца столбцом свободных членов.

.
Δ 1=
в1
в2
а12
а22
а13
а23
в3
а32
а33
Δ3=
Δ 2=
а11 а12 в1
а21 а22 в2
а31 а32
в3
а11 в1
а21 в2
а13
а23
а31 в3
а33
Теорема: Если определитель системы Δ не
равен 0, то система имеет единственное
решение, которое находится по формулам:
Х1 = Δ1/ Δ;
х2== Δ2/ Δ;
х3== Δ3/ Δ
Теорема: Если определитель системы Δ=0, и
хотя бы один из определителей ∆1, ∆2, ∆3
отличен от нуля, то система несовместна(т.е.
не имеет решений).
Теорема:Если определитель системы ∆=0, и
∆1=∆2=∆3=0, то система имеет бесконечное
множество решений. (неопределенная
система).
12. Матричный метод решения СЛАУ
Системе3х
линейных
уравнений
соответствует матричное уравнение
АХ=В
А=
а11
а21
а31
а
а
а
12
22
32
23
33
а
а
а
13
х1
х
Х = 2
х
3
АХ=В
А-1АХ= А-1В
ЕХ = А-1В
Х = А-1В
в1
в2
В=
в3
14.
 Метод не работает, если число уравнений не равно числу неизвестных, или когда матрица системы хотя и квадратна, но вырождена (тогда не сущесМетод не работает, если число уравнений не равно
Метод не работает, если число уравнений не равно числу неизвестных, или когда матрица системы хотя и квадратна, но вырождена (тогда не сущесМетод не работает, если число уравнений не равночислу неизвестных, или когда матрица системы хотя
и квадратна, но вырождена (тогда не существует
обратной матрицы, т.е определитель основной
матрицы равен нулю).
English Русский Правила
Калькулятор матриц — eMathHelp
Этот калькулятор складывает, вычитает, умножает, делит и возводит в степень две матрицы с показанными шагами. Он также найдет определитель, инверсию, rref (уменьшенную форму эшелона строк), нулевое пространство, ранг, собственные значения и собственные векторы и умножит матрицу на скаляр.
Операция:AddSubtractMultiplyDivideВозведение в степеньMultiply by scalarTransposeFind determinantDiagonalizeFind inverseFind rankFind сокращенной эшелонированной формы строки (rref)Find row spaceFind column spaceFind null space and nullityFind traceFind собственные значения и собственные векторыFind LU DecompositionFind QR Factorization Найти SVDFНайти инверсию Мура-Пенроуза (псевдоинверсию)Найти матрицу миноровНайти кофактор матрицаНайти сопряженную (сопряженную) матрицуВыполнить исключение Гаусса-ЖорданаНайти характеристический многочленНайти матрицу переходаНайти экспоненту
Размер матрицы: $$$\раз$$$ Матриз: Размер матрицы: $$$\раз$$$ Матриз: Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже.
Ваш ввод
Вычислить $$$\left[\begin{array}{ccc}1 & 0 & 0\\0 & 0 & 4\\0 & 1 & 0\end{массив}\right] + \left[\begin{ array}{ccc}2 & 1 & 4\\5 & 7 & 1\\1 & 2 & 5\end{массив}\right].$$$
Решение
$$$\left[ \begin{array}{ccc}{\color{DarkBlue}1} & {\color{Chocolate}0} & {\color{Red}0}\\{\color{BlueViolet}0} & {\color{DarkMagenta } 0} & {\ color{Blue}4}\\{\color{Brown}0} & {\color{GoldenRod}1} & {\color{Violet}0}\end{массив}\right] + \ left[\begin{array}{ccc}{\color{DarkBlue}2} & {\color{Chocolate}1} & {\color{Red}4}\\{\color{BlueViolet}5} & {\color {DarkMagenta} 7} & {\ color{Blue}1}\\{\color{Brown}1} & {\color{GoldenRod}2} & {\color{Violet}5}\end{массив}\right] = \left[\begin{array}{ccc}{\color{DarkBlue}\left(1\right)} + {\color{DarkBlue}\left(2\right)} & {\color{Chocolate}\left (0 \ справа)} + {\ цвет {Шоколад} \ влево (1 \ вправо)} & {\ цвет {Красный} \ влево (0 \ вправо)} + {\ цвет {Красный} \ влево (4 \ вправо) }\\{\color{BlueViolet}\left(0\right)} + {\color{BlueViolet}\left(5\right)} & {\color{DarkMagenta}\left(0\right)} + {\ color{DarkMagenta}\left(7\right)} & {\color{Blue}\left(4\right)} + {\color{Blue}\left(1\right)}\\{\color{Brown} \ влево (0 \ вправо)} + {\ цвет {Коричневый} \ влево (1 \ вправо)} & {\ цвет {GoldenRod} \ влево (1 \ вправо)} + {\ цвет {GoldenRod} \ влево (2 \ справа)} & {\ цвет {Фиолетовый} \ влево (0 \ вправо)} + {\ цвет {Фиолетовый} \ влево (5 \ вправо)} \ конец {массив} \ вправо] = \ влево [\ начать {массив} {ccc}3 & 1 & 4\\5 & 7 & 5\\1 & 3 & 5\end{массив}\right]$$$
Ответ
$$$\left[\begin{array}{ccc}1 & 0 & 0\\0 & 0 & 4\\0 & 1 & 0\end{массив}\right] + \left[\begin{array}{ccc}2 & 1 & 4\\5 & 7 & 1\\1 & 2 & 5\end{array}\right] = \left[\begin{array}{ccc} 3 & 1 & 4\\5 & 7 & 5\\1 & 3 & 5\end{массив}\right]$$$A
матриц символов — Googlesuche
2 Тип: Бегренце diesuche auf deutschsprachige Ergebnisse. Du kannst deinesuchsprache in den Einstellungen ändern.
Du kannst deinesuchsprache in den Einstellungen ändern.Калькулятор матриц — Symbolab
www.symbolab.com › … › Матрицы и векторы
Чтобы перемножить две матрицы, их внутренние размеры должны совпадать. Например, даны две матрицы A и B, где A представляет собой матрицу размера m x p, а B …
Жордан Гаусса (RREF) · Умножение матрицы, калькулятор мощности · Калькулятор обратной матрицы
Умножение матрицы, калькулятор мощности — Symbolab
www.symbolab.com › … › Матрицы
Бесплатный калькулятор умножения и мощности матриц — решение умножения матриц и степени …
Расчет матриц и векторов — Symbolab Mathe Lösungen
de.symbolab.com › Step-by-Step › Матрицы и векторы
Для матриц нет такой вещи как деление, вы можете умножать, но не можете делить. Умножение на обратное… Подробнее. Gib eine Aufgabe ein.
Матрица || Как использовать symbolab для решения матрицы — YouTube
www. youtube.com › смотреть
youtube.com › смотреть
01.02.2022 · Матрица || Как использовать symbolab для решения матрицы. Компьютерная инженерия. Компьютерная инженерия …
Добавлено: 2:10
Прислано: 01.02.2022
Практика Symbolab – Apps bei Google Play
play.google.com › магазин › приложения › подробности › id=com.symbolab.practice
Bewertung 3,5 (24) · Kostenlos · AndroidПрактика, практика, практика! Нет лучшего способа укрепить вашу уверенность в математике и навыки. Получите максимум от учебного времени с помощью Symbolab Practice …
Как сделать матрицу, которую могут читать wolfram и symbolab (в идеале…
tex.stackexchange.com › вопросы › как сделать-a…
Кстати, Wolfram Alpha не обнаружит умножение матриц, поскольку формат матриц не соответствует умножению, …
Сложение векторов Symbolab
txomz.ksztalceniejutra.pl
|U| = Square Root ( Инструмент для вычисления тензорного произведения, своего рода умножение, применимое к тензорам, векторам или матрицам, волоскам.
Какую площадь имеют части квадрата со стороной а на которые он разбивается своими диагоналями: Какую площадь имеют части квадрата со стороной a, на которые он …?
Сторона квадрата равна 1 Какую площадь имеют части квадрата на которые он разбивается своими диагоналями — Знания.site
Ответы 4
Ответ: 1/4
Решение: Sквадрата = 1×1 = 1
Часть квадрата= 1/4, т,к делится на четыре равные части. Все просто)
Автор:
chung
Оценить ответ:
0
я умный
Автор:
urijah
Оценить ответ:
0
я эйнштейн
Ответ: 1/4
Решение: Sквадрата = 1×1 = 1
Часть квадрата= 1/4, т,к делится на четыре равные части. Все просто)
Все просто)
Знаешь ответ? Добавь его сюда!
Последние вопросы
Физика
2 часа назад
Помогите пожалуйста
1.Чему равна постоянная дифракционной решётки, если при освещении её
монохроматическим светом с длиной волны 650 нм лучи, отклоняющиеся
на угол 10°, образуют максимум третьего порядка?
2. Разность хода лучей от двух когерентных источников света с длиной
волны 450 нм, сходящихся в одной точке, равна 4.5 • 10 6 м. Будет ли
наблюдаться усиление или ослабление света в этой точке?
3.Период дифракционной решётки 2,5 мкм. Найдите наибольший порядок
спектра для зелёного света ) 600 нм.
Физика
10 часов назад
Тело массой 4 кг, находясь на высоте 12 метров, свободно падает.
 Найти кинетическую энергию и скорость тела на высоте 6 м (посередине) . Найти кинетическую энергию и скорость тела в момент удара о Землю.
Найти кинетическую энергию и скорость тела на высоте 6 м (посередине) . Найти кинетическую энергию и скорость тела в момент удара о Землю.Физика
14 часов назад
Помоги, пожалуйста, прорешать оба варианта. Нужно к среде (3 мая) ЗАДАНИЯ ВНИЗУ!!!!
Математика
14 часов назад
4,8у+3,7у=11,9 Ачимы помогити🥰🥰🥰🥰 Решить уравнение
Математика
14 часов назад
5.8*(4.5-x) решите уравнение пожайлуста!
Математика
17 часов назад
Вычислите удобный способом
15/29*(19/25*7/9)*5/7
История
17 часов назад
Помогите пожалуйста
История
17 часов назад
Рассмотрите репродукцию картины художника В.
 В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура
В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура1.Используя сюжет картины и пункт 1 &26, составьте перечень качеств, которыми обладал Тимур.
2.Как объясняют спасение русской земли от тимура современные учёные?
3.Как объясняли это современники событий?
История
18 часов назад
рассказ от имени путешественника или первопроходца (цель, участники, маршрут). по теме Русские путешественники и первопроходцы XVII
Другие предметы
18 часов назад
можно ли на др маме подарить отчима?
Математика
19 часов назад
помогите якласс
Математика
19 часов назад
помогите якласс
Математика
20 часов назад
ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО !!!
В магазине продавалось w книг русских писателей и на d книг больше зарубежных писателей.
 Сколько всего книг было в магазине?
Сколько всего книг было в магазине?Мальвина и Пьеро вместе собирали голубику и собрали v штук. А Артемон собрал в k раз больше. Сколько всего голубики собрали Мальвина, Пьеро и Артемон?
В x группах занимается по w девочек, а в одной группе — p мальчиков.
Во сколько раз больше занимается мальчиков, чем девочек?
В у группах занимается по х мальчиков, а в одной группе — r девочек.
Во сколько раз меньше занимается мальчиков, чем девочек
Русский язык
1 день назад
Произведите синтаксический разбор предложений, и составте схемы.
1) Гвардия уже вышла из Петербурга 10-го августа, и сын, оставшийся для обмундирования вМоскве, должен был догнать ее по дороге в Радзивилов.
2) У Ростовых были именинницы Натальи, мать и меньшая дочь.
3) Графиня с красивой старшею дочерью и гостями, не перестававшими сменять один другого, сидели в гостиной.

4) Граф встречал и провожал гостей, приглашая всех к обеду.
5) Проводив одного гостя, граф возвращался к тому или той, которые еще были в гостиной.
Математика
1 день назад
ужас мне так лень сюда заходить
How much to ban the user?
1 hour 1 day 100 years
Сторона квадрата равна 1. Какую площадь имеют части квадрата, на которые он разбивается своими диагоналями? — Знания.site
Ответы 1
Сторона квадрата – 1
S☐ = 1² = 1
Диагонали квадрата делят его на 4 равные части → каждая площадь его частей будет равна 1/4
Ответ. 1/4
Автор:
nico17
Оценить ответ:
0
Знаешь ответ? Добавь его сюда!
Последние вопросы
Физика
2 часа назад
Помогите пожалуйста
1.
 Чему равна постоянная дифракционной решётки, если при освещении её
Чему равна постоянная дифракционной решётки, если при освещении еёмонохроматическим светом с длиной волны 650 нм лучи, отклоняющиеся
на угол 10°, образуют максимум третьего порядка?
2. Разность хода лучей от двух когерентных источников света с длиной
волны 450 нм, сходящихся в одной точке, равна 4.5 • 10 6 м. Будет ли
наблюдаться усиление или ослабление света в этой точке?
3.Период дифракционной решётки 2,5 мкм. Найдите наибольший порядок
спектра для зелёного света ) 600 нм.
Физика
10 часов назад
Тело массой 4 кг, находясь на высоте 12 метров, свободно падает. Найти кинетическую энергию и скорость тела на высоте 6 м (посередине) . Найти кинетическую энергию и скорость тела в момент удара о Землю.
Физика
14 часов назад
Помоги, пожалуйста, прорешать оба варианта.
 Нужно к среде (3 мая) ЗАДАНИЯ ВНИЗУ!!!!
Нужно к среде (3 мая) ЗАДАНИЯ ВНИЗУ!!!!Математика
14 часов назад
4,8у+3,7у=11,9 Ачимы помогити🥰🥰🥰🥰 Решить уравнение
Математика
14 часов назад
5.8*(4.5-x) решите уравнение пожайлуста!
Математика
17 часов назад
Вычислите удобный способом
15/29*(19/25*7/9)*5/7
История
17 часов назад
Помогите пожалуйста
История
17 часов назад
Рассмотрите репродукцию картины художника В.
 В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура
В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура1.Используя сюжет картины и пункт 1 &26, составьте перечень качеств, которыми обладал Тимур.
2.Как объясняют спасение русской земли от тимура современные учёные?
3.Как объясняли это современники событий?
История
18 часов назад
рассказ от имени путешественника или первопроходца (цель, участники, маршрут). по теме Русские путешественники и первопроходцы XVII
Другие предметы
18 часов назад
можно ли на др маме подарить отчима?
Математика
19 часов назад
помогите якласс
Математика
19 часов назад
помогите якласс
Математика
20 часов назад
ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО !!!
В магазине продавалось w книг русских писателей и на d книг больше зарубежных писателей.
 Сколько всего книг было в магазине?
Сколько всего книг было в магазине?Мальвина и Пьеро вместе собирали голубику и собрали v штук. А Артемон собрал в k раз больше. Сколько всего голубики собрали Мальвина, Пьеро и Артемон?
В x группах занимается по w девочек, а в одной группе — p мальчиков.
Во сколько раз больше занимается мальчиков, чем девочек?
В у группах занимается по х мальчиков, а в одной группе — r девочек.
Во сколько раз меньше занимается мальчиков, чем девочек
Русский язык
1 день назад
Произведите синтаксический разбор предложений, и составте схемы.
1) Гвардия уже вышла из Петербурга 10-го августа, и сын, оставшийся для обмундирования вМоскве, должен был догнать ее по дороге в Радзивилов.
2) У Ростовых были именинницы Натальи, мать и меньшая дочь.
3) Графиня с красивой старшею дочерью и гостями, не перестававшими сменять один другого, сидели в гостиной.

4) Граф встречал и провожал гостей, приглашая всех к обеду.
5) Проводив одного гостя, граф возвращался к тому или той, которые еще были в гостиной.
Математика
1 день назад
ужас мне так лень сюда заходить
How much to ban the user?
1 hour 1 day 100 years
Видео-урок: Площадь квадрата по диагоналям
Стенограмма видео
В этом видео мы найдем площадь
квадрата по длине диагонали. Мы также посмотрим, как мы можем найти
длина диагонали с учетом площади. Начнем с краткого обзора
то, что мы уже должны знать. Во-первых, мы знаем, что квадрат
четырехугольник или четырехугольник со всеми четырьмя сторонами одинаковой длины. В квадрате весь интерьер
углы тоже будут 90 градусов. Если нам известна длина стороны
квадрат, назовем его 𝑙, тогда мы знаем, что каждая сторона также будет стороной
длина 𝑙.
В квадрате весь интерьер
углы тоже будут 90 градусов. Если нам известна длина стороны
квадрат, назовем его 𝑙, тогда мы знаем, что каждая сторона также будет стороной
длина 𝑙.
Чтобы найти площадь квадрата, мы умножит длину на длину, что будет 𝑙 раз 𝑙. Мы могли бы также написать это как 𝑙 в квадрате. Но что будет, если вместо нам дана длина квадрата, нам дана длина диагонали, которую мы мог позвонить 𝑑? Как же тогда мы можем выработать область? Начнем с того, что мы можем вычислить длину стороны этого квадрата, а затем использовать эту формулу, чтобы найти другая формула площади квадрата с использованием диагоналей.
Вспомним, что квадрат имеет
получил четыре угла по 90 градусов. Это означает, что мы можем создать право
треугольник внутри нашего квадрата и, следовательно, мы могли бы применить пифагорейский
теорема. Эта теорема применима к правому
только треугольники. И это говорит о том, что площадь
гипотенуза равна сумме квадратов двух других сторон.
Эта теорема применима к правому
только треугольники. И это говорит о том, что площадь
гипотенуза равна сумме квадратов двух других сторон.
Применение теоремы Пифагора к тогда в нашем треугольнике гипотенуза будет 𝑑, поэтому мы начнем с 𝑑 в квадрате равно 𝑙 в квадрате плюс 𝑙 в квадрате. Это, конечно, упростит до 𝑑 квадрат равен двум 𝑙 в квадрате. И тогда помните, что мы пытаемся чтобы найти длину 𝑙 через диагональ. Это означает, что нам нужно разделить обе части уравнения на два. Следовательно, 𝑑 в квадрате над двумя равно 𝑙 в квадрате. Итак, чтобы найти 𝑙, мы берем квадрат корень из обеих сторон, в результате чего 𝑙 равен квадратному корню из 𝑑 в квадрате больше двух.
Давайте помнить, что мы пытаемся
найдите площадь квадрата, что мы можем сделать теперь, когда у нас есть 𝑙 по диагонали
длина 𝑑.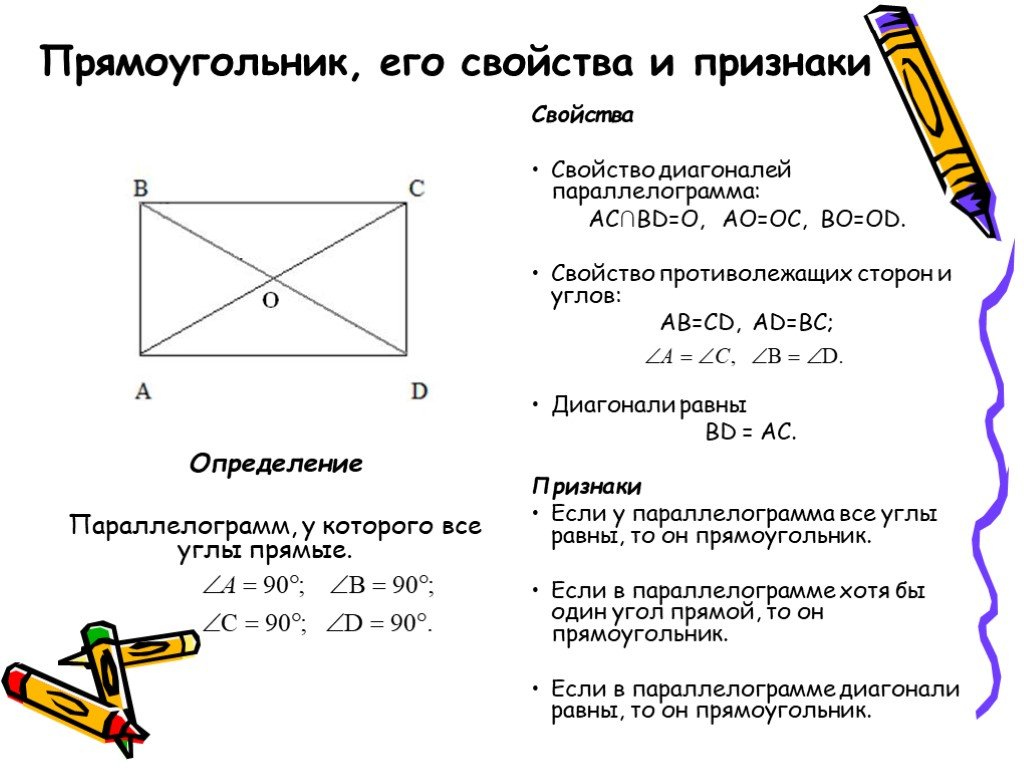 Мы возьмем нашу формулу и заполним
в значениях для 𝑙, чтобы дать нам, что площадь квадрата равна квадрату
корень из 𝑑 в квадрате, умноженный на квадратный корень из 𝑑 в квадрате
два.
Мы возьмем нашу формулу и заполним
в значениях для 𝑙, чтобы дать нам, что площадь квадрата равна квадрату
корень из 𝑑 в квадрате, умноженный на квадратный корень из 𝑑 в квадрате
два.
Когда у нас есть квадратный корень из число, умноженное само на себя, мы просто остаемся с этим числом. В этом случае у нас останется 𝑑 в квадрате над двумя. Теперь мы нашли формулу для площадь квадрата через длину диагонали. То есть площадь квадрата равно 𝑑 в квадрате над двумя, где 𝑑 — длина диагонали. Когда мы пройдем остальную часть этого видео, мы в основном будем смотреть на квадраты, где нам дана длина диагонали. Но, конечно, всегда Важно помнить формулу площади через длину стороны. Давайте посмотрим на нашу первую вопрос.
Найдите площадь квадрата, диагональ равна девяти сантиметрам.
Давайте начнем с моделирования нашего
квадрат. Мы знаем, что у него будет четыре
равные стороны и четыре угла по 90 градусов. Мы можем вспомнить, что легко
найдите площадь квадрата, если известна длина одной из сторон. Однако здесь нам дается
длина диагонали. Итак, нам нужно запомнить
другая формула, то есть площадь квадрата равна 𝑑 в квадрате над
два, где 𝑑 — длина диагонали.
Мы знаем, что у него будет четыре
равные стороны и четыре угла по 90 градусов. Мы можем вспомнить, что легко
найдите площадь квадрата, если известна длина одной из сторон. Однако здесь нам дается
длина диагонали. Итак, нам нужно запомнить
другая формула, то есть площадь квадрата равна 𝑑 в квадрате над
два, где 𝑑 — длина диагонали.
Нам дано, что диагональ
составляет девять сантиметров. Таким образом, мы можем заполнить это в
формулу так, чтобы площадь была равна девяти в квадрате на два. Как девять в квадрате девять умножить
к девяти мы получим ответ 81 больше двух. Наши подразделения здесь будут возведены в квадрат
сантиметры. Итак, мы нашли площадь
квадрат с диагональю девять сантиметров, что составляет 81 на два квадрата
сантиметры. Конечно, мы могли бы также дать
наш ответ в виде десятичных 40,5 квадратных сантиметров.
До сих пор в этом видео мы видели как найти площадь квадрата по длине диагонали. Но можем ли мы найти способ найти длина диагонали, если нам известна площадь? Что ж, на самом деле мы можем сделать это, переставляя формулу площади квадрата по диагонали. Если принять площадь равной буква 𝐴, то что нам действительно нужно сделать, так это переставить ее так, чтобы у нас была 𝑑 в качестве предметом этого уравнения. Когда мы умножаем обе части уравнение на два, мы получим два 𝐴 равно 𝑑 в квадрате. Чтобы найти 𝑑, мы возьмем квадратный корень из обеих частей уравнения, что дает нам квадратный корень из двух 𝐴 равно 𝑑.
Теперь у нас есть еще одна формула для найдите длину диагонали 𝑑, зная площадь 𝐴 квадрата. Давайте посмотрим, как мы можем поместить это в практика в следующем вопросе.
Учитывая, что площадь каждого квадрата
на шахматной доске 81 квадратный сантиметр, найдите длину диагонали
шахматная доска.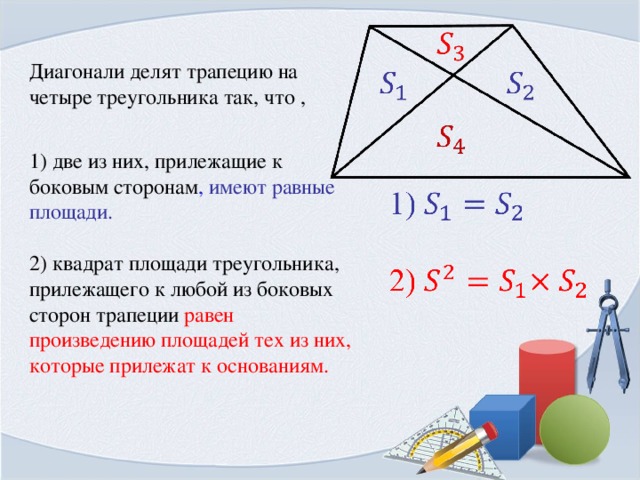
Здесь нам говорят, что площадь каждый из этих меньших квадратов на шахматной доске будет равен 81 квадратному сантиметру. Это не просто включает все черные квадраты, например, но он также будет включать каждый белый квадрат как хорошо. Нам нужно узнать диагональ длина шахматной доски. И мы должны помнить, что существует Формула, связывающая длину диагонали квадрата с его площадью. Формула состоит в том, что 𝑑, длина диагонали равна квадратному корню из двух 𝐴, где 𝐴 — площадь. Мы можем получить эту формулу перестановка площади квадрата по формуле. Эта площадь равна 𝑑 в квадрате больше двух, где 𝑑 — диагональ.
Прежде чем мы сможем использовать формулу, которая
𝑑 равно квадратному корню из двух 𝐴, нам сначала нужно найти площадь
целая шахматная доска. Вместо того, чтобы считать каждый
квадрат, чтобы увидеть, сколько полей на этой шахматной доске, мы могли бы просто посчитать
что в каждой строке восемь квадратов и в каждом столбце восемь квадратов.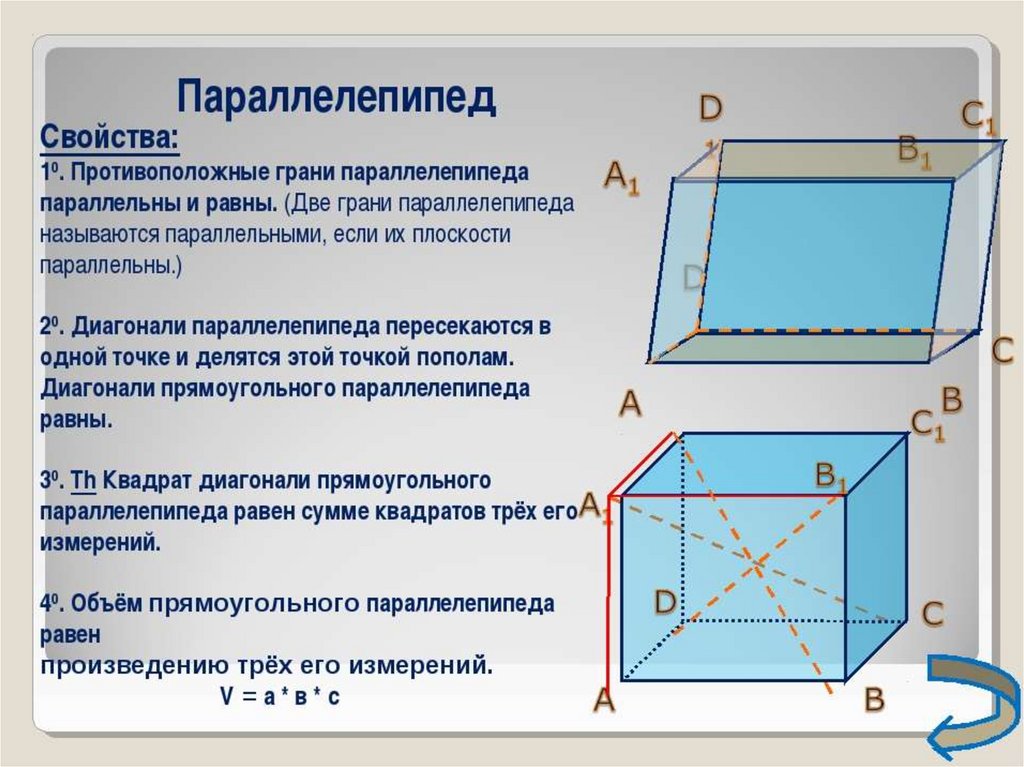 Это также подтвердит, что мы делаем
действительно есть квадратная шахматная доска. Поскольку у нас есть восемь квадратов в каждом
ряд и восемь в каждом столбце, то общее количество квадратов будет 64
квадраты. Чтобы найти общую площадь всех
этих квадратов, мы знаем, что есть 64 квадрата, и каждый из них будет иметь площадь 81
квадратных сантиметров. Оценка этого даст нам
общая площадь 5184 квадратных сантиметра.
Это также подтвердит, что мы делаем
действительно есть квадратная шахматная доска. Поскольку у нас есть восемь квадратов в каждом
ряд и восемь в каждом столбце, то общее количество квадратов будет 64
квадраты. Чтобы найти общую площадь всех
этих квадратов, мы знаем, что есть 64 квадрата, и каждый из них будет иметь площадь 81
квадратных сантиметров. Оценка этого даст нам
общая площадь 5184 квадратных сантиметра.
В качестве альтернативного метода
подсчитайте это, если представить, что один квадрат имеет площадь 81 квадратный сантиметр,
это означало бы, что длина каждого из этих квадратов будет девять
сантиметры. Так как у нас есть восемь квадратов вдоль
длина каждой из сторон квадрата и восемь умножить на девять равно 72, то мы могли бы
проработайте площадь. Площадь здесь будет длиной
на длину, которая будет 72 умножить на 72, что также даст нам площадь
площадью 5184 квадратных сантиметра.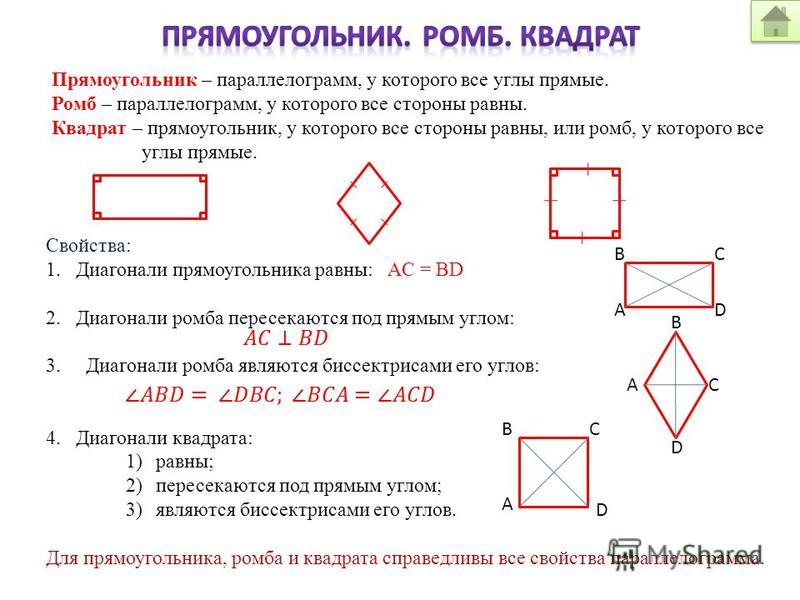 Мы можем заполнить значение, которое
площадь 𝐴 равна 5184 в нашей формуле, учитывая, что квадратный корень также
включает в себя это значение площади, а не только два. Мы можем упростить это, чтобы получить 𝑑
равен квадратному корню из 10368.
Мы можем заполнить значение, которое
площадь 𝐴 равна 5184 в нашей формуле, учитывая, что квадратный корень также
включает в себя это значение площади, а не только два. Мы можем упростить это, чтобы получить 𝑑
равен квадратному корню из 10368.
Вместо того, чтобы тянуться к нашему
калькулятор, давайте посмотрим, сможем ли мы упростить это значение 10368, посмотрев, есть ли
квадратный множитель его. Мы могли бы написать, что это равно
до квадратного корня из 144, умноженного на 72. Разбив это на два отдельных
квадратных корней, мы можем вычислить квадратный корень из 144 как 12. Но, конечно, 72 также имеет
квадратный коэффициент. Мы можем выписать квадратный корень из 72
как квадратный корень из 36, умноженный на два. Тогда мы могли бы упростить нашу
расчет 12 раз шесть раз квадратный корень из двух до 72 корень из двух. Тогда мы можем дать наш ответ, что
длина диагонали шахматной доски равна 72 корням из двух. А единицами будут сантиметры
поскольку мы работаем с длиной, а не с площадью.
А единицами будут сантиметры
поскольку мы работаем с длиной, а не с площадью.
Посмотрим на другой вопрос.
Найдите длину диагонали квадрат, площадь которого равна площади прямоугольника, имеющего размеры 10 см и 35 сантиметров.
Здесь лучше всего начать с моделируем две наши фигуры, квадрат и прямоугольник. Прямоугольник имеет длину и ширина 10 сантиметров и 35 сантиметров. И нам нужно найти диагональ длина квадрата. Информация, которую нам дают позволяют нам вычислить длину диагонали в том, что площадь наших двух четырехугольников та же. У нас нет длины информацию о квадрате, поэтому давайте посмотрим, сможем ли мы вычислить площадь этого прямоугольник.
Мы можем вспомнить, что площадь
прямоугольник равен произведению длины на ширину. Затем мы заполним наши два
значения 35 и 10, и вычисление 35, умноженное на 10, легко и просто, 350
квадратных сантиметров. Итак, площадь нашего квадрата будет
также быть 350 квадратных сантиметров. Нам нужно запомнить формулу
которая соединяет площадь квадрата с его диагональю. Площадь квадрата равна
диагональ 𝑑 в квадрате над двумя. Так как мы хотим найти диагональ
учитывая площадь, то мы можем использовать переставленную форму этой формулы, чтобы получить, что
𝑑 равно квадратному корню из двух 𝐴, где 𝐴 — площадь квадрата.
Итак, площадь нашего квадрата будет
также быть 350 квадратных сантиметров. Нам нужно запомнить формулу
которая соединяет площадь квадрата с его диагональю. Площадь квадрата равна
диагональ 𝑑 в квадрате над двумя. Так как мы хотим найти диагональ
учитывая площадь, то мы можем использовать переставленную форму этой формулы, чтобы получить, что
𝑑 равно квадратному корню из двух 𝐴, где 𝐴 — площадь квадрата.
Мы можем ввести значение для
область, которую мы знаем, сохраняя букву 𝑑, поскольку это неизвестное, которое мы хотим найти
вне. 𝑑 равно квадратному корню из
два умножить на 350, что упрощает до 𝑑 равно квадратному корню из
700. Предположим, что мы используем
метод без калькулятора, нам нужно еще больше упростить этот квадратный корень. Мы должны это заметить
хороший квадратный коэффициент 100. И, следовательно, мы можем разбить
наш расчет в квадратный корень из 100, умноженный на квадратный корень из семи,
что упрощается до 𝑑 равно 10 корень семь. Поскольку 𝑑 — длина диагонали, то
мы можем дать окончательный ответ из 10 корней из семи сантиметров.
Поскольку 𝑑 — длина диагонали, то
мы можем дать окончательный ответ из 10 корней из семи сантиметров.
Давайте посмотрим на последний вопрос где нам нужно будет использовать обе формулы площади квадрата.
Найдите разницу между площадь квадрата со стороной 17 см и площадь квадрата со стороной длина диагонали 20 сантиметров.
В этом вопросе нам говорят, что есть два квадрата. Нам дана длина стороны одного и длина диагонали другого. Итак, давайте начнем с рисования этих квадраты. Но не волнуйтесь, если они не вполне в масштабе. Предположим, что этот первый квадрат тот, у которого длина стороны 17 сантиметров. И, конечно же, потому что это квадрат, мы знаем, что все стороны будут 17 сантиметров. И второй квадрат, мы могли бы сделать с диагональю 20 сантиметров.
Нас спрашивают о районах
эти квадраты. На самом деле, нам нужно отработать
разница между областями. Но давайте для начала подумаем, как мы
найти площадь каждого квадрата. В первом квадрате у нас есть
длина стороны, так что давайте вспомним нашу первую формулу. Площадь квадрата равна
длина, умноженная на длину, или, альтернативно, длина в квадрате. Мы можем заполнить длину стороны 𝑙
в нашу формулу, поэтому мы будем вычислять 17, умноженное на 17. Используя любое умножение
метод, мы получим ответ 289. И поскольку это область, мы будем
имеют единицы площади квадратные сантиметры.
На самом деле, нам нужно отработать
разница между областями. Но давайте для начала подумаем, как мы
найти площадь каждого квадрата. В первом квадрате у нас есть
длина стороны, так что давайте вспомним нашу первую формулу. Площадь квадрата равна
длина, умноженная на длину, или, альтернативно, длина в квадрате. Мы можем заполнить длину стороны 𝑙
в нашу формулу, поэтому мы будем вычислять 17, умноженное на 17. Используя любое умножение
метод, мы получим ответ 289. И поскольку это область, мы будем
имеют единицы площади квадратные сантиметры.
Теперь, когда мы нашли площадь
этого первого квадрата, давайте посмотрим, как мы можем найти площадь второго квадрата, где
нам дана длина диагонали вместо длины стороны. Мы можем вспомнить вторую формулу
для площади квадрата, который говорит, что он равен 𝑑 в квадрате над двумя, где 𝑑
длина диагонали. Подставляем длину диагонали 𝑑
как 20 сантиметров, у нас есть формула, что площадь равна 20 в квадрате над
два. 20 умножить на 20 даст нам
400 и деление на два дает нам площадь 200 квадратных сантиметров.
Подставляем длину диагонали 𝑑
как 20 сантиметров, у нас есть формула, что площадь равна 20 в квадрате над
два. 20 умножить на 20 даст нам
400 и деление на два дает нам площадь 200 квадратных сантиметров.
Мы не должны забывать в этот момент что мы не ответили на вопрос. Нам еще нужно найти разница. Поэтому берем большую площадь из 289 и вычесть 200, что дает нам окончательный ответ, что разница между площадь этих двух квадратов равна 89 квадратных сантиметров.
Давайте теперь подведем итог тому, что мы
узнал в этом видео. Мы начали с повторения того, что следует
быть знакомой формулой, что площадь квадрата равна 𝑙 умножить на 𝑙, где 𝑙
это длина стороны. Затем мы увидели, как можно использовать
Теорема Пифагора, позволяющая вывести еще одну формулу площади квадрата.
учитывая длину диагонали 𝑑, то есть площадь квадрата равна 𝑑
в квадрате над двумя. Затем мы увидели, как мы можем переставить
что формула 𝐴, площадь, равна 𝑑 в квадрате над двумя, что дает нам формулу 𝑑
равно квадратному корню из двух 𝐴. Эта формула позволяет нам более
быстро найти длину диагонали, зная площадь квадрата.
Затем мы увидели, как мы можем переставить
что формула 𝐴, площадь, равна 𝑑 в квадрате над двумя, что дает нам формулу 𝑑
равно квадратному корню из двух 𝐴. Эта формула позволяет нам более
быстро найти длину диагонали, зная площадь квадрата.
Диагональ квадрата — формула, свойства, примеры
Диагональ квадрата — это отрезок, соединяющий любые две несмежные вершины. Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Формула диагонали квадрата используется для вычисления длины диагонали квадрата, когда известна длина его стороны.
Градусы | Минуты |
| 9014 7 1 | 60′ |
2 | 120′ |
3 | 180′ |
4 | 240′ |
| 9 0147 5 | 300′ |
| 1. | Что такое диагональ квадрата? |
| 2. | Что такое Диагональ формулы квадрата? |
| 3. | Вывод диагонали квадрата по формуле |
| 4. | Примеры использования диагональной формулы квадрата |
5. | Часто задаваемые вопросы о диагонали квадратной формулы |
Что такое диагональ квадрата?
Квадрат имеет две диагонали, каждая из которых образована соединением противоположных вершин квадрата. Обратите внимание на следующий квадрат, чтобы соотнести свойства диагоналей, приведенные ниже.
- Диагонали квадрата равны по длине.
- Они перпендикулярны друг другу.
- Они делят квадрат на два равных равнобедренных прямоугольных треугольника.
Что такое Диагональ формулы квадрата?
Диагональ формулы квадрата равна d = a√2; где «d» — диагональ, а «а» — сторона квадрата. Формула диагонали квадрата выводится по теореме Пифагора. Диагональ делит квадрат на два равнобедренных прямоугольных треугольника. Обе диагонали равны и делят друг друга пополам под прямым углом. Давайте разберемся, как вывести формулу для нахождения диагонали квадрата.
Вывод диагонали квадрата по формуле
В квадрате длина обеих диагоналей одинакова. Длина диагонали «d» квадрата со стороной «а» вычисляется по теореме Пифагора. Обратите внимание на следующий квадрат, чтобы увидеть, что длина диагонали обозначена буквой «d», а длина стороны обозначена буквой «a».
Длина диагонали «d» квадрата со стороной «а» вычисляется по теореме Пифагора. Обратите внимание на следующий квадрат, чтобы увидеть, что длина диагонали обозначена буквой «d», а длина стороны обозначена буквой «a».
Диагональ квадрата Формула
Рассмотрим треугольник ADC в квадрате. Мы знаем, что все углы квадрата равны 9.0 °, поэтому, используя теорему Пифагора, мы можем найти гипотенузу, которая в данном случае равна «d».
d 2 = а 2 + а 2
d = √(а 2 + а 2 )
90 004 d = √(2a 2 )d = √2 × √a 2
= √2a
Следовательно, диагональ формулы квадрата: d = a√2
клубок
Часто задаваемые вопросы о диагонали квадратной формулы
Что такое диагональ квадрата в математике?
Диагональ квадрата — это отрезок, соединяющий две несмежные вершины. Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Свойства диагоналей квадрата следующие:
Квадрат имеет две диагонали, которые равны по длине и делят друг друга пополам под прямым углом. Свойства диагоналей квадрата следующие:
- Они одинаковой длины.
- Они перпендикулярны друг другу.
- Они делят квадрат на два равных равнобедренных прямоугольных треугольника.
Какова формула диагонали квадрата?
Квадрат имеет две диагонали одинаковой длины, которые можно рассчитать по формуле d = a√2, где а — сторона квадрата.
Как рассчитать диагональ квадрата по формуле диагонали?
Чтобы вычислить длину диагонали квадрата, мы используем следующие шаги:
- Шаг 1: Проверьте длину стороны квадрата, a.
- Шаг 2: Подставьте значение «а» в формулу диагонали квадрата, d = a√2.
- Шаг 3: Запишите полученное значение в соответствующей единице измерения.
Как получить диагональ квадратной формулы?
Диагональ квадратной формулы может быть получена с помощью теоремы Пифагора.
- Шаг 1: Проведите диагонали квадрата.
- Шаг 2: Образуются два прямоугольных треугольника. Рассмотрим один из треугольников.
- Шаг 3: Две стороны прямоугольного треугольника будут одинаковыми, так как все стороны квадрата равны.
- Шаг 4: Примените теорему Пифагора и вычислите длину гипотенузы треугольника, являющегося диагональю квадрата.
Таким образом, диагональ d = √(a 2 + a 2 ) = (√2)а = а√2; где «а» — сторона квадрата.
Что такое «а» в диагонали формулы квадрата?
Так как квадрат имеет четыре равные стороны, поэтому в формуле диагонали квадрата «а» представляет сторону квадрата. Таким образом, диагональ квадратной формулы задается как d = a√2.
Диагональ квадрата равна его стороне?
Нет, диагональ квадрата не равна его стороне. Поскольку все углы квадрата равны 90°, диагональ квадрата становится гипотенузой треугольников, образуемых в квадрате.
Как найти диагональ квадрата, зная площадь?
Если известна площадь квадрата, можно вычислить длину стороны квадрата. Затем значение длины стороны можно использовать для нахождения диагонали квадрата с помощью формулы d = a√2. Например, если площадь квадрата составляет 81 кв. Сначала найдем длину его стороны, так как мы знаем, что площадь квадрата = a 2 . Следовательно, сторона «а» = √81 = 9 единиц. Теперь мы будем использовать это значение в формуле d = a√2, d = 9√2 = 12,72 единицы.
Затем значение длины стороны можно использовать для нахождения диагонали квадрата с помощью формулы d = a√2. Например, если площадь квадрата составляет 81 кв. Сначала найдем длину его стороны, так как мы знаем, что площадь квадрата = a 2 . Следовательно, сторона «а» = √81 = 9 единиц. Теперь мы будем использовать это значение в формуле d = a√2, d = 9√2 = 12,72 единицы.
Как найти диагональ квадрата, если дана сторона?
Диагональ квадрата можно вычислить, если известна сторона. Диагональ квадратной формулы = a√2; где «а» — длина стороны. Данную длину стороны подставляют в эту формулу, чтобы получить длину диагонали. Например, если длина стороны квадрата равна 10 см, мы подставим в формулу значение d = a√2. Это означает, что длина диагонали (d) = a√2 = 10√2 = 14,14 см.
Как найти диагональ квадрата с периметром?
Диагональ квадрата можно вычислить, если известен периметр квадрата. Давайте разберемся в этом на примере. Например, если периметр квадрата равен 32 единицам, найдем диагональ, выполнив следующие шаги:
- Шаг 1: Мы знаем, что формула для нахождения периметра квадрата = 4 × длина стороны.


 Найти кинетическую энергию и скорость тела на высоте 6 м (посередине) . Найти кинетическую энергию и скорость тела в момент удара о Землю.
Найти кинетическую энергию и скорость тела на высоте 6 м (посередине) . Найти кинетическую энергию и скорость тела в момент удара о Землю. В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура
В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура Сколько всего книг было в магазине?
Сколько всего книг было в магазине?
 Чему равна постоянная дифракционной решётки, если при освещении её
Чему равна постоянная дифракционной решётки, если при освещении её Нужно к среде (3 мая) ЗАДАНИЯ ВНИЗУ!!!!
Нужно к среде (3 мая) ЗАДАНИЯ ВНИЗУ!!!! В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура
В Верещагина «Апофеоз войны». таким оставалось поле сражения после победы тимура Сколько всего книг было в магазине?
Сколько всего книг было в магазине?

 Смотрите подробный материал о развитии логики у детей.
Смотрите подробный материал о развитии логики у детей.
 Всего стало 33 стержня.
Всего стало 33 стержня.







 Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.
Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.
 Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.
Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении. У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?
У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?
 15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
 Соревнование длилось ровно 45 минут. За это время все соревнующиеся в сумме съели 179 пирожков.
Соревнование длилось ровно 45 минут. За это время все соревнующиеся в сумме съели 179 пирожков. Значит, Ква-Квариус и Грамотигр вместе съели 69 пирожков.
Значит, Ква-Квариус и Грамотигр вместе съели 69 пирожков.

 Владелец магазина предоставил скидку в размере 5 рупий на общую покупку 3 игрушек за 30 рупий. Затем среди 5 рупий каждый человек взял 1 рупию, а оставшиеся 2 рупии отдали нищему возле магазина.
Владелец магазина предоставил скидку в размере 5 рупий на общую покупку 3 игрушек за 30 рупий. Затем среди 5 рупий каждый человек взял 1 рупию, а оставшиеся 2 рупии отдали нищему возле магазина. Теперь вы хотите получить 100 фруктов за 100 рупий. Итак, сколько бананов, манго и яблок вы купите ??
Теперь вы хотите получить 100 фруктов за 100 рупий. Итак, сколько бананов, манго и яблок вы купите ??
 Запишите каждое из следующих предложений в символьной форме, используя переменные операторов p и q .
Запишите каждое из следующих предложений в символьной форме, используя переменные операторов p и q .  Запишите обратное, обратное и контрапозитивное значение каждого из следующих импликаций.
Запишите обратное, обратное и контрапозитивное значение каждого из следующих импликаций.  Покажите, что (i) ¬( p ∧ q ) ≡ ¬ p ∨¬ q (ii) ¬( p → 90 263 q ) ≡ p ∧¬ q .
Покажите, что (i) ¬( p ∧ q ) ≡ ¬ p ∨¬ q (ii) ¬( p → 90 263 q ) ≡ p ∧¬ q . 

 Если бесплатное бронирование и осмотр закончились, а вы ещё не уехали — минуты простоя тарифицируются по опции «Парковка».
Если бесплатное бронирование и осмотр закончились, а вы ещё не уехали — минуты простоя тарифицируются по опции «Парковка».
 От качества данных процессов существенно зависит развитие будущего плода.
От качества данных процессов существенно зависит развитие будущего плода. С первого дня цикла и слизистая матки начинает готовиться к вероятной беременности. Для имплантации, т. е. внедрения образовавшегося зародыша в стенку матки, создается оптимальная среда. Для этого вследствие влияния гормонов происходит утолщение эндометрия, он покрывается сетью сосудов и накапливает необходимые для будущего зародыша питательные вещества.
С первого дня цикла и слизистая матки начинает готовиться к вероятной беременности. Для имплантации, т. е. внедрения образовавшегося зародыша в стенку матки, создается оптимальная среда. Для этого вследствие влияния гормонов происходит утолщение эндометрия, он покрывается сетью сосудов и накапливает необходимые для будущего зародыша питательные вещества.

 Если сперматозоиды находят яйцеклетку, они начинают выделять специальные ферменты, способные разрыхлить ее оболочку. Как только один из сперматозоидов проникает внутрь яйцеклетки, другие этого уже сделать не могут вследствие восстановления плотности ее оболочки. Таким образом, одна яйцеклетка может быть оплодотворена только одним сперматозоидом.
Если сперматозоиды находят яйцеклетку, они начинают выделять специальные ферменты, способные разрыхлить ее оболочку. Как только один из сперматозоидов проникает внутрь яйцеклетки, другие этого уже сделать не могут вследствие восстановления плотности ее оболочки. Таким образом, одна яйцеклетка может быть оплодотворена только одним сперматозоидом. Женский организм создает все необходимые условия для безопасного развития плода.
Женский организм создает все необходимые условия для безопасного развития плода. Термин имплантация обозначает процесс внедрения эмбриона в слой эндометрия.
Термин имплантация обозначает процесс внедрения эмбриона в слой эндометрия. Происходит сплетение кровеносными сосудами эмбриона с организмом мамы, что позволяет ему сразу же начать добывать полезные и нужные для развития вещества. Это жизненно необходимо, поскольку к данному времени запас, который несла в себе зрелая яйцеклетка, оказывается исчерпанным.
Происходит сплетение кровеносными сосудами эмбриона с организмом мамы, что позволяет ему сразу же начать добывать полезные и нужные для развития вещества. Это жизненно необходимо, поскольку к данному времени запас, который несла в себе зрелая яйцеклетка, оказывается исчерпанным. После первого дня задержки менструации при ее регулярном цикле уже возможно определить беременность с помощью теста самостоятельно.
После первого дня задержки менструации при ее регулярном цикле уже возможно определить беременность с помощью теста самостоятельно.

 В этом случае просто сделайте «математику» ниже:
В этом случае просто сделайте «математику» ниже:

 12
12 01
01
 Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала.
Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала.
 График функции
График функции Окружность
Окружность Разложение вектора на составляющие по осям координат
Разложение вектора на составляющие по осям координат Уравнение плоскости, проходящей через данную точку
Уравнение плоскости, проходящей через данную точку Предел функции при х->х0
Предел функции при х->х0 Геометрический смысл производной
Геометрический смысл производной Дифференцирование функций, заданных параметрически
Дифференцирование функций, заданных параметрически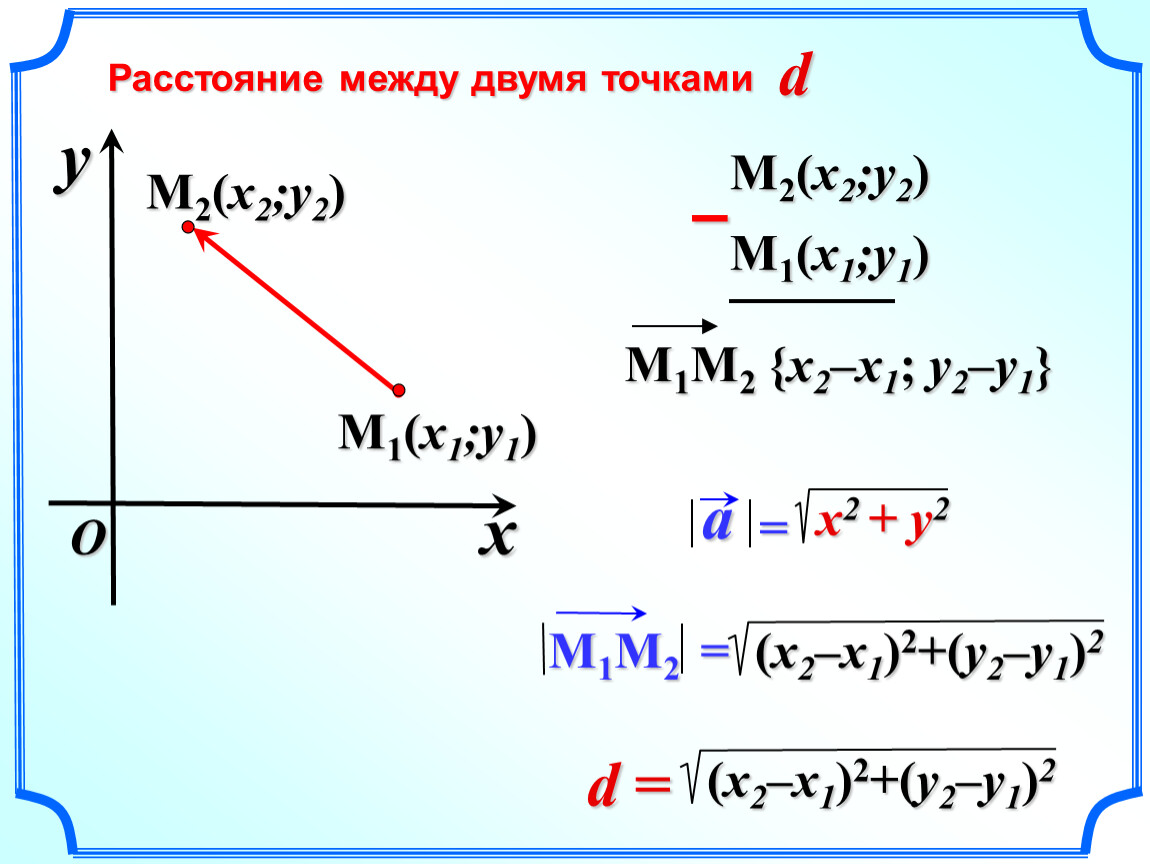 ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА Понятие об интегралах, не берущихся в элементарных функциях
Понятие об интегралах, не берущихся в элементарных функциях Интегралы от разрывных функций
Интегралы от разрывных функций Инвариантность формы полного дифференциала
Инвариантность формы полного дифференциала Вычисление криволинейного интеграла
Вычисление криволинейного интеграла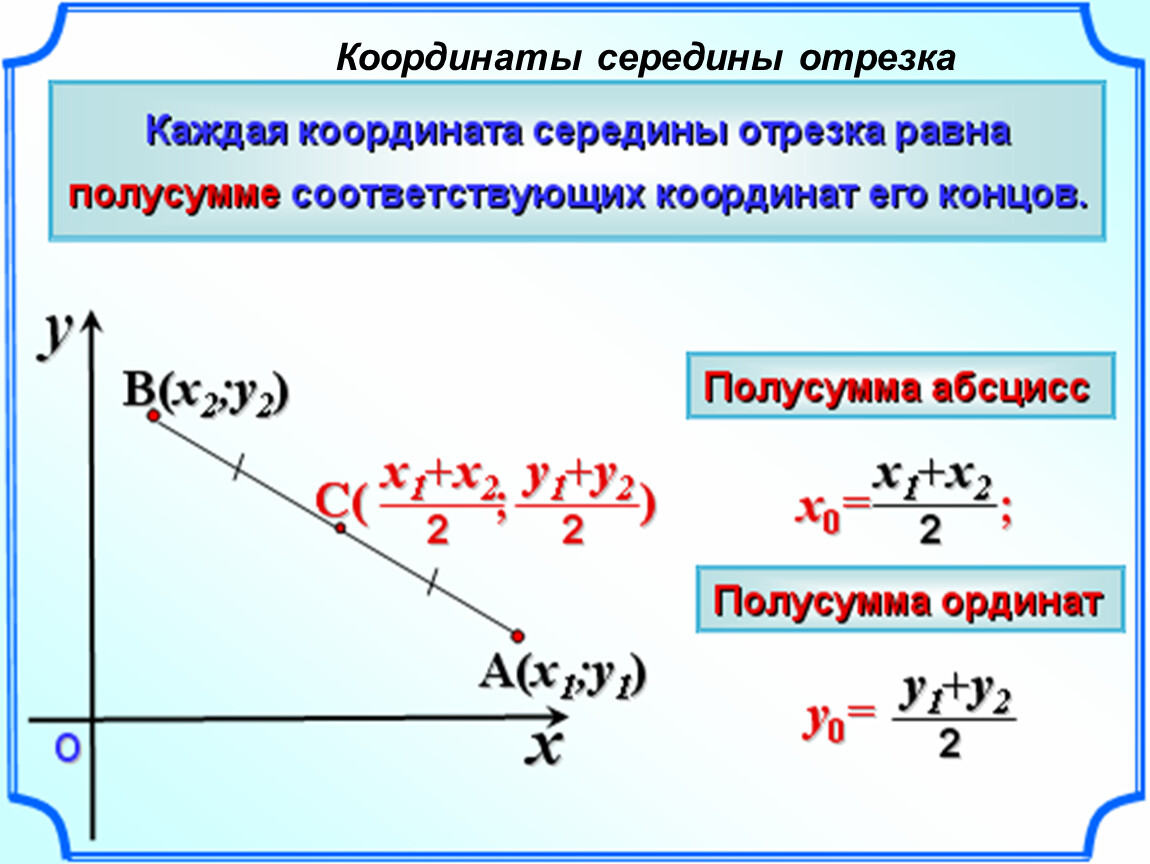 Числовые ряды с комплексными членами
Числовые ряды с комплексными членами Метод вариации произвольных постоянных
Метод вариации произвольных постоянных Расстояние между двумя точками в координатной геометрии можно рассчитать, найдя длину отрезка, соединяющего заданные координаты.
Расстояние между двумя точками в координатной геометрии можно рассчитать, найдя длину отрезка, соединяющего заданные координаты.




 Рассмотрим два комплексных числа z 1 = a + ib и z 2 = c + id. Напомним, что каждому комплексному числу на комплексной плоскости соответствует точка на координатной плоскости. Тогда расстояние между двумя комплексными числами z 1 и z 2 это:
Рассмотрим два комплексных числа z 1 = a + ib и z 2 = c + id. Напомним, что каждому комплексному числу на комплексной плоскости соответствует точка на координатной плоскости. Тогда расстояние между двумя комплексными числами z 1 и z 2 это: То же самое работает и с y-координатами. Таким образом, расстояние между двумя точками также можно записать как √[(x 1 — х 2 ) 2 + (у 1 — у 2 ) 2 ].
То же самое работает и с y-координатами. Таким образом, расстояние между двумя точками также можно записать как √[(x 1 — х 2 ) 2 + (у 1 — у 2 ) 2 ].





 Очень хорошо получается. . . Я думаю, что программное обеспечение прекрасно помогает студентам в течение всего года, дополняя любые материалы, которые они получают в обычном классе.
Очень хорошо получается. . . Я думаю, что программное обеспечение прекрасно помогает студентам в течение всего года, дополняя любые материалы, которые они получают в обычном классе.  Отличная программа!
Отличная программа! 
 Восклицательное предложение находится:
Восклицательное предложение находится:  23 молекуласының (қж) алатын көлемін есепте.
23 молекуласының (қж) алатын көлемін есепте. 23=11.2 л
23=11.2 л 02.2023
Химия
сұрақ қойды
02.2023
Химия
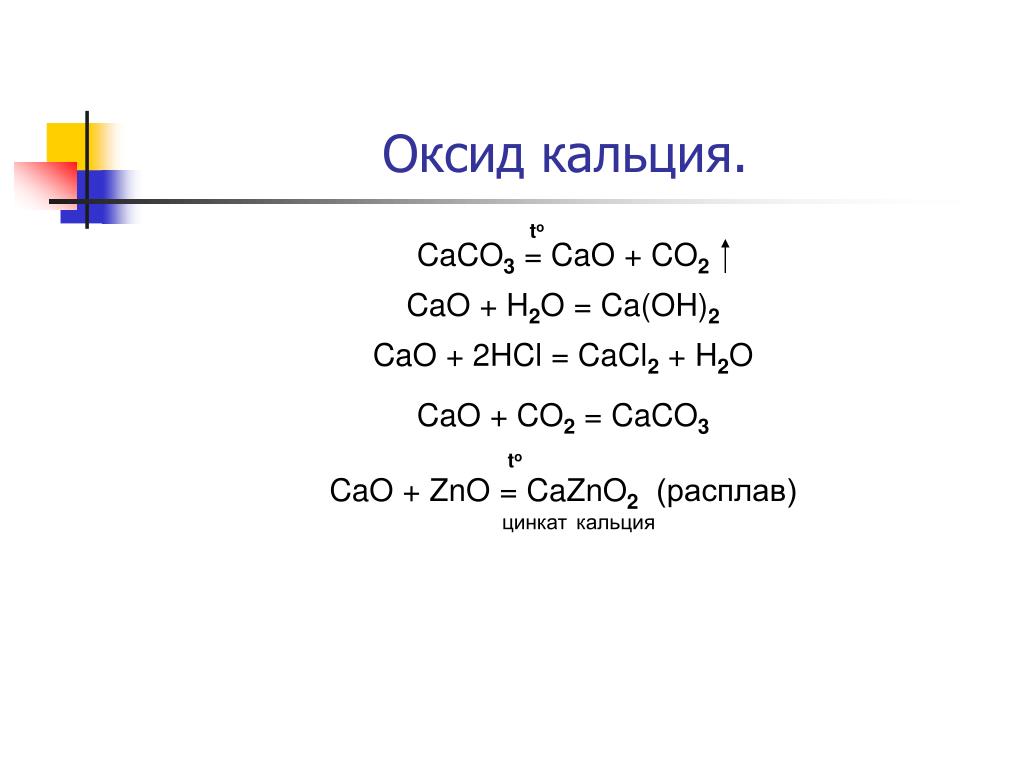
сұрақ қойды Концентрированная солнечная энергия служит источником высокотемпературного технологического тепла. Теоретическая чистая потребность в энергии оценивается в 2,5 МДж/моль CO 9 .0008 2 захвачено.
Концентрированная солнечная энергия служит источником высокотемпературного технологического тепла. Теоретическая чистая потребность в энергии оценивается в 2,5 МДж/моль CO 9 .0008 2 захвачено.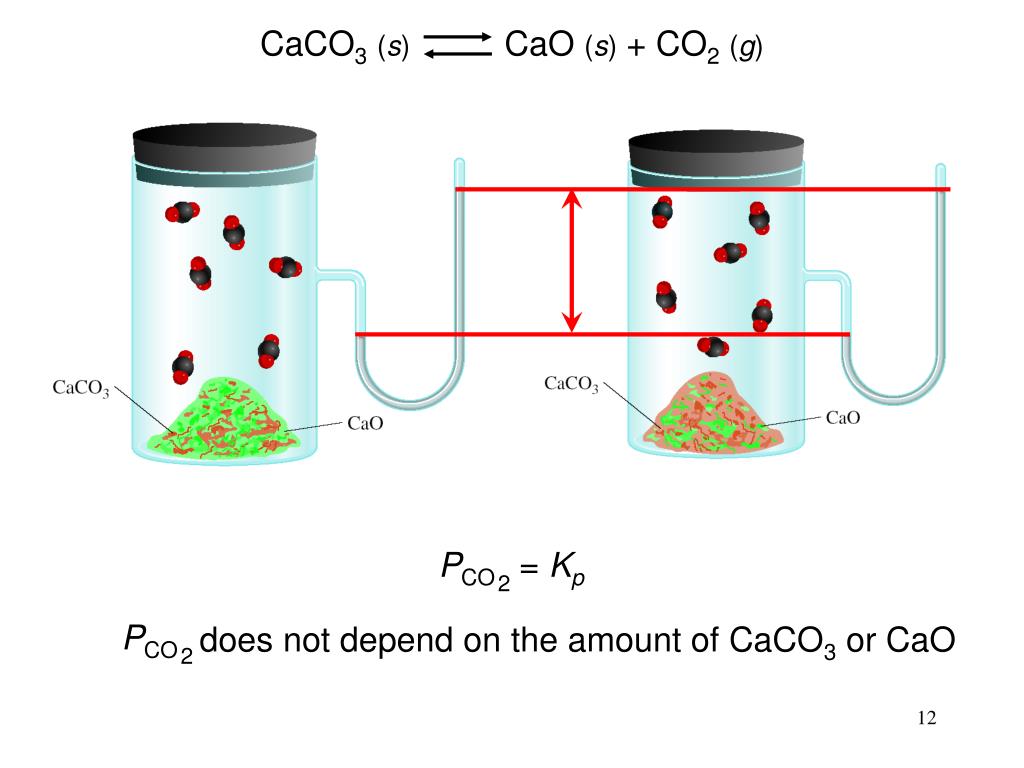 2. Схема солнечного реактора с псевдоожиженным слоем для последовательного проведения циклов карбонизации-прокаливания с использованием солнечной энергии
2. Схема солнечного реактора с псевдоожиженным слоем для последовательного проведения циклов карбонизации-прокаливания с использованием солнечной энергии




 Вот как это работает:
Вот как это работает:
 В любом случае, теперь я могу прочитать требуемые значения из уравнения:
В любом случае, теперь я могу прочитать требуемые значения из уравнения: