Квадрат качественная сталь 10,5х10,5 мм размеры 2,7 м со склада в Москве
Цена: 195 990i/т
т
м.п.
Размер: 10,5
Длина: 2,7 м
Сталь: Р12
Предлагаем купить Квадрат качественная сталь 10,5 мм из стали р12 оптом или в розницу с доставкой по Москве и Московской области. Качественный металлопрокат по цене 195 990i/т со склада. Квадрат качественная сталь 10,5 мм из стали р12 всегда в наличии в большом количестве. Имеется система скидок постоянным покупателям. Для уточнения информации по заказу и доставке товара Квадрат качественная сталь 10,5 мм из стали р12 звоните менеджерам по телефону + 7 (495) 989-1820 и они с радостью Вас проконсультируют по всем имеющимся вопросам.
Похожие товары
Размер:
Все6810,512141618202225283032353638404550556065707580859095100110120125130135140150160170180200205230245250260280300320370Длина:
Все2,7 м3 м4-6 мн/дСталь:
Все3Х2В8Ф4Х5В2ФС5Х2ВМНФ5ХНМ7Х312Х2Н4Аш12Х1313Х11Н2В2МФ14Г214Х17Н218Х2Н4ВАш20Х20Х2Н4А20Х1320ХГСА20ХГСНМАвд20ХСНВФА25ХГСА30Х2НВФА30ХГСА30ХГСНВФА30ХН2МФА30ХНВА38Х2МЮА38ХГН38ХН3МА40Х40Х2Н2МА40ХН40ХН2МА42Х1МФА45ХНМ50ХН55С260ХН65Г95Х18шА40ГОХН3МР6М5Р12Р18Ст10Ст20Ст 20Ст35Ст45Ст 45Ст 50У8АУ10У10АХ6ВФХ12МФШХ15ШХ15СГШХ20СГЭИ366(У16)ст20ст45| Наименование: Квадрат качественная сталь | Длина | Сталь | Цена | Кол-во т | м. п. п. | |
|---|---|---|---|---|---|---|
| 6 мм | 3 м | ст45 | 196 990i/т | В корзину | ||
| 8 мм | 4-6 м | У8А | 196 990i/т | В корзину | ||
| 10,5 мм | 2,7 м | Р12 | 195 990i/т | В корзину | ||
| 12 мм | н/д | У8А | 195 990i/т | В корзину | ||
| 12 мм | н/д | ст45 | 195 990i/т | п.»> | В корзину | |
| 14 мм | н/д | ст45 | 195 990i/т | В корзину | ||
| 14 мм | н/д | У8А | 195 990i/т | В корзину | ||
| 16 мм | н/д | ст20 | 192 990i/т | В корзину | ||
| 16 мм | н/д | ст45 | 194 990i/т | В корзину | ||
| 16 мм | н/д | У8А | 192 990i/т | п.»> | В корзину | |
| 18 мм | н/д | У8А | 194 990i/т | В корзину | ||
| 20 мм | н/д | ст20 | 195 990i/т | В корзину |
Собственное
производство
Собственный
склад
Оперативная
доставка
10000 видов
продукции
Грамотная
консультация
Оставить заявку
E-mail*
Дополнительные комментарии:
Квадрат 10х10 L=5,80-6,0м. Профсталь
Квадрат 10х10 L=5,80-6,0м. ПрофстальПрофСталь
Личный кабинет
Корзина
0Корзина
0- Главная
- Интернет-магазин
- Квадрат
- Квадрат 10х10 L=5,80-6,0м
- Описание
- О доставке и оплате
Квадрат 10х10 L=5,80-6,0м ГОСТ 2591-2006
Доставка
Доставка металлопроката осуществляется грузовыми машинами открытого типа, оборудованными кранами манипуляторами, что позволяет производить выгрузку металла. Цены на доставку вы можете рассчитать онлайн.
Цены на доставку вы можете рассчитать онлайн.
Оплата
Наличный расчёт
У нас можно приобрести металлопрокат за наличные (наличный расчет) оплачивая в офисе непосредственно перед погрузкой.
Безналичный расчёт
Для юридических лиц имеется возможность приобрести металлопрокат по счету (безналичный расчет). Для этого необходимо связаться с менеджером по телефону или электронной почте.
Расчет на месте
Оплата (наличный расчет) непосредственно при получении металлопроката при условии доставки транспортом Компании
Банковской картой
Онлайн оплата банковской картой онлайн происходит через ПАО СБЕРБАНК с использованием Банковских карт следующих платежных систем:
Visa International
К оплате принимаются все виды платежных карточек VISA, за исключением Visa Electron. В большинстве случаев карта Visa Electron не применима для оплаты через интернет, за исключением карт, выпущенных отдельными банками. О возможности оплаты картой Visa Electron вам нужно выяснять у банка-эмитента вашей карты.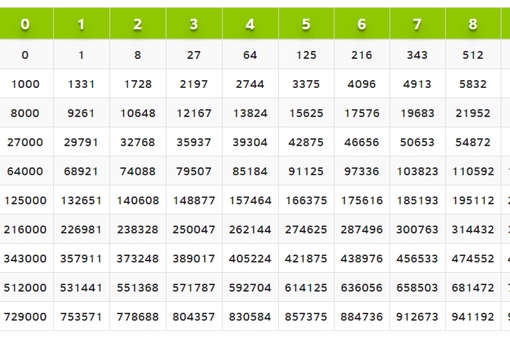
MasterCard Worldwide, Maestro и МИР
К оплате принимаются все виды MasterCard, Maestro и МИР.
Дополнительная комиссия не взимается. Поступление денежных средств происходит в online-режиме.
Вам нужно знать Номер карты, Имя держателя, Дата окончания действия, Код CVC2/CVV2. Если на вашей карте код CVC / CVV отсутствует, то, возможно, карта не пригодна для CNP транзакций (т.е. таких транзакций, при которых сама карта не присутствует, а используются её реквизиты), и вам следует обратиться в банк для получения подробной информации.
При выборе способа оплаты «Оплата банковской картой онлайн», Вы будете перенаправлены на платежный шлюз ОАО «Сбербанк России» для ввода реквизитов Вашей карты.
Пожалуйста, приготовьте Вашу пластиковую карту заранее. Дополнительно нужно ввести ФИО, email, контактный телефон, а также номер брони для идентификации плательщика. Соединение с платежным шлюзом и передача информации осуществляется в защищенном режиме с использованием протокола шифрования SSL.
В случае если Ваш банк поддерживает технологию безопасного проведения интернет-платежей Verified By Visa или MasterCard Secure Code для проведения платежа также может потребоваться ввод специального пароля. Способы и возможность получения паролей для совершения интернет-платежей Вы можете уточнить в банке, выпустившем карту.
Настоящий сайт поддерживает 256-битное шифрование. Конфиденциальность сообщаемой персональной информации обеспечивается ОАО «Сбербанк России». Введенная информация не будет предоставлена третьим лицам, за исключением случаев, предусмотренных законодательством РФ. Проведение платежей по банковским картам осуществляется в строгом соответствии с требованиями платежных систем МИР, Visa Int. и MasterCard Europe Sprl.
Возврат денежных средств
Срок рассмотрения заявки на возврат составляет 14 дней. Возврат осуществляется на расчетный счет или банковскую карту, с которой был произведен платеж. Срок возврата составляет от 15 до 30 банковских дней, в зависимости от условий Банка, в котором была выпущена банковская карта.
Карточка организации (PDF)
С нами удобно!
Всегда точно в срок, экономия времени
Все по ГОСТу,
без брака
Выгодные цены.
Любые объемы
Контроль на всех этапах.
Личный кабинет
Возможно, вы захотите посмотреть
Сизы
Изделия
Фиксаторы
Электроды
Проволока вязальная
Заглушки
Сантехника
Изделия кованые
Круги отрезные
Шарниры
Итого к оплате:
0,00₽
| Длина, м | Масса шт, кг | Цена, за метр: | Цена за штуку: | Цена за тонну: |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
Выберите количество
Калькулятор идеального квадрата
Создано Люцией Заборовской, доктором медицинских наук, кандидатом наук
Отзыв Стивена Вудинга
Последнее обновление: 23 ноября 2022 г.
- Что такое число в форме идеального квадрата?
- Как пользоваться калькулятором идеального квадрата?
- Как вычислить идеальный квадрат?
- Список идеальных квадратов
Ищете калькулятор идеальных квадратов? Воспользуйтесь нашим простым инструментом и быстро узнайте, принадлежит ли ваш номер номеру благородный список идеальных квадратов . 🖼️
Ознакомьтесь с нашей статьей ниже , чтобы узнать определение идеального квадрата , полный список чисел идеального квадрата от 0 до 1000 и несколько простых шагов по вычислению всего этого.
Что такое число в совершенном квадрате?
Число в идеальном квадрате — это число, которое можно получить, умножив на два одинаковых целых числа ; другими словами, правильный квадратный корень — это целое число.
💡 Целое число — это имя целого числа , которое может быть отрицательным, положительным или равным 0. Целое число не может содержать дроби или десятичные дроби.
Целое число не может содержать дроби или десятичные дроби.
- Примеры целых чисел: -5, 0, 3, 235.
- Примеры чисел, которые не являются целыми числами : 1,2, 3¾, 0,25.
Ищете другой тип для завершения калькулятора идеального квадрата? Мы также можем отличить совершенный квадратный трехчлен , представленный в виде ax² + bx + c . Эта конкретная формула также должна удовлетворять условию b² = 4ac .
Мы говорили о квадратах , теперь пришло время подумать о корнях в математике — проверьте наш универсальный калькулятор корня или инструмент кубического корня. 🥕
Как пользоваться калькулятором идеального квадрата?
В этом разделе вы узнаете, как пользоваться калькулятором идеального квадрата с шагами!
Ваш ввод
Вы можете ввести любое число, любое желаемое значение и длину (ну, до определенного момента).
 Не стесняйтесь вводить целых уравнений ; попробуйте умножение (5*67), деление (3/675), сложение (1+1) или вычитание (1,56-0,86).
Не стесняйтесь вводить целых уравнений ; попробуйте умножение (5*67), деление (3/675), сложение (1+1) или вычитание (1,56-0,86).Ваш результат
Ваш результат будет включать не только простое сообщение о том, является ли ваше число идеальным квадратом, но и наш полный расчет квадрата также покажет простое пошаговое объяснение.
Идеальный квадрат слишком прост для вас? Попробуйте что-нибудь продвинутого уровня 🔬, например, наш калькулятор сложных корней или калькулятор среднеквадратичных значений.
Как вычислить идеальный квадрат?
Чтобы проверить правильность вашего квадрата, вы можете просто вычислить квадратный корень из заданного числа . Если квадратный корень — целое число, ваше число — идеальный квадрат.
Подсчитаем квадраты следующих чисел: 49 и 53 .
√49 = 7 — 7 — целое число → число 49 — это полный квадрат.
√53 = 7,280109 — 7,280109 не является целым числом → число 53 не является полным квадратом.
Что делать, если у вас нет калькулятора, а ваше число довольно велико?
Давайте попробуем более интересный метод:
Полезно знать, что все квадраты заканчиваются на 1, 4, 5, 6, 9или 00 . Вот как вы можете выполнить быстрый первый выбор и решить, какое число может быть и не может быть идеальным квадратом.
- Если ваш номер заканчивается на 1 , 4 или 9 , его цифра десятков всегда должна быть даже (0, 2, 4, 6, 8), чтобы он был правильным квадратом.
- Если ваш номер заканчивается на 5 , цифра десятков всегда будет 2 .
- Если ваш номер заканчивается на 6 , цифра десятков всегда равна нечетный (1, 3, 5, 7 и 9)
Также нужно знать, что цифровой корень числа должен быть равен 0, 1, 4 или 7 .
 Если вычисленный цифровой корень не является одним из упомянутых значений, ваше число не может быть идеальным квадратом.
Если вычисленный цифровой корень не является одним из упомянутых значений, ваше число не может быть идеальным квадратом.
💡 Мы можем легко вычислить цифровой корень числа, сложив все цифры числа, а затем, если в полученной сумме две цифры, просуммировать и их. (Например, 1234567 → 1+2+3+4+5+6+7 = 28 → 2 + 8 = 10 → 1 + 0 = 1) .
Давайте попробуем этот метод, используя два следующих номера: 36573 и 21904 .
1-й пример:
36576Номер заканчивается на 1, 4, 5, 6, 9 или 00?
Да, наше число может быть идеальным квадратом.
Наше число оканчивается на 6. Является ли его десятка нечетным числом?
Да, это цифра десятков — 7. Наше число может быть идеальным квадратом.
Какой цифровой корень нашего числа?
36573 = 3+6+5+7+3 = 24 = 2+4 = 6Цифровой корень нашего числа не равен 0, 1, 4 или 7.
 Наше число не может быть полным квадратом.
Наше число не может быть полным квадратом.
2-й пример:
21904Номер заканчивается на 1, 4, 5, 6, 9 или 00?
Да, наше число может быть идеальным квадратом.
Наше число оканчивается на 4. Является ли его десятка четным числом?
Да, его десятая цифра равна 0. Наше число может быть идеальным квадратом.
Какой цифровой корень нашего числа?
21904 = 2+1+9+0+4 = 16 = 1+6 = 7Цифровой корень нашего числа равен одному из следующих чисел: 0, 1, 4 или 7. Таким образом, это , вероятно, полный квадрат .
Список идеальных квадратов
В таблице ниже вы найдете все квадраты, которые ищете; перечислим все правильные квадраты от 0 до 1000 .
0 = 0² = 0 * 0 |
1 = 1² = 1 * 1 |
9 = 3² = 3 * 3 |
16 = 4² = 4 * 4 |
25 = 5² = 5 * 5 |
36 = 6² = 6 * 6 |
49 = 7² = 7 * 7 |
64 = 8² = 8 * 8 |
81 = 9² = 9 * 9 |
100 = 10² = 10 * 10 |
121 = 11² = 11 * 11 | 144 = 12² = 12 * 12 |
169 = 13² = 13 * 13 |
196 = 14² = 14 * 14 |
225 = 15² = 15 * 15 |
256 = 16² = 16 * 16 | 9027 5
289 = 17² = 17 * 17 |
324 = 18² = 18 * 18 |
361 = 19² = 19 * 19 |
400 = 20² = 20 * 20 |
441 = 21² = 21 * 21 |
484 = 22² = 22*22 |
529 = 23² = 23 * 23 |
576 = 24² = 24 * 24 |
676 = 26² = 26 * 26 |
729 = 27² = 27 * 27 |
784 = 28² = 28 * 28 | 902 75
841 = 29² = 29 * 29 |
900 = 30² = 30 * 30 |
961 = 31² = 31 * 31 |
Люция Заборовска, доктор медицинских наук, кандидат наук
Ваш номер:
Ознакомьтесь с 71 похожим арифметическим калькулятором ➗
Абсолютное изменениеАбсолютное значениеСложение и вычитание дробей… Еще 68
Как возвести в квадрат число в Python? 6 способов (с кодом)
Python является наиболее предпочтительным языком программирования, когда речь идет о работе с большими объемами данных. Он обладает множеством встроенных библиотек, которые помогут вам выполнять несколько операций, таких как возведение числа в квадрат. В этой статье мы узнаем обо всех методах возведения в квадрат числа в Python с различными вариантами использования. Итак, приступим!
Он обладает множеством встроенных библиотек, которые помогут вам выполнять несколько операций, таких как возведение числа в квадрат. В этой статье мы узнаем обо всех методах возведения в квадрат числа в Python с различными вариантами использования. Итак, приступим!
Прежде чем перейти к методам, давайте сначала повторим, что мы собираемся делать. Возведение числа в квадрат означает умножение числа само на себя. Допустим, у вас есть число x, тогда его квадрат равен x².
Ниже приведены 6 методов, с помощью которых можно найти квадрат числа:
1) УмножениеСамый простой способ найти квадрат числа в Python — умножить число само на себя. Это самый простой выход из всех, где мы используем оператор умножения ‘*’.
Пример:
номер по умолчанию (a):
вернуть а * а
печать (число (5))
Результат:
2) Использование оператора экспоненты
Вы также можете найти квадрат заданного числа с помощью оператора экспоненты в Python. Он представлен «**» . При применении этого метода оператор экспоненты возвращает экспоненциальную степень, в результате чего получается квадрат числа. Обратите внимание, что выражение «a**b» будет определено как «a в степени b».
Он представлен «**» . При применении этого метода оператор экспоненты возвращает экспоненциальную степень, в результате чего получается квадрат числа. Обратите внимание, что выражение «a**b» будет определено как «a в степени b».
Пример:
n = 5 результат = п ** 2 print(result)
Вывод:
3) Использование метода pow()
все типы математических операторов на данные. pow() — это один из методов математической библиотеки, который может помочь вам найти квадрат числа. Вы также можете использовать метод pow(), чтобы найти другую экспоненциальную степень данного числа.
Чтобы использовать этот метод, мы должны сначала импортировать математическую библиотеку, используя ключевое слово «импорт». Позже метод pow() принимает два параметра , где первый параметр является числом, а второй параметр указывает экспоненциальную степень числа.
В нашем случае вторым параметром будет «2», так как мы хотим найти квадрат числа. Взгляните на приведенный ниже пример для лучшего понимания метода pow():
Пример:
н = 5 результат = мощность (n, 2) print(result)
Вывод:
4) Возведение в квадрат списка чисел
единственная переменная. Когда список имеет целочисленное значение, вы можете найти квадрат каждого числа внутри списка, умножив его на себя с помощью цикла for.
Пример:
sample_list = [2,4,6,8] результат = [число ** 2 для числа в sample_list] печать (результат)
Вывод:
[4, 16, 36, 64]
5) Использование цикла while
Одним из наименее используемых методов нахождения квадрата числа в Python является использование цикла while. Пока цикл повторяет блок кода, пока данное условие не станет ложным. Следовательно, мы будем находить квадрат числа с помощью цикла while, пока условие не станет ложным.
Следовательно, мы будем находить квадрат числа с помощью цикла while, пока условие не станет ложным.
Пример:
n = 1
в то время как n <= 5:
напечатать (n, '\t', n ** 2)
п += 1
Вывод:
1 1 2 4 3 9 4 16 5 25
6) Квадрат массива
Чтобы найти квадрат массива, содержащего целые числа, проще всего воспользоваться библиотекой NumPy. Numpy — это встроенная библиотека Python, которая помогает выполнять все виды числовых операций с данными с помощью простых и эффективных шагов.
Квадратный метод NumPy поможет вам вычислить квадрат каждого элемента в массиве и предоставить вам окончательный результат. Чтобы использовать библиотеку NumPy, вы должны импортировать ее с помощью ключевого слова «import».
Пример:
импортировать numpy как np
массив = np.массив ([2,4,6,8])
print("Квадратное значение arr: \n", np. square(arr))
square(arr))
Вывод:
Квадрат Значение обр: [4 16 36 64]
Программа для ввода числа от пользователя
Это одна из задач Python для начинающих, которую решает любой программист. В приведенной ниже программе пользователь вводит целое число, а квадрат этого целого числа печатается в качестве вывода. Здесь мы использовали метод умножения, чтобы найти квадрат. Проверьте код ниже:
n = int(input("Введите целое число в квадрат: "))
вывод =n*n
печать (вывод)
Вывод:
Введите целое число в квадрат: 45 2025
Программа для возведения в квадрат N чисел
Иногда нам нужен список квадратов чисел. Во-первых, число «n» определяется пользователем. Следующая программа на Python печатает квадраты всех чисел до n. Здесь мы использовали оператор экспоненты с циклом for.
n = int(input("Введите количество целых чисел в квадрате: "))
для i в диапазоне (1, n+1):
квадрат = я ** 2
печать (квадрат)
Вывод:
Введите количество целых чисел в квадрат: 3 1 4 9
Программа для возведения в квадрат чисел в диапазоне
После того, как мы узнаем, как печатать квадраты 'n' чисел, мы также можем использовать это для диапазона чисел и печатать их.

 Не стесняйтесь вводить целых уравнений ; попробуйте умножение (5*67), деление (3/675), сложение (1+1) или вычитание (1,56-0,86).
Не стесняйтесь вводить целых уравнений ; попробуйте умножение (5*67), деление (3/675), сложение (1+1) или вычитание (1,56-0,86). Если вычисленный цифровой корень не является одним из упомянутых значений, ваше число не может быть идеальным квадратом.
Если вычисленный цифровой корень не является одним из упомянутых значений, ваше число не может быть идеальным квадратом. Наше число не может быть полным квадратом.
Наше число не может быть полным квадратом.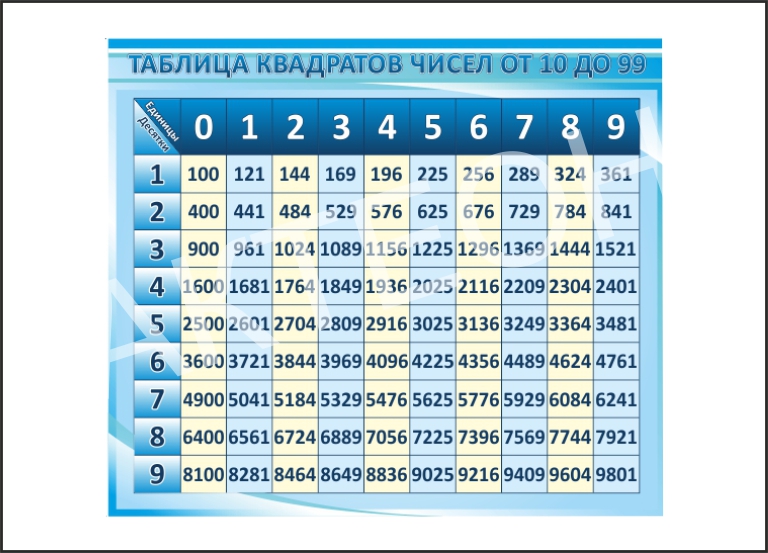 square(arr))
square(arr))
 Подставляем
Подставляем При x > 0 имеем:
При x > 0 имеем:





 Вычислить интеграл
Вычислить интеграл 7
7
 \]
\]
 {2}+C \), где \(C \) — любая константа (при условии, что это действительное число).
{2}+C \), где \(C \) — любая константа (при условии, что это действительное число). \]Это означает, что \( F(x) \pm G(x) \) является первообразной \( f(x) \pm g(x) \), так что \[ \int (f(x) \pm g(x)) ~\mathrm{d}x = F(x) \pm G(x) + C. \]
\]Это означает, что \( F(x) \pm G(x) \) является первообразной \( f(x) \pm g(x) \), так что \[ \int (f(x) \pm g(x)) ~\mathrm{d}x = F(x) \pm G(x) + C. \] Теперь предположим, что вы хотите обратить этот процесс вспять, и спросите себя: какая функция (функции) могла бы иметь производную \(f(x) = 0 \)? Очевидно, \( F(x) = 3 \) — один ответ. Вы говорите, что \(F(x) = 3\) является первообразной \(f(x) = 0\).
Теперь предположим, что вы хотите обратить этот процесс вспять, и спросите себя: какая функция (функции) могла бы иметь производную \(f(x) = 0 \)? Очевидно, \( F(x) = 3 \) — один ответ. Вы говорите, что \(F(x) = 3\) является первообразной \(f(x) = 0\). Другими словами, так же, как и с производными:
Другими словами, так же, как и с производными: 9{2}} ~\mathrm{d}x \]
9{2}} ~\mathrm{d}x \]



 Интеграция есть процесс, обратный дифференциации. Вместо дифференцирования функции нам дается производная функции и требуется вычислить функцию по производной. Этот процесс называется интеграцией или антидифференциацией. Рассмотрим функцию f(x) = sin(x), производную этой функции, если f'(x) = cos(x). Итак, интегрирование f'(x) должно вернуть функцию f(x). Обратите внимание, что для каждой функции f(x) = sin(x) + C производная одинакова, потому что после дифференцирования константа становится равной нулю. Таким образом, первообразные не уникальны, для каждой функции ее первообразные бесконечны.
Интеграция есть процесс, обратный дифференциации. Вместо дифференцирования функции нам дается производная функции и требуется вычислить функцию по производной. Этот процесс называется интеграцией или антидифференциацией. Рассмотрим функцию f(x) = sin(x), производную этой функции, если f'(x) = cos(x). Итак, интегрирование f'(x) должно вернуть функцию f(x). Обратите внимание, что для каждой функции f(x) = sin(x) + C производная одинакова, потому что после дифференцирования константа становится равной нулю. Таким образом, первообразные не уникальны, для каждой функции ее первообразные бесконечны. Правило обратной степени — это одно из правил, которые помогают нам интегрировать многочлены и другие функции. Правило обратной мощности
Правило обратной степени — это одно из правил, которые помогают нам интегрировать многочлены и другие функции. Правило обратной мощности  Интегралы можно понять через графики. Ясно, что интегралы есть не что иное, как антипроизводные. Рассмотрим функцию f(x) и скажем, что она является антипроизводной, если задана F(x). В этом случае F'(x) = f(x). Рассматривайте приведенный ниже график как график функции f(x), это означает, что график производных функции F(x) задан и целью является определение интегральной функции F(x).
Интегралы можно понять через графики. Ясно, что интегралы есть не что иное, как антипроизводные. Рассмотрим функцию f(x) и скажем, что она является антипроизводной, если задана F(x). В этом случае F'(x) = f(x). Рассматривайте приведенный ниже график как график функции f(x), это означает, что график производных функции F(x) задан и целью является определение интегральной функции F(x). Подынтегральные выражения есть не что иное, как производные от интегралов. Они дают информацию о скорости увеличения/уменьшения и максимумах и минимумах интегралов. Рассмотрим график функции f(x),
Подынтегральные выражения есть не что иное, как производные от интегралов. Они дают информацию о скорости увеличения/уменьшения и максимумах и минимумах интегралов. Рассмотрим график функции f(x),
 е. не имеет ни нижнего предела, ни верхнего предела. В то время как определенные интегралы дают значение функции в пределе. т. е. определенные интегралы интегрируются по определенному интервалу. Неопределенные интегралы имеют постоянную интегрирования, тогда как определенный интеграл не имеет постоянной интегрирования.
е. не имеет ни нижнего предела, ни верхнего предела. В то время как определенные интегралы дают значение функции в пределе. т. е. определенные интегралы интегрируются по определенному интервалу. Неопределенные интегралы имеют постоянную интегрирования, тогда как определенный интеграл не имеет постоянной интегрирования. 0003
0003


 Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,2. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Вероятность того, что это вопрос по теме «Внешние углы», равна 0,2. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
 Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежат 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежат 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.


 Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
 Найдите вероятность
Найдите вероятность Какова вероятность, что доклад профессора
Какова вероятность, что доклад профессора

 Найдите вероятность того, что А.
Найдите вероятность того, что А.


 Это независимые события, вероятность их
Это независимые события, вероятность их Брать
один из наших многочисленных практических тестов по теории вероятностей для прогона часто задаваемых вопросов. Ты
получите невероятно подробные результаты оценки в конце практического теста по теории вероятностей, чтобы
помочь вам определить свои сильные и слабые стороны. Выберите один из наших практических тестов по теории вероятностей прямо сейчас
и начать!
Брать
один из наших многочисленных практических тестов по теории вероятностей для прогона часто задаваемых вопросов. Ты
получите невероятно подробные результаты оценки в конце практического теста по теории вероятностей, чтобы
помочь вам определить свои сильные и слабые стороны. Выберите один из наших практических тестов по теории вероятностей прямо сейчас
и начать!
 edu
edu  Основной принцип подсчета и примеры.
Основной принцип подсчета и примеры. 



 Решение здесь.
Решение здесь. 
 )/3
)/3 eNotes без рекламы
eNotes без рекламы в 20:13:27.
в 20:13:27.
 89
89 )
/
флок (англ.)
/
шок (англ.)
/
сотня
/
большая сотня (англ.)
/
гросс
/
тысяча
/
большой гросс
)
/
флок (англ.)
/
шок (англ.)
/
сотня
/
большая сотня (англ.)
/
гросс
/
тысяча
/
большой гросс Наш калькулятор позволяет получить ответ в одно действие.
Наш калькулятор позволяет получить ответ в одно действие. Например, килояблоко — это 1000 яблок.
Например, килояблоко — это 1000 яблок. Com понравилось. Приходите снова!
Com понравилось. Приходите снова!
 2 × 100
2 × 100 Например, он может помочь узнать какой процент составляет число 1 от числа 5? Введите первое число (например ‘1’) и второе число (например ‘5’). После чего нажмите кнопку ‘Посчитать’.
Например, он может помочь узнать какой процент составляет число 1 от числа 5? Введите первое число (например ‘1’) и второе число (например ‘5’). После чего нажмите кнопку ‘Посчитать’. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. е. 1,45 .
е. 1,45 . Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  На какую часть вопроса Энди ответил правильно?
На какую часть вопроса Энди ответил правильно? Чему равно 3/15 в наименьшем члене?
Чему равно 3/15 в наименьшем члене? Мы будем использовать это позже в уроке.
Мы будем использовать это позже в уроке. И то, и другое довольно просто и легко сделать, но я лично предпочитаю метод преобразования в десятичный, так как он требует меньше шагов.
И то, и другое довольно просто и легко сделать, но я лично предпочитаю метод преобразования в десятичный, так как он требует меньше шагов.
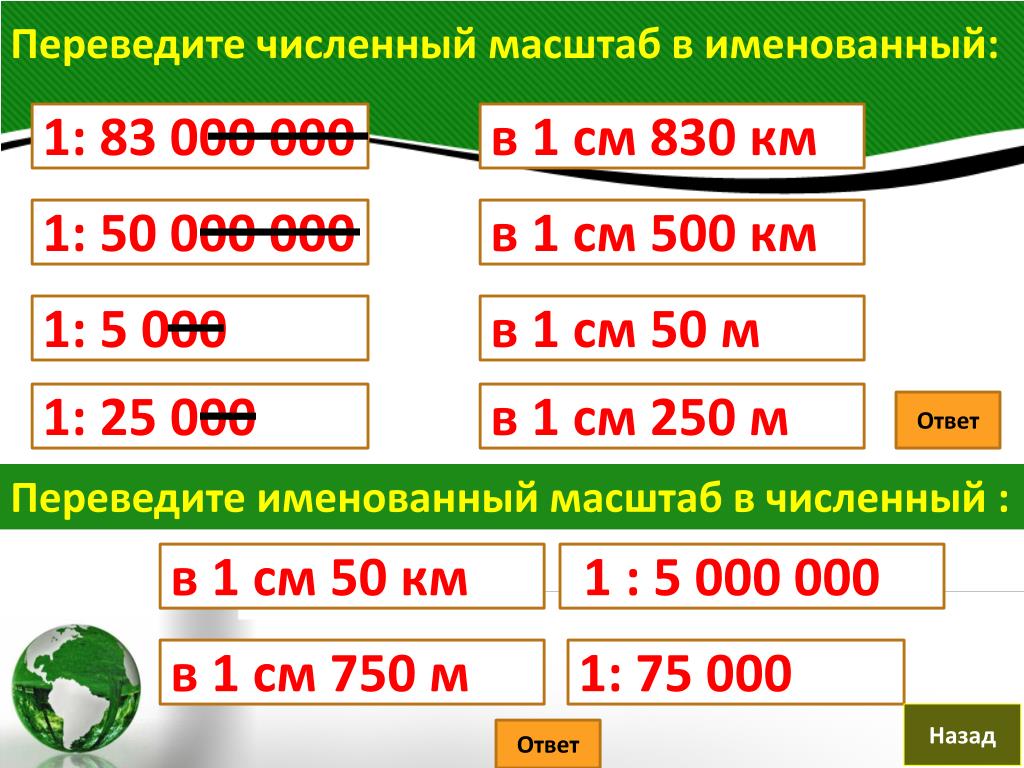
 Поскольку 1000 м = 100000 см, то на карте каждый отрезок в 100 000 раз меньше отрезка участка в местности. 1 : 100 000 = 0,000001. Говорят, что такая карта выполнена в масштабе одна стотысячная (по названию десятичной дроби, которую можно получить как соотношение двух чисел масштаба 1 и 100000).
Поскольку 1000 м = 100000 см, то на карте каждый отрезок в 100 000 раз меньше отрезка участка в местности. 1 : 100 000 = 0,000001. Говорят, что такая карта выполнена в масштабе одна стотысячная (по названию десятичной дроби, которую можно получить как соотношение двух чисел масштаба 1 и 100000).
 Для перевода в метры от числа в знаменателе забираем два нуля, если в километры – забираем пять нулей.
Для перевода в метры от числа в знаменателе забираем два нуля, если в километры – забираем пять нулей. Какой масштаб использовал ученик, если в реальности расстояние составляет 400 м.
Какой масштаб использовал ученик, если в реальности расстояние составляет 400 м.


 При применении поворота (о начале), масштабирования (в котором мы будем перемещать в начало координат, а затем обратно) и перемещения, имеет ли значение, в каком порядке мы это делаем? Почему?
При применении поворота (о начале), масштабирования (в котором мы будем перемещать в начало координат, а затем обратно) и перемещения, имеет ли значение, в каком порядке мы это делаем? Почему?

 После нескольких недель работы команда была готова использовать весы со своими участниками исследования.
После нескольких недель работы команда была готова использовать весы со своими участниками исследования. «Даже если вы переведете его в термин, который имеет смысл с грамматической точки зрения, он все равно не будет иметь истинного значения в местном контексте. Нам пришлось пройти через весь этот процесс, чтобы выбрать термин с сопоставимым значением».
«Даже если вы переведете его в термин, который имеет смысл с грамматической точки зрения, он все равно не будет иметь истинного значения в местном контексте. Нам пришлось пройти через весь этот процесс, чтобы выбрать термин с сопоставимым значением».


 Сообщение ученика о рациональных выражениях известных из основной школы. Таким образом, учение об уравнениях невозможно без учения о законах действий.
Сообщение ученика о рациональных выражениях известных из основной школы. Таким образом, учение об уравнениях невозможно без учения о законах действий. е. уравнение, имеющее те же корни, и только их.
е. уравнение, имеющее те же корни, и только их.
 -7.
-7.

 В частности, равносильными считаются две системы, не имеющие решений.
В частности, равносильными считаются две системы, не имеющие решений.


 В этой области математики существуют вопросы, на которые математики еще не дали ответа. Возможно, кто-то из вас найдет ответы на эти вопросы.
В этой области математики существуют вопросы, на которые математики еще не дали ответа. Возможно, кто-то из вас найдет ответы на эти вопросы.

 Поэтому может возникнуть опасная ситуация – переменная примет такое значение, что знаменатель обратится в ноль. Чтобы этого не произошло, заранее исключим из рассмотрения нули знаменателя и определяем область допустимых значений.
Поэтому может возникнуть опасная ситуация – переменная примет такое значение, что знаменатель обратится в ноль. Чтобы этого не произошло, заранее исключим из рассмотрения нули знаменателя и определяем область допустимых значений. Упрощаем уравнение с помощью разрешенных преобразований:
Упрощаем уравнение с помощью разрешенных преобразований: {2}\) равен 1. Значит, удобно использовать теорему Виета:
{2}\) равен 1. Значит, удобно использовать теорему Виета:

 С моей точки зрения, большинство учеников слабы в математике. Они сталкиваются с трудностями при решении математических задач. Я тоже столкнулся с той же проблемой, когда учился в 10 классе.
С моей точки зрения, большинство учеников слабы в математике. Они сталкиваются с трудностями при решении математических задач. Я тоже столкнулся с той же проблемой, когда учился в 10 классе. Вы должны попытаться связать это понятие со своей повседневной жизнью и создать свою собственную формулу запоминания понятий.
Вы должны попытаться связать это понятие со своей повседневной жизнью и создать свою собственную формулу запоминания понятий. Когда числитель и знаменатель состоят из многочленов, такие дроби называются рациональными выражениями.
Когда числитель и знаменатель состоят из многочленов, такие дроби называются рациональными выражениями. Знаменатель рационального выражения никогда не может быть равен нулю. Подобно алгебраическим выражениям, оно содержит неизвестные переменные. Чтобы упростить рациональное выражение, мы приводим его к простейшей форме.
Знаменатель рационального выражения никогда не может быть равен нулю. Подобно алгебраическим выражениям, оно содержит неизвестные переменные. Чтобы упростить рациональное выражение, мы приводим его к простейшей форме.
 Чтобы разделить рациональное выражение на другое рациональное выражение, мы должны умножить первое выражение на обратную величину второго выражения.
Чтобы разделить рациональное выражение на другое рациональное выражение, мы должны умножить первое выражение на обратную величину второго выражения.

 См. схему на этой веб-странице.
См. схему на этой веб-странице. com/a/bT1zMoB
com/a/bT1zMoB
 Профессионально-общественная аккредитация
Профессионально-общественная аккредитация Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав Обычно предприятия, работающие с торговыми кредитами, предоставляют покупателям 30, 60 или 90 дней для оплаты, при этом транзакция регистрируется в счете-фактуре.
Обычно предприятия, работающие с торговыми кредитами, предоставляют покупателям 30, 60 или 90 дней для оплаты, при этом транзакция регистрируется в счете-фактуре.

 Бухгалтерский учет с товарными кредитами может различаться в зависимости от того, использует ли компания кассовый учет или учет по методу начисления. Бухгалтерский учет обязателен для всех публичных компаний. При учете по методу начисления компания должна признавать доходы и расходы в момент их совершения.
Бухгалтерский учет с товарными кредитами может различаться в зависимости от того, использует ли компания кассовый учет или учет по методу начисления. Бухгалтерский учет обязателен для всех публичных компаний. При учете по методу начисления компания должна признавать доходы и расходы в момент их совершения. Они считаются обязательствами, которые компания должна понести.
Они считаются обязательствами, которые компания должна понести. Многие из этих финтех-компаний сотрудничают с продавцами в точках продаж, чтобы обеспечить финансирование покупок под 0% или под низкие проценты. Эти партнерские отношения помогают снизить торговые кредитные риски для продавцов, а также поддерживают рост для покупателей.
Многие из этих финтех-компаний сотрудничают с продавцами в точках продаж, чтобы обеспечить финансирование покупок под 0% или под низкие проценты. Эти партнерские отношения помогают снизить торговые кредитные риски для продавцов, а также поддерживают рост для покупателей. LiquidX, например, теперь предлагает электронную торговую площадку, ориентированную на страхование торговых кредитов для участников со всего мира.
LiquidX, например, теперь предлагает электронную торговую площадку, ориентированную на страхование торговых кредитов для участников со всего мира.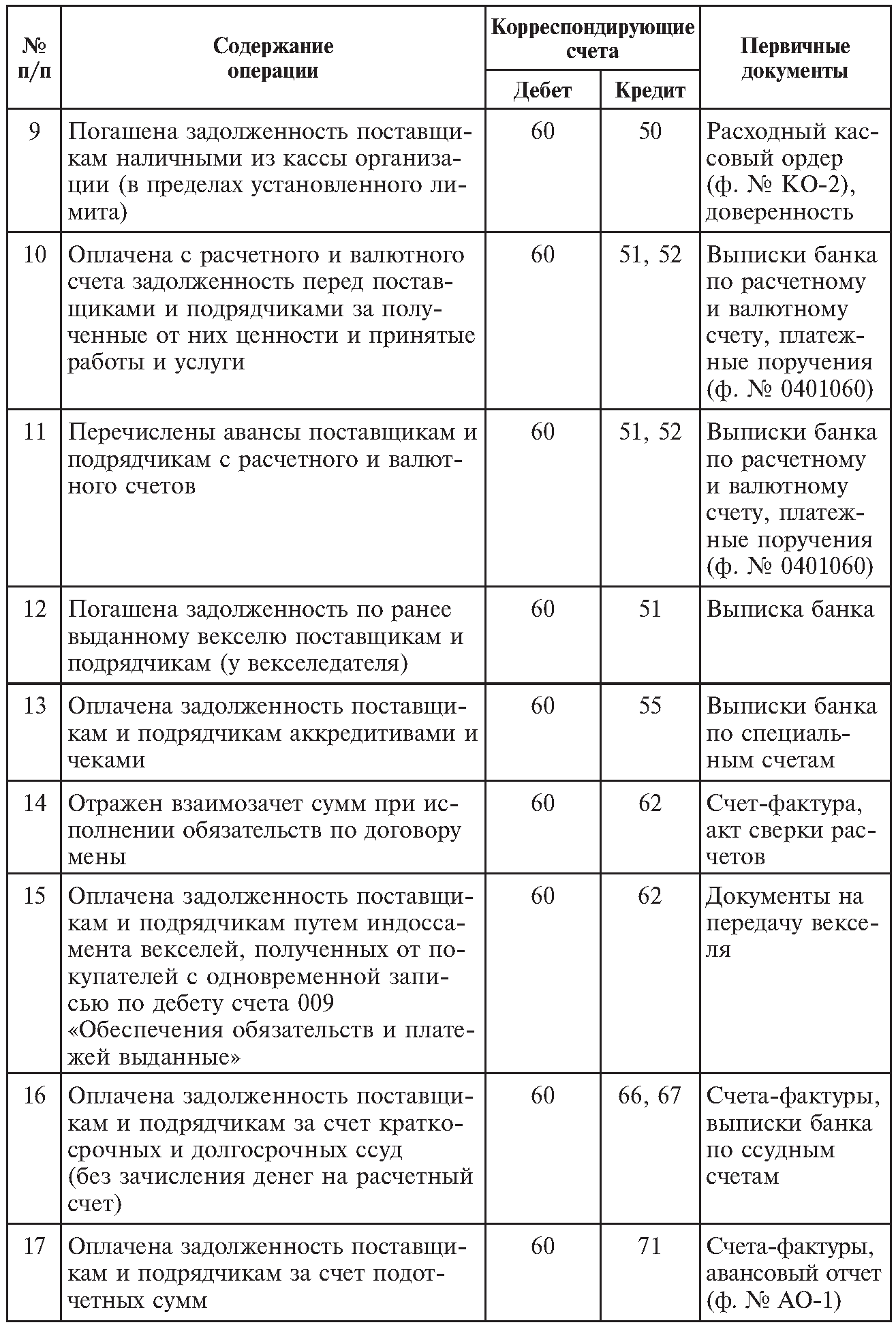 Без хорошего кредитного рейтинга коммерческий кредит не может быть предложен бизнесу.
Без хорошего кредитного рейтинга коммерческий кредит не может быть предложен бизнесу.
 Затраты обычно проявляются в виде штрафных санкций за просрочку платежа или процентных начислений на непогашенную задолженность. Если платежи не производятся, это также может негативно сказаться на кредитоспособности вашего бизнеса, а также на отношениях с вашим поставщиком.
Затраты обычно проявляются в виде штрафных санкций за просрочку платежа или процентных начислений на непогашенную задолженность. Если платежи не производятся, это также может негативно сказаться на кредитоспособности вашего бизнеса, а также на отношениях с вашим поставщиком. Это означает, что бизнес берет на себя риски при расширении финансирования. Безнадежные долги можно списать, но неплатежи клиента всегда могут нанести ущерб бизнесу.
Это означает, что бизнес берет на себя риски при расширении финансирования. Безнадежные долги можно списать, но неплатежи клиента всегда могут нанести ущерб бизнесу. Процентная скидка применяется, если оплата производится до даты, согласованной в условиях.
Процентная скидка применяется, если оплата производится до даты, согласованной в условиях. Торговый кредит – это беспроцентная ссуда. Однако торговый кредит может быть дорогим, если платеж не произведен к согласованной дате, в связи с чем заемщик может понести высокие расходы либо из-за пени за просрочку платежа, либо из-за процентной ставки, взимаемой продавцом с непогашенной суммы.
Торговый кредит – это беспроцентная ссуда. Однако торговый кредит может быть дорогим, если платеж не произведен к согласованной дате, в связи с чем заемщик может понести высокие расходы либо из-за пени за просрочку платежа, либо из-за процентной ставки, взимаемой продавцом с непогашенной суммы. Бесплатный телефон (включая все мобильные).
Бесплатный телефон (включая все мобильные).


 Это, вероятно, будет считаться несправедливым условием, и если банк берет деньги с общего счета для оплаты вашего единственного долга, вам следует подать жалобу.
Это, вероятно, будет считаться несправедливым условием, и если банк берет деньги с общего счета для оплаты вашего единственного долга, вам следует подать жалобу.