Иррациональные неравенства и способы их решения примеры. Некоторые моменты о том, как выполняется решение неравенств
Ведение беременности
Неравенства и системы неравенств — это одна из тем, которая проходится в средней школе по алгебре. По уровню сложности она является не самой трудной, т. к. имеет незамысловатые правила (о них немного позже). Как правило, решение систем неравенств школьники усваивают достаточно легко. Это связано ещё и с тем, что учителя попросту «натаскивают» своих учеников по данной теме. И они не могут этого не делать, ведь она изучается и в дальнейшем с применением иных математических величин, а также проверяется на ОГЭ и ЕГЭ. В школьных учебниках тема, посвящённая неравенствам и системам неравенств, раскрыта очень подробно, поэтому если вы собираетесь её изучить, то лучше всего прибегнуть именно к ним. Данная статья лишь пересказывает большие материалы, и в ней могут быть некоторые опущения.
Понятие системы неравенств
Если обратиться к научному языку, то можно дать определение понятию «система неравенств». Это такая математическая модель, которая представляет собой несколько неравенств. От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.
Это такая математическая модель, которая представляет собой несколько неравенств. От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.
Системы неравенств и системы уравнений
В процессе изучения новой темы очень часто возникают недопонимания. С одной стороны, всё ясно и скорее хочется приступить к решению заданий, а с другой — какие-то моменты остаются в «тени», не совсем хорошо осмысливаются. Также некоторые элементы уже полученных знаний могут переплетаться с новыми. В результате такого «наложения» зачастую случаются ошибки.
Поэтому перед тем как приступить к разбору нашей темы, следует вспомнить про отличия уравнений и неравенств, их систем. Для этого нужно ещё раз пояснить, что представляют собой данные математические понятия. Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Виды неравенств
Выделяют два вида неравенств: числовые и с неизвестной переменной. Первый тип представляет собой предоставленные величины (цифры), неравные друг другу, например, 8 > 10. Второй — это неравенства, содержащие в себе неизвестную переменную (обозначается какой-либо буквой латинского алфавита, чаще всего X). Данная переменная требует своего нахождения. В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).
В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).
Два последних вида по степени своего построения и уровню сложности решения делятся на простые и сложные. Простые называют ещё линейными неравенствами. Они, в свою очередь, подразделяются на строгие и нестрогие. Строгие конкретно «говорят», что одна величина обязательно должна быть либо меньше, либо больше, поэтому это в чистом виде неравенство. Можно привести несколько примеров: 8 x + 9 > 2, 100 — 3 x > 5 и т. д. Нестрогие включают в себя ещё и равенство. То есть одна величина может быть больше или равна другой величине (знак «≥») либо меньше или равна другой величине (знак «≤»). Ещё в линейных неравенствах переменная не стоит в корне, квадрате, не делится на что-либо, из-за чего они называются «простыми». Сложные включают в себя неизвестные переменные, нахождение которых требует выполнения большего количества математических операций. Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах.
Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах.
Свойства неравенств
К свойствам неравенств относятся следующие положения:
- Знак неравенства меняется на обратный, если применяется операция по перемене следования сторон (например, если t 1 ≤ t 2 , то t 2 ≥ t 1).
- Обе части неравенства позволяют прибавить к себе одно и то же число (например, если t 1 ≤ t 2 , то t 1 + число ≤ t 2 + число).
- Два и более неравенств, имеющие знак одного направления, позволяют складывать их левые и правые части (например, если t 1 ≥ t 2 , t 3 ≥ t 4 , то t 1 + t 3 ≥ t 2 + t 4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же положительное число (например, если t 1 ≤ t 2 и число ≤ 0, то число · t 1 ≥ число · t 2).

- Два и более неравенств, имеющие положительные члены и знак одного направления, позволяют умножать себя друг на друга (например, если t 1 ≤ t 2 , t 3 ≤ t 4 , t 1 , t 2 , t 3 , t 4 ≥ 0 то t 1 · t 3 ≤ t 2 · t 4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же отрицательное число, но при этом знак неравенства меняется (например, если t 1 ≤ t 2 и число ≤ 0, то число · t 1 ≥ число · t 2).
- Все неравенства обладают свойством транзитивности (например, если t 1 ≤ t 2 и t 2 ≤ t 3 , то t 1 ≤ t 3).
Теперь после изучения основных положений теории, относящейся к неравенствам, можно приступить непосредственно к рассмотрению правил решения их систем.
Решение систем неравенств. Общие сведения. Способы решения
Как уже говорилось выше, решением выступают значения переменной, подходящие ко всем неравенствам данной системы. Решение систем неравенств — это осуществление математических действий, которые в итоге приводят к решению всей системы или доказывают, что у неё решений не имеется. В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «икс» принадлежит пустому множеству»). Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «икс» принадлежит пустому множеству»). Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
Графический способ
Позволяет решить систему неравенств с несколькими неизвестными величинами (от двух и выше). Благодаря данному методу система линейных неравенств решается достаточно легко и быстро, поэтому он является самым распространённым способом. Это объясняется тем, что построение графика сокращает объём написания математических операций. Особенно становится приятным немного отвлечься от ручки, взять в руки карандаш с линейкой и приступить к дальнейшим действиям с их помощью, когда выполнено много работы и хочется небольшого разнообразия. Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.
Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.
Чтобы выполнить решение системы неравенств с помощью графического способа, необходимо все члены каждого неравенства перенести в их левую часть. Знаки поменяются на противоположные, справа следует записать ноль, затем нужно записать каждое неравенство отдельно. В итоге из неравенств получатся функции. После этого можно доставать карандаш и линейку: теперь потребуется нарисовать график каждой полученной функции. Всё множество чисел, которое окажется в интервале их пересечения, будет являться решением системы неравенств.
Алгебраический способ
Позволяет решить систему неравенств с двумя неизвестными переменными. Также неравенства должны обладать одинаковым знаком неравенства (т. е. обязаны содержать либо только знак «больше», либо только знак «меньше» и пр.) Несмотря на свою ограниченность, этот способ к тому же и более сложный. Он применяется в двух этапах.
Он применяется в двух этапах.
Первый включает себя действия по избавлению от одной из неизвестных переменных. Сначала нужно её выбрать, затем проверить на наличие чисел перед этой переменной. Если их нет (тогда переменная будет выглядеть, как одиночная буква), то ничего не изменяем, если есть (вид переменной будет, например, таким — 5y или 12y), то тогда необходимо сделать так, чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно умножить каждый член неравенств на общий множитель, например, если в первом неравенстве записано 3y, а во втором 5y, то необходимо все члены первого неравенства умножить на 5, а второго — на 3. Получится 15y и 15y соответственно.
Второй этап решения. Нужно левую часть каждого неравенства перенести в их правые части с изменением знака каждого члена на противоположный, справа записать нуль. Затем наступает самое интересное: избавление от выбранной переменной (по-другому это называется «сокращение») во время складывания неравенств. Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.
Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.
Способ подстановки
Позволяет решить систему неравенств при наличии возможности ввести новую переменную. Обычно этот способ применяется, когда неизвестная переменная в одном члене неравенства возведена в четвёртую степень, а в другом члене имеет квадрат. Таким образом, данный метод направлен на понижение степени неравенств в системе. Неравенство образца х 4 — х 2 — 1 ≤ 0 данным способом решается так. Вводится новая переменная, например, t. Пишут: «Пусть t = х 2 «, далее модель переписывают в новом виде. В нашем случае получится t 2 — t — 1 ≤0. Это неравенство нужно решить методом интервалов (о нём немного позже), потом обратно вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы будут решением системы.
Метод интервалов
Это самый простой способ решения систем неравенств, и в то же время он является универсальным и распространённым. Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:
Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:
- Все члены каждого неравенства переносятся в левую часть с изменением знака на противоположный (справа пишется ноль).
- Неравенства выписываются отдельно, определяется решение каждого из них.
- Находятся пересечения неравенств на числовой прямой. Все числа, находящиеся на этих пересечениях, будут являться решением.
Какой способ использовать?
Очевидно тот, который кажется наиболее лёгким и удобным, но бывают такие случаи, когда задания требуют определённого метода. Чаще всего в них написано, что нужно решать либо с помощью графика, либо методом интервалов. Алгебраический способ и подстановка используются крайне редко или не используются вообще, поскольку они достаточно сложные и запутанные, да и к тому же больше применяемы для решения систем уравнений, а не неравенств, поэтому следует прибегать к рисованию графиков и интервалов. Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
Если что-то не получается
Во время изучения той или иной темы по алгебре, естественно, могут возникнуть проблемы с её пониманием. И это нормально, ведь наш мозг устроен так, что он не способен уяснить сложный материал за один раз. Часто требуется перечитать параграф, воспользоваться помощью учителя или заняться практикой по решению типовых заданий. В нашем случае они выглядят, например, так: «Решите систему неравенств 3 x + 1 ≥ 0 и 2 x — 1 > 3». Таким образом, личное стремление, помощь сторонних людей и практика помогают в понимании любой сложной темы.
Решебник?
А ещё очень хорошо подойдёт решебник, только не для списывания домашних заданий, а для самопомощи. В них можно найти системы неравенств с решением, посмотреть на них (как на шаблоны), попытаться понять, как именно автор решения справился с поставленной задачей, а затем попытаться выполнить подобное в самостоятельном порядке.
Выводы
Алгебра — это один из самых сложных предметов в школе. Ну что же тут поделать? Математика всегда была такой: кому-то она даётся легко, а кому-то с затруднением. Но в любом случае следует помнить, что общеобразовательная программа построена так, что с ней может справиться любой ученик. К тому же, надо иметь в виду огромное количество помощников. Некоторые из них были упомянуты выше.
Урок и презентация на тему: «Системы неравенств. Примеры решений»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 9 класса
Интерактивное учебное пособие для 9 класса «Правила и упражнения по геометрии»
Электронное учебное пособие «Понятная геометрия» для 7-9 классов
Система неравенств
Ребята, вы изучили линейные и квадратные неравенства, научились решать задачи на эти темы. Теперь давайте перейдем к новому понятию в математике – система неравенств. Система неравенств похожа на систему уравнений. Вы помните системы уравнений? Системы уравнений вы изучали в седьмом классе, постарайтесь вспомнить, как вы их решали.
Теперь давайте перейдем к новому понятию в математике – система неравенств. Система неравенств похожа на систему уравнений. Вы помните системы уравнений? Системы уравнений вы изучали в седьмом классе, постарайтесь вспомнить, как вы их решали.
Введем определение системы неравенств.
Несколько неравенств с некоторой переменой х образуют систему неравенств, если нужно найти все значения х, при которых каждое из неравенств образует верное числовое выражение.
Любое значение x, при которых каждое неравенство принимает верное числовое выражение, является решением неравенства. Также может называться и частным решением.
А что есть частное решение? Например, в ответе мы получили выражение х>7. Тогда х=8, или х=123, или какое-либо другое число большее семи – частное решение, а выражение х>7 – общее решение. Общее решение образуется множеством частных решений.
Как мы объединяли систему уравнений? Правильно, фигурной скобкой, так вот с неравенствами поступают также. Давайте рассмотрим пример системы неравенств: $\begin{cases}x+7>5\\x-3
Если система неравенств состоит из одинаковых выражений, например, $\begin{cases}x+7>5\\x+7
Так, что же значит: найти решение системы неравенств?
Решение неравенства – это множество частных решений неравенства, которые удовлетворяют сразу обоим неравенствам системы.
Общий вид системы неравенств запишем в виде $\begin{cases}f(x)>0\\g(x)>0\end{cases}$
Обозначим $Х_1$ – общее решение неравенства f(x)>0.
$Х_2$ – общее решение неравенства g(x)>0.
$Х_1$ и $Х_2$ — это множество частных решений.
Решением системы неравенств будут числа, принадлежащие, как $Х_1$, так и $Х_2$.
Давайте вспомним операции над множествами. Как нам найти элементы множества, принадлежащие сразу обоим множествам? Правильно, для этого есть операция пересечения. Итак, решением нашего неравенство будет множество $А= Х_1∩ Х_2$.
Примеры решений систем неравенств
Давайте посмотрим примеры решения систем неравенств.
Решите систему неравенств.
а) $\begin{cases}3x-1>2\\5x-10 b) $\begin{cases}2x-4≤6\\-x-4
Решение.
а) Решим каждое неравенство отдельно.
$3х-1>2; \; 3x>3; \; x>1$.
$5x-10
Отметим наши промежутки на одной координатной прямой.
Решением системы будет отрезок пересечения наших промежутков. Неравенство строгое, тогда отрезок будет открытым.
Неравенство строгое, тогда отрезок будет открытым.
Ответ: (1;3).
Б) Также решим каждое неравенство отдельно.
$2x-4≤6; 2x≤ 10; x ≤ 5$.
$-x-4 -5$.
Решением системы будет отрезок пересечения наших промежутков. Второе неравенство строгое, тогда отрезок будет открытым слева.
Ответ: (-5; 5].
Давайте обобщим полученные знания.
Допустим, необходимо решить систему неравенств:
$\begin{cases}f_1 (x)>f_2 (x)\\g_1 (x)>g_2 (x)\end{cases}$.
Тогда, интервал ($x_1; x_2$) – решение первого неравенства.
Интервал ($y_1; y_2$) – решение второго неравенства.
Решение системы неравенств – есть пересечение решений каждого неравенства.
Системы неравенств могут состоять из неравенств не только первого порядка, но и любых других видов неравенств.
Важные правила при решении систем неравенств.
Если одно из неравенств системы не имеет решений, то и вся система не имеет решений.
Если одно из неравенств выполняется для любых значений переменой, то решением системы будет решение другого неравенства. 2+36
2+36
Как решать линейные неравенства? Для начала неравенство надо упростить: раскрыть скобки, привести подобные слагаемые.
Рассмотрим примеры решения линейных неравенств с одной переменной.
Раскрываем скобки . Если перед скобками стоит множитель, умножаем его на каждое слагаемое в скобках. Если перед скобками стоит знак «плюс», знаки в скобках не меняются. Если перед скобками стоит знак «минус», знаки в скобках меняются на противоположные.
Приводим подобные слагаемые.
Получили неравенство вида ax+b≤cx+d. Переносим неизвестные в одну сторону, известные — в другую с противоположными знаками (можно было сначала перенести неизвестные в одну сторону, известные в другую, а уже потом привести подобные слагаемые).
Обе части неравенства делим на число, стоящее перед иксом. Так как 8 больше нуля, знак неравенства не меняется:
Title=»Rendered by QuickLaTeX.com»>
Так как , точку -2 отмечаем на числовой прямой закрашенной. от -2, на минус бесконечность.
Так как неравенство нестрогое и точка закрашенная, в ответ -2 записываем с квадратной скобкой.
Чтобы от десятичных дробей перейти к целым числам, можно обе части неравенства умножить на 10 (это не обязательно. Можно работать с десятичными дробями).
Title=»Rendered by QuickLaTeX.com»>
При умножении обеих частей на положительное число знак неравенства не меняется. Умножать на 10 надо каждое слагаемое. При умножении произведения на 10 используем сочетательное свойство умножения , то есть умножаем на 10 только один множитель.
Раскрываем скобки:
Приводим подобные слагаемые:
Переносим неизвестные в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Поскольку -6 — отрицательное число, знак неравенства меняется на противоположный:
Title=»Rendered by QuickLaTeX.com»>
Сокращаем дробь:
Title=»Rendered by QuickLaTeX.com»>
Так как неравенство строгое, на числовой прямой -2/3 отмечаем выколотой точкой. Штриховка идёт вправо, на плюс бесконечность:
Штриховка идёт вправо, на плюс бесконечность:
Неравенство строгое, точка выколотая, поэтому в ответ -2/3 записываем с круглой скобкой:
Title=»Rendered by QuickLaTeX.com»>
Раскрываем скобки. Если перед произведением двух скобок стоит знак «минус», удобно сначала выполнить умножение, и только потом раскрывать скобки, изменяя знак каждого слагаемого на противоположный:
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Приводим подобные слагаемые:
Title=»Rendered by QuickLaTeX.com»>
Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Обе части неравенства делим на число, стоящее перед иксом. Так как -10
Поскольку неравенство строгое, 1,6 отмечаем на числовой прямой выколотой точкой. Штриховка от 1,6 идёт влево, на минус бесконечность:
Так как неравенство строгое и точка выколотая, 1,6 в ответ записываем с круглой скобкой.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Неравенство это выражение с, ≤, или ≥. Например, 3x — 5 Решить неравенство означает найти все значения переменных, при которых это неравенство верно.
Каждое из этих чисел является решением неравенства, а множество всех таких решений является его множеством решений . Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами .
Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами .
Линейные неравенства
Принципы решения неравенств аналогичны принципам решения уравнений.
Принципы решения неравенств
Для любых вещественных чисел a, b,
и c
:
Принцип прибавления неравенств : Если a Принцип умножения для неравенств : Если a 0 верно, тогда ac
Если a bc также верно.
Подобные утверждения также применяются для a ≤ b.
Когда обе стороны неравенства умножаются на отрицательное число, необходимо полностью изменить знак неравенства.
Неравенства первого уровня, как в примере 1 (ниже), называются линейными неравенствами .
Пример 1 Решите каждое из следующих неравенств. Затем изобразите множество решений.
a) 3x — 5
b) 13 — 7x ≥ 10x — 4
Решение
Любое число, меньше чем 11/5, является решением.
Множество решений есть {x|x
Чтобы сделать проверку, мы можем нарисовать график y 1 = 3x — 5 и y 2 = 6 — 2x. Тогда отсюда видно, что для x
Тогда отсюда видно, что для x
Множеством решений есть {x|x ≤ 1}, или (-∞, 1]. График множества решений изображён ниже.
Двойные неравенства
Когда два неравенства соединены словом и , или , тогда формируется двойное неравенство .
Двойное неравенство, как
-3 и 2x + 5 ≤ 7
называется соединённым , потому что в нём использовано и . Запись -3
Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.
Пример 2 Решите -3 Решение У нас есть
Множество решений {x|x ≤ -1 или x > 3}. Мы можем также написать решение с использованием обозначения интервала и символ для объединения или включения обоих множеств: (-∞ -1] (3, ∞). График множества решений изображен ниже.
Для проверки, нарисуем y 1 = 2x — 5, y 2 = -7, и y 3 = 1. Заметьте, что для {x|x ≤ -1 или x > 3}, y 1 ≤ y 2 или y 1 > y 3 .
Неравенства с абсолютным значением (модулем)
Неравенства иногда содержат модули. Следующие свойства используются для их решения.
Следующие свойства используются для их решения.
Для а > 0 и алгебраического выражения x:
|x|
|x| > a эквивалентно x или x > a.
Подобные утверждения и для |x| ≤ a и |x| ≥ a.
Например,
|x|
|y| ≥ 1 эквивалентно y ≤ -1 или y ≥ 1;
и |2x + 3| ≤ 4 эквивалентно -4 ≤ 2x + 3 ≤ 4.
Пример 4 Решите каждое из следующих неравенств. Постройте график множества решений.
a) |3x + 2|
b) |5 — 2x| ≥ 1
Решение
a) |3x + 2|
Множеством решением есть {x|-7/3
b) |5 — 2x| ≥ 1
Множеством решением есть {x|x ≤ 2 или x ≥ 3}, или (-∞, 2] }
Иррациональные неравенства и способы их решения
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Иррациональные
неравенства
и способы их решения
2. Занятие №1.
Цель: Рассмотреть неравенства вида:Основным методом решения иррациональных
неравенств является метод сведения исходного
неравенства к равносильной системе рациональных
неравенств или совокупности таких систем.
Чтобы избежать ошибок при решении
иррациональных неравенств, следует рассматривать
только те значения переменной, при которых все
входящие в неравенство функции определены, т.е. найти
ОДЗ этого неравенства, а затем обоснованно
осуществлять равносильный переход на всей ОДЗ или
ее частях.
1.Рассмотрим иррациональное неравенство вида
Решение. ОДЗ неизвестного будет определяться из
решения неравенства
К тому же,
(x)>0, т.
 к
кПоэтому данное неравенство равносильно следующей
системе неравенств.
4. Пример 1.
Решить неравенство5. Пример 1.
Решить неравенство6. Тогда, решением заданного неравенства будет пересечение множеств решений системы
7. 2.Рассмотрим неравенство вида:
Решение. ОДЗ неизвестного будет определяться из условияНо, в отличие от предыдущего, (x) может принимать как положительные,
так и отрицательные значения. Поэтому в процессе решения должны
рассматривать два случая: (x) <0 и (x)
. В первом случае данное
неравенство равносильно следующей системе неравенств:
Но в этой системе можно опустить последнее неравенство, т.к.
при (x)<0 оно выполняется всегда. Т.о. имеем
8. В случае же Заданное неравенство равносильно следующей системе неравенств:
( x) 0В случае же
Заданное неравенство равносильно следующей
системе неравенств:
Тогда, из последней системы видно, что первое неравенство можно
опустить, т.
 к. из f(x)>( (x))2 следует справедливость f(x)
к. из f(x)>( (x))2 следует справедливость f(x)Решением неравенства будет объединение множеств решений обоих случаев.
9. Пример 2.
Решить неравенство10. Пример 2. Решить неравенство:
Рассмотрим два случая:11. Занятие №2
• Цель: Рассмотреть неравенства вида:При решении иррациональных неравенств
используются те же методы, что и при решении
иррациональных уравнений: возведение обеих
частей неравенства в одну и ту же натуральную
степень, введение новых переменных и т.д.
Однако при решении иррациональных неравенств
необходимо следить за тем, чтобы выполняемые
преобразования приводили к равносильному
неравенству.
12. 1.Неравенство вида
равносильно системе неравенств:2.Неравенство вида
равносильно неравенству f(x) <q(x).
13. Пример 3.
Решить неравенство14. Пример 3.Решить неравенство:
15. Пример 4.
Решить неравенство16. Пример4.Решить неравенство:
17.
 Занятие №3.• Цель: Рассмотреть решения неравенств
Занятие №3.• Цель: Рассмотреть решения неравенствметодом интервалов.
• При решении иррациональных неравенств
методом интервалов надо всегда помнить,
что нули функций рассматриваются только
входящие в ОДЗ.
18. Пример 5. Решим иррациональное неравенство методом интервалов :
19. Занятие №4.
• Цель: Рассмотреть решенияиррациональных неравенств введением
новой переменной
20. Пример 6. Решим неравенство введением новой переменной
21. ешим неравенствопеременно
22. Занятие №5.
• Цель: Рассмотреть решенияиррациональных неравенств методом
замены множителя .
23. Пример №7. Решим неравенство методом замены множителя
24. Домашнее задание. Решить неравенство:
Пример 1.Пример 2.
Пример 3.
Пример 4.
Пример 5.
25. ВЫВОДЫ:
Рассмотрели иррациональные неравенства испособы их решения.
Основным методом решения иррациональных неравенств
является метод сведения исходного неравенства к
равносильной системе рациональных неравенств или
совокупности таких систем
возведение обеих частей
неравенства в одну и ту же
натуральную степень
введение новой переменной , метод интервалов ,
метод замены множителя .

26. СПАСИБО ЗА УРОК!
English Русский Правила
Некоторые ошибки в решении иррациональных неравенств в учебнике по математике 10 класс | Материалы конференции AIP
Пропустить пункт назначения
Исследовательская статья| 02 марта 2021 г.
Тьянг Даниэль Чандра
Информация об авторе и статье
Автор, ответственный за переписку: tjang.daniel.fmipa@um.ac.id
Материалы конференции AIP 2330, 040031 (2021)
https://doi.org/10.1063/5.0043229
- Разделенный экран
- Взгляды
- Содержание артикула
- Рисунки и таблицы
- Видео
- Аудио
- Дополнительные данные
- Экспертная оценка
- Нажмите здесь, чтобы открыть pdf в другом окне PDF для
- Делиться
- Твиттер
- Фейсбук
- Реддит
Перепечатки и разрешения
- Поиск по сайту
Иконка Цитировать Цитировать
Цитата
Тджанг Даниэль Чандра; Некоторые ошибки в решении иррациональных неравенств в учебнике по математике 10 класс. AIP Conference Proceedings 2 марта 2021 г.; 2330 (1): 040031. https://doi.org/10.1063/5.0043229
AIP Conference Proceedings 2 марта 2021 г.; 2330 (1): 040031. https://doi.org/10.1063/5.0043229
Скачать файл цитаты:
- Ris (Zotero)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- КонецПримечание
- РефВоркс
- Бибтекс
Расширенный поиск |Поиск по цитированию
В статье описаны некоторые ошибки при решении иррациональных неравенств в учебнике по математике для 10 класса. Основная ошибка заключается в том, что возводят в квадрат обе части неравенства без учета знака члена каждой части неравенства. Предлагаются некоторые предложения по исправлению ошибок и приводятся примеры для иллюстрации.
Темы
Учебники
1.
Гадери
M.
Сравнительный анализ учебников по естественным наукам и руководства для учителей в Иране с Америкой (наука в любое время
).
Procedia — Soc Behav Sci.
2010
;
2
(
2
):
5427
–
40
.
https://doi.org/10.1016/j.sbspro.2010.03.886
2.
Сукино
.
Математика джилид 1A untuk SMA/MA Kelas X Семестр 1 Келомпок Ваджиб
.
Джакарта: Эрланга
;
2016
.
3.
Bartle
RG
,
Sherbert
DR 900 03
. No TitleIntroduction to Real Analysis, четвертое издание.
Иллинойс
:
John Wiley & Sons, Inc
;
2011
.
4.
Bagni
G.
Иррациональное неравенство: учебно-дидактический контракт
.
Преподаватель истории математики.
1996
;
133
–
40
.
Этот контент доступен только в формате PDF.
9.7: Решение рациональных неравенств — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 49968
- Чау Д Тран
- Береговой колледж
Цели обучения
- Решение рациональных неравенств
- Решите неравенство с рациональными функциями
Будьте готовы
Прежде чем приступить к работе, пройдите этот тест на готовность.
- Найдите значение \(x-5\), когда ⓐ \(x=6\) ⓑ \(x=-3\) ⓒ \(x=5\)
Если вы пропустили эту задачу, просмотрите пример 1. 2. .16.
2. .16. - Решите: \(8-2 x<12\)
Если вы пропустили эту задачу, просмотрите пример 2.6.13. - Запишите в виде интервала: \(-3 \leq x<5 \)
Если вы пропустили эту проблему, просмотрите пример 2.6.4.
Решение рациональных неравенств
Мы научились решать линейные неравенства после того, как научились решать линейные уравнения. Техники были почти такими же, за одним важным исключением. Когда мы умножаем или делим на отрицательное число, знак неравенства меняется на противоположный.
Только что научившись решать рациональные уравнения, мы теперь готовы решать рациональные неравенства. Рациональное неравенство — это неравенство, содержащее рациональное выражение.
Рациональное неравенство 9{2}} \leq \dfrac{3}{x}\quad \) являются рациональными неравенствами, поскольку каждое из них содержит рациональное выражение.
Когда мы решим рациональное неравенство, мы будем использовать многие методы, которые мы использовали при решении линейных неравенств. Мы особенно должны помнить, что когда мы умножаем или делим на отрицательное число, знак неравенства должен измениться.
Мы особенно должны помнить, что когда мы умножаем или делим на отрицательное число, знак неравенства должен измениться.
Еще одно отличие состоит в том, что мы должны тщательно рассмотреть, какое значение может сделать рациональное выражение неопределенным и поэтому должно быть исключено.
Когда мы решаем уравнение и получаем \(x=3\), мы знаем, что есть одно решение, равное 3.
Когда мы решаем неравенство и получаем \(x>3\), мы знаем, что решений много. Мы графически отображаем результат, чтобы лучше показать все решения, и начинаем с 3. Три становится критической точкой, а затем мы решаем, следует ли заштриховать слева или справа от нее. Числа справа от 3 больше, чем 3, поэтому мы заштриховываем вправо.
Чтобы решить рациональное неравенство, мы сначала должны написать неравенство только с одним частным слева и 0 справа.
Затем мы определяем критические точки, чтобы использовать их для разделения числовой прямой на интервалы. Критическая точка — это число, которое делает рациональное выражение нулевым или неопределенным.
Затем мы оценим множители числителя и знаменателя и найдем частное в каждом интервале. Это позволит определить интервал или интервалы, содержащие все решения рационального неравенства.
Мы записываем решение в интервальной нотации, стараясь определить, включены ли конечные точки.
Пример \(\PageIndex{1}\)
Решите и запишите решение в интервальной записи: \(\dfrac{x-1}{x+3} \geq 0\)
Решение
Шаг 1 . Запишите неравенство в виде одного частного слева и нуля справа.
Наше неравенство имеет следующий вид.\[\dfrac{x-1}{x+3} \geq 0 \nonumber \]
Шаг 2 . Определите критические точки — точки, в которых рациональное выражение будет равно нулю или неопределенно.
Рациональное выражение будет равно нулю, если числитель равен нулю. Так как \(x-1=0\) при \(x=1\), то 1 является критической точкой.
Рациональное выражение будет неопределенным, если знаменатель равен нулю. Поскольку \(x+3=0\) при \(x=-3\), то -3 является критической точкой.
Поскольку \(x+3=0\) при \(x=-3\), то -3 является критической точкой.
Критические точки 1 и -3.
Шаг 3 . Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Числовая строка делится на три интервала:
\[(-\infty,-3) \quad (-3,1) \quad (1,\infty) \nonnumber \]
Шаг 4 . Проверьте значение в каждом интервале. Над числовой прямой показывают знак каждого множителя рационального выражения в каждом интервале. Ниже числовой строки укажите знак частного.
Чтобы найти знак каждого фактора в интервале, мы выбираем любую точку в этом интервале и используем ее в качестве контрольной точки. Любая точка интервала даст выражению тот же знак, поэтому мы можем выбрать любую точку интервала.
\[\text { Интервал }(-\infty,-3) \nonumber \]
Число -4 находится в интервале \((-\infty,-3)\). Проверка \(x=-4\) в выражении в числителе и знаменателе.
Числитель:
\[\begin{array}{l} {x-1} \\ {-4-1} \\ {-5} \\ {\text {Отрицательный}} \end{массив} \номер\]
Знаменатель:
\[\begin{array}{l} {x+3} \\ {-4+3} \\ {-1} \\ {\text {Отрицательный}} \end{массив} \nonumber \]
Над числовой строкой отметьте множитель \(x-1\) отрицательным и отметьте множитель \(x+3\) отрицательным.
Поскольку отрицательное число, деленное на отрицательное, является положительным, отметьте положительное частное в интервале \((-\infty,-3)\).
\[\text {Интервал } (-3,1) \номер \]
Число 0 находится в интервале \((-3,1)\). Тест \(х=0\).
Числитель:
\[\begin{array}{l} {x-1} \\ {0-1} \\ {-1} \\ {\text {Отрицательный}} \end{массив} \ nonumber \]
Знаменатель:
\[\begin{array}{l} {x+3} \\ {0+3} \\ {3} \\ {\text {Positive}} \end{array } \nonumber \]
Над числовой строкой отметьте множитель \(x-1\) отрицательным и отметьте \(x+3\) положительным.
Поскольку отрицательное число, деленное на положительное, равно отрицательному, частное в интервале \((-3,1)\ помечается как отрицательное).
\[\text {Интервал }(1, \infty) \nonumber \]
Число 2 находится в интервале \((1, \infty)\). Тест \(х=2\).
Числитель:
\[\begin{array}{l} {x-1} \\ {2-1} \\ {1} \\ {\text {Positive}} \end{array} \nonumber \]
Знаменатель:
\[\begin{array}{l} {x+3} \\ {2+3} \\ {5} \\ {\text {Положительный}} \end{массив} \nonumber \]
Над числовой строкой отметьте множитель \(x-1\) положительным и отметьте \(x+3\) положительным.
Поскольку положительное число, деленное на положительное, является положительным, отметьте положительное частное в интервале \((1, \infty)\).
Шаг 5 . Определите промежутки, на которых неравенство верно. Запишите решение в интервальной записи.
Мы хотим, чтобы частное было больше или равно нулю, поэтому числа в интервалах \((-\infty,-3)\) и \((1, \infty) \) являются решениями.
А как же критические точки?
Критическая точка \(x=-3\) делает знаменатель равным 0, поэтому ее нужно исключить из решения и отметить скобкой.
Критическая точка \(x=1\) делает все рациональное выражение равным 0. Неравенство требует, чтобы рациональное выражение было больше или равно. Итак, 1 является частью решения и мы будем отмечать его скобкой.
Вспомним, что когда у нас есть решение, состоящее из более чем одного интервала, мы используем символ объединения \(\cup \), чтобы соединить два интервала. Решение в интервальной записи \((-\infty,-3) \cup[1, \infty)\).
Упражнение \(\PageIndex{1}\)
Решите и запишите решение в интервальной записи: \(\dfrac{x-2}{x+4} \geq 0\)
- Ответ
\((-\infty,-4) \cup[2, \infty)\)
Упражнение \(\PageIndex{2}\)
Решите и запишите решение в интервальной записи: \(\dfrac{x+2}{x-4} \geq 0\)
- Ответ
\((-\infty,-2] \cup(4, \infty)\)
Мы суммируем шаги для удобства.
Как решить рациональное неравенство
Шаг 1. Запишите неравенство в виде одного частного слева и нуля справа.
Шаг 2. Определите критические точки – точки, в которых рациональное выражение будет равно нулю или неопределенно.
Шаг 3. Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Шаг 4. Проверьте значение в каждом интервале. Над числовой прямой показывают знак каждого множителя числителя и знаменателя в каждом интервале. Ниже числовой строки укажите знак частного.
Шаг 5. Определите интервалы, на которых неравенство верно. Запишите решение в интервальной записи.
Следующий пример требует, чтобы мы сначала привели рациональное неравенство в правильную форму.
Пример \(\PageIndex{2}\)
Решите и запишите решение в интервальной записи: \(\dfrac{4 x}{x-6}<1\)
Решение
\[\ dfrac{4 x}{x-6}<1 \nonumber \]
Вычтите 1, чтобы получить ноль справа.
\[\dfrac{4 x}{x-6}-1<0 \nonumber \]
Перепишите 1 в виде дроби с помощью ЖК-дисплея.
\[\dfrac{4 x}{x-6}-\frac{x-6}{x-6}<0 \nonumber \]
Вычтите числители и поместите разницу над общим знаменателем.
\[\dfrac{4 x-(x-6)}{x-6}<0 \nonumber \]
Упростить.
\[\dfrac{3 x+6}{x-6}<0 \nonumber \]
Умножьте числитель, чтобы показать все множители.
\[\dfrac{3(x+2)}{x-6}<0 \nonumber \]
Найдите критические точки.
Частное будет равно нулю, если числитель равен нулю. Частное не определено, когда знаменатель равен нулю.
Частное не определено, когда знаменатель равен нулю.
\[\begin{array}{rlrl} {x+2} & {=0} & {x-6} & {=0} \\ {x} & {=-2} & {x} & { =6} \end{массив} \номер\]
Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Проверка значения в каждом интервале.
| \((-\infty,-2)\) | \((-2,6)\) | \((6, \infty)\) | |
|---|---|---|---|
| \(х+2)\) | х+2 -3+2 -1 — | х+2 0+2 2 + | х+2 7+2 9 + |
| \(х-6\) | х-6 -3-6 -9 — | х-6 0-6 -6 — | х-6 7-6 1 + |
Над числовой линией укажите знак каждого множителя рационального выражения в каждом интервале. {2}-2 x-15}>0\). 9{2}-2 x-15}>0 \номер \]
{2}-2 x-15}>0\). 9{2}-2 x-15}>0 \номер \]
Разложите знаменатель на множители.
\[\dfrac{5}{(x+3)(x-5)}>0 \nonumber \]
Найдите критические точки. Частное равно 0, когда числитель равен 0. Поскольку числитель всегда равен 5, частное не может быть 0.
Частное будет неопределенным, если знаменатель равен нулю.
\[\begin{aligned} &(x+3)(x-5)=0\\ &x=-3, x=5 \end{aligned} \nonumber \]
Используйте критические точки для разделения числовую прямую на интервалы. 9{2}=0} && {x-6=0} && {x+1=0} \\ {x=0} && {x=6} && {x=-1} \end{массив} \nonumber \ ]
Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Над числовой линией укажите знак каждого фактора в каждом интервале. Под числовой прямой покажите знак частного.
Поскольку 0 исключен, решение представляет собой два интервала \((-1,0) \cup(0,6)\), \((-1,0)\) и \((0,6) \).
Упражнение \(\PageIndex{7}\) 9{2}}
<\dfrac{3}{x}\).- Ответить
\((3,6)\)
Решение неравенства с рациональными функциями
При работе с рациональными функциями иногда полезно знать, когда функция больше или меньше определенного значения. Это приводит к рациональному неравенству.
Это приводит к рациональному неравенству.
Пример \(\PageIndex{5}\)
Учитывая функцию \(R(x)=\dfrac{x+3}{x-5}\), найдите значения x, при которых функция меньше или равно 0,
Решение
Мы хотим, чтобы функция была меньше или равна 0.
\[R(x) \leq 0 \nonumber \]
Подставим рациональное выражение вместо \(R(x)\) .
\[\dfrac{x+3}{x-5} \leq 0 \quad x \neq 5 \nonumber \]
Найдите критические точки.
\[\begin{array}{rlrl} {x+3=0} && {x-5=0} \\ {x=-3} && {x=5} \end{array} \nonumber \]
Используйте критические точки, чтобы разделить числовую прямую на интервалы.
Тестовые значения в каждом интервале. Над числовой линией покажите знак каждого фактора в каждом интервале. Под числовой прямой покажите знак частного. Запишите решение в интервальной записи. Поскольку 5 исключено, мы не включаем его в интервал.
\[[-3,5) \nonumber \]
Упражнение \(\PageIndex{9}\)
Учитывая функцию \(R(x)=\dfrac{x-2}{x+4} \), найдите значения \(x\), при которых функция меньше или равна 0.
- Ответить
\((-4,2]\)
Упражнение \(\PageIndex{10}\)
Учитывая функцию \(R(x)=\dfrac{x+1}{x-4}\), найдите значения \(x\), которые делают функция меньше или равна 0.
- Ответ
\([-1,4)\)
В экономике функция \(C(x)\) используется для представления стоимости производства \(x\) единиц товара. Среднюю стоимость единицы можно найти, разделив \(C(x)\) на количество товаров \(x\). Тогда средняя стоимость единицы равна \(c(x)=\dfrac{C(x)}{x}).
Пример \(\PageIndex{6}\)
Функция \(C(x)=10 x+3000\) представляет себестоимость производства \(x\), количества изделий. Найти:
- Функция средней стоимости, \(c(x)\)
- Сколько изделий нужно произвести, чтобы их средняя стоимость была меньше 40 долларов.
Решение
- \[C(x)=10 x+3000 \номер\]
Функция средней стоимости имеет вид \(c(x)=\dfrac{C(x)}{x})\). Чтобы найти функцию средней стоимости, разделите функцию стоимости на \(x\).
Чтобы найти функцию средней стоимости, разделите функцию стоимости на \(x\).
\[\begin{aligned} &c(x)=\dfrac{C(x)}{x}\\ &c(x)=\dfrac{10 x+3000}{x} \end{aligned} \nonumber \]
Функция средней стоимости равна \(c(x)=\dfrac{10 x+3000}{x} \)
- Мы хотим, чтобы функция \(c(x)\) была меньше 40.
\[c(x)<40 \nonumber \]
Подставить рациональное выражение forc(x).
\[\dfrac{10 x+3000}{x}<40, \quad x \neq 0 \nonumber \]
Вычтите 40, чтобы получить 0 справа.
\[\dfrac{10 x+3000}{x}-40<0 \номер\]
Перепишите левую часть как одно частное, найдя ЖК-дисплей и выполнив вычитание.
\[\begin{align} \dfrac{10 x+3000}{x}-40\left(\dfrac{x}{x}\right) &<0\\ \dfrac{10 x+3000}{ x}-\dfrac{40 x}{x} &<0\\ \dfrac{10 x+3000-40 x}{x} &<0 \\ \dfrac{-30 x+3000}{x} &< 0 \end{aligned} \nonumber \]
Разложите числитель на множители, чтобы показать все множители.
\[\begin{array}{ll} {\dfrac{-30(x-100)}{x}<0} \\ {-30(x-100)=0} && {x=0} \ конец {массив} \номер \]
Найдите критические точки.
\[\begin{array}{rl} {-30 \neq 0} & {x-100=0} \\ &{x=100} \end{array} \nonumber \]
Более 100 элементов должны быть произведены, чтобы средняя стоимость не превышала 40 долларов за единицу.
Упражнение \(\PageIndex{11}\)
Функция \(C(x)=20 x+6000\) представляет собой стоимость производства \(x\), количества изделий. Найти:
- Сколько изделий нужно произвести, чтобы их средняя стоимость была меньше 60 долларов.
- Ответить
- \(с(х)=\dfrac{20 х+6000}{х}\)
- Необходимо произвести более 150 единиц продукции, чтобы средняя стоимость не превышала 60 долларов за единицу.
Упражнение \(\PageIndex{12}\)
Функция \(C(x)=5 x+900\) представляет собой стоимость производства \(x\), количества изделий. Найти:
- Сколько изделий нужно произвести, чтобы их средняя стоимость была меньше 20 долларов.
- Ответить
- \(с(х)=\dfrac{5 х+900}{х}\)
- Необходимо произвести более 60 единиц продукции, чтобы средняя стоимость не превышала 20 долларов США за единицу.





 2. .16.
2. .16.




 Студенты могут практиковать римские цифры от 1 до 40, используя таблицу и использовать ее для дальнейшего преобразования чисел.
Студенты могут практиковать римские цифры от 1 до 40, используя таблицу и использовать ее для дальнейшего преобразования чисел. Например: LI, L > I, поэтому LI = L + I = 50 + 1 = 51,9.0176
Например: LI, L > I, поэтому LI = L + I = 50 + 1 = 51,9.0176 Он состоит из записи чисел от 1 до 40, использовавшейся римлянами в древние времена.
Он состоит из записи чисел от 1 до 40, использовавшейся римлянами в древние времена. Пары простых чисел-близнецов от 1 до 40: (3, 5), (5, 7), (11, 13), (17, 19) и (29) , 31). Следовательно, между римскими цифрами 1 и 40 находится 5 простых чисел-близнецов.
Пары простых чисел-близнецов от 1 до 40: (3, 5), (5, 7), (11, 13), (17, 19) и (29) , 31). Следовательно, между римскими цифрами 1 и 40 находится 5 простых чисел-близнецов.
 строчные римские цифры плюс
строчные римские цифры плюс 

 Это практический инструмент для всех, кто работает с промежутками времени в разных единицах измерения и хочет сэкономить время и избежать ошибок в расчетах.
Это практический инструмент для всех, кто работает с промежутками времени в разных единицах измерения и хочет сэкономить время и избежать ошибок в расчетах.

 С научной точки зрения.
С научной точки зрения.


 Не помешало и то, что Эмиля играл всемирно известный бас Эцио Пинца. Конечно, мы получили небольшой вкус этой магии в возрождении Театра Линкольн-центра Бартлетта Шера с великолепным выступлением Паоло Сота, получившим премию «Тони».
Не помешало и то, что Эмиля играл всемирно известный бас Эцио Пинца. Конечно, мы получили небольшой вкус этой магии в возрождении Театра Линкольн-центра Бартлетта Шера с великолепным выступлением Паоло Сота, получившим премию «Тони». Возможно, это была битва с Actors Equity за роль Джонатана Прайса в евразийской роли Инженера, или использование вертолета на сцене в заголовках, или, может быть, это была иногда банальная лирика, которая сделала этот блокбастер несколько ругаемым гигантом. Как столы повернулись. После одного идиотского мюзикла без мелодии за другим, Мисс Сайгон похожа на Моя прекрасная леди и мы с нетерпением ждем предстоящего возрождения. Трудно представить, чтобы кто-то останавливал шоу в конце второго акта, как вдохновленный Прайс в «Американской мечте».
Возможно, это была битва с Actors Equity за роль Джонатана Прайса в евразийской роли Инженера, или использование вертолета на сцене в заголовках, или, может быть, это была иногда банальная лирика, которая сделала этот блокбастер несколько ругаемым гигантом. Как столы повернулись. После одного идиотского мюзикла без мелодии за другим, Мисс Сайгон похожа на Моя прекрасная леди и мы с нетерпением ждем предстоящего возрождения. Трудно представить, чтобы кто-то останавливал шоу в конце второго акта, как вдохновленный Прайс в «Американской мечте». «Наследие (Последняя воля и завещание)» из «Двадцатый век»
«Наследие (Последняя воля и завещание)» из «Двадцатый век»  Каждый год, который Бродвей ждет от Финна очередного великолепного нового саундтрека, слишком долго.
Каждый год, который Бродвей ждет от Финна очередного великолепного нового саундтрека, слишком долго. обязательно похоже на это — или как в Follies , где вся последовательность Лавленда, по сути, может быть так называемой 11-часовой мультипесней. Однако в Company мы получаем потрясающий подарок от Сондхейма в «Being Alive», столь же страстном и столь же честном заявлении о желании быть любимым, как когда-либо написанном, положенном на неотразимую музыку, которая только становится глубже при повторном прослушивании. .
обязательно похоже на это — или как в Follies , где вся последовательность Лавленда, по сути, может быть так называемой 11-часовой мультипесней. Однако в Company мы получаем потрясающий подарок от Сондхейма в «Being Alive», столь же страстном и столь же честном заявлении о желании быть любимым, как когда-либо написанном, положенном на неотразимую музыку, которая только становится глубже при повторном прослушивании. .
 Он может быть очень эмоциональным (см. «Телефонный провод» в «Дом веселья» или «Неудача слов» в «Дорогом Эване Хансене») или дерзким и громким («Мы смотрим на тебя, Эльфаба»). Вот некоторые из любимых 11-часовых номеров сотрудников TodayTix, которые вы можете посмотреть на YouTube!
Он может быть очень эмоциональным (см. «Телефонный провод» в «Дом веселья» или «Неудача слов» в «Дорогом Эване Хансене») или дерзким и громким («Мы смотрим на тебя, Эльфаба»). Вот некоторые из любимых 11-часовых номеров сотрудников TodayTix, которые вы можете посмотреть на YouTube! Она заставляет ноты звучать легко и непринужденно. В ее игре есть настоящая боль, но она наполнена той радостью, которую приносит знание настоящей боли. Есть много версий этой песни, и наблюдение за каждым человеком всегда является откровением, но выступление Патти здесь действительно выделяется по всем этим причинам.
Она заставляет ноты звучать легко и непринужденно. В ее игре есть настоящая боль, но она наполнена той радостью, которую приносит знание настоящей боли. Есть много версий этой песни, и наблюдение за каждым человеком всегда является откровением, но выступление Патти здесь действительно выделяется по всем этим причинам. Вам знакомо это чувство, когда вы ставите перед собой цель что-то сказать, и мучительный момент между произнесением этого и ожиданием ответа. Этот краткий момент колебания прямо перед тем, как вы должны сказать что-то, на что, как вы знаете, вы получите реакцию, а затем прилив страха и облегчения прекрасно передан во всей этой композиции.
Вам знакомо это чувство, когда вы ставите перед собой цель что-то сказать, и мучительный момент между произнесением этого и ожиданием ответа. Этот краткий момент колебания прямо перед тем, как вы должны сказать что-то, на что, как вы знаете, вы получите реакцию, а затем прилив страха и облегчения прекрасно передан во всей этой композиции. Прелесть «Официантки» в том, что она похожа на настоящую жизнь: смешно, сложно, грустно, а также в равной степени очень тяжело и достойно празднования. Прелесть этой песни в том, что она позволяет Дженне просто «быть» — в ней нет ничего фальшивого, принудительного или перформативного. Это так грубо и честно. Я люблю «She Used to Be Mine», потому что она одновременно кажется песней, написанной только для этого персонажа, и песней, которая кажется написанной для каждого человека в комнате. Мое любимое исполнение номера — сценарист шоу Сара Барейлес и оригинальная бродвейская Дженна Джесси Мюллер на церемонии вручения премии «Тони». Убедитесь, что вы взяли несколько салфеток, прежде чем нажимать кнопку воспроизведения.
Прелесть «Официантки» в том, что она похожа на настоящую жизнь: смешно, сложно, грустно, а также в равной степени очень тяжело и достойно празднования. Прелесть этой песни в том, что она позволяет Дженне просто «быть» — в ней нет ничего фальшивого, принудительного или перформативного. Это так грубо и честно. Я люблю «She Used to Be Mine», потому что она одновременно кажется песней, написанной только для этого персонажа, и песней, которая кажется написанной для каждого человека в комнате. Мое любимое исполнение номера — сценарист шоу Сара Барейлес и оригинальная бродвейская Дженна Джесси Мюллер на церемонии вручения премии «Тони». Убедитесь, что вы взяли несколько салфеток, прежде чем нажимать кнопку воспроизведения. Однако Сэм убеждает ее думать иначе, но не раньше, чем Ода Мэй заглянет в ее возможный богатый образ жизни. Это очень запоминающаяся, воодушевляющая песня, которая полностью контрастирует с остальной музыкой и приносит легкое облегчение от очень эмоциональной истории любви и потери. Это идеальное число 11 часов!
Однако Сэм убеждает ее думать иначе, но не раньше, чем Ода Мэй заглянет в ее возможный богатый образ жизни. Это очень запоминающаяся, воодушевляющая песня, которая полностью контрастирует с остальной музыкой и приносит легкое облегчение от очень эмоциональной истории любви и потери. Это идеальное число 11 часов! если делать или делать достаточно хорошо / достаточно оригинально / стоит всех усилий, мой профессиональный медицинский совет будет смотреть это видео 400 раз в день Приходи на сладкую сладкую гармонию в 1:57 и оставайся для Мэнди, шепчущей: «Я люблю тебя». » в 4:17 «Возможно, выбор был ошибочным / Выбор не был / Вы должны двигаться дальше». Вы шутите надо мной, Стивен Джошуа Сондхейм??? (hbd btw xo)
если делать или делать достаточно хорошо / достаточно оригинально / стоит всех усилий, мой профессиональный медицинский совет будет смотреть это видео 400 раз в день Приходи на сладкую сладкую гармонию в 1:57 и оставайся для Мэнди, шепчущей: «Я люблю тебя». » в 4:17 «Возможно, выбор был ошибочным / Выбор не был / Вы должны двигаться дальше». Вы шутите надо мной, Стивен Джошуа Сондхейм??? (hbd btw xo) Любая песня с конфетти-пушкой в конце обязательно привлечет мое внимание! Затем я работал над шоу время от времени в течение многих лет, и после сотен (может быть, тысяч?!) прослушиваний я все еще люблю его.
Любая песня с конфетти-пушкой в конце обязательно привлечет мое внимание! Затем я работал над шоу время от времени в течение многих лет, и после сотен (может быть, тысяч?!) прослушиваний я все еще люблю его. Кроме того, тот факт, что тот, кто играет Эвана, буквально должен рыдать, — это физический подвиг, которого я никогда не пойму.
Кроме того, тот факт, что тот, кто играет Эвана, буквально должен рыдать, — это физический подвиг, которого я никогда не пойму.

 «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.
«Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа. «Отбрасывая» логарифмы, делаем это грамотно.
«Отбрасывая» логарифмы, делаем это грамотно.
 Если вы получите ответ, что решение неравенства – все числа, от минус до плюс бесконечности, то это значит, что неравенство выполняется при любых значениях p
Решим неравенство
Перенесем все в левую часть.
Раскрываем скобки.
Приводим подобные члены.
Раскрываем скобки.
Приводим подобные члены.
Изменим знаки выражений на противоположные.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Окончательный ответ: p-любое.
Это значит, что оно истинно при любых значениях p.
Решим еще одно неравенство, в которой в качестве переменно будет не p, а у
Перенесем все в левую часть.
Раскрываем скобки, используя распределительный закон умножения
Раскрываем скобки, помня, что при раскрытии скобок знаки выражений меняются на противоположные
Приводим подобные члены.
Если вы получите ответ, что решение неравенства – все числа, от минус до плюс бесконечности, то это значит, что неравенство выполняется при любых значениях p
Решим неравенство
Перенесем все в левую часть.
Раскрываем скобки.
Приводим подобные члены.
Раскрываем скобки.
Приводим подобные члены.
Изменим знаки выражений на противоположные.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Окончательный ответ: p-любое.
Это значит, что оно истинно при любых значениях p.
Решим еще одно неравенство, в которой в качестве переменно будет не p, а у
Перенесем все в левую часть.
Раскрываем скобки, используя распределительный закон умножения
Раскрываем скобки, помня, что при раскрытии скобок знаки выражений меняются на противоположные
Приводим подобные члены. Изменяем порядок действий. Ставим слагаемые так, чтобы нам было удобно применять формулу корней квадратного уравнения в дальнейшем
Решаем вспомогательное уравнение.
Решаем это квадратное уравнение через дискриминант.
Находим дискриминант по стандартной формуле
Дискриминант равен нулю, значит, уравнение имеет один корень.
Старший коэффициент положителен.
Квадратичная функция принимает только неотрицательные значения.
Следующее неравенство равносильно предыдущему.
Окончательный ответ: y — любое.
При решении неравенства мы по показали, что его решениями являются все действительные числа. А это значит, что при любых у выполняется неравенство, что и требовалось доказати.
Решим еще одно неравенство, в котором неизвестной будет переменная x
Для начала перенесем все в левую часть.
Теперь умножаем друг на другу, пользуясь стандартным правилом.
Изменяем порядок действий. Ставим слагаемые так, чтобы нам было удобно применять формулу корней квадратного уравнения в дальнейшем
Решаем вспомогательное уравнение.
Решаем это квадратное уравнение через дискриминант.
Находим дискриминант по стандартной формуле
Дискриминант равен нулю, значит, уравнение имеет один корень.
Старший коэффициент положителен.
Квадратичная функция принимает только неотрицательные значения.
Следующее неравенство равносильно предыдущему.
Окончательный ответ: y — любое.
При решении неравенства мы по показали, что его решениями являются все действительные числа. А это значит, что при любых у выполняется неравенство, что и требовалось доказати.
Решим еще одно неравенство, в котором неизвестной будет переменная x
Для начала перенесем все в левую часть.
Теперь умножаем друг на другу, пользуясь стандартным правилом. Приводим подобные члены в скобках
Раскрываем скобки, меняя знаки выражений на противоположные
Приводим подобные члены и изменяем порядок действий.
Изменим знаки выражений на противоположные. При этом x в квадрате окажется без знака минуса, а
— 2 изменится +2
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Окончательный ответ: x –любое, так выражение x в квадрате +2 в любом случаем принимает положительное значение
Таким мы доказали то, что нам требовалось.
Приводим подобные члены в скобках
Раскрываем скобки, меняя знаки выражений на противоположные
Приводим подобные члены и изменяем порядок действий.
Изменим знаки выражений на противоположные. При этом x в квадрате окажется без знака минуса, а
— 2 изменится +2
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Окончательный ответ: x –любое, так выражение x в квадрате +2 в любом случаем принимает положительное значение
Таким мы доказали то, что нам требовалось. Здесь, как вы увидите, в этом нет необходимости, поэтому вы можете решить это так же, как уравнение. Сначала умножьте обе части на 2, чтобы исключить знаменатель:
Здесь, как вы увидите, в этом нет необходимости, поэтому вы можете решить это так же, как уравнение. Сначала умножьте обе части на 2, чтобы исключить знаменатель: Если бы вы выбрали , то увидели бы, что данное неравенство принимает вид: , что работает, потому что
Если бы вы выбрали , то увидели бы, что данное неравенство принимает вид: , что работает, потому что  Однако что, если это отрицательное число? Помните, что когда вы умножаете или делите на отрицательное число в неравенстве, вы должны перевернуть знак. Но здесь вы не знаете, означает ли умножение на умножение на положительное или отрицательное число, поэтому вы не знаете, в каком направлении должен указывать знак. Важным соображением при работе с неравенствами является то, что вы никогда не сможете умножать или делить на переменную, если не знаете знак переменной. В результате возможны и I, и II, но ни один из них не гарантирован:
Однако что, если это отрицательное число? Помните, что когда вы умножаете или делите на отрицательное число в неравенстве, вы должны перевернуть знак. Но здесь вы не знаете, означает ли умножение на умножение на положительное или отрицательное число, поэтому вы не знаете, в каком направлении должен указывать знак. Важным соображением при работе с неравенствами является то, что вы никогда не сможете умножать или делить на переменную, если не знаете знак переменной. В результате возможны и I, и II, но ни один из них не гарантирован: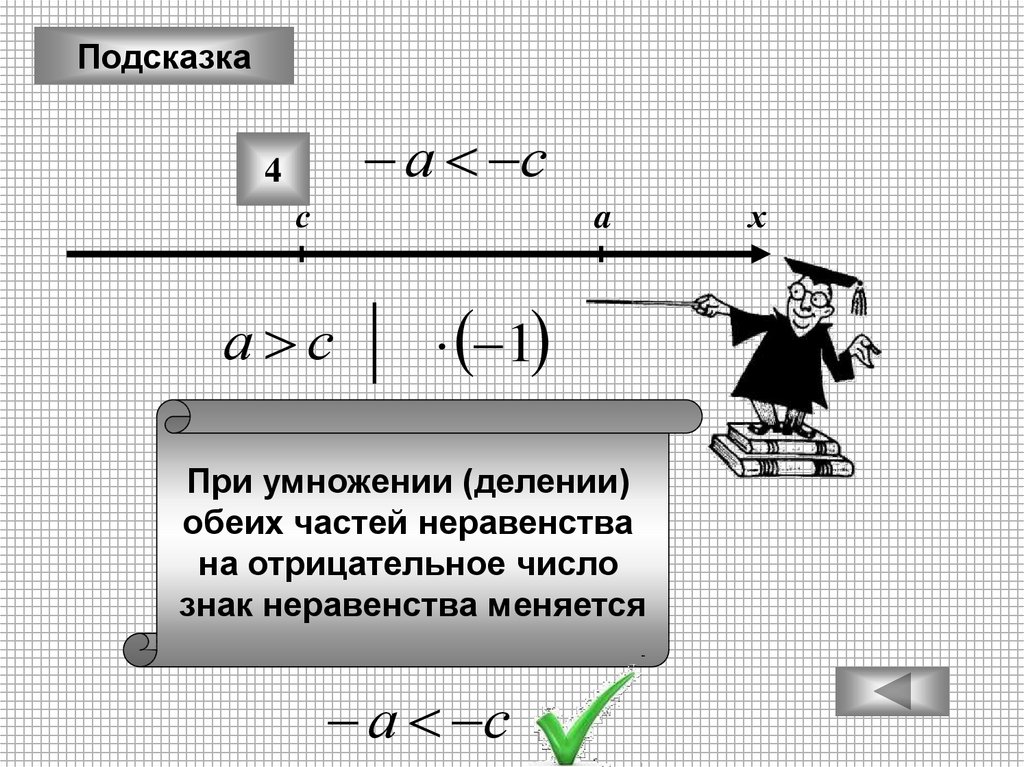 Таким образом, вы можете решить эту проблему, проделав одно и то же с обеими сторонами неравенства. Начиная с , вы можете:
Таким образом, вы можете решить эту проблему, проделав одно и то же с обеими сторонами неравенства. Начиная с , вы можете: Если вы вычтете 6 из обеих сторон, вы получите:
Если вы вычтете 6 из обеих сторон, вы получите: В этой задаче вам не нужно делать этот шаг.
В этой задаче вам не нужно делать этот шаг. Здесь это означает, что если вы сделаете (логический) первый шаг деления обеих частей на , вам нужно изменить знак неравенства с больше на меньше, чтобы получить:
Здесь это означает, что если вы сделаете (логический) первый шаг деления обеих частей на , вам нужно изменить знак неравенства с больше на меньше, чтобы получить: Если вы умножаете или делите на отрицательное число, вы должны изменить знак неравенства. Этой ситуации (как вы увидите здесь) обычно легко избежать.
Если вы умножаете или делите на отрицательное число, вы должны изменить знак неравенства. Этой ситуации (как вы увидите здесь) обычно легко избежать. Когда мы умножаем или делим на отрицательное число, мы должны перевернуть знак неравенства, поскольку мы в основном «переворачиваем» отношение над 0 на числовой прямой. (Число, которое больше, когда оно положительное, становится «более отрицательным» и, следовательно, меньше, когда оно отрицательное, и наоборот).
Когда мы умножаем или делим на отрицательное число, мы должны перевернуть знак неравенства, поскольку мы в основном «переворачиваем» отношение над 0 на числовой прямой. (Число, которое больше, когда оно положительное, становится «более отрицательным» и, следовательно, меньше, когда оно отрицательное, и наоборот).
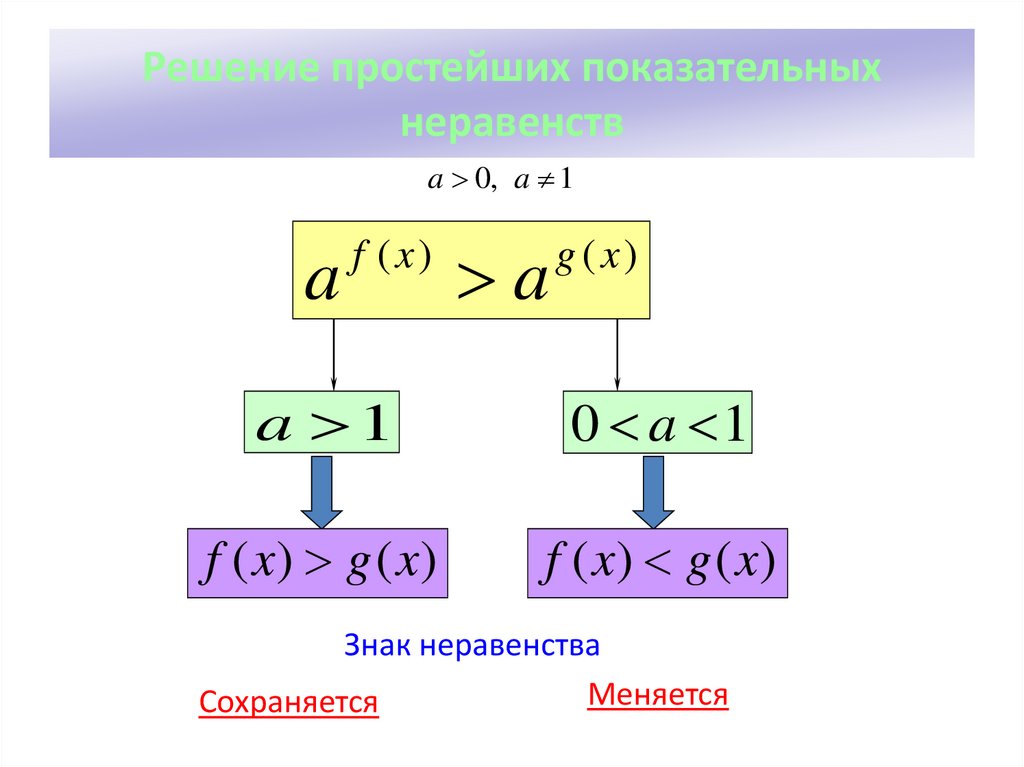 Для этого отнимите 6 с обеих сторон.
Для этого отнимите 6 с обеих сторон.

 49
49
_hrom_images/lekciya_15_(himiya)_hrom_2.jpg)
 Он достаточно ломкий, но при этом имеет несравненный плюс по сравнению со многими другими металлами – устойчивость к заражению коррозией; именно поэтому он является важным компонентом при производстве нержавеющей стали, а также используется для нанесения на поверхность других металлов, более склонных к коррозии. Хром обладает плохой тепло- и электропроводностью.
Он достаточно ломкий, но при этом имеет несравненный плюс по сравнению со многими другими металлами – устойчивость к заражению коррозией; именно поэтому он является важным компонентом при производстве нержавеющей стали, а также используется для нанесения на поверхность других металлов, более склонных к коррозии. Хром обладает плохой тепло- и электропроводностью. Если раскалить Cr, то способен вступить в реакцию с водяными парами.
Если раскалить Cr, то способен вступить в реакцию с водяными парами.
 Мысленно отделяем последний элемент (с уже определённой степенью окисления) от двух других элементов. Нам требуется, чтобы СО двух первых и последнего элементов в сумме была равна нулю.
Мысленно отделяем последний элемент (с уже определённой степенью окисления) от двух других элементов. Нам требуется, чтобы СО двух первых и последнего элементов в сумме была равна нулю.



 1993; Мерц, 1993].
1993; Мерц, 1993]. Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности.
Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности. Термодинамически наиболее стабильными состояниями являются +3 и +2, тогда как степени окисления +3 и +6 наиболее распространены в водном растворе. Кинетически хром +3 инертен замещению: для водообмена k(сек-1) = 2,5 х 10(-6) из-за наличия полузаполненного состояния d(t2g)3,4A2g. С другой стороны, протонирование/депротонирование происходит довольно быстро. Полимеризация протекает очень медленно, но ускоряется при более высоких значениях pH; кислотное расщепление протонированных олигомеров также происходит довольно медленно. Хром +6 как ион хромата сильно окисляется при низких значениях pH и в меньшей степени в щелочном растворе. Ион хромата действительно образует некоторые поликислоты и полианионы. Эти факторы необходимо учитывать при анализе образцов на содержание общего хрома и количество каждой степени окисления.
Термодинамически наиболее стабильными состояниями являются +3 и +2, тогда как степени окисления +3 и +6 наиболее распространены в водном растворе. Кинетически хром +3 инертен замещению: для водообмена k(сек-1) = 2,5 х 10(-6) из-за наличия полузаполненного состояния d(t2g)3,4A2g. С другой стороны, протонирование/депротонирование происходит довольно быстро. Полимеризация протекает очень медленно, но ускоряется при более высоких значениях pH; кислотное расщепление протонированных олигомеров также происходит довольно медленно. Хром +6 как ион хромата сильно окисляется при низких значениях pH и в меньшей степени в щелочном растворе. Ион хромата действительно образует некоторые поликислоты и полианионы. Эти факторы необходимо учитывать при анализе образцов на содержание общего хрома и количество каждой степени окисления.
 В. Ященко, 2020. Вариант 8, задача 15
В. Ященко, 2020. Вариант 8, задача 15 Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?
Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили? Лучше всего оформлять решение неравенства именно так.
Лучше всего оформлять решение неравенства именно так. Такое, что не решается обычными способами.
Такое, что не решается обычными способами.


 в математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Возьмем новое понятие — дискриминант. Вспомните слово «дискриминация». Что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отношение к различным людям. Оба слова (и дискриминант, и дискриминация) происходят от латинского discriminans — «различающий». Дискриминант различает квадратные уравнения по числу корней.
в математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Возьмем новое понятие — дискриминант. Вспомните слово «дискриминация». Что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отношение к различным людям. Оба слова (и дискриминант, и дискриминация) происходят от латинского discriminans — «различающий». Дискриминант различает квадратные уравнения по числу корней. 9 класс — презентация онлайн
9 класс — презентация онлайн
 ах² + bх + с = 0,
ах² + bх + с = 0, В любом квадратном уравнении есть два значения переменной.
В любом квадратном уравнении есть два значения переменной.
 Опять же, два линейных фактора также решаются, чтобы получить решение уравнения. корни, полученные из уравнения, должны удовлетворять заданному квадратному уравнению. 92-4ac}}{2a}\) и найти два корня данного квадратного уравнения.
Опять же, два линейных фактора также решаются, чтобы получить решение уравнения. корни, полученные из уравнения, должны удовлетворять заданному квадратному уравнению. 92-4ac}}{2a}\) и найти два корня данного квадратного уравнения.
 H.S. = x 2 — 8x + 12
H.S. = x 2 — 8x + 12 H.S. = х 2 — 8х + 12
H.S. = х 2 — 8х + 12 Х.С. = x 2 — 5x + 6
Х.С. = x 2 — 5x + 6 ……………(i)
……………(i) H.S. x = 3x 2 — 5x — 2
H.S. x = 3x 2 — 5x — 2
 H .S доказано, что верно
H .S доказано, что верно С. доказано, что верно
С. доказано, что верно ………..(i)
………..(i) IF.C.8.A
— Используйте процесс факторизации и завершения квадрата квадратичной функции, чтобы показать нули, экстремальные значения и симметрию графика, и интерпретируйте их с точки зрения контекста.
IF.C.8.A
— Используйте процесс факторизации и завершения квадрата квадратичной функции, чтобы показать нули, экстремальные значения и симметрию графика, и интерпретируйте их с точки зрения контекста. 


 Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. е. 1,45 .
е. 1,45 . Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
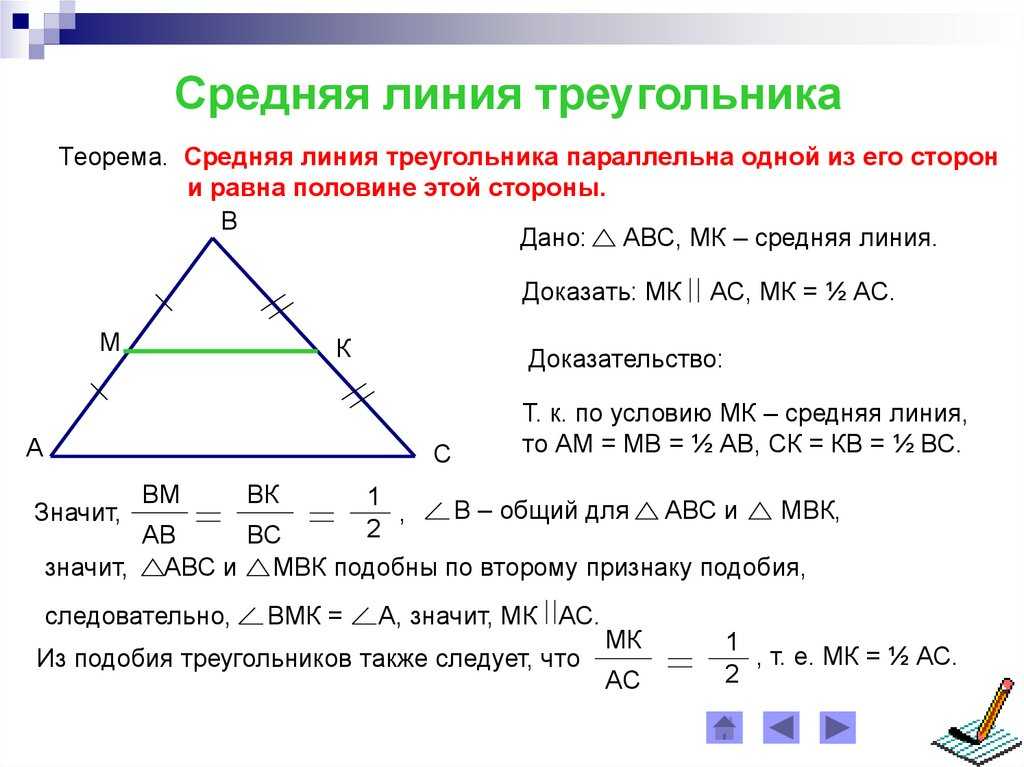
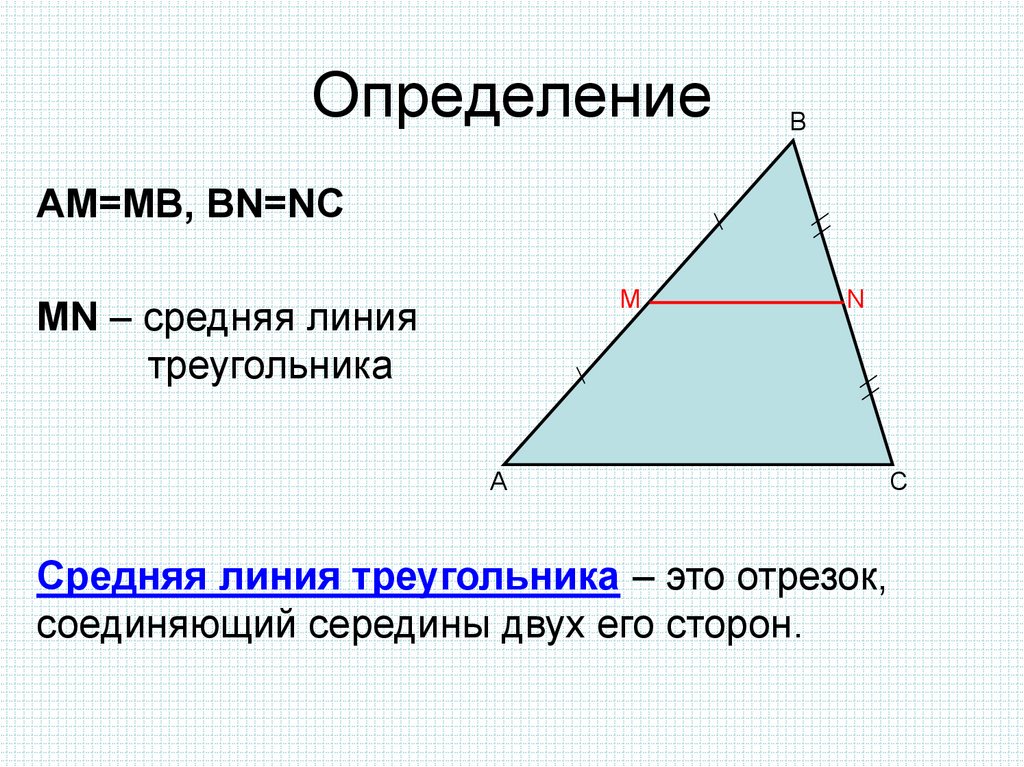
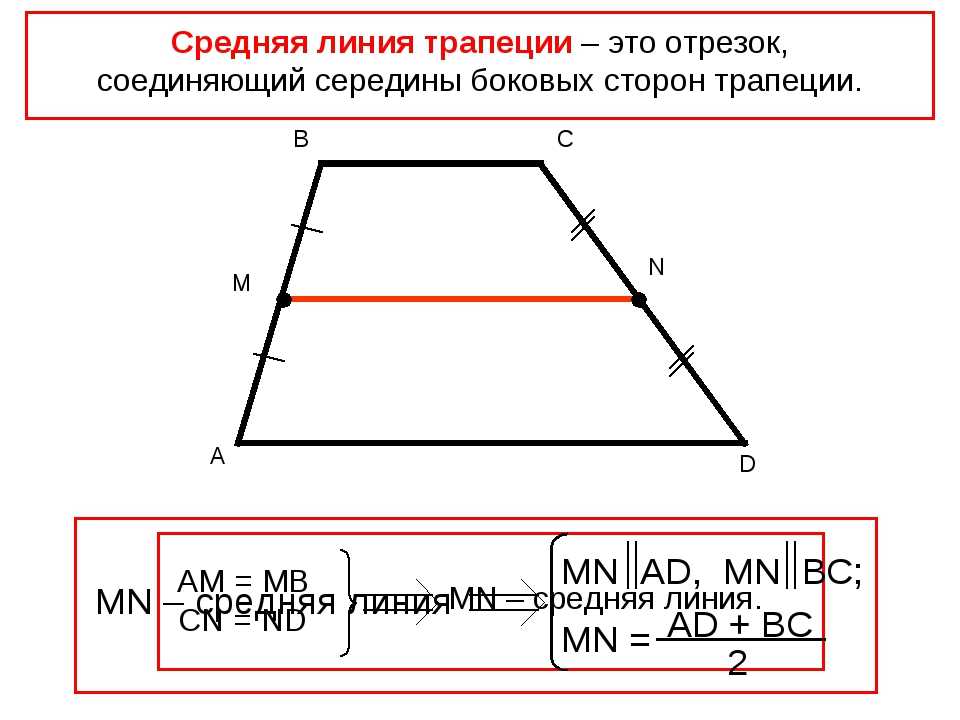
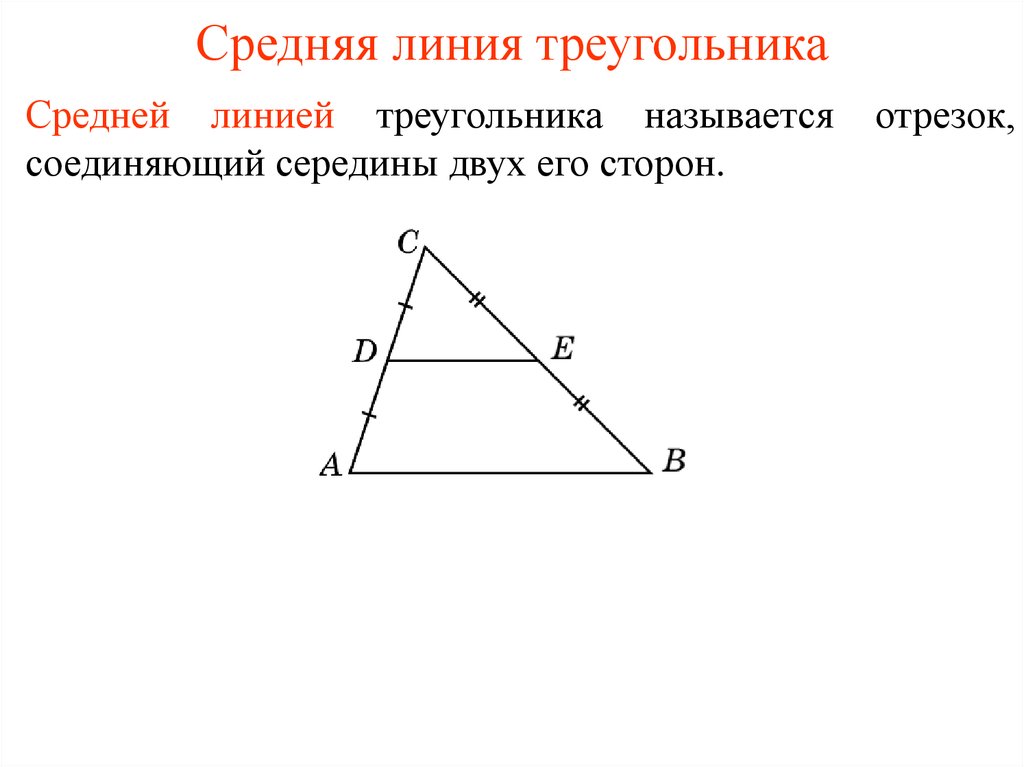
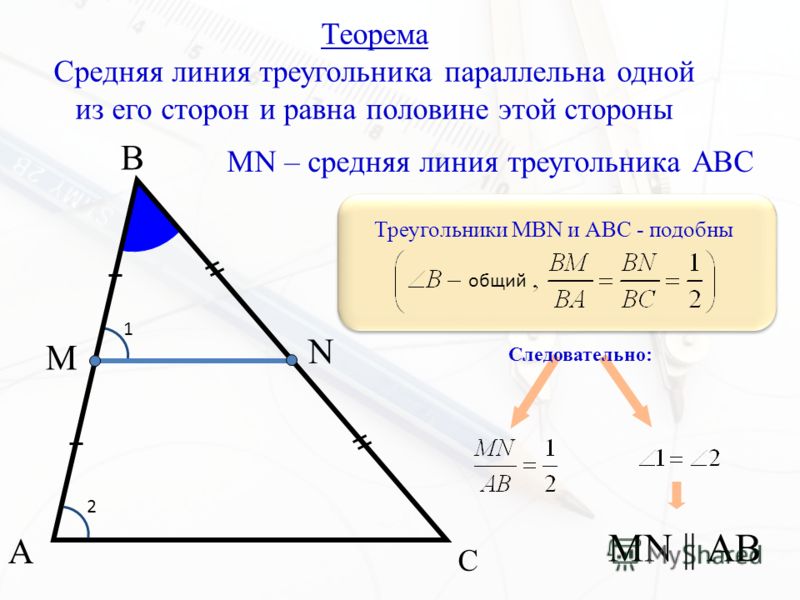 В любом треугольнике можно провести три средних линии.
В любом треугольнике можно провести три средних линии.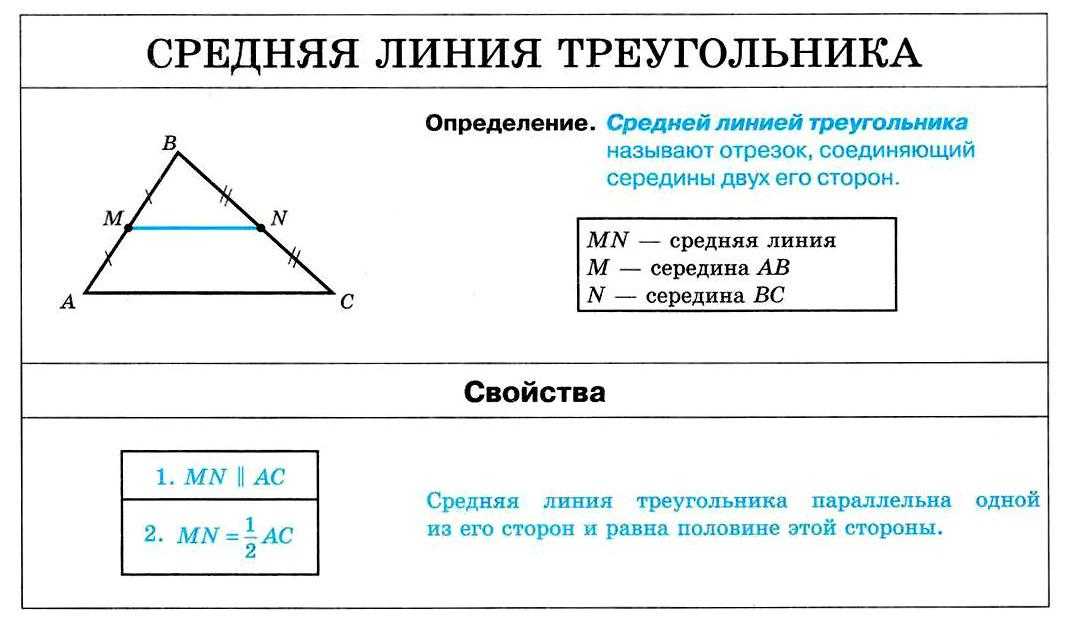
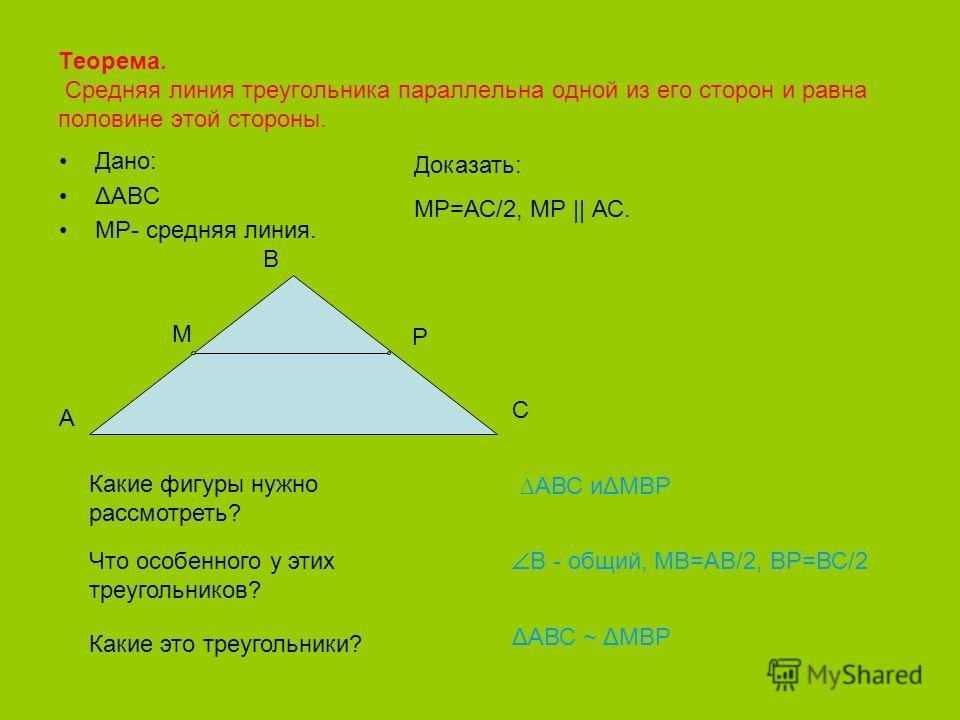
 Значит, доказано, что средняя линия равна половине основания.
Значит, доказано, что средняя линия равна половине основания. Найти площадь большого прямоугольного треугольника.
Найти площадь большого прямоугольного треугольника.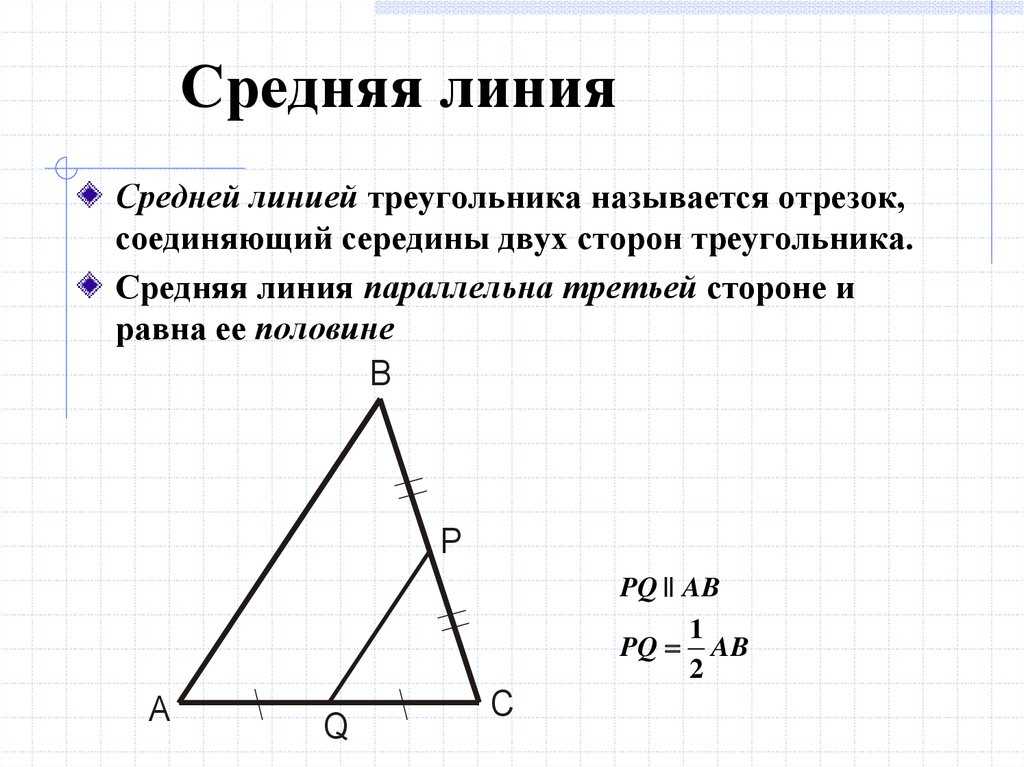
 Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была на блоге статья, в которой сии факты я предлагал просто запомнить, теперь подробнее…
Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была на блоге статья, в которой сии факты я предлагал просто запомнить, теперь подробнее…
 Поскольку мы знаем длины сторон, мы знаем, что точка C , середина стороны AS , точно равна 12 см с любого конца. Точка R на AH точно равна 18 см с любого конца.
Поскольку мы знаем длины сторон, мы знаем, что точка C , середина стороны AS , точно равна 12 см с любого конца. Точка R на AH точно равна 18 см с любого конца.

 Сторона 9{2}482,5 дюйма2.
Сторона 9{2}482,5 дюйма2. Шаги просты, а результаты визуально приятны:
Шаги просты, а результаты визуально приятны: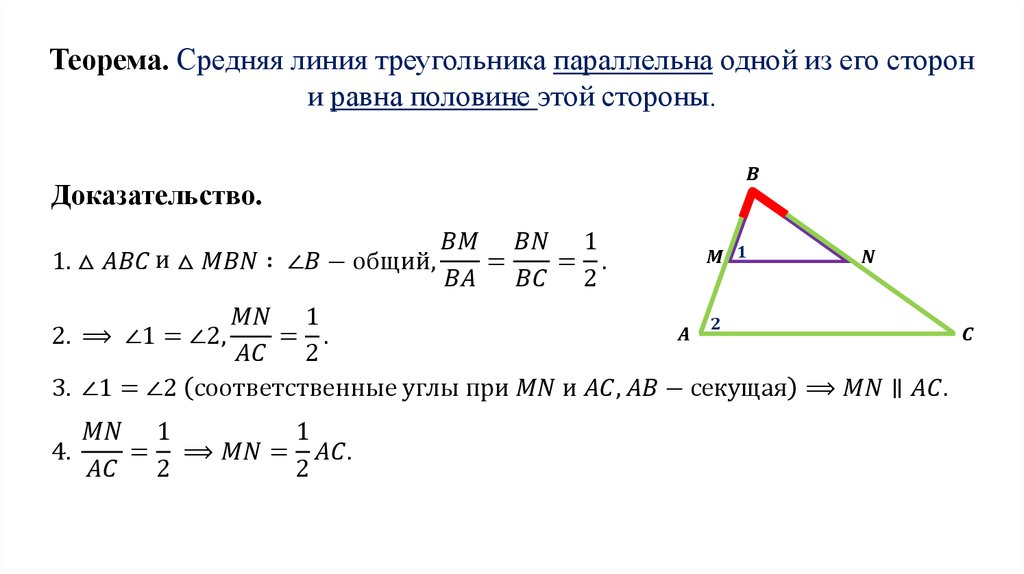 Даже если это не так, вы все равно найдете этот инструмент полезным.
Даже если это не так, вы все равно найдете этот инструмент полезным.