Архивы Калькулятор онлайн — РадиоСхема
Просмотр архива тегов
Alex
Подмножество конечного множества <<< Все Калькуляторы Подмно́жество в теории множеств — это понятие части множества. Определение Множество называется подмножеством множества , если все элементы, принадлежащие , также…
Alex
Пересечение множеств чисел <<< Все Калькуляторы Пересечение и Пересече́ние мно́жеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем…
Alex
Перенос слагаемых в уравнении <<< Все Калькуляторы
Alex
Найти объединение множеств
<<< Все Калькуляторы
Объедине́ние мно́жеств в теории множеств — множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств и обычно обозначается ∪ , но иногда можно…
Объединение двух множеств и обычно обозначается ∪ , но иногда можно…
Alex
Вычисление Неравенство Бернулли <<< Все Калькуляторы Нера́венство Берну́лли утверждает: если , то для всех Доказательство Доказательство неравенства проводится методом математической индукции по n. При n = 1…
Alex
Метод наименьших квадратов онлайн <<< Все Калькуляторы Метод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от…
Alex
Логарифм и Антилогарифм
<<< Все Калькуляторы
Логари́фм числа по основанию — определяется как показатель степени, в которую надо возвести основание , чтобы получить число . Обозначение: , произносится: «логарифм по…
Обозначение: , произносится: «логарифм по…
Alex
Решение кубических уравнений онлайн <<< Все Калькуляторы Куби́ческое уравне́ние — алгебраическое уравнение третьей степени, общий вид которого следующий: Для графического анализа кубического уравнения в декартовой…
Alex
Количество подмножеств в множестве <<< Все Калькуляторы
Alex
Калькулятор квадратных уравнений
<<< Все Калькуляторы
Квадра́тное уравне́ние — алгебраическое уравнение общего вида
где — неизвестное, , , — коэффициенты, причём
Выражение называют квадратным трёхчленом. …
…
Арксеканс онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор вычислит арксинус, арккосинус, арктангенс, арккотангенс, арксеканс и арккосеканс и определит значение угла как в градусной, так и в радианной мере.

Введите число
арксинус (arcsin)арккосинус (arccos)арктангенс (arctg)арккотангенс (arcctg)арксеканс (arcsec)арккосеканс (arccosec)
Что такое арксеканс угла
Арксекансом (arcsec x) числа x, является угол α заданный в радианной мере, такой, что sec α = x.
Вычислить арксеканс, означает найти угол α, секанс которого равен числу x.
Область значений (определяющее неравенства угла α в радианной и градусной мерах):
0 ≤ α α ≤ π
0° ≤ α α ≤ 180°
Область определения (определяющее неравенство числа x):
1 ≤ x ≤ −1
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
| Рабочий лист радикальных дробей | Glencoe/McGraw-Hill Algebra 2 Assessment | ПРАКТИКА КВАДРАТНЫХ КОРНЕЙ |
бесплатно загружаемый инструмент алгебры | пример бесплатных задач по математике для 7 класса | решение уравнений с переменными листы |
калькулятор матриц онлайн | Программное обеспечение по алгебре решает шаг за шагом | длинное алгебраическое уравнение |
ответов на рабочие листы Гленко Макгроу | «все формулы алгебры» | 8-й класс по естественным наукам, 4 квадрата, рабочий лист |
бесплатная саксонская математическая алгебра 1 ответы | уравнения балансировки онлайн | онлайн-график с поиском точки пересечения линии |
реальных примеров эллипсов | Калькулятор кубической факторизации | BBC переставляет формулы |
сделать синтетическое деление на TI 83 плюс | Elementary Linear Algebra 9th Edition Solutions Manual +скачать | перестановка и комбинация |
решение абстрактной алгебры Фрели | как найти кубический корень по формуле TI 89 | вопросов о способностях с ответами |
Распечатка 12-дюймовой линейки | добавление алгебраических уравнений | стихов о тригонометрии |
Бумага по математике для 8 класса | сурд рабочий лист | нахождение корня уравнения с помощью Matlab + метод деления пополам |
«Креативный дизайн программного обеспечения» TI-89 | Калькулятор алгебры, решающий задачи | Разделение мономов рабочий лист |
ти89 фактор | Калькулятор дифференциальных уравнений второго порядка | печатные листы по математике для третьего класса |
«Алгебра 2» pdf | Java-программа для нахождения кубического корня из числа | онлайн-помощь по математике |
перевести смешанную дробь в десятичную | вопросов по математике для VIII класса | оценить по алгебре |
Как использовать расчет cos на TI-83 | бесплатных саксонских тестов по математике для печати | «онлайн-тест CLEP» колледж |
обратная функция квадратного уравнения | Платон чит по основам математики в Интернете | Формула для масштабного коэффициента |
найти нули полиномиального уравнения | план урока по длинному делению для 2 класса | почему нам не нужен общий знаменатель для умножения и деления |
| Рабочий лист уравнений дроби | алгебраические плитки для теста по математике штата Нью-Йорк | Калькулятор неправильных интегралов |
ti графический онлайн калькулятор java | english ks2 документы для печати | как упорядочить дроби от наименьшей к наибольшей |
ks3+линейные уравнения и простые квадратные уравнения | онлайн факторинг | отрицательный и положительный математический калькулятор |
Тест по математике для 8-го класса штата Нью-Йорк | математический лист с формулами из 8 кругов | формула наибольшего общего делителя |
калькулятор ти-83, счетверенное уравнение с функциями | Physics+James S Walker+ решения торрент | забавных способов разделить смешанные дроби |
алгебраический решатель или помощник | бесплатная помощь по алгебре для 9 класса | Математические стихи — Площадь и объем |
Алгебра Решатель | алгебра, задачи | математические мелочи |
получить ответы на действия над подкоренными выражениями | оценка выражений печатные листы | решение текстовых задач по квадратным уравнениям, рабочий лист |
листов разложения | показателей степени в алгебраических выражениях | наклон матлаб |
метод подстановки в алгебре | математические мелочи по тригонометрии | математика ks3 рабочий лист |
пример квадратного уравнения путем извлечения квадратного корня | ответы a+plus по алгебре 2 | умножение матриц практика алгебра 1 |
| Рабочий лист часов , напишите дробь | 7 класс Алгебра квадратные корни | Предварительная алгебра для учеников холла |
10-й стандартный бесплатный онлайн-тест по математике | ti 89 кубический корень | Калькуляторы деления многочленов |
бесплатных печатных задач по алгебре для 6-х классов | контрольные работы по математике для 8 класса | Калькулятор уравнений балансировки |
решение системы вкладышей | Калькулятор уравнений Casio | математика учит меня координатам год 9 сат |
математических мошеннических сайтов | уравнений по алгебре для 4 класса | алгебра 2 и перестановки |
умножение на 8 листов | Алгебра в колледже для чайников | калькулятор числа миксов онлайн |
алгебраические упрощения степени | переменных рабочих листов 5 класс | обучающие математические коэффициенты для чайников |
математические мелочи 3 класс | как умножать выражения и похожие термины | алгебраический решатель скачать бесплатно |
математические мелочи элементарные | деление, упрощение алгебры квадратных корней | словесные проблемы с отсутствующими листами переменных |
упрощение алгебраических выражений | классная математика 4 детей. | рабочая тетрадь Glencoe для предварительной алгебры |
Бесплатно загружаемые рабочие листы порядка действий для семиклассников | налоговые листы | что вы знаете о квадратных уравнениях и функциях |
Калькулятор наименьшего общего кратного | вычислений | Презентация Power Point урока математики «Круги» для пятого класса |
Мастерство Математика Алгебра Рабочие листы | Предварительный тест по алгебре для 5-го класса Ирвин | Заполнение рабочего листа Square+ |
рабочие листы по математике для пятого класса | второй заказ ODE45 | алгебра 1 практическая рабочая тетрадь ответы |
помощник по математическому анализу | алгебра 1+ответы | алгебра решить |
Бесплатное решение математических задач | ks3 научные бесплатные документы | в ти-89 как найти корень уравнения |
| Рабочий лист для преобразования десятичных дробей в дроби | интерактивные полиномиальные игры факторинга | математический аппарат ревизия год9 |
Предварительное тестирование Glenco PreAlgebra | смешанное число как десятичное | линейных неравенств онлайн |
бесплатный калькулятор задач по алгебре II | легкая алгебра упрощение | умножение одночленов и многочленов в PowerPoint |
конвертировать html в электронную книгу ti 89 | Как мы используем радикальные выражения в реальной жизни? | как вы делаете деление в десятых долях |
сложение, вычитание, умножение и деление бесплатных игр | математика в колледже для чайников | ОБРАЗЦЫ ТЕСТА ПО МАТЕМАТИКЕ ДЛЯ 3-ГО КЛАССА ДЛЯ NYS TEST |
решение задач перестановки и комбинации | ks3 решение математических уравнений балансировки | Графический онлайн-калькулятор texas tools |
заполните квадрат как до 10 года | вычислитель по правилу Крамера TI-85 | бесплатных рабочих листов для 3-х классов по геометрии |
бесплатных рабочих листов по алгебре для пятого класса | разложение суммы в кубе | Печатные рабочие листы с домашними заданиями для 3 класса |
мелочи о математике | ти-89 факториал | математические мелочи со своими ответами |
Уравнение Коши-Эйлера ti89 | графический калькулятор параболы | Рабочий лист по математике с ответами |
Решение квадратных корней | «уравнение с двумя переменными» | продвинутая алгебра 2 проверка математики |
Рабочий лист по геометрии 6 класс | онлайн-конструктор графиков с предварительным расчетом | простые таблицы алгебры |
ответ на рабочие листы Glencoe/Mcgraw Hill | калькулятор метода исключения | бесплатных математических тестов ks3 |
виртуальный 6 класс алгебра | наименее распространенный многократный калькулятор | ПРЕЗЕНТАЦИИ POWERPOINT ДЛЯ РЕШЕНИЯ ЗАДАЧ ПО МАТЕМАТИКЕ В ТРЕТЬЕМ КЛАССЕ |
алгебра разложения квадратных корней | бесплатный онлайн-решатель задач с предварительным исчислением | обзор элементарной алгебры |
Выразите радикал в упрощенной форме квадратный корень из 180 | алгебра и тригонометрия: функции и приложения ответы | упрощающий подсчет радикалов |
МакДугал Литтел TAKS практика | решать неоднородные уравнения | 12. |
математических мелочей о графиках | Онлайн калькулятор от наименьшей до наибольшей | «Вступительный тест по алгебре» |
тригонометрия 5-е издание домашнее задание ответы | матрицы второй степени | пример приложения с использованием матриц/предварительного исчисления |
Практические статистические задачи | образец экзамена по алгебре | бесплатный онлайн калькулятор алгебры |
Алгебратор | решать сложение и вычитание дробей | матлаб + палиндром |
бесплатные распечатки для занятий в третьем классе | Бесплатные математические задачи по алгебре | упростить дроби matlab |
решение квадратных уравнений в стандартной форме | Пробные тесты для 6-го класса, штат Нью-Джерси | СОВЕТЫ ПО РЕШЕНИЮ ТРИГОНОМЕТРИИ ДЕСЯТОГО КЛАССА |
Алгебра Гленко 1 Книга | математика gmat практика | бесплатная копия книги McDougal Littell Book 3 для 8-го класса онлайн |
«Корни на ТИ-83» | перестановок для 3-х классов | алгебра KS3 отрицательные числа неизвестные рабочие листы |
как использовать синтетическое деление на TI-84 plus | метод наименьших квадратов ti-89 | образец IQ тест шестой класс |
что такое погонный метр | ТИ-84 бесплатный онлайн калькулятор | программ базовой алгебры бесплатно |
www. | разложение полиномов третьего порядка на множители | мелочи по математической тригонометрии |
Алгебра с умными ответами | алгебраические правила сложения минусов с вычитанием | TAKS Практика по математике для 6-го класса |
рабочий лист град/2 математика | листов «Таблица функций» 8 класс | как построить график для y = 2x-1 |
функции уравнения, уроки 7 класс, бесплатно | рудин ч 8 раствор | коэффициент разности двух идеальных квадратов |
Бесплатный онлайн математический калькулятор деление | Математические крестики-нолики факторинг | научи мою 8-летнюю математику бесплатно онлайн |
исследовательских проектов по математике | SAT математические задачи на коэффициенты и оценки | математика алгебра онлайн |
решить одновременное уравнение на ti 84 | решение для переменной в функции журнала | корней функции второго порядка matlab |
уравнение теплопроводности, цилиндрическое, неоднородное | бесплатных рабочих листов, образец теста на конец класса | полная книга способностей в pdf |
творческих задач по алгебре | clep алгебра примеры | индуистская алгебра |
Решение уравнений, рабочий лист 8 класс | Таблица эквивалентных дробей | рабочие листы «вычитание целых чисел» |
полиграфическая бумага | покажи мне бесплатные математические примеры для девятого класса онлайн | Алгебра Макдугала Литтелла 1 интегрированный курс Copyright 1998 |
Excel математические распечатки | Формула процентов | Математические читы |
Вероятность/комбинации 5 класс | БЫСТРЫЕ БЕСПЛАТНЫЕ ОТВЕТЫ НА ДОМАШНЕЕ ЗАДАНИЕ ПО АЛГЕБРЕ | ответов на Алгебра 2 Макдугал Литтел |
Бесплатный образец бумаги по математике для 5-го класса | сложение знаменателей алгебра | читы по математике prentice hall |
игры с упрощением алгебраических выражений | инструмент наименьшего общего знаменателя | бесплатных рабочих листов для 8-го класса |
Наших пользователей: Ваша программа спасла мою оценку в этом семестре. Это было очень полезно. Математика не может быть проще с Algebrator. Спасибо! Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?Поисковые фразы, использованные 30.10.2010:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Уравнения и неравенства, содержащие переменную под знаком модуля
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
• СОДЕРЖАНИЕ
Понятие
модуля
Уравнения,
содержащие
переменную
под знаком модуля
Неравенства,
содержащие
переменную
под знаком модуля
3. Понятие модуля
Модулем числа а называется расстояние от началаотсчета до точки с координатой а
а|
|
Например:
|-7|=7
-7
Таким образом:
х
а
0
|
7 | =7
0
а, если а 0,
а
а, если а 0
х
7
оглавление
4.
 Уравнения.содержащие переменную под знаком модуля
Уравнения.содержащие переменную под знаком модуля| f(x) | = a
| f(x) | = |g(x) |
| f(x) | = g(x)
| f(x) | + | g(x) | = h(x)
5. Уравнение вида | f(x) | = a
Если а < 0, то уравнение решений не имеет
Если а = 0, то f(x) = 0
Если а > 0, то f(x) = а или f(x) = — а
Пример:
Решить уравнение: | 2х – 5 | = 13
Решение: 2х – 5 = 13 или 2х – 5 = — 13
2х = 13 + 5
2х = — 13 + 5
2х = 18
х =9
2х = — 8
х = -4
Ответ: х = 9 , х = — 4
Задачи для самостоятельного решения
оглавление
другой вид
6. Уравнение вида | f(x) | = a
Решите уравнение• 1) | 2х — 3| = 7
Ответ
• 2) .|х2 – х — 5| = 1 Ответ
• 3) | |х| — 2 |= 2
Ответ
оглавление
другой вид
• Ответ: х = 5, х = — 2
• Показать решение
назад
• Ответ: x = — 2, x = 3
• Показать решение
х
1
назад
17
2
• Ответ: x= 4, x= — 4 , x = 0
• Показать решение
назад
РЕШЕНИЕ:
| 2х – 3 | = 7
2х – 3 = 7 или
2х = 7 + 3 или
2х = 10 или
х = 5 или
2х – 3 = — 7
2х = — 7 + 3
2х = — 4
х =- 2
назад
РЕШЕНИЕ:
| х2 – х — 5 | = 1
х2 – х — 5 = 1 или
х2 – х — 6 = 0
D = 25
x1 = — 2, x2 = 3
х2 – х — 5 = -1
х2 – х — 4 = 0
D = 17
1 17
х1, 2
2
назад
РЕШЕНИЕ:
| |x| -2 | = 2
|x| -2 = 2
или |x| -2 = — 2
|x| = 2+ 2
|x| = — 2 +2
|x| = 4
|x| = 0
x = 4 или х = — 4
x = 0
назад
13.
 Уравнение вида | f(x) | = g(x)• 1) определить условие, при котором уравнение имеет решение:
Уравнение вида | f(x) | = g(x)• 1) определить условие, при котором уравнение имеет решение:g(x) ≥ 0
• 2) f(x) = g(x) или f(x) = — g(x)
• 3) Решить уравнения и выбрать корни, удовлетворяющие
условиюg(x) ≥ 0
• Пример: Решить уравнение:| х + 2| = 2( 3 – х)
• Определим при каких значениях х уравнение имеет решение
2( 3 – х) ≥ 0 => х ≤ 3
• Распишем данное уравнение на два:
х + 2 = 2( 3 – х) или х + 2 = — 2( 3 – х)
х = 4/3
х = 8 не удовлетворяет условию х ≤ 3
• Ответ: х = 4/3
Задачи для самостоятельного
решения
другой вид
Уравнение вида | f(x) | = g(x)
Решите уравнения
1) |5х + 2| = 3 – 3х
2) |х2 — 2х| = 3 — 2х
Ответ:
Ответ
другой вид
• Ответ: х = 1/8, х = — 2,5
• Показать решение
назад
• Ответ: х = 3 , х = 1
• Показать решение
назад
РЕШЕНИЕ:
• |5х + 2| = 3 – 3х
• Определим при каких значениях х уравнение
имеет решение: 3 – 3х ≥ 0 => х ≤ 1
• Распишем данное уравнение на два:
• 5х + 2 = 3 – 3х или 5х + 2 = — (3 – 3х)
• 5х + 3х = 3 – 2
5х — 3х = — 3 – 2
• 8х = 1
2х = — 5
• х = 1/8
х = — 2,5
• Оба корня удовлетворяют условию х ≤ 1
назад
РЕШЕНИЕ:
• |х2 -2 х| = 3 — 2х
• Определим при каких значениях х уравнение имеет
решение: 3 — 2х ≥ 0 => х ≤ 1,5
• Распишем данное уравнение на два:
• х2 –2 х =3 — 2х
или
х2 – 2х = — (3 — 2х )
• х2 = 3
х2 – 4х +3 = 0
• х= 3
х1 = 1 х2 = 3
Корни 3 и 3 не удовлетворяют условию х ≤ 1,5
Ответ: х = 3 х = 1
назад
19.
 Уравнение вида | f(x) | = | g(x)|
Уравнение вида | f(x) | = | g(x)|1способ: f(x) = g(x) или f(x) = — g(x)
2способ: возвести обе части уравнения в квадрат
Пример Решить уравнение: |х + 2| = |2х — 6|
1 способ: х + 2 = 2х – 6 или х + 2 = — (2х – 6)
х = 8
3х = 4
х = 4/3
2 способ: (|х + 2|)2 = (|2х — 6|)2 Воспользуемся свойством |а|2=а2
(х + 2)2 = (2х — 6)2
3х2 – 28х + 32 = 0 => х = 8, х = 4/3
Задачи для самостоятельного
решения
другой вид
Уравнение вида | f(x) | = |g(x)|
Решите уравнения
1) |х2 + х — 2| = |х +2|
2) |3 + х |= |х|
Ответ:
Ответ
другой вид
• Ответ: х = -2, х = 0, х = 2
• Показать решение
назад
• Ответ: х = -1,5
• Показать решение
назад
• РЕШЕНИЕ
|х2 + х — 2| = |х +2|
х2 + х — 2 = х +2 или х2 + х — 2 = — (х +2)
х2 = 4
х2 + 2х = 0
х = 2, х = — 2
х(х + 2) = 0
х = 0 х = -2
Ответ: х = -2, х = 0, х = 2
назад
• РЕШЕНИЕ
|3 + х| = |х|
3+х =х
или
3= 0
решений нет
Ответ: х = -1,5
назад
3+х =-х
2х = -3
х = -1,5
25.
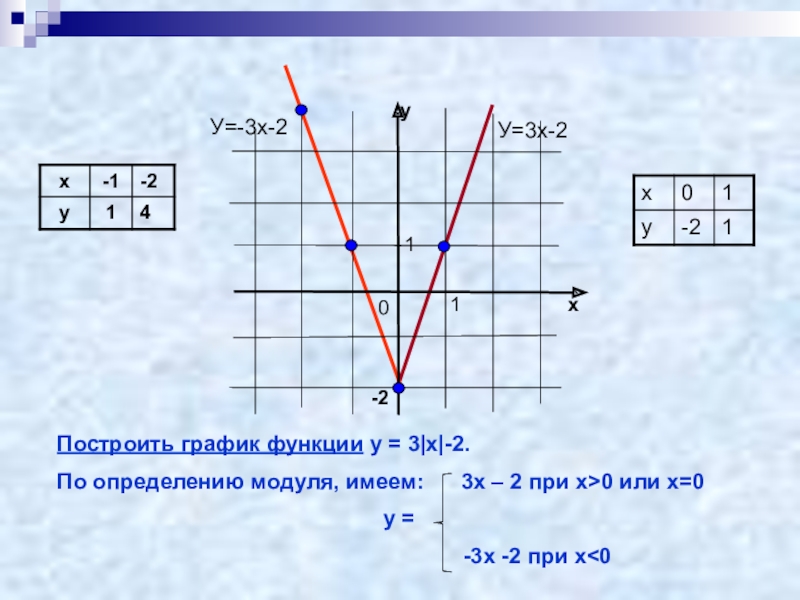 Уравнение вида | f(x) | + | g(x)| = h(x)• При решении уравнений данного вида используется
Уравнение вида | f(x) | + | g(x)| = h(x)• При решении уравнений данного вида используетсяправило раскрытия модуля.
• Пример: Решить уравнение:|х-3| + |2х-1| =8
1
• Найдем нули функций, стоящих под знаком модуля: х= 3, х= 2
• Отметим эти точки на числовой прямой и определим знаки функций на
получившихся промежутках
1
2
х 3
2х 1
3
Рассмотрим решение уравнения на каждом промежутке
1
х
2
1
х 3
2
Задачи для самостоятельного
решения
х 3
Ответ:
оглавление
26. Уравнение вида | f(x) | + | g(x)| = h(x)
• Пример: Решить уравнение: |х-3| + |2х-1| =8х
1
1 2
3
х 3
2х 1
2
Раскроем модули с учетом знака функций на этом промежутке
— ( х-3 ) – ( 2х-1 ) = 8
— 3х +4 = 8
4
удовлетворяет условию
х
3
х
1
2
назад
27. Уравнение вида | f(x) | + | g(x)| = h(x)
Пример: Решить уравнение:|х-3| + |2х-1| =81
2
3
х 3
2х 1
1
х 3
2
Раскроим модули с учетом знака функций на этом промежутке
— ( х-3 ) + ( 2х-1 ) = 8
х+2=8
х=6 не удовлетворяет условию 1 х 3
2
назад
28.
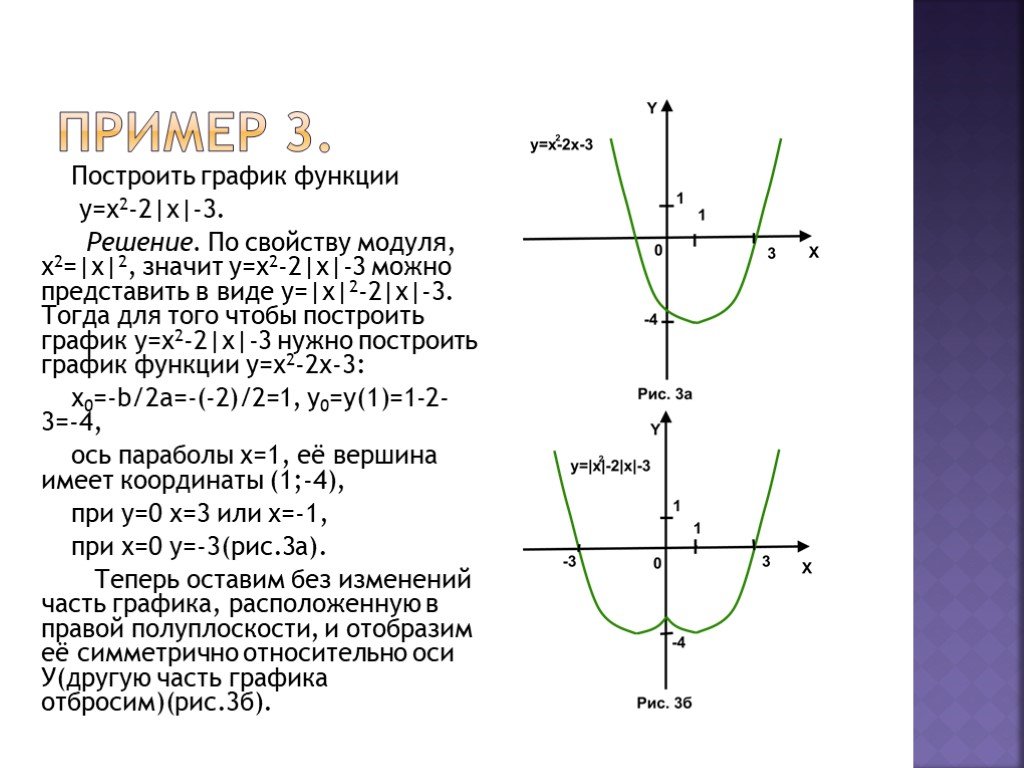 Уравнение вида | f(x) | + | g(x)| = h(x)Пример: Решить уравнение:|х-3| + |2х-1| =8
Уравнение вида | f(x) | + | g(x)| = h(x)Пример: Решить уравнение:|х-3| + |2х-1| =81
2
3
х 3
х 3
2х 1
• Раскроем модули с учетом знака функций на этом
промежутке
( х-3 ) + ( 2х-1 ) = 8
3х — 4 = 8
х=4 удовлетворяет условию х 3
назад
29. Уравнение вида | f(x) | + | g(x)| = h(x)
Объединим все ответы1
2
1
х
2
х
4
3
3
1
х 3
2
решений нет
Ответ: х
4
3
Задачи для самостоятельного
решения
х 3
2х 1
х 3
х 4
х 4
назад
30. Раскрытие модуля
а, если а 0,а
а, если а 0
• Решить уравнение: | 2х — 4| = х +6
Раскроем модуль.
Если 2х – 4 ≥ 0 , т. е. х ≥ 2,
то 2х – 4 = х +6
х = 10 – удовлетворяет условию х ≥ 2
Если 2х – 4 < 0, т. е. х < 2,
то -(2х – 4) = х +6
х = — 2/3 – удовлетворяет условию х < 2
Ответ: х = -2/3, х = 10
Второй способ
оформления
31. Раскрытие модуля
а, если а 0,а
а, если а 0
• Решить уравнение: | 2х — 4| = х +6
Раскроем модуль.

Найдем нули функции, стоящей внутри знака модуля
2х – 4 = 0 => х = 2
Отметим точку с координатой 2 на прямой.
—
2
+
Определим знаки функции на получившихся промежутках
Рассмотрим неравенство отдельно на каждом промежутке:
Если х < 2, то 2х – 4 < 0 => -(2х – 4) = х +6
х = — 2/3 – удовлетворяет условию х < 2
Если х ≥ 2, то 2х – 4 ≥ 0 => 2х – 4 = х +6
х = 10 – удовлетворяет условию х ≥ 2
Ответ: х = -2/3, х = 10
назад
32. Уравнение вида | f(x) | + | g(x)| = h(x)
Решите уравнения2 х 3 х 1 2х 1
3 х 3 х 5 2х
х 2 х 2 2х
Ответ:
Ответ:
Ответ:
оглавление
• Ответ:
x 2
2
3
х 4
• Показать решение
назад
• Ответ:
x 2
• Показать решение
назад
• Ответ:
x ;0
• Показать решение
назад
36. Уравнение вида | f(x) | + | g(x) | = h(x)
• Задача 1. Решить уравнение 2 х 3 х 1 2х 1Найдем нули функций (х-3) и (х+1) , отметим эти точки на числовой
прямой и определим знаки этих функций на получившихся
промежутках
+
х-3
х+1
+
3 +
-1
х 1
2 х 3 ( х 1) 2х 1
2 х 6 х 1 2 х 1
5х 6
6
х
5
не
удовлетворяет условию
х 1
1 х 3
2 х 3 ( х 1) 2х 1
2 x 6 х 1 2 х 1
3x 8
2
x 2
3
удовлетворяет условию
х 3
2 х 3 ( х 1) 2х 1
2 x 6 х 1 2 х 1
х 4
удовлетворяет условию
х 3
1 х 3
Ответ:
x 2
2
х 4
3
назад
37.
 Уравнение вида | f(x) | + | g(x) | = h(x)• Задача 1. Решить уравнение 3 х 3 х 5 2 х
Уравнение вида | f(x) | + | g(x) | = h(x)• Задача 1. Решить уравнение 3 х 3 х 5 2 хНайдем нули функций (3-х) и (х+5) , отметим эти точки на числовой
прямой и определим знаки этих функций на получившихся
промежутках
+
+
3-х
х+5
+
3 +
-5
х 5
5 х 3
3 х 3( х 5) 2х
3 х 3х 15 2х
18 0
3 х 3( х 5) 2х
3 x 3х 11 2х
6x 12
решений нет
x 2
удовлетворяет условию
х 3
3 х 3( х 5) 2х
3 x 3х 15 2х
х 9,5
не удовлетворяет условию
х 3
5 х 3
Ответ:
x 2
назад
38. Уравнение вида | f(x) | + | g(x) | = h(x)
• Задача 1. Решить уравнение х 2 х 2 2хНайдем нули функций (х-3) и (х+1) , отметим эти точки на числовой
прямой и определим знаки этих функций на получившихся
промежутках
+
х-2
х
+
2 +
0
х 0
х 2 х 2 2х
х 2 х 2 2х
2 2
верно при всех х
0 х 2
х 2 х 2 2х
x 2 х 2 2х
2x 0
с учетом условия
х 0
х ;0
x 0
удовлетворяет условию
0 х 2
Ответ:
х 2
х 2 х 2 2х
x 2 х 2 2х
х ;0
x 1
не удовлетворяет условию
х 2
назад
40.
 Неравенствасодержащие переменную под знаком модуля
Неравенствасодержащие переменную под знаком модуля|x| <a
| f(x) | < a
| f(x) | < |g(x) |
| f(x) | > |g(x) |
|x| >a
| f(x) | > a
| f(x) | + | g(x) | < h(x)
| f(x) | + | g(x) | > h(x)
41. Неравенства вида |x| < a
Неравенства вида |x| < a• Опираясь на понятие модуля:
|x| < a — это значит: расстояние от начала координат до точек,
удовлетворяющих данному условию должно быть меньше а.
На координатной прямой эти точки будут находиться правее нуля
до точки с координатой (а) и левее нуля до точки с координатой (а)
-а
х а; а
х
а
Пример: Решите неравенство |х| ≤ 6
Решение: Отметим на координатной прямой точки с координатами 6 и 6.
Решением будет множество точек, находящихся на отрезке 6;6
Ответ:
-6
6;6
6
Другой вид
х
42. Неравенства вида |x| > a
Неравенства вида |x| > aОпираясь на понятие модуля:
|x| > a — это значит: расстояние от начала координат до точек,
удовлетворяющих данному условию должно быть больше а.
На координатной прямой эти точки будут находиться правее с
координатой (а) и левее точки с координатой (-а)
-а
х
а
х ; а а;
Пример: Решите неравенство: | х| > 9
Решение: Отметим на координатной прямой точки с координатами
-9 и 9. Решением неравенства будет являться множество точек,
координаты которых меньше – 9 или больше 9
-9
Ответ : х ; 9 9;
9
х
Задачи для самостоятельного
решения
43. Решите неравенства
х 8Ответ : 8 х 8
х 3 8
Ответ : 11 х 11
х 2 16 Ответ : х 14 или х 14
13 2 х 5 Ответ : х 4 или х 4
x 2 16 0
Ответ : 4 х 4
Показать решение
75 3 x 2 0 Ответ : х 5 или х 5 Показать решение
ДРУГОЙ ВИД
44. Решение неравенства
x 2 16 0x 2 16
Извлекаем корень из обеих частей уравнения,
2
не забывая свойства : х х
х 4
-4
4
х
Ответ : 4 х 4
НАЗАД
45. Решение неравенства
75 3 x 2 03 x 2 75
x 2 25
Извлекаем корень из обеих частей уравнения,
не забывая свойства : х х
2
х 5
-5
5
х
Ответ : х 5 или х 5
Другой вид
46.
 Неравенства вида |f(x)| < aНеравенства вида |f(x)| < a
Неравенства вида |f(x)| < aНеравенства вида |f(x)| < a• Аналогично неравенству вида |x| < a , решением данного
неравенства будет являться множество точек, удовлетворяющих
условию — a < f(x) < a
Пример 1: Решите неравенство: | 2х — 3| ≤ 11
Решение: Это неравенство равносильно двойному неравенству
— 11 ≤ 2х — 3 ≤ 11
— 11 + 3 ≤ 2х ≤ 11 + 3
-8 ≤ 2х ≤14
-4 ≤ х ≤7
Ответ : х 4; 7
Другой вид
47. Неравенства вида |f(x)| > a
Неравенства вида |f(x)| > a• Аналогично неравенству вида |x| > a , решением данного
неравенства будет являться множество точек, удовлетворяющих
условиям f(x) < — a или f(x) > a
Пример 1: Решите неравенство: | х + 6| ≥ 4
Решение: Это неравенство равносильно неравенствам:
х + 6 ≤ — 4 или х + 6 ≥ 4
х ≤-4-6
х≥ 4-6
х≥ -2
х ≤ — 10
Ответ : х ; 10 2;
Задачи для
самостоятельного решения
48. Решите неравенства
2 х 3Ответ:
х 3 1 5
Ответ:
2 х 4 2 12
Ответ:
13 2 4 3х 5
Ответ:
ДРУГОЙ ВИД
2 х 3
Ответ : 1 х 5
Показать решение
назад
х 3 1 5
Ответ : 9 х 3
Показать решение
назад
2 х 4 2 12
Ответ : х 3 или х 7
Показать решение
назад
13 2 4 3х 5
8
Ответ : х 0 или х
3
Показать решение
назад
53.
 Решение неравенства2 х 3
Решение неравенства2 х 33 2 х 3
3 2 х 3 2
5 х 1
5 х 1
1 х 5
-1
5
Ответ : 1 х 5
х
НАЗАД
54. Решение неравенства
х 3 1 5х 3 6
6 х 3 6
6 3 х 6 3
9 х 3
-9
3
Ответ : 9 х 3
х
НАЗАД
55. Решение неравенства
2 х 4 2 122 х 4 10
2 х 4 10 или 2 х 4 10
2 х 6 или 2 х 14
х 3 или х 7
-3
7
Ответ : х 3 или х 7
х
НАЗАД
56. Решение неравенства
13 2 4 3х 52 4 3х 5 13
2 4 3х 8
4 3х 4
4 3 х 4 или 4 3 х 4
3 х 8 или 3 х 0
8
х
или х 0
3
0
8
3
8
Ответ : х 0 или х
3
х
НАЗАД
57. Неравенства вида
f ( x) g ( x)Неравенства вида f ( x) g ( x) или f ( x) g ( x)
можно решать двумя способами:
1. возведением обеих частей в квадрат
2. раскрывая модули по определению
Пример: Решить неравенство: 3х 2 х 1
1 способ: Т. к. обе части неравенства неотрицательны, то их можно
2
2
3
х
2
х
1
возвести в квадрат
Используя известное свойство, получим: (3х 2) 2 ( х 1) 2
Перенесем все слагаемы в левую часть и разложим на множители
по формуле разность квадратов:
(3х 2) ( х 1) (3х 2) ( х 1) 0
2 х 3 4 х 1 0
Решая методом интервалов, получим:
1 3
х
;
4 2
Второй
способ
58.
 Неравенства видаf ( x) g ( x)
Неравенства видаf ( x) g ( x)Пример: Решить неравенство: 3х 2 х 1
2 способ: Найдем нули функции, стоящей внутри знака модуля, отметим эти
числа на числовой прямой и определим знаки этих функций на
получившихся промежутках:
—
—
+
-1
Решим неравенство на каждом промежутке:
х 1
3х-2
+
1 х
2
3
2
3
х+1
+
х
2
3
(3x 2) ( x 1)
(3 x 2) ( x 1)
(3x 2) ( x 1)
2x 3
4x 1
1
x
4
2x 3
x 1,5
x 1,5
с учетом данного условия:
-1
1
1,5
Решений нет
1
4
2
3
1 2
х
;
4 3
2
3
3
2
2 3
х
;
3 2
Объединяем второе и третье решение
1 3
х
;
4
2
59. Решите неравенство
2 х 2x 1Ответ:
ДРУГОЙ ВИД
2 х 2x 1
1
Ответ : x ; 3 ;
3
Показать решение
другой вид
61. Решение неравенства
2 х 2x 12 x
2
Возведем обе части в квадрат
2 x 1
2
Перенесем все в левую часть
и разложим по формуле разность квадратов
( 2 x 2 x 1)( 2 x 2 x 1) 0
( 3 x 1)( x 3) 0
—
+
Решаем неравенство методом интервалов
—
1
31
Ответ : x ; 3 ;
3
-3
х
НАЗАД
Неравенства вида
f ( x) g ( x) h( x)
• Неравенства данного вида решаются
методом раскрытия модулей, как и
уравнения такого типа .

• Рассмотрим решение данного вида
неравенств на примере:
63. Неравенства вида
f ( x) g ( x) h( x)3х 2 х 1 2 x
Пример: Решить неравенство:
2 способ: Найдем нули функции, стоящей внутри знака модуля, отметим эти
числа на числовой прямой и определим знаки этих функций на
получившихся промежутках:
—
—
+
-1
Решим неравенство на каждом промежутке:
х 1
1 х
2
3
2
3
(3x 2) ( x 1) 2 x (3x 2) ( x 1) 2 x
4x 3
3
x
4
с учетом данного условия:
1
3
4
Решений нет
6x 1
1
x
6
-1
3х-2
+
1
6
х+1
+
х
2
3
(3 x 2) ( x 1) 2 x
0x 3
Неравенство верно при всех х
2
3
1 2
х
;
6 3
2
3
2
х
;
3
Объединяем второе и третье решение
1
х
;
4
English Русский Правила
2-x-1=0$ по модулю $11$. Я уже знаю, что решения $x=4$ по модулю $11$ и $x=8$ по модулю $11$, но я получил этот результат, попробовав. Я также знаю, что могу получить эти решения, используя обычную квадратичную формулу и выполняя некоторые сравнения следующим образом:
$$x=\frac{1\pm \sqrt{5}}{2}\equiv_{11}\frac{1\pm \sqrt{16}}{2}\equiv_{11}\frac{1\pm 4}{2}$$
$$x_+\equiv_{11}\frac{1+ 4}{2}\equiv_{11}\frac{5}{2}\equiv_{11}\frac{16}{2}=8$$
$$x_-\equiv_{11}\frac{1- 4}{2}\equiv_{11}\frac{-3}{2}\equiv_{11}\frac{8}{2}=4$$
Однако в этом методе я должен суммировать $11$ с некоторыми числами, пока не получу число, которое находится в $\mathbb{F}_{11}$. Что, если я продолжаю суммировать и суммировать, а в $\mathbb{F}_{11}$ ничего не получится? Когда можно сделать вывод, что уравнение не имеет решения? Есть ли лучший способ сделать это? 92$, поэтому мы могли бы продолжать вычитать 11$ из $x$ (или прибавлять 11$) до тех пор, пока $x$ не окажется в нужном диапазоне.
Я также знаю, что могу получить эти решения, используя обычную квадратичную формулу и выполняя некоторые сравнения следующим образом:
$$x=\frac{1\pm \sqrt{5}}{2}\equiv_{11}\frac{1\pm \sqrt{16}}{2}\equiv_{11}\frac{1\pm 4}{2}$$
$$x_+\equiv_{11}\frac{1+ 4}{2}\equiv_{11}\frac{5}{2}\equiv_{11}\frac{16}{2}=8$$
$$x_-\equiv_{11}\frac{1- 4}{2}\equiv_{11}\frac{-3}{2}\equiv_{11}\frac{8}{2}=4$$
Однако в этом методе я должен суммировать $11$ с некоторыми числами, пока не получу число, которое находится в $\mathbb{F}_{11}$. Что, если я продолжаю суммировать и суммировать, а в $\mathbb{F}_{11}$ ничего не получится? Когда можно сделать вывод, что уравнение не имеет решения? Есть ли лучший способ сделать это? 92$, поэтому мы могли бы продолжать вычитать 11$ из $x$ (или прибавлять 11$) до тех пор, пока $x$ не окажется в нужном диапазоне. Таким образом, вы должны попробовать каждую возможность между $0$ и $10$: или, используя переформулирование этого вычисления «прибавьте $11$ к $5$, пока не получите квадратное число», вы должны повторить процесс $10$ раз (пока достигнув $5+11\times 10=115$), чтобы установить, что решения не существует. (Хотя, конечно, в этом случае есть два решения.)
(Хотя, конечно, в этом случае есть два решения.)
, так что
$$2x\equiv \begin{случаи} +4+1=5\эквив16\\ -4+1=-3\экв8 \end{случаи} $$
, следовательно, $x\equiv8$ и $4$.
Суть здесь в том, что $5$ является квадратичным вычетом по модулю $11$. Можно узнать, какие числа являются квадратичными остатками (а какие нет), не обязательно зная их «квадратный корень», но для небольших простых чисел, таких как $11$, пробежаться по возможностям так же быстро, как и применить любую причудливую теорию.
$\endgroup$ 92-x-12=(x-4)(x+3).$$ Решения равны $4$ и $-3,$ по модулю $11$ они равны $$4 \quad \text{и} \quad 8.$$ $\endgroup$ $\begingroup$Если проблема заключается в нахождении квадратного корня из $5\bmod 11$, это можно сделать с помощью того, что я называю «методом возведения в степень».
Поскольку $11-1$ делится на $2$, но не на $4$, любой квадратичный вычет $r$ будет иметь квадратный корень, являющийся также степенью $r\bmod 11$. Затем квадратный корень можно вычислить как степень, что требует $O(\log n)$ умножения, где $n$ — показатель степени. 92\экв5$. (Если бы это не удалось, квадратный корень и, следовательно, квадратное уравнение не имели бы решения.) Таким образом, мы можем с уверенностью ввести эти значения для квадратных корней из $5$ с ограниченным методом проб и ошибок и исходить из этого.
Затем квадратный корень можно вычислить как степень, что требует $O(\log n)$ умножения, где $n$ — показатель степени. 92\экв5$. (Если бы это не удалось, квадратный корень и, следовательно, квадратное уравнение не имели бы решения.) Таким образом, мы можем с уверенностью ввести эти значения для квадратных корней из $5$ с ограниченным методом проб и ошибок и исходить из этого.
абстрактная алгебра — $\Bbb F_2[X]$ модули с 8 элементами
Пусть $L$ полный список неизоморфных $\Bbb{F}_2[X]$-модулей порядка $8$. Тогда по аргументу подсчета, который вы привели выше, $L$ должен содержаться в следующем списке: 93+X+1$ неприводимы в $\Bbb{F}_2[X]$, так как не имеют корней в $\Bbb{F}_2$.
Снова применяя структурную теорему к окончательным формам каждого из этих (классов изоморфизма) модулей, мы можем заключить, что $L$ — это в точности указанный список.
Также обратите внимание, что 1-8 в $L$ — это полный список неизоморфных циклических $\Bbb{F}_2[X]$-модулей порядка $8$.

 ком
ком 3 Обзор раздела газового законодательства
3 Обзор раздела газового законодательства mathamatics.com
mathamatics.com Это не только помогло мне с домашним заданием, но и научило решать проблемы.
Это не только помогло мне с домашним заданием, но и научило решать проблемы.  алгебра Ферстера и тригонометрия Companiton web
алгебра Ферстера и тригонометрия Companiton web
 T — Неизвестная функция29:TT и NCI-h2385 — Синаптическая передача сигнала
T — Неизвестная функция29:TT и NCI-h2385 — Синаптическая передача сигнала
 : Высшая школа, 1991. – 157 с. Практикум предназначен для выполнения самостоятельных практических заданий по предмету «Математическая статистика». Он состоит из семи параграфов и приложений.
: Высшая школа, 1991. – 157 с. Практикум предназначен для выполнения самостоятельных практических заданий по предмету «Математическая статистика». Он состоит из семи параграфов и приложений.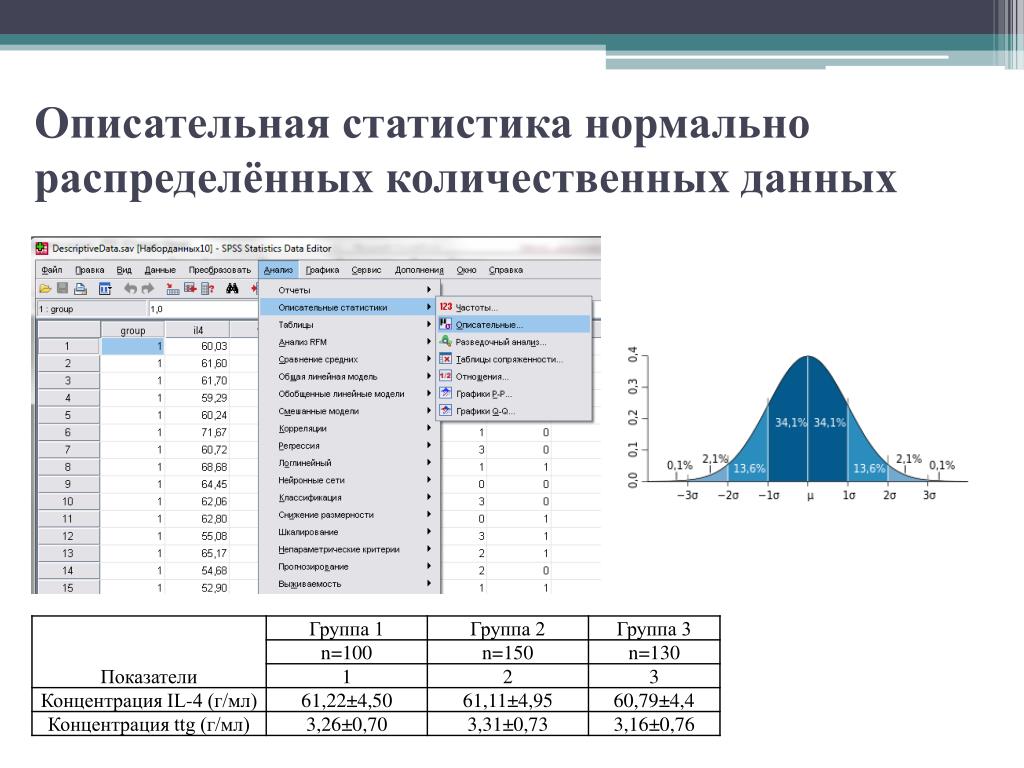 : Диалектика Год: 2008 Cтраниц: 316 Формат: pdf/djvu Размер: 14 мб Язык: русский Цель этой книги заключается в том, чтобы…
: Диалектика Год: 2008 Cтраниц: 316 Формат: pdf/djvu Размер: 14 мб Язык: русский Цель этой книги заключается в том, чтобы…
 В книге приводится масса примеров из реальных источников, имеющих отношение к повседневной жизни: от последних открытий в медицине, исследований преступности и тенденций этнического состава жителей страны до опросов на тему знакомств в Интернете, использования сотовых телефонов и худшего автомобиля тысячелетия.
В книге приводится масса примеров из реальных источников, имеющих отношение к повседневной жизни: от последних открытий в медицине, исследований преступности и тенденций этнического состава жителей страны до опросов на тему знакомств в Интернете, использования сотовых телефонов и худшего автомобиля тысячелетия.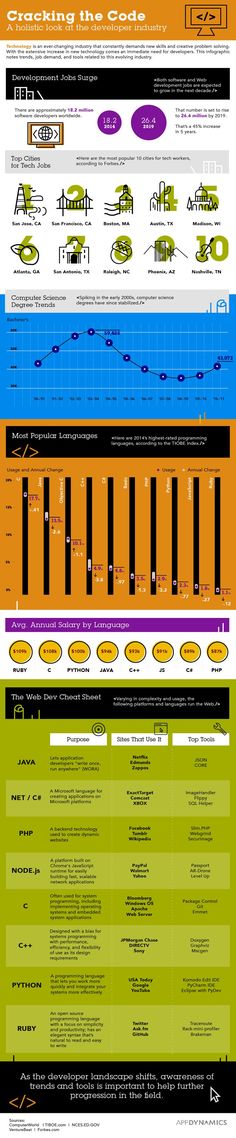 Не забывайте о том, что с помощью статистических данных вас могут попытаться ввести в заблуждение, поэтому учитесь справляться с такими проблемами.
Не забывайте о том, что с помощью статистических данных вас могут попытаться ввести в заблуждение, поэтому учитесь справляться с такими проблемами.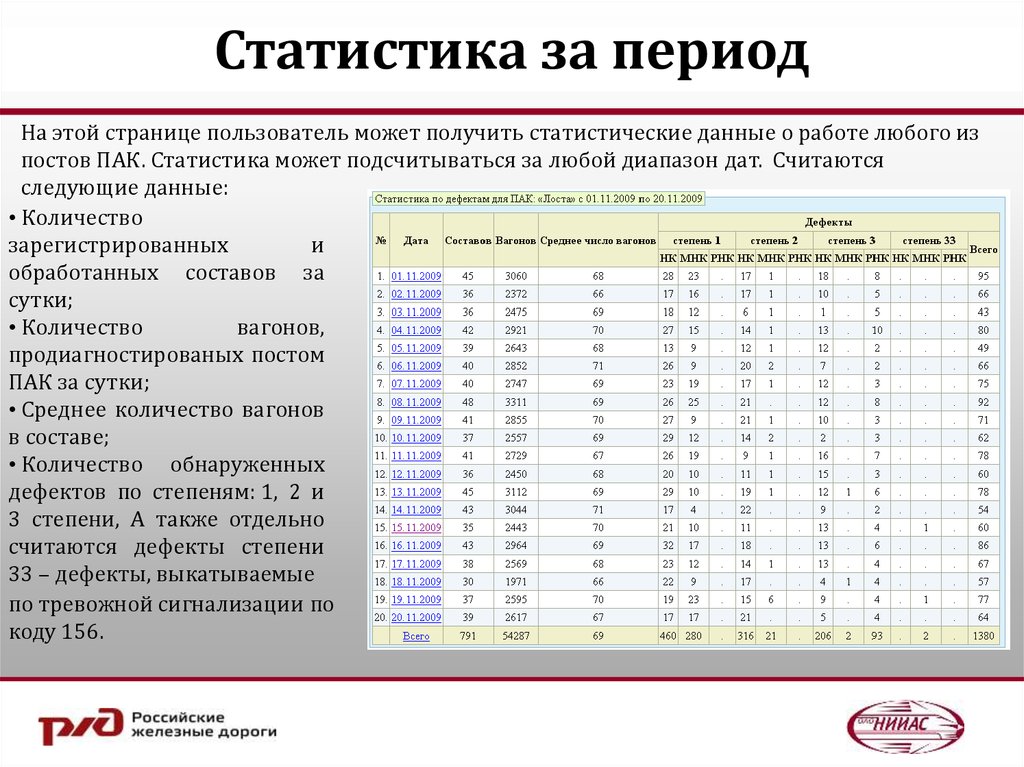 ..
.. Благодаря этой книге вы разовьете способность разбираться в статистических результатах и принимать на их основе важные решения (например, о результатах новейших медицинских исследований).
Благодаря этой книге вы разовьете способность разбираться в статистических результатах и принимать на их основе важные решения (например, о результатах новейших медицинских исследований). …
…
 Рамси Дебора. Статистика для чайников. Файл формата pdf. размером 8,12 МБ.
Рамси Дебора. Статистика для чайников. Файл формата pdf. размером 8,12 МБ. Издано в 2008 году.
Издано в 2008 году. ..
.. : Диалектика, 2008. 316 с. Цель этой книги заключается в том, чтобы научить вас понимать и критически оценивать невероятное количество статистической информации, с которой вам приходится сталкиваться ежедневно диаграммы, графики, таблицы, а также газетные заголовки
: Диалектика, 2008. 316 с. Цель этой книги заключается в том, чтобы научить вас понимать и критически оценивать невероятное количество статистической информации, с которой вам приходится сталкиваться ежедневно диаграммы, графики, таблицы, а также газетные заголовки Файл формата djvu. размером 6,10 МБ.
Файл формата djvu. размером 6,10 МБ.

 Благодаря книге «Статистика для чайников» вы разовьете способность разбираться в статистических результатах и принимать на их основе важные решения (например, о результатах новейших медицинских исследований). Не забывайте о том, что с помощью статистических данных вас могут попытаться ввести в заблуждение, поэтому учитесь справляться с такими проблемами. В книге «Статистика для чайников» приводится масса примеров из реальных источников, имеющих отношение к повседневной жизни: от последних открытий в медицине, исследований преступности и тенденций этнического состава жителей страны до опросов на тему знакомств в Интернете, использования сотовых телефонов и худшего автомобиля тысячелетия. Читая главы книги «Статистика для чайников», вы начнете понимать, как пользоваться диаграммами, графиками и таблицами, а также научитесь оценивать результаты последних опросов, экспериментов и других исследований. Вы даже узнаете, как с помощью сверчков измерить температуру воздуха и как сорвать джек-пот в лотерее.
Благодаря книге «Статистика для чайников» вы разовьете способность разбираться в статистических результатах и принимать на их основе важные решения (например, о результатах новейших медицинских исследований). Не забывайте о том, что с помощью статистических данных вас могут попытаться ввести в заблуждение, поэтому учитесь справляться с такими проблемами. В книге «Статистика для чайников» приводится масса примеров из реальных источников, имеющих отношение к повседневной жизни: от последних открытий в медицине, исследований преступности и тенденций этнического состава жителей страны до опросов на тему знакомств в Интернете, использования сотовых телефонов и худшего автомобиля тысячелетия. Читая главы книги «Статистика для чайников», вы начнете понимать, как пользоваться диаграммами, графиками и таблицами, а также научитесь оценивать результаты последних опросов, экспериментов и других исследований. Вы даже узнаете, как с помощью сверчков измерить температуру воздуха и как сорвать джек-пот в лотерее. Десять критериев хорошего опроса
Глава 21. Десять распространенных статистических ошибок
Источники
Индекс
список рисунков
Список таблиц
Список боковых панелей
Задняя обложка
Озадачены статистикой? Не бойтесь — это удобное руководство предлагает четкие и практические объяснения статистических идей,
методы, формулы и расчеты, а также множество примеров, показывающих, как эти концепции применимы к вашей
повседневная жизнь. Вы увидите, как убрать погрешность из опросов общественного мнения и как анализировать и интерпретировать
данные для повышения производительности в классе или на рабочем месте.
Узнайте, как:
Интерпретируйте и критикуйте графики и диаграммы
Определить шансы с вероятностью
Делайте предположения с уверенностью, используя уровни достоверности
Настроить и провести проверку гипотезы
Вычислить статистические формулы
об авторе
Дебора Рамси получила докторскую степень. по статистике Университета штата Огайо (OSU) в 1993. По окончании учебы она
поступил на факультет статистического факультета Канзасского государственного университета, выиграв выдающуюся награду.
Десять критериев хорошего опроса
Глава 21. Десять распространенных статистических ошибок
Источники
Индекс
список рисунков
Список таблиц
Список боковых панелей
Задняя обложка
Озадачены статистикой? Не бойтесь — это удобное руководство предлагает четкие и практические объяснения статистических идей,
методы, формулы и расчеты, а также множество примеров, показывающих, как эти концепции применимы к вашей
повседневная жизнь. Вы увидите, как убрать погрешность из опросов общественного мнения и как анализировать и интерпретировать
данные для повышения производительности в классе или на рабочем месте.
Узнайте, как:
Интерпретируйте и критикуйте графики и диаграммы
Определить шансы с вероятностью
Делайте предположения с уверенностью, используя уровни достоверности
Настроить и провести проверку гипотезы
Вычислить статистические формулы
об авторе
Дебора Рамси получила докторскую степень. по статистике Университета штата Огайо (OSU) в 1993. По окончании учебы она
поступил на факультет статистического факультета Канзасского государственного университета, выиграв выдающуюся награду. В 1998 году она получила президентскую награду за преподавание и получила должность и продвижение по службе. В 2000 году она вернулась в ОГУ в качестве
Директор Учебного центра математики и статистики, где она работает сегодня. Деб является редактором
«Учебные материалы» Журнала статистического образования; она также публиковала статьи и давала профессиональные
презентации на тему статистического образования, с особым акцентом на статистическую грамотность (навыки для
понимание статистики в повседневной жизни и на рабочем месте) и иммерсивная среда обучения
(среда, которая способствует самостоятельному открытию идей учащимися).
Статистика для чайников
Дебора Рамси
ISBN: 0764554239John Wiley & Sons © 2003 (356 страниц)
Эта ссылка предлагает объяснения статистических идей,
методы, формулы и расчеты, а также примеры
которые показывают, как эти концепции применимы к вашей повседневной жизни. Оглавление
Статистика для чайников
Введение
Часть I — Статистика естественного движения населения о статистике
Глава 1
— Статистика повседневной жизни
Глава 2
— Статистика пошла не так
Глава 3
— Инструменты торговли
Часть II.
В 1998 году она получила президентскую награду за преподавание и получила должность и продвижение по службе. В 2000 году она вернулась в ОГУ в качестве
Директор Учебного центра математики и статистики, где она работает сегодня. Деб является редактором
«Учебные материалы» Журнала статистического образования; она также публиковала статьи и давала профессиональные
презентации на тему статистического образования, с особым акцентом на статистическую грамотность (навыки для
понимание статистики в повседневной жизни и на рабочем месте) и иммерсивная среда обучения
(среда, которая способствует самостоятельному открытию идей учащимися).
Статистика для чайников
Дебора Рамси
ISBN: 0764554239John Wiley & Sons © 2003 (356 страниц)
Эта ссылка предлагает объяснения статистических идей,
методы, формулы и расчеты, а также примеры
которые показывают, как эти концепции применимы к вашей повседневной жизни. Оглавление
Статистика для чайников
Введение
Часть I — Статистика естественного движения населения о статистике
Глава 1
— Статистика повседневной жизни
Глава 2
— Статистика пошла не так
Глава 3
— Инструменты торговли
Часть II. Основы обработки чисел
Глава 4
— Получение картины — диаграммы и графики
Глава 5
— Средние значения, медианы и многое другое
Часть III. Определение шансов
Глава 6
— Каковы шансы? — Понимание вероятности
Глава 7
— Азартные игры, чтобы выиграть
Часть IV. Пробираясь сквозь результаты
Глава 8
— Меры относительного положения
Глава 9- Внимание! Результаты проб различаются!
Глава 10. Оставляя место для погрешности
Часть V. Уверенные предположения
Глава 11. Дело оценки — интерпретация и оценка уверенности
Интервалы
Глава 12. Расчет точных доверительных интервалов
Глава 13. Обычно используемые доверительные интервалы — формулы и примеры
Часть IV. Выставление претензии на проверку (гипотезы)
Глава 14. Заявления, тесты и выводы
Глава 15. Обычно используемые проверки гипотез — формулы и примеры
Часть VII. Статистические исследования.
Глава 16 — Опросы, опросы и еще раз опросы
Глава 17. Эксперименты. Медицинские прорывы или вводящие в заблуждение результаты?
Глава 18. Поиск связей — корреляции и ассоциации
Глава 19- Статистика и зубная паста — контроль качества
Часть VIII — Часть десятков
Глава 20.
Основы обработки чисел
Глава 4
— Получение картины — диаграммы и графики
Глава 5
— Средние значения, медианы и многое другое
Часть III. Определение шансов
Глава 6
— Каковы шансы? — Понимание вероятности
Глава 7
— Азартные игры, чтобы выиграть
Часть IV. Пробираясь сквозь результаты
Глава 8
— Меры относительного положения
Глава 9- Внимание! Результаты проб различаются!
Глава 10. Оставляя место для погрешности
Часть V. Уверенные предположения
Глава 11. Дело оценки — интерпретация и оценка уверенности
Интервалы
Глава 12. Расчет точных доверительных интервалов
Глава 13. Обычно используемые доверительные интервалы — формулы и примеры
Часть IV. Выставление претензии на проверку (гипотезы)
Глава 14. Заявления, тесты и выводы
Глава 15. Обычно используемые проверки гипотез — формулы и примеры
Часть VII. Статистические исследования.
Глава 16 — Опросы, опросы и еще раз опросы
Глава 17. Эксперименты. Медицинские прорывы или вводящие в заблуждение результаты?
Глава 18. Поиск связей — корреляции и ассоциации
Глава 19- Статистика и зубная паста — контроль качества
Часть VIII — Часть десятков
Глава 20. Десять критериев хорошего опроса
Глава 21. Десять распространенных статистических ошибок
Источники
Индекс
список рисунков
Список таблиц
Список боковых панелей
Статистика для чайников
Дебора Рамси, доктор философии
Опубликовано
Уайли Паблишинг, Инк.
111 Ривер Ст.
Хобокен, Нью-Джерси 07030
http://www.wiley.com
Авторское право © 2003 Wiley Publishing, Inc.,
Индианаполис, Индиана
Издано Wiley Publishing, Inc., Индианаполис, Индиана.
Опубликовано одновременно в Канаде
Никакая часть данной публикации не может быть воспроизведена, сохранена в поисковой системе или передана в любой форме.
или любыми средствами, электронными, механическими, фотокопированием, записью, сканированием или иным, за исключением случаев, когда
разрешено в соответствии со статьями 107 или 108 Закона 1976 Закона об авторском праве США, без предварительного
письменное разрешение Издателя или разрешение путем оплаты соответствующей платы за копию
в Центр защиты авторских прав, 222 Rosewood Drive, Danvers, MA 01923, 978-750-8400, факс 978-
646-8700.
Десять критериев хорошего опроса
Глава 21. Десять распространенных статистических ошибок
Источники
Индекс
список рисунков
Список таблиц
Список боковых панелей
Статистика для чайников
Дебора Рамси, доктор философии
Опубликовано
Уайли Паблишинг, Инк.
111 Ривер Ст.
Хобокен, Нью-Джерси 07030
http://www.wiley.com
Авторское право © 2003 Wiley Publishing, Inc.,
Индианаполис, Индиана
Издано Wiley Publishing, Inc., Индианаполис, Индиана.
Опубликовано одновременно в Канаде
Никакая часть данной публикации не может быть воспроизведена, сохранена в поисковой системе или передана в любой форме.
или любыми средствами, электронными, механическими, фотокопированием, записью, сканированием или иным, за исключением случаев, когда
разрешено в соответствии со статьями 107 или 108 Закона 1976 Закона об авторском праве США, без предварительного
письменное разрешение Издателя или разрешение путем оплаты соответствующей платы за копию
в Центр защиты авторских прав, 222 Rosewood Drive, Danvers, MA 01923, 978-750-8400, факс 978-
646-8700. Запросы к Издателю о разрешении следует направлять в Юридический отдел,
Wiley Publishing, Inc., 10475 Crosspoint Blvd., Indianapolis, IN 46256, 317-572-3447, факс 317-572-
4447, e-mail:
Запросы к Издателю о разрешении следует направлять в Юридический отдел,
Wiley Publishing, Inc., 10475 Crosspoint Blvd., Indianapolis, IN 46256, 317-572-3447, факс 317-572-
4447, e-mail: Определение шансов
Глава 6
— Каковы шансы? — Понимание вероятности
Глава 7
— Азартные игры, чтобы выиграть
Часть IV. Пробираясь сквозь результаты
Глава 8
— Меры относительного положения
Глава 9- Внимание! Результаты проб различаются!
Глава 10. Оставляя место для погрешности
Часть V. Уверенные предположения
Глава 11. Дело оценки — интерпретация и оценка уверенности
Интервалы
Глава 12. Расчет точных доверительных интервалов
Глава 13. Обычно используемые доверительные интервалы — формулы и примеры
Часть IV. Выставление претензии на проверку (гипотезы)
Глава 14. Заявления, тесты и выводы
Глава 15. Обычно используемые проверки гипотез — формулы и примеры
Часть VII. Статистические исследования.
Глава 16 — Опросы, опросы и еще раз опросы
Глава 17. Эксперименты. Медицинские прорывы или вводящие в заблуждение результаты?
Глава 18. Поиск связей — корреляции и ассоциации
Глава 19- Статистика и зубная паста — контроль качества
Часть VIII — Часть десятков
Глава 20. Десять критериев хорошего опроса
Глава 21.
Определение шансов
Глава 6
— Каковы шансы? — Понимание вероятности
Глава 7
— Азартные игры, чтобы выиграть
Часть IV. Пробираясь сквозь результаты
Глава 8
— Меры относительного положения
Глава 9- Внимание! Результаты проб различаются!
Глава 10. Оставляя место для погрешности
Часть V. Уверенные предположения
Глава 11. Дело оценки — интерпретация и оценка уверенности
Интервалы
Глава 12. Расчет точных доверительных интервалов
Глава 13. Обычно используемые доверительные интервалы — формулы и примеры
Часть IV. Выставление претензии на проверку (гипотезы)
Глава 14. Заявления, тесты и выводы
Глава 15. Обычно используемые проверки гипотез — формулы и примеры
Часть VII. Статистические исследования.
Глава 16 — Опросы, опросы и еще раз опросы
Глава 17. Эксперименты. Медицинские прорывы или вводящие в заблуждение результаты?
Глава 18. Поиск связей — корреляции и ассоциации
Глава 19- Статистика и зубная паста — контроль качества
Часть VIII — Часть десятков
Глава 20. Десять критериев хорошего опроса
Глава 21. Десять распространенных статистических ошибок
Источники
Индекс
список рисунков
Список таблиц
Список боковых панелей
Статистика для чайников
Дебора Рамси
ISBN: 0764554239
John Wiley & Sons © 2003 (356 страниц)
Эта ссылка предлагает объяснения статистических идей,
методы, формулы и расчеты, а также примеры
которые показывают, как эти концепции применимы к вашей повседневной жизни. Оглавление
Статистика для чайников
Введение
Часть I — Статистика естественного движения населения о статистике
Глава 1
— Статистика повседневной жизни
Глава 2
— Статистика пошла не так
Глава 3
— Инструменты торговли
Часть II. Основы обработки чисел
Глава 4
— Получение картины — диаграммы и графики
Глава 5
— Средние значения, медианы и многое другое
Часть III. Определение шансов
Глава 6
— Каковы шансы? — Понимание вероятности
Глава 7
— Азартные игры, чтобы выиграть
Часть IV. Пробираясь сквозь результаты
Глава 8
— Меры относительного положения
Глава 9- Внимание! Результаты проб различаются!
Глава 10.
Десять распространенных статистических ошибок
Источники
Индекс
список рисунков
Список таблиц
Список боковых панелей
Статистика для чайников
Дебора Рамси
ISBN: 0764554239
John Wiley & Sons © 2003 (356 страниц)
Эта ссылка предлагает объяснения статистических идей,
методы, формулы и расчеты, а также примеры
которые показывают, как эти концепции применимы к вашей повседневной жизни. Оглавление
Статистика для чайников
Введение
Часть I — Статистика естественного движения населения о статистике
Глава 1
— Статистика повседневной жизни
Глава 2
— Статистика пошла не так
Глава 3
— Инструменты торговли
Часть II. Основы обработки чисел
Глава 4
— Получение картины — диаграммы и графики
Глава 5
— Средние значения, медианы и многое другое
Часть III. Определение шансов
Глава 6
— Каковы шансы? — Понимание вероятности
Глава 7
— Азартные игры, чтобы выиграть
Часть IV. Пробираясь сквозь результаты
Глава 8
— Меры относительного положения
Глава 9- Внимание! Результаты проб различаются!
Глава 10. Оставляя место для погрешности
Часть V. Уверенные предположения
Глава 11. Дело оценки — интерпретация и оценка уверенности
Интервалы
Глава 12. Расчет точных доверительных интервалов
Глава 13. Обычно используемые доверительные интервалы — формулы и примеры
Часть IV. Выставление претензии на проверку (гипотезы)
Глава 14. Заявления, тесты и выводы
Глава 15. Обычно используемые проверки гипотез — формулы и примеры
Часть VII. Статистические исследования.
Глава 16 — Опросы, опросы и еще раз опросы
Глава 17. Эксперименты. Медицинские прорывы или вводящие в заблуждение результаты?
Глава 18. Поиск связей — корреляции и ассоциации
Глава 19- Статистика и зубная паста — контроль качества
Часть VIII — Часть десятков
Глава 20. Десять критериев хорошего опроса
Глава 21. Десять распространенных статистических ошибок
Источники
Индекс
список рисунков
Список таблиц
Список боковых панелей
Задняя обложка
Озадачены статистикой? Не бойтесь — это удобное руководство предлагает четкие и практические объяснения статистических идей,
методы, формулы и расчеты, а также множество примеров, показывающих, как эти концепции применимы к вашей
повседневная жизнь.
Оставляя место для погрешности
Часть V. Уверенные предположения
Глава 11. Дело оценки — интерпретация и оценка уверенности
Интервалы
Глава 12. Расчет точных доверительных интервалов
Глава 13. Обычно используемые доверительные интервалы — формулы и примеры
Часть IV. Выставление претензии на проверку (гипотезы)
Глава 14. Заявления, тесты и выводы
Глава 15. Обычно используемые проверки гипотез — формулы и примеры
Часть VII. Статистические исследования.
Глава 16 — Опросы, опросы и еще раз опросы
Глава 17. Эксперименты. Медицинские прорывы или вводящие в заблуждение результаты?
Глава 18. Поиск связей — корреляции и ассоциации
Глава 19- Статистика и зубная паста — контроль качества
Часть VIII — Часть десятков
Глава 20. Десять критериев хорошего опроса
Глава 21. Десять распространенных статистических ошибок
Источники
Индекс
список рисунков
Список таблиц
Список боковых панелей
Задняя обложка
Озадачены статистикой? Не бойтесь — это удобное руководство предлагает четкие и практические объяснения статистических идей,
методы, формулы и расчеты, а также множество примеров, показывающих, как эти концепции применимы к вашей
повседневная жизнь. Вы увидите, как убрать погрешность из опросов общественного мнения и как анализировать и интерпретировать
данные для повышения производительности в классе или на рабочем месте.
Узнайте, как:
Интерпретируйте и критикуйте графики и диаграммы
Определить шансы с вероятностью
Делайте предположения с уверенностью, используя уровни достоверности
Настроить и провести проверку гипотезы
Вычислить статистические формулы
об авторе
Дебора Рамси получила докторскую степень. по статистике Университета штата Огайо (OSU) в 1993. По окончании учебы она
поступил на факультет статистического факультета Канзасского государственного университета, выиграв выдающуюся награду.
В 1998 году она получила президентскую награду за преподавание и получила должность и продвижение по службе. В 2000 году она вернулась в ОГУ в качестве
Директор Учебного центра математики и статистики, где она работает сегодня. Деб является редактором
«Учебные материалы» Журнала статистического образования; она также публиковала статьи и давала профессиональные
презентации на тему статистического образования, с особым акцентом на статистическую грамотность (навыки для
понимание статистики в повседневной жизни и на рабочем месте) и иммерсивная среда обучения
(среда, которая способствует самостоятельному открытию идей учащимися).
Вы увидите, как убрать погрешность из опросов общественного мнения и как анализировать и интерпретировать
данные для повышения производительности в классе или на рабочем месте.
Узнайте, как:
Интерпретируйте и критикуйте графики и диаграммы
Определить шансы с вероятностью
Делайте предположения с уверенностью, используя уровни достоверности
Настроить и провести проверку гипотезы
Вычислить статистические формулы
об авторе
Дебора Рамси получила докторскую степень. по статистике Университета штата Огайо (OSU) в 1993. По окончании учебы она
поступил на факультет статистического факультета Канзасского государственного университета, выиграв выдающуюся награду.
В 1998 году она получила президентскую награду за преподавание и получила должность и продвижение по службе. В 2000 году она вернулась в ОГУ в качестве
Директор Учебного центра математики и статистики, где она работает сегодня. Деб является редактором
«Учебные материалы» Журнала статистического образования; она также публиковала статьи и давала профессиональные
презентации на тему статистического образования, с особым акцентом на статистическую грамотность (навыки для
понимание статистики в повседневной жизни и на рабочем месте) и иммерсивная среда обучения
(среда, которая способствует самостоятельному открытию идей учащимися). Статистика для чайников
Дебора Рамси
ISBN: 0764554239John Wiley & Sons © 2003 (356 страниц)
Эта ссылка предлагает объяснения статистических идей,
методы, формулы и расчеты, а также примеры
которые показывают, как эти концепции применимы к вашей повседневной жизни. Оглавление
Статистика для чайников
Введение
Часть I — Статистика естественного движения населения о статистике
Глава 1
— Статистика повседневной жизни
Глава 2
— Статистика пошла не так
Глава 3
— Инструменты торговли
Часть II. Основы обработки чисел
Глава 4
— Получение картины — диаграммы и графики
Глава 5
— Средние значения, медианы и многое другое
Часть III. Определение шансов
Глава 6
— Каковы шансы? — Понимание вероятности
Глава 7
— Азартные игры, чтобы выиграть
Часть IV. Пробираясь сквозь результаты
Глава 8
— Меры относительного положения
Глава 9- Внимание! Результаты проб различаются!
Глава 10. Оставляя место для погрешности
Часть V. Уверенные предположения
Глава 11. Дело оценки — интерпретация и оценка уверенности
Интервалы
Глава 12.
Статистика для чайников
Дебора Рамси
ISBN: 0764554239John Wiley & Sons © 2003 (356 страниц)
Эта ссылка предлагает объяснения статистических идей,
методы, формулы и расчеты, а также примеры
которые показывают, как эти концепции применимы к вашей повседневной жизни. Оглавление
Статистика для чайников
Введение
Часть I — Статистика естественного движения населения о статистике
Глава 1
— Статистика повседневной жизни
Глава 2
— Статистика пошла не так
Глава 3
— Инструменты торговли
Часть II. Основы обработки чисел
Глава 4
— Получение картины — диаграммы и графики
Глава 5
— Средние значения, медианы и многое другое
Часть III. Определение шансов
Глава 6
— Каковы шансы? — Понимание вероятности
Глава 7
— Азартные игры, чтобы выиграть
Часть IV. Пробираясь сквозь результаты
Глава 8
— Меры относительного положения
Глава 9- Внимание! Результаты проб различаются!
Глава 10. Оставляя место для погрешности
Часть V. Уверенные предположения
Глава 11. Дело оценки — интерпретация и оценка уверенности
Интервалы
Глава 12. Расчет точных доверительных интервалов
Глава 13. Обычно используемые доверительные интервалы — формулы и примеры
Часть IV. Выставление претензии на проверку (гипотезы)
Глава 14. Заявления, тесты и выводы
Глава 15. Обычно используемые проверки гипотез — формулы и примеры
Часть VII. Статистические исследования.
Глава 16 — Опросы, опросы и еще раз опросы
Глава 17. Эксперименты. Медицинские прорывы или вводящие в заблуждение результаты?
Глава 18. Поиск связей — корреляции и ассоциации
Глава 19- Статистика и зубная паста — контроль качества
Часть VIII — Часть десятков
Глава 20. Десять критериев хорошего опроса
Глава 21. Десять распространенных статистических ошибок
Источники
Индекс
список рисунков
Список таблиц
Список боковых панелей
Статистика для чайников
Дебора Рамси, доктор философии
Опубликовано
Уайли Паблишинг, Инк.
111 Ривер Ст.
Хобокен, Нью-Джерси 07030
http://www.wiley.com
Авторское право © 2003 Wiley Publishing, Inc.,
Индианаполис, Индиана
Издано Wiley Publishing, Inc., Индианаполис, Индиана.
Расчет точных доверительных интервалов
Глава 13. Обычно используемые доверительные интервалы — формулы и примеры
Часть IV. Выставление претензии на проверку (гипотезы)
Глава 14. Заявления, тесты и выводы
Глава 15. Обычно используемые проверки гипотез — формулы и примеры
Часть VII. Статистические исследования.
Глава 16 — Опросы, опросы и еще раз опросы
Глава 17. Эксперименты. Медицинские прорывы или вводящие в заблуждение результаты?
Глава 18. Поиск связей — корреляции и ассоциации
Глава 19- Статистика и зубная паста — контроль качества
Часть VIII — Часть десятков
Глава 20. Десять критериев хорошего опроса
Глава 21. Десять распространенных статистических ошибок
Источники
Индекс
список рисунков
Список таблиц
Список боковых панелей
Статистика для чайников
Дебора Рамси, доктор философии
Опубликовано
Уайли Паблишинг, Инк.
111 Ривер Ст.
Хобокен, Нью-Джерси 07030
http://www.wiley.com
Авторское право © 2003 Wiley Publishing, Inc.,
Индианаполис, Индиана
Издано Wiley Publishing, Inc., Индианаполис, Индиана. Опубликовано одновременно в Канаде
Никакая часть данной публикации не может быть воспроизведена, сохранена в поисковой системе или передана в любой форме.
или любыми средствами, электронными, механическими, фотокопированием, записью, сканированием или иным, за исключением случаев, когда
разрешено в соответствии со статьями 107 или 108 Закона 1976 Закона об авторском праве США, без предварительного
письменное разрешение Издателя или разрешение путем оплаты соответствующей платы за копию
в Центр защиты авторских прав, 222 Rosewood Drive, Danvers, MA 01923, 978-750-8400, факс 978-
646-8700. Запросы к Издателю о разрешении следует направлять в Юридический отдел,
Wiley Publishing, Inc., 10475 Crosspoint Blvd., Indianapolis, IN 46256, 317-572-3447, факс 317-572-
4447, e-mail:
Опубликовано одновременно в Канаде
Никакая часть данной публикации не может быть воспроизведена, сохранена в поисковой системе или передана в любой форме.
или любыми средствами, электронными, механическими, фотокопированием, записью, сканированием или иным, за исключением случаев, когда
разрешено в соответствии со статьями 107 или 108 Закона 1976 Закона об авторском праве США, без предварительного
письменное разрешение Издателя или разрешение путем оплаты соответствующей платы за копию
в Центр защиты авторских прав, 222 Rosewood Drive, Danvers, MA 01923, 978-750-8400, факс 978-
646-8700. Запросы к Издателю о разрешении следует направлять в Юридический отдел,
Wiley Publishing, Inc., 10475 Crosspoint Blvd., Indianapolis, IN 46256, 317-572-3447, факс 317-572-
4447, e-mail: Рамси электронная книга
Рамси электронная книга Я бы не стал вас винить, если бы вы сейчас цинично относились к статистике, о которой читаете в СМИ, — временами я тоже. Хорошей новостью является то, что в то время как большое количество вводящей в заблуждение и неверной информации ждет вас, также создается много отличного материала; например, многие исследования и методы, использующие данные, помогают улучшить качество нашей жизни. Ваша работа заключается в том, чтобы уметь отделять хорошее от плохого и быть уверенным в своей способности сделать это. Благодаря глубокому пониманию статистики и статистических процедур вы обретете силу и уверенность в работе с числами в повседневной жизни, на работе и в классе. Вот о чем эта книга.
Я бы не стал вас винить, если бы вы сейчас цинично относились к статистике, о которой читаете в СМИ, — временами я тоже. Хорошей новостью является то, что в то время как большое количество вводящей в заблуждение и неверной информации ждет вас, также создается много отличного материала; например, многие исследования и методы, использующие данные, помогают улучшить качество нашей жизни. Ваша работа заключается в том, чтобы уметь отделять хорошее от плохого и быть уверенным в своей способности сделать это. Благодаря глубокому пониманию статистики и статистических процедур вы обретете силу и уверенность в работе с числами в повседневной жизни, на работе и в классе. Вот о чем эта книга. (А вы думали, что статистика — это просто обработка чисел!)
(А вы думали, что статистика — это просто обработка чисел!) Вы едите продукты, цены на которые основаны на маркетинговых данных. Вы идете на прием к врачу, где вам измеряют артериальное давление, температуру, вес и делают анализ крови; после того, как вся информация будет собрана, вы получите отчет, показывающий ваши цифры и то, как вы сравниваете их со статистическими нормами.
Вы едите продукты, цены на которые основаны на маркетинговых данных. Вы идете на прием к врачу, где вам измеряют артериальное давление, температуру, вес и делают анализ крови; после того, как вся информация будет собрана, вы получите отчет, показывающий ваши цифры и то, как вы сравниваете их со статистическими нормами.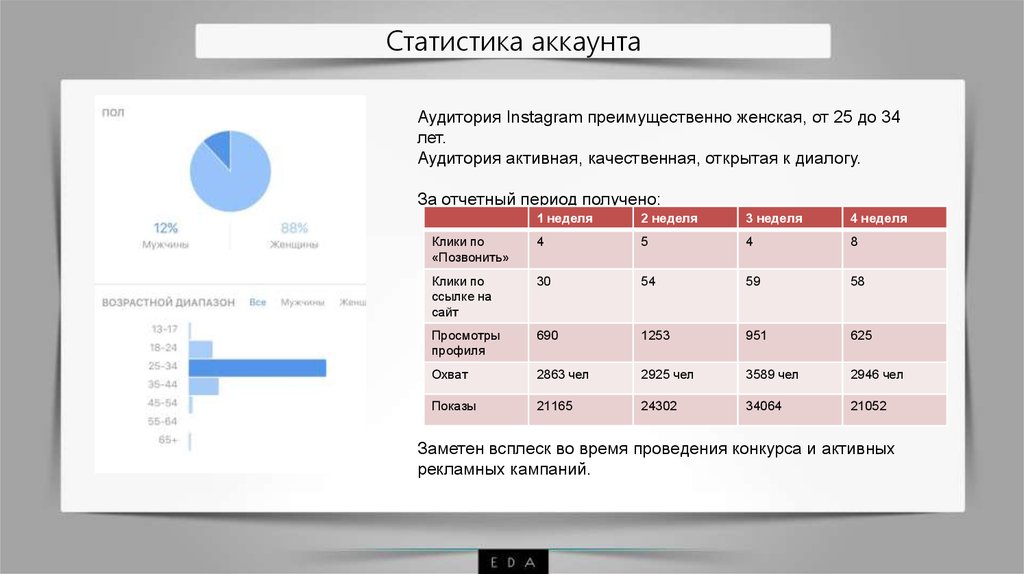
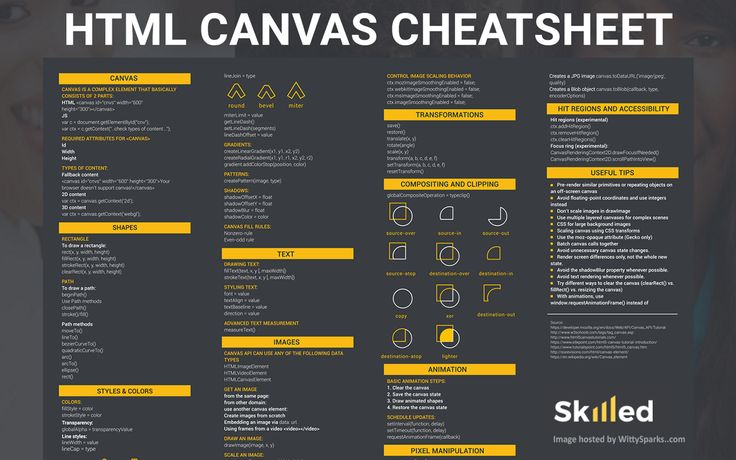 (Черт возьми, по крайней мере, вам нужен жаргон, потому что я использую его на протяжении всей книги; не беспокойтесь, я всегда его просматриваю.)
(Черт возьми, по крайней мере, вам нужен жаргон, потому что я использую его на протяжении всей книги; не беспокойтесь, я всегда его просматриваю.) Этот шаг сводится к выяснению того, какой процесс вы будете использовать для получения необходимых данных. В этом разделе я дам обзор двух основных типов исследований — опросов и экспериментов — и объясню, почему так важно оценить, как было разработано исследование, прежде чем верить его результатам.
Этот шаг сводится к выяснению того, какой процесс вы будете использовать для получения необходимых данных. В этом разделе я дам обзор двух основных типов исследований — опросов и экспериментов — и объясню, почему так важно оценить, как было разработано исследование, прежде чем верить его результатам.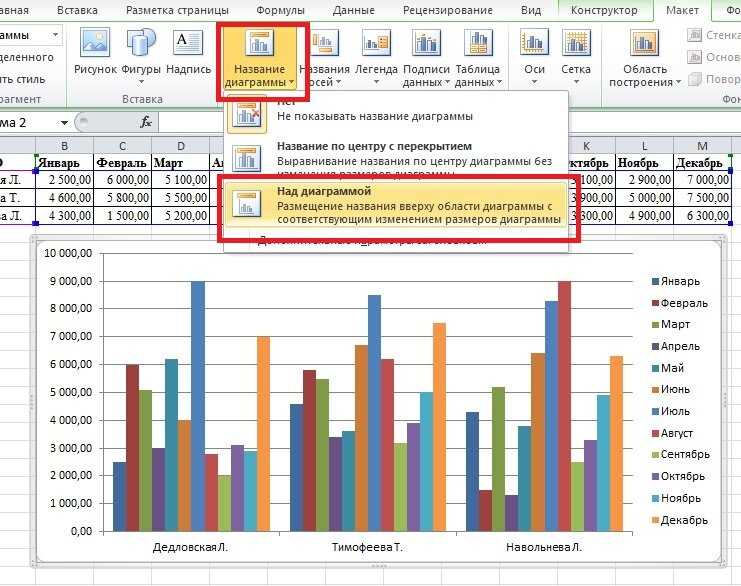
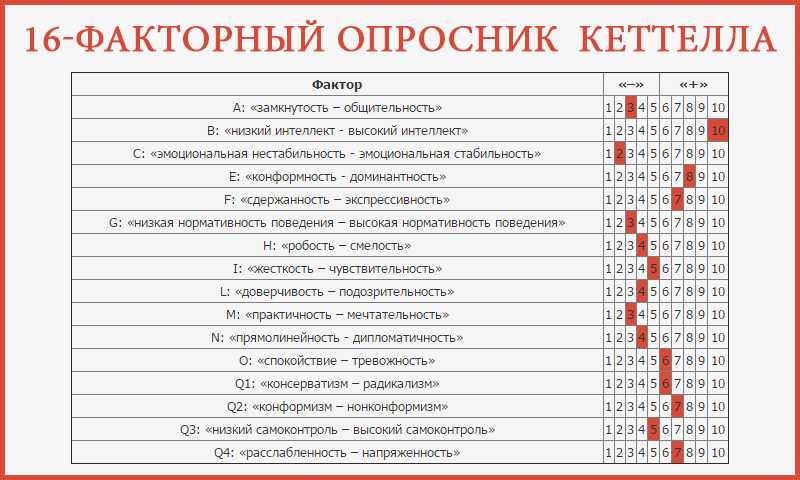 Инструменты, необходимые для сортировки опросов, находятся в главе 16.
Инструменты, необходимые для сортировки опросов, находятся в главе 16. Некоторые потенциальные проблемы, возникающие в ходе экспериментов, включают исследователей и/или испытуемых, которые знают, какое лечение они получали, факторы, не учитываемые в исследовании, влияющие на результат (например, вес субъекта при изучении дозировки препарата), или отсутствие контрольной группы. (не оставляя исходного уровня для сравнения результатов).
Некоторые потенциальные проблемы, возникающие в ходе экспериментов, включают исследователей и/или испытуемых, которые знают, какое лечение они получали, факторы, не учитываемые в исследовании, влияющие на результат (например, вес субъекта при изучении дозировки препарата), или отсутствие контрольной группы. (не оставляя исходного уровня для сравнения результатов).
 Естественно, пока не выйдет новый iPhone мы не узнаем, будет он намного лучше нашего (В1), таким же (В3) или сильно уступающим в качестве (В3). Посчитав прибыль во всех случаях, в итоге получим матрицу:
Естественно, пока не выйдет новый iPhone мы не узнаем, будет он намного лучше нашего (В1), таким же (В3) или сильно уступающим в качестве (В3). Посчитав прибыль во всех случаях, в итоге получим матрицу: Критерий максимума (максимаксный) является оптимистическим, т.е. мы надеемся на самый благоприятный для нас исход.представляется как max (max i).
Критерий максимума (максимаксный) является оптимистическим, т.е. мы надеемся на самый благоприятный для нас исход.представляется как max (max i). Критерий Сэвиджа (минимаксный). Суть его заключается в выборе стратегии, не допускающей слишком высоких потерь. Для этого используется матрица рисков, в которой вычисляется максимальная прибыль при каждом варианте действия игрока, и среди результатов выбирается наименьший. Его формула выглядит как min (max i)
Критерий Сэвиджа (минимаксный). Суть его заключается в выборе стратегии, не допускающей слишком высоких потерь. Для этого используется матрица рисков, в которой вычисляется максимальная прибыль при каждом варианте действия игрока, и среди результатов выбирается наименьший. Его формула выглядит как min (max i)

 Для выбора оптимальной стратегии в онлайн режиме необходимо задать размерность матрицы. Затем в новом диалоговом окне выбрать необходимые критерии и коэффициенты. Также можно вставить данные из Excel.
Размерность платежной матрицы (целевая функция ЗПР в условиях неопределенности)
Для выбора оптимальной стратегии в онлайн режиме необходимо задать размерность матрицы. Затем в новом диалоговом окне выбрать необходимые критерии и коэффициенты. Также можно вставить данные из Excel.
Размерность платежной матрицы (целевая функция ЗПР в условиях неопределенности)


 75
75 Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы.
Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы.

 В некотором смысле теория игр — это наука о стратегии или, по крайней мере, об оптимальном принятии решений независимыми и конкурирующими субъектами в стратегической обстановке.
В некотором смысле теория игр — это наука о стратегии или, по крайней мере, об оптимальном принятии решений независимыми и конкурирующими субъектами в стратегической обстановке.  40с. Многие считают математика Джона Нэша первым значительным продолжением работы фон Неймана и Моргенштерна.
40с. Многие считают математика Джона Нэша первым значительным продолжением работы фон Неймана и Моргенштерна.
 )
) Этот сценарий различных вариантов выбора в течение долгого времени до достижения равновесия чаще всего разыгрывается в деловом мире, когда две фирмы определяют цены на продукты с высокой степенью взаимозаменяемости, такие как авиабилеты или безалкогольные напитки.
Этот сценарий различных вариантов выбора в течение долгого времени до достижения равновесия чаще всего разыгрывается в деловом мире, когда две фирмы определяют цены на продукты с высокой степенью взаимозаменяемости, такие как авиабилеты или безалкогольные напитки. Теория игр переключила внимание с установившегося равновесия на рыночный процесс.
Теория игр переключила внимание с установившегося равновесия на рыночный процесс.
 Однако сторонние консультанты или внешние стороны, помогающие проекту, могут быть поощрены другими способами, не связанными с успехом проекта.
Однако сторонние консультанты или внешние стороны, помогающие проекту, могут быть поощрены другими способами, не связанными с успехом проекта. д.), наиболее распространенными являются кооперативные и некооперативные теории игр. Кооперативная теория игр имеет дело с тем, как взаимодействуют коалиции или кооперативные группы, когда известны только выигрыши. Это игра между коалициями игроков, а не между отдельными людьми, и в ней ставится вопрос о том, как формируются группы и как они распределяют выигрыш между игроками.
д.), наиболее распространенными являются кооперативные и некооперативные теории игр. Кооперативная теория игр имеет дело с тем, как взаимодействуют коалиции или кооперативные группы, когда известны только выигрыши. Это игра между коалициями игроков, а не между отдельными людьми, и в ней ставится вопрос о том, как формируются группы и как они распределяют выигрыш между игроками. Это означает, что на каждого победителя приходится проигравший. В качестве альтернативы это означает, что полученная коллективная чистая выгода равна потерянной коллективной чистой выгоде. Почти каждое спортивное событие представляет собой игру с нулевой суммой, в которой одна команда побеждает, а другая проигрывает.
Это означает, что на каждого победителя приходится проигравший. В качестве альтернативы это означает, что полученная коллективная чистая выгода равна потерянной коллективной чистой выгоде. Почти каждое спортивное событие представляет собой игру с нулевой суммой, в которой одна команда побеждает, а другая проигрывает. Это означает, что каждый участник должен постоянно принимать решения, в то время как их противник принимает решения. По мере того, как компании разрабатывают свои планы маркетинга, разработки продуктов и операционных планов, конкурирующие компании одновременно делают то же самое.
Это означает, что каждый участник должен постоянно принимать решения, в то время как их противник принимает решения. По мере того, как компании разрабатывают свои планы маркетинга, разработки продуктов и операционных планов, конкурирующие компании одновременно делают то же самое.
 Рассмотрим пример двух преступников, арестованных за преступление. У прокуратуры нет веских доказательств, чтобы осудить их. Однако для получения признания чиновники выводят заключенных из одиночных камер и допрашивают каждого в отдельных камерах. Ни один из заключенных не имеет возможности общаться друг с другом. Официальные лица представляют четыре сделки, часто отображаемые в виде поля 2 x 2.
Рассмотрим пример двух преступников, арестованных за преступление. У прокуратуры нет веских доказательств, чтобы осудить их. Однако для получения признания чиновники выводят заключенных из одиночных камер и допрашивают каждого в отдельных камерах. Ни один из заключенных не имеет возможности общаться друг с другом. Официальные лица представляют четыре сделки, часто отображаемые в виде поля 2 x 2. Равновесие Нэша предполагает, что в дилемме заключенного оба игрока сделают ход, который лучше для них по отдельности, но хуже для них в совокупности.
Равновесие Нэша предполагает, что в дилемме заключенного оба игрока сделают ход, который лучше для них по отдельности, но хуже для них в совокупности.
 Наихудший возможный результат реализуется, если никто не добровольно. Например, рассмотрим компанию, в которой процветает бухгалтерское мошенничество, хотя высшее руководство не знает об этом. Некоторые младшие сотрудники бухгалтерского отдела знают о мошенничестве, но не решаются сообщить об этом высшему руководству, потому что это приведет к увольнению сотрудников, причастных к мошенничеству, и, скорее всего, к судебному преследованию.
Наихудший возможный результат реализуется, если никто не добровольно. Например, рассмотрим компанию, в которой процветает бухгалтерское мошенничество, хотя высшее руководство не знает об этом. Некоторые младшие сотрудники бухгалтерского отдела знают о мошенничестве, но не решаются сообщить об этом высшему руководству, потому что это приведет к увольнению сотрудников, причастных к мошенничеству, и, скорее всего, к судебному преследованию.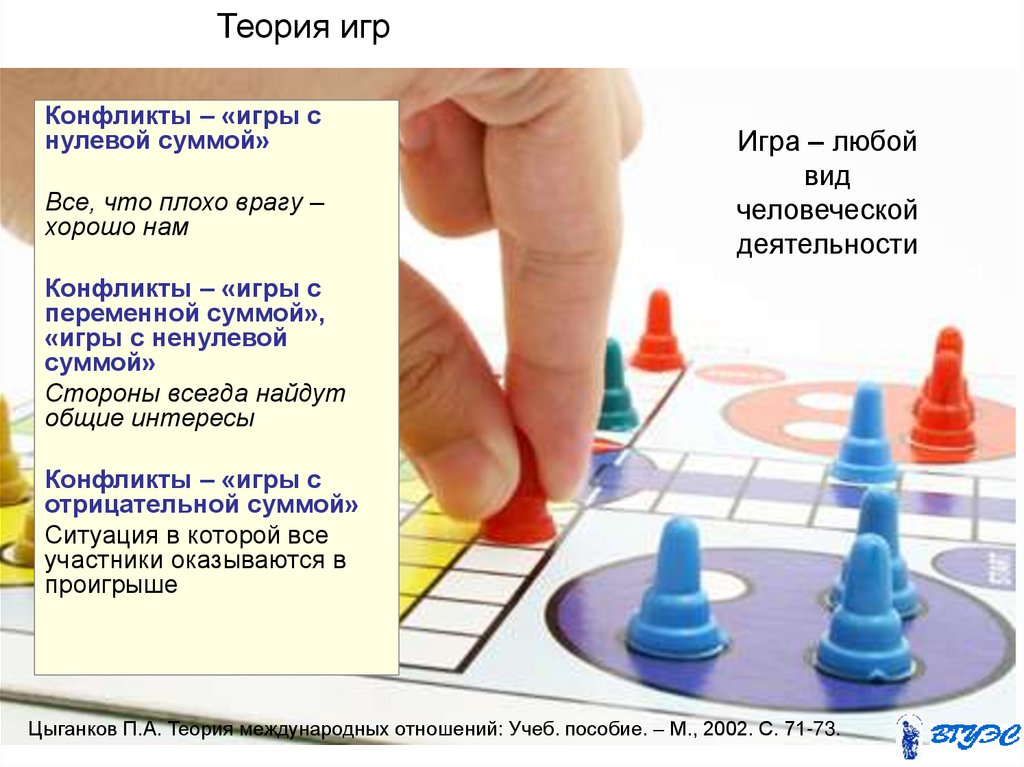
 Их новый продукт может привести к увеличению рыночной капитализации компании в пятьдесят раз. С другой стороны, неудачный запуск продукта сделает компанию банкротом. В любой ситуации участник готов рискнуть для достижения наилучшего результата, даже если возможен худший результат.
Их новый продукт может привести к увеличению рыночной капитализации компании в пятьдесят раз. С другой стороны, неудачный запуск продукта сделает компанию банкротом. В любой ситуации участник готов рискнуть для достижения наилучшего результата, даже если возможен худший результат. В бизнесе это может быть ситуация, когда компания решает масштабироваться и выйти на новый рынок, независимо от того, решила ли конкурирующая компания также выйти на рынок. В «Дилемме заключенного» доминирующей стратегией будет признание.
В бизнесе это может быть ситуация, когда компания решает масштабироваться и выйти на новый рынок, независимо от того, решила ли конкурирующая компания также выйти на рынок. В «Дилемме заключенного» доминирующей стратегией будет признание. Вместо этого питчер должен смешивать свою стратегию от подачи к подаче, чтобы создать ощущение непредсказуемости, от которого он надеется извлечь выгоду.
Вместо этого питчер должен смешивать свою стратегию от подачи к подаче, чтобы создать ощущение непредсказуемости, от которого он надеется извлечь выгоду. Теория игр может анализировать набор моделей поведения, но не может точно предсказать человеческий фактор.
Теория игр может анализировать набор моделей поведения, но не может точно предсказать человеческий фактор. Во-первых, все игроки являются рациональными акторами, стремящимися к максимизации полезности и обладающими полной информацией об игре, правилах и последствиях. Игрокам не разрешается общаться или взаимодействовать друг с другом. Возможные исходы не только известны заранее, но и не могут быть изменены. Теоретически количество игроков в игре может быть бесконечным, но в большинстве игр будет только два игрока.
Во-первых, все игроки являются рациональными акторами, стремящимися к максимизации полезности и обладающими полной информацией об игре, правилах и последствиях. Игрокам не разрешается общаться или взаимодействовать друг с другом. Возможные исходы не только известны заранее, но и не могут быть изменены. Теоретически количество игроков в игре может быть бесконечным, но в большинстве игр будет только два игрока. Это остается областью активных исследований и прикладной науки по сей день.
Это остается областью активных исследований и прикладной науки по сей день. Йена, Германия: Густав Фишер. [На немецком языке.] [Google Scholar]
Йена, Германия: Густав Фишер. [На немецком языке.] [Google Scholar] Тенденции Экол. Эвол. 11 , 92-98. ( 10.1016/0169-5347(96)81050-0) [PubMed] [CrossRef] [Google Scholar]
Тенденции Экол. Эвол. 11 , 92-98. ( 10.1016/0169-5347(96)81050-0) [PubMed] [CrossRef] [Google Scholar] Жене. 47 , 306-307. ( 10.1038/ng.3260) [PubMed] [CrossRef] [Google Scholar]
Жене. 47 , 306-307. ( 10.1038/ng.3260) [PubMed] [CrossRef] [Google Scholar] Теор. Народ. биол. 36 , 125-143. ( 10.1016/0040-5809(89)
Теор. Народ. биол. 36 , 125-143. ( 10.1016/0040-5809(89) Дж. Эксп. Зоол. Б 316 , 1-9. ( 10.1002/jez.b.21377) [PubMed] [CrossRef] [Google Scholar]
Дж. Эксп. Зоол. Б 316 , 1-9. ( 10.1002/jez.b.21377) [PubMed] [CrossRef] [Google Scholar] 1163/156853979X00449) [CrossRef] [Google Scholar]
1163/156853979X00449) [CrossRef] [Google Scholar] Дж. Теор. биол. 111 , 475-491. ( 10.1016/S0022-5193(84)80235-0) [CrossRef] [Google Scholar]
Дж. Теор. биол. 111 , 475-491. ( 10.1016/S0022-5193(84)80235-0) [CrossRef] [Google Scholar]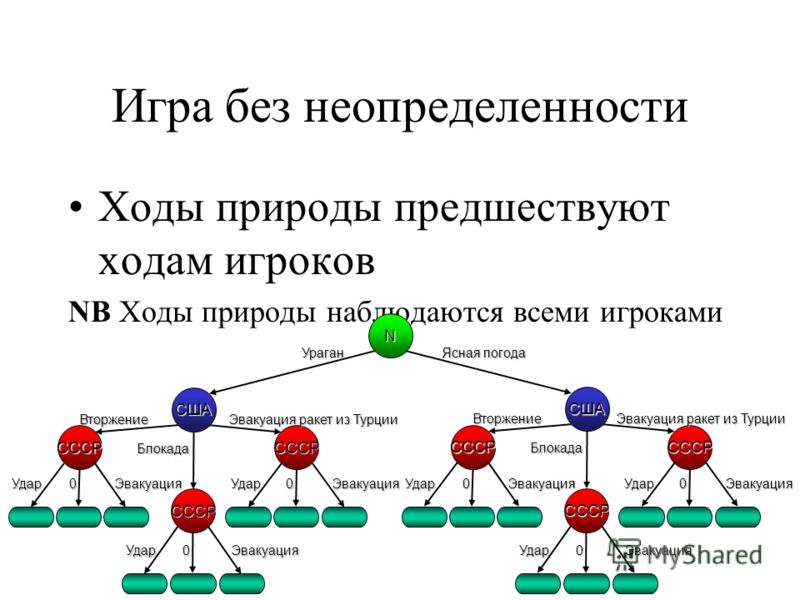 Хантингфорд Ф.А., Тейлор А.С., Смит И.П., Торп К.Е. 1995.
Поведенческие и физиологические исследования агрессии крабов-плавунцов. Дж. Эксп. Мар биол. Экол. 193 , 21-39. ( 10.1016/0022-0981(95)00108-5) [CrossRef] [Google Scholar]
Хантингфорд Ф.А., Тейлор А.С., Смит И.П., Торп К.Е. 1995.
Поведенческие и физиологические исследования агрессии крабов-плавунцов. Дж. Эксп. Мар биол. Экол. 193 , 21-39. ( 10.1016/0022-0981(95)00108-5) [CrossRef] [Google Scholar] Дж. Р. Кребс, Н. Б. Дэвис), стр. 282–309. Оксфорд, Великобритания: Научные публикации Блэквелла.
Дж. Р. Кребс, Н. Б. Дэвис), стр. 282–309. Оксфорд, Великобритания: Научные публикации Блэквелла. Дж. Теор. биол. 144 , 517-546. ( 10.1016/S0022-5193(05)80088-8) [PubMed] [CrossRef] [Google Scholar]
Дж. Теор. биол. 144 , 517-546. ( 10.1016/S0022-5193(05)80088-8) [PubMed] [CrossRef] [Google Scholar] Эвол. Экол. 2 , 115-138. ( 10.1007/BF02067272) [CrossRef] [Google Scholar]
Эвол. Экол. 2 , 115-138. ( 10.1007/BF02067272) [CrossRef] [Google Scholar] С., Эрре Э.А. 2001.
Проверка правила Гамильтона на соревновании между родственниками. Природа 409 , 510-513. ( 10.1038/35054057) [PubMed] [CrossRef] [Google Scholar]
С., Эрре Э.А. 2001.
Проверка правила Гамильтона на соревновании между родственниками. Природа 409 , 510-513. ( 10.1038/35054057) [PubMed] [CrossRef] [Google Scholar] ( 10.1016/S0003-3472(83)80027-X) [CrossRef] [Google Scholar]
( 10.1016/S0003-3472(83)80027-X) [CrossRef] [Google Scholar]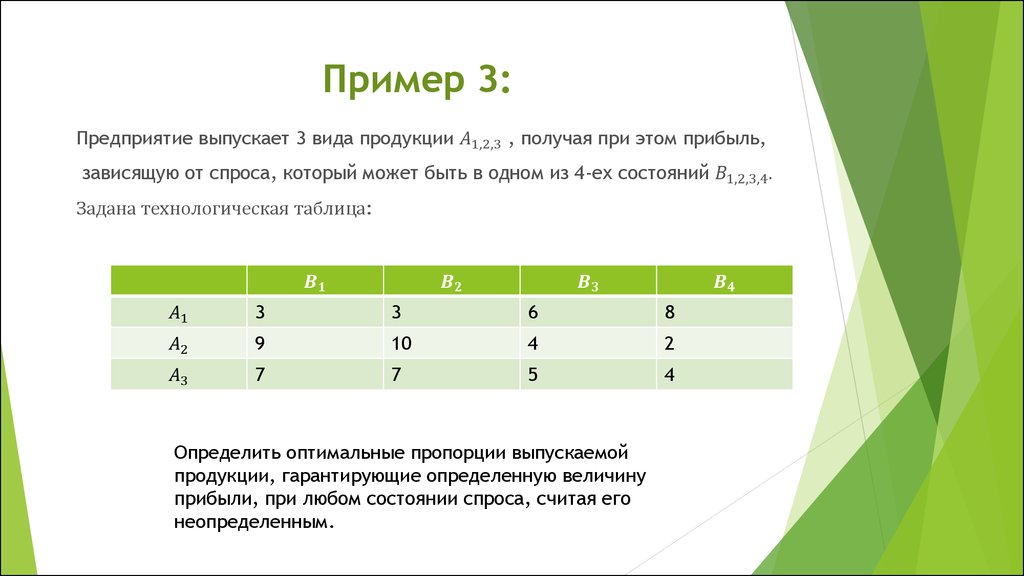 Местертон-Гиббонс М., Алан Дугаткин Л. 1995.
К теории иерархий доминирования: эффекты оценки, размер группы и различия в боевых способностях. Поведение Экол. 6 , 416-423. ( 10.1093/beheco/6.4.416) [CrossRef][Google Scholar]
Местертон-Гиббонс М., Алан Дугаткин Л. 1995.
К теории иерархий доминирования: эффекты оценки, размер группы и различия в боевых способностях. Поведение Экол. 6 , 416-423. ( 10.1093/beheco/6.4.416) [CrossRef][Google Scholar] биол. Преподобный Кэмб. Фил. соц. 81 , 33-74. ( 10.1017/S146479310500686X) [PubMed] [CrossRef] [Google Scholar]
биол. Преподобный Кэмб. Фил. соц. 81 , 33-74. ( 10.1017/S146479310500686X) [PubMed] [CrossRef] [Google Scholar]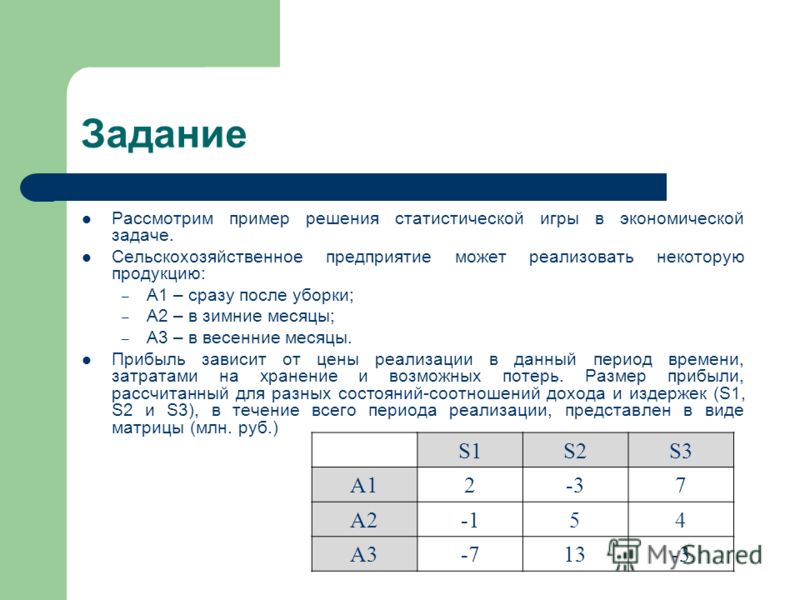 Дж. Аним. Экол. 91 , 1036-1046. ( 10.1111/1365-2656.13691) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Дж. Аним. Экол. 91 , 1036-1046. ( 10.1111/1365-2656.13691) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] 1988.
Различия между взаимным альтруизмом, родственным отбором и сотрудничеством и модель начальной эволюции благотворного поведения. этанол Социобиол. 9 , 189-209. ( 10.1016/0162-3095(88)
1988.
Различия между взаимным альтруизмом, родственным отбором и сотрудничеством и модель начальной эволюции благотворного поведения. этанол Социобиол. 9 , 189-209. ( 10.1016/0162-3095(88) Поведение наук о мозге. 7 , 115-116. ( 10.1017/S0140525X00026479) [CrossRef] [Google Scholar]
Поведение наук о мозге. 7 , 115-116. ( 10.1017/S0140525X00026479) [CrossRef] [Google Scholar] Леймар О. 1997.
Повторяющиеся игры: подход в пространстве состояний. Дж. Теор. биол. 184 , 471-498. ( 10.1006/jtbi.1996.0286) [CrossRef] [Google Scholar]
Леймар О. 1997.
Повторяющиеся игры: подход в пространстве состояний. Дж. Теор. биол. 184 , 471-498. ( 10.1006/jtbi.1996.0286) [CrossRef] [Google Scholar] ( 10.1002/bs.3830280108) [CrossRef] [Google Scholar]
( 10.1002/bs.3830280108) [CrossRef] [Google Scholar] 2019.03.015) [CrossRef] [Google Scholar]
2019.03.015) [CrossRef] [Google Scholar] Аним. Поведение 34 , 1562-1566. ( 10.1016/S0003-3472(86)80225-1) [CrossRef] [Google Scholar]
Аним. Поведение 34 , 1562-1566. ( 10.1016/S0003-3472(86)80225-1) [CrossRef] [Google Scholar] 1999.
Включение правил реагирования в эволюционные игры. Природа 401 , 368-371. ( 10.1038/43872) [PubMed] [CrossRef] [Google Scholar]
1999.
Включение правил реагирования в эволюционные игры. Природа 401 , 368-371. ( 10.1038/43872) [PubMed] [CrossRef] [Google Scholar] Социобиол. 35 , 1-11. ( 10.1007/BF00167053) [CrossRef] [Google Scholar]
Социобиол. 35 , 1-11. ( 10.1007/BF00167053) [CrossRef] [Google Scholar] Аним. Поведение 63 , 547-555. ( 10.1006/anbe.2001.1937) [CrossRef] [Google Scholar]
Аним. Поведение 63 , 547-555. ( 10.1006/anbe.2001.1937) [CrossRef] [Google Scholar] ( 10.1086/718315) [PubMed] [CrossRef] [Google Scholar]
( 10.1086/718315) [PubMed] [CrossRef] [Google Scholar] 23 , 416-419. ( 10.1016/j.tree.2008.04.011) [PubMed] [CrossRef] [Google Scholar]
23 , 416-419. ( 10.1016/j.tree.2008.04.011) [PubMed] [CrossRef] [Google Scholar] проц. Р. Соц. Б 280 , 20122573. ( 10.1098/rspb.2012.2573) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
проц. Р. Соц. Б 280 , 20122573. ( 10.1098/rspb.2012.2573) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
 5. Прямоугольная система координат
5. Прямоугольная система координат Линейно независимая система векторов
Линейно независимая система векторов 4. Уравнение плоскости в векторной форме
4. Уравнение плоскости в векторной форме . то самое черчение, которое изъяли из школьной программы.
. то самое черчение, которое изъяли из школьной программы. Если мы попробуем расположить эти…
Если мы попробуем расположить эти… Не замечаем потому, что её состояние не меняется, а значит, из сферы…
Не замечаем потому, что её состояние не меняется, а значит, из сферы… Детерминанты также имеют широкое применение в технике, науке, экономике и социальных науках. Теперь займемся определителем матрицы.
Детерминанты также имеют широкое применение в технике, науке, экономике и социальных науках. Теперь займемся определителем матрицы.


 Но, кроме решения систем, вы, скорее всего, не увидите ничего интересного в ближайшие несколько лет.
Но, кроме решения систем, вы, скорее всего, не увидите ничего интересного в ближайшие несколько лет. ..
.. ..формула для определителя 2×2: ad − cb .
..формула для определителя 2×2: ad − cb .
 Символ называется радикалом , термин под этим символом называется радикалом и , а все выражение называется радикальным выражением .
Символ называется радикалом , термин под этим символом называется радикалом и , а все выражение называется радикальным выражением . Порядок операций требует, чтобы мы складывали члены в подкоренной формуле, прежде чем находить квадратный корень.
Порядок операций требует, чтобы мы складывали члены в подкоренной формуле, прежде чем находить квадратный корень.  Мы также можем использовать правило произведения, чтобы выразить произведение нескольких подкоренных выражений в виде одного подкоренного выражения.
Мы также можем использовать правило произведения, чтобы выразить произведение нескольких подкоренных выражений в виде одного подкоренного выражения.

 (где a ≠0)
(где a ≠0)
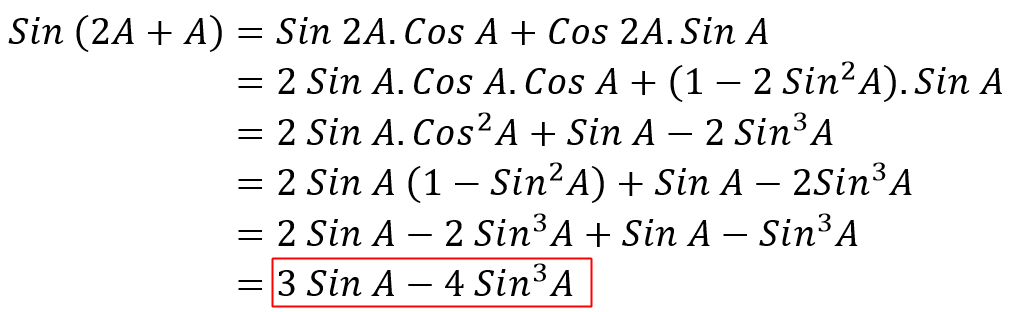 )
) )
) )
) )
) )
) )
) )
) 3a если sina+cosa=0,8 — вопрос №1918398 — Учеба и наука
3a если sina+cosa=0,8 — вопрос №1918398 — Учеба и наука 04.16
04.16 2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение… )/3
)/3
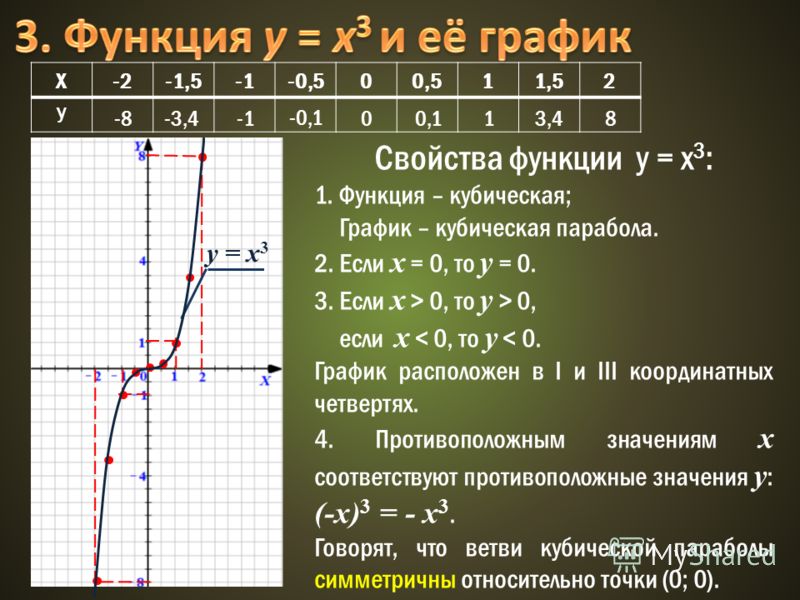 05.13
05.13  by 2013-2016
by 2013-2016 2-9x,null,0,0,,,black,1,none»/>
2-9x,null,0,0,,,black,1,none»/> в 18:48:45.
в 18:48:45.

 д.). Не забываем параллельно добавлять нули и в знаменателе:
д.). Не забываем параллельно добавлять нули и в знаменателе:

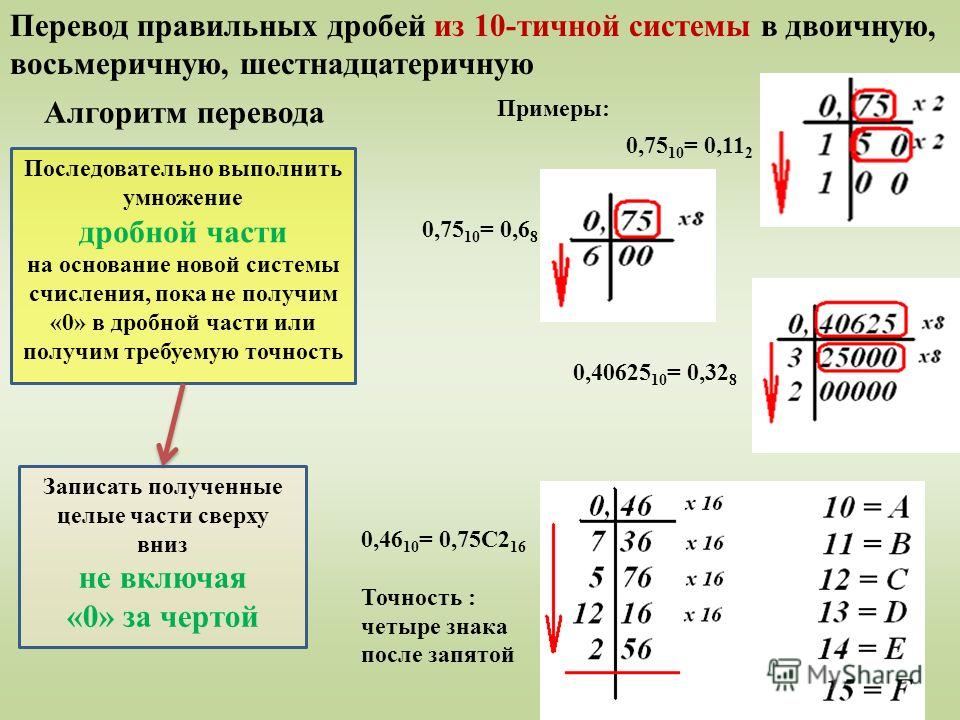 5 класс
5 класс Например, Дэвид, ученик класса Чада, работает машинистом. Машинисты производят металлические детали с точностью до одной тысячной дюйма. Если вы постоянно работаете с десятичными дробями, вы можете забыть, как работать с дробями, поэтому Дэвид хочет знать, как преобразовать эти десятичные дроби в дроби. Лучший способ проиллюстрировать, как это сделать, — просто привести пример.
Например, Дэвид, ученик класса Чада, работает машинистом. Машинисты производят металлические детали с точностью до одной тысячной дюйма. Если вы постоянно работаете с десятичными дробями, вы можете забыть, как работать с дробями, поэтому Дэвид хочет знать, как преобразовать эти десятичные дроби в дроби. Лучший способ проиллюстрировать, как это сделать, — просто привести пример. числитель и знаменатель и умножьте каждый на 10 для каждой цифры справа от запятой. В этом случае у нас есть 3 цифры справа. Поэтому умножаем каждую на 1000 (10×10×10).
числитель и знаменатель и умножьте каждый на 10 для каждой цифры справа от запятой. В этом случае у нас есть 3 цифры справа. Поэтому умножаем каждую на 1000 (10×10×10). Вы когда-нибудь были на строительной площадке, и ваш начальник попросил вас отрезать кусок трубы или, может быть, кусок дерева? Каково было измерение? Может быть, это было что-то вроде 8 ⅜ дюймов. Может быть, это было 2 фута 2 ¼ дюйма. Это довольно стандартно.
Вы когда-нибудь были на строительной площадке, и ваш начальник попросил вас отрезать кусок трубы или, может быть, кусок дерева? Каково было измерение? Может быть, это было что-то вроде 8 ⅜ дюймов. Может быть, это было 2 фута 2 ¼ дюйма. Это довольно стандартно. Что нам нужно сделать в первую очередь, так это преобразовать 0,9384 в дюймы, прежде чем переходить к долям дюйма. Начните с того, сколько дюймов в футе.
Что нам нужно сделать в первую очередь, так это преобразовать 0,9384 в дюймы, прежде чем переходить к долям дюйма. Начните с того, сколько дюймов в футе. 2608\times16=4.1728[/латекс]
2608\times16=4.1728[/латекс] Нам нужно изменить десятичную дробь дюйма на шестнадцатые, поэтому умножьте это на 16.
Нам нужно изменить десятичную дробь дюйма на шестнадцатые, поэтому умножьте это на 16. Правильный способ записи дроби —
Правильный способ записи дроби — Мы будем рассматривать разные знаменатели, чтобы понять, как эти термины читаются с этим числителем.
Мы будем рассматривать разные знаменатели, чтобы понять, как эти термины читаются с этим числителем. Здесь 3 x 5/2 x 5 дает 15/10.
Здесь 3 x 5/2 x 5 дает 15/10.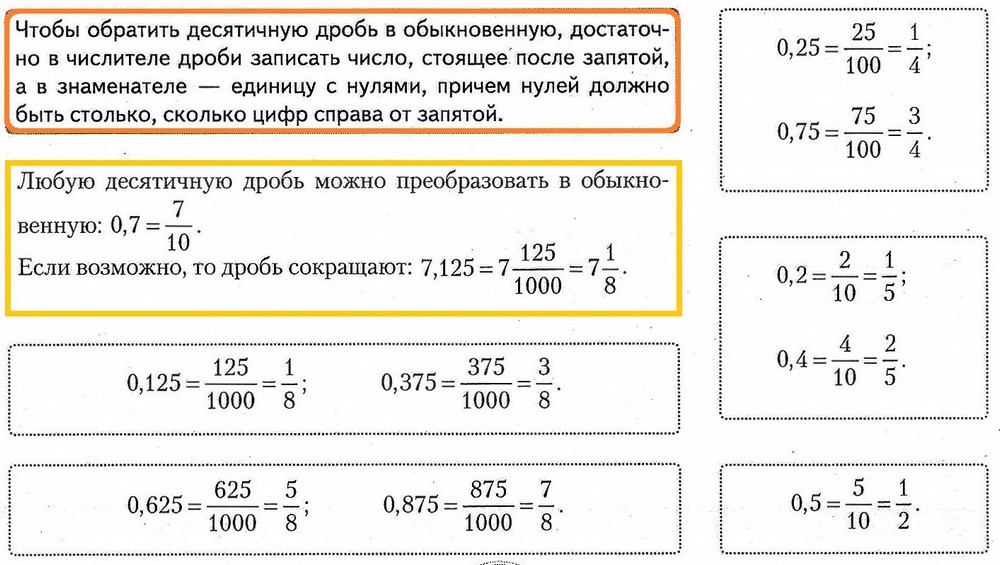 Вы также будете использовать их для выражения процентов. Например, 97% можно записать как 97/100 для простоты вычисления.
Вы также будете использовать их для выражения процентов. Например, 97% можно записать как 97/100 для простоты вычисления. Первым шагом к лучшему пониманию десятичных чисел является ежедневное выполнение задач с десятичными дробями. Идея взять ручку и бумагу для решения задач скучна и неинтересна для учащихся. Им нужны развлекательные способы, чтобы побудить их к практике сумм.
Первым шагом к лучшему пониманию десятичных чисел является ежедневное выполнение задач с десятичными дробями. Идея взять ручку и бумагу для решения задач скучна и неинтересна для учащихся. Им нужны развлекательные способы, чтобы побудить их к практике сумм.
