Острый угол
Содержание:
- Какой угол называется острым в математике
- Определение, основные признаки и свойства
- Примеры решения задач
Содержание
- Какой угол называется острым в математике
- Определение, основные признаки и свойства
- Примеры решения задач
Какой угол называется острым в математике
Угол представляет собой геометрическую фигуру, которая образована с помощью пары лучей. Данные линии называют сторонами. Они берут начало в одной точке, называемой вершиной. Согласно основным признаком геометрической фигуры, можно сформулировать ее понятие.
Данные линии называют сторонами. Они берут начало в одной точке, называемой вершиной. Согласно основным признаком геометрической фигуры, можно сформулировать ее понятие.
Угол является геометрической фигурой, состоящей из пары лучей в виде ее сторон, которые выходят из одной точки или вершины.
Данные фигуры в геометрии подразделяют на типы в зависимости от градусной величины, расположению относительно друг друга и относительно окружности. Основными видами являются:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- прямой;
- тупой;
- острый;
- развернутый.
Градусная мера, которой обладает острый угол, менее 90 градусов. Данный вид геометрической фигуры можно встретить в каждом четырехугольнике, если он не является прямоугольным квадратом или произвольным параллелограммом. Острый угол можно полностью вписать во внутреннее пространство прямого, а одна из его сторон является биссектрисой. Пример острого угла АОВ изображен на рисунке:
Острый угол можно полностью вписать во внутреннее пространство прямого, а одна из его сторон является биссектрисой. Пример острого угла АОВ изображен на рисунке:
Определение, основные признаки и свойства
ОпределениеОстрый угол – это геометрическая фигура, градусная мера которой составляет менее 90 градусов.
Источник: webmath.ruДля всех острых углов характерна градусная мера в интервале от 0 до 90 градусов. Простым способом распознавания типа угла является использование предмета, который имеет прямой угол. Его прикладывают к искомому элементу таким образом, чтобы их вершины были совмещены. Примером такого инструмента является линейка. Возможно два варианта результата измерений:
- прямой угол целиком вмещает в себя начерченный, тогда измеряемый угол является острым;
- нарисованный угол помещает в себя прямой, тогда рассматриваемый угол является тупым.
Точным инструментом для измерения градусной меры является транспортир, который состоит из линейки и полуокружности. Пользоваться им несложно. Достаточно приложить центр транспортира к вершине фигуры таким образом, чтобы любой из его сторон совпадал с гранью линейки. Второй луч покажет градусы, соответствующие геометрической фигуре.
Пользоваться им несложно. Достаточно приложить центр транспортира к вершине фигуры таким образом, чтобы любой из его сторон совпадал с гранью линейки. Второй луч покажет градусы, соответствующие геометрической фигуре.
Транспортир также применяют, когда необходимо начертить тупой или острый угол:
- провести один луч;
- начало линии совместить с центром инструмента;
- приложить линейку к нужному числу градусов и провести линию.
Особенности рассматриваемой геометрической фигуры:
- если один из смежных углов острый, то второй в любом случае окажется тупым;
- каждый треугольник обладает как минимум одним острым углом;
- есть треугольники, все углы которых являются острыми, их называют остроугольными.
Примеры решения задач
Задача 1
С помощью рисунка необходимо найти острые углы.
Источник: webmath.ruРешение
Стороны фигуры, изображенной на первом рисунке, перпендикулярны друг другу. Поэтому его нельзя назвать острым. На втором рисунке начерчен угол, который меньше, чем прямой.
Поэтому его нельзя назвать острым. На втором рисунке начерчен угол, который меньше, чем прямой.
Согласно определению, данный угол является острым. Если сравнить угол, который изображен на третьем рисунке, с прямым, то можно сделать вывод, что он тупой, так как его градусная мера составляет больше, чем 90 градусов.
Источник: webmath.ruОтвет: острым является угол, который изображен на втором рисунке.
Задача 2
Имеется пара смежных углов. Один из них больше, чем второй на 30 градусов. Требуется определить, какой из этих углов является острым.
Решение
Обозначим меньший угол буквой х. Тогда (х+30) является большим углом. Известно, что сумма смежных углов составляет 180 градусов. Можно записать справедливое равенство:
х + (х + 30) = 180
2х = 150
х = 75
75 < 90
Ответ: меньший угол, который составляет 75 градусов, будет острым.
Насколько полезной была для вас статья?
Рейтинг: 5. 00 (Голосов: 2)
00 (Голосов: 2)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
что это такое, признаки и свойства, примеры решения задач
Содержание:
- Что такое острый угол
- Признаки и свойства острых углов
- Примеры решения задач
Содержание
- Что такое острый угол
- Признаки и свойства острых углов
- Примеры решения задач
Что такое острый угол
Острым углом принято обозначать такой угол, который меньше по сравнению с прямым, то есть имеет градусную меру больше, чем ноль, но меньше, чем 90°.
Изобразим на рисунке, как выглядит острый угол, исходя из рассмотренного определения:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: www.treugolniki.ru
На уроках геометрии и математике при решении различных задач школьники пользуются специальными измерительными и чертежными инструментами. Одним из таких полезных приспособлений является транспортир. С его помощью можно достаточно быстро и просто выполнить построение острого угла какой-либо градусной меры.
Порядок действий при построении острого угла с применением транспортира:
- Отметить некую точку на листе бумаги, которая будет играть роль вершины заданного угла.
- Используя полученную точку, построить луч, вершина которого совпадает с ней. Данный луч является одной из сторон искомого угла.
- С помощью транспортира совместим вершину угла с отверстием, расположенным по центру инструмента, таким образом, чтобы отмеченный на нем ноль градусов совпал с определенной ранее стороной угла.

- Предположим, что необходимо рассмотренным способом начертить угол в 72°. На шкале транспортира в данном случае потребуется найти отметку в соответствии с заданной градусной мерой и нарисовать точку.
- Далее следует соединить полученную точку с вершиной угла с помощью луча, который является второй стороной искомого угла.
Перенесем рассмотренную схему изображения острого угла в 72°. Заметим, что отчет градусной меры допустимо начинать с нижней или верхней шкалы, отмеченной на транспортире:
Источник: www.treugolniki.ru
Признаки и свойства острых углов
Перечислим свойства, которые характерны для любого острого угла:
- При рассмотрении пары смежных углов, один из которых меньше по сравнению с прямым, то есть определяется как острый, можно сделать вывод, что второй из смежных углов является тупым.
- Какой-либо произвольный треугольник обладает как минимум одним острым углом.

- Треугольники, которые образованы тремя острыми углами, носят название остроугольных.
Признаком любого острого угла является его градусная мера, которая в любом случае будет меньше, чем 90°. В геометрии часто встречаются задачи, когда необходимо идентифицировать тот или иной угол по его признаку. Тогда целесообразно воспользоваться еще одним полезным инструментом под названием угольник.
В качестве примера воспользуемся угольником и соединим его вершину с вершиной искомого угла, который необходимо идентифицировать. При этом расположим угольник так, чтобы его грань проходила по какой-нибудь одной стороне рассматриваемого угла. В результате другая сторона измерительного инструмента перекроет вторую сторону угла. Изобразим схематично принцип выполнения этой процедуры:
Источник: www.treugolniki.ru
Примеры решения задач
Задача 1На рисунке изображено несколько углов.Требуется выяснить, какой из представленных углов является острым.
Решение
Воспользуемся определением острого угла и вспомним, что его градусная мера меньше, чем 90°.
Рассмотрим изображение угла на рисунке (а). Заметим, что в данном случае одна сторона угла играет роль перпендикуляра по отношению ко второй. Тогда угол, который расположен между ними, составляет 90°. Сделаем вывод, что такой угол является прямым.
Далее обратимся к рисунку (б). Построим к одной из сторон угла перпендикуляр. Изобразим это действие наглядно, дополнив начальное изображение:
Заметим, что угол меньше по сравнению с прямым. Это утверждение полностью соответствует понятию острого угла. Сделаем вывод о том, что угол, изображенный на рисунке (б), является острым.
Перейдем к третьему варианту. Аналогично предыдущему примеру, построим перпендикулярную прямую к углу, изображенному на рисунке (в), которая проходит через его вершину:
Заметим, что искомый угол больше по сравнению с прямым, то есть имеет такую градусную меру, которая превышает 90°. Данный угол можно идентифицировать как тупой. Он не является острым.
Данный угол можно идентифицировать как тупой. Он не является острым.
Ответ: острым является угол, изображенный на рисунке (б).
Задача 2Имеется пара смежных углов. Один из них имеет градусную меру, которая на 30° меньше, чем у второго. Необходимо определить, чему равен острый угол.
Решение
Введем обозначение х для неизвестного острого угла. В таком случае угол, градусная мера которого больше, можно записать в виде следующего выражения:
х + 30
Вспомним, что острый угол обладает полезным свойством. При рассмотрении пары смежных углов, один из которых меньше по сравнению с прямым, то есть определяется как острый, можно сделать вывод, что второй из смежных углов является тупым. В сумме смежные углы составляют 180°. Запишем справедливое равенство:
х + (х+30) = 180
2х = 150
х = 75
Угол, который ранее был обозначен за х, составляет 75°. Заметим, что такая градусная мера меньше, чем 90°. На основании этого факта острый угол равен 75°.
Ответ: 75°.
Задача 3На рисунке изображена окружность с центром в точке О. К окружности построена касательная СА, которая играет роль одной из сторон угла с вершиной в точке С. Вторая сторона угла пересекает точку О. Градусная мера полученной дуги АD составляет 100°. Необходимо вычислить, чему равен угол АСО.
Решение
Построим в заданной окружности радиус, который обозначим как ОА. Перенесем действия на рисунок:
Заметим, что полученный треугольник АОС имеет прямой угол, то есть по определению является прямоугольным:
АОС = 90°
Вспомним, что в сумме все углы в треугольнике составляют 180°. На основании этого соотношения вычислим градусную меру угла СОА:
СОА = 180 – АОD = 180 – 100 = 80
В результате угол АОС составит:
АОС = 90 – 80 = 10
Ответ: 10°
Задача 4На рисунке изображены два смежных угла. Необходимо вычислить, чему равен угол АОЕ при условии, что ОЕ является биссектрисой угла АОС. Аналогично, ОD играет роль биссектрисы угла СОВ. Градусная мера угла ВОD составляет 25°. Необходимо вычислить угол АОЕ.
Аналогично, ОD играет роль биссектрисы угла СОВ. Градусная мера угла ВОD составляет 25°. Необходимо вычислить угол АОЕ.
Решение
Исходя из того, что биссектриса делит угол на две равные части, вычислим градусную меру угла СОВ:
СОВ = \(25 \cdot 2\) = 50
Развернутый угол АОВ составляет 180° по определению. Тогда можно найти величину угла АОС:
АОС = 180 – 50 = 130
Зная, что биссектриса ОЕ делит угол АОС на два равных угла, получим, что искомый угол АОЕ равен:
АОЕ = \(130 \div 2\) = 65
Ответ: 65°.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Острый угол Определение и значение
- Лучшие определения
- Викторина
- Подробнее об остром угле
- Примеры
- Культура
Угол, градусная мера которого лежит в пределах от 0° до 90°. Сравните тупой угол.
Сравните тупой угол.
ВИКТОРИНА
МОЖЕТЕ ЛИ ВЫ ОТВЕЧАТЬ НА ЭТИ ОБЫЧНЫЕ ГРАММАТИЧЕСКИЕ СПОРЫ?
Есть грамматические дебаты, которые никогда не умирают; и те, которые выделены в вопросах этой викторины, наверняка снова всех разозлят. Знаете ли вы, как отвечать на вопросы, которые вызывают самые ожесточенные споры по грамматике?
Вопрос 1 из 7
Какое предложение правильное?
Слова рядом с острым углом
acus, acusector, acutance, острый, острый акцент, острый угол, острый свод, неотложная помощь, острая болезнь, острая доза, остро
Научный словарь American Heritage® Copyright © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
ПОДРОБНЕЕ ОБ ОСТРОМ УГЛЕ
Что такое острый угол
? Острый угол — это угол, который измеряется между 90° и 0°, что означает, что он меньше прямого угла (L-образная форма), но имеет по крайней мере некоторое пространство между двумя образующими его линиями. Форма «V» является примером острого угла .
Форма «V» является примером острого угла .
Угол – это пространство между двумя пересекающимися линиями или плоскостями (поверхностями) или фигура, образованная таким пересечением. Углы обычно измеряются в градусах (°). (Они не связаны с градусами, используемыми для измерения температуры.)
Острые углы — это основная концепция геометрии с большим количеством приложений. Инженерия и архитектура полагаются на знание углов и способов их точного измерения.
Почему
острый угол важен в геометрии?Вы когда-нибудь пользовались транспортиром? Если да, то вы, вероятно, помните, что использовали его для измерения углов. Три основных вида углов: прямые углы, тупые углы , и острые углы. Если базовая геометрическая фигура состоит из прямых линий (извините, кругов), она содержит по крайней мере один из этих трех типов углов.
В квадрате четыре внутренних угла являются четырьмя углами квадрата. Все эти углы прямые (каждый равен 90°). Если вы возьмете один из этих углов и переместите одну линию ближе к другой, сузив пространство между ними, угол будет меньше 90° и будет острым углом. Угол больше 90° называется тупой угол. Если продолжать увеличивать угол, в конечном итоге он составит 180° и будет выглядеть точно как прямая линия.
Все эти углы прямые (каждый равен 90°). Если вы возьмете один из этих углов и переместите одну линию ближе к другой, сузив пространство между ними, угол будет меньше 90° и будет острым углом. Угол больше 90° называется тупой угол. Если продолжать увеличивать угол, в конечном итоге он составит 180° и будет выглядеть точно как прямая линия.
Понимание разницы между углами — один из первых уроков геометрии, а понимание этой основной идеи — отправная точка для изучения более сложных геометрических понятий. Острые углы (а также прямые и тупые углы) важны во многих областях, которые полагаются на геометрию и точное измерение форм. Просто подумайте о том, сколько углов в вашем доме, и вы поймете, насколько важны углы для архитектуры.
Знаете ли вы…?
Сумма трех углов треугольника всегда равна 180°. Это означает, что по крайней мере два угла треугольника всегда будут острыми углами. Треугольник, состоящий из трех одинаковых острых углов по 60°, называется равносторонним треугольником.
Каковы реальные примеры
острых углов ?Как только вы узнаете, как выглядят острые углы, вы, вероятно, начнете замечать их в повседневных предметах.
Matisfun.com
Линия роста волос Дрейка действительно раньше была острым углом??? 💀 https://t.co/gyHLB7gW0Z
— Джон (@__Cephei) 15 ноября 2019 г.
Каждый раз, когда я сгибаю колено под острым углом, я чувствую натяжение и легкий щелчок за правым коленом 😂
— Trap Money 🐂 (@fwitter_life) 15 ноября 2019 г.
Проверьте себя!
Острый угол — это угол, который равен:
A. Равен 90°
B. Меньше 90°
C. Больше 90°Как использовать острый угол в предложении
Проехав несколько лиг, мы повернули под острым углом, который вывел нас на главную дорогу, и в тот же день мы прибыли в Ику.
Путешествие в Перу, на побережье, в Сьерру, через Кордильеры и Анды, в первобытные леса|J. Дж. фон Чуди
Их наружные отверстия подобны двум щелям, которые не лежат параллельно, а образуют друг с другом острый угол.
Книга курьезов|I. Platts
Судно было сломано на миделе, корма и нос торчали из воды под острым углом.
Героический рекорд британского флота|Арчибальд Херд
В этой первой форме мотыги острие повернуто так, что образует острый угол с рукояткой, к которой оно прикреплено.
Элементы народной психологии|Вильгельм Вундт
Продолжая двигаться на юго-запад, мы подошли под острым углом к большой главной дороге между Лхасой и Ладаком, так называемому тасаму.
Транс-Гималаи, Том. 2 (из 2)|Свен Хедин
Культурные определения острого угла
острый угол
Угол, размер которого меньше девяноста градусов, но больше нуля градусов.
(Сравните тупой угол и прямой угол.)
Новый словарь культурной грамотности, третье издание Авторское право © 2005 г., издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Определения острого угла и примеры
Определения острого угла и примеры
Острый угол
Острый угол — это тип угла между двумя точками на плоскости. Прямой острый угол – это угол, который равен 90 градусам. Острый угол можно измерить транспортиром или линейкой.
Примером острого угла является угол между двумя точками на полу. Если кто-то стоит перед одной точкой и поднимает левую ногу так, что пятка касается второй точки, то его левая лодыжка образует с полом острый угол.
Что такое острый угол?
Острый угол — это мера в градусах между двумя углами, обычно измеряемая от вершины одного угла до вершины другого.
Острые углы обычно используются в геометрии и тригонометрии для измерения расстояний и углов между точками и могут быть представлены символом.
Некоторые примеры острых углов включают 30 градусов, 45 градусов, 60 градусов и 90 градусов. Острые углы также можно измерить транспортиром или линейкой.
Определение острого угла
Острый угол — это угловая мера, имеющая меньшее численное значение, чем прямой угол. Острые углы также известны как «согнутые углы». В геометрии острые углы используются для определения размера и формы объектов. Чем меньше угол, тем точнее определение.
Градус острого угла
Есть несколько вещей, которые вы должны знать об острых углах.
1) Угол между двумя прямыми всегда острый.
2) Острые углы измеряются в градусах.
3) Прямой угол равен 120 градусам.
4) Острый угол можно найти, сложив углы, образованные пересекающими его прямыми.Реальные примеры острых углов
Есть несколько реальных примеров острых углов, с которыми вы можете столкнуться в повседневной жизни.
Например, когда вы ведете машину и видите грузовик, припаркованный под углом к дороге. Это острый угол, потому что он не указывает прямо на автомобиль. Другой пример: вы идете по тротуару и видите бордюр под острым углом от земли.
Острый угол Свойства треугольника
Есть несколько свойств, которые следует учитывать при работе с острыми углами. Во-первых, острый угол — это любой угол, который меньше 90 градусов. Во-вторых, острый угол считается меньшим, если он составляет от 30 до 59°.градусов и больше, если он измеряет 60 или более градусов. Наконец, острые углы можно описать с помощью радианов или градусов.
Формула острого угла
Формула острого угла — это математическая формула, используемая для расчета величины угла между двумя точками.
Острый угол между двумя точками является мерой того, насколько широкий угол измеряется от его большей стороны. Чем меньше значение, тем уже угол.
Примеры острого угла
Острый угол — это угол, размер которого меньше 90 градусов.




 (Сравните тупой угол и прямой угол.)
(Сравните тупой угол и прямой угол.) Острые углы обычно используются в геометрии и тригонометрии для измерения расстояний и углов между точками и могут быть представлены символом.
Острые углы обычно используются в геометрии и тригонометрии для измерения расстояний и углов между точками и могут быть представлены символом.


 Вы можете преобразовать практически любой тип документа в PDF: DOCX, XLSX, PPTX, HTML, TXT, PDF, EPUB, PNG, BMP, GIF, JPG, ODD, SVG, SWF, TIFF, CSV и многие другие (прокрутите ниже, чтобы увидеть полный список).
Вы можете преобразовать практически любой тип документа в PDF: DOCX, XLSX, PPTX, HTML, TXT, PDF, EPUB, PNG, BMP, GIF, JPG, ODD, SVG, SWF, TIFF, CSV и многие другие (прокрутите ниже, чтобы увидеть полный список). Загрузите все свои документы, и наш онлайн-конвертер PDF создаст из них PDF-файлы.
Загрузите все свои документы, и наш онлайн-конвертер PDF создаст из них PDF-файлы. Просто попробуйте конвертацию и посмотрите на результат.
Просто попробуйте конвертацию и посмотрите на результат.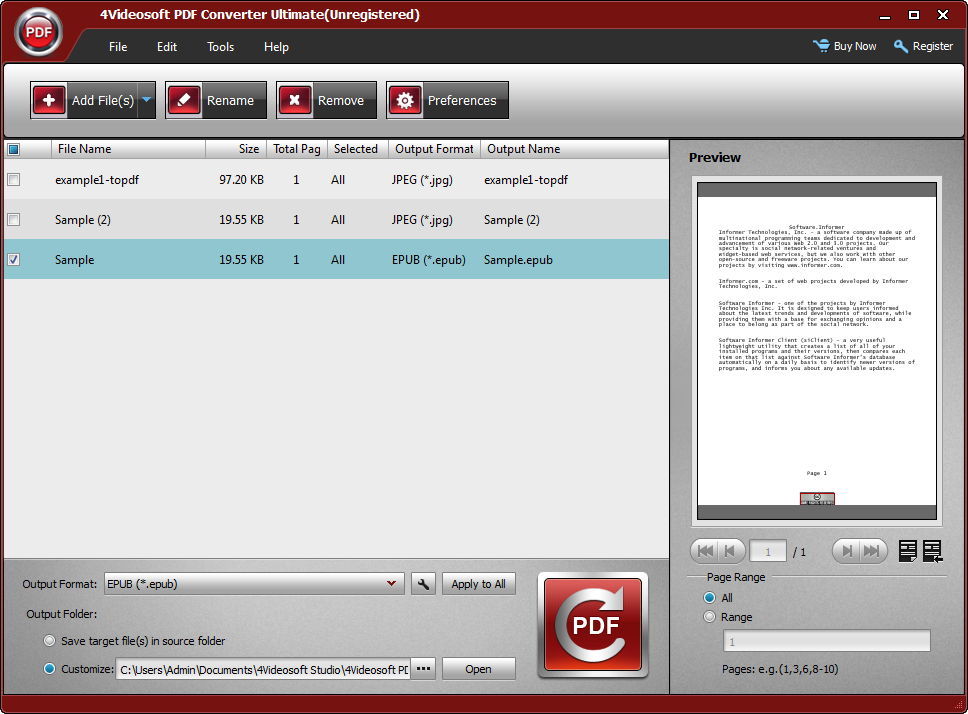

 Он также может разбивать PDF по закладкам или пустым страницам. Total PDF Converter изменит дату файла или сохранит исходные метки времени. Просто установите соответствующий флажок. Подписывайте PDF-документы своей цифровой подписью в процессе преобразования файлов. Объединение нескольких PDF-файлов в один многостраничный документ с помощью мощного пакетного конвертера PDF. Total PDF Converter может автоматически поворачивать ваши документы. Конвертер PDF в Word для вашего удобства поддерживает форматы Doc и DOCX. Преобразовать PDF в JPG? Настройте финальное изображение в соответствии с вашими потребностями. Установите желаемое качество изображения JPEG, чтобы уменьшить размер файла. Приложение также извлекает выбранные страницы и конвертирует их в JPEG. Конвертируйте файлы PDF/PS/EPS/PRN с помощью нашего понятного интерфейса с множеством подсказок для начинающих. Самый широкий список типов выходных файлов: DOC, DOCX, RTF, XLS, HTML, BMP, JPEG, GIF, WMF, EMF, PNG, EPS, PS, TIFF, TXT, CSV, PDF/A и PDF! Total PDF Converter может объединять несколько файлов PDF в одно изображение TIFF.
Он также может разбивать PDF по закладкам или пустым страницам. Total PDF Converter изменит дату файла или сохранит исходные метки времени. Просто установите соответствующий флажок. Подписывайте PDF-документы своей цифровой подписью в процессе преобразования файлов. Объединение нескольких PDF-файлов в один многостраничный документ с помощью мощного пакетного конвертера PDF. Total PDF Converter может автоматически поворачивать ваши документы. Конвертер PDF в Word для вашего удобства поддерживает форматы Doc и DOCX. Преобразовать PDF в JPG? Настройте финальное изображение в соответствии с вашими потребностями. Установите желаемое качество изображения JPEG, чтобы уменьшить размер файла. Приложение также извлекает выбранные страницы и конвертирует их в JPEG. Конвертируйте файлы PDF/PS/EPS/PRN с помощью нашего понятного интерфейса с множеством подсказок для начинающих. Самый широкий список типов выходных файлов: DOC, DOCX, RTF, XLS, HTML, BMP, JPEG, GIF, WMF, EMF, PNG, EPS, PS, TIFF, TXT, CSV, PDF/A и PDF! Total PDF Converter может объединять несколько файлов PDF в одно изображение TIFF. Или поместите каждую страницу многостраничного PDF-файла в новый файл TIFF. Настройте вывод: установите новые поля в дюймах в соответствии с вашими стандартами (готово к печати). Каждый файл PDF отображается на панели предварительного просмотра. Вы можете увеличивать/уменьшать масштаб или просматривать документ в полном размере. Опция предварительного просмотра позволяет легко найти нужный PDF-файл. Добавьте текстовые или графические водяные знаки в верхний или нижний колонтитул выходного файла. Он также идеально подходит для штамповки бейтса! Хотите больше заказов? Добавление пагинации (доступна порядковая нумерация папок). Total PDF Converter может извлекать для вас четные и нечетные страницы. В отличие от бесплатных конвертеров PDF, наше приложение обрабатывает тысячи документов, сохраняя структуру папок. Независимо от того, какой у вас MS Office, наше приложение может конвертировать PDF в DOC и DocX. Мы также предлагаем PDF Converter SDK для Web\SQL server\ASP\.
Или поместите каждую страницу многостраничного PDF-файла в новый файл TIFF. Настройте вывод: установите новые поля в дюймах в соответствии с вашими стандартами (готово к печати). Каждый файл PDF отображается на панели предварительного просмотра. Вы можете увеличивать/уменьшать масштаб или просматривать документ в полном размере. Опция предварительного просмотра позволяет легко найти нужный PDF-файл. Добавьте текстовые или графические водяные знаки в верхний или нижний колонтитул выходного файла. Он также идеально подходит для штамповки бейтса! Хотите больше заказов? Добавление пагинации (доступна порядковая нумерация папок). Total PDF Converter может извлекать для вас четные и нечетные страницы. В отличие от бесплатных конвертеров PDF, наше приложение обрабатывает тысячи документов, сохраняя структуру папок. Независимо от того, какой у вас MS Office, наше приложение может конвертировать PDF в DOC и DocX. Мы также предлагаем PDF Converter SDK для Web\SQL server\ASP\. NET\C#. С помощью ActiveX вы можете легко внедрить наш PDF-конвертер в свое приложение и распространить его среди конечных пользователей. Total PDF Converter имеет полную поддержку командной строки (получите готовую командную строку из графического интерфейса).
NET\C#. С помощью ActiveX вы можете легко внедрить наш PDF-конвертер в свое приложение и распространить его среди конечных пользователей. Total PDF Converter имеет полную поддержку командной строки (получите готовую командную строку из графического интерфейса).
 Настольная версия не требует подключения к Интернету, поэтому утечки невозможны.
Настольная версия не требует подключения к Интернету, поэтому утечки невозможны.

 75 . Найдите АС.
75 . Найдите АС. у.).
у.).
 Choose the right form:
Choose the right form:
 6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.
6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.
 Если выполнить перевод pdf в txt формат довольно легко, то для перевода pdf в word требовались специальные программы, которые не так дешево и стоят.
Если выполнить перевод pdf в txt формат довольно легко, то для перевода pdf в word требовались специальные программы, которые не так дешево и стоят. Вот и все собственно.
Вот и все собственно.
 04.2023, 17:06:35 • Подано по адресу:
Топ-лист программного обеспечения для работы с PDF
• Проверенные решения
04.2023, 17:06:35 • Подано по адресу:
Топ-лист программного обеспечения для работы с PDF
• Проверенные решения
 Он имеет функцию OCR, которая позволяет легко редактировать отсканированные PDF-файлы. PDFelement позволяет легко конвертировать PDF-файлы и упрощает вашу работу.
Он имеет функцию OCR, которая позволяет легко редактировать отсканированные PDF-файлы. PDFelement позволяет легко конвертировать PDF-файлы и упрощает вашу работу.

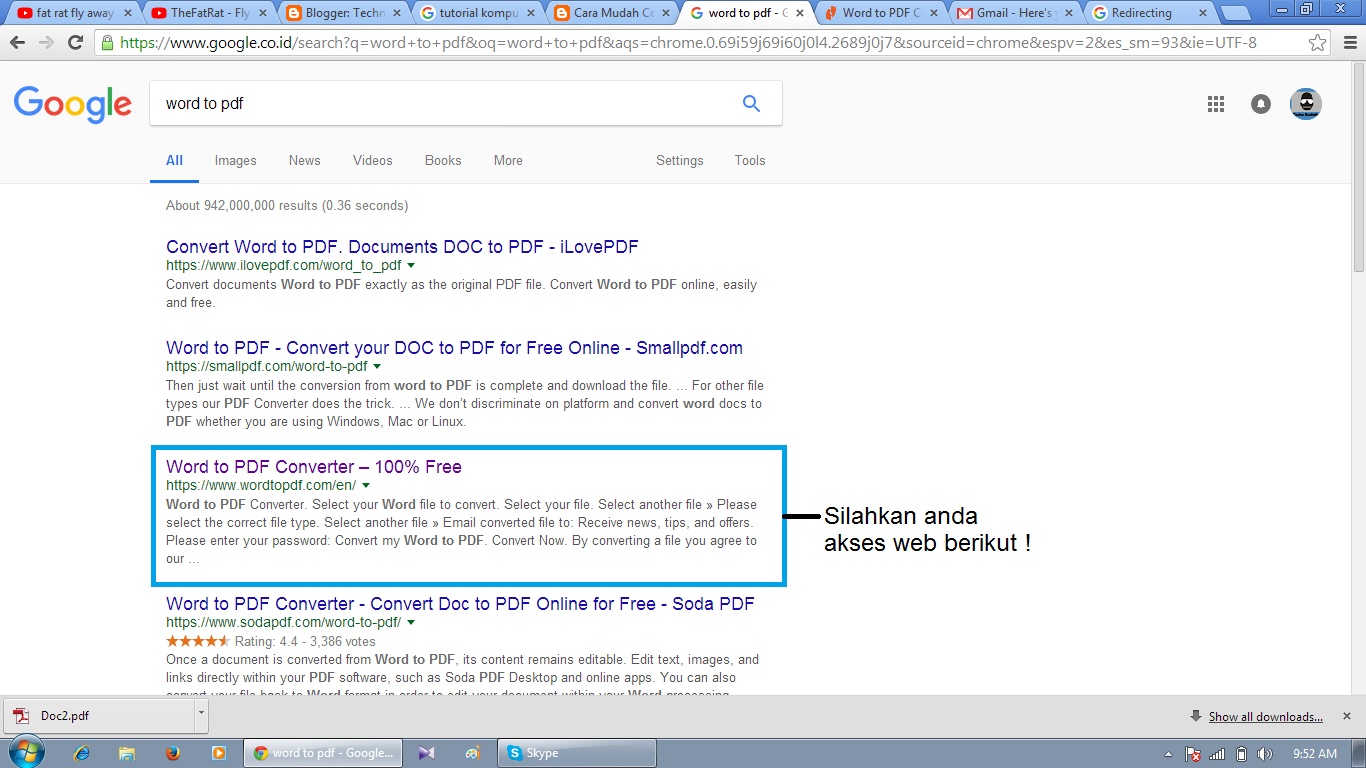 Он позволяет легко конвертировать Word, Excel и другие форматы в PDF простым щелчком мыши. Этот автономный конвертер Word в PDF полностью совместим с Excel, Word, PowerPoint, HTML и форматами изображений. Он также позволяет конвертировать PDF-документы, защищенные паролем. Функция OCR может преобразовывать отсканированные документы в редактируемые тексты, а также изменять размер страниц.
Он позволяет легко конвертировать Word, Excel и другие форматы в PDF простым щелчком мыши. Этот автономный конвертер Word в PDF полностью совместим с Excel, Word, PowerPoint, HTML и форматами изображений. Он также позволяет конвертировать PDF-документы, защищенные паролем. Функция OCR может преобразовывать отсканированные документы в редактируемые тексты, а также изменять размер страниц. Однако вам необходимо загрузить его на свое устройство, чтобы конвертировать PDF-файлы в автономном режиме. Загрузите его с официального сайта на свое устройство и следуйте инструкциям по установке.
Однако вам необходимо загрузить его на свое устройство, чтобы конвертировать PDF-файлы в автономном режиме. Загрузите его с официального сайта на свое устройство и следуйте инструкциям по установке. Этот автономный конвертер документов в PDF широко считается отраслевым стандартом, позволяя вам тратить меньше времени на занятую работу и больше времени на завершение проектов после ознакомления с его мощными функциями. Он преобразует документ, сохраняя исходный макет, поэтому вам не нужно тратить время на внесение изменений.
Этот автономный конвертер документов в PDF широко считается отраслевым стандартом, позволяя вам тратить меньше времени на занятую работу и больше времени на завершение проектов после ознакомления с его мощными функциями. Он преобразует документ, сохраняя исходный макет, поэтому вам не нужно тратить время на внесение изменений. Второй — использовать Microsoft Office для Mac. Если вы предпочитаете использовать специальное PDF-решение для преобразования Word в PDF в автономном режиме, получите Wondershare PDFelement, который также доступен для пользователей Mac.
Второй — использовать Microsoft Office для Mac. Если вы предпочитаете использовать специальное PDF-решение для преобразования Word в PDF в автономном режиме, получите Wondershare PDFelement, который также доступен для пользователей Mac. Здесь вам нужно выбрать опцию «Экспортировать как PDF».
Здесь вам нужно выбрать опцию «Экспортировать как PDF». Он также имеет функцию пакетного преобразования. Его можно использовать для сжатия больших файлов до меньших размеров, а также для добавления дополнительных страниц в документ PDF.
Он также имеет функцию пакетного преобразования. Его можно использовать для сжатия больших файлов до меньших размеров, а также для добавления дополнительных страниц в документ PDF.
 После выбора сервера просто нажмите кнопку «Конвертировать сейчас». Вы можете скачать преобразованный файл PDF после преобразования.
После выбора сервера просто нажмите кнопку «Конвертировать сейчас». Вы можете скачать преобразованный файл PDF после преобразования. Затем нажмите «Преобразовать в PDF», чтобы сделать это.
Затем нажмите «Преобразовать в PDF», чтобы сделать это.
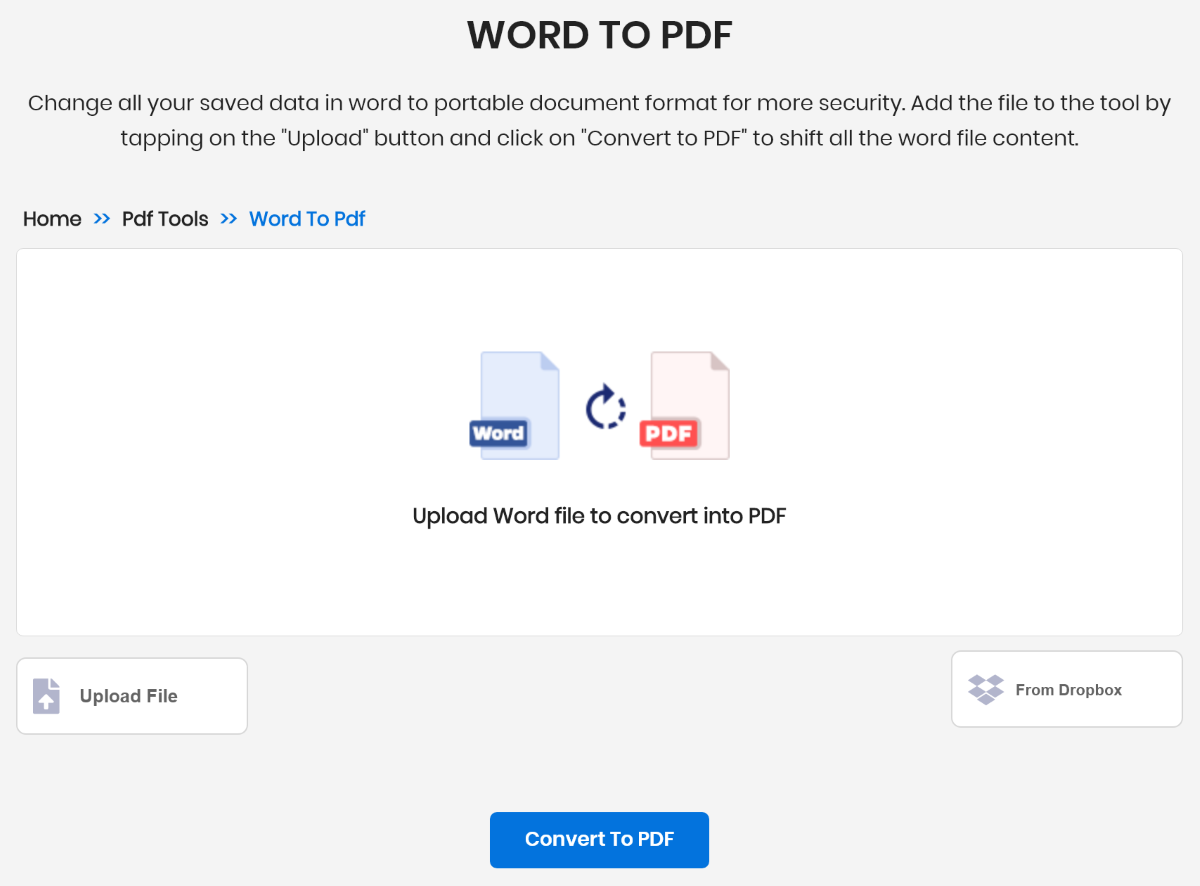 Если вы хотите безопасно конвертировать PDF в Word, используйте автономный конвертер PDF в Word, который может обеспечить безопасную обработку файлов и их сохранение на вашем устройстве в автономном режиме.
Если вы хотите безопасно конвертировать PDF в Word, используйте автономный конвертер PDF в Word, который может обеспечить безопасную обработку файлов и их сохранение на вашем устройстве в автономном режиме.

 К счастью, вы можете использовать функцию печати в PDF, которая работает в большинстве браузеров. Все, что вам нужно сделать, это:
К счастью, вы можете использовать функцию печати в PDF, которая работает в большинстве браузеров. Все, что вам нужно сделать, это: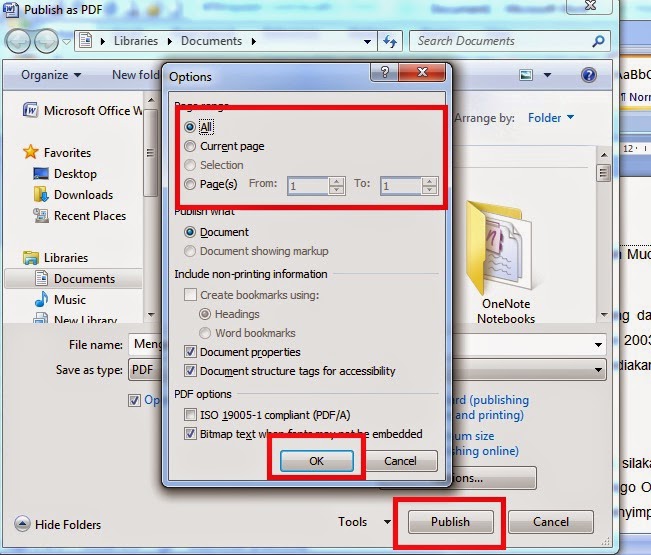 Откройте файл PDF, и это файл на английском языке. Теперь наша миссия состоит в том, чтобы изменить язык файла PDF.
Откройте файл PDF, и это файл на английском языке. Теперь наша миссия состоит в том, чтобы изменить язык файла PDF.
 Например, он может помочь узнать какие простые множители у числа 12? Выберите начальное число (например ’12’). После чего нажмите кнопку ‘Посчитать’.
Например, он может помочь узнать какие простые множители у числа 12? Выберите начальное число (например ’12’). После чего нажмите кнопку ‘Посчитать’. Есть 6 множителей из 12, среди которых 12 — самый большой множитель, а 2 и 3 — его простые множители. Разложение на простые множители числа 12 может быть выполнено путем умножения всех его простых множителей так, чтобы произведение было равно 12. Давайте узнаем о все множителя числа 12 , разложения на простые множители числа 12 , пары факторов из 12 и дерево факторов из 12 в этой статье.
Есть 6 множителей из 12, среди которых 12 — самый большой множитель, а 2 и 3 — его простые множители. Разложение на простые множители числа 12 может быть выполнено путем умножения всех его простых множителей так, чтобы произведение было равно 12. Давайте узнаем о все множителя числа 12 , разложения на простые множители числа 12 , пары факторов из 12 и дерево факторов из 12 в этой статье. Это означает, что 12 полностью делится на все эти числа. Помимо этого, 12 также имеет отрицательные факторы, которые могут быть перечислены как -1, -2, -3, -4, -6 и -12. Для отрицательных множителей нам нужно умножить отрицательный множитель на отрицательный, например, (-6) × (-2) = 12.
Это означает, что 12 полностью делится на все эти числа. Помимо этого, 12 также имеет отрицательные факторы, которые могут быть перечислены как -1, -2, -3, -4, -6 и -12. Для отрицательных множителей нам нужно умножить отрицательный множитель на отрицательный, например, (-6) × (-2) = 12. Мы записываем это конкретное число вместе с его парой и составляем список, как показано на рисунке выше. Когда мы проверяем и перечисляем все числа до 9, мы автоматически получаем вместе с ним другой парный коэффициент. Например, начиная с 1, мы пишем 1 × 12 = 12, 2 × 6 = 12 и так далее. Здесь (1, 12) образует первую пару, (2, 6) образует вторую пару, и список продолжается, как показано. Итак, когда мы пишем 1 как множитель 12, мы получаем другой множитель как 12; и поскольку мы пишем 2 как множитель 12, мы получаем 6 как другой множитель. Таким образом, мы получаем все факторы.
Мы записываем это конкретное число вместе с его парой и составляем список, как показано на рисунке выше. Когда мы проверяем и перечисляем все числа до 9, мы автоматически получаем вместе с ним другой парный коэффициент. Например, начиная с 1, мы пишем 1 × 12 = 12, 2 × 6 = 12 и так далее. Здесь (1, 12) образует первую пару, (2, 6) образует вторую пару, и список продолжается, как показано. Итак, когда мы пишем 1 как множитель 12, мы получаем другой множитель как 12; и поскольку мы пишем 2 как множитель 12, мы получаем 6 как другой множитель. Таким образом, мы получаем все факторы. Простые делители числа 12 отличаются от делителей числа 12. Как мы видели в предыдущем разделе, делители числа 12 могут быть перечислены как 1, 2, 3, 4, 6 и 12. Однако все они не являются простыми. числа. Итак, давайте найдем простые делители числа 12, используя простую факторизацию в следующем разделе.
Простые делители числа 12 отличаются от делителей числа 12. Как мы видели в предыдущем разделе, делители числа 12 могут быть перечислены как 1, 2, 3, 4, 6 и 12. Однако все они не являются простыми. числа. Итак, давайте найдем простые делители числа 12, используя простую факторизацию в следующем разделе. Итак, мы снова делим 6 на 2, что равно 6 ÷ 2 = 3. После этого делим 3 на 3, чтобы получить 1 как частное,
Итак, мы снова делим 6 на 2, что равно 6 ÷ 2 = 3. После этого делим 3 на 3, чтобы получить 1 как частное,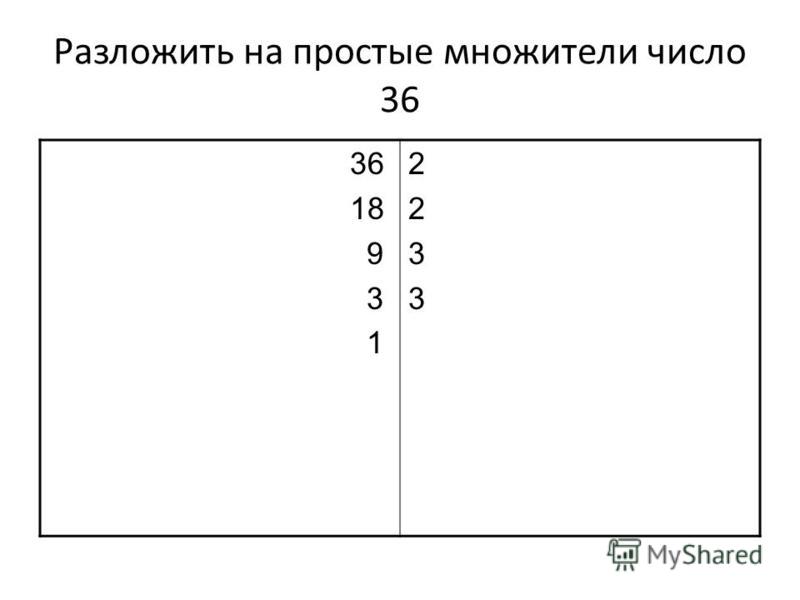
 Это означает, что произведение парных множителей 12 всегда равно 12. Пары множителей 12 можно записать, как показано в таблице ниже:
Это означает, что произведение парных множителей 12 всегда равно 12. Пары множителей 12 можно записать, как показано в таблице ниже:
 Например, 12 = 2 × 2 × 3 = 2 2 × 3. Мы получаем простую факторизацию 12 как 2 2 × 3. Просто прибавьте единицу (1) к показателям 2 и 1 по отдельности и умножьте их суммы. . (2 + 1) × (1 + 1) = 3 × 2 = 6. Это означает, что 12 имеет всего 6 делителей.
Например, 12 = 2 × 2 × 3 = 2 2 × 3. Мы получаем простую факторизацию 12 как 2 2 × 3. Просто прибавьте единицу (1) к показателям 2 и 1 по отдельности и умножьте их суммы. . (2 + 1) × (1 + 1) = 3 × 2 = 6. Это означает, что 12 имеет всего 6 делителей.
 Мы делаем математику увлекательной. Проверьте, как!
Мы делаем математику увлекательной. Проверьте, как! Теперь мы можем найти наибольший общий делитель (НОД) чисел 12 и 18, который равен 6.
Теперь мы можем найти наибольший общий делитель (НОД) чисел 12 и 18, который равен 6. Таким образом, простые делители или простые множители числа 12 равны 2 и 3.
Таким образом, простые делители или простые множители числа 12 равны 2 и 3.
 Это самый простой способ получить ответ на вопрос, сколько факторов в числе 12 отрицательных, так как есть множество других способов, которые могут вас озадачить.
Это самый простой способ получить ответ на вопрос, сколько факторов в числе 12 отрицательных, так как есть множество других способов, которые могут вас озадачить. Они кратны отдельным числам. Здесь это числа, кратные 3 и 4.
Они кратны отдельным числам. Здесь это числа, кратные 3 и 4.

 14159..
14159.. Однако я понимаю, что это может быть проблемой, потому что я потеряю решения, приведенные здесь:
Однако я понимаю, что это может быть проблемой, потому что я потеряю решения, приведенные здесь:

 Сколько информации содержится в сообщениях о том,
что рыбак поймал карася, окуня, поймал рыбу?
Сколько информации содержится в сообщениях о том,
что рыбак поймал карася, окуня, поймал рыбу?
 6 бит.
6 бит.

 Объем всей информации в книге:
2400*150 = 360 000 байт.
Объем всей информации в книге:
2400*150 = 360 000 байт.
 В рулетке общее количество лунок равно 128. Какое
количество информации мы получаем в зрительном сообщения об остановке
шарика в одной из лунок?
В рулетке общее количество лунок равно 128. Какое
количество информации мы получаем в зрительном сообщения об остановке
шарика в одной из лунок?
 Формула Шеннона
Формула Шеннона 
 рч = 40/50 = 0,8; рб = 10/50 = 0,2;
iч = log2(1/0,2) ≈ 2,32;
iб = log2(1/0,8) ≈ 0,32
рч = 40/50 = 0,8; рб = 10/50 = 0,2;
iч = log2(1/0,2) ≈ 2,32;
iб = log2(1/0,8) ≈ 0,32 7-11: Методическое пособие. — М., БИНОМ. Лаборатория знаний. 2007.
Угринович Н.Д. Практикум по информатике и информационным технологиям.Учебное пособие для общеобразовательных учреждений. Изд. 2-е, испр./ Н.Д. Угринович, Л.Л. Босова, Н.И. Михайлова – М.:БИНОМ. Лаборатория знаний, 2004
CD «Компьютерный практикум Windows-CD». Приложение к пособию Угринович Н. Д. Преподавание курса «Информатика и ИКТ» в основной и старшей школе. 7-11: Методическое пособие. — М., БИНОМ. Лаборатория знаний. 2007.
http://ru.wikipedia.org/wiki/%D0%A8%D0%B5%D0%BD%D0%BD%D0%BE%D0%BD_%D0%9A.
7-11: Методическое пособие. — М., БИНОМ. Лаборатория знаний. 2007.
Угринович Н.Д. Практикум по информатике и информационным технологиям.Учебное пособие для общеобразовательных учреждений. Изд. 2-е, испр./ Н.Д. Угринович, Л.Л. Босова, Н.И. Михайлова – М.:БИНОМ. Лаборатория знаний, 2004
CD «Компьютерный практикум Windows-CD». Приложение к пособию Угринович Н. Д. Преподавание курса «Информатика и ИКТ» в основной и старшей школе. 7-11: Методическое пособие. — М., БИНОМ. Лаборатория знаний. 2007.
http://ru.wikipedia.org/wiki/%D0%A8%D0%B5%D0%BD%D0%BD%D0%BE%D0%BD_%D0%9A. Двое вытягиваются последовательно, не меняя местами после каждого розыгрыша.
Двое вытягиваются последовательно, не меняя местами после каждого розыгрыша. Событие B транслируется в 2 события: Синий + (Белый или Красный) или (Белый или Красный) + Синий. Вероятности каждого из этих событий, сложенные вместе, будут (2/16) * (14/15) + (14/16) * (2/15) = 0,2333333333; следовательно, А более вероятно.
Событие B транслируется в 2 события: Синий + (Белый или Красный) или (Белый или Красный) + Синий. Вероятности каждого из этих событий, сложенные вместе, будут (2/16) * (14/15) + (14/16) * (2/15) = 0,2333333333; следовательно, А более вероятно.

 Таким образом, их вероятности можно объединить с умножением.
Таким образом, их вероятности можно объединить с умножением. Мы не можем рассчитать вероятность P(A), если не знаем две вероятности, которые в сумме дают 0,88.
Мы не можем рассчитать вероятность P(A), если не знаем две вероятности, которые в сумме дают 0,88. Какова приблизительная вероятность того, что из стандартной колоды из 52 игральных карт вытащатся два туза подряд?
Какова приблизительная вероятность того, что из стандартной колоды из 52 игральных карт вытащатся два туза подряд? Затем вычтите это из 1 (100%), чтобы вычислить возможность рисования пары разных цветов.
Затем вычтите это из 1 (100%), чтобы вычислить возможность рисования пары разных цветов. Это составляет знаменатель дроби: это количество равновероятных возможных исходов.
Это составляет знаменатель дроби: это количество равновероятных возможных исходов.







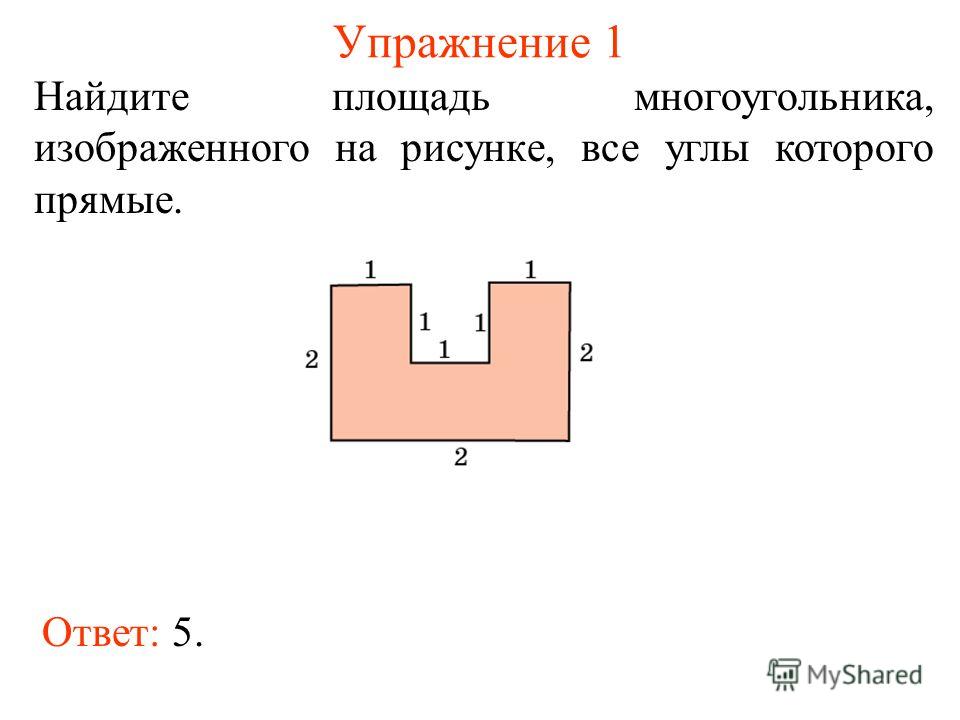
 Друзья! К вашему вниманию пару задачек с многоугольником и вписанной в него окружностью. Существует формула, которой связывается радиус указанной окружности и периметр с площадью такого многоугольника. Вот она:
Друзья! К вашему вниманию пару задачек с многоугольником и вписанной в него окружностью. Существует формула, которой связывается радиус указанной окружности и периметр с площадью такого многоугольника. Вот она: Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь. *Свойство подобия фигур.
*Свойство подобия фигур.
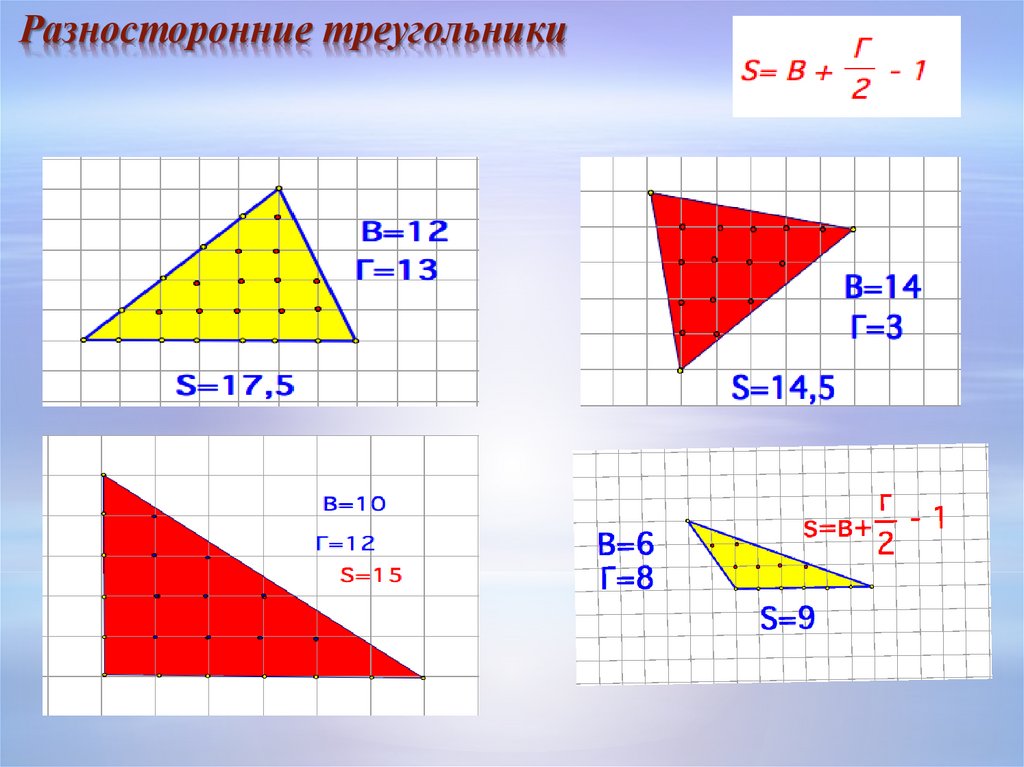
 Поскольку многоугольники представляют собой замкнутые плоские формы, то площадь многоугольника — это пространство, которое он занимает в двумерной плоскости. Единица площади любого многоугольника всегда выражается в квадратных единицах. Обратите внимание на следующий рисунок, на котором показана площадь многоугольника на двумерной плоскости.
Поскольку многоугольники представляют собой замкнутые плоские формы, то площадь многоугольника — это пространство, которое он занимает в двумерной плоскости. Единица площади любого многоугольника всегда выражается в квадратных единицах. Обратите внимание на следующий рисунок, на котором показана площадь многоугольника на двумерной плоскости.
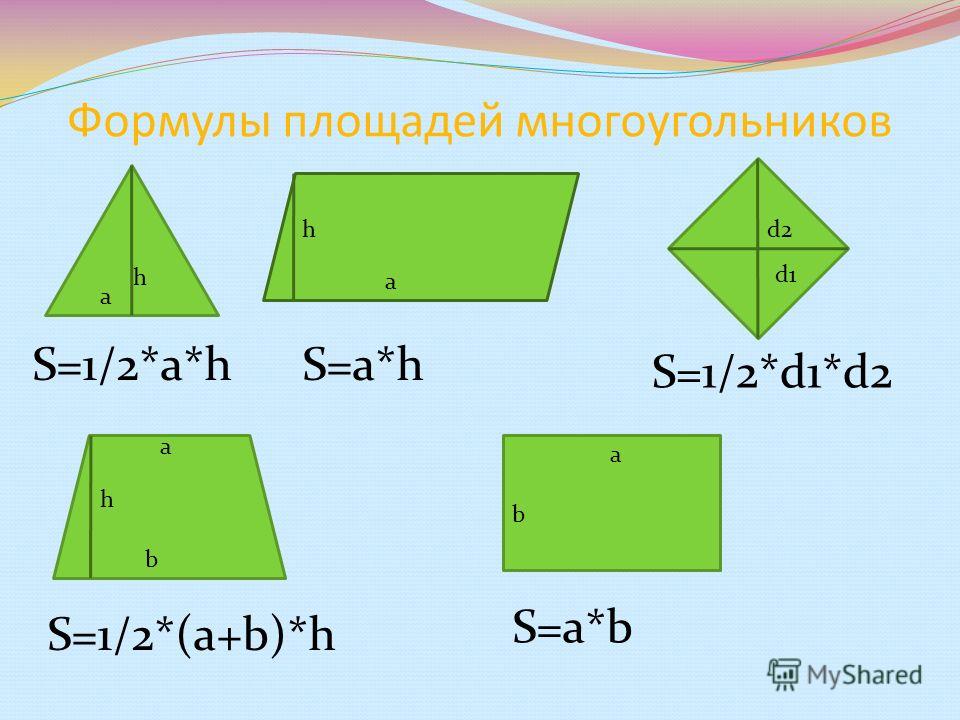
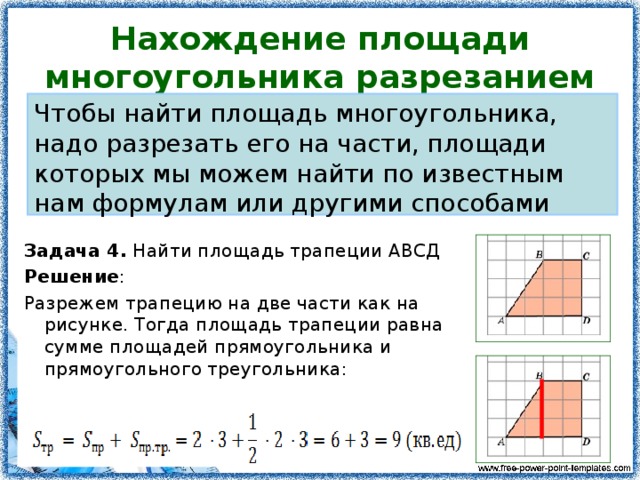 Таким образом, эта дифференциация также вносит различие в вычисление площади многоугольников. Площадь некоторых общеизвестных многоугольников определяется как:
Таким образом, эта дифференциация также вносит различие в вычисление площади многоугольников. Площадь некоторых общеизвестных многоугольников определяется как: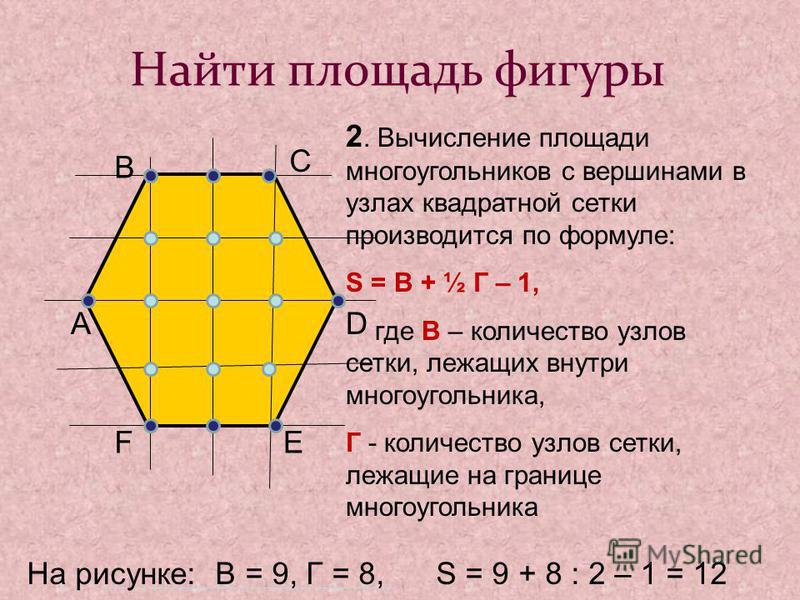 Таким образом, метод расчета площади правильных многоугольников основан на формулах, связанных с каждым многоугольником. Давайте посмотрим на формулы некоторых часто используемых правильных многоугольников:
Таким образом, метод расчета площади правильных многоугольников основан на формулах, связанных с каждым многоугольником. Давайте посмотрим на формулы некоторых часто используемых правильных многоугольников: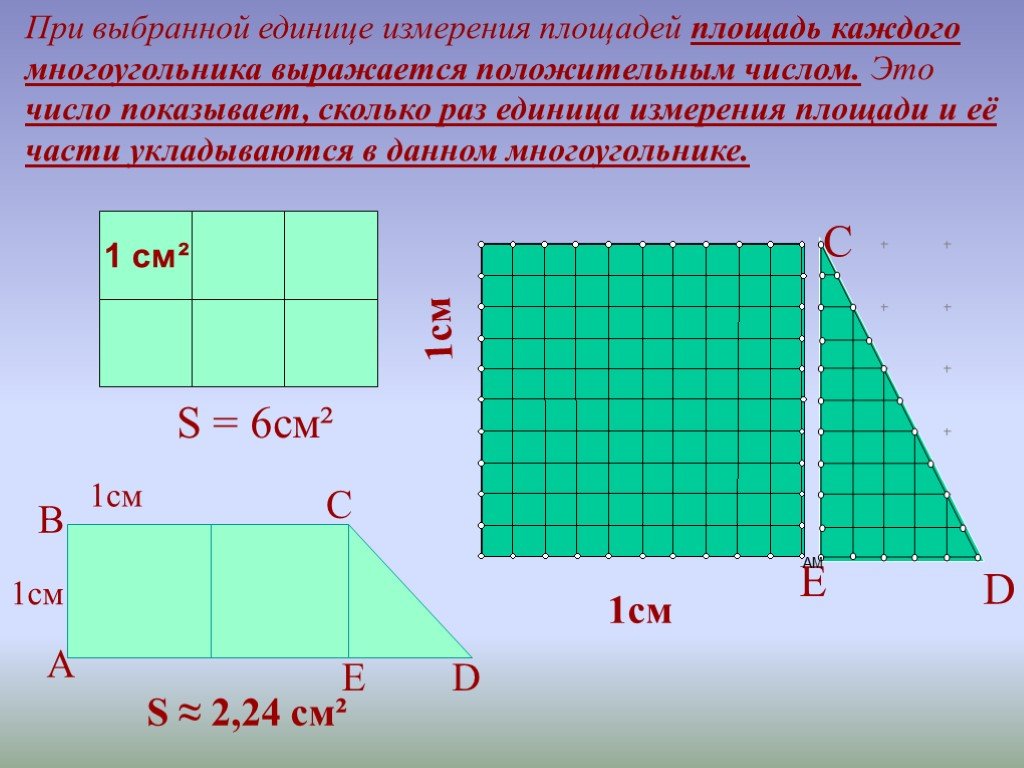 92\)
92\)  2}\) = 2 единицы 92}\) = 2 единицы
2}\) = 2 единицы 92}\) = 2 единицы Запишем единицу площади многоугольника в квадратных единицах , где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).
Запишем единицу площади многоугольника в квадратных единицах , где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).
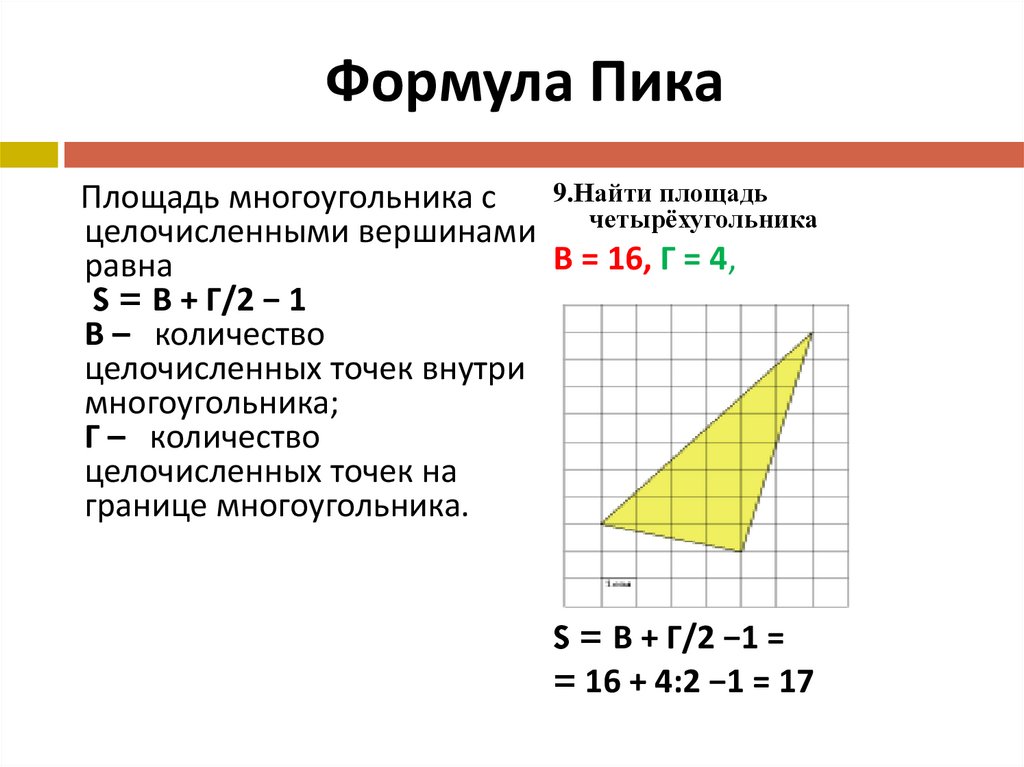 С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.
С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.