2.2. Примеры составления математических моделей экономических задач
Экономико-математическая модель – математическое описание исследуемого экономического процесса или объекта. Эта модель выражает закономерности экономического процесса в абстрактном виде с помощью математических соотношений. Использование математического моделирования в экономике позволяет углубить количественный экономический анализ, расширить область экономической информации, интенсифицировать экономические расчеты.
Рассмотрим примеры экономико-математических моделей, которые относятся к задачам линейного программирования.
1.Задача об использовании ресурсов (задача планирования производства).
При
производстве
видов продукции используетсявидов
ресурсов. Известно:запасы ресурсов;расход каждогого
вида ресурса на изготовление единицый
продукции;прибыль,
получаемая при реализации единицый
продукции. Составить план выпуска
продукции, обеспечивающий максимальную
прибыль.
Решение. Обозначим объем выпускай продукции. Учитывая, чтоприбыль от реализации всего объемай продукции,затратыго вида ресурса на весь объем выпускай продукции, неотрицательность переменных задачи, запишем математическую модель задачи.
2. Задача о составлении рациона питания (задача о диете, задача о смесях).
Животные должны получать ежедневно питательных веществ в количестве не менее. В рацион животных входят кормавидов. Известно:содержаниего питательного вещества в единицего вида корма;стоимость единицыго вида корма. Составить суточный рацион кормления животных, обеспечивающий минимальные затраты.
Решение. Обозначим объемго вида корма, входящего в суточный рацион. Так какколичествого питательного вещества, содержащегося вм виде корма, входящего в суточный рацион,стоимостьго корма, то математическая модель имеет вид
3. Транспортная
задача.
Транспортная
задача.
Однородный груз сосредоточен у поставщиковв объемах. Данный груз необходимо доставитьпотребителямв объемах. Известныстоимость перевозки единицы груза от каждогого поставщика каждомуму потребителю. Требуется составить такой план перевозок, при котором:
–мощности всех поставщиков были реализованы;
–спросы всех потребителей были удовлетворены;
–суммарные затраты на перевозку были минимальны.
Исходные данные транспортной задачи записываются в виде таблицы
Пункты отправления | Пункты назначения | Запасы | ||||
… | … | |||||
… | … | |||||
… | … | … | … | … | … | … |
… | … | |||||
… | … | … | … | … | … | … |
… | … | |||||
Потребности | … | … | ||||
Решение. Обозначим
объемы
перевозок от каждогого
поставщика каждомуму
потребителю. Математическая постановка
задачи состоит в определении минимального
значения функции
Обозначим
объемы
перевозок от каждогого
поставщика каждомуму
потребителю. Математическая постановка
задачи состоит в определении минимального
значения функции
при условиях
Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.
,
то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.
404 Cтраница не найдена
Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь.
Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Математическое моделирование — Решения MATLAB и Simulink
Математические модели имеют решающее значение для понимания и точного прогнозирования поведения сложных систем. Эти модели позволяют решать критически важные задачи, такие как:
Эти модели позволяют решать критически важные задачи, такие как:
- Прогнозирование и оптимизация поведения системы
- Проектирование систем управления
- Характеристика реакции системы
Продукты MathWorks предоставляют все инструменты, необходимые для разработки математических моделей. MATLAB ® поддерживает подходы как к численному, так и к символьному моделированию и обеспечивает аппроксимацию кривых, статистику, оптимизацию, решение ОДУ и УЧП, исчисление и другие основные математические инструменты. Симулинк ® добавляет среду для моделирования и симуляции поведения многодоменных систем, а также для разработки встроенных систем.
«В отличие от компаний, которые полагаются на готовые решения для количественного анализа, мы видим, что наш процесс постоянно совершенствуется. У нас есть возможность постоянно улучшать наши алгоритмы и модели в MATLAB, и это большое преимущество».
Виллем Джелема, Робеко
Построение моделей на основе данных и научных принципов
С помощью семейств продуктов MATLAB и Simulink вы можете моделировать системы практически любого типа, включая:
- Линейные и нелинейные
- Статическая и динамическая
- Детерминированный и стохастический
- Дискретный и непрерывный
Вы можете выбрать одну из нескольких сред моделирования, что позволит вам описать вашу систему программно, символически или с помощью блок-схем и конечных автоматов. Создание управляемых данными или физических моделей дает множество различных преимуществ, таких как извлечение информации из данных, информирование процессов проектирования с помощью проектирования на основе моделей, обеспечение виртуального ввода в эксплуатацию или создание операционных цифровых двойников.
Создание управляемых данными или физических моделей дает множество различных преимуществ, таких как извлечение информации из данных, информирование процессов проектирования с помощью проектирования на основе моделей, обеспечение виртуального ввода в эксплуатацию или создание операционных цифровых двойников.
Разработка моделей на основе данных
Когда у вас есть физическое понимание, вы можете создавать модели на основе первых принципов, используя аналитические или символические подходы. Методы моделирования на основе данных особенно полезны, когда у вас нет достаточной информации о вашей системе. В этом случае вы можете обеспечить точность модели, выбрав метод моделирования, подходящий для ваших экспериментальных или исторических данных. Используйте инструменты подгонки кривой статистики, чтобы исследовать отношения между вашими данными. Вы можете использовать модели линейной и нелинейной регрессии, классификацию, кластеризацию и инструменты подбора поверхности. Динамические модели, позволяющие выразить влияние прошлого опыта системы на ее текущее и будущее поведение, можно моделировать с помощью нейронных сетей и методов идентификации системы. Методы, управляемые данными, также можно использовать для настройки коэффициентов вашей модели из первых принципов, чтобы они соответствовали экспериментальным данным с использованием методов моделирования серого ящика и методов оптимизации отклика.
Методы, управляемые данными, также можно использовать для настройки коэффициентов вашей модели из первых принципов, чтобы они соответствовали экспериментальным данным с использованием методов моделирования серого ящика и методов оптимизации отклика.
Узнать больше
- Моделирование углекислого газа в атмосфере и набор инструментов для подбора кривой
- Прогнозирование нагрузки и цен на электроэнергию с помощью MATLAB (47:43)
- Разработка прогностических моделей (MathWorks Consulting)
- Цифровые двойники для профилактического обслуживания
Примеры кода
- Классический маятник: некоторые вопросы, связанные с алгоритмом Классический маятник: некоторые вопросы, связанные с алгоритмом
Изучить продукты
- Curve Fitting Toolbox™
- Simscape™
- Stateflow™
- Статистика и машинное обучение Toolbox™
- Symbolic Math Toolbox™
- System Identification Toolbox™
Разработка моделей на основе математических, инженерных и научных принципов
Можно выбрать один из нескольких подходов к созданию математических моделей на основе первых принципов. Например, вы можете:
Например, вы можете:
- Используйте символьные вычисления для получения уравнений и аналитических моделей, описывающих вашу систему
- Создание блок-схем сложных многодоменных систем
- Использовать методы конечных элементов для систем, описываемых уравнениями в частных производных
Подробнее
- Моделирование поршня (8:57)
- Инженерный проект и документация с MATLAB (36:59)
- Структурный и термический анализ с помощью MATLAB (43:48)
- Моделирование пониженного порядка
Изучить продукты
- Curve Fitting Toolbox™
- Simscape™
- Stateflow™
- Статистика и машинное обучение Toolbox™
- Symbolic Math Toolbox™
- System Identification Toolbox™
Разработка моделей для предметно-ориентированных приложений
Продукты MathWorks для конкретных приложений позволяют разрабатывать математические модели для приложений в следующих областях:
- Вычислительная оптимизация финансового портфеля, оценка рисков и экономическое прогнозирование
- Физическое моделирование механических, электрических, гидравлических и приводных систем
- Моделирование и калибровка трансмиссии
- Анализ экспрессии генов в вычислительной биологии, анализ последовательностей и моделирование путей
- Экологическое и аэродинамическое моделирование аэрокосмических систем
- Моделирование систем управления, проектирование и проверка контроллеров, моделирование систем с обратной связью
Оценка и оптимизация моделей
После разработки модели вы можете испытывать ее в различных условиях, управлять результатами моделирования и визуализировать их, а также оптимизировать их точность.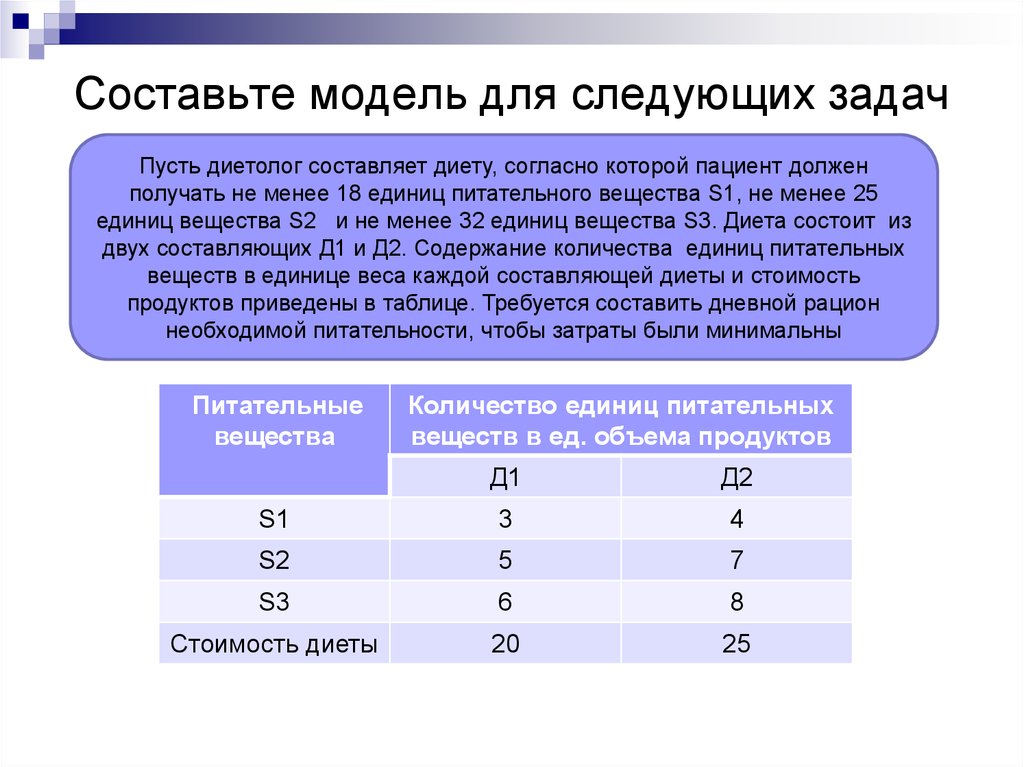 Вы также можете документировать свою работу и делиться моделью с коллегами.
Вы также можете документировать свою работу и делиться моделью с коллегами.
Моделирование вашей модели
Моделирование позволяет прогнозировать поведение вашей системы в различных условиях или проверять вашу модель путем сравнения результатов моделирования с тестовыми данными. Инструменты MathWorks упрощают управление всеми аспектами моделирования модели. Вы можете:
- Определение условий моделирования с использованием DoE, распределений вероятностей и других тестовых векторов
- Запустите симуляцию, используя числовые решатели мирового класса и параллельные вычисления
- Результаты постобработки с использованием возможностей анализа данных MATLAB, управления данными и визуализации
Подробнее
- Использование статистики для анализа неопределенностей в моделях систем
- Ускорение анализа методом конечных элементов в MATLAB с помощью параллельных вычислений
Обзор продуктов
- Global Optimization Toolbox™
- Компилятор MATLAB™
- Набор инструментов для оптимизации™
- Simulink Design Optimization™
- Тест Simulink
Оптимизируйте свою модель
После того, как вы построили свою модель, вы можете оптимизировать параметры и проверить модель на соответствие реальному поведению системы. Инструменты оптимизации MathWorks позволяют усовершенствовать модель существующей системы или оптимизировать проект новой системы путем корректировки проектных переменных в соответствии с конкретными критериями производительности.
Инструменты оптимизации MathWorks позволяют усовершенствовать модель существующей системы или оптимизировать проект новой системы путем корректировки проектных переменных в соответствии с конкретными критериями производительности.
Узнать больше
- Надежность и надежность
- Robeco разрабатывает модели количественного отбора акций и оптимизации портфеля с помощью инструментов MathWorks
Обзор продуктов
- Global Optimization Toolbox™
- Компилятор MATLAB™
- Набор инструментов для оптимизации™
- Simulink Design Optimization™
- Тест Simulink
Документируйте и делитесь своей моделью
С помощью инструментов создания отчетов MATLAB и Simulink вы можете автоматически документировать этапы построения модели и результаты моделирования и поддерживать их в актуальном состоянии при проектировании. Вы можете использовать настольные и веб-инструменты MathWorks для развертывания, чтобы поделиться своими оптимизированными моделями и связанными приложениями с коллегами.
Подробнее
- Что такое компилятор MATLAB? (2:23)
- Интеграция и развертывание ваших алгоритмов в корпоративных системах (MathWorks Consulting)
Обзор продуктов
- Global Optimization Toolbox™
- Компилятор MATLAB™
- Набор инструментов для оптимизации™
- Simulink Design Optimization™
- Тест Simulink
Выберите веб-сайт
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и предложения. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка
Европа
Обратитесь в местный офис
Экономическое моделирование: примеры и значение
Вы были одним из тех детей, у которых был огромный набор Lego? Или, случайно, вы не из тех взрослых, которые до сих пор любят играть с этими великолепными наборами? Даже, может быть, вы один из организованных коллекционеров, которые мечтали о Соколе Тысячелетия из Лего? Это может вас удивить, но знаете ли вы, что сборка наборов Lego может иметь что-то общее с наукой?
Как вы можете догадаться из названия этого раздела, конструирование моделей Lego похоже на научные модели, а экономисты строили научные модели с самого начала экономической науки. Подобно деталям Lego и полным наборам Lego при конструировании миниатюрной Эйфелевой башни, экономические модели отображают происходящие явления в реальности.
Подобно деталям Lego и полным наборам Lego при конструировании миниатюрной Эйфелевой башни, экономические модели отображают происходящие явления в реальности.
Вы, конечно, знаете, что Эйфелева башня из Лего — это не настоящая Эйфелева башня! Это просто его представление, базовая версия. Это именно то, что делают экономические модели. Поэтому, если вы играли с наборами Lego, вы будете четко понимать этот раздел, а если вы уже знакомы с экономическими моделями, этот раздел может дать некоторые советы по сборке наборов Lego, так что продолжайте прокручивать!
Экономическое моделирование Значение
Значение экономического моделирования связано со значением научного моделирования. Науки вообще пытаются понять происходящие явления. От физики до политологии ученые пытаются уменьшить неопределенность и хаос с помощью правил и моделей.
Но что такое модель? Модели — это упрощенная версия реальности. Они рисуют картину, чтобы мы могли понять чрезвычайно сложные вещи. С другой стороны, экономика сильно отличается от естественных наук. Экономисты не могут наблюдать явления, происходящие в чашке Петри, как это делают биологи. Кроме того, отсутствие контролируемых экспериментов и неясность причинно-следственной связи между событиями, происходящими в социальном мире, в определенной степени препятствует экспериментам в экономике. Поэтому это отсутствие вариантов при проведении экспериментов заменяется моделированием в экономике.
С другой стороны, экономика сильно отличается от естественных наук. Экономисты не могут наблюдать явления, происходящие в чашке Петри, как это делают биологи. Кроме того, отсутствие контролируемых экспериментов и неясность причинно-следственной связи между событиями, происходящими в социальном мире, в определенной степени препятствует экспериментам в экономике. Поэтому это отсутствие вариантов при проведении экспериментов заменяется моделированием в экономике.
При этом, поскольку реальность чрезвычайно сложна и хаотична, они принимают некоторые правила перед построением модели. Эти предположения обычно уменьшают сложность реальности.
Модели — это конструкции с общими предположениями, которые помогают нам понять явления, происходящие в природе, и предсказать будущее в соответствии с нашим пониманием этих явлений.
Например, физики время от времени допускают вакуум для этих моделей, а экономисты предполагают, что агенты рациональны и обладают полной информацией о рынке. Мы знаем, что это не реально. Мы все знаем, что воздух существует, и мы не живем в вакууме, так как все мы знаем, что экономические агенты могут принимать иррациональные решения. Тем не менее, они полезны по разным причинам.
Мы знаем, что это не реально. Мы все знаем, что воздух существует, и мы не живем в вакууме, так как все мы знаем, что экономические агенты могут принимать иррациональные решения. Тем не менее, они полезны по разным причинам.
Экономические модели — это особые типы моделей, специально ориентированные на то, что происходит в экономике. Они представляют реальность с помощью различных методов, таких как графическое представление или наборы математических уравнений.
Экономические модели — это подтип научных моделей, которые сосредоточены на происходящих в экономике явлениях и пытаются представить, исследовать и понять эти явления при определенных условиях и предположениях.
Тем не менее, поскольку экономика и общество представляют собой чрезвычайно сложные системы, экономические модели различаются, а их методологии меняются. Все они имеют разные подходы и характеристики для ответа на разные вопросы.
Типы экономических моделей
В этом разделе мы рассмотрим широко используемые общие типы экономических моделей. Как упоминалось ранее, экономические модели существуют в разных методологиях, и их последствия различаются, поскольку реальность, которую они пытаются обнаружить, различна. Наиболее часто используемые экономические модели могут быть представлены как визуальные экономические модели, математические экономические модели и экономические симуляции.
Как упоминалось ранее, экономические модели существуют в разных методологиях, и их последствия различаются, поскольку реальность, которую они пытаются обнаружить, различна. Наиболее часто используемые экономические модели могут быть представлены как визуальные экономические модели, математические экономические модели и экономические симуляции.
Типы экономических моделей: визуальные экономические модели
Наглядные экономические модели, пожалуй, самые распространенные в учебниках. Если вы пойдете в книжный магазин и возьмете книгу по экономике, вы увидите десятки графиков и диаграмм. Визуальные экономические модели относительно просты и понятны. Они пытаются уловить происходящие в реальности события с помощью различных схем и графиков.
Наиболее известными визуальными экономическими моделями являются, пожалуй, кривые IS-LM, графики совокупного спроса и предложения, кривые полезности, графики рынков факторов производства и границы производственных возможностей.
Подведем итоги границы производственных возможностей, чтобы ответить на вопрос, почему мы классифицируем ее как визуальную экономическую модель.
На рис. 1 ниже мы можем увидеть, вероятно, первый график в каждом современном учебнике по экономике — границу производственных возможностей или кривую возможностей продукта.
Рис. 1 – Граница производственных возможностей
Эта кривая представляет возможные объемы производства обоих товаров, x и y. Тем не менее, мы будем рассматривать не саму модель, а ее аспекты. Эта модель предполагает, что в экономике существует два товара. Но на самом деле мы можем видеть много товаров в любой экономике, и большую часть времени существует сложная взаимосвязь между товарами и нашим бюджетом. Эта модель упрощает реальность и дает нам ясное объяснение посредством абстракции.
Другим хорошо известным примером визуальных экономических моделей является представление отношений между агентами в экономике с помощью диаграмм рынков факторов производства.
Рис. 2 – Отношения на рынках факторов производства
Этот тип диаграммы является примером визуального экономического моделирования. Мы знаем, что на самом деле отношения в экономике гораздо сложнее, чем на этой диаграмме. Тем не менее, этот тип моделирования в некоторой степени помогает нам понять и разработать политику.
Мы знаем, что на самом деле отношения в экономике гораздо сложнее, чем на этой диаграмме. Тем не менее, этот тип моделирования в некоторой степени помогает нам понять и разработать политику.
С другой стороны, объем визуальных экономических моделей относительно ограничен. Таким образом, экономика сильно зависит от математических моделей для преодоления ограничений визуальных экономических моделей.
Типы экономических моделей: математические экономические модели
Математические экономические модели разрабатываются для преодоления ограничений визуальных экономических моделей. Обычно они следуют правилам алгебры и исчисления. Следуя этим правилам, математические модели пытаются объяснить отношения между переменными. Тем не менее, эти модели могут быть чрезвычайно абстрактными, и даже самые простые модели содержат значительное количество переменных и их взаимодействий. Одной из известных математических экономических моделей является модель Солоу-Лебедя, широко известная как модель роста Солоу. 9{1-\alpha-\beta}\)
9{1-\alpha-\beta}\)
Здесь производственная функция обозначена через \(Y\), капитал через \(K\), человеческий капитал через \(H\), труд через \(L\) , а технология с \(A\). Тем не менее, наша главная цель здесь не в том, чтобы углубиться в модель роста Солоу, а в том, чтобы показать, что она содержит множество переменных.
Рис. 3 – Модель роста Солоу
Например, на Рисунке 3 показана модель роста Солоу, развитие технологий изменит наклон линии требуемых инвестиций в положительную сторону. В дополнение к этому модель утверждает, что увеличение потенциального выпуска может существовать только по отношению к развитию технологий в стране.
Модель роста Солоу — относительно простая модель. Современные экономические модели могут содержать страницы уравнений или приложений, связанных с понятием вероятности. Поэтому для расчета этих типов чрезвычайно сложных систем мы обычно используем модели экономического моделирования или экономическое моделирование.
Типы экономических моделей: экономическое моделирование
Как упоминалось ранее, современные экономические модели обычно исследуются с помощью компьютеров при использовании экономического моделирования. Это очень сложные динамические системы. Поэтому вычисления становятся необходимыми. Экономисты, как правило, осведомлены о механике системы, которую они конструируют. Они устанавливают правила и позволяют машинам делать математическую часть. Например, если мы хотим разработать модель роста Солоу с международной торговлей и несколькими товарами, подойдет вычислительный подход.
Это очень сложные динамические системы. Поэтому вычисления становятся необходимыми. Экономисты, как правило, осведомлены о механике системы, которую они конструируют. Они устанавливают правила и позволяют машинам делать математическую часть. Например, если мы хотим разработать модель роста Солоу с международной торговлей и несколькими товарами, подойдет вычислительный подход.
Использование экономических моделей
Экономические модели могут использоваться по многим причинам. Экономисты и политики постоянно обмениваются идеями об установлении повестки дня. Как упоминалось ранее, экономические модели используются для лучшего понимания реальности.
Кривые LM зависят от соотношения между процентными ставками и денежной массой. Предложение денег зависит от фискальной политики. Таким образом, этот тип экономического моделирования может быть полезен для будущих политических предложений. Еще один важный пример — кейнсианские экономические модели помогли Соединенным Штатам пережить Великую депрессию. Следовательно, экономические модели могут помочь нам понять и оценить экономические события при планировании наших стратегий.
Следовательно, экономические модели могут помочь нам понять и оценить экономические события при планировании наших стратегий.
Пример экономического моделирования
Мы привели множество примеров экономических моделей. Тем не менее, лучше углубиться и детально разобраться в структуре одной экономической модели. Лучше начать с основ. Таким образом, здесь мы фокусируемся на модели спроса и предложения.
Как мы уже говорили, все модели начинаются с предположений, и модель спроса и предложения не является исключением. Во-первых, мы предполагаем, что рынки совершенно конкурентны. Почему мы это предполагаем? Прежде всего, упростить реальность монополий. Поскольку существует много покупателей и продавцов, монополий не существует. И фирмы, и потребители должны быть ценополучателями. Это гарантирует, что фирмы продают в соответствии с ценой. Наконец, мы должны исходить из того, что информация доступна и легкодоступна для обеих сторон. Если потребители не знают, что они получают, цена может быть изменена для увеличения прибыли фирм.
Теперь, после установления наших основных предположений, мы можем перейти к более подробному изложению. Мы знаем, что существует благо. Назовем этот товар \(x\), а цену этого товара — \(P_x\). Мы знаем, что существует некоторый спрос на этот товар. Мы можем продемонстрировать объем спроса с помощью \(Q_d\) и объем предложения с помощью \(Q_s\). Мы предполагаем, что если цена ниже, то спрос будет выше.
Таким образом, мы можем сказать, что общий спрос является функцией цены. Таким образом, мы можем сказать следующее:
\(Q_d = \alpha P + \beta\)
где \(\alpha\) — отношение спроса к цене, а \(\beta\) — константа.
Рис. 4 – График спроса и предложения на рынке факторов производства
В реальной жизни эта взаимосвязь может оказаться слишком сложной. Тем не менее, это не означает, что мы не можем упростить. Поскольку мы знаем, что сделки возможны только там, где предложение равно спросу, мы можем найти равновесную цену на этот товар на этом рынке.
Вы понимаете, насколько это упрощено, если сравнивать с реальностью?
При построении этой модели мы сначала заложили некоторые допущения, а уже после этого решили, что анализировать, и упростили реальность. После этого мы использовали наши знания и создали общую модель для приложения к реальности. Тем не менее, мы должны иметь в виду, что эта модель имеет ограничения. В действительности рынки почти никогда не бывают полностью конкурентными, а информация не так изменчива и широко распространена, как мы предполагали. Это проблема не только этой конкретной модели. В общем, все модели имеют ограничения. Если мы поймем ограничения модели, она будет более полезной для будущих приложений.
Ограничения экономических моделей
Как и все модели, экономические модели также имеют некоторые ограничения.
Известный британский статистик Джордж Э. П. Покс сказал следующее:
Все модели ошибочны, но некоторые из них полезны.
Это довольно важный аргумент. Как мы упоминали ранее, модели могут быть чрезвычайно полезны для улучшения нашего понимания явлений. Тем не менее, все модели имеют ограничения, а некоторые могут содержать недостатки.
Как мы упоминали ранее, модели могут быть чрезвычайно полезны для улучшения нашего понимания явлений. Тем не менее, все модели имеют ограничения, а некоторые могут содержать недостатки.
Вы помните, что мы делали, конструируя нашу чрезвычайно простую модель? Мы начали с предположений. Ложные предположения могут привести к ложным результатам. Они могут по своей сути звучать в рамках модели. Тем не менее, они не могут объяснить реальность, если не построены на реалистичных предположениях.
Построив допущения для модели, мы упростили реальность. Социальные системы чрезвычайно сложны и хаотичны. Поэтому для расчета и погони за необходимым мы убираем некоторые условия и упрощаем действительность. С другой стороны, чрезмерное упрощение может привести к нереалистичным решениям. Мы должны тщательно проанализировать то, что мы не учитываем в уравнениях.
После этапа упрощения создается математическое соотношение. Математика является важной частью экономического моделирования.

 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав Это значительно упрощает вычисления.
Это значительно упрощает вычисления. Практикуйте и изучайте правила и через некоторое время у Вас будет выходить не хуже. До встречи в следующих уроках!
Практикуйте и изучайте правила и через некоторое время у Вас будет выходить не хуже. До встречи в следующих уроках! Получим
Получим
 Вычислим
определитель
го
порядка
Вычислим
определитель
го
порядка Тогда по свойству 3. определитель
представится в виде суммы двух
определителей
Тогда по свойству 3. определитель
представится в виде суммы двух
определителей В нашем случае транспонировании
приводит к замене на наоборот. Поэтому имеем два равенства
В нашем случае транспонировании
приводит к замене на наоборот. Поэтому имеем два равенства
 Эти продукты складываются, и сумма является определителем A. Знак слагаемых положительный для четных перестановок и отрицательный для нечетных перестановок.
Эти продукты складываются, и сумма является определителем A. Знак слагаемых положительный для четных перестановок и отрицательный для нечетных перестановок.


 Размерность уменьшается и может быть уменьшена далее шаг за шагом до скаляра.
Размерность уменьшается и может быть уменьшена далее шаг за шагом до скаляра.

 Для случая линейной (N×N) системы уравнений с det(A), не равным 0, решение можно представить в следующем виде:
Для случая линейной (N×N) системы уравнений с det(A), не равным 0, решение можно представить в следующем виде:
 Есть два основных варианта: 9Определитель 0283 минорами и определитель перестановками .
Есть два основных варианта: 9Определитель 0283 минорами и определитель перестановками . 2?\)
2?\)
 \]
\] \конец{выравнивание}\]
\конец{выравнивание}\]
 (2)
(2)
 2}{16}\)
2}{16}\)

 {2}$ и т. д. 9{\circ} \right)$. Квадрат — это особый вид прямоугольника (равносторонний) и особый вид параллелограмма (равносторонний и равноугольный).
{2}$ и т. д. 9{\circ} \right)$. Квадрат — это особый вид прямоугольника (равносторонний) и особый вид параллелограмма (равносторонний и равноугольный). {2}$ 9{2}$
{2}$ 9{2}$
 7 0.10
7 0.10
 См. Рисунок 4-3. Каждому местоположению на текущей конструкционной плоскости присваивается значение координаты. На протяжении всей книги AutoCAD 2D вы будете работать с одной и той же вспомогательной плоскостью. Вспомогательные плоскости полностью описаны в книге AutoCAD 3D.
См. Рисунок 4-3. Каждому местоположению на текущей конструкционной плоскости присваивается значение координаты. На протяжении всей книги AutoCAD 2D вы будете работать с одной и той же вспомогательной плоскостью. Вспомогательные плоскости полностью описаны в книге AutoCAD 3D.
 Последний пункт очень важен для вас при рисовании в AutoCAD. AutoCAD запоминает последнюю введенную точку и сохраняет ее в символе @. Символ @ означает «Последнее абсолютное координатное местоположение».
Последний пункт очень важен для вас при рисовании в AutoCAD. AutoCAD запоминает последнюю введенную точку и сохраняет ее в символе @. Символ @ означает «Последнее абсолютное координатное местоположение». (Рис. Шаг 3)
(Рис. Шаг 3) 5,0
5,0  См. пример ниже.
См. пример ниже. Сохраните его в папке: Курсы CAD/AutoCAD 2D/Lab Exercises
Сохраните его в папке: Курсы CAD/AutoCAD 2D/Lab Exercises Можно ввести более одного U, чтобы вернуться еще дальше. Убедитесь, что вы нажимаете ENTER или SPACE после каждого.)
Можно ввести более одного U, чтобы вернуться еще дальше. Убедитесь, что вы нажимаете ENTER или SPACE после каждого.)  (Рис. Шаг 4)
(Рис. Шаг 4) Если объекты выбраны до ввода команды ERASE, приглашение не появляется.
Если объекты выбраны до ввода команды ERASE, приглашение не появляется.

 Перед относительными декартовыми координатами должен стоять символ @.
Перед относительными декартовыми координатами должен стоять символ @. (Рисунок Шаг 3A и 3B)
(Рисунок Шаг 3A и 3B)

 Если вы видите только один объект, даже если он может иметь одинаковые пурпурный и красный цвета, ваш рисунок точен.
Если вы видите только один объект, даже если он может иметь одинаковые пурпурный и красный цвета, ваш рисунок точен.


 Если 3 не
градусов долготы мы не знаем из числа самого по себе, если оно
должен представлять непроецированную координату на чертеже САПР или если
это число, которое имеет какое-то значение в определенных географических координатах
система.
Если 3 не
градусов долготы мы не знаем из числа самого по себе, если оно
должен представлять непроецированную координату на чертеже САПР или если
это число, которое имеет какое-то значение в определенных географических координатах
система.
 Из Новый
Тема Object Dialog мы видим, что помимо классического
задание точек, линий и площадей по координатам, рисующим
объект в режиме соединения точек Коллектор также может указывать линии и
области с использованием криволинейных сегментов, где номера координат указывают дуги окружности , эллипс
дуги или сплайнов .
Из Новый
Тема Object Dialog мы видим, что помимо классического
задание точек, линий и площадей по координатам, рисующим
объект в режиме соединения точек Коллектор также может указывать линии и
области с использованием криволинейных сегментов, где номера координат указывают дуги окружности , эллипс
дуги или сплайнов .
 АлгоритмАЛГОРИТМ
АлгоритмАЛГОРИТМ Методы Гаусса и Жордана-Гаусса.
Методы Гаусса и Жордана-Гаусса.
 -1
*B
-1
*B


 Si una matriz se puede reducir a su forma reducida por filas, entonces su inversa Existe y se puede calcular utilizando el método de Gauss Jordan.
Si una matriz se puede reducir a su forma reducida por filas, entonces su inversa Existe y se puede calcular utilizando el método de Gauss Jordan. org
org ..
.. систем отсчета.
систем отсчета.
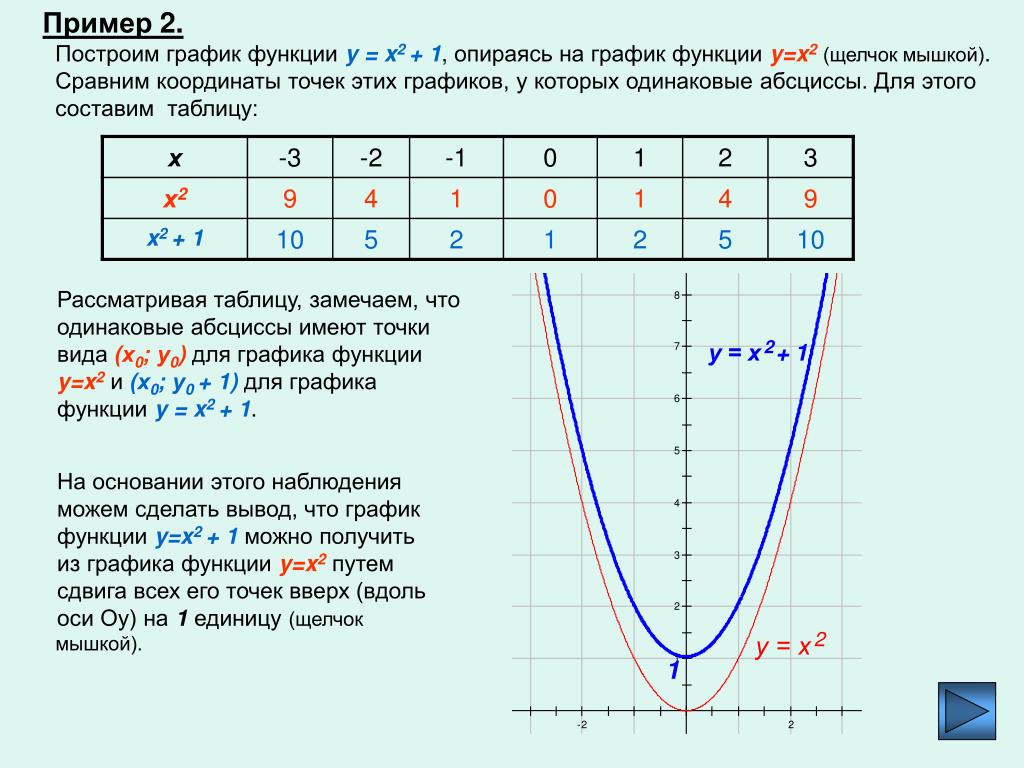
 Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.

 И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим: Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:  е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим: Рассмотрим характерные примеры.
Рассмотрим характерные примеры. Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А. Часто ее приписывают древнегреческим мудрецам, однако, скорее всего, она присутствовала и в других культурах, в которых была развита математика и геометрия (например, в древнеегипетской). В древности эта задача имела и вполне практическое применение, ведь знание того, как найти середину отрезка при помощи простейших измерительных приборов, было полезно, например, в землемерстве, землеустройстве и строительстве. Сегодня, при наличии сложной измерительной техники, такое задание скорее представляет упражнение для развития интеллектуальных способностей и пространственной фантазии школьников.
Часто ее приписывают древнегреческим мудрецам, однако, скорее всего, она присутствовала и в других культурах, в которых была развита математика и геометрия (например, в древнеегипетской). В древности эта задача имела и вполне практическое применение, ведь знание того, как найти середину отрезка при помощи простейших измерительных приборов, было полезно, например, в землемерстве, землеустройстве и строительстве. Сегодня, при наличии сложной измерительной техники, такое задание скорее представляет упражнение для развития интеллектуальных способностей и пространственной фантазии школьников. Затем устанавливаем иглу циркуля в другой конец отрезка и повторяем процедуру очерчивания полукруга.Проделав описанную процедуру, видим, что наши окружности пересекаются в двух точках. Берем линейку и соединяем эти две точки прямой линией. Получаем линию перпендикулярную исходному отрезку. Именно точка пересечения этой линии и отрезка и является серединой последнего.
Затем устанавливаем иглу циркуля в другой конец отрезка и повторяем процедуру очерчивания полукруга.Проделав описанную процедуру, видим, что наши окружности пересекаются в двух точках. Берем линейку и соединяем эти две точки прямой линией. Получаем линию перпендикулярную исходному отрезку. Именно точка пересечения этой линии и отрезка и является серединой последнего. Именно в этом и состоит логика подобного решения задачи о построении середины отрезка при помощи циркуля.
Именно в этом и состоит логика подобного решения задачи о построении середины отрезка при помощи циркуля. Например, это применимо, когда речь идет о возрастных интервала х. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.
Например, это применимо, когда речь идет о возрастных интервала х. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012. 2/N. Иными словами дисперсия – это средний квадрат отклонения от среднего арифметического значения. определяет, насколько в среднем отклоняются конкретные показатели ряда от их среднего значения. Оно является абсолютной мерой колеблемости признака, а потому четко интерпретируется.
2/N. Иными словами дисперсия – это средний квадрат отклонения от среднего арифметического значения. определяет, насколько в среднем отклоняются конкретные показатели ряда от их среднего значения. Оно является абсолютной мерой колеблемости признака, а потому четко интерпретируется.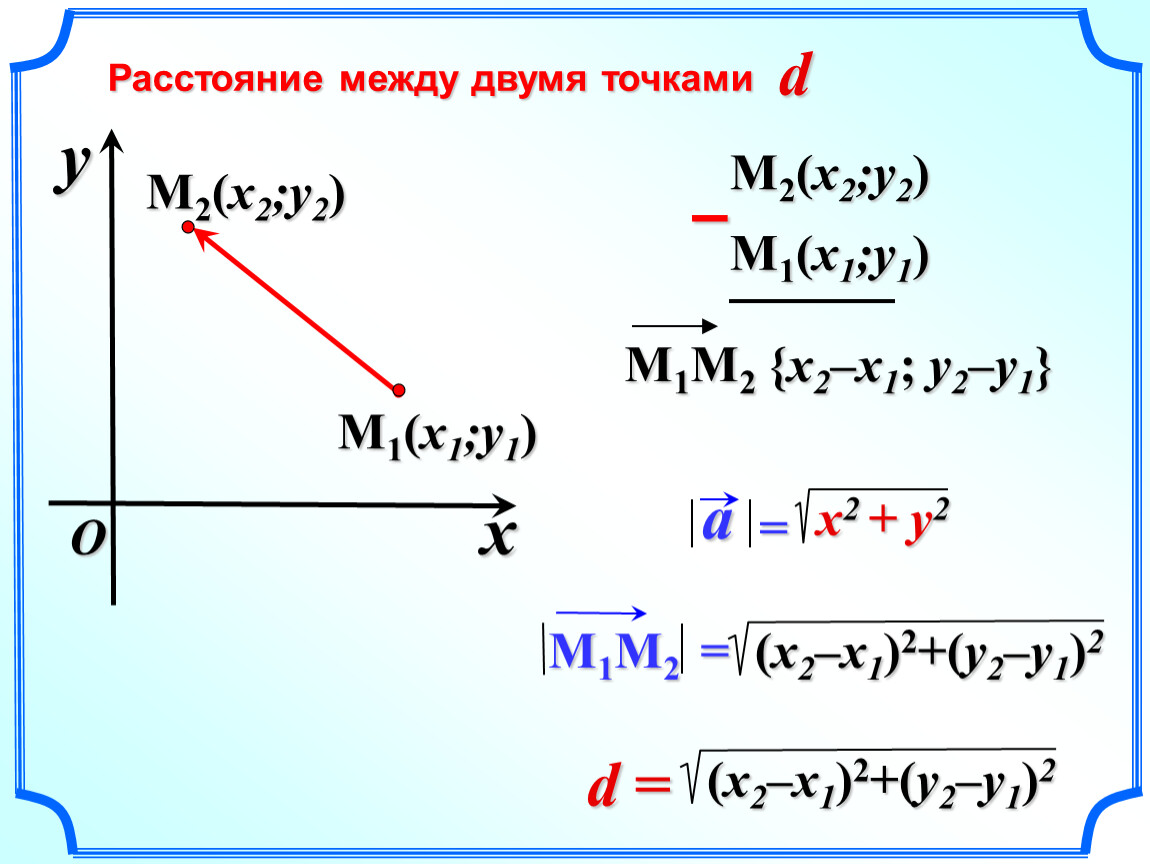 Точка K — середина ребра A 1 B 1 . Найдите координаты этой точки.
Точка K — середина ребра A 1 B 1 . Найдите координаты этой точки. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы. Рассмотрим пример.
Рассмотрим пример.

 Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.

 И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим: Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:  е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим: Рассмотрим характерные примеры.
Рассмотрим характерные примеры. Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
 Используем соответствующие формулы:
Используем соответствующие формулы:-16514864281403904547626faedcb85fd.jpg) Теперь мы знаем, что параметрический
уравнения прямой в пространстве представляют собой неединственную систему из трех уравнений: 𝑥 равно 𝑥
sub 𝐴 плюс 𝑡𝑙, 𝑦 равно 𝑦 sub 𝐴 плюс 𝑡𝑚 и 𝑧 равно 𝑧 sub 𝐴 плюс
𝑡𝑛. И вот где 𝐴 точка на
линия с координатами 𝑥 под 𝐴, 𝑦 под 𝐴 и 𝑧 под 𝐴; вектор с
компоненты 𝑙, 𝑚, 𝑛 — вектор направления прямой; а 𝑡 — действительный параметр
между отрицательным и положительным ∞.
Теперь мы знаем, что параметрический
уравнения прямой в пространстве представляют собой неединственную систему из трех уравнений: 𝑥 равно 𝑥
sub 𝐴 плюс 𝑡𝑙, 𝑦 равно 𝑦 sub 𝐴 плюс 𝑡𝑚 и 𝑧 равно 𝑧 sub 𝐴 плюс
𝑡𝑛. И вот где 𝐴 точка на
линия с координатами 𝑥 под 𝐴, 𝑦 под 𝐴 и 𝑧 под 𝐴; вектор с
компоненты 𝑙, 𝑚, 𝑛 — вектор направления прямой; а 𝑡 — действительный параметр
между отрицательным и положительным ∞. Итак, с 𝑝 один равен один, два,
три и 𝑝 два равно три, шесть, минус пять, наша середина имеет координаты один
плюс три на два, два плюс шесть на два и три плюс минус пять на
два. Это четыре больше двух, восемь больше
два, и минус два на два, что является точкой с координатами два, четыре и
отрицательный.
Итак, с 𝑝 один равен один, два,
три и 𝑝 два равно три, шесть, минус пять, наша середина имеет координаты один
плюс три на два, два плюс шесть на два и три плюс минус пять на
два. Это четыре больше двух, восемь больше
два, и минус два на два, что является точкой с координатами два, четыре и
отрицательный.

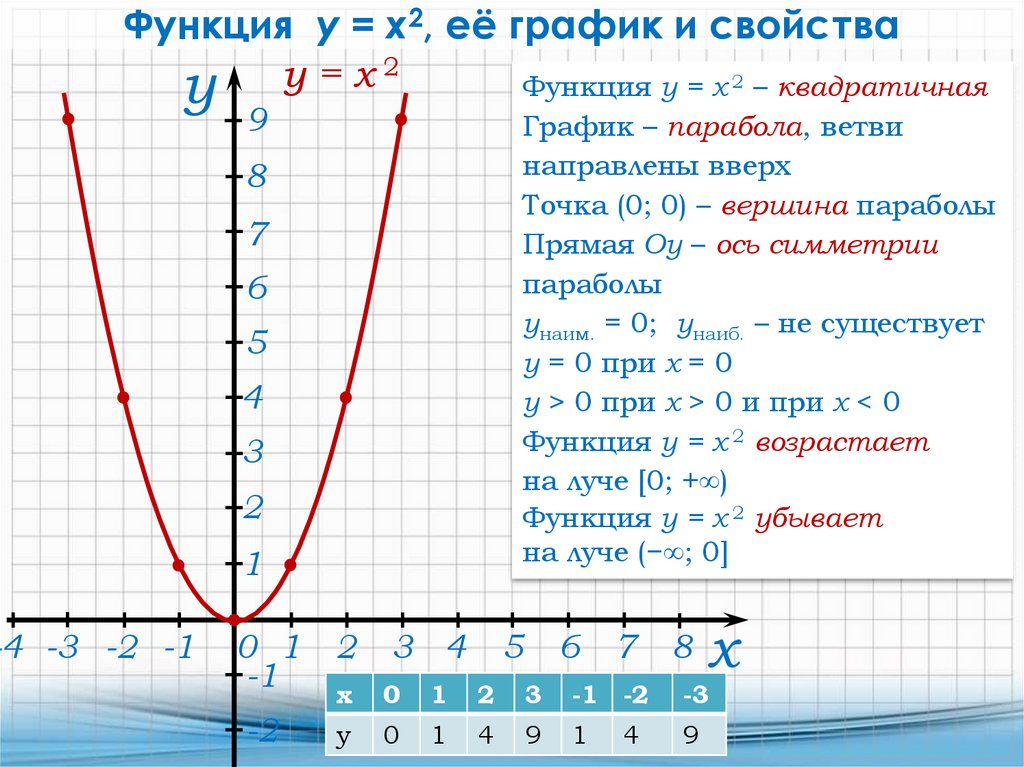
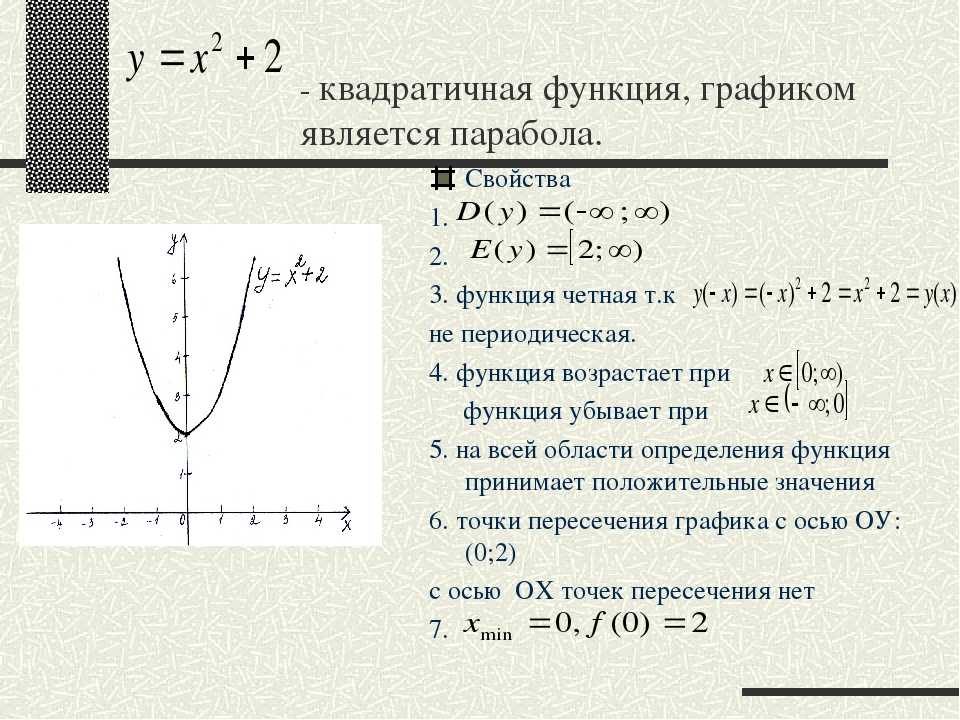
 D(y)=
D(y)=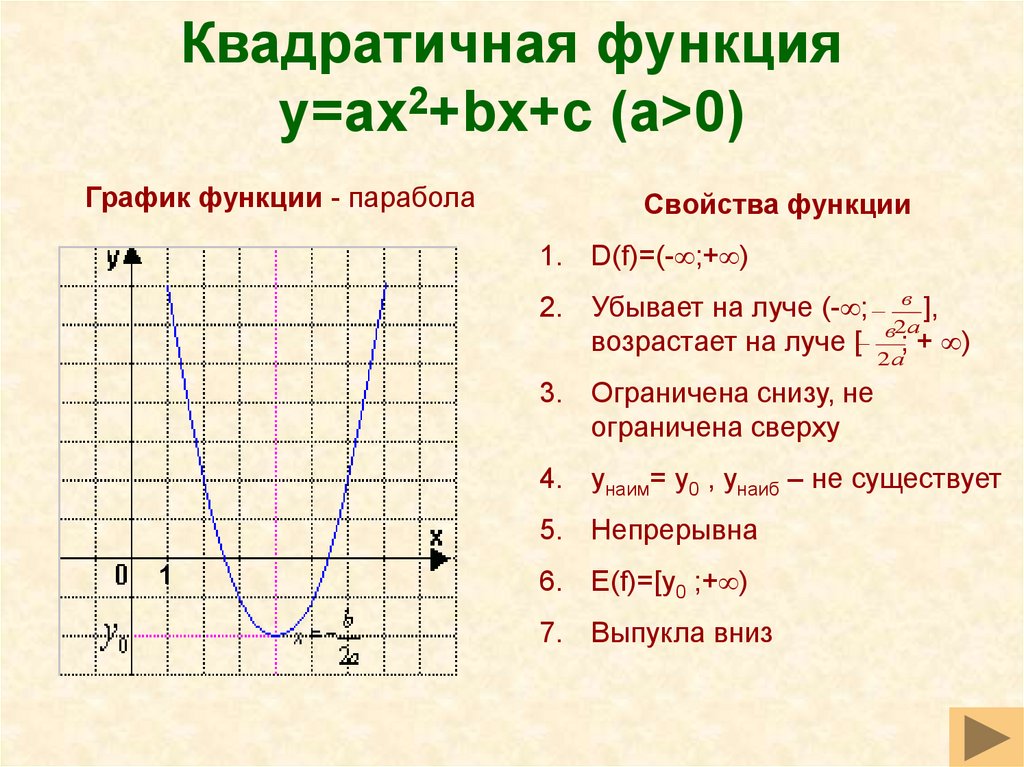 (Напомним: областью определения функции называется совокупность значений независимой переменной, см.раздел «Функции и их графики»)
(Напомним: областью определения функции называется совокупность значений независимой переменной, см.раздел «Функции и их графики»)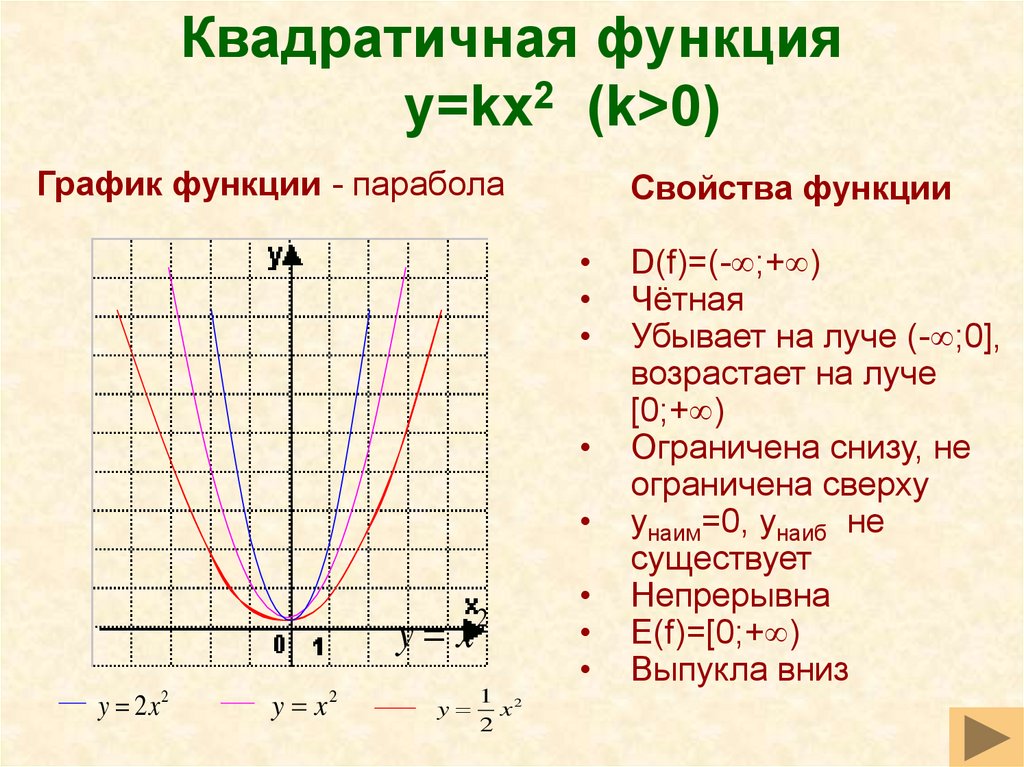 Противоположным значениям аргумента соответствуют равные значения функции.
Противоположным значениям аргумента соответствуют равные значения функции.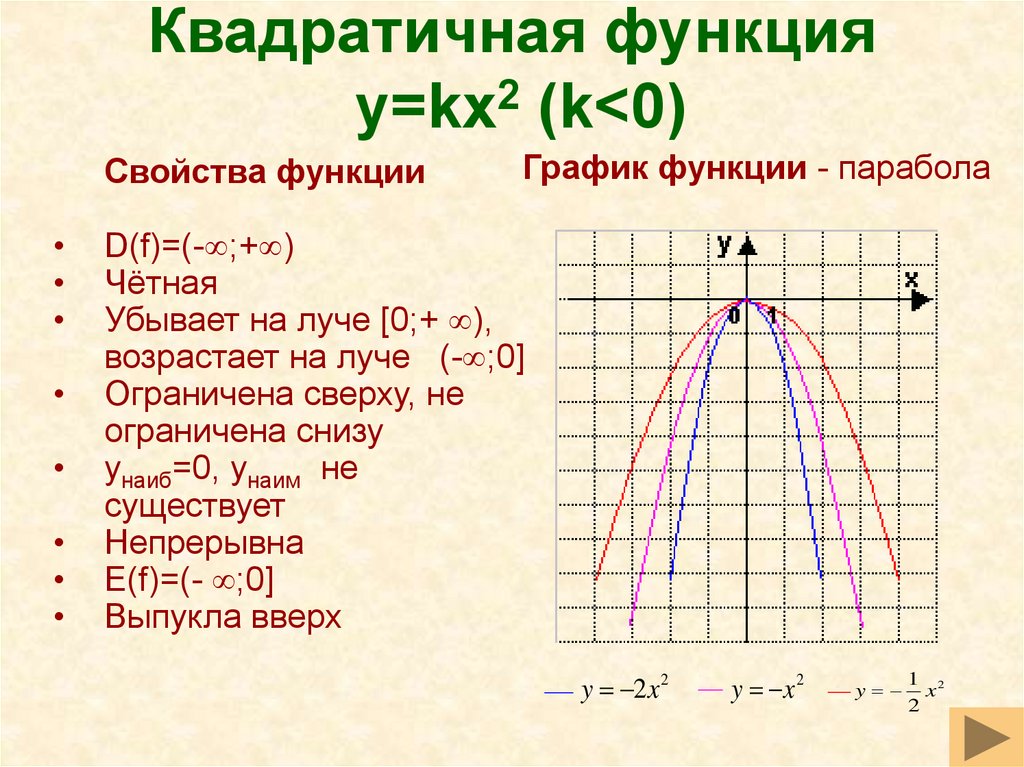
 Уравнение, представляющее параболическую функцию, является квадратным уравнением со второй степенью по x.
Уравнение, представляющее параболическую функцию, является квадратным уравнением со второй степенью по x.


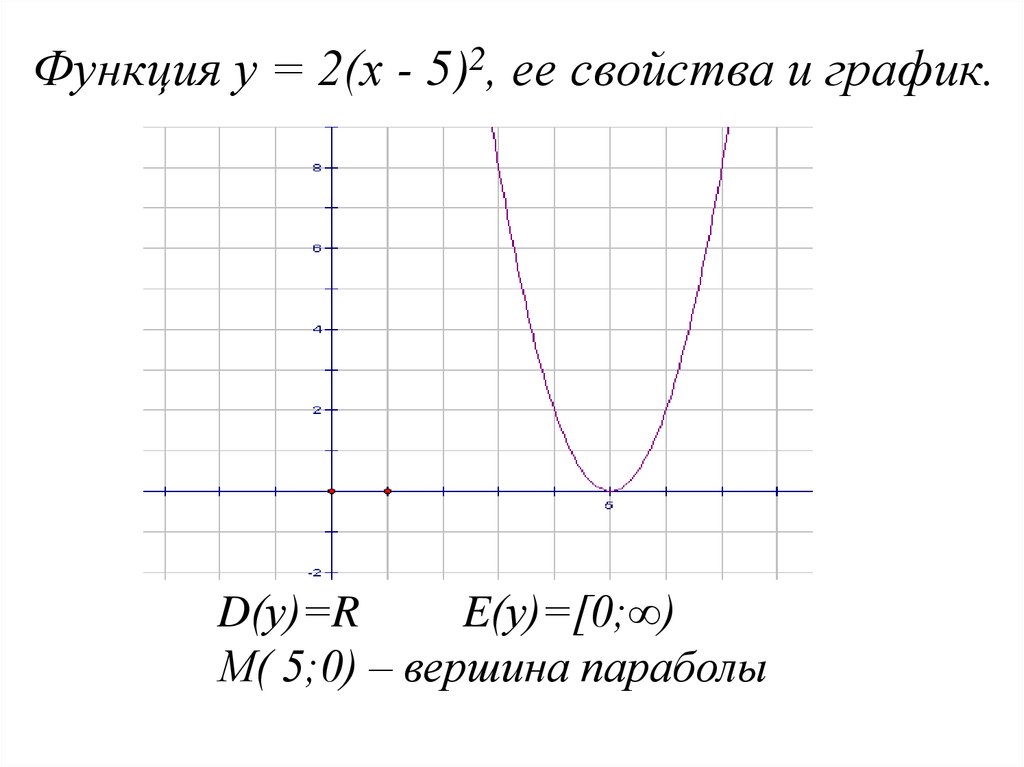
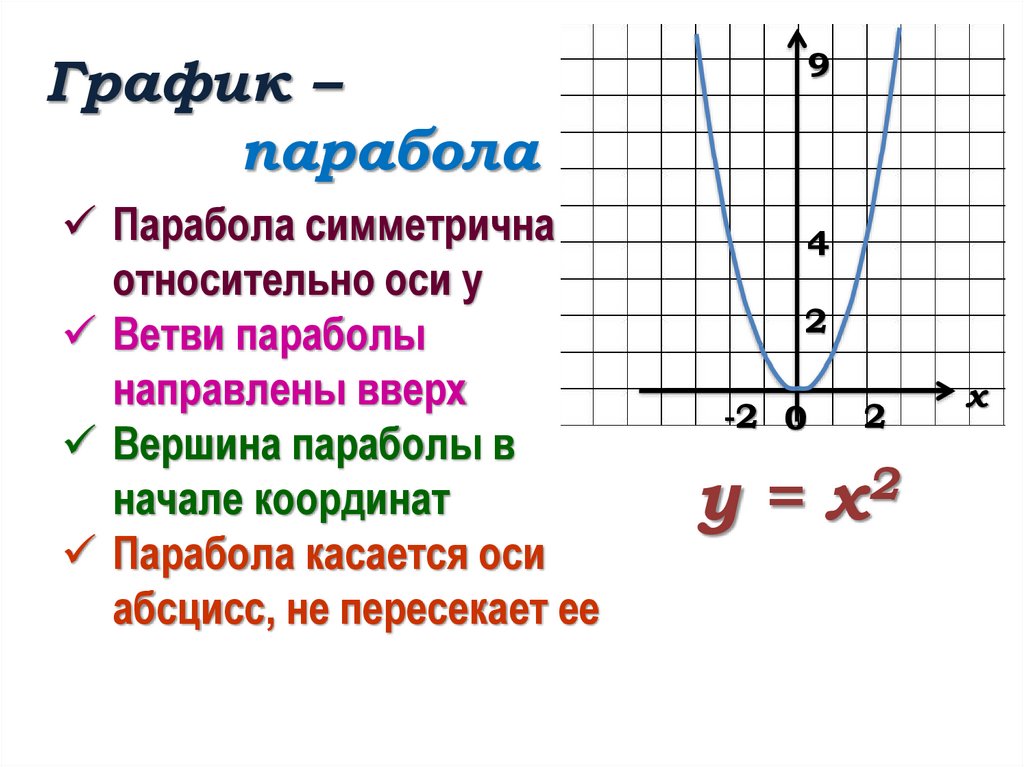 Диапазон параболической функции представлен на оси Y.
Диапазон параболической функции представлен на оси Y.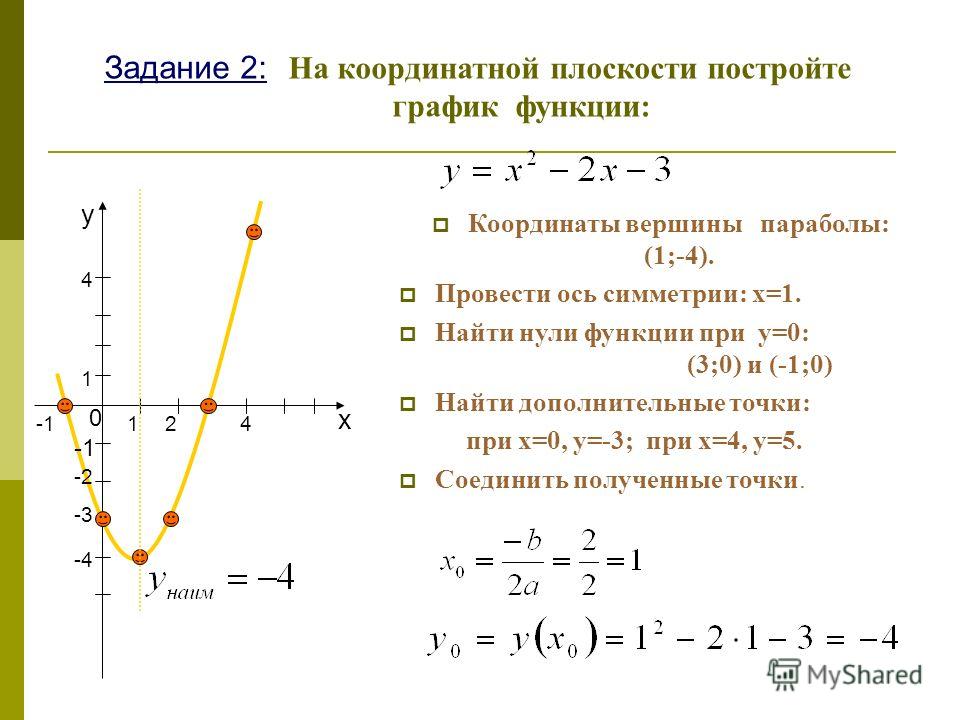
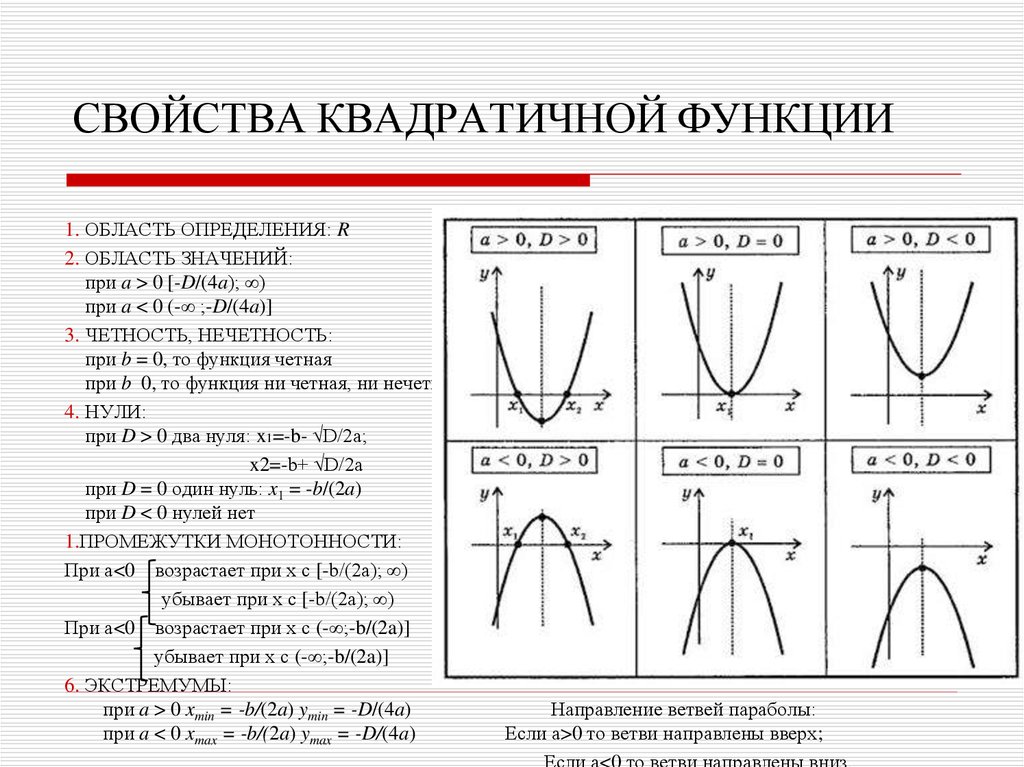
 В любом случае вершина является поворотной точкой на графе. График также симметричен, а вертикальная линия проходит через вершину, называемую 9.0103 ось симметрии .
В любом случае вершина является поворотной точкой на графе. График также симметричен, а вертикальная линия проходит через вершину, называемую 9.0103 ось симметрии . Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. [latex]x[/latex]-перехваты, те точки, где парабола пересекает [latex]x[/latex]-ось, находятся в [latex]\left(-3,0\right)[/latex] и [латекс]\влево(-1,0\вправо)[/латекс]. 9{2}+k[/latex]
Для параболы, которая открывается вверх, вершина находится в самой нижней точке графика, в данном случае [латекс]\влево(-2,-1\вправо)[/латекс]. [latex]x[/latex]-перехваты, те точки, где парабола пересекает [latex]x[/latex]-ось, находятся в [latex]\left(-3,0\right)[/latex] и [латекс]\влево(-1,0\вправо)[/латекс]. 9{2}+k[/latex]

 И они пробуют свои силы. Если в процессе этого появляется некий побочный продукт, полезный для общества, то хорошо. Например, создание электрических батарей стало возможным благодаря работе Джеймса Максвелла по изучению магнетизма и электричества, однако шотландский физик занимался наукой не ради батареек.
И они пробуют свои силы. Если в процессе этого появляется некий побочный продукт, полезный для общества, то хорошо. Например, создание электрических батарей стало возможным благодаря работе Джеймса Максвелла по изучению магнетизма и электричества, однако шотландский физик занимался наукой не ради батареек. д. Эти числа составляют значительную часть математических операций для проведения вычислений.
д. Эти числа составляют значительную часть математических операций для проведения вычислений. Множество натуральных чисел задано N = 1, 2, 3, 4, 5, 6, 7,…
Множество натуральных чисел задано N = 1, 2, 3, 4, 5, 6, 7,… Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается буквой Q.
Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается буквой Q.

 Более высокие уровни ереси могут быть связаны с религией или наукой — не соглашайтесь с ортодоксальными предположениями здесь, и вас сочтут вполне возможно сумасшедшим. Высший уровень ереси в современном мире — математическая ересь . Несогласие с математической ортодоксией равносильно тому, чтобы «быть полноценным чудаком». Вам просто не позволено сомневаться в определенных идеях математики, не будучи осужденным как интеллектуальный прокаженный.
Более высокие уровни ереси могут быть связаны с религией или наукой — не соглашайтесь с ортодоксальными предположениями здесь, и вас сочтут вполне возможно сумасшедшим. Высший уровень ереси в современном мире — математическая ересь . Несогласие с математической ортодоксией равносильно тому, чтобы «быть полноценным чудаком». Вам просто не позволено сомневаться в определенных идеях математики, не будучи осужденным как интеллектуальный прокаженный.
 )
) Я, например, не думаю, что математики знают, что такое прямые. И поскольку их теории построены на их метафизических заявлениях о «линиях и точках», теории должны быть пересмотрены с нуля.
Я, например, не думаю, что математики знают, что такое прямые. И поскольку их теории построены на их метафизических заявлениях о «линиях и точках», теории должны быть пересмотрены с нуля.
 Точки не могут иметь длину, ширину или глубину. И тем не менее, все формы якобы построены из них. Поэтому вы можете спросить: «Подождите, как фигуры, имеющие размеры, могут состоять из набора точек, не имеющих измерений?»
Точки не могут иметь длину, ширину или глубину. И тем не менее, все формы якобы построены из них. Поэтому вы можете спросить: «Подождите, как фигуры, имеющие размеры, могут состоять из набора точек, не имеющих измерений?» Буквальное основание, на котором строится вся теоретическая структура современной геометрии, — «точка» — сомнительно. Ошибки на этом уровне могут иметь катастрофические последствия.
Буквальное основание, на котором строится вся теоретическая структура современной геометрии, — «точка» — сомнительно. Ошибки на этом уровне могут иметь катастрофические последствия. Хотя неспециалисты могут назвать его «кругом», это всего лишь приближение к математическому кругу, который иногда называют «идеальным кругом».
Хотя неспециалисты могут назвать его «кругом», это всего лишь приближение к математическому кругу, который иногда называют «идеальным кругом».
 Его «диаметр» тоже представляет собой простое целое число — количество пикселей, из которых он состоит. Поместите одно целое число в числитель и одно целое число в знаменатель, и вы получите рациональное число пи.
Его «диаметр» тоже представляет собой простое целое число — количество пикселей, из которых он состоит. Поместите одно целое число в числитель и одно целое число в знаменатель, и вы получите рациональное число пи. Не существует «одного истинного отношения, называемого «пи», по той же причине, по которой не существует «единого истинного отношения высоты стола к длине». Каждая таблица и круг построены конечным числом единиц, расположенных по-разному, и поэтому их соотношения будут различаться.
Не существует «одного истинного отношения, называемого «пи», по той же причине, по которой не существует «единого истинного отношения высоты стола к длине». Каждая таблица и круг построены конечным числом единиц, расположенных по-разному, и поэтому их соотношения будут различаться.



 Это только начало совершенно новой теории математики, которую я называю «математикой базовых единиц». Это основы базовой геометрии:
Это только начало совершенно новой теории математики, которую я называю «математикой базовых единиц». Это основы базовой геометрии:
 И, как это бывает, пока круг не построен из крошечного количества основных единиц, отношение числа пи составит около 3,14159.(Хотя, если мы будем предельно точны, мы должны обозначать дроби, поскольку десятичное расширение может быть сомнительным в рамках базовых единиц. Но это будущая статья.). Не существует «общего» или «идеального» круга. Существуют конкретные реальные окружности, каждая из которых представляет собой составной объект, построенный конечным числом точек.
И, как это бывает, пока круг не построен из крошечного количества основных единиц, отношение числа пи составит около 3,14159.(Хотя, если мы будем предельно точны, мы должны обозначать дроби, поскольку десятичное расширение может быть сомнительным в рамках базовых единиц. Но это будущая статья.). Не существует «общего» или «идеального» круга. Существуют конкретные реальные окружности, каждая из которых представляет собой составной объект, построенный конечным числом точек. В этой статье я не могу осветить все возражения против геометрии базовых единиц, но объясню еще несколько способов ее осмысления и поясню, почему она превосходит стандартную ортодоксальность.
В этой статье я не могу осветить все возражения против геометрии базовых единиц, но объясню еще несколько способов ее осмысления и поясню, почему она превосходит стандартную ортодоксальность. Возможно, сейчас это не имеет большого значения, но по мере того, как технология приближается к базовым размерам физического пространства, это может иметь большое значение.
Возможно, сейчас это не имеет большого значения, но по мере того, как технология приближается к базовым размерам физического пространства, это может иметь большое значение. Чем ровнее край круга, тем больше площадь круга.)
Чем ровнее край круга, тем больше площадь круга.) Эти объекты просто не будут коррелировать с нашей вселенной. Кто знает, возможно, мы могли бы сказать правду о другой физической вселенной с меньшими базовыми единицами.
Эти объекты просто не будут коррелировать с нашей вселенной. Кто знает, возможно, мы могли бы сказать правду о другой физической вселенной с меньшими базовыми единицами. Объект строится, пока вы наблюдаете за ним. То же самое происходит и в математике; объекты строятся так, как вы их себе представляете. Об этом еще много будет сказано в следующих статьях.
Объект строится, пока вы наблюдаете за ним. То же самое происходит и в математике; объекты строятся так, как вы их себе представляете. Об этом еще много будет сказано в следующих статьях. Это неправильно. Окружности и многоугольники состоят из конечного числа точек , а не линий. Линии ничего не составляют; они сами являются составными объектами.
Это неправильно. Окружности и многоугольники состоят из конечного числа точек , а не линий. Линии ничего не составляют; они сами являются составными объектами.
 Ященко И. В. Тренировочная работа 35 Вопрос 9 Найдите корень выражения
Ященко И. В. Тренировочная работа 35 Вопрос 9 Найдите корень выражения Найти главную линейную часть приращения площади этого квадрата и оценить относительную ошибку ( в процентах) при замене приращения его главной частью.
[46]
Найти главную линейную часть приращения площади этого квадрата и оценить относительную ошибку ( в процентах) при замене приращения его главной частью.
[46] Примем, что при смешении приращение площади поверхности раздела за отрезок времени dt прямо пропорционально разности между максимально возможным и текущим значением межфазной поверхности.
[51]
Примем, что при смешении приращение площади поверхности раздела за отрезок времени dt прямо пропорционально разности между максимально возможным и текущим значением межфазной поверхности.
[51] Подъем поплавка или поршня, линейно связанный с приращением площади отверстия, выражает непосредственно величину расхода.
[54]
Подъем поплавка или поршня, линейно связанный с приращением площади отверстия, выражает непосредственно величину расхода.
[54] [57]
[57] Найдите площадь квадрата, проведенного по диагонали исходного квадрата (8 см Х 8 см)». eNotes Editorial , 28 января 2013 г., https://www.enotes.com/homework-help/side-square-8-cm-find-area-square-drown-diagonal-77955.
По состоянию на 28 апреля 2023 г.
Найдите площадь квадрата, проведенного по диагонали исходного квадрата (8 см Х 8 см)». eNotes Editorial , 28 января 2013 г., https://www.enotes.com/homework-help/side-square-8-cm-find-area-square-drown-diagonal-77955.
По состоянию на 28 апреля 2023 г.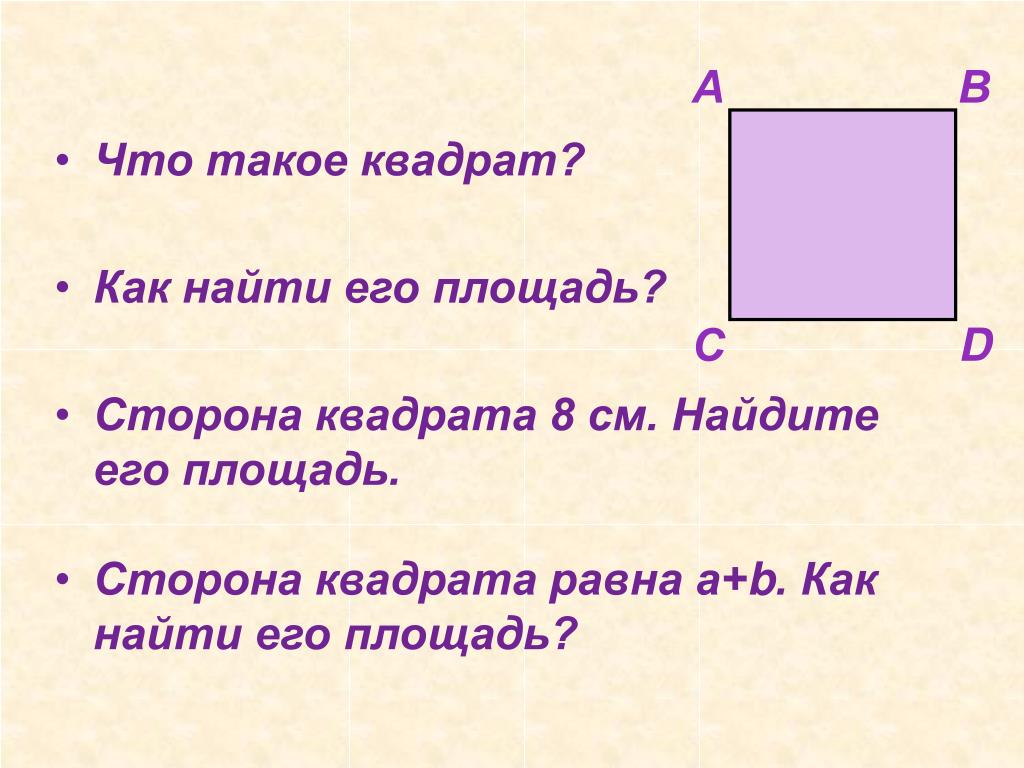
 в 18:48:45.
в 18:48:45. 2 cm है। वर्ग का क्षेत्रफल ज्ञात करें?
2 cm है। वर्ग का क्षेत्रफल ज्ञात करें?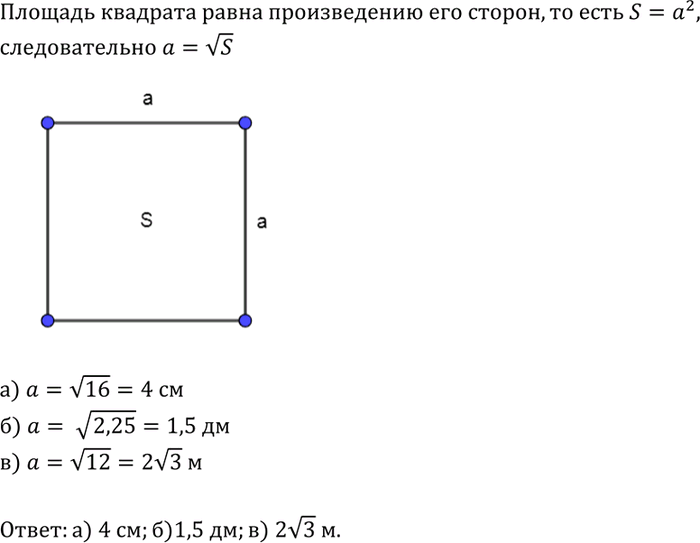 2, то найдите площадь треугольника ADB? 92, то найдите длину…
2, то найдите площадь треугольника ADB? 92, то найдите длину…