Как решить линейное уравнение с одним неизвестным (переменной): примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Решение уравнений с одним неизвестным (переменной)
В данной публикации мы рассмотрим определение и общий вид записи уравнения с одним неизвестным, а также приведем алгоритм его решения с практическими примерами для лучшего понимания.
Определение и запись уравнения
Алгоритм и примеры решения уравнений с одим неизвестным
Простые варианты
Сложные варианты
Определение и запись уравнения
Математическое выражение вида ax + b = 0 называется уравнением с одним неизвестным (переменной) или линейным уравнением. Здесь:
a и b – любые числа: a – коэффициент при неизвестном, b – свободный коэф.
x – переменная. Для обозначения может использоваться любая буква, но общепринятыми являются латинские x, y и z.
Уравнение можно представить в равнозначном виде ax = -b. После этого мы смотрим на коэффициенты.
При a ≠ 0 единственный корень x = -b/a.
При a = 0 уравнение примет вид 0 ⋅ x = -b. В таком случае:
если b ≠ 0, корней нет;
если b = 0, корнем является любое число, т.к. выражение 0 ⋅ x = 0 верно при любом значении x.
Алгоритм и примеры решения уравнений с одим неизвестным
Простые варианты
Рассмотрим простые примеры при a = 1 и наличии всего одного свободного коэффициента.
При решении более сложного уравнения с одной переменной, очень часто требуется сначала его упростить, прежде чем находить корень. Для этого могут применяться следующие приемы:
раскрытие скобок;
перенос всех неизвестных в одну сторону от знака “равно” (обычно в левую), а известных в другую (правую, соответственно).
приведение подобных членов;
освобождение от дробей;
разделение обеих частей на коэффициент при неизвестном.
Переносим все неизвестные влево, а известные вправо (не забываем при переносе менять знак на противоположный): 6x – 3x – x = 2 – 18.
Выполняем приведение подобных членов: 2x = -16.
Делим обе части уравнения на число 2 (коэффициент при неизвестной): x = -8.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Решение уравнений с одним неизвестным, сводящихся к линейным
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Решение уравнений с одним неизвестным, сводящихся к линейным
2. Устная работа
Какое равенство называется уравнением? Что такое корень уравнения? Сколько корней может иметь уравнение? Что значит –решить уравнение? Какое уравнение называют линейным?
3. Математический диктант
Как называется уравнение -2х=17 Придумайте какоенибудь линейное уравнение с одним неизвестным х При каком условии уравнение сх=5 имеет один корень? При каком условии уравнение ах=-3 не имеет корней? Как называется уравнение 17х=-2 Придумайте какоенибудь линейное уравнение с одним неизвестным у При каком условии уравнение ау=3 не имеет корней? При каком условии уравнение ру=-5 имеет единственный корень?
4.
Объяснение нового материалаСловесная формулировка Запись в общем виде пример 1. Если к обеим частям верного равенства прибавить одно и то же число или из обеих частей верного равенства вычесть одно и то же число, то получится верное равенство Если а=в и рлюбое число, то а+р=в+р а-р=в-р 7=7 7+2=7+2 7-2=7-2 2. Если обе части верного равенства умножить или разделить на одно и то же число, не равное нулю, то получится верное равенство Если а=в и р не равно 0, то ар=вр, ар:вр 27=27 27*3=27*3 27:3=27:3
5. Объяснение нового материала
Решим уравнение 9х-23=5х-11 9х-5х=-11+23 4х=12 х=12:4 х=3 Ответ: х=3 Какие свойства использовались при решении этого уравнения?
6. Основные свойства уравнений
Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный. Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
Перенести члены, содержащие неизвестное в левую часть, не содержащие неизвестное- в правую. Привести подобные члены. Разделить обе части уравнения на коэффициент при неизвестном, если он не равен нулю.
9. Решение задач
Выполнить Выполнить Выполнить Выполнить №86(1,3) самостоятельно №87(1,3) №88(1,3) №89(1,3)
10. Итоги урока
Сформулируйте свойства решения уравнения. Расскажите схему решения линейного уравнения одним неизвестным.
11. Домашнее задание
Выучить п.7 Выполнить № 88(2,4), №89(2,4), №97(2) Принести тетрадь для контрольных работ
English
Русский
Правила
Решение линейных уравнений с одним неизвестным
Все математические ресурсы GMAT
22 диагностических теста
693 практических теста
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
GMAT Math Help »
Проблемные вопросы »
Алгебра »
Линейные уравнения, одно неизвестное »
Решение линейных уравнений с одним неизвестным
При каком значении следующее уравнение не имеет решения?
Возможные ответы:
Уравнение всегда должно иметь хотя бы одно решение независимо от значения .
Правильный ответ:
Объяснение:
Максимально упростите обе части уравнения и решите в уравнении через:
имеет ровно одно решение, если знаменатель не равен 0, то есть . Мы убеждаемся, что это значение не дает решения, заменяя:
Уравнение не имеет решения и является правильным ответом.
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
900 16
Объяснение:
Сообщить об ошибке
Решить для :
Возможные ответы: 9 0005
Правильный ответ:
Объяснение:
Сообщить об ошибке
Решить для:
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Что такое координата средней точки и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула средней точки:
Сообщить об ошибке
Что такое координата средней точки и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула средней точки:
Сообщить об ошибке
Что такое координата середины и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула средней точки:
Сообщить об ошибке
Решить следующее уравнение:
.
Возможные ответы:
Правильный ответ:
Объяснение:
Начнем с выделения выражения абсолютного значения:
Это дает нам два случая удаления абсолютного значения:
и
Затем мы решаем для каждого случая:
Сообщить об ошибке
Решить для :
Возможно Ответы:
Уравнение не имеет решения.
Правильный ответ:
Объяснение:
Сообщить об ошибке. 0004
Уравнение не имеет решения.
Правильный ответ:
Объяснение:
Сообщить об ошибке
← Предыдущий 1 2 3 4 Далее →
Уведомление об авторских правах
Все ресурсы по математике GMAT
22 Диагностические тесты
693 практических теста
Вопрос дня
Карточки
Learn by Concept
Решение уравнений с одной неизвестной переменной Практические вопросы
Узнайте, как решать уравнения с одной неизвестной переменной , уравнения с переменными с обеих сторон, уравнения со скобками и уравнения с дробями — даже если у вас аллергия на алгебра!
Этот математический обзор алгебраических уравнений предназначен для освежения ваших знаний перед вступительными экзаменами, такими как ATI TEAS V, HESI, ACT или SAT.
Какой тип математики входит в экзамен ATI TEAS? Секция ATI TEAS по математике проверяет участников на порядок операций, отношения, дроби, метрическую беседу и т. Д. Эта викторина по математике ATI TEAS проверит вашу способность решать умножение и деление десятичных чисел.
Как решать уравнения с одной неизвестной переменной
Я покажу вам, как решать уравнения с одним неизвестным, например, 2x + 5 = 10. Я также покажу вам, как решать уравнения с переменными с обеих сторон, например, 2 (x + 5) = 7x + 3. Кроме того, я составлю уравнения с дробями х/2 + 1/3 = х/4 + 2/3.
Далее вам нужно переместить переменную в одну часть уравнения, а числа — в другую. Это наша цель — выяснить, что представляет собой переменная (обычно «x»). Мы хотим, чтобы наш окончательный ответ говорил что-то вроде x=5.
Чтобы изолировать переменную с одной стороны и число с другой стороны, мы можем использовать несколько «правил». Одним из правил является принцип сложения, который гласит, что мы можем добавить или вычесть число из самого себя, чтобы удалить его из одной части уравнения, но мы должны сделать то же самое с другой частью уравнения, чтобы сохранить его сбалансированным.
Другим принципом является принцип умножения, аналогичный принципу сложения. Принцип умножения гласит, что мы можем умножить или разделить переменную на число, чтобы изолировать ее в одной части уравнения, но мы должны сделать то же самое с другой частью уравнения.
Решение уравнений с одной неизвестной переменной
Эти практические вопросы помогут вам решать уравнения с одной неизвестной переменной.
1. х + 3 = 5*
х = 5
х = 9
х = 2
х = 66
2. 2x + 7 = 21*
х = 7
х = 89
х = 68
х = 12
3. 2(2x – 4) = x + 4*
х = 8
х = 4
х = 2
х = 12
4. х/10 = 5*
х = 78
х = 100
х = 25
х = 50
5. х/2 + 7 = х/6 – 1*
х = 48
х = 24
х = -25
х = -24
6. 2(х/2 + 4) = 5х – 5*
х = 3 1/4 ИЛИ 13/4
х = 3 5/8 ИЛИ 29/8
х = 3
Ни один из вариантов не правильный
7. 5х + 3 = 2х + 12*
х = 3
х = 9
х = 7
х = 6
8. х/3 = 5/6*
х = 9 1/3 ИЛИ 29/3
х = 2/9
х = 15/6 ИЛИ 2 1/2
х = 6
(ПРИМЕЧАНИЕ. Когда вы нажмете «Отправить», будет обновлена эта же страница. Прокрутите вниз, чтобы увидеть результаты.)
После того, как вы закончите сдавать тест и нажмете «Отправить», страница обновится, и вам нужно будет прокрутить вниз чтобы увидеть, что вы сделали правильно и неправильно. Кроме того, под этой викториной находится макет викторины с ключом для ответа (если вы хотите распечатать викторину, просто скопируйте и вставьте ее). Не забудьте поделиться этой викториной с друзьями! Однако, пожалуйста, не публикуйте повторно на других сайтах.
Решение уравнений с одной неизвестной переменной Практические вопросы
Юниум — федеральная сеть образовательных центров для школьников по всей России. Мы проводим занятия по подготовке к ЕГЭ и ГИА. Каждый год наши выпускники поступают в лучшие ВУЗы страны, а их результаты выше, чем в среднем по России.
Сообщение:
Запрос успешно отправлен. В ближайшее время расширенный доступ будет предоставлен.
– Oбразование как Стиль Жизни
Присылайте свои колонки
и предложения
У вас есть интересная новость
или материал из сферы образования
или популярной науки? Расскажите нам!
Просветительский медиа-проект об образовании,
посвящённый самым актуальным и полезным
концепциям, теориям и методикам, технологиям
и исследованиям, продуктам и сервисам. Мы
говорим о том, как развиваются и изменяются
образование и наука. Копирование материалов возможно только
с разрешения редакции Newtonew.
ЕГЭ спецпроект
ProTeachers
MOOC 2016
Большая переменная
Физика: игра света
Маршрут в будущее
Считаные годы
Образование XXI века
Мы используем файлы cookie для улучшения пользовательского опыта. Подробнее вы можете посмотреть в нашем пользовательском соглашении.
App Store
Google Play
Подписаться на рассылку
Подписаться на рассылку
Авторизация на сайте
Вход через соц.сети:
ВКонтакте
Facebook
Google
Новый пользователь
Введите ваш email:
Введите пароль:
Повторите пароль:
назад
Напомнить пароль
Введите email, на который вы зарегистрированы:
назад
Пароль выслан
Мы выслали ваш пароль для входа в систему на указанный email.
Рубрика: Обзор функций онлайн калькулятораАвтор: Калькулятор Онлайн
0
Арксинус Запись: asin(x), arcsin(x) Параметры: x — Число Примеры: plot(asin(x),x=-1. .1) plot(asin(x),x=-1..1) plot(re(asin(x)),im(asin(x)),x=-2..2)
det a
det a
Вы искали det a? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и det a матрицы, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «det a».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как det a,det a матрицы,det a матрицы что это,det в матрице это,det матрицы,det что такое,det это,вычисление детерминанта матрицы,вычисление определителей,вычисление определителей матрицы,вычисление определителя,вычисления определителя матрицы,вычислите определители,вычислите определитель,вычислите определитель матрицы,вычислить определители,вычислить определители матриц,вычислить определитель,вычислить определитель матрица,вычислить определитель матрицы,вычислить определитель матрицы а,вычислить определитель матрицы онлайн по правилу треугольника,вычислить определитель матрицы по правилу треугольника онлайн,вычислить определитель методом треугольника,вычислить определитель по правилу треугольника,вычислить определитель по правилу треугольника онлайн,детерминант как найти,детерминант матрицы,детерминант матрицы как найти,детерминант матрицы это,как вычислить определитель,как вычислить определитель матрицы,как вычислить определитель матрицы 2 на 2,как найти детерминант матрицы,как найти определитель в матрице,как найти определитель матрицы 2 на 2,как обозначается определитель матрицы,как определить определитель матрицы,как посчитать определитель,как решить определитель,как считать определители,как считать определитель,как считать определитель матрицы,математика определитель,математика определитель матрицы,матрица вычислить определитель,матрица и определители,матрица и определитель,матрица метод треугольника,матрица метод треугольников,матрица найти определитель,матрица определители,матрица определитель,матрица определитель вычислить,матрица определитель которой равен нулю называется,матрица правила треугольника,матрица правило треугольника,матрица свойства определителей,матрицы det,матрицы det a,матрицы вычисление определителей,матрицы вычисления определителя,матрицы и определители,матрицы метод треугольника,матрицы метод треугольников,матрицы определение определителя,матрицы определители,матрицы определитель определение,матрицы определитель свойства,матрицы определить,матрицы решение методом треугольника,матрицы свойства определителей,метод треугольника матрица,метод треугольников матрица,найти детерминант матрицы,найти определитель,найти определитель матрица,найти определитель матрицы,нахождение определителя,нахождение определителя матрицы,нахождение определителя матрицы методом треугольника,нахождения определителя матрицы,определение матрицы определителя,определение определитель,определение определитель матрицы,определение определителя,определение определителя матрицы,определители как считать,определители матриц,определители матрица,определители матрицы,определитель,определитель 2 на 2,определитель в математике,определитель в матрице,определитель и матрица,определитель как посчитать,определитель математика,определитель матрица,определитель матрицы,определитель матрицы 2 на 2,определитель матрицы 3х3 правило треугольника,определитель матрицы всегда целое число,определитель матрицы детерминант матрицы,определитель матрицы как искать,определитель матрицы как считать,определитель матрицы математика,определитель матрицы методом треугольника,определитель матрицы не всегда можно вычислить,определитель матрицы определение,определитель матрицы прямоугольной,определитель матрицы свойства,определитель матрицы формула,определитель матрицы что это,определитель матрицы это,определитель матрицы это что,определитель методом треугольника,определитель равен,определитель треугольной матрицы,определить матрицу,определить матрицы,подсчет определителя,поиск определителя матрицы,правила треугольника матрица,правило треугольников в матрице,правило треугольников матрица,правило треугольников матрицы,примеры определитель матрицы,расчет определителя,расчет определителя матрицы,решение матриц методом треугольника,решение матрицы методом треугольника,решение определителей,решение определителя,решить определитель,свойства определителей матриц,свойства определителей матрица,свойства определителей матрицы,свойства определителей матрицы с примерами,свойства определитель матрицы,свойства определителя матрицы,свойство матрицы определителя,свойство определителя матрицы,способы нахождения определителя матрицы,формула детерминант,формула лейбница для матриц,формула определителя,что такое det,что такое det в матрице,что такое в матрице det,что такое определитель матрицы. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и det a. Просто введите задачу в окошко и нажмите
«решить» здесь (например, det a матрицы что это).
Решить задачу det a вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Онлайн-калькулятор для расчета определителя 3×3
Онлайн-калькулятор для расчета определителя 3×3
Онлайн-калькулятор вычисляет значение определителя матрицы 3×3 по правилу Сарруса и с разложением Лапласа в строке или столбце.
Определитель 3х3
det A=|a11a12a13a21a22a23a31a32a33|
Введите коэффициенты
↹#. 000
а 11 =
а 12 =
а 13 =
а 21 =
а 22 =
а 23 =
а 31 =
а 32 =
а 33 =
Расчет значения определителя
Расчет по правилу Сарруса
Для матрицы 3×3 определитель можно вычислить по правилу Сарруса. Правило Сарруса использует диагонали для расчета. Калькулятор показывает этапы расчета. Для иллюстрации элементы главных диагоналей окрашены в зеленый цвет, а элементы второстепенных диагоналей — в синий. Серым цветом первые два столбца повторяются для облегчения чтения диагоналей.
Вычисление с использованием разложения Лапласа
Общий метод вычисления определителя дается теоремой разложения Лапласа. Теорему можно использовать из любой строки или столбца. Калькулятор показывает расширение для выбранной строки или столбца. Вы можете выбрать строку или столбец, которые будут использоваться для расширения.
Расчет с помощью алгоритма Гаусса
Примечание:
Если ведущие коэффициенты равны нулю, то столбцы или строки меняются местами соответственно, чтобы было возможно деление на старший коэффициент. Значение определителя правильное, если после преобразований нижняя треугольная матрица равна нулю, а все элементы главной диагонали равны 1.
Объяснение методов
Определитель матрицы 3×3 по правилу Сарруса
Определитель вычисляется следующим образом по правилу Сарруса. Схематически первые два столбца определителя повторяются, так что большая и малая диагонали могут быть виртуально соединены линейной линией. Затем делают произведения главных диагональных элементов и добавляют эти произведения. С второстепенными диагоналями вы должны сделать то же самое. Разница между ними дает определитель матрицы.
Теорема Лапласа о расширении
Теорема Лапласа о развитии предлагает метод вычисления определителя, в котором определитель развивается после строки или столбца. Размерность уменьшается и может быть уменьшена далее шаг за шагом до скаляра.
det A=∑i=1n-1i+j⋅aijdetAij ( Расширение по j-му столбцу )
det A=∑j=1n-1i+j⋅aijdetAij ( Разложение по i-й строке )
где A ij , подматрица A, которая возникает, когда i-я строка и j- й столбец удален.
Пример разложения Лапласа по первой строке матрицы 3×3.
det A=|a11a12a13a21a22a23a31a32a33|
Первый элемент определяется коэффициентом a 11 и субдетерминант, состоящий из элементов с зеленым фоном.
|a11a12a13a21a22a23a31a32a33|=>a11|a22a23a32a33|
Второй элемент задается коэффициентом a 12 и субдетерминантом, состоящим из элементов с зеленым фоном.
|a11a12a13a21a22a23a31a32a33|=>a12|a21a23a31a33|
Третий элемент определяется коэффициентом a 13 и субдетерминантом, состоящим из элементов с зеленым фоном.
|a11a12a13a21a22a23a31a32a33|=>a13|a21a22a31a32|
С тремя элементами определитель может быть записан как сумма определителей 2×2.
det A=|a11a12a13a21a22a23a31a32a33|=a11|a22a23a32a33|-a12|a21a23a31a33|+a13|a21a22a31a32|
Важно учитывать, что знаки элементов чередуются следующим образом.
|+-+-+-+-+|
Метод Гаусса
В методе Гаусса определитель преобразуется таким образом, что элементы нижней матрицы треугольника становятся равными нулю. Для этого вы используете правила коэффициента строки и добавление строк. Добавление строк не меняет значения определителя. Факторы ряда должны рассматриваться как множители перед определителем. Если определитель треугольный и элементы главной диагонали равны единице, то множитель перед определителем соответствует значению самого определителя.
det A=|a11a12…a1naj1aj2…ajn⋮an1an2…ann|=λ|1a12…a1n01…ajn⋮00…1|=λdet A’=λ
Калькулятор определителя матрицы
Определитель квадратной матрицы A = ( a i j )
размерности n является действительным числом, которое линейно зависит от каждого вектора-столбца матрицы. Обозначим через det ( A )
или | А |
определитель квадратной матрицы А.
Свойства определителей
Определитель равен 0, если
Две строки в матрице равны.
В матрице хотя бы одна строка или столбец равны нулю.
Матрица уникальна.
Вычитание строки i из строки j n раз не меняет значения определителя.
Если поменять местами две строки или столбца, знак определителя изменится с положительного на отрицательный или с отрицательного на положительный.
Определитель единичной матрицы равен 1,
det ( I п ) = 1
Определители A и его транспонирования равны,
дет ( А Т ) = дет ( А )
det (A — 1) = 1 det (A) = [det (A)] — 1
Если матрицы A и B имеют одинаковую размерность,
det ( A B ) = det ( A ) × det ( B )
det ( c A ) = c n x det ( A )
det ( А ) знак равно а п а 22 … а п п знак равно ∏ я знак равно 1 п а я я
, если матрица A треугольная
а я j = 0
эт я ≠ j
, определитель равен произведению диагоналей матрицы.
Методы расчета детерминанта
Расширение кофактора (разложение Лапласа)
Расширение кофактора используется для небольших матриц, поскольку оно становится неэффективным для больших матриц по сравнению с методами разложения матриц.
Формула для вычисления расширения Place дается следующим образом:
Где k — фиксированный выбор i ∈ {1, 2, …, n}, а det (A k j ) — минор элемента a i j .
Пример
Формула Лейбница
Где Sn ∈ {1, 2, …, n} — множество перестановок от 1 до n, и sign — это функция, определяющая знак множества Sn, которая возвращает +1 для четных перестановок и -1 для нечетных перестановок.
Пример
Исключение Гаусса
Исключение Гаусса также используется для нахождения определителя путем преобразования матрицы в форму сокращенного эшелона строк путем замены строк или столбцов местами, добавления к строке и умножения на другую строку, чтобы показать максимум нулей.
У этого термина существуют и другие значения, см. Сложение (значения).
Сложение (прибавление) — одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае — два числа). Более строго сложение — бинарная операция, определённая на некотором множестве, элементы которого мы будем называть числами, при которой двум числовым аргументам (слагаемым) a и b сопоставляется итог (сумма), обычно обозначаемый с помощью знака «плюс»: a+b.
Содержание
1 Определение сложения
1.1 Абстрактная алгебра
2 Свойства сложения в арифметике
3 Обозначение операции
4 Запись при помощи буквы Σ
5 См. также
Определение сложения
Абстрактная алгебра
В абстрактной алгебре сложением может называться любая бинарная, коммутативная и ассоциативная операция. В случае, если на этом множестве определено также умножение, то сложение предполагается дистрибутивным по отношению к нему.
Свойства сложения в арифметике
Сложение обладает следующими свойствами:
коммутативностью (переместительный закон):
ассоциативностью (сочетательный закон):
дистрибутивностью относительно умножения (распределительный закон):
В других системах (чисел, объектов) любое из этих свойств может не выполняться.
Обозначение операции
Первое появление знаков «плюс» и «минус».
Знак плюс для операции сложения плюса (а также знак минуса) придумали в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в «Арифметике» Иоганна Видмана, изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа вскоре получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
У этого термина существуют и другие значения, см. Сложение (значения).
Сложение (прибавление) — одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае — два числа). Более строго сложение — бинарная операция, определённая на некотором множестве, элементы которого мы будем называть числами, при которой двум числовым аргументам (слагаемым) a и b сопоставляется итог (сумма), обычно обозначаемый с помощью знака «плюс»: a+b.
Содержание
1 Определение сложения
1.1 Абстрактная алгебра
2 Свойства сложения в арифметике
3 Обозначение операции
4 Запись при помощи буквы Σ
5 См. также
Определение сложения
Абстрактная алгебра
В абстрактной алгебре сложением может называться любая бинарная, коммутативная и ассоциативная операция. В случае, если на этом множестве определено также умножение, то сложение предполагается дистрибутивным по отношению к нему.
Свойства сложения в арифметике
Сложение обладает следующими свойствами:
коммутативностью (переместительный закон):
ассоциативностью (сочетательный закон):
дистрибутивностью относительно умножения (распределительный закон):
В других системах (чисел, объектов) любое из этих свойств может не выполняться.
Обозначение операции
Первое появление знаков «плюс» и «минус».
Знак плюс для операции сложения плюса (а также знак минуса) придумали в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в «Арифметике» Иоганна Видмана, изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа вскоре получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
математика (BrE) | математика (AmE) является сокращенной формой математика
На этой странице перечислены основные математические символы с их названиями и примерами на английском языке.
+ плюс/дополнение
Знак плюс означает:
а. понятие
положительное
Любое число больше нуля является положительным числом и может быть записано со знаком плюс или без него.
Таким образом, +5 (плюс пять) и 5 (пять) — одно и то же число.
б. операция сложения
3 + 5 = 8 три плюс пять равно восьми пять прибавить к трем, получится восемь три прибавить к пяти, получится восемь
Сложение дает нам сумму . В 3 + 5 = 8 сумма равна восьми.
—
знак минус/знак вычитания
Знак минус означает:
а. понятие отрицательного
Любое число меньше нуля является отрицательным числом и записывается со знаком минус перед ним.
-3 минус три
б. операция вычитания
8 — 5 = 3 восемь минус пять равно трем пять вычесть из восьми равно трем если из восьми вычесть пять, то получится три если из восьми вычесть пять, то получится три
Вычитание дает нам разницы . В 8 — 5 = 3 разница три.
×
знак умножения / знак умножения
Знак умножения на означает:
умножение
5 x 6 = 30 пять раз шесть равно тридцати пять умножить на шесть равно тридцати пять шестерок равно тридцати если умножить 5 на 6 получится тридцать
Умножение дает нам произведение . В 5 х 6 = 30 произведение равно 30.
÷ ИЛИ /
знак деления
Знак деления представляет:
подразделение
15 ÷ 3 = 5 15 / 3 = 5 пятнадцать разделить на три равно пяти пять получится пятнадцать трижды если пятнадцать разделить на три получится пять если три разделить на пятнадцать получится пять
Деление
дает нам частное . В 15 ÷ 3 = 5 частное равно пяти.
Подытожим вышеописанные четыре операции следующим образом:
операция
результат
дополнение
«плюс»
2 + 2 = 4
сумма
вычитание
«минус»
5 — 3 = 2
разница
умножение
«раз»
3 х 5 = 15
товар
отделение
«делится на»
21/7 = 3
частное
=
знак равенства
Знак равенства представляет равенство :
3 + 4 = 7 три плюс четыре равно семь
Обратите внимание, что мы обычно говорим, что равно НЕ равно:
два плюс два равно четыре
два плюс два равно четырем
< меньше
3 < 4 три меньше четырех
>
больше
4 > 3 четыре больше трех
≠
НЕ равно
x ≠ z x не равно z
≥
больше или равно
x ≥ z x больше или равно z
≤
меньше или равно
z ≤ x z меньше или равно x
¾
дробь
см. дроби
.
десятичный разделитель | точка
Десятичный разделитель отделяет целое число от его дробной части справа:
1,23
В английском языке десятичным разделителем обычно является точка (.). Обратите внимание, что в некоторых языках десятичным разделителем является запятая (,).
см. десятичные дроби
,
разделитель тысяч
В английском языке разделитель тысяч разделяет целые числа на группы по три справа.
10 987 654 321
В английском языке разделителем тысяч обычно является запятая (,). Обратите внимание, что в некоторых языках разделителем тысяч является точка (.), а иногда и пробел ( ).
см. тыс.
%
знак процента
Знак процентов указывает число или отношение в виде доли от 100 ( процентов ).
40% сорок процентов Только сорок процентов людей проголосовали за нее. Какой процент проголосовал за нее? Сорок процентов.
√
квадратный корень
√16 = 4 квадратный корень из шестнадцати равен четырем квадратный корень из шестнадцати равен четырем
5-значный плюс/минус 5-значный Сложение и вычитание с некоторыми
Эти рабочие листы обеспечивают практику сложения и вычитания 5-значного числа. Эти рабочие листы по математике предназначены для практики сложения и вычитания пятизначных чисел. Эти рабочие листы подходят для учащихся старших классов начальной или средней школы, которые работают над улучшением своих математических навыков. Сложение и вычитание — одни из основных математических функций, которые мы используем в повседневной деятельности. Научите своих учеников или детей складывать и вычитать пятизначные числа, используя эти замечательные рабочие листы. Это набор из 100 рабочих листов для печати, которые предназначены для того, чтобы помочь учащимся научиться решать задачи на сложение и вычитание. Этот набор содержит 100 печатных листов со смешанными задачами на сложение и вычитание с 5-значными числами. Учащиеся могут использовать эти рабочие листы для овладения математическими навыками на практике, в учебной группе или для взаимного обучения. Родители могут работать со своими детьми, чтобы дать им дополнительную практику, сохранить их навыки свежими во время школьных каникул или помочь им освоить новый математический навык.
Вы получите: • 1 PDF-файл. Включены в файл PDF 100 рабочих листов. Все страницы разные. • Готов к печати. Международный формат бумаги A4, книжная ориентация, ширина 210 мм x длина 297 мм (11,69″ x 8,27″). • Распечатать всего 100 страниц.
Мгновенная загрузка • Это цифровой продукт. Никакой физический продукт не будет отправлен. • Ваши файлы будут доступны для скачивания после подтверждения оплаты. • Я не принимаю возврат, обмен или отмену. Но, пожалуйста, свяжитесь со мной, если у вас есть какие-либо проблемы с вашим заказом.
Надеюсь, вам понравится пользоваться этими предметами. Пожалуйста, дайте мне знать, если у вас есть какие-либо вопросы, комментарии или проблемы.
Имейте в виду, что вам не разрешено продавать эти продукты, но не стесняйтесь делать фотокопии для любых образовательных нужд.
Улучшите свои математические навыки дома. Осуществляйте ежедневную практику, и вы будете лучше, чем вчера. Сделайте математику частью своей повседневной жизни, чтобы практиковать ее, даже не задумываясь. Практика делает совершенным, и математика не является исключением. Составьте для себя расписание занятий и старайтесь повторять свои математические задачи по 15–20 минут в день. Ваши навыки будут расти со временем без особых усилий с вашей стороны. Математика может быть веселой. Воспринимайте это как игру. Вы — ваш единственный конкурент. Не сравнивайте себя с другими и сосредоточьтесь на своих целях. Сосредоточьтесь только на своих целях и собственном путешествии, и вы неизбежно продолжите совершенствоваться.
Линейные уравнения – примеры с объяснением (7 класс, математика)
4.2
Средняя оценка: 4.2
Всего получено оценок: 938.
4.2
Средняя оценка: 4.2
Всего получено оценок: 938.
Линейные уравнения это первый шаг на пути изучения огромного количества самых разных уравнений. Именно в этой теме ученики усваивают важнейшие приемы решения. Чтобы не упустить ни одну из мелочей курса математики 6 класса, разберемся в вопросе подробнее.
Что такое уравнение?
В общем случае, уравнением называется тождество с одной неизвестной.
Тождеством зовется равенство. То есть уравнение это два равных между собой выражения, одно из которых или оба содержат неизвестное. Важным является условие присутствия только одной неизвестной в одном уравнении.
Можно написать уравнение с двумя и большим количеством переменных, но такое выражение решить не получится. Запомните, даже в системах уравнений, количество переменных должно равняться количеству уравнений. Например, система:
х+3=2
у+х=3
Z+у=4 – имеет решение. А вот уравнение:
Х+у=12 – однозначных решений не имеет. Почему?
Решением называется строго определенные числа, которые удовлетворяю требованиям равенства. То есть:
Х+3=5
Неизвестная имеет только одно решение. В уравнении х+у=12 – решений бесконечно много. Число х может быть любым, как только мы выберем и подставим любое число, изменится в соответствии с нашим выбором и у. Поэтому и говорят, что у такого уравнения нет определенных решений.
Виды уравнений
Выделяют следующие виды уравнений:
Выделяют так же системы уравнений, где несколько тождеств имеют одинаковые значения переменных. В таких уравнениях часто используют способ подстановки, заменяя одну переменную другой.
Способы решения линейного уравнения
Любое уравнение можно решить двумя способами:
Аналитическим, то есть с помощью математических вычислений. Этот способ хорош своей точностью
Графическим, то есть с помощью построения на графике. Этот способ хорош возможностью использования практически в любой ситуации. К нему прибегают, когда найти корень с помощью вычислений невозможно.
Рассмотрим каждый из способов.
Графический способ
Для понимания графического способа нужно вспомнить, что такое функция. Функция это зависимость одной переменной от другой. Выражение, которое мы записали в начале: х+у=12 – как раз является функцией. Перенесем х в левую сторону выражения и запишем функцию в классическом виде.
у=12-х – функция имеет форму линии, откуда и название функции и соответствующего ей уравнения. Значение корня любого уравнения это одна или несколько точек на графике функции. Точки эти задаются пересечением с графиком другой функции.
Например, уравнение х+7=13 можно разбить на две функции:
у=х+7
у=13 – в первом случае это прямая линия. Во втором, прямая линия, которая проходит параллельно оси Оу через точку 13 на оси Ох. Точка пересечения двух графиков и будет решением уравнения.
Аналитический способ
Аналитический способ решения линейных уравнений подразумевает перенос величин из одной части выражения в другую с заменой знака. Смысл переноса в том, чтобы собрать все неизвестные в одной части уравнения, а все числа в другой.
Приведем пример линейного уравнения: 2х-7х+15=0
2х-7х+15=0 – соберем все значения х в правой части, а числа в левой
2х-7х=-15
-5х=-15 – теперь поделим обе части выражения на коэффициент при неизвестном, т. е. на число -5
х=3
Что мы узнали?
Мы поговорили о видах уравнений. Разобрали, какие уравнения нельзя решить и привели объяснение. Выделили и разобрали на примерах два способа решений линейных уравнений.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Марина Богданова
8/10
Ольга Симанович
10/10
Валя Никитина
9/10
Герман Крутов
9/10
Татьяна Гужиева
10/10
Валерий Периков
6/10
Ярик Старовский
10/10
Наталья Карасёва
7/10
Романчитос Канаев
7/10
Валерий Цыганков
9/10
Оценка статьи
4. 2
Средняя оценка: 4.2
Всего получено оценок: 938.
А какая ваша оценка?
Практика. Линейные уравнения и их системы 7 класс онлайн-подготовка на Ростелеком Лицей
Решение линейных уравнений
Пример 1. Решить уравнение: .
Решение
Вспомним, что деление, по определению, операция, обратная умножению (деление на какое-либо число – это то же самое, что и умножение на обратное к этому числу):
Разделим обе части уравнения на или умножим на :
Упростим выражение в левой части уравнения:
Упростим выражение в правой части уравнения:
Таким образом, решением уравнения будет:
Ответ: .
Пример 2. Решить уравнение: .
Решение
Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .
Упростим уравнение – выполним действия в обеих частях уравнения: .
Разделим обе части уравнения на :
Решением уравнения является .
Ответ: .
Пример 3. Решить уравнение: .
Решение
Раскроем скобки в правой и левой частях уравнения. Для выражения в левой части уравнения используем распределительный закон: .
Тогда . Вспомним, что если перед скобками стоит знак минус, то при раскрытии скобок все знаки всех слагаемых внутри скобок меняются на противоположный: .
Перепишем уравнение после применения преобразований: .
Как и в предыдущем примере, перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .
Выполнив действия в обеих частях уравнения, получим тождество: .
Таким образом, данное равенство верно всегда, при любых значениях переменной.
Ответ: – любое число.
Пример 4. Решить уравнение: .
Решение
Раскроем скобки в правой и левой частях уравнения, используя распределительный закон .
Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .
Получаем .
Данное равенство неверно всегда, т.е. оно не выполняется ни при каких значениях переменной.
Ответ: нет решений.
Пример 5. Решить уравнение: .
Решение
Избавимся от знаменателей дробей – умножим обе части уравнения на общий знаменатель всех дробей, т.е. число :
Получим: .
Выполним сокращения и избавимся от знаменателей: .
Раскроем скобки:
Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .
Выполнив действия в обеих частях уравнения, получим следующее уравнение: .
Найдем :
Ответ: .
Системы линейных уравнений
В общем виде системы линейных уравнений выглядят следующим образом: где – переменные, – произвольные числа.
Есть несколько методов решения систем уравнений.
Метод подстановки.
Метод сложения.
Графический метод.
Решение систем линейных уравнений
Пример 6. Решить систему: .
Решение (несколько способов)
1. Метод подстановки – необходимо в уравнении выразить одну переменную через другую и подставить во второе уравнение.
Из первого уравнения выразим , для этого перенесем из левой части уравнения в правую: .
Затем умножим обе части первого уравнения на : .
Теперь подставим во второе уравнение полученное выражение: .
Теперь во втором уравнении только одна переменная , решим его (мы уже умеем это делать – получилось обычное линейное уравнение с одной переменной).
Раскроем скобки во втором уравнении: .
Во втором уравнении перенесем все слагаемые с переменной в левую часть, а без переменной – в правую: .
Выполним действия в обеих частях второго уравнения: .
Найдем : .
Подставим в первое уравнение найденное значение переменной:
Решением системы будет: .
Ответ: .
2. Метод сложения – нужно преобразовать уравнения так, чтобы при одной переменной в разных уравнениях были противоположные коэффициенты, после этого нужно сложить правые и левые части уравнений.
Избавимся от переменной . Умножим первое уравнение на : .
Подставим найденное значение в любое из уравнений исходной системы, например, в первое: .
Выразим : . Решением системы будет: .
Ответ: .
3. Графический метод
Сначала перепишем каждое из уравнений так, чтобы они задавали линейную функцию в привычном для нас виде , т. е. выразим через :
Графиком линейной функции является прямая. Построим обе прямые по двум точкам. Вместо возьмем произвольные значения и подставим их в соответствующие уравнения прямых:
Отметим точки на координатной плоскости и проведем через них прямые (Рис. 1).
Рис. 1. Иллюстрация к примеру 6
Видно, что точкой пересечения прямых является точка с координатами . Поскольку точка лежит на каждой из прямых, а прямая – это множество решений уравнения, то точка пересечения прямых является решением каждого из уравнений, т.е. является решением системы. Координаты точки пересечения и будут решением системы.
Дополнительно нужно подставить координаты точки в исходную систему, чтобы убедиться в правильности: .
Ответ: .
Пример 7. Решить систему: .
Решение
Сначала упростим уравнения системы – избавимся от знаменателей дробей. Для этого умножим каждое уравнение на общий знаменатель дробей, которые в него входят (чтобы найти это число, нужно рассмотреть наименьшее общее кратное чисел, которые стоят в знаменателе):
Получим:
Выполним сокращения и избавимся от знаменателей:
Раскроем скобки:
Приведем подобные слагаемые:
Умножим второе уравнение на :
Сложим уравнения системы:
Получим уравнение:
Выполним действия:
Найдем :
Подставим в первое уравнение найденное значение переменной:
Решением системы будет: .
Ответ: .
Задачи, решение которых сводятся к линейным уравнениям и их системам
Задача 1
Провод длиной 456 метров разрезали на 3 части (Рис. 2), причем первая часть в 4 раза длиннее третьей, а вторая – на 114 метров длиннее третьей. Найти длину каждой части провода.
Рис. 2. Иллюстрация к задаче 1
Решение
1. Провод длиной 456 метров разрезали на 3 части:
Первая часть в 4 раза длиннее третьей:
Вторая часть на 114 метров длиннее третьей:
Теперь все выражено через часть 3, поэтому все замены можно переписать так:
2. Обозначим длину части 3 за :
Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую:
Выполним действия:
Найдем – длину части :
3. Найдем длину части :
м
Часть :
м
Ответ: 228 метров; 171 метров; 57 метров.
Задача 2
Из села в город легковой автомобиль доехал за 2 ч, а грузовой – за 5 ч (Рис. 3). Найти скорость движения каждого автомобиля, если скорость грузового автомобиля на 48 км/ч меньше скорости легкового.
Рис. 3. Иллюстрация к задаче 2
Решение
Введем обозначения:
Легковой автомобиль: – его скорость, – время, – путь, который он проходит.
Грузовой автомобиль: –скорость, – время, – путь, который он проходит.
Перепишем условие задачи в новых обозначениях:
– автомобили проехали одно и то же расстояние
Воспользуемся следующей формулой: . Тогда:
Так как , то . Используем оставшееся условие и получим следующую систему: .
Такую систему будем решать методом подстановки – подставим первое уравнение во второе: .
Раскроем скобки: .
Перенесем все слагаемые с переменной в одну часть уравнения, а без переменной – в другую: .
Найдем :
Таким образом, скорость легкового автомобиля: км/ч.
Найдем скорость грузового автомобиля: подставим найденное значение в уравнение :
км/ч
Ответ: 80 км/ч; 32 км/ч.
Задача 3
Токарь планировал изготавливать ежедневно по 24 детали, чтобы выполнить задание вовремя. Но он изготавливал ежедневно на 15 деталей больше (Рис. 4) и уже за 6 дней до окончания срока работы сделал 21 деталь сверх плана. За сколько дней токарь планировал выполнить задание?
Рис. 4. Иллюстрация к задаче 3
Решение
Введем обозначения:
Токарь планировал: сделать работу со скоростью за время .
Получилось: сделал работу со скоростью за время .
Перепишем условие задачи в новых обозначениях:
деталь/день
деталь/день
Воспользуемся формулой:
Тогда:
Если , то .
Подставим в предыдущее уравнение: .
Раскроем скобки: .
Перенесем все слагаемые с переменной в левую часть уравнения, а без переменной – в правую: .
Выполним действия: .
Найдем :
Ответ: 17 дней.
Задачи. Системы линейных уравнений
Задача 4
Лодка за 3 ч движения по течению реки и 4 ч против течения проходит 114 км (Рис. 5). Найти скорость лодки по течению и ее скорость против течения, если за 6 ч движения против течения она проходит такой же путь, как и за 5 ч по течению.
Рис. 5. Иллюстрация к задаче 4
Решение
Введем обозначения:
Скорость лодки по течению: .
Скорость лодки против течения: .
Воспользуется формулой: .
Лодка за 3 ч движения по течению реки и 4 ч против течения проходит 114 км, тогда .
За 6 ч движения против течения она проходит такой же путь, как и за 5 ч по течению: .
Запишем полученную систему линейных уравнений: .
Воспользуется методом подстановки. Во втором уравнении выразим через – разделим обе части уравнения на : .
Подставим полученное значение в первое уравнение: .
Выполним действие: .
Найдем : .
Найдем : .
Ответ: км/ч; км/ч.
Задача 5
В двух ящиках лежат яблоки. Если из первого ящика переложить во второй 45 яблок, то в обоих ящиках их станет поровну (Рис. 6). Если же из второго ящика переложить в первый 20 яблок, то в первом станет в 3 раза больше яблок, чем во втором (Рис. 7). Сколько яблок лежит в каждом ящике?
Рис. 6. Иллюстрация к задаче 5
Рис. 7. Иллюстрация к задаче 5
Решение
Пусть изначально в первом ящике было яблок, а во втором – яблок. Если из первого ящика переложить во второй 45 яблок, то в обоих ящиках их станет поровну:
Если же из второго ящика переложить в первый яблок, то в первом станет в раза больше яблок, чем во втором: . Запишем полученную систему линейных уравнений: .
Раскроем скобки во втором уравнении: .
В обоих уравнениях выразим через : .
Воспользуемся методом подстановки – подставим выражение во второе уравнение: .
Во втором уравнении перенесем все слагаемые с переменной в левую часть, а без переменной – в правую: .
Найдем – количество яблок во втором ящике: . Подставим найденное значение в первое уравнение и найдем – количество яблок в первом ящике:
Ответ: .
Задача 6
Один металлический сплав содержит меди, другой – меди (Рис. 8). Сколько килограммов каждого сплава надо взять, чтобы получить 120 кг сплава, содержащего меди (Рис. 9)?
Рис. 8. Иллюстрация к задаче 6
Рис. 9. Иллюстрация к задаче 6
Решение
Пусть необходимо взять кг первого сплава и кг второго сплава. Тогда .
Теперь посчитаем массу меди, она составляет: .
Мы знаем, что – это от чего-то (Рис. 10), значит, — это , т.е. от – это .Аналогично от – это , а от – это .
Рис. 10. Иллюстрация к задаче 6
Запишем уравнение: . Запишем полученную систему линейных уравнений: .
В первом уравнении выразим через : .
Воспользуемся методом подстановки – подставим первое уравнение во второе: .
Раскроем скобки во втором уравнении: .
Во втором уравнении оставим слагаемые с переменной в левой части уравнения, а без переменной перенесем в правую: .
Выполним действия: . Найдем – количество кг второго сплава, которое необходимо взять: .
Найдем – количество кг первого сплава: .
Ответ: кг; кг.
Задача 7
Сумма цифр двузначного числа равна . Если поменять местами его цифры, то получим число, которое больше данного на . Найти данное число.
Решение
Обозначим двузначное число так: . Сумма цифр двузначного числа равна : .
Если поменять местами его цифры, то получим следующее число: . Так как в числе десятков и единиц, то , а в числе десятков и единиц, значит, .
Число на больше, чем , поэтому .
Перенесем все слагаемые с переменной в левую часть, а без переменной – в правую:
Запишем полученную систему линейных уравнений: .
В первом уравнении выразим через : .
Воспользуемся методом подстановки – подставим это выражение во второе уравнение: .
Во втором уравнении раскроем скобки: .
Перенесем все слагаемые с переменной в левую часть, а без переменной – в правую и выполним действия: .
Найдем – число единиц в числе :
Найдем – число десятков в числе :
Таким образом, исходным числом является .
Ответ: .
Заключение
На этом уроке мы потренировались решать различные уравнения и системы линейных уравнений, а также задачи, которые к ним сводятся.
Список рекомендованной литературы
Никольский С. М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. ФГОС, изд-во «Просвещение», 2017.
Три утенка и четыре гусенка весят г, а четыре утенка и три гусенка весят г. Сколько весит один гусенок?
Linear Equations Class 10 — NCERT Solutions, MCQ, Exemplar [2023-24]
Вы учитесь. ..
Обновлено для NCERT 2023-24 Книги
Получите решения NCERT для главы 3, класс 10 — Пара линейных уравнений с двумя переменными в Teachoo. Ответы на все вопросы упражнения, примеры и дополнительные вопросы были снабжены видео каждого вопроса
Мы изучали линейные уравнения с двумя переменными в классе 9, мы будем изучать пара линейных уравнений в этой главе.
В этой главе мы узнаем
Что такое Линейные уравнения с двумя переменными
Преобразование утверждений в уравнения и построение графика этих линейных уравнений
Возможный тип графиков для пары линейных уравнений с двумя переменными — две пересекающиеся линии, две параллельные линии, совпадающие прямые
Нахождение s Решение уравнений по графикам
Непротиворечивость уравнений путем нахождения отношения a 1 /a 2 , b 1 /b 2 , c 1 /c 9004 1 2
и проверка того, являются ли линии
Совпадающие линии (Бесконечное множество решений)
Параллельные линии ( Нет решений)
Решение пары линейных уравнений
Замена Метод
Исключение Метод
Перекрестное умножение Метод
Решение сложных уравнений типа 2/x + 3/y = 4 путем замены переменных (например, подстановка p = 1/x, q = 1/y и решение)
Решение вопросов-утверждений путем сначала составления уравнений, а затем решения
Щелкните ссылку на упражнение или тему ниже, чтобы начать выполнение главы 9. 0003
Примечание. При нажатии на ссылку открывается первый вопрос. Чтобы открыть любой другой вопрос упражнения, перейдите в конец страницы. Существует список со стрелками, содержащий все вопросы ( важных вопросов, также отмечены)
Серийный номер
Пример 3.1
Пример 3.2
Пример 3.3
Примеры
Вопросы по делу (MCQ)
MCQ от NCERT Exemplar
График пары линейных уравнений
Метод перекрестного умножения
Уравнения, сведенные к паре линейных уравнений
Важные вопросы по линейным уравнениям
Концептуальные вопросы
Составление уравнений графически и алгебраически
Нахождение соотношений (согласованность)
Графическое решение уравнений
Замена
Ликвидация
Метод перекрестного умножения
Смешанные вопросы — Уравнение
Смешанные вопросы — Составим уравнение
Что в нем?
Обновлено для NCERT 2023-24 Books
Получите решения NCERT для главы 3, класс 10 — Пара линейных уравнений с двумя переменными в Teachoo. Ответы на все вопросы упражнения, примеры и дополнительные вопросы были предоставлены с видео каждого вопроса
Мы изучали линейные уравнения с двумя переменными в классе 9, мы будем изучать пар из линейных уравнений в этой главе.
В этой главе мы узнаем
Что такое Линейные уравнения с двумя переменными
Преобразование утверждений в уравнения и построение графика этих линейных уравнений
Возможный тип графиков для пары линейных уравнений с двумя переменными — две пересекающиеся линии, две параллельные линии, совпадающие прямые
Нахождение Решение уравнений по графикам
Непротиворечивость уравнений путем нахождения отношения 1 /а 2 , б 1 /б 2 , в 1 /с 2
и проверка того, являются ли линии
Совпадающие линии (Бесконечное множество решений)
Параллельные линии ( Нет решений)
Решение пары линейных уравнений
Замена Метод
Ликвидация Метод
Перекрестное умножение Метод
Решение сложных уравнений типа 2/x + 3/y = 4 путем замены переменных (например, подстановка p = 1/x, q = 1/y и решение)
Решение вопросов-утверждений путем сначала составления уравнений, а затем решения
Щелкните ссылку на упражнение или тему ниже, чтобы начать выполнение главы
Примечание. При нажатии на ссылку открывается первый вопрос. Чтобы открыть любой другой вопрос упражнения, перейдите в конец страницы. Есть список со стрелками, в котором есть все вопросы (с важные вопросы также отмечены)
Teachoo дает вам лучший опыт, когда вы вошли в систему. Пожалуйста, войдите 🙂
Войти
Teachoo ответит на все ваши вопросы, если вы черный пользователь!
Присоединиться к Teachoo Черный
Уравнение, сводимое к паре линейных уравнений с примерами
Мы обсудим решение таких пар уравнений, которые не являются линейными, но могут быть приведены к линейному виду с помощью подходящих замен.
вопрос 1. Решите следующую систему уравнений
, х, у ≠ 0,
Решение: Положим 1/x = u и 1/y = v
⇒ 12u + 4v = 1 …(i)
3u + 2v = 0 …(ii)
Умножьте уравнение (ii) на 4, чтобы сделать коэффициенты u равными
12u + 4v = 1…(iii)
12u + 8v = 0 …(iv)
–4v = 1
v = -1/4
Ввод значения v в уравнение (i)
Следовательно,
1/x = u или 1/x = 1/6 ⇒ x = 6
1/y = v или 1/y = 1/-4 ⇒ y = –4
Решение x = 6, y = –4.
вопрос 2. Решите следующую систему уравнений
.
Решение:
10/ х + у + 2/х- у = 4…(i)
15/х + у — 5/х -у = -2 … (ii)
Положим 1/x + y = u и 1/x — y = v
10u + 2v = 4 …(iii)
15u — 5v = -2…(iv)
Умножение уравнения (iii) на 5 и уравнения (iv) на 2 для исключения v
50u + 10v = 20
30у — 10в = -4
80u = 16
и = 16/80 = 1/5
Подставляя значение u в уравнение (iii), мы получаем
10 х 1/5 + 2в = 4
2 + 2v = 4
2т = 2
v = 1
∴ 1/х + у = 1/5, 1/х -у = 1
или х + у = 5 …(v)
х — у = 1 …(vi)
Складывая уравнения (v) и (vi), получаем
2x = 6 ⇒ x = 3
Подставляя значение x в уравнение (v), получаем
3 + у = 5
у = 2
Решение х = 3; у = 2
ЗАДАЧИ СЛОВА:
Для решения повседневных задач с помощью одновременных линейных уравнений с двумя переменными или приводимых к ним уравнений поступают следующим образом:0003
(i) Представить неизвестные величины теми же переменными x и y, которые подлежат определению.
(ii) Найдите условия, данные в задаче, и переведите вербальные условия в пару одновременных линейных уравнений.
(iii) Решите эти уравнения и получите требуемые величины в соответствующих единицах измерения.
Тип проблем:
(i) Определение двух чисел, когда задано отношение между ними.
(ii) Проблемы с дробями, цифрами числа, возрастом людей.
(iii) Проблемы течения реки, времени и расстояния.
(iv) Проблемы, связанные с менструацией и геометрией.
(v) Проблемы, связанные со временем и работой.
(vi) Проблемы, связанные с смесями, раскладушками, переносом и утерей, скидками.
вопрос 3. Сумма цифр двузначного числа равна 9. Кроме того, девять раз это число вдвое больше числа, полученного путем изменения порядка цифр. Найдите число.
Решение: Пусть цифра в разряде единиц = y.
Пусть цифра десятков = х.
∴ Данное число равно 10x + y.
Согласно вопросу,
х + у = 9 … (i)
Когда цифры перевернуты, y становится цифрой десятков, а x становится цифрой единиц.
∴ Обратное число 10y + x.
Согласно вопросу,
9(10х + у) = 2(10у + х)
90x + 9y = 20y + 2x
90x — 2x = 20y — 9y
88х — 11у = 0
8x – y = 0 …(ii)
8х = у … (iii)
Подставляя значение y в уравнение (ii), мы имеем
х + 8х = 9
9x = 9
х = 1.
Из уравнения (iii) y = 8,
Необходимое число 18.
вопрос 4. Найдите два числа такие, что сумма удвоенного первого и трехкратного второго равна 89 и первое в четыре раза больше второго в пять раз на 13.
Решение: Пусть два числа будут x и y.
Тогда образуются уравнения 2x + 3y = 89 ….(i)
4x – 5y = 13 …(ii)
При решении уравнения (i) и (ii), мы получаем
х = 22
и у = 15
Следовательно, требуемые числа 22 и 15.
вопрос 5. Числитель дроби на 4 меньше знаменателя. Если числитель уменьшить, а знаменатель увеличить на 1, то знаменатель в восемь раз больше числителя.
«Русский Арт»: лучшие наряды звезд с красной дорожки премии RU.TV 10
«Сталин все планировал лично». Как устранили главного украинского нациста
По Одессе ударили с тыла. Следующим будет Киев
Культура
Из песни слова — выкинешь: как западные артисты изменяют треки о России
Туризм
«Автопутешествия — это круто!» Дирижер-дальнобойщик о «свободе на колесах»
Триумф зеленой повестки: электричество в Европе стало бесплатным
Сергей Савчук
Зеленский нужен Западу на южном фронте
Петр Акопов
Прорыв украинской ДРГ на Белгородчине обеспечит великую медиапобеду Киева
Ирина Алкснис
Лыжные гонки
Экс-тренер сборной России по лыжным гонкам ответил на обвинения в допинге
Формула-1
«Хонда» станет мотористом «Астон Мартин» с 2026 года
Футбол
Капитан «Спартака» Джикия опубликовал пост в соцсетях в поддержку Соболева
Футбол
«Барселона» потерпела второе поражение подряд в ранге чемпиона Испании
Хоккей
Ротенберг сообщил о переходе Толчинского в СКА
TOP, BOTTOM(full)
TOP, BOTTOM(full)
BOTTOM
Открывается c отступом от верхнего края когда по ширине меньше ширины окна.
Открывается c отступом от верхнего края когда по ширине меньше ширины окна.
Открывается c отступом от верхнего края когда по ширине меньше ширины окна.
Открывается c отступом от верхнего края когда по ширине меньше ширины окна.
На фулл скрине открывается с белой подложкой на всю высоту, контент вверху.
На фулл скрине открывается с белой подложкой на всю высоту, контент вверху.
На фулл скрине открывается с белой подложкой на всю высоту, контент вверху.
На фулл скрине открывается с белой подложкой на всю высоту, контент вверху.
center
Открывается по центру когда по ширине меньше ширины окна.
Открывается по центру когда по ширине меньше ширины окна.
Открывается по центру когда по ширине меньше ширины окна.
Открывается по центру когда по ширине меньше ширины окна.
На фулл скрине открывается с белой подложкой на всю высоту, контент вверху.
На фулл скрине открывается с белой подложкой на всю высоту, контент вверху.
На фулл скрине открывается с белой подложкой на всю высоту, контент вверху.
На фулл скрине открывается с белой подложкой на всю высоту, контент вверху.
Пример полей
Заголовок поля
Вход на сайт
Почта
Пароль
Восстановить пароль
Зарегистрироваться
Срок действия ссылки истек
Назад
Регистрация на сайте
Почта
Пароль
Я принимаю условия соглашения и даю своё согласие на обработку персональных данных в соответствии
с Политикой конфиденциальности
Федерального Государственного Унитарного Предприятия «Международное информационное агентство «Россия сегодня»,
расположенного по адресу: Россия, 119021, г. Москва, Зубовский бульвар, д. 4.
Войти с логином и паролем
Ваши данные
Восстановление пароля
Почта
Назад
Восстановление пароля
Ссылка для восстановления пароля отправлена на адрес
Восстановление пароля
Новый пароль
Подтвердите пароль
Написать автору
Тема
Сообщение
Почта
ФИО
Нажимая на кнопку «Отправить», Вы соглашаетесь с Политикой конфиденциальности
Задать вопрос
Ваше имя
Ваш город
Ваш E-mail
Ваше сообщение
Сообщение отправлено!
Спасибо!
Произошла ошибка!
Попробуйте еще раз!
Обратная связь
Чем помочь?
Если ни один из вариантов не подходит, нажмите здесь для связи с нами
Обратная связь
Чтобы воспользоваться формой обратной связи, Вы должны войти на сайт.
Разблокировать аккаунт
Вы были заблокированы за нарушение правил комментирования материалов
Срок блокировки — от 12 до 48 часов, либо навсегда.
Если Вы не согласны c блокировкой, заполните форму.
Назад
Разблокировать аккаунт
Имя в чате
Дата сообщения
Время отправки сообщения
Блокировался ваш аккаунт ранее?
Сколько раз?
Удалили мое сообщение
Ваше сообщение было удалено за нарушение правил комментирования материалов
Если Вы не согласны c блокировкой, заполните форму.
Назад
Удалили мое сообщение
Чтобы связаться с нами, заполните форму ниже:
Ваше сообщение
Перетащите, или выберите скриншот
Связаться с нами
Если вы хотите пожаловаться на ошибку в материале, заполните форму ниже:
Ссылка на материал
Опишите проблему
Перетащите, или выберите скриншот
Связаться с нами
Чтобы связаться с нами, заполните форму ниже:
Ваше сообщение
Перетащите, или выберите скриншот
Показать
Папа римский заявил, что не задумывается об отставке
РИМ, 16 фев — РИА Новости. Папа Римский Франциск заявил, что не задумывается об уходе в отставку, считая папское служение пожизненным. В четверг утром итальянский журнал иезуитов La Civiltà Cattolica привел выдержки из бесед понтифика с членами ордена в ходе поездок в ДР Конго и Южный Судан. На этих встречах папе Франциску задали вопрос, рассматривает ли он возможность досрочного ухода на покой по примеру своего предшественника Бенедикта XVI. «Нет, мне это не приходило в голову», — ответил понтифик. Он напомнил, что вскоре после избрания на папский престол он подписал документ о своем отречении на случай серьезного ухудшения состояния здоровья. По его словам, подобное заявление в прошлом уже написал папа Пий XII на случай, если бы Адольф Гитлер решил перевезти его в Германию. «Это не значит, что отставные папы должны стать, скажем так, «модой», нормальным явлением», — подчеркнул папа Франциск, добавив, что не знает, где находится его документ. «У Бенедикта хватило смелости сделать это, потому что он не хотел продолжать из-за своего здоровья. На данный момент у меня нет этого в повестке», — сказал Франциск во время встречи с иезуитами в Киншасе. «Я считаю, что служение папы Римского является ad vitam (пожизненным – ред.). Я не понимаю, почему бы ему таким не быть. Просто подумайте, что служение патриархов всегда на всю жизнь, и важна историческая традиция. Если вместо этого мы прислушаемся к болтовне, тогда надо менять папу каждые полгода», — заключил он. Папа Римский Франциск страдает от сильных болей в коленном суставе, из-за чего он вынужден пользоваться креслом-коляской. В июле 2021 года в римской больнице «Агостино Джемелли» папе Франциску была сделана плановая хирургическая операция по поводу дивертикулярной болезни сигмовидной ободочной кишки. Операция продолжалась около трех часов и потребовала резекции левой части толстого кишечника. Папа Франциск провел в клинике десять суток.
в мире, ватикан, франциск (хорхе марио бергольо), папа римский
Религия, В мире, Ватикан, Франциск (Хорхе Марио Бергольо), Папа Римский
РИМ, 16 фев — РИА Новости. Папа Римский Франциск заявил, что не задумывается об уходе в отставку, считая папское служение пожизненным.
В четверг утром итальянский журнал иезуитов La Civiltà Cattolica привел выдержки из бесед понтифика с членами ордена в ходе поездок в ДР Конго и Южный Судан. На этих встречах папе Франциску задали вопрос, рассматривает ли он возможность досрочного ухода на покой по примеру своего предшественника Бенедикта XVI.
В РПЦ прокомментировали идею устроить встречу патриарха и папы в Черногории
27 января, 18:55
«Нет, мне это не приходило в голову», — ответил понтифик. Он напомнил, что вскоре после избрания на папский престол он подписал документ о своем отречении на случай серьезного ухудшения состояния здоровья. По его словам, подобное заявление в прошлом уже написал папа Пий XII на случай, если бы Адольф Гитлер решил перевезти его в Германию. «Это не значит, что отставные папы должны стать, скажем так, «модой», нормальным явлением», — подчеркнул папа Франциск, добавив, что не знает, где находится его документ.
«У Бенедикта хватило смелости сделать это, потому что он не хотел продолжать из-за своего здоровья. На данный момент у меня нет этого в повестке», — сказал Франциск во время встречи с иезуитами в Киншасе. «Я считаю, что служение папы Римского является ad vitam (пожизненным – ред. ). Я не понимаю, почему бы ему таким не быть. Просто подумайте, что служение патриархов всегда на всю жизнь, и важна историческая традиция. Если вместо этого мы прислушаемся к болтовне, тогда надо менять папу каждые полгода», — заключил он.
Папа Римский Франциск страдает от сильных болей в коленном суставе, из-за чего он вынужден пользоваться креслом-коляской. В июле 2021 года в римской больнице «Агостино Джемелли» папе Франциску была сделана плановая хирургическая операция по поводу дивертикулярной болезни сигмовидной ободочной кишки. Операция продолжалась около трех часов и потребовала резекции левой части толстого кишечника. Папа Франциск провел в клинике десять суток.
В Ватикане похоронили почетного папу римского Бенедикта XVI
5 января, 13:51
IX римскими цифрами — Что такое IX римскими цифрами?
Что такое IX римскими цифрами?
IX римскими цифрами равно числу 9.
Это потому, что:
I = 1
Х = 10
Как видно на нашей главной странице с римскими цифрами под заголовком «Принцип вычитания», потому что меньшее число (в данном случае I равно 1) пишется перед большим числом (в данном случае X равно 10) , то меньшее число отнимается от большего числа.
Таким образом, даже если оно записано как IX, все уравнение работает как:
X (10) минус I (1), что равно 9.
Если I было записано как после X, два числа суммируются, так как меньшее число следует за большим. Таким образом, в этом примере XI в римских цифрах будет равняться X + I или 10 + 1, что равняется 11.
Математические вопросы, содержащие римские цифры IX
Почему бы не попробовать решить некоторые математические уравнения, каждое из которых содержит римское число 9, IX, в них где-то?
1. Что такое V плюс IX?
Мы уже знаем из вышеизложенного, что римские цифры IX = 9, поэтому все, что нам нужно сделать, чтобы решить этот вопрос, это добавить 9 к числу, представленному буквой V, что равно 5.
Таким образом, ответ равен 5 + 9, что равно 14 (или XIV римскими цифрами). Н.Б. Обратите внимание, что 14 не пишется как XIIII, поскольку число 4 в римских цифрах — это IV, что снова использует принцип вычитания, который мы используем для вычисления числа IX.
2. Что такое XI–IX?
Это уравнение палиндрома было бы немного сложнее, если бы мы не показали выше, как переводится число XI!
Ранее мы видели, что XI равно числу 11, потому что это X (10) плюс I (1). Таким образом, взяв IX (9) из XI (11), мы получим ответ 2 (или II римскими цифрами).
3. Сколько IX умножить на III?
Простая сумма умножения. IX (9) умножить на III (3) равно 27 (или XXVII римскими цифрами).
4. Чему равно число IX, умноженное на LIV?
Немного более хитрое уравнение умножения, но очень похожее на приведенное выше, если вы знаете, что такое LIV в римских цифрах.
LIV это L (50) плюс V (5) минус I (1)… помните принцип вычитания, потому что I предшествует V! Итак, LIV = 50 + 5 – 1, что равно 54.
Теперь, когда мы знаем, что LIV = 54, и мы знаем, что IX = 9, мы просто перемножаем их вместе, чтобы получить довольно большое число 486. Римскими цифрами , это CDLXXXVI. Хотите понять всю сумму? Это:
D (500) – C (100) плюс L (50) плюс X (10) плюс X (10) плюс X (10) плюс V (5) плюс I (1).
Фу!
Иногда при работе с большими римскими числами, такими как это, и особенно когда требуется вычитание, иногда вам может быть проще решить это, если вы разделите уравнение на две или более частей.
В этом примере лучше (особенно когда вы только начинаете учиться читать римские цифры) отработать первую часть CD (500 минус 100), чтобы получить начальное число 400, а затем просто прибавить остальное к нему
5. Сколько XLV делится на IX?
Еще одна хитрость, которую нужно закончить, снова включала этот принцип вычитания для определения того, чему соответствует XLV.
Поскольку меньшее число, X (10), стоит перед большим числом, L (50), нам нужно вычесть X из L, поэтому мы вычитаем 10 из 50, что дает нам 40. Затем мы просто добавляем V ( 5), что дает в сумме 45.
Деление 45 на IX (9) дает ответ 5 (или V римскими цифрами).
Помните, если вам трудно разобраться в римских цифрах, вы, конечно, не одиноки, и даже людям, которые читали и конвертировали их в течение длительного времени, все же нужно уделить время, чтобы убедиться они правильно перевели его в современные цифры.
Не стесняйтесь использовать инструмент преобразования римских цифр на нашей главной странице римских цифр, который может преобразовать обе римские цифры в современные числа, или введите число, чтобы преобразовать его в римские цифры, так как это может помочь увидеть правильный номер, чтобы вы могли понять, как он составлен.
Связанные страницы:
Римские цифры 1-100
Римские цифры для часов
L римскими цифрами
Римские цифры LV
LVI Римские цифры
MMXXI римскими цифрами
XIX Римские цифры
XXI Римские цифры
XLIX Римские цифры
XXIV Римские цифры
XXVI Римские цифры
XXVII Римские цифры
99 римскими цифрами
Татуировка с римскими цифрами
Теория музыки с римскими цифрами
Ввел ли Гай Марий римскую цифру VII?
Примеры римских цифр в древней истории
Роль римских цифр в искусстве и архитектуре
Использование римских цифр в астрономии
Использование римских цифр в юридических документах
Римская цифра Clocks Hour 9
Галерея ClipArt Plain Clocks Hour 9 предлагает 60 изображений часов, показывающих время с 9 часов.
Сложение степеней в круге: marta_inj — LiveJournal
Деление степеней не дается. Впрочем, неудивительно. Вот что пишут по этому поводу:
Как известно разные всякие операции, и те которые производятся над числами, и те, что над объектами реального мира — можно разделить на «прямые» и «обратные». Последние выполнить гораздо труднее. (Например: забить в доску гвоздь (особенно если по самую шляпку) куда как проще чем потом его обратно оттуда вытащить.) А в математике для обратных операций еще и приходится расширять множество чисел. Вот как раз из соображений справедливости: прямая операция применима к любому числу, или любой паре чисел, если двухместная, и её результат всегда принадлежит к тому же множеству объектов, что и её операнды, а обратная, видите ли, нет.
Сначала у людей были только натуральные числа — с их помощью яблоки считали (и корзины, куда их собирались складывать), ну или мамонтов на пастбище — дело то как раз происходило примерно в те самые времена. Складывать можно, разумеется, любые натуральные числа — получается опять натуральное число. Но вот вычитать…
Сначала постановили что вычитать большее из меньшего безсмысленно. (Ну в самом деле, как можно взять из корзины семь яблок, если их там только три? Никак!)
Но потом (а к тому времени деньги уже давно были в ходу) придумали ноль и отрицательные числа и стали трактовать их как «долг». То есть смысл для таких операций, хоть и не сразу, но нашелся.
Операция умножения тоже применима к любым натуральным числам, а вот обратная к ней — деление на равные части — для многих пар даёт остаток. А деление меньшего на большее сначала тоже считали бессмысленным, но потом (причем куда раньше изобретения ноля) признали полезным для обозначения частей целого и узаконили как «натуральные дроби».
Операция возведения в степень, изображающая многократное умножение числа самого на себя, придумана по аналогии с операцией умножения, заменяющей многократное сложение числа самого с собою. Но вот обратная к ней, известная как нахождение корня такой-то степени… На этом, кстати, сломались древние греки: обнаружили что диагональ квадрата несоизмерима с его стороной. (Теорему Пифагора они уже знали.) То есть, если длину стороны принять за единицу, то точная длина диагонали не выражается никакой натуральной дробью. В результате чего, посыпав голову пеплом, отказались от чисел вообще, перейдя исключительно к геометрическим построениям!
Много-много позже такие числа всё-таки узаконили, обозвав, правда, «иррациональными». (Причем их оказалось гораздо больше чем «рациональных». И это при том, что даже натуральных чисел, коие всего лишь подмножество рациональных, и то — бесконечность!) Некоторым наиболее популярным иррациональным числам дали собственные имена. Наиболее известные из них это числа Пи и Е, ну еще может быть Тау (коэффициент ряда Фибоначчи равный один плюс корень из пяти и всё это делённое на два). Тут пришла пора распространить действие всех известных на тот момент операций на все известные на тот момент числа, и этот фокус более-менее получился — ну кроме некоторых исключительных случаев. Причем казалось-бы самых простых. Вот не получается деление на ноль. Но ноль — он ведь один единственный. Для него одного вполне можно сделать исключение. (И к тому же — если очень хочется — можно считать что деление любого числа на ноль даёт бесконечность. А деление его же на бесконечность — соответственно даёт ноль.) В остальном с участием в умножении и делении отрицательных и нецелых чисел никаких сложностей больше не возникло. Перешли к возведению в степень. Отрицательную степень стали трактовать как многократное деление единицы на это число. (А возведение в нулевую — соответственно умножение или деление ноль раз — вот единица и остаётся.) Возведение в дробную степень — как нахождение корня… На радостях ввели обратную к степенной функции — логарифмическую, и тут…
Да не тут, а гораздо раньше. Еще когда только-только придумали отрицательные числа и взялись их не только складывать но и умножать, обнаружили что произведение двух отрицательных чисел неизменно даёт положительное. А значит сыскать такое число, умножив которое само на себя можно было бы получить отрицательный результат (даже для самого простейшего случая — единицы) решительно невозможно. Таковых чисел просто нет!
То есть квадратных корней для отрицательного числа не дождёшься, в то время как у положительного числа их сразу два. Нечестно, несправедливо, судью (ну или кто там всем этим заведует) на мыло! А давайте, сказали великовозрастные детишки-математики, такое число просто выдумаем. Выдумали, обозначили буквой i и обозвали «мнимым», потому как ничему реальному не соответствует и существует исключительно в их воображении.
Присмотрелись по-внимательнее — батюшки-светы! Выдумали то только одно мнимое число (то, которое будучи умножено само на себя, даёт в результате минус единицу), а получили столько же сколько «реальных» — целую числовую ось. Вредное число i, если умножить на него любое реальное число, делает его мнимым. И эта мнимая числовая ось не имеет с действительной ничего общего… А, нет — имеет. Одну точку. Ту, которая ноль. Ноль — он такой: что на него ни умножь — всё в ноль превратит. За сим, что действительный ноль, что мнимый — всё ноль.
Алгебраическая сумма.
Положительные и отрицательные числа. Целые числа. Сложение целых чисел.12+
8 месяцев назад
Математика от Баканчиковой326 подписчиков
Сегодня мы будем говорить об алгебраической сумме. Этот урок будет полезен ученикам 6 и 7 классов. Но вначале, мы напомним Вам, что такое целые числа, для чего они нужны, как обозначаются. Покажем, как строится числовая прямая, где на ней находятся положительные, отрицательные и противоположные числа. Затем объясним, как складываются отрицательные числа. Особо остановимся на том, как складывать положительные и отрицательные числа. На примере про деревья, Вы точно поймете и будете без ошибок выполнять подобные действия. Мы дадим Вам определение и объясним, из чего складывается алгебраическая сумма, приведем конкретные примеры и покажем, как можно вычислять алгебраическую сумму.
00:00 Начало видео.
00:30 Для чего нужны целые числа?
01:48 Вспоминаем построение числовой прямой.
03:04 Противоположные числа. Отрицательные и положительные числа. 04:40 Что такое целые числа?
05:46 Действия с целыми числами.
06:29 Сложение отрицательных чисел.
09:10 Как складывать положительные и отрицательные числа?
13:04 Что такое алгебраическая сумма?
15:21 Примеры алгебраической суммы.
18:38 Примеры вычисления алгебраической суммы.
Рекомендуем Вам посмотреть следующие видео:
Выражения с переменной. Как прочитать и объяснить выражения с переменной. Примеры выражений. Алгебра 7 класс. https://youtu.be/YDwS5Bl9Szo
Что такое компоненты. Рассказ о Пете и Диме или зачем нужны компоненты. https://rutube.ru/video/2a05adba43e67d1ea1b5cab6d8e6d18a/
Компоненты сложения. Результат сложения. Компоненты вычитания. Результат вычитания. https://rutube.ru/video/817bf00c7751d685ff04a14f983f186b/
Компоненты умножения. Результат умножения. Компоненты деления. Результат деления. https://rutube.ru/video/f9c294622103e8a2c9d8ef149d8e757f/
Буквенные выражения. Определение. Значение буквенного выражения. https://rutube.ru/video/9df8b54b78d677bd9751979e94aece76/
5-11 класс. Порядок действий в математике. Примеры на порядок действий. Оформление решений. https://rutube.ru/video/7c0d132e7a5a520f24ed240f458a8b0e/
Степень с натуральным показателем. Компоненты степени. https://rutube.ru/video/d70872cb3e43dad6eb4ad3bf16eaaa7c/
#АлгебраическаяСумма #ЦелыеЧисла #МатематикаОтБаканчиковой #алгебраическаясуммамногочленов #построениечисловойпрямой #алгебраическаясумма #целыечисла #сложениецелыхчисел #противоположныечисла #чтотакоецелыечисла #целыечисла #обозначениецелыхчисел #действиясцелымичислами #сложениеотрицательныхчисел #сложениеположительныхиотрицательныхчисел #примерыалгебраическойсуммы #примерывычисленияалгебраическойсуммы #обозначениецелыхчисел #алгебра7класс #математика6класс #вычитаниеотрицательныхчисел #сложениеивычитаниеотрицательныхчисел #сложениевычитаниеотрицательныхиположительныхчисел
вычитание отрицательных чисел, сложение и вычитание отрицательных чисел, сложение вычитание отрицательных и положительных чисел, построение числовой прямой, алгебраическая сумма, целые числа, сложение целых чисел, противоположные числа, что такое целые числа, целые числа, обозначение целых чисел, действия с целыми числами, сложение отрицательных чисел, сложение положительных и отрицательных чисел, примеры алгебраической суммы, примеры вычисления алгебраической суммы, обозначение целых чисел, алгебра 7 класс, математика 6 класс
Отрицательные силы — Математика GCSE
Введение
Как работать с отрицательными силами
Рабочий лист отрицательных степеней
Распространенные заблуждения
Практикуйте вопросы об отрицательной силе
Отрицательные силы Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Как работать с отрицательными силами
Рабочий лист отрицательных степеней
Распространенные заблуждения
Практикуйте вопросы об отрицательной силе
Отрицательные силы Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем об отрицательных степенях, в том числе о том, что они собой представляют, как их упрощать и вычислять, а также как комбинировать их с другими законами экспонент.
Существуют также рабочие листы полномочий и корней, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли. 9{2}}=\frac{1}{9} .
Отрицательная степень не означает , что основание является отрицательным числом. Если основание положительное число, знаменатель дроби остается положительным.
Давайте посмотрим, почему отрицательная степень — это дробь, использующая степени числа 10.
При делении каждой строки на 10 мощность уменьшается на 1 .
Когда мы достигаем 100 (нулевой показатель степени), мы делим основание само на себя, любое основание в степени 9{-1} .
По мере того, как мы продолжаем делить на 10, знаменатель дроби становится все больше, а это означает, что исходное число становится все меньше и меньше (приближаясь к 0).
Что такое отрицательные силы?
Положительная обратная связь
Другим термином для отрицательной мощности является положительная обратная величина .
обратная числа — это значение, которое можно умножить на исходное число, чтобы получить ответ 1 . 9{-3}=\frac{1}{64} .
Помните: Дробь также может быть преобразована в десятичную.
Как работать с отрицательными степенями
Для использования отрицательных степеней:
Упростите любые силы, используя законы индексов.
Оценить или решить (при необходимости).
Как работать с отрицательными силами
Рабочая таблица полномочий и корней (включая отрицательные силы)
Получите бесплатный рабочий лист с отрицательными способностями, содержащий более 20 вопросов и ответов о способностях и корнях. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО Икс
Рабочий лист сил и корней (включая отрицательные силы)
Получите бесплатный рабочий лист отрицательных сил, содержащий более 20 вопросов и ответов о силах и корнях. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры отрицательных степеней
Пример 1: упростить и оценить 9{-3} .
Запишите свой ответ в виде смешанного числа.
Упростите любые силы, используя законы индексов.
Поскольку мы начинаем с основания \frac{3}{4}, возведенного в степень -3, мы знаем, что отрицательная степень дает положительную обратную величину основания (помните, что обратная величина — это число, которое вы умножьте на, чтобы получить ответ 1 ).
Итак, на что нам нужно умножить \frac{3}{4}, чтобы получить значение 1 ?
Расширить свое понимание системы счисления, включив в него степени
Вычисления с корнями и целыми индексами
Упрощение выражений с суммами, произведениями и степенями, включая законы индексов
Все еще зависает?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе обучения математике GCSE.
Мы используем необходимые и необязательные файлы cookie, чтобы улучшить работу нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой в отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять вашими настройками файлов cookie или изменять их. Принять
Отрицательные показатели — полный курс алгебры
Навыки в A L G E B R A
Содержание | Главная
20
Степень дроби
Делительные степени одного основания
Отрицательные показатели
Секция 2
Показатель степени 0
Научное обозначение
Степень дроби
«Чтобы возвести дробь в степень, возведите числитель и знаменатель в эту степень.»
Пример 1.
Для, согласно значению показателя степени и правилу умножения дробей:
Пример 2. Применить правила экспоненты:
Решение . Мы должны принять 4-ю силу всего. Но чтобы взять степень степени — умножьте показатели:
Задача 1. Применить правила экспонент.
Чтобы увидеть ответ, наведите указатель мыши на цветную область. Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»). Сначала решай задачу сам!
а)
=
x 2 у 2
б)
=
8 x 3 27
в)
=
г)
=
д)
=
x 2 — 2 x + 1 x 2 + 2 x + 1
Трехчлен Perfect Square
Делительные степени одного основания
В следующем уроке мы увидим следующее правило сокращения дроби:
топор ай
=
х у
«И числитель, и знаменатель могут быть разделены на общий множитель. »
Рассмотрим эти примеры:
2 · 2 · 2 · 2 · 2 2 · 2
=
2 · 2 · 2
___2 · 2___ 2 · 2 · 2 · 2 906 83 · 2
=
__1__ 2 · 2 · 2
Если мы запишем их с показателями, то
2 2
=
2 3
2 2 2 5
=
1 2 3
В каждом случае мы вычитаем показателей. Но когда показатель степени в знаменателе больше, мы пишем 1 над разницей.
Пример 3.
x 3
=
х 5
x 8
=
1 x 5
Вот правило:
Проблема 2. Упростите следующее. (Не пишите отрицательную степень.)
а)
=
х 3
б)
x 2 x 5
=
1 x 3
в)
x x 5
=
1 x 4
г)
x 2 x
=
х
д)
=
− х 4
е)
=
1 x 2
Проблема 3. Упростите каждое из следующих действий. Затем вычислите каждое число.
а)
=
2 3
=
8
б)
2 2 2 5
=
1 2 3
=
1 8
в)
2 2 5
=
1 2 4
=
1 16
г)
2 2 2
=
2
д)
=
−2 4
=
−16.
См. Урок 13.
е)
=
1 2 2
=
1 4
Пример 4. Упрощение путем сокращения до наименьших членов:
Раствор. Рассмотрите каждый элемент по очереди:
Проблема 4. Упростите, приведя к наименьшим терминам. (Не пишите отрицательные степени.
а)
=
г 3 5 x 3
б)
=
−
8 а 3 5 б 3
в)
=
−
3 z _ 5 x 4 y 3
г)
=
с 3 16
д)
( x + 1) 3 ( x — 1) ( x — 1) 3 ( x + 1) 901 30
=
( x + 1) 2 ( x − 1) 2
Отрицательные показатели степени
Теперь мы собираемся расширить значение экспоненты не только на положительное целое число. Мы сделаем это таким образом, чтобы выполнялись обычные правила экспонент. То есть мы хотим, чтобы следующие правила выполнялись для любые показателей степени: положительные, отрицательные, 0 — четные дроби.
а м а н
=
а м + п
То же основание
( аб ) п
=
а н б н
Сила продукта
( a м ) n
=
а мин
Сила Силы
Начнем с определения числа с отрицательным показателем степени .
а − п
=
1 а н
Это число, обратное этому числу с положительным показателем степени.
a − n это взаимный из а н .
Пример 5.
2 −3
=
1 2 3
=
1 8
База 2 не меняется. Отрицательная экспонента становится положительной — в знаменателе.
Пример 6. Сравните следующее. То есть оценить каждый:
3 −2 −3 −2 (−3) −2 (−3) −3
Ответы.
3 −2
=
1 3 2
=
1 9
.
Далее,
−3 −2 является отрицательным числом из 3 −2 . (См. Урок 13.) База по-прежнему равна 3.
.
−3 −2
= −
1 9
.
Что касается (−3) −2 , скобки указывают, что основание равно −3:
.
(−3) −2
=
1 (−3) 2
=
1 9
.
Наконец,
(−3) −3
=
1 (−3) 3
=
−
1 27
.
Таким образом, отрицательная экспонента не дает отрицательного числа. Это может сделать только отрицательное основание. И тогда показатель степени должен быть нечетным
Пример 7. Упростите
а 2 а 5
.
Решение . Поскольку мы изобрели отрицательные показатели степени, теперь мы можем вычесть 90 704 из любых 90 705 показателей степени следующим образом:
а 2 а 5
= a 2 − 5 = a −3
Теперь у нас есть следующее правило для любых показателей m , н :
На самом деле именно потому, что мы хотели, чтобы это правило выполнялось, мы
определили a − n как
1 а н
.
Мы хотим
а 2 а 5
=
а −3
Но
а 2 а 5
=
1 а 3
Следовательно, мы определяем a −3 как
.
1 а 3
.
Пример 8.
а −1
=
1 а
a −1 теперь является символом обратной или мультипликативной инверсии числа к любому числу a . Он появляется в следующем правиле (Урок 6):
а · а −1 = 1
Проблема 5. Оцените следующее.
а) (
2 3
) −1
=
3 2
.
3 2
является обратным числом
.
2 3
.
б) (
2 3
) −4
=
81 16
.
81 16
является величиной, обратной 4-й степени числа
.
2 3
.
Задача 6. Покажите: a m · b − n =
а м б н
.
а м · б − n = а м ·
1 б н
=
а м б н
.
Определение подразделения
Пример 9. Используйте правила экспонент, чтобы вычислить (2 −3 · 10 4 ) −2 .
Решение.
(2 −3 · 10 4 ) −2
=
2 6 · 10 −8
Сила силы
=
Проблема 6
=
_64_ 100 000 000
Задача 7. Оцените следующее.
а)
2 −4
=
1 2 4
=
1 16
б)
5 −2
=
1 5 2
=
1 25
в)
10 −1
=
1 10 1
=
1 10
г)
(−2) −3
=
1 (−2) 3
=
1 −8
=
−
1 8
д)
(−2) −4
=
1 (−2) 4
=
1 16
е)
−2 −4
=
−
1 2 4
=
−
1 16
г) (½) −1 =
2. 2 — это , обратное ½.
Задача 8. Используйте правила экспонент, чтобы оценить следующее.
а)
10 2 · 10 −4 = 10 2 − 4 = 10 −2 = 1/100.
б)
(2 −3 ) 2
=
2 −6
=
1 2 6
=
1 64
в)
(3 −2 · 2 4 ) −2
=
3 4 · 2 −8
=
3 4 2 8
=
81 256
г)
2 −2 · 2
=
2 −2+1
=
2 −1
=
1 2
Задача 9. Перепишите без знаменателя.
а)
x 2 x 5
=
x 2−5
=
x −3
б)
г г 6
=
г 1−6
=
г −5
в)
=
x −3 г −4
г)
=
а −1 б −6 в −7
д)
1 х
=
x −1
е)
1 x 3
=
x −3
г)
( x + 1) x
=
( х + 1) х -1
ч)
( х + 2) 2 ( х + 2) 6
=
( х + 2) −4
Пример 10. Перепишите без знаменателя и оцените:
Ответить . Правило вычитания показателей —
— выполняется, даже если показатель степени отрицателен.
Следовательно,
=
10 −3 + 5 − 2 + 4
=
10 4
=
10 000.
Показатель степени 2 входит в числитель как −2; показатель -4 идет туда как +4.
Задача 10. Перепишите без знаменателя и оцените.
а)
2 2 2 −3
= 2 2 + 3 = 2 5 = 32
б)
10 2 10 −2
= 10 2 + 2 = 10 4 = 10 000
в)
= 10 2 − 5 − 4 + 6 = 10 −1 =
1 10
г)
= 2 5 − 6 + 9 − 7 = 2 1 = 2
Проблема 11. Можно сдвинуть множители между числителем и знаменателем [Как?]
Путем изменения знака степени.
Пример 11. Перепишем без знаменателя:
Ответ.
Показатель степени 3 входит в числитель как −3; показатель степени -4 идет туда как +4.
Задача 12. Перепишите только с положительными показателями.
Belt conveyor drive with conical-cylindrical reduction gear | Download drawings, blueprints, Autocad blocks, 3D models
Drawings content
Компановка — фрагмент.dwg
Редуктор схема.dwg
Промежуточный вал.dwg
Вал.dwg
Масштаб 1к2. dwg
Рама.dwg
Эпюра Промежуточный вал.dwg
Спецификация.dwg
Быстроходный вал.dwg
Колесо. dwg
Общий вид привода.dwg
Тихоходный вал.dwg
Спецификация 1.dwg
Расчёт цилиндрической передачи.doc
Расчёт конической передачи. doc
Выбор двигателя.doc
Расчёт долговечности подшипников.doc
Краткая характеристика.doc
Выбор и расчёт шпонок на смятие.doc
Библиографический список. doc
Содержание.doc
Предварительный расчёт валов редуктора.doc
Радиоуправляемый МАЗ 537 в масштабе 1 к 2,5
Тема сайта
Системная
Тёмная
Светлая
Чёрная
Авторизация
Войти
Спецпроекты
Я автор
Популярное
Авто
Ностальгия
Антифишки
Новости
Фишкина солянка
Тоже интересное
Чистилище
Полит. солянка
Мемолента
Демотиваторы
Гифки
Еда
Спорт
Кубики
Военное
Фото
Книги
Открытки
Анекдоты
Дикая природа
Игры
Путешествия
Кино
Лица проекта
Юмор
Селфи для фишек
Факты
Животные
Истории
Лонгриды
Тесты
ИнфоFishki
Кое-что важное
Полная версия
Реклама на фишках
Firework
Предложения проекту
FAQ
Техподдержка
Закрыли доступ?
Согласие на обработку ПД
На что жалуетесь?
Прямой выход M.
1K2
6 324,00 фунтов стерлингов
Inc НДС 20%
Чтобы приобрести этот продукт, пожалуйста:
Свяжитесь с нами
Рейтинг клиентов: (0)
Масштабируемый 16-портовый маршрутизатор MADI
(Снято с производства)
1024×1024-канальный маршрутизатор MADI с 16 портами
Два 8-портовых слота ввода-вывода могут быть оснащены модулями ввода-вывода MADI BNC, SC Fiber и SFP.
Смарт Модуль ввода-вывода SFP для анализа качества сигнала, информации об уровне сигнала, регистрации ошибок и т. д.
Аудиоканалы могут маршрутизироваться группами или индивидуально
Сценарии LUA
Управление моментальными короткими замыканиями
Режим двойника — зеркалирование/избыточность маршрутизатора Р
DirectOut M.1K2 (Снято с производства)
DirectOut M.1K2 — это масштабируемый 16-портовый маршрутизатор MADI, обеспечивающий мощную матрицу маршрутизации до 1024 x 1024 аудиоканалов, которая заполняет пробел между небольшими устройствами маршрутизации и большими поперечинами. решения. Устройство оснащено двумя слотами ввода-вывода, в которые можно установить модули ввода-вывода BNC, SC или SFP с 8 портами MADI. Он может работать с одним 8-портовым модулем ввода/вывода и при необходимости модернизироваться до 16 портов.
Безопасная и надежная эксплуатация M.1K2 обеспечивает высочайшую надежность благодаря двум источникам питания с резервированием фаз с отдельными входами IEC и переключателями питания переменного тока на задней панели. Кроме того, два порта MADI могут быть настроены как резервные пары. В случае возникновения проблемы между модулями происходит автоматическое переключение без щелчка, и пользователь информируется об этом через программный интерфейс. 4 объекта групповой политики можно использовать для сигнализации о событиях или интеграции в студии. Поддержка SNMP обеспечивает сетевой мониторинг состояния устройства.
Doppelgänger (зеркалирование устройств) Один (или более) M. 1K2 может быть настроен для работы в качестве ведомого по отношению к одному ведущему устройству. Все данные конфигурации (точки коммутации, конфигурация портов, метки и т. д.) постоянно синхронизируются.
Автоматизация LUA Scripting Engine — функции и предопределенные последовательности команд (например, залпы) можно настроить с помощью сценариев, которые запускаются определяемыми горячими клавишами.
Синхронизация M.1K2 может тактироваться любым входом MADI, синхронизацией слов, опорным входом видео или может служить генератором тактовой частоты. Системные часы подаются на два дополнительных выхода Word Clock.
PolySync Каждый порт MADI может иметь собственную опорную синхронизацию, что расширяет возможности применения M.1K2 в средах со смешанной синхронизацией.
MADImatrix Все аудиосигналы могут маршрутизироваться произвольно, группами или по отдельности. Незвуковые сигналы также могут быть маршрутизированы. Все входные сигналы обновляются, сохраняя пользовательские биты на выходе неизменными.
Матрица эмбеддера/деэмбеддера Последовательные данные (MIDI, RS-232, RS-422/485), встроенные в сигнал MADI или из аппаратных интерфейсов, могут маршрутизироваться отдельно от аудиосигнала.
Проверка сигнала Новая плата ввода-вывода «SFP.IO SMART» предлагает анализ качества сигнала MADI и запрос информации с использованием соответствующих модулей SFP. Специальная информация об уровне сигнала, средах SFP и их рабочих характеристиках предоставляется через веб-интерфейс M.1K2. Любые возникающие ошибки постоянно регистрируются.
Маркировка Для маркировки ввода/вывода предусмотрена мощная функция импорта/экспорта CSV. Переключаемые слои отображают либо настраиваемые имена, либо номер порта/канала.
Управление моментальными снимками Моментальные снимки, содержащие все настройки маршрутизации, меток, портов и часов в одном пакете, можно группировать в проекты и обмениваться ими между различными устройствами M. 1K2. Отдельные части снимка могут быть восстановлены в любое время.
Управление пользователями Индивидуальное управление функциями на основе определяемых классов разрешений может быть настроено для разных пользователей, позволяя этим пользователям совместно управлять устройствами в сложных средах в соответствии с их уровнем разрешений.
Удаленный доступ Удаленное управление осуществляется через сетевое соединение и интерфейс веб-браузера. Возможен одновременный доступ из других местоположений, который не ограничивается конкретной операционной системой. Обновления прошивки могут быть установлены через Ethernet.
Несколько подключаемых модулей позволяют различными способами осуществлять внешнее управление устройством. В настоящее время поддерживаются следующие методы:
Когда вам нужно измерить что-то маленькое, эти портативные весы идеально подходят для этой работы! Это идеальные весы для измерения продуктов питания, специй, лекарств, чая, дрожжей или других мелких предметов. Мы разработали эти мини-весы, чтобы ими было легко пользоваться, где бы вы их ни брали. Он оснащен цифровым ЖК-экраном с подсветкой для лучшей видимости. Мы добавили измерительную поверхность из нержавеющей стали, которую легко чистить и за которой легко ухаживать. Кроме того, весы поставляются со встроенной крышкой для надежной защиты, где бы они ни находились. Благодаря возможности конвертации между унциями, граммами, тройскими унциями, пеннивейтами, гранами и каратами, эти весы чрезвычайно универсальны. На приборе всего 3 кнопки: Тара, Вкл/Выкл и Режим. Эти кнопки находятся на сенсорном ЖК-экране. Все электронные весы AWS оснащены высокоточной тензометрической технологией, которая обеспечивает точность день за днем. Кроме того, наши электронные весы оснащены технологией автоматического включения: одним нажатием кнопки на весах вы легко получите точное измерение веса. BT2-1KG точно измеряет вес от 0,1 до 1000 граммов.
Основные характеристики
Размеры карманов позволяют брать их с собой куда угодно
Сенсорный ЖК-дисплей
Функция автоматического отключения
Крышка служит лотком для взвешивания
E легко переключаться между граммами, унциями, тройскими унциями , пеннивейты, караты и граны
Перчатки с полиуретановым покрытием 5 степень защиты от порезов размер 10 серые
Главная
>Электрооборудование
>Инструмент, измерительные приборы и средства защиты
>Защитные материалы и спецодежда
>Защитные перчатки
>HAUPA
>Перчатки с полиуретановым покрытием 5 степень защиты от порезов размер 10 серые | 120304/10 Haupa (#771319)
Наименование
Наличие
Цена
опт с НДС
Дата обновления
Добавить в корзину
Срок поставки
Перчатки с полиуретановым покрытием, 5 степень защиты от порезов, размер 10, серые | 120304/10 | Haupa
1
504. 18
р.
01.05.2023
От 1 дня
Условия поставки перчаток с полиуретановым покрытием 5 степень защиты от порезов размер 10 серые | 120304/10 Haupa
Купить перчатки с полиуретановым покрытием 5 степень защиты от порезов размер 10 серые | 120304/10 Haupa могут физические и юридические лица, по безналичному и наличному расчету,
отгрузка производится с пункта выдачи на следующий день после поступления оплаты.
Цена перчаток с полиуретановым покрытием 5 степень защиты от порезов размер 10 серые | 120304/10 Haupa зависит от общей суммы заказа, на сайте указана оптовая цена.
Доставим перчатки с полиуретановым покрытием 5 степень защиты от порезов размер 10 серые | 120304/10 Haupa на следующий день после оплаты, по Москве и в радиусе 200 км от МКАД, в другие регионы РФ отгружаем транспортными компаниями.
Похожие товары
Перчатки с полиуретановым покрытием размер 10 черн (пара) HAUPA 120300/10
по запросу
Перчатки с полиуретановым покрытием 5 степень защиты от порезов размер 11 серые | 120304/11 Haupa
по запросу
Перчатки с полиуретановым покрытием 5 степень защ размер 9 сер (пара) HAUPA 120304/9
по запросу
Mathway | Популярные задачи
1
Найти число возможных исходов
7 выбор 3
2
Найти число возможных исходов
8 выбор 3
3
Найти число возможных исходов
5 выбор 2
4
Найти число возможных исходов
4 выбор 2
5
Найти число возможных исходов
8 выбор 4
6
Найти число возможных исходов
10 выбор 3
7
Найти число возможных исходов
7 выбор 4
8
Найти число возможных исходов
6 выбор 3
9
Найти число возможных исходов
9 выбор 3
10
Найти число возможных исходов
3 выбор 2
11
Найти число возможных исходов
6 выбор 4
12
Найти число возможных исходов
5 выбор 4
13
Найти число возможных исходов
7 перестановка 3
14
Найти число возможных исходов
7 выбор 2
15
Найти число возможных исходов
10 выбор 5
16
Найти число возможных исходов
10 выбор 6
17
Найти число возможных исходов
13 выбор 5
18
Найти число возможных исходов
3 выбор 3
19
Найти число возможных исходов
4 выбор 1
20
Найти число возможных исходов
4 выбор 4
21
Найти число возможных исходов
5 выбор 1
22
Найти число возможных исходов
6 перестановка 3
23
Найти число возможных исходов
8 выбор 5
24
Найти число возможных исходов
9 перестановка 4
25
Найти число возможных исходов
13 выбор 3
26
Найти число возможных исходов
12 выбор 2
27
Найти число возможных исходов
12 выбор 4
28
Найти число возможных исходов
12 выбор 3
29
Найти число возможных исходов
9 выбор 5
30
Найти число возможных исходов
9 выбор 2
31
Найти число возможных исходов
7 выбор 5
32
Найти число возможных исходов
6 перестановка 6
33
Найти число возможных исходов
8 перестановка 5
34
Найти число возможных исходов
8 перестановка 3
35
Найти число возможных исходов
7 перестановка 5
36
Найти число возможных исходов
52 выбор 5
37
Найти число возможных исходов
5 перестановка 3
38
Найти число возможных исходов
12 выбор 5
39
Найти число возможных исходов
3 выбор 1
40
Найти число возможных исходов
11 выбор 5
41
Найти число возможных исходов
10 выбор 2
42
Найти число возможных исходов
15 выбор 3
43
Найти число возможных исходов
52 выбор 4
44
Найти число возможных исходов
9 выбор 4
45
Найти число возможных исходов
9 перестановка 3
46
Найти число возможных исходов
7 перестановка 4
47
Найти число возможных исходов
7 перестановка 2
48
Найти число возможных исходов
11 выбор 4
49
Найти число возможных исходов
11 выбор 2
50
Найти число возможных исходов
11 выбор 3
51
Найти число возможных исходов
10 перестановка 5
52
Найти число возможных исходов
5 выбор 5
53
Найти число возможных исходов
6 выбор 1
54
Найти число возможных исходов
8 перестановка 4
55
Найти число возможных исходов
8 выбор 6
56
Найти число возможных исходов
13 выбор 4
57
Вычислить
e
58
Найти уравнение, перпендикулярное прямой
-7x-5y=7
59
Найти число возможных исходов
13 выбор 2
60
Найти число возможных исходов
10 перестановка 2
61
Найти число возможных исходов
10 перестановка 3
62
Найти число возможных исходов
10 выбор 7
63
Найти число возможных исходов
20 выбор 4
64
Найти число возможных исходов
6 перестановка 4
65
Найти число возможных исходов
5 перестановка 4
66
Найти число возможных исходов
6 выбор 5
67
Найти число возможных исходов
52 выбор 3
68
Найти число возможных исходов
4 выбор 0
69
Найти число возможных исходов
9 перестановка 7
70
Найти число возможных исходов
6 выбор 2
71
Найти число возможных исходов
5 перестановка 5
72
Найти число возможных исходов
5 перестановка 2
73
Найти число возможных исходов
6 выбор 6
74
Найти число возможных исходов
7 выбор 6
75
Найти число возможных исходов
8 перестановка 6
76
Найти число возможных исходов
7 перестановка 7
77
Найти число возможных исходов
9 перестановка 5
78
Найти число возможных исходов
2 перестановка 2
79
Найти число возможных исходов
10 выбор 8
80
Найти число возможных исходов
12 выбор 7
81
Найти число возможных исходов
15 выбор 5
82
Найти обратный элемент
[[1,0,1],[2,-2,-1],[3,0,0]]
83
Определить область значений
1/4x-7
84
Найти число возможных исходов
10 перестановка 7
85
Найти число возможных исходов
12 выбор 6
86
Найти число возможных исходов
2 выбор 1
87
Найти число возможных исходов
30 выбор 3
88
Найти число возможных исходов
9 выбор 6
89
Найти число возможных исходов
8 перестановка 2
90
Найти число возможных исходов
7 выбор 1
91
Найти число возможных исходов
6 перестановка 2
92
Найти число возможных исходов
4 перестановка 2
93
Найти число возможных исходов
4 перестановка 3
94
Найти число возможных исходов
3 перестановка 3
95
Найти число возможных исходов
46 выбор 6
96
Найти число возможных исходов
5 перестановка 1
97
Найти число возможных исходов
52 выбор 7
98
Найти число возможных исходов
52 перестановка 5
99
Найти число возможных исходов
9 выбор 1
100
Найти число возможных исходов
9 перестановка 6
5° Брендинг
Спиральный
Мы дизайнеры, стратеги, строители, мыслители, мечтатели, писатели и исполнители. Мы помогаем нашим друзьям из высших учебных заведений с институциональным брендингом и коммуникациями на каждом этапе опыта избирателя — от услуг по зачислению до отношений с выпускниками и развития.
Наша работаЗачем работать с нами
Брендинг
Исследования и открытия / Фирменный стиль / Разработка логотипа / Слоган и матрица сообщений …
Интернет
Стратегия (CMS, IA, управление) / Дизайн и создание / Разработка контента / Обучение и поддержка …
Регистрация
Обзор и стратегия потока коммуникаций / Брендинг путешествия / Инструменты посещения кампуса / Цифровое творчество ….
Это любой, кто ценит свой бренд, хочет развиваться и предан проекту. У нас было много таких.
Список клиентов
«Мне посчастливилось работать с брендингом 5° в двух разных организациях с довольно большим промежутком времени между обеими кампаниями. Одна вещь, которую я действительно ценю, это то, что они не пытались развернуть один и тот же дизайн формочек для печенья в разных учреждениях. Я думаю, это стало возможным, потому что они действительно поддерживают партнерство и сотрудничество, необходимые для представления каждого клиента. Они веселые и забавные, и они заботятся о людях, которые составляют нашу команду. Это просто отличный рецепт успеха».
— ААРОН ПОРТЕР | БЫВШИЙ ВИЦЕ-ПРЕЗИДЕНТ ОТДЕЛА ЗАЧИСЛЕНИЯ | УНИВЕРСИТЕТ КАРСОНА-НЬЮМАНА
С момента нашей первой встречи до последнего телефонного звонка (и даже после него) 5° продемонстрировали непревзойденный опыт, рассудительность, креативность и основательность в своем подходе к нашему плану. Я уже работал над проектами по брендингу и реконструкции веб-сайтов и был поражен их вниманием к деталям. Они определенно превзошли мои ожидания! Они включили наши исследования и идеи и объединили свой собственный опыт христианского высшего образования, чтобы представить конечный продукт, который осуществил и превзошел наши мечты».
— ДЖЕННА ДЖОНСОН I ПОМОЩНИК ДИРЕКТОРА ПО ИНТЕГРИРОВАННОМУ МАРКЕТИНГУ ЧАРЛСТОНСКОГО ЮЖНОГО УНИВЕРСИТЕТА
«UMHB, безусловно, ценит наше сотрудничество с 5° Branding. У нас была возможность объединиться с 5° для нескольких кампаний по приему, и каждый раз продукт кажется лучше, потому что они не торопятся, чтобы узнать ваш кампус. Во многом успех UMHB можно объяснить прекрасным партнерством с 5°».
— БРЕНТ Р. БЕРКС, ЭД.Д. | ДИРЕКТОР ПО ПРИЕМУ И РЕКРУТИНГУ, УНИВЕРСИТЕТ МЭРИ ХАРДИН-БЕЙЛОР
Мы делаем это с равными частями процесса, технологий, опыта, мужества и магии.
Чем мы занимаемся
Быть самим собой: задача маленького гуманитарного колледжа
Максимальное использование 1 мая — и после
Чем хороша ваша школа? Что делает его другим?
Создание (и сохранение) Команды зачисления будущего
Отображение пути будущего студента в вашем маркетинговом плане
Три способа привлечь лучших кандидатов в высшие учебные заведения в условиях жесткого рынка
Политики маркетинга дополнительных тестов для будущих студентов
Ребрендинг в миссии: История Женевского колледжа
Привлечение неопределившихся специальностей в вашу школу
Посетите блог
Будьте в курсе последних тенденций и лучших практик в сфере высшего образования, подписавшись на нашу рассылку.
Имя
Электронная почта
Встречайте 5° — 5° Брендинг
Мы верим, что бренд обладает силой. Способность двигать людей и менять жизнь к лучшему. Великий бренд является аутентичным, с сильным чувством личности, места и цели. Мы работаем с известными образовательными брендами, чтобы помочь определить их подлинность, дифференцировать их предложения и донести их преимущества до аудитории, которая больше всего нуждается в этом.
Мы отличаемся тремя способами.
Один, фокус. Нам известно частное высшее образование. Мы являемся продуктом независимого высшего образования и твердо верим в его необходимость в качестве силы добра в нашей культуре.
Два, список клиентов. На протяжении многих лет мы имели честь работать со многими независимыми школами. Мы знаем об уникальных проблемах и возможностях, с которыми сегодня сталкиваются частные или религиозные учреждения. Мы хотим поддерживать и укреплять этот список школ-партнеров.
Три, доверие. В результате прежних и нынешних отношений клиенты продолжают обращаться к 5° за стратегией, креативом и результатами, которым они доверяют.
Познакомьтесь с руководством. Ли Инско / Опыт работы с клиентами, партнер
Ли здесь известен как «лучший друг клиента» — честь, которую он заслужил годами, активно слушая, видя потребности, затыкая дыры и успокаивая людей. Он также обладает способностью видеть проблему с высоты 30 000 футов, не упуская деталей, талант, который является естественным для Ли.
Ли имеет более чем 25-летний опыт работы в сфере коммуникаций с высшим образованием, в течение двенадцати лет работал вице-президентом по продажам в Details Communications и в течение десяти лет был директором по маркетингу в Сэмфордском университете, прежде чем стать соучредителем 5° в 2014 году. Этот опыт в сочетании с неустанным исследования и желание учиться сослужили хорошую службу клиентам, и они пожинают плоды его опыта.
Майк Робинсон / креативный директор, партнер
С 1996 года Майк создает первоклассные креативы для клиентов по всему миру. Он работал как в агентстве, так и в национальном министерстве. Выпускник Самфорда, он сочетает в себе уникальное понимание рынка высшего образования с желанием проникнуть в суть клиента, чтобы создать персональные и эффективные коммуникационные решения. Как хранитель нашего культурного пульса, он хорошо осведомлен о проблемах, затрагивающих образовательные и некоммерческие организации.
Клиенты извлекли пользу из способности Майка понять и выявить их особенности. Помимо работы с клиентами, он следит за тем, чтобы команда 5° синхронизировалась с нашими собственными сообщениями, миссией и ценностями.
Ким Кэмпбелл / бренд-стратег, руководитель проекта
Ким работает в области маркетинга и высшего образования более десяти лет. Она обладает уникальным пониманием проблем, с которыми регулярно сталкиваются команды высшего образования по маркетингу и коммуникациям. Ким также имеет опыт разработки маркетинговых стратегий для традиционных студентов и нетрадиционных взрослых учащихся. Некоторые из клиентов 5 °, которые воспользовались ее опытом, — это Южный университет Чарльстона, Женевский колледж, Университет Пьемонта, Богословская семинария Бетани и Университет Пайквилля.
Обладая обширным опытом в области развития брендов, маркетинговой стратегии и управления проектами, Ким участвовала в проектах для различных учреждений. Она может перемещаться между этапами общей картины проекта и «второстепенными» элементами, которые иногда могут быть решающими или решающими. Ким наблюдает за повседневными операциями, которые ведут многие проекты 5 ° от первоначального обнаружения до реализации
Райан Морабито / эксперт по бренду, стратег
Эксперт по бренд-маркетингу с более чем двадцатилетним опытом работы в сфере высшего образования Райан сотрудничает с более чем сотней колледжей и университетов в разработке и реализации долгосрочных и краткосрочных маркетинговых инициатив. Он преднамеренный и творческий мыслитель, а также признанный лидер в проведении высококачественных исследований рынка, оптимизации узнаваемости бренда и разработке стратегических моделей, которые фокусируют операционные усилия и приводят к результатам.
Райан преуспевает в концептуализации, разработке и запуске комплексных маркетинговых программ и их реализации в срок и в рамках бюджета. Он обладает сильной способностью стратегически рассматривать организационные проблемы, руководить межфункциональными командами, развивать партнерские отношения, эффективно общаться и управлять несколькими проектами.
5° выбило наш брендинг и веб-сайт из парка! Мы уже пожинаем плоды нашей тяжелой совместной работы. Студентам, как будущим, так и нынешним, нравится новый внешний вид, и они говорят о том, как легко найти то, что они ищут. Выпускники больше гордятся своей альма-матер. Преподаватели и сотрудники в восторге от того, что мы предлагаем общественности, и общественность ЗАМЕТИЛА!
С момента нашей первой встречи до последнего телефонного звонка (и даже после него) 5° продемонстрировали непревзойденный опыт, рассудительность, креативность и основательность в своем подходе к нашему плану. Я уже работал над проектами по брендингу и реконструкции веб-сайтов и был поражен их вниманием к деталям. Они определенно превзошли мои ожидания! Они включили наши исследования и идеи и объединили свой собственный опыт христианского высшего образования, чтобы представить конечный продукт, который осуществил и превзошел наши мечты. Д
— Дженна Джонсон I, исполнительный директор по маркетингу и коммуникациям, Южный университет Чарлстона,
.
UMHB, безусловно, ценит наше партнерство с 5° Branding. У нас была возможность объединиться с 5° для нескольких кампаний по приему, и каждый раз продукт кажется лучше, потому что они не торопятся, чтобы узнать ваш кампус. Во многом успех UMHB можно объяснить прекрасным партнерством с 5° .
— Брент Р. Беркс, изд. | Директор по приему и найму, Университет Мэри Хардин-Бейлор
Я много лет работал с 5° Branding над множеством проектов и бесчисленное количество раз рекомендовал их коллегам. Они точны и надежны, и я не мог представить себе работу с лучшей группой. Их работа обязательно привлечет внимание ваших потенциальных клиентов, и я настоятельно рекомендую их.
— Томас М. Хюбнер-младший, доктор философии. | Президент Общественного колледжа Меридиан
«Я имел удовольствие работать с 5° Branding над комплексным проектом редизайна учреждения, в котором я работал несколько лет назад. Они были творческими, тщательными и профессиональными. Их вклад был искренним, их подход был деликатным, а их конечный продукт отражал наше стремление к переменам. Надеюсь на сотрудничество с ними в будущем!
— Доктор Том Джонс | Бывший президент Баптистского колледжа Уильямса
5° Брендинг был незаменимым активом для нашей команды здесь, на Среднем Западе. От начала до конца они не выполнили обещанное и перевыполнили, что обеспечивает нам долгосрочный успех.
«Эти ребята отлично работают! Я очень ценю дополнительные усилия, которые они прилагают, чтобы не только понять проект, но и по-настоящему понять нас как учреждение и нашу целевую аудиторию. Недавно мы работали с ними над редизайном сайта. Креативное направление, которое они предложили, стало огромным преимуществом для всего проекта. В отличие от других поставщиков, с которыми я работал, они действительно были заинтересованы в проекте и хотели, чтобы мы добились успеха.
— Крис Харди | Директор веб-коммуникаций, Университет Мессии
«Я работал с командой 5° в нескольких учреждениях. Проекты, над которыми мы сотрудничали, варьируются от комплексной инициативы по брендингу до целевых кампаний по набору персонала. В каждом проекте они превзошли установленные ожидания. Совсем недавно LeTourneau понадобилась сплоченная кампания по набору персонала, чтобы сообщить о своей позиции национального лидера среди христианских университетов в STEM, а также продвигать сильные стороны программ бизнеса, образования и гуманитарных наук. 5° С брендингом все в порядке!
— Терри Дейл Круз, доктор философии. | Бывший вице-президент по регистрации, Университет ЛеТурно
Мы считаем 5° Branding бесценными членами нашей медиа-команды. Рабочие отношения, которыми мы наслаждаемся с их командой, стали возможными благодаря их невероятному творчеству, полированной готовой продукции и неизменной готовности пройти лишнюю милю. Мы не можем рекомендовать их достаточно!
— Лиза Уолдроп | Директор по СМИ и коммуникациям, Шелтонский государственный общественный колледж
Моя команда выбрала компанию 5° для проведения ребрендинга. С самого начала было ясно, что команда поняла, как получить представление о нашем бренде и воплотить это понимание в успешный ребрендинг. Команда руководила нами на всех этапах исследований, открытий и анализа. Мы были настолько впечатлены их работой, что выбрали их для продвижения нового бренда и создания нового веб-сайта. Работа с веб-сайтом была столь же феноменальной, как и следовало ожидать от 5°. Я очень рекомендую их.
— Брайан Мюррей | Старший директор по маркетингу и коммуникациям Среднеамериканской баптистской теологической семинарии
Наша команда работала с 5° над несколькими маркетинговыми проектами. Они действительно стали продолжением нашей команды. От публикаций о наборе персонала до веб-дизайна и поддержки программирования, команда 5° работала с нами и помогала создавать решения, которые нашли большой отклик у наших будущих студентов, наших преподавателей и наших сотрудников. Более того, они нашли время, чтобы понять масштаб того, что наша команда может поддерживать в долгосрочной перспективе, разрабатывая устойчивые стратегии. Одна из вещей, которые я больше всего ценю в наших отношениях с 5°, это то, что они не пытаются заново изобретать наш бренд и отказываться от всего, что мы делали в прошлом. Вместо этого они тратят много времени на знакомство с нашим кампусом и нашими студентами, чтобы помочь в создании кампаний по зачислению, основанных на том, кто мы на самом деле. Такое очень трудно найти на рынке!
— Эми Кертис | Бывший менеджер по веб-коммуникациям, MidAmerica Nazarene University
Мне понравилось тесно сотрудничать с 5° в проекте редизайна наших материалов для взрослых и традиционных приемных материалов. Они нашли время, чтобы познакомиться с нашим учреждением, а также узнать о сходствах и различиях между различными форматами программ, которые мы предлагаем. Они предложили творческие подходы, которые привели к удивительным готовым продуктам! Люди до сих пор постоянно спрашивают нас, кто разработал наши материалы, и мы быстро указываем им на людей из 5°!
— Доктор Стейси Бартлетт | Начальник штаба Пойнтского университета
5° Брендинг понимает маркетинг высшего образования. Это эксперты, которых мы все надеемся найти. Было приятно работать с 5° в течение последнего десятилетия. Они честны, заслуживают доверия, скромны, креативны, тщательны и с ними весело сотрудничать. И к нам относятся так, как будто мы их единственный клиент, что само по себе является искусством. Настоятельно рекомендуется!
— Эд Гобл | Креативный директор Кэмпбеллсвиллского университета
Работать с 5° было потрясающе. Они не торопились, чтобы узнать о нашем колледже, и придумали потрясающие маркетинговые материалы, которые действительно отражали атмосферу нашего кампуса. Это казалось огромной работой, но они шаг за шагом вели нас через процесс, упрощая его выполнение. Мне нравится с ними работать!
— Джессика Хефке | Старший заместитель директора по управлению зачислением и коммуникациям Вестминстерского колледжа
Было очень приятно работать с 5° Branding, поскольку они помогли нам провести ребрендинг нашей семинарии, включая введение нового названия и нового местоположения в 400 милях к югу. 5° смог отразить сердцебиение нашей школы на печатной странице и наше присутствие в Интернете. Мы искренне ценим их профессионализм и умение вести нас через весь процесс.
— Кэти Чут | Бывший директор по коммуникациям Gateway Seminary
Наша команда работала с 5 Degrees Branding над двумя крупными редизайнами веб-сайтов, и они превзошли все наши ожидания.
Здесь:
00″ data-percent-format=»10.00%» data-date-format=»DD.MM.YYYY» data-time-format=»HH:mm» data-features=»["after_table_loaded_script"]» data-search-value=»» data-lightbox-img=»» data-head-rows-count=»1″ data-pagination-length=»50,100,All» data-auto-index=»off» data-searching-settings=»{"columnSearchPosition":"bottom","minChars":"0"}» data-lang=»default» data-override=»{"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default"}» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
Для этого могут применяться следующие приемы:
Узоры и орнаменты на посуде»
Объяснение нового материалаСловесная формулировка
Одним из правил является принцип сложения, который гласит, что мы можем добавить или вычесть число из самого себя, чтобы удалить его из одной части уравнения, но мы должны сделать то же самое с другой частью уравнения, чтобы сохранить его сбалансированным.
2(2x – 4) = x + 4*
2(2x – 4) = x + 4*
Когда вы нажмете «Отправить», будет обновлена эта же страница. Прокрутите вниз, чтобы увидеть результаты.) 
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и det a. Просто введите задачу в окошко и нажмите
«решить» здесь (например, det a матрицы что это).
000
Размерность уменьшается и может быть уменьшена далее шаг за шагом до скаляра.
До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа вскоре получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
.. Что такое Сложение?
также
До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа вскоре получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
В 8 — 5 = 3 разница три.
дроби
Этот набор содержит 100 печатных листов со смешанными задачами на сложение и вычитание с 5-значными числами. 
Этот способ хорош возможностью использования практически в любой ситуации. К нему прибегают, когда найти корень с помощью вычислений невозможно.
2
Решить уравнение: .
е. выразим через :
Запишем полученную систему линейных уравнений: .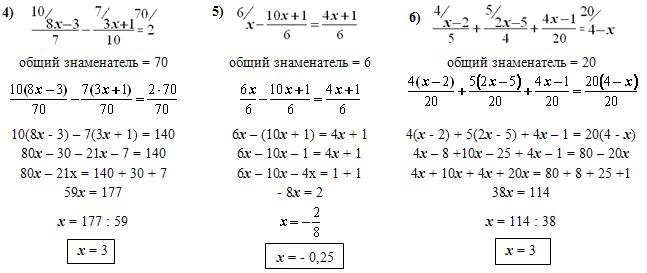
10), значит, — это , т.е. от – это .Аналогично от – это , а от – это .
Так как в числе десятков и единиц, то , а в числе десятков и единиц, значит, .
М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. ФГОС, изд-во «Просвещение», 2017.
..
0003
Ответы на все вопросы упражнения, примеры и дополнительные вопросы были предоставлены с видео каждого вопроса
При нажатии на ссылку открывается первый вопрос. Чтобы открыть любой другой вопрос упражнения, перейдите в конец страницы. Есть список со стрелками, в котором есть все вопросы (с важные вопросы также отмечены)
ru/20230216/frantsisk-1852402124.html
На этих встречах папе Франциску задали вопрос, рассматривает ли он возможность досрочного ухода на покой по примеру своего предшественника Бенедикта XVI. «Нет, мне это не приходило в голову», — ответил понтифик. Он напомнил, что вскоре после избрания на папский престол он подписал документ о своем отречении на случай серьезного ухудшения состояния здоровья. По его словам, подобное заявление в прошлом уже написал папа Пий XII на случай, если бы Адольф Гитлер решил перевезти его в Германию. «Это не значит, что отставные папы должны стать, скажем так, «модой», нормальным явлением», — подчеркнул папа Франциск, добавив, что не знает, где находится его документ. «У Бенедикта хватило смелости сделать это, потому что он не хотел продолжать из-за своего здоровья. На данный момент у меня нет этого в повестке», — сказал Франциск во время встречи с иезуитами в Киншасе. «Я считаю, что служение папы Римского является ad vitam (пожизненным – ред.). Я не понимаю, почему бы ему таким не быть. Просто подумайте, что служение патриархов всегда на всю жизнь, и важна историческая традиция.
Если вместо этого мы прислушаемся к болтовне, тогда надо менять папу каждые полгода», — заключил он. Папа Римский Франциск страдает от сильных болей в коленном суставе, из-за чего он вынужден пользоваться креслом-коляской. В июле 2021 года в римской больнице «Агостино Джемелли» папе Франциску была сделана плановая хирургическая операция по поводу дивертикулярной болезни сигмовидной ободочной кишки. Операция продолжалась около трех часов и потребовала резекции левой части толстого кишечника. Папа Франциск провел в клинике десять суток.
xn--p1ai/
На этих встречах папе Франциску задали вопрос, рассматривает ли он возможность досрочного ухода на покой по примеру своего предшественника Бенедикта XVI.
). Я не понимаю, почему бы ему таким не быть. Просто подумайте, что служение патриархов всегда на всю жизнь, и важна историческая традиция. Если вместо этого мы прислушаемся к болтовне, тогда надо менять папу каждые полгода», — заключил он.
Римскими цифрами , это CDLXXXVI. Хотите понять всю сумму? Это:
Затем мы просто добавляем V ( 5), что дает в сумме 45.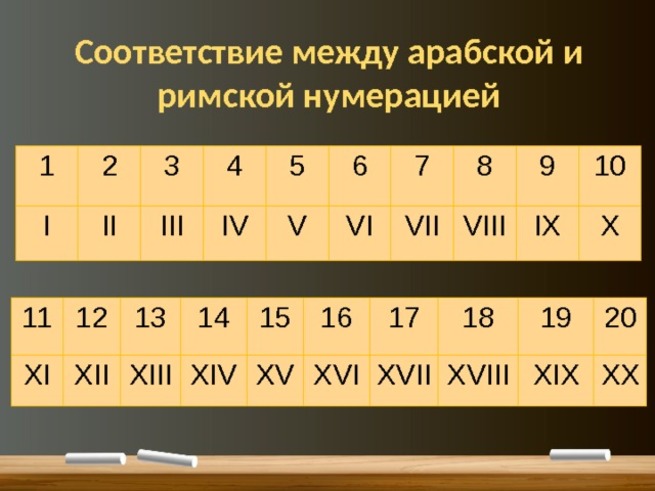
(Теорему Пифагора они уже знали.) То есть, если длину стороны принять за единицу, то точная длина диагонали не выражается никакой натуральной дробью. В результате чего, посыпав голову пеплом, отказались от чисел вообще, перейдя исключительно к геометрическим построениям!
Но ноль — он ведь один единственный. Для него одного вполне можно сделать исключение. (И к тому же — если очень хочется — можно считать что деление любого числа на ноль даёт бесконечность. А деление его же на бесконечность — соответственно даёт ноль.) В остальном с
Таковых чисел просто нет!
Положительные и отрицательные числа. Целые числа. Сложение целых чисел.12+
04:40 Что такое целые числа?
05:46 Действия с целыми числами.
06:29 Сложение отрицательных чисел.
09:10 Как складывать положительные и отрицательные числа?
13:04 Что такое алгебраическая сумма?
15:21 Примеры алгебраической суммы.
18:38 Примеры вычисления алгебраической суммы.
Рекомендуем Вам посмотреть следующие видео:
Выражения с переменной. Как прочитать и объяснить выражения с переменной. Примеры выражений. Алгебра 7 класс. https://youtu.be/YDwS5Bl9Szo
Что такое компоненты. Рассказ о Пете и Диме или зачем нужны компоненты. https://rutube.ru/video/2a05adba43e67d1ea1b5cab6d8e6d18a/
Компоненты сложения. Результат сложения. Компоненты вычитания. Результат вычитания. https://rutube.ru/video/817bf00c7751d685ff04a14f983f186b/
Компоненты умножения. Результат умножения. Компоненты деления. Результат деления. https://rutube.ru/video/f9c294622103e8a2c9d8ef149d8e757f/
Буквенные выражения. Определение. Значение буквенного выражения. https://rutube.ru/video/9df8b54b78d677bd9751979e94aece76/
5-11 класс.
Порядок действий в математике. Примеры на порядок действий. Оформление решений. https://rutube.ru/video/7c0d132e7a5a520f24ed240f458a8b0e/
Степень с натуральным показателем. Компоненты степени. https://rutube.ru/video/d70872cb3e43dad6eb4ad3bf16eaaa7c/
#АлгебраическаяСумма #ЦелыеЧисла #МатематикаОтБаканчиковой #алгебраическаясуммамногочленов #построениечисловойпрямой #алгебраическаясумма #целыечисла #сложениецелыхчисел #противоположныечисла #чтотакоецелыечисла #целыечисла #обозначениецелыхчисел #действиясцелымичислами #сложениеотрицательныхчисел #сложениеположительныхиотрицательныхчисел #примерыалгебраическойсуммы #примерывычисленияалгебраическойсуммы #обозначениецелыхчисел #алгебра7класс #математика6класс #вычитаниеотрицательныхчисел #сложениеивычитаниеотрицательныхчисел #сложениевычитаниеотрицательныхиположительныхчисел
вычитание отрицательных чисел, сложение и вычитание отрицательных чисел, сложение вычитание отрицательных и положительных чисел, построение числовой прямой, алгебраическая сумма, целые числа, сложение целых чисел, противоположные числа, что такое целые числа, целые числа, обозначение целых чисел, действия с целыми числами, сложение отрицательных чисел, сложение положительных и отрицательных чисел, примеры алгебраической суммы, примеры вычисления алгебраической суммы, обозначение целых чисел, алгебра 7 класс, математика 6 класс
Включает рассуждения и прикладные вопросы.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
»
Упростите каждое из следующих действий. Затем вычислите каждое число.
Мы сделаем это таким образом, чтобы выполнялись обычные правила экспонент. То есть мы хотим, чтобы следующие правила выполнялись для любые показателей степени: положительные, отрицательные, 0 — четные дроби.
(См. Урок 13.) База по-прежнему равна 3.
Упростите 
2 — это , обратное ½.
Перепишите без знаменателя.
Перепишите без знаменателя и оцените:
Можно сдвинуть множители между числителем и знаменателем [Как?]
dwg
doc
doc
солянка
1K2
решения. Устройство оснащено двумя слотами ввода-вывода, в которые можно установить модули ввода-вывода BNC, SC или SFP с 8 портами MADI. Он может работать с одним 8-портовым модулем ввода/вывода и при необходимости модернизироваться до 16 портов.
1K2 может быть настроен для работы в качестве ведомого по отношению к одному ведущему устройству. Все данные конфигурации (точки коммутации, конфигурация портов, метки и т. д.) постоянно синхронизируются.
Незвуковые сигналы также могут быть маршрутизированы. Все входные сигналы обновляются, сохраняя пользовательские биты на выходе неизменными.
1K2. Отдельные части снимка могут быть восстановлены в любое время.
0 (виртуальный COM-порт)
bigcommerce.com/s-j40z9v89c/product_images/uploaded_images/aws.png
Мы разработали эти мини-весы, чтобы ими было легко пользоваться, где бы вы их ни брали. Он оснащен цифровым ЖК-экраном с подсветкой для лучшей видимости. Мы добавили измерительную поверхность из нержавеющей стали, которую легко чистить и за которой легко ухаживать. Кроме того, весы поставляются со встроенной крышкой для надежной защиты, где бы они ни находились. Благодаря возможности конвертации между унциями, граммами, тройскими унциями, пеннивейтами, гранами и каратами, эти весы чрезвычайно универсальны. На приборе всего 3 кнопки: Тара, Вкл/Выкл и Режим. Эти кнопки находятся на сенсорном ЖК-экране. Все электронные весы AWS оснащены высокоточной тензометрической технологией, которая обеспечивает точность день за днем. Кроме того, наши электронные весы оснащены технологией автоматического включения: одним нажатием кнопки на весах вы легко получите точное измерение веса. BT2-1KG точно измеряет вес от 0,1 до 1000 граммов.
Мы помогаем нашим друзьям из высших учебных заведений с институциональным брендингом и коммуникациями на каждом этапе опыта избирателя — от услуг по зачислению до отношений с выпускниками и развития.
Одна вещь, которую я действительно ценю, это то, что они не пытались развернуть один и тот же дизайн формочек для печенья в разных учреждениях. Я думаю, это стало возможным, потому что они действительно поддерживают партнерство и сотрудничество, необходимые для представления каждого клиента. Они веселые и забавные, и они заботятся о людях, которые составляют нашу команду. Это просто отличный рецепт успеха».
Она может перемещаться между этапами общей картины проекта и «второстепенными» элементами, которые иногда могут быть решающими или решающими. Ким наблюдает за повседневными операциями, которые ведут многие проекты 5 ° от первоначального обнаружения до реализации
Он обладает сильной способностью стратегически рассматривать организационные проблемы, руководить межфункциональными командами, развивать партнерские отношения, эффективно общаться и управлять несколькими проектами.
Д
Они были творческими, тщательными и профессиональными. Их вклад был искренним, их подход был деликатным, а их конечный продукт отражал наше стремление к переменам. Надеюсь на сотрудничество с ними в будущем!
В отличие от других поставщиков, с которыми я работал, они действительно были заинтересованы в проекте и хотели, чтобы мы добились успеха.
Рабочие отношения, которыми мы наслаждаемся с их командой, стали возможными благодаря их невероятному творчеству, полированной готовой продукции и неизменной готовности пройти лишнюю милю. Мы не можем рекомендовать их достаточно!
Они действительно стали продолжением нашей команды. От публикаций о наборе персонала до веб-дизайна и поддержки программирования, команда 5° работала с нами и помогала создавать решения, которые нашли большой отклик у наших будущих студентов, наших преподавателей и наших сотрудников. Более того, они нашли время, чтобы понять масштаб того, что наша команда может поддерживать в долгосрочной перспективе, разрабатывая устойчивые стратегии. Одна из вещей, которые я больше всего ценю в наших отношениях с 5°, это то, что они не пытаются заново изобретать наш бренд и отказываться от всего, что мы делали в прошлом. Вместо этого они тратят много времени на знакомство с нашим кампусом и нашими студентами, чтобы помочь в создании кампаний по зачислению, основанных на том, кто мы на самом деле. Такое очень трудно найти на рынке!
Они нашли время, чтобы познакомиться с нашим учреждением, а также узнать о сходствах и различиях между различными форматами программ, которые мы предлагаем. Они предложили творческие подходы, которые привели к удивительным готовым продуктам! Люди до сих пор постоянно спрашивают нас, кто разработал наши материалы, и мы быстро указываем им на людей из 5°!
Они не торопились, чтобы узнать о нашем колледже, и придумали потрясающие маркетинговые материалы, которые действительно отражали атмосферу нашего кампуса. Это казалось огромной работой, но они шаг за шагом вели нас через процесс, упрощая его выполнение. Мне нравится с ними работать!