12 лучших российских сериалов с высоким рейтингом
- ForbesLife
- Иван Афанасьев Автор
Собрали для вас лучшие российские сериалы с высоким рейтингом — от комедийных до триллеров с захватывающим сюжетом. Список шоу, которые стоит посмотреть и добавить в свой топ сериалов — в подборке Forbes Life
«Вампиры средней полосы» (2021)
Количество сезонов: 1 (8 серий) и новогодний спецвыпуск
Режиссеры: Антон Маслов, Андрей Богатырев
Вампиры живут среди нас.
Будучи меньшинством, они вынуждены не убивать людей и чтить кодекс поведения, за соблюдением которого следят Хранители из числа простых смертных. Когда в Смоленске находят несколько обескровленных трупов, к вурдалакам возникают вопросы. Теперь семейство вампиров во главе с древним Святославом Вернидубовичем должно выяснить, кто посягнул на существующий порядок.
Несмотря на мрачную завязку, это одна из лучших комедий, что выходили в России в последние годы. По настроению больше похожий на «Что мы делаем в тени», чем на серьезный vamp-movie, «Вампиры средней полосы» покоряет необычным подходом к кровопийцам (они, например, потребляют донорскую кровь из обычных пластиковых бутылок) и атмосферой российской глубинки. Плюс — шикарный актерский состав: от Глеба Калюжного до Юрия Стоянова, наконец-то получившего достойную роль. После просмотра вы наверняка захотите съездить в Смоленск — и начать смотреть российские сериалы чаще.
«Хрустальный» (2021)
Количество сезонов: 1 (10 серий)
Режиссер: Душан Глигоров
В городе с поэтичным названием маньяк насилует и убивает мальчиков. Расследовать страшные события отправляют из Москвы Сергея Смирнова, выросшего в этих местах. Переживший здесь травму детства, изменившую его навсегда, он вынужден вновь погрузиться в тяжелые воспоминания, чтобы выйти на след убийцы.
Один из наиболее рейтинговых детективных сериалов последнего времени, «Хрустальный» на первый взгляд кажется еще одним «Методом» (сценарист тот же — Олег Маловичко). На самом деле все куда сложнее: это шоу о той России, которую редко показывают в кино и на телевидении — мрачной и опасной, таящей в себе тайны, скрываемые под печатями коррупции, нетерпимости и страха. Обратите внимание на актеров, особенно Николая Шрайбера, звезду ролей второго и третьего плана, наконец-то получившего достойную его таланта роль.
«Мир! Дружба! Жвачка!» (2020)
Количество сезонов: 2 (16 серий)
Режиссеры: Илья Аксенов, Антон Федоров
1990-е. Санька, парень из обычной российской семьи того времени — безработный папа-писатель и предприимчивая мама-продавщица, — попадает в переплет, по глупости угнав машину члена местной кавказской ОПГ. Теперь ему и его друзьям предстоит выпутаться и вывести себя и родных из-под удара, а поможет им в этом недавно прибывший из Афганистана дядя Алик со своей бандой.
Телесериал для тех, кто считает, что про «лихие 90-е» уже нельзя сказать ничего нового. Классический, на первый взгляд криминальный сюжет подан глазами подростков, у которых жизнь только начинается — эдакий «Очень странные вещи», но без демогоргонов и мистики, зато с Yuppi, «Каратекой» на NES и прогулками по газовым трубам.
Посмотреть на Россию после распада СССР под таким углом — весьма необычно, свежо и познавательно. А еще тут есть Юра Борисов в роли ветерана Афгана — и он каждый раз неизбежно перетягивает на себя все внимание в кадре.
«Чики» (2020)
Количество сезонов: 1 (8 серий)
Режиссер: Эдуард Оганесян
Юг России. Три молодые секс-работницы, Света, Марина и Люда, вынуждены зарабатывать на жизнь на обочине. Однажды в родной край возвращается их экс-коллега Жанна — она успела съездить в Москву, навести там шороху и вернуться с планами открыть бизнес на малой родине и предлагает девчонкам «вписаться» в эту смелую затею. Те соглашаются, хотя и понимают, что из желающих им помешать выстроится целая очередь.
Отечественный сериал в жанре драмы, за которым было интересно наблюдать еще на этапе производства, когда некоторые жители города Прохладный, где проходили съемки, пытались всячески помешать процессу.
Если вы хотите увидеть действительно реалистичную и честную драму о том, чем живет Россия за пределами Садового кольца, посмотрите «Чик». Это шоу для тех, кто не боится узнавать новое о своей стране и делать открытия. Как минимум сериал открыл публике великолепных актеров — от Варвары Шмыковой до Сергея Гилева.
«Обратная сторона Луны» (2012)
Количество сезонов: 2 (32 серии)
Режиссер: Александр Котт
2011 год. Капитан полиции Михаил Соловьев давно охотится за маньяком, убивающим молодых девушек. Однажды, почти загнав преступника в угол, он попадает под машину — и вместо того, чтобы умереть, оказывается в 1979 году, где все его принимают за отца, тоже работающего в милиции. Пытаясь разобраться в причинах происходящего, он включается в работу и понимает, что маньяк существует и в этой версии реальности.
Редкий пример на нашем телевидении, когда русский ремейк зарубежного сериала оказался не только не хуже, но и лучше оригинала.
Адаптация британского «Жизнь на Марсе» (который, кстати, переснимали и в США) интересна не только необычным сюжетом, но и взглядом на историю СССР глазами современного человека — критическим и ностальгическим одновременно. Плюс — одна из самых сильных ролей Павла Деревянко.
«Перевал Дятлова» (2020)
Количество сезонов: 1 (8 серий)
Режиссеры: Валерий Федорович, Евгений Никишов, Павел Костомаров, Степан Гордеев
Зима 1959-го. В Уральских горах пропадает группа студентов во главе с опытным туристом Игорем Дятловым. Позже их всех находят погибшими. Для расследования инцидента из Москвы отправляют майора КГБ Костина. Оказавшись на месте, он понимает, что все возможные версии, от убийства до лавины, могут оказаться неверными: причина смерти молодых людей видится куда более невероятной.
Популярный миф о «группе Дятлова», сгинувшей на подступах к горе Холатчахль, уже успел обрасти сотнями теорий и версий произошедшего.
Необычный и по-настоящему интересный российский сериал в жанре фантастики знаменателен хотя бы тем, что возвращает погибшим человеческий облик — из «персонажей» они превращаются в людей, а их история — в настоящую трагедию. Их, кстати, сыграли в основном молодые и малоизвестные актеры, которые вполне могут стать звездами нашего кино — от Марии Луговой до Юрия Дейнекина.
«Шторм» (2019)
Количество сезонов: 1 (8 серий)
Режиссер: Борис Хлебников
Опытный следователь Градов берется за инцидент с обвалом крыши Дворца спорта, при котором погибло много людей, включая детей. Почти взяв «за жабры» главного подозреваемого, кандидата в мэры города, он узнает, что возлюбленная тяжело больна, и предлагает виновному откупиться огромной взяткой. Теперь уже за Градовым устанавливает слежку его коллега и друг, следователь Осокин, пытаясь выяснить, откуда у того взялись миллионы на лечение.
Сериал, который стоит посмотреть любому человеку, живущему в России, — он как нельзя лучше описывает истоки коррупции в нашей стране. По итогам 2019 года «Шторм» входил в списки лучших ТВ-шоу за год — да и сейчас смотрится очень свежо. Не в последнюю очередь благодаря шикарным актерским работам: Максим Лагашкин в роли «честного мента» — фантастическая роль.
«Обоюдное согласие» (2022)
Количество сезонов: 1 (6 серий)
Режиссер: Валерия Гай Германика
Анна — молодая учительница литературы, подвергшаяся групповому изнасилованию на яхте своих друзей. Наутро после происшествия она приходит в полицию, чтобы подать заявление, но есть проблема: преступники — высокопоставленные чиновники и приближенные к ним люди, до которых так просто не добраться. Происшествие меняет жизнь не только девушки, но и всего города.
Наделавшая шуму в 2000-х, Валерия Гай Германика вернулась с новым провокационным шоу: сериал постоянно играется со зрителем, подкидывая тому ложные зацепки, намекая, что «не все так однозначно». В этом списке «Обоюдное согласие» — самый свежий сериал, но нет сомнений, что он останется в памяти надолго. Так обстоятельно на животрепещущую для России тему не высказывался еще никто. Кстати, обратите внимание на исполнителя роли следователя, ведущего дело Анны: его играет Андрей Козлов, один из самых известных магистров шоу «Что? Где? Когда?», дебютировавший в кино в качестве актера.
«Эпидемия» (2019)
Количество сезонов: 2 (16 серий)
Режиссеры: Павел Костомаров, Дмитрий Тюрин
В Москве разгорается страшная эпидемия неизвестной заразы: заболевшие передают вирус по воздуху и умирают через три-четыре дня после заражения.
Живущий за городом Сергей вынужден на время оставить семью и ехать в столицу, чтобы вытащить оттуда бывшую жену с сыном. Вместе с другими выжившими им предстоит бежать из города, спасаясь от вируса и мародеров.
Фантастический survival-сериал, впечатливший самого Стивена Кинга, стал первой ласточкой (к сожалению, залетной) успеха наших ТВ-шоу за рубежом, попавший во всевозможные топы и продленный на второй сезон, который, кстати, начали показывать совсем недавно. Метафорически предсказавший и пандемию коронавируса, и раскол в российском обществе, он и сейчас смотрится пугающе актуально. Сильный актерский состав: что на первом, что на втором плане — сплошь звезды, от Кирилла Кяро и Виктории Исаковой до Юры Борисова и Анны Михалковой.
Happy End (2021)
Количество сезонов: 1 (8 серий)
Режиссер: Евгений Сангаджиев
Вынужденные бежать в Москву из родного города, 19-летние Вера и Влад оказываются без работы и жилья.
Единственным выходом для них становится вебкам-бизнес. Оказавшись в мире виртуального секса, молодые люди начинают делать на этом неплохие деньги. Но скоро становится ясно, что долго так жить нельзя, по крайней мере без последствий.
Один из наиболее провокационных сериалов последних лет, большой дебют артиста «Гоголь-центра» Евгения Сангаджиева и мощные актерские работы Лены Трониной и Дениса Власенко оправдывают свой высокий рейтинг как минимум глубоким погружением в тему вебкам-порно. Но куда важнее — это актуальная история о молодых людях, потерявшихся в столице и по жизни в целом, выбравших наиболее легкий путь, который, конечно, куда более тернист, чем им казалось.
«Последний министр» (2020)
Количество сезонов: 2 (30 серий) и новогодний спецвыпуск
Режиссер: Роман Волобуев
В вымышленном Министерстве перспективного планирования умирает престарелый министр.
На его место избирают Евгения Тихомирова, нерадивого политика, в прошлом утопившего на позиции мэра подконтрольный ему город. Под его руководством фиктивный орган власти неожиданно начинает действовать, пытаясь приносить пользу людям — правда, не всегда удачно и часто довольно нелепо.
Фарсовая сатира, ставшая первым успешным проектом во времена бума онлайн-кинотеатров в период пандемии ковида. Ни один новый российский сериал до сих пор не достиг такого уровня точности в высмеивании болячек российской политики, как «Последний министр». А самодур Тихомиров в исполнении Яна Цапника быстро стал народным персонажем.
«Псих» (2020)
Количество сезонов: 1 (8 серий)
Режиссер: Федор Бондарчук
Олег — психолог премиум-класса, к которому выстраивается большая очередь из столичных-клиентов: от чиновников до светских львиц.
При этом он сам давным-давно не в порядке: зависим от наркотиков, живет с резиновой куклой и не может найти жену, которая таинственно пропала уже почти год как. Нарастающие психозы и внутренняя агрессия рискуют бесконтрольно вырваться на свободу.
Детективный сюжет «Психа» не должен сбивать с толку: это в первую очередь экзистенциальная драма о том, как мы все устали от жизни. Временами через него даже прорывается комедия, но такая, от которой смеешься, параллельно борясь с нервным тиком. Дебют Федора Бондарчука на малом экране со сходящим с ума Константином Богомоловым определенно заслуживает похвал — это один из наиболее тонких сериалов на российском телевидении.
BenQ V7000i – действительно большая картинка без компромиссов. Обзор лазерного ультракороткофокусного 4K-проектора для домашнего кинотеатра
Если для вас картинка диагональю 85 дюймов
представляется недостаточной для просмотра фильмов и несоответствующей по
масштабу звуковому сопровождению в исполнении вашей кинотеатральной системы
окружающего звучания, то выход лишь один – проектор.
А если при этом вы не
хотите или не можете реализовать в вашей гостиной классическую проекционную
систему, то решением будет использование ультракороткофокусного проектора, например,
BenQ V7000i.
А началось всё с проекционных телевизоров. В конце прошлого века, когда наиболее востребованная диагональ экрана телевизоров (тогда ещё кинескопных) была 25-29 дюймов, проекционные аппараты могли предложить картинку с нереальной для того времени диагональю 50 и даже 60 дюймов. И выглядели те проекционные модели как настоящие телевизоры, поскольку объединяли в одном корпусе проектор, работающий в режиме обратной проекции, экран и акустические системы.
Прошли годы. Диагональ экрана массовых моделей
телевизоров неуклонно росла, а многие любители домашних кинопросмотров выбрали
проекторы, которые обеспечивали картинку с диагональю более 100 дюймов. Но построение
домашнего кинотеатра на базе классического проектора сопряжено с решением
целого ряда проблем – от организации затемнения помещения до прокладки проводки
к проектору, и только большие энтузиасты готовы их решать.
А что же делать
остальным любителям кино, которые предпочитают смотреть его на действительно
большом экране? И тут на выручку приходят старые добрые проекционные телевизоры
– точнее, ультракороткофокусные проекторы, например, BenQ V7000i, сочетающие
большую диагональ экрана с удобством инсталляции и эксплуатации. Впрочем, обо
всём по порядку.
Изучаем
Кроме возможности получения изображения большого размера, у проекционного способа формирования картинки есть ещё одно важное преимущество – он более естественный для человеческого глаза. Наше зрение воспринимает окружающие предметы через отражённый от них солнечный или электрический свет. Подобный тип восприятия визуальной информации является привычным для человека, и именно на этом принципе основана работа проектора. В отличие от проекторов, экран телевизора излучает свет в направлении зрителя, и такое изображение воспринимается мозгом как искусственное.
Ультракороткофокусная оптика
позволяет расположить BenQ V7000i непосредственно рядом с экраном – чаще всего аппарат
устанавливают на телевизионную тумбу под экраном.
Таким образом, во-первых, нет
необходимости подвешивать проектор под потолок и прокладывать к нему достаточно
длинные кабели, поскольку он расположен рядом с остальными компонентами системы,
а, во-вторых, такое расположение исключает попадание
зрителей между проектором и экраном – то есть, просмотру ничего не сможет
помешать.
Одной из главных проблем использования
классического проектора вместо телевизора является необходимость организации
затемнения помещения. Ультракороткофокусный проектор BenQ V7000i способен
отчасти избавить от этих забот. Высокий световой поток, достигающий 2 500
люмен, в сочетании с небольшим проекционным расстоянием обеспечивают очень
яркую картинку – при прямом солнечном свете её воспринимать, конечно, будет
сложно, но и кромешной тьмы для просмотра создавать не требуется. BenQ V7000i вполне
комфортно можно смотреть при фоновом электрическом свете или с задернутыми
неплотными шторами при дневном свете. Впрочем, на прямом солнце пасуют и
обычные телевизоры.
Подспорьем в получении яркой картинки от ультракороткофокусного проектора будет специальный ALR-экран (Ambient Light Rejecting), блокирующий до 85% паразитной засветки благодаря использованию чёрно-белых линейных линз Френеля. Слой из чёрных линз поглощает фоновый свет, а белые элементы отражают излучение проектора непосредственно на зрителя. Часто такой экран идет в комплекте с ультракороткофокусными проекторами, но BenQ решил дать свободу выбора необходимой диагонали экрана и не привязывать покупателя к варианту, идущему в комплекте.
Необходимый высокий световой поток в проекторе BenQ V7000i обеспечивает не привычная ртутная лампа высокого давления, а лазерно-фосфорный источник света, который отличается когерентностью излучения, то есть, способностью сохранять во времени разность фаз составляющих излучение волн в пространстве. В результате удается получить более сочные и натуральные цвета.
Другой отличительной особенностью лазерного
источника света стало практически полное отсутствие инерции при изменении
яркости свечения, что позволяет реализовать на качественно новом уровне
повышение контрастности изображения, которое в проекторах с лампой высокого
давления достигалось с помощью куда более инерционной динамической диафрагмы
объектива.
Третьим преимуществом лазерного источника света в сравнении с лампой высокого давления стал существенно больший ресурс, вполне сравнимый с ресурсом LED или OLED панели обычного телевизора. Если проекционная лампа в проекторе фактически была расходным материалом с ресурсом от 2 до 5 тысяч часов работы, то для лазерного источника проектора BenQ V7000i производитель декларирует ресурс 20 тысяч часов.
И на этом длинный перечень преимуществ не заканчивается – лазерный источник света набирает номинальную яркость при включении существенно быстрее лампы, а при выключении ему не нужен продолжительный отвод тепла, которое для лампы высокого давления строго обязателен. То есть, включение и выключение BenQ V7000i ничем не отличается от управления обычным телевизором.
Источник света в BenQ V7000i базируется на
сборке лазерных диодов синего цвета и фосфорного колеса, преобразующего синий
свет в белый. Синий лазер был выбран, поскольку мощность излучения лазерных
диодов зависит от длины волны света, и наибольшую интенсивность можно достичь в
синем спектре.
Компания BenQ с
давних времён была надёжным партнёром компании Texas Instruments в
продвижении микрозеркальной технологии формирования изображения. Именно в
проекторах BenQ первыми появлялись самые свежие версии
микрозеркальных чипов. Не стала исключением и модель BenQ V7000i. Здесь применяется
одночиповая технология DLP на базе микрозеркальной DMD-сборки от Texas
Instruments
с диагональю 0,47” и с физическим разрешением 1 920 x 1 080 точек.
Разрешение 4K
(3 840 x 2 160)
достигается с помощью оптического актуатора XPR (Expanded Pixel Resolution).
Причём, это вовсе не какой-то искусственный метод повышения разрешения – в
результате его работы на экране формируется изображение с реальным разрешением
4K.
Технология “оптического сдвига” использует инерционность человеческого зрения –
на экран последовательно проецируются несколько изображений с оптическим
смещением, которое и производит актуатор XPR. Высокая скорость смены этих
изображений не позволяет глазу фиксировать эти «переключения» и кадр
воспринимается как единое целое – с кратно более высоким разрешением.
Замечу, что
аналогичным способом формируется цветная картинка в одночиповых микрозеркальных
проекторах – красный, зелёный и синий цветовые компоненты последовательно
выводятся на экран, а глаз интегрирует полноцветное изображение.
Проектор BenQ V7000i поддерживает видео с расширенным динамическим диапазоном HDR10. Есть фирменный режим HDR PRO, в котором повышается детализация в ярких и тёмных сценах. Референсная цветопередача достигается не только заводской калибровкой проектора и реализацией специального режима Filmmaker Mode, но и за счет широчайшего покрытия цветового пространства DCI-P3, достигающего по заверениям производителя рекордного уровня 98%.
Как уже отмечалось ранее, проектор
BenQ V7000i оснащён аудиосистемой, что позволяет ему работать
автономно – для сопровождения кинофильмов наличие внешней системы окружающего
звучания не обязательно. При этом, речь не идет о небольшом широкополосном
динамике, которым обычно комплектуются презентационные модели – здесь за
акустически прозрачной тканью, которой отделана передняя панель проектора, скрываются
две трёхполосных (!!!) акустических системы, на каждую из которых работает
усилитель мощностью 5 Ватт.
Виртуальное окружающее звучание моделируется DSP-процессором. Конечно,
полноразмерную систему окружающего звучания домашнего кинотеатра встроенная
аудиосистема не заменит, но большинство штатной акустики телевизоров переиграет
точно. В разработке и настройке аудиосистемы проектора BenQ V7000i принимала
участие компания TreVolo.
С современным телевизором проектор BenQ V7000i роднят смарт-функции операционной системы Android TV, реализованные во внешнем донгле BenQ QS01, подключаемом к порту HDMI. С одной стороны, такое решение уменьшает количество доступных портов HDMI до одного, да и внешнее устройство, подключенное к проектору, усложняет инсталляцию. С другой, подобный функционал развивается сегодня очень быстро – со временем для получения новых возможностей вам будет достаточно заменить недорогой донгл, а не менять весь проектор. В этом смысле такое решение обеспечивает большую гибкость.
Донгл BenQ QS01 базируется
на процессоре Amlogic S905Y2 с четырьмя
ядрами Cortex-A53 и оснащается
2 ГБ оперативной и 16 ГБ постоянной памяти.
Интеграция в домашнюю компьютерную
сеть реализована только через двухдиапазонный Wi-Fi (2.4 ГГц / 5
ГГц, 802.11 a/b/g/n/ac). Есть здесь
и адаптер Bluetooth 4.2 LE. Донгл оснащен портами HDMI 2.0b и microUSB для
подачи питания. Проектор комплектуется двумя пультами ДУ – более крупный
позволяет в полном объёме управлять настройками проектора, а пульт поменьше белого
цвета оптимизирован в том числе и для управления донглом и содержит специальные
кнопки для вызова Google Assistant, Amazon Prime Video и других сервисов. При
этом, с помощью этого пульта можно управлять основными функциями проектора, что
позволяет в повседневной эксплуатации обходится им, а большой пульт
использовать только для настройки проектора.
Без помощи донгла проектор BenQ
V7000i может воспроизводить медиафайлы с внешних USB-накопителей, для подключения которых
есть два порта USB
2.0 и один – USB
3.0. Поддерживается воспроизведение видео в форматах MPEG1, MPEG4, H.263, H.264, H.265 и Motion JPEG во всех популярных контейнерах.
Единственный
момент – встроенный плеер не поддерживает воспроизведение полных образов дисков
в файлах ISO и в структуре директорий. Впрочем, относить это к
недостаткам я не стал, поскольку подобной возможности нет ни у одной модели
телевизоров, с которыми мне приходилось сталкиваться.
Установка и настройка
Для тестирования ультракороткофокусного
проектора BenQ V7000i был выбран фирменный ALR-экран BenQ ALR 100″ с диагональю 100 дюймов,
специально разработанный для проекторов BenQ V7000i / V7050i. При установке BenQ
V7000i относительно экрана нужно чётко попасть в нужное место и зафиксировать
там устройство – для экрана с диагональю 100 дюймов проектор должен
располагаться на расстоянии 22,2 см от
поверхности экрана и в 25,2 см ниже нижней его кромки. Для максимальной
диагонали 120 дюймов эти цифры будут 33,1 см и 31,3 см соответственно. Причём, позиционировать
проектор относительно экрана придется механическим способом – никаких
регулировок, кроме регулировки фокуса, оптическая система проектора не
предоставляет.
Впрочем, это обычная ситуация с ультракороткофокусными
проекторами. В помощь установщику производитель предусмотрел возможность
регулировки высоты всех четырёх ножек проектора, а также снабдил BenQ
V7000i двумя выдвигающимися линейками для контроля расстояния до поверхности
экрана.
Системное меню проектора BenQ V7000i предоставляет доступ к расширенному набору настроек картинки, включая детальные настройки цветовой температуры, гаммы, расширенное управление цветовыми компонентами и так далее. Но проекторы BenQ для домашнего кинотеатра калибруются на заводе и демонстрируют натуральную цветопередачу уже “из коробки”. Потому достаточно было отключить всевозможные “улучшайзеры” передачи движения и активировать режим Filmmaker Mode.
При тестировании проектора BenQ V7000i использовался как встроенный в него мультимедийный
проигрыватель, который воспроизводил контент с внешнего жесткого диска с
интерфейсом USB,
так и внешний проигрыватель OPPO BDP-203, подключенный по HDMI.
Кроме дисков UltraHD Blu-ray с разрешением 4K в программу
испытаний был включен материал Full HD с дисков Blu-ray, а также фильмы со стриминговых
сервисов.
Смотрим и слушаем
Можно смотреть вечно – на струящуюся воду, языки пламени и… отъезжающую при включении верхнюю панель проектора BenQ V7000i. Кроме визуального эффекта, эта деталь выполняет очень важную функцию. Дело в том, что в ульракороткофокусных проекторах объектив фактически расположен хоть и под углом, но вверх внешней линзой, которая открыта не только для пыли, но и для посягательств маленьких кинолюбителей и домашних питомцев. Защитная панель в проекторе BenQ V7000i надёжно предохраняет от возможных неприятностей. А ещё это просто красиво!
Проектор BenQ
V7000i продемонстрировал насыщенную мельчайшими деталями
картинку с натуральной цветопередачей. Обычно особое внимание при оценке
уделяется способности воспроизвести глубокий чёрный цвет, но здесь сразу
обращаешь внимание на сочность, но не крикливость практически всей палитры. Проектор
тщательно прорабатывает тончайшие оттенки цвета и яркостные переходы, а
натуральная цветопередача и серьезный запас контрастности дарят по-настоящему
трёхмерный кадр.
Второй момент – даже в условиях фонового освещения яркости проектора вполне хватило для формирования выразительной картинки – никакой деградации тёмных участков кадра не наблюдалось, а на видеоматериале с расширенным динамическим диапазоном HDR изображение становилось ещё более глубоким и объемным.
Третьим пунктом (по порядку, а не по значимости) отметим качественную работу видеопроцессора – самые динамичные движения в кадре воспроизводятся с минимальным размытием и отсутствием ореолов. Спортивные состязания или динамичные экшн-сцены современных блокбастеров представляются BenQ V7000i без намёка на стробирование или фризы. Идеально выполняется проектором и скалирование материала Full HD с дисков Blu-ray до разрешения 4K.
И, наконец, про звуковое сопровождение
видеоряда – встроенная в BenQ V7000i
аудиосистема TreVolo продемонстрировала
довольно выразительное звучание с детальными высокими частотами и плотным басом.
При этом, мне не удалось перегрузить акустику – конечно, громоподобными
взрывами она поразить воображение не сможет, но сопроводить фильм чистым
саундтреком без искажений встроенной аудиосистеме вполне по силам – и даже
подобие какого-то объёма она создавать умеет.
Паспортные данные:
Тип – лазерный ультракороткофокусный 4K-проектор | Полное название – BenQ V7000i | Световой поток, ANSI-лм – 2 500 | Источник света – лазерный, ресурс 20 000 часов | Разрешение изображения, пикс. – 4K UHD 3 840 x 2 160 | Физический формат кадра – 16:9 | Матрицы: тип, размер (дюймов) – 1 х DMD Ti 0,47 | Разрешение матрицы физическое, пикс. – 1 920 x 1 080 (формирование разрешения 4K происходит через механизм оптического сдвига изображения XPR) | Поддержка видеопотока – до 4K/60 Гц HDR10 | Диагональ экрана, дюймов — 70 – 120 | Расстояние установки проектора от экрана диагональю 100 дюймов, см – 22,2 | Видеовходы – HDMI v2.0 (2) (один с поддержкой ARC) | Аудиовыход – цифровой оптический Toslink | Возможности интеграции в компьютерную сеть – Wi-Fi 802.11ac (2.4 ГГц / 5 ГГц) – через донгл BenQ QS01, входящий в комплект | Встроенные динамики, Вт – 2 x 5 | Дополнительно – моторизованная панель для защиты объектива, внешний донгл BenQ QS01 с Android TV, два пульта дистанционного управления | Потребляемая мощность, Вт – 480 | Габариты (Ш x В x Г), см – 50,0 x 15,7 x 38,8 | Масса, кг – 10,0
Оценки
Плюсы: выразительная детальная картинка с натуральной цветопередачей, широкий цветовой охват, заводская калибровка, поддержка HDR10, большой ресурс лазерного источника света, возможности Android TV, встроенная аудиосистема, стильный дизайн с моторизованной защитной шторкой
Минусы: нет проекционного экрана в комплекте, необходимость обеспечить жёсткую фиксацию проектора относительно экрана, интеграция в компьютерную сеть только по Wi-Fi
Дизайн – 100
Качество изготовления – 95
Изображение – 95
Функции – 95
Итого – 95
Вывод:
Современному
лазерному ультракороткофокусному проектору вполне по силам конкурировать с
топовыми телевизорами.
Предлагая огромную картинку, размер которой даже для
флагманских моделей телевизоров всё ещё недоступен, BenQ V7000i обладает
полноценным функционалом смарт-ТВ и высокой яркостью, достаточной для того,
чтобы не утруждаться с организацией специальных мер по затемнению комнаты. А
установка проектора непосредственно под экраном избавит от обычных проблем
инсталляции классической проекционной системы. Бонусом станет стильный дизайн
BenQ V7000i с моторизованной защитной шторкой.
Что такое цветовой охват вообще и DCI—P3 в частности, и почему он должен быть как можно шире можно узнать здесь.
Анатолий Максименко
3 мая 2023 года
Реклама ООО «ЦС Импекс»
Токен 4CQwVszH9pSaLkUKfFE
Теги: Домашний кинотеатр, Проектор, BenQ, 4K, HDR, Лазерный проектор, проектор для домашнего кинотеатра, кинотеатральный проектор, Ультракороткофокусный проектор, BenQ V7000i, HDR-PRO, BenQ V7050i
Подписывайтесь на нашу ленту в Яндекс.
Дзен
Добро пожаловать в наш калькулятор псевдоинверсии , где мы узнаем все, что нужно знать о псевдоинверсии Мура-Пенроуза. Мы покажем вам , как вычислить псевдообратную для любой матрицы, и рассмотрим некоторые ее важные свойства. Мы даже покажем вам, как вычислить псевдообратную матрицу 3 на 2. Итак, берите чашечку кофе и приступим!
Краткое введение в матрицы
Прежде чем мы сможем правильно объяснить, что такое псевдоинверсия, мы должны охватить некоторые основы — и что может быть более фундаментальным строительным блоком линейной алгебры, чем матрица? 9{-1}А-1. Это также известно как обратная Мура-Пенроуза или просто псевдообратная . Когда определитель матрицы равен нулю, ее нельзя инвертировать. Мы бы назвали матрицу единственной — она не имеет обратной . Это печально, потому что обратное значение ценно при решении системы уравнений .
Однако есть и хорошие новости: если мы сможем найти какое-то значение, равное почти решению, мы все равно сможем делать некоторые действительно полезные вещи. Нахождение этого приближенного решения — это именно то, что позволяет нам сделать псевдообратная матрица.
Система уравнений определяется как A⋅x⃗=b⃗A\cdot\vec{x} = \vec{b}A⋅x=b, где AAA — известная матрица, а b⃗\vec{b}b — известный вектор. Нам нужно найти неизвестный вектор x⃗\vec{x}x. В идеальной линейной задаче, которую вы найдете на занятиях по алгебре, есть только одно верное решение , x⃗\vec{x}x. Мы бы назвали такую проблему «четко определенной» . Тем не менее, реальные проблемы, которые переформулированы с помощью A⋅x⃗=b⃗A\cdot\vec{x} = \vec{b}A⋅x=b, редко бывают четко определены 9ТА+=Q⋅M−1⋅PT.
Как пользоваться псевдообратным калькулятором?
К счастью для нас, наш псевдообратный калькулятор работает намного быстрее, чем формула! Имея под рукой матрицу, выполните следующие простые действия.
- Выберите размеры вашей матрицы . Матрица с nnn строк и mmm столбцов обычно называется матрицей размера n×mn\times mn×m. Итак, если ваша матрица состоит из трех чисел в высоту и двух чисел в ширину, ее размеры составляют 3 × 23 × 23 × 2.
- Введите значения вашей матрицы построчно . Используйте символьную матрицу в верхней части калькулятора в качестве справочной информации, когда решаете, какое значение куда следует поместить.
- Найдите визуализированные результаты в нижней части калькулятора .
Отображаются как ваша полная матрица, так и ее псевдообратная, на случай, если вы захотите убедиться, что правильно ввели свои значения.
Для чего используется псевдоинверсия?
Как мы уже говорили ранее, мы использовали псевдообращение Мура-Пенроуза в линейной алгебре к найти приближенные решения плохо определенных систем уравнений. Но что хорошего в приближенном решении?
Поиск наилучшего решения плохо определенной системы уравнений является важнейшим элементом многих реальных технологий.
Приближенные решения лежат в основе всей концепции сопоставления данных с , поэтому псевдоинверсия может помочь вам предсказывать погоду, прогнозировать деловые и экономические тенденции и диагностировать медицинские проблемы.
Наилучшее решение становится еще лучше, когда вы понимаете полученную линию наилучшего соответствия не обязательно должно быть линейным , но может быть квадратичным или экспоненциальным . Если вы видите закономерность в своих данных, вы можете подогнать к ней любую линию , а обратная модель Мура-Пенроуза может помочь вам найти эту линию.
Поскольку необратимая матрица не имеет обратной , мы не можем вычислить ее число условия , что лишает нас ценной информации. В подобных случаях псевдоинверсия может заменить на обычной инверсией в 9.0003 номер условия формула .
Пример расчета псевдообратного уравнения Мура-Пенроуза
Все расчеты хороши в теории, но как насчет практики? Действительно ли это так сложно, как кажется?
Давайте рассмотрим два примера: в одном мы используем короткие пути, которые дает нам линейная независимость, и в другом нам приходится выбирать более длинный путь.
Начнем с матрицы AAA:
A=[132433]\footnotesize A = \begin{bmatrix} 1 & 3 \\ 2 & 4 \\ 3 & 3 \\ \end{bmatrix}A=[123343] 9Т\\ &= \begin{bmatrix} -0,342 и -0,158 и 0,553\ 0,289 и 0,211 и -0,237\ \end{bmatrix} \end{split}A+=(AT⋅A)−1⋅AT=[−0,3420,289−0,1580,2110,553−0,237]
И вот оно: псевдоинверсия нашего 3-by -2 матрица.
Это было достаточно просто, но теперь давайте займемся линейно зависимой матрицей 3 на 2 и ее псевдообратной, где мы вынуждены использовать расширенный метод. Рассмотрим нашу следующую матрицу BBB:
B=[122436]\footnotesize B = \begin{bmatrix} 1 & 2 \\ 2 & 4 \\ 3 & 6 \end{bmatrix}B=[123246] 9Т\\ &= \begin{bmatrix} 0,014 и 0,029 и 0,043\ 0,029 и 0,057 и 0,086\ \end{bmatrix} \end{split}M−1∴B+=[701]=[0.014]=Q⋅M−1⋅PT=[0.0140.0290.0290.0570.0430.086]
И так , мы нашли псевдообратную линейно зависимую матрицу !
Часто задаваемые вопросы
В чем разница между нормальной инверсией и псевдоинверсией?
Нет «разницы» между псевдоинверсией и инверсией.
Псевдоинверсия — это просто обобщение инверсии — пытается выполнить ту же работу. Псевдообращение A + стремится удовлетворить A·A + ≈ Ɪ, где Ɪ — единичная матрица.
- Если обратное не существует, псевдообратное — это самое близкое, что мы можем получить к обратному.
- Если обратное существует, то псевдообратное точно равно обратному.
Псевдообратный квадрат?
Псевдоинверсия A + будет иметь транспонированную форму исходной матрицы . Матрица размера n × m имеет псевдообратную форму размера m × n. Другими словами, если A имеет, например, 2 строки и 3 столбца, то A + будет иметь 3 строки и 2 столбца. Таким образом, + будет квадратным, только если A будет квадратным .
Что такое псевдообратная нулевая матрица?
A Нулевая матрица Z — матрица, содержащая только нули. Она не имеет обратной, так как ее определитель всегда равен 0.
Псевдообратная нулевая матрица обычно является транспонированной нулевой матрицей, т. е. Z + = З Т .
Что такое псевдообратная диагональная матрица?
Диагональная матрица D — это матрица, которая имеет ненулевые элементы только по диагонали, а все остальные элементы равны нулю. Из-за уникальной структуры D вычислить D + очень просто: просто замените элементы по диагонали на их обратные величины.
Калькулятор обратной матрицы с шагами
Знакомство с калькулятором обратной матрицы
Калькулятор обратной матрицы с шагами — это интерактивный матричный инструмент, который упрощает процедуру обращения матриц. Калькулятор обратной матрицы работает для расчета обратной матрицы онлайн.
Обратная матрица — это матрица, которая умножается на исходную матрицу и дает единичную матрицу. А обратная матрица — это своего рода нахождение дробей действительных чисел. Вы можете легко вычислить эти дроби и для этого вам нужно найти обратную матрицу калькулятора с дробями.
Этот калькулятор обратной матрицы уменьшает вашу работу по вычислению обратной матрицы вручную. Этот онлайн-калькулятор матриц упрощает вашу учебу или работу одним щелчком мыши.
Вы также можете умножать на матрицы с помощью калькулятора матричного скалярного умножения
При использовании решателя обратных матриц следует помнить, что при вводе значений в инструмент значения матрицы должны быть не единственными. Поскольку обратная сингулярная матрица не может быть вычислена математически, поэтому в калькуляторе обратной матрицы необходимо ввести только невырожденную матрицу.
Матричная обратная операция является одним из широко используемых методов матричных вычислений. И доказано, что эта матрица обратного калькулятора имеет большое значение, поскольку она может легко сократить вашу ручную работу и даст вам решение обратной матрицы одним щелчком мыши. Онлайн-калькулятор матриц оказывается полезным для студентов и математиков при решении линейной алгебраической задачи методом обращения матриц.
Вы также можете использовать калькулятор суммы матриц и калькулятор вычитания матриц, чтобы вычислить сложение матриц и вычитание матриц.
Как пользоваться калькулятором обратной матрицы?
Инверсия матрицы — сложная процедура, включающая несколько различных матричных операций. При определении обратной матрицы необходимо вычислить определитель, сопряженную и единицу матрицы.
Для расчета определителя матрицы сопряженной вы можете воспользоваться нашим онлайн-калькулятором определителя и калькулятором матрицы сопряженной.
Все ручные операции удлиняют процесс обращения матриц, однако при использовании матричного калькулятора процедура сокращается до двух шагов. Да, только два шага и обратная матрица будут вычислены, избегая всех этих скрытых операций.
Два простых шага, перечисленных ниже, помогут вам использовать онлайн-калькулятор обратимой матрицы.
Введите ввод
Каждый цифровой инструмент работает таким образом, вы вводите данные, а вывод предоставляется вам.
Чтобы рассчитать обратную матрицу онлайн, первый шаг, который вам нужно выполнить, — это ввести необходимые данные.
В калькуляторе обратного преобразования матриц требуется только два ввода: первый — это размер вашей матрицы, а второй — элементы внутри матрицы.
Укажите размеры
Поэтому сначала выберите, в каком порядке ваша невырожденная матрица должна быть инвертирована. Выбор порядка матрицы является первым входом, требуемым в решателе обратных матриц.
Связанный: Попробуйте использовать решатель умножающих матриц и калькулятор определителя с шагами для умножения матриц и для получения определителя матриц.
Введите значения элементов
Затем вы должны ввести значения элементов в вашей матрице. Если вы используете решатель обратных матриц для изучения процедуры, вы также можете выбрать случайные значения из калькулятора.
Получить вывод
После ввода входных данных решатель обратной матрицы предоставит вам выходные данные обратной матрицы.
Матрица, обратная
Чтобы получить результаты, просто перейдите к кнопке расчета и нажмите на нее. За доли секунды калькулятор обратной матрицы с шагами предоставит вам обратную исходную невырожденную матрицу.
Часто задаваемые вопросы
Можем ли мы вычислить инверсию всех матриц?
С помощью калькулятора обратной матрицы с шагами можно определить обратную невырожденную матрицу. Однако обратная сторона всех матриц не может быть определена, с помощью матричных инструментов вычисляется только обратная обратимая матрица.
Как получить исходную матрицу после ее инвертирования?
После того, как вы инвертировали свою матрицу с помощью калькулятора обратной матрицы с шагами и хотите получить исходную матрицу с помощью вычислений. Вам нужно всего лишь предпринять следующие шаги, чтобы получить оригинальную матрицу:
Шаг #1: Откройте калькулятор обратимой матрицы, чтобы ввести свою перевернутую матрицу.
Шаг № 2: Нажмите кнопку расчета, чтобы получить обратную матрицу.
1. Арифметика. Алгебра. АнализЭлементарная математика с точки зрения высшей, Т.1. Арифметика. Алгебра. Анализ
Написанная в форме лекций для учителей, книга и за давностью лет не потеряла своей значимости,, свежести, привлекательности.
n = w
Учение о малых колебаниях, в частности, о колебаниях маятника.
Оставайтесь с нами, чтобы узнать больше об этой увлекательной теме!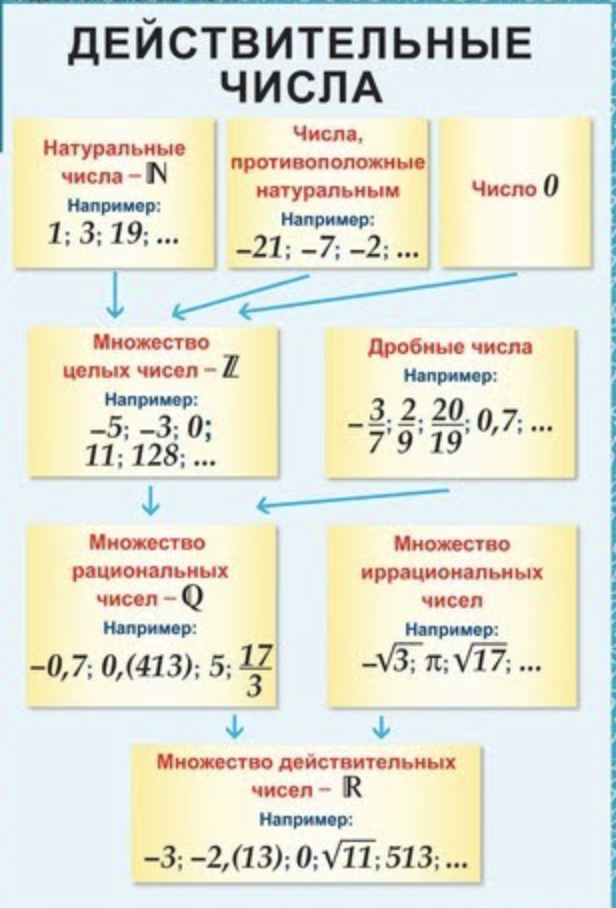
..), квадратный корень из двух (1,414213…) и золотое сечение (1,618033…).
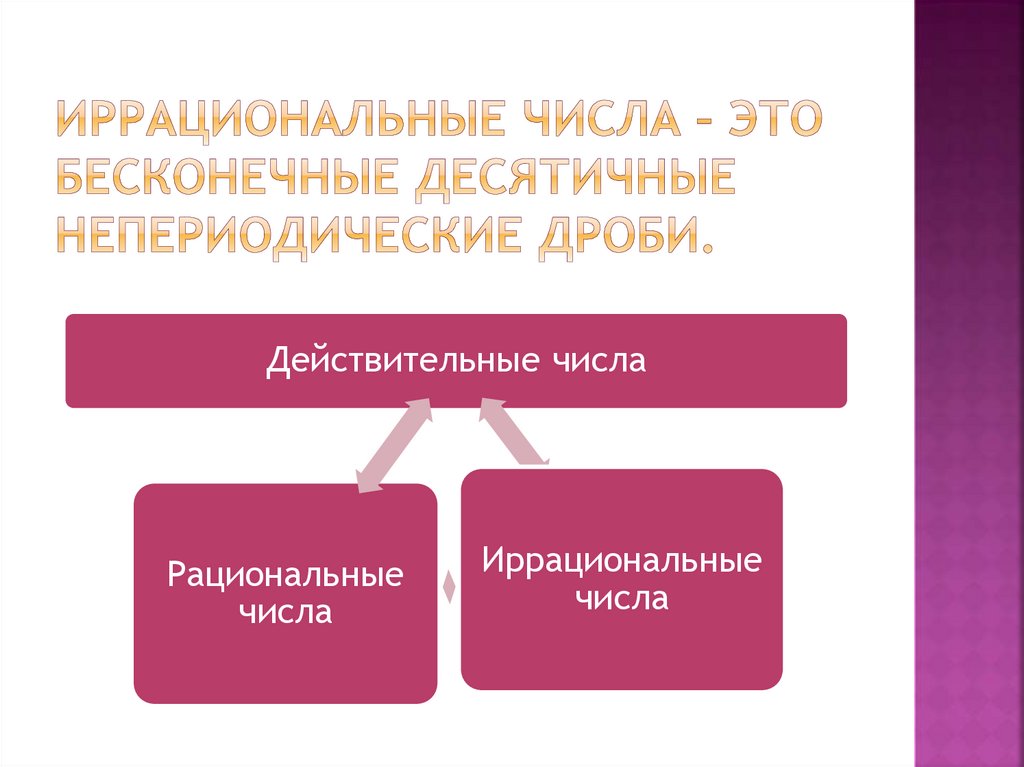В зависимости от ситуации и того, насколько точным должен быть ответ, эти методы могут варьироваться от разложения в ряд до численных приближений.
Пи также часто используется в физике, например, чтобы выяснить, как движутся планеты и куда они движутся.
С их помощью и экспертными знаниями учащиеся узнают больше об иррациональных числах и смогут использовать полученные знания в различных областях математики.
(Изображение предоставлено Shutterstock)
)
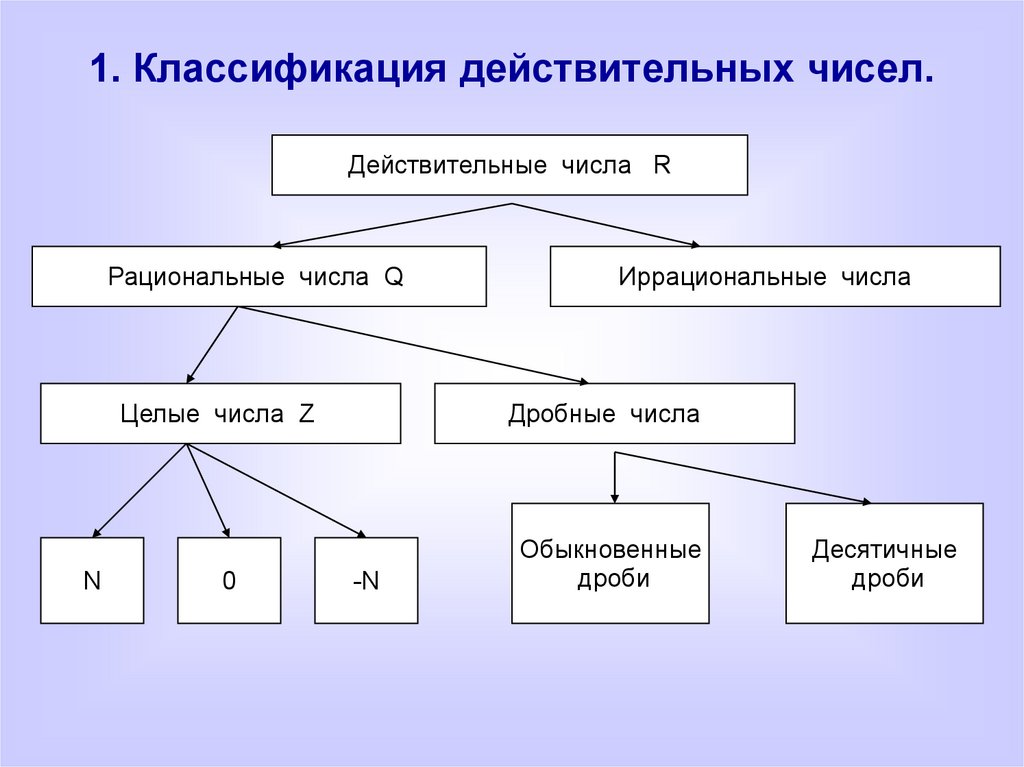
Поскольку иррациональные числа — это все те действительные числа, которые не являются рациональными, иррациональные числа значительно перевешивают рациональные числа; они составляют все остальные несчетные действительные числа.
Разделите лист формата А2 еще раз пополам, и вы получите два листа бумаги формата А3 и так далее.
Но большая часть этого неверна. Фи тесно связана с последовательностью Фибоначчи , еще одним источником многих заблуждений.
Павлова
Бехтерева
Для более высокой скорости тестирования можно объединить два прибора CL-6000i вместе, чтобы обеспечить производительность почти до 1 000 тестов в час.
На сегодняшний день оборудованием Mindray пользуются почти в 190 странах мира.
Мы снижаем наше воздействие на окружающую среду и внедряем принципы устойчивого развития и экономики замкнутого цикла во все, что мы делаем.
Мы вносим свой вклад в обеспечение продовольственной безопасности с помощью широкого спектра решений AgTech, удобрений, альтернативных белков и других продуктов, которые позволяют продуктам питания сохранять более длительный срок хранения и сокращать количество пищевых отходов.
)
)
)
)
)
)
)
)
12.21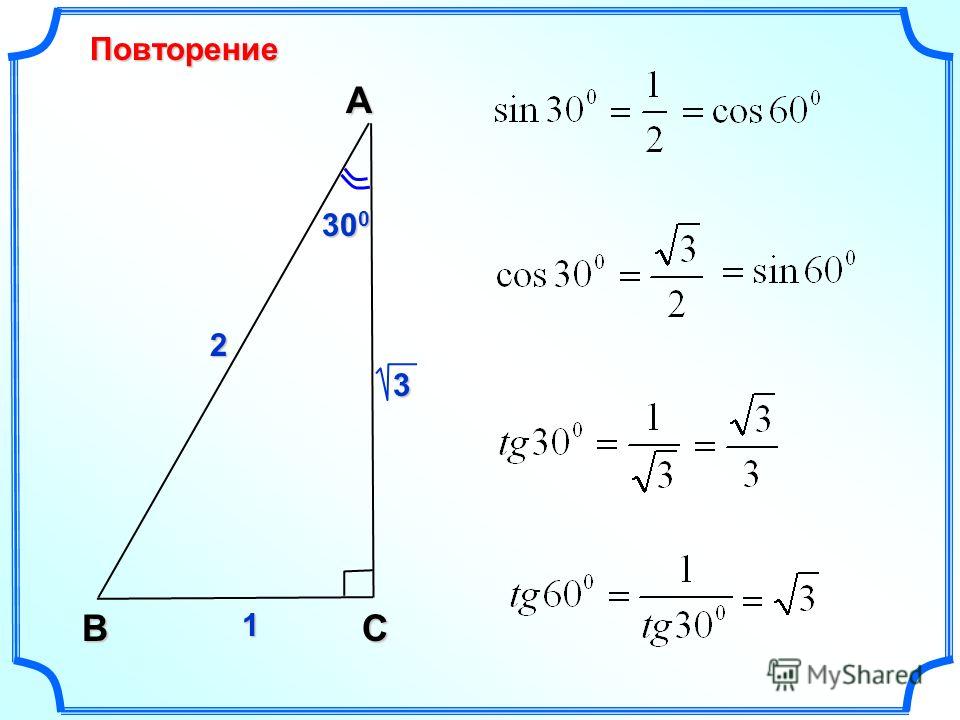
Модули их импульсов равны 0.05 кг м/с и 0.03 кг м/с.столкнувшись шарики слипаются.чему равен импульс шариков
)/3
..
T-отношения некоторых конкретных углов
>
T-соотношения некоторых конкретных углов Упражнение 11
>
Вопрос 2
Если Вы не можете вывести тригонометрическую формулу, значит, что-то упущено на предыдущих этапах. Если вы выводите с трудом и долго, считайте, что вам повезло — вы нашли то самое место, куда надо прикладывать усилия для получения результата. Скоро научитесь делать это быстро. (Однако если Вам предстоит экзамен, перед экзаменом подзубрите формулы.)
М. Гельфанд, С.М. Львовский, А. Л. Тоом
1 градус: нужно разделить окружность на 360… Читать дальше
Стало все нагдядно и просто и с этим пришло понимание формул.
Здесь мы вкратце познакомимся с тем, что такое тригонометрические функции и как они вводятся, а также узнаем основные формулы, которыми будет достаточно нам пользоваться для решения задач с ней.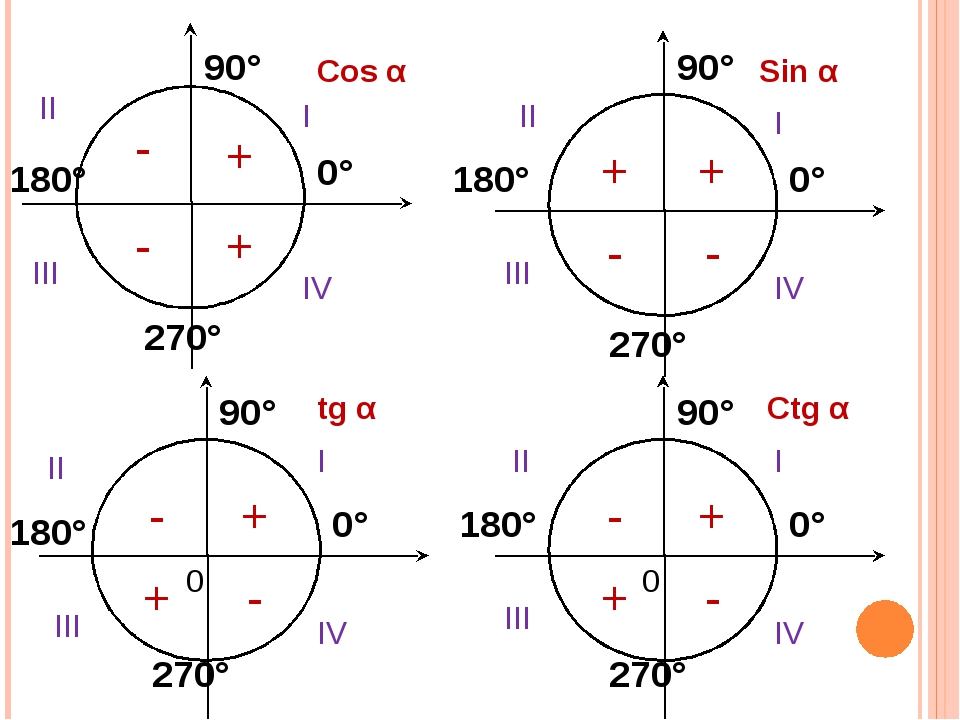
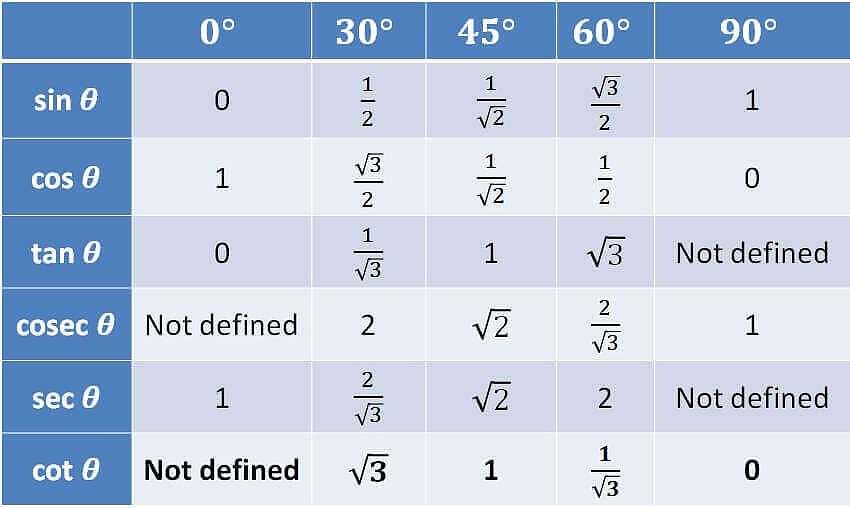
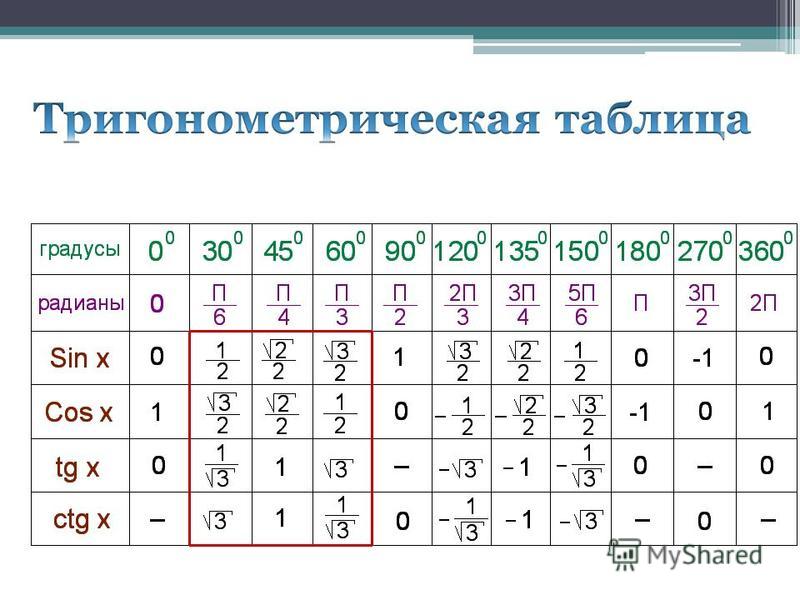
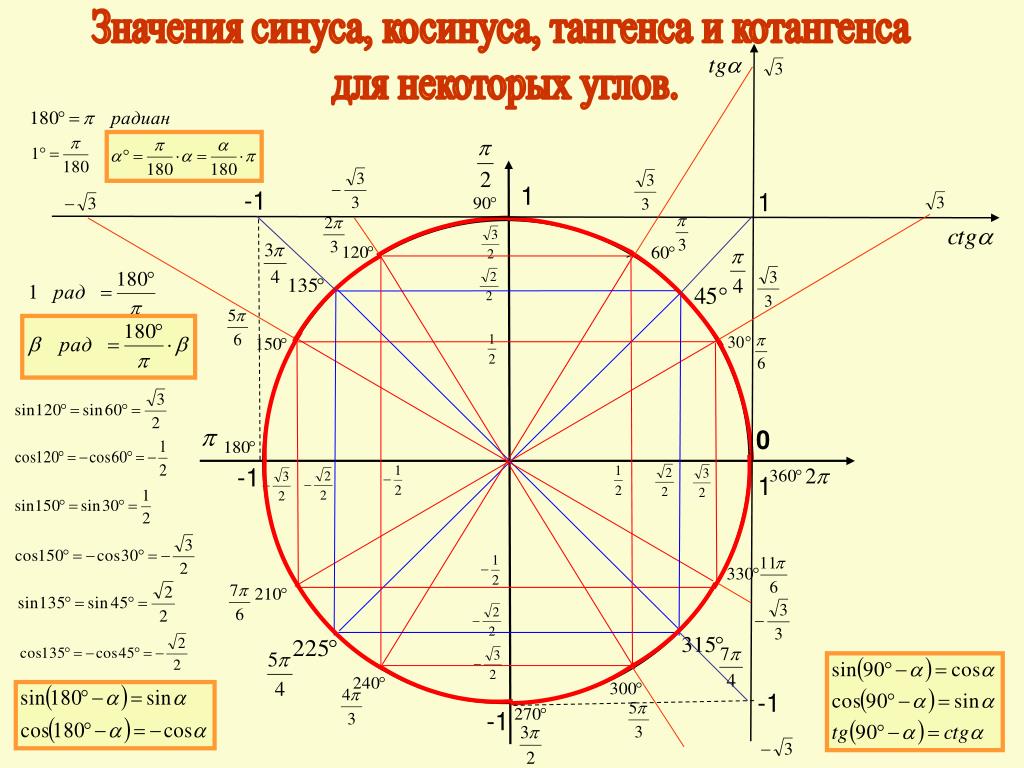
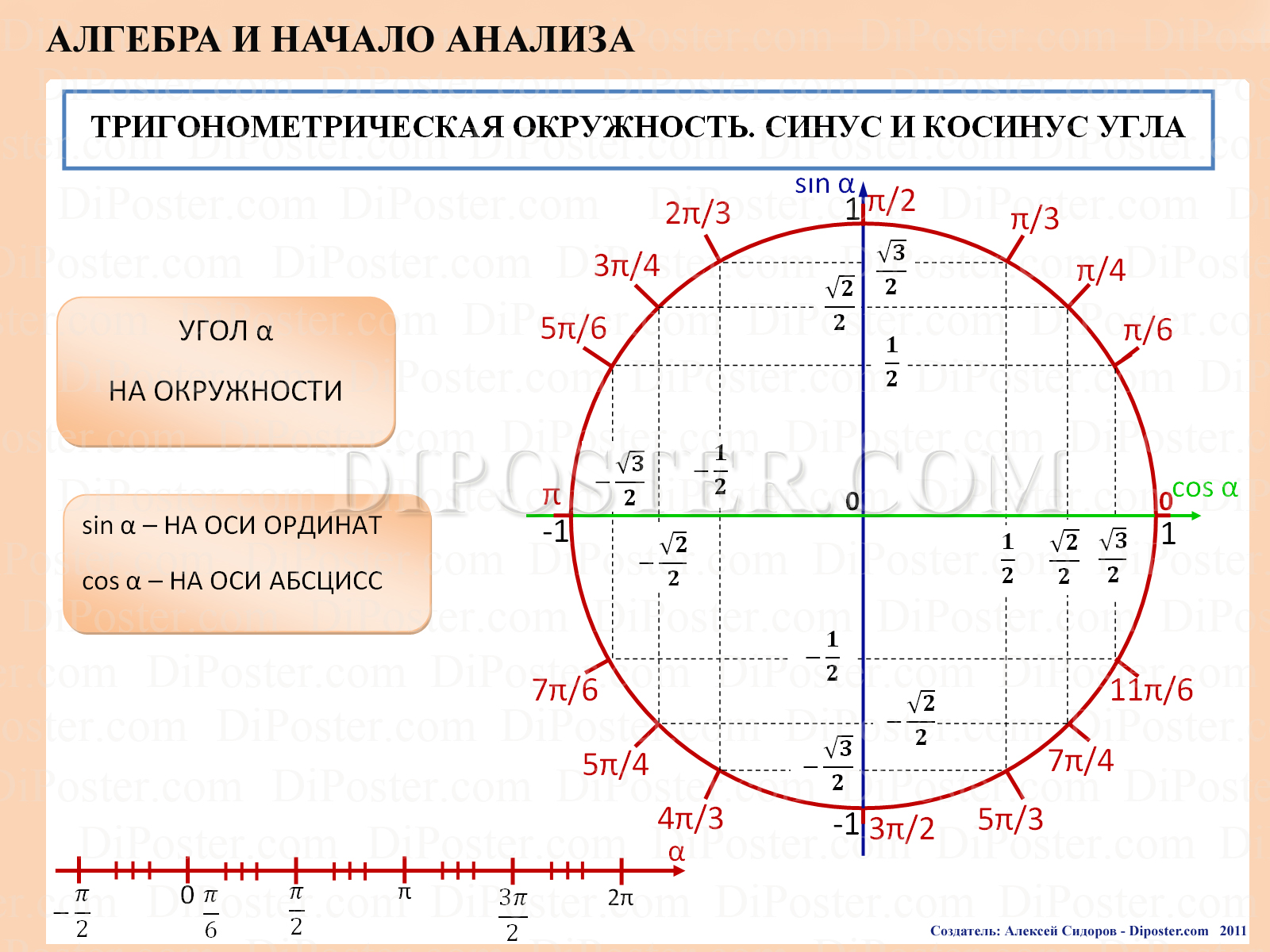
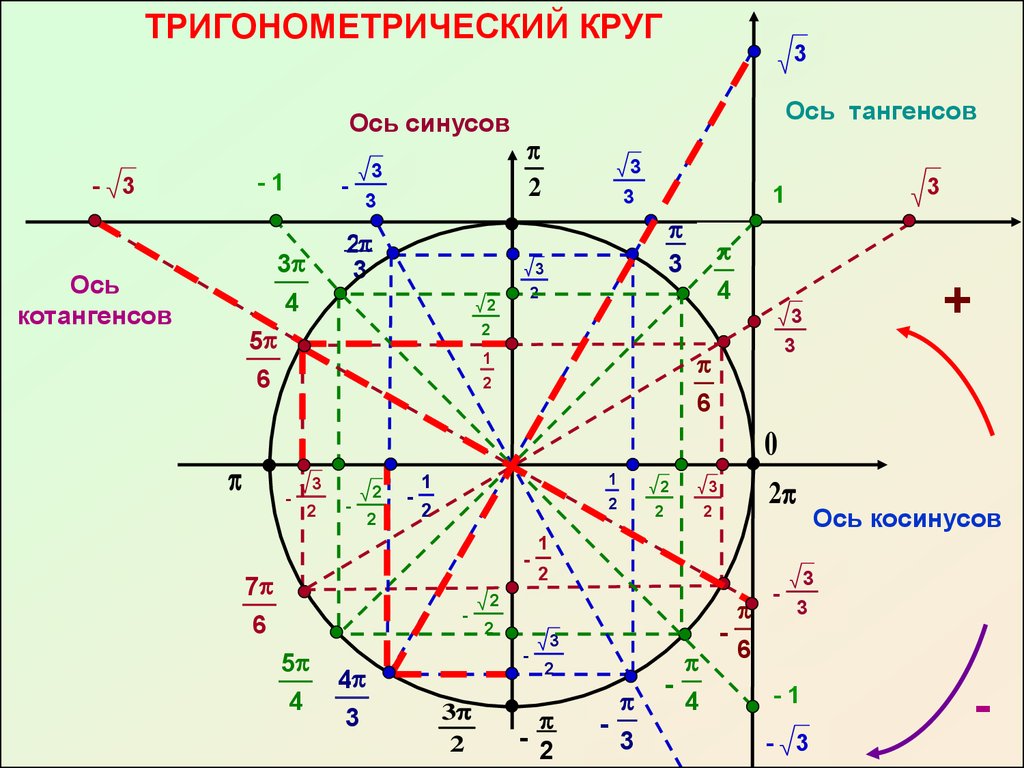
А давайте проделаем с ней некоторые преобразования — поделим и левую и правую части на гипотенузу. Получаем основное тригонометрическое тождество, одно из важнейших соотношений тригонометрии. Оно связывает синус и косинус одним выражением, что позволяет легко находить одно из другого, а также, позволяет упрощать некоторые выражения.
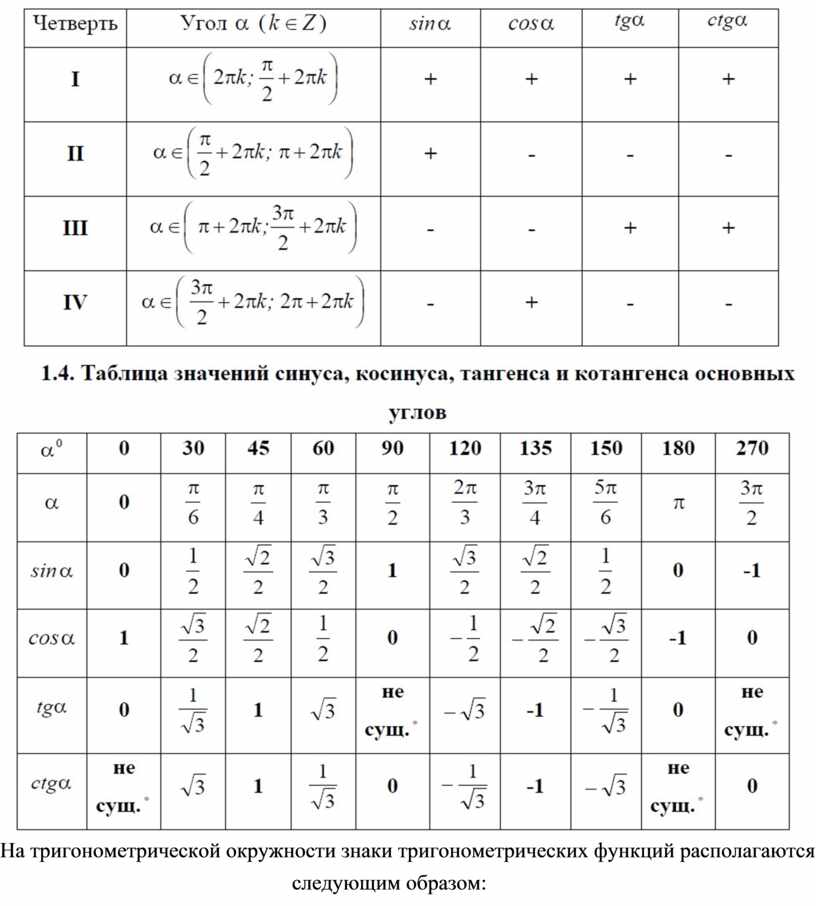
И вычисленные значения лежат в таблице, называемой таблицей Брадиса, в которой можно легко посмотреть эти значения. Да и она не нужна сейчас, когда у всех под рукой калькуляторы. Ниже приведена таблица основных значений, которые достаточно знать наизусть. Видно корреляцию значений, что можно заметить, например, в том же самом основном тождестве. Также видно, что значение синуса 90 у нас 1, то есть, противолежащая сторона к углу в 90° — это гипотенуза, и при делении ее на саму себя будет 1. Из тождества косинус 90° будет 0. Некоторые значения тангенса и котангенса отсутствуют в ней вследствие деления на 0 в формулах выше.
Видно, что максимальное значение синуса, также, как и косинуса — это единица (при 90°). И что же будет при 91°? Как видно, синус будет уменьшаться вместе с координатой у точки пересечения, и он будет равен sin(89°). Координата х же, которой будет равен косинус, будет отрицательной, из-за чего получаем отрицательный косинус.
Также предлагайте темы для будущих разборов.
Он в центре, у вас на макушке, но это большой черт возьми.
)
( Что с этим парнем? О, инцидент с голым мужчиной на моей стене… )
У нас есть вертикальные части (синус, тангенс), горизонтальные части (косинус, котангенс) и «гипотенусы» (секанс, косеканс). (Примечание: метки показывают, куда «поднимается» каждый элемент. Косеканс — это полное расстояние от вас до потолка.) 92$) мы видим, как связаны стороны каждого треугольника.
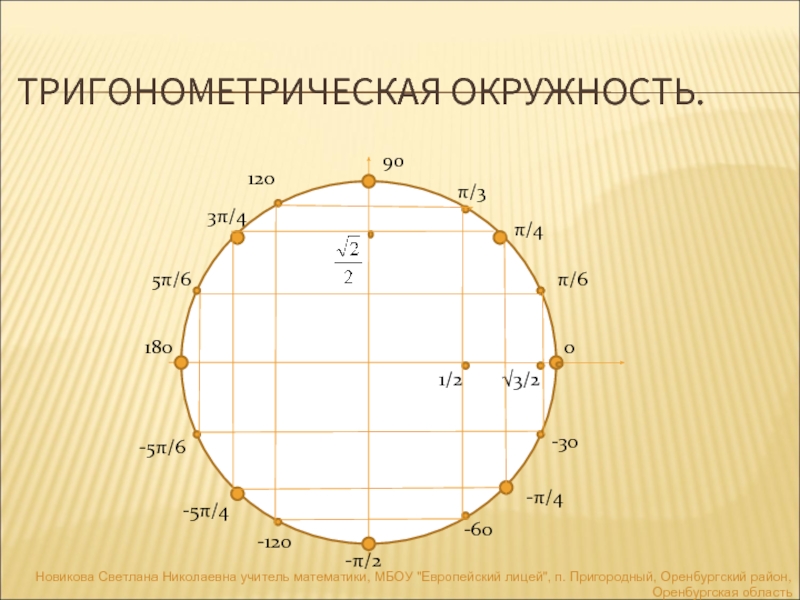Это нормально. Он по-прежнему имеет высоту, в зеленом цвете.
(Воистину, адское путешествие.)
Узоры и орнаменты на посуде»
Найти Область определения и область значений функцииНАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ
Область определения и область значений функцииОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ
Проверь себяПРОВЕРЬ СЕБЯ
Узнайте больше о желаемом домене с помощью этих советов по поиску владельцев доменного имени, а также с помощью инструмента поиска WHOIS от Shopify.
Вы можете переместить свой веб-сайт в другой домен, если хотите изменить URL-адрес. Когда вы перемещаете свой веб-сайт в другой домен, важно следовать передовым методам SEO, чтобы свести к минимуму потерю трафика. Перенаправляя старый домен на новый действующий домен, вы сигнализируете Google, что новый домен теперь является домом для старого контента веб-сайта.
co
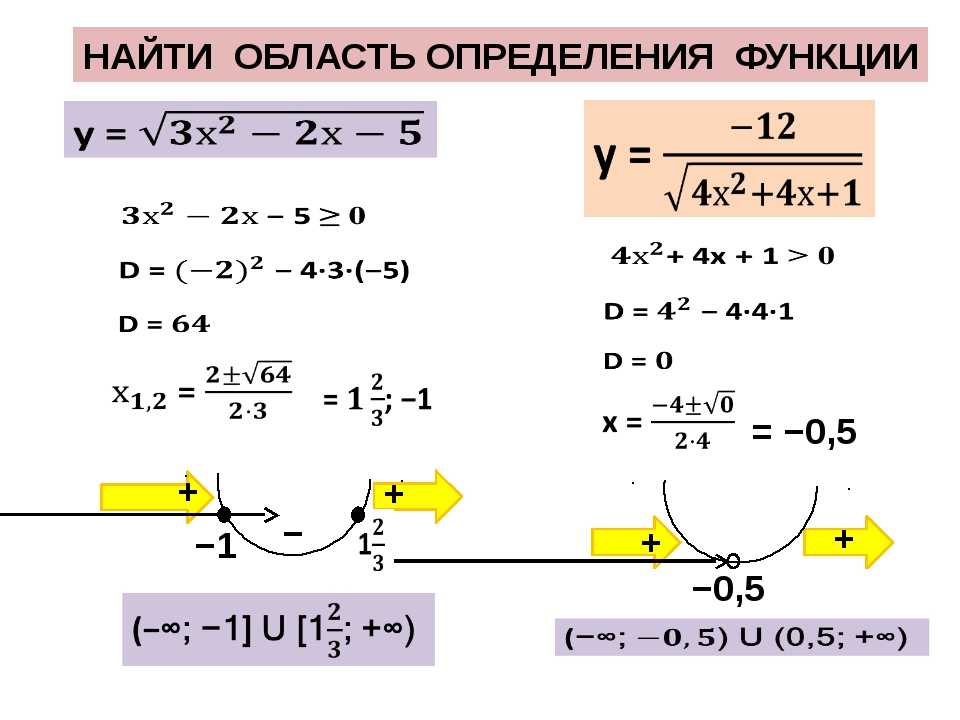io
tech
top
ws
site
run
vet
realty
vote
У нас есть документация и видео, чтобы ответить на ваши вопросы, когда вы начинаете, строите и развиваете свой онлайн-бизнес.
org/Question»>
Хостинг позволяет создавать новые веб-сайты, чтобы они были видны клиентам в Интернете, а системы безопасности работали. Все планы создания сайтов электронной коммерции Shopify включают услуги хостинга.
Выражение ???\sqrt{x+9}??? не определено, где ???x+9??? отрицательно. Например, если ???x=-10???, то ???x+9??? равно ???-1???. Аналогично, если ???x??? любое число меньше, чем ???-9???, ???x+9??? будет отрицательным. Однако ???-9??? само по себе нормально, потому что ???\sqrt{x+9}??? тогда будет ???0???, что не является неопределенным.
)
)
)
)
)
)
)
)
2
3
14159..
)/3
2), t=\tan x/2, \ $, но я не могу найти правильное решение.
Также я пробовал квадратировать обе стороны, но все равно ничего.
$$
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.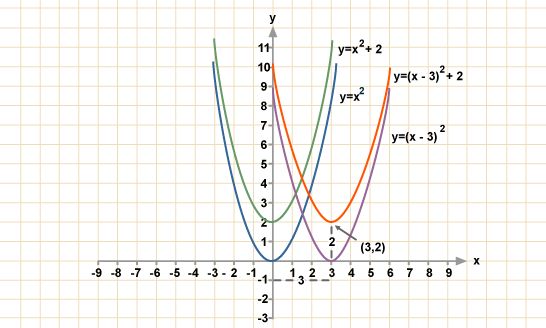
.. Задача 8E: Найдите расстояние между каждой парой точек: a -3,-7 и 2, 5 c -a,-b и a,b b 0, 0 и -2, 6 d… Задача 9E: Найдите середину отрезка, соединяющего каждую пару точек: a 0, -3 и 4, 0 c 3, 2 и… Задача 10E Задача 11E: Точки A и B имеют симметрию относительно начала координат O. Найдите координаты B, если A является… Задача 12E: Точки A и B имеют симметрию относительно точки C 2,3. Найдите координаты B, если A является… Задача 13E: Точки A и B имеют симметрию относительно точки C. Найдите координаты C для заданной точки: a A… Задача 14E: Точки A и B имеют симметрию относительно оси x. Найдите координаты B, если A является… Задача 15E Задача 16E: Точки A и B имеют симметрию относительно вертикальной линии, где x=2. Найдите координаты A… Задача 17E: Точки A и B имеют симметрию относительно оси y. Найдите координаты A, если B это… Задача 18E Задача 19E: Точки A и B имеют симметрию относительно вертикальной линии x=a или горизонтальной линии y=b. Задайте… Задача 20E: В упражнениях с 20 по 22 примените формулу средней точки.
M 3,-4является серединой AB-, в которой A является… Задача 21EЗадача 22EЗадача 23E: Прямоугольник ABCD имеет три вершины в точках A2,-1,B6,-1 и C6,3. Найдите четвертую вершину и… Задача 24E: Прямоугольник MNPQ имеет три вершины в точках M0, 0, Na, 0 и Q0, b. Найдите четвертую вершину P и… Задача 25E: Используйте формулу расстояния, чтобы определить тип треугольника, который имеет эти вершины: a A0, 0, B4,0,… Задача 26E: Используйте метод из примера 4, чтобы найти уравнение прямой, описывающей все равноудаленные точки… Задача 27E. Воспользуйтесь методом из примера 4, чтобы найти уравнение прямой, описывающей все равноудаленные точки… Задача 28E. Для компланарных точек A, B и C , предположим, что вы использовали формулу расстояния, чтобы показать, что… Задача 29EЗадача 30EЗадача 31EЗадача 32E: На оси абсцисс имеются две точки, расположенные на расстоянии 6 единиц от точек 3,1….Задача 33E: Треугольник с вершинами M-4,0,N3,- 1 и Q2,4 заключены в рамки, как показано. Найдите площадь.
.. Задача 34E: Используйте метод бокса, предложенный в упражнении 33, чтобы найти площадь RST с R-2,4,S-1,-2 и T6,5…. Задача 35E: Определите площадь ABC, если A=2,1,B=5,3, а C является отражением B относительно оси X. Задача 36E: Найдите площадь ABC В упражнении 35, но предположим, что C является отражением B по оси Y. Задача 37E. Найдите точный объем твердого тела, которое получается, когда треугольная область с вершинами находится в точках 0, 0, 5,…. Задача 38E. Найдите точный объем твердого тела, которое получается, когда треугольная область с вершинами 0, 0, 6,… Задача 39E: Найдите точный объем твердого тела, которое получается, когда прямоугольная область с вершинами находится в точках 0, 0,… Задача 40E: Найдите точный объем тела, которое получается, когда область, ограниченная осями в квадранте I… Задача 41E: Найдите точную площадь поперечной поверхности каждого твердого тела в упражнении 40. Найдите точный объем образовавшегося твердого тела… Задача 42E: Найдите объем твердого тела, образовавшегося, когда треугольная область имеет вершины в точках 2, 0, 4, 0.
, и 2,… Задача 43E: По определению, эллипс — это геометрическое место точек, сумма расстояний которых от двух фиксированных точек F1 и… Задача 44E: По определению, гипербола — это геометрическое место точек, положительная разность которых расстояния от двух… Задача 45EЗадача 46E: Используйте формулу расстояния, чтобы показать, что уравнение параболы с фокусом F0,2 и директрисой… Задача 47E: После 90 вращение против часовой стрелки вокруг начала координат, изображение A3, 1 точка B-1, 3. Что… Задача 48E: Рассмотрим точку Ca,b. Каким будет образ C после поворота против часовой стрелки на 90 вокруг… Задача 49E Задача 50E: Графики парабол eith уравнений y=x2 и прямой y=18-x2 пересекаются в двух точках. Найти… Задача 51E format_list_bulleted 
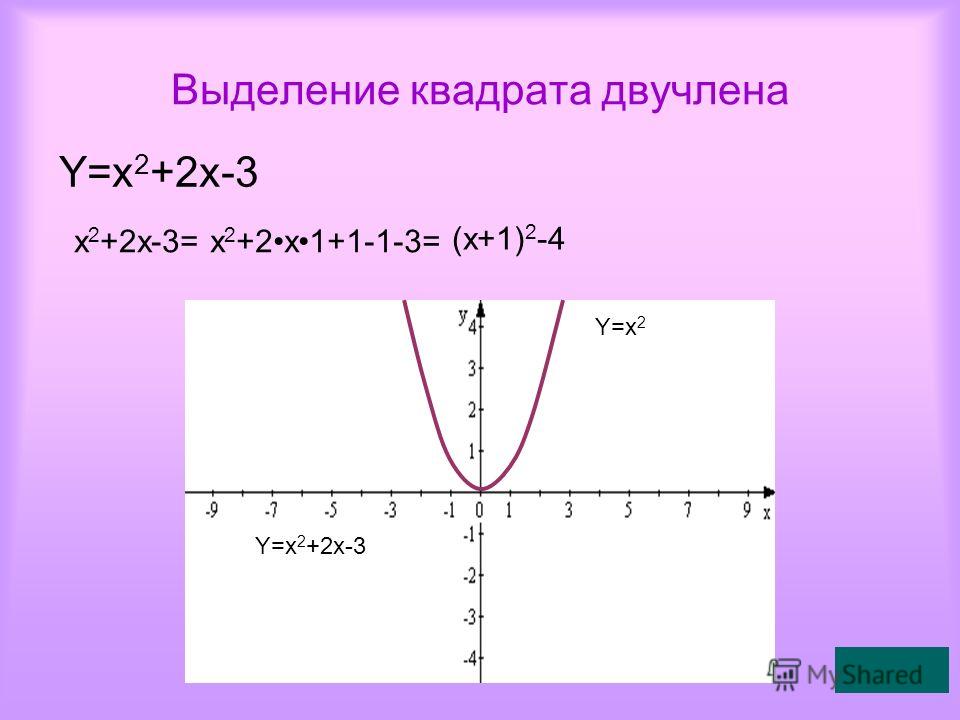
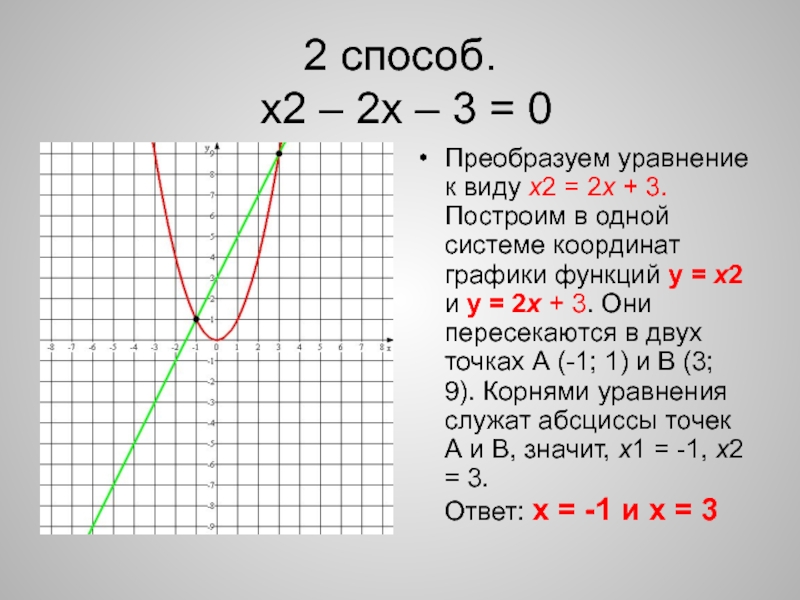
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 1 
Для вычисления
логарифмов эффективна формула
рисунок выше).
Для каждого числа z из области сходимости
В частности, радиус сходимости степенного ряда (24.33) можно вычислить по формуле
25. Подставив в него выражение Найдем
Если- функция независимой переменнойТо в общем
Найти решениеДифференциального уравнения первого
Когда мы добавляем бесконечное число членов, как мы это делаем со степенным рядом, сумма этих членов будет либо конечным числом, либо бесконечной.
Это всего лишь один пример использования радиуса конвергенции, и существует множество других приложений, которые работают за кулисами компьютерного программного обеспечения и помогают нам каждый день!
} \\ & \hspace{5ex} \text{Используя тест отношения, сходимость происходит, когда: } \; Л < 1, \; L = \lim_{n\to\infty} \left\lvert\frac{a_{n+1}}{a_{n}} \right\rvert\\ \\ & \hspace{4ex} \text{1.1) Подставив наш ряд в формулу проверки отношения, мы получим: } \\ \\ & \hspace{9{1}} \cdot \infty \cdot x\right\rvert\\ \\ & \hspace{4ex} \text{1.4) Для дальнейшего упрощения мы сократим члены, содержащие бесконечности.} \\ & \hspace{ 9ex} \text{Поступая так, получаем:} \\ \\ & \hspace{9ex} L = \left\lvert\frac{x}{1}\right\rvert\\ \\ & \hspace{4ex} \text{1.5) Применение критериев сходимости } \; L < 1 \text{, получаем:} \\ \\ & \hspace{9ex} \left\lvert\frac{x}{1}\right\rvert < 1\\ \\ \\ & \hspace{2ex } \text{2) Теперь давайте решим новое уравнение сходимости для определения радиуса сходимости.}\\ \\ & \hspace{4ex} \text{2.1) Решив неравенство сходимости для радиуса сходимости, получим: } \\ \\ & \hspace{9ex} \left\lvert\frac{x}{1}\right\rvert < 1 \; \Длинная праваястрелка\; \text{радиус} = \boxed{1} \\ \\ & \hspace{4ex} \boxed{\text{Радиус сходимости} = \boxed{1}}\\ & \end{align}$$
Он также использует систему компьютерной алгебры (CAS), основанную на JS, которая выполняет некоторые алгебраические шаги в процессе вычислений. Поскольку калькулятор работает на основе кода JS, он полностью работает внутри встроенного механизма JS вашего браузера и предоставляет мгновенные решения и шаги (не требуется перезагрузка страницы).
Просто введите свою функцию и диапазон переменных в заданных разделах ввода и нажмите кнопку расчета, чтобы получить мгновенный вывод вместе с подробной процедурой.
е. радиус конвергенции
569805089977
Посмотрите обучающий видео урок
как правильно склонять числительные.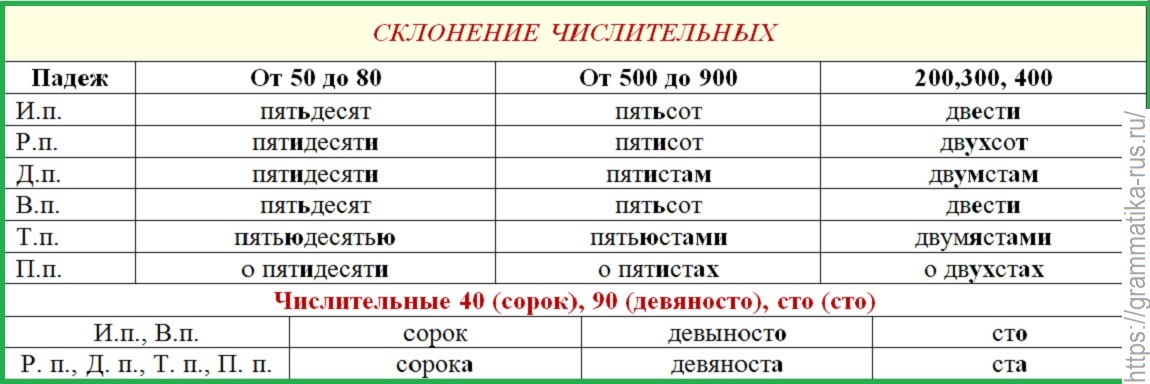
Всего в русском языке существует шесть падежей, каждый из которых имеет свой вспомогательный вопрос.
У числительных на -десят два окончания, так как изменяются обе части: пятидесяти, пятьюдесятью.
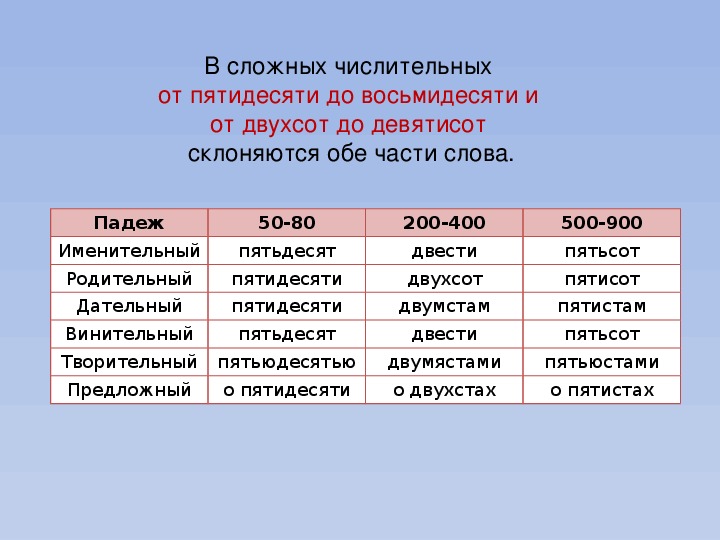europa.eu
..]
..]
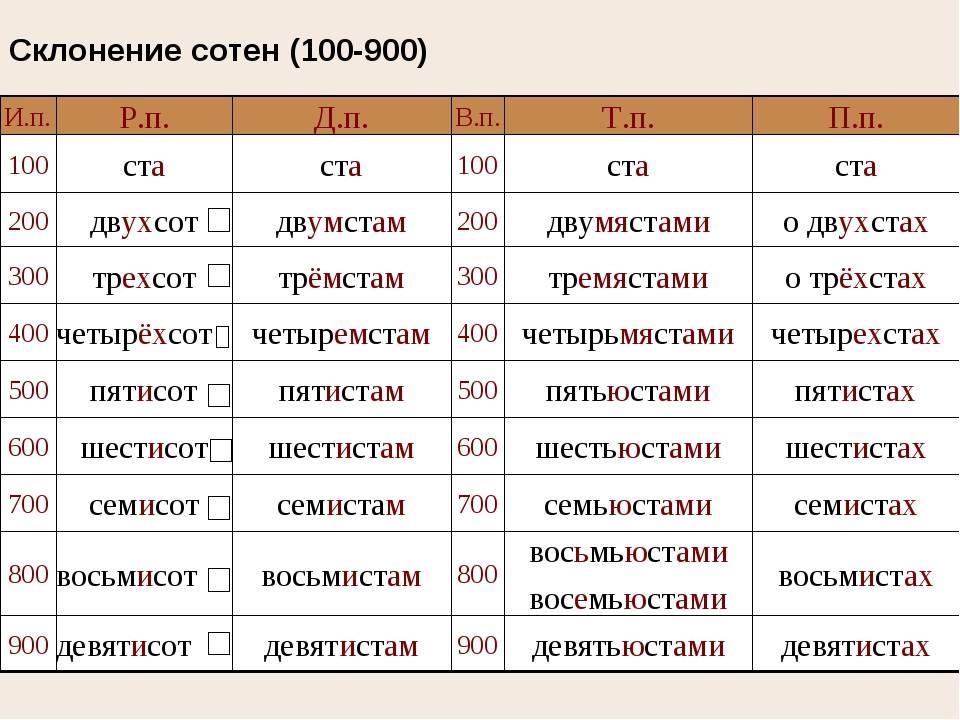..] F O RT Y-ДВЕ ТЫСЯЧИ ВОСЕМЬДЕСЯТ ГЕН DR E D ПЯТЬДЕСЯТ — S E VE N ЕВРО И ДЕСЯТЬ ЕВРОЦЕНТОВ (‘7 142 857,10), представитель d b y СЕМЬДЕСЯТ ОДИН M I LL ION FO U R СТО ДВАДЦАТЬ ВОСЕМЬ ТЫСЯЧ ОДИН ТЫСЯЧА F IV E СТО СЕМЬДЕСЯТ ОДИН c o мм на акции […]
142.857,10 ‘), срединный представитель e SETENTA Y UN MILLO NE S CUATROCIENTAS VEINT IO CHO MIL QUI NI EN TAS SETENTA Y UNA ac […]
е. ndas эквивалент […]
. .]
..]
..]
..]
..]
..]
..]
..]
..]
..]
org
Сто a n d восемь d e le Гации отсутствовали.
. .]
es
Упражнение 7А.
Упражнение 7А.
>
Вопрос 1
…