199 — сто девяносто девять. натуральное нечетное число. 46е простое число. в ряду натуральных чисел находится между числами 198 и 200. Все о числе сто девяносто девять.
- Главная
- О числе 199
199 — сто девяносто девять. Натуральное нечетное число. 46е простое число. В ряду натуральных чисел находится между числами 198 и 200.
Like если 199 твое любимое число!
Распространенные значения и факты
199 регион — г. Москва
- Столица
- Москва
- Автомобильный код
- 77, 97, 99, 177, 197, 199, 777
- Федеральный округ
- Центральный
- Экономический район
- Центральный
- Дата образования
- Основана в 1147 г.
- Территория
- 1 080, 8 кв. км 0,01 % от РФ 88 место в РФ
- Население
- Общая численность 11 551, 930 тыс. чел. 7,13 % от РФ 1 место в РФ
Изображения числа 199
Склонение числа «199» по падежам
| Падеж | Вспомогательное слово | Характеризующий вопрос | Склонение числа 199 |
|---|---|---|---|
| Именительный | Есть | Кто? Что? | сто девяносто девять |
| Родительный | Нет | Кого? Чего? | ста девяноста девяти |
| Дательный | Дать | Кому? Чему? | ста девяноста девяти |
| Винительный | Видеть | Кого? Что? | сто девяносто девять |
| Творительный | Доволен | Кем? Чем? | ста девяноста девятью |
| Предложный | Думать | О ком? О чём? | ста девяноста девяти |
Перевод «сто девяносто девять» на другие языки
- Азербайджанский
- yüz doxsan doqquz
- Албанский
- 199
- Английский
- one hundred ninety nine
- Арабский
- 199
- Армянский
- հարյուր իննսուն ինը
- Белорусский
- 199
- Болгарский
- сто деветдесет и девет
- Вьетнамский
- 199
- Голландский
- 199
- Греческий
- εκατόν ενενήντα εννέα
- Грузинский
- ას ოთხმოცდაცხრამეტი
- Иврит
- 199
- Идиш
- 199
- Ирландский
- 199
- Исландский
- 199
- Испанский
- ciento noventa y nueve
- Итальянский
- 199
- Китайский
- 199
- Корейский
- 백아흔아홉
- Латынь
- centum nonaginta novem,
- Латышский
- 199
- Литовский
- 199
- Монгольский
- нэг зуун ерэн есөн
- Немецкий
- 199
- Норвежский
- 199
- Персидский
- 199
- Польский
- sto dziewięćdziesiąt dziewięć
- Португальский
- 199
- Румынский
- 199
- Сербский
- сто деведесет девет
- Словацкий
- sto deväťdesiat deväť
- Словенский
- 199
- Тайский
- 199
- Турецкий
- 199
- Украинский
- сто дев’яносто дев’ять
- Финский
- satayhdeksänkymmentäyhdeksän
- Французский
- 199
- Хорватский
- 199
- Чешский
- sto devadesát devět
- Шведский
- 199
- Эсперанто
- cent naŭdek naŭ
- Эстонский
- 199
- Японский
- 199
Перевод «199» на другие языки и системы
Римскими цифрами
- Римскими цифрами
- CXCIX
Сервис перевода арабских чисел в римские
Арабско-индийскими цифрами
- Арабскими цифрами
- ١٩٩
- Восточно-арабскими цифрами
- ۱۹۹
- Деванагари
- १९९
- Бенгальскими цифрами
- ১৯৯
- Гурмукхи
- ੧੯੯
- Гуджарати
- ૧૯૯
- Ория
- ୧୯୯
- Тамильскими цифрами
- ௧௯௯
- Телугу
- ౧౯౯
- Каннада
- ೧೯೯
- Малаялам
- ൧൯൯
- Тайскими цифрами
- ๑๙๙
- Лаосскими цифрами
- ໑໙໙
- Тибетскими цифрами
- ༡༩༩
- Бирманскими цифрами
- ၁၉၉
- Кхемерскими цифрами
- ១៩៩
- Монгольскими цифрами
- ᠑᠙᠙
В других системах счисления
- 199 в двоичной системе
- 11000111
- 199 в троичной системе
- 21101
- 199 в восьмеричной системе
- 307
- 199 в десятичной системе
- 199
- 199 в двенадцатеричной системе
- 147
- 199 в тринадцатеричной системе
- 124
- 199 в шестнадцатеричной системе
- C7
QR-код, MD5, SHA-1 числа 199
Адрес для вставки QR-кода числа 199, размер 500×500:
http://pro-chislo.ru/data/moduleImages/QRCodes/199/44229e68df29e16d225b13f06094cf2d.png
- MD2 от 199
- 6961d9b99c6bc452ebe5e331233c24bd
- MD4 от 199
- 50e1bc5c5d17ff1601d0db130f5647c0
- MD5 от 199
- 84d9ee44e457ddef7f2c4f25dc8fa865
- SHA1 от 199
- 2952aeca0fe15cf310ede96c437acb94b2b208f1
- SHA256 от 199
- 5a39cadd1b007093db50744797c7a04a34f73b35ed444704206705b02597d6fd
- SHA384 от 199
- 5ce4bdda7f6ec2474836cec064539ec32555e53be99b9628cb74d1b9530ff11c2e67f5af082685a649e8e61f8606e1c0
- SHA512 от 199
- f729827708b4e0a559425f6fcb0b62f1c36a53f0d3341f852bf285a5360d3356243ea353305fbd30b01ff009c8c628ee7df635dd44b142ab5e357a8c09b01b6b
- GOST от 199
- 67aff1da85914e8a268b5b4b4844cebca2ac0d186605334ccb5ecc1e69c3338f
- Base64 от 199
- MTk5
199й день в году
199й день в не високосном году — 18 июля
День хозяйственный подразделений
День пожарного надзора
199й день в високосном году — 17 июля
День морской авиации ВМФ России
Математические свойства числа 199
- Простые множители
- 199
- Делители
- 1, 199
- Количество делителей
- 2
- Сумма делителей
- 200
- Простое число
- Да (46е простое число)
- Предыдущее простое
- 197
- Следующее простое
- 211
- 199е простое число
- 1217
- Число Фибоначчи
- Нет
- Число Белла
- Нет
- Число Каталана
- Нет
- Факториал
- Нет
- Регулярное число (Число Хемминга)
- Нет
- Совершенное число
- Нет
- Полигональное число
- Нет
- Квадрат
- 39601
- Квадратный корень
- 14.
 106735979666
106735979666 - Натуральный логарифм (ln)
- 5.2933048247245
- Десятичный логарифм (lg)
- 2.2988530764097
- Синус (sin)
- -0.88179883606755
- Косинус (cos)
- -0.47162571251991
- Тангенс (tg)
- 1.869700511781
Комментарии о числе 199
← 198
200 →
- Распространенные значения и факты
- Изображения числа 199
- Склонение числа «199» по падежам
- Перевод «сто девяносто девять» на другие языки
- Перевод «199» на другие языки и системы
- QR-код, MD5, SHA-1 числа 199
- 199й день в году
- Математические свойства числа 199
- Комментарии о числе 199
Склонение числительного 199 (Сто девяносто девять) по падежам
Склонение числительного 199 по падежам: именительный, родительный, дательный,
винительный, творительный, предложный. Удобный поиск склонений для слов,
более 83451 слов в нашей базе. Посмотрите обучающий видео урок
как правильно склонять числительные.
Посмотрите обучающий видео урок
как правильно склонять числительные.
| Падеж | Вопрос | Слово |
|---|---|---|
| именительный | Кто, что? | сто девяносто девять |
| родительный | Кого, чего? | ста девяноста девяти |
| дательный | Кому, чему? | ста девяноста девяти |
| винительный | Кого, что? | сто девяносто девять |
| творительный | Кем, чем? | ста девяноста девятью |
| предложный | О ком, о чём? | о ста девяноста девяти |
Важно знать о склонении слов
Склонение существительных
Изменение имён существительных по падежам характеризуется изменением их окончаний, которые называются падежными формами. Всего в русском языке существует шесть падежей, каждый из которых имеет свой вспомогательный вопрос.
Всего в русском языке существует шесть падежей, каждый из которых имеет свой вспомогательный вопрос.
Для того, чтобы определить падеж имени существительного, нужно попробовать задать к нему один из вспомогательных вопросов.
Также существуют несклоняемые имена существительные, т.е. те, которые имеют во всех падежах одну и ту же форму. К несклоняемым относятся как имена нарицательные (например, «кофе» или «какао»), так и имена собственные (например, «Гёте»).
Как правило, несклоняемыми существительными оказываются слова, заимствованные из иностранных языков. Они могут относиться ко всем трем родам.
Склонение имен числительных
Склонение числительных не имеет единого образца, оно представлено несколькими типами:
- Числительное один склоняется как прилагательное в единственном числе: один — одного (новый — нового).
- Числительные от пяти до десяти и числительные на -дцать и -десят склоняются как существительные 3-склонения.
 У числительных на -десят два окончания, так как изменяются обе части: пятидесяти, пятьюдесятью.
У числительных на -десят два окончания, так как изменяются обе части: пятидесяти, пятьюдесятью. - Числительные сорок, девяносто, сто, полтора и полтораста, изменяясь по падежам, имеют только две формы: именительный и винительный падежи — сорок, девяносто, сто, полтора, полтораста; родительный, дательный, творительный, предложный падежи — сорока, девяноста, ста, полутора, полутораста.
- Числительные от двухсот до четырехсот и от пятисот до девятисот склоняются по особому типу.
- Собирательные числительные также склоняются по особому типу. Числительные оба, обе имеют два разных варианта склонения.
- Простые порядковые числительные склоняются как прилагательные: первый (новый) — первого (нового). У сложных порядковых числительных только одно окончание. У составных порядковых числительных изменяется только последняя часть.
- У дробных числительных при склонении изменяются обе части.
Склонение прилагательных
Склонение прилагательных – это изменение их по родам, падежам и числам.
Однако не все прилагательные изменяются и по родам, и по числам, и по падежам. Краткие прилагательные не изменяются по падежам, а прилагательные в форме простой сравнительной степени вообще не склоняются.
Для того, чтобы правильно склонять имена прилагательные, нужно знать их падежные вопросы в обоих числах.
Важно понимать, что окончание прилагательного можно проверить окончанием вопроса.
Видеоурок. Правила употребления и склонения числительных
Склонение других чисел
сто шестьдесят пять сто шестьдесят восемь сто шестьдесят девять сто семьдесят сто семьдесят два сто семьдесят три сто семьдесят четыре сто семьдесят пять сто семьдесят один сто семьдесят восемь
Ещё никто не оставил комментария, вы будете первым.
Начинается с цифры
1 2 3 4 5 6 7 8 9
девять тысяч девятьсот девяносто девять
Определение из Викисловаря, бесплатного словаря
Перейти к навигацииПерейти к поиску
Содержание
- 1
- 1.1 Альтернативные формы
- 1.2 Число
- 1.2.1 Связанные термины
- 1.2.2 Переводы
английский
Альтернативные формы
- девять тысяч девятьсот девяносто девять (США)
- девяносто девятьсот девяносто девять (Великобритания)
Числовой[править]
девять тысяч девятьсот девяносто девять
- Кардинальное число, встречающееся после девяти тысяч девятисот девяноста восьми и до десяти тысяч, представленное арабскими цифрами как 9 999.
 Обозначается римскими цифрами как IXCMXCIX.
Обозначается римскими цифрами как IXCMXCIX.
Связанные термины[править]
- Порядковый номер: девять тысяч девятьсот девяносто девятый.
Переводы[править]
Кардинальный номер 9 999
|
Совершено в Орхусе (Дания) двадцать четвертого числа [. eur-lex.europa.eu eur-lex.europa.eu | Hecho en Aarhus (Dinamarca), el […] veinticuatro de ju nio de mil nove ci entos noventa y 03o 9 0.0303 9 0.0303 9 eur-lex.europa.eu eur-lex.europa.eu | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Совершено в Роттердаме на десятый день […] сентября be r , одна тысяча девятьсот a n d девяносто — e i ght 9.0030 ghteur-lex.europa.eu eur-lex.europa.eu | Хечо в Роттердаме [. eur-lex.europa.eu eur-lex.europa.eu | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
СОВЕРШЕНО В ЛОНДОНЕ двадцать седьмого числа […] день ноября mb e r одна тысяча девятьсот a n d 33 девяносто — t w o . eur-lex.europa.eu eur-lex.europa.eu | Hecho en Londres el da […] veintisiete de nov ie mbre de mil n ovecientos noventa y dos . eur-lex.europa.eu eur-lex.europa.eu | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Совершено в Париже тринадцатого числа […]
день января ар г , одна тысяча девятьсот a n d девяносто — t h re e. npsglobal.org npsglobal.org | Хечо-ан-Парс […] el da trece de e nero de mil no vecient os noventa 3streytrey 0 .npsglobal.org npsglobal.org | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Одна тысяча т ч р е е 9003 0030 a n d девяносто девять г r и ts для различных […] уровня образования были распределены среди семисот […] и девяноста семей в Испании и Латинской Америке, включая гранты для учащихся специальных учебных заведений. focus.abengoa.es focus.abengoa.es | Sealamos en lugar [. пункт лос-диверсос нивелес де […] enseanza distribuidas entre setecientas noventa familias de Espaa e Iberoamrica, destacando las asignadas para Educacin Especial. focus.abengoa.es focus.abengoa.es | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Увеличение капитала завершено в конце апреля подпиской […] и оплата 1 310 482 акций, рай си п г одиннадцать m i lli o n сто 9n 3 д тридцать девять тысяч а п d девяносто — s e ve евро (’11 139 097). zeltia.es zeltia.es | A finales de abril se cerr la ampliacin [. с подпиской […] desembol so de un tot al de 1.310.482 acciones, ca pt ndos 0 3 t un 0033 de один раз mil lones ciento treinta y nueve mil noventa y si et e евро […] (11.139.097′). zeltia.es zeltia.es | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Совершено в Рио-де-Жанейро пятого числа […] день J un e , одна тысяча девятьсот a n 3 d 3 900 — т wo . data.iucn.org data.iucn.org | Hecho en Ro de […] Janeiro el cinco de juni o d e mil n ovecientos noventa y dos dos. data. data.iucn.org | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
СОВЕРШЕНО в Монреале 28 числа […] Май уе а р одна тысяча девятьсот a n d девяносто — n i […] Арабский, китайский, французский, […] Русский и испанский языки, причем все тексты имеют одинаковую силу. eur-lex.europa.eu eur-lex.europa.eu | HECHO en Montreal el da […] veintiocho d e Mayo de mil no vecient os noventa y nueve en 0 0033 аол, рабе, […]китаянки, франки, англы […] y ruso, siendo todos los textos igualmente autnticos. eur-lex.europa. eur-lex.europa.eu | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На дату Плана слияния, […] ТЕЛЕФНИЦА МВИЛЕС o wn e d одна тысяча f iv e 903 а н д девяносто девять ( 1 ,5 99) собственные акции. telefonica.com telefonica.com | Por otra parte, TELEFNICA MVILES […] титульный номер эпохи а-ля феча дель Проекто […] de Fu si n de mil quinienta s noventa y nueve (1 30 .593 ) es prop ia s en a ut ocartera. telefonica.com telefonica.com | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
СОВЕРШЕНО в Гётеборге (Швеция) тридцатого числа [. eur-lex.europa.eu eur-lex.europa.eu | HECHO en Gotemburgo (Suecia), a […] treinta de no viemb re de mil no veciento s noventa y nueve . eur-lex.europa.eu eur-lex.europa.eu | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В соответствии с последней статьей корпоративного устава уставный капитал […] Banco Popular […]
Эспаол, SA . и с СТО Т H IR TY-ТРИ МИЛЛИОНА ТРИСТА FIF TE E N ТЫСЯЧА СТО 3 0 9 Н Г С IX Т Д — ДЕВЯТЬ E U RO S (‘133,315,169), представитель d 303 b один миллиард т h r e e сотня t h 3 milty-three 3 3 ли о п сто пятьдесят один тысяча с i x сто девяносто ( 3 , 3 3 , 3 3 151 690) [. доли по 9 штук в каждой0003 […] номинальной стоимостью ДЕСЯТЬ ЕВРОЦЕНТОВ (‘0,10), полностью оплачены. bancopopular.es bancopopular.es | De acuerdo con el artculo final de sus Estatutos Sociales, el Capital […] социальный банк […] Popular Espaol, S.A., e s de CIENTO T RE INTA Y TRES MILLONES TRESCIENTOS QUI NC E MIL C IE NTO SESE NT A Y NUEVE EUR OS (133.315.169 ‘), репрезентадо p или mil trescientesientos от ci en до cincuenta y un mil seis c ienta s noventa a ccion es (1.333.151.690) de […] DIEZ CNTIMOS де евро […] (0,10 ‘) de valor номинальное cada una, totalmente desembolsadas. bancopopular.es bancopopular.es | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Совершено в Маастрихте седьмого дня […] Февраль уе а р одна тысяча девятьсот а п д 3 3 90 ty — t w o . eur-lex.europa.eu eur-lex.europa.eu | Hecho en […] Maastricht, el siete de f ebrer o d e mil n ovecientos noventa y 3 dos. eur-lex.europa.eu eur-lex.europa.eu | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
СОВЕРШЕНО в Риме, этот […] двадцать четвертый день J un e , одна тысяча девятьсот a n d девяносто — f a […] оригинал, на английском языке [. и французском языках, причем оба текста имеют одинаковую силу. unesdoc.unesco.org unesdoc.unesco.org | HECHO в Риме, эл. […] veinticuatro де июль Nio D E MIL N Oveciento S Noventa Y Cinco, E N UN S OLO O RI GINL, […] en los idiomas francs e […] ingls, siendo los dos textos igualmente autnticos. unesdoc.unesco.org unesdoc.unesco.org | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Принимает этот семнадцатый день […] 9 июня0030 ye a r одна тысяча девятьсот a n d девяносто 033 — n i ne следующие [.. .] Конвенция, которая может […] упоминается как Конвенция о наихудших формах детского труда 1999 г. observatoire-avocats.org observatoire-avocats.org | приемный, кон […] fecha 17 de j unio de mil no vecient os noventa 0 30 y el si guiente […] Convenio, que podr ser citado el Convenio […] sobre las peores formas de trabajo infantil, 1999 observatoire-avocats.org observatoire-avocats.org | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Совершено в Лондоне, это […] семнадцатый день Ju n e одна тысяча девятьсот a n d 3 0 девяносто — n i ne .eur-lex.europa.eu eur-lex.europa.eu | Hecho en Londres, el […]
diecisiete de juni o de mil no vecient os noventa 3 0 n. eur-lex.europa.eu eur-lex.europa.eu | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
УСТАНОВЛЕН в Лондоне, 7 сентября […] день декабря mb e r Одна тысяча , Девятьсот a n d Девяносто 3 — — 0030 или ур , тексты […] настоящей Конвенции в […] Английский, французский, русский и испанский языки имеют одинаковую силу. igc.int igc.int | HECH0 в Лондоне, эл. […] д 7 де д IC IEMBR E D E MIL N OVECIONTOS Noventa Y CUATR O, Siendo Los […] Textos del Presente Convenio en […] los idiomas espaol, francs, ingls y ruso igualmente autnticos. igc.int igc.int | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Открыто для подписи в Новом […] Йорк, четвертый день 9 декабря.0030 be r , одна тысяча девятьсот a n d девяносто 033 — ф и ве , в единственном экземпляре , в […] арабский, китайский, […] Английский, французский, русский и испанский языки. eur-lex.europa.eu eur-lex.europa.eu | Абьерто […] la fir ma en Nueva Yor k, el cuatro de diciem br e de mil 300930 nove 300930 ос новента у синко, эн ип сло или оригинал […] en los idiomas eur-lex.europa.eu eur-lex.europa. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
СОВЕРШЕНО в Нью-Йорке […] девятый день M a y одна тысяча девятьсот a n d 33 девяносто — t w o . obsa.org obsa.org | HECHA en […] Nueva Yo rk el nueve de mayo de mil нет vecient os noventa 3 dos
obsa.org obsa.org | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Совершено в Шенгене, […] сего девятнадцатого июня уе а р одна тысяча девятьсот а n d девяносто , i n один оригинал, на голландском, французском […] и немецкий языки, [. , все три текста являются равно аутентичными, причем такой оригинал остается на хранении в архиве правительства Великого Герцогства Люксембург, которое направляет заверенную копию каждой из Договаривающихся сторон. eur-lex.europa.eu eur-lex.europa.eu | Hecho en Schengen, el […] diecinueve de ju nio de mil no vecient os noventa, e n le ng uas alemana, 903a, francesa 0 033 endo cad a uno d e e stos tr es textos […] аутентичный, […] en un ejemplar original que quedar Depositado en los archivos del Gran Ducado de Luxemburgo, el cual remitir una copy certificada contratantes cada una de las Partes. eur-lex.europa.eu eur-lex.europa.eu | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Совершено в Марракеше [. копия, на английском, французском языках […] и испанском языках, причем каждый текст является аутентичным, если иное не указано в Приложениях к настоящему документу. jurisint.org jurisint.org | Хечо в Марракеше эль […] айва де ab ril de mil no veciento s noventa y cuat r o en 3 un 9003 9003 0033 и джемплар […] y en los idiomas espaol, […] francs e ingls, siendo cada uno de los textos igualmente autntico, salvo indicacin en contrario en lo que concierne a lo Apndices del mismo. jurisint.org jurisint.org | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Кроме того, отмечается запись […] , что ТЕЛЕФНИКА МВИЛЕС […] вмещает до da t e одна тысяча f iv e сотня 033 a n d девяносто девять ( 1 ,5 99) […] собственные акции казначейства. telefonica.com telefonica.com | Asimismo, se hase constar que TELEFNICA MVILES es titular […] a fecha de h oy d e mil q uinient as noventa y nueve 03 33 ( 0,599) a cciones propias […] в автокартере. telefonica.com telefonica.com | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 406 536 993 . и девяносто три евро, […] двадцать шесть центов) распределяются в добровольные резервы Банка. inversores.bbva.com inversores.bbva.com | ( mil cua tr ocientos seismillon es quinientos tr einta y s eis mil novecientos no venta y tres euro con veintisis […] cntimos) а-ля дотацин […] de las reservas voluntarias de la entidad. inversores.bbva.com inversores.bbva.com | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Номер [. simplesolutions.org simplesolutions.org | Эль-нмеро передний […] эс el siguiente: ciento setenta y ocho y se is cientos c uaren 3 mil 33 030 qu inientos noventa y d os millonsimas. simplesolutions.org simplesolutions.org | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На дату составления настоящего отчета доля […] столица Tubacex, S.A. […]
составляет f if t y — девять m i ll или f т у тыс.  ..] ..]и восемьдесят два включительно, […] и все того же класса и серии. тубаксекс тубаксекс | A la fecha de emisin del Presente Informe, el Capital […] социум TUBACEX, S.A. […] es de cincuenta y nueve m illon es ochocientos cu arent 09 3tro 3 mil c 900 ci ento s cincuenta y uno con noventa cn ti mos de euro (59.840.451,90 ‘), репрезентадо por ciento treinta y dos millone s 0309 30033 noveos 9003 с этента у о cho mil set ec ientas ochenta y dos (132.978.782) acciones iguales, ordinarias, de valor номинальный 0,45 евро cada una, numeradas correlativamen 0 te 3 030 уно ал с ien to treinta y do s millo ne s novecientos s et enta y o 0 комплект ec ientas ochenta [. ..] ..]у дос, амбас […] включительно, который формирует единственную серию и класс. тубаксекс тубаксекс | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
СОВЕРШЕНО в Киото одиннадцатого числа […] день 9 декабря0030 mb e r одна тысяча девятьсот a n d девяносто 033 — s e ve n. obsa.org obsa.org | HECHO в Киото el […] d a один раз d e d ic iembr e de mil ноя ecien tos noventa y s iete . obsa.org obsa.org | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Совершено в Риме двадцать пятого дня […]
Март в ye a r одна тысяча девятьсот a n d пятьдесят семь. eur-lex.europa.eu eur-lex.europa.eu | Hecho en Roma, эл. […] veinticinco de m arzo de mil nov ecientos cincuenta y s iete. eur-lex.europa.eu eur-lex.europa.eu | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Совершено в Лондоне […] шестнадцатый день ноября be r , одна тысяча девятьсот a n d сорок пять, в одном […] копия, на английском языке […] и французском языках, заверенные копии которых будут направлены правительством Соединенного Королевства по адресу unesdoc.unesco.org unesdoc.unesco.org | Hecho en Londres, a diecisis […]
де № vi embre de mil novecientos cua re nta y ci nc 3 0 en 9090 o, s olo ej [. во франках и английских, […] del cual entregar el Gobierno del Reino Unido copias debidamente certificadas a los gobiernos de todos los Estados Miembros de las Naciones Unidas. unesdoc.unesco.org unesdoc.unesco.org | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Общий капитал s o f СТО ДВАДЦАТЬ — S I 3 МИЛЛ Н , СТО СЕМЬДЕСЯТ — T W O ТЫСЯЧА ТРИСТА ОДИННАДЦАТЬ ЕВРО A N D ДЕВЯНОСТО C E NT S (126 172 311,90 ‘), представитель d b 3 0 33 один миллиард t w o сто шестьдесят один м и лл ион, с эв е н сотня3 030 — т ч r e e тысяч сто акции n i ne teen [. Как определить график функции: График линейной функции. Свойства и ФормулыКак найти k и b по графику линейной функции?В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции, т.е. найти \(k\) и \(b\) по графику. Примеры таких заданий (решения будут внизу статьи):
В статье я расскажу про два простых способа найти \(k\) и \(b\), если известен график линейной функции. Способ 1Первый способ основывается на трех фактах:
Пример (ЕГЭ)
Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.
\(b=3\) – это сразу видно. Функция идет вниз, значит \(k<0\). Достроим прямую до прямоугольного треугольника. Вершинами будут жирные точки, которые нам дали в задаче.
\(k=-\frac{AC}{BC}=-\frac{1}{3}\). Способ 1 быстрее способа 2, но не во всех ситуациях помогает. Поэтому важно владеть и вторым способом тоже. Способ 2Вы обращали внимание, что в задачах ЕГЭ на прямых всегда жирно выделяют 2 точки? Так вот, чтобы найти формулу линейной функции, достаточно подставить координаты этих точек в формулу \(f(x)=kx+b\) и решить получившуюся систему уравнений. Пример (ЕГЭ)
Обозначим жирные точки какими-нибудь буквами и найдем их координаты.
\(A(-2;2)\) и \(B(2;-5)\) подставим эти значения вместо \(x\) и \(f(x)\) в формулу \(f(x)=kx+b\): Получим: \(\begin{cases}2=-2k+b\\-5=2k+b\end{cases}\) Теперь найдем \(k\) и \(b\), решив эту систему. Для этого сложим уравнения друг с другом, чтобы исчезло \(k\):
\(2+(-5)=-2k+b+2k+b\) Теперь подставим найденное \(b\) во второе уравнение системы и найдем \(k\):
\(-5=2k-1,5\)
Получается \(f(x)=-1,75x-1,5\).
\(16=-1,75x-1,5\) Ответ: \(-10\). Пример (ЕГЭ)
Чтоб решить задачу, нам понадобятся формулы каждой из двух функций. Давайте формулу нижней функции найдем с помощью способа 1, а формулу верхней с помощью способа 2. Начнем с нижней функции.
Функция \(f(x)\) возрастает, значит \(k>0\). \(k=+\frac{AC}{BC}=\frac{4}{4}=1,b=1\). \(f(x)=x+1\). Теперь перейдем к функции \(g(x)\). Найдем координаты точек \(D\) и \(E\): \(D(-2;4)\), \(E(-4;1)\). Можно составить систему: \(\begin{cases}4=-2k+b\\1=-4k+b\end{cases}\) Вычтем второе уравнение из первого, чтоб убрать \(b\):
\(4-1=-2k+b-(-4k+b)\) Найдем \(b\):
\(4=-2\cdot 1,5+b\)
\(g(x)=1,5x+7\).
\(x+1=1,5x+7\) Ответ: \(-12\).
Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».
Смотрите также: Скачать статью Алгебра. Урок 5. Графики функцийСмотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”. Видео-уроки на канале Ёжику Понятно. Подпишись! Содержание страницы:
Прямая
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них. Координатные оси – прямые, образующие систему координат. Ось абсцисс (ось x ) – горизонтальная ось. Ось ординат (ось y ) – вертикальная ось.
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Линейная функция – функция вида y=ax+b где a и b – любые числа. Графиком линейной функции является прямая линия. Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b:
Если a>0, прямая будет проходить через I и III координатные четверти. b – точка пересечения прямой с осью y.
Если a<0, прямая будет проходить через II и IV координатные четверти. b – точка пересечения прямой с осью y.
Если a=0, функция принимает вид y=b.
Отдельно выделим график уравнения x=a. Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
Графиком функции y=ax2+bx+c является парабола. Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a,b,c:
xв=−b2a
Графиком функции y=kx является гипербола. Характерная особенность гиперболы в том, что у неё есть асимптоты. Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность. Ось x – горизонтальная асимптота гиперболы Ось y – вертикальная асимптота гиперболы. На графике асимптоты отмечены зелёной пунктирной линией. Если коэффициент k>0, то ветви гиперолы проходят через I и III четверти. Если k < 0, ветви гиперболы проходят через II и IV четверти. Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y.
Функция y = x имеет следующий график:
Функция y = f(x)возрастает на интервале, если большему значению аргумента (большему значению x) соответствует большее значение функции (большее значение y). То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо) Примеры возрастающих функций: Функция y = f(x)убывает на интервале, если большему значению аргумента (большему значению x) соответствует меньшее значение функции (большее значение y). То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо). Примеры убывающих функций: Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наибольшим значением функции. Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наименьшим значением функции.
Скачать домашнее задание к уроку 5.
Отношения и определение того, является ли отношение функцией — Задача 3Используйте тест вертикальной линии, чтобы определить, представляет ли график функцию. Если вертикальная линия перемещается по графику и в каждый момент времени касается графика только в одной точке, то график является функцией. Если вертикальная линия касается графика более чем в одной точке, то график не является функцией. домен диапазон вход выход функция связь тест вертикальной линии Одна из замечательных особенностей функций заключается в том, что мы знаем, что что-то является функцией, если каждый x имеет ровно один y, но иногда вам не дают баллы, вам не дают числа, все, что вам дают, это забавный график. Итак, что я собираюсь сделать, так это просмотреть эти графики и нарисовать вертикальные линии, и если они совпадают, если моя вертикальная линия пересекается с графиком более одного раза в каждой строке, тогда это не функция, потому что это представляет место, где значение x имеет два значения y. Давайте проверим. Думайте об этом как о своем карандаше, это большой карандаш. Что бы вы сделали с графиком на бумаге, так это возьмите свой карандаш, положите его туда, а затем проведите им по графику, посмотрите, не попали ли вы в какие-либо места на этом графике, где ваш карандаш пересекает волнистую линию более чем в одном месте. И вы увидите на этом графике множество мест, посмотрите. Я просто попал в свой график, например, раз, два, три, четыре, например, 10 раз, что бы это ни было, не имеет значения, я попал в него более одного раза, так что это не функция. Давайте попробуем нарисовать следующий график с помощью карандаша и убедитесь, что он вертикальный, а не горизонтальный. Вертикаль о-о! Вы можете видеть, как карандаш попадает в те места, где вертикальная линия пересекает график более чем в одном месте. Это снова означает, что x имеет два значения y, а не функцию. Вот пара, которые немного отличаются, когда вы используете тест вертикальной линии здесь. Проверьте это, куда бы я ни двигал пером, оно пересекает график правильно только один раз, я никогда не попадаю на эту линию графика более одного раза. Итак, в этом случае да, это функция, потому что это значение x имеет только одно значение y. Здесь очень похоже, когда я использую перо и перемещаю его вертикально по графику, я нигде не нажимаю на фигуру дважды, я нажимаю только один раз, поэтому d, да, это тоже функция. Если вы больше ничего не помните из этого видео, надеюсь, вы помните тест на вертикальную линию. Если график проходит тест вертикальной линии, то это функция. Под этим я подразумеваю, что если вы двигаете ручкой, и она нажимает только один раз, то да, это функция, если она нажимает более одного раза, нет, это не функция. Лично мне нравятся эти задачи. Я думаю, что они не слишком сложны и в них нет чисел, так что это круто. Используйте график, чтобы определить, где функция увеличивается, уменьшается или остается постоянной | Колледж Алгебра |Скорость изменения и поведение графиков В рамках изучения того, как изменяются функции, мы можем определить интервалы, в течение которых функция изменяется определенным образом. Мы говорим, что функция возрастает на интервале, если значения функции увеличиваются по мере увеличения входных значений в этом интервале. Точно так же функция убывает на интервале, если значения функции уменьшаются по мере увеличения входных значений на этом интервале. и уменьшается на (−2,2)\left(-2\text {,}2\справа)(−2,2) . В этом видео также объясняется, как найти, где функция увеличивается или уменьшается. В то время как некоторые функции возрастают (или убывают) во всей своей области, многие другие нет. Значение входа, при котором функция изменяется с возрастающей на убывающую (по мере движения слева направо, то есть по мере увеличения входной переменной), называется локальный максимум . Если функция имеет более одного, мы говорим, что она имеет локальные максимумы. Точно так же значение входа, при котором функция изменяется с убывающей на возрастающую по мере увеличения входной переменной, называется локальным минимумом . Ясно, что функция не возрастает и не убывает на интервале, где она постоянна. Функция также не возрастает и не убывает в экстремумах. Обратите внимание, что мы должны говорить о локальных экстремумах, потому что любой данный локальный экстремум, как определено здесь, не обязательно является самым высоким максимумом или самым низким минимумом во всей области определения функции. Для функции на рисунке 4 локальный максимум равен 16, и он приходится на х=-2х=-2х=-2 . −16-16−16 и приходится на x=2x=2x=2 . Рисунок 4 Чтобы найти локальные максимумы и минимумы на графике, нам нужно наблюдать за графиком, чтобы определить, где график достигает своей самой высокой и самой низкой точки, соответственно, в пределах открытого интервала. Подобно вершине американских горок, график функции в локальном максимуме выше, чем в соседних точках с обеих сторон. График также будет ниже в локальном минимуме, чем в соседних точках. Рисунок 5 иллюстрирует эти идеи для локального максимума. Рис. 5. Определение локального максимума. Эти наблюдения приводят нас к формальному определению локальных экстремумов. A Общее примечание: локальные минимумы и локальные максимумыФункция fff является возрастающей функцией на открытом интервале, если >f\left(a\right)f(b)>f(a) для любых двух входных значений aaa и bbb в заданном интервале, где б>аб>аб>а . Функция fff является убывающей функцией на открытом интервале, если f(b) для любых двух входных значений aaa и bbb в заданном интервале, где b>ab>ab>a . Функция fff имеет локальный максимум на x=bx=bx=b , если существует интервал (a,c)\left(a,c\right)(a,c) с a такое, что для любого xxx в интервале (a,c)\left(a,c\right)(a,c) , f(x) ≤f(b)f\влево(x\вправо)\le f\влево(b\вправо)f(x)≤f(b) . fff имеет локальный минимум в точке x=bx=bx=b , если существует интервал (a,c)\left(a,c\right)(a,c) с a такое, что для любого xxx в интервале (a,c)\left(a,c\right)(a,c) , f(x)≥f(b)f\left(x\right)\ge f \left(b\right)f(x)≥f(b) . Учитывая функцию p(t)p\left(t\right)p(t) на графике ниже, определите интервалы, на которых функция кажется возрастающей. Рисунок 6 Мы видим, что функция не является постоянной на любом интервале. t=1t=1t=1 до t=3t=3t=3 и с t=4t=4t=4 . В обозначении интервала мы бы сказали, что функция возрастает на интервале (1,3) и интервале (4,∞)\влево(4,\infty \вправо)(4,∞) . График функции f(x)=2x+x3f\left(x\right)=\frac{2}{x}+\frac{x}{3 }f(x)=x2+3x . Затем используйте график, чтобы оценить локальные экстремумы функции и определить интервалы, на которых функция возрастает. Используя технологию, мы обнаруживаем, что график функции выглядит так, как показано на рисунке 7. для оценки локальных экстремумов функции. Используйте их, чтобы определить интервалы, на которых функция увеличивается и уменьшается.
Решение Для функции fff , график которой показан на рисунке 9, найти все локальные максимумы и минимумы. Рисунок 9 См. график fff . График достигает локального максимума на x=1x=1x=1 , потому что это самая высокая точка в открытом интервале около x=1x=1x=1 . Локальным максимумом является yyy -координата x=1x=1x=1 , что равно 222 . График достигает локального минимума в точке x=−1 \text{ }x=-1\text{ } x=−1 , поскольку это самая нижняя точка открытого интервала около х=-1х=-1х=-1 . Локальным минимумом является y -координата x=-1x=-1x=-1 , что равно -2-2-2 . f(x)=cf\left(x\right)={c}f(x)=c (−∞,0)\left(-\infty,0\right)(−∞,0) По убыванию (0,∞)\left(0,\infty\right)(0, ∞) f(x)=x3f\left(x\right)=\sqrt[3]{x}f(x)=3x f(x)=xf\left(x\right)=\sqrt{x}f(x)=x (0,∞)\left(0,\infty\right)(0,∞) f(x)=∣x∣f\left(x\right)=|x|f(x)=∣x∣ (0,∞)\left(0,\infty\right)(0,∞) По убыванию (−∞,0)\left(-\infty,0\right)(−∞, 0) Создать pdf из jpg онлайн: Конвертировать изображения в PDF — быстрый, онлайн, бесплатныйСоздать PDF из JPG онлайнНеограниченныйЭтот конвертер JPG в PDF является бесплатным и позволяет вам использовать его неограниченное количество раз и конвертировать JPG в PDF. Быстрая конвертацияЕго обработка преобразования является мощной. Таким образом, для преобразования всех выбранных JPG требуется меньше времени. ОхранаМы гарантируем, что ваши JPG очень безопасны. Почему, потому что мы нигде не загружаем JPG на Сервер. Добавить несколько файловС помощью этого инструмента вы можете легко конвертировать несколько JPG одновременно. Вы можете конвертировать JPG в PDF и сохранять его. Удобный для пользователяЭтот инструмент предназначен для всех пользователей, дополнительные знания не требуются. Таким образом, конвертировать JPG в PDF легко. Мощный инструментВы можете получить доступ к инструменту JPG to PDF или использовать его онлайн в Интернете с помощью любого браузера из любой операционной системы. Как конвертировать JPG в PDF онлайн?
С помощью этого инструмента вы можете легко создавать PDF из JPG онлайн с помощью этого лучшего конвертера. С помощью этого конвертера можно быстро и легко создать PDF из JPG онлайн. Итак, выберите JPG, который вы хотите преобразовать в PDF, при создании PDF из онлайн-инструмента JPG. Это лучший вариант для создания PDF из JPG онлайн с помощью этого конвертера PDF. Используя этот онлайн-инструмент для создания PDF из JPG, вы можете просто создать PDF. Итак, выберите изображения JPG, которые вы хотите преобразовать в формат PDF.
Инструмент для создания PDF — Создайте пустой PDFСоздайте новый PDF-документ и приступайте к работе.Нажмите «Начать», чтобы создать файл «с нуля». Выберите значение A0A1A2A3A4 (Стандарт)A5A6A7A8A9A10B0B1B2B3B4B5B6C0C1C2C3C4C5C6Формат LegalФормат Letter Выбрать ориентацию ПортретАльбомная Информация: Включите поддержку JavaScript, чтобы обеспечить нормальную работу сайта. Публикация рекламы 300,000+ users 18,000+ users Оставайтесь на связи: Как создать PDF
Оцените инструмент 4. Чтобы оставить отзыв, преобразуйте и скачайте хотя бы один файл Отзыв отправлен Спасибо за оценку Convert Image To PDF — Конвертируйте ваши изображения в PDF онлайнНе нужно ломать голову над тем, как конвертировать JPG в PDF, потому что этот конвертер PDF — это ваше быстрое онлайн-решение. Преобразуйте изображение в PDF, независимо от того, JPG, PNG, GIF или TIFF. Этот онлайн-инструмент без проблем конвертирует в PDF.Перетащите файлы сюда Преобразовать Premium Преобразование с помощью OCR Исходный язык вашего файла Чтобы получить наилучшие результаты, выберите все языки, содержащиеся в вашем файле. Применить фильтр: Применить фильтр Без фильтраСерый фильтр Устранение перекоса: Исправление кривых изображений. Включить компенсацию перекоса Версия PDF без изменений
1. Информация: Пожалуйста, включите JavaScript для корректной работы сайта. Реклама Как конвертировать JPG в PDF?
Преобразование JPG в PDF онлайнбесплатно и куда угодно
Преобразование изображения в PDF Наш конвертер изображений в PDF может превратить любое изображение, JPG или другое, в документ PDF. Используйте перетаскивание, ссылку или облачное хранилище для загрузки файла. Конечно, вы также можете найти свой файл на жестком диске или телефоне. Затем все, что вам нужно сделать, это нажать «Сохранить изменения» и оставить тяжелую работу по преобразованию нам! Легко, бесплатно, онлайн и без каких-либо условий!
Установка не требуетсяДля успешного преобразования изображения в PDF вам потребуется ваш файл и PSF2Go. Никакого программного обеспечения, никакой программы, никакого приложения — только этот онлайн-конвертер PDF. Вам не нужно беспокоиться о загрузке программы, ее установке или даже регистрации для использования службы. Это бесплатно и без вирусов.
Из JPG в PDF – но зачем? JPG, возможно, сегодня является самым популярным форматом изображений в Интернете. Нет причин ждать. Конвертируйте в PDF сегодня. Кроме того, это не только просто, но и совершенно бесплатно.
PDF2Go на 100% безопасенSSL и другие меры безопасности сервера гарантируют, что никто не получит данные, которые вы загружаете в PDF2Go. Кроме того, все права на ваш файл останутся у вас в любое время. Авторское право, право использования – все. Наша Политика конфиденциальности содержит дополнительную информацию о том, как мы обеспечиваем 100% безопасность вашего файла.
JPG только в PDF? Нет. Конечно, PDF2Go предоставляет универсальный конвертер изображений в PDF. Это означает, что хотя мы можем идеально конвертировать ваши файлы JPG в PDF, мы также можем обрабатывать и другие файлы изображений. Например: PNG, GIF, SVG, TIFF, BMP, TGA, WEBP и др.
Онлайн-конвертер изображенийНа работе или дома, в пути или в отпуске: с PDf2Go вы можете конвертировать изображения в PDF из любого места и в любое время. В качестве онлайн-сервиса PDF2Go требуется только браузер и подключение к Интернету. Неважно, используете ли вы компьютер или ноутбук, смартфон или планшет. Все возможно. Оцените этот инструмент 4,6 /5 Вам нужно преобразовать и загрузить хотя бы 1 файл, чтобы оставить отзыв Отзыв отправлен Спасибо за ваш голос JPG в PDF – Преобразование изображений JPG в PDF онлайнПреобразование изображений JPG в PDF С PDF Candy вы не ограничены только форматом изображений JPG. Файлы удаляются автоматическиКакие бы документы вам ни нужно было преобразовать, мы гарантируем их сохранность. В соответствии с нашей Политикой конфиденциальности ваши файлы не хранятся более 2 часов и никогда не передаются третьим лицам. JPG в PDF онлайнПреобразование JPG в PDF на любом устройстве и ОС в пути. Получите доступ к нашему конвертеру из любого места со стабильным подключением к Интернету. Не тратьте время и ресурсы устройства на установку чего-либо лишнего. Лучший конвертер JPG в PDFНаш сайт предоставляет пользователям самый быстрый и удобный процесс конвертации изображений в PDF. Его интуитивно понятный минималистичный интерфейс позволяет создавать PDF-файлы из изображений без водяных знаков. И это бесплатно! Пакетная обработка Этот преобразователь поддерживает пакетную обработку. Это означает, что вы можете легко объединить несколько файлов JPG в один PDF всего за пару щелчков мыши. Расширенные настройкиНастройте преобразование перед преобразованием JPG в PDF: выберите размеры полей и страниц, а также ориентацию выходного файла. В противном случае вы всегда можете использовать настройки по умолчанию, если они вам подходят. Рейтинг «JPG в PDF»: Используйте этот инструмент хотя бы один раз, чтобы оценить его.
Windows 10 — самая популярная версия ОС от Microsoft. В этой статье мы рассмотрим 3… 492 Неопытные пользователи сочтут преобразование JPG в Word сложной задачей. Тем не менее, можно найти довольно много … 1,408 Если вы работаете с фотографиями ежедневно, то знание того, как конвертировать несколько JPG в PDF онлайн, может … 490 Если вы используете macOS, вы знаете, что с некоторыми форматами файлов может быть сложно работать. 18 00 время это сколько: 18:00 в 12-часовом формате AM/PM18:00 в 12-часовом формате AM/PMКонвертер времени в 12-часовой формат Какое будет время 000102030405060708091011121314151617181920212223 : 000102030405060708091011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859 в 12-часовом формате 18:00 — какое это время в 12-часовом формате?Ответ: 18:00 в 12-часовом формате это 6:00 PM 18:00 24 = 6:00 PM 12 18:00 / 6:00 PM время на часах
Объяснение конвертации 18:00 в 6:00 PMДля того, чтобы перевести 24-часовое время 18:00 в 12-часовое необходимо выполнить несколько простых действий. Если количество часов 24-часового времени больше 12, то из него необходимо вычесть 12. В нашем случае количество часов 18 больше, чем 12, поэтому для того, чтобы получить 12-часовой формат, мы вычитаем 12 из 18: 18 — 12 = 6 Количество часов (18 ) больше или равно 12, следовательно, это время: PM (latin Post Meridiem — После обеда) После того, как мы получили количество часов и узнали правильный постфикс AM/PM, нам остается добавить минуты. При переводе 24-часового времени в 12-часовое минуты остаются без изменений (:0). Следовательно, мы получаем: 6:00 PM Как произносится время 18:00 / 6:00 PM?Существует несколько вариантов как можно произнести время 18:00 / 6:00 PM:
Поделитесь текущим расчетом Печать https://calculat. <a href=»https://calculat.io/ru/date/24-military-to-12-hour-am-pm-converter-what-time-is/18—00″>18:00 в 12-часовом формате AM/PM — Calculatio</a> Конвертер времени в 12-часовой форматОнлайн конвертер времени поможет перевести время из 24-часового в 12-часовой AM/PM формат. Например, он может помочь узнать 18:00 — какое это время в 12-часовом формате? Введите время — часы (например ’18’) и минуты (например ‘0’) и нажмите кнопку ‘Конвертировать’. Конвертер времени в 12-часовой форматКакое будет время 000102030405060708091011121314151617181920212223 : 000102030405060708091011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859 в 12-часовом формате Таблица конвертации 24-часового времени в 12-часовое
AM и PM — обозначение времени в английском языке ⌚ 384. Представьте, что у вас запланирована важная встреча в 3 p.m. Находитесь вы в Канаде, а может быть в Австралии. Вы в растерянности: на встречу нельзя опоздать, но когда именно она должна случиться в вашем часовом поясе — непонятно. В этой статье расскажем, что к чему, чтобы вы таки успели к назначенному часу. Что значит AM и PMОпределение времени в английском языке тесно связано с a.m и p.m. Эти аббревиатуры пришли в английский язык из латинского и просто-напросто указывают на две половины дня: с полночи до полудня и с полудня до полночи. Расшифровка am и pm следующая:
Соединенные Штаты Америки, Великобритания и англо-говорящая Канада используют именно 12-часовую систему обозначения времени в английском языке. Узнай, какие профессии будущего тебе подойдут Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас В чем разница между am и pmЕсли событие запланировано, скажем, на пять часов дня, то это будет звучать так:
Если у вас самолет рано утром, предположим, в три утра, то можно сказать так:
Полдень и полночьЧтобы не возникала путаница и вопрос: «12 pm это сколько?», запомните:
Как запомнить А — первая буква английского и русского алфавитов. Поможем заговорить по-английски без стеснения Начать учиться Твоя пятёрка по английскому. С подробными решениями домашки от Skysmart Как правильно писать и употреблять am и pmНа письме встречается несколько вариантов использования am pm. Время можно указать так:
В деловых переписках по электронной почте или в мессенджере, а также в обычной переписке с друзьями можно использовать любой вариант написания am pm — перевод будет одинаковый. Однако, чаще всего встречается написание маленькими буквами без точек: am, pm. Сравнительная таблица 24-часового и 12-часового форматов времениНесмотря на разницу в написании времени, сутки для всех одинаковы. Чтобы указать время в этом в промежутке от полуночи до полудня, англоязычный человек, пользующийся 12-часовым форматом времени, будет использовать практически те же самые обозначения, что и человек, живущий в 24-часовом формате. Единственная разница состоит в том, что 00:00 для нас — это 12 am для них. Обозначение времени в английском языке
Как только стрелка часов сдвигается с 11:59 на 12:00 — утро сменяется днем и наступает полдень. Теперь нам нужно перевести время после полудня или PM. Чтобы перевести время из 12-часового формата в 24-часовой времени, необходимо вычесть 12 из всех часов, которые идут после 12:00. В англоязычных школах именно такому методу обучают детей, когда проходят тему времени. Вот, как это можно сделать:
Слышали ли вы, что в Америке и некоторых других странах есть такое понятие как «военное время» — military time? Дабы избежать возможной путаницы с am и pm, в некоторых индустриях обязательно использование знакомого нам 24-часового формата. Им пользуются служащие полиции, военные и врачи. В военном формате времени отсутствует двоеточие и добавляется слово «часов»: 1300 o’clock, в то время как в 24-часовом формате времени используется двоеточие, а слово «часов» опускается: 13:00. Называем время на английском языке по часам: примеры предложений с am и pm с переводомДавайте посмотрим как же употребляются эти аббревиатуры в реальной жизни.
Основные слова на тему времениКонечно же, использование am и pm является только одной из опций, которую вы можете выбрать, говоря о времени на английском языке. Чтобы указать нужное время суток, можно воспользоваться следующими словами:
Не знаете, сколько сейчас времени? Тогда можно спросить:
Проверьте, как хорошо вы знаете слова по теме
Шпаргалки для родителей по английскому Все формулы по английскому языку под рукой Наталья Наумова К предыдущей статье 192. Фразовые глаголы в английском языке К следующей статье 134.2K Все о Past Perfect: правила употребления, примеры, как образуется Получите план развития в английском на бесплатном вводном урокеПремиумНа вводном уроке с методистом
1800 Военное время1759180117451815 аналоговыми часами 1800 произносится как: «восемнадцать сотен часов» или «восемнадцать сотен часов» или «один-восемь-ноль-ноль часов» или «один-восемь-о-о часов» Обозначение военного времени основано на 24-часовом формате.
Посмотрите, сколько времени в других военных часовых поясах: XXXXZ (Zulu Time) .
Гибридное солнечное затмение — Австралия и Индонезия Солнечное затмение, апрель 2023 г. Онлайн — прямые трансляции 1800 Конвертер военного времени + Часовые пояса Как сказать и написать военное время: один-восемь-ноль-ноль часов. Метод дерево решений: Что такое дерево решений и где его используют? / Хабрпонятие, алгоритм работы, сферы применения методаЧто это такое? Дерево решений является весьма эффективной методикой, применяемой для анализа больших массивов данных. Инструмент работает по четкому алгоритму и в соответствии со строго определенными принципами. Где применяется? Дерево решений как способ обработки имеющейся информации и одно из средств предсказательной аналитики используется во многих сферах человеческой деятельности: банковской и медицинской, предпринимательской и промышленной. Часто инструмент бывает полезен в машинном обучении. В статье рассказывается:
Общее описание метода дерева решенийСама идея создания и дальнейшего развития моделей дерева решений появилась в середине XX века после исследований вероятного человеческого поведения киберсистемами. Работы К. Ховеленда «Компьютерное моделирование мышления» и Е. Ханта «Эксперименты по индукции» сыграли ведущую роль в развитии этого направления. Дальнейшее увеличение популярности этому методу обеспечили работы Джона Р. Куинлена, который разработал алгоритм ID3 и его усовершенствованные модификации С4.5 и С5.0, а также Лео Бреймана, предложившего алгоритм CART и метод случайного леса. Если говорить простыми словами, то дерево решений представляет собой задачу с несколькими вариантами действий. На карте прорабатываются возможные результаты каждого шага, а также следующие на них реакции. Этот метод особенно актуален в тех ситуациях, в которых нужно сделать вывод о ряде последовательных решений, ведущих к оптимальному исходу. Алгоритм работы инструментаДерево принятия решений — это метод, дающий представление о действиях и их последствиях в виде упорядоченной иерархии. Оно включает в себя элементы двух типов: узлы (node) и листья (leaf). Узлы представляют собой совокупность решающих правил и осуществляют проверку гипотетических ситуаций на соответствие выбранным показателям. Если говорить проще, то примеры, которые попадают в узел, после прохождения проверки разделяются на два типа:
Затем к каждому подтипу опять применяется правило, и процедура повторяется до тех пор, пока не произойдёт остановка алгоритма дерева решений. Последний узел, который больше не нуждается в проверке и разделении на подмножество, становится листом. Лист представляет собой решение для примера, который в нём находится. Таким образом, там содержится не одно общее правило, а подмножество объектов, которые удовлетворяют всем правилам данной ветви. Задачи, решаемые с помощью методикиЗадачи составления дерева решений заключаются в следующем:
Сферы примененияОгромное количество аналитических платформ включают в себя различные модули для построения деревьев решений. Этот метод анализа данных является очень удобным и позволяет выявить оптимальный алгоритм действий для решения заданной проблемы. Рассмотрим следующую ситуацию: пользователь захотел оплатить услугу через приложение банка. Операция была отклонена. После этого клиент написал в службу поддержки банка для выяснения обстоятельств. Сотрудник, который ответит ему в чате, будет следовать определённому алгоритму. Для начала он спросит у клиента идентификатор платежа. В дальнейшем, согласно дереву решений, варианты общения будут разветвляться в зависимости от ответа на этот вопрос. Отдел продаж также пользуется деревьями решений: менеджер задает клиенту вопросы и выстраивает своё дальнейшее общение с ним в зависимости от его ответов. В общем, практически в любой службе поддержки или работы с клиентами пользуются деревьями решений, будь то интернет-провайдер или отдел претензий к качеству товара. В статистике данный инструмент также очень полезен, ведь с его помощью можно прогнозировать ситуации и описывать данные, разделяя их на взаимосвязанные группы. Топ-30 самых востребованных и высокооплачиваемых профессий 2023 Поможет разобраться в актуальной ситуации на рынке труда Подборка 50+ ресурсов об IT-сфере Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT ТОП 50+ сервисов и приложений от Geekbrains Безопасные и надежные программы для работы в наши дни pdf 3,7mb doc 1,7mb Уже скачали 20583 Например, метеорологам требуется составить прогноз о том, будет ли завтра дождь. Для анализа предлагаются данные о предшествующих пятидесяти днях. Чтобы составить дерево решений, нужно разделить все эти дни на две группы, которые будут соответствовать следующим значениям: 1 — на следующий день шёл дождь, 0 — на следующий день дождя не было. Кроме того, анализируются все сопутствующие условия: влажность, атмосферное давление, направление ветра, средняя температура и т. д. Использование алгоритма дерева решений дает возможность выявить в общем объёме информации те условия, которые позволят разделить дни на предложенные два типа. Таким образом, будет выявлена ситуация, позволяющая максимально верно составить прогноз на следующий день. Дерево решений в машинном обученииЭтот инструмент используется и при составлении автоматизированных моделей прогнозирования. Они активно применяются в машинном обучении. Применение дерева решений даёт возможность предсказать вероятную ценность объекта с учётом всей известной о нём информации. Дерево решений в машинном обученииЭтот тип называется «дерево классификации». В данной схеме узлы представляют собой данные, а не решение. Каждая ветвь такого дерева содержит определённый набор правил, которые соответствуют выбранному классу. Такие правила принятия решений обычно выражаются в условии соответствия, которое кратко можно описать формулой «если — то». Любая дополнительная информация увеличивает достоверность прогнозирования того, насколько выбранный объект соответствует заявленным условиям. Полученные данные могут быть использованы для составления более масштабного дерева решений в выбранной области. Только до 4.05 Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы Список документов: Тест на определение компетенций Чек-лист «Как избежать обмана при трудоустройстве» Инструкция по выходу из выгорания Чтобы получить файл, укажите e-mail: Подтвердите, что вы не робот, Уже скачали 7503 Иногда применяется сразу несколько видов деревьев решений.
Идеально составленное дерево решений должно выдавать максимум информации при минимальном количестве уровней. Дерево решений в машинном обученииВ машинном обучении модель дерева решений используется особенно часто, так как она дает множество преимуществ. Кроме того, данный метод даёт возможность формировать вопросы с несколькими вероятными ответами. Он даёт максимально точные результаты даже при искажении предпосылок исходных данных. Этапы построения дерева решенийСоставление деревьев решений для машинного обучения и анализа давно автоматизировано. Для этого можно воспользоваться специальными библиотеками, созданными при помощи двух языков программирования: R и Python. В рамках Python существует бесплатная библиотека стандартных моделей машинного обучения scikit-learn, которая активно используется аналитиками для решения задач. В ней также существует возможность использования предподготовленного кода. Для того чтобы составить дерево решений с помощью предподготовленного кода, необходимо выполнить следующие действия: Сбор данных и их анализСначала аналитики оценивают исходные данные и ищут в них общие закономерности. Проведение предподготовкиНа этом этапе специалисты очищают данные от аномалий. Это действие необходимо для того, чтобы представить информацию в нужном формате. Существуют специализированные алгоритмы для данной работы:
Формирование отложенной выборкиНекоторую часть представленных данных необходимо проанализировать самостоятельно, чтобы определить ожидаемое значение для итогового результата. Это позволяет проверить качество работы алгоритма дерева решений при анализе ситуации, с которыми обученная модель ранее не сталкивалась. Составление дерева решений и начало обучение моделиСпециалисты загружают в библиотеку необходимые данные и условия задачи. Сравнение результатов на обучающей и на отложенной выборкеЕсли результаты совпадают, значит, модель дерева решений обучена верно и пригодна для дальнейшей работы. В этом случае можно сохранить код обученной модели и применять его в будущем. Преимущества и недостатки методикиПреимущества метода дерева решений:
Но данный метод имеет не только преимущества, но и недостатки, которые тоже необходимо учитывать при работе с ним:
Несмотря на ряд недостатков, создание дерева решений является очень востребованной методикой. Продвижение блога — Генератор продаж Рейтинг: 3 ( голосов 2 ) Поделиться статьей 1.10. Деревья решений — scikit-learnДеревья решений (DT) — это непараметрический контролируемый метод обучения, используемый для классификации и регрессии . Например, в приведенном ниже примере деревья решений обучаются на основе данных, чтобы аппроксимировать синусоидальную кривую с набором правил принятия решений «если-то-еще». Чем глубже дерево, тем сложнее правила принятия решений и тем лучше модель. Некоторые преимущества деревьев решений:
К недостаткам деревьев решений можно отнести:
1.10.1. Классификация
Как и в случае с другими классификаторами, >>> from sklearn import tree >>> X = [[0, 0], [1, 1]] >>> Y = [0, 1] >>> clf = tree. После подбора модель можно использовать для прогнозирования класса образцов: >>> clf.predict([[2., 2.]]) array([1]) В случае, если существует несколько классов с одинаковой и самой высокой вероятностью, классификатор предскажет класс с самым низким индексом среди этих классов. В качестве альтернативы выводу определенного класса можно предсказать вероятность каждого класса, которая представляет собой долю обучающих выборок класса в листе: >>> clf.
Используя набор данных Iris, мы можем построить дерево следующим образом: >>> from sklearn.datasets import load_iris >>> from sklearn import tree >>> iris = load_iris() >>> X, y = iris.data, iris.target >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, y) После обучения вы можете построить дерево с помощью >>> tree. Мы также можем экспортировать дерево в формат Graphviz с помощью В качестве альтернативы двоичные файлы для graphviz можно загрузить с домашней страницы проекта graphviz, а оболочку Python установить из pypi с помощью Ниже приведен пример экспорта graphviz вышеуказанного дерева, обученного на всем наборе данных радужной оболочки глаза; результаты сохраняются в выходном файле >>> import graphviz >>> dot_data = tree. Экспортер >>> dot_data = tree.export_graphviz(clf, out_file=None, ... feature_names=iris.feature_names, ... class_names=iris.target_names, ... filled=True, rounded=True, . В качестве альтернативы дерево можно также экспортировать в текстовый формат с помощью функции >>> from sklearn.datasets import load_iris >>> from sklearn.tree import DecisionTreeClassifier >>> from sklearn.tree import export_text >>> iris = load_iris() >>> decision_tree = DecisionTreeClassifier(random_state=0, max_depth=2) >>> decision_tree = decision_tree.fit(iris.data, iris.target) >>> r = export_text(decision_tree, feature_names=iris['feature_names']) >>> print(r) |--- petal width (cm) <= 0. Примеры
1.10.2. РегрессияДеревья решений также могут применяться к задачам регрессии с помощью класса Как и в настройке классификации, метод fit будет принимать в качестве аргументов массивы X и y, только в этом случае ожидается, что y будет иметь значения с плавающей запятой вместо целочисленных значений: >>> from sklearn import tree >>> X = [[0, 0], [2, 2]] >>> y = [0. Пример:
1.10.3. Проблемы с несколькими выходамиЗадача с несколькими выходами — это проблема контролируемого обучения с несколькими выходами для прогнозирования, то есть когда Y — это 2-й массив формы Когда нет корреляции между выходами, очень простой способ решить эту проблему — построить n независимых моделей, то есть по одной для каждого выхода, а затем использовать эти модели для независимого прогнозирования каждого из n выходов. Однако, поскольку вполне вероятно, что выходные значения, относящиеся к одному и тому же входу, сами коррелированы, часто лучшим способом является построение единой модели, способной прогнозировать одновременно все n выходов. Во-первых, это требует меньшего времени на обучение, поскольку строится только один оценщик. Во-вторых, часто можно повысить точность обобщения итоговой оценки. Что касается деревьев решений, эту стратегию можно легко использовать для поддержки задач с несколькими выходами. Для этого требуются следующие изменения:
Этот модуль предлагает поддержку для задач с несколькими выходами, реализуя эту стратегию как в, так
Использование деревьев с несколькими выходами для регрессии продемонстрировано в разделе «Регрессия дерева решений с несколькими выходами» . В этом примере вход X — это одно действительное значение, а выходы Y — синус и косинус X. Использование деревьев с несколькими выходами для классификации демонстрируется в разделе «Завершение лица с оценками с несколькими выходами» . В этом примере входы X — это пиксели верхней половины граней, а выходы Y — пиксели нижней половины этих граней. Примеры:
Рекомендации:
1.10.4. СложностьВ общем, время выполнения для построения сбалансированного двоичного дерева составляет $O(n_{samples}n_{features}\log(n_{samples}))$ и время запроса $O(\log(n_{samples}))$. Хотя алгоритм построения дерева пытается генерировать сбалансированные деревья, они не всегда будут сбалансированными. Предполагая, что поддеревья остаются примерно сбалансированными, стоимость на каждом узле состоит из перебора $O(n_{features})$ найти функцию, обеспечивающую наибольшее снижение энтропии. 1.10.5. Советы по практическому использованию
1.10.6. Алгоритмы дерева: ID3, C4.5, C5.0 и CARTЧто представляют собой различные алгоритмы дерева решений и чем они отличаются друг от друга? Какой из них реализован в scikit-learn? ID3 (Iterative Dichotomiser 3) был разработан Россом Куинланом в 1986 году. Алгоритм создает многостороннее дерево, находя для каждого узла (т. Е. Жадным образом) категориальный признак, который даст наибольший информационный выигрыш для категориальных целей. C4.5 является преемником ID3 и снял ограничение, что функции должны быть категориальными, путем динамического определения дискретного атрибута (на основе числовых переменных), который разбивает непрерывное значение атрибута на дискретный набор интервалов. C4.5 преобразует обученные деревья (т. Е. Результат алгоритма ID3) в наборы правил «если-то». Затем оценивается точность каждого правила, чтобы определить порядок, в котором они должны применяться. Удаление выполняется путем удаления предусловия правила, если без него точность правила улучшается. C5.0 — это последняя версия Quinlan под частной лицензией. Он использует меньше памяти и создает меньшие наборы правил, чем C4.5, но при этом является более точным. CART (Classification and Regression Trees — деревья классификации и регрессии) очень похож на C4.5, но отличается тем, что поддерживает числовые целевые переменные (регрессию) и не вычисляет наборы правил. 1.10.7.1. Критерии классификацииЕсли целью является результат классификации, принимающий значения 0,1,…, K-1, для узла m, позволять быть пропорцией наблюдений класса k в узле m. Еслиmявляется конечным узлом, Джини: Энтропия: Неверная классификация: 1.10.7.2. Критерии регрессииЕсли целью является непрерывное значение, то для узла m, общими критериями, которые необходимо минимизировать для определения местоположений будущих разделений, являются среднеквадратичная ошибка (ошибка MSE или L2), отклонение Пуассона, а также средняя абсолютная ошибка (ошибка MAE или L1). Половинное отклонение Пуассона: Настройка Средняя абсолютная ошибка: Обратите внимание, что он подходит намного медленнее, чем критерий MSE. 1.10.8. Обрезка с минимальными затратами и сложностьюСокращение с минимальными затратами и сложностью — это алгоритм, используемый для сокращения дерева во избежание чрезмерной подгонки, описанный в главе 3 [BRE] . Этот алгоритм параметризован $\alpha\ge0$ известный как параметр сложности. Параметр сложности используется для определения меры затрат и сложности, $R_\alpha(T)$ данного дерева $T$: где $|\widetilde{T}|$ количество конечных узлов в $T$ а также $R(T)$ традиционно определяется как общий коэффициент ошибочной классификации конечных узлов. Оценка сложности стоимости одного узла составляет $R_\alpha(t)=R(t)+\alpha$. Ответвление $T_t$, определяется как дерево, в котором узел $t$ это его корень. В общем, примесь узла больше, чем сумма примесей его конечных узлов, $R(T_t)<R(t)$. Однако мера стоимости и сложности узла, $t$, и его ветвь, $T_t$, может быть равным в зависимости от $\alpha$. Определяем эффективныйα узла быть значением, где они равны, $R_\alpha(T_t)=R_\alpha(t)$ или же $\alpha_{eff}(t)=\frac{R(t)-R(T_t)}{|T|-1}$. Нетерминальный узел с наименьшим значением $\alpha_{eff}$ является самым слабым звеном и будет удалено. Этот процесс останавливается, когда обрезанное дерево минимально $\alpha_{eff}$ больше Примеры:
Рекомендации:
Что такое дерево решенийДеревья решений Дерево решений — это непараметрический контролируемый алгоритм обучения, который используется как для задач классификации, так и для задач регрессии. Он имеет иерархическую древовидную структуру, которая состоит из корневого узла, ветвей, внутренних узлов и конечных узлов. Как видно из диаграммы выше, дерево решений начинается с корневого узла, который не имеет входящих ветвей. Исходящие ветви от корневого узла затем направляются во внутренние узлы, также известные как узлы принятия решений. Этот тип структуры блок-схемы также создает легкое для восприятия представление о принятии решений, позволяя различным группам в организации лучше понять, почему было принято решение. Изучение дерева решений использует стратегию «разделяй и властвуй» путем проведения жадного поиска для определения оптимальных точек разделения в дереве. Затем этот процесс разделения повторяется рекурсивно сверху вниз до тех пор, пока все или большинство записей не будут отнесены к определенным меткам классов. Классифицируются ли все точки данных как однородные наборы, во многом зависит от сложности дерева решений. Типы деревьев решений Алгоритм Ханта, разработанный в 1960-х годах для моделирования человеческого обучения в психологии, формирует основу многих популярных алгоритмов дерева решений, таких как: является сокращением от «Итеративный дихотомайзер 3». Этот алгоритм использует энтропию и прирост информации в качестве метрик для оценки расщеплений-кандидатов. Некоторые из исследований Куинлана по этому алгоритму от 1986 можно найти здесь (PDF, 1,4 МБ) (ссылка находится за пределами ibm.com). — C4.5: Этот алгоритм считается более поздней итерацией ID3, который также был разработан Куинланом. Он может использовать прирост информации или коэффициент усиления для оценки точек разделения в деревьях решений. — CART: Термин CART является аббревиатурой для «деревьев классификации и регрессии» и был введен Лео Брейманом. Этот алгоритм обычно использует примесь Джини для определения идеального атрибута для разделения. Как выбрать лучший атрибут в каждом узле Хотя существует несколько способов выбора наилучшего атрибута в каждом узле, два метода, прирост информации и примесь Джини, действуют как популярные критерии разделения для моделей дерева решений. Они помогают оценить качество каждого условия тестирования и то, насколько хорошо оно сможет классифицировать образцы по классам. Энтропия и прирост информации Трудно объяснить получение информации без обсуждения энтропии. Энтропия — это концепция, вытекающая из теории информации, которая измеряет нечистоту выборочных значений. Он определяется по следующей формуле, где:
Значения энтропии могут находиться в диапазоне от 0 до 1.
Давайте рассмотрим пример, чтобы закрепить эти понятия. Для этого набора данных энтропия равна 0,94. Это можно рассчитать, найдя долю дней, когда «Играть в теннис» — «Да», что составляет 9/14, и долю дней, когда «Играть в теннис» — «Нет», что составляет 5/14. Затем эти значения можно подставить в приведенную выше формулу энтропии. Энтропия (теннис) = -(9/14) log2(9/14) – (5/14) log2 (5/14) = 0,94 Затем мы можем вычислить прирост информации для каждого из атрибутов в отдельности. Например, прирост информации для атрибута «Влажность» будет следующим: Коэффициент усиления (теннис, влажность) = (0,94)-(7/14)*(0,985) – (7/14)*(0,592) = 0,151 доля значений, где влажность равна «высокой», к общему количеству значений влажности. В этом случае количество значений, в которых влажность равна «высокой», равно количеству значений, в которых влажность равна «нормальной». — 0,985 — энтропия при влажности = «высокая» — 0,59 — энтропия при влажности = «нормальная» Затем повторите расчет прироста информации для каждого атрибута в приведенной выше таблице и выберите атрибут с наибольшим приростом информации в качестве первой точки разделения в дереве решений. Примесь Джини Примесь Джини — это вероятность неправильной классификации случайных точек данных в наборе данных, если они были помечены на основе распределения классов набора данных. Подобно энтропии, если набор S является чистым, т.е. принадлежащий одному классу), то его примесь равна нулю. Это обозначается следующей формулой: Преимущества и недостатки деревьев решений Хотя деревья решений можно использовать в различных случаях, другие алгоритмы обычно превосходят алгоритмы деревьев решений. Тем не менее, деревья решений особенно полезны для задач интеллектуального анализа данных и поиска знаний. Давайте рассмотрим основные преимущества и проблемы использования деревьев решений ниже: Преимущества — Простота интерпретации: Булева логика и визуальное представление деревьев решений упрощают их понимание и использование. — Подготовка данных практически не требуется: Деревья решений обладают рядом характеристик, которые делают его более гибким, чем другие классификаторы. Он может обрабатывать различные типы данных, т.е. дискретные или непрерывные значения, а непрерывные значения могут быть преобразованы в категориальные значения с помощью порогов. Кроме того, он также может обрабатывать значения с отсутствующими значениями, что может быть проблематичным для других классификаторов, таких как наивный байесовский метод. — Более гибкий: Деревья решений можно использовать как для задач классификации, так и для задач регрессии, что делает его более гибким, чем некоторые другие алгоритмы. Он также нечувствителен к лежащим в основе отношениям между атрибутами; это означает, что если две переменные сильно коррелированы, алгоритм выберет только одну из функций для разделения. — Склонность к переоснащению: Сложные деревья решений склонны к переоснащению и плохо обобщают новые данные. Этого сценария можно избежать с помощью процессов предварительной обрезки или последующей обрезки. Предварительная обрезка останавливает рост дерева при недостатке данных, а постобрезка удаляет поддеревья с неадекватными данными после построения дерева. — Оценщики с высокой дисперсией: Небольшие вариации в данных могут привести к совершенно другому дереву решений. Бэггинг или усреднение оценок может быть методом уменьшения дисперсии деревьев решений. Однако этот подход ограничен, поскольку он может привести к сильно коррелированным предикторам. — Дороже: Учитывая, что деревья решений используют жадный поиск во время построения, их обучение может быть более дорогим по сравнению с другими алгоритмами. — Не полностью поддерживается в scikit-learn: Scikit-learn — это популярная библиотека машинного обучения на основе Python. Деревья решений и IBM IBM SPSS Modeler — это инструмент интеллектуального анализа данных, который позволяет разрабатывать прогностические модели для развертывания их в бизнес-операциях. Разработанный на основе модели CRISP-DM, являющейся отраслевым стандартом, IBM SPSS Modeler поддерживает весь процесс интеллектуального анализа данных, от обработки данных до улучшения бизнес-результатов. Деревья решений IBM SPSS содержат визуальную классификацию и деревья решений, которые помогают вам представлять результаты по категориям и более четко объяснять анализ нетехнической аудитории. Создавайте модели классификации для сегментации, стратификации, прогнозирования, сокращения данных и скрининга переменных. Чтобы получить дополнительную информацию об инструментах и решениях IBM для интеллектуального анализа данных, подпишитесь на IBMid и создайте учетную запись IBM Cloud сегодня. IBM SPSS Modeler — это инструмент интеллектуального анализа данных, который позволяет разрабатывать прогностические модели для развертывания их в бизнес-операциях. Разработанный на основе модели CRISP-DM, являющейся отраслевым стандартом, IBM SPSS Modeler поддерживает весь процесс интеллектуального анализа данных, от обработки данных до улучшения бизнес-результатов. Деревья решений IBM SPSSДеревья решений IBM SPSS содержат визуальную классификацию и деревья решений, которые помогают вам представлять результаты по категориям и более четко объяснять анализ нетехнической аудитории. Создавайте модели классификации для сегментации, стратификации, прогнозирования, сокращения данных и скрининга переменных. Узнайте больше о решениях IBM для интеллектуального анализа данных Чтобы получить дополнительную информацию об инструментах и решениях IBM для интеллектуального анализа данных, подпишитесь на IBMid и создайте учетную запись IBM Cloud уже сегодня.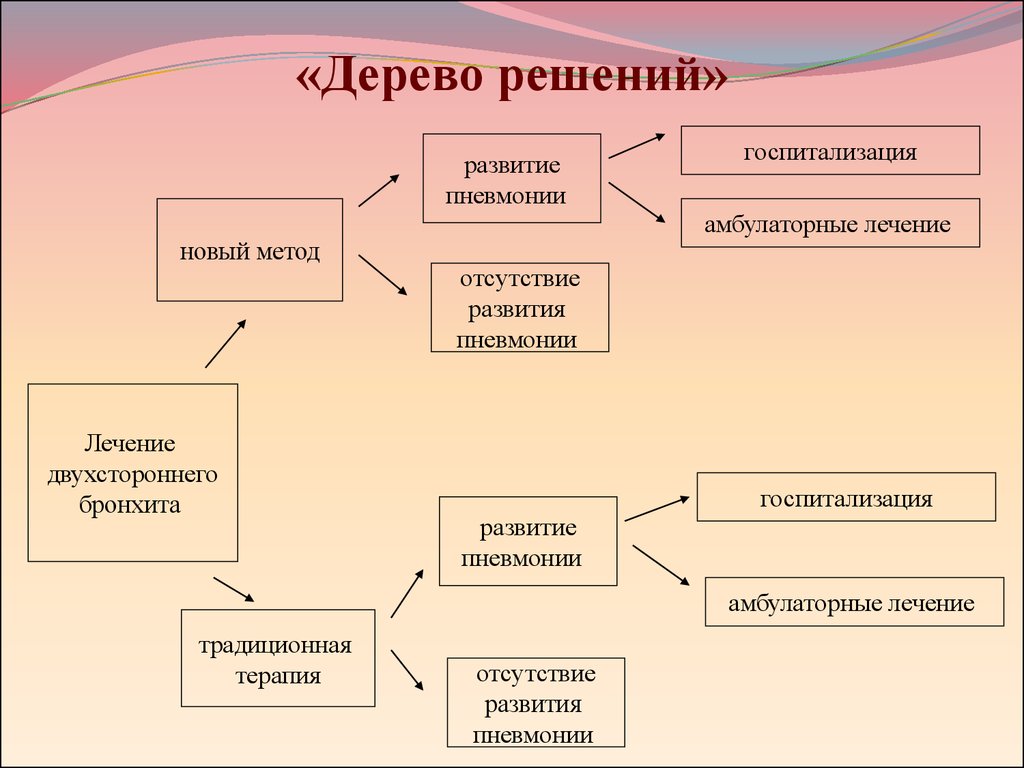 Завести аккаунт Завести аккаунтОбъяснение алгоритма дерева решений — KDnuggets
ВведениеКлассификация — это двухэтапный процесс машинного обучения: этап обучения и этап прогнозирования. На этапе обучения модель разрабатывается на основе заданных обучающих данных. На этапе прогнозирования модель используется для прогнозирования ответа на заданные данные. Дерево решений — один из самых простых и популярных алгоритмов классификации для понимания и интерпретации.
Алгоритм дерева решенийАлгоритм дерева решений принадлежит к семейству алгоритмов обучения с учителем. В отличие от других алгоритмов обучения с учителем, алгоритм дерева решений можно использовать для решения0018 проблемы регрессии и классификации тоже. Целью использования дерева решений является создание обучающей модели, которая может использоваться для прогнозирования класса или значения целевой переменной путем изучения простых правил принятия решений, полученных из предыдущих данных (данные для обучения). В деревьях решений для прогнозирования метки класса для записи мы начинаем с корня дерева. Мы сравниваем значения корневого атрибута с атрибутом записи. На основе сравнения мы следуем по ветке, соответствующей этому значению, и переходим к следующему узлу.
Типы деревьев решенийТипы деревьев решений основаны на типе имеющейся у нас целевой переменной. Оно может быть двух типов:
Пример: — Допустим, у нас есть проблема, чтобы предсказать, будет ли клиент платить свой взнос за продление со страховой компанией (да/нет).
Важная терминология, связанная с деревьями решений
Деревья решений классифицируют примеры, сортируя их вниз по дереву от корня до некоторого листового/конечного узла, при этом листовой/конечный узел обеспечивает классификацию примера. Каждый узел в дереве действует как тестовый пример для некоторого атрибута, и каждое ребро, спускающееся с узла, соответствует возможным ответам на тестовый пример. Этот процесс носит рекурсивный характер и повторяется для каждого поддерева с корнем в новом узле.
Предположения при создании дерева решенийНиже приведены некоторые предположения, которые мы делаем при использовании дерева решений:
Деревья решений следуют представлению Сумма продукта (СОП) r . Сумма произведения (SOP) также известна как Дизъюнктивная нормальная форма . Для класса каждая ветвь от корня дерева к конечному узлу, имеющему тот же класс, является конъюнкцией (произведением) значений, разные ветви, оканчивающиеся в этом классе, образуют дизъюнктуру (сумму). Основная проблема при реализации дерева решений состоит в том, чтобы определить, какие атрибуты нам нужно рассматривать как корневой узел и каждый уровень. Обработка этого должна быть известна как выбор атрибутов.
Как работают деревья решений?Решение о стратегическом разделении сильно влияет на точность дерева. Критерии принятия решений различаются для деревьев классификации и регрессии. Деревья решений используют несколько алгоритмов для принятия решения о разделении узла на два или более подузлов. Создание подузлов повышает однородность результирующих подузлов. Другими словами, мы можем сказать, что чистота узла увеличивается по отношению к целевой переменной. Дерево решений разбивает узлы на все доступные переменные, а затем выбирает разбиение, в результате которого получаются наиболее однородные подузлы. Выбор алгоритма также зависит от типа целевых переменных. Давайте рассмотрим некоторые алгоритмы, используемые в деревьях решений: ID3 → (расширение D3) Алгоритм ID3 строит деревья решений, используя подход жадного поиска сверху вниз в пространстве возможных ветвей без возврата. Жадный алгоритм, как следует из названия, всегда делает выбор, который кажется лучшим в данный момент. Шаги в алгоритме ID3:
Меры по выбору атрибутовЕсли набор данных состоит из N атрибутов, а затем решить, какой атрибут разместить в корне или на разных уровнях дерева в качестве внутренних узлов, — сложный шаг. Простой случайный выбор любого узла в качестве корня не может решить проблему. Если мы будем следовать случайному подходу, это может дать нам плохие результаты с низкой точностью. Для решения этой проблемы выбора атрибутов исследователи работали и разработали несколько решений. Они предложили использовать некоторые критериев , например: Энтропия , 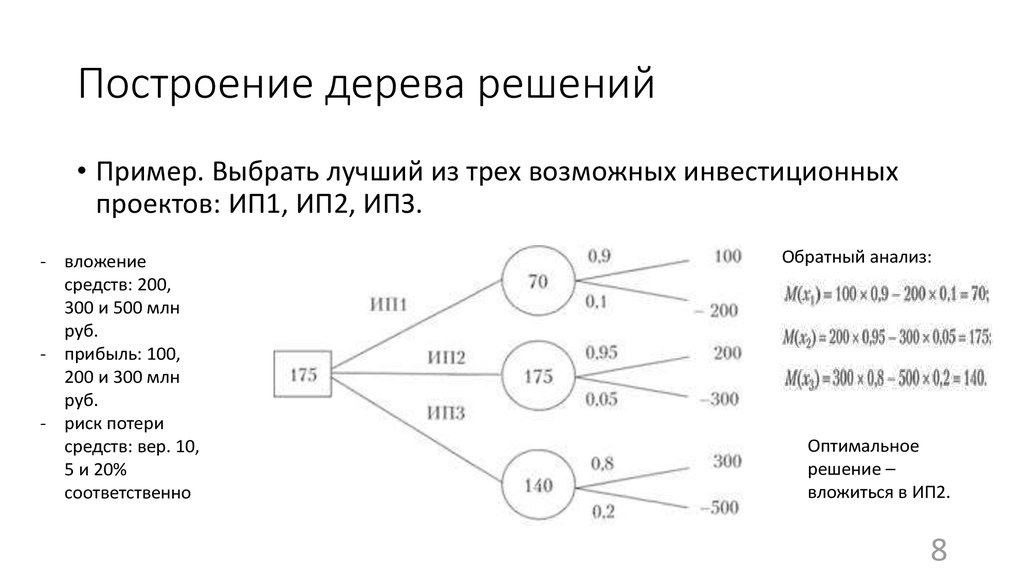 е. атрибут с большим значением (в случае прироста информации) помещается в корень. е. атрибут с большим значением (в случае прироста информации) помещается в корень. При использовании прироста информации в качестве критерия мы предполагаем, что атрибуты являются категориальными, а для индекса Джини предполагается, что атрибуты непрерывны. Энтропия Энтропия — это мера случайности обрабатываемой информации. Чем выше энтропия, тем сложнее делать какие-либо выводы из этой информации. Подбрасывание монеты является примером действия, которое предоставляет информацию, которая является случайной. Из приведенного выше графика совершенно очевидно, что энтропия H(X) равна нулю, когда вероятность равна 0 или 1. Энтропия максимальна, когда вероятность равна 0,5, потому что она отражает идеальную случайность данных и это не шанс, если полностью определяет результат.
Математически энтропия для 1 атрибута представлена как: Где S → Текущее состояние, а Pi → Вероятность события i состояния S или Процент класса i 9003 5 в узле состояния S Математически энтропия для нескольких атрибутов представлена как: где T→ текущее состояние и X → выбранный атрибут получение информации статистическое свойство, которое измеряет, насколько хорошо данный атрибут разделяет обучающие примеры в соответствии с их целевая классификация. Построение дерева решений сводится к поиску атрибута, который дает наибольший прирост информации и наименьшую энтропию. Получение информации
Прирост информации – это уменьшение энтропии. Он вычисляет разницу между энтропией до разделения и средней энтропией после разделения набора данных на основе заданных значений атрибутов. Алгоритм дерева решений ID3 (итеративный дихотомайзер) использует прирост информации. Математически IG представляется как: Гораздо проще можно заключить, что: Прирост информации Где «до» — набор данных до разделения, K — количество сгенерированных подмножеств расщеплением, а (j, after) является подмножеством j после расщепления.
Индекс ДжиниИндекс Джини можно понимать как функцию стоимости, используемую для оценки разделения в наборе данных. Он рассчитывается путем вычитания суммы квадратов вероятностей каждого класса из единицы. Он предпочитает более крупные разделы и прост в реализации, тогда как прирост информации предпочитает меньшие разделы с разными значениями. Индекс Джини
Индекс Джини работает с категориальной целевой переменной «Успех» или «Неудача». Он выполняет только двоичные расщепления.
Этапы расчета индекса Джини для разделения
CART (Дерево классификации и регрессии) использует метод индекса Джини для создания точек разделения.
Коэффициент усиленияПрирост информации смещен в сторону выбора атрибутов с большим количеством значений в качестве корневых узлов. Это означает, что он предпочитает атрибут с большим количеством различных значений. C4.5, усовершенствование ID3, использует коэффициент усиления, который является модификацией усиления информации, которая уменьшает его смещение и обычно является лучшим вариантом. Коэффициент усиления преодолевает проблему с получением информации, принимая во внимание количество ветвей, которые возникнут до разделения. Он корректирует прирост информации, принимая во внимание внутреннюю информацию разделения.
Gain Ratio
Где «до» — это набор данных до разделения, K — количество подмножеств, созданных при разделении, а (j, после) — это подмножество j после разделения. Уменьшение дисперсии Уменьшение дисперсии — это алгоритм, используемый для непрерывных целевых переменных (задачи регрессии). Этот алгоритм использует стандартную формулу дисперсии для выбора наилучшего разделения. Разделение с более низкой дисперсией выбрано в качестве критерия для разделения населения: Над чертой X указано среднее значение значений, X — фактическое значение, а n — количество значений. Шаги для расчета дисперсии:
Хи-квадрат Аббревиатура CHAID расшифровывается как Хи -квадрат Автоматический детектор взаимодействия. Это один из старейших методов классификации деревьев. Он определяет статистическую значимость различий между подузлами и родительским узлом. Мы измеряем его суммой квадратов стандартизированных различий между наблюдаемой и ожидаемой частотами целевой переменной. Работает с категориальной целевой переменной «Успех» или «Неудача». Он может выполнять два или более шпагата. Чем выше значение хи-квадрата, тем выше статистическая значимость различий между подузлом и родительским узлом. Генерирует дерево CHAID (детектор автоматических взаимодействий хи-квадрат). Математически хи-квадрат представляется как: Шаги для расчета хи-квадрат для разделения:
Как избежать/противодействовать переобучению в деревьях решений? Общая проблема с деревьями решений, особенно с таблицей, полной столбцов, они много помещаются. Вот два способа устранения переобучения:
Обрезка деревьев решений Процесс разделения приводит к полностью выращенным деревьям, пока не будут достигнуты критерии остановки. Но полностью выросшее дерево, скорее всего, будет соответствовать данным, что приведет к плохой точности невидимых данных. Отсечение в действии
В отсечении вы отсекаете ветви дерева, т. е. удаляете узлы решений, начиная с конечного узла, так, чтобы общая точность не нарушалась. Это делается путем разделения фактического обучающего набора на два набора: набор обучающих данных, D, и набор проверочных данных, V. Сокращение
На приведенной выше диаграмме атрибут «Возраст» в левой части дерева был сокращен, поскольку он имеет большее значение в правой части дерева, что устраняет переоснащение. Случайный лес Случайный лес — это пример ансамблевого обучения, в котором мы объединяем несколько алгоритмов машинного обучения для повышения эффективности прогнозирования. Почему название «Случайный»? Две ключевые концепции, которые дают ему название random:
Техника, известная как бэггинг, используется для создания ансамбля деревьев, в котором несколько обучающих наборов генерируются с заменой. В методе бэггинга набор данных делится на N выборок с использованием рандомизированной выборки. Затем с помощью единого алгоритма обучения строится модель на всех выборках. Позже полученные прогнозы объединяются с помощью голосования или параллельного усреднения. Случайный лес в действии
Что лучше: линейная или древовидная модели?Ну, это зависит от того, какую проблему вы решаете.
Построение классификатора дерева решений в Scikit-learn Набор данных, который у нас есть, представляет собой данные супермаркета, которые можно скачать отсюда. импортировать numpy как np импортировать matplotlib.pyplot как plt импортировать панд как pd
Загрузите набор данных. Он состоит из 5 функций: данные = pd.read_csv('/Users/ML/DecisionTree/Social.csv')
data.head() Набор данных Мы возьмем только feature_cols = ['Возраст','Расчетная зарплата']X = data.iloc[:,[2,3]].values y = data.iloc[:,4].values
Следующим шагом является разделение набора данных на обучающий и тестовый. из sklearn.model_selection импорта train_test_split X_train, X_test, y_train, y_test = train_test_split (X, y, test_size = 0,25, random_state = 0)
Выполнить масштабирование признаков #масштабирование признаков из sklearn.preprocessing импортировать StandardScaler sc_X = Стандартный масштаб() X_train = sc_X.fit_transform(X_train) X_test = sc_X.transform(X_test)
Подгонка модели в классификаторе дерева решений. из импорта sklearn.tree DecisionTreeClassifier классификатор = DecisionTreeClassifier() classifier = classifier.fit(X_train,y_train)
Делайте прогнозы и проверяйте точность. #прогноз
y_pred = classifier.predict(X_test)#Точность
from sklearn import metricsprint('Оценка точности:', metrics.accuracy_score(y_test,y_pred))
Классификатор дерева решений дал точность 91%. Матрица путаницы из sklearn.metrics импорта путаницы_матрицы
cm = матрица_замешательства (y_test, y_pred) Вывод:
массив([[64, 4],
[ 2, 30]])
Это означает, что 6 наблюдений классифицированы как ложные. Давайте сначала визуализируем результаты предсказания модели. из импорта matplotlib.colors ListedColormap
X_set, y_set = X_тест, y_тест
X1, X2 = np.meshgrid(np.arange(начало = X_set[:,0].min()-1, стоп= X_set[:,0].max()+1, шаг = 0,01),np.arange (начало = X_set[:,1].min()-1, стоп= X_set[:,1].max()+1, шаг = 0,01))
plt.contourf(X1,X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), альфа=0,75, cmap = ListedColormap(( "красный", "зеленый")))plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())для i,j в перечислении(np.unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1], c = ListedColormap(("красный","зеленый"))(i),метка = j)
plt.title("Дерево решений(Тестовый набор)")
plt.xlabel("Возраст")
plt.ylabel("Ориентировочная зарплата")
plt.legend()
plt.show()
Давайте также визуализируем дерево: Вы можете использовать функцию export_graphviz Scikit-learn для отображения дерева в блокноте Jupyter. export_graphviz функция преобразует классификатор дерева решений в точечный файл, а pydotplus преобразует этот точечный файл в png или отображаемую форму на Jupy тер. из sklearn.tree import export_graphviz
из sklearn.externals.six импортировать StringIO
из IPython.display импортировать изображение
импортировать pydotplusdot_data = StringIO()
export_graphviz (классификатор, out_file = dot_data,
заполнено = верно, округлено = верно,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
график = pydotplus.graph_from_dot_data(dot_data.getvalue())
Изображение(graph.create_png())
Дерево решений.
В диаграмме дерева решений каждый внутренний узел имеет правило принятия решения, которое разделяет данные. Здесь результирующее дерево не обрезано. Это необрезанное дерево необъяснимо и нелегко понять. В следующем разделе давайте оптимизируем его путем обрезки. Оптимизация классификатора дерева решений критерий : необязательный (по умолчанию = «джини») или Выбрать меру выбора атрибута: этот параметр позволяет нам использовать меру выбора различных атрибутов. Поддерживаемые критерии: «джини» для индекса Джини и «энтропия» для получения информации. splitter : строка, необязательная (по умолчанию = «best») или Split Strategy: этот параметр позволяет нам выбрать стратегию разделения. Поддерживаемые стратегии: «лучшие» для выбора наилучшего разделения и «случайные» для выбора наилучшего случайного разделения. max_depth : int или None, необязательно (по умолчанию = None) или Максимальная глубина дерева: максимальная глубина дерева. Если None, то узлы расширяются до тех пор, пока все листья не будут содержать выборок меньше, чем min_samples_split. Более высокое значение максимальной глубины вызывает переоснащение, а более низкое значение — недостаточное (Источник). В Scikit-learn оптимизация классификатора дерева решений выполняется только путем предварительной обрезки. Максимальная глубина дерева может использоваться как управляющая переменная для предварительной обрезки. # Создать объект классификатора дерева решений
classifier = DecisionTreeClassifier(criterion="entropy", max_depth=3)# Обучить классификатор дерева решений
classifier = classifier.fit(X_train,y_train)#Предсказать ответ для тестового набора данных
y_pred = classifier.predict(X_test)# Точность модели, как часто классификатор верен?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
Ну, скорость классификации увеличилась до 94%, что лучше, чем в предыдущей модели. Теперь давайте снова визуализируем обрезанное дерево решений после оптимизации. точка_данных = StringIO()
export_graphviz (классификатор, out_file = dot_data,
заполнено = верно, округлено = верно,
special_characters = True, feature_names = feature_cols, class_names = ['0','1'])
график = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())
Дерево решений после обрезки
Эта сокращенная модель менее сложна, объяснима и проста для понимания, чем предыдущий график модели дерева решений.
Заключение В этой статье мы подробно рассмотрели дерево решений; Это работает, меры выбора атрибутов, такие как получение информации, коэффициент усиления и индекс Джини, построение модели дерева решений, визуализация и оценка набора данных супермаркета с использованием пакета Python Scikit-learn и оптимизация производительности дерева решений с помощью настройки параметров. Задания модуль алгебра: Модуль Алгебра — ЁПМодуль Алгебра — ЁПМодуль алгебра первой части содержит десять (6 – 15) заданий, каждое из которых оценивается в один балл. Действия с дробями Понятие обыкновенной и десятичной дроби. Сложение, вычитание, умножение, деление дробей. Сравнение дробей. Перевод обыкновенной дроби в десятичную и обратно. Действия со степенями Понятие степени. Свойства степеней. Возведение отрицательного числа в степень. Задание №7Координатная прямая Понятие координатной прямой. Расположение чисел на координатной прямой. Сравнение чисел, расположенных на координатной прямой. Сопоставление чисел, изображенных на прямой с некоторым числом. Модуль числа Понятие модуля числа. Квадратный корень из числа Понятие квадратного корня. Задание №8Преобразования и вычисления Свойства квадратного корня, свойства степеней. Вынесение множителя за знак квадратного корня. ФСУ Формулы сокращенного умножения. Стандартный вид числа Понятие стандартного вида числа. Перевод приставок в множитель. Задание №9Уравнения Системы уравнений Статистика, вероятности. Задание №11Виды графиков Прямая. Действия с графиками Растяжение графиков. Сдвиги графиков. Задание №12Числовые последовательности Понятие числовой последовательности. Нахождение n-ных членов последовательности. Принцип работы с числовыми последовательностями. Арифметическая прогрессия. Понятие арифметической прогрессии. Разность арифметической прогрессии. Рекуррентная формула. Сумма первых n членов арифметической прогрессии. Геометрическая прогрессия Понятие геометрической прогрессии. Знаменатель прогрессии. Рекуррентная формула. Сумма первых n членов геометрической прогрессии. Полезные формулы. Задание №13Формулы сокращенного умножения ФСУ. Упрощение выражений Разложение на множители: вынесение общего множителя, группировка, применение ФСУ. Приведение выражений к общему знаменателю. Задание №14Расчеты по формулам. Задание №15Неравенства Линейные неравенства. Квадратные неравенства. Рациональные неравенства. ОДЗ. Системы неравенств Понятие системы неравенств. Отбор решений. В модуле алгебра второй части содержится три задания (21 – 23), каждое из которых оценивается в два балла. Задание №21Алгебраические выражения, уравнения, системы уравнений, неравенства, системы неравенств. Задание №22Текстовые задачи Задание №23Функции и их свойства. Графики функций.
ОГЭ 2018. Модуль «Алгебра» — презентация онлайн1. ОГЭ 2018 гМодуль«Алгебра» Автор: Фролова Л.А. 1 2. Характеристика модуля:Модуль «Алгебра» состоит из 2-х частей.Часть 1. 14 заданий (1-14) с кратким ответом. Каждое задание оценивается в 1 балл. Часть 2. 3 задания (21-23) с развёрнутым ответом. Задание 21. Автор: Фролова Л.А. 2 3. Задание 22.Задание 23.Автор: Фролова Л.А. 3 4. Часть 1Автор: Фролова Л.А.4 5. Задание 1Характеристика задания: задание 1 представляетсобой задачу на арифметические действия с дробями — как десятичными, так и обыкновенными. Рекомендации: уделить самое пристальное внимание, отработав с учащимися как действия с десятичными дробями, так и действия с обыкновенными дробями и комбинациями десятичных и обыкновенных дробей.  Если Еслирациональный способ вычислений не очевиден, следует решить задачу стандартным образом и не тратить время на его поиск. Автор: Фролова Л.А. 5 6. Пример заданияОбратим все дроби в неправильныеобыкновенные дроби и раскроем скобки (в данном случае это наиболее рациональный способ): Ответ: 28 Автор: Фролова Л.А. 6 7. Задание 2Характеристика задания: задание 2 ОГЭ поматематике, открывающее блок «Реальная математика» в каждом из экзаменационных вариантов, представляет собой задачу на чтение и анализ данных, представленных в виде таблиц, либо задачу, связанную с записью чисел в стандартном виде и их сравнением. Автор: Фролова Л.А. 7 Автор: Фролова Л.А. 8 9. Задание 3Характеристика задания: задание 3 ОГЭ поматематике представляет собой задачу на взаимное расположение чисел на числовой (координатной) прямой, их сравнение и оценку Автор: Фролова Л.  А. А.9 10. Пример заданияАвтор: Фролова Л.А.10 11. Задание 4Характеристика задания: Задание 4 ОГЭ поматематике продолжает линию заданий 1 и 3 и является задачей на преобразование числовых и буквенных выражений и вычисление их значений. При этом задачи открытого банка по этой позиции варианта ОГЭ можно разделить на две чётко разграниченные группы: •задачи на действия с целыми степенями • задачи на действия с корнями Автор: Фролова Л.А. 11 Автор: Фролова Л.А. 12 13. Задание 5Характеристика задания: задание 5 ОГЭ по математикепредставляет собой задачу на чтение и анализ данных, представленных в виде графиков. Все такие задачи делятся на две чётко разграниченные группы: • в первой требуется найти точку оси абсцисс, ответив на вопрос типа «какого числа значение величины было равно данному?», •во второй — найти наибольшее или наименьшее значение некоторой величины, т.  е. точку оси ординат. е. точку оси ординат.Ошибочные ответы обычно обусловлены невнимательностью: перепутаны наибольшее и наименьшее значения, вместо температуры в ответе указана дата и т. п Автор: Фролова Л.А. 13 Автор: Фролова Л.А. 14 Автор: Фролова Л.А. 15 16. Задание 6Характеристика задания: Задание 6 ОГЭ по математике представляетсобой несложное рациональное уравнение — линейное или квадратное либо сводящееся в одно-два действия к одному из них целое или дробнолинейные уравнение. Квадратные уравнения представлены в открытом банке ОГЭ по математике всеми типами: неполные (с нулевым вторым или третьим коэффициентом) Методические рекомендации с разбором задач и полные (приведённые и неприведённые). Для того чтобы успешно справиться с подобным заданием на ОГЭ, достаточно уметь решать линейные и квадратные уравнения, помнить правило переноса слагаемого из одной части уравнения в другую (знак этого слагаемого меняется на противоположный), обладать определёнными вычислительными навыками, связанными с арифметическими действиями над целыми числами и дробями.  Автор: Фролова Л.А. 16 Автор: Фролова Л.А. 17 18. Задание 7Характеристика задания: задание 7 ОГЭ по математике представляетсобой несложную арифметическую текстовую задачу на проценты, отношения величин или производительность. Для решения этих практико-ориентированных задач достаточно уметь выполнять арифметические действия с целыми числами и дробями (вычисления по действиям), деление с остатком и последующее округление с недостатком или избытком и т. п. В таких задачах желательно делать проверку, в том числе и на здравый смысл — с помощью прикидки и оценки. В некоторых случаях, когда речь идёт о небольших числах, ответ можно получить и с помощью обычного перебора. Значительную часть заданий открытого банка ОГЭ на этой позиции в вариантах экзаменационных работ составляют именно задачи на проценты. Автор: Фролова Л.А. 18 19. Пример заданияПринтер печатает 7 страниц за 6 секунд.Сколько страниц напечатает принтер за 5 минут? Р е ш е н и е.  Пять минут — это 5 · 60 = 300 секунд. Поскольку 300 : 6=50, за 5 минут принтер напечатает 50 · 7=350 страниц. Ответ: 350 Автор: Фролова Л.А. 19 20. Задание 8Характеристика задания: задание 8 ОГЭ по математикепредставляет собой задачу на чтение и анализ информации, представленной в виде диаграмм — круговых или столбчатых. В простейших случаях надо определить, оценить или соотнести с условием долю, которую занимает в общей площади круговой диаграммы сектор, соответствующий одной из характеристик, подсчитать число столбиков, удовлетворяющих тому или иному требованию, либо сравнить некоторые из них по высоте. Немного сложнее задачи, требующие определённого расчёта или сопоставления данных. Заметим, что диаграммы применяются для наглядного, качественного сравнения тех или иных показателей или характеристик. Решение подобных задач не предполагает использования транспортира (для круговых диаграмм) или линейки (для столбчатых диаграмм) Автор: Фролова Л.  А. А.20 Автор: Фролова Л.А. 21 Автор: Фролова Л.А. 22 23. Задание 9Автор: Фролова Л.А.23 Автор: Фролова Л.А. 24 25. Задание 10Характеристика задания: задания, связанные сфункциями и их графиками (именно к ним относится задание 10 ОГЭ), ежегодно включаются в варианты ОГЭ по математике. По большей части это задания на чтение графиков функций, содержащие вопросы о свойствах функций, задания, в которых требуется установить соответствие между функциями, заданными формулами, и графиками этих функций, либо вариации последних, предполагающие ответ на вопрос, какая из нескольких данных формул задаёт функцию, график которой приведён в условии, или какой из нескольких данных графиков соответствует функции, заданной указанной в условии формулой. Автор: Фролова Л.А. 25 Автор: Фролова Л.А. 26 Автор: Фролова Л.А. 27 28. Задание 11Автор: Фролова Л.А.28 Автор: Фролова Л.  А. А.29 Автор: Фролова Л.А. 30 Автор: Фролова Л.А. 31 Автор: Фролова Л.А. 32 33. Задание 12Характеристика задания: задание 12 ОГЭ по математике — это задачана преобразование рациональных алгебраических выражений и вычисление их значений. Решение задач на преобразование выражений предполагает, как правило, последовательное упрощение данных выражений. При этом используются свойства степеней и формулы сокращённого умножения. Упрощение выражений обычно сводится к приведению подобных членов и сокращению дробей после некоторых предварительных действий, важнейшим из которых является разложение на множители. Последнее, в свою очередь, заключается в выполнении одного или нескольких из следующих четырёх правил: 1) «примени формулу или свойство»; 2) «сгруппируй слагаемые»; 3) «вынеси за скобку»; 4) «добавь и вычти». Автор: Фролова Л.А. 33 Автор: Фролова Л.А. 34 35. Задание 13Характеристика задания: задание 13 представляет собой задачу навычисление по данной формуле.  В условиях таких задач даются формулы В условиях таких задач даются формулыиз разных областей знаний, причём значения всех величин за исключением одной в этих формулах известны. Требуется найти значение именно этой величины. Есть подобные задачи и в ЕГЭ по математике — как базового, так и профильного уровня. Отметим, что для решения этих задач вовсе не обязательно быть специалистом, например, в области биологии или химии, здесь проверяется именно умение вычислять значение искомой величины по данной формуле и данным константам, т. е. по сути это задачи на «понимание при чтении», в данном случае чтении условия. При этом в само условие, вообще говоря, можно не вникать, более того, это и не нужно: достаточно выписать данную формулу, значения данных в условие величин, подставить эти значения в выписанную формулу и найти из неё единственную неизвестную величину Автор: Фролова Л.А. 35 Автор: Фролова Л.А. 36 37. Задание 14Характеристика задания: задание 14 ОГЭ поматематике представляет собой линейное или квадратное неравенство либо систему двух простейших линейных неравенств.  Автор: Фролова Л.А. 37 Автор: Фролова Л.А. 38 Часть 2 Автор: Фролова Л.А. 39 40. Задание 21Автор: Фролова Л.А.40 Автор: Фролова Л.А. 41 42. Задание 22Характеристика задания: Задание 22 ОГЭ поматематике представляет собой традиционную текстовую задачу по одной из трёх тем: «Движение», «Производительность и работа», «Проценты и концентрация». Некоторые из этих задач можно решить арифметически, не прибегая к составлению уравнению, другие требуют составления одного или двух уравнений и их решения. Автор: Фролова Л.А. 42 • Пример задания. Маша и Даша за день пропалывают 5 грядок, Даша и Глаша — 6 грядок, а Глаша и Маша — 7 грядок. Сколько грядок за день смогут прополоть девочки, работая втроём? • Р е ш е н и е. Вообразим, что сначала Маша и Даша работали один день, затем Даша и Глаша работали один день, а потом Глаша и Маша работали ещё один день. Получается, что каждая из девочек работала два дня, или что бригада, состоящая из Маши, Глаши и Даши, прополола 5+6+7=18 грядок за два дня.  Значит, за один Значит, за одиндень эта бригада прополет вдвое меньше грядок, т. е. 9. • Ответ: 9 Автор: Фролова Л.А. 43 44. Задание 23•Характеристика задания: задание 23 ОГЭ по математике представляет собой задачупо теме «Графики функций». Это задание можно отнести к относительно сложным, но следует понимать, что сложность эта относительна и в данном случае обусловлена либо формулой, задающей функцию и предполагающей предварительные алгебраические преобразования для получения одной из базовых функций школьного курса (из области определения которой в некоторых случаях придётся исключить одну или две точки), либо самим условием, требующим исследования взаимного расположения графиков двух функций и ответа на определённые вопросы о числе их общих точек в зависимости от некоторой величины. •Что качается формулы, задающей функцию, то, как уже отмечалось, после несложных преобразований этой формулы (сокращения дроби, раскрытия модуля, приведения подобных слагаемых) получается формула, задающая элементарную функцию, графиком которой (или частью графика которой) является прямая, парабола, гипербола или их части — возможно, с удалёнными (выколотыми) точками (последние могут появиться в случае задания функции с помощью алгебраической дроби, область определения которой находится из условия неравенства нулю её знаменателя) Автор: Фролова Л.  А. А.44 Автор: Фролова Л.А. 45 46. Шкала пересчёта суммарного балла за выполнение модуля «Алгебра» в отметку по алгебреШкала пересчёта суммарного балла завыполнение модуля «Алгебра» в отметку по алгебре «3» — 6 – 8 баллов; «4» — 9 – 12 баллов; «5» — 13 – 17 баллов. Автор: Фролова Л.А. 46 АЛГЕБРА 1222 — Колледж РасмуссенаАЛГЕБРА 1222 Вопросы и ответыАЛГЕБРА 1222 ДокументыПоказаны с 1 по 78 из 78Сортировать по: {[$select.selected.label]} ALGEBRA 1222 Тесты Вопросы и ответыПоказано с 1 по 8 из 49Посмотреть все
Новые загруженные документыПодробнее Назад в отдел Алгебра I — Математический класс миссис ОуэнАлгебра IПерейдите по ссылкам, чтобы получить доступ к календарю или раздаточному материалу по правилам, политикам и процедурам: Календарь Правила, Поли и процедуры Четвертый квартал
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Через 2 года мой братишка будет в 2 раза старше, чем 2 года назад, а я через 3 года буду в 3 раза старше, чем 3 года назад. Пользуйтесь нашим приложением Что такое число в кубе? (Примеры и рабочие листы)
Когда вы умножаете целое число (не дробь) само на себя, а затем еще раз само на себя, результатом будет число в кубе . Например, 3 x 3 x 3 = 27. Простой способ записать 3 в кубе: 3 3 . Это означает, что три умножить само на себя три раза. Самый простой способ выполнить это вычисление — выполнить первое умножение (3×3), а затем умножить ответ на то же число, с которого вы начали; 3 х 3 х 3 = 9x 3 = 27.
Кубические числа могут быть немного более запутанными, чем числа в квадрате, просто из-за дополнительного умножения. По сути, вы вычисляете трехмерную форму, а не плоскую. Вот плоский (или двумерный) квадрат 4 x 4:
равно 16.
Вот трехмерный куб 4 x 4:
Чтобы вычислить количество блоков (число в кубе), на этот раз мы должны умножить 4 x 4 x 4 или 4 3 , что равно 64. В KS2 вам не нужно узнать куб цифры наизусть, но вы должны иметь общее представление о том, что они собой представляют и как их вычислить. Часто детям дается образец чисел, например, числа нижнего конца куба, и может быть предложено попытаться разобраться в этом образце.
Вот список чисел в кубе до 12×12:
Куб отрицательного числа всегда будет отрицательным, точно так же, как куб положительного числа всегда будет положительным.
Например; -5 3 = -5 х -5 х- -5 = (25 х -5) = -125.
Так же, как и целые числа (целые числа), десятичное число также легко возвести в куб. Не волнуйтесь, вам не нужно запоминать их на ключевом этапе 2 (или, возможно, даже отрабатывать)!
Вот несколько рабочих листов, предназначенных специально для того, чтобы разобраться с числами в кубе и отработать свои навыки. 6-й класс – Рисование точек на кубиках 8-й класс – Знай свои квадраты и кубики 8-й класс – Кубические числа и кубические корни 08 Если вам нравятся кубические числа и головоломки, и вы действительно хотите бросить себе вызов, почему бы не заглянуть на веб-сайт BBC Bitesize или не попробовать некоторые из головоломок и задач, поставленных командой NRich из Кембриджского университета? https://nrich. http://www.bbc.co.uk/guides/z2ndsrd
900 09 АВТОР, МС ЭЛИСОН – УЧИТЕЛЬ МАТЕМАТИКИ.НАПИСАНО: Шарлотта Поттер Разложение многочлена с X в кубе
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 106735979666
106735979666 У числительных на -десят два окончания, так как изменяются обе части: пятидесяти, пятьюдесятью.
У числительных на -десят два окончания, так как изменяются обе части: пятидесяти, пятьюдесятью. Обозначается римскими цифрами как IXCMXCIX.
Обозначается римскими цифрами как IXCMXCIX. ..]
день J un e , одна тысяча девятьсот a n 3 d 3 900 — e i gh т.
..]
день J un e , одна тысяча девятьсот a n 3 d 3 900 — e i gh т. ..]
el diez de sept ie mbre de mil no veciento s noventa y ocho .
..]
el diez de sept ie mbre de mil no veciento s noventa y ocho .
 ..]
la co nc esin de mil tre scientas noventa y nueve A estud 3 ed
..]
la co nc esin de mil tre scientas noventa y nueve A estud 3 ed ..]
..] iucn.org
iucn.org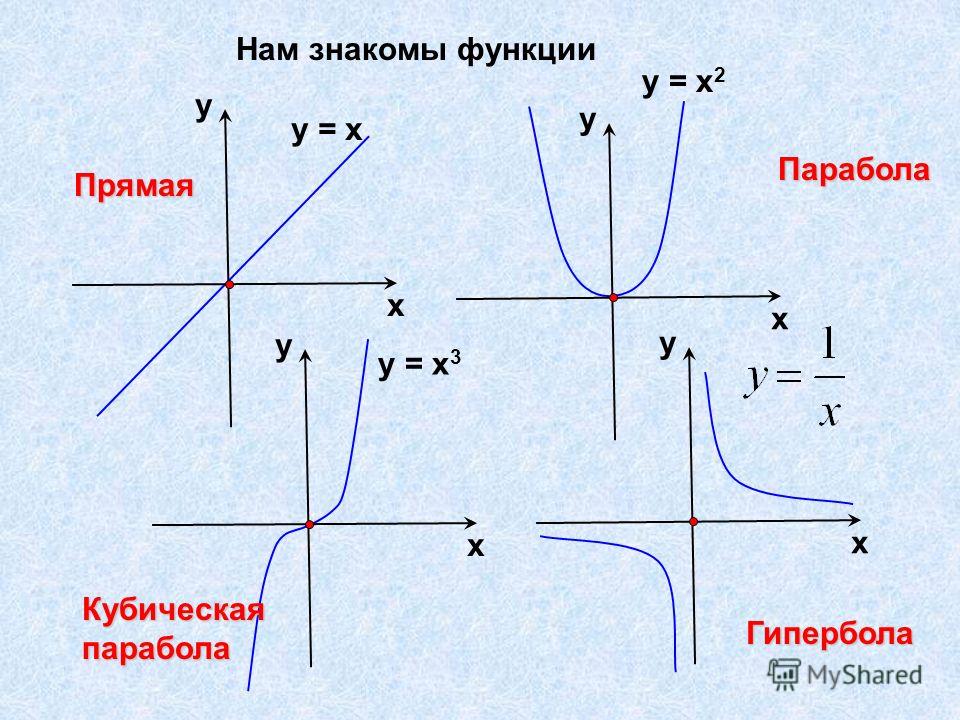 Получается \(g(x)=-\frac{1}{3}x+3\).
Получается \(g(x)=-\frac{1}{3}x+3\).
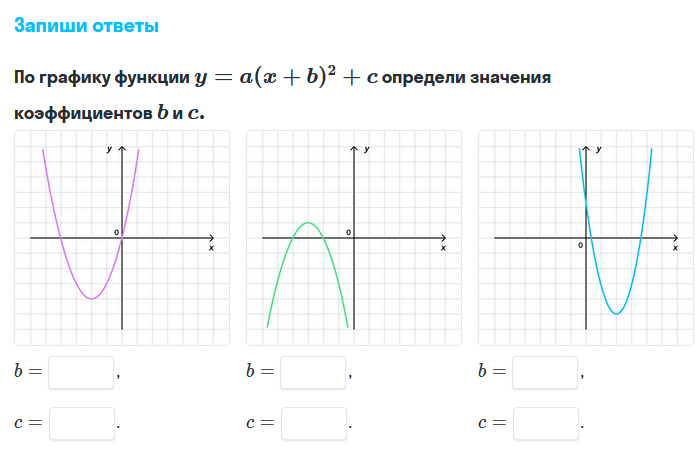 Остается последний шаг – вычислим при каком иксе функция, то есть \(f(x)\), равна \(16\):
Остается последний шаг – вычислим при каком иксе функция, то есть \(f(x)\), равна \(16\):
 Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем \(f(x)\) и \(g(x)\).
Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем \(f(x)\) и \(g(x)\).
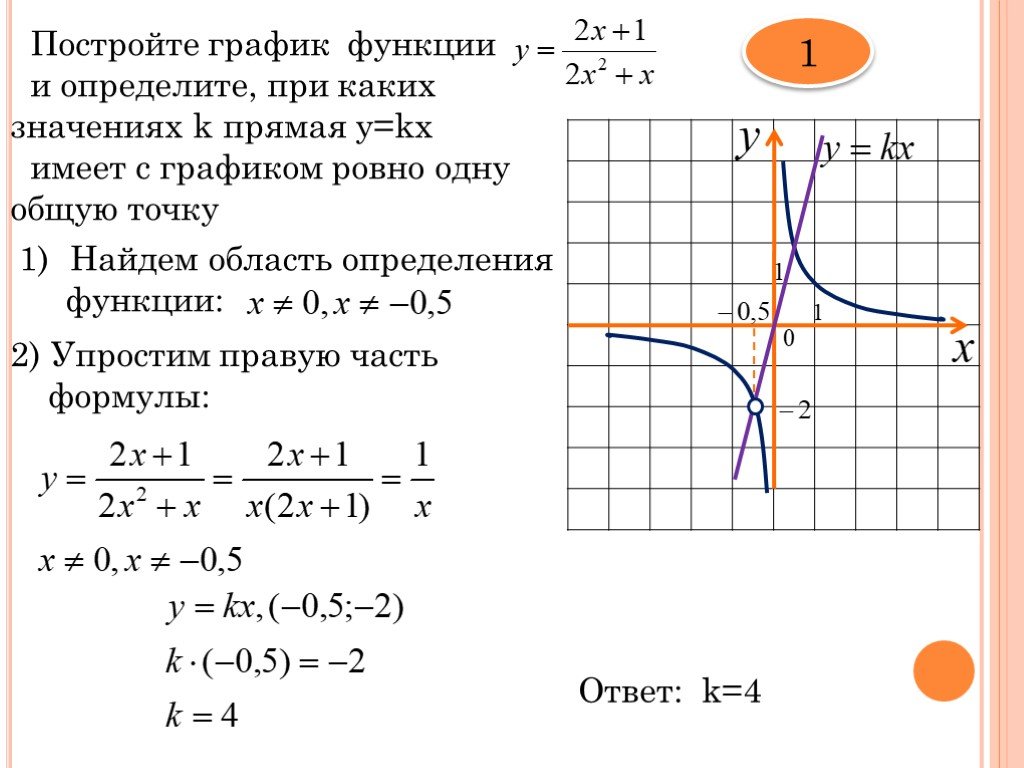
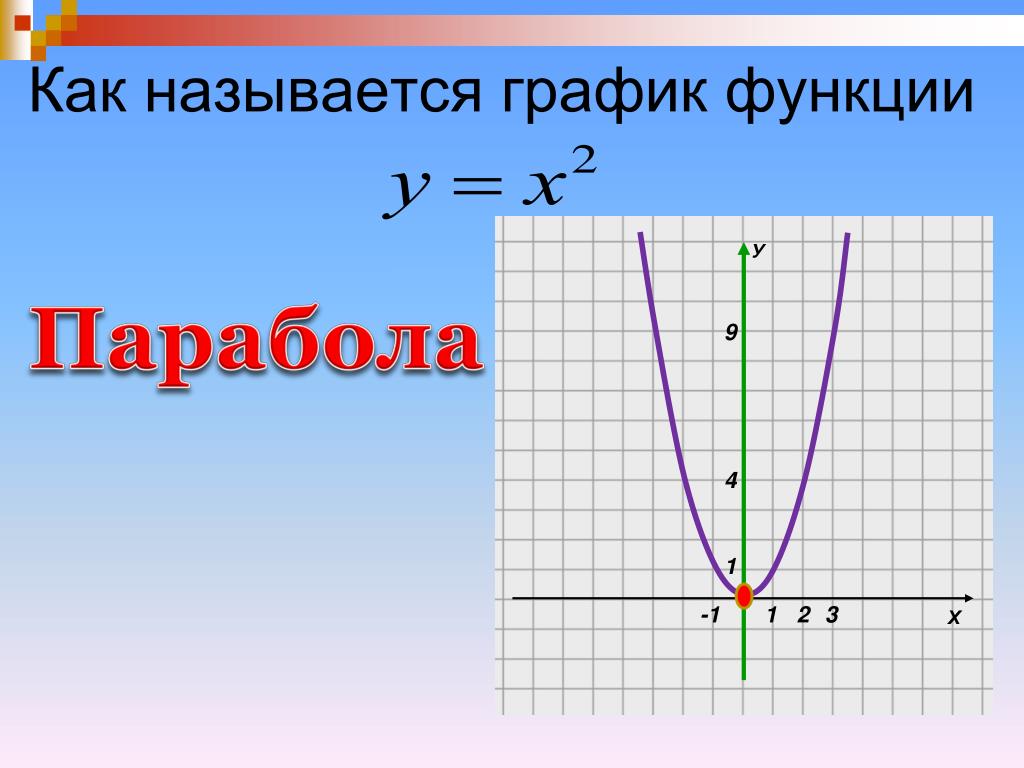
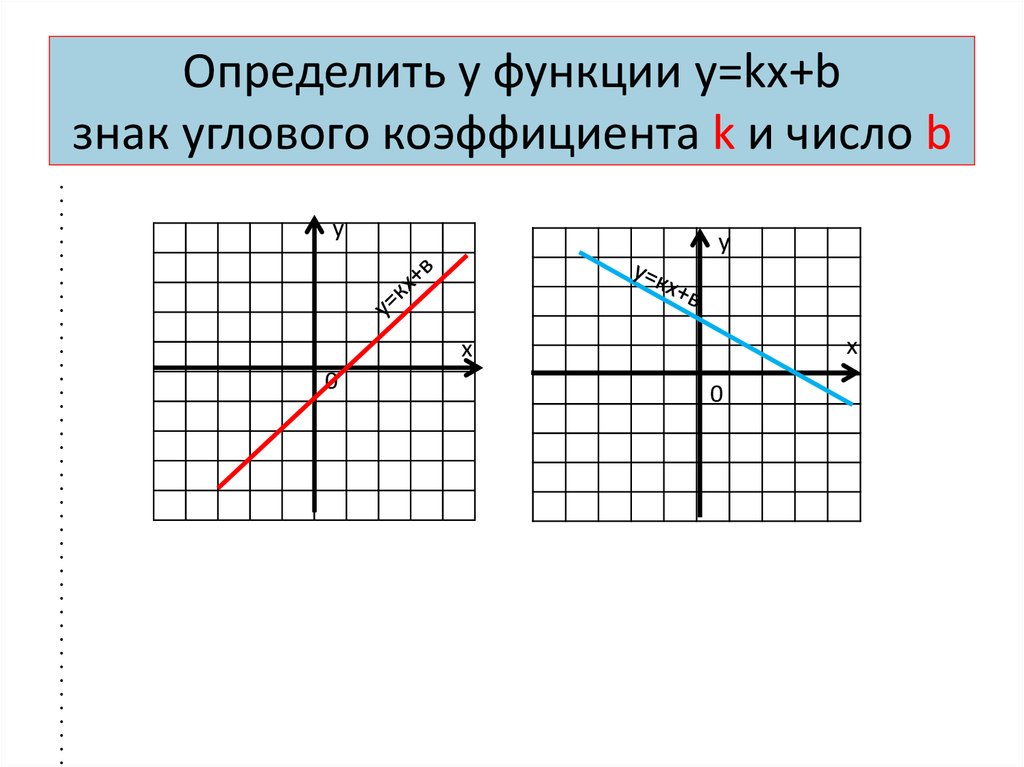
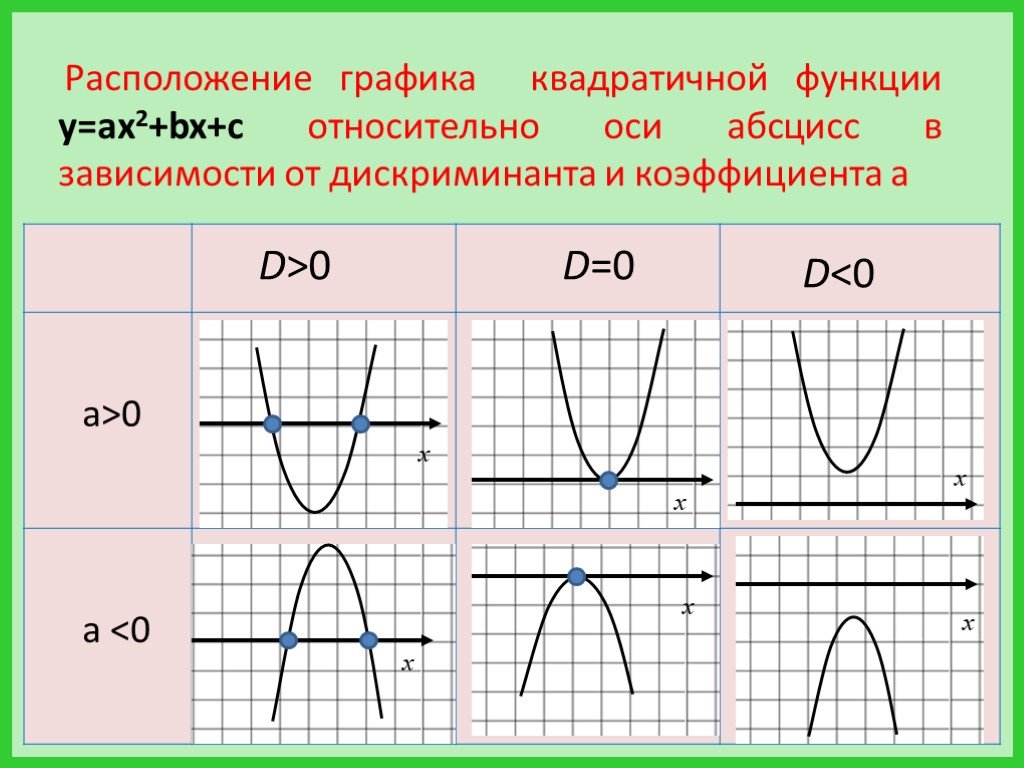
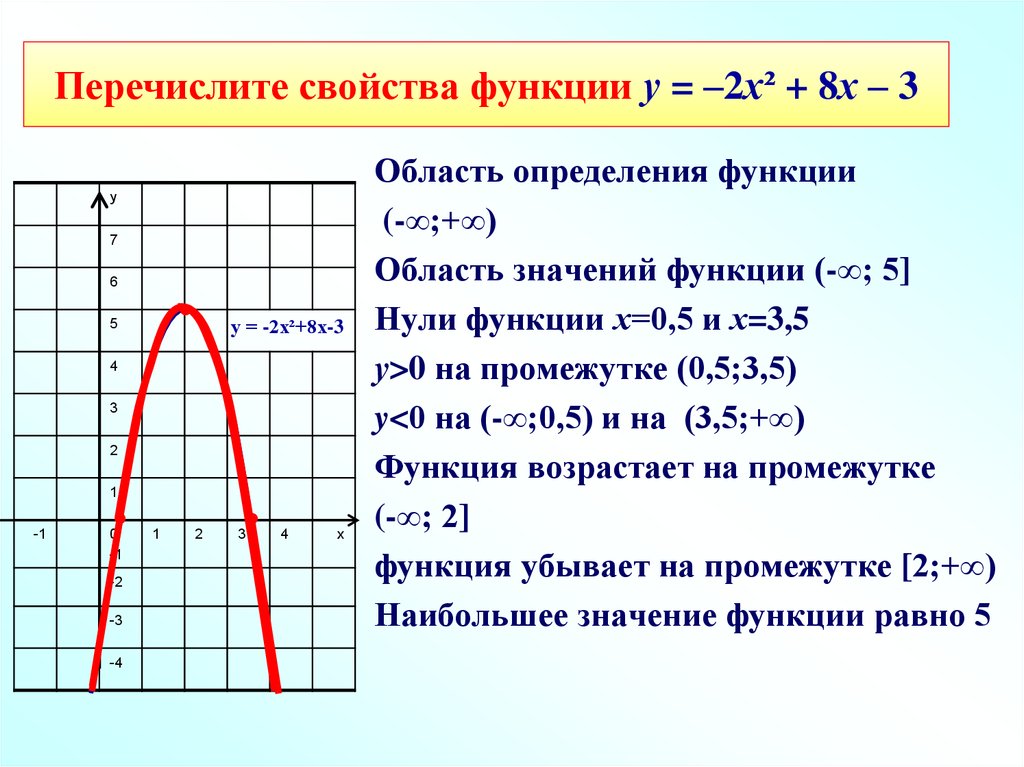
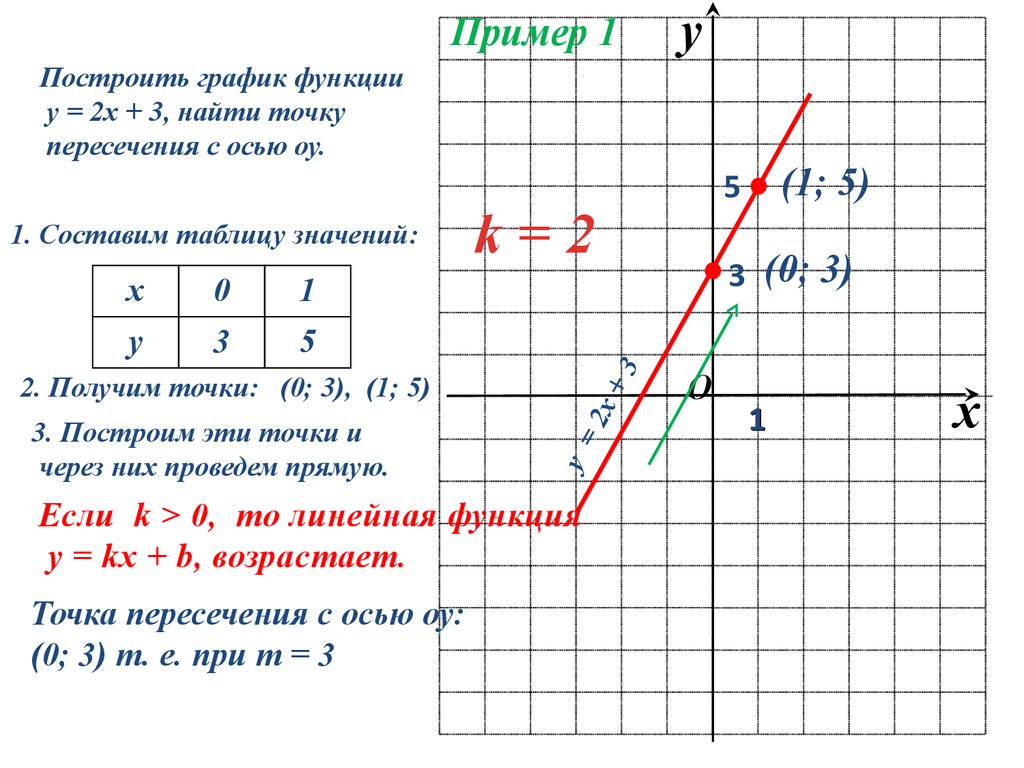 Итак, о чем я хочу поговорить здесь, так это о том, как вы можете сказать, что что-то является функцией, просто основываясь на графике, и вы увидите, что это на самом деле довольно просто. Он использует так называемый тест вертикальной линии.
Итак, о чем я хочу поговорить здесь, так это о том, как вы можете сказать, что что-то является функцией, просто основываясь на графике, и вы увидите, что это на самом деле довольно просто. Он использует так называемый тест вертикальной линии.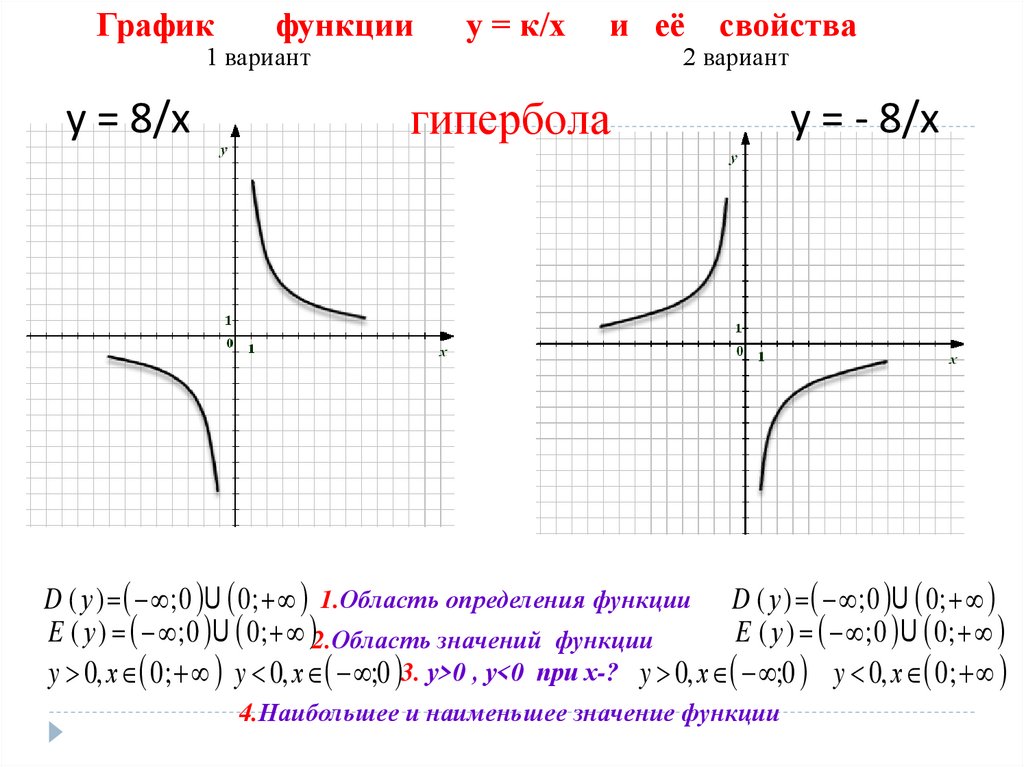 Это значение x прямо здесь, что бы оно ни было, имеет множество значений y, есть значение y, есть еще одно, нет никого, это не функция. Каждый x получает только одно значение y.
Это значение x прямо здесь, что бы оно ни было, имеет множество значений y, есть значение y, есть еще одно, нет никого, это не функция. Каждый x получает только одно значение y.
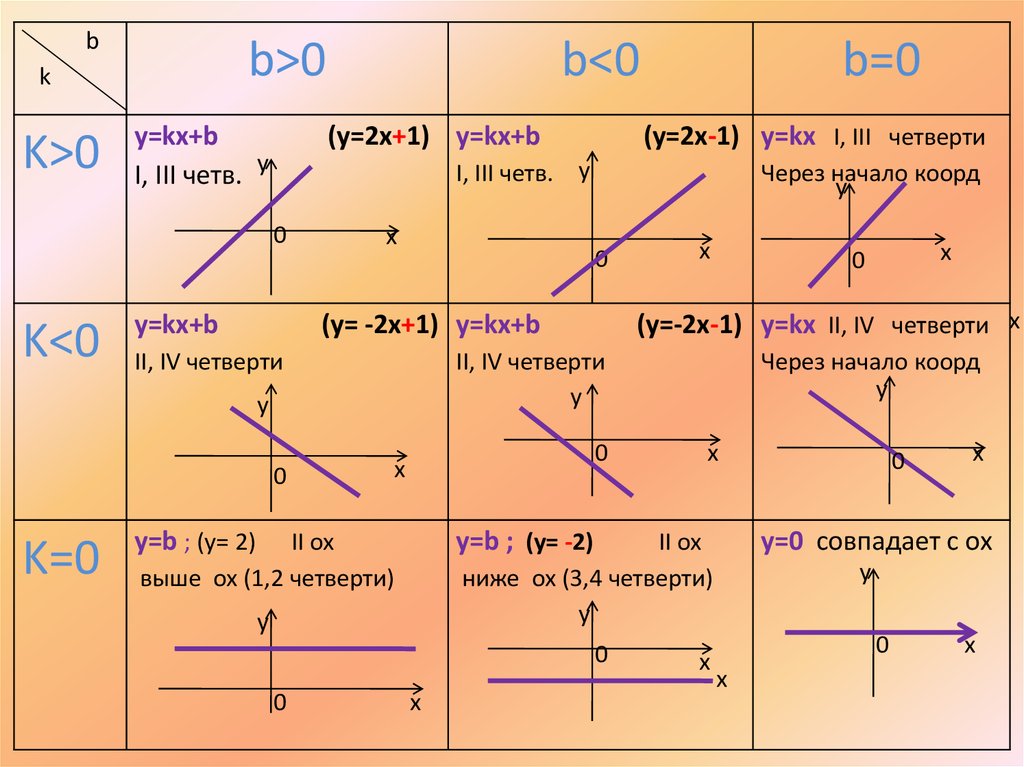 Средняя скорость изменения возрастающей функции положительна, а средняя скорость изменения убывающей функции отрицательна. На рис. 3 показаны примеры увеличения и уменьшения интервалов функции. 9{\text{}}\left(2,\infty\right)(-∞,−2)∪ (2,∞)
Средняя скорость изменения возрастающей функции положительна, а средняя скорость изменения убывающей функции отрицательна. На рис. 3 показаны примеры увеличения и уменьшения интервалов функции. 9{\text{}}\left(2,\infty\right)(-∞,−2)∪ (2,∞) Форма множественного числа — «локальные минимумы». Вместе локальные максимумы и минимумы называются локальными экстремумами или локальными экстремальными значениями функции. (Форма единственного числа — «экстремум».) Часто термин местный заменяется термином относительный 9.0058 . В этом тексте мы будем использовать термин локальный .
Форма множественного числа — «локальные минимумы». Вместе локальные максимумы и минимумы называются локальными экстремумами или локальными экстремальными значениями функции. (Форма единственного числа — «экстремум».) Часто термин местный заменяется термином относительный 9.0058 . В этом тексте мы будем использовать термин локальный . Локальный минимум равен
Локальный минимум равен
 Аналогично,
Аналогично,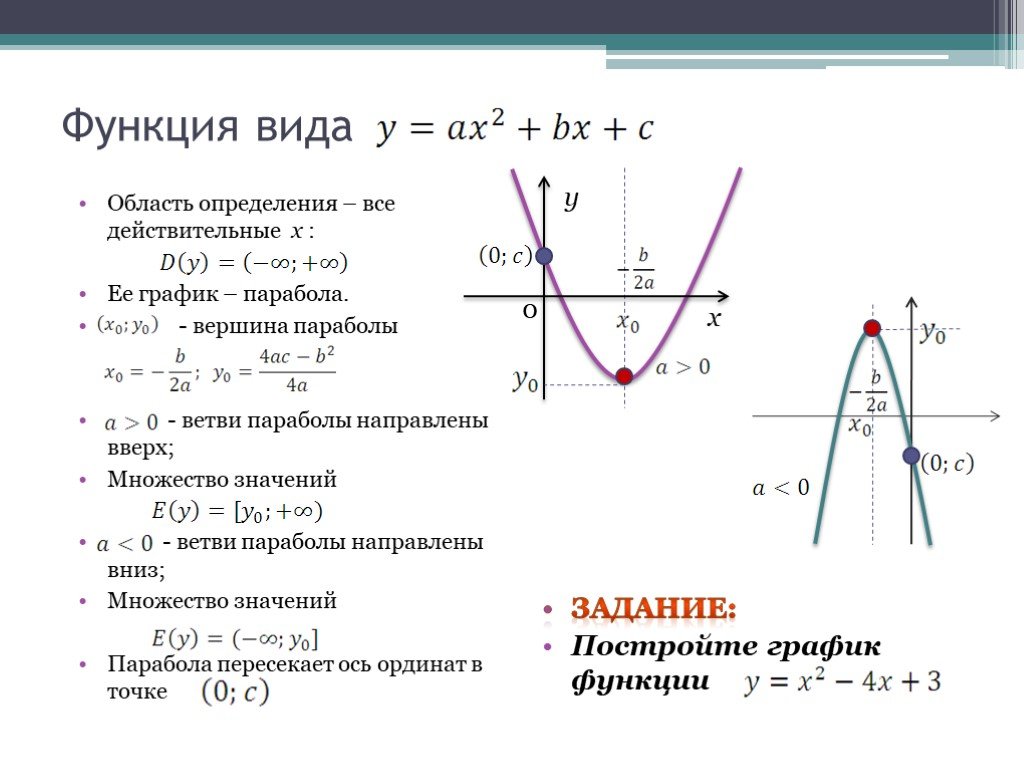 Функция увеличивается там, где она наклонена вверх, когда мы движемся вправо, и уменьшается там, где она наклонена вниз, когда мы двигаемся вправо. Функция увеличивается с
Функция увеличивается там, где она наклонена вверх, когда мы движемся вправо, и уменьшается там, где она наклонена вниз, когда мы двигаемся вправо. Функция увеличивается с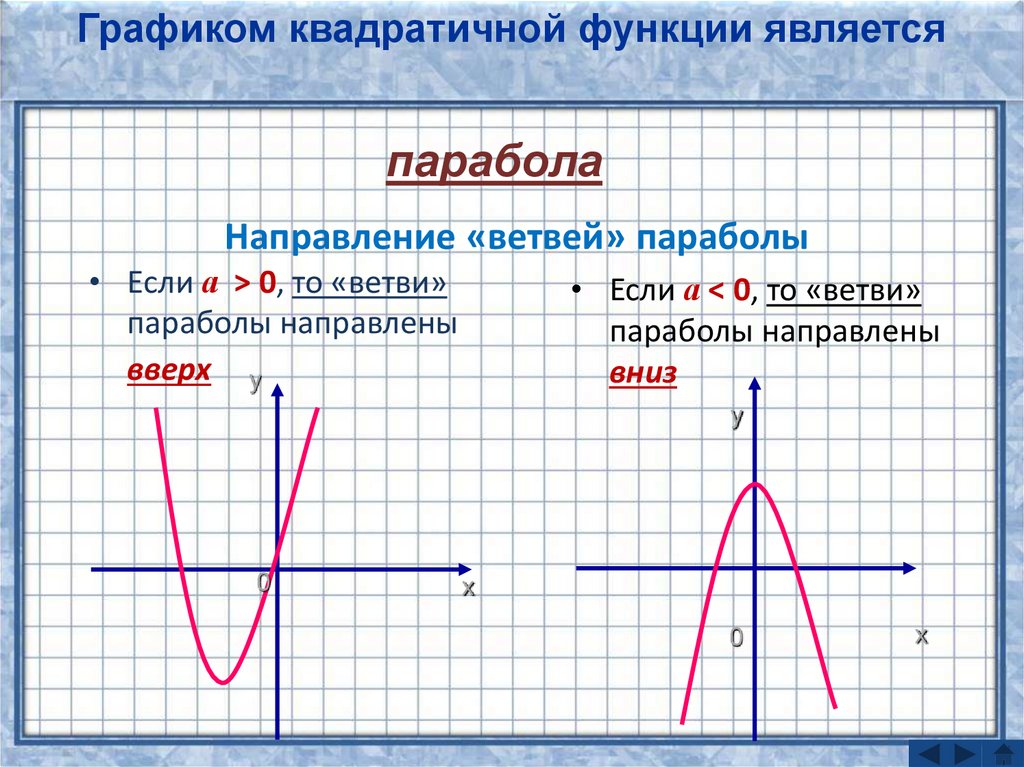 Похоже, что существует нижняя точка или локальный минимум между 9{2}-15x+20\\f(x)=x3−6×2−15x+20
Похоже, что существует нижняя точка или локальный минимум между 9{2}-15x+20\\f(x)=x3−6×2−15x+20
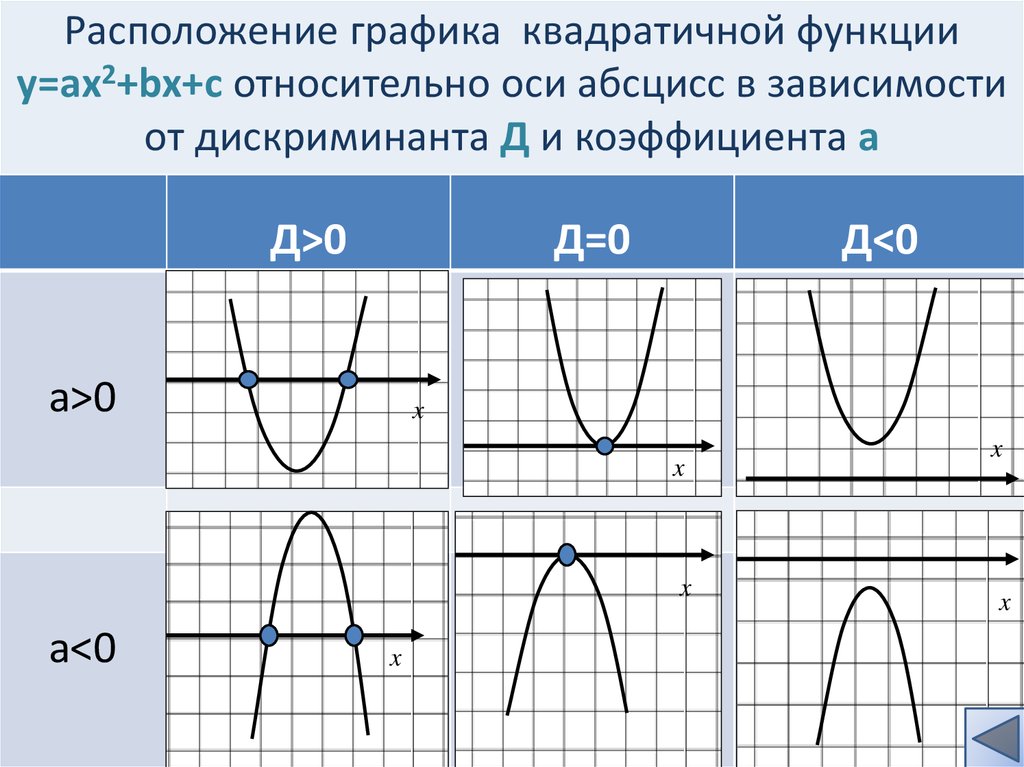
 После выбора изображений JPG в этом инструменте вы увидите, что этот инструмент автоматически начнет создавать PDF-файлы всех изображений. Вы также можете увидеть кнопку загрузки на каждом PDF-файле ниже после конвертации из JPG. Вы также можете использовать функцию этого инструмента. Например, вы можете изменить ориентацию страницы, задать поля, повернуть изображение, настроить размер страницы и т. д. Вы также можете загрузить один PDF-файл одновременно, включая несколько PDF-файлов. Наконец, используя этот онлайн-инструмент для создания PDF из JPG, вы можете легко создавать PDF из JPG.
После выбора изображений JPG в этом инструменте вы увидите, что этот инструмент автоматически начнет создавать PDF-файлы всех изображений. Вы также можете увидеть кнопку загрузки на каждом PDF-файле ниже после конвертации из JPG. Вы также можете использовать функцию этого инструмента. Например, вы можете изменить ориентацию страницы, задать поля, повернуть изображение, настроить размер страницы и т. д. Вы также можете загрузить один PDF-файл одновременно, включая несколько PDF-файлов. Наконец, используя этот онлайн-инструмент для создания PDF из JPG, вы можете легко создавать PDF из JPG.
 0 / 5
0 / 5
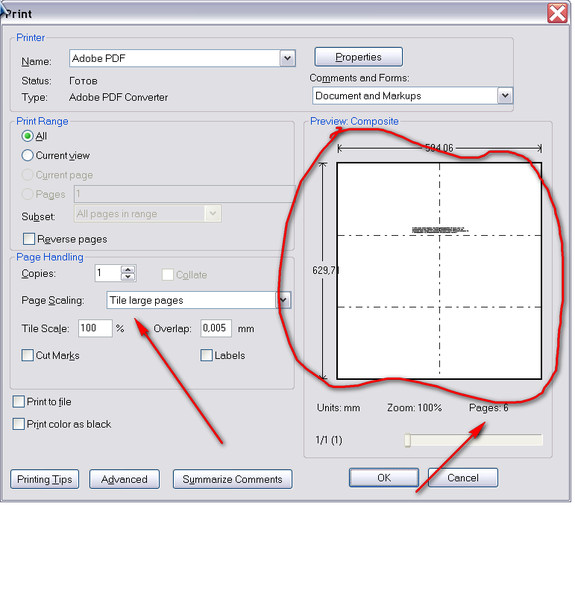 41.51.61.72.0
41.51.61.72.0 Все, что вам нужно, это ваше изображение и стабильное подключение к Интернету.
Все, что вам нужно, это ваше изображение и стабильное подключение к Интернету. И все же ему не хватает некоторых преимуществ, которые может предоставить PDF как формат документа. Совместимость, а также оптимизация для принтера — лишь некоторые из них.
И все же ему не хватает некоторых преимуществ, которые может предоставить PDF как формат документа. Совместимость, а также оптимизация для принтера — лишь некоторые из них.
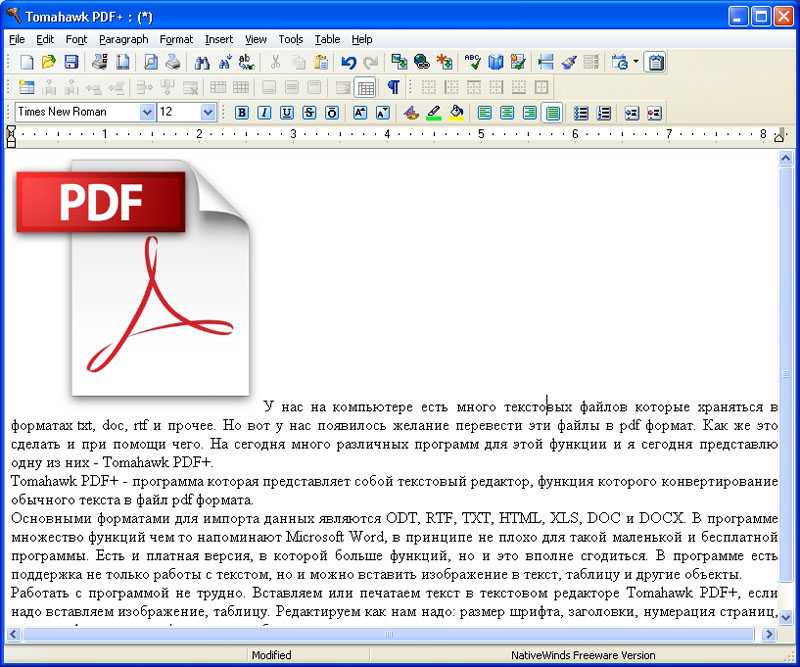 Этот конвертер JPG в PDF поддерживает JPG, JPEG, PNG и другие наиболее популярные форматы изображений.
Этот конвертер JPG в PDF поддерживает JPG, JPEG, PNG и другие наиболее популярные форматы изображений.
 Вы можете загружать файлы в облачное хранилище или создавать PDF-файлы и делиться ими по URL-адресу. Обратите внимание, что все файлы безвозвратно удаляются с наших серверов через 2 часа после обработки, и если вам нужно поделиться ими дольше, воспользуйтесь функцией «Поделиться» на странице загрузки. В этом случае файл будет доступен в течение 7 дней.
Вы можете загружать файлы в облачное хранилище или создавать PDF-файлы и делиться ими по URL-адресу. Обратите внимание, что все файлы безвозвратно удаляются с наших серверов через 2 часа после обработки, и если вам нужно поделиться ими дольше, воспользуйтесь функцией «Поделиться» на странице загрузки. В этом случае файл будет доступен в течение 7 дней.
 io/ru/date/24-military-to-12-hour-am-pm-converter-what-time-is/18—00
io/ru/date/24-military-to-12-hour-am-pm-converter-what-time-is/18—00 9K
9K
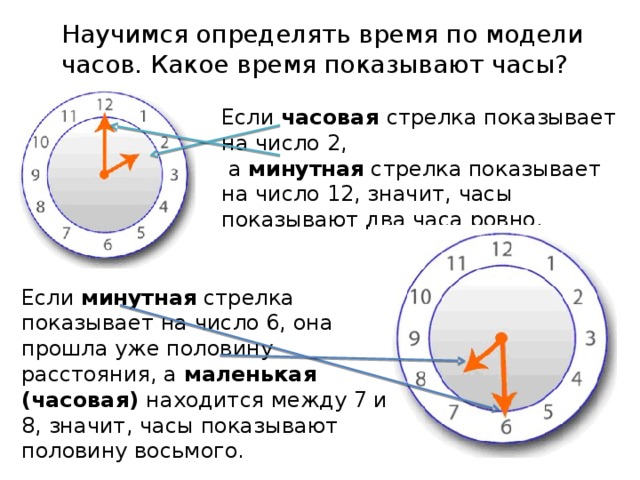 Новый день, когда наступает полночь, тоже начинается с буквы А: am.
Новый день, когда наступает полночь, тоже начинается с буквы А: am.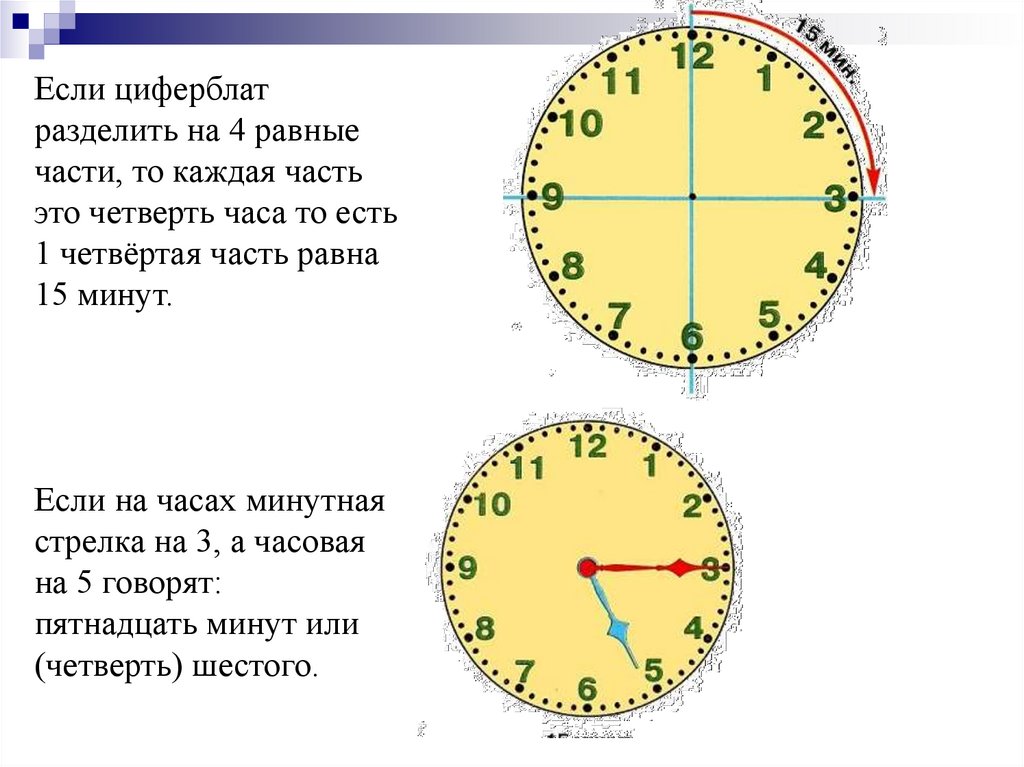 Мы уже выяснили с вами выше, в 12-часовом формате времени 12:00 am равняется 00:00. Время с 12:00 am до 12:00 pm равнозначно времени с 00:00 (полночь) до 12:00 (полдень) в 24-часовом формате времени.
Мы уже выяснили с вами выше, в 12-часовом формате времени 12:00 am равняется 00:00. Время с 12:00 am до 12:00 pm равнозначно времени с 00:00 (полночь) до 12:00 (полдень) в 24-часовом формате времени.

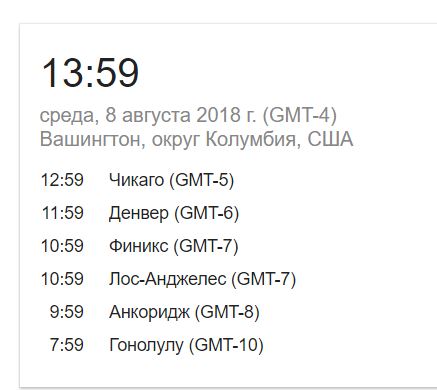 m. – Она придет на ужин к семи вечера.
m. – Она придет на ужин к семи вечера.

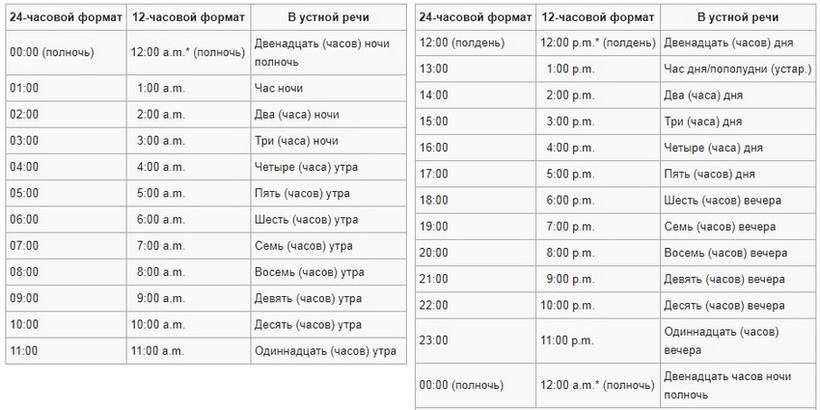

 2K
2K Время суток записывается в формате ччмм, где чч (0-23)
— полные часы, прошедшие с полуночи, мм (00-59) — количество минут, прошедших с последнего полного часа.
Чтобы преобразовать часы больше 12 в 12-часовые часы, просто вычтите 12 из заданных часов, и это даст вам время после полудня.
… более …
Время суток записывается в формате ччмм, где чч (0-23)
— полные часы, прошедшие с полуночи, мм (00-59) — количество минут, прошедших с последнего полного часа.
Чтобы преобразовать часы больше 12 в 12-часовые часы, просто вычтите 12 из заданных часов, и это даст вам время после полудня.
… более …
 M.
M.
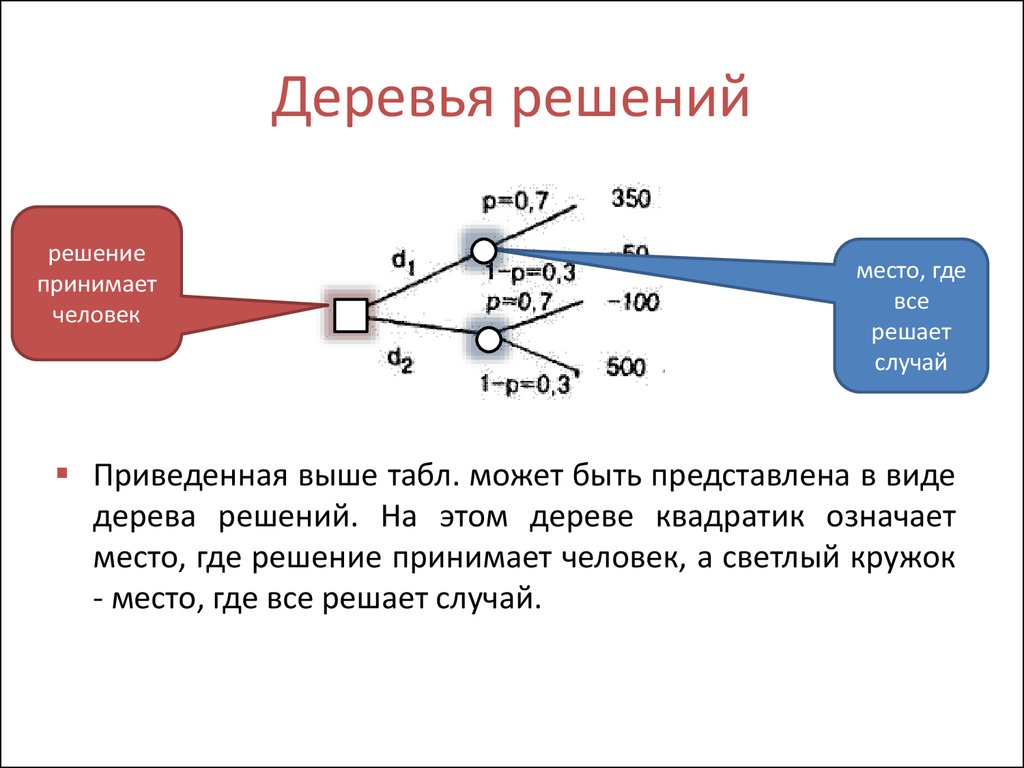
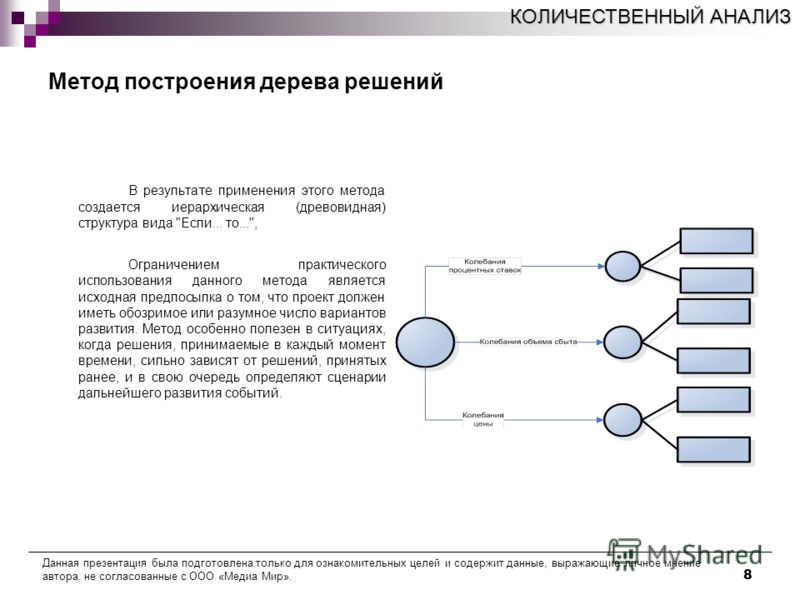 Ведь пример оказывается в листе, только если будет соответствовать всем установленным критериям на пути к нему. Очевидно, что к каждому листу ведёт только одна «дорога», что предполагает единственное верное решение и следование одному оптимальному алгоритму.
Ведь пример оказывается в листе, только если будет соответствовать всем установленным критериям на пути к нему. Очевидно, что к каждому листу ведёт только одна «дорога», что предполагает единственное верное решение и следование одному оптимальному алгоритму.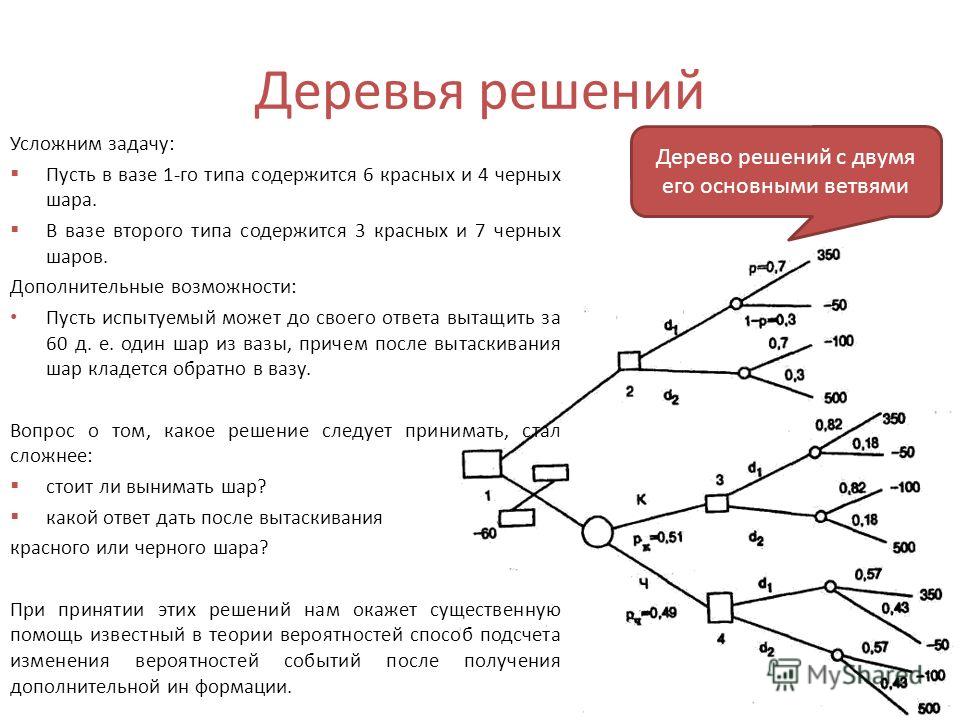 Дерево решений, например, используется для составления готовых скриптов для общения с потребителями в сфере продаж товаров и услуг.
Дерево решений, например, используется для составления готовых скриптов для общения с потребителями в сфере продаж товаров и услуг.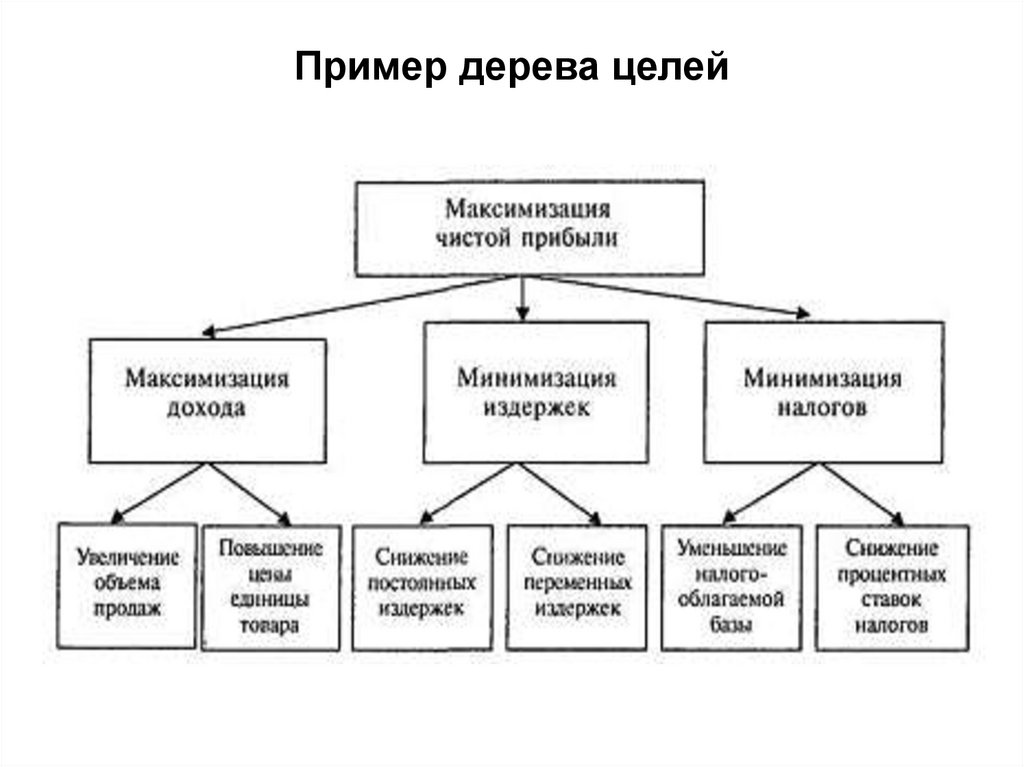 Самой простой и популярной задачей, которая ставится перед деревом решений, является бинарная классификация. Она представляет собой деление заявленных примеров на два типа, один из которых является положительным (успех), а второй — отрицательным (неудача).
Самой простой и популярной задачей, которая ставится перед деревом решений, является бинарная классификация. Она представляет собой деление заявленных примеров на два типа, один из которых является положительным (успех), а второй — отрицательным (неудача).
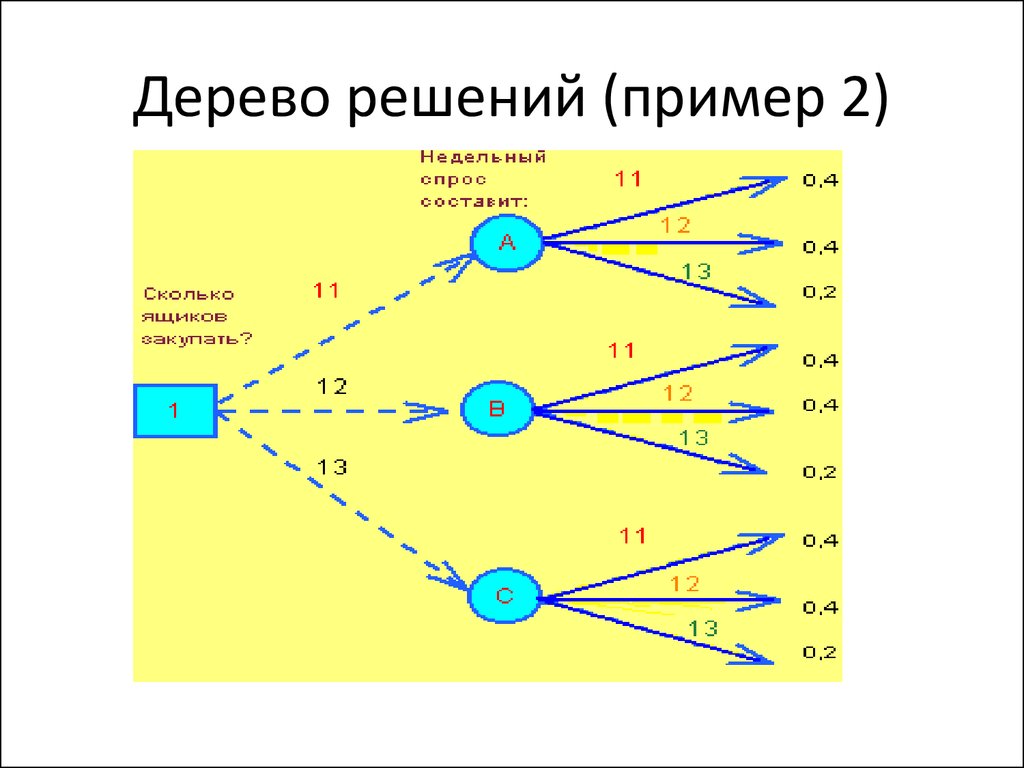 Условия формулируются отдельно по каждому решению или значению и прогнозируют вероятность определённого результата при соблюдении условий.
Условия формулируются отдельно по каждому решению или значению и прогнозируют вероятность определённого результата при соблюдении условий. Это позволяет наиболее точно предсказать результат и выявить оптимальный алгоритм для достижения желаемого итога. В качестве комбинированного подхода используются следующие методы:
Это позволяет наиболее точно предсказать результат и выявить оптимальный алгоритм для достижения желаемого итога. В качестве комбинированного подхода используются следующие методы: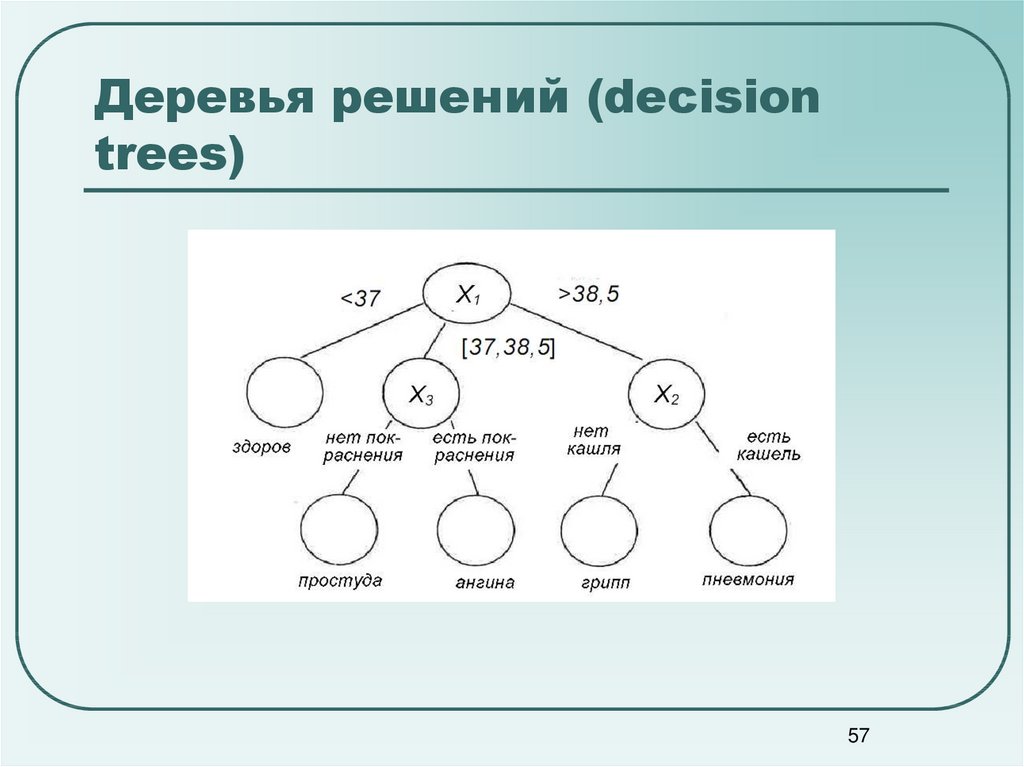 Этот инструмент экономически выгоден, так как затраты на его использование уменьшаются с каждой дополнительной точкой данных. Деревья решений позволяют анализировать как числовые, так и категориальные данные.
Этот инструмент экономически выгоден, так как затраты на его использование уменьшаются с каждой дополнительной точкой данных. Деревья решений позволяют анализировать как числовые, так и категориальные данные. Затем они формируют ответ на вопрос о том, почему для решения данной задачи должен использоваться именно такой инструмент. Кроме того, на этом этапе вычисляются факторы, которые оказывают влияние на зависимую переменную.
Затем они формируют ответ на вопрос о том, почему для решения данной задачи должен использоваться именно такой инструмент. Кроме того, на этом этапе вычисляются факторы, которые оказывают влияние на зависимую переменную.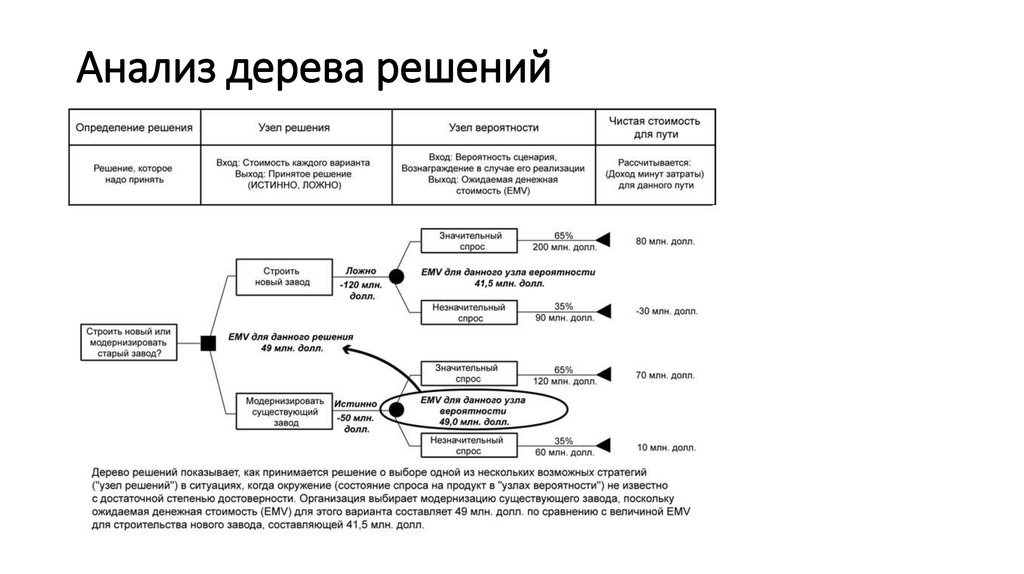 На основе представленной информации происходит автоматическая генерация правил работы дерева решений.
На основе представленной информации происходит автоматическая генерация правил работы дерева решений.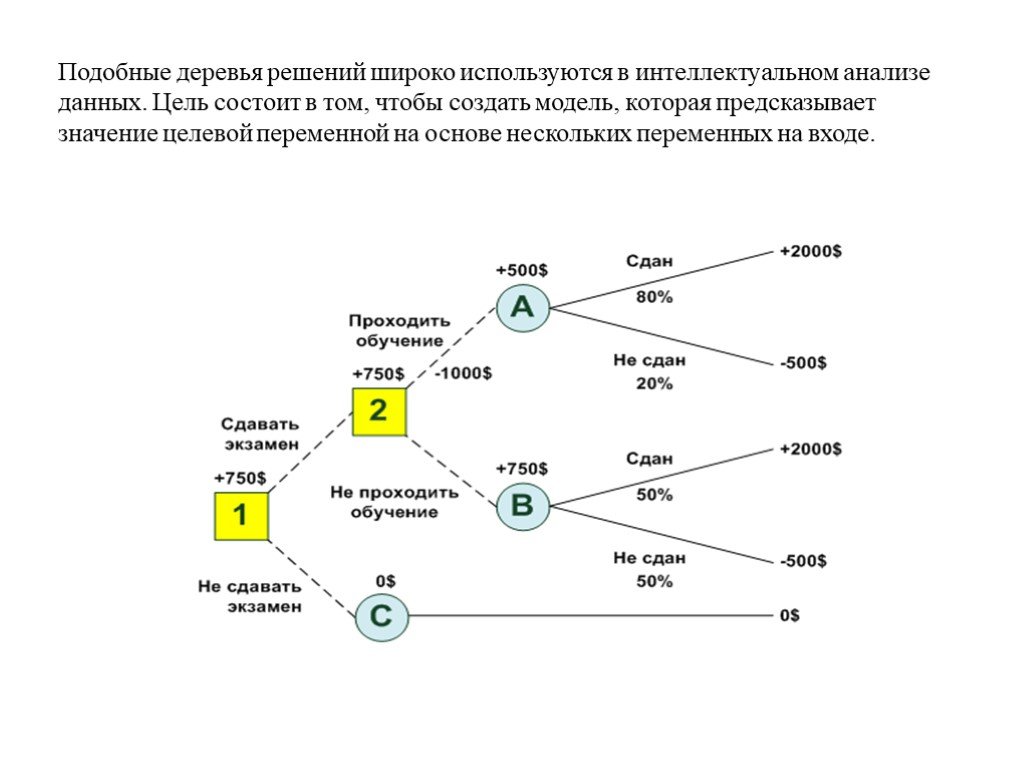
 Она актуальна в различных ситуациях и способна сослужить хорошую службу. Если вы являетесь новичком в данной сфере, то попробуйте начать с небольших задач. Постепенно вы наберетесь опыта и сможете грамотно использовать этот инструмент для работы с более глобальными вопросами.
Она актуальна в различных ситуациях и способна сослужить хорошую службу. Если вы являетесь новичком в данной сфере, то попробуйте начать с небольших задач. Постепенно вы наберетесь опыта и сможете грамотно использовать этот инструмент для работы с более глобальными вопросами.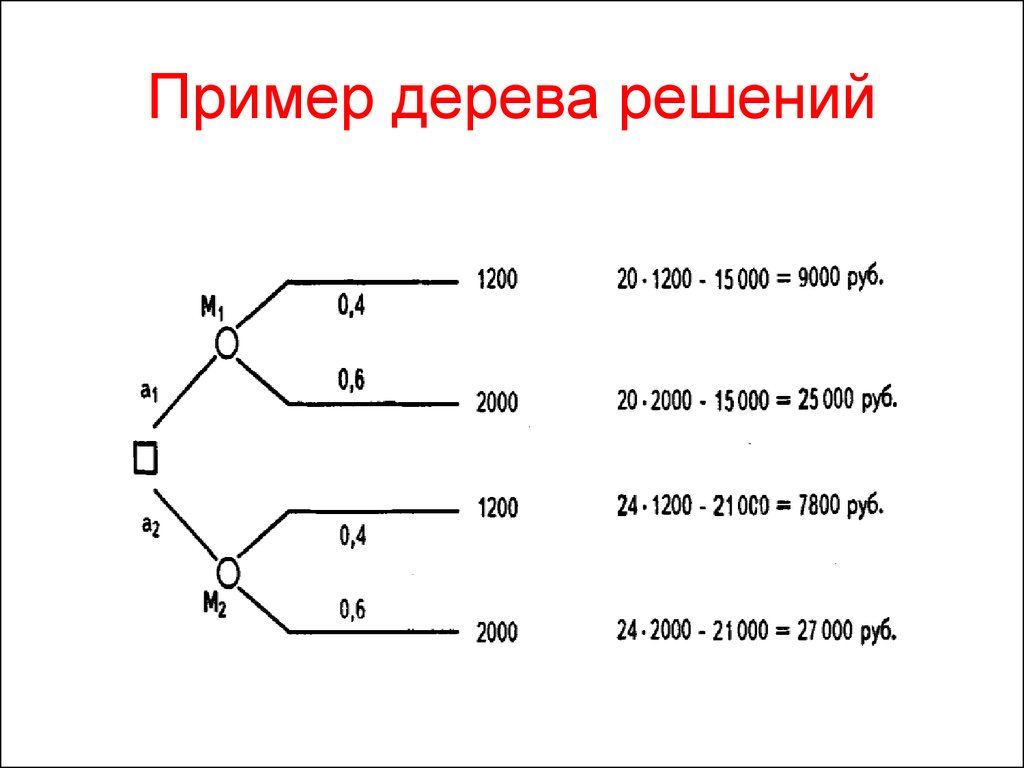 Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной, изучая простые правила принятия решений, выведенные из характеристик данных. Дерево можно рассматривать как кусочно-постоянное приближение.
Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной, изучая простые правила принятия решений, выведенные из характеристик данных. Дерево можно рассматривать как кусочно-постоянное приближение.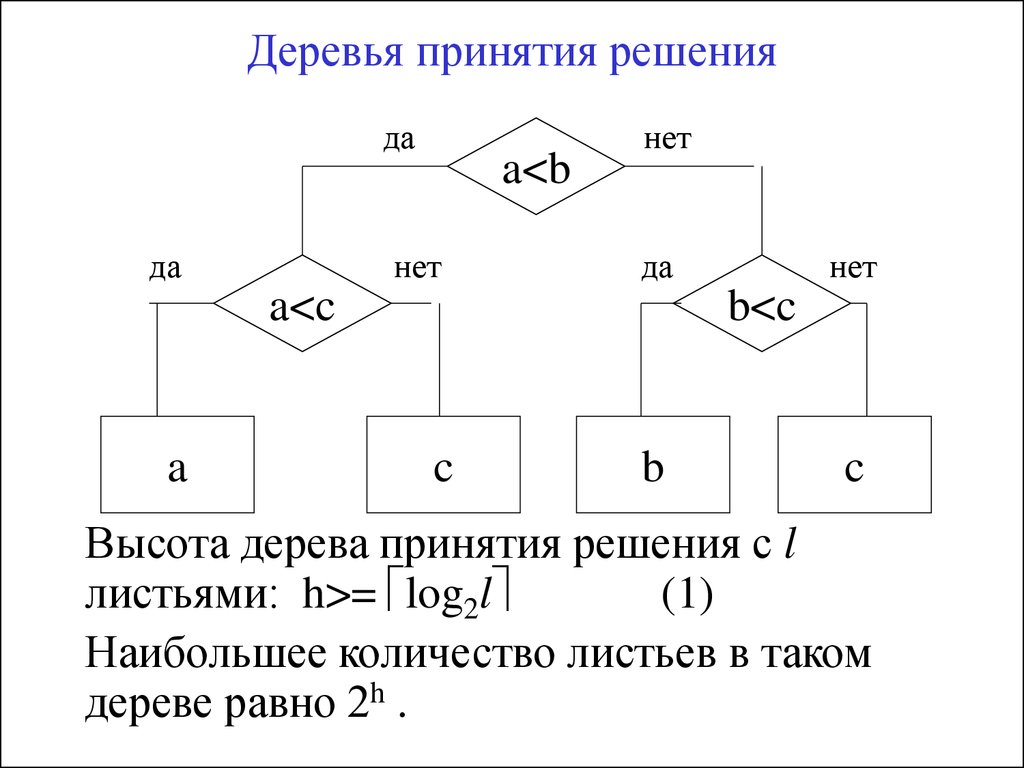
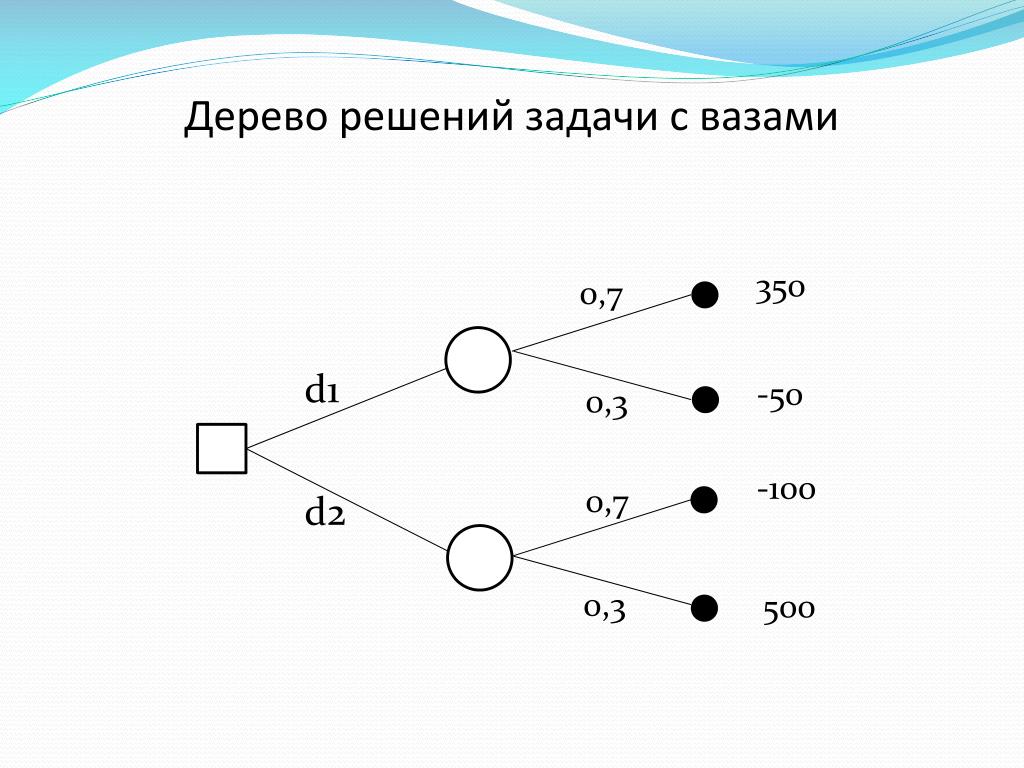 Это называется переобучением. Чтобы избежать этой проблемы, необходимы такие механизмы, как обрезка, установка минимального количества выборок, необходимых для конечного узла, или установка максимальной глубины дерева.
Это называется переобучением. Чтобы избежать этой проблемы, необходимы такие механизмы, как обрезка, установка минимального количества выборок, необходимых для конечного узла, или установка максимальной глубины дерева. Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой.
Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой.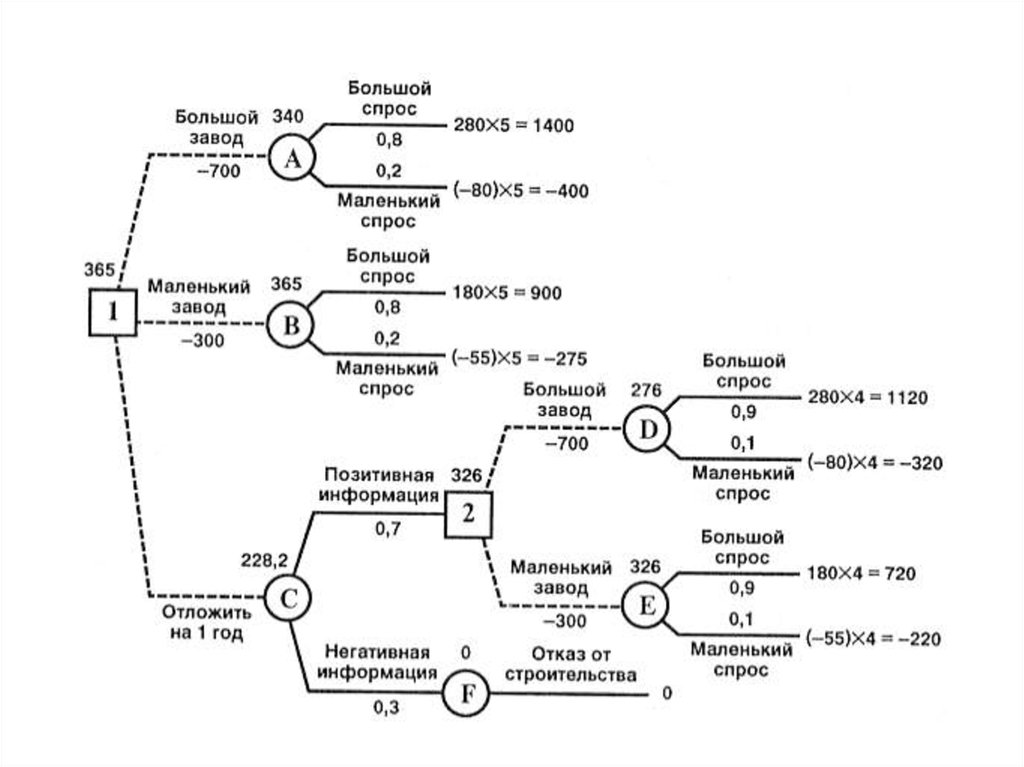 DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)
DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)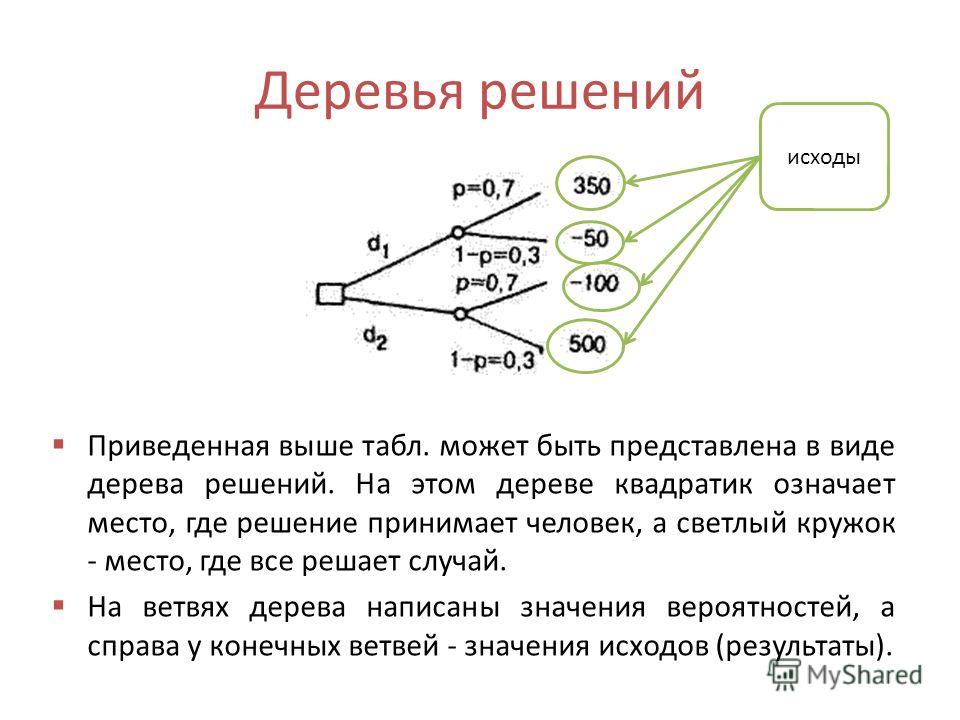 predict_proba([[2., 2.]])
array([[0., 1.]])
predict_proba([[2., 2.]])
array([[0., 1.]]) plot_tree(clf)
plot_tree(clf)  export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris")
export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris")  .. special_characters=True)
>>> graph = graphviz.Source(dot_data)
>>> graph
.. special_characters=True)
>>> graph = graphviz.Source(dot_data)
>>> graph 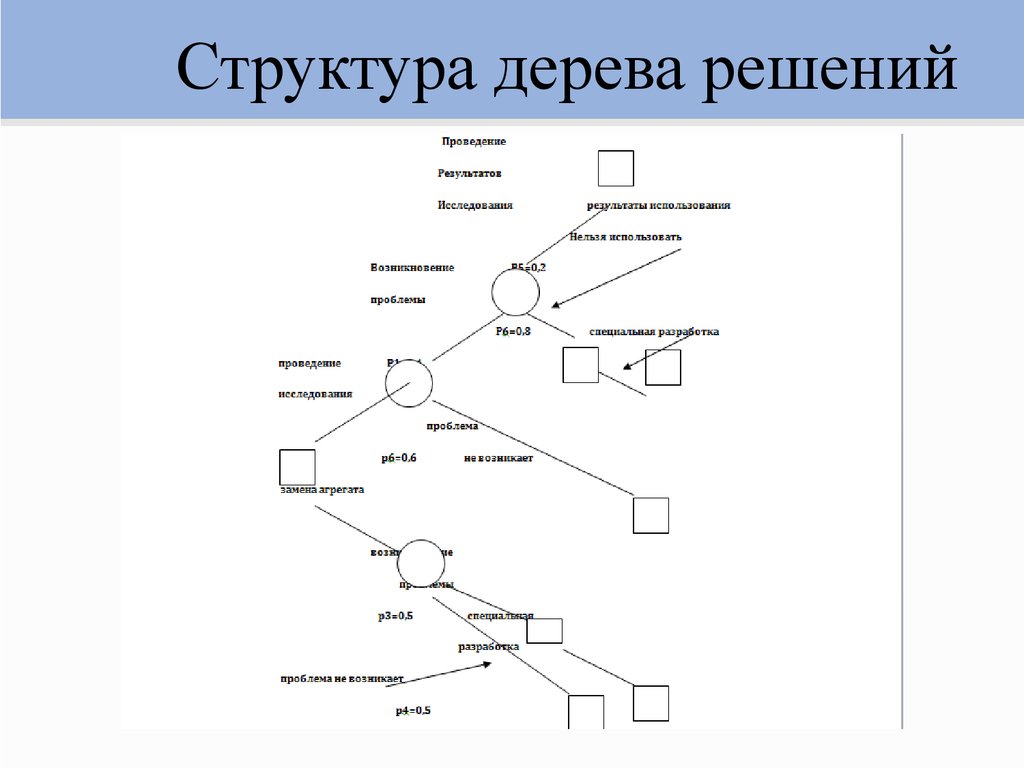 80
| |--- class: 0
|--- petal width (cm) > 0.80
| |--- petal width (cm) <= 1.75
| | |--- class: 1
| |--- petal width (cm) > 1.75
| | |--- class: 2
80
| |--- class: 0
|--- petal width (cm) > 0.80
| |--- petal width (cm) <= 1.75
| | |--- class: 1
| |--- petal width (cm) > 1.75
| | |--- class: 2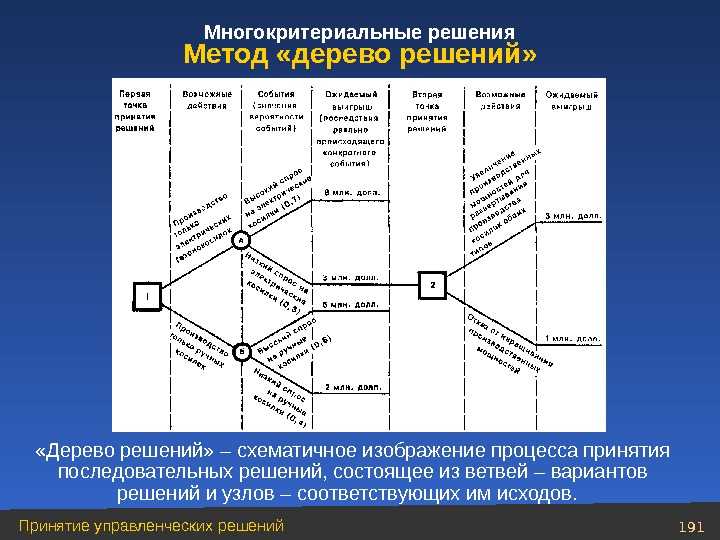 5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])
5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])
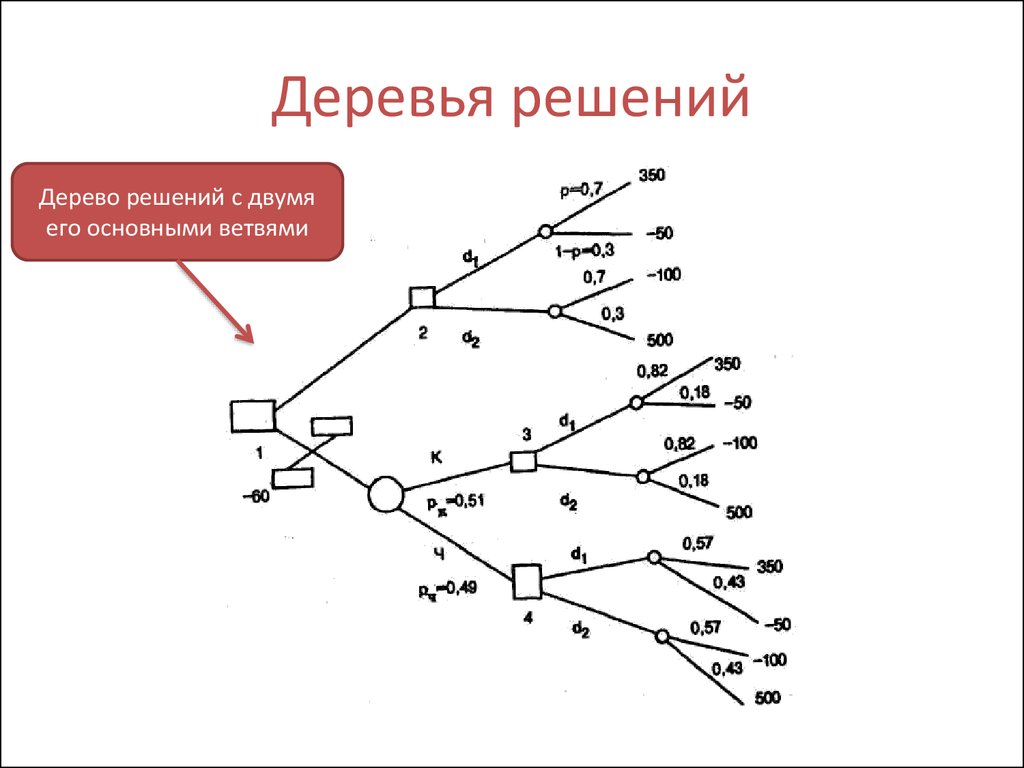
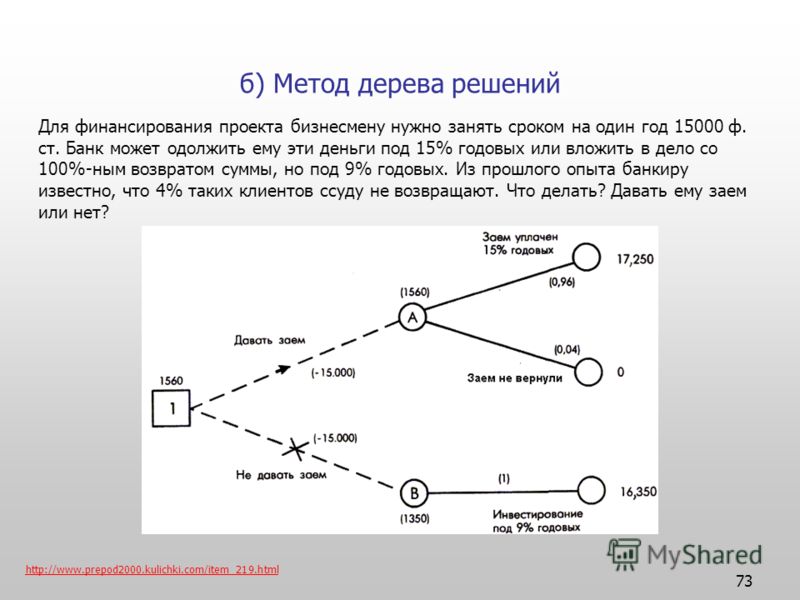 {2}\log(n_{samples}))$
{2}\log(n_{samples}))$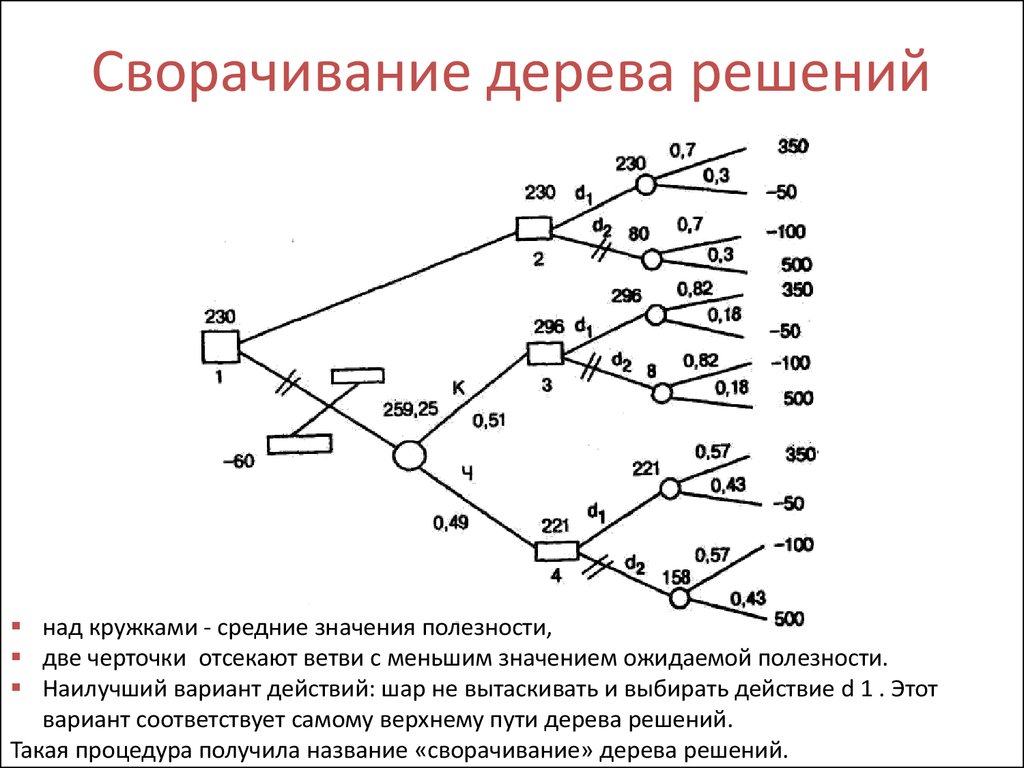 Используйте
Используйте 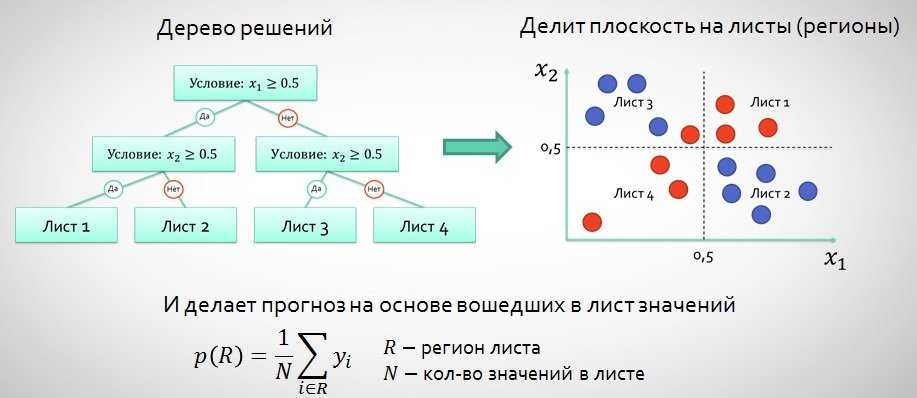 Рассмотрим
Рассмотрим 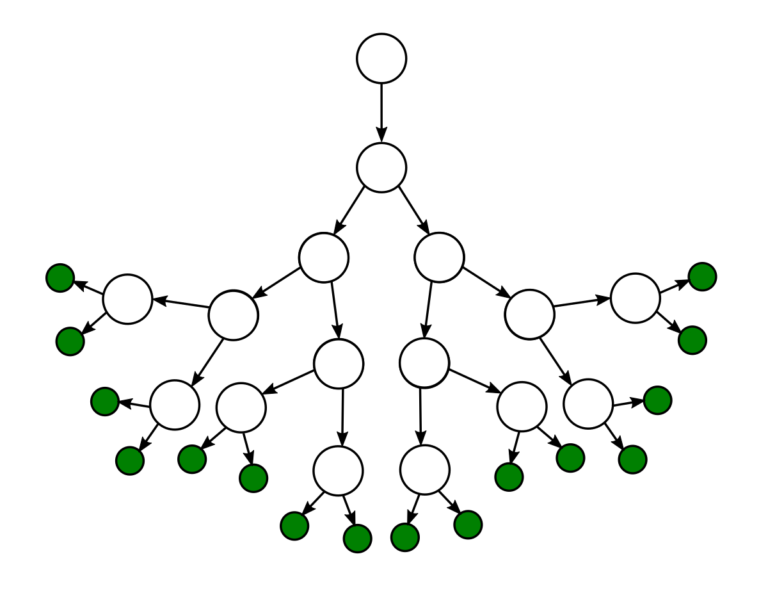
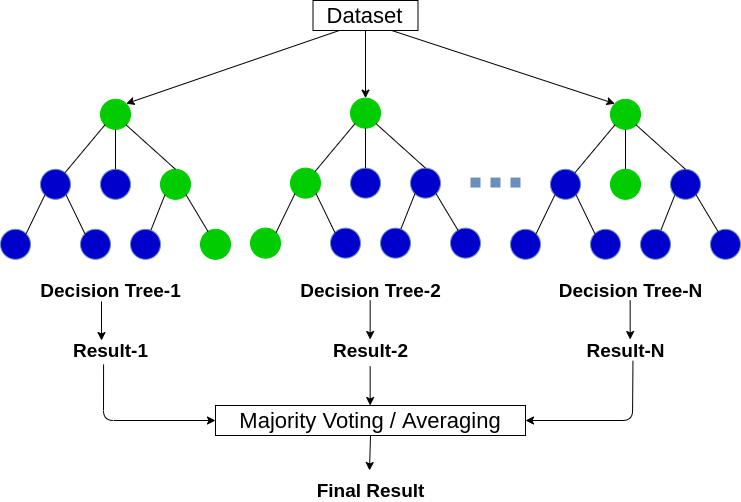 Деревья вырастают до максимального размера, а затем обычно применяется этап обрезки, чтобы улучшить способность дерева обобщать невидимые данные.
Деревья вырастают до максимального размера, а затем обычно применяется этап обрезки, чтобы улучшить способность дерева обобщать невидимые данные. *)$ пока не будет достигнута максимально допустимая глубина, $N_m < \min_{samples}$ или же $N_m = 1$.
*)$ пока не будет достигнута максимально допустимая глубина, $N_m < \min_{samples}$ или же $N_m = 1$. 2$$
2$$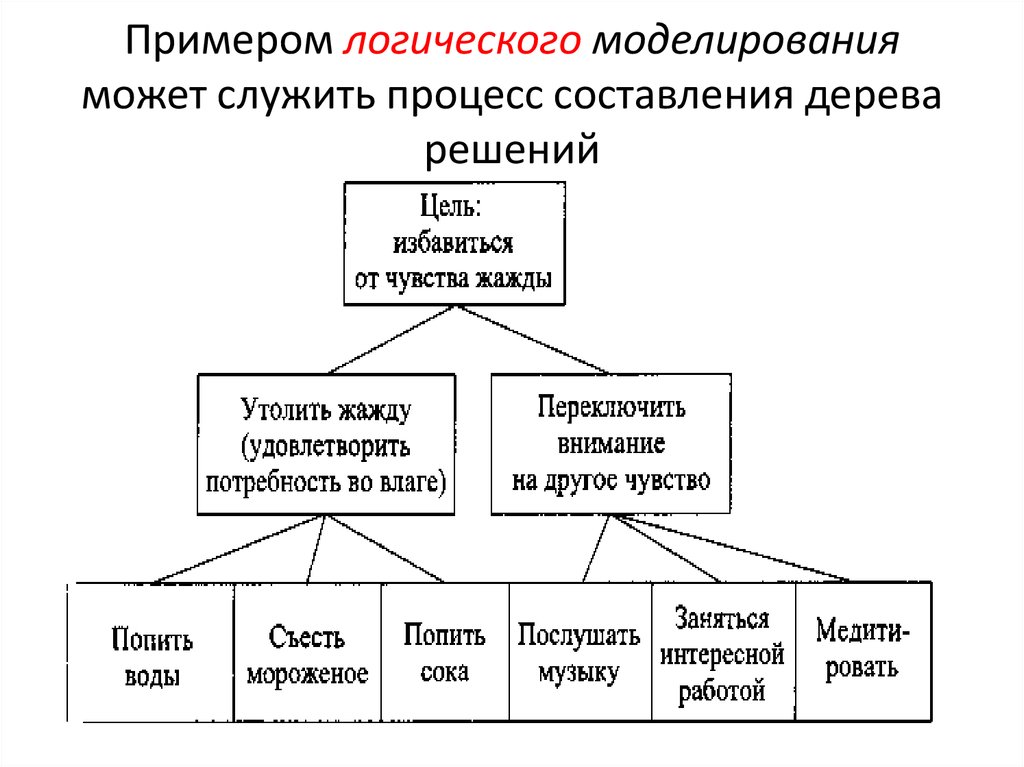 В качестве альтернативы scikit-learn использует взвешенную общую примесь конечных узлов для $R(T)$. Как показано выше, примесь узла зависит от критерия. Обрезка с минимальными затратами и сложностью находит поддеревоT что сводит к минимуму $R_\alpha(T)$.
В качестве альтернативы scikit-learn использует взвешенную общую примесь конечных узлов для $R(T)$. Как показано выше, примесь узла зависит от критерия. Обрезка с минимальными затратами и сложностью находит поддеревоT что сводит к минимуму $R_\alpha(T)$.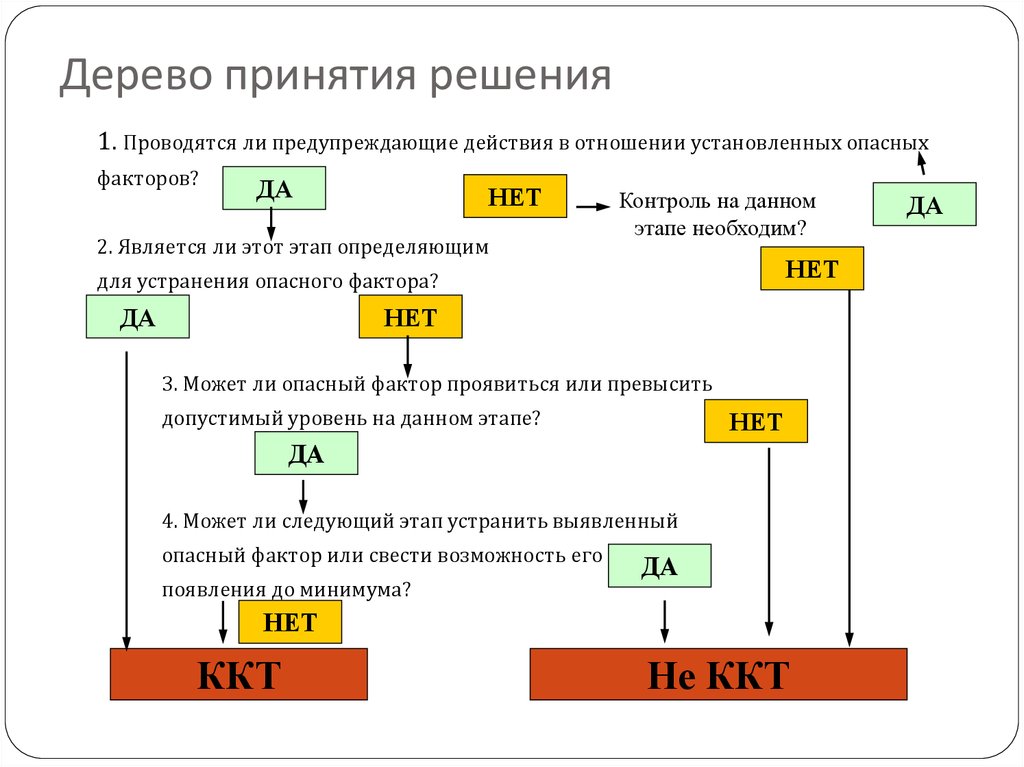 Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984.
Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984.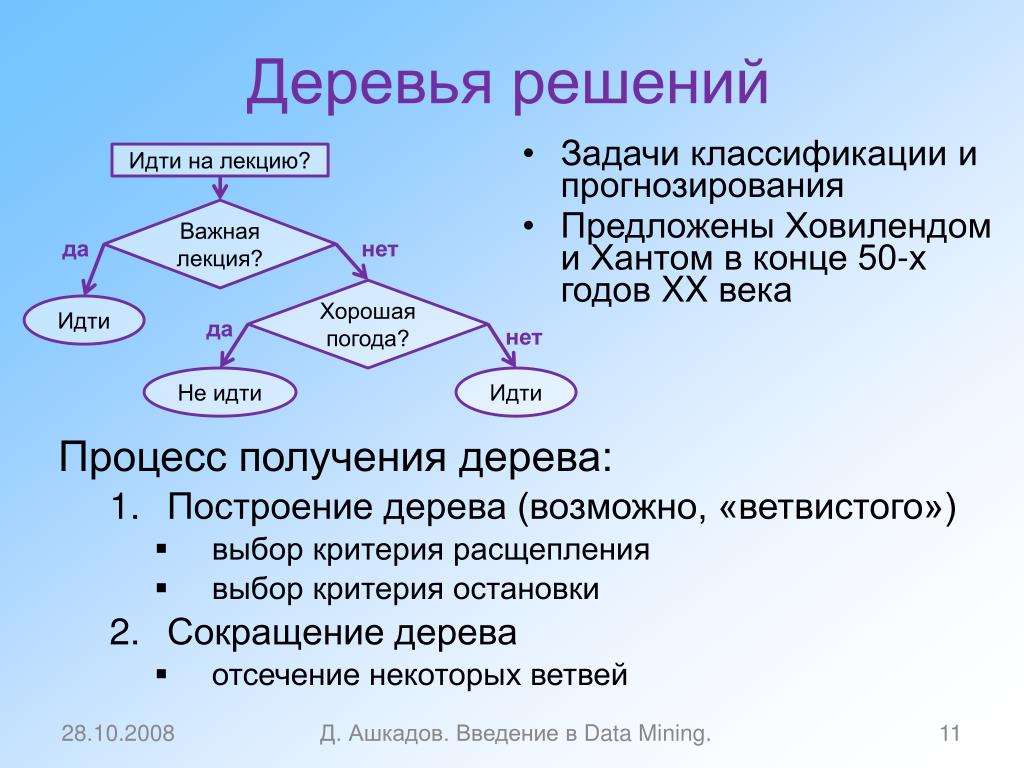 На основе доступных функций оба типа узлов выполняют оценку для формирования однородных подмножеств, которые обозначаются конечными узлами или конечными узлами. Листовые узлы представляют все возможные результаты в наборе данных. В качестве примера, давайте представим, что вы пытаетесь оценить, стоит ли вам заниматься серфингом, вы можете использовать следующие правила принятия решений, чтобы сделать выбор:
На основе доступных функций оба типа узлов выполняют оценку для формирования однородных подмножеств, которые обозначаются конечными узлами или конечными узлами. Листовые узлы представляют все возможные результаты в наборе данных. В качестве примера, давайте представим, что вы пытаетесь оценить, стоит ли вам заниматься серфингом, вы можете использовать следующие правила принятия решений, чтобы сделать выбор: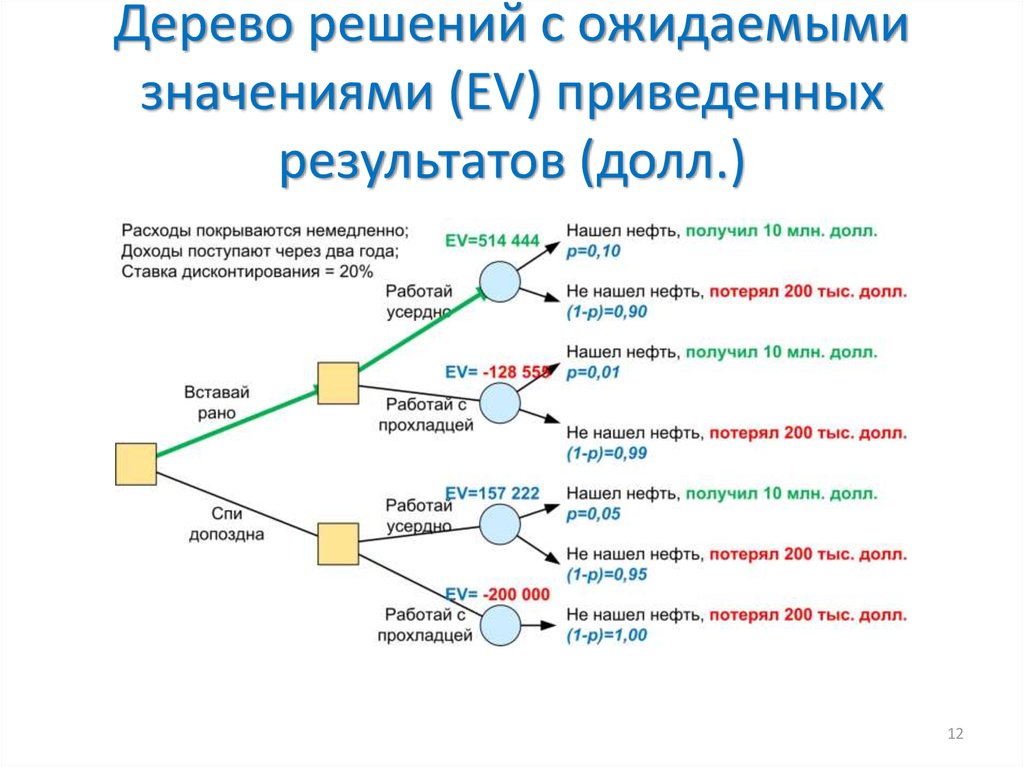 Меньшие деревья легче могут получить чистые листовые узлы, т.е. точки данных в одном классе. Однако по мере роста дерева становится все труднее поддерживать эту чистоту, и это обычно приводит к тому, что в данное поддерево попадает слишком мало данных. Когда это происходит, это называется фрагментацией данных и часто может привести к переоснащению. В результате деревья решений отдают предпочтение маленьким деревьям, что согласуется с принципом экономии в бритве Оккама; то есть «сущности не должны умножаться сверх необходимости». Иными словами, деревья решений должны усложнять только в случае необходимости, поскольку самое простое объяснение часто является лучшим. Чтобы уменьшить сложность и предотвратить переоснащение, обычно используется обрезка; это процесс, который удаляет ветви, разделяющиеся на объекты с низкой важностью. Затем соответствие модели можно оценить в процессе перекрестной проверки. Другой способ, которым деревья решений могут поддерживать свою точность, — это формирование ансамбля с помощью алгоритма случайного леса; этот классификатор предсказывает более точные результаты, особенно когда отдельные деревья не коррелируют друг с другом.
Меньшие деревья легче могут получить чистые листовые узлы, т.е. точки данных в одном классе. Однако по мере роста дерева становится все труднее поддерживать эту чистоту, и это обычно приводит к тому, что в данное поддерево попадает слишком мало данных. Когда это происходит, это называется фрагментацией данных и часто может привести к переоснащению. В результате деревья решений отдают предпочтение маленьким деревьям, что согласуется с принципом экономии в бритве Оккама; то есть «сущности не должны умножаться сверх необходимости». Иными словами, деревья решений должны усложнять только в случае необходимости, поскольку самое простое объяснение часто является лучшим. Чтобы уменьшить сложность и предотвратить переоснащение, обычно используется обрезка; это процесс, который удаляет ветви, разделяющиеся на объекты с низкой важностью. Затем соответствие модели можно оценить в процессе перекрестной проверки. Другой способ, которым деревья решений могут поддерживать свою точность, — это формирование ансамбля с помощью алгоритма случайного леса; этот классификатор предсказывает более точные результаты, особенно когда отдельные деревья не коррелируют друг с другом.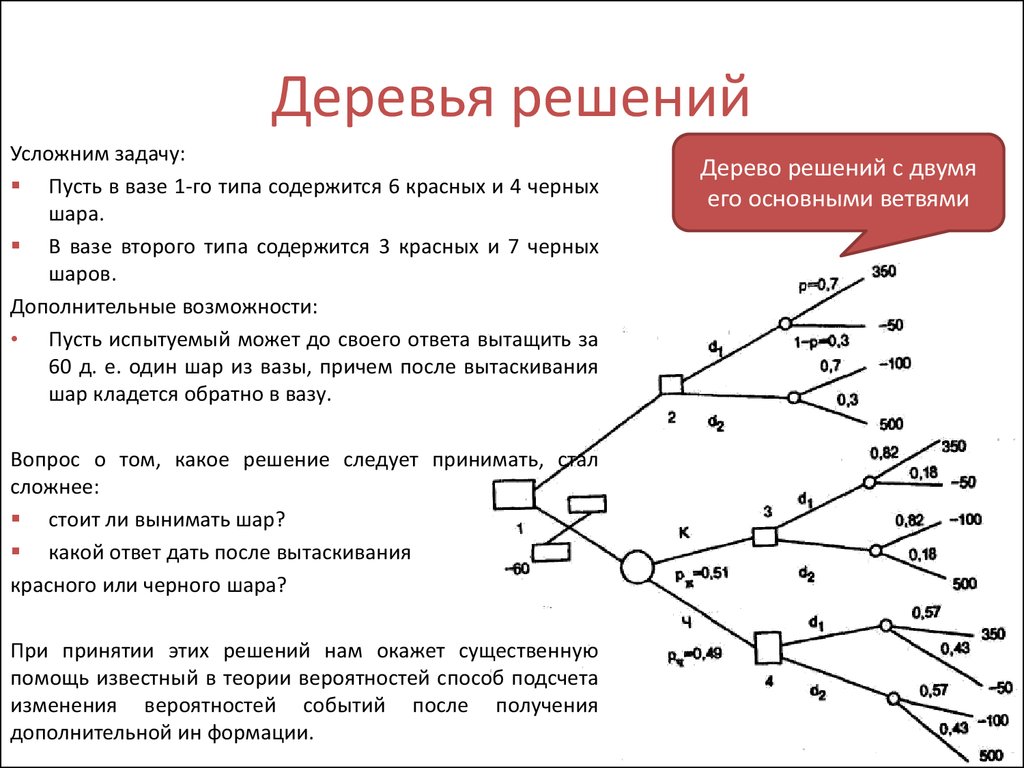
 Примесь Джини измеряет, как часто случайно выбранный атрибут неправильно классифицируется. При оценке с использованием примеси Джини более низкое значение является более идеальным.
Примесь Джини измеряет, как часто случайно выбранный атрибут неправильно классифицируется. При оценке с использованием примеси Джини более низкое значение является более идеальным.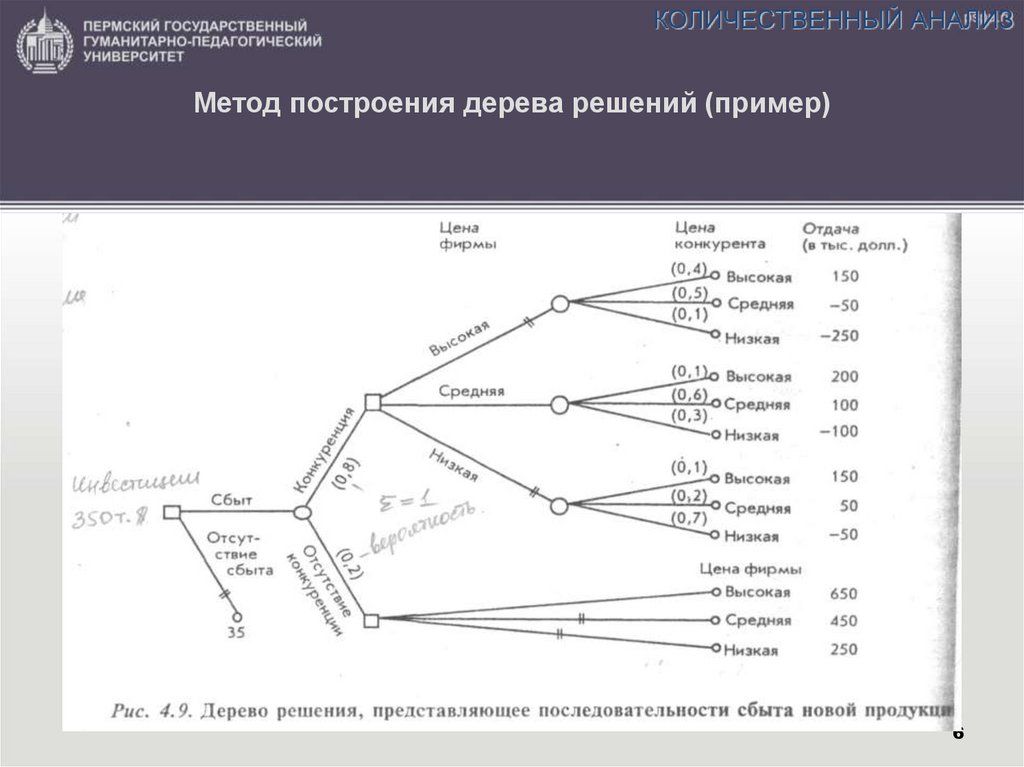 Если все выборки в наборе данных S принадлежат одному классу, то энтропия будет равна нулю. Если половина выборок относится к одному классу, а другая половина — к другому классу, энтропия будет максимальной, равной 1. Чтобы выбрать лучший признак для разделения и найти оптимальное дерево решений, атрибут с наименьшим следует использовать количество энтропии. Прирост информации представляет собой разницу в энтропии до и после разделения по данному атрибуту. Атрибут с наибольшим приростом информации даст наилучшее разделение, поскольку он лучше всего справляется с классификацией обучающих данных в соответствии с его целевой классификацией. Прирост информации обычно представляется следующей формулой, где:
Если все выборки в наборе данных S принадлежат одному классу, то энтропия будет равна нулю. Если половина выборок относится к одному классу, а другая половина — к другому классу, энтропия будет максимальной, равной 1. Чтобы выбрать лучший признак для разделения и найти оптимальное дерево решений, атрибут с наименьшим следует использовать количество энтропии. Прирост информации представляет собой разницу в энтропии до и после разделения по данному атрибуту. Атрибут с наибольшим приростом информации даст наилучшее разделение, поскольку он лучше всего справляется с классификацией обучающих данных в соответствии с его целевой классификацией. Прирост информации обычно представляется следующей формулой, где: 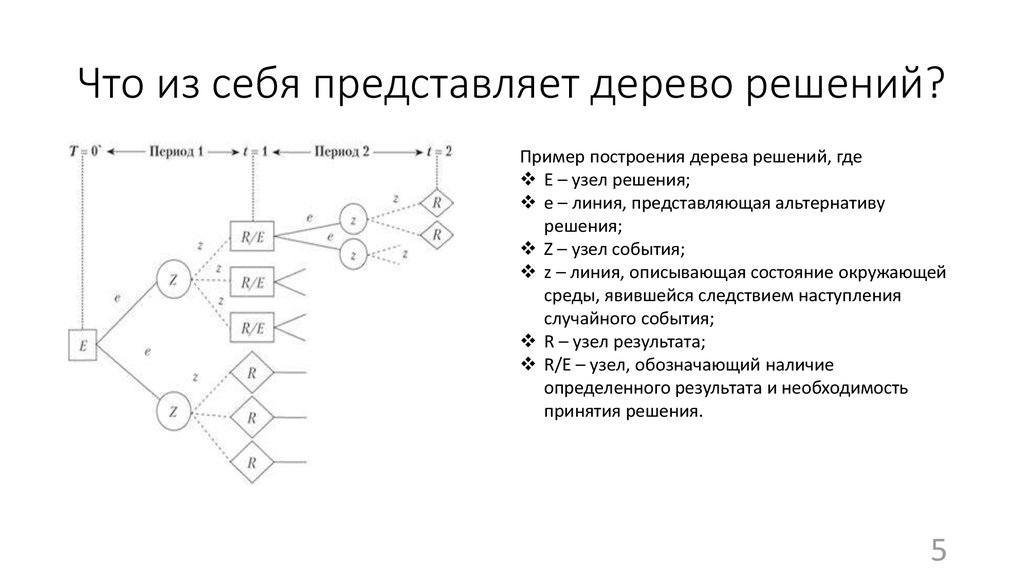 Представьте, что у нас есть следующий произвольный набор данных:
Представьте, что у нас есть следующий произвольный набор данных:  В этом случае Outlook дает наибольший прирост информации. Оттуда процесс повторяется для каждого поддерева.
В этом случае Outlook дает наибольший прирост информации. Оттуда процесс повторяется для каждого поддерева. Иерархическая природа дерева решений также позволяет легко увидеть, какие атрибуты являются наиболее важными, что не всегда понятно с другими алгоритмами, такими как нейронные сети.
Иерархическая природа дерева решений также позволяет легко увидеть, какие атрибуты являются наиболее важными, что не всегда понятно с другими алгоритмами, такими как нейронные сети.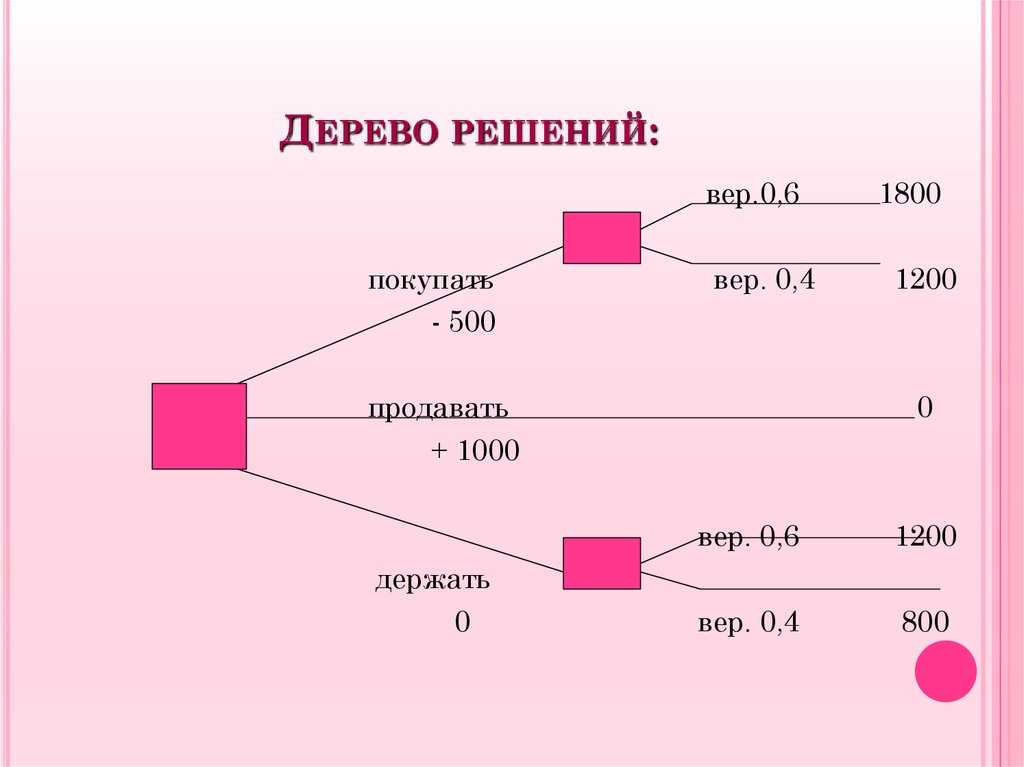
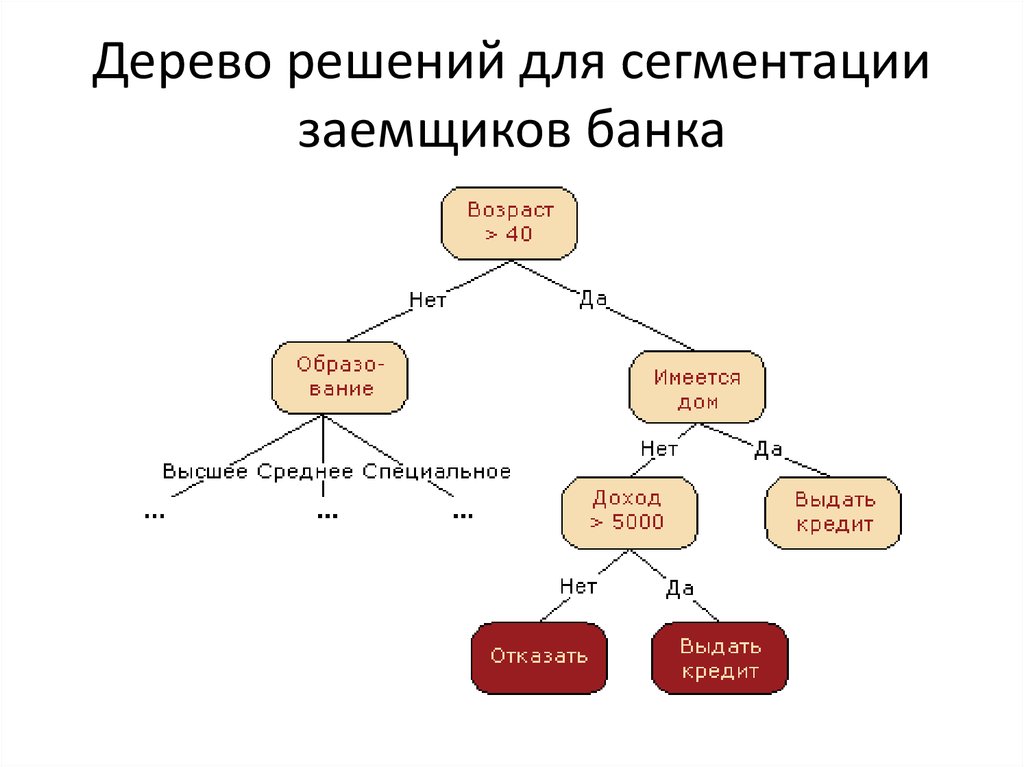 Хотя в этой библиотеке есть модуль дерева решений (DecisionTreeClassifier, ссылка находится за пределами ibm.com), текущая реализация не поддерживает категориальные переменные.
Хотя в этой библиотеке есть модуль дерева решений (DecisionTreeClassifier, ссылка находится за пределами ibm.com), текущая реализация не поддерживает категориальные переменные.

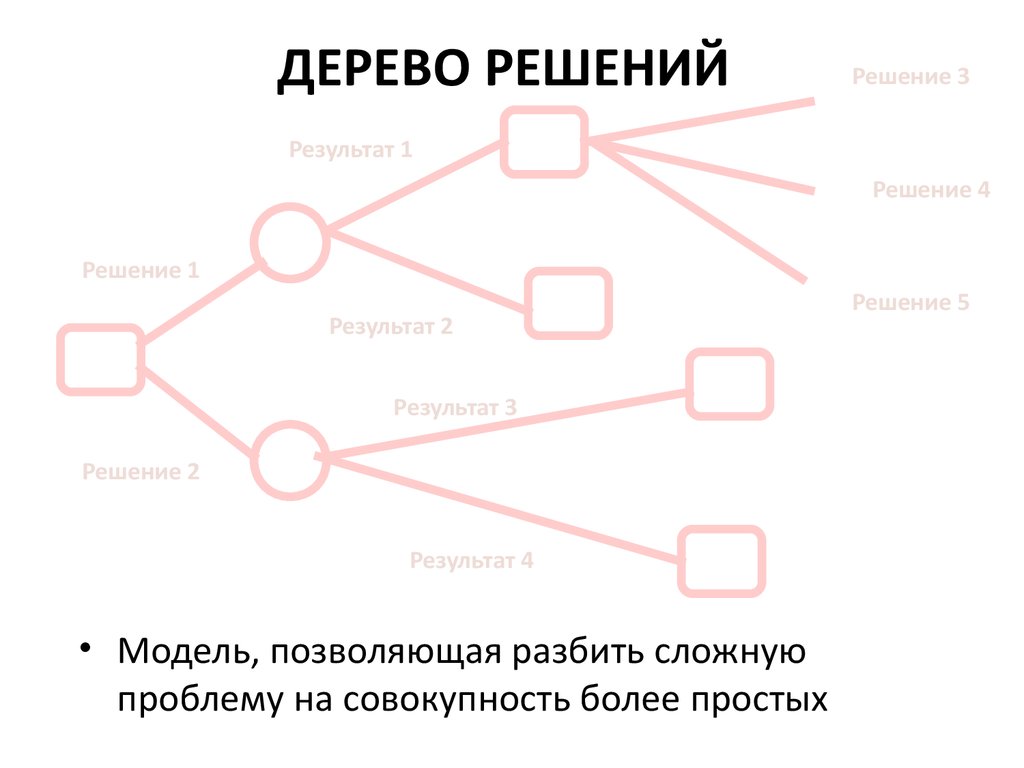 Здесь мы знаем, что доход клиентов является существенной переменной, но страховая компания не располагает подробной информацией о доходах всех клиентов. Теперь, когда мы знаем, что это важная переменная, мы можем построить дерево решений для прогнозирования доходов клиентов на основе рода занятий, продукта и различных других переменных. В этом случае мы прогнозируем значения для непрерывных переменных.
Здесь мы знаем, что доход клиентов является существенной переменной, но страховая компания не располагает подробной информацией о доходах всех клиентов. Теперь, когда мы знаем, что это важная переменная, мы можем построить дерево решений для прогнозирования доходов клиентов на основе рода занятий, продукта и различных других переменных. В этом случае мы прогнозируем значения для непрерывных переменных.
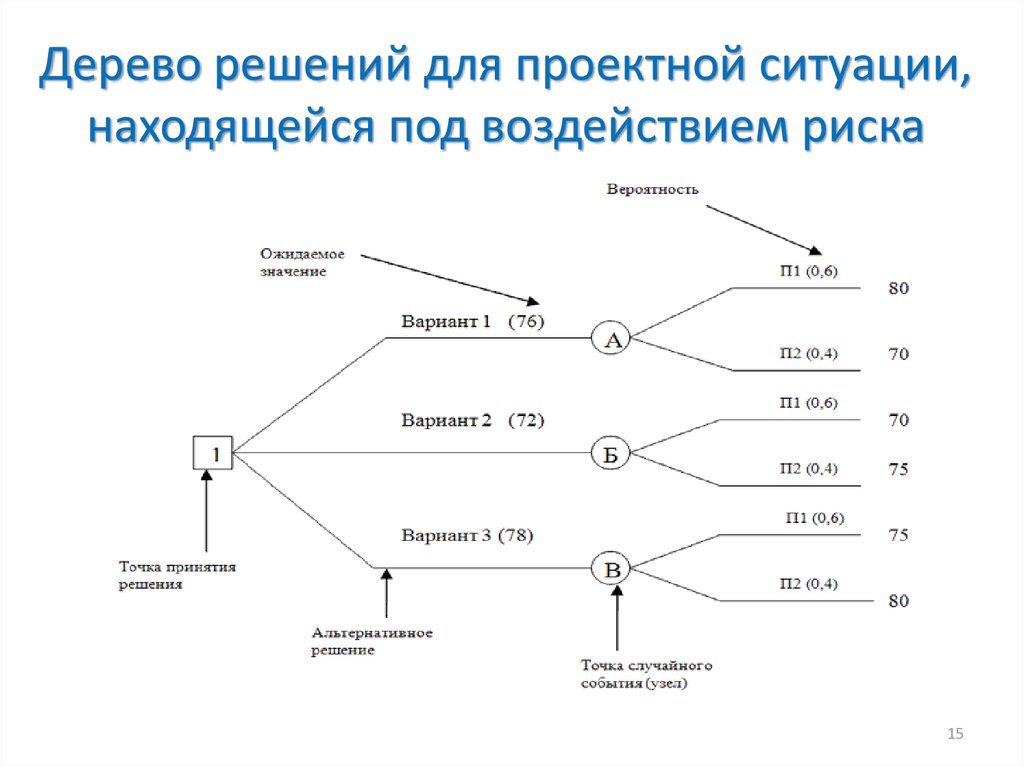 У нас есть различные меры выбора атрибутов для определения атрибута, который можно рассматривать как корневую ноту на каждом уровне.
У нас есть различные меры выбора атрибутов для определения атрибута, который можно рассматривать как корневую ноту на каждом уровне.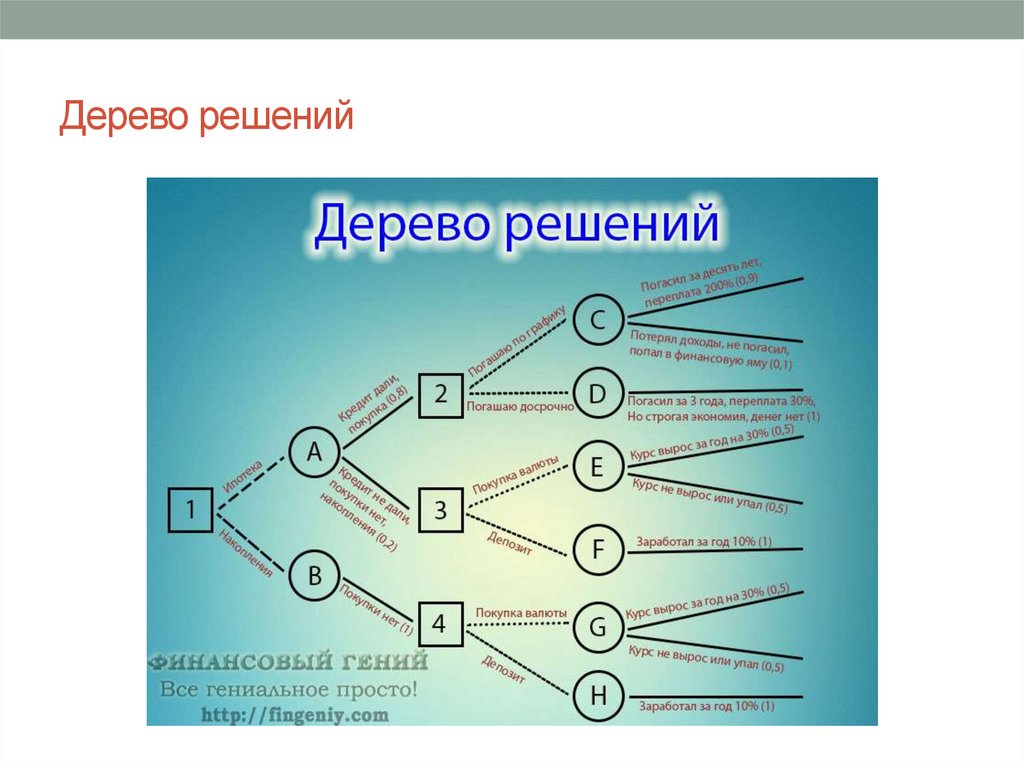 Выполняет многоуровневое разбиение при вычислении деревьев классификации)
Выполняет многоуровневое разбиение при вычислении деревьев классификации) 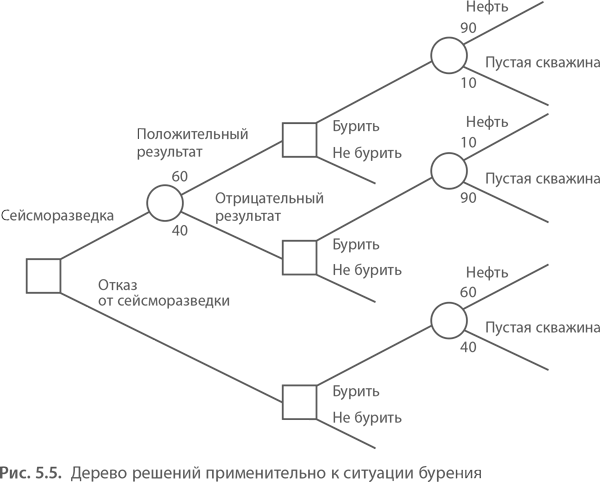
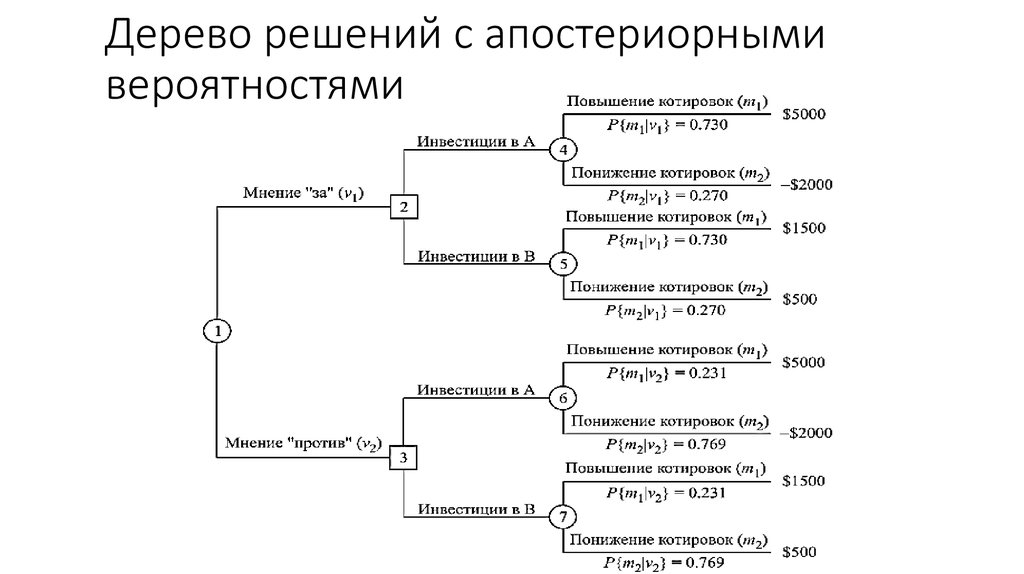
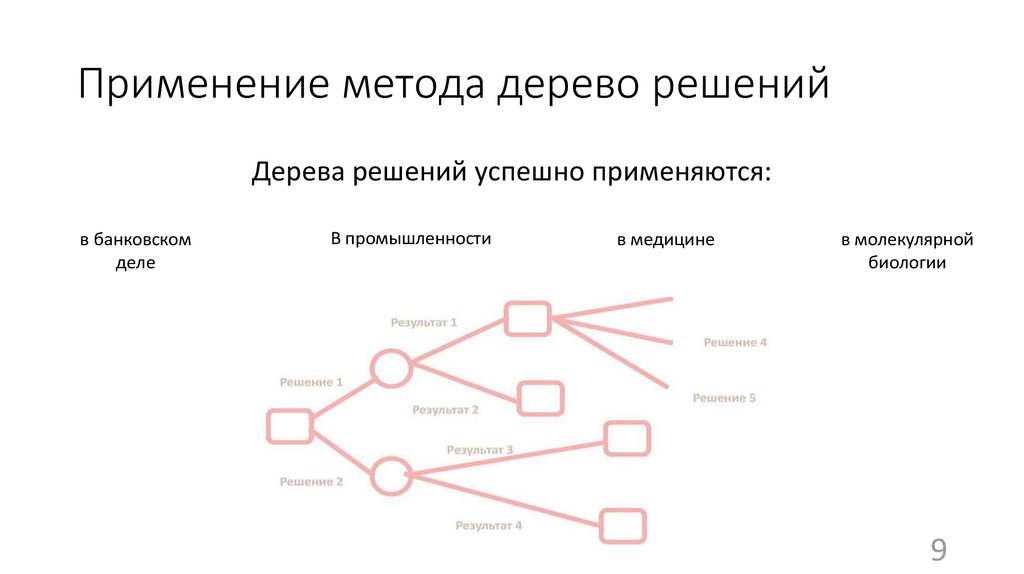
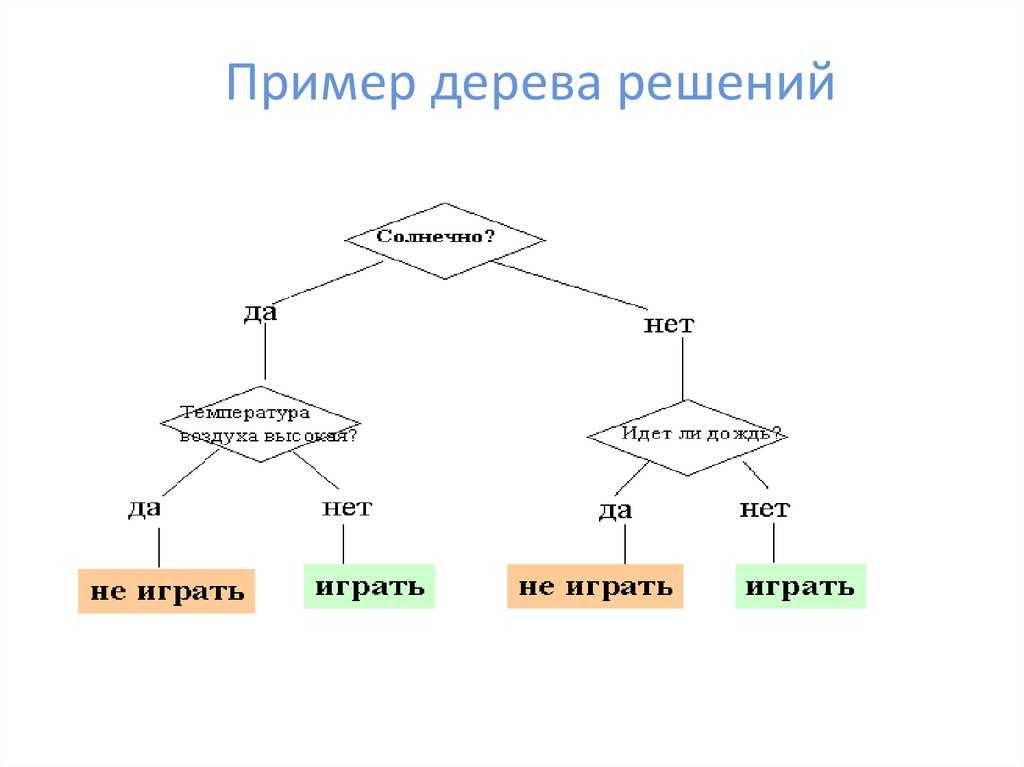
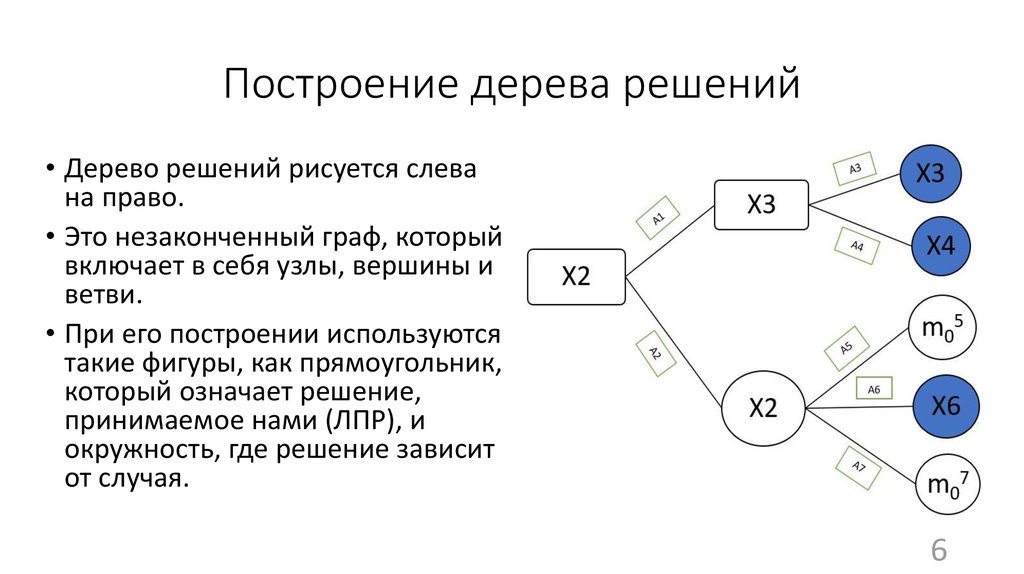 д. С помощью прироста информации вы разделитесь на «Пол» (при условии, что он имеет самый высокий прирост информации), и теперь переменные «Возрастная группа» и «Рейтинг» могут быть одинаково важны, и с помощью коэффициента прироста он будет наказывать переменная с более четкими значениями, которые помогут нам определить разделение на следующем уровне.
д. С помощью прироста информации вы разделитесь на «Пол» (при условии, что он имеет самый высокий прирост информации), и теперь переменные «Возрастная группа» и «Рейтинг» могут быть одинаково важны, и с помощью коэффициента прироста он будет наказывать переменная с более четкими значениями, которые помогут нам определить разделение на следующем уровне.
 Иногда кажется, что дерево запомнило обучающий набор данных. Если для дерева решений не установлено ограничение, это даст вам 100% точность в наборе обучающих данных, потому что в худшем случае для каждого наблюдения будет создан 1 лист. Таким образом, это влияет на точность прогнозирования выборок, не входящих в обучающую выборку.
Иногда кажется, что дерево запомнило обучающий набор данных. Если для дерева решений не установлено ограничение, это даст вам 100% точность в наборе обучающих данных, потому что в худшем случае для каждого наблюдения будет создан 1 лист. Таким образом, это влияет на точность прогнозирования выборок, не входящих в обучающую выборку. Подготовьте дерево решений, используя отдельный набор обучающих данных, D. Затем продолжайте обрезать дерево соответствующим образом, чтобы оптимизировать точность набор проверочных данных, версия
Подготовьте дерево решений, используя отдельный набор обучающих данных, D. Затем продолжайте обрезать дерево соответствующим образом, чтобы оптимизировать точность набор проверочных данных, версия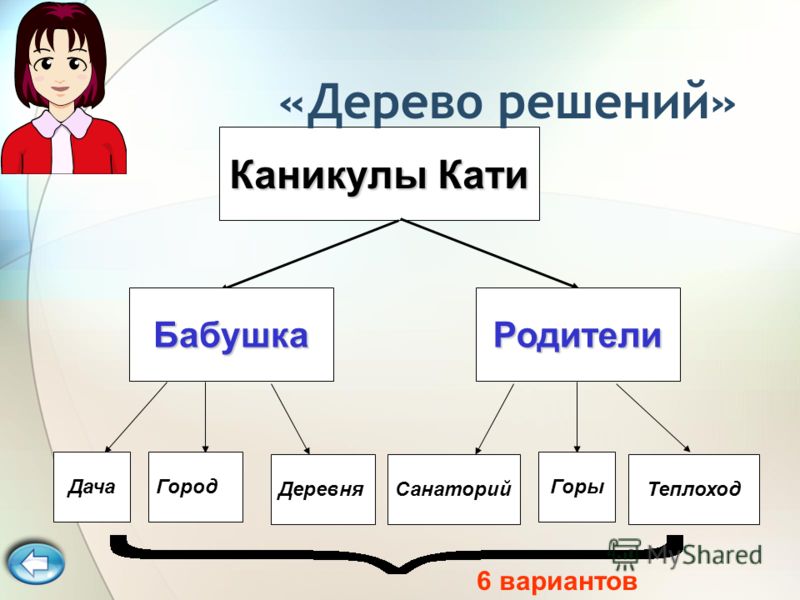
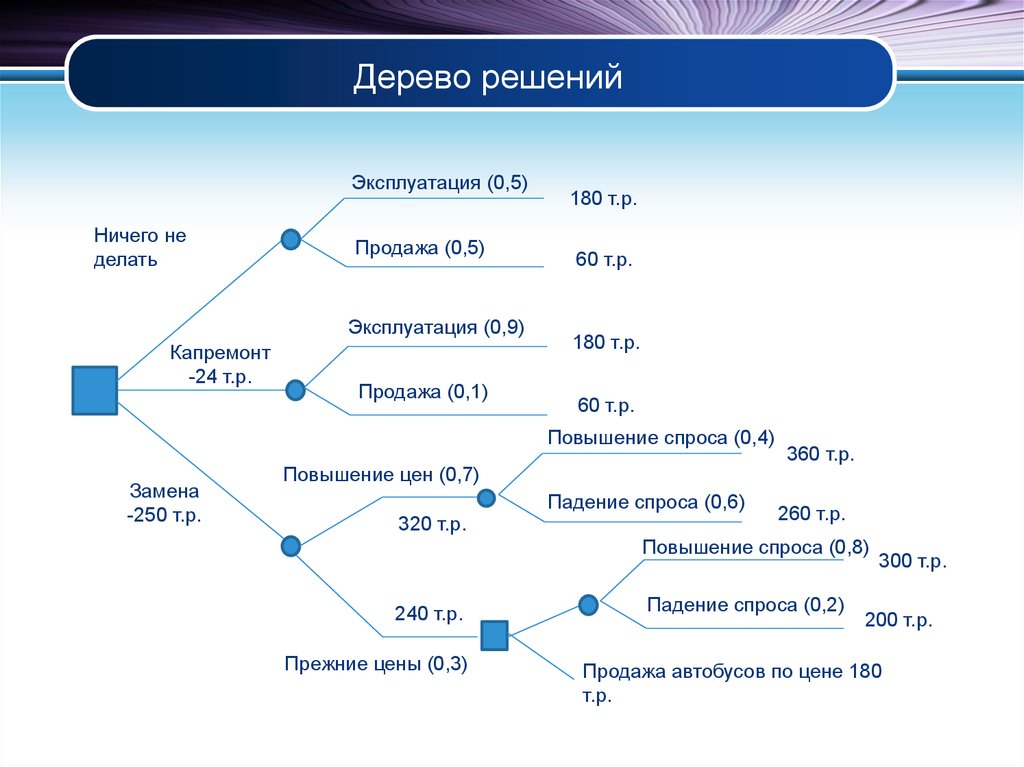
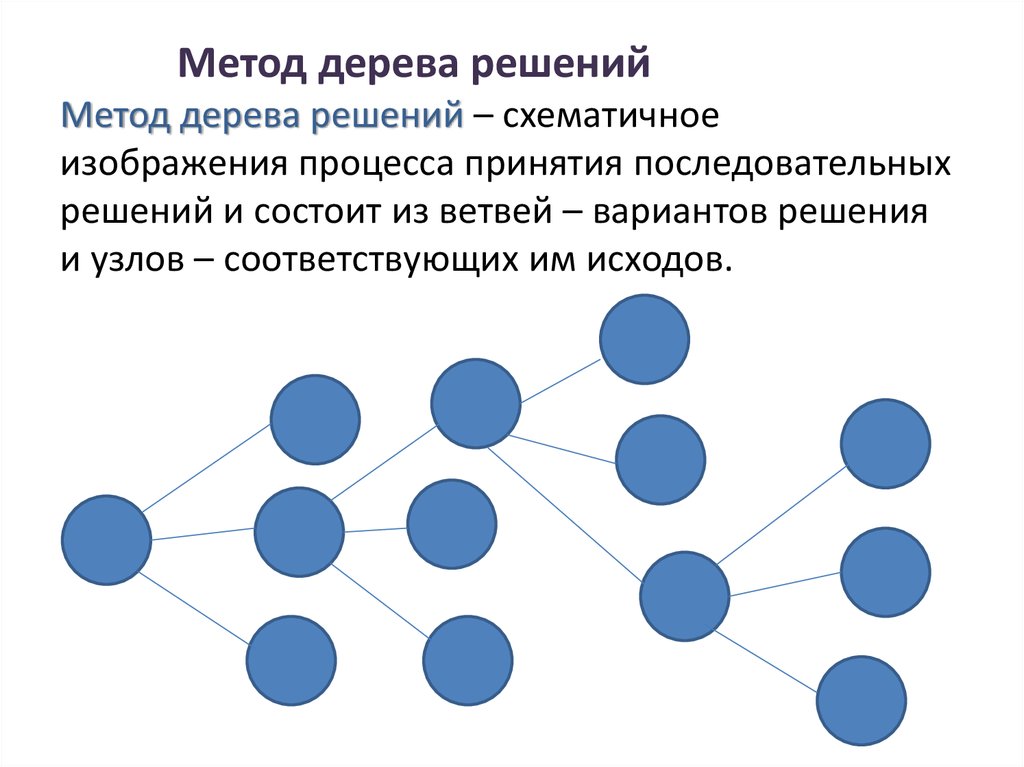

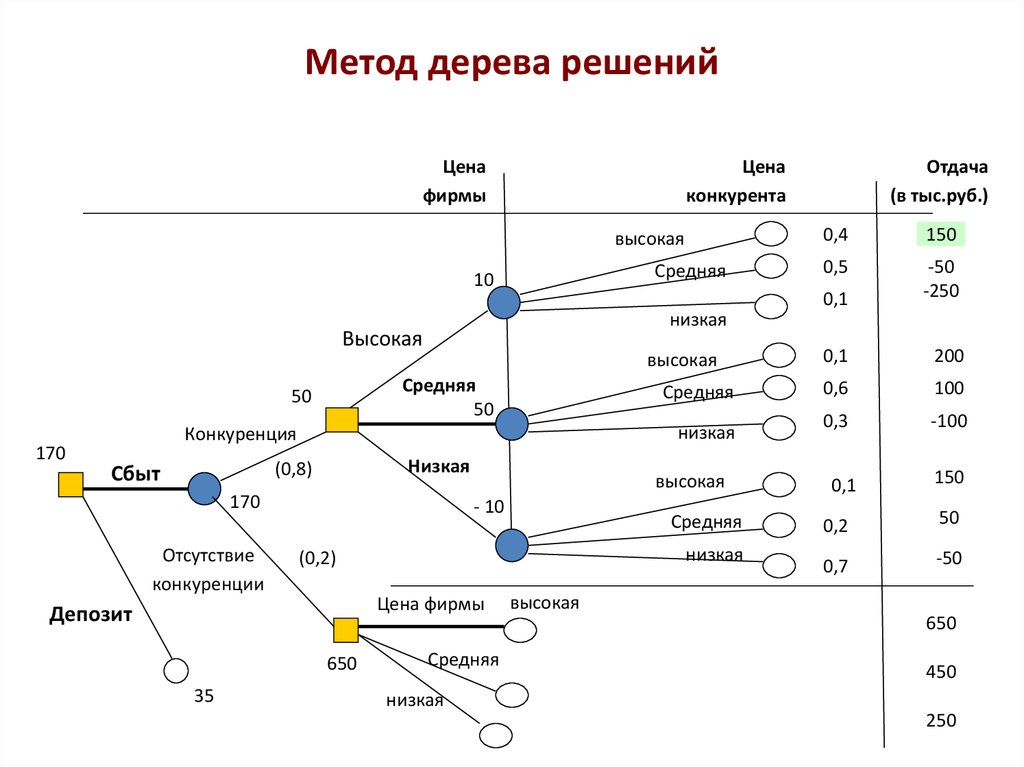 Для построения деревьев вам также необходимо установить Graphviz и pydotplus.
Для построения деревьев вам также необходимо установить Graphviz и pydotplus.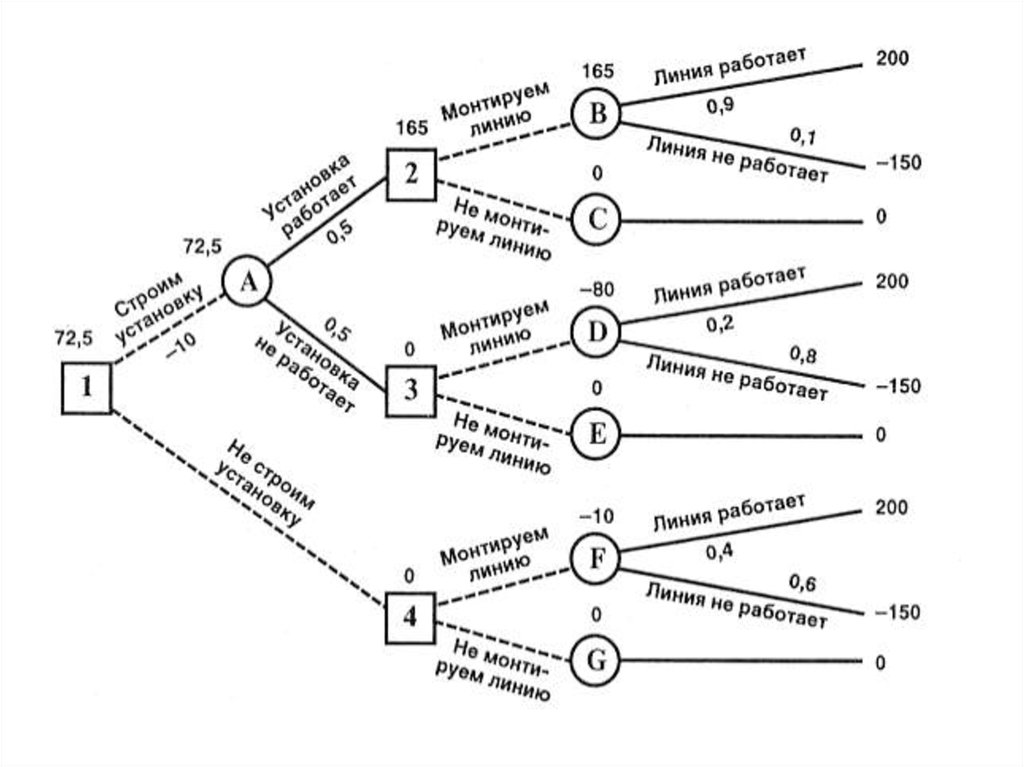 Джини называют коэффициентом Джини, который измеряет загрязненность узла. Вы можете сказать, что узел чистый, когда все его записи принадлежат одному и тому же классу, такие узлы известны как конечные узлы.
Джини называют коэффициентом Джини, который измеряет загрязненность узла. Вы можете сказать, что узел чистый, когда все его записи принадлежат одному и тому же классу, такие узлы известны как конечные узлы.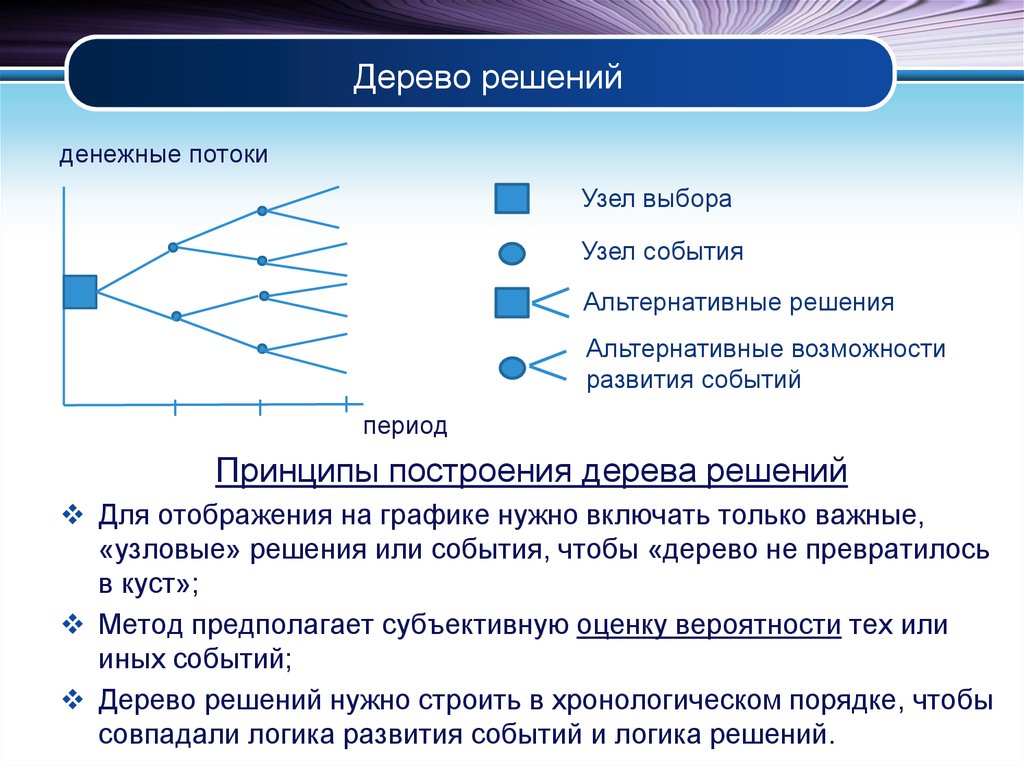
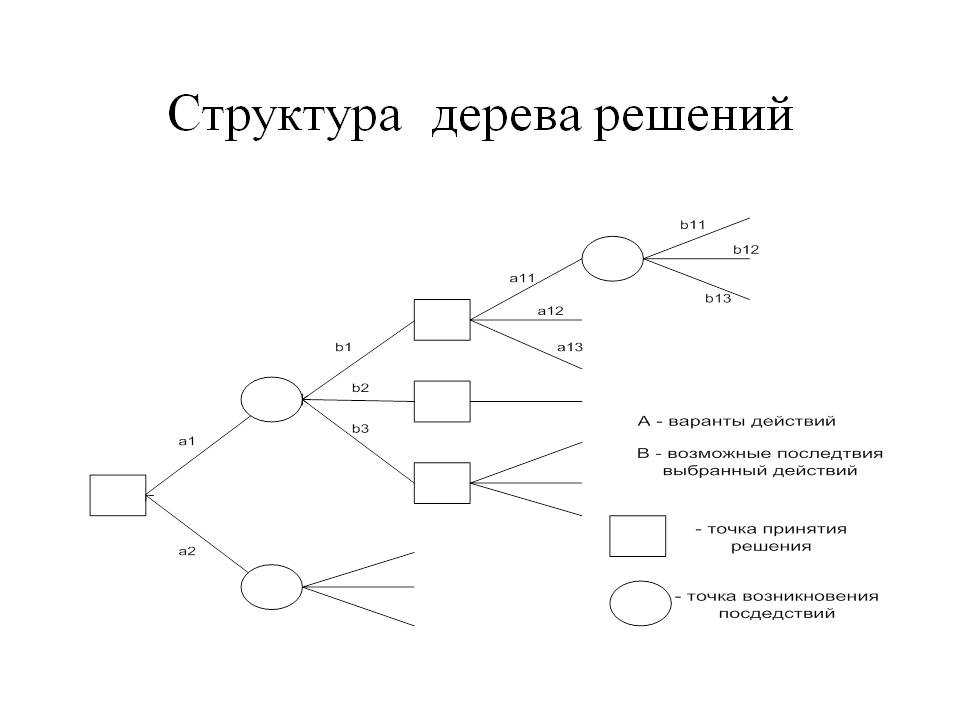
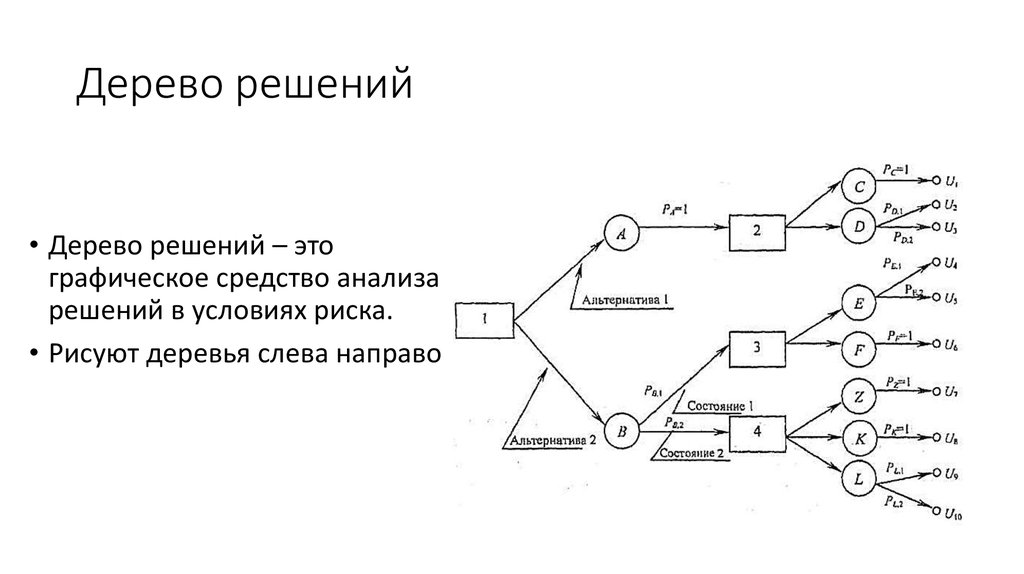
 Парабола. Гипербола. Квадратный корень.
Парабола. Гипербола. Квадратный корень. Применение ФСУ в различных выражениях.
Применение ФСУ в различных выражениях.  Задачи на проценты, сплавы и смеси. Задачи на совместную работу. Движение по прямой. Разные задачи.
Задачи на проценты, сплавы и смеси. Задачи на совместную работу. Движение по прямой. Разные задачи. в приложении
в приложении в приложении
в приложении

 И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим: Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы: Выполним некоторые операции над векторами в координатах и получим:
Выполним некоторые операции над векторами в координатах и получим: 
 Заданы координаты точки C1(1, 1, 0), а также определена точка M, являющаяся серединой диагонали BD1 и имеющая координаты M (4, 2, -4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C1(1, 1, 0), а также определена точка M, являющаяся серединой диагонали BD1 и имеющая координаты M (4, 2, -4) . Необходимо рассчитать координаты точки А.
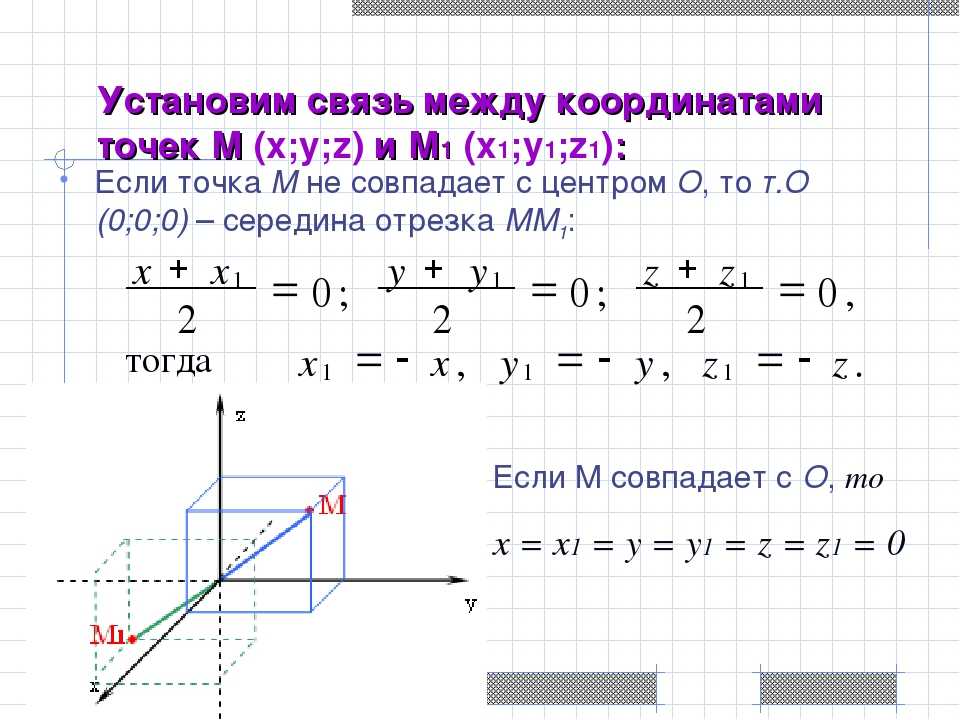 Координата С — это середина отрезка А и В. Исходя из этого нужно определить значение координаты \[x_{C}\] .
Координата С — это середина отрезка А и В. Исходя из этого нужно определить значение координаты \[x_{C}\] .
 Которая соответственно перпендикулярна относительной одной из осей.
Которая соответственно перпендикулярна относительной одной из осей.

 \]
\] {2}}=\sqrt{58}\]
{2}}=\sqrt{58}\] В этом случае координата x перемещается с 4 на 2 или вниз на 2, поэтому новая координата x должна быть 2-2 = 0. Координата y перемещается с 4 на -5 или вниз на 9., поэтому новая координата y должна быть -5-9 = -14.
В этом случае координата x перемещается с 4 на 2 или вниз на 2, поэтому новая координата x должна быть 2-2 = 0. Координата y перемещается с 4 на -5 или вниз на 9., поэтому новая координата y должна быть -5-9 = -14.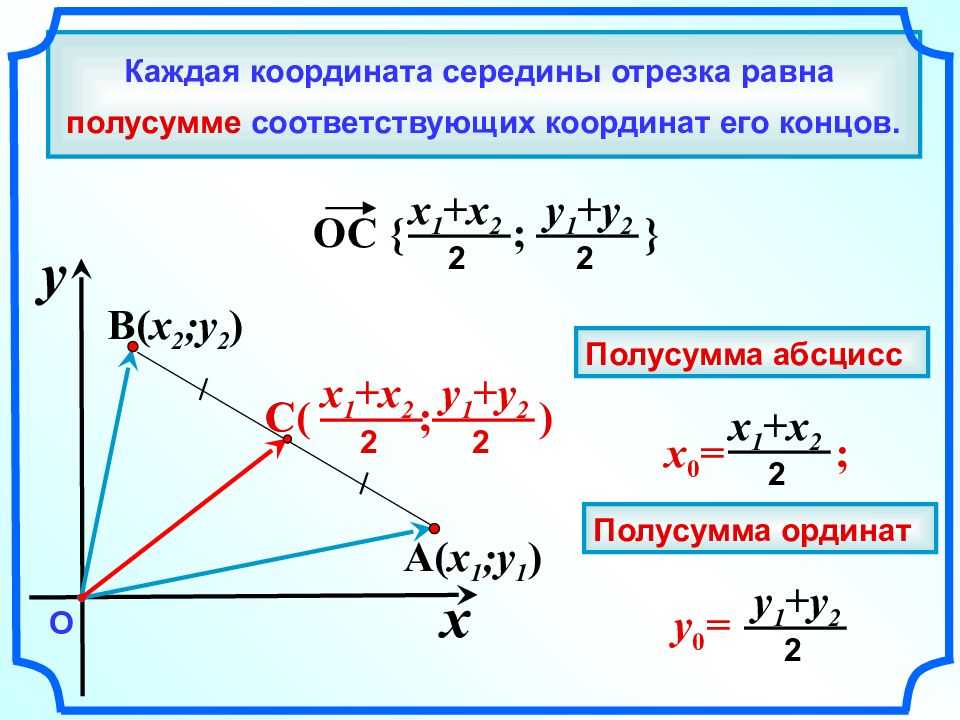 Точка B равна (x, y). Середина AB равна (17, –4). Какова ценность Б?
Точка B равна (x, y). Середина AB равна (17, –4). Какова ценность Б? Общая длина отрезка должна быть в два раза больше расстояния от точки А до середины.
Общая длина отрезка должна быть в два раза больше расстояния от точки А до середины. Формула известна как формула раздела . Начнем!
Формула известна как формула раздела . Начнем!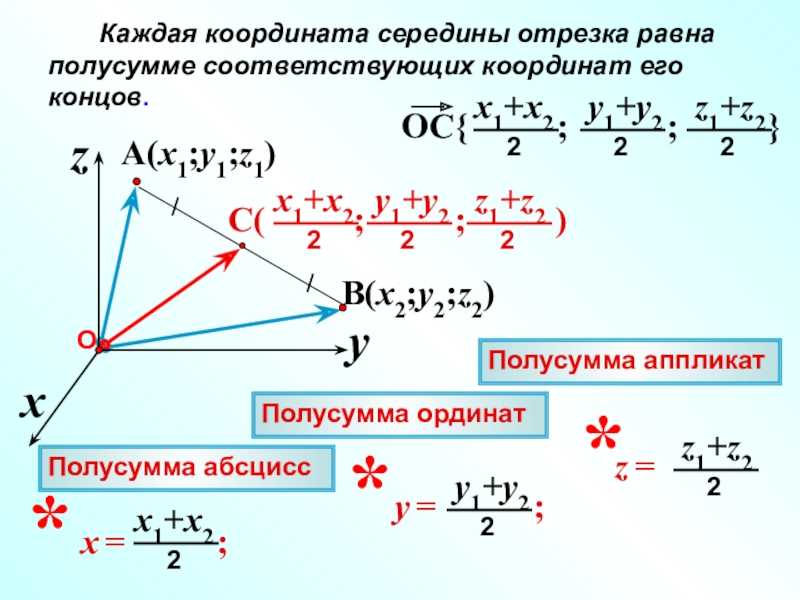 Как я упоминал ранее, существует (в общем) несколько методов решения задачи координатной геометрии. Это один из таких случаев. Идея состоит в том, чтобы развить ваш уровень мышления и дать вам представление о том, какие методы хороши, а какие нет.
Как я упоминал ранее, существует (в общем) несколько методов решения задачи координатной геометрии. Это один из таких случаев. Идея состоит в том, чтобы развить ваш уровень мышления и дать вам представление о том, какие методы хороши, а какие нет. Позвольте мне написать это лучше:
Позвольте мне написать это лучше: Вот симуляция, которая показывает две точки A и B , а также точку C , разделяющую соединяющий их отрезок в некотором отношении.
Вот симуляция, которая показывает две точки A и B , а также точку C , разделяющую соединяющий их отрезок в некотором отношении.
 2. Найдите площадь полной поверхности цилиндра.
2. Найдите площадь полной поверхности цилиндра.
 maths.org/public/leg.php?code=-308
maths.org/public/leg.php?code=-308 com
com
 Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.
Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны. )
) Катет, лежащий против угла в , равен половине гипотенузы. Получаем, что BH = 3,5.
Катет, лежащий против угла в , равен половине гипотенузы. Получаем, что BH = 3,5. Аналогично, NQ = 1.
Аналогично, NQ = 1.
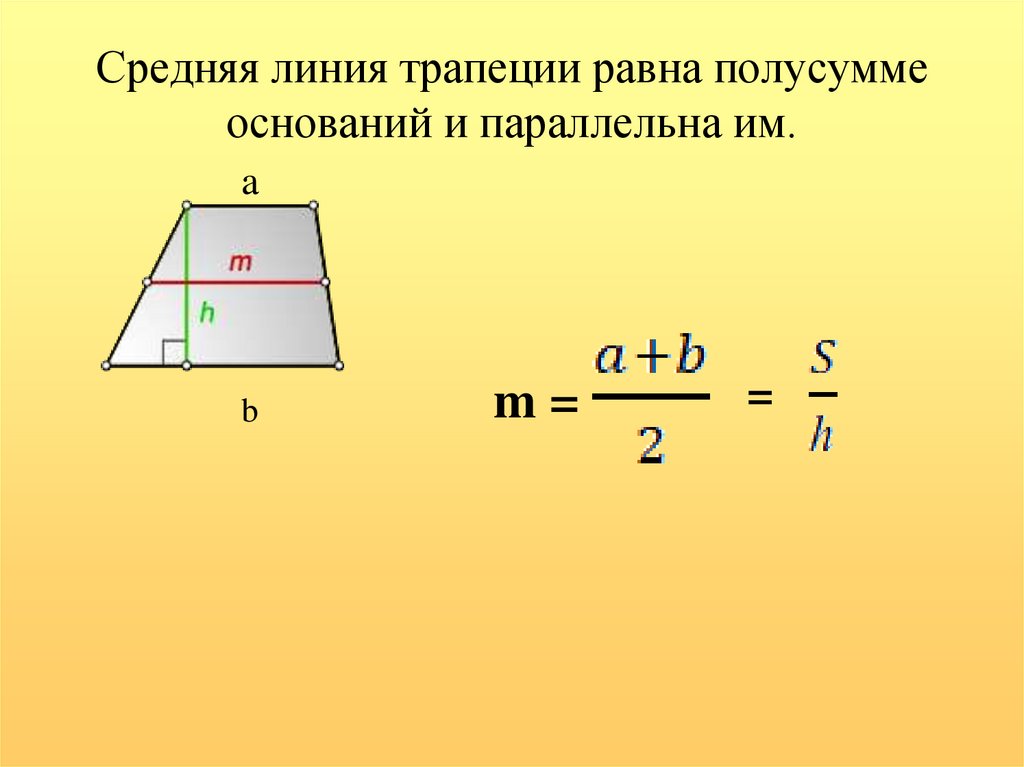
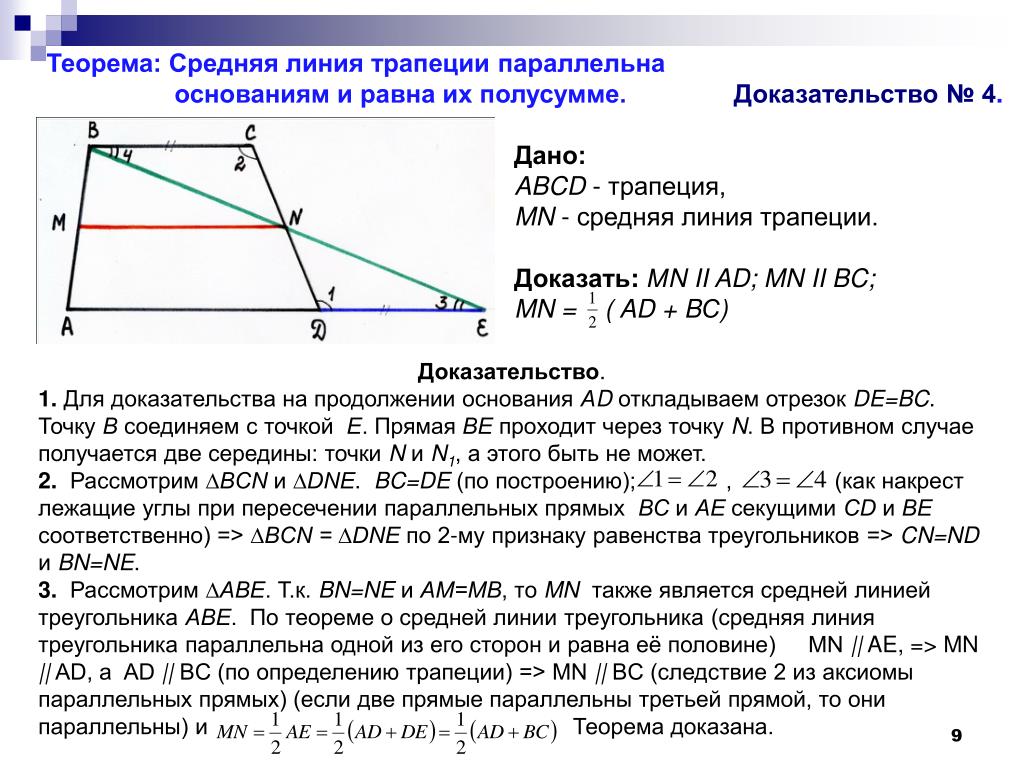
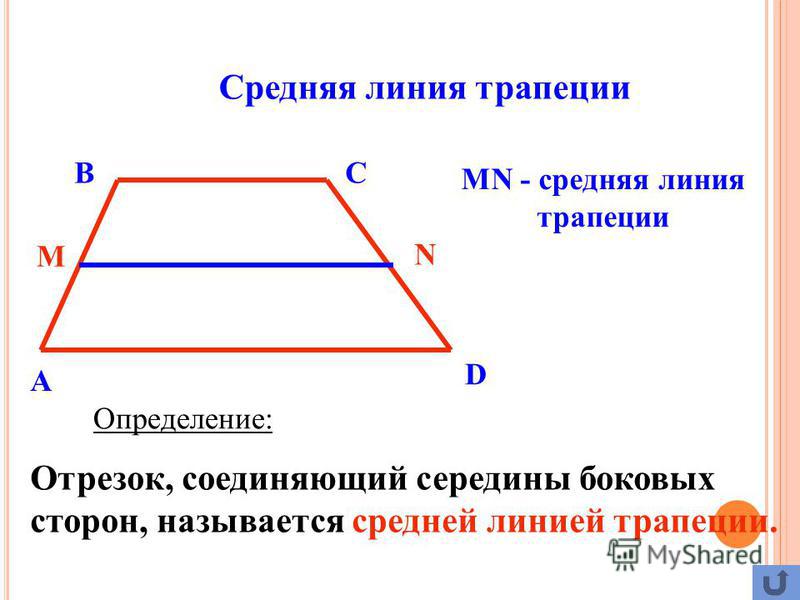 Найдите радиус r вписанной в трапецию окружности.
Найдите радиус r вписанной в трапецию окружности.
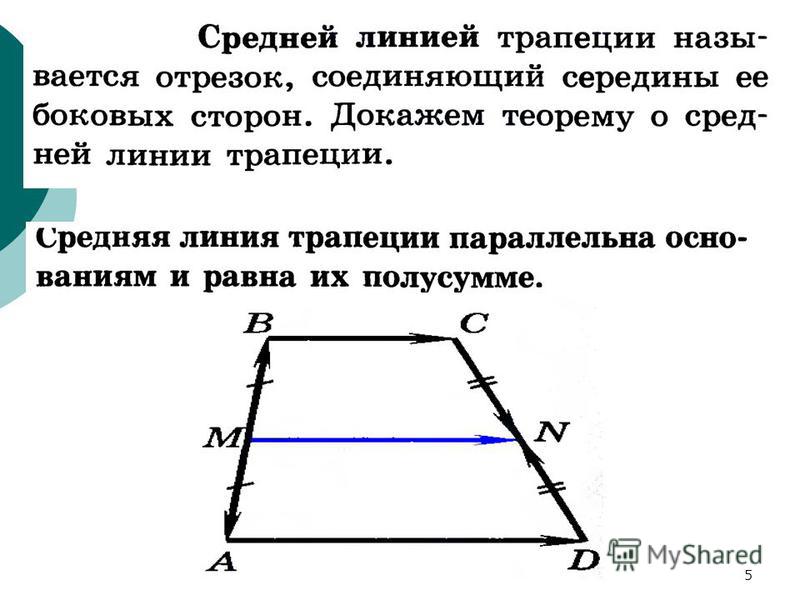
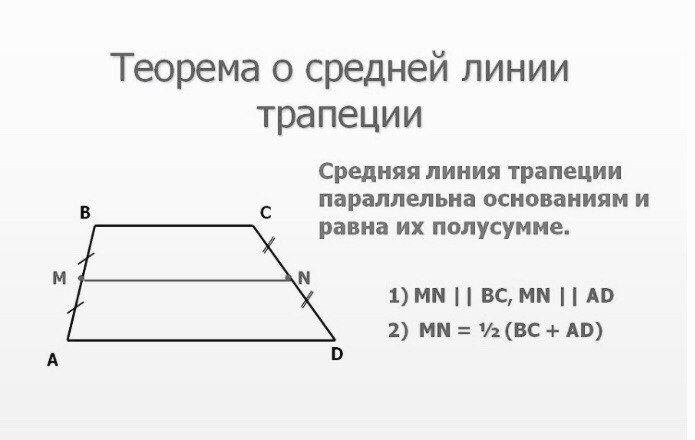 \circ\)
\circ\)
 Параллельные линии идут в одном направлении и всегда находятся на одинаковом расстоянии друг от друга.
Параллельные линии идут в одном направлении и всегда находятся на одинаковом расстоянии друг от друга.

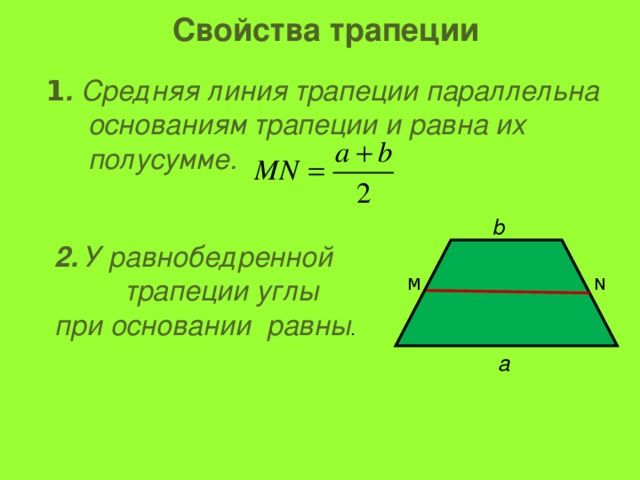

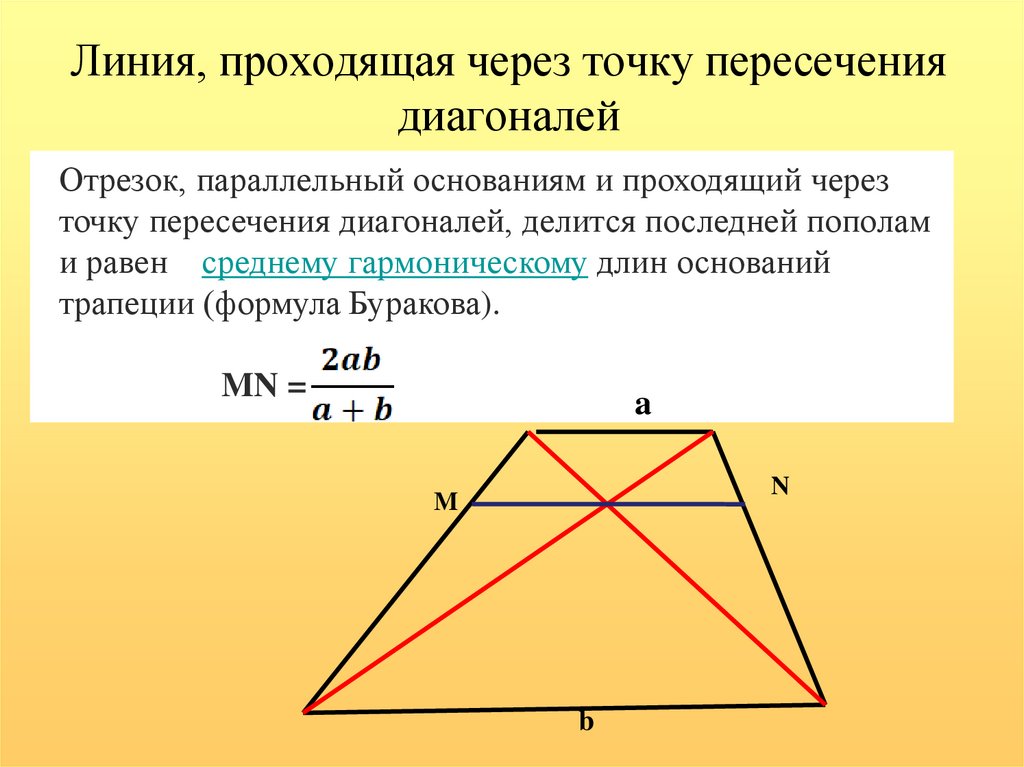 com.
com.  Средний сегмент встречается с каждой ногой в средней точке. Средняя точка находится на равном расстоянии от обоих концов линий ног.
Средний сегмент встречается с каждой ногой в средней точке. Средняя точка находится на равном расстоянии от обоих концов линий ног.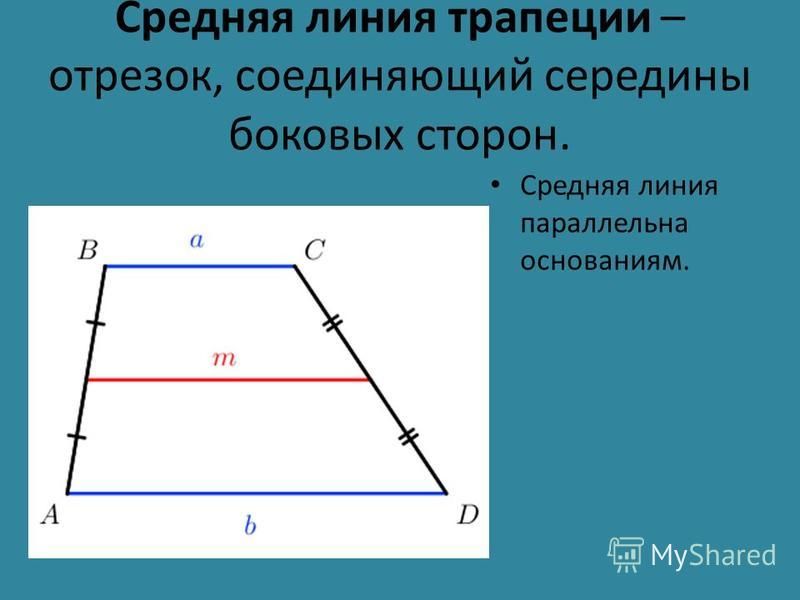 Помните, что средний сегмент должен начинаться в середине каждой ноги.
Помните, что средний сегмент должен начинаться в середине каждой ноги.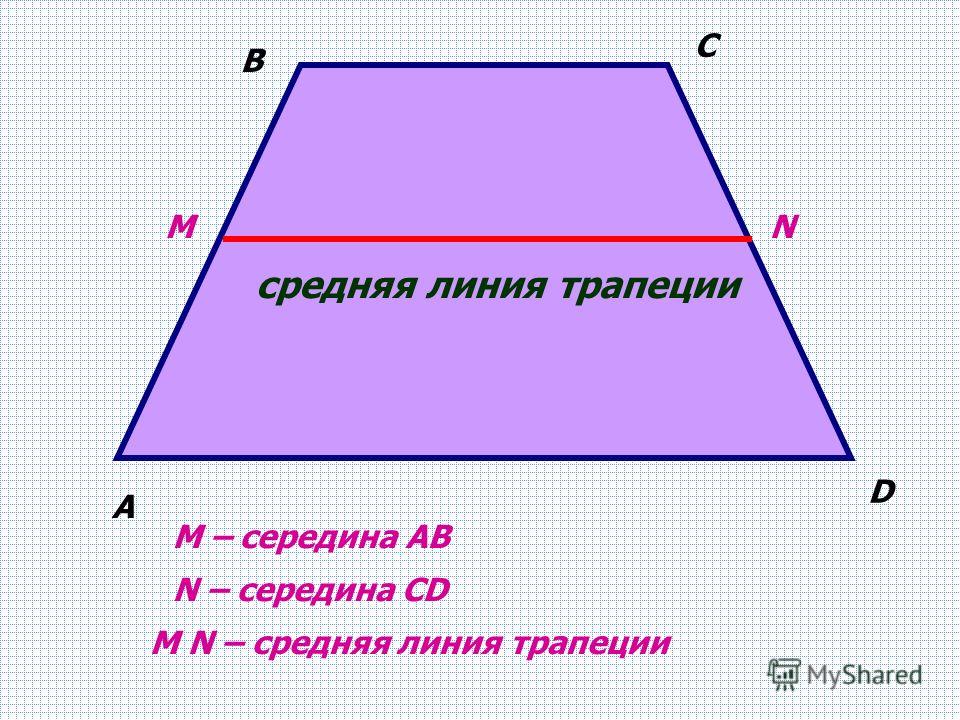
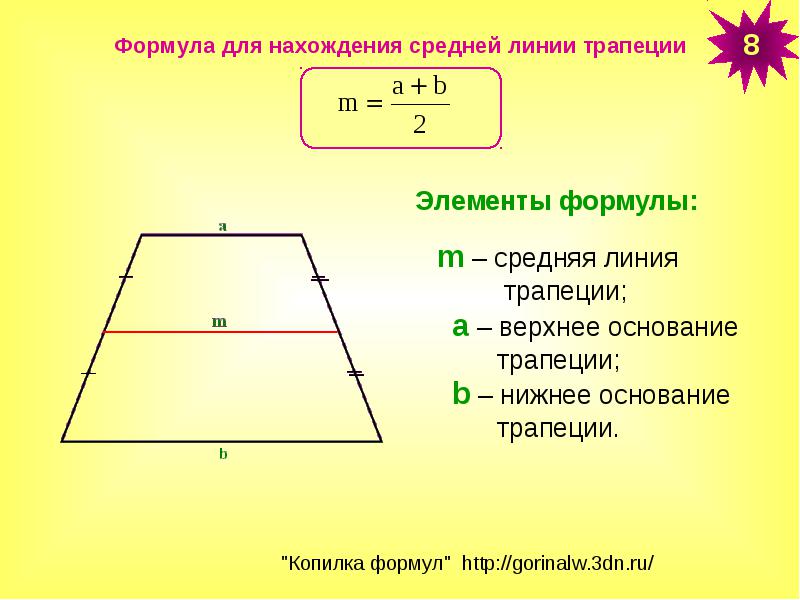 Начните с умножения обеих сторон на 2:
Начните с умножения обеих сторон на 2:
 Две другие параллельные стороны будут называться основаниями .
Две другие параллельные стороны будут называться основаниями . Здесь мы можем легко сыграть в средней части. Помните, что средний сегмент должен начинаться в середине каждой ноги.
Здесь мы можем легко сыграть в средней части. Помните, что средний сегмент должен начинаться в середине каждой ноги.
 Начните с умножения обеих сторон на 2:
Начните с умножения обеих сторон на 2: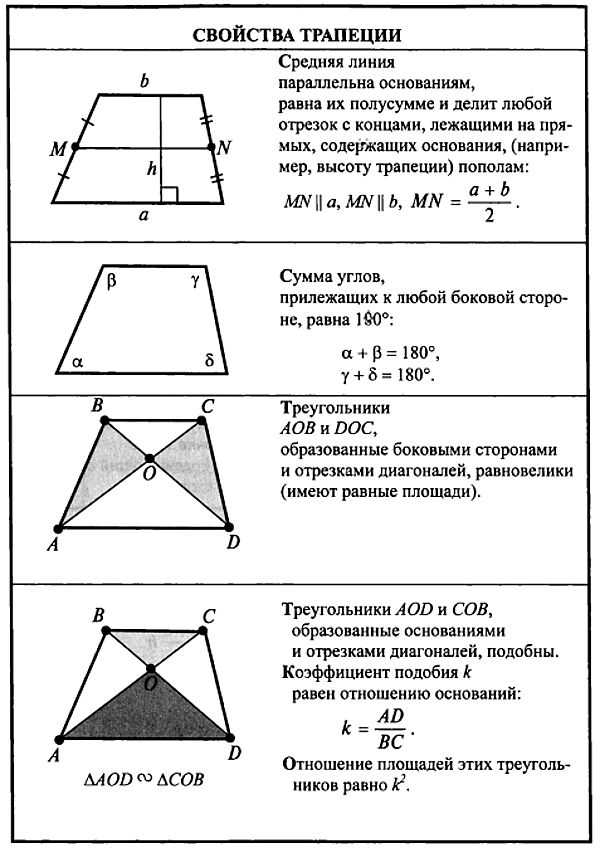
 Отсюда мы можем показать, что EF — средняя линия треугольника ΔADG. Таким образом, согласно теореме о середине треугольника, он параллелен DG и равен половине DG .
Отсюда мы можем показать, что EF — средняя линия треугольника ΔADG. Таким образом, согласно теореме о середине треугольника, он параллелен DG и равен половине DG .