Тема: Эксцентриситет гиперболы
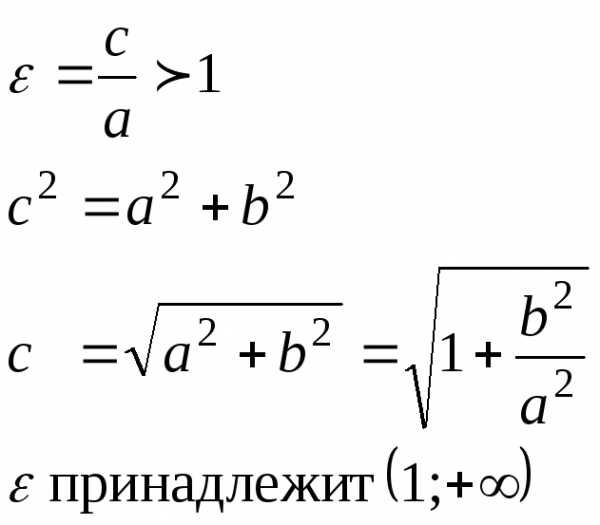
1) 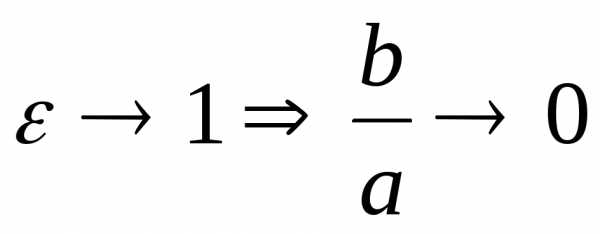
Полуось  —
Действительная
—
Действительная
Полуось b – мнимая
Ветви гиперболы
все ближе приближаются к 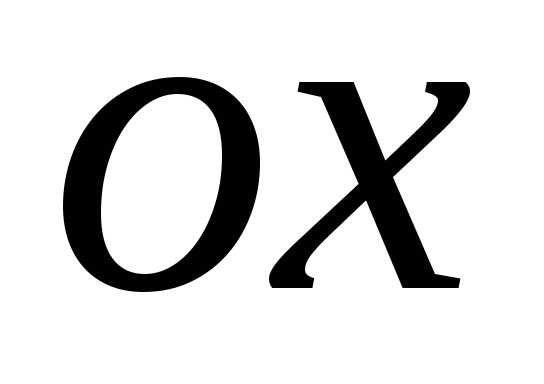
2) 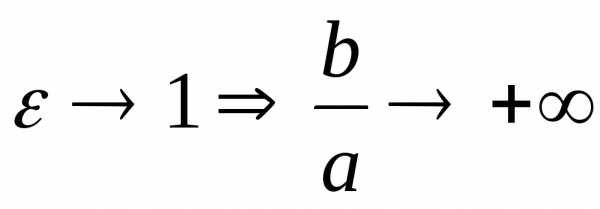
Ветви отодвигаются
от 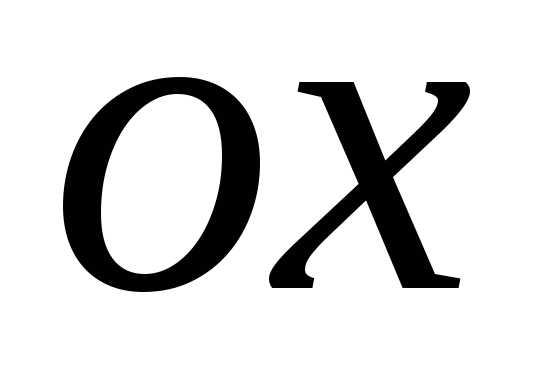
Парабола – множество точек в плоскости для которых расстояние до данной точки называемой фокусом и данной прямой называемой директриса равны.
N y
M – точка параболы
P0/2 P/2 F –фокус х
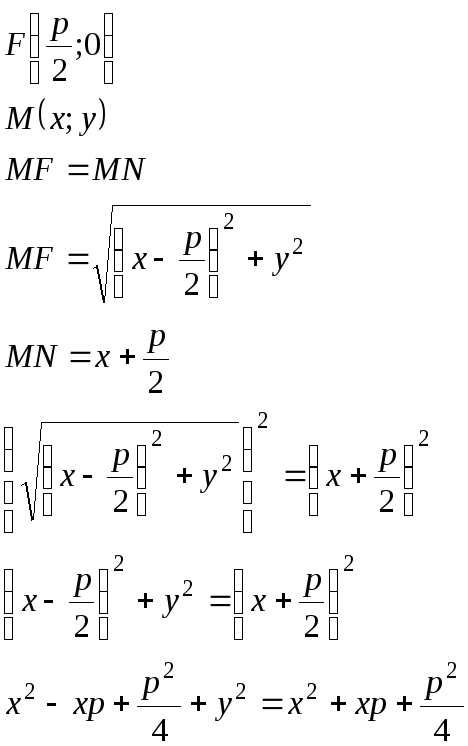
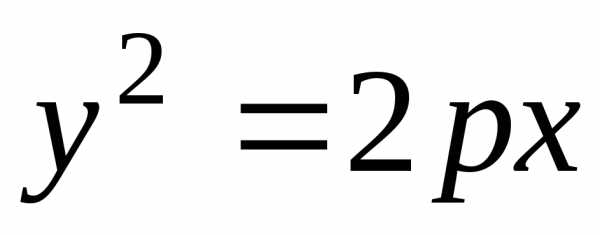 ,
, 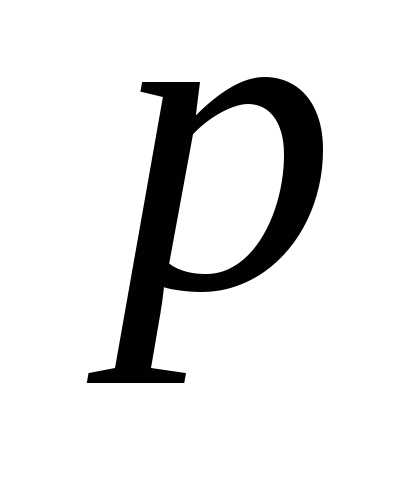 -расстояние
от директрисы до фокуса
-расстояние
от директрисы до фокуса
Можно доказать, что последнее равенство равносильно первому. Оно называется каноническим уравнением параболы.
Тема: Исследование формы параболы.
т.к. координата у входит в уравнение во второй степени, то кривая симметрична относительно оси

 может быть только больше или равным
нулю. Значит, параболы существуют только
в правой полуплоскости.
может быть только больше или равным
нулю. Значит, параболы существуют только
в правой полуплоскости.при,

из уравнения видно, что парабола проходит из начала координат, т.е. при
так как парабола симметрично относительно
 ,
то достаточно построить ее часть лежащую
в I четверти.
,
то достаточно построить ее часть лежащую
в I четверти.
у
0 х
Замечание:
К числу канонических следует отнести также следующие уравнения параболы
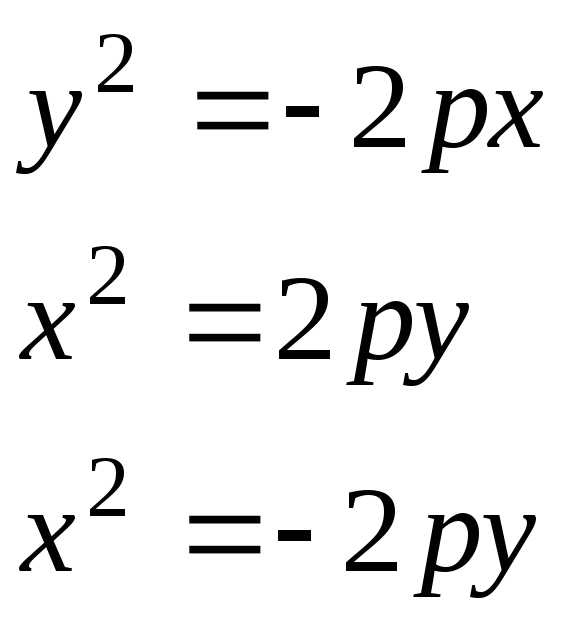
Эксцентриситет параболы =1
Тема: Матрица. Понятие матрицы. Основные определения.
Матрицей называется прямоугольная таблица чисел или функций расположенных по строкам и столбцам.
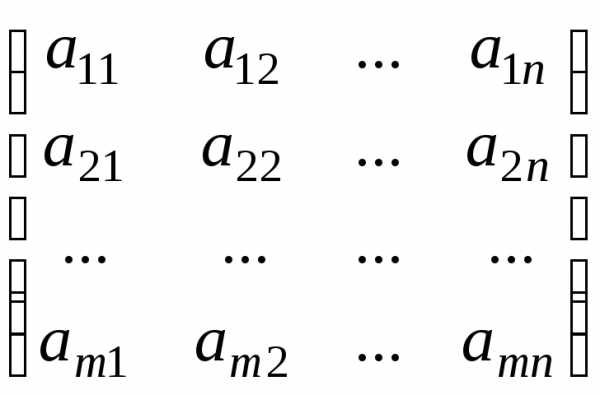
 —
размерность матрицы
—
размерность матрицы
Матрица называется квадратной, если m=n
Если матрица
имеет размерность  ,
такая матрица называется матрица —
трока.
,
такая матрица называется матрица —
трока.
Если матрица
имеет размерность 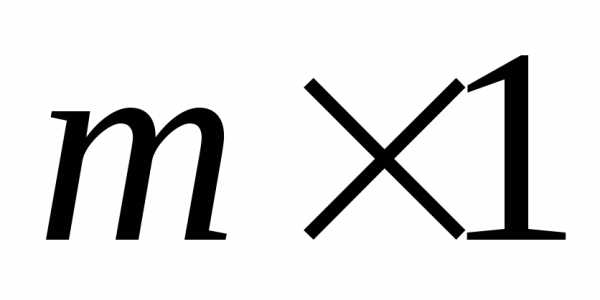 ,
такая матрица называется матрица –
столбец
,
такая матрица называется матрица –
столбец
Матрица
размерностью  ,
называется матрицей n-ого
порядка.
,
называется матрицей n-ого
порядка.
А,В,С
Две матрицы одинаковой размерности равны друг другу, если равны их элементы, стоящие на одинаковых местах.
Элементы матрицы, у которых номер строки равен номеру столбца, образуют главную диагональ матрицы.
Тема: Действие над матрицами
Пусть даны две матрицы одинаковой размерности. Их суммой (или разностью) называется такая матрица той же размерности, все элементы которой получены сложением (или вычитанием) соответствующих элементов данных матриц.
Умножение матрицы на число
Произволением матрицы на число является матрица той же размерности, все элементы которой получены умножением соответствующих элементов данной матрицы на это число.
Транспонирование матриц.
Перемена местами строк и столбцов матрицы таким образом, что строка № i становится столбцом № I, и наоборот, называется транспонированием матрицы.

Умножение матриц друг на друга.
Произведением матрицы А размерности 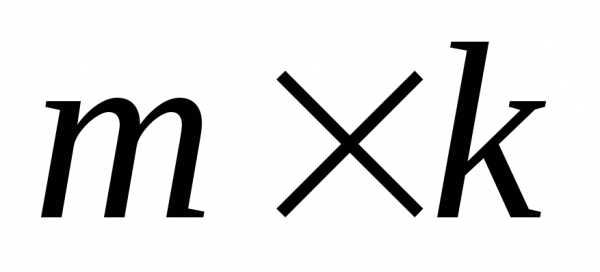 на матрицу B размерностью
на матрицу B размерностью 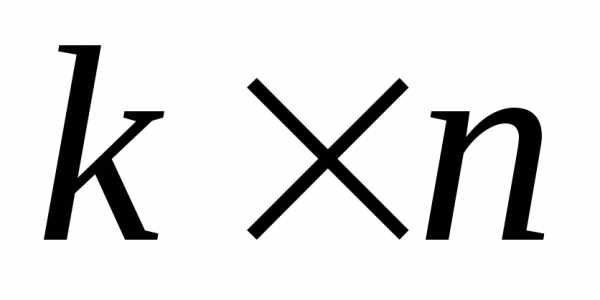 называется такая матрица с размерностью
называется такая матрица с размерностью  ,
каждый элемент которой получен из
элементов матриц А и В по правилу «строка
на столбец».
,
каждый элемент которой получен из
элементов матриц А и В по правилу «строка
на столбец».
Из определения следует, что нельзя перемножать матрицы произвольных размерностей.
Условие перемножаемости: число столбцов первой матрицы должно быть равно числу строк второй матрицы.
Правило «Строка на столбец»
Рассмотрим его на примере:
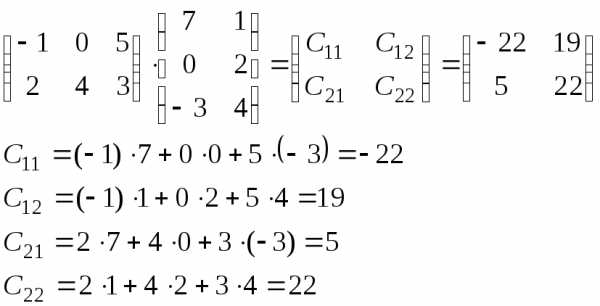
Замечание:
Из определения произведения матриц следует, что умножение матриц не перестановочно, потому что после перемены местами сомножителей может оказаться, что такое умножение не возможно.
studfiles.net
1 Тема: Матрицы и определители
Таблицу вида
 называют
прямоугольной матрицей размера
называют
прямоугольной матрицей размера  .
Элементы
.
Элементы назыаются элементами матрицы.
m
– число строк,
n-
число столбцов. Матрица размера
назыаются элементами матрицы.
m
– число строк,
n-
число столбцов. Матрица размера  называется квадратной матрицей.
называется квадратной матрицей.
Операции над матрицами определяются с помощью операции над их элементами.
Две матрицы А и В размера
 равны, если равны их элементы
равны, если равны их элементы .
.Суммой матриц А и В размера есть матрица размера
 ,
каждый ее элемент равен сумме
соответствующих элементов.
,
каждый ее элемент равен сумме
соответствующих элементов.Произведение матрицы А размера
 на
число есть матрица размера
на
число есть матрица размера ,
каждый элемент которой равен произведению
,
каждый элемент которой равен произведению на число.
на число.Произведение матрицы А размера
 на матрицу В размера
на матрицу В размера есть
матрица С размера
есть
матрица С размера .
.
Матрицей
обратной для А называется матрица 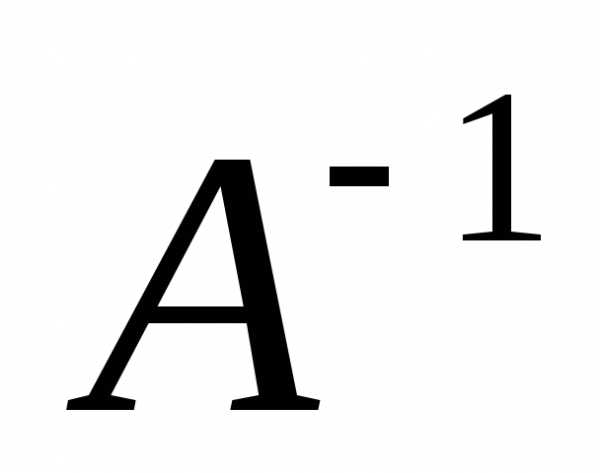 ,
для которой.
,
для которой.
Квадратная матрица называется невырожденной, если она имеет обратную матрицу.
Число линейно независимых строк(или столбцов) матрицы называют ее рангом.
Определителем квадратной матрицы А n-го порядка называют число
 (2)
(2)
Минором 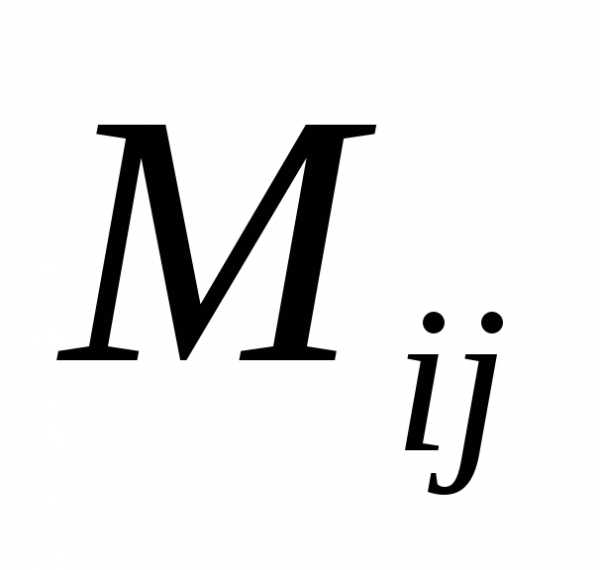 элемента
элемента  в определителе
n-го
порядка
(2) есть определитель
в определителе
n-го
порядка
(2) есть определитель
(n—1)-го порядка, получающийся из определителя (2), если из него вычеркнуть i-строку и j-й столбец.
Алгебраическое
дополнение  элемента
элемента  есть
коэффициент при
есть
коэффициент при в
разложении определителя или.
Определитель можно выразить через
элементы его строки или столбца и их
алгебраические дополнения следующим
образом:(разложение
Лапласа).
в
разложении определителя или.
Определитель можно выразить через
элементы его строки или столбца и их
алгебраические дополнения следующим
образом:(разложение
Лапласа).
Определитель второго порядка .
Определитель третьего порядка .
Свойства определителей
Определитель не меняется при транспонировании
При перемене местами двух строк(столбцов) определитель меняет знак.
Если квадратная матрица содержит две одинаковые строки (столца), то ее определитель равен нулю.
Если все элементы какой –либо строки (столбца) определителя умножить на число с, то на это число умножится и сам определитель.
Если элементы любой строки(столбца) представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, в первом из которых элементы отмеченной строки равны первым слагаемым, во втором –вторым.
Определитель не меняется при строчном (столбцевом) перобразовании
Сумма произведении элементов любой строки(столбца) на алгебраические дополнения элементов другой строки(столбца) равна нулю.
Если все элементы определителя n-го порядка расположенные выше (или ниже) главной диагонали равны 0, то определитель равен произведению элементов расположенных на главной диагонали.
2 Тема: Система линейных уравнений.
Система n линейных уравнений c n неизвестными имеет вид:
 (1)
(1)
Решением системы уравнений называется всякая совокупность чисел a1, a2, an, которая, будучи поставлена в систему на место неизвестных X 1,X 2 ,…,X n, обращает все уравнения системы в тождество.
Система уравнений называется совместной, если она имеет одно единственное решение, и несовместной, если не имеет решений.
Совместная система уравнений называется определенной, если она имеет одно единственное решение, и неопределенной, если она имеет, по крайней мере, два различных решения.
Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и тоже множество решений.
Определителем системы называется определитель, составленный из коэффициентов aij.
Линейное уравнение называется однородным, если его свободный член равен нулю.
Система линейных уравнений называется однородной, если все входящие в неё уравнения являются линейными однородными уравнениями.
Однородная система n линейных уравнений с n неизвестными имеет ненулевые решения тогда и только тогда, когда определитель её равен нулю.
Для нахождения решения системы линейных уравнений применяют метод Гаусса и правило Крамера.
Метод Гаусса решения системы заключается в последовательном исключении переменных.
Теорема: Для того, чтобы система линейных неоднородных уравнений была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу её основной матрицы.
Пусть дана система двух линейных уравнений с двумя неизвестными. Тогда:
если r = R =0, т.е. если все коэффициенты a1 ,a 2, b1 ,b 2, c 1, c2 равны нулю, то любая пара действительных чисел является решением системы.
если r =0, R =1, т.е. a1 =a 2=b1 =b 2=0 и c +c≠0, то система не имеет решений.
если r =1, R =1, то система имеет бесконечно много решений, но не любая пара действительных чисел есть её решение.
если r =1, R =2, то система не имеет решений.
если r =2, R =2, то система имеет единственное решение, которое можно найти по правилу Крамера.
Формулы
Крамера имеют вид: 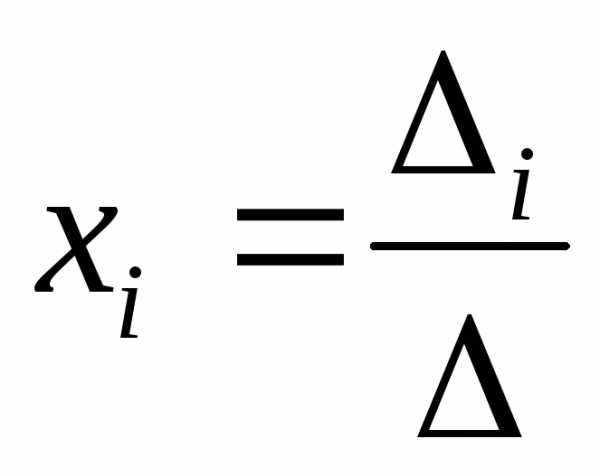 .
.
studfiles.net
Лекция № 3. Тема 3 : Матрицы
3.1. Основные виды матриц
Определение 1. Матрицей называется совокупность чисел, располо-женных в т строках и п столбцах и обозначается

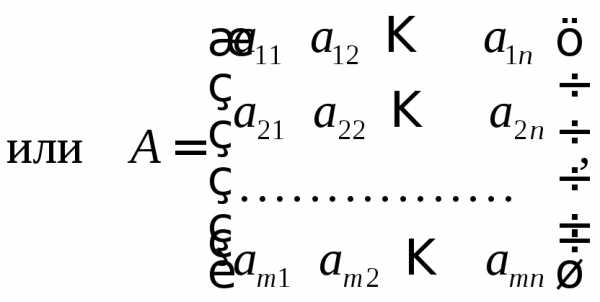
Число, стоящее на
пересечении 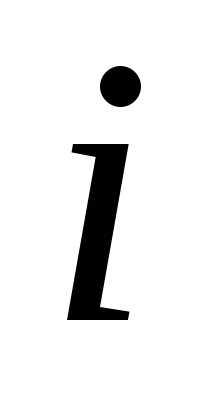 -ой
строки и
-ой
строки и -го
столбца, обозначается
-го
столбца, обозначается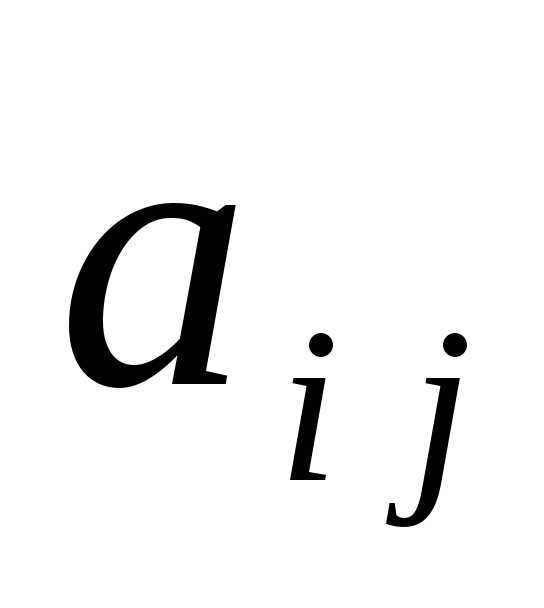 и называется элементом матрицы;размерность
матрицы.
и называется элементом матрицы;размерность
матрицы.
Существуют следующие виды матриц:
Матрица – строка
Матрица – столбец

Нулевая матрица все ее элементы нули.
Единичная матрица

Диагональная матрица
 .
.Симметрическая матрица – для ее элементов выполняется равенство
 для всех
для всех
Важной характеристикой
квадратной матрицы А является её опреде-литель, который
обозначается  Если
Если ,
то матрицаА назы-вается невырожденной.
В противном случае – вырожденной.
,
то матрицаА назы-вается невырожденной.
В противном случае – вырожденной.
Определение 2. Две матрицы 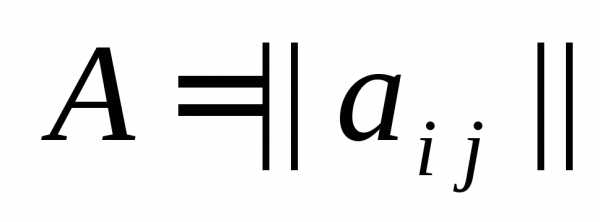 и
и 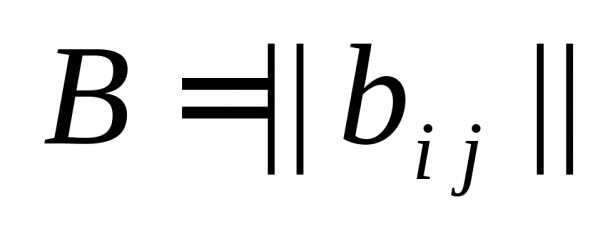 одинаковой раз-мерности называются
равными, если равны все их соответствующие
эле-менты
одинаковой раз-мерности называются
равными, если равны все их соответствующие
эле-менты 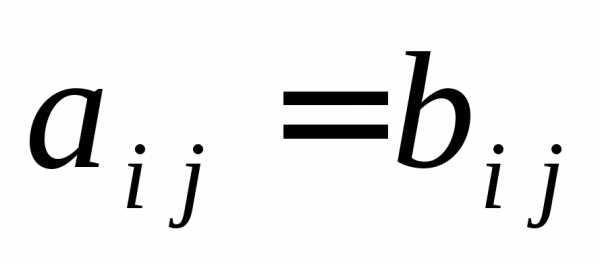 для всех
для всех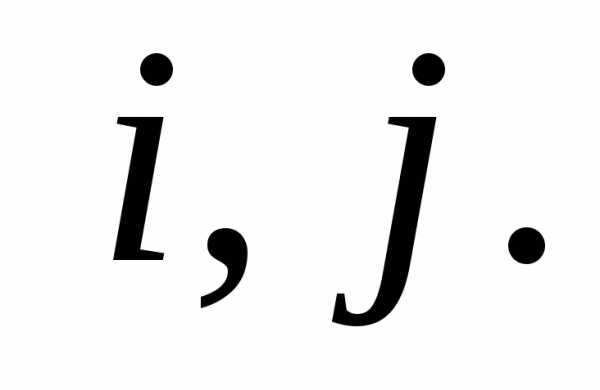
3.2. Действия над матрицами
1. Транспонирование матриц.
Определение 3. Транспонированием матрицы называется замена её строк столбцами с сохранением их номеров.
Транспонированная матрица обозначается А Т.
Пример 1. Найти А Т, если
матрица 
Тогда 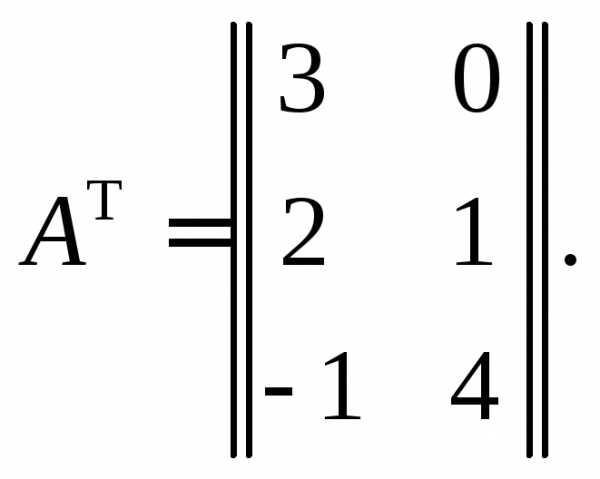
2. Сложение матриц.
Определение 4. Суммой двух матриц 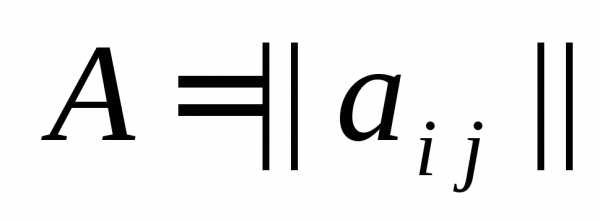 и
и 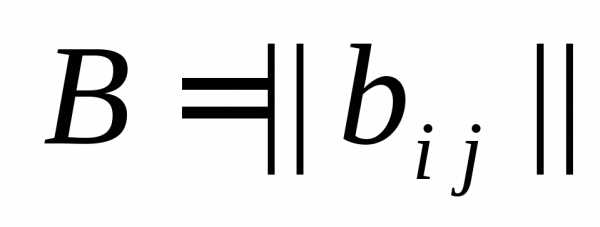 одинаковой
размерности называется матрица С той же размерности, элементы которой
определяются равенствами
и обозначается.
одинаковой
размерности называется матрица С той же размерности, элементы которой
определяются равенствами
и обозначается.
3. Умножение матрицы на число.
Определение 5. Произведением матрицы 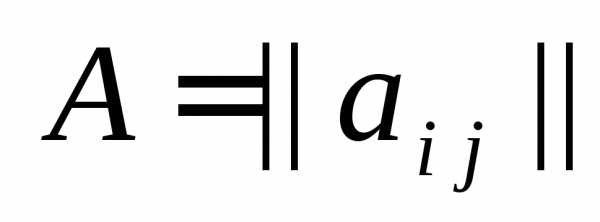 на некоторое число
на некоторое число  называется матрица
называется матрица  ,
элементы которой равны элементам матрицы А,
умноженным на это число
,
элементы которой равны элементам матрицы А,
умноженным на это число  ,
т.е.
,
т.е.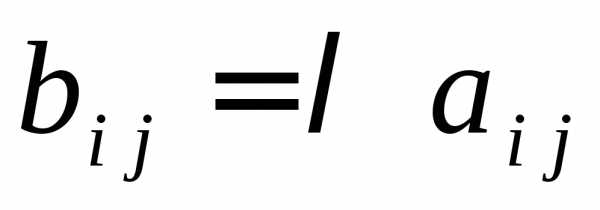 и обозначается
и обозначается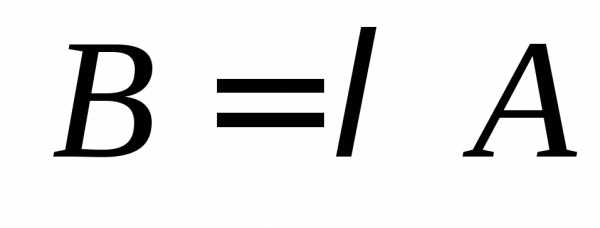 .
.
Пример 2. Найти матрицу , если
4. Умножение матриц.
Определение 6. Произведением матрицы 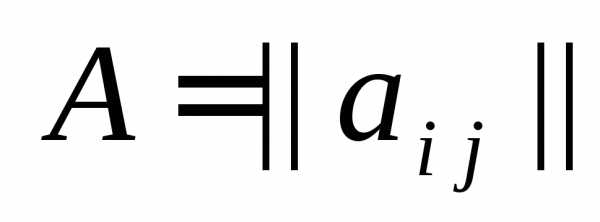 размерности
размерности  и матрицы
и матрицы 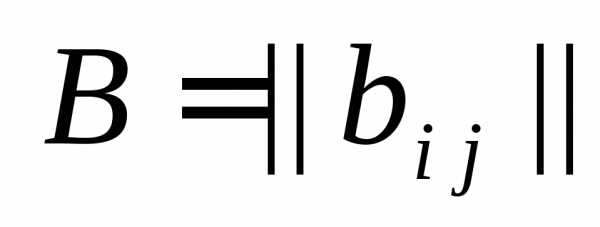 размерности
размерности  ,называется матрица
,называется матрица 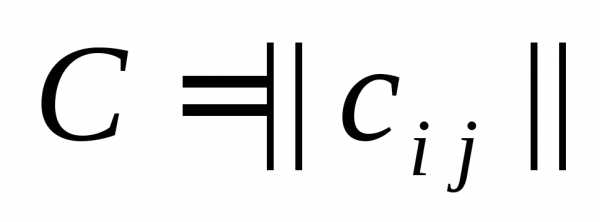 ,
размерности
,
размерности  ,
элементы которой удовлетворяют
равенству
,
элементы которой удовлетворяют
равенству
и обозначается 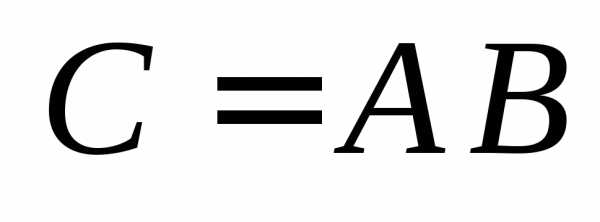 .
.
Замечание 1. Как видно из определения, произведение двух матриц будет определено, если число столбцов первой матрицы равно числу строк второй.
Пример 3. Найти произведение матриц
Тогда
Замечание 2. Легко убедиться в том, что в общем случае произведение матриц не обладает коммутативным свойством, т.е. что видно из следующего примера.
Пример 4. Найти произведение матриц
Тогда имеем
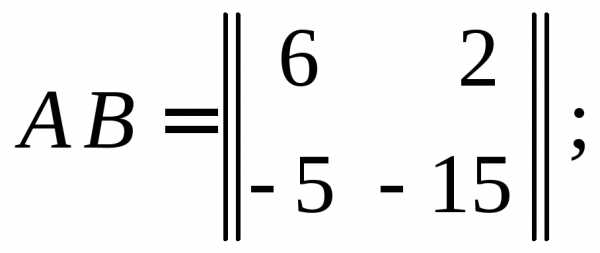
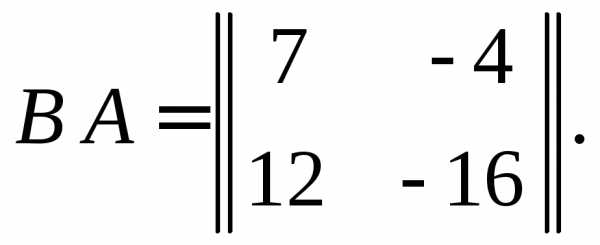
3.3. Обратная матрица
Определение 7. Обратной матрицей матрицы А называется матрица 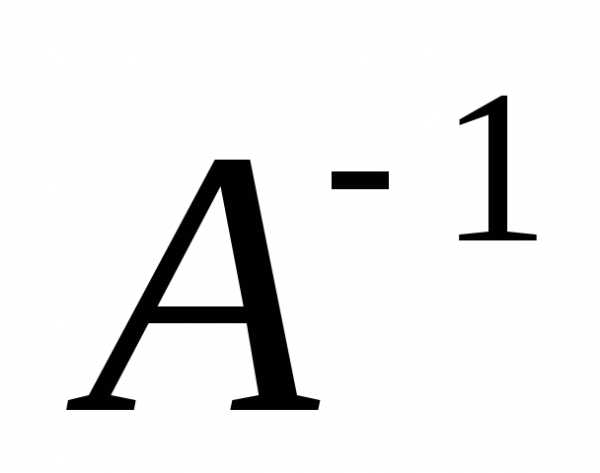 , для
которой выполняется равенство
, для
которой выполняется равенство
Из этого определения
следует, что понятие обратной матрицы
является взаимообратным и определено
только для квадратных матриц. При этом
для существования обратной матрицы
необходимо, чтобы матрица А была невырожденной, т.е.  .
.
Покажем, что
обратной матрицей  для случая матрицыА размер-ности
для случая матрицыА размер-ности  будет матрица
будет матрица
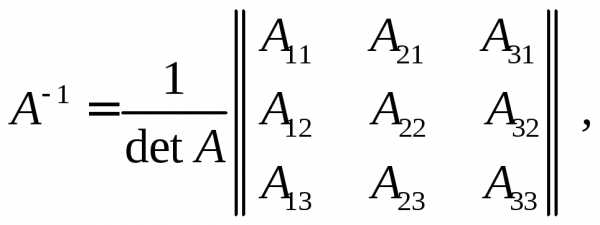
где 
алгебраические дополнения элемента
алгебраические дополнения элемента 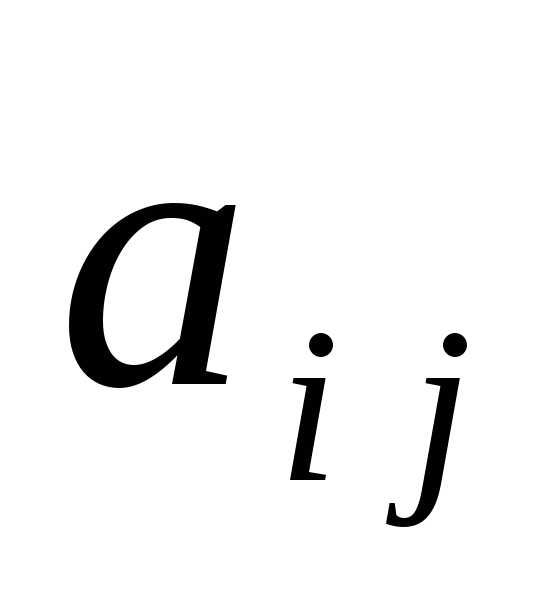 .
.
Тогда
Например,
и т.д.
Так же можно
проверить и равенство 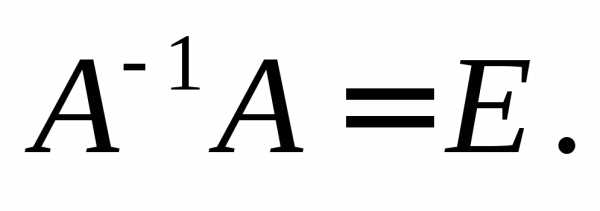
Замечание 4. Аналогично для матрицы А размерности  обратная матрица
обратная матрица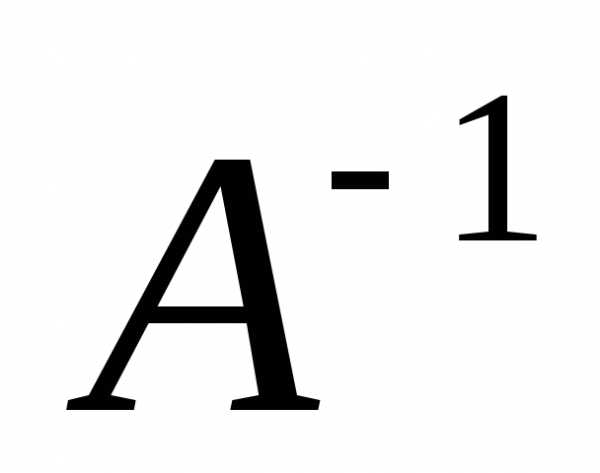 имеет вид
имеет вид
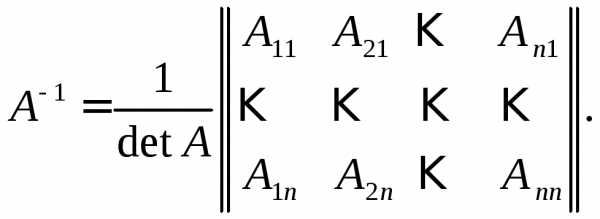
3.4. Решение систем линейных уравнений с помощью обратной матрицы
Рассмотрим систему линейных алгебраических уравнений
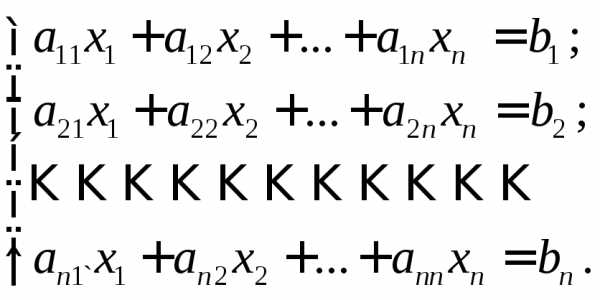 (1)
(1)
Введем следующие матрицы
Тогда, используя правило умножения матриц, систему (1) можно пред-ставить в следующем виде (матричная форма системы уравнений (1))
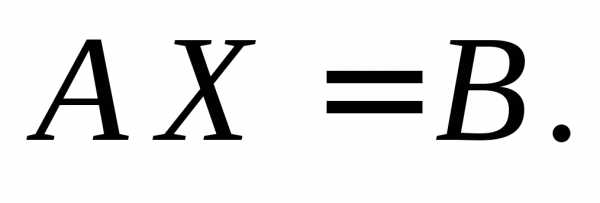 (2)
(2)
Пусть  тогда для матрицыА существует обратная
тогда для матрицыА существует обратная 
Умножая обе части
равенства (2) слева на 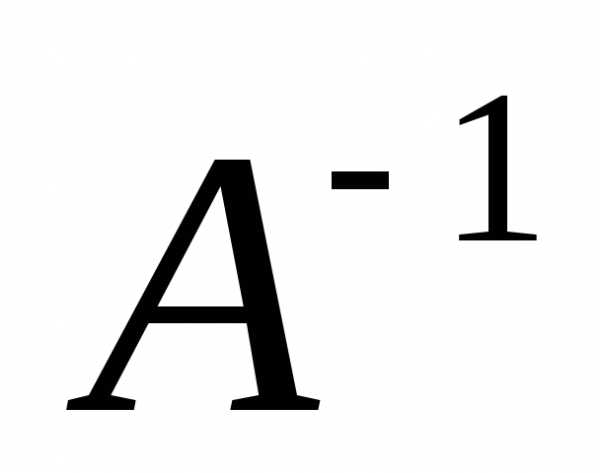 ,получим
,получим
(3)
В силу равенств
и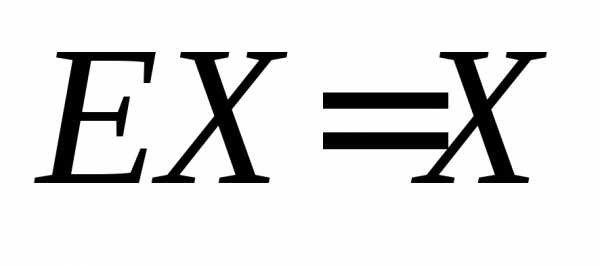 формула (3) принимает вид
формула (3) принимает вид
(4)
Не трудно убедиться в том, что выражение (4), полученное для Х, действительно является решением уравнения (1). Подставляя это выражение в уравнение (2), имеем
Замечание 5. Решение, полученное по формуле (4), то же самое, что было получено по формулам Крамера. Этот факт, вытекающий из единственности решения системы (1), можно непосредственно проверить, если подставить в формулу (4) выражение для обратной матрицы.
Пример 5. Матричным методом решить систему уравнений
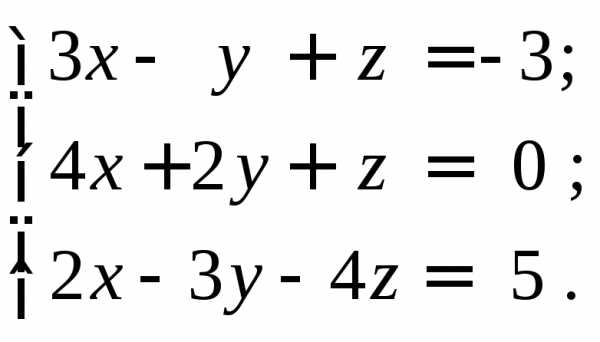
Здесь
Тогда
следовательно, обратная матрица существует.
Вычисляем алгебраические дополнения
аналогично далее
Таким образом, получим окончательное решение
studfiles.net
Тема 1. Матрицы. Определители
Матрицы и их виды
Определение 1.1 Матрицейразмера  называется
прямоугольная таблица чисел, состоящая
изmстрок иnстолбцов. Число в соответствующей
позиции называется элементом матрицы.
называется
прямоугольная таблица чисел, состоящая
изmстрок иnстолбцов. Число в соответствующей
позиции называется элементом матрицы.
В общем виде матрица записывается:
 — матрица
размера
— матрица
размера  ,
,
или коротко 
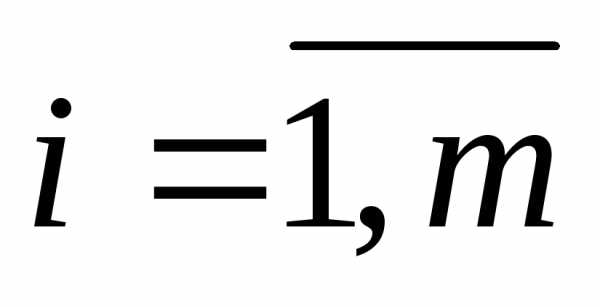 ,
, ;
;
 – элемент матрицы, стоящий в
– элемент матрицы, стоящий в –
той строке и
–
той строке и – том столбце.
– том столбце.
Пример.
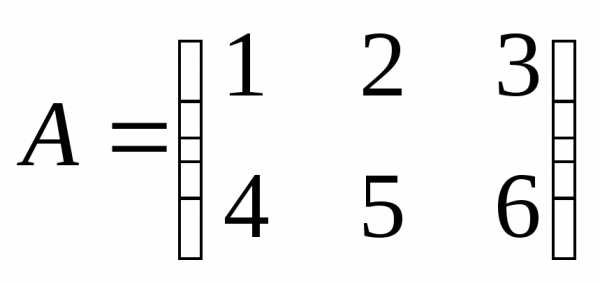 — матрица размера
— матрица размера .
Элемент
.
Элемент .
.
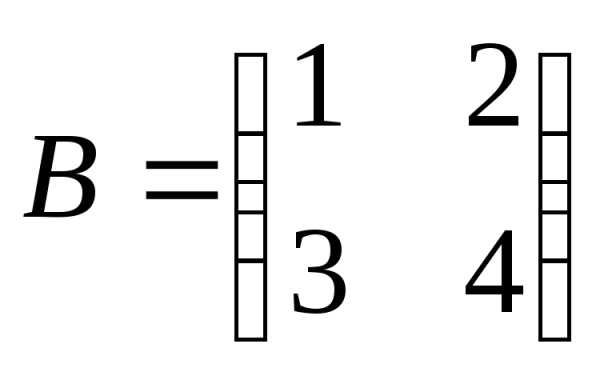 — матрица размера
— матрица размера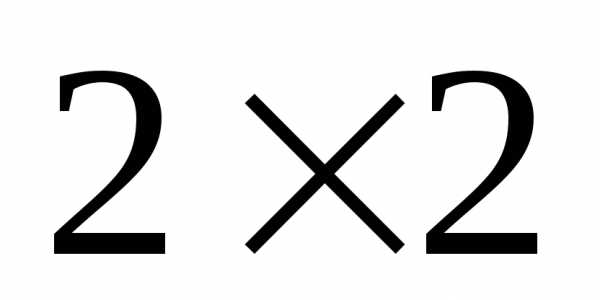 .
Элемент
.
Элемент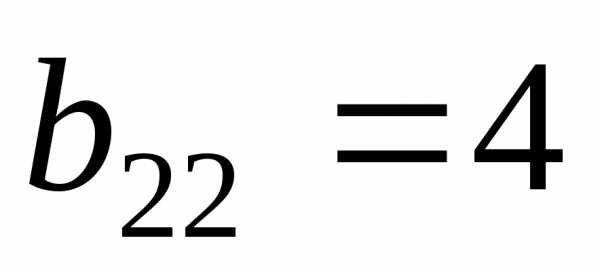 .
.
Матрица характеризуется:
1) размером,
2) элементами.
Определение 1.2 Две матрицы одного размера называютсяравными, если все их соответствующие элементы равны.
Пусть даны матрицы 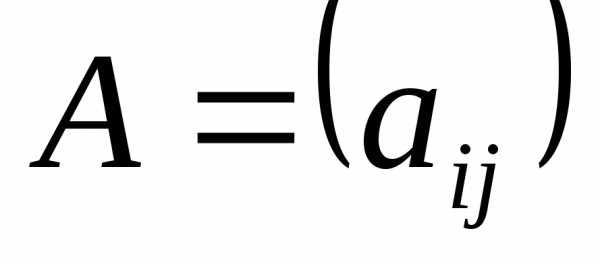 и
и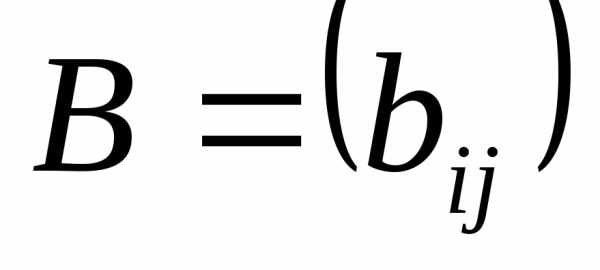 одного размера.
одного размера.
Тогда 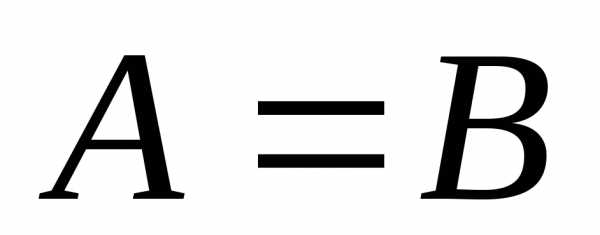 ,
если
,
если =
=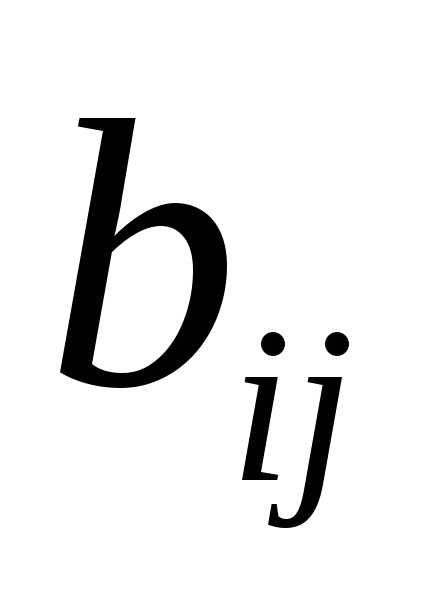 ,
где
,
где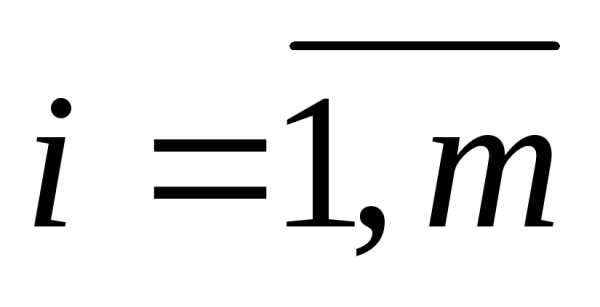 ,
,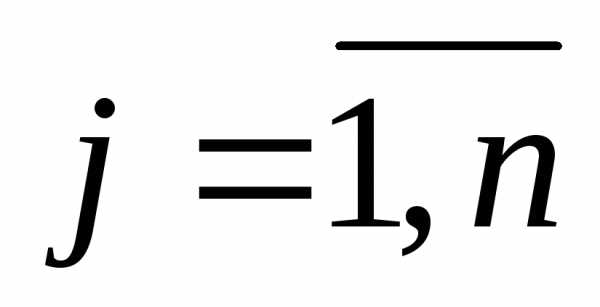 .
.
Пример.
1) 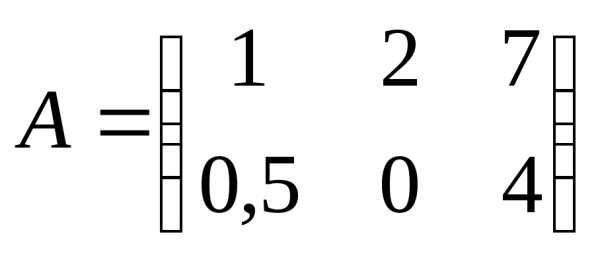 ,
2)
,
2)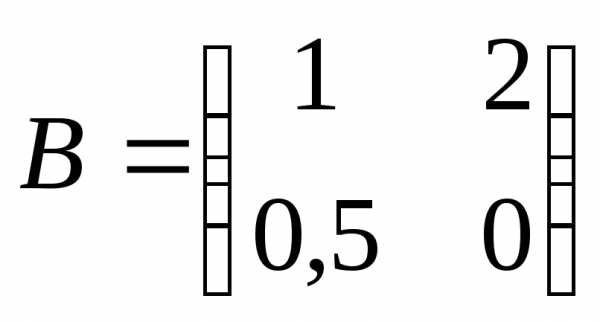 .
.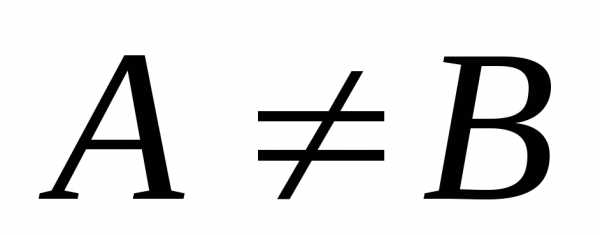 ,
так как размеры матриц не совпадают.
,
так как размеры матриц не совпадают.
3) 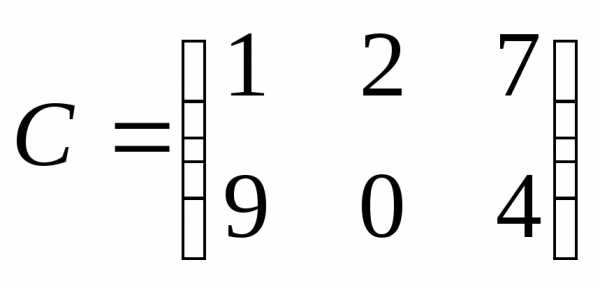 .
.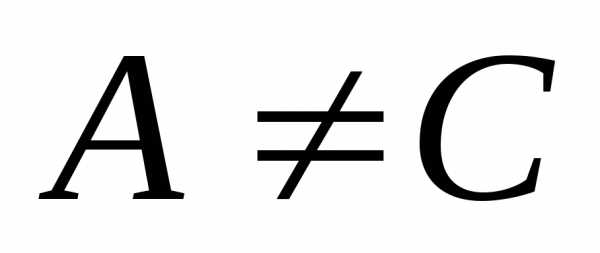 ,
так как
,
так как .
.
Виды матриц
Название | Пример | Размер | Элементы |
1. Прямоугольная |
| | – |
2. Квадратная |
| | – |
3. Матрица — столбец |
| | – |
4. Матрица — строка | , | | – |
5. Нулевая матрица |
| или |
|
6. Единичная матрица |
| |
|
7. Диагональная матрица |
| | Элементы |
8. Треугольная матрица (верхняя) |
| |
1.2 Операции над матрицами
Определение 1.3 Суммойдвух матриц
размера называется
матрица того же размера, каждый элемент
которой есть сумма соответствующих
элементов слагаемых матриц, т.е.
называется
матрица того же размера, каждый элемент
которой есть сумма соответствующих
элементов слагаемых матриц, т.е.
, ,
,
где
,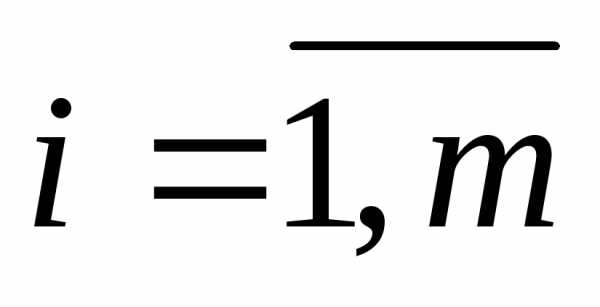 ,
,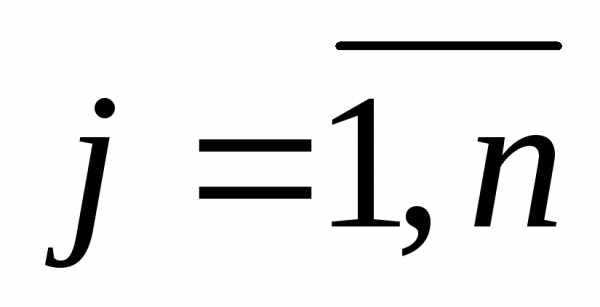 .
.
Пример.
Сложение матриц производится поэлементно.
Определение 1.4 Разностью двух матриц
размера называется
матрица
называется
матрица 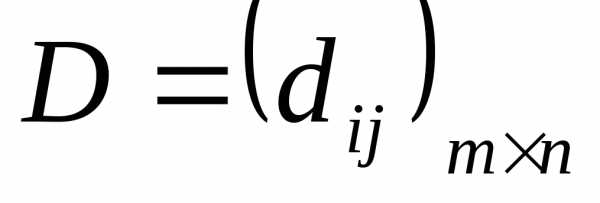 ,
каждый элемент которой есть разность
соответствующих элементов двух матриц
т.е.
,
каждый элемент которой есть разность
соответствующих элементов двух матриц
т.е.
,
где
Пример.
.
Определение 1.5. Произведениемматрицы на число  называется матрица того же размера,
каждый элемент которой является
произведением соответствующего элемента
исходной матрицы на это число, т.е.
называется матрица того же размера,
каждый элемент которой является
произведением соответствующего элемента
исходной матрицы на это число, т.е.
,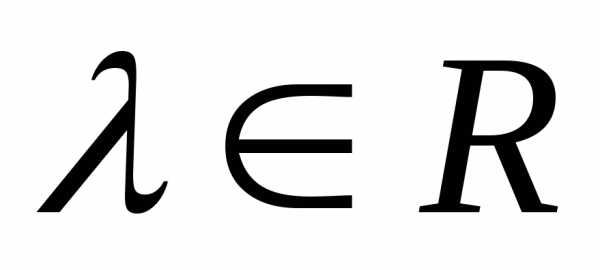
 .
.
Пример. .
Умножение матрицы на число производится поэлементно.
Матрица называетсяпротивоположной матрице A.
Операции сложения матриц и умножения матрицы на число называются линейными операциями над матрицами.
Свойства линейных операций над матрицами
Пусть A,B,C– матрицы,и β – действительные числа.
1) Коммутативность сложения
5)
2) Ассоциативность сложения
6)
3) Дистрибутивность относительно суммы матриц
7)
4) Дистрибутивность относительно суммы чисел
8)
Определение 1.6 Произведением двух матриц, первая из которых имеет
размер ,
а вторая
,
а вторая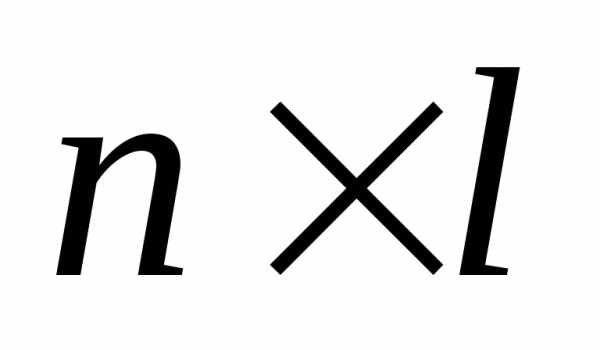 называется матрица размером
называется матрица размером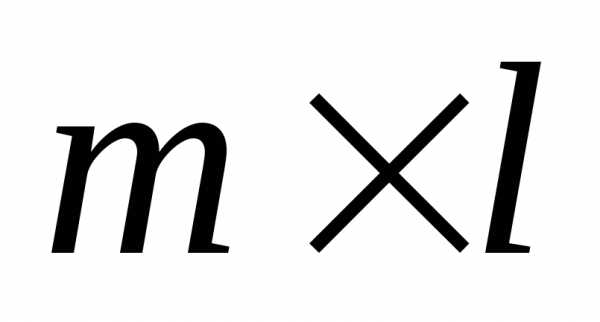 ,
каждый элемент которой, стоящий в позиции
,
каждый элемент которой, стоящий в позиции является суммой произведений элементов
является суммой произведений элементов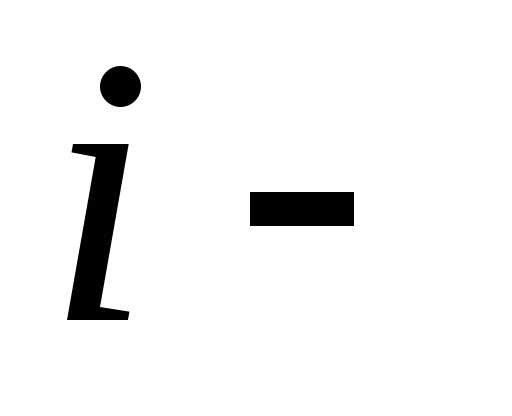 той
строки 1-го сомножителя и соответствующих
элементовj-того столбца
2-го множителя. (Правило: строка на
столбец).
той
строки 1-го сомножителя и соответствующих
элементовj-того столбца
2-го множителя. (Правило: строка на
столбец).
где
Пример.
1) 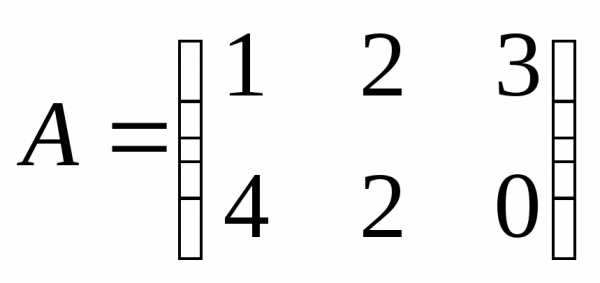 ,
,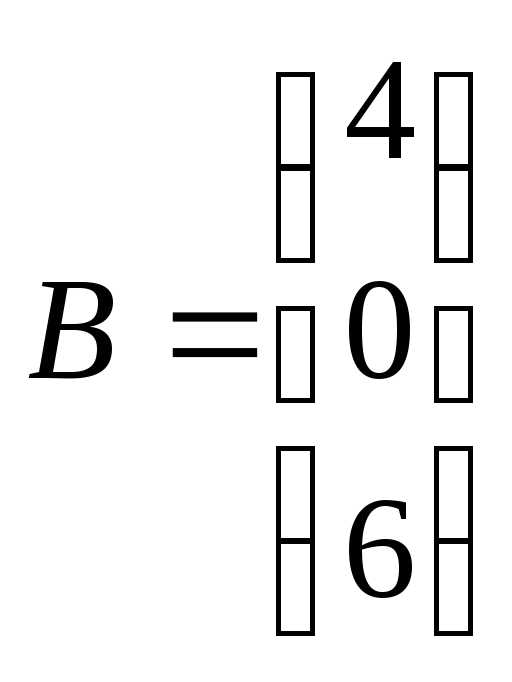 .матрица-столбец
.матрица-столбец
2) 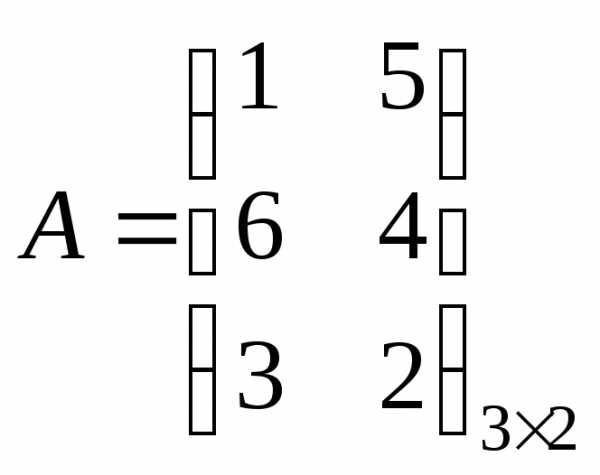 ;
;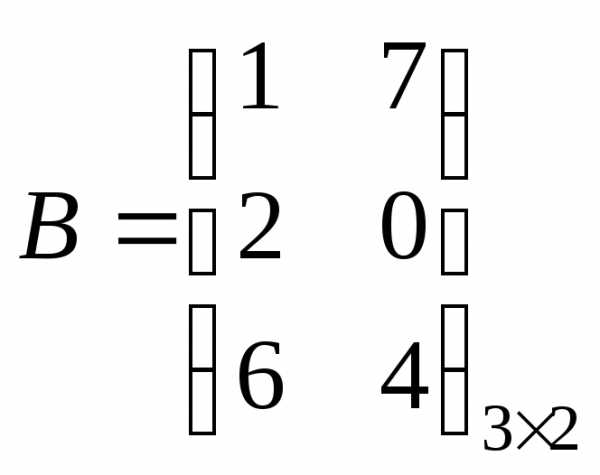
 — умножение невозможно, из-за несоответствия
размеров матриц.
— умножение невозможно, из-за несоответствия
размеров матриц.
3) Найти 
4) Найти 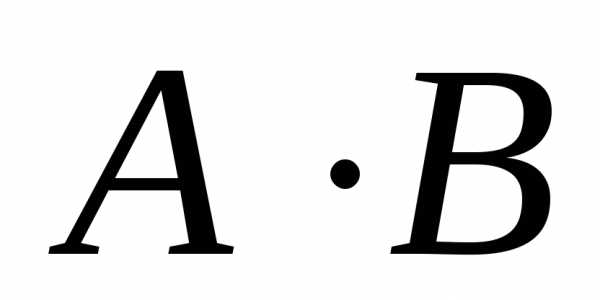 и
и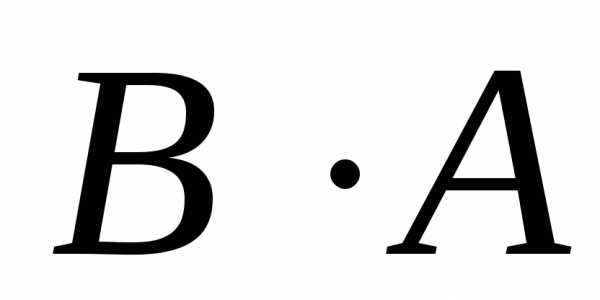 .
.
 ,
,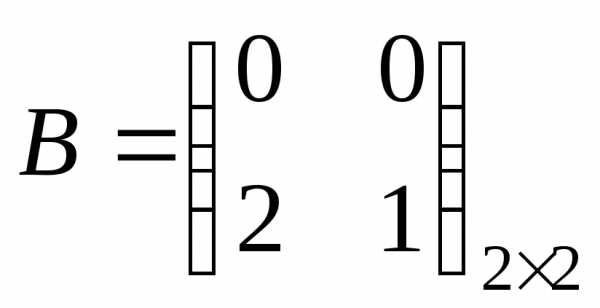
;
Таким образом, получили, что 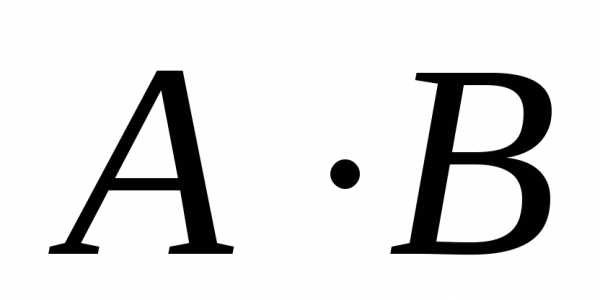
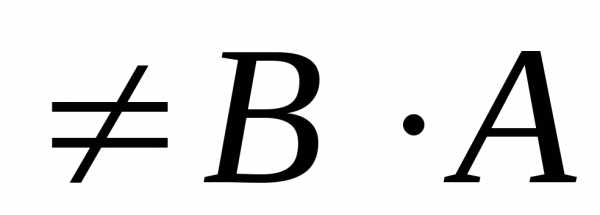 .
.
Умножение матриц не обладает свойством
коммутативности, т.е. 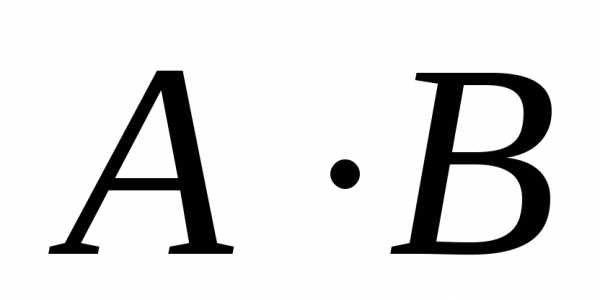
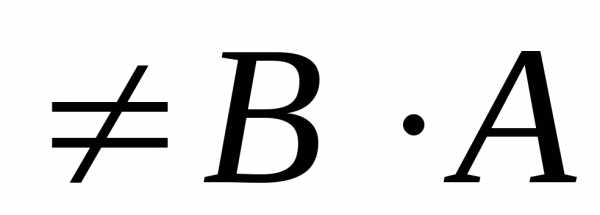 в общем случае.
в общем случае.
Две матрицы А и В, для которых выполняется
равенство
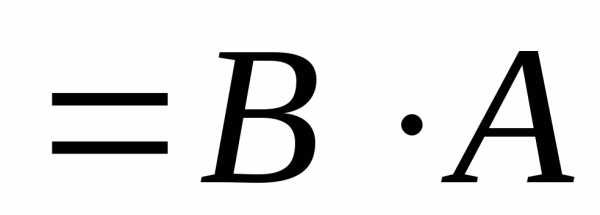 называютсякоммутативными.
называютсякоммутативными.
Легко показать, что где А – квадратная матрица, Е – единичная матрица того же размера.
Если для заданных матриц операция умножения определена, то справедливы следующие свойства:
Определение 1.7 Матрица называетсятранспонированной по отношению к данной, если ее строки являются столбцами данной матрицы, т.е.
,.
Пример.
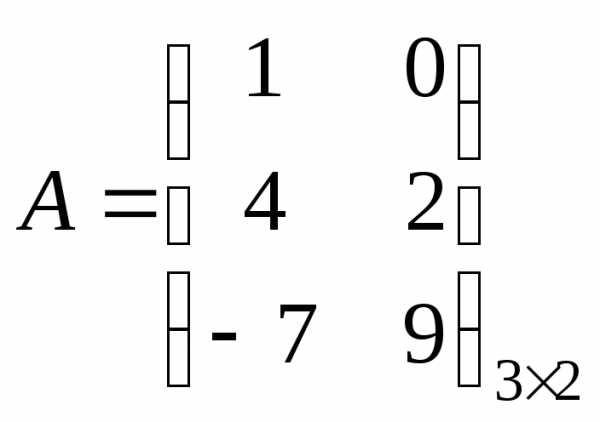 ,
,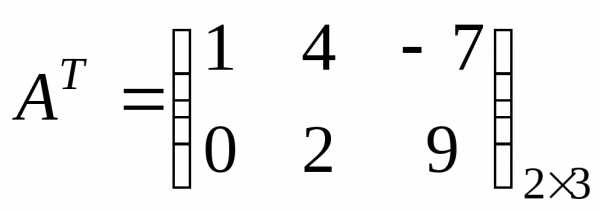 .
.
studfiles.net
«Матрицы, матричный метод решения СЛУ».
Матрицей размера m´n называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде
A =
или сокращенно в виде A = (ai j) (i = ; j = ). Числа ai j, составляющие данную матрицу, называются ееэлементами; первый индекс указывает на номер строки, второй – на номер столбца. Две матрицы A = (ai j) и B = (bi j) одинакового размера называютсяравными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если ai j = bi j.
Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
Виды матриц.
Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой иливектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.
Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера m´n, все элементы которой равны нулю, называютсянулевой матрицей и обозначается через 0.
Элементы матрицы с одинаковыми индексами называютэлементамиглавной диагонали.
Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратнойпорядка n.
Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:
.
Если все элементы ai i диагональной матрицы равны 1, то матрица называетсяединичнойи обозначается буквой Е:
E = .
Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю.
Транспонированиемназывается такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.
Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу
AT = ,
которая будет транспонированной по отношению к матрице А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.
Действие над матрицами.
Произведением матрицы А на число lназывается матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число l: l A = (l ai j).
Т.е. для того чтобы умножить матрицу A на число l нужно каждый элемент матрицы A умножить на это число.
Суммойдвух матриц А = (ai j) и B = (bi j) одного размера называется матрица C = (ci j) того же размера, элементы которой определяются по формуле ci j = ai j + bi j.
Т.е. чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах.
Или:
=
ПроизведениеАВ матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.
Произведением двух матриц А = (ai j) и B = (bj k), где i = , j= , k= , заданных в определенном порядке АВ, называется матрица С = (c i k), элементы которой определяются по следующему правилу:
c i k = ai 1 b1 k + ai 2 b2 k +… + ai m bm k = ai s bs k.
Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Т.е. перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы.
Обратная матрица.
Квадратная матрица А называется невырожденной, илинеособенной, если ее определитель отличен от нуля, ивырожденной,или особенной, если D = 0.
Понятие обратной матрицы вводится только для квадратных матриц.
Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A-1 и удовлетворяющая условию .
Справедлива следующая теорема:
Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.
находится следующим образом
,
где Aij – алгебраические дополнения элементов aij данной матрицы A.
Итак, чтобы найти обратную матрицу нужно:
1. Найти определитель матрицы A.
2. Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу, элементами которой являются числа Aij.
3. Найти матрицу, транспонированную полученной матрице А, и умножить её на – это и будет обратная матрица.
Аналогично для матриц второго порядка, обратной будет следующая матрица .
Матричный метод решения СЛУ
Рассмотрим систему, состоящую из n линейных уравнений с n неизвестными:
Вводя матрицу коэффициентов перед неизвестными А, матрицу-столбец неизвестных Х и матрицу-столбец свободных членов В, систему можно переписать в матричной форме:
Предположим, что матрица А — неособенная, т.е. А ≠ 0. Решим матричное уравнение, а следовательно и систему (4) с помощью обратной матрицы А,
где, А = * Ặ =>
X = * Ặ =>
Для системы трех уравнений с тремя неизвестными:
решение запишется в виде:
Лекция №3.
Рекомендуемые страницы:
lektsia.com
Тема 1. «Матрицы и действия над ними»
1. Определение матрицы
2. Виды матриц
Квадратная матрица называется диагональной, если элементы по главной диагонали отличны от нуля, а остальные элементы нулевые:
Квадратные матрицы вида
Прямоугольная матрица вида
Матрица, состоящая из одной строки называется матрицей-строкой или строчной матрицей.
Суммой (разностью) двух матриц одинаковой размерности называется матрица, элементы которой равны сумме (разности) соответствующих элементов матриц слагаемых.
Пример
Произведением матрицы на число называется матрица, полученная из данной умножением всех ее элементов на число.
Линейные операции обладают следующими свойствами:
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной.
Умножение матриц определяется для согласованных матриц.
Например:
В случае, когда АВ=ВА, матрицы А и В называют перестановочными или коммутативными.
Ответ:Пример
Ответ:Свойства операции транспонирования:
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В:
Пример
Ответ:Свойства операции умножение матриц:
Решение (Пример 1):
Получаем:
Ответ:
Спасибо за внимание!
|
rpp.nashaucheba.ru
Презентация по математике «Матрицы и действия с ними»
Презентация по математике «Матрицы и действия с ними» — скачать бесплатно53335531463039513235404944384142294843374734365045565452
XСкопируйте код и вставьте его на свой сайт.
Матрицы и действия с ними
Описание презентации по отдельным слайдам:
 1 слайд
1 слайдТема 1. «Матрицы и действия над ними» Основные понятия: Определение матрицы Виды матриц Действия над матрицами
 2 слайд
2 слайд1. Определение матрицы Прямоугольная таблица чисел вида называется матрицей. — элементы матрицы. Размер матрицы Главная диагональ матрицы Побочная диагональ матрицы
 3 слайд
3 слайд2. Виды матриц Прямоугольная Квадратная Нулевая Единичная Диагональная Симметричная Вырожденная Равные Треугольная Квазитреугольная (ступенчатая или трапециевидная) Матрица-строка или строчная матрица Матрица-столбец или столбцевая матриц
 4 слайд
4 слайдМатрица называется прямоугольной, если количество ее строк не совпадает с количеством столбцов: Матрица называется квадратной, если количество ее строк совпадает с количеством столбцов:
 5 слайд
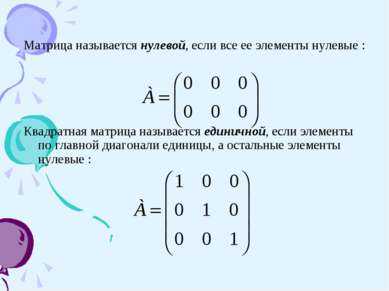
5 слайдМатрица называется нулевой, если все ее элементы нулевые : Квадратная матрица называется единичной, если элементы по главной диагонали единицы, а остальные элементы нулевые :
 6 слайд
6 слайдКвадратная матрица называется диагональной, если элементы по главной диагонали отличны от нуля, а остальные элементы нулевые: Квадратная матрица называется симметричной, если относительно главной диагонали для всех ее элементов выполняется условие :
 7 слайд
7 слайдКвадратная матрица называется вырожденной, если ее определитель равен нулю. Матрицы А и В (одинаковых размерностей) называются равными, если :
 8 слайд
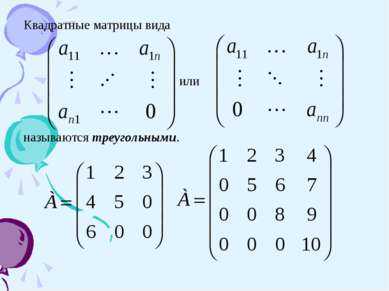
8 слайдКвадратные матрицы вида или называются треугольными.
 9 слайд
9 слайдПрямоугольная матрица вида называется квазитреугольной (ступенчатая или трапециевидная)
 10 слайд
10 слайдМатрица, состоящая из одной строки называется матрицей-строкой или строчной матрицей. Матрица, состоящая из одного столбца называется матрицей-столбцом или столбцевой матрицей
 12 слайд
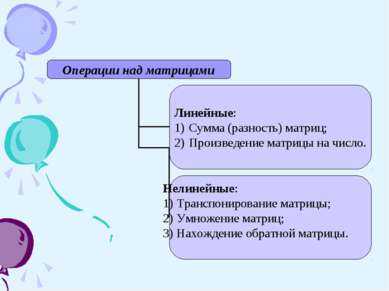
12 слайдСуммой (разностью) двух матриц одинаковой размерности называется матрица, элементы которой равны сумме (разности) соответствующих элементов матриц слагаемых. Например: Пример
 13 слайд
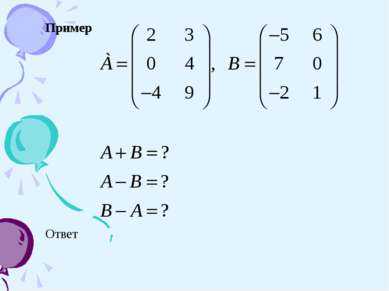
13 слайдПример Ответ
 14 слайд
14 слайдПроизведением матрицы на число называется матрица, полученная из данной умножением всех ее элементов на число. Например: Пример
 15 слайд
15 слайдЛинейные операции обладают следующими свойствами:
 16 слайд
16 слайдМатрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной. Например: Свойства
 17 слайд
17 слайдУмножение матриц определяется для согласованных матриц. Произведением матрицы на матрицу называется матрица , для которой , т.е. каждый элемент матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.
 18 слайд
18 слайдСпасибо за внимание! Презентацию подготовил студент группы СО-11 Бирюков Владислав
Чтобы скачать материал, введите свой email, укажите, кто Вы, и нажмите кнопку
Нажимая кнопку, Вы соглашаетесь получать от нас email-рассылку
Если скачивание материала не началось, нажмите еще раз «Скачать материал».
84468461854286128646885588729033
337313373733750338143391134093341513416634179342413425334268
У вас есть презентация, загружайте:
Для того чтобы загрузить презентацию на сайт, необходимо зарегистрироваться.
uslide.ru

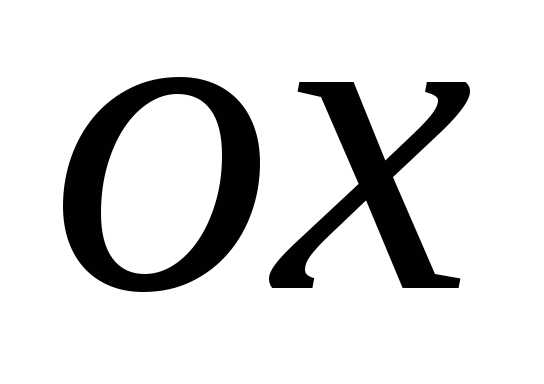
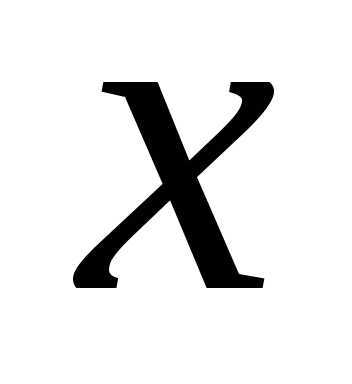 может быть только больше или равным
нулю. Значит, параболы существуют только
в правой полуплоскости.
может быть только больше или равным
нулю. Значит, параболы существуют только
в правой полуплоскости.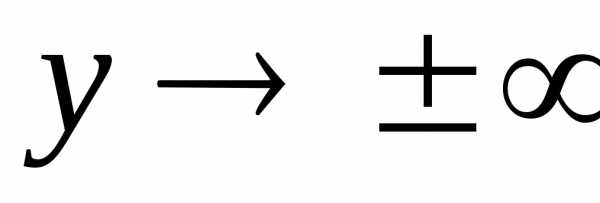
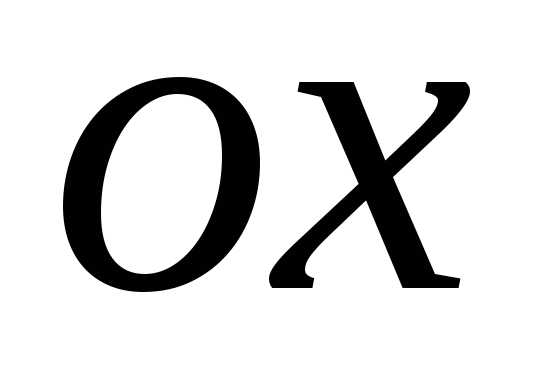 ,
то достаточно построить ее часть лежащую
в I четверти.
,
то достаточно построить ее часть лежащую
в I четверти. равны, если равны их элементы
равны, если равны их элементы .
. ,
каждый ее элемент равен сумме
соответствующих элементов.
,
каждый ее элемент равен сумме
соответствующих элементов. на
число есть матрица размера
на
число есть матрица размера ,
каждый элемент которой равен произведению
,
каждый элемент которой равен произведению на число.
на число. на матрицу В размера
на матрицу В размера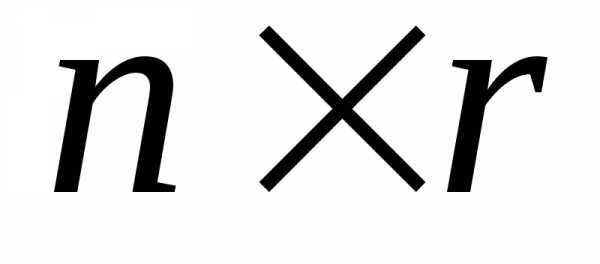 есть
матрица С размера
есть
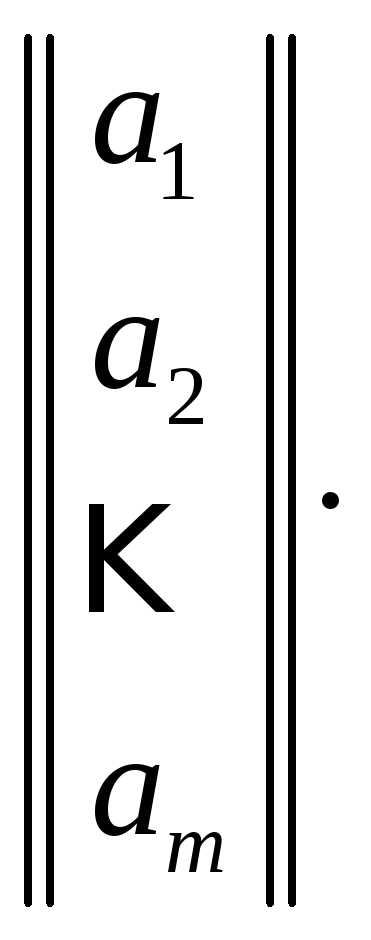
матрица С размера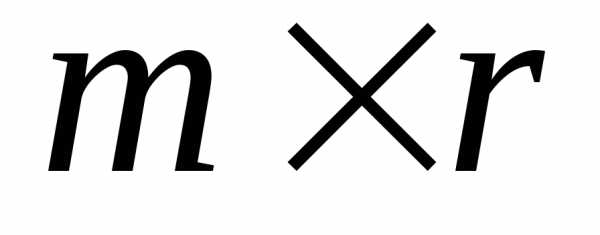 .
.

 .
.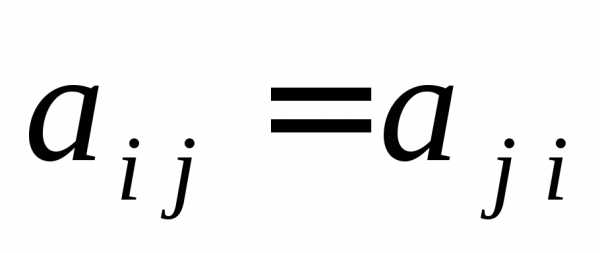 для всех
для всех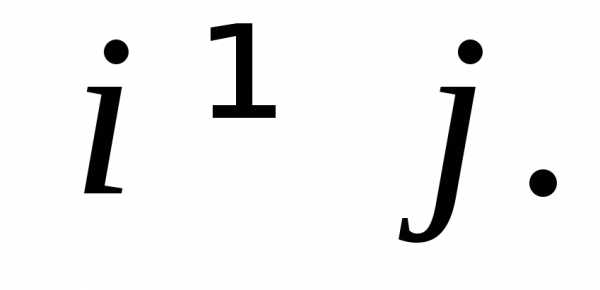
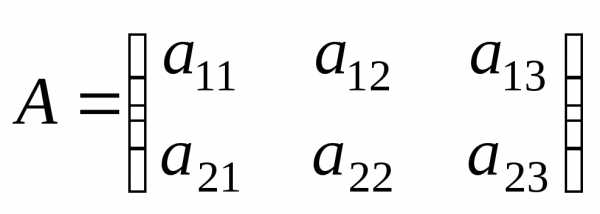 ,
,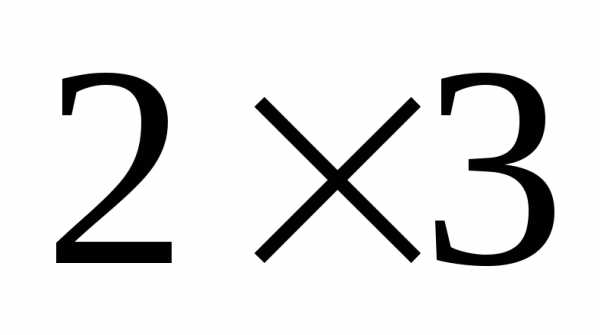


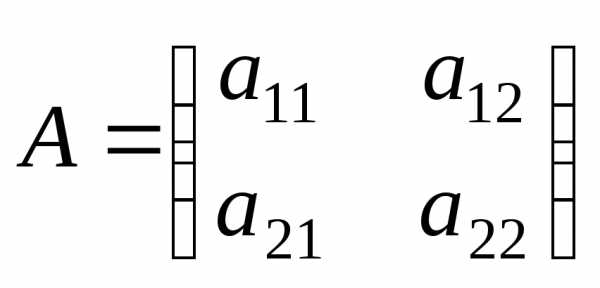 ,
,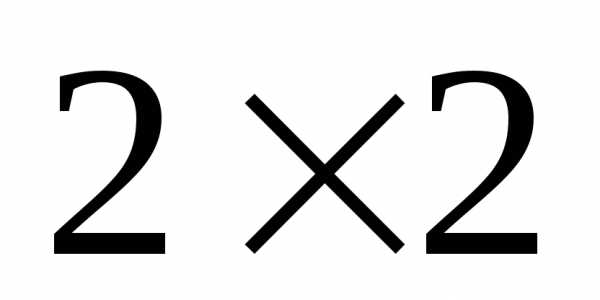

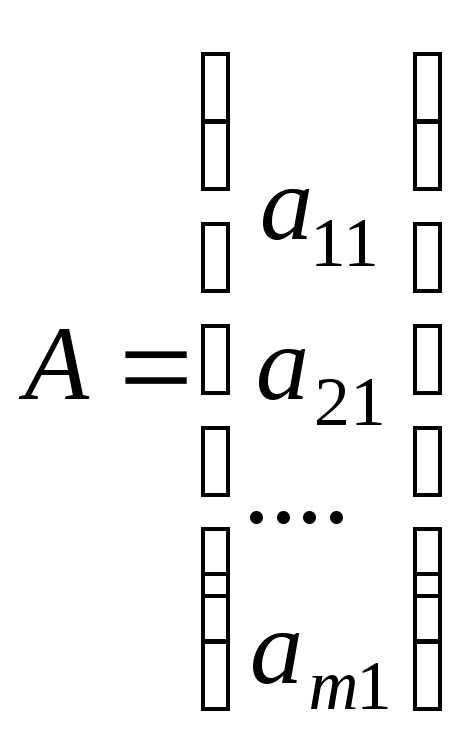 ,
,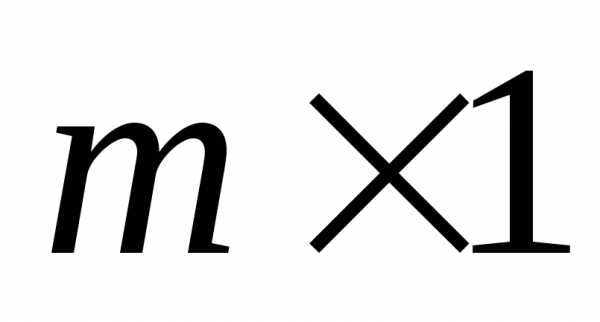
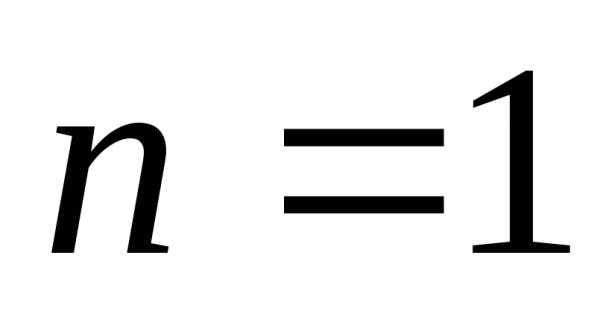
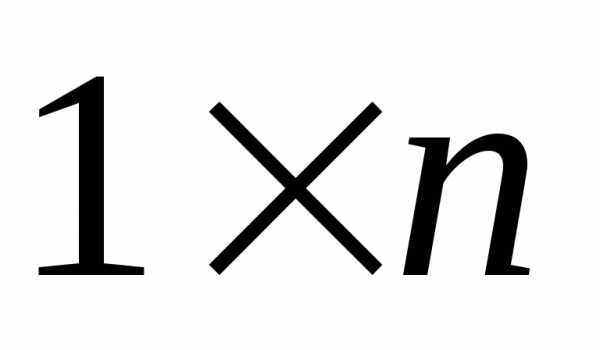
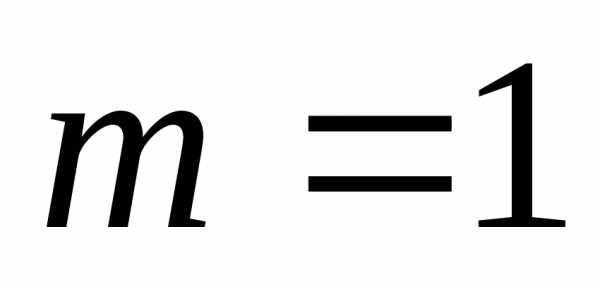
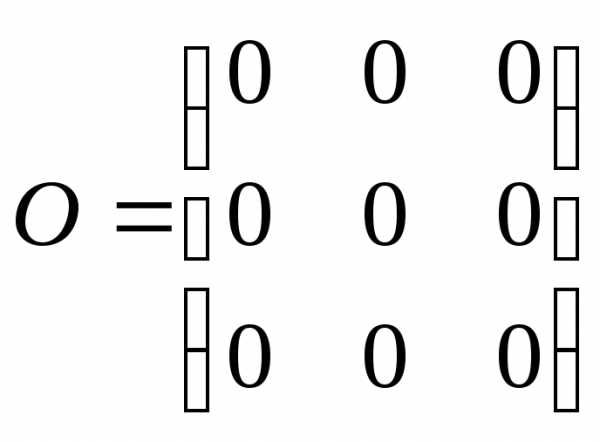 ,
,
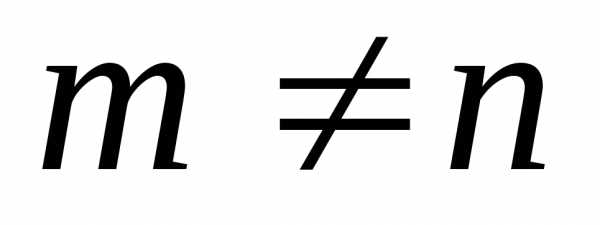
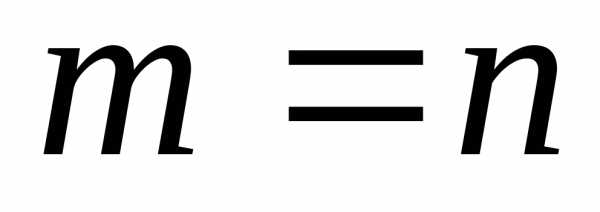
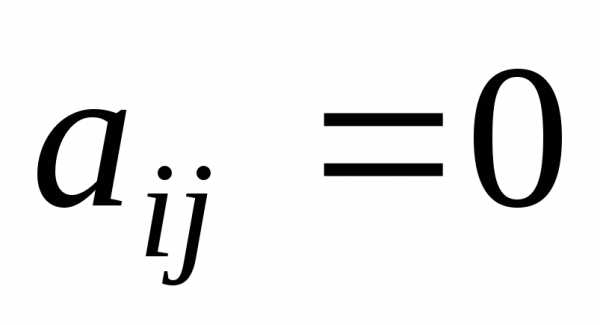
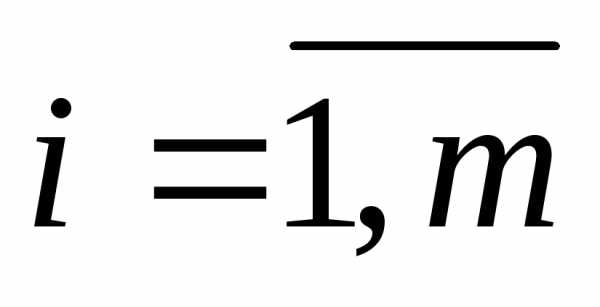 ,
,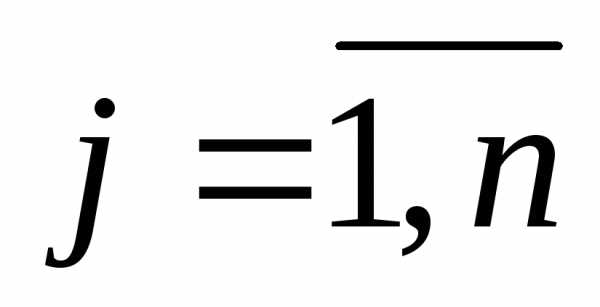 .
. ,
,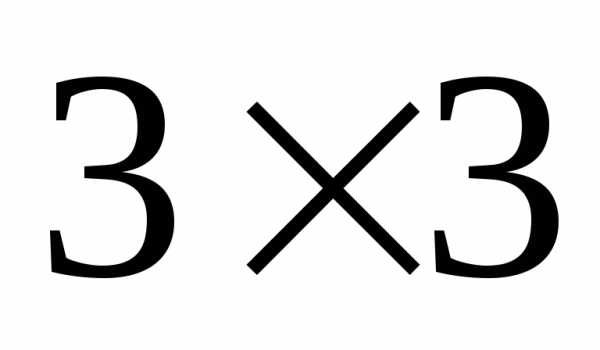
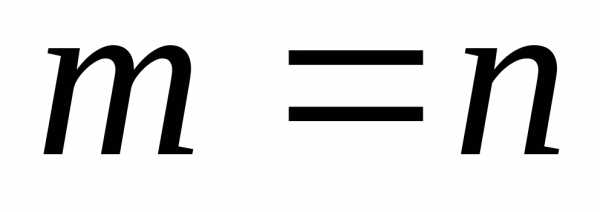
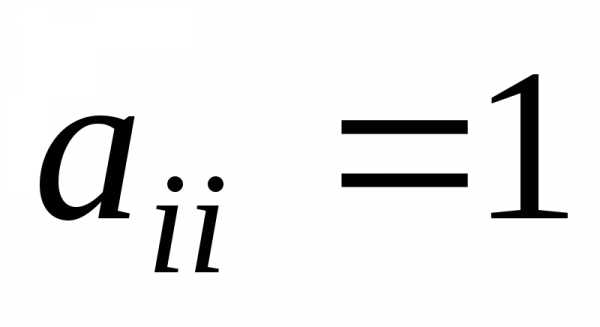
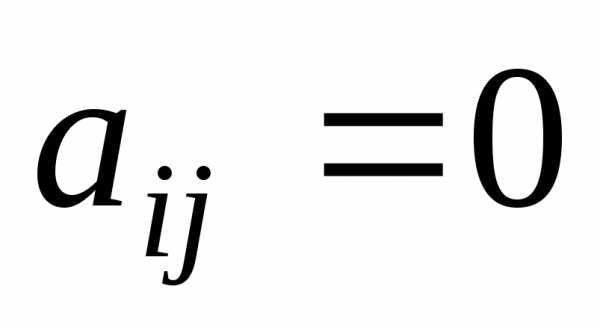
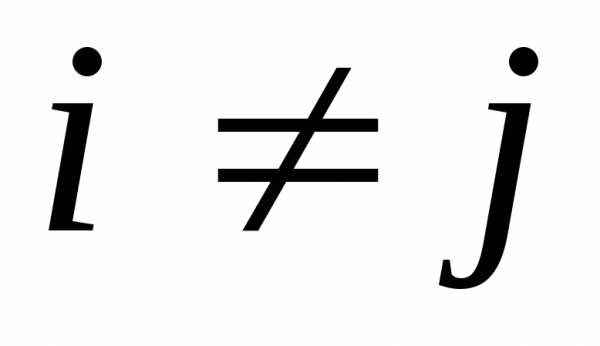
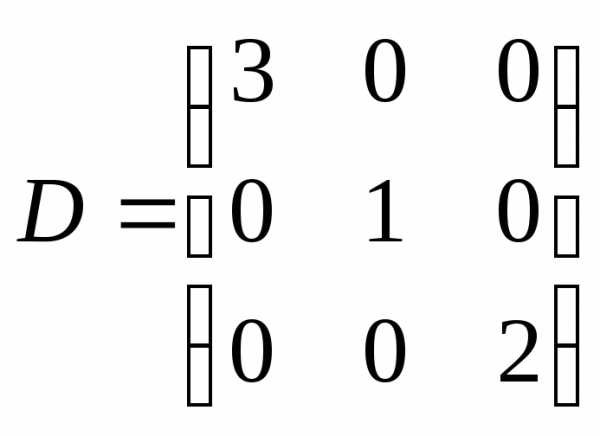 ,
,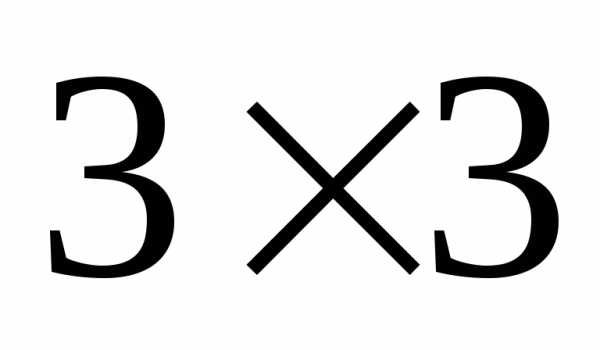
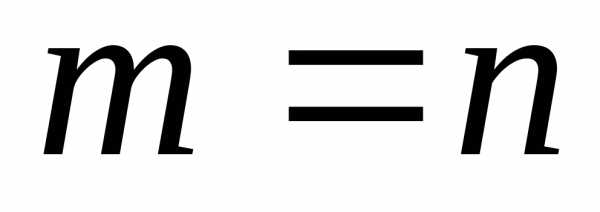
 образуют
главную диагональ
образуют
главную диагональ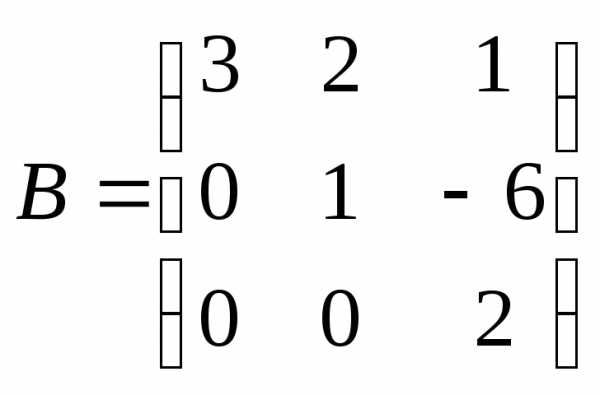 ,
,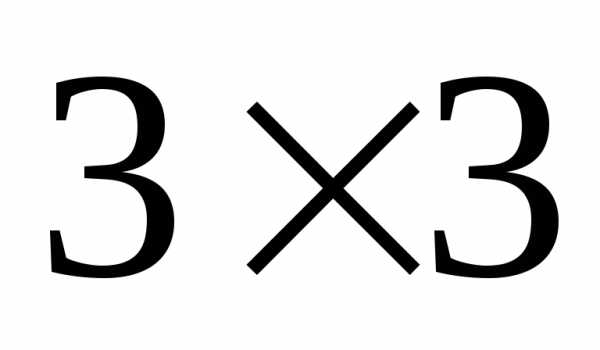
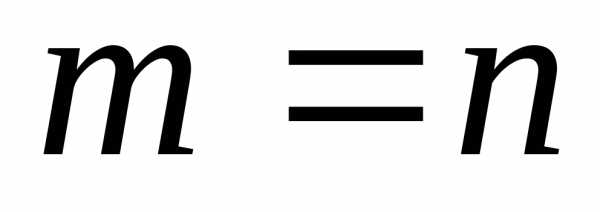
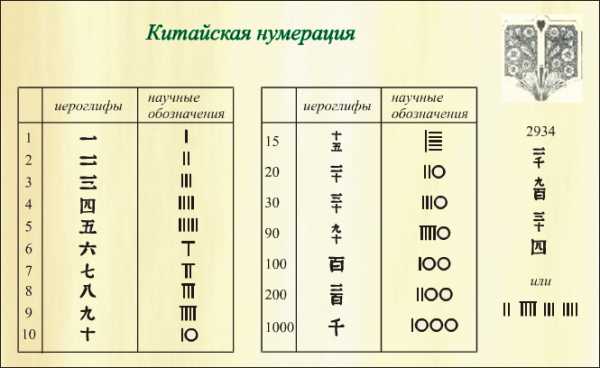
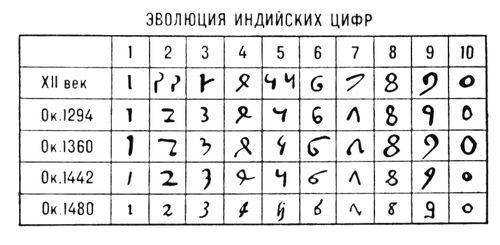
 Цифры на арабском языке на транспортных билетах, ценниках на рынке, на рекламных листовках.
Цифры на арабском языке на транспортных билетах, ценниках на рынке, на рекламных листовках.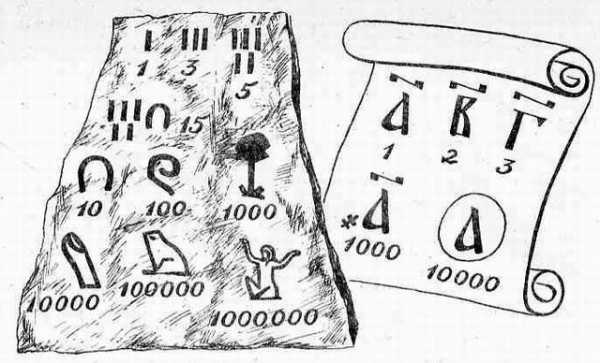
















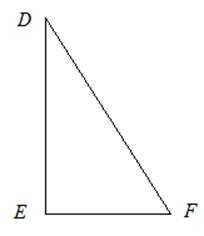
 Все о треугольниках ГЕОМЕТРИЯ 7 КЛАСС
Все о треугольниках ГЕОМЕТРИЯ 7 КЛАСС Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, последовательно соединенных отрезками
Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, последовательно соединенных отрезками Виды треугольников: l остроугольные l Тупоугольные l прямоугольные
Виды треугольников: l остроугольные l Тупоугольные l прямоугольные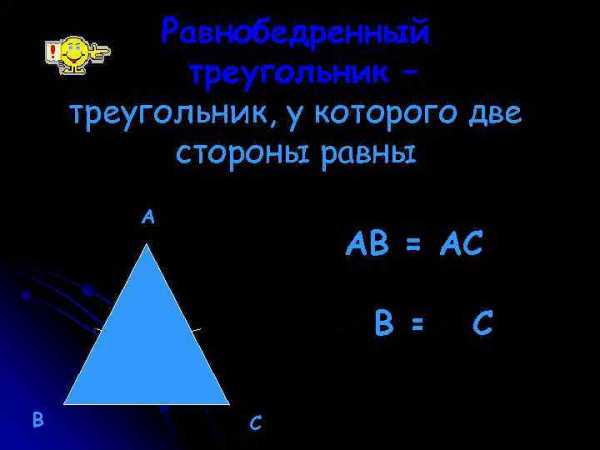 Равнобедренный треугольник – треугольник, у которого две стороны равны А АВ = АС B = В С C
Равнобедренный треугольник – треугольник, у которого две стороны равны А АВ = АС B = В С C Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника. В равных треугольниках против соответственно равных сторон лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника. В равных треугольниках против соответственно равных сторон лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны. Первый признак равенства треугольников: l Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Первый признак равенства треугольников: l Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Второй признак равенства треугольников: l Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников: l Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Третий признак равенства треугольников: l Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
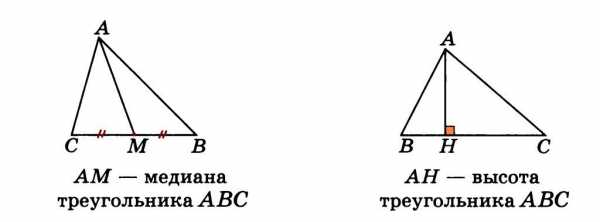
Третий признак равенства треугольников: l Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.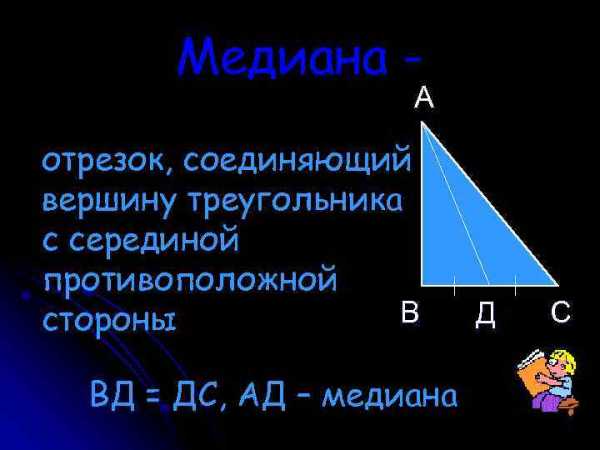 Медиана — А отрезок, соединяющий вершину треугольника с серединой противоположной В стороны ВД = ДС, АД – медиана Д С
Медиана — А отрезок, соединяющий вершину треугольника с серединой противоположной В стороны ВД = ДС, АД – медиана Д С Биссектриса — отрезок биссектрисы А угла треугольника, соединяющий вершину треугольника с точкой противоположной В стороны ВАК = САК, АК — биссектриса К С
Биссектриса — отрезок биссектрисы А угла треугольника, соединяющий вершину треугольника с точкой противоположной В стороны ВАК = САК, АК — биссектриса К С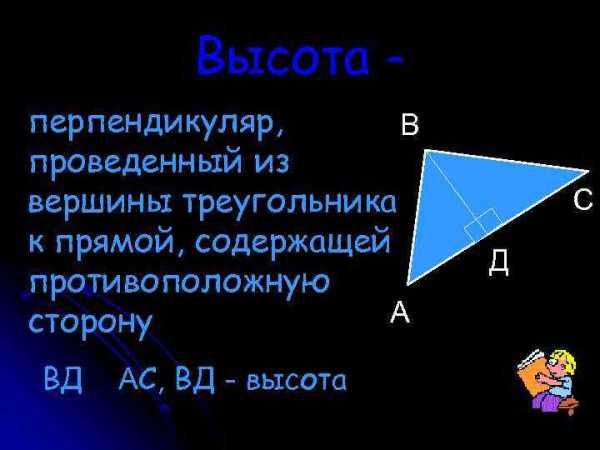 Высота перпендикуляр, В проведенный из вершины треугольника к прямой, содержащей противоположную А сторону ВД АС, ВД — высота С Д
Высота перпендикуляр, В проведенный из вершины треугольника к прямой, содержащей противоположную А сторону ВД АС, ВД — высота С Д В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке
В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой Внешним углом треугольника называется угол, смежный с каким – нибудь углом этого треугольника Внешний Угол Внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним
Внешним углом треугольника называется угол, смежный с каким – нибудь углом этого треугольника Внешний Угол Внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним Прямоугольный треугольник к г и а п о т т е н е у з т к а т е т а
Прямоугольный треугольник к г и а п о т т е н е у з т к а т е т а Некоторые свойства прямоугольных треугольников • сумма двух острых углов прямо- угольного треугольника равна 90° • катет 30 о • прямоугольного треуголь ника, лежащий против угла в 30°, равен половине гипотенузы если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°
Некоторые свойства прямоугольных треугольников • сумма двух острых углов прямо- угольного треугольника равна 90° • катет 30 о • прямоугольного треуголь ника, лежащий против угла в 30°, равен половине гипотенузы если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30° Признаки равенства прямоугольных треугольников • Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны • Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны
Признаки равенства прямоугольных треугольников • Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны • Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны Признаки равенства прямоугольных треугольников • если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны • если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны
Признаки равенства прямоугольных треугольников • если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны • если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны Соотношение между сторонами и углами треугольника • В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона • В прямоугольном треугольнике гипотенуза больше катета • Если два угла треугольника равны, то треугольник равнобедренный
Соотношение между сторонами и углами треугольника • В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона • В прямоугольном треугольнике гипотенуза больше катета • Если два угла треугольника равны, то треугольник равнобедренный Неравенство треугольника Каждая сторона треугольника меньше суммы двух других сторон Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ
Неравенство треугольника Каждая сторона треугольника меньше суммы двух других сторон Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ
 Построение треугольника по трем сторонам C • A • • B
Построение треугольника по трем сторонам C • A • • B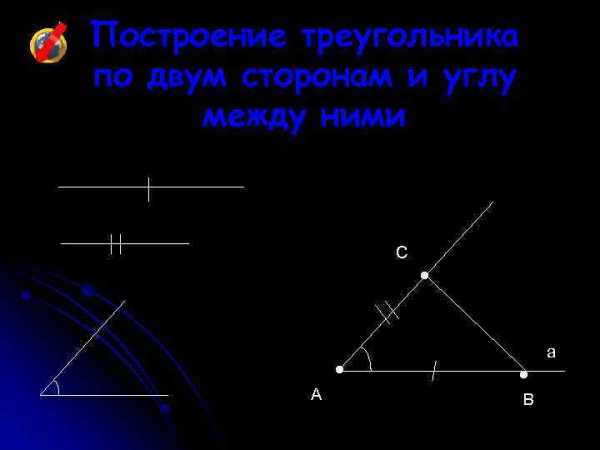 Построение треугольника по двум сторонам и углу между ними C A • • • B a
Построение треугольника по двум сторонам и углу между ними C A • • • B a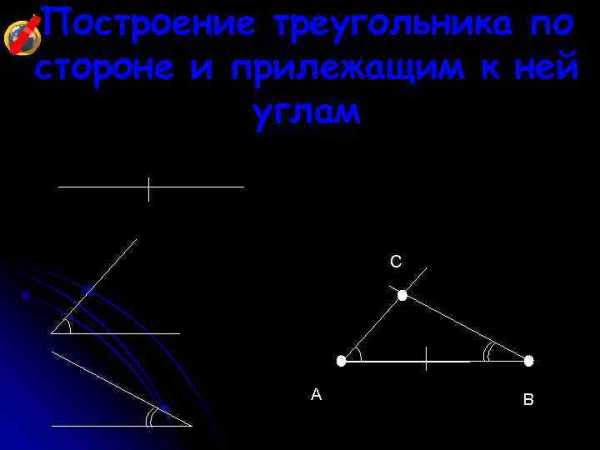 Построение треугольника по стороне и прилежащим к ней углам C A B
Построение треугольника по стороне и прилежащим к ней углам C A B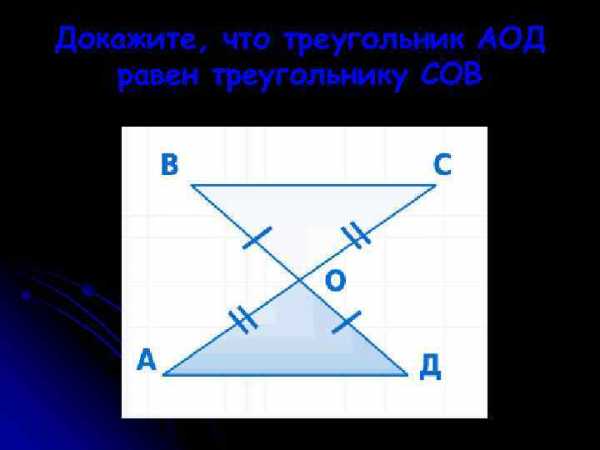 Докажите, что треугольник АОД равен треугольнику СОВ
Докажите, что треугольник АОД равен треугольнику СОВ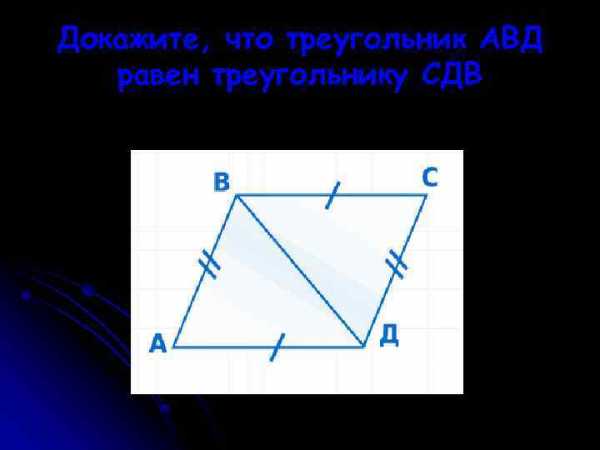 Докажите, что треугольник АВД равен треугольнику СДВ
Докажите, что треугольник АВД равен треугольнику СДВ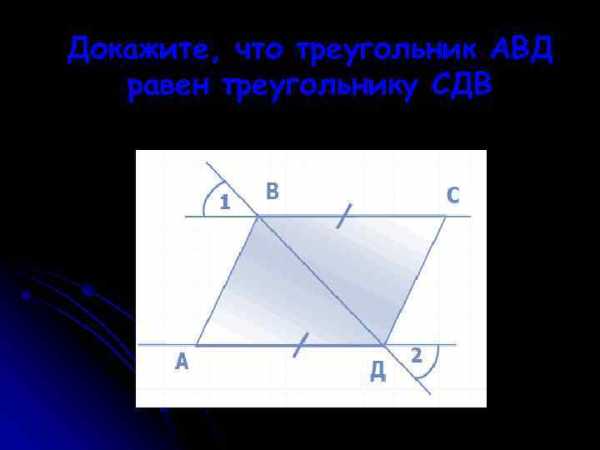 Докажите, что треугольник АВД равен треугольнику СДВ
Докажите, что треугольник АВД равен треугольнику СДВ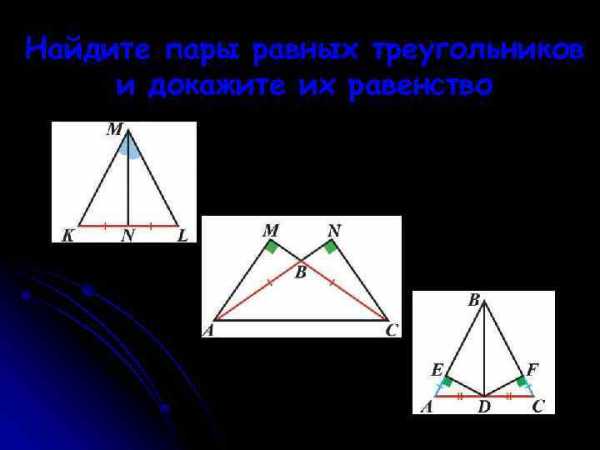 Найдите пары равных треугольников и докажите их равенство
Найдите пары равных треугольников и докажите их равенство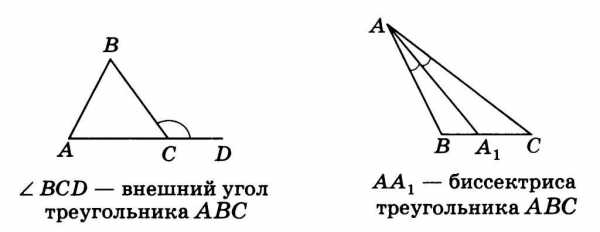
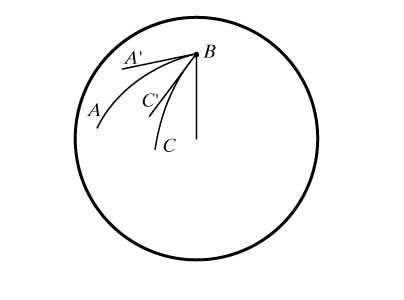
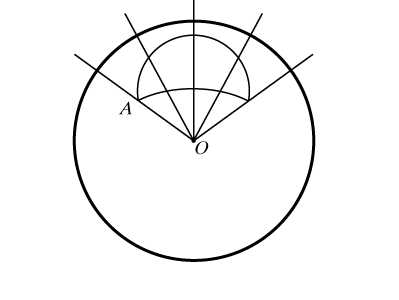
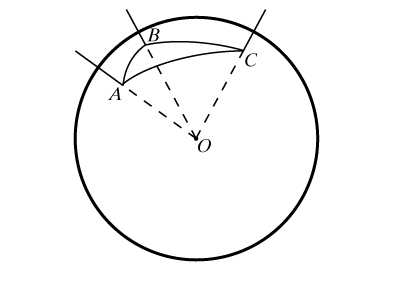
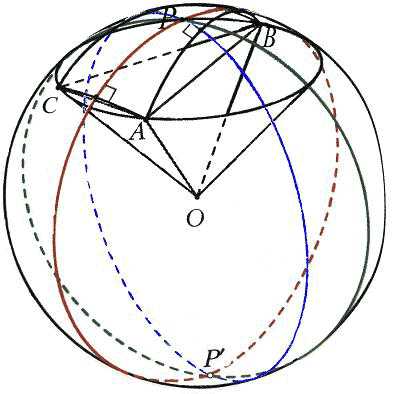
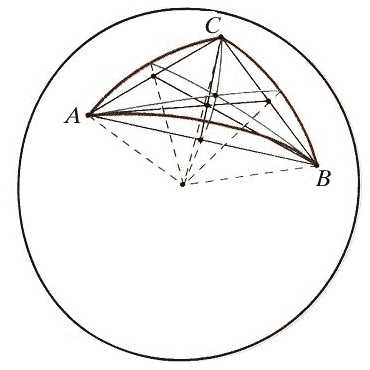
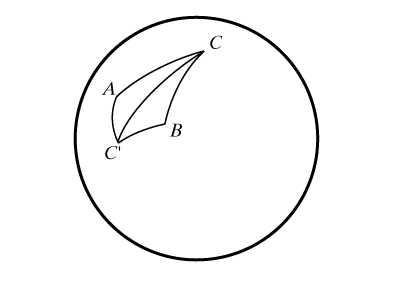
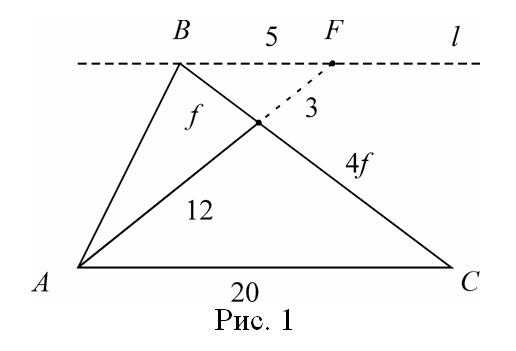 проходящую через вершину В параллельно стороне АС и продолжим АМ до пересечения с прямой в точке F. Ясно, что треугольники АМС и ВМF подобны (коэффициент подобия равен 4). Получаем, что BF = 5, MF = 3, т.е. появились новые данные, которые помогут решить задачу. Обратим внимание на два частных случая для прямой . Если АМ – медиана (ВМ : МС = 1 : 1), то BF = AC и MF = AM (происходит продолжение медианы на свою длину) (рис.2).
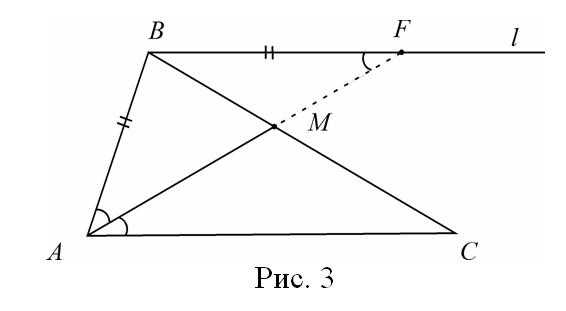
проходящую через вершину В параллельно стороне АС и продолжим АМ до пересечения с прямой в точке F. Ясно, что треугольники АМС и ВМF подобны (коэффициент подобия равен 4). Получаем, что BF = 5, MF = 3, т.е. появились новые данные, которые помогут решить задачу. Обратим внимание на два частных случая для прямой . Если АМ – медиана (ВМ : МС = 1 : 1), то BF = AC и MF = AM (происходит продолжение медианы на свою длину) (рис.2).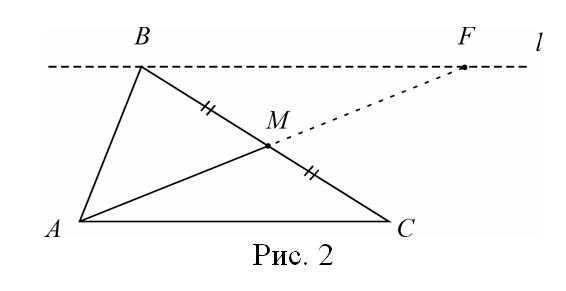
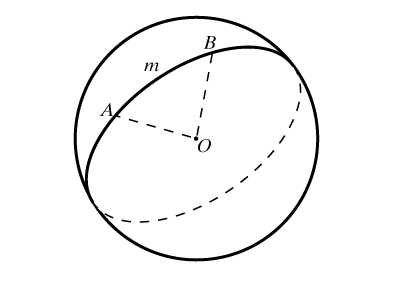
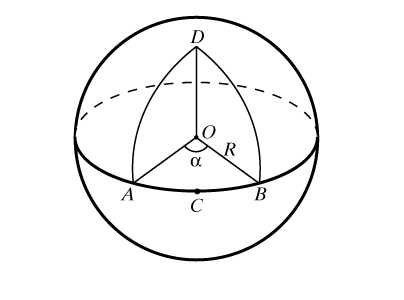
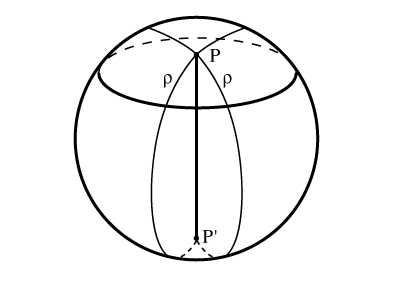
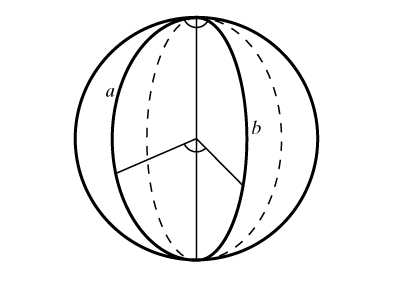
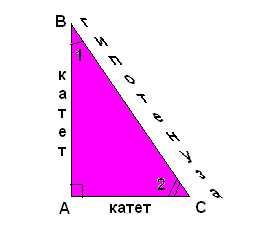 Добрый день, друзья! Сегодня из «Сборника задач для поступающих во ВТУЗы» мы будем решать задачи по геометрии прямоугольного треугольника.
Добрый день, друзья! Сегодня из «Сборника задач для поступающих во ВТУЗы» мы будем решать задачи по геометрии прямоугольного треугольника.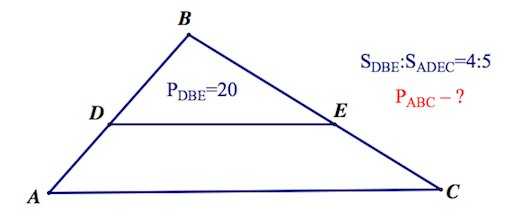





 a = ≈ 12
a = ≈ 12










 Продолжаем решать простейшие геометрические задачки.
Продолжаем решать простейшие геометрические задачки.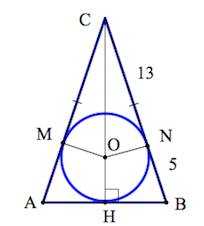
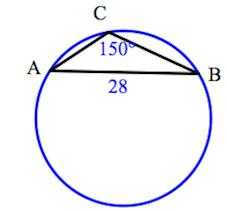



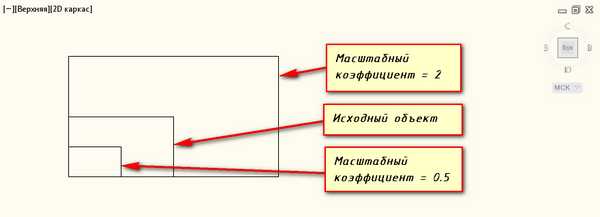
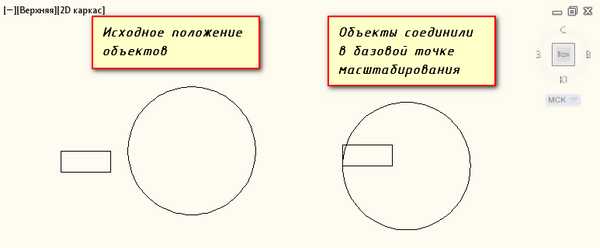
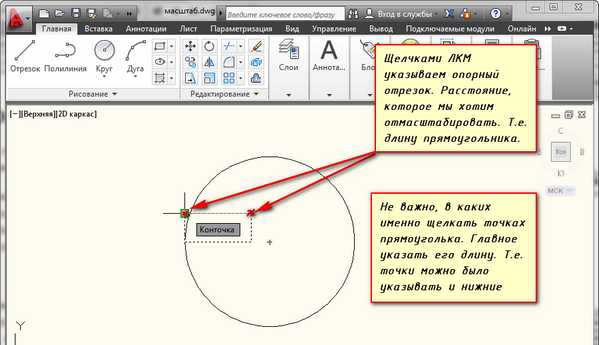
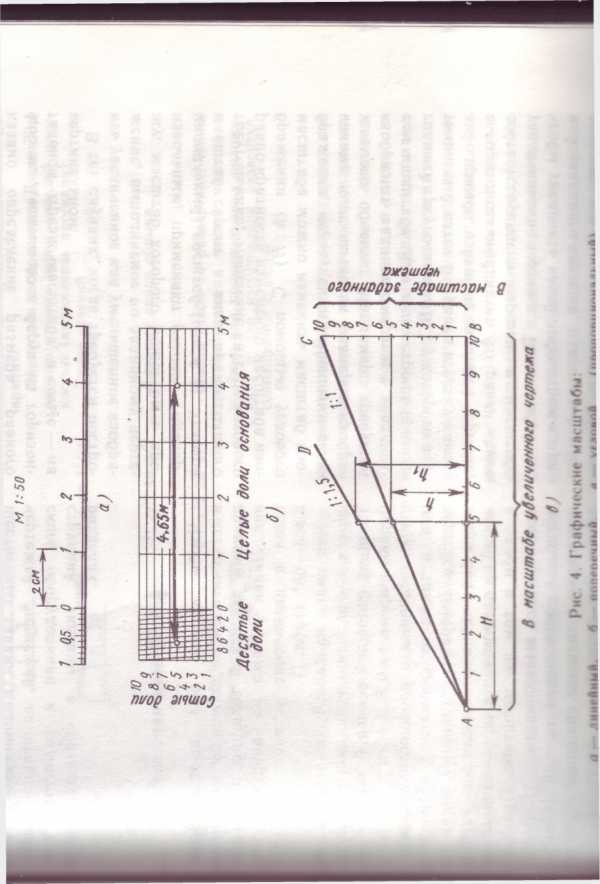
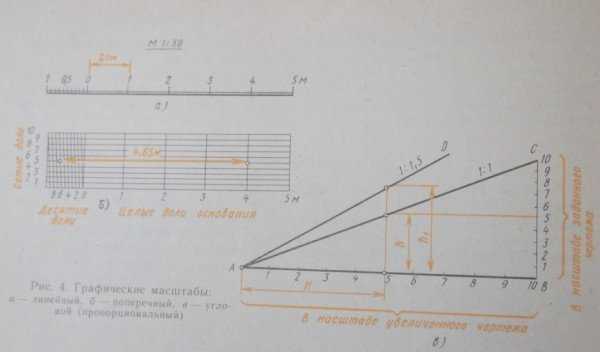 Изображение в натуральную величину 1:1.В процессе проектирования генеральных планов больших объектов используют следующие масштабы: 1:2000; 1: 5000; 1:10000; 1:20000; 1: 25000; 1:50000.
Изображение в натуральную величину 1:1.В процессе проектирования генеральных планов больших объектов используют следующие масштабы: 1:2000; 1: 5000; 1:10000; 1:20000; 1: 25000; 1:50000.