Большой тест с ответами по социологии (часть 2) – пройти тест онлайн бесплатно
180 вопросов
Показать
Скрыть правильные ответы
Вопрос:
Люди, длительное время проживающие на одной и той же территории, образуют …
Варианты ответа:
- класс
- территориальную общность
- нацию
- малую группу
Вопрос:
Элемент структуры общества, его «ячейка», одна из первых форм социальной общности людей и социальных отношений – это …
Варианты ответа:
- малая социальная группа
- большая социальная группа
- производственный коллектив
- семья
Вопрос:
Две социальные группы, которые современные российские социологи (Т.И. Заславская и В.В. Радаев) относят к категории «новые бедные» — это …
Варианты ответа:
- работники совместных предприятий
- работники «бюджетной сферы»
- предприниматели
- граждане с высокой семейной нагрузкой
Вопрос:
К этническим группам относятся …
Варианты ответа:
- расы, племена, народы, кланы
- этносы, находящиеся на стадии присваивающего хозяйства
- малые народности
- классы, страты, территориальные группы, граждане государств
Вопрос:
«Стигма» – это …
Варианты ответа:
zaochnik.com
социология (тест к зачёту)_с ответами
Тест по социологии
1 Общество современного типа
характеризуется… (выберите верные
утверждения):
а) имеет развитое сельское хозяйство
б) социальный статус индивида определяется
положением семьи, рода
в) в ответ на побои мужа жены падают
иск в суд
г) неразвиты контакты с окружающими
странами
2. Что из ниже перечисленного не относится
к городскому образу жизни:
а) снижение значимости соседских
отношений
б) неустойчивость социального статуса
в) повышенная формальность в
межиндивидуальных контактах
г) единство культурных норм
3. Концепция социальной стратификации
изучает:
а) межличностные отношения в
студенческой группе
б) иерархическое строение общества
в) межгосударственные отношения
г) систему конфликтных отношений
4. Классовая принадлежность индивида
определяется:
а) этническим происхождением
б) участием в деятельности общественной
организации
в) заработной платой и доходами
г) местом жительству (город — село)
5. Социология- это наука, которая изучает:
а) национальный, состав общества
б) экономические отношения между странами
в) рождаемость, смертность, возрастной
состав населения
г) взаимодействие социальных групп,
отношения между ними
д)_______________________________________________________
6. К какому времени относится формирование
социологии как науки:
а) ХV-ХVIвв.
б) XVII-XVIIIвв.
в) ХIХ-ХХ вв.
г) она еще не сформировалась как наука.
7. Семья из четырех человек (родители и
дети-школьники) за несколько лет сумела
купить 4-х комнатную квартиру, мебель,
съездила дважды по турпутевкам в круиз
по Волге, дети посещают платные курсы
по информатике. К какому социальному
классу ее можно отнести:
а) среднему — высшему
б) среднему — среднему
в) предпринимательскому
г) низшему
8. Результаты инженерной деятельности
больше всего влияют на:
а) политическую систему общества
б) межгосударственные отношения
в) профессиональный состав общества
г) внутрисемейные отношения
д) функциональную структуру предприятия
9. Что, из ниже перечисленного не относится
к элементам культуры:
а) городская свалка
б) программа политической партии
в) полезные ископаемые и сибирская
тайга
г) танцы, спорт, свадьбы
д) теория относительности
10. Собирая материал для своей будущей
книги, исследователь изучал архивы,
подшивки старых газет и журналов, смотрел
кинохронику. Каким методом он пользовался:
а) математическим моделированием
б) экспериментом
в) опросом
г) изучение документов (контент-анализ)
11. Понятия:
а) социальная структура (1)
б) престиж (3)
в) класс – большая социальная группа,
отличающаяся от других по критериям
доступа к общественному богатству
(распределению благ в обществе), власти,
социальному престижу
г) социальная стратификация — иерархическая
система неравенства
д) социальная роль (2)
е) этноцентризм – тенденция оценивать
другие культуры на основе собственной;
вера в биологическое и культурное
превосходство членов собственной группы
над другими группами
Определения:
1) определенный порядок взаимосвязей
между элементами социума;
2) ожидаемое поведение в типических
обстоятельствах;
3) степень уважения определенного
статуса.
Задание: связать определения с понятиями
и написать недостающие.
12. Что из нижеприведенного можно отнести
к социальным процессам, идущим в крупных
городах:
а) ремонт дорог и тротуаров
б) решение администрации городов о
запрете на выгул собак без намордников
в) формирование финансово-промышленных
групп в сфере городского хозяйства
г) приватизация земли промышленными
предприятиями и учреждениями
13. Это то, что дает возможность:
а) структурировать время
б) ощущать себя полезным человеком
в) вступать в разнообразные связи и
отношения
г) получать деньги
д) создавать различные блага
е) занимать определенный статус.
О чем идет речь? (трудовая
деятельность, работа)
14. Студент Иванов И.И. пришел в гости к
сокурсникам — узбекам. Ради гостя они
приготовили плов и пригласили к трапезе.
Узбеки ели плов руками. Иванов подумал:
«Какие отсталые, даже столовыми приборами
не умеют пользоваться». Как можно
охарактеризовать его позицию:
а) культурный релятивизм
б) этноцентризм
15. Выйдя замуж, молодая женщина взяла
фамилию мужа, но жить стали у её родителей,
не желая идти в общежитие. Свой бюджет,
питание, покупку других товаров вели
отдельно от ее родителей. С позиции
социологии семьи дайте характеристику
данной супружеской паре.
Патриархат, т.к. она взяла фамилию
мужа; матрилокальная семья, так как
супружеская пара живет с родителями
жены. С одной стороны, это нуклеарная
семья, т.к. живут вместе два поколения,
с другой стороны, дети не зависят от
родителей и являются новообразованной
(прокреационной) семьей, значит, имеем
расширенную семью
16. Среди факторов, влияющих на формирование
личностных свойств индивида, социальными
являются:
а) климат и ландшафт данного региона
б) знак Зодиака, под которым родился
ребенок
в) генетический код родителей
г) расширенная форма семьи
д) большой выбор мультиков в домашней
фильмотеке
17. Законодательное собрание Пермской
области приняло решение — обратиться
к ректорам пермских вузов, чтобы они
приняли на льготных основаниях в вузы
выпускников коми-пермяцких школ. Какая
форма межнациональных отношений нашла
выражение в этом решении:
а) амальгамизация
б) этническое преследование
в) ассимиляция
г) защита прав этнического меньшинства
18. Что из ниже перечисленного не относится
к характеристикам села:
а) постоянное проживание в нем жителей
б) расширенный выпуск тканей
в) местное самоуправление
г) развитое многообразие культурных
стилей
19. Какие из ниже перечисленных групп
входили в социальную структуру
дореволюционного российского общества:
а) купцы II гильдии
б) каста неприкасаемых
в) разночинцы — народники
г) муллы и священники
д) атеисты
20. Нижеследующие утверждения соотнесите
с типами общества:
а) известный политик В.В.Ж., славящийся
своей эксцентричностью в Гос. Думе, в
быту был тихим и мирным человеком гезельшафт
б) «Братки» решили не жадничать и вложили
деньги на создание своей политической
организации «Наша Пермь» гезельшафт
в) Участковый милиционер не реагировал
на жалобы женщин, к которым приставали
его дружки гемайншафт
21. Как Вы думаете, какое общество менее
стабильно:
а) общество «закрытого типа»
б) многоэтническое общество
в) общество, в котором имеются видимые
социально-экономические различия между
группами
г) общество «открытого типа»
д) общество с авторитарной властью
22. Традиционное общество характеризуется:
а) наличием многопартийной политической
системы
б) преобладанием профессий умственного
труда
в) удовлетворением многообразных
потребностей через деятельность
специализированных институтов
г)различиями прав социальных
общностей
23. Неформальный социальный контроль
более всего распространен:
а) на крупном промышленном предприятии
б) на стадионе во время футбольного
матча
в) в небольшом селе
г) в областной клинической больнице
24. В какие периоды общественного развития
выше интенсивность и всеобщность
социальной мобильности (необходимо
кратко обосновать свой ответ):
в период бурного экономического роста
(восходящая вертикальная мобильность)
и в кризисное время (нисходящая
мобильность), т.е. в переходные периоды,
когда теряется стабильность в обществе
и возникает потребность или необходимость
изменять социальный статус (также во
время войн и революций).
25. Термин социология впервые был
применен: (нет ответа – правильный
Конт)
а) Платоном
б) Парсонсом
в) Э. Дюркгеймом
г) М. Ломоносовым
д) М. Вебером
26. Студент пермского вуза перевелся
учиться по своей специальности в
столичный вуз. Рассмотрите данный факт
с позиции социальной мобильности
(горизонтальная, вертикальная, статус):
горизонтальная – смена территории;
статус остался тот же – студент.
27. Более 80% своего бюджета семья из 4-х
человек (работающие муж и жена,
дети-школьники) ежемесячно тратила на
проживание и покупку товаров первой
необходимости. К какой социальной группе
можно ее отнести:
а) состоятельные
б) средний – средний класс
в) бедные (относительно бедные)
г) предпринимательская
28. Социальная структура советского
общества выражалась в формуле (2+1).
Расшифруйте содержание формулы и
покажите ее социологическую некорректность.
Два класса+интеллигенция (рабочие,
крестьяне + интеллегенция)
Сущ-ла многоклассовая с-ма: номенклатура
(большие права), интел-я, переходный
класс м-ду интел-й и раб-ми, собственно
крестьяне и рабочие и переходный м-ду
крест-ми и раб-ми
29. Как можно объяснить с помощью теории
«гезельшафта» кризисное состояние
современного российского общества
(дайте краткое объяснение)
Рынок как система взаимодействий
выступает не только в экономике, но и в
др. сферах ж. (политике, образовании,
здравоохранении, …)
Сложная система управления, недостаточная
согласованность в разделении полномочий
между центром и регионами.
Установки типа «цель оправдывает
средства» и отсутствие конкретных
правил и предписаний приводит к эрозии
морали и права.
Рациональное индивидуализированное
критическое сознание приводит к
несоблюдению правовых норм
30. Семья «Х» заготовила на зиму со своего
огорода овощи, фрукты, варенья, соленья
и довольствовалась небольшой заработной
платой мужа, которой хватало на покупку
хлеба, сахара, чая и т.д. «Главное —
душевный покой, всех денег не заработаешь»
— гак отвечал «X» на
замечание соседа, что можно побольше
вкалывать?Традиционный (работать
столько, сколько необходимо для
удовлетворения минимальных потребностей)
Семья «У» только и была озабочена поиском
дополнительного заработка и доходов,
хотя жила в большой и благоустроенной
квартире, имела две машины и полный
достаток. Рыночный (иметь больше,
больше работать)
Студент «Z» сумел сдать
на «4» и «5» сессию умело, использовав
шпаргалки своих товарищей и халатность
преподавателей, хотя на лекции и
лабораторные занятия не ходил вовсе.псевдорыночный (иметь больше, меньше
работать)
Какие социокультурные типы здесь
представлены?
31. Как называются виды брака:
Одна женщина, несколько мужчин – полиандрия
Один мужчина несколько женщин — полигиния
Несколько мужчин, несколько женщин —
групповой брак
32. Иванов женился на девушке из горного
аула, он — выпускник вуза, она имеет
среднее образование. Какой это брак
эндогамный или экзогамный? экзогамный
studfiles.net
Тест итогового контроля по Социологии с ответами
1.Родоначальником теории стратификации считают:
а) П.Сорокина
б) К.Маркса
в) М.Вебера
г) Т.Парсонса
2.М.Вебер выделял следующие виды социального действия (укажите все правильные варианты):
а) целерациональное
б) ценностно-рациональное
в) аффективное
г) девиантное
3.Определите, кому из мыслителей принадлежит мысль о том, что естественное состояние человечества – это «война всех против всех»:
а) Ф.Аквинскому
б) М.Веберу
в) Т.Гоббсу
г) Н.Макиавелли
4.Автором социологической теории бюрократии является:
а) Ф.Тённис
б) М.Вебер
в) Э.Гидденс
г) А.Кравченко
5.Родоначальниками теории гражданского общества можно назвать:
а) К.Маркса и Ф.Энгельса
б) Т.Гоббса и Дж.Локка
в) П.Лаврова и П.Ткачёва
г) Р.Дарендорфа и Л.Козера
6.Термин «социология» ввёл в научное употребление:
а) О.Конт
б) М.Вебер
в) Г.Спенсер
г) Э.Дюркгейм
- Направление в социологии исходящее из положения, что новое «положительное» знание должно быть свободно от всяких домыслов, опираться на естествознание:
а) понимающая социология
б) позитивизм
в) интеракционизм
г) этнометодология
8.Понятие «социальная аномия» ввёл:
а) М.Вебер
б) Э.Дюркгейм
в) О.Конт
г) Г.Спенсер
9.Систему социологических взглядов Г.Спенсера называют:
а) понимающей
б) органической
в) неорганической
г) традиционной
10.В западной социологии XX века можно выделить следующие направления (укажите все правильные варианты):
а) неопозитивизм
б) структурный функционализм
в) иррационализм
г) бихевиоризм
11.Автором концепции постиндустриального общества является:
а) Д.Белл
б) Дж.Хоманс
в) Л.Козер
г) К.Маркс
12.Представителями психологического направления в русской социологической мысли конца XIX-начала XX века были (укажите все правильные ответы):
а) П. Струве
б) Л. Петражицкий
в) Е. де Роберти
г) П. Сорокин
13.К.Маркс разработал:
а) цивилизационный подход к обществу;
б) теорию трёх стадий;
в) формационный подход к обществу
г) культурологический подход к обществу
14.Термин «теории среднего уровня» был введен в социологию:
а) П. Сорокиным
б) Э. Дюркгеймом
в) Р. Мертоном
г) К. Марксом
15.Предметом социологии является:
а) политическая система
б) общество
в) межличностные отношения
г) производственные отношения
16.В структуре социологического знания можно выделить следующие уровни (укажите все правильные ответы):
а) теоретическая социология
б) теории высшего уровня
в) теории среднего уровня
г) прикладная социология
17.Соответствие между гипотезами, выдвинутыми Дж.Хомансом для объяснения социального действия, и их пониманием:
| ценности | чем ценнее вознаграждение, тем выше вероятность повторения действия |
| фрустрации-агрессии | не получив награду, личность возмущается |
| успеха | действие должно быть разумным и понятным |
| голодания-насыщения | чем чаще получалось вознаграждение, тем быстрее развивается привыкание |
| стимула | действие, которое вознаграждается, имеет тенденцию к повторению |
18.Соответствие между характеристиками этапов социального развития этноса, по Н.Данилевскому, и их названиями:
| становление некоторых организационных форм жизни этноса | этнографический |
| расцвет | культурный |
| становление | государственный |
| естественный конец | угасающий |
19.Соответствие между отраслями социологии и их характеристикой:
| практическая социология | взаимодействие человека с окружающей средой, с учетом природных и социальных процессов, и их результатов |
| социология права | социальные свойства и социальная роль права как средство социальной регуляции |
| политическая социология | социальные действия и отношения в политической сфере |
20.Последовательность развития общественно-экономических формаций, по К.Марксу:
а) первобытнообщинная
б) рабовладельческая
в) феодальная
г) капиталистическая
д) коммунистическая
21.С точки зрения марксизма, понятие базиса общества включает в себя (укажите все правильные варианты):
а) производительные силы
б) производственные отношения
в) образование
г) политическую сферу
22.Духовная сфера жизни общества включает в себя (укажите все правильные варианты):
а) культуру
б) науку
в) производство
г) религию
23.Социальная мобильность замедляется в периоды:
а) стабилизации в обществе
б) революций, гражданских войн
в) иностранной интервенции
г) реформ
24.Горизонтальная мобильность означает:
а) повышение социального статуса
б) понижение социального статуса
в) социальное перемещение при сохранении статуса индивида
г) сумма социальной мобильности индивида в течение жизни
25.Высокий уровень эмоциональности взаимоотношений отличают группы:
а) вторичные
б) первичные
в) рефрентные
г) квазигруппы
26.Во вторичных группах в человеке ценят прежде всего:
а) его индивидуальность
б) его эмоциональность
в) его функциональность
г) его внутренний мир
27.Если под одной крышей живёт несколько родственных семей, больше двух поколений, такая семья называется:
а) нуклеарной
б) расширенной
в) супружеской
г) полигамной
28.Главное предназначение социальных институтов:
а) удовлетворять общественные потребности, придавать обществу стабильность
б) обеспечивать обществу динамизм, подвижность, изменчивость
в) давать дипломы выпускникам
г) обеспечивать господство одной политической силы
29.Достигаемым называется статус, который:
а) приобретается через личные усилия и конкуренцию
б) достаётся при рождении
в) навязывается обществом вне зависимости от усилий личности
г) указывает на место индивида в политической системе общества
- Постиндустриальное общество в развитых странах пришло на смену индустриальному:
а) в VIII-VI вв. до н.э. в результате неолитической революции
б) в XVIII в. в результате промышленной революции
в) в 1917 г. в результате социалистической революции
г) во второй половине XX в.
- Выявите ошибочное суждение:
а) организации – это, прежде всего, социальные группы, ориентированные на достижение взаимосвязанных и специфических целей
б) организации свойственна высокая степень формализации их внутренней структуры в том смысле, что правила, регламентация, распорядок охватывают практически все сферы поведения ее членов
в) в организации основное значение придается индивидуальным личным качествам, а не умению выполнять определенные функции
г) организации присуще наличие координирующего и управляющего органов
- К факторам индивидуальной мобильности относятся (выделите все правильные варианты):
а) уровень полученного образования
б) социальные революции
в) физические и умственные способности
г) внешние данные
- Характерными признаками социальной организации является (укажите все правильные ответы):
а) наличие ценностно-нормативных стандартов
б) наличие иерархической структуры
в) монорелигиозность
г) наличие возможности вертикальной мобильности для индивида
- К признакам малой группы относится (укажите все правильные признаки):
а) ограниченное число членов группы
б) нестабильность состава
в) большая интенсивность взаимодействия членов группы
г) производственный статус
- Реальная или воображаемая группа, с которой индивид соотносит себя как с эталоном носит название:
а) референтной
б) номинальной
в) статистической
г) реальной
- Нуклеарная семья:
а) состоит из мужа, жены и детей
б) включает представителей нескольких поколений
в) всегда включает представителей только одного поколения
г) является формой полигамного брака
- Совокупность социальных перемещений людей в обществе называется:
а) социальным взаимодействием
б) социальным прогрессом
в) социальной мобильностью
г) социальным регрессом
- Дистанцией социальной мобильности называется:
а) расстояние между двумя соседними статусами
б) несоответствие между статусом и ролью
в) процентная доля населения, участвующая в социальных перемещениях
г) количество ступенек, на которые удалось подняться или пришлось спуститься индивидам
- К каналам социальной мобильности относятся (укажите все правильные ответы):
а) армия
б) демонстрация
в) церковь
г) собственность
- Иерархия социального неравенства в определенном обществе, в определенный отрезок времени – это
а) родство
б) ранжирование
в) стратификация
г) дифференциация
- Открытой стратификационной системой является:
а) кастовая
б) рабовладельческая
в) сословная
г) классовая
- Под социальными институтами понимаются:
а) взаимодействие индивидов
б) межличностные отношения
в) формы управления
г) устойчивые формы организации совместной деятельности
- Под социальной структурой понимаются:
а) совокупность статусов и ролей
б) социальная система
в) взаимодействие людей
г) формы управления
- Современное общество охватывает два этапа развития, соответствующих двум типам общества:
а) простому и сложному
б) первобытнообщинному и рабовладельческому
в) индустриальному и постиндустриальному
г) аграрному и индустриальному
- В современной социологии в качестве признаков общества выделяют (укажите все правильные ответы):
а) наличие территории, совпадающей с государственными границами
б) наличие разделения властей
в) общность культуры
г) самодостаточность
- Необходимость выполнения несовместимых ролей носит название:
а) ролевое поведение
б) ролевой конфликт
в) ролевой набор
г) столкновение ролей
- Социализация продолжается:
а) от рождения до поступления в школу
б) во время обучения в школе
в) от рождения до глубокой старости
г) в процессе трудовой деятельности
- Главным результатом процесса социализации является:
а) формирование личности
б) формирование темперамента
в) получение образования
г) реализация индивидом активного избирательного права
- Какие факторы влияют на формирование личности в процессе социализации:
а) исключительно биологические
б) исключительно социальные
в) совокупность биологических и социальных факторов
г) ни те, ни другие
- Народная культура включает:
а) изящное искусство, так называемую серьезную музыку и высокоинтеллектуальную литературу
б) мифы, легенды, сказания, эпос, сказки, песни, танцы
в) популярную и эстрадную музыку, цирк, любовно-сексуальные романы, триллеры, газетные «сенсации» и т.д.
г) строения, памятники, автомобили, книги и т.д.
- Какой вид культуры обозначает такую субкультуру, которая не просто отличается от доминирующей культуры, но и противостоит ей, находится в конфликте с государственными ценностями?
а) элитарная
б) народная
в) массовая
г) контркультура
- Назовите главного агента первичной социализации личности:
а) государство
б) семья
в) этническая группа
г) СМИ
- В социологии существует ряд теорий, раскрывающих причины девиантного поведения. Какая из них объясняет рост девиации разложением системы ценностей, социальных институтов, обусловленных кризисом всего общества?
а) теория культурного переноса
б) теория аномии
в) теория стигматизации
г) теория физических типов
- Основными элементами культуры общества являются (укажите все правильные ответы):
а) социальные ценности
б) язык и знаковая система
в) правовая система
г) социальные нормы
- Социальные нормы означают:
а) требование правительства к гражданам соблюдать установленные законы
б) юридические документы, содержащие законодательные постановления
в) предписания, требования, пожелания и ожидания соответствующего (общественно одобряемого) поведения
г) публичное одобрение со стороны официальных организаций
- Социальными санкциями называются:
а) только наказания
б) только поощрения
в) наказания и поощрения
г) ни то, ни другое
- К неформальным позитивным санкциям относятся:
а) публичное одобрение со стороны официальных организаций
б) наказания, предусмотренные правовыми актами
в) публичное одобрение, не исходящее от официальных организаций
г) наказания, не предусмотренные официальными инстанциями
- Девиантное поведение является:
а) преступным
б) отклоняющимся
в) максимально одобряемым в обществе
г) формой поведения в традиционном обществе
- Социализация предполагает:
а) только воздействие индивида на общество
б) только воздействие общества на индивида
в) отсутствие взаимного воздействия индивида и общества
г) двусторонний процесс воздействия общества на индивида и индивида на общество
- Статусный набор – это:
а) совокупность всех статусов, принадлежащих одному индивиду
б) совокупность всех ролей, принадлежащих одному статусу
в) совокупность всех статусов, существующих в обществе
г) права, которые имеет индивид, занимающий определённый статус
- Главным (интегральным) статусом называется:
а) наиболее характерный для данного индивида статус
б) положение индивида в малой группе
в) гражданский статус человека
г) национальность
- К статусообразующим характеристикам современного постиндустриального общества относятся (укажите все правильные ответы):
а) доход
б) престиж
в) семейное положение
г) авторитет
- Ролевой идентификацией называется:
а) дистанцирование от роли
б) промежуточное звено между статусом и ролью
в) максимальное слияние с ролью
г) динамическая сторона статуса
- Поведение, ожидаемое от того, кто имеет определенный социальный статус
а) действие
б) девиантное
в) ролевое
г) организованное
- К основным социологическим теориям личности можно отнести (укажите все правильные ответы):
а) ролевую концепцию
б) поведенческую концепцию
в) структурный функционализм
г) теорию «зеркального «Я»
- В психоаналитической концепции личности З.Фрейда выделяются следующие подструктуры (укажите все правильные ответы):
а) подсознание
б) самосознание
в) мегасознание
г) сверхсознание
- Последовательность признаков самостоятельности, которые ребенок обретает в процессе своей социализации:
а) коммуникационный
б) социальный
в) экономический
г) политический
- Соответствие между понятиями и их определением:
| десоциализация | процесс отучения от старых норм, ценностей, ролей и правил поведения |
| социализация | процесс усвоения культурных норм и освоения социальных ролей |
| ресоциализация | процесс обучения новым ценностям, нормам, ролям и правилам поведения взамен старых |
- В случае, если участники социального взаимодействия стремятся навязать противнику свою волю, изменить его поведение или вообще устранить его, происходит следующий социальный процесс:
а) конкуренция
б) кооперация
в) сотрудничество
г) конфликт
- Циклическое развитие общества исследуется в трудах:
а) К.Маркса
б) А.Тойнби
в) Э.Дюркгейма
г) Д.Белла
- Одну из стадий исторического развития называют ещё «информационное общество». О какой стадии идёт речь?
а) доиндустриальное общество
б) восточное общество
в) американское общество
г) постиндустриальное общество
- Прогресс означает развитие:
а) по восходящей
б) по нисходящей
в) циклическое
г) обратное
- Развитие сферы услуг характеризует прежде всего:
а) доиндустриальное общество
б) индустриальное общество
в) постиндустриальное общество
г) социалистическое общество
- На наличие у социальных конфликтов позитивного потенциала указывала (укажите все правильные ответы):
а) теория социального конфликта Р.Дарендорфа и Л.Козера
б) структурный функционализм Т.Парсонса
в) марксистская социологическая теория
г) психоаналитическая концепция
- Неорганическая модернизация является (укажите все правильные ответы):
а) моментом собственного развития страны
б) ответом на внешний вызов со стороны более развитых стран
в) способом «догоняющего» развития
г) способом развития культурного своеобразия страны
- Географический детерминизм – географическое и социологическое понятие обозначающее:
а) определяющее влияние экономических условий на социальную структуру общества
б) зависимость политики государства от действий местных властей
в) взаимозависимость между обществом и окружающей, природной средой
г) влияние, которое человек оказывает на географическую среду
- Социальный прогресс:
а) является частью научно-технического прогресса
б) знаменует попятное движение общества
в) указывает на то, что разные народы движутся во времени с различной скоростью
г) глобальный процесс, знаменующий движение человеческого общества на всём протяжении исторического времени
- Соответствие между типами социального конфликта и их характеристикой
| игра | конфликт в рамках правил |
| схватка | непримиримые противоречия и можно рассчитывать на победу |
| дебаты | возможен спор и обе стороны могут рассчитывать на компромисс |
79.Соответствие между авторами и разработанными ими признаками определения типизации развития обществ:
| Г.Ленски, Дж.Ленски | способ добывания средств к существованию |
| Н.Данилевский, О.Шпенглер | культурно-исторический тип |
| Д.Белл, Э.Тоффлер | уровень развития техники и технологии |
| К.Маркс, Ф.Энгельс | способ производства материальных благ |
- Последовательность этапов развития этноса, по Н.Данилевскому:
- этнографический
- государственный
- культурный
- угасания
- Последовательность глобальных революционных процессов в истории человечества:
а) неолитический
б) промьшленный
в) менеджеров
г) компьютерный
- Последовательность формирования этноса:
а) клан
б) семья
в) род
г) племя
д) народность
е) нация
- Соответствие между стадиями развития истории общества, по О.Конту, и их характеристикой:
| метафизическая | явления природы и общества объясняются при помощи абстрактных философских принципов |
| теологическая | явления природы и общество объясняются действием сверхъестественных сил |
| позитивно-научная | исследование реальных фактов |
- Лицо, выступающее в качестве источника первичной информации в процессе опроса или в ходе наблюдения – это
а) субъект
б) объект
в) респондент
г) испытуемый
- Закрытыми вопросами в социологических исследованиях называют:
а) вопросы на темы, связанные с государственной тайной
б) вопросы на темы, ранее не исследовавшиеся
в) вопросы, предполагающие выбор ответа из ограниченного числа вариантов
г) вопросы, предполагающие выбор ответа из неограниченного числа вариантов
- Общность, на которую социолог распространяет выводы исследования
а) единицы отбора
б) выборочная совокупность
в) генеральная совокупность
г) континуум
- Последовательность процедур, относящихся к методической, технической стороне контент-анализа:
а) формулировка задач
б) выделение категорий и единиц содержания
в) сведение грамматических структур к единым формам
г) обеспечение сопоставимости полученных данных
- Последовательность этапов проведения социологического исследования:
а) подготовка исследования
б) сбор первичной социологической информации
в) подготовка собранной информации к обработке и ее обработка
г) анализ обработанной информации
д) подготовка отчета по результатам исследования
- Соответствие между содержанием и функциями общественного мнения:
| объединяет на основе идентичных оценок большие аудитории | интегративная |
| служит для оценки по различным вопросам | экспертная |
| оказывает влияние на социальное поведение | регулятивная |
- Основными методами социологических исследований являются:
а) исторический
б) контент-анализ
в) эксперимент
г) наблюдение
- Видами наблюдения являются:
а) включённое
б) невключённое
в) выключенное
г) независимое
- Соответствие между понятиями и их определениями:
| выборочная совокупность | совокупность единиц, отобранных для исследования, по которой можно судить обо всем объекте |
| репрезентативность выборки | соответствие структуры выборки структуре генеральной |
| генеральная совокупность | все множество объектов исследования |
- Соответствие между понятиями и их определениями:
| квантификация | числовое выражение качественных признаков исследуемых социальных объектов |
| корреляция | связь между несколькими социальными переменными исследования |
| социальная квота | доля, часть элементов социального объекта, отобранных для социологического изучения н анализа |
- Соответствие между понятиями и их определениями:
| метод | последовательность операций, общая система действий и способов организации исследования |
| техника | совокупность специальных приемов для эффективного использования различных методов исследований |
| социологическое исследование | система процедур, проводимых с целью получить точные объективные данные об изучаемом явлении |
| процедура | совокупность технических приемов, связанных с данным методом, включая частные операции, их последовательность и взаимосвязь |
Правильные ответы выделены курсивом. Правильность выполнения тестов контролируется самим студентом и (при необходимости) совместно студентом и преподавателем, ведущим данную дисциплину. Критериями оценки являются:
«отлично» — не менее 90% правильных ответов;
«хорошо» — не менее 70% правильных ответов;
«удовлетворительно» — не менее 55% правильных ответов.
testdoc.ru
Тест с ответами по социологии для 2 курса
Номер вопроса | Правильный ответ | Вариант ответа | Вопрос и варианты ответа |
1 | | | Когда возникла социология? |
| | 1 | В XVII веке |
| | 2 | В XVIII веке |
| + | 3 | В XIX веке |
| | 4 | В XX веке |
2 | | | В чем различие общих и специальных социологических теорий? |
| | 1 | В достоверности знаний |
| | 2 | В глубине познания действительности |
| | 3 | В методах изучения |
| + | 4 | В разном масштабе охвата социальной реальности |
3 | | | Кто первым ввел в научный оборот термин «социология»? |
| | 1 | И. Кант |
| | 2 | М. Вебер |
| | 3 | Г. Спенсер |
| + | 4 | О. Конт |
4 | | | Кем была разработана концепция общественной формации? |
| | 1 | Г. Гегелем |
| | 2 | Л. Фейербахом |
| + | 3 | К. Марксом |
| | 4 | Ш. Фурье |
5 | | | Кто был создателем «плюралистической социологии» в России? |
| | 1 | Н. Михайловский |
| + | 2 | М. Ковалевский |
| | 3 | С. Южаков |
| | 4 | Б. Чичерин |
6 | | | Кем был введен в научный оборот термин «постиндустриальное общество»? |
| | 1 | У. Ростоу |
| | 2 | З. Бжезинским |
| | 3 | А. Туренном |
| + | 4 | Д. Беллом |
7 | | | Какое состояние общественных отношений является оптимальным? |
| | 1 | Стагнации |
| | 2 | Застоя |
| + | 3 | Социальной стабильности |
| | 4 | Кризиса |
| | | |
| | | |
| | | |
8 | | | Кем разработана теория социальной стратификации и социальной мобильности? |
| | 1 | Т. Парсонсом |
| | 2 | Р. Дарендорфом |
| | 3 | Дюверже |
| + | 4 | П. Сорокиным |
9 | | | Какой социальный институт был самым ранним? |
| | 1 | Государство |
| | 2 | Право |
| + | 3 | Семья |
| | 4 | Церковь |
10 | | | Кто из основателей социологии положил начало исследованию феномена бюрократии? |
| | 1 | Л. Гумплович |
| + | 2 | М. Вебер |
| | 3 | Э. Дюркгейм |
| | 4 | В. Парето |
11 | | | В чем заключается главная цель любого социологического исследования? |
| | 1 | Формулировка основных гипотез |
| | 2 | Ответы на поставленные вопросы |
| + | 3 | Познание социальных свойств, связей и отношений избранного объекта. |
| | 4 | Получение информации |
12 | | | Кем была создана органическая теория общества? |
| | 1 | О. Контом |
| + | 2 | Г. Спенсером |
| | 3 | М. Вебером |
| | 4 | Э. Дюркгеймом |
13 | | | Кем использовались в качестве метода исследования «идеальные типы»? |
| | 1 | О. Контом |
| | 2 | К. Марксом |
| | 3 | Э. Дюркгеймом |
| + | 4 | М. Вебером |
14 | | | Кто разработал субъективный метод в российской социологии? |
| | 1 | Н. Кареев |
| + | 2 | П. Лавров |
| | 3 | Е.В. де Роберти |
| | 4 | П. Новгородцев |
15 | | | Кто является создателем теории «больших циклов» (длинных волн)? |
| + | 1 | Н. Кондратьев |
| | 2 | П. Сорокин |
| | 3 | А. Гастев |
| | 4 | С. Струмилин |
| | | |
16 | | | С какой сферы начинается органическая модернизация? |
| | 1 | С экономики |
| | 2 | С социальной сферы |
| + | 3 | С культуры и общественного сознания |
| | 4 | С политики |
17 | | | Какое понятие отражает постепенные, плавные социальные преобразования? |
| | 1 | Революция |
| + | 2 | Эволюция |
| | 3 | Технизация |
| | 4 | Институционализация |
18 | | | Когда возникла «массовая культура»? |
| | 1 | В XVII веке |
| | 2 | В XVIII веке |
| | 3 | В XIX веке |
| + | 4 | В XX веке |
19 | | | Чем определяется главный социальный статус индивида? |
| | 1 | Семейным положением |
| | 2 | Партийной принадлежностью |
| + | 3 | Должностью |
| | 4 | Членством в спортивном обществе |
20 | | | Кто является приверженцем общей теории социального конфликта? |
| | 1 | Л. Коузер |
| | 2 | С. Хантингтон |
| | 3 | А. Раппопорт |
| + | 4 | К. Боулдинг |
testdoc.ru
Тест по социологии — Декан-НН
1. Кого можно считать основателем социологии?
1. М. Вебер
2. Платон
3. Э. Дюркгейм
4. О. Конт
5. Аристотель
2. Какое определение социологии более точное?
1. Социология – наука об обществе
2. Социология изучает поведение людей
3. Социология – наука о возникновении, развитии и функционировании социальных общностей и социальных процессов, о социальных отношениях как механизмах взаимосвязи и взаимодействия между этими общностями, между общностью и личностью
4.Социология изучает механизмы взаимодействия между организациями и социальными институтами
5. Вся совокупность связей и отношений, которые носят название социальных
3. Понятие «социальное действие» ввел в научный оборот…
1.О.Конт
2. Г. Спенсер
3. М.Вебер
4. Э. Дюркгейм
5. Т. Парсонс
4. Кто рассматривал общество как биологический организм?
1. Г. Спенсер
2. М. Вебер
3. В. Паретто
4. К. Маркс
5. Т. Парсонс
5. Как называется исторически сложившиеся устойчивые формы организации совместной деятельности людей?
1. Социальная группа
2. Гражданское общество
3. Социальный институт
4. Социальная общность.
5. Трудовой коллектив
6. Какое определение общества наиболее полно и корректно?
1. Общество – это то же, что и государство
2. Общество всегда совпадает с территорией определенной страны,
поэтому основной признак – это географические границы
3. Понятие «общество» совпадает с понятием «культура»
4. Общество – люди, взаимодействующие на очерченной территории и имеющие общую культуру
5. Общество – самая крупная группа людей
7. Для какого типа общества характерна социальная солидарность, сплоченность?
1. Массовое общество
2. Индустриальное общество
3. Постиндустриальное общество
4. Постмодерное общество
5. Традиционное общество
8. Что, по мнению Т.Парсонса, сохраняет общество как стабильную систему?
1. Дифференциация и интеграция
2. Органическая солидарность, которая в процессе развития общества, пришла на смену механической солидарности
3. Определенные механизмы и структуры, которые выполняют функции
адаптации, целеполагания, интеграции и поддержания образца
4. Социальные конфликты, которые сплачивают противоборствующие стороны
5. Всевозрастающая рационализация общества
9. Какому типу общества характерны такие черты, как разделение руда, усиление социального разнообразия, расширение возможностей личного выбора?
1. Аграрное общество
2. Традиционное общество
3.Общество охотников и собирателей
4. Индустриальное общество
5. Индустриальное и постиндустриальное общество
10. Как называется процесс возрастающего влияния различных факторов международного значения на социальную действительность в отдельных странах?
1. Модернизация
2. Индустриализация
3. Информатизация
4. Глобализация
5. Интеграция
11. Методологический раздел программы эмпирического социологического исследования включает в себя:
1. Описание методы обработки и анализа данных
2. Описание цели, задач, объекта, предмета исследования, интерпретацию понятий
3. Обоснование выборки, обоснование методов сборки данных
4. Организационный план исследования
5.Распределение обязанностей между исполнителями и учет финансовых ресурсов
12. Что такое объект социологического исследования?
1. Это содержательная, методическая, организационная конкретизация цели
2. Это то, что существует вне зависимости от исследователя и на что может быть направлен процесс исследования
3. Это значимые свойства, стороны, особенности явления, которые подлежат непосредственному изучению
4. Это значимая сторона социального явления, подлежащая системному анализу
5. Определенные общественные отношения.
13. Наиболее распространенным методом сбора социологической информации является:
1. Опрос
2.Наблюдение
3. Эксперимент
4. Социометрический тест
5. Анализ документов
14. В социологическом исследовании перевод понятий в систему эмпирически проверяемых показателей, индексов и шкал это:
1. Теоретическая интерпретация понятий
2. Эмпирическая интерпретация понятий
3. Операционализация понятий
4. Анализ и интерпретация эмпирических данных
5. Системный анализ объекта исследования
15. Под репрезентативностью в социологическом эмпирическом исследовании понимают:
1. Предположение о свойствах изучаемых объектах
2. Часть объектов генеральной совокупности, отобранных с помощью специальных приемов для получения информации
3. Совокупность всех возможных социальных объектов, которые подлежат изучению в пределах программы социологического явления
4. Свойство выборочной совокупности воспроизводить параметры и значительные элементы генеральной совокупности
5. Социальное противоречие, требующее разрешения
16. Какой принцип определения малой социальной группы является наиболее существенным?
1. Количество участников
2. Степень формализации статусов и ролей
3. Длительность существования
4. Тесные межличностные контакты, близость участников и взаимодействия
5. Наличие системы контроля
17. Что такое конформизм?
1. Тенденция к согласованности между членами группы, что приводит к узкому взгляду на тот или иной вопрос
2. Поведение, контролируемое посредством группового давления
3. Поведение, в котором проявляются способности группового лидера
4. Действия, направленные на поддержку социальных изменений
5. Вид группового мышления
18. Примером квазигруппы будет…
1.Толпа
2. Студенческая группа
3. Семья
4. Дружеская тусовка
5. Трудовой коллектив
19. Отождествления себя с другим субъектом, группой, социальным образом в процессе социализации называется…
1. Социализация
2. Идентификация
3. Институционализация
4. Приспособление
5. Ассимиляция
20. Кого нельзя назвать агентами первичной социализации?
1. Семья
2. Школа
3. Воспитатели
4. Трудовой коллектив
5. Сверстники
21. Вторичная социализация включает в себя…
1. Профессиональную социализацию
2. Воспитание в школе
3. Воспитание в семье
4. Нормы и правила поведения, которые ребенок узнает в кругу сверстников. 5. Нормы и правила поведения, которые человек получает от родителей, воспитателей, учителей
22. Социальный статус – это…
1. Совокупность действий, которые должен выполнять человек, занимающий определенное место в социальной системе
2. Определенная позиция в социальном пространстве
3. Устойчивая связь элементов в социальной системе
4.Нормативно регулируемое участие индивида в конкретном процессе социального взаимодействия
5. Совокупность взаимосвязанных и взаимодействующих социальных групп, социальных институтов и отношений между ними
23. Какие из перечисленных статусов и ролей личности нельзя назвать предписанными?
1.Мужчина
2. Афроамериканец
3. Мужские и женские роли, характерные для данной культуры
4. Муж
5. Пожилой человек
24. Выберите наиболее полный набор важнейших дифференцирующих признаков слоя.
1. Национальность, вероисповедание, происхождение, доход
2. Образование, профессия, доход, престиж
3. Профессия, национальность, доход
4. Профессия, доход, половозрастные характеристики
5. Доход, образование, происхождение, характер потребления благ
25. Какое из перечисленных понятий не имеет прямого отношеня к социальной структуре общества
1. Стратификация
2. Социализация
3. Социальная мобильность
4. Маргинальность
5. Социальный класс
26. Выберете наиболее точную формулировку такого явления, как социальная мобильность:
1. Это получение человеком новой профессии
2. Это борьба социальных групп за улучшение своего собственного положения
3. Это переход общества как социальной системы на более высокую ступень развития
4. Это изменение условий жизни индивидов
5. Это продвижение по иерархической социальной вертикали или
горизонтали социальных групп или индивидов
27. Как называется система упорядоченных взаимодействий, где появляется набор устойчивых социальных ожиданий.
1. Социальные действия
2. Социальная общность
3. Социальные отношения
4. Социальные институты
5. Социальная организация
28. Что такое девиантное поведение?
1. Поведение, отклоняющееся от принятых в обществе норм и ценностей
2. Система взаимообусловленных социальных действий
3. Поведение, ориентируемое на действия других людей
4. Поведение, которое характеризует лидера в группе
5. Поведение, направленное на социальные изменения
29. Социальная группа, ориентированная на достижение взаимосвязанных специфических целей и на формирование высокоформализованных структур – это
1. Социальный институт
2. Социальная общность
3. Формальная группа
4. Организация
5. Институт социализации
30. Как называется процесс определения и закрепления социальных норм, правил, статусов и ролей, приведение их в систему, которая способна действовать в направлении удовлетворения некоторой общественной потребности?
1. Социализация
2. Организация
3 Институционализация
4. Модернизация
5. Стратификация
nn.dekane.ru
Тест с ответами по социологии
1.Прочитайте высказывания. Выберите верный вариант ответа.
«У социологии слабые связи с философией и историей».
а) да
б) нет+
2.Совпадают ли предметная область социологии и истории?
а) Да
б) нет+
3.Примером какого исследования является работа Э.Дюркгейма «Самоубийство» ?
а) Теоретического
б) Лабораторного
в) практического
г) + эмпирического
4.В чем заключается влияние математики на социологию?
а) математика является методологической основой развития социологии
б) для социологии прежде всего важны математические методы, используемые в социологических исследованиях +
в) математика является информационной базой существования социологии как науки
5.Что является предметом социологии по Г.Спенсеру?
а) общество, развивающееся в сторону целостности через конфликты и противоречия
б) общество как социальный организм, в котором дифференциация считается интеграцией благодаря стественной эволюции его социальных институтов +
в) общество, основу которого составляют взаимодействия людей, движимых волей
6.Как П.Сорокин понимал предмет социологии?
а) систематическое изучение общества, в котором особое внимание уделяется современным индустриальным системам
б) изучение общества как реальной совокупности
в) заимодействующих индивидов, в которой положение (статус) социального субъекта зависит от его действий в институтах+
7.Примером какого исследования является работа М. Вебера “Протестантская этика и дух капитализма” ?
а) теоретического+
б) лабораторного
в) практического
г) полевого
8.Что из перечисленного не относится к функциям социологии?
а) теоретико-познавательная
б) диагностическая
в) эвристическая
г) прогностическая
д) организационно-технологическая
е) социального проектирования и конструирования+
ж) инструментальная
9.Какое из утверждений является верным?
а) Социология изучает все социальные явления
б) Социология изучает большое число объектов
в) Социология изучает различные формы жизнедеятельности одного и того же объекта+
10. К уровням социологического знания относятся …
а) общесоциологические теории+
б) общенаучные теории
в) прикладная социология+
г) теории среднего уровня+
11.Какими являются теории, которые находятся между эмпирической и теоретической социологией?
а) макросоциологические
б) среднего уровня +
в) социального обмена
12.Что относится к основным социологическим парадигмам?
а) антропоценрическая +
б) социоцентрическая +
в) этноцентрическая
13.Основоположником чего был А. Шюц ?
а) системного метода
б) метода структурно-функционального анализа
в) феноменологического метода+
14. На какие группы можно разделить социологические парадигмы?
а) структурно-функциональные +
б) целевые+
в) интерпретативные +
г) интегральные
д) гипотетические
15. Основатель синергетики?
а) И.Стенгерс
б) И.Пригожин +
в) Г.Хакен
16. Что относится к уровням социологического знания?
а) общесоциологические теории+
б) общенаучные теории
в) теории среднего уровня +
г) прикладная социология+
shooltest.ru
Контрольный тест по социологии (вариант 2) » СтудИзба
Тесты / Социология
9 383
0
Вопросы написаны с порядковым номером
подчёркнутым шрифтом. Варианты ответов даны со знаком минус («
—«) перед ним, а правильные ответы выделены
жирным шрифтом со знаком плюс («
+«) перед ним.
1. Социология как наука возникла— в начале 20 века
+ в середине 19 века — в 18 веке
— в эпоху античности
2. Социология относится к следующему типу знания— философскому
+ опытно-рациональному — обыденномуКстати, если Вам нужна компания по оказанию бухгалтерских услуг, то можно найти её по адресу: lev-cons.ru. На этом сайте также можно найти большое количество других услуг по похожим тематикам!
3. Опытно-рациональный тип познания отличается от обыденного— практической применимостью знаний
+ стремлением к обоснованию своих выводов — умозрительностью
— очевидностью
4. Изучение философии дает социологу+ умение обобщать — умение конкретизировать
— овладение эмпирическими методами
умение применять полученные знания на практике
5. С точки зрения О.Конта, для позитивной стадии развития человеческого мышления характерно— стремление к абсолютному знанию
+ умение за фактами видеть закономерности — стремление извлечь пользу из любого знания
— поиск конечных причин явлений
6. Принцип операционализации означает— повторяемость, воспроизводимость понятий
— косвенную проверку научных выводов
— формирование общего понятия на основе синтеза нескольких частных понятий
+ представление общего понятия в виде эмпирически верифицируемых составляющих
7. Количественное измерение качественных признаков называется— верификацией
+ квантификацией — операционализацией
— аксиологизацией
8. Уровни социологического знания выделяются в зависимости от соотношения+ теории и эмпирии — целей и задач исследования
— масштабов исследования
— длительности исследования
9. С точки зрения Р.Мертона, ведущую роль в современной социологии играет— общесоциологическая теория
— эмпирия
— прикладное исследование
+ теория среднего уровня
10. Из перечисленных наук номотетической не является
— социология
— психология
+ история — правоведение
11. Основоположники социологии пытались приблизить ее методы к методам— философии
+ естественных наук — психологии
12. Э.Дюркгейм считал, что социальные факты следует изучать+ как вещи — как идеально-типические конструкции
— как реальность
13. С точки зрения Э.Дюркгейма, социальные факты следует объяснять— данными органов чувств
— рациональными доводами
+ другими социальными фактами — доводами философии
14. Э.Дюркгейм считал, что предпонятие— абсолютно бесполезно для науки
+ служит указателем для научного поиска — улавливает важнейшие признаки явления
15. Свое учение назвал «понимающей социологией»+ М.Вебер — О.Конт
— Э.Дюркгейм
— Т.Парсонс
16. М.Вебер считал, что социология должна— вырабатывать ценности
+ критически анализировать ценности — указать человеку, какие ценности ему лучше выбрать
— избегать ценностной проблематики
17. Утверждение М.Вебера о том, что «методически корректная научная аргументация в области социальных наук должна быть признана правильной и китайцем» означает, что— социологическое знание должно быть предельно простым и понятным всем
+ социологическое знание должно иметь общезначимый характер — социология должна так убедительно представить социальный идеал, что его примет даже представитель другой культуры
18. М.Вебер считал, что главной задачей университета является— воспитание нравственных качеств
— формирование мировоззрения
+ передача специальных знаний
19. Вопрос: «Следует ли содействовать тому, чтобы определенная ситуация развивалась в определенном направлении?» является— научным
+ оценочным — одновременно и научным, и оценочным
20. М.Вебер определял понимание как+ знание смысла человеческого действия — выявление причинно-следственных связей
— идентификацию с объектом исследования
— анализ душевной жизни человека
21. Вебер считал идеальный тип— социальным идеалом
— гипотезой
— схемой
+ утопией — средним типом
22. А.Шюц считал, что— методы естественных наук являются единственно научными методами
— методы общественных наук абсолютно отличны от методов естественных наук
+ нет различий в методических принципах естественных и общественных наук — методы общественных наук – частный случай методов естественных наук
23. А.Щюц считал, что отождествление опыта с чувственным наблюдением— обеспечивает объективность социологического исследования
— позволяет идентифицировать себя с участниками событий
+ исключает из исследования целый ряд областей социальной реальности — обеспечивает глубокое понимание социальной реальности
24. А.Щюц считал, что социальная реальность является + интерсубъективной — субъективной
— объективной
25. А.Щюц назвал «конструкциями конструкций»— конструкции обыденного сознания
+ научные конструкции — мировоззренческие конструкции
— идеологические конструкции
26. П.Сорокин полагал, что социология отличается от других генерализирующих наук об обществе тем, что— изучает свою сферу социальной реальности
+ имеет дело со всеми сферами социальной реальности — глубже и полнее познает социальную реальность
— дает более общую картину каждой сферы социальной реальности
27. П.Сорокин полагал, что специальная социология изучает— общие свойства социальных систем
+ определенный класс социокультурных явлений — основные типы взаимоотношений людей
— повторяющиеся социальные процессы
28. Наукой о порядке и прогрессе называл социологию+ О.Конт — К.Маркс
— Г.Спенсер
— М.Вебер
29. Высказывание «Если ограничить науку принципом непосредственной полезности, то это лишает науку будущего» принадлежит+ О.Конту — Г.Спенсеру
— К.Марксу
— М.Веберу
— Э.Дюркгейму
30. Основоположником органической школы (органицизм) является— О.Конт
+ Г.Спенсер — Э.Дюркгейм
— М.Вебер
31. Для Чикагской социологической школы характерно:— теоретическая направленность
+ эмпирическая направленность — методологическая направленность
32. К представителям франкфуртской школы относятся:— А.Шюц, П.Бурдье
— Н.Луман, П.Бергер
— Ф.Теннис, П.Сорокин
+ Т.Адорно, Г.Маркузе
33. Асфальтированные аллеи являются у П.Монсона символом— социальной структуры
— социальных изменений
+ социальных институтов — социальных взаимодействий
34. «Протаптывание тропинок» и «зарастание аллей», по П.Монсону, символ— социального контроля
— отклоняющегося поведения
+ социальных изменений
35. Движение «кораблей в море» характеризует, по мнению П.Монсона, направление, называемое— позитивизм
— структурализм
+ экзистенциализм — неомарксизм
36. Структурализм (по П.Монсону) рассматривает общество + независимо от поведения отдельных индивидов — как результат поступков отдельных индивидов
— как результат свободного выбора индивидов
37. З.Бауман считает, что определение своего отношения к здравому смыслу является важным для+ социальных наук — естественных наук
— философского знания
38. Социология, в отличие от здравого смысла (согласно З.Бауману):+ отрицает самоочевидность явлений — не опирается на рациональный анализ явлений
— уменьшает «степень свободы» индивидов
Рейтинг статьи:
| Поделитесь ссылкой пожалуйста: |
|
Похожие статьи
Контрольный тест по социологии (вариант 1)
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
studizba.com










 a.
a. b.
b. d.
d. и
и  . Найдите градусную меру каждого угла треугольника.
. Найдите градусную меру каждого угла треугольника. ; в) —
; в) — ; г) —
; г) — =1 и cos
=1 и cos и cos
и cos ; г) sin
; г) sin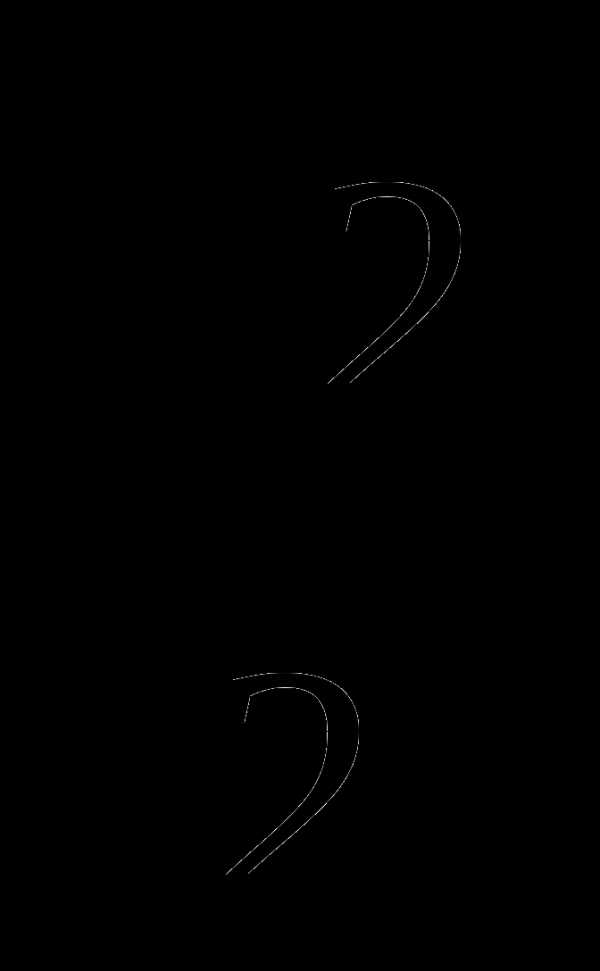 и cos
и cos ), если cos
), если cos , sin
, sin ,
,  <
< ;
;  ; в)
; в)  ;
; cos
cos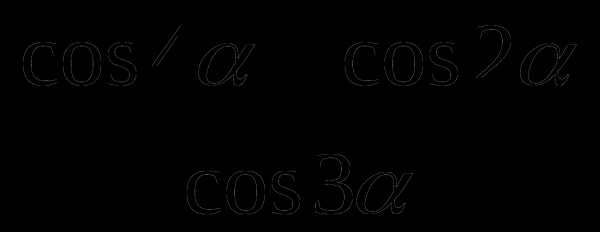 .
. ; в)
; в) 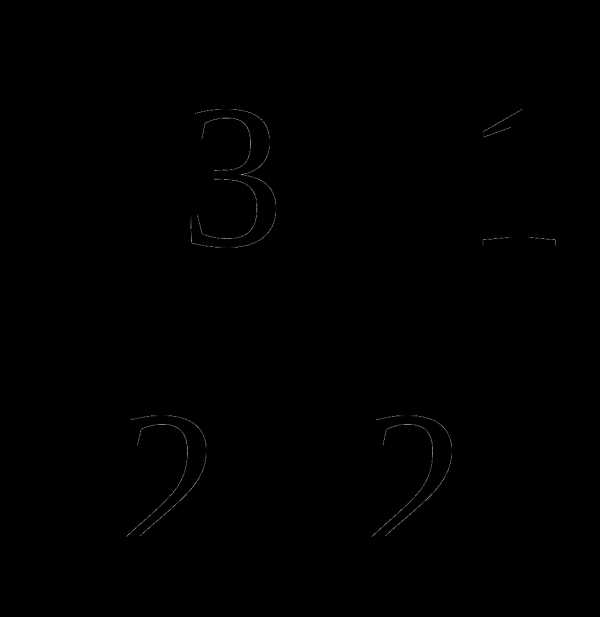 ;
; ; г) другой ответ.
; г) другой ответ.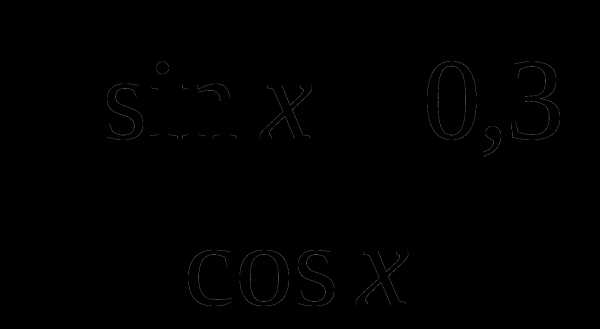 не имеет смысла?
не имеет смысла? ; б)
; б)  ; г)
; г)  ,
, 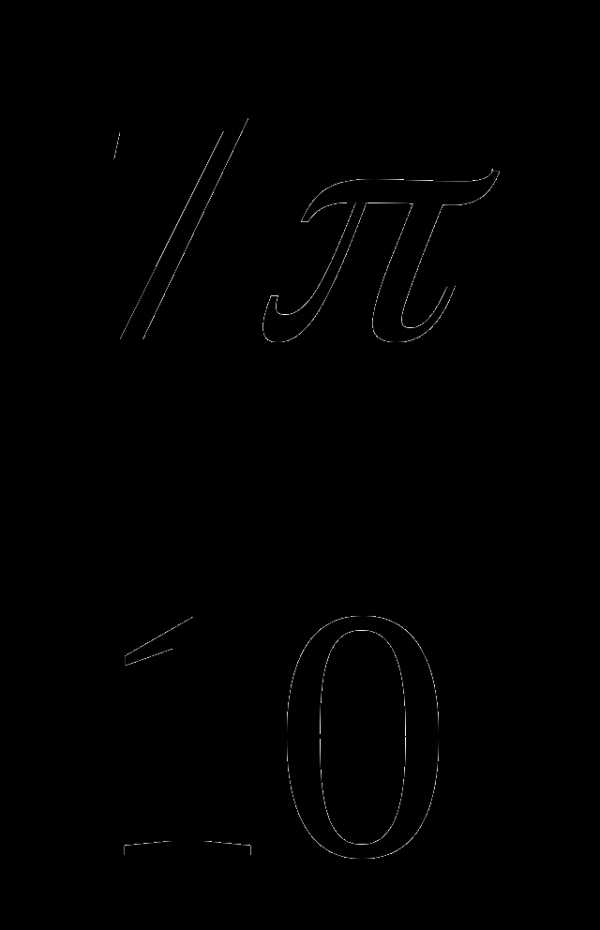 ; в)
; в) ,
,  ;
;
 и cos
и cos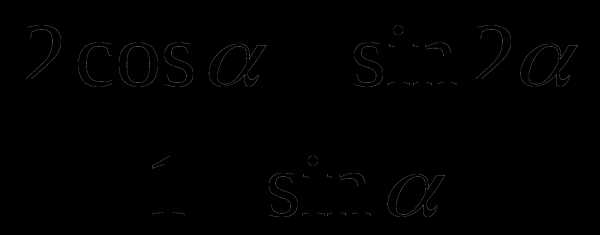 .
. 4; г) другой ответ.
4; г) другой ответ. -2; в)
-2; в)  ;
; ; г) другой ответ.
; г) другой ответ.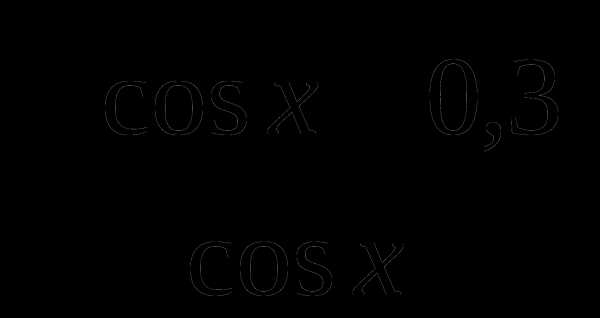 не имеет смысла?
не имеет смысла? . Найдите градусную меру каждого угла треугольника.
. Найдите градусную меру каждого угла треугольника. и ctg
и ctg .
. (
( ; в)
; в)  ; г) другой ответ.
; г) другой ответ. не имеет смысла?
не имеет смысла? ; г)
; г)  ,
,  ; в)
; в) ,
,  ,
,  и
и  ; в) —
; в) — и ctg
и ctg ; в) tg
; в) tg и ctg
и ctg ;
;  .
.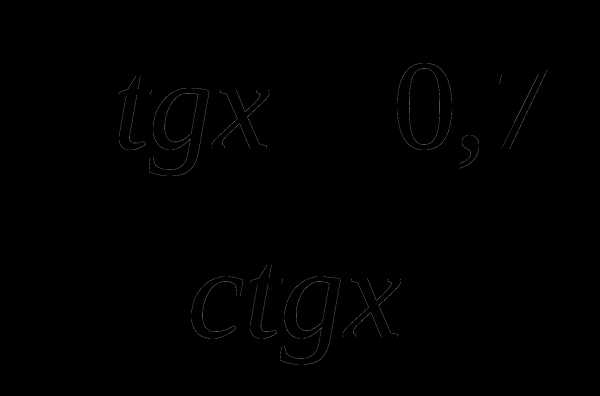 не имеет смысла?
не имеет смысла?

 .
(5.12)
.
(5.12)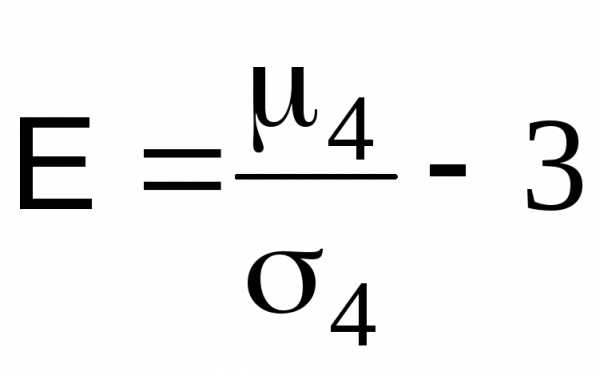 .
(5.13)
.
(5.13)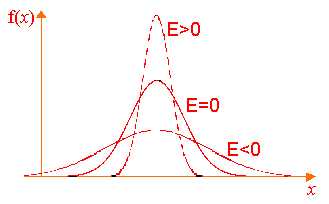

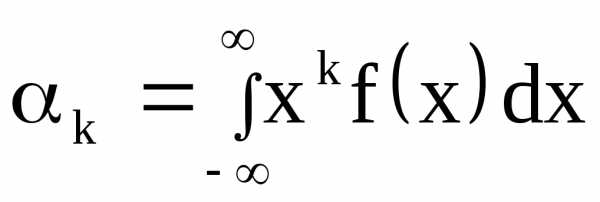
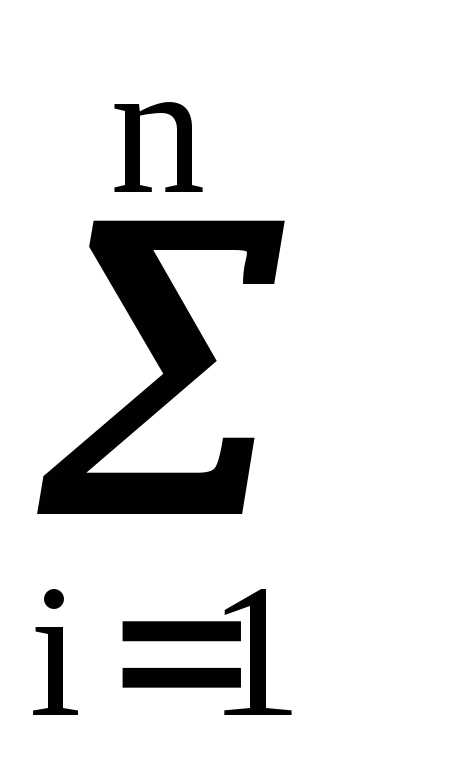 (xi – mx)S pi.
(xi – mx)S pi. (xi – mx)pi =
(xi – mx)pi = xi pi –
xi pi –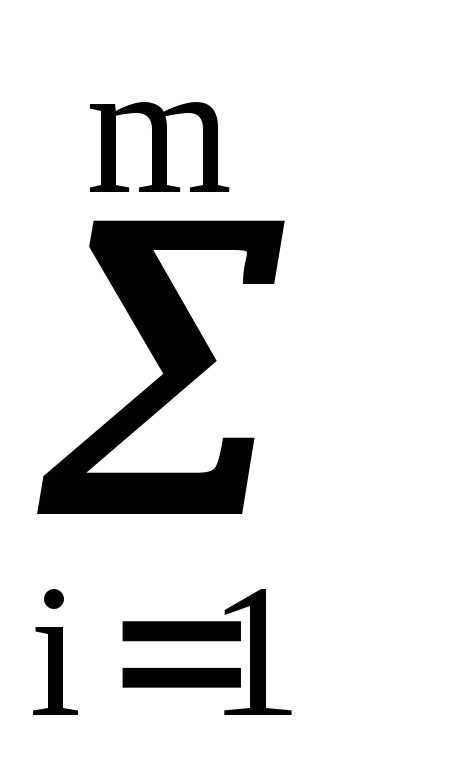 mx pi = mx–mx
mx pi = mx–mx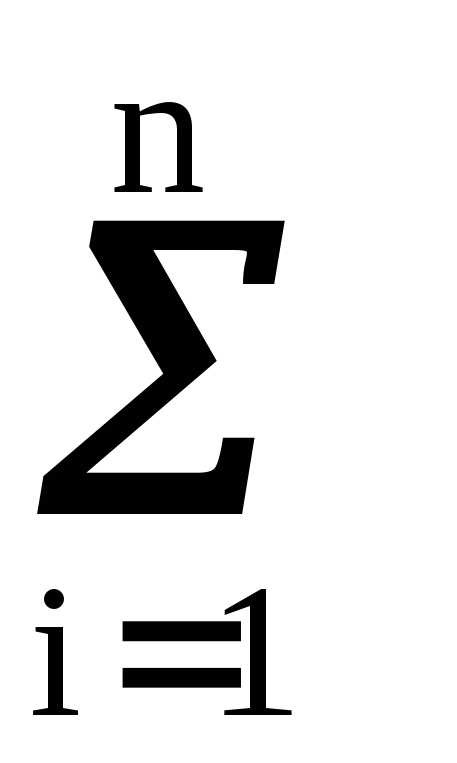 pi =mx–mx=
0.
pi =mx–mx=
0.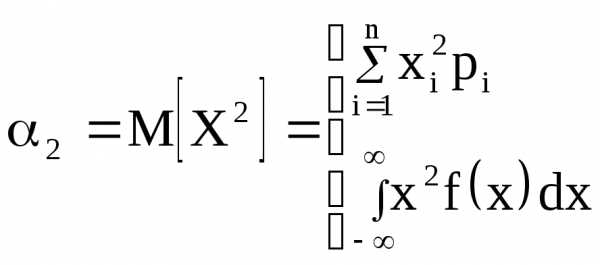


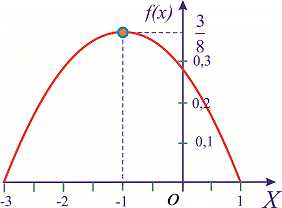



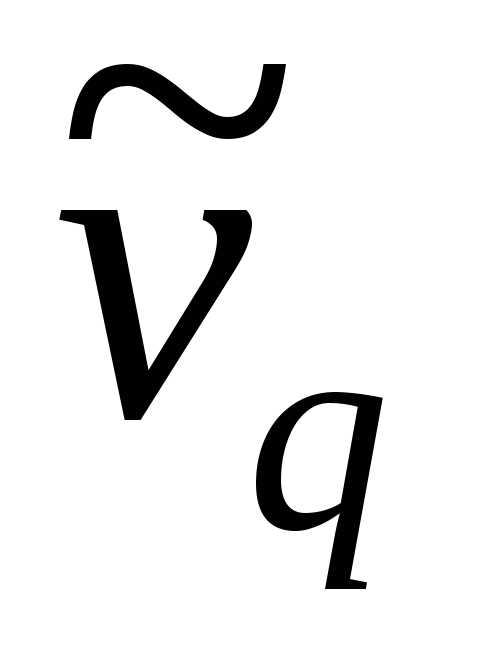 ) порядка q называют
взвешенную среднюю арифметическую q—x степеней
вариантов, т.е.
) порядка q называют
взвешенную среднюю арифметическую q—x степеней
вариантов, т.е. (20)
(20)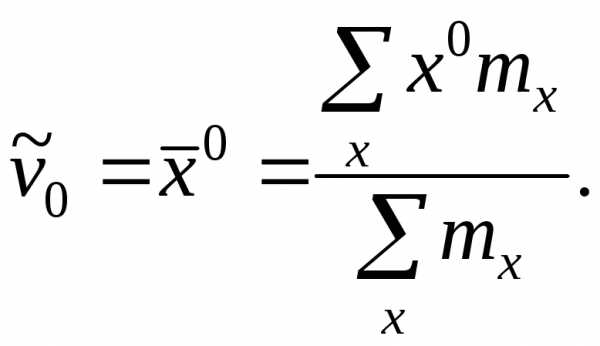

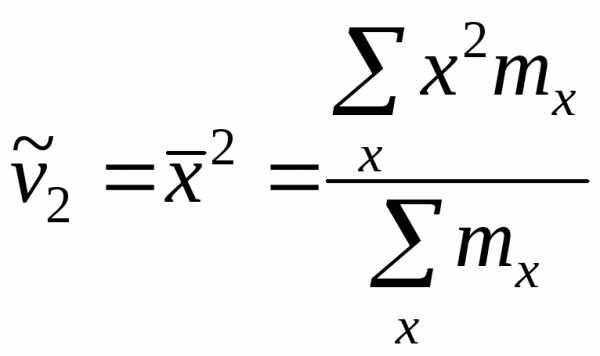 и
т.д.
и
т.д. )
порядкаq называют
взвешенную среднюю арифметическую q—x степеней
отклонений вариантов от их средней
арифметической, т.е.
)
порядкаq называют
взвешенную среднюю арифметическую q—x степеней
отклонений вариантов от их средней
арифметической, т.е.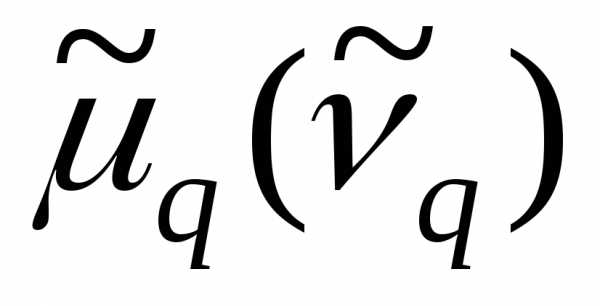 часто будем
называть просто центральным моментом
(начальным моментом), не употребляя
термин «эмпирический».
часто будем
называть просто центральным моментом
(начальным моментом), не употребляя
термин «эмпирический». —
число сочетаний из q элементов по р элементов (p≤.q).
—
число сочетаний из q элементов по р элементов (p≤.q). —с, поэтому центральный момент q—го
порядка
—с, поэтому центральный момент q—го
порядка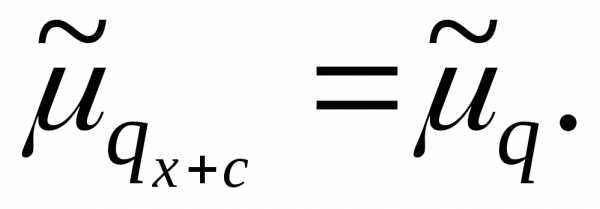
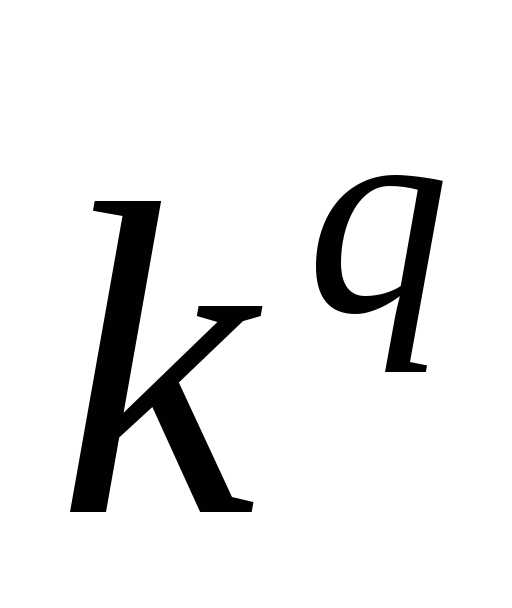 раз.
раз.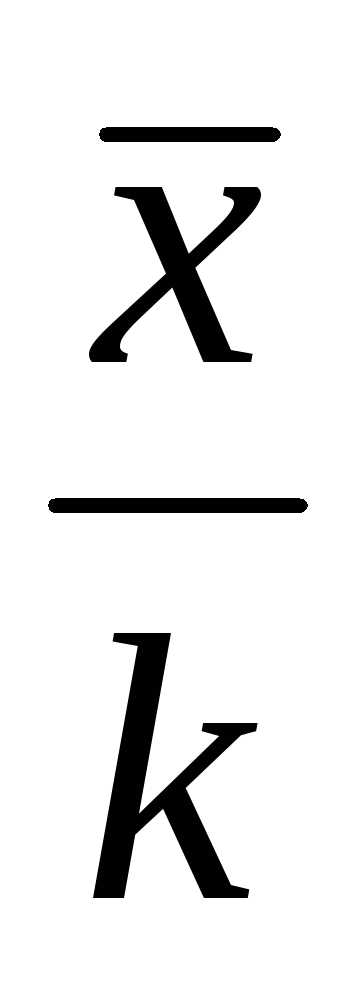 ,
поэтому
центральный момент q-гo порядка
,
поэтому
центральный момент q-гo порядка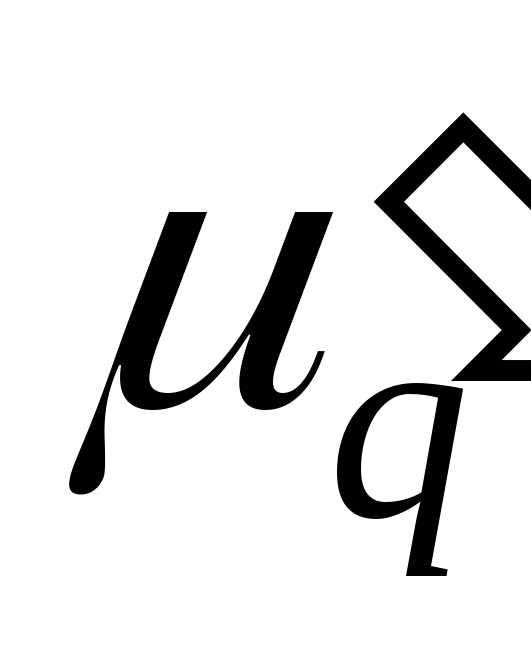 (центральный
момент q—го
порядка для измененного ряда), легко
вычислить центральный момент q-го
порядка для первоначального ряда:
(центральный
момент q—го
порядка для измененного ряда), легко
вычислить центральный момент q-го
порядка для первоначального ряда: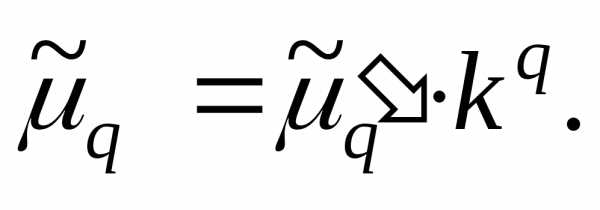 (26)
(26)
 называют отношение центрального момента
третьего порядка к кубу среднеквадратического
отклонения:
называют отношение центрального момента
третьего порядка к кубу среднеквадратического
отклонения: , то эмпирический коэффициент асимметрии
отрицателен; говорят, что в этом случае
имеет место левосторонняя асимметрия. Если же в вариационном ряду преобладают
варианты, большие
, то эмпирический коэффициент асимметрии
отрицателен; говорят, что в этом случае
имеет место левосторонняя асимметрия. Если же в вариационном ряду преобладают
варианты, большие  , то эмпирический коэффициент асимметрии
положителен; в этом случае имеет место правосторонняя асимметрия. При
левосторонней асимметрии левая ветвь
полигона длиннее правой. При правосторонней,
более длинной является правая ветвь.
, то эмпирический коэффициент асимметрии
положителен; в этом случае имеет место правосторонняя асимметрия. При
левосторонней асимметрии левая ветвь
полигона длиннее правой. При правосторонней,
более длинной является правая ветвь. называют уменьшенное на 3 единицы
отношение центрального момента четвертого
порядка к четвертой степени
среднеквадратического отклонения:
называют уменьшенное на 3 единицы
отношение центрального момента четвертого
порядка к четвертой степени
среднеквадратического отклонения: .
(28)
.
(28)

















 По моему мнению, многие люди обожают лето из-за его теплоты, красоты и заманчивости. Лично для меня, лето ассоциируется с теплым утренним днем или ветреным пасмурным вечером. Большую часть своего лета я, как и большинство людей провожу на улице. Я трачу свое время, разгуливая по паркам и переулкам. Не знаю почему, но мой слегка грязный, ничем не привлекательный город манит меня. Я люблю прогуливаться вечерами по мостикам, которые ведут через реку. Во время этих прогулок, я много размышляю о разных вещах. О смысле жизни, и чем-то подобном.
По моему мнению, многие люди обожают лето из-за его теплоты, красоты и заманчивости. Лично для меня, лето ассоциируется с теплым утренним днем или ветреным пасмурным вечером. Большую часть своего лета я, как и большинство людей провожу на улице. Я трачу свое время, разгуливая по паркам и переулкам. Не знаю почему, но мой слегка грязный, ничем не привлекательный город манит меня. Я люблю прогуливаться вечерами по мостикам, которые ведут через реку. Во время этих прогулок, я много размышляю о разных вещах. О смысле жизни, и чем-то подобном. Лето- это та пора года, когда можно не «заморачиваться» на счет одежды. Зимой, каждый человек одевается, так скажем, тщательно. Свитер, куртка, шапка и так далее. Согласитесь, ведь надоедает носить на себе эти килограммы вещей? А что нужно летом? Шорты, футболка и обувь.
Лето- это та пора года, когда можно не «заморачиваться» на счет одежды. Зимой, каждый человек одевается, так скажем, тщательно. Свитер, куртка, шапка и так далее. Согласитесь, ведь надоедает носить на себе эти килограммы вещей? А что нужно летом? Шорты, футболка и обувь. Лето- это то время, когда хочется жить и наслаждаться каждым прожитым моментом. Прекрасные летние закаты, утренняя роса, вечерняя прохлада и дневная жара- именно так, я бы охарактеризовал летнюю пору. Живите и любите, вот что я хочу вам пожелать. До конца лета, осталось несколько недель и нужно сделать так, чтобы это лето стало для вас незабываемым.
Лето- это то время, когда хочется жить и наслаждаться каждым прожитым моментом. Прекрасные летние закаты, утренняя роса, вечерняя прохлада и дневная жара- именно так, я бы охарактеризовал летнюю пору. Живите и любите, вот что я хочу вам пожелать. До конца лета, осталось несколько недель и нужно сделать так, чтобы это лето стало для вас незабываемым.