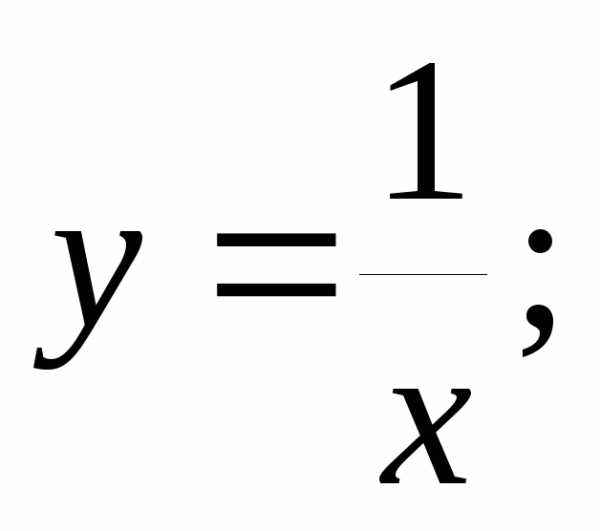Квадратный корень из степени
Квадратный корень из степени
Цели: рассмотреть извлечение квадратного корня из степени числа
Ход урока
I Сообщение темы и цели урока
II Повторение и закрепление пройденного материала
Ответы на вопросы по домашнему заданию ( разбор нерешенных задач)
Контроль усвоения материала
— Сформулируйте теорему о квадратном корне из произведения чисел
— Сформулируйте теорему о квадратном корне из частного
Вычислите значение выражения:

III Изучение нового материала
Сначала рассмотрим числовые примеры. Найдем значение выражения √х2 при х = 8 и при х = — 7. Получаем: √82 = √64 = 8 и √(-7)2 = √49 = 7
В каждом из этих примеров квадратный корень из квадрата числа равнялся модулю этого числа: √82 = │8│ = 8 и √(-7)2 = │-7│ = 7. Обобщим результаты этих примеров и докажем теорему.
Теорема: при любом значении х верно равенство √х2 = │х│. (1)
Рассмотрим два случая.
а) Если х ≥ 0, то по определению арифметического корня √х2 = х. Так как
х ≥ 0, то х = │х│ и равенство может быть записано в виде √х2 = │х│.
б) Если х < 0, то величина – х > 0 и получаем √х2 = √(- х) = — х. Так как х < 0, то – х = │х│ и равенство можно записать в виде √х2 = │х│.
Значит, при любом значении х выполнено равенство √х2 = │х│
Такое тождество очень часто применяется при извлечении квадратного корня из степени с четным показателем. При этом, чтобы извлечь корень из степени с четным показателем, надо представить подкоренное выражение в виде квадрата некоторого выражения и использовать рассмотренное тождество.
Пример 1.
Извлечем корень из √а8
Представим степень а8 в виде квадрата степени а4, т.е. а8 = (а4 )2 и используем тождество (1): √а8 = √(а4 )2 = │а4│= а4. Учтено, что при всех значениях а величина а4 ≥ 0 и │а4│= а4.
Пример 2.
Извлечем корень из √с6 при с < 0.
Представим с6 в виде с6 = ( с3)2 и используем тождество (1). Получаем √с6 =√(с3)2 = │с3│ = — с3. Учтено, что с < 0, тогда с3 < 0 и │с3│= -с3 (по определению модуля).
Пример 3
Найдем значение выражения √63504.
Разложим число 63504 на произведение простых множителей и получим: 63504 = 16*81*49=24 34 72. Теперь найдем √63504 = √24 34 72 =√24 √34 √72 = √(22)2 √(32)2 √72 =22 32 7 = 252
Полученное тождество позволяет решать и более сложные задачи.
Пример 4.
Найдем значение выражения √(7-√13)*√(7+√13).
Учтем теорему о корне из произведения и формулу разности квадратов. Получаем: √(7-√13)*√(7+√13)= √(7-√13)*(7+√13)=√72-(√13)2 = √49-13 = √36 = 6.
IV Формирование умений и навыков
№ 393(а, б, в, г), № 401(а, б, е, ж), № 404
V Итоги урока
1. Сформулируйте теорему о корне из квадрата числа (выражения).
2. Как извлечь корень из степени с четным показателем?
VI Домашнее задание
№ 393, № 402, № 403
infourok.ru
Корень из числа: определения, примеры
Квадратный корень, арифметический квадратный корень
Чтобы понять определение корня из числа, и квадратного корня в частности, нужно иметь представление о степени с натуральным показателем. В этом пункте мы часто будем сталкиваться со второй степенью числа — квадратом числа.
Начнем с определения квадратного корня.
Определение
Квадратный корень из числа a — это число, квадрат которого равен a.
Чтобы привести примеры квадратных корней, возьмем несколько чисел, например, 5, −0,3, 0,3, 0, и возведем их в квадрат, получим соответственно числа 25, 0,09, 0,09 и 0 (52=5·5=25, (−0,3)2=(−0,3)·(−0,3)=0,09, (0,3)2=0,3·0,3=0,09 и 02=0·0=0). Тогда по данному выше определению число 5 является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 – это квадратный корень из нуля.
Следует отметить, что не для любого числа a существует действительное число, квадрат которого равен a. А именно, для любого отрицательного числа a не существует ни одного действительного числа b, квадрат которого равнялся бы a. В самом деле, равенство a=b2 невозможно для любого отрицательного a, так как b2 – неотрицательное число при любом b. Таким образом, на множестве действительных чисел не существует квадратного корня из отрицательного числа. Иными словами, на множестве действительных чисел квадратный корень из отрицательного числа не определяется и не имеет смысла.
Отсюда вытекает логичный вопрос: «А для любого ли неотрицательного a существует квадратный корень из a»? Ответ – да. Обоснованием этого факта можно считать конструктивный способ, используемый для нахождения значения квадратного корня.
Тогда встает следующий логичный вопрос: «Каково число всех квадратных корней из данного неотрицательного числа a – один, два, три, или еще больше»? Вот ответ на него: если a равно нулю, то единственным квадратным корнем из нуля является нуль; если же a – некоторое положительное число, то количество квадратных корней из числа a равно двум, причем корни являются противоположными числами. Обоснуем это.
Начнем со случая a=0. Сначала покажем, что нуль действительно является квадратным корнем из нуля. Это следует из очевидного равенства 02=0·0=0 и определения квадратного корня.
Теперь докажем, что 0 – единственный квадратный корень из нуля. Воспользуемся методом от противного. Предположим, что существует некоторое число b, отличное от нуля, которое является квадратным корнем из нуля. Тогда должно выполняться условие b2=0, что невозможно, так как при любом отличном от нуля b значение выражения b2 является положительным. Мы пришли к противоречию. Это доказывает, что 0 – единственный квадратный корень из нуля.
Переходим к случаям, когда a – положительное число. Выше мы сказали, что всегда существует квадратный корень из любого неотрицательного числа, пусть квадратным корнем из a является число b. Допустим, что существует число c, которое тоже является квадратным корнем из a. Тогда по определению квадратного корня справедливы равенства b2=a и c2=a, из них следует, что b2−c2=a−a=0, но так как b2−c2=(b−c)·(b+c), то (b−c)·(b+c)=0. Полученное равенство в силу свойств действий с действительными числами возможно лишь тогда, когда b−c=0 или b+c=0. Таким образом, числа b и c равны или противоположны.
Если же предположить, что существует число d, являющееся еще одним квадратным корнем из числа a, то рассуждениями, аналогичными уже приведенным, доказывается, что d равно числу b или числу c. Итак, число квадратных корней из положительного числа равно двум, причем квадратные корни являются противоположными числами.
Для удобства работы с квадратными корнями отрицательный корень «отделяется» от положительного. С этой целью вводится определение арифметического квадратного корня.
Определение
Арифметический квадратный корень из неотрицательного числа a – это неотрицательное число, квадрат которого равен a.
Для арифметического квадратного корня из числа a принято обозначение . Знак называется знаком арифметического квадратного корня. Его также называют знаком радикала. Поэтому можно часть слышать как «корень», так и «радикал», что означает один и тот же объект.
Число под знаком арифметического квадратного корня называют подкоренным числом, а выражение под знаком корня – подкоренным выражением, при этом термин «подкоренное число» часто заменяют на «подкоренное выражение». Например, в записи число 151 – это подкоренное число, а в записи выражение a является подкоренным выражением.
При чтении слово «арифметический» часто опускается, например, запись читают как «квадратный корень из семи целых двадцати девяти сотых». Слово «арифметический» произносят лишь тогда, когда хотят особо подчеркнуть, что речь идет именно о положительном квадратном корне из числа.
В свете введенного обозначения из определения арифметического квадратного корня следует, что и для любого неотрицательного числа a.
Квадратные корни из положительного числа a с помощью знака арифметического квадратного корня записываются как и . Например, квадратные корни из числа 13 есть и . Арифметический квадратный корень из нуля равен нулю, то есть, . Для отрицательных чисел a записи мы не будем придавать смысла вплоть до изучения комплексных чисел. Например, лишены смысла выражения и .
На базе определения квадратного корня доказываются свойства квадратных корней, которые часто применяются на практике.
Нахождение квадратных корней заслуживает детального изучения, этой теме посвящена отдельная статья извлечение квадратных корней.
В заключение этого пункта заметим, что квадратные корни из числа a являются решениями квадратного уравнения вида x2=a относительно переменной x.
К началу страницы
www.cleverstudents.ru
Как представить корень в виде степени
Как представить корень в виде степени?
Для этого нужно от корня перейти к степени с дробным показателем:
В частности,
Например,
Во многих случаях преобразование выражений с корнями проще выполнять, представив корни в виде степеней.
www.algebraclass.ru
Квадратный корень из степени
Прежде чем преступать к изучению новой темы, давайте вспомним определение модуля числа.
Итак, модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А (а).
Также модулем положительного числа называется само это число.
Модуль числа нуль равен нулю.
А модулем отрицательного числа называется противоположное ему число.
Задание: найти значение выражения , при и при .
Легко заметить, что в первом примере в ответе тоже получается . Обратите внимание, в каждом из рассмотренных примеров, корень из квадрата числа равен модулю этого числа.
Теорема: При любом значении х верно равенство:
Следовательно, При любом значение выражения совпадает со значением выражения .
Равенство является тождеством.
Это тождество применяется при извлечении квадратного корня из степени с чётным показателем. Чтобы извлечь корень из степени с чётным показателем, достаточно представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством: .
Например: преобразуем выражения:
Задание 2: найдите значение выражения.
Итоги:
При любом значении икс верно равенство: .
Это равенство является тождеством и применяется при извлечении квадратного корня из степени с чётным показателем.
Чтобы извлечь корень из степени с чётным показателем, достаточно представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством: .
videouroki.net
Корень квадратный из числа
Мы с вами уже уяснили себе, что каждому математическому действию соответствует аналогичное, но обратное по направлению действие.
Для сложения таким обратным действием является вычитание, для умножения — деление. Теперь попробуем выяснить, какое действие является обратным для возведения в степень. Поскольку возведение в степень — это многократное умножение, то, очевидно, обратным действием будет многократное деление.
Например, 32 можно разделить на 2 и получить 16, затем 16 разделить на 2 и получить 8; затем 8 разделить на 2 и получить 4; затем 4 разделить на 2 и получить 2; наконец, затем 2 разделить на 2 и получить 1. В краткой форме эти действия можно записать как 32:2:2:2:2:2=1. (Наша задача заключалась в том, чтобы добраться до 1.) Поскольку мы произвели деление 5 раз и добрались до 1, то можно сказать, что 2 — это корень пятой степени из 32.
Если мы рассмотрим число 81, то увидим, что 81:3:3:3:3=1, таким образом, 3 является корнем четвертой степени из 81. (Почему, собственно, корнем? Откуда взялось это слово? Это можно объяснить таким образом: число 32 растет из основания 2, а 81 — из основания 3 так же, как растение произрастает из корней.)
Такая математическая операция обозначается как $\sqrt{}$. На разнообразие корней указывает число в верхней левой части корня. Так, корень пятой степени из 32 можно записать как $\sqrt[5]{32}$, корень четвертой степени из 81 можно записать как $\sqrt[4]{81}$. Значок $\sqrt{ }$ называется знаком радикала, а числа, содержащие корни, называются радикалами. Слово «радикал» пришло к нам из латыни, где оно означает просто «корень».
Мы редко встречаемся с корнями высоких степеней, чаще всего приходится иметь дело с операциями, обратными возведению во вторую степень, то есть в квадрат. Извлечение корня второй степени называется извлечением квадратного корня, а $\sqrt[2]{}$ называется квадратным корнем, причем двойка слева часто опускается. В дальнейшем под значком $\sqrt{}$ без цифры в верхнем левом углу мы всегда будем иметь в виду квадратный корень.
Что же такое квадратный корень из числа? 25 — это квадрат 5, таким образом, можно сказать, что 5 — это квадратный корень из 25, или $\sqrt{25}=5$. Поэтому следует говорить «пять — это корень второй степени из 25», но обычно употребляют формулировку «квадратный корень». (Точно так же корень третьей степени называют кубическим корнем.)
Следующая проблема заключается в том, чтобы выяснить, как найти корень такой- то из некоего числа. Здесь можно идти путем от противоположного. Предположим, мы знаем, что $2^5=32$, это означает, что если 32 пять раз разделить на 2, то результатом будет 1. (Если мы возвели число в какую-то степень, нетрудно пойти в обратном порядке.)
На практике арифметический метод определения корней заключается в серии обратных действий. Попробуем извлечь квадратный корень из 625. Схема вычислений будет следующей:
Первую цифру ответа, 2, мы получаем подбором. Мы знаем, что 2×2=4, это ближайшее возможное число, меньшее 6, поскольку 3×3=9, что больше 6. Затем проводим вычитание и выносим две цифры вместо одной, как это принято при обычном делении в столбик. (Если бы мы извлекали кубический корень, мы выносили бы три цифры, в случае корня четвертой степени — четыре цифры и так далее.) Чтобы получить следующую цифру, надо разделить 225 на 45. Цифру 45 вы получаете, удваивая первую цифру ответа, что дает вам 4. Вторая цифра должна быть равна второй цифре вашего ответа, таким образом, ее тоже можно найти подбором, так, чтобы получить число, ближайшее к 225. Цифра 5 подходит наиболее точно, так как 5х45=225.
Этот процесс может показаться вам очень трудным, и вы будете совершенно правы. Вычислять корни чисел арифметическим способом очень трудно, но результаты оказываются полезными при различных расчетах.
Рассмотрим следующий пример. Чему равен $\sqrt{2}$? Какое число надо возвести в квадрат, чтобы получить 2?
Мы можем сразу определить, что среди целых чисел такого числа нет, ведь 1×1=1, а 2х2=4. Первое число слишком мало, а второе слишком велико. Следовательно, ответ будет дробным числом.
А может ли вообще существовать квадратный корень в виде дробного числа? Почему же нет? Согласно нашему определению экспоненциальных выражений $(1\frac25)^2$ — это $1\frac25 \times 1\frac25$, и ответом является число $1\frac{24}{25}$. А это, в свою очередь, означает, что $\sqrt{1\frac{24}{25}}$ равен $1\frac{2}{5}$. Теперь мы убедились, что не только квадратный корень может быть дробным числом. И в обоих случаях справедливы те же правила, что и в случае целых чисел.
Кроме того, случайно оказалось, что число $1\frac{2}{5}$, будучи умноженное на себя самое, дает результат, близкий к 2. Отсюда следует, что $1\frac{2}{5}$ близко к $\sqrt{2}$. Только $\frac{1}{25}$ отделяет нас от искомого ответа, так как $(1\frac{2}{5})^2$ — это $1\frac{24}{25}$, а нам нужно получить число $1\frac{25}{25}$, то есть 2.
Но можно получить и более точный ответ. Если помножить дробное число $1\frac{41}{100}$ на себя самое, мы получим $1\frac{9881}{10000}$, что гораздо ближе к 2. Может показаться, что, если делать более точные вычисления, мы рано или поздно найдем точное значение дробного числа, которое является корнем квадратным из 2, хотя, возможно, это будет очень сложное число.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Квадратный корень из степени: правила и примеры
Квадратным корнем из числа a называют такое число, квадрат которого равен a. Например, числа -5 и 5 являются квадратными корнями из числа 25. То есть, корни уравнения x^2=25, являются квадратными корнями из числа 25. Теперь необходимо научиться извлекать квадратный корень из степени.
Есть два основных правила:
Правило №1
Если a>=0 и n – некоторое натуральное число, то справедливо следующее равенств: √(a^(2*n)) =a^n.
Например, √x^14 = √x^(2*7) = x^7
Правило №2
Для произвольного числа a справедливо следующее равенство:
√a^2 = |a|.
Например, √(-5)^2 = |-5|=5; Кстати, следует заметить, что первая формула является частным случаем второй формулы.
Рассмотрим еще несколько примеров:
Упростить выражение √a^16.
Так как у нас неизвестно какие значения может принимать а, то воспользоваться первым правилом нельзя, ибо оно предназначено только для положительных а. Представим это выражение в виде (a^8)^2 и воспользуемся свойством два:
√a^16 =√ (a^8)^2 = |a^8|
Теперь раскроем модуль. Так как a^8 >=0 при любом а, то |a^8| = a^8.
Получаем, что √a^16 = a^8.
Упростить выражение √a^10, при аа у нас отрицательное, значит использовать первое правило нельзя, пользуемся вторым.
а^10= (а^5)^2.
Имеем √a^10 = |a^5|.
Раскрываем модуль. Так как а по условию меньше нуля, тогда и a^5 тоже меньше нуля, а значит |a^5|=-а^5.
Получаем √a^10 = -а^5, при а<0.
Нужна помощь в учебе?
Предыдущая тема: Квадратный корень из произведения и дроби: правила и примеры
Следующая тема:   Вынесение множителя из под корня и внесение под корень: примеры
Все неприличные комментарии будут удаляться.
www.nado5.ru
Корень квадратный — это… Что такое Корень квадратный?
Квадра́тный ко́рень из (корень 2-й степени) — это решение уравнения вида . Несмотря на то, что в первую очередь под и подразумеваются числа, в различных рассмотрениях они могут быть математическими объектами различной природы, в том числе такими как матрицы и операторы. При использовании термина следует уточнять его значение в конкретном разделе математики.
Применение операции корня к числам
Квадратный корень из числа — это такое число, квадрат которого (результат умножения на себя) равен , то есть решение уравнения относительно переменной .[1][2]
Рациональные числа
Корень из рационального числа является рациональным числом, только если и (после сокращения общих множителей) являются квадратами натуральных чисел.
Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к ним с помощью линейных рекуррент, а с другой стороны ограничивает точность приближения: , где зависит от [3][4].
Действительные числа
При натуральных уравнение не всегда разрешимо в рациональных числах, что и привело к появлению новых числовых полей. Древнейшее из таких расширений — поле вещественных (действительных) чисел.
Теорема. Для любого положительного числа a существует ровно два вещественных корня, которые равны по модулю и противоположны по знаку. [5]
Неотрицательный квадратный корень из положительного числа называется арифметическим квадратным корнем и обозначается с использованием знака радикала .[6]
Комплексные числа
Над полем комплексных чисел решений всегда два, отличающихся только знаком (за исключением квадратного корня из нуля). Корень из комплексного числа часто обозначают как , однако использовать это обозначение нужно осторожно. Распространенная ошибка:
Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
- ,
то (см. Формула Муавра)
- ,
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k=0 и k=1, таким образом в итоге в ответе получаются два различных результата.
Квадратный корень как элементарная функция
Вещественный анализ
График функцииКвадратным корнем называют также функцию вещественной переменной , которая каждому ставит в соответствие арифметическое значение корня.[7] Эта функция является частным случаем степенной функции с . Эта функция является гладкой при , в нуле же она непрерывна справа, но не дифференцируема.
Комплексный анализ
Обобщения
Квадратные корни вводятся как решения уравнений вида и для других объектов: матриц [8], функций [9], операторов[10] и т. п. В качестве операции при этом могут использоваться достаточно произвольные мультипликативные операции, например, суперпозиция.
В алгебре применяется следующее формальное определение: Пусть — группоид и . Элемент называется квадратным корнем из если .
Квадратный корень в элементарной геометрии
Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырех действий арифметики, квадратные корни и ничего сверх того. [11]
Квадратный корень в информатике
Во многих языках программирования функционального уровня (а также языках разметки типа sqrt, от англ. square root «квадратный корень».
Алгоритмы нахождения квадратного корня
Нахождение или вычисление квадратного корня заданного числа называется извлечением (квадратного) корня.
Арифметическое извлечение квадратного корня
Для квадратов чисел верны следующие равенства:
- 1 = 12
- 1 + 3 = 22
- 1 + 3 + 5 = 32
и так далее.
То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и сочтя количество выполненных действий. Например, так:
- 9 − 1 = 8
- 8 − 3 = 5
- 5 − 5 = 0
Выполнено 3 действия, квадратный корень числа 9 равен 3.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня.
Геометрическое извлечение квадратного корня
В частности, если , а , то [12]
Столбиком
Этот способ позволяет найти приближённоё значение корня из любого действительного числа с любой наперёд заданной точностью.
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Пусть извлекается корень из целого числа A. В отличие от деления снос производится группами по 2 цифры, причём группы следует отмечать, начиная с десятичной запятой (в обе стороны), дописывая необходимым количеством нулей.
- Найти an, квадрат которого наиболее близко подходит к группе старших разрядов числа A, оставаясь меньше последнего.
- Провести вычитание из старших разрядов A квадрата числа an.
- Удвоить an.
- Сдвинуть остаток от вычитания на 2 разряда влево, а величину 2an — на один разряд влево. Под сдвигом в данном алгоритме понимается умножение/деление на степени 10, что соответственно является сдвигом влево и вправо.
- Приписать справа от остатка вычитания два следующих старших разряда числа A.
- Сравнить полученное число с нулём.
- Если полученное число не равно 0, то найти такое 2an − 1, которое, будучи умноженным на , даст в результате число, меньшее полученного на четвёртом шаге, но наиболее близкое к нему по значению. Перейти к п.3.
- Если в п.5 получено равенство, то перейти к п.4, предварительно приписв справа от an нуль.
- После получения количества цифр, равного , прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.
Примечания
- ↑ «Корнем n-й степени из числа x называется число, n-я степень которого совпадает с x. При n = 2 и n = 3 корни называются соответственно квадратным и кубическим.» — определение из статьи «Алгебра» энциклопедии «Кругосвет»
- ↑ «Извлечь корень n-й степени из числа а — это значит найти такое число (или числа) x, которое при возведении в n-ю степень даст данное число ()… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.
- ↑ Теорема Лиувилля о приближении алгебраических чисел
- ↑ См. А. Я. Хинчин, Цепные дроби, М. ГИФМЛ, 1960, §§ 4, 10.
- ↑ Фихтенгольц, Григорий Михайлович. Курс дифференциального и интегрального исчисления Том. 1. Введение, § 4 // Мат. анализ на EqWorld
- ↑ Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). М., 1974 г., п. 1.2.1
- ↑ Фихтенгольц, гл. 2, § 1
- ↑ См., например: Гантмахер Ф. Р., Теория матриц, М.: Гос. изд-во технико-теоретической литературы, 1953, или: Воеводин В., Воеводин В., Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ, Спб.: БХВ-Петербург, 2006.
- ↑ См., например: Ершов Л. В., Райхмист Р. Б., Построение графиков функций, М.: Просвещение, 1984, или: Каплан И. А., Практические занятия по высшей математике, Харьков: Изд-во ХГУ, 1966.
- ↑ См., например: Хатсон В., Пим Дж., Приложения функционального анализа и теории операторов, М.: Мир, 1983, или: Халмош П., Гильбертово пространство в задачах, М.: Мир, 1970.
- ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. (ГЛАВА III Геометрические построения. Алгебра числовых полей)
- ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. Стр. 148
См. также
Ссылки
Wikimedia Foundation. 2010.
dic.academic.ru



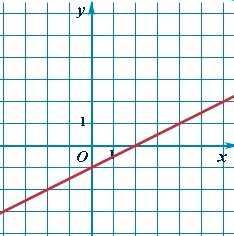
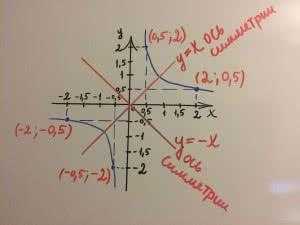
 гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти
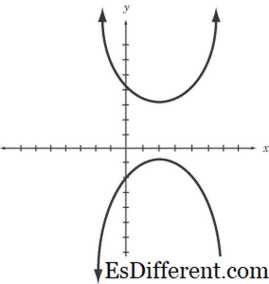
гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти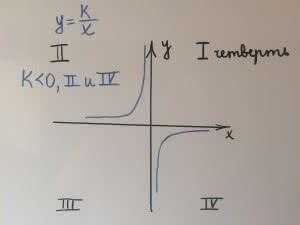 гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти
гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти



 и отлична от нуля.
и отлична от нуля.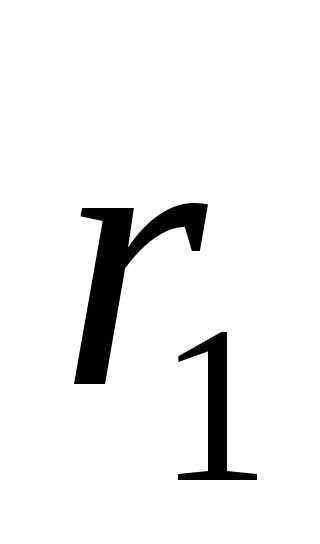
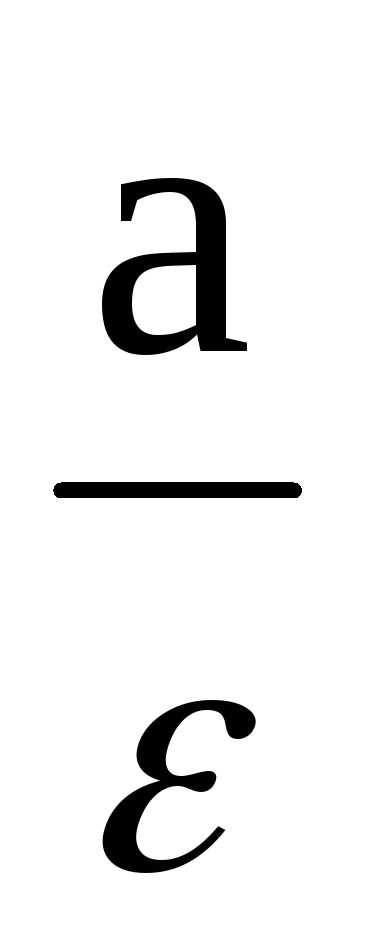
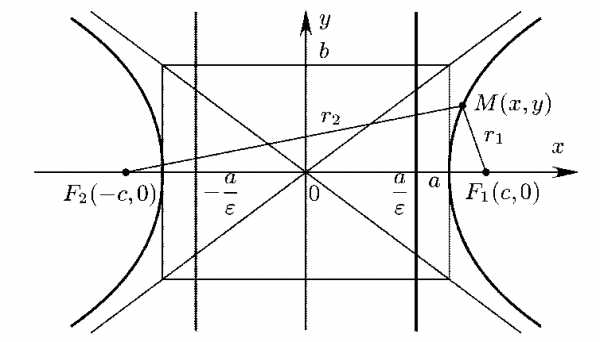
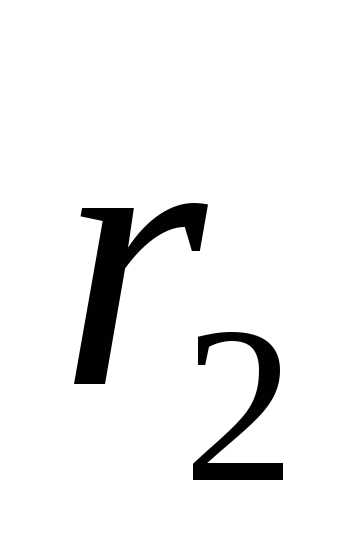 — фокусные радиусы точки
— фокусные радиусы точки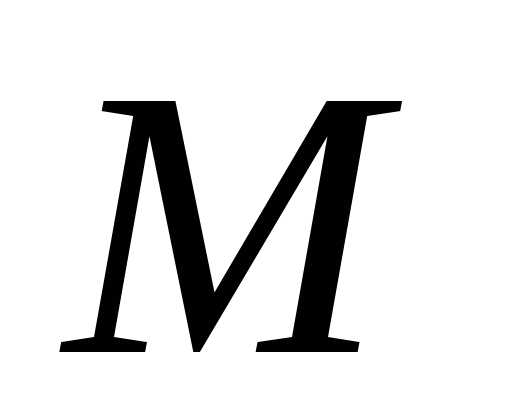 .
.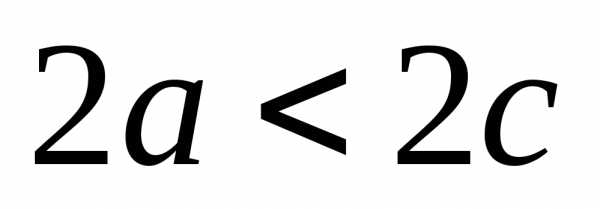 (по
определению) следовательно
(по
определению) следовательно  .
.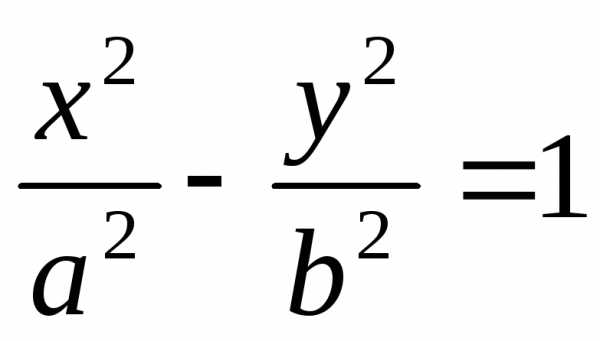 , (11)
, (11)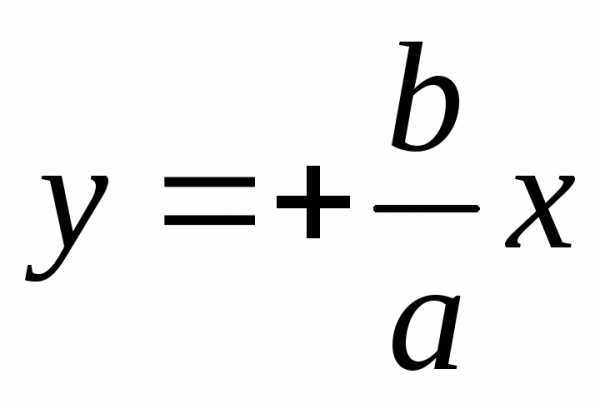 – это уравнение прямой с угловым
коэффициентом
– это уравнение прямой с угловым
коэффициентом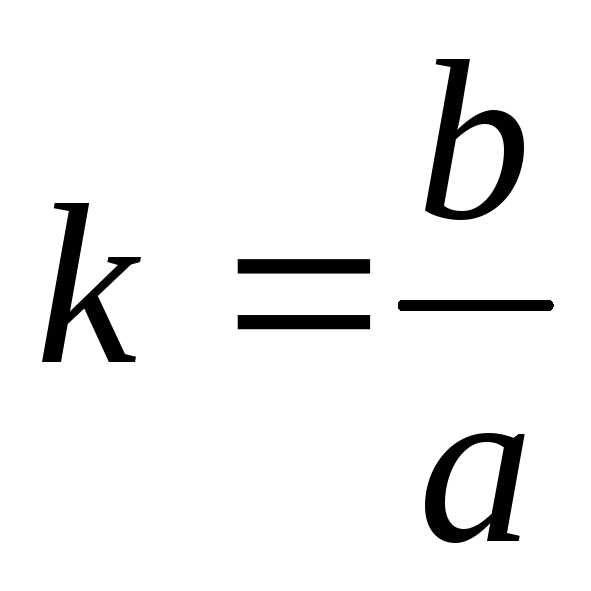 .
При.
.
При. называютсяасимптотамигиперболы.
называютсяасимптотамигиперболы.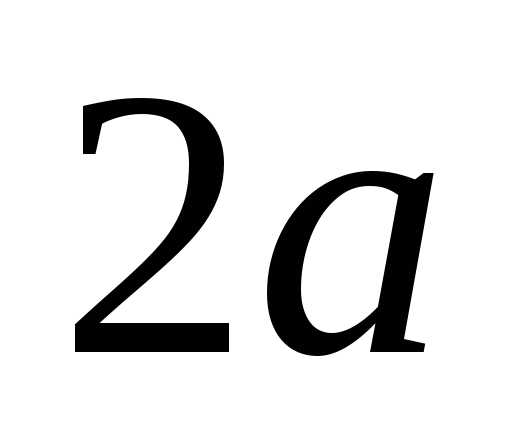 и
и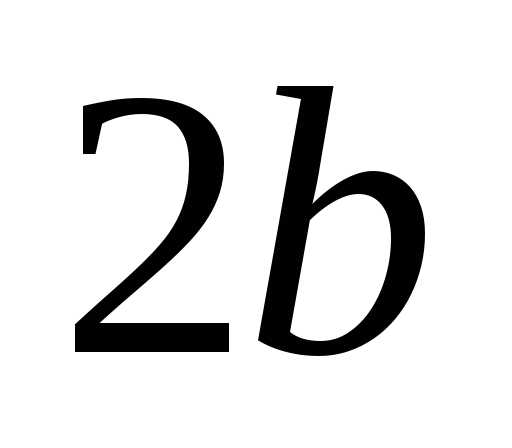 — оси гиперболы.
— оси гиперболы.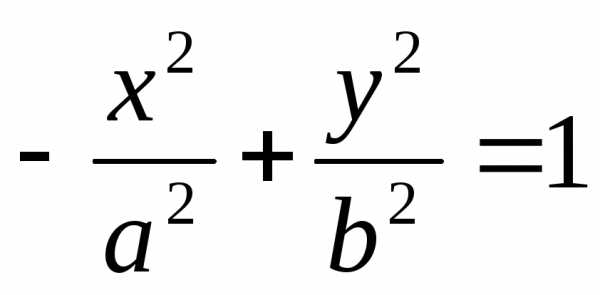 задает гиперболу, сопряженную с первой.
задает гиперболу, сопряженную с первой.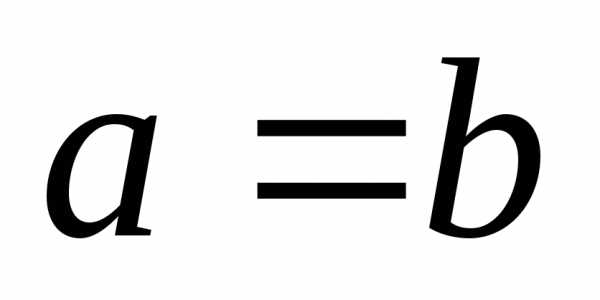 называется равносторонней:
называется равносторонней: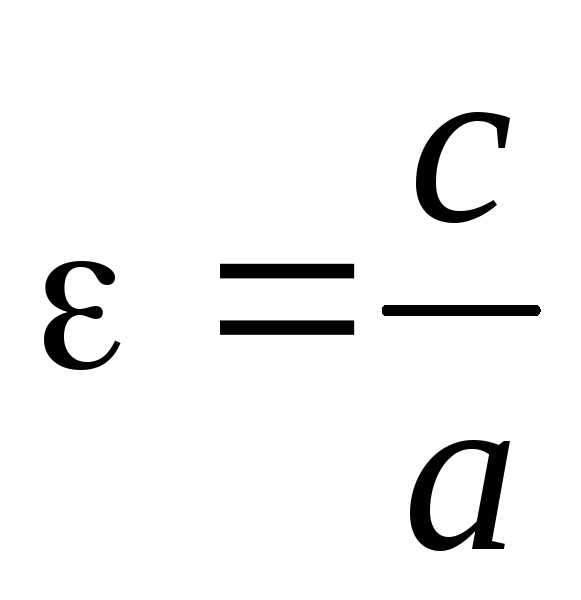 . (12)
. (12)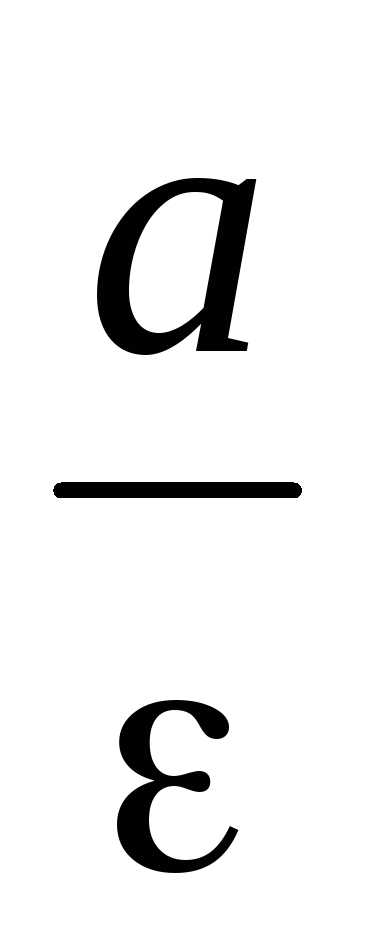 от него, называютсядиректрисамигиперболы.
от него, называютсядиректрисамигиперболы.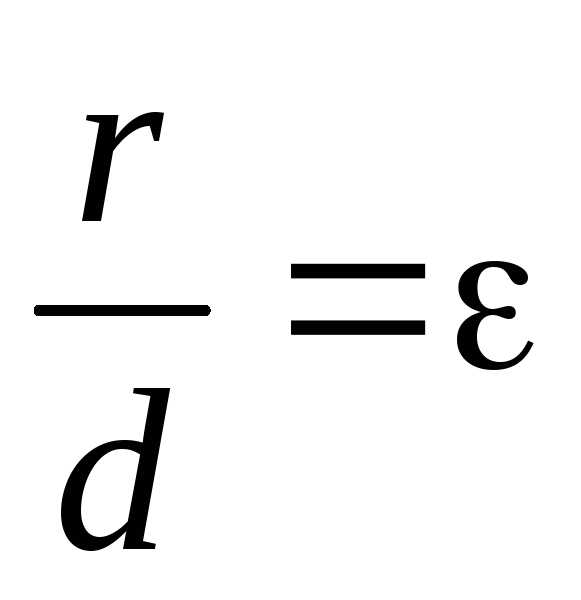 , (13)
, (13)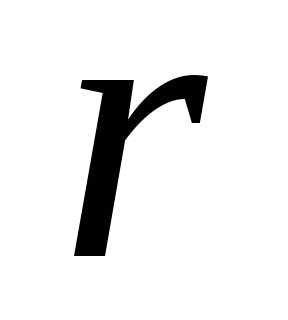 – расстояние от точки до фокуса
– расстояние от точки до фокуса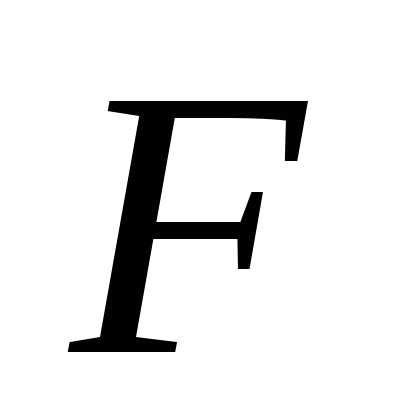 ,
а
,
а – расстояние до соответствующей
директрисы.
– расстояние до соответствующей
директрисы. .
(14)
.
(14) –фокус,
–фокус, 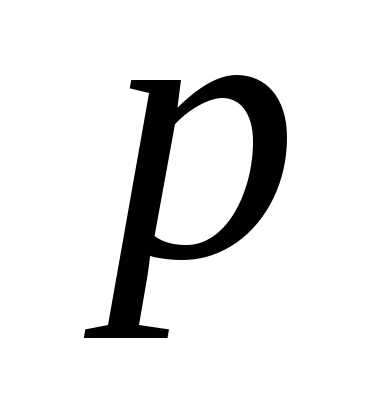 – расстояние от фокуса до директрисы
– параметр параболы,– фокальный радиус точки.
– расстояние от фокуса до директрисы
– параметр параболы,– фокальный радиус точки.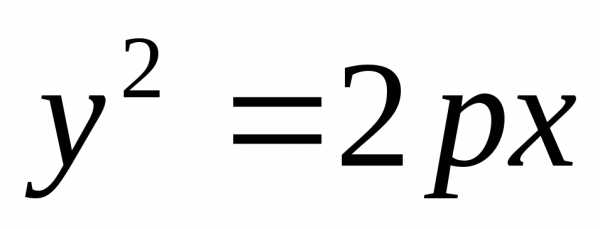 (15)
(15)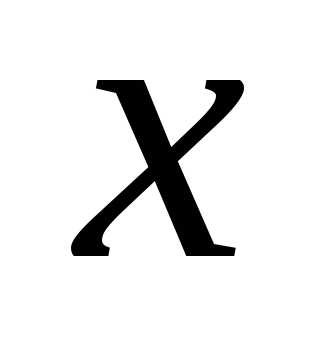 ,
при
,
при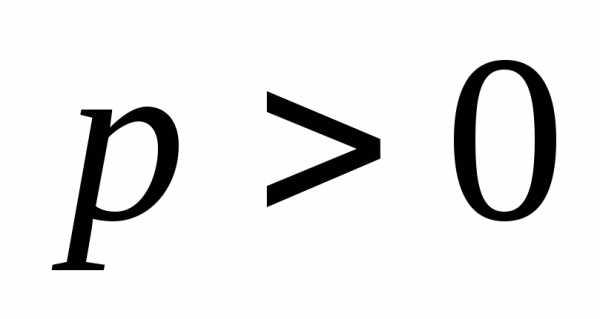 ветви параболы направлены вправо.
Уравнение
ветви параболы направлены вправо.
Уравнение задает параболу,
симметричную относительно оси ординат,
ветви которой при
задает параболу,
симметричную относительно оси ординат,
ветви которой при 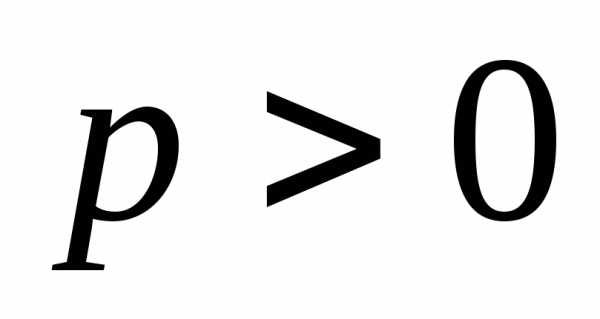 направлены вверх.
направлены вверх.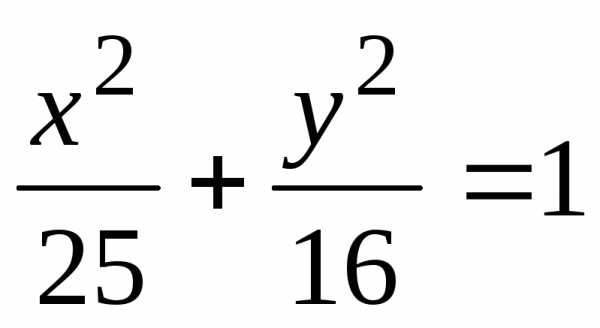
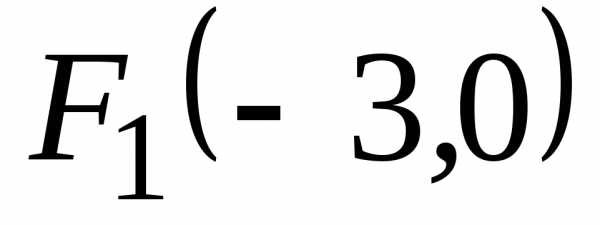 и
и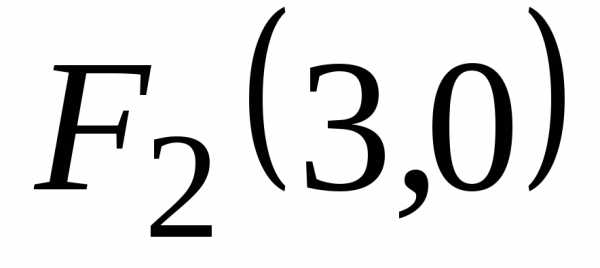 ,
эксцентриситет
,
эксцентриситет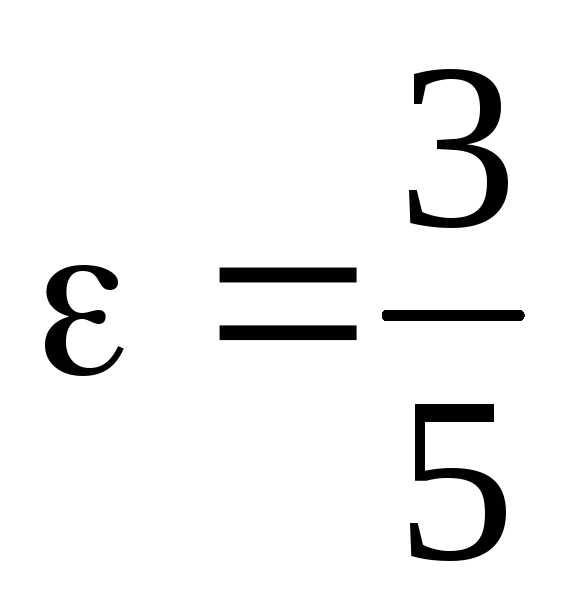
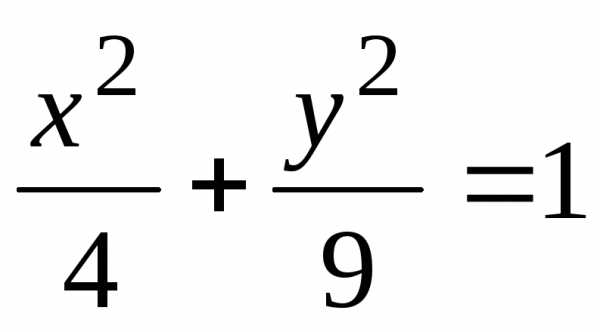
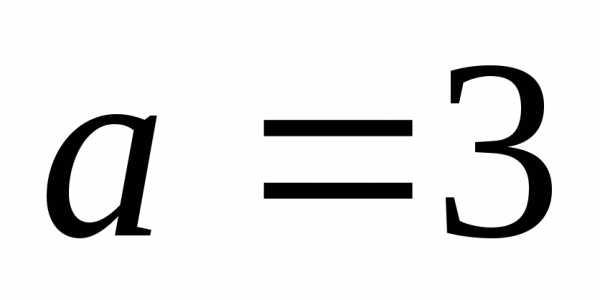 ,
а малая полуось
,
а малая полуось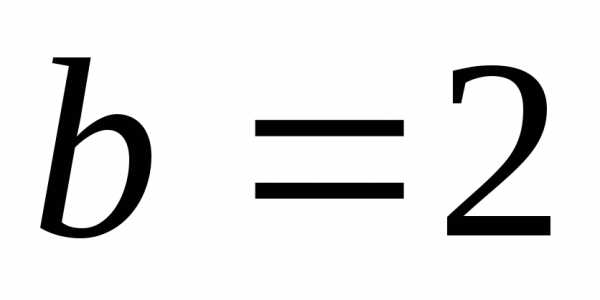 .
При этом ось эллипса и его фокусы
расположены на оси
.
При этом ось эллипса и его фокусы
расположены на оси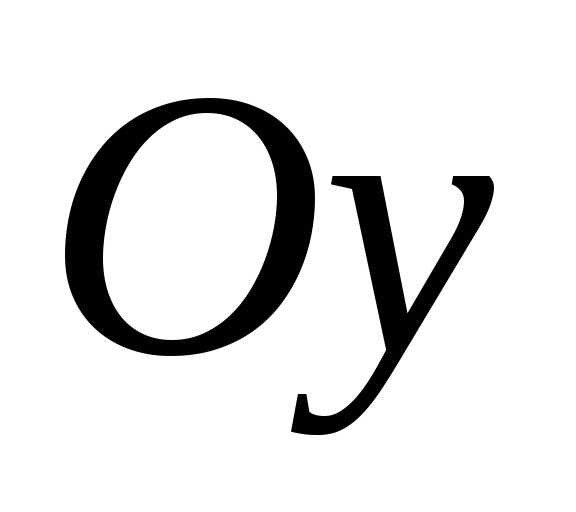 .
Найдем
.
Найдем по формуле
по формуле и
и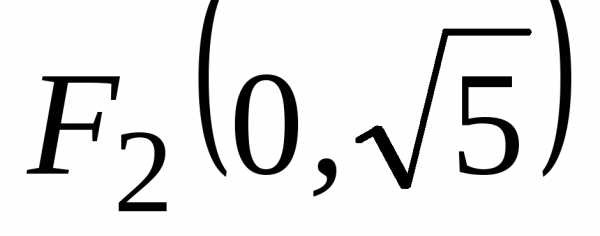 ,
а его эксцентриситет
,
а его эксцентриситет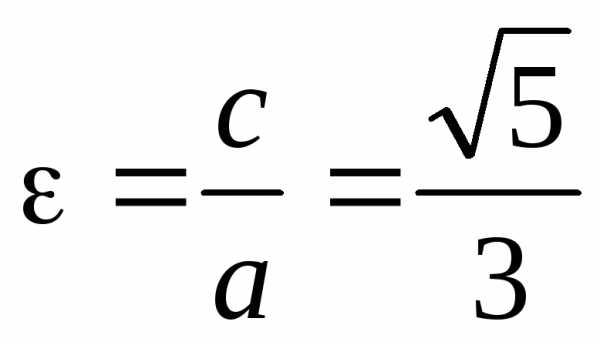
 ,
а его эксцентриситет
,
а его эксцентриситет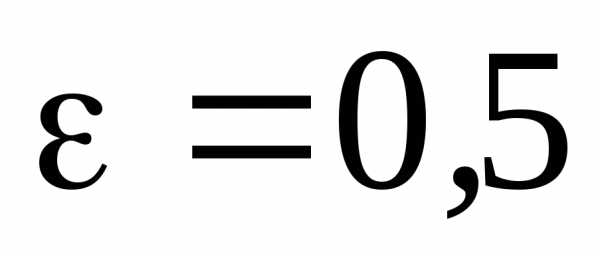 .
Найти расстояние между фокусами эллипса.
.
Найти расстояние между фокусами эллипса.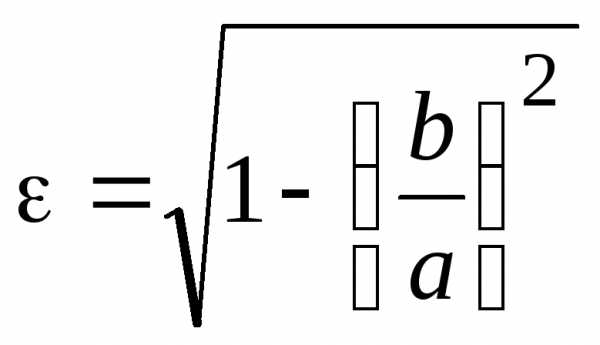 ,
или
,
или  ,
откуда.
,
откуда.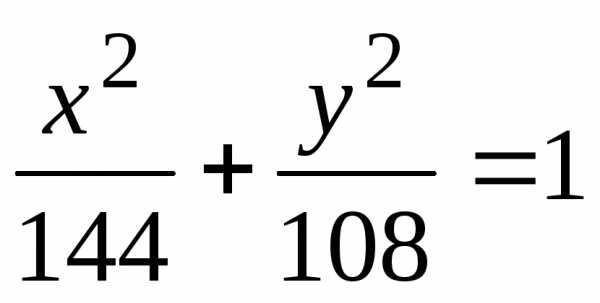 .
.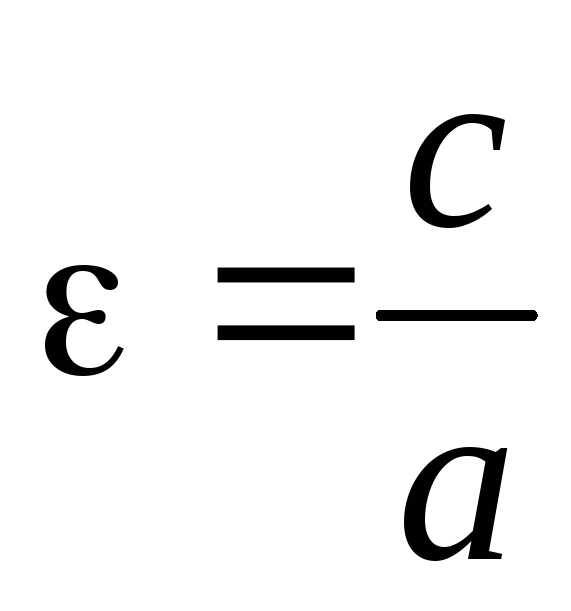 ,
то;и расстояние между фокусами
,
то;и расстояние между фокусами и, сравнив с общей формулой асимптот,
найдем отношение
и, сравнив с общей формулой асимптот,
найдем отношение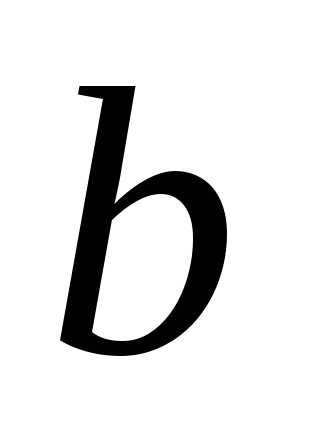 к
к :
: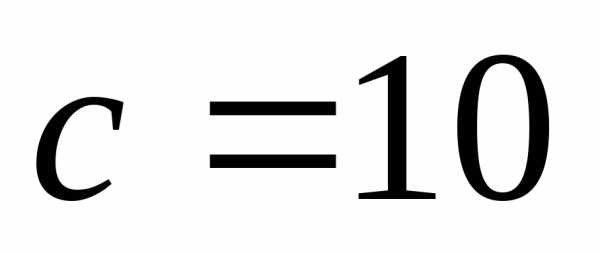 .
Так как для гиперболы,
то для нахождения
.
Так как для гиперболы,
то для нахождения и
и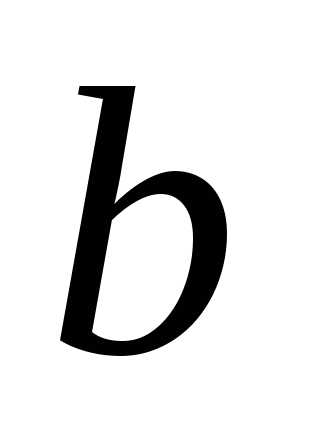 получим систему уравнений
получим систему уравнений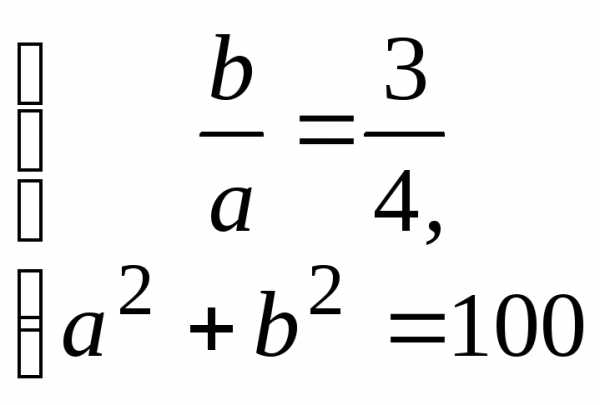
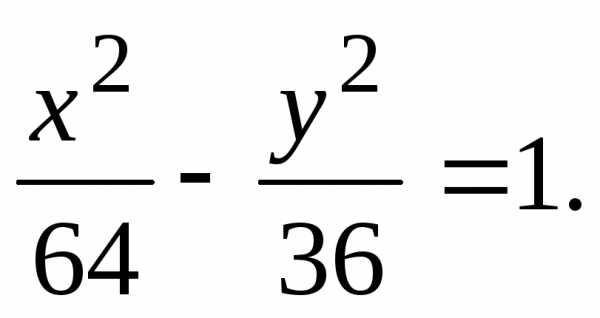
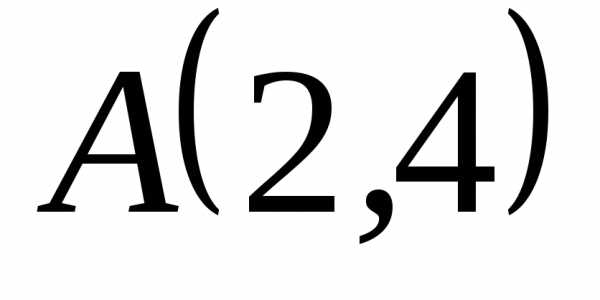 и симметрична относительно оси
и симметрична относительно оси .
Написать ее уравнение.
.
Написать ее уравнение.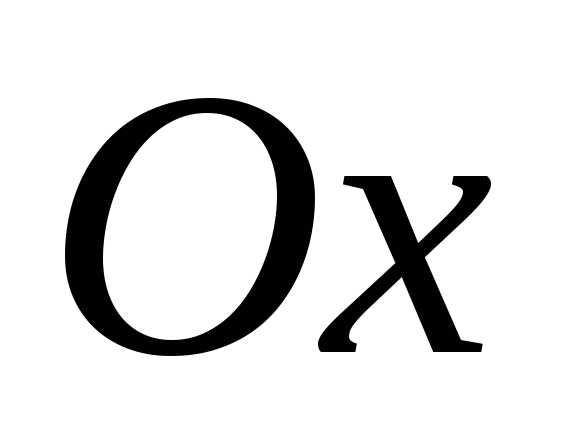 и проходит через точку
и проходит через точку с положительной абсциссой, то она имеет
вид, представленный на рис.
с положительной абсциссой, то она имеет
вид, представленный на рис. в уравнение такой параболы
в уравнение такой параболы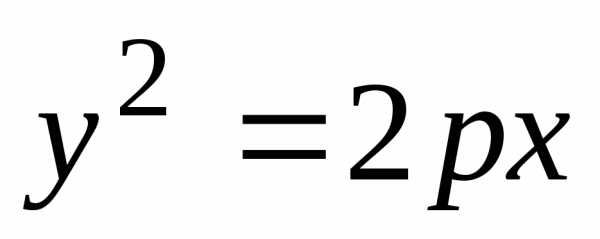 ,
получим,
т.е.
,
получим,
т.е.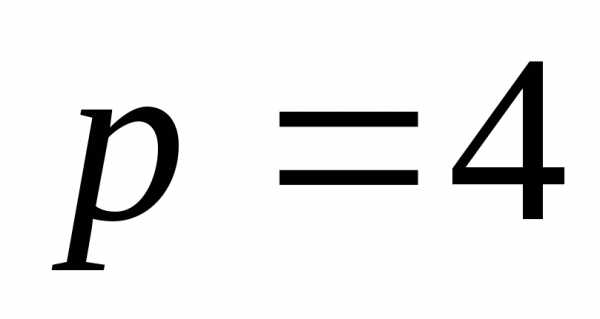 .
.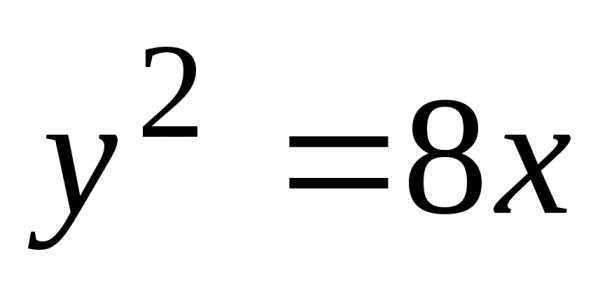
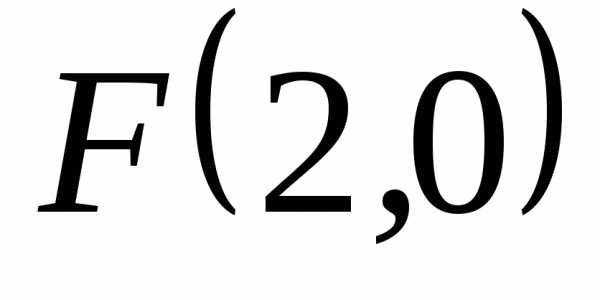 ,
уравнение директрисы
,
уравнение директрисы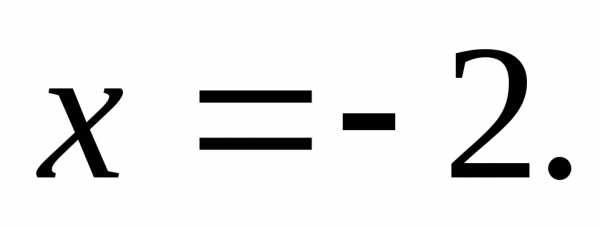
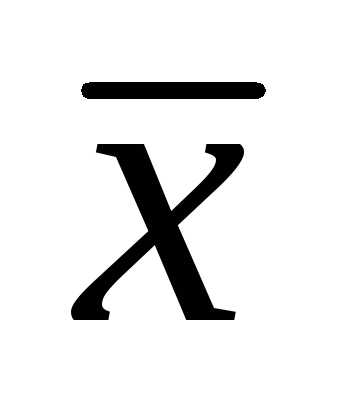 и
и получаем уравнение окружности
получаем уравнение окружности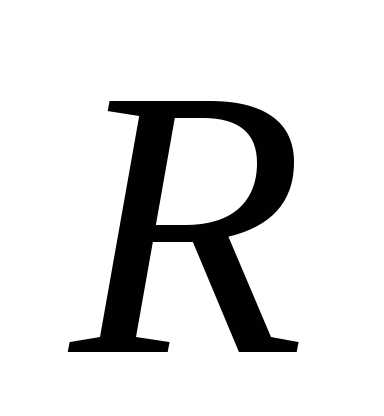 с центром в начале координат. Уравнение
окружности того же радиуса с центром в
точке
с центром в начале координат. Уравнение
окружности того же радиуса с центром в
точке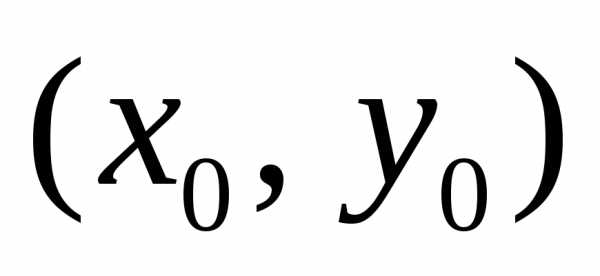 имеет вид
имеет вид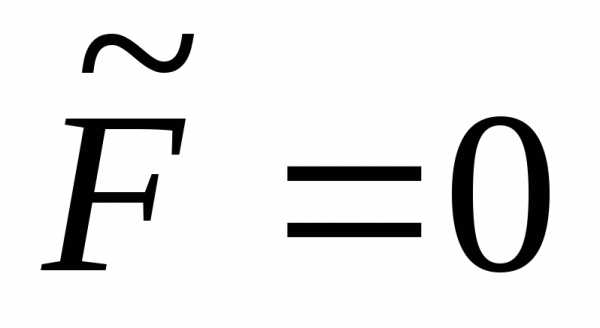 ,
то окружность вырождается в точку.
Наконец, если
,
то окружность вырождается в точку.
Наконец, если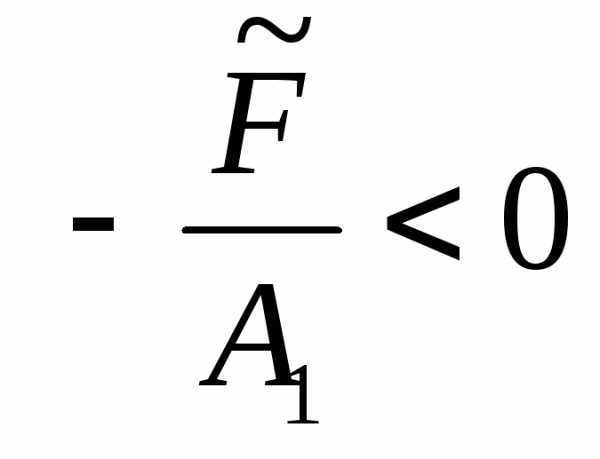 ,
то уравнениене определяет какой-либо кривой на
плоскости (мнимая окружность).
,
то уравнениене определяет какой-либо кривой на
плоскости (мнимая окружность).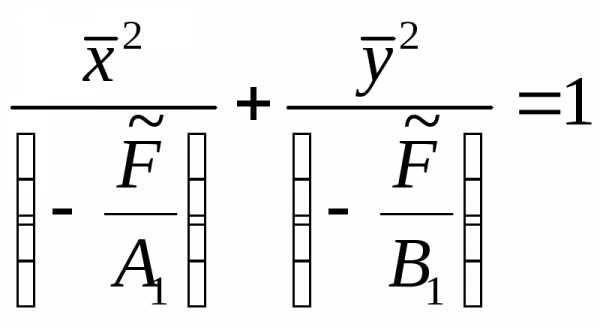 .
.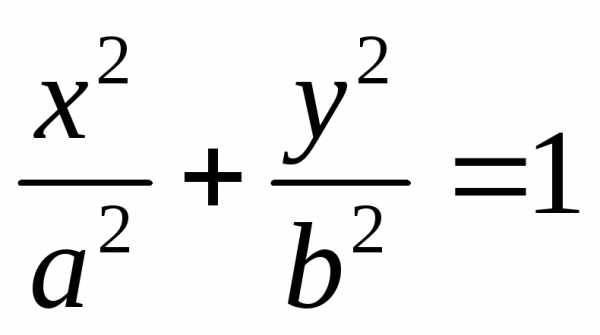 .
.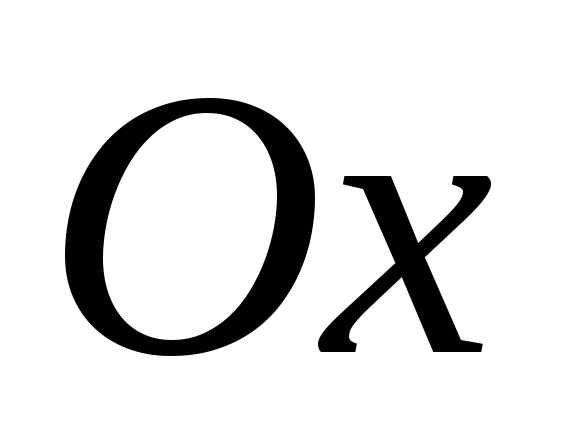 и
и называютсяосями
симметрии эллипса,
а точки
—вершинами
эллипса.
Пусть
называютсяосями
симметрии эллипса,
а точки
—вершинами
эллипса.
Пусть 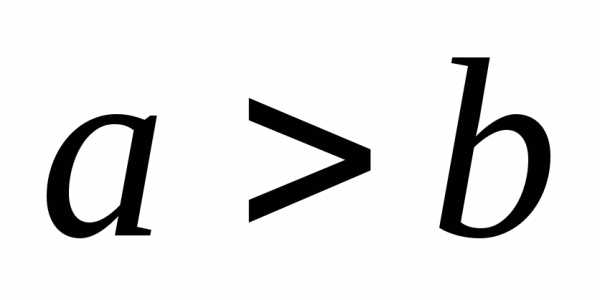 .
Отрезок
.
Отрезок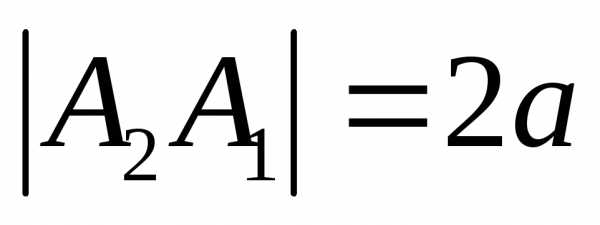 называетсябольшой
осью эллипса (
называетсябольшой
осью эллипса ( —большой
полуосью эллипса),
а отрезок
—большой
полуосью эллипса),
а отрезок  —малой осью
эллипса (
—малой осью
эллипса (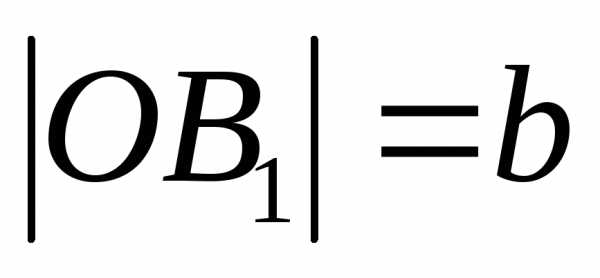 — малой
полуосью эллипса).
Эллипс имеет два фокуса ,
где.
Расстояние между фокусами равно
— малой
полуосью эллипса).
Эллипс имеет два фокуса ,
где.
Расстояние между фокусами равно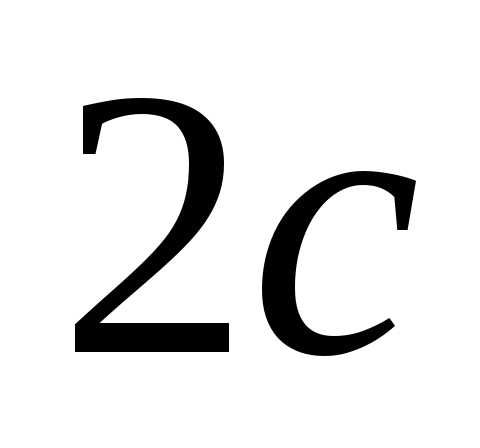 .
Форма эллипса зависит от отношения
.
Форма эллипса зависит от отношения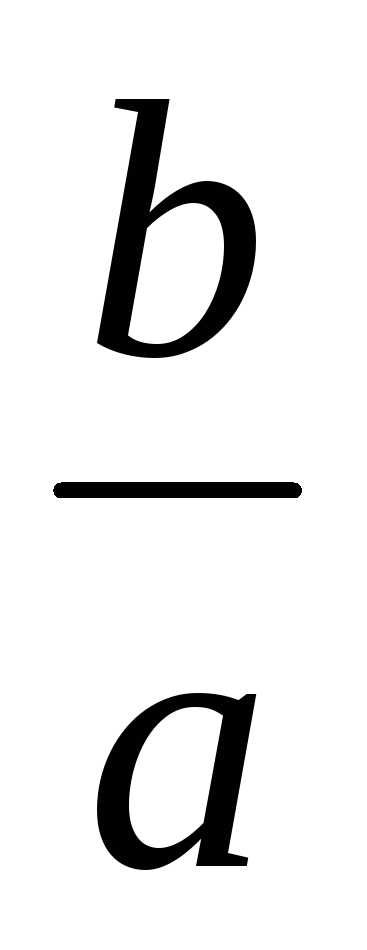 .
При
.
При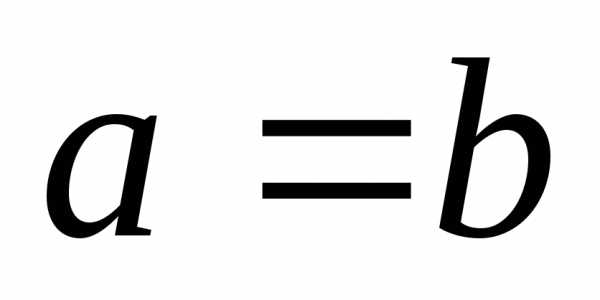 эллипс превращается в окружность.
Отклонение от окружности (сплющенность)
эллипса характеризуется параметром
эллипс превращается в окружность.
Отклонение от окружности (сплющенность)
эллипса характеризуется параметром ,
который называетсяэксцентриситетом
эллипса.
Для окружности
,
который называетсяэксцентриситетом
эллипса.
Для окружности 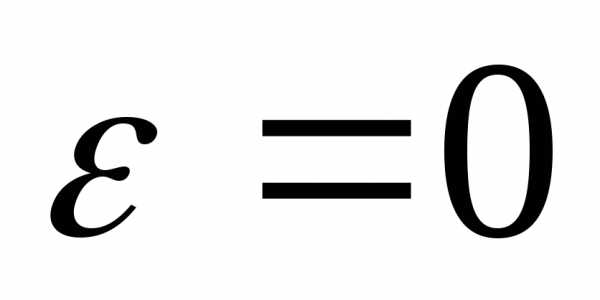 ,
для эллипса.
При
,
для эллипса.
При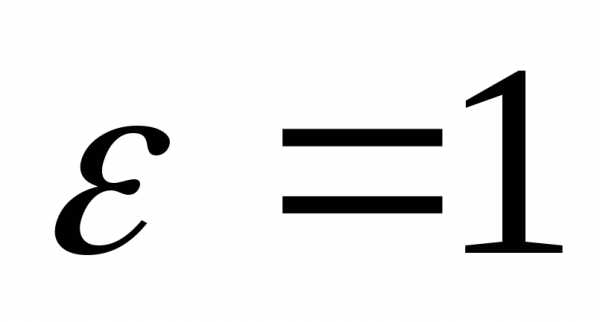 эллипс вырождается в отрезок (
эллипс вырождается в отрезок (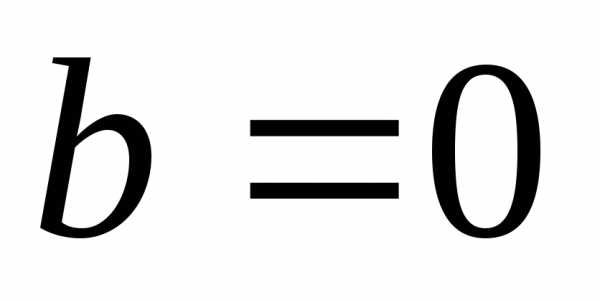 ).
Справедливость этих утверждений легко
увидеть из соотношения
).
Справедливость этих утверждений легко
увидеть из соотношения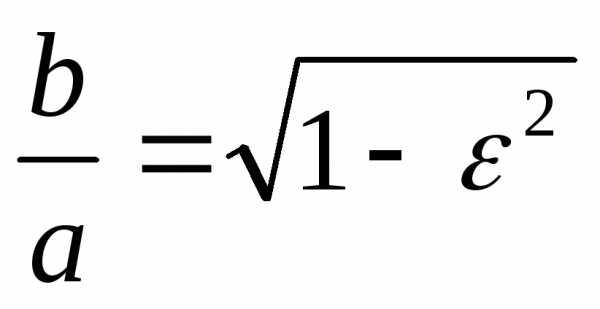 .
. ,
лежащую на эллипсе. Длины
,
лежащую на эллипсе. Длины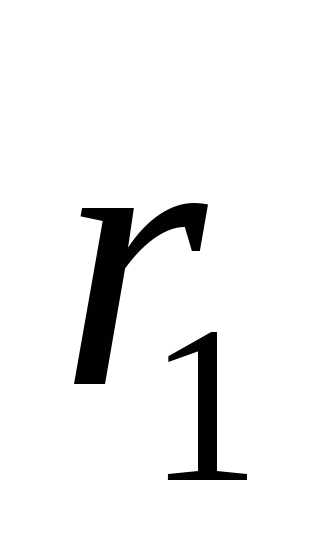 и
и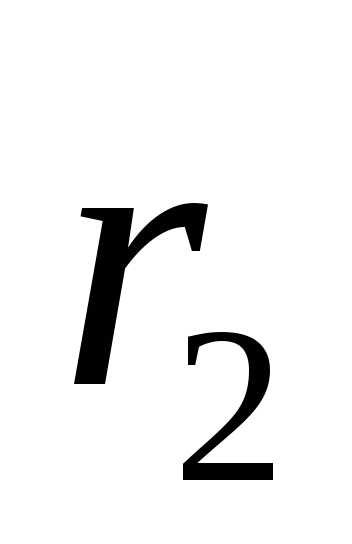 соответственно отрезков
соответственно отрезков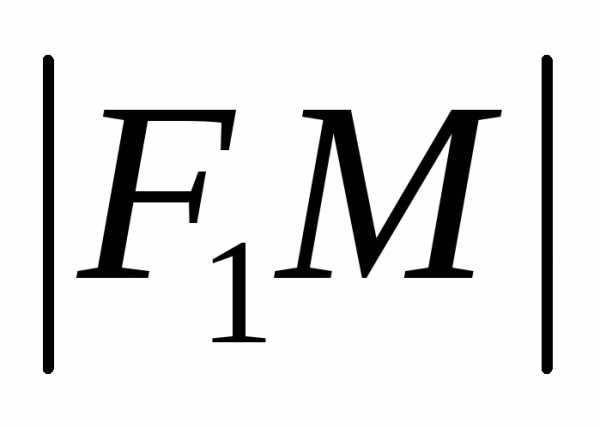 и
и называютсяфокальными
радиусами эллипса.
Заметим, что
.
Приведем соотношения, связывающие
фокальные радиусы с эксцентриситетом
эллипса:.
называютсяфокальными
радиусами эллипса.
Заметим, что
.
Приведем соотношения, связывающие
фокальные радиусы с эксцентриситетом
эллипса:.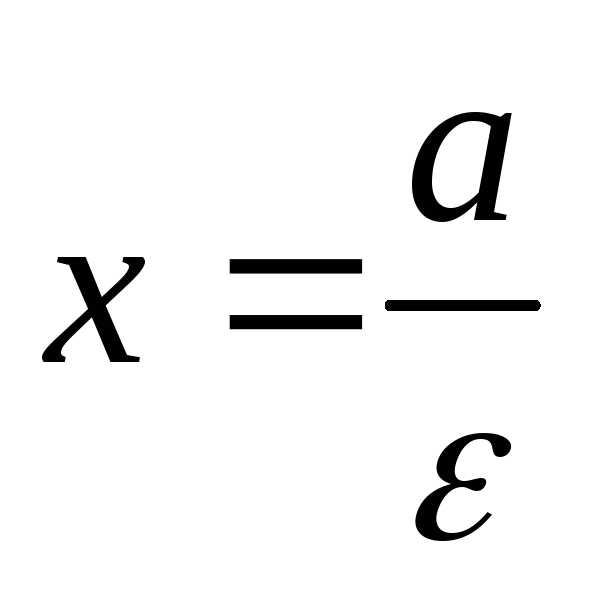 и
и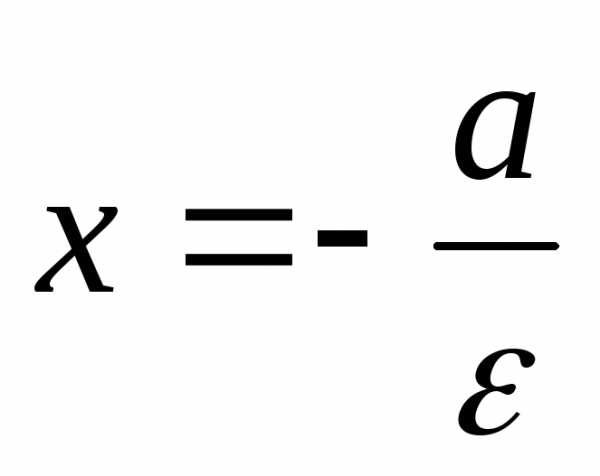 называютсядиректрисами
эллипса.
Рассмотрим правую директрису
называютсядиректрисами
эллипса.
Рассмотрим правую директрису 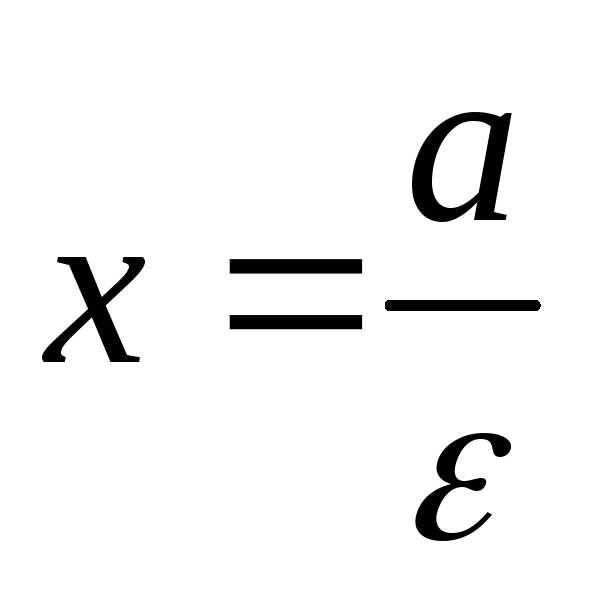 и правый же фокус эллипса
и правый же фокус эллипса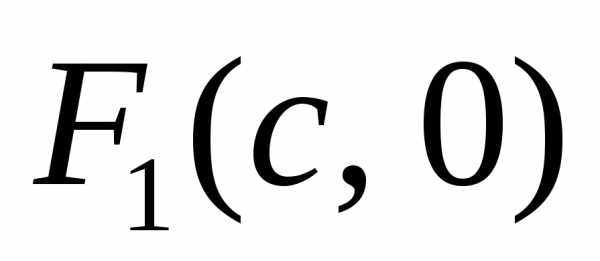 .
Точка
.
Точка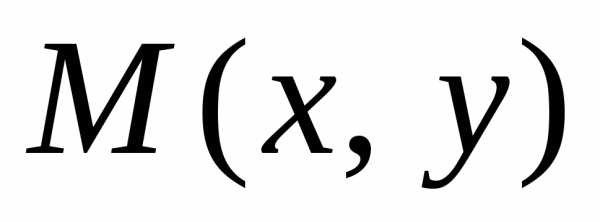 ,
лежащая на эллипсе, находится на
расстоянии
,
лежащая на эллипсе, находится на
расстоянии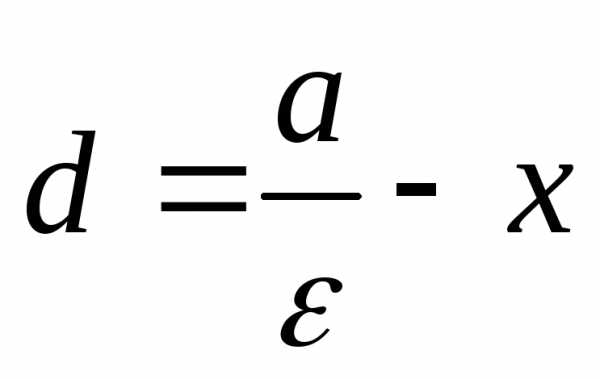 от рассматриваемой директрисы. Преобразуя
это равенство
от рассматриваемой директрисы. Преобразуя
это равенство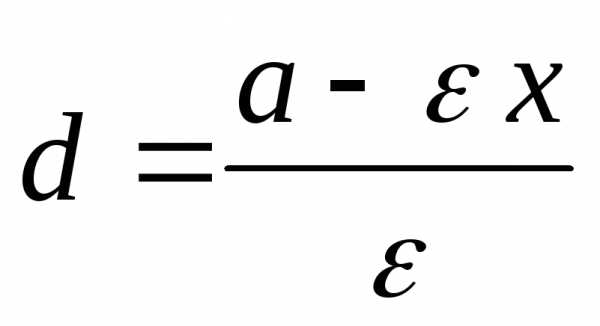 и замечая, что,
получим формулу
и замечая, что,
получим формулу (отношение фокального радиуса любой
точки эллипса к расстоянию между этой
точкой и соответствующей директрисой
есть величина постоянная, равная
эксцентриситету эллипса). Аналогичное
соотношение можно получить для другого
фокуса и другой директрисы.
(отношение фокального радиуса любой
точки эллипса к расстоянию между этой
точкой и соответствующей директрисой
есть величина постоянная, равная
эксцентриситету эллипса). Аналогичное
соотношение можно получить для другого
фокуса и другой директрисы. ).
).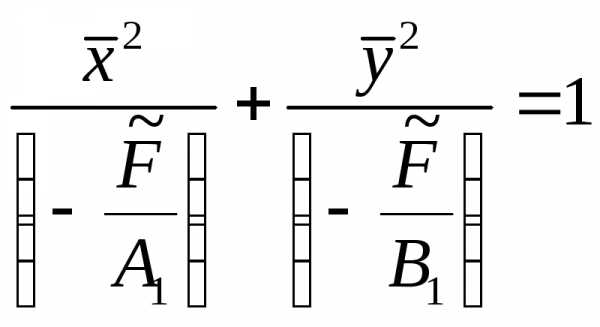 ,
,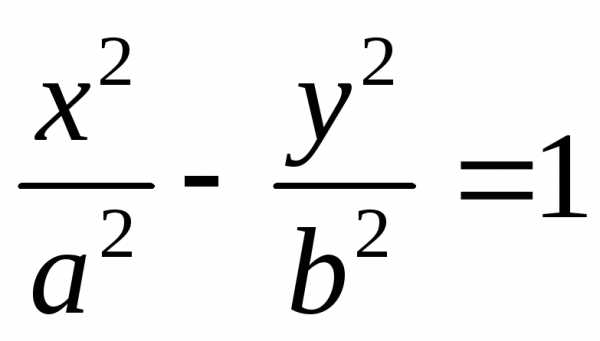

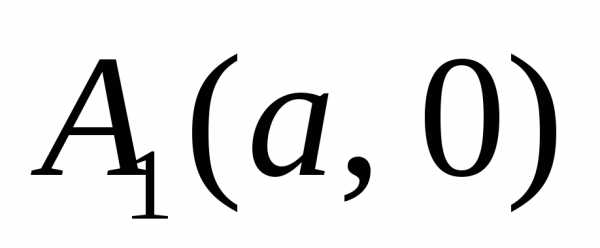 и
и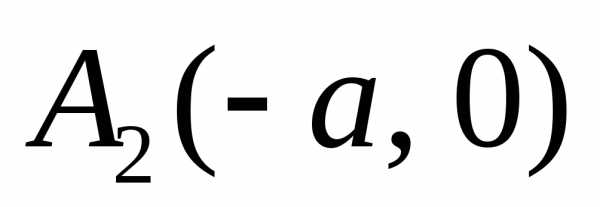 называютсявершинами
гиперболы,
а отрезок
называютсявершинами
гиперболы,
а отрезок 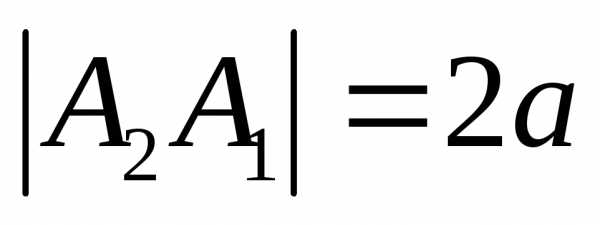 —действительной
осью гиперболы (
—действительной
осью гиперболы (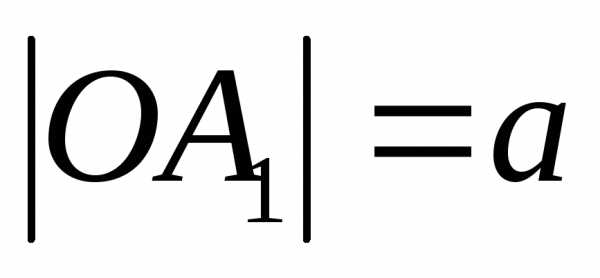 —действительной
полуосью гиперболы).
Точки
—действительной
полуосью гиперболы).
Точки  и
и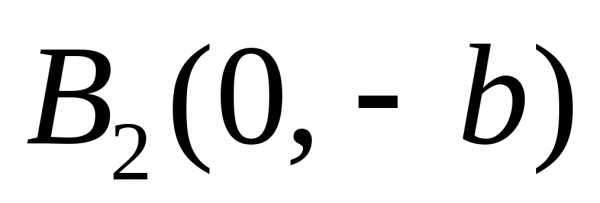 ,
лежащие на координатной оси
,
лежащие на координатной оси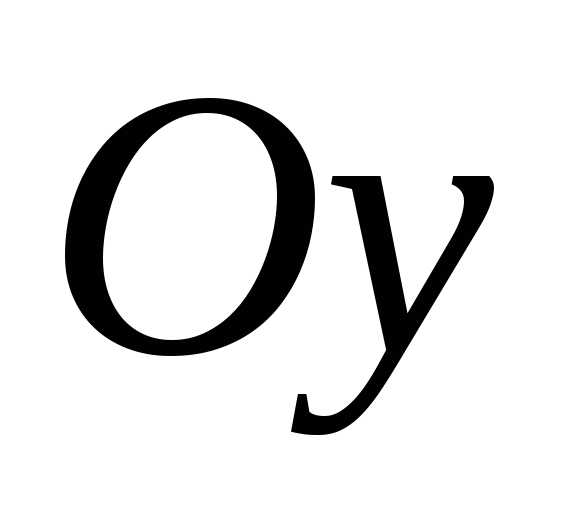 ,
можно назватьмнимыми вершинами
гиперболы,
а отрезок
,
можно назватьмнимыми вершинами
гиперболы,
а отрезок 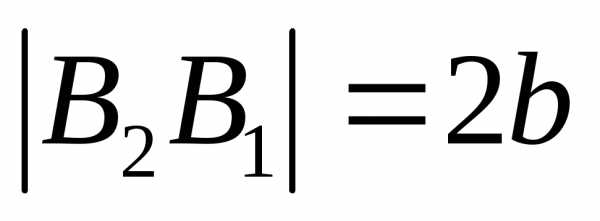 —мнимой
осью гиперболы (
—мнимой
осью гиперболы ( —мнимой
полуосью гиперболы).
Прямоугольник со сторонами
—мнимой
полуосью гиперболы).
Прямоугольник со сторонами 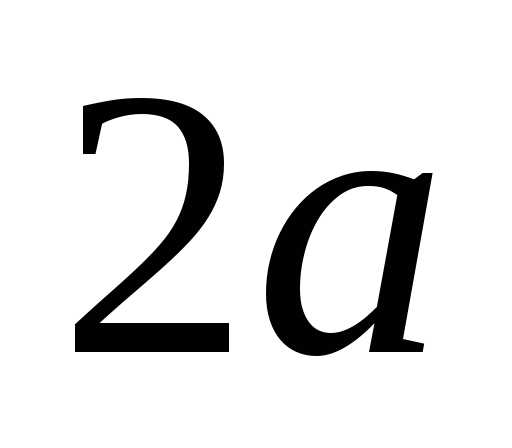 и
и ,
на которых лежат вершины гиперболы,
называютосновным
прямоугольником гиперболы. Прямые
,
на которых лежат вершины гиперболы,
называютосновным
прямоугольником гиперболы. Прямые 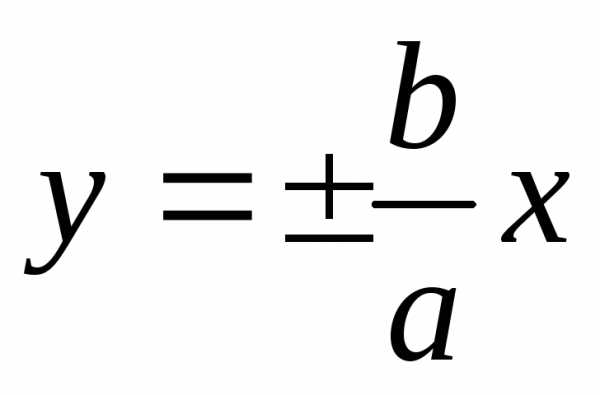 (частями которых являются диагонали
прямоугольника гиперболы) носят названиеасимптот
гиперболы.
Построение гиперболы удобно начинать
с построения прямоугольника и асимптот
гиперболы. Если
(частями которых являются диагонали
прямоугольника гиперболы) носят названиеасимптот
гиперболы.
Построение гиперболы удобно начинать
с построения прямоугольника и асимптот
гиперболы. Если 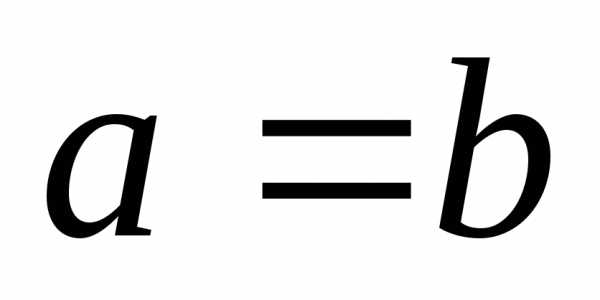 ,
то гипербола называетсяравносторонней,
ее уравнение имеет вид
.
Различаютправую
ветвь гиперболы (проходит
через вершину
,
то гипербола называетсяравносторонней,
ее уравнение имеет вид
.
Различаютправую
ветвь гиперболы (проходит
через вершину 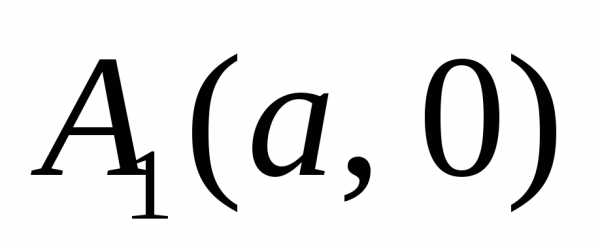 )
илевую
ветвь гиперболы (проходит
через вершину
)
илевую
ветвь гиперболы (проходит
через вершину 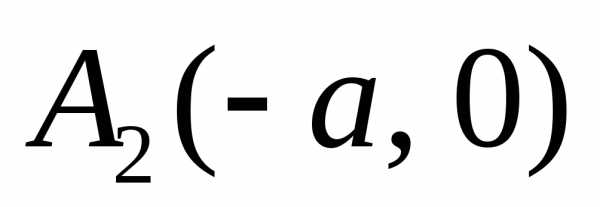 ).
). 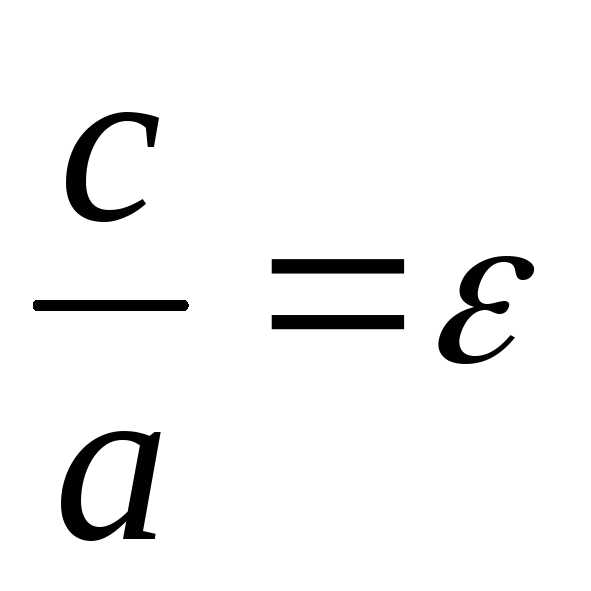 называетсяэксцентриситетом
гиперболы и
характеризует степень сжатости гиперболы.
Заметим, что
называетсяэксцентриситетом
гиперболы и
характеризует степень сжатости гиперболы.
Заметим, что 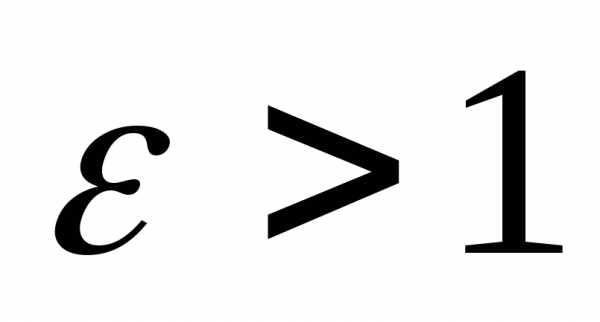 .
Отношение полуосей гиперболы является
функцией эксцентриситета
.
Отношение полуосей гиперболы является
функцией эксцентриситета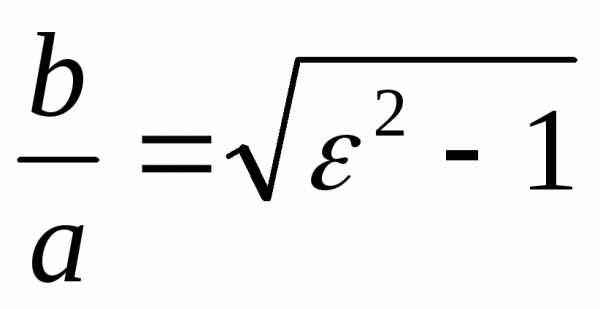 .
При
.
При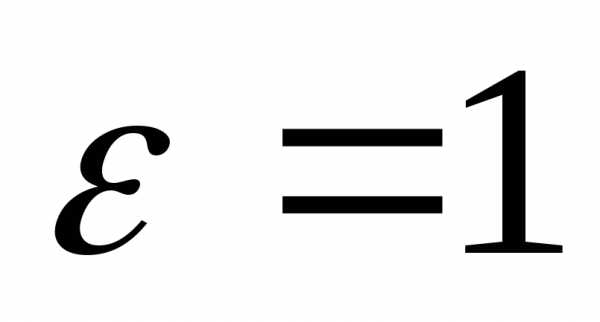 гипербола сжимается до двух лучей. При
росте эксцентриситета гипербола
«расправляется» и ее ветви стремятся
к прямым
гипербола сжимается до двух лучей. При
росте эксцентриситета гипербола
«расправляется» и ее ветви стремятся
к прямым .
.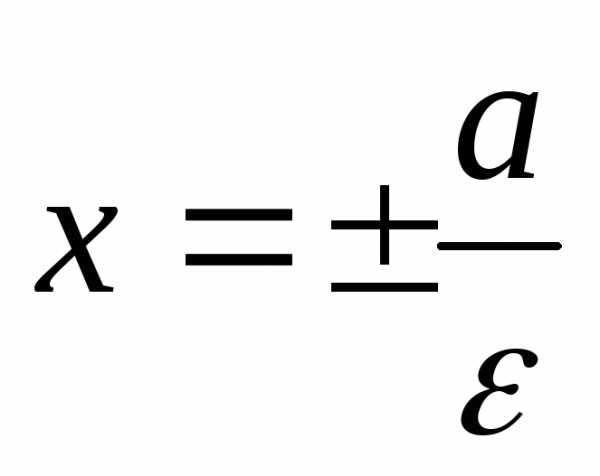 называютсядиректрисами
гиперболы.
Директрисы гиперболы имеют то же свойство
называютсядиректрисами
гиперболы.
Директрисы гиперболы имеют то же свойство 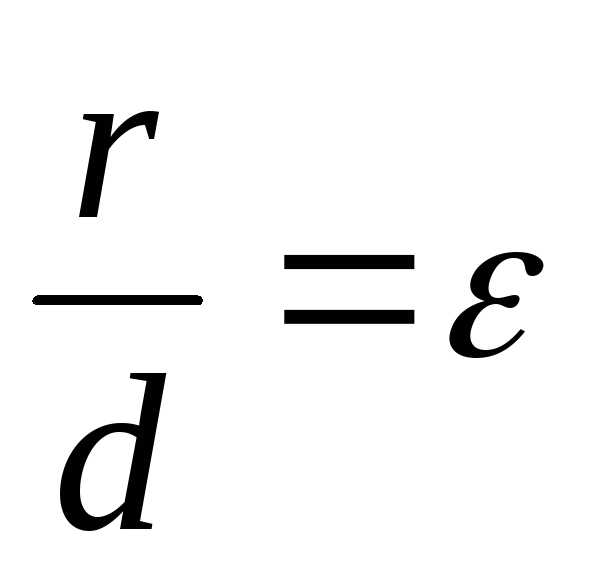 ,
что и директрисы эллипса.
,
что и директрисы эллипса.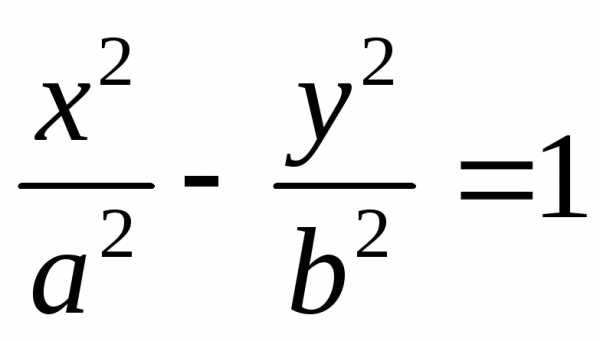 и
и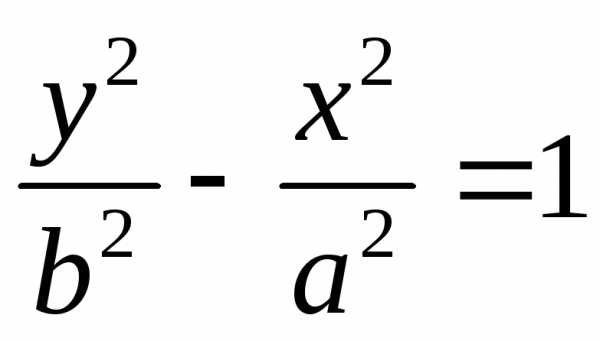 ,
имеющие разные действительные и мнимые
оси, но одинаковые асимптоты, называютсясопряженными гиперболами.
,
имеющие разные действительные и мнимые
оси, но одинаковые асимптоты, называютсясопряженными гиперболами. ).
).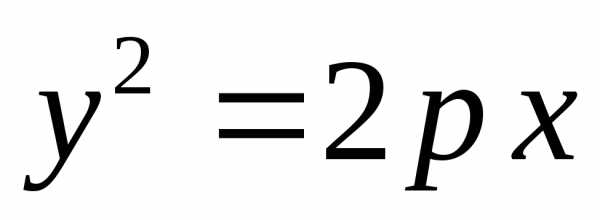 ,
,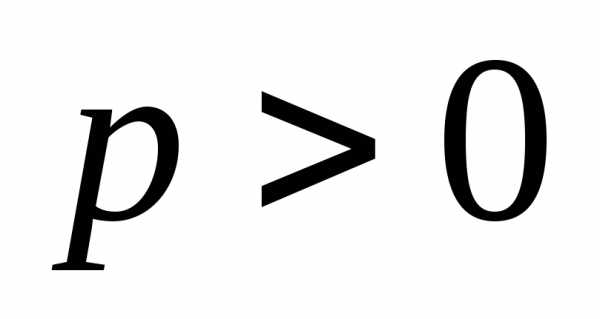 —параметр
параболы. Парабола
не является центральной кривой. Вершина
параболы находится в начале координат,
а фокус – в точке
—параметр
параболы. Парабола
не является центральной кривой. Вершина
параболы находится в начале координат,
а фокус – в точке 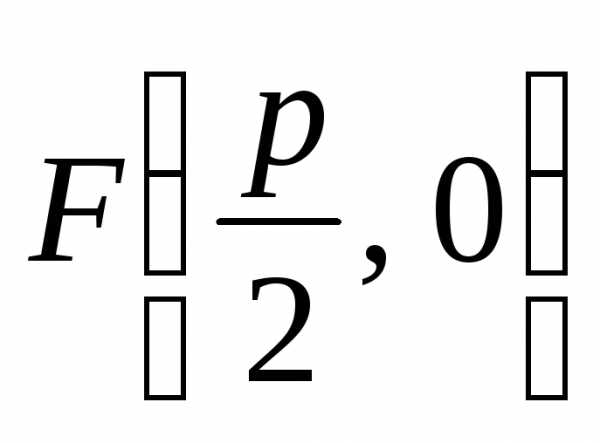 .
.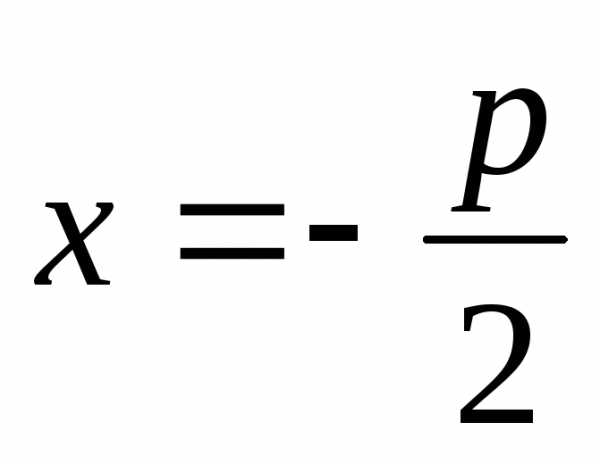 .
Ось
.
Ось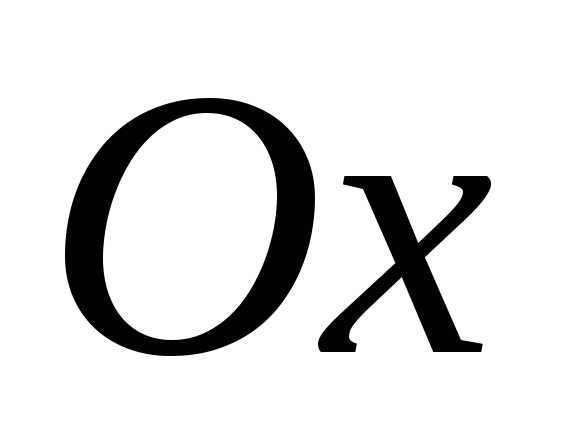 является осью симметрии параболы.
Фокальный радиус любой точки параболы
равен ее расстоянию до директрисы, т.е.
является осью симметрии параболы.
Фокальный радиус любой точки параболы
равен ее расстоянию до директрисы, т.е.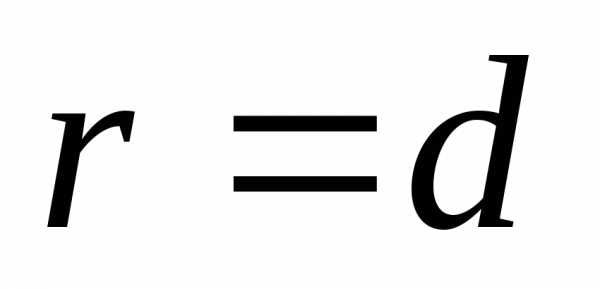 .
Об этом равенстве говорит геометрическое
определение параболы. Параболой
называется множество всех точек
плоскости, каждая из которых одинаково
удалена от данной точки, называемой
фокусом, и данной прямой, называемой
директрисой.
.
Об этом равенстве говорит геометрическое
определение параболы. Параболой
называется множество всех точек
плоскости, каждая из которых одинаково
удалена от данной точки, называемой
фокусом, и данной прямой, называемой
директрисой. из уравнения
из уравнения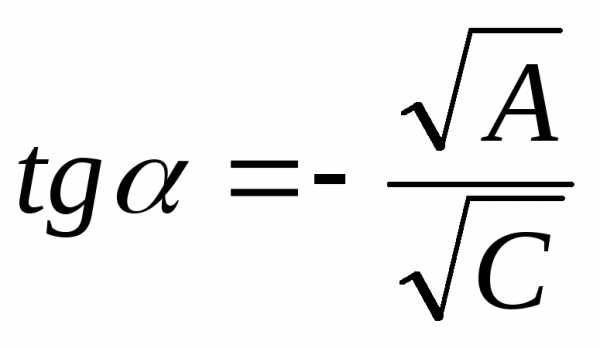 ,
можно обратить коэффициент
,
можно обратить коэффициент в нуль (если взять угол
в нуль (если взять угол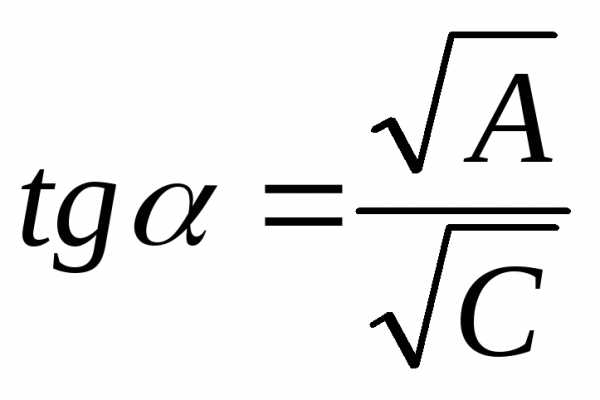 ,
то обратится в нуль
,
то обратится в нуль ).
В обоих случаях станет нулевым и
коэффициент
).
В обоих случаях станет нулевым и
коэффициент .
Далее совершая параллельный перенос
осей координат, можно найти координаты
вершины параболы и ее уравнение.
.
Далее совершая параллельный перенос
осей координат, можно найти координаты
вершины параболы и ее уравнение. ,
то общее уравнение кривой второго
порядка примет вид
,
то общее уравнение кривой второго
порядка примет вид ; 2) эллипс при
; 2) эллипс при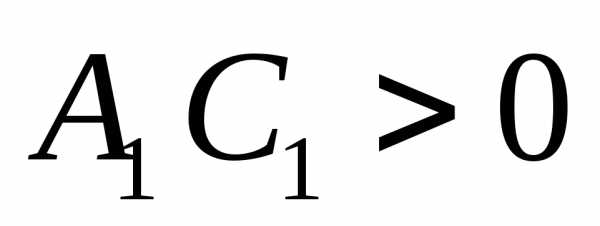 ;
;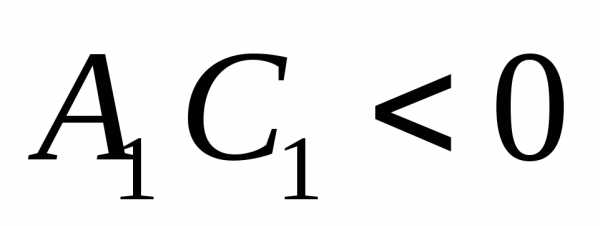 ;
;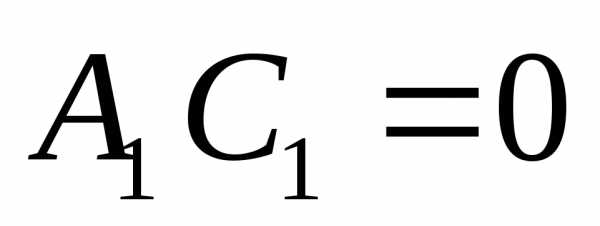 .
.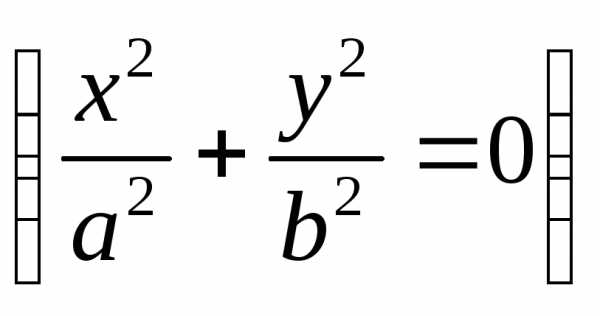 или в мнимый эллипс
или в мнимый эллипс ;
;






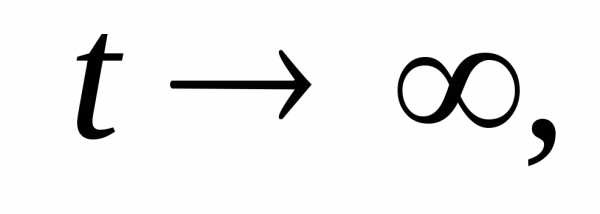
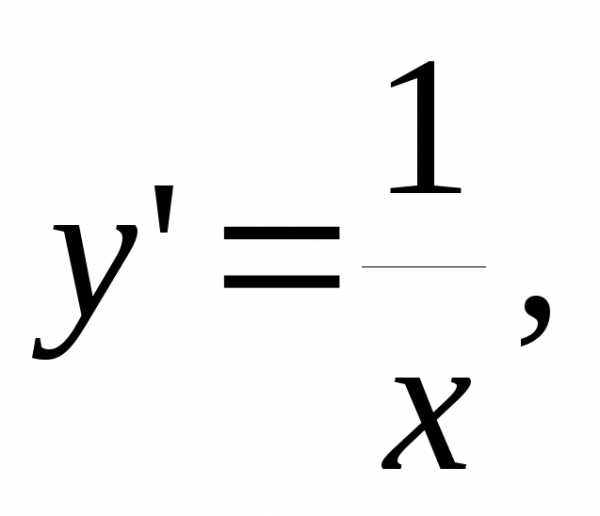
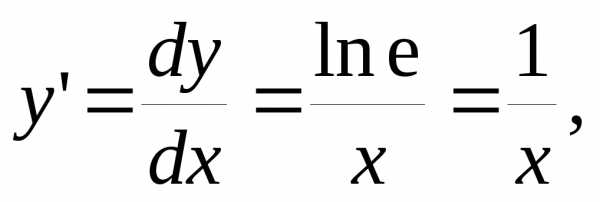 ри
имеем и видно, что
выражение под знаком логарифма есть
второй замечательный предел – числоe– основание натуральных логарифмов.
По определению,ln
e = 1,и
тогда : или, короче,
ри
имеем и видно, что
выражение под знаком логарифма есть
второй замечательный предел – числоe– основание натуральных логарифмов.
По определению,ln
e = 1,и
тогда : или, короче,