курс | Группа | Специальность | Задания |
1 | БД-18ф | Банковское дело | https://yadi.sk/d/htOHN-oycydhZA |
1 | ГС-18 | Гостиничный сервис | https://yadi.sk/d/6l8eHGwdywRbWA |
1 | ДОУ-18ф | Документационное обеспечение управления и архивоведение | https://yadi.sk/d/Po3sdkJ9eCz-AA |
1 | ДОУ-18 | Документационное обеспечение управления и архивоведение | https://yadi.sk/d/l8qmw4mUIUkIWw |
1 | ПС-18 | Почтовая связь | https://yadi.sk/d/9v166BEX3vx9yw |
1 | Ю-18ф | Право и организация социального обеспечения | https://yadi.sk/d/vBNcWC9GDDhHlA |
1 | Ю-18 | Право и организация социального обеспечения | https://yadi.sk/d/4XJR_LAURcplOg |
2 | ГС-17 | Гостиничный сервис | https://yadi.sk/d/HzlqaMurmZfYgQ |
2 | БД-17ф | Банковское дело | https://yadi.sk/d/xxkVRVYr_Lnc2A |
2 | БД-17 | Банковское дело | https://yadi.sk/d/ujFthuSf4sO5sw |
2 | ДОУ-17ф | Документационное обеспечение управления и архивоведение | https://yadi.sk/d/Gc_HsB4PKdTE_w |
2 | ДОУ-17 | Документационное обеспечение управления и архивоведение | https://yadi.sk/d/x-QJBixJvBjOkg |
2 | Т-17ф | Туризм | https://yadi.sk/d/FC6uPZiyn3i_qg |
2 | ПС-17 | Почтовая связь | https://yadi.sk/d/f19_I3RtgkUxPg |
2 | Ю-17ф | Право и организация социального обеспечения | https://yadi.sk/d/1qZGGcLCZsVZGg |
2 | Ю-17 | Право и организация социального обеспечения | https://yadi.sk/d/Bti91yQMQ9e7QQ |
3 | БД-16 | Банковское дело | https://yadi.sk/d/Pj_c18Wyl4esJw |
3 | ГС-16 | Гостиничный сервис | https://yadi.sk/d/nWsV4h-J6qbXkw |
3 | ДОУ-16 | Документационное обеспечение управления и архивоведение | https://yadi.sk/d/gP5RTDfEI7xxcw |
3 | ПС-16 | Почтовая связь | https://yadi.sk/d/A1uSqd8xJPD4bg |
3 | Ю-16 | Право и организация социального обеспечения | https://yadi.sk/d/vNgADJZqyhCz9A |
3 | ГС-16ф | Гостиничный сервис | https://yadi.sk/d/8nkEWzPcOI-VzQ |
3 | ДОУ-16ф | Документационное обеспечение управления и архивоведение | https://yadi.sk/d/cyzb_8DShv6_RQ |
3 | Ю-16ф | Право и организация социального обеспечения | https://yadi.sk/d/aqdnatI-LP9F6Q |
www.ikest.ru
Интерактивные, творческие, дополнительные задания для организации самостоятельной работы студентов
В самостоятельную работу студентов входит подготовка к семинарам, к опросам по изученному материалу, а также самостоятельное изучение по специальной литературе некоторых тем для понимания вопросов дефектологии.
Примерный перечень заданий для самостоятельной работы студентов
Изучение различных видов документации.
Работа со словарями и справочной литературой, учебными пособиями и периодическими психолого-педагогическими изданиями.
Выполнение учебно-исследовательского задания.
Подготовка выступления по заданной теме по нескольким источникам.
Составление краткого плана выступления, его тезисов.
Анализирование конкретных педагогических ситуаций, выделение проблем и дальнейшее предложение различных вариантов их решения.
Разработка конкретных методик изучения определенного педагогического явления, используя которые можно проанализировать полученные результаты.
Темы для самостоятельной работы
Темы для самостоятельной работы студентов ориентированы на актуальные проблемы специальной психологии и коррекционной педагогики; определяются в процессе собеседования преподавателя со студентами с целью максимального содействия развитию становлению профессиональной компетентности обучающегося. Самостоятельная работа студентов базируется на их собственном опыте, накопленном в ходе изучения практики работы педагога в учреждениях коррекционного типа.
Предметное содержание специальной педагогики и специальной психологии.
Понятие нормы и патологии в современных науках о человеке.
Понятие нарушенного (отклоняющегося) развития.
Причины отклонений в развитии и факторы, их определяющие.
Общие и специфические закономерности нормального и нарушенного (отклоняющегося) развития.
Модально-неспецифические закономерности нарушенного (отклоняющегося) развития.
Механизмы формирования системных отклонений.
Параметры и виды психического дизонтогенеза (В.В. Лебединский).
Система психолого-педагогического изучения детей с нарушенным (отклоняющимся) развитием.
Компенсация и коррекция, как основные категории специальной педагогики и специальной психологии.
Депривационные феномены в условиях нарушенного (отклоняющегося) развития.
Российская система специального (коррекционного) образования.
Социальная адаптация детей с нарушенным (отклоняющимся) развитием.
Педагогическая интеграция детей с нарушенным (отклоняющимся) развитием.
Семья, воспитывающая ребенка с нарушенным (отклоняющимся) развитием.
Олигофрения (устойчивое недоразвитие).
Задержка психического развития (задержанное развитие).
Нарушения основных школьных навыков (чтения, письма, счета).
Синдром дефицита внимания с гиперактивностью.
Общество и люди с ограниченными возможностями здоровья.
Методические указания для обучающихся по освоению дисциплины
Данный курс предполагает комплекс заданий в рамках аудиторной и самостоятельной работы. Оценка успешности освоения данного курса будет комплексной – по результатам работы на лекциях и семинарах, выполнении заданий по темам курса и по результатам внеаудиторной самостоятельной работы студента.
В ходе изучения данного курса студенту могут быть предложены различные виды заданий для самостоятельной работы и выступления на семинарах. По желанию студент может выбрать сам понравившееся задание и подготовить его.
При самостоятельном изучении вопросов студенту необходимо:
Внимательно прочитать и понять тему (проблему).
Подобрать учебную и научную литературу по изучаемой теме (проблеме).
Прочитать материал учебника, осмыслить полученную информацию.
Записать в тетрадь основные положения вопроса в виде тезисов.
Дополнить данные положения, обратившись к другим источникам.
Если при подготовке к занятиям встречаются вопросы, в понимании которых возникают затруднения, то необходимо получить консультацию у преподавателя.
Оформить собранный материал по вопросу и представить его преподавателю.
Задания для самостоятельной работы студентов:
Выполнение учебно-исследовательского задания.
Подготовка выступления по заданной теме по нескольким источникам.
Сравнение позиций инклюзивного и коррекционного образования.
Составление краткой аннотации прочитанного, плана выступления, его тезисов.
Анализ конкретных педагогических ситуаций, выделение проблем и дальнейшее предложение различных вариантов их решения.
Учебно-методическое и информационное обеспечение курса
а) основная литература:
Гонеев, А.Д. Основы коррекционной педагогики: учеб. пособие для студ. вузов, обучающихся по спец. «Педагогика» / А.Д. Гонеев, Н.И. Лифинцева, Н.. Ялпаева; ред. В.А. Сластенин. — 7-е изд., стер. — М.: Академия, 2011. — 268 с.
Специальная психология: учеб. для студ. пед. вузов, обучающихся по дефектологическим спец. / В.И. Лубовский [и др.]; ред. В.И. Лубовский. — 6-е изд., испр. и доп. — М.: Академия , 2009. — 557 с.
Специальная педагогика: учеб. пособие для студ. пед. вузов / Л.И. Аксенова [и др.]; Под ред. Н. М. Назаровой. — 10-е изд., стер. — М.: ACADEMiA, 2010. — 395 с.
б) дополнительная литература:
Воспитание и обучение детей и подростков с тяжелыми и множественными нарушениями развития / И. М. Бгажнокова [и др.]; ред. И. М. Бгажнокова. — М.: Владос, 2010. — 239 с.
Гилленбранд, К. Коррекционная педагогика: обучение трудных школьников: Учеб. пособие для студ. вузов / К. Гиллебранд. — 2-е изд. — М.: AcademiA, 2007. — 237 с.
Иванов, Е.С. Детский аутизм: диагностика и коррекция: учеб. пособие / Е.С. Иванов, Л.Н. Демьянчук, Р.В. Демьянчук. — СПб.: Дидактика Плюс, 2004. — 76 с.
Неретина, Т.Г. Специальная педагогика и коррекционная психология: учеб.-метод. комплекс / Т. Г. Неретина; Моск. психолого-соц. ин-т. — 2-е изд. — М.: Флинта : МПСИ, 2010. — 375 с.
Никишина, В.Б. Практическая психология в работе с детьми с задержкой психического развития: пособие для психологов и педагогов / В. Б. Никишина. — М.: Владос, 2003. — 126 с.
Обучение детей с нарушениями интеллектуального развития (олигофренопедагогика): учеб. пособие для студ. вузов / Под ред. Б.П. Пузанова. — 4-е изд., стер. — М.: AcademiA, 2008. — 269 с.
Программы специальных (коррекционных) образовательных учреждений VIII вида: 5-9 кл.: В 2 сб. Сб. 1 / В. В. Воронкова [и др.]; ред. В. В. Воронкова. — М.: Владос, 2010. — 223 с.
Программы специальных (коррекционных) образовательных учреждений VIII вида: 5-9 кл.: В 2 сб. Сб. 2 / С.Л. Мирский [и др.]; ред. В.В. Воронкова. — М.: Владос, 2010. — 223с.
Ратнер, Ф.Л. Интегрированное обучение детей с ограниченными возможностями в обществе здоровых детей: научное издание / Ф.Л. Ратнер, А.Ю. Юсупова. — М.: Владос, 2006. — 175 с.
Специальная семейная педагогика. Семейное воспитание детей с отклонениями в развитии: учеб. пособие / Н. А. Борисова [и др.]; ред.: В.И. Селиверстов, О.А. Денисова, Л.М. Кобрина. — М.: Владос, 2009. — 358 с.
в) перечень ресурсов информационно—телекоммуникационной сети «Интернет» и ЭБС
http://lib.herzen.spb.ru – Фундаментальная библиотека РГПУ им. А.И. Герцена
Каталог образовательных интернет-ресурсов: http://www.edu.ru/index.php?page_id=6 Библиотека портала: http://www.edu.ru/index.php?page_id=242
Научная электронная библиотека eLIBRARY.RU:http://elibrary.ru/defaultx.asp
Гуманитарная электронная библиотека: http://www.lib.ua-ru.net/katalog/41.html
Научная онлайн-библиотека Порталус: http://www.portalus.ru/
Библиотека Гумер: http://www.gumer.info/
Служба Twirps.com:http://www.twirpx.com/about/
Электронная библиотека учебников. Учебники по педагогике: http://studentam.net/content/category/1/2/5/
Интернет библиотека электронных книг Elibrus:http://elibrus.1gb.ru/psi.shtml
г) информационные технологии, используемые при осуществлении образовательного процесса по дисциплине (модулю), включая перечень программного обеспечения и информационных справочных систем
программное обеспечение–PowerPoint,AdobeAcrobat
Материально-техническая база
мультимедиа проектор, компьютер.
Приложения:
studfiles.net
Упражнения для тренинга со студентами
Упражнение «Превращаем проблему в цели»
Цель: выявить проблемы, существующие у студентов при взаимодействии с социальным окружением, и переформулировать их в цели.
Количество участников: 15-20 человек.
Время проведения: 30-45 минут.
Материальное обеспечение: ручки, бумага писчая, вопросы для каждого участника.
Ход занятия:
Педагог предлагает студентам составить список проблем, которые они хотели бы как можно быстрее разрешить.
В составлении списка проблем им могут помочь следующие вопросы:
1.Что я действительно хочу сделать, что иметь, чего достичь?
2.Что еще может доставить мне удовольствие?
3.В каких сферах жизни я хотел бы усовершенствовать свои способности?
4.Что в последнее время занимало мои мысли, волновало или сердило меня?
5.На что я чаще всего жалуюсь?
6.Что создаст мне больше всего забот?
7.Что заставляет меня чувствовать себя тревожно или напряженно? Что дает мне возможность чувствовать себя уютно?
8.Что меня больше всего расстраивает?
9.Что стало в последнее время меня раздражать?
10.Что я хотел бы изменить в моем отношении к самому себе?
11.Что мне надо изменить в себе?
12.На что у меня уходит слишком много времени?
13.Что мне очень сложно сделать? От чего я быстро устаю?
14.Как я мог бы лучше распределять свое время?
15.Как я мог бы разумнее расходовать свои деньги?
Затем студенты выбирают и описывают проблему, которую они хотели бы решить прежде всего и представляют ее как можно более объективно.
После описания проблемы участники формулируют цель, которой они могли бы достичь, и отвечают на следующий вопрос: «Что мне необходимо сделать для того, чтобы моя проблема перестала существовать или, по крайней мере, стала менее острой?».
Упражнение «Заверши фразу»
Цель: выявить имеющиеся представления по обсуждаемой теме; проанализировать опыт взаимодействия с социальным окружением.
Количество участников: до 25 человек.
Время проведения: 20 минут.
Ход занятия:
Педагог предлагает студентам завершить ряд фраз, касающихся темы или содержания, атмосферы, организации взаимодействия.
Педагог может предложить студентам завершить следующие фразы:
— «Думаю, что настоящий друг…»;
— «Студенты, с которыми я учусь…»;
— «Моими сильными сторонами взаимодействия являются…»;
— «В процессе взаимодействия с людьми…»;
— «По отношению человека к человеку можно судить о…» и т.д.
Метод реализуется следующим образом: педагог произносит незавершенную фразу и указывает на участника, которому предлагает ее завершить. С одной и той же фразой педагог может обращаться к двум – трем студентам. Желательно, чтобы каждый завершил хотя бы одну фразу.
Упражнение «Контакты»
Цель: развивать умение устанавливать и поддерживать контакты с людьми.
Время проведения: 30-60 минут.
Количество участников: до 15 человек.
Ход занятия:
Педагог предлагает студентам разыграть некоторые ситуации.
Примерные ситуации:
«Перед вами человек, которого вы видите первый раз, но он вам очень понравился и вызвал желание с ним ознакомиться. Некоторое время вы раздумываете, а затем обращаетесь к нему. Время на установление контакта, приветствие и проведение беседы – 2-3 минуты».
Затем по сигналу педагога студенты должны в течение 1 минуты закончить начатую беседу, попрощаться и перейти вправо к новому участнику.
Эти правила распространяются и на нижеследующие ситуации:
«В вагоне метро вы случайно оказались рядом с довольно известным киноактером. Вы обожаете его, и, конечно, хотели бы с ним поговорить. Ведь это такая удача». Роль актера играют сидящие во внутреннем круге студенты.
«Вам нужна довольно крупная сумма денег. Нужно поговорить с родителями. И вот вы подошли к отцу (матери)».
«Вы узнали, что один из ваших друзей дурно отзывался о вас в неформальной обстановке. Надо с ним поговорить. Конечно, это не очень приятно, но лучше сразу все выяснить, чем строить догадки и переживать по этому поводу. Случай представился: вы одни, никого рядом нет».
Примечание:
— педагогу следует обратить внимание всех участников на то, как ни вступают в контакт, начинают встречу, какие приемы и способы коммуникации используют, как поддерживают разговор и заканчивают беседу;
— после очередной смены партнеров, задавая ситуацию, педагог определяет конкретные роли для каждого круга. Например, во внешнем круге участники играют роль родителей, во внутреннем – детей;
— задача педагога в этом упражнении – подобрать такие ситуации, чтобы было интересно решать поставленную проблему.
Ролевая игра «Ребятушки-козлятушки»
Цель: определить успешные стратегии поведения при взаимодействии.
Количество участников: до 20 человек.
Время проведения: 30-50 минут.
Ход занятия:
Педагог напоминает студентам старую сказку про волка и семерых козлят, а затем распределяет роли среди участников.
Группа разделяется на две части: одни играют роль «козлят-экспертов», другие – «претендентов», пытающихся убедить «козлят» в своей благонадежности.
Задача «козлят» — в диалоге с претендентом на попадание к ним в дом понять, действительно ли этот неизвестный является тем, за кого себя выдает, или это «волк». Из нескольких претендентов «козлята» должны выбрать тех, кто на самом деле получил роль «мамы-козы», «брата», «дяди-козла» и прочих некровожадных родственников.
«Претенденты» имеют скрытые задания не забывать о том, что они «волки», «лисы», «тигры» и т.д.
Однако эти задания надо от «козлят» скрывать. Каждый «претендент» должен сообщить коллегам о выбранном им образе.
Для того, чтобы убедить «козлят» в своей благонадежности, предоставляется фиксированное время. «Претендент» может говорить и делать все, что угодно, «козлята» тоже могут разговаривать с ним и между собой на любые темы. По истечении заданного времени «козлята» решат, можно ли пускать «претендента» в дом. В любом случае «претендент» не раскрывает свою роль до окончания игры.
Обсуждение итогов игры.
«Претенденты» раскрывают свои роли. Своими впечатлениями делятся сначала те, кто получил отказ. Затем обсуждаются действия тех, кто добился успеха.
Игра «Гороховый король».
Цель: развивать коммуникативные умения; развивать речь; создать благоприятную атмосферу.
Количество участников: до 20 человек.
Время проведения: до 30 минут.
Материальное обеспечение: горох (по 5 штук каждому участнику).
Ход занятия:
Каждому студенту раздается по пять горошин. Студенты ходят по аудитории и вступают друг с другом в разговор. Встречаясь, им необходимо друг другу по очереди задавать такие вопросы, чтобы в ответ они услышали слово «Да» или «Нет».
Если студент, отвечающий на вопрос, произносит одно из этих слов, то отдает собеседнику одну горошину. После этого они расходятся и ищут следующих партнеров для разговора.
У кого горошины закончились, тот выбывает из коммуникации. У кого после завершения будет самое большое количество горошин, тот – «Гороховый король».
Взаимодействуя, студентам необходимо выполнять следующие правила:
— нельзя молчать;
— нельзя избегать контакта и уходить от вопроса.
Метод «Пустой стул»
Цель: расширить представления студентов по обсуждаемой теме; обратить внимание на разнообразие мнений, точек зрения на предложенную тему; развить умение студентов осуществлять выбор и аргументировать его.
Количество участников: до 25 человек.
Время проведения: 40-50 минут.
Материальное обеспечение: листы бумаги с написанными тезисами.
Ход занятия:
Педагог выбирает тему, готовит 4 высказывания, представляющие разные точки зрения на обсуждаемый вопрос и расставляет мебель по кругу. Каждое высказывание записывает на отдельном большом листе бумаги и размещает на полу, образуя круг. Все студенты встают и, переходя от листа к листу, знакомятся с содержанием высказываний. Затем каждый из них выбирает то высказывание, с которым согласен, и садится возле него. Таким образом, создаются малые группы для дискуссии.
Каждая группа в течение 10-15 минут обсуждает содержание высказывания, фиксируя аргументы, подтверждающие ее выбор.
После обсуждения в малых группах перед каждой из них ставится один стул, на который садится представитель группы, чтобы высказать совместно выработанное мнение по обсуждаемой теме и начать дискуссию Время выступления – 2-3 минуты.
Завершив выступление, он возвращается к малой группе. Каждый студент может продолжить дискуссию, высказывая свое мнение, поддерживая аргументами позицию группы или подчеркивая неточности предыдущих вступлений. Для того, чтобы включиться в обсуждение, он должен занять пустой стул, стоящий перед его малой группой. Студент может занять пустой стул только один раз.
Педагог завершает дискуссию за 5 минут до конца занятия, чтобы подвести итоги работы групп.
Примечание:
— количество высказываний не должно превышать четырех;
— при наличии у студентов затруднений в определении своей позиции, педагог может предложить выбрать то высказывание, которое согласуется с его убеждениями;
— при большом количестве студентов в малых группах и желании активного участия всех членов команды, педагог может ограничивать время выступления представителей команд.
Упражнение «Плохо — хорошо»
Цель: развить умение объективно оценивать ситуацию взаимодействия.
Количество участников: до 25 человек.
Время проведения: 30-40 минут.
Материальное обеспечение: писчая бумага, ручки.
Ход занятия:
Каждый студент получает лист бумаги и ручку.
Педагог предлагает студентам вспомнить проблему, ситуацию, которая из тревожит (например, сдача экзаменов, неприятный разговор и т.д.).
Студенты делят листок на две половины. Слева они записывают 10 позиций-аспектов жизненной проблемы, которые имеют негативные последствия для них, справой стороны – 10 позиций, в которых отмечены положительные стороны данной ситуации.
При обсуждении упражнения педагог показывает, что в каждой жизненной ситуации необходимо уметь находить положительные стороны, за счет этого сохранять самообладание и спокойствие.
Упражнение «Три ответа»
Цель: развить умения определять адекватный способ поведения при взаимодействии.
Количество человек: до 15 студентов.
Время проведения: 30-50 минут.
Ход занятия:
Каждый студент придумывает ситуацию, в которой ему приходится отвечать воображаемому собеседнику. Эту ситуацию он сообщает группе, а потом демонстрирует три варианта ответов. Один из вариантов должен демонстрировать уверенное поведение, второй – агрессивное, напористое, наступательное, третий – неуверенное.
Все три варианта демонстрируются без предварительного предупреждения о том, какой конкретно вариант сейчас будет показан. После показа свои впечатления об услышанном и увиденном варианте ответа сообщает группа.
Каждый из студентов должен поделиться своими догадками по поводу того, какой из трех вариантов прозвучал. Можно раздать карточки с кратко изложенными ситуациями, например:
1.В автобусе проверка билетов. У вас по каким-то причинам билета нет. К вам подходит контролер. Вы говорите ему…
2.Собака вашего соседа испортила ваш половик. Вы звоните в дверь соседа. Он показывается на пороге. Вы говорите ему…
3.Преподаватель задает вам вопрос, который вы прослушали. Вы отвечаете ему…
4.Группа молодых веселых людей в кинотеатре мешает вам громким разговором. Вы обращаетесь к ним…
5.Ваш сосед настаивает на том, чтобы вы переключили телевизор на другую программу, где идет многосерийный фильм (спортивная передача), а вы смотрите то, что нравится вам. Вы говорите ему…
6.Ваш приятель не отдал вам в назначенный срок взятые в долг деньги. Вы говорите…
7.В поликлинике какой-то тип прорывается к врачу вне очереди. Все молчат. Вы говорите…
8.Родители просят сходить вас в магазин. Вы устали. Вы говорите им…
Упражнение «Шаг навстречу»
Цель: развить умение студентов делать комплимент, говорить приятное.
Количество участников: до 15-20 человек.
Время проведения: 30-40 минут.
Ход занятия:
Педагог просит двух студентов (это в данном случае важно) выйти к доске и стать лицом друг к другу с разных сторон.
Затем педагог дает им следующее задание: сделать шаг навстречу друг другу и сказать что-либо приятное. Студенты шагают до тех пор, пока не приблизятся друг к другу.
Примечание:
Обычно само задание вызывает смех среди присутствующих и смущение тех, кто стоит перед аудиторией.
Иногда кто-нибудь из студентов предлагает: «Попросите их говорить неприятное, они пойдут быстрее». После этой реплики педагогу необходимо обратиться ко всем студентам с просьбой проанализировать увиденное и услышанное.
Вернуться на главную сайта Личностный рост и саморазвитие
| < Предыдущая | Следующая > |
|---|
mirrosta.ru
Задания для студентов с первыми буквам фамилий: А-Й
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Семинар 4 Перспективы развития права международных организаций как отрасли международного права (семинарское занятие)
Цели:целью семинарского занятия является усвоение студентами понятия, значения и особенностей международно-правовых норм, регламентирующих статус межправительственных организаций и межправительственных органов, структуру, полномочия и порядок деятельности органов, юридическую силу их актов. Цель занятия состоит также в выработке у студентов умения чётко различать правовой статус межправительственных и неправительственных организаций.
Задачи:задачей семинарского занятия является приобретение студентами практических навыков раскрывать содержание основных международных конвенций. Кроме того, задача занятия состоит в усвоении студентами правила, что право международных организаций состоит из двух частей : внутреннего и внешнего права.
План:
1. Право международных организаций как самостоятельная отрасль международного права.
2. Правовая природа международных конференций. Юридическое значение решений международных конференций.
3. Правовая природа международных организаций как важной юридической формы международного сотрудничества государств.
4. Виды международных организаций.
5. Организация Объединенных Наций. Цели и принципы. Членство. Система органов ООН, их компетенция. Проблема повышения эффективности ООН.
6. Правовой статус специализированных учреждений ООН.
7. Региональные международные организации.
8. Европейский Союз.
9. Содружество независимых государств.
10. Всемирная торговая организация.
Задания для студентов с первыми буквам фамилий: А-Й
Темы рефератов, эссе, презентаций :
1. Всемирная торговая организация, её роль в развитии международного экономического права.
2. Роль решений международных организаций в регулировании международных экономических отношений.
3. Совершенствование и модификация ГАТТ. ГАТТ 1994 г.
4. Передача государствами своих полномочий в компетенцию международных экономических организаций.
5. Правовая природа НАТО.
6. Международный Суд ООН.
7. Европейский Союз: международно-правовая характеристика
8. Интерпол и Европол как межведомственные организации
9. Компетенция Генеральной Ассамблеи.
10. Компетенция Международного суда ООН.
11. Компетенция Совета Безопасности, порядок принятия решений.
12. Компетенция ЭКОСОС, система органов и порядок принятия решений.
13. Консенсус как метод принятия решений в международных организациях.
14. Критерии членства в международной организации
15. Лига арабских государств: правовые проблемы деятельности
16. Лига наций: правовые проблемы деятельности
17. МВФ: правовые проблемы деятельности
Индивидуальные домашние задания:
№1
Тема задания:подготовка письменного заключения
Описание задания: Подготовьте письменное заключение по вопросу о том, законно ли было принятие Палестинской Администрацией в Специализированное учреждение ООН- ЮНЕСКО. Вопросы для письменного заключения составляются по конкретным фактическим обстоятельствам. При составлении заключения обучающимся необходимо квалифицированно применить нормы международного права. Заключение должно быть развернутым с убедительной аргументацией сделанных выводов.
№2
Тема задания:докажите, чья позиция была правильной и соответствующей принципам и нормам международного права
Описание задания: Совет Безопасности ООН на своём заседании обсуждал вопрос о военном вмешательстве в Сирию. За принятие такой резолюции проголосовали США, Франция и Великобритания, а Россия и Китай, обладая правом «вето» как постоянные члены Совета Безопасности ООН, проголосовали «против» и решение принято не было. Обоснуйте со ссылкой на конкретные статьи Устава ООН и других международно-правовых актов правомерность позиций России и Китая, применивших право «вето» при решении данного вопроса.
№3
Тема задания:проведите различие между международной межправительственной организацией и интеграционным объединением
Описание задания: Проведите различие между международной межправительственной организацией как, например, ООН и интеграционным объединением, к примеру, Европейский Союз. Что более приемлемо для государств-участников : быть членом международной организации или участником интеграционного объединения? Обоснуйте , ограничивает ли суверенитет государства его участие в интеграционном объединении. Что больше способствует унификации национального права государств-участников , их вхождение в международные организации или интеграционные объединения? Что больше даёт развитию экономики государства его членство в международной организации или участие в интеграционном объединении?
№4
Тема задания:приведите доказательства в пользу вступления или не вступления РФ в ОПЕК.
Описание задания: В соответствии со своим уставом органы ОПЕК (Организации государств — поставщиков нефти) вправе принимать решения о приостановке или сокращении размера добычи нефти. Три нефтедобывающих страны: Россия, Венесуэла и Норвегия не являются членами ОПЕК и самостоятельно принимают решения о размерах добычи нефти, о партнёрах по поставке нефти и о цене на нефть. Должностные лица ОПЕК выразили неудовольствие по поводу такой позиции этих государств и обратились к ним с просьбой уменьшить объём добываемой нефти. Аргументируйте со ссылками на конкретные статьи соответствующих международно-правовых актов правомерность позиций: с одной стороны должностных лиц ОПЕК, а с другой стороны правительств трёх, не входящих в ОПЕК нефтедобывающих стран: России , Венесуэлы, Норвегии.
№5
Тема задания:Сформулируйте рекомендации по оптимизации процедуры оспаривания частными лицами распространения на них действия решений Совета Безопасности ООН.
Описание задания: 21 марта 2011 года все финансовые средства, находящиеся на банковских счетах ООО «Адиак» были заморожены. Руководство ООО «Адиак» не согласно с предоставленными объяснениями. В российских официальных инстанциях, куда обратилось руководство ООО «Адиак» за разъяснениями, было сообщено, что в отношении ООО «Адиак» были выполнены требования ряда резолюций СБ ООН — 1267 (1999), 1333 (2000), 1390 (2002) о блокировании финансовых активов, находящихся под контролем, в том числе косвенным, террористической организации «Аль-Каида». Данное хозяйственное общество было включено в Сводный перечень, предусмотренный указанными резолюциями, поскольку по полученной компетентными органами информации соответствовала названному выше признаку. Руководство ООО «Адиак» категорически не согласно с возложенными на ООО обвинениями и примененными к нему мерами. Со ссылкой на документы ООН укажите, какие действия должны быть предприняты руководством ООО «Адиак» по исключению ООО «Адиак» из Сводного перечня и последующему размораживанию его финансовых активов.
Список используемой литературы:
1. Международное право ( общая часть) .Учебник. Изд-во «Статут»,Казань 2013 г.
2. Международное публичное право. Учебник. Издание пятое переработанное и дополненное. Отв. ред. д.ю.н., проф. Бекяшев К.А., М., изд-во «Проспект», 2013.
3. Международное право. Учебник. Под ред. А.Н. Вылегжанина. М. «ЮРАЙТ», 2013.
4. Международное право. Учебник. 3-е издание. Отв. ред. Кузнецов В.И., Тузмухамедов Б.Р., изд-во «Норма» М., 2012
5. Марченко М.Н. Основные принципы организации и деятельности судебной системы Европейского Союза // «Российское правосудие».,2010, №3
6. Организация Объединённых Наций и защита прав человека; под ред. А.Х. Абашидзе.//ГОСУДАРСТВО И ПРАВО №8 // 2011.
7. Моисеев Е.Г. СНГ и ЕврАзЭС : история и современность– Российский ежегодник международного права, Спб., 2012.
8. Жело В.В Право международных организаций//Учебное пособие. ЮФУ 2010.
9. Князькин С.А. – Отдельные аспекты защиты прав человека через механизм ООН// Российский ежегодник международного права, Спб., 2012.
10. Замятин В.Ю. Современные аспекты ответственности международных организаций // Московский журнал международного права. — М.: Междунар. отношения, 2004, №3.
11. Рачков И.В. Ответственность государства за деяния международной организации // Вестник Московского университета. — М.: Изд-во Моск. ун-та, 2006, № 1.
12. Якушев Ю.В. К вопросу о соотношении правосубъектности международных межправительственных организаций и их способности нести ответственность за международно-противоправные деяния // Международное право — International Law. — М.: Изд-во РУДН, 2007, № 3 (31).
13. Якушев Ю.В. Проекты статей об ответственности международных организаций // Вестник Российского университета дружбы народов. Серия: Юридические науки. — М.: Изд-во РУДН, 2006, № 3 (21).
14. Гвоздецкий Д.С. Консультативное заключение Международного Суда ООН (1949) — важный этап становления института дипломатической защиты международных организаций // Закон и право. — М.: ЮНИТИ-ДАНА, 2008, № 6.
15. Кургузова Я.С. Международно-правовое регулирование защиты сотрудников международных организаций // Законодательство и экономика. — М., 2003, № 3.
16. Митрофанов М.В. Привилегии и иммунитеты служащих международных организаций // Вестник Московского университета. — М.: Изд-во Моск. ун-та, 1981, № 2.
17. Капустин А.Я. Организация Объединенных наций и развитие современного международного права (к 60-летию ООН) // Вестник Российского университета дружбы народов. Серия: Юридические науки. — М.: Изд-во РУДН, 2005, № 2 (18).
18. Малеев Ю.Н. Организация Объединенных Наций — 60 лет. Сколько еще? // Международное право — International Law. — М.: Изд-во РУДН, 2005, № 3 (23).
19. А. Кутейников//Новое в исследовании международных организаций// Журнал теории международных отношений и мировой политики. №1(32), 2013 г.
megapredmet.ru
Задания для студентов.docx — Сценарий внеклассного мероприятия «Конкурс знатоков …
189. 5 тур (9+2)
190. «Текстовый марафон»
191.
(1)Пасхальная ночь! (2)Все уходили из дома, дети оставались одни с няней
и гувернанткой. (3)Ночь была — как пещера: пустая, но полная ожиданием часа, когда
прокатится над Москвой и Москвойрекой первый удар колокола, с колокольни Ивана
Великого. (4)И, кидаясь в его голос, заждавшимся трепетом своих голосов все
колокола Москвы и всех московских окрестностей заголосят, заликуют неслыханным
хоровым трезвоном, испуская в чёрную, как глухое сукно, ночь такое количество
звуков, что, перегоняя все горелки детских игр и все симфонические концерты
старших, перезванивая колокольным сияющим щебетом все колокольчики русских
дорог и все весенние рощи, звуки, захлебнувшись собой, вырвутся из своего царства. (5)
И тогда над Москвойрекой полетит к ним на помощь воинство царства соседнего —
слепящее серебро, золото, олово, медь, слившиеся, жар всех Жарптиц всех русских
сказок, и, взлетая вверх, под тучи, обронит в холодные весенние воды, окаймлённые
огоньками, перья всех цветов и красок со всех художнических палитр.
192.
(6)Помосковски это называлось — «ракеты». (7)А вокруг Царьпушки царята
всех пушек, не в силах стерпеть, выпустят на свободу из жерл ядра свои
суворовским и кутозовским грохотами, — и уж ничего нельзя будет понять, ни
увидеть, ни услыхать…
193.
(8)Припав к окнам с открытыми форточками и подрагивая от холода, мы,
тайно или с доброго разрешения вскочив с постелей, ждали, когда вспыхнет
кремлёвским заревом темнота над крышами Палашевского переулка. (9)Тогда и свой
голос подаст оттуда ближняя наша церковка.
194.
(10)Но во дворе раздавались голоса и шаги, и мы, забыв запрет, сон, всё, —
кидались навстречу объятьям, пасхе, куличу и подаркам. (11)И свежий, весенний,
пахнущий землёй воздух, ворвавшийся со двора со взрослыми!
195.
(12)Бледным золотом апрельских лучей наводненная зала, парадно накрыт
стол, треугольник (как ёлка!) творожной пасхи, боярскими шапками (бобрового меха!)
куличи, горшки гиацинтов, густо пахнущих, как только сирень умеет, и таких
невероятных окрасок, точно их феерическая розовость, фиолетовость, голубизна —
приснилась. (13)Но они стоят на столе! (14)Ярмарочное цветение крашеных яиц, и
огромный, сердоликом (чуть малиновее) окорок ветчины.
196.
(15)Как горели лбы (тайком, нагнувшись под стол, о них разбиваемых
крутых яиц — подражание Андрюше), как пряно пахло от ломтей кулича, как
пачкались в выковыривании изюминок и цукатов пальцы и как, противной горой,
наваливалось пресыщение, когда крошка самого вкусного отказывалась лезть в рот!
(16)Каплями янтаря и рубина остатки вин в отставленных рюмках! (17)И ненасытное
счастье безраздельного обладания: новые книги, новые цветные карандаши, новые
перочинные ножи, шкатулки, альбомы, новые яйца: стеклянные, каменные, фарфоровые
— не считая бренности шоколадных, сахарных…
197.
(По А.И. Цветаевой*)
198.
199.
10
znanio.ru
Задания для студентов
(с использованием Интернет, справочной и учебной литературы).
Подготовить мини-справку об историческом термине.
Ознакомиться с сочинением на историческую тему и составить краткую аннотацию.
Составить сравнительную таблицу по избранному сюжету, например, сравнительный анализ формационного, цивилизационного, альтернативного, сравнительно-исторического подходов к изучению истории; сравнение взглядов историков разных направлений или на ту или иную проблему и т.д.
Сделать подборку высказываний известных людей по тем или иным историческим событиям, сюжетам, личностям, явлениям.
Обнаружить ложную историческую информацию в сообщениях СМИ.
Вопросы для проверки знаний.
В чем состоят особенности периодизации, которая положена в основу курса «История» по Федеральному Государственному стандарту третьего поколения? В чем заключаются характерные черты исторического сознания россиян (старшего поколения, молодежи, различных социально-профессиональных групп)? Какие вопросы российской истории требуют более полного исследования и всестороннего освещения?
Какие известные историки жили, работали, похоронены в Петербурге? Какие труды по истории железнодорожного транспорта, Петербургского государственного университета путей сообщения имеются в библиотеке ПГУПС? Как складывались судьбы историков в разные эпохи?
Какие исторические архивы имеются в Петербурге? Что такое внешняя и внутренняя критика источника? Чем занимаются археологи, источниковеды, палеографы и другие специалисты?
Что может служить истиной в споре между историками? Действительно ли история «никого и ничему не учит»?
Какие сюжеты российской истории подвергаются наибольшим искажениям со стороны некоторых зарубежных историков? Почему и для чего это делается? Какие сюжеты отечественной истории подвергаются наибольшим искажениям со стороны некоторых российских историков, политиков, деятелей культуры? Почему и для чего это делается? Какие сюжеты мировой истории и почему подвергаются наибольшим искажениям со стороны российских историков, политиков и деятелей культуры? Какое место занимают исторические сюжеты во взаимоотношениях России с соседями по ближнему и дальнему зарубежью?
Литература:
Абрамова Н. Г. Вспомогательные исторические дисциплины: учебное пособие.- М., 2008.
Бердинских В. А. Ремесло историка в России.- М., 2009.
Голиков А. Г. Источниковедение отечественной истории: учебное пособие для студентов вузов.- 3-е изд.- М., 2009.
Згурский Г. В. Словарь исторических терминов.- М., 2008.
Репина Л.П., Зверева В.В., Парамонова М.Ю. История исторического знания: пособие для вузов. — М., 2006.
Смоленский Н. И. Теория и методология истории: учебное пособие.- М., 2007.
Соболева Н. А. Очерки истории российской символики: от тамги до символов государственного суверенитета.- М., 2006.
Тойнби А.Дж. Постижение истории: избранное, 1934-1961.- М., 2008.
Тема 2. Особенности становления государственности в россии и в мире. Основные вопросы семинара:
Теории происхождения государства и этапы становления государственности.
Цивилизации Древнего мира: специфика развития государства, общества и культуры.
Становление европейской цивилизации.
Образование Древнерусского государства.
Русские земли в XI-XII вв.
studfiles.net
Помощь с домашними заданиями для студентов / / Студуслуги
Домашнее задание для студентов ни в коем случае нельзя сравнить с заданиями школьников. если в школе мы все понимали, что от нас требуют согласно предоставленному материалу, то в высшем учебном заведении не всегда все так открыто и понятно. Многие домашние задания завуалированы, чтобы студент сам мог сделать вывод о том, какой конечный результат он должен получить. Чтобы разобраться с тем, какую помощь с домашними заданиями оказывают учебные центры для студентов, сначала нужно привести подробную классификацию таких заданий, чтобы студентам стало понятно, с чем им предстоит столкнуться с первого и до последнего курса обучения.
Итак, четкого разделения домашних заданий нет. Классификацию для себя составляют сами специалисты по оказанию помощи студентам. Мы подобрали несколько вариантов такого разделения. Основной вариант построен таким образом, что домашние задания находятся на нисходящих ступенях проверки выполнения домашнего задания. Другими словами, сначала идут те виды домашних заданий, которые требуют максимального внимания и сосредоточения сил, а затем, те виды заданий, которые можно практически не делать, так как такой труд редко оценивается по достоинству. Чтобы студентам было проще воспринимать информацию статьи, разделим домашние задания по степеням сложности по шкале от одного до десяти, где 10- предел сложности.
Сложность от 7 до 10
Это самый трудный вид домашнего задания. Это вид работ встречается примерно в 10% заданий. Таким заданиям преподаватель уделяет пристальное внимание, поскольку в его интересах не упустить ни малейшей детали. Он смотрит как написана работа, как раскрыта тема, соблюдены ли правила оформления и структуры текста. Это неполный список правил, которые распространены на такие задания. Так пристально могут проверять задание только эксперты в области практических заданий. Нельзя сказать, что данный вид задания играет большую роль для образования студентов. Излишняя скрупулёзность может сыграть злую шутку как с преподавателем, так и со студентом. Это своего рода вид экспериментального преподавания, которым могут заниматься те преподаватели, которые целиком и полностью отданы своему ремеслу.
Как делать такую работу? Сначала надо смириться с тем, что все-таки придется поддастся всем тем правилам, которые были установлены для таких заданий. Иногда даже полезно уделять особое внимание домашним заданиям, относясь к ним чуточку внимательнее и ответственнее. Если же студент считает, что к простенькому домашнему заданию предъявляются слишком уж требовательные нормы, то стоит обратиться на кафедру, чтобы была проведена открытая лекция, чтобы было оценено, как именно преподаватель ведет занятия. На основании этого можно будет сделать вывод о том, какого объема домашние задания даются студентам, и соответствуют ли они нормам.
Сложность от 4 до 6
Это оптимальный и самый распространенный вид домашнего задания. Данный вид домашнего задания встречается где-то в 60% случаев. По факту, это стандартная домашняя работа, на выполнение которой требует разумное количество времени. Проверяют же домашнее задание без излишнего энтузиазма, часто хватает формального наличия выполненного домашнего задания.При этом данный вид домашней работы следует делать вовремя, качественно и в полном объёме. Если несколько раз грубо нарушить предъявляемые требования (срок, объём оформление), то преподаватель может лично в отношении студента применить санкции в виде плохой оценки или проверки будущего домашнего задания по виду, описанному выше. Так что лучше стараться делать такие задания грамотно и аккуратно. Нужно ценитьдеятельность и справедливость преподавателя. Студент должен доставлять ему удовольствие от полноты и грамотности выполнения домашнего задания. И тогда, в дальнейшем, учащегося могут перевести в ту привилегированную группу, которой позволено практически никогда не делать домашнее задание. НА самом деле и такое случается. если студент представит себя, как ответственного и грамотного исполнителя домашнего задания, то в последствии ему будет проще сдавать не только работы, заданные на дом, но и экзамены.
Сложность от 1 до 3
Такие домашние работы встречается в 30% случаев. если говорить формально, то преподаватели задают домашнюю работу, однако по факту, её никто не проверяет. Часто такая ситуация случается, когда в университете происходят чрезвычайные события. Например, аккредитация. В это время руководству и преподавателя не до вашего домашнего задания. Их основная задача – пройти аккредитацию. Также, такое возможно в ситуации, описанной выше. То есть студент может зарекомендовать себя, как ответственный и грамотный исполнитель, а в последствии домашняя работа станет относиться именно к этой группе. Но даже в этом случае не стоит пренебрежительно относиться к домашним заданиям. Не исключен вариант, что преподаватель все же захочет проверить работу студента, а в дальнейшем он будет удивлен неграмотности и неаккуратности представленного материала. Так что, перед тем, как самостоятельно относить работу к этой категории, стоит подумать о том, действительно ли она к ней относится или нет.
Подводим итоги
Итак, мы рассказали вам о том, какие категории домашних заданий мы знаем. Наверняка студенты также согласятся с таким разделением заданий. Но не стоит также забывать и о том, что о качества домашнего задания зависит отношение преподавателя к студенту. если испортить отношение к себе, то в дальнейшем будет непросто сдавать сессию. Так что, качество домашнего задания – это залог успешной учёбы.
studuslugi.ru


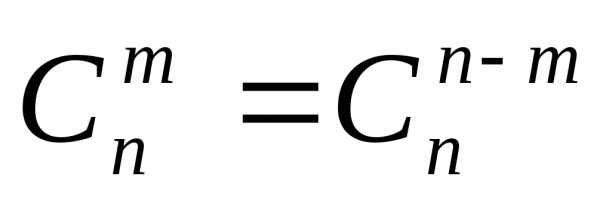 (1.8)
(1.8)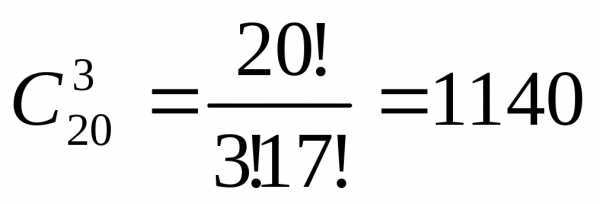

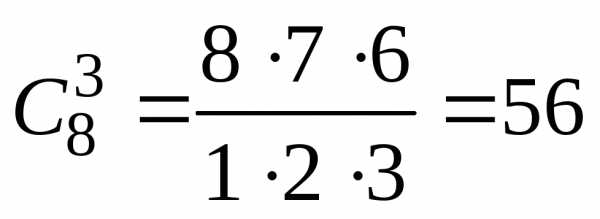 .
.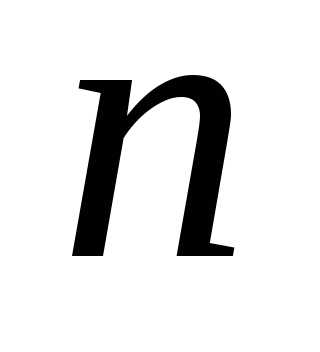 различных сортов. Пусть предметы одного
сорта не различаются.
различных сортов. Пусть предметы одного
сорта не различаются.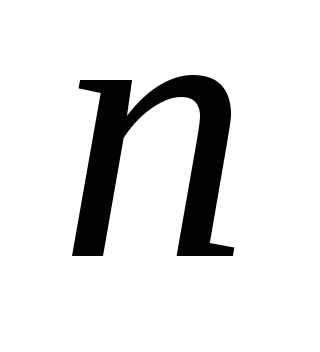 элементов по
элементов по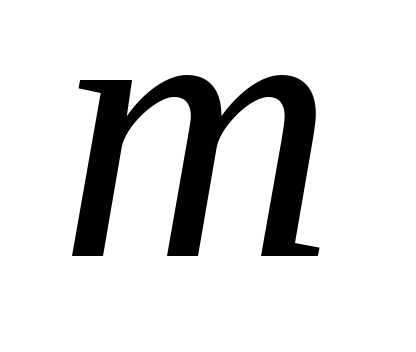 называется
выборка
называется
выборка 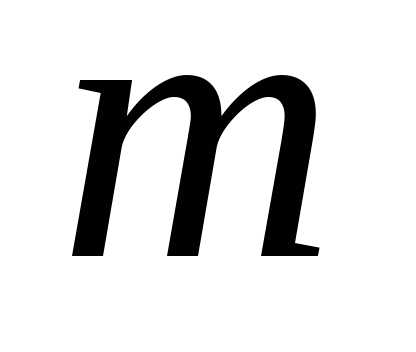 предметов из неограниченного количества
предметов
предметов из неограниченного количества
предметов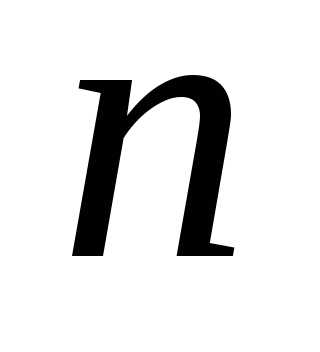 различных сортов. Такие выборки должны
отличаться хотя бы одним элементом,
т.е. порядок элементов во внимание не
принимается
различных сортов. Такие выборки должны
отличаться хотя бы одним элементом,
т.е. порядок элементов во внимание не
принимается и вычисляется по формуле
и вычисляется по формуле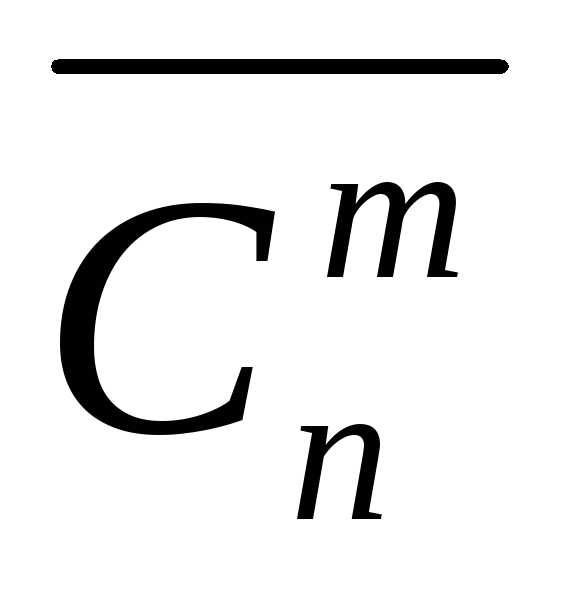 .
(1.11)
.
(1.11)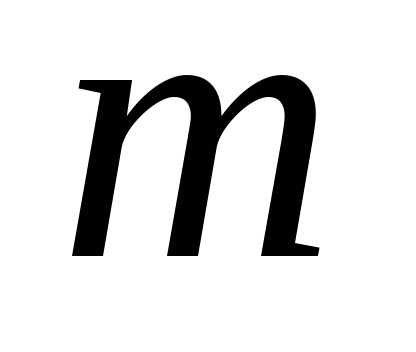 типов в него входит. Назовем кратностью
элемента число повторений данного
элемента в сочетании с повторениями.
Например, в сочетанииэлемент
типов в него входит. Назовем кратностью
элемента число повторений данного
элемента в сочетании с повторениями.
Например, в сочетанииэлемент имеет кратность
имеет кратность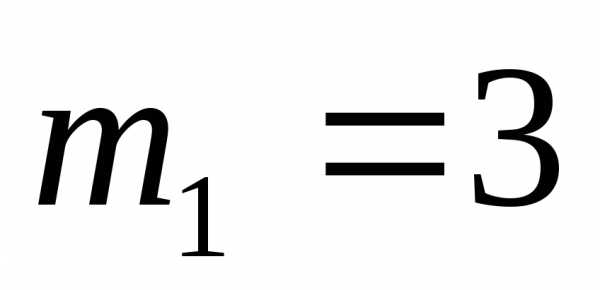 ,
элемент
,
элемент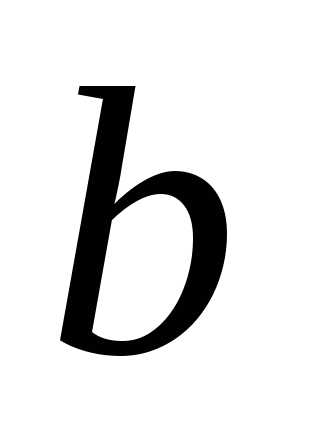 имеет кратность
имеет кратность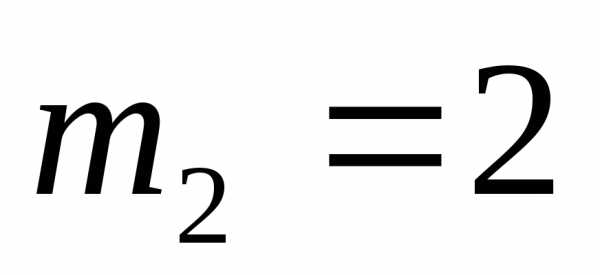 ,
элемент
,
элемент имеет кратность
имеет кратность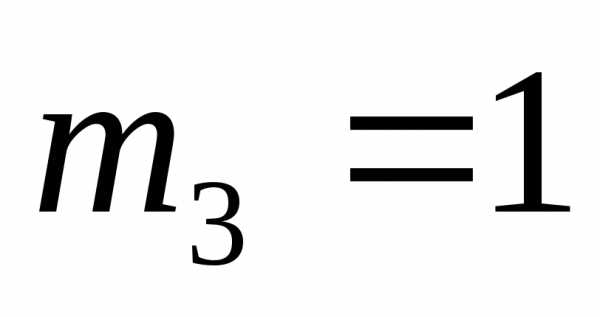 ,
элемент
,
элемент имеет кратность
имеет кратность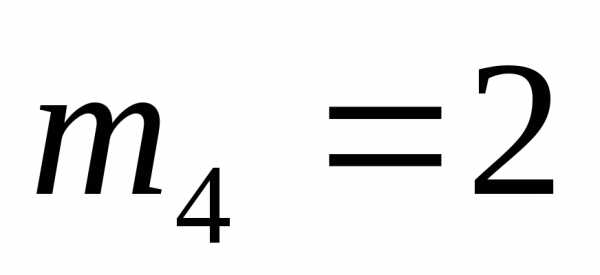 .
Сумма всех кратностей равна порядку
сочетания,
т.е..
Поставим каждому сочетанию в соответствие
последовательность из нулей и единиц,
составленную по такому правилу: напишем
подряд столько единиц, сколько элементов
первого типа в него входит, затем нуль,
затем напишем столько единиц, сколько
элементов второго типа в него входит,
затем нуль и т.д. Например, сочетанию с
повторениями
.
Сумма всех кратностей равна порядку
сочетания,
т.е..
Поставим каждому сочетанию в соответствие
последовательность из нулей и единиц,
составленную по такому правилу: напишем
подряд столько единиц, сколько элементов
первого типа в него входит, затем нуль,
затем напишем столько единиц, сколько
элементов второго типа в него входит,
затем нуль и т.д. Например, сочетанию с
повторениями соответствует последовательность
11101101011. Если некоторый элемент не
содержится в данном сочетании с
повторениями, т.е. его кратность равна
нулю, то тогда группа единиц не пишется
и в последовательности появится 0 по
меньшей мере два раза. В элементах
последовательности из нулей и единиц,
соответствующих сочетаниям с повторениями
из
соответствует последовательность
11101101011. Если некоторый элемент не
содержится в данном сочетании с
повторениями, т.е. его кратность равна
нулю, то тогда группа единиц не пишется
и в последовательности появится 0 по
меньшей мере два раза. В элементах
последовательности из нулей и единиц,
соответствующих сочетаниям с повторениями
из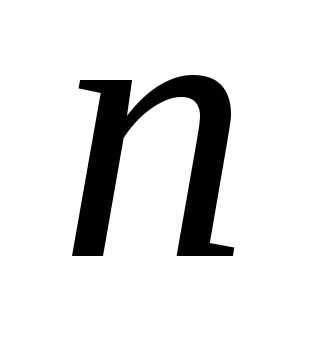 элементов по
элементов по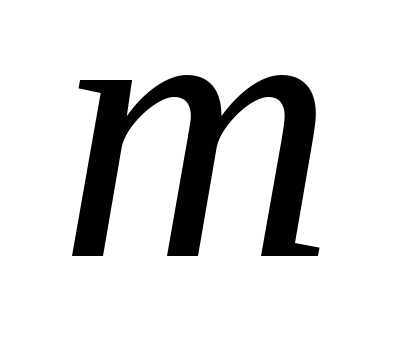 цифра 1 встречается
цифра 1 встречается раз, а цифра 0 встречается
раз, а цифра 0 встречается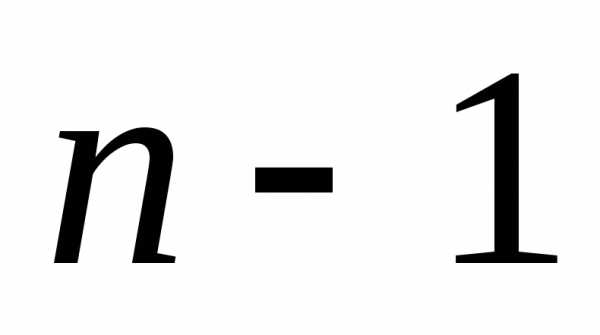 раз. Для сочетания
раз. Для сочетания соответственно 8 и 3. Всевозможные
сочетания с повторениями получатся,
если подвергнуть перестановке нули и
единицы в соответствующей последовательности.
соответственно 8 и 3. Всевозможные
сочетания с повторениями получатся,
если подвергнуть перестановке нули и
единицы в соответствующей последовательности.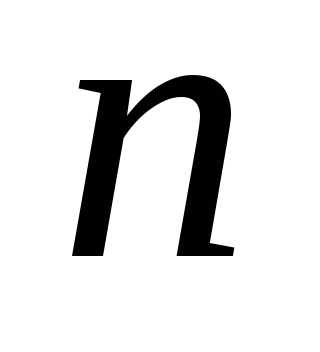 элементов по
элементов по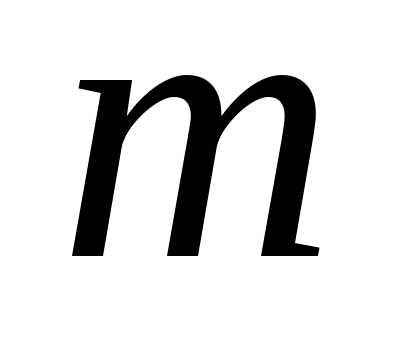 соответствует последовательность из
соответствует последовательность из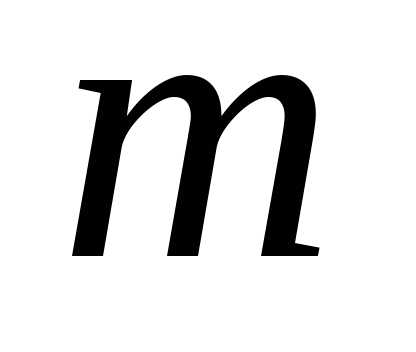 единиц и
единиц и нулей. Следовательно, число сочетаний
с повторениями из
нулей. Следовательно, число сочетаний
с повторениями из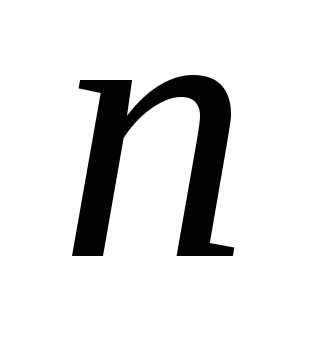 элементов по
элементов по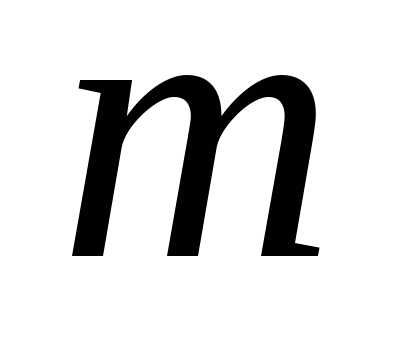 равно числу последовательностей из
равно числу последовательностей из единиц и
единиц и нулей. Это число определяется числом
перестановок с повторениями
нулей. Это число определяется числом
перестановок с повторениями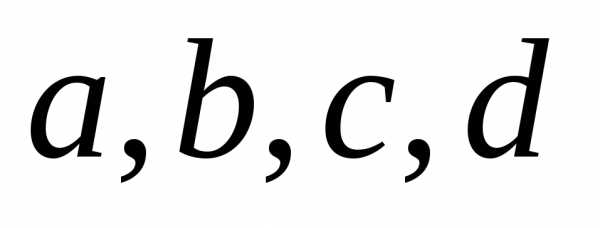 по 2 с повторениями будут.
Им соответствуют следующие последовательности
из нулей и единиц
по 2 с повторениями будут.
Им соответствуют следующие последовательности
из нулей и единиц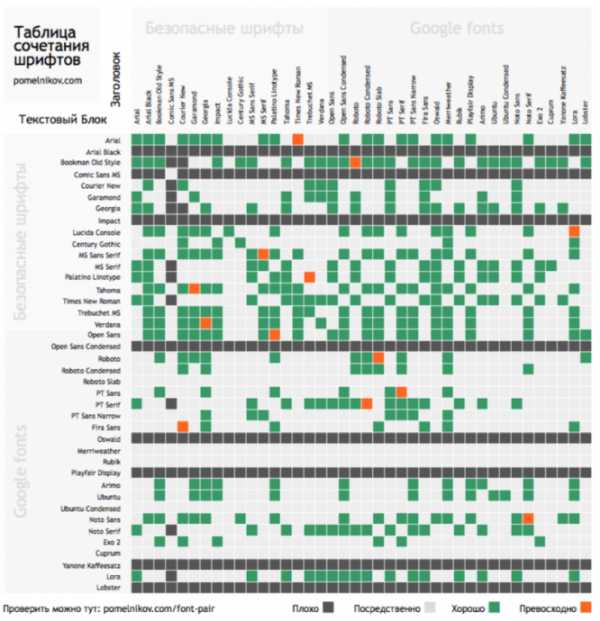 Скачать таблицу в .pdf
Скачать таблицу в .pdf
 Отношение толщины основных штрихов к высоте прямого знака, основная толщина (жирность) шрифта. Изменения этого отношения образуют сверхсветлое (Ultra Light, Extra Light, Thin), Светлое (Light), нормальное (Book, Regular, Roman), Полужирное (Medium, Demi Bold, Semibold), Жирное (Bold, Heavy), сверхжирное (Extra Bold, Black, Ultra Bold) начертания.
Отношение толщины основных штрихов к высоте прямого знака, основная толщина (жирность) шрифта. Изменения этого отношения образуют сверхсветлое (Ultra Light, Extra Light, Thin), Светлое (Light), нормальное (Book, Regular, Roman), Полужирное (Medium, Demi Bold, Semibold), Жирное (Bold, Heavy), сверхжирное (Extra Bold, Black, Ultra Bold) начертания. Элементы дополняющие шрифт, придающие ему стиль и особенности. К аксессуарам относят засечки, декор, фактуры, росчерки, скругления, узоры, особые элементы и эффекты.
Элементы дополняющие шрифт, придающие ему стиль и особенности. К аксессуарам относят засечки, декор, фактуры, росчерки, скругления, узоры, особые элементы и эффекты. Жмя на картинку для хорошего качества
Жмя на картинку для хорошего качества



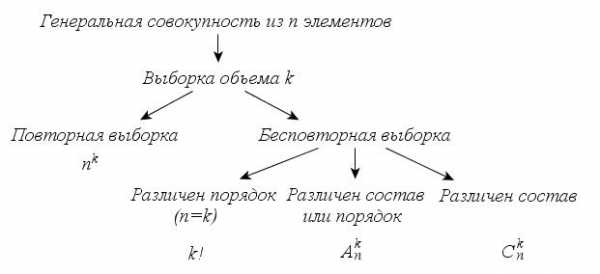










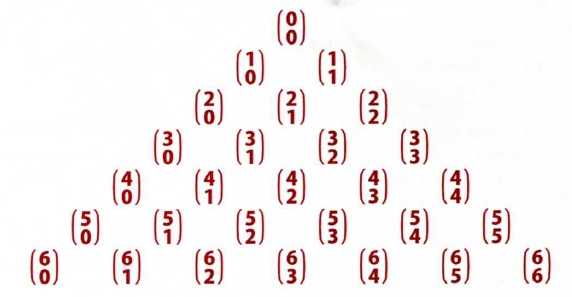











 имеет место следующее равенство:
имеет место следующее равенство: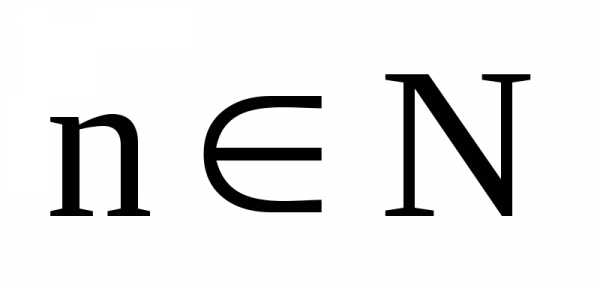 – натуральное число. Так как комплексное
числоимеет модуль
– натуральное число. Так как комплексное
числоимеет модуль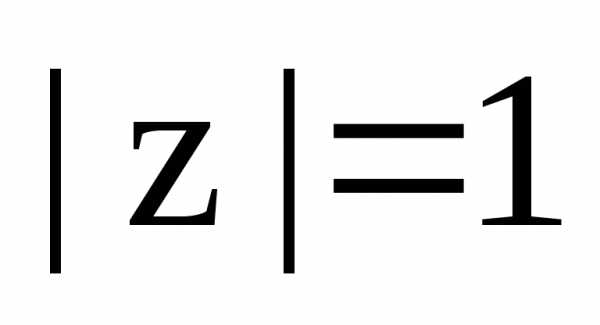 ,
то справедливость формулы Муавра в этом
случае следует из следствия 2 теоремы
об умножении комплексных чисел в
тригонометрической форме записи.
,
то справедливость формулы Муавра в этом
случае следует из следствия 2 теоремы
об умножении комплексных чисел в
тригонометрической форме записи.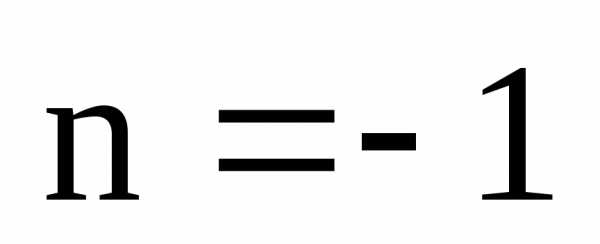 .
Тогда
.
Тогда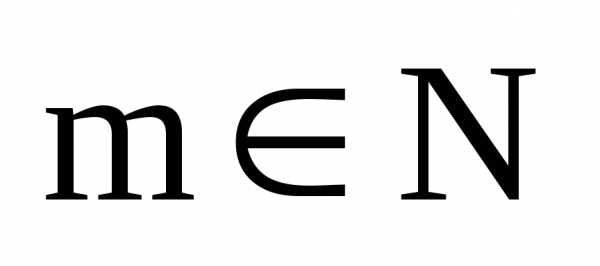 – натуральное число. Тогда по свойству
целых степеней, которые справедливы в
любом поле, в том числе и в поле комплексных
чисел, имеем:
– натуральное число. Тогда по свойству
целых степеней, которые справедливы в
любом поле, в том числе и в поле комплексных
чисел, имеем:
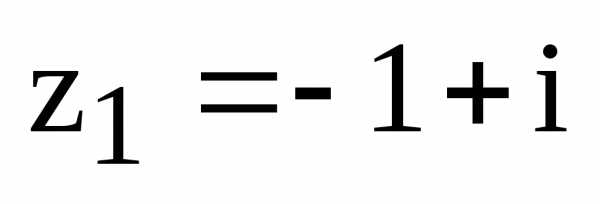 и
и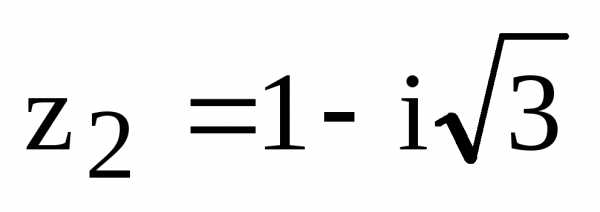 в тригонометрической форме и найдите
их произведение
в тригонометрической форме и найдите
их произведение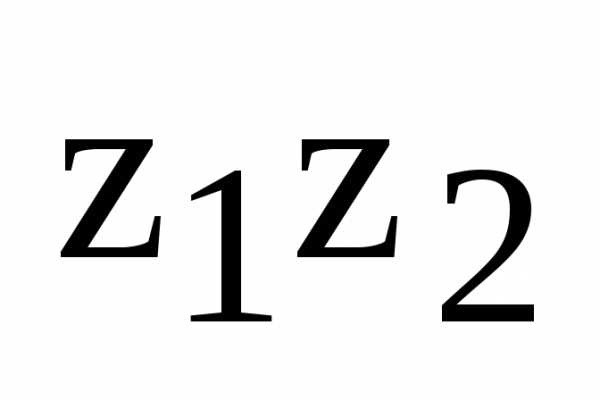 и частное
и частное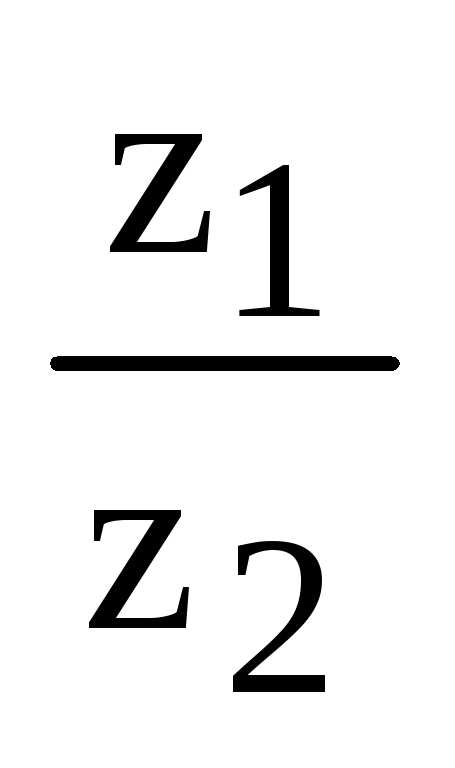 .
. на комплексной плоскости находится во
второй четверти, поэтому
на комплексной плоскости находится во
второй четверти, поэтому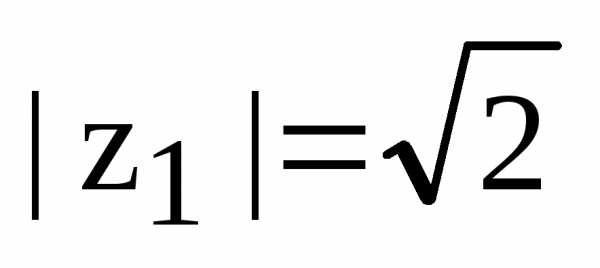 ,
.
,
.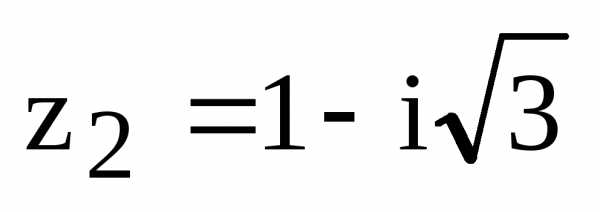 на комплексной плоскости находится во
четвертой четверти, поэтому
на комплексной плоскости находится во
четвертой четверти, поэтому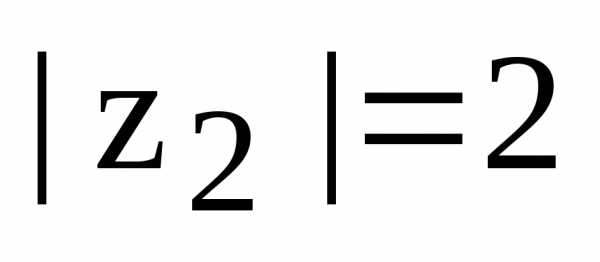 ,
.
,
.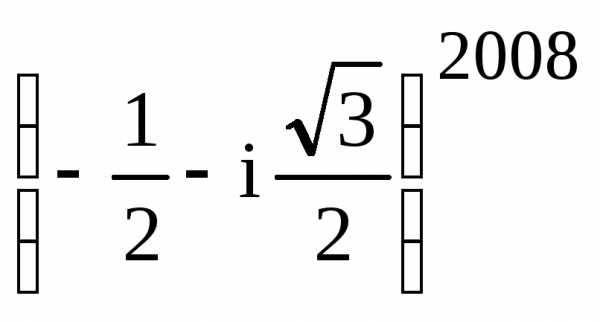 .
.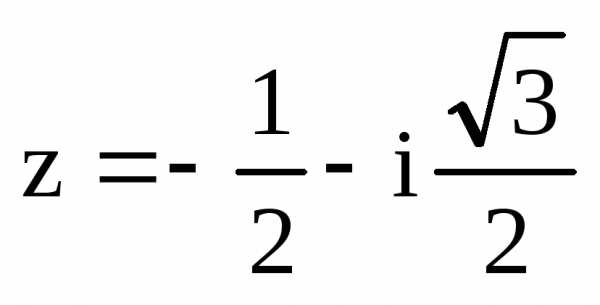 на комплексной плоскости находится в
третьей четверти, поэтому
на комплексной плоскости находится в
третьей четверти, поэтому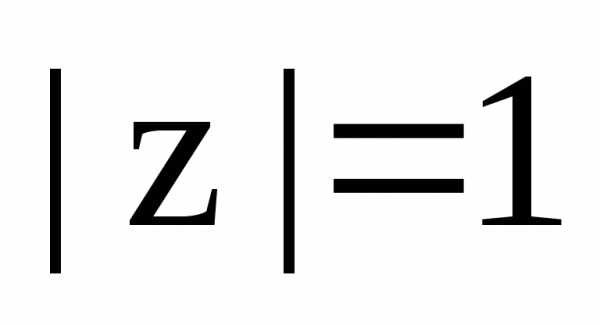 ,
,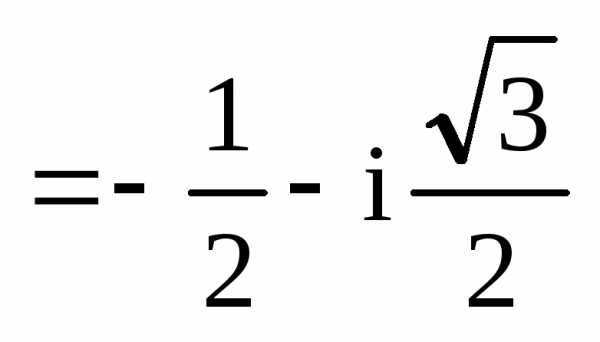 .
.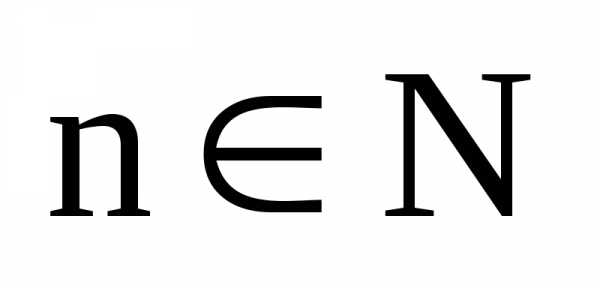 и
и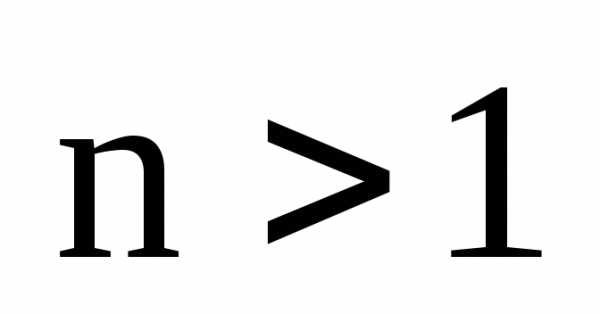 .
Корнемn-й степени из
комплексного числаzназывается комплексное число
.
Корнемn-й степени из
комплексного числаzназывается комплексное число ,
такое, что
,
такое, что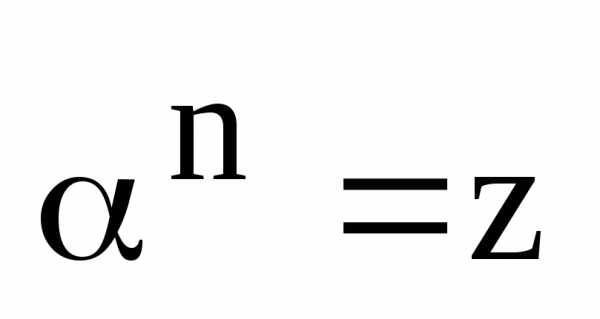 .
.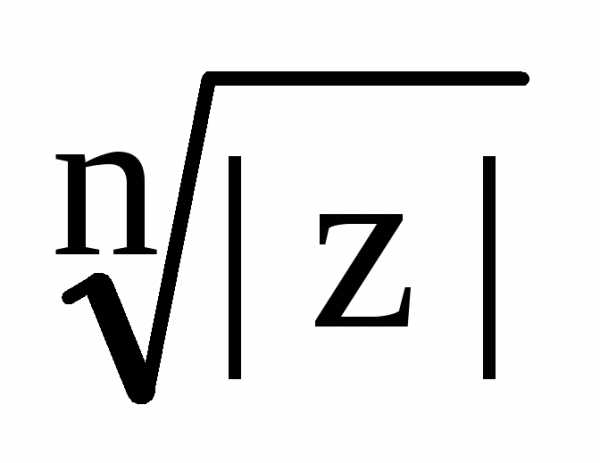 – арифметический кореньn-й
степени из положительного числа
– арифметический кореньn-й
степени из положительного числа .
.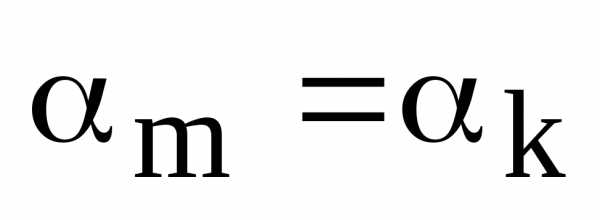 ,
гдеи
,
гдеи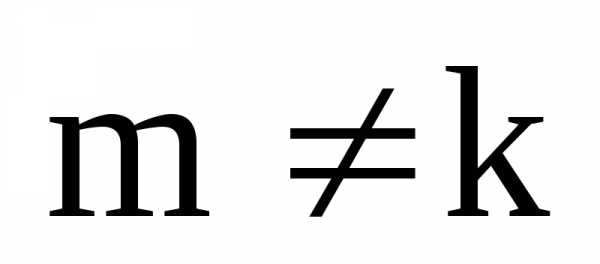 .
Тогда по теореме о равенстве двух
комплексных чисел в тригонометрической
форме записи следует, что равны их
аргументы.
.
Тогда по теореме о равенстве двух
комплексных чисел в тригонометрической
форме записи следует, что равны их
аргументы. может отличаться от числа
может отличаться от числа на число кратное числу
на число кратное числу (т.е. на целое число оборотов) и аналогично
для аргумента числа
(т.е. на целое число оборотов) и аналогично
для аргумента числа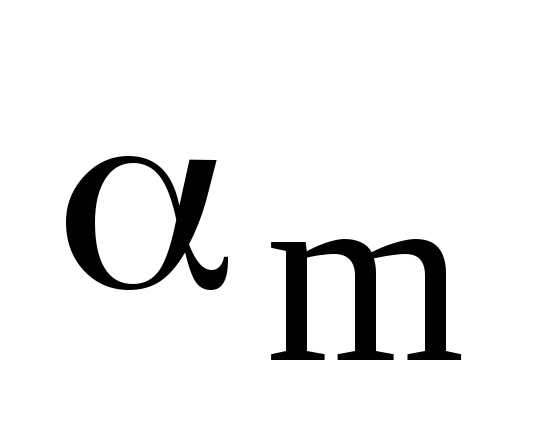 .
Отсюда следует, что,
где
.
Отсюда следует, что,
где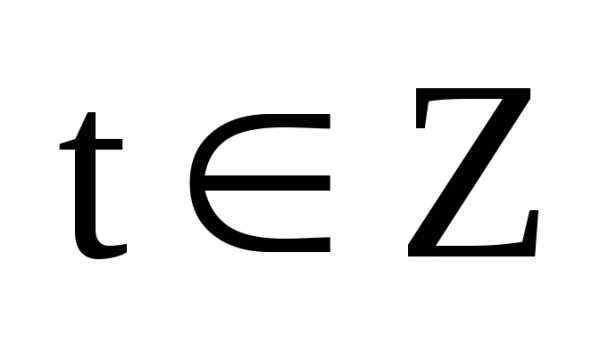 .
Умножим это равенство наn:.
Отсюда следует, чтои т.к. по нашему предположению
.
Умножим это равенство наn:.
Отсюда следует, чтои т.к. по нашему предположению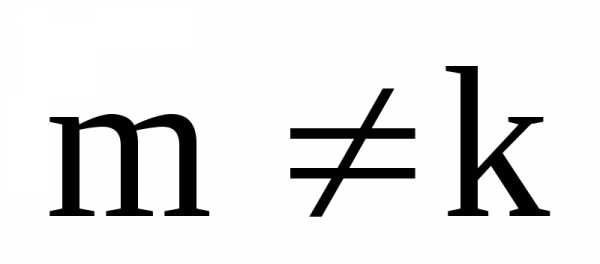 ,
то,
чего не может быть, т.к.и.
Получили противоречие. Следовательно,
среди корней в множестве (10) нет равных,
ч.т.д.
,
то,
чего не может быть, т.к.и.
Получили противоречие. Следовательно,
среди корней в множестве (10) нет равных,
ч.т.д.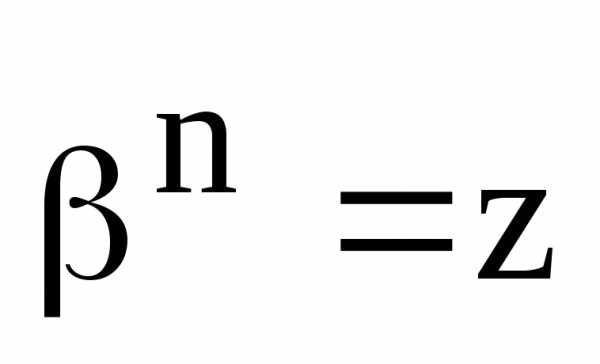 .
Так как.
Отсюда, из тех же соображений, что и во
второй части доказательства, следуют
равенства
.
Так как.
Отсюда, из тех же соображений, что и во
второй части доказательства, следуют
равенства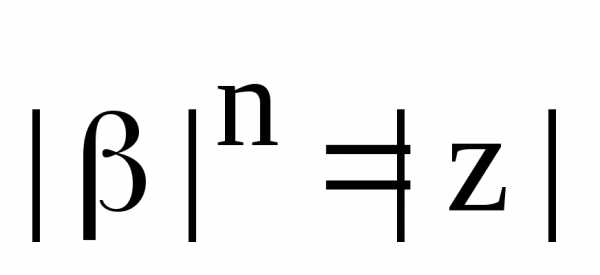 и,
где
и,
где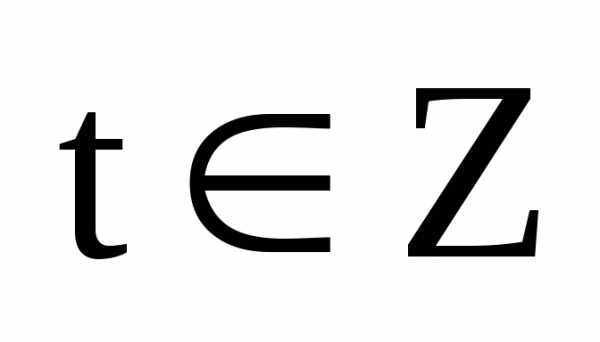 .
Из первого равенства получаем, что
.
Из первого равенства получаем, что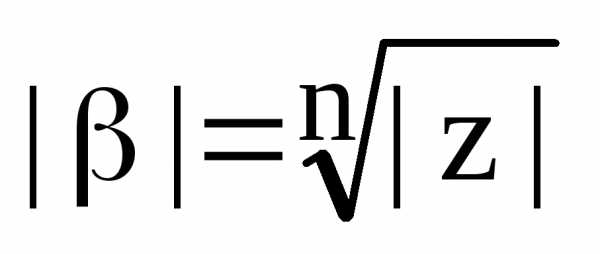 ,
а из второго следует
,
а из второго следует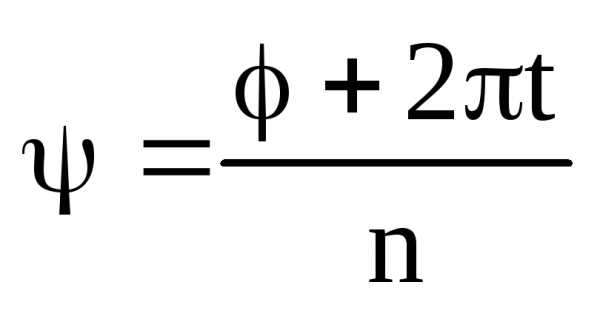 .
.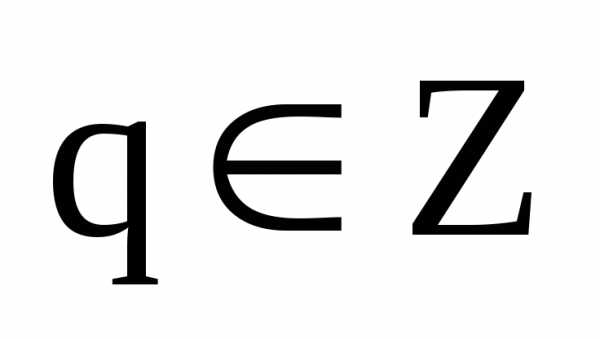 ,
а остатокrтакже является
целым числом, но.
Отсюда
,
а остатокrтакже является
целым числом, но.
Отсюда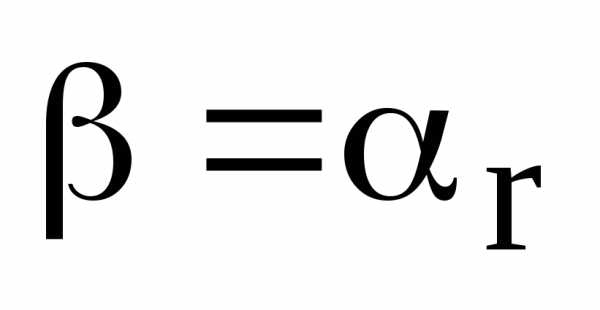 является корнем из множества корней
(4), ч.т.д.
является корнем из множества корней
(4), ч.т.д.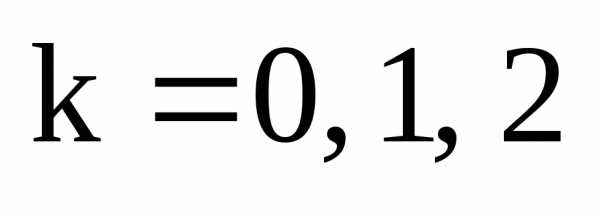 .
.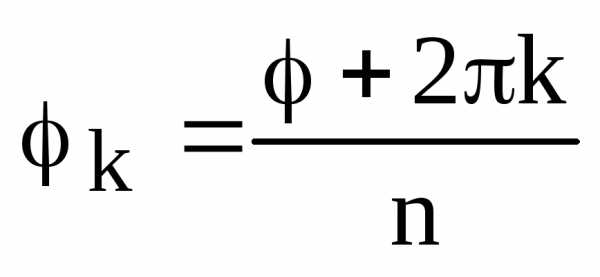 ,.
,. с центром в начале координат. Из формулы
(5) мы видим, что угол между такими двумя
соседними точками одинаковый. Отсюда
делаем вывод, что все корни располагаются
на окружности равномерно. Если соединить
все соседние точки (корни) отрезками
прямой, то получим правильныйn-угольник.
с центром в начале координат. Из формулы
(5) мы видим, что угол между такими двумя
соседними точками одинаковый. Отсюда
делаем вывод, что все корни располагаются
на окружности равномерно. Если соединить
все соседние точки (корни) отрезками
прямой, то получим правильныйn-угольник.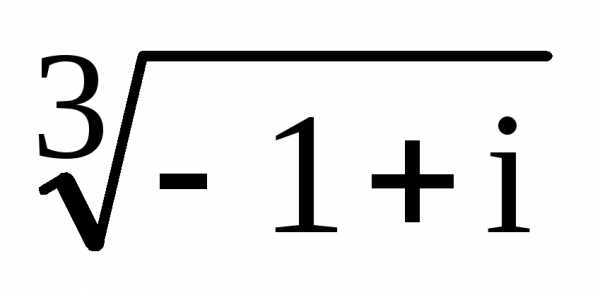 на комплексной плоскости.
на комплексной плоскости.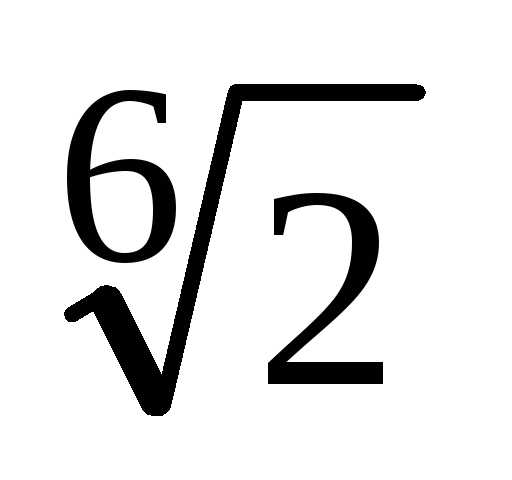 с центром в начале координат и отмечаем
на ней точки полярный угол которых
равен:
с центром в начале координат и отмечаем
на ней точки полярный угол которых
равен: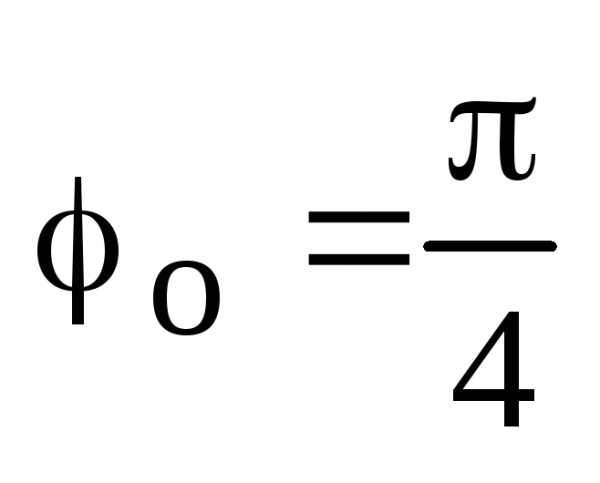 ,
, 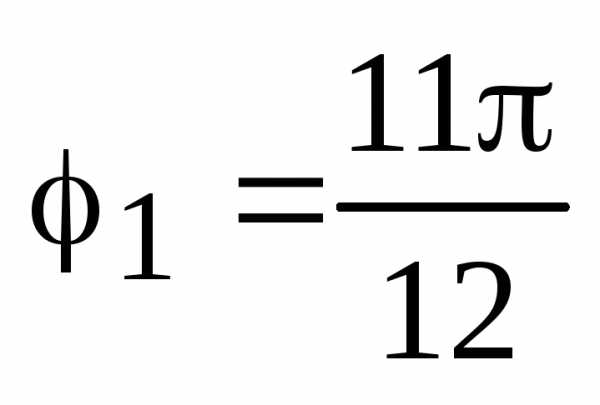 ,
,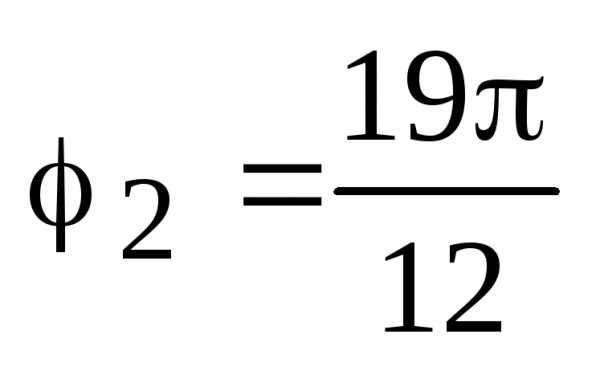 .
.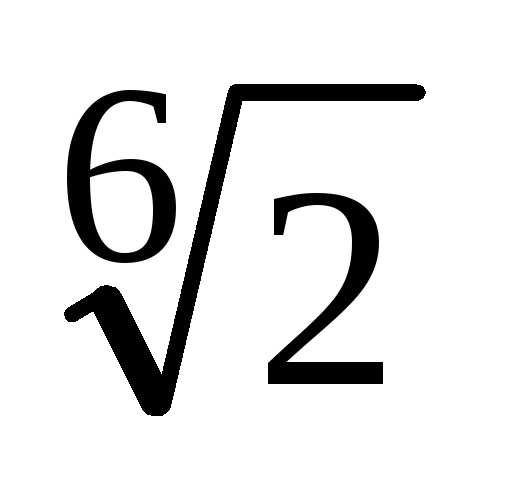
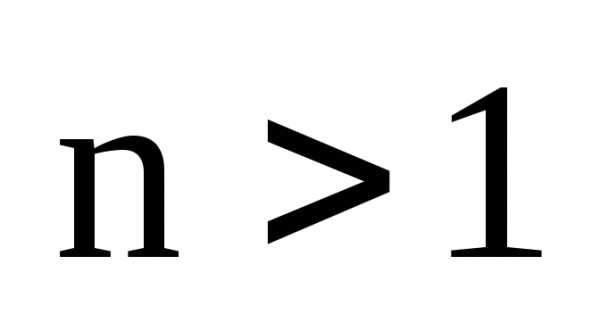 – натуральное число. По формуле корней
из комплексного числа, существует ровноnкорней из комплексного
числа.
Для вычисления этих корней запишем
единицу в тригонометрической форме:
– натуральное число. По формуле корней
из комплексного числа, существует ровноnкорней из комплексного
числа.
Для вычисления этих корней запишем
единицу в тригонометрической форме: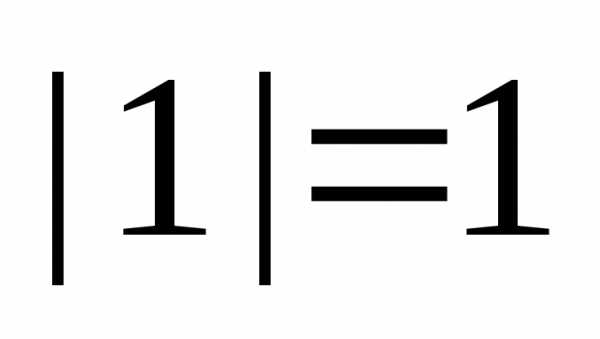 ,
, .
.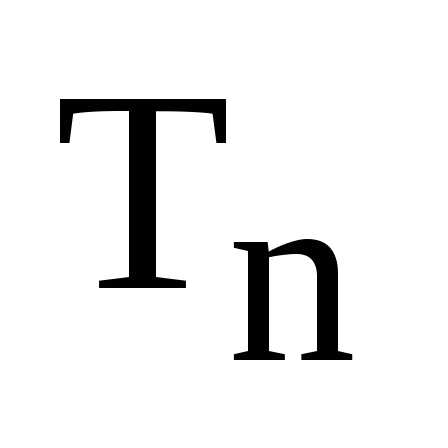 .
По формуле корней получаем:
.
По формуле корней получаем: .
(9)
.
(9)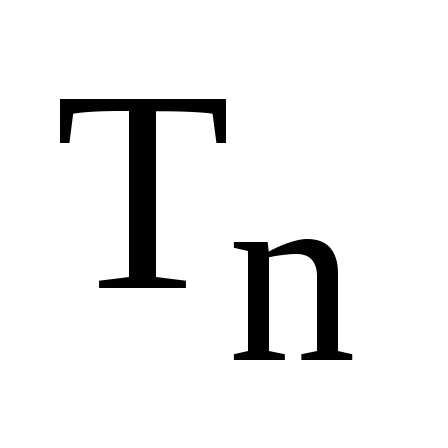 из 1 можем записать так:
из 1 можем записать так: замкнуто относительно умножения. Пусть
замкнуто относительно умножения. Пусть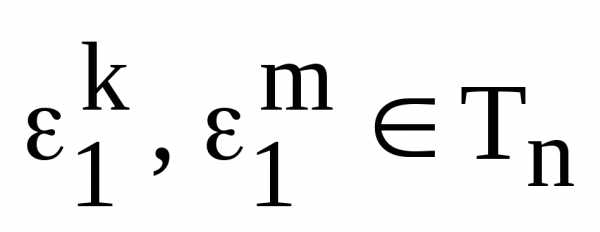 – два произвольных корня из 1, т.е..
Найдем их произведение:
– два произвольных корня из 1, т.е..
Найдем их произведение: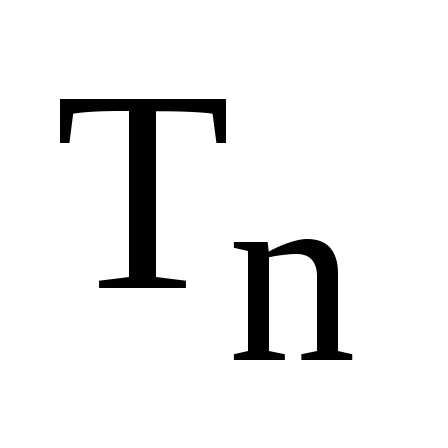 определена операция умножения и т.к.
она ассоциативна и коммутативна в поле
комплексных чисел, то она ассоциативна
и коммутативна и на множестве
определена операция умножения и т.к.
она ассоциативна и коммутативна в поле
комплексных чисел, то она ассоциативна
и коммутативна и на множестве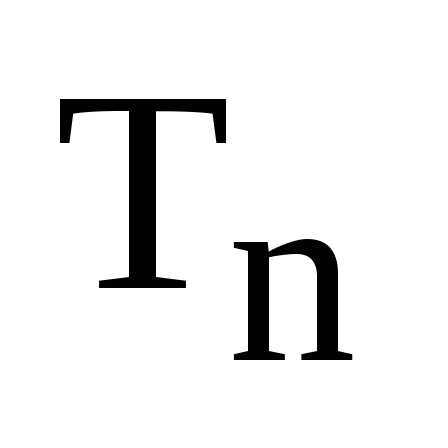 .
Далее,
.
Далее,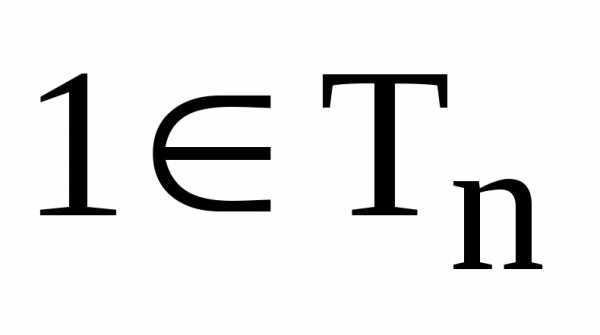 .
Покажем, что любой элемент из
.
Покажем, что любой элемент из имеет обратный элемент также принадлежащий
множеству
имеет обратный элемент также принадлежащий
множеству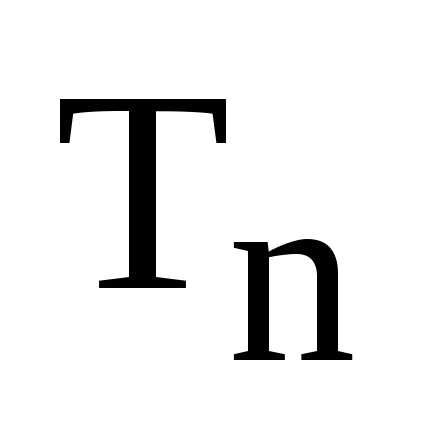 :
: .
.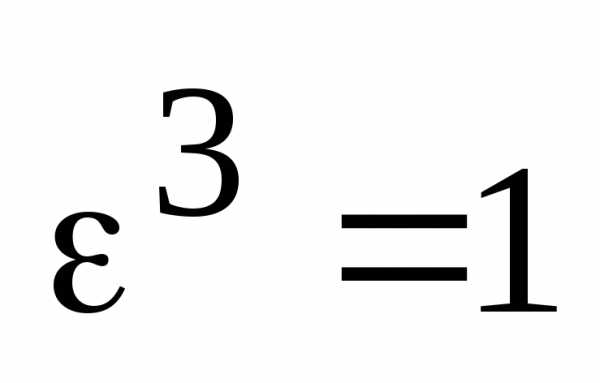 .
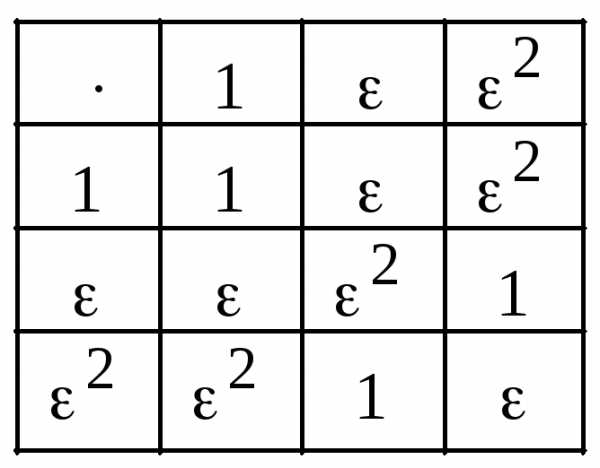
.
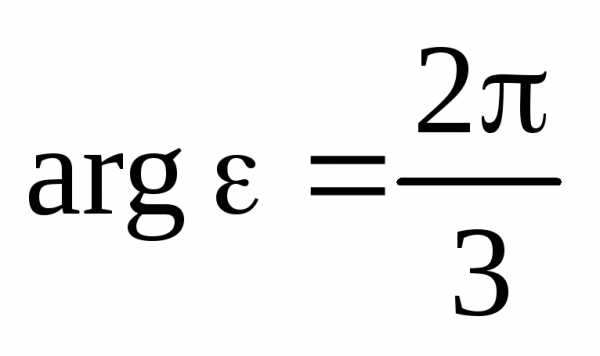 ,
,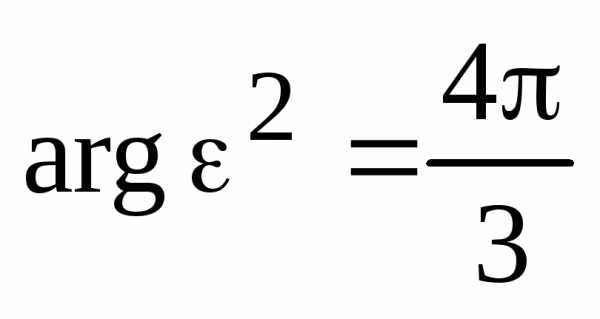 .
.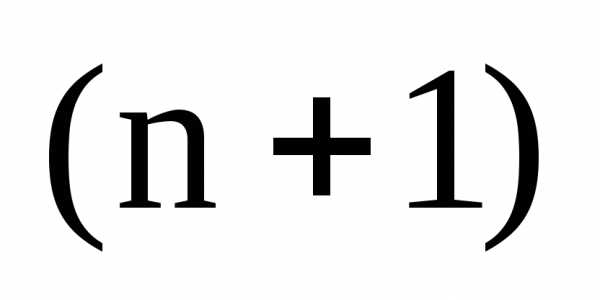 -й
степени из 1.
-й
степени из 1. ,m– их число,– их кратности,t– число
квадратных трехчленов с действительными
коэффициентамии отрицательными дискриминантами,– кратности соответствующих комплексных
корней,
,m– их число,– их кратности,t– число
квадратных трехчленов с действительными
коэффициентамии отрицательными дискриминантами,– кратности соответствующих комплексных
корней,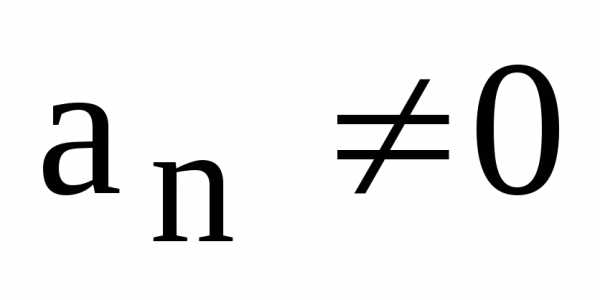 – старший коэффициент многочлена
– старший коэффициент многочлена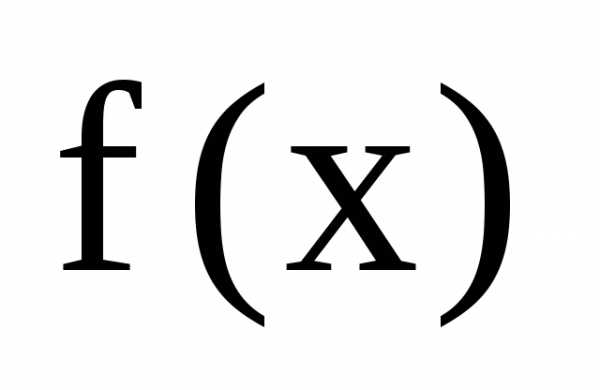 ,n– его степень.
,n– его степень.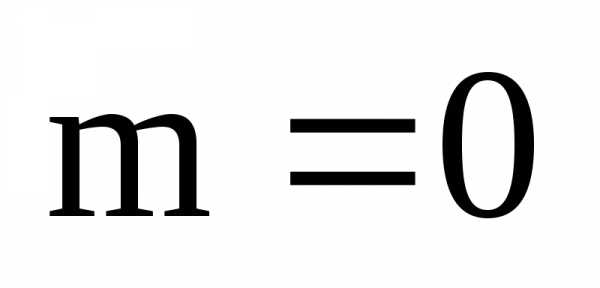 и многочлен не имеет действительных
корней. Аналогично, многочлен может не
иметь комплексных корней, тогда
и многочлен не имеет действительных
корней. Аналогично, многочлен может не
иметь комплексных корней, тогда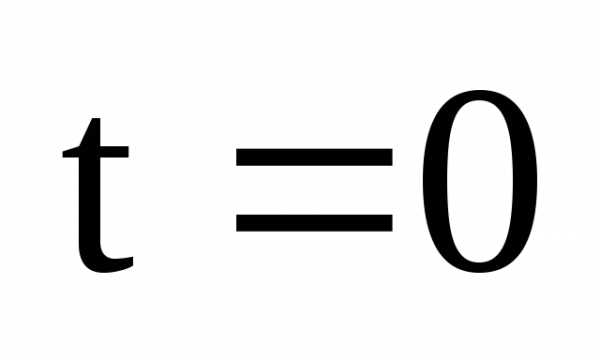 .
Далее, очевидно, что степень многочлена
.
Далее, очевидно, что степень многочлена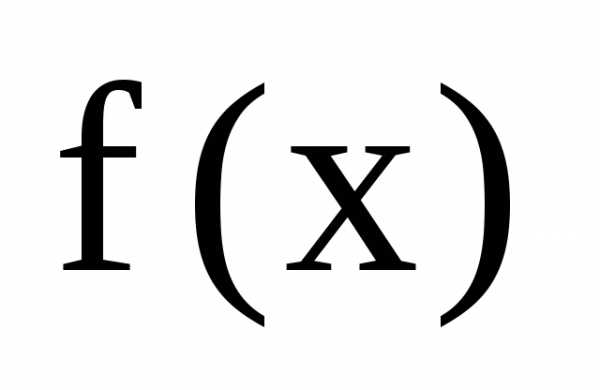
 ,
то комплексно сопряженное ему число
,
то комплексно сопряженное ему число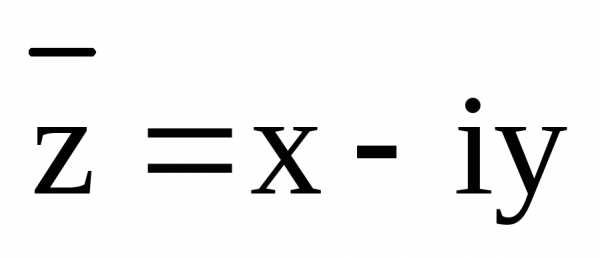 также является корнем этого многочлена.
Действительно, если
также является корнем этого многочлена.
Действительно, если ,
то.
,
то.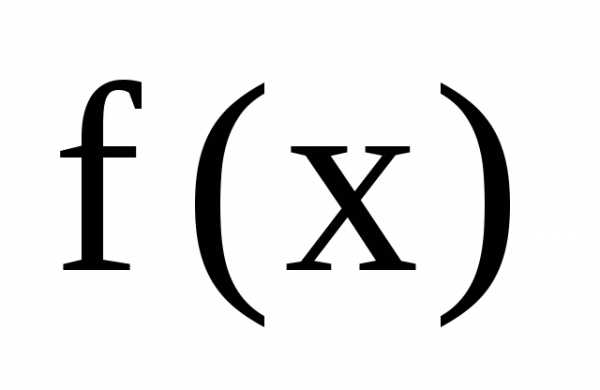 ,m– их число,– их кратности,– все различные комплексно сопряженные
корни многочлена
,m– их число,– их кратности,– все различные комплексно сопряженные
корни многочлена ,t– число пар всех различных
комплексно сопряженных корней,– их кратности,
,t– число пар всех различных
комплексно сопряженных корней,– их кратности,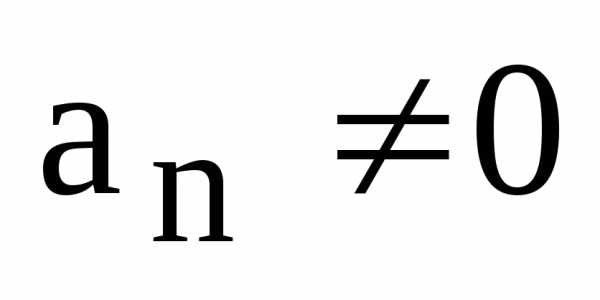 – старший коэффициент многочлена
– старший коэффициент многочлена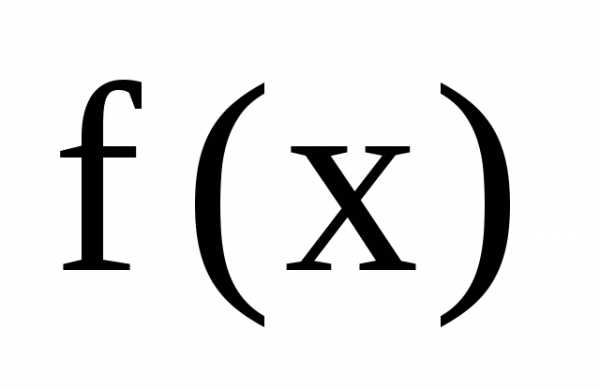 ,n– его степень.
,n– его степень.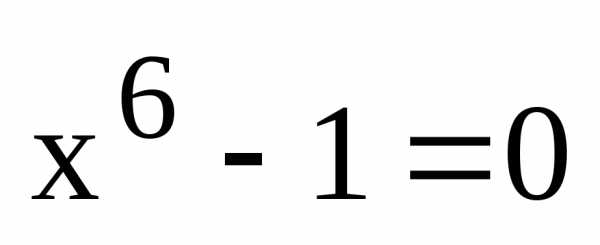 .
Так как
.
Так как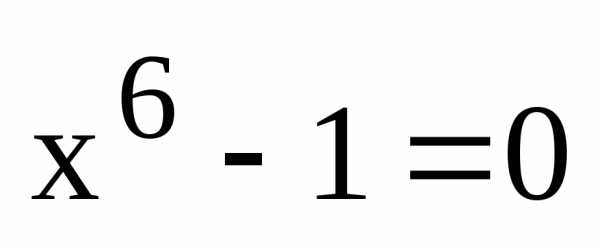 ,
мы найдем тем самым все корни многочлена.
,
мы найдем тем самым все корни многочлена.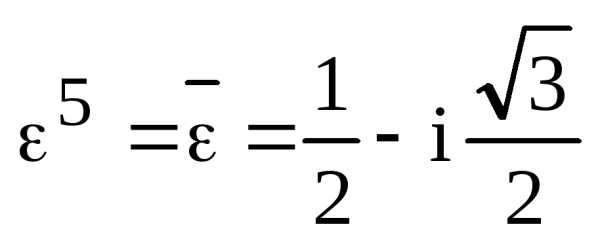 .
.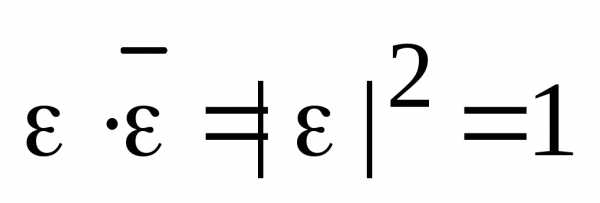 ,,,
,,,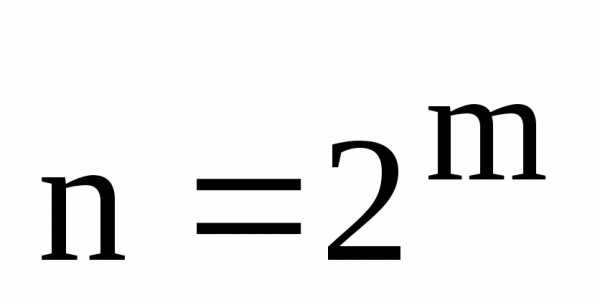 ,
, ,
,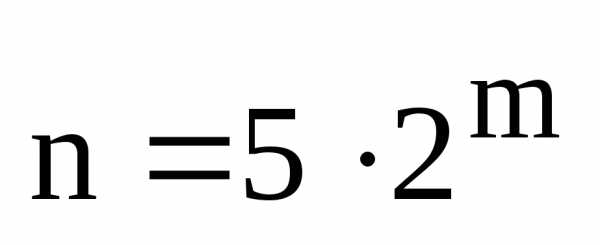 и
и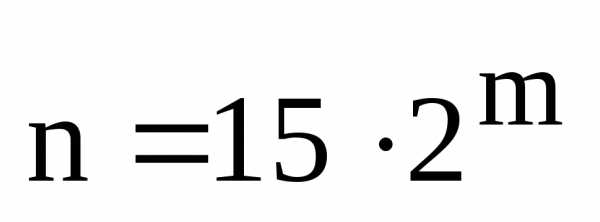 ,
,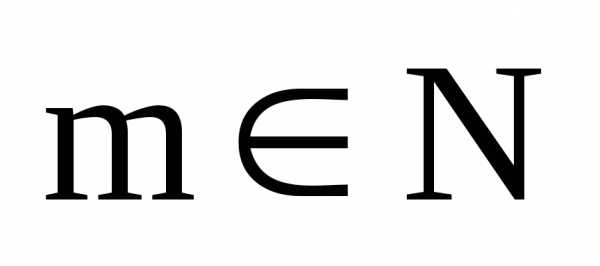 .
Очень важно, что с помощью линейки
проводятся только отрезки прямых, а
длины отрезков измеряются с помощью
циркуля, а не делений на линейке. Так,
используя эти инструменты можно построить
отрезок, длина которого выражается
числом, полученным из 1 с помощью четырех
арифметических действий (сложения,
вычитания, умножения, деления) и
извлечением квадратного корня. Т.е.
вначале есть только отрезок, длина
которого принимается за 1. Тогда можно
построить отрезок, длина которого равна
рациональному числу или квадратному
корню из рационального числа. Далее,
если отрезок длины а уже построен с
помощью циркуля и линейки, то можно
построить с помощью этих инструментов
отрезок длиныb, если
числоbвыражается через
а с помощью арифметических действий и
квадратного корня. Говорят, что такое
число выражается в квадратных радикалах.
.
Очень важно, что с помощью линейки
проводятся только отрезки прямых, а
длины отрезков измеряются с помощью
циркуля, а не делений на линейке. Так,
используя эти инструменты можно построить
отрезок, длина которого выражается
числом, полученным из 1 с помощью четырех
арифметических действий (сложения,
вычитания, умножения, деления) и
извлечением квадратного корня. Т.е.
вначале есть только отрезок, длина
которого принимается за 1. Тогда можно
построить отрезок, длина которого равна
рациональному числу или квадратному
корню из рационального числа. Далее,
если отрезок длины а уже построен с
помощью циркуля и линейки, то можно
построить с помощью этих инструментов
отрезок длиныb, если
числоbвыражается через
а с помощью арифметических действий и
квадратного корня. Говорят, что такое
число выражается в квадратных радикалах. в
в алгебраической форме.
в
в алгебраической форме.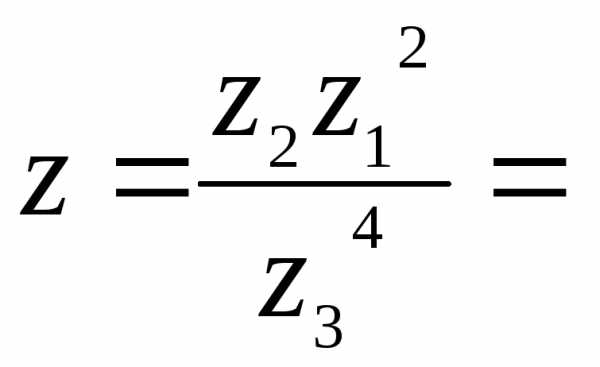
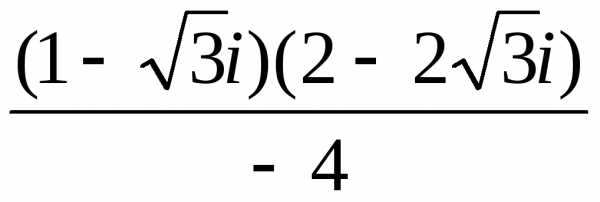
 аргумент комплексного числа
аргумент комплексного числа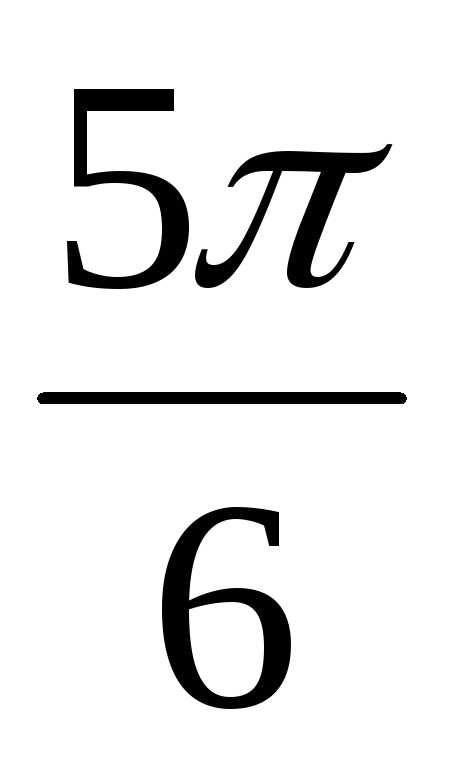 + isin )
+ isin ) 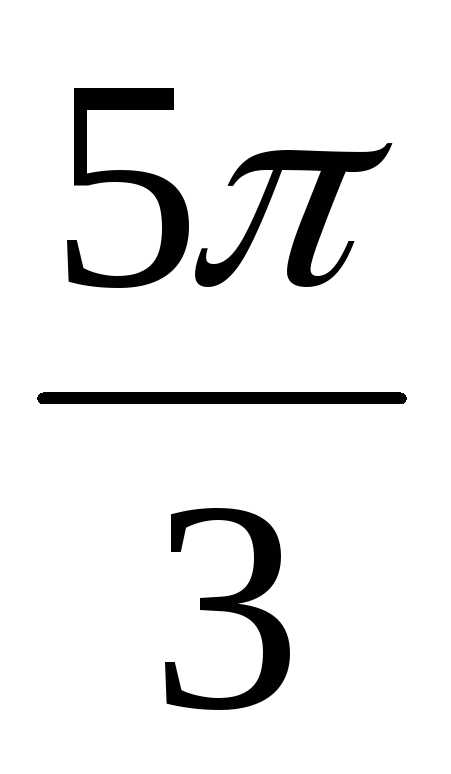 + isin
+ isin  )
) 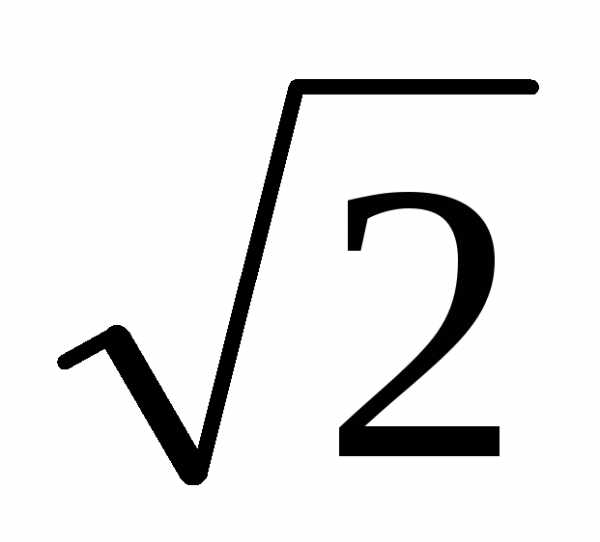 (cos
(cos 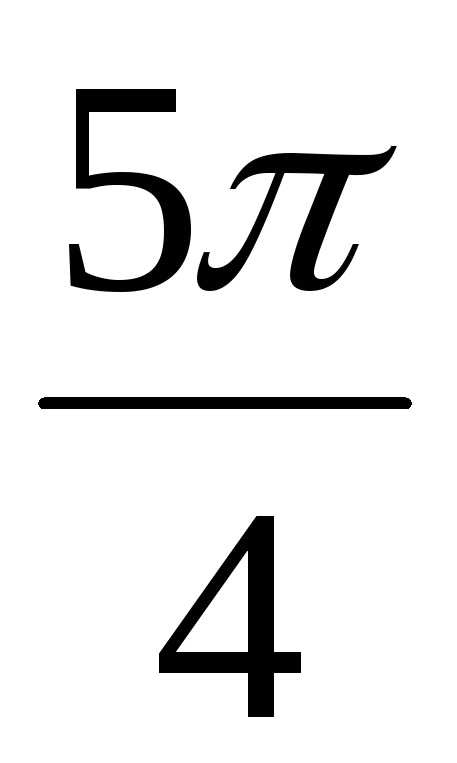 + isin
+ isin 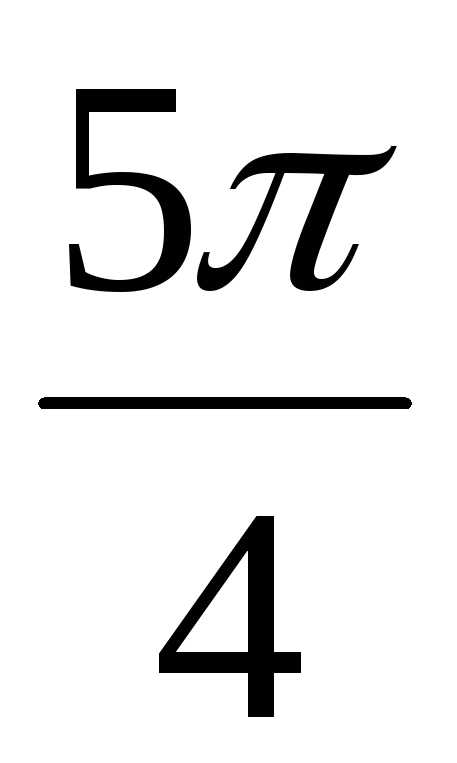 )
) 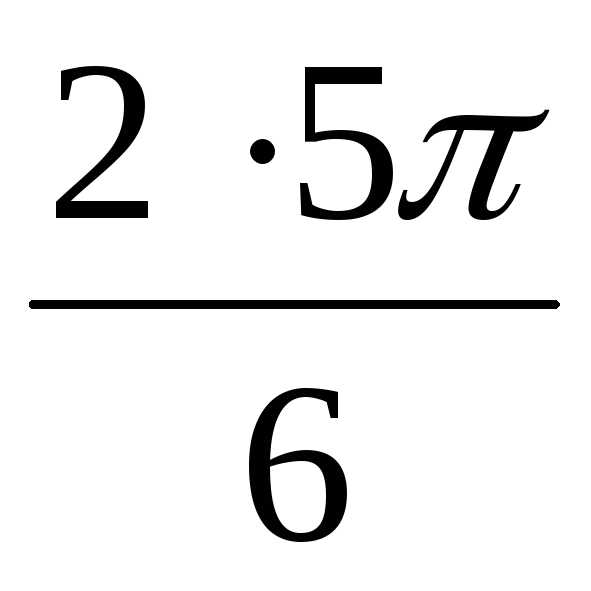 + isin
+ isin 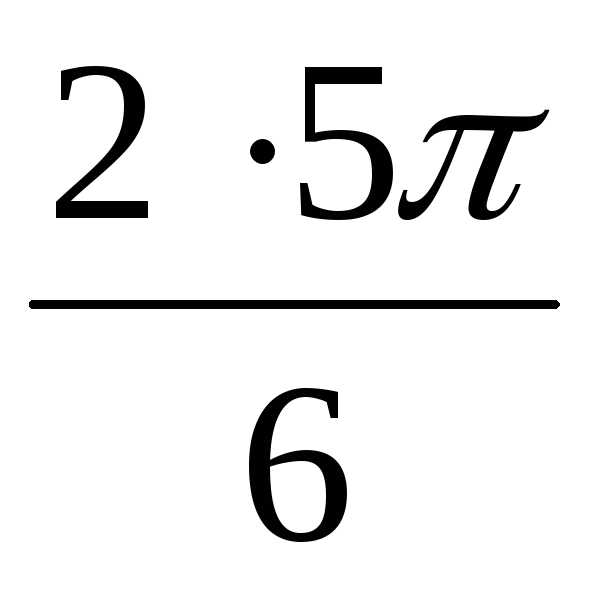 )
= =
)
= = )4 (cos
)4 (cos  + isin
+ isin 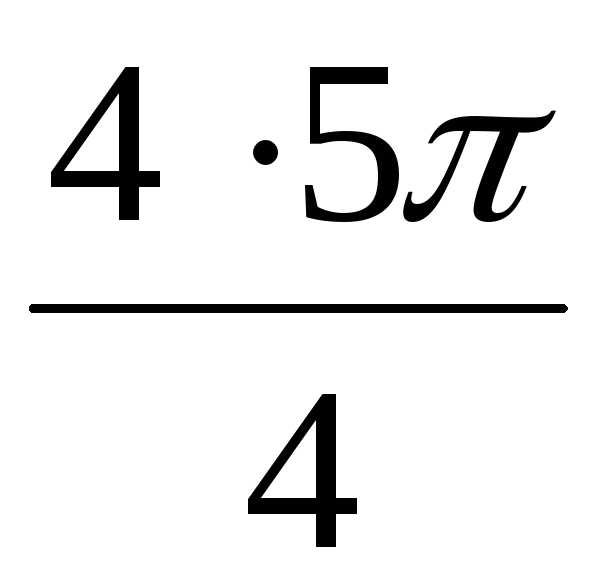 )=
= 4(cos 5 + isin 5)
= 4(cos (4 + )
+ isin (4 + ))
= 4(cos + i sin )
)=
= 4(cos 5 + isin 5)
= 4(cos (4 + )
+ isin (4 + ))
= 4(cos + i sin )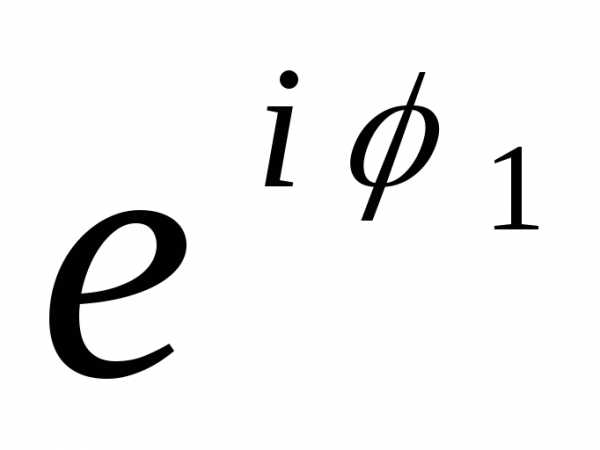 =2e
=2e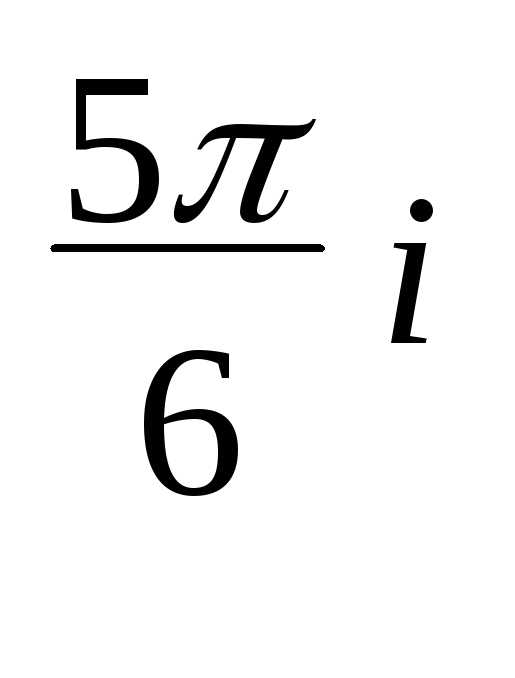
 = 2e
= 2e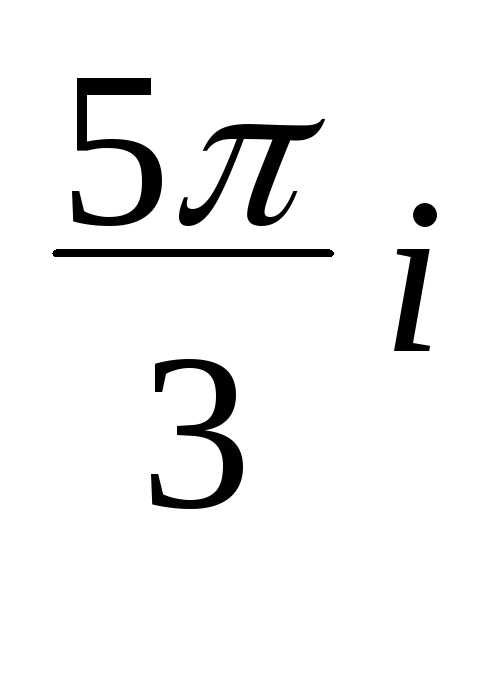
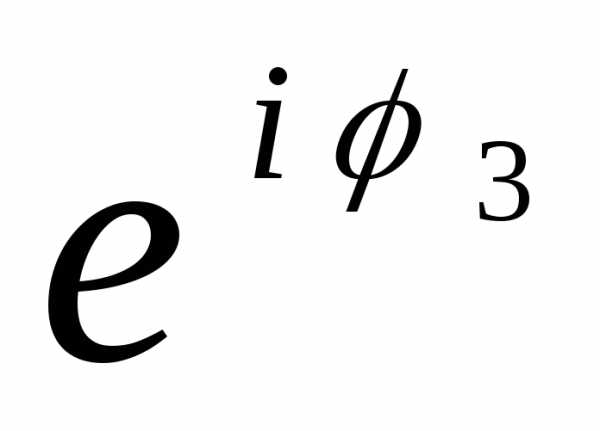 =
= e
e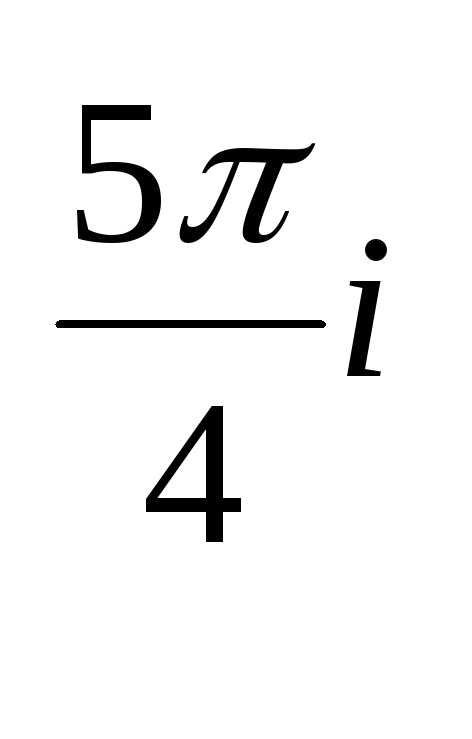
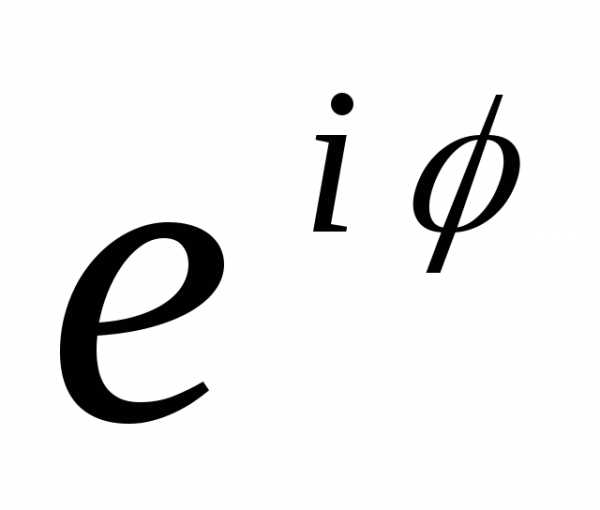 ) n = r n
) n = r n 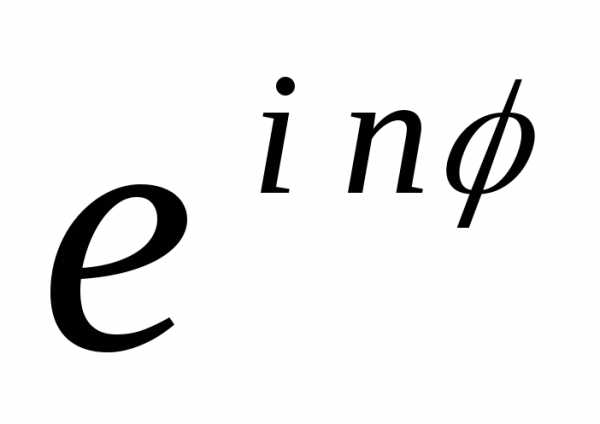
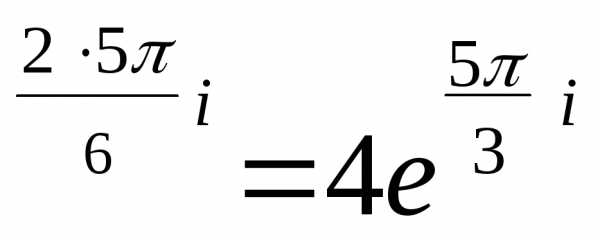
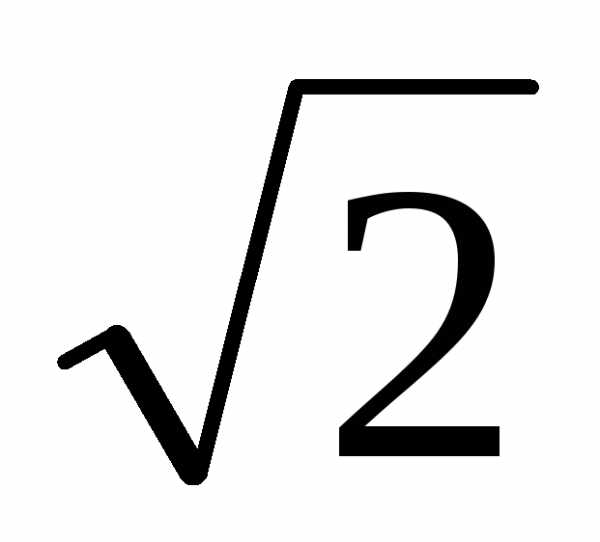 )4
)4 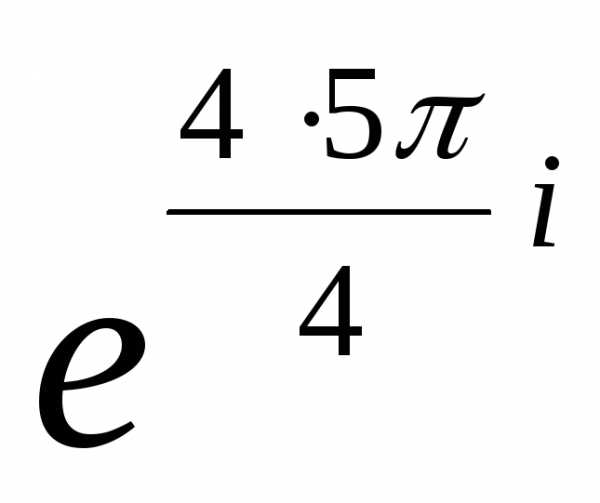 =
4
=
4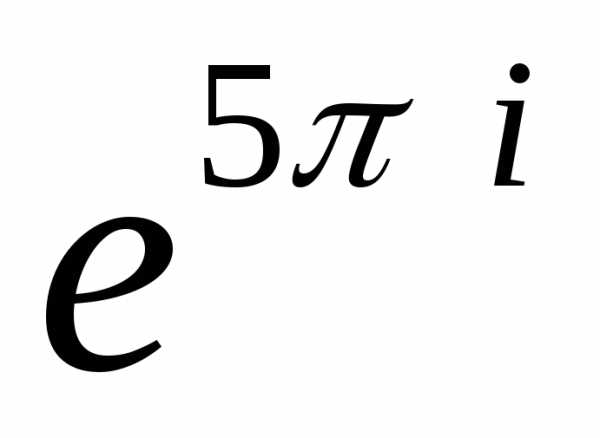
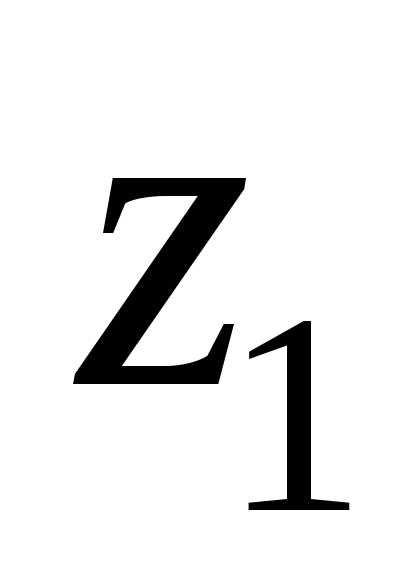 и
и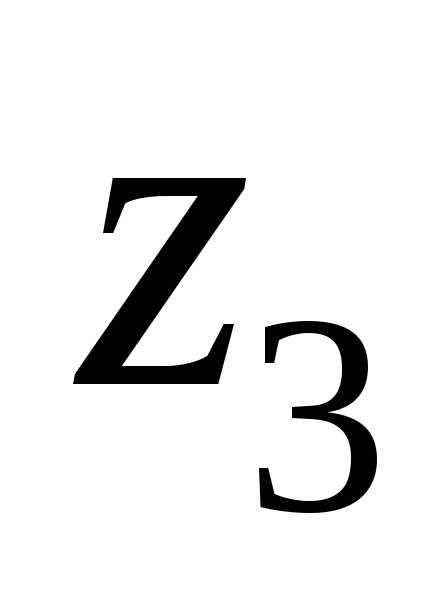 на комплексной плоскости, которое равно
модулю их разности.
на комплексной плоскости, которое равно
модулю их разности.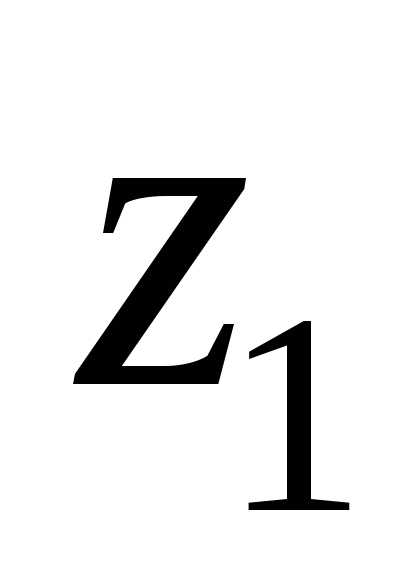 и
и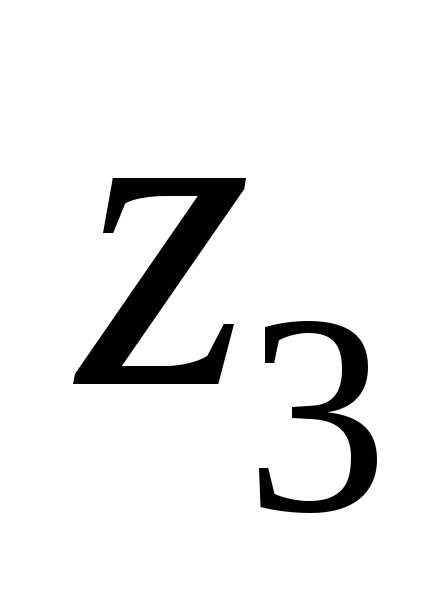 будет
будет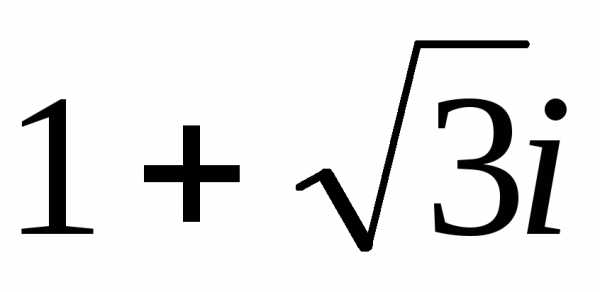 —
алгебраическая форма;
—
алгебраическая форма;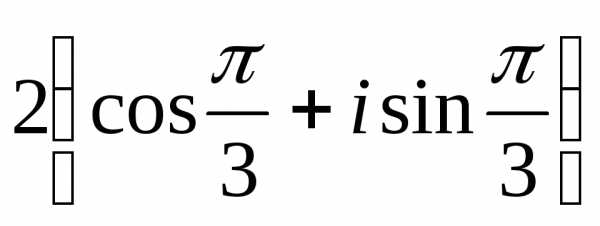 —
тригонометрическая форма;
—
тригонометрическая форма;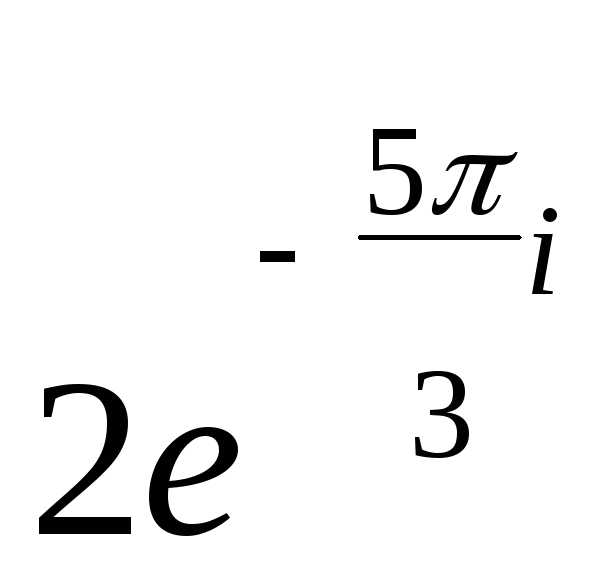 —
показательная форма; 2)
—
показательная форма; 2)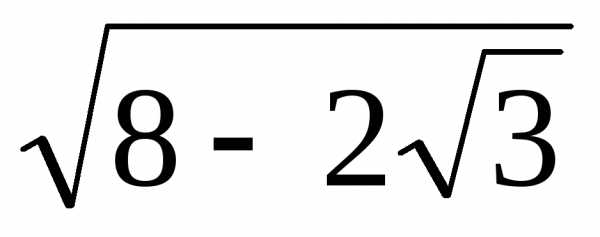
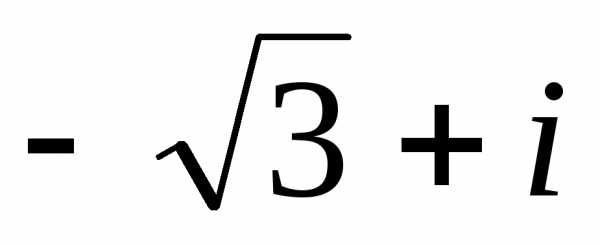 иz22 =
иz22 = 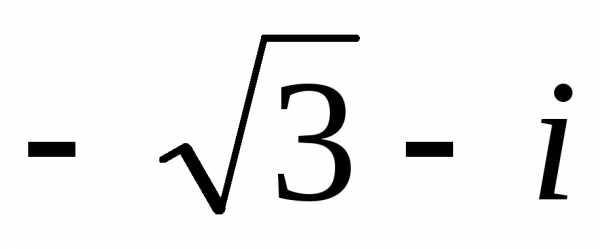 )
на множестве комплексных чисел.
)
на множестве комплексных чисел.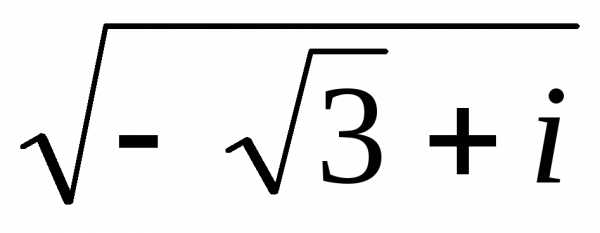 иz2 =
иz2 = 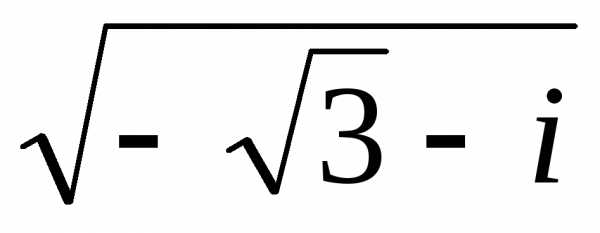
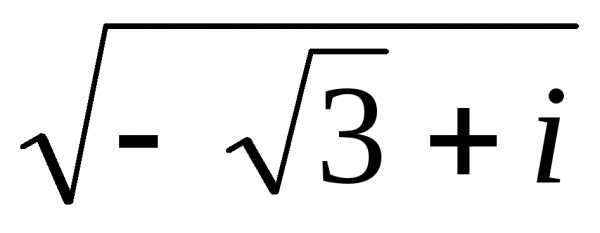 =u + iv.
Тогда
=u + iv.
Тогда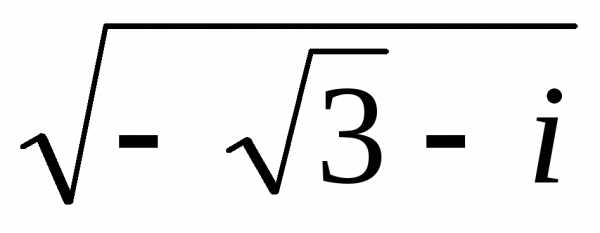 =w — it.
Тогда
=w — it.
Тогда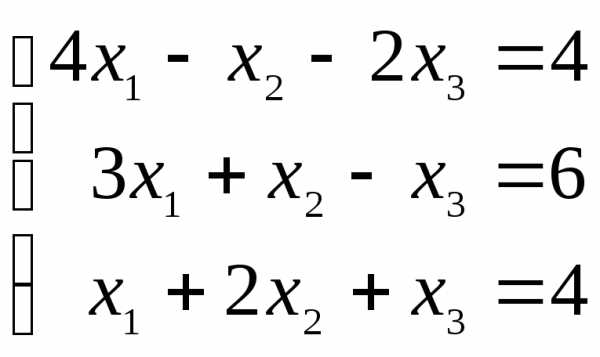 тремя
способами:
тремя
способами:

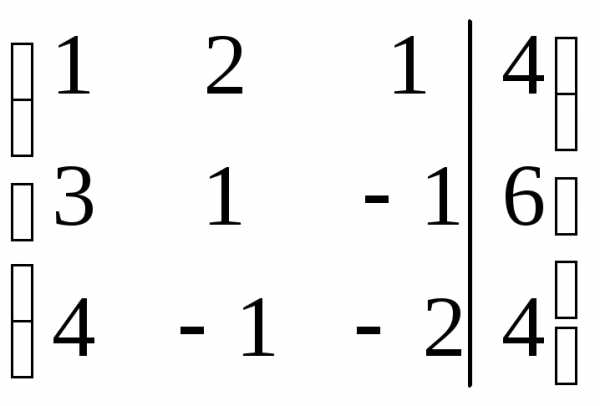
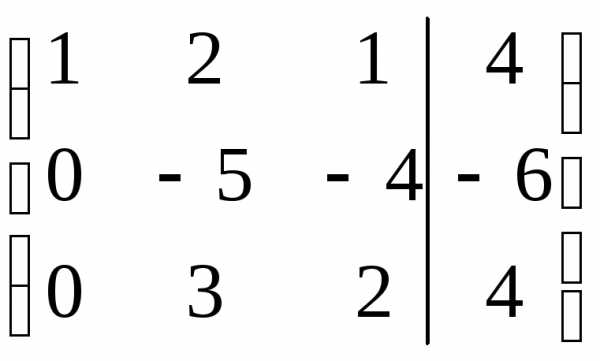
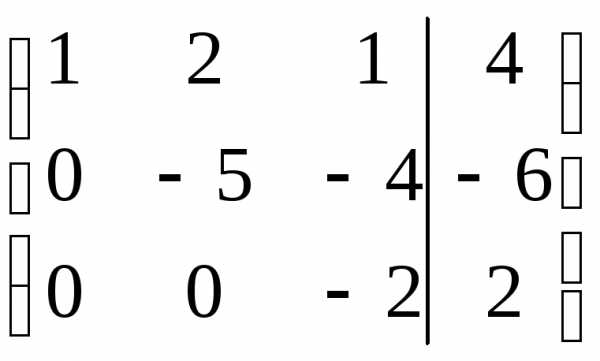
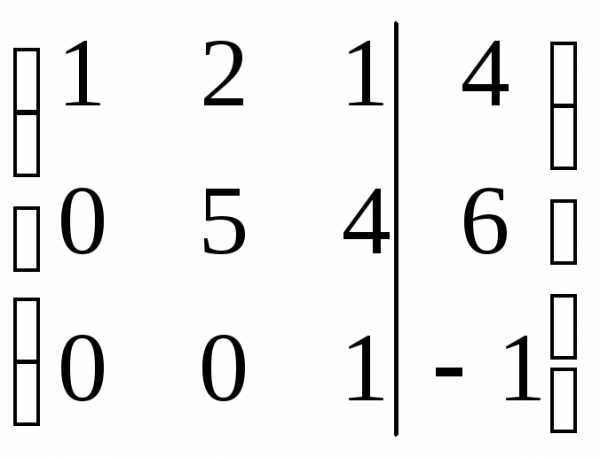


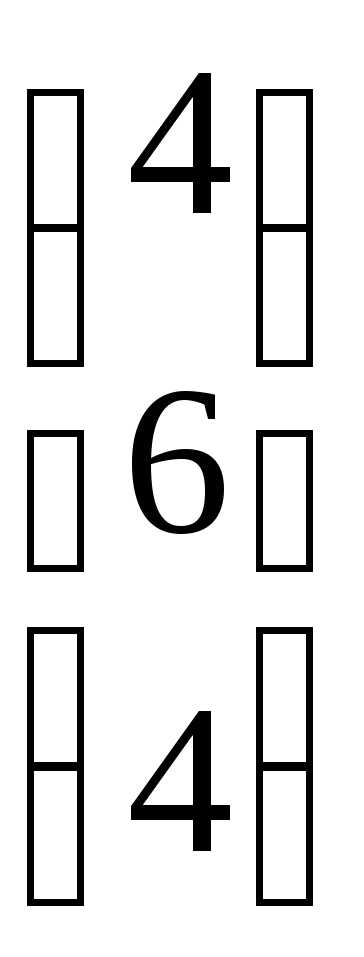
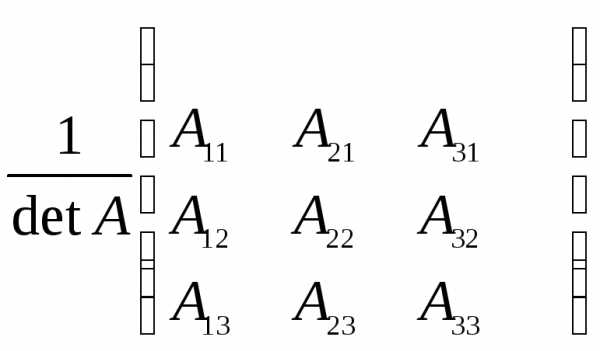 , где Аij — алгебраические дополнения соответствующих элементов.
, где Аij — алгебраические дополнения соответствующих элементов.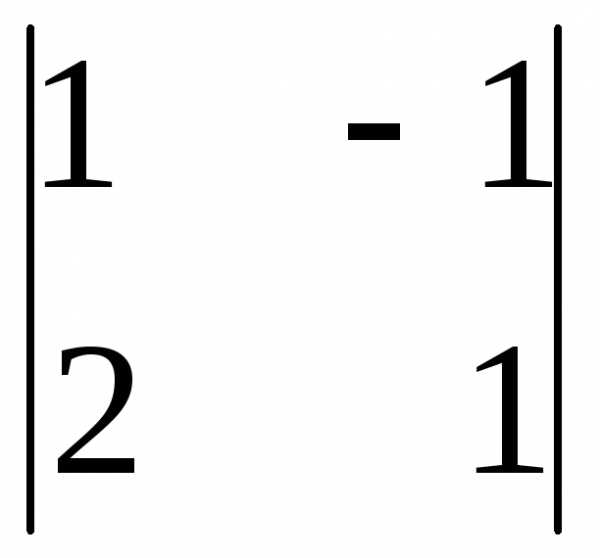 = 1 · 1 – 2 · (-1) = 3
= 1 · 1 – 2 · (-1) = 3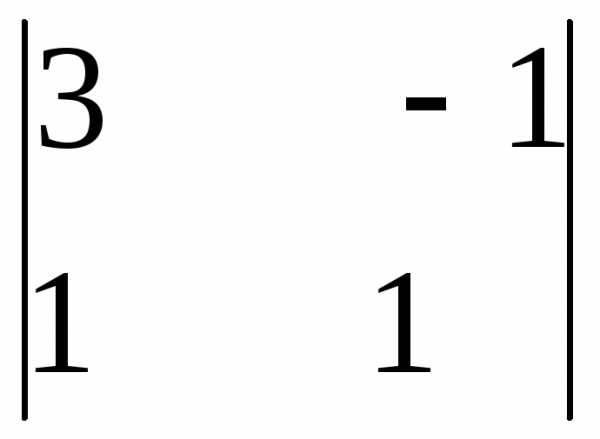 =
— (3 · 1 – 1 · (-1)) = — 4
=
— (3 · 1 – 1 · (-1)) = — 4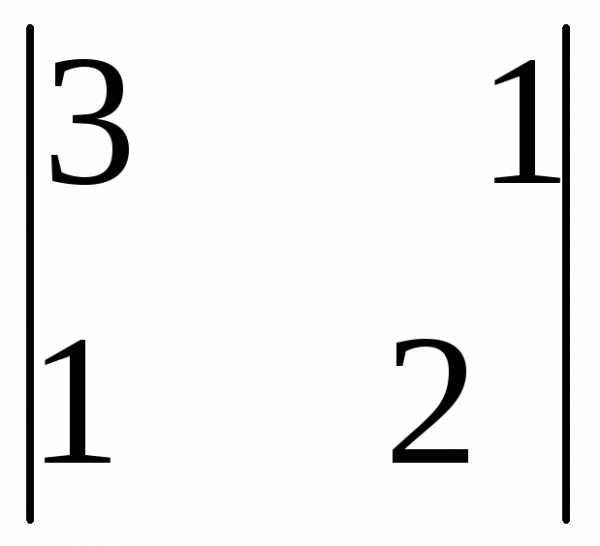 = 3 · 2 – 1 · 1 = 5
= 3 · 2 – 1 · 1 = 5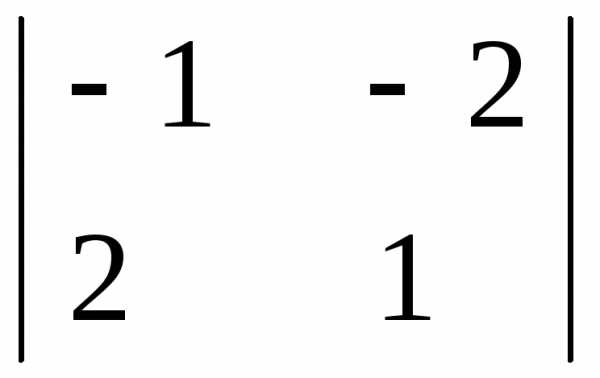 = — ((-1) · 1 – 2 · (-2) = — 3
= — ((-1) · 1 – 2 · (-2) = — 3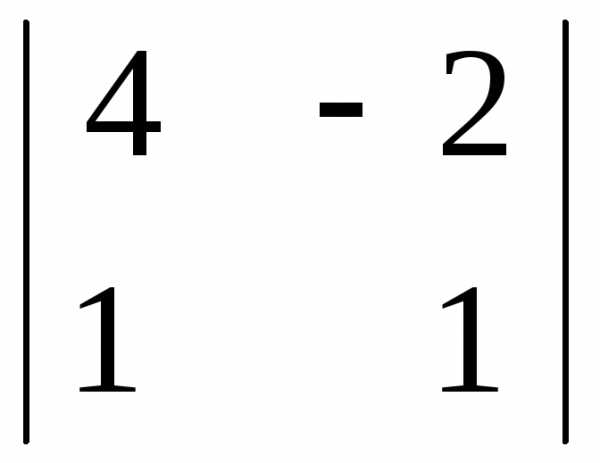 = 4 · 1 – 1 · (-2) = 6
= 4 · 1 – 1 · (-2) = 6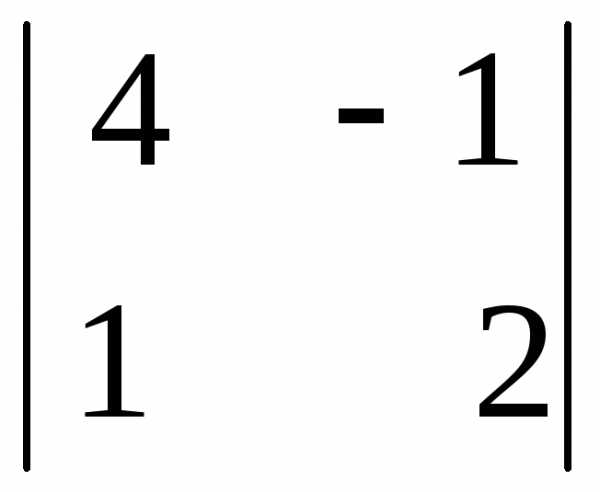 = — (4 · 2 – 1 · (-1)) = — 9
= — (4 · 2 – 1 · (-1)) = — 9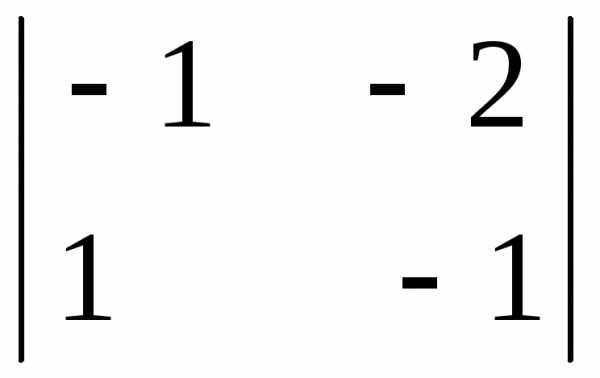 = (-1) · (-1) – (- 2) · 1 = 3
= (-1) · (-1) – (- 2) · 1 = 3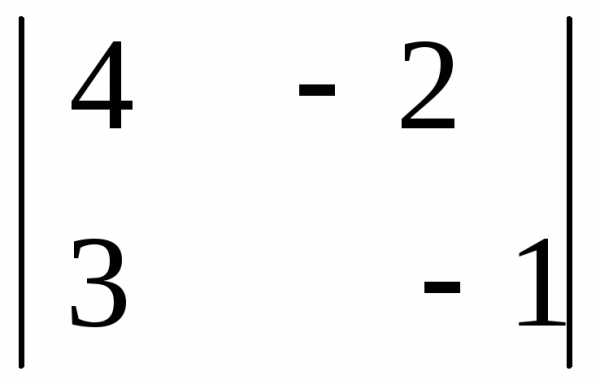 = — (4 · (-1) – 3 · (-2)) = — 2
= — (4 · (-1) – 3 · (-2)) = — 2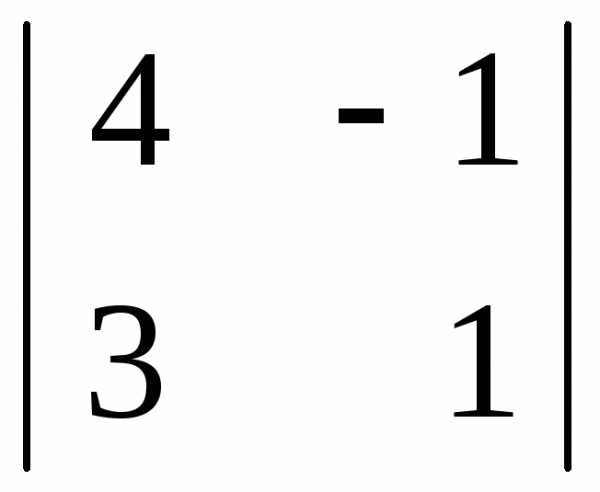 = 4 · 1 – 3 · (-1) = 7
= 4 · 1 – 3 · (-1) = 7
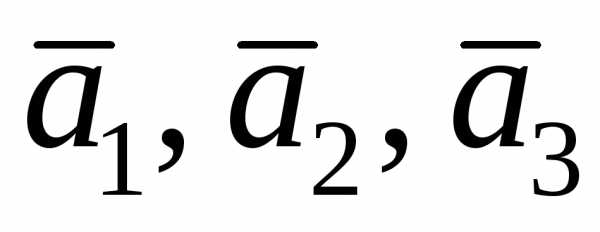 образуют базис, и определить, какая это
тройка векторов: правая или левая.
образуют базис, и определить, какая это
тройка векторов: правая или левая.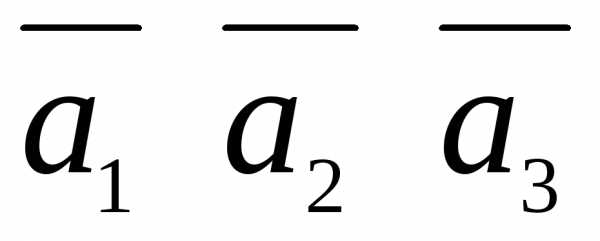 :
: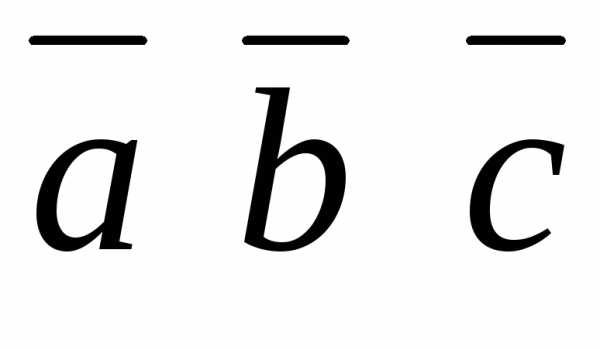 ≠
0, значит данные векторы не компланарны.
Таким образом, они линейно независимы
и образуют базис. При этом, они образуют
правую тройку векторов, т.к. их смешанное
произведение – число положительное:
≠
0, значит данные векторы не компланарны.
Таким образом, они линейно независимы
и образуют базис. При этом, они образуют
правую тройку векторов, т.к. их смешанное
произведение – число положительное: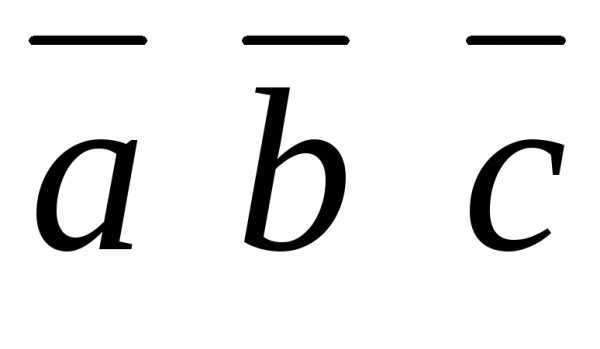 =
23 0.
=
23 0. образуют
базис, тройка векторов
образуют
базис, тройка векторов 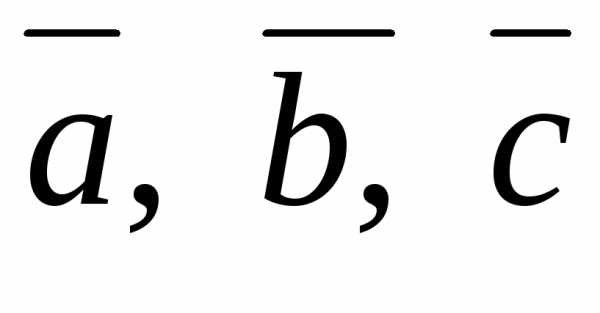 –
правая.
–
правая.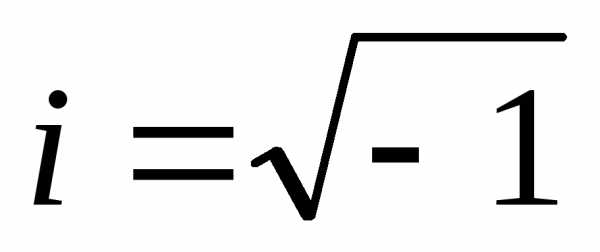 называетсямнимой единицейи
называетсямнимой единицейи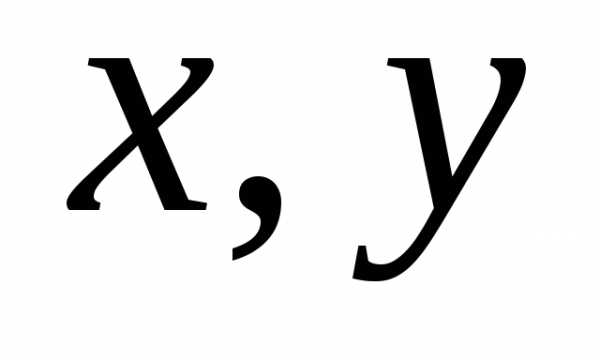 — действительные числа:
— действительные числа: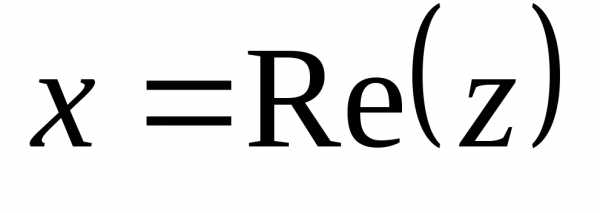 называетсядействительной (вещественной)
частью;
называетсядействительной (вещественной)
частью; —мнимой частьюкомплексного числа
—мнимой частьюкомплексного числа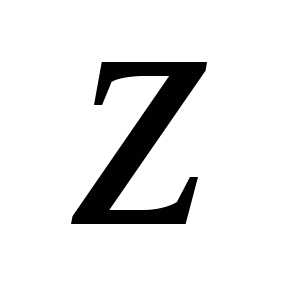 .
Комплексные числа виданазываютсячисто мнимыми числами.
Множество всех комплексных чисел
обозначается буквой
.
Комплексные числа виданазываютсячисто мнимыми числами.
Множество всех комплексных чисел
обозначается буквой .
.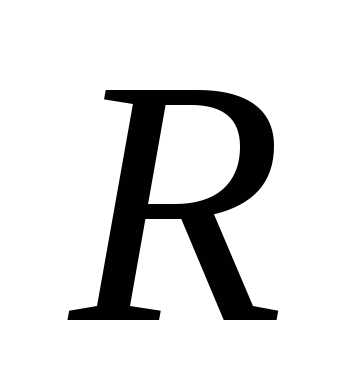 является частью множества
является частью множества
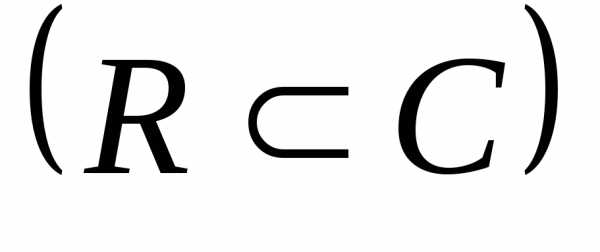 :.
С другой стороны, существуют комплексные
числа, не принадлежащие множеству
:.
С другой стороны, существуют комплексные
числа, не принадлежащие множеству .
Например,и
.
Например,и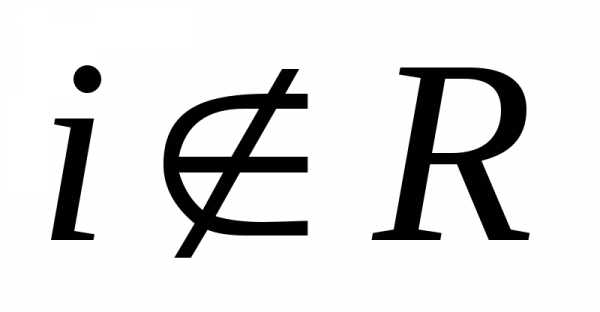 ,
т.к.
,
т.к. .
.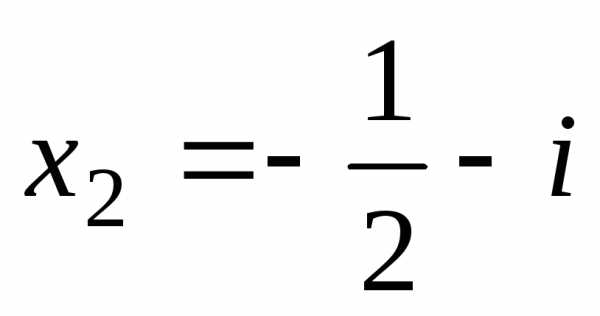 .
.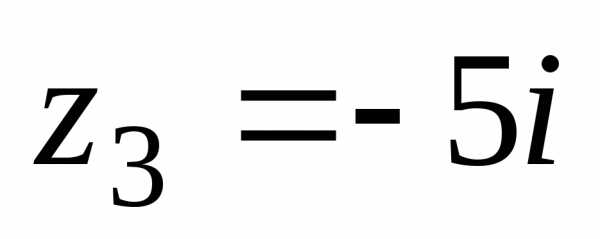 ,
,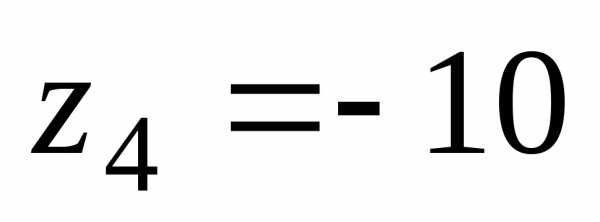 .
.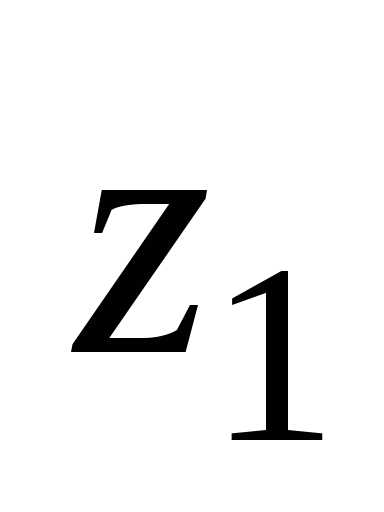 ,
, ,
представляющей плоскость с декартовой
системой координат
,
представляющей плоскость с декартовой
системой координат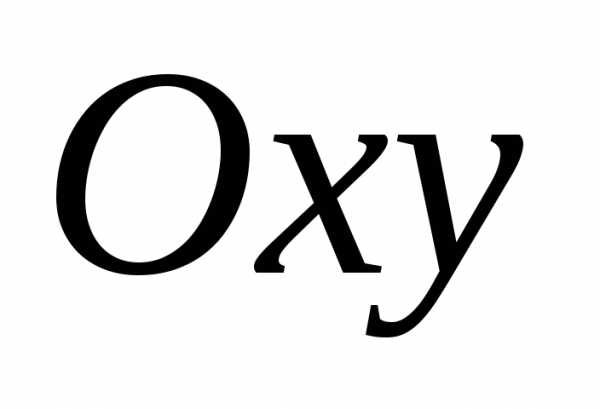 .
Начало вектора лежит в точке
.
Начало вектора лежит в точке ,
а конец — в точке с координатами
,
а конец — в точке с координатами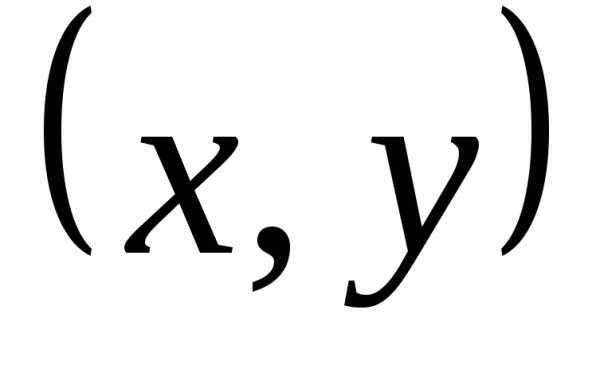 (рис
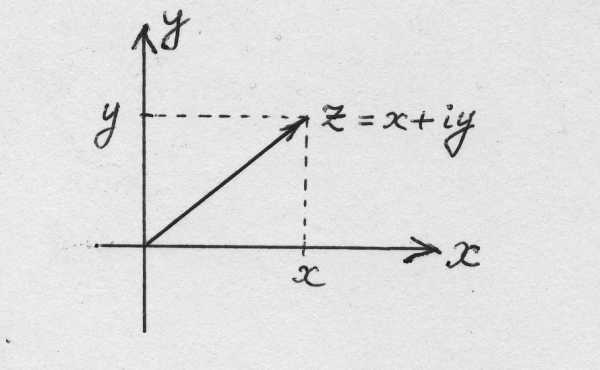
1.) Ось
(рис
1.) Ось называется
вещественной осью, а ось
называется
вещественной осью, а ось — мнимой осью комплексной плоскости
— мнимой осью комплексной плоскости .
.
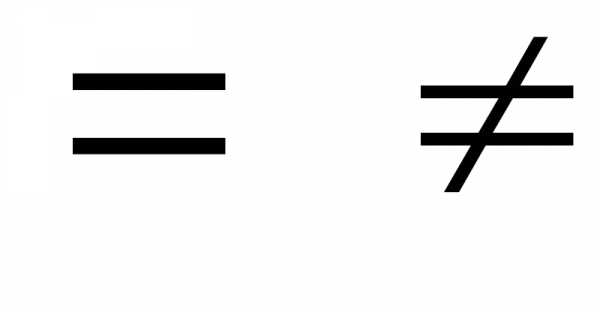 ..
Если же хотя бы одно из равенств:нарушено, то
..
Если же хотя бы одно из равенств:нарушено, то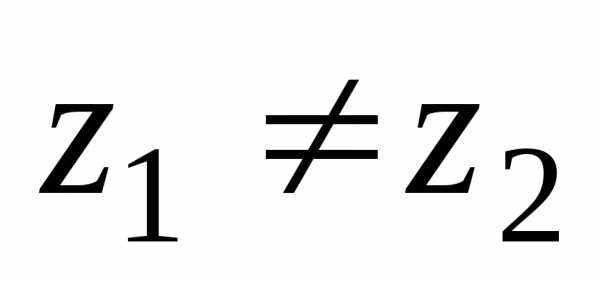 .Записи типа
не имеют смысла.
.Записи типа
не имеют смысла.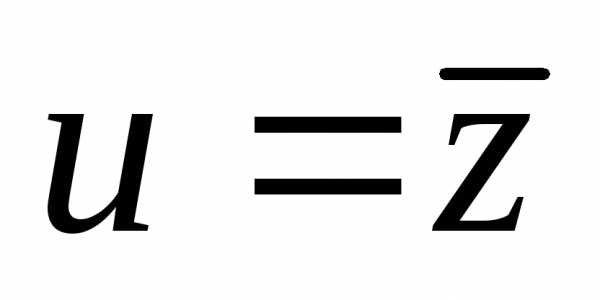 .
Очевидно, что
.
Очевидно, что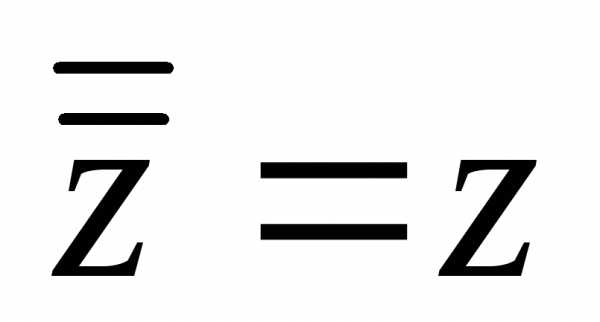 .
Везде далее черта сверху над комплексным
числом будет означать комплексное
сопряжение.
.
Везде далее черта сверху над комплексным
числом будет означать комплексное
сопряжение.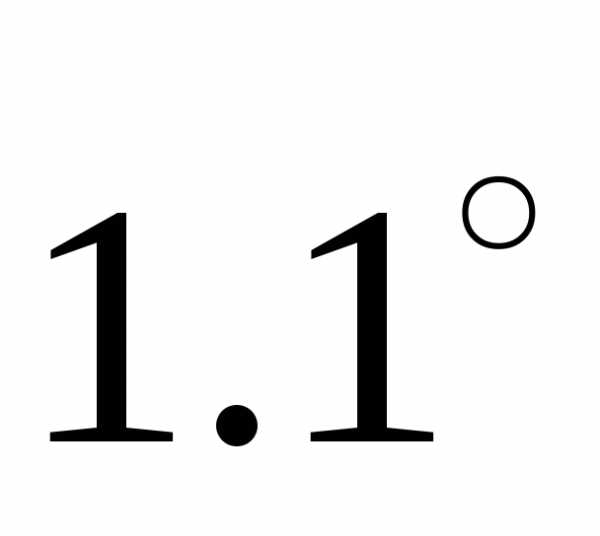 — свойство коммутативности;
— свойство коммутативности;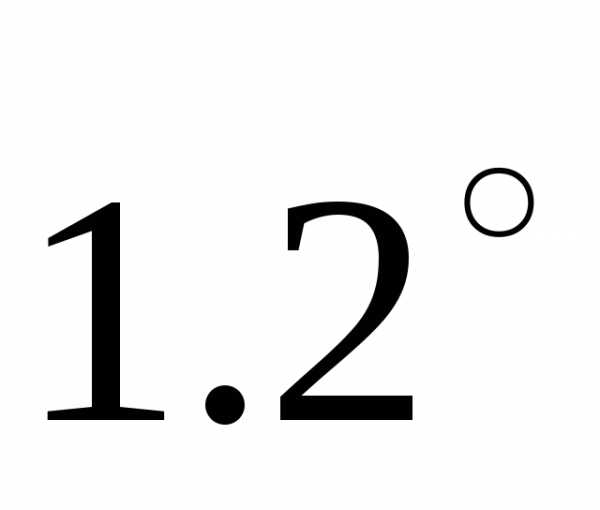 — свойство ассоциативности.
— свойство ассоциативности.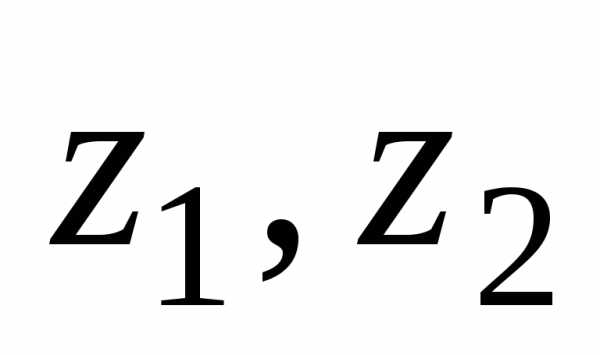 означает сложение отвечающих им на
плоскости
означает сложение отвечающих им на
плоскости векторов по правилу параллелограмма.
векторов по правилу параллелограмма.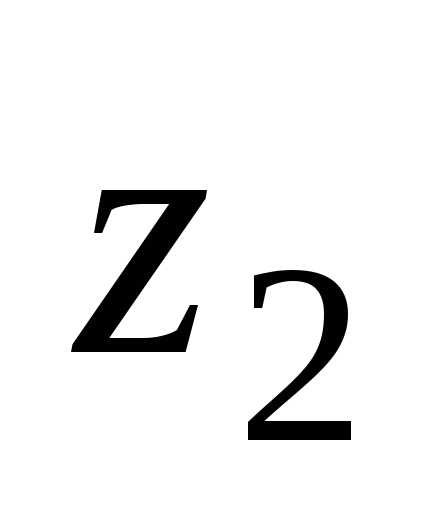 из числа
из числа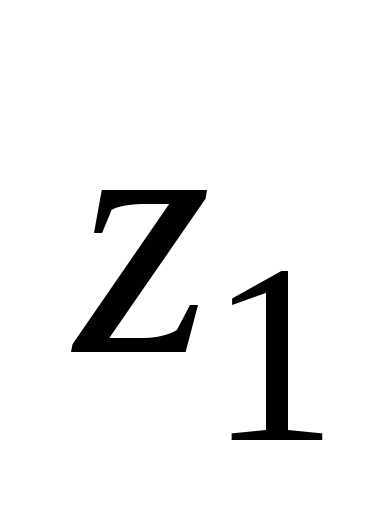 производится так:
производится так: — свойство коммутативности;
— свойство коммутативности; — свойство ассоциативности;
— свойство ассоциативности; — закон дистрибутивности.
— закон дистрибутивности.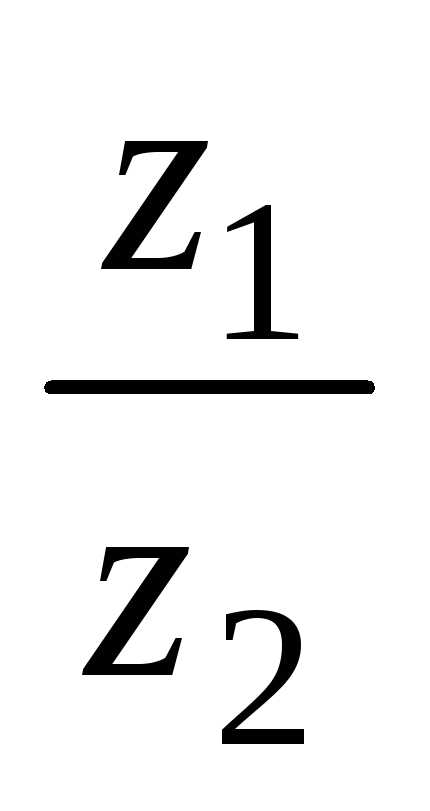 выполнимо только при
выполнимо только при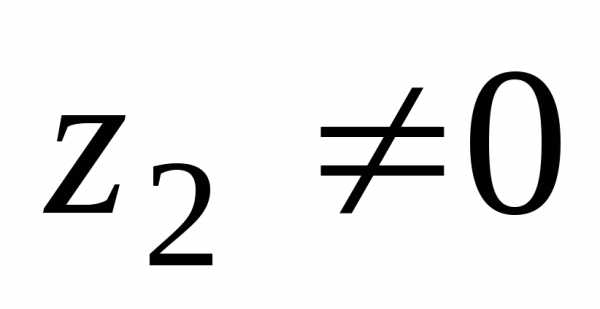 и производится так:
и производится так: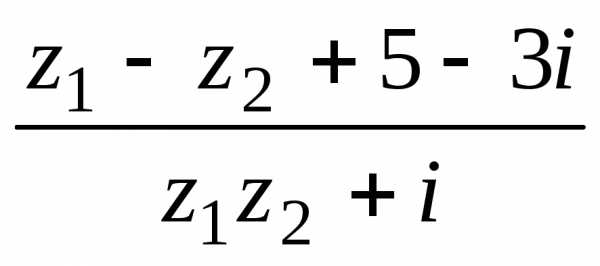 ,
если.
,
если.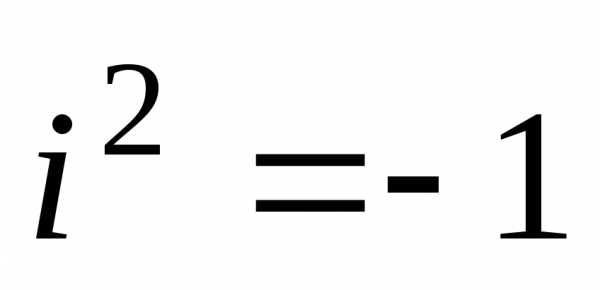 .
.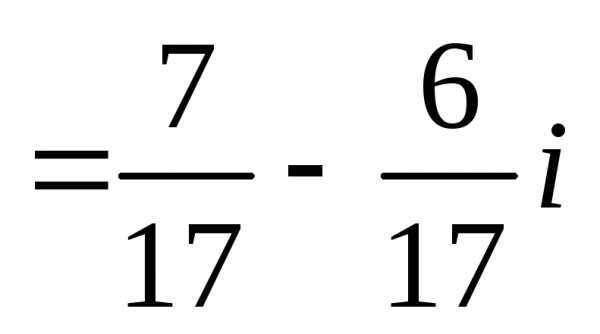 .(ош!)
.(ош!)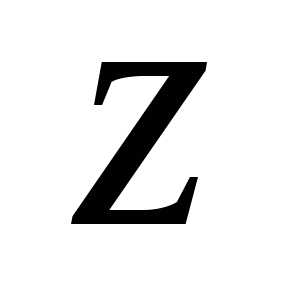 обозначается
обозначается )
это — неотрицательное число
)
это — неотрицательное число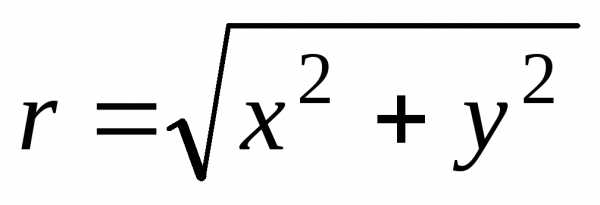 ,
т.е. .
,
т.е. .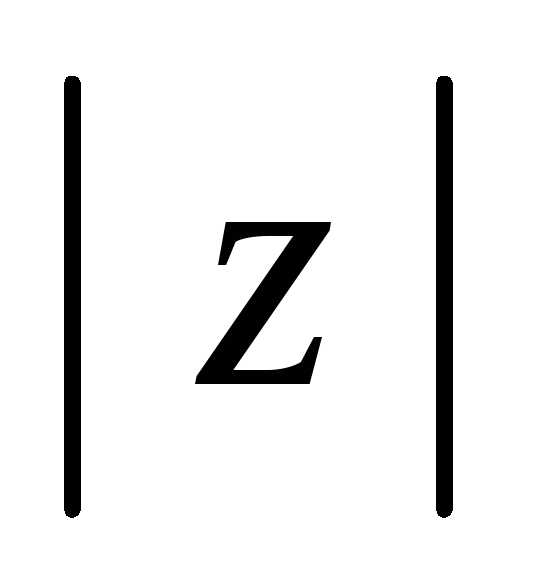 — длина вектора, представляющего число
— длина вектора, представляющего число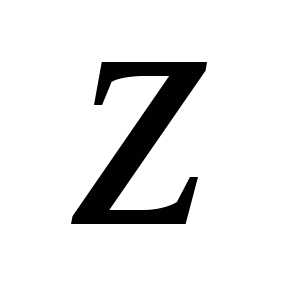 на комплексной плоскости
на комплексной плоскости .
Уравнение
.
Уравнение определяет множество всех чисел
определяет множество всех чисел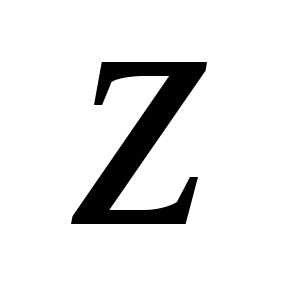 (векторов на
(векторов на ),
концы которых лежат на единичной
окружности
),
концы которых лежат на единичной
окружности .
.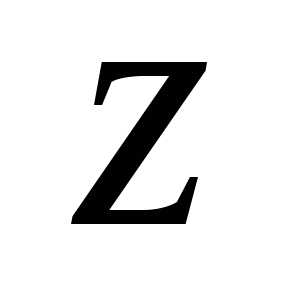 обозначается
обозначается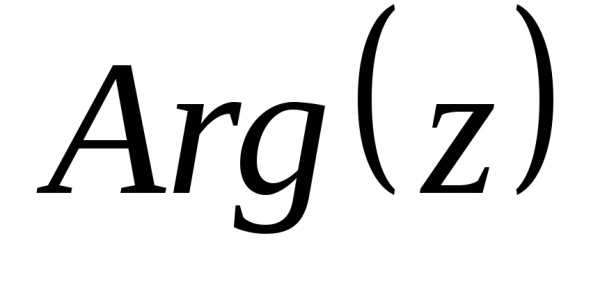 )
это – угол
)
это – угол в радианах между вещественной осью
в радианах между вещественной осью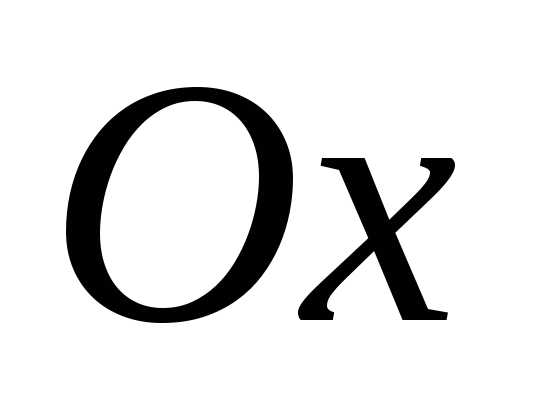 и числом
и числом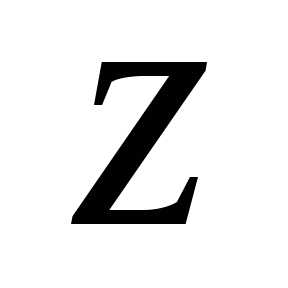 на комплексной плоскости
на комплексной плоскости ,
причем
,
причем  положителен, если он отсчитывается от
положителен, если он отсчитывается от до
до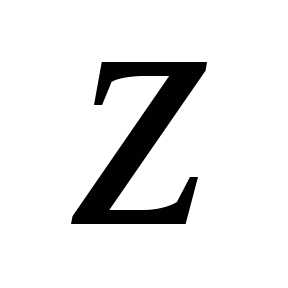 против часовой стрелки, и
против часовой стрелки, и отрицателен, если
отрицателен, если отсчитывается от оси
отсчитывается от оси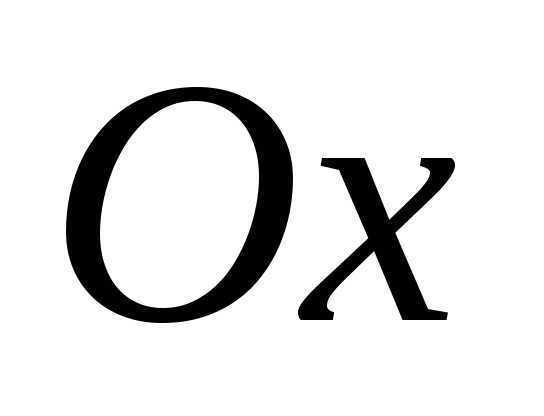 до
до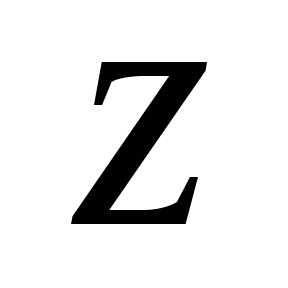 по часовой стрелке.
по часовой стрелке.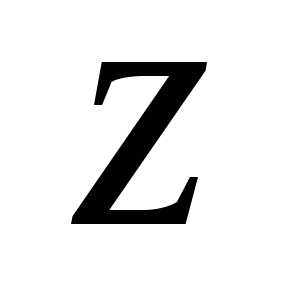 определяется неоднозначно, с точностью
до слагаемого
определяется неоднозначно, с точностью
до слагаемого ,
где
,
где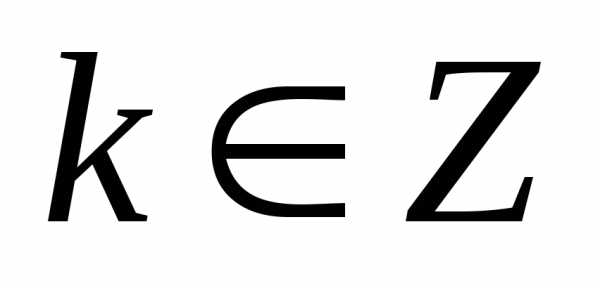 .
Однозначно аргумент числа
.
Однозначно аргумент числа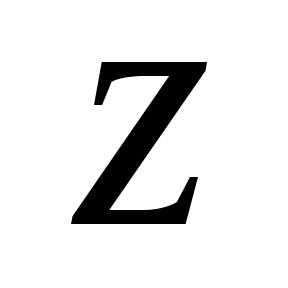 определяется в пределах одного обхода
единичной окружности
определяется в пределах одного обхода
единичной окружности на плоскости
на плоскости .Обычно требуется найти
.Обычно требуется найти 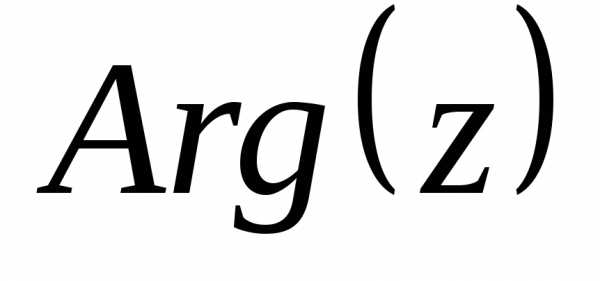 в пределах интервала
в пределах интервала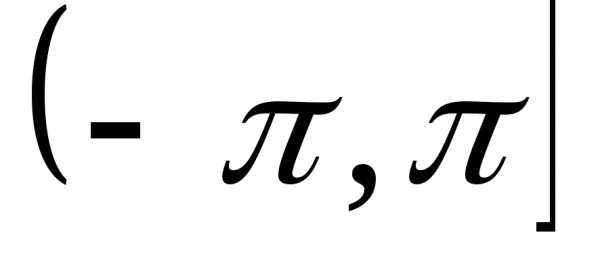 , такое значение называется главным
значением аргумента числа
, такое значение называется главным
значением аргумента числа 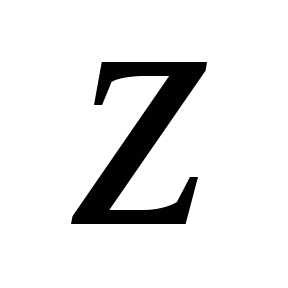 и обозначается
и обозначается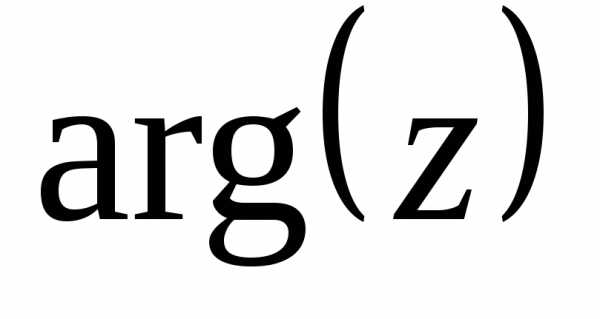 .
.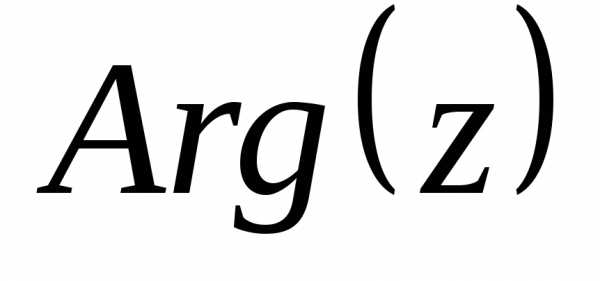 и
и числа
числа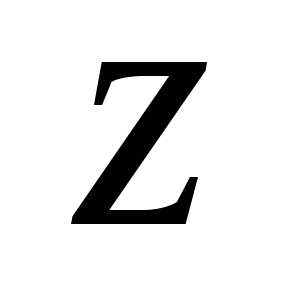 можно найти из уравнения
можно найти из уравнения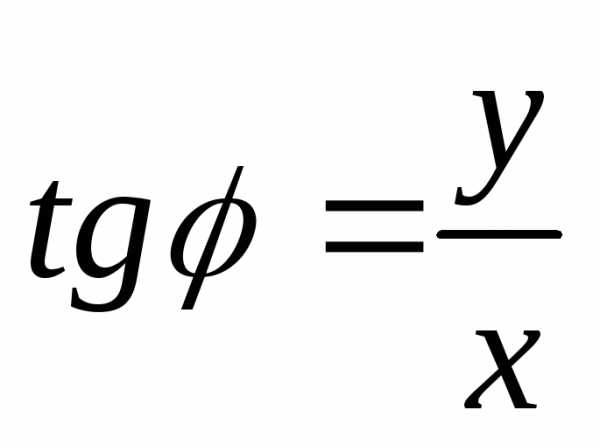 ,
при этомобязательнонужно
учитывать, в какой четверти плоскости
,
при этомобязательнонужно
учитывать, в какой четверти плоскости лежит конец вектора
лежит конец вектора — точка
— точка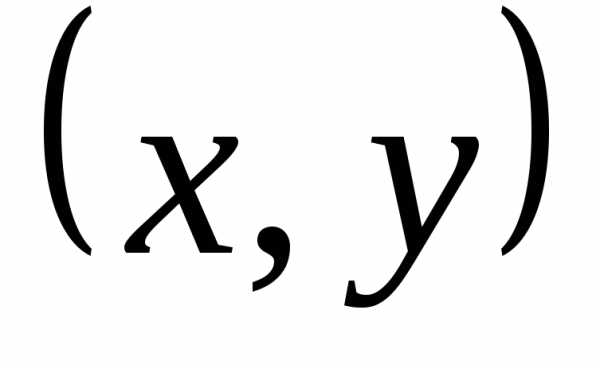 :
: ),
то;
),
то; ),
то;
),
то; ),
то;
),
то; ),
то.
),
то. точки
точки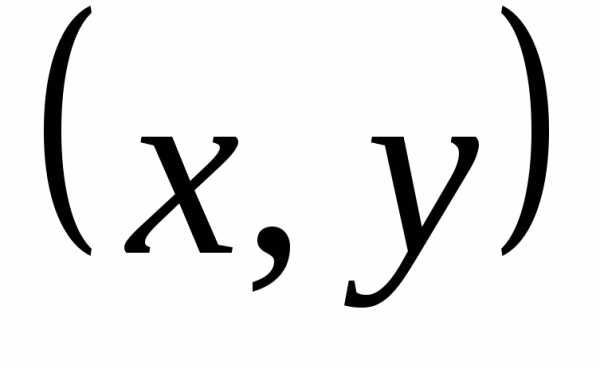 — конца вектора
— конца вектора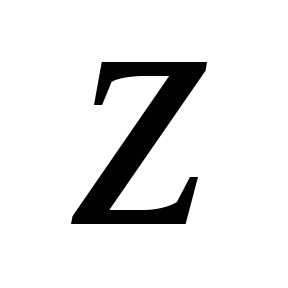 на плоскости
на плоскости .
.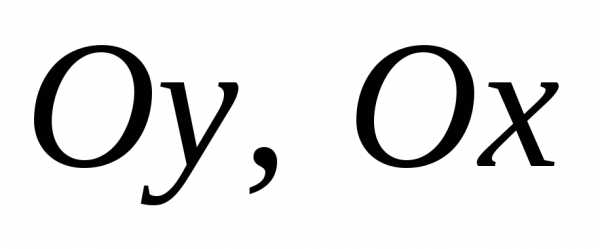 ,
разделяющих четверти 1,2,3,4 комплексной
плоскости
,
разделяющих четверти 1,2,3,4 комплексной
плоскости ,
находятся сразу же по графическим
изображениям этих чисел на плоскости
,
находятся сразу же по графическим
изображениям этих чисел на плоскости .
.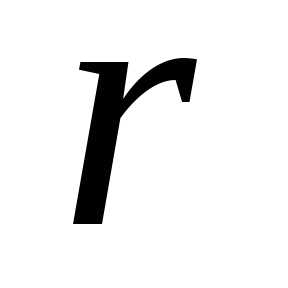 —
модуль,
—
модуль, —
аргумент комплексного числа
—
аргумент комплексного числа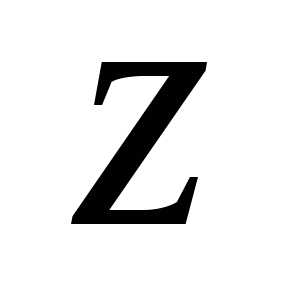 .
Такое представление комплексных чисел
вытекает из равенств.
.
Такое представление комплексных чисел
вытекает из равенств.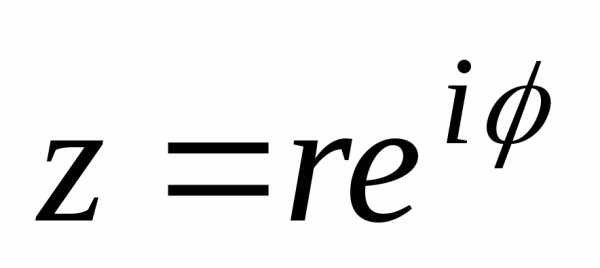 ,
(3)
,
(3)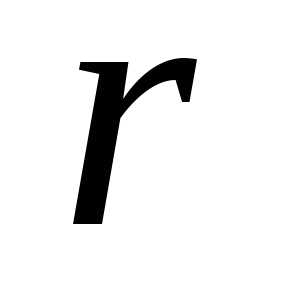 —
модуль,
—
модуль, —
аргумент числа
—
аргумент числа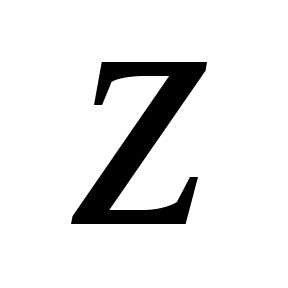 .
Возможность представления комплексных
чисел в показательной форме (3) вытекает
из тригонометрической формы (2) и формулы
Эйлера:
.
Возможность представления комплексных
чисел в показательной форме (3) вытекает
из тригонометрической формы (2) и формулы
Эйлера: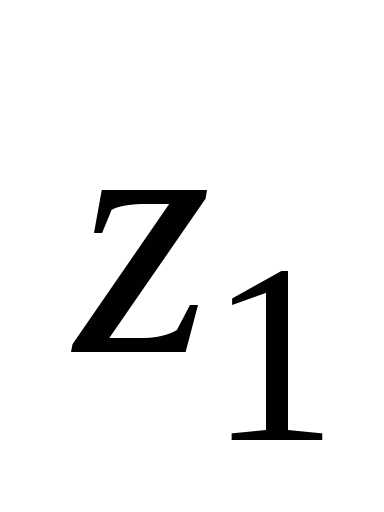 ,
,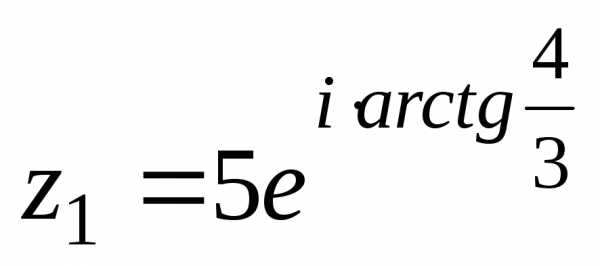 — показательная (экспоненциальная)
форма записи числа
— показательная (экспоненциальная)
форма записи числа .
.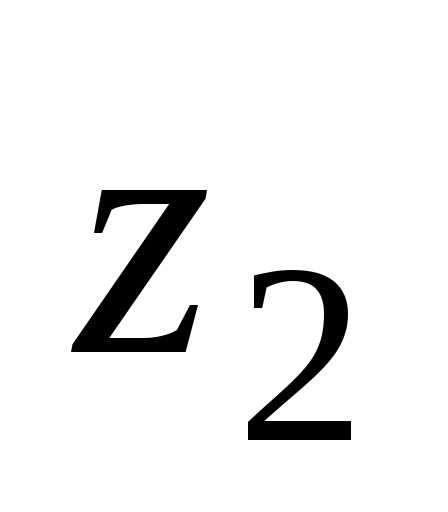 ,
,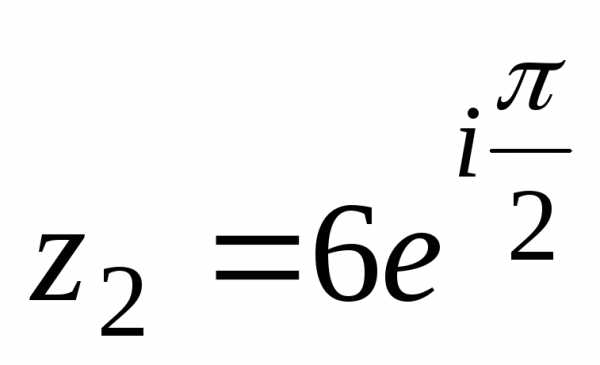 — показательная (экспоненциальная)
форма записи числа
— показательная (экспоненциальная)
форма записи числа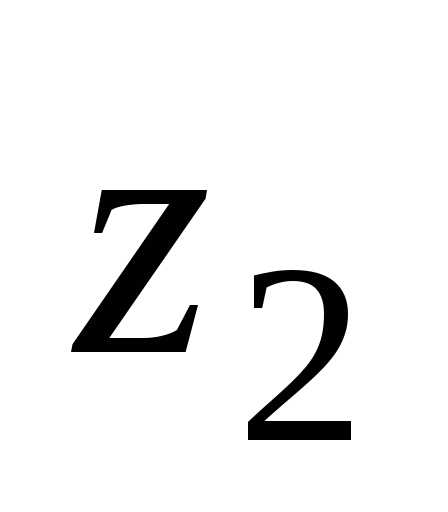 .
. ,
,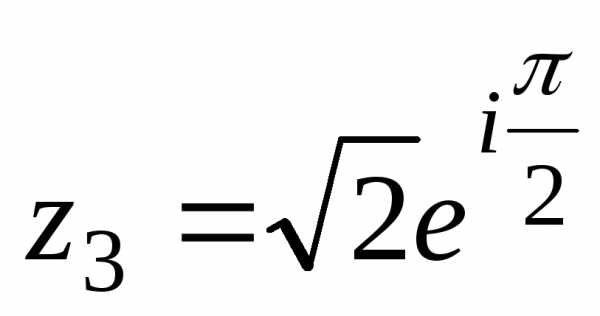 — показательная (экспоненциальная)
форма записи числа
— показательная (экспоненциальная)
форма записи числа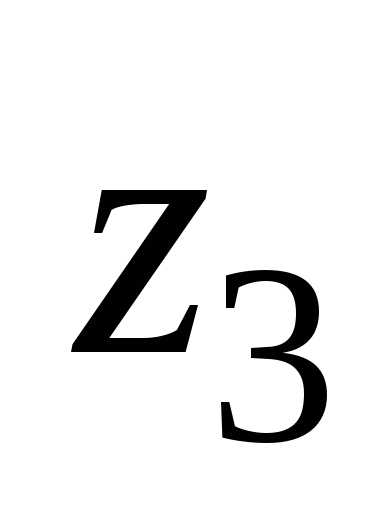 .
. ,
,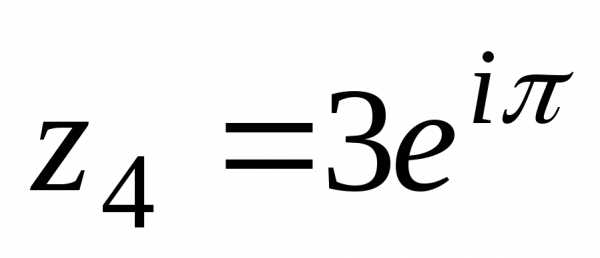 — показательная (экспоненциальная)
форма записи числа
— показательная (экспоненциальная)
форма записи числа .
.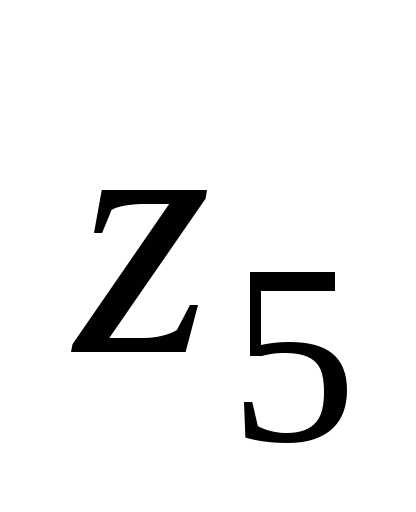 ,
,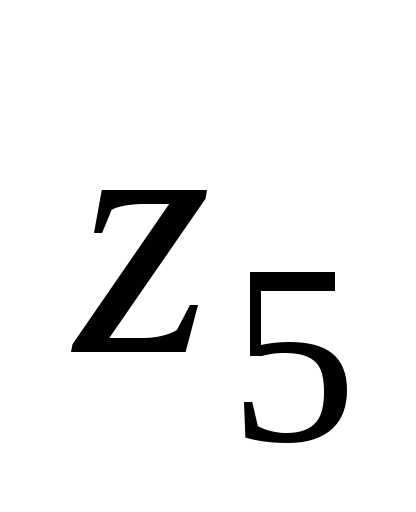 .
.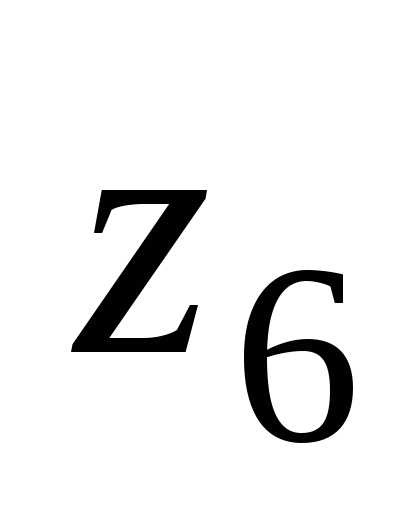 ,
,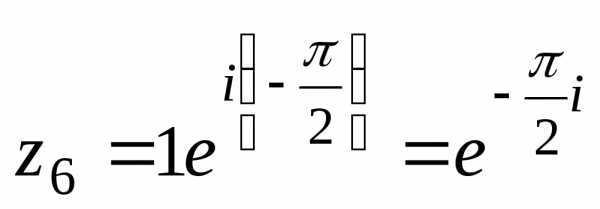 — показательная (экспоненциальная)
форма числа
— показательная (экспоненциальная)
форма числа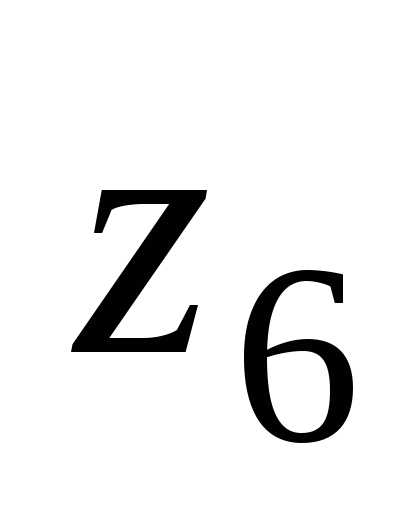 .
.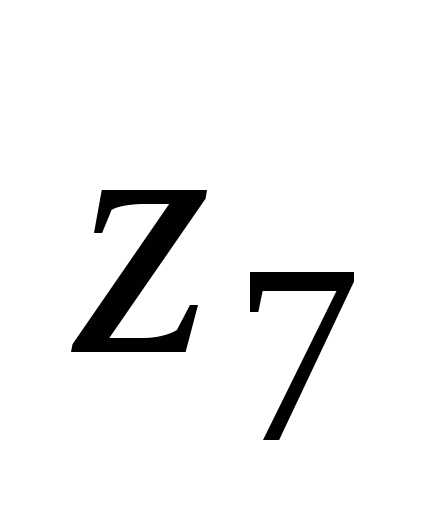 ,
,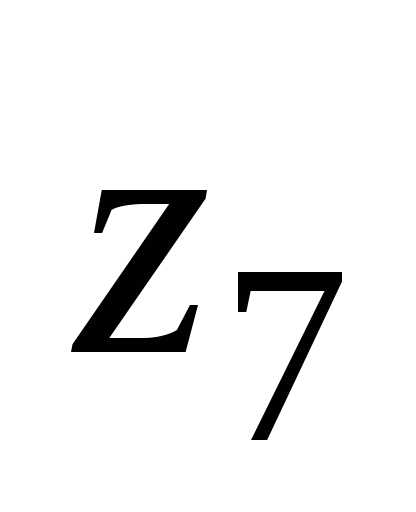 .
. ,
,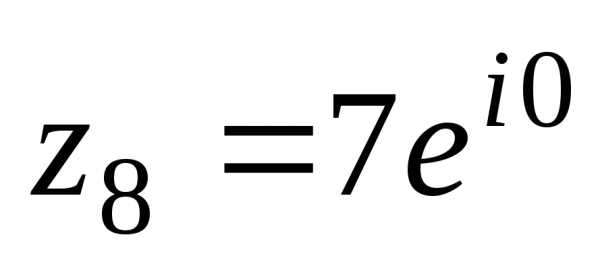 — показательная (экспоненциальная)
форма записи числа
— показательная (экспоненциальная)
форма записи числа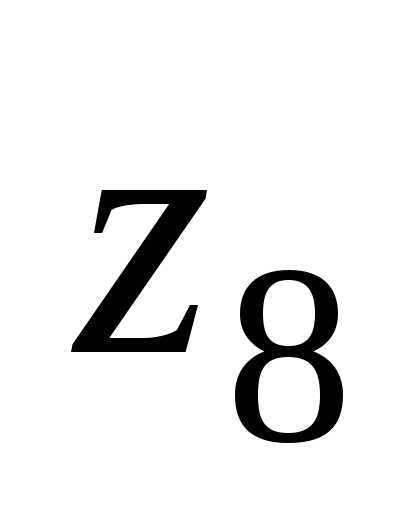 .
.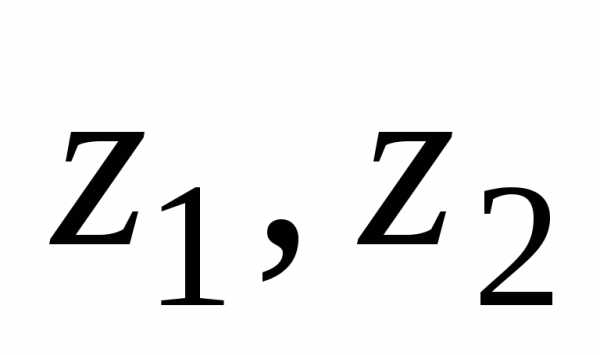 .
.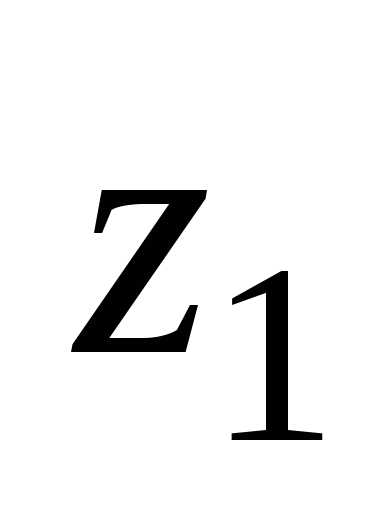 на число
на число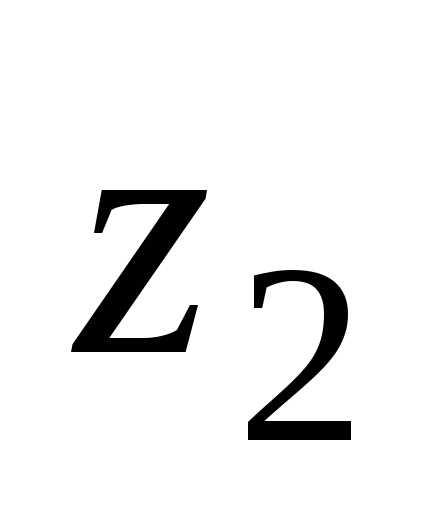 получается комплексное число
получается комплексное число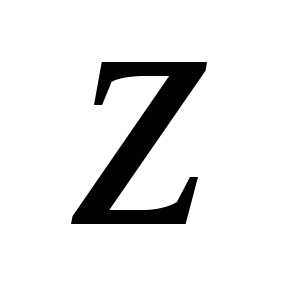 ,
модуль
,
модуль которого равен отношению модулей
которого равен отношению модулей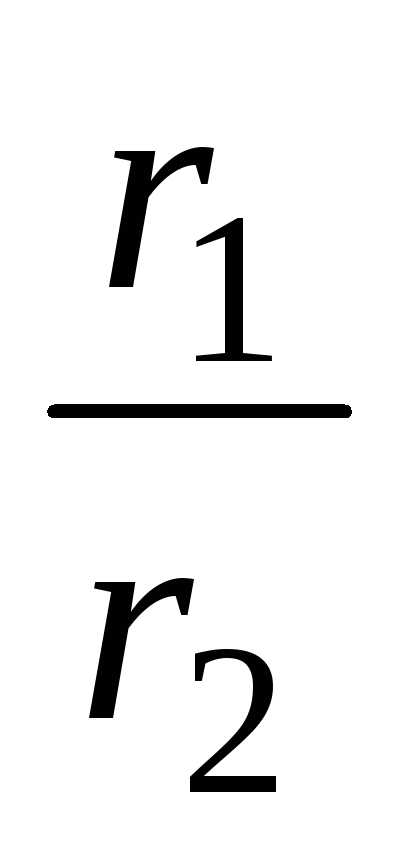 ,
а аргумент
,
а аргумент — разности
— разности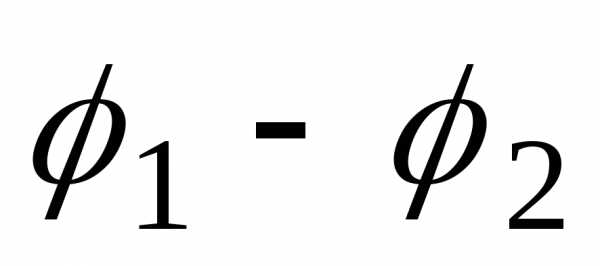 аргументов чисел
аргументов чисел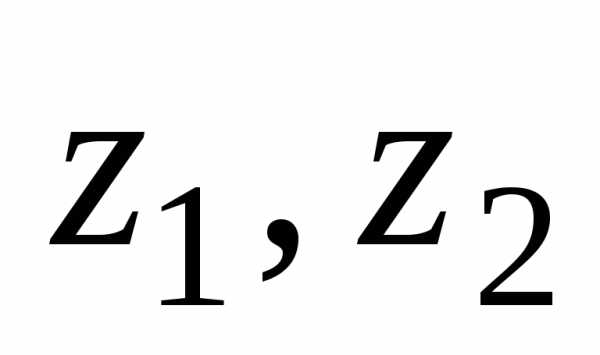 .
.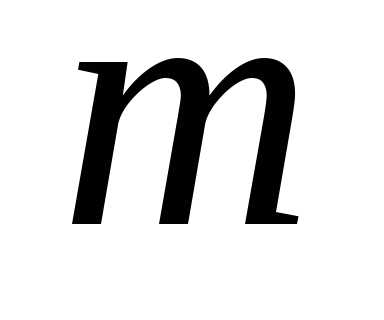 комплексного
числа,
следует действовать так: сначала найти
модуль
комплексного
числа,
следует действовать так: сначала найти
модуль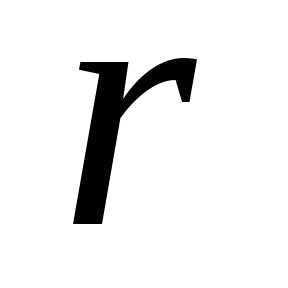 и аргумент
и аргумент этого числа; представить
этого числа; представить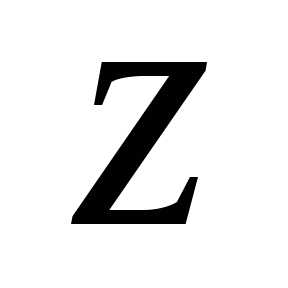 в показательной форме
в показательной форме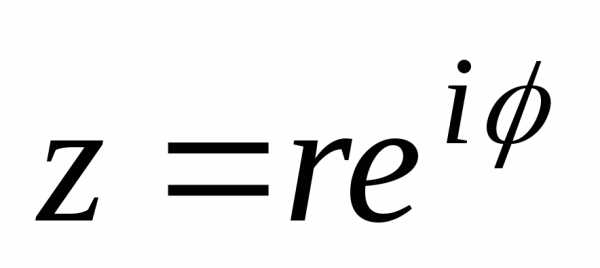 ;
найти
;
найти ,
выполнив следующую последовательность
действий
,
выполнив следующую последовательность
действий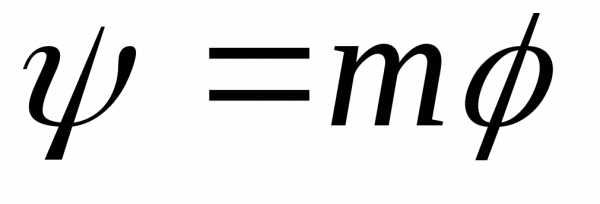 числа
числа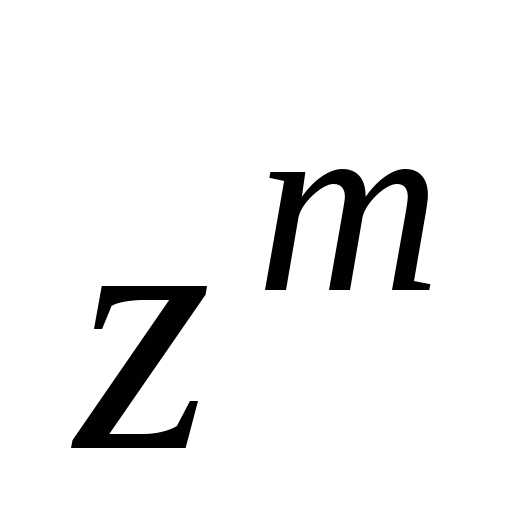 может не принадлежать интервалу
может не принадлежать интервалу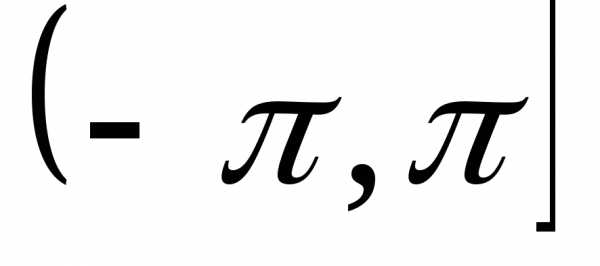 .
В этом случае следует по полученному
значению
.
В этом случае следует по полученному
значению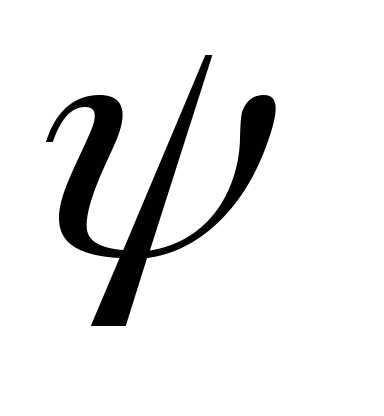 найти главное значениеаргумента
найти главное значениеаргумента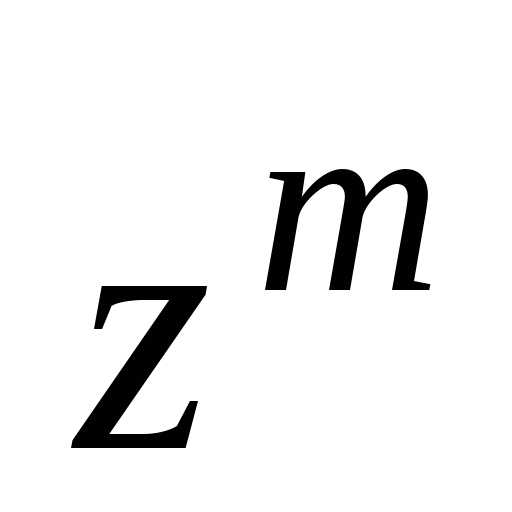 ,
прибавляя (или вычитая) число
,
прибавляя (или вычитая) число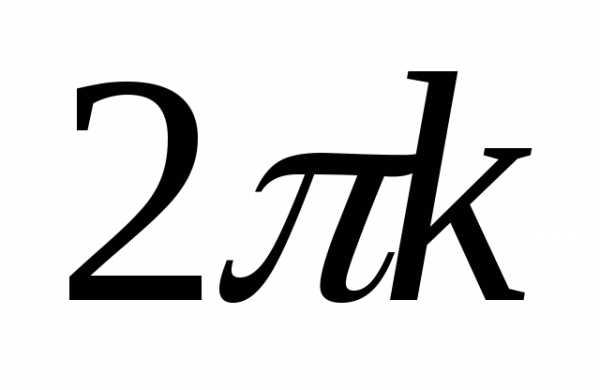 с таким значением
с таким значением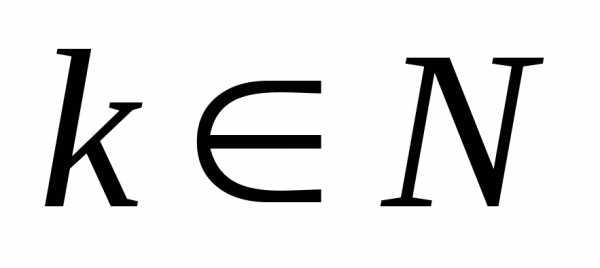 ,
чтобы
,
чтобы
 .
После этого, нужно заменить в формулах
(5)
.
После этого, нужно заменить в формулах
(5)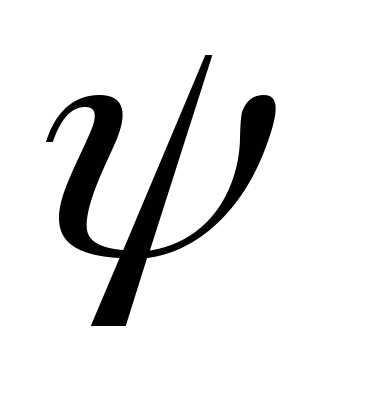 на
на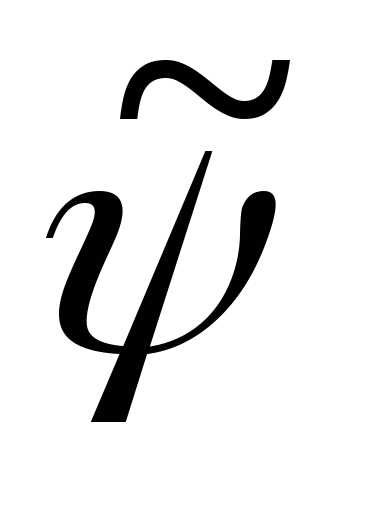 .
. и
и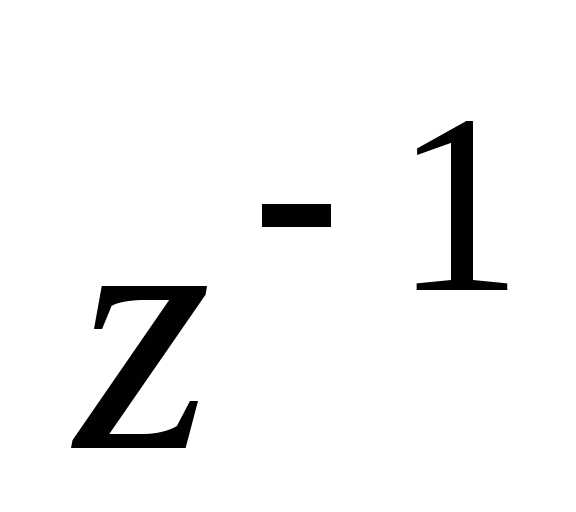 ,
если.
,
если.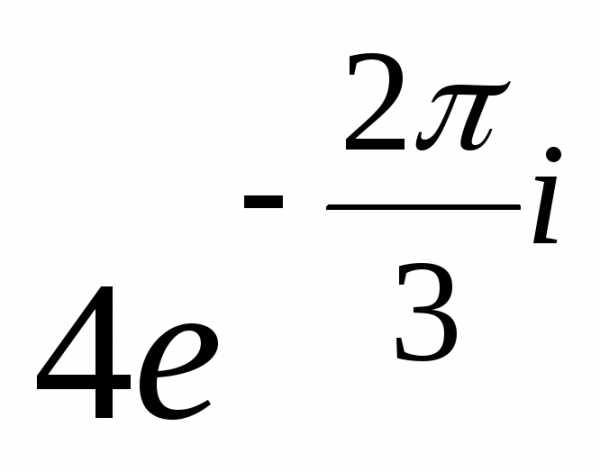 (см. число
(см. число из примера 6).
из примера 6).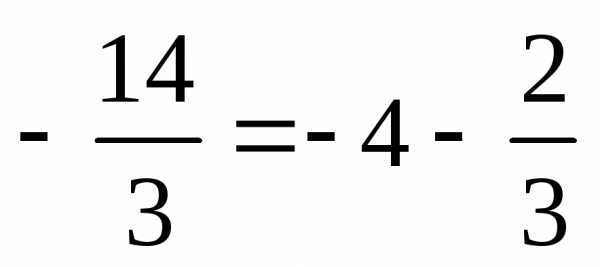 .
.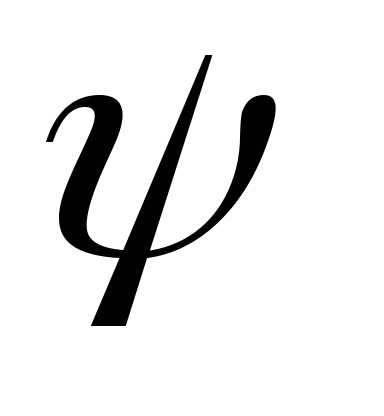 можно заменить наи, значит,
можно заменить наи, значит,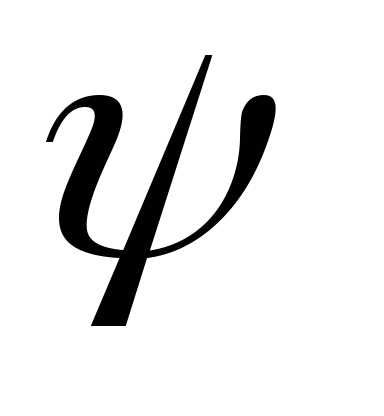 на.
Следовательно,
на.
Следовательно,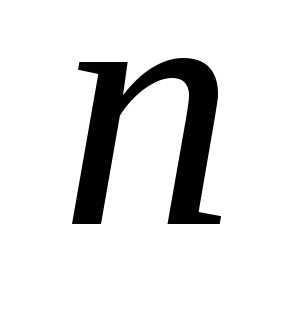 -й
степени
-й
степени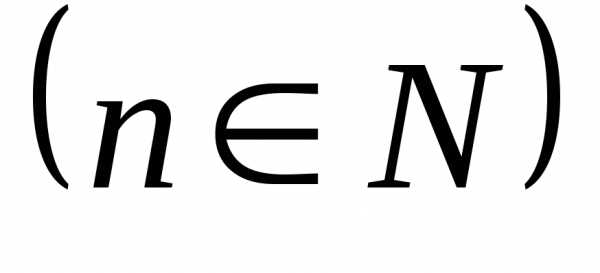 из комплексного числапроводится по формуле Муавра-Лапласа
из комплексного числапроводится по формуле Муавра-Лапласа имеет ровно
имеет ровно различных значений.
различных значений.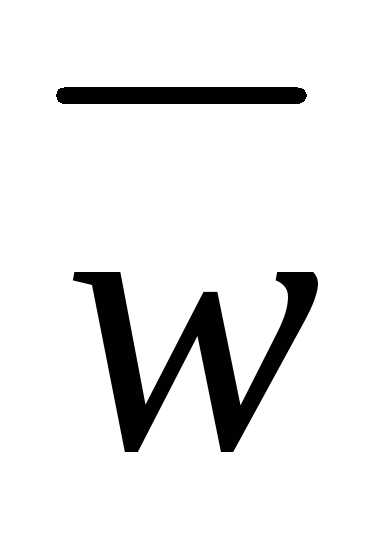 =x – yiназывается сопряженным числом по
отношению кw = x + yi.
=x – yiназывается сопряженным числом по
отношению кw = x + yi.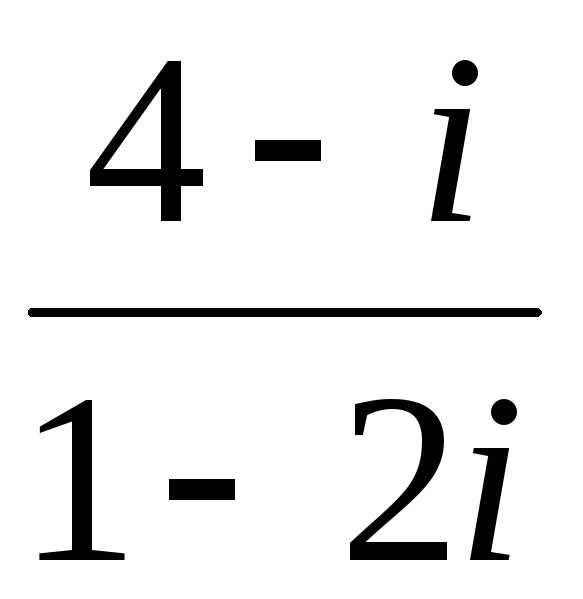 = [домножаем числитель и знаменатель
дроби на число, сопряженное знаменателю]
=
= [домножаем числитель и знаменатель
дроби на число, сопряженное знаменателю]
=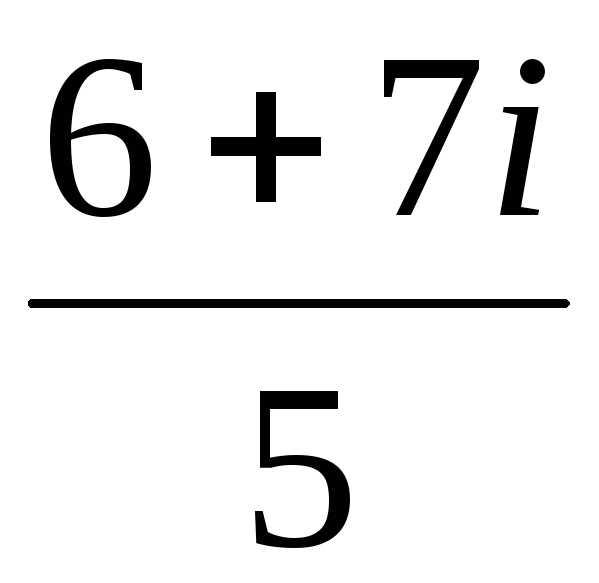 есть выражение, а не число, поэтому его
нельзя рассматривать как ответ.
есть выражение, а не число, поэтому его
нельзя рассматривать как ответ.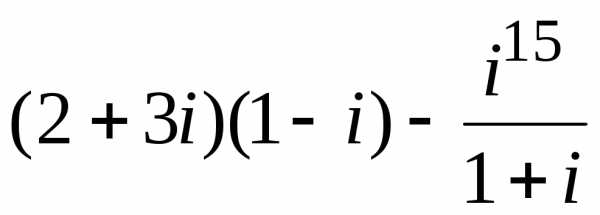 =
=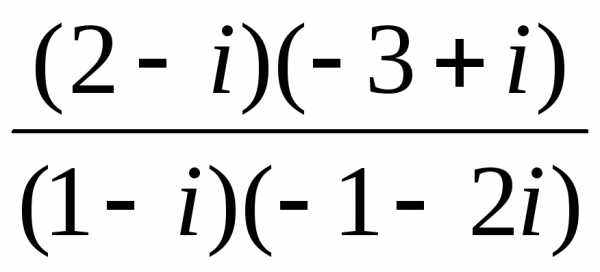 =
[домножаем числитель и знаменатель
дроби на числа, сопряженные обоим числам
знаменателя] =
=
[домножаем числитель и знаменатель
дроби на числа, сопряженные обоим числам
знаменателя] =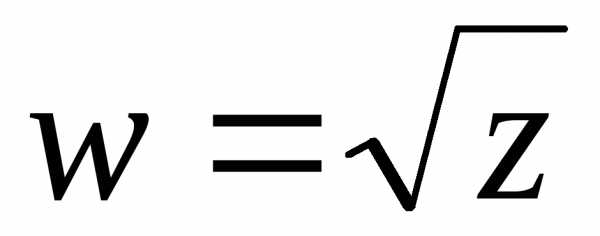 называется квадратным корнем из
комплексного числаz,
если
называется квадратным корнем из
комплексного числаz,
если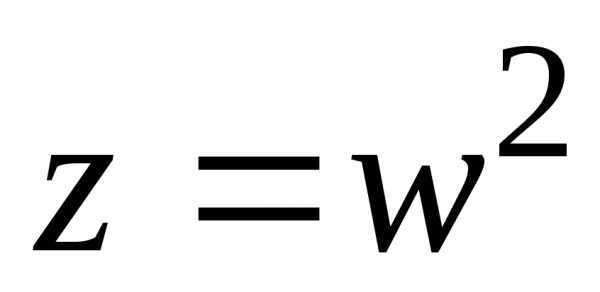 [1, с. 191].
[1, с. 191].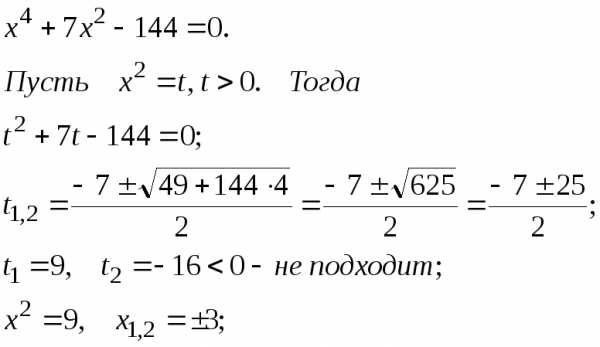 Ответ:{‑3 + 4i;
3 ‑ 4i}.
Ответ:{‑3 + 4i;
3 ‑ 4i}.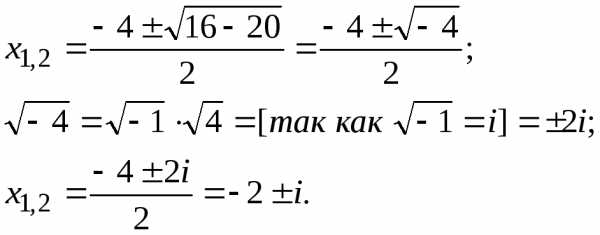 Ответ:{‑2 +i;
‑2 –i}.
Ответ:{‑2 +i;
‑2 –i}. .
.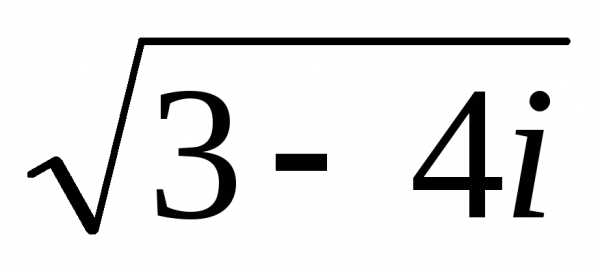 :
: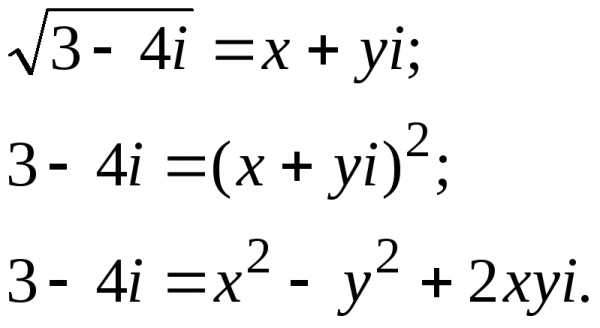
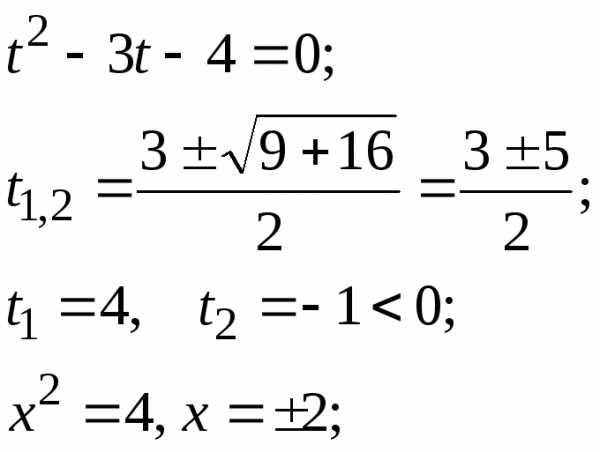
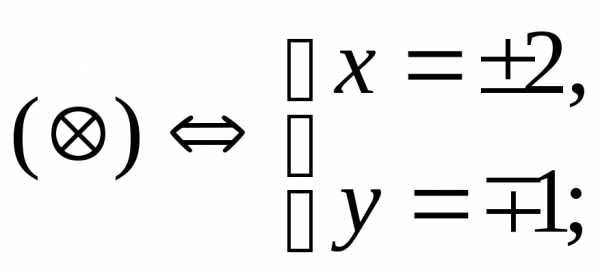
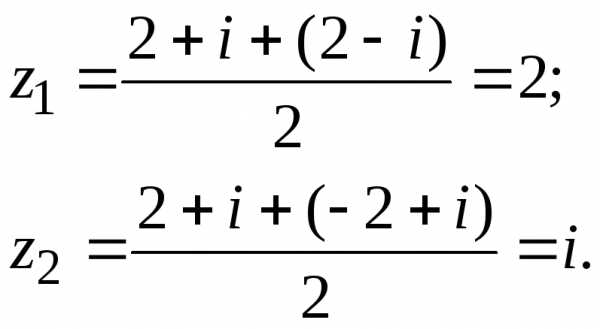 Ответ:{2;i}.
Ответ:{2;i}.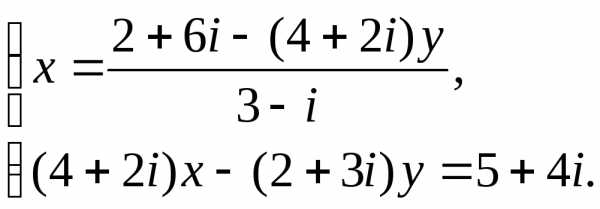

 ешение.
У числаz1действительная часть равна ‑2, а
мнимая ‑ 0. Следовательно, изображением
числаz1служит
точка (‑2, 0) (рис. 1.1).
ешение.
У числаz1действительная часть равна ‑2, а
мнимая ‑ 0. Следовательно, изображением
числаz1служит
точка (‑2, 0) (рис. 1.1).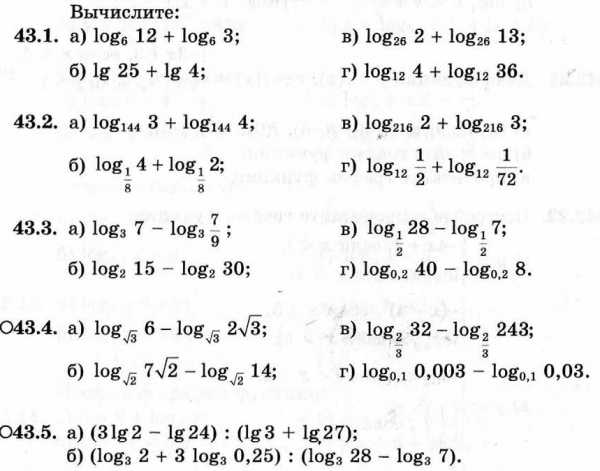

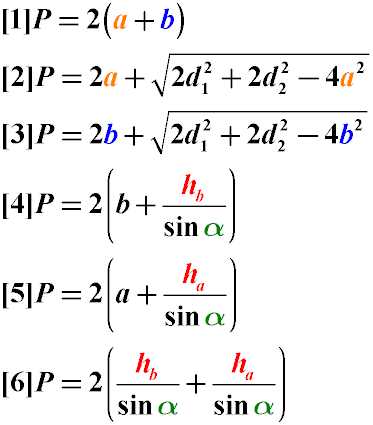
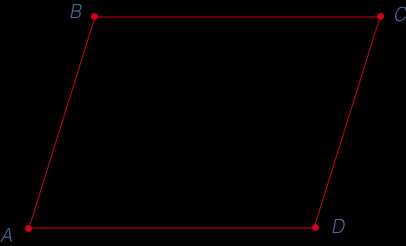
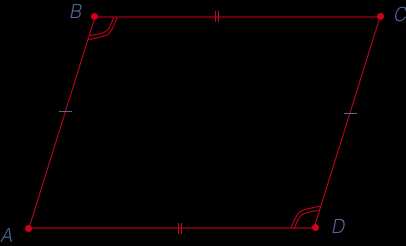
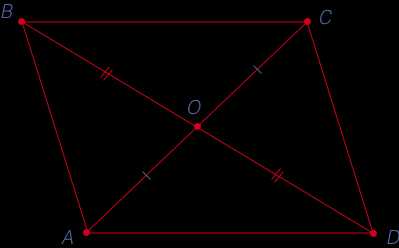
 Треугольники, из которых состоит тетраэдр, называются его гранями.
Треугольники, из которых состоит тетраэдр, называются его гранями. Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.
Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.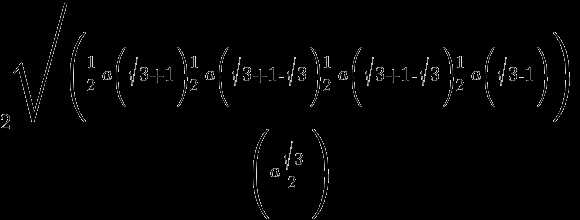
 по
векторам
по
векторам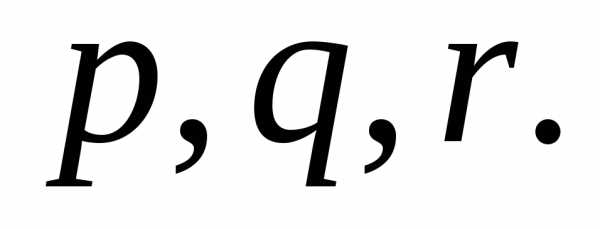
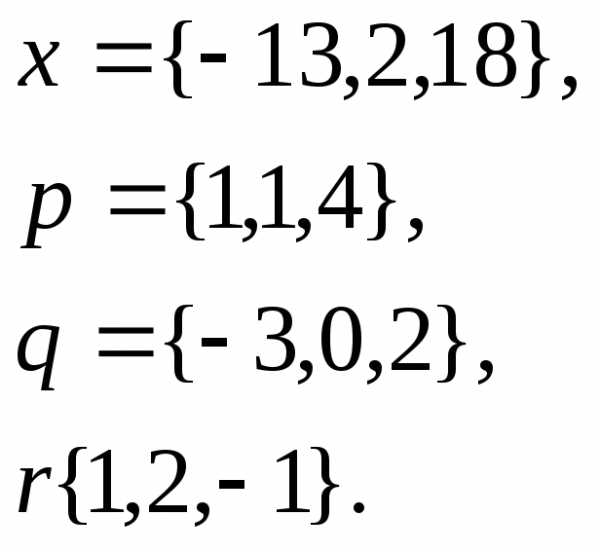
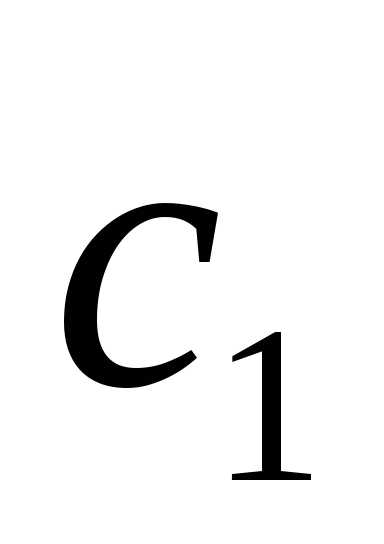 и
и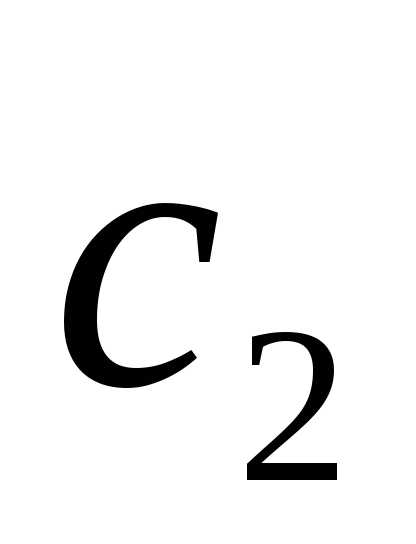 ,
построенные по векторам
,
построенные по векторам и
и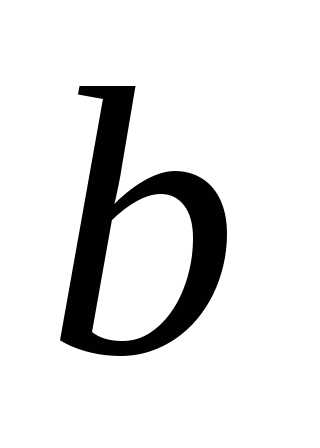 ?
?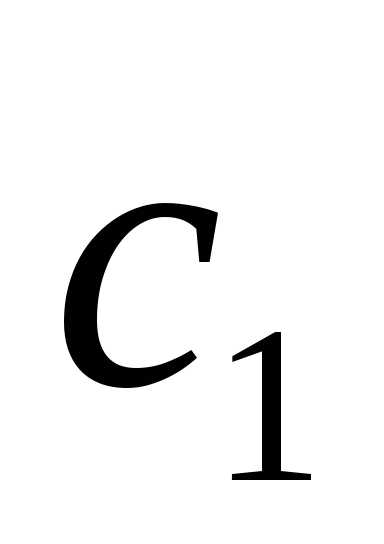 и
и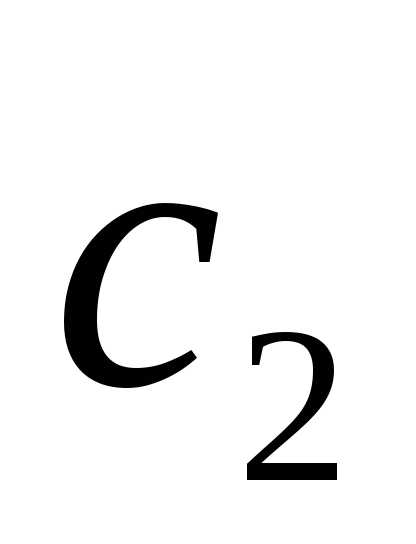 коллинеарны.
коллинеарны.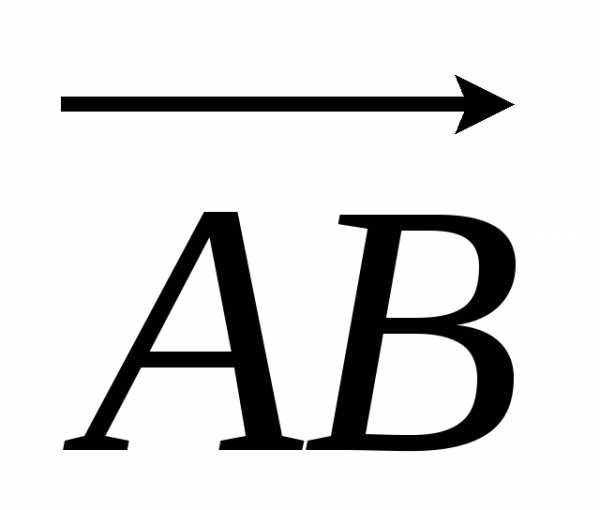 и
и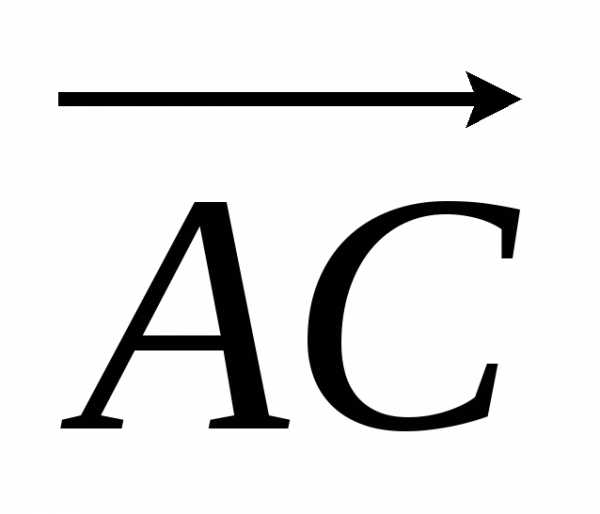 .
.
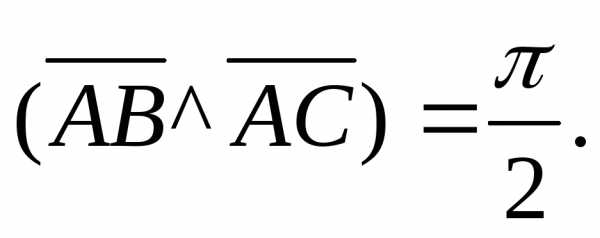
 и
и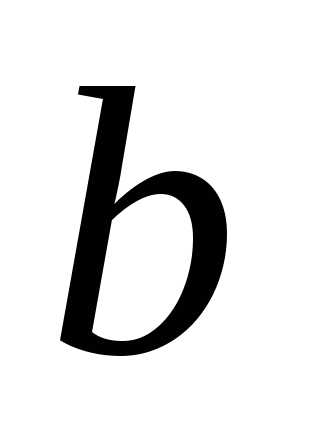 .
.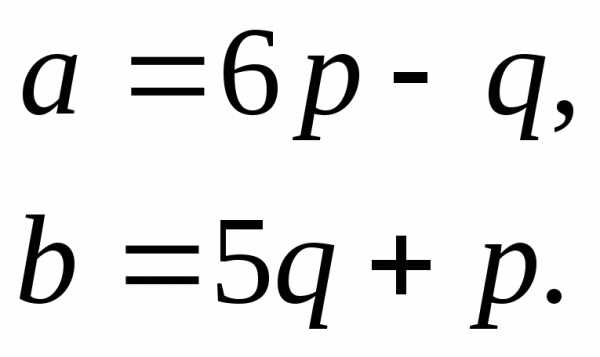
 ,
,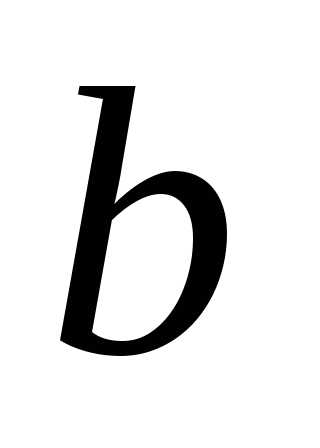 и
и .
. ,
,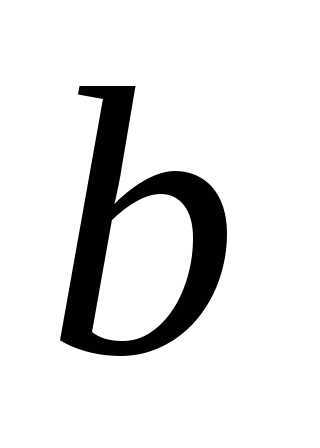 ине
компланарны.
ине
компланарны. на грань
на грань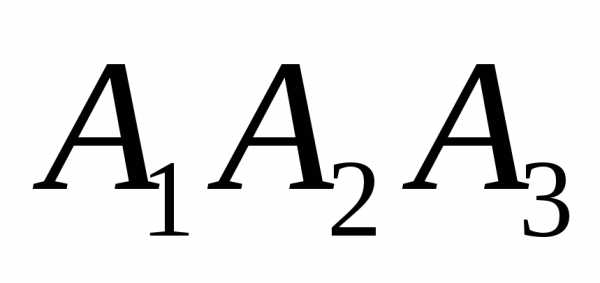 .
.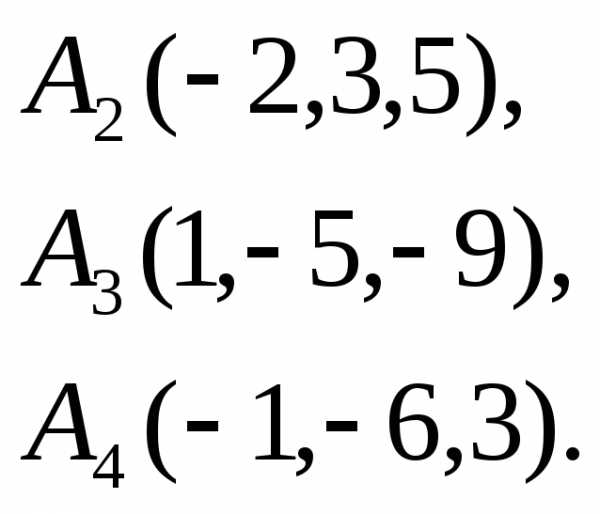
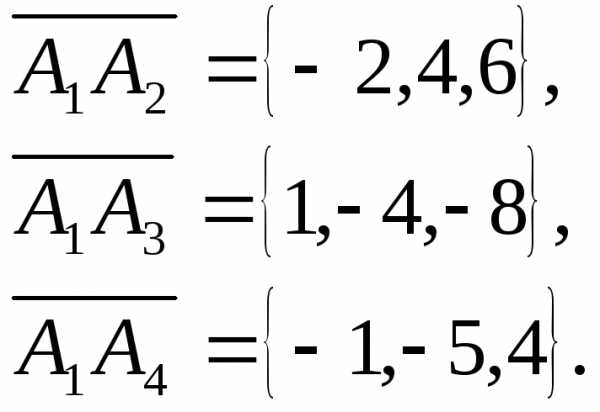
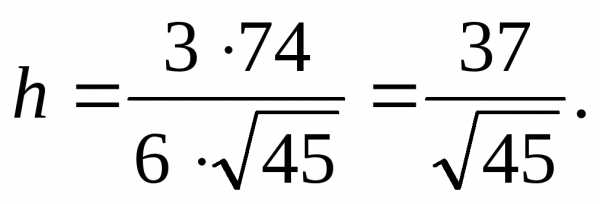
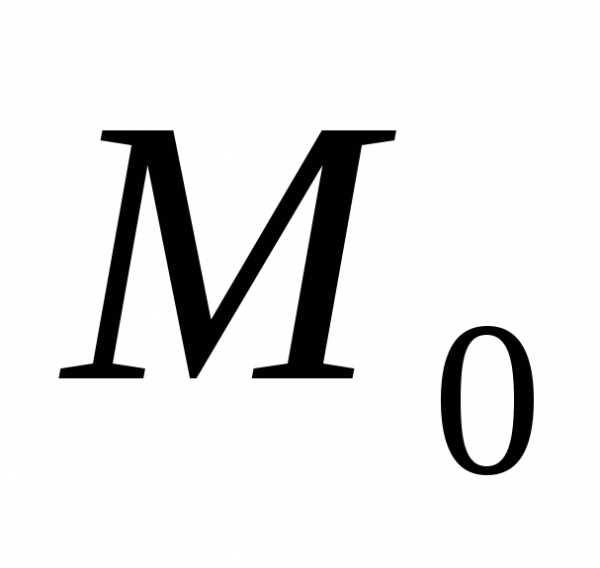 до
плоскости, проходящей через точки.
до
плоскости, проходящей через точки.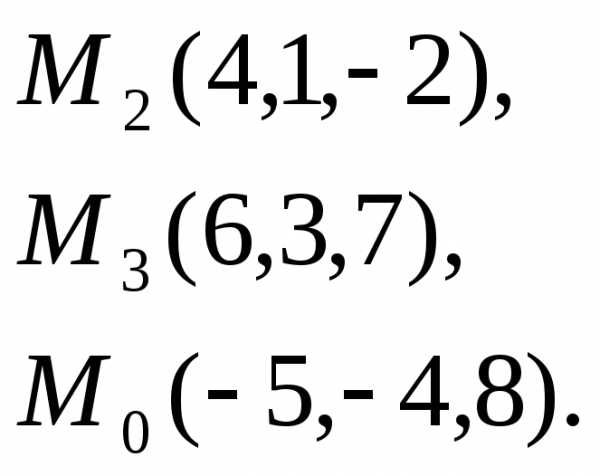
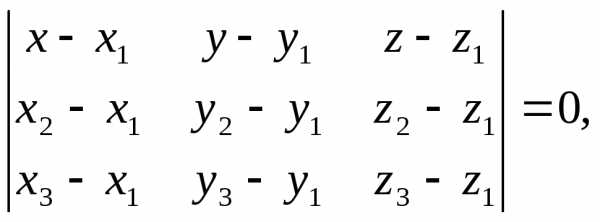
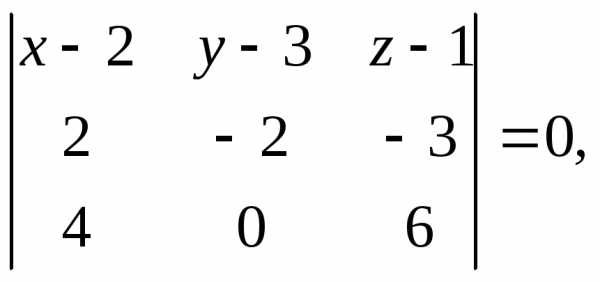
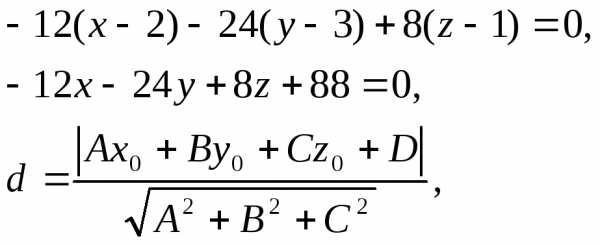
 перпендикулярно
вектору
перпендикулярно
вектору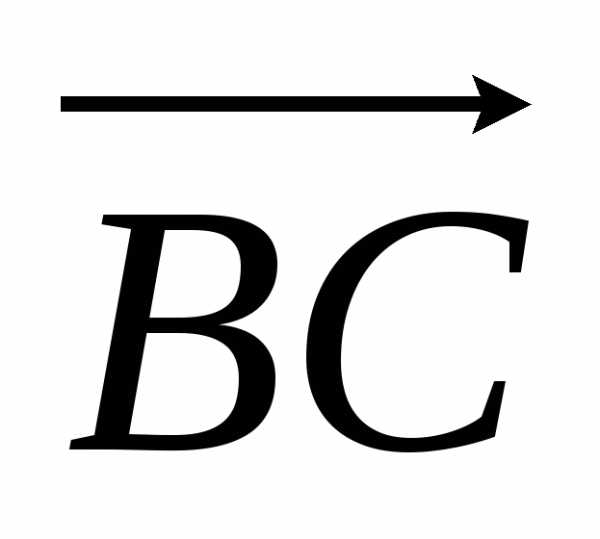 .
.
 ,
равноудаленной от точек
,
равноудаленной от точек и
и .
.
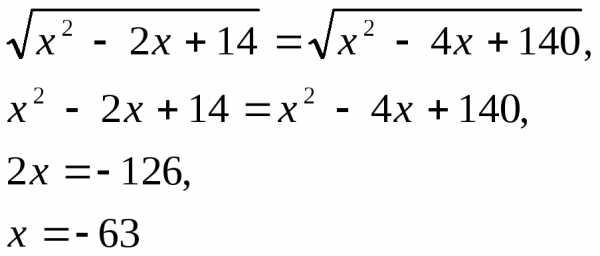
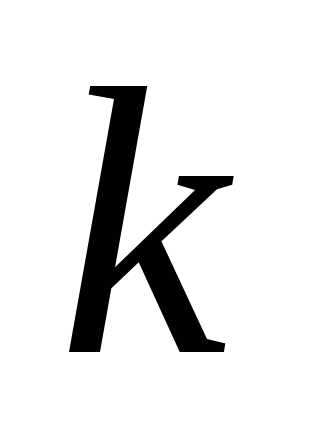 -коэффициент
гомотетии с центром в начале координат.
Верно ли, что точка
-коэффициент
гомотетии с центром в начале координат.
Верно ли, что точка принадлежит
образу плоскости
принадлежит
образу плоскости ?
? переходит
в плоскость
переходит
в плоскость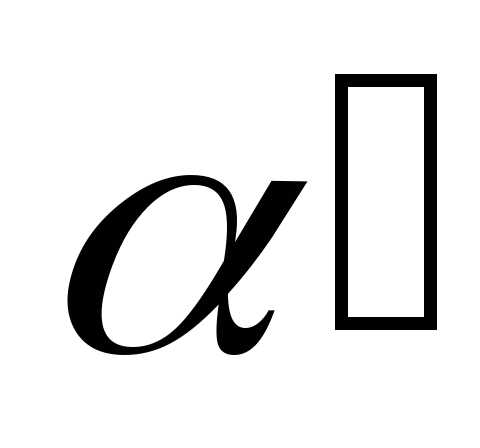 .
.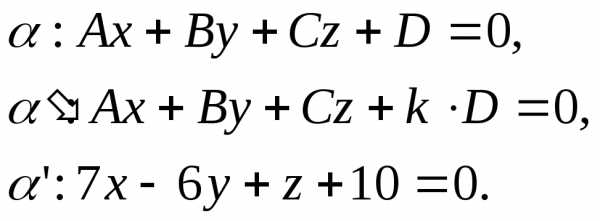
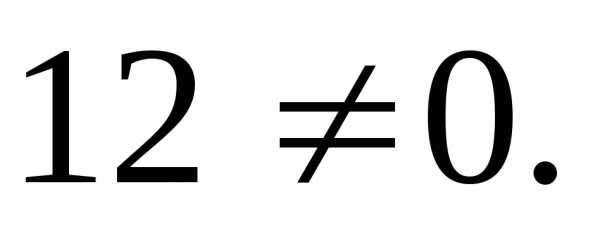
 не
принадлежит образу плоскости
не
принадлежит образу плоскости .
.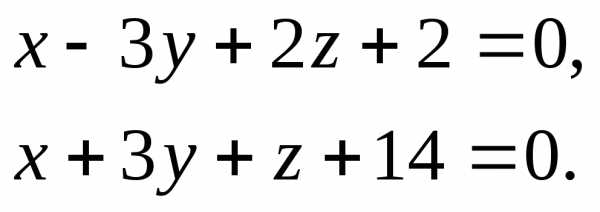
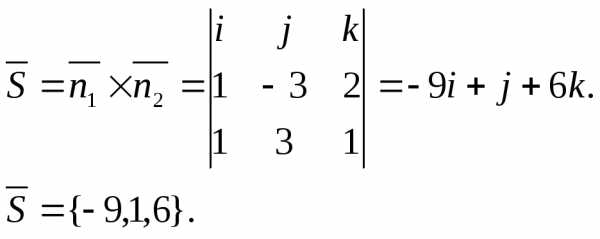
 значение
значение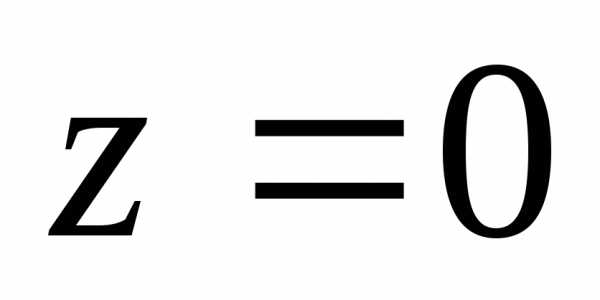 .
.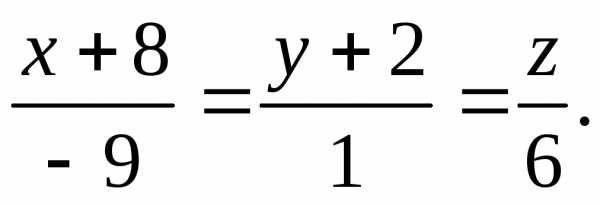

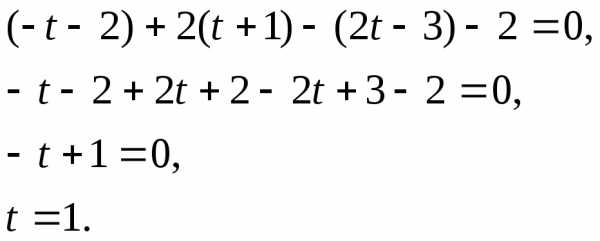
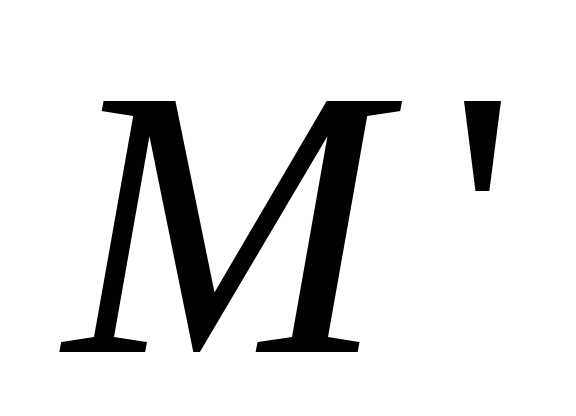 ,
симметричную точке
,
симметричную точке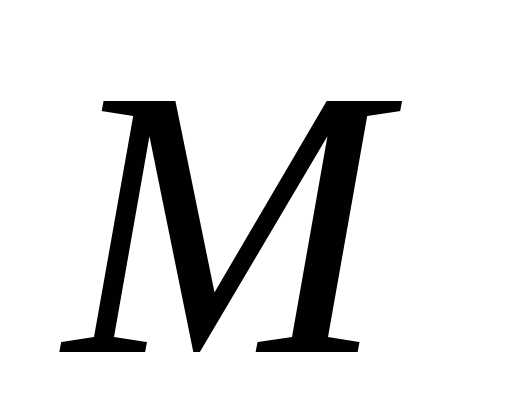 относительно
прямой.
относительно
прямой.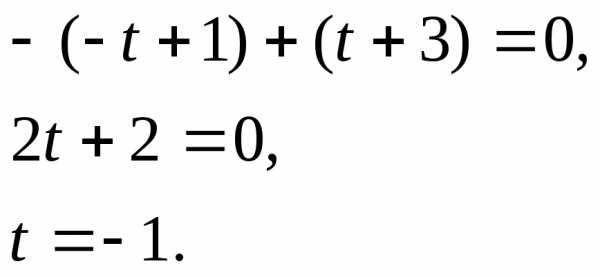
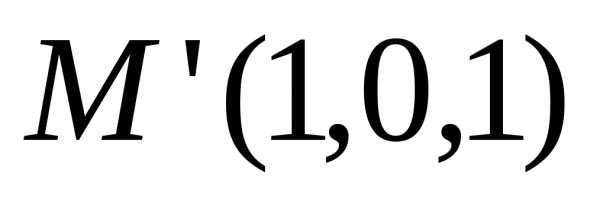 —
искомая точка.
—
искомая точка.