Действия над комплексными числами
Над комплексными числами можно выполнять следующие действия:
- сложение;
- вычитание;
- умножение;
- деление;
- возведение комплексного числа в степень;
- извлечение корня $n$—й степени из комплексного числа.
Операции сложения и вычитания выполняются для чисел, представленных в алгебраической форме.
Умножение, деление и возведение в степень выполняются для чисел, представленных в любой форме записи.
Извлечение корня выполняется для чисел, представленных в тригонометрической форме.
Определение 1
Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
- $a$ — вещественная (действительная) часть;
- $b$ — мнимая часть.
Определение 2
Запись некоторого комплексного числа $z$ в виде $z=r\cdot (\cos \varphi +i\sin \varphi )$ называется тригонометрической формой записи, где число $r$ — модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ — аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac{b}{a} $.
Определение 3
Запись некоторого комплексного числа $z$ в виде $z=r\cdot e^{i\varphi } $ называется показательной формой записи, где число $r$ — модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ — аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac{b}{a} $.
Примечание 1
При необходимости извлечения корня из комплексного числа, записанного в показательной форме, необходимо предварительно привести его к тригонометрической форме представления.
Сумма комплексных чисел
Суммой двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством \[z_{1} +z_{2} =(a_{1} +b_{1} i)+(a_{2} +b_{2} i)=(a_{1} +a_{2} )+(b_{1} +b_{2} )\cdot i.\]
Разность комплексных чисел
Разностью двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством \[z_{1} -z_{2} =(a_{1} +b_{1} i)-(a_{2} +b_{2} i)=(a_{1} -a_{2} )+(b_{1} -b_{2} )\cdot i.\]
Пример 1
Выполнить действия: 1) $z_{1} +z_{2} $2) $z_{1} -z_{2} $ для заданных комплексных чисел $z_{1} =2+4i$ и $z_{2} =1-3i$.
Решение:
1) По определению имеем: $z_{1} +z_{2} =(a_{1} +a_{2} )+(b_{1} +b_{2} )\cdot i$
Для исходных чисел получаем:
\[z_{1} +z_{2} =(2+4i)+(1-3i)=(2+1)+(4-3)i=3+i\]
2) По определению имеем: $z_{1} -z_{2} =(a_{1} -a_{2} )+(b_{1} -b_{2} )\cdot i$
Для исходных чисел получаем:
\[z_{1} +z_{2} =(2+4i)-(1-3i)=(2-1)-(4+3)i=1-7i.\]
Произведение комплексных чисел
Произведением двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^{2} =-1$.
Произведением двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ является комплексное число, которое определяется равенством
\[z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )].\]
Пример 2
Выполнить умножение комплексных чисел представленных в алгебраической форме:
$z_{1} =1+3i$ и $z_{2} =2-2i$.Решение:
Для исходных чисел, учитывая определение, получаем:
\[z_{1} \cdot z_{2} =(1+3i)\cdot (2-2i)=\]
\[1\cdot 2+3\cdot 2i+1\cdot (-2i)+3i\cdot (-2i)=2+6i-2i-6i^{2} =2+4i+6=8+4i\]
Пример 3
Выполнить умножение комплексных чисел представленных в тригонометрической форме:
$z_{1} =3\sqrt{3} \cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )$ и $z_{2} =2\cdot (\cos \pi +i\cdot \sin \pi )$.Решение:
1) По определению имеем: $z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )]$
Для исходных чисел получаем:
\[\begin{array}{l} {z_{1} \cdot z_{2} =\left(3\sqrt{3} \cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )\right)\cdot \left(2\cdot (\cos \pi +i \cdot \sin \pi )\right)=6\cdot \sqrt{3} \cdot \left[\cos \left(\frac{\pi }{2} +\pi \right)+i\cdot \sin \left(\frac{\pi }{2} +\pi \right)\right]=} \\ {=6\sqrt{3} \cdot \left(\cos \frac{3\pi }{2} +i\cdot \sin \frac{3\pi }{2} \right)} \end{array}\]Частное комплексных чисел
Частным двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i \sin \varphi _{2} )$ является комплексное число, которое определяется равенством
\[z_{1} \div z_{2} =\frac{r_{1} }{r_{2} } \cdot [\cos (\varphi _{1} -\varphi _{2} )+i\sin (\varphi _{1} -\varphi _{2} )].\]
Примечание 2
Чтобы выполнить операцию деления комплексных чисел, представленных в алгебраической форме, необходимо:
- представить запись операции деления в виде дроби;
- числитель и знаменатель дроби умножить на число сопряженное знаменателю;
- привести полученное выражение к алгебраической записи.
Пример 4
Выполнить деление комплексных чисел, представленных в алгебраической форме:
$z_{1} =2+i$ и $z_{2} =1-i$.Решение:
Для исходных чисел получаем:
\[\frac{z_{1} }{z_{2} } =\frac{2+i}{1-i} =\frac{(2+i)(1+i)}{(1-i)(1+i)} =\frac{2+i+2i+i^{2} }{1^{2} -i^{2} } =\frac{2+3i-1}{1+1} =\frac{1+3i}{2} = \frac{1}{2} +\frac{3}{2} i\]Пример 5
Выполнить деление комплексных чисел представленных в тригонометрической форме:
$z_{1} =3\cdot \left(\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} \right)$ и $z_{2} =2\cdot (\cos 2\pi +i\cdot \sin 2\pi )$.Решение:
По определению имеем: $z_{1} \div z_{2} =\frac{r_{1} }{r_{2} } \cdot [\cos (\varphi _{1} -\varphi _{2} )+i\sin (\varphi _{1} -\varphi _{2} )]$
Для исходных чисел получаем:
\[\begin{array}{l} {\frac{z_{1} }{z_{2} } =3\cdot \left(\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} \right)\div \left(2\cdot (\cos 2\pi +i\cdot \sin 2\pi )\right)=\frac{3}{2} \cdot \left[\cos \left(\frac{2\pi }{3} -2\pi \right)+i\cdot \sin \left(\frac{2\pi }{3} -2\pi \right)\right]=} \\ {= \frac{3}{2} \cdot \left(\cos \left(-\frac{4\pi }{3} \right)+i\cdot \sin \left(-\frac{4\pi }{3} \right)\right)} \end{array}\]Степерь комплексного числа
Степенью порядка $n$ некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством
\[z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi ).\]
Данная формула называется формулой Муавра.
Пример 6
Выполнить действие $z^{3} $, где $z=3\cdot \left(\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} \right)$.
Решение:
По формуле Муавра получим:
\[z^{3} =3^{3} \cdot \left(\cos \left(3\cdot \frac{\pi }{4} \right)+i\cdot \sin \left(3\cdot \frac{\pi }{4} \right)\right)=27\cdot \left(\cos \frac {3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right).\]Пример 7
Выполнить действие $z^{100} $, где $z=1\cdot \left(\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} \right)$.
Решение:
По формуле Муавра получим:
\[z^{100} =1^{100} \cdot \left(\cos \left(100\cdot \frac{\pi }{2} \right)+i\cdot \sin \left(100\cdot \frac{\pi }{2} \right)\right)=1\cdot \left(\cos 50\pi +i\cdot \sin 50\pi \right)=1\cdot \left(\cos 0+i\cdot \sin 0\right).\]
Корень комплексного числа
Корнем $n$-й степени некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством
\[\sqrt[{n}]{z} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1.\]
Пример 8
Выполнить действие $\sqrt[{3}]{z} $, где $z=4\cdot (\cos \pi +i\cdot \sin \pi )$.
Решение:
Для $k=0$ получаем: $w_{1} =\sqrt[{3}]{z} =\sqrt[{3}]{4} \cdot \left(\cos \frac{\pi }{3} +i\cdot \sin \frac{\pi }{3} \right)$.
Для $k=1$ получаем: $w_{2} =\sqrt[{3}]{z} =\sqrt[{3}]{4} \cdot \left(\cos \frac{\pi +2\pi }{3} +i\cdot \sin \frac{\pi +2\pi }{3} \right)=\sqrt[{3}] {4} \cdot \left(\cos \pi +i\cdot \sin \pi \right)$.
Для $k=2$ получаем: $w_{3} =\sqrt[{3}]{z} =\sqrt[{3}]{4} \cdot \left(\cos \frac{\pi +4\pi }{3} +i\cdot \sin \frac{\pi +4\pi }{3} \right)=\sqrt[{3}] {4} \cdot \left(\cos \frac{5\pi }{3} +i\cdot \sin \frac{5\pi }{3} \right)$.
spravochnick.ru
Математический портал. Высшая математика. Математический анализ.
Комплексные числа — числа вида $x+iy,$ где $x,y\in \mathbb{R,}$ а
$\,i,$ такое число, что $ i^2=-1.$ Множество комплексных чисел
обозначается $\mathbb{C}.$
Действия над комплексными числами.
Сложение комплексных чисел:
$$(x_1+iy_1)+(x_2+iy_2)=(x_1+x_2)+i(y_1+y_2).$$
Умножение двух комплексных чисел:
$$(x_1+iy_1)(x_2+iy_2)=x_1x_2-y_1y_2+(x_1y_2+x_2y_1)i.$$
Умножение комплексного числа на действительное:
$$\lambda(x+iy)=\lambda x+i\lambda y.$$
Деление комплексных чисел:
$$\frac{x_1+iy_1}{x_2+iy_2}=\frac{(x_1+iy_1)(x_2-iy_2)}{(x_2+iy_2)(x_2-iy_2)}=\frac{x_1x_2+y_1y_2+i(y_1x_2-x_1y_2)}{x_2^2+y_2^2}=$$ $$\frac{x_1x_2+y_1y_2}{x_2^2+y_2^2}+\frac{y_1x_2-x_1y_2}{x_2^2+y_2^2}i.$$
Действительные числа $x$ и $y$ комплексного числа $z=x+iy,$ называются действительной и мнимой частью числа $z$ и обозначаются, соответственно, $Re z=x$ и $Im z=y.$
Два комплексных числа $z_1=x_1+iy_1$ и $z_2=x_2+iy_2$ называются равными в том и только том случае, если $x_1=x_2,$ $y_1=y_2.$
Запись $z=x+iy$ называют алгебраической формой комплексного числа $z.$
Числа $z_1=x+iy$ и $z_2=x-iy$ называют сопряженными.
Примеры:
Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:
1.421. $(2+3i)(3-i).$
Решение:
$(2+3i)(3-i)=6-2i+9i-3i^2=6+7i+3=9+7i.$
Ответ: $9+7i.$
1.424. $(2i-i^2)^2+(1-3i)^3.$
Решение.
$(2i-i^2)^2+(1-3i)^3=(2i+1)^2+1-3(3i)^2+3(3i)-(3i)^3=$ $=4i^2+4i+1-27i^2+9i-27i^3=-4+4i+1+27-9i+27i=24+22i.$
Ответ: $24+22i.$
1.425. $\frac{2-i}{1+i}.$
Решение.
$$\frac{2-i}{1+i}=\frac{(2-i)(1-i)}{(1+i)(1-i)}=\frac{2-2i-i+i^2}{1-i^2}=\frac{2-3i-1}{1+1}=\frac{1-3i}{2}=\frac{1}{2}-\frac{3}{2}i.$$
Ответ: $\frac{1}{2}-\frac{3}{2}i.$
{jumi[*4]}
1.428. $\frac{(1+i)(3+i)}{3-i}-\frac{(1-i)(3-i)}{3+i}.$
Решение.
$$\frac{(1+i)(3+i)}{3-i}-\frac{(1-i)(3-i)}{3+i}=\frac{(1+i)(3+i)(3+i)}{(3-i)(3+i)}-$$ $$-\frac{(1-i)(3-i)(3-i)}{(3+i)(3-i)}=\frac{9+15i+7i^2+i^3}{9-i^2}-\frac{9-15i+7i^2-i^3}{9-i^2}=$$ $$=\frac{9+15i-7-i-9+15i+7-i}{10}=\frac{28}{10}i=\frac{14}{5}i.$$
Ответ: $\frac{14}{5}i.$
Найти действительные решения следующего уравнения:
1. 430. $(1+i)x+(-2+5i)y=-4+17i.$
Решение.
$(1+i)x+(-2+5i)y=-4+17i\Rightarrow$
$x+xi-2y+5yi=-4+17i\Rightarrow$
$(x-2y)+(x+5y)i=-4+17i\Rightarrow$
$$\left\{\begin{array}{lcl}x-2y=-4\\x+5y=17\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=2y-4\\2y-4+5y=17\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x=2\\y=3\end{array}\right. .$$
Ответ: $x=2; y=3.$
Домашнее задание.
Выполнить действия над комплексными числами, представив результат в алгебраичекой форме:
1.422. $(1+2i)^2.$
Ответ: $-3+4i.$
1.423. $(1-i)^3-(1+i)^3.$
Ответ: $-4i.$
1.426. $\frac{1}{1+4i}+\frac{1}{4-i}.$
Ответ: $\frac{5}{17}-\frac{3}{17}i.$
1.427. $\left(\frac{1-i}{1+i}\right)^3.$
Ответ: $i.$
Найти действительные решения следующего уравнения:
1.431. $12((2x+i)(1+i)+(x+y)(3-2i))=17+6i.$
Ответ: $x=1/3; y=1/4.$
Решить следующие системы линейных уравнений:
1.432. $(3-i)z_1+(4+2i)z_2=1+3i;$
$(4+2i)z_1-(2+3i)z_2=7.$
Ответ: $z_1=1; z_2=i.$
1.433. $(2+i)z_1+(2-i)z_2=6;$
$(3+2i)z_1+(3-2i)z_2=8.$
Ответ: $z_1=2+i; z_2=2-i.$
mathportal.net
Действия с комплексными числами
Время проведения –2 часа.
Цель работы:отработать навыки выполнения действий с комплексными числами; научиться решать квадратные уравнения, дискриминант которых отрицателен.
Вопросы для подготовки к работе:
1. Понятие мнимой единицы;
2. Понятие комплексного числа;
3. Понятие модуля и аргумента комплексного числа;
4. Равенство комплексных чисел;
5. Решение квадратных уравнений, дискриминант которых отрицателен;
6. Действие над комплексными числами в алгебраической форме;
7. Геометрическая интерпретация комплексного числа;
8. Тригонометрическая форма комплексного числа;
Содержание работы:
1. Решение квадратных уравнений, дискриминант которых отрицателен;
2. Выполнение действий над комплексными числами;
3. Геометрическая интерпретация комплексного числа;
4. Представление комплексного числа в тригонометрической форме.
Литература:[1, с.17-23]
Порядок выполнения задания:
При выполнении первого задания необходимо учитывать следующее: в комплексных числах можно извлечь квадратный корень из отрицательного числа, так как , где — мнимая единица. Следовательно, в поле комплексных чисел разрешимо любое квадратное уравнение, в том числе с отрицательным дискриминантом.
Пример: Решить уравнение
Решение:
Найдем дискриминант , , следовательно, уравнение имеет мнимые корни, которые находят по формуле
Ответ:
Для выполнения второго, третьего заданий необходимо уметь применять операции над комплексными числами и знать правило равенства комплексных чисел.
Отметим, что с комплексными числами, записанными в алгебраической форме, операции сложения, вычитания и умножения можно производить также, как с действительными биномами, деление выполняют путем умножения делимого и делителя на число, сопряженное делителю. Правило равенства: два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей.
Пример: Найдите сумму, разность, произведение, частное двух комплексных чисел
Решение:
, где
Ответ: , , ,
Пример: Найдите действительные решения уравнения
Решение:
В соответствии с правилом равенства получаем:
Ответ:
Для выполнения четвертого, пятого заданий необходимо знать тригонометрическую форму записи комплексного числа и его геометрическую интерпретацию.
Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу ставится в соответствие точка М координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу (ось называют действительной), а коэффициент при мнимой части – ординату точки (ось называют мнимой).
Расстояние от начала системы координат до точки, соответствующей комплексному числу , называют модулем этого числа, который вычисляют по формуле: . Угол между положительной полуосью и лучом называют аргументом комплексного числа . Выражение называют тригонометрической формой комплексного числа.
Пример: Изобразить на комплексной плоскости число и записать его в тригонометрической форме.
Решение:
Комплексному числу соответствует точка плоскости
Для комплексного числа имеем: , (по чертежу).
Поэтому в тригонометрической форме комплексное число имеет вид:
Ответ:
Вариант 1
1. Решить уравнение
1)
2)
3)
4)
2. Выполнить действия над комплексными числами, представив результат в алгебраической форме
1)
2)
3)
4)
5)
6)
7)
3. Найти действительные решения уравнения
1)
2)
4. Изобразите на комплексной плоскости следующие комплексные числа
1)
2)
5. Записать комплексное число в тригонометрической форме
Вариант 2
1. Решить уравнение
1)
2)
3)
4)
2. Выполнить действия над комплексными числами, предствавив результат в алгебраической форме
1)
2)
3)
4)
5)
6)
7)
3. Найти действительные решения уравнения
1)
2)
4. Изобразите на комплексной плоскости следующие комплексные числа
1)
2)
5. Записать комплексное число в тригонометрической форме
Практическая работа № 8
infopedia.su
§ 2.Действия над комплексными числами
П.2.1.Сложение комплексных чисел
Суммой двух комплексных чисел z1=х1+iy1 и z2=х2+iy2 называется комплексное число, определяемое равенством
z1+z2=(x1+x2)+i(y1+y2). (2.1)
Сложение комплексных чисел обладает переместителъным (коммутативным) и сочетательным (ассоциативным) свойствами:
z1+z2=z2+z1
(z1+z2)+z3=z1+(z2+z3).
Из определения (2.1) следует, что геометрически комплексные числа складываются как векторы (см. рис. 164).
Непосредственно из рисунка видно, что |z1+z2|≤|z1|+|z2|. Это соотношение называется неравенством треугольника.
П.2.2.Вычитание комплексных чисел
Вычитание определяется как действие, обратное сложению. Разностью двух комплексных чисел z1 и z2 называется такое комплексное число z, которое, будучи сложенным с z2, дает число zl т. е. z=z1-z2, если z+z2=z1.
Если z1=x1+iy1, z2=x2+iy2, то из этого определения легко получить z:
z=z1-z2=(x1-x2)+i(y1-y2). (2.2)
Из равенства (2.2) следует, что геометрически комплексные числа вычитаются как векторы (см. рис. 165).
Непосредственно из рисунка видно, что |z1-z2|≥|z1|-|z2|. Отметим, что
т. е. модуль разности двух комплексных чисел равен расстоянию d между точками, изображающими эти числа на плоскости.
Поэтому, например, равенство |z-2i|=1 определяет на комплексной плоскости множество точек z, находящихся на расстоянии 1 от точки z0=2i, т. е. окружность с центром в z0=2i и радиусом 1.
П.2.3. Умножение комплексных чисел
Произведением к омплексных чисел z1 =х1 +iy1 и z2=х2+iy2 называется комплексное число, определяемое равенством
z=z1 z2 =(x1 x2- у1 у2)+i(x1 y2+y1x 2 ). (2.3)
Отсюда, в частности, следует важнейшее соотношение
i 2 =- 1. (2.4)
Действительно, i2=ii=(0+1 i )(0+1i )=(0-1)+i(0+0)=-1. Благодаря соотношению (2.4) формула (2.3) получается формально путем перемножения двучленов x1+ iy1 и х2+iy2:
(х1 +iy1 )(x2+iy2) =x1x 2 +x1 iy2+i у1 х2+iy1iy 2 =x1 x2 +i2y1 y2+i (x1 y2+y1 x2)=x1 x2-y1 y2+i(x1 y2+y1x 2 ).
Например,
(2-3i)(- 5+4i)=-10+8i+15i-12i2=-10+23i+12=2+23i.
Заметим, что z*z=(х+iy)(x-iy)=х2+у2 — действительное число.
Умножение комплексных чисел обладает переместительным, сочетательным и распределительным (дистрибутивным) свойствами:
z1z2=z2z1
(z1z2)z3=z1(z2z3).
z1(z2+z3)=z1z2+z1z3.
В этом легко убедиться, используя определение (2.3).
Найдем произведение комплексных чисел z1=r1(cosφ1+isinφ1) и z2=r2(cosφ2+isinφ2), заданных в тригонометрической форме:
z1z2=r1(cosφ1+isinφ1)r2(cosφ2+isinφ2)=
r1r2(cosφ1cosφ2+isinφ1cosφ2+rcosφ1siπφ2-sinφ1sinφφ2)=
=r1r2((cosφ1cosφ2-siπφ1sinφ2)+i(sinφ1cosφ2+cosφ1 sinφ2))=
=r1r2(cos(φ1+φ2)+i sin(φ1+φ2)),
т. е.
z1z2=r1r2(cos(φ1+φ2)+isin(φ1+φ2)).
Мы показали, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
Это правило распространяется на любое конечное число множителей. В частности, если есть n множителей и все они одинаковые, то
zn=(r(cosφ+isinφ))n=rn(cosnφ+isinnφ). (2.5)
Формула (2.5) называется формулой Муавра.
studfiles.net
7 раб
Методические рекомендации к выполнению практической работы №7.
Действия над комплексными числами в алгебраической и тригонометрической форме.
Понятие комплексного числа и его геометрическая интерпретация.
Действия над комплексными числами в алгебраической форме.
Тригонометрическая форма комплексного числа.
Действия над комплексными числами в тригонометрической форме.
1. Понятие комплексного числа и его геометрическая интерпретация.
Определение 1:
Комплексными числами называются числа
вида 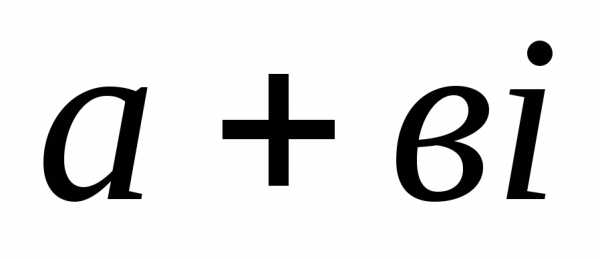 ,
где
,
где и
и — действительные числа, а число
— действительные числа, а число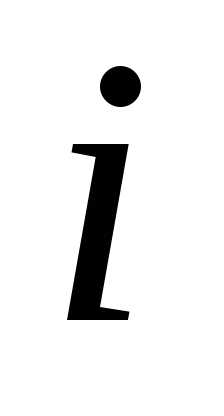 ,
определяемое равенством
,
определяемое равенством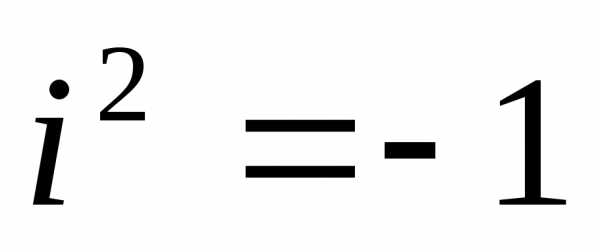 ,
называется мнимой единицей, если для
этих чисел понятия равенства и действия
сложения и умножения определены следующим
образом:
,
называется мнимой единицей, если для
этих чисел понятия равенства и действия
сложения и умножения определены следующим
образом:
1). Два комплексных
числа 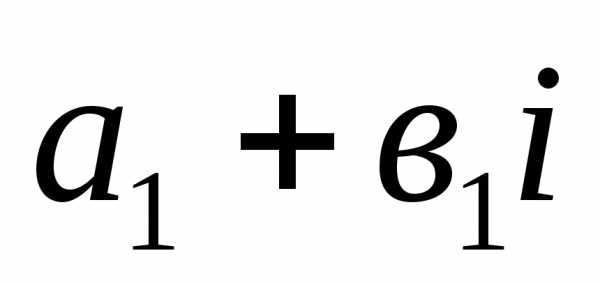 и
и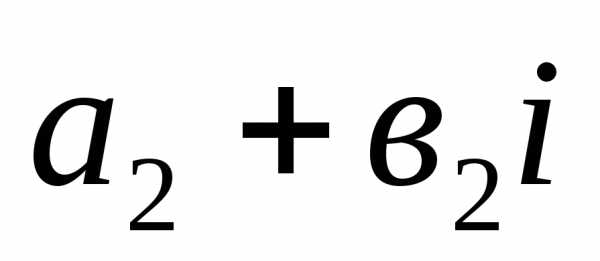 называются равными, если
называются равными, если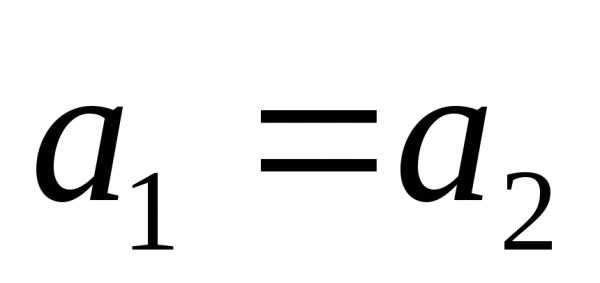 ,
,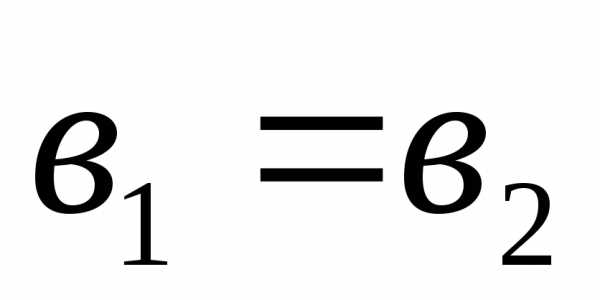 ;
;
2).
Суммой двух комплексных чисел 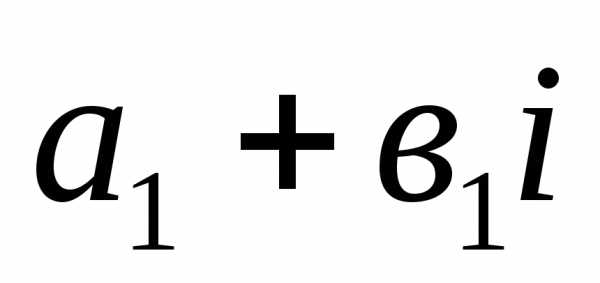 и
и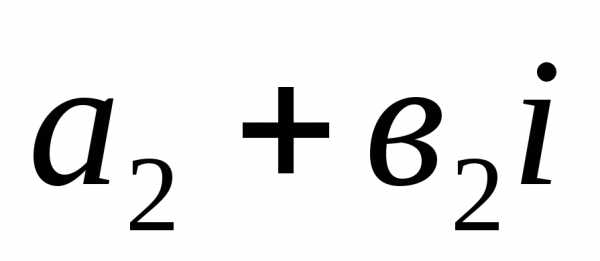 называется комплексное число;
называется комплексное число;
3).
Произведением двух комплексных чисел 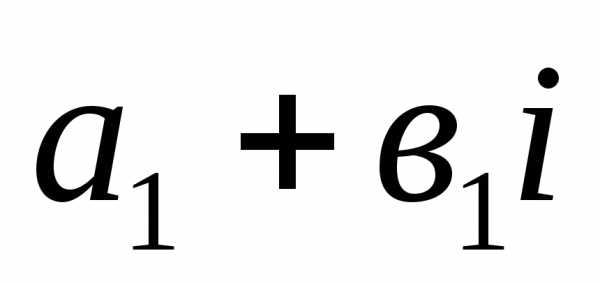 и
и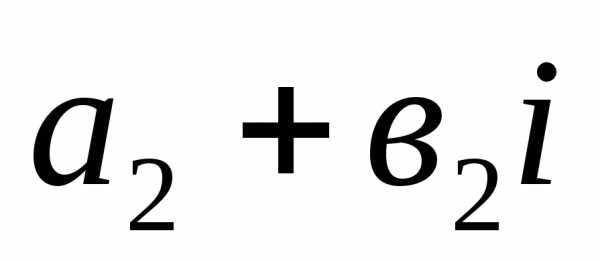 называется комплексное число;
называется комплексное число;
Запись комплексного
числа в виде называется алгебраической
формой записи комплексного числа, где  называется действительной
частью комплексного числа, а
называется действительной
частью комплексного числа, а  —мнимой
частью.
—мнимой
частью.
Пример1: 7+3i
Любое действительное
число содержится в множестве комплексных
чисел. Поэтому его можно записать так: 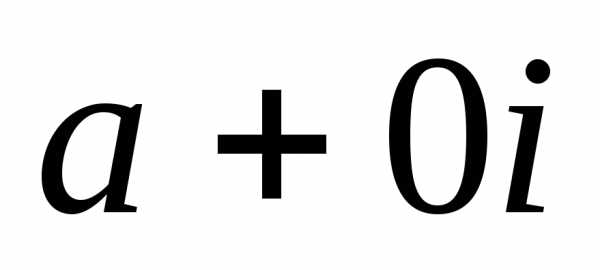 .
.
Пример: 4=4+0i
Определение 2: Комплексное число  называетсякомплексно
сопряженным
называетсякомплексно
сопряженным
с
числом 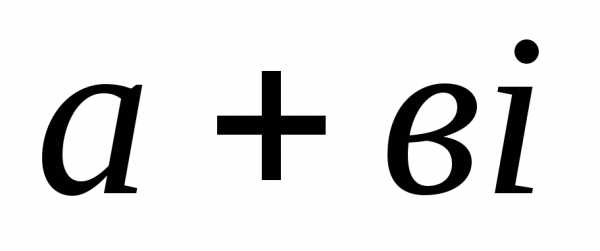 и
обозначается
и
обозначается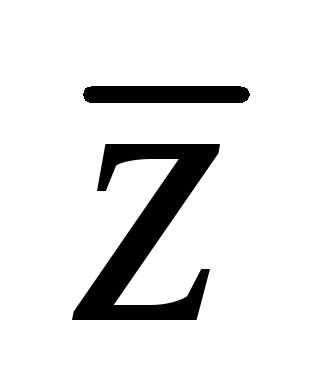 ,
то есть.
,
то есть.
Пример2: 2+5i и 2-5i
Определение 3: Модулем комплексного числа
называется число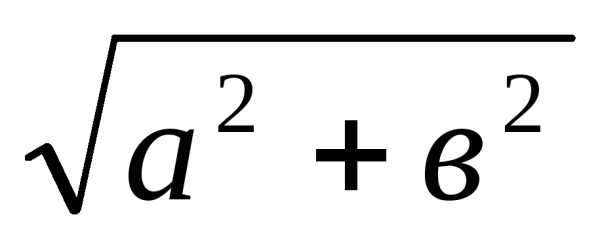 :.
Причем
:.
Причем .
.
Комплексное число можно изобразить двумя способами:
1. Точкой плоскости с координатами (а;в).
При этом действительные числа изображаются точками оси абсцисс, которую называют действительной осью, а чисто мнимые числа- точками оси ординат, которую называют мнимой осью.
2. В виде вектора
с началом в начале координат ( )
и концом в точке М(а;в) ().
)
и концом в точке М(а;в) ().
Каждой точке
плоскости с координатами (а;в) соответствует
один и только один вектор с началом в
точке О(0;0) и концом в точке М(а;в),поэтому
комплексное число 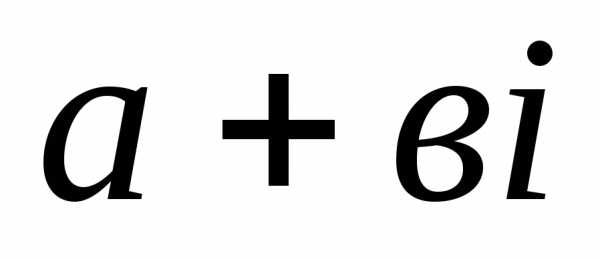 можно изобразить в виде вектора
можно изобразить в виде вектора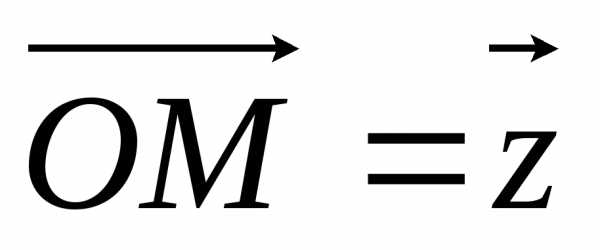 .
.
Определение 4: Угол φ
между действительной осью ОХ и вектором 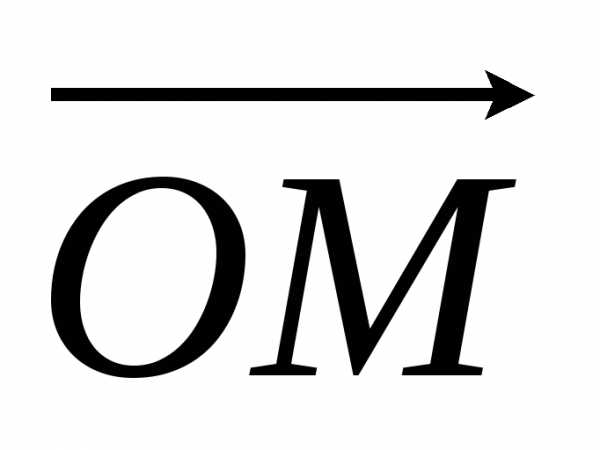 ,
отсчитываемый от положительного
направления действительной оси,
называетсяаргументом комплексного числа. Если отсчет ведется
против движения часовой стрелки, то
величина угла считается положительной,
иначе- отрицательной.
,
отсчитываемый от положительного
направления действительной оси,
называетсяаргументом комплексного числа. Если отсчет ведется
против движения часовой стрелки, то
величина угла считается положительной,
иначе- отрицательной.
Любое комплексное
число имеет бесконечное множество
аргументов, отличающихся друг от друга
на число, кратное  .
Наименьшее по абсолютной величине
значение аргумента из промежутканазываетсяглавным
значением аргумента.
.
Наименьшее по абсолютной величине
значение аргумента из промежутканазываетсяглавным
значением аргумента.
Из определения тригонометрических функций следует:
Пример3:
Изобразить геометрическую интерпретацию комплексного числа, найти модуль комплексного числа и главное значение аргумента.
а). 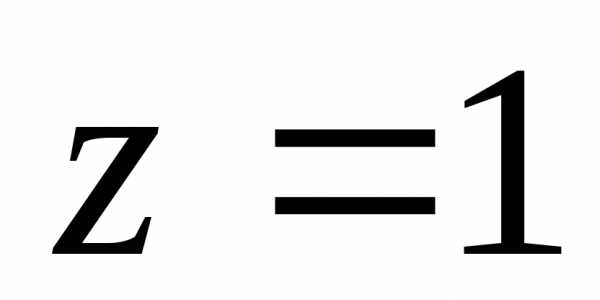 ;
б).
;
б).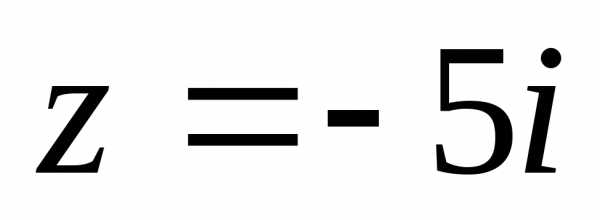 ;
в)..
;
в)..
Решение:
а). 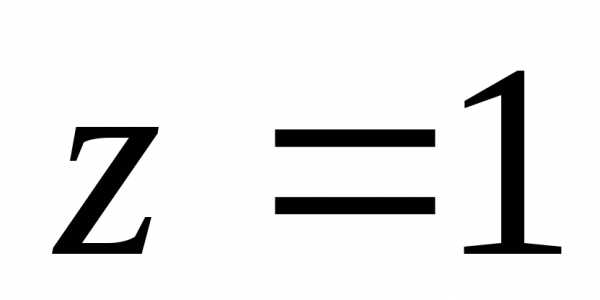
;
б). 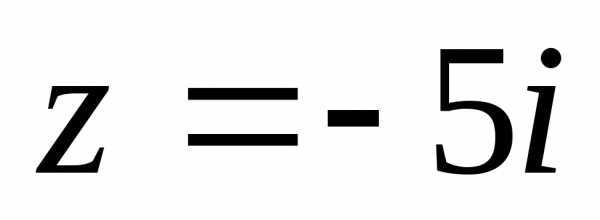
;
в).
2. Действия над комплексными числами в алгебраической форме.
Сложение и умножение комплексных чисел мы ввели в определении комплексного числа. Введем правила вычитания и деления комплексных чисел: ;
.
Но удобнее всего действия над комплексными числами производить с помощью правил соответствующих действий над многочленами и понятием мнимой единицы.
Пример4:
Выполнить действия:
а). 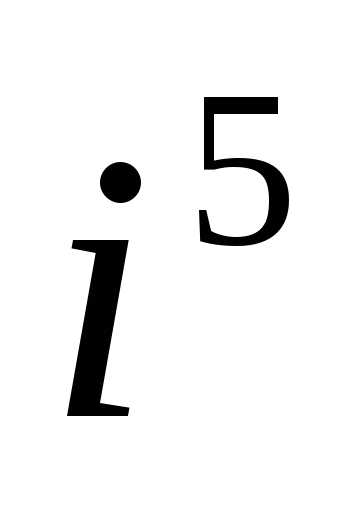 ;
б).
;
б).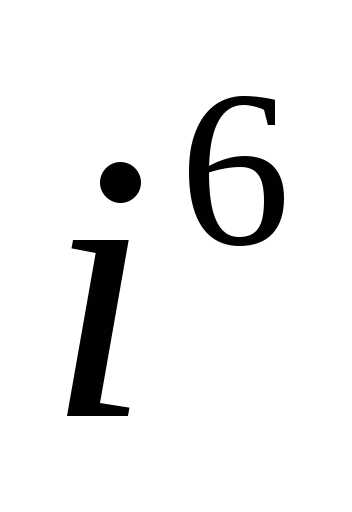 ;
в).
;
в). ;
г).;
д).;
е).;
;
г).;
д).;
е).;
ж). 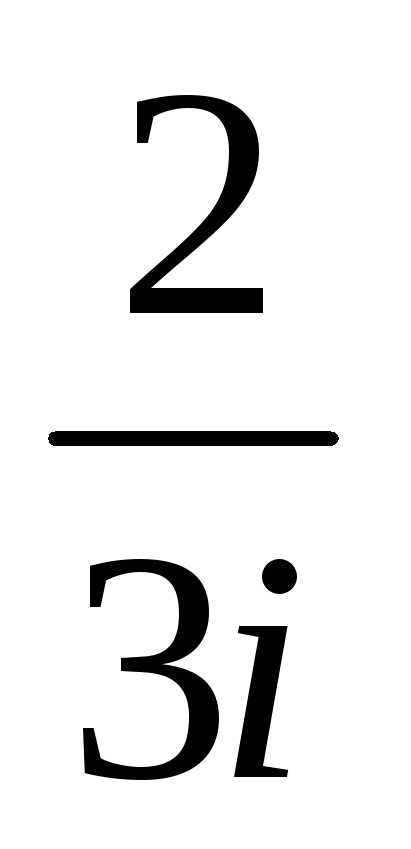 ;
з).
;
з).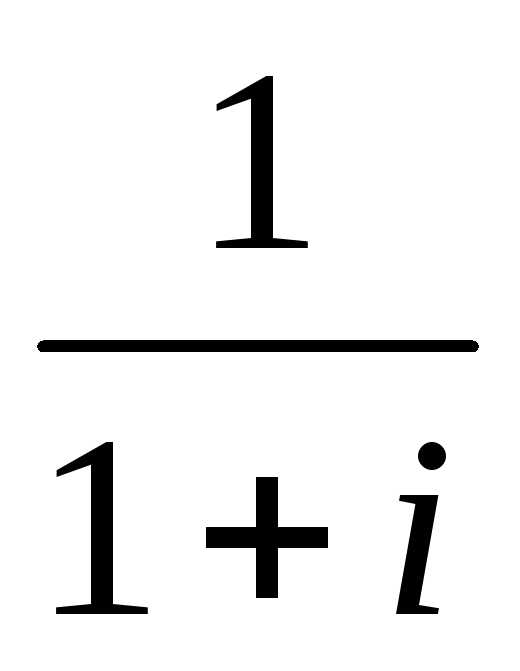 ;
и).
;
и).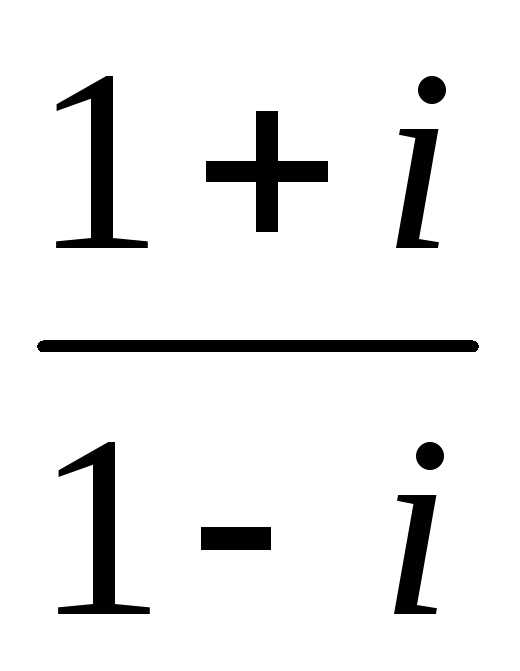 ;
к).
;
к).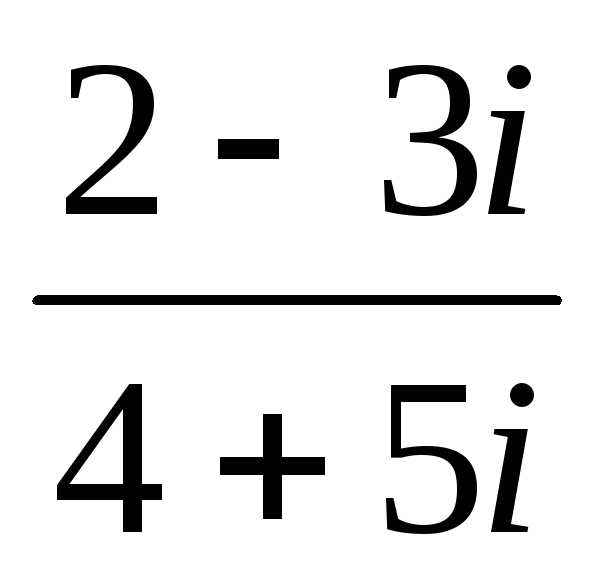 .
.
Решение:
а). ;
б). ;
в). ;
г).;
д). ;
е). ;
ж). ;
з). ;
и). ;
к). .
3. Тригонометрическая форма комплексного числа.
Изобразим комплексное число геометрически:
Обозначим модуль комплексного числа .
Аргументом комплексного числа называется угол φ, который вычисляется с помощью формул:
но , тогда
и
Подставим получившиеся формулы в , получим:
,тогда
— тригонометрическая форма комплексного числа.
Алгоритм перехода из алгебраической формы комплексного числа в тригонометрическую:
Найти: .
Изобразить геометрически число , для нахождения четверти числа φ.
Составить уравнения: и найти φ.
Записать z в тригонометрической форме .
Примеры: а).Перевести числа из алгебраической формы в тригонометрическую.
1).  .
.
1. .
2. Изобразим геометрически:
Значит φ принадлежит I четверти.
3. 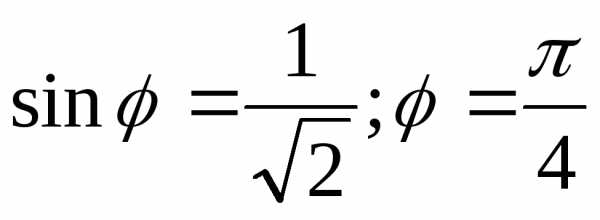 .
.
4..
2). 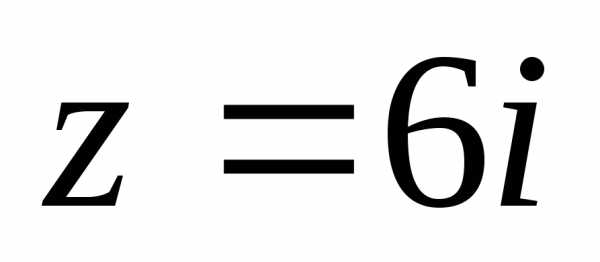 .
.
1. .
2. Изобразим геометрически:
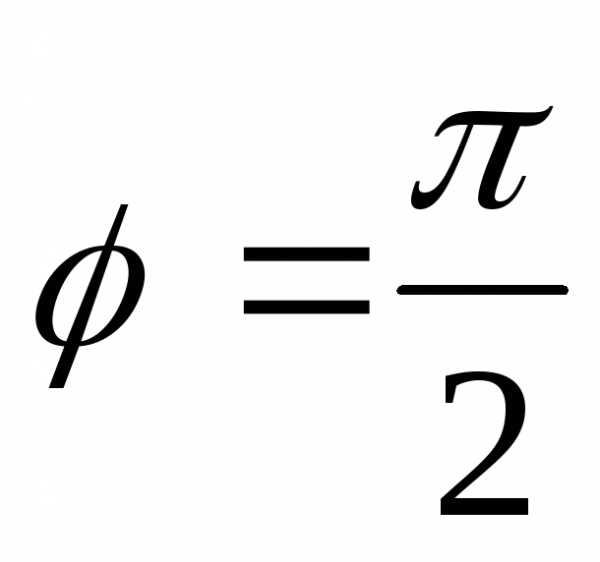 ,
так как z
принадлежит положительной полуоси ОУ.
,
так как z
принадлежит положительной полуоси ОУ.
Значит 3 пункт можно опустить.
4. .
3).
1. .
2. Изобразим геометрически:
φ принадлежит II четверти.
3. .
4.
б). перевести из тригонометрической формы в алгебраическую:
1).
Решение:
.
2).
Решение:
.
4. Действия над комплексными числами в тригонометрической форме.
Пусть даны два числа в тригонометрической форме: и.
1). При умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются:
.
2). При делении двух комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются:
.
3). При возведении комплексного числа вn-ую степень используется формула:
, которая называется формулой Муавра.
4). Для извлечения корня n-ой степени из комплексного числа используется формула:
.
Примеры:
Дано: ,.
Найти: 1). 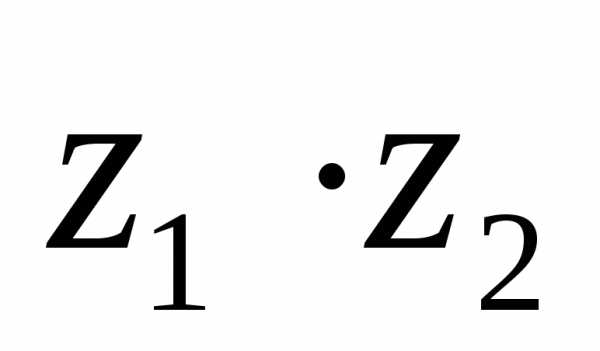 ,
2).
,
2). ,
3).
,
3).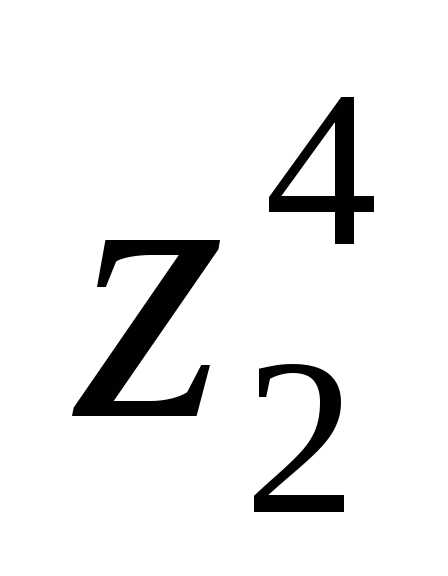 ,
4).
,
4).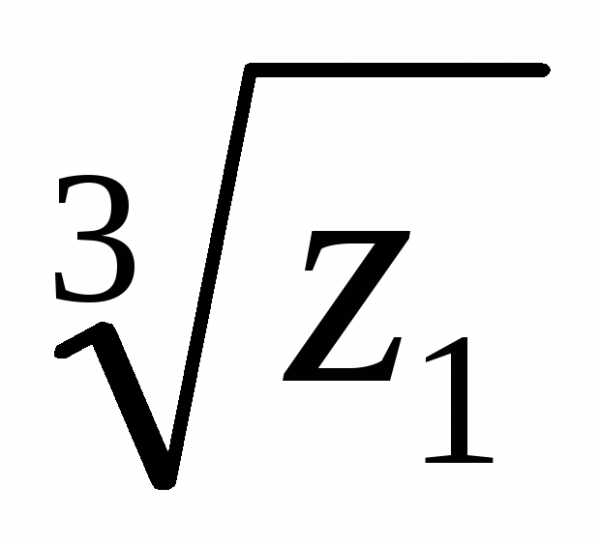 .
.
Решение: 1).
2).
3).
4).


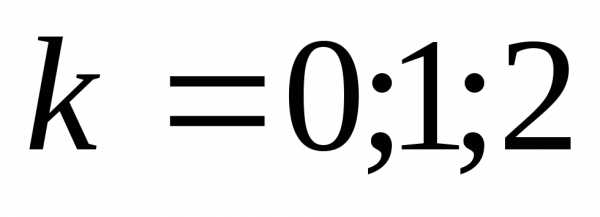
Практическая работа№7.
Тема: Действия над комплексными числами в алгебраической и тригонометрической форме.
Цель: Научить выполнять различные действия с комплексными числами; переводить комплексные числа из алгебраической формы и обратно;
Задания:
I-B II-B
1. Выполнить действия с комплексными числами в алгебраической форме:
1)., 1).,
2). 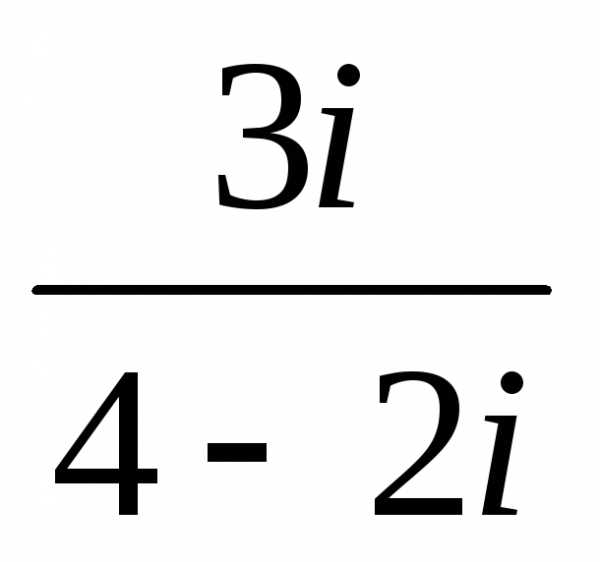 ,
3).
,
3).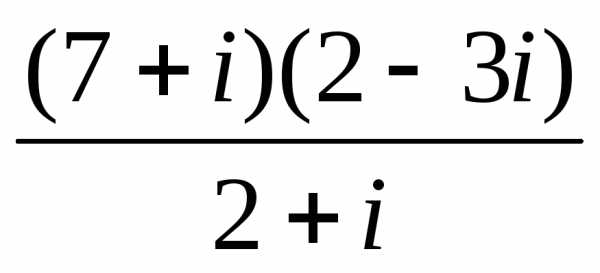 .
2).
.
2).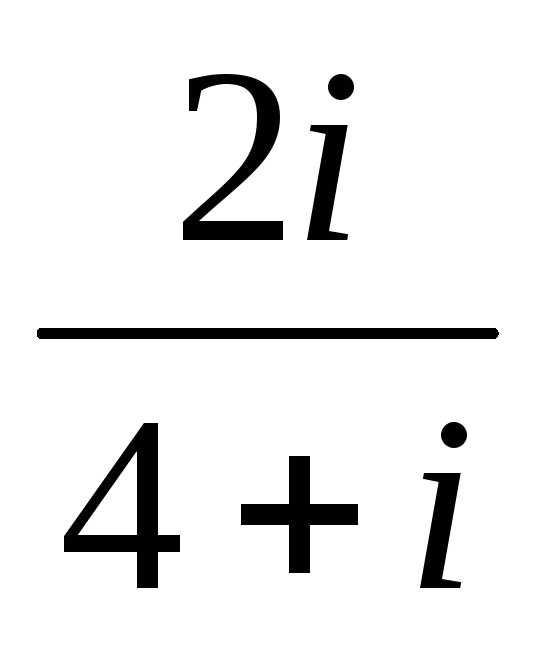 ,
3).
,
3).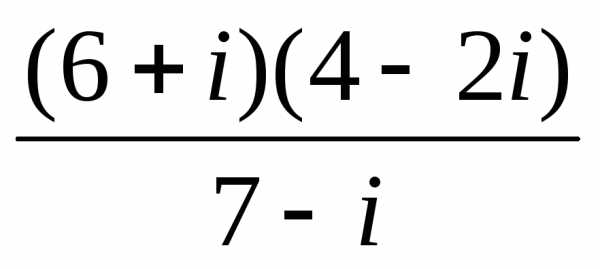 .
.
2. Записать комплексные числа в тригонометрической форме:
1). 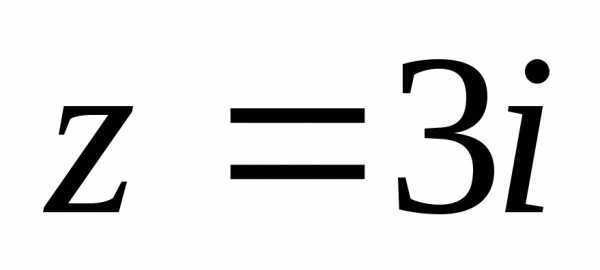 ,
2).
,
2).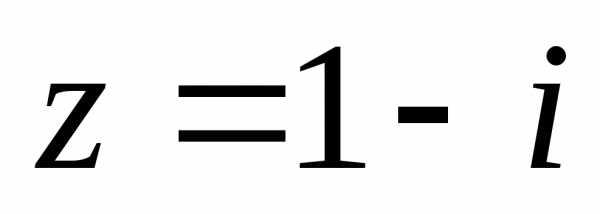 ,
3)..
1).
,
3)..
1).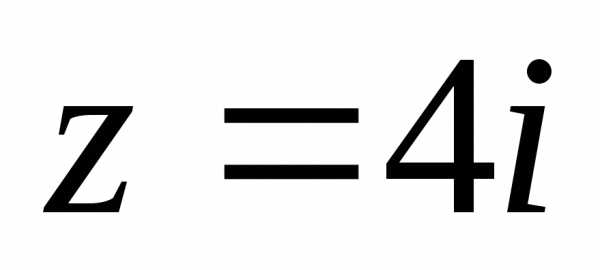 ,
2).,
3).
,
2).,
3). .
.
3. Выполнить
действия с комплексными числами в
тригонометрической форме: 1). 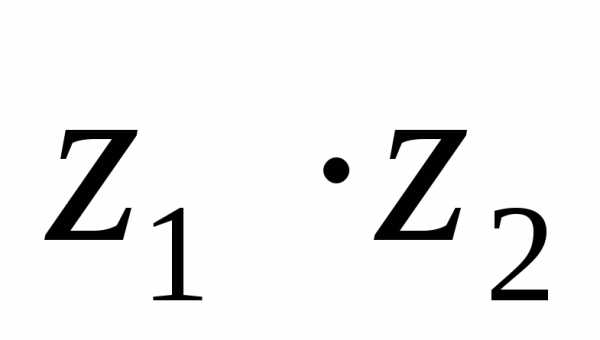 , 2).
, 2).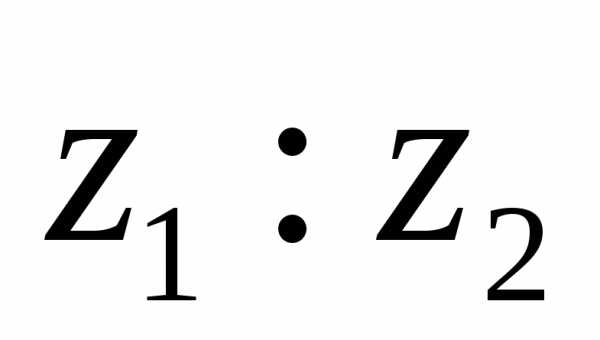 ,
если:
,
если:
, ,
. .
Ответы к практической работе № 6:
I-B. II-B.
1.
1).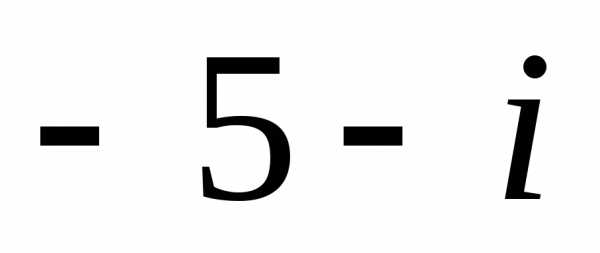 ,
1. 1).
,
1. 1).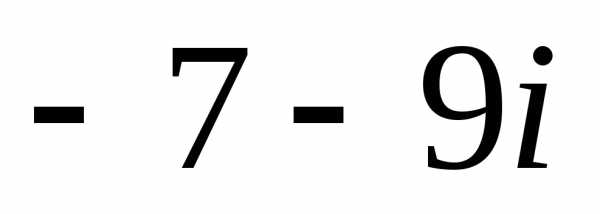
2). 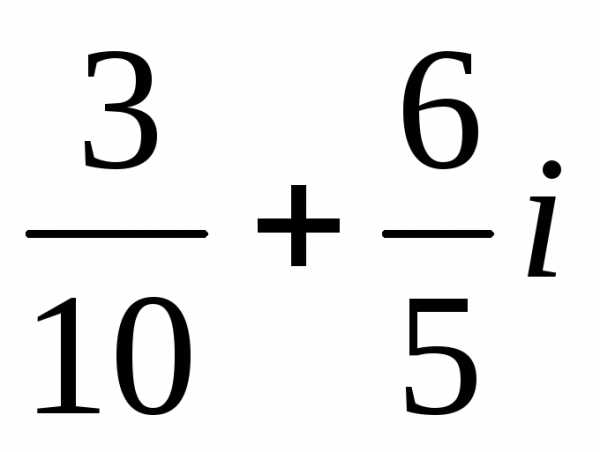 ,
2).
,
2).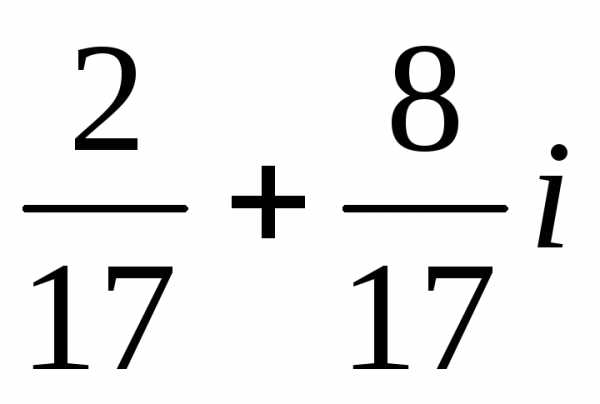 ,
,
3).
.
3). .
.
2. 1). , 2. 1).,
2). , 2).,
3). . 3)..
3. 1). 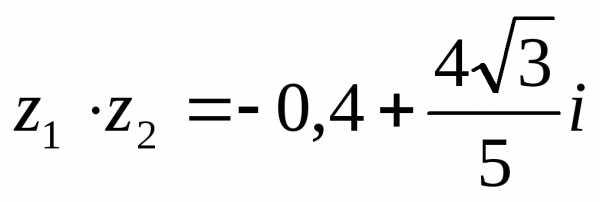 ,
3. 1).,
,
3. 1).,
2). 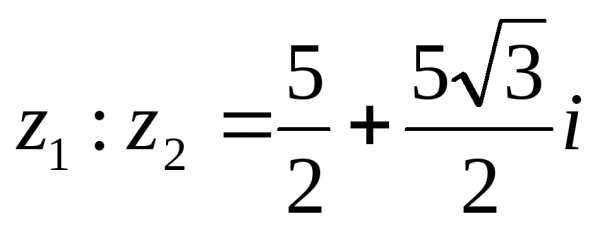 .
2)..
.
2)..
studfiles.net
Алгебраические действия над комплексными числами
1. Сложение и вычитание двух комплексных чисел:
Следствие.
Комплексные числа 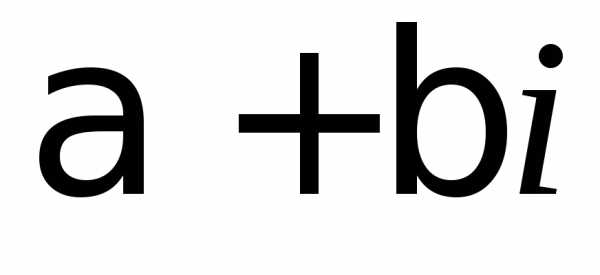 и
и называются взаимно сопряженными и
обозначаются,Следовательно,
называются взаимно сопряженными и
обозначаются,Следовательно,
для двух взаимно сопряженных чисел:
сумма – действительное число,
разность – чисто мнимое число.
2. Умножение двух комплексных чисел:
•
Произведение взаимно сопряженных чисел
–действительное число.
• Если
числа  и
и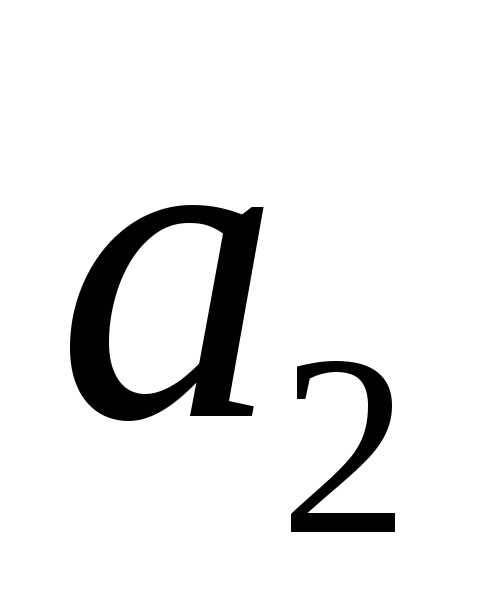 заданы в тригонометрической форме, то
заданы в тригонометрической форме, то
• Если
числа  и
и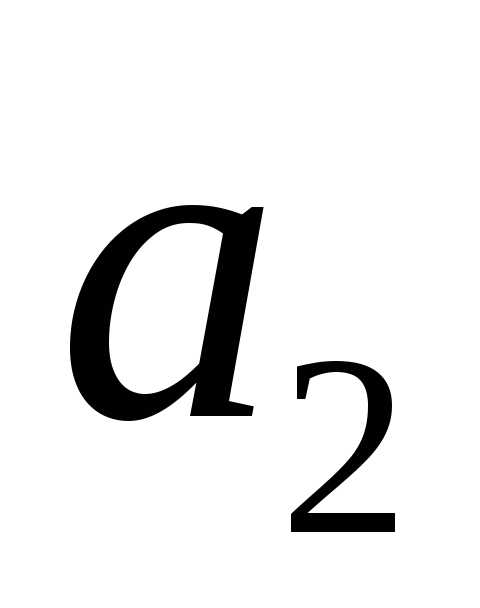 заданы в показательной форме, то
заданы в показательной форме, то
3. Деление двух комплексных чисел всегда возможно и осуществляется:
• в алгебраической форме с помощью умножения делимого и делителя на число, взаимно сопряженное делителю:
• в тригонометрической и показательной форме следующим образом:
если то
или 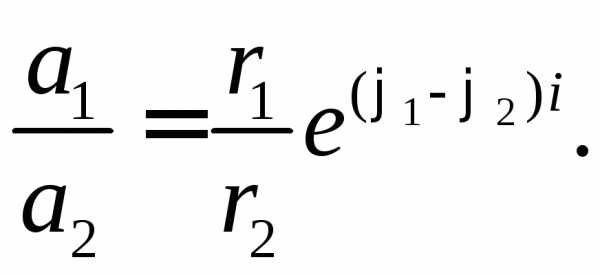
Примеры 1)
2)
3)
4)
5) 
6) Если комплексное число тообратное ему число
4. Возведение в n-ю степень комплексного числа
если  то
то
В
частности, имеем: 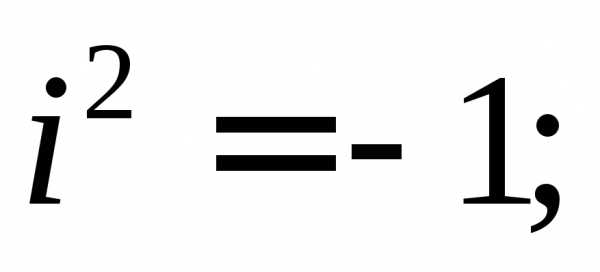
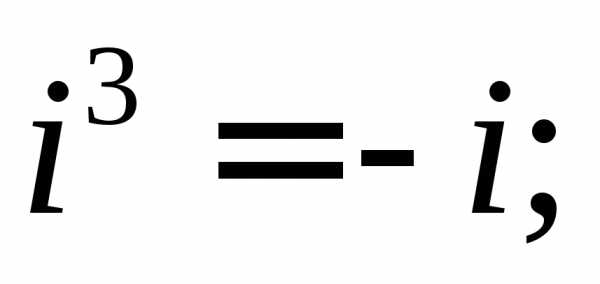
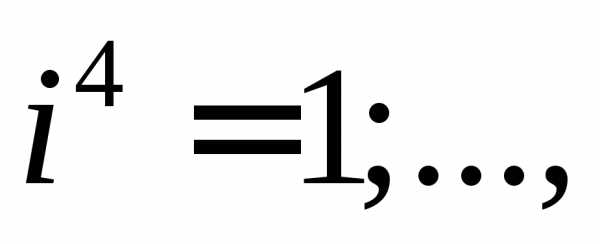
Если 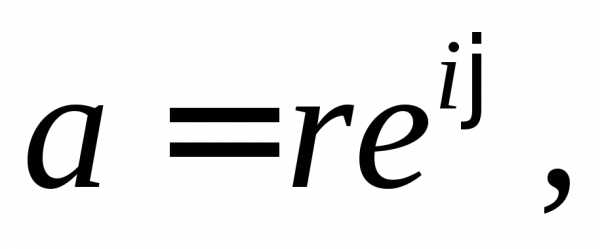 то.
то.
5. Извлечение
корня n-ой
степени как
действие, обратное возведению в степень:
если
и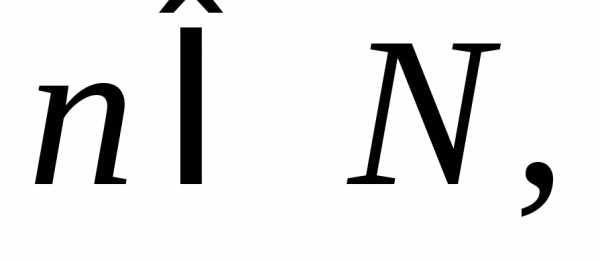 то
то
где
Если 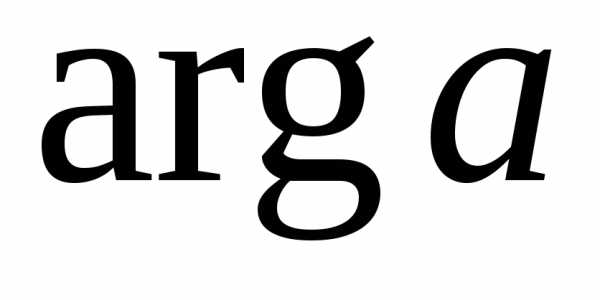 принимает значения:
принимает значения:
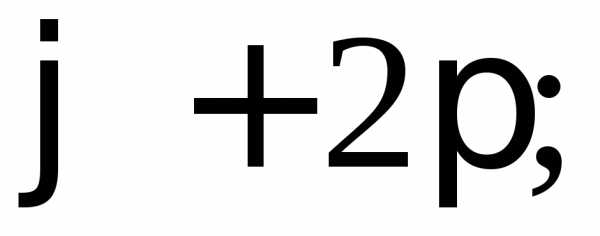
 …,то значения
…,то значения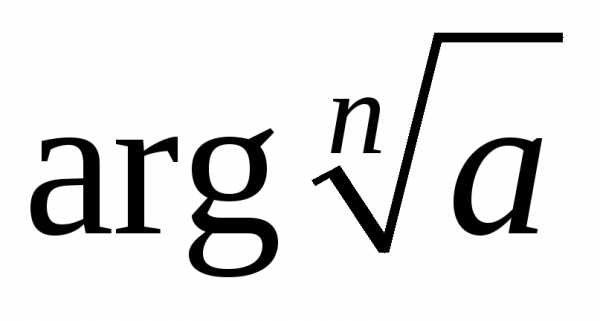 будут отличаться друг от друга на
будут отличаться друг от друга на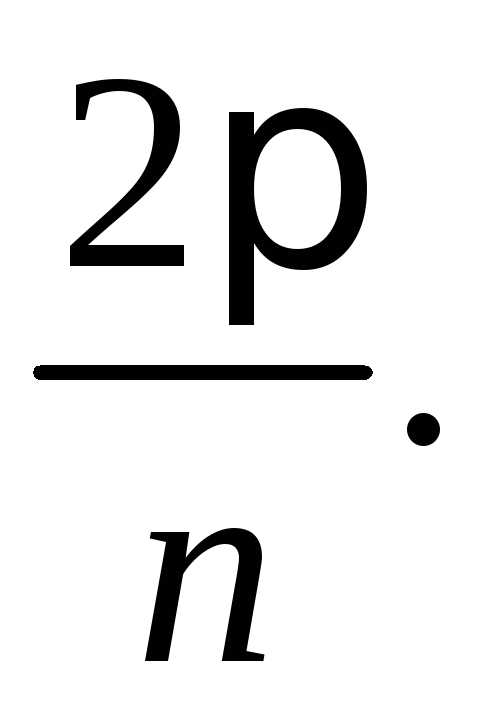 При дальнейших
При дальнейших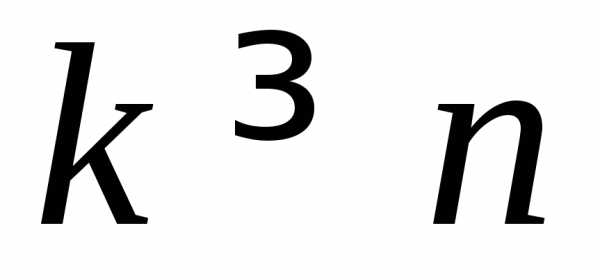 значения
значения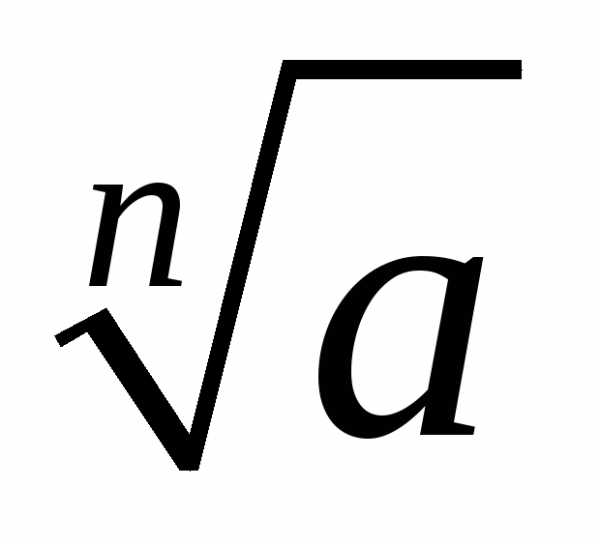 будут повторяться. В геометрической
интерпретации точки, изображающие
будут повторяться. В геометрической
интерпретации точки, изображающие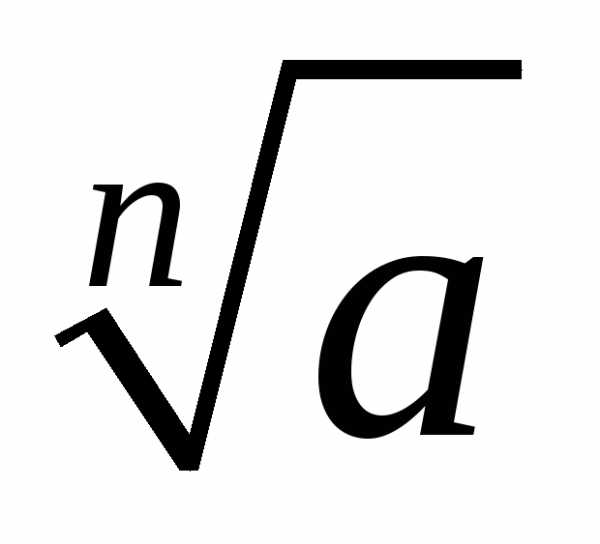 ,
являются вершинами правильногоn-угольника
с центром в начале координат. На рис. 2
изображены шесть значений
,
являются вершинами правильногоn-угольника
с центром в начале координат. На рис. 2
изображены шесть значений 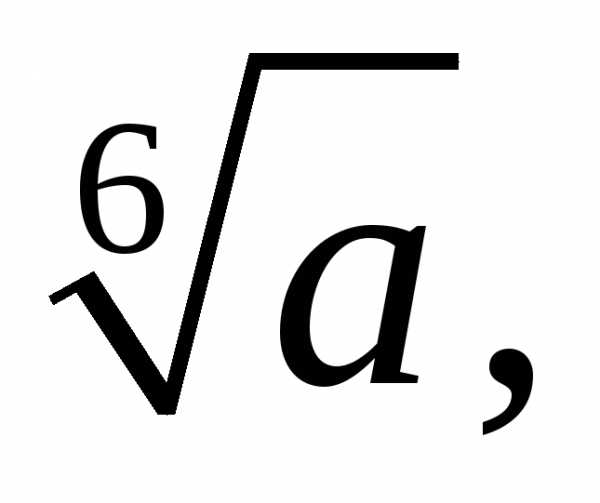 где
где
Пример 1. k = 0, 1, 2, 3.
Получаем четыре значения корня:
1) 2)
3) 4)
Пример 2. k = 0, 1.
Получаем
два значения 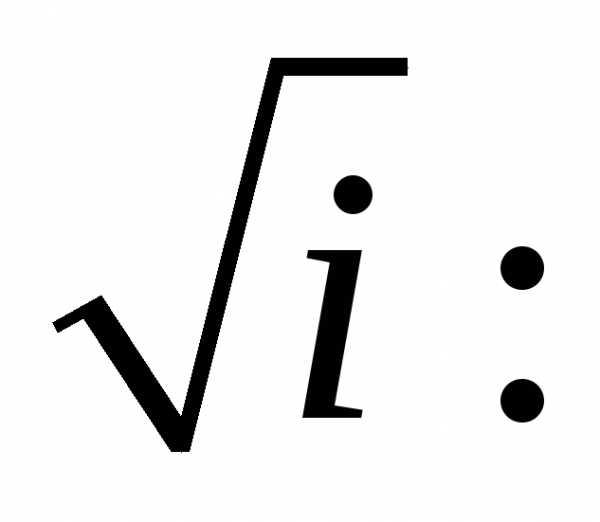 1)
1) 2)
2)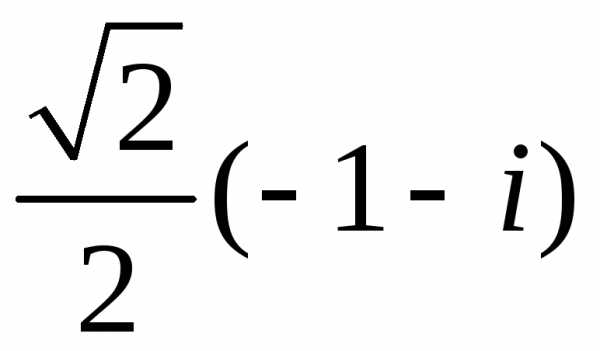 (рис. 3).
(рис. 3).
1.3. Алгебраические выражения и действия над ними
В алгебре изучаются действия с выражениями, содержащими как числовые, так и буквенные значения. При этом буквам может при необходимости придаваться конкретное численное значение.
• Одночленом называется произведение нескольких
сомножителей, являющихся числами или
буквами. Отдельные числа и буквы также
считаются одночленами. Например, 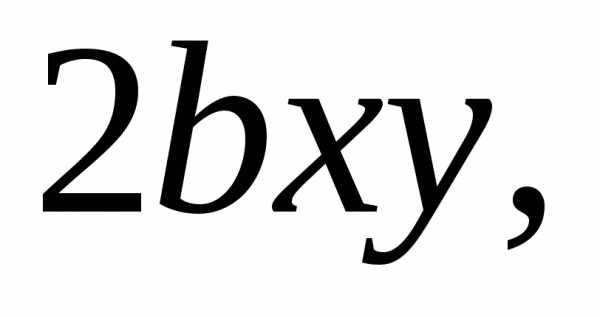
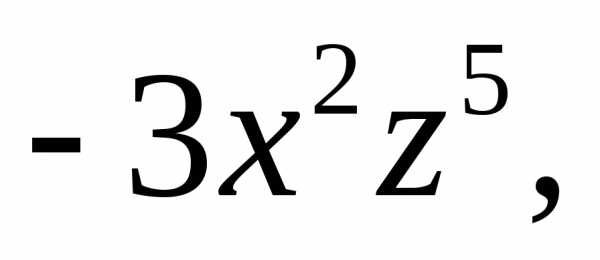 6,у – одночлены.
6,у – одночлены.
• Многочленом называется сумма одночленов. Например, – многочлены.
Основу всех алгебраических операций представляют следующие законы сложения и умножения:
Переместительный закон:
Сочетательный закон:
Распределительный закон:
При выполнении преобразований алгебраических выражений используются следующие приемы.
• Приведение подобных членов. Если несколько слагаемых имеют одинаковые буквенные части, то их числовые коэффициенты складываются, а буквенная часть сохраняется. Например,
• Вынесение множителя за скобки производится на основе распределительного закона и правил действий со степенями.
Пример 1.
Раскрытие скобок также производится с помощью распределительного закона. Необходимо помнить, что если множитель перед скобками имеет отрицательный знак, то при их раскрытии меняются знаки всех слагаемых.
Пример 2.
Пример 3.
• Деление многочленов. Для деления многочлена, зависящего от одной переменной х, на аналогичный многочлен меньшей степени используют следующую процедуру деления столбиком:
1) расположим слагаемые в многочленах в порядке убывания степени неизвестной; 2) разделим первое слагаемое делимого многочлена на первое слагаемое делителя и результат напишем в частное; 3) умножим результат на делитель и вычтем его из делимого; 4) произведем с полученным при вычитании многочленом действия аналогичные пунктам 2) и 3). Будем повторять эту операцию, пока при вычитании не получится либо ноль, либо многочлен степени меньшей, чем у делителя. Этот многочлен называется остатком.
Пример 4. Выполнить деление многочлена на многочлен
3
–
х4 – 7х3 + 12х2 – 5х + 3 х2 – 2х + 33х4 – 6х3 + 9х2 3х2 – х + 1
–х3 + 3х2 – 5х + 3– х3 + 2х2 – 3х
–
х2 – 2х + 3х2 – 2х + 3
0
Следовательно,
studfiles.net
Действия над комплексными числами — Мегаобучалка
1. При сложении двух комплексных чисел отдельно складываются их действительные части и мнимые части:
z1 + z2 = (a1 + a2) + (b1 + b2)i. (1)
2. При умножении двух комплексных чисел получается комплексное число:
z1z2 = (a1a2– b1b2) + (a1b2 + a2b1)i, (2).
3. При делении двух комплексных чисел получается комплексное число:
, (3).
@ Задача 1. Найти сумму двух комплексных чисел 2 + 3i и – 4 + 6i.
Решение: Комплексные числа суммируются по правилу (1): (2 + 3i) + (– 4 + 6i) = (2 – 4) + (3 + 6)i = – 2 + 9i.
@ Задача 2. Найти произведение двух комплексных чисел 2 + 3i и – 4 + 5i.
Решение: Комплексные числа умножаются по правилу (2):
(2 + 3i)·(– 4 + 5i) = (2·(– 4) – 3·5) + (2·5 + 3·(– 4))i = – 23 – 2i.
@ Задача 3. Найти частное двух комплексных чисел 2 + 4i и 1 + i.
Решение: Комплексные числа делятся по правилу (3):
.
Тригонометрическая форма комплексного числа
Всякое комплексное число z = a + bi можно изобразить точкой A(a,b) плоскости, такой что a = Rez, а b = Imz. Тогда a и b можно выразить через полярные координаты r и j: a = rcosj, b = rsinj, где r и j называются модулем и аргументом комплексного числа.
Таким образом, комплексное число z = a + bi можно представить в тригонометрической форме
.
Экспоненциальной формой комплексного числа называется число .
@ Задача 4. Представить в тригонометрической форме комплексное число .
Решение: Так как , то комплексное число представляется в тригонометрической форме в виде
.
Корни квадратного и биквадратного уравнений
Корни квадратного уравнения ax2 + bx + c = 0 с отрицательным дискриминантом D = b2 – 4ac < 0 являются комплексными числами и находятся по формулам .
Корни биквадратного уравнения x4 + px2 + q = 0 с отрицательным дискриминантом D = p2 – 4q < 0 являются комплексными числами и находятся по формулам:
,
.
@ Задача 5. Решить квадратное уравнение x2 – 4x + 8 = 0.
Решение: Дискриминант квадратного уравнения отрицательный: D = 42 – 4×8 = – 16 < 0 и, следовательно, корни квадратного уравнения равны .
@ Задача 6. Решить биквадратное уравнение
x4 – 4x2 + 16 = 0.
Решение: Дискриминант биквадратного уравнения отрицательный: D = 42 – 4×16 = – 48 < 0. Т.к. и , то и .
§1.7 Прямые и плоскости в аффинном пространстве. Выпуклые множества и их свойства.
В n-мерном пространстве задаётся упорядоченной системой линейно независимых векторов , выходящих из одной точки O. Аффинными координатами точки M называют такие числа xi, что
Tочку O и систему векторов называют репером или аффинным базисом; прямые, проходящие через вектора — координатными осями.
На аффинной плоскости (n = 2) координату x1 называют абсциссой, а x2 – ординатой точки M. В пространстве же координаты точки называют её абсциссой, ординатой и аппликатой. Аналогичным образом именуют и координатные оси.
megaobuchalka.ru

 Статьи
26.02.2016 в 15:20
Статьи
26.02.2016 в 15:20

 Если в бюджетных блока питания обычно предусматриваются два вида защиты: от кратковременного перенапряжения во внешней сети и короткого замыкания внутри блока, то качественные устройства поддерживают более продвинутый пакет безопасности. Лучшие образцы оснащаются интеллектуальной схемой на основе специального чипа и способны своевременно реагировать на чрезмерное потребление тока, перегрев и пониженное напряжение. Кроме того, недорогие блоки не имеют защиты, предотвращающей их включение без штатной нагрузки, в то время как дорогим решениям такой режим работы не страшен.
Если в бюджетных блока питания обычно предусматриваются два вида защиты: от кратковременного перенапряжения во внешней сети и короткого замыкания внутри блока, то качественные устройства поддерживают более продвинутый пакет безопасности. Лучшие образцы оснащаются интеллектуальной схемой на основе специального чипа и способны своевременно реагировать на чрезмерное потребление тока, перегрев и пониженное напряжение. Кроме того, недорогие блоки не имеют защиты, предотвращающей их включение без штатной нагрузки, в то время как дорогим решениям такой режим работы не страшен. Еще одной характерной особенностью бюджетных блоков питания является использование минимально допустимых номиналов электролитических конденсаторов, устанавливаемых в выходных фильтрах. От их ёмкости напрямую зависит время отключения, на протяжении которого БП способен поддерживать требуемые уровни напряжения, позволяя компьютеру экстренно завершить критические операции. При кратковременном пропадании сетевого питания, возможно даже продолжение работы ПК без перезагрузки. Проще говоря, некоторые качественные модели БП имеют «встроенный источник бесперебойного питания».
В современных БП используется импульсный принцип преобразования входного напряжения, который позволяет увеличить эффективность устройства и значительно уменьшить его габариты, но отличается высоким уровнем реактивной мощности. Последняя не передается в нагрузку как раз в силу особенностей потребления тока и расходуется на электромагнитное излучение, паразитные помехи и нагрев. Отношение активной мощности к полной в англоязычной литературе называется power factor, а на русский язык этот термин переводится как коэффициент мощности. Законодательство большинства стран прямо регламентирует характер сетевой нагрузки и предписывает снижать уровень импульсных колебаний до приемлемых значений с помощью различных приемов компенсации (Power Factor Correction).
Еще одной характерной особенностью бюджетных блоков питания является использование минимально допустимых номиналов электролитических конденсаторов, устанавливаемых в выходных фильтрах. От их ёмкости напрямую зависит время отключения, на протяжении которого БП способен поддерживать требуемые уровни напряжения, позволяя компьютеру экстренно завершить критические операции. При кратковременном пропадании сетевого питания, возможно даже продолжение работы ПК без перезагрузки. Проще говоря, некоторые качественные модели БП имеют «встроенный источник бесперебойного питания».
В современных БП используется импульсный принцип преобразования входного напряжения, который позволяет увеличить эффективность устройства и значительно уменьшить его габариты, но отличается высоким уровнем реактивной мощности. Последняя не передается в нагрузку как раз в силу особенностей потребления тока и расходуется на электромагнитное излучение, паразитные помехи и нагрев. Отношение активной мощности к полной в англоязычной литературе называется power factor, а на русский язык этот термин переводится как коэффициент мощности. Законодательство большинства стран прямо регламентирует характер сетевой нагрузки и предписывает снижать уровень импульсных колебаний до приемлемых значений с помощью различных приемов компенсации (Power Factor Correction).

 Простой интерфейс, полный русский перевод, базовый принцип работы. Я бы не рекомендовал конечному потребителю ориентироваться на этот калькулятор. Получаемые значения объективно ниже рекомендуемых, не учитывается запас мощности и КПД блоков питания, отсутствует тонкая настройка параметров.
Простой интерфейс, полный русский перевод, базовый принцип работы. Я бы не рекомендовал конечному потребителю ориентироваться на этот калькулятор. Получаемые значения объективно ниже рекомендуемых, не учитывается запас мощности и КПД блоков питания, отсутствует тонкая настройка параметров. Удобный интерфейс, отсутствие русского языка, много опций, доступно большое количество параметров. Хороший итоговый вывод, показаны реальное потребление, рекомендуемая мощность БП и сила тока. Генерируется ссылка на готовые вычисления, а также, в качестве рекламы, предлагаются рекомендуемые модели БП.
Удобный интерфейс, отсутствие русского языка, много опций, доступно большое количество параметров. Хороший итоговый вывод, показаны реальное потребление, рекомендуемая мощность БП и сила тока. Генерируется ссылка на готовые вычисления, а также, в качестве рекламы, предлагаются рекомендуемые модели БП. Я лично пользуюсь этим калькулятором достаточно давно. К слову, предыдущий калькулятор сделан на API вычислителя от Enermax. Точные расчёты и вывод итогов с учётом запаса мощности. Стоит уточнить, что по факту калькулятор ориентирован на блоки питания производства Enermax, то есть при покупке бюджетных аналогов следует добавлять 20-30% к итоговым расчётам.
Я лично пользуюсь этим калькулятором достаточно давно. К слову, предыдущий калькулятор сделан на API вычислителя от Enermax. Точные расчёты и вывод итогов с учётом запаса мощности. Стоит уточнить, что по факту калькулятор ориентирован на блоки питания производства Enermax, то есть при покупке бюджетных аналогов следует добавлять 20-30% к итоговым расчётам. У меня он так и не заработал (см. скриншот). На шаге выбора модели процессора список просто не раскрылся. Сомневаюсь, что даже при корректной работе этот калькулятор может соперничать с более продвинутыми аналогами.
У меня он так и не заработал (см. скриншот). На шаге выбора модели процессора список просто не раскрылся. Сомневаюсь, что даже при корректной работе этот калькулятор может соперничать с более продвинутыми аналогами. [spoiler effect=»slide» show=»Скриншот проверки утилиты на VirusTotal (Развернуть)» hide=»Скриншот проверки утилиты на VirusTotal (Свернуть)»]
[spoiler effect=»slide» show=»Скриншот проверки утилиты на VirusTotal (Развернуть)» hide=»Скриншот проверки утилиты на VirusTotal (Свернуть)»]
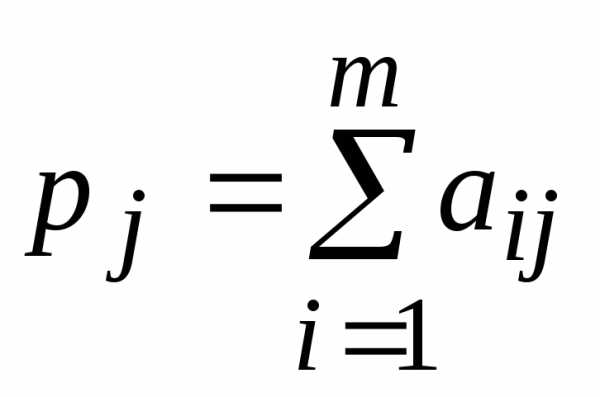
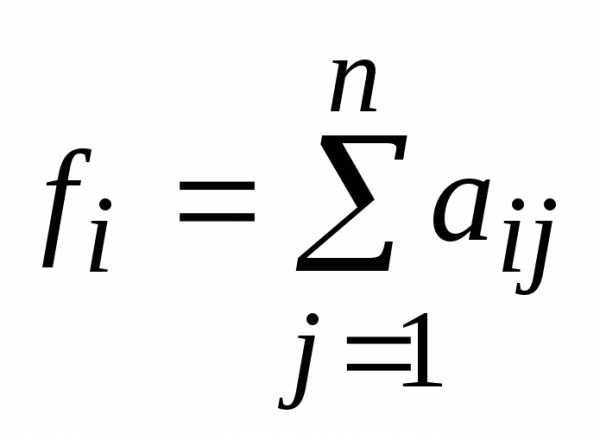
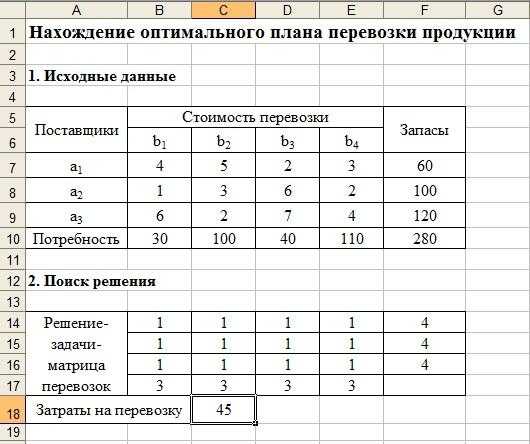
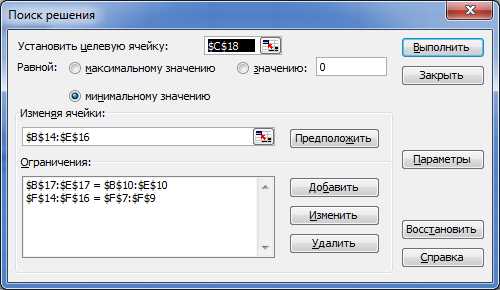
 — пример нечётной функции. — пример чётной функции. ни чётная, ни нечётная.
— пример нечётной функции. — пример чётной функции. ни чётная, ни нечётная. — пример нечётной функции. — пример чётной функции. ни чётная, ни нечётная.
— пример нечётной функции. — пример чётной функции. ни чётная, ни нечётная. называют событие
называют событие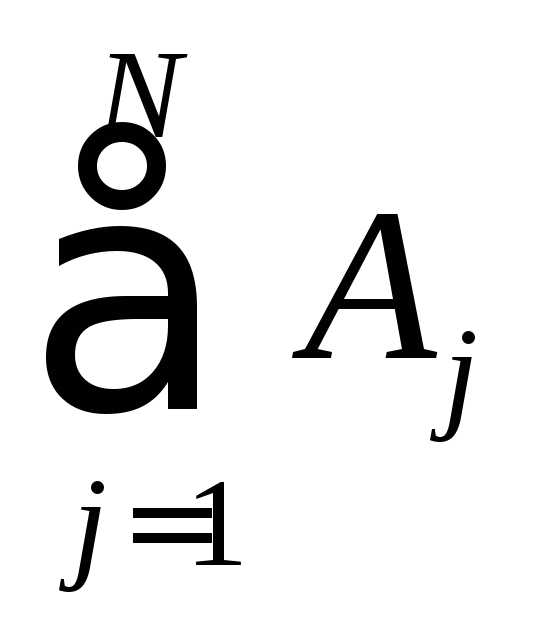 ,
которое наблюдается каждый раз, когда
наступаетхотя бы одно изсобытий
,
которое наблюдается каждый раз, когда
наступаетхотя бы одно изсобытий .
В частности, объединением
событий A и B
называют событие A+B (у некоторых авторов
.
В частности, объединением
событий A и B
называют событие A+B (у некоторых авторов 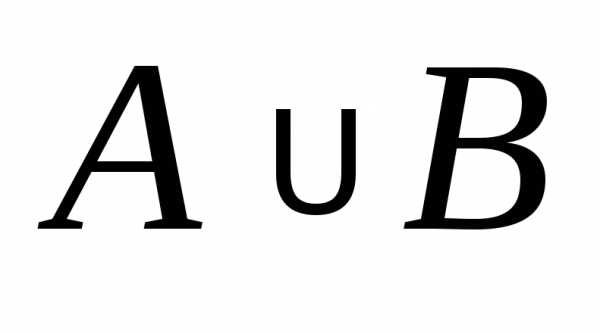 ),
которое наблюдается, когданаступает или A, или B или оба этих события одновременно(Рис. 7).
Признаком пересечения в текстовых
формулировках событий служит союз“или”.
),
которое наблюдается, когданаступает или A, или B или оба этих события одновременно(Рис. 7).
Признаком пересечения в текстовых
формулировках событий служит союз“или”.
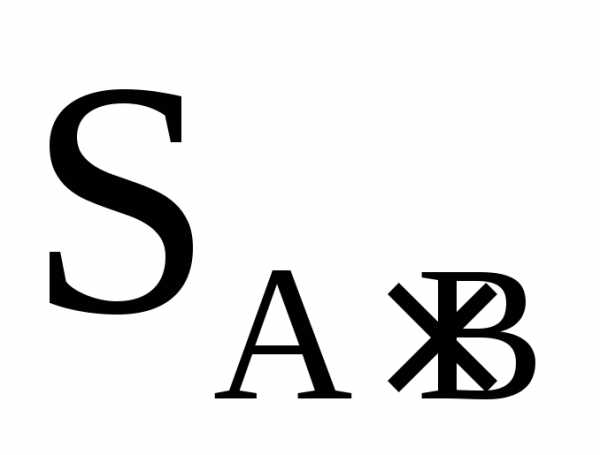 .
И исходы, соответствующие
событию B,
располагаются как в правой части
заштрихованной
фигуры, так и в помеченной
.
И исходы, соответствующие
событию B,
располагаются как в правой части
заштрихованной
фигуры, так и в помеченной 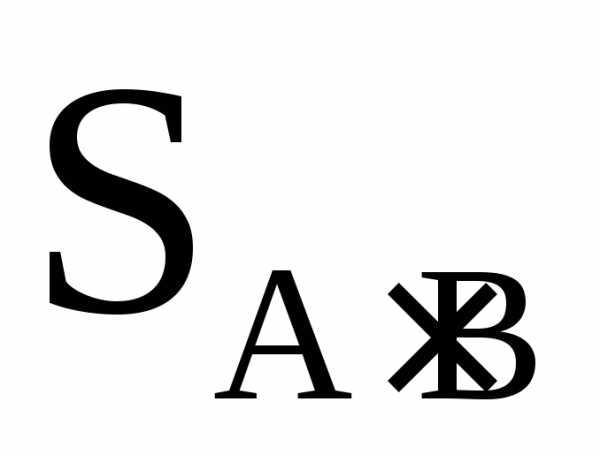 центральной части. Таким образом,
при сложении
центральной части. Таким образом,
при сложении и
и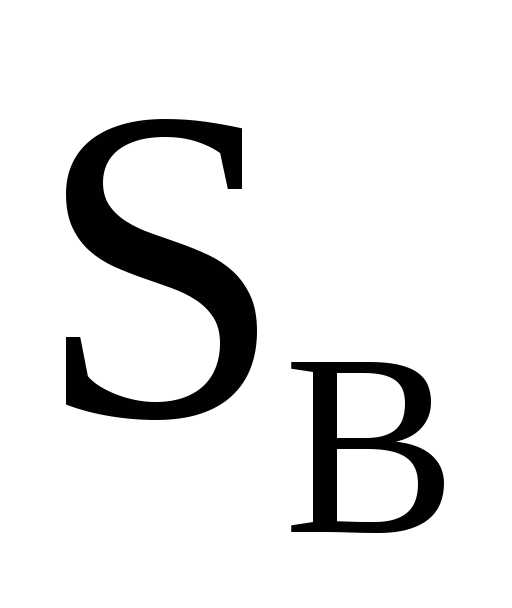 площадка
площадка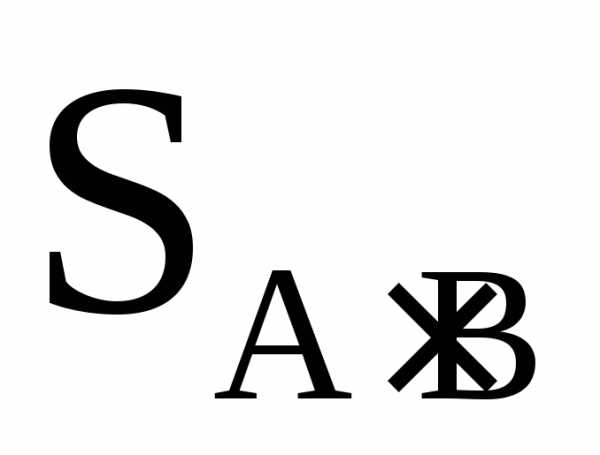 реально войдет в эту сумму дважды, а
точное выражение для площади заштрихованнойфигуры имеет
вид.
реально войдет в эту сумму дважды, а
точное выражение для площади заштрихованнойфигуры имеет
вид. определяется выражением
определяется выражением …
… ,образуют
полную группу,
то для них
,образуют
полную группу,
то для них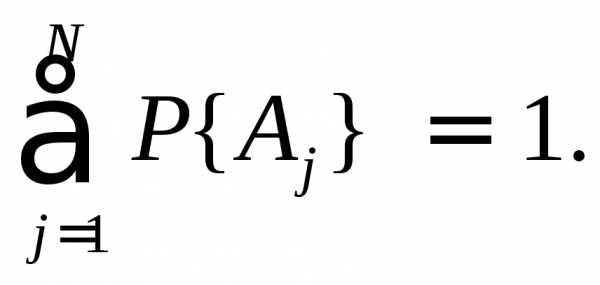
 …
…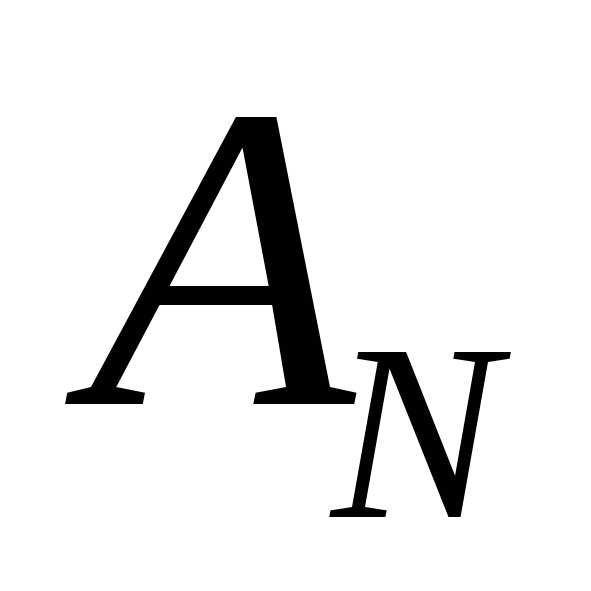 »
является утверждение «ни одно из событий
»
является утверждение «ни одно из событий …
… не реализуется». Т.е., иначе говоря, «в
опыте будут наблюдаться события
не реализуется». Т.е., иначе говоря, «в
опыте будут наблюдаться события ,
и
,
и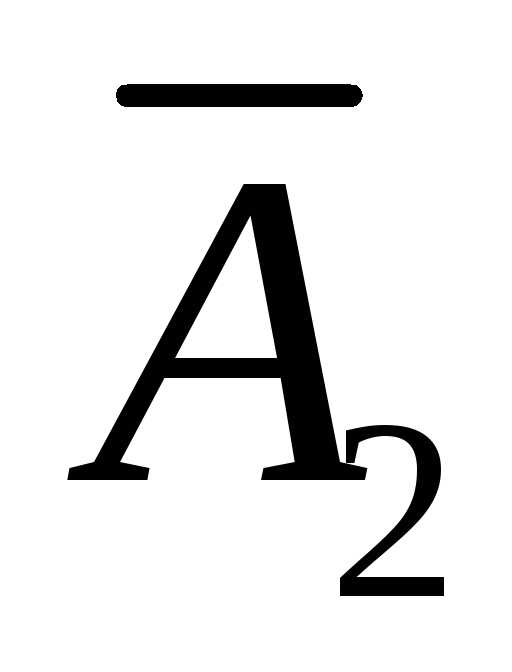 ,
и …, и
,
и …, и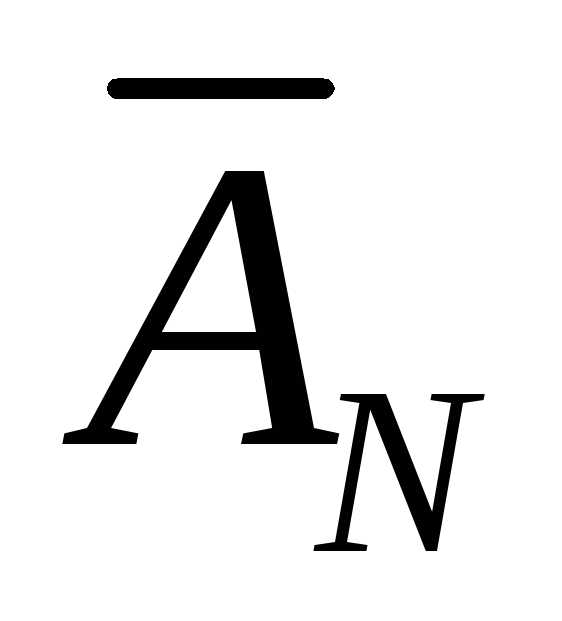 »,
что представляет собой уже пересечение
событий, противоположных исходному
набору. Отсюда, с учетом ( 2 .0), для
объединения произвольного числа событий
получаем
»,
что представляет собой уже пересечение
событий, противоположных исходному
набору. Отсюда, с учетом ( 2 .0), для
объединения произвольного числа событий
получаем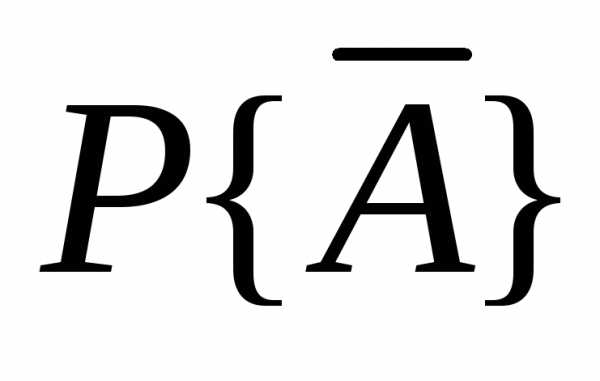 ,
получить из ( 2 .0) нужную величину
,
получить из ( 2 .0) нужную величину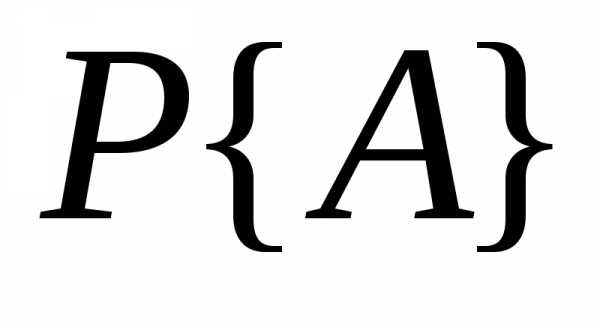 никакого труда уже не представляет.
никакого труда уже не представляет.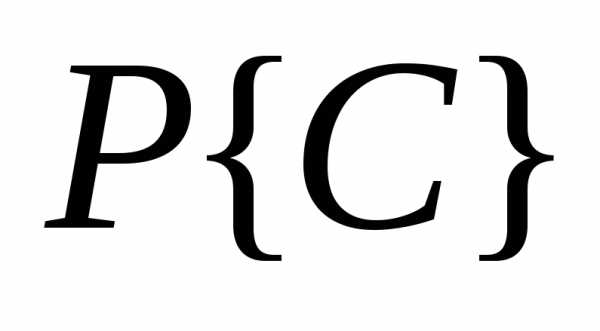 и
и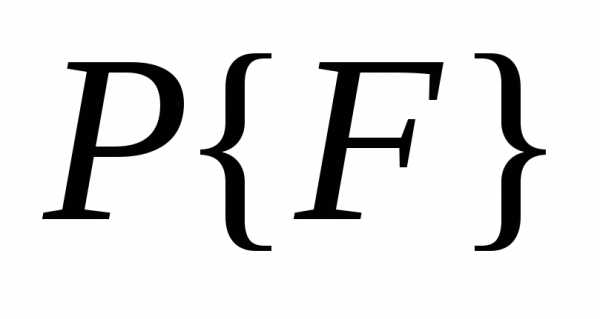 получить
конфликтующие с ( 1 .0) в
принципе невозможно, то для
получить
конфликтующие с ( 1 .0) в
принципе невозможно, то для  попытка использования
( 2 .0) вместо ( 2 .0) привела бы к явно
некорректному значению .
Важно помнить, что подобное значение
вероятности принципиально невозможно,
и при получении столь парадоксального
результата незамедлительно приступать
к поиску ошибки.
попытка использования
( 2 .0) вместо ( 2 .0) привела бы к явно
некорректному значению .
Важно помнить, что подобное значение
вероятности принципиально невозможно,
и при получении столь парадоксального
результата незамедлительно приступать
к поиску ошибки. = P{
выбрано бракованное изделие } = 0,3 и
= P{
выбрано бракованное изделие } = 0,3 и = P{
выбрано годное изделие } = 0,7.
= P{
выбрано годное изделие } = 0,7. = “первая
микросхема – годная, вторая — бракованная”;
= “первая
микросхема – годная, вторая — бракованная”;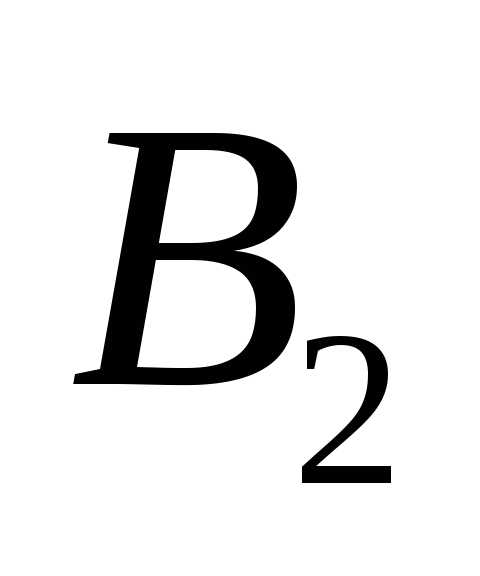 =
“первая микросхема – бракованная,
вторая – годная”.
=
“первая микросхема – бракованная,
вторая – годная”. не являются эквивалентными.
На самом деле, ,
т.к. формулировкасобытия B требует, чтобы среди микросхем ровно одна, но совсем не
обязательно первая была годной
(а другая – бракованной). Поэтому, хотя событие
не являются эквивалентными.
На самом деле, ,
т.к. формулировкасобытия B требует, чтобы среди микросхем ровно одна, но совсем не
обязательно первая была годной
(а другая – бракованной). Поэтому, хотя событие 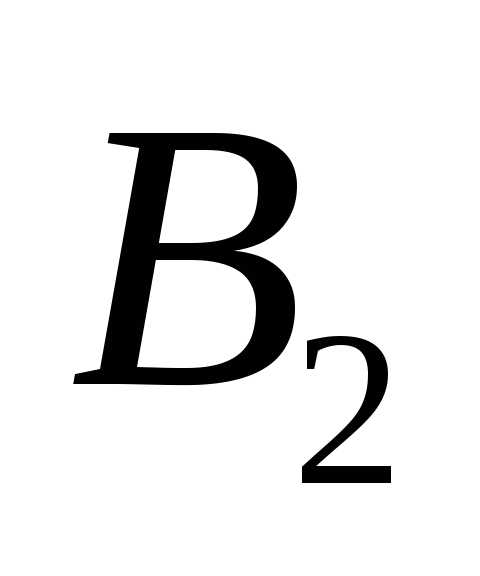 не является дублем события
не является дублем события ,
а должно учитываться независимо.
Учитывая несовместность событий
,
а должно учитываться независимо.
Учитывая несовместность событий  и
и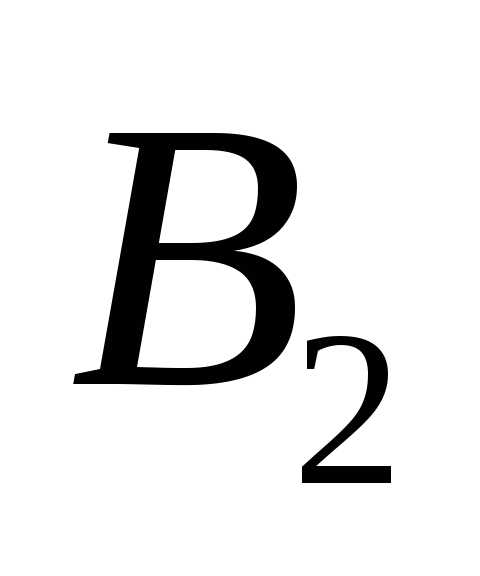 , вероятность их логической суммы будет
равна
, вероятность их логической суммы будет
равна  легко, то
именно с этого и надо начинать решение
задачи, завершая его применением
соотношения ( 2 .0).
легко, то
именно с этого и надо начинать решение
задачи, завершая его применением
соотношения ( 2 .0). = “белый шар
извлекли при первой же попытке”;
= “белый шар
извлекли при первой же попытке”; = “сначала вынули
красный шар, а затем — белый”;
= “сначала вынули
красный шар, а затем — белый”; =
“дважды вынули красный шар, а на третий
раз — белый”…
=
“дважды вынули красный шар, а на третий
раз — белый”… может быть формально бесконечно
протяженной.
может быть формально бесконечно
протяженной.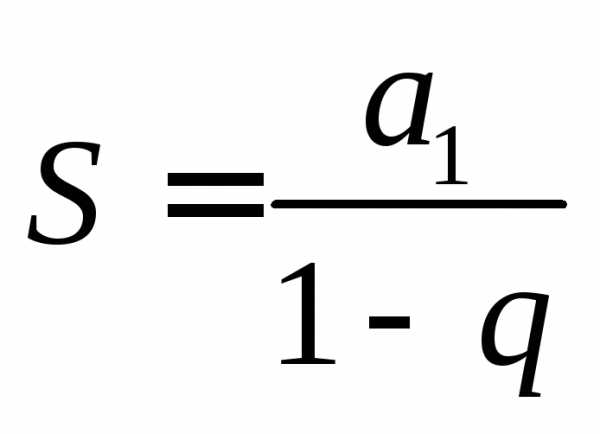 .
. называют событие
называют событие  ,
заключающееся в наступлениивсех событий
,
заключающееся в наступлениивсех событий в одном опыте. В частности, пересечением
двух
в одном опыте. В частности, пересечением
двух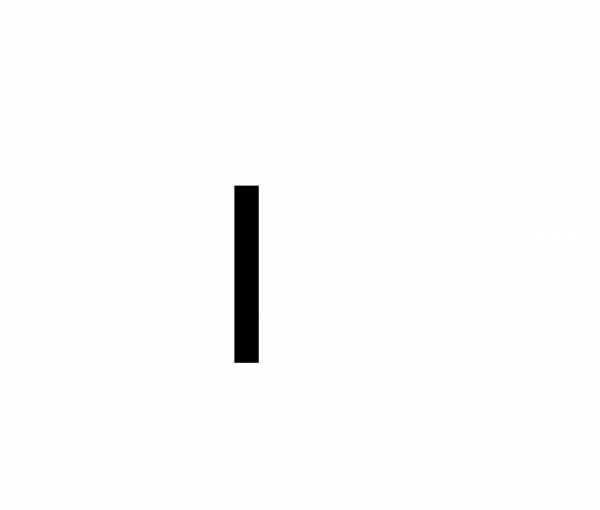 и
и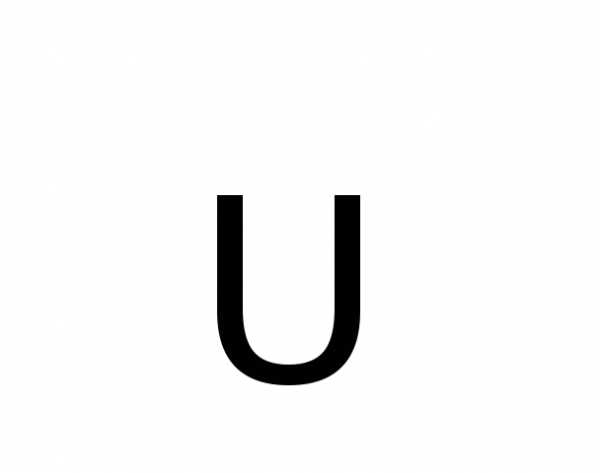 соответственно,
но в настоящем пособии эти символы не
используются.
Как правило, явной потребности в подобных
специфичных
символах не возникает,
а использование вместо символа
соответственно,
но в настоящем пособии эти символы не
используются.
Как правило, явной потребности в подобных
специфичных
символах не возникает,
а использование вместо символа 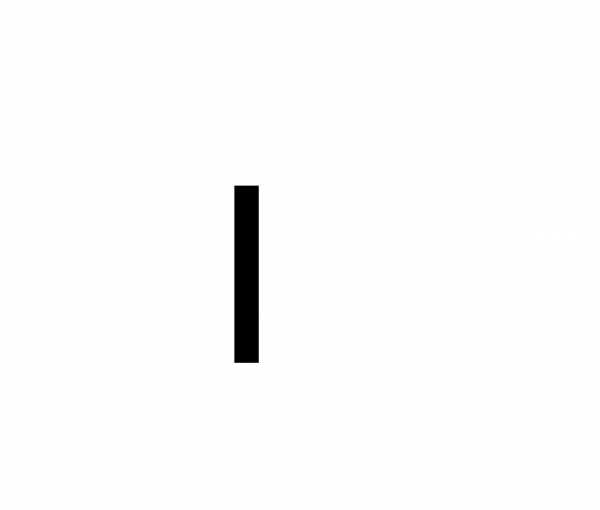 значка произведения и вместо
значка произведения и вместо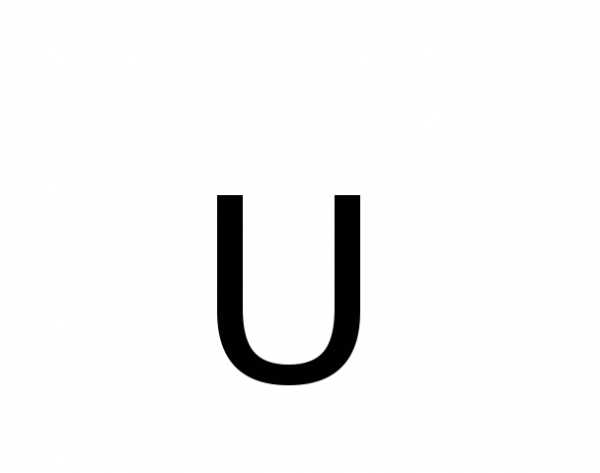 –
знака суммы к неясностям, как правило,
не приводит, но позволяет достичь большей
компактности записи.
–
знака суммы к неясностям, как правило,
не приводит, но позволяет достичь большей
компактности записи. ,
событиюB
– группа точек с пометкой
,
событиюB
– группа точек с пометкой 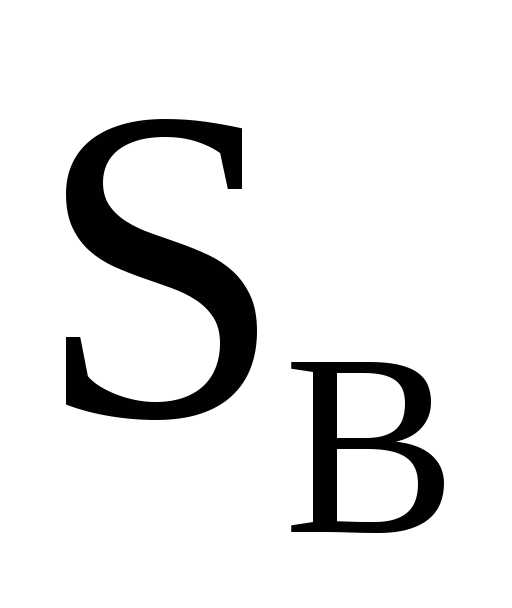 ,
а исходам общим для этих событий –
центральная область с площадью
,
а исходам общим для этих событий –
центральная область с площадью  .
.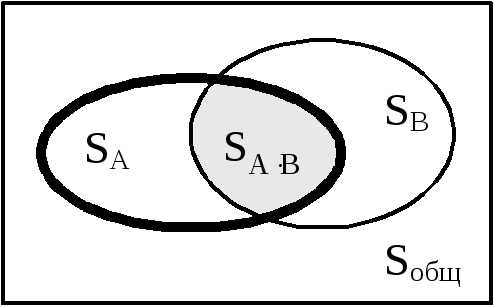
 ,
выделенная на Рис. 6жирной линией.
Соответственно, вероятность наблюдения
в этих условиях событияB(помимо обязательного событияA)
определялась бы соотношением площадей
,
выделенная на Рис. 6жирной линией.
Соответственно, вероятность наблюдения
в этих условиях событияB(помимо обязательного событияA)
определялась бы соотношением площадей 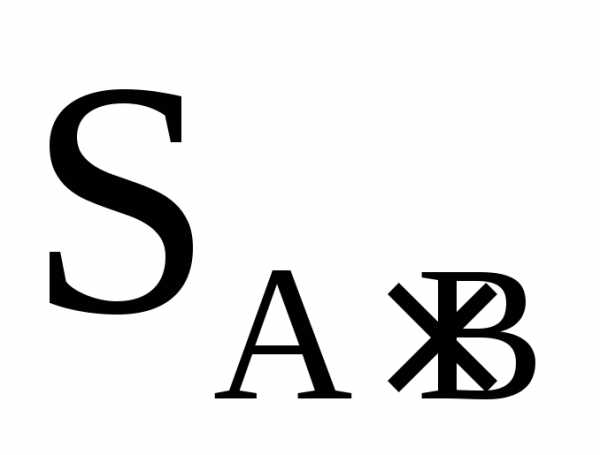 и
и .
Применительно же к условиям исходного
эксперимента указанное отношение есть
ни что иное, как условная вероятность
событияB
.
Применительно же к условиям исходного
эксперимента указанное отношение есть
ни что иное, как условная вероятность
событияB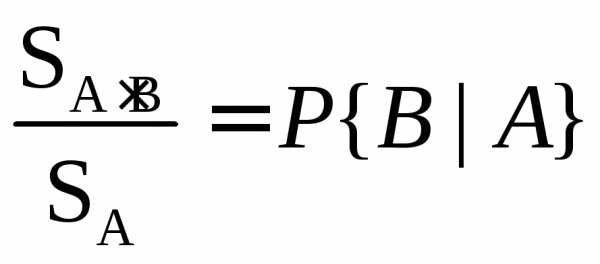 .
. определяется выражением
определяется выражением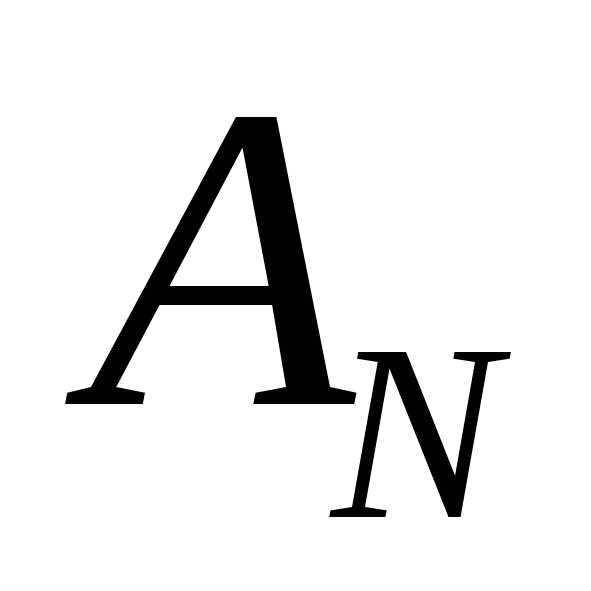 ,
вычисленная при условии,
что все события начиная с
,
вычисленная при условии,
что все события начиная с  и до
и до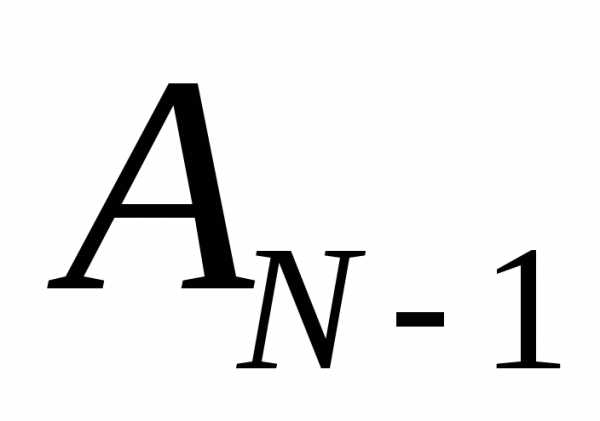 совершились.
совершились. — “неудачей”. Рассмотрим событие
— “неудачей”. Рассмотрим событие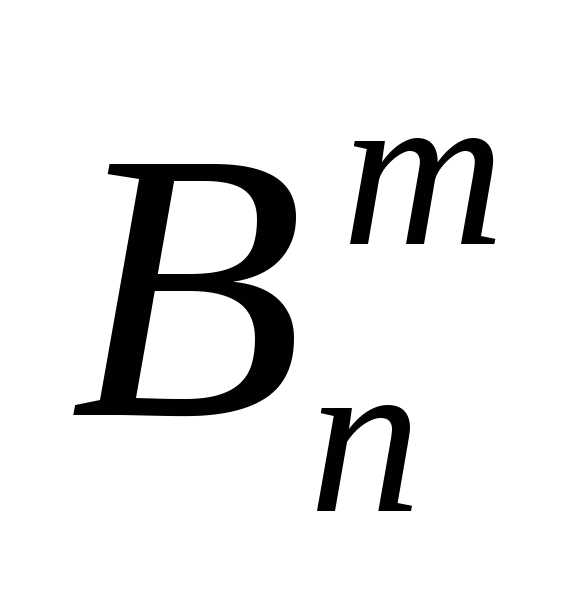 ={
в n испытаниях произошло ровно m “успехов”}.
={
в n испытаниях произошло ровно m “успехов”}.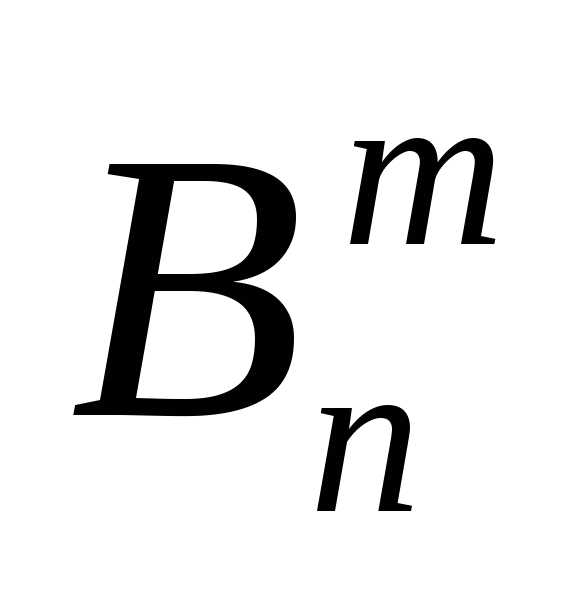 )
=
)
= 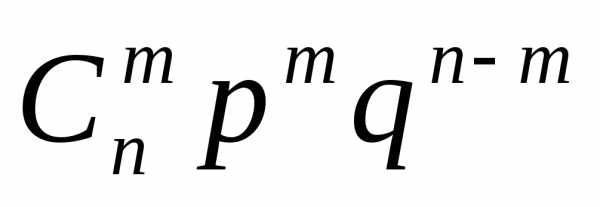 , m = 1, 2, …, n , (1.6)
, m = 1, 2, …, n , (1.6)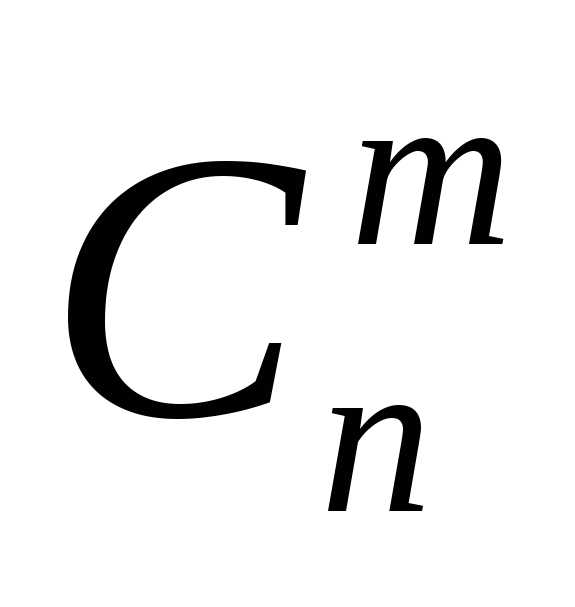 — число сочетаний из n элементов по m :
— число сочетаний из n элементов по m :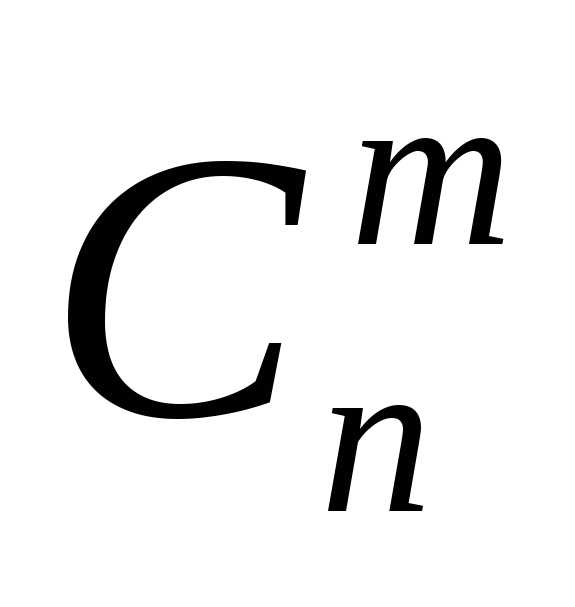 =
= 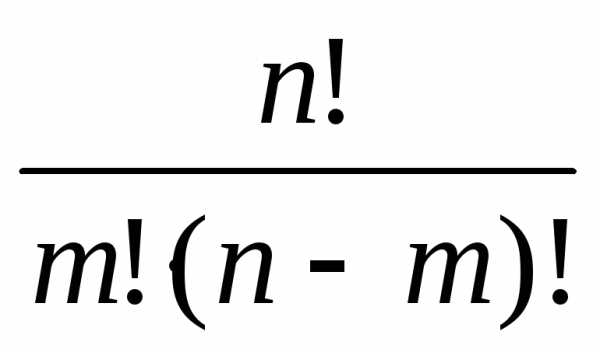 =.
=.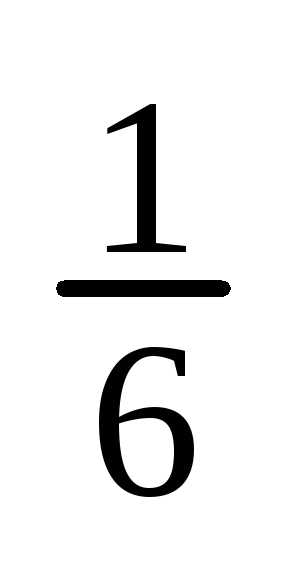 , а вероятность “неудачи” — q=
1 —
, а вероятность “неудачи” — q=
1 — 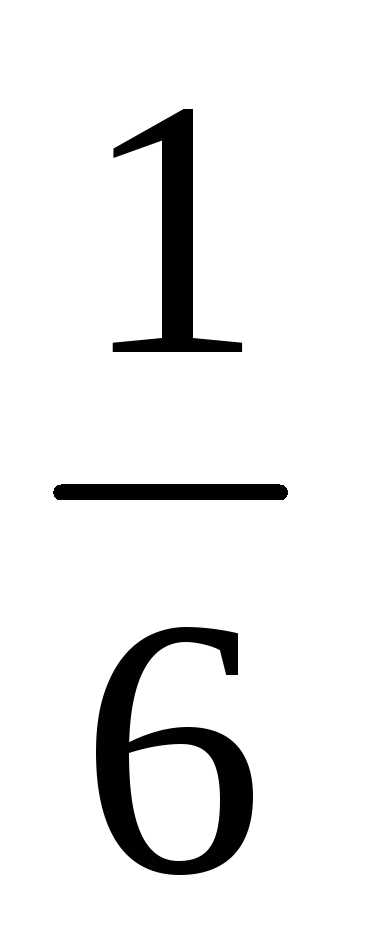 =
= .
Тогда по формуле Бернулли вероятность
того, что результате трехразового
бросания кубика два раза выпадет сторона
с шестью очками, будет равна
.
Тогда по формуле Бернулли вероятность
того, что результате трехразового
бросания кубика два раза выпадет сторона
с шестью очками, будет равна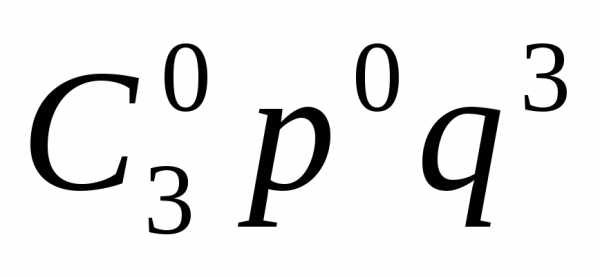 +
+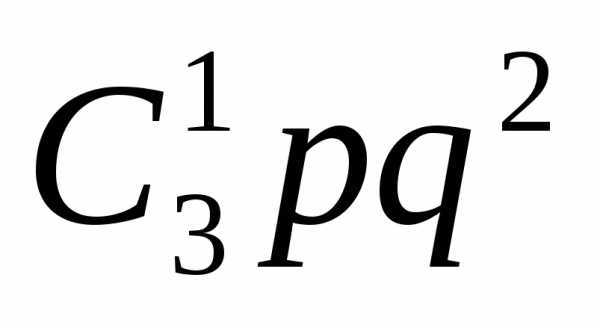 +
+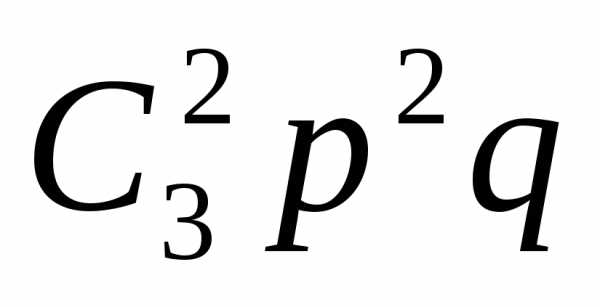 =
= .
(1.7)
.
(1.7) .
.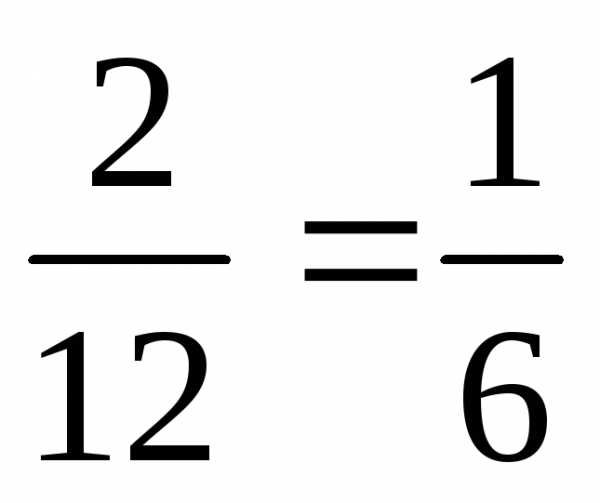 .
Таким образом, информация о наступлении
событияA оказала влияние на вероятность события C.
.
Таким образом, информация о наступлении
событияA оказала влияние на вероятность события C.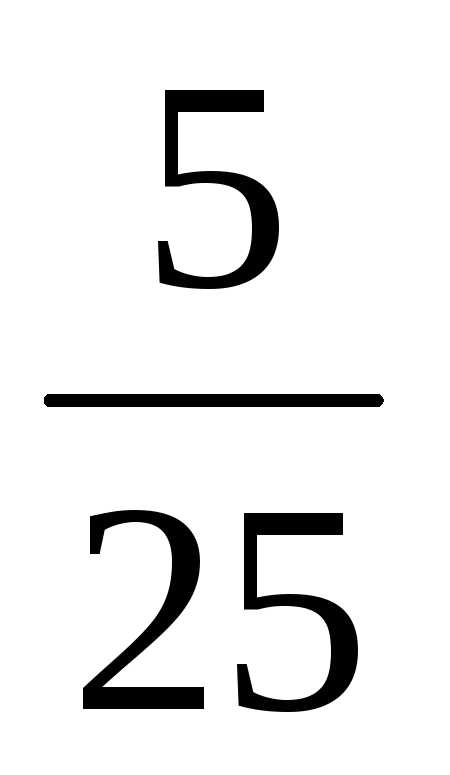 ;
;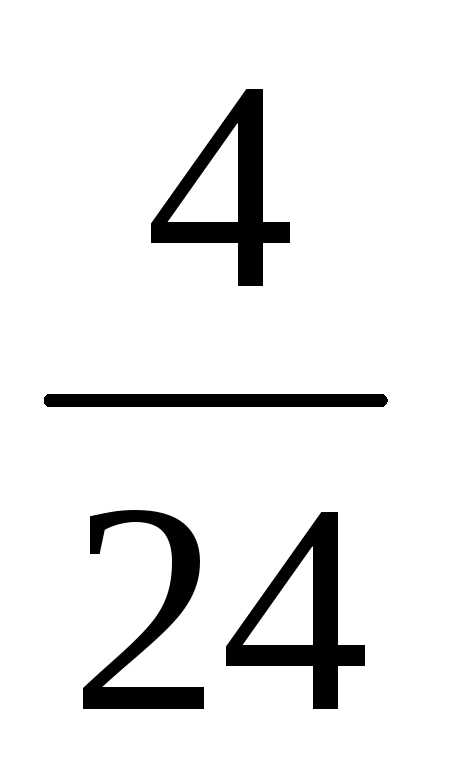 ;
;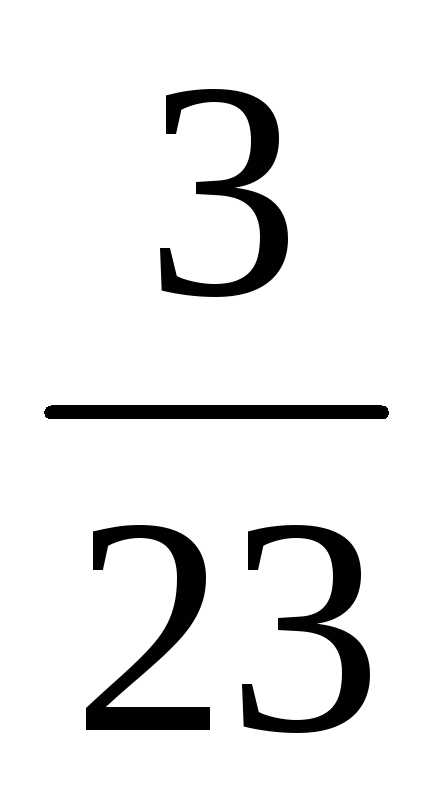 .
.
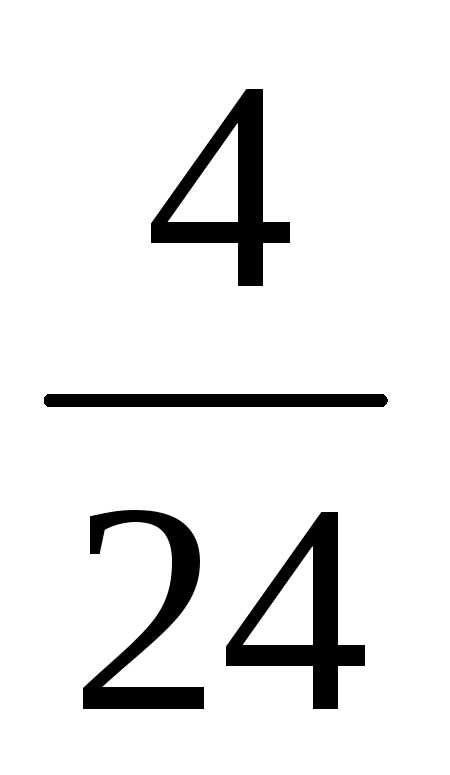
 =
=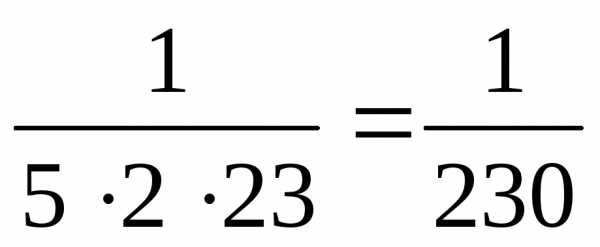 .
. 
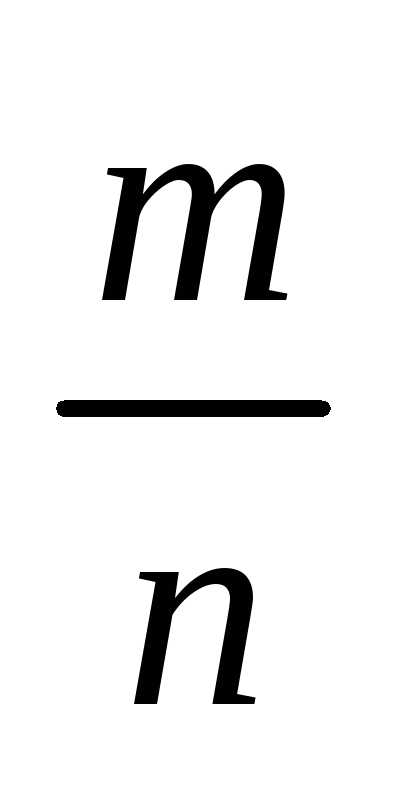 , (1)
, (1) ,…,а
,…,а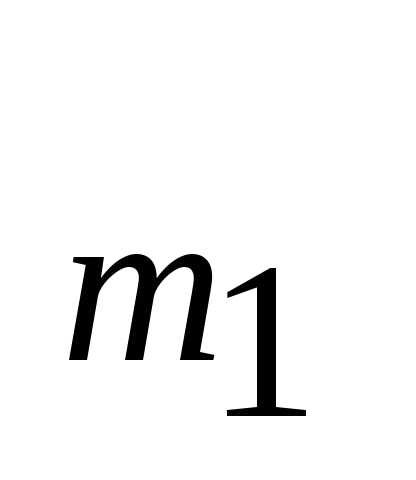 }
и {b, b
}
и {b, b ,…,b
,…,b }.
}. n,
называются такие комбинации, каждая из
которых содержит ровно m элементов и отличается от любой другой
хотя бы одним элементом. Число сочетаний
из n элементов по m элементов обозначается С
n,
называются такие комбинации, каждая из
которых содержит ровно m элементов и отличается от любой другой
хотя бы одним элементом. Число сочетаний
из n элементов по m элементов обозначается С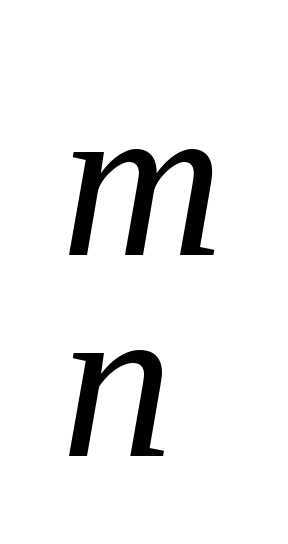 и находится по формуле
и находится по формуле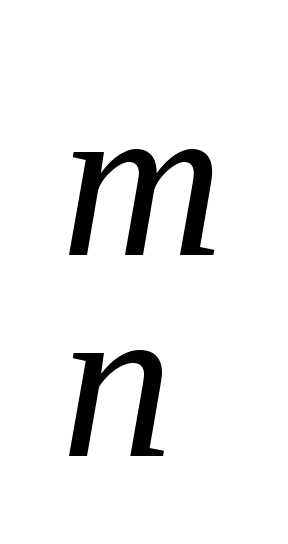 =
= ,
,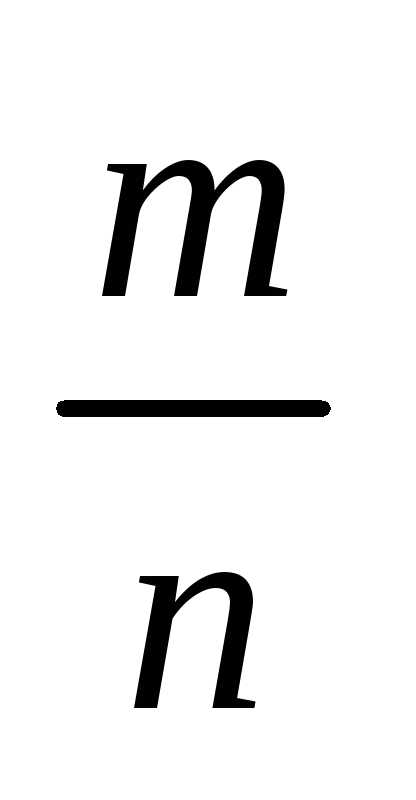 .
Общее числоn возможных различных способов отбора
равно числу способов, которыми можно
отобрать 5 билетов из 100: n = C
.
Общее числоn возможных различных способов отбора
равно числу способов, которыми можно
отобрать 5 билетов из 100: n = C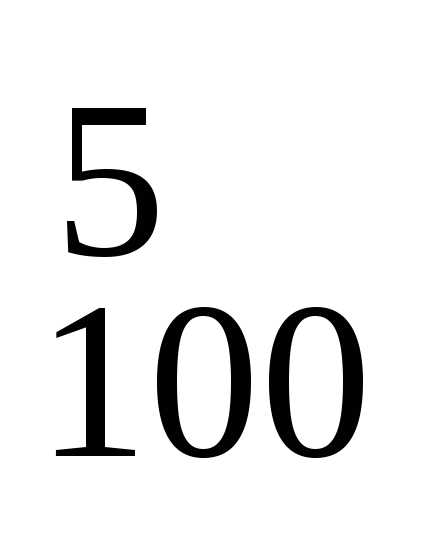 .
.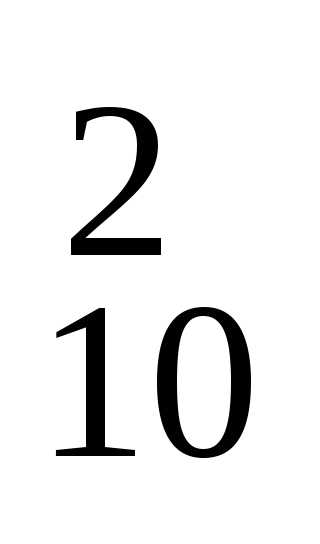 ;
а число различных способов отбора трех
«пустых» билетов из 90: m2 = C
;
а число различных способов отбора трех
«пустых» билетов из 90: m2 = C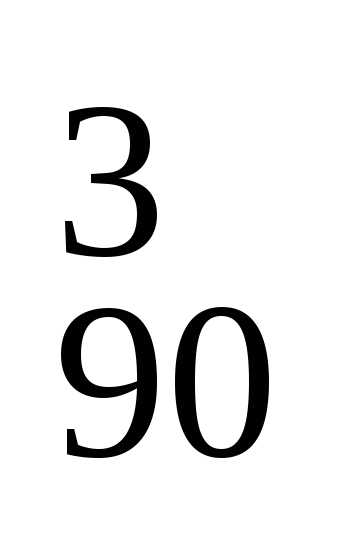 .
Используя правило произведения, получаем: m = m1·m2 – число способов, благоприятствующих
событию А.
Следовательно, искомая вероятность
.
Используя правило произведения, получаем: m = m1·m2 – число способов, благоприятствующих
событию А.
Следовательно, искомая вероятность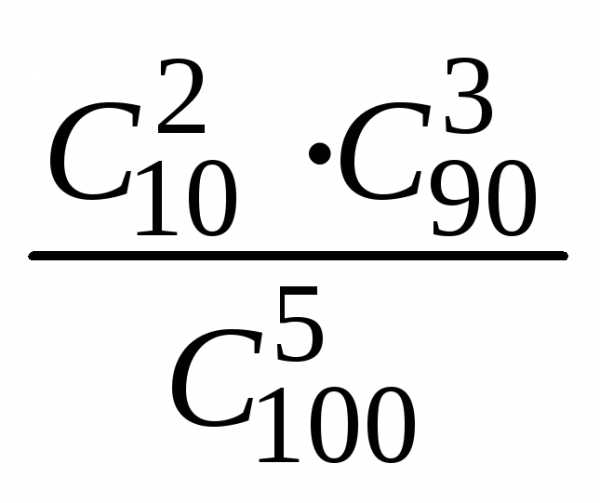 =
=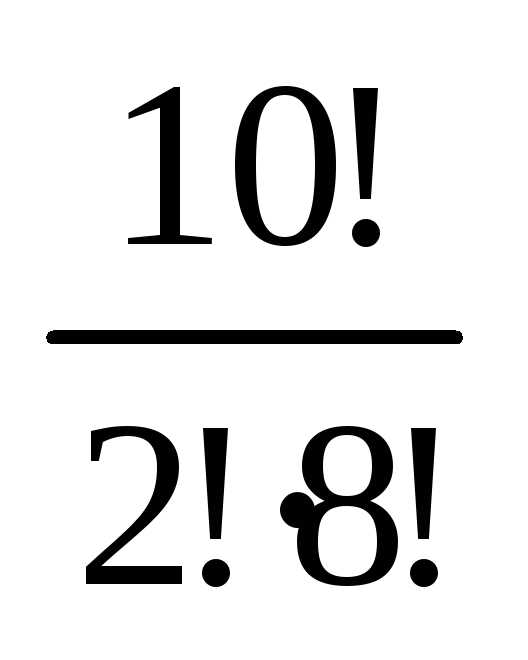 ·
· :
: ≈
0,07.
≈
0,07. )
= 1, где
)
= 1, где – событие противоположное событиюА.
– событие противоположное событиюА.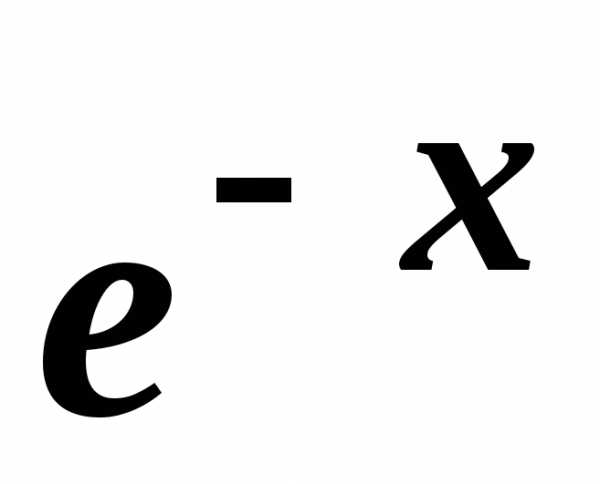 для
0 ≤ x< 1, e ≈ 2,7183
для
0 ≤ x< 1, e ≈ 2,7183