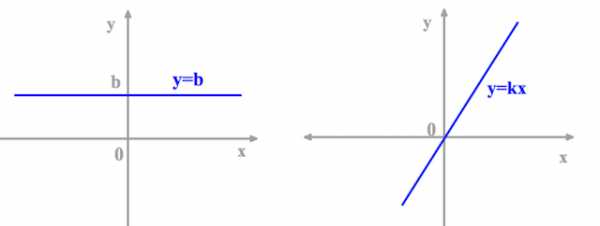_ — сложившееся у окружающих мнение о нравственном облике человека (группы), основанное на его предшествующем поведении
_ — опущение в речи слов, легко подразумеваемых или восстанавливаемых по контексту
(*ответ*) Эллипсис
Энтимема
Хиазм
Симплока
_ — переход от общего к частному, необходимый вывод следствий из принятых посылок
(*ответ*) Дедукция
Алгоритм
Импликация
Экспликация
_ — переход от частного к общему, вероятностное обобщение опытных данных
(*ответ*) Индукция
Амфибрахий
Анафора
Хорей
_ — применение в споре или в доказательствах софизмов; словесные ухищрения, вводящие в заблуждение
(*ответ*) Софистика
Демагогия
Паралингвистика
Антиноммы
_ — развернутое уподобление, подробности которого складываются в систему намеков; причем прямой смысл изображения не теряется, но дополняется возможностью его переносного истолкования
(*ответ*) Аллегория
Идиома
Метафора
Оксюморон
_ — разделение суждений в зависимости от способа установления их истинности
(*ответ*) Аналитические и синтетические суждения
Ассерторические и аподиктические суждения
Суждения конъюнкции и дизъюнкции
Суждения импликации и эквиваленции
_ — речь какой-либо социальной или профессиональной группы, отличающаяся от общеразговорного языка особым составом слов и выражений
(*ответ*) Жаргон
Катахреза
Арго
Сленг
_ — речь определенных социально замкнутых групп
(*ответ*) Арго
Жаргон
Сленг
Фразеологизм
_ — риторический прием; воззвание (часто неожиданное) к одному из слушателей или читателей, к воображаемому лицу или неодушевленному предмету
(*ответ*) Апострофа
Восклицание
Аффектация
Гипербола
_ — свойственное только данному языку неразложимое словосочетание, значение которого не совпадает со значением составляющих его слов, взятых в отдельности
(*ответ*) Идиома
Инверсия
Оксюморон
Асиндетон
_ — семантически неоправданное сочетание слов, например, «малиновый звон»
(*ответ*) Катахреза
Метафора
Амфимакр
Анафора
_ — слова или выражения, употребляемые людьми определенных возрастных групп, профессий или классовых прослоек
(*ответ*) Сленг
Арго
Жаргон
Фразеологизм
_ — сложившееся у окружающих мнение о нравственном облике человека (группы), основанное на его предшествующем поведении и выражающееся в признании его авторитета в том, чего от него ожидают в дальнейшем
(*ответ*) Репутация
Рейтинг
Престиж
Имидж
www.soloby.ru
Профессиональная этика КОТ 2 Примеры вопросов
КОТ 2 Реализация норм юридической этики на практике
Социальные нормы, регулирующие повеление человека в обществе, его отношение к другим людям, к обществу и к себе, – это …
Согласно М С. Строговичу под нравственностью понимаются
нормы, закрепляющие права человека
соблюдение норм морали
действующие в обществе социальные нормы, регулирующие поступки, поведение людей, их взаимоотношения
санкционированные государством обычаи
Аристотель выделял такой вид справедливости как
справедливость свободы
справедливость равенства
справедливость бытия
справедливость братства
Категория этики, объединяющая все, имеющее положительное нравственное значение, отвечающее требованиям нравственности, служащее отграничению нравственного от безнравственного, противостоящего злу, – это …
Философская наука, изучающая мораль как одну из важнейших сторон жизнедеятельности человека, общества, — это этика.
Категория этики, означающая отношение личности к обществу, другим людям, выражающееся в нравственной обязанности по отношению к ним в конкретных условиях, – это…
обязанность
повинность
долг
обязательство
Новое существительное ethica (этика) для обозначения науки, которая изучает добродетели, в IV веке до н. э. ввел…
Платон
Аристотель
Гераклит
Сократ
Судья НЕ может заниматься
научной деятельностью
преподавательской деятельностью
предпринимательской деятельностью
творческой деятельностью
В соответствии с частью 1 статьи 46 Конституции РФ
никому не гарантируется судебная зашита его прав и свобод
круг субъектов, которым не гарантируется судебная зашита их прав и свобод определяется федеральным законом
круг субъектов, которым гарантируется судебная защита их прав и свобод определяется федеральным законом
каждому гарантируется судебная зашита его прав и свобод
Основы судебного этикета заложены в…
ФЗ «Об исполнительном производстве»
Гражданском кодексе РФ
процессуальном законодательстве
Уголовном кодексе РФ
Право последней реплики в гражданском процессе всегда принадлежит:
представителю ответчика
ответчику
представителю истца
истцу
Согласно части 4 статьи 154 АПК РФ лицо, нарушающее порядок в судебном заседании или не подчиняющееся законным распоряжениям председательствующего, после предупреждения может быть …
удалено из зала судебного заседания
подвергнуто телесному наказанию
заключено под стражу
дисквалифицировано
Правовая культура является частью
системы права
российского законодательства
духовной культуры
материальной культуры
К аспектам, в которых может пониматься термин «мораль» НЕ относятся:
мораль как особая форма общественного сознания
мораль как вид общественных отношений
мораль как способ достижения целей
мораль как вид гражданско-правового договора
Поступок как первичный элемент нравственной деятельности включает в себя:
привлечение к ответственности
деяние
мотив
причинно-следственную связь
Соблюдение моральных норм контролируется
только правоохранительными органами
только государством
обществом в целом
только лицами, специально наделенными соответствующими полномочиям
Совокупность поступков человека, имеющих нравственное значение, совершаемых им в относительно продолжительный период в постоянных или изменяющихся условиях, принято называть…
деянием
бездействием
поведением
юридическим составом
Мнение о нравственном облике человека, сложившееся у окружающих, основанное на его предшествующем поведении,
добродетель
репутация
честь
достоинство
Судьями в Российской Федерации могут быть граждане:
имеющие высшее юридическое образование
имеющие любое высшее образование
имеющие стаж работы по юридической профессии не менее 2 лет
имеющие стаж работы по юридической профессии не менее 5 лет
достигшие 18 лет
достигшие 25 лет
Гражданин Российской Федерации, поступающий на государственную службу Российской Федерации либо муниципальную службу, обязан ознакомиться с положениями …
Кодекса судейской этики
Кодекса профессиональной этики адвоката
Типового кодекса этики и служебного поведения государственных служащих Российской Федерации и муниципальных служащих
Профессионального кодекса нотариусов Российской Федерации
При освещении судебной деятельности в средствах массовой информации судья НЕ вправе …
разъяснять в устной форме принятый судебный акт по рассмотренному делу
давать комментарии по существу дел, по которым не принято окончательных судебных актов
давать информацию о процессуальных стадиях рассмотрения дела
разъяснять в письменной форме принятый судебный акт по рассмотренному делу
Согласно части 1 статьи 48 Конституции РФ
в случаях, предусмотренных законом, лицу гарантируется право на получение квалифицированной юридической помощи
каждому гарантируется право на получение квалифицированной юридической помощи
каждому гарантируется право на получение юридической помощи
право на получение квалифицированной юридической помощи гарантируется только подозреваемому и обвиняемому в совершении преступления
Необходимость соблюдения правил адвокатской профессии вытекает из факта…
наличие стажа по юридической профессии не менее 2 лет
сдачи квалификационного экзамена
присвоения статуса адвоката
получения высшего юридического образования
Если в действиях лица, нарушающего порядок в судебном заседании, имеются признаки преступления, судья
направляет соответствующие материалы в органы дознания или предварительного следствия для возбуждения
уголовного дела в отношении нарушителя
выносит приговор в отношении нарушителя
направляет материалы в соответствующий суд
выносит нарушителю предупреждение
По мнению А.Д. Бойкова культура судебной деятельности НЕ включает в себя:
профессиональное мастерство работников суда
судебную этику
проблему морали и права
совершенство законодательства
Согласно статье 158 ГПК РФ участники процесса свои показания и объяснения дают стоя, а отступление от данного правила допускается только с …
разрешения председательствующего
согласия лиц. участвующего в деле
согласия прокурора, участвующего в деле
разрешения председателя суда
Право последней реплики в уголовном процессе принадлежит:
защитнику
потерпевшему
государственному обвинителю
подсудимому
Достигнутый обществом уровень правового регулирования социальных отношений, правовой защищенности личности, обеспечения правопорядка, – это …
правовой идеализм
модернизация
правовая система
правовая культура
Моральные последствия поступка – это
исключительно неблагоприятные последствия
всегда привлечение лица к административной ответственности
нарушение прав и свобод человека
самооценка его человеком н оценка со стороны окружающих
В основу формулирования моральных норм положены
обычаи
идеалы, навязываемые государством
реальные принципы, идеалы, понятия о добре и зле
привычки
К аспектам, в которых может пониматься термин «мораль» относятся:
мораль как источник российского права
мораль как вид общественных отношений
мораль как вид юридической ответственности
мораль как особая форма общественного сознания
мораль как вид гражданско-правового договора
мораль как один из способов нормативного регулирования поведения человека
test-for-you.ru
Тема 2. Понятие морали. Моральные нормы, ценности, категории нравственного сознания
I
S:
Можно ли утверждать, что мораль составляет
ядро культуры:
+:Да
-:Нет
I
S:
Что такое нравственность?
+:Идеальное
поведение людей
-:Реальное
поведение людей
I
S:
Что означает понятие «императивность
морали»:
+:Обязательность,
повелительность
-:Наличие
цели
-:Наличие
идеального положения вещей
I
S:
Что является этическим принципом:
+:Гуманизм
-:Добро
-:Ревность
I
S:
Когда возникла мораль?
+:В
первобытном обществе
-:В
рабовладельческом обществе
-:В
средневековом обществе
I
S:
Что является основным показателем
нравственности?
-:Любые
отношения между людьми
+:Отношение
к человеку не как к вещи, а как к ценности
I
S:
Как понимал этику И. Кант:
-:Как
науку о культуре
+:Как
науку о долге
-:Как
науку о нравственности
I
S:
Что означает понятие «стихийность
морали»:
-:Моральные
нормы создаются каждым человеком
отдельно
+:Моральные
нормы формируются непосредственно в
общественной жизни как -:выражение
насущных потребностей
-:Моральные
нормы создаются специальными органами,
стихийно созванными
I
S:
В каких двух видах существует мораль:
+:Как
характеристика личности
+:Как
характеристика групповых, в целом
общественных отношений
-:Как
характеристика институциональных
отношений
I
S:
Что является этической категорией?
+:Добро
-:Материализм
-:Деонтология
I
S:
Что не входит в состав этики, как науки,
согласно взглядам современных
отечественных ученых:
-:Прикладная
этика
+:Метаэтика
-:Деонтология
I
S:
К какой функции морали относится умение
человека делать предъявляемые к нему
требования своими личными мотивами
поведения?
-:к
регулятивной
-:оценочно-императивной
+:воспитательно-гуманистической
-:познавательной
-:прогностической
I
S:
Где и в чем, прежде всего, проявляются
санкции морали?
-:в
специально организованных институтах
+:в
общественном мнении
I
S:
Где имеет место моральная регуляция?
+:в
семье
+:в
науке
-:в
политике
I
S:
Существуют ли универсальные моральные
принципы?
+:Да
-:Нет
I
S:
К какому типу моральной регуляции
относится моральная саморегуляция?
-:К
обычному варианту моральной регуляции
+:К
высшему типу моральной регуляции
I
S:
К какой функции морали относится
установление моральной ценности
различных явлений действительности?
-:к
регулятивной
+:оценочно-императивной
-:воспитательно-гуманистической
-:познавательной
-:прогностической
I
S:
Каков наиболее авторитетный субъект
моральной оценки?
-:Индивид
-:Группа
+:Общественность
I
S:
Взаимозависимы ли мотив и результат
действия?
+:Взаимозависимы
-:Невзаимозависимы
-:В
большинстве случаев взаимозависимы,
но есть примеры расхождения мотива и
результата
I
S:
Что (кто) является объектом моральной
оценки
+:Индивиды
-:Сферы
общественной жизни
-:Явления
природы
I
S:
Существуют ли случаи неадекватной
моральной самооценки?
+:Да
-:Нет
I
S:
К какой функции морали относится
постижение человеком своего призвания
в мире?
-:К
регулятивной
-:Оценочно-императивной
-:Воспитательно-гуманистической
+:Познавательной
-:Прогностической
I
S:
Что такое нравственный идеал личности?
+:Воплощение
идеи морально безупречного человека
-:Гуманистический
идеал
-:Воплощение
всех известных добродетелей
I
S:
Кто из представителей нижеприведенных
направлений отрицал свободу?
+:Фаталисты
-:Волюнтаристы
I
S:
Какие человеческие характеристики
способствуют постижению философского
понятия свободы?
+:Уровень
образования
+:Уровень
культуры
-:Квалификация
-:Состояние
здоровья
I
S:
Какое из нижеприведенных суждений
верно?
-:Счастье
зависит от объективных условий
+:Счастье
зависит от внутреннего мира человека
-:Субъективное
ощущение счастья должно быть объективно
обусловлено
I
S:
К какой моральной категории близко
понятие «долг»?
+:Ответственность
-:Совесть
-:Стыд
I
S:
К какому моральному понятию очень близко
понятие «стыд»?
-:Честь
+:Совесть
-:Ответственность
I
S:
В каком виде чаще всего выражается
справедливость?
-:Как
проблема равенства
+:Как
проблема свободы
I
S:
Как формулируется правило талиона
(«золотого принципа нравственности»)
+:Поступай
по отношению к другим так, как хочешь,
чтобы они поступали по отношению к тебе
-:Око
за око, зуб за зуб
I
S:
Какой этический принцип противоположен
«золотому принципу нравственности»?
-:Не
отвечай злом на зло
+:Если
тебя ударили по одной щеке, подставь
другую
I
S:
Аксиология – область этических знаний,
которая изучает….
+:Ценности
-:Нормы
-:Проблемы
свободы
I
S:
Дескриптивная этика – область этических
знаний, которая изучает….
-:Проблемы
должного и долга
-:Ценности
+:Нравы,
обычаи и мораль конкретного этноса
I
S:
Деонтология – область этических знаний,
которая изучает….
-:Ценности
отдельных народов
-:Общегосударственные
нормы
+:Проблемы
должного и долга
I
S:
Что такое толерантность?
+:Терпимое
отношение, стремление уважать взгляды
других
-:Справедливость
в отношениях с людьми
-:Субординация
в отношениях с другими
I
S:
Как соотносятся понятия «духовность»
и «религиозность»?
-:Обозначают
приблизительно одно и то же
+:Понятие
«духовность» шире понятия «религиозность»
и включает его в себя в качестве одного
из компонентов
-:Понятие
«религиозность» шире понятия «духовность»
и включает его в себя в качестве одного
из компонентов
-:Оба
понятия обозначают принципиально разные
вещи
I
S:
Менталитет – это…..
-:То
же, что и мораль
+:Совокупность
взглядов на мир, мировосприятие,
мироощущение
-:Совокупность
взглядов на свободу и закон
-:То
же, что и толерантность
I
S:
Что такое гуманизм?
-:Доброта
-:Совестливость
+:Человечность
I
S:
Этика – это философская дисциплина,
изучающая
-:культуру
и искусство
-:развитие
человеческого общества
+:мораль
и нравственность
-:внутреннюю
природу человека
I
S:
Термин «этика» имеет происхождение
+:древнегреческое
-:русское
-:немецкое
-:латинское
I
S:
Профессиональная этика отражает
особенности нравственного сознания,
взаимоотношений и поведения людей,
обусловленные
-:особенностями
личности руководителя
-:требованиями
повышения эффективности профессиональной
деятельности
-:личными
взаимоотношениями в коллективе
+:спецификой
профессиональной деятельности
I
S:
Что такое мораль?
+:Совокупность
правил и норм поведения
-:Само
поведение людей
-:Отношения
между людьми
I
S:
Что такое нравственность?
+:Идеальное
поведение людей
-:Реальное
поведение людей
I
S:
Перечислите три важные составляющие
духовного идеала
-:Истина
+:Красота
+:Добро
-:Свобода
-:Честь
I
S:
Слово этика происходит от греческого
слова «ЭТОС» и первоначально означало:
-:манера
-:стойбище
-:нрав
+:привычка
I
S:
К какому роду литературного произведения
относятся жанры, роман, повести, рассказа,
очерка?
+:Эпос
-:лирика
-:драма
-:поэзия
I
S:
Одним из недостатков морали, по мнению
Ф. Ницше, является:
-:отстаивание
своих интересов индивидом
+:отречение
от своих интересов
-:следование
желаниям
-:воплощение
своих желаний
I
S:
Как моральное существо, человек
совершает сознательные поступки, а как
биопсихическое:
+:бессознательные
-:неразумные
-:агрессивные
-:аморальные
I
S:
Неспособность человека отстоять
нравственные принципы, в которые он
верит, из-за опасения за личные интересы,
боязни навлечь на себя неблагоприятные
последствия, называется
-:чванством
-:косностью
-:лицемерием
+:малодушием
I
S:
Отличие между стыдом и совестью состоит
в том, что стыд возникает, когда человек
что-то должен был, но не смог
проконтролировать, а совесть говорит
в нем тогда, когда он должен был и мог
проконтролировать, но
-:несознательно
не стал этого делать
-:сознательно
не стал этого делать
+:подсознательно
не стал это делать
-:бессознательно
не стал это делать
I
S:
Поступок, по своему содержанию
представляющий нарушение требований
нравственности, называется:
+:проступком
-:грехом
-:преступлением
-:деянием
I
S:
Объектом этики является:
+:поведение
человека
-:поведение
живых существ
-:в
поступок человека
-:добродетельность
человека
I
S:
Моральный принцип предписывающий
человеку готовность пожертвовать своим
интересом в пользу интересов другого
называется:
-:коллективизм
+:альтруизм
-:индивидуализм
-:эгоизм
I
S:
Слепая приверженность требованиям
какой-либо морали, без разумного их
обоснования и понимания их общественного
значения, безусловное соблюдение этих
требований, называется:
-:догматизмом
-:конформизмом
+:малодушием
-:косностью
I
S:
Абсолютизм исходит из ___________человеческой
воли, т. е. ее подчинения чему-то внешнему.
-:гетерономности
+:автономности
-:слабости
-:бессилия.
I
S:
Самосовершенствование человека в
буддизме происходит через
+:самопожертвование
-:самообразование
-:самоотречение
-:самовоспитание
I
S:
Сложившееся у окружающих мнение о
нравственном облике человека на основании
его предшествующего поведения называется:
-:характеристикой
-:мнением
-:биографией
+:репутацией
I
S:
Самой древней морально-правовой
системой является:
+:Надписи
Ашока
-:Законы
Ману
-:Законы
Хаммурапи
-:Законы
Моисея
I
S:
Средневековый способ определения
виновности или правоты обвиняемого
путем испытания огнем, раскаленным
железом и т.п. называется _________:
+:ордалия
-:оргия
-:пытка
-:инквизиция
I
S:
Деятельность будет считаться
исключительно моральной, если она
мотивирована:
-:долгом
+:правильно
-:обоснованно
-:с
учетом обстоятельств
I
S:
В отличие от человека, склонного
принимать все на себя, в том числе и даже
чужую вину, человека, имеющего устойчивую
склонность перекладывать негативную
ответственность на внешние факторы, на
других людей или на объективные
обстоятельства, называют ____
+:экстерналом
-:интерналом
-:экстравертом
-:интровертом
I
S:
Согласно утилитаризму, соблюдение
моральных норм позволяет достичь:
+:наибольшее
количество счастья для наибольшего
количества людей
-:наибольшее
количество счастья для наиболее достойных
людей
-:обществу
наибольшего количества материальных
благ
-:мира
и согласия в обществе
I
S:
Предметом этики является:
-:поведение
человека на основе свободного выбора
-:правила
вежливого поведения
+:раскрытие
сущности морали
-:мотивы
поступка человека
I
S:
Свод норм регламентирующих поведение,
практически каждый шаг мусульманина
от рождения до смерти, получил название:
-:фикх
-:хадис
+:шариат
-:сура
I
S:
Структура морального______ представляет
собой систему взаимосвязанных понятий,
таких как свобода воли, добро и зло,
добродетель и долг, нормы морали, стыд
и совесть, честь достоинство, справедливость
и т. д.
+:сознания
-:поступка
-:деятельности
-:отношения
I
S:
Счастье в его обыденном понимании
это_____
-:наиболее
полное удовлетворение своих желаний
-:случайная
удача и дар судьбы
+:отсутствие
желаний и полное спокойствие
-:быть
здоровым и богатым
I
S:
Поступок будет однозначно морален,
если он совершен___
-:по
зову совести
-:ради
общественной пользы
+:из
чувства долга
-:ради
собственного удовольствия
I
S:Психическое
состояние, выражающее неосознанную
потребность субъекта, называется___
+:желание
-:стремление
-:влечение
-:возбуждение
I
S:Основу
моральных норм составляют
-:моральные
ценности
+:добрые
отношения между людьми
-:традиции
-:научно
обоснованные теории
I
S:Различные
способы воздаяния, поощрения, наказания
для обеспечения выполнения всеми людьми
предписываемых им требований называются
-:принципами
-:санкциями
-:заповедями
+:императивами
I
S:Формирование
достоинства человека связано с его
оценкой
+:своих
властных полномочий
-:своей
одаренности
-:своей
внешности
-:своей
ценности
I
S:Поведение
человека в обществе регулируется
определенными нормами, именуемыми:
-:социальными
+:политическими
-:государственными
-:стандартными
I
S:Процесс
осознания и выбора причины поступка
называется
+:лицемерием
-:мотивацией
-:атараксией
-:малодушием
I
S:Предписывание
заведомо безнравственным поступкам
возвышенные мотивы и человеколюбивые
цели, называется
+:лицемерием
-:мотивацией
-:атараксией
-:малодушием
I
S:Моральная
значимость человека, оценивается
обществом двумя этическими понятиями:
-:честь
и достоинство
-:честность
и верность
-:порядочность
и доброжелательность
+:покорность
и независимость
I
S:Ханжество,
как показная строгость нравов соотноситься
с _______
-:обманом
-:хитростью
-:клеветой
-:лицемерием
I
S:Все
этические теории можно подразделить
на два основных вида:
+:аксиологические
и деонтологические
-:аксиологические
и психологические
-:психологические
и деонтологические
-:утилитарные
и психологические.
I
S:Вне
общества человек становится __
+:имморальным
существом
-:аморальным
существом
-:высоконравственным
существом
-:тем
кто он есть на самом деле
I
S:Одно
из главных понятий этики стоицизма,
обозначающее душевную невозмутимость,
называется ____
-:нирвана
-:умиротворенность
+:апатия
-:дуккха
I
S:Чувство
несправедливости связано с эмоцией ___
+:обиды
-:жалости
-:злобы
-:страха
I
S:Рабская
приверженность человека отжившим
привычкам и традициям, неспособность
воспринимать и поддерживать новое,
диктуемое актуальными потребностями
современности, называется ______
+:косностью
-:лицемерием
-:конформизмом
-:малодушием
I
S:Религиозное
понимание вины, при котором оценка
проступка дается не обществом или
человеком, а Богом называется________
-:Раскаянием
+:грехом
-:предательством
-:богохульством
I
S:Способность
человека к состраданию является
генетической основой
-:стыда
-:депрессии
-:совести
+:жалости
I
S:Что
такое калокагатия?
+:гармония
внешнего и внутреннего
-:подражание
I
S:Главной
нравственной ценностью в религии
является приобщение к
-:церкви
-:культуре
+:Богу
-:потустороннему
I
S:Социально-психологическая
ориентация, складывающаяся не в результате
самостоятельных решений общественных
и нравственных проблем, а пассивного,
приспособительского принятия готового
порядка вещей, называется _____
+:конформизмом
-:косностью
-:лицемерием
-:малодушием
I
S:Принцип
морали, согласно которому человек должен
совершать свой моральный выбор строго
и неуклонно следуя канону; безотносительно
к конкретным обстоятельствам и даже
вопреки целесообразности называется:
+:ригоризм
-:волюнтаризм
-:фатализм
-:героизм
I
S:Деонтология
– это
-:наука
о должном
+:учение
о долге
-:разновидность
онтологии
-:учение
о сущем
I
S:К
основным жизненным ценностям обычно
относят:
-:счастье;
любовь; творчество; социальное положение;
-:любовь;
семейное положение; долголетие
+:материальное
положение; здоровье:
-:счастье;
интеллект; слава;
I
S:
Общественное мнение и самооценка могут
не совпасть. Если самооценка занижена,
то это ведет к:
-:высокомерию
+:скромности
-:гордости
-:тщеславию
I
S:
Объектом этики является:
+:поведение
человека
-:поведение
живых существ
-:в
поступок человека
-:добродетельность
человека
I
S:
Если низкая самооценка совпадает с
низким общественным мнением, то человек
осознает себя:
-:ничтожеством
-:одиноким
+:ненужным
-:брошенным
на произвол судьбы
I
S:
Слепая приверженность требованиям
какой-либо морали, без разумного их
обоснования и понимания их общественного
значения, безусловное соблюдение этих
требований, называется:
-:догматизмом
+:конформизмомом
-:малодушием
-:косностью
I
S:
Первой ответной реакцией на несправедливость
является
-:спор
+:месть
-:бранная
речь
-:проявление
агрессии
I
S:
Легендарные спартанские нравы были
созданы Ликургом. Это была воинская,
героическая мораль, вырабатывавшая
воинскую доблесть и презрение к труду,
это мораль утверждала:
-:роскошь
-:богатство
-:привилегированность
аристократии
+:право
на насилие
I
S:
Сопереживание, окрашенное в негативные
тона, называют _____
-:состраданием
+:эмпатией
-:симпатией
-:стыдом
I
S:
Категорический императив гласит:
+:поступай
только согласно такой максиме,
руководствуясь которой ты в то же время
-:можешь
пожелать, чтобы она стала всеобщим
законом
+:поступай
согласно такой цели, руководствуясь
которой ты в то же время можешь
-:пожелать,
чтобы она стала желанной для всех
-:поступай
так, чтобы ты всегда относился к
человечеству и в своем лице, и в лице
всякого -:другого так же, как к цели, и
никогда не относился бы к нему только
как к средству
-:поступай
так, чтобы ты всегда относился к
человечеству и в своем лице, и в лице
всякого -:другого так же, как к средству,
и никогда не относился бы к нему только
как к цели
I
S:
Мотивы и поведение человека, который
рассматривает и направляет свои поступки
и взаимоотношения с окружающими с точки
зрения личной материальном выгоды,
называется_______
+:корыстолюбием
-:конформизмом
-:косностью
-:лицемерием
I
S:
Общественное мнение и самооценка могут
не совпасть. Если самооценка завышена,
то это ведет к___
+:высокомерию
-:гордости
-:скромности
-:тщеславию
I
S:
Известно положение римского права
гласит: «Наказание не может быть вечным,
но ___ пребывает вовек»
-:грех
+:вина
-:преступление
-:позор
I
S:
Право вообще — это внешняя форма выражения
свободы человека и справедливого
отношения к нему. Внутренней же формой
свободы и справедливости является:
+:мораль
-:закон
-:совесть
-:разум
I
S:
Моральный принцип, предписывающий
человеку готовность пожертвовать своим
интересом в пользу интересов другого
называется
-:коллективизм
+:альтруизм
-:индивидуализм
-:эгоизм
I
S:
Человек имеет развитое чувство
собственного достоинства, если он
может__
+:доставлять
радость людям
-:обходится
без посторонней помощи
-:быть
вежливым в обращении
-:верным
своему слову
studfiles.net
§ 6. Достоинство и честь. Юридическая этика: Учебник для вузов
§ 6. Достоинство и честь
Достоинство — категория этики, означающая особое моральное отношение человека к самому себе и отношение к нему со стороны общества, окружающих, основанное на признании ценности человека как личности.
Сознание человеком собственного достоинства есть форма самосознания и самоконтроля. Человек не совершает определенного поступка, считая, что это ниже его достоинства. Достоинство — выражение ответственности человека за свое поведение перед самим собой, форма самоутверждения личности. Достоинство обязывает совершать нравственные поступки, сообразовывать свое поведение с требованиями нравственности.
В то же время достоинство личности требует от других уважения к ней, признания за человеком соответствующих прав и возможностей и обосновывает высокую требовательность к нему со стороны окружающих. В этом отношении достоинство зависит от положения человека в обществе, состояния общества, способности его обеспечить практическое утверждение неотчуждаемых прав человека, признание самоценности личности.
Понятие достоинства личности опирается на принцип равенства всех людей в моральном отношении, основывается на равном праве каждого человека на уважение, запрет унижать его достоинство, независимо от того, какое социальное положение он занимает. Достоинство человека — одна из высших нравственных ценностей.
Честь как категория этики означает моральное отношение человека к самому себе и отношение к нему со стороны общества, окружающих, когда моральная ценность личности связывается с моральными заслугами человека, с его конкретным общественным положением, родом деятельности и признаваемыми за ним моральными заслугами (честь офицера, честь судьи, честь ученого, врача, предпринимателя).
Честь и достоинство тесно связаны. Однако в отличие от достоинства, основанного на признании равенства всех людей, честь оценивает людей дифференцированно.
Исторически честь в моральном сознании общества появилась в виде Представлений о родовой и сословной чести, предписывающей человеку определенный образ жизни, деятельности, поведения, не унижающий достоинства сословия, к которому он принадлежит.
Таковы были представления об офицерской чести в условиях, когда офицерский корпус комплектовался в основном из дворянства. Они были связаны с особой щепетильностью в отношении действий, которые затрагивали или могли затронуть честь офицера и дворянина.
В России, как и в других европейских странах, способом решения вопросов чести являлась дуэль. Запрещенная строжайшими указами Петра I еще в 1702 г., дуэль тем не менее существовала и до манифеста Екатерины TI 1787 г. и позже. Приказ по военному ведомству от 20 мая 1884 г. по существу узаконил дуэль в армии. (Установленная в армии процедура, предшествовавшая офицерской дуэли, описана А. И. Куприным в повести «Поединок».) В спорах по поводу допустимости или недопустимости дуэли в обществе не все юристы выступали на стороне ее противников. Так, известный криминалист Спасович утверждал, что «обычай поединка является среди цивилизации как символ того, что человек может и должен в известных случаях жертвовать самым дорогим своим благом — жизнью — за вещи, которые с материалистической точки зрения не имеют значения и смысла: за веру, родину и честь. Вот почему обычаем этим нельзя поступиться».
Честь обязывает человека оправдывать и поддерживать репутацию, которой он обладает лично и которая принадлежит социальной группе, коллективу, в котором он состоит.
Репутация — мнение о нравственном облике человека, сложившееся у окружающих, основанное на его предшествующем поведении. Репутация определенной социальной группы складывается на основании поведения принадлежащих к ней индивидуумов в течение достаточно длительного периода их деятельности. Репутация, разумеется, не остается неизменной, как и сами люди, ее создающие.
Кодекс чести судьи Российской Федерации, принятый в 1993 г., обязывает судью в любой ситуации сохранять личное достоинство, заботиться о своей чести, избегать всего, что могло бы причинить ущерб репутации.
Поделитесь на страничке
Следующая глава >
fil.wikireading.ru
Тест с ответами по этике
1. Что подразумевается под предметом этики?
а) культура;
б) мораль;+
в) прекрасное;
г) социальные отношения
2. Каким этическим нормам уделяется основное внимание в рамках западной европейской культуры?
а) польза, выгода, трудолюбие;
б) справедливость, добро, благо;+
в) честь, свобода, вера.
3. Какие существуют виды барьеров общения?
а) межъязыковые;+
б) мировоззренческие;
в) психологические;+
г) соматические;
д) социальные;+
е) технические;+
4.Этическая категория, которая лежит в основе высказывания «Все равны перед законом и судом»?
а) долг;
б) достоинство;
в) ответственность;
г) справедливость;+
д) честь
5.Каковы правила представления по канону?
а) женщина первая представляется мужчине;
б) лица с более высоким статусом представляются людям со статусом более низким;
в) младшие по возрасту представляются старшим;+
г) мужчина первым представляется женщине+
6. Где не используется литературный язык?
а) в научной речи;
б) в невербальном общении;+
в) в официально-деловой речи;
г) в письменной речи;
д) в профессиональном общении
7. Компоненты, которые включает в себя культура делового общения:
а) все ответы верны;+
б) психологию делового общения;
в) служебный этикет;
г) технику делового общения;
д) этику делового общения
8. Что из ниже перечисленного относится к стилям руководства?
а) Политический
б) Либеральный+
в) Демократический+
г) Авторитарный+
9.Как называется моральный принцип, который выражается в желании помочь другим:
а) альтруизм;+
б) толерантность;
в) честолюбие;
г) эмпатия
10. На чем из ниже перечисленного основано в деловой этике недопустимость вмешательства в дела конкурентов, ущемление их интересов?
а) равенстве;
б) свободе;+
в) справедливости;
г) честности
11.Как называется набор наиболее важных предположений, которые принимаются членами организации, и получают выражение в заявляемых организацией ценностях, задающих людям ориентиры их поведения и действий:
а) должностные обязанности;
б) кодекс чести;
в) корпоративная культура;+
г) правила внутреннего распорядка
12.Что такое ответственность?
а) категория этики, означающая отношение личности к обществу, другим людям, выражающаяся в нравственной обязанности по отношению к ним в конкретных условиях;
б) категория этики, опирающаяся на принцип равенства всех людей в моральном отношении;
в) категория этики, характеризующая личность с точки зрения выполнения ею нравственных требований, соответствия ее моральной деятельности нравственному долгу;+
г) категория этики, характеризующая моральную ценность личности в связи с его статусом, родом деятельности и признаваемыми за ним моральными заслугами;
д) категория этики, характеризующая способность человека осуществлять нравственный самоконтроль, внутреннюю самооценку с точки зрения соответствия своего поведения требованиям нравственности, самостоятельно формулировать для себя нравственные задачи и требовать от себя их выполнения
13.Кто из данных деятелей относится к наиболее известным русским купцам-меценатам?
а) Алексеев
б) Морозов+
в) Третьяков+
г) Прохоров+
14. Какие компоненты относятся к социальным компонентам деловой репутации организации?
а) Социальная жизнь
б) Социальные блага+
в) Социальные гарантии по ТК РФ+
г) Социальная ответственность+
15. Какие компоненты относятся к компонентам деловой репутации организации?
а) Моральная
б) Рыночная+
в) Финансовая+
г) Социальная+
16. К какому году, по оценке специалистов, появляется субъект этики деловых отношений в рамках постсоветской России?
а) 1992 году;+
б) 1995 году;
в) 1998 году
17.Как называется подсистема этикета, которая определяет пространственную организацию общения?
а) вербальный этикет;
б) мимика и жесты;
в) этикетная атрибутика;
г) этикетная проксемика+
18.Через что проходит самосовершенствование человека в буддизме?
а) самобичевание;
б) самовоспитание;
в) самообразование;
г) самоотречение;+
д) самопожертвование
19.Как называется сложившееся у окружающих мнение о нравственном облике личности или коллектива, которое основано на его предшествующем поведении и выражающееся в признании его заслуг?
а) авторитет;
б) имидж;
в) популярность;
г) престиж;
д) репутация+
20. Что такое тактичность?
а) внутренний голос человека;
б) определенный круг обязательств и исполнение своих обязанностей, сложившихся на основе профессиональных или общественных отношений;
в) сделал, и что хотел сделать;
г) способность и привычка человека вести себя, уважая достоинство другого человека;+
д) способность человека осуществлять внутренний нравственный самоконтроль;
21.Что относится к основным категориям этики?
а) добро и зло;+
б) пространство и время;
в) свобода;
г) совесть
22. Верно ли убеждение, что различные сферы человеческой деятельности обусловливают специфику профессиональной этики?
Да+
Нет
test-s-otvetami.ru
Тесты по Профессиональной этике | Социальная сеть работников образования
Примерные образцы тестовых заданий
1. Этика как наука существует:
a) более 20 веков;
b) более 10 веков;
c) с конца 18 века;
d) с IV века до нашей эры.
2. Этика — это наука:
a) которая изучает добродетели;
b) об общепринятых и повторяющихся формах поведения людей
c) о морали, нравственности;
d) о нравах, обычаях.
3. Мораль — это:
a) общепринятые в рамках социальной общности (группы)правила, образцы поведения или действия в определенной ситуации;
b) форма общественного сознания, в которой отражаются идеи, представления, принципы и правила поведения людей в обществе;
c) общепринятые и повторяющиеся формы поведения людей, которые служат средством передача социального и культурного опыта от поколения к поколению;
d) правила поведения людей при совершении обрядов и форм деятельности.
4. Социальные нормы — это:
a) общепринятые в рамках социальной общности (группы)правила, образцы поведения или действия в определенной ситуации;
b) форма общественного сознания, в которой отражаются идеи, представления, принципы и правила поведения людей в обществе;
c) общепринятые и повторяющиеся формы поведения людей, которые служат средством передача социального и культурного опыта от поколения к поколению;
d) правила поведения людей при совершении обрядов и форм деятельности.
5. Ритуалы — это:
a) правила поведения людей при совершении обрядов и форм деятельности.
b) общепринятые и повторяющиеся формы поведения людей, которые служат средством передачи социального и культурного опыта от поколения к поколению.
c) правила поведения, которые устанавливаются и охраняются государством.
d) наиболее обобщенные и стабильные правила поведения людей в том или ином обществе, которые выверены временем и длительно существуют.
6. Традиции — это:
a) правила поведения, которые устанавливаются и охраняются государством.
b) представляют собой правила поведения, которые устанавливаются самими общественными организациями и охраняются с помощью мер общественного воздействия, предусмотренных уставами этих организаций.
c) духовно-нравственные правила человеческого общежития, основанные на представлении людей о Боге как творце мироздания.
d) наиболее обобщенные и стабильные правила поведения людей в том или ином обществе, которые выверены временем и длительно существуют.
7. Права — это:
a) представляют собой правила поведения, которые устанавливаются самими общественными организациями и охраняются с помощью мер общественного воздействия, предусмотренных уставами этих организаций.
b) правила поведения, которые устанавливаются и охраняются государством.
c) духовно-нравственные правила человеческого общежития, основанные на представлении людей о Боге как творце мироздания.
d) наиболее обобщенные и стабильные правила поведения людей в том или ином обществе, которые выверены временем и длительно существуют.
8. Религия — это:
a. духовно-нравственные правила человеческого общежития, основанные на представлении людей о Боге как творце мироздания.
b) передача социального и культурного опыта от поколения к поколению;
c) правила поведения людей при совершении обрядов и форм деятельности.
d) наиболее обобщенные и стабильные правила поведения людей в том или ином обществе, которые выверены временем и длительно существуют.
9. Нормы общественных организаций — представляют собой:
a) наиболее обобщенные и стабильные правила поведения людей в том или ином обществе, которые выверены временем и длительно существуют.
b) правила поведения, которые устанавливаются и охраняются государством.
c) правила поведения, которые устанавливаются самими общественными организациями и охраняются с помощью мер общественного воздействия, предусмотренных уставами этих организаций.
d) общепринятые и повторяющиеся формы поведения людей, которые служат средством передачи социального и культурного опыта от поколения к поколению.
10. Основателем этики признаётся:
a) Платон (428-328 до н.э.)
b) великий древнегреческий философ Сократ (469-399 до н.э.).
c) Аристотель (384-322 до н.э.),
d) Сенека (4 до н.э. – 65 н.э.)
11. Термин «этика» (ethica) впервые использовал для обозначения науки, которая изучает добродетели:
a) Платон (428-328 до н.э.)
b) великий древнегреческий философ Сократ (469-399 до н.э.).
c) Аристотель (384-322 до н.э.),
d) Сенека (4 до н.э. – 65 н.э.)
12. В истории развития этики как науки можно выделить:
a) 3 этапа: античная этика, средневековая этика, современная этика.
b) 2 этапа: античная этика, современная этика.
c) 5 этапов: предэтика, античная этика, средневековая этика, этика Нового времени, современная этика.
d) 4 этапа: античная этика, средневековая этика, этика Нового времени, современная этика.
14. Автор термина “Мораль”:
a. Гомер;
b. Тацит;
c. Цицерон.
15. Нравственность — термин:
a. французский;
b. китайский;
c. русский.
16. “Домострой” — памятник этической мысли:
a. Древней Греции;
b. Индии;
c. России.
17. “Любовь к ближнему” — моральная норма этики:
a. античной;
b. конфуцианской;
c. христианской.
18. Этический утилитаризм — это этика:
a. феодальных экономических отношений;
b. рабовладельческих рыночных отношений;
c. буржуазных рыночных отношений.
19. Эвдемонизм — это:
a. долг;
b. красота;
c. счастье.
20. Гедонизм — это:
a. аскетизм;
b. чувственное наслаждение.
c. патриотизм;
21. Логос — это закон:
a. Римской империи;
b. Российской империи;
c. Космоса.
22. Аскетизм — это:
a. отказ от чувственно-физических наслаждений;
b. печаль;
c. развлечение;
23. Понятие “греха” впервые сформулировано:
a. Платоном;
b. Аристотелем;
c. Фомой Аквинским.
24. “Деонтология” — это:
a. учение о правилах поведения;
b. учение об общественных нравах и обычаях;
c. учение о проблемах морали и нравственности, раздел этики.
b) профессиональная этика.
25. “Категорический императив” встречается в учении:
a. Маркса;
b. Гегеля;
c. Канта.
26. Религиозное начало преобладало в этике:
a. античности;
b. Нового времени;
c. Средних веков.
27. Рационализм — отличительная черта этики:
a. протестантизма.
b. язычества;
c. православия;
28. Этикет — это :
a. религиозное учение;
b. памятник древней этической мысли;
c. культура поведения.
29. Этику к “практической философии” относил:
a. Аристотель.
b. Гегель;
c. Маркс;
30. Эмотивизм — это направление в этике:
a. марксизма;
b. экзистенциализма;
c. неопозитивизма.
31. “Научить человека быть счастливым” — это точка зрения:
a. разумного эгоизма;
b. гедонизма;
c. эвдемонизма.
32. Эмотивизм это направление в этике:
a. марксизма;
b. экзистенциализма;
c. неопозитивизма.
33. “Человек должен быть свободным” считает этика:
a. этического утилитаризма;
b. экзистенциализма;
c. неотомизма
34. Добро и зло — это:
a) самооценивающее чувство, переживание, один из древнейших интимноличностных регуляторов поведения людей.
b) нравственная задача, которую человек формулирует для себя сам на основании нравственных требований, обращенных ко всем.
c) наиболее общие формы моральной оценки, разграничивающие нравственное и безнравственное.
35. В этике справедливость — категория,
a) означающая такое положение вещей, которое рассматривается как должное, отвечающее представлениям о сущности человека, его неотъемлемых правах, исходящее из признания равенства между всеми людьми и необходимости соответствия между деянием и воздаянием за добро и зло;
b) специфически моральная категория;
c) специфически правовая категория.
36. Долг представляет собой:
a) нравственную задачу, которую человек формулирует для себя сам на основании нравственных требований, обращенных ко всем.
b) самооценивающее чувство, переживание, один из древнейших интимноличностных регуляторов поведения людей.
c) категория этики, характеризующая личность с точки зрения выполнения ею нравственных требований, соответствия ее моральной деятельности нравственному долгу, рассматриваемого с позиций возможностей личности
37. Совесть — это:
a) самооценивающее чувство, переживание, один из древнейших интимноличностных регуляторов поведения людей.
b) нравственная задача, которую человек формулирует для себя сам на основании нравственных требований, обращенных ко всем.
c) категория этики, характеризующая способность человека осуществлять нравственный самоконтроль, внутреннюю самооценку с позиций соответствия своего поведения требованиям нравственности, самостоятельно формулировать для себя нравственные задачи и требовать от себя их выполнения.
d) обязанность и необходимость давать отчет в своих действиях, поступках, отвечать за их возможные последствия
38. Ответственность — это:
a) выражение ответственности человека за свое поведение перед самим собой, форма самоутверждения личности.
b) нравственную задачу, которую человек формулирует для себя сам на основании нравственных требований, обращенных ко всем.
c) категория этики, характеризующая личность с точки зрения выполнения ею нравственных требований, соответствия ее моральной деятельности нравственному долгу, рассматриваемого с позиций возможностей личности.
d) обязанность и необходимость давать отчет в своих действиях, поступках, отвечать за их возможные последствия.
39. Достоинство — это:
a) категория этики, означающая особое моральное отношение человека к самому себе и отношение к нему со стороны общества, окружающих, основанное на признании ценности человека как личности.
b) категория этики, характеризующая личность с точки зрения выполнения ею нравственных требований, соответствия ее моральной деятельности нравственному долгу, рассматриваемого с позиций возможностей личности.
c) мнение о нравственном облике человека, сложившееся у окружающих, основанное на его предшествующем поведении.
d) выражение ответственности человека за свое поведение перед самим собой, форма самоутверждения личности.
40. Репутация— это:
a) самооценивающее чувство, переживание, один из древнейших интимноличностных регуляторов поведения людей.
b) нравственная задача, которую человек формулирует для себя сам на основании нравственных требований, обращенных ко всем.
c) мнение о нравственном облике человека, сложившееся у окружающих, основанное на его предшествующем поведении.
d) выражение ответственности человека за свое поведение перед самим собой, форма самоутверждения личности.
41. Право — это:
a) нравственная задача, которую человек формулирует для себя сам на основании нравственных требований, обращенных ко всем.
b) необходимые, взаимосвязанные и взаимопроникающие системы регуляции общественной жизни.
c) совокупность установленных или санкционированных государством общеобязательных правил поведения (норм), соблюдение которых обеспечивается мерами государственного воздействия
42. Мораль и право – это:
a) необходимые, взаимосвязанные и взаимопроникающие системы регуляции общественной жизни.
b) совокупность установленных или санкционированных государством общеобязательных правил поведения (норм), соблюдение которых обеспечивается мерами государственного воздействия
c) выполняют единую социальную функцию – регулирование поведения людей в обществе.
d) признание достоинства и ценности личности.
43. Презумпция невиновности означает:
a) нравственная задача, которую человек формулирует для себя сам на основании нравственных требований, обращенных ко всем.
b) мнение о нравственном облике человека, сложившееся у окружающих, основанное на его предшествующем поведении.
c) выражение ответственности человека за свое поведение перед самим собой, форма самоутверждения личности.
d) признание достоинства и ценности личности.
44. Презумпция невиновности впервые была сформулирована:
a) в Декларации прав человека и гражданина, принятой во Франции в 1789 году,
b) в Международном пакте о гражданских и политических правах от 19 декабря 1966 года
c) в Конституции Российской Федерации 1993 года
45. Культура уголовного процесса представляет собой:
a) уровень, степень развития какой-либо отрасли хозяйственной или умственной деятельности.
b) качественную характеристику этого вида государственной деятельности, опирающуюся на общее понятие культуры, а также представления о юридической культуре.
c) достижения общества в производственной, общественной и духовной жизни.
nsportal.ru
Тест по курсу «Профессиональная этика»
Вид работы: Тест
Предмет: Профессиональная этика
- Термин “этика” появился:
а) в Античности;
б) Средние века;
в) эпоху Возрождения.
- Что изучает наука этика?
а) мораль, нравственность;
б) традиции, обычаи, народное творчество;
в) поведение каждого конкретного человека в обществе;
г) социальные проблемы общества;
д) политическое устройство общества.
- Понятие “нравственность”:
а) совпадает по содержанию с понятием “мораль”;
б) совпадает по содержанию с понятием “этика”;
в) обозначает основные понятия морального самосознания;
г) обозначает область поступков людей, реальных нравов, сложившихся в обществе.
- Специфика нравственных отношений состоит в том, что:
а) они возникают естественным образом, стихийно;
б) они представляют собой особый вид общественных отношений;
в) они являются компонентом, стороной других видов общественных отношений.
- Мораль регулирует:
а) мышление и намерения людей;
б) наиболее значимые сферы жизнедеятельности людей;
в) все сферы жизнедеятельности людей.
- Основное требование профессиональной этики состоит:
а) в выполнении приказов и инструкций;
б) защите прав человека;
в) соблюдении моральной справедливости.
- Добро – это:
а) моральный выбор человека, ведущий к успеху;
б) моральная категория, предельно выражающая то, что важно и значимо для жизни человека и общества;
в) моральная категория, выражающая определенную степень человеческого совершенства.
- Нравственная категория, выражающаяся в моральной обязанности по отношению к другим людям в конкретных условиях; – это:
а) честь;
б) долг;
в) справедливость;
г) ответственность;
д) совесть.
- Совесть – это:
а) внутренний голос человека;
xn--d1aux.xn--p1ai


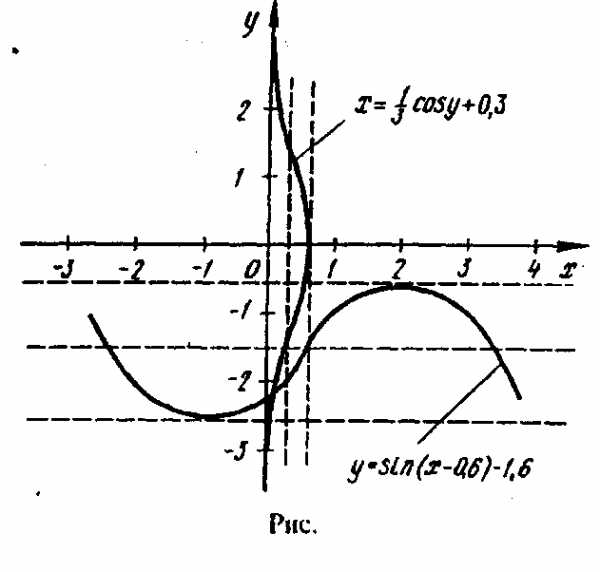
 (4)
(4)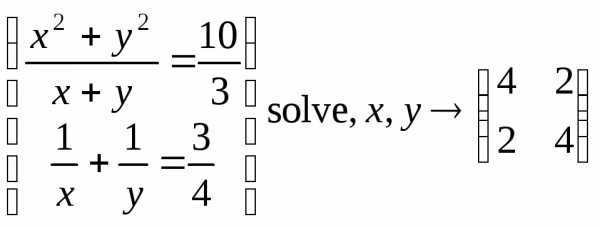 ,
,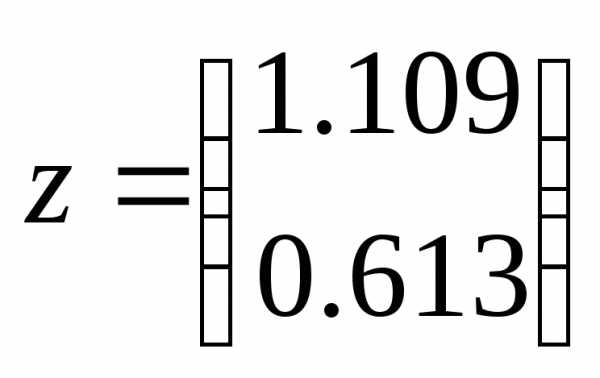
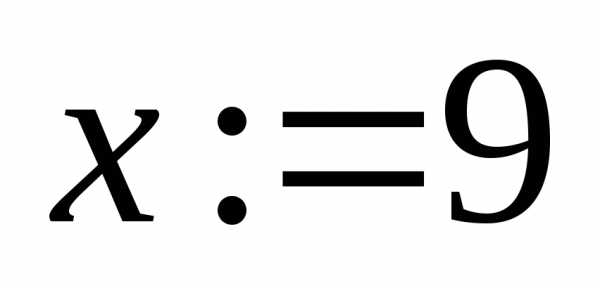 ,
то система сообщит, что решение задачи
не найдено. Неизвестные и их начальные
значения можно задавать в векторном
виде. Пример (установите начало нумерации
элементов матриц с 1):
,
то система сообщит, что решение задачи
не найдено. Неизвестные и их начальные
значения можно задавать в векторном
виде. Пример (установите начало нумерации
элементов матриц с 1):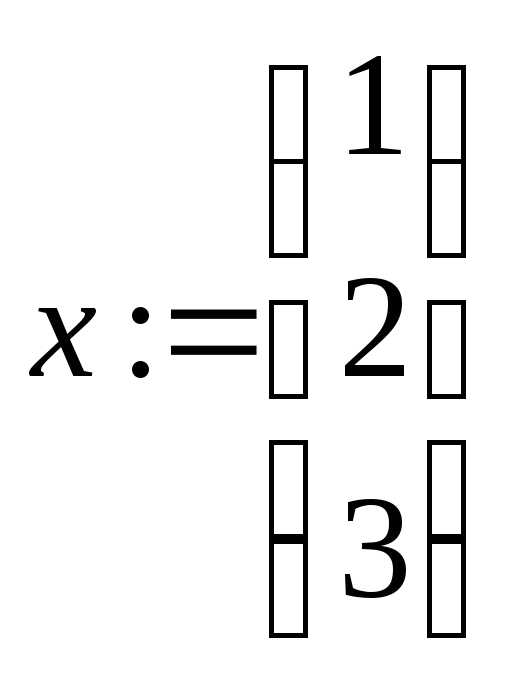
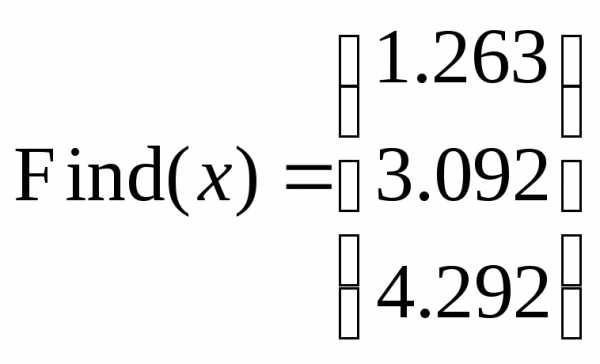 .
.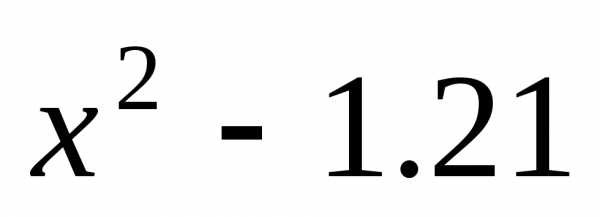 ,
,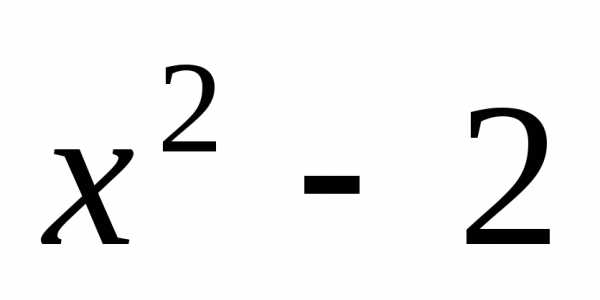 .
В других случаях для разложения на
множители приходится находить корни
многочлена. Как это можно сделать в
системе МС, описано выше. Следует, однако,
учесть, что функцияpolyroots
гарантирует хорошие результаты только
для многочленов невысокой степени.
Аналогичным недостатком обладает и
директива solve
для символьного нахождения корней.
Рассмотрим следующий пример. Пусть
.
В других случаях для разложения на
множители приходится находить корни
многочлена. Как это можно сделать в
системе МС, описано выше. Следует, однако,
учесть, что функцияpolyroots
гарантирует хорошие результаты только
для многочленов невысокой степени.
Аналогичным недостатком обладает и
директива solve
для символьного нахождения корней.
Рассмотрим следующий пример. Пусть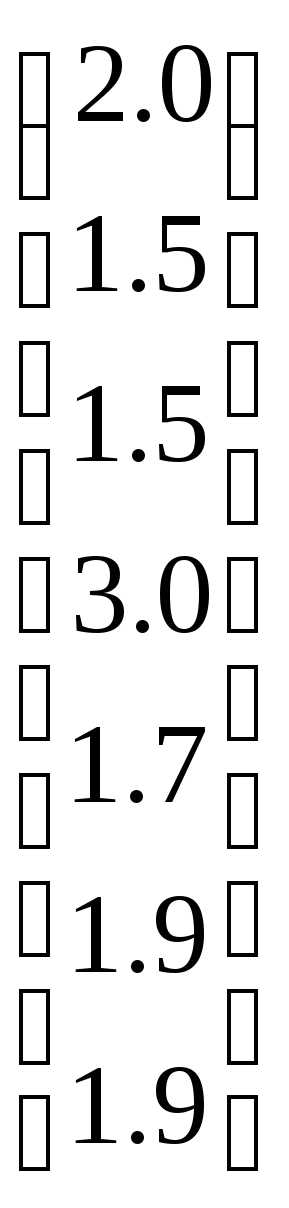

 .
Вычислим корни:
.
Вычислим корни:  .
.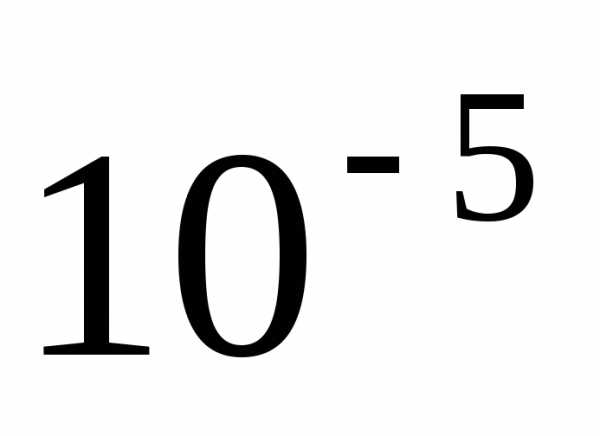 ,.
Найдем корни с помощью функцииpolyroots.
Увидим, что изменения происходят уже в
третьем знаке после десятичной точки,
причем простой вещественный корень 2
превращается в комплексный:
,.
Найдем корни с помощью функцииpolyroots.
Увидим, что изменения происходят уже в
третьем знаке после десятичной точки,
причем простой вещественный корень 2
превращается в комплексный:
 .
.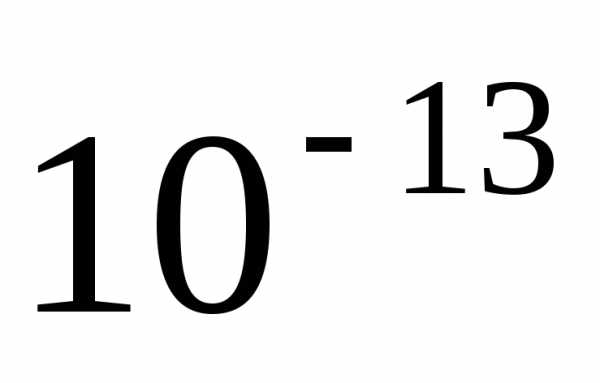 ,
а для корней, полученных с помощью
функцииpolyroots,
– порядок
,
а для корней, полученных с помощью
функцииpolyroots,
– порядок 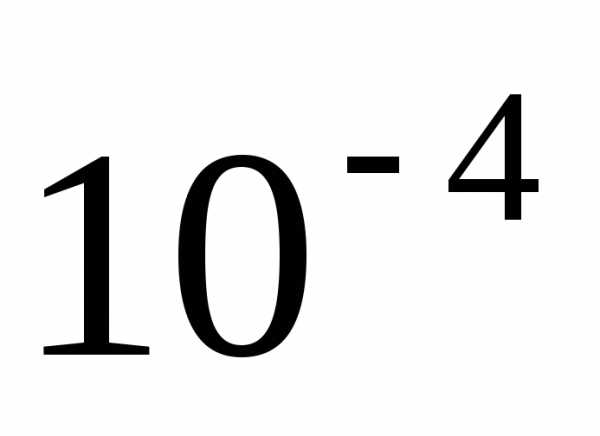 .
.
 .
. .
.
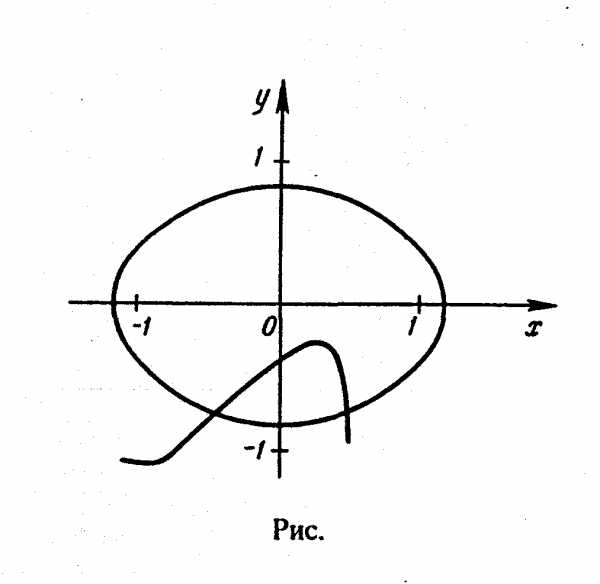
 определяются приближенно (например,
графически).
определяются приближенно (например,
графически).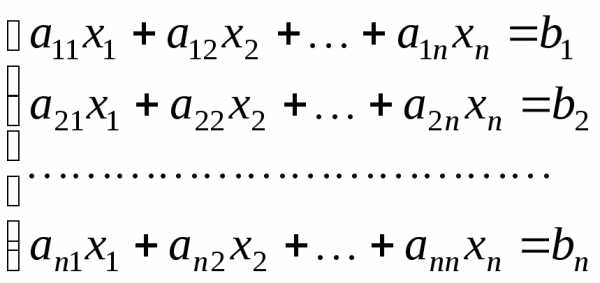 (3.1)
(3.1)
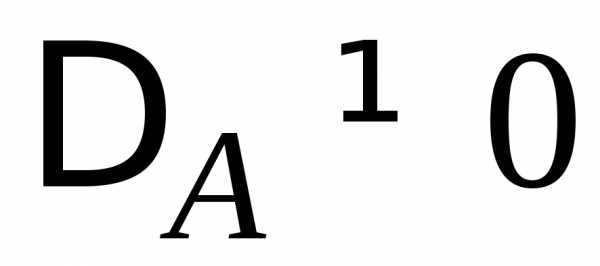 ,
где
,
где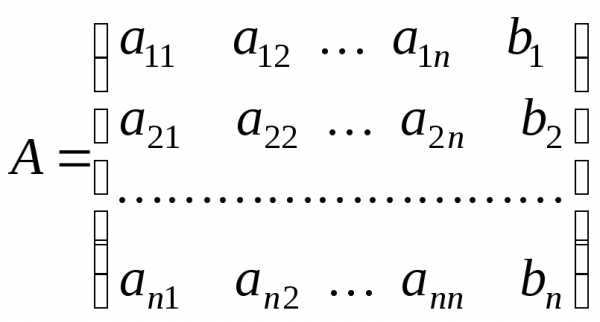
матрица коэффициентов
матрица коэффициентов  системы (3.1)
системы (3.1) матрицыА выберем наибольший по модулю, называемый
главным
элементом.
Пусть им будет элемент
матрицыА выберем наибольший по модулю, называемый
главным
элементом.
Пусть им будет элемент 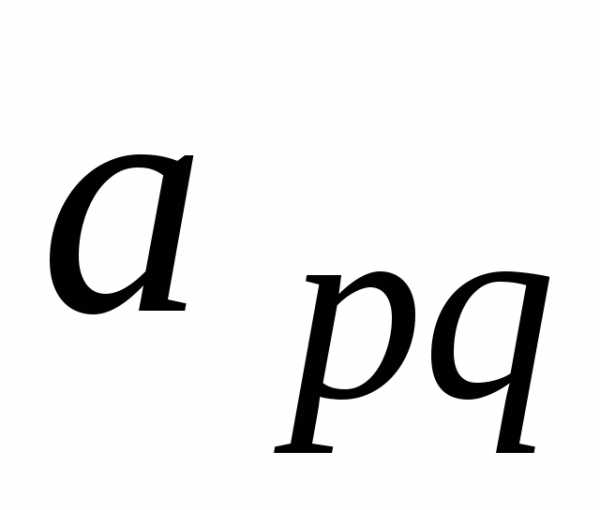 .
Строка с номеромр,
содержащая главный элемент, называется
главной строкой.
.
Строка с номеромр,
содержащая главный элемент, называется
главной строкой. для всех
для всех .
Затем преобразуем матрицу следующим
образом: из каждой неглавной строки
вычитаем почленно главную строку,
умноженную наmi . В результате получим матрицу, у которой
все элементы q-го
столбца, за исключением
.
Затем преобразуем матрицу следующим
образом: из каждой неглавной строки
вычитаем почленно главную строку,
умноженную наmi . В результате получим матрицу, у которой
все элементы q-го
столбца, за исключением 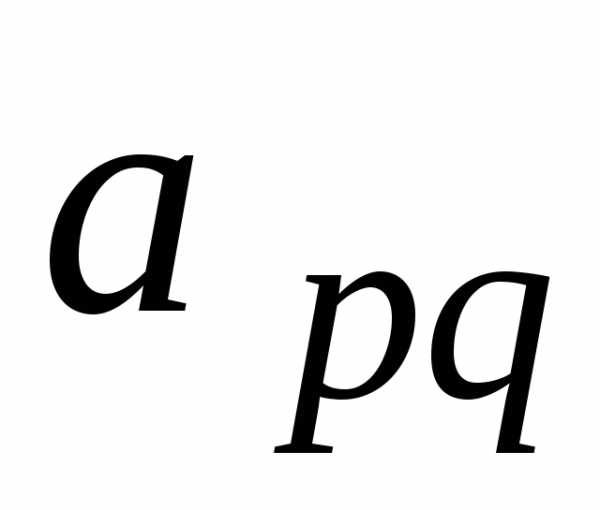 ,
равны нулю. Отбрасываем этот столбец и
главную строку и
,
равны нулю. Отбрасываем этот столбец и
главную строку и с меньшим на единицу числом строк и
столбцов. Над матрицей
с меньшим на единицу числом строк и
столбцов. Над матрицей повторяем аналогичные операции, после
чего получаем матрицуА2 и т. д. Такие преобразования продолжаем
до тех пор, пока не получим матрицу,
содержащую одну строку, которую считаем
тоже главной. Затем объединяем все
главные строки, начиная с последней.
После некоторой перестановки они
образуют треугольную матрицу, эквивалентную
исходной. На этом заканчивается этап
вычислений, называемый прямым
ходом. Решив
систему с полученной треугольной
матрицей коэффициентов, найдём
последовательно значения неизвестных
.
Этот этап вычислений называетсяобратным
ходом. Смысл
выбора главного элемента состоит в том,
чтобы сделать достаточно малым число mi и тем самым уменьшить погрешность
вычислений.
повторяем аналогичные операции, после
чего получаем матрицуА2 и т. д. Такие преобразования продолжаем
до тех пор, пока не получим матрицу,
содержащую одну строку, которую считаем
тоже главной. Затем объединяем все
главные строки, начиная с последней.
После некоторой перестановки они
образуют треугольную матрицу, эквивалентную
исходной. На этом заканчивается этап
вычислений, называемый прямым
ходом. Решив
систему с полученной треугольной
матрицей коэффициентов, найдём
последовательно значения неизвестных
.
Этот этап вычислений называетсяобратным
ходом. Смысл
выбора главного элемента состоит в том,
чтобы сделать достаточно малым число mi и тем самым уменьшить погрешность
вычислений.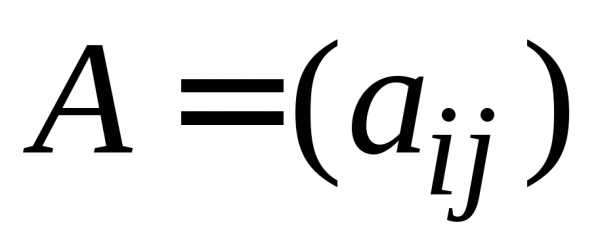 ,
где(i, j = 1, 2,…, n).
Для нахождения элементов обратной
матрицы
,
где(i, j = 1, 2,…, n).
Для нахождения элементов обратной
матрицы  ,
где (i, j = 1, 2,… n)
воспользуемся основным соотношением:
,
где (i, j = 1, 2,… n)
воспользуемся основным соотношением: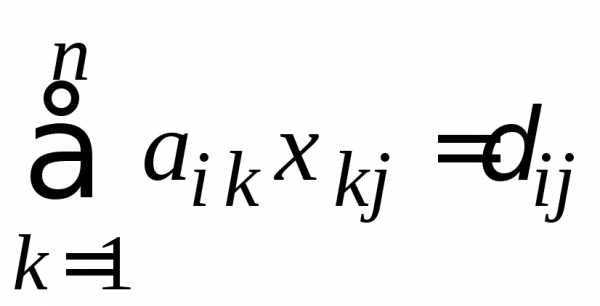 (i = 1, 2, …, n; j – фиксировано),
где
(i = 1, 2, …, n; j – фиксировано),
где 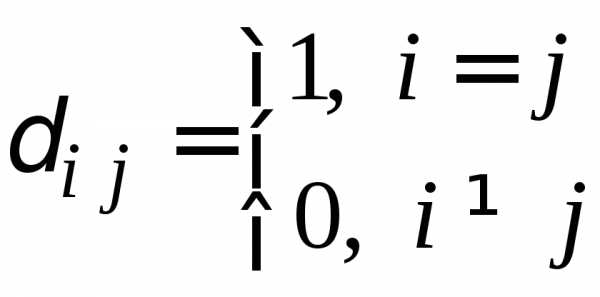 .
. ,
то существует единственная неподвижная
точка
,
то существует единственная неподвижная
точка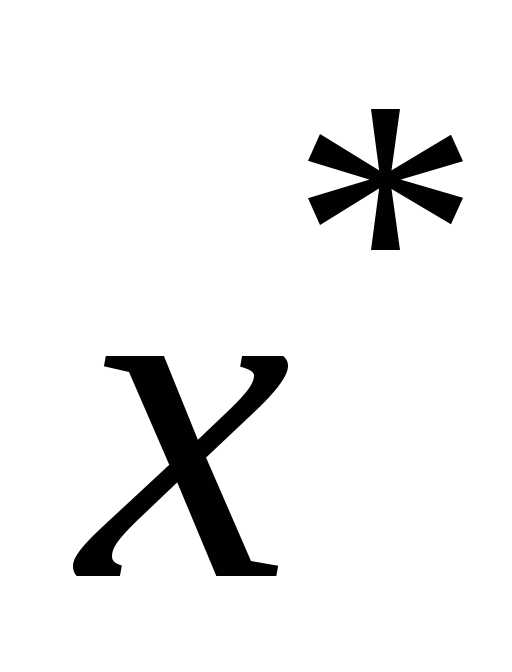 ,
такая, что
,
такая, что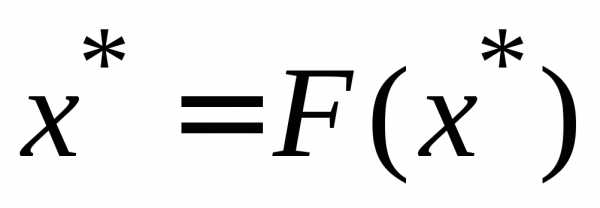 .
При этом итерационная последовательность,
.
При этом итерационная последовательность,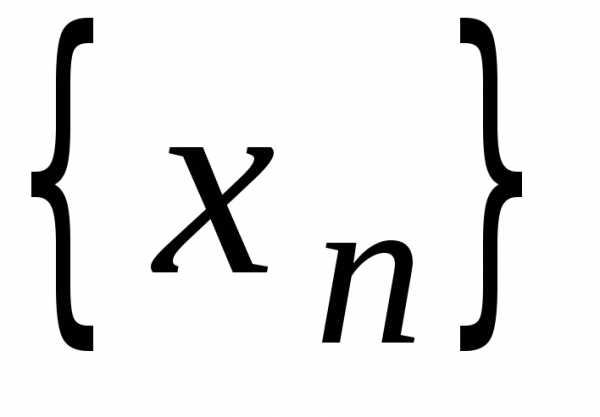 ,
полученная с помощью отображенияF с любым начальным членом х(0),
сходится к
,
полученная с помощью отображенияF с любым начальным членом х(0),
сходится к 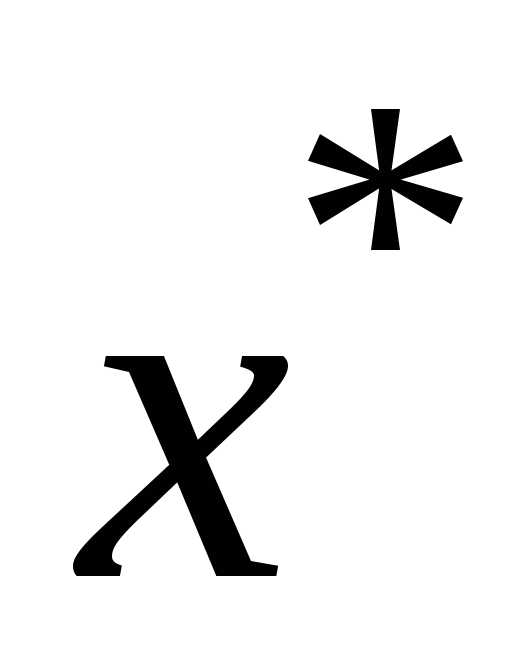 .
.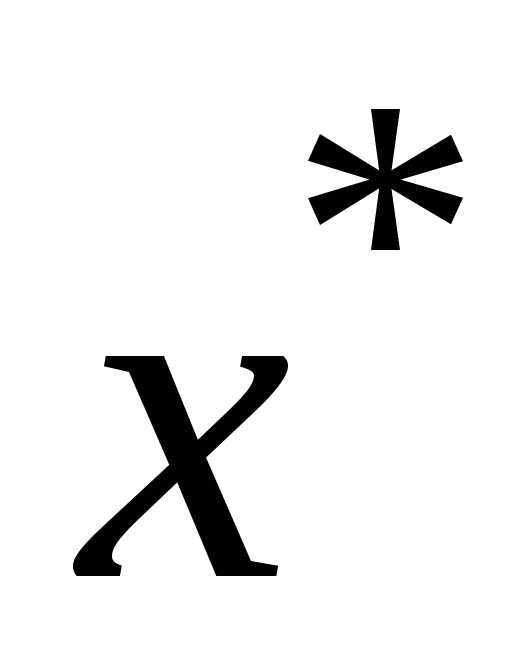 отображенияF и приближением х(к) даётся формулами:
отображенияF и приближением х(к) даётся формулами: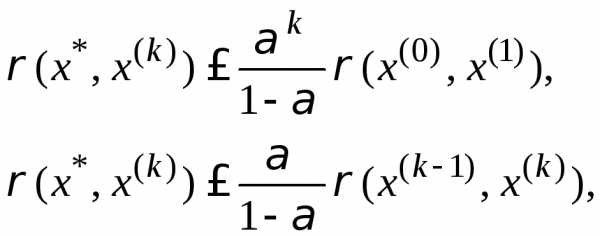 (3.3)
(3.3)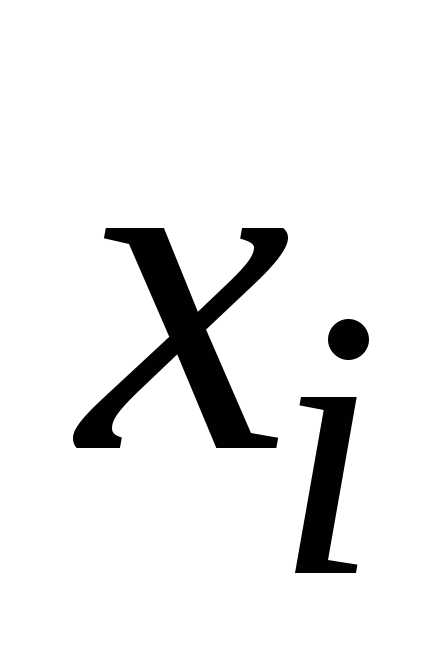 .
.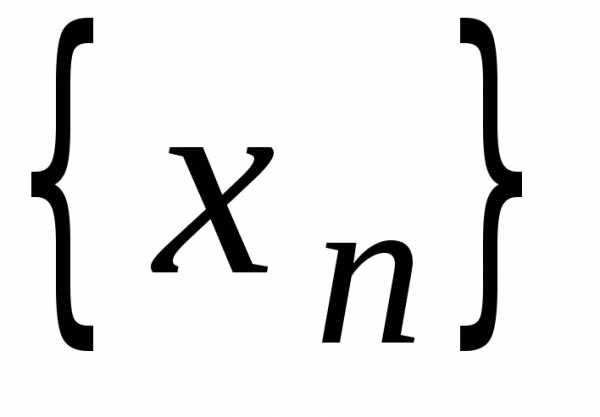 .
.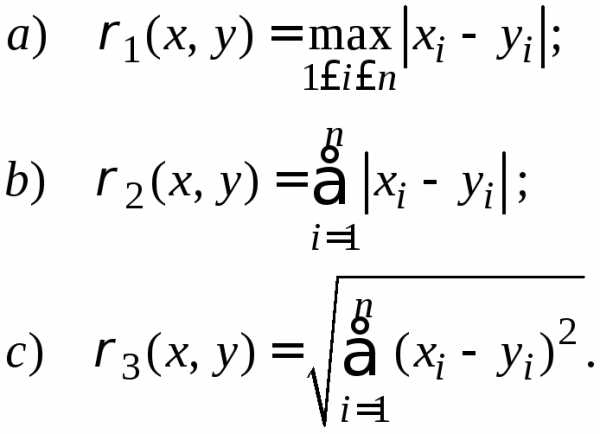 (3.4)
(3.4) :
: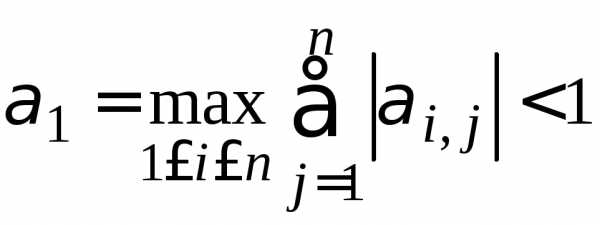 ,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по строкам, должна быть меньше
единицы.
,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по строкам, должна быть меньше
единицы.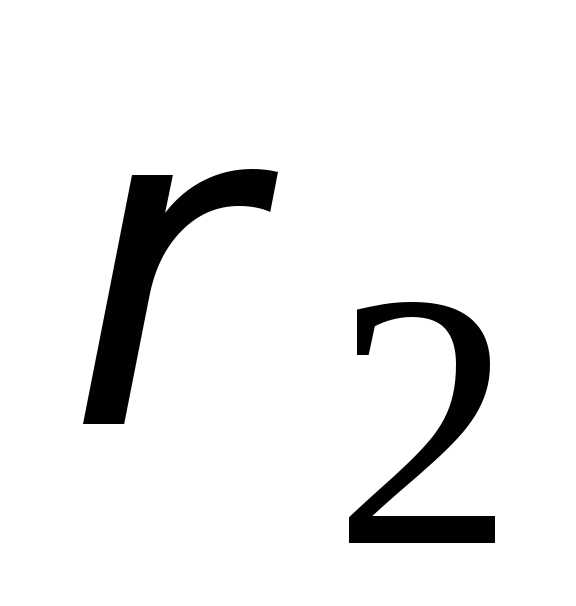 :
: ,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по столбцам, должна быть
меньше единицы.
,
т. е. максимальная из сумм модулей
коэффициентов в правой части системы
(3.2), взятых по столбцам, должна быть
меньше единицы. :
: 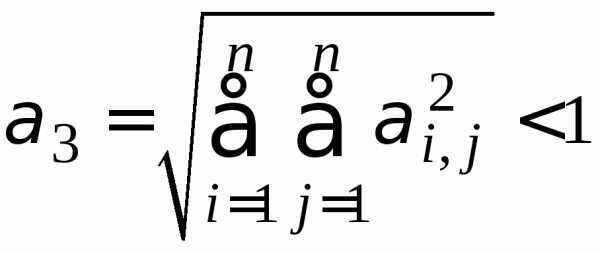 ,
т. е. сумма квадратов при неизвестных в
правой части системы (3.2) должна быть
меньше единицы
,
т. е. сумма квадратов при неизвестных в
правой части системы (3.2) должна быть
меньше единицы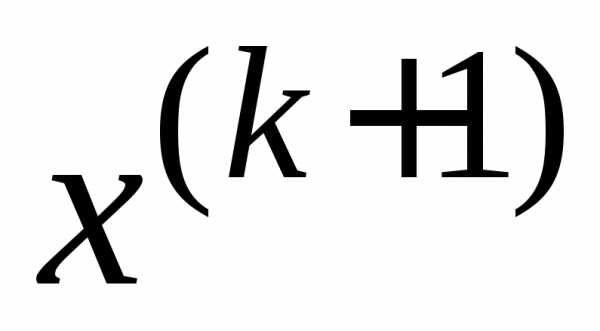 проводится по следующим формулам:
проводится по следующим формулам: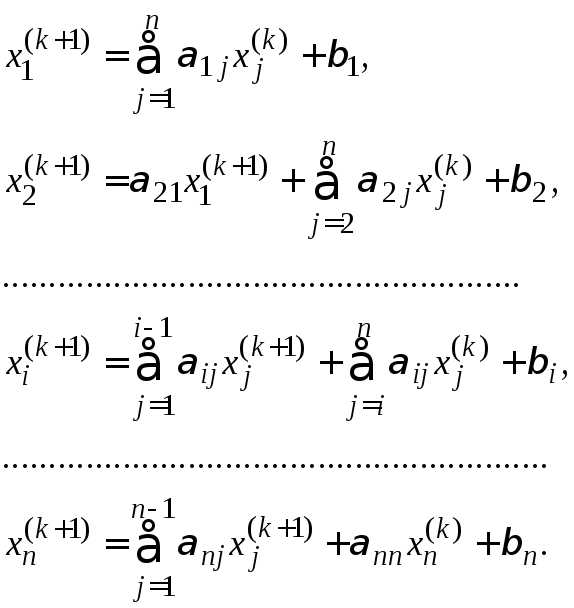
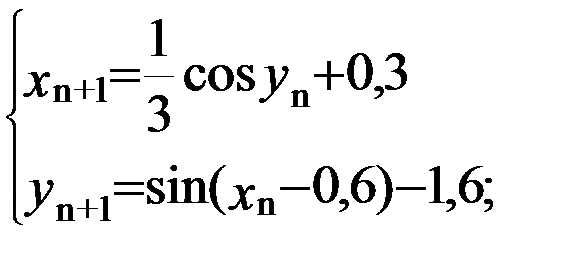
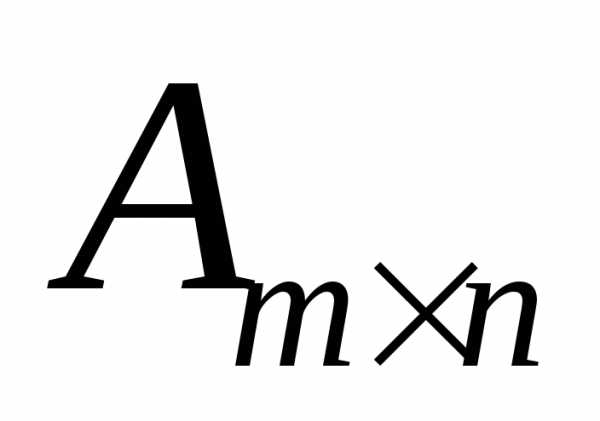 означает, что матрица
означает, что матрица имеет
имеет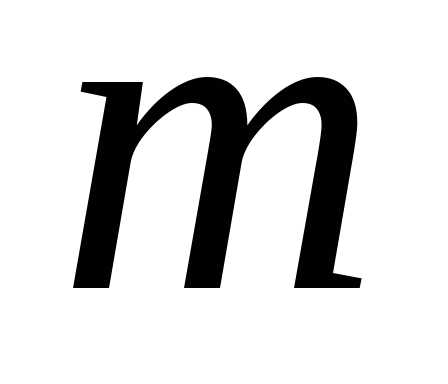 строк и
строк и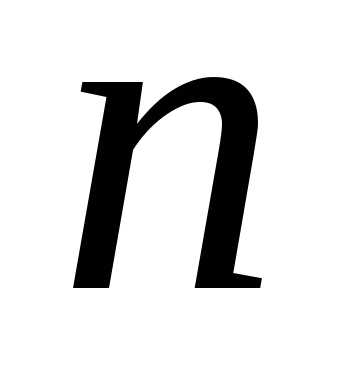 столбцов,
столбцов, элемент, находящийся на пересечении
элемент, находящийся на пересечении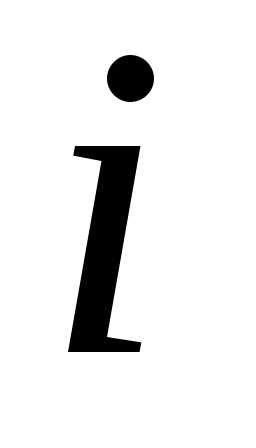 –й
строки и
–й
строки и –го
столбца.
–го
столбца. ,
для всех.
,
для всех.
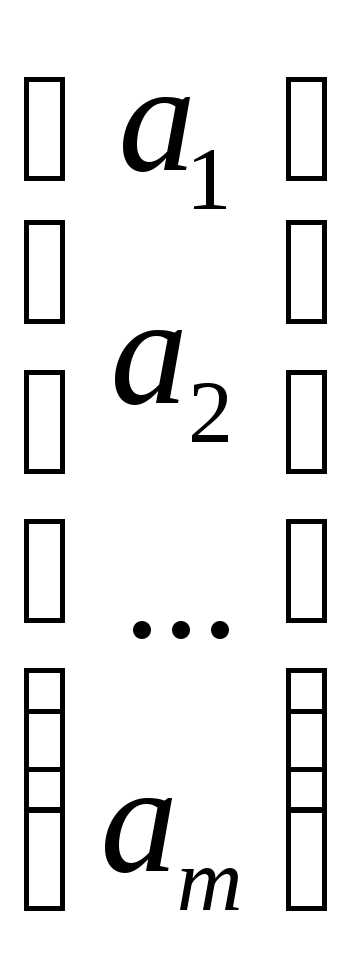

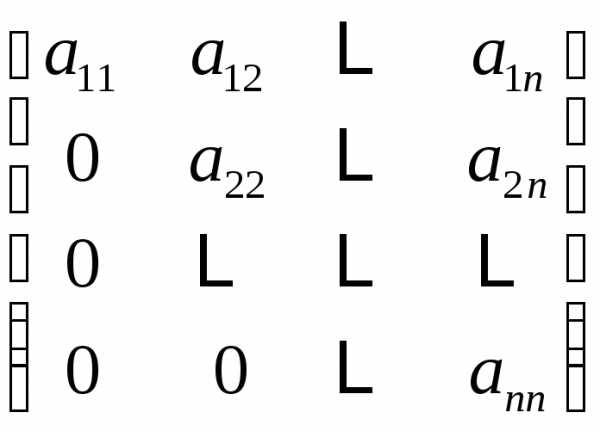
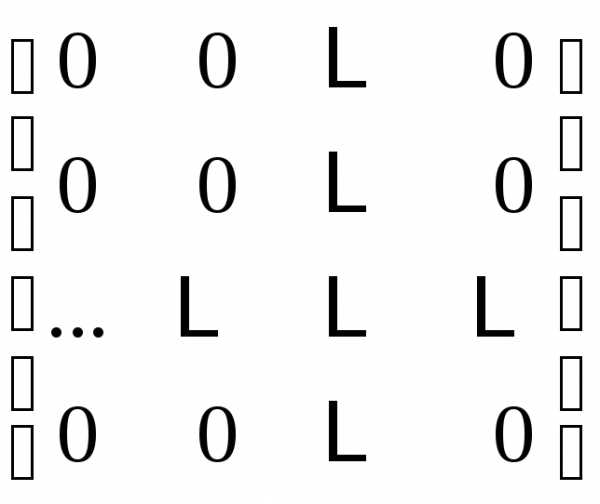
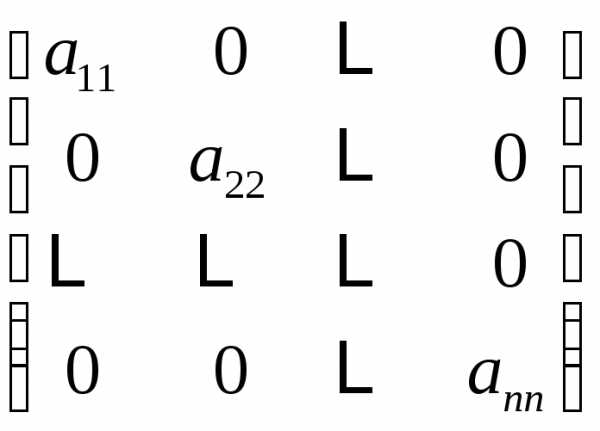
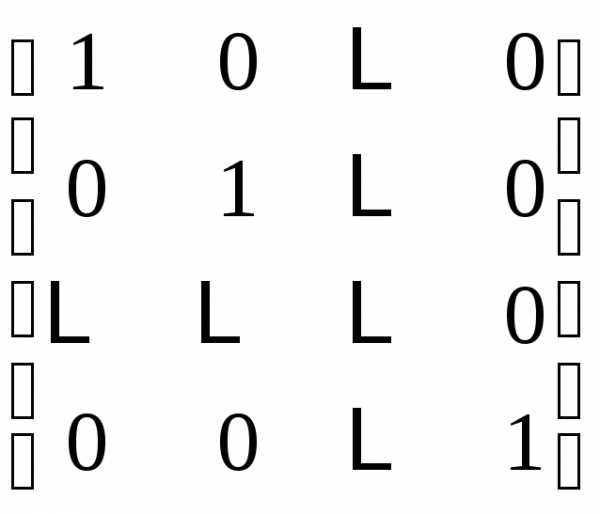
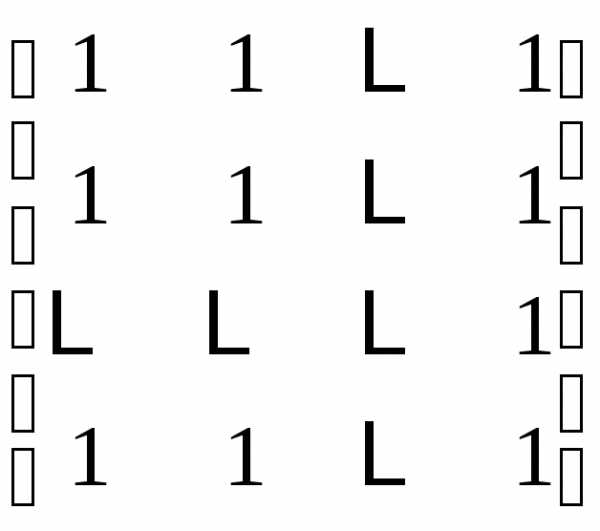

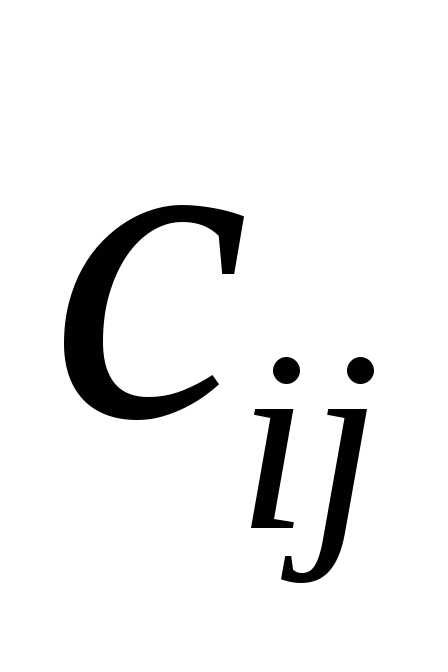 есть сумма произведений всех элементов
есть сумма произведений всех элементов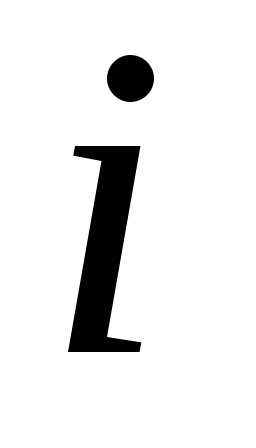 –й
строки
–й
строки на соответсвующие элементы
на соответсвующие элементы –го
столбца
–го
столбца .
.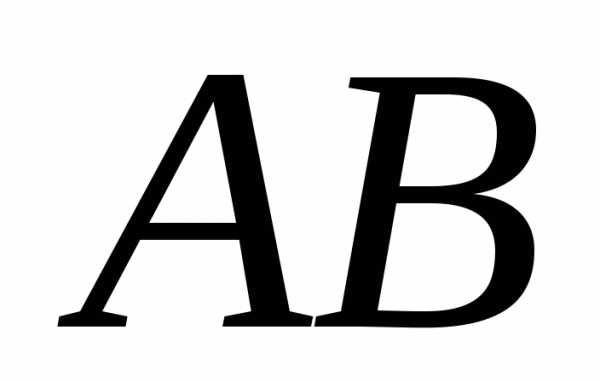 – существует, то произведение
– существует, то произведение может и не существовать. Вообще говоря,.
То есть умножение матриц не коммутативно.
Если же,
то
может и не существовать. Вообще говоря,.
То есть умножение матриц не коммутативно.
Если же,
то и
и называют коммутативными. Например,
диагональные матрицы одного порядка
коммутативны.
называют коммутативными. Например,
диагональные матрицы одного порядка
коммутативны.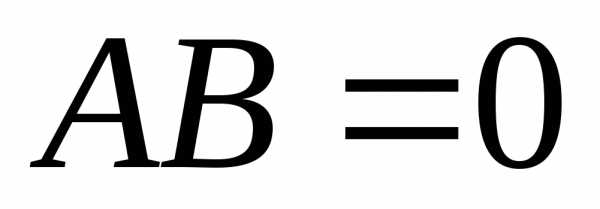 ,
то необязательно
,
то необязательно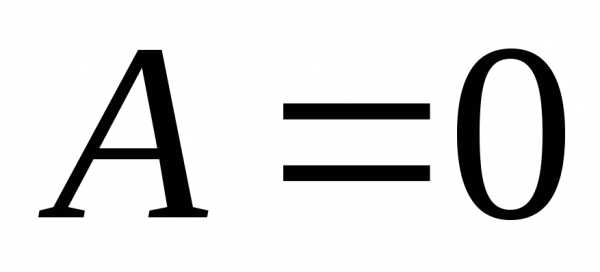 или
или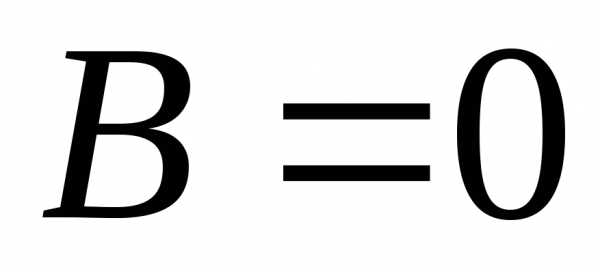 .
Т.е., произведение ненулевых матриц
может дать нулевую матрицу. Например
.
Т.е., произведение ненулевых матриц
может дать нулевую матрицу. Например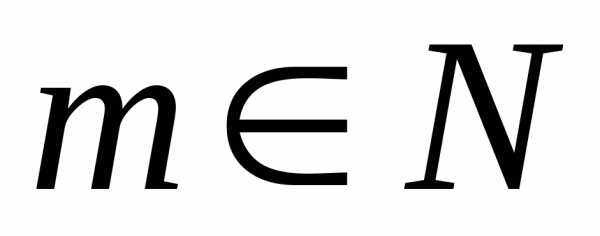 ,
то
,
то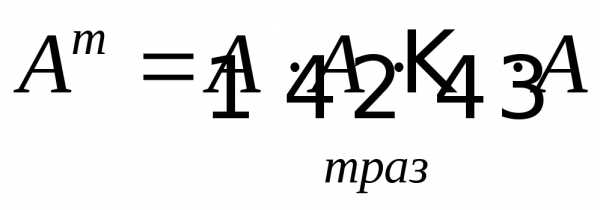 .
.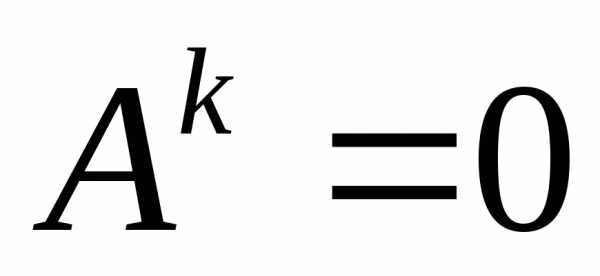 не следует, что
не следует, что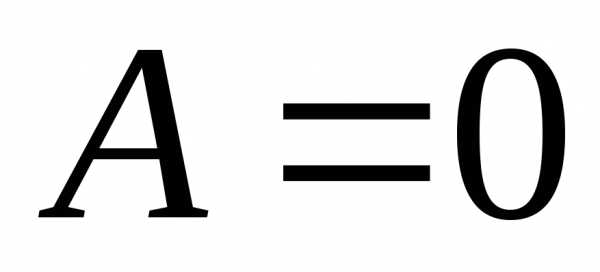 .
.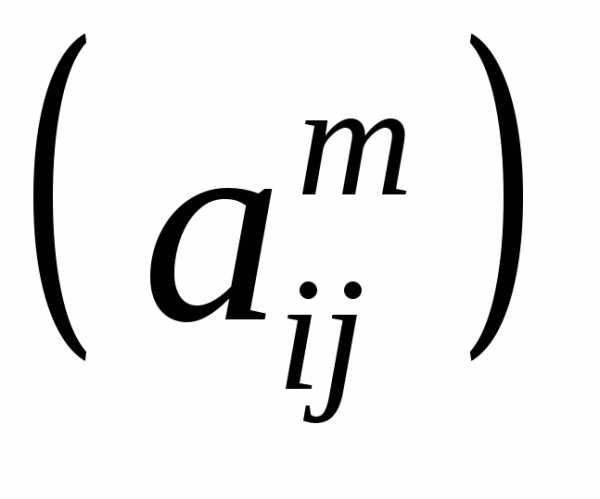 .
.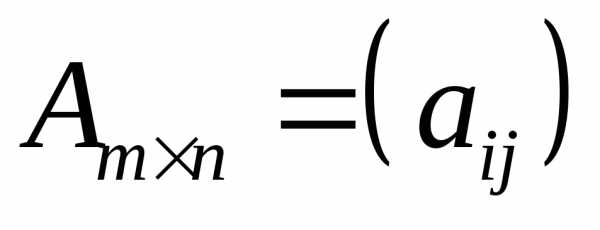 ,
, 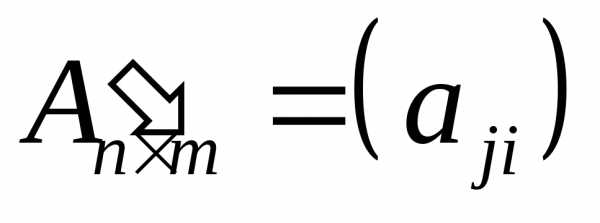
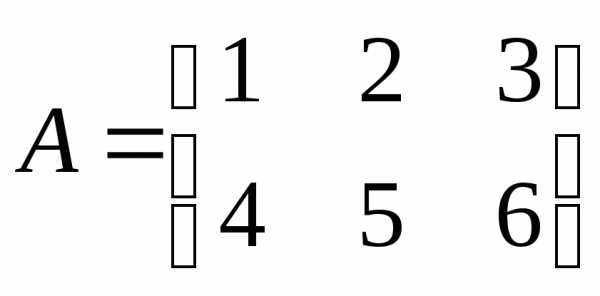 ,
, 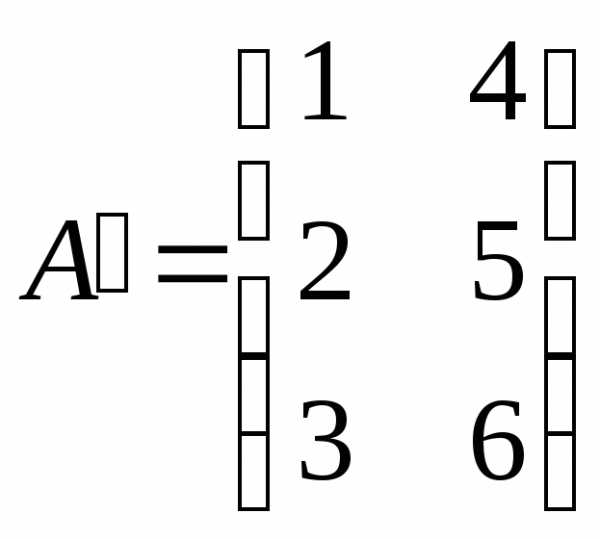 .
.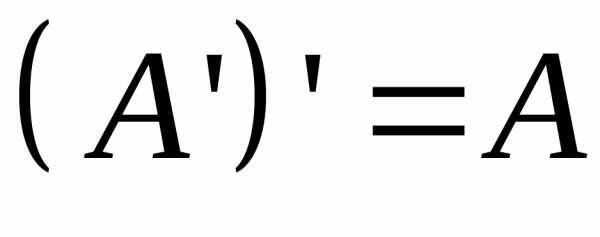
 .
.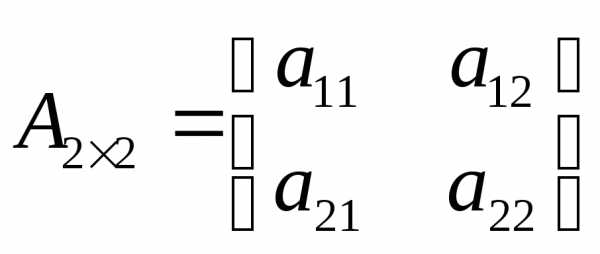 вычисляется
по правилу:
вычисляется
по правилу: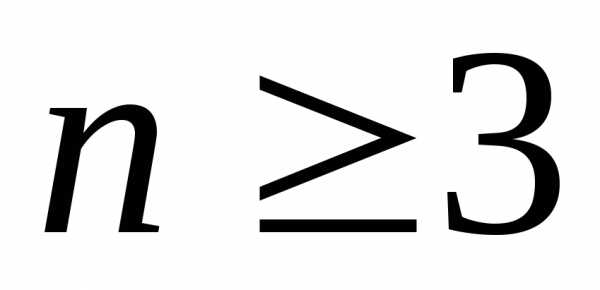 )
необходимо ввести понятия минора и
алгебраического дополнения элемента.
)
необходимо ввести понятия минора и
алгебраического дополнения элемента.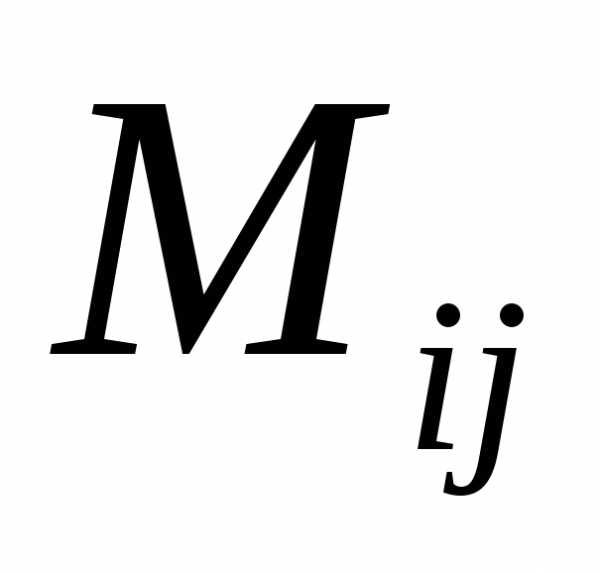 элемента
элемента  называют определитель, который получают
из матрицы
называют определитель, который получают
из матрицы ,
вычеркивая-ю
строку и
,
вычеркивая-ю
строку и -й
столбец.
-й
столбец. размером
размером :
: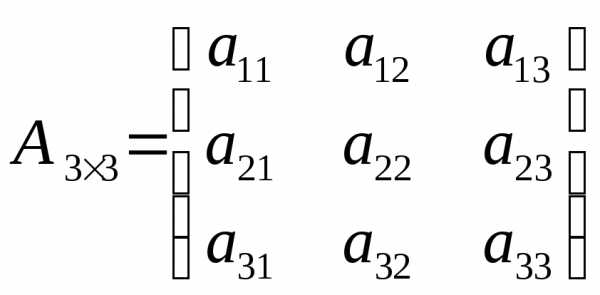 ,
, элемента
элемента называют его минор, умноженный на
называют его минор, умноженный на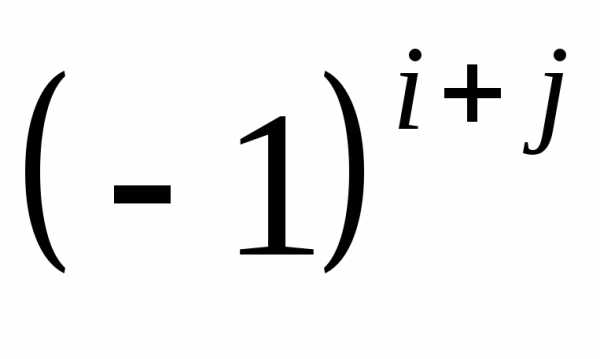 .
.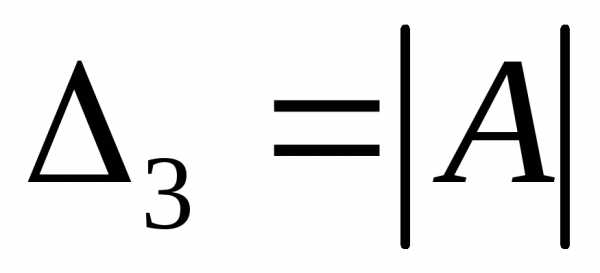 по элементам первой строки, получим:
по элементам первой строки, получим: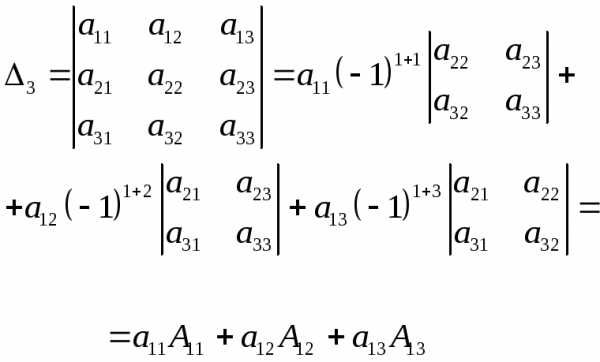
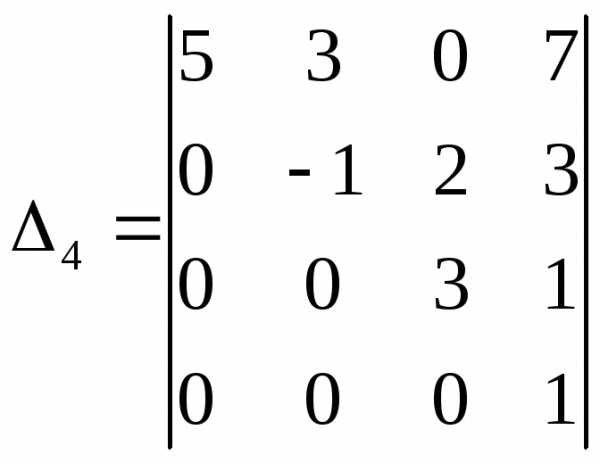
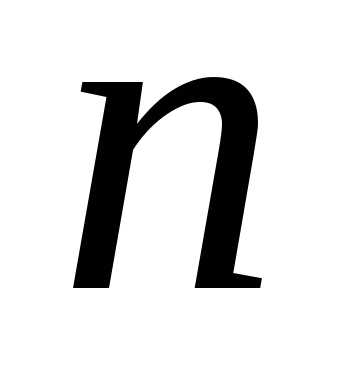 -го
порядка к вычислению
-го
порядка к вычислению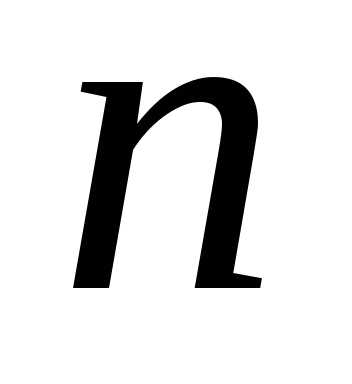 определителей
определителей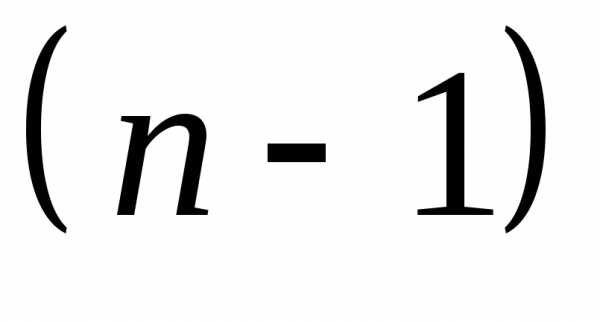 -го
порядка и, в конечном итоге, к вычислению
определителей второго порядка.
-го
порядка и, в конечном итоге, к вычислению
определителей второго порядка.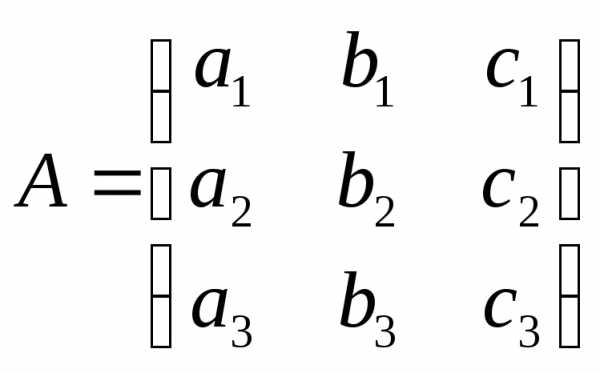
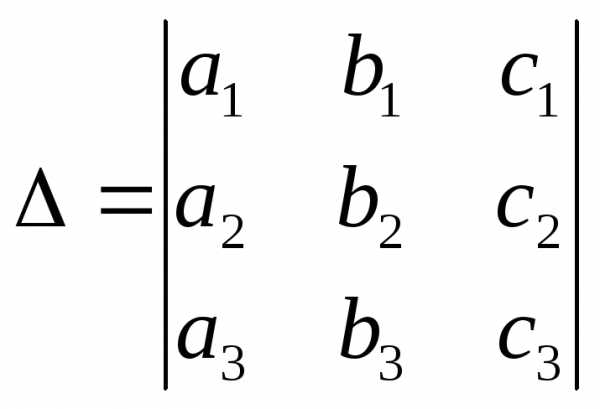
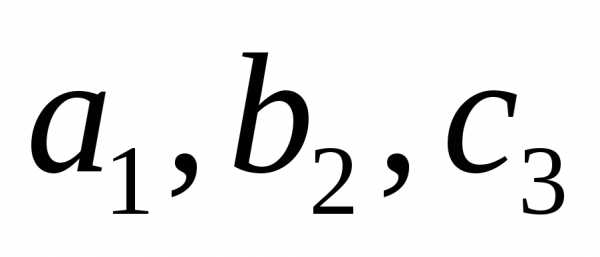 называется
главной , а диагональ, образованная
элементами
называется
главной , а диагональ, образованная
элементами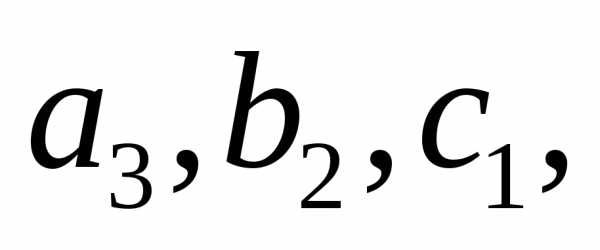 -побочной.
-побочной.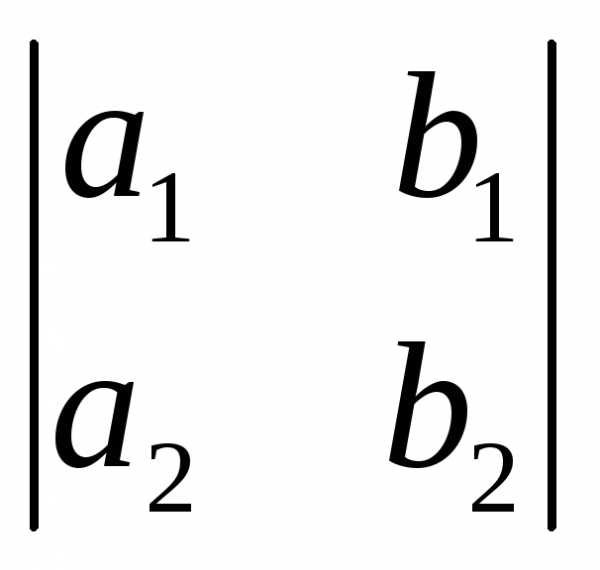 ,
соответствующим матрице
,
соответствующим матрице ,
называется число, равное.
,
называется число, равное.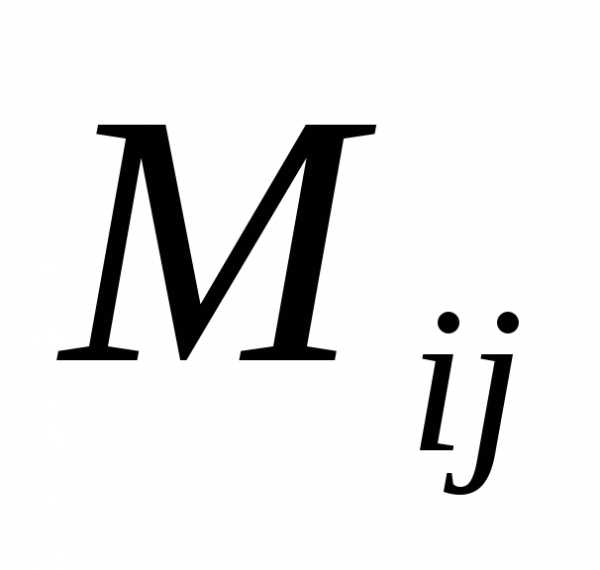 элемента
элемента определителя называется определитель,
полученный из данного, вычеркиваниемi-й
строки и j-го
столбца, на пересечении которых расположен
этот элемент.
определителя называется определитель,
полученный из данного, вычеркиваниемi-й
строки и j-го
столбца, на пересечении которых расположен
этот элемент. элемента
элемента называется
минор этого элемента
называется
минор этого элемента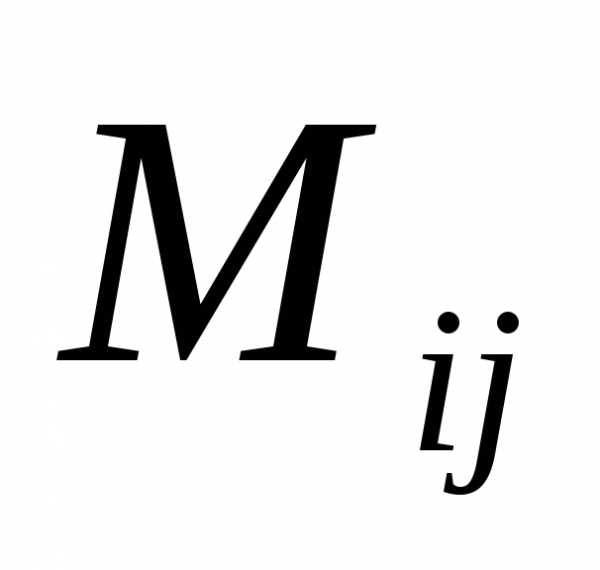 ,
умноженный на
,
умноженный на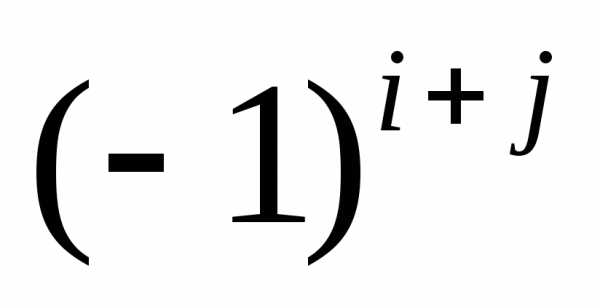 , т.е.
, т.е.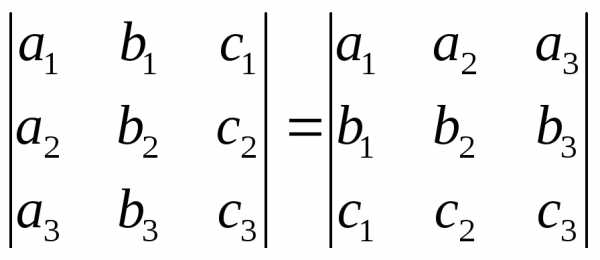
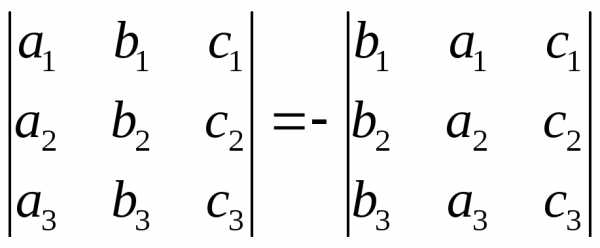
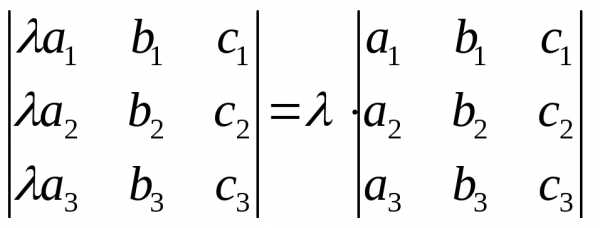
 — начало координат,Ox—
ось абсцисс, Oy-ось
ординат,
— начало координат,Ox—
ось абсцисс, Oy-ось
ординат,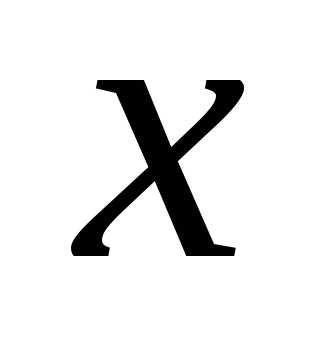 —
абсциссой,
—
абсциссой, – ординатой,
– ординатой, –
аппликатой точки М.
–
аппликатой точки М.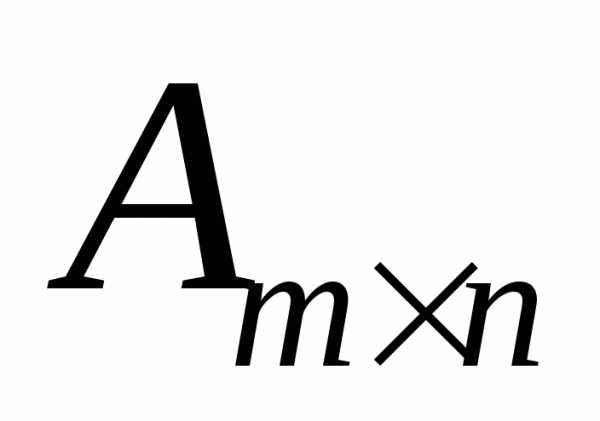 означает, что матрица
означает, что матрица имеет
имеет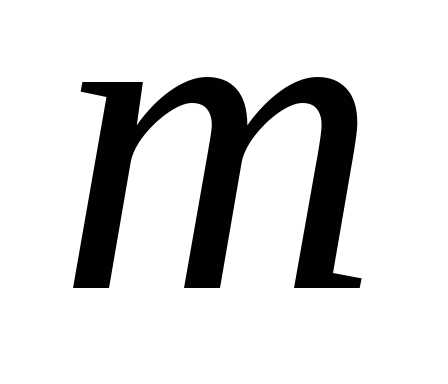 строк и
строк и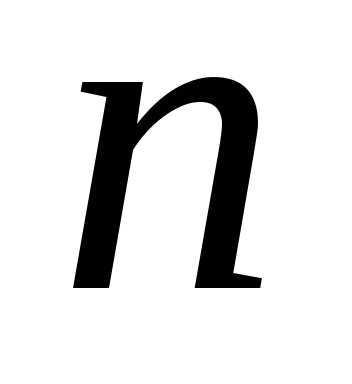 столбцов,
столбцов, элемент, находящийся на пересечении
элемент, находящийся на пересечении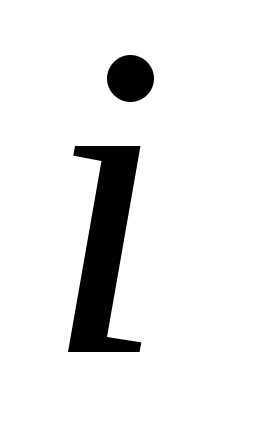 –й
строки и
–й
строки и –го
столбца.
–го
столбца.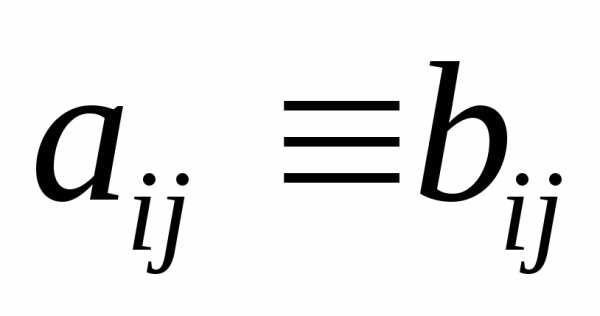 ,
для всех.
,
для всех.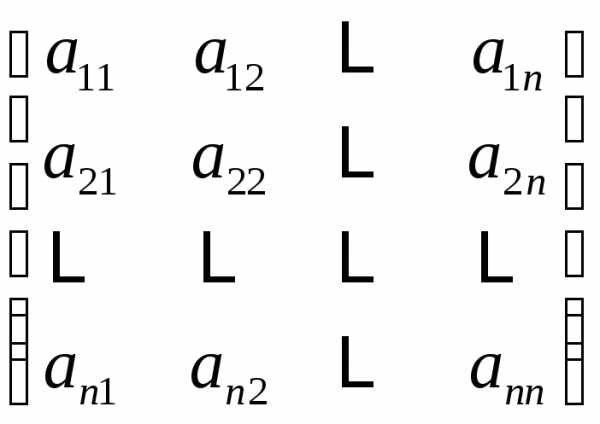
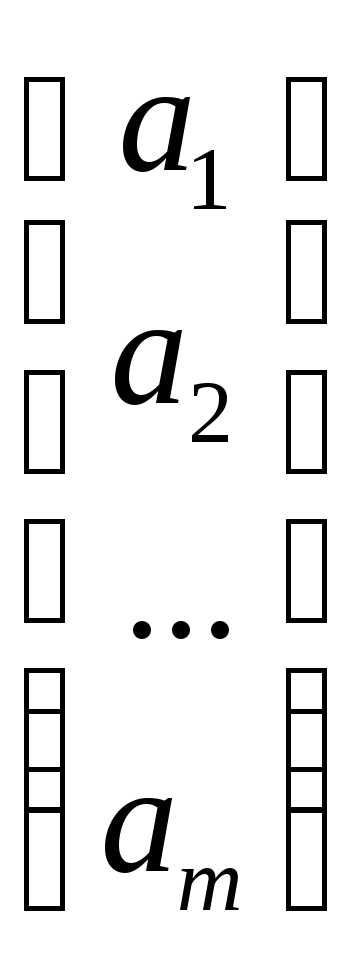

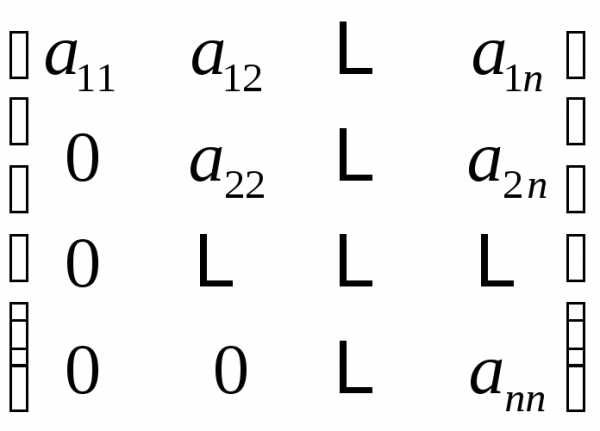
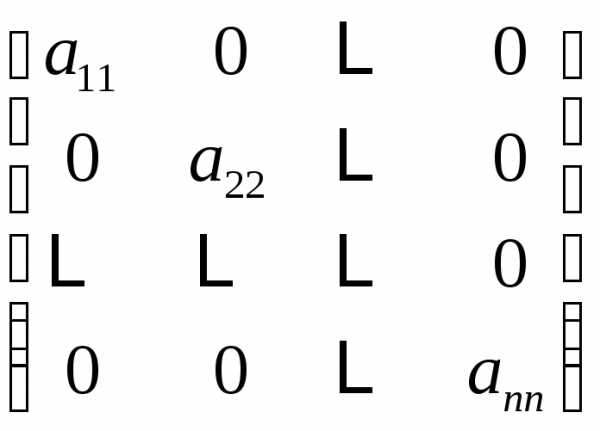
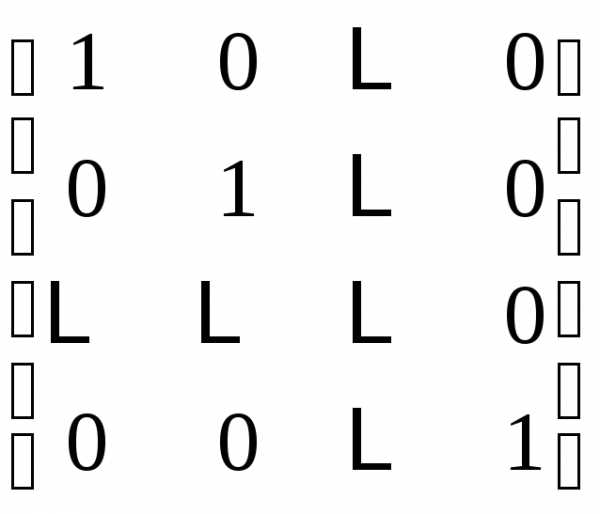
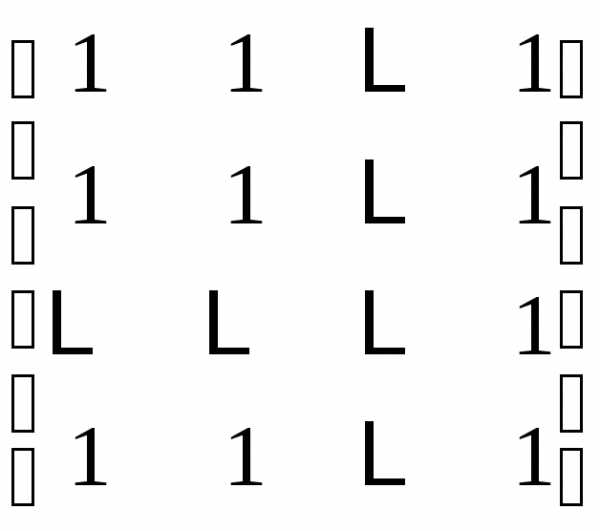

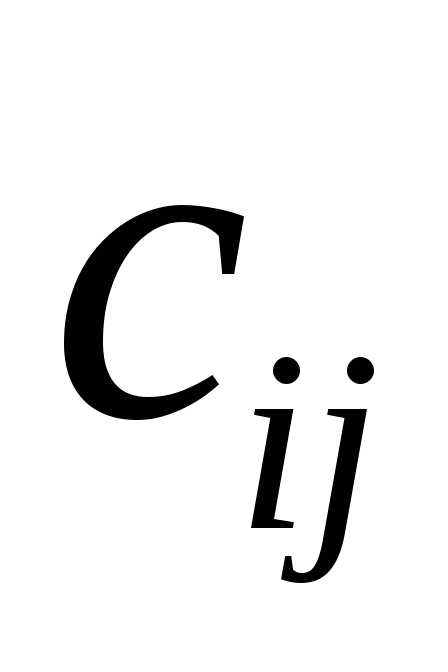 есть сумма произведений всех элементов
есть сумма произведений всех элементов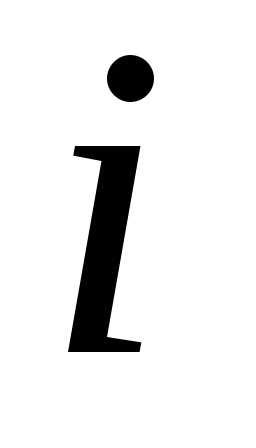 –й
строки
–й
строки на соответсвующие элементы
на соответсвующие элементы –го
столбца
–го
столбца .
.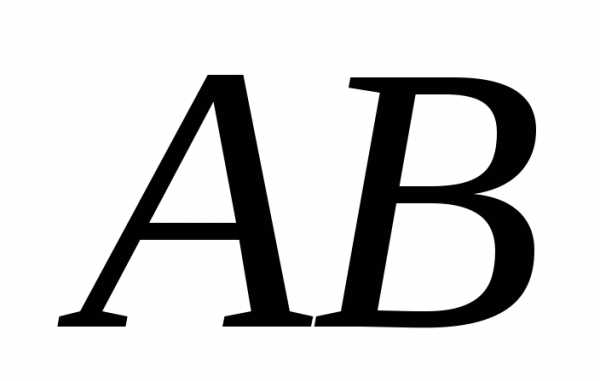 – существует, то произведение
– существует, то произведение может и не существовать. Вообще говоря,.
То есть умножение матриц не коммутативно.
Если же,
то
может и не существовать. Вообще говоря,.
То есть умножение матриц не коммутативно.
Если же,
то и
и называют коммутативными. Например,
диагональные матрицы одного порядка
коммутативны.
называют коммутативными. Например,
диагональные матрицы одного порядка
коммутативны.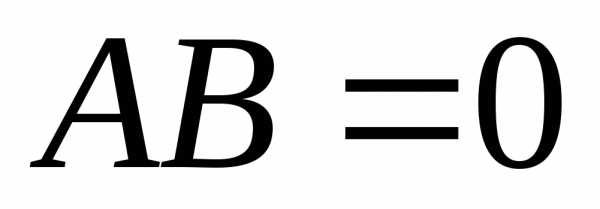 ,
то необязательно
,
то необязательно или
или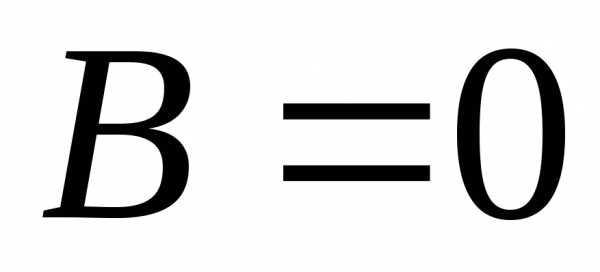 .
Т.е., произведение ненулевых матриц
может дать нулевую матрицу. Например
.
Т.е., произведение ненулевых матриц
может дать нулевую матрицу. Например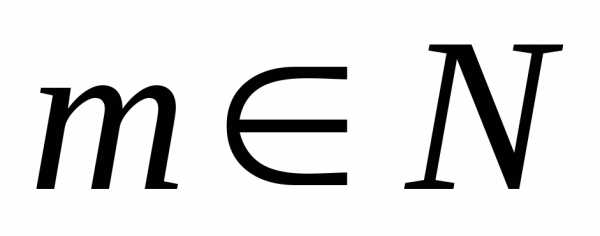 ,
то
,
то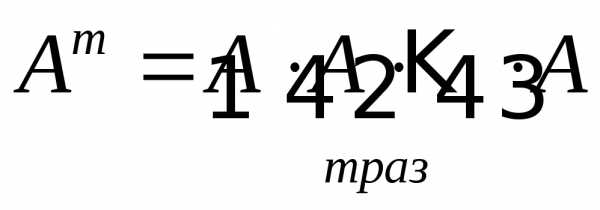 .
.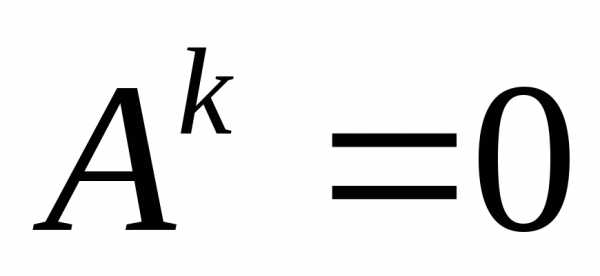 не следует, что
не следует, что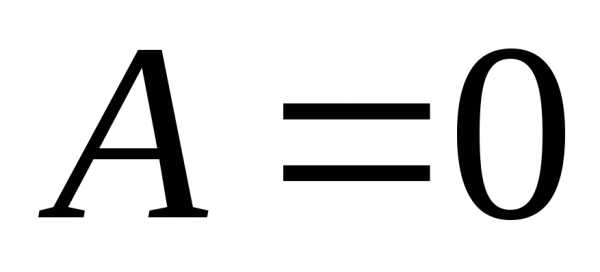 .
.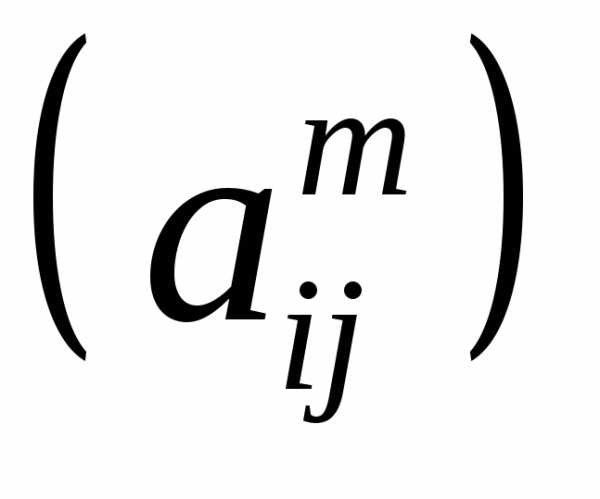 .
.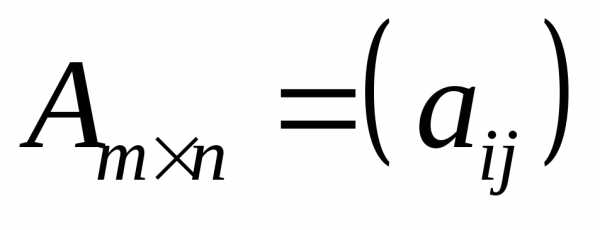 ,
, 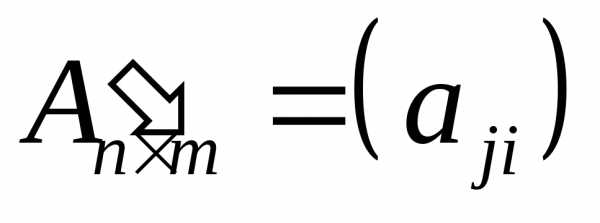
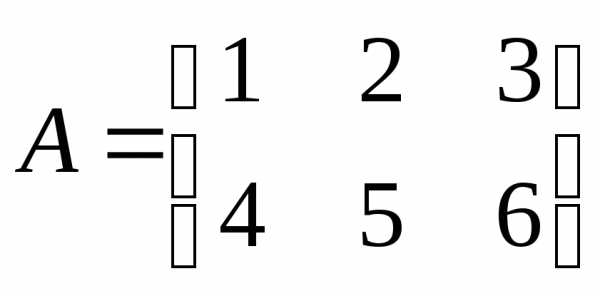 ,
, 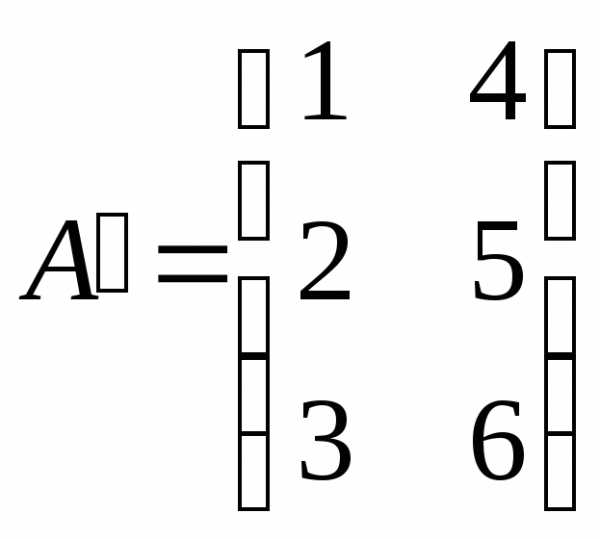 .
.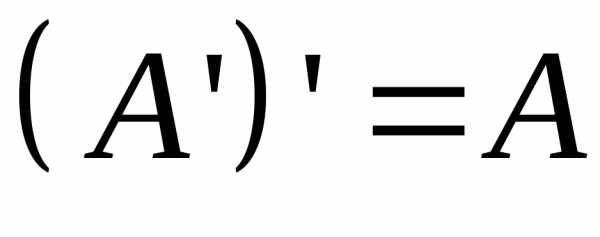
 .
.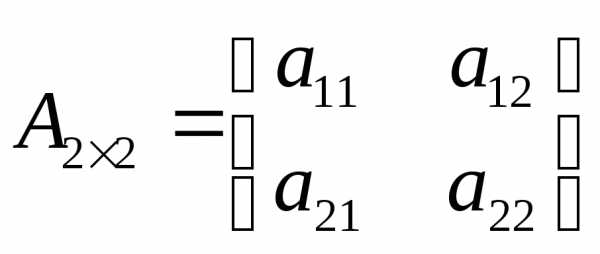 вычисляется
по правилу:
вычисляется
по правилу: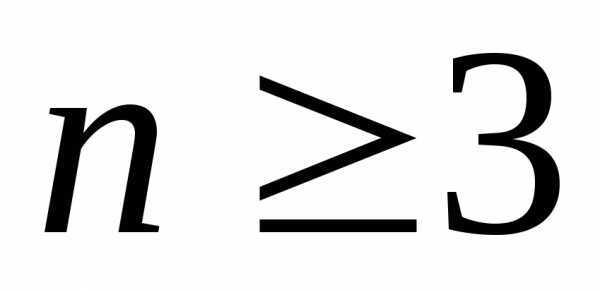 )
необходимо ввести понятия минора и
алгебраического дополнения элемента.
)
необходимо ввести понятия минора и
алгебраического дополнения элемента.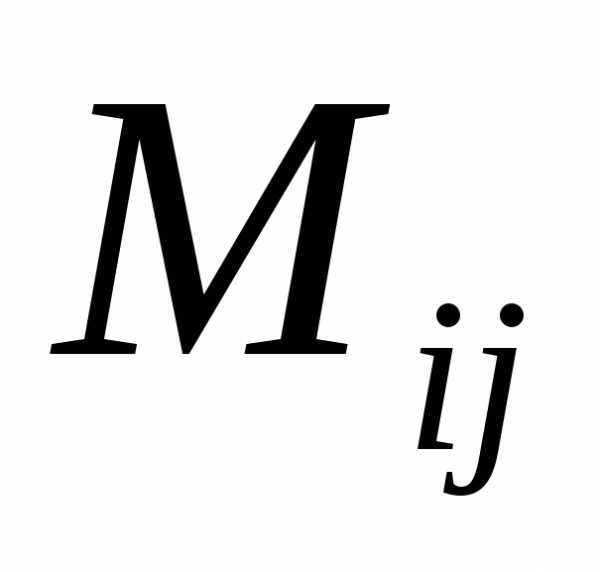 элемента
элемента  называют определитель, который получают
из матрицы
называют определитель, который получают
из матрицы ,
вычеркивая
,
вычеркивая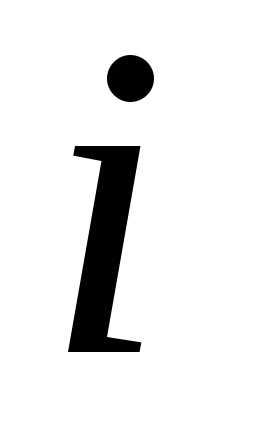 -ю
строку и
-ю
строку и -й
столбец.
-й
столбец. размером
размером :
: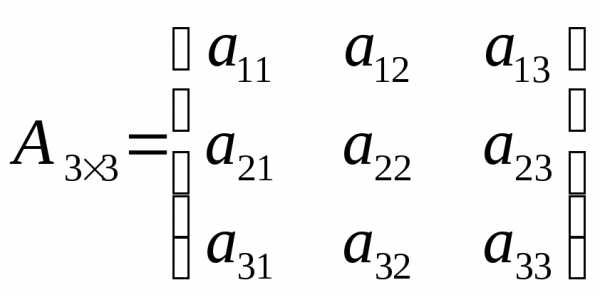 ,
, элемента
элемента называют его минор, умноженный на
называют его минор, умноженный на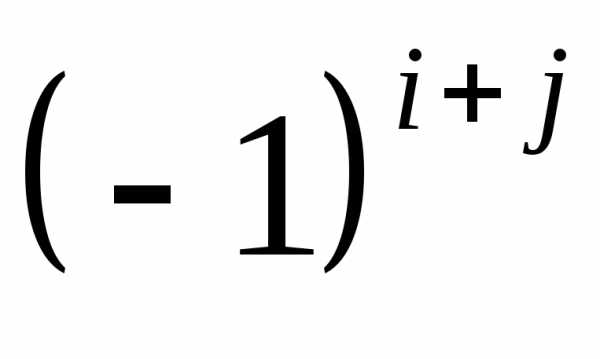 .
.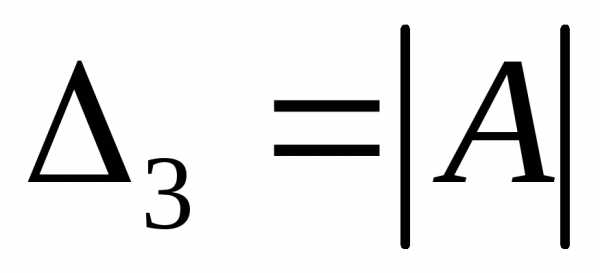 по элементам первой строки, получим:
по элементам первой строки, получим: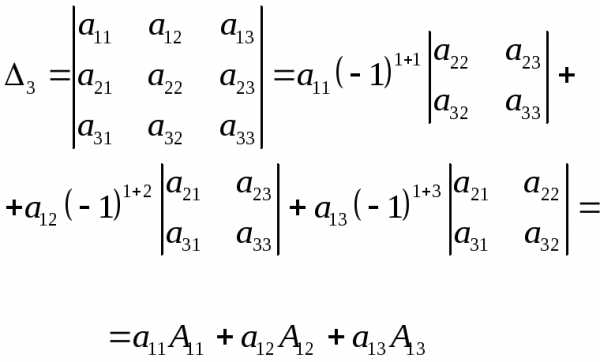

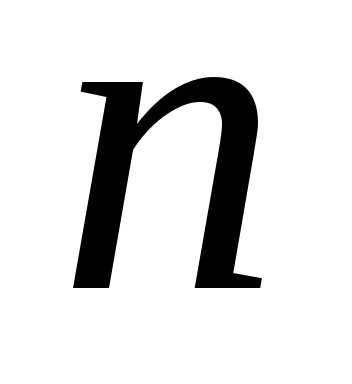 -го
порядка к вычислению
-го
порядка к вычислению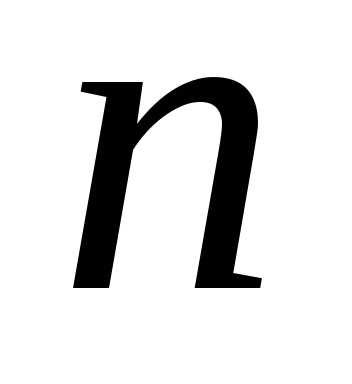 определителей
определителей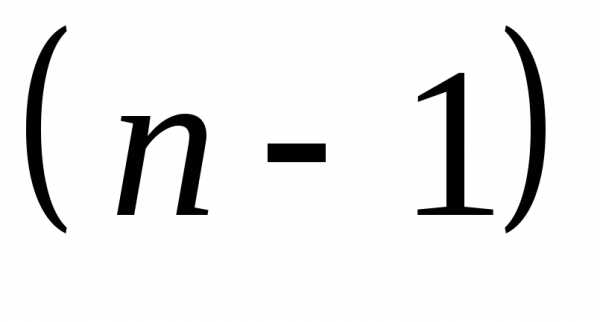 -го
порядка и, в конечном итоге, к вычислению
определителей второго порядка.
-го
порядка и, в конечном итоге, к вычислению
определителей второго порядка.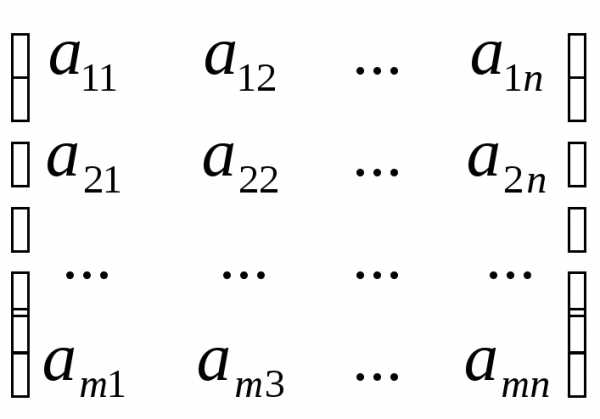
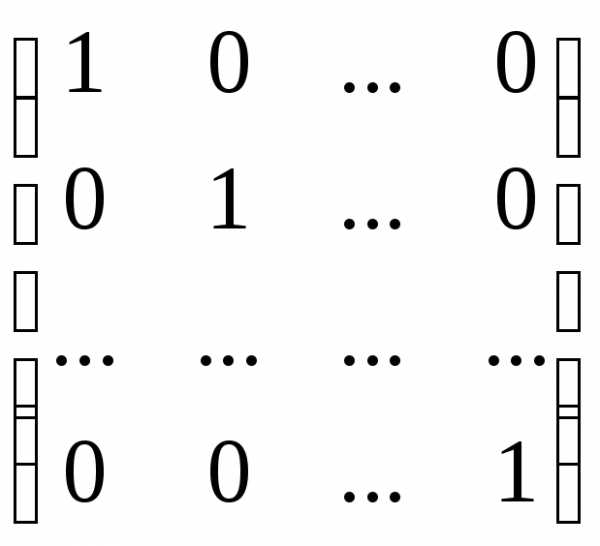 = E,
= E,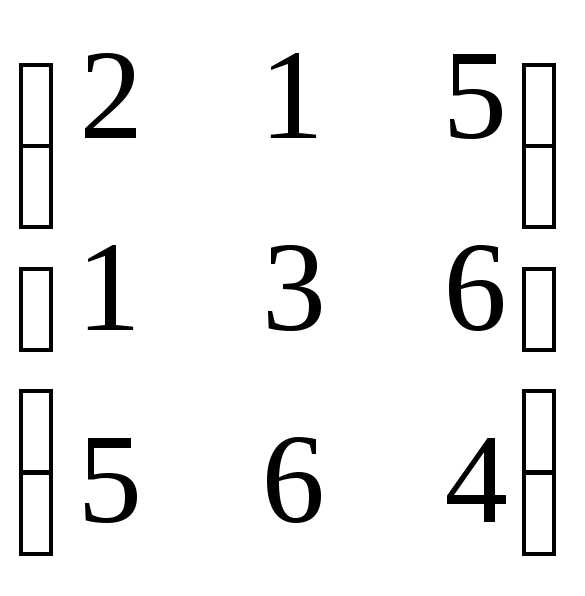 -симметрическая
матрица
-симметрическая
матрица называетсядиагональной матрицей.
называетсядиагональной матрицей.
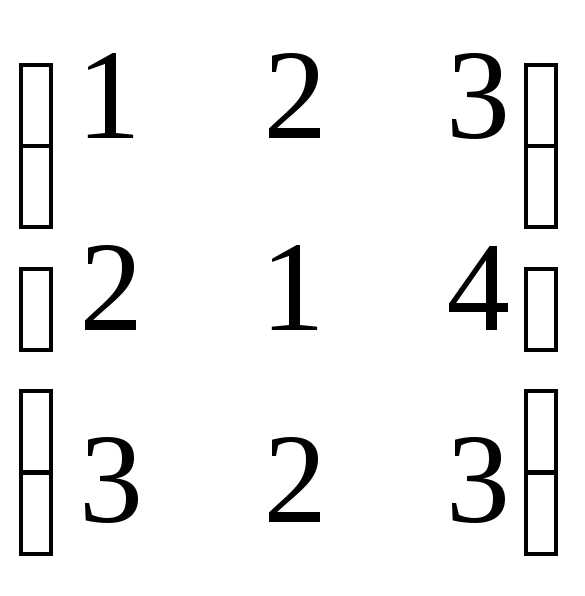 ;
B
=
;
B
=  ,
найти 2А + В.
,
найти 2А + В. ,
2А + В =
,
2А + В = 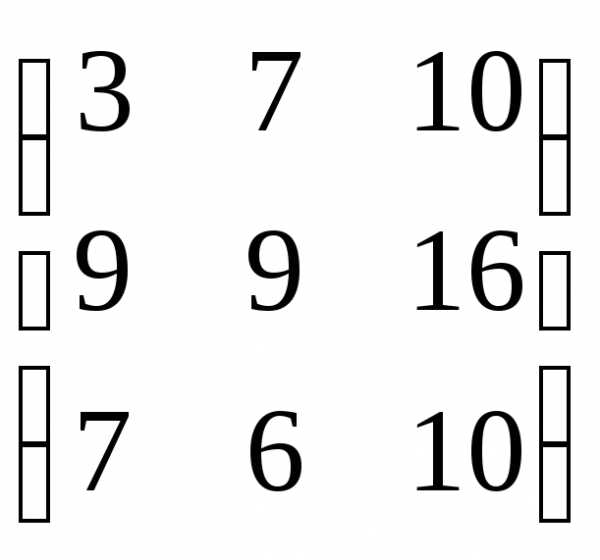 .
.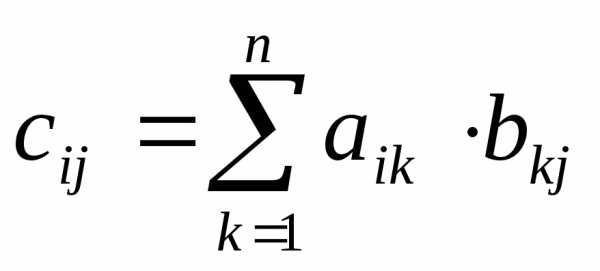 .
. ;
В = АТ=
;
В = АТ=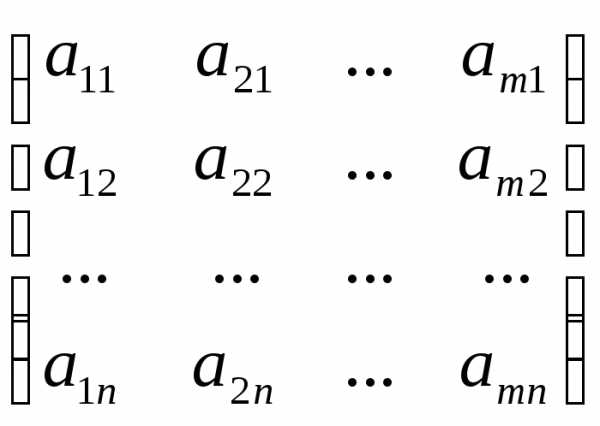 ;
;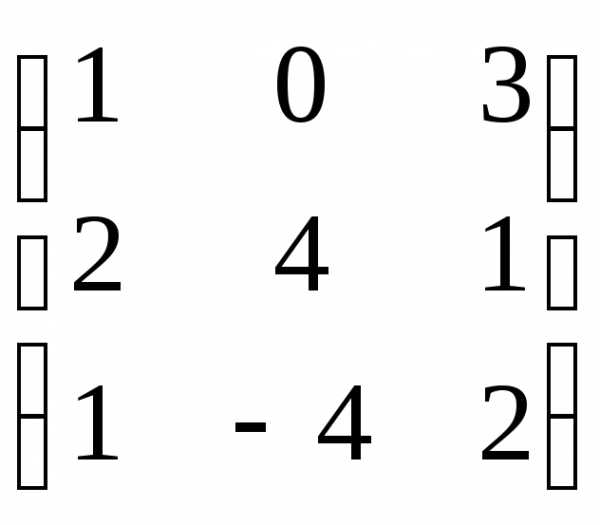 ,
В =
,
В = 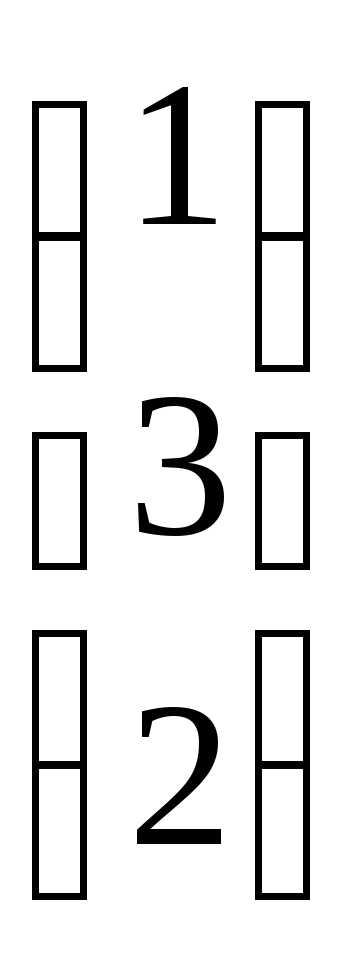 ,
С =
,
С = 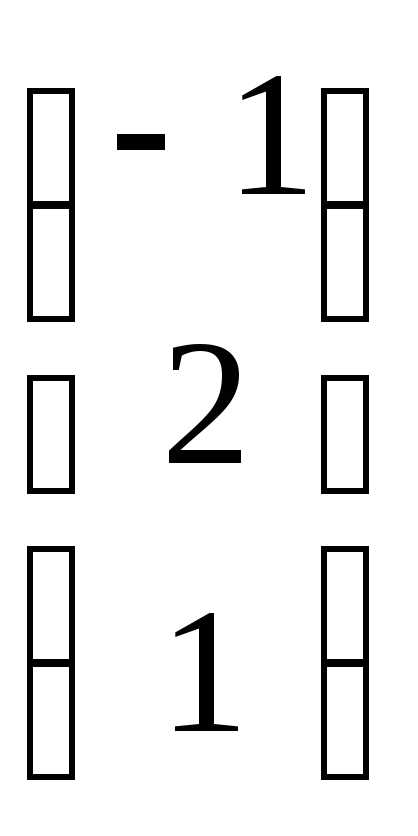 и число
= 2. Найти АТВ+С.
и число
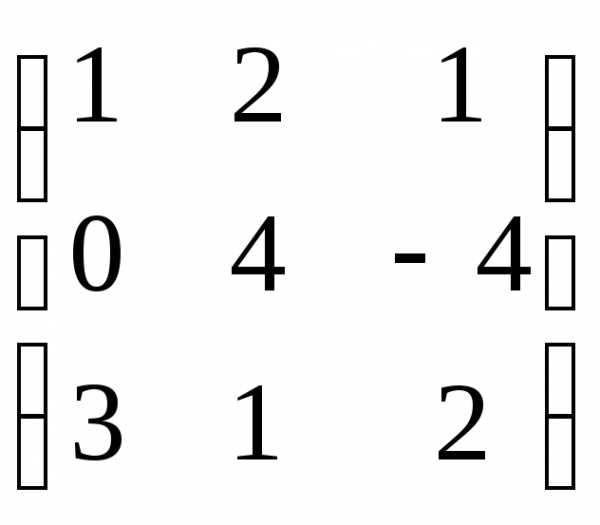
= 2. Найти АТВ+С.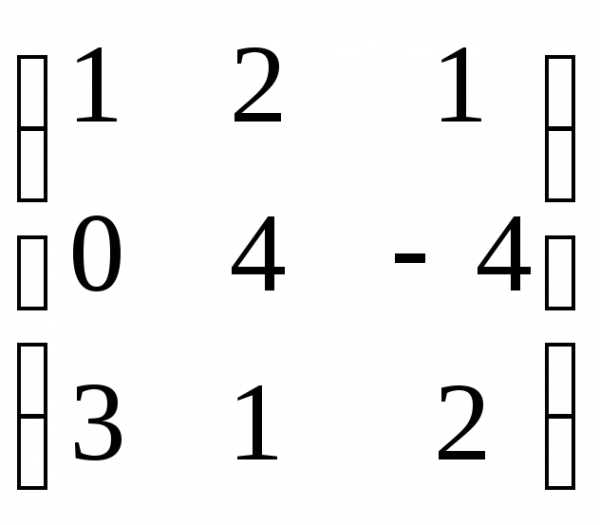 ;
ATB
=
;
ATB
= 
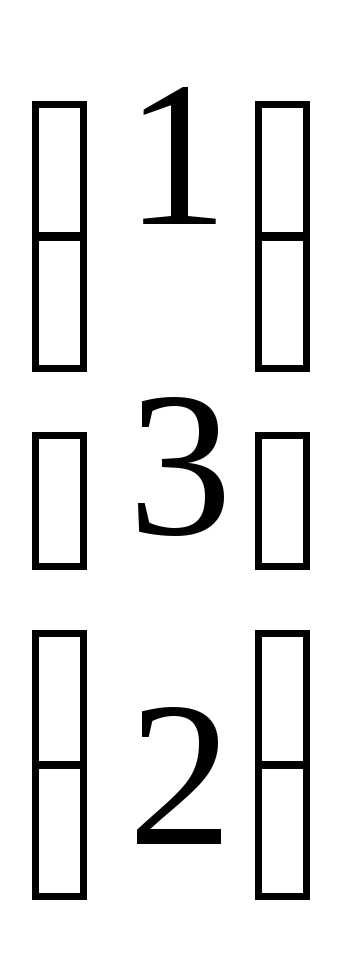 =
= 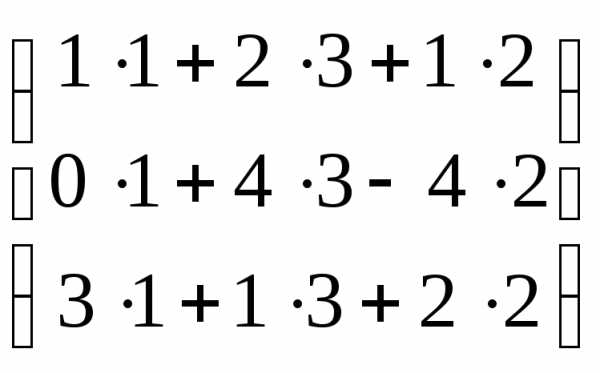 =
= 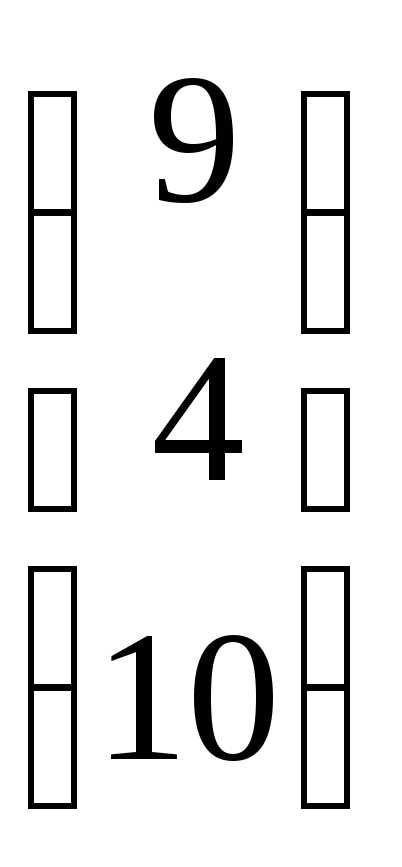 ;
;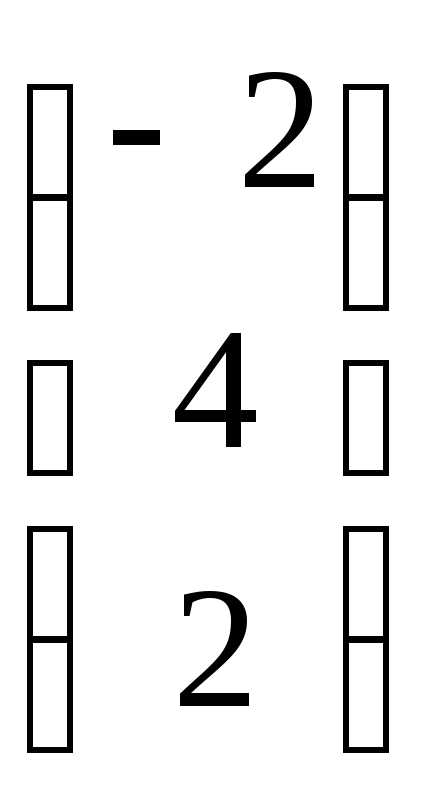 ;
АТВ+С
=
;
АТВ+С
= 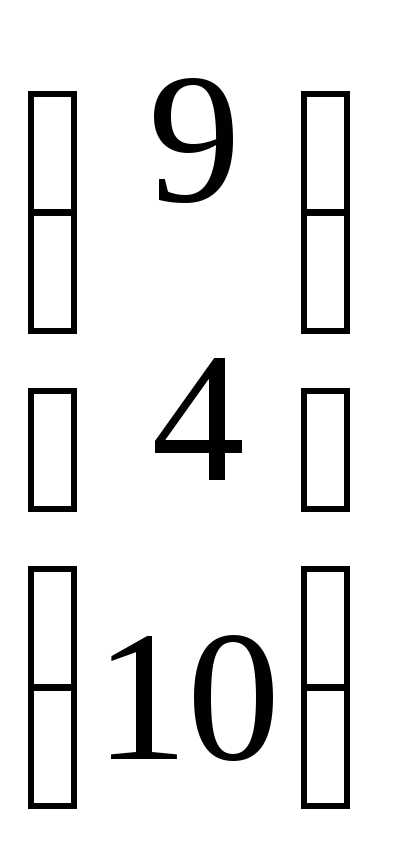 +
+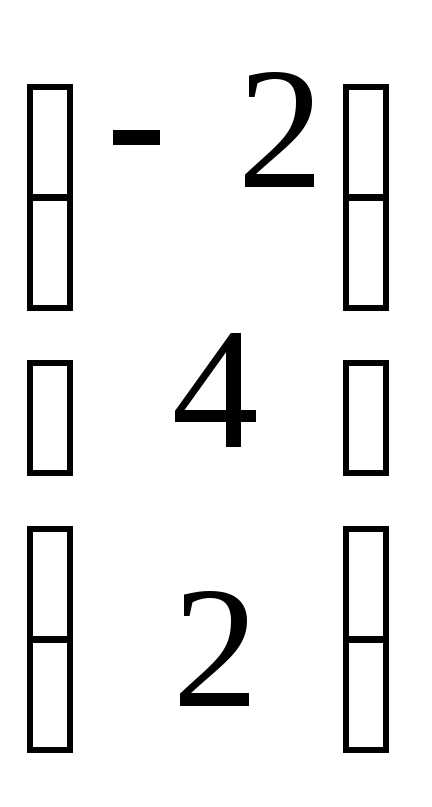 =
= 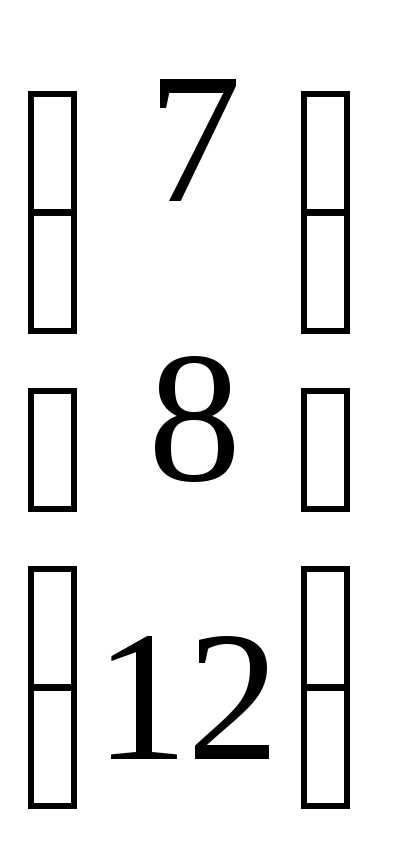 .
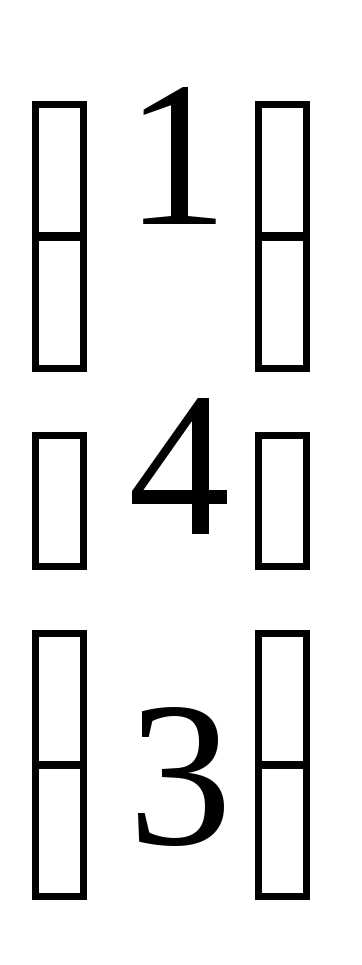
.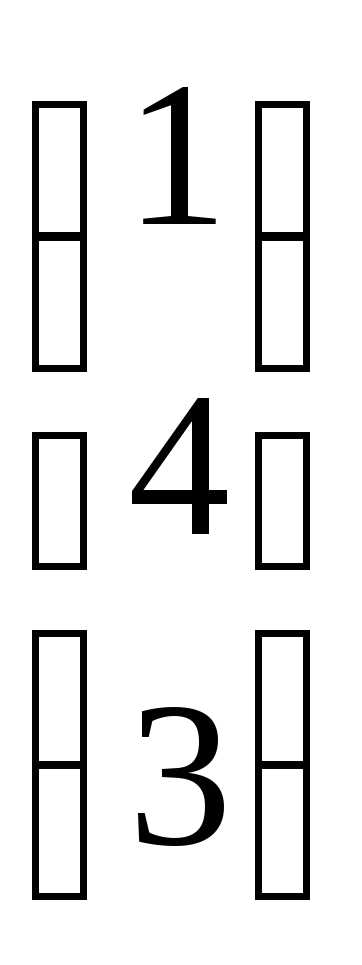 и В =
и В =  .
.
 =
= 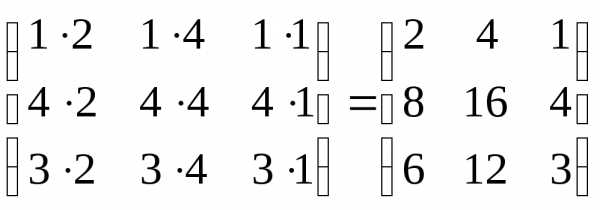 .
.
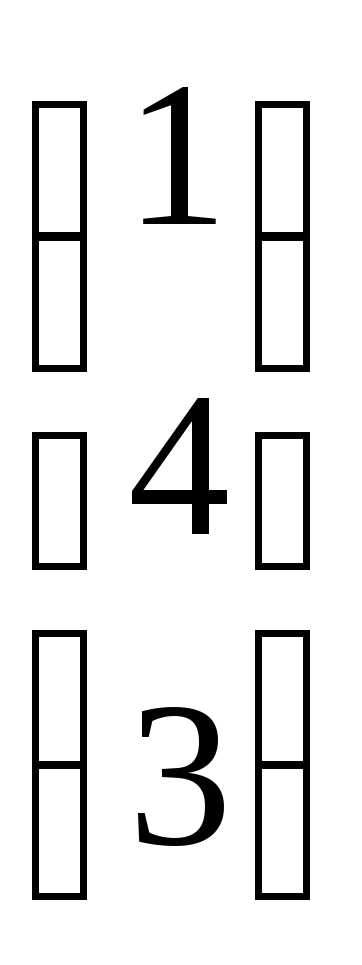 = 21
+ 44
+ 13
= 2 + 16 + 3 = 21.
= 21
+ 44
+ 13
= 2 + 16 + 3 = 21. ,
В =
,
В = 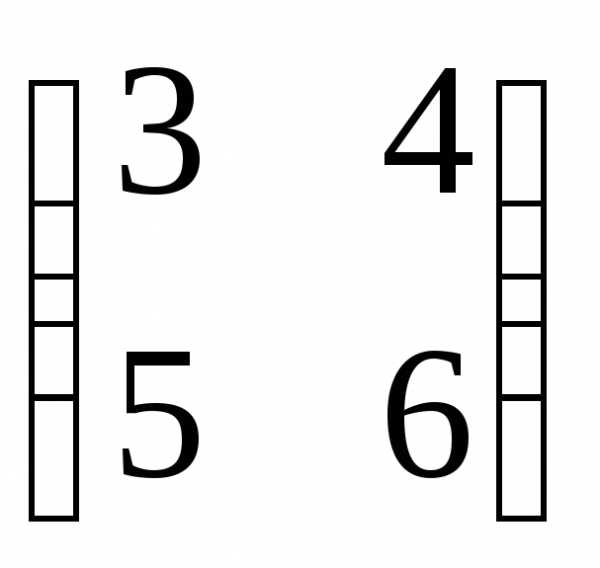

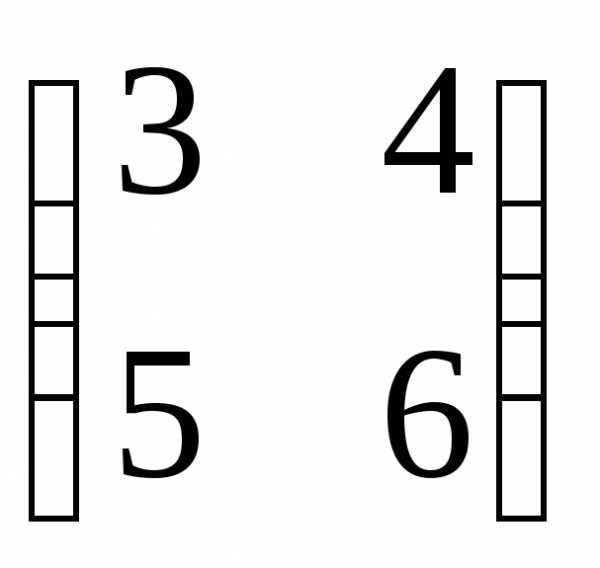 =
=
=
= 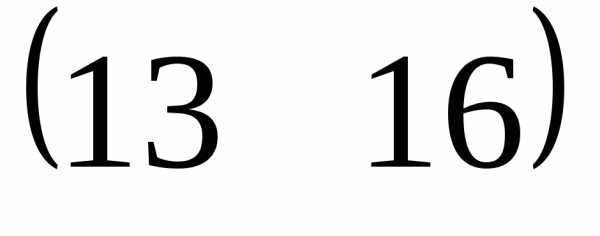 .
.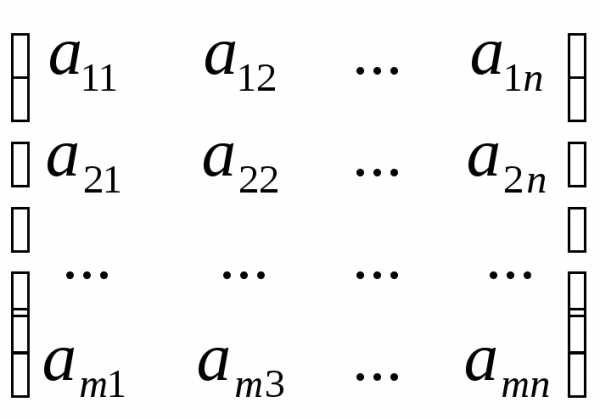

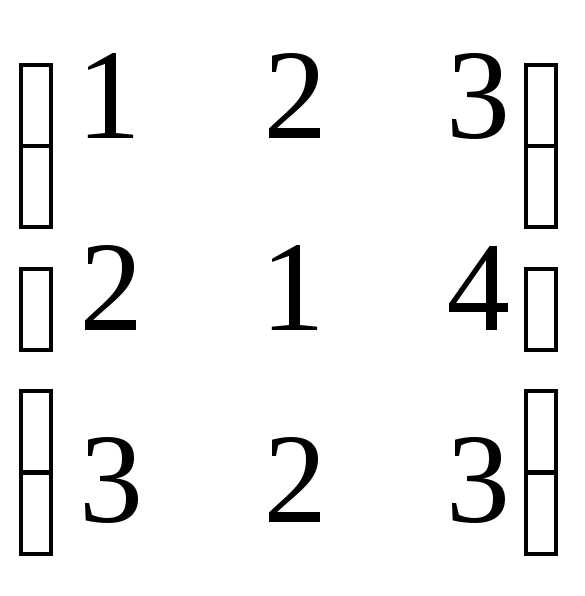 ;
B
=
;
B
= 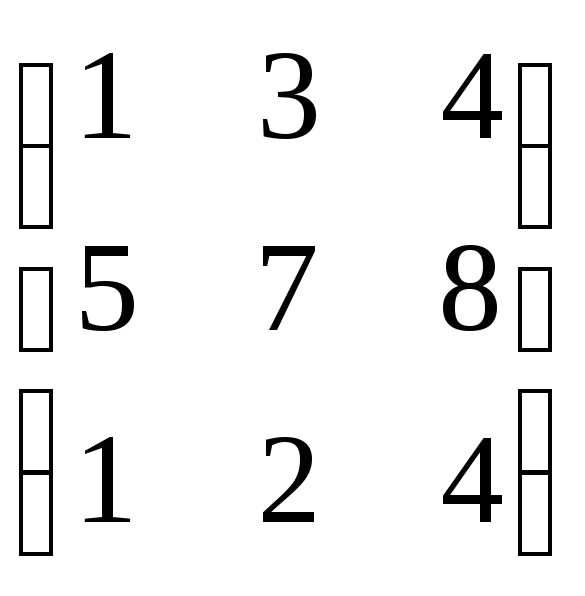 ,
найти 2А + В.
,
найти 2А + В.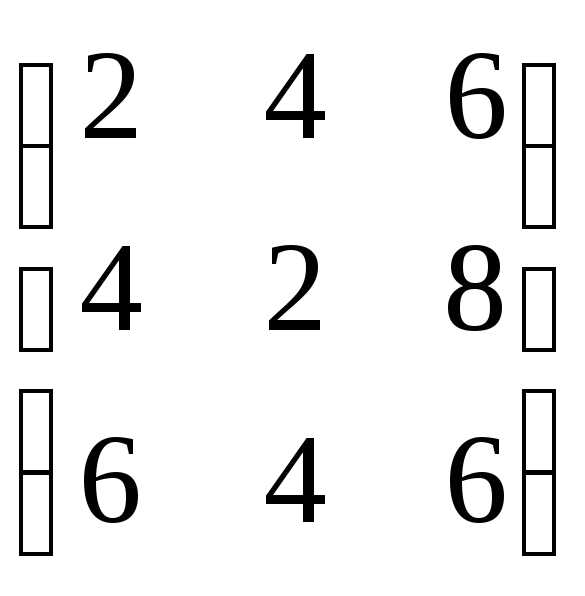 ,
2А + В =
,
2А + В =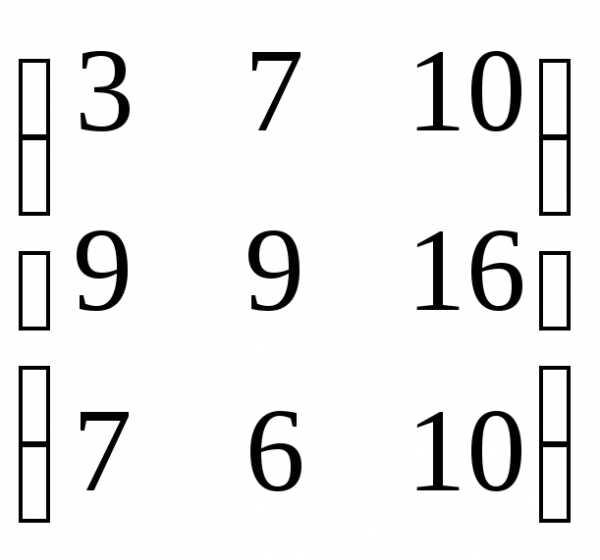 .
.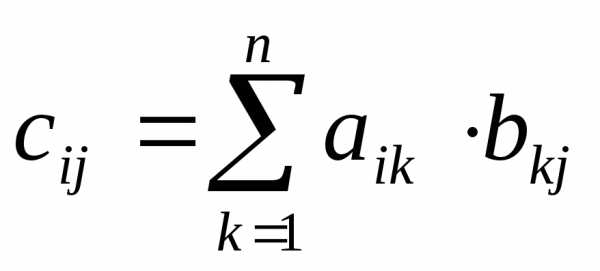 .
.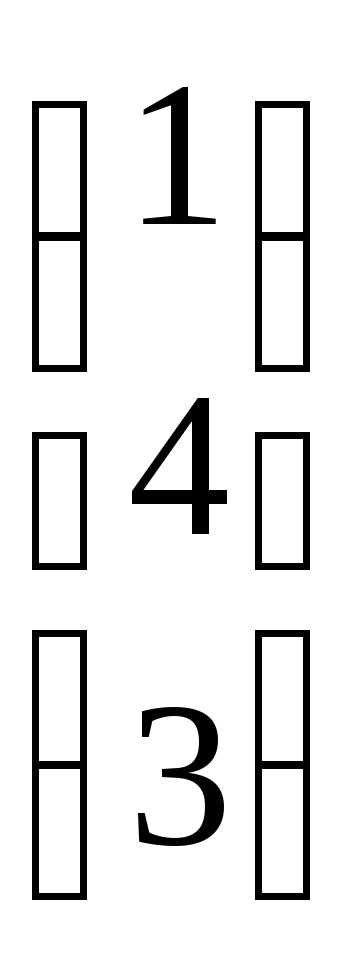 и В =
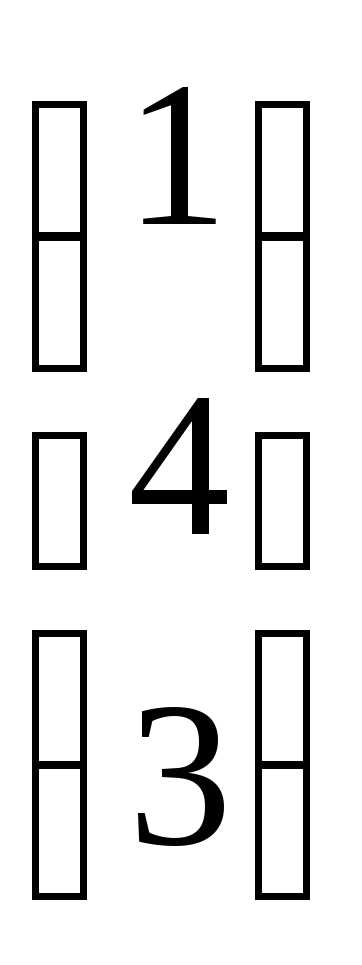
и В = .
.
 =
=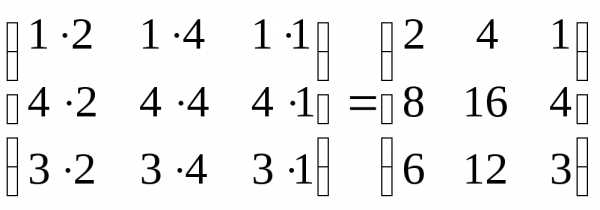 .
.
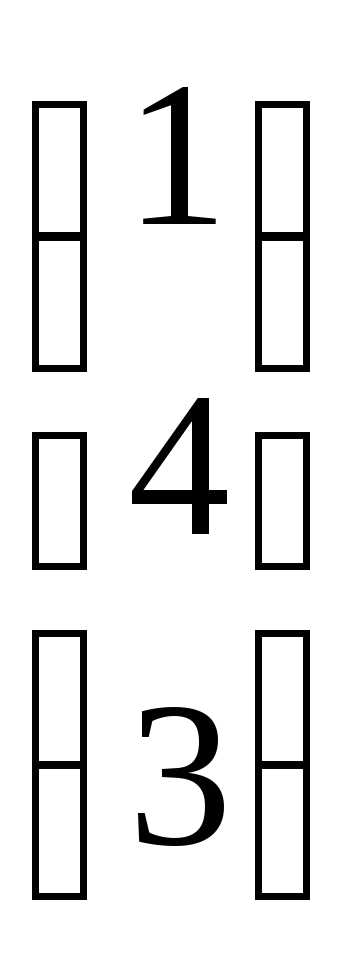 = 21
+ 44
+ 13
= 2 + 16 + 3 = 21.
= 21
+ 44
+ 13
= 2 + 16 + 3 = 21. ,
В =
,
В =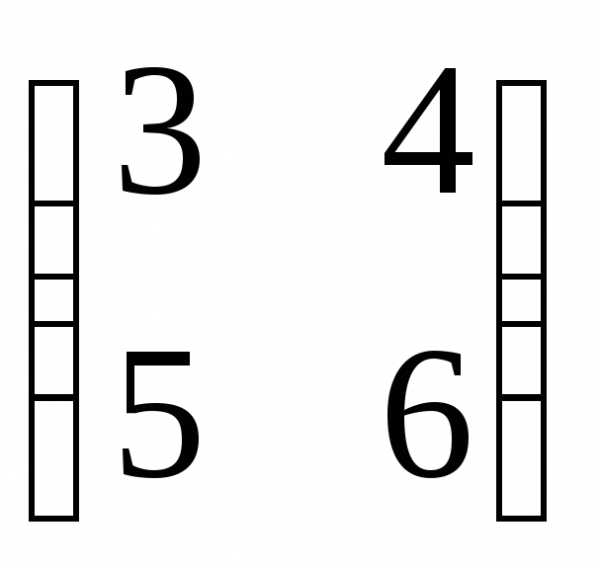
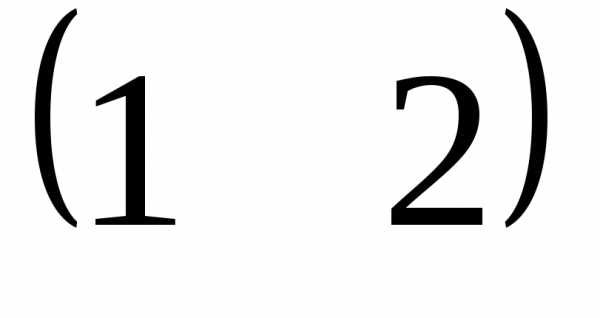
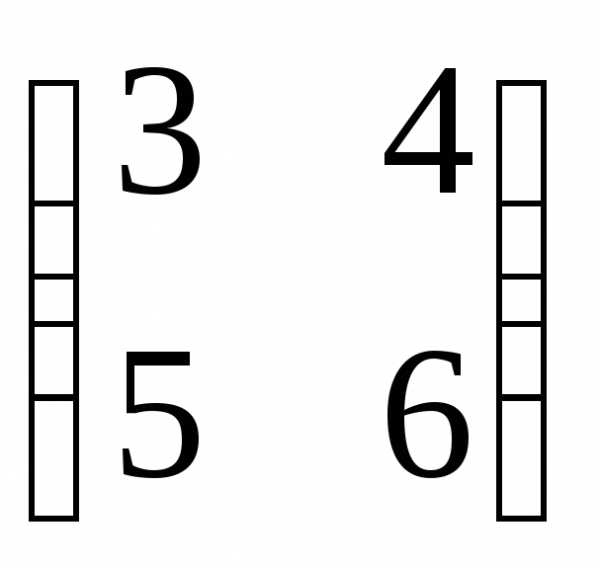 ==
==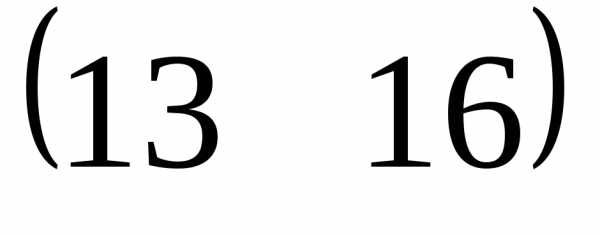 .
. называется число, которое может быть
вычислено по элементам матрицы по
формуле:
называется число, которое может быть
вычислено по элементам матрицы по
формуле: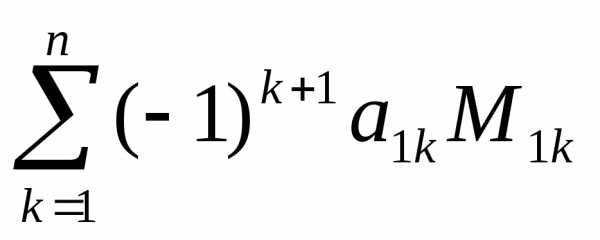 ,
где
,
где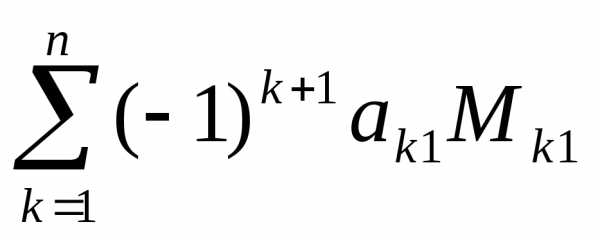
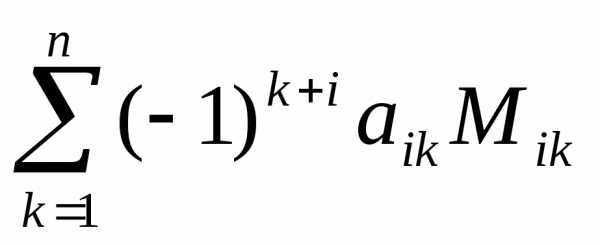 ,
i
= 1,2,…,n.
,
i
= 1,2,…,n.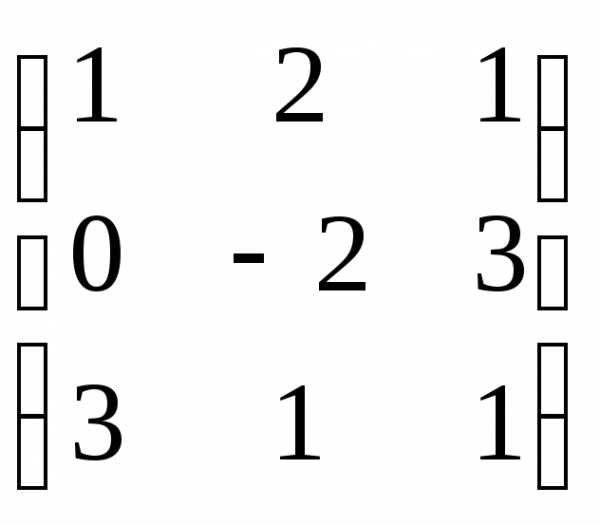
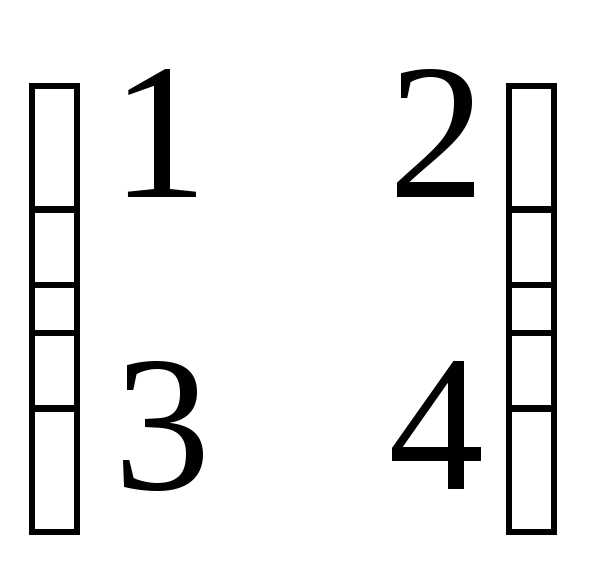 ,
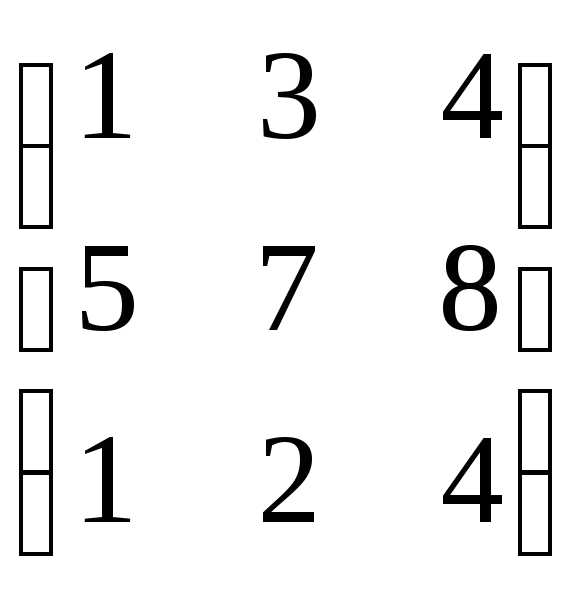
В =
,
В =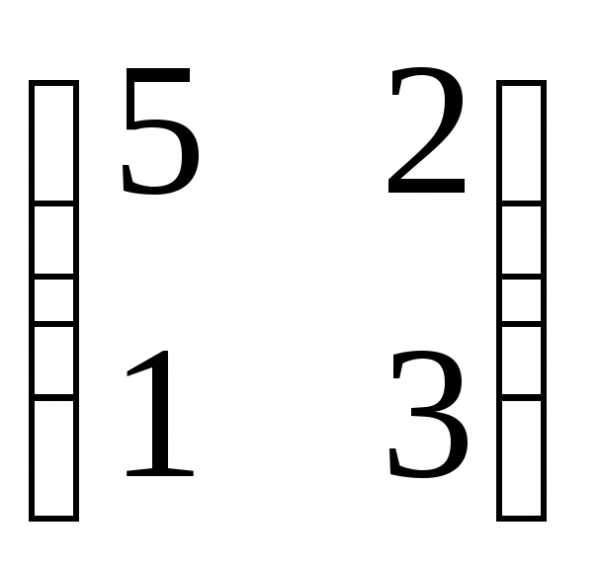 .
Найти
det (AB).
.
Найти
det (AB).
 спользуя
свойства определителей, его нужно
преобразовать так, чтоб в каком, либо
столбце или строке стало три элемента
нуля.
спользуя
свойства определителей, его нужно
преобразовать так, чтоб в каком, либо
столбце или строке стало три элемента
нуля. еперь
во второй строке появилось два нуля.
Далее, ко второму столбцу прибавим
четвёртый, умноженный на два.
еперь
во второй строке появилось два нуля.
Далее, ко второму столбцу прибавим
четвёртый, умноженный на два.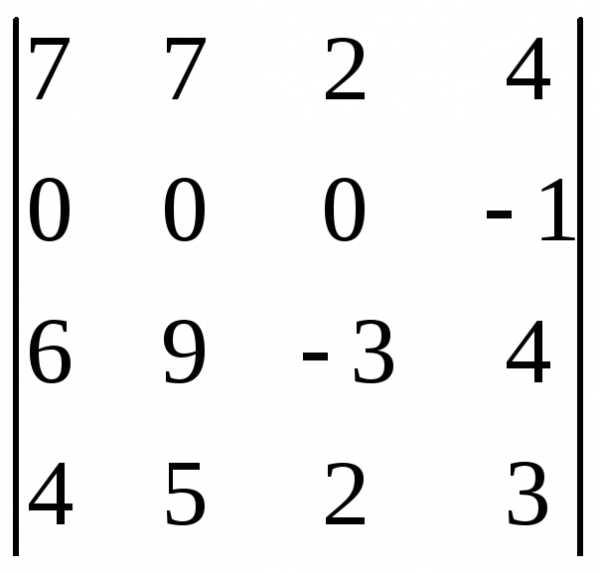 то
и требовалось сделать. Далее раскроем
данный определитель по второй строке.
то
и требовалось сделать. Далее раскроем
данный определитель по второй строке.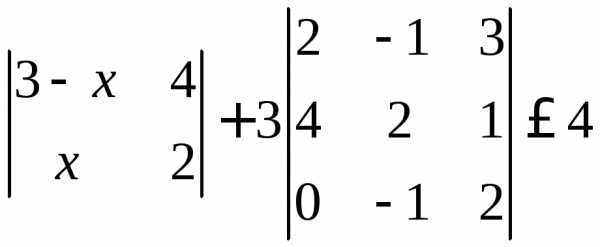
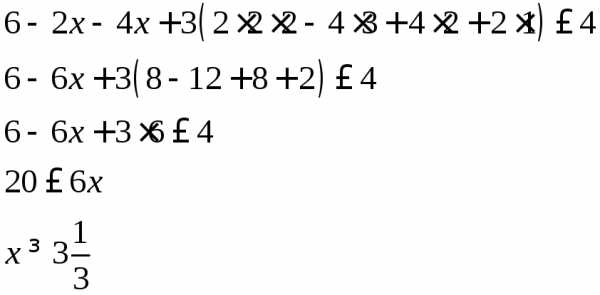

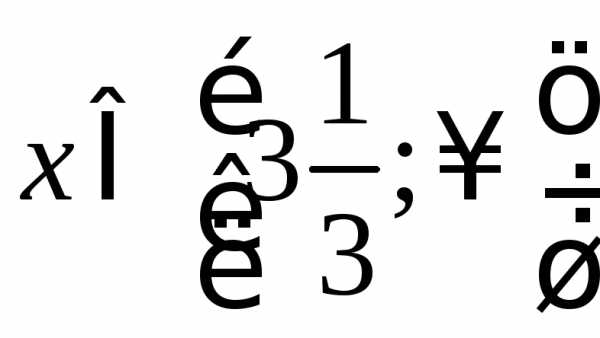
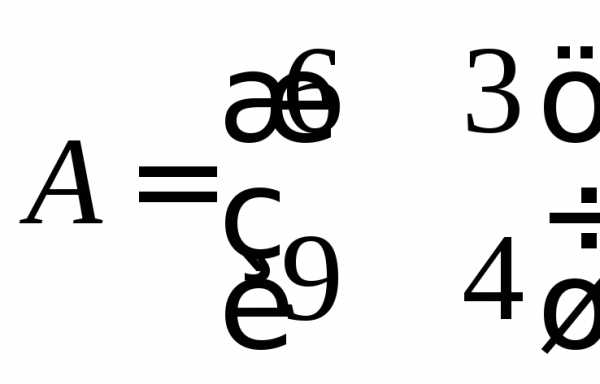 ,
, 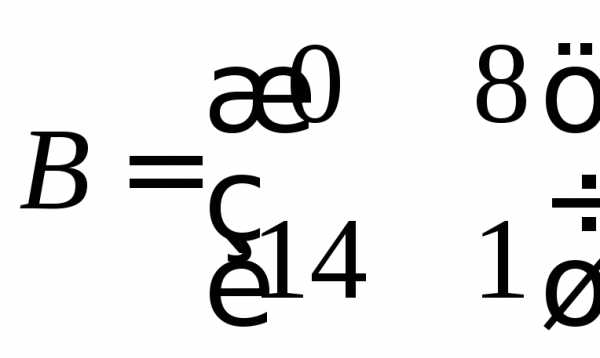 ,
,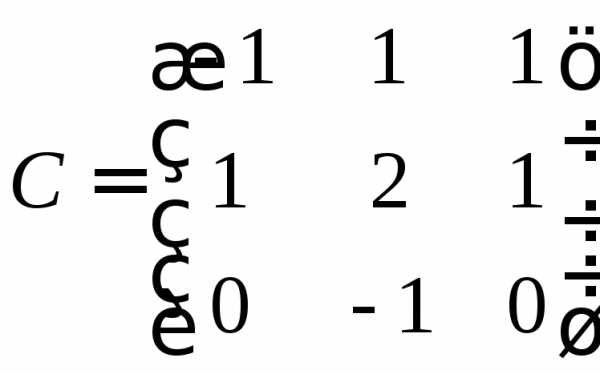 ,
,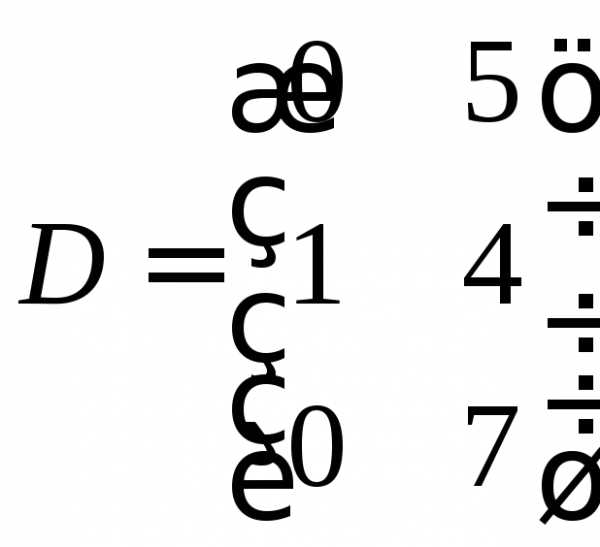
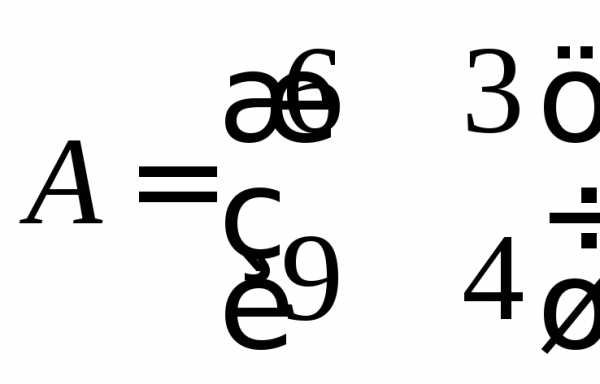
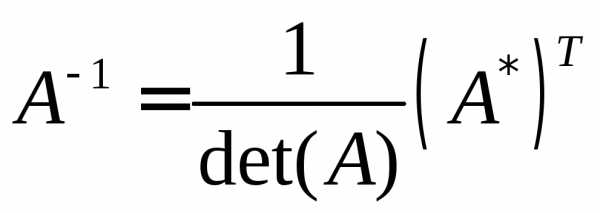 ,
, 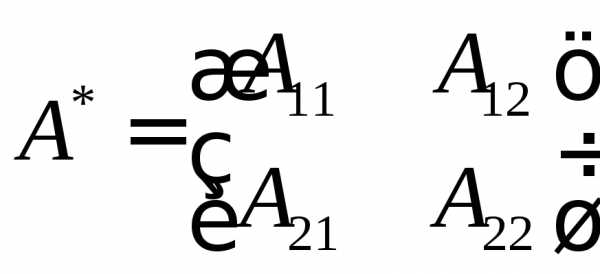
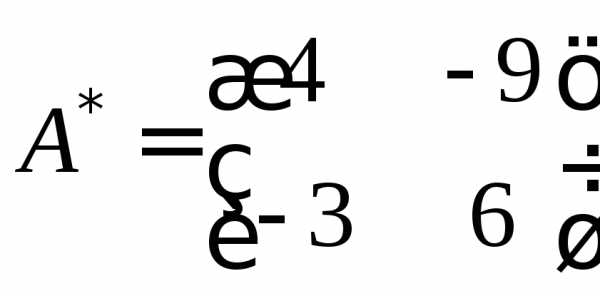
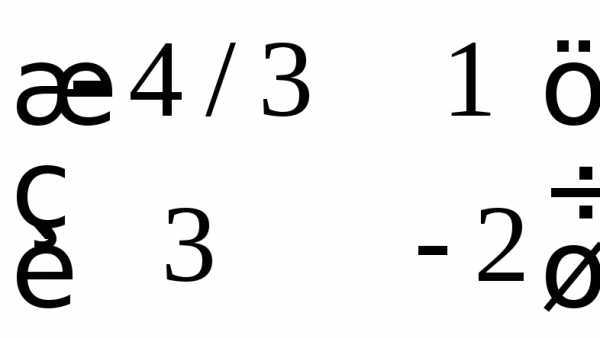
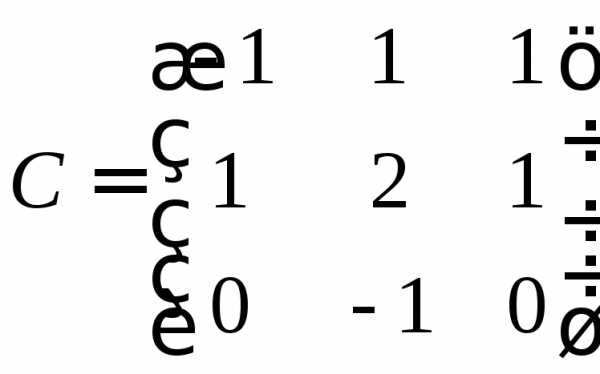 .
.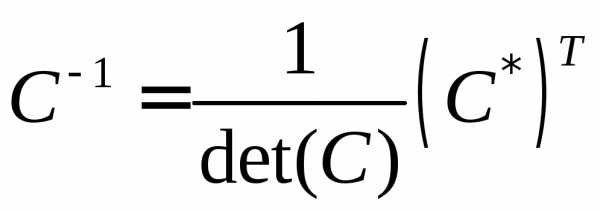 ,
, 
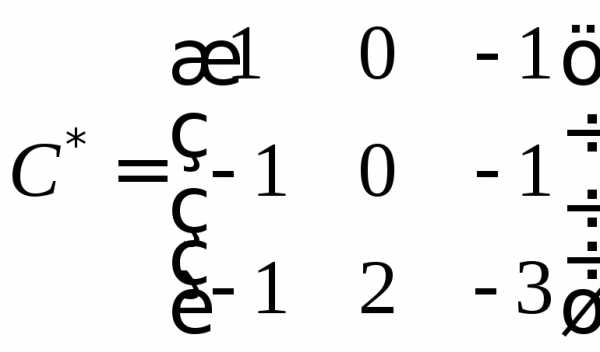
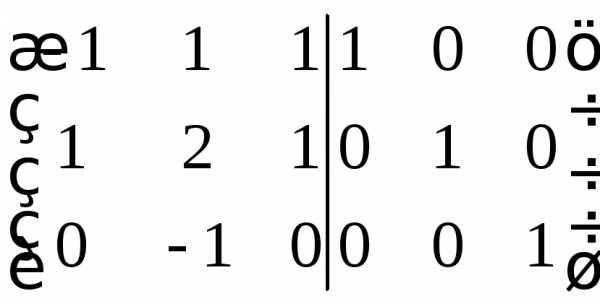
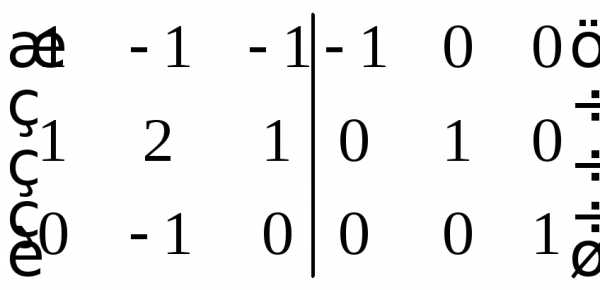


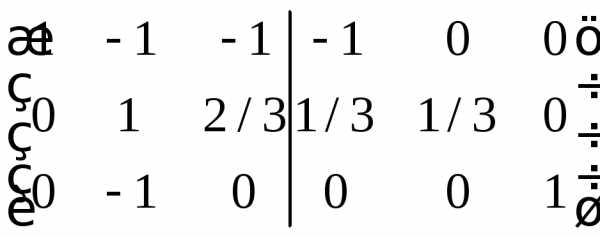


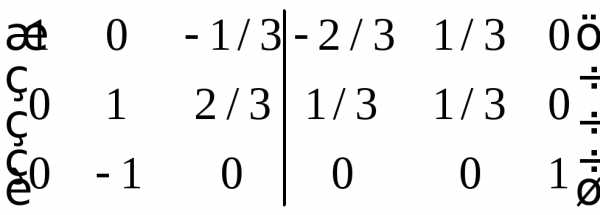

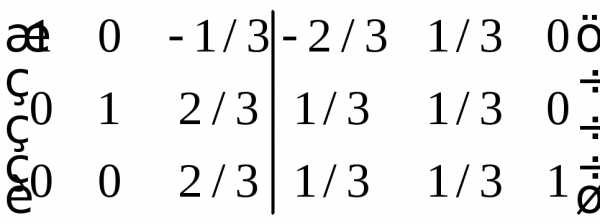





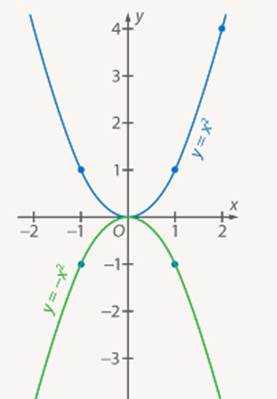
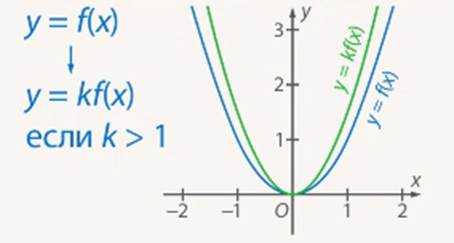




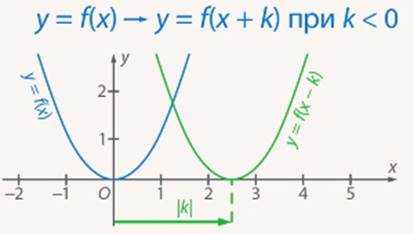


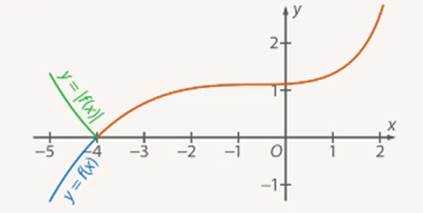




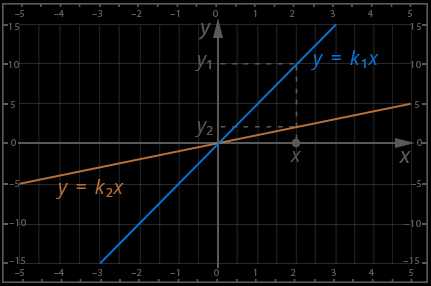
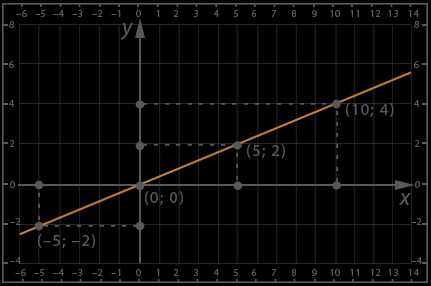
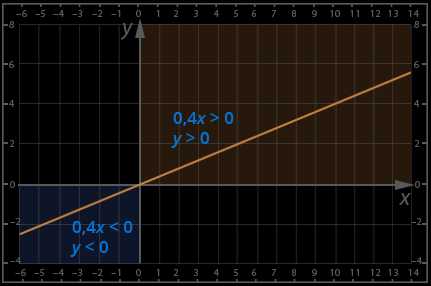

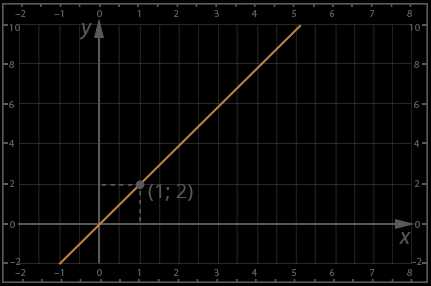
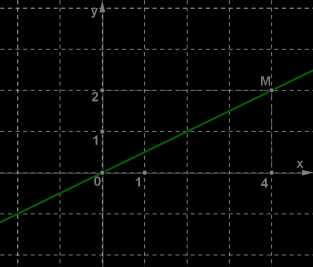
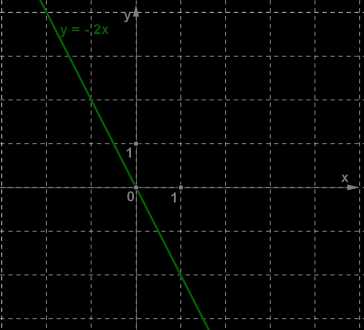
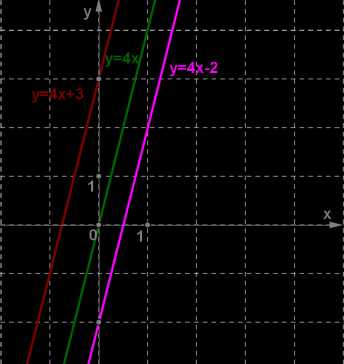
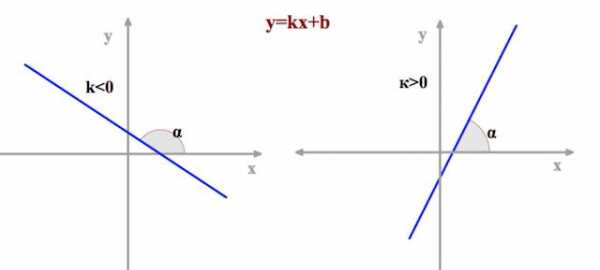
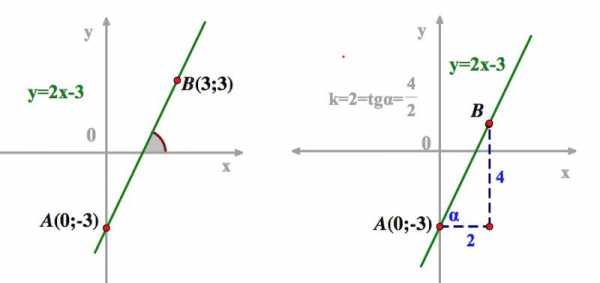
 Графики линейных функций, имеющие один и тот же угловой коэффициент, параллельны друг другу ( см. рис. слева (ниже)).
Графики линейных функций, имеющие один и тот же угловой коэффициент, параллельны друг другу ( см. рис. слева (ниже)). Частные случаи:
Частные случаи: