Теория случайных чисел
Раздел 1. Теория случайных чисел.
Все события делятся на детерминированные, случайные и неопределенные.
Если событие наступает в эксперименте всегда, оно называется достоверным , если никогда – невозможным . Это детерминированные события.
Статистическое определение вероятности: Если в опыте, повторяющемся n раз, событие появляется mA раз, тогда относительная частота наступления события:
. Р(А) – вероятность наступления события А.Для достоверного события W: Р(W)=1. Для невозможного события Æ: Р(Æ)=0.
0 £ P(A) £ 1, т.к. 0£mA £n — 0 £ hn(A) £ 1
W mA =n hn(A)=1
Æ mA =0 hn(A)=0
Все мыслимые взаимоисключающие исходы опыта называются элементарными событиями . Наряду с ними можно наблюдать более сложные события – комбинации элементарных.
Несколько событий в данном опыте называются равновозможными , если появление одного из них не более возможно, чем другого.
Классическое определение вероятности: Если n-общее число элементарных событий и все они равновозможные, то вероятность события А:
,где mA — число исходов, благоприятствующих появлению события А.
Раздел 2. Сложные события.
Теория сложных событий позволяет по вероятностям простых событий определять вероятности сложных. Она базируется на теоремах сложения и умножения вероятностей.
1) Суммой (объединением) двух событий А и В называется новое событие А+В, заключающееся в проявлении хотя бы одного из этих событий.
2) Произведением (пересечением) двух событий А и В называется новое событие АВ, заключающееся в одновременном проявлении обоих событий. А*В=АВ, АА=А, АВА=АВ.
3) Событие А влечет за собой появление события В, если в результате наступления события А всякий раз наступает событие В. АÌВ
А=В: АÌВ, ВÌА
Два события называются несовместными , если появление одного из них исключает возможность появления другого.
Если события несовместны, то АВ=Æ.
События А1 , А2 , …Аn образуют полную группу событий в данном опыте, если они являются несовместными и одно из них обязательно происходит:
Ai Aj = Æ (i ¹ j, i,j=1,2…n)
A1 +A2 +…+An = W
— событие противоположное событию А, если оно состоит в не появлении события А.
А и — полная группа событий, т.к. А+
=W, А=Æ.Теорема сложения вероятностей.
Вероятность суммы несовместных событий равна сумме вероятностей событий:
Р(А+В+С+…) = Р(А) + Р(В) + Р(С) +…
Следствие. Если события A1 +A2 +…+An — полная группа событий, то сумма их вероятностей равна 1.
P(A+ ) = P(A) + P(
) = 1Вероятность наступления двух совместных событий равна:
Р(А+В) = Р(А) + Р(В) — Р(АВ)
Р(А+В+С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) – Р(АВС)
Теорема. Если АÌВ, то Р(А) £ Р(В).
В=В1 +В2 (В1 =А) Р(В)=Р(В1 ) + Р(В2 )= Р(А) + Р(В2 )
Теорема умножения вероятностей. Условные вероятности.
Опыт повторяется n раз, mB раз наступает событие В, mАВ раз наряду с событием В наступает событие А.
hn(B) =
hn(AB) =Рассмотрим относительную частоту наступления события А, когда событие В уже наступило:
— условная вероятность события А по событию В – вероятность события А, когда событие В уже наступило.Свойства условных вероятностей.
Свойства условных вероятностей аналогичны свойствам безусловных вероятностей.
1. 0 £ Р(А/В) £ 1, т.к.
; АВ Ì В, Р(АВ) £ Р(В)2. Р(А/А)=1
3. ВÌА, — Р(А/В)=1
4.
5. Р[(A+C)/B] = Р(А/В) + Р(C/В) – Если события А и С несовместны
Р[(A+C)/B] = Р(А/В) + Р(C/В) — Р(АC/В) – Если события А и С совместны
Теорема . Вероятность произведения двух событий равна произведению вероятности одного события на условную вероятность другого.
Свойства независимых событий.
Если события А и В независимы, то независимы и каждая из пар: А и В, А и
, и В, .Если события Н1 , Н2 , …Нn независимы, то заменяя любые из них на противоположные, вновь получаем независимые события.
Формула полной вероятности.
Вероятность события В, которое может произойти совместно только с одним из событий Н1 , Н2 , …Нn , образующих полную группу событий, вычисляется по формуле:
События А1 , А2 , …Аn называют гипотезами .
Теорема гипотез (формула Байеса).
Если до опыта вероятности гипотез были Р(Н1 ), Р(Н2 )…Р(НN ), а в результате опыта произошло событие А, то условные вероятности гипотез находятся по формуле:
Пример. На трех технологических линиях изготавливаются микросхемы. Найти: 1) вероятность того, что случайно выбранное изделие оказывается бракованным; 2) вероятность того, что если изделие дефектно, то оно изготовлено на 1 линии.
Рассмотрим события: Н1 , Н2 ,…Нi ,…,НN (полная группа событий)– изделие изготавливается i линией; А{изделие с браком}.
1) Р(А)=0,25*0,05+0,35*0,04+0,4*002=0,0345=3,45%
2)
Схема последовательных испытаний Бернулли.
Проводится серия из n испытаний, в каждом из которых с вероятностью р может произойти событие А, с вероятностью q=1-р событие
.Вероятность наступления события А не зависит от числа испытаний n и результатов других испытаний.
Такая схема испытаний с двумя исходами (событие А наступило либо не наступило) называется схемой последовательных испытаний Бернулли.
Пусть при n испытаниях событие А наступило k раз, (n-k) раз событие
. — число различных комбинаций события АВероятность каждой отдельной комбинации:
Вероятность того, что в серии из n испытаний событие А, вероятность которого равна р, появится k раз:
— условие нормировки. Пример. Вероятность изготовления нестандартной детали равна р=0,25, q=0.75. Построить многоугольник распределения вероятностей числа нестандартных деталей среди 8 изготовленных.N=8 p=0.25 q=0.75
Если k0 – наивероятнейшее число, то оно находится в пределах:
np-q £ k0 £ np+q
Если число (np+q) нецелое, то k0 – единственное
Если число (np+q) целое, то существует 2 числа k0 .
Предельные теоремы в схеме Бернулли.
mirznanii.com
Вероятностная теория чисел // Алексей Буфетов ≪ ∀ x, y, z
Цель данного курса — показать, как вероятностные методы и интуиция помогают отвечать на теоретико-числовые вопросы. Я расскажу про два существенно разных сюжета.
1. Правильные гипотезы
Верно ли, что простых чисел-близнецов бесконечно много? Верно ли, что любое четное число раскладывается в сумму двух простых? Ответы на эти вопросы, формально говоря, еще не получены. Однако, существуют правдоподобные гипотезы, дающие куда более точную информацию: так, если — количество простых чисел-близнецов, меньших , то (значение константы также предсказывается). Эта гипотеза следует из простых вероятностных соображений и подтверждается численными данными. Вероятностные «прикидки» позволяют сделать предположения и в ряде других известных вопросов (например, гипотеза Гольдбаха, гипотеза Римана), которые тоже подтверждаются численными экспериментами.
Кажется странным, что в детерминированной ситуации (число уж либо простое, либо нет) оказывается полезным вероятностный подход. Причину можно попытаться описать следующим образом: простые числа определяются свойствами относительно умножения, а относительно сложения никакой ощутимой «структуры» у них нет. Поэтому относительно сложения они ведут себя «случайным» образом.
2. Типичное число простых множителей натурального числа
Пусть — число различных простых делителей натурального числа n. Выберем n равномерно случайно из для большого . Чему равно типичное значение ?
Оказывается, для почти всех мы имеем . Более того, мы докажем теорему Эрдеша-Каца для . Эта теорема утверждает, что имеет порядок и описывается гауссовским распределением.
На этом материале мы познакомимся с базовыми теоремами теории вероятностей: законом больших чисел и центральной предельной теоремой.
Программа:
Базовые понятия: конечное вероятностное пространство, случайные величины, независимость. Множество как вероятностное пространство. Делимость на различные простые как (асимптотически) независимые события. Вероятностная модель Крамера простых чисел.
Улучшенная модель Крамера. Гипотезы: асимптотика количества простых чисел-близнецов, асимптотика количества разложений четного числа в сумму двух простых.
Закон больших чисел и центральная предельная теорема для бернуллиевских величин. Эквивалентная формулировка гипотезы Римана: функция Мебиуса «случайна».
Теорема Эрдеша-Каца: почти всякое натуральное число имеет примерно простых делителей. Более того, число простых делителей удовлетворяет центральной предельной теореме.
По курсу предполагается выдача листочков с задачами. Никаких предварительных знаний по теории вероятностей и теории чисел не предполагается.
Материалы: Листок 1 [pdf 182 KB], Листок 2 [pdf 199 KB]
Алексей Игоревич Буфетов
Летняя школа «Современная математика», г. Дубна
20-27 июля 2016 г.
forany.xyz
Закон больших чисел и теория вероятностей — научная основа анализа статистических данных
В решении важнейшей задачи установление и количественное выражение закономерностей и взаимозависимости социальных явлений статистическая наука опирается на закон больших чисел (ЗБЧ), смысл которого состоит в том, что правильности и закономерности социальных явлений могут быть обнаружены только при их массовом наблюдении.
Специфика статистического количественного анализа социальных фактов, в которых проявляется смысл закона больших чисел, заключается в том, что сделанный на его основе вывод, обнаруженная тенденция, закономерность относятся к совокупности («большому числу») как таковой. Иными словами, закон больших чисел лежит в основе самой логики статистического умозаключения; на основе ЗБЧ выявляется массовая закономерность.
Для статистических закономерностей весьма характерно сложное переплетение внутренних и внешних причин, необходимого и случайного. Эти закономерности образуются в результате действия внутренних необходимых причин.
Множество вариаций и случайных отклонений сглаживаются (элиминируют) именно в массе, что приводит к образованию статистических закономерностей.Проявление такой закономерности и есть результат действия закона больших чисел, которое состоит в том, что совокупность большого числа случайных явлений имеет определенные, не зависящие от случая характеристики, выражаемые количественными, показателями. То есть представление о ЗБЧ и его действии нельзя отрывать от представления о статистической закономерности как формы, в которую облекается закономерность массового явления, изучаемая статистикой с количественной стороны. Причем ЗБЧ проявляется тем отчетливее, чем крупнее статистическая совокупность.
Массовые закономерности, а вместе с ними и ЗБЧ, проявляются в самых различных областях действительности. Особенно наглядны они в области демографии, криминальной статистике.
В малом числе наблюдений (например, отдельные преступления) случайные факторы не дают возможности обнаружить закономерность. Напротив, при суммировании большого числа единичных явлений случайности парализуют друг друга, что позволяет установить законы, которые при малых масштабах маскируются индивидуальными отклонениями.
Статистическая закономерность — это не особая форма движения материи, а лишь внешнее проявление этого движения в статистических распределениях и обобщающих статистических характеристиках. Статистически установленные правильности в изменениях количественных показателей, повторяемость и устойчивость фактов свидетельствуют лишь о том, что в исследуемом массовом явлении заложена известная закономерность, вскрытие которой составляет задачу соответствующей науки (например, криминологии, социологии).
Закономерности массового явления, объективные связи, заложенные в этом явлении, находят свое выражение не в отдельных показателях, а в средней величине, в характере распределения.
Стоит отмстить, что закон больших чисел не создает уровней, а лишь регулирует случайные отклонения от заданных природой данного явления уровней.
Таким образом, закон больших чисел основывается иа понятии случайности и вероятности уменьшение степени случайности и возрастание степени вероятности наличия определенного признака происходит по мере увеличения статистической совокупности.
Естественнонаучное обоснование, точная формулировка и условия применимости закона больших чисел даются в теории вероятностей. Другими словами, теория вероятностей является математическим обоснованием закона больших чисел. Объект теории вероятностей измерение объективной возможности результатов, возникающих в массе однородных случайных событий, и выведение на этом основании количественных закономерностей, которым они подчиняются.
С ее помощью вычисляются шансы возможного наступления случайного события. Случайный характер варьирующих от единицы к единице совокупности признаков позволяет оценивать, насколько велика вероятность появления того или иного признака в ней. Отношение количества фактически появившихся интересующих пае фактов к общему количеству’ всех возможных фактов, выраженное в виде процента или десятичной дроби, называется частостью или опытной (эмпирической) вероятностью.
Вероятность — «математическая, числовая характеристика стелет! возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях».
Вероятность обычно обозначается буквой Р. Например, выражение Р(Л) = 0,5 означает, что вероятность наступления события А равна 0,5.
Вероятность принято классифицировать по следующей шкале:
16) 0,00 — полностью исключено;
17) 0,10 — в высшей степени неопределенно;
18) 0,20 — весьма неправдоподобно; I
0,30-0,40 — неправдоподобно;
0,60 — вероятно;
0,70 — весьма вероятно;
0,80 0,90 —в высшей степени вероятно; 1,00 — полностью достоверно.
Выводы
Таким образом, вероятность получает определенное количественное выражение, несмотря па то, что наличие того или иного признака или его колебания является случайным [6].
Если в урну поместить черный шар и белый шар, то при выемке одного шара из урны одинаково возможно появление любого из них. При этом проявляется альтернативная изменчивость, которая заключается в возможности лишь двух исходов: из урны можно вынуть только белый шар либо только черный шар. То же происходит и при подбрасывании монеты. Это обстоятельство одинаковой возможности выпадения любой стороны монеты называется равновновозможностью. Событие называется равновозможным, если нет причин, делающих одно из этих событий более возможным, чем другое. Событие называется несовместимым в том случае, когда появление одного делает появление другого невозможным.
Результат каждого единичного опыта с монетой или шарами также зависит от двух групп факторов: основных, связанных со свойствами явления, и случайных, не связанных с этими свойствами. Однако удобством монетной или урновой модели является, во-первых, то, что в ней легко отделить основные причины и свойства явления от побочных; во-вторых, па этой модели легко проследить, как действует каждая группа причин и что является результатом действия каждой из них.
Чтобы априори, т. е. до опыта, определить вероятность наступления какого- либо случайного явления, нужно знать число шансов, благоприятствующих его наступлению, а также число всех возможных шансов (как благоприятствующих, так и неблагоприятствующих). Отношение первой величины ко второй называется математической вероятностью. Она выражается в виде дроби, где в числителе указывается число благоприятствующих шансов, а в знаменателе—число всех возможных шансов. Например, при подбрасывании монеты возможно два исхода. Если считать выпадение орла благоприятным исходом, то вероятность его равна I /2. Если считать благоприятным исходом появление черного шара из урны, в которой находится 70 черных шаров и 30 белых шаров, то вероятность благоприятного исхода при выемке одного шара равна 70/100, а вероятность неблагоприятного исхода равна 30/100 [6].
Вероятность основное понятие теории вероятностей, которая, по образному- выражению автора классических трудов по теории вероятностей П. С. Лапласа (1749-1827), есть здравый смысл, переложенный па вычисление.
В числовом выражении вероятность равна доле признака во всей совокупности, как, например, доле черных или белых шаров в урне. Но доля характеризует состав совокупности, а вероятность является оценкой степени объективной возможности того или иного результата при отборе наудачу одной единицы из всей совокупности.
Вероятность органически связана с категориями причины и следствия. В самом деле, наблюдаемые на поверхности процессов частности — не что иное, как следствие тех или иных внутренних причин, определяющих вероятность явления. Таким образом, вероятность выражает объективную меру связи, причины со следствием, выступает мощным средством исследования причинности в массовых явлениях. Теория вероятностей показывает, что при достаточно большом (но не исчерпывающем) числе наблюдений могут быть выявлены и измерены правильности и закономерности, которые присущи изучаемой совокупности.
Применение теории вероятностей к социальным явлениям, в частности к преступности, обусловлено наряду с независимостью отдельных событий (иррегулярностью преступлений) еще и их известной устойчивостью.
Преступность представляет собой типичную статистическую совокупность, обладающую относительно устойчивыми характеристиками, позволяющими конкретно изучать се и даже прогнозировать се изменения.
megaobuchalka.ru
Теория вероятности
Вероятность и распределение вероятности.
1. Предмет теории вероятности. Вероятность и статистика.
2. Основные категории теории вероятности.
3. Классическое и статистическое определение вероятности.
4. Теорема сложения вероятностей.
5. Теорема умножения вероятностей.
6. Следствие теорем сложения и умножения вероятностей.
7. Вероятность гипотез. Формула Байеса.
8. Независимые события. Биномиальное распределение.
9. Вероятность редких событий. Формула Пуассона.
10. Локальная теорема де Муавра-Лапласа.
11. Интегральная формула Лапласа.
12. Зависимые события. Гипергеометрическое распределение.
13. Нормальное распределение.
14. Сравнительная оценка параметров эмпирического и нормального распределений. Критерий Пирсона.
1. Предмет теории вероятности. Вероятность и статистика.
Теория вероятности и математическая статистика – это наука, занимающаяся изучением закономерностей массовых случайных явлений , то есть статистических закономерностей. Такие же закономерности, только в более узкой предметной области социально-экономических явлений, изучает статистика. Между этими науками имеется общность методологии и высокая степень взаимосвязи. Практически любые выводы сделанные статистикой рассматриваются как вероятностные.
Особенно наглядно вероятностный характер статистических исследований проявляется в выборочном методе, поскольку любой вывод сделанный по результатам выборки оценивается с заданной вероятностью.
С развитием рынка постепенно сращивается вероятность и статистика, особенно наглядно это проявляется в управлении рисками, товарными запасами, портфелем ценных бумаг и т.п. За рубежом теория вероятности и математическая статистика применятся очень широко. В нашей стране пока широко применяется в управлении качеством продукции, поэтому распространение и внедрение в практику методов теории вероятности актуальная задача.
2. Основные категории теории вероятности.
Как и всякая наука, теория вероятности и математическая статистика оперируют рядом основных категорий:
— События;
— Вероятность;
— Случайность;
— Распределение вероятностей и т.д.
События – называется произвольное множество некоторого множества всех возможных исходов, могут быть:
— Достоверные;
— Невозможные;
— Случайные.
Достоверным называется событие, которое заведомо произойдет при соблюдении определенных условий.
Невозможным называется событие, которое заведомо не произойдет при соблюдении определенных условий.
Случайным называют события, которые могут произойти либо не произойти при соблюдении определенных условий.
События называют единственновозможными , если наступление одного из них это событие достоверное.
События называют равновозможными , если ни одно из них не является более возможным, чем другие.
События называют несовместимыми , если появление одного из них исключает возможность появления другого в том же испытании.
3. Классическое и статистическое определение вероятности.
Вероятность – численная характеристика реальности появления того или иного события.
Классическое определение вероятности : если множество возможных исходов конечное число, то вероятностью события Е считается отношение числа исходов благоприятствующих этому событию к общему числу единственновозможных равновозможных исходов.
Множество возможных исходов в теории вероятности называется пространством элементарных событий.
Пространство элементарных событий всегда можно описать числом nS=2, nS=6.
Если обозначить число исходов благоприятствующих событию n(E), то вероятность события Е будет выглядеть
. Для наших примеров .Исходя из классического определения вероятности, можно вывести ее основные свойства :
1) Вероятность достоверного события равна 1.
2) Вероятность невозможного события равна 0.
3) Вероятность случайного события находится в пределах от 0 до 1.
Классическое определение вероятности связано с непосредственным подсчетом вероятности, требует точного знания числа всех возможных исходов, и удобно для расчета вероятности достаточно простых событий.
Расчет вероятности более сложных событий — это сложная задача, требующая определения чисел всех возможных комбинаций появления этих событий. Подобными расчетами занимается специальная наука – комбинаторика . Поэтому на практике часто используется статистическое определение вероятности.
Доказано, что при многократном повторении опыта частости довольно устойчивы и колеблятся около некоторого постоянного числа, представляющего собой вероятность события.
Таким образом, в условиях массовых испытаний распределение частостей превращается в распределение вероятности случайной перемены.
Достоинство статистического определения вероятности в том, что для ее расчета не обязательно знать конечное число исходов.
Если классическое определение вероятности осуществляется априори (до опыта), то статистическое апосториори (после опыта по результатам).
Распределение частостей дискретного ряда, выраженных конечными числами, называется дискретным распределением вероятности .
Если осуществляются исследования массовых событий частостей, которые распределяются непрерывно и могут быть выражены какой-либо функцией, называются непрерывным распределением вероятности .
На графике такое распределение отражается непрерывной плавной линией, а площадь ограниченная этой линией и осью абсцисс всегда равна 1.
4. Теорема сложения вероятностей.
Суммой или объединением событий Е1 и Е2 , называют событием Е, состоящим в появлении события Е1 или Е2 или обоих этих событий.
Площадь прямоугольника – это пространство элементарных событий (число единственно возможных равновозможных исходов). Площади кругов Е1 и Е2 соответственно – это числа исходов благоприятствующих событиям Е1 и Е2 .
— число появлений исходов благоприятствующих событиям Е1 или Е2 или обоих этих событий.То есть вероятность появления хотя бы одного из двух несовместимых событий равна сумме вероятности этих событий.
Данная формула является частным случаем теоремы сложения вероятностей .
Доказывается общий случай теоремы методом математической индукции, путем последовательной разбивки сложного события на пары.
Пример : По результатам наблюдения за продажей мужских костюмов получены следующие данные о вероятности продажи костюмов разных размеров.
Совокупность единственно возможных событий называется полной группой или полной системой .
Сумма вероятностей событий, образующих полную систему равна 1.
образуют полную систему, тогда вероятность появления хотя бы одного события равна 1.В то же время
не совместны, тогда по теории сложения вероятностей .Пример : Из каждых 10 посетителей магазина 6 не делают покупок.
Вероятность появления хотя бы одного из этих событий равна 1.Два единовременно возможных события, образующих полную группу, называются противоположными (например: орел и решка).
Сумма вероятностей противоположных событий равна 1.
Если случайное событие Е имеет весьма малую вероятность, то практически можно считать, что в единичном испытании это событие не произойдет. Если
.mirznanii.com
теория случайных чисел — Что такое теория вероятности и кто ее разработал? — 22 ответа
теория вероятности википедия
В разделе Наука, Техника, Языки на вопрос Что такое теория вероятности и кто ее разработал? заданный автором спросонья лучший ответ это Эйнштейн
Ответ от 22 ответа[гуру]Привет! Вот подборка тем с ответами на Ваш вопрос: Что такое теория вероятности и кто ее разработал?
Ответ от Ms. Dum-Dum[гуру]
что за идиоты…эйнштейн разработал теорию относительности..а теория вероятностей началась с того, что пытались разобраться в вероятности выйгрыша в карты или кости в веке эдак 16м…основоположниками стали Героламо Гардано ,Пьер де Ферма и Блеиз Паскаль…все трое были математиками-физиками…
потом позже стали уже рассматривать случаи с вероятностью, где переменная может быть любым реальным числом на промежутке, а необязательно целым..то бишь продолжительные случаи, и не дискретные…появились всякого рода распределения и т.д.
А уже основноположником современной теории вероятности стал русский математик Андрей Николаевич Колмогоров.
Теорияв вероятностей подвергает анализу феномен случайности. Центральные объекты теории: случайные производные, стокастический процесс и события. Две самые фундаментальные теоремы в теории вероятностей: закон больших чисел и теорема центрального лимита.
Ответ от Впросонках[гуру]
Теорию вероятности разработал А. Энштейн.
Ответ от Евровидение[гуру]
Всё. Я пошел в раздел для взрослых)
Ответ от Пользователь удален[гуру]
Теорию вероятноси создал не Энштейн, конечно же, а кто-то другой положил начало. Знаю, что ее начали создавать для того, чтобы описать азартные игры (кости, карты, рулетка). Сейчас теория вероятности- очень сложная наука с очень сложным математическим аппаратом, и одна из самых прикладых в математике.
Определение не помню, но это же понятно должно быть… Например, вероятность выпадения орла при броске монеты — 50 процентов.
Прикольный аватар, кстати. Это ты?
Ответ от Leonid[гуру]
Ребята, это раздел науки и техники, а не юмора.. .Оно конечно, Эйнштейн великий физик, — но при чём тут теория ВЕРОЯТНОСТЕЙ? ! Вы хоть бы в энциклопедию заглянули, а? Или хоть вспомнить, что теория ОТНОСИТЕЛЬНОСТИ — это одно, а ВЕРОЯТНОСТЕЙ — это ДРУГОЕ! !
Значит, по теме. или можно почитать подробнее. Вкратце — огромное число явлений и в жизни, и в науке (теория газов или квантовая механика) , и в технике (шум, теория передачи сигналов) связано со случайными процессами. И теория вероятностей изучает закономерности, которые там имеют место. Потому что случайне-то они случайные — но все эти случайности подчиняются строгим закономерностям, у них есть определённые свойства и параметры и т. д.
Ответ от Антон Корень[гуру]
Теория вероятностей — направление в науке , утверждающее , что можно с любой заданной точностью предсказать поведение случайного процесса , если иметь достаточную информацию об ограниченом количестве фрагментов этого случайного процесса …Основоположники …действительно море , хотя на сегодняшний день и называют в их ряду чаще всего Паскаля …
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
История теории вероятностей на Википедии
Посмотрите статью на википедии про История теории вероятностей
Обсуждение шаблона Десятилетия на Википедии
Посмотрите статью на википедии про Обсуждение шаблона Десятилетия
Применения случайности на Википедии
Посмотрите статью на википедии про Применения случайности
Теория вероятностей на Википедии
Посмотрите статью на википедии про Теория вероятностей
Тобольск на Википедии
Посмотрите статью на википедии про Тобольск
Ответить на вопрос:
22oa.ru
Теория вероятности Википедия

Тео́рия вероя́тностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
История[ | ]
 Христиан Гюйгенс
Христиан Гюйгенс  Андрей Николаевич Колмогоров
Андрей Николаевич КолмогоровВозникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей[1]. Под влиянием поднятых и рассматриваемых ими вопросов решением тех же задач занимался и Христиан Гюйгенс. При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год)[2].
Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний.
В XVIII веке важное значение для развития теории вероятностей имели работы Томаса Байеса, сформулировавшего и доказавшего Теорему Байеса.
В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Карл Гаусс детально исследовал нормальное распределение случайной величины (см. график выше), также называемое «распределением Гаусса».
Во второй половине XIX века значительный вклад внес ряд европейских и русских учёных: П. Л. Чебышёв,
ru-wiki.ru











 Источник фото: онлайн-сервис интеллектуального развития детей https://iqsha.ru
Источник фото: онлайн-сервис интеллектуального развития детей https://iqsha.ru









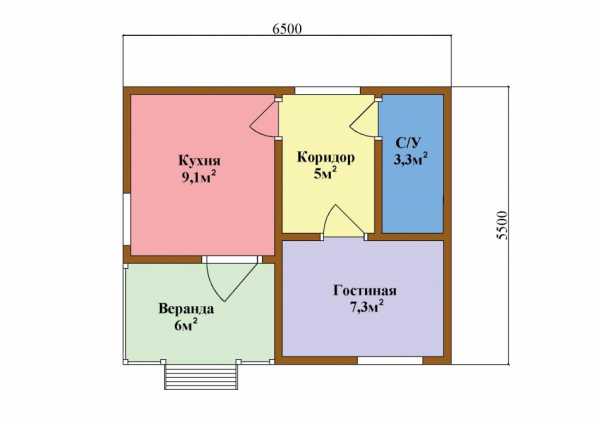



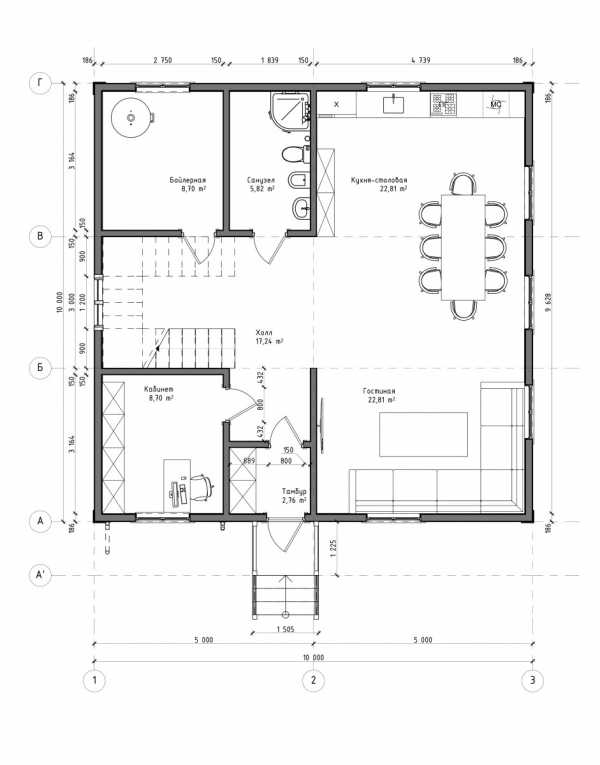










































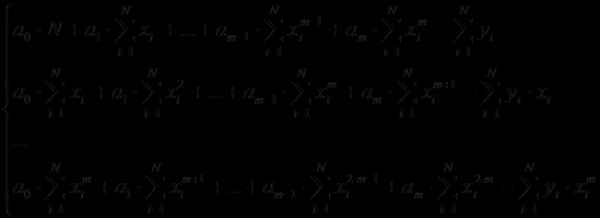

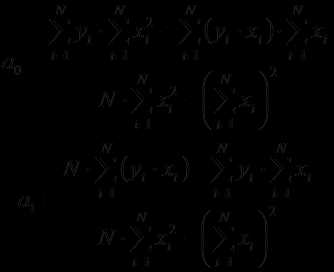
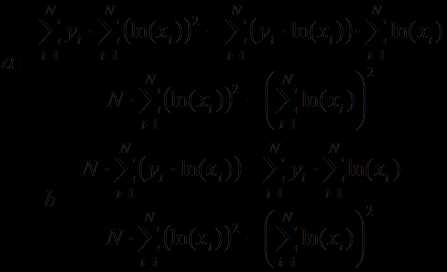
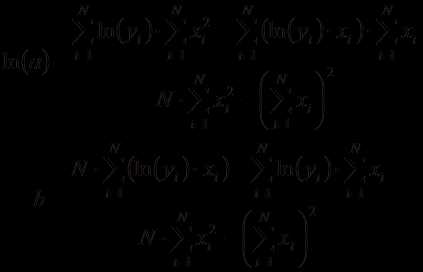
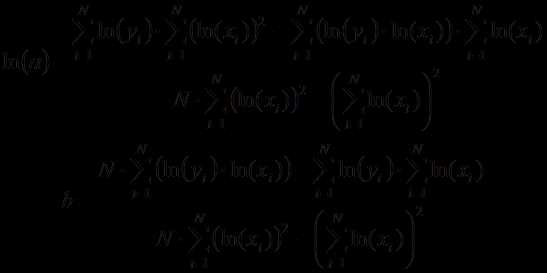




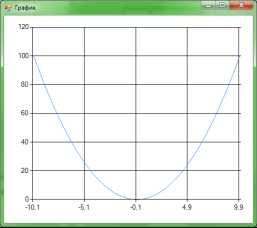
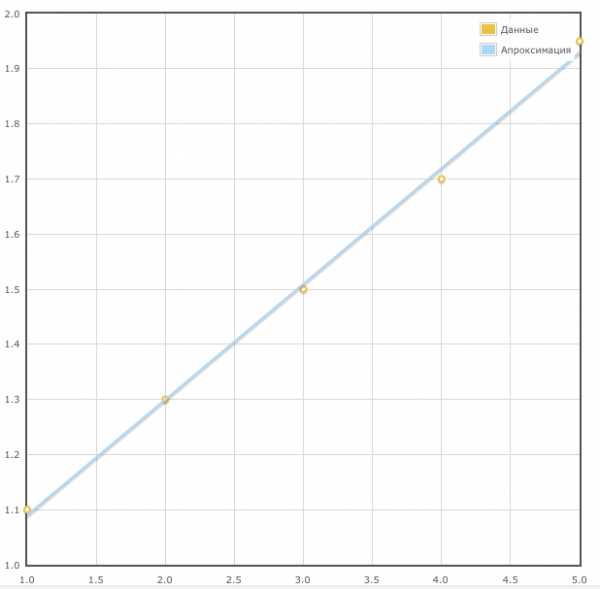
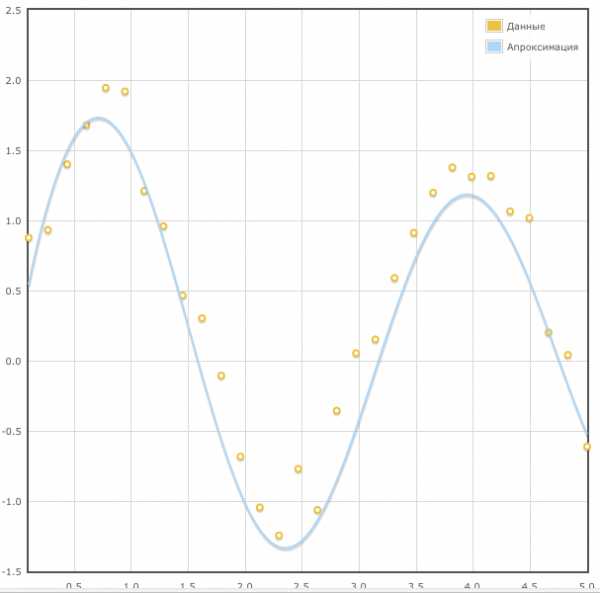


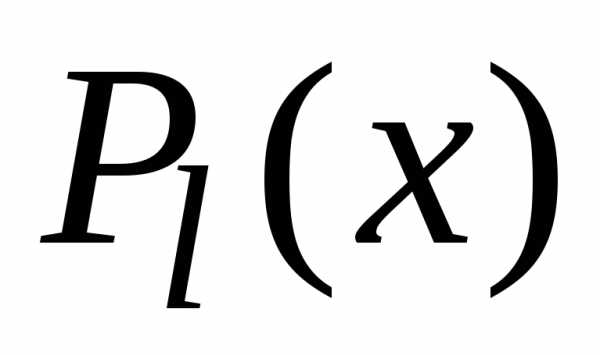 ,
гдеl<n-1.
В простейшем случае строится полином
первой степени, т.е. линейная функция: F(x) =ax+b. Коэффициенты a и b находятся с помощью метода наименьших
квадратов по следующим формулам:
,
гдеl<n-1.
В простейшем случае строится полином
первой степени, т.е. линейная функция: F(x) =ax+b. Коэффициенты a и b находятся с помощью метода наименьших
квадратов по следующим формулам: ,
, 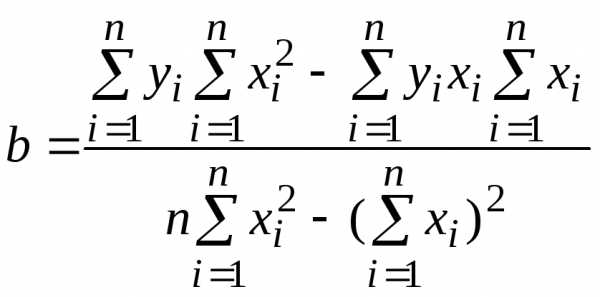 .
. .
Эти измерения дали таблицу, состоящую
из К+1 (К=3-5) значений количества распадовдля моментов времени
.
Эти измерения дали таблицу, состоящую
из К+1 (К=3-5) значений количества распадовдля моментов времени .
.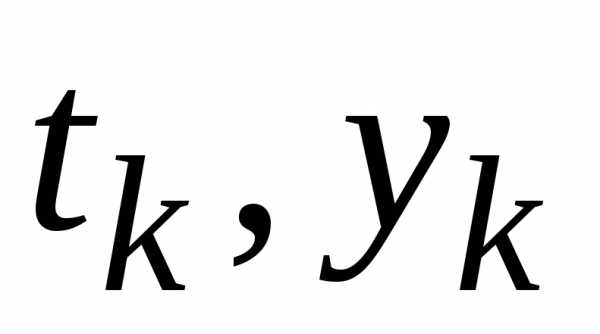 ,
отыскивая параметры линейной зависимости.
Тангенс угла наклона линейной зависимости
определяет константу радиоактивного
распада
,
отыскивая параметры линейной зависимости.
Тангенс угла наклона линейной зависимости
определяет константу радиоактивного
распада .
.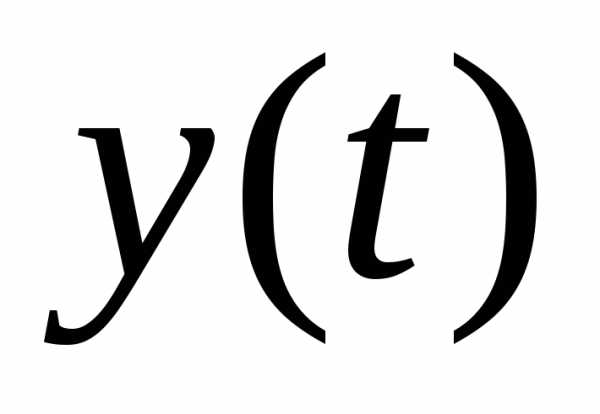 вместе с экспериментальными точками.
Заметим, что закон радиоактивного
распада является вероятностным и
выполняется сравнительно точно для
больших значений
вместе с экспериментальными точками.
Заметим, что закон радиоактивного
распада является вероятностным и
выполняется сравнительно точно для
больших значений .
Периоды полураспада радиоактивных
изотопов изменяются в очень широких
пределах. Например, период полураспада
изотопа азота равен 10 минутам, а период
полураспада изотопа хлора 300 000 лет
[1]. В заданиях период полураспада равен
часам (и ответ следует выдавать в часах).
.
Периоды полураспада радиоактивных
изотопов изменяются в очень широких
пределах. Например, период полураспада
изотопа азота равен 10 минутам, а период
полураспада изотопа хлора 300 000 лет
[1]. В заданиях период полураспада равен
часам (и ответ следует выдавать в часах).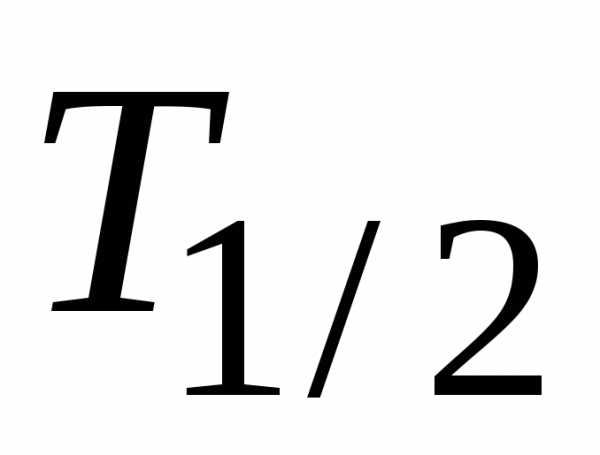 следует его связь с постоянной распада:
следует его связь с постоянной распада: ,
.
,
. — номер студента в группе, а
— номер студента в группе, а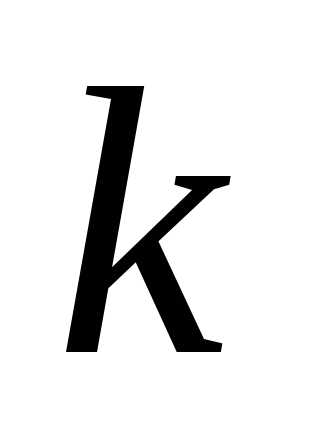 —
номер измерения (,
время в этой формуле измеряется в часах.
Между номером студента и периодом
полураспада имеется линейная зависимость.
—
номер измерения (,
время в этой формуле измеряется в часах.
Между номером студента и периодом
полураспада имеется линейная зависимость. и экспериментальными точками, выписать
значения постоянной распада и времени
полураспада в часах.
и экспериментальными точками, выписать
значения постоянной распада и времени
полураспада в часах. :
:
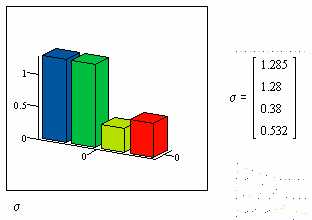

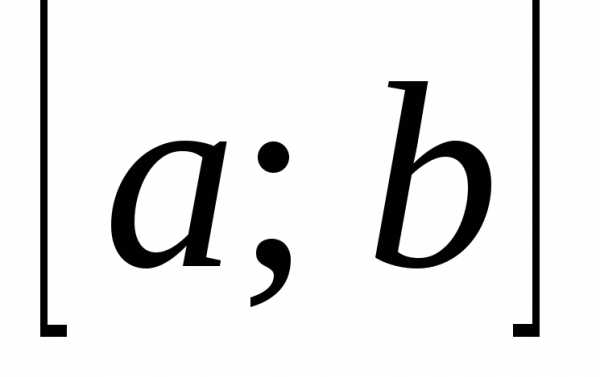 задана функция
задана функция и определена система функций
и определена система функций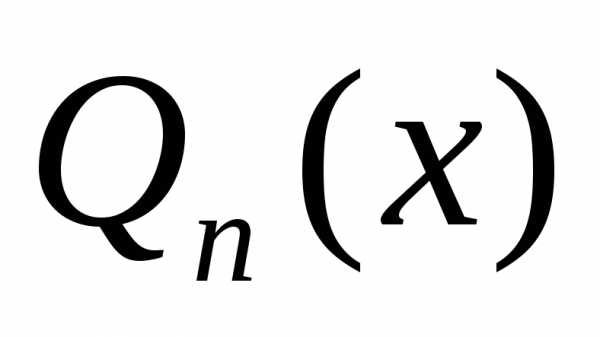 называют многочленом наилучшего
среднеквадратического приближения
функции
называют многочленом наилучшего
среднеквадратического приближения
функции на отрезке
на отрезке ,
если расстояние от многочлена до данной
функции по среднеквадратичной норме
(среднеквадратичное отклонение) является
наименьшим. Иначе говоря, выполняется
условие:
,
если расстояние от многочлена до данной
функции по среднеквадратичной норме
(среднеквадратичное отклонение) является
наименьшим. Иначе говоря, выполняется
условие: называют задачей об интегральном
среднеквадратичном приближении
(аппроксимации) функции
называют задачей об интегральном
среднеквадратичном приближении
(аппроксимации) функции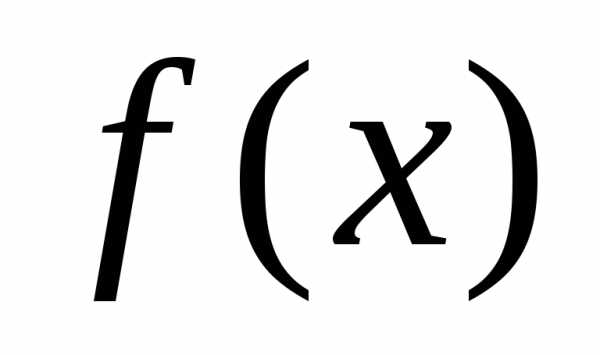 на отрезке
на отрезке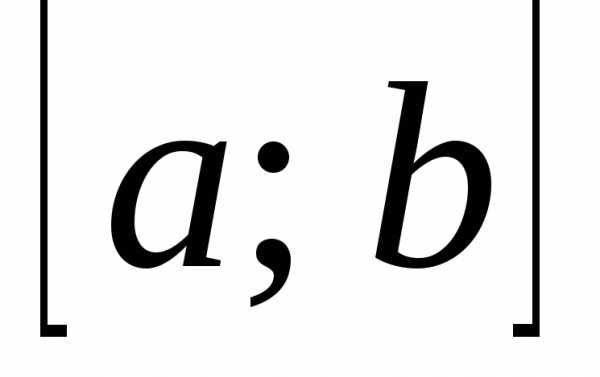 обобщённым многочленом. Эта задача
сводится к нахождению коэффициентовиз условия (1).
обобщённым многочленом. Эта задача
сводится к нахождению коэффициентовиз условия (1).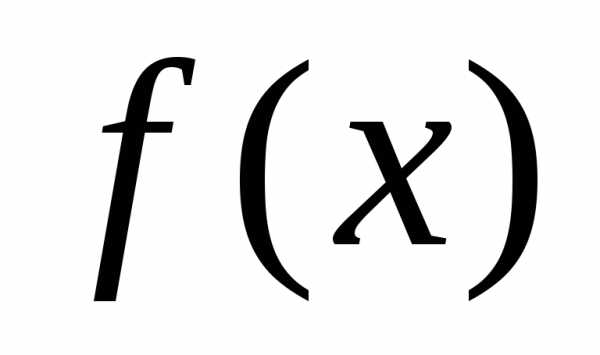 и система функцийопределены на множестве точек,
то приближение функции
и система функцийопределены на множестве точек,
то приближение функции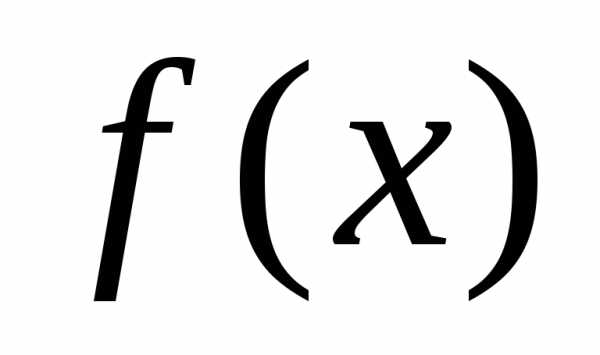 многочленом
многочленом называют точечным среднеквадратичным
приближением на множестве точек.
При этом для обобщённого многочлена
наилучшего приближения
называют точечным среднеквадратичным
приближением на множестве точек.
При этом для обобщённого многочлена
наилучшего приближения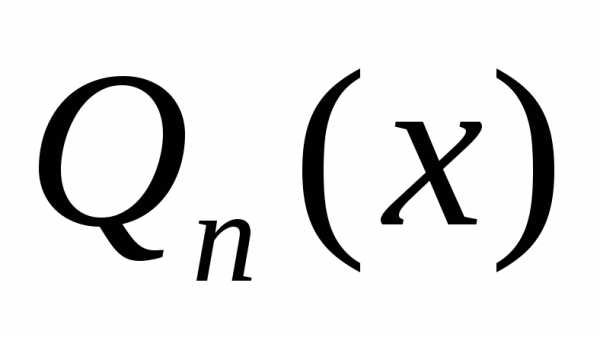 среднеквадратичное отклонениена системе точек.
среднеквадратичное отклонениена системе точек.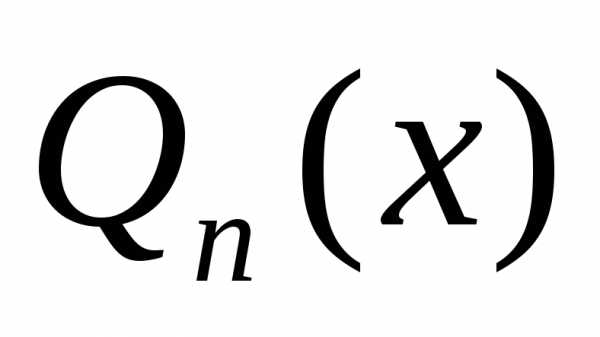 функции
функции на отрезке
на отрезке упрощается, если система функцийобладает свойством ортогональности на
данном отрезке.
упрощается, если система функцийобладает свойством ортогональности на
данном отрезке.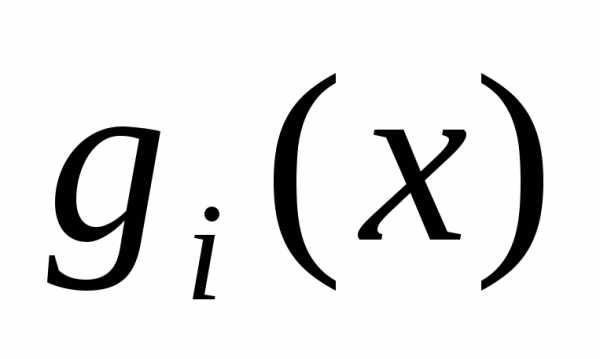 и
и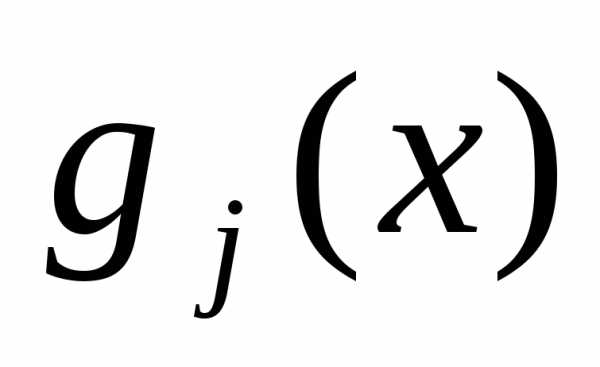 на отрезке
на отрезке называется определённый интеграл от
их произведения на этом отрезке. Обозначим
скалярное произведение, каки
запишем:
называется определённый интеграл от
их произведения на этом отрезке. Обозначим
скалярное произведение, каки
запишем: .
.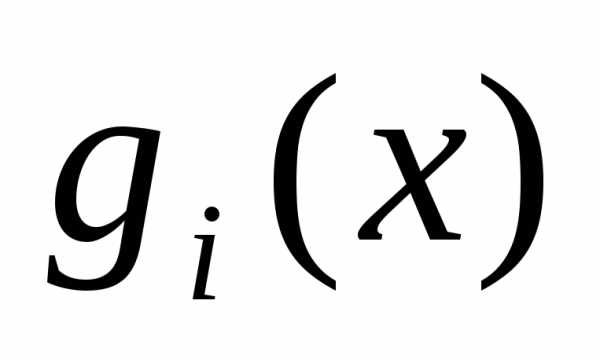 на отрезке
на отрезке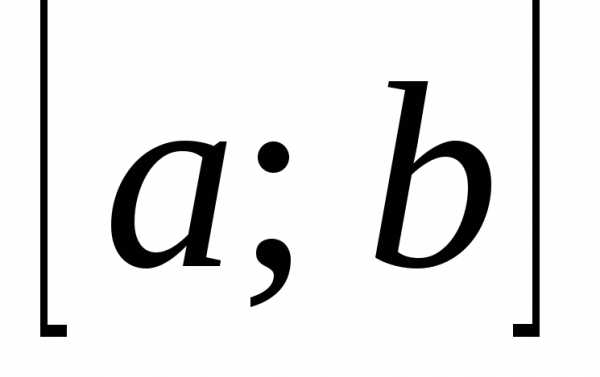 называется число.
Функция
называется число.
Функция ,
для которой существует интеграл
,
для которой существует интеграл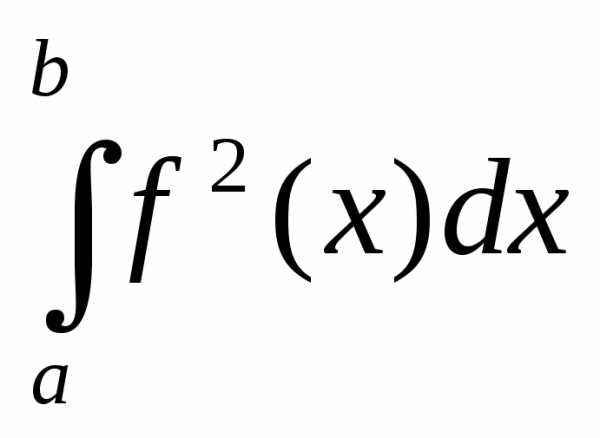 ,
называется интегрируемой с квадратом
на отрезке
,
называется интегрируемой с квадратом
на отрезке .
.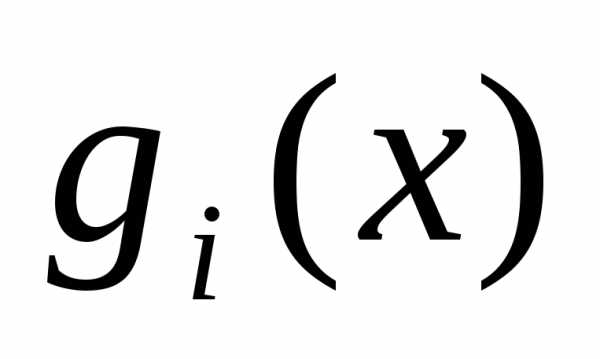 и
и называются ортогональными на отрезке
называются ортогональными на отрезке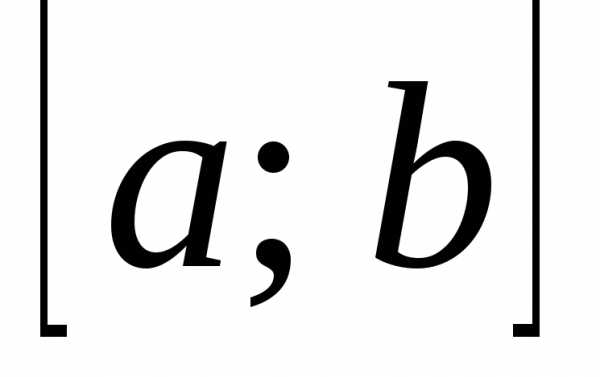 ,
если их скалярное произведение на этом
отрезке равно нулю, то есть
,
если их скалярное произведение на этом
отрезке равно нулю, то есть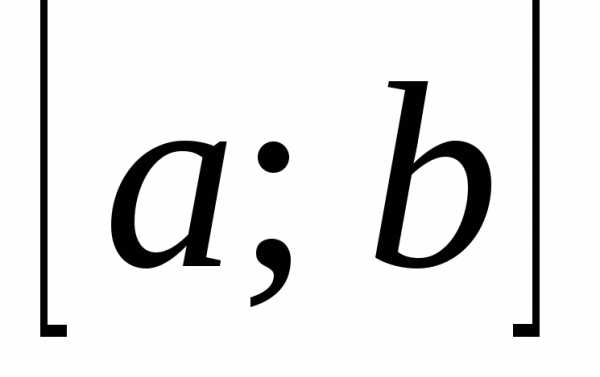 ,
если все функции этой системы попарно
ортогональны на этом отрезке.
,
если все функции этой системы попарно
ортогональны на этом отрезке.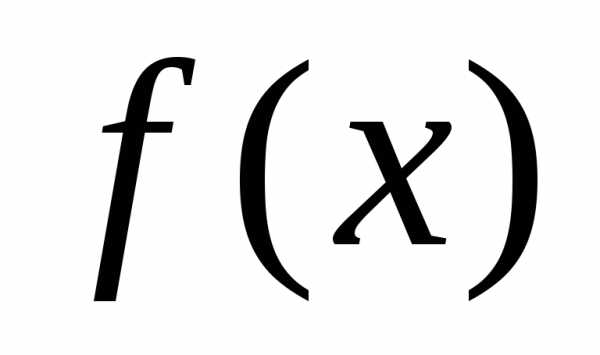 относительно ортогональной системы
функций, если они определяются по
формулам
относительно ортогональной системы
функций, если они определяются по
формулам ,
интегрируемой с квадратом на отрезке
,
интегрируемой с квадратом на отрезке ,
обобщённый многочленп-го порядка
,
обобщённый многочленп-го порядка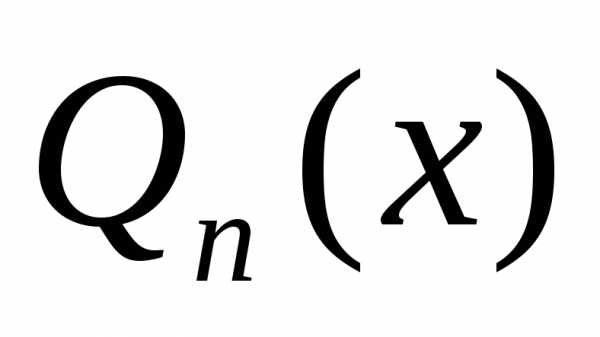 с коэффициентами Фурье функции
с коэффициентами Фурье функции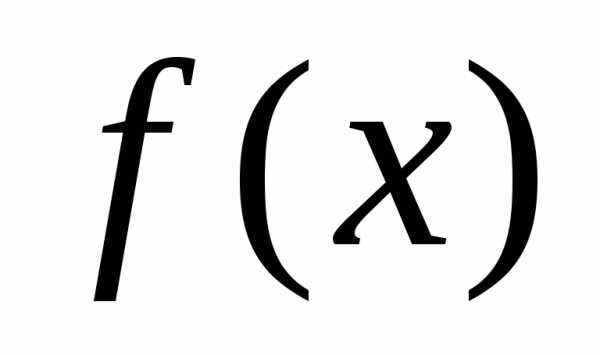 относительно ортогональной на отрезке
относительно ортогональной на отрезке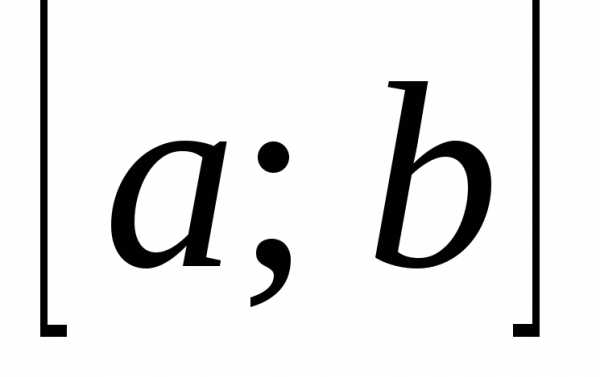 системы функцийявляется многочленом наилучшего
среднеквадратичного отклонения этой
функции, причём квадрат наименьшего
среднеквадратичного отклонения
определяется соотношением
системы функцийявляется многочленом наилучшего
среднеквадратичного отклонения этой
функции, причём квадрат наименьшего
среднеквадратичного отклонения
определяется соотношением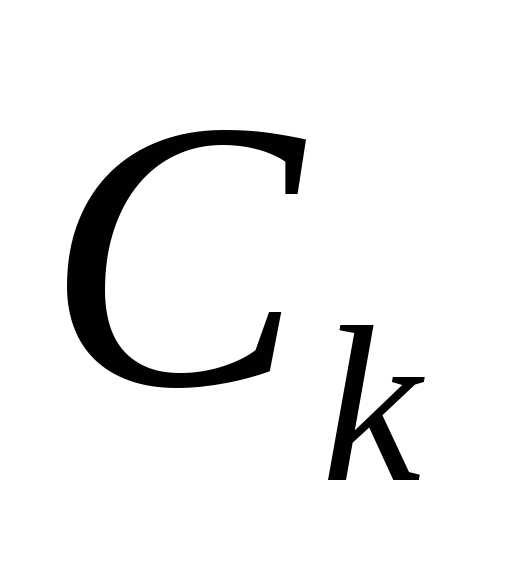 —
коэффициенты Фурье, определяемые по
формулам (3).
—
коэффициенты Фурье, определяемые по
формулам (3).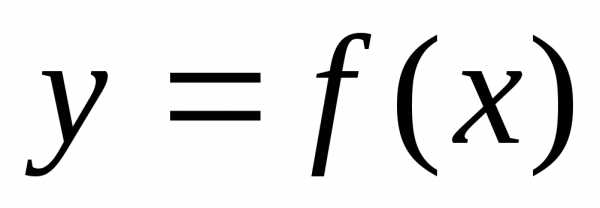 ,
явным образом выражающей зависимостьу отх. Естественно требовать,
чтобы график искомой функции
,
явным образом выражающей зависимостьу отх. Естественно требовать,
чтобы график искомой функции изменялся плавно и не слишком уклонялся
от экспериментальных точек
изменялся плавно и не слишком уклонялся
от экспериментальных точек .
Поиск такой функциональной зависимости
называют “сглаживанием” экспериментальных
данных.
.
Поиск такой функциональной зависимости
называют “сглаживанием” экспериментальных
данных.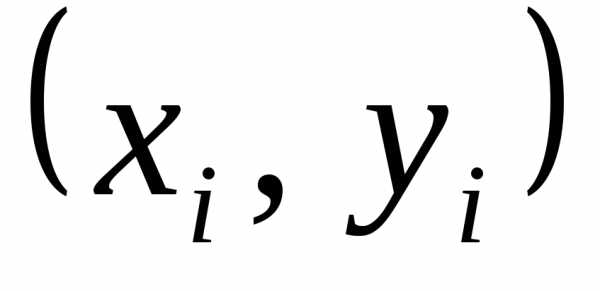 является минимальной, то есть функция
является минимальной, то есть функция и
и :
: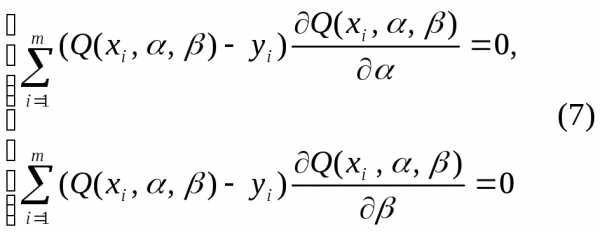 .
.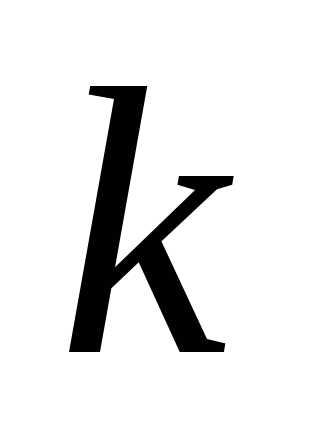 и
и :
: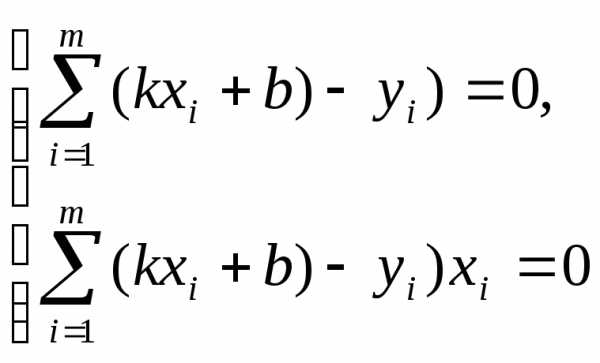
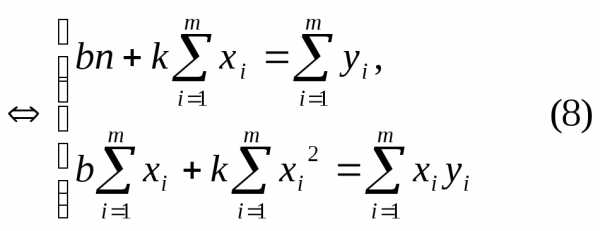 .
.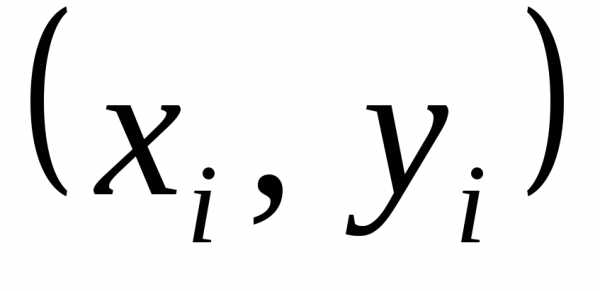 не располагаются вблизи прямой, то
выбирают новые переменные
не располагаются вблизи прямой, то
выбирают новые переменные давали бы точки
давали бы точки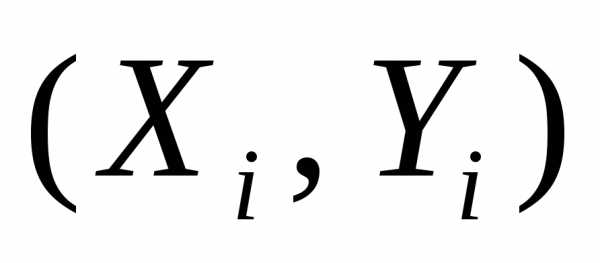 менее уклоняющиеся от прямой. Для
аппроксимирующей прямойкоэффициенты можно определить из
уравнений (8), где вместо
менее уклоняющиеся от прямой. Для
аппроксимирующей прямойкоэффициенты можно определить из
уравнений (8), где вместо и
и подставляют соответствующие значения
подставляют соответствующие значения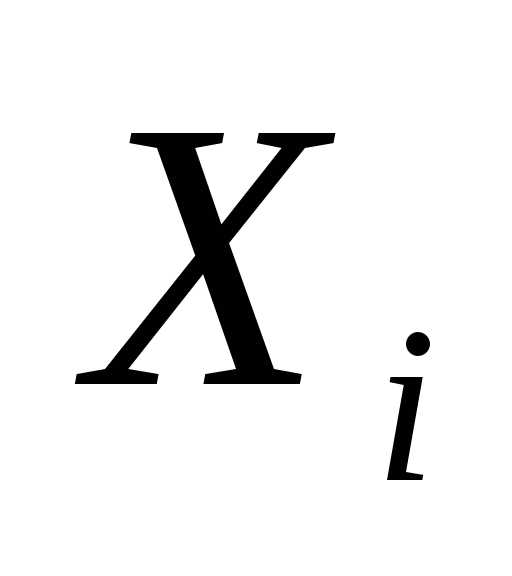 и
и .
Нахождение зависимостей (9) называют,
выравниваем экспериментальных данных.
Функциональная зависимость
.
Нахождение зависимостей (9) называют,
выравниваем экспериментальных данных.
Функциональная зависимость определена неявно уравнениемразрешимым относительноу в частных
случаях.
определена неявно уравнениемразрешимым относительноу в частных
случаях.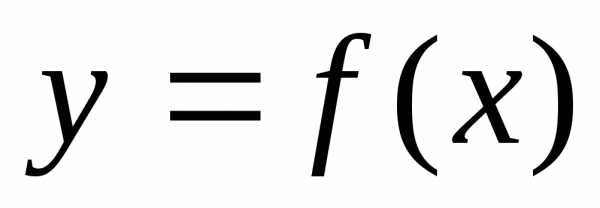 ,
используя аппроксимирующие зависимости
с двумя параметрами
,
используя аппроксимирующие зависимости
с двумя параметрами и
и ,
и определить наилучшие значения
параметров, если опытные данные
представлены таблицей:
,
и определить наилучшие значения
параметров, если опытные данные
представлены таблицей:

 лежат приблизительно на одной прямой.
Положими составим таблицу для экспериментальных
данных в новых переменных:
лежат приблизительно на одной прямой.
Положими составим таблицу для экспериментальных
данных в новых переменных: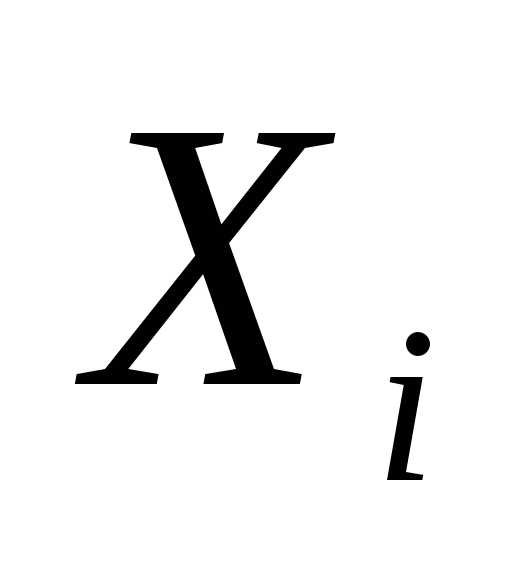

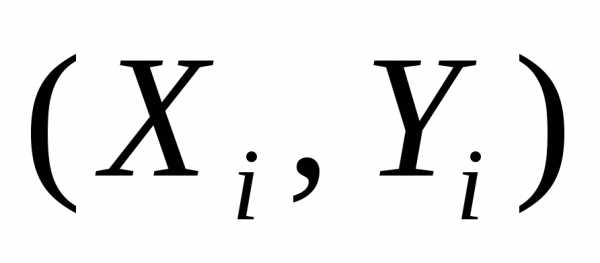 лежат приблизительно на одной прямой,
в чём легко убедиться, построив их в
системе координат
лежат приблизительно на одной прямой,
в чём легко убедиться, построив их в
системе координат .
Наилучшие значения параметров
.
Наилучшие значения параметров и
и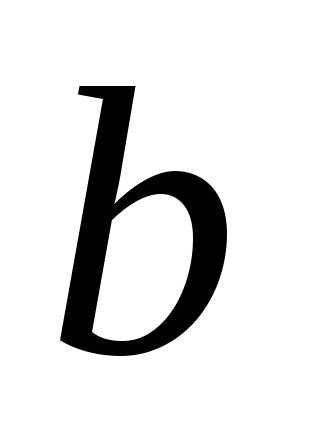 находятся из системы уравнений (8):
находятся из системы уравнений (8): и
и имеет вид.
Отсюда легко получить прямую зависимость
между переменными в виде степенной
функции:
имеет вид.
Отсюда легко получить прямую зависимость
между переменными в виде степенной
функции: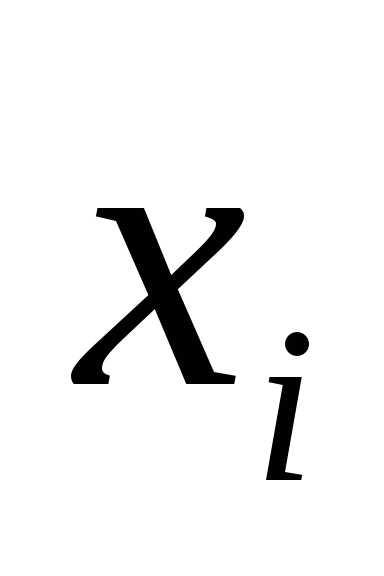

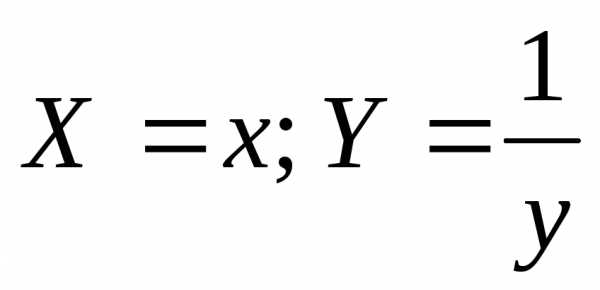
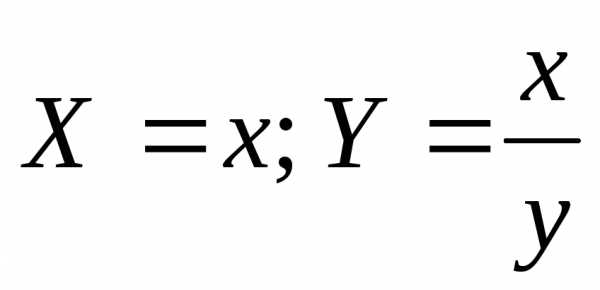
 .
. будет наименьшим.
будет наименьшим.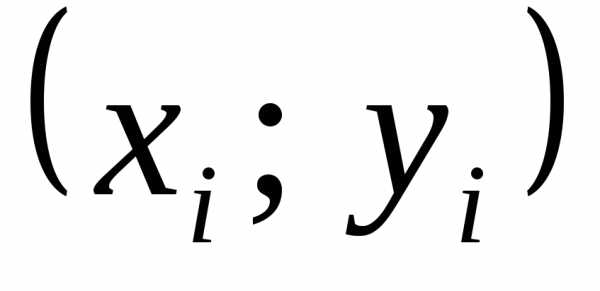 на координатную сетку
на координатную сетку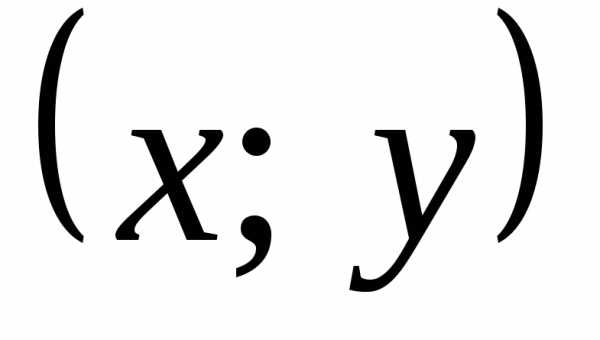 .
.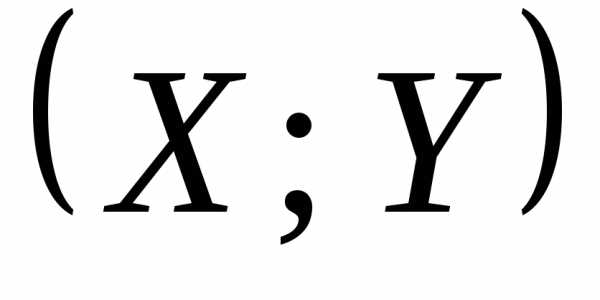 так, чтобы преобразованные экспериментальные
данные
так, чтобы преобразованные экспериментальные
данные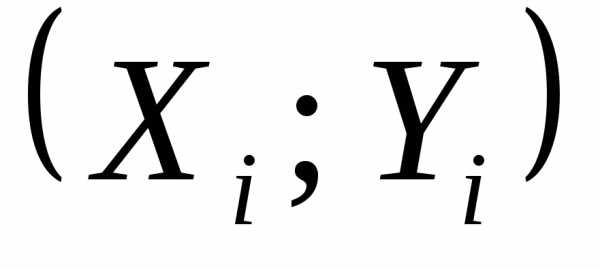 наименее уклонялись от прямой.
наименее уклонялись от прямой.
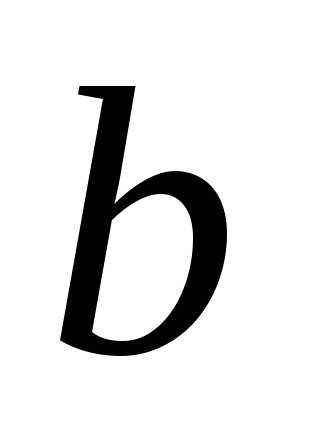 в уравнении прямой.
в уравнении прямой.