Бином Ньютона — Википедия. Что такое Бином Ньютона
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
- (a+b)n=∑k=0n(nk)an−kbk=(n0)an+(n1)an−1b+⋯+(nk)an−kbk+⋯+(nn)bn{\displaystyle (a+b)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}a^{n-k}b^{k}={n \choose 0}a^{n}+{n \choose 1}a^{n-1}b+\dots +{n \choose k}a^{n-k}b^{k}+\dots +{n \choose n}b^{n}}
где (nk)=n!k!(n−k)!=Cnk{\displaystyle {n \choose k}={\frac {n!}{k!(n-k)!}}=C_{n}^{k}} — биномиальные коэффициенты, n{\displaystyle n} — неотрицательное целое число.
В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома Ньютона для более общего случая, когда показатель степени — произвольное действительное (или даже комплексное) число. В этом случае бином представляет собой бесконечный ряд (см. ниже).
Доказательство
Доказательство
Обобщения
Формула бинома Ньютона является частным случаем разложения функции (1+x)r{\displaystyle (1+x)^{r}} в ряд Тейлора:
- (1+x)r=∑k=0∞(rk)xk{\displaystyle (1+x)^{r}=\sum _{k=0}^{\infty }{r \choose k}x^{k}},
где r может быть комплексным числом (в частности, отрицательным или вещественным). Коэффициенты этого разложения находятся по формуле:
- (rk)=1k!∏n=0k−1(r−n)=r(r−1)(r−2)⋯(r−(k−1))k!{\displaystyle {r \choose k}={1 \over k!}\prod _{n=0}^{k-1}(r-n)={\frac {r(r-1)(r-2)\cdots (r-(k-1))}{k!}}}
При этом ряд
- (1+z)α=1+αz+α(α−1)2z2+…+α(α−1)⋯(α−n+1)n!zn+…{\displaystyle (1+z)^{\alpha }=1+\alpha {}z+{\frac {\alpha (\alpha -1)}{2}}z^{2}+…+{\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}z^{n}+…}.
сходится при |z|≤1{\displaystyle |z|\leq 1}.
В частности, при z=1m{\displaystyle z={\frac {1}{m}}} и α=x⋅m{\displaystyle \alpha =x\cdot m} получается тождество
- (1+1m)xm=1+x+xm(xm−1)2m2+…+xm(xm−1)⋯(xm−n+1)n!mn+….{\displaystyle \left(1+{\frac {1}{m}}\right)^{xm}=1+x+{\frac {xm(xm-1)}{2\;m^{2}}}+…+{\frac {xm(xm-1)\cdots (xm-n+1)}{n!\;m^{n}}}+\dots .}
Переходя к пределу при m→∞{\displaystyle m\to \infty } и используя второй замечательный предел limm→∞(1+1m)m=e{\displaystyle \lim _{m\to \infty }{\left(1+{\frac {1}{m}}\right)^{m}}=e}, выводим тождество
- ex=1+x+x22+⋯+xnn!+…,{\displaystyle e^{x}=1+x+{\frac {x^{2}}{2}}+\dots +{\frac {x^{n}}{n!}}+\dots ,}
которое именно таким образом было впервые получено Эйлером.
Мультиномиальная теорема
Бином Ньютона может быть обобщен до полинома Ньютона — возведения в степень суммы произвольного числа слагаемых:
- (x1+x2+⋯+xm)n=∑kj⩾0k1+k2+⋯+km=n(nk1,k2,…,km)x1k1…xmkm,{\displaystyle (x_{1}+x_{2}+\cdots +x_{m})^{n}=\sum \limits _{k_{j}\geqslant 0 \atop k_{1}+k_{2}+\cdots +k_{m}=n}{n \choose k_{1},k_{2},\ldots ,k_{m}}x_{1}^{k_{1}}\ldots x_{m}^{k_{m}},}
где (nk1,k2,…,km)=n!k1!k2!⋯km!{\displaystyle \textstyle {\binom {n}{k_{1},k_{2},\ldots ,k_{m}}}={\frac {n!}{k_{1}!k_{2}!\cdots k_{m}!}}} — мультиномиальные коэффициенты. Сумма берётся по всем неотрицательным целым индексам kj{\displaystyle k_{j}}, сумма которых равна n (то есть по всем композициям числа n длины m). При использовании полинома Ньютона считается, что выражения xj0=1{\displaystyle x_{j}^{0}=1}, даже если xj=0{\displaystyle x_{j}=0}.
Мультиномиальная теорема легко доказывается либо индукцией по m, либо из комбинаторных соображений и комбинаторного смысла мультиномиального коэффициента.
При m=2{\displaystyle m=2}, выражая k2=n−k1{\displaystyle k_{2}=n-k_{1}}, получаем бином Ньютона.
Полные полиномы Белла
Пусть Bn(as)=Bn(a1,…,an){\displaystyle B_{n}(a_{s})=B_{n}(a_{1},\dots ,a_{n})} и B0=1{\displaystyle B_{0}=1} ,тогда полные полиномы Белла обладают биномиальным разложением:
- Bn(as+bs)=∑i+j=n(ni, j)Bi(as)Bj(bs).{\displaystyle B_{n}({{a_{s}}+{b_{s}}})=\sum _{i+j=n}{n \choose i,\ j}{B_{i}}({a_{s}}){B_{j}}({b_{s}}).}
История
Долгое время считалось, что для натуральных показателей степени эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Однако историки науки обнаружили, что формула была известна ещё китайскому математику Яну Хуэю (англ.), жившему в XIII веке, а также исламским математикам ат-Туси (XIII век) и ал-Каши (XV век). В середине XVI века Михаэль Штифель описал биномиальные коэффициенты и также составил их таблицу до степени 18.
Исаак Ньютон около 1677 года обобщил формулу для произвольного показателя степени (дробного, отрицательного и др.). Из биномиального разложения Ньютон, а позднее и Эйлер, выводили всю теорию бесконечных рядов.
В художественной литературе
В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо сложном.[1]
Когда ему исполнился двадцать один год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность. После этого он получил кафедру математики в одном из наших провинциальных университетов, и, по всей вероятности, его ожидала блестящая карьера.
Оригинальный текст (англ.)
The Final Problem At the age of twenty-one he wrote a treatise upon the binomial theorem, which has had a European vogue. On the strength of it he won the mathematical chair at one of our smaller universities, and had, to all appearances, a most brilliant career before him.
- «подумаешь, бином Ньютона! Умрёт он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвёртой палате».
См. также
Примечания
Литература
Ссылки
wiki.sc
Бином ньютона — это… Что такое Бином ньютона?
Бином Ньютона — это формула
- ,
где — биномиальные коэффициенты, n — неотрицательное целое число.
Доказательство
Докажем это равенство, используя метод математической индукции:
База индукции: n = 1
(a + b)1 = a + b
Шаг индукции:
Пусть утверждение для n верно:
Тогда надо доказать утверждение для n + 1:
Начнём доказательство:
Извлечём из первой суммы слагаемое при k = 0
Извлечём из второй суммы слагаемое при k = n
Теперь сложим преобразованные суммы:
Что и требовалось доказать
Комментарий:
- — одно из тождеств биномиальных коэффициентов
Для ненатуральных степеней
где r может быть комплексным числом (в частности, отрицательным или вещественным). Коэффициенты находятся по формуле:
При этом ряд
- .
сходится при .
В частности, при и получается тождество
Переходя к пределу при и используя второй замечательный предел , выводим тождество
именно таким образом впервые полученное Эйлером.
История
Считается, что эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Тем не менее, она была известна ещё китайскому математику Яну Хуэю, жившему в XIII веке. Возможно, её открыл персидский учёный, поэт и философ Омар Хайям.
Исаак Ньютон обобщил формулу для прочих показателей степени.
В художественной литературе
В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо сложном.
- В рассказе А. Конан Дойля «Последнее дело Холмса» Холмс говорит о математике профессоре Мориарти:
- «Когда ему исполнился двадцать один год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность. После этого он получил кафедру математики в одном из наших провинциальных университетов, и, по всей вероятности, его ожидала блестящая будущность».
Об этой специфической роли бинома Ньютона в культуре писал известный математик В. А. Успенский [1].
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
Бином Ньютона — Мегаэнциклопедия Кирилла и Мефодия — статья
Бино́м Нью́тона — математическая формула вида \((a + b)^n\), выражающая целую положительную степень суммы двух слагаемых (двучлена, бинома) через степени этих слагаемых. Частными случаями бинома Ньютона при n = 2 и n = 3 являются формулы для квадрата и куба суммы а и b: (а + b)2 = а2 + 2ab + b2, (а + b)3 = а3 + 3a2b + 3ab2 + b3. При n = 4 получают формулу (а + b)4 = a4+ 4a3b + 6a2b2 + 4ab3 + b4.Для целого положительного n формула имеет вид (1):
\((a + b)^n = a^n + \binom{n}{1}a^{n-1}b + \binom{n}{2}a^{n-2}b{^2} + \binom{n}{3}a^{n-3}b{^3} + … + \binom{n}{n-1}ab^{n-1} + b{^n} \)
или вид (2):
\((a + b)^n = a^n +{n! \over1!(n-1)!}a^{n-1}b + {n! \over2!(n-2)!}a^{n-2}b^2 + … + b^{n2}\)Для вычислений удобнее формула (3):
\((a + b)^n = a^n + na^{n-1}b + {n(n-1) \over 1*2}a^{n-2}b^2 + {n(n-1)(n-2)\over 1*2*3}a^{n-3}b3+…+b^n.\)
Бином Ньютона для дробных и отрицательных показателей
Пусть имеем выражение \((a + b)^n\), где n — дробное или отрицательное число. Пусть \(| a | >| b |. \)Представим \((a + b)^n\) в виде \(a^n(1 + x)^n\). Величина \(x = {b \over a}\)абсолютное ее значение меньше единицы. Выражение \((1 + x)^n\) можно вычислить с любой степенью точности по формуле (3).
Обобщенная формула бинома Ньютона
\((a_1+a_2+a_3+ … +a_k)^n = \sum {n! \over n_1! n_2! … n_k!}a{_1^{n_1}}a{_2^{n_2}\dots a{_k^{n_k}}}\)n — целое положительное число.
Числа 1, n, \(n(n-1)\over 1*2\) называются биномиальными коэффициентами. Биномиальные коэффициенты всегда являются целыми положительными числами. Крайние коэффициенты равны единице; коэффициенты членов, равноотстоящих от концов, одинаковы; коэффициенты возрастают от краев к середине; сумма всех коэффициентов равна 2n. Сумма двух соседних коэффициентов в разложении (а + b)n равна коэффициенту в разложении (а + b)n+1; например, суммы 1+3, 3+3, 3+1 соседних коэффициентов в формуле для (а + b)3 дают коэффициенты 4, 6, 4 в формуле для (а + b)4. Пользуясь этим свойством, можно получить путем сложения биномиальные коэффициенты для любого n. Результаты располагают в виде таблицы — треугольника Паскаля.Формула бинома Ньютона для целых положительных показателей была известна задолго до Исаака Ньютона, но он в 1676 году указал на возможность распространения этого разложения и на случай дробного или отрицательного показателя. Строгое обоснование указанных Ньютоном возможностей дал Н. Абель в 1826 году. В случае дробного или отрицательного n все биномиальные коэффициенты отличны от нуля, а правая часть формулы получает бесконечный ряд членов (биномиальный ряд). Бином Ньютона играет роль во многих областях математики, в частности в алгебре и теории чисел.- М.Я. Выгодский. Справочник по элементарной математике. М: Наука, 1979.
megabook.ru
БИНОМ НЬЮТОНА — это… Что такое БИНОМ НЬЮТОНА?
- БИНОМ НЬЮТОНА
БИНОМ НЬЮТОНА, математическое правило разложения алгебраического выражения (а+b)n в ряд степеней численных значений х и у (где n — положительное число). При n-2 разложение выглядит таким образом: (х+у)2=х2+2ху+у2.
Научно-технический энциклопедический словарь.
Смотреть что такое «БИНОМ НЬЮТОНА» в других словарях:
Бином ньютона — Бином Ньютона это формула , где биномиальные коэффициенты, n неотрицательное целое число. Содержание 1 Доказательство … Википедия
бином ньютона — БИНОМ, а, м. (или бином ньютона). Ирон. О чем л. кажущемся сложным, запутанным. Возм. распространилось под влиянием романа М. Булгакова «Мастер и Маргарита» … Словарь русского арго
Бином Ньютона — Бином Ньютона формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид , где биномиальные коэффициенты, неотрицательное целое число. В таком виде эта формула была известна… … Википедия
Бином Ньютона — алгебраическая формула, открытая Ньютоном, выражающая какую угодно степень двучлена, а именно: (х + а)n = хn + n/1(axn 1) + [n/(n 1)/1.2](а2хn 2) + …[n(n 1)(n 2)…(n m+1)/1.2.3…m](anxn m) + … или, в компактной форме, пользуясь символом n! =… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Бином Ньютона — Разг. Шутл. О чём л. сложном, запутанном. Елистратов, 41 … Большой словарь русских поговорок
Подумаешь, бином Ньютона! — Из романа (гл. 18 «Неудачливые визитеры») «Мастер и Маргарита» (1940) Михаила Афанасьевича Булгакова (1891 1940). Слова Коровьева Фагота, комментирующего диалог между Воландом и буфетчиком Андреем Фокичем Соковым. Последний пришел жаловаться на… … Словарь крылатых слов и выражений
бином — а, м. binôme, лат. binomia m. 1. мат. Алгебраическое выражение, представляющее сумму или разность одночленов; двучлен. БАС 2. Боюсь, еслиб я и осмелился представить здесь самое простое развитие двучленника (бинома) Ньютонова необходимого для сего … Исторический словарь галлицизмов русского языка
Ньютона бином — Бином Ньютона это формула , где биномиальные коэффициенты, n неотрицательное целое число. Содержание 1 Доказательство … Википедия
БИНОМ — (от лат. bis дважды, и греч. nomos часть, отдел). Двучлен (в алгебре). Бином Ньютона общая формула для возведения двучленного количества в любую степень. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. БИНОМ в… … Словарь иностранных слов русского языка
Бином — (лат. bis дважды, nomen имя) или двучлен частный случай полинома (многочлена), состоящего из двух слагаемых мономов (одночленов). Например: Для вычисления степеней биномов используется бином Ньютона: А также … Википедия
Книги
- Девственная селедка. Мимолетности, или Подумаешь, бином Ньютона!, 576 с. В этот сборник включены два романа: Девственная селедка и Мимолетности, или Подумаешь, бином Ньютона! . Теперь Вы можете, не прерываясь, узнать о судьбе героев. Какие странные штуки… Издатель: Омега — Л, Производитель: Омега — Л, Подробнее Купить за 575 грн (только Украина)
- Алгебра. Часть 2. Тождественные преобразования со степенями и корнями. Функции. Неравенства. Прогрессии. Логарифмы. Исследование уравнений. Мнимые и комплексные числа. Алгебраические уравнения. Неопределенные уравнения. Соединения и бином Ньютона, Киселев А.П., Учебник по алгебре, написанный выдающимся педагогом А. П. Киселевым в далеком 1888 году, выдержал с тех пор множество переизданий и на долгое время стал классическим для преподавания алгебры… Серия: — Издатель: URSS, Подробнее Купить за 529 руб
- Девственная селедка. Мимолетности, или Подумаешь, бином Ньютона!, Вильмонт Екатерина Николаевна, В этот сборник включены два романа: «Девственная селедка» и»Мимолетности, или Подумаешь, бином Ньютона!». Теперь Вы можете, не прерываясь, узнать о судьбе героев. Какие странные штуки иной… Издатель: Астрель, Подробнее Купить за 449 руб
dic.academic.ru
Бином Ньютона — Википедия
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
- (a+b)n=∑k=0n(nk)an−kbk=(n0)an+(n1)an−1b+⋯+(nk)an−kbk+⋯+(nn)bn{\displaystyle (a+b)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}a^{n-k}b^{k}={n \choose 0}a^{n}+{n \choose 1}a^{n-1}b+\dots +{n \choose k}a^{n-k}b^{k}+\dots +{n \choose n}b^{n}}
где (nk)=n!k!(n−k)!=Cnk{\displaystyle {n \choose k}={\frac {n!}{k!(n-k)!}}=C_{n}^{k}} — биномиальные коэффициенты, n{\displaystyle n} — неотрицательное целое число.
В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома Ньютона для более общего случая, когда показатель степени — произвольное действительное (или даже комплексное) число. В этом случае бином представляет собой бесконечный ряд (см. ниже).
Доказательство
Доказательство
Видео по теме
Обобщения
Формула бинома Ньютона является частным случаем разложения функции (1+x)r{\displaystyle (1+x)^{r}} в ряд Тейлора:
- (1+x)r=∑k=0∞(rk)xk{\displaystyle (1+x)^{r}=\sum _{k=0}^{\infty }{r \choose k}x^{k}},
где r может быть комплексным числом (в частности, отрицательным или вещественным). Коэффициенты этого разложения находятся по формуле:
- (rk)=1k!∏n=0k−1(r−n)=r(r−1)(r−2)⋯(r−(k−1))k!{\displaystyle {r \choose k}={1 \over k!}\prod _{n=0}^{k-1}(r-n)={\frac {r(r-1)(r-2)\cdots (r-(k-1))}{k!}}}
При этом ряд
- (1+z)α=1+αz+α(α−1)2z2+…+α(α−1)⋯(α−n+1)n!zn+…{\displaystyle (1+z)^{\alpha }=1+\alpha {}z+{\frac {\alpha (\alpha -1)}{2}}z^{2}+…+{\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}z^{n}+…}.
сходится при |z|≤1{\displaystyle |z|\leq 1}.
В частности, при z=1m{\displaystyle z={\frac {1}{m}}} и α=x⋅m{\displaystyle \alpha =x\cdot m} получается тождество
- (1+1m)xm=1+x+xm(xm−1)2m2+…+xm(xm−1)⋯(xm−n+1)n!mn+….{\displaystyle \left(1+{\frac {1}{m}}\right)^{xm}=1+x+{\frac {xm(xm-1)}{2\;m^{2}}}+…+{\frac {xm(xm-1)\cdots (xm-n+1)}{n!\;m^{n}}}+\dots .}
Переходя к пределу при m→∞{\displaystyle m\to \infty } и используя второй замечательный предел limm→∞(1+1m)m=e{\displaystyle \lim _{m\to \infty }{\left(1+{\frac {1}{m}}\right)^{m}}=e}, выводим тождество
- ex=1+x+x22+⋯+xnn!+…,{\displaystyle e^{x}=1+x+{\frac {x^{2}}{2}}+\dots +{\frac {x^{n}}{n!}}+\dots ,}
которое именно таким образом было впервые получено Эйлером.
Мультиномиальная теорема
Бином Ньютона может быть обобщен до полинома Ньютона — возведения в степень суммы произвольного числа слагаемых:
- (x1+x2+⋯+xm)n=∑kj⩾0k1+k2+⋯+km=n(nk1,k2,…,km)x1k1…xmkm,{\displaystyle (x_{1}+x_{2}+\cdots +x_{m})^{n}=\sum \limits _{k_{j}\geqslant 0 \atop k_{1}+k_{2}+\cdots +k_{m}=n}{n \choose k_{1},k_{2},\ldots ,k_{m}}x_{1}^{k_{1}}\ldots x_{m}^{k_{m}},}
где (nk1,k2,…,km)=n!k1!k2!⋯km!{\displaystyle \textstyle {\binom {n}{k_{1},k_{2},\ldots ,k_{m}}}={\frac {n!}{k_{1}!k_{2}!\cdots k_{m}!}}} — мультиномиальные коэффициенты. Сумма берётся по всем неотрицательным целым индексам kj{\displaystyle k_{j}}, сумма которых равна n (то есть по всем композициям числа n длины m). При использовании полинома Ньютона считается, что выражения xj0=1{\displaystyle x_{j}^{0}=1}, даже если xj=0{\displaystyle x_{j}=0}.
Мультиномиальная теорема легко доказывается либо индукцией по m, либо из комбинаторных соображений и комбинаторного смысла мультиномиального коэффициента.
При m=2{\displaystyle m=2}, выражая k2=n−k1{\displaystyle k_{2}=n-k_{1}}, получаем бином Ньютона.
Полные полиномы Белла
Пусть Bn(as)=Bn(a1,…,an){\displaystyle B_{n}(a_{s})=B_{n}(a_{1},\dots ,a_{n})} и B0=1{\displaystyle B_{0}=1} ,тогда полные полиномы Белла обладают биномиальным разложением:
- Bn(as+bs)=∑i+j=n(ni, j)Bi(as)Bj(bs).{\displaystyle B_{n}({{a_{s}}+{b_{s}}})=\sum _{i+j=n}{n \choose i,\ j}{B_{i}}({a_{s}}){B_{j}}({b_{s}}).}
История
Долгое время считалось, что для натуральных показателей степени эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Однако историки науки обнаружили, что формула была известна ещё китайскому математику Яну Хуэю (англ.), жившему в XIII веке, а также исламским математикам ат-Туси (XIII век) и ал-Каши (XV век). В середине XVI века Михаэль Штифель описал биномиальные коэффициенты и также составил их таблицу до степени 18.
Исаак Ньютон около 1677 года обобщил формулу для произвольного показателя степени (дробного, отрицательного и др.). Из биномиального разложения Ньютон, а позднее и Эйлер, выводили всю теорию бесконечных рядов.
В художественной литературе
В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо сложном.[1]
Когда ему исполнился двадцать один год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность. После этого он получил кафедру математики в одном из наших провинциальных университетов, и, по всей вероятности, его ожидала блестящая карьера.
Оригинальный текст (англ.)
The Final Problem At the age of twenty-one he wrote a treatise upon the binomial theorem, which has had a European vogue. On the strength of it he won the mathematical chair at one of our smaller universities, and had, to all appearances, a most brilliant career before him.
- «подумаешь, бином Ньютона! Умрёт он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвёртой палате».
См. также
Примечания
Литература
Ссылки
wiki2.red
бином ньютона — это… Что такое бином ньютона?
- бином ньютона
- БИНОМ, -а, м. (или бином ньютона). Ирон. О чем-л. кажущемся сложным, запутанным.
Словарь русского арго. — ГРАМОТА.РУ. В. С. Елистратов. 2002.
- бином
- биомицин
Смотреть что такое «бином ньютона» в других словарях:
Бином ньютона — Бином Ньютона это формула , где биномиальные коэффициенты, n неотрицательное целое число. Содержание 1 Доказательство … Википедия
БИНОМ НЬЮТОНА — БИНОМ НЬЮТОНА, математическое правило разложения алгебраического выражения (а+b)n в ряд степеней численных значений х и у (где n положительное число). При n 2 разложение выглядит таким образом: (х+у)2=х2+2ху+у2 … Научно-технический энциклопедический словарь
Бином Ньютона — Бином Ньютона формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид , где биномиальные коэффициенты, неотрицательное целое число. В таком виде эта формула была известна… … Википедия
Бином Ньютона — алгебраическая формула, открытая Ньютоном, выражающая какую угодно степень двучлена, а именно: (х + а)n = хn + n/1(axn 1) + [n/(n 1)/1.2](а2хn 2) + …[n(n 1)(n 2)…(n m+1)/1.2.3…m](anxn m) + … или, в компактной форме, пользуясь символом n! =… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Бином Ньютона — Разг. Шутл. О чём л. сложном, запутанном. Елистратов, 41 … Большой словарь русских поговорок
Подумаешь, бином Ньютона! — Из романа (гл. 18 «Неудачливые визитеры») «Мастер и Маргарита» (1940) Михаила Афанасьевича Булгакова (1891 1940). Слова Коровьева Фагота, комментирующего диалог между Воландом и буфетчиком Андреем Фокичем Соковым. Последний пришел жаловаться на… … Словарь крылатых слов и выражений
бином — а, м. binôme, лат. binomia m. 1. мат. Алгебраическое выражение, представляющее сумму или разность одночленов; двучлен. БАС 2. Боюсь, еслиб я и осмелился представить здесь самое простое развитие двучленника (бинома) Ньютонова необходимого для сего … Исторический словарь галлицизмов русского языка
Ньютона бином — Бином Ньютона это формула , где биномиальные коэффициенты, n неотрицательное целое число. Содержание 1 Доказательство … Википедия
БИНОМ — (от лат. bis дважды, и греч. nomos часть, отдел). Двучлен (в алгебре). Бином Ньютона общая формула для возведения двучленного количества в любую степень. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. БИНОМ в… … Словарь иностранных слов русского языка
Бином — (лат. bis дважды, nomen имя) или двучлен частный случай полинома (многочлена), состоящего из двух слагаемых мономов (одночленов). Например: Для вычисления степеней биномов используется бином Ньютона: А также … Википедия
Книги
- Девственная селедка. Мимолетности, или Подумаешь, бином Ньютона!, 576 с. В этот сборник включены два романа: Девственная селедка и Мимолетности, или Подумаешь, бином Ньютона! . Теперь Вы можете, не прерываясь, узнать о судьбе героев. Какие странные штуки… Издатель: Омега — Л, Производитель: Омега — Л, Подробнее Купить за 575 грн (только Украина)
- Алгебра. Часть 2. Тождественные преобразования со степенями и корнями. Функции. Неравенства. Прогрессии. Логарифмы. Исследование уравнений. Мнимые и комплексные числа. Алгебраические уравнения. Неопределенные уравнения. Соединения и бином Ньютона, Киселев А.П., Учебник по алгебре, написанный выдающимся педагогом А. П. Киселевым в далеком 1888 году, выдержал с тех пор множество переизданий и на долгое время стал классическим для преподавания алгебры… Серия: — Издатель: URSS, Подробнее Купить за 529 руб
- Девственная селедка. Мимолетности, или Подумаешь, бином Ньютона!, Вильмонт Екатерина Николаевна, В этот сборник включены два романа: «Девственная селедка» и»Мимолетности, или Подумаешь, бином Ньютона!». Теперь Вы можете, не прерываясь, узнать о судьбе героев. Какие странные штуки иной… Издатель: Астрель, Подробнее Купить за 449 руб
russian_argo.academic.ru
Бином Ньютона — это… Что такое Бином Ньютона?
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
- ,
где — биномиальные коэффициенты, — неотрицательное целое число.
В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное рациональное число (возможно, отрицательное). В этом случае бином представляет собой бесконечный ряд (см. ниже).
Доказательство
Докажем это равенство индукцией по n:
База индукции:
Шаг индукции: Пусть утверждение для верно:
Тогда надо доказать утверждение для :
Начнём доказательство:
Извлечём из первой суммы слагаемое при
Извлечём из второй суммы слагаемое при
Теперь сложим преобразованные суммы:
Что и требовалось доказать
Комментарий:
- — одно из тождеств биномиальных коэффициентов
Обобщения
Формула бинома Ньютона является частным случаем разложения функции в ряд Тейлора:
где r может быть комплексным числом (в частности, отрицательным или вещественным). Коэффициенты этого разложения находятся по формуле:
При этом ряд
- .
сходится при .
В частности, при и получается тождество
Переходя к пределу при и используя второй замечательный предел , выводим тождество
которое именно таким образом было впервые получено Эйлером.
Мультиномиальная теорема
Бином Ньютона может быть обобщен до полинома Ньютона — возведения в степень суммы произвольного числа слагаемых:
где — мультиномиальные коэффициенты. Сумма берется по всем неотрицательным целым индексам , сумма которых равна n. При использовании полинома Ньютона, считается, что выражения , даже в случае .
Мультиномиальная теорема легко доказывается либо по индукции по m, либо из комбинаторных соображений и комбинаторного смысла мультиномиального коэффициента.
При , выражая через , получаем бином Ньютона.
Биномиальные многочлены [источник не указан 799 дней]
Семейство многочленов G называется биномиальным, если оно представляется в виде суммы произведений набора множителей g:
где
- ≠0.
Биномиальные многочлены обладают биномиальным разложением:
Биномиальная группа [источник не указан 799 дней]
Группа из одномерных матриц с нулевым элементом заданной на нём операцией ,
где
Единицей группы является , нулём — Обратный элемент
где
История
Долгое время считалось, что для натуральных показателей степени эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Однако историки науки обнаружили, что формула была известна ещё китайскому математику Яну Хуэю, жившему в XIII веке, а также исламским математикам ат-Туси (XIII век) и ал-Каши (XV век).
Исаак Ньютон около 1676 года обобщил формулу для произвольного показателя степени (дробного, отрицательного и др.). Из биномиального разложения Ньютон, а позднее и Эйлер, выводили всю теорию бесконечных рядов.
В художественной литературе
В художественной литературе «бином Ньютона» появляется в нескольких запоминающихся контекстах, где речь идёт о чём-либо сложном.[1]
Когда ему исполнился двадцать один год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность. После этого он получил кафедру математики в одном из наших провинциальных университетов, и, по всей вероятности, его ожидала блестящая будущность.
Оригинальный текст (англ.)
The Final Problem
At the age of twenty-one he wrote a treatise upon the binomial theorem, which has had a European vogue. On the strength of it he won the mathematical chair at one of our smaller universities, and had, to all appearances, a most brilliant career before him.
Примечания
См. также
dik.academic.ru
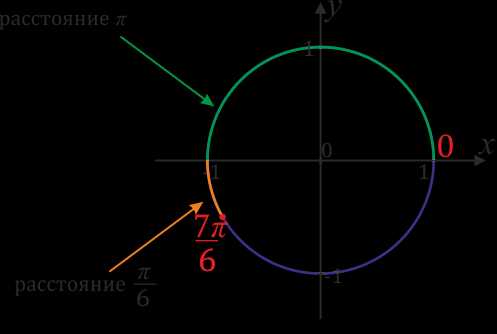
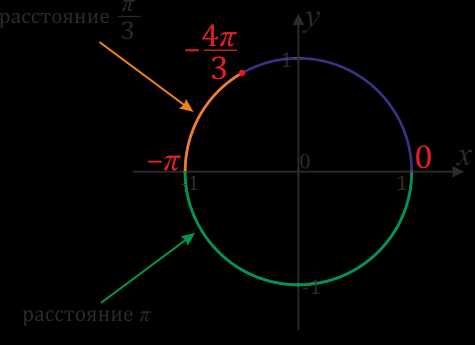
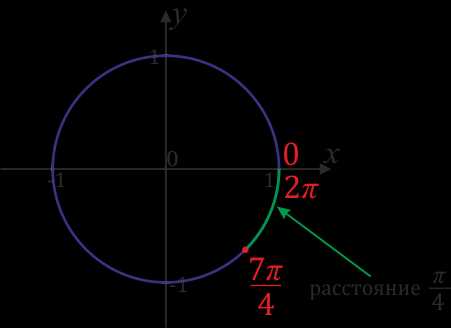
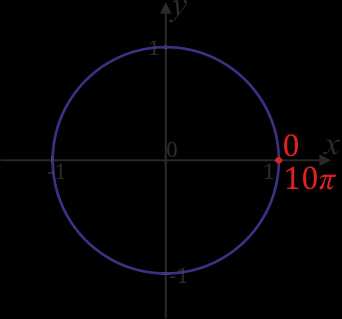
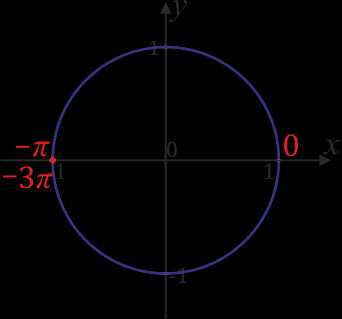
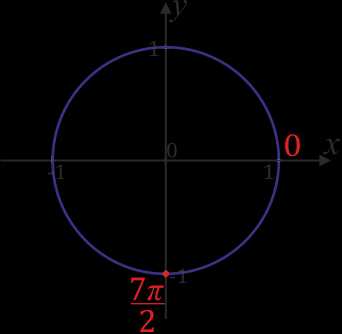
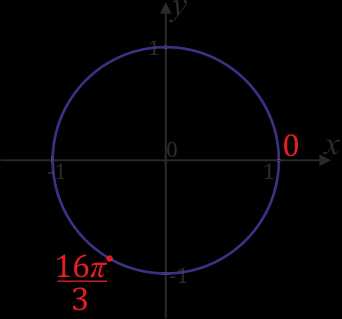
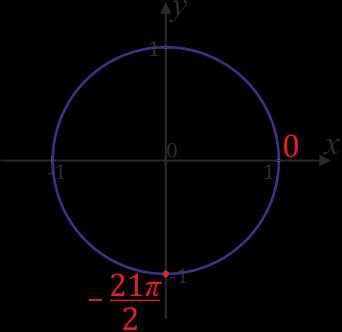
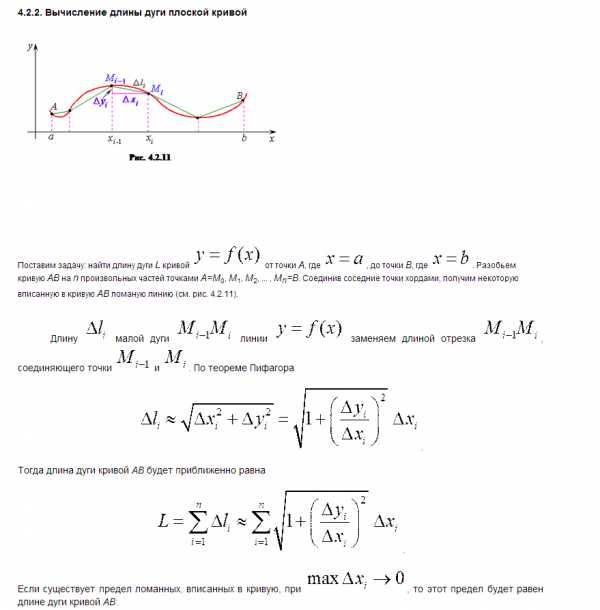
на отрезке
.
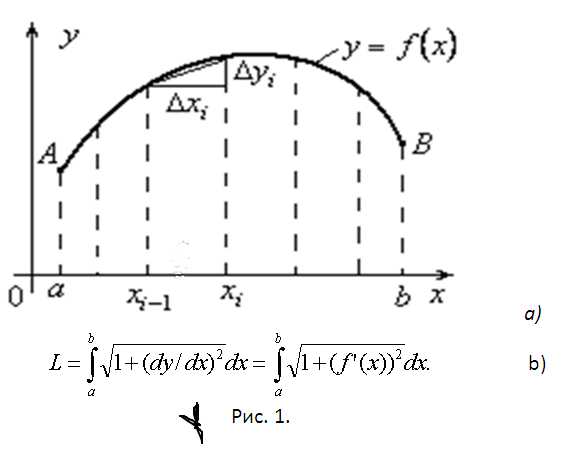
Разобьем отрезок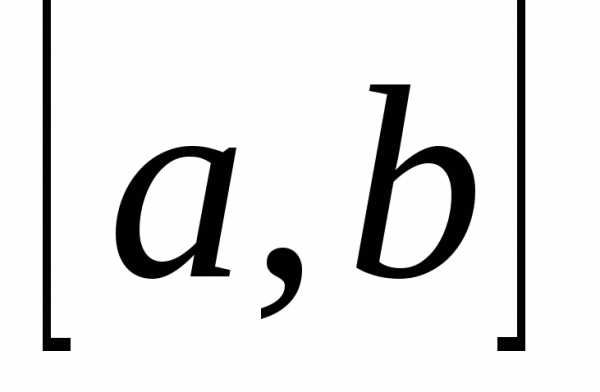
точками наnчастей.
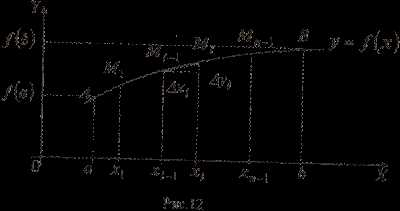
Из каждой точки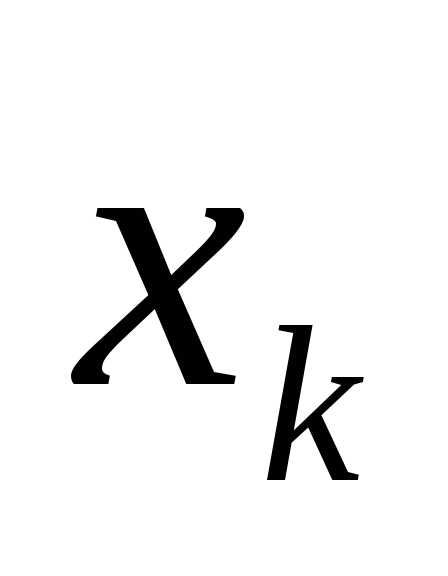
восстановим перпендикуляр к осиOx;
тогда дугаABразобьется
наnчастей точками(рис.4). Заменим каждый участок дуги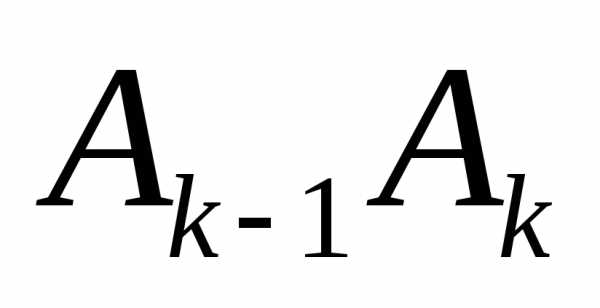
участком прямой
.
,
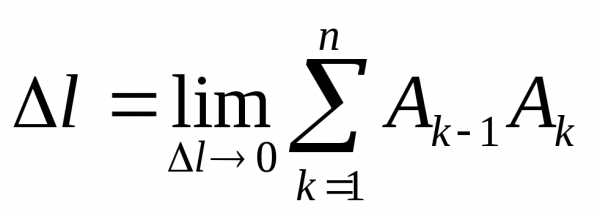а значит, и при,
т.е.
(8)
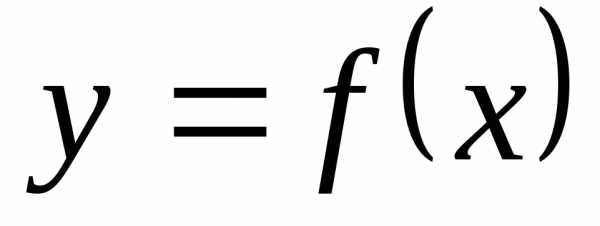и ее производная
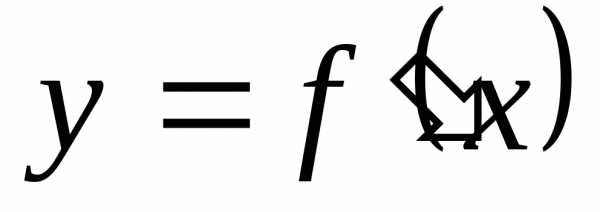непрерывны на отрезке
.
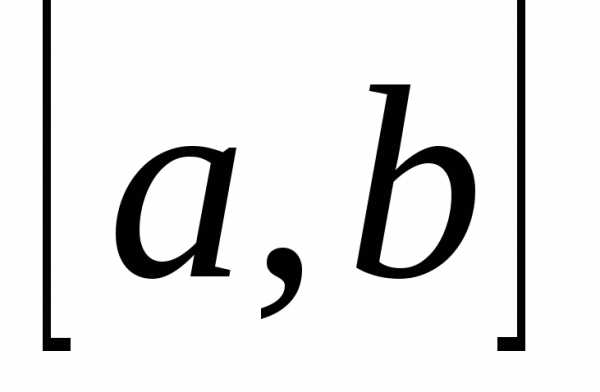Согласно теореме Пифагора имеем.
Обозначим.
Так каки,
то на основании теоремы Лагранжа получим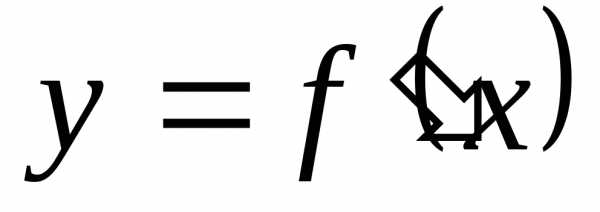
существует предел (8) интегральной суммы.
Таким образом,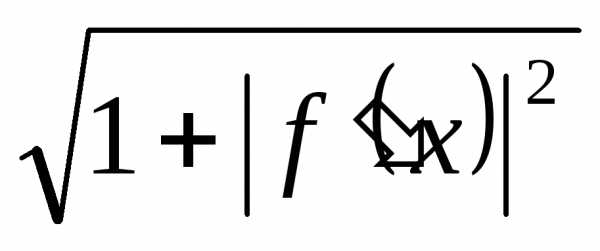
на отрезке
:
.
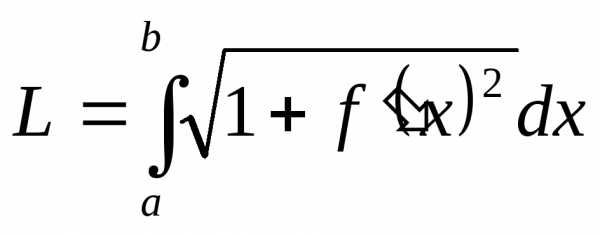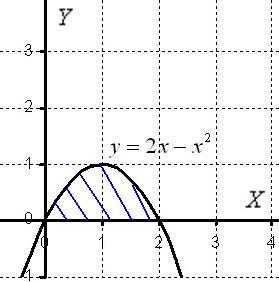
(10)
,
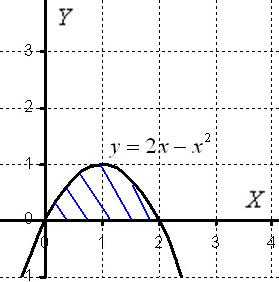
отсеченной прямой
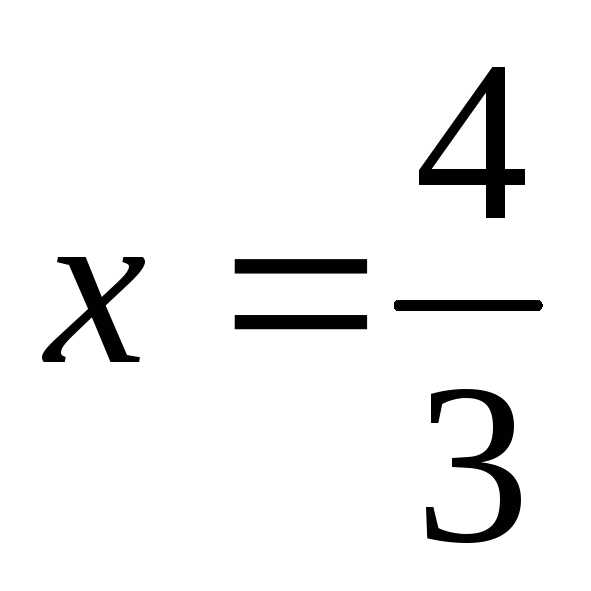(рис.5).
;
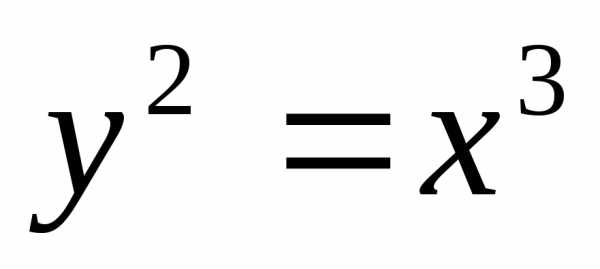имеем,
откуда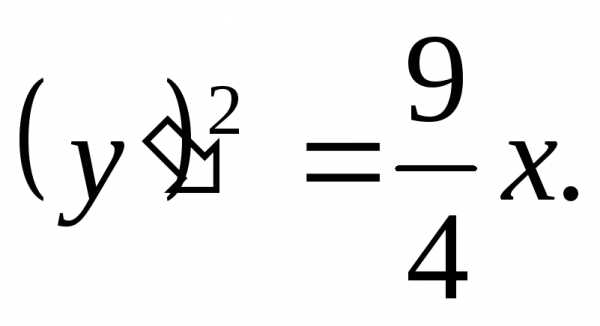
В силу симметрии достаточно вычислить
длину половины кривой
.
По формуле (10) получим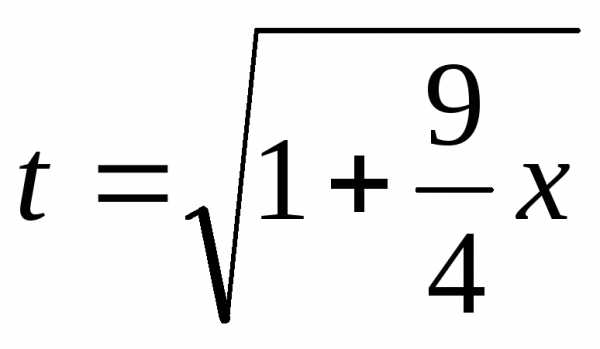
.
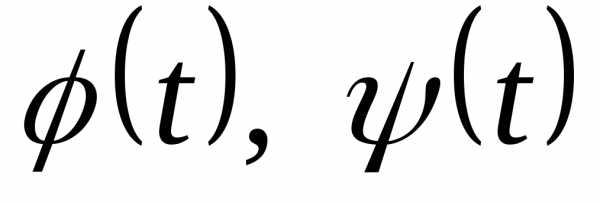— непрерывные и имеющие непрерывные
производные функции, причем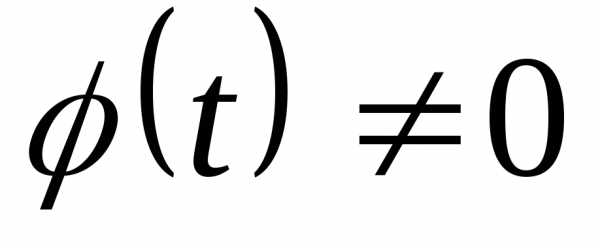
.
Пусть.
В интеграле (10) произведем подстановку;
так как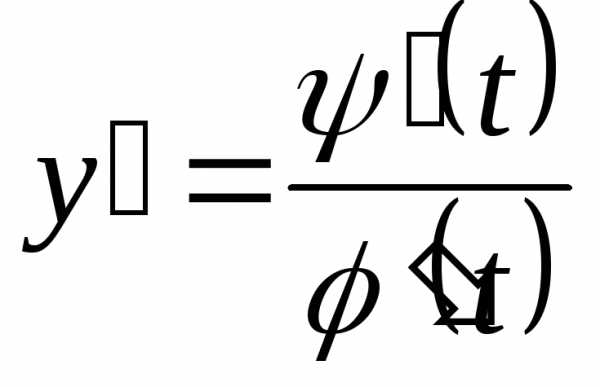
,
то получим
в пределах.
Тогда по формуле (11) находим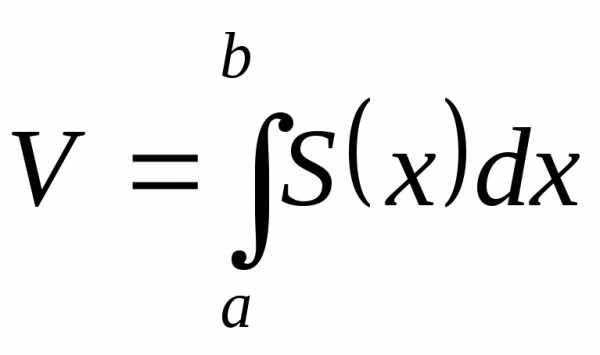
,
получим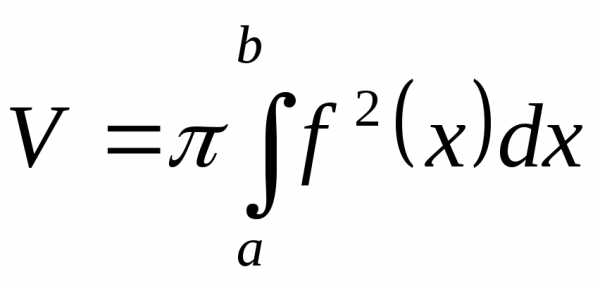
(13)
,
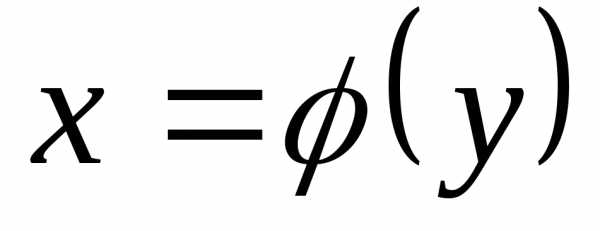осьюOyи прямымиy=aиy=b, вращается
вокруг осиOy, то объем
полученного тела вычисляется по формуле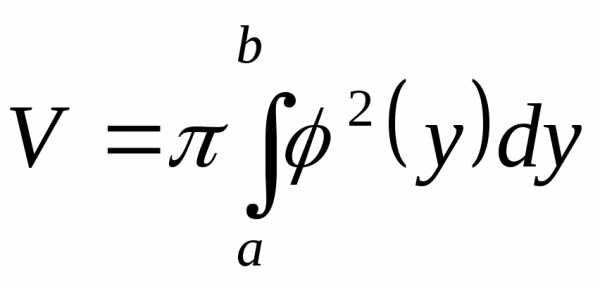
(14)
,
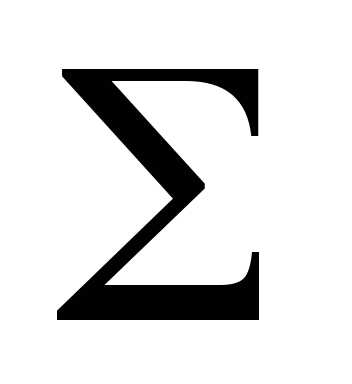к которому стремится площадь поверхности,
образованной вращением вокруг осиOxломаной,
вписанной в дугуAB, при
стремлении к нулю наибольшей из ее
сторон
,
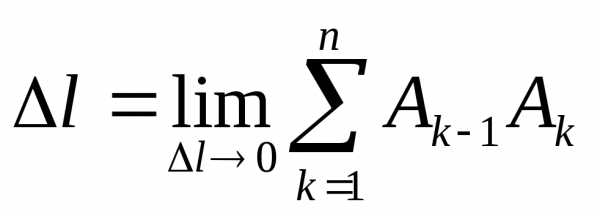а значит, и при,
т.е.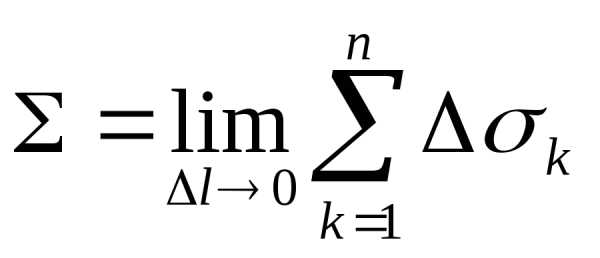
.